【中国计量学院考研专业课真题】信号系统与信号处理2012
2016年中国计量大学考研真题805信号系统与信息处理

七、(12分)某线性系统如图6所示:
(1)求系统的单位冲激响应h(t)和系统函数H(s);
(2)求系统的频率响应函数 ,并画出幅频特性曲线。
图6
【完】
图5
五、(20分)一线性时不变连续时间系统的微分方程为
若输入信号 ,起始状态为 试求:
(1)系统的零输入响应 和零状态响应 ;
(2)系统函数 ,单位冲激响应 ;
(3)若 ,求系统的零状态响应。
六、(15分)已知某一因果系统的差分方程为
(1)求该系统的系统函数 ;
(2)求系统的频率特性并画出幅频特性曲线, ,判断此系统具有何种滤波器特性。
(1) ;(2) ;(3) ;
图4
三、(12分)已知线性时不变因果系统的差分方程为
(1)求该系统的系统函数H(z),并指出其收敛域;
(2)求满足上述差பைடு நூலகம்方程的一个稳定、但非因果系统的单位样值响应h(n)。
四、(15分)如图5(a)所示系统,已知乘法器的输入 , ,系统频率特性如图5(b)所示,(1)求出 的频谱 ;(2)画出 和 的频谱图;(3)写出 的表达式。
(A)滤波器的相频特性斜率成正比
(B)滤波器的截止频率成正比
(C)滤波器的相频特性斜率成反比
(D)滤波器的截止频率成反比
9.欲使信号通过线性系统不产生失真,则该系统应具有()。
(A)幅频特性为线性,相频特性也为线性
(B)幅频特性为线性,相频特性为常数
(C)幅频特性为常数,相频特性为线性
(D)幅频特性为常数,相频特性也为常数
(A) (B) (C) (D)
5.连续周期信号 的频谱 的特点是( )。
(A)周期、连续频谱(B)周期、离散频谱
清华大学2012年828信号与系统考研真题-新祥旭考研辅导

清华大学2012年828信号与系统考研真题-回忆一、问答题,每小题6分1、假设h(t)下所围面积为Ah, f(t)下所围面积为Af, g(t)=h(t)*f(t)(两者卷积),g(t)下所围面积为Ag, 试证Ag=Ah*Af(两者之积)。
2、若t趋于无穷时,对于任意输入,其零状态响应均不为0,试问该系统是BIBO 稳定系统吗?3、不记得了,比较基础的题,不做也罢。
4、已知F{x(n)} = X(exp(jw)),Y(exp(jw))=∫X(exp(jw))dw (积分限是从(w - pi/2)到(w + pi/2), 试用x(n)来表示y(n).5、已知F{x(t)} = X(jw),试求∫x(t-y)*exp(-(y^2)/2)dy的傅式变换。
(y的积分是从负无穷到正无穷)(提示F{exp(-pi*(t^2))} = exp(-a*(f^2)),大概这样,记不清了)6、已知x1(n)和x2(n)分别为长为N1、N2的序列,试用DFT和IDFT表示两者的卷积。
7、x(k)=∑x(i)(求和限是从n到正无穷),已知Z{x(n)} = X(z),求Z{x(k)}。
8、请问X(exp(j0))和∫x(t)dt (积分线从负无穷到正无穷),请问两者的物理意义分别是什么。
二、(12分)已知冲击响应h(t,y)(y表示另一常数,书上用的tao表示,我表示不来,嘻嘻),拉式的系统函数H(S),傅式的系统函数H(jw),均可用来表示输入x(t)和输出y(t),但输入以及冲击响应或系统函数均要满足一定的关系,是分别阐明。
三、(20分)已知x1(t) = u(t) –u(t - 2), x2(t) =u(t) –2u(t - 1) + u(t - 2)1、试分别画出x1(t)和x2(t)的可实现的匹配滤波器。
2、试画出x1(t)、x2(t)分别通过x2(t)的匹配滤波器后系统的输出。
3、试求x2(t)通过其匹配滤波器后的最大输出信噪比。
武汉大学2012信号与系统真题

(1)系统函数为 H ( s) (2)由 1 k1k2e sT 0 即: k1k2e
T jT
e
e j 2 k , k 0 , 1, 2 ...
可知系统函数极点的实部满足 k1k2e T 1
1 ln k1k2 T 为使系统稳定,系统函数的极点必须全部位于左半 S 平面,即,这时应满足 条件:
武汉大学
2012 年攻读硕士学位研究生入学考试试题(共用) (满分值 150 分)
科目名称:信号与系统(C 卷)
一、 (20 分)系统如图 1-1 所示,
科目代码:934
注意:所有答题内容必须写在答题纸上,凡写在试题或草稿纸上的一律无效。
图 1-1
(1) (5 分)求系统函数 H ( s)
R( s ) ; E (s)
k1[ f (t ) k2 y(t T )t ) k1k2 y(t T ) 当 f (t ) (t ) 时, y(t ) h(t )
h( t ) 1 k ( t) 1 k 2k h ( t ) T
当 t 0 时, h(0) k1 (t )
解得:
0 ,这时 k1k2 应满足条件: k1k2 1
(3)由前式可解得极点的虚部为: 极点分布图为:
2 k , k 0, 1, 2... T
jω
6π T 4π T 2π T
1 lnk1k2 T
σ
2π T 4π T 6π T
(4)由于 e sT 表示时延 T,可以写出时域输入输出关系为:
所以有:
1 E ( s ) iL (0 ) vC (0 ) 1 1 s V0 ( s ) vC (0 ) 1 s s 2s s 1 iL (0 ) vC (0 ) E (s) 1 s 2 vC (0 ) 2 s 2s 1 s s 2s 1
(完整word版)信号与系统考试试题及答案,推荐文档

长沙理工大学拟题纸课程编号 1拟题教研室(或老师)签名 教研室主任签名 符号说明:)sgn(t 为符号函数,)(t δ为单位冲击信号,)(k δ为单位脉冲序列,)(t ε为单位阶跃信号,)(k ε为单位阶跃序列。
一、填空(共30分,每小题3分)1. 已知)()4()(2t t t f ε+=,求_______)("=t f 。
)('4)(2)("t t t f δε+2. 已知}4,2,4,3{)(},1,2,2,1{)(=-=k h k f ,求______)()(=*k h k f 。
}4,6,8,3,4,10,3{)()(-=*k h k f3. 信号通过系统不失真的条件为系统函数_______)(=ωj H 。
0)(t j Kej H ωω-=4. 若)(t f 最高角频率为m ω,则对)4(t f 取样的最大间隔是______。
m T ωπωπ4max max ==5. 信号t t t f ππ30cos 220cos 4)(+=的平均功率为______。
101122222=+++==∑∞-∞=n n F P6. 已知一系统的输入输出关系为)3()(t f t y =,试判断该系统是否为线性时不变系统______。
故系统为线性时变系统。
7. 已知信号的拉式变换为)1)(1(1)(2-+=s s s F ,求该信号的傅立叶变换)(ωj F =______。
故傅立叶变换)(ωj F 不存在。
8. 已知一离散时间系统的系统函数2121)(---+=z z z H ,判断该系统是否稳定______。
故系统不稳定。
9. =+-+⎰∞∞-dt t t t )1()2(2δ______。
310. 已知一信号频谱可写为)(,)()(3ωωωωA e A j F j -=是一实偶函数,试问)(t f 有何种对称性______。
关于t=3的偶对称的实信号。
二、计算题(共50分,每小题10分)1. 已知连续时间系统的单位冲激响应)(t h 与激励信号)(t f 的波形如图A-1所示,试由时域求解该系 统的零状态响应)(t y ,画出)(t y 的波形。
中国计量大学信号系统与信号处理2007年考研初试真题

一、简答题(共 8 小题,每小题 6 分,共 48 分,) 1、(1)计算函数值
f (t ) d [e t (t )]
dt (2)计算函数值
f (t)
2
(t
)
sin2t
dt
t
2、(1) 判断由方程 y(t) 2x(t) 10描述的系统是否为线性时不变系统。
(2)已知离散系统的系统函数 h(n) anu(n 1) ,判断该系统的因果性、 稳定性。
3、计算如图 1-1 所示矩形脉冲 f1(t)的频谱密度函数,画出幅度频谱图。
f (t)
1
2
0
2t
图 1-1
4、已知某线性时不变系统的系统函数 H ( j) 如图 1-2 所示,系统没有延时,
输入信号 f (t) 2 cos 2t ,求该系统的输出信号 y(t ) 。
H (jω) 6
-3 0
中国计量学院 2007 年攻读硕士学位研究生入学试题
考试科目名称: 信号系统与信号处理
考试科目代码:
409
考 生 姓 名:
考 生 编 号:
考生须知:
1、所有答案必须写在答题纸上,做在试卷 或草稿纸上无效。
2、答案必须写清题号,字迹要清楚,保持 卷面清洁。
3、试卷、草稿纸必须随答题纸一起交回。
本试卷共 八 大题,共 四 页。
储,其差分方程为 y(n) y(n 1) x(n),求系数 与 之间的关系,
以使该系统对恒定输入(常数输入)具有与上述系统同样的响应;
5、假设输入 x(n)由两个分量组成,即 x(n) C w(n),式中,C 是常数, 而 w(n)是在 附近频率上的掺杂噪声,若设计一个系统来估计 C 值,
中国民航大学硕士研究生入学考试_12年硕士“信号与系统(A卷)”

科目名称:信号与系统 (A 卷)注意:1.答案全部写在答题纸上,写在试卷上不计分;2.答题时一律使用蓝、黑色墨水笔或圆珠笔作答,用其它笔答题不给分;3.考试时间:3小时,总分:150分。
注:本试卷中,u (t )表示单位阶跃函数,u (n )表示单位阶跃序列。
其中第二题需要使用计算器。
一、(共50分)解答下列各题,必须给出必要的解答过程。
1.(5分)“信号与系统”课程阐述的是“线性时不变系统”的原理和分析方法,那么系统的线性和时不变性是否存在必然联系?为什么?2.(5分)信号1()2cos 6f t t ⎛⎫= ⎪⎝⎭和1()2cos 6f n n ⎛⎫=⎪⎝⎭是否都是周期信号?为什么?3.(5分)设d ()e cos()()d t f t t t tδ-⎡⎤=⎣⎦,画出()f t 的波形。
4.(2分)信号傅里叶分析的研究与应用起始于科学家傅里叶。
请问你对傅里叶本人及其从事的研究知道多少?尽可能写出你所知道的信息。
5.(6分)对于周期1T (角频率1ω)的信号()f t ,证明其双边傅里叶级数频谱中,只有将1n ω与1n ω-对应的谱线矢量相加,其结果才表示()f t 的n 次谐波,n 为正整数。
6.(5分)信号()f t 的傅里叶变换为(j )F ω,()f t 的波形如图1所示,求(j )d F ωω+∞-∞⎰。
7.(6分)设理想低通滤波器的频响函数j311(j )=6e ()()55H u u ωωωω-⎡⎤+--⎢⎥⎣⎦,现激励()8Sa 6t e t ⎛⎫= ⎪⎝⎭,求该滤波器的响应()r t 。
共5 页 第 1 页图18.(5分)某LTI 系统的系统函数22()22s H s s s +=++,求该系统在激励()t δ时的零状态响应。
9.(5分)一个LTI 系统的激励和响应分别为()e t 、()r t ,系统的数学模型为22d ()d ()d ()23()()d d d r t r t e t r t e t t t t++=+。
中国计量学院2012级本科生本硕创新计划项目
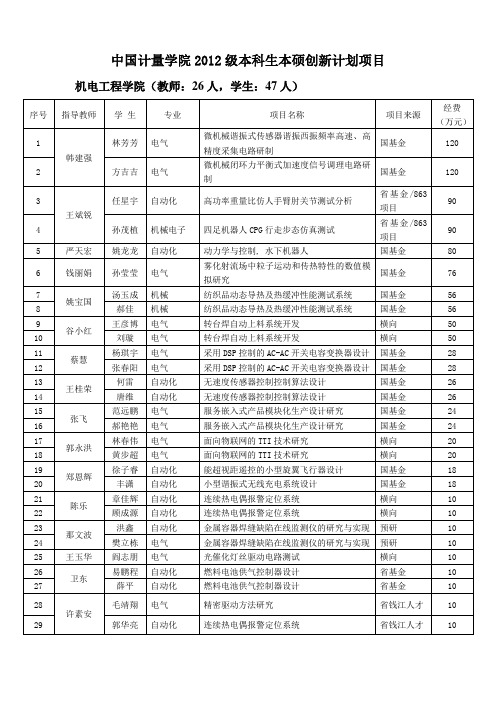
中国计量学院2012级本科生本硕创新计划项目机电工程学院(教师:26人,学生:47人)
计量测试工程学院(教师:44人,学生:69人)
信息工程学院(教师:7人,学生:12人)
光学与电子科技学院(教师:35人,学生:35人)
材料科学与工程学院(教师:22人,学生:22人)
质量与安全工程学院(教师:7人,学生:9人)
经济与管理学院(教师:6人,学生:11人)
理学院(教师:10人,学生:16人)
注释:曹飞龙导师组*成员有“曹飞龙,赵建伟,张永全”。
生命科学学院(教师:9人,学生:16人)
法学院(教师:1人,学生:2 人)
人文学院(教师:5人,学生:5人)
马克思主义学院(教师:1人,学生:2人)。
中国计量大学2020年《805信号系统与信号处理》考研专业课真题试卷

《信号系统与信号处理》试卷 第 1 页 共 1 页 中国计量大学
2020年硕士研究生招生考试试题
考试科目代码:805 考试科目名称:信号系统与信号处理 所有答案必须写在报考点提供的答题纸上,答在试卷或草稿纸上无效。
(注:本试卷中的()u t 代表单位阶跃信号。
)
一、简答题(13小题,共70分)
1.(1)(2分)计算积分
1()[(2)(2)]t e t t t dt δδ+∞
−+−++∫ ;
(2)(2分)计算积分
(1)(2)u t u t dt ∞−∞
−−∫;
(3)(2分)计算积分sin()t dt t ∞−∞
∫; 2.(4分)已知某系统的输入、输出关系为2()()3y t t f t =+,试判断该系统是否为 线性系统和时不变系统。
3.(6分)某连续周期信号()f t 的傅里叶级数展开后的频谱,具有哪三个特点?
4.(6分)写出以下三个连续时间系统各自的单位冲激响应()h t :()(1)y t f t =−, -()()t
y t f d ττ∞=∫ ,()[()]/y t d f t dt = 。
5.(6分)已知图1(a )所示的信号)(1t f 的傅里叶变换为()1F j ω,求图1(b )
所示的信号)(2t f 与)(1t f 的关系及)(2t f 的傅里叶变换()2F j ω。
《信号与系统》考研试题解答第一章信号与系统

第一章信号与系统一、单项选择题X1.1 (北京航空航天大学 2000 年考研题)试确定下列信号的周期:( 1) x(t )3cos 4t3;(A ) 2( B )( C )2(D )2( 2) x(k ) 2 cosk sin8k 2 cosk642(A ) 8 ( B ) 16 ( C )2 (D ) 4X1.2 (东南大学 2000 年考研题)下列信号中属于功率信号的是。
(A ) cost (t)(B ) e t (t)(C ) te t (t )t( D ) eX1.3 (北京航空航天大学 2000 年考研题)设 f(t)=0 ,t<3,试确定下列信号为 0 的 t 值:(1) f(1- t)+ f(2- t);(A ) t>-2 或 t>-1 ( B ) t=1 和 t=2(C ) t>-1( D ) t>-2(2) f(1- t) f(2- t) ;(A ) t>-2 或 t>-1 ( B ) t=1 和 t=2(C ) t>-1 ( D ) t>-2(3) ft ;3(A ) t>3 (B ) t=0 (C ) t<9 (D ) t=3X1.4 (浙江大学 2002 年考研题)下列表达式中正确的是 。
(A ) ( 2t )(t)( B ) ( 2t)1(t)2(C ) ( 2t )2 (t )( D )2 (t)1(2 )2X1.5 (哈尔滨工业大学 2002 年考研题)某连续时间系统的输入f( t) 和输出 y(t)满足y(t) f (t ) f (t 1) ,则该系统为。
(A )因果、时变、非线性 ( B )非因果、时不变、非线性 (C )非因果、时变、线性( D )因果、时不变、非线性X1.6 (东南大学 2001 年考研题)微分方程 y (t) 3y (t) 2 y(t) f (t 10) 所描述的系统为。
(A)时不变因果系统(B)时不变非因果系统(C)时变因果系统(D)时变非因果系统X1.7 (浙江大学2003 年考研题)y(k) f ( k 1) 所描述的系统不是。
郑君里信号系统考研《信号与系统》考研真题与考研笔记

郑君里信号系统考研《信号与系统》考研真题与考研笔记第一部分考研真题精选一、选择题1下列信号属于功率信号的是()。
[中国传媒大学2017研]A.e-tε(t)B.cos(2t)ε(t)C.te-tε(t)D.Sa(t)【答案】B查看答案【解析】如果信号f(t)的能量有界(0<E<∞,P=0),称f(t)为能量有限信号,简称为能量信号。
如果信号f(t)的功率有界(0<P<∞,E=∞),称f(t)为功率有限信号,简称为功率信号。
ACD三项的能量均为有限值,因此为能量信号。
B项,cos(2t)ε(t)是单边周期信号,因此能量无界,但是功率为有限值,因此B为功率信号。
2下列信号中,选项()不是周期信号,其中m,n是整数。
[山东大学2019研]A.f(t)=cos2t+sin5tB.f(t)=f(t+mT)C.x(n)=x(n+mN)D.x(n)=sin7n+e iπn【答案】D查看答案【解析】A项,cos2t的周期为T1=2π/2=π,sin5t的周期为T2=2π/5,由于T1/T2=5/2,是有理数,因此为周期信号,且周期为T=2T1=5T2=2π。
BC两项,一个连续信号满足f(t)=f(t+mT),m=0,±1,±2,…,则称f (t)为连续周期信号,满足上式条件的最小的T值称为f(t)的周期。
一个离散信号f(k),若对所有的k均满足f(k)=f(k+mN),m=0,±1,±2,…,则称f(k)为连续周期信号,满足上式条件的最小的N值称为f(k)的周期。
D项,sin7n的周期N1=2π/7,e iπn的周期为N2=2π/π=2,N1/N2=π/7为无理数,因此为非周期信号。
3下列关于单位冲激函数或单位样本函数的表达式,选项()不正确。
[山东大学2019研]A.B.δ(t)*f(t)=f(t)C.D.【答案】D查看答案【解析】冲激函数的极限形式的定义式应该为4下列叙述正确的有()。
【华南理工大学2012年考研专业课真题】信号与系统2012

k 6
⎧ 0, k = 1,3,5, 7,... , c、t0 是实数; − t0 ⎩ce ,k ≠ 1,3,5, 7,....
−15
2. x(1) = 2e
;
3. X ( s ) 为有理拉氏变换式; 4. X ( s ) 仅有两个极点和一个零点; 5. X ( s ) 的收敛域为 Re{s} > −15 ; 确定 x (t ) =?
π n 8 π C. cos [ n − 1] 8
π n 4 π D. cos [ n − 1] 4
B. cos
6. 已知一离散时间 LTI 系统的单位脉冲响应 h[n]和系统的输入 x[n]如图 2 所示,
图2
y[n]为系统输出,则 y[3]=(
)
第
4
页
A. 2
B . 3;
C. 5
D. 6
7.有一单位冲激响应为 h(t ) 的因果LTI系统,其输入x(t)和输出y(t)的关系由线性常系 若 数微分方程所关联:y′′(t ) + 5ay′(t ) + 6a 2 y (t ) = x′(t ) − ax(t ), a > 0 , g (t ) = e− at ∫ h(τ )dτ ,
10.考虑一个离散时间序列 x[ n ] ,它的傅立叶变换是 X (e ) ,由 x[ n ] 形成两个新序 列 x1[ n] 和 x2 [ n] ,其中 x1[ n] = x[3n] ,而 x 2 [n] = ⎨
jω
⎧ x1[n], n = 0,±3,±6, Λ ⎩0, 其余n
,它们的傅
第
2
页
立 叶 变 换 分 别 是 X 1 (e jω ) 和 X 2 (e jω ) , 求 X 1 (e jω ) 与 X (e ) 的 关 系 _______________________; X 2 (e ) 与 X 1 (e ) 的关系____________________。
信号与系统期中考试标准答案
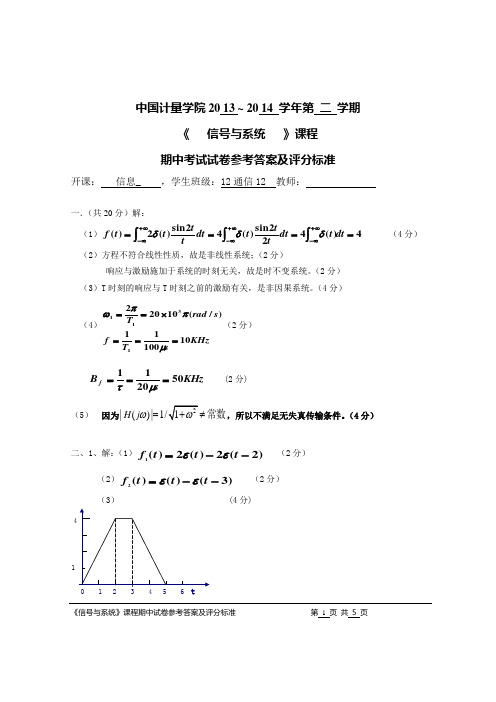
《信号与系统》课程期中试卷参考答案及评分标准 第 1 页 共 5 页中国计量学院20 13 ~ 20 14 学年第 二 学期《 信号与系统 》课程 期中考试试卷参考答案及评分标准开课: 信息_ ,学生班级:12通信12 教师:一.(共20分)解: (1)4)(422sin )(42sin )(2)(====⎰⎰⎰∞+∞-∞+∞-∞+∞-dt t dt ttt dt t t t t f δδδ (4分)(2)方程不符合线性性质,故是非线性系统;(2分)响应与激励施加于系统的时刻无关,故是时不变系统。
(2分)(3)T 时刻的响应与T 时刻之前的激励有关,是非因果系统。
(4分)(4)KHz sT f s rad T 1010011)/(102021311===⨯==μππω(2分)KHz sB f 502011===μτ(2分) (5)因为|()|1/ω=常数H j ,所以不满足无失真传输条件。
(4分)二、1、解:(1))2(2)(2)(1--=t t t f εε (2分)(2))3()()(2--=t t t f εε (2分)(3) (4分)1《信号与系统》课程期中试卷参考答案及评分标准 第 2 页 共 5 页2、(8分)解:f(t)为周期信号,T=2,其基波角频率Ω=π。
在间隔(-1,1)内,f(t)表示为δ(t),f(t)的傅里叶级数展开式为 21)(1,)(11===⎰∑-ΩΩ-∞-∞=dt e t Tc ec t f tin n tjn n n δ其中, 所以,∑-∑=-=∑=∑=∞-∞=∞-∞=-∞-∞=-∞-∞=n n tjn n ntjn n nn n eF c ec F t f F )()(221][][)]([πωδπΩωπδΩΩ3、(8分)解:211)(j ωω+=Hωωϕa r c t a n )(-=)4sin(21sin π-⇒t t ,)sin(sin 632512-⇒t t ,)sin(sin 7231013-⇒t t所以,)723sin(101)632sin(51)4sin(21)( -+-+-=t t t t y π三.(12分) 解:⎪⎫⎛==⎰--)(21ωττωττωSa A dt Ae j F t j (4分)(4分)(2) 2 (4分)四、(10分)将f(t)展开成三角函数形式的傅立叶级数,考虑到f(t)偶对称性质,故正弦分量bn 全为零,其中:12/2/21T ωπππ===,τπ=,E A = !!!!第 3 页共 5 页故:01/2a = ,1sin(/2)2*/2A A a πππππ== 3sin(3/2)2*3/23A A a πππππ==等,如下,其它偶次项0n a =)7cos 715cos 513cos 31(cos 22)( +-+-+=t t t t A A t f π (5分) 考虑到该系统是一个带通滤波器,只将2到7 rad/s 的频率成分保留,故除3,5,7三个频率分量保留外,其它分量全部滤除!!又因为该系统的通带内的增益为1,所以输出信号的直接就是f(t)的三个频率分量!!如下所示:)7c o s 715c o s 513c o s 31(2)(t t t A t f +--=π (5分)五、解:1《信号与系统》课程期中试卷参考答案及评分标准 第 4 页 共 5 页(8分)2、将y(t)与2cos30000πt 相乘,得到信号的频谱为:将2y(t) cos30000πt 经过截止频率为15kHz 的低通滤波器,则可以恢复到m(t)的频谱,即恢复为m(t).所以解密器与加密器的结构完全相同。
2012年 华中科技大学电信系考研 824《信号与线性系统》真题及答案(科学硕士)

二O 一二年华中科技大学招收硕士研究生 824《信号与线性系统》真题及答案(科学硕士)满分150,答题时间180分钟适用专业:通信与信息系统、信号与信息处理、电路与系统、电磁场与微波技术一、填空题(3分/空,共30分)1.连续时间信号24()j t x t eπ⎛⎫+ ⎪⎝⎭=的平均功率为 瓦;2.积分()sin 21t t dt δ∞-∞'-⎰的值= ;3.离散信号[]cos cos 54x n n n ππ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭的基波周期为 ;4.卷积积分()()()21*1t u t u t +--⎡⎤⎣⎦= ; 5.信号()sin sin 2*1t tt t ππππ-的傅里叶变换为 ;(注:*表示卷积) 6.周期序列[][][]310410h x n u n k u n k +∞=-∞=+----∑的傅里叶系数10a= ;7.已知()x t 的奈奎斯特抽样角频率为N ω,则()()cos N x t t ω的奈奎斯特抽样角频率为 ;8.一连续时间LTE 系统,,输入输出方程为()()()()2y t y t y t x t '''--=,如果该系统既不是因果系统也不是稳定系统,它的冲激响应为 ;9.序列[]()()01kk x n n k δ∞==--∑的z 变换为 ,收敛域为 。
二、选择题(2分/题,共20分)1.输入输出方程为[][]()()sin 1y n x n n δ=-的系统是( )的系统。
(a )线性、因果、稳定 (b )线性、非因果、稳定(c )线性、非因果、不稳定 (d )非线性、因果不稳定 2.以下冲激响应函数中,( )不对应稳定LTE 系统。
(a )()()cos h t tu t = (b )()()t h t te u t -= (c )()()22t h t e u t =-+ (d )()sin /h t t t =3.一个奇的且为纯虚数的信号,其傅里叶变换为一个( )。
中国计量大学自动控制原理2012--2014年考研真题

0.2S + 1 B(s)
Kh
四、(15 分)
已知一单位反馈系统的开环传递函数为:G(s)
=
K0 (s + 4) s(s + 2)
。
1. 试证明该系统根轨迹的复数部分为一圆,并画出根轨迹。(8 分)
2. 分析K0从 0→∞变化时系统阻尼比的变化情况;(4 分)
3. 分析K0从 0→∞变化时系统超调量的变化情况。(3 分)
二、(15 分) 已知系统的单位脉冲响应为 g(t) = 10e−0.2t + 5e−0.5t ,
(1) 求系统的传递函数;(10 分) (2) 确定系统的单位阶跃响应达到稳态值的 95%所需的时间。(5 分)
三、(15 分)
控制系统如下图所示。若要求系统的超调量 M p = 0.25 ,峰值时间 tp = 2s 。
db
0 20
0
0.02
-20
-40
20
200
0
ω
-20
七、(20 分) 已知采样系统结构如图所示,其中采样周期 T = 0.1 s。
R(S)
-T
1-e −TS S
k
C(S)
2S +1
(1)求开环脉冲传递函数和闭环脉冲传递函数;(15 分) (2)确定闭环系统稳定的 k 值范围。(5 分)
《自动控制原理》试卷 第 2 页 共 3 页
一、(15 分) 控制系统如下图所示:
R(s)
- G1(s)
G2(s)
-
H4(s)
-
G3(s)
H2(s)
C(s)
G4(s)
-
G5(s)
G6(s)
H3(s)
H1(s)
2020年中国计量大学考研真题805信号系统与信号处理(2020年)

《信号系统与信号处理》试卷 第 1 页 共 1 页 中国计量大学
2020年硕士研究生招生考试试题
考试科目代码:805 考试科目名称:信号系统与信号处理 所有答案必须写在报考点提供的答题纸上,答在试卷或草稿纸上无效。
(注:本试卷中的()u t 代表单位阶跃信号。
)
一、简答题(13小题,共70分)
1.(1)(2分)计算积分
1()[(2)(2)]t e t t t dt δδ+∞
−+−++∫ ;
(2)(2分)计算积分
(1)(2)u t u t dt ∞−∞
−−∫;
(3)(2分)计算积分sin()t dt t ∞−∞
∫; 2.(4分)已知某系统的输入、输出关系为2()()3y t t f t =+,试判断该系统是否为 线性系统和时不变系统。
3.(6分)某连续周期信号()f t 的傅里叶级数展开后的频谱,具有哪三个特点?
4.(6分)写出以下三个连续时间系统各自的单位冲激响应()h t :()(1)y t f t =−, -()()t
y t f d ττ∞=∫ ,()[()]/y t d f t dt = 。
5.(6分)已知图1(a )所示的信号)(1t f 的傅里叶变换为()1F j ω,求图1(b )
所示的信号)(2t f 与)(1t f 的关系及)(2t f 的傅里叶变换()2F j ω。
刘A学长提供。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ω
五、 (15 (15 分)已知某 LTI 系统的激励为 e(t ) = (e − t + e −3t )ε (t ) ,系统的零状态响应为:
r (t ) = (2e −t − e −4t )ε (t ) ,求: (1)系统函数; (2)系统的单位冲激响应; (3)系统微分
方程。
《信号系统与信号处理》试卷
0
1
t
四、 ( 10 分 ) 某 连 续 LTI 时 间 系 统 的 频 率 响 应 H ( jω ) 如 下 图 所 示 , 输 入 信 号
f (t) = 1 + 0.6 cost + 0.4 cos3t + 0.2 cos5t ,画出输入信号的单边傅里叶频谱,求系统
的输出 y (t ) 。
H ( jω )
该信号的谱线间隔是多少?带宽是多少?
1 1 7. 求信号 f (t ) = [ε (t + ) − ε (t − )]cosω0t 的频谱 F ( jω) 。 2 2
8. 确定下列信号的奈奎斯特频率。
(1) f (t ) = sa (50πt ) (2) f ( t ) = sa 2 (60πt )
(6 分) (6 分) (6 分)
k 9. 已知序列 x(k ) = a [ε (k ) − ε (k − 8)],a > 0 ,求其 z 变换 X ( z ) ,并指出其收敛域和极
《信号系统与信号处理》试卷
第1页 共3页
点、零点。 的? (6 分)
(6 分)
10. 叙述周期信号的频谱特点。离散周期信号的频谱是否是离散的?是否是周期
二、 (10 分)已知下图所示信号 x1 (t ) 和 x2 (t ) ,试画出它们的卷积 y (t ) = x1 (t ) ∗ x2 (t ) 的图 形。
x1 (t )
x 2 (t )
1 0 1
t
1/2 1 -1/2 2 3 4 5
t
三、 (10 分)求下图所示信号的频谱密度函数。
f(t) 1
-1
1 (3)若 f (t ) = Sa ( t ) ,求 y (t ) 。 2
f(t)
+ +
y(t)
∑
H 1 ( jω )
延时 T
【完】
《信号系统与信号处理》试卷
第3页 共3页
第2页 共3页
六、 (15 (15 分)一个因果离散时间 LTI 系统描述为
3 1 y (k − 1) + y (k − 2) = x(k ) 4 8 其中, x(k ) , y(k ) 分别为系统的输入和输出。 y (k ) −
(1) 确定系统函数 H ( z) ; (2) 确定系统的冲激响应 h(k ) ;
2.已知某系统的输入输出信号分别为 x(k ) 和 y(k ) ,则下面
(3 分) 是因果、线性和
时不变系统。
(4 分) (b) y(k +1) − x(k ) y(k ) = kx(k + 2) (d) y(k ) − y(k +1) = x(k + 2)
(a) y(k ) + y(k +1) = kx(k ) (c) y(k ) − y(k −1) = x(k )
(6 分)
2 1 1 1 5. 信号 x(t ) = 2 sin( t ) + 4 cos( t ) + 4 cos( t − π ) 是否为周期信号?若是,求其周期。 3 2 3 5
(6 分)
6.已知周期矩形脉冲信号 x(t ) 的矩形宽度 τ = 1µs ,周期 T = 2µs ,幅度 E = 1V ,试问
jω (3) 确定系统的频率响应 H (e ) 。
七、 (2 (20 分)某系统如下图所示,其中 H1 ( jω ) 为理想低通滤波器,即
− j ωt e 0 H 1 ( jω ) = 0
,ω ≤1 ,ω >1
(1)求该理想低通滤波器的冲激响应 h1 (t ) ; (2)若 f (t ) = Sa (2t ) ,求 y (t ) ;
(注:本试卷中的 ε (t ) 代表单位阶跃信号。 ) 一、简答题( 简答题(10 小题, 小题,共 70 分) sin πt (2)计算积分 ∫ t 2δ (t − 6)dt
−∞ +∞
(3 分) (3 分) (3 分)
(3)计算序列和 ∑2i δ (i − 2)
i=−∞
+∞
(4)已知 y(t ) = x(t ) ∗ h(t ), ,计算 x(t − 2) ∗ h(t − 5) . (3 分) (5)已知信号 f (t ) 的带宽为 B,求信号 y(t ) = f (2t − 5) 的带宽.(3 分) (6)已知输入信号 x(t ) 的频率范围为 0∼ ω1 ,某低通系统的带宽为 ω2 ,且 ω2 > ω1 , 求该系统的输出信号 y(t ) = x(t ) ∗ h(t) 的频率范围。
3.已知一连续时间 LTI 系统的单位冲激响应 h(t) = ε (t ) − ε (t −1) ,计算该系统的单位
阶跃响应 g(t ) 。
(6 分)
↓ ↓
4.若离散时间系统的单位脉冲响应为 h( k ) = {1,−1,2} ,求系统在 f ( k ) = {1, 2,−2,1} 激
励下的零状态响应。
