Lingo 求解运输问题
lingo运输问题的实验报告

数学与计算科学学院实验报告
实验项目名称运输问题求解
所属课程名称运筹学B
实验类型综合
实验日期 2014年10月25日
姓名张丽芬
学号 0102
成绩
附录1:源程序
附录2:实验报告填写说明
1.实验项目名称:要求与实验教学大纲一致.
2.实验目的:目的要明确,要抓住重点,符合实验教学大纲要求.
3.实验原理:简要说明本实验项目所涉及的理论知识.
4.实验环境:实验用的软、硬件环境.
5.实验方案(思路、步骤和方法等):这是实验报告极其重要的内容.概括整个实验过程.
对于验证性实验,要写明依据何种原理、操作方法进行实验,要写明需要经过哪几个步骤来实现其操作.对于设计性和综合性实验,在上述内容
基础上还应该画出流程图、设计思路和设计方法,再配以相应的文字说明.对于创新性实验,还应注明其创新点、特色.
6.实验过程(实验中涉及的记录、数据、分析):写明具体实验方案的具体实施步骤,包括实验过程中的记录、数据和相应的分析.
7.实验结论(结果):根据实验过程中得到的结果,做出结论.
8.实验小结:本次实验心得体会、思考和建议.
9.指导教师评语及成绩:指导教师依据学生的实际报告内容,给出本次实验报告的评价.。
运输问题课程设计lingo

运输问题课程设计lingo一、教学目标本章节的教学目标是让学生掌握运输问题的基本概念、Lingo模型的构建及求解方法。
通过本章节的学习,学生应能够:1.理解运输问题的背景和意义,掌握运输问题的基本概念和分类。
2.学会使用Lingo软件构建运输问题的模型,并运用该软件求解运输问题。
3.能够运用所学知识分析和解决实际生活中的运输问题。
二、教学内容本章节的教学内容主要包括以下几个部分:1.运输问题的基本概念:运输问题的发展历程、基本概念、分类及应用领域。
2.Lingo软件的使用:Lingo软件的界面及功能、模型的构建、求解及优化。
3.运输问题的Lingo模型求解:单源、多源、循环、分配等类型的运输问题的Lingo模型构建及求解。
4.实际案例分析:分析现实生活中遇到的运输问题,运用Lingo软件求解,并提出解决方案。
三、教学方法为了达到本章节的教学目标,将采用以下教学方法:1.讲授法:讲解运输问题的基本概念、Lingo软件的使用方法及运输问题的Lingo模型求解方法。
2.案例分析法:分析实际案例,引导学生运用所学知识解决实际问题。
3.讨论法:学生分组讨论,培养学生的合作能力和解决问题的能力。
4.实验法:让学生动手操作Lingo软件,亲自构建和求解运输问题模型,提高学生的实际操作能力。
四、教学资源为了支持本章节的教学内容和教学方法的实施,将准备以下教学资源:1.教材:《运输问题与Lingo建模》。
2.参考书:关于运输问题、Lingo软件使用的相关书籍。
3.多媒体资料:运输问题案例视频、Lingo软件操作演示视频。
4.实验设备:计算机、投影仪等。
五、教学评估本章节的教学评估将采用多元化的评估方式,全面、客观地评价学生的学习成果。
评估方式包括:1.平时表现:通过课堂参与、提问、讨论等环节,记录学生的表现,占总评的30%。
2.作业:布置与本章节内容相关的作业,要求学生独立完成,占总评的20%。
3.考试:设计针对本章节内容的考试,测试学生对运输问题及Lingo建模的掌握程度,占总评的50%。
用lingo解决运输问题

用lingo解决运输问题(一)实验目的1. 运输问题求解的编程实现2(掌握使用matlab、Lingo、Excel的求解功能求解运输问题,并对结果进行分析。
(二)实验内容《运筹学》清华三版P98页 3.3题Lingo程序代码及运行结果(选取部分):<1>3.3(1):程序代码:model:sets:xiao/1..4/:s;chan/1..3/:h;link(chan,xiao):x,y;endsetsdata:y=3 7 6 42 43 24 3 8 5;h=5 2 3;s=3 3 2 2;enddatamin=@sum(link:x*y);@for(xiao(j):@sum(chan(i):x(i,j))=s(j));@for(chan(i):@sum(xiao(j):x(i,j))=h(i)); 运行结果及结果分析:Objective value: 32.00000产地1分别将数量为3和2的产品运往销地甲和丁;产地2将数量为2的产品运往销地丙;产地3将数量为3的产品运往销地乙;该运输问题的最小费用为32.<2>3.3(2):程序代码:model:sets:xiao/1..4/:s;chan/1..3/:h;link(chan,xiao):x,y; endsetsdata:y=10 6 7 1216 10 5 95 4 10 10;h=4 9 4;s=5 2 4 6;enddatamin=@sum(link:x*y); @for(xiao(j):@sum(chan(i):x(i,j))=s(j));@for(chan(i):@sum(xiao(j):x(i,j))=h(i));运行结果及结果分析:Objective value: 118.0000产地1将数量为1、2、1的产品分别运往销地甲、乙、丙;产地将数量为3、6的产品运往销地丙、丁;产地3将数量为4的产品运往销地甲。
Lingo软件在运输问题中的应用研究

Lingo软件在运输问题中的应用研究问题:万通公司有三个仓库:H1,H2,H3,B商品在这三仓库中的库存分别为150 吨、145 吨、160 吨;已知有四家商场(S1,S2,S3,S4) 需要购买该公司的B商品,他们的需求量分别为80 吨、118 吨、137 吨、113 吨。
问如何利用现有库存资源满足这四家商场的需求,并使得总运输成本最低。
从这三个仓库向四家商场送货的ij i j构建数学模型如下:目标函数:Min=26* X11 +21* X12…+21* X33 +23* X34库存约束:ΣX1j <=150;ΣX2j <=145;ΣX3j <=160;j=1,2,3,4需求约束:ΣX i1=80;ΣX i2 =118;ΣX i3 =137;ΣX i4 =113;i=1,2,3非负约束:X ij>=0使用Lingo软件,编制程序如下:model:sets:h/h1,h2,h3/:capacity;s/s1,s2,s3,s4/:demand;links(h,s):cost,x;endsetsdata:capacity=150,145,160;demand=80,118,137,113;cost=26,21,23,20,21,19,12,21,16,19,21,23;enddatamin=@sum(links(i,j):cost*x);@for(s(j):@sum(h(i):x(i,j))=demand(j));@for(h(i):@sum(s(j):x(i,j))<=capacity(i));End运行后的结果如下:Global optimal solution found.Objective value: 7486.000Infeasibilities: 0.000000Total solver iterations: 6Variable Value Reduced CostCAPACITY( H1) 150.0000 0.000000CAPACITY( H2) 145.0000 0.000000CAPACITY( H3) 160.0000 0.000000DEMAND( S1) 80.00000 0.000000DEMAND( S2) 118.0000 0.000000 DEMAND( S3) 137.0000 0.000000 DEMAND( S4) 113.0000 0.000000 COST( H1, S1) 26.00000 0.000000 COST( H1, S2) 21.00000 0.000000 COST( H1, S3) 23.00000 0.000000 COST( H1, S4) 20.00000 0.000000 COST( H2, S1) 21.00000 0.000000 COST( H2, S2) 19.00000 0.000000 COST( H2, S3) 12.00000 0.000000 COST( H2, S4) 21.00000 0.000000 COST( H3, S1) 16.00000 0.000000 COST( H3, S2) 19.00000 0.000000 COST( H3, S3) 21.00000 0.000000 COST( H3, S4) 23.00000 0.000000 X( H1, S1) 0.000000 8.000000 X( H1, S2) 30.00000 0.000000 X( H1, S3) 0.000000 9.000000 X( H1, S4) 113.0000 0.000000 X( H2, S1) 0.000000 5.000000 X( H2, S2) 8.000000 0.000000 X( H2, S3) 137.0000 0.000000 X( H2, S4) 0.000000 3.000000 X( H3, S1) 80.00000 0.000000 X( H3, S2) 80.00000 0.000000 X( H3, S3) 0.000000 9.000000 X( H3, S4) 0.000000 5.000000Row Slack or Surplus Dual Price1 7486.000 -1.0000002 0.000000 -18.000003 0.000000 -21.000004 0.000000 -14.000005 0.000000 -20.000006 7.000000 0.0000007 0.000000 2.0000008 0.000000 2.000000 从结果中能看出,最低费用为7486元,最有运输方案是仓库1向商场2供货30吨,向商场4供货113吨,仓库2向商场2进货8吨,向商场3供货137吨,仓库3向商场1供货80吨,向商场2供货80吨。
用lingo解决运输问题

用lingo解决运输问题(一)实验目的1. 运输问题求解的编程实现2.掌握使用matlab、Lingo、Excel的求解功能求解运输问题,并对结果进行分析。
(二)实验内容《运筹学》清华三版P98页 3.3题Lingo程序代码及运行结果(选取部分):<1>3.3(1):程序代码:model:sets:xiao/1..4/:s;chan/1..3/:h;link(chan,xiao):x,y;endsetsdata:y=3 7 6 42 43 24 3 8 5;h=5 2 3;s=3 3 2 2;enddatamin=@sum(link:x*y);@for(xiao(j):@sum(chan(i):x(i,j))=s(j));@for(chan(i):@sum(xiao(j):x(i,j))=h(i));运行结果及结果分析:Objective value: 32.00000产地1分别将数量为3和2的产品运往销地甲和丁;产地2将数量为2的产品运往销地丙;产地3将数量为3的产品运往销地乙;该运输问题的最小费用为32.<2>3.3(2):model:sets:xiao/1..4/:s;chan/1..3/:h;link(chan,xiao):x,y;endsetsdata:y=10 6 7 1216 10 5 95 4 10 10;h=4 9 4;s=5 2 4 6;enddatamin=@sum(link:x*y);@for(xiao(j):@sum(chan(i):x(i,j))=s(j));@for(chan(i):@sum(xiao(j):x(i,j))=h(i));运行结果及结果分析:Objective value: 118.0000产地1将数量为1、2、1的产品分别运往销地甲、乙、丙;产地将数量为3、6的产品运往销地丙、丁;产地3将数量为4的产品运往销地甲。
最小费用为118.<3>3.3(3):程序代码:model:sets:xiao/1..5/:s;chan/1..4/:h;link(chan,xiao):x,y;endsetsdata:y=10 20 5 9 102 10 8 30 61 20 7 10 4h=5 6 2 9;s=4 4 6 2 4;enddatamin=@sum(link:x*y);@for(xiao(j):@sum(chan(i):x(i,j))=s(j));@for(chan(i):@sum(xiao(j):x(i,j))<=h(i));运行结果及结果分析:Objective value: 90.00000产地1分别将数量为1、2的产品运往销地丙、丁;产地2分别将数量为4、2的产品运往销地甲、戊;产地3将数量为2的产品运往销地戊;产地4分别将数量为4、5的产品运往销地乙、丙;最小运费为90.<4>3.3(4):程序代码:model:sets:xiao/1..5/:s;chan/1..5/:h;link(chan,xiao):x,y;endsetsdata:y=10 18 29 13 2213 10000 21 14 160 6 11 3 100009 11 23 18 1924 28 36 30 34;h=100 120 140 80 60;s=100 120 100 60 80;enddatamin=@sum(link:x*y);@for(xiao(j):@sum(chan(i):x(i,j))=s(j));@for(chan(i):@sum(xiao(j):x(i,j))<=h(i));运行结果及结果分析:Objective value: 5520.000产地1将数量为100的产品运往销地甲;产地2分别将数量为40、80的产品运往销地丙、戊;产地3分别将数量为的产品运往销地乙、丙、丁;产地4将数量为80的产品运往销地乙;产地5将数量为20的产品运往销地乙。
Lingo 求解运输问题

定义了三个集合,其中links在前两 输入程序 个集合warehouses 和vendors的基 础上定义 data: model: 表示集合 links中的元素就是集合 capacity=60 55 51 43 41 52; !6发点8收点运输问题; warehouses 和vendors demand=35 37 的元素组合 22 32 41 32 43 38; sets: cost=6 2 6 7 4 2 9 5 成的有序二元组,从数学上看 link warehouses/wh1..wh6/: capacity; 49和 53 8 5 8 2 的笛卡儿 是warehouses vendors vendors/v1..v8/: demand; 52197433 积,也就是说 links(warehouses,vendors): cost, volume; 76739271 links={ ( S |Swarehouses , endsets 2, 3T 9) 57 265 !目标函数; 5 Tvendors} 5 2 2 8 1 4 3; min=@sum(links: cost*volume); enddatacost和volume也就是 因此,其属性 end !需求约束; 一个6*8 的矩阵(或者说是含有48 @for(vendors(J): 个元素的二维数组)。 @sum(warehouses(I): volume(I,J))=demand(J)); MATRIX LINGO 建模语言也称为矩阵生成器( !产量约束; GENERATOR)。类似warehouses 和vendors直接把元素列举 @for(warehouses(I): 出来的集合,称为基本集合 (primary set),而把links这种基于其 @sum(vendors(J): volume(I,J))<=capacity(I)); 它集合而派生出来的二维或多维集合称为派生集合 (derived set)。 !这里是数据 ;
利用Lingo解一个具体的运输问题例子
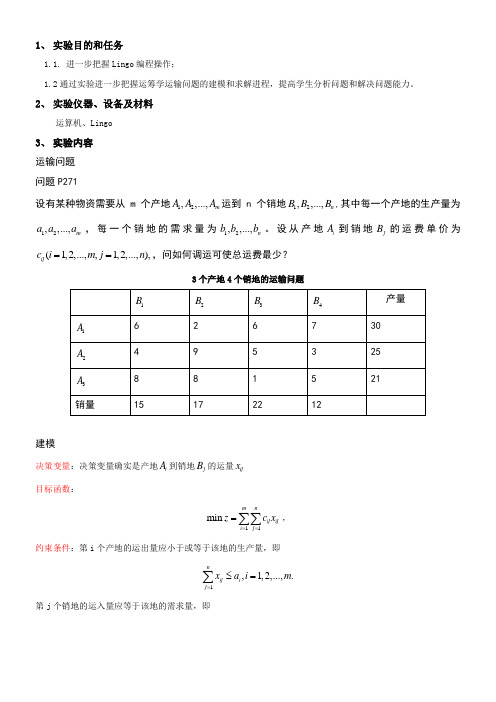
1、 实验目的和任务1.1. 进一步把握Lingo 编程操作;1.2通过实验进一步把握运筹学运输问题的建模和求解进程,提高学生分析问题和解决问题能力。
2、 实验仪器、设备及材料运算机、Lingo3、 实验内容运输问题问题P271设有某种物资需要从m 个产地12,,...,m A A A 运到n 个销地12,,...,n B B B ,其中每一个产地的生产量为12,,...,m a a a ,每一个销地的需求量为12,,...,n b b b 。
设从产地i A 到销地j B 的运费单价为(1,2,...,,1,2,...,),ij c i m j n ==,问如何调运可使总运费最少?3个产地4个销地的运输问题建模决策变量:决策变量确实是产地i A 到销地j B 的运量ij x目标函数:11min m nij ij i j z c x ===∑∑,约束条件:第i 个产地的运出量应小于或等于该地的生产量,即1,1,2,...,.n ij i j xa i m =≤=∑第j 个销地的运入量应等于该地的需求量,即1,1,2,....m ij j i xb j n ===∑求解进程编写模型程序:model :! 3 Warehouse,4 Customer Transportation Problem;sets :Warehouse/1..3/:a;Customer/1..4/:b;Routes(warehouse,customer):c,x;endsets!here are the parameters;data :a=30,25,21;b=15,17,22,12;c=6,2,6,7,4,9,5,3,8,8,1,5;enddata! The objective;[obj] min =@sum (routes:c*x);!The supply constraints;@for (warehouse(i):[sup]@sum (customer(j):x(i,j))<=a(i));!The demand constraints;@for (customer(j):[dem] @sum (warehouse(i):x(i,j))=b(j));end计算结果:Global optimal solution found.Objective value: 161.0000Total solver iterations: 6Variable Value Reduced CostA( 1) 30.00000 0.000000A( 2) 25.00000 0.000000A( 3) 21.00000 0.000000B( 1) 15.00000 0.000000B( 2) 17.00000 0.000000B( 3) 22.00000 0.000000B( 4) 12.00000 0.000000C( 1, 1) 6.000000 0.000000C( 2, 1) 4.000000 0.000000C( 2, 2) 9.000000 0.000000C( 2, 3) 5.000000 0.000000C( 2, 4) 3.000000 0.000000C( 3, 1) 8.000000 0.000000C( 3, 2) 8.000000 0.000000C( 3, 3) 1.000000 0.000000C( 3, 4) 5.000000 0.000000X( 1, 1) 2.000000 0.000000X( 1, 2) 17.00000 0.000000X( 1, 3) 1.000000 0.000000X( 1, 4) 0.000000 2.000000X( 2, 1) 13.00000 0.000000X( 2, 2) 0.000000 9.000000X( 2, 3) 0.000000 1.000000X( 2, 4) 12.00000 0.000000X( 3, 1) 0.000000 7.000000X( 3, 2) 0.000000 11.00000X( 3, 3) 21.00000 0.000000X( 3, 4) 0.000000 5.000000Row Slack or Surplus Dual PriceOBJ 161.0000 -1.000000SUP( 1) 10.00000 0.000000SUP( 2) 0.000000 2.000000SUP( 3) 0.000000 5.000000DEM( 1) 0.000000 -6.000000DEM( 2) 0.000000 -2.000000DEM( 3) 0.000000 -6.000000事实上,咱们关切更多的是那些非零变量,因此,可选择“Lingo|solution..”弹出一个对话框(介绍此对话框),选择“nonzeros only”,即可只列出非零变量:Global optimal solution found.Objective value: 161.0000Total solver iterations: 6Variable Value Reduced CostA( 1) 30.00000 0.000000A( 2) 25.00000 0.000000A( 3) 21.00000 0.000000B( 1) 15.00000 0.000000B( 2) 17.00000 0.000000B( 3) 22.00000 0.000000C( 1, 3) 6.000000 0.000000C( 1, 4) 7.000000 0.000000C( 2, 1) 4.000000 0.000000C( 2, 2) 9.000000 0.000000C( 2, 3) 5.000000 0.000000C( 2, 4) 3.000000 0.000000C( 3, 1) 8.000000 0.000000C( 3, 2) 8.000000 0.000000C( 3, 3) 1.000000 0.000000C( 3, 4) 5.000000 0.000000X( 1, 1) 2.000000 0.000000X( 1, 2) 17.00000 0.000000X( 1, 3) 1.000000 0.000000X( 2, 1) 13.00000 0.000000X( 2, 4) 12.00000 0.000000X( 3, 3) 21.00000 0.000000Row Slack or Surplus Dual PriceSUP( 2) 0.000000 2.000000SUP( 3) 0.000000 5.000000DEM( 1) 0.000000 -6.000000DEM( 2) 0.000000 -2.000000DEM( 3) 0.000000 -6.000000DEM( 4) 0.000000 -5.000000结果分析由于Lingo软件中采纳集,数据段和循环函数的编写方式,因此便于程序推行到一样形式利用,例如,只需修改运输问题中产地和销地的个数,和参数a,b,c的值,就能够够求解任何运输问题。
数学建模-(货机装运lingo)

数学建模-(货机装运lingo)货机装运是指将货物从一个起点运输到一个终点,在这个过程中需要考虑到货物的重量、体积、运输方式等多种因素。
在货机装运过程中,一个关键问题是如何最大化运载效率,即在保证运输安全和合法的前提下,尽可能地提高货机的装载量,从而降低单位运输成本。
在数学建模中,可以使用lingo等工具进行货机装运的优化。
具体来说,可以将该问题抽象为一个数学模型,以最大化货机的装载量为目标函数,同时考虑到运输安全、货物重量、体积等约束条件。
下面以一个具体例子来说明如何使用lingo进行货机装运的优化:假设有一架货机,其载重量为10000公斤,可以装载两种货物A和B,每种货物的重量和体积如下:货物类型重量(公斤)体积(立方米)A 600 1.5B 400 0.8同时,从起点到终点的运输费用如下:货物类型运输费用(元/公斤)A 10B 15要求在保证运输安全和合法的前提下,最大化货机的装载量,即:subject to:A +B <= 10000(装载量不超过10000公斤)其中,A和B表示货机装载的货物A和B的数量,V是货机的装载体积,运输费用是由货物类型和运输距离等因素决定的,这里简化为一个固定值。
使用lingo进行求解的过程如下:1.首先,在lingo中创建一个新的模型文件,并定义目标函数和约束条件:2.对模型进行求解,并设置模型参数:model:solve;parameters:V = 15;end;在上述代码中,V表示货机的装载体积,这里假设为15立方米。
solve表示对模型进行求解,通过设置end来结束参数定义。
3.对求解结果进行分析和优化,例如考虑不同装载体积下的最优解:for V := 15 to 20 dobeginwriteln('Optimal value for V=',V,': ',model.obj);在以上代码中,for循环遍历不同的装载体积值(15到20),分别求解模型并输出优化结果。
LINGO求解运输问题

一.实验目的1、学会使用LINGO 软件求解运输问题的步骤与方法。
2、掌握使用LINGO 对运输问题的求解功能,并对结果进行分析。
二.实验内容1.已知某企业有甲、乙、丙三个分厂生产一种产品,其产量分别为7、9、7个单位,需运往A 、B 、C 、D 四个门市部,各门市部需要量分别为3、5、7、8个单位。
已知单位运价如下表。
试确定运输计划使总运费最少。
2.现在要在五个工人中确定四个人来分别完成四项工作中的一项工作。
由于每个工人的技术特长不同,他们完成各项工作所需的工时也不同。
每个工人完成各项工作所需工时如下表所示,试找出一个工作分配方案,使总工时最小。
三. 模型建立1.由题设知,总产量为:7+9+7=23个单位,总销量为:3+5+7+8=23个单位,所以这是一个产销平衡的运输问题。
设)4,3,2,1;3,2,1(==j i x ij 代表从第i 个产地运往第j 个销地的数量,z 为总运费。
i a 表示第i 个产地的产量,j b 表示第j 个销地的销量ij c 表示从第i 个产地运往第j 个销地的单位产品运输费用。
则该问题的数学模型为:34114131max 0,1,2,3;1,2,3,4ij iji j ij i j ij j i ij Z c x x a x b x i j =====⎧=⎪⎪⎪=⎨⎪⎪≥==⎪⎩∑∑∑∑2. 设0-1变量,1,0ij i x i ⎧=⎨⎩当第个人完成某j 项工作,当第个人不完成某j 项工作则该问题的数学模型为:54115141min 1,1,01ij iji j ij i ij j ij Z c x x j x i x i j =====⎧= =1,2,3,4⎪⎪⎪= = 1,2,3,4,5⎨⎪⎪= =1,2,3,4,5;=1,2,3,4⎪⎩∑∑∑∑或,四. 模型求解(含经调试后正确的源程序)1、编写程序1-1.m 如下:model : sets :warehouses/wh1..wh3/: capacity; vendors/v1..v4/: demand;links(warehouses,vendors): cost, volume; endsets data :capacity=7 9 7; demand=3 5 7 8; cost= 12 13 10 11 10 12 14 10 14 11 15 12; enddatamin =@sum (links(I,J): cost(I,J)*volume(I,J));@for(vendors(J):@sum(warehouses(I): volume(I,J))=demand(J));@for(warehouses(I):@sum(vendors(J): volume(I,J))<=capacity(I));end2、编写程序2-1.m如下:model:sets:workers/w1..w5/;jobs/j1..j4/;links(workers,jobs): cost,volume;Endsetsdata:cost=9 4 3 74 65 65 4 7 57 5 2 310 6 7 4;enddatamin=@sum(links: cost*volume);@for(workers(I): @sum(jobs(J): volume(I,J))<=1);@for(jobs(J): @sum(workers(I): volume(I,J))=1);@for(links(i,j): @bin(volume(i,j)));End五.结果分析最优调运方案为:甲→C:7单位;甲→D:0单位;乙→A:3单位;乙→D:6单位;丙→B:5单位;丙→D:2单位。
用lingo编程解决运输问题大全
LINGO是用来求解线性和非线性优化问题的简易工具。
LINGO内置了一种建立最优化模型的语言,可以简便地表达大规模问题,利用LINGO高效的求解器可快速求解并分析结果。
当你在windows下开始运行LINGO系统时,会得到类似下面的一个窗口:外层是主框架窗口,包含了所有菜单命令和工具条,其它所有的窗口将被包含在主窗口之下。
在主窗口内的标题为LINGO Model – LINGO1的窗口是LINGO的默认模型窗口,建立的模型都都要在该窗口内编码实现。
下面举两个例子。
例1.1如何在LINGO中求解如下的LP问题:,6002100350..32min 212112121≥≤+≥≥++x x x x x x x t s x x在模型窗口中输入如下代码:min =2*x1+3*x2; x1+x2>=350; x1>=100;2*x1+x2<=600;然后点击工具条上的按钮 即可。
例1.2 使用LINGO 软件计算6个发点8个收点的最小费用运输问题。
产销单位运价如下表。
销地产地B 1B 2B 3B 4B 5B 6B 7B 8产量A 1 6 2 6 7 4 2 5 9 60 A 2 4 9 5 3 8 5 8 2 55 A 3 5 2 1 9 7 4 3 3 51 A 4 7 6 7 3 9 2 7 1 43 A 5 2 3 9 5 7 2 6 5 41 A 6 5 5 2 2 8 1 4 3 52 销量3537223241324338使用LINGO软件,编制程序如下:model:!6发点8收点运输问题;sets:warehouses/wh1..wh6/: capacity; vendors/v1..v8/: demand;links(warehouses,vendors): cost, volume;endsets!目标函数;min=@sum(links: cost*volume);!需求约束;@for(vendors(J):@sum(warehouses(I):volume(I,J))=demand(J));!产量约束;@for(warehouses(I):@sum(vendors(J):volume(I,J))<=capacity(I));!这里是数据;data:capacity=60 55 51 43 41 52;demand=35 37 22 32 41 32 43 38; cost=6 2 6 7 4 2 9 54 95 3 8 5 8 25 2 1 9 7 4 3 37 6 7 3 9 2 7 12 3 9 5 7 2 6 55 5 2 2 8 1 4 3;enddataend然后点击工具条上的按钮即可。
用LINGO软件解决运输问题研究

用LINGO软件解决运输问题研究
用LINGO软件解决运输问题研究
摘要:运输问题是运筹学中常见问题。
针对这种问题我们也曾学习过传统的方法,运输问题可以利用表上作业法来解决。
当数据不多且复杂性地时,表上作业法比较好操作,但是现实中我们面对的问题往往数据更多且更为复杂。
而lingo是针对运筹学问题的一个很好的软件应用。
在此,简要的介绍lingo软件在运输问题上的运用,并给出相关例子供读者参考,以便能在遇到类似问题时更准确的解答。
关键词:lingo软件应用运输问题
一、lingo软件简介
lingo是linear interactive and general optimizer的缩写,即”交互式的线性和通用优化求解器”,由美国lindo系统公司(lindo system inc.)推出的,可以用于求解非线性规划,也可以用于一些线性和非线性方程组的求解等,功能十分强大,是求解优化模型的最佳选择。
其特色在于内置建模语言,提供十几个内部函数,可以允许决策变量是整数(即整数规划,包括0-1 整数规划),方便灵活,而且执行速度非常快。
能方便与excel,数据库等其他软件交换数据。
lingo 是使建立和求解线性、非线性和整数最佳化模型更快更简单更有效率的综合工具。
lingo 提供强大的语言和快速的求解引擎来阐述和求解最佳化模型。
1. 简单的模型表示。
实验2 Lingo求解运输问题和整数规划

a=1.25,8.75,0.5,5.75,3,7.25;
b=1.25,0.75,4.75,5,6.5,7.75;
!quantities of the demand and supply(供需量);
d=3,5,4,7,6,11; e=20,20;
x,y=5,1,2,7;
enddata
init:
!initial locations for the supply(初始点);
j 1 i1
2
s.t.
cij d i , i 1,...,6
线性规划模型
j 1
6
cij e j ,
j 1,2
用例中数据计算,
最优解为
i
i 1
12 345 6
ci1( 料 场A) 3 5 0 7 0 1
ci2( 料 场B) 0 0 4 0 6 10
总吨公里数为136.2
Location(Linear)
月份型 monthM..monthN OCT..JAN
OCT, NOV, DEC, JAN
年份月份型
monthYearM..mo nthYearN
OCT2001..JAN OCT2001,
2002
NOV2001,
DEC2001,
JAN2002
运算符的优先级
三类运算符:
算术运算符 逻辑运算符 关系运算符 优先级 运算符 最高 #NOT# —(负号)
43
A5
2 3 9 57 2
65
41
A6
5 5 2 28 1
43
52
销量
35 37 22 32 41 32 43 38
a i 6 0 5 5 1 4 3 4 1 5 2 30 2 b i 3 3 5 2 7 3 2 4 2 3 1 4 2 3 3 2 88
lingo软件在运输问题中的应用

172科技创新导报 Science and Technology Innovation Herald2008 NO.36Science and Technology Innovation Herald管 理 科 学随着社会经济的发展,运输业在经济生活中的地位越来越重要,国内国际的物流、人流最终都离不开具体的运输环节。
在社会产品的最终成本中,运输成本约占10%-30%,所以,开展合理运输,节约运输成本,对于降低社会产品的总成本起着重要作用。
因此,运输企业需要在众多运输方案中选择总运费最小的。
这样的问题,在物流运筹学中称为运输问题。
在求解运输问题方面,我们通常介绍的是表上作业法。
这是一种手工做法。
当输出地个数M,和输入地个数N比较大时,这种手工的表上作业法就显得很繁琐了,这时我们要处理的是至少M+1行N+1列的表格。
因此,我们考虑用计算机来处理这个问题。
可以用来求解运输问题的软件常见的有,lingo、lindo、MATLAB、office中的excel等。
他们各有特色,今天,我就通过一个实例来介绍lingo软件在运输问题中的应用。
傲来公司有三个仓库:H1、H2、H3,A商品在这三仓库中的库存分别为100吨,95吨,110吨;另知有四家大型超市(S1、S2、S3、S4)需要该公司的A商品,他们的需求量分别是55吨,80吨,90吨,75吨 。
我们面临的问题是如何利用现有库存资源满足这四家超市的需求,并使总运输成本最低。
从三个仓库向四家超市送货的运输成本价(元/吨)如表1所示。
表1该运输问题的目标很明了,就是总运费最小化。
所以我们令Xij表示从仓库Hi到超市Sj运送的商品吨数。
从而有运输问题的数学模型:目标函数:MIN=25*X11+20*X12….+20*X33+22*X34库存约束:∑X1j<=100;∑X2j<=95;∑X3j<=110;j=1,2,3,4需求约束:∑Xi1=55;∑Xi2=80;∑Xi3=90;∑Xi4=75;i=1,2,3非负约束:Xij>=0用lingo求解的过程如下:model:!3仓库,4超市运输问题模型;sets:h/h1 h2 h3/:capacity;s/s1 s2 s3 s4/:demand;links(h,s):cost,x;endsets!目标函数;min=@sum(links(i,j):cost(i,j)*x(i,j));!需求函数;@for(s(j):@sum(h(i):x(i,j))=demand(j));!供用约束;@for(h(i):@sum(s(j):x(i,j))<=capacity(i));!数据段;data:capacity=100 95 110;demand=55 80 90 75;cost=25 20 22 19 20 18 11 20 15 1820 22;enddata在lingo8.0,windows2000环境中运行结果如下:Global optimal solution found.Objective value: 4720.000Total solver iterations: 4Variable Value Reduced CostCAPACITY( H1)100.0000 0.000000CAPACITY( H2) 95.0000 0.000000CAPACITY( H3)110.0000 0.000000DEMAND( S1) 55.00000 0.000000DEMAND( S2) 80.00000 0.000000DEMAND( S3) 90.00000 0.000000DEMAND( S4) 75.00000 0.000000COST( H1, S1)25.00000 0.000000COST( H1, S2)20.00000 0.000000COST( H1, S3)22.00000 0.000000COST( H1, S4)19.00000 0.000000COST( H2, S1)20.00000 0.000000COST( H2, S2)18.00000 0.000000COST( H2, S3)11.00000 0.000000COST( H2, S4)20.00000 0.000000COST( H3, S1)15.00000 0.000000COST( H3, S2)18.00000 0.000000COST( H3, S3)20.00000 0.000000COST( H3, S4)22.00000 0.000000X( H1, S1) 0.000000 8.000000X( H1, S2) 20.00000 0.000000X( H1, S3) 0.000000 9.000000X( H1, S4) 75.00000 0.000000X( H2, S1) 0.000000 5.000000X( H2, S2) 5.000000 0.000000X( H2, S3) 90.00000 0.000000X( H2, S4) 0.000000 3.000000X( H3, S1) 55.00000 0.000000X( H3, S2) 55.00000 0.000000X( H3, S3) 0.000000 9.000000X( H3, S4) 0.000000 5.000000Row Slack or Surplus Dual Price1 4720.000 -1.0000002 0.000000 -17.000003 0.000000 -20.000004 0.000000 -13.000005 0.000000 -19.000006 5.000000 0.0000007 0.000000 2.0000008 0.000000 2.000000该结果显示最低运费为4720元,最优运输方案是仓库1向超市2供货20吨,仓库1向超市4供货75吨,仓库2向超市2供货5吨,仓库2向超市3供货90吨,仓库3向超市1供货55吨,仓库3向超市2供货55吨。
数学建模_线性规划_运输问题lingo程序

X15 20.00000 0.000000
X16 0.000000 5.000000
X21 0.000000 7.000000
X22 0.000000 2.000000
X23 0.000000 17.00000
X24 0.000000 6.000000
X25 10.00000 0.000000
2 0.000000 -2.000000
3 0.000000 -6.000000
4 0.000000 -5.000000
5 0.000000 -1.000000
6 0.000000 0.000000
7 0.000000 -6.000000
8 0.000000 -4.000000
9 0.000000 -7.000000
MinZ=20x11+15x12+16x13+5x14+4x15+7x16+17x21+15x22+33x23+12x24+8x25+6x26+9x31+12x32+18x33+16x34+30x35+13x36+12x41+8x42+11x43+27x44+19x45+14x46+7x52+10x53+21x54+10x55+32x56+6x64+11x65+13x66
运输点1接收点1运输点23020接收点2运输点33040接收点3运输点41020接收点4运输点520接收点540运输点6接收点6这样的方案费用最小为1620
应用LINGO软件求解运输问题

2012——2013学年第一学期合肥学院数理系实验报告课程名称:运筹学实验项目:应用LINGO软件求解运输问题实验类别:综合性□设计性□√验证性□专业班级:姓名:学号:实验地点:实验时间:指导教师:成绩:一.实验目的1、学会使用LINGO 软件求解运输问题的步骤与方法。
2、掌握使用LINGO 对运输问题的求解功能,并对结果进行分析。
二.实验内容1.已知某企业有甲、乙、丙三个分厂生产一种产品,其产量分别为7、9、7个单位,需运往A 、B 、C 、D 四个门市部,各门市部需要量分别为3、5、7、8个单位。
已知单位运价如下表。
试确定运输计划使总运费最少。
2.现在要在五个工人中确定四个人来分别完成四项工作中的一项工作。
由于每个工人的技术特长不同,他们完成各项工作所需的工时也不同。
每个工人完成各项工作所需工时如下表所示,试找出一个工作分配方案,使总工时最小。
三. 模型建立1.由题设知,总产量为:7+9+7=23个单位,总销量为:3+5+7+8=23个单位,所以这是一个产销平衡的运输问题。
设)4,3,2,1;3,2,1(==j i x ij 代表从第i 个产地运往第j 个销地的数量,z 为总运费。
i a 表示第i 个产地的产量,j b 表示第j 个销地的销量ij c 表示从第i 个产地运往第j 个销地的单位产品运输费用。
则该问题的数学模型为:34114131max 0,1,2,3;1,2,3,4ij iji j ij ij ij j i ij Z c x x a x b x i j =====⎧=⎪⎪⎪=⎨⎪⎪≥==⎪⎩∑∑∑∑2. 设0-1变量,1,0ij i x i ⎧=⎨⎩当第个人完成某j 项工作,当第个人不完成某j 项工作 则该问题的数学模型为:54115141min 1,1,01ij iji j ij i ij j ijZ c x x j x i x i j =====⎧= =1,2,3,4⎪⎪⎪= = 1,2,3,4,5⎨⎪⎪= =1,2,3,4,5;=1,2,3,4⎪⎩∑∑∑∑或,四. 模型求解(含经调试后正确的源程序)1、编写程序1-1.m 如下:model :sets :warehouses/wh1..wh3/: capacity;vendors/v1..v4/: demand;links(warehouses,vendors): cost, volume;endsetsdata :capacity=7 9 7;demand=3 5 7 8;cost= 12 13 10 1110 12 14 1014 11 15 12;enddatamin =@sum (links(I,J): cost(I,J)*volume(I,J));@for(vendors(J):@sum(warehouses(I): volume(I,J))=demand(J));@for(warehouses(I):@sum(vendors(J): volume(I,J))<=capacity(I));end2、编写程序2-1.m如下:model:sets:workers/w1..w5/;jobs/j1..j4/;links(workers,jobs): cost,volume;Endsetsdata:cost=9 4 3 74 65 65 4 7 57 5 2 310 6 7 4;enddatamin=@sum(links: cost*volume);@for(workers(I): @sum(jobs(J): volume(I,J))<=1);@for(jobs(J): @sum(workers(I): volume(I,J))=1);@for(links(i,j): @bin(volume(i,j)));End五.结果分析1、运行结果:Global optimal solution found.Objective value: 239.0000Infeasibilities: 0.000000Total solver iterations: 6Variable Value Reduced Cost CAPACITY( WH1) 7.000000 0.000000 CAPACITY( WH2) 9.000000 0.000000 CAPACITY( WH3) 7.000000 0.000000 DEMAND( V1) 3.000000 0.000000 DEMAND( V2) 5.000000 0.000000 DEMAND( V3) 7.000000 0.000000 DEMAND( V4) 8.000000 0.000000COST( WH1, V1) 12.00000 0.000000COST( WH1, V2) 13.00000 0.000000COST( WH1, V3) 10.00000 0.000000COST( WH1, V4) 11.00000 0.000000COST( WH2, V1) 10.00000 0.000000COST( WH2, V2) 12.00000 0.000000COST( WH2, V3) 14.00000 0.000000COST( WH2, V4) 10.00000 0.000000COST( WH3, V1) 14.00000 0.000000COST( WH3, V2) 11.00000 0.000000COST( WH3, V3) 15.00000 0.000000COST( WH3, V4) 12.00000 0.000000VOLUME( WH1, V1) 0.000000 1.000000 VOLUME( WH1, V2) 0.000000 3.000000 VOLUME( WH1, V3) 7.000000 0.000000 VOLUME( WH1, V4) 0.000000 0.000000 VOLUME( WH2, V1) 3.000000 0.000000 VOLUME( WH2, V2) 0.000000 3.000000 VOLUME( WH2, V3) 0.000000 5.000000 VOLUME( WH2, V4) 6.000000 0.000000 VOLUME( WH3, V1) 0.000000 2.000000 VOLUME( WH3, V2) 5.000000 0.000000 VOLUME( WH3, V3) 0.000000 4.000000 VOLUME( WH3, V4) 2.000000 0.000000Row Slack or Surplus Dual Price1 239.0000 -1.0000002 0.000000 -12.000003 0.000000 -11.000004 0.000000 -11.000005 0.000000 -12.000006 0.000000 1.0000007 0.000000 2.0000008 0.000000 0.000000所以,最优调运方案为:甲→C:7单位;甲→D:0单位;乙→A:3单位;乙→D:6单位;丙→B:5单位;丙→D:2单位。
lingo编程程序求解选址-运输问题

sets:factory/1..3/:s1,s2,s3,s4;!工厂四种产品供应量;warhouse/1..13/:lwar,fd,eva,yun,war1,war2,war3,war4,wq1,wq2,wq3,wq4;!配送中心最大仓储量、评价值、固定运营成本、库存成本以及库存量;customer/1..24/:d1,d2,d3,d4;!客户四种产品的需求量;tr/1..13/:z;link1(factory,warhouse):d,x1,x2,x3,x4;!工厂到客户的运输距离,四种产品的运输量;link2(warhouse,customer):dd,xx1,xx2,xx3,xx4,xxx1,xxx2,xxx3,xxx4;!物流中心到客户运输距离、运输量,未超出安全距离的运输量;endsetsdata:!供用量;s1=;s2=;s3=;s4=;!最大库存;lwar=;!安全距离;fd=;!需求量;d1=;d2=;d3=;d4=;!运输成本;tc=;ttc=;yun=;!运营成本;u=;!超出最佳半径的惩罚成本;w1=;w2=;w3=;!单位库存成本;war1=;war2=;war3=;war4=;d=;!各钢厂到备选配送中心距离;dd=;!备选配送中心到需求点的距离;enddataf1=@sum(link1(i,j):x1(i,j)*tc*d(i,j))+@sum(link1(i,j):x2(i,j)*tc*d(i,j) )+@sum(link1(i,j):x3(i,j)*tc*d(i,j))+@sum(link1(i,j):x4(i,j)*tc*d(i,j)) +@sum(link2(j,k):xx1(j,k)*ttc*dd(j,k))+@sum(link2(j,k):xx2(j,k)*ttc*dd( j,k))+@sum(link2(j,k):xx3(j,k)*ttc*dd(j,k))+@sum(link2(j,k):xx4(j,k)*tt c*dd(j,k))+@sum(warhouse(j):z(j)*yun)+@sum(link2(j,k):@smax(dd(j,k)-600,0)*(xx1+xx2+xx3+xx4-xxx1-xxx2-xxx3-xx x4)*u)+@sum(warhouse(j):wq1(j)*war1+wq2(j)*war2+war3*wq3(j)+wq4(j)*war4 );f2=@sum(link2(j,k):xxx1+xxx2+xxx3+xxx4);max=(7731050000-f1)/6485240000+f2/1125;!每种产品的安全距离运输量;@for(link2:xxx1=@if(dd#gt#600,0,xx1));@for(link2:xxx2=@if(dd#gt#600,0,xx2));@for(link2:xxx3=@if(dd#gt#600,0,xx3));@for(link2:xxx4=@if(dd#gt#600,0,xx4));!超过安全距离的惩罚成本;tt=@sum(link2(j,k):@smax(dd-600,0)*(xx1-xxx1)*u)+@sum(link2(j,k):@smax( dd-600,0)*(xx2-xxx2)*u)+@sum(link2(j,k):@smax(dd-600,0)*(xx3-xxx3)*u)+@sum(link2(j,k):@smax(dd -600,0)*(xx4-xxx4)*u);!工厂供应约束;@for(factory(i):@sum(warhouse(j):x1(i,j))<=s1(i));@for(factory(i):@sum(warhouse(j):x2(i,j))<=s2(i));@for(factory(i):@sum(warhouse(j):x3(i,j))<=s3(i));@for(factory(i):@sum(warhouse(j):x4(i,j))<=s4(i));!配送中心库存量;@for(warhouse(j):wq1=-@sum(customer(k):xx1(j,k))+@sum(factory(i):x1(i,j)));@for(warhouse(j):wq2=-@sum(customer(k):xx2(j,k))+@sum(factory(i):x2(i,j)));@for(warhouse(j):wq3=-@sum(customer(k):xx3(j,k))+@sum(factory(i):x3(i,j)));@for(warhouse(j):wq4=-@sum(customer(k):xx4(j,k))+@sum(factory(i):x4(i,j)));!配送中心流出量小于流入量;@for(warhouse(j):@sum(customer(k):xx1(j,k))<=@sum(factory(i):x1(i,j)));@for(warhouse(j):@sum(customer(k):xx2(j,k))<=@sum(factory(i):x2(i,j))); @for(warhouse(j):@sum(customer(k):xx3(j,k))<=@sum(factory(i):x3(i,j))); @for(warhouse(j):@sum(customer(k):xx4(j,k))<=@sum(factory(i):x4(i,j))); !满足顾客需求;@for(customer(k):@sum(warhouse(j):xx1(j,k)*z(j))=d1(k));@for(customer(k):@sum(warhouse(j):xx2(j,k)*z(j))=d2(k));@for(customer(k):@sum(warhouse(j):xx3(j,k)*z(j))=d3(k));@for(customer(k):@sum(warhouse(j):xx4(j,k)*z(j))=d4(k));@sum(tr(j):z(j))<=13;!限制选择配送中心数量;@for(tr(j):@bin(z(j)));!z是0-1变量;end。
LINGO软件求解运输问题与表上作业法的比较
2 = U1 V2 9 0 + ; : 十 V2 4 U3 V1 1 一 U3 V2 7 U4 V2 1 U4 V3 0 U4 V4 3 Us V1 ;一 + ;5 + ;一 + ;= 十 ;一 + ;一 + ;
设 U —0 分别求 出 U。 s和 ~ , 4 , ~U 如表 4所示 .
18 3
湛 江师 范学 院学报 ( 自然科 学 )
第 3 卷 1
表上 做 出记 号 , 同时 由于 B 的需求 已经满 足 , 以划 去该列 其他 的各个 运价 . 可 计算结 果 如表 2 示 : 所
表 2 第 l轮 求解 表 表 3 初始 调 运 方案 表
以此类 推 , 经过 8轮求解 , 求得 初始 调运方 案如 表 3所示 :
表 4 第 1轮检 验 表 表 5 最 优 调 运方 案表
设没有 调运 量的运 价为 C , 果 不 小 于 + , 如 检验 通 过 ; 否则 在 该 运 价上 做 记 号 , 等待 下 一 步 调 整. 以此类 推 , 过 4轮 调整后 , 经 通过 检验 , 有 的 均大 于 【 所 ,十 , 此调运 方案 为最 优方案 , 如表 5所示 . 求解结 果 : 3 0 X2—2 ,X3一3 ,X 2 0 X4=1 , 1: 0 X5=1 , 3 0 Xl =1 , 2 O l O —3 , 0 X5: 3 , 2 0 X5—1 ;即产 地 1向销 :
张 家 善
( 江师范学院 商学院 , 东 湛江 544) 湛 广 2 0 8
摘
要 : 为 一 类 特 殊 的 线性 规 划 问题 , 输 问题 的 求 解 统上 采 用表 上 作 业 法 . 是 其 求 解 过 程 复 杂 、 琐 , 作 运 但 繁
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
对冒号“:”前面的集合的每个元素(下标),冒号“:”后 面的约束关系式都要成立 。
2020/5/23
18
例5 分配问题(指派问题,Assignment Problem)
(1)集合段(SETS):以“ SETS:” 开始, “ENDSETS” 结束,定义必要的集合变量(SET)及其元素(MEMBER, 含义类似于数组的下标)和属性(ATTRIBUTE,含义类似于 数组)。
基本集合的定义语法
基本集合的定义格式为(方括号“[ ]”中的内容是可选项, 可以没 有):
setname [/member_list/] [: attribute_list];
例2 直接用LINGO来解如下二次规划问题:
Max 98x1 277x2 x12 0.3x1x2 2x22 1
s.t. x1 x2 100
2
x1 2x2
3
x1, x2 0 为整数
4
输入窗口如下:
程序语句输入的备注:
•LINGO总是根据“MAX=”或“MIN=”寻找目标函数,而除注 释语句和TITLE语句外的其他语句都是约束条件,因此语句的 顺序并不重要 。 •限定变量取整数值的语句为“@GIN(X1)”和“@GIN(X2)”, 不可以写成“@GIN(2)”,否则LINGO将把这个模型看成没有 整数变量。 •LINGO中函数一律需要以“@”开头,其中整型变量函数 (@BIN、@GIN)和上下界限定函数(@FREE、@SUB、 @SLB)与LINDO中的命令类似。而且0/1变量函数是@BIN函 数。
例1 如何在LINGO中求解如下的LP问题:
min 2x1 3x2 s.t.
x1 x2 350
x1
100
2x1 x2 600
x1, x2 0
在模型窗口中输入如下代码:
min=2*x1+3*x2; x1+x2>=350; x1>=100; 2*x1+x2<=600;
然后点击工具条上的按钮 即可。
A1 A2 A3 A4 A5 A6 销量
6 2 6 7 4 2 5 9 60 4 9 5 3 8 5 8 2 55 5 2 1 9 7 4 3 3 51 7 6 7 3 9 2 7 1 43 2 3 9 5 7 2 6 5 41 5 5 2 2 8 1 4 3 52 35 37 22 32 41 32 43 38
LINGO简介
(Linear Interactive General Optimizer)
LINGO(Linear Interactive General Optimizer) 是用来求解线性和非线性优化问题的简易工具。
LINGO内置了一种建立最优化模型的语言,可以简 便地表达大规模问题,利用LINGO高效的求解器可 快速求解并分析结果。
何定义这样的属性?
集合的属性相当于以集合的元素为下标的数组。这里的 c 相 ij
当于二维数组。它的两个下标分别来自集合warehouses 和 vendors ,因此可以定义一个由二元对组成的新的集合,然 后将 c 定义成这个新集合的属性。
ij
输入程序
定义了三个集合,其中links在前两 个集合warehouses 和vendors的基
•语句是组成LINGO模型的基本单位,每个语句都以分号结尾,编 写程序时应注意模型的可读性。例如:一行只写一个语句,按照 语句之间的嵌套关系对语句安排适当的缩进,增强层次感。
•以感叹号开始的是说明语句(说明语句也需要以分号结束)。
LINGO模型最基本的组成要素
一般来说, LINGO中建立的优化模型可以由五个部分组成,或 称为五“段”(SECTION):
model: !6发点8收点运输问题; sets: warehouses/wh1..wh6/: capacity; vendors/v1..v8/: demand; links(warehouses,vendors): cost, volume; endsets !目标函数;
data: capacity=60 55 51 43 41 52; demand=35 37 22 32 41 32 43 38; cost=6 2 6 7 4 2 9 5 49538582 52197433 76739271 23957265 5 5 2 2 8 1 4 3;
(5)计算段(CALC):以“CALC: ”开始, “ENDCALC”结 束,对一些原始数据进行计算处理。
在实际问题中,输入的数据通常是原始数据,不一定能在模 型中直接使用,可以在这个段对这些原始数据进行一定的“预 处理”,得到模型中真正需要的数据。
逻辑运算符
运算结果只有“真”(TRUE)和“假”(FALSE)两个值(称为“逻 辑值”),LINGO中用数字1代表TRUE,其他值(典型的值是0)都 是FALSE。 在LINGO中,逻辑运算(表达式)通常作为过滤条件使用,逻辑运 算符有9种,可以分成两类: #AND#(与),#OR#(或),#NOT#(非):逻辑值之间的运算,它们操 作的对象本身已经是逻辑值或逻辑表达式,计算结果也是逻辑值。
类型 数字型 字符-数字型
隐式列举格式 1..n stringM..stringN
日期(星期)型 dayM..dayN
示例
1..5 Car101..car2 08 MON..FRI
示例集合表示的元素 1, 2, 3, 4, 5 Car101, car102, … , car208
MON, TUE, WED, THU, FRI
#EQ#(等于),#NE#(不等于),#GT#(大于),#GE#(大于等于),#LT#(小 于),#LE#(小于等于):是“数与数之间”的比较,也就是它们操作 的对象本身必须是两个数, 计算得到的结果是逻辑值。
关系运算符
表示是“数与数之间”的大小关系,在LINGO中用来表示优 化模型的约束条件。LINGO中关系运算符有3种: <(即<=,小于等于),=(等于),>(即>=,大于等于) (在优化模型中约束一般没有严格小于、严格大于关系)
min=@sum(links: cost*volume); !需求约束;
enddata end
@for(vendors(J):
@sum(warehouses(I): volume(I,J))=demand(J));
!产量约束;
@for(warehouses(I):
@sum(vendors(J): volume(I,J))<=capacity(I));
月份型 年份-月份型
monthM..monthN
OCT..JAN
monthYearM..monthYe OCT2001..JA
arN
N2002
OCT, NOV, DEC, JAN
OCT2001, NOV2001, DEC2001, JAN2002
(2)目标与约束段:目标函数、约束条件等,没有段的开 始和结束标记,因此实际上就是除其它四个段(都有明确的段 标记)外的LINGO模型。
建立模型: (产大于销) 设xij为从第i个产地调运给第j个销地的物资数量
68
min
z= i=1
j=1cijxij
8
s.t. xij≤ai (i=1,2,……,6)
j=1
6
xij=bj (j=1,2,……,8)
i=1
xij0 ( i=1,2,……,6 ;j=1,2,……,8)
使用LINGO软件,编制程序如下:
model:
础上定义
data:
!6发点8收点运输问题; sets:
表示集合calipnakcsit中y=的60元55素5就1 4是3集41合52; warehoudseems 和anvde=n3d5o3r7s的22元32素4组1 3合2 43 38;
enwvlidenanskredest(hosworsua/rvsee1hs./.ovwu8hs/e1:s.d.,wvemehn6adn/o:drc;sa)p: accoistyt,;volum成 是 积eli;的 w,nka有 也rs=e序 就h{c(oo二 是usSs4572t元 说e=,9263s6组和 T51792)3935,6ve8797|7从Sn5422w4d数8376oa2rr2315学9se的h5上o笛u看s卡elsi,儿nk
!这里是数据;
然后点击工具条上的按钮 即可。
本例中集合的概念
利用集合的概念,可以定义产地warehouses和销地vendors两个
集合,分别有6个和8个元素(下标),其属性分别为产量capacity
和销量demand。但从各个产地到销地的单位运价
c
i
和决策变量
j
(运送量)xij 与集合warehouses和集合vendors都有关系的。该如
LINGO的基本用法的几点注意事项
•LINGO中不区分大小写字母;变量和行名可以超过8个字符, 但不能超过32个字符,且必须以字母开头。
•用LINGO解优化模型时已假定所有变量非负(除非用限定变量取 值范围的函数@free或@sub或@slb另行说明)。
•变量可以放在约束条件的右端(同时数字也可放在约束条件的左 端)。但为了提高LINGO求解时的效率,应尽可能采用线性表达 式定义目标和约束(如果可能的话)。
这里一般要用到LINGO的内部函数,尤其是与集合相关的 求和函数@SUM和循环函数@FOR等。
(3)数据段(DATA):以 “DATA:” 开始, “ENDDATA”结束, 对集合的属性(数组)输入必要的常数数据。 格式为:“attribute(属性) = value_list(常数列表);” 常数列表(value_list)中数据之间可以用逗号“,”分开,也可以用 空格分开(回车等价于一个空格) 。
