2014北京市高考压轴卷 数学(理科) 含解析
北京市高考数学压轴卷 理(含解析)(1)

2014北京市高考压轴卷理科数学一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的1.已知11xyi i=-+,其中,x y 是实数,i 是虚数单位,则x yi +的共轭复数为( ) A .12i + B .12i - C .2i + D .2i -2.已知函数3()f x x x =--,123,,x x x R ∈,且120x x +>,230x x +>,310x x +>,则123()()()f x f x f x ++的值为()A.正B.负C.零D.可正可负3.已知某几何体的三视图如下,则该几何体体积为( )A .4+52π B .4+32π C .4+2π D .4+π 4.如图所示为函数π()2sin()(0,0)2f x x ωϕωϕ=+>≤≤的部分图像,其中A ,B 两点之间的距离为5,那么(1)f -=( ) A .-1 B .3-C 3D .15.(5分)已知两条不重合的直线m、n和两个不重合的平面α、β,有下列命题:①若m⊥n,m⊥α,则n∥α;②若m⊥α,n⊥β,m∥n,则α∥β;③若m、n是两条异面直线,m⊂α,n⊂β,m∥β,n∥α,则α∥β;④若α⊥β,α∩β=m,n⊂β,n⊥m,则n⊥α.其中正确命题的个数是()A.1B.2C.3D.46.设函数是定义在上的可导函数,其导函数为,且有,则不等式的解集为A. B.C. D.7.已知F1(﹣c,0),F2(c,0)为椭圆的两个焦点,P为椭圆上一点且,则此椭圆离心率的取值范围是()A.B.C.D.8.已知定义在R上的偶函数f(x)满足f(1+x)=f(1﹣x),且x∈[0,1]时,,则方程在区间[﹣3,3]上的根的个数为()A.5 B.4 C.3 D.2二、填空题:本大题共6小题,每小题5分,共30分.把答案填在答题卡的相应位置.9.已知集合{}{}22,1,3,3,21,1A a aB a a a=+-=--+,若{}3A B=-I,则实数a的值为________________.10.已知如图所示的流程图(未完成),设当箭头a指向①时输出的结果S=m,当箭头a指向②时,输出的结果S=n,求m+n的值.11.若n S 是等差数列}{n a 的前n 项和,且8320S S -=,则11S 的值为 . 12.展开式中有理项共有 项.13.在平面直角坐标系xOy 中,过坐标原点的一条直线与函数xx f 2)(=的图象交于P 、Q 两点,则线段PQ 长的最小值是_______14.设a ∈R ,若x >0时均有[(a ﹣1)x ﹣1](x 2﹣ax ﹣1)≥0,则a= .三、解答题:本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤.解答写在答题卡上的指定区域内.15.已知向量)4cos ,4(cos ),1,4sin 3(2x x n x m ==.记x f ⋅=)( (I)求)(x f 的周期;(Ⅱ)在∆ABC 中,角A 、B 、C 的对边分别是a 、b 、c ,且满足(2a —c)cos B=b cosC , 若13f (A )+=∆ABC 的形状. 16.在一次对某班42名学生参加课外篮球、排球兴趣小组(每人参加且只参加一个兴趣小组) 篮球 排球 总计 男同学 16 6 22 女同学 8 12 20 总计241842(Ⅰ)据此判断是否有95%的把握认为参加“篮球小组”或“排球小组”与性别有关?(Ⅱ)在统计结果中,如果不考虑性别因素,按分层抽样的方法从两个兴趣小组中随机抽取7名同学进行座谈.已知甲、乙、丙三人都参加“排球小组”. ①求在甲被抽中的条件下,乙丙也都被抽中的概率;②设乙、丙两人中被抽中的人数为X ,求X 的分布列及数学期望E(X).下面临界值表供参考:2()P K k≥0.15 0.10 0.05 0.025 0.010 0.005 0.001 k0 2.072 2.706 3.841 5.024 6.635 7.879 10.828参考公式:2()()()()Ka b c d a c b d=++++命题意图:考查分类变量的独立性检验,条件概率,随机变量的分布列、数学期望等,中等题.17.已知正四棱柱1111-ABCD A B C D中,12,4==AB AA.(Ⅰ)求证:1BD A C⊥;(Ⅱ)求二面角11--A A C D的余弦值;(Ⅲ)在线段1CC上是否存在点P,使得平面11A CD⊥平面PBD,若存在,求出1CPPC的值;若不存在,请说明理由.18.已知椭圆2222:1(0)x yC a ba b+=>>的左右焦点分别为12,F F,点3)B为短轴的一个端点,260OF B∠=︒.(Ⅰ)求椭圆C的方程;(Ⅱ)如图,过右焦点2F,且斜率为(0)≠k k的直线l与椭圆C相交于,E F两点,A为椭圆的右顶点,直线,AE AF分别交直线3=x于点,M N,线段MN的中点为P,记直线2PF的斜率为'k.求证: '⋅k k为定值.19.已知数列{}n a 的各项均为正数,记12()n A n a a a =+++L ,231()n B n a a a +=+++L ,342(),1,2,n C n a a a n +=+++=L L .(Ⅰ)若121,5a a ==,且对任意n ∈*N ,三个数(),(),()A n B n C n 组成等差数列,求数列{}n a 的通项公式.(Ⅱ)证明:数列{}n a 是公比为q 的等比数列的充分必要条件是:对任意n ∈*N ,三个数(),(),()A n B n C n 组成公比为q 的等比数列.20.已知函数2()2ln f x x x ax =-+(a ∈R ).(Ⅰ)当2a =时,求()f x 的图象在1x =处的切线方程;(Ⅱ)若函数()()g x f x ax m =-+在1[e]e ,上有两个零点,求实数m 的取值范围;(Ⅲ)若函数()f x 的图象与x 轴有两个不同的交点12(0)(0)A x B x ,,,,且120x x <<, 求证:12()02x x f +'<(其中()f x '是()f x 的导函数).2014北京市高考压轴卷数学理word 版参考答案 1. 【答案】D 【解析】1()1,2,1,12x x xi yi x y i =-=-∴==+故选D . 2. 【答案】B【解析】∵3()f x x x =--,∴函数()f x 在R 上是减函数且是奇函数,∵120x x +>,∴12x x >-,∴12()()f x f x <-,∴12()()f x f x <-,∴12()()0f x f x +<, 同理:23()()0f x f x +<,31()()0f x f x +<,∴123()()()0f x f x f x ++<.3. 【答案】A【解析】该几何体是一个圆柱与一个长方体的组成,其中重叠了一部分2π,所以该几何体的体积为52213422πππ⨯⨯+-=+.故选A . 4. 【答案】A. 【解析】5. 【答案】C【解析】①若m⊥n,m⊥α,则n 可能在平面α内,故①错误 ②∵m⊥α,m∥n,∴n⊥α,又∵n⊥β,∴α∥β,故②正确 ③过直线m 作平面γ交平面β与直线c , ∵m、n 是两条异面直线,∴设n∩c=O, ∵m∥β,m ⊂γ,γ∩β=c∴m∥c, ∵m ⊂α,c ⊄α,∴c∥α,∵n ⊂β,c ⊂β,n∩c=O,c∥α,n∥α ∴α∥β;故③正确④由面面垂直的性质定理:∵α⊥β,α∩β=m,n ⊂β,n⊥m,∴n⊥α.故④正确 故正确命题有三个,故选C6. 【答案】C.【解析】由,得:,即,令,则当时,,即在是减函数,,,,在是减函数,所以由得,,即,故选7. 【答案】C.【解析】设P(m,n ),=(﹣c﹣m,﹣n)•(c﹣m,﹣n)=m2﹣c2+n2,∴m2+n2=2c2,n2=2c2﹣m2①.把P(m,n )代入椭圆得 b2m2+a2n2=a2b2②,把①代入②得 m2=≥0,∴a2b2≤2a2c2,b2≤2c2,a2﹣c2≤2c2,∴≥.又 m2≤a2,∴≤a2,∴≤0,a2﹣2c2≥0,∴≤.综上,≤≤,故选 C.8. 【答案】A.【解析】由f(1+x)=f(1﹣x)可得函数f(x)的图象关于x=1对称,方程在区间[﹣3,3]根的个数等价于f(x)与y=图象的交点的个数,而函数y=图象可看作y=的图象向下平移1个单位得到,作出它们的图象如图:可得两函数的图象有5个交点,故选A9. 【答案】a=-1.【解析】若a-3=-3,则a=0,此时:}1,1,3{},3,1,0{--=-=B A ,}3,1{-=⋂∴B A ,与题意不符,舍 若2a-1=-3,则a=-1,此时:}2,4,3{},3,1,0{--=-=B A ,}3{-=⋂∴B A ,∴a=-1 若a2+1=-3,则a 不存在 综上可知:a=-1 10. 【答案】20.【解析】当箭头指向①时,计算S 和i 如下. i =1,S =0,S =1; i =2,S =0,S =2; i =3,S =0,S =3; i =4,S =0,S =4; i =5,S =0,S =5; i =6结束. ∴S=m =5.当箭头指向②时,计算S 和i 如下. i =1,S =0, S =1; i =2,S =3; i =3,S =6; i =4,S =10; i =5,S =15; i =6结束. ∴S=n =15. ∴m+n =20. 11. 【答案】44【解析】由83456786520S S a a a a a a -=++++==,解得64a =,又由611111611211()114422a a a S a ⨯+====12. 【答案】3. 【解析】展开式通项公式为T r+1==若为有理项时,则为整数,∴r=0、6、12,故展开式中有理项共有3项,故答案为:3 13.【答案】4.【解析】设过坐标原点的一条直线方程为y kx =,因为与函数xx f 2)(=的图象交于P 、Q 两点,所以0k >,且联列解得22,2,,2P k Q k k k ⎛⎫⎛⎫--⎪ ⎪ ⎪ ⎪⎝⎝,所以 ()222122284PQ kk k k ⎛⎫⎛⎫=+=+≥ ⎪ ⎪ ⎪⎝⎭⎝⎭14. 【答案】【解析】(1)a=1时,代入题中不等式明显不成立.(2)a≠1,构造函数y 1=(a ﹣1)x ﹣1,y 2=x 2﹣ax ﹣1,它们都过定点P (0,﹣1). 考查函数y 1=(a ﹣1)x ﹣1:令y=0,得M (,0),∴a>1;考查函数y 2=x 2﹣ax ﹣1,显然过点M (,0),代入得:,解之得:a=,或a=0(舍去). 故答案为:15. 【解析】2311()3cos cos cos 4442222x x x x x f x =+=++1sin 262x π⎛⎫=++⎪⎝⎭(I )π4=T(Ⅱ 根据正弦定理知:()2cos cos (2sin sin )cos sin cos a c B b C A C B B C -=⇒-= 12sin cos sin()sin cos 23A B B C A B B π⇒=+=⇒=⇒=∵13()f A +=∴ 113sin 262263A A πππ+⎛⎫+++= ⎪⎝⎭或23π3A π⇒=或 π 而203A π<<,所以3A π=,因此∆ABC 为等边三角形.……………12分16. 【解析】(Ⅰ)由表中数据得K 2的观测值k =42×(16×12-8×6)224×18×20×22=25255≈4.582>3.841. ……2分所以,据此统计有95%的把握认为参加“篮球小组”或“排球小组”与性别有关.……4分 (Ⅱ)①由题可知在“排球小组”的18位同学中,要选取3位同学. 方法一:令事件A 为“甲被抽到”;事件B 为“乙丙被抽到”,则P(A∩B)=33318C C ,P(A)=217318C C .所以P(B|A)=P(A∩B )P(A)=33217C C =217×16 =1136. ……7分 方法二:令事件C 为“在甲被抽到的条件下,乙丙也被抽到”, 则P(C)=22217C C =217×16=1136. ②由题知X 的可能值为0,1,2.依题意P(X =0)=316318C C =3551;P(X =1)=21162318C C C =517;P(X =2)=12162318C C C =151. 从而X 的分布列为X 0 1 2 P3551517151……10分 于是E(X)=0×3551+1×517+2×151=1751=13. ……12分17. 【解析】证明:(Ⅰ)因为1111ABCD A B C D -为正四棱柱,所以1AA ⊥平面ABCD ,且ABCD 为正方形. ………1分 因为BD ⊂平面ABCD ,所以1,BD AA BD AC ⊥⊥. ………2分 因为1AA AC A =I ,所以BD ⊥平面1A AC . ………3分因为1AC ⊂平面1A AC , 所以1BD A C ⊥. ………4分 (Ⅱ) 如图,以D 为原点建立空间直角坐标系-D xyz .则11(0,0,0),(2,0,0),(2,2,0),(0,2,0),(2,0,4),(2,2,4),D A B C A B 11(0,2,4),(0,0,4)C D ………5分所以111(2,0,0),(0,2,4)D A DC ==-uuuu r uuu r. 设平面11A D C 的法向量111(,,)x y z =n .所以 1110,D A D C ⎧⋅=⎪⎨⋅=⎪⎩uuuu r uuu r n n .即1110,240x y z =⎧⎨-=⎩……6分 令11z =,则12y =. 所以(0,2,1)=n . 由(Ⅰ)可知平面1AA C的法向量为(2,2,0)DB =uu u r. ……7分所以cos ,5DB <>==uu u rn . ……8分 因为二面角11--A A C D 为钝二面角, 所以二面角11--A A C D的余弦值为5-. ………9分 (Ⅲ)设222(,,)P x y z 为线段1CC 上一点,且1(01)CP PC λλ=≤≤uu r uuu r. 因为2221222(,2,),(,2,4)CP x y z PC x y z =-=---uu r uuu r.所以222222(,2,)(,2,4)x y z x y z λ-=---. ………10分 即22240,2,1x y z λλ===+. 所以4(0,2,)1P λλ+. ………11分 设平面PBD 的法向量333(,,)x y z =m .因为4(0,2,),(2,2,0)1DP DB λλ==+uu u r uu u r ,所以 0,0DP DB ⎧⋅=⎪⎨⋅=⎪⎩uu u r uu u r m m .即3333420,1220y z x y λλ⎧+=⎪+⎨⎪+=⎩. ………12分 令31y =,则3311,2x z λλ+=-=-. 所以1(1,1,)2λλ+=--m . ………13分 若平面11A CD ⊥平面PBD ,则0⋅=m n .即1202λλ+-=,解得13λ=.所以当113CP PC =时,平面11A CD ⊥平面PBD . ………14分 18.【解析】(Ⅰ)由条件2,a b ==…………2分故所求椭圆方程为13422=+y x . …………4分 (Ⅱ)设过点2(1,0)F 的直线l 方程为:)1(-=x k y . …………5分由22(1),143y k x x y =-⎧⎪⎨+=⎪⎩可得:01248)34(2222=-+-+k x k x k …………6分因为点2(1,0)F 在椭圆内,所以直线l 和椭圆都相交,即0>∆恒成立. 设点1122(,),(,)E x y F x y ,则34124,34822212221+-=+=+k k x x k k x x . …………8分 因为直线AE 的方程为:)2(211--=x x y y , 直线AF 的方程为:)2(222--=x x y y , ………9分 令3x =,可得)2,3(11-x y M ,)2,3(22-x y N ,所以点P 的坐标12121(3,())222y y x x +--. ………10分直线2PF 的斜率为12121()0222'31y y x x k +---=-12121()422y y x x =+-- 122112121212()42()4x y x y y y x x x x +-+=⋅-++1212121223()4142()4kx x k x x k x x x x -++=⋅-++ …………12分 2222222241282341434341284244343k k k k k k k k k k k -⋅-⋅+++=⋅--⋅+++34k=- 所以k k '⋅为定值43-. …………13分19. 【解析】 (Ⅰ) 因为对任意n *∈N ,三个数(),(),()A n B n C n 是等差数列, 所以()()()()B n A n C n B n -=-. ………1分 所以1122n n a a a a ++-=-, ………2分 即21214n n a a a a ++-=-=. ………3分 所以数列{}n a 是首项为1,公差为4的等差数列. ………4分 所以1(1)443n a n n =+-⨯=-. ………5分(Ⅱ)(1)充分性:若对于任意n *∈N ,三个数(),(),()A n B n C n 组成公比为q 的等比数列,则()(),()()B n qA n C n qB n ==. ………6分 所以[]()()()(),C n B n q B n A n -=-得2211(),n n a a q a a ++-=-即2121n n a qa a qa ++-=-. ………7分因为当1n =时,由(1)(1),B qA =可得21a qa =, ………8分 所以210n n a qa ++-=. 因为0n a >, 所以2211n n a a q a a ++==. 即数列{}n a 是首项为1a ,公比为q 的等比数列, ………9分 (2)必要性:若数列{}n a 是公比为q 的等比数列,则对任意n *∈N ,有1n n a a q +=. ………10分因为0n a >,所以(),(),()A n B n C n 均大于0.于是12)2311212(......(),()......n n n nq a a a a a a B n q A n a a a a a a +++++++===++++++ ………11分231)342231231(......(),()......n n n n q a a a a a a C n q B n a a a a a a ++++++++++===++++++ ………12分 即()()B n A n =()()C n B n =q ,所以三个数(),(),()A n B n C n 组成公比为q 的等比数列. ………13分综上所述,数列{}n a 是公比为q 的等比数列的充分必要条件是:对任意n ∈N ﹡,三个数(),(),()A n B n C n 组成公比为q 的等比数列. ………14分20. 【解析】(Ⅰ)当2a =时,2()2ln 2f x x x x =-+,2()22f x x x'=-+,切点坐标为(11),, 切线的斜率(1)2k f '==,则切线方程为12(1)y x -=-,即21y x =-. 2分(Ⅱ)2()2ln g x x x m =-+,则22(1)(1)()2x x g x x xx-+-'=-=,∵1[e]e x ∈,,故()0g x '=时,1x =.当11ex <<时,()0g x '>;当1e x <<时,()0g x '<.故()g x 在1x =处取得极大值(1)1g m =-. 4分 又211()2e e g m =--,2(e)2e g m =+-,2211(e)()4e 0e e g g -=-+<,则1(e)()e g g <,∴()g x 在1[e]e,上的最小值是(e)g . 6分()g x 在1[e]e ,上有两个零点的条件是2(1)10,11()20,eeg m g m =->⎧⎪⎨=--≤⎪⎩解得2112e m <≤+, ∴实数m 的取值范围是21(12]e +,. 8分(Ⅲ)∵()f x 的图象与x 轴交于两个不同的点12(0)(0)A x B x ,,,,∴方程22ln 0x x ax -+=的两个根为12x x ,,则211122222ln 0,2ln 0,x x ax x x ax ⎧-+=⎪⎨-+=⎪⎩两式相减得1212122(ln ln )()x x a x x x x -=+--.又2()2ln f x x x ax=-+,2()2f x x a x'=-+,则1212124()()2x x f x x a x x +'=-+++1212122(ln ln )4x x x x x x -=-+-. 下证1212122(ln ln )40x x x x x x --<+-(*),即证明2111222()ln 0x x x x x x -+<+,12x t x =, ∵120x x <<,∴01t <<,即证明2(1)()ln 01t u t t t -=+<+在01t <<上恒成立. 10分∵22222(1)2(1)114(1)()(1)(1)(1)t t t u t t t t t t t -+---'=+=-=+++,又01t <<,∴()0u t '>, ∴()u t 在(0,1)上是增函数,则()(1)0u t u <=,从而知2111222()ln 0x x x x x x -+<+,故(*)式<0,即12()02x x f +'<成立………….12分。
2014北京高考数学试卷(答案)

z
E 0, 2,0 , B 1,0,0 , C 2,1,0 , F 0,1,1 , P 0,0, 2
设面 ABF 的法向量为 n x0 , y0 , z0 , AB 1,0,0 ,
AF 0,1,1
A
F E y
G
H D C B M x
sin x b 与恒成立矛盾,故 b ≥1 , x 综上知: b 的最小值为 1 . x2 y 2 1, 19.⑴椭圆的标准方程为: 4 2 sin x bx 0
c 2 ; a 2 ⑵由题意知,直线 OA 的斜率存在,设为 k ,则直线 OA 的方程为 y kx , OA⊥OB ,
x1 2t y1 t H 2t , t , 2 2t z 2 2t 1
又
H 面 ABF , BH 2t 1, t , 2 2t
n BH 0 t 2t 2 0 , t
2 2
2 4 2 2 4 2 4 , H , , , PH , , 3 3 3 3 3 3 3
2014 高考答案与解析
2014 北京高考数学(理科)解析
2 .故 A 1.集合 A x | x2 2 x 0 0 ,
B 0 , 2 ,选 C.
上为增函数,符合题意. 2. A. y x 1 在 1,
B. y ( x 1)2 在 (0 , 1) 上为减函数,不合题意. C. y 2 x 为 ( , ) 上的减函数,不合题意. D. y log0.5 ( x 1) 为 (1, ) 上的减函数,不合题意. 故选 A.
π 若 b 1 ,则 h x cos x b 0 在 0 上有唯一解 x0 ,且 x 0 x0 时, h x 0 , 2 故 h x 在 0 x0 上单调递增,此时 h x h 0 0 ,
2014年北京高考理科数学试题含答案(Word版)

2014年北京高考数学(理科)试题一.选择题(共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项)1.已知集合2{|20},{0,1,2}A x x x B =-==,则A B =( ).{0}A .{0,1}B .{0,2}C .{0,1,2}D 2.下列函数中,在区间(0,)+∞上为增函数的是( ).A y = 2.(1)B y x =- .2x C y -= 0.5.l o g (1)D y x =+ 3.曲线1cos 2sin x y θθ=-+⎧⎨=+⎩(θ为参数)的对称中心( ) .A 在直线2y x =上 .B 在直线2y x =-上.C 在直线1y x =-上 .D 在直线1y x =+上4.当7,3m n ==时,执行如图所示的程序框图,输出的S 值为( ).7A .42B .210C .840D5.设{}n a 是公比为q 的等比数列,则"1"q >是"{}"n a 为递增数列的( ).A 充分且不必要条件 .B 必要且不充分条件.C 充分必要条件 .D 既不充分也不必要条件6.若,x y 满足20200x y kx y y +-≥⎧⎪-+≥⎨⎪≥⎩且z y x =-的最小值为-4,则k 的值为( ).2A .2B - 1.2C 1.2D -7.在空间直角坐标系Oxyz 中,已知()2,0,0A ,()2,2,0B ,()0,2,0C,(D ,若 1S ,2S ,3S 分别表示三棱锥D ABC -在xOy ,yOz ,zOx 坐标平面上的正投影图形的 面积,则( )(A )123S S S == (B )12S S =且 31S S ≠(C )13S S =且 32S S ≠ (D )23S S =且 13S S ≠8.有语文、数学两,成绩评定为“优秀”“合格”“不合格”三种.若A 同学每科成绩不低于B 同学,且至少有一科成绩比B 高,则称“A 同学比B 同学成绩好.”现有若干同学, 他们之间没有一个人比另一个成绩好, 且没有任意两个人语文成绩一样,数学成绩也一样的.问满足条件的最多有多少学生( )(A )2 (B )3 (C )4 (D )5二、填空题(共6小题,每小题5分,共30分)9.复数211i i +⎛⎫= ⎪-⎝⎭________. 10.已知向量a 、b 满足1a =,()2,1b =,且()0a b R λλ+=∈,则λ=________.11.设双曲线C 经过点()2,2,且与2214y x -=具有相同渐近线,则C 的方程为________; 渐近线方程为________.12.若等差数列{}n a 满足7890a a a ++>,7100a a +<,则当n =________时{}n a 的前n 项和最大.13. 把5件不同产品摆成一排,若产品A 与产品C 不相邻,则不同的摆法有_______种.14. 设函数)sin()(ϕω+=x x f ,0,0>>ωA ,若)(x f 在区间]2,6[ππ上具有单调性,且 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛6322πππf f f ,则)(x f 的最小正周期为________.试题分析:对等比数列}{n a ,若1 q ,则当0,1a 时数列}{n a 是递减数列;若数列}{n a 是递增数列,则二.填空题:本大题共6小题,每小题5分,共30分.请将答案天灾答题卡对应题的位置上,答错位置,书写不清,模棱两可均不得分.9.【答案】1-【解析】 试题分析:i i i i i i i ==+-+=-+22)1)(1()1(112,所以1)11(22-==-+i ii . 10.【答案】5【解析】三.解答题(共6题,满分80分)15. (本小题13分)如图,在ABC ∆中,8,3==∠AB B π,点D 在BC 边上,且71cos ,2=∠=ADC CD (1)求BAD ∠sin(2)求AC BD ,的长16. (本小题13分).李明在10场篮球比赛中的投篮情况如下(假设各场比赛互相独立):(1)从上述比赛中随机选择一场,求李明在该场比赛中投篮命中率超过6.0的概率.(2)从上述比赛中选择一个主场和一个客场,求李明的投篮命中率一场超过6.0,一场不超过6.0的概率.(3)记x 是表中10个命中次数的平均数,从上述比赛中随机选择一场,记X 为李明在这比赛中的命中次数,比较)(X E 与x 的大小(只需写出结论)17.(本小题14分)如图,正方形AMDE 的边长为2,C B ,分别为MD AM ,的中点,在五棱锥ABCDE P - 中,F 为棱PE 的中点,平面ABF 与棱PC PD ,分别交于点H G ,.(1)求证:FG AB //;(2)若⊥PA 底面ABCDE ,且PE AF ⊥,求直线BC 与平面ABF 所成角的大小,并 求线段PH 的长.18.(本小题13分) 已知函数()cos sin ,[0,]2f x x x x x π=-∈, (1)求证:()0f x ≤;(2)若sin x a b x <<在(0,)2π上恒成立,求a 的最大值与b 的最小值.19.(本小题14分)已知椭圆22:24C x y +=,(1)求椭圆C 的离心率.(2)设O 为原点,若点A 在椭圆C 上,点B 在直线2y =上,且OA OB ⊥,求直线AB 与圆222x y +=的位置关系,并证明你的结论.20.(本小题13分)对于数对序列1122(,),(,),,(,)n n P a b a b a b ,记111()T P a b =+,112()max{(),}(2)k k k k T P b T P a a a k n -=++++≤≤,其中112max{(),}k k T P a a a -+++表示1()k T P -和12k a a a +++两个数中最大的数,(1)对于数对序列(2,5),(4,1)P P ,求12(),()T P T P 的值.(2)记m 为,,,a b c d 四个数中最小值,对于由两个数对(,),(,)a b c d 组成的数对序列(,),(,)P a b c d 和'(,),(,)P a b c d ,试分别对m a =和m d =的两种情况比较2()T P 和2(')T P 的大小.(3)在由5个数对(11,8),(5,2),(16,11),(11,11),(4,6)组成的所有数对序列中,写出一个数对序列P 使5()T P 最小,并写出5()T P 的值.(只需写出结论).。
2014年北京市高考理科数学试卷及答案解析(word版).wps

6. D
若 k ≥ 0 , z y x 没有最小值,不合题意.
若 k 0 ,则不等式组所表示的平面区域如图所示.
由图可知,
z
y
x
在点
2 k
,0
处取最小值.
故
0
2 k
4
,解得
k
1 2
,即选项
D
正确.
7. D( S2 S3 且 S1 ≠ S3 )
y
2
kx-y+2=0
x+y-2=0
O
2
2x -
CD 2, cos ADC 1 7
(1)求 sin BAD (2)求 BD, AC 的长
16. (本小题 13 分). 李明在 10 场篮球比赛中的投篮情况如下(假设各场比赛互相独立):
(1)从上述比赛中随机选择一场,求李明在该场比赛中投篮命中率超过 0.6 的概率. (2)从上述比赛中选择一个主场和一个客场,求李明的投篮命中率一场超过 0.6 ,一
学,
他们之间没有一个人比另一个成绩好,且没有任意两个人语文成绩一样,数学成绩也一样
的.问满足条件的最多有多少学生( )
(A) 2
(B) 3
(C) 4
(D) 5
二、填空题(共 6 小题,每小题 5 分,共 30 分)
9.复数
1 1
i i
2
________.
10.已知向量 a 、 b 满足 a 1, b 2,1 ,且 a b 0 R,则 ________.
求线段 PH 的长.
18.(本小题 13 分)
已知函数 f (x) x cos x sin x, x [0, ], 2
(1)求证: f (x) 0 ;
2014年北京高考数学理科试题及答案

2014年普通高等学校招生全国统一考试
数学(理)(北京卷)
本试卷共 5 页,150 分。考试时长 120 分钟,考生务必将答案答在答题卡上,在试卷上作答无效。考 试结束后,将本试卷和答题卡一并收回。
第一部分(选择题 共 40 分)
一、选择题共 8 小题,每小题 5 分,共 40分。在每小题列出的四个选项中,选出符合题目要求的一项。
场次 投篮次数 命中次数 场次 投篮次数 命中次数
主场 1
22
12
客场 1
18
8
主场 2
15
12
客场 2
13
12
主场 3
12
8
客场 3
21
7
主场 4
23
8
客场 4
18
15
主场 5
24
20
客场 5
25
12
(Ⅰ)从上述比赛中随机选择一场,求李明在该场比赛中投篮命中率超过 0.6 的概率;
(Ⅱ)从上述比赛中随机选择一个主场和一个客场,求李明的投篮命中率一场超过 0.6,另一场不超过
(1) 已知集合 A {x | x2 2x 0}, B {0, 1, 2},若 A B
(A) {0}
(B) {0, 1}
(C) {0, 2}
(D) {0, 1, 2}
(2) 下列函数中,在区间 (0, }上为增函数的是
(A) y x 1
(B) y=(x 1)2
(C) y 2 x
(D) y log (x 1) 0.5
P
F
G
E
H
D A
B
C
M
(18)(本小题 13 分)已知函数 f (x) x cos x (Ⅰ)求证: f (x) 0 ;(Ⅱ)若 a sin x
2014年高考理科数学北京卷(含详细答案)

.
设平面ABF的法向量为 ,则 ,即 .
令 ,则 .所以 ,设直线BC与平面ABF所成角为 ,
则 .
设点H的坐标为
因为点H在棱PC上,所以可设 ,即 ,
所以 .
因为 是平面ABF的法向量,所以 ,即 .
解得 ,所以点H的坐标为ቤተ መጻሕፍቲ ባይዱ
所以 .
【提示】由线面平行推出线线平行,利用线面垂直、线线垂直这个条件,作出有关辅助线,建立空间直角坐标系求解.
圆心 到直线AB的距离 .此时直线AB与圆 相切.
当 时,直线AB的方程为 ,即 ,
圆心 到直线AB的距离 .
又 , ,故 ,
此时直线AB与圆 相切.
【提示】根据给出的椭圆方程找出离心率,然后利用椭圆方程与直线的关系及两线垂直,求出直线与圆的位置关系.
【考点】圆与圆锥曲线的综合,椭圆的简单性质
20.【答案】(1)
A.2人
B.3人
C.4人
D.5人
第Ⅱ卷(非选择题共110分)
二、填空题:本大题共6小题,每小题5分.共30分,把答案填写在题中的横线上.
9.复数 .
10.已知向量a,b满足 a ,b ,且 a b 0 ,则 .
11.设双曲线 经过点 ,且与 具有相同渐近线,则 的方程为;渐近线方程为.
12.若等差数列 满足 , ,则当 时, 的前 项和最大.
【提示】由循环语句、条件语句执行程序,直至结束.
【考点】循环结构
5.【答案】D
【解析】当 时,数列 递减;当 ,数列 递增时, ,故选D.
【提示】根据等比数列的性质,结合充分条件和必要条件的定义进行判断即可得到结论.
【考点】充分、必要条件,等比数列的性质
2014年北京市高考数学试卷及解析(理科)

2014年北京市高考数学试卷(理科)一、选择题(共8小题,每小题5分,共40分、在每小题列出的四个选项中,选出符合题目要求的一项)1、(5分)已知集合A={x|x2﹣2x=0},B={0,1,2},则A∩B=()A、{0}B、{0,1}C、{0,2}D、{0,1,2}2、(5分)下列函数中,在区间(0,+∞)上为增函数的是()A、y=B、y=(x﹣1)2C、y=2﹣xD、y=log0.5(x+1)3、(5分)曲线(θ为参数)的对称中心()A、在直线y=2x上B、在直线y=﹣2x上C、在直线y=x﹣1上D、在直线y=x+1上4、(5分)当m=7,n=3时,执行如图所示的程序框图,输出的S的值为()A、7B、42C、210D、8405、(5分)设{a n}是公比为q的等比数列,则“q>1”是“{a n}为递增数列”的()A、充分而不必要条件B、必要而不充分条件C、充分必要条件D、既不充分也不必要条件6、(5分)若x,y满足,且z=y﹣x的最小值为﹣4,则k的值为()A、2B、﹣2C、D、﹣7、(5分)在空间直角坐标系Oxyz中,已知A(2,0,0),B(2,2,0),C(0,2,0),D(1,1,),若S1,S2,S3分别表示三棱锥D﹣ABC在xOy,yOz,zOx 坐标平面上的正投影图形的面积,则()A、S1=S2=S3B、S2=S1且S2≠S3C、S3=S1且S3≠S2D、S3=S2且S3≠S18、(5分)学生的语文、数学成绩均被评定为三个等级,依次为“优秀”“合格”“不合格”、若学生甲的语文、数学成绩都不低于学生乙,且其中至少有一门成绩高于乙,则称“学生甲比学生乙成绩好”、如果一组学生中没有哪位学生比另一位学生成绩好,并且不存在语文成绩相同、数学成绩也相同的两位学生,则这一组学生最多有()A、2人B、3人C、4人D、5人二、填空题(共6小题,每小题5分,共30分)9、(5分)复数()2=、10、(5分)已知向量,满足||=1,=(2,1),且+=(λ∈R),则|λ|=、11、(5分)设双曲线C经过点(2,2),且与﹣x2=1具有相同渐近线,则C 的方程为;渐近线方程为、12、(5分)若等差数列{a n}满足a7+a8+a9>0,a7+a10<0,则当n=时,{a n}的前n项和最大、13、(5分)把5件不同产品摆成一排,若产品A与产品B相邻,且产品A与产品C不相邻,则不同的摆法有种、14、(5分)设函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0)若f (x)在区间[,]上具有单调性,且f()=f()=﹣f(),则f(x)的最小正周期为、三、解答题(共6小题,共80分,解答应写出文字说明、演算步骤或证明过程)15、(13分)如图,在△ABC中,∠B=,AB=8,点D在边BC上,且CD=2,cos∠ADC=、(1)求sin∠BAD;(2)求BD,AC的长、16、(13分)李明在10场篮球比赛中的投篮情况统计如下(假设各场比赛相互独立);场次投篮次数命中次数场次投篮次数命中次数主场12212客场1188主场21512客场21312主场3128客场3217主场4238客场41815主场52420客场52512(1)从上述比赛中随机选择一场,求李明在该场比赛中投篮命中率超过0.6的概率;(2)从上述比赛中随机选择一个主场和一个客场,求李明的投篮命中率一场超过0.6,一场不超过0.6的概率;(3)记是表中10个命中次数的平均数,从上述比赛中随机选择一场,记X为李明在这场比赛中的命中次数,比较EX与的大小(只需写出结论)、17、(14分)如图,正方形AMDE的边长为2,B,C分别为AM,MD的中点,在五棱锥P﹣ABCDE中,F为棱PE的中点,平面ABF与棱PD,PC分别交于点G,H、(1)求证:AB∥FG;(2)若PA⊥底面ABCDE,且PA=AE,求直线BC与平面ABF所成角的大小,并求线段PH的长、18、(13分)已知函数f(x)=xcosx﹣sinx,x∈[0,](1)求证:f(x)≤0;(2)若a<<b对x∈(0,)上恒成立,求a的最大值与b的最小值、19、(14分)已知椭圆C:x2+2y2=4,(1)求椭圆C的离心率(2)设O为原点,若点A在椭圆C上,点B在直线y=2上,且OA⊥OB,求直线AB与圆x2+y2=2的位置关系,并证明你的结论、20、(13分)对于数对序列P:(a1,b1),(a2,b2),…,(a n,b n),记T1(P)=a1+b1,T k(P)=b k+max{T k﹣1(P),a1+a2+…+a k}(2≤k≤n),其中max{T k﹣1(P),a1+a2+…+a k}表示T k(P)和a1+a2+…+a k两个数中最大的数,﹣1(Ⅰ)对于数对序列P:(2,5),(4,1),求T1(P),T2(P)的值;(Ⅱ)记m为a,b,c,d四个数中最小的数,对于由两个数对(a,b),(c,d)组成的数对序列P:(a,b),(c,d)和P′:(c,d),(a,b),试分别对m=a和m=d两种情况比较T2(P)和T2(P′)的大小;(Ⅲ)在由五个数对(11,8),(5,2),(16,11),(11,11),(4,6)组成的所有数对序列中,写出一个数对序列P使T5(P)最小,并写出T5(P)的值(只需写出结论)、参考答案与试题解析一、选择题(共8小题,每小题5分,共40分、在每小题列出的四个选项中,选出符合题目要求的一项)1、(5分)已知集合A={x|x2﹣2x=0},B={0,1,2},则A∩B=()A、{0}B、{0,1}C、{0,2}D、{0,1,2}分析:解出集合A,再由交的定义求出两集合的交集、解答:解:∵A={x|x2﹣2x=0}={0,2},B={0,1,2},∴A∩B={0,2}故选:C、点评:本题考查交的运算,理解好交的定义是解答的关键、2、(5分)下列函数中,在区间(0,+∞)上为增函数的是()A、y=B、y=(x﹣1)2C、y=2﹣xD、y=log0.5(x+1)分析:根据基本初等函数的单调性,判断各个选项中函数的单调性,从而得出结论、解答:解:由于函数y=在(﹣1,+∞)上是增函数,故满足条件,由于函数y=(x﹣1)2在(0,1)上是减函数,故不满足条件,由于函数y=2﹣x在(0,+∞)上是减函数,故不满足条件,由于函数y=log0.5(x+1)在(﹣1,+∞)上是减函数,故不满足条件,故选:A、点评:本题主要考查函数的单调性的定义和判断,基本初等函数的单调性,属于基础题、3、(5分)曲线(θ为参数)的对称中心()A、在直线y=2x上B、在直线y=﹣2x上C、在直线y=x﹣1上D、在直线y=x+1上分析:曲线(θ为参数)表示圆,对称中心为圆心,可得结论、解答:解:曲线(θ为参数)表示圆,圆心为(﹣1,2),在直线y=﹣2x上,故选:B、点评:本题考查圆的参数方程,考查圆的对称性,属于基础题、4、(5分)当m=7,n=3时,执行如图所示的程序框图,输出的S的值为()A、7B、42C、210D、840分析:算法的功能是求S=7×6×…×k的值,根据条件确定跳出循环的k值,计算输出S的值、解答:解:由程序框图知:算法的功能是求S=7×6×…×k的值,当m=7,n=3时,m﹣n+1=7﹣3+1=5,∴跳出循环的k值为4,∴输出S=7×6×5=210、故选:C、点评:本题考查了循环结构的程序框图,根据框图的流程判断算法的功能是解答本题的关键、5、(5分)设{a n}是公比为q的等比数列,则“q>1”是“{a n}为递增数列”的()A、充分而不必要条件B、必要而不充分条件C、充分必要条件D、既不充分也不必要条件分析:根据等比数列的性质,结合充分条件和必要条件的定义进行判断即可得到结论、解答:解:等比数列﹣1,﹣2,﹣4,…,满足公比q=2>1,但{a n}不是递增数列,充分性不成立、若a n=﹣1为递增数列,但q=>1不成立,即必要性不成立,故“q>1”是“{a n}为递增数列”的既不充分也不必要条件,故选:D、点评:本题主要考查充分条件和必要条件的判断,利用等比数列的性质,利用特殊值法是解决本题的关键、6、(5分)若x,y满足,且z=y﹣x的最小值为﹣4,则k的值为()A、2B、﹣2C、D、﹣分析:对不等式组中的kx﹣y+2≥0讨论,当k≥0时,可行域内没有使目标函数z=y﹣x取得最小值的最优解,k<0时,若直线kx﹣y+2=0与x轴的交点在x+y﹣2=0与x轴的交点的左边,z=y﹣x的最小值为﹣2,不合题意,由此结合约束条件作出可行域,化目标函数为直线方程的斜截式,由图得到最优解,联立方程组求出最优解的坐标,代入目标函数得答案、解答:解:对不等式组中的kx﹣y+2≥0讨论,可知直线kx﹣y+2=0与x轴的交点在x+y﹣2=0与x轴的交点的右边,故由约束条件作出可行域如图,当y=0,由kx﹣y+2=0,得x=,∴B(﹣)、由z=y﹣x得y=x+z、由图可知,当直线y=x+z过B(﹣)时直线在y轴上的截距最小,即z最小、此时,解得:k=﹣、故选:D、点评:本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题、7、(5分)在空间直角坐标系Oxyz中,已知A(2,0,0),B(2,2,0),C(0,2,0),D(1,1,),若S1,S2,S3分别表示三棱锥D﹣ABC在xOy,yOz,zOx 坐标平面上的正投影图形的面积,则()A、S1=S2=S3B、S2=S1且S2≠S3C、S3=S1且S3≠S2D、S3=S2且S3≠S1分析:分别求出三棱锥在各个面上的投影坐标即可得到结论、解答:解:设A(2,0,0),B(2,2,0),C(0,2,0),D(1,1,),则各个面上的射影分别为A',B',C',D',在xOy坐标平面上的正投影A'(2,0,0),B'(2,2,0),C'(0,2,0),D'(1,1,0),S1=、在yOz坐标平面上的正投影A'(0,0,0),B'(0,2,0),C'(0,2,0),D'(0,1,),S2=.在zOx坐标平面上的正投影A'(2,0,0),B'(2,0,0),C'(0,0,0),D'(0,1,),S3=,则S3=S2且S3≠S1,故选:D、点评:本题主要考查空间坐标系的应用,求出点对于的投影坐标是解决本题的关键、8、(5分)学生的语文、数学成绩均被评定为三个等级,依次为“优秀”“合格”“不合格”、若学生甲的语文、数学成绩都不低于学生乙,且其中至少有一门成绩高于乙,则称“学生甲比学生乙成绩好”、如果一组学生中没有哪位学生比另一位学生成绩好,并且不存在语文成绩相同、数学成绩也相同的两位学生,则这一组学生最多有()A、2人B、3人C、4人D、5人分析:分别用ABC分别表示优秀、及格和不及格,根据题干中的内容推出文成绩得A,B,C的学生各最多只有1个,继而推得学生的人数、解答:解:用ABC分别表示优秀、及格和不及格,显然语文成绩得A的学生最多只有1个,语文成绩得B得也最多只有一个,得C最多只有一个,因此学生最多只有3人,显然(AC)(BB)(CA)满足条件,故学生最多有3个、故选:B、点评:本题主要考查了合情推理,关键是找到语句中的关键词,培养了推理论证的能力、二、填空题(共6小题,每小题5分,共30分)9、(5分)复数()2=﹣1、分析:由复数代数形式的除法运算化简括号内部,然后由虚数单位i的运算性质得答案、解答:解:()2=、故答案为:﹣1、点评:本题考查了复数代数形式的除法运算,考查了虚数单位i的运算性质,是基础题、10、(5分)已知向量,满足||=1,=(2,1),且+=(λ∈R),则|λ|=、分析:设=(x,y)、由于向量,满足||=1,=(2,1),且+=(λ∈R),可得,解出即可、解答:解:设=(x,y)、∵向量,满足||=1,=(2,1),且+=(λ∈R),∴=λ(x,y)+(2,1)=(λx+2,λy+1),∴,化为λ2=5、解得、故答案为:、点评:本题考查了向量的坐标运算、向量的模的计算公式、零向量等基础知识与基本技能方法,属于基础题、11、(5分)设双曲线C经过点(2,2),且与﹣x2=1具有相同渐近线,则C 的方程为;渐近线方程为y=±2x、分析:利用双曲线渐近线之间的关系,利用待定系数法即可得到结论、解答:解:与﹣x2=1具有相同渐近线的双曲线方程可设为﹣x2=m,(m≠0),∵双曲线C经过点(2,2),∴m=,即双曲线方程为﹣x2=﹣3,即,对应的渐近线方程为y=±2x,故答案为:,y=±2x、点评:本题主要考查双曲线的性质,利用渐近线之间的关系,利用待定系数法是解决本题的关键,比较基础、12、(5分)若等差数列{a n}满足a7+a8+a9>0,a7+a10<0,则当n=8时,{a n}的前n项和最大、分析:可得等差数列{a n}的前8项为正数,从第9项开始为负数,进而可得结论、解答:解:由等差数列的性质可得a7+a8+a9=3a8>0,∴a8>0,又a7+a10=a8+a9<0,∴a9<0,∴等差数列{a n}的前8项为正数,从第9项开始为负数,∴等差数列{a n}的前8项和最大,故答案为:8、点评:本题考查等差数列的性质和单调性,属中档题、13、(5分)把5件不同产品摆成一排,若产品A与产品B相邻,且产品A与产品C不相邻,则不同的摆法有36种、分析:分3步进行分析:①用捆绑法分析A、B,②计算其中A、B相邻又满足B、C相邻的情况,即将ABC看成一个元素,与其他产品全排列,③在全部数目中将A、B相邻又满足A、C相邻的情况排除即可得答案、解答:解:先考虑产品A与B相邻,把A、B作为一个元素有种方法,而A、B可交换位置,所以有2=48种摆法,又当A、B相邻又满足A、C相邻,有2=12种摆法,故满足条件的摆法有48﹣12=36种、故答案为:36、点评:本题考查分步计数原理的应用,要优先分析受到限制的元素,如本题的A、B、C、14、(5分)设函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0)若f (x)在区间[,]上具有单调性,且f()=f()=﹣f(),则f(x)的最小正周期为π、分析:由f()=f()求出函数的一条对称轴,结合f(x)在区间[,]上具有单调性,且f()=﹣f()可得函数的半周期,则周期可求、解答:解:由f()=f(),可知函数f(x)的一条对称轴为x=,则x=离最近对称轴距离为、又f()=﹣f(),则f(x)有对称中心(,0),由于f(x)在区间[,]上具有单调性,则≤T⇒T≥,从而=⇒T=π、故答案为:π、点评:本题考查f(x)=Asin(ωx+φ)型图象的形状,考查了学生灵活处理问题和解决问题的能力,是中档题、三、解答题(共6小题,共80分,解答应写出文字说明、演算步骤或证明过程)15、(13分)如图,在△ABC中,∠B=,AB=8,点D在边BC上,且CD=2,cos∠ADC=、(1)求sin∠BAD;(2)求BD,AC的长、分析:根据三角形边角之间的关系,结合正弦定理和余弦定理即可得到结论、解答:解:(1)在△ABC中,∵cos∠ADC=,∴sin∠ADC====,则sin∠BAD=sin(∠ADC﹣∠B)=sin∠ADC•cosB﹣cos∠ADC•sinB=×﹣=、(2)在△ABD中,由正弦定理得BD==,在△ABC中,由余弦定理得AC2=AB2+CB2﹣2AB•BCcosB=82+52﹣2×8×=49,即AC=7、点评:本题主要考查解三角形的应用,根据正弦定理和余弦定理是解决本题本题的关键,难度不大、16、(13分)李明在10场篮球比赛中的投篮情况统计如下(假设各场比赛相互独立);场次投篮次数命中次数场次投篮次数命中次数主场12212客场1188主场21512客场21312主场3128客场3217主场4238客场41815主场52420客场52512(1)从上述比赛中随机选择一场,求李明在该场比赛中投篮命中率超过0.6的概率;(2)从上述比赛中随机选择一个主场和一个客场,求李明的投篮命中率一场超过0.6,一场不超过0.6的概率;(3)记是表中10个命中次数的平均数,从上述比赛中随机选择一场,记X为李明在这场比赛中的命中次数,比较EX与的大小(只需写出结论)、分析:(1)根据概率公式,找到李明在该场比赛中超过0.6的场次,计算即可,(2)根据互斥事件的概率公式,计算即可、(3)求出平均数和EX,比较即可、解答:解:(1)设李明在该场比赛中投篮命中率超过0.6为事件A,由题意知,李明在该场比赛中超过0.6的场次有:主场2,主场3,主场5,客场2,客场4,共计5场所以李明在该场比赛中投篮命中率超过0.6的概率P(A)=,(2)设李明的投篮命中率一场超过0.6,一场不超过0.6的概率为事件B,同理可知,李明主场命中率超过0.6的概率,客场命中率超过0.6的概率,故P(B)=P1×(1﹣P2)+P2×(1﹣P1)=;(3)=(12+8+12+12+8+7+8+15+20+12)=11.4EX=点评:本题主要考查了概率的计算、数学期望,平均数,互斥事件的概率,属于中档题、17、(14分)如图,正方形AMDE的边长为2,B,C分别为AM,MD的中点,在五棱锥P﹣ABCDE中,F为棱PE的中点,平面ABF与棱PD,PC分别交于点G,H、(1)求证:AB∥FG;(2)若PA⊥底面ABCDE,且PA=AE,求直线BC与平面ABF所成角的大小,并求线段PH的长、分析:(1)运用线面平行的判定定理和性质定理即可证得;(2)由于PA⊥底面ABCDE,底面AMDE为正方形,建立如图的空间直角坐标系Axyz,分别求出A,B,C,E,P,F,及向量BC的坐标,设平面ABF的法向量为n=(x,y,z),求出一个值,设直线BC与平面ABF所成的角为α,运用sinα=|cos|,求出角α;设H(u,v,w),再设,用λ表示H的坐标,再由n=0,求出λ和H的坐标,再运用空间两点的距离公式求出PH的长、解答:(1)证明:在正方形AMDE中,∵B是AM的中点,∴AB∥DE,又∵AB⊄平面PDE,∴AB∥平面PDE,∵AB⊂平面ABF,且平面ABF∩平面PDE=FG,∴AB∥FG;(2)解:∵PA⊥底面ABCDE,∴PA⊥AB,PA⊥AE,如图建立空间直角坐标系Axyz,则A(0,0,0),B(1,0,0),C(2,1,0),P(0,0,2),E(0,2,0),F(0,1,1),,设平面ABF的法向量为=(x,y,z),则即,令z=1,则y=﹣1,∴=(0,﹣1,1),设直线BC与平面ABF所成的角为α,则sinα=|cos<,>|=||=,∴直线BC与平面ABF所成的角为,设H(u,v,w),∵H在棱PC上,∴可设,即(u,v,w﹣2)=λ(2,1,﹣2),∴u=2λ,v=λ,w=2﹣2λ,∵是平面ABF 的法向量,∴=0,即(0,﹣1,1)•(2λ,λ,2﹣2λ)=0,解得λ=,∴H(),∴PH==2、点评:本题主要考查空间直线与平面的位置关系,考查直线与平面平行、垂直的判定和性质,同时考查直线与平面所成的角的求法,考查运用空间直角坐标系求角和距离,是一道综合题、18、(13分)已知函数f(x)=xcosx﹣sinx,x∈[0,](1)求证:f(x)≤0;(2)若a<<b对x∈(0,)上恒成立,求a的最大值与b的最小值、分析:(1)求出f′(x)=cosx﹣xsinx﹣cosx=﹣xsinx,判定出在区间∈(0,)上f′(x)=﹣xsinx<0,得f(x)在区间∈[0,]上单调递减,从而f(x)≤f (0)=0、(2)当x>0时,“>a”等价于“sinx﹣ax>0”,“<b”等价于“sinx﹣bx <0”构造函数g(x)=sinx﹣cx,通过求函数的导数讨论参数c求出函数的最值,进一步求出a,b的最值、解答:解:(1)由f(x)=xcosx﹣sinx得f′(x)=cosx﹣xsinx﹣cosx=﹣xsinx,此在区间∈(0,)上f′(x)=﹣xsinx<0,所以f(x)在区间∈[0,]上单调递减,从而f(x)≤f(0)=0、(2)当x>0时,“>a”等价于“sinx﹣ax>0”,“<b”等价于“sinx﹣bx <0”令g(x)=sinx﹣cx,则g′(x)=cosx﹣c,当c≤0时,g(x)>0对x∈(0,)上恒成立,当c≥1时,因为对任意x∈(0,),g′(x)=cosx﹣c<0,所以g(x)在区间[0,]上单调递减,从而,g(x)<g(0)=0对任意x∈(0,)恒成立,当0<c<1时,存在唯一的x0∈(0,)使得g′(x0)=cosx0﹣c=0,g(x)与g′(x)在区间(0,)上的情况如下:x(0,x0)x0(x0,)g′(x)+﹣g(x)↑↓因为g(x)在区间(0,x0)上是增函数,所以g(x0)>g(0)=0进一步g(x)>0对任意x∈(0,)恒成立,当且仅当综上所述当且仅当时,g(x)>0对任意x∈(0,)恒成立,当且仅当c≥1时,g(x)<0对任意x∈(0,)恒成立,所以若a<<b对x∈(0,)上恒成立,则a的最大值为,b的最小值为1点评:本题考查利用导数求函数的单调区间;利用导数求函数的最值;考查解决不等式问题常通过构造函数解决函数的最值问题,属于一道综合题、19、(14分)已知椭圆C:x2+2y2=4,(1)求椭圆C的离心率(2)设O为原点,若点A在椭圆C上,点B在直线y=2上,且OA⊥OB,求直线AB与圆x2+y2=2的位置关系,并证明你的结论、分析:(1)化椭圆方程为标准式,求出半长轴和短半轴,结合隐含条件求出半焦距,则椭圆的离心率可求;(2)设出点A,B的坐标分别为(x0,y0),(t,2),其中x0≠0,由OA⊥OB得到,用坐标表示后把t用含有A点的坐标表示,然后分A,B的横坐标相等和不相等写出直线AB的方程,然后由圆x2+y2=2的圆心到AB的距离和圆的半径相等说明直线AB与圆x2+y2=2相切、解答:解:(1)由x2+2y2=4,得椭圆C的标准方程为、∴a2=4,b2=2,从而c2=a2﹣b2=2、因此a=2,c=、故椭圆C的离心率e=;(2)直线AB与圆x2+y2=2相切、证明如下:设点A,B的坐标分别为(x0,y0),(t,2),其中x0≠0、∵OA⊥OB,∴,即tx0+2y0=0,解得、当x0=t时,,代入椭圆C的方程,得、故直线AB的方程为x=,圆心O到直线AB的距离d=、此时直线AB与圆x2+y2=2相切、当x0≠t时,直线AB的方程为,即(y0﹣2)x﹣(x0﹣t)y+2x0﹣ty0=0、圆心O到直线AB的距离d=、又,t=、故=、此时直线AB与圆x2+y2=2相切、点评:本题考查椭圆的简单几何性质,考查了圆与圆锥曲线的综合,训练了由圆心到直线的距离判断直线和圆的位置关系,体现了分类讨论的数学思想方法,考查了计算能力和逻辑思维能力,是压轴题、20、(13分)对于数对序列P:(a1,b1),(a2,b2),…,(a n,b n),记T1(P)=a1+b1,T k(P)=b k+max{T k﹣1(P),a1+a2+…+a k}(2≤k≤n),其中max{T k﹣1(P),a1+a2+…+a k}表示T k(P)和a1+a2+…+a k两个数中最大的数,﹣1(Ⅰ)对于数对序列P:(2,5),(4,1),求T1(P),T2(P)的值;(Ⅱ)记m为a,b,c,d四个数中最小的数,对于由两个数对(a,b),(c,d)组成的数对序列P:(a,b),(c,d)和P′:(c,d),(a,b),试分别对m=a和m=d两种情况比较T2(P)和T2(P′)的大小;(Ⅲ)在由五个数对(11,8),(5,2),(16,11),(11,11),(4,6)组成的所有数对序列中,写出一个数对序列P使T5(P)最小,并写出T5(P)的值(只需写出结论)、分析:(Ⅰ)利用T1(P)=a1+b1,T k(P)=b k+max{T k﹣1(P),a1+a2+…+a k}(2≤k ≤n),可求T1(P),T2(P)的值;(Ⅱ)T2(P)=max{a+b+d,a+c+d},T2(P′)=max{c+d+b,c+a+b},分类讨论,利用新定义,可比较T2(P)和T2(P′)的大小;(Ⅲ)根据新定义,可得结论、解答:解:(Ⅰ)T1(P)=2+5=7,T2(P)=1+max{T1(P),2+4}=1+max{7,6}=8;(Ⅱ)T2(P)=max{a+b+d,a+c+d},T2(P′)=max{c+d+b,c+a+b}、当m=a时,T2(P′)=max{c+d+b,c+a+b}=c+d+b,∵a+b+d≤c+d+b,且a+c+d≤c+b+d,∴T2(P)≤T2(P′);当m=d时,T2(P′)=max{c+d+b,c+a+b}=c+a+b,∵a+b+d≤c+a+b,且a+c+d≤c+a+d,∴T2(P)≤T2(P′);∴无论m=a和m=d,T2(P)≤T2(P′);(Ⅲ)数对(4,6),(11,11),(16,11),(11,8),(5,2),T5(P)最小;T1(P)=10,T2(P)=26;T3(P)42,T4(P)=50,T5(P)=52点评:本题考查新定义,考查学生分析解决问题的能力,正确理解与运用新定义是解题的关键。
北京市高考数学压轴卷 理(含解析)1

2014北京市高考压轴卷理科数学一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的1.已知11xyi i=-+,其中,x y 是实数,i 是虚数单位,则x yi +的共轭复数为( ) A .12i + B .12i - C .2i + D .2i -2.已知函数3()f x x x =--,123,,x x x R ∈,且120x x +>,230x x +>,310x x +>,则123()()()f x f x f x ++的值为()A.正B.负C.零D.可正可负3.已知某几何体的三视图如下,则该几何体体积为( )A .4+52π B .4+32π C .4+2π D .4+π 4.如图所示为函数π()2sin()(0,0)2f x x ωϕωϕ=+>≤≤的部分图像,其中A ,B 两点之间的距离为5,那么(1)f -=( )A .-1B .CD .15.(5分)已知两条不重合的直线m、n和两个不重合的平面α、β,有下列命题:①若m⊥n,m⊥α,则n∥α;②若m⊥α,n⊥β,m∥n,则α∥β;③若m、n是两条异面直线,m⊂α,n⊂β,m∥β,n∥α,则α∥β;④若α⊥β,α∩β=m,n⊂β,n⊥m,则n⊥α.6.设函数是定义在上的可导函数,其导函数为,且有,则不等式的解集为A. B.C. D.7.已知F1(﹣c,0),F2(c,0)为椭圆的两个焦点,P为椭圆上一点且,B D8.已知定义在R上的偶函数f(x)满足f(1+x)=f(1﹣x),且x∈[0,1]时,,则方程在区间[﹣3,3]上的根的个数为()9.已知集合{}{}22,1,3,3,21,1A a aB a a a=+-=--+,若{}3A B=-,则实数a的值为________________.10.已知如图所示的流程图(未完成),设当箭头a指向①时输出的结果S=m,当箭头a指向②时,输出的结果S=n,求m+n的值.11.若n S 是等差数列}{n a 的前n 项和,且8320S S -=,则11S 的值为 . 12.展开式中有理项共有 项.13.在平面直角坐标系xOy 中,过坐标原点的一条直线与函数xx f 2)(=的图象交于P 、Q 两点,则线段PQ 长的最小值是_______14.设a ∈R ,若x >0时均有[(a ﹣1)x ﹣1](x 2﹣ax ﹣1)≥0,则a= .三、解答题:本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤.解答写在答题卡上的指定区域内.15.已知向量)4cos ,4(cos ),1,4sin 3(2x x n x m ==.记x f ⋅=)( (I)求)(x f 的周期;(Ⅱ)在∆ABC 中,角A 、B 、C 的对边分别是a 、b 、c ,且满足(2a —c)cos B=b cosC , 若12f (A )=,试判断∆ABC 的形状. 16.在一次对某班42名学生参加课外篮球、排球兴趣小组(每人参加且只参加一个兴趣小组)(Ⅰ)据此判断是否有95%的把握认为参加“篮球小组”或“排球小组”与性别有关?(Ⅱ)在统计结果中,如果不考虑性别因素,按分层抽样的方法从两个兴趣小组中随机抽取7名同学进行座谈.已知甲、乙、丙三人都参加“排球小组”. ①求在甲被抽中的条件下,乙丙也都被抽中的概率;②设乙、丙两人中被抽中的人数为X ,求X 的分布列及数学期望E(X).下面临界值表供参考:参考公式:2()()()()K a b c d a c b d =++++命题意图:考查分类变量的独立性检验,条件概率,随机变量的分布列、数学期望等,中等题. 17.已知正四棱柱1111-ABCD A B C D 中,12,4==AB AA . (Ⅰ)求证:1BD AC ⊥;(Ⅱ)求二面角11--A AC D 的余弦值;(Ⅲ)在线段1CC 上是否存在点P ,使得平面11ACD ⊥平面PBD ,若存在,求出1CPPC 的值;若不存在,请说明理由.18.已知椭圆2222:1(0)x y C a b a b+=>>的左右焦点分别为12,F F ,点B 为短轴的一个端点,260OF B ∠=︒. (Ⅰ)求椭圆C 的方程;(Ⅱ)如图,过右焦点2F ,且斜率为(0)≠k k 的直线l 与椭圆C 相交于,E F 两点,A 为椭圆的右顶点,直线,AE AF 分别交直线3=x 于点,M N ,线段MN 的中点为P ,记直线2PF 的斜率为'k .求证: '⋅k k 为定值.19.已知数列{}n a 的各项均为正数,记12()n A n a a a =+++L ,231()n B n a a a +=+++L ,342(),1,2,n C n a a a n +=+++=L L .(Ⅰ)若121,5a a ==,且对任意n ∈*N ,三个数(),(),()A n B n C n 组成等差数列,求数列{}n a 的通项公式.(Ⅱ)证明:数列{}n a 是公比为q 的等比数列的充分必要条件是:对任意n ∈*N ,三个数(),(),()A n B n C n 组成公比为q 的等比数列.20.已知函数2()2ln f x x x ax =-+(a ∈R ).(Ⅰ)当2a =时,求()f x 的图象在1x =处的切线方程;(Ⅱ)若函数()()g x f x ax m =-+在1[e]e ,上有两个零点,求实数m 的取值范围;(Ⅲ)若函数()f x 的图象与x 轴有两个不同的交点12(0)(0)A x B x ,,,,且120x x <<, 求证:12()02x x f +'<(其中()f x '是()f x 的导函数).2014北京市高考压轴卷数学理word 版参考答案 1. 【答案】D 【解析】1()1,2,1,12x x xi yi x y i =-=-∴==+故选D . 2. 【答案】B【解析】∵3()f x x x =--,∴函数()f x 在R 上是减函数且是奇函数,∵120x x +>,∴12x x >-,∴12()()f x f x <-,∴12()()f x f x <-,∴12()()0f x f x +<, 同理:23()()0f x f x +<,31()()0f x f x +<,∴123()()()0f x f x f x ++<.3. 【答案】A【解析】该几何体是一个圆柱与一个长方体的组成,其中重叠了一部分2π,所以该几何体的体积为52213422πππ⨯⨯+-=+.故选A . 4. 【答案】A. 【解析】5. 【答案】C【解析】①若m⊥n,m⊥α,则n 可能在平面α内,故①错误 ②∵m⊥α,m∥n,∴n⊥α,又∵n⊥β,∴α∥β,故②正确 ③过直线m 作平面γ交平面β与直线c , ∵m、n 是两条异面直线,∴设n∩c=O, ∵m∥β,m ⊂γ,γ∩β=c∴m∥c, ∵m ⊂α,c ⊄α,∴c∥α,∵n ⊂β,c ⊂β,n∩c=O,c∥α,n∥α ∴α∥β;故③正确④由面面垂直的性质定理:∵α⊥β,α∩β=m ,n ⊂β,n⊥m,∴n⊥α.故④正确 故正确命题有三个, 故选C6. 【答案】C. 【解析】由,得:,即,令,则当时,,即在是减函数,,,,在是减函数,所以由得,,即,故选7. 【答案】C.【解析】设P(m,n ),=(﹣c﹣m,﹣n)•(c﹣m,﹣n)=m2﹣c2+n2,∴m2+n2=2c2,n2=2c2﹣m2①.把P(m,n )代入椭圆得 b2m2+a2n2=a2b2②,把①代入②得 m2=≥0,∴a2b2≤2a2c2,b2≤2c2,a2﹣c2≤2c2,∴≥.又 m2≤a2,∴≤a2,∴≤0,a2﹣2c2≥0,∴≤.综上,≤≤,故选 C.8. 【答案】A.【解析】由f(1+x)=f(1﹣x)可得函数f(x)的图象关于x=1对称,方程在区间[﹣3,3]根的个数等价于f(x)与y=图象的交点的个数,而函数y=图象可看作y=的图象向下平移1个单位得到,作出它们的图象如图:可得两函数的图象有5个交点,故选A9. 【答案】a=-1.【解析】若a-3=-3,则a=0,此时:}1,1,3{},3,1,0{--=-=B A ,}3,1{-=⋂∴B A ,与题意不符,舍 若2a-1=-3,则a=-1,此时:}2,4,3{},3,1,0{--=-=B A ,}3{-=⋂∴B A ,∴a=-1 若a2+1=-3,则a 不存在 综上可知:a=-1 10. 【答案】20.【解析】当箭头指向①时,计算S 和i 如下. i =1,S =0,S =1; i =2,S =0,S =2; i =3,S =0,S =3; i =4,S =0,S =4; i =5,S =0,S =5; i =6结束. ∴S=m =5.当箭头指向②时,计算S 和i 如下. i =1,S =0, S =1; i =2,S =3; i =3,S =6; i =4,S =10; i =5,S =15; i =6结束. ∴S=n =15. ∴m+n =20. 11. 【答案】44【解析】由83456786520S S a a a a a a -=++++==,解得64a =,又由611111611211()114422a a aS a ⨯+==== 12. 【答案】3. 【解析】展开式通项公式为T r+1==若为有理项时,则为整数,∴r=0、6、12,故展开式中有理项共有3项, 故答案为:3 13.【答案】4.【解析】设过坐标原点的一条直线方程为y kx =,因为与函数xx f 2)(=的图象交于P 、Q 两点,所以0k >,且联列解得,P Q ⎛ ⎝,所以4PQ ==≥14. 【答案】【解析】(1)a=1时,代入题中不等式明显不成立.(2)a≠1,构造函数y 1=(a ﹣1)x ﹣1,y 2=x 2﹣ax ﹣1,它们都过定点P (0,﹣1). 考查函数y 1=(a ﹣1)x ﹣1:令y=0,得M (,0),∴a>1;考查函数y 2=x 2﹣ax ﹣1,显然过点M (,0),代入得:,解之得:a=,或a=0(舍去). 故答案为:15.【解析】211()cos cos cos 4442222x x x x x f x +++1sin 262x π⎛⎫=++⎪⎝⎭(I )π4=T(Ⅱ 根据正弦定理知:()2cos cos (2sin sin )cos sin cos a c B b C A C B B C -=⇒-= 12sin cos sin()sin cos 23A B B C A B B π⇒=+=⇒=⇒=∵()f A =∴1sin 262263A A πππ⎛⎫+++= ⎪⎝⎭或23π3A π⇒=或 π 而203A π<<,所以3A π=,因此∆ABC 为等边三角形.……………12分16. 【解析】(Ⅰ)由表中数据得K 2的观测值k =42×(16×12-8×6)224×18×20×22=25255≈4.582>3.841. ……2分所以,据此统计有95%的把握认为参加“篮球小组”或“排球小组”与性别有关.……4分 (Ⅱ)①由题可知在“排球小组”的18位同学中,要选取3位同学. 方法一:令事件A 为“甲被抽到”;事件B 为“乙丙被抽到”,则P(A∩B)=33318C C ,P(A)=217318C C .所以P(B|A)=P(A∩B )P(A)=33217C C =217×16 =1136. ……7分 方法二:令事件C 为“在甲被抽到的条件下,乙丙也被抽到”,则P(C)=22217C C =217×16=1136. ②由题知X 的可能值为0,1,2.依题意P(X =0)=316318C C =3551;P(X =1)=21162318C C C =517;P(X =2)=12162318C C C =151. 从而X 的分布列为……10分于是E(X)=0×3551+1×517+2×151=1751=13. ……12分 17. 【解析】证明:(Ⅰ)因为1111ABCD A B C D -为正四棱柱,所以1AA ⊥平面ABCD ,且ABCD 为正方形. ………1分因为BD ⊂平面ABCD ,所以1,BD AA BD AC ⊥⊥. ………2分 因为1AA AC A =,所以BD ⊥平面1A AC . ………3分 因为1AC ⊂平面1A AC , 所以1BD AC ⊥. ………4分(Ⅱ) 如图,以D 为原点建立空间直角坐标系-D xyz .则11(0,0,0),(2,0,0),(2,2,0),(0,2,0),(2,0,4),(2,2,4),D A B C A B 11(0,2,4),(0,0,4)C D ………5分所以111(2,0,0),(0,2,4)D A DC ==-u u u u r u u u r . 设平面11A D C 的法向量111(,,)x y z =n .所以 1110,0D A D C ⎧⋅=⎪⎨⋅=⎪⎩uuuu r uuu r n n .即1110,240x y z =⎧⎨-=⎩……6分 令11z =,则12y =.所以(0,2,1)=n .由(Ⅰ)可知平面1AAC 的法向量为 (2,2,0)DB =u u u r . ……7分所以cos ,5DB <>==uu u r n . ……8分 因为二面角11--A AC D 为钝二面角,所以二面角11--A AC D的余弦值为. ………9分 (Ⅲ)设222(,,)P x y z 为线段1CC 上一点,且1(01)CP PC λλ=≤≤uu r uuu r .因为2221222(,2,),(,2,4)CP x y z PC x y z =-=---uu r uuu r .所以222222(,2,)(,2,4)x y z x y z λ-=---. ………10分 即22240,2,1x y z λλ===+. 所以4(0,2,)1P λλ+. ………11分 设平面PBD 的法向量333(,,)x y z =m . 因为4(0,2,),(2,2,0)1DP DB λλ==+uu u r uu u r ,所以 0,0DP DB ⎧⋅=⎪⎨⋅=⎪⎩uu u r uu u r m m .即3333420,1220y z x y λλ⎧+=⎪+⎨⎪+=⎩. ………12分 令31y =,则3311,2x z λλ+=-=-. 所以1(1,1,)2λλ+=--m . ………13分 若平面11ACD ⊥平面PBD ,则0⋅=m n .即1202λλ+-=,解得13λ=. 所以当113CP PC =时,平面11ACD ⊥平面PBD . ………14分 18.【解析】(Ⅰ)由条件2,a b ==…………2分 故所求椭圆方程为13422=+y x . …………4分 (Ⅱ)设过点2(1,0)F 的直线l 方程为:)1(-=x k y . …………5分 由22(1),143y k x x y =-⎧⎪⎨+=⎪⎩可得:01248)34(2222=-+-+k x k x k …………6分 因为点2(1,0)F 在椭圆内,所以直线l 和椭圆都相交,即0>∆恒成立.设点1122(,),(,)E x y F x y ,则34124,34822212221+-=+=+k k x x k k x x . …………8分 因为直线AE 的方程为:)2(211--=x x y y , 直线AF 的方程为:)2(222--=x x y y , ………9分 令3x =,可得)2,3(11-x y M ,)2,3(22-x y N , 所以点P 的坐标12121(3,())222y y x x +--. ………10分 直线2PF 的斜率为12121()0222'31y y x x k +---=- 12121()422y y x x =+-- 122112121212()42()4x y x y y y x x x x +-+=⋅-++1212121223()4142()4kx x k x x k x x x x -++=⋅-++ …………12分 2222222241282341434341284244343k k k k k k k k k k k -⋅-⋅+++=⋅--⋅+++ 34k=- 所以k k '⋅为定值43-. …………13分 19. 【解析】 (Ⅰ) 因为对任意n *∈N ,三个数(),(),()A n B n C n 是等差数列, 所以()()()()B n A n C n B n -=-. ………1分所以1122n n a a a a ++-=-, ………2分 即21214n n a a a a ++-=-=. ………3分 所以数列{}n a 是首项为1,公差为4的等差数列. ………4分 所以1(1)443n a n n =+-⨯=-. ………5分(Ⅱ)(1)充分性:若对于任意n *∈N ,三个数(),(),()A n B n C n 组成公比为q 的等比数列,则()(),()()B n qA n C n qB n ==. ………6分 所以[]()()()(),C n B n q B n A n -=-得2211(),n n a a q a a ++-=-即2121n n a qa a qa ++-=-. ………7分因为当1n =时,由(1)(1),B qA =可得21a qa =, ………8分 所以210n n a qa ++-=.因为0n a >, 所以2211n n a a q a a ++==. 即数列{}n a 是首项为1a ,公比为q 的等比数列, ………9分(2)必要性:若数列{}n a 是公比为q 的等比数列,则对任意n *∈N ,有1n n a a q +=. ………10分 因为0n a >,所以(),(),()A n B n C n 均大于0.于是12)2311212(......(),()......n n n nq a a a a a a B n q A n a a a a a a +++++++===++++++ ………11分 231)342231231(......(),()......n n n n q a a a a a a C n q B n a a a a a a ++++++++++===++++++ ………12分 即()()B n A n =()()C n B n =q ,所以三个数(),(),()A n B n C n 组成公比为q 的等比数列. ………13分综上所述,数列{}n a 是公比为q 的等比数列的充分必要条件是:对任意n ∈N ﹡,三个数(),(),()A n B n C n 组成公比为q 的等比数列. ………14分20. 【解析】(Ⅰ)当2a =时,2()2ln 2f x x x x =-+,2()22f x x x'=-+,切点坐标为(11),, 切线的斜率(1)2k f '==,则切线方程为12(1)y x -=-,即21y x =-. 2分 (Ⅱ)2()2ln g x x x m =-+,则22(1)(1)()2x x g x x x x-+-'=-=, ∵1[e]e x ∈,,故()0g x '=时,1x =.当11ex <<时,()0g x '>;当1e x <<时,()0g x '<. 故()g x 在1x =处取得极大值(1)1g m =-. 4分 又211()2e e g m =--,2(e)2e g m =+-,2211(e)()4e 0e eg g -=-+<,则1(e)()e g g <, ∴()g x 在1[e]e,上的最小值是(e)g . 6分 ()g x 在1[e]e ,上有两个零点的条件是2(1)10,11()20,e eg m g m =->⎧⎪⎨=--≤⎪⎩解得2112e m <≤+, ∴实数m 的取值范围是21(12]e +,. 8分 (Ⅲ)∵()f x 的图象与x 轴交于两个不同的点12(0)(0)A x B x ,,,,∴方程22l n 0x x a x -+=的两个根为12x x ,,则211122222l n 0,2l n 0,x x a x x x a x ⎧-+=⎪⎨-+=⎪⎩两式相减得1212122(ln ln )()x x a x x x x -=+--.又2()2ln f x x x ax =-+,2()2f x x a x '=-+,则1212124()()2x x f x x a x x +'=-+++1212122(ln ln )4x x x x x x -=-+-. 下证1212122(ln ln )40x x x x x x --<+-(*),即证明2111222()ln 0x x x x x x -+<+,12x t x =, ∵120x x <<,∴01t <<,即证明2(1)()ln 01t u t t t -=+<+在01t <<上恒成立. 10分 ∵22222(1)2(1)114(1)()(1)(1)(1)t t t u t t t t t t t -+---'=+=-=+++,又01t <<,∴()0u t '>, ∴()u t 在(0,1)上是增函数,则()(1)0u t u <=,从而知2111222()ln 0x x x x x x -+<+, 故(*)式<0,即12()02x x f +'<成立………….12分。
2014北京高考数学真题(理科)及答案
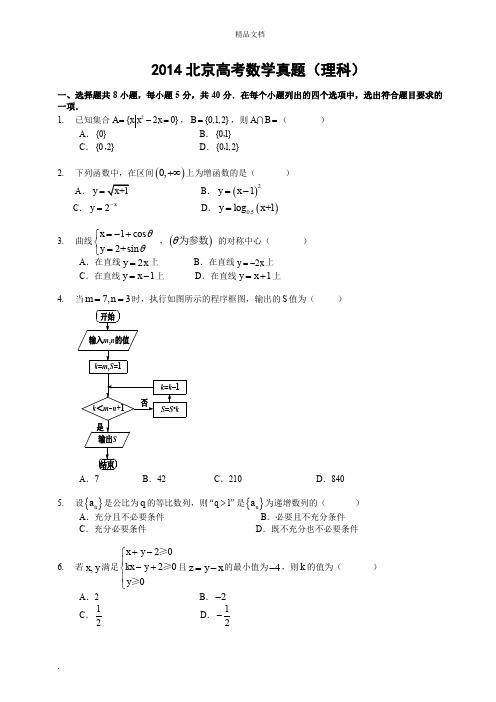
2014北京高考数学真题(理科)一、选择题共8小题,每小题5分,共40分.在每个小题列出的四个选项中,选出符合题目要求的一项.1. 已知集合2{20}A x x x =-=,{0,1,2}B =,则AB =( )A .{0}B .{01},C .{02},D .{01,2},2. 下列函数中,在区间()0,+∞上为增函数的是()A .+1y x =B .()21y x =-C .2xy -= D .()0.5log +1y x =3. 曲线1cos 2+sin x y θθ=-+⎧⎨=⎩,()θ为参数 的对称中心()A .在直线2y x =上B .在直线2y x =-上C .在直线1y x =-上D .在直线1y x =+上4. 当7,3m n ==时,执行如图所示的程序框图,输出的S 值为()否k =k 1S =S •k结束输出S 是k <m n +1k =m ,S =1输入m ,n 的值开始A .7B .42C .210D .8405. 设{}n a 是公比为q 的等比数列,则1q >“”是{}n a 为递增数列的( )A .充分且不必要条件B .必要且不充分条件C .充分必要条件D .既不充分也不必要条件6. 若,x y 满足20200x y kx y y +-⎧⎪-+⎨⎪⎩≥≥≥且z y x =-的最小值为4-,则k 的值为()A .2B .2-C .12 D .12-7. 在空间直角坐标系Oxyz 中,已知()2,0,0A ,()2,2,0B ,()0,2,0C ,(1,1,2)D ,若123S ,S ,S 分别表示三棱锥D ABC -在,,xOy yOz zOx 坐标平面上的正投影图形的面积,则()A .123S S S ==B .12S =S 且31S S ≠C .13S =S 且32S S ≠D .23S =S 且13S S ≠8. 有语文、数学两学科,成绩评定为“优秀”“合格”“不合格”三种.若A 同学每科成绩不低于B同学,且至少有一科成绩比B 高,则称“A 同学比B 同学成绩好.”现有若干同学,他们之中没有一个人比另一个成绩好,且没有任意两个人语文成绩一样,数学成绩也一样的.问满足条件的最多有多少学生( )A .2B .3C .4D .5第二部分(非选择题 共110分)二、填空题共6小题,每小题5分,共30分.9. 复数21i 1i +⎛⎫= ⎪-⎝⎭ .10. 已知向量u r α、rb 满足1=r a ,()2,1=r b ,且()λλ+=∈0R r r a b ,则λ= .11. 设双曲线C 经过点()2,2,且与2214y x -=具有相同渐近线,则C 的方程为 ;渐近线方程为 .12. 若等差数列{}n a 满足7890a a a ++>,7100a a +<,则当n = 时,{}n a 的前n 项和最大.13. 把5件不同产品摆成一排,若产品A 与产品B 相邻,且产品A 与产品C 不相邻,则不同的摆法有 种.14. 设函数()()sin f x A x ωϕ=+(A ωϕ是常数,0A >,0ω>).若()f x 在区间ππ,62⎡⎤⎢⎥⎣⎦上具有单调性,且π2ππ236f f f ⎛⎫⎛⎫⎛⎫==- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,则()f x 的最小正周期为 .三、解答题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.15. (本小题共13分) 如图,在ABC ∆中,3B π∠=,8AB =,点D 在BC 上,且=2CD ,1cos 7ADC ∠=(I )求sin BAD ∠; (II )求,BD AC 的长.DCBA16(本小题共13分)李明在10场篮球比赛中的投篮情况(假设各场比赛相互独立):(1) 从上述比赛随机选择一场,求李明在该场比赛中的投篮命中率超过0.6的概率;(2) 从上述比赛中随机选择一个主场和客场,求李明的投篮命中率一场超过0.6,一场不超过0.6的概率; (3) 记x 是表中10个命中次数的平均数,从上述比赛中随机选择一场,记X 为李明在这场比赛中命中次数,比较E X ()与x 的大小(只需要写出结论)17.(本小题共14分)如图,正方形AMDE 的边长为2,,B C 分别为AM 、MD 的中点,在五棱锥P ABCDE -中,F 为棱PE 的中点,平面ABF 与棱PD ,PC 分别交于点G 、H (Ⅰ)求证://AB FG ; (Ⅱ)若P A A B C D E ⊥平面,且=P A A E ,求直线BC 与平面ABF 所成角的大小,并求线段PH 的长.MPHGFEDCBA18.(本小题共13分)已知函数()cos sin ,[0,]2f x x x x x π=-∈(I )求证:()0f x …; (II )若sin x a b x <<在(0,)2π上恒成立,求与a 的最大值与b 的最小值.19.(本小题共14分)已知椭圆22:24C x y +=(I )求椭圆C 的离心率;(II )设O 为坐标原点,若点A 在椭圆C 上,点B 在直线2y =上,且OA OB ⊥,求直线AB 与圆222x y +=的位置关系,并证明你的结论.20(本小题共13分)对于数对序列()11,P a b ,()22,a b ,⋅⋅⋅,(),n n a b ,记()111T P a b =+,()(){}()112max ,2k k k k T P b T P a a a k n -=+++⋅⋅⋅+剟,其中(){}112max ,k k T P a a a -++⋅⋅⋅+表示()1k T P -和12k a a a ++⋅⋅⋅+两个数中最大的数, (1)对于数对序列()2,3P ,()4,1,求()1T P ,()2T P 的值.(2)记m 为a b c d 、、、四个数中最小值,对于由两个数对(),a b ,(),c d 组成的数对序列 ()(),,,P a b c d 和()()',,,P c d a b ,试分别对m a =和m d =时两种情况比较()2T P 和()2'T P 的大小.(3)在由5个数对()11,8,()5,2,()16,11,()11,11,()4,6组成的所有数对序列中,写出一个数对序列P 使()5T P 最小,并写出()5T P 的值.(只需写出结论)参考答案一、 选择题(共8小题,每小题5分,共40分)1.C 2.A 3.B 4.C5.D6.D7.D8.B二、填空题(共6小题,每小题5分,共30分)9.1- 10.5 11.221312x y -=; 2y x =±12.8 13.36 14.π三、解答题(共6小题,共80分)15.(共13分) 【解析】 (1)243sin 1cos 7ADC ADC ∠=-∠=sin sin()sin cos cos sin 4311333727214BAD ADC B ADC B ADC B∴∠=∠-∠=∠⋅∠-∠⋅∠=⨯-⨯=(2)在ABD ∆中,sin sin sin AB AD BDADB B BAD ==∠∠∠,即:8433337214AD BD ==解得: 3,7BD AD == 在ACD ∆中,222222cos 172272497AC AD DC AD DC ADC=+-⋅⋅∠=+-⨯⨯⨯=7AC ∴=16.(共13分)解:(1)设李明在该场比赛中投篮命中率超过0.6的概率为事件A , 由题可知,李明在该场比赛中命中率超过0.6的场次有: 主场2、主场3、主场5、客场2、客场4,共计5场 所以李明在该场比赛中投篮命中率超过0.6的概率()51102P A ==. (2)设李明一场投篮命中率超过0.6,一场命中率不超过0.6的概率为事件B ,同理可知,李明主场命中率超过0.6的概率135P =,客场命中率超过0.6的概率225P =故()()()122133221311=+=555525P B P P P P =⨯-+⨯-⨯⨯. (3)()E X x =.17.(共14分) 【解析】 (1) 证明://,,ED AM ED AM PED PED ⊄⊂面面//AM PED ∴面,AM ABF AB ABF ⊂⊂面即面ABF PED FG =面面Ç//AB FG ∴(2) 如图建立空间坐标系A xyz -,各点坐标如下:(0,0,0),E(0,2,0),B(1,0,0),C(2,1,0),F(0,1,1),P(0,0,2)A设ABF 面的法向量为000(,,z )n x y =,(1,0,0)AB =,(0,1,1),AF =n AB n AF ⎧⋅=⎪⎨⋅=⎪⎩,即00x y z =⎧⎨+=⎩,令1y =得:(0,1,1)n =- 又(1,1,0)BC =,11sin ,222BC n ∴<>==⨯直线BC 与平面ABF 所成角为6π 设111(,,z )H x y ,由,PH tPC =则111(,,z 2)t(2,1,2)x y -=-(21,,22)H t t t ∴--又,(21,,22)H ABF BH t t t ∈=--面0n BH ∴⋅=,2220,3t t t ∴+-=∴=,422(,,)333H ∴,424,,333PH ⎛⎫= ⎪⎝⎭|PH|=2∴18.(共13分)解:(1)证明:()()'cos sin cos sin ,f x x x x x x x =+--=-∵π0,2x ⎡⎤∈⎢⎥⎣⎦,∴()'0f x …,即()f x 在π0,2⎡⎤⎢⎥⎣⎦上单调递增,∴()f x 在π0,2⎡⎤⎢⎥⎣⎦上的最大值为()00f =,所以()0f x …. (2)一方面令()si n x g x x =,π0,2x ⎛⎫∈ ⎪⎝⎭,则()2cos sin 'x x xg x x ⋅-=,由(1)可知,()'0g x <, 故()g x 在π0,2⎛⎫ ⎪⎝⎭上单调递减,从而()π22πg x g ⎛⎫>= ⎪⎝⎭,故2πa …,所以m a x 2πa =. 令()sin h x x bx =-,π0,2x ⎛⎫∈ ⎪⎝⎭,则()'cos h x x b =-,当1b …时,()'0h x <,故()h x 在π0,2x ⎛⎫∈ ⎪⎝⎭上单调递减,从而()()00h x h <=,所以()s i n 0h x x b x =-<恒成立.当1b <时,()'cos 0h x x b =-=在π0,2⎛⎫ ⎪⎝⎭有唯一解0x ,且()00,x x ∈,()'0h x >,故()h x 在()00,x 上单调递增,从而()()00h x h >=, 即sin sin 0sin x x bx x bx b x ->⇒>⇒>与sin xb x<恒成立矛盾, 综上,1b …,故min 1b =.19.(共14分)(1)椭圆的标准方程为:22142x y +=,故2,2a b ==,则2c =,故离心率2e 2c a ==; (2)由题可得,直线OA 的斜率存在,设为k ,则直线OA 的方程为y kx =,OA OB ⊥,○1当0k =时,()2,0A ±,已知()0,2B ,此时直线AB 方程为20x y +-=或+2=0x y -,原点到直线AB 的距离均为2,故满足直线AB 与圆222x y +=相切;○2当0k ≠时,直线OB 方程为1y x k=-, 联立22142y kx x y =⎧⎪⎨+=⎪⎩得,()221+24k x =,故2222,1212k A k k ⎛⎫ ⎪++⎝⎭或2222,1212k k k ⎛⎫-- ⎪++⎝⎭, 联立12y x k y ⎧=-⎪⎨⎪=⎩得,()2,2B k -,由A 的对称性,那么不妨去点2222,1212k A kk ⎛⎫⎪++⎝⎭进行计算,于是直线AB 方程为()()22222212122222112212kk k ky x k x k k kkk --++-=+=+++++,()()22212112+220k k x k k y k -+-+++=原点到直线AB 的距离()()222222+2=212+112k d k kkk=-+++,此时与圆222x y +=相切;综上所述,直线AB 与圆222x y +=相切.20.(共13分)解:(1)()1257T P =+=,()(){}{}211max ,241max 7,6178T P T P =++=+=+=;(2)当m a =时,()1T P a b =+,(){}{}2,+max +max ,a c T P d a b a d b c =++=+;()1'+T P c d =,(){}{}2'max ,max ,T P b c d c a b c a d b c d =+++=++=++; 因为a 是a b c d 、、、中最小的数,所以{}max ,a b c b c ++…,从而()()22'T P T P …;当m d =时,()1T P a b =+,(){}{}2,+max +max ,a c T P d a b a d b c =++=+; (){}{}2'max ,max ,T P b c d c a b c a d a b c =+++=++=++;因为d 是a b c d 、、、中最小的数,所以{}max ,d b c b c ++…,从而()()22'T P T P …; 综上,这两种情况下都有()()22'T P T P ….(3)52.分布为:(4,6)(16,11)(11,11)(11,8)(5,2)。
2014年高考理科数学北京卷(含答案解析)

绝密★启用前2014年普通高等学校招生全国统一考试(北京卷)数学(理科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分,考试时间120分钟.第Ⅰ卷(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合2{|20}A x x x =-=,{0,1,2}B =,则A B = ( )A .{0}B .{0,1}C .{0,2}D .{0,1,2}2.下列函数中,在区间(0,)+∞上为增函数的是( )A.y B .2(1)y x =- C .2x y -=D .0.5log (1)y x =+3.曲线1cos ,2sin ,x y θθ=-+⎧⎨=+⎩(..为参数)的对称中心( )A .在直线2y x =上B .在直线2y x =-上C .在直线1y x =-上D .在直线1y x =+上4.当7m =,3n =时,执行如图所示的程序框图,输出的S 值为( )A .7B .42C .210D .840 5.设{}n a 是公比为q 的等比数列,则“1q >”是“{}n a 为递增数列”的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件6.若x ,y 满足20,20,0,x y kx y y +-⎧⎪-+⎨⎪⎩≥≥≥且z y x =-的最小值为4-,则k 的值为( )A .2B .2-C .12D .12-7.在空间直角坐标系O xyz -中,已知()2,0,0A ,()2,2,0B ,(0),2,0C,(D .若1S ,2S ,3S 分别是三棱锥D ABC -在xOy ,yOz ,zOx 坐标平面上的正投影图形的面积,则( ) A .123S S S ==B .21S S =且23S S ≠C .31S S =且32S S ≠D .32S S =且31S S ≠8.学生的语文、数学成绩均被评定为三个等级,依次为“优秀”“合格”“不合格”.若学生甲的语文、数学成绩都不低于学生乙,且其中至少有一门成绩高于乙,则称“学生甲比学生乙成绩好”.如果一组学生中没有哪位学生比另一位学生成绩好,并且不存在语文成绩相同、数学成绩也相同的两位学生,那么这组学生最多有( )A .2 人B .3 人C .4 人D .5 人第Ⅱ卷(非选择题 共110分)二、填空题:本大题共6小题,每小题5分.共30分,把答案填写在题中的横线上.9.复数21i ()1i+=- . 10.已知向量a ,b 满足|a |1=,b (2,1)=,且λa +b =0()λ∈R ,则||λ= .11.设双曲线C 经过点(2,2),且与2214y x =-具有相同渐近线,则C 的方程为 ;渐近线方程为 .12.若等差数列{}n a 满足7890a a a ++>,7100a a +<,则当n = 时,{}n a 的前n 项和最大.13.把5件不同产品摆成一排.若产品A 与产品B 相邻,且产品A 与产品C 不相邻,则不同的摆法有 种.14.设函数()sin()f x A x ωϕ=+(,,A ωϕ是常数,0A >,0)ω>.若()f x 在区间ππ,62⎡⎤⎢⎥⎣⎦上具有单调性,且π2ππ()()()236f f f ==-,则()f x 的最小正周期为 . 三、解答题:本大题共6小题,共80分.解答应写出必要的文字说明、证明过程或演算步骤.15.(本小题满分13分)如图,在ABC △中,π3B ∠=,8AB =,点D 在BC 边上,且2CD =,1cos 7ADC ∠=.(Ⅰ)求sin BAD ∠; (Ⅱ)求BD ,AC 的长.-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无------------------------------------姓名________________ 准考证号_____________16.(本小题满分13分)(Ⅰ)从上述比赛中随机选择一场,求李明在该场比赛中投篮命中率超过0.6的概率;(Ⅱ)从上述比赛中随机选择一个主场和一个客场,求李明的投篮命中率一场超过0.6,一场不超过0.6的概率;(Ⅲ)记x为表中10个命中次数的平均数.从上述比赛中随机选择一场,记X为李明在这场比赛中的命中次数.比较EX与x的大小.(只需写出结论)17.(本小题满分14分)如图,正方形AMDE的边长为2,B,C分别为AM,MD的中点.在五棱锥P ABCDE-中,F为棱PE的中点,平面ABF与棱PD,PC分别交于点G,H.(Ⅰ)求证:AB FG;(Ⅱ)若PA⊥底面ABCDE,且PA AE=,求直线BC与平面ABF所成角的大小,并求线段PH的长. 18.(本小题满分13分)已知函数()cos sinf x x x x=-,π0,2x⎡⎤∈⎢⎥⎣⎦.(Ⅰ)求证:()0f x≤;(Ⅱ)若sin xa bx<<对π(0,)2x∈恒成立,求a的最大值与b的最小值.19.(本小题满分13分)已知椭圆C:2224x y+=.(Ⅰ)求椭圆C的离心率;(Ⅱ)设O为原点.若点A在椭圆C上,点B在直线2y=上,且OA OB⊥,试判断直线AB与圆222x y+=的位置关系,并证明你的结论.20.(本小题满分13分)对于数对序列P:11(,)a b,22(,)a b,⋅⋅⋅,(),n na b,记111()T P a b=+,()k kT P b=+ 112max{(),}k kT P a a a-+⋅⋅⋅++(2)k n≤≤,其中112(ma}x{),k kT P a a a-++⋅⋅⋅+表示1()kT P-和12ka a a++⋅⋅⋅+两个数中最大的数.(Ⅰ)对于数对序列P:(2,5),(4,1),求1()T P,2()T P的值;(Ⅱ)记m为a,b,c,d四个数中最小的数,对于由两个数对(,)a b,(,)c d组成的数对序列P:(,)a b,(,)c d和P':(,)c d,(,)a b,试分别对m a=和m d=两种情况比较2()T P和2()T P'的大小;(Ⅲ)在由五个数对(11,8),(5,2),(16,11),(11,11),(4,6)组成的所有数对序列中,写出一个数对序列P使5()T P最小,并写出5()T P的值.(只需写出结论)2014年普通高等学校招生全国统一考试(北京卷)数学(理科)答案解析第Ⅰ卷一、选择题 1.【答案】C 【解析】{}0,2A =,{0,2}{0,1,2}{0,2}AB ∴==,故选C.【提示】用描述法、列举法写出集合,求其交集. 【考点】交集及其运算 2.【答案】A【解析】由基本初等函数的性质得,选项B 中的函数在(0,1)上递减,选项C ,D 中的函数在(0,)+∞上为减函数,所以排除B ,C ,D ,故选A.【提示】根据基本初等函数的单调性,判断各个选项中函数的单调性,从而得出结论. 【考点】对数函数的单调性与特殊点 3.【答案】B【解析】曲线方程消去参数化为22(1)(2)=1x y ++-,其对称中心点为(1,2)-,验证知其在直线2y x =-上,故选B.【提示】曲线方程消去参数化为普通方程,求经过对称中心的一条直线. 【考点】曲线的参数方程 4.【答案】C【解析】=1765=210S ⨯⨯⨯,故选C.【提示】由循环语句、条件语句执行程序,直至结束. 【考点】循环结构 5.【答案】D【解析】当101a q <>,时,数列{}n a 递减;当10a <,数列{}n a 递增时,01q <<,故选D.【提示】根据等比数列的性质,结合充分条件和必要条件的定义进行判断即可得到结论. 【考点】充分、必要条件,等比数列的性质 6.【答案】D【解析】可行域如图所示,当0k >时,知z y x =-无最小值,当0k <时,目标函数线过可行域内A 点时z 有最小值.联立020y kx y =⎧⎨-+=⎩解得2,0A k ⎛⎫⎪⎝⎭,故min 2=0+=4z k 即1=2k -,故选D.【提示】给出约束条件和目标函数在此区域的最小值,求未知参数. 【考点】简单线性规划 7.【答案】D【解析】设顶点D 在三个坐标平面xOy 、yOz 、zOx 上的正投影分别为1D 、2D 、3D ,则11AD BD ==2AB =, ∴11S 22=22=⨯⨯,22122OCD S S ==⨯=△,33122OAD S S ==⨯△,故选D.【提示】分别求出三棱锥在各个面上的投影坐标即可得到结论. 【考点】空间直角坐标系 8.【答案】B【解析】假设A 、B 两位学生的数学成绩一样,由题意知他们语文成绩不一样,这样他们的语文成绩总有人比另一个人高,语文成绩较高的学生比另一个学生“成绩好”,与已知条件“他们之中没有一个比另一个成绩好”相矛盾.因此,没有任意两位学生数学成绩是相同的.因为数学成绩只有3种,因而学生数量最大为3,即3位学生的成绩分别为(优秀,不合格)、(合格,合格)、(不合格,优秀)时满足条件,故选B. 【提示】分别用ABC 分别表示优秀、及格和不及格,根据题干中的内容推出成绩得A ,B ,C 的学生各最多只有1个,继而推得学生的人数. 【考点】排列组合数的应用第Ⅱ卷二、填空题 9.【答案】1-【解析】22221i (1i)2i 11i (1i)(1i)2⎡⎤+-⎛⎫⎛⎫==-⎢⎥ ⎪ ⎪--+⎝⎭⎝⎭=⎣⎦. 【提示】复数的乘、除运算,直接计算出结果. 【考点】复数代数形式的四则运算 10.【解析】0a b λ+=,a b λ∴=-,||5||||b a λ∴===. 【提示】已知向量和向量的模,及两向量之间的关系,求||λ的值. 【考点】向量的线性运算11.【答案】22=1312x y -2y x ±=【解析】设双曲线C 的方程为224y x λ-=,将(2,2)代入得2222=3=4λ--, ∴双曲线C 的方程为22=1312x y -.令22=04y x -得渐近线方程为2y x =±.【提示】利用双曲线简单的几何性质,求经过一点,与已知曲线有相同渐近线的双曲线. 【考点】双曲线的简单几何性质 12.【答案】8 【解析】7898=30a a a a ++>,710890a a a a +=+<,8900a a ∴><,,∴8n =时,数列{}n a 的前n 项和最大.【提示】可得等差数列{}n a 的前8项为正数,从第9项开始为负数,进而可得结论. 【考点】等差数列性质 13.【答案】36【解析】32132362336A A A =⨯⨯=.【提示】根据题目的要求,利用分步乘法计数原理与排列与组合,求出其中的不同摆法. 【考点】乘法原理,排列数的应用 14.【答案】π【解析】结合图像得π2πππ2326+=422T +-,即πT =.【提示】结合二次函数的图象与单调性,求最小正周期T. 【考点】二次函数的图象与周期性 三、解答题 15.【答案】(1)14(2)37BD AC ==,【解析】(1)在ADC △中,因为1cos 7ADC ∠=,所以sin ADC ∠=. 所以sin sin()BAD ADC B ∠=∠-∠sin cos cos sin ADC B ADC B =∠-∠1127=-=(2)在ABD △中,由正弦定理得sin 3sin AB BAD BD ADB ∠===∠,在ABC △中,由余弦定理得2222cos AC AB BC AB BC B =+-22185285492=+-⨯⨯⨯=,所以7AC =.【提示】根据三角形边角之间的关系,结合正弦定理和余弦定理即可得到结论.【考点】三角函数的基本关系式,正弦定理,余弦定理 16.【答案】(1)0.5 (2)1325(3)EX x =【解析】(1)根据投篮统计数据,在10场比赛中,李明投篮命中率超过0.6的有5场,分别是主场2,主场3,主场5,客场2,客场4.所以在随机选择的一场比赛中,李明的投篮命中率超过0.6的概率是0.5.(2)设事件A 为“在随机选择的一场主场比赛中李明的投篮命中率超过0.6”,事件B 为“在随机选择的一场客场比赛中李明的投篮命中率超过0.6”,事件C 为“在随机选择的一个主场和一个客场中,李明的投篮命中率一场超过0.6,一场不超过0.6”.则C ABAB =,A B ,独立根据投篮统计数据,32()()55P A P B ==,.()()()P C P AB P AB =+33225555=⨯+⨯1325=所以在随机选择的一个主场和一个客场中,李明的投篮命中率一场超过0.6,一场不超过0.6的概率为1325. (3)EX x =.【提示】由互斥事件与独立事件的概率,设出基本事件,并求出概率. 【考点】离散型随机变量的期望与方差,相互独立事件的概率乘法公式 17.【答案】(1)在正方形中,因为B 是AM 的中点,所以AB DE ∥.又因为AB ⊄平面PDE ,所以AB PDE ∥平面,因为AB ⊂平面ABF ,且平面ABF平面PDE FG =,所以AB FG ∥.(2)因为PA ⊥底面ABCDE ,所以PA AB ⊥,PA AE ⊥.如图建立空间直角坐标系Axyz ,则(0,0,0)A ,(1,0,0)B ,(2,1,0)C ,(0,0,2)P ,(0,1,1)F ,(1,1,0)BC =.设平面ABF 的法向量为(,,)n x y z =,则0n AB n AF ⎧=⎪⎨=⎪⎩,即00x y z =⎧⎨+=⎩. 令1,z =,则1y =-.所以(0,1,1)n =-,设直线BC 与平面ABF 所成角为α, 则1sin |cos ,|2|||n BC n BC n BC α===|.设点H 的坐标为(,,).u v w因为点H 在棱PC 上,所以可设(01)PH PC λλ=<<,即(,,2)(2,1,2)u v w λ-=-, 所以2,,22u v w λλλ===-.因为n 是平面ABF 的法向量,所以0n AH =,即(0,1,1)(2,,22)0λλλ--=.解得23λ=,所以点H 的坐标为422,,333⎛⎫⎪⎝⎭所以2PH =.【提示】由线面平行推出线线平行,利用线面垂直、线线垂直这个条件,作出有关辅助线,建立空间直角坐标系求解. 【考点】直线与平面所成的角18.【答案】(1)由()cos sin f x x x x =-得()cos sin cos sin f x x x x x x x '=--=-.因为在区间π0,2⎛⎫ ⎪⎝⎭上()sin 0f x x x '=-<,所以()f x 在区间π0,2⎡⎤⎢⎥⎣⎦上单调递减,从而()(0)0f x f ≤=.(2)当0x >时,“sin xa x>”等价于“sin 0x ax ->”,“sin x b x <”等价于“sin 0x bx -<”. 令()g x sin x cx =-,则()cos g x x c '=-.当0c ≤时,()0g x >对任意π0,2x ⎛⎫∈ ⎪⎝⎭恒成立.当1c ≥时,因为对任意π0,2x ⎛⎫∈ ⎪⎝⎭,()cos 0g x x c '=-<,所以()g x 在区间π0,2⎡⎤⎢⎥⎣⎦上单调递减.从而()(0)0g x g <=对任意π0,2x ⎛⎫∈ ⎪⎝⎭恒成立.当01c <<时,存在唯一的0π0,2x ⎛⎫∈ ⎪⎝⎭,使得00()cos 0g x x c '=-=.()g x 与()g x '在区间π0,⎛⎫⎪上的情况如下:因为()g x 在区间[]00,x 上是增函数,所以0()(0)0g x g >=.进一步,“()0g x >对任意π0,2x ⎛⎫∈ ⎪⎝⎭恒成立”当且仅当ππ1022g ⎛⎫=-≥ ⎪⎝⎭,即20πc <≤.综上所述,当且仅当2πc ≤时,()0g x >对任意π0,2x ⎛⎫∈ ⎪⎝⎭恒成立;当且仅当1c≥时,()<0g x 对任意π0,2x ⎛⎫∈⎪⎝⎭恒成立.所以,若sin x a b x <<对任意π0,2x ⎛⎫∈ ⎪⎝⎭恒成立,则a 最大值为2π,b 的最小值为1 【提示】直接利用导数的几何意义,证明函数.第(2)问是求解未知参量的最值,函数求导,由函数值变化判断单调区间,进而求解最值. 【考点】导数的几何意义,利用导数判断参数的范围19.【答案】(1)由题意,椭圆C 的标准方程为22142x y +=.所以224,2a b ==,从而2222c a b =-=.因此2,a c ==故椭圆C 的离心率2c e a ==(2)直线AB 与圆222x y +=相切.证明如下:设点A ,B 的坐标分别为00(,)x y ,(,2)t ,其中00x ≠. 因为OA OB ⊥,所以0OA OB =,即0020tx y +=,解得02y t x =-. 当0x t =时,202t y =,代入椭圆C 的方程,得t =AB 的方程为x =.圆心O 到直线AB 的距离d .此时直线AB 与圆222x y +=相切.当0x t ≠时,直线AB 的方程为0022()y y x t x t--=--,即0000(2)()20y x x ty x t y ---+-=,圆心O 到直线AB的距离d =.又220024x y +=,02y t x =-,故d ===此时直线AB 与圆222x y +=相切.【提示】根据给出的椭圆方程找出离心率,然后利用椭圆方程与直线的关系及两线垂直,求出直线与圆的位置关系.【考点】圆与圆锥曲线的综合,椭圆的简单性质 20.【答案】(1)12()7()8T P T P ==, (2)22()()T P T P '≤(3)1()10T P =,2()26T P =,3()42T P =,4()50T P =,5()52T P =【解析】(1)1()257T P =+=,21()1max{(),24}T P T P =++1max{7,6}=+=8. (2)2()T P {}max ,a b d a c d =++++,2()T P '={}max ,c d b c a b ++++. 当m =a 时,2()T P '={}max ,c d b c a b ++++=c d b ++,因为c d b c b d ++≤++,且a c d c b d ++≤++,所以2()T P ≤2()T P '. 当m =d 时,2()T P '{}max ,c d b c a b =++++c a b =++,因为a b d ++≤c a b ++,且a c d c a b ++≤++所以2()T P ≤2()T P '. 所以无论m a =还是m d =,22()()T P T P '≤都成立.(3)数对序列P :(4,6),(11,11),(16,11),(11,8),(5,2)的5()T P 值最小, 1()10T P =,2()26T P =,3()42T P =,4()50T P =,5()52T P =【提示】给出数学概念的新定义,根据新定义,求值比较大小. 【考点】分析法和综合法。
2014年全国普通高等学校招生统一考试理科数学(北京卷带解析)试题

2014年全国普通高等学校招生统一考试理科(北京卷)数学试题1、【题文】已知集合,,则()A.B.C.D.2、【题文】下列函数中,在区间上为增函数的是()A.B.C.D.3、【题文】曲线,(为参数)的对称中心()A.在直线上B.在直线上C.在直线上D.在直线上4、【题文】当时,执行如图所示的程序框图,输出的值为()A.7 B.42 C.210 D.8405、【题文】设是公比为的等比数列,则“”是“为递增数列”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件6、【题文】若、满足,且的最小值为,则的值为()A.2 B.C.D.7、【题文】在空间直角坐标系中,已知.若分别是三棱锥在坐标平面上的正投影图形的面积,则()A.B.且C.且D.且8、【题文】学生的语文、数学成绩均被评为三个等级,依次为“优秀”“合格”“不合格”.若学生甲的语文、数学成绩都不低于学生乙,且其中至少有一门成绩高于乙,则称“学生甲比学生乙成绩好”.如果一组学生中没有哪位学生比另一位学生成绩好,并且不存在语文成绩相同、数学成绩也相同的两位学生,那么这组学生最多有()A.2人B.3人C.4人D.5人9、【题文】复数 .10、【题文】已知向量、满足,,且(),则 .11、【题文】设双曲线经过点(2,2),且与具有相同渐近线,则的方程为;渐近线方程为 .12、【题文】若等差数列满足,则当时,的前项和最大.13、【题文】把5件不同产品摆成一排,若产品与产品相邻,且产品与产品不相邻,则不同的摆法有种.14、【题文】设函数(是常数,).若在区间上具有单调性,且,则的最小正周期为 .15、【题文】如图,在中,,点在边上,且,.(1)求;(2)求,的长.(1)从上述比赛中随机选择一场,求李明在该场比赛中投篮命中率超过0.6的概率;(2)从上述比赛中随机选择一个主场和一个客场,求李明的投篮命中率一场超过0.6,一场不超过0.6的概率;(3)记为表中10个命中次数的平均数,从上述比赛中随机选择一场,记为李明在这场比赛中的命中次数,比较与的大小(只需写出结论)17、【题文】如图,正方体的边长为2,,分别为,的中点,在五棱锥中,为棱的中点,平面与棱,分别交于,. (1)求证:;(2)若底面,且,求直线与平面所成角的大小,并求线段的长.18、【题文】已知函数.(1)求证:;(2)若对恒成立,求的最大值与的最小值.19、【题文】已知椭圆:.(1)求椭圆的离心率;(2)设为原点,若点在椭圆上,点在直线上,且,试判断直线与圆的位置关系,并证明你的结论.20、【题文】对于数对序列,记,,其中表示和两个数中最大的数.(1)对于数对序列,求的值;(2)记为,,,四个数中最小的数,对于由两个数对组成的数对序列和,试分别对和两种情况比较和的大小;(3)在由五个数对组成的所有数对序列中,写出一个数对序列使最小,并写出的值.(只需写出结论).。
2014年北京高考数学理科试题及答案

绝密★启封并使用完毕前2014年普通高等学校招生全国统一考试数学(理)(北京卷)本试卷共5页,150分。
考试时长120分钟,考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并收回。
第一部分(选择题 共40分)一、选择题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
(1) 已知集合2{|20}A x x x =-=,{0,1,2}B =,若AB =(A) {0} (B) {0,1} (C) {0,2} (D) {0,1,2}(2) 下列函数中,在区间(0,}+∞上为增函数的是(A) y = (B) 2=(1)y x - (C) 2x y -= (D) 0.5log (1)y x =+(3) 曲线1cos 2sin x y =-+⎧⎨=+⎩θθ ,(θ为参数)的对称中心(A) 在直线2y x =上 (B) 在直线2y x =-上 (C) 在直线1y x =-上 (D) 在直线1y x =+上(4) 当7m =,3n =时,执行如图所示的程序框图,输出的s 值为 (A) 7 (B) 42 (C) 210 (D) 840(5) 设{}n a 是公比为q 的等比数列,则“1q >”是“{}n a ”为递增数列的 (A) 充分且不必要条件 (B) 必要且不充分条件 (C) 充分且必要条件 (D) 既非充分也非必要条件(6) 若,x y 满足20200x y kx y y +-≥⎧⎪-+≥⎨⎪≥⎩且z y x =-的最小值为4-,则k 的值是(A) 2 (B) 2- (C)1 (D) 1- S k(7) 在空间坐标系O xyz -中,已知(2,0,0)A ,(2,2,0)B ,(0,2,0)C ,D ,若1S ,2S ,3S 分别表示三棱锥D ABC -在xOy ,yOz ,zOx 则坐标平面上的正投影图形的面积,则(A) 1S =2S =3S (B) 1S =2S 且31S S ≠ (C) 1S =3S 且32S S ≠ (D) 2S =3S 且13S S ≠(8) 有语文、数学两学科,成绩评定为“优秀”“合格”“不合格”三种.若A 同学每科成绩不低于B 同学,且至少有一颗成绩比B 高,则称 “A 同学比B 同学成绩好,”现在若干同学,他们之中没有一个人比另一个人成绩好,且没有任意两个人语文成绩一样,数学成绩也一样的。
2014年高考真题——理科数学(北京卷)解析版 Word版含解析

课标理数【2014·北京理卷】一、选择题1. [2014•北京理卷]1.已知集合2{|20},{0,1,2}A x x x B =-==,则AB =( ).{0}A .{0,1}B .{0,2}C .{0,1,2}D【答案】C【解析】∵{}2,0=A ,∴{}{}{}2,02,1,02,0== B A . 2.[2014•北京理卷]下列函数中,在区间(0,)+∞上为增函数的是( ).A y = 2.(1)B y x =- .2x C y -= 0.5.log (1)D y x =+【答案】A【解析】由初等函数的性质得选项B 在()1,0上递减,选项C 、D 在()+∞,0为减函数,所以排除B 、C 、D. 3.[2014•北京理卷] 曲线1cos 2sin x y θθ=-+⎧⎨=+⎩(θ为参数)的对称中心( ).A 在直线2y x =上 .B 在直线2y x =-上 .C 在直线1y x =-上 .D 在直线1y x =+上【答案】B【解析】曲线方程消参化为()()12122=-++y x ,其对称中心为()2,1-,验证知其满足x y 2-=.4.[2014•北京理卷]当7,3m n ==时,执行如图所示的程序框图,输出的S 值为( ).7A .42B .210C .840D【答案】C【解析】2105671=⨯⨯⨯=S . 5.[2014•北京理卷]设{}n a 是公比为q 的等比数列,则"1"q >是"{}"n a 为递增数列的( ).A 充分且不必要条件 .B 必要且不充分条件 .C 充分必要条件 .D 既不充分也不必要条件【答案】D【解析】当01<a 时,1>q 数列{}n a 递减;01<a 时,数列{}n a 递增,10<<q . 理数6.E5[2014•北京理卷]若,x y 满足20200x y kx y y +-≥⎧⎪-+≥⎨⎪≥⎩且z y x =-的最小值为-4,则k 的值为( ).2A .2B - 1.2C 1.2D -【答案】D【解析】可行域如图所示,当0>k 时,知x y z -=无最小值,当0<k 时,目标函数线过可行域内A 点时z 有最小值,联立⎩⎨⎧=+-=020y kx y ,解之得⎪⎭⎫⎝⎛-0,2k A ,420min -=+=k z ,即21-=k .7.[2014•北京理卷]在空间直角坐标系Oxyz 中,已知()2,0,0A ,()2,2,0B ,()0,2,0C,(D ,若 1S ,2S ,3S 分别表示三棱锥D ABC -在xOy ,yOz ,zOx 坐标平面上的正投影图形的 面积,则( )(A )123S S S == (B )12S S =且 31S S ≠ (C )13S S =且 32S S ≠ (D )23S S =且 13S S ≠ 【答案】D【解析】设顶点D 在三个坐标面xoy 、yoz 、zox 的正投影分为'1D 、'2D 、'3D ,则211='='BD AD ,2=AB ,∴2222211=⨯⨯⨯=S ,2222122=⨯⨯=='OCD S S ,2222133=⨯⨯=='OAD S S .8.[2014•北京理卷]有语文、数学两学科,成绩评定为“优秀”“合格”“不合格”三种.若A 同学每科成绩不低于B 同学,且至少有一科成绩比B 高,则称“A 同学比B 同学成绩好.”现有若干同学, 他们之间没有一个人比另一个成绩好,且没有任意两个人语文成绩一样,数学成绩也一样 的.问满足条件的最多有多少学生( )(A )2 (B )3 (C )4 (D )5 【答案】B【解析】假设AB 两个同学的数学成绩一样,由题意知他们语文成绩不一样,这样他们的语文成绩总有人比另一个人高,语文成绩较高的同学比另一个同学“成绩好”,与已知条件“他们之中没有一个比另一个成绩好”相矛盾.因此,没有任意两个同学数学成绩是相同的.因为数学成绩只有3种,因而同学数量最大为3.即 3位同学成绩分别为(优秀,不合格)、(合格,合格)、(不合格,优秀)时满足条件. 二、填空题9.[2014•北京理卷]2=-+y x 02=+-y kx A=-x y复数211i i +⎛⎫= ⎪-⎝⎭________.【答案】1-【解析】()()()122111112222-=⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛+-+=⎪⎭⎫ ⎝⎛-+i i i i i i . 10.[2014•北京理卷]已知向量a 、b 满足1a =,()2,1b =,且()0a b R λλ+=∈,则λ=________.【答案】5【解析】∵0=+b a λ,∴b a -=λ,∴515||||===a b λ. 11.[2014•北京理卷]设双曲线C 经过点()2,2,且与2214y x -=具有相同渐近线,则C 的方程为________; 渐近线方程为________.【答案】112322=-y x ;x y 2±= 【解析】设双曲线C 的方程为λ=-224x y ,将()2,2代入λ=-=-324222,∴双曲线方程为112322=-y x .令0422=-x y 得渐近线方程为x y 2±=. 12.[2014•北京理卷]若等差数列{}n a 满足7890a a a ++>,7100a a +<,则当n =________时{}n a 的前n 项和最大. 【答案】8【解析】∵038987>=++a a a a ,098107<+=+a a a a ,∴0,098<>a a ,∴8=n 时数列{}n a 前n 和最大. 13.[2014•北京理卷]把5件不同产品摆成一排,若产品A 与产品C 不相邻,则不同的摆法有_______种. 【答案】36【解析】36326132233=⨯⨯=A A A . 14.[2014•北京理卷]设函数)sin()(ϕω+=x x f ,0,0>>ωA ,若)(x f 在区间]2,6[ππ上具有单调性,且 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛=⎪⎭⎫⎝⎛6322πππf f f ,则)(x f 的最小正周期为________. 【答案】π【解析】结合图象得26223224ππππ+-+≥T ,即π≥T .15.[2014•北京理卷] 如图,在ABC ∆中,8,3==∠AB B π,点D 在BC 边上,且71cos ,2=∠=ADC CD (1)求BAD ∠sin (2)求AC BD ,的长解:(I )在ADC ∆中,因为17COS ADC ∠=,所以sin ADC ∠=. 所以sin sin()BAD ADC B ∠=∠-∠sin cos cos sin ADC B ADC B =∠-∠=1433237121734=⨯-⨯. (Ⅱ)在ABD ∆中,由正弦定理得AA-6π2π32π8sin 3sin AB BAD BD ADB ⋅∠===∠, 在ABC ∆中,由余弦定理得2222cos AC AB BC AB BC B =+-⋅⋅22185285492=+-⨯⨯⨯=, 所以7AC =.16.[2012•北京理卷]李明在10场篮球比赛中的投篮情况如下(假设各场比赛互相独立):(1)从上述比赛中随机选择一场,求李明在该场比赛中投篮命中率超过6.0的概率. (2)从上述比赛中选择一个主场和一个客场,求李明的投篮命中率一场超过6.0,一 场不超过6.0的概率.(3)记x 是表中10个命中次数的平均数,从上述比赛中随机选择一场,记X 为李明 在这比赛中的命中次数,比较)(X E 与x 的大小(只需写出结论).解:(I)根据投篮统计数据,在10场比赛中,李明投篮命中率超过0.6的场次有5场,分别是主场2,主场3,主场5,客场2,客场4.所以在随机选择的一场比赛中,李明的投篮命中率超过0.6的概率是05.(Ⅱ)设事件A 为“在随机选择的一场主场比赛中李明的投篮命中率超过0.6”,事件B 为“在随机选择的一场客场比赛中李明的投篮命中率超过0.6”,事件C 为“在随机选择的一个主场和一个客场中,李明的投篮命中率一场超过0.6,一场不超过0.6”。
2014年北京高考数学理科试题及答案

绝密★启封并使用完毕前2014年普通高等学校招生全国统一考试数学(理)(北京卷)本试卷共5页,150分。
考试时长120分钟,考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并收回.第一部分(选择题 共40分)一、选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项. (1) 已知集合2{|20}A x x x =-=,{0,1,2}B =,若AB =(A ) {0} (B) {0,1} (C ) {0,2} (D) {0,1,2}(2) 下列函数中,在区间(0,}+∞上为增函数的是(A) y = (B) 2=(1)y x - (C) 2x y -= (D) 0.5log (1)y x =+(3) 曲线1cos 2sin x y =-+⎧⎨=+⎩θθ ,(θ为参数)的对称中心(A) 在直线2y x =上 (B ) 在直线2y x =-上 (C ) 在直线1y x =-上 (D) 在直线1y x =+上(4) 当7m =,3n =时,执行如图所示的程序框图,输出的s 值为 (A) 7 (B) 42 (C ) 210 (D ) 840(5) 设{}n a 是公比为q 的等比数列,则“1q >”是“{}n a ”为递增数列的 (A) 充分且不必要条件 (B) 必要且不充分条件 (C ) 充分且必要条件 (D ) 既非充分也非必要条件(6) 若,x y 满足20200x y kx y y +-≥⎧⎪-+≥⎨⎪≥⎩且z y x =-的最小值为4-,则k 的值是(A) 2 (B ) 2- (C )12 (D ) 12- S k(7) 在空间坐标系O xyz -中,已知(2,0,0)A ,(2,2,0)B ,(0,2,0)C ,D ,若1S ,2S ,3S 分别表示三棱锥D ABC -在xOy ,yOz ,zOx 则坐标平面上的正投影图形的面积,则(A ) 1S =2S =3S (B) 1S =2S 且31S S ≠ (C) 1S =3S 且32S S ≠ (D) 2S =3S 且13S S ≠(8) 有语文、数学两学科,成绩评定为“优秀”“合格”“不合格”三种.若A 同学每科成绩不低于B 同学,且至少有一颗成绩比B 高,则称 “A 同学比B 同学成绩好,”现在若干同学,他们之中没有一个人比另一个人成绩好,且没有任意两个人语文成绩一样,数学成绩也一样的。
2014年北京高考理科数学试题含答案(Word版)

2014 年北京高考数学(理科)试题一 .选择题(共 8小题,每题 5 分,共 40分 .在每题列出的四个选项中,选出切合题目要求的一项)1.已知会合A{ x | x22x0}, B{0,1, 2} ,则A B ()A.{0}B.{ 0, 1}C.{ 0, 2}D.{ 0,1, 2}2.以下函数中,在区间(0,) 上为增函数的是()A.y x1B. y( x12)C.y 2 x D . y l o 0g. 5x( 1 )3.曲线x1cos(为参数)的对称中心()y2sinA. 在直线y2x 上B.在直线y2x 上C. 在直线y x1上D.在直线y x 1上4.当m7, n 3 时,履行以下图的程序框图,输出的S 值为()A.7B.42C.210D.8405.设{ a n}是公比为q的等比数列,则" q1" 是 "{ a n }" 为递加数列的()A. 充足且不用要条件B. 必需且不充足条件C. 充足必需条件D. 既不充足也不用要条件x y206.若x, y知足kx y20 且z y x 的最小值为-4,则 k 的值为()y0A.2B.21D .1 C .2 27.在空间直角坐标系Oxyz 中,已知 A 2,0,0 , B 2,2,0 , C 0,2,0,D 1,1, 2,若S1, S2, S3分别表示三棱锥D ABC 在xOy,yOz, zOx坐标平面上的正投影图形的面积,则()(A)S1S2S3(B)S1S2且 S3S1(C)S1S3且 S3S2(D)S2S3且 S1S38.有语文、数学两,成绩评定为“优异”“合格”“不合格”三种 .若A同学每科成绩不低于 B 同学,且起码有一科成绩比B高,则称“ A 同学比 B 同学成绩好.”现有若干同学,他们之间没有一个人比另一个成绩好,且没有随意两个人语文成绩同样,数学成绩也同样的 .问知足条件的最多有多少学生()(A)2(B)3(C)4(D)5二、填空题(共 6 小题,每题 5 分,共30 分)12i________.9.复数i110.已知向量a、b知足a 1 ,b2,1,且 a b 0R ,则________.11.设双曲线C经过点2,2,且与 y2x21拥有同样渐近线,则 C 的方程为________;4渐近线方程为 ________.12.若等差数列a n知足a7a8 a90 , a7a10 0 ,则当 n________时a n的前n项和最大 .13.把 5 件不一样产品摆成一排,若产品 A 与产品 C 不相邻,则不一样的摆法有_______种.14.设函数 f ( x) sin( x) , A0,0 ,若 f (x) 在区间 [6,] 上拥有单一性,且2f f 2,则 f (x) 的最小正周期为________.f236试题剖析:平等比数列{ a n} ,若 q 1 ,则当 a1 ,0 时数列 { a n} 是递减数列;若数列{ a n } 是递加数列,则二.填空题:本大题共 6 小题,每题 5 分,共 30 分. 请将答案天灾答题卡对应题的位置上,答错地点,书写不清,含糊其词均不得分.9.【答案】 1【分析】试题剖析:1i(1 i )22i i ,因此 (1i )2i 21. 1i(1 i )(1 i )21i10.【答案】 5【分析】三.解答题(共 6 题,满分80 分)15. (本小题 13 分)如图,在ABC 中,B, AB 8,点D在BC边上,且 CD1 2,cos ADC37( 1)求sin BAD(2)求BD, AC的长16.(本小题 13 分) .李明在 10 场篮球竞赛中的投篮状况以下(假定各场竞赛相互独立):(1)从上述竞赛中随机选择一场,求李明在该场竞赛中投篮命中率超出0.6 的概率.(2)从上述竞赛中选择一个主场和一个客场,求李明的投篮命中率一场超出0.6 ,一场不超出0.6 的概率.(3)记x 是表中10 个命中次数的均匀数,从上述竞赛中随机选择一场,记X为李明在这竞赛中的命中次数,比较E(X)与x 的大小(只要写出结论)17.(本小题14 分)如图,正方形AMDE的边长为2,B,C分别为AM ,MD的中点,在五棱锥P ABCDE 中,F为棱PE 的中点,平面ABF与棱PD , PC 分别交于点G, H.( 1)求证:AB // FG;( 2)若PA底面ABCDE,且AF PE ,求直线BC 与平面ABF所成角的大小,并求线段PH的长 .18.(本小题13 分)f (x)xcosxsin,[0, ],已知函数x x2( 1)求证:f ( x)0 ;( 2)若a sin x b在 (0,) 上恒建立,求a的最大值与 b 的最小值.x219.(本小题14 分)已知椭圆 C : x2 2 y2( 1)求椭圆C的离心率( 2)设O为原点,若点.4 ,A 在椭圆C上,点B 在直线y 2 上,且OA OB ,求直线AB与圆x2y2 2 的地点关系,并证明你的结论.20.(本小题13 分)关于数对序列P(a1,b1),( a2,b2 ),,( a n, b n ) ,记T1(P)a1b1,T k ( P)b k max{T k 1(P), a1a2a k }(2k n) ,此中max{T k 1( P), a1a2a k }表示 T k 1(P)和 a1a2a k两个数中最大的数,( 1)关于数对序列P(2,5), P(4,1) ,求 T1 (P),T2 (P) 的值.( 2)记m为a,b,c, d四个数中最小值,对于由两个数对(a, b),( c, d )组成的数对序列P(a,b),( c,d ) 和 P '(a,b),( c, d) ,试分别对m a 和m d 的两种状况比较T2 ( P) 和 T2 (P ') 的大小 .( 3)在由 5 个数对(11,8),(5,2),(16,11),(11,11),(4,6)构成的全部数对序列中,写出一个数对序列P 使 T5( P) 最小,并写出 T5 (P) 的值.(只要写出结论).。
(新课标Ⅱ)2014高考数学压轴卷 理(含解析)

2014新课标II 高考压轴卷理科数学选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.的共轭复数为(3. 由y=f (x )的图象向左平移个单位,再把所得图象上所有点的横坐标伸长到原来的2倍得到y=2sin 的图象,则 f (x )为( ) 2sin4.已知函数,则的值是( )D5. 设随机变量~X N (3,1),若(4)P X p >=,,则P(2<X<4)= ( A)12p + ( B)l —p (C)l-2p (D)12p - 6. 6.运行右面框图输出的S 是254,则①应为(A) n ≤5 (B) n ≤6 (C)n ≤7 (D) n ≤8 7. 若曲线在点(a ,f (a ))处的切线与两条坐标轴围成的三角形的面积为18,则a=( )8.已知A 、B是圆22:1O x y +=上的两个点,P 是AB 线段上的动点,当AOB ∆的面积最大时,则AO AP ⋅-2AP 的最大值是( )A.1-B.0C.81D.219.一个四面体的四个顶点在空间直角坐标系xyz O -中的坐标分别是(0,0,0),(1,2,0),(0,2,2),(3,0,1),则该四面体中以yOz 平面为投影面的正视图的面积为 A .3 B .25 C .2 D .2710. .已知函数2()cos()f n n n π=,且()(1)n a f n f n =++,则123100a a a a ++++=A . 0B .100-C .100D .1020011.设x ,y 满足约束条件,若目标函数z=ax+by (a >0,b >0)的最大值为12,则+的最小值为( )C 12.设双曲线﹣=1(a >0,b >0)的右焦点为F ,过点F 作与x 轴垂直的直线l 交两渐近线于A 、B 两点,且与双曲线在第一象限的交点为P ,设O 为坐标原点,若=λ+μ(λ,μ∈R ),λμ=,则该双曲线的离心率为( )BCD二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡的相应位置. 13.某棉纺厂为了了解一批棉花的质量,从中随机抽取了100根棉花纤维的长度(棉花纤维的长度是棉花质量的重要指标),所得数据都在区间[5,40]中,其频率分布直方图如图所示.从抽样的100根棉花纤维中任意抽取一根,则其棉花纤维的长度小于20mm 的概率为 .14.已知1cos21sin cos ααα-=,1tan()3βα-=-,则tan(2)βα-的值为 .15.函数43y x x =++(3)x >-的最小值是 .16.已知函数f(x)=x 3+x ,对任意的m ∈[-2,2],f(mx -2)+f(x)<0恒成立,则x 的取值范围为________.三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.解答写在答题卡上的指定区域内.17.已知函数3cos 32cos sin 2)(2-+=x x x x f ,R ∈x . (Ⅰ)求函数(3)1y f x =-+的最小正周期和单调递减区间;(Ⅱ)已知ABC ∆中的三个内角,,A B C 所对的边分别为,,a b c ,若锐角A 满足()26A f π-=7a =,sin sin 14B C +=,求ABC ∆的面积. 18.随机询问某大学40名不同性别的大学生在购买食物时是否读营养说明,得到如下列联表:⑴根据以上列联表进行独立性检验,能否在犯错误的概率不超过0.01的前提下认为性别与是否读营养说明之间有关系?⑵从被询问的16名不读营养说明的大学生中,随机抽取2名学生,求抽到男生人数ξ的分布列及其均值(即数学期望).(注:))()()(()(22d b c a d c b a bc ad n K ++++-=,其中d c b a n +++=为样本容量.)19.已知正四棱柱1111-ABCD A B C D 中,12,4==AB AA . (Ⅰ)求证:1BD AC ⊥;(Ⅱ)求二面角11--A AC D 的余弦值;(Ⅲ)在线段1CC 上是否存在点P ,使得平面11ACD ⊥平面PBD ,若存在,求出1CPPC 的值;若不存在,请说明理由.20.已知动圆P 与圆221:(3)81F x y ++=相切,且与圆222:(3)1F x y -+=相内切,记圆心P 的轨迹为曲线C ;设Q 为曲线C 上的一个不在x 轴上的动点,O 为坐标原点,过点2F 作OQ的平行线交曲线C 于,M N 两个不同的点. (Ⅰ)求曲线C 的方程;(Ⅱ)试探究||MN 和2||OQ 的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由;(Ⅲ)记2QF M ∆的面积为1S ,2OF N ∆的面积为2S ,令12S S S =+,求S 的最大值. 21.已知0t >,函数()3x tf x x t-=+. (1)1t =时,写出()f x 的增区间;(2)记()f x 在区间[0,6]上的最大值为()g t ,求()g t 的表达式;(3)是否存在t ,使函数()y f x =在区间(0,6)内的图象上存在两点,在该两点处的切线互相垂直?若存在,求t 的取值范围;若不存在,请说明理由.请考生在第22、23、24题中任选一题作答,如果多做,则按所做的第一题计分.作答时请写清题号.22.选修4﹣1:几何证明选讲如图,AB 是⊙O 的直径,AC 是弦,直线CE 和⊙O 切于点C ,AD 丄CE ,垂足为D . (I ) 求证:AC 平分∠BAD;(II ) 若AB=4AD ,求∠BAD 的大小.23.选修4﹣4:坐标系与参数方程将圆x2+y2=4上各点的纵坐标压缩至原来的,所得曲线记作C;将直线3x﹣2y﹣8=0绕原点逆时针旋转90°所得直线记作l.(I)求直线l与曲线C的方程;(II)求C上的点到直线l的最大距离.24. 选修4﹣5:不等式选讲设函数,f(x)=|x﹣1|+|x﹣2|.(I)求证f(x)≥1;(II)若f(x)=成立,求x的取值范围.2014新课标II高考压轴卷理科数学参考答案1. 【答案】A.【解析】由A={0,1,2},B={x|x=2a,a∈A}={0,2,4},所以A∩B={0,1,2}∩{0,2,4}={0,2}.所以A∩B中元素的个数为2.故选C.2. 【答案】A.【解析】由z•i=2﹣i,得,∴.故选:A.3. 【答案】B.【解析】由题意可得y=2sin的图象上各个点的横坐标变为原来的,可得函数y=2sin(6x﹣)的图象.再把函数y=2sin (6x ﹣)的图象向右平移个单位,即可得到f (x )=2sin[6(x ﹣)﹣)]=2sin (6x ﹣2π﹣)=2sin的图象,故选B .4. 【答案】C. 【解析】=f (log 2)=f (log 22﹣2)=f (﹣2)=3﹣2=,故选C .5. 【答案】C.【解析】因为(4)(2)P X P X p >=<=,所以P(2<X<4)= 1(4)(2)12P X P X p ->-<=-,选C. 6. 【答案】C.【解析】本程序计算的是212(12)2222212n nn S +-=+++==--,由122254n +-=,得12256n +=,解得7n =。
2014年北京高考真题-理科数学含答案

2014年北京高考数学(理科)试题一.选择题(共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项)1.已知集合2{|20},{0,1,2}A x x x B =-==,则A B =( ).{0}A .{0,1}B .{0,2}C .{0,1,2}D 2.下列函数中,在区间(0,)+∞上为增函数的是( ).1A y x =+ 2.(1)B y x=- .2x C y -= 0.5.l o g (1)D y x =+ 3.曲线1cos 2sin x y θθ=-+⎧⎨=+⎩(θ为参数)的对称中心( ).A 在直线2y x =上 .B 在直线2y x =-上.C 在直线1y x =-上 .D 在直线1y x =+上4.当7,3m n ==时,执行如图所示的程序框图,输出的S 值为( ).7A .42B .210C .840D5.设{}n a 是公比为q 的等比数列,则"1"q >是"{}"n a 为递增数列的( ).A 充分且不必要条件 .B 必要且不充分条件.C 充分必要条件 .D 既不充分也不必要条件6.若,x y 满足20200x y kx y y +-≥⎧⎪-+≥⎨⎪≥⎩且z y x =-的最小值为-4,则k 的值为( ).2A .2B - 1.2C 1.2D -7.在空间直角坐标系Oxyz 中,已知()2,0,0A ,()2,2,0B ,()0,2,0C ,()1,1,2D ,若 1S ,2S ,3S 分别表示三棱锥D ABC -在xOy ,yOz ,zOx 坐标平面上的正投影图形的 面积,则( )(A )123S S S == (B )12S S =且 31S S ≠(C )13S S =且 32S S ≠ (D )23S S =且 13S S ≠8.有语文、数学两学科,成绩评定为“优秀”“合格”“不合格”三种.若A 同学每科成绩不 低于B 同学,且至少有一科成绩比B 高,则称“A 同学比B 同学成绩好.”现有若干同学,他们之间没有一个人比另一个成绩好,学科 网且没有任意两个人语文成绩一样,数学成绩也一样 的.问满足条件的最多有多少学生( )(A )2 (B )3 (C )4 (D )5二、填空题(共6小题,每小题5分,共30分)9.复数211i i +⎛⎫= ⎪-⎝⎭________. 10.已知向量a 、b 满足1a =,()2,1b =,且()0a b R λλ+=∈,则λ=________.11.设双曲线C 经过点()2,2,且与2214y x -=具有相同渐近线,则C 的方程为________; 渐近线方程为________.12.若等差数列{}n a 满足7890a a a ++>,7100a a +<,则当n =________时{}n a 的前n 项和最大.13. 把5件不同产品摆成一排,若产品A 与产品C 不相邻,则不同的摆法有_______种.14. 设函数)sin()(ϕω+=x x f ,0,0>>ωA ,若)(x f 在区间]2,6[ππ上具有单调性,且 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛6322πππf f f ,则)(x f 的最小正周期为________. 三.解答题(共6题,满分80分)15. (本小题13分)如图,在ABC ∆中,8,3==∠AB B π,点D 在BC 边上,且71cos ,2=∠=ADC CD (1)求BAD ∠sin(2)求AC BD ,的长16. (本小题13分).李明在10场篮球比赛中的投篮情况如下(假设各场比赛互相独立):(1)从上述比赛中随机选择一场,求李明在该场比赛中投篮命中率超过6.0的概率.(2)从上述比赛中选择一个主场和一个客场,学科 网求李明的投篮命中率一场超过6.0,一 场不超过6.0的概率.(3)记x 是表中10个命中次数的平均数,从上述比赛中随机选择一场,记X 为李明在这比赛中的命中次数,比较)(X E 与x 的大小(只需写出结论)17.(本小题14分)如图,正方形AMDE 的边长为2,C B ,分别为MD AM ,的中点,在五棱锥ABCDE P - 中,F 为棱PE 的中点,平面ABF 与棱PC PD ,分别交于点H G ,.(1)求证:FG AB //;(2)若⊥PA 底面ABCDE ,且PE AF ⊥,求直线BC 与平面ABF 所成角的大小,并 求线段PH 的长.18.(本小题13分) 已知函数()cos sin ,[0,]2f x x x x x π=-∈, (1)求证:()0f x ≤;(2)若sin x a b x <<在(0,)2π上恒成立,求a 的最大值与b 的最小值.19.(本小题14分)已知椭圆22:24C x y +=,(1)求椭圆C 的离心率. (2)设O 为原点,若点A 在椭圆C 上,点B 在直线2y =上,且OA OB ⊥,求直线AB 与圆222x y +=的位置关系,并证明你的结论.20.(本小题13分)对于数对序列1122(,),(,),,(,)n n P a b a b a b ,记111()T P a b =+,112()max{(),}(2)k k k k T P b T P a a a k n -=++++≤≤,其中112max{(),}k k T P a a a -+++表示1()k T P -和12k a a a +++两个数中最大的数,(1)对于数对序列(2,5),(4,1)P P ,求12(),()T P T P 的值.(2)记m 为,,,a b c d 四个数中最小值,学科 网对于由两个数对(,),(,)a b c d 组成的数对序列(,),(,)P a b c d 和'(,),(,)P a b c d ,试分别对m a =和m d =的两种情况比较2()T P 和2(')T P 的大小.(3)在由5个数对(11,8),(5,2),(16,11),(11,11),(4,6)组成的所有数对序列中,写出一个数对序列P 使5()T P 最小,并写出5()T P 的值.(只需写出结论).。
2014年普通高等学校招生全国统一考试数学理试题(北京卷,扫描版,解析版)

2014年普通高等学校招生全国统一考试
数学(理)(北京卷)
本试卷共5页,150分。
考试时长120分钟。
考试生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题共40分)
一、选择题共8小题。
每小题5分.共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
第二部分(非选择题共110分) 二.填空题共6小题。
每小题5分。
共30分。
三、解答题共6小题,共80分。
解答应写出文字说明,演算步骤或证明过程。
绝密★考试结束前
2014年普通高等学校招生全国统一考试
数学(理)(北京卷)参考答案一、选择题(共8小题。
每小题5分.共40分)
二.填空题(共6小题。
每小题5分。
共30分)
三、解答题(共6小题,共80分)
11
12
13
14。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014北京市高考压轴卷理科数学一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的 1.已知11xyi i=-+,其中,x y 是实数,i 是虚数单位,则x yi +的共轭复数为( ) A .12i + B .12i - C .2i + D .2i -2.已知函数3()f x x x =--,123,,x x x R ∈,且120x x +>,230x x +>,310x x +>,则123()()()f x f x f x ++的值为()A.正B.负C.零D.可正可负3.已知某几何体的三视图如下,则该几何体体积为( )A .4+52π B .4+32π C .4+2π D .4+π 4.如图所示为函数π()2sin()(0,0)2f x x ωϕωϕ=+>≤≤的部分图像,其中A ,B 两点之间的距离为5,那么(1)f -=( )A .-1B .CD .15.(5分)已知两条不重合的直线m、n和两个不重合的平面α、β,有下列命题:①若m⊥n,m⊥α,则n∥α;②若m⊥α,n⊥β,m∥n,则α∥β;③若m、n是两条异面直线,m⊂α,n⊂β,m∥β,n∥α,则α∥β;④若α⊥β,α∩β=m,n⊂β,n⊥m,则n⊥α.其中正确命题的个数是()6.设函数是定义在上的可导函数,其导函数为,且有,则不等式的解集为A. B.C. D.7.已知F1(﹣c,0),F2(c,0)为椭圆的两个焦点,P为椭圆上一点且,则此椭圆离心率的取值范围是()B8.已知定义在R上的偶函数f(x)满足f(1+x)=f(1﹣x),且x∈[0,1]时,,则方程在区间[﹣3,3]上的根的个数为()9.已知集合{}{}22,1,3,3,21,1A a a B a a a =+-=--+,若{}3A B =-,则实数a 的值为________________.10.已知如图所示的流程图(未完成),设当箭头a 指向①时输出的结果S =m ,当箭头a 指向②时,输出的结果S =n ,求m +n 的值.11.若n S 是等差数列}{n a 的前n 项和,且8320S S -=,则11S 的值为 . 12.展开式中有理项共有 项.13.在平面直角坐标系xOy 中,过坐标原点的一条直线与函数xx f 2)(=的图象交于P 、Q 两点,则线段PQ 长的最小值是_______14.设a ∈R ,若x >0时均有[(a ﹣1)x ﹣1](x 2﹣ax ﹣1)≥0,则a= .三、解答题:本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤.解答写在答题卡上的指定区域内.15.已知向量)4cos ,4(cos ),1,4sin 3(2x x x ==.记x f ⋅=)( (I)求)(x f 的周期;(Ⅱ)在∆ABC 中,角A 、B 、C 的对边分别是a 、b 、c ,且满足(2a —c)cos B=b cosC , 若f (A )=,试判断∆ABC 的形状. 16.在一次对某班42名学生参加课外篮球、排球兴趣小组(每人参加且只参加一个兴趣小组)情况调查中,经统计得到如下2×2列联表:(单位:人)(Ⅱ)在统计结果中,如果不考虑性别因素,按分层抽样的方法从两个兴趣小组中随机抽取7名同学进行座谈.已知甲、乙、丙三人都参加“排球小组”. ①求在甲被抽中的条件下,乙丙也都被抽中的概率;②设乙、丙两人中被抽中的人数为X ,求X 的分布列及数学期望E(X). 下面临界值表供参考:参考公式:2()()()()K a b c d a c b d =++++命题意图:考查分类变量的独立性检验,条件概率,随机变量的分布列、数学期望等,中等题. 17.已知正四棱柱1111-ABCD A BC D 中,12,4==AB AA . (Ⅰ)求证:1BD AC ⊥;(Ⅱ)求二面角11--A AC D 的余弦值;(Ⅲ)在线段1CC 上是否存在点P ,使得平面11ACD ⊥平面PBD ,若存在,求出1CPPC 的值;若不存在,请说明理由.18.已知椭圆2222:1(0)x y C a b a b+=>>的左右焦点分别为12,F F ,点B 为短轴的一个端点,260OF B ∠=︒. (Ⅰ)求椭圆C 的方程;(Ⅱ)如图,过右焦点2F ,且斜率为(0)≠k k 的直线l 与椭圆C 相交于,E F 两点,A 为椭圆的右顶点,直线,AE AF 分别交直线3=x 于点,M N ,线段MN 的中点为P ,记直线2PF 的斜率为'k .求证: '⋅k k 为定值.19.已知数列{}n a 的各项均为正数,记12()n A n a a a =+++L ,231()n B n a a a +=+++L ,342(),1,2,n C n a a a n +=+++=L L .(Ⅰ)若121,5a a ==,且对任意n ∈*N ,三个数(),(),()A n B n C n 组成等差数列,求数列{}n a 的通项公式.(Ⅱ)证明:数列{}n a 是公比为q 的等比数列的充分必要条件是:对任意n ∈*N ,三个数(),(),()A n B n C n 组成公比为q 的等比数列.20.已知函数2()2ln f x x x ax =-+(a ∈R ).(Ⅰ)当2a =时,求()f x 的图象在1x =处的切线方程;(Ⅱ)若函数()()g x f x ax m =-+在1[e]e ,上有两个零点,求实数m 的取值范围;(Ⅲ)若函数()f x 的图象与x 轴有两个不同的交点12(0)(0)A x B x ,,,,且120x x <<, 求证:12()02x x f +'<(其中()f x '是()f x 的导函数).2014北京市高考压轴卷数学理word 版参考答案1. 【答案】D 【解析】1()1,2,1,12x x xi yi x y i =-=-∴==+故选D . 2. 【答案】B【解析】∵3()f x x x =--,∴函数()f x 在R 上是减函数且是奇函数,∵120x x +>,∴12x x >-,∴12()()f x f x <-,∴12()()f x f x <-,∴12()()0f x f x +<, 同理:23()()0f x f x +<,31()()0f x f x +<,∴123()()()0f x f x f x ++<.3. 【答案】A【解析】该几何体是一个圆柱与一个长方体的组成,其中重叠了一部分2π,所以该几何体的体积为52213422πππ⨯⨯+-=+.故选A . 4. 【答案】A. 【解析】5. 【答案】C【解析】①若m⊥n,m⊥α,则n 可能在平面α内,故①错误 ②∵m⊥α,m∥n,∴n⊥α,又∵n⊥β,∴α∥β,故②正确 ③过直线m 作平面γ交平面β与直线c , ∵m、n 是两条异面直线,∴设n∩c=O, ∵m∥β,m ⊂γ,γ∩β=c∴m∥c, ∵m ⊂α,c ⊄α,∴c∥α,∵n ⊂β,c ⊂β,n∩c=O,c∥α,n∥α ∴α∥β;故③正确④由面面垂直的性质定理:∵α⊥β,α∩β=m ,n ⊂β,n⊥m,∴n⊥α.故④正确 故正确命题有三个,故选C6.【答案】C.【解析】由,得:,即,令,则当时,,即在是减函数,,,,在是减函数,所以由得,,即,故选7.【答案】C.【解析】设P(m,n ),=(﹣c﹣m,﹣n)•(c﹣m,﹣n)=m2﹣c2+n2,∴m2+n2=2c2,n2=2c2﹣m2①.把P(m,n )代入椭圆得b2m2+a2n2=a2b2②,把①代入②得m2=≥0,∴a2b2≤2a2c2,b2≤2c2,a2﹣c2≤2c2,∴≥.又m2≤a2,∴≤a2,∴≤0,a2﹣2c2≥0,∴≤.综上,≤≤,故选C.8.【答案】A.【解析】由f(1+x)=f(1﹣x)可得函数f(x)的图象关于x=1对称,方程在区间[﹣3,3]根的个数等价于f(x)与y=图象的交点的个数,而函数y=图象可看作y=的图象向下平移1个单位得到,作出它们的图象如图:可得两函数的图象有5个交点,故选A【解析】①若a-3=-3,则a=0,此时:}1,1,3{},3,1,0{--=-=B A ,}3,1{-=⋂∴B A ,与题意不符,舍 ②若2a-1=-3,则a=-1,此时:}2,4,3{},3,1,0{--=-=B A ,}3{-=⋂∴B A ,∴a=-1 ③若a2+1=-3,则a 不存在 综上可知:a=-1 10. 【答案】20.【解析】当箭头指向①时,计算S 和i 如下. i =1,S =0,S =1; i =2,S =0,S =2; i =3,S =0,S =3; i =4,S =0,S =4; i =5,S =0,S =5; i =6结束. ∴S=m =5.当箭头指向②时,计算S 和i 如下. i =1,S =0, S =1; i =2,S =3; i =3,S =6; i =4,S =10; i =5,S =15; i =6结束. ∴S=n =15. ∴m+n =20. 11. 【答案】44【解析】由83456786520S S a a a a a a -=++++==,解得64a =,又由611111611211()114422a a a S a ⨯+====【解析】展开式通项公式为T r+1==若为有理项时,则为整数,∴r=0、6、12,故展开式中有理项共有3项, 故答案为:3 13.【答案】4.【解析】设过坐标原点的一条直线方程为y kx =,因为与函数xx f 2)(=的图象交于P 、Q 两点,所以0k >,且联列解得,P Q ⎛ ⎝,所以4PQ ==≥14. 【答案】【解析】(1)a=1时,代入题中不等式明显不成立.(2)a ≠1,构造函数y 1=(a ﹣1)x ﹣1,y 2=x 2﹣ax ﹣1,它们都过定点P (0,﹣1). 考查函数y 1=(a ﹣1)x ﹣1:令y=0,得M (,0),∴a >1;考查函数y 2=x 2﹣ax ﹣1,显然过点M (,0),代入得:,解之得:a=,或a=0(舍去). 故答案为:15. 【解析】211()cos cos cos 4442222x x x x x f x +=++1sin 262x π⎛⎫=++⎪⎝⎭(I )π4=T(Ⅱ 根据正弦定理知:()2cos cos (2sin sin )cos sin cos a c B b C A C B B C -=⇒-=12sin cos sin()sin cos 23A B B C A B B π⇒=+=⇒=⇒=∵()f A =∴1sin 262263A A πππ⎛⎫++=+= ⎪⎝⎭或23π3A π⇒=或 π 而203A π<<,所以3A π=,因此∆ABC 为等边三角形.……………12分16. 【解析】(Ⅰ)由表中数据得K 2的观测值k =42×(16×12-8×6)224×18×20×22=25255≈4.582>3.841. ……2分 所以,据此统计有95%的把握认为参加“篮球小组”或“排球小组”与性别有关.……4分 (Ⅱ)①由题可知在“排球小组”的18位同学中,要选取3位同学. 方法一:令事件A 为“甲被抽到”;事件B 为“乙丙被抽到”,则P(A∩B)=33318C C ,P(A)=217318C C .所以P(B|A)=P(A∩B )P(A)=33217C C =217×16 =1136. ……7分 方法二:令事件C 为“在甲被抽到的条件下,乙丙也被抽到”, 则P(C)=22217C C =217×16=1136. ②由题知X 的可能值为0,1,2.依题意P(X =0)=316318C C =3551;P(X =1)=21162318C C C =517;P(X =2)=12162318C C C =151. 从而X 的分布列为……10分 于是E(X)=0×3551+1×517+2×151=1751=13. ……12分17. 【解析】证明:(Ⅰ)因为1111ABCD A BC D -为正四棱柱,所以1AA ⊥平面ABCD ,且ABCD 为正方形. ………1分 因为BD ⊂平面ABCD ,所以1,BD AA BD AC ⊥⊥. ………2分因为1AA AC A =,所以BD ⊥平面1A AC . ………3分因为1AC ⊂平面1A AC , 所以1BD AC ⊥. ………4分 (Ⅱ) 如图,以D 为原点建立空间直角坐标系-D xyz .则11(0,0,0),(2,0,0),(2,2,0),(0,2,0),(2,0,4),(2,2,4),D A B C A B11(0,2,4),(0,0,4)C D ………5分所以111(2,0,0),(0,2,4)D A DC ==-uuuu r uuu r . 设平面11A D C 的法向量111(,,)x y z =n .所以 1110,D A D C ⎧⋅=⎪⎨⋅=⎪⎩uuuu ruuu rn n .即1110,240x y z =⎧⎨-=⎩……6分 令11z =,则12y =. 所以(0,2,1)=n .由(Ⅰ)可知平面1AAC 的法向量为 (2,2,0)DB =u u u r. ……7分所以cos ,DB <>==uu u rn ……8分 因为二面角11--A AC D 为钝二面角,所以二面角11--A AC D的余弦值为. ………9分 (Ⅲ)设222(,,)P x y z 为线段1CC 上一点,且1(01)CP PC λλ=≤≤uu r uuu r. 因为2221222(,2,),(,2,4)CP x y z PC x y z =-=---uu r uuu r.所以222222(,2,)(,2,4)x y z x y z λ-=---. ………10分即22240,2,1x y z λλ===+. 所以4(0,2,)1P λλ+. ………11分 设平面PBD 的法向量333(,,)x y z =m .因为4(0,2,),(2,2,0)1DP DB λλ==+uu u r uu ur ,所以 0,0DP DB ⎧⋅=⎪⎨⋅=⎪⎩uu u r uu u rm m .即3333420,1220y z x y λλ⎧+=⎪+⎨⎪+=⎩. ………12分 令31y =,则3311,2x z λλ+=-=-. 所以1(1,1,)2λλ+=--m . ………13分 若平面11ACD ⊥平面PBD ,则0⋅=m n . 即1202λλ+-=,解得13λ=. 所以当113CP PC =时,平面11ACD ⊥平面PBD . ………14分 18.【解析】(Ⅰ)由条件2,a b =…………2分故所求椭圆方程为13422=+y x . …………4分 (Ⅱ)设过点2(1,0)F 的直线l 方程为:)1(-=x k y . …………5分由22(1),143y k x x y =-⎧⎪⎨+=⎪⎩可得:01248)34(2222=-+-+k x k x k …………6分因为点2(1,0)F 在椭圆内,所以直线l 和椭圆都相交,即0>∆恒成立. 设点1122(,),(,)E x y F x y ,则34124,34822212221+-=+=+k k x x k k x x . …………8分因为直线AE 的方程为:)2(211--=x x y y , 直线AF 的方程为:)2(222--=x x y y , ………9分 令3x =,可得)2,3(11-x y M ,)2,3(22-x yN , 所以点P 的坐标12121(3,())222y y x x +--. ………10分直线2PF 的斜率为12121()0222'31y y x x k +---=-12121()422yy x x =+-- 122112121212()42()4x y x y y y x x x x +-+=⋅-++ 1212121223()4142()4kx x k x x kx x x x -++=⋅-++ …………12分 2222222241282341434341284244343k k k k k k k k k k k -⋅-⋅+++=⋅--⋅+++ 34k =-所以k k '⋅为定值43-. …………13分19. 【解析】 (Ⅰ) 因为对任意n *∈N ,三个数(),(),()A n B n C n 是等差数列,所以()()()()B n A n C n B n -=-. ………1分 所以1122n n a a a a ++-=-, ………2分 即21214n n a a a a ++-=-=. ………3分 所以数列{}n a 是首项为1,公差为4的等差数列. ………4分 所以1(1)443n a n n =+-⨯=-. ………5分(Ⅱ)(1)充分性:若对于任意n *∈N ,三个数(),(),()A n B n C n 组成公比为q 的等比数列,则()(),()()B n qA n C n qB n ==. ………6分所以[]()()()(),C n B n q B n A n -=-得2211(),n n a a q a a ++-=-即2121n n a qa a qa ++-=-. ………7分因为当1n =时,由(1)(1),B qA =可得21a qa =, ………8分所以210n n a qa ++-=. 因为0n a >, 所以2211n n a a q a a ++==. 即数列{}n a 是首项为1a ,公比为q 的等比数列, ………9分 (2)必要性:若数列{}n a 是公比为q 的等比数列,则对任意n *∈N ,有1n n a a q +=. ………10分因为0n a >,所以(),(),()A n B n C n 均大于0.于是12)2311212(......(),()......n n n nq a a a a a a B n q A n a a a a a a +++++++===++++++ ………11分 231)342231231(......(),()......n n n n q a a a a a a C n q B n a a a a a a ++++++++++===++++++ ………12分即()()B n A n =()()C n B n =q ,所以三个数(),(),()A n B n C n 组成公比为q 的等比数列. ………13分综上所述,数列{}n a 是公比为q 的等比数列的充分必要条件是:对任意n ∈N ﹡,三个数(),(),()A n B n C n 组成公比为q 的等比数列. ………14分20. 【解析】(Ⅰ)当2a =时,2()2ln 2f x x x x =-+,2()22f x x x'=-+,切点坐标为(11),, 切线的斜率(1)2k f '==,则切线方程为12(1)y x -=-,即21y x =-. ····························· 2分(Ⅱ)2()2ln g x x x m =-+,则22(1)(1)()2x x g x x xx-+-'=-=,∵1[e]e x ∈,,故()0g x '=时,1x =.当11ex <<时,()0g x '>;当1e x <<时,()0g x '<.故()g x 在1x =处取得极大值(1)1g m =-. ·············································································· 4分 又211()2e e g m =--,2(e)2e g m =+-,2211(e)()4e 0e e g g -=-+<,则1(e)()eg g <,∴()g x 在1[e]e,上的最小值是(e)g . ······················································································· 6分()g x 在1[e]e ,上有两个零点的条件是2(1)10,11()20,eeg m g m =->⎧⎪⎨=--≤⎪⎩解得2112e m <≤+, ∴实数m 的取值范围是21(12]e+,. ··························································································· 8分(Ⅲ)∵()f x 的图象与x 轴交于两个不同的点12(0)(0)A x B x ,,,,∴方程22ln 0x x ax -+=的两个根为12x x ,,则211122222ln 0,2ln 0,x x ax x x ax ⎧-+=⎪⎨-+=⎪⎩两式相减得1212122(ln ln )()x x a x x x x -=+--.又2()2ln f x x x ax =-+,2()2f x x a x'=-+,则1212124()()2x x f x x a x x +'=-+++1212122(ln ln )4x x x x x x -=-+-. 下证1212122(ln ln )40x x x x x x --<+-(*),即证明2111222()ln 0x x x x x x -+<+,12x t x =, ∵120x x <<,∴01t <<,即证明2(1)()ln 01t u t t t -=+<+在01t <<上恒成立. ·················· 10分 ∵22222(1)2(1)114(1)()(1)(1)(1)t t t u t t t t t t t -+---'=+=-=+++,又01t <<,∴()0u t '>, ∴()u t 在(0,1)上是增函数,则()(1)0u t u <=,从而知2111222()ln 0x x x x x x -+<+, 故(*)式<0,即12()02x x f +'<成立………….12分。
