计量经济学多重共线性分析
计量经济学实验五 多重共线性的检验与修正 完成版
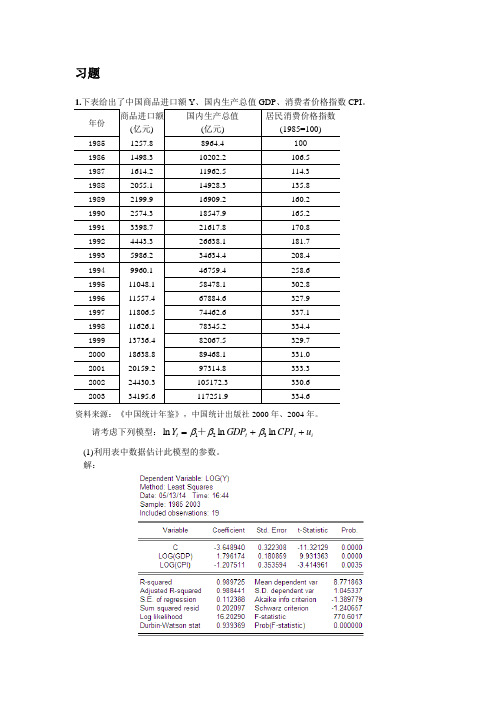
习题1.下表给出了中国商品进口额Y 、国内生产总值GDP 、消费者价格指数CPI 。
年份 商品进口额 (亿元)国内生产总值(亿元)居民消费价格指数(1985=100)1985 1257.8 8964.4 1001986 1498.3 10202.2 106.5 1987 1614.2 11962.5 114.3 1988 2055.1 14928.3 135.8 1989 2199.9 16909.2 160.2 1990 2574.3 18547.9 165.2 1991 3398.7 21617.8 170.8 1992 4443.3 26638.1 181.7 1993 5986.2 34634.4 208.4 1994 9960.1 46759.4 258.6 1995 11048.1 58478.1 302.8 1996 11557.4 67884.6 327.9 1997 11806.5 74462.6 337.1 1998 11626.1 78345.2 334.4 1999 13736.4 82067.5 329.7 2000 18638.8 89468.1 331.0 2001 20159.2 97314.8 333.3 2002 24430.3 105172.3 330.6 200334195.6117251.9334.6资料来源:《中国统计年鉴》,中国统计出版社2000年、2004年。
请考虑下列模型:i t t t u CPI GDP Y ++=ln ln ln 321βββ+ (1)利用表中数据估计此模型的参数。
解:ln 3.6489 1.796ln 1.2075ln t t t Y GDP CPI =--+t= (-11.32) (9.93) (-3.415)20.988770.6.0.1124R F S E ===(2)你认为数据中有多重共线性吗?多重共线性的检验 1)综合统计检验法若 在OLS 法下:R 2与F 值较大,但t 检验值较小,则可能存在多重共线性。
计量经济学:多重共线性

计量经济学:多重共线性多重共线性52=.53085123 第四章专门讨论古典假定中⽆多重共线性假定被违反的情况,主要内容包括多重共线性的实质和产⽣的原因、多重共线性产⽣的后果、多重共线性的检测⽅法及⽆多重共线性假定违反后的处置⽅法。
第⼀节什么是多重共线性⼀、多重共线性的含义第三章讨论多元线性回归模型的估计时,强调了假定⽆多重共线性,即假定各解释变量之间不存在线性关系,或者说各解释变量的观测值之间线性⽆关。
在计量经济学中所谓的多重共线性(Multi-Collinearity),不仅包括解释变量之间精确的线性关系,还包括解释变量之间近似的线性关系。
从数学意义上去说明多重共线性,就是对于解释变量k X 、、X X 32,如果存在不全为0的数k λλλ,2,1 ,能使得n ,2, ,1i 033221 ==++++ki k i i X X X λλλλ ( 4.1 )则称解释变量k X X X ,,,32 之间存在着完全的多重共线性。
⽤矩阵表⽰,解释变量的数据矩阵为X=213112232223111k k nnkn X X X X X X X X X ??(4.2)当Rank(X )在实际经济问题中,完全的多重共线性并不多见。
常见的情形是解释变量k X X X ,,,32 之间存在不完全的多重共线性。
所谓不完全的多重共线性,是指对于解释变量k X 、、X X 32,存在不全为0的数k λλλ,2,1 ,使得n ,2, ,1i 033221 ==+++++i ki k i i u X X X λλλλ(4.3)其中,i u 为随机变量。
这表明解释变量k X 、、X X 32只是⼀种近似的线性关系。
如果k 个解释变量之间不存在完全或不完全的线性关系,则称⽆多重共线性。
若⽤矩阵4表⽰,这时X 为满秩矩阵,即Rank(X )=k 。
需要强调,解释变量之间不存在线性关系,并⾮不存在⾮线性关系,当解释变量存在⾮线性关系时,并不违反⽆多重共线性假定。
计量经济学第四章多重共线性

R-squared
0.989654
Adjusted R-squared 0.986955 S.E. of regression 1437.448 Sum squared resid 47523916 Log likelihood -256.7013 Durbin-Watson stat 1.654140
4
(二)不完全的多重共线性
实际中,常见的情形是解释变量之间存在不 完全的多重共线性。
对于解释变量 X 2 , X 3, X k,存在不全为0的数
1
,
2
,
,使得
k
1 2X2 3X3 ...k Xk u 0
5
(三)解释变量的关系小节
可能表现为三种情形: r为相关系数 (1) rxixj 0 ,解释变量间毫无线性关系。这时多元
Var(ˆ2 )
9
二、不完全多重共线性产生的后果
1、参数估计值的方差增大
Var( βˆ 2 ) = σ 2
1 x22i (1-
r223 )
=
σ2
1
x22i (1 - r223 )
当 r23增大时,
^
Var( 2)
也增大
10
方差膨胀因子 (Variance Inflation Factor)
17 17
2、交叉相关系数(Cross correlation)
相关系数计算的是两组样本的同期相关程 度,交叉相关则可以表示不同期之间的相关 程度。
Eviews操作: Group窗口的view/cross correlation/输入 滞后期设定/ 输出结果阅读:看是否超出2倍标准差线
18
2倍 标准 差线
1、参数估计值有很大的偶然性。 2、参数显著性检验未通过。 3、经济意义检验未通过。 4、相关系数大。
计量经济学实验报告四---多重共线性

计量经济学实验报告四
[实验名称] 多重共线性
[实验目的] 用Eviews 软件检验模型的多重共线性.
[实验内容] (1)根据表列出的家庭消费支出Y与可支配收入X1和个人财富X2的统计数据,在Eviews软件下,OLS的估计结果为
所以模型为Yˆ=245.52+0.57X1-0.0058X2
(3.53)(0.79)(-0.08)
R2=0.962 F=88.845 D.W.=2.708
由拟合优度知,收入和财富一起解释了消费支出的96%.然而两者的t检验都在5%的显著性水平下是不显著的.不仅如此,财富变量的符号也与经济理论不相符合.但从F的检验值看,对收入与财富的参数同时为零的假设显然是拒绝的.因此,显著的F检验值与不显著t检验值,说明了收入与财富存在较高的相关性,使得无法分辨二者各自对消费的影响.只作消费支出关于收入的一元回归模型.如下
所以模型为Yˆ=244.55+0.509X1
(3.813)(14.24)
R2=0.962 F=202.87 D.W.=2.68
我们将上面模型与之相比,新引入的变量并没有带来拟合优度的显著变化,所以该引入的变量不是一个独立的解释变量.因此应该只作消费支出关于收入或财富的一元回归模型来对二元模型进行修正.。
计量经济学07计量多重共线性

Y/C1 △ Y
0.6072 0.6028 0.5996 0.5613 0.5339 0.5697
588 587 1088 1628 1441
0.5552 1651 0.5067 2920
0.5684 1762 0.5762 1854 0.5339 2960 0.5083 4584 0.4624 8637 0.4284 12610 0.4581 12294 0.5041 9093
横截面数据:生产函数中,资本投入与劳动力投入往 往出现高度相关情况,大企业二者都大,小企业都小。
(2)滞后变量的引入
在经济计量模型中,往往需要引入滞后经济变量来 反映真实的经济关系。例如消费变动的影响因素不仅有 本期可支配收入,还应考虑以往各期的可支配收入;固 定资产存量变动的影响因素不仅有本期投资,还应考虑 以往若干期的投资。同一变量的前后期之值很可能有较 强的线性相关性,模型中引入了滞后变量,多重共线性 就难以避免。
第七章 多重共线性
(Multicollinearity)
一、多重共线性的概念 二、实际经济问题中的多重共线性 三、多重共线性的后果 四、多重共线性的检验 五、克服多重共线性的方法 六、案例
一、多重共线性的概念
对于模型
Yi= 0+ 1X1i+ 2X2i+ + kXki+ i
i=1,2,…,n 其基本假设之一是解释变量是互相独立的。
求出X1与X2的简单相关系数r,若|r|接近1,则说明两变量 存在较强的多重共线性。
(2) 对多个解释变量的模型,采用综合统计检验法
若 在OLS法下:R2与F值较大,但t检验值较小,说明各 解释变量对Y的联合线性作用显著,但各解释变量间存在共 线性而使得它们对Y的独立作用不能分辨,故t检验不显著。
计量经济学(第四章多重共线性)

06
总结与展望
研究结论总结
多重共线性现象普遍存在于经济数据中,对计量 经济学模型的估计和解释产生了重要影响。
通过使用多种诊断方法,如相关系数矩阵、方差膨 胀因子(VIF)和条件指数(CI),可以有效地识别 多重共线性问题。
在存在多重共线性的情况下,普通最小二乘法 (OLS)估计量虽然仍然是无偏的,但其方差可能 变得很大,导致估计结果不稳定。
主成分分析法的优点
可以消除多重共线性的影响,同 时降低自变量的维度,简化模型。
岭回归法
岭回归法的基本思想
通过在损失函数中加入L2正则化项(即所有自变量的平方和),使得回归系数的估计更加稳定, 从而消除多重共线性的影响。
岭回归法的步骤
首先确定正则化参数λ的值,然后求解包含L2正则化项的损失函数最小化问题,得到岭回归系数的估 计值。
逐步回归法的优点
可以自动选择重要的自变量,同时消除多重共线性的影响。
主成分分析法
主成分分析法的基本思想
通过正交变换将原始自变量转换 为互不相关的主成分,然后选择 少数几个主成分进行回归分析。
主成分分析法的步骤
首先对原始自变量进行标准化处理, 然后计算相关系数矩阵并进行特征值 分解,得到主成分及其对应的特征向 量。最后,选择少数几个主成分作为 新的自变量进行回归分析。
岭回归法的优点
可以有效地处理多重共线性问题,同时避免过拟合现象的发生。此外,岭回归法还可以提供对所 有自变量的系数进行压缩估计的功能,使得模型更加简洁易懂。
05
实证研究与结果分
析
数据来源及预处理
数据来源
本研究采用的数据集来自于公开的统 计数据库,涵盖了多个经济指标和影 响因素的观测值。
数据预处理
计量经济学第三节 多重共线性

第三节多重共线性
假定六:解释变量之间不是完全线性相关的。
目的与要求:1.多重共线性的概念?
2.多重共线性产生的主要原因是什么?
3.多重共线性会导致什么后果?
4.多重共线性的检验方法 5.多重共线性的解决方法
一、多重共线性的概念
对于模型 Yi=0+1X1i+2X2i++kXki+i i=1,2,…,n 其基本假设之一是解释变量是互相独立的。 如果某两个或多个解释变量之间出现了完全 的线性相关性或接近线性相关,则称该模型出现 了多重共线性。
如投资函数 :
t
It 0 1X 可以变换成 It X
t / 0
2X
t 1
u
:
/ 1
t
X
t 1
t
/ 2
X
t
u
X
X
(2).进行变换,采用相对量作为解释变量
例如,某产品的销售量Y 取决于其出厂价格X1、
市场价格X2和市场总供应量X3。设定模型为
消选取相关性最强的
变量建立一元回归模型
在一元回归模型中引入第二个变量, 选择要求:模
型中每个解释变量影响显著,参数符号正确,校正的
~ 判定系数值 R 2 有所提高.
在选取的二元回归模型中以同样方式引入第三个变
量……
(四).增加样本观测值。
ln y 0 1 ln x 1 2 ln x 2 3 ln x 3 u
由于X1、X2、X3高度相关,我们可以用X1 /X2代替X1、 X2对y的影响。模型变为:
ln y
/ 0
/ 1
计量经济学第四章 多重共线性

x2i
3 2
x3i
x3i
参数的估计值为:
ˆ2
x32i x2i yi x2i x3i x3i yi
(
x22i )(
x32i ) (
x2i
x 3i
)2
x32i
2
x3i yi x32i 2 2
x32i x32i
x2i x3i x22i
x2i x3i
ˆ1 Y ˆ2 X 2 ˆ3 X 3
ˆ2
x32i x2i yi x2i x3i x3i yi ( x22i )( x32i ) ( x2i x3i )2
ˆ3
x22i x3i yi x2i x3i x2i yi •
(
x22i )(
x32i ) (
x2i
x 3i
)
2
x2i yi x3i yi
x2i x3i x32i
4.2多重共线性的后果
如果X1和X2完全线性相关,则存在非0的λ使得:
1 2 X 2i 3 X 3i 0
则有:
1 2 X 2 3 X 3 0
2 X 2i X 2 3 X3i X3 0
X 2i X3i X 2iYi
X
2 3i
X
3iYi
VAR
COV
(βˆ )
2
(XX)1
2
N X 2i
X 3i
X2i
X
2 2i
X 2i X 3i
计量经济第六章多重共线性

• 2、数据采集的范围有限,或采集 的样本量小于模型的自变量个数。
• 如在罕见疾病的研究过程中,由于病 情罕见、病因又相当复杂,而只能在 少数的患者身上采集大量的变量信息。
3、模型中采用滞后变量
在计量经济模型中,往往需要引入 滞后变量来反映真实的经济关系。 例如,消费=f(当期收入, 前期收入) 显然,两期收入间有较强的线性相 关性。
up
三、方差膨胀因子法
• 自变量间的共线性程度越大时,VIF值也随之 增大。所以也可利用方差膨胀因子来检验 多重共线性问题。 • 一般来说,当VIF >10时,表明 涉及的两个 变量存在高度线性相关,模型存在不完全 多重共线性。
P111 【经典实例】
• 计算得到的方差膨胀因子值分别为
VIF1 =10000,VIF2 =10000,VIF3 =9.6525,VIF4 =11.5875
2 2 2 1
同理易得
ˆ ) Var( 2
• EVIEWS遇到完全多重共线性时,会 显示 • Near singular matrix,无法进行估 计
2、不完全多重共线性下的后果
(1)估计量的方差增大 2 2 x 2 ˆ) 由于 Var ( 1 2 x12x2 (x1 x2 )2
• 可以看出,除了 VIF3 10 ,其余的方 差膨胀因子值均大于10,表明模型中 存在较严重的多重共线性问题。
up
第三节 多重共线性的修正 一、改变模型的形式 二、删除自变量 三、减少参数估计量的方差 四、其它方法 习题
up
• 一、改变模型的形式
• (一)变换模型的函数形式
• 例如将线性回归模型转化为对数模 型或者多项式模型。 • (二)改变模型的自变量的形式
计量经济学之多重共线性

计量经济学之多重共线性引言多重共线性是计量经济学中一个重要的概念,在经济学研究中扮演着重要的角色。
在本文中,我们将深入探讨多重共线性的概念、原因和影响,并介绍一些常见的解决方案和应对方法。
什么是多重共线性?多重共线性是指在回归分析中,自变量之间存在高度相关性的情况。
具体来说,多重共线性指的是自变量之间线性相关性较高,可能导致回归分析的结果不准确或难以解释。
多重共线性的原因多重共线性的产生有多种原因,以下是一些常见的原因:1.样本选择偏倚:当样本中存在特定的特征或者数据的选择方式导致一些变量的相关性增强。
2.变量的定义重复:有些变量可能在定义上重复,导致它们之间存在高度相关性。
3.缺少重要变量:当回归模型中存在遗漏的重要变量时,其他变量可能会代替这些遗漏的变量,导致多重共线性。
4.数据测量误差:测量误差也可能导致自变量之间存在高度相关性。
多重共线性的影响多重共线性可能会对回归模型产生一系列的问题和影响:1.估计系数不准确:多重共线性会导致回归系数的估计不准确,使得对自变量的解释变得困难。
2.系数符号相反:多重共线性可能导致估计系数的符号与理论预期相反。
3.误差项的方差增加:多重共线性会导致误差项的方差增加,从而降低了模型的精确度。
4.解释力度减弱:多重共线性会降低模型的解释力度,使得我们难以解释模型的结果。
解决多重共线性的方法针对多重共线性问题,我们可以采取以下方法来解决:1.增大样本量:增大样本量可以降低变量之间的相关性,从而减轻多重共线性的影响。
2.删除相关变量:通过检验变量之间的相关性,删除相关性较高的变量,可以减轻多重共线性的程度。
3.主成分分析:主成分分析是一种降维的方法,可以将相关性较高的变量合并为一个主成分,从而避免了多重共线性的问题。
4.增加惩罚项:在回归模型中增加惩罚项,如岭回归或lasso回归,可以减轻多重共线性的影响。
5.使用时间序列数据:对于存在多重共线性的房地产数据等时间序列数据,可以使用时间序列模型来避免多重共线性的问题。
计量经济学:多重共线性
影响比较大的,略去影响较小的。
元线性回归模型并进行OLS估计,拟合优度最大且接近1时,说明
这个变量与其他所有解释变量间存在共线性。
第三节 多重共线性的检验
辅助回归法中的方差膨胀因子:
对 于 多 元 线 性 回 归 模: 型Yi 0 1 X 1i ... k X ki ui 为 判 断 诸 自 变 量 间 是存 否在 多 重 共 线 性 , 进如 行下 辅 助 回 归 : X ji 0 1 X 1i ... j 1,i X j 1,i j 1,i X j 1,i ... k X ki v i , j 1,2,...,k 若 上 述 辅 助 回 归 的 可系 决数 为 R2 X j的 方 差 膨 胀 因 子 为 : j, 则 定 义 自 变 量 1 VIF j 1 R2 j
第一节 多重共线性的概念
若有c0+c1X1i+c2X2i+…+ckXki=0 i=1,2,…,n。其中: ci不全为0,则称
解释变量间存在完全多重共线性
若存在:c0+c1X1i+c2X2i+…+ckXki≈0 i=1,2,…,n。 其中:ci不全为0,
则称为解释变量间存在近似多重共线性。
完全共线性的情况并不多见,一般出现的是在一定程度上的共线性,
第二节 多重共线性的来源与后果
4、参数估计值不稳定,经济含义不合理
样本观测值稍有变动、增加或减少解释变量等都会使参数估计值发生较大变 化,甚至出现符号错误,从而不能正确反映解释变量对被解释变量的影响。
5、模型的预测功能失效
较大的方差容易使预测区间变大,从而使预测失去意义
注意:只要模型满足经典假设,则在近似多重共线性情况下,OLS估计量仍 然满足无偏性、线性性和有效性。但此时,无偏性并不意味着对某一给定样 本,其参数估计值就等于真实值。有效性也不意味着参数估计量的方差一定 很小。
计量经济学 第3章 多重共线性

剔除P值大的自变量
和前面的回归结果比较,收入弹性增 大了,但是价格弹性的绝对值却下降 了。不过需要注意的是,简化了的模 型的系数估计是有偏的
程序(gretl)
• • • • • • • • • • • open E:\data\data31.xls setobs 1 1962 --time-series ly=log(y) lx1=log(x1) lx2=log(x2) lx3=log(x3) lx4=log(x4) model1 <- ols ly 0 lx1 lx2 lx3 lx4 corr lx1 lx2 lx3 lx4 vif model2 <- ols ly 0 lx1 lx2
程序(EViews)
• • • • • • • • • • • • wfopen E:\data\data31.xls @freq A 1962 genr ly=log(y) genr lx1=log(x1) genr lx2=log(x2) genr lx3=log(x3) genr lx4=log(x4) equation eq1.ls ly c lx1 lx2 lx3 lx4 freeze eq1.results cor lx1 lx2 lx3 lx4 eq1.varinf equation eq2.ls ly c lx1 lx2 freeze eq2.results
第3章 多重共线性
学习目标 案例简介 案例分析 问题探讨与思考 练习
学习目标
• 理解多重共线性定义及存在多重共线性所带来的影响 • 掌握如何辨别模型中是否存在多重共线性现象 • 能够对多重共线性加以处理
案例简介
通过对人均鸡肉消费量和人均实际可支配收入、鸡肉的实际零售价格、猪肉的实际零售价格 及牛肉的实际零售价格之间的关系进行分析,以验证鸡肉的需求价格弹性及相关的交叉弹性 等。
计量经济学 第七章 多重共线性

第七章 多重共线性“多重共线性”一词由R. Frisch 1934年提出,它原指模型的解释变量间存在线性关系。
7.1多重共线性及产生的原因 7.1.1.非多重共线性假定111211212221121111k k T T Tk x x xx xx X x x x ---=如果rk (X 'X ) = rk (X ) < k 或`0X X =称解释变量是完全共线性相关。
在实际经济问题中,完全多重共线性和完全无多重共线性两种极端情况都是极少的,大多数情况是解释变量存在不完全的多重共线性,或者近似的多重共线性,可一表示为:1122110k k x x x u λλλ--++++= 7.1.2.多重共线性的经济解释(1)经济变量在时间上有共同变化的趋势。
如在经济上升时期,收入、消费、就业率等都增长,当经济收缩期,收入、消费、就业率等又都下降。
当这些变量同时进入模型后就会带来多重共线性问题。
0.E+001.E+112.E+113.E+114.E+11808284868890929496980002GDPCONS0.E +001.E +112.E +113.E +114.E +110.0E +005.0E +101.0E +111.5E +112.0E +112.5E +11C O N SG D P o f H o n g K o n g(2)解释变量与其滞后变量同作解释变量。
滞后变量与原因变量在经济意义上没有本质区别,只是时间上的差异,原因变量与解释变量有相关关系,滞后变量也会有相关关系。
(见下图) (3)解释变量之间往往存在密切的关联度。
对同一经济现象的解释变量,往往存在密切的相关关系,如生产函数,资本大,需投入的劳动力也应趆多。
0.E+001.E+112.E+113.E+114.E+11GDP0.E+001.E+112.E+113.E+114.E+110.E+001.E+112.E+113.E+114.E+11GDP(-1)GDP7.2.多重共线性的后果(1) 当 `0X X =,X 为降秩矩阵,则 (X 'X ) -1不存在,βˆ= (X 'X )-1 X 'Y 不可计算。
计量经济学多重共线性的分析

检验多重共线性
➢ 检验简单相关系数
进一步选择Covariance Analysis的Correlation,得到变 量之间的偏相关系数矩阵,观察偏相关系数。
可以发现,Y与X1、X2、X3的相关系数都在0.9以上 ,但输出结果中,解释变量X1、X3的回归系数却无 法通过显著性检验。认为解释变量之间存在多重共 线性。
➢ 收集整理实验数据 ➢ 建立线性回归模型 ➢ 检验多重共线性 ➢ 用逐步回归法克服多重共线性
收集整理实验数据
1978年至2011年我国税收收入与国民生产总值情况
(来源于中国统计年鉴)
建立线性回归模型
➢ 用普通最小二乘法估计模型
利用实验数据分别建立Y关于X1、X2、X3的散点图 (SCAT Xi Y)
建立线性回归模型
➢ 用普通最小二乘法估计模型
利用实验数据分别建立Y关于X1、X2、X3的散点图 (SCAT Xi Y)
根据散点图可以看出Y与 X1、X2、X3都呈现正 的线性相关,
建立线性回归模型
➢ 建立一个多元线性回归模型
输出结果,只有X2的系数通过显著性检验, 其他没有通过,而F值很大,通过了显著性 检验,判断模型存在多重共线性。
用逐步回归法克服多重共线性
➢ 找出最简单的回归形式
Y=24023.76+4.1804X1 (5.887) (36.5072) R2=0.977979
D.W.=0.1937
Y=-1592.676+2.6322X2 (-1.1194) (116.4316) R2=0.997792 D.W.=0.6285
用逐步回归法克服多重共线性
➢ 逐步回归
第一步,引入变量X1
用逐步回归法克服多重共线性
《计量经济学》第四章 多重共线性

σ2
R j 2 = X j 对其余 k − 2 个解释变量进行回归的 R 2 σ2 ˆ 还可写成 var( β j ) = VIF j 2
∑x
j
VIF的倒数被称为容许度(TOL j) 的倒数被称为容许度( 的倒数被称为容许度
TOL j = 1 = 1− Rj2 VIFj
采用普通最小二乘法得到以下估计结果
3
财政收入模型的EViews估计结果 财政收入模型的EViews估计结果 EViews
Variable 农业增加值NZ 农业增加值 工业增加值GZ 工业增加值 建筑业增加值JZZ 建筑业增加值 总人口TPOP 总人口 最终消费CUM 最终消费 受灾面积SZM 受灾面积 截距项 R-squared Adjusted R-squared S.E. of regression Sum squared resid Log likelihood Durbin-Watson stat Coefficient -1.535090 0.898788 -1.527089 0.151160 0.101514 -0.036836 -11793.34 0.995015 0.993441 481.5380 4405699. -193.4165 1.873809 Std. Error 0.129778 0.245466 1.206242 0.033759 0.105329 0.018460 3191.096 Mean dependent var S.D. dependent var Akaike info criterion Schwarz criterion F-statistic Prob(F-statistic) t-Statistic -11.82861 3.661558 -1.265989 4.477646 0.963783 -1.995382 -3.695704 Prob. 0.0000 0.0017 0.2208 0.0003 0.3473 0.0605 0.0015 5897.824 5945.854 15.41665 15.75537 632.0999 0.000000 4
计量经济学实验报告 多重共线性检验

计量经济学上机实验报告多重共线性检验实验背景近年来,中国旅游业一直保持高速发展,旅游业作为国民经济新的增长点,在整个社会经济发展中的作用日益显现。
中国的旅游业分为国内旅游和入境旅游两大市场,入境旅游外汇收入年均增长22.6%,与此同时国内旅游也迅速增长。
改革开放20多年来,特别是进入90年代后,中国的国内旅游收入年均增长14.4%,远高于同期GDP 9.76%的增长率。
为了规划中国未来旅游产业的发展,需要定量地分析影响中国旅游市场发展的主要因素。
模型•其中,•Yt——第t年全国旅游收入•X2——国内旅游人数(万人)•X3——城镇居民人均旅游支出(元)•X4——农村居民人均旅游支出(元)•X5——公路里程(万公里)•X6——铁路里程(万公里)Y = 0.0639689468*X2 + 0.2098186372*X3 + 5.283346538*X4 - 3.352906602*X5 - 53.38584085*X6 - 2220.150544数据来源中国统计局网站样本区间1994——2009实验过程及结果(一)实证结果Dependent Variable: YMethod: Least SquaresDate: 04/06/11 Time: 15:49Sample: 1994 2009Included observations: 16Variable Coefficient Std. Error t-Statistic Prob.X2 0.063969 0.007714 8.292875 0.0000X3 0.209819 1.319292 0.159039 0.8768X4 5.283347 1.918838 2.753409 0.0204X5 -3.352907 2.376484 -1.410869 0.1886X6 -53.38584 434.6829 -0.122816 0.9047C -2220.151 2210.044 -1.004573 0.3388R-squared 0.994274 Mean dependent var 4270.119Adjusted R-squared 0.991411 S.D. dependent var 2720.860S.E. of regression 252.1678 Akaike info criterion 14.17806Sum squared resid 635886.0 Schwarz criterion 14.46778Log likelihood -107.4245 F-statistic 347.2644Durbin-Watson stat 1.224560 Prob(F-statistic) 0.000000R2很高,F显著,但x3、x5、x6不显著,X5、X6的符号甚至是负的。
计量经济学试题计量经济学中的多重共线性问题与解决方法

计量经济学试题计量经济学中的多重共线性问题与解决方法计量经济学试题-多重共线性问题与解决方法在计量经济学中,多重共线性是一个重要的问题。
它指的是当两个或多个自变量之间存在高度相关性时,会导致模型估计的结果不准确或者不可靠。
多重共线性问题在经济学研究中经常出现,因此探索解决方法是非常必要的。
一、多重共线性问题的原因多重共线性问题通常由于样本中的自变量之间存在强烈的线性相关性而引发。
例如,当一个自变量可以通过其他自变量的线性组合来表示时,就会出现多重共线性问题。
这种情况下,模型估计的结果会变得不稳定,标准误差会变得很大,使得对自变量的解释变得困难。
二、多重共线性问题的影响多重共线性问题对计量经济模型的影响是多方面的。
首先,它会导致模型估计结果的不稳定性。
当自变量之间存在高度相关性时,即使是微小的样本误差也会导致模型估计结果的显著变化。
其次,多重共线性问题会导致标准误差的上升,使得参数的显著性检验变得困难。
最后,多重共线性问题还会导致模型解释力的下降,使得对自变量对因变量的影响进行准确的解释变得困难。
三、解决多重共线性问题的方法1. 删除变量:当发现自变量之间存在高度相关性时,一种解决方法是删除其中一个变量。
如果某个自变量可以用其他变量线性表示,就可以考虑将其删除。
然而,删除变量的过程需要谨慎,以免造成结果的失真。
2. 采用主成分分析:主成分分析是一种常用的处理多重共线性问题的方法。
它通过对自变量进行线性组合,生成新的主成分变量,从而消除原始自变量之间的相关性。
通过采用主成分分析,可以得到一组无关的自变量,从而解决多重共线性问题。
3. 利用岭回归:岭回归是一种通过增加正则化项来减小模型参数估计标准误差的方法。
通过岭回归,可以有效地解决多重共线性问题。
岭回归对相关自变量的系数进行惩罚,从而减小系数估计的方差。
这种方法可以提高模型的准确性和稳定性。
4. 使用其他估计方法:在实际应用中,还可以采用其他估计方法来解决多重共线性问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Y=23812.76+1.5479X3 (5.2876) (33.047) R2=0.973264 D.W.=0.2997
可见,Y受X2的影响最大,选择(2)式作
为初始的回归模型。
可编辑ppt
12
上述初始回归模型,寻 找最佳回归方程。为求简明,先列出回归结果如 下表,过程截图放在说明部分。
Y=-3204.732+2.8134X2-0.1091X3 (-1.644) (18.427) (-1.997) R2=0.9979 D.W.=0.613
可编辑ppt
16
用逐步回归法克服多重共线性
➢逐步回归
第二步,引入变量X3
可编辑ppt
17
用逐步回归法克服多重共线性
➢逐步回归
第一步与第二步表明,X1与X3是多余的。故 最终的拟合模型为:
检验,判断模型存在可编多辑p重pt 共线性。
7
检验多重共线性
➢检验简单相关系数
进一步选择Covariance Analysis的Correlation,得到变 量之间的偏相关系数矩阵,观察偏相关系数。
可以发现,Y与X 1 、X 2 、X 3 的相关系数都在0.9以
上,但输出结果中,解释变量X1、X3的回归系数却
可编辑ppt
2
实验步骤
➢收集整理实验数据 ➢建立线性回归模型 ➢检验多重共线性 ➢用逐步回归法克服多重共线性
可编辑ppt
3
收集整理实验数据
1978年至2011年我国税收收入与国民生产总值情况
(来源于中国统计年鉴)
可编辑ppt
4
建立线性回归模型
➢ 用普通最小二乘法估计模型
利用实验数据分别建立Y关于X1、X2、X3的散点图( SCAT Xi Y)
可编辑ppt
14
用逐步回归法克服多重共线性
➢逐步回归
第一步,引入变量X1
可编辑ppt
15
用逐步回归法克服多重共线性
➢逐步回归
第一步:在初始模型中引入 X 3 ,模型拟合优度提高, 但是参数符号不合理,且变量没有通过了t检验,故去 掉C、X3
Y=24023.76+4.1804X2 (-1.1194) (116.4316) R2=0.9978 D.W.=0.6285
10
用逐步回归法克服多重共线性
➢找出最简单的回归形式
分别作Y与X1、X2、X3间的回归(LS Y C Xi )
可编辑ppt
11
用逐步回归法克服多重共线性
➢找出最简单的回归形式
Y=24023.76+4.1804X1 (5.887) (36.5072) R2=0.977979
D.W.=0.1937
Y=-1592.676+2.6322X2 (-1.1194) (116.4316) R2=0.997792 D.W.=0.6285
无法通过显著性检验。认为解释变量之间存在多重
共线性。
可编辑ppt
8
用逐步回归法克服多重共线性
➢找出最简单的回归形式
分别作Y与X1、X2、X3间的回归(LS Y C Xi )
可编辑ppt
9
用逐步回归法克服多重共线性
➢找出最简单的回归形式
分别作Y与X1、X2、X3间的回归(LS Y C Xi )
可编辑ppt
可编辑ppt
13
用逐步回归法克服多重共线性
➢逐步回归
第一步:在初始模型中引入 X 1 ,模型拟合优度提高, 但是参数符号不合理,且变量没有通过了t检验,故去 掉C、X1
Y=24023.76+4.1804X2 (-1.1194) (116.4316) R2=0.9978 D.W.=0.6285
Y=-3665.342-0.3671X1+2.8591X2 (-1.7503) (-1.334) (16.672) R2=0.9979 D.W.=0.644
可编辑ppt
5
建立线性回归模型
➢ 用普通最小二乘法估计模型
利用实验数据分别建立Y关于X1、X2、X3的散点图( SCAT Xi Y)
根据散点图可以看出Y 与X1、X2、X3都呈现 正的线性相关,
可编辑ppt
6
建立线性回归模型
➢建立一个多元线性回归模型
输出结果,只有X2的系数通过显著性检验,
其他没有通过,而F值很大,通过了显著性
计量经济学多重共线性分析
可编辑ppt
1
计量经济学多重共线性分析
根据1980年至2011年我国国民生产总值与社 会固定资产投资、社会消费品零售总额和建筑 业总产值的关系,建立并检验影响国民生产总 值的函数模型,以掌握掌握多重共线性问题出 现的来源、后果、检验及修正的原理,以及相 关的Eviews操作方法。
Y=24023.76+4.1804X2
可编辑ppt
18
可编辑ppt
19
