成都市高二数学零诊复习资料
四川省成都市玉林中学高高二数学下期零诊试题 第23课时 统计复习资料

第23课时 统计 自主梳理抽样方法:1.简单随机抽样(1)定义:设一个总体含有N 个个体,从中____________抽取n 个个体作为样本(n≤N),如果每次抽取时总体内的各个个体被抽到的机会都________,就把这种抽样方法叫做简单随机抽样.(2)最常用的简单随机抽样的方法:__________和____________.2.系统抽样的步骤假设要从容量为N 的总体中抽取容量为n 的样本.(1)先将总体的N 个个体进行________;(2)确定____________,对编号进行________.当N n (n 是样本容量)是整数时,取k =N n; (3)在第1段用________________确定第一个个体编号l (l≤k);(4)按照一定的规则抽取样本.通常是将l 加上间隔k 得到第2个个体编号________,再加k 得到第3个个体编号________,依次进行下去,直到获取整个样本.3.分层抽样(1)定义:一般地,在抽样时,将总体分成互不交叉的层,然后按照一定的比例,从各层独立地抽取一定数量的个体,将各层取出的个体合在一起作为样本,这种抽样方法是一种分层抽样.(2)分层抽样的应用范围:当总体是由________________________________组成时,往往选用分层抽样.4.在频率分布直方图中,纵轴表示__________________,数据落在各小组内的频率用________________表示,所有长方形面积之和________.5.作频率分布直方图的步骤(1)求极差(即一组数据中________与________的差);(2)决定________与________;(3)将数据________;(4)列________________;(5)画________________.6.频率分布折线图和总体密度曲线(1)频率分布折线图:连接频率分布直方图中各小长方形上端的________,就得频率分布折线图.(2)总体密度曲线:随着__________的增加,作图时____________增加,组距减小,相应的频率折线图会越来越接近于一条光滑曲线,统计中称这条光滑曲线为总体密度曲线.7.当样本数据较少时,茎叶图表示数据的效果较好,一是统计图上没有原始数据丢失,二是方便记录与表示,但茎叶图一般只便于表示两位有效数字的数据.8.众数、中位数、平均数(1)在一组数据中,出现次数________的数据叫做这组数据的众数.(2)将一组数据按大小依次排列,把处在________位置的一个数据(或中间两个数据的平均数)叫做这组数据的中位数.(3)如果有n 个数x 1,x 2,……,x n ,那么x =____________叫做这n 个数的平均数.9.标准差和方差(1)标准差是样本数据到平均数的一种____________.(2)标准差:s = ________________________.(3)方差:s 2=________________________________(x n 是样本数据,n 是样本容量,x 是样本平均数).1.(1)逐个不放回地 相等 (2)抽签法 随机数法2.(1)编号 (2)分段间隔k 分段 (3)简单随机抽样 (4)(l +k) (l +2k)3.(2)差异明显的几个部分4.频率与组距的比值 小长方形的面积 等于15.(1)最大值 最小值 (2)组距 组数 (3)分组 (4)频率分布表 (5)频率分布直方图6.(1)中点 (2)样本容量 所分的组数8.(1)最多 (2)中间 (3)x 1+x 2+…+x n n9.(1)平均距离 (2)1n1-x 2+2-x 2+…+n -x 2] (3)1n[(x 1-x )2+(x 2-x )2+…+(x n -x )2] 探究点一 抽样方法例1 某高级中学有学生270人,其中一年级108人,二、三年级各81人,现要抽取10人参加某项调查,考虑选用简单随机抽样、分层抽样和系统抽样三种方案,使用简单随机抽样和分层抽样时,将学生按一、二、三年级依次统一编号为1,2,…,270;使用系统抽样时,将学生统一随机编号为1,2,…,270,并将整个编号依次分为10段.如果抽得号码有下列四种情况:①7,34,61,88,115,142,169,196,223,250;②5,9,100,107,111,121,180,195,200,265;③11,38,65,92,119,146,173,200,227,254;④30,57,84,111,138,165,192,219,246,270.关于上述样本的下列结论中,正确的是( )A .②、③都不能为系统抽样B .②、④都不能为分层抽样C .①、④都可能为系统抽样D .①、③都可能为分层抽样解:D [③中每部分选取的号码间隔一样(都是27),可能为系统抽样方法,排除A ;②可能为分层抽样,排除B ;④不是系统抽样,排除C ,故选D .]变式迁移1 将参加夏令营的600名学生编号为:001,002,…,600.采用系统抽样方法抽取一个容量为50的样本,且随机抽得的号码为003.这600名学生分住在三个营区,从001到300在第Ⅰ营区,从301到495在第Ⅱ营区,从496到600在第Ⅲ营区,三个营区被抽中的人数依次为( ) A .26,16,8 B .25,17,8 C .25,16,9 D .24,17,9解:B [由题意,系统抽样间隔k =60050=12,故抽到的个体编号为12k +3 (其中k =0,1,2,3,…,49).令12k +3≤300,解得k≤24.∴k=0,1,2,…,24,共25个编号.所以从Ⅰ营区抽取25人;令300<12k +3≤495,解得25≤k≤41.∴k=25,26,27,…,41,共17个编号.所以从Ⅱ营区抽取17人;因此从第Ⅲ营区抽取50-25-17=8(人).]探究点二 频率分布直方图例2 (2011·福州调研)如图是某市有关部门根据该市干部的月收入情况,作抽样调查后画出的样本频率分布直方图,已知图中第一组的频数为4 000,请根据该图提供的信息解答下列问题:(图中每组包括左端点,不包括右端点,如第一组表示收入在[1 000,1 500))(1)求样本中月收入在[2 500,3 500)的人数;(2)为了分析干部的收入与年龄、职业等方面的关系,必须从样本的各组中按月收入再用分层抽样方法抽出100人作进一步分析,则月收入在[1 500,2 000)的这段应抽多少人?(3)试估计样本数据的中位数.解 (1)∵月收入在[1 000,1 500)的概率为0.000 8×500=0.4,且有4 000人,∴样本的容量n =4 0000.4=10 000; 月收入在[1 500,2 000)的频率为0.000 4×500=0.2;月收入在[2 000,2 500)的频率为0.000 3×500=0.15;月收入在[3 500,4 000)的频率为0.000 1×500=0.05.∴月收入在[2 500,3 500)的频率为1-(0.4+0.2+0.15+0.05)=0.2.∴样本中月收入在[2 500,3 500)的人数为0.2×10 000=2 000.(2)∵月收入在[1 500,2 000)的人数为0.2×10 000=2 000,∴再从10 000人中用分层抽样方法抽出100人,则月收入在[1 500,2 000)的这段应抽取100×2 00010 000=20(人). (3)由(1)知月收入在[1 000,2 000)的频率为0.4+0.2=0.6>0.5,∴样本数据的中位数为1 500+0.5-0.40.000 4=1 500+250=1 750(元). 变式迁移2 为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图如图,由于不慎将部分数据丢失,但知道前4组频数成等比数列,后6组的频数成等差数列,设最大频率为a ,视力在4.6到5.0之间的学生数为b ,则a ,b 值分别为( )A .0.27,78B .0.27,83C .2.7,78D .2.7,83解:A [由频率分布直方图知组距为0.1.4.3~4.4间的频数为100×0.1×0.1=1.4.4~4.5间的频数为100×0.1×0.3=3.又前4组的频数成等比数列,∴公比为3.从而4.6~4.7间的频数最大,且为1×33=27.∴a=0.27.根据后6组频数成等差数列,且共有100-13=87(人).设公差为d ,则6×27+6×52d =87. ∴d=-5,从而b =4×27+4×32×(-5)=78.]探究点三 用样本数字特征估计总体数字特征例3 甲、乙、丙三名射箭运动员在某次测试中各射箭20次,三人的测试成绩如表所示:s 1、s 2、s 3( )A .s 3>s 1>s 2B .s 2>s 1>s 3C .s 1>s 2>s 3D .s 2>s 3>s 1解:B [由已知可得甲、乙、丙的平均成绩均为8.5.方法一 ∵s 21=1n[(x 1-x )2+(x 2-x )2+…+(x n -x )2], ∴s 1=120-2+-2+-2+-2] =2520. 同理s 2=2920,s 3=2120,∴s 2>s 1>s 3. 方法二 ∵s 21=1n(x 21+x 22+…+x 2n )-x 2, ∴s 21=120(5×72+5×82+5×92+5×102)-8.52=73.5-72.25=1.25=54, ∴s 1=2520.同理s 2=2920,s 3=2120, ∴s 2>s 1>s 3.]变式迁移3 甲、乙两名射击运动员参加某大型运动会的预选赛,他们分别射击了5次,成绩如下表(单位:环):如果甲、乙两人中只有1.解:甲解析 x 甲=x 乙=9,s 2甲=15[(9-10)2+(9-8)2+(9-9)2+(9-9)2+(9-9)2]=25, s 2乙=15[(9-10)2+(9-10)2+(9-7)2+(9-9)2+(9-9)2]=65>s 2甲,故甲更稳定,故选甲.探究点四 用茎叶图分析数据例4 随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm ),获得身高数据的茎叶图如图.(1)根据茎叶图判断哪个班的平均身高较高;(2)计算甲班的样本方差;(3)现从乙班这10名同学中随机抽取两名身高不低于173 cm 的同学,求身高为176 cm 的同学被抽中的概率.解 (1)由茎叶图可知:甲班身高集中于160~179之间,而乙班身高集中于170~180之间.因此乙班平均身高高于甲班.(2)x =158+162+163+168+168+170+171+179+179+18210=170,甲班的样本方差为110[(158-170)2+(162-170)2+(163-170)2+(168-170)2+(168-170)2+(170-170)2+(171-170)2+(179-170)2+(179-170)2+(182-170)2]=57.2.(3)设身高为176 cm 的同学被抽中的事件为A ,从乙班10名同学中抽中两名身高不低于173 cm 的同学有:(181,173),(181,176),(181,178),(181,179),(179,173),(179,176),(179,178),(178,173),(178,176),(176,173)共10个基本事件,而事件A 含有4个基本事件,∴P(A)=410=25.变式迁移3 (2011·汉沽模拟)某班甲、乙两学生的高考备考成绩如下:甲:512 554 528 549 536 556 534 541 522 538乙:515 558 521 543 532 559 536 548 527 531(1)用茎叶图表示两学生的成绩;(2)分别求两学生成绩的中位数和平均分.解 (1)两学生成绩的茎叶图如图所示.(2)将甲、乙两学生的成绩从小到大排列为:甲:512 522 528 534 536 538 541 549 554 556乙:515 521 527 531 532 536 543 548 558 559从以上排列可知甲学生成绩的中位数为536+5382=537. 乙学生成绩的中位数为532+5362=534. 甲学生成绩的平均分为500+12+22+28+34+36+38+41+49+54+5610=537, 乙学生成绩的平均分为500+15+21+27+31+32+36+43+48+58+5910=537.课后练习:1.某校高三年级有男生500人,女生400人,为了解该年级学生的健康情况,从男生中任意抽取25人,从女生中任意抽取20人进行调查,这种抽样方法是( )A.简单随机抽样法B.抽签法C.随机数法D.分层抽样法D[由分层抽样的定义可知,该抽样为按比例的抽样.]2.某中学开学后从高一年级的学生中随机抽取90名学生进行家庭情况调查,经过一段时间后再次从这个年级随机抽取100名学生进行学情调查,发现有20名同学上次被抽到过,估计这个学校高一年级的学生人数为( )A.180 B.400 C.450 D.2 000C[设这个学校高一年级人数为x,则90x=20100,∴x=450.]3.一个单位有职工800人,其中具有高级职称的为160人,具有中级职称的为320人,具有初级职称的为200人,其余人员120人.为了解职工收入情况,决定采用分层抽样的方法,从中抽取容量为40的样本.则从上述各层中依次抽取的人数分别是( )A.12,24,15,9 B.9,12,12,7 C.8,15,12,5 D.8,16,10,6 D[由题意,各种职称的人数比为160∶320∶200∶120=4∶8∶5∶3,所以抽取的具有高、中、初级职称的人数和其他人员的人数分别为40×420=8,40×820=16,40×520=10,40×320=6.]4.如图,样本A和B分别取自两个不同的总体,它们的样本平均数分别为x A和x B,样本标准差分别为s A和s B,则( )A.x A>x B,s A>s BB.x A<x B,s A>s BC.x A>x B,s A<s BD.x A<x B,s A<s BB[A中的数据都不大于B中的数据,所以x A<x B,但A中的数据比B中的数据波动幅度大,所以s A>s B.]5. 10名工人某天生产同一种零件,生产的件数分别是15,17,14,10,15,17,17,16,14,12,设其平均数为a,中位数为b,众数为c,则有( )A.a>b>c B.b>c>a C.c>a>b D.c>b>aD[平均数a=110(15+17+14+10+15+17+17+16+14+12)=14.7.中位数b=15,众数c=17.∴c>b>a.]3.为了了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图如图,由于不慎将部分数据丢失,但知道后五组频数和为62,设视力在4.6到4.8之间的学生数为a,最大频率为0.32,则a的值为( )A .64B .54C .48D .27B [前两组中的频数为100×(0.05+0.11)=16. ∵后五组频数和为62,∴前三组为38.∴第三组为22.又最大频率为0.32的最大频数为0.32×100=32,∴a=22+32=54.]4.下图是某学校举行的运动会上,七位评委为某体操项目打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )A .84,4.84B .84,1.6C .85,1.6D .85,4C [去掉最高分93,最低分79,平均数为15(84+84+86+84+87)=85, 方差s 2=15[(84-85)2+(84-85)2+(86-85)2+(84-85)2+(87-85)2]=85=1.6.] 5.有一个容量为66的样本,数据的分组及各组的频数如下:[11.5,15.5) 2 [15.5,19.5) 4 [19.5,23.5) 9[23.5,27.5) 18 [27.5,31.5) 11 [31.5,35.5) 12[35.5,39.5) 7 [39.5,43.5) 3根据样本的频率分布估计,数据落在[31.5,43.5)的概率约是( )A .16B .13C .12D .23B [由条件可知,落在[31.5,43.5)的数据有12+7+3=22(个),故所求概率约为2266=13.]9.一个总体有100个个体,随机编号为0,1,2,…,99,依编号顺序平均分成10组,组号依次为1,2,3,…,10,现用系统抽样方法抽取一个容量为10的样本,规定如果在第1组中随机抽取的号码为m ,那么在第k 组中抽取的号码个位数字与m +k 的个位数字相同,若m =6,则在第7组中抽取的号码是________.解析 由题意知,第7组中抽取的号码的个位数与6+7的个位数相同,即为3;又第7组中号码的十位上的数为6,所以在第7组中抽取的号码是63.10.一个总体分为A ,B 两层,用分层抽样方法从总体中抽取一个容量为10的样本.已知B层中每个个体被抽到的概率都为112,则总体中的个体数为________ 解析 分层抽样中,每个个体被抽到的概率都相等,则10x =112⇒x =120. 11.甲、乙两人在10天中每天加工零件的个数用茎叶图表示如下图,中间一列的数字表示零件个数的十位数,两边的数字表示零件个数的个位数,则这10天甲、乙两人日加工零件的平均数分别为______和_________________________.24 23解析 x 甲=110(10×2+20×5+30×3+17+6+7)=24, x 乙=110(10×3+20×4+30×3+17+11+2)=23. 12.将容量为n 的样本中的数据分成6组,绘制频率分布直方图,若第一组至第六组数据的频率之比为2∶3∶4∶6∶4∶1,且前三组数据的频数之和等于27,则n 等于________.60解析 ∵第一组至第六组数据的频率之比为2∶3∶4∶6∶4∶1,∴前三组频数为2+3+420·n=27,故n =60. 13.如图所示是某公司(员工总人数300人)2012年员工年薪情况的频率分布直方图,由此可知,员工中年薪在2.4万元~2.6万元之间的共有________人.答案 72解析 由所给图形,可知员工中年薪在2.4万元~2.6万元之间的频率为1-(0.02+0.08+0.08+0.10+0.10)×2=0.24,所以员工中年薪在2.4万元~2.6万元之间的共有300×0.24=72(人).14.某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关的数据如表所示:(1)(2)用分层抽样方法在收看新闻节目的观众中随机抽取5名,大于40岁的观众应该抽取几名?(3)在上述抽取的5名观众中任取2名,求恰有1名观众的年龄为20至40岁的概率.解 (1)因为在20至40岁的58名观众中有18名观众收看新闻节目,而大于40岁的42名观众中有27名观众收看新闻节目,所以,经直观分析,收看新闻节目的观众与年龄是有关的.(4分)(2)从题中所给条件可以看出收看新闻节目的共45人,随机抽取5人,则抽样比为545=19,故大于40岁的观众应抽取27×19=3(人).(8分) (3)抽取的5名观众中大于40岁的有3人,在20至40岁的有2人,记大于40岁的人为a 1,a 2,a 3,20至40岁的人为b 1,b 2,则从5人中抽取2人的基本事件有(a 1,a 2),(a 1,a 3),(a 2,a 3),(b 1,b 2),(a 1,b 1),(a 1,b 2),(a 2,b 1),(a 2,b 2),(a 3,b 1),(a 3,b 2)共10个,其中恰有1人为20至40岁的有6个,故所求概率为610=35.(14分) 15.为了了解一个小水库中养殖的鱼的有关情况,从这个水库中多个不同位置捕捞出100条鱼,称得每条鱼的质量(单位:kg ),并将所得数据分组,画出频率分布直方图(如图所示).(1)在下面表格中填写相应的频率;(2)估计数据落在[1.15,1.30中的概率为多少;(3)将上面捕捞的100条鱼分别作一记号后再放回水库.几天后再从水库的多处不同位置捕捞出120条鱼,其中带有记号的鱼有6条.请根据这一情况来估计该水库中鱼的总条数.解 (1)组距),故可得下表:(6分) (2)因为0.30+0.15+0.02=0.47,所以数据落在[1.15,1.30)中的概率约为0.47.(9分) (3)因为120×1006=2 000, 所以水库中鱼的总条数约为2 000.(12分)16.某市2010年4月1日-4月30日对空气污染指数的监测数据如下(主要污染物为可吸入颗粒物):61,76,70,56,81,91,92,91,75,81,88,67,101,103,95,91,77,86,81,83,82,82,64,79,86,85,75,71,49,45.(1)完成频率分布表.(2)作出频率分布直方图.(3)根据国家标准,污染指数在0~50之间时,空气质量为优;在51~100之间时,为良;在101~150之间时,为轻微污染;在151~200之间时,为轻度污染.请你依据所给数据和上述标准,对该市的空气质量给出一个简短评价.解 (1)频率分布表:(2)(3)答对下述两条中的一条即可:①该市有一个月中空气污染指数有2天处于优的水平,占当月天数的115;有26天处于良的水平,占当月天数的1315;处于优或良的天数为28,占当月天数的1415.说明该市空气质量基本良好.②轻微污染有2天,占当月天数的115;污染指数在80以上的接近轻微污染的天数15,加上处于轻微污染的天数2,占当月天数的1730,超过50%;说明该市空气质量有待进一步改善.。
2024届成都七中高二零诊模拟考试试卷(全科)24届高二文科数学零诊模拟考试试卷答案
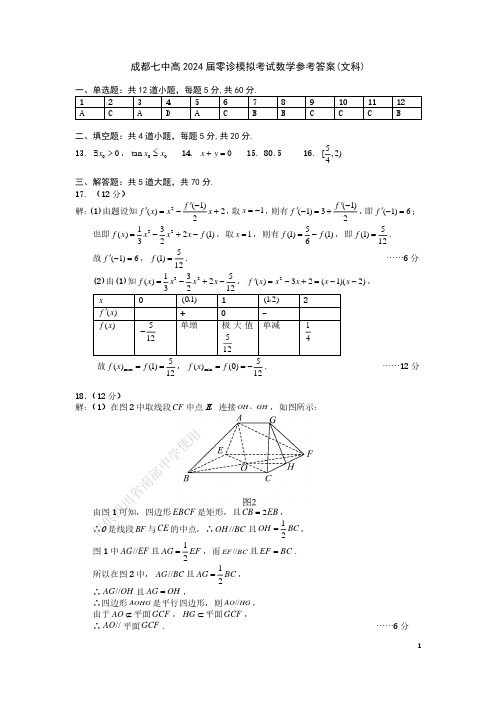
1成都七中高2024届零诊模拟考试数学参考答案(文科)二、填空题:共4道小题,每题5分,共20分.13. 00x ∃>,00tan x x ≤ 14. 0x y += 15. 80.5 16. 5[,2)4三、解答题:共5道大题,共70分. 17. (12分)解:(1)由题设知2(1)()22f f x x x '−'=−+,取1x =−,则有(1)(1)32f f '−'−=+,即(1)6f '−=; 也即3213()2(1)32f x x x x f =−+−,取1x =,则有5(1)(1)6f f =−,即5(1)12f =.故(1)6f '−=,5(1)12f =. ……6分(2)由(1)知32135()2f x x x x =−+−,2()32(1)(2)f x x x x x '=−+=−−,故max ()(1)12f x f ==,min ()(0)12f x f ==−. ……12分CF 中点H ,连接OH GH 、,如图所示:EBCF 是矩形,且2CB EB =,的中点,∴//OH BC 且12OH BC =,12EF ,而//EF BC 且EF BC =.BC 且12AG BC =,,是平行四边形,则//AO HG , HG ⊂平面GCF ,学使用四川省南部中学使用仅供2224t tt−=+,解得2,1()3t t==或舍去.故t的取值为23. ……12分21.(12分)解:(1)由()xf x e ax=−知()xf x e a'=−,1)当a e≤时,且有[1,)x∈+∞,()0f x'≥,()f x单增,故无极值;2)当a e>时,有(1,ln)x a∈,()0f x'<,()f x单减,而(ln,)x a∈+∞,()0f x'>,()f x单增,故()(ln)lnf x f a a a a==−极小值,()f x无极大值.综上,当a e≤时,()f x无极值;当a e>时,()f x极小值为lna a a−,()f x无极大值. ……4分(2)由(1)可知()1xf x e'=−,即有1111lntt t tλλ+>+−−,整理可令得(1)(1)()ln01tF t ttλλ+−=−>+, ……6分而22221(1)(1)(1)()(1)(1)t tF tt t t tλλλλ+−−'=−=++,……7分 1)当1λ≥时,且(1,)t∈+∞,有22(1)()0(1)tF tt tλ−'≥>+,()F t单增,()(1)0F t F>=,满足题设;……9分 2)当01λ<<时,且21(1,)tλ∈,有()0F t'<,()F t单减,()(1)0F t F<=,不满足题设;……11分综上,λ的取值范围为[1,)+∞. ……12分22.(10分)解:(1)由2sin2cosaρθθ=+,得22sin2cosaρρθρθ=+,故曲线的直角坐标方程为,即222()(1)1x a y a−+−=+;由sin()4πρθ−=,得sin cos2ρθρθ−=,故直线的直角坐标方程为. ……4分(2)点P的直角坐标为(2,0)−,在直线上,而直线的标准参数方程为(t为参数),将其代入,整理可得.由题设知222(3)4(44)2(1)0a a a∆=+−+=−>,解得.又,.当1,1a a>−≠且时,有12,0t t>,则1212||||||||3)PM PN t t t t a+=+=+=+=解得2a=;当1a≤−时,有12t t≤,则1212||||||||||1|PM PN t t t t a+=+=−==−=,解得4a=−.故a的值为2或-4. ……10分C2222x y y ax+=+l2y x=+ll22xy⎧=−⎪⎪⎨⎪=⎪⎩2222x y y ax+=+()2440t t a−+++=1a≠12t t+=1244t t a=+仅供四川省南部中学使用3。
成都七中高二数学零诊期末复习-不等式

高中数学复习----不等式一、不等式的性质及均值不等式1.实数的三岐性:设R b a ∈,,那么0>-⇔>b a b a ;0=-⇔=b a b a ;0<-⇔<b a b a ; 2.不等式的性质:(1)对称性:a b b a <⇔>,(2)传递性:c a c b b a >⇒>>,;(3)加法原理:c b c a b a ±>±⇒>;(4)乘法原理cbc a bc ac c b a c b c a bc ac c b a <<⇒<>>>⇒>>,0,;,0,;(5)可加性:d b c a d c ba +>+⇒⎩⎨⎧>>,(减法可以转化为加法来进行d b c a d c d c ba ->-⇒->-⇒⎩⎨⎧<>; (6)可乘性:bd ac d c b a >⇒>>>>0,0;(除法可转化为乘法来进行) (7)乘方原理:)1,(0>∈>⇒>>n N n b a b a n n ; (8)开方原理:)1,(0>∈>⇒>>n N n b a b a n n ;(9)三角不等式b a b a b a +≤±≤-,(其中左等号成立的充要条件是0≤ab ;右等号成立的充要条件是0≥ab ; 3.均值不等式(1)ab b a ≥+222(R b a ∈,当且仅当b a =时”=”成立) (2)ab ba ≥+2(0,0>>b a 当且仅当b a =时’=”成立) (应用于求最值要注意三个条件:一正,二定,三相等缺一不可. (3)均值不等式的拓展:)0,0(2211222>>+≤+≤≤+b a b a ba ab b a 4.典型例题例1.已知0,0<<>>d c b a ,求证:0<<cbd a ;例2.若01<<-a 比较21a +与11+a 的大小;例3.设12log 2)(,13log )(+=+=x x x g x x f ,其中0>x 且1≠x ,试比较)(x f 和)(x g 的大小.例4.设1,0,0=+>>y x y x 求yx 11+的最小值.例5.设1,0,=+>b a b a ,求1212+++b a 的最大值.例6.已知1,0,0=+>>b a b a 求证: 9)11)(11(≥++ba ;5.巩固训练A 组1.下列推理正确的是( )(A)b a bc ac >⇒> (B)b a b a >⇒>22 (C)b a ba <⇒>11 (D)b a b a <⇒<2.已知c b a ,,满足a b c <<且0<ac ,那么下列选项中一定成立的是( ) (A)ac ab > (B)0)(<-a b c (C)22ab cb < (D)0)(>-c a ac3.若x c x b x a e x 31ln ,ln 2,ln ),1,(===∈-则( )(A)c b a << (B)b a c << (C)c a b << (D)a c b <<4.已知1>x ,则14422-++x x 的最小值为( )(A)2 (B)6 (C)8 (D)95.设R b a ∈,,已知命题;:b a p =命题22:222b a b a q +≤⎪⎭⎫⎝⎛+,则p 是q 成立的( ) (A)必要不充分条件(B)充分不必要条件(C)充分必要条件(D)不充分也不必要条件6.若55ln ,33ln ,22ln ===c b a ,则c b a ,,三个数按从小到大排列为 ; 7.若0,0>>y x ,且191=+yx ,则y x +的最小值为 ; 8.某公司一年购买某种货物400吨,每次都购买x 吨,运费为4万元/次.一年的总存储费用为x 4万元,要使一年的总运费与总存储费用之和最小,则=x 吨.B 组1.已知,10<<<b a 则a a b b b alog ,,log 1的大小关系是 ;2已知点),(y x 在直线12=+y x 上,则y x 42+的最小值是 ; 3.如果2>+abb a ,则0>ab 且 ; 4.已知不等式9)1)((≥++yax y x 对任意正实数y x ,恒成立,则正实数a 的最小值为 ;5.设数列{}n a 中,n n n f a 2)(==若21n n ≠,比较)2(21n n f +与2)()(21n f n f +的大小; 二.不等式的证明及含绝对值的不等式1不等式的证明是不等式的难点之一,证明的主要方法有:比较法,分析法和综合法.(1)比较法:是证明不等式的最基本的方法,可分为作差比较法,作商比较法(2)分析法:指从证明的不等式出发,”执果索因”,从结论出发找命题成立的充分条件,直到找到明显成立的不等式或已经证明的不等式为止,这种方法叫分析法.(3)综合法:从一个正确的不等式出发,根据不等式的性质及均值不等式对该不等式变形,直到得出所求证的不等式为止,即”执因索果”注:除了以上方法外还有反证法,放缩法,数学归纳法,换元法,函数法与数形结合法等 2.含绝对值的不等式(1)实数的绝对值的定义⎪⎩⎪⎨⎧<-=>=)0()0(0)0(a a a a a a ; (2)对R b a ∈,有)0(,≠==b ba b ab a ab (3)对+∈∈R a R x ,有a x a a x a x <<-⇔<⇔<22a x a x a x a x -<>⇔>⇔>或22*)(2121N n a a a a a a n n ∈+++≤+++3.典型例题例1.已知+∈R b a ,,且1=+b a ,求证:222)(by ax by ax +≥+;例2.已知实数n m b a ,,,其中m 与n 为正数,求证:nm b a n b m a ++≥+222)(;例3. 已知R c b a ∈,,,求证:)(2222222c b a a c c b b a ++≥+++++;例4:若233=+q p ,求证:2≤+q p例5.证明:113121222<+++n;例6(1)已知1,1<<b a 求证;11>--ba ab; (2)求实数λ的取值范围,使不等式11>--ba ab λλ对满足1,1<<b a 的一切实数b a ,恒成立;4.巩固训练A 组1.不等式ba b a 11,>>同时成立的充要条件是( ) (A)0>>b a (B)b a >>0 (C)011<<a b (D)011>>ba(A)b a +有最小值)12(2+ (B)b a +有最大值2)12(+ (C)ab 有最小值)12(+ (D)ab 有最小值)12(2+3.若0,,>c b a 且324)(-=+++bc c b a a ,则c b a ++2的最小值为( ) (A)13- (B)13+ (C)232+ (D)232-4.设实数y x ,满足1)1(22=-+y x .若对满足条件的y x ,,0≥++c y x 恒成立,则c 的取值范围是( )(A)),12[+∞- (B)]12,(--∞ (C)),12[+∞+ (D)]12,(+-∞ 5.设x x f lg )(=,若c b a <<<0且)()()(b f c f a f >>,则下列结论中正确的是( ) (A)0)1)(1(>--c a (B)1>ac (C)1=ac (D)1<ac6.已知b n m a y x =+=+2222,,其中b a ,为常数,则ny mx +的最大值为 ;7.设+∈R m b a ,,且ma mb a b ++<,则a 与b 的大小关系为 ; B 组1.在(1) x y 2=;(2)x y 2log =;(3)2x y =;(4)x y cos =,这四个函数中,当1021<<<x x 时,使2)()()2(2121x f x f x x f +>+恒成立的函数有 ; 2.设1,0,0=+>>y x y x ,则a y x ≤+恒成立的a 的最小值是 ; 3.设x x b x x a x -+=--=>1,1,1,则a 与b 的大小关系是 ; 4.已知0,0>>b a 且R y x b a ∈=+,,1,求证:xy bx ay by ax ≥++))((5.已知2122≤+≤y x ,证明:32122≤++≤y xy x ;6.已知3,1,222=++=++>>c b a c b a c b a ,求证:3132<+<-c b7.已知72)(2+-=x x x f 且3<-m x ,求证:156)()(+<-m m f x f8.已知数列{}n a 中,12-=n n a ,求证:*)(31213221N n n a a a a a a n n ∈->++++三、不等式的解法及不等式的综合应用1.解不等式的过程实质上是一个等价转化的过程,最终都要转化为一元一次或一元二次不等式,要掌握以下几类不等式解法 (1)一元一次不等式的解法; (2)一元二次不等式的解法; (3)简单的高次不等式的解法; (4)分式不等式解法;(5)含绝对值不等式的解法; (6)了解指、对数不等式的解法; (7)了解无理不等式的解法; 2.不等式的综合应用(1)不等式知识贯穿于高中数学的始终,是构建高中数学知识交汇点的一个典型平台。
2023-2024学年四川省成都市高二上册期末调研考试数学(理)试题(含解析)

2023-2024学年四川省成都市高二上册期末调研考试数学(理)试题第Ⅰ卷(选择题,共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.双曲线2214y x -=的渐近线方程为()A.12y x =±B.14y x =±C.2y x=± D.4y x=±【正确答案】C【分析】根据给定双曲线方程直接求出其渐近线方程即可.【详解】双曲线2214y x -=的渐近线方程为.2y x=±故选:C2.在空间直角坐标系Oxyz 中,点(4,1,9)P 到点(2,4,3)Q 的距离为()A.5B.6C.7D.8【正确答案】C【分析】根据空间两点的距离坐标公式即可.【详解】根据空间两点的距离坐标公式可得.7PQ ==故选:C3.在一次游戏中,获奖者可以获得5件不同的奖品,这些奖品要从编号为1-50号的50种不同奖品中随机抽取确定,用系统抽样的方法为获奖者抽取奖品编号,则5件奖品的编号可以是()A.3,13,23,33,43 B.11,21,31,41,50C.3,6,12,24,48 D.3,19,21,27,50【正确答案】A【分析】根据系统抽样的知识求得正确答案.【详解】依题意,组距为50105=,所以A 选项符合,BCD 选项不符合.故选:A4.命题“0m ∀∈≤N ”的否定是()A.00m ∃∉≥NB.00m ∃∈>NC.00m ∃∈≤ND.0m ∀∈>N 【正确答案】B【分析】利用含有一个量词的命题的否定的定义判断.【详解】解:因为命题0m ∀∈≤N 是全程量词命题,所以其否定是存在量词命题,即00m ∃∈>N ,故选:B5.若,,a b c ∈R ,则“a b >”是“a c b c +>+”的()A.充分不必要条件 B.必要不充分条件C.充要条件 D.既不充分也不必要条件【正确答案】C【分析】根据充要条件的定义即可判断.【详解】根据不等式的性质可得a b a c b c >⇔+>+,∴“a b >”是“a c b c +>+”的充要条件.故选:C6.已知直线:0l Ax By C ++=(A ,B 不同时为0),则下列说法中错误的是()A.当0B =时,直线l 总与x 轴相交B.当0C =时,直线l 经过坐标原点O C.当0A C ==时,直线l 是x 轴所在直线D 当0AB ≠时,直线l 不可能与两坐标轴同时相交【正确答案】D【分析】根据直线的知识对选项进行分析,从而确定正确答案.【详解】依题意,直线:0l Ax By C ++=(A ,B 不同时为0).A 选项,当0B =时,0A ≠,直线方程可化为Cx A=-,此时直线l 总与x 轴有交点,A 选项正确.B 选项,当0C =时,直线方程为0Ax By +=,此时直线l 经过原点O ,B 选项正确.C 选项,当0A C ==时,0B ≠,直线方程可化为0y =,此时直线l 是x 轴所在直线,C 选项正确.D 选项,当0AB ≠时,如10x y -+=,直线l 过点()()1,0,0,1-,即直线l 与两坐标轴同时相交,D 选项错误.故选:D.7.执行如图所示的程序语句,若输入5x =,则输出y 的值为()INPUTx IF x<0THEN y=-x+1ELSE y=-x^2+3END IF PRINTy ENDA.4B.7C.22- D.28-【正确答案】C【分析】分析程序框图的运行过程知,本题的功能为计算并输出分段函数21,03,0x x y x x -+<⎧=⎨-+≥⎩的值,因为输入5x =,所以执行的是23y x =-+,进而可得解.【详解】由算法语句知,该程序的功能是计算并输出分段函数21,03,0x x y x x -+<⎧=⎨-+≥⎩的值,当5x =时,满足0x ≥,∴执行23y x =-+,∴输出的y 值为22-.故选:C8.已知F 是抛物线24y x =的焦点,M 是抛物线上一点,且满足120OFM ∠=︒(O 为坐标原点),则FM 的值为()A.4B.3C. D.2【正确答案】A【分析】设FM t =,求得M 点坐标并代入抛物线方程,从而求得t ,也即求得FM .【详解】依题意,()1,0F ,设FM t =,由于120OFM ∠=︒,不妨设M 在第一象限,则()1cos60,sin 60M t t +︒︒,即131,22M t ⎛⎫+⎪ ⎪⎝⎭,将M 点坐标代入24y x =得2314142t t ⎛⎫=+ ⎪⎝⎭,即()()238160,4340t t t t --=-+=,由于0t >,所以4t =,即4FM =.故选:A9.已知圆221:(2)(1)9O x y -+-=和直线:10l x y -+=.若圆2O 与圆1O 关于直线l 对称,则圆2O 的方程为()A.22(3)9x y -+= B.22(3)9x y +-=C.22(2)(3)9x y -+-= D.22(3)(2)9x y -+-=【正确答案】B【分析】求出圆1O 的圆心关于直线l 的对称点,即为圆2O 的圆心坐标,进而可得圆2O 的方程.【详解】圆2O 与圆1O 关于直线l 对称,则圆心()12,1O 与圆()2,O a b 关于:10l x y -+=对称可得211022112a bb a ++⎧-+=⎪⎪⎨-⎪=-⎪-⎩,化简得3030a b a b -+=⎧⎨+-=⎩,解得0,3a b ==又两圆半径相等,故圆2O 的方程为22(3)9x y +-=故选:B10.已知13,22m ⎡⎤∈-⎢⎣⎦,命题2:2320p m m --≤,命题22:1623x y q m m +=--表示焦点在x 轴上的椭圆.则下列命题中为真命题的是()A.p q ∧ B.p q∨ C.p q⌝∨ D.p q⌝∧【正确答案】B【分析】首先判断命题p 、q 的真假,再根据复合命题的真假性判断即可.【详解】解:由22320m m --≤,即()()2120m m +-≤,解得122m -≤≤,因为13,22⎡⎤-⎢⎥⎣⎦1,22⎡⎤-⎢⎥⎣⎦,所以命题p 为真命题,则p ⌝为假命题,若方程221623x ym m +=--表示焦点在x 轴上的椭圆,则60230623m m m m ->⎧⎪->⎨⎪->-⎩,解得332m <<,又13,22m ⎡⎤∈-⎢⎥⎣⎦,所以命题q 为假命题,则q ⌝为真命题,所以p q ∧为假命题,p q ∨为真命题,p q ⌝∨为假命题,p q ⌝∧为假命题.故选:B11.在平面直角坐标系xOy 内,对任意两点()11,A x y ,()22,B x y ,定义A ,B 之间的“曼哈顿距离”为1212AB x x y y =-+-,记到点O 的曼哈顿距离小于或等于1的所有点(,)x y 形成的平面区域为Ω.现向221x y +=的圆内随机扔入N 粒豆子,每粒豆子落在圆内任何一点是等可能的,若落在Ω内的豆子为M 粒,则下面各式的值最接近圆周率的是()A.N MB.2N MC.3N MD.4N M【正确答案】B【分析】设(),P x y ,根据1OP ≤得1x y +≤,作出平面区域Ω,根据几何概型计算求解即可.【详解】设(),P x y ,则|1|P y O x =+≤,当0,0x y ≤≥时,1x y +≤;当0,0x y ≥<时,1x y -≤;当0,0x y <≥时,1x y -+≤;当0,0x y <<时,1x y --≤.则平面区域Ω为下图中的四边形ABCD及其内部,其面积为2S ==,根据几何概型公式可得:2πM N =,2πN M∴=.故选:B12.已知有相同焦点1F ,2F 的椭圆22122:1(0)x y C a b a b+=>>与双曲线22222:1(0,0)x y C m n m n-=>>在第一象限的交点为A ,若2AOF △(O 为坐标原点)是等边三角形,则abmn的值为()A.2+B.2C.232D.223+【正确答案】A【分析】根据已知图形特征结合椭圆,双曲线中,a b c ,关系及公交点求解即可.【详解】2AOF △(O 为坐标原点)是等边三角形,260°AOF ∠=且21OA OF OF ==,则2190°F AF ∠=,且122F F c =,则21,AF c AF ==,))121221,21,a AF AF c m AF AF c =+==-=-)2222221322c b a c c c ⎛⎫+⎪=-=-= ⎪⎝⎭,)2222221322c n c m c c ⎛⎫- ⎪=-=-= ⎪⎝⎭所以22b n =,即得b n =,所以112423222cab a a mn m m++=====+故选:A第Ⅱ卷(非选择题,共90分)二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡上.13.椭圆22110036x y +=上一点P 与它的一个焦点的距离等于6,那么点P 与另一个焦点的距离等于______.【正确答案】14【分析】设左、右焦点为12,F F ,利用椭圆的定义即得解.【详解】设左、右焦点为12,F F ,设1||6PF =,由题得10,a =因为12||||2210=20PF PF a +==⨯,所以2||14PF =.所以点P 与另一个焦点的距离等于14.故1414.为了解某校高三学生的数学成绩,随机地抽查了该校100名高三学生的期中考试数学成绩,得到频率分布直方图如图所示.请根据以上信息,估计该校高三学生数学成绩的中位数为______.(结果保留到小数点后两位)【正确答案】71.67【分析】依据频率分布直方图,计算0.5p =时对应的数值,即为中位数.【详解】解:()0.0050.04100.450.5+⨯=< ,()0.0050.040.03100.750.5++⨯=> ,所以中位数在[)70,80之间,设中位数为m ,则有700.03100.50.4510m -⨯⨯=-,所以57071.673m =+≈故答案为.71.6715.甲,乙两人下棋,若两人下成和棋的概率是13,甲获胜的概率是14,则乙获胜的概率是______.【正确答案】512【分析】利用互斥事件概率加法公式直接求解.【详解】解:甲,乙两人下棋,两人下成和棋的概率是13,甲获胜的概率是14,∴乙获胜的概率11134512P =--=.故512.16.已知双曲线22221(0,0)x y a b a b-=>>的左,右焦点1F ,2F ,经过1F 斜率为的直线l 与双曲线的左支相交于P ,Q 两点.记12PF F △的内切圆的半径为a ,则双曲线的离心率为______.1或212+【分析】分两种情况求解离心率,设内切圆圆心为T,分别与三边相切于,,M N H,连接1TF,计算得到212HF HF c+=,1HF c a=-,得到1tan aTF Hc a∠=-,根据二倍角公式得到212ee e-=-解得答案.【详解】当P点在第二象限时,设内切圆圆心为T,分别与三边相切于,,M N H,连接1TF,2121212PF PF NF MF HF HF a-=-=-=,又212HF HF c+=,1HF c a=-,则1tan aTF Hc a∠=-,直线1PF的斜率为221ac aac a-=⎛⎫- ⎪-⎝⎭,整理得到:212ee e-=-1e=+或212e=-(舍去).当P点在第三象限时,同理设内切圆圆心为T,分别与三边相切于,,M N H,连接1TF,2121212PF PF NF MF HF HF a-=-=-=,又212HF HF c+=,1HF c a=-,则1tan aTF Hc a∠=-,直线1PF的斜率为221ac aac a--=⎛⎫- ⎪-⎝⎭,整理得到:212e e e -=-12e =+或1e =.1+或212+三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.已知点(4,2)P -,直线:3450l x y --=.(1)求经过点P 且与直线l 平行的直线的方程;(2)求经过点P 且与直线l 垂直的直线的方程.【正确答案】(1)34200x y -+=(2)43100x y ++=【分析】(1)设出所求平行直线的方程,利用P 点坐标求得正确答案.(2)利用点斜式求得所求直线的方程.【小问1详解】设经过点P 且与直线l 平行的直线的方程为340x y C -+=,将()4,2P -代入得1280,20C C --+==,所以所求直线方程为34200x y -+=【小问2详解】直线:3450l x y --=的斜率为34,与直线l 垂直的直线的斜率为43-,所以经过点P 且与直线l 垂直的直线的方程为()4243y x -=-+,即43100x y ++=.18.甲,乙两台机床同时生产一种零件,统计5天中两台机床每天所出的次品件数,数据如下图:(1)判断哪台机床的性能更稳定,请说明理由;(2)从甲机床这五天的数据中任意抽取两天的数据,求至多有一天的次品数超过1件的概率.【正确答案】(1)乙机床更稳定,理由见解析;(2)910【分析】(1)计算甲、乙两种机床的生产次品的平均数和方差,说明稳定性;(2)分别计算从五天中任意抽取两天的方法种数和这两天中至多有一天次品数超过1的方法种数,利用古典概型公式计算概率即可.【小问1详解】甲机床的次品数为0,1,0,2,2,平均数为1,方差为()()()()()22222101110121210.85⎡⎤⨯-+-+-+-+-=⎣⎦;乙机床的次品数为.1,平均数为1,方差为()()()()()22222111011121110.45⎡⎤⨯-+-+-+-+-=⎣⎦;∴甲、乙两个机床生产的次品的平均数相等,甲机床次品数的方差大于乙机床次品数的方差,所以乙机床性能更稳定.【小问2详解】设从五天的数据中抽取两天,至多有一天的次品数超过1件为事件A ,则从甲机床这五天的数据中任意抽取两天的数据,抽取的方法有25C 10n ==种,至多有一天的次品数超过1件()211332C C C 9n A =+=,则()910P A =.19.已知圆22:60A x y x +-=与直线32x =相交于M ,N 两点.(1)求||MN 的长;(2)设圆C 经过点M ,N 及(2,2)B .若点P 在圆C 上,点Q 在圆A 上,求||PQ 的最大值.【正确答案】(1)(2)7+【分析】(1)根据圆的方程确定圆心与半径,求圆心到直线的距离,结合直线与圆相交弦长公式求解即可得||MN 的长;(2)根据圆C 经过点M ,N ,可得圆心在圆心C 在x 轴上,设(),0C a ,半径为1r ,即可求得圆C 的方程,再根据两圆上动点距离最值即可得||PQ 的最大值.【小问1详解】圆22:60A x y x +-=化成标准方程为()2239x y -+=,则圆心为()3,0A ,半径3r =,圆A 与直线32x =相交于M ,N 两点,则圆心A 到直线32x =的距离为33322d =-=,所以MN ===【小问2详解】由于圆A 与直线32x =相交于M ,N 两点,所以333333,2222M N ⎛⎫⎛⎫- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,或333333,2222N M ⎛⎫⎛⎫- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,,又圆C 经过点M ,N ,则圆心C 在x 轴上,设(),0C a ,半径为1r ,则1CM CB r ==,1r ==,解得11,a r =-=则圆()22:113C x y ++=,若点P 在圆C 上,点Q 在圆A上,所以max 1||437PQ AC r r =++=++=+.20.某工厂统计2022年销售网点数量与售卖出的产品件数的数据如下表:销售网点数x (单位:个)1719202123售卖出的产品件数y (单位:万件)2122252730假定该工厂销售网点的个数与售卖出的产品件数呈线性相关关系,(1)求2022年售卖出的产品件数y (单位:万件)关于销售网点数x (单位:个)的线性回归方程;(2)根据(1)中求出的线性回归方程,预测2022年该工厂建立40个销售网点时售卖出的产品件数.参考公式:()()()112211ˆn niii ii i nniii i x x y y x y nxybx x xnx ====---==--∑∑∑∑,ˆˆa y bx=-.【正确答案】(1)167.ˆyx =-;(2)约57万件.【分析】(1)由参考公式可算出销售网点数x (单位:个)的线性回归方程;(2)将40x =代入由(1)算得的回归方程可得答案.【小问1详解】由题,可得1719202123205x ++++==,2122252730255y ++++==,51172119222025212723302532i ii x y==⨯+⨯+⨯+⨯+⨯=∑,5222222117192021232020ii x==++++=∑.则22532520253216202020520ˆ.b-⨯⨯===-⨯,2520167.ˆa =-⨯=-.故回归方程为.167.ˆyx =-【小问2详解】将40x =代入回归方程,则64757ˆy=-=.故2022年该工厂建立40个销售网点时售卖出的产品件数约57万件.21.已知椭圆2222:1(0)x y E a b a b +=>>经过点12⎫⎪⎭,离心率为2.(1)求椭圆E 的方程;(2)设经过右焦点2F 的两条互相垂直的直线分别与椭圆E 相交于A ,B 两点和C ,D 两点.求四边形ACBD 的面积的最小值.【正确答案】(1)2214x y +=(2)3225【分析】(1)依题意得到关于a 、b 、c 的方程组,解得即可;(2)首先求出右焦点坐标,当直线AB 的斜率不存在或为0时直接求出四边形的面积,当直线AB 的斜率存在且不为0时,设直线(:AB y k x =-,()11,A x y ,()22,B x y ,联立直线与椭圆方程,消元、列出韦达定理,利用弦长公式表示出AB ,同理得到CD ,最后由面积公式及基本不等式计算可得.【小问1详解】依题意可得2222231142a b c e a c a b⎧+=⎪⎪⎪==⎨⎪=-⎪⎪⎩,解得21a b c ⎧=⎪=⎨⎪=⎩,所以椭圆方程为2214x y +=.【小问2详解】由(1)可知)2F ,当直线AB 的斜率不存在或为0时,1141222ACBDS AB CD =⋅=⨯⨯=,其中通径为221b a=,当直线AB 的斜率存在且不为0时,设直线(:AB y k x =-,()11,A x y ,()22,B x y ,则直线(1:CD y x k=-,由(2214y k x xy ⎧=-⎪⎨⎪+=⎩消去y 得()2222141240k x x k +-+-=,()()()()222224141241610k kk ∆=--+⨯-=+>,所以212214x x k+=+,212212414k x x k -=+,所以AB =()224114k k +==+,同理可得()2222141414114k k CD k k ⎛⎫⎛⎫-+ ⎪ ⎪ ⎪+⎝⎭⎝⎭==+⎛⎫+⋅- ⎪⎝⎭,所以()()222281121414ACBDSk k k kAB CD =⋅+⨯⨯++=+,因为()()()()()222222214425114424k k k k k ⎡⎤++++⎢⎥++≤=⎢⎥⎣⎦,所以()()22221322525148ACBD S k k +≥=⨯+,当且仅当1k =±时等号成立,综上可得四边形ACBD 的面积的最小值为3225.22.已知点(1,0)F ,经过y 轴右侧一动点A 作y 轴的垂线,垂足为M ,且||||1AF AM -=.记动点A 的轨迹为曲线C .(1)求曲线C 的方程;(2)设经过点(1,0)B -的直线与曲线C 相交于P ,Q 两点,经过点(1,)((0,2)D t t ∈,且t 为常数)的直线PD 与曲线C 的另一个交点为N ,求证:直线QN 恒过定点.【正确答案】(1)()240y x x =>(2)证明见解析【分析】(1)设()(),0A x y x >,根据距离公式得到方程,整理即可;(2)设()11,P x y 、()22,Q x y 、()33,N x y ,表示出直线PQ 的方程,由点()1,0B -在直线PQ 上,代入可得124y y =,同理可得()13231y y ty y y ++=,再表示出直线QN ,代入可得()()()131441y y ty y x +-=-,即可得到直线QN 过定点坐标.【小问1详解】解:设()(),0A x y x >,则()0,M y ,因为||||1AF AM -=1x -=,又0x>1x =+,整理得()240y x x =>.【小问2详解】证明:设()11,P x y 、()22,Q x y 、()33,N x y ,所以121222121212444PQ y y y y k y y x x y y --===-+-,所以直线PQ 的方程为()11124y y x x y y -=-+,因为点()1,0B -在直线PQ 上,所以()111241y x y y -=--+,即21112414y y y y ⎛⎫-=-- ⎪+⎝⎭,解得124y y =①,同理可得直线PN 的方程为()11134y y x x y y -=-+,又()1,D t 在直线PN 上,所以()111341t y x y y -=-+,易得1y t ≠,解得()13231y y ty y y ++=②,所以直线QN 的方程为()22234y y x x y y -=-+,即()23234y y y x y y +=+③,将②式代入③式化简得()1311234y y ty y x y y y +=+,又124y y =,即()131344y y ty y x y +=+,即()()()131441y y ty y x +-=-,所以直线QN 恒过定点41,t ⎛⎫ ⎪⎝⎭.。
四川省成都市2023-2024学年高二下学期7月零诊摸底模拟数学试题1答案

成都市2022级高中毕业年级摸底模拟测试数学参考答案及评分标准一、单选题(共40分)1.(本题5分)已知等比数列的前项和为,若,,则( )A .20B .30C .40D .50【详解】因为是等比数列,所以成等比数列,即成等比数列,显然,故选:B2.(本题5分)的展开式中的系数是( )A .48B .-48C .72D .-72【详解】由题意,多项式的展开式中,的系数等于.故选:A.3.(本题5分)已知离散型随机变量的分布列为0123若,则( )4.(本题5分)曲线的单调增区间是( )A .B .C .和D .和5.(本题5分)已知数列满足,则“为等比数列”是“(,)”的( ){}n a n n S 310S =620S =9S ={}n a ()363963,,0S S S S S S --≠,910,10,20S -99201030S S =⇒-=()6(2)x y x y +-52x y ()6(2)x y x y +-52x y 221166C (2)C (2)48-+-=ξξPm 4929n()1E ξ=()31D ξ+=22ln y x x =-()0,1[)1,+∞(],1-∞-()0,1()1,0-[)1,+∞{}n a 12a ={}n a m n m n a a a +⋅=m ∀*n ∈NA .充分条件但不是必要条件B .必要条件但不是充分条件6.(本题5分)已知函数的导函数的图象如下,则下面判断正确的是( )A .在区间上是增函数B .在上是减函数C .当时,取极大值D .在上是增函数【详解】在区间,导数值有正有负,A 不正确;在区间上导数值大于零,是增函数,B 不正确;在区间上导数值小于零,在区间上导数值大于零,所以当时,取极小值,C 不正确;在区间上导数值大于零,是增函数,D 正确.故选:D 7.(本题5分)在教育部和各省份教育厅组织的九省联考后,预计在4月份左右完全按照高考模式进行高考志愿模拟填报,对于某校的甲、乙、丙、丁4名同学,现有数学与应用数学、计算机、信息安全与密码管理三个专业可供选择,每名同学只能填报其中一个专业,每个专业至少有一名同学填报,则甲同学不填报数学与应用数学专业的方案种数为( )A .8B .16C .12D .24【详解】4名同学填报3个专业的方法共有种,其中甲同学填报数学与应用数学专业的方法有两种情况,若数学与应用数学专业有2名同学报考,则从乙、丙、丁三人中选择1人连同甲同学一起报考数学与应用数学专业,则有种情况,若数学与应用数学专业只有甲这1名同学报考,则从乙、丙、丁中选择2人报考其他两个专业之一,则共有种情况,故甲同学不填报数学与应用数学专业的方案一共有种.故选:D .()y f x =()f x '()2,1-()f x ()1,2()f x 4x =()f x ()4,5()f x ()2,1-()1,2()f x ()3,4()4,54x =()f x ()4,5()f x 2343C A 36=1232C A 6=2132C C 6=366624--=8.(本题5分)已知椭圆的左、右焦点分别为,点在椭圆上,且,的面积为的焦距为( )二、多选题(共18分)9.(本题6分)对于的展开式,下列说法正确的是( )A .展开式共有8项B .展开式的各项系数之和为1C .展开式中的常数项是11210.(本题6分)若函数有且仅有极大值,则( )A .B .()2222:10x y E a b a b +=>>12,F F A E 122AF AF =12AF F △E 832x x ⎛⎫- ⎪⎝⎭()()2ln 0b cf x a x ac x x =++≠0a >0ab >2③当时,如图所示,结合二次函数的图象可得故选:CD.11.(本题6分)已知数列的前项和分别为,若,则( )A .B .C .的前10项和为D .的前10项和为80b ac ∆=+>{}{},n n a b n ,n n S T 121,22n n n a n T +=-=-10100S =101024b =11n n a a +⎧⎫⎨⎬⎩⎭9191n b ⎧⎫⎨⎬⎩⎭10231024三、填空题(共15分)12.(本题5分)若定义域都为R 的函数及其导函数,满足对任意实数x 都有,则.【详解】对,两边同时求导导数得,则,,,,从而.故答案为:202413.(本题5分)托马斯·贝叶斯(Thomas Bayes )在研究“逆向概率”的问题中得到了一个公式:,这个公式被称为贝叶斯公式(贝叶斯定理),其中称为B 的全概率,假设小红口袋中有4个白球和4个红球,小兰口袋中有2个白球和2个红球,现从小红自己口袋中任取2个球放入小兰口袋中,小兰再从自己口袋中()f x ()f x '()()202522025f x f x x --=-()20241k f k ='=∑()()202522025f x f x x --=-()()20252f x f x ''+-=()()120242f f ''+=()()220232f f ''+=L ()()101210132f f ''+=()20241210122024k f k ='=⨯=∑()()()()()1i i i njjj P A P B A P A B P A P B A ==∑()()1nj j j P A P B A =∑袤七尺.该羡除是一个多面体,如图,四边形,均为等腰梯形,,面面,梯形、的高分别为3,7,且,,,则 ,异面直线所成角的余弦值是 .【详解】过分别作,的高,垂足分别为平面平面,又平面平面,又面,故可得∵,,又如图,以为坐标原点,建立空间直角坐标系,四、解答题(共77分)15.(本题13分)已知数列的前项和为,且,数列为等比数列,且.(1)求数列的通项公式;(2)若数列满足,记数列的前项和为,数列的前项和为,试比较与的大小.【详解】(1)∵数列的前项和为,且,∴当时,,当时,,故,ABCDFE ABCD ABEF AB CD EF ∥∥ABCD ⊥ABEF ABCD ABEF 6AB =10CD =8EF =DE =,AD BF A CD EF ABCD ⊥ABEF ////AB CD ABCD ⋂ABEF AB =AM ⊂ABEF AN AM ⊥AN AB ⊥AN AM ⊥AM AB ⊥A {}n a n n S 2n S n ={}n b 252,16b b =={}{},n n a b {}n c nn b c a =12n n n c c +⎧⎫⎨⎬⋅⎩⎭n n A 11n c ⎧⎫⎨⎬+⎩⎭n n B n A n B {}n a n n S 2n S n =1n =111a S ==2n ≥121n n n a S S n -=-=-21n a n =-(1)求函数的单调区间;2.17.(本题15分)如图,在四棱锥中,平面平面ABCD ,,,M为棱PC 的中点.(1)证明:平面PAD ;(2)若,(i )求二面角的余弦值;()f x x ()()f x f k x k +->P ABCD -PDC ⊥,AD DC AB DC ⊥∥112AB CD AD ===//BM 1PC PD ==P DM B --(ii )在线段PA 上是否存在点Q ,使得点Q 到平面BDM?若存在,求出PQ 的值;若不存在,说明理∴,∴四边形ABMN 是平行四边形,又平面PAD ,(2)∵∵M 为棱PC 的中点,∴(i )设平面BDM 的一个法向量为1,2MN CD MN CD =∥BM ⊄MN ⊂5,1,PC PD CD ==()10,1,,1,1,02M B ⎛⎫ ⎪⎝⎭(10,1,,1,1,02DM DB ⎛⎫== ⎪⎝⎭投篮.无论之前投篮情况如何,甲每次投篮的命中率均为0.6,乙每次投篮的命中率均为0.8.由抽签确定第1次投篮的人选,第1次投篮的人是甲、乙的概率各为0.5.(1)求第2次投篮的人是乙的概率;(2)求第次投篮的人是甲的概率;(3)已知:若随机变量服从两点分布,且,则.记前次(即从第1次到第次投篮)中甲投篮的次数为,求.i i X ()()110,1,2,,i i i P X P X q i n ==-===⋅⋅⋅11n ni i i i E X q ==⎛⎫= ⎪⎝⎭∑∑n n Y ()E Y19.(本题17分)已知抛物线:,直线与抛物线交于,两点,为坐标原点.(1)若直线过的焦点.(i)当的面积最小时,求直线的方程;(ii)当,记的外接圆与的另一个交点为,求;(2)设圆(,)与交于四点,,,,记弦,的中点分别为,,求证:线段被定点平分,并求定点坐标.C 24y x =AB C A B O AB C F AOB AB 8AB =AOB ΓC P OP ()()2227x y b r -+-=b ∈R 0r >C O Q A B AB OQ M N。
四川省成都市玉林中学高高二数学下期零诊试题 第11课时 平面向量与空间向量复习资料(1)

第11课时 平面向量与空间向量【知识点梳理】 1.向量的有关概念(1)向量的定义:既有______又有______的量叫做向量.在空间中,具有______和______的量叫做空间向量.(2)表示方法:用 来表示向量.有向线段的长度表示向量的大小,箭头所指的方向表示向量的方向.用字母a ,b ,…或用AB →,BC →,…表示.(3)模:向量的______叫向量的模,记作________或_______.(4)零向量:长度为零的向量叫做零向量,记作0;零向量的方向是________.(5)单位向量:长度为____单位长度的向量叫做单位向量.与a 平行的单位向量e =____________.(6)平行向量:方向______或______的______向量;平行向量又叫____________,任一组平行向量都可以移到同一直线上.规定:0与任一向量______.(7)相等向量:长度______且方向______的向量. (8)共线向量定理 对平面上(或空间内)任意两个向量a ,b (b ≠0),a∥b 的充要条件是_________________.推论 如图所示,点P 在l 上的充要条件是:OP →=OA →+t a ①其中a 叫直线l 的方向向量,t ∈R ,在l 上取AB →=a ,则①可化为OP →=___________________或OP →=(1-t )OA →+tOB →.(9)共面向量定理如果两个向量a ,b 不共线,那么向量p 与向量a ,b 共面的充要条件是存在惟一的有序实数对(x ,y ),使p =x a +y b ,推论的表达式为MP →=xMA →+yMB →或对空间任意一点O 有,OP →=__________________或OP →=xOA →+yOB →+zOM →,其中x +y +z =____. 2.向量的加法运算及其几何意义(1)已知非零向量a ,b ,在平面内(或空间内)任取一点A ,作AB →=a ,BC →=b ,则向量AC→叫做a 与b 的 ,记作 ,即 =AB →+BC →= ,这种求向量和的方法叫做向量加法的 .(2)以同一点O 为起点的两个已知向量a ,b 为邻边作平行四边形OACB ,则以O 为起点的对角线OA →就是a 与b 的和,这种作两个向量和的方法叫做向量加法的 .(3)加法运算律a +b =________ (交换律);(a +b )+c =____________(结合律). 3.向量的减法及其几何意义(1)相反向量与a ____________、____________的向量,叫做a 的相反向量,记作______. (2)向量的减法①定义a -b =a +________,即减去一个向量相当于加上这个向量的____________.②如图,AB →=a ,,AD →=b ,则AC →= ,DB →=____________.4.向量数乘运算及其几何意义(1)定义:实数λ与向量a 的积是一个向量,记作______,它的长度与方向规定如下: ①|λa |=______;②当λ>0时,λa 与a 的方向______;当λ<0时,λa 与a 的方向______;当λ=0时,λa =______.(2)运算律设λ,μ是两个实数,则①λ(μa )=________.(结合律)②(λ+μ)a =________.(第一分配律) ③λ(a +b )=__________.(第二分配律) 5.向量基本定理(1)平面向量基本定理如果e 1,e 2是同一平面内的两个________向量,那么对于这一平面内的任意向量a ,__________一对实数λ1,λ2,使a =______________.我们把不共线的向量e 1,e 2叫做表示这一平面内所有向量的一组________. (2)空间向量基本定理如果三个向量a ,b ,c 不共面,那么对空间任一向量p ,存在有序实数组{x ,y ,z },使得p =____________________________,把{a ,b ,c }叫做空间的一个基底. 6.向量的数量积及运算律 (1)数量积及相关概念 ①两向量的夹角已知两个非零向量a ,b ,在平面(或空间)任取一点O ,作OA →=a ,OB →=b ,则________叫做向量a 与b 的夹角,记作________,其范围是________________,若〈a ,b 〉=π2,则称a与b ______________,记作a ⊥b . ②两向量的数量积已知两个非零向量a ,b ,则______________________叫做向量a ,b 的数量积,记作________,即______________________________. (2)向量数量积的运算律①结合律:(λa )·b =____________________; ②交换律:a·b =________;③分配律:a·(b +c )=________________.【课堂讲解】题型一 向量的模及夹角问题例1已知|a |=4,|b |=3,(2a -3b )·(2a +b )=61.(1)求a 与b 的夹角θ;(2)求|a +b |; (3)若AB →=a ,BC →=b ,求△ABC 的面积.【解析】(1)∵(2a -3b )·(2a +b )=61,∴4|a |2-4a·b -3|b |2=61.又|a |=4,|b |=3,∴64-4a·b -27=61,∴a·b =-6.∴cos θ=a·b |a||b |=-64×3=-12.又0≤θ≤π,∴θ=2π3.(2)|a +b |=a +b 2=|a |2+2a·b +|b |2=16+-+9=13.(3)∵AB →与BC →的夹角θ=2π3,∴∠ABC =π-2π3=π3.又|AB →|=|a |=4,|BC →|=|b |=3,∴S △ABC =12|AB →||BC →|sin ∠ABC =12×4×3×32=3 3.题型二 两向量的平行与垂直问题例2 已知a =(cos α,sin α),b =(cos β,sin β),且k a +b 的长度是a -k b 的长度的3倍(k >0).(1)求证:a +b 与a -b 垂直; (2)用k 表示a ·b ;(3)求a ·b 的最小值以及此时a 与b 的夹角θ.【解析】1.非零向量a ⊥b ⇔a ·b =0⇔x 1x 2+y 1y 2=0.2.当向量a 与b 是非坐标形式时,要把a 、b 用已知的不共线的向量表示.但要注意运算技巧,有时把向量都用坐标表示,并不一定都能够简化运算,要因题而异.解 (1)由题意得,|a |=|b |=1,∴(a +b )·(a -b )=a 2-b 2=0,∴a +b 与a -b 垂直.(2)|k a +b |2=k 2a 2+2k a ·b +b 2=k 2+2k a ·b +1,(3|a -k b |)2=3(1+k 2)-6k a ·b .由条件知,k 2+2k a ·b +1=3(1+k 2)-6k a ·b ,从而有,a ·b =1+k 24k(k >0).(3)由(2)知a ·b =1+k 24k =14(k +1k )≥12,当k =1k时,等号成立,即k =±1.∵k >0,∴k =1.此时cos θ=a ·b |a ||b |=12,而θ∈[0,π],∴θ=π3.故a ·b 的最小值为12,此时θ=π3.题型三 向量基本定理的应用例3 如图所示,在△OAB 中,OC →=14OA →,OD →=12OB →,AD 与BC 交于点M ,设OA →=a ,OB →=b ,以a 、b为基底表示OM →.【解析】本题利用方程的思想,设OM →=ma +nb ,通过建立关于m 、n 的方程求解,同时注意体会应用向量法解决平面几何问题的方法.解 设OM →=m a +n b (m ,n ∈R ),则AM →=OM →-OA →=(m -1)a +n b ,AD →=OD →-OA →=12b -a =-a +12b .因为A ,M ,D 三点共线,所以m -1-1=n 12,即m +2n =1.而CM →=OM →-OC →=⎝ ⎛⎭⎪⎫m -14a +n b ,CB →=OB →-OC →=b -14a =-14a +b ,因为C ,M ,B 三点共线,所以m -14-14=n 1,即4m +n =1.由⎩⎪⎨⎪⎧m +2n =1,4m +n =1, 解得⎩⎪⎨⎪⎧m =17,n =37.所以OM →=17a +37b .【自主测评】 一.选择题1. 设a ,b 为不共线向量, AB →=a +2b ,BC →=-4a -b ,CD →=-5a -3b ,则下列关系式中正确的是 ( ) A.AD →=BC → B.AD →=2BC → C.AD →=-BC → D.AD →=-2BC →2. 如图所示,平面内的两条相交直线OP 1和OP 2将该平面分割成四个部分Ⅰ、Ⅱ、Ⅲ、Ⅳ(不包括边界).若OP →=aOP 1→+bOP 2→,且点P 落在第Ⅲ部分,则实数a ,b 满足 ( )A .a >0,b >0B .a >0,b <0C .a <0,b >0D .a <0,b <0答案:B [由于点P 落在第Ⅲ部分,且OP →=aOP 1→+bOP 2→,则根据实数与向量的积的定义及平行四边形法则知a >0,b <0.]3. 已知△ABC 中,AB →=a ,AC →=b ,a·b <0,S △ABC =154,|a |=3,|b |=5,则∠BAC 等于 ( )A .30°B .-150°C .150°D .30°或150°4. 设0≤θ≤2π时,已知两个向量OP 1→=(cos θ,sin θ),OP 2→=(2+sin θ,2-cos θ),则向量P 1P 2→长度的最大值是 ( )A. 2B. 3 C .3 2 D .2 35.在平行四边形ABCD 中,AC 为一条对角线,若AB →=(2,4),AC →=(1,3),则BD →等于( ) A .(-2,-4) B .(-3,-5) C .(3,5) D .(2,4)6. 已知a =(2,3),b =(-4,7),则a 在b 上的投影为 ( )A.135B.655 C.6513D.1313B [因为a·b =|a|·|b |·cos〈a ,b 〉,所以,a 在b 上的投影为|a |·cos〈a ,b 〉=a·b|b |=21-842+72=1365=655.]7. 在△ABC 中,已知D 是AB 边上一点,AD →=2DB →,CD →=13CA →+λCB →,则λ等于( ) A.23 B.13 C .-13 D .-238. 如图所示,在正方体ABCD —A 1B 1C 1D 1中,O 是底面ABCD 的中心,M 、N 分别是棱DD 1、D 1C 1的中点,则直线OM ( )A .既垂直于AC ,又垂直于MNB .垂直于AC ,但不垂直于MN C .垂直于MN ,但不垂直于ACD .与AC 、MN 都不垂直二.填空题9. 平面上有三个点A (-2,y ),B (0,2y ),C (x ,y ),若A B →⊥BC →,则动点C 的轨迹方程为________________.y 2=8x (x ≠0)解析 由题意得AB →=⎝ ⎛⎭⎪⎫2,-y 2,BC →=⎝ ⎛⎭⎪⎫x ,y 2,又AB →⊥BC →,∴AB →·BC →=0,即⎝⎛⎭⎪⎫2,-y 2·⎝ ⎛⎭⎪⎫x ,y 2=0,化简得y 2=8x (x ≠0).10. 已知点A (1,-2),若向量|AB →与a =(2,3)同向,|AB →|=213,则点B 的坐标为________.(5,4) 解析 ∵向量AB →与a 同向,∴设AB →=(2t,3t ) (t >0).由|AB →|=213,∴4t 2+9t 2=4×13.∴t 2=4.∵t >0,∴t =2.∴AB →=(4,6).设B 为(x ,y ),∴⎩⎪⎨⎪⎧x -1=4,y +2=6. ∴⎩⎪⎨⎪⎧x =5,y =4.11. 在正方体ABCD —A 1B 1C 1D 1中,给出以下向量表达式:①(A 1D 1→-A 1A →)-AB →; ②(BC →+BB 1→)-D 1C 1→;③(AD →-AB →)-2DD 1→; ④(B 1D 1→+A 1A →)+DD 1→.其中能够化简为向量BD 1→的是________.(填所有正确的序号)①②解析 ①(A 1D 1→-A 1A →)-AB →=AD 1→-AB →=BD 1→;②(BC →+BB 1→)-D 1C 1→=BC 1→-D 1C 1→=BD 1→; ③(AD →-AB →)-2DD 1→=BD →-2DD 1→≠BD 1→; ④(B 1D 1→+A 1A →)+DD 1→=B 1D 1→+(A 1A →+DD 1→)=B 1D 1→≠BD 1→.12.如图所示,PD 垂直于正方形ABCD 所在平面,AB =2,E 为PB 的中点,cos 〈DP →,AE →〉=33,若以DA ,DC ,DP 所在直线分别为x ,y ,z 轴建立空间直角坐标系,则点E 的坐标为________.(1,1,1)解析 设DP =y >0,则A (2,0,0),B (2,2,0),P (0,0,y ),E ⎝⎛⎭⎪⎫1,1,y 2,DP →=(0,0,y ),AE →=⎝ ⎛⎭⎪⎫-1,1,y 2.∴cos 〈DP →,AE →〉=DP →·AE →|DP →||AE →|=12y 2y 2+y 24=y 8+y 2=33. 解得y =2,∴E (1,1,1).13. O 是平面上一点,A ,B ,C 是平面上不共线三点,动点P 满足OP →=OA →+λ(AB →+AC →),λ=12时,则PA →·(PB →+PC →)的值为________. 答案:0 解析 由OP →=OA →+λ(AB →+AC →),λ=12,得AP →-12(AB →+AC →),即点P 为△ABC 中BC 边的中点,∴PB →+PC →=0.∴PA →·(PB →+PC →)=PA →·0=0. 三.解答题14. 已知点G 是△ABO 的重心,M 是AB 边的中点.(1)求GA →+GB →+GO →;(2)若PQ 过△ABO 的重心G ,且,OA →=a ,OB →=b ,OP →=m a ,OQ →=n b ,求证:1m +1n=3(1)解 ∵点G 是△ABO 的重心,∴GA →+GB →+GO →=0.(2)证明 ∵M 是AB 边的中点,∴OM →=12(a +b ).∵G 是△ABO 的重心,∴OG →=23OM →=13(a+b ).∵P 、G 、Q 三点共线,∴PG →∥GQ →,有且只有一个实数λ,使PG →=λGQ →.,∴(13-m )a +13b =λ[-13a +(n -13)b ].又因为a 、b 不共线,所以113311()33m n λλ⎧-=-⎪⎪⎨⎪=-⎪⎩,消去λ,整理得3mn =m +n ,故1m +1n=3.15. 设向量a =(4cos α,sin α),b =(sin β,4cos β),c =(cos β,-4sin β).(1)若a 与b -2c 垂直,求tan(α+β)的值; (2)求|b +c |的最大值;(3)若tan αtan β=16,求证:a ∥b .解 因为a 与b -2c 垂直,所以a ·(b -2c )=4cos αsin β-8cos αcos β+4sin αcos β+8sin αsin β=4sin(α+β)-8cos(α+β)=0.因此tan(α+β)=2.(2)解 由b +c =(sin β+cos β,4cos β-4sin β),得|b +c |=β+cos β2+β-4sin β2=17-15sin 2β≤4 2.又当β=-π4时,等号成立,所以|b +c |的最大值为4 2.(3)证明 由tan αtan β=16得4cos αsin β=sin α4cos β,所以a ∥b .16. 已知向量a =(cos(-θ),sin(-θ)),b =(cos ⎝ ⎛⎭⎪⎫π2-θ,sin ⎝ ⎛⎭⎪⎫π2-θ). (1)求证:a ⊥b ;(2)若存在不等于0的实数k 和t ,使x =a +(t 2+3)b ,y =-k a +t b ,满足x ⊥y ,试求此时k +t 2t的最小值.(1)证明 ∵a·b =cos(-θ)·cos ⎝ ⎛⎭⎪⎫π2-θ+sin ()-θ·sin ⎝ ⎛⎭⎪⎫π2-θ=sin θcos θ-sin θcos θ=0.∴a ⊥b .(2)解 由x ⊥y 得,x·y =0,即[a +(t 2+3)b ]·(-k a +t b )=0,∴-k a 2+(t 3+3t )b2+[t -k (t 2+3)]a·b =0,∴-k |a |2+(t 3+3t )|b |2=0.又|a |2=1,|b |2=1,∴-k +t 3+3t =0,∴k =t 3+3t .∴k +t 2t =t 3+t 2+3t t =t 2+t +3=⎝ ⎛⎭⎪⎫t +122+114.故当t =-12时,k +t 2t 有最小值114.。
四川省成都市玉林中学高高二数学下期零诊试题 第17课时 基本不等式及其应用复习资料(B)

第17课时(B ) 基本不等式及其应用【知识点梳理】 1.基本不等式ab ≤a +b2(1)基本不等式成立的条件:____________.(2)等号成立的条件:当且仅当________时取等号. 2.几个重要的不等式(1)a 2+b 2≥________ (a ,b ∈R ).(2)b a +a b≥____(a ,b 同号).(3)ab ≤⎝⎛⎭⎪⎫a +b 22 (a ,b ∈R ).(4)⎝ ⎛⎭⎪⎫a +b 22____a 2+b 22. 3.算术平均数与几何平均数设a >0,b >0,则a ,b 的算术平均数为________,几何平均数为________,基本不等式可叙述为:________________________________________________. 4.利用基本不等式求最值问题已知x >0,y >0,则(1)如果积xy 是定值p ,那么当且仅当________时,x +y 有最____值是________(简记:积定和最小).(2)如果和x +y 是定值p ,那么当且仅当________时,xy 有最____值是__________(简记:和定积最大).1.(1)a >0,b >0 (2)a =b 2.(1)2ab (2)2 (4)≤3.a +b2 ab 两个正数的算术平均数不小于它们的几何平均数 4.(1)x =y 小 2p (2)x =y 大p 241.“a >b >0”是“ab <a 2+b 22”的( ) A .充分而不必要条件 B .必要而不充分条件 C .充要条件 D .既不充分也不必要条件2.(2011·南平月考)已知函数f (x )=⎝ ⎛⎭⎪⎫12x ,a 、b ∈(0,+∞),A =f ⎝ ⎛⎭⎪⎫a +b 2,B =f (ab ),C =f ⎝ ⎛⎭⎪⎫2ab a +b ,则A 、B 、C 的大小关系是( ) A .A ≤B ≤C B .A ≤C ≤B C .B ≤C ≤A D .C ≤B ≤A 3.下列函数中,最小值为4的函数是( )A .y =x +4xB .y =sin x +4sin x (0<x <π)C .y =e x +4e -xD .y =log 3x +log x 814.(2011·大连月考)设函数f (x )=2x +1x-1(x <0),则f (x )有最________值为________.5.(2010·山东)若对任意x >0,xx 2+3x +1≤a 恒成立,则a 的取值范围为________________. 【课堂讲解】题型一 利用基本不等式求最值例1 (1)已知x >0,y >0,且1x +9y=1,求x +y 的最小值;(2)已知x <54,求函数y =4x -2+14x -5的最大值;(3)若x ,y ∈(0,+∞)且2x +8y -xy =0,求x +y 的最小值.解题导引 基本不等式的功能在于“和与积”的相互转化,使用基本不等式求最值时,给定的形式不一定能直接适合基本不等式,往往需要拆添项或配凑因式(一般是凑和或积为定值的形式),构造出基本不等式的形式再进行求解.基本不等式成立的条件是“一正、二定、三相等”,“三相等”就是必须验证等号成立的条件.解 (1)∵x >0,y >0,1x +9y=1,∴x +y =(x +y )⎝⎛⎭⎪⎫1x +9y=y x+9xy+10≥6+10=16. 当且仅当y x =9x y 时,上式等号成立,又1x +9y=1, ∴x =4,y =12时,(x +y )min =16.(2)∵x <54,∴5-4x >0.y =4x -2+14x -5=-⎝ ⎛⎭⎪⎫5-4x +15-4x +3 ≤-2-4x15-4x+3=1, 当且仅当5-4x =15-4x,即x =1时,上式等号成立,故当x =1时,y max =1. (3)由2x +8y -xy =0,得2x +8y =xy , ∴2y +8x=1.∴x +y =(x +y )⎝ ⎛⎭⎪⎫8x +2y =10+8y x +2x y=10+2⎝ ⎛⎭⎪⎫4y x+x y≥10+2×2×4y x ·xy=18,当且仅当4y x =xy,即x =2y 时取等号.又2x +8y -xy =0,∴x =12,y =6.∴当x =12,y =6时,x +y 取最小值18.题型二 基本不等式在证明不等式中的应用例2 已知a >0,b >0,a +b =1,求证:(1+1a )(1+1b)≥9.解题导引 “1”的巧妙代换在不等式证明中经常用到,也会给解决问题提供简捷的方法.在不等式证明时,列出等号成立的条件不仅是解题的必要步骤,而且也是检验转化是否有误的一种方法.证明 方法一 因为a >0,b >0,a +b =1,所以1+1a =1+a +b a =2+ba.同理1+1b=2+a b.所以(1+1a )(1+1b )=(2+b a )(2+ab)=5+2(b a +a b)≥5+4=9.所以(1+1a )(1+1b )≥9(当且仅当a =b =12时等号成立).方法二 (1+1a )(1+1b )=1+1a +1b +1ab=1+a +b ab +1ab =1+2ab, 因为a ,b 为正数,a +b =1,所以ab ≤(a +b 2)2=14,于是1ab ≥4,2ab≥8,因此(1+1a )(1+1b )≥1+8=9(当且仅当a =b =12时等号成立).变式迁移2 已知x >0,y >0,z >0.求证:⎝ ⎛⎭⎪⎫y x +z x ⎝ ⎛⎭⎪⎫x y +z y ⎝ ⎛⎭⎪⎫x z +yz ≥8.题型三 基本不等式的实际应用例3某单位用2 160万元购得一块空地,计划在该空地上建造一栋至少10层,每层2 000平方米的楼房.经测算,如果将楼房建为x (x ≥10)层,则每平方米的平均建筑费用为560+48x (单位:元).(1)写出楼房平均综合费用y 关于建造层数x 的函数关系式;(2)该楼房应建造多少层时,可使楼房每平方米的平均综合费用最少?最少值是多少?(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用=购地总费用建筑总面积)解题导引 1.用基本不等式解应用题的思维程序为:由题设写出函数→变形转化→利用基本不等式→求得最值→结论2.在应用基本不等式解决实际问题时,要注意以下四点:(1)先理解题意,设变量,一般把要求最值的变量定为函数;(2)建立相应的函数关系式,把实际问题抽象为函数最值问题;(3)在定义域内求函数最值;(4)正确写出答案.解 (1)依题意得y =(560+48x )+2 160×10 0002 000x=560+48x +10 800x(x ≥10,x ∈N *).(2)∵x >0,∴48x +10 800x≥248×10 800=1 440,当且仅当48x =10 800x,即x =15时取到“=”,此时,平均综合费用的最小值为560+1 440=2 000(元).答 当该楼房建造15层时,可使楼房每平方米的平均综合费用最少,最少值为2 000元.【课后检测】 一、选择题1.设a >0,b >0,若3是3a 与3b的等比中项,则1a +1b的最小值为( )A .8B .4C .1D.14 B [因为3a ·3b=3,所以a +b =1,1a +1b=(a +b )⎝ ⎛⎭⎪⎫1a +1b =2+b a +a b≥2+2b a ·a b =4,当且仅当b a =a b 即a =b =12时,“=”成立.] 2.已知不等式(x +y )⎝ ⎛⎭⎪⎫1x +a y ≥9对任意正实数x ,y 恒成立,则正实数a 的最小值为( ) A .2B .4C .6D .8B [不等式(x +y )⎝ ⎛⎭⎪⎫1x +a y ≥9对任意正实数x ,y 恒成立,则1+a +y x +ax y≥a +2a +1≥9,∴a ≥2或a ≤-4(舍去). ∴正实数a 的最小值为4.]3.已知a >0,b >0,则1a +1b+2ab 的最小值是( )A .2B .2 2C .4D .5C [因为1a +1b +2ab ≥21ab+2ab=2⎝⎛⎭⎪⎫1ab+ab ≥4,当且仅当1a =1b 且1ab=ab ,即a =b =1时,取“=”号.] 4.一批货物随17列货车从A 市以a km/h 的速度匀速直达B 市,已知两地铁路线长400 km ,为了安全,两列车之间的距离不得小于⎝ ⎛⎭⎪⎫a 202km ,那么这批货物全部运到B 市,最快需要( )A .6 hB .8 hC .10 hD .12 hB [第一列货车到达B 市的时间为400a h ,由于两列货车的间距不得小于⎝ ⎛⎭⎪⎫a 202km ,所以第17列货车到达时间为400a +16·⎝ ⎛⎭⎪⎫a 202a =400a +16a400≥8,当且仅当400a =16a 400,即a =100 km/h时成立,所以最快需要8 h .] 5.设x ,y 满足约束条件⎩⎪⎨⎪⎧3x -y -6≤0x -y +2≥0x ≥0,y ≥0,若目标函数z =ax +by (a >0,b >0)的最大值为12,则2a +3b的最小值为( ) AA.256 B.83C.113D .4 6. 已知a >0,b >0,a +b =2,则y =1a +4b的最小值是( )A.72B .4 C.92D .5C [∵a +b =2,∴a +b2=1.∴1a +4b =(1a +4b )(a +b 2)=52+(2a b +b 2a )≥52+22a b ·b 2a =92(当且仅当2a b =b 2a,即b =2a 时,“=”成立),故y =1a +4b 的最小值为92.]7. “a >b >0”是“ab <a 2+b22”的( )A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件 答案:A8. 已知函数f (x )=⎝ ⎛⎭⎪⎫12x ,a 、b ∈(0,+∞),A =f ⎝ ⎛⎭⎪⎫a +b 2,B =f (ab ),C =f ⎝ ⎛⎭⎪⎫2ab a +b ,则A 、B 、C 的大小关系是( )A .A ≤B ≤C B .A ≤C ≤B C .B ≤C ≤AD .C ≤B ≤A 答案:A 二、填空题9.若正实数x ,y 满足2x +y +6=xy ,则xy 的最小值是________.18解析 由x >0,y >0,2x +y +6=xy ,得xy ≥22xy +6(当且仅当2x =y 时,取“=”),即(xy )2-22xy -6≥0,∴(xy -32)·(xy +2)≥0.又∵xy >0,∴xy ≥32,即xy ≥18.故xy 的最小值为18.10.在平面直角坐标系xOy 中,过坐标原点的一条直线与函数f (x )=2x的图象交于P ,Q 两点,则线段PQ 长的最小值是________.4解析 过原点的直线与f (x )=2x交于P 、Q 两点,则直线的斜率k >0,设直线方程为y =kx ,由⎩⎪⎨⎪⎧y =kx ,y =2x,得⎩⎪⎨⎪⎧x =2k ,y =2k或⎩⎪⎨⎪⎧x =-2k ,y =-2k ,∴P (2k,2k ),Q (-2k ,-2k )或P (-2k,-2k ),Q (2k,2k ).∴|PQ |=2k+2k2+2k +2k 2=22k +1k≥4.11.已知f (x )=32x -(k +1)3x+2,当x ∈R 时,f (x )恒为正值,则k 的取值范围为__________________.(-∞,22-1)解析 由f (x )>0得32x -(k +1)·3x +2>0,解得k +1<3x +23,而3x+23≥22,∴k +1<22,k <22-1.12. 设函数f (x )=2x +1x-1(x <0),则f (x )有最________值为________.答案:大 -22-1 13.若对任意x >0,xx 2+3x +1≤a 恒成立,则a 的取值范围为________________.答案:[15,+∞)三、解答题14. (1)已知0<x <43,求x (4-3x )的最大值;(2)点(x ,y )在直线x +2y =3上移动,求2x +4y的最小值.解 (1)∵0<x <43,∴0<3x <4.∴x (4-3x )=13(3x )(4-3x )≤13⎝ ⎛⎭⎪⎫3x +4-3x 22=43,(4分)当且仅当3x =4-3x ,即x =23时,“=”成立.∴当x =23时,x (4-3x )的最大值为43.(6分)(2)已知点(x ,y )在直线x +2y =3上移动,∴x +2y =3.∴2x+4y≥22x 4y=22x +2y=223=4 2.当且仅当⎩⎪⎨⎪⎧2x =4y ,x +2y =3,即x =32,y =34时,“=”成立.∴当x =32,y =34时,2x +4y的最小值为4 2.15. 已知x >0,y >0,z >0.求证:⎝ ⎛⎭⎪⎫y x +z x ⎝ ⎛⎭⎪⎫x y +z y ⎝ ⎛⎭⎪⎫x z +y z ≥8. 证明 ∵x >0,y >0,z >0, ∴y x +z x ≥2yz x >0,x y +z y ≥2xz y >0, x z +y z ≥2xy z>0. ∴⎝ ⎛⎭⎪⎫y x +z x ⎝ ⎛⎭⎪⎫x y +z y ⎝ ⎛⎭⎪⎫x z +y z ≥8yz ·xz ·xy xyz=8.当且仅当x =y =z 时等号成立.所以(y x +z x )(x y +z y )(x z +yz)≥8.16.经观测,某公路段在某时段内的车流量y (千辆/小时)与汽车的平均速度v (千米/小时)之间有函数关系y =920vv 2+3v +1 600(v >0).(1)在该时段内,当汽车的平均速度v 为多少时车流量y 最大?最大车流量为多少? (2)为保证在该时段内车流量至少为10千辆/小时,则汽车的平均速度应控制在什么范围内?解 (1)y =920v v 2+3v +1 600=920v +1 600v+3≤9202v ×1 600v+3=92083≈11.08.(4分) 当v =1 600v,即v =40千米/小时时,车流量最大,最大值为11.08千辆/小时(6分)(2)据题意有920vv 2+3v +1 600≥10,(8分)化简得v 2-89v +1 600≤0,即(v -25)(v -64)≤0, 所以25≤v ≤64.所以汽车的平均速度应控制在[25,64]这个范围内. .。
四川省成都市2023-2024学年高二下学期期末数学试题含答案

成都市高二数学期末零诊模拟试卷(答案在最后)一、单项选择题1.下列导数运算错误的是()A.()e xf x x =,则()()1e xf x x +'= B.()πsin 3f x =,则()πcos 3f x ='C.()f x =()f x '= D.()ln x f x x =,则()21ln x f x x -'=【答案】B 【解析】【分析】根据求导法则,求导公式逐个选项计算即可.【详解】A 选项,()e xf x x =,则()()()()''e e ee 1e x xxx x f x x x x x =+=+=+',A 正确;B 选项,()πsin 3f x =,()πsin 03f x '⎛⎫ ⎪⎝⎭'==,B 错误;C 选项,()()12f x x ==,()1212f x x -='=C 正确;D 选项,()ln x f x x =,()()()22ln ln 1ln x x x x x f x x x ''⋅-⋅-==',D 正确.故选:B2.已知数列21,n a n =-32n b n =-,则由这两个数列公共项从小到大排列得到的数列为{}n c ,则数列{}n c 的通项公式为()A.32n c n =-B.41n c n =-C.53n c n =-D.65n c n =-【答案】D 【解析】【分析】根据两数列的项的特征,易推得由公共项构成的新数列项的特征,写出通项公式化简即得.【详解】因数列{}n a 是首项为1,公差为2的等差数列,而数列{}n b 是首项为1,公差为3的等差数列,则这两个数列的公共项从小到大排列构成的新数列{}n c 是首项为1,公差为6的等差数列,故1(1)665n c n n =+-⨯=-.故选:D.3.已知一批沙糖桔的果实横径(单位:mm )服从正态分布()245,5N ,其中果实横径落在[]40,55的沙糖桔为优质品,则这批沙糖桔的优质品率约为()(若()2,X N μσ~,则()0.6827P X μσμσ-≤≤+≈,()220.9545P X μσμσ-≤≤+≈)A.0.6827B.0.8186C.0.8413D.0.9545【答案】B 【解析】【分析】根据正态分布三段区间的概率值以及正态分布的性质求解即可.【详解】因为所种植沙糖桔的果实横径(单位:mm )服从正态分布()245,5N ,其中45,5μσ==,所以果实横径在[]40,55的概率为()2P X μσμσ-≤≤+()()112222P X P X μσμσμσμσ=-≤≤++-≤≤+0.477250.341350.8186≈+=.故选:B .4.函数()2ln f x x x =-单调递减区间是()A.0,2⎛ ⎝⎦B.2⎫+⎪⎪⎣⎭∞C.,,0,22∞⎛⎛⎫-- ⎪ ⎪⎝⎦⎝⎭D.,0,22⎡⎫⎛-⎪ ⎢⎪ ⎣⎭⎝⎦【答案】A 【解析】【分析】求导后,令()0f x '≤,解出即可.【详解】()221212,0x f x x x x x-'=-=>,令()0f x '≤,解得202x <≤,所以单调递减区间为0,2⎛ ⎝⎦.故选:A.5.如图,左车道有2辆汽车,右车道有3辆汽车等待合流,则合流结束时汽车通过顺序共有()种.A.10B.20C.60D.120【答案】A 【解析】【分析】合流结束时5辆车需要5个位置,第一步从5个位置选2个位置安排左边的2辆汽车,第二步剩下3个位置安排右边的3辆汽车,从而由分步乘法计数原理可得结果.【详解】设左车辆汽车依次为12,A A ,右车辆汽车依次为123,,B B B ,则通过顺序的种数等价于将12,A A 安排在5个顺序中的某两个位置(保持12,A A 前后顺序不变),123,,B B B 安排在其余3个位置(保持123,,B B B 前后顺序不变),123,,B B B ,所以,合流结束时汽车通过顺序共有2353C C 10=.故选:A.6.已知a =,b =,ln 44c =,其中e 2.71828= 为自然对数的底数,则()A.b a c <<B.b c a<< C.a b c<< D.c b a<<【答案】A 【解析】【分析】首先将,,a b c 化成统一形式,构造函数()ln xf x x=()0x >,研究单调性进而比较大小即可.【详解】由题意得a ==,b ==,ln 42ln 2ln 2442c ===;设()ln x f x x =,则21ln ()xf x x-'=,当0e x <<时,()0f x '>,所以()f x 单调递增,又02e <<<<,所以(2)f f f <<ln 22<<,所以b a c <<.故选:A .7.已知AB 是圆O :222x y +=的直径,M ,N 是圆O 上两点,且120MON ∠=︒,则()OM ON AB +⋅的最小值为()A.0B.-2C.-4D.-【答案】C 【解析】【分析】取MN 的中点C ,结合垂径定理与数量积的运算表示出()OM ON AB +⋅后,借助三角函数值域即可得解.【详解】设MN 的中点为C ,∵120MON ∠=︒,OM ON =,则302OC =°=,∵C 为MN 的中点,∴2OM ON OC +=,设向量OC 与AB的夹角为()0πθθ≤≤,∴()22cos 4cos OM ON AB OC AB OC AB θθ+⋅=⋅==,又[]cos 1,1θ∈-,∴()OM ON AB +⋅的最小值为4-.故选:C.8.当0x >时,24e 2ln 1x x x ax ⋅-≥+恒成立,则实数a 最大值为()A.4eB.4C.24e D.8【答案】B 【解析】【分析】本题考查利用导数解决不等式恒成立问题,根据题意易于分离参数得24e 2ln 1x x x a x⋅--≤,再利用切线放缩化简求出a 的取值范围.【详解】因为0x >,由24e 2ln 1xx x ax ⋅-≥+,得24e 2ln 1x x x a x⋅--≤.令()()242ln 4e 2ln 1e 2ln 10x x x x x x f x x x x+⋅----==>令()1,[0,)xg x e x x ∞=--∈+,则()10xg x e ='-≥在[0,)+∞上恒成立,故函数()1,[0,)xg x e x x ∞=--∈+在[0,)+∞上单调递增,所以()()00g x g ≥=即e 1x x ≥+,由e 1x x ≥+,得2ln 4e 2ln 41x x x x +≥++,所以()2ln 412ln 14x x x f x x++--≥=.当且仅当2ln 40x x +=时,取“=”,此时ln 2x x =-,由ln y x =与2y x =-图象可知0(0,x ∃∈+∞)使00ln 2x x =-,此时min ()4f x =.所以4a ≤,即a 有最大值为4.故选:B.二、多项选择题9.已知等比数列{}n a 的公比为q ,前n 项和为n S ,若13465,135a a a a +=+=,则()A.114a = B.3q =C.1134n n a -=⨯ D.()1314nn S =-【答案】BD 【解析】【分析】利用题设等式进行等比数列的基本量运算,求得1,a q ,代入公式即可一一判断.【详解】依题,21321(1)5(1)135a q a q q ⎧+=⎨+=⎩,解得11,23a q ⎧=⎪⎨⎪=⎩故A 错误,B 正确;则111132n n n a a q--==⨯,1)(1)131(1)1(3144n n n n a q S q -==---=-,故C 错误,D 正确.故选:BD.10.已知函数()31f x x x =-+,则()A.()f x 有两个极值点B.()f x 有一个零点C.点()0,1是曲线()y f x =的对称中心D.直线2y x =是曲线()y f x =的切线【答案】ABC 【解析】【分析】利用导数研究函数的单调性,结合极值点的概念、零点的存在性定理即可判断AB ;根据奇函数图象关于原点对称和函数图象的平移变换即可判断C ;根据导数的几何意义即可判断D.【详解】A :()231f x x '=-,令()0f x ¢>得3x >或3x <-,令()0f x '<得33x -<<,所以()f x 在(,3-∞-,,)3+∞上单调递增,(,33-上单调递减,所以3x =±时取得极值,故A 正确;B :因为323(1039f -=+>,3231039f =->,()250f -=-<,所以函数()f x 只在,3⎛-∞- ⎪⎝⎭上有一个零点,即函数()f x 只有一个零点,故B 正确;C :令3()h x x x =-,该函数的定义域为R ,()()()()33h x x x x x h x -=---=-+=-,则()h x 是奇函数,(0,0)是()h x 的对称中心,将()h x 的图象向上移动一个单位得到()f x 的图象,所以点(0,1)是曲线()y f x =的对称中心,故C 正确;D :令()2312f x x '=-=,可得1x =±,又()(1)11f f =-=,当切点为(1,1)时,切线方程为21y x =-,当切点为(1,1)-时,切线方程为23y x =+,故D 错误.故选:ABC.【点睛】关键点点睛:本题主要考查利用导数研究函数的性质和函数图象的平移变换,其中选项C ,构造函数3()h x x x =-,奇函数图象关于原点对称推出()f x 的对称性是解决本题的关键.11.如图,在棱长为2的正方体1111ABCD A B C D -中,O 为正方体的中心,M 为1DD 的中点,F 为侧面正方形11AA D D 内一动点,且满足1//B F 平面1BC M ,则()A.三棱锥1D DCB -的外接球表面积为12πB.动点F 的轨迹的线段为π2C.三棱锥1F BC M -的体积为定值D.若过A ,M ,1C 三点作正方体的截面Ω,Q 为截面Ω上一点,则线段1AQ 长度的取值范围为26,3⎡⎢⎣【答案】ACD 【解析】【分析】选项A :三棱锥1D DCB -的外接球即为正方体的外接球,结合正方体的外接球分析;选项B :分别取1AA ,11A D 的中点H ,G ,连接1B G ,GH ,1HB ,1AD ;证明平面1//B GH 平面1BC M ,从而得到点F 的轨迹;选项C :根据选项B 可得出//GH 平面1BC M ,从而得到点F 到平面1BC M 的距离为定值,即可判断;选项D :设N 为1BB 的中点,从而根据面面平行的性质定理可得到截面Ω即为面1AMC N ,从而线段1AQ 长度的最大值为线段11A C 的长,最小值为四棱锥11A AMC N -以1A 为顶点的高.【详解】对于A :由题意可知:三棱锥1D DCB -的外接球即为正方体的外接球,可知正方体的外接球的半径R =所以三棱锥1D DCB -的外接球表面积为24π12πR =,故A 正确;对于B :如图分别取1AA ,11A D 的中点H ,G ,连接1B G ,GH ,1HB ,1AD ,由正方体的性质可得11//B H C M ,且1B H ⊂平面1B GH ,1C M ⊄平面1B GH ,所以1//C M 平面1B GH ,同理可得:1//BC 平面1B GH ,且111BC C M C ⋂=,1BC ,1C M ⊂平面1BC M ,所以平面1//B GH 平面1BC M ,而1//B F 平面1BC M ,所以1B F ⊂平面1B GH ,所以点F 的轨迹为线段GH ,长度为,故B 不正确;对于C :由选项B 可知,点F 的轨迹为线段GH ,因为//GH 平面1BC M ,则点F 到平面1BC M 的距离为定值,同时1BC M 的面积也为定值,则三棱锥1F BC M -的体积为定值,故C 正确;对于D :如图,设平面Ω与平面11AA B B 交于AN ,N 在1BB 上,因为截面Ω⋂平面11AA D D AM =,平面11//AA D D 平面11BB C C ,所以1//AM C N ,同理可证1//AN C M ,所以截面1AMC N 为平行四边形,所以点N 为1BB 的中点,在四棱锥11A AMC N -中,侧棱11A C 最长,且11A C =设棱锥11A AMC N -的高为h ,因为1AM C M ==1AMC N 为菱形,所以1AMC 的边1AC ,又1AC =则112AMC S =⨯=△1111111142223323C AA M AA M V SD C -=⋅=⨯⨯⨯⨯=△,所以1111114333A AMC AMC C AA M V S h V --=⋅===△,解得h =,综上,可知1AQ 长度的取值范围是26,3⎡⎢⎣,故D 正确.故选:ACD .【点睛】关键点睛:由面面平行的性质得到动点的轨迹,再由锥体的体积公式即可判断C ,D 选项关键是找到临界点,求出临界值.三、填空题12.在322x x ⎛⎫+ ⎪⎝⎭的展开式中,3x 项的系数为_____________.【答案】6【解析】【分析】写出展开式的通项,利用通项计算可得.【详解】二项式322x x ⎛⎫+ ⎪⎝⎭展开式的通项为()32631332C 2C rrrr r rr T x x x --+⎛⎫== ⎪⎝⎭,{}0,1,2,3r ∈,令633r -=,解得1r =,所以3113322C 6T x x ==,所以展开式中3x 的系数为6.故答案为:613.已知双曲线C :()2222100x y a b a b-=>>,的左、右焦点分别为1F ,2F ,O 为原点,若以12F F 为直径的圆与C 的渐近线的一个交点为P ,且1=F P ,则C 的离心率为_____________.【答案】2【解析】【分析】根据题意,得到1||||OP OF c ==,且1F P ==,在1OPF 中,利用余弦定理求得11cos 2F OP ∠=-,得到22πππ33F OP ∠=-=,结合2tan b F OP a ∠==,利用离心率的定义,即可求解.【详解】由以12F F 为直径的圆与C 的渐近线的一个交点为P ,可得1||||OP OF c ==,又1F P ==,在1OPF 中,由余弦定理22211111cos 22OP OF PF F OP OP OF +-∠==-,得12π3F OP ∠=,所以22πππ33F OP ∠=-=,根据直线OP 为渐近线可得2tan OP b k F OP a =∠=,所以b a =2c e a ==.故答案为:2.14.某班组织开展知识竞赛,抽取四名同学,分成甲、乙两组:每组两人,进行对战答题.规则如下:每次每名同学回答6道题目,其中有1道是送分题(即每名同学至少答对1题).若每次每组对的题数之和为3的倍数,则原答题组的人再继续答题;若对的题数之和不是3的倍数,就由对方组接着答题,假设每名同学每次答题之间相互独立,且每次答题顺序不作考虑,第一次由甲组开始答题,则第7次由甲组答题的概率为______.【答案】365729【解析】【分析】先用古典概型计算公式求每次每组对的题数之和是3的倍数的概率,设第n 次由甲组答题的概率为n P ,由全概率公式得到1n P +与n P 的递推公式,根据递推公式求数列{}n P 的通项公式,令7n =,可得问题答案.【详解】记答题的两位同学答对的题数分别为1x ,1y ,则1x ,{}11,2,3,4,5,6y ∈当()()()()()()()()()()()()(){}11,1,2,1,5,2,1,2,4,3,3,3,6,4,2,4,5,5,1,5,4,6,3,6,6x y ∈时,11x y +是3的倍数,故两位同学答对的题数之和是3的倍数的概率为121663=⨯,两位同学答对的题数之和不是3的倍数的概率为23.记第n 次由甲组答题的概率为n P ,则由乙组答题的概率为1n P -,()112133n n n P P P +=+-,即11233n n P P +=-+,进一步有1111232n n P P +⎛⎫-=-- ⎪⎝⎭,又11111222p -=-=,所以数列12n P ⎧-⎫⎨⎬⎩⎭是以12为首项,以13-为公比的等比数列,所以1111223n n P -⎛⎫-=- ⎪⎝⎭.令7n =,则67111365223729P ⎛⎫=+⨯-= ⎪⎝⎭.故答案为:365729【点睛】关键点点睛:设n P 表示第n 次由甲组答题的概率,由全概率公式得()112133n n n P P P +=+-⇒11233n n P P +=-+,得到数列{}n P 的递推公式是解决该题的关键.四、解答题15.设公差不为0的等差数列{}n a 的首项为1,且2514,,a a a 成等比数列.(1)求数列{}n a 的通项公式;(2)已知数列{}n b 为正项数列,且212n n a b +=,设数列11n n b b +⎧⎫⎨⎬+⎩⎭的前n 项和为n S ,求证:n S <.【答案】(1)21n a n =-(2)证明见解析【解析】【分析】(1)设等差数列{}n a 的公差为d ,则0d ≠,根据等比中项的性质及等差数列通项公式得到方程,求出d ,即可求出通项公式;(2)由(1)得2nb n =,即n b =,从而得到11n n b b +=-+,再利用裂项相消法计算可得.【小问1详解】设等差数列{}n a 的公差为d ,则0d ≠,2a Q ,5a ,14a 成等比数列,则22145a a a =,即2111()(13)(4)a d a d a d ++=+,将11a =代入上式,解得2d =或0d =(舍去).21n a n ∴=-;【小问2详解】由(1)得212n n a b n +==,又0n b >,所以n b =,所以11n n b b+===+,则1n S=-+-++…1=-<.16.如图,在底面ABCD 是矩形的四棱锥P ABCD -中,1,2,AB BC PA PD ====,点P 在底面ABCD 上的射影为点(O O 与B 在直线AD 的两侧),且2PO =.(1)求证:AO PD ⊥;(2)求平面ABP 与平面BCP 夹角的余弦值.【答案】(1)证明见解析(2)10【解析】【分析】(1)作出辅助线,得到线线垂直,结合,OA OD AOD ⊥ 为等腰直角三角形,进而得到AO ⊥平面POD ,得到答案;(2)建立空间直角坐标系,写出点的坐标,得到两个平面的法向量,由法向量夹角的余弦公式求出答案.【小问1详解】证明:连接OD ,因为PO ⊥平面,,ABCD OA OD ⊂平面ABCD ,所以,PO OA PO OD ⊥⊥.又2PA PD PO ===,所以OA OD ==又2AD =,故222OA OD AD +=,所以,OA OD AOD ⊥ 为等腰直角三角形.而PO OD O = ,,PO OD ⊂平面POD ,所以AO ⊥平面POD ,因为PD ⊂平面POD ,所以AO PD ⊥.【小问2详解】由(1)知,,,OA OD OP 两两垂直,以,,OA OD OP 所在直线分别为x 轴,y 轴,z 轴建立如图所示的空间直角坐标系.则)(),0,0,2AP ,由9045135OAB ∠=+=,得45BAx ∠=,可得点B 坐标为,,022⎛⎫ ⎪ ⎪⎝⎭,同理得232,22C ⎛⎫⎪⎪⎝⎭.所以()()2,,,2,22AP BP BC ⎛⎫==--= ⎪ ⎪⎝⎭,设()111,,m x y z =为平面ABP 的法向量,则00m AP m BP ⎧⋅=⎪⎨⋅=⎪⎩,即11111202022z x y z ⎧+=⎪⎨--+=⎪⎩令11z =,则11y x ==,得平面ABP的一个法向量)m =.设()222,,n x y z =为平面BCP 的法向量,则00n BP n BC ⎧⋅=⎪⎨⋅=⎪⎩,即2222220220x y z ⎧--+=⎪⎨⎪=⎩,令21x =,则221,y z ==,得平面BCP的一个法向量(n =.设平面ABP 与平面BCP 的夹角为α,则cos cos ,10m n m n m n α⋅====,所以平面ABP 与平面BCP夹角的余弦值为10.17.某植物园种植一种观赏花卉,这种观赏花卉的高度(单位:cm )介于[]15,25之间,现对植物园部分该种观赏花卉的高度进行测量,所得数据统计如图所示.(1)求a 的值;(2)若从高度在[)15,17和[)17,19中分层抽样抽取5株,在这5株中随机抽取3株,记高度在[)15,17内的株数为X ,求X 的分布列及数学期望()E X ;(3)以频率估计概率,若在所有花卉中随机抽取3株,记高度在[)15,17内的株数为Y ,求Y 的数学期望.【答案】(1)0.125a =(2)分布列见详解,65(3)0.3【解析】【分析】(1)根据题意结合频率和为1列式求解即可;(2)根据分层抽样可知高度在[)15,17和[)17,19的株数分别为2和3,结合超几何分布求分布列和期望;(3)根据题意分析可知()3,0.1Y B ~,结合二项分布的期望公式运算求解.【小问1详解】由题意可知:每组的频率依次为0.1,0.15,2,0.3,0.2a ,因为0.10.1520.30.21a ++++=,解得0.125a =.【小问2详解】由(1)可得高度在[)15,17和[)17,19的频率分别为0.1和0.15,所以分层抽取的5株中,高度在[)15,17和[)17,19的株数分别为2和3,可知X 可取0,1,2,则有:()303235C C 10C 10P X ===,()213235C C 31C 5P X ===,()123235C C 32C 10P X ===,所以X 的分布列为:X012P11035310X 的期望为()1336012105105E X =⨯+⨯+⨯=.【小问3详解】因为高度在[)15,17的频率为0.1,用频率估计概率,可知高度在[)15,17的概率为0.1,由题意可知:()3,0.1Y B ~,所以()30.10.3E Y =⨯=.18.已知椭圆2222:1(0)xy E a b a b +=>>的左焦点为F ,上顶点为B ,离心率2e =,直线FB 过点(1,2)P .(1)求椭圆E 的标准方程;(2)过点F 的直线l 与椭圆E 相交于M ,N 两点(M 、N 都不在坐标轴上),若MPF NPF =∠∠,求直线l 的方程.【答案】(1)2212x y +=;(2)550x y ++=.【解析】【分析】(1)根据给定条件,求出,,a b c 即得椭圆E 的标准方程.(2)根据给定条件,借助倾斜角的关系可得1MP NP k k ⋅=,设出直线l 的方程,与椭圆方程联立,利用韦达定理结合斜率的坐标公式求解即得.【小问1详解】令(,0)F c -,由2c e a ==,得,a b c ==,则直线FB 的斜率1k =,由直线FB 过点(1,2)P ,得直线FB 的方程为1y x =+,因此1,b c a ===所以椭圆C 的标准方程为2212x y +=.【小问2详解】设MPF NPF θ∠=∠=,直线MP 的倾斜角为β,直线NP 的倾斜角为α,由直线FP 的斜率1k =知直线FP 的倾斜角为π4,于是ππ,44αθβθ=+=+,即有π2αβ+=,显然,αβ均不等于π2,则πsin()sin 2tan tan 1πcos cos()2αααβαα-=⋅=-,即直线,MP NP 的斜率满足1MP NP k k ⋅=,由题设知,直线l 的斜率不为0,设直线l 的方程为1,1x my m =-≠,由22122x my x y =-⎧⎨+=⎩,消去x 并整理得,22(2)210m y my +--=,显然0∆>,设1122(,),(,)M x y N x y ,则12122221,22m y y y y m m +==-++,由1MP NP k k ⋅=,得121222111y y x x --⋅=--,即1212(1)(1)(2)(2)0x x y y -----=,则1212(2)(2)(2)(2)0my my y y -----=,整理得21212(1)(22)(0)m y y m y y ---+=,即2221(22)2022m m m m m --⋅--=++,于是25410m m --=,而1m ≠,解得,15m =-,所以直线l 的方程为115x y =--,即550x y ++=.【点睛】关键点点睛:本题第2问,由MPF NPF =∠∠,结合直线倾斜角及斜率的意义求得1MP NP k k ⋅=是解题之关键.19.已知函数()22ln f x x x a x =-+.(1)当2a =时,试求函数图象在点()()1,1f 处的切线方程;(2)讨论函数()f x 的单调性;(3)若函数()f x 有两个极值点1x ,2x (12x x <),且不等式()()2211m x mf x ->恒成立,其中m ∈Z ,试求整数m 的取值范围.【答案】(1)230x y --=(2)见解析(3)3m ≤-或m 1≥,且m ∈Z .【解析】【分析】(1)求当2a =时,函数的导数,求得切线的斜率和切点,由点斜式方程即可得到切线方程;(2)求出()f x 的导数,令()0f x '=,得2220x x a -+=,对判别根式讨论,令导数大于零得到增区间,令导数小于零,得到减区间;(3)函数()f x 有两个极值点1x ,2x ,由(2)可知,102a <<,构造函数1()12ln 1h x x x x x =-++-102x ⎛⎫<< ⎪⎝⎭,利用导数求得()h x 的范围,分0m >或0m <或0m <的整数,对不等式()()2211m x mf x ->分离参数,分别求解.【小问1详解】当2a =时,()222ln f x x x x =-+,故()222f x x x -'=+.故()212221f =-'+=,又()21121f =-=-,故函数图象在点()()1,1f 处的切线方程为()()121y x --=-,即230x y --=.【小问2详解】()22ln f x x x a x =-+的定义域为()0,∞+,所以()22222a x x af x x x x='-+=-+,令()0f x '=,得2220x x a -+=,(i )当480a ∆=-≤,即12a ≥时,()0f x '≥在()0,∞+上恒成立,所以函数()f x 在(0,)+∞上单调递增;(ii )当480a ∆=->,即12a <时,由2220x x a -+=,得1,212x ±=,①若102a <<,由()0f x '>,得11202x -<<或1122x +>,()f x ∴的单调递增区间是112(0,2-,1()2++∞;由()0f x '<,得11211222a a x -+<<,()f x ∴的单调递减区间是112112(22a a--+-;②若0a =,则2()2f x x x =-,函数()f x 在(0,1)上递减,在(1,)+∞上递增;③若a<0,由()0f x '<,得11202x <<,则函数()f x 在1(0,)2+上递减;由()0f x '>,得12x +>,则函数()f x 在1()2++∞上递增.综上,当12a ≥时,()f x 的单调递增区间是(0,)+∞;当102a <<时,()f x的单调递增区间是1(0,2,1(,)2++∞,单调递减区间是11(,)22+;当0a ≤时,()f x的单调递增区间是1()2++∞,单调递减区间是1(0,)2+.【小问3详解】由(2)可知,函数()f x 有两个极值点1x ,2x ,则102a <<,由()0f x '=,得2220x x a -+=,则121x x =+,1x =,21122x +=,由102a <<,可得1102x <<,2112x <<,()()()22222111111111111112221222ln 222ln 2ln 1x x x x x x x x x x f x x x a x x x x x -+--+--+===-1111112ln 1x x x x =-++-,令1()12ln 1h x x x x x =-++-102x ⎛⎫<< ⎪⎝⎭,则21()12ln (1)h x x x '=-+-,因为102x <<,1112x -<-<-,21(1)14x <-<,2141(1)x -<-<--,又2ln 0x <,所以()0h x '<,即102x <<时,()h x 单调递减,又3ln 21()22h --=,所以3()ln 2,02h x ⎛⎫∈-- ⎪⎝⎭,不等式()()2211m x mf x ->,m ∈Z 恒成立,若0m >且m ∈Z ,则()21211f x m m m m x -=->,即10m m-≥,设()1k m m m=-,()k m 在()0,∞+上单调递增,且()10k =,所以由10m m-≥可得,m 1≥且m ∈Z ,若0m <且m ∈Z ,则()21211f x m m m m x -=-<,即13ln 22m m -≤--,设()1k m m m=-,()k m 在(),0∞-上单调递增,而()10k -=,()132222k -=-+=-,()18333ln 2332k -=-+=-<--,所以3m ≤-且m ∈Z ,若0m =,则不等式()()2211m x mf x ->,m ∈Z 不成立,综上:3m ≤-或m 1≥,且m ∈Z .【点睛】方法点睛:不等式恒成立问题常见方法:①分离参数()a f x ≥恒成立(()max a f x ≥即可)或()a f x ≤恒成立(()min a f x ≤即可);②数形结合(()y f x =图象在()y g x =上方即可);③讨论最值()min 0f x ≥或()max 0f x ≤恒成立;④讨论参数,排除不合题意的参数范围,筛选出符合题意的参数范围.。
成都七中2022-2023学年度2024届高二(下)零诊模拟考试数学试题(理科)含答案

成都七中高 2024 届零诊模拟考试数学试题(理科)时间: 120 分钟 满分:150 分一、单选题:共12道小题,每题5分,共60分.1.设121iz i i-=++,则z 的虚部为 A.i B.3i C.1 D.32.直线1:10l x ay +-=与直线2:10l ax y ++=平行,则a= A.0 B.1 C.-1 D.1或-13.一组数据包括47、48、51、54、55,则这组数据的标准差为B.C.10 D.504.已知函数()f x 在其定义域R 上的导函数为()f x ',当x R ∈时,()0 f x '>是“()f x 单调递增”的 A.充要条件B.既不充分也不必要条件C.必要不充分条件D.充分不必要条件5.如图所示的算法框图思路源于我国古代数学名著《九章算术》中的“更相减相术”,执行该算法框图,若输入的a 、b 分别为36、96,则输出的a=( )A.0B.8C.12D.246.直线2x =与抛物线2:2(0)C y px p =>交于D 、E 两点,若0OD OE ⋅=,其中O 为坐标原点,则C 的准线方程为( )A.14x =-B.12x =-C.1x =-D.2x =-7.函数lg y x =的图象经过变换10:2x xy y ϕ''⎧=⎨=+⎩后得到函数()y f x ''=的图象,则()f x =A.1lg x -+B.1lg x +C.3lg x -+D.3lg x +8.有甲、乙、丙、丁四名学生参加歌唱比赛,其中只有一位获奖,有人走访了四人,甲说:“是乙或丙获奖.”乙说:“甲、丙都未获奖.”丙说:“我获奖了.”丁说:“是乙获奖.”四位歌手的话只有两句是对的,则获奖的歌手是 A.甲 B.乙 C.丙 D.丁9.设曲线C 的参数方程为1cos 1sin x y θθ=+⎧⎨=+⎩(θ为参数,且,22πθπ⎡⎤∈⎢⎥⎣⎦),曲线C 上动点P 到直线:143x y l +=的最短距离为A.0B.15C.25D.110.关于圆周率π,数学史上出现过很多有创意的求法,如著名的浦丰实验和查理斯实验.受其启发,可通过设计如下实验来估计π值:先请100名同学每人随机写下一组正实数对(x ,y),且要求x ,y 均小于1;再统计x 、y 和1作为三边长能形成钝角三角形的数对(x ,y)的个数m ;最后利用统计结果估计π值.假如某次实验结果得到m=28,那么本次实验可以将π值估计为 A.227 B.4715 C.7825 D.531711.点A 、B 在以PC 为直径的球O 的表面上,且AB BC ⊥,AB=BC=2,已知球O 的表面积是12π,设直线PB 和AC 所成角的大小为α,直线PB 和平面PAC 所成角的大小为β,四面体PABC 内切球半径为r ,下列说法中正确的个数是①BC ⊥平面PAB ;②平面PAC ⊥平面ABC ; ③sin cos αβ=:④12r > A.1 B.2 C.3 D.412.函数()1sin(11)x f x e x =--在[0,)+∞上的零点个数为A.1B.2C.3D.4二、填空题:共4道小题,每题5分,共20分.13.命题“0tan x x x ∀>>,”的否定为_____________.14.函数()cos xf x x=的图象在x π=处的切线方程为_____________.15.某区为了解全区12000名高二学生的体能素质情况,在全区高二学生中随机抽取了1000名学生进行体能测试,并将这1000名的体能测试成绩整理成如下频率分布直方图.根据此频率分布直方图,这1000名学生平均成绩的估计值为____________.16. 双曲线2222:1(,0)x y H a b a b -=>其左、右焦点分别为12,F F ,倾斜角为3π的直线2PF 与双曲线H 在第一象限交于点P ,设12F PF 内切圆半径为r ,若223PF r ≥∣,则双曲线H 的离心率的取值范围为______. 三、解答题:共5道大题,共70分.17.(12分)设函数321(1)()2(1)34f f x x x x f '-=-+-(1)求()1f '-、()1f 的值; (2)求()f x 在[0,2]上的最值.18.(12分)信创产业即信息技术应用创新产业,是一条规模庞大、体系完整的产业链,是数字经济的重要抓手之一.在政府、企业等多方面的共同努力下,中国信创产业市场规模不断扩大,市场释放出前所未有的活力.下表为2018—2022年中国信创产业规模(单位:千亿元),其中2018—2022年对应的代码依次为1~5.(1)从2018—2022年中国信创产业规模中任取2个数据,求这2个数据都大于10的概率.(2)由上表数据可知,可用指数型函数模型x y a b =⋅拟合y 与x 的关系,请建立关于x 的回归方程(a ,b 的值精确到0.01),并预测2023年中国信创产业规模能否超过20千亿元. 参考数据:其中ln i i v y =,5115i i v v ==∑参考公式:对于一组数据()11,u w ,()22,u w ,…,(),n n u w ,其回归直线ˆˆˆwu αβ=+的斜率和截距的最小二乘估计公式分别为1221ˆni ii nii u w nwunu β=-=-=-∑∑,ˆˆw u αβ=- 19.(12分)如图,三棱柱111ABC A B C -中,侧面11ACC A 为矩形,AB AC ⊥且AB=AC=2,D 为11B C 的中点,1122AA B C ==. (1)证明:1//AC 平面1A BD ;(2)求平面1AB C 与平面1AA D 所成锐二面角的余弦值20.(12分)椭圆2222:1(0)x y C a b a b+=>>上顶点为B ,左焦点为F ,中心为0.已知T 为x 轴上动点,直线BT 与椭圆C 交于另一点D ;而P 为定点,坐标为(2,3)-,直线PT 与y 轴交于点Q.当T 与F 重合时,有||||PB PT =,且2BT BP BQ =+. (1)求椭圆C 的标准方程;(2)设T 的横坐标为t ,当(0,2)t ∈时,求DTQ 面积的最大值. 21.(12分)设函数()x f x e ax =-,其中a R ∈.(1)讨论函数()f x 在[1,)+∞上的极值;(2)若函数f(x)有两零点()1212,x x x x <,且满足1211x x λλ+>+,求正实数λ的取值范围. 22.(10分)在平面直角坐标系xOy 中,以O 为极点,x 轴的正半轴为极轴,建立极坐标系,曲线C和直线l 的极坐标方程分别为2sin 2cos a ρθθ=+和sin 4x πρ⎛⎫-= ⎪⎝⎭且二者交于M ,N 两个不同点.(1)写出曲线C 和直线l 的直角坐标方程;(2)若点P 的极坐标为(2,),||||PM PN π+=a 的值.理科数学参考答案13.00x ∃>,00tan x x ≤ 14.0x y += 15.80.516.5,24⎡⎫⎪⎢⎣⎭三、解答题:共5道大题,共70分. 17.解:(1)由题设知2(1)()22f f x x x ''-=-+,取1x =-,则有(1)(1)32f f ''--=+,即(1)6f '-=: 也即3213()2(1)32f x x x x f =-+-,取1x =,则有5(1)(1)6f f =-,即5(1)12f =故(1)6f '-=,5(1)12f =.(2)由(1)知32135()23212f x x x x =-+-,2()32(1)(2)f x x x x x '=-+=--,故max 5()(1)12f x f ==,min 5()(0)12f x f ==- 18.解:(1)从2018—2022年中国信创产业规模中任取2个数据有(8.1,9.6),(8.1,11.5),(8.1,13.8),(8.1,16.7),(9.6,11.5),(9.6,13.8),(9.6,16.7),(11.5,13.8),(11.5,16.7),(13.8,16.7),共10种情况,其中这2个数据都大于10的有(11.5,13.8),(11.5,16.7),(13.8,16.7),共3种情况,所以2个数据都大于10的概率310P =(2)x y a b =⋅两边同时取自然对数得()ln ln ln ln x y a b a x b =⋅=+,则v lna xlnb =+. 因为5213, 2.45,55i i x v x ====∑,所以5152221538.5253 2.45ln 0.17755535i i i ii x v xvb xx =-=--⨯⨯===-⨯-∑∑ ·1 2.450.1773 1.919lna v x nb =-=-⨯=,所以 1.9190.177v x =+ 即ln 1.9190.177y x =+,所以 1.9190.177ˆe 6.81 1.19x x y+==⨯, 即y 关于x 的回归方程为ˆ 6.81 1.19x y=⨯. 2023年的年份代码为6,把x=6代入ˆ 6.81 1.19x y =⨯, 得66.81 1.19 6.81 2.8419.3420y =⨯=⨯≈<,所以预测2023年中国信创产业规模不会超过20千亿元. 19.公众号:高中试卷君解:(1)连接1AB 与A 、B 交于点O ,连接OD111ABC A B C -为三棱柱,11ABB A ∴为平行四边形,点O 为1AB 的中点 又D 为11B C 的中点,则1//AC OD ,又OD ⊂平面1A BD ,1AC ⊂/平面11,//A BD AC ∴平面1A BD . (2)CA AB ⊥,1CA AA ⊥,AB∩1AA A =,CA ∴⊥平面11ABB A1AB ⊂面11ABB A ,1CA AB ∴⊥ 222211(22)22AB CB AC ∴=-=-=AB=2,12AB =,122BB =,∴22211AB AB BB +=,即1AB AB ⊥以A 为坐标原点,AB ,1AB ,AC 分别为x 轴,y 轴,z 轴建立空间直角坐标系,A(0,0,0),1(2,2,0)A -,B(2,0,0),1(0,2,0)B ,1(2,2,2)C -,D(-1,2,1)1(2,2,0)AA ∴=-,1(1,0,1)A D =1AB AB ⊥,AB AC ⊥,1AB AC A ⋂=AB ∴⊥平面1AB C ,则平面1AB C 的一个法向量为1(1,0,0)n =设平面1AA D 的法向量为2(,,)n x y z =,则121200AA n A D n ⎧⋅=⎪⎨⋅=⎪⎩,即2200x y x z -+=⎧⎨+=⎩令x=1,y=1,z=-1,∴2(1,1,1)n =-,设平面1AB C 与平面1AA D 所成二面角的大小为θ1212|1cos 31n n n n θ⋅⨯∴====∴平面1AB C 与平面1AA D20.解:(1)设F(-c,0),由2BT BP BQ =+知2(-c )=-2+0,即c=1, 由||||PB PT=知2222(20))[2(1)]0)b--+=---+,即b =则a=2,故椭圆C 的标准方程为22143x y +=(2)直线BT 的方程为x y =,与22143x y +=联立,可得()222243120t y y t +-+-=,且0>,有223124D t y t -=+,即D y =直线PT 的方程为2x y +=-,令x=0,可得Q y =由sin sin 3DTQ Q DDTQPTBPTBS y y y y QT DT DTQ QT DT SSSPT BT BTP PT BT ⋅-⋅⋅∠⋅====-⋅⋅∠⋅即2224DTQt t St -=+,(0,2)t ∈ 而22214t tt -≤+,当2t +=2t =时取等,且()0,2t ∈ 故DTQ 面积的最大值为221.解:(1)由()x f x e ax =-知()x f x e a '=-,1)当a e ≤时,且有[1,)x ∈+∞,()0f x '≥,()f x 单增,故无极值;2)当a e >时,有(1,ln )x a ∈,()0f x '<,()f x 单减,而(ln ,)x a ∈+∞,()0f x '>,()f x 单增,故()(ln )ln f x f a a a a ==-极小值,()f x 无极大值.综上,当a e ≤时,()f x 无极值;当a e >时,()f x 极小值为ln a a -,()f x 无极大值.(2)由(1)可知当a e >时,(ln )(1ln )0f a a a =-<,1(00f =>),且x f x →+∞→+∞,(), 由零点存在定理可知120ln x a x <<<,而题设可知12120x x e ax e ax -=-=,消去a 可得221121x x x x x e e e x -==,令211x t x =>,且21ln t x x =-,即2ln 1t t x t =-,1ln 1t x t =-, 将其代入1211x x λλ+>+,整理可令得(1)(1)()ln 01t F t t t λλ+-=->+而()22221(1)1(1)()(1)(1)t t F t t t t t λλλλ'--+=-=++,1)当1λ≥时,且(1,)t ∈+∞,有22(1)()0(1)t F t t t λ'-≥>+,()F t 单增,F(t)>F(1)=0,满足题设; 2)当0<λ<1时,且211,t λ⎛⎫∈ ⎪⎝⎭,有()0F t '<,()F t 单减,F(t)<f(l)=0,不满足题设;综上,λ的取值范围为[1,)+∞.22.解:(1)由2sin 2cos a ρθθ=+,得22sin 2cos a ρρθρθ=+,故曲线C 的直角坐标方程为2222x y y ax +=+,即222()(1)1x a y a -+-=+;由sin 4πρθ⎛⎫-= ⎪⎝⎭sin cos 2ρθρθ-=故直线l 的直角坐标方程为2y x =+.(2)点P 的直角坐标为(-2,0),在直线l 上,而直线l的标准参数方程为2x y ⎧=-+⎪⎪⎨⎪=⎪⎩(t 为参数),将其代入2222x y y ax +=+,整理可得2)440t t a -++=. 由题设知222(3)4(44)2(1)0a a a ∆=+-+=->,解得1a ≠又12t t +=,1244t t a =+当a>-1,且a≠1时,有12,0t t >,则)12123PM PN t t t t a ++=+===+ 解得a=2;当1a ≤-时,有120t t ≤,则12121PM PN t t t t ++=-===- 得a=-4.故a 的值为2或-4..。
四川省成都市玉林中学高高二数学下期零诊试题 第1课时 集合与常用逻辑用语复习资料

第1课时集合与常用逻辑用语【知识点梳理】1.集合元素的三个特征:确定性、互异性、无序性.2.元素与集合的关系是属于或不属于关系,用符号∈或∉表示.3.集合的表示法:列举法、描述法、图示法、区间法.4.集合间的基本关系对任意的x∈A,都有x∈B,则A⊆B(或B⊇A).若A⊆B,且在B中至少有一个元素x∈B,但x∉A,则A B(或B A).若A⊆B且B⊆A,则A=B.5.集合的运算及性质设集合A,B,则A∩B={x|x∈A且x∈B},A∪B={x|x∈A或x∈B}.设全集为U,则∁U A={x|x∈U且x∉A}.A∩∅=∅,A∩B⊆A,∩⊆,A∩B=A⇔A⊆B.A∪∅=A,A∪B⊇A,A∪B⊇B,A∪B=B⇔A⊆B.A∩∁U A=∅;A∪∁U A=U.6.命题用语言、符号或式子表达的,可以判断真假的陈述句叫做命题,其中判断为真的语句叫做真命题,判断为假的语句叫做假命题.7.四种命题及其关系(1)四种命题一般地,用p和q分别表示原命题的条件和结论,用¬p和¬q分别表示p和q的否定,于是四种命题的形式就是原命题:若p则q(p⇒q);逆命题:若q则p(q⇒p);否命题:若¬p则¬q(¬p⇒¬q);逆否命题:若¬q则¬p(¬q⇒¬p).(2)四种命题间的关系(3)四种命题的真假性①两个命题互为逆否命题,它们有相同的真假性.②两个命题为逆命题或否命题,它们的真假性没有关系.8.充分条件与必要条件若p⇒q,则p叫做q的充分条件;若q⇒p,则p叫做q的必要条件;如果p⇔q,则p 叫做q的充要条件.9.逻辑联结词命题中的或,且,非叫做逻辑联结词.“p且q”记作p∧q,“p或q”记作p∨q,“非p”记作¬p.10.命题p∧q,p∨q,¬11.全称量词与存在量词(1)短语“所有的”“任意一个”在逻辑中通常叫做全称量词,并用符号“∀”表示.含有全称量词的命题,叫做全称命题,可用符号简记为∀x∈M,p(x),它的否定∃x∈M,綈p (x ).(2)短语“存在一个”“至少有一个”在逻辑中通常叫做存在量词,并用符号“∃”表示.含有存在量词的命题,叫做特称命题,可用符号简记为∃x ∈M ,p (x ),它的否定∀x ∈M ,¬p (x ).【课堂讲解】1.集合的运算例1 设全集是实数集R ,A ={x |2x 2-7x +3≤0},B ={x |x 2+a <0}.(1)当a =-4时,求A ∩B 和A ∪B ;(2)若(∁R A )∩B =B ,求实数a 的取值范围.解题导引 解决含参数问题的集合运算,首先要理清题目要求,看清集合间存在的相互关系,注意分类讨论、数形结合思想的应用以及空集的特殊性.解 (1)A ={x |12≤x ≤3}. 当a =-4时,B ={x |-2<x <2},∴A ∩B ={x |12≤x <2}, A ∪B ={x |-2<x ≤3}.(2)∁R A ={x |x <12或x >3}. 当(∁R A )∩B =B 时,B ⊆∁R A ,即A ∩B =∅.①当B =∅,即a ≥0时,满足B ⊆∁R A ;②当B ≠∅,即a <0时,B ={x |--a <x <-a },要使B ⊆∁R A ,需-a ≤12, 解得-14≤a <0. 综上可得,a 的取值范围为a ≥-14. 变式迁移3 (2011·阜阳模拟)已知A ={x ||x -a |<4},B ={x ||x -2|>3}.(1)若a =1,求A ∩B ;(2)若A ∪B =R ,求实数a 的取值范围.解 (1)当a =1时,A ={x |-3<x <5},B ={x |x <-1或x >5}.∴A ∩B ={x |-3<x <-1}.(2)∵A ={x |a -4<x <a +4},B ={x |x <-1或x >5},且A ∪B =R ,∴⎩⎪⎨⎪⎧a -4<-1a +4>5⇒1<a <3. ∴实数a 的取值范围是(1,3).2.充要条件的探索已知两个关于x 的一元二次方程mx 2-4x +4=0和x 2-4mx +4m 2-4m -5=0,且m ∈Z .求两方程的根都是整数的充要条件.解 ∵mx 2-4x +4=0是一元二次方程,∴m ≠0. [2分]另一方程为x 2-4mx +4m 2-4m -5=0,两方程都要有实根,∴⎩⎪⎨⎪⎧ Δ1=-m ,Δ2=16m 2-m 2-4m -,解得m ∈[-54,1]. [6分]∵两根为整数,故和与积也为整数,∴⎩⎪⎨⎪⎧ 4m∈Z 4m ∈Z 4m 2-4m -5∈Z ,∴m 为4的约数, [8分]∴m =-1或1,当m =-1时,第一个方程x 2+4x -4=0的根为非整数,而当m =1时,两方程均为整数根,∴两方程的根均为整数的充要条件是m =1. [12分]【突破思维障碍】本题涉及到参数问题,先用转化思想将生疏复杂的问题化归为简单、熟悉的问题解决,两方程有实根易想Δ≥0.求出m 的范围,要使两方程根都为整数可转化为它们的两根之和与两根之积都是整数.【易错点剖析】易忽略一元二次方程这个条件隐含着m ≠0,不易把方程的根都是整数转化为两根之和与两根之积都是整数.3.全称命题与特称命题的否定例3写出下列命题的“否定”,并判断其真假.(1)p :∀x ∈R ,x 2-x +14≥0; (2)q :所有的正方形都是矩形;(3)r :∃x ∈R ,x 2+2x +2≤0;(4)s :至少有一个实数x ,使x 3+1=0.解题导引 (1)全(特)称命题的否定与一般命题的否定有着一定的区别,全(特)称命题的否定是将其全称量词改为存在量词(或把存在量词改为全称量词),并把结论否定;而一般命题的否定则是直接否定结论即可.(2)要判断“綈p ”命题的真假,可以直接判断,也可以判断p 的真假.因为p 与綈p 的真假相反且一定有一个为真,一个为假.解 (1)綈p :∃x ∈R ,x 2-x +14<0,这是假命题, 因为∀x ∈R ,x 2-x +14=(x -12)2≥0恒成立,即p 真,所以綈p 假. (2)綈q :至少存在一个正方形不是矩形,是假命题.(3)綈r :∀x ∈R ,x 2+2x +2>0,是真命题,这是由于∀x ∈R ,x 2+2x +2=(x +1)2+1≥1>0成立.(4)綈s :∀x ∈R ,x 3+1≠0,是假命题,这是由于x =-1时,x 3+1=0.变式迁移3 (2009·天津)命题“存在x 0∈R,2x 0≤0”的否定是( )A .不存在x 0∈R,2x 0>0B .存在x 0∈R,2x 0≥0C .对任意的x ∈R,2x ≤0D .对任意的x ∈R,2x >0答案 D解析 本题考查全称命题与特称命题的否定.原命题为特称命题,其否定应为全称命题,而“≤”的否定是“>”,所以其否定为“对任意的x ∈R,2x >0”.4.全称与特称量词的应用例4已知命题p :“∀x ∈[1,2],x 2-a ≥0”,命题q :“∃x 0∈R ,x 20+2ax 0+2-a =0”,若命题“p 且q ”是真命题,求实数a 的取值范围.【答题模板】解 由“p 且q ”是真命题,则p 为真命题,q 也为真命题. [3分]若p 为真命题,a ≤x 2恒成立,∵x ∈[1,2],∴a ≤1. [6分]若q 为真命题,即x 2+2ax +2-a =0有实根,Δ=4a 2-4(2-a )≥0,即a ≥1或a ≤-2, [10分]综上,所求实数a 的取值范围为a ≤-2或a =1. [12分]【突破思维障碍】含有逻辑联结词的命题要先确定构成命题的(一个或两个)命题的真假,求出参数存在的条件,命题p 转化为恒成立问题,命题q 转化为方程有实根问题,最后再求出含逻辑联结词的命题成立的条件.若直接求p 成立的条件困难,可转化成求綈p 成立的条件,然后取补集.【易错点剖析】“p 且q ”为真是全真则真,要区别“p 或q ”为真是一真则真,命题q 就是方程x 2+2ax+2-a =0有实根,所以Δ≥0.不是找一个x 0使方程成立.【课后检测】(每个题后附答案,最好能附详细解答,8选+5填+3解答)一.选择题1. (2010·北京)集合P ={x ∈Z |0≤x <3},M ={x ∈Z |x 2≤9},则P ∩M 等于( )A .{1,2}B .{0,1,2}C .{1,2,3}D .{0,1,2,3}答案 B解析 由题意知:P ={0,1,2},M ={-3,-2,-1,0,1,2,3},∴P ∩M ={0,1,2}.2.(2010·天津)设集合A ={x ||x -a |<1,x ∈R },B ={x |1<x <5,x ∈R }.若A ∩B =∅,则实数a 的取值范围是( )A .{a |0≤a ≤6}B .{a |a ≤2或a ≥4}C .{a |a ≤0或a ≥6}D .{a |2≤a ≤4}答案 C解析 由|x -a |<1得-1<x -a <1,即a -1<x <a +1.由图可知a +1≤1或a -1≥5,所以a ≤0或a ≥6.3.设全集U 是实数集R ,M ={x |x 2>4},N ={x |2x -1≥1},则右图中阴影部分所表示的集合是( )A.{x|-2≤x<1} B.{x|-2≤x≤2}C.{x|1<x≤2} D.{x|x<2}答案 C解析题图中阴影部分可表示为(∁U M)∩N,集合M为{x|x>2或x<-2},集合N为{x|1<x≤3},由集合的运算,知(∁U M)∩N={x|1<x≤2}.4.关于命题“若抛物线y=ax2+bx+c的开口向下,则{x|ax2+bx+c<0}≠∅”的逆命题、否命题、逆否命题,下列结论成立的是( )A.都真 B.都假C.否命题真 D.逆否命题真答案 D解析本题考查四种命题之间的关系及真假判断.对于原命题:“若抛物线y=ax2+bx+c的开口向下,则{x|ax2+bx+c<0}≠∅”,这是一个真命题,所以其逆否命题也为真命题,但其逆命题:“若{x|ax2+bx+c<0}≠∅,则抛物线y=ax2+bx+c的开口向下”是一个假命题,因为当不等式ax2+bx+c<0的解集非空时,可以有a>0,即抛物线的开口可以向上.因此否命题也是假命题.5.(2011·枣庄模拟)集合A={x||x|≤4,x∈R},B={x|x<a},则“A⊆B”是“a>5”的( )A.充分不必要条件 B.必要不充分条件C.充要条件 D.既不充分也不必要条件答案 B解析A={x|-4≤x≤4},若A⊆B,则a>4,a>4a>5,但a>5⇒a>4.故选B.4.6.(2011·龙岩月考)已知条件p:|x+1|>2,条件q:x>a,且¬p是¬q的充分不必要条件,则a的取值范围是( )A.a≥1 B.a≤1C.a≥-3 D.a≤-3答案 A解析¬p是¬q的充分不必要条件的等价命题为q是p的充分不必要条件,即q⇒p,而p q,条件p化简为x>1或x<-3,所以当a≥1时,q⇒p.7.已知命题“∀a,b∈R,如果ab>0,则a>0”,则它的否命题是( )A.∀a,b∈R,如果ab<0,则a<0B.∀a,b∈R,如果ab≤0,则a≤0C.∃a,b∈R,如果ab<0,则a<0D.∃a,b∈R,如果ab≤0,则a≤0答案 B解析∀a,b∈R是大前堤,在否命题中也不变,又因ab>0,a>0的否定分别为ab≤0,a≤0,故选B.8.(2011·宁波调研)下列有关命题的说法正确的是( )A.命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1”B.“x=-1”是“x2-5x-6=0”的必要不充分条件C.命题“∃x∈R,使得x2+x+1<0”的否定是“∀x∈R,均有x2+x+1<0”D.命题“若x=y,则sin x=sin y”的逆否命题为真命题答案 D二.填空题9.(2010·江苏)设集合A={-1,1,3},B={a+2,a2+4},A∩B={3},则实数a=____.答案 1解析∵3∈B,由于a2+4≥4,∴a+2=3,即a=1.10.(2011·惠州模拟)已知p :(x -1)(y -2)=0,q :(x -1)2+(y -2)2=0,则p 是q 的____________条件.答案 必要不充分解析 由(x -1)(y -2)=0得x =1或y =2,由(x -1)2+(y -2)2 =0得x =1且y =2,所以由q 能推出p ,由p 推不出q, 所以填必要不充分条件.11.(2010·安徽)命题“对∀x ∈R ,|x -2|+|x -4|>3”的否定是______________.答案 ∃x ∈R ,|x -2|+|x -4|≤312.(2009·天津)设全集U =A ∪B ={x ∈N *|lg x <1},若A ∩(∁U B )={m |m =2n +1,n =0,1,2,3,4},则集合B =________.答案 {2,4,6,8}解析 A ∪B ={x ∈N *|lg x <1}={1,2,3,4,5,6,7,8,9},A ∩(∁U B )={1,3,5,7,9},∴B ={2,4,6,8}.13.已知命题p :“∀x ∈R ,∃m ∈R 使4x -2x +1+m =0”,若命题¬p 是假命题,则实数m 的取值范围为__________.答案 m ≤1解析 命题綈p 是假命题,即命题p 是真命题,也就是关于x 的方程4x -2x +1+m =0有实数解,即m =-(4x -2x +1),令f (x )=-(4x -2x +1),由于f (x )=-(2x -1)2+1,所以当x-Ray时f (x )≤1,因此实数m 的取值范围是m ≤1.三.解答题14. (2011·岳阳模拟)已知集合A ={x |x -5x +1≤0},B ={x |x 2-2x -m <0}, (1)当m =3时,求A ∩(∁R B );(2)若A ∩B ={x |-1<x <4},求实数m 的值.解 由x -5x +1≤0, 所以-1<x ≤5,所以A ={x |-1<x ≤5}.(3分)(1)当m =3时,B ={x |-1<x <3},则∁R B ={x |x ≤-1或x ≥3},(6分)所以A ∩(∁R B )={x |3≤x ≤5}.(10分)(2)因为A ={x |-1<x ≤5},A ∩B ={x |-1<x <4},(12分)所以有42-2×4-m =0,解得m =8.此时B ={x |-2<x <4},符合题意,故实数m 的值为8.(14分)15. 已知数列{a n }的前n 项和S n =p n +q (p ≠0,且p ≠1),求证:数列{a n }为等比数列的充要条件为q =-1.证明 充分性:当q =-1时,a 1=S 1=p +q =p -1.(2分)当n ≥2时,a n =S n -S n -1=p n -1(p -1).当n =1时也成立.(4分)于是a n +1a n =p n p -p n -1p -=p (n ∈N *), 即数列{a n }为等比数列.(6分)必要性:当n =1时,a 1=S 1=p +q .当n ≥2时,a n =S n -S n -1=p n -1(p -1).∵p ≠0,p ≠1,∴a n +1a n =p n p -p n -1p -=p .(10分) ∵{a n }为等比数列,∴a 2a 1=a n +1a n =p ,即p p -p +q=p , 即p -1=p +q .∴q =-1.(13分)综上所述,q =-1是数列{a n }为等比数列的充要条件.(14分)16. 命题p :关于x 的不等式x 2+2ax +4>0对一切x ∈R 恒成立,q :函数f (x )=(3-2a )x 是增函数,若p 或q 为真,p 且q 为假,求实数a 的取值范围.解 设g (x )=x 2+2ax +4,由于关于x 的不等式x 2+2ax +4>0对一切x ∈R 恒成立,所以函数g (x )的图象开口向上且与x 轴没有交点,故Δ=4a 2-16<0,∴-2<a <2.(4分)又∵函数f (x )=(3-2a )x 是增函数,∴3-2a >1,∴a <1.(6分)又由于p 或q 为真,p 且q 为假,可知p 和q 一真一假.(1)若p 真q 假,则⎩⎪⎨⎪⎧-2<a <2,a ≥1, ∴1≤a <2;(8分)(2)若p 假q 真,则⎩⎪⎨⎪⎧a ≤-2,或a ≥2,a <1,∴a ≤-2.(10分) 综上可知,所求实数a 的取值范围为1≤a <2,或a ≤-2.(12分)。
四川省成都市玉林中学高高二数学下期零诊试题 第13课时 数列的概念与简单表示法复习资料

第13课时 数列的概念与简单表示法【知识点梳理】 1.数列的定义按________________着的一列数叫数列,数列中的______________都叫这个数列的项;在函数意义下,数列是________________________的函数,数列的一般形式为:______________________,简记为{a n },其中a n 是数列的第____项. 2.通项公式:如果数列{a n }的______与____之间的关系可以____________来表示,那么这个式子叫做数列的通项公式.但并非每个数列都有通项公式,也并非都是唯一的. 3.数列常用表示法有:_________、________、________. 4.数列的分类: 数列按项数来分,分为____________、__________;按项的增减规律分为________、________、__________和__________.递增数列⇔a n +1______a n ;递减数列⇔a n +1______a n ;常数列⇔a n +1______a n .5.a n 与S n 的关系:已知S n ,则a n =⎩⎪⎨⎪⎧,n =1,,n ≥2.【课堂讲解】例1.在数列{a n }中,a 1=1,a n +1=a n +2n -1,求a n . 解析 由a n +1=a n +2n -1,得a n +1-a n =2n -1.所以a 2-a 1=1,a 3-a 2=2,a 4-a 3=22, a 5-a 4=23,…a n -a n -1=2n -2(n ≥2),将以上各式左右两端分别相加,得a n -a 1=1+2+22+…+2n -2=2n -1-1,所以a n =2n -1(n ≥2),又因为a 1=1适合上式,故a n =2n -1(n ≥1).例2:已知数列{a n }的通项a n =(n +1)⎝ ⎛⎭⎪⎫1011n (n ∈N *),试问该数列{a n }有没有最大项?若有,求出最大项的项数;若没有,说明理由.解 方法一 令⎩⎪⎨⎪⎧n +⎝ ⎛⎭⎪⎫1011n ≥n ·⎝ ⎛⎭⎪⎫1011n -1n +⎝ ⎛⎭⎪⎫1011n n +⎝ ⎛⎭⎪⎫1011n +1⇔⎩⎪⎨⎪⎧ 10n +10≥11n 11n +11≥10n +20⇔⎩⎪⎨⎪⎧n ≤10n ≥9,∴n =9或n =10时,a n 最大, 即数列{a n }有最大项,此时n =9或n =10.方法二 ∵a n +1-a n =(n +2)·⎝ ⎛⎭⎪⎫1011n +1-(n +1)·⎝ ⎛⎭⎪⎫1011n=⎝ ⎛⎭⎪⎫1011n ·9-n 11 当n <9时,a n +1-a n >0,即a n +1>a n ; 当n =9时,a n +1-a n =0,即a n +1=a n ; 当n >9时,a n +1-a n <0,即a n +1<a n . 故a 1<a 2<a 3<…<a 9=a 10>a 11>a 12>…,∴数列{a n }中有最大项,为第9、10项.例3. 已知各项均为正数的数列{a n }的前n 项和满足S n >1,且6S n =(a n +1)(a n +2),n ∈N *.求{a n }的通项公式.解析 由a 1=S 1=16(a 1+1)(a 1+2),解得a 1=1或a 1=2,由已知a 1=S 1>1,因此a 1=2. 又由a n +1=S n +1-S n=16(a n +1+1)(a n +1+2)-16(a n +1)(a n +2), 得a n +1-a n -3=0或a n +1=-a n . 因a n >0,故a n +1=-a n 不成立,舍去. 因此a n +1-a n -3=0.即a n +1-a n =3,从而{a n }是公差为3,首项为2的等差数列,故{a n }的通项为a n =3n -1.例4.(1)已知{a n }的前n 项和S n =3n+b ,求{a n }的通项公式.(2)已知在正项数列{a n }中,S n 表示前n 项和且2S n =a n +1,求a n . 解 (1)a 1=S 1=3+b ,当n ≥2时,a n =S n -S n -1=(3n +b )-(3n -1+b )=2·3n -1. 当b =-1时,a 1适合此等式; 当b ≠-1时,a 1不适合此等式.∴当b =-1时,a n =2·3n -1;当b ≠-1时,a n =⎩⎪⎨⎪⎧3+b (n =1)2·3n -1(n ≥2). (2)由2S n =a n +1,得S n =⎝⎛⎭⎪⎫a n +122,当n =1时,a 1=S 1=⎝ ⎛⎭⎪⎫a 1+122,得a 1=1;当n ≥2时,a n =S n -S n -1 =⎝ ⎛⎭⎪⎫a n +122-⎝ ⎛⎭⎪⎫a n -1+122, 整理,得(a n +a n -1)(a n -a n -1-2)=0, ∵数列{a n }各项为正,∴a n +a n -1>0. ∴a n -a n -1-2=0.∴数列{a n }是首项为1,公差为2的等差数列. ∴a n =a 1+(n -1)×2=2n -1. 【课后检测】(每个题后附答案,最好能附详细解答,8选+5填+3解答) 一.选择题1.设数列{a n }的前n 项和S n =n 2,则a 8的值为 ( A )A .15B .16C .49D .642.已知数列{a n }的通项公式是a n =2n3n +1,那么这个数列是 ( A )A .递增数列B .递减数列C .摆动数列D .常数列 3.已知数列{a n }的前n 项和为S n ,且S n =2(a n -1),则a 2等于 ( A )A .4B .2C .1D .-2 4.(2011·烟台模拟)数列{a n }中,若a n +1=a n2a n +1,a 1=1,则a 6等于 ( D )A .13 B.113 C .11 D.1115.数列{a n }满足a n +a n +1=12 (n ∈N *),a 2=2,S n 是数列{a n }的前n 项和,则S 21为 ( B )A .5 B.72 C.92 D.1326.数列{a n }:1,-58,715,-924,…的一个通项公式是( )A .a n =(-1)n +12n -1n 2+n (n ∈N +)B .a n =(-1)n -12n +1n 3+3n (n ∈N +)C .a n =(-1)n +12n -1n 2+2n (n ∈N +)D .a n =(-1)n -12n +1n 2+2n(n ∈N +)解析 观察数列{a n }各项,可写成:31×3,-52×4,73×5,-94×6,故选D.答案 D7.把1,3,6,10,15,21这些数叫做三角形数,这是因为这些数目的点子可以排成一个正三角形(如图所示).则第七个三角形数是( ). A .27B .28C .29D .30解析 观察三角形数的增长规律,可以发现每一项与它的前一项多的点数正好是本身的序号,所以根据这个规律计算即可.根据三角形数的增长规律可知第七个三角形数是1+2+3+4+5+6+7=28. 答案 B8.设数列{a n }满足:a 1=2,a n +1=1-1a n,记数列{a n }的前n 项之积为Πn ,则Π 2 011的值为( )A .-12B .-1 C.12D .2解析:由a 2=12,a 3=-1,a 4=2可知,数列{a n }是周期为3的周期数列,从而Π 2 011=Π1=2. 答案:D 二.填空题9. 数列{a n }满足a n +1=⎩⎪⎨⎪⎧2a na n <12,2a n-112≤a n ,若a 1=67,则a 2 010的值为________.3710.已知S n 是数列{a n }的前n 项和,且有S n =n 2+1,则数列{a n }的通项a n =__________________.⎩⎪⎨⎪⎧2 (n =1)2n -1 (n ≥2,n ∈N *) 11.将全体正整数排成一个三角形数阵:1 2 3 4 5 6 7 8 9 10 11 12 13 14 15… … … … … …根据以上排列规律,数阵中第n (n ≥3)行从左至右的第3个数是____________.n 2-n +6212. 已知数列{}n a 的前n 项和为n S ,11a =,12n n S a +=,,则n S =1)23(-=n n S解析 因为n n n S S a -=++11,所以由12+=n n a S 得,)(21n n n S S S -=+,整理得123+=n n S S ,所以231=+n n S S ,所以数列}{n S 是以111==a S 为首项,公比23=q 的等比数列,所以1)23(-=n n S13. 已知数列{a n }的通项公式为a n =(n +2)(78)n,则当a n 取得最大值时,n 等于________.解析:由题意知⎩⎪⎨⎪⎧a n ≥a n -1,a n ≥a n +1,∴⎩⎪⎨⎪⎧n +78nn +78n -1,n +78n n +78n +1.∴⎩⎪⎨⎪⎧n ≤6,n ≥5.∴n =5或6.答案:5或6 三.解答题14. 数列{a n }的通项公式是a n =n 2-7n +6. (1)这个数列的第4项是多少?(2)150是不是这个数列的项?若是这个数列的项,它是第几项? (3)该数列从第几项开始各项都是正数? 解析:(1)当n =4时,a 4=42-4×7+6=-6.(2)令a n =150,即n 2-7n +6=150,解得n =16,即150是这个数列的第16项. (3)令a n =n 2-7n +6>0,解得n >6或n <1(舍),∴从第7项起各项都是正数.15. 已知数列{a n }的前n 项和S n =2n 2-3n +1,求{a n }的通项公式. 解 当n =1时,a 1=S 1=2×12-3×1+1=0;当n ≥2时,a n =S n -S n -1=(2n 2-3n +1)-2(n -1)2+3(n -1)-1=4n -5; 又n =1时,a n =4×1-5=-1≠a 1,∴a n =⎩⎪⎨⎪⎧0, n =1,4n -5, n ≥2.16根据下列条件,确定数列{a n }的通项公式. (1)a 1=1,a n +1=3a n +2; (2)a 1=1,a n +1=(n +1)a n ;(3)a 1=2,a n +1=a n +ln ⎝⎛⎭⎪⎫1+1n ..解 (1)∵a n +1=3a n +2,∴a n +1+1=3(a n +1),∴a n +1+1a n +1=3, ∴数列{a n +1}为等比数列,公比q =3, 又a 1+1=2,∴a n +1=2·3n -1,∴a n =2·3n -1-1.(2)∵a n +1=(n +1)a n ,∴a n +1a n=n +1.∴a n a n -1=n ,a n -1a n -2=n -1, ……a 3a 2=3, a 2a 1=2, a 1=1.累乘可得,a n =n ×(n -1)×(n -2)×…×3×2×1=n !. 故a n =n !.(3)∵a n +1=a n +ln ⎝ ⎛⎭⎪⎫1+1n ,∴a n +1-a n =ln ⎝ ⎛⎭⎪⎫1+1n =ln n +1n.∴a n -a n -1=lnnn -1,a n -1-a n -2=ln n -1n -2,……a 2-a 1=ln 21,累加可得,a n -a 1=lnnn -1+ln n -1n -2+…+ln 21=ln n -ln(n -1)+ln(n -1)-ln(n -2)+…+ln 2-ln 1 =ln n .又a 1=2,∴a n =ln n +2.。
2023-2024学年四川省成都实验外国语学校高二(下)零诊数学试卷(含答案)

2023-2024学年四川省成都实验外国语学校高二(下)零诊数学试卷一、单选题:本题共8小题,每小题5分,共40分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.设等差数列{a n}的前n项和为S n,已知a2+2a4+a10=68,则S9=( )A. 272B. 270C. 157D. 1532.直线l:x+y=1,圆C:x2+y2−2x−2y−2=0.则直线l被圆C所截得的弦长为( )A. 2B. 23C. 27D. 143.若f′(x)是函数f(x)的导函数,f(x)=x22+3xf′(3),则f′(−3)=( )A. −152B. −92C. 32D. 1524.某校举办了数学知识竞赛,并将1000名学生的竞赛成绩(满分100分,成绩取整数)整理成如图所示的频率分布直方图,则以下四个说法正确的个数为( )①a的值为0.005②估计这组数据的众数为75③估计这组数据的下四分位数为60④估计成绩高于80分的有300人A. 1B. 2C. 3D. 45.已知数列{a n}满足a1=1,a na n−1=n−1n,(n≥2),则a n=( )A. n−1B. 1n−1C. n D. 1n6.设函数f(x)=2x−2x−alnx在(1,2)上单调递减,则实数a的取值范围是( )A. [4,5]B. (5,+∞)C. [4,+∞)D. [5,+∞)7.某学校有A,B两家餐厅,王同学第1天午餐时随机地选择一家餐厅用餐.如果第1天去A餐厅,那么第2天去A餐厅的概率为0.6;如果第1天去B餐厅,那么第2天去A餐厅的概率为0.4.计算王同学第2天去A餐厅用餐的概率( )A. 0.24B. 0.36C. 0.5D. 0.528.设函数f(x)=e x (2x−1)−ax +a ,其中a <1,若存在唯一的整数x 0,使得f(x 0)<0,则a 的取值范围是( )A. [−32e ,1)B. [−32e ,34)C. [32e ,34)D. [32e ,1)二、多选题:本题共3小题,共18分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
零诊复习资料(仅供7班使用) 第2讲函数的性质【知识梳理】一、单调性1.定义:设D 是函数()f x 定义域的子区间,对任意12,x x D ∈,当12x x <时: (1)都有()()12f x f x <⇔()f x 在区间D 上是增函数; (2) 都有()()12f x f x >⇔()f x 在区间D 上是减函数.2.判定:(1)定义法;(2)图象法:(3)结论法(所学初等函数的单调性); (4)复合函数的单调性:同增异减,小心范围.3.用定义证单调性的步骤:任取——作差——变形——定号——结论. 二、奇偶性1.定义:对函数()f x 定义域内的任意x : (1)都有()()f x f x -=-⇔()f x 为奇函数; (2)都有()()f x f x -=⇔()f x 为偶函数.点拨:奇、偶函数的定义域关于原点对称.2.性质:(1)奇函数()f x ⇔图象关于原点对称;若()0f 有意义,则()00f =; (2)偶函数()f x ⇔图象关于y 轴对称()()f x f x ⇔=;(3)在关于原点对称的两个区间上:奇函数同单调;偶函数异单调.3.用定义判奇偶性的步骤:求定义域——定()f x -与()f x 的关系——下结论. 三、对称性:轴对称,中心对称.对函数()f x 的定义域内的任何一个自变量x :1.若都有()()f a x f a x -=+,则()f x 的图象关于直线x a =对称;若都有()()f a x f b x -=+,则()f x 的图象关于直线2a bx +=对称。
2.若都有()()f a x f a x -=-+,则()f x 的图象关于点(),0a 对称;若都有()()f a x f b x -=-+,则()f x 的图象关于点,02a b +⎛⎫⎪⎝⎭对称。
若都有()()22f x f a x b +-=,则()y f x =的图象关于点(),a b 对称.四、周期性1.定义:如果存在非零常数T ,对函数()f x 定义域内任意的x ,都有()()f x T f x +=,则称函数()f x 是周期函数,T 是它的一个周期.2.性质:(1)若T 是()f x 的一个周期,则(),0kT k Z k ∈≠也是()f x 的周期; (2)若T 是()f x 的一个周期,则()f x ω()0ω≠是周期函数,且一个周期是||ωT.3.结论:(1)若()y f x =图象有两条对称轴,()x a x b a b ==≠,则()y f x =必是周期函数,且一周期为2||T a b =-;(2)若()y f x =图象有两个对称中心(,0),(,0)()A a B b a b ≠,则()y f x =是周期函数,且一周期为2||T a b =-;(3)如果函数()y f x =的图象有一个对称中心(,0)A a 和一条对称轴()x b a b =≠,则函数()y f x =必是周期函数,且一周期为4||T a b =-;(4)若函数()f x 满足下列条件之一,则()f x 是周期函数,且一个周期为2T a =()0a ≠:①()()f a x f x +=-;②1()()f x a f x +=;③1()()f x a f x +=-.例2.(1)若定义在R 上的奇函数()f x 以T 为周期,则函数()f x 在区间[,]T T -上至少有 5个零点.(2)函数()f x 的定义域为R ,若()1f x +和()1f x -都是奇函数,则函数()()g x f x =,{}1,1,3,5x ∈-的值域是{}0.(3)定义在R 上的偶函数()f x 满足(2)()f x f x +=-,且在[6,4]--上是增函数,在锐角ABC ∆中,令(sin sin )m f A B =+,(cos cos )n f A C =+,则m 和n 的大小关系为_______m n <.(4)函数()12sin 1f x x x π=+-在区间[]2,4-上的所有零点之和等于8.(5)设()f x 是连续的偶函数,且在()0,+∞是单调函数,则方程()34x f x f x +⎛⎫= ⎪+⎝⎭所有根之和为8-.第3讲初等函数【知识梳理】1.指数与对数的运算性质: (1)指数式与对数式的互化:log (0,1,0)b a a N b N a a N =⇔=>≠>。
(2)对数的运算性质()0,1,0,0a a M N >≠>>:①恒等式:N a N a =log ;log b a a b =。
②()log log log a a a MN M N =+;log log log a a a MM N N=-;log log n a a M n M =。
③换底公式及推论:log log log c a c b b a =;log log n m a a mb b n=;log log n n a a b b =;1log log a b b a =。
2x y a a a =>≠log (0,1)y x a a =>≠点拨:y a =与log (0,1)a y x a a =>≠互为反函数,其图象关于y x =对称。
3.y x α=(Q α∈)例1.(1)若,518,9log 18==ba 用a 和b 表示45log 36=(2)已知2(3)4log 3233.5x f x =+,则8(2)(4)(8)(2)f f f f ++++=L _______(3)已知函数()lg ,010,16,10.2x x f x x x ⎧<≤⎪=⎨-+>⎪⎩若,,a b c 互不相等,且()()()f a f b f c ==,则abc 的取值范围是()10,12.解:(1)18185log 5bb =⇒=,又18log 9a =,()1818183618181818log 45log 9log 5log 4518log 36log 92log 22122log 9a ba b a ba a aa ++++∴=====++--+。
(2)令23k x =,则222log 3log 34log 34xk x x k ==⇒=故8(2)(4)(8)(2)f f f f ++++=L ()412388233.52012+++++⨯=L (3)设0a b c <<<,如图有:例5.已知函数)32(log )(221+-=ax x x f(1)若()f x 的定义域为R ,求实数a(2)若()f x 的值域为R ,求实数a (3)若()f x 在]1,(-∞内为增函数,求实数a 解:令223u x ax =-+,12log y u =。
(1)()f x 的定义域为R 2230x ax ⇔-+>恒成立。
(24120a a a ∴∆=-<⇔∈。
(2)()f x 的值域为R 223u x ax ⇔=-+能取()0,+∞的一切值()0,u ⇔+∞⊆的值域,()24120,a a a ∴∆=-≥⇔∈-∞+∞U 。
(3)()f x 在]1,(-∞内为增函数223u x ax ⇔=-+在]1,(-∞内递减且恒正,[)min111,24202a a a u a a ≥≥⎧⎧∴⇔⇔∈⎨⎨=-><⎩⎩。
第4讲函数与方程【知识梳理】1.函数零点的定义:对于函数()y f x =()x D ∈,把使()0f x =成立的实数x 叫做函数()y f x =()x D ∈的零点.2.等价关系:方程()0f x =有实数根?函数()y f x =的图像与x 轴有交点?函数()y f x =有零点.3.零点存在性定理:如果函数()y f x =在区间[],a b 上的图像是连续不断的一条曲线,并且有()()0f a f b ⋅<,那么函数()y f x =在区间(),a b 内有零点,即存在(),c a b ∈,使得()0f c =,这个c 也就是()0f x =的根.(定理之逆不成立) 推论:若()y f x =在区间[],a b 上是连续的单调函数,并且有()()0f a f b ⋅<,则函数()y f x =在区间(),a b 内有唯一零点。
4.二分法:对于在区间[],a b 上连续不断,且()()0f a f b ⋅<的函数()y f x =,通过不断地把函数()f x 的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法.口诀:定区间,找中点,中值计算两边看;同号去,异号算,零点落在异号间; 周而复始怎么办?精确度上来判断.点拨:连续的异号零点可用二分法求其近似值。
【典例精析】例6.(1)已知1x 是函数()25x f x x =+-的零点,2x 是函数()2log 5g x x x =+-的零点.则12x x +=5;(2)已知1x 是()225x f x x =+-函数的零点,2x 是函数()()22log 125g x x x =-+-的零点.则12x x +=72解:(1)()()2225025log 5log 50xx f x x x x x g x x x ⎧=+-=⎧=-+⎪⇔⎨⎨=-+=+-=⎪⎩⎩由图(1)知12x x +=5.(2)()()()()122522250252log 1250log 12x xx f x x g x x x x x -⎧=-+⎪⎧=+-=⎪⎪⇔⎨⎨=-+-=⎪⎪⎩-=-+⎪⎩由图(2)知12x x +=72第6讲三角函数【知识梳理】1.象限角与轴线角2.定义()0r => 3.单位圆与三角函数线 思考1:sin 1αα=⇔=;sin 1αα=-⇔=;cos 1αα=⇔=;cos 1αα=-⇔=4.同角关系:(1)平方关系:22sin cos 1αα+=;(2)商数关系:sin tan cos ααα=; 5.诱导公式:纵变横不变,符号看象限.思考2:(1)若()22410,0x y x y +=>>,则22xy u x y =∈+⎛ ⎝⎦(2)若tan 2α=,则3sin 3cos 2sin cos αααα-=+725-思考3:(1)2sin 236y x ⎛⎫=-++ ⎪⎝⎭的图象的对称轴为;对称中心为(2)函数sin y x =的图象与直线y x =有多少个公共点? 7.图象变换第7讲平面向量【知识梳理】1.向量的线性运算:加法、减法、数乘.2.重要结论: (1)任意向量MN u u u u r :MN MP PN MP=+=+u u u u r u u u r u u u r u u u r (2)若,,O A B 三点不共线,则,,P A B (3)P 为线段AB 的中点2OA OBOP +⇔=u u u r u u u r u u u r ;(4)在ABCD Y 中:①()()a b a b a b +⊥-⇔r r r r r r||=||;②a b a b a b ⊥⇔-r r r r r r |+|=||。
