题目：圆图的研究及应用 - 浙江大学电子邮件系统
图2
图 3
首先对负载阻抗归一化。在图3 中为A 点，读出其导纳值。第一个元件为并联电容，它将 使电路的导纳值沿着等g圆顺时针方向移动。由于最后一个元件为串联电感，它需要使电路的阻 抗值沿r=1的圆顺时针方向移动到达O点，从而实现与传输线的特性阻抗匹配。因此B应该位于 g=0．47的圆与r=1的圆的交点。确定B的阻抗值。计算出A点到B点的容纳之差，去归一化的值。 从而得到电容值。 Alliss大功率发射系统转动天线的匹配网络: Alliss大功率发射系统的转动天线部分突破了传统的短波天线匹配方法，采用集中参数器 件所组成的匹配网络来代替分布参数元件构成的阻抗转换器，从而使大功率发射系统的功率传 输手段进入一个新的技术发展阶段：高精度和高效率的阶段。该系统采用电感和电容组成并联 式双Ⅱ网络，在5.9-26.1MHz的10个频段的范围内，在发射机的功率输出系统与转动天线的发射 体之间分微小频段进行精确调配。匹配网络下图所示。
r rs容抗时总阻抗垂 直往下移动，移动距离根据所串接电抗值而 定。 图 1 （4）一并联阻抗 Z1 r1 / / jx1 与另一电抗并接，合成总阻抗Z1，也只是电抗部分发生变化， 它在图上沿 rp r1 的圆移动，当并接感抗时，Z1点沿 rp r1 的圆反时针方向移动。当并接容抗
图 6. 左半圆图与右半圆图
但是必须注意到，用圆图化简和卡诺图不同的是： （1）任何紧挨着的2”个最小项不一定能合并，例如图7中10、11、14、15能合并，但10、13、 14、15则不能合并． （2）表面上几何不相邻的最小项有可能能合并．例：17、49、21、53能合并． 现举两例进行说明： 例1．用圆图法化简下面的多变量“与或”逻辑函数式： Y=L(A,B,C,D,E,F) = A’B’C’D’F + A’CD’E’ + A’B’C’DF + A’CDE’ + BC’D’F + BC’DF + ACD’E’ + AB’C’D’F+ ACDE’ + AB’C’DF 解：画出圆图，如图1所示，将逻辑函数各“与或”项用“*”填入图中． A’B’C’D’F项是虚径线D’F与实弧线A’B’C’交点，它是相邻最小项Σ1，3合并的结果； A’CD’E’项是虚径线D’E’与虚弧线A’C的交点，它是相邻最小项E8，9，24，25合并的结果； A’B’C’DF项是虚径线DF与实弧线A’B’C’交点，它是相邻最小项Σ5，7合并的结果； A’CDE’项是虚径线DE’与虚弧线A’C的交点，它是相邻最小项Σ12，13，28，29合并的结果； BC’D’F项是虚径线D’F与虚弧线BC’的交点，它是相邻最小项Σ17，19，49，51合并的结果； BC’DF项是虚径线DF与虚弧线BC’的交点，它是相邻最小项Σ21，23，53，55合并的结果； ACD’E’项是虚径线D’E’与虚弧线AC的交点，它是相邻最小项E4o，41，56，57合并的结果； AB’C’D’F项是虚径线D’F与实弧线AB’C’的交点，它是相邻最小项233，35合并的结果； ACDE’项是虚径线DE’与虚弧线AC的交点，它是相邻最小项Σ44，45，60，61合并的结果； AB’C’DF是虚径线DF与实弧线AB’C’的交点，它是相邻最小项E37，39合并的结果．
图 4 图4 中C1．A、C1．B为同步调整电容，L1．A、L1．B为同步调整电感，C2、C3为平 衡电容。由于平衡一不平衡转换器输入端的阻抗比较低，通过的电流较大，因此采 用双Ⅱ网络将电流一分为二，既能保护元器件，又能降低热损耗。
二、用圆图化简多变量逻辑函数
曹思汗
我们在求解一些传输线问题时经常会利用圆图（如阻抗或导纳圆图）来进行分析，其中圆 图中的 各种圆代表了丰富的物理意义（如等 圆，等r/g圆，等x/b圆），同时圆图将传输线上 的电路状态变换等效到了圆图上沿圆周的旋转，使该过程清晰直观地呈现出来。
除了可以进行传输线分析，圆图还可以用来对多变量的表达式进行化简运算。利用圆图化 简较之前学过的用卡诺图化简有很大的优越性。卡诺图在进行化简前，必须先将函数表达式变 换成“与或”的形式，即最小项之和，然后才能将每个最小项对应的填入卡诺图。然而这种方 法对于是由“或与”形式，即最大项之积，给出的函数表达式是非常繁琐的，且易如出错。然 而如果利用新引入的圆图来进行化简能省去对函数表达式变换的步骤。 化简圆图是这样定义的：首先为圆图上的经线与纬线选定对应的变量，为方便起见，我们 先以6变量A ~ F函数为例，其中纬线对应变量为A，B，C，经线对应变量D，E，F。和卡诺图一样， 我们也利用循环代码（格林码）为相邻经线和相邻纬线进行编码。如图5
图 8
3. 按多变量圆图法合并最小项规则合并最大项。 根据规则1，将圆图中方框5，6，7，8中的“*”分别合并，合并结果分别是： （A+B+D+E）,(A+B+D’+E), (A’+B+D+E), (A’+B+D’+E). 根据规则2，将圆图中椭圆框1，2，3，4中的“*”分别合并，合并的结果是： （A+B+C+E’）,(A+B’+C+E’), (A’+B’+C+E’), (A’+B+C+E’). 根据规则3，将椭圆1和2，3和4分别合并，得（A+C+E’）, (A’+C+E’). 再根据规则2，将椭圆1，2，3，4全合并，得（C+E’），将方框5和6，7和8分别合并，得 （A+B+E）, (A’+B+E),再将方框与5，6，7，8全合并得（B+E）. 所以，最后得到最简化的“或与”逻辑式为：Z= L(A,B,C,D,E,F)=(B+E)(C+E’). 综上，利用圆图化简多变量逻辑函数式较卡诺图有很大的优越性，尤其是对以最大项形式给出 的表达式的化简有很好的便利性，同时圆图也保留了卡诺图化简的直观性与清晰性。
时，Z1点沿 rp r1 圆顺时针方向移动，其移动的距离与所并联的电抗X 值的关系由下式决定：
1/ X 2 1/ X 1 1/ X 。式中X1为原并联电抗的电抗值；X 为所并接电抗元件的电抗值；
X2为并接后的合成电抗值。 （5）将此图应用于阻抗匹配的方法：把所要求达到匹配的阻抗作为基值，对所需要匹配 的阻抗归一化，纳入阻抗变换图中，如果需要匹配的原为串联阻抗，按直角坐标确定其位置， 如原为并联阻抗的方法，把它移到与r。=1的圆或rs=1的直线上，接着再沿 rp =1的圆(并一电抗) 或沿rs=1的直线(串一电抗)接到r=1，x =0点，这就达到匹配了。 由于存在一些事先没有估计到的因素，按计算出来的元件数值装配以后，实际上并不一定 达到完全匹配。这就需要进行实际调整。 在直角坐标系中，反射系数 的表述为：
题目：圆图的研究及应用
姓名： 郑唤欢 学号： 3080103129 曹思汗 3080100873 朱海燕 3080103999
专业： 信息与通信工程
电子科学与技术
圆图的研究及应用
（郑唤欢
（1 信息与通信工程
1
曹思汗
2 电子科学与技术
2
朱海燕 ）
3 信息与通信工程 3080103999）
3
3080103129
r ji | | e j
的实部为 r ，虚部为
i 。在极坐标系中，反射系数J1的幅值为 | | ，相位为 。
导纳值的增减变化与阻抗圆图相同，增减的方向如图中所示。二者的差异值得注意，主要 表现在： （1)在导纳圆图上， 沿电导常数圆逆时针方向移动表现为感纳(以绝对值表示)增加(电感量减 小)。 （2)在导纳圆图上，沿电导常数圆顺时针方向移动表现为容纳增加(电容量增加)。 （3)在导纳圆图上，电纳小于零(感纳)的圆位于水平坐标轴的上半部，这时在电纳圆上，顺 时针方向表现为电导的增加；而电纳大于零(容纳)的点位于水平坐标轴的下半部，逆时针方向 为电导增加的方向。 除了书上介绍的短路线匹配外，反 型匹配网络和Alliss大功率发射系统转动天线的匹配 网络。 反 型匹配网络： 实现阻抗匹配的网络有多种，这里仅举一例加以说明。其他类型的网络可以类推。图11为 反 型网络。假定工作频率为1MHz，求匹配元件的值。
一、圆图在电阻网络中的应用
郑唤欢
史密斯圆图的实轴代表了阻抗或反射系数的实部，而其虚轴则代表了阻抗或反射系数的虚 部，因此等r圆的圆心位于坐标的原点。史密斯圆图的实质就是Z平面和r平面两个复平面之间的 映射。图1是阻抗(归一化值)变换图，图l中有两个系统，一为直角坐标系统，计算图1导纳圆图 算阻抗串联，一为圆坐标系统，计算阻抗的并联，因此可在此图1 中进行计算阻抗的串联与导 纳的换算等。具体做法如下： （1）将Z（z）以特征阻抗 Z c 归一化， 即
z( z)
Z ( z ) 1 u ( z ) Zc 1 u ( z )
（2）在图1 中任何一点代表一个阻抗， 其中直角坐标系的坐标r。，X。表示该点阻抗 的串联电阻与电抗值， 同时通过该点圆坐标系 r一圆及X 圆则代表该阻抗的并联电阻与电抗 值。 （3）串联阻抗 Z1 r1 jx1 与另一个电抗 串接合成总阻抗z ，只是电抗部分发生变化， 在图上沿
图 7 根据规则（1），图7中各小方框和椭圆框中的“*”可以分别合并； 根据规则（3），椭圆框圈1和圈2合并得A’C’D’F，圈3和圈4合并得A’C’DF，圈5和圈6合并得 AC’D’F，圈7和圈8合并得AC’DF. 根据规则 （2） ， 方框 （1） 和 （2） 合并得A’CE’， （3） 和 （4） 合并得ACE’， 然后再合并 （1） ,(2),(3),(4) 得CE’，椭圆框1，2和3，4合并得A’C’F，5，6和7，8合并得AC’F，然后再将1，2，3，4，5，6， 7，8合并在一起得C’F。 故最后得到最简化的“与或”逻辑式为Y= CE’+C’F. 例2. 利用圆图法化简“或与”逻辑函数式： Z=L(A,B,C,D,E,F)=(A+B+C)(A+B+C+D+E)(A+B+C+D’+E)(A’+B+C)(A’+C+B’+D’+E)(A+B’+C+ E’)(A’+B’+C+E’) 解：一般常规化简方法是利用摩根定理将“和之积”化为”积之和”形式，然后再用代数法或 卡诺图法进行化简，但对多变量“和之积”逻辑函数化简，无论采用现存的何种方法都显得非 常麻烦，且易出错。圆图法它不需要变换逻辑形式，可直接在图上化简。 具体步骤是： 1. 画出多变量圆图，其中循环代码用变量的最大项表示。 2. 将逻辑函数Z的各个“或与”项用“*”号填入图中。 例如（A+B+C）项是实弧线（A+B+C）与8条实经线相交所组成的相邻8个最大项合并的结 果，因此可在这8个交点上标“*”，其它项也按此法一一填入图中。见图8
挑战杯历届全国特等奖、一等奖作品
国家历届挑战杯特等奖、一等奖作品第一届“挑战杯”全国大学生课外学术科技作品竞赛由清华大学于1989年承办：清华大学摘得“挑战杯”一等奖获奖名单如下：北京大学刘闯在地理信息系统中土地评价模型的建模研究清华大学陈邕涛等中华学习机CAI软件开发工具清华大学吴丹策等电脑照相及微机图像处理系统清华大学金龙文等竹草木漂白系列新工艺的研究华中理工大学吴敏等建筑方案“将居民安置在发种种的小镇中”新疆石河子医学院王惠民门脉系的内分泌学意义第二届“挑战杯”全国大学生课外学术科技作品竞赛由浙江大学于1991年承办：上海交通大学摘得“挑战杯”一等奖获奖名单如下：浙江大学微机遥感图像显示操作及处理系统郑州大学方兴未艾福利企业国防科技大学Hyperview（v1.01）系统北方交通大学铁道部及各地区财务基准收益率的测定上海交通大学光纤中自然聚焦光场的环形结构上海医科大学他莫昔芬枸橡酸新工艺的研究及其原理的讨论上海交通大学农村民居建筑调研华中理工大学微量泄漏检测仪北京航天航空大学简繁五笔汉字系统及其为通道汉卡四川成都电子科技大学通信母板自动测试系统第三届“挑战杯”全国大学生课外学术科技作品竞赛由上海交通大学于1993年承办：北京大学获得“挑战杯”一等奖获奖名单如下：北京大学基于具有更佳频率分辨率的正交子波变换及自适应VQ技术的图像压缩北京大学危机与出路.....从九二深圳股市看中国B股清华大学铁基合金薄膜中铁原子磁矩的反常增大等作品获奖东北大学超级电子档案系统吉林大学镧系离子荧光探针探测天花粉蛋白结构和分子间能量传递武汉大学信安－Ｉ型计算机网络信息保护系统浙江大学ＰＬＴ陶瓷期间合金电极成型新技术四川师范大学四川西部蝶类资源调查天津财经学院建立会计逻辑学体系的构想北方交通大学多渠道多方式利用外资发展我国的铁路的探讨中国科技大学本原矩阵指数的一个猜想证明上海交通大学浦东开发区环境调查及综合防治上海医科大学Ｚ曲线显示和分析ＤＮＡ系列的直观工具南京理工大学激光全息场再现图像的离子自动检测华东理工大学化学气相淀积反应器中超细粒子形成过程研究及产物形态控制华中理工大学将城市引入农村，农村引入城市－繁忙江南水乡的僻静水上花园齐齐哈尔工学院黑龙江省甜菜糖业产品结构调整战略研究报告北京航空航天大学空中机器人系统北京航空航天大学智能化电力电容在线检测仪第四届“挑战杯”全国大学生课外学术科技作品竞赛由武汉大学于1995年承办：复旦大学摘得“挑战杯”一等奖获奖名单如下：复旦大学载能束合成新型共价氮化碳超硬材料研究河北大学BaZrXTil-03固溶体的合成，结构与物性武汉大学高性能镍／金属氢化物电池和锂离子蓄电池暨南大学物体三维形貌测试技术的研究等作品获奖北京大学物体三维形貌测试技术的研究云南大学村落文化贫困地区农村妇女生育健康服务模式——武定县中山大学《劳动法》与外来工的权益保障北京大学光ＷＤＭ（波分复用）中的激光波长控制清华大学高速中西文激光打印／照排控制器北京师范大学论教师的教学效能感南京理工大学走出困境再创辉煌——重庆军工企业走上发展之路的启示北京科技大学双拇指型多指手大连理工大学大学物理实验ＣＡＩ教学软件包华中理式大学新型宜人化计算机辅助设计绘图系统——开目ＣＡＤ华北师范大学松树花粉的培养和它萌发时营养万分的变化吉林工业大学梁的大挠度强迫振动的非线性响应的分析的新方法苏州丝绸工学院真丝新村料的研制及产品开发北京航天航空大学遥控多用途空中飞行平台第五届“挑战杯”全国大学生课外学术科技作品竞赛由南京理工大学于19９７年承办：清华大学摘得“挑战杯”一等奖获奖名单清华大学《十字路口看乡企》——中国农村乡镇企业转制问题调查报告清华大学蛋白质去折叠与折叠机制的研究清华大学基于界面设计的多层膜技术获得新型合金清华大学文本无关的说话人语音语音识别系统北京大学两家名油企业生活后勤体制变革北京大学股市中操纵市场行为及防范的法律对策北京大学 Runge—lenz矢量与升降算子武汉大学武汉市再就业工程调研报告南京理工大学小波变换中的视觉门限模型和图像的层次分割优生权编码复旦大学通用工件识别系统生成工具VisionExport南京大学水煤奖添加剂NDF上海交通大学柔体机器人（组件）云南大学边疆民族地区生态环境变迁与脱贫致富——云南省怒江傈族自治州经济开发新模式研究北京航空航天大学三翼面微型无人驾驶验证机国科学技术大学酶反应的理论研究——方法及在葡萄糖异构酶中的应用四川联合大学利用红矾母液和铬酐下脚料生产蒙囿吸收铬鞣粉剂石油大学河南西峡恐龙蛋化石层及恐龙绝灭原因初探中国政法大学青少年创造能力培养和知识产权保护教育调查报告吉林工业大学轿车车身焊装用微机控制自动螺柱焊机第六届“挑战杯”全国大学生课外学术科技作品竞赛由重庆大学于1999年承办：复旦大学获得“挑战杯”一、二等奖获奖名单北京航空航天大学鱼类运动仿生研究及其柔体舰艇模型东北大学微型足球机器人系统江苏理工大学高性能铝合金材料的应用研究复旦大学指间区纹的进化和遗传南京大学体内可降解吸收医用高分子材料及其制品大连海事大学椭圆波导中的场中国科学技术大学关于α和β环糊精与苯衍生物之间的包含驱动力及包合结构的新模型上海交通大学面向软件无线电的数字发射机（激励器部分）东南大学中文个人数字助理（ASICPDA-2000）北方交通大学大规模发展交通仿真及公交智能调度指挥平台开发重庆大学 AV-100S型双面表格自动阅读机苏州大学真丝新材料-差别化柞桑弹力真丝的研制与产品开发北京大学从法院状告新闻媒体谈起——一起名誉侵权官司引发的思考复旦大学适应环境变化，构建新型企业——上海国有外贸企业改革调查华东师范大学师范大学生专业思想状况调查哈尔滨理工大学侵华日军731部队罪证网站国立华侨大学基于可持续发展的水资源定价试探华中理工大学基于针式传感器的多功能扫描探针显微装置南京大学电动自行车综合测试仪吉林工学院轿车深冲件应用国产冷轧IF钢板研究江苏理工大学 4LGT-130型稻麦联合收割机的研制重庆大学虚拟式小波变换信号分析仪重庆医科大学手握（傻瓜）式纯水检测仪华东理工大学清洁化生产取代芳胺磺酸中国科学技术大学超支化聚（胺-酯）的合成及其光固化性能研究吉林工学院汽车内饰件粘合剂的研制同济大学茶多酚提取新工艺及其系列产品开发无锡轻工大学 UASB-CAAS系统处理高浓度有机废水的工程技术无锡轻工大学维生素在光滑球拟酵母发酵生产丙铜酸中的关键作用广西师范大学湘西洛塔植物区系及开发利用研究重庆大学心肌收缩能力的一种无伤性检测和评估方法研究山西大学 Hie Senberg 方程的换算表示复旦大学国内首家微波硫灯的研制桂林工学院 NETWARE高级编程接口及未公开的核心技术武汉交通科技大学二维条码自动识别应用技术研究西安电子科技大学高速分组无线网长沙铁道学院空调客车状态参数集中管理系统成都电子科技大学校园网上的学生管理信息系统中国科学技术大学基于中文实时语音技术的有声电子系统北京理工大学《圣林3.0》实时三维图象引擎武汉大学系列安全容错智能卡应用系统重庆邮电学院多链路中国NO.7的信令分析仪华中理工大学基于LAN/INTERNET的H.323视频会议系统西安电子科技大学自控光阀及其在防弧光领域的应用清华大学细菌基因快速鉴测仪中国地质大学（武汉）油气资源储量评价系统华东理工大学无规共聚高分子相平衡的研究武汉大学新型固相微萃取探针复旦大学智能酒气电子鼻山东工业大学弹性管束热交换器的结构、动态特性及自动控制过程仿真重庆建筑大学新型高效掺合料北京大学社区的构成清华大学走近21世纪的中国环境技术中国人民大学面对挑战，中国对外经济的立足点北京师范大学困境与出路——城镇企业下岗职工再就业状况调查北京师范大学面向21世纪发展远程教育——关于中国远程教育中若干问题的调查与思考中国政法大学中国农民法律意识现状探讨西南政法大学典权的过程分析及性质研究山西大学刚玉之路河海大学江苏省水资源可持结发展模式探讨中国药科大学我国药品价格现状分析及管理对策的研究杭州商学院论国有企业激励机制湖南财经学院买方市场：高教与经济增长—发展高教是推动经济增长的重要途径华中农业大学农业科技推广中的几点思考第七届“挑战杯”全国大学生课外学术科技作品竞赛由西安交通大学于2001年承办：复旦大学和东南大学获得“挑战杯”特等奖北京大学锆基固体电解质纳米晶薄膜材料的制备及微结构与电学性质研究清华大学结构光三维扫描仪北京航空航天大学数字立体电视其计算机成像系统南开大学发光锌纳米分子复旦大学上海越族后裔与台湾高山族的渊源华东师范大学师范生对教育类课程看法的调查报告东南大学 OSC2001微型掌上数字存储示波器东南大学南京市流动民工现状调查山东大学换热器动态仿真及智能控制系统山东大学紫外倍频晶体K2AL2B207的生长技术汕头大学 LCD生产过程的基板自动对位贴合及ITO、SPACER自动检测系统电子科技大学考虑交易费用与风险情况下移动平均交易规则的检验四川大学论对抽象行政行为的司法监督重庆大学“移民者的乐园”——三峡库区“棚户现象”调查研究与城市（镇）迁建、移民问题思考渝州大学绿色贸易壁垒及重庆之应对贵阳中医学院《针穴II》虚拟三维教学系统西安交通大学金纳米球壳微粒的空腔谐振吸收特性）西安交通大学一种适用于小C臂X光机的数字成像系统一等奖北京大学中国高龄老人健康状况和健康预期寿命研究北京航空航天大学环形翼飞机北京航空航天大学弹射座椅地面综合测试仪及其嵌入式系统北京航空航天大学多机器鱼协调及机器鱼的机动性研究北京科技大学喷丝板自动检测系统北京科技大学灵丘贫锰银矿综合利用技术研究北京理工大学哈勃常数的实验估计北京理工大学发动机润滑系统仿真软件包北京师范大学教师反馈、学生的归因模式与学生学业成绩关系的研究：一项行动研究及其对学校心理健康教育的启示中国人民大学真茵寡聚糖诱导子诱导悬浮培养红豆杉细胞的信号转导途径及其过程模型的研究天津理工学院缔合色心型X线影像板河北大学陆马峰的发育与筑巢行为的研究河北科技大学 L-抗坏血酸-2-三聚磷酸酯的合成研究华北电力大学民事举证责任倒置问题探析大连海事大学船舶运动控制试验平台大连理工大学冰柜监控管理系统大连理工大学单金属、双金属催化剂表面CO氧化反应的模拟模型大连理工大学医学层析图象三维几何重建与可视化仿真东北大学般若企业互联网络综合应用平台吉林工学院溶液法银纳米微粉的光化学制备哈尔滨理工大学地下管线定位仪东华大学中国绿色服装发展探究复旦大学转动基板的激光测温复旦大学知识产权新课题——基因专利复旦大学以企业信息化迎接B2B挑战华东师范大学 GSEEK码路天使——中西文著者号码自动生成系统上海财经大学高级管理层激励与上市公司经营绩效上海交通大学全光通信系统仿真软件上海师范大学如何在中国农村普及信息技术教育同济大学多高层建筑结构设计系统（简称MTS）东南大学均压型行波形超声波电机苏州大学真丝调拒水拒油防污多功能整理新技术研究及产品开发苏州大学非接触式高精度数字图像面积测量仪苏州大学激发型抗人CD40单克隆抗体的研制及产品开发扬州大学 Xa21基因导入水稻广亲和恢复系SWR20提高白叶枯病抗性中国药科大学脆壁克鲁维酵母菌乳糖酶的开发与应用浙江大学基于综合推理的集成化智能书法创作合肥工业大学关于安徽农村税费改革的调查和建议中国科学技术大学语音合成芯片郑州工程学院王涛河南省高校大学生创新能力现状调查与对策研究郑州工程学院袁少勇在WTO框架下：中国粮食流通体制改革研究华中师范大学我国城市社区的阶层化趋势研究武汉大学用人市场对大学毕业生质量评价的社会学分析武汉理工大学谈广义M集的演化及其在图形防伪中的应用中国地质大学(武汉) 全球古大陆再造软件开发研究国防科学技术大学 Windows变速器国防科学技术大学数字水印新技术华南农业大学车八岭保护区及其邻近地区的木兰科植物种群及其群落特征的研究中山大学中国南沙群岛海域浮游原生动物生物多样性研究中山大学珠江三角洲富裕农村主观剩余劳动力问题研究华南热带农业学院蝗虫霉菌的培养及致病性初步实验西南石油学院油藏压裂模拟设计与分析软件系统重庆大学可穿戴式计算机——Netdaily云南大学便携式高精度数字燃油流量计云南大学传统法文化的断裂与现代法治的真空——少数民族农村法治秩序建构路径选择的社区个案研究长安大学 The Problems and the Solutions on Ecological Architecture in Developing Countries西安电子科技大学单片机模糊控制软件仿真和生成平台西安理工大学 Sn02：F透明电热膜加热管兰州大学纳米微阵电极组装体系的制备和初步研究宁夏大学宁夏移民区可持续发展模式研究宁夏大学历史上固原地区人地关系的两次转型对生态建设的启示新疆大学维－汉－英三向背单词系统、电脑词典第八届“挑战杯”全国大学生课外学术科技作品竞赛由华南理工大学于2003年承办：清华大学获得“挑战杯”复旦大学获得挑战杯永久纪念碑一座一等奖获奖名单北京大学司法判决书中“双高”现象并存的另一种解释进路北京大学贫困学生怎么上大学？——中国高校学生贷款运行机制案例分析及其国际比较北京航空航天大学仿生飞翼布局飞机北京航空航天大学纳米光催化空气消毒净化器清华大学北京市流动儿童受教育状况及心理健康现状调查报告中国地质大学（北京）大学生创新精神和实践能力培养的调查研究——团体创新模式分析中国农业大学 AISCR-1-100微机控制全自动智能除雪机器人中国人民大学资本市场融资条件与产品市场竞争双重约束下的中国上市公司融资行为研究北京城市学院北京市乞丐现状调查报告天津大学桩基承台前方设挡土结构的大型码头结构河北科技师范学院杏树新害虫---JT虫生物学特性及无公害防治研究山西财经大学货币需求中的认知因素分析大连理工大学基于元胞自动机和Penna模型的生态系统模拟模型吉林大学国有经济控制力及控制方式新探吉林大学兽疫链球菌突变株产生的透明质酸的纯化及表征北华大学气动蠕动式缆索机器人哈尔滨医科大学中药复方抗心律失常药物筛选平台的建立复旦大学手晃电子显示棒上海财经大学城市轨道交通投资对周边地价变动影响的实证分析上海交通大学新型水葫芦打捞船上海交通大学基于 Inter PXA250的无线个人客户端的开发(wireless personal client)同济大学轨道交通运输组织仿真系统开发同济大学城市之桥—上海世博会人行过江“花”桥的结构概念设计同济大学四轮独立驱动燃料电池微型汽车东南大学通用手持概念仪器东南大学江苏省企业电子商务应用调查研究报告南京大学一种新型的磁力吸盘南京大学他们怎样生存——三峡移民迁前生存状况调查南京工业大学绿色紧凑的冷冻式空气干燥机南京理工大学鱼类旋涡射流推进理论及其应用南京师范大学稀土有机配合物生态转光剂的制备南京师范大学推进乡镇机构改革的对策研究——苏南、苏北若干典型乡镇机构改革的比较分析南京邮电学院基于动态路由控制的高性能IP宽带接入网关中国矿业大学花生收获机华东船舶工业学院仿生波动推进器绍兴文理学院组织的镶嵌、链接和整合——中国轻纺城地方商会个案分析浙江工业大学“AH-Assemble”汇编语言集成开发平台浙江师范大学村委会选举中乡镇政府的角色转换——以浙江省昌镇村委会选举为个案中国科学技术大学σ键超共轭作用在丙烯旋转能垒中的重要性中国科学技术大学最小超对称标准模型下的R宇称破坏机制对CERN LHC上轻子对产生过程的影响中国科学技术大学 Bcl-rambo β的发现和功能研究福建农林大学甘蔗近缘属植物斑茅的杂交利用与抗逆性评价福州大学基于评价方法属性层次的组合评价研究华侨大学三维自然纹理的反求设计与制造厦门大学从“三农”问题透视乡镇政权——以福建省枫亭镇和大济镇为例山东理工大学竹红菌甲素--一种新型抗生素的抑菌作用研究郑州工程学院大学生诚信缺失徂源及对策——转型期大学生信用行为分析湖北大学论诚信的劣变与对教育理性的质问----关于当代大学生诚信状况的分析以及对当代教育的反思华中科技大学北京、武汉高校人才培养与学生素质状况调查报告武汉大学绿色铅酸蓄电池及其生产工艺武汉化工学院水性聚酯树脂的合成及其涂料研制中国地质大学（武汉）求解动态TSP问题的新型演化算法国防科技大学新概念路标系统与无人驾驶汽车模型湖南大学 RSY-1肉类水分快速测定仪湖南大学入世过渡期：银行不良资产处置模式的比较分析与路径选择湖南师范大学传统文化与党风廉政建设湖南师范大学走向权利时代的民工权益——来自深圳民工的调查中南大学三峡移民的文化差异与文化融合——以湖南岳阳地区新市、杨林两地三峡移民为样本分析的调查报告中南大学基于等离子体聚合膜技术的压电免疫传感器的研究及其在急性白血病免疫分型中的应用广州大学岭南城市广场与公园热环境研究华南理工大学新型高分子点阵发光显示屏华南农业大学园艺植物自然分类系统及其汉拉英名称对照广东商学院 21世纪中国人口老龄化与银色产业开发四川大学通过分子复合实现聚乙烯醇的吹塑成膜西南石油学院现代试井分析技术及软件系统第三军医大学以纳米金为报告系统的病原体快速检测基因芯片第三军医大学抑制胆固醇合成对乳腺癌细胞离子跨膜流动、细胞骨架形成及细胞通讯功能影响的研究重庆工学院一个非常值得关注的“三农”问题——重庆市农村养老问题调查研究云南师范大学微波加热技术在催化化学反应中的应用长安大学环保型野生植物杀虫剂的研究西安科技大学基于虚拟仪器技术的多种机械量测试系统西安交通大学透平叶片型线设计及优化软件西安交通大学金纳米棒状微粒的吸收光谱宁夏大学数字显微镜模拟目镜及病理远程诊断系统新疆大学新疆家蚕抗菌肽基因工程产品的开发与应用第九届“挑战杯”全国大学生课外学术科技作品竞赛由复旦大学于2005年承办：复旦大学获得“挑战杯”复旦大学以总分４２０分的最高分夺得第九届“挑战杯”；北京大学、中国矿业大学、南京大学等２０所高校捧得“优胜杯”；清华大学由于累计３次捧杯，获得“挑战杯‘永久纪念杯’”。
概率论与数理统计及其应用_习题答案_(浙大_盛骤谢式千版本)
《概率论与数理统计》习题解答教材：《概率论与数理统计及其应用》，浙江大学盛骤、谢式千编，高等教育出版社，2004年7月第一版目录第一章随机事件及其概率1第二章随机变量及其分布9第三章随机变量的数字特征25第四章正态分布33第五章样本及抽样分布39第六章参数估计42第七章假设检验53第一章 随机事件及其概率1、解：（1）{}67,5,4,3,2=S （2）{} ,4,3,2=S （3）{} ,,,TTH TH H S =（4）{}6,5,4,3,2,1,,T T T T T T HT HH S =2、设A , B 是两个事件，已知81)(,21)(,41)(===AB P B P A P ，求)(B A P ，)(B A P ，)(AB P ，)])([(AB B A P 解：81)(,21)(,41)(===AB P B P A P ∴)()()()(AB P B P A P B A P -+= 85812141=-+= )()()(AB P B P B A P -=838121=-=87811)(1)(=-=-=AB P AB P)])([(AB B A P )]()[(AB B A P -=)()(AB P B A P -= )(B A AB ⊂218185=-=3、解：用A 表示事件“取到的三位数不包含数字1”2518900998900)(191918=⨯⨯==C C C A P4、在仅由0，1，2，3，4，5组成且每个数字至多出现一次的全体三位数字中，任取一个三位数，（1）该数是奇数的概率；（2）求该数大于330的概率。
解：用A 表示事件“取到的三位数是奇数”，用B 表示事件“取到的三位数大于330”(1) 455443)(2515141413⨯⨯⨯⨯==A C C C C A P =0.48 2） 455421452)(251514122512⨯⨯⨯⨯+⨯⨯=+=A C C C A C B P =0.485、袋中有5只白球，4只红球，3只黑球，在其中任取4只，求下列事件的概率 （1）4只中恰有2只白球，1只红球，1只黑球； （2）4只中至少有2只红球； （3）4只中没有白球解：用A 表示事件“4只中恰有2只白球，1只红球，1只黑球”（1）412131425)(C C C C A P ==495120=338（2）用B 表示事件“4只中至少有2只红球”16567)(4124418342824=++=C C C C C C B P 或4124838141)(C C C C B P +-==16567495201= （3）用C 表示事件“4只中没有白球”99749535)(41247===C C C P 6、解：用A 表示事件“某一特定的销售点得到k 张提货单”nkn k n MM C A P --=)1()( 7、解：用A 表示事件“3只球至少有1只配对”，B 表示事件“没有配对”（1）3212313)(=⨯⨯+=A P 或321231121)(=⨯⨯⨯⨯-=A P （2）31123112)(=⨯⨯⨯⨯=B P 8、（1）设1.0)(,3.0)(,5.0)(===AB P B P A P ，求(),(),(),(),P A B P B A P A B P A A B(),()P AB A B P A AB ；（2）袋中有6只白球，5只红球每次在袋中任取一只球，若取到白球，放回，并放入1只白球，若取到红球不放回也不再放回另外的球，连续取球四次，求第一、二次取到白球且第三、四次取到红球的概率。
科学技术史知到章节答案智慧树2023年浙江大学
科学技术史知到章节测试答案智慧树2023年最新浙江大学第一章测试1.二十四节气是我国劳动人民在长期实践中总结出来的，它主要反映____地区的其后特点和农事概况。
（）参考答案:黄河中下游2.金代数学家____的《测海圆镜》是最早一部系统论述“天元术”的著作，对我国古代数学成就“天元术”的发展做出重要贡献。
（）参考答案:李冶3.西晋地理学家裴秀主持编绘了_____，这是中国历史上第一部见于记载的历史地图集。
最大贡献是提出了中国古代的制图理论——“制图六体”。
（）参考答案:《禹贡地域图》4.我国最早最系统的一部水道著作是北魏郦道元所著的_____。
( )参考答案:《水经注》5.以下哪几项属于元代著名发明家、农学家王祯的成就？（）参考答案:转轮排字盘;编著《农书》;木刻活字6.宋元时期中国古代传统数学的发展过程中一个重要的阶段，宋元数学四大家包括___、____（）参考答案:秦九韶;朱世杰7.东汉时期蔡伦用麻类、绳头、渔网和树皮等造出了质量优良的“蔡侯纸”，对发明和推广造纸术做出了重要贡献。
（）参考答案:错第二章测试1.古希腊哲学与科学的始祖，人类历史上第一次用理性方式寻求万物本原的学者是。
（）参考答案:泰勒斯2.四体液学说的提出者，制定了医生道德规范的是古希腊著名医学家_____。
（）参考答案:希波克拉底3.《天文学大成》的作者是_____。
（）参考答案:托勒密4.古希腊科学家阿基米德流传至今的物理学著作有_____。
（）参考答案:《平面图形的平衡或其重心》;《论浮体》5.亚里士多德被誉为古希腊第一位百科全书式的学者，其研究领域涉及物理学、生物学、哲学、天文学等多个学科。
（）参考答案:对第三章测试1.中世纪时期的自然哲学，占主导地位的是____的自然哲学。
（）参考答案:亚里士多德2.亚里士多德的自然哲学学说中，主要包括____。
（）参考答案:月上和月下世界的划分;质料和形式说;四因说3.经验主义强调自下而上，从经验观察出发，以下哪几位属于16-17世纪经验主义的代表哲学家？( ）参考答案:洛克;培根4.科学史学科的创始人亚历山大·柯瓦雷提出了亚里士多德主义的再次兴起，这是科学史上的几个经典命题之一。
(完整版)史密斯圆图及应用
ZZ~~LL
1 1
(z) 1e j2z
史密斯(Smith)圆图 即根据这些公式绘出 的极坐标圆图
一、阻抗圆图
阻抗圆图的组成 – 等反射系数圆族 – 等相位线族 – 等电阻圆族 – 等电抗圆族
阻抗圆图——等反射系数圆族
– 无耗传输线上离终端距离为z处的反射系 数
(z) 1 e j(12 z)
1 cos(1 2 z) j sin(1 2 z)
1史密斯圆图及其应用简化阻抗和导纳的计算同时满足工程上的其他需要阻抗反射系数反射系数阻抗导纳阻抗匹配归一化阻抗与反射系数之间的关系史密斯smith圆图即根据这些公式绘出的极坐标圆图一阻抗圆图阻抗圆图的组成等反射系数圆族等相位线族等电阻圆族等电抗圆族阻抗圆图等反射系数圆族无耗传输线上离终端距离为z处的反射系数阻抗圆图等反射系数圆族在ujv复平面上等反射系数模的轨迹是以坐标原点为圆心1为半径的圆不同的反射系数模就对应不同大小的圆1所有的反射系数圆都位于单位圆内反射系数模和驻波系数一一对应又称为等驻波系数圆族坐标原点为匹配点
– 实轴对应纯电阻轨迹，即x＝0。
• 正实轴OD直线为电压波腹点（电流波节点） 的轨迹，且归一化电阻等于驻波系数值；
• 负实轴OC直线为电压波节点（电流波腹点） 的轨迹，且归一化电阻等于驻波系数的倒数
– 最外圆为纯电抗圆，即||=1的全反射圆
阻抗圆图----特点
圆图上有两个特殊的面
– 圆图的上半平面 x>0，感性电抗的轨迹 – 圆图的下半平面 x<0，容性电抗的轨迹
– 已知负载阻抗ZL，确定传输线上第一个电 压波腹点与波节点距离负载的距离；
– 已知驻波系数VSWR及距离负载电压波节 点的位置，确定负载阻抗ZL
阻抗圆图的应用----阻抗变换
第六章 数理统计的基本概念 - 浙江大学邮件系统
31
2 极大似然估计
注意到，L ,
1
n
e
1
n
i1
xi
n
是的增函数，
取到最大值时，L达到最大。
故 X1 min X1, X 2 , , X n ,
又lnL
nln
1
n i 1
Xi
ˆ
令 dlnL d
n
解：似然函数L f xi , i 1
n
xi
1n 2来自 n 1
xi
i 1
i1
lnL
n 2
ln
n
1 ln xi
i 1
令
dlnL
d
n 2
1
2
1
n
ln xi 0
i 1
lnL 称为对数似然函数.
利用lnL
i
0, i
1,
2,...,
k.解得ˆi，i
1,
2,...,
k.
3. 若L 关于某个i 是单调增减函数，此时i的极大似然
估计在其取值范围的边界取得；
4. 若ˆ是 的极大似然估计，则g 的极大似然估计为g ˆ 。
n i 1
(xi 1)2
2 2
d
d 2
ln
L(
2
)
n
2
2
1
2
4
n
( xi
i 1
1)2
2019浙江大学信号系统与数字电路考研真题与答案解析16页word文档
《2019浙江大学信号系统与数字电路考研复习精编》《复习精编》是惟学浙大精品考研专业课系列辅导材料中的核心产品。
本书严格依据学校官方最新指定参考书目，并结合考研的精华笔记、题库和内部考研资讯进行编写，是惟学浙大老师的倾力之作。
通过本书，考生可以更好地把握复习的深度广度，核心考点的联系区分，知识体系的重点难点，解题技巧的要点运用，从而高效复习、夺取高分。
考试分析——解析考题难度、考试题型、章节考点分布以及最新试题，做出考试展望等；复习之初即可对专业课有深度把握和宏观了解。
复习提示——揭示各章节复习要点、总结各章节常见考查题型、提示各章节复习重难点与方法。
知识框架图——构建章节主要考点框架、梳理全章主体内容与结构，可达到高屋建瓴和提纲挈领的作用。
核心考点解析——去繁取精、高度浓缩初试参考书目各章节核心考点要点并进行详细展开解析、以星级多寡标注知识点重次要程度便于高效复习。
历年真题与答案解析——反复研究近年真题，洞悉考试出题难度和题型；了解常考章节与重次要章节，有效指明复习方向。
《复习精编》具有以下特点：（1）立足教材，夯实基础。
以指定教材为依据，全面梳理知识，注意知识结构的重组与概括。
让考生对基本概念、基本定理等学科基础知识有全面、扎实、系统的理解、把握。
（2）注重联系，强化记忆。
复习指南分析各章节在考试中的地位和作用，并将各章节的知识体系框架化、网络化，帮助考生构建学科知识网络，串联零散的知识点，更好地实现对知识的存储,提取和应用。
（3）深入研究，洞悉规律。
深入考研专业课考试命题思路，破解考研密码，为考生点拨答题技巧。
1、全面了解，宏观把握。
备考初期，考生需要对《复习精编》中的考前必知列出的院校介绍、师资力量、就业情况、历年报录情况等考研信息进行全面了解，合理估量自身水平，结合自身研究兴趣，科学选择适合自己的研究方向，为考研增加胜算。
2、稳扎稳打，夯实基础。
基础阶段，考生应借助《复习精编》中的考试分析初步了解考试难度、考试题型、考点分布，并通过最新年份的试题分析以及考试展望初步明确考研命题变化的趋势；通过认真研读复习指南、核心考点解析等初步形成基础知识体系，并通过做习题来进一步熟悉和巩固知识点，达到夯实基础的目的。
概率论与数理统计 - 浙江大学邮件系统
T
0
S t
1 T
d
1 T
tT S d
t
周期性
＝＝＝
1
T
T
0
S
d
常数
RX t,t E S t S t
T
0
S
t
S
t
1 T
d
1 T
tT S S d
t
周期性
＝＝＝
1
T
T 0
S
S
记为
d＝＝RX
所以随机相位周期过程是平稳的。
15
例4：考虑随机电报信号，P X
t
I
1 2
而与起始时间t1无关。
严平稳过程的数字特征：
设严平稳过程X t 是二阶矩过程，则
记为
（1）X t E X t E X 0＝＝X 常数
（2）RX t ,t E X t X t
记为
E X 0 X ＝＝RX
定义：给定二阶矩过程X t ,t T，如果
对任意的t,t T ,
k0 j0
N
ak amk 2
k 0
0mk N
只与m有关，所以{Yn }是平稳序列。
例3：设S t 是一周期为T的函数，是在0,T 上服从均匀分布的随机 变量，称X t S t 为随机相位周期过程，试讨论它的平稳性。
解：由假设，的概率密度为:
f
1 T
0
0 T
其他
于是, E X
t
E S t
或称这两个过程是联合 宽 平稳的
例: 一族随机变量Xt (t T )独立同分布, 则随机过程{Xt ;t T}是严平稳的.
证 : 设Xt的分布函数为F，对任意不同t1,,tn ,任意h， P( X t1 x1,..., X tn xn ) P( X t1 x1)...P( X tn xn )
微波大作业Smith圆图的应用
微波大作业班级：作者：应用史密斯圆图提取慢波微带线特征阻抗方法摘要：慢波微带线的多种不连续性和相邻慢波单元的耦合影响了特征阻抗的准确计算,因此在慢波微带线的设计阶段需要一种手段来提取其特征阻抗。
提出一种利用史密斯圆图提取慢波微带线特征阻抗的方法,该方法通过观察慢波微带线的反射系数在史密斯圆图中的图像估计其特征阻抗的大小,并通过反射系数极值计算特征阻抗。
以梳状慢波微带线为例检验该方法,特征阻抗的提取结果与利用S参数提取的结果十分接近,从而证明该方法是一种可行的慢波微带线特征阻抗提取方法。
关键词：慢波微带线特征阻抗史密斯圆图1.引言在微波集成电路活单片微波集成电路中，电路的小型化是有限考虑的设计目标。
慢波微带线可以提高所传到的电磁波的相位常数β，今儿缩短单位电长度微带线的物理长度，一次成为射频器件小型化的一种长度。
慢波微带线的主要特性参量有特征阻抗Zc和相位常数β。
相位常数可以直接测量，儿特征阻抗需要通过间接手段获得。
一般是先计算微带线分布参数和其不连续性引起的寄生参数。
由于寄生参数的计算是基于近似公式并且常常忽略相邻慢波单元的耦合，所以分布参数的计算结果存在误差，进而影响到特征阻抗的精确计算。
因为对特征阻抗的计算存在误差，所以在慢波微带线设计阶段就需要一种手段来估计算结果。
而通过反射系数在史密斯圆图上的图像来提取特征阻抗，恰恰可以解决这个问题2.史密斯圆图的原理史密斯圆图是由菲利普·史密斯(Phillip Smith)于1939年发明的，当时他在美国的RCA公司工作。
一年後，一位名为Kurakawa的日本工程师也声称发明了这种图表。
史密斯曾说过，“在我能够使用计算尺的时候，我对以图表方式来表达数学上的关联很有兴趣”。
史密斯圆图基本在于以下的算式当中的Γ代表其线路的反射系数(reflection coefficient)，即S参数（S-parameter）里的S11，ZL是归一负载值，即ZL / Z0。
浙江大学
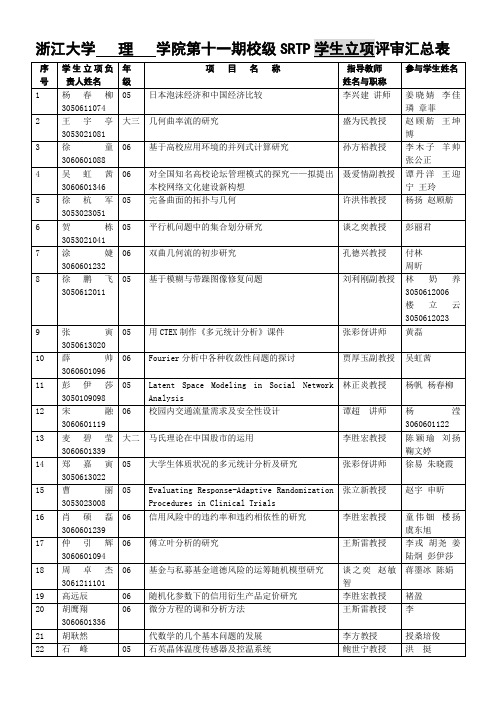
教师立项负责人姓名
职称
项目名称
参与学生姓名
1
朱建新
教授
波在有损耗的波导中传播的快速计算
金烁汪熠巫泽俊蒋豪
2
张立新
教授
非线性时间序列的建模极其在经济、金融中的应用——（1）异方差模型
赵一泽裘欢朱栩青强璐
3
黄正达
教授
非线性数值代数以及优化中的算法设计及评判
何纪辽
4
朱建新
教授
一类复矩阵的特征问题高精度计算及其应用
许升高
康亮
24
张广东
06
半导体磁阻效应现象研究
鲍德松高工
何丕模教授
林滨滨
25
骆子喻
06
二维颗粒对振动频率的响应
鲍德松高工
何丕模教授
张雷锋
26
谢晟
06
半金属薄膜制备及拉曼光谱测量
李海洋教授
尹鑫茂
吴靖
27
王俊淇
许翱鹏
06
半金属薄膜制备及Hall效应测量
李海洋教授
无
28
车彦明
06
基于半导体探测器和核乳胶的射线探测和物质相互作用的研究
欧阳安蛟
副教授
韩旭、赵子龙、
魏丹青
95
刘思甜
06
基于职业指导的大学生能力素质指标体系的研究
钟建安
副教授
刘思甜，谢琳，卫然
96
王佳淼
06
不同心理暗示下人们对网上购物的信任度变化
钟建安
副教授
杨力
97
张茜
06
关于手写输入的工程心理学研究
张彤副教授
张茜，许诺，张玥，周慧娜
98
嵌合型猪圆环病毒PCV1-2 及PCV2 ORF2 真核表达
嵌合型猪圆环病毒PCV1-2及PCV2 ORF2真核表达质粒对商品猪的免疫保护研究1程旭，宋益，盛瑜，高崧，刘秀梵扬州大学农业部畜禽传染病学重点开放实验室，江苏扬州（225009）E-mail：gsong@摘要：应用本实验室构建的嵌合型猪圆环病毒PCV1-2及真核表达质粒pcDNA3.1/V5-His-orf2作为免疫原免疫母源抗体ELISA效价在0.07-0.60不等的商品猪，九头猪随机分为四组，第1组为3头，其余3组均为2头。
第1组肌肉注射免疫TCID50为10 3.5的PCV1-2病毒/头，第2组肌肉注射真核表达质粒200µg/头, 第3组肌肉注射空载体（pcDNA3.1）200µg/头, 第4组不免疫作为攻毒对照组。
在免疫后42天，PCV1-2组及真核表达质粒组产生了PCV2抗体。
免疫后42天所有组攻毒PCV2和PRRSV，剂量分别为2×104.5TCID50/头和106TCID50/头。
攻毒后21天攻毒对照组猪淋巴结比免疫组猪显著肿大，免疫组猪血清、淋巴结中PCV2病毒载量低于对照组，攻毒对照组猪淋巴结中PCV2抗原含量高于免疫组，这些结果表明嵌合型猪圆环病毒PCV1-2及真核表达质粒肌肉注射免疫商品猪后，对PCV2感染能产生保护性免疫应答，有可能成为候选疫苗。
关键词：嵌合型猪圆环病毒PCV1-2，真核表达质粒，免疫保护猪圆环病毒（porcine circovirus，PCV）是由Tisher等于1974年在PK15细胞中发现[1]。
该病毒为20面体对称，无囊膜，以滚环方式进行复制，其基因组是一种环状、单股负链DNA。
该病毒有两个基因型：PCV1和PCV2。
前者无致病性，广泛存在于猪群中；后者首先由Allan 等从患断奶仔猪多系统衰竭综合征（postweaning multisystemic wasting syndrome,PMWS）的猪群中分离并证明为PMWS的重要病原[2]，该病以进行性消瘦，呼吸困难，淋巴结肿大，发育迟缓，黄疸及皮肤苍白等为主要特征[3，4]。