2014年全国数学竞赛初三决赛试题(含答案)
试卷:2014年上海市新知杯初中数学试题(含答案解析)

2014上海市初三数学竞赛试卷(2014年12月7日 上午9:00—11:00)解答本试卷可以使用科学计算器一、填空题(每小题10分,共80分)1.化简:3223222a a b ab b a ab b--+=-+ 2. 若y xa x z+=,z y b y x +=,x z c z y +=,则()()()b c a c a b a b c +-+-+-的值为3. 已知ABCD 是等腰梯形, ABIICD ,AB=6,CD=16,△ACE 是直角三角形,∠AEC=900,CE=BC=AD ,则AE 的长为4. 方程2014xyz xy yz zx x y z ++++++=的非负整数解(x ,y ,z )的组数为5.在三角形ABC 中,∠ABC=440,D 是边BC 上的一点,满足DC=2AB, ∠BAD=240,则∠ACB 的大小为6. 在直角坐标平面xOy 上,由不等式221x y x y ⎧≤⎪≤⎨⎪-≤⎩确定的区域的面积为7. 使得关于x 的方程2221130a x ax a ++-=有两个整数根的所有正实数a 是8. 设20142的所有正约数为d 1,d 2,…,d k ,则12111 (201420142014)k d d d +++=+++二、解答题(第9、10 题,每题15 分,第11、12 题,每题20 分,共70 分) 9. 解关于x 的方程:(1)xx x x x a x x+--=++10.如图,在凸四边形ABCD 中,已知∠ABC +∠CDA =3000,AB CD BC AD ⨯=⨯, 求证:AB CD AC BD ⨯=⨯11. 已知边长为a 的正方形ABCD 的内部有n 个圆,每个圆的面积都不大于1,且与正方形ABCD 的边平行的直线都至多与一个圆相交,求证:这n 个圆的面积之和小于a 。
12. (1)证明:可以将全体正整数分成3组A 1,A 2,A 3,使得对每一个整数15n ≥,在A 1,A 2,A 3的每一组中都能取出两个不同的数,它们的和为n(2)证明:将全体正整数任意分成4组A 1,A 2,A 3,A 4,则存在整数15n ≥,在A 1,A 2,A 3 ,A 4中一定有一组A i ,在A i 中不存在两个不同的数,它们的和为n2014上海市初三数学竞赛试卷解答(2014年12月7日上午9:00—11:00)解答本试卷可以使用科学计算器一、填空题(每小题10分,共80分)1.化简:3223222a ab ab ba ab b--+= -+2. 若y xax z+=,z yby x+=,x zcz y+=,则()()()b c a c a b a b c+-+-+-的值为3. 已知ABCD是等腰梯形,ABIICD,AB=6,CD=16,△ACE是直角三角形,∠AEC=900,CE=BC=AD,则AE的长为4. 方程2014xyz xy yz zx x y z ++++++=的非负整数解(x ,y ,z )的组数为5.在三角形ABC 中,∠ABC=440,D 是边BC 上的一点,满足DC=2AB, ∠BAD=240,则∠ACB 的大小为6. 在直角坐标平面xOy 上,由不等式221x y x y ⎧≤⎪≤⎨⎪-≤⎩确定的区域的面积为7. 使得关于x 的方程2221130a x ax a ++-=有两个整数根的所有正实数a 是8. 设20142的所有正约数为d 1,d 2,…,d k ,则12111 (201420142014)k d d d +++=+++二、解答题(第9、10 题,每题15 分,第11、12 题,每题20 分,共70 分) 9. 解关于x 的方程:(1)xx x x x a x x+--=++⨯=⨯, 10.如图,在凸四边形ABCD中,已知∠ABC+∠CDA =3000,AB CD BC AD⨯=⨯求证:AB CD AC BD11. 已知边长为a的正方形ABCD的内部有n个圆,每个圆的面积都不大于1,且与正方形ABCD的边平行的直线都至多与一个圆相交,求证:这n个圆的面积之和小于a。
2014全国数学竞赛初三决赛试卷

2014年全国初中数学联赛决赛试卷含参考答案一、选择题:(本题满分42分,每小题7分) 1.已知,x y 为整数,且满足22441111211()()()3x y x y x y++=--,则x y +的可能的值有( ) A. 1个 B. 2个 C. 3个 D. 4个【答】 C.由已知等式得2244224423x y x y x y xy x y x y++-⋅=⋅,显然,x y 均不为0,所以x y +=0或32()xy x y =-.若32()xy x y =-,则(32)(32)4x y +-=-.又,x y 为整数,可求得12,x y =-⎧⎨=⎩,或21.x y =-⎧⎨=⎩,所以1x y +=或1x y +=-.因此,x y +的可能的值有3个.2.已知非负实数,,x y z 满足1x y z ++=,则22t xy yz zx =++的最大值为 ( ) A .47 B .59 C .916 D .1225【答】 A.21222()2()()4t xy yz zx x y z yz x y z y z =++=++≤+++212(1)(1)4x x x =-+-2731424x x =-++2734()477x =--+,易知:当37x =,27y z ==时,22t xy yz zx =++取得最大值47.3.在△ABC 中,AB AC =,D 为BC 的中点,BE AC ⊥于E ,交AD 于P ,已知3BP =,1PE =,则AE = ( )A.2BCD【答】 B .因为AD BC ⊥,BE AC ⊥,所以,,,P D C E 四点共圆,所以12BD BC BP BE ⋅=⋅=,又2BC BD =,所以BD =DP =.又易知△AEP ∽△BDP ,所以AE PEBD DP =,从而可得PE AE BD DP =⋅=.4.6张不同的卡片上分别写有数字2,2,4,4,6,6,从中取出3张,则这3张卡片上所写的数字可以作为三角形的三边长的概率是 ( )A .12 B .25 C .23 D .34【答】 B.若取出的3张卡片上的数字互不相同,有2×2×2=8种取法;若取出的3张卡片上的数字有相同的,有3×4=12种取法.所以,从6张不同的卡片中取出3张,共有8+12=20种取法.要使得三个数字可以构成三角形的三边长,只可能是:(2,4,4),(4,4,6),(2,6,6),(4,6,6),由于不同的卡片上所写数字有重复,所以,取出的3张卡片上所写的数字可以作为三角形的三边长的情况共有4×2=8种.因此,所求概率为82205=.5.设[]t 表示不超过实数t 的最大整数,令{}[]t t t =-.已知实数x 满足33118x x +=,则1{}{}x x+= ( )A .12 B.3 C.1(32D .1 【答】 D . 设1x a x +=,则32223211111()(1)()[()3](3)x x x x x a a x x x x x+=++-=++-=-,所以2(3)18a a -=,因式分解得2(3)(36)0a a a -++=,所以3a =.由13x x +=解得1(32x =±,显然10{}1,0{}1x x <<<<,所以1{}{}x x+=1.6.在△ABC 中,90C ∠=︒,60A ∠=︒,1AC =,D 在BC 上,E 在AB 上,使得△ADE 为等腰直角三角形, 90ADE ∠=︒ ,则BE 的长为 ( )A.4- B.2 C.11)2D1 【答】 A.过E 作EF BC ⊥于F ,易知△ACD ≌△DFE ,△EFB ∽△ACB .设EF x =,则2BE x =,22AE x =-,)DE x =-,1DF AC ==,故2221)]x x +=-,即2410x x -+=.又01x <<,故可得2x =故24BE x ==-二、填空题:(本题满分28分,每小题7分)A1.已知实数,,a b c 满足1a b c ++=,1111a b c b c a c a b++=+-+-+-,则abc =____.【答】 0. 由题意知1111121212c a b++=---,所以 (12)(12)(12)(12)(12)(12)(12)(12)(12)a b b c a c a b c --+--+--=---整理得22()8a b c abc -++=,所以abc =0. 2.使得不等式981715n n k <<+对唯一的整数k 成立的最大正整数n 为 . 【答】144. 由条件得7889k n <<,由k 的唯一性,得178k n -≤且189k n +≥,所以2118719872k k n n n +-=-≥-=,所以144n ≤.当144n =时,由7889k n <<可得126128k <<,k 可取唯一整数值127. 故满足条件的正整数n 的最大值为144.3.已知P 为等腰△ABC 内一点,AB BC =,108BPC ∠=︒,D 为AC 的中点,BD 与PC 交于点E ,如果点P 为△ABE 的内心,则PAC ∠= .【答】48︒.由题意可得PEA PEB CED AED ∠=∠=∠=∠,而180PEA PEB AED ∠+∠+∠=︒,所以60PEA PEB CED AED ∠=∠=∠=∠=︒, 从而可得30PCA ∠=︒.又108BPC ∠=︒,所以12PBE ∠=︒,从而24ABD ∠=︒. 所以902466BAD ∠=︒-︒=︒, 11()(6630)1822PAE BAD CAE ∠=∠-∠=︒-︒=︒,所以183048PAC PAE CAE ∠=∠+∠=︒+︒=︒.4.已知正整数,,a b c 满足:1a b c <<<,111a b c ++=,2b ac =,则b = .【答】36.设,a c 的最大公约数为(,)a c d =,1a a d =,1c c d =,11,a c 均为正整数且11(,)1a c =,11a c <,则2211b ac d a c ==,所以22|d b ,从而|d b ,设1b b d =(1b 为正整数),则有2111b a c =,而11(,)1a c =,所以11,a c 均为完全平方数,设2211,a m c n ==,则1b mn =,,m n 均为正整数,且(,)1m n =,m n <.又111a b c ++=,故111()111d a b c ++=,即22()111d m n mn ++=.注意到222212127m n mn ++≥++⨯=,所以1d =或3d =.若1d =,则22111m n mn ++=,验算可知只有1,10m n ==满足等式,此时1a =,不符合题意,故舍去.若3d =,则2237m n mn ++=,验算可知只有3,4m n ==满足等式,此时27,36,48a b c ===,符合题意.因此,所求的36b =.三、(本题满分20分)设实数,a b 满足22(1)(2)40a b b b a +++=,(1)8a b b ++=,求2211a b+的值. 解 由已知条件可得222()40a b a b ++=,()8ab a b ++=.设a b x +=,ab y =,则有2240x y +=,8x y +=, …………5分 联立解得(,)(2,6)x y =或(,)(6,2)x y =. ………10分若(,)(2,6)x y =,即2a b +=,6ab =,则,a b 是一元二次方程2260t t -+=的两根,但这个方程的判别式2(2)24200∆=--=-<,没有实数根; ………… … 15分若(,)(6,2)x y =,即6a b +=,2ab =,则,a b 是一元二次方程2620t t -+=的两根,这个方程的判别式2(6)8280∆=--=>,它有实数根.所以2222222222211()262282a b a b ab a b a b a b ++--⨯+====. ………20分四、.(本题满分25分)如图,在平行四边形ABCD 中,E 为对角线BD 上一点,且满足ECD ACB ∠=∠,AC 的延长线与△ABD 的外接圆交于点F . 证明:DFE AFB ∠=∠.证明 由ABCD 是平行四边形及已知条件知ECD ACB DAF ∠=∠=∠. ………5分又A 、B 、F 、 D 四点共圆,所以BDC ABD AFD ∠=∠=∠,………… ….10分 所以△ECD ∽△DAF , …… …15分 所以ED CD ABDF AF AF==. ………20分 又EDF BDF BAF ∠=∠=∠,所以△EDF ∽△BAF ,故DFE AFB ∠=∠.…………… ………25分五、(本题满分25分)设n 是整数,如果存在整数,,x y z 满足3333n x y z xyz =++-,则称n 具有性质P .FB(1)试判断1,2,3是否具有性质P ;(2)在1,2,3,…,2013,2014这2014个连续整数中,不具有性质P 的数有多少个? 解 取1x =,0y z ==,可得33311003100=++-⨯⨯⨯,所以1具有性质P ;取1x y ==,0z =,可得33321103110=++-⨯⨯⨯,所以2具有性质P ;…………………5分 若3具有性质P ,则存在整数,,x y z 使得33()3()()x y z x y z xy yz zx =++-++++,从而可得33|()x y z ++,故3|()x y z ++,于是有39|()3()()x y z x y z xy yz zx ++-++++,即9|3,这是不可能的,所以3不具有性质P . ……………………10分(2)记333(,,)3f x y z x y z xyz =++-,则33(,,)()3()3f x y z x y z xy x y xyz =++-+- 3()3()()3()x y z x y z x y z xy x y z =++-+++-++=3()3()()x y z x y z xy yz zx ++-++++2221()()2x y z x y z xy yz zx =++++--- 2221()[()()()]2x y z x y y z z x =++-+-+-. 即(,,)f x y z 2221()[()()()]2x y z x y y z z x =++-+-+- ①……………………15分不妨设x y z ≥≥,如果1,0,1x y y z x z -=-=-=,即1,x z y z =+=,则有(,,)31f x y z z =+; 如果0,1,1x y y z x z -=-=-=,即1x y z ==+,则有(,,)32f x y z z =+; 如果1,1,2x y y z x z -=-=-=,即2,1x z y z =+=+,则有(,,)9(1)f x y z z =+; 由此可知,形如31k +或32k +或9k (k 为整数)的数都具有性质P .……………………20分 又若33|(,,)()3()()f x y z x y z x y z xy yz zx =++-++++,则33|()x y z ++,从而3|()x y z ++,进而可知39|(,,)()3()()f x y z x y z x y z xy yz zx =++-++++.综合可知:当且仅当93n k =+或96n k =+(k 为整数)时,整数n 不具有性质P .又2014=9×223+7,所以,在1,2,3,…,2013,2014这2014个连续整数中,不具有性质P 的数共有224×2=448个. …………………25分。
全国初三初中数学竞赛测试带答案解析

全国初三初中数学竞赛测试班级:___________ 姓名:___________ 分数:___________一、选择题1.已知m 、n 是两个连续正整数,m<n ,且a=mn ,设x=,y=.下列说法正确的是( ).A .x 为奇数,y 为偶数B .x 为偶数,y 为奇数C .x 、y 都为奇数D .x 、y 都为偶数2.设a 、b 、c 和S 分别为三角形的三边长和面积,关于x 的方程b 2x 2+(b 2+c 2-a 2)x+c 2=0的判别式为Δ.则Δ与S 的大小关系为( ).A .Δ=16S 2B .Δ=-16S 2C .Δ=16SD .Δ=-16S3..设a 为的小数部分,b 为的小数部分.则的值为( ). A .+-1B .-+1C .--1D .++14.如图,D 、E 分别为△ABC 的边AB 、AC 上的点,△ACD 与△BCD 的周长相等,△ABE 与△CBE 的周长相等,记△ABC 的面积为S.若∠ACB=90°,则AD·CE 与S 的大小关系为( ).A 、S=AD·CEB 、S>AD·CEC 、S<AD·CED 、无法确定5.如图,在△ABC 中,AB=8,BC=7,AC=6,延长边BC 到点P ,使得△PAB 与△PCA 相似.则PC 的长是( ).A .7B .8C .9D .106.如图,以PQ=2r(r ∈Q)为直径的圆与一个以R(R ∈Q)为半径的圆相切于点P.正方形ABCD 的顶点A 、B 在大圆上,小圆在正方形的外部且与边CD 切于点Q.若正方形的边长为有理数,则R 、r 的值可能是( ).A.R=5,r="2"B.R=4,r=3/2C.R=4,r="2"D.R=5,r=3/2二、填空题1.已知方程x 2+x-1=0的两个根为α、β.则的值为 .2.把1,2,…,2 008个正整数分成1 004组:a 1,b 1;a 2,b 2;…;a 1 004,b 1 004,且满足a 1+b 1=a 2+b 2=…=a 1004+b 1004.对于所有的i(i=1,2,…,1 004),a i b i 的最大值为 .3.AD、BE、CF为△ABC的内角平分线.若BD+BF=CD+CE=AE+AF,则∠BAC的度数为 .4.下列四个命题:①一组对边相等且一组对角相等的四边形是平行四边形; ②一组对边相等且一条对角线平分另一条对角线的四边形是平行四边形;③一组对角相等且这一组对角的顶点所联结的对角线被另一条对角线平分的四边形是平行四边形;④一组对角相等且这一组对角的顶点所联结的对角线平分另一条对角线的四边形是平行四边形.其中,正确命题的序号是 .三、解答题1.(20分)已知△ABC中,∠A>∠B>∠C,且∠A=2∠B.若三角形的三边长为整数,面积也为整数,求△ABC面积的最小值.2.(25分)已知G是△ABC内任一点,BG、CG分别交AC、AB于点E、F.求使不等式S△BGF ·S△CGE≤kS2△ABC恒成立的k的最小值.3.(25分)已知(x+)(y+)=1.求证:x+y=0.全国初三初中数学竞赛测试答案及解析一、选择题1.已知m、n是两个连续正整数,m<n,且a=mn,设x=,y=.下列说法正确的是( ).A.x为奇数,y为偶数B.x为偶数,y为奇数C.x、y都为奇数D.x、y都为偶数【答案】C【解析】考查知识点:两个连续正整数之间的关系,平方根的意义,奇数和偶数的概念。
2014年全国初中数学竞赛试题参考答案及评分标准

2014年全国初中数学竞赛试题参考答案及评分标准一、选择题(共10小题,每小题6分,满分60分.) 1.已知x 、y 、z 满足2x =3y-x =5z+x ,则5x-yy+2z的值为( )(A )1 (B )13 (C )-13 (D )12【答】B .解:设 2x =3y-x =5z+x =1k 则x=2k ,y-z=3k ,z+x=5k ,即x=2k ,y=6k ,z=3k 。
所以5x-y y+2z =5·2k-6k 6k+6k =13,故选B.2.已知等腰三角形的周长为12,则腰长a 的取值范围是( )(A )a >3 (B )a <6 (C )3<a <6 (D )4<a <7 【答】C.解:腰长为a ,则底长为12-2a ,由2a >12-2a 及12-2a >0可得3<a <6 故选C. 3.设 21x x 、 是一元二次方程032=-+x x的两根,则 1942231+-x x 等于( )(A )-4 (B )8 (C )6 (D )0 【答】D.解:将21x x 、代入方程,将目标整式降次,利用两根之和求解.4.如果a b ,为给定的实数,且1a b <<,那么1121a a b a b ++++,, ,这四个数据的平均数与中位数之差的绝对值是( ) (A )1 (B )214a - (C )12 (D )14【答】D.解:由题设知,1112a a b a b <+<++<+,所以这四个数据的平均数为1(1)(1)(2)34244a ab a b a b+++++++++=, 中位数为 (1)(1)44224a ab a b++++++=, 于是 4423421444a b a b ++++-=. 故选D.5. 如图,正方形A BCD 和EFGC 中,正方形EFGC 的边长为a ,用a 的代数式表示阴影部分△AEG 的面积为( )(A )232a (B )223a (C )212a (D )2a【答】C .6.若△ABC 的三条边a,b,c 满足关系式a 4+b 2c 2- a 2c 2-b 4=0,则△ABC 的形状是( ) (A )等腰三角形 (B )等边三角形(C )直角三角形 (D )等腰三角形或直角三角形 【答】D.解法一:原方程左边变形为 (a 4-b 4)+(b 2c 2-a 2c 2)=0, (a 2+b 2)(a 2-b 2)+(b 2-a 2+)c 2=0,∴(a 2-b 2)(a 2+b 2-c 2)=0, ∴a=b 或c 2=a 2+b 2.∴△ABC 为等腰三角形或直角三角形. 解法二:应用配方法a 4+b 2c 2- a 2c 2-b 4=0, (a 4-a 2c 2)-(-b 2c 2+b 4)=0 (a 2-22c )2 -(22c -b 2)2=0 ∴(a 2-b 2)(a 2+b 2-c 2)=0, ∴a 2-b 2=0,或a 2+b 2-c 2=0. ∴a=b 或c 2=a 2+b 2. ∴△ABC 为等腰三角形或直角三角形. 故选D.7.一批志愿者组成了一个“爱心团队”,以募集爱心基金.第一个月他们就募集到资金1万元,随着影响的扩大,第n (n ≥2)个月他们募集到的资金都将会比上个月增加20%,则当该月所募集到的资金首次突破10万元时(参考数据: 51.22.5≈,61.2 3.0≈,71.2 3.6≈),相应的n 的值为( )(A )11 (B )12 (C )13 (D )14 【答】D.8.如图:点D 是△ABC 的边BC 上一点,若∠CAD = ∠DAB = 60°,AC = 3 ,AB = 6,则AD 的长度是( )(A )2 (B )2.5 (C )3 (D )3.5 【答】A.解:如图,作BE ⊥AC 交CA 的延长线于E ,在Rt △ABE 中, ∠BAE= 60° ∴∠ABE= 30° ∴AE=21AB = 3 由勾股定理得BE =33∴21BCA s △AC ·BE =329 ∵∠CAD = ∠DAB = 60°同理得△ADC 和△ABD 中AD 边上的高分别是323和33 ∴=CD A s △343AD ,=B DA s △323AD 又CD A s △+B DA s △=BC A s △ ∴343AD + 323AD =329 ∴AD = 2 故选A9.若m=20132+20132×20142+20142,则m ( )(A )是完全平方数,还是奇数 (B )是完全平方数,还是偶数 (C )不是完全平方数,但是奇数 (D )不是完全平方数,但是偶数 【答】A.解 :原式=20132-2×2013×2014+20142+2×2013×2014+20132×20142=(2013-2014)2+2×2013×2014+(2013×2014)2=1+2×2013×2014+(2013×2014)2=(2013×2014+1)2所以(2013×2014+1)2是一个完全平方数,末尾数字是9,所以也是奇数. 故选A. 10、设非零实数a ,b ,c 满足2302340a b c a b c ++=⎧⎨++=⎩,,则222ab bc caa b c ++++的值为( ) (A )12-(B )0 (C )12(D )1 【答】A.解:由已知得(234)(23)0a b c a b c a b c ++=++-++=,故 2()0a b c ++=.于是 2221()2ab bc ca a b c ++=-++, 所以22212ab bc ca a b c ++=-++.故选A.二、填空题(共5小题,每小题6分,满分30分)11.已知整数1234a a a a ⋅⋅⋅,,,,满足下列条件:10a =,21|1|a a =-+,32|2|a a =-+,43|3|a a =-+,…,依次类推,则2012a 的值为 .【答】1006-12.如图,四边形ABCD 中,AB =BC ,∠ABC =∠CDA =90°, BE ⊥AD 于点E ,且四边形ABCD 的面积为8,则BE = .【答】解:.如图,可以通过旋转变换将△ABE 绕点B 逆时针旋转90°,得到△CBF.证明出四边形BFDE 是正方形,且它的面积是8,则边长是或者过点B 作BF ⊥BE ,交DC 延长线于F. 证明△ABE ≌△CBF ,其余思路同上。
九年级数学竞赛试题(含答案)-

初三数学竞赛试题(本卷满分:120分,时间:120分钟)一、选择题(每小题5分、共40分)1、如果多项式200842222++++=b a b a p ,则p 的最小值是( )(A) 2005 (B) 2006 (C) 2007 (D) 20082、菱形的两条对角线之和为L,面积为S,则它的边长为( ). (A)2124L S - (B)2124L S + (C)21S L 42- (D)21S L 42+3、方程1)1(32=-++x x x 的所有整数解的个数是( )(A )5个 (B )4个 (C )3个 (D )2个 4、已知梯形ABCD 中,AD ∥BC ,对角线AC 、BD 交于O ,△AOD 的面积为4, △BOC 的面积为9,则梯形ABCD 的面积为( )(A )21 (B )22 (C )25 (D )26 5、方程|xy |+|x+y|=1的整数解的组数为( )。
(A )8 (B) 6 (C) 4 (D) 2 6、已知一组正数12345,,,,x x x x x 的方差为:222222123451(20)5S x x x x x =++++-,则关于数据123452,2,2,2,2x x x x x + + + + +的说法:①方差为S 2;②平均数为2;③平均数为4;④方差为4S 2。
其中正确的说法是( )(A) ①② (B) ①③ (C) ②④ (D )③④7、一名模型赛车手遥控一辆赛车,先前进1m ,然后,原地逆时针方向旋转角a(0°<α<180°)。
被称为一次操作.若五次操作后,发现赛车回到出发点,则角α为 ( )(A) 7 2° (B )108°或14 4° (C )144° (D ) 7 2°或144°8、如图,已知圆心为A 、B 、C 的三个圆彼此相切,且均与直线l 相切.若⊙A、⊙B、⊙C 的半径分别为a 、b 、c(0<c<a<b),则a 、b 、c 一定满足的关系式为 ( ) (A )2b=a+c (B )=b c a +(C )b ac 111+= (D)ba c 111+=二、填空题(每小题5分,共30分)9、已知a ﹑b 为正整数,a=b-2005,若关于x 方程x 2-ax+b=0有正整数解,则a 的最小值是________. 10、如图,在△ABC 中,AB=AC, AD ⊥BC, CG ∥AB, BG 分别交AD,AC 于E,F.若b a BE EF =,那么BEGE等于 .A BCG F E D11、已知二次函数c bx ax y ++=2的图象与x 轴交于点(-2,0),(x1,0),且1<x1<2,与y 轴正半轴的交点在(0,2)的下方,下列结论:①a<b<0;②2a+c>0;③4a+c<0;④2a-b+1.其中正确的结论是_____________.(填写序号)12、如图,⊙O 的直径AB 与弦EF 相交于点P ,交角为45°, 若22PF PE +=8,则AB 等于 .13、某商铺专营A ,B 两种商品,试销一段时间,总结得到经营利润y 与投人资金x(万元)的经验公式分别是yA=x 71,yB=x 73。
初三数学竞赛试题及答案

初三数学竞赛试题一、选择题(下列各题的备选答案中,只有一个答案是正确的,将正确答案的序号填入题后的括号内,每小题2分,共20分)1.下列各式中,最简二次根式为( )A.B 。
D 。
2。
方程(x+1)x=0的根是()A。
x1=1,x2=0 B.x1=—1,x2=1 C。
x1=—1,x2=0 D.x1=x2=03。
如图,PA、PB分别切⊙O于A、B,点C 为优弧上一点,∠ACB=60°,则∠APB的度数是()A。
60° B.120° C.30°或120° D.30°4.二次函数y=—x2-4x+2的顶点坐标、对称轴分别是( )A。
(—2,6),x=—2 B。
(2,6),x=2 C。
(2,6),x=-2 D.(-2,6),x=25。
已知Rt△ABC∽Rt△A′B′C′,∠C=∠C′=90°,且AB=2A′B′,则sinA 与sinA′的关系为()A。
sinA=2sinA′ B。
2sinA=sinA′ C.sinA=sinA′ D。
不确定6.在下面四种边长相等的正多边形的组合中,能作平面镶嵌的组合是()7.如图,点P是x轴正半轴上的一个动点,过点P做x轴的垂线PQ交双曲线y=1x于点Q,连结OQ,当点P向右运动时,Rt△QOP的面积()A.逐渐增大 B。
逐渐减小 C。
保持不变D。
无法确定8。
已知⊙O1和⊙O2的半径分别为2和m,圆心距为n,且2和m都是方程x2-10x+n=0的两根,则两圆的位置关系是()A。
相交 B.外离 C.内切 D.外切9。
将某氢氧化钠溶液加水,则描述溶液pH值与加水量(m)间变化规律的图象大致是()10.如图,AB是⊙O的弦,C是AB的三等分点,连结OC并延长交⊙O于点D。
若OC=3,CD=2,则圆心O到弦AB的距离是()A。
B。
9CD。
二、填空题(每小题2分,共20分)11.已知点P(—3,2),点P′是点P关于原点的对称点,则点P′的坐标是____。
全国初三初中数学竞赛测试带答案解析

全国初三初中数学竞赛测试班级:___________ 姓名:___________ 分数:___________一、选择题1.如图,已知在Rt△ABC中,AB=35,一个边长为12的正方形CDEF内接于△ABC.则△ABC的周长为( ).(A)35 (B)40 (C)81 (D)842.设n=9+99+…+99…9(99个9).则n的十进制表示中,数码1有( )个.A.50B.90C.99D.1003.已知f(x)=x2+6ax-a,y=f(x)的图像与x轴有两个不同的交点(x1,0),(x2,0),且=8a-3.则a的值是( ).A.1B.2C.0或D.4.若不等式ax2+7x-1>2x+5对-1≤a≤1恒成立,则x的取值范围是( ).A.2≤x≤3B.2<x<3C.-1≤x≤1D.-1<x<15.在Rt△ABC中,∠B=60°,∠C=90°,AB=1,分别以AB、BC、CA为边长向△ABC外作等边△ABR、等边△BCP、等边△CAQ,联结QR交AB于点T.则△PRT的面积等于( ).(A) (B) (C) (D)6.在3×5的棋盘上,一枚棋子每次可以沿水平或者垂直方向移动一小格,但不可以沿任何斜对角线移动.从某些待定的格子开始,要求棋子经过全部的小正方格恰好一次,但不必回到原来出发的小方格上.在这15个小方格中,有( )个可以是这枚棋子出发的小方格.A.6B.8C.9D.10二、填空题1.正方形ABCD的边长为5,E为边BC上一点,使得BE=3,P是对角线BD上的一点,使得PE+PC的值最小.则PB= .2.设a、b、c为整数,且对一切实数x,(x-a)(x-8)+1="(x-b)(x-c)" 恒成立.则a+b+c的值为 .3.如图,在以O为圆心的两个同心圆图2中,MN为大圆的直径,交小圆于点P、Q,大圆的弦MC交小圆于点A、B.若OM=2,OP= 1,MA=AB=BC,则△MBQ的面积为 .4.从1, 2,…, 2 006中,至少要取出个奇数,才能保证其中必定存在两个数,它们的和为2 008.三、解答题1.(20分)实数x、y、z、w满足x≥y≥z≥w≥0,且5x+4y+3z+6w=100.求x+y+z+w的最大值和最小值.2.(25分)如图,在Rt△ABC中,∠B=90°,它的内切圆分别与边BC、CA、AB相切于点D、E、F,联结AD与内切圆相交于另一点P,联结PC、PE、PF.已知PC⊥PF.求证:(1)EP/DE=PD/DC;(2)△EPD是等腰三角形.3.(25分)在中,有多少个不同的整数(其中,[x]表示不大于x的最大整数)?全国初三初中数学竞赛测试答案及解析一、选择题1.如图,已知在Rt△ABC中,AB=35,一个边长为12的正方形CDEF内接于△ABC.则△ABC的周长为( ).(A)35 (B)40 (C)81 (D)84【答案】D【解析】分析:首先设BC=a,AC=b,由勾股定理与正方形的性质,可得:a2+b2=352,Rt△AFE∽Rt△ACB,再由相似三角形的对应边成比例,可得12(a+b)=ab,解方程组即可求得.解答:解:如图,设BC=a,AC=b,则a2+b2=352=1225.①又Rt△AFE∽Rt△ACB,所以=,即=,故12(a+b)=ab.②由①②得(a+b)2=a2+b2+2ab=1225+24(a+b),解得a+b=49(另一个解-25舍去),所以a+b+c=49+35=84.故答案为D.2.设n=9+99+…+99…9(99个9).则n的十进制表示中,数码1有( )个.A.50B.90C.99D.100【答案】C【解析】由于9=10-1,99=100-1,…,所以n="9+99+999+…+" =10+102+103+…1099-99×1.然后据此等式求出n的值后,即能得出n的十进制表示中,数码1有多少个.解:n=9+99+999+…+=10+102+103+…1099-99×1,=1111111…10(99个1)-99,=11111…1011(99个1).所以在十进制表示中,数码1有99个.故答案为:99.根据式中数据的特点将式中的数据变为10的n次方相加的形式是完成本题的关键.3.已知f(x)=x2+6ax-a,y=f(x)的图像与x轴有两个不同的交点(x1,0),(x2,0),且=8a-3.则a的值是( ).A.1B.2C.0或D.【答案】D【解析】本题考查二次函数与一元二次方程关系的综合应用问题。
-初中数学竞赛题(含答案)

初中数学竞赛一、选择题(每小题7分,共56分.以下每题的4个结论中,仅有一个是正确的,请将正确答案的英文字母填在题后的圆括号内)1.在-|-3|3,-(-3)3,(-3)3,-33中,最大的是( B ). (A)-|-3|3 (B)-(-3)3 (C)(-3)3 (D)-332. “a 的2倍与b 的一半之和的平方,减去a 、b 两数平方和的4倍”用代数式表示应为( )(A)2a+(21b 2)-4(a+b)2 (B)(2a+21b)2-a+4b 2(c)(2a+21b)2-4(a 2+b 2) (D)(2a+21b)2-4(a 2+b 2)23.若a 是负数,则a+|-a|( C ),(A)是负数 (B)是正数 (C)是零 (D)可能是正数,也可能是负数 4.如果n 是正整数,那么表示“任意负奇数”的代数式是( ). (A)2n+l (B)2n-l (C)-2n+l (D)-2n-l5.已知数轴上的三点A 、B 、C 分别表示有理数a 、1、-l ,那么|a+1|表示( ). (A)A 、B 两点的距离 (B)A 、C 两点的距离 (C)A 、B 两点到原点的距离之和 (D)A 、C 两点到原点的距离之和6.如图,数轴上标出若干个点,每相邻两点相距1个单位,点A 、B 、C 、D 对应的数分别是整数a 、b 、c 、d ,且d-2a =10,那么数轴的原点应是( ). (A)A 点 (B)B 点 (C)C 点 (D)D 点7.已知a+b =0,a≠b ,则化简a b (a+1)+ba(b+1)得( ).(A)2a (B)2b (C)+2 (D)-28.已知m<0,-l<n<0,则m ,mn ,mn 2由小到大排列的顺序是 ( ).(A)m ,mn ,mn 2 (B)mn ,mn 2,m (C)mn 2,mn ,m (D)m ,mn 2,mn 二、填空题(每小题?分,共84分)9.计算:31a -(21a -4b -6c)+3(-2c+2b)=10.计算:0.7×194+243×(-15)+0.7×95+41×(-15)=ll.某班有男生a(a>20)人,女生20人,a-20表示的实际意义是12.在数-5,-3,-1,2,4,6中任取三个相乘,所得的积中最大的是13.下表中每种水果的重量是不变的,表的左边或下面的数是所在行或所在列水果的总重量,则表中问号“?”表示的数是 梨 梨 苹果 苹果 30 梨 型 梨 梨 28 荔枝 香蕉 苹果 梨 20 香蕉 香蕉 荔枝 苹果 ? 19 20 25 3014.某学生将某数乘以-1.25时漏了一个负号,所得结果比正确结果小0.25,则正确结果应是 .15.在数轴上,点A 、B 分别表示-31和51,则线段AB 的中点所表示的数是 .16.已知2a x b n-1与-3a 2b 2m (m 是正整数)是同类项,那么(2m-n)x =17.王恒同学出生于20世纪,他把他出生的月份乘以2后加上5,把所得的结果乘以50后加上出生年份,再减去250,最后得到2 088,则王恒出生在 年 月. 18.银行整存整取一年期的定期存款年利率是2.25%,某人1999年12月3日存入1 000元,2000年12月3日支取时本息和是 元,国家利息税税率是20%,交纳利息税后还有 元.19.有一列数a 1,a 2,a 3,a 4,…,a n ,其中 a 1=6×2+l ; a 2=6×3+2; a 3=6×4+3; a 4=6×5+4;则第n 个数a n = ;当a n =2001时,n = . 20.已知三角形的三个内角的和是180°,如果一个三角形的三个内角的度数都是小于120的质数,则这个三角形三个内角的度数分别是第十五届江苏省初中数学竞赛参考答案初一年级第一试一、1.B 2.C 3.C 4.C 5.B 6.B 7.D 8.D二、9.一6a+1 06. 10.一43.6.11.男生比女生多的人数.1 2.90. 1 3.1 6. 1 4.0.1 2 5. 1 5.-1511 6.1. 1 7.1988;1. 18.1022.5;101 8. 1 9.7n+6;2 8 5.2 O .2,8 9,8 9或2,7 1,1 07(每填错一组另扣2分).一、选择题1.已知x=2是关于x 的方程3x-2m=4的根,则m 的值是( ) (A)5 (B)-5 (C)1 (D)-12.已知a+2=b-2=2c=2001,且a+b+c=2001k ,那么k 的值为( )。
历年初中数学竞赛真题库含答案
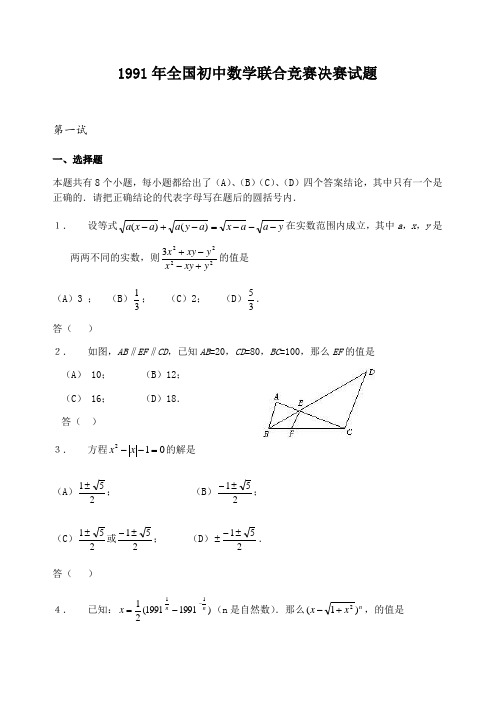
1991年全国初中数学联合竞赛决赛试题第一试一、选择题本题共有8个小题,每小题都给出了(A )、(B )(C )、(D )四个答案结论,其中只有一个是正确的.请把正确结论的代表字母写在题后的圆括号内.1. 设等式y a a x a y a a x a ---=-+-)()(在实数范围内成立,其中a ,x ,y 是两两不同的实数,则22223yxy x y xy x +--+的值是 (A )3 ; (B )31; (C )2; (D )35. 答( )2. 如图,AB ‖EF ‖CD ,已知AB =20,CD =80,BC =100,那么EF 的值是(A ) 10; (B )12;(C ) 16; (D )18.答( )3. 方程012=--x x 的解是(A )251±; (B )251±-; (C )251±或251±-; (D )251±-±. 答( )4.已知:)19911991(2111n n x --=(n 是自然数).那么n x x )1(2+-,的值是(A)11991-; (B)11991--;(C)1991)1(n -; (D)11991)1(--n .答( )5. 若M n 1210099321=⨯⨯⨯⨯⨯ ,其中M为自然数,n 为使得等式成立的最大的自然数,则M(A)能被2整除,但不能被3整除;(B)能被3整除,但不能被2整除;(C)能被4整除,但不能被3整除;(D)不能被3整除,也不能被2整除.答( )6. 若a ,c ,d 是整数,b 是正整数,且满足c b a =+,d c b =+,a d c =+,那么 d c b a +++的最大值是(A)1-;(B)5-;(C)0;(D)1.答( )7. 如图,正方形OPQR 内接于ΔABC .已知ΔAOR 、ΔBOP 和ΔCRQ 的面积分别是11=S ,32=S 和13=S ,那么,正方形OPQR 的边长是 (A)2;(B)3;(C)2 ;(D)3.答( )8. 在锐角ΔABC 中,1=AC ,c AB =, 60=∠A ,ΔABC 的外接圆半径R ≤1,则 (A)21< c < 2 ; (B)0< c ≤21; 答( )(C )c > 2; (D )c = 2.答( )二、填空题1.E是平行四边形ABCD 中BC 边的中点,AE 交对角线BD 于G ,如果ΔBEG 的面积是1,则平行四边形ABCD 的面积是 . 2.已知关于x 的一元二次方程02=++c bx ax 没有实数解.甲由于看错了二次项系数,误求得两根为2和4;乙由于看错了某一项系数的符号,误求得两根为-1和4,那么,=+ac b 32 .3.设m ,n ,p ,q 为非负数,且对一切x >0,qpn m x x x x )1(1)1(+=-+恒成立,则 =++q p n m 22)2( .4.四边形ABCD 中,∠ ABC 135=,∠BCD 120=,AB 6=,BC 35-=,CD = 6,则AD = .第二试x + y , x - y , x y , yx 四个数中的三个又相同的数值,求出所有具有这样性质的数对(x , y ).二、ΔABC中,AB<AC<BC,D点在BC上,E点在BA的延长线上,且BD=BE=AC,ΔBDE的外接圆与ΔABC的外接圆交于F点(如图).求证:BF=AF+CF三、将正方形ABCD分割为2n个相等的小方格(n是自然数),把相对的顶点A,C染成红色,把B,D染成蓝色,其他交点任意染成红、蓝两色中的一种颜色.证明:恰有三个顶点同色的小方格的数目必是偶数.1992年全国初中数学联合竞赛决赛试题第一试一.选择题本题共有8个题,每小题都给出了(A), (B), (C), (D)四个结论,其中只有一个是正确的.请把正确结论的代表字母写在题后的圆括号内.1.满足1=+-ab b a 的非负整数),(b a 的个数是(A)1; (B)2; (C)3; (D)4.2.若0x 是一元二次方程)0(02≠=++a c bx ax 的根,则判别式ac b 42-=∆与平方式20)2(b ax M +=的关系是(A)∆>M (B)∆=M (C)∆>M ; (D)不确定.3.若01132=+-x x ,则44-+x x 的个位数字是(A)1; (B)3; (C)5; (D)7.答( )4.在半径为1的圆中有一内接多边形,若它的边长皆大于1且小于2,则这个多边形的边数必为(A)7; (B)6; (C)5; (D)4.答( )5.如图,正比例函数)0(>==a ax y x y 和的图像与反比例函数)0(>=k xk y 的图像分别相交于A 点和C 点.若AOB Rt ∆和COD ∆的面积分别为S 1和S 2,则S 1与S 2的关系是 (A)21S S > (B)21S S =(C)21S S < (D)不确定 答( )6.在一个由88⨯个方格组成的边长为8的正方形棋盘内放一个半径为4的圆,若把圆周经过的所有小方格的圆内部分的面积之和记为1S ,把圆周经过的所有小方格的圆内部分的面积之和记为2S ,则21S S 的整数部分是 (A)0; (B)1; (C)2; (D)3.答( )7.如图,在等腰梯形ABCD 中, AB //CD , AB=2CD ,︒=∠60A ,又E 是底边AB 上一点,且FE=FB=AC , FA=AB .则AE :EB 等于(A)1:2 (B)1:3(C)2:5 (D)3:10答( )8.设9321,,,,x x x x ⋅⋅⋅均为正整数,且921x x x <⋅⋅⋅<<,220921=+⋅⋅⋅++x x x ,则当54321x x x x x ++++的值最大时,19x x -的最小值是(A)8; (B)9; (C)10; (D)11.答( )二.填空题1.若一等腰三角形的底边上的高等于18cm ,腰上的中线等15cm ,则这个等腰三角形的面积等于________________.2.若0≠x ,则x x x x 44211+-++的最大值是__________.3.在ABC ∆中,B A C ∠∠=∠和,90 的平分线相交于P 点,又AB PE ⊥于E 点,若3,2==AC BC ,则=⋅EB AE .4.若b a ,都是正实数,且0111=+--b a b a ,则=+33)()(ba ab . 第二试一、设等腰三角形的一腰与底边的长分别是方程062=+-a x x 的两根,当这样的三角形只有一个时,求a 的取值范围.二、如图,在ABC ∆中,D AC AB ,=是底边BC 上一点,E 是线段AD 上一点,且A CED BED ∠=∠=∠2.求证:CD BD 2=.三、某个信封上的两个邮政编码M 和N 均由0,1,2,3,5,6这六个不同数字组成,现有四个编码如下:A :320651B :105263C :612305D :316250已知编码A 、B 、C 、D 各恰有两个数字的位置与M 和N 相同.D 恰有三个数字的位置与M 和N 相同.试求:M 和N.1993年全国初中数学联合竞赛决赛试题第一试一.选择题本题共有8个小题,每小题都给出了(A), (B), (C), (D)四个结论,其中只有一个是正确的.请把正确结论的代表字母写在题后的圆括号内.1.多项式1612+-x x 除以12-x 的余式是(A)1; (B)-1; (C)1-x ; (D)1+x ;2.对于命题Ⅰ.内角相等的圆内接五边形是正五边形.Ⅱ.内角相等的圆内接四边形是正四边形,以下四个结论中正确的是(A )Ⅰ,Ⅱ都对 (B )Ⅰ对,Ⅱ错 (C )Ⅰ错,Ⅱ对. (D )Ⅰ,Ⅱ都错.3.设x 是实数,11++-=x x y .下列四个结论:Ⅰ.y 没有最小值;Ⅱ.只有一个x 使y 取到最小值;Ⅲ.有有限多个x (不止一个)使y 取到最大值;Ⅳ.有无穷多个x 使y 取到最小值.其中正确的是(A )Ⅰ (B )Ⅱ (C )Ⅲ (D )Ⅳ4.实数54321,,,,x x x x x 满足方程组⎪⎪⎪⎩⎪⎪⎪⎨⎧=++=++=++=++=++.;;;;52154154354324321321a x x x a x x x a x x x a x x x a x x x其中54321,,,,a a a a a 是实常数,且54321a a a a a >>>>,则54321,,,,x x x x x 的大小顺序是(A)54321x x x x x >>>>; (B )53124x x x x x >>>>;(C )52413x x x x x >>>>; (D )24135x x x x x >>>>.5.不等式73)1(12+<-<-x x x 的整数解的个解(A )等于4 (B )小于4 (C )大于5 (D )等于56.在ABC ∆中,BC AO O A =∠,,是垂心是钝角,则)cos(OCB OBC ∠+∠的值是 (A)22- (B)22 (C)23 (D)21-. 答( )7.锐角三角ABC 的三边是a , b , c ,它的外心到三边的距离分别为m , n ,p ,那么m :n :p 等于 (A)c b a 1:1:1; (B)c b a :: (C)C B A cos :cos :cos (D)C B A sin :sin :sin .答( )8.13333)919294(3-+-可以化简成 (A))12(333+; (B))12(333- (C)123- (D)123+答( )二.填空题1. 当x 变化时,分式15632212++++x x x x 的最小值是___________. 2.放有小球的1993个盒子从左到右排成一行,如果最左面的盒里有7个小球,且每四个相邻的盒里共有30个小球,那么最右面的盒里有__________个小球.3.若方程k x x =--)4)(1(22有四个非零实根,且它们在数轴上对应的四个点等距排列,则k =____________.4.锐角三角形ABC 中,︒=∠30A .以BC 边为直径作圆,与AB , AC分别交于D , E ,连接DE , 把三角形ABC 分成三角形ADE 与四边形BDEC ,设它们的面积分别为S 1, S 2,则S 1:S 2=___________. 第二试一.设H 是等腰三角形ABC 垂心,在底边BC 保持不变的情况下让顶点A 至底边BC 的距离变小,这时乘积HBC ABC S S ∆∆⋅的值变小,变大,还是不变?证明你的结论.二.ABC ∆中, BC =5, AC =12, AB =13, 在边AB ,AC 上分别取点D , E , 使线段DE 将ABC ∆分成面积相等的两部分.试求这样的线段DE 的最小长度.三.已知方程0022=++=++b cx x c bx x 及分别各有两个整数根21,x x 及21,x x '',且,021>x x 021>''x x . (1)求证:;0,0,0,02121<'<'<<x x x x (2)求证:1-b ≤c ≤1+b ; (3)求c b ,所有可能的值.1994年全国初中数学联赛试题第一试(4月3日上午8:30—9:30)考生注意:本试共两道大题,满分80分.一、选择题(本题满分48分,每小题6分)本题共有8个小题都给出了A,B、C,D,四个结论,其中只有一个是正确的,请把你认为正确结论的代表字母写在题后答案中的圆括号内,每小题选对得6分;不选、选错或选出的代表字母超过一个(不论是否写在圆括号内),一律得0分.〔答〕( )2.设a,b,c是不全相等的任意实数,若x=a2-bc,y=b2-ca,z=c2-ab,则x,y,zA.都不小于0B.都不大于0C.至少有一个小0于D.至少有一个大于0〔答〕( )3.如图1所示,半圆O的直径在梯形ABCD的底边AB上,且与其余三边BC,CD,DA相切,若BC=2,DA=3,则AB的长A.等于4B.等于5C.等于6D.不能确定〔答〕( )A.1 B.-1 C.22001D.-22001〔答〕( )5.若平行直线EF,MN与相交直线AB,CD相交成如图2所示的图形,则共得同旁内角A.4对B.8对C.12对D.16对〔答〕( )〔答〕( )7.设锐角三角形ABC的三条高AD,BE,CF相交于H。
初三数学竞赛试卷

初三数学竞赛试卷考试范围:xxx ;考试时间:xxx 分钟;出题人:xxx 姓名:___________班级:___________考号:___________1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上一、选择题1.已知:岛P 位于岛Q 的正西方,由岛P ,Q 分别测得船R 位于南偏东30°和南偏西45°方向上,符合条件的示意图是( )A .B .C .D .2.如图,在x 轴的正半轴上依次截取OA 1=A 1A 2=A 2A 3=A 3A 4=A 4A 5,过点A 1、A 2、A 3、A 4、A 5分别作x 轴的垂线与反比例函数(x≠0)的图象相交于点P 1、P 2、P 3、P 4、P 5,得直角三角形OP 1A 1、A 1P 2A 2、A 2P 3A 3、A 3P 3A 4、A 4P 5A 5,并设其面积分别为S 1、S 2、S 3、S 4、S 5,则S 1+S 2+S 3+S 4+S 5的值为()A .2B .C .3D .3.如图,直线AB 、CD 相交于点E ,DF ∥AB . 若∠D =70°,则∠CEB 等于( ) A .70° B .80° C .90° D .110°4.如果收入80元记作+80元,那么支出20元记作( )A .+20元B .﹣20元C .+100元D .﹣100元5.如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=5,F为DE的中点.若△CEF的周长为18,则OF的长为()A.3.2 B.3.5 C.3.6 D.3.76.下列命题中的真命题是 ( )A.对角线互相垂直的四边形是菱形B.中心对称图形都是轴对称图形C.两条对角线相等的梯形是等腰梯形D.等腰梯形是中心对称图形7.不等式组的解集在数轴上表示正确的是( )8.两圆的圆心距为5,它们的半径分别是一元二次方程x2-5x+4=0的两根,则两圆()A.外切 B.相交 C.内切 D.外离9.计算结果为()A.2 B.4 C.8 D.1610.已知半径分别为3 cm和1cm的两圆相交,则它们的圆心距可能是()A.1 cm B.3 cm C.5cm D.7cm二、判断题11.如图1,已知点A(a,0),B(0,b),且a、b满足,▱ABCD的边AD与y轴交于点E,且E为AD中点,双曲线y=经过C、D两点.(1)求k的值;(2)点P在双曲线y= 上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求满足要求的所有点P、Q的坐标;(3)以线段AB为对角线作正方形AFBH(如图3),点T是边AF上一动点,M是HT的中点,MN⊥HT,交AB于N,当T在AF上运动时,的值是否发生改变?若改变,求出其变化范围;若不改变,请求出其值,并给出你的证明.12.( 12分)如图,在Rt △ABC 中,∠ACB=90°,AC=3,BC=4,过点B 作射线BB 1使得BB 1∥AC .动点D 从点A 出发沿射线AC 方向以每秒5个单位的速度运动,同时动点E 从点C 沿射线AC 方向以每秒3个单位的速度运动.过点D 作DH ⊥AB 于H ,过点E 作EF ⊥AC 交射线BB 1于F ,G 是EF 中点,连接DG .设点D 运动的时间为t 秒.(1)当t 为何值时,AD=AB ,并求出此时DE 的长度; (2)当△DEG 与△ACB 相似时,求t 的值.13.已知双曲线y =(x >0),直线l 1:y ﹣=k (x ﹣)(k <0)过定点F 且与双曲线交于A ,B 两点,设A (x 1,y 1),B (x 2,y 2)(x 1<x 2),直线l 2:y =﹣x +.(1)若k =﹣1,求△OAB 的面积S ;(2)若AB =,求k 的值;(3)设N (0,2),P 在双曲线上,M 在直线l 2上且PM ∥x 轴,问在第二象限内是否存在一点Q ,使得四边形QMPN 是周长最小的平行四边形,若存在,请求出Q 点的坐标。
2014年全国初中数学联合竞赛试题参考答案和评分标准

初三数学竞赛试题 2014年全国初中数学联合竞赛试题参考答案及评分标准A.B. C. D.2014年全国初中数学联合竞赛试题参考答案及评分标准2.【答】 A.,易知:当,时,取得最大值.4.【答】 B.若取出的3张卡片上的数字互不相同,有2×2×2=8种取法;若取出的3张卡片上的数字有相同的,有3×4=12种取法.所以,从6张不同的卡片中取出3张,共有8+12=20种取法.6.【答】 A.过作于,易知△≌△,△∽△.设,则,,,,故,即.又,故可得.故.1.【答】 0.由题意知,所以2.【答】144.由条件得,由的唯一性,得且,所以,所以.当时,由可得,可取唯一整数值127.故满足条件的正整数的最大值为144.4.【答】36.设的最大公约数为,,,均为正整数且,,则,所以,从而,设(为正整数),则有,而,所以均为完全平方数,设,则,均为正整数,且,.又,故,即.注意到,所以或.若,则,验算可知只有满足等式,此时,不符合题意,故舍去.解由已知条件可得,.设,,则有,,……………………5分若,即,,则是一元二次方程的两根,但这个方程的判别式,没有实数根;……………………15分若,即,,则是一元二次方程的两根,这个方程的判别式,它有实数根.所以. ……………………20分解取,,可得,所以1具有性质.取,,可得,所以5具有性质.…………………5分为了一般地判断哪些数具有性质,记,则=.即……………………10分如果,即,则有;如果,即,则有;如果,即,则有;由此可知,形如或或(为整数)的数都具有性质.因此,1,5和2014都具有性质. ……………………20分若2013具有性质,则存在整数使得.注意到,从而可得,故,于是有,即,但2013=9×223+6,矛盾,所以2013不具有性质. ……………………25分2014年全国初中数学联合竞赛试题参考答案及评分标准,易知:当,时,取得最大值.【答】 B.若取出的3张卡片上的数字互不相同,有2×2×2=8种取法;若取出的3张卡片上的数字有相同的,有3×4=12种取法.所以,从6张不同的卡片中取出3张,共有8+12=20种取法.要使得三个数字可以构成三角形的三边长,只可能是:(2,4,4),(4,4,6),(2,6,6),(4,6,6),由于不同的卡片上所写数字有重复,所以,取出的3张卡片上所写的数字可以作为三角形的三边长的情况共有4×2=8种.A.B. C. D.【答】 A.设,则,,,,故,即.又,故可得.故.。
华杯赛试题及答案初三

华杯赛试题及答案初三一、选择题(每题3分,共30分)1. 下列哪个数是无理数?A. πB. 3.14C. 0.33333...(无限循环)D. √2答案:A2. 如果一个二次方程ax² + bx + c = 0(a ≠ 0)的判别式Δ = b² - 4ac小于0,那么这个方程:A. 有一个实数根B. 有两个实数根C. 没有实数根D. 有无穷多个解答案:C3. 已知函数f(x) = 2x - 1,求f(-2)的值。
A. -5B. -3C. 3D. 5答案:A...(此处省略其他选择题)二、填空题(每题4分,共20分)1. 一个直角三角形的两条直角边分别为3和4,那么斜边的长度是______。
答案:52. 某工厂原计划每天生产100个零件,实际每天生产120个零件,那么实际生产效率比计划提高了______%。
答案:20%...(此处省略其他填空题)三、解答题(每题10分,共50分)1. 已知一个长方体的长、宽、高分别为a、b、c,求该长方体的体积。
答案:长方体的体积V = a × b × c。
2. 解方程:x² - 5x + 6 = 0。
答案:首先计算判别式Δ = b² - 4ac = (-5)² - 4 × 1 × 6 = 1,然后求解 x = (-b ± √Δ) / 2a = (5 ± 1) / 2,得到 x₁= 2,x₂ = 3。
...(此处省略其他解答题)结束语本次华杯赛试题涵盖了初三数学的主要知识点,包括代数、几何、函数等。
希望同学们通过练习这些题目,能够加深对数学知识的理解,提高解题能力。
同时,也希望同学们在实际的华杯赛中取得优异的成绩。
祝各位同学学习进步,数学竞赛取得好成绩!。
九年级数学竞赛试题(含答案)

初三数学竞赛试题(本卷满分:120分,时间:120分钟)一、选择题(每小题5分、共40分)1、如果多项式200842222++++=b a b a p ,则p 的最小值是( )(A) 2005 (B) 2006 (C) 2007 (D) 20082、菱形的两条对角线之和为L,面积为S,则它的边长为( ). (A)2124L S - (B)2124L S + (C)21S L 42- (D)21S L 42+3、方程1)1(32=-++x x x 的所有整数解的个数是( )(A )5个 (B )4个 (C )3个 (D )2个 4、已知梯形ABCD 中,AD ∥BC ,对角线AC 、BD 交于O ,△AOD 的面积为4, △BOC 的面积为9,则梯形ABCD 的面积为( )(A )21 (B )22 (C )25 (D )26 5、方程|xy |+|x+y|=1的整数解的组数为( )。
(A )8 (B) 6 (C) 4 (D) 2 6、已知一组正数12345,,,,x x x x x 的方差为:222222123451(20)5S x x x x x =++++-,则关于数据123452,2,2,2,2x x x x x + + + + +的说法:①方差为S 2;②平均数为2;③平均数为4;④方差为4S 2。
其中正确的说法是( )(A) ①② (B) ①③ (C) ②④ (D )③④7、一名模型赛车手遥控一辆赛车,先前进1m ,然后,原地逆时针方向旋转角a(0°<α<180°)。
被称为一次操作.若五次操作后,发现赛车回到出发点,则角α为 ( )(A) 7 2° (B )108°或14 4° (C )144° (D ) 7 2°或144°8、如图,已知圆心为A 、B 、C 的三个圆彼此相切,且均与直线l 相切.若⊙A、⊙B、⊙C 的半径分别为a 、b 、c(0<c<a<b),则a 、b 、c 一定满足的关系式为 ( ) (A )2b=a+c (B )=b c a +(C )b ac 111+= (D)ba c 111+=二、填空题(每小题5分,共30分)9、已知a ﹑b 为正整数,a=b-2005,若关于x 方程x 2-ax+b=0有正整数解,则a 的最小值是________. 10、如图,在△ABC 中,AB=AC, AD ⊥BC, CG ∥AB, BG 分别交AD,AC 于E,F.若b a BE EF =,那么BEGE等于 .A BCG F E D11、已知二次函数c bx ax y ++=2的图象与x 轴交于点(-2,0),(x1,0),且1<x1<2,与y 轴正半轴的交点在(0,2)的下方,下列结论:①a<b<0;②2a+c>0;③4a+c<0;④2a-b+1.其中正确的结论是_____________.(填写序号)12、如图,⊙O 的直径AB 与弦EF 相交于点P ,交角为45°, 若22PF PE +=8,则AB 等于 .13、某商铺专营A ,B 两种商品,试销一段时间,总结得到经营利润y 与投人资金x(万元)的经验公式分别是yA=x 71,yB=x 73。
初三数学竞赛试题(含答案)-

初三数学竞赛试题 班级 姓名 一、选择题(共8小题,每小题5分,共40分)1.要使方程组⎩⎨⎧=+=+23223y x a y x 的解是一对异号的数,则a 的取值范围是( )(A )334<<a (B )34<a (C )3>a (D )343<>a a 或 2.一块含有︒30角的直角三角形(如图),它的斜边AB =8cm, 里面空 心DEF ∆的各边与ABC ∆的对应边平行,且各对应边的距离都是1cm,那么DEF ∆的周长是( )(A)5cm (B)6cm (C) cm )(36- (D) cm )(33+3.将长为15cm 的木棒截成长度为整数的三段,使它们构成一个三角形的三边,则不同的截法有( )(A)5种 (B) 6种 (C)7种 (D)8种4.作抛物线A 关于x 轴对称的抛物线B ,再将抛物线B 向左平移2个单位,向上平移1个单位,得到的抛物线C 的函数解析式是1122-+=)x (y ,则抛物线A 所对应的函数表达式是 ( )(A)2322-+-=)x (y (B) 2322++-=)x (y(C) 2122---=)x (y (D) 2322++-=)x (y5.书架上有两套同样的教材,每套分上、下两册,在这四册教材中随机抽取两册,恰好组成一套教材的概率是( )(A)32 (B) 31 (C) 21 (D) 61 6.如图,一枚棋子放在七边形ABCDEFG 的顶点处,现顺时针方向移动这枚棋子10次,移动规则是:第k 次依次移动k 个顶点。
如第一次移动1个顶点,棋子停在顶点B 处,第二次移动2个顶点,棋子停在顶点D 。
依这样的规则,在这10次移动的过程中,棋子不可能分为两停到的顶点是( )(A)C,E,F (B)C,E,G (C)C,E (D)E,F.7.一元二次方程)a (c bx ax 002≠=++中,若b ,a 都是偶数,C 是奇数,则这个方程( )(A)有整数根 (B)没有整数根 (C)没有有理数根 (D)没有实数根8.如图所示的阴影部分由方格纸上3个小方格组成,我们称这样的图案为L 形,那么在由54⨯ 个小方格组成的方格纸上可以画出不同位置的L 形图案个数是( )(A)16 (B) 32 (C) 48 (D) 64二、填空题:(共有6个小题,每小题5分,满分30分)9.已知直角三角形的两直角边长分别为3cm,4cm ,那么以两直角边为直径的两圆公共弦的长为 cm.10.将一组数据按由小到大(或由大到小)的顺序排列,处于最中间位置的数(当数据的个数是奇数时),或最中间两个数据的平均数(当数据的个数是偶数时)叫做这组数据的中位数,现有一组数据共100个数,其中有15个数在中位数和平均数之间,如果这组数据的中位数和平均数都不在这100个数中,那么这组数据中小于平均数的数据占这100个数据的百分比是11.ABC ∆中,c ,b ,a 分别是C ,B ,A ∠∠∠的对边,已知232310-=+==C ,b ,a ,则C sin c B sin b +的值是等于 。
2014年全国初中数学竞赛九年级预选赛试题参考答案

2014年全国初中数学竞赛九年级预选赛试题参考答案本卷由蕲春县濒湖晨光学校石子据外来试题影相录制并解答,正确性不保一.选择题(共5小题,每小题6分,满分30分)1.甲、乙两人分别从两地同时出发,若相向而行,则a 小时相遇;若同向而行,则b 小时甲追上乙.那么甲的速度是乙的速度的( )倍. A .a +b b B .b a +b C .a +b b -a D .a +b a -b【分析】a (v 甲+v 乙)=b (v 甲-v 乙),由此可得C 正确. 2.方程(x 2+x -1)x +3=1的所有整数解共有( )个. A .5 B .4 C .3 D .2【分析】分三种情况:①a 0=1,a ≠0,x +3=0,x =-3,此时x 2+x -1=5≠0;②1n =1,x 2+x -1=1,x =-2或1;③(-1)2n =1,x 2+x -1=-1,x =-1或0,但x =0时,不满足;故x =-3, -2, -1,1,选B .3.已知A (-1,2)、B (3,2),C 是坐标轴上的一点,若△ABC 是直角三角形,则满足条件的C 点共有( )个. A .3 B .4 C .5 D .6【分析】本题参照图解的5种情况,选C .4.用三种边长相等的正多边形地砖铺地,其顶点拼在一起,刚好能完全铺满地面.已知正多边形的边数分别为x 、y 、z ,则 1x +1y +1z 的值为( ).A .1B .23C .12D .13【分析】据平面密铺的定义,参与密铺的三个多边形各出一个内角,三内角之和为360°.即 (x -2)180° x +(y -2)180° x +(z -2)180° x =360°,或者先求外角再求内角,所列方程则为: 180°-360°x +180°- 360°y +180°- 360°z =360°,整理两者,均可得 1x +1y +1z =12;选C . 5.一名模型赛车手遥控一辆赛车,先前进1m ,然后原地逆时针旋转α(0°<α<180°),被称为一次操作.若5次操作后,发现赛车回到出发点,则α为( ). A .72° B .108°或144° C . 144° D .72°或144° 【分析】考虑两种情况,如下两图所示,本题选D .第5二.填空题(共5小题,每小题6分,满分30分) 6.代数式x 2+4 +(12-x )2+9 的最小值是 .【分析】考虑数形结合,运用勾股定理构图如下:AP +BP ≥AB =52+122 =13.第6题图BA123x12-x32P’CPN M BA7.如图,⊙O 的直径AB 与弦EF 相交于P ,交角为45°,若PE 2+PF 2=8,则AB = . 【分析】作OC ⊥EF 于C , FD ⊥AB 于D ,连接OE 、OF , 设OC =a , PD =b ,则PC =a , OP =2a , BF =b , PF =2b , CE =CF =a +2b , PE =2a +2b ,记OE =OF =R ,在△OCE 中,a 2+(a +2b )2 =R 2,则R 2=2a 2+22ab +2b 2 ;又PE 2+PF 2=8,即(2a +2)2+(2b )2=8,所以a 2+2ab +b 2 =2,故R =2,AB =2R =4. 8.已知a 、b 为正整数, a =b -2005,若关于x 的方程x 2-ax +b =0有正整数解,则a 的最小值是 .【分析】由根与系数关系知:x 1+x 2=a ,x 1x 2=b ,又a =b -2005,∴ x 1+x 2 =x 1x 2-2005, x 1x 2-x 1-x 2+1=2006,∴(x 1-1)(x 2-1)=1×2006=2×1003=2×17×59=34×59,(x 1,x 2) =(2,2007),(3,1004),(35,60),由此知a =x 1+x 2=2009,1007,95,则最小值是95. 9.双曲线y =k x 和y =1 x 在第一象限内的图象如图所示,P 在y =kx的图象上,PC ⊥x 轴于C ,交y =1 x 的图象于A ,PD ⊥y 轴于D ,交y =1 x 的图象于B ,当P 点在y =kx的图象上运动时, 下列结论:①△OBD 与△OAC 的面积相等;②四边形P AOB 的面积保持不变;③P A =PB ;④ 若A 是PC 的中点,则B 是DP 的中点.其中一定正确的的序号是 .FEDCBA【分析】由k 的几何意义知S △OBD =S △OAC = 12;S 四边形P AOB =k -1;仅当P (k ,k )时,P A =PB ;令P (2a ,2b ),则A (2a ,b ),B (a ,2b ),由此知B 是DP 的中点. 故①②④ 均正确.10.如图,一个圆作滚动运动,它从A 位置开始,滚运与它相同的其他6个圆的上部,到达B 位置.则该圆共滚过 圈.【分析】设圆的半径为R ,则总路径长是120360·2π·2R ·2+60360·2π·2R ·4=163πR ,则共转了163πR ÷2πR = 83(圈). 三.解答题(共4题,每题15分,满分60分)11.如图,菱形ABCD 的边长为2,BD =2,E 、F 分别是AD 、CD 上两个动点,且满足AE +CF =2.(1)判断△BEF 的形状,并说明理由; (2)记△BEF 的面积为S ,求S 的取值范围. 【解】(1)△BEF 是等边三角形,理由如下:∵AE +DE =AE +CF =2,∴DE =CF ,又菱形ABCD 的边长为2,BD =2,∴△ABD 与△BCD 均为等边三角形,∴∠ABD =∠C =60°, BD =BC , ∴△BDE ≌△BCF ,∴ BE =BF ,∠DBE =∠CBF ,∵∠CBF +∠DBF =60°, ∴∠DBE +∠DBF =60°,即∠EBF =60°,∴△BEF 是等边三角形. (2)∵△BEF 为等边三角形,∴S =3 4BF 2,当E →D ,F →C ,BF 最大,BF =2; 当BF ⊥CD 时,BF 最小,BF = 3 ;故3 34≤S ≤ 3 .12.预计用1500元购买甲商品x 个,乙商品y 个,不料甲商品每个涨价1.5元,乙商品每个涨价1元,尽管购买甲商品的个数比预定数量少10个,但总金额仍多用29元;若甲商品每个只涨价1元,并且购买甲商品的数量只比预定数量少5个,那么甲、乙两商品支付的总金额是1563.5元. (1)求x 、y 的关系式;(2)若预计购买甲商品的个数的2倍与预计购买乙商品的个数的和大于205而小于210,求x、y的值.【解】(1)设甲商品原单价为a元,乙商品原单价为b元,则ax+by=1500 ①(a+1.5)(x-10)+(b+1)y=1529 ②(a+1)(x-5)+(b+1)y=1563.5 ③联立可得0.5x+y=93,即y=93-0.5x;(2)205<2x+y<210,又y=93-0.5x,∴7423<x<78,又x为整数,∴x=75,76,77,但x=75,77时,y不是整数,∴x=76,y=55.13.在正实数范围内,只存在一个数是关于x的方程x2+kx+3x-1=3x+k的解,求实数k的取值范围.【解】原方程可化为2x2-3x-k-3=0 ,首先考虑增根:k=2x2-3x-3,令x=1,则k=-4;k=-4时,2x2-3x+1=0,(2x-1)(x-1)=0,x1=12,x2=1(增根舍去)令f(x)=2x2-3x-k-3,∵a=2>0在x轴的正半轴上,于是分两种情况:ⅰ)△=0时,k=-338,此时x=34;ⅱ)x1x2≤0,即-k+32≤0,k≥-3.特别地,当k=-3时,2x2-3x=0,x1=32,x2=0(舍去)综上所述,k=-4,-338或k≥-3.14.如图,A(0,1),B是y轴的负半轴上的一个动点,以AB为边作菱形ABCD,其对角线的交点M恰好落在x轴上.记D(x,y).(1)求M点的坐标;(2)求y与x的函数关系式,并写出自变量x的取值范围;(3)若P是(2)中函数图象上的动点,Q(0,t)是定点,是否存在平行于x轴的直线l,使得直线l被以线段PQ为直径的圆截得的弦长始终为定值?若存在,求t的取值范围和直线l的解析式(用含t的代数式表示);若不存在,请说明理由.14x 2【解】(1)M (x2,0);(2)作DE ⊥OA 于E ,则OE =y ,AE =1-y ,DE =x ,AD =AB =1+y ,在Rt △ADE 中,(1-y )2+x 2=(1+y )2,故 y =14x 2,由于B 是y 轴的负半轴上的一个动点,所以x ≠0; (3)设)4,(2m m p ,则圆心)812,2(2m t m E +,作EF ⊥MN 于F ,MN 就是直线l :n y =被⊙E 所截得的弦长,则22222)812()2(m t n m EQ EN --+==,222)812(m t n EF --=,则在△EFN 中,222222)812()812()2(m t n m t n m FN -----+=22)1(41n nt m t n -+-+=,考虑到m 为变量,当1+=n t 时,1-=t n ,122-=-=t n nt FN ≥0,此时t ≥1,即12-=t MN , 即当1-=t y 时,弦长12-=t MN (定值),t ≥1.原题上传后,李先传先生就第2现已作修正,并提示第3问的解法,用垂径定理解决弦长,从而避开圆的方程,根据提示,录排如上. 此法避免了圆的方程. 附第3问用圆的方程求解设)4,(2m m P ,则圆心为)82,2(2m t m +,圆的方程为 ])4([41)82()2(222222m t m m t y m x -+=--+-,化简,得041412222=+--+-t m yt y m y mx x设直线的方程为n y =,则041412222=+--+-t m nt n m n mx x ,设交点的横坐标为21,x x ,aac b x x 4221-=-,本处1=a ,则t m nt n m n m ac b x x 22222221444-++-=-=-=2244)1(n nt m t n -+-+考虑到m 为变量,当1+=n t 时,1-=t n ,)1(44221-==-t n x x ≥0,此时t ≥1,即当1-=t y 时,上式为定值,即弦长为1221-=-t x x ,t ≥1.本题经动态试验,选择二图上传,可见无论x 的取值范围如何,其结论都正确:对不同的t 值,弦长不同;对同一t 值,弦长一定;这一定值是相对于确定的t 值而言,寓动于静.MN = 2.82843厘米2MN = 2.82843厘米2本题第3问初次做感觉很难.。
2014年全国初中数学联赛决赛(初三)试题及其解答

PAE 1 (BAD CAE) 1 (66 30) 18 ,
2
2
所以 PAC PAE CAE 18 30 48 .
EP
C
D
A
4.已知正整数 a, b, c 满足:1 a b c , a b c 111, b2 ac ,则 b
.
【答】36.
设 a, c 的最大公约数为 (a, c) d , a a1d , c c1d , a1, c1 均为正整数且 (a1, c1) 1, a1 c1,则
F
故12 x2 [ 2(1 x)]2 ,即 x2 4x 1 0 .又 0 x 1,故可得 x 2 3 .
A
B E
故 BE 2x 4 2 3 .
二、填空题:(本题满分 28 分,每小题 7 分)
1.已知实数 a, b, c 满足 a b c 1, 1 1 1 1,则 abc ____. abc bca cab
8.
a2 b2 a2b2
a2b2
22
二.(本题满分 25 分)如图,在平行四边形 ABCD 中,E 为对角线 BD 上一点,且满足 ECD ACB ,
AC 的延长线与△ ABD 的外接圆交于点 F . 证明: DFE AFB .
D
证明 由 ABCD 是平行四边形及已知条件知 ECD ACB DAF .
【答】 0.
由题意知 1 1 1 1,所以 1 2c 1 2a 1 2b
(1 2a)(1 2b) (1 2b)(1 2c) (1 2a)(1 2c) (1 2a)(1 2b)(1 2c)
整理得 2 2(a b c) 8abc ,所以 abc 0.
2014 年全国初中数学联合竞赛试题参考答案 第 2 页(共 6 页)
初三数学竞赛试题(含答案)

初三数学竞赛试题(含答案)8个时,即第4个数)称为()。
A)中位数(B)平均数(C)众数(D)极差11.如图,在正方形ABCD中,E、F分别是AB、CD的中点,连接AE、BF,交于点G,则△ABG的面积是()。
A)1/4(ABCD)(B)1/6(ABCD)(C)1/8(ABCD)(D)1/12(ABCD)12.已知函数f(x)在区间[0,1]上连续,且f(0)=0,f(1)=1,则方程f(x)=1/2在区间(0,1)内至少有()个实根。
A)0(B)1(C)2(D)313.如图,在三角形ABC中,D、E分别是AB、AC的中点,F是BC上一点,且AF平分△ABC的周长,则△ABC的面积是()。
A)4S△ADE(B)2S△ADE(C)S△ADE(D)S△ABC14.如图,正方形ABCD中,点E、F分别在AB、BC上,且AE=CF,则△DEF的面积是()。
A)1/4AB2(B)1/6AB2(C)1/8AB2(D)1/12AB2三、解答题:(共有3个小题,每小题20分,满分60分)15.已知函数f(x)=x3-3x2+2x+1,g(x)=f(x)-2x+3,h(x)=g(x)-2x+3,求h(x)的最高项系数。
16.如图,ABCD是一个正方形,O是BD上一点,且OD=2BD,连接AC、CO,交于点E,求△ABE的面积。
17.如图,在长方形ABCD中,点E、F分别在AB、BC 上,且AE=CF,连接EF,交AC于点G,求证:△ADG与△CDF的面积相等。
解:根据题意,可以得到以下方程组:begin{cases}frac{6-2a}{5}=y \\3a-4<x<6-2aend{cases}$要使方程组的解是一对异号的数,只需 $y3$ 或 $a3$ 时,$x$ 的取值范围为 $3a-40$,即 $0<x<6-2a$。
因此,答案为$\boxed{\frac{3}{2}<a<3}$。
2014年全国高中数学联合竞赛上海赛区获奖名单

12 黄小雨 男 上海中学 高二 210
13 李嘉昊 男 上海中学 高三 207
14 陆一平 男 上海中学 高三 204
15 柏旻皓 男 上海中学 高三 20二附属中学 高二 197
48 来俊杰 男 华东师范大学第二附属中学 高三 156
49 程梓兼 男 复旦大学附属中学 高一 156
50 任达伟 男 上海中学 高三 156
51 杨泽凡 男 西南位育中学 高三 154
52 周峥文 男 华东师范大学第二附属中学 高三 152
53 徐恩泽 男 华东师范大学第二附属中学 高二 149
22 蔡洪润 男 大境中学 高三 76
23 严逸君 男 华东师范大学第二附属中学 高三 76
24 金尚丰 男 上海中学 高二 76
25 严韫洲 男 市北初级中学 初三 76
26 钱昱东 男 七宝中学 高三 75
27 金陆骅 男 奉贤中学 高三 74
42 张晋之 男 交通大学附属中学 高三 120
43 卢宇晟 男 上海中学 高三 119
44 盛夏 男 华东师范大学第二附属中学 高三 118
45 崔涵 男 华东师范大学第二附属中学 高二 118
46 尹秋阳 男 上海市实验学校 高三 118
47 雷世骐 男 市北初级中学 初三 118
60 洪泰格 男 上海中学 高二 112
61 秦寅臻 男 复旦大学附属中学 高二 112
62 张健瑞 男 上海市实验学校 高二 112
63 杨成昊 男 上海中学东校 高二 112
64 张文杰 男 华东师范大学第二附属中学 高一 112
人教版 初三数学竞赛专题:平面几何的定值问题(包含答案)
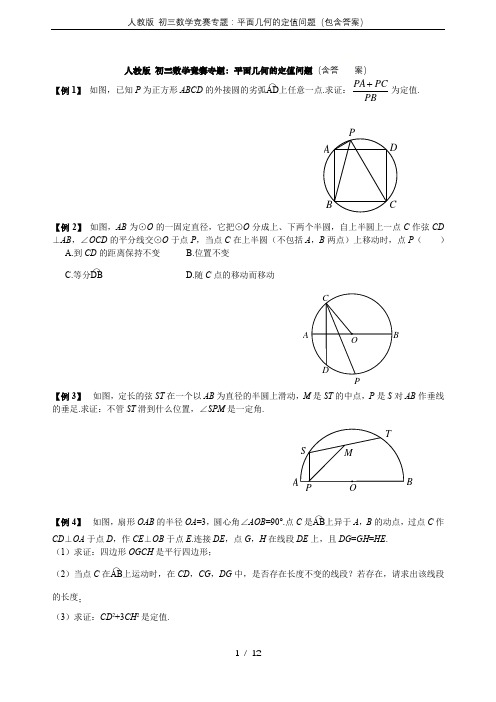
人教版 初三数学竞赛专题:平面几何的定值问题(含答案)【例1】 如图,已知P 为正方形ABCD 的外接圆的劣弧AD⌒上任意一点.求证:PA PC PB为定值.【例2】 如图,AB 为⊙O 的一固定直径,它把⊙O 分成上、下两个半圆,自上半圆上一点C 作弦CD ⊥AB ,∠OCD 的平分线交⊙O 于点P ,当点C 在上半圆(不包括A ,B 两点)上移动时,点P ( ) A.到CD 的距离保持不变 B.位置不变C.等分DB⌒ D.随C 点的移动而移动【例3】 如图,定长的弦ST 在一个以AB 为直径的半圆上滑动,M 是ST 的中点,P 是S 对AB 作垂线的垂足.求证:不管ST 滑到什么位置,∠SPM 是一定角.【例4】 如图,扇形OAB 的半径OA =3,圆心角∠AOB =90°.点C 是AB⌒上异于A ,B 的动点,过点C 作CD ⊥OA 于点D ,作CE ⊥OB 于点E .连接DE ,点G ,H 在线段DE 上,且DG =GH =HE .(1)求证:四边形OGCH 是平行四边形;(2)当点C 在AB ⌒上运动时,在CD ,CG ,DG 中,是否存在长度不变的线段?若存在,请求出该线段的长度;(3)求证:CD 2+3CH 2是定值.P AB CDAPB【例5】 如图1,在平面直角坐标系xOy 中,点M 在x 轴的正半轴上,⊙M 交x 轴于A ,B 两点,交y 轴于C ,D 两点,且C 为弧AE 的中点,AE 交y 轴于G 点.若点A 的坐标为(-2,0),AE =8. (1)求点C 的坐标;(2)连接MG ,BC ,求证:MG ∥BC ;(3)如图2,过点D 作⊙M 的切线,交x 轴于点P .动点F 在⊙M 的圆周上运动时,PFOF的比值是否发生变化?若不变,求出比值;若变化,说明变化规律.(图1)(图2)【例6】 如图,已知等边△ABC 内接于半径为1的圆O ,P 是⊙O 上的任意一点.求证:P A 2+PB 2+PC 2为定值.【能力训练】1.如图,点A ,B 是双曲线xy 3上的两点,分别经过A ,B 两点向x 轴,y 轴作垂线段.若S 阴影=1,则BOACE HG D A=+21S S _______.(第1题图) (第3题图) (第4题图)2.从等边三角形内一点向三边作垂线段,已知这三条垂线段的长分别为1,3,5,则这个等边三角形的面积是__________.3.如图,OA ,OB 是⊙O 任意两条半径,过B 作BE ⊥OA 于E ,又作OP ⊥AB 于P ,则定值OP 2+EP 2为_________.4.如图,在菱形ABCD 中,∠ABC =120°,F 是DC 的中点,AF 的延长线交BC 的延长线于点E ,则直线BF 与直线DE 所夹的锐角的度数为( )A.30°B.40°C.50°D.60°5.如图,在⊙O 中,P 是直径AB 上一动点,在AB 同侧作A A '⊥AB ,AB B B ⊥',且A A '=AP ,B B '=BP .连接B A '',当点P 从点A 移动到点B 时,B A ''的中点的位置( ) A .在平分AB 的某直线上移动 B.在垂直AB 的某直线上移动 C.在弧AMB 上移动 D.保持固定不移动(第5题图) (第6题图) 6.如图,A ,B 是函数xky =图象上的两点,点C ,D ,E ,F 分别在坐标轴上,且分别与点A ,B ,O 构成正方形和长方形.若正方形OCAD 的面积为6,则长方形OEBF 的面积是( ) A.3 B.6 C.9 D.127.(1)经过⊙O 内或⊙O 外一点P 作两条直线交⊙O 于A ,B 和C ,D 四点,得到如图①~⑥所表示的六种不同情况.在六种不同情况下,P A ,PB ,PC ,PD 四条线段之间在数量上满足的关系式可以用同一个式子表示出来.请你首先写出这个式子,然后只就如图②所示的圆内两条弦相交的一般情况给出它的证明.A ABCDEFAB'(2)已知⊙O 的半径为一定值r ,若点P 是不在⊙O 上的一个定点,请你过点P 任作一直线交⊙O 于不重合的两点E ,F . PE ·PF 的值是否为定值?为什么?由此你发现了什么结论?请你把这一结论用文字叙述出来.8.在平面直角坐标系中,边长为2的正方形OABC 的两顶点A ,C 分别在y 轴,x 轴的正半轴上,点O 在原点,现将正方形OABC 绕O 点顺时针旋转,当A 点第一次落在直线x y =上时停止旋转.旋转过程中,AB 边交直线x y =于点M ,BC 边交x 轴于点N .(1)求OA 在旋转过程中所扫过的面积;(2)旋转过程中,当MN 与AC 平行时,求正方形OABC 旋转度数;(3)设△MBN 的周长为P ,在正方形OABC 旋转的过程中,P 值是否有变化?请证明你的结论.⑥⑤④③②①P(B )A PB9.如图,AB 是半圆的直径,AC ⊥AB ,AC =AB .在半圆上任取一点D ,作DE ⊥CD ,交直线AB 于点E ,BF ⊥AB ,交线段AD 的延长线于点F .(1)设弧AD 是x °的弧,若要点E 在线段BA 的延长线上,则x 的取值范围是_______.(2)不论点D 取在半圆的什么位置,图中除AB =AC 外,还有两条线段一定相等.指出这两条相等的线段,并予证明.(第9题图) (第10题图)(第11题图)10.如图,内接于⊙O 的四边形ABCD 的对角线AC 与BD 垂直相交于点K ,设⊙O 的半径为R .求证: (1)2222DK CK BK AK +++是定值; (2)2222DA CD BC AB +++是定值.11.如图,设P 是正方形ABCD 外接圆劣弧弧AB 上的一点,求证:DPCP BPAP ++的值为定值.1.等腰△ABC 的底边BC 为定长2,H 为△ABC 的垂心.当顶点A 在保持△ABC 为等腰三角形的情况下 改变位置时,面积S △ABC ·S △HBC 的值保持不变,则S △ABC ·S △HBC =________.2.已知A ,B ,C ,D ,E 是反比例函数xy 16=(x >0)图象上五个整数点(横、纵坐标均为整数),分别过这些点向横轴或纵轴作垂线段,以垂线段所在的正方形边长为半径作四分之一圆周的两条弧,组成如图所示的五个橄榄形(阴影部分),则这五个橄榄形的面积总和是__________(用含π的代数式表示).P D CB A A折叠,使点A ,B 落在六边形ABCDEF 的内部,记∠C +∠D + )A. ∠1+∠2=900°-2α B. ∠1+∠2=1080°-2α C. ∠1+∠2=720°-α D. ∠1+∠2=360°-21α(第3题图) (第4题图)4.如图,正△ABO 的高等于⊙O 的半径,⊙O 在AB 上滚动,切点为T ,⊙O 交AO ,BO 于M ,N ,则弧MTN ( )A.在0°到30°变化B.在30°到60°变化C.保持30°不变D.保持60°不变5.如图,AB 是⊙O 的直径,且AB =10,弦MN 的长为8.若MN 的两端在圆上滑动时,始终与AB 相交,记点A ,B 到MN 的距离分别为h 1,h 2,则∣h 1-h 2∣等于( )A.5B.6C.7D.8(第5题图) 12GF EDCHBAB6.如图,已知△ABC 为直角三角形,∠ACB =90°,AC =BC ,点A ,C 在x 轴上,点B 坐标为(3,m )(m >0),线段AB 与y 轴相交于点D ,以P (1,0)为顶点的抛物线过点B ,D . (1)求点A 的坐标(用m 表示) (2)求抛物线的解析式;(3)设点Q 为抛物线上点P 至点B 之间的一动点,连接PQ 并延长交BC 于点E ,连接BQ 并延长交AC 于点F .试证明:FC (AC +EC )为定值.7.如图,已知等边△ABC 内接于圆,在劣弧AB 上取异于A ,B 的点M .设直线AC 与BM 相交于K ,直线CB 与AM 相交于点N .证明线段AK 和BN 的乘积与M 点的选择无关.(第7题图) (第8题图)8.如图,设H 是等腰三角形ABC 两条高的交点,在底边BC 保持不变的情况下让顶点A 至底边BC 的距离变小,这时乘积S △ABC ·S △HBC 的值变小、变大,还是不变?证明你的结论.9.如图,在平面直角坐标系xOy 中,抛物线10941812--=x x y 与x 轴的交点为点A ,与y 轴的交点为点B .过点B 作x 轴的平行线BC ,交抛物线于点C ,连接AC .现有两动点P ,Q 分别从O ,C 两点同时出发,点P 以每秒4个单位的速度沿OA 向终点A 移动,点Q 以每秒1个单位的速度沿CB 向点B 移动.点P 停止运动时,点Q 也同时停止运动.线段OC ,PQ 相交于点D ,过点D 作DE ∥OA ,交CA 于E ,射线QE 交x 轴于点F .设动点P ,Q 移动的时间为t (单位:秒). (1)求A ,B ,C 三点的坐标和抛物线的顶点坐标;(2)当t 为何值时,四边形PQCA 为平行四边形?请写出计算过程; (3)当290<<t 时,△PQF 的面积是否总是定值?若是,求出此值;若不是,请说明理由; (4)当t 为何值时,△PQF 为等腰三角形,请写出解答过程.NKMB AC HCBA(第9题图) (第10题图) 10.已知抛物线C 1:12121+-=x x y ,点F (1,1). (1)求抛物线C 1的顶点坐标;(2)若抛物线C 1与y 轴的交点为A ,连接AF ,并延长交抛物线C 1于点B ,求证:211=+BFAF . (3)抛物线C 1上任意一点P (x P ,y P )(0<x P <1),连接PF ,并延长交抛物线C 1于点 Q (x Q ,y Q ),试判断211=+QFPF 是否成立?请说明理由.11.已知A ,B 是平面上的两个顶点,C 是位于AB 一侧的一个动点,分别以AC ,BC 为边在△ABC 外作正方形ACDE 和正方形BCFG .求证:不论C 在直线AB 同一侧的任何位置,EG 的中点P 的位置不变. 参考答案例 1 延长PC 至E ,使CE =AP ,连结BE ,则△BCE ≌△BAP ,及△PBE 为等腰直角三角形,故PA PC CE PC PEPB PB PB++=== 例2 B 提示:连结AC ,BC ,可以证明P 为APB 的中点. 例3 ∵SP ⊥OP ,OM ⊥ST ,∴S ,M ,O ,P 四点共圆,于是∠SPM =∠SOM =12∠SOT 为定角. 例4 (1)连结OC 交DE 于M ,则OM =CM , EM =DM ,而DG = HE ,则HM =GM 故四边形OGCH 是平行四边形. (2)DG 不变.DE =OC =OA =3 .DG =13DE =13×3=1. (3)设CD =x ,延长OG 交CD 于N ,则CN =DN =12 x ,229CE x =- , 2214DN x = .∴22394ON x =-,而ON =32CH ,∴22143CH x =-.故CD 2+3CH 2=x 2+3(4-13x 2)=x 2+12-x 2为定值. 例5 ⑴C (0,4) ⑵先求得AM =CM =5,连接MC 交AE 于N ,由△AO G ∽△ANM ,得OG AO MN AN =,O G =32,38OG OM OC OB ==,又∠BOC =∠G OM ,∴△G OM ∽△COB ,∠G MO =∠CBO ,得M G ∥BC .⑶连结DM ,则DM ⊥PD ,DO ⊥PM ,DO 2=OM •OP ,OP =163.动点F 在⊙M 的圆周上运动时,从特殊位置探求OFPF的值.当F 与点A 重合时,2316523OF AO PF AP ===-;当点F 与点B 重合时,8316583OF OB PF PB ===+;当点F 不与点A ,B 重合时,连接OF 、PF 、MF ,∴DM 2=MO •MP ,∴FM 2=MO •MP ,即FM MPOM FM=,又∠OMP =∠FMP ,∴△MFO ∽△MPF ,35OF MO PF MF ==,故OF PF 的比值不变,比值为35. 例6 ∠BPC =120°,在△BPC 中,由余弦定理得BC 2=PB 2+PC 2-2PB •PC =BC 2,又由上托勒密定理得BC •P A +PC •AB ,而AB =BC =AC ,∴P A =PB +PC ,从而P A 2+ PB 2+ PC 2= (PB +PC )2+ PB 2+ PC 2=2 (PB 2+PC 2+PB •PC )=2BC 2=2×()23=6.故P A 2+PB 2+PC 2为定值.A 级 1.4提示:∵S 1+S 阴= S 2+S 阴=xy =3,∴S 1+S 2=2xy -2S 阴=6-2=4.2.273 提示:1+3+5=9是等边三角形的高. 3.r 2提示:先考查OB 与OA 垂直的情形.4.D 提示:延长BF 交DE 于点M ,连接BD ,则△BCD 为等边三角形,BF 平分∠CBD .∵F 为CD 中点,且AD ∥CE ,∴△ADF 与△ECF 关于点F 中心对称.∴CE =AD =CD ,∴∠CEM=30°,∠DMF=60°,5.D 提示:A′B′的中点均在⊙O 的上半圆的中点处. 6.B 提示:S 正方形OCAD =OD •OC =A A x y k ==6,∴S OEBF =OE •OF =x B •y B k ==6. 7.⑴略⑵当点P在⊙O 内时,过P 作直径CD ,则PE •PF =PD •PC =r 2-OP 2为定值;当点P 在⊙O 外时,PE •PF 为定值22OP r -.结论:过不在圆上的一个定点任作一条直线与圆相交,则这点到直线与圆相交点的两条线段长的积为定值. 8.⑴2π⑵22.5° ⑶P 值无变化.理由如下:如图,延长BA 交y 轴于E 点,可证明△OAE ≌△OCN ,得OE =ON ,AE =CN ,又∠MOE =∠MON =45°,OM =ON ,∴△OME ≌△OMN ,得MN =ME =AM +AE =AM +CN .∴P =MN +BN +BM =AM +CM +CN +BN +BM =AB +AC =4.9.⑴0<x <90 ⑵BE =BF 提示:连接BD ,可证明△BDF ∽△ADB ,△BDE ∽△ADC . 10.⑴作OP ⊥BD 于P ,OQ ⊥AC 于Q ,连接AO ,则AO 2=()()221122BK DK CK AK ⎡⎤⎡⎤-++⎢⎥⎢⎥⎣⎦⎣⎦,又AK •CK =BK •DK ,得AK 2+BK 2+CK 2+DK 2=4R 2为定值. ⑵作直径DE ,连接AE ,BE ,CE ,AB 2+CD 2=4R 2,AD 2+BC 2=4R 2,故AB 2+BC 2+CD 2+DA 2=8K 2为定值. 11.设正方形的边长为a ,根据托勒密定理,对于四边形APBC 和四边形APBD ,有CP •a =AP •a +BP •2a ,DP •a =BP •a +AP •2a ,两式相加并整理得(CP +DP )a =(AP +BP )(a +2a ),从而21AP BPCP DP+=-+为定值.B 级1.1 提示:不妨设∠A 为锐角,AD ,BE ,CF 为△ABC 的三条高,H 为垂心,由AB =AC 知∠HBD =∠HCD =∠HAE ,∠HDC =∠CDA =90°,故R t △CHD ∽R t △ACD .∴AD DC DC HD =,即AD •HD =DC 2=14BC 2=1.∴S △ABC •S △HBC =2111224BC AD BC HD BC ⎛⎫⎛⎫⋅⋅⋅= ⎪ ⎪⎝⎭⎝⎭=1.当∠A ≥90°时,结论成立.2.13π-26 提示:∵A ,B ,C ,DE 是反比例函数y =16x(x >0)图象上五个整数点,由图象可知,这些点的横坐标分别为1,2,4,8,16.∴五个正方形的边长分别为1,3,4,2,1.∴这五人橄榄形的面积总和是2221111112211122222444424242πππ⎡⎤⎛⎫⎛⎫⎛⎫⨯-⨯⨯+⨯-⨯⨯+⨯-⨯⨯ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦=5π-10+8π-16=13π-26. 3.B 提示:如图,设F A 的延长线与CB 的延长线交于点P ,G A ′的延长线与HB ′的延长线交于点P ′.由对称性可知∠1=2∠APP ′,∠2=2∠BPP ′.∴∠1+∠2=2∠APB .∵∠APB =540°-α,∴∠1+∠2=1080°-2α. 4.D 5.B 提示:如图,设AB 与MN 交于点C ,过点O 作OD ⊥MN 于D ,连接FO 并延长交EB 于G .由垂径定理,得OD =2254-=3.由△AFO ≌△B G O ,得AF =B G ,即h 1=B G .由AF ⊥MN ,BE ⊥MN ,得△FOD ∽△F G E .∴12OD FO GE FG ==.∴E G =2OD =6,∴12h h AF BE -=-=E G =6. 6.⑴A (3-m ,0) ⑵y =x 2-2x +1 ⑶过点Q 作QM ⊥AC 于M ,过点Q 作QN ⊥BC 于N ,设Q 点的坐标为(x ,x 2-2x +1),则QM =CN =(x -1)2,MC =QN=3-x .∵QM ∥CE ,∴PQM ∽△PEC .∴QM PMEC PC=,即()2112x x EC--=,得EC =2(x -1).∵QN ∥CF ,∴△BQN ∽△BFC .∴QN BN FC BC =,即()24134x x FC ---=,得FC =41x +.又AC =4,∴FC (AC +EC )=()44211x x +-⎡⎤⎣⎦+=8为定值. 7.提示:易证△ABK ∽△BNA ,故AK •BN =AB 2为定值,即AK 与BN 的乘积与M 点的选择无关. 8.提示:S △ABC •S △HBC =116BC 4,由于BC 是不变的,所以当点A 至BC 的距离变小时,乘积S △ABC •S △HBC 保持不变. 9.⑴A (18,0),B (0,-10),顶点坐标为(4,-989)⑵若四边形PQCA 为平行四边形,由于QC ∥P A ,故只要QC =P A 185. ⑶即可,而P A =18-4t ,CQ =t ,故18-4t =t ,得t =设点P 运动t s ,则OP =4t ,CQ =t ,0<t <4.5.说明P在线段OA 上,且不与点O ,A 重合.由于QC ∥OP 知△QDC ∽△PDO ,故144QD QC t DP OP t ===.同理QC ∥AF ,故14QC CE AF EA ==,即14t AF =,∴AF =4t =OP .∴PF =P A +AF =P A +OP =18.又点Q 到直线PF 的距离d =10,∴S △PQF =12•PF •d =12×18×10=90.于是S △PQF 的面积总为定值90. ⑷由前面知道,P (4t ,0),F (18+4t ,0),Q (8-t ,-10),0≤t ≤4.5.构造直角三角形后易得PQ 2=(4t -8+t )2+102=,FQ 2=(18+4t -8+t )2+102=(5t +10)2+100.①若FP =FQ ,即182=(5t +10)2+100,故25(t +2)2=224,(t +2)2=24425.∵2≤t +2≤6.5,∴t +2=244414255=.∴t = 4145-2. ②若QP =QF ,即(5t -8)2+100=(5t +10)2+100,即(5t -8)2=(5t +10)2,无0≤t ≤4.5的t 满足. ③若PQ =PF ,即(5t -8)2+100=182,∴(5t -8)2=224.由于224≈15,又0≤5t ≤22.5,∴-8≤5t -8≤14.5,14.52=22984124⎛⎫= ⎪⎝⎭<224.故没有t (0≤t ≤4.5)满足此方程.综上所述,当t =4145-2时,△PQ R 为等腰三角形. 10.⑴C 1的顶点坐标为(1,12). ⑵略 ⑶作PM ⊥AB 于M ,作QN ⊥AB 交AB 延长线于N ,∴PM =1-y P ,FM =1-x P .在R t △PMF 中,PF 2=(1-y P )2+(1-x P )2=1-2y P +y P 2+1-2x P +x P 2,又∵点P 在抛物线上,∴y P =12x P 2-x P +1,∴PF 2=1-x P 2+2x P -2+y P 2+1-2x P +x P 2=y P 2,∴PF =y P ,同理,QF =y Q ,易证△PMF ∽△QNF ,则PM QN PF QF =,∴11Q P y y PF QF --=,即11PF QF PF QF --=,∴11PF QF+=2. 11.先从特殊情况出发.当△ABC 是等腰直角三角形时,点P 与点C 重合,此时点P 的位置在AB 的中垂线上,且到AB的距离为12AB ,如图①所示.下面就一般情况来证明上面的结论(结论②所示).过C ,E ,G 分别作直线AB 的垂线CH ,EM ,G N ,垂足分别是H ,M ,N .容易证明△AEM ≌△ACH ,△B G N ≌△BCH .从而有AM =CH =BN ,EM =AH ,G N =BH .这样,线段AB 的中点O 也是线段MN 的中点,连接OP ,则OP 是梯形EMN G 的中位线,从而OP ⊥AB ,OP =12(EM +G N )= 12(AH +BH )=12AB .∴无论点C 在AB 同一侧的位置如何,E G 中点P 的位置不变.。
初三数学竞赛试题及答案精选

全国初中数学联赛试题第一试一、选择题1.已知a=355,b=444,c=533,则有[ ]A.a<b<c B.c<b<a C.c<a<b D.a<c<bA.1 B.2 C.3 D.43.如果方程(x-1)(x2-2x-m)=0的三根可以作为一个三角形的三边之长,那么实数m的取值范围是4.如果边长顺次为25、39、52与60的四边形内接于一圆,那么此圆的周长为[ ]A.62πB.63π C.64πD.65π5.设AB是⊙O的一条弦,CD是⊙O的直径,且与弦AB相交,记M=|S △CAB-S△DAB|,N=2S△OAB,则[ ]A.M>N B.M=N C.M<N D.M、N的大小关系不确定6.设实数a、b满足不等式||a|-(a+b)|<|a-|a+b||,则[ ]A.a>0且b>0 B.a<0且b>0C.a>0且b<0 D.a<0且b<0二、填空题1.在12,22,32…,952这95个数中,十位数字为奇数的数共有____个。
4.以线段AB为直径作一个半圆,圆心为O,C是半圆周上的点,且OC2=AC·BC,则∠CAB=______.第二试一、已知∠ACE=∠CDE=90°,点B在CE上,CA=CB=CD,经A、C、D三点的圆交AB于F(如图)求证F为△CDE的内心。
二、在坐标平面上,纵坐标与横坐标都是整数理由。
三、试证:每个大于6的自然数n,都可以表示为两个大于1且互质的自然数之和。
初中数学联赛参考答案第一试一、选择题1.讲解:这类指数幂的比较大小问题,通常是化为同底然后比较指数,或化为同指数然后比较底数,本题是化为同指数,有c=(53)11=12511<24311=(35)11=a<25611=(44)11=b。
选C。
利用lg2=0.3010,lg3=0.4771计算lga、lgb、lgc也可以,但没有优越性。
2.讲解:这类方程是熟知的。
先由第二个方程确定z=1,进而可求出两个解:(2,21,1)、(20,3,1).也可以不解方程组直接判断:因为x≠y(否则不是正整数),故方程组①或无解或有两个解,对照选择支,选B。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014年全国初中数学联赛决赛试题一、选择题:(本题满分42分,每小题7分) 1.已知,x y 为整数,且满足22441111211()()()3x y x y x y++=--,则x y +的可能的值有( ) A. 1个 B. 2个 C. 3个 D. 4个【答】 C.由已知等式得2244224423x y x y x y xy x y x y++-⋅=⋅,显然,x y 均不为0,所以x y +=0或32()xy x y =-. 若32()xy x y =-,则(32)(32)4x y +-=-.又,x y 为整数,可求得12,x y =-⎧⎨=⎩,或21.x y =-⎧⎨=⎩,所以1x y +=或1x y +=-.因此,x y +的可能的值有3个.2.已知非负实数,,x y z 满足1x y z ++=,则22t xy yz zx =++的最大值为 ( ) A .47 B .59 C .916 D .1225【答】 A.21222()2()()4t xy yz zx x y z yz x y z y z =++=++≤+++212(1)(1)4x x x =-+-2731424x x =-++2734()477x =--+,易知:当37x =,27y z ==时,22t xy yz zx =++取得最大值47.3.在△ABC 中,AB AC =,D 为BC 的中点,BE AC ⊥于E ,交AD 于P ,已知3BP =,1PE =,则AE = ( )A .62B .2C .3D .6 【答】 B.因为AD BC ⊥,BE AC ⊥,所以,,,P D C E 四点共圆,所以12BD BC BP BE ⋅=⋅=,又2BC BD =,所以6BD =,所以3DP =.又易知△AEP ∽△BDP ,所以AE PEBD DP =,从而可得1623PE AE BD DP =⋅=⋅=. 4.6张不同的卡片上分别写有数字2,2,4,4,6,6,从中取出3张,则这3张卡片上所写的数字可以作为三角形的三边长的概率是 ( )A .12 B .25 C .23 D .34【答】 B.若取出的3张卡片上的数字互不相同,有2×2×2=8种取法;若取出的3张卡片上的数字有相同的,有3×4=12种取法.所以,从6张不同的卡片中取出3张,共有8+12=20种取法.要使得三个数字可以构成三角形的三边长,只可能是:(2,4,4),(4,4,6),(2,6,6),(4,6,6),由于不同的卡片上所写数字有重复,所以,取出的3张卡片上所写的数字可以作为三角形的三边长的情况共有4×2=8种.因此,所求概率为82205=. 5.设[]t 表示不超过实数t 的最大整数,令{}[]t t t =-.已知实数x 满足33118x x +=,则1{}{}x x+= ( )A .12 B .35- C .1(35)2- D .1 【答】 D. 设1x a x +=,则32223211111()(1)()[()3](3)x x x x x a a x x x x x+=++-=++-=-,所以2(3)18a a -=,因式分解得2(3)(36)0a a a -++=,所以3a =.由13x x +=解得1(35)2x =±,显然10{}1,0{}1x x <<<<,所以1{}{}x x+=1. 6.在△ABC 中,90C ∠=︒,60A ∠=︒,1AC =,D 在BC 上,E 在AB 上,使得△ADE 为等腰直角三角形, 90ADE ∠=︒ ,则BE 的长为 ( )A .423-B .23-C .1(31)2- D .31-【答】 A.过E 作EF BC ⊥于F ,易知△ACD ≌△DFE ,△EFB ∽△ACB . 设EF x =,则2BE x =,22AE x =-,2(1)DE x =-,1DF AC ==,故2221[2(1)]x x +=-,即2410x x -+=.又01x <<,故可得23x =-.故2423BE x ==-.二、填空题:(本题满分28分,每小题7分) 1.已知实数,,a b c 满足1a b c ++=,1111a b c b c a c a b++=+-+-+-,则abc =____.【答】 0. 由题意知1111121212c a b++=---,所以 (12)(12)(12)(12)(12)(12)(12)(12)(12)a b b c a c a b c --+--+--=---整理得22()8a b c abc -++=,所以abc =0.FEBCAD2.使得不等式981715n n k <<+对唯一的整数k 成立的最大正整数n 为 . 【答】144. 由条件得7889k n <<,由k 的唯一性,得178k n -≤且189k n +≥,所以2118719872k k n n n +-=-≥-=,所以144n ≤.当144n =时,由7889k n <<可得126128k <<,k 可取唯一整数值127. 故满足条件的正整数n 的最大值为144.3.已知P 为等腰△ABC 内一点,AB BC =,108BPC ∠=︒,D 为AC 的中点,BD 与PC 交于点E ,如果点P 为△ABE 的内心,则PAC ∠= .【答】48︒.由题意可得PEA PEB CED AED ∠=∠=∠=∠,而180PEA PEB AED ∠+∠+∠=︒,所以60PEA PEB CED AED ∠=∠=∠=∠=︒, 从而可得30PCA ∠=︒.又108BPC ∠=︒,所以12PBE ∠=︒,从而24ABD ∠=︒. 所以902466BAD ∠=︒-︒=︒, 11()(6630)1822PAE BAD CAE ∠=∠-∠=︒-︒=︒,所以183048PAC PAE CAE ∠=∠+∠=︒+︒=︒.4.已知正整数,,a b c 满足:1a b c <<<,111a b c ++=,2b ac =,则b = . 【答】36.设,a c 的最大公约数为(,)a c d =,1a a d =,1c c d =,11,a c 均为正整数且11(,)1a c =,11a c <,则2211b ac d a c ==,所以22|d b ,从而|d b ,设1b b d =(1b 为正整数),则有2111b a c =,而11(,)1a c =,所以11,a c 均为完全平方数,设2211,a m c n ==,则1b mn =,,m n 均为正整数,且(,)1m n =,m n <.又111a b c ++=,故111()111d a b c ++=,即22()111d m n mn ++=. 注意到222212127m n mn ++≥++⨯=,所以1d =或3d =.若1d =,则22111m n mn ++=,验算可知只有1,10m n ==满足等式,此时1a =,不符合题意,故舍去.若3d =,则2237m n mn ++=,验算可知只有3,4m n ==满足等式,此时27,36,48a b c ===,符合题意.因此,所求的36b =.EDAB PC三、(本题满分20分)设实数,a b 满足22(1)(2)40a b b b a +++=,(1)8a b b ++=,求2211a b +的值.解 由已知条件可得222()40a b a b ++=,()8ab a b ++=.设a b x +=,ab y =,则有2240x y +=,8x y +=, …………5分 联立解得(,)(2,6)x y =或(,)(6,2)x y =. ………10分若(,)(2,6)x y =,即2a b +=,6ab =,则,a b 是一元二次方程2260t t -+=的两根,但这个方程的判别式2(2)24200∆=--=-<,没有实数根; ………… … 15分若(,)(6,2)x y =,即6a b +=,2ab =,则,a b 是一元二次方程2620t t -+=的两根,这个方程的判别式2(6)8280∆=--=>,它有实数根.所以2222222222211()262282a b a b ab a b a b a b ++--⨯+====. ………20分 四、.(本题满分25分)如图,在平行四边形ABCD 中,E 为对角线BD 上一点,且满足ECD ACB ∠=∠, AC 的延长线与△ABD 的外接圆交于点F . 证明:DFE AFB ∠=∠.证明 由ABCD 是平行四边形及已知条件知ECD ACB DAF ∠=∠=∠. ………5分又A 、B 、F 、 D 四点共圆, 所以BDC ABD AFD ∠=∠=∠,………… ….10分 所以△ECD ∽△DAF , …… …15分所以ED CD ABDF AF AF==. ………20分 又EDF BDF BAF ∠=∠=∠,所以△EDF ∽△BAF ,故DFE AFB ∠=∠.…………… ………25分五、(本题满分25分)设n 是整数,如果存在整数,,x y z 满足3333n x y z xyz =++-,则称n 具有性质P . (1)试判断1,2,3是否具有性质P ;(2)在1,2,3,…,2013,2014这2014个连续整数中,不具有性质P 的数有多少个?解 取1x =,0y z ==,可得33311003100=++-⨯⨯⨯,所以1具有性质P ;取1x y ==,0z =,可得33321103110=++-⨯⨯⨯,所以2具有性质P ;…………………5分若3具有性质P ,则存在整数,,x y z 使得33()3()()x y z x y z xy yz zx =++-++++,从而可得33|()x y z ++,故3|()x y z ++,于是有39|()3()()x y z x y z xy yz zx ++-++++,即9|3,这是不可能的,所以3不具有性质P . ……………………10分FCA BDE(2)记333(,,)3f x y z x y z xyz =++-,则33(,,)()3()3f x y z x y z xy x y xyz =++-+- 3()3()()3()x y z x y z x y z xy x y z =++-+++-++=3()3()()x y z x y z xy yz zx ++-++++2221()()2x y z x y z xy yz zx =++++--- 2221()[()()()]2x y z x y y z z x =++-+-+-. 即(,,)f x y z 2221()[()()()]2x y z x y y z z x =++-+-+- ①……………………15分不妨设x y z ≥≥,如果1,0,1x y y z x z -=-=-=,即1,x z y z =+=,则有(,,)31f x y z z =+; 如果0,1,1x y y z x z -=-=-=,即1x y z ==+,则有(,,)32f x y z z =+; 如果1,1,2x y y z x z -=-=-=,即2,1x z y z =+=+,则有(,,)9(1)f x y z z =+; 由此可知,形如31k +或32k +或9k (k 为整数)的数都具有性质P .……………………20分又若33|(,,)()3()()f x y z x y z x y z xy yz zx =++-++++,则33|()x y z ++,从而3|()x y z ++,进而可知39|(,,)()3()()f x y z x y z x y z xy yz zx =++-++++.综合可知:当且仅当93n k =+或96n k =+(k 为整数)时,整数n 不具有性质P . 又2014=9×223+7,所以,在1,2,3,…,2013,2014这2014个连续整数中,不具有性质P 的数共有224×2=448个. …………………25分。
