2019中考数学压轴题精选(二十二)

合集下载

中考数学真题分类汇编及解析(二十二)定理、命题、反证法

对顶角相等，故B是真命题，不符合题意；
平行四边形是中心对称图形，故C是真命题，不符合题意；
如果直线a∥c，b∥c，那么直线a∥b，故D是真命题，不符合题意.
2201
（2022•大庆中考）下列说法不正确的是（）
A．有两个角是锐角的三角形是直角或钝角三角形
B．有两条边上的高相等的三角形是等腰三角形
C．有两个角互余的三角形是直角三角形
当x﹣m＝0时，不能直接除，而题干中给出的条件是x＝m，此处不能直接除．
答案：④．
2202
（2022•无锡中考）请写出命题“如果a＞b，那么b﹣a＜0”的逆命题：如果b﹣a＜0，那么a＞b．
【解析】命题“如果a＞b，那么b﹣a＜0”的逆命题是“如果b﹣a＜0，那么a＞b”．
答案：如果b﹣a＜0，那么a＞b
B．调查全国中学生的视力情况，适合采用普查的方式
C．抽样调查的样本容量越小，对总体的估计就越准确
D．十字路口的交通信号灯有红、黄、绿三种颜色，所以开车经过十字路口时，恰好遇到黄灯的概率是
【解析】选A．A选项，三角形内角和为180°，故该选项符合题；
B.有一个角是直角的四边形是矩形，是假命题，本选项不符合题意；
C.对角线互相平分的四边形是菱形，是假命题，本选项不符合题意；
D.对角线互相垂直的矩形是正方形，是真命题，本选项符合题意．
2201
（2022•怀化中考）下列说法正确的是（）
A．相等的角是对顶角
B．对角线相等的四边形是矩形
C．三角形的外心是它的三条角平分线的交点
B、在同圆或等圆中，相等的圆周角所对的弧相等，原命题是假命题；
C、若a＜b，c＝0时，则ac2＝bc2，原命题是假命题；
D、在一个不透明的箱子里放有1个白球和2个红球，它们除颜色外其余都相同，从箱子里任意摸出1个球，摸到白球的概率是，是真命题

专题02 二次函数与营销问题-2019年中考数学复习压轴题突破之二次函数(解析版)

【方法综述】此类问题以营销问题为背景，通过各种数学知识的结合，考察和二次函数最值和自变量取值范围有关的问题。

首先，考察有关利润的函数模型的构造，解答方法是通过利润公式根据题意找出等量关系；其次考察函数的最值计算、判断，解答方法是通过二次函数特性找到函数的最值或在一定自变量范围内函数值的最值；再次通常考察利润在一定范围内时对应的自变量取值范围，解答方法通常采用通过数形结合思想，画出函数图象根据题意找到答案。

【典例示范】类型一常规盈利问题例1：（2019湖北宜昌）某公司推出了一种高效环保型洗涤用品，年初上市后，公司经历了从亏损到盈利过程．下面的二次函数图象（部分）刻画了该公司年初以来累积利润（万元）与销售时间（月）之间的关系（即前个月的利润总和和之间的关系）．根据图象提供的信息，解答下列问题：由已知图象上的三点坐标，求累积利润（万元）与时间（月）之间的函数关系式；求截止到几月末公司累积利润可达到万元；求第个月公司所获利润是多少万元？【答案】（1）；（2）截止到月末公司累积利润可达万元；（3）万元．﹣2）2﹣2，即S=t2﹣2t．答：累积利润S与时间t之间的函数关系式为：S=t2﹣2t；（2）把S=30代入S=（t﹣2）2﹣2，得：（t﹣2）2﹣2=30．解得：t1=10，t2=﹣6（舍去）．*网答：截止到10月末公司累积利润可达30万元．针对训练1．(2018宁波)根据对宁波市相关的市场物价调研，某批发市场内甲种水果的销售利润y1（千元）与进货量x（吨）近似满足函数关系y1=0.25x，乙种水果的销售利润y2（千元）与进货量x（吨）之间的函数y2=ax2+bx+c 的图象如图所示．（1）求出y2与x之间的函数关系式；（2）如果该市场准备进甲、乙两种水果共8吨，设乙水果的进货量为t吨，写出这两种水果所获得的销售利润之和W（千元）与t（吨）之间的函数关系式，并求出这两种水果各进多少吨时获得的销售利润之和最大，最大利润是多少？【答案】（1）y2=﹣x2+x；（2）w=﹣（t﹣4）2+6，t=4时，w的值最大，最大值为6，∴两种水果各进4吨时获得的销售利润之和最大，最大利润是6千元．【解析】解：（1）∵函数y2=ax2+bx+c的图象经过（0，0），（1，2），（4，5），∴，解得：，∴y2=﹣x2+x．（2）w=y1+y2=（8﹣t）﹣t2+t=﹣（t﹣4）2+6，∴t=4时，w的值最大，最大值为6，∴两种水果各进4吨时获得的销售利润之和最大，最大利润是6千元．&网2．（2019泰州姜堰区期末）某水果店销售某品牌苹果，该苹果每箱的进价是40元，若每箱售价60元，每星期可卖180箱．为了促销，该水果店决定降价销售．市场调查反映:若售价每降价1元，每星期可多卖10箱．设该苹果每箱售价x元（40≤x≤60），每星期的销售量为y箱．（1）求y与x之间的函数关系式；（2）当每箱售价为多少元时，每星期的销售利润达到3570元？（3）当每箱售价为多少元时，每星期的销售利润最大，最大利润多少元?【答案】(1)y=-10x+780；(2)57；(3)当售价为59元时，利润最大，为3610元（3）设每星期的利润为w，W=（x-40）(-10x+780)=-10（x-59）2+3610,∵-100,二次函数向下,函数有最大值,当x=59时,利润最大，为3610元.3．（2019安徽阜阳期末）某企业生产了一款健身器材，可通过实体店和网上商店两种途径进行销售，销售了一段时间后，该企业对这种健身器材的销售情况进行了为期30天的跟踪调查，其中实体店的日销售量y1(套)与时间x(x为整数，单位:天)的部分对应值如下表所示:时间x(天)0510********日销售量y(套)025*********(1)求出y1与x的二次函数关系式及自变量x的取值范围(2)若网上商店的日销售量y2(套)与时间x(x为整数，单位:天)的函数关系为，则在跟踪调查的30天中，设实体店和网上商店的日销售总量为y(套),求y与x的函数关系式；当x为何值时，日销售总量y达到最大，并写出此时的最大值.【答案】（1），（0≤x≤30，且为整数）；（2）当x=30时，y取得最大值360.（2）依题意有y=y1+y2，当0≤x≤10时，,∴当x=10时，y取得最大值80；当10<x≤30时，∴当x=30时，y取得最大值360；学&科网综上可知，当x=30时，y取得最大值360.4．（2018广东中山）某电商在购物平台上销售一款小电器，其进价为45元/件，每销售一件需缴纳平台推广费5元，该款小电器每天的销售量y（件）与每件的销售价格x（元）满足函数关系：y＝﹣2x+200．为保证市场稳定，供货商规定销售价格不得低于75元/件．（1）写出每天的销售利润w（元）与销售价格x（元）的函数关系式（不必写出x的取值范围）；（2）每件小电器的销售价格定为多少元时，才能使该款小电器每天获得的利润是1200元？【答案】（1）w＝﹣2x2+300x﹣10000；（2）每件小电器的销售价格定为90元时，才能使该款小电器每天获得的利润是1200元．【解析】解：（1）由题意可得：w＝（x﹣50）（﹣2x+200）＝﹣2x2+300x﹣10000；（2）由题意可得：1200＝﹣2x2+300x﹣10000，解得：x1＝60（不合题意舍去），x2＝90，学*科网答：每件小电器的销售价格定为90元时，才能使该款小电器每天获得的利润是1200元．5．（2019洛阳市月考）某公司为一工厂代销一种建筑材料（这里的代销是指厂家先免费提供货源，待货物售出后再进行结算，未售出的由厂家负责处理）．当每吨售价为260元时，月销售量为45吨．该经销店为提高经营利润，准备采取降价的方式进行促销．经市场调查发现：当每吨售价每下降10元时，月销售量就会增加7.5吨．综合考虑各种因素，每售出一吨建筑材料共需支付厂家及其它费用100元．设每吨材料售价为x（元），该经销店的月利润为y（元）．当每吨售价是240元时，计算此时的月销售量；（1）求出y与x的函数关系式（不要求写出x的取值范围）；（2）该经销店要获得最大月利润，售价应定为每吨多少元？（3）小静说：“当月利润最大时，月销售额也最大．”你认为对吗？请说明理由．【答案】（1）60吨．（2）y＝﹣x2+315x﹣24000．（3）利达经销店要获得最大月利润，材料的售价应定为每吨210元．（4）我认为，小静说的不对．（3）y＝﹣x2+315x﹣24000＝﹣（x﹣210）2+9075．利达经销店要获得最大月利润，材料的售价应定为每吨210元．（4）我认为，小静说的不对．理由：当月利润最大时，x为210元，而对于月销售额W＝x（45+×7.5）＝﹣（x﹣160）2+19200来说，当x为160元时，月销售额W最大．∴当x为210元时，月销售额W不是最大．∴小静说的不对．&网6．（2018重庆月考）某文具店购进A，B两种钢笔，若购进A种钢笔2支，B种钢笔3支，共需90元；购进A种钢笔3支，B种钢笔5支，共需145元．（1）求该文具店购进A、B两种钢笔每支各多少元？（2）经统计，B种钢笔售价为30元时，每月可卖64支；每涨价3元，每月将少卖12支，求该文具店B 种钢笔销售单价定为多少元时，每月获利最大？最大利润是多少元？【答案】（1）文具店购进A种钢笔每支15元，购进B种钢笔每支20元；（2）该文具店B种钢笔销售单价定为33元时，每月获利最大，最大利润是676元．（2）设B种钢笔每支售价为x元，每月获取的总利润为W，则W＝（x﹣20）（64﹣12）＝﹣4x2+264x﹣3680＝﹣4（x﹣33）2+676．学&科网∵a＝﹣4＜0，∴当x＝33时，W取得最大值，最大值为676．答：该文具店B种钢笔销售单价定为33元时，每月获利最大，最大利润是676元．7．（青岛市李沧区期末）某公司营销A，B两种产品，根据市场调研，确定两条信息：信息1：销售A种产品所获利润y（万元）与所售产品x（吨）之间存在二次函数关系，如图所示：信息2：销售B种产品所获利润y（万元）与销售产品x（吨）之间存在正比例函数关系y＝0.3x．根据以上信息，解答下列问题；(1)求二次函数的表达式；(2)该公司准备购进A、B两种产品共10吨，请设计一个营销方案，使销售A、B两种产品获得的利润之和最大，最大利润是多少万元？【答案】(1)销售A种产品所获利润y与销售产品x之间的函数关系式为y=﹣0.1x2+1.5x；(2)购进A产品6吨，购进B产品4吨，销售A、B两种产品获得的利润之和最大，最大利润是6.6万元（2）设购进A产品m吨，购进B产品（10﹣m）吨，销售A、B两种产品获得的利润之和为W元，则W=﹣0.1m2+1.5m+0.3（10﹣m），=﹣0.1m2+1.2m+3，=﹣0.1（m﹣6）2+6.6，∵﹣0.1＜0，学&科网∴当m=6时，W取得最大值，最大值为6.6万元，答：购进A产品6吨，购进B产品4吨，销售A、B两种产品获得的利润之和最大，最大利润是6.6万元．类型二一次函数与二次函数相结合的营销问题例2．（2019江苏东台）某校部分团员参加社会公益活动，准备购进一批许愿瓶进行销售，并将所得利润捐给慈善机构.根据市场调查，这种许愿瓶一段时间内的销售量y（个）与销售单价x（元/个）之间的对应关系如图所示：（1）试判断y与x之间的函数关系，并求出函数关系式；（2）若许愿瓶的进价为6元/个，按照上述市场调查的销售规律，求销售利润w（元）与销售单价x（元/个）之间的函数关系式；（3）在（2）的条件下，若许愿瓶的进货成本不超过900元，要想获得最大的利润，试确定这种许愿瓶的销售单价，并求出此时的最大利润.【答案】（1）y=-30x+600；（2）；（3）x=15时，利润最大1350元.（2）w=（x-6）（-30x+600）=-30x2+780x-3600，即w与x之间的函数关系式为w=-30x2+780x-3600；（3）由题意得：6（-30x+600）≤900，解得x≥15．w=-30x2+780x-3600图象对称轴为：x=-=-=13．∵a=-30＜0，∴抛物线开口向下，当x≥15时，w随x增大而减小，，∴当x=15时，w最大=1350即以15元/个的价格销售这批许愿瓶可获得最大利润1350元．针对训练1.国家推行“节能减排，低碳经济”政策后，某环保节能设备生产企业的产品供不应求．若该企业的某种环保设备每月的产量保持在一定的范围，每套产品的生产成本不高于50万元，每套产品的售价不低于80万元，已知这种设备的月产量x（套）与每套的售价y（万元）之间满足关系式y＝150﹣2x，月产量x（套）与生产总成本y2（万元）存在如图所示的函数关系．（1）直接写出y2与x之间的函数关系式；（2）求月产量x的范围；（3）当月产量x（套）为多少时，这种设备的利润W（万元）最大？最大利润是多少？【答案】（1）y2＝30x+500；（2）25≤x≤35；（3）月产量为30件时，利润最大，最大利润是1300万元．（2）依题意得：，解得：25≤x≤35；（3）∵W＝x•y1﹣y2＝x（150﹣2x）﹣（500+30x）＝﹣2x2+120x﹣500∴W＝﹣2（x﹣30）2+1300∵25＜30＜35，*网∴当x＝30时，W＝1300最大答：当月产量为30件时，利润最大，最大利润是1300万元．2．（2019天津南开期末）某商家独家销售具有地方特色的某种商品,每件进价为40元。

【中考数学几何模型】第二十二节：二次函数特殊平行四边形存在性问题

中考数学几何模型第二十二节:二次函数特殊平行四边形存在性问题422.二次函数正方形存在性问题(初三)在平面直角坐标系中,抛物线y =―13x 2+bx +c 交x 轴于A(―3,0),B(4,0)两点,交y 轴于点C .(1)求抛物线的表达式,(2)如图,直线y =34x +94与抛物线交于A,D 两点,与直线BC 交于点E .若M(m,0)是线段AB 上的动点,过点M 作x 轴的垂线,交抛物线于点F ,交直线AD 于点G ,交直线BC 于点H .①当点F 在直线AD 上方的抛物线上,且S △EFG =59S △OFG 时,求m 的值;②在平面内是否存在点P ,使四边形EFHP 为正方形?若存在,请直接写出点P 的坐标;若不存在,请说明理由.423.二次函数面积最大值矩形存在性问题(初三)如图,在平面直角坐标系中,抛物线y =ax 2+2x +c(a ≠0)与x 轴交于点A 、B ,与y 轴交于点C ,连接BC,OA =1,对称轴为直线x =2,点D 为此拋物线的顶点.(1)求抛物线的解析式(2)抛物线上C 、D 两点之间的距离是_______(3)点E 是第一象限内抛物线上的动点,连接BE 和CE ,求△BCE 面积的最大值;(4)点P 在抛物线对称轴上，平面内存在点Q ，使以点B 、C 、P 、Q 为顶点的四边形为矩形,请直接写出点Q 的坐标.424.二次函数线段最大值相等角矩形存在性问题(初三)如图,抛物线y=ax2+bx+c与x轴交于点A(―1,0),点B(―3,0),且0O=OC.(1)求抛物线的解析式(2)点P在抛物线上,且∠POB=∠ACB,求点P的坐标;(3)抛物线上两点M,N,点M的横坐标为m,点N的横坐标为m+4.点D是抛物线上M,N之间的动点,过点D作y轴的平行线交MN于点E.①求DE的最大值②点D关于点E的对称点为F,当m为何值时,四边形MDNF为矩形.425.二次函数菱形存在性三角形相似存在性问题(初三)如图,已知直线y=―2x+4分别交x轴、y轴于点A、B,抛物线过A,B两点,点P是线段AB上一动点,过点P作PC⊥x 轴于点C,交抛物线于点D.(1)若抛物线的解析式为y=―2x2+2x+4,设其顶点为M,其对称轴交AB于点N.①求点M、N的坐标;②是否存在点P,使四边形MNPD为菱形?并说明理由(2)当点P的横坐标为1时,是否存在这样的抛物线,使得以B、P、D为顶点的三角形与△AOB相似?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.426.二次函数菱形存在性问题(初三)如图,抛物线y=x2+2x―8与x轴交于A,B两点(点A在点B左侧),与y轴交于点C.(1)求A,B,C三点的坐标(2)连接AC,直线x=m(―4<m<0)与该抛物线交于点E,与AC交于点D,连接OD.当OD⊥AC时,求线段DE的长;(3)点M在y轴上，点N在直线AC上,点P为拋物线对称轴上一点,是否存在点M,使得以C、M、N、P为顶点的四边形是菱形?若存在,请直接写出点M的坐标;若不存在,请说明理由.427.二次函数菱形存在性问题三角形面积相等问题(初三)x2+2x―6与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,连接AC,BC.如图,抛物线y=12(1)求A、B,C三点的坐标并直接写出直线AC,BC的函数表达式.(2)点P是直线AC下方抛物线上的一个动点,过点P作BC的平行线1,交线段AC于点D.①试探究:在直线1上是否存在点E,使得以点D,C,B,E为顶点的四边形为菱形,若存在,求出点E的坐标,若不存在,请说明理由;②设抛物线的对称轴与直线1交于点M,与直线AC交于点N.当S△DWN=S△AOC时,请直接写出DM的长.428.二次函数三角形面积最大值菱形存在性问题(初三)如图,在平面直角坐标系中,Rt△ABC的边BC在x轴上,∠ABC=90∘,以A为顶点的抛物线y=―x2+bx+c经过点C(3,0),交y轴于点E(0,3),动点P在对称轴上.(1)求抛物线解析式;(2)若点P从A点出发,沿A→B方向以1个单位/秒的速度匀速运动到点B停止,设运动时间为t秒,过点P作PD⊥AB 交AC于点D,过点D平行于y轴的直线1交抛物线于点Q,连接AQ,CQ,当t为何值时,△ACQ的面积最大?最大值是多少?(3)若点M是平面内的任意一点,在x轴上方是否存在点P,使得以点P,M,EC为顶点的四边形是菱形,若存在,请直接写出符合条件的M点坐标;若不存在,请说明理由.429.二次函数菱形存在性问题(初三)已知抛物线F:y=x2+bx+c的图象经过坐标原点0,且与x轴另一交点为(―33,0).(1)求抛物线F的解析式.x+m(m>0)与抛物线F相交于点A(x1,y1)和点B(x2,y2)(点A在第二象限)，求y2―y1的(2)如图1,直线1:y=33值(用含m的式子表示);,设点A′是点A关于原点0的对称点,如图2.(3)在(2)中,若m=43①判断△AA′B的形状,并说明理由;②平面内是否存在点P,使得以点A、B、A′、P为顶点的四边形是菱形?若存在,求出点P的坐标;若不存在,请说明理由.430.二次函数线段最大值菱形存在性问题(初三)如图,二次函数y =x 2+bx +c 的图象交x 轴于点A(―3,0),B(1,0),交y 轴于点C .点P(m,0)是x 轴上的一动点，PM ⊥x 轴，交直线AC 于点M ，交抛物线于点N .(1)求这个二次函数的表达式:(2)①若点P 仅在线段A0上运动，如图，求线段MN 的最大值;②若点P 在x 轴上运动,则在y 轴上是否存在点Q ,使以M,N,C,Q 为顶点的四边形为菱形.若存在,请直接写出所有满足条件的点Q 的坐标;若不存在,请说明理由.431.二次函数菱形存在性问题(初三)如图,一次函数y =33x ―3图象与坐标轴交于点A 、B ,二次函数y =33x 2+bx +c 图象过A 、B 两点.(1)求二次函数解析式(2)点B 关于抛物线对称轴的对称点为点C ,点P 是对称轴上一动点,在抛物线上是否存在点Q ,使得以B 、C 、P 、Q 为顶点的四边形是菱形?若存在,求出Q 点坐标;若不存在,请说明理由.答案422【解】(1)∵抛物线y =―13x 2+bx +c 交x 轴于A(―3,0),B(4,0)两点,∴y =―13(x +3)(x ―4)=―13x 2+13x +4;(2)①如图1,∵B(4,0),C(0,4),∴设BC 的解析式为:y =kx +n,则{4k +n =0n =4,解得{k =―1n =4∴BC 的解析式为:y =―x +4,∴―x +4=34x +94,解得:x =1,∴E(1,3),∵M(m,0),且MH ⊥x 轴,∴G (m,34m +94),F (m,―13m 2+13m +4),∴FG =―13m 2+13m +4―(34m +94)=―13m 2―512m +74∵S △EFG =59S △OEG ,△EFG 和△OEG 的水平宽度相同,∴FG =59ON,∴―13m 2―512m +74=59×94解得:m 1=34,m 2=―2;②存在,由①知:E(1,3),且∠CBM =45∘∴过点E 作AB 的平行线,与抛物线的交点就是正方形EFHP 的顶点F.∴FH =EF,∠EFH =∠FHP =∠HPE =90∘,∵M(m,0),且MH ⊥x 轴,∴H(m,―m +4),F (m,―13m 2+13m +4),分两种情况:第一种情况:当―3⩽m <1时,如图1,点F 在EP 的左侧∴FH =(―m +4)―(―13m 2+13m +4)=13m 2―43m,∴13m 2―43m =1―m,解得:m 1=1+132(舍),m 2=1―132,∴H(1―132,7+132),∴P (1,7+132),第二种情况:当1<m <4时,点F 在PE 的右边,如图2,同理得―13m 2+43m =m ―1,解得:m 1=1+132,m 2=1―132(舍)，同理得P (1,7―132);综上,点P 的坐标为:(1,7+132)或(1,7―132).423【解】(1)∵OA =1,∴A(―1,0),又∵对称轴为x =2,∴B(5,0),将A,B 代入解析式得:{0=a ―2+c0=25a +10+c ,解得{a =―12c =52,∴y =―12x 2+2x +52(2)由(1)得:C (0,52),D (2,92),∴由两点距离公式可得:CD =22,故答案为22;(3)∵B(5,0),C (0,52),∴直线BC 的解析式为:y =―12x +52,设E (x,―12x 2+2x +52),且0<x <5,如图,作EF ⊥x 轴交BC 于点F,则F (x,―12x +52),∴EF =―12x 2+2x +52―(―12x +52)=―12x 2+52x,S △BCE =12×EF ×BO =12×(―12x 2+52x )×5=―54(x ―52)2+12516当x =52时,S △BCE 有最大值为12516;(4).设P(2,y),Q(m,n),由(1)知B(5,0),C (0,52),分三种情况讨论:①若BC 为矩形的对角线,由中点坐标公式得:{5+0=2+m 0+52=y +n ,解得:{m =3n =52―y ,又∵∠BPC =90∘,∴PC 2+PB 2=BC 2,即:22+(52―y )2+32+y 2=52+(52)2,解得y =4或y =―32,∴n =―32或n =4,∴Q (3,―32)或Q(3,4)，②若BP 为矩形的对角线,由中点坐标公式得{5+2=0+m 0+y =52+n ,解得:{m =7n =y ―52,又∵∠BCP =90∘,BC 2+CP 2=BP 2即:52+(52)2+22+(52―y )2=32+y 2,解得y =132,∴Q(7,4),③若BQ 为矩形的对角线,由中点坐标公式得:{5+m =2+00+n =y +52,解得:{m =―3n =y +52,又∵∠BCQ =90∘,∴BC 2+CQ 2=BQ 2,即:52+(52)2+m 2+(52―n )2=(5―m)2+n 2,解得n =―72,∴Q (―3,―72),综上,点Q 的坐标为(3,―32)或(3,4),或(7,4)或(―3,―72).解法二,也可以构造利用一线三等角三角形相似来解决。

2019中考数学压轴题精编(含参考答案与试题解析共300页)

2019中考数学压轴题精编(含参考答案与试题解析共300页)中考数学压轴题精选（共120题，共两部分：前一部分为试题+参考答案与试题解析，后一部分为纯试题汇编）第一部分1．（2014•黔南州）如图，在平面直角坐标系中，顶点为（4，﹣1）的抛物线交y轴于A点，交x轴于B，C两点（点B在点C的左侧），已知A点坐标为（0，3）．（1）求此抛物线的解析式（2）过点B作线段AB的垂线交抛物线于点D，如果以点C为圆心的圆与直线BD相切，请判断抛物线的对称轴l 与⊙C有怎样的位置关系，并给出证明；（3）已知点P是抛物线上的一个动点，且位于A，C两点之间，问：当点P运动到什么位置时，△PAC的面积最大？并求出此时P点的坐标和△PAC的最大面积．考点：二次函数综合题．专题：压轴题．分析：（1）已知抛物线的顶点坐标，可用顶点式设抛物线的解析式，然后将A点坐标代入其中，即可求出此二次函数的解析式；（2）根据抛物线的解析式，易求得对称轴l的解析式及B、C的坐标，分别求出直线AB、BD、CE的解析式，再求出CE的长，与到抛物线的对称轴的距离相比较即可；（3）过P作y轴的平行线，交AC于Q；易求得直线AC的解析式，可设出P点的坐标，进而可表示出P、Q的纵坐标，也就得出了PQ的长；然后根据三角形面积的计算方法，可得出关于△PAC的面积与P点横坐标的函数关系式，根据所得函数的性质即可求出△PAC的最大面积及对应的P点坐标．解答：解：（1）设抛物线为y=a（x﹣4）2﹣1，∵抛物线经过点A（0，3），∴3=a（0﹣4）2﹣1，；∴抛物线为；（3分）（2）相交．证明：连接CE，则CE⊥BD，当时，x1=2，x2=6．A（0，3），B（2，0），C（6，0），对称轴x=4，∴OB=2，AB==，BC=4，∵AB⊥BD，∴∠OAB+∠OBA=90°，∠OBA+∠EBC=90°，∴△AOB∽△BEC，∴=，即=，解得CE=，∵＞2，∴抛物线的对称轴l与⊙C相交．（7分）（3）如图，过点P作平行于y轴的直线交AC于点Q；可求出AC的解析式为；（8分）设P点的坐标为（m，），则Q点的坐标为（m，）；∴PQ=﹣m+3﹣（m2﹣2m+3）=﹣m2+m．∵S△PAC=S△PAQ+S△PCQ=×（﹣m2+m）×6=﹣（m﹣3）2+；∴当m=3时，△PAC的面积最大为；此时，P点的坐标为（3，）．（10分）点评：此题考查了二次函数解析式的确定、相似三角形的判定和性质、直线与圆的位置关系、图形面积的求法等知识．2．（2014•巴中）如图，在平面直角坐标系xOy中，抛物线y=ax2+bx﹣4与x轴交于点A（﹣2，0）和点B，与y 轴交于点C，直线x=1是该抛物线的对称轴．（1）求抛物线的解析式；（2）若两动点M，H分别从点A，B以每秒1个单位长度的速度沿x轴同时出发相向而行，当点M到达原点时，点H立刻掉头并以每秒个单位长度的速度向点B方向移动，当点M到达抛物线的对称轴时，两点停止运动，经过点M的直线l⊥x轴，交AC或BC于点P，设点M的运动时间为t秒（t＞0）．求点M的运动时间t与△APH的面积S的函数关系式，并求出S的最大值．考点：二次函数综合题．分析：（1）根据抛物线y=ax2+bx﹣4与x轴交于点A（﹣2，0），直线x=1是该抛物线的对称轴，得到方程组，解方程组即可求出抛物线的解析式；（2）由于点M到达抛物线的对称轴时需要3秒，所以t≤3，又当点M到达原点时需要2秒，且此时点H 立刻掉头，所以可分两种情况进行讨论：①当0＜t≤2时，由△AMP∽△AOC，得出比例式，求出PM，AH，根据三角形的面积公式求出即可；②当2＜t≤3时，过点P作PM⊥x轴于M，PF⊥y轴于点F，表示出三角形APH的面积，利用配方法求出最值即可．解答：解：（1）∵抛物线y=ax2+bx﹣4与x轴交于点A（﹣2，0），直线x=1是该抛物线的对称轴，∴，解得：，∴抛物线的解析式是：y=x2﹣x﹣4，（2）分两种情况：①当0＜t≤2时，∵PM∥OC，∴△AMP∽△AOC，∴=，即=，∴PM=2t．解方程x2﹣x﹣4=0，得x1=﹣2，x2=4，∵A（﹣2，0），∴B（4，0），∴AB=4﹣（﹣2）=6．∵AH=AB﹣BH=6﹣t，∴S=PM•AH=×2t（6﹣t）=﹣t2+6t=﹣（t﹣3）2+9，当t=2时S的最大值为8；②当2＜t≤3时，过点P作PM⊥x轴于M，作PF⊥y轴于点F，则△COB∽△CFP，又∵CO=OB，∴FP=FC=t﹣2，PM=4﹣（t﹣2）=6﹣t，AH=4+（t﹣2）=t+1，∴S=PM•AH=（6﹣t）（t+1）=﹣t2+4t+3=﹣（t﹣）2+，当t=时，S最大值为．综上所述，点M的运动时间t与△APQ面积S的函数关系式是S=，S的最大值为．点评：本题是二次函数的综合题型，其中涉及到运用待定系数法求二次函数的解析式，三角形的面积，二次函数的最值等知识，综合性较强，难度适中．运用数形结合、分类讨论及方程思想是解题的关键．．3．（2014•潍坊）如图，抛物线y=ax2+bx+c（a≠0）与y轴交于点C（0，4），与x轴交于点A和点B，其中点A的坐标为（﹣2，0），抛物线的对称轴x=1与抛物线交于点D，与直线BC交于点E．（1）求抛物线的解析式；（2）若点F是直线BC上方的抛物线上的一个动点，是否存在点F使四边形ABFC的面积为17，若存在，求出点F的坐标；若不存在，请说明理由；（3）平行于DE的一条动直线l与直线BC相交于点P，与抛物线相交于点Q，若以D、E、P、Q为顶点的四边形是平行四边形，求点P的坐标．考点：二次函数综合题．分析：（1）先把C（0，4）代入y=ax2+bx+c，得出c=4①，再由抛物线的对称轴x=﹣=1，得到b=﹣2a②，抛物线过点A（﹣2，0），得到0=4a﹣2b+c③，然后由①②③可解得，a=﹣，b=1，c=4，即可求出抛物线的解析式为y=﹣x2+x+4；（2）假设存在满足条件的点F，连结BF、CF、OF，过点F作FH⊥x轴于点H，FG⊥y轴于点G．设点F 的坐标为（t，﹣t2+t+4），则FH=﹣t2+t+4，FG=t，先根据三角形的面积公式求出S△OBF=OB•FH=﹣t2+2t+8，S△OFC=OC•FG=2t，再由S四边形ABFC=S△AOC+S△OBF+S△OFC，得到S四边形ABFC=﹣t2+4t+12．令﹣t2+4t+12=17，即t2﹣4t+5=0，由△=（﹣4）2﹣4×5=﹣4＜0，得出方程t2﹣4t+5=0无解，即不存在满足条件的点F；（3）先运用待定系数法求出直线BC的解析式为y=﹣x+4，再求出抛物线y=﹣x2+x+4的顶点D（1，），由点E在直线BC上，得到点E（1，3），于是DE=﹣3=．若以D、E、P、Q为顶点的四边形是平行四边形，因为DE∥PQ，只须DE=PQ，设点P的坐标是（m，﹣m+4），则点Q的坐标是（m，﹣m2+m+4）．分两种情况进行讨论：①当0＜m＜4时，PQ=（﹣m2+m+4）﹣（﹣m+4）=﹣m2+2m，解方程﹣m2+2m=，求出m的值，得到P1（3，1）；②当m＜0或m＞4时，PQ=（﹣m+4）﹣（﹣m2+m+4）=m2﹣2m，解方程m2﹣2m=，求出m的值，得到P2（2+，2﹣），P3（2﹣，2+）．解答：解：（1）∵抛物线y=ax2+bx+c（a≠0）过点C（0，4），∴c=4 ①．∵对称轴x=﹣=1，∴b=﹣2a ②．∵抛物线过点A（﹣2，0），∴0=4a﹣2b+c ③，由①②③解得，a=﹣，b=1，c=4，∴抛物线的解析式为y=﹣x2+x+4；（2）假设存在满足条件的点F，如图所示，连结BF、CF、OF，过点F作FH⊥x轴于点H，FG⊥y轴于点G．设点F的坐标为（t，﹣t2+t+4），其中0＜t＜4，则FH=﹣t2+t+4，FG=t，∴S△OBF=OB•FH=×4×（﹣t2+t+4）=﹣t2+2t+8，S△OFC=OC•FG=×4×t=2t，∴S四边形ABFC=S△AOC+S△OBF+S△OFC=4﹣t2+2t+8+2t=﹣t2+4t+12．令﹣t2+4t+12=17，即t2﹣4t+5=0，则△=（﹣4）2﹣4×5=﹣4＜0，∴方程t2﹣4t+5=0无解，故不存在满足条件的点F；（3）设直线BC的解析式为y=kx+n（k≠0），∵B（4，0），C（0，4），∴，解得，∴直线BC的解析式为y=﹣x+4．由y=﹣x2+x+4=﹣（x﹣1）2+，∴顶点D（1，），又点E在直线BC上，则点E（1，3），于是DE=﹣3=．若以D、E、P、Q为顶点的四边形是平行四边形，因为DE∥PQ，只须DE=PQ，设点P的坐标是（m，﹣m+4），则点Q的坐标是（m，﹣m2+m+4）．①当0＜m＜4时，PQ=（﹣m2+m+4）﹣（﹣m+4）=﹣m2+2m，由﹣m2+2m=，解得：m=1或3．当m=1时，线段PQ与DE重合，m=1舍去，∴m=3，P1（3，1）．②当m＜0或m＞4时，PQ=（﹣m+4）﹣（﹣m2+m+4）=m2﹣2m，由m2﹣2m=，解得m=2±，经检验适合题意，此时P2（2+，2﹣），P3（2﹣，2+）．综上所述，满足题意的点P有三个，分别是P1（3，1），P2（2+，2﹣），P3（2﹣，2+）．点评：本题是二次函数的综合题型，其中涉及到运用待定系数法求二次函数、一次函数的解析式，四边形的面积，平行四边形的判定等知识，综合性较强，难度适中．运用数形结合、分类讨论及方程思想是解题的关键．4．（2014•重庆）如图，已知抛物线y=﹣x2+2x+3与x轴交于A，B两点（点A在点B的左边），与y轴交于点C，连接BC．（1）求A，B，C三点的坐标；（2）若点P为线段BC上一点（不与B，C重合），PM∥y轴，且PM交抛物线于点M，交x轴于点N，当△BCM 的面积最大时，求△BPN的周长；（3）在（2）的条件下，当△BCM的面积最大时，在抛物线的对称轴上存在一点Q，使得△CNQ为直角三角形，求点Q的坐标．考点：二次函数综合题．分析：（1）依据抛物线的解析式直接求得C的坐标，令y=0解方程即可求得A、B点的坐标；（2）△BCM的面积最大，则过点M作直线L∥BC，直线L应与抛物线相切，即只有一个交点，设直线L 的解析式为y=﹣x+b，则﹣x2+2x+3=﹣x+b的，△=9﹣4b+12=0求得b的值，从而求得三角形的三边长，求得周长；（3）分三种情况：①当∠CQN=90°时；②当∠CNQ=90°时；③当∠NCQ=90°时；讨论求解．解答：解：（1）由抛物线的解析式y=﹣x2+2x+3，∴C（0，3），令y=0，﹣x2+2x+3=0，解得x=3或x=﹣1；∴A（﹣1，0），B（3，0）．（2）过点M作直线L∥BC，当与抛物线相切时，三角形BCM的面积最大，∵直线BC的解析式为y=﹣x+3，设直线L的解析式为y=﹣x+b，则﹣x2+2x+3=﹣x+b，只有一个解，整理得x2﹣3x+b﹣3=0，∴△=9﹣4b+12=0，解得b=，代入﹣x2+2x+3=﹣x+b，解得x=，把x=代入y=﹣x2+2x+3，M（，），代入直线BCy=﹣x+3，则P（，），N（，0），∴BN=，PN=，PB=，∴C△BCN=BN+PN+PB=3+．（3）作抛物线的对称轴x=1，设Q（1，h），①∠CQN=90°时，则CN2=CQ2+QN2，∴32+32=22+h2+12+（h﹣3）2，整理得h2﹣6h﹣2=0，解得：h=或，∴Q（1，）或Q（1，）；②当∠CNQ=90°时，则Q点应在x轴的下方，∴CQ2=CN2+QN2，∴12+（3﹣h）2=22+h2+32+32，解得h=﹣2，∴Q（1，﹣2）；③当∠NCQ=90°时，则Q应在x轴的上方，∴NQ2=CQ2+CN2h2+22=12+（h﹣3）2+32+32，解得h=4，∴Q（1，4）．点评：此题考查了二次函数与坐标轴的交点的性质、三角形面积的确定、二次函数的应用等知识，难度较大．二次函数这部分经常利用数形结合以及分类讨论思想相结合，综合性较强注意不要漏解．5．（2014•福州）如图，抛物线y=（x﹣3）2﹣1与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，顶点为D．（1）求点A，B，D的坐标；（2）连接CD，过原点O作OE⊥CD，垂足为H，OE与抛物线的对称轴交于点E，连接AE，AD，求证：∠AEO=∠ADC；（3）以（2）中的点E为圆心，1为半径画圆，在对称轴右侧的抛物线上有一动点P，过点P作⊙E的切线，切点为Q，当PQ的长最小时，求点P的坐标，并直接写出点Q的坐标．考点：二次函数综合题．分析：（1）根据二次函数性质，求出点A、B、D的坐标；（2）如何证明∠AEO=∠ADC？如答图1所示，我们观察到在△EFH与△ADF中：∠EHF=90°，有一对对顶角相等；因此只需证明∠EAD=90°即可，即△ADE为直角三角形，由此我们联想到勾股定理的逆定理．分别求出△ADE三边的长度，再利用勾股定理的逆定理证明它是直角三角形，由此问题解决；（3）依题意画出图形，如答图2所示．由⊙E的半径为1，根据切线性质及勾股定理，得PQ2=EP2﹣1，要使切线长PQ最小，只需EP长最小，即EP2最小．利用二次函数性质求出EP2最小时点P的坐标，并进而求出点Q的坐标．解答：（1）解：顶点D的坐标为（3，﹣1）．令y=0，得（x﹣3）2﹣1=0，解得：x1=3+，x2=3﹣，∵点A在点B的左侧，∴A（3﹣，0），B（3+，0）．（2）证明：如答图1，过顶点D作DG⊥y轴于点G，则G（0，﹣1），GD=3．令x=0，得y=，∴C（0，）．∴CG=OC+OG=+1=，∴tan∠DCG=．设对称轴交x轴于点M，则OM=3，DM=1，AM=3﹣（3﹣）=．由OE⊥CD，易知∠EOM=∠DCG．∴tan∠EOM=tan∠DCG==，解得EM=2，∴DE=EM+DM=3．在Rt△AEM中，AM=，EM=2，由勾股定理得：AE=；在Rt△ADM中，AM=，DM=1，由勾股定理得：AD=．∵AE2+AD2=6+3=9=DE2，∴△ADE为直角三角形，∠EAD=90°．设AE交CD于点F，∵∠AEO+∠EFH=90°，∠ADC+AFD=90°，∠EFH=∠AFD（对顶角相等），∴∠AEO=∠ADC．（3）解：依题意画出图形，如答图2所示：由⊙E的半径为1，根据切线性质及勾股定理，得PQ2=EP2﹣1，要使切线长PQ最小，只需EP长最小，即EP2最小．设点P坐标为（x，y），由勾股定理得：EP2=（x﹣3）2+（y﹣2）2．∵y=（x﹣3）2﹣1，∴（x﹣3）2=2y+2．∴EP2=2y+2+（y﹣2）2=（y﹣1）2+5当y=1时，EP2有最小值，最小值为5．将y=1代入y=（x﹣3）2﹣1，得（x﹣3）2﹣1=1，解得：x1=1，x2=5．又∵点P在对称轴右侧的抛物线上，∴x1=1舍去．∴P（5，1）．此时点Q坐标为（3，1）或（，）．点评：本题是二次函数压轴题，涉及考点众多，难度较大．第（2）问中，注意观察图形，将问题转化为证明△ADE 为直角三角形的问题，综合运用勾股定理及其逆定理、三角函数（或相似形）求解；第（3）问中，解题关键是将最值问题转化为求EP2最小值的问题，注意解答中求EP2最小值的具体方法．6．（2014•济宁）如图，抛物线y=x2+bx+c与x轴交于A（5，0）、B（﹣1，0）两点，过点A作直线AC⊥x轴，交直线y=2x于点C；（1）求该抛物线的解析式；（2）求点A关于直线y=2x的对称点A′的坐标，判定点A′是否在抛物线上，并说明理由；（3）点P是抛物线上一动点，过点P作y轴的平行线，交线段CA′于点M，是否存在这样的点P，使四边形PACM 是平行四边形？若存在，求出点P的坐标；若不存在，请说明理由．考点：二次函数综合题．分析：（1）利用待定系数法求出抛物线的解析式；（2）首先求出对称点A′的坐标，然后代入抛物线解析式，即可判定点A′是否在抛物线上．本问关键在于求出A′的坐标．如答图所示，作辅助线，构造一对相似三角形Rt△A′EA∽Rt△OAC，利用相似关系、对称性质、勾股定理，求出对称点A′的坐标；（3）本问为存在型问题．解题要点是利用平行四边形的定义，列出代数关系式求解．如答图所示，平行四边形的对边平行且相等，因此PM=AC=10；利用含未知数的代数式表示出PM的长度，然后列方程求解．解答：解：（1）∵y=x2+bx+c与x轴交于A（5，0）、B（﹣1，0）两点，∴，解得．∴抛物线的解析式为y=x2﹣x﹣．（2）如答图所示，过点A′作A′E⊥x轴于E，AA′与OC交于点D，∵点C在直线y=2x上，∴C（5，10）∵点A和A′关于直线y=2x对称，∴OC⊥AA′，A′D=AD．∵OA=5，AC=10，∴OC===．∵S△OAC=OC•AD=OA•AC，∴AD=．∴AA′=，在Rt△A′EA和Rt△OAC中，∵∠A′AE+∠A′AC=90°，∠ACD+∠A′AC=90°，∴∠A′AE=∠ACD．又∵∠A′EA=∠OAC=90°，∴Rt△A′EA∽Rt△OAC．∴，即．∴A′E=4，AE=8．∴OE=AE﹣OA=3．∴点A′的坐标为（﹣3，4），当x=﹣3时，y=×（﹣3）2+3﹣=4．所以，点A′在该抛物线上．（3）存在．理由：设直线CA′的解析式为y=kx+b，则，解得∴直线CA′的解析式为y=x+…（9分）设点P的坐标为（x，x2﹣x﹣），则点M为（x，x+）．∵PM∥AC，∴要使四边形PACM是平行四边形，只需PM=AC．又点M在点P的上方，∴（x+）﹣（x2﹣x﹣）=10．解得x1=2，x2=5（不合题意，舍去）当x=2时，y=﹣．∴当点P运动到（2，﹣）时，四边形PACM是平行四边形．点评：本题是二次函数的综合题型，考查了二次函数的图象及性质、待定系数法、相似、平行四边形、勾股定理、对称等知识点，涉及考点较多，有一定的难度．第（2）问的要点是求对称点A′的坐标，第（3）问的要点是利用平行四边形的定义列方程求解．7．（2014•泰安）二次函数y=ax2+bx+c的图象经过点（﹣1，4），且与直线y=﹣x+1相交于A、B两点（如图），A点在y轴上，过点B作BC⊥x轴，垂足为点C（﹣3，0）．（1）求二次函数的表达式；（2）点N是二次函数图象上一点（点N在AB上方），过N作NP⊥x轴，垂足为点P，交AB于点M，求MN的最大值；（3）在（2）的条件下，点N在何位置时，BM与NC相互垂直平分？并求出所有满足条件的N点的坐标．考点：二次函数综合题．分析：（1）首先求得A、B的坐标，然后利用待定系数法即可求得二次函数的解析式；（2）设M的横坐标是x，则根据M和N所在函数的解析式，即可利用x表示出M、N的坐标，利用x表示出MN的长，利用二次函数的性质求解；（3）BM与NC互相垂直平分，即四边形BCMN是菱形，则BC=MC，据此即可列方程，求得x的值，从而得到N的坐标．解答：解：（1）由题设可知A（0，1），B（﹣3，），根据题意得：，解得：，则二次函数的解析式是：y=﹣﹣x+1；（2）设N（x，﹣x2﹣x+1），则M、P点的坐标分别是（x，﹣x+1），（x，0）．∴MN=PN﹣PM=﹣x2﹣x+1﹣（﹣x+1）=﹣x2﹣x=﹣（x+）2+，则当x=﹣时，MN的最大值为；（3）连接MN、BN、BM与NC互相垂直平分，即四边形BCMN是菱形，由于BC∥MN，即MN=BC，且BC=MC，即﹣x2﹣x=，且（﹣x+1）2+（x+3）2=，解得：x=﹣1，故当N（﹣1，4）时，MN和NC互相垂直平分．点评：本题是待定系数法求二次函数的解析式，以及二次函数的性质、菱形的判定的综合应用，利用二次函数的性质可以解决实际问题中求最大值或最小值问题．8．（2014•泸州）如图，已知一次函数y1=x+b的图象l与二次函数y2=﹣x2+mx+b的图象C′都经过点B（0，1）和点C，且图象C′过点A（2﹣，0）．（1）求二次函数的最大值；（2）设使y2＞y1成立的x取值的所有整数和为s，若s是关于x的方程=0的根，求a的值；（3）若点F、G在图象C′上，长度为的线段DE在线段BC上移动，EF与DG始终平行于y轴，当四边形DEFG 的面积最大时，在x轴上求点P，使PD+PE最小，求出点P的坐标．考点：二次函数综合题．分析：（1）首先利用待定系数法求出二次函数解析式，然后求出其最大值；（2）联立y1与y2得，求出点C的坐标为C（，），因此使y2＞y1成立的x的取值范围为0＜x＜，得s=1+2+3=6；将s的值代入分式方程，求出a的值；（3）第1步：首先确定何时四边形DEFG的面积最大．如答图1，四边形DEFG是一个梯形，将其面积用含有未知数的代数式表示出来，这个代数式是一个二次函数，根据其最值求出未知数的值，进而得到面积最大时点D、E的坐标；第2步：利用几何性质确定PD+PE最小的条件，并求出点P的坐标．如答图2，作点D关于x轴的对称点D′，连接D′E，与x轴交于点P．根据轴对称及两点之间线段最短可知，此时PD+PE最小．利用待定系数法求出直线D′E的解析式，进而求出点P的坐标．解答：解：（1）∵二次函数y2=﹣x2+mx+b经过点B（0，1）与A（2﹣，0），∴，解得∴l：y1=x+1；C′：y2=﹣x2+4x+1．y2=﹣x2+4x+1=﹣（x﹣2）2+5，∴y max=5；（2）联立y1与y2得：x+1=﹣x2+4x+1，解得x=0或x=，当x=时，y1=×+1=，∴C（，）．使y2＞y1成立的x的取值范围为0＜x＜，∴s=1+2+3=6．代入方程得解得a=；（3）∵点D、E在直线l：y1=x+1上，∴设D（p，p+1），E（q，q+1），其中q＞p＞0．如答图1，过点E作EH⊥DG于点H，则EH=q﹣p，DH=（q﹣p）．在Rt△DEH中，由勾股定理得：DE2+DH2=DE2，即（q﹣p）2+[（q﹣p）]2=（）2，解得q﹣p=2，即q=p+2．∴EH=2，E（p+2，p+2）．当x=p时，y2=﹣p2+4p+1，∴G（p，﹣p2+4p+1），∴DG=（﹣p2+4p+1）﹣（p+1）=﹣p2+p；当x=p+2时，y2=﹣（p+2）2+4（p+2）+1=﹣p2+5，∴F（p+2，﹣p2+5）∴EF=（﹣p2+5）﹣（p+2）=﹣p2﹣p+3．S四边形DEFG=（DG+EF）•EH=[（﹣p2+p）+（﹣p2﹣p+3）]×2=﹣2p2+3p+3∴当p=时，四边形DEFG的面积取得最大值，∴D（，）、E（，）．如答图2所示，过点D关于x轴的对称点D′，则D′（，﹣）；连接D′E，交x轴于点P，PD+PE=PD′+PE=D′E，由两点之间线段最短可知，此时PD+PE最小．设直线D′E的解析式为：y=kx+b，则有，解得∴直线D′E的解析式为：y=x﹣．令y=0，得x=，∴P（，0）．点评：本题是二次函数压轴题，综合考查了二次函数与一次函数的图象与性质、待定系数法、函数最值、分式方程的解、勾股定理、轴对称﹣最短路线等知识点，涉及考点众多，难度较大．本题难点在于第（3）问，涉及两个最值问题，第1个最值问题利用二次函数解决，第2个最值问题利用几何性质解决．9．（2014•益阳）如图，直线y=﹣3x+3与x轴、y轴分别交于点A、B，抛物线y=a（x﹣2）2+k经过点A、B，并与X轴交于另一点C，其顶点为P．（1）求a，k的值；（2）抛物线的对称轴上有一点Q，使△ABQ是以AB为底边的等腰三角形，求Q点的坐标；（3）在抛物线及其对称轴上分别取点M、N，使以A，C，M，N为顶点的四边形为正方形，求此正方形的边长．考点：二次函数综合题．分析：（1）先求出直线y=﹣3x+3与x轴交点A，与y轴交点B的坐标，再将A、B两点坐标代入y=a（x﹣2）2+k，得到关于a，k的二元一次方程组，解方程组即可求解；（2）设Q点的坐标为（2，m），对称轴x=2交x轴于点F，过点B作BE垂直于直线x=2于点E．在Rt△AQF 与Rt△BQE中，用勾股定理分别表示出AQ2=AF2+QF2=1+m2，BQ2=BE2+EQ2=4+（3﹣m）2，由AQ=BQ，得到方程1+m2=4+（3﹣m）2，解方程求出m=2，即可求得Q点的坐标；（3）当点N在对称轴上时，由NC与AC不垂直，得出AC为正方形的对角线，根据抛物线的对称性及正方形的性质，得到M点与顶点P（2，﹣1）重合，N点为点P关于x轴的对称点，此时，MF=NF=AF=CF=1，且AC⊥MN，则四边形AMCN为正方形，在Rt△AFN中根据勾股定理即可求出正方形的边长．解答：解：（1）∵直线y=﹣3x+3与x轴、y轴分别交于点A、B，∴A（1，0），B（0，3）．又∵抛物线抛物线y=a（x﹣2）2+k经过点A（1，0），B（0，3），∴，解得，故a，k的值分别为1，﹣1；（2）设Q点的坐标为（2，m），对称轴x=2交x轴于点F，过点B作BE垂直于直线x=2于点E．在Rt△AQF中，AQ2=AF2+QF2=1+m2，在Rt△BQE中，BQ2=BE2+EQ2=4+（3﹣m）2，∵AQ=BQ，∴1+m2=4+（3﹣m）2，∴m=2，∴Q点的坐标为（2，2）；（3）当点N在对称轴上时，NC与AC不垂直，所以AC应为正方形的对角线．又∵对称轴x=2是AC的中垂线，∴M点与顶点P（2，﹣1）重合，N点为点P关于x轴的对称点，其坐标为（2，1）．此时，MF=NF=AF=CF=1，且AC⊥MN，∴四边形AMCN为正方形．在Rt△AFN中，AN==，即正方形的边长为．点评：本题是二次函数的综合题型，其中涉及到的知识点有二元一次方程组的解法，等腰三角形的性质，勾股定理，二次函数的性质，正方形的判定与性质，综合性较强，难度适中．10．（2014•兰州）如图，抛物线y=﹣x2+mx+n与x轴交于A、B两点，与y轴交于点C，抛物线的对称轴交x轴于点D，已知A（﹣1，0），C（0，2）．（1）求抛物线的表达式；（2）在抛物线的对称轴上是否存在点P，使△PCD是以CD为腰的等腰三角形？如果存在，直接写出P点的坐标；如果不存在，请说明理由；（3）点E时线段BC上的一个动点，过点E作x轴的垂线与抛物线相交于点F，当点E运动到什么位置时，四边形CDBF的面积最大？求出四边形CDBF的最大面积及此时E点的坐标．考点：二次函数综合题．分析：（1）由待定系数法建立二元一次方程组求出求出m、n的值即可；（2）由（1）的解析式求出顶点坐标，再由勾股定理求出CD的值，再以点C为圆心，CD为半径作弧交对称轴于P1，以点D为圆心CD为半径作圆交对称轴于点P2，P3，作CE垂直于对称轴与点E，由等腰三角形的性质及勾股定理就可以求出结论；（3）先求出BC的解析式，设出E点的坐标为（a，﹣a+2），就可以表示出F的坐标，由四边形CDBF 的面积=S△BCD+S△CEF+S△BEF求出S与a的关系式，由二次函数的性质就可以求出结论．解答：解：（1）∵抛物线y=﹣x2+mx+n经过A（﹣1，0），C（0，2）．解得：，∴抛物线的解析式为：y=﹣x2+x+2；（2）∵y=﹣x2+x+2，∴y=﹣（x﹣）2+，∴抛物线的对称轴是x=．∴OD=．∵C（0，2），∴OC=2．在Rt△OCD中，由勾股定理，得CD=．∵△CDP是以CD为腰的等腰三角形，∴CP1=CP2=CP3=CD．作CH⊥x轴于H，∴HP1=HD=2，∴DP1=4．∴P1（，4），P2（，），P3（，﹣）；（3）当y=0时，0=﹣x2+x+2∴x1=﹣1，x2=4，∴B（4，0）．设直线BC的解析式为y=kx+b，由图象，得，解得：，∴直线BC的解析式为：y=﹣x+2．如图2，过点C作CM⊥EF于M，设E（a，﹣a+2），F（a，﹣a2+a+2），∴EF=﹣a2+a+2﹣（﹣a+2）=﹣a2+2a（0≤x≤4）．∵S四边形CDBF=S△BCD+S△CEF+S△BEF=BD•OC+EF•CM+EF•BN，=+a（﹣a2+2a）+（4﹣a）（﹣a2+2a），=﹣a2+4a+（0≤x≤4）．=﹣（a﹣2）2+∴a=2时，S四边形CDBF的面积最大=，∴E（2，1）．点评：本题考查了待定系数法求一次函数的解析式的运用，二次函数的解析式的运用，勾股定理的运用，等腰三角形的性质的运用，四边形的面积的运用，解答时求出函数的解析式是关键．11．（2014•钦州）如图，在平面直角坐标系中，抛物线y=﹣x2+bx+c与x轴交于A、D两点，与y轴交于点B，四边形OBCD是矩形，点A的坐标为（1，0），点B的坐标为（0，4），已知点E（m，0）是线段DO上的动点，过点E作PE⊥x轴交抛物线于点P，交BC于点G，交BD于点H．（1）求该抛物线的解析式；（2）当点P在直线BC上方时，请用含m的代数式表示PG的长度；（3）在（2）的条件下，是否存在这样的点P，使得以P、B、G为顶点的三角形与△DEH相似？若存在，求出此时m的值；若不存在，请说明理由．考点：二次函数综合题．分析：（1）将A（1，0），B（0，4）代入y=﹣x2+bx+c，运用待定系数法即可求出抛物线的解析式；（2）由E（m，0），B（0，4），得出P（m，﹣m2﹣m+4），G（m，4），则PG=﹣m2﹣m+4﹣4=﹣m2﹣m；（3）先由抛物线的解析式求出D（﹣3，0），则当点P在直线BC上方时，﹣3＜m＜0．再运用待定系数法求出直线BD的解析式为y=x+4，于是得出H（m，m+4）．当以P、B、G为顶点的三角形与△DEH相似时，由于∠PGB=∠DEH=90°，所以分两种情况进行讨论：①△BGP∽△DEH；②△PGB∽△DEH．都可以根据相似三角形对应边成比例列出比例关系式，进而求出m的值．解答：解：（1）∵抛物线y=﹣x2+bx+c与x轴交于点A（1，0），与y轴交于点B（0，4），∴，解得，∴抛物线的解析式为y=﹣x2﹣x+4；（2）∵E（m，0），B（0，4），PE⊥x轴交抛物线于点P，交BC于点G，∴P（m，﹣m2﹣m+4），G（m，4），∴PG=﹣m2﹣m+4﹣4=﹣m2﹣m；（3）在（2）的条件下，存在点P，使得以P、B、G为顶点的三角形与△DEH相似．∵y=﹣x2﹣x+4，∴当y=0时，﹣x2﹣x+4=0，解得x=1或﹣3，∴D（﹣3，0）．当点P在直线BC上方时，﹣3＜m＜0．设直线BD的解析式为y=kx+4，将D（﹣3，0）代入，得﹣3k+4=0，解得k=，∴直线BD的解析式为y=x+4，∴H（m，m+4）．分两种情况：①如果△BGP∽△DEH，那么=，即=，由﹣3＜m＜0，解得m=﹣1；②如果△PGB∽△DEH，那么=，即=，由﹣3＜m＜0，解得m=﹣．综上所述，在（2）的条件下，存在点P，使得以P、B、G为顶点的三角形与△DEH相似，此时m的值为﹣1或﹣．点评：本题是二次函数的综合题型，其中涉及到运用待定系数法求二次函数、一次函数的解析式，线段的表示，相似三角形的性质等知识，综合性较强，难度适中．运用数形结合、方程思想及分类讨论是解题的关键．12．（2014•贵港）如图，抛物线y=ax2+bx﹣3a（a≠0）与x轴交于点A（﹣1，0）和点B，与y轴交于点C（0，2），连接BC．（1）求该抛物线的解析式和对称轴，并写出线段BC的中点坐标；（2）将线段BC先向左平移2个单位长度，在向下平移m个单位长度，使点C的对应点C1恰好落在该抛物线上，求此时点C1的坐标和m的值；（3）若点P是该抛物线上的动点，点Q是该抛物线对称轴上的动点，当以P，Q，B，C四点为顶点的四边形是平行四边形时，求此时点P的坐标．考点：二次函数综合题．分析：（1）把点A（﹣1，0）和点C（0，2）的坐标代入所给抛物线可得a、b的值，进而得到该抛物线的解析式和对称轴，再求出点B的坐标，根据中点坐标公式求出线段BC的中点坐标即可；（2）根据平移的性质可知，点C的对应点C1的横坐标为﹣2，再代入抛物线可求点C1的坐标，进一步得到m的值；（3）B、C为定点，可分BC为平行四边形的一边及对角线两种情况探讨得到点P的坐标．解答：解：（1）∵抛物线y=ax2+bx﹣3a（a≠0）与x轴交于点A（﹣1，0）和点B，与y轴交于点C（0，2），∴，解得．∴抛物线的解析式为y=﹣x2+x+2=﹣（x﹣1）2+2，∴对称轴是x=1，∵1+（1+1）=3，∴B点坐标为（3，0），∴BC的中点坐标为（1.5，1）；（2）∵线段BC先向左平移2个单位长度，再向下平移m个单位长度，使点C的对应点C1恰好落在该抛物线上，∴点C1的横坐标为﹣2，当x=﹣2时，y=﹣×（﹣2）2+×（﹣2）+2=﹣，∴点C1的坐标为（﹣2，﹣），m=2﹣（﹣）=5；（3）①若BC为平行四边形的一边，∵BC的横坐标的差为3，∵点Q的横坐标为1，∴P的横坐标为4或﹣2，∵P在抛物线上，∴P的纵坐标为﹣3，∴P1（4，﹣3），P2（﹣2，﹣3）；②若BC为平行四边形的对角线，则BC与PQ互相平分，∵点Q的横坐标为1，BC的中点坐标为（1.5，1），∴P点的横坐标为1.5+（1.5﹣1）=2，∴P的纵坐标为﹣×22+×2+2=2，∴P3（2，2）．综上所述，点P的坐标为：P1（4，﹣3），P2（﹣2，﹣3），P3（2，2）．点评：考查了二次函数综合题，涉及待定系数法求函数解析式，抛物线的对称轴，中点坐标公式，平移的性质，平行四边形的性质，注意分BC为平行四边形的一边或为对角线两种情况进行探讨．13．（2014•厦门）如图，已知c＜0，抛物线y=x2+bx+c与x轴交于A（x1，0），B（x2，0）两点（x2＞x1），与y 轴交于点C．（1）若x2=1，BC=，求函数y=x2+bx+c的最小值；（2）过点A作AP⊥BC，垂足为P（点P在线段BC上），AP交y轴于点M．若=2，求抛物线y=x2+bx+c顶点的纵坐标随横坐标变化的函数解析式，并直接写出自变量的取值范围．考点：二次函数综合题．分析：（1）根据勾股定理求得C点的坐标，把B、C点坐标代入y=x2+bx+c即可求得解析式，转化成顶点式即可．（2）根据△AOM∽△COB，得到OC=2OB，即：﹣c=2x2；利用x22+bx2+c=0，求得c=2b﹣4；将此关系式代入抛物线的顶点坐标，即可求得所求之关系式．解答：解：（1）∵x2=1，BC=，∴OC==2，∴C（0，﹣2），把B（1，0），C（0，﹣2）代入y=x2+bx+c，得：0=1+b﹣2，解得：b=1，∴抛物线的解析式为：y=x2+x+﹣2．转化为y=（x+）2﹣；∴函数y=x2+bx+c的最小值为﹣．（2）∵∠OAM+∠OBC=90°，∠OCB+∠OBC=90°，∴∠OAM=∠OCB，又∵∠AOM=∠BOC=90°，∴△AOM∽△COB，∴，∴OC=•OB=2OB，∴﹣c=2x2，即x2=﹣．∵x22+bx2+c=0，将x2=﹣代入化简得：c=2b﹣4．抛物线的解析式为：y=x2+bx+c，其顶点坐标为（﹣，）．令x=﹣，则b=﹣2x．y==c﹣=2b﹣4﹣=﹣4x﹣4﹣x2，∴顶点的纵坐标随横坐标变化的函数解析式为：y=﹣x2﹣4x﹣4（x＞﹣）．点评：本题考查了勾股定理、待定系数法求解析式、三角形相似的判定及性质以及抛物线的顶点坐标的求法等．14．（2014•重庆）如图，抛物线y=﹣x2﹣2x+3 的图象与x轴交于A、B两点（点A在点B的左边），与y轴交于点C，点D为抛物线的顶点．（1）求A、B、C的坐标；（2）点M为线段AB上一点（点M不与点A、B重合），过点M作x轴的垂线，与直线AC交于点E，与抛物线交于点P，过点P作PQ∥AB交抛物线于点Q，过点Q作QN⊥x轴于点N．若点P在点Q左边，当矩形PQMN的周长最大时，求△AEM的面积；（3）在（2）的条件下，当矩形PMNQ的周长最大时，连接DQ．过抛物线上一点F作y轴的平行线，与直线AC 交于点G（点G在点F的上方）．若FG=2DQ，求点F的坐标．考点：二次函数综合题．分析：（1）通过解析式即可得出C点坐标，令y=0，解方程得出方程的解，即可求得A、B的坐标．（2）设M点横坐标为m，则PM=﹣m2﹣2m+3，MN=（﹣m﹣1）×2=﹣2m﹣2，矩形PMNQ的周长d=﹣2m2﹣8m+2，将﹣2m2﹣8m+2配方，根据二次函数的性质，即可得出m的值，然后求得直线AC的解析式，把x=m代入可以求得三角形的边长，从而求得三角形的面积．（3）设F（n，﹣n2﹣2n+3），根据已知若FG=2DQ，即可求得．解答：解：（1）由抛物线y=﹣x2﹣2x+3可知，C（0，3），令y=0，则0=﹣x2﹣2x+3，解得x=﹣3或x=1，∴A（﹣3，0），B（1，0）．（2）由抛物线y=﹣x2﹣2x+3可知，对称轴为x=﹣1，设M点的横坐标为m，则PM=﹣m2﹣2m+3，MN=（﹣m﹣1）×2=﹣2m﹣2，∴矩形PMNQ的周长=2（PM+MN）=（﹣m2﹣2m+3﹣2m﹣2）×2=﹣2m2﹣8m+2=﹣2（m+2）2+10，∴当m=﹣2时矩形的周长最大．∵A（﹣3，0），C（0，3），设直线AC解析式为；y=kx+b，解得k=1，b=3，∴解析式y=x+3，当x=﹣2时，则E（﹣2，1），∴EM=1，AM=1，∴S=•AM•EM=．（3）∵M点的横坐标为﹣2，抛物线的对称轴为x=﹣1，∴N应与原点重合，Q点与C点重合，∴DQ=DC，把x=﹣1代入y=﹣x2﹣2x+3，解得y=4，∴D（﹣1，4）∴DQ=DC=，∵FC=2DQ，∴FG=4，设F（n，﹣n2﹣2n+3），则G（n，n+3），∵点G在点F的上方，∴（n+3）﹣（﹣n2﹣2n+3）=4，解得：n=﹣4或n=1．∴F（﹣4，﹣5）或（1，0）．点评：本题考查了二次函数与坐标轴的交点的求法，矩形的性质，一元二次方程的解法，二次函数最值的求法，综合性较强，难度适中．运用数形结合、方程思想是解题的关键．15．（2014•德州）如图，在平面直角坐标系中，已知点A的坐标是（4，0），并且OA=OC=4OB，动点P在过A，B，C三点的抛物线上．。

中考数学专题二十二：梯形(含详细参考答案)

中考数学专题复习第二十二讲梯形【基础知识回顾】一、梯形的定义、分类、和面积：1、定义：一组对边平行，而另一组对边的四边形，叫做梯形。

其中，平行的两边叫做两底间的距离叫做梯形的2、分类：梯形3、梯形的面积：梯形= （上底+下底） X 高【赵老师提醒：要判定一个四边形是梯形，除了要注明它有一组对边外，还需注明另一组对边不平行或的这组对边不相等】二、等腰梯形的性质和判定：1、性质：⑴等腰梯形的两腰相等，相等⑵等腰梯形的对角线⑶等腰梯形是对称图形一般梯形特殊梯形等腰梯形：两腰的梯形叫做等腰梯形直角梯形：一腰与底的梯形叫做直角梯形2、判定：⑴用定义：先证明四边形是梯形，再证明其两腰相等⑵同一底上两个角的梯形是等腰梯形⑶对角线的梯形是等腰梯形【赵老师提醒：1、梯形的性质和判定中同一底上的两个角相等“不被成”两底角相等2、等腰梯形所有的判定方法都必须先证它是梯形3、解决梯形问题的基本思路是通过做辅助线将梯形转化为形式常见的辅助线作法有要注意根据题目的特点灵活选用辅助线】【重点考点例析】考点一：梯形的基本概念和性质例1 （2012•内江）如图，四边形ABCD是梯形，BD=AC且BD⊥AC，若AB=2，CD=4，则S梯形ABCD= 9．思路分析：过点B作BE∥AC交DC的延长线于点E，过点B 作BF⊥DC于点F，判断出△BDE是等腰直角三角形，求出BF，继而利用梯形的面积公式即可求解．解答：解：过点B作BE∥AC交DC的延长线于点E，过点B 作BF⊥DC于点F，则AC=BE，DE=DC+CE=DC+AB=6，又∵BD=AC 且BD⊥AC，∴△BDE是等腰直角三角形，∴BF=DE=3，故可得梯形ABCD的面积为（AB+CD）×BF=9．故答案为：9．点评：此题考查了梯形的知识，平移一条对角线是经常用到的一种辅助线的作法，同学们要注意掌握，解答本题也要熟练等腰直角三角形的性质，难度一般．对应训练1.（2012•无锡）如图，梯形ABCD中，AD∥BC，AD=3，AB=5，BC=9，CD的垂直平分线交BC于E，连接DE，则四边形ABED 的周长等于（）A．17B．18C．19D．201．考点：；．分析：由CD的垂直平分线交BC于E，根据线段垂直平分线的性质，即可得DE=CE，即可得四边形ABED的周长为AB+BC+AD，继而求得答案．解答：解：∵CD的垂直平分线交BC于E，∴DE=CE，∵AD=3，AB=5，BC=9，∴四边形ABED的周长为：AB+BE+DE+AD=AB+BE+EC+AD=AB+BC+AD=5+9+3=17．故选A．点评：此题考查了线段垂直平分线的性质．此题比较简单，注意掌握数形结合思想与转化思想的应用是解此题的关键．考点二：等腰梯形的性质例2 （2012•呼和浩特）已知：在等腰梯形ABCD中，AD∥BC，AC⊥BD，AD=3，BC=7，则梯形的面积是（）A．25B．50C．25 D．思路分析：过点D作DE∥AC交BC的延长线于点E，作DF⊥BC 于F，证平行四边形ADEC，推出AC=DE=BD，∠BDE=90°，根据等腰三角形性质推出BF=DF=EF= BE，求出DF，根据梯形的面积公式求出即可．解答：解：过点D作DE∥AC交BC的延长线于点E，∵AD∥BC （已知），即AD∥CE，∴四边形ACED是平行四边形，∴AD=CE=3，AC=DE，在等腰梯形ABCD中，AC=DB，∴DB=DE （等量代换），∵AC⊥BD，AC∥DE，∴DB⊥DE，∴△BDE是等腰直角三角形，作DF⊥BC于F，则DF=BE=5，S梯形ABCD=（AD+BC）•DF=（3+7）×5=25，故选A．点评：本题主要考查对等腰三角形性质，平行四边形的性质和判定，等腰梯形的性质，等腰直角三角形等知识点的理解和掌握，能求出高DF的长是解此题的关键．对应训练2．（2012•厦门）如图，在等腰梯形ABCD中，AD∥BC，对角线AC与BD相交于点O，若OB=3，则OC= 3．2．3考点：．分析：先根据梯形是等腰梯形可知，AB=CD，∠BCD=∠ABC，再由全等三角形的判定定理得出△ABC≌△DCB，由全等三角形的对应角相等即可得出∠DBC=∠ACB，由等角对等边即可得出OB=OC=3．解答：解：∵梯形ABCD是等腰梯形，∴AB=CD，∠BCD=∠ABC，在△ABC与△DCB中，∵,∴△ABC≌△DCB，∴∠DBC=∠ACB，∴OB=OC=3．故答案为：3．点评：本题考查的是等腰梯形的性质及全等三角形的判定与性质，熟知在三角形中，等角对等边是解答此题的关键．考点三：等腰梯形的判定例3 （2012•襄阳）如图，在梯形ABCD中，AD∥BC，E为BC的中点，BC=2AD，EA=ED=2，AC与ED相交于点F．（1）求证：梯形ABCD是等腰梯形；（2）当AB与AC具有什么位置关系时，四边形AECD是菱形？请说明理由，并求出此时菱形AECD的面积．考点：；；．分析：（1）由AD∥BC，由平行线的性质，可证得∠DEC=∠EDA，∠BEA=∠EAD，又由EA=ED，由等腰三角形的性质，可得∠EAD=∠EDA，则可得∠DEC=∠AEB，继而证得△DEC≌△AEB，即可得梯形ABCD是等腰梯形；（2）由AD∥BC，BE=EC=AD，可得四边形ABED和四边形AECD均为平行四边形，又由AB⊥AC，AE=BE=EC，易证得四边形AECD是菱形；过A作AG⊥BE 于点G，易得△ABE是等边三角形，即可求得答案AG的长，继而求得菱形AECD的面积．解答：（1）证明：∵AD∥BC，∴∠DEC=∠EDA，∠BEA=∠EAD，又∵EA=ED，∴∠EAD=∠EDA，∴∠DEC=∠AEB，又∵EB=EC，∴△DEC≌△AEB，∴AB=CD，∴梯形ABCD是等腰梯形．（2）当AB⊥AC时，四边形AECD是菱形．证明：∵AD∥BC，BE=EC=AD，∴四边形ABED和四边形AECD均为平行四边形．∴AB=ED，∵AB⊥AC，∴AE=BE=EC，∴四边形AECD是菱形．过A作AG⊥BE于点G，∵AE=BE=AB=2，∴△ABE是等边三角形，∴∠AEB=60°，∴AG=，∴S菱形AECD=EC•AG=2×=2。

2019年中考数学压轴题70题精选

2019年中考数学压轴题70题精选注意事项：认真阅读理解，结合历年的真题，总结经验，查找不足！重在审题，多思考，多理解！【001】如图，抛物线2(1)y a x =-+a ≠0〕经过点(2)A -，0，抛物线的顶点为D ，过O 作射线OM AD ∥、过顶点D 平行于x 轴的直线交射线OM 于点C ，B 在x 轴正半轴上，连结BC 、〔1〕求该抛物线的解析式；〔2〕假设动点P 从点O 出发，以每秒1个长度单位的速度沿射线OM 运动，设点P 运动的时间为()t s 、问当t 为何值时，四边形DAOP 分别为平行四边形？直角梯形？等腰梯形？〔3〕假设OC OB =，动点P 和动点Q 分别从点O 和点B 同时出发，分别以每秒1个长度单位和2个长度单位的速度沿OC 和BO 运动，当其中一个点停止运动时另一个点也随之停止运动、设它们的运动的时间为t ()s ，连接PQ ，当t 为何值时，四边形BCPQ 的面积最小？并求出最小值及此时PQ 的长、【002】如图，在平面直角坐标系中，矩形ABCD 的三个顶点B 〔4，0〕、C 〔8，0〕、D 〔8，8〕.抛物线y=ax 2+bx 过A 、C 两点.(1)直接写出点A 的坐标，并求出抛物线的解析式；(2)动点P 从点A 出发、沿线段AB 向终点B 运动，同时点Q 从点C 出发，沿线段CD向终点D 运动、速度均为每秒1个单位长度，运动时间为t 秒.过点P 作PE ⊥AB 交AC 于点E ，①过点E 作EF ⊥AD 于点F ，交抛物线于点G.当t 为何值时，线段EG 最长?②连接EQ 、在点P 、Q 运动的过程中，判断有几个时刻使得△CEQ 是等腰三角形? 请直接写出相应的t 值。

【003】如图13，二次函数)0(2<++=p q px x y 的图象与x 轴交于A 、B 两点，与y 轴交于点C 〔0，-1〕，ΔABC 的面积为45。

〔1〕求该二次函数的关系式；〔2〕过y 轴上的一点M 〔0，m 〕作y 轴的垂线，假设该垂线与ΔABC 的外接圆有公共点，求m 的取值范围；〔3〕在该二次函数的图象上是否存在点D ，使四边形ABCD 为直角梯形？假设存在，求出点D 的坐标；假设不存在，请说明理由。

九年级数学第二十二章第1节《二次函数的图象和性质》解答题专题 (10)含解析

第二十二章第1节《二次函数的图象和性质》解答题专题 (10)1．已知关于x 的方程2(41)40kx k x -++=．（1）当k 取何值时，方程有两个实数根；（2）若二次函数2(41)4y kx k x =-++的图象与x 轴两个交点的横坐标均为整数，且k 为正整数，求k 值并用配方法求出抛物线的顶点坐标．2．抛物线2y x bx c =-++（b ，c 为常数）与x 轴交于点()1,0x 和()2,0x ，与y 轴交于点A ，点E 为抛物线顶点．（Ⅰ）当121,3x x =-=时，求点A ，点E 的坐标；（Ⅱ）若顶点E 在直线y x =上，当点A 位置最高时，求抛物线的解析式；（Ⅲ）若11,0x b =->，当(1,0)P 满足PA PE +值最小时，求b 的值．3．已知抛物线2y x bx c =++与x 轴交于()1,0A x ，()2,0B x 两点，且12xx <，若222133x x k +=（k 为正整数），我们把该抛物线称为“B 系抛物线”．特例感知（1）当2b =，15c =-时，请判断抛物线2y x bx c =++是否是“B 系抛物线”，并说明理由．推广验证（2）若234c b =-，且b 为负整数，请判断抛物线2y x bx c =++是否是“B 系抛物线”，并说明理由．拓展应用（3）在（2）的条件下，若M 为该抛物线的顶点，且ABM ∆为等腰直角三角形，求该抛物线的解析式．4．已知：如图抛物线26y ax bx =++与x 轴交于点()6,0B ()2,0C -与y 轴交于点A ．（1）求抛物线的解析式；（2）如图点P 是线段AB 上方抛物线上的一个动点连结PA 、PB ．设PAB △的面积为S ．点P 的横坐标为m ．①试求S 关于m 的函数关系式；②请说明当点P 运动到什么位置时PAB △的面积有最大值？③过点P 作x 轴的垂线交线段AB 于点D 再过点P 做//PE x 轴交抛物线于点E 连结DE 请问是否存在点P 使PDE △为等腰直角三角形？若存在请直接写出点P 的坐标；若不存在请说明理由．5．在平面直角坐标系xOy 中抛物线()2420y axax a a =-+≠的顶点为P 且与y 轴交于点A 与直线y a =-交于点BC （点B 在点C 的左侧）.（1）求抛物线()2420y axax a a =-+≠的顶点P 的坐标（用含a 的代数式表示）；（2）横、纵坐标都是整数的点叫做整点记抛物线与线段AC 围成的封闭区域（不含边界）为“W 区域”.①当2a =时请直接写出“W 区域”内的整点个数；②当“W 区域”内恰有2个整点时结合函数图象直接写出a 的取值范围.6．在平面直角坐标系xOy 中，已知，点A （3，0）、B （－2，5）、C （0，－3）．求经过点A 、B 、C 的抛物线的表达式．7．在平面直角坐标系xOy 中，抛物线25y ax bx a =+-与y 轴交于点A ，将点A 向左平移4个单位长度，得到点B ，点B 在抛物线上．（1）求点B 的坐标（用含a 的式子表示）；（2）求抛物线的对称轴；（3）已知点()1,2P a --，()4,2Q -．若抛物线与线段PQ 恰有一个公共点，结合函数图象，求a 的取值范围．8．如图1在平面直角坐标系xOy 中抛物线y=-（x-a ）（x-4）（a ＜0）与x 轴交于A 、B 两点（点A 在点B 的左侧）与y 轴交于点C 点D 为抛物线的顶点．（1）若D 点坐标为（32524，）求抛物线的解析式和点C 的坐标；（2）若点M 为抛物线对称轴上一点且点M 的纵坐标为a 点N 为抛物线在x 轴上方一点若以C 、B 、M 、N 为顶点的四边形为平行四边形时求a 的值；（3）直线y=2x+b 与（1）中的抛物线交于点D 、E （如图2）将（1）中的抛物线沿着该直线方向进行平移平移后抛物线的顶点为D′与直线的另一个交点为E′与x 轴的交点为B′在平移的过程中求D′E′的长度；当∠E′D′B′=90°时求点B′的坐标．9．二次函数y=ax 2+bx+c （a≠0）的图象向左平移4个单位，再向上平移3个单位，得到二次函数y=x 2﹣2x+1，求：b ，c 的值． 10．在平面直角坐标系中，抛物线y 14=x 2沿x 轴正方向平移后经过点A （x 1，y 2），B （x 2，y 2），其中x 1，x 2是方程x 2﹣2x ＝0的两根，且x 1＞x 2，（1）如图．求A ，B 两点的坐标及平移后抛物线的解析式；（2）平移直线AB 交抛物线于M ，交x 轴于N ，且14AB MN =，求△MNO 的面积；（3）如图，点C 为抛物线对称轴上顶点下方的一点，过点C 作直线交抛物线于E 、F ，交x 轴于点D ，探究CD CDCE CF+的值是否为定值？如果是，求出其值；如果不是，请说明理由．11．已知：关于x 的二次函数2y x ax =-+（a ＞0），点A （n ，y 1）、B （n+1，y 2）、C （n+2，y 3）都在这个二次函数的图象上，其中n 为正整数．（1）y 1=y 2，请说明a 必为奇数；（2）设a=11，求使y 1≤y 2≤y 3成立的所有n 的值；（3）对于给定的正实数a ，是否存在n ，使△ABC 是以AC 为底边的等腰三角形？如果存在，求n 的值（用含a 的代数式表示）；如果不存在，请说明理由．12．如图①定义：直线:(0,0)l y mx n m n =+<>与x 、y 轴分别相交于A 、B 两点将AOB ∆绕着点O 逆时针旋转90°得到COD ∆过点A 、B 、D 的抛物线P 叫做直线l 的“纠缠抛物线”反之直线l 叫做P 的“纠缠直线"两线“互为纠缠线”．（1）若:22l y x =-+则纠缠物线P 的函数解析式是____________．（2）判断并说明22y x k =-+与212y x x k k=--+是否“互为纠缠线”．（3）如图②若纠缠直线:24l y x =-+纠缠抛物线P 的对称轴与CD 相交于点E 点F 在l 上点Q 在P 的对称轴上当以点C 、E 、Q 、F 为顶点的四边形是以CE 为一边的平行四边形时求点Q 的坐标．13．已知二次函数y ＝ax 2（a ≠0）的图象经过点（﹣2，3）（1）求a 的值，并写出这个二次函数的解析式；（2）求出此抛物线上纵坐标为3的点的坐标． 14．关于x 的二次函数y 1＝x 2+kx+k ﹣1（k 为常数）（1）对任意实数k ，函数图象与x 轴都有交点（2）若当x≥75时，函数y 的值都随x 的增大而增大，求满足条件的最小整数k 的值（3）K 取不同的值时，函数抛物线的顶点位置也会变化，但会在某一函数图象上，求该函数图象的解析式（4）若当自变量x 满足0≤x≤3时，与其对应的函数值y 的最小值为10，求此时k 的值． 15．如图，在平面直角坐标系中，抛物线2y ax bx =+经过(2,4)A --，(2,0)B . （1）求抛物线2y ax bx =+的解析式.（2）若点M是该抛物线对称轴上的一点，求AM OM的最小值.16．在同一个直角坐标系中作出y＝12x2，y＝12x2－1的图象．(1)分别指出它们的开口方向、对称轴以及顶点坐标；(2)抛物线y＝12x2－1与抛物线y＝12x2有什么关系？17．如图：已知抛物线的顶点为A（1，4），抛物线与y轴交于点B（0，3）与x轴交于C、D两点，点P是x轴上的一个动点.（1）求抛物线的解析式；（2）当PA+PB的值是最小时，求点P的坐标.18．在平面直角坐标系中xOy中，抛物线y＝x2﹣4x+m+2的顶点在x轴上．（1）求抛物线的表达式；（2）点Q是x轴上一点，①若在抛物线上存在点P，使得∠POQ＝45°，求点P的坐标．②抛物线与直线y＝1交于点E，F（点E在点F的左侧），将此抛物线在点E，F（包含点E和点F）之间的部分沿x轴向左平移n个单位后得到的图象记为G，若在图象G上存在点P，使得∠POQ＝45°，求n的取值范围．19．如图，已知抛物线y=ax2+bx+3与x轴交于A、B两点，过点A的直线l与抛物线交于点C，其中A点的坐标是（1，0），C点坐标是（4，3）．（1）求抛物线的解析式；（2）在（1）中抛物线的对称轴上是否存在点D，使△BCD的周长最小？若存在，求出点D的坐标，若不存在，请说明理由；（3）若点E是（1）中抛物线上的一个动点，且位于直线AC的下方，试求△ACE的最大面积及E点的坐标．20．如图抛物线y=-x2+bx+c与x轴交于A、B两点交y轴正半轴于C点D为抛物线的顶点A （-10）B（30）．（1）求出二次函数的表达式．（2）点P在x轴上且∠PCB=∠CBD求点P的坐标．（3）在x轴上方抛物线上是否存在一点Q使得以QCBO为顶点的四边形被对角线分成面积相等的两部分？如果存在请直接写出点Q的坐标；如果不存在请说明理由．【答案与解析】1．（1）0k ≠；（2）k=1，（52，94-）.(1)要使方程有两个实数根，必须满足两个条件：[]2(41)440k k k ⎧∆=-+-⨯≥⎨≠⎩从而可求出k 的取值范围；(2)令y=0，得到一个一元二次方程，用含有k 的代数式表示方程的解，根据题意求出k 的值.(1)依题意得[]2(41)4400k k k ⎧∆=-+-⨯≥⎨≠⎩，整理得24k-100k ⎧∆=≥⎨≠⎩（）∵当k 取任何值时，2(41)0k -≥， ∴0k ≠∴当0k ≠时，方程总有两个实数根.(2)解方程2(41)40kx k x -++=，得14x =，21x k=． ∵12x x 和均为整数且k 为正整数，∴取k=1． ∴254y x x =-+222555()()422x x =-+-+ 259()24x =--∴抛物线的顶点坐标为（52，94-）．【点睛】本题考查二次函数综合题，解题的关键是掌握根的判别式和抛物线的顶点坐标的求法.2．（Ⅰ）()0,3A ，(1,4)E ；（Ⅱ）214y x x =-++；（Ⅲ）3b = （Ⅰ）将（-1，0），（3，0）代入抛物线的解析式求得b 、c 的值，确定解析式，从而求出抛物线与y 轴交于点A 的坐标，运用配方求出顶点E 的坐标即可；（Ⅱ）先运用配方求出顶点E 的坐标，再根据顶点E 在直线y x =上得出吧b 与c 的关系，利用二次函数的性质得出当b=1时，点A 位置最高，从而确定抛物线的解析式；（Ⅲ）根据抛物线经过（-1，0）得出c=b+1，再根据（Ⅱ）中顶点E 的坐标得出E 点关于x 轴的对称点E '的坐标，然后根据A 、P 两点坐标求出直线AP 的解析式，再根据点在直线AP 上，此时PA PE +值最小，从而求出b 的值.解：（Ⅰ）把点(-1,0)和(3,0)代入函数2y x bx c =-++，有10930b c b c --+=⎧⎨-++=⎩．解得2,3b c == 2223(1)4y x x x ∴=-++=--+(0,3),(1,4)A E ∴（Ⅱ）由222424b c b y x bx c x +⎛⎫=-++=--+ ⎪⎝⎭，得24,24b c b E ⎛⎫+ ⎪⎝⎭∵点E 在直线y x =上，2424b c b+∴=221111(1)4244c b b b ∴=-+=--+2110,(1)44A b ⎛⎫∴--+ ⎪⎝⎭ 当1b =时，点A 是最高点此时，214y x x =-++（Ⅲ）：抛物线经过点(1,0)-，有10b c --+=1c b ∴=+24,,(0,)24b c b E A c ⎛⎫+ ⎪⎝⎭ 2(2),,(0,1)24b b E A b ⎛⎫+∴+ ⎪⎝⎭∴E 关于x 轴的对称点E '为2(2),24b b ⎛⎫+- ⎪⎝⎭设过点A ，P 的直线为y kx t =+.把(0,1),(1,0)A b P +代入y kx t =+，得(1)(1)y b x =-+-把点2(2),24b b E '⎛⎫+- ⎪⎝⎭代入(1)(1)y b x =-+-.得2(2)(1)142b b b +⎛⎫=-+- ⎪⎝⎭，即2680b b --=解得，3b =0,3b b >∴=舍去.317b ∴=+ 【点睛】本题主要考查的是二次函数的综合应用，解答本题主要应用了待定系数法求二次的解析式、最短距离，数形结合思想及待定系数法的应用是解题的关键，属于中考压轴题．3．（1）是；理由见解析；（2）是；理由见解析；（3）23y 4x x =--．（1）根据“B 系抛物线”代入2b =，15c =-，然后计算与x 轴交点坐标，然后判断22213x x +的值判断即可；（2）将234c b =-代入表达式后计算与x 轴交点坐标，然后判断22213x x +的值判断即可；（3）过M 作MH ⊥AB ，然后根据（2）得到AB 长度和M 的横坐标，然后计算即可．解：（1）当2b =，15c =-时，代入2y x bx c =++即2215y x x =+-令y =0，即20215x x +=-∴(3)(x 5)0x -+= ∴125,3x x =-=∴22213x x +=2233?(-5)3k +=即28k=∴是“B 系抛物线” （2）∵234c b =-∴2234y x bx b =+-令y =0，即22304x bx b =+-∴13()()022x b x b -+= ∵b 为非负数 ∴1213,22x b x b ==- ∴2231()3?()322b b k -+=即233b k =此时2k b = ∴是“B 系抛物线”；（3）如图，当△ABM 为等腰直角三角形时，过M 作MH ⊥AB ，其中AB=2b ，点M 横坐标为2b - 将2b x =-代入2234y x bx b =+-即2223()()224b b y b b b =-+--= ∴MH=-2b∵△ABM 为等腰直角三角形 ∴MH=12AB ∴21×22b b -=解的120(),1b b ==-舍去∴抛物线的解析式234y x x =--【点睛】本题主要考查二次函数性质，理解“B 系抛物线”是解题的关键． 4．（1）2162y x bx =-++；（2）①()2327322S m =--+②当m=3时S 有最大值③点P 的坐标为（4,6）或（55-）．（1）由()2(6)(2)412y a x x a x x =-+=-- 则-12a=6求得a 即可；（2）①过点P 作x 轴的垂线交AB 于点D 先求出AB 的表达式y=-x+6设点21,262P m m m ⎛⎫-++ ⎪⎝⎭则点D （m-m+6）然后再表示()222113327332669322222S PD OB PD m m m m m m ⎛⎫=⨯⨯==-+++-=-+=--+ ⎪⎝⎭即可；②由在()2327322S m =--+中32-＜0故S 有最大值；③△PDE 为等腰直角三角形则PE=PD 然后再确定函数的对称轴、E 点的横坐标进一步可得|PE|=2m-4即21266242m m m m -+++-=-求得m 即可确定P 的坐标．解：（1）由抛物线的表达式可化为()22(6)6=(2)412y a x x a x ax bx x =+-++-=- 则-12a=6解得：a=12-故抛物线的表达式为：2162y x bx =-++；（2）①过点P 作x 轴的垂线交AB 于点D由点A(0,6)、B 的坐标可得直线AB 的表达式为：y=-x+6 设点21,262P m m m ⎛⎫-++ ⎪⎝⎭则点D （m-m+6） ∴()222113327332669=322222S PD OB PD m m m m m m ⎛⎫=⨯⨯==-+++-=-+--+ ⎪⎝⎭； ②∵()2327322S m =--+32-＜0 ∴当m=3时S 有最大值； ③∵△PDE 为等腰直角三角形 ∴PE=PD ∵点21,262P m m m ⎛⎫-++ ⎪⎝⎭函数的对称轴为：x=2则点E 的横坐标为：4-m 则|PE|=2m-4 即21266242m m m m -+++-=- 解得：m=4或-2或517+517-2和517 当m=4时21262m m -++=6；当m=517-21262m m -++=3175．故点P 的坐标为（4,6）或（5173175）．【点睛】本题属于二次函数综合应用题主要考查了一次函数、等腰三角形的性质、图形的面积计算等知识点掌握并灵活应用所学知识是解答本题的关键． 5．（1）顶点P 的坐标为()2,2a -；（2）① 6个；② 112a <≤112a -≤<-．（1）由抛物线解析式直接可求；（2）①由已知可知A （02）C （2+2 -2）画出函数图象观察图象可得；②分两种情况求：当a ＞0时抛物线定点经过（2-2）时a=1抛物线定点经过（2-1）时a=12则12＜a≤1；当a ＜0时抛物线定点经过（22）时a=-1抛物线定点经过（21）时a=-12则-1≤a<-12．解：（1）∵y=ax 2-4ax+2a=a （x-2）2-2a ∴顶点为（2-2a ）；（2）如图①∵a=2∴y=2x 2-8x+2y=-2 ∴A （02）C （2-2） ∴有6个整数点；②当a ＞0时抛物线定点经过（2-2）时a=1 抛物线定点经过（2-1）时12a =； ∴112a <≤．当0a <时抛物线顶点经过点（22）时1a =-；抛物线顶点经过点（21）时12a =-； ∴ 112a -≤<-． ∴综上所述：112a <≤112a -≤<-．【点睛】本题考查二次函数的图象及性质；熟练掌握二次函数的图象及性质是解题的关键．6．223y x x =--设抛物线的解析式为y=ax 2+bx+c ，再把三个已知点的坐标代入得到关于a 、b 、c 的方程组，解方程组即可得到二次函数的解析式．解：设经过点A 、B 、C 的抛物线的表达式为2(0)y ax bx c a =++≠．则9304253a b c a b c c ++=⎧⎪-+=⎨⎪=-⎩，解得：123a b c =⎧⎪=-⎨⎪=-⎩． ∴经过点A 、B 、C 的抛物线的表达式为223y x x =--．【点睛】本题考查了用待定系数法求二次函数的解析式：在利用待定系数法求二函数关系式时，要根据题目给定的条件，选择恰当的方法设出关系式，从而代入数值求解． 7．（1）()4,5B a --；（2）2x =-；（3）205a -≤< （1）根据解析式得到点A 的坐标，利用平移即可得到带你B 的坐标；（2）根据点A 、B 的对称性即可求出对称轴；（3）分两种情况：a>0或a<0时，分别确定点P 、Q 的位置，根据抛物线与线段PQ 恰有一个公共点求出答案.（1）∵抛物线25y ax bx a =+-与y 轴交于点A ，∴点A(0，-5a)，∵将点A 向左平移4个单位长度，得到点B ， ∴B(-4，-5a)；（2）对称轴是x=0422-=-；（3）如图：当a<0时，∵A(0，-5a), ()1,2P a --,且-5a>-2a ， ∴点P 在抛物线下方，∵()4,2Q -，抛物线与线段PQ 恰有一个公共点，B(-4，-5a)， ∴点Q 在抛物线上方或是在抛物线上，即25a ≥-，解得25a ≥-， ∴205a -≤<时抛物线与线段PQ 恰有一个公共点；当a>0时，∵A(0，-5a), ()1,2P a --，且-5a<-2a<0， ∴点P 在抛物线上方，在x 轴下方， ∵()4,2Q -，B(-4，-5a)， ∴点Q 在抛物线上方，∴此时抛物线与线段PQ 没有公共点；综上，205a -≤<时抛物线与线段PQ 恰有一个公共点. 【点睛】此题考查抛物线的性质，利用解析式求点坐标，点平移的规律，抛物线对称轴，抛物线与线段交点问题.8．（1）y=-x 2+3x+4C （04）；（2）a 11326221-；（3）D ′E ′5B′（-10）．（1）将点D 的坐标代入函数解析式求得a 的值；利用抛物线解析式来求点C 的值．（2）需要分类讨论：BC 为边和BC 为对角线两种情况根据“平行四边形的对边平行且相等平行四边形的对角线相互平分”的性质列出方程组利用方程思想解答．（3）根据平移规律得到D ′E ′的长度、平移后抛物线的解析式然后由函数图象上点的坐标特征求得点B ′的坐标．（1）依题意得：254=-（32-a ）（32-4）．解得a=-1．∴抛物线解析式为：y=-（x+1）（x-4）或y=-x 2+3x+4． ∴C （04）．（2）由题意知：A （a0）B （40）C （0-4a ）．对称轴为直线x=42a +则M （42a +a ）． ①MN ∥BC 且MN=BC 根据点的平移特征可知N （42a --3a ）．则-3a=-（42a --a ）（42a --4）．解得：②当BC 为对角线时设N （xy ）．根据平行四边形的对角线互相平分可得：4424a x a y a +⎧+=⎪⎨⎪+=-⎩．解得425a x y a-⎧=⎪⎨⎪=-⎩．则-5a=-（42a --a ）（42a --4）．解得a=63±．（舍去正值） ∴a 12=63-．（3）把D （32524，）代入y=2x+b 得到：2×32+b=254．则b=134．故直线解析式为：y=2x+134．联立2132434y x y x x ⎧=+⎪⎨⎪=-++⎩．解得1132254x y ⎧=⎪⎪⎨⎪=⎪⎩（舍去）221294x y ⎧=-⎪⎪⎨⎪=⎪⎩．∴E （-1294）∴．根据抛物线的平移规律则平移后线段D′E′始终等于设平移后的D′（m2m+134）则E′（m-22m-34）．平移后抛物线的解析式为：y=-（x-m ）2+2m+134．则D′B′：y=-12x+n 过点（m2m+134） ∴y=-12x+52m+134则B′（5m+1320）． ∴-12（5m+132）+52m+134=0．解得m 1=-32m 2=-138． ∴B ′1（-10）B′2（-1380）（与D′重合舍去）．综上所述B′（-10）．【点睛】本题主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养．要会利用数形结合的思想把代数和几何图形结合起来利用点的坐标的意义表示线段的长度从而求出线段之间的关系． 9．b=﹣10，c=22．此题实际上是将抛物线y=x 2﹣2x+1向下平移3个单位，向右平移4个单位得到抛物线y=ax 2+bx+c （a≠0），由此求得b ，c 的值．解：将y=x 2﹣2x+1向下平移3个单位，向右平移4个单位，得：y=（x ﹣1﹣4）2﹣3=（x ﹣5）2﹣3=x 2﹣10x+22．故：b=﹣10，c=22．【点睛】本题考查了二次函数图象的平移，熟练掌握平移的规律：左加右减，上加下减，并用规律求函数解析式是关键．10．（1）点A 坐标为（2，0），点B 坐标为（0，1），21(2)4y x =-;（2）12或28；（3）CD CDCE CF+为定值，定值为1．（1）解方程x 2﹣2x ＝0得x 1＝2，x 2＝0．即可求得点A 坐标为（2，0），抛物线解析式为()2124y x =- ，把x ＝0代入抛物线解析式得y ＝1，即可得点B 坐标为（0，1）；（2）如图，过M 作MH ⊥x 轴，垂足为H ，由AB ∥MN ，即可得△ABO ∽△MHN ，根据相似三角形的性质可得14BO HN AB MH AO MN ===，由此求得MH ＝4，HN ＝8，将y ＝4代入抛物线()2124y x =-求得x 1＝﹣2，x 2＝6，所以M 1（﹣2，4），N 1（6，0），M 2（6，4），N 2（14，0）,由此求得△MNO 的面积即可；（3）设C （2，m ），求得CD 解析式为y ＝kx +m ﹣2k ，令y ＝0得kx +m ﹣2k ＝0，由此求得点D 为（2k mk-，0）；把CD 的解析式与抛物线的解析式联立221(2)4y kx m ky x =+-⎧⎪⎨=-⎪⎩，消去y 得，kx +m ﹣2k ＝14（x ﹣2）2．化简得x 2﹣4（k +1）x +4﹣4m +8k ＝0，由根与系数关系得，x 1+x 2＝4k +4，x 1•x 2＝4﹣4m +8k ．过E 、F 分别作EP ⊥CA 于P ，FQ ⊥CA 于Q ，由AD ∥EP ，AD ∥FQ ，可得CD CDCE CF+＝AD AD EP FQ AD EP FQ EP FQ ++=⋅⋅ ＝（2k mk -﹣2）×()()121212424x x x x x x +-⋅-++＝()()()4444482444k m k m k k +--⋅-+-++＝1，由此可得CD CD CE CF+为定值，定值为1．（1）解方程x 2﹣2x ＝0得x 1＝2，x 2＝0． ∴点A 坐标为（2，0），抛物线解析式为()2124y x =- ．把x ＝0代入抛物线解析式得y ＝1． ∴点B 坐标为（0，1）．（2）如图，过M 作MH ⊥x 轴，垂足为H ∵AB ∥MN ∴△ABO ∽△MHN∴14BO HN AB MH AO MN === ∴MH ＝4，HN ＝8将y ＝4代入抛物线()2124y x =- 可得x 1＝﹣2，x 2＝6∴M 1（﹣2，4），N 1（6，0），M 2（6，4），N 2（14，0）, ∴11164122M N O S ∆=⨯⨯= 221144282M N O S ∆=⨯⨯=（3）设C （2，m ），设直线CD 为y ＝kx +b 将C （2，m ）代入上式，m ＝2k +b ，即b ＝m ﹣2k ． ∴CD 解析式为y ＝kx +m ﹣2k ，令y ＝0得kx +m ﹣2k ＝0， ∴点D 为（2k mk-，0）联立221(2)4y kx m k y x =+-⎧⎪⎨=-⎪⎩，消去y 得，kx +m ﹣2k ＝14（x ﹣2）2．化简得，x 2﹣4（k +1）x +4﹣4m +8k ＝0由根与系数关系得，x 1+x 2＝4k +4，x 1•x 2＝4﹣4m +8k ．过E 、F 分别作EP ⊥CA 于P ，FQ ⊥CA 于Q ， ∴AD ∥EP ，AD ∥FQ ， ∴CD CD CE CF+＝AD ADEP FQ AD EP FQ EP FQ ++=⋅⋅ ＝（2k mk-﹣2）×()()121212424x x x x x x +-⋅-++＝()()()4444482444k mk m k k +--⋅-+-++ ＝1∴CD CDCE CF +为定值，定值为1．【点睛】本题是二次函数综合题，考查了一次函数与二次函数图象的交点问题，解决第（3）问的关键是确定CD CD CE CF+＝AD ADEP FQ AD EP FQ EP FQ ++=⋅⋅，再利用根与系数的关系解决． 11．解：（1）∵点A （n ，y 1）、B （n+1，y 2）都在二次函数2y x ax =-+（a ＞0）的图象上，∴()()2212y n an y n 1a n 1=-+=-+++，． ∵y 1=y 2，∴()()22n an n 1a n 1-+=-+++，整理得：a=2n+1． ∵n 为正整数，∴a 必为奇数．（2）当a=11时，∵y 1＜y 2＜y 3，∴()()()()222n 11n n 111n 1n 211n 2-+≤-+++≤-+++．化简得：0102n 184n ≤-≤-．解得：n 4≤． ∵n 为正整数，∴n=1、2、3、4．（3）存在．假设存在，则AB=AC ，如图所示，过点B 作BN ⊥x 轴于点N ，过点A 作AD ⊥BN 于点D ，CE ⊥BN 于点E ，∵x A =n ，x B =n+1，x C =n+2，∴AD=CE=1．在Rt △ABD 与Rt △CBE 中，AB=BC ，AD=CE ， ∴Rt △ABD ≌Rt △CBE （HL ）．∴∠BAD=∠CBE ，即BN 为顶角的平分线．由等腰三角形性质可知，点A 、C 关于BN 对称． ∴BN 为抛物线的对称轴，点B 为抛物线的顶点， ∴()a an 1212+=-=⨯-．∴a n 12=-．∴存在n ，使△ABC 是以AC 为底边的等腰三角形，an 12=-．（1）将点A 和点B 的坐标代入二次函数的解析式，利用y 1=y 2得到用n 表示a 的式子，即可得到答案；（2）将a=11代入解析式后，由题意列出不等式组，求得此不等式组的正整数解．（3）本问为存在型问题，如图所示，可以由三角形全等及等腰三角形的性质，判定点B为抛物线的顶点，点A 、C 关于对称轴对称，于是得到()a a n 1212+=-=⨯-，从而可以求出a n 12=-． 12．答案见解析.（1）若l ：y=-2x+2则点A 、B 、C 、D 的坐标分别为：（10）、（02）、（01）、（-20）则抛物线的表达式为：y=a （x+2）（x-1）即可求解；（2）同理：点A 、B 、C 、D 的坐标分别为：（k0）、（02k ）、（0k ）、（-2k0）则抛物线的表达式为：y=a （x+2k ）（x-k ）即可求解；（3）以点C 、E 、Q 、F 为顶点的四边形是以CE 为一边的平行四边形时由题意得：|x Q -x F |=1即：m+1=±1即可求解．解：（1）若l ：y=-2x+2则点A 、B 、C 、D 的坐标分别为：（10）、（02）、（01）、（-20）则抛物线的表达式为：y=a （x+2）（x-1）将点B 的坐标代入上式得：2=a （0+2）（0-1）解得：a=-1故答案为：y=-x 2-x+2；(2)同理：点A 、B 、C 、D 的坐标分别为：（k0）、（02k ）、（0k ）、（-2k0）则抛物线的表达式为：y=a （x+2k ）（x-k ）将点B 的坐标代入上式并解得：a=1-k 故抛物线的表达式为：y=211-(2)()2x k x k x x k k k +-=--+ 故y=-2x+2k 与y ＝212x x k k--+“互为纠缠线”；点A 、B 、C 、D 的坐标分别为：（20）、（04）、（02）、（-40）同理可得：抛物线的表达式为：y=21--42x x + 抛物线的对称轴为：x=-1设点F （m-2m+4）点Q （-1n ）将点C 、D 的坐标代入一次函数表达式并求得：直线CD 的表达式为：y=12x+2 点CE 横坐标差为1故纵坐标差为12以点C 、E 、Q 、F 为顶点的四边形是以CE 为一边的平行四边形时由题意得：|x Q -x F |=1即：m+1=±1解得：m=0或-2当m=0时点F （04）则点Q （-192）；同理当m=-2时点Q （-1172）；综上点Q 坐标为：Q （-192）或Q （-1172）．【点睛】本题考查的是二次函数综合运用涉及到一次函数、平行四边形性质等其中（3）要注意分类求解避免遗漏．13．（1）34，234y x = （2）（﹣2，3），（2，3）（1）根据二次函数图象上点的坐标满足其解析式，把点（-2，3）代入解析式得到关于a 的方程，然后解方程即可；（2）把y=3代入解析式求出x 的值即可．解：（1）∵抛物线y ＝ax 2经过点（﹣2，3），∴4a ＝3，∴a=34， ∴二次函数的解析式为234y x =；（2）∵抛物线上点的纵坐标为3， ∴3＝34x 2，解得x ＝±2， ∴此抛物线上纵坐标为3的点的坐标为（﹣2，3），（2，3）．【点睛】考查了待定系数法求解析式，二次函数图象上点的坐标特征，函数解析式与图象上的点之间的关系，点在图象上，则满足解析式；反之，满足解析式则在函数图象上．14．（1）见解析；（2）﹣150；（3）y ＝﹣x 2﹣2x ﹣1；（4）11．（1）计算△，根据△的值进行判断；（2）根据二次函数的增减性即可判断；（3）得到抛物线的顶点，写成方程组，消去k 得y =-x 2-2x -1，即可判断；（4）函数配方后得y =x 2+kx +k -1=22124k k x k ⎛⎫+-+- ⎪⎝⎭，根据对称轴的位置分三种情况进行讨论可得结论.解：（1）∵△＝k 2﹣4（k ﹣1）＝k 2﹣4k+4＝（k ﹣2）2≥0，∴对任意实数k ，函数图象与x 轴都有交点；（2）∵a＝1＞0，抛物线的对称轴x b k 2a 2=-=-， ∴在对称轴的右侧函数y 的值都随x 的增大而增大，即当x k 2-＞时，函数y 的值都随x 的增大而增大， ∵x≥75时，函数y 的值都随x 的增大而增大， ∴k 2-≤75，k≥﹣150， ∴k 的最小整数是﹣150， ∴满足条件的最小整数k 的值是﹣150；（3）∵y＝x 2+kx+k ﹣1＝（x k 2+）22k 4-+k ﹣1， ∴抛物线的顶点为（k 2-，2k 4-+k ﹣1）， ∴2k x 2k y k 14⎧=-⎪⎪⎨⎪=-+-⎪⎩，消去k 得，y ＝﹣x 2﹣2x ﹣1，由此可见，不论k 取任何实数，抛物线的顶点都满足函数y ＝﹣x 2﹣2x ﹣1，即抛物线的顶点在二次函数y ＝﹣x 2﹣2x ﹣1的图象上；（4）∵y＝x 2+kx+k ﹣1＝（x k 2+）22k 4-+k ﹣1， ∴抛物线的顶点为（k 2-，2k 4-+k ﹣1），又∵0≤x≤3时，与其对应的函数值y 的最小值为10， ①当k 2-≤0时，即k≤0，此时x ＝0时，y 取得最小值是10，则有10＝k ﹣1，k ＝11． ②当k 2-≥3时，即k≤﹣6，此时x ＝3时，y 取得最小值是10，则有10＝32+3k+k ﹣1， k 12=，不符合题意； ③当0k 2-＜＜3时，即﹣6＜k ＜0，此时x k 2=-时，y 取得最小值是10，即2k 4-+k ﹣1＝10，此方程无实根，综上所述，k 的值是11．【点睛】本题主要考查了二次函数的性质，解决本题的关键是要熟悉函数关系式和方程的关系、函数的性质.15．（1）抛物线的解析式为212y x x =-+；（2）AM OM +的最小值为42. （1）利用待定系数法可求出该抛物线的解析式；（2）根据O 、B 两点正好关于抛物线的对称轴对称，那么只需连接A 、B ，直线AB 和抛物线对称轴的交点即为符合要求的M 点，而AM +OM 的最小值正好是AB 的长，过点A 作AN ⊥x 轴于点N ．在Rt △ABN 中，根据勾股定理即可得出结论．（1）把A （﹣2，﹣4），B （2，0）两点的坐标代入y =ax 2+bx 中，得：424420a b a b -=-⎧⎨+=⎩，解方程组，得：a 12=-，b =1，∴解析式为y 12=-x 2+x ．（2）由y 12=-x 2+x 12=-（x ﹣1）212+，可得抛物线的对称轴为直线x =1，并且对称轴垂直平分线段OB ，∴OM =BM ，∴OM +AM =BM +AM ．连接AB 交直线x =1于M 点，则此时OM +AM 最小．过点A 作AN ⊥x 轴于点N ．在Rt △ABN 中，AB 222244AN BN =+=+=42，因此OM +AM 最小值为42．【点睛】本题是二次函数的综合题，难点在于点M 位置的确定，正确理解二次函数的轴对称性以及两点之间线段最短是解题的关键．16．见解析试题分析：观察图像结合函数表达式可以得到两个函数开口向上，对称轴也都是y 轴，顶点坐标分别是(0,0),（0，-1）；根据二次函数的性质及图像知道抛物线y＝12x2－1与抛物线y＝12x2形状相同，对称轴相同，但是位置不同，开口方向也相同，所以可以得到抛物线y＝12x2－1可由抛物线y＝12x2向下平移1个单位长度得到的．解：如图所示：(1)抛物线y＝12x2开口向上，对称轴为y轴，顶点坐标(0，0)；抛物线y＝12x2－1开口向上，对称轴为y轴，顶点坐标(0，－1)．(2)抛物线y＝12x2－1可由抛物线y＝12x2向下平移1个单位长度得到．17．（1）y=﹣（x﹣1）2+4；（2）当PA+PB的值是最小时，点P的坐标是（37，0）.试题分析：（1）由题意可设抛物线解析式为“顶点式”，再代入点B的坐标可求得解析式；（2）由题意作出点B关于x轴的对称轴点E，连接AE交x轴于点P，P为所求的点，由A、E的坐标可求得直线AE的解析式，再由AE的解析式就可求得点P的坐标.试题解析：(1)∵抛物线的顶点A的坐标为（1，4），∴设抛物线的表达式为y＝a(x－1)2＋4.∵抛物线过点B(0，3)，∴3＝a(0－1)2＋4.解得a＝－1.∴二次函数的表达式为y＝－(x－1)2＋4，即y＝－x2＋2x＋3.(2)作点B关于x轴的对称点E(0，－3)，连接AE交x轴于点P，点P即为所求点．设AE所在直线的表达式为y＝kx＋b，分别代入A，E坐标，得43k bb+=⎧⎨=-⎩，解得73kb=⎧⎨=-⎩，∴y＝7x－3.当y＝0时，x＝3 7 .∴点P 的坐标为(37，0)． 18．（1）y ＝x 2﹣4x +4；（2）①点P 的坐标为（1，1）或（4，4）；②在图象G 上存在点P ，使得∠POQ ＝45°，n 的取值范围为0≤n ≤4．（1）根据抛物线顶点在x 轴上，列式计算可得m 的值；（2）由∠POQ ＝45°，作直线y ＝x ，交抛物线y ＝x 2﹣4x +4于点P ，联立解析式求出P 点坐标即可；（3）分两种情况考虑：当点P ，Q 在y 轴右侧时与点P ，Q 在y 轴左侧时，列出不等式求解即可.解：（1）∵抛物线y ＝x 2﹣4x +m +2的顶点在x 轴上，∴()()2412441m ⨯⨯+--⨯＝0，解得：m ＝2， ∴抛物线的表达式为y ＝x 2﹣4x +4．（2）①作直线y ＝x ，交抛物线y ＝x 2﹣4x +4于点P ，如图1所示．联立直线OP 及抛物线的表达式成方程组，得：244y x y x x =⎧⎨=+⎩﹣，解得：1111x y =⎧⎨=⎩，2244x y =⎧⎨=⎩， ∴点P 的坐标为（1，1）或（4，4）．②当y ＝1时，x 2﹣4x +4＝1，解得：x 1＝1，x 2＝3，∴点E 的坐标为（1，1），点F 的坐标为（3，1）．分两种情况考虑：（i ）当点P ，Q 在y 轴右侧时，∵抛物线y ＝x 2﹣4x +4与直线y ＝x 交于点（1，1）， ∴当1≤3﹣n ≤3时，图象G 上存在点P ，使得∠POQ ＝45°，解得：0≤n ≤2；（ii ）当点P ，Q 在y 轴左侧时，同①可得出，抛物线y ＝x 2﹣4x +4与直线y ＝﹣x 交于点（﹣1，﹣1）或（﹣4，﹣4），∴当﹣1≤3﹣n ≤1时，图象G 上存在点P ，使得∠POQ ＝45°，解得：2≤n ≤4．综上所述：若在图象G 上存在点P ，使得∠POQ ＝45°，n 的取值范围为0≤n ≤4．【点睛】本题考查二次函数的图像和性质，正确理解∠POQ＝45°的意义，运用数形结合的思想解决问题是解题关键.19．（1）y=x2﹣4x+3；（2）存在，抛物线对称轴上存在点D（2，1），使△BCD的周长最小；（3）△ACE的最大面积278，此时E点坐标为（52，34）．（1）利用待定系数法求二次函数解析式解答即可．（2）利用待定系数法求出直线AC的解析式，然后根据轴对称确定最短路线问题，直线AC 与对称轴的交点即为所求点D．（3）根据直线AC的解析式，设出过点E与AC平行的直线，然后与抛物线解析式联立消掉y得到关于x的一元二次方程，利用根的判别式△=0时，△ACE的面积最大，然后求出此时与AC平行的直线，然后求出点E的坐标，并求出该直线与x轴的交点F的坐标，再求出AF ，再根据直线l 与x 轴的夹角为45°求出两直线间的距离，再求出AC 间的距离，然后利用三角形的面积公式列式计算即可得解．解：（1）∵抛物线y=ax 2+bx+3经过点A （1，0），点C （4，3），∴a b 30{16a 4b 33++=++=，解得a 1{b 4==-． ∴抛物线的解析式为y=x 2﹣4x+3．（2）存在．∵点A 、B 关于对称轴对称，∴点D 为AC 与对称轴的交点时△BCD 的周长最小． ∵y=x 2﹣4x+3=（x ﹣2）2﹣1，∴抛物线的对称轴为直线x=2．设直线AC 的解析式为y=kx+b （k≠0），则k b 0{4k b 3+=+=，解得：k 1{b 1==-．∴直线AC 的解析式为y=x ﹣1．当x=2时，y=2﹣1=1．∴抛物线对称轴上存在点D （2，1），使△BCD 的周长最小．（3）如图，设过点E 与直线AC 平行线的直线为y=x+m ，联立243y x my x x =+⎧⎨=-+⎩，消掉y 得，x 2﹣5x+3﹣m=0．由△=（﹣5）2﹣4×1×（3﹣m ）=0得m=134-．∴m=134-时，点E 到AC 的距离最大，△ACE 的面积最大．此时x=52，y=5133244-=-．∴点E 的坐标为（52，34-）．设过点E 的直线与x 轴交点为F ，则F （134，0）．∴AF=139144-=．∵直线AC 的解析式为y=x ﹣1，∴∠CAB=45°．∴点F 到AC 的距离为9292428⨯=．又∵223(41)32AC =+-=．∴△ACE 的最大面积192273228=⨯⨯=，此时E 点坐标为（52，34-）． 20．（1）y=-x 2+2x+3；（2）P （60）或P 3,02⎛⎫ ⎪⎝⎭；（3）存在点Q 113113,⎛⎫++ ⎪ ⎪⎝⎭或17,24⎛⎫- ⎪⎝⎭．（1）将点A 、B 坐标代入解析式求出b 、c 的值即可得；（2）∠PCB=∠CBD 有两种情况①P 在B 的右侧时延长BD 交y 轴于点H 由∠OCB=∠OBC=45°可证明∠HCB=∠CBP 从而△PCB ≌△HBC 由直线BD 即可求得：OH=OP=6从而得到P 点坐标；②P 在B 的左侧时此时PC ∥BD 根据一次函数解析式即可求出P ；（3）分以下两种情况分别求解①点Q 在y 轴右侧时由OB=OC 可得出OQ 是∠BOC 的平分线联立二次函数解析式与直线OQ 的解析式即可求解；②点Q 在y 轴左侧时可得这条对角线只能是BQ 过点C 作x 轴的平行线EF 过点QB 分别作EF 的垂线垂足分别为FE 延长FQ 交x 轴于点G 设点Q 的坐标为(mn)根据S △BOQ =S △CBQ =S 梯形FQBE -S △FCQ -S △BEC 可得出关于mn 的关系式再与二次函数的解析式联立即可求解．解：（1）将点A （-10）B （30）代入y=-x 2+bx+c 得10930b c b c --+=⎧⎨-++=⎩解得23b c =⎧⎨=⎩∴二次函数的表达式为y=-x 2+2x+3；（2）①当点P 在点B 右侧时延长BD 交y 轴于点H∵y=-x 2+2x+3=-（x-1）2+4∴点D 的坐标为（14）设直线BD 的解析式为y=kx+b 则304k b k b +=⎧⎨+=⎩解得26k b =-⎧⎨=⎩即直线BD 的解析式为y=-2x+6 ∴点H 的坐标为（06）∵OB=OC=3∴∠OBC=∠OCB=45°∴∠HCB=∠CBP=135°又∠PCB=∠CBDBC=BC∴△PCB ≌△HBC∴CH=PB∴OH=OB=6故此时点P 的坐标为（60）；②当点P （P′）在点B 左侧时直线BD 的表达式为：y=-2x+6∵∠P′CB=∠CBD 则P′C ∥BD则直线P′C 的表达式为：y=-2x+3当y=0x=32故此时点P′的坐标为3,02⎛⎫ ⎪⎝⎭综上所述点P 的坐标为（60）或3,02⎛⎫⎪⎝⎭；（3）存在．理由如下：①当点Q 在y 轴右侧时以QCBO 为顶点的四边形被对角线分成面积相等的两部分这条对角线只能是OQS △COQ =S △BOQ 如图而OB=OC 故OQ 是∠BOC 的平分线即OQ 的函数表达式为：y=x将y=x 与y=-x 2+2x+3联立得-x 2+2x+3=x 解得113+ 故此时点Q 的坐标为（1132+1132+）； ②当点Q 在y 轴左侧时以QCBO 为顶点的四边形被对角线分成面积相等的两部分这条对角线只能是BQS △BOQ =S △CBQ 如图过点C 作x 轴的平行线EF 过点QB 分别作EF 的垂线垂足分别。

中考数学精讲篇中考压轴题突破二、解答题压轴题突破重难点突破十几何图形综合题

(2)如解图，连接 EF，由(1)知△BCE≌△ADF，∴AF＝BE，又∵AF∥BE， ∴四边形 ABEF 为平行四边形， ∴S△AEF＝S△AEB，同理 S△DEF＝S△DEC， ∴T＝S△AEB＋S△DEC. ∵T＝S△AED＋S△ADF＝S△AED＋S△BCE，
S ∴S＝S△AEB＋S△AED＋S△BCE＋S△DEC＝2T，∴T＝2.
(1)解：①在 Rt△ABC 中，∵BC＝2，AC＝4， ∴AB＝ 22＋42＝2 5.∵AD＝CD＝2，∴BD＝2 2. 由翻折可知 BP＝BA＝2 5. ②证明：∵△BCD 是等腰直角三角形， ∴∠BDC＝45°，∴∠ADB＝∠BDP＝135°，
∴∠PDC＝135°－45°＝90°.∴∠BCD＝∠PDC＝90°，∴DP∥BC. ∵PD＝AD＝BC＝2，∴四边形 BCPD 是平行四边形．
重难点突破十几何图形综合题
类型一：与全等三角形有关的问题 (安徽：2018，2014，2011T23)
如图，在△ABC 中，∠ACB＝90°，AC＝BC，延长 AB 至点 D，使 DB＝ AB，连接 CD，以 CD 为边作△CDE，其中∠DCE＝90°，CD＝CE，连接 BE. (1)求证：△ACD≌△BCE； (2)若 AB＝6 cm，则 BE＝______cm； (3)BE 与 AD 有何位置关系？请说明理由．
证明：(1)∵∠ACB＝90°，AC＝BC， ∴∠ABC＝45°＝∠PBA＋PBC， ∵∠APB＝135°， ∴∠PAB＋PBA＝45°， ∴∠PBC＝∠PAB， ∵∠APB＝∠BPC＝135°， ∴△PAB∽△PBC.
(2)∵△PAB∽△PBC， PA PB AB
∴PB＝PC＝BC，在 Rt△ABC 中，AC＝BC， ∴ABBC＝ 2， ∴PA＝ 2PB，PB＝ 2PC， ∴PA＝2PC.

2019年全国各地中考数学压轴题分类汇编几何综合（浙江专版）含答案

2019年全国各地中考数学压轴题分类汇编（浙江专版）几何综合打印版答案在最后1.（2019・杭州）如图，已知正方形ABCD的边长为1,正方形CEFG的面积为Si，点E在。

C边上,点G在3。

的延长线上，设以线段4£>和£>£为邻边的矩形的面积为，，且£=$2.（1）求线段CE的长；（2）若点H为BC边的中点，连接HQ,求证：HD=HG.2.（2019・杭州）如图，已知锐角三角形ABC内接于圆O,ODLBC于点Q,连接Q4.(1)若ZBAC=60°,①求证：OD=—OA.2②当。

4=1时，求△A3C面积的最大值.(2)点E在线段QA上，OE=OD,连接DE,设ZABC=mZOED,ZACB=nZOED(m,"是正数），若ZABCCZACB,求证：m-n+2^0.3.(2019.宁波)如图，矩形EFGH的顶点E,G分别在菱形ABCD的边A£>,BC上，顶点F,H在菱形ABCD的对角线BD上.(1)求证：BG=DE；(2)若E为AD中点，FH=2,求菱形ABCD的周长.4.(2019-宁波)定义：有两个相邻内角互余的四边形称为邻余四边形，这两个角的夹边称为邻余线.(1)如图1,在△ABC中，AB=AC,AD是AABC的角平分线，E,F分别是B。

，AD上的点.求证：四边形ABEF是邻余四边形.(2)如图2,在5X4的方格纸中，A,B在格点上，请画出一个符合条件的邻余四边形ABEF,使A3是邻余线，E,尸在格点上.(3)如图3,在(1)的条件下，取EF中点连结并延长交AB于点0延长EF交AC于点N.若N为A C的中点，DE=2BE,Q3=3,求邻余线仙的长.5.(2019-宁波)如图1,经过等边△ABC的顶点A,C(圆心。

在△ABC内)，分别与AB,CB的延长线交于点D,E,连结DE,BFLEC交AE于点F.(1)求证：BD=BE.(2)当AF：EF=3：2,AC=6时，求AE的长.(3)设tanZDAE—y.EF①求y关于x的函数表达式；②如图2,连结OF,OB,若左AEC的面积是△OFB面积的10倍，求y的值.副图26.(2019・温州)如图，在ZVIBC中，ZBAC=90°,点E在BC边上，且CA=CE,过A,C,E三点的OO交AB于另一点F,作直径AD,连结QE并延长交AB于点G,连结CD,CF.(1)求证：四边形DCFG是平行四边形.(2)当BE=4,CD=^AB时,求。

中考数学压轴题100题含答案解析

中考数学压轴题100题精选【含答案】【001】如图，已知抛物线y a(x 3 3( a z 0)经过点A2 °)，抛物线的顶点为D , 过O作射线OM // AD •过顶点D平行于x轴的直线交射线OM于点C , B在x轴正半轴上，连结BC •(1)求该抛物线的解析式；(2)若动点P从点0出发，以每秒1个长度单位的速度沿射线OM运动，设点P运动的时间为t(s) •问当t为何值时，四边形DAOP分别为平行四边形？直角梯形？等腰梯形？(3)若0C °B，动点P和动点Q分别从点0和点B同时出发，分别以每秒1个长度单位和2 个长度单位的速度沿OC和BO运动，当其中一个点停止运动时另一个点也随之停止运动•设它们的运动的时间为t (s)，连接PQ，当t为何值时，四边形BCPQ的面积最小？并求出最小值及此时PQ的长.【002】如图16,在Rt A ABC中，/ C=90 , AC = 3 , AB = 5 .点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动，到达点A后立刻以原来的速度沿AC返回；点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P、Q的运动，DE保持垂直平分PQ,且交PQ于点D，交折线QB-BC-CP于点E.点P、Q同时出发，当点Q到达点B时停止运动,点P也随之停止.设点P、Q运动的时间是t秒(t >0).(1) 当t = 2时，AP = ，点Q到AC的距离是:(2) 在点P从C向A运动的过程中，求△ APQ的面积S与t的函数关系式；(不必写出t的取值范围)(3) 在点E从B向C运动的过程中，四边形QBED能否成为直角梯形？若能，求t的值.若不能，请说明理由；(4) 当DE经过点C时，请直接写出t的值.【003】如图，在平面直角坐标系中，已知矩形ABCD的三个顶点B (4, 0)、C ( 8, 0)、D ( 8,8) •抛物线y=ax2+bx过A、C两点.(1) 直接写出点A的坐标，并求出抛物线的解析式；(2) 动点P从点A出发.沿线段AB向终点B运动，同时点Q从点C出发，沿线段CD 向终点D运动.速度均为每秒1个单位长度，运动时间为t秒•过点P作PE丄AB交AC于点E,①过点E作EF丄AD于点F，交抛物线于点G.当t为何值时，线段EG最长?②连接EQ.在点P、Q运动的过程中，判断有几个时刻使得△ CEQ是等腰三角形？请直接写出相应的t值。

2019届中考数学压轴题精练：由比例线段产生的函数关系问题(含2019试题-含详解)

图6
例 2 2019 年上海市徐汇区中考模拟第 25 题
在 Rt△ABC 中，∠C＝90°，AC＝6， sin B = 3 ，⊙B 的半径长为 1，⊙B 交边 CB 于点 P，点 O 是边 AB 上的 5
动点．（1）如图 1，将⊙B 绕点 P 旋转 180°得到⊙M，请判断⊙M 与直线 AB 的位置关系；（2）如图 2，在（1）的条件下，当△OMP 是等腰三角形时，求 OA 的长；（3）如图 3，点 N 是边 BC 上的动点，如果以 NB 为半径的⊙N 和以 OA 为半径的⊙O 外切，设 NB＝y，OA＝x，
一点特身尔传过辱加马克也种的锋找悟分己两把这了森竟发钟就理在球迷同道突换张些提面疯断他况干出攻贾和进且埃放伊长方亮握来巴度错始太多阿力脚利守下还须门去拥更曼对不样击比行给是磕倒得班夏快被单逼平各次炸:认刻控国人做姜论要奇正有助纳熟好们会求等奥个本刚想起说续路溜技危席诉场丽如照七大前向验可型里达速防然到斯肯中着所员十反直后忍踢劳暴险都吃预新能必量狂聚简禁插线情强洛索赛王上化经完军维从赫尽才硬解问看图时让吼没算接手似呼滥足态味普惊拉松我取又回毫护架最意德致少迫年宁日排腰罗么状底娥停撞高尼败体落六潮无敢远将定拿留耗明头实鲁激泽告麦当命卫粗退背洞边练景吊周权变候为话亲文切结而7望粘3主配但毕胜感打充封功别皮令牧般雷制成声谁术黑整悉翻引遭蒂那托瓦法全弓已扳喊心飞消题焦区林却规现走表住予死余雨波安舞丹丰据积入盯够虎脑幕战先应再挥获掀开轻诱空迹什怕伦博站压摆之风三名急烧很动鱼冕集作射冲子轰镜继因季受隔第用见紧格谋升塞势怎跑犯转失部输步精招信哪虑果误你惜响仿教识抢生办羞暇奏域弹自斗补常知地气带象酸只事富队欢透运霸布兵号坐间跳节内葡甚束历墙希零伤巨撤支嗅梅缩占星草计位几许亏像并岁优句差领根二台米条产滚库注牙何真老考效贴准冠群0局随决歇丝合吸乎拼容含神原保距亚猛近以热越重觉破萄警依刺刀难渗茨虽段陷挤吉父恩悲秒铲跟五章至非玩糙胆承4火叫1嫦害久臂按穿病机套横范默庆电童确扩离未密存佯华四漏英腩叹限易糊目漂贺倍小双肋迎鸣蒙管科择荡该选堵掉姆援2扑祝系曾调约仍摸啊闪此沉备外仅阶忘友处八散增敲彩爆佛寻攒严扰客若纠乔宠泪萨闻今艳清乐豪纸沛首请眼皇记于数或歌荷任呵抗闷终帅水市匹柱恐驻夸称字悬置相阵者额便赢创价脸挺盖答交工登覆唱早围牌兴宫商质灯烦需匆担迪绪佳讯较服颜付极胸乌麻天白杨捧即霍追包车澡趣连纵使她视媒闹宾评收超扁关花哨折色铁红巾贸智甲颠帮晚漠忙儿恨吧否搁判公票威音烂陆团赴哀爱8键亨嘴口裁掌遁赞享串另抱吹笔美造著签念资9旁显千魁贵孙舒诺牲顾尖黄物磨海觑油丑仰词家女鲜挡业.咱示语士兰靠温审其繁苛郁抵流厢轮报刁室每伸疑立胁榜竞驶忌愿恶言琐投笑呢衣敬假诚冷式标喝酒勒移扬谭素嘹裔睹谈偏耶费河角举万听广慰俱坦喜负掩牺桶夹责枯惨际钢总绅齐幸九烈砸赶钻呆观及频采脱洗耽试瞬满赋陪杯猥除猝影辛孩瓶厅冰介腿礼讶欧愧召众洲街拐房男啤指怪慢省挑官饮昧山既纪汗怀朋光通哦谢展掏端餐屋乖云虾拔绍微低吟豫材苦斤粉冒息膊避西顿施巧卖挽梦畅罪哈百代略春画拭钱卡楼吗尤类宴导萃喂杰悸逃龄滑译扫谷疼鬼擦颇胳城借份嘛庭半貌馆妇菜古冻北缺东异犹播复宿爽朝淡杂姐舫

中考数学压轴题

2019中考数学压轴题1.眉山如图1;在平面直角坐标系中;抛物线y ＝﹣94x 2+bx+c 经过点A ﹣5;0和点B1;0. 1求抛物线的解析式及顶点D 的坐标；2点P 是抛物线上A 、D 之间的一点;过点P 作PE ⊥x 轴于点E;PG ⊥y 轴;交抛物线于点G.过点G 作GF ⊥x 轴于点F.当矩形PEFG 的周长最大时;求点P 的横坐标；3如图2;连接AD 、BD;点M 在线段AB 上不与A 、B 重合;作∠DMN ＝∠DBA ; MN 交线段AD 于点N;是否存在这样点M;使得△DMN 为等腰三角形若存在;求出AN 的长；若不存在;请说明理由.2.甘肃如图;已知二次函数y ＝x 2+bx +c 的图象与x 轴交于点A 1;0、B 3;0;与y 轴交于点C ．1求二次函数的解析式； 2若点P 为抛物线上的一点;点F 为对称轴上的一点;且以点A 、B 、P 、F 为顶点的四边形为平行四边形;求点P 的坐标；3点E 是二次函数第四象限图象上一点;过点E 作x 轴的垂线;交直线BC 于点D ;求四边形AEBD 面积的最大值及此时点E 的坐标． 3.广安如图;抛物线y =−x 2+bx +c 与x 轴交于A 、B 两点(A 在B 的左侧);与y 轴交于点N ;过A 点的直线l ：y =kx +n 与y 轴交于点C ;与抛物线y =−x 2+bx +c 的另一个交点为D ;已知A(−1,0);D(5,−6);P 点为抛物线y =−x 2+bx +c 上一动点(不与A 、D 重合)．(1)求抛物线和直线l 的解析式；(2)当点P 在直线l 上方的抛物线上时;过P 点作PE//x 轴交直线l 于点E ;作PF//y 轴交直线l 于点F ;求PE +PF 的最大值；(3)设M 为直线l 上的点;探究是否存在点M ;使得以点N 、C ;M 、P 为顶点的四边形为平行四边形若存在;求出点M 的坐标；若不存在;请说明理由．4.武威如图;抛物线y ＝ax 2+bx +4交x 轴于A ﹣3;0;B 4;0两点;与y 轴交于点C ;连接AC ;BC ．点P 是第一象限内抛物线上的一个动点;点P 的横坐标为m ．1求此抛物线的表达式；2过点P 作PM ⊥x 轴;垂足为点M ;PM 交BC 于点Q ．试探究点P 在运动过程中;是否存在这样的点Q ;使得以A ;C ;Q 为顶点的三角形是等腰三角形．若存在;请求出此时点Q 的坐标;若不存在;请说明理由；3过点P 作PN ⊥BC ;垂足为点N ．请用含m 的代数式表示线段PN 的长;并求出当m 为何值时PN 有最大值;最大值是多少5.无锡已知二次函数42-+=bx ax y a ＞0的图像与x 轴交于A 、B 两点;A 在B 左侧;且OA B A C O D E F G P y x 图1 图2 A B C D y xM N O＜OB;与y轴交于点C．D为顶点;直线AC交对称轴于点E;直线BE交y轴于点F;AC：CE ＝2：1．1求C点坐标;并判断b的正负性；2设这个二次函数的图像的对称轴与直线AC交于点D;已知DC：CA＝1：2;直线BD与y 轴交于点E;连接BC．①若△BCE的面积为8;求二次函数的解析式；②若△BCD为锐角三角形;请直接写出OA的取值范围．6.菏泽如图;抛物线与x轴交于A;B两点;与y轴交于点C0;﹣2;点A的坐标是2;0P为抛物线上的一个动点;过点P作PD⊥x轴于点D;交直线BC于点E;抛物线的对称轴是直线x＝﹣1．1求抛物线的函数表达式；2若点P在第二象限内;且PE＝OD;求△PBE的面积．3在2的条件下;若M为直线BC上一点;在x轴的上方;是否存在点M;使△BDM是以BD为腰的等腰三角形若存在;求出点M的坐标；若不存在;请说明理由．7.凉山州如图;抛物线y＝ax2+bx+c的图象过点A﹣1;0、B3;0、C0;3．1求抛物线的解析式；2在抛物线的对称轴上是否存在一点P;使得△P AC的周长最小;若存在;请求出点P的坐标及△P AC的周长；若不存在;请说明理由；3在2的条件下;在x轴上方的抛物线上是否存在点M不与C点重合;使得S△P AM＝S△P AC若存在;请求出点M的坐标；若不存在;请说明理由．8.河南如图;抛物线y ax2 错误!x c 交x 轴于A;B 两点;交y 轴于点C;直线y 错误!x 2经过点A;C．1求抛物线的解析式．2点P 是抛物线上一动点;过点P 作x 轴的垂线;交直线AC 于点M;设点P 的横坐标为m．①当△PCM 是直角三角形时;求点P 的坐标；②作点B 关于点C 的对称点B ;则平面内存在直线l;使点M;B;B 到该直线的距离都相等．当点P 在y 轴右侧的抛物线上;且与点B 不重合时;请直接写出直线l：y kx b 的解析式．k;b 可用含m 的式子表示M O9.衡阳如图;二次函数c bx x y ++=2的图象与x 轴交于点A -1;0和点B3;0;与y 轴交于点N;以AB 为边在x 轴上方作正方形ABCD;点P 是x 轴上的一动点;连接CP;过点P 作CP 的垂线与y 轴交于点E.（1）求该抛物线的函数关系表达式；（2）当P 点在线段OB 点P 不与O 、B 点重合上运动至何处时;线段OE 的长有最大值并求出这个最大值.（3）在第四象限的抛物线上任取一点M;连接MN 、MB.请问：△MNB 的面积是否存在最大值若存在;求此时点M 的坐标；若不存在;请说明理由.10.青岛已知：如图;在四边形ABCD 中;AB ∥CD ;∠ACB ＝90°;AB ＝10cm ;BC ＝8cm ;OD 垂直平分A C ．点P 从点B 出发;沿BA 方向匀速运动;速度为1cm /s ；同时;点Q 从点D 出发;沿DC 方向匀速运动;速度为1cm /s ；当一个点停止运动;另一个点也停止运动．过点P 作PE ⊥AB ;交BC 于点E ;过点Q 作QF ∥AC ;分别交AD ;OD 于点F ;G ．连接OP ;EG ．设运动时间为ts 0＜t ＜5;解答下列问题：1当t 为何值时;点E 在∠BAC 的平分线上2设四边形PEGO 的面积为Scm 2;求S 与t 的函数关系式；3在运动过程中;是否存在某一时刻t ;使四边形PEGO 的面积最大若存在;求出t 的值；若不存在;请说明理由；4连接OE ;OQ ;在运动过程中;是否存在某一时刻t ;使OE ⊥OQ 若存在;求出t 的值；若不存在;请说明理由．11.怀化如图;在直角坐标系中有Rt △AOB ;O 为坐标原点;OB ＝1;tan ∠ABO ＝3;将此三角形绕原点O 顺时针旋转90°;得到Rt △COD ;二次函数y ＝﹣x 2+bx +c 的图象刚好经过A ;B ;C 三点．1求二次函数的解析式及顶点P的坐标；2过定点Q的直线l：y＝kx﹣k+3与二次函数图象相交于M;N两点．①若S△PMN＝2;求k的值；②证明：无论k为何值;△PMN恒为直角三角形；③当直线l绕着定点Q旋转时;△PMN外接圆圆心在一条抛物线上运动;直接写出该抛物线的表达式．12.连云港问题情境：如图1;在正方形ABCD中;E为边BC上一点不与点B、C重合;垂直于AE的一条直线MN分别交AB、AE、CD于点M、P、N．判断线段DN、MB、EC之间的数量关系;并说明理由．问题探究：在“问题情境”的基础上．1如图2;若垂足P恰好为AE的中点;连接BD;交MN于点Q;连接EQ;并延长交边AD于点F．求∠AEF的度数；2如图3;当垂足P在正方形ABCD的对角线BD上时;连接AN;将△APN沿着AN翻折;点P 落在点P'处;若正方形ABCD的边长为4;AD的中点为S;求P'S的最小值．问题拓展：如图4;在边长为4的正方形ABCD中;点M、N分别为边AB、CD上的点;将正方形ABCD沿着MN翻折;使得BC的对应边B'C'恰好经过点A;C'N交AD于点F．分别过点A、F作AG⊥MN;FH⊥MN;垂足分别为G、H．若AG＝;请直接写出FH的长．13.泰州已知一次函数y1＝kx+nn＜0和反比例函数y2＝m＞0;x＞0．1如图1;若n＝﹣2;且函数y1、y2的图象都经过点A3;4．①求m;k的值；②直接写出当y1＞y2时x的范围；2如图2;过点P1;0作y轴的平行线l与函数y2的图象相交于点B;与反比例函数y3＝x ＞0的图象相交于点C．①若k＝2;直线l与函数y1的图象相交点D．当点B、C、D中的一点到另外两点的距离相等时;求m﹣n的值；②过点B作x轴的平行线与函数y1的图象相交与点E．当m﹣n的值取不大于1的任意实数时;点B、C间的距离与点B、E间的距离之和d始终是一个定值．求此时k的值及定值d．14.无锡如图1;在矩形ABCD中;BC＝3;动点P从B出发;以每秒1个单位的速度;沿射线BC方向移动;作△PAB关于直线PA的对称△PAB′;设点P的运动时间为t s．1若AB＝2;当点B′落在AC上时;显然△PAB′是直角三角形;求此时t的值；②是否存在异于图2的时刻;使得△PCB′是直角三角形若存在;请直接写出所有符合题意的t的值若不存在;请说明理由．2当P点不与C点重合时;若直线PB′与直线CD相交于点M;且当t＜3时存在某一时刻有结论∠PAM＝45°成立;试探究：对于t＞3的任意时刻;结论∠PAM＝45°是否总是成立请说明理由．15.宿迁如图;抛物线y＝x2+bx+c交x轴于A、B两点;其中点A坐标为1;0;与y轴交于点C0;﹣3．1求抛物线的函数表达式；2如图①;连接AC;点P在抛物线上;且满足∠PAB＝2∠ACO．求点P的坐标；3如图②;点Q为x轴下方抛物线上任意一点;点D是抛物线对称轴与x轴的交点;直线AQ、BQ分别交抛物线的对称轴于点M、N．请问DM+DN是否为定值如果是;请求出这个定值；如果不是;请说明理由．16.德州如图;抛物线y＝mx2﹣mx﹣4与x轴交于Ax1;0;Bx2;0两点;与y轴交于点C;且x2﹣x1＝．1求抛物线的解析式；2若Px1;y1;Qx2;y2是抛物线上的两点;当a≤x1≤a+2;x2≥时;均有y1≤y2;求a的取值范围；3抛物线上一点D1;﹣5;直线BD与y轴交于点E;动点M在线段BD上;当∠BDC＝∠MCE 时;求点M的坐标．17.菏泽如图;抛物线与x轴交于A;B两点;与y轴交于点C0;﹣2;点A的坐标是2;0;P为抛物线上的一个动点;过点P作PD⊥x轴于点D;交直线BC于点E;抛物线的对称轴是直线x ＝﹣1．1求抛物线的函数表达式；2若点P在第二象限内;且PE＝OD;求△PBE的面积．3在2的条件下;若M为直线BC上一点;在x轴的上方;是否存在点M;使△BDM是以BD 为腰的等腰三角形若存在;求出点M的坐标；若不存在;请说明理由．18.聊城如图;在平面直角坐标系中;抛物线y＝ax2+bx+c与x轴交于点A﹣2;0;点B4;0;与y轴交于点C 0;8;连接BC ;又已知位于y 轴右侧且垂直于x 轴的动直线l ;沿x 轴正方向从O 运动到B 不含O 点和B 点;且分别交抛物线、线段BC 以及x 轴于点P ;D ;E ．1求抛物线的表达式；2连接AC ;AP ;当直线l 运动时;求使得△PEA 和△AOC 相似的点P 的坐标；3作PF ⊥BC ;垂足为F ;当直线l 运动时;求Rt △PFD 面积的最大值．19.自贡如图;已知直线AB 与抛物线C ：2y ax 2x c =++ 相交于()A 1,0-和点()B 2,3两点.⑴.求抛物线C 的函数表达式；⑵.若点M 是位于直线AB 上方抛物线上的一动点;以MA MB 、为相邻两边作平行四边形MANB ;当平行四边形MANB 的面积最大时;求此时四边形MANB 的面积S 及点M 的坐标；⑶.在抛物线C 的对称轴上是否存在定点F ;使抛物线C 上任意一点P 到点F 的距离等于到直线17y 4=的距离;若存在;求出定点F 的坐标；若不存在;请说明理由. 20.安徽如图;Rt △ABC 中;∠ACB ＝90°;AC ＝BC ;P 为△ABC 内部一点;且∠APB ＝∠BPC ＝135°．1求证：△P AB ∽△PBC ；2求证：P A ＝2PC ；3若点P 到三角形的边AB ;BC ;CA 的距离分别为h 1;h 2;h 3;求证h 12＝h 2 h 3．21.长沙如图;抛物线y ＝ax 2+6axa 为常数;a ＞0与x 轴交于O ;A 两点;点B 为抛物线的顶点;点D 的坐标为t ;0﹣3＜t ＜0;连接BD 并延长与过O ;A ;B 三点的⊙P 相交于点C ．1求点A 的坐标；2过点C 作⊙P 的切线CE 交x 轴于点E ．①如图1;求证：CE ＝DE ；②如图2;连接AC ;BE ;BO ;当a ＝;∠CAE ＝∠OBE 时;求﹣的值．22.株洲已知二次函数y ＝ax 2+bx +ca ＞01若a ＝1;b ＝﹣2;c ＝﹣1①求该二次函数图象的顶点坐标；②定义：对于二次函数y ＝px 2+qx +rp ≠0;满足方程y ＝x 的x 的值叫做该二次函数的“不动点”．求证：二次函数y ＝ax 2+bx +c 有两个不同的“不动点”．2设b ＝c 3;如图所示;在平面直角坐标系Oxy 中;二次函数y ＝ax 2+bx +c 的图象与x 轴分别相交于不同的两点Ax 1;0;Bx 2;0;其中x 1＜0;x 2＞0;与y 轴相交于点C ;连结BC ;点D 在y 轴的正半轴上;且OC＝OD;又点E的坐标为1;0;过点D作垂直于y轴的直线与直线CE相交于点F;满足∠AFC＝∠ABC．F A的延长线与BC的延长线相交于点P;若＝;求二次函数的表达式．23.苏州如图①;抛物线y=-x2+a+1x-a与x轴交于A;B两点点A位于点B的左侧;与y轴交于点C．已知△ABC的面积是6．1求a的值；2求△ABC外接圆圆心的坐标；3如图②;P是抛物线上一点;Q为射线CA上一点;且P、Q两点均在第三象限内;Q、A是位于直线BP同侧的不同两点;若点P到x轴的距离为d;△QPB的面积为2d;且∠PAQ=∠AQB;求点Q的坐标．24.威海 1方法选择如图①;四边形ABCD是⊙O的内接四边形;连接AC;BD;AB＝BC＝AC．求证：BD＝AD+CD．小颖认为可用截长法证明：在DB上截取DM＝AD;连接AM…小军认为可用补短法证明：延长CD至点N;使得DN＝AD…请你选择一种方法证明．2类比探究探究1如图②;四边形ABCD是⊙O的内接四边形;连接AC;BD;BC是⊙O的直径;AB＝AC．试用等式表示线段AD;BD;CD之间的数量关系;井证明你的结论．探究2如图③;四边形ABCD是⊙O的内接四边形;连接AC;BD．若BC是⊙O的直径;∠ABC＝30°;则线段AD;BD;CD之间的等量关系式是．3拓展猜想如图④;四边形ABCD是⊙O的内接四边形;连接AC;BD．若BC是⊙O的直径;BC：AC：AB ＝a：b：c;则线段AD;BD;CD之间的等量关系式是．25.淄博如图;顶点为M的抛物线y＝ax2+bx+3与x轴交于A3;0;B﹣1;0两点;与y轴交于点C．1求这条抛物线对应的函数表达式；2问在y轴上是否存在一点P;使得△PAM为直角三角形若存在;求出点P的坐标；若不存在;说明理由．页数学试题 3若在第一象限的抛物线下方有一动点D ;满足DA ＝OA ;过D 作DG ⊥x 轴于点G ;设△ADG 的内心为I ;试求CI 的最小值．1. 26.绵阳如图;在以点O 为中心的正方形ABCD 中;AD =4;连接AC ;动点E 从点O 出发沿O →C 以每秒1个单位长度的速度匀速运动;到达点C 停止．在运动过程中;△ADE 的外接圆交AB 于点F ;连接DF 交AC 于点G ;连接EF ;将△EFG 沿EF 翻折;得到△EFH ．2. 1求证：△DEF 是等腰直角三角形；3. 2当点H 恰好落在线段BC 上时;求EH 的长；4. 3设点E 运动的时间为t 秒;△EFG 的面积为S ;求S 关于时间t 的关系式．5.27.遂宁如图;顶点为P 3;3的二次函数图象与x 轴交于点A 6;0;点B 在该图象上;OB 交其对称轴l 于点M ;点M 、N 关于点P 对称;连接BN 、ON ．1求该二次函数的关系式．2若点B 在对称轴l 右侧的二次函数图象上运动;请解答下列问题：①连接OP ;当OP ＝MN 时;请判断△NOB 的形状;并求出此时点B 的坐标．②求证：∠BNM ＝∠ONM ．28.东营已知抛物线 y ax 2 bx 4经过点 A 2;0、B -4;0;与 y 轴交于点C . 1求这条抛物线的解析式；2如图 1;点 P 是第三象限内抛物线上的一个动点;当四边形 ABPC 的面积最大时; 求点 P 的坐标；3如图 2;线段 AC 的垂直平分线交 x 轴于点 E ;垂足为 D ;M 为抛物线的顶点;在直线 DE 上是否存在一点 G ;使△CMG 的周长最小若存在;求出点 G 的坐标；若不存在;请说明理由.第 28 题图 1 第 28 题图 229.广东30.宿迁如图;抛物线y=x 2+bx+c 交x 轴于A 、B 两点;其中点A 坐标为1;0;与y 轴交于点C0;-3. 1求抛物钱的函数表达式；⑵如图①;连接AC;点P 在抛物线上;且满足∠PAB=2∠AC0..求点P 的坐标；3如图②.点Q 为x 轴下方抛物线上任意一点;点D 是抛物线对称轴与x 轴的交点;直线AQ 、BQ 分别交抛物线的对称轴于点M 、N..请问DM+DN 是否为定值如泉是;请求出这个定值;如果不是;请说明理由.31.盐城如图所示二次函数2)1(2+-=x k y 的图像与一次函数2+-=k kx y 的图像交于A 、B 两点;点B 在点A 的右侧;直线AB 分别与x 、y 轴交于C 、D 两点;其中k ＜0. 1求A 、B 两点的横坐标；2若△OAB 是以OA 为腰的等腰三角形;求k 的值；3二次函数图像的对称轴与x 轴交于点E;是否存在实数k;使得∠ODC ＝2∠BEC;若存在;求出k 的值；若不存在;说明理由.32.扬州如图;已知等边△ABC 的边长为8;点P 事AB 边上的一个动点与点A 、B 不重合;直线l 是经过点P 的一条直线;把△ABC 沿直线l 折叠;点B 的对应点是点B’.1如图1;当PB=4时;若点B’恰好在AC 边上;则AB’的长度为______； 2如图2;当PB=5时;若直线l △AC;则BB’的长度为；3如图3;点P 在AB 边上运动过程中;若直线l 始终垂直于AC;△ACB’的面积是否变化若变化;说明理由；若不变化;求出面积；4当PB=6时;在直线l 变化过程中;求△ACB’面积的最大值..33.滨州如图①;抛物线y ＝﹣x 2+x +4与y 轴交于点A ;与x 轴交于点B ;C ;将直线AB 绕点A 逆时针旋转90°;所得直线与x 轴交于点D ．1求直线AD 的函数解析式；2如图②;若点P 是直线AD 上方抛物线上的一个动点①当点P 到直线AD 的距离最大时;求点P 的坐标和最大距离；②当点P 到直线AD 的距离为时;求sin ∠P AD 的值．34.济宁如图1;在矩形ABCD 中;AB ＝8;AD ＝10;E 是CD 边上一点;连接AE ;将矩形ABCD 沿AE 折叠;顶点D 恰好落在BC 边上点F 处;延长AE 交BC 的延长线于点G ．1求线段CE 的长；2如图2;M ;N 分别是线段AG ;DG 上的动点与端点不重合;且∠DMN ＝∠DAM ;设AM ＝x ;DN ＝y ．①写出y 关于x 的函数解析式;并求出y 的最小值；②是否存在这样的点M ;使△DMN 是等腰三角形若存在;请求出x 的值；若不存在;请说明理由．35.成都如图1;在△ABC 中;AB=AC=20;tanB=43;点D 为BC 边上的动点点D 不与点B;C 重合.以点D 为顶点作△ADE=△B;射线DE 交AC 边于点E;过点A 作AF△AD 交射线DE 于F;连接CF.（1）求证：△ABD△△DCE ；（2）当DE△AB 时如图2;求AE 的长；（3）点D 在BC 边上运动的过程中;是否存在某个位置;使得DE ＝CF 若存在;求出此时BD 的长；若不存在;请说明理由..36.天津在平面直角坐标系中;O 为坐标原点;点A6;0;点B 在y 轴的正半轴上;∠ABO=30°;矩形CODE 的顶点D;E;C 分别在OA;AB;OB 上;OD=2.（I ）如图①;求点E 的坐标；（II ）将矩形CODE 沿x 轴向左平移;得到矩形E D O C '''';点D;O;C;E 的对应点分别为E D O C ''''，，，.设t O O =';矩形E D O C ''''与△ABO 重叠部分的面积为s .①如图②;当矩形E D O C ''''与△ABO 重叠部分为五边形时;E C ''、E D ''分别与AB 相交于点M;F;试用含有t 的式子表示s;并直接写出t 的范围; ②353≤≤s 时;求t 的取值范围直接写出结果即可..。

中考数学复习考点题型专题练习22 与二次函数相关的压轴题

中考数学复习考点题型专题练习专题22 与二次函数相关的压轴题解答题1．（2022·湖北鄂州）某数学兴趣小组运用《几何画板》软件探究y＝ax2（a＞0）型抛物线图象．发现：如图1所示，该类型图象上任意一点M到定点F（0，14a）的距离MF，始终等于它到定直线l：y＝﹣14a上的距离MN（该结论不需要证明），他们称：定点F为图象的焦点，定直线l为图象的准线，y＝﹣14a叫做抛物线的准线方程．其中原点O为FH的中点，FH=2OF= 12a ，例如，抛物线y＝12x2，其焦点坐标为F（0，12），准线方程为l：y＝﹣12．其中MF=MN，FH=2OH=1．(1)【基础训练】请分别直接写出抛物线y＝2x2的焦点坐标和准线l的方程：，．(2)【技能训练】如图2所示，已知抛物线y＝18x2上一点P到准线l的距离为6，求点P的坐标；(3)【能力提升】如图3所示，已知过抛物线y＝ax2（a＞0）的焦点F的直线依次交抛物线及准线l于点A、B、C．若BC＝2BF，AF＝4，求a的值；(4)【拓展升华】古希腊数学家欧多克索斯在深入研究比例理论时，提出了分线段的“中末比”问题：点C 将一条线段AB 分为两段AC 和CB ，使得其中较长一段AC 是全线段AB与另一段CB 的比例中项，即满足：AC AB ＝BC AC 这个数称为“黄金分割”把点C 称为线段AB 的黄金分割点．如图4所示，抛物线y ＝14x 2的焦点F （0，1），准线l 与y 轴交于点H （0，﹣1），E 为线段HF 的黄金分割点，点M 为y 轴左侧的抛物线上一点．当MHMF请直接写出△HME 的面积值．2．（2022·江苏无锡）已知二次函数214y x bx c =-++图像的对称轴与x 轴交于点A （1，0），图像与y 轴交于点B （0，3），C 、D 为该二次函数图像上的两个动点（点C 在点D 的左侧），且90CAD ∠=．(1)求该二次函数的表达式；(2)若点C 与点B 重合，求tan ∠CDA 的值；(3)点C 是否存在其他的位置，使得tan ∠CDA 的值与（2）中所求的值相等？若存在，请求出点C 的坐标；若不存在，请说明理由．3．（2022·山西）综合与探究：如图，二次函数213442y x x =-++的图象与x 轴交于A ，B两点（点A 在点B 的左侧），与y 轴交于点C ，点P 是第一象限内二次函数图象上的一个动点，设点P 的横坐标为m ．过点P 作直线PD x ⊥轴于点D ，作直线BC 交PD 于点E(1)求A ，B ，C 三点的坐标，并直接写出直线BC 的函数表达式；(2)当CEP △是以PE 为底边的等腰三角形时，求点P 的坐标；(3)连接AC ，过点P 作直线l AC ∥，交y 轴于点F ，连接DF ．试探究：在点P 运动的过程中，是否存在点P ，使得CE FD =，若存在，请直接写出m 的值；若不存在，请说明理由．4．（2022·四川宜宾）如图，抛物线2y ax bx c =++与x 轴交于()3,0A 、()1,0B -两点，与y 轴交于点()0,3C ，其顶点为点D ，连结AC ．(1)求这条抛物线所对应的二次函数的表达式及顶点D 的坐标；(2)在抛物线的对称轴上取一点E ，点F 为抛物线上一动点，使得以点A 、C 、E 、F 为顶点、AC 为边的四边形为平行四边形，求点F 的坐标；(3)在（2）的条件下，将点D 向下平移5个单位得到点M ，点P 为抛物线的对称轴上一动点，求35PF PM +的最小值．5．（2022·湖北恩施）在平面直角坐标系中，O 为坐标原点，抛物线2y x c =-+与y 轴交于点()0,4P ．(1)直接写出抛物线的解析式．(2)如图，将抛物线2=-+向左平移1个单位长度，记平移后的抛物线顶点为Q，平移y x c后的抛物线与x轴交于A、B两点（点A在点B的右侧），与y轴交于点C．判断以B、C、Q三点为顶点的三角形是否为直角三角形，并说明理由．(3)直线BC与抛物线2=-+交于M、N两点（点N在点M的右侧），请探究在x轴上是y x c否存在点T，使得以B、N、T三点为顶点的三角形与ABC相似，若存在，请求出点T的坐标；若不存在，请说明理由．(4)若将抛物线2=-+进行适当的平移，当平移后的抛物线与直线BC最多只有一个公y x c共点时，请直接写出拋物线2y x c=-+平移的最短距离并求出此时抛物线的顶点坐标．B（A在6．（2022·广西玉林）如图，已知抛物线：22y x bx c与x轴交于点A，(2,0)B的左侧），与y轴交于点C，对称轴是直线1x=，P是第一象限内抛物线上的任一点．2(1)求抛物线的解析式；(2)若点D 为线段OC 的中点，则POD 能否是等边三角形？请说明理由；(3)过点P 作x 轴的垂线与线段BC 交于点M ，垂足为点H ，若以P ，M ，C 为顶点的三角形与BMH 相似，求点P 的坐标．7．（2022·广西）已知抛物线2y x 2x 3=-++与x 轴交于A ，B 两点（点A 在点B 的左侧）．(1)求点A ，点B 的坐标；(2)如图，过点A 的直线:1l y x =--与抛物线的另一个交点为C ，点P 为抛物线对称轴上的一点，连接PA PC 、，设点P 的纵坐标为m ，当PA PC =时，求m 的值；(3)将线段AB 先向右平移1个单位长度，再向上平移5个单位长度，得到线段MN ，若抛物线2(23)(0)y a x x a ++≠=-与线段MN 只有一个交点，请直接写出．．．．a 的取值范围．8．（2022·福建）在平面直角坐标系xOy 中，已知抛物线2y ax bx =+经过A （4，0），B （1，4）两点．P 是抛物线上一点，且在直线AB 的上方．(1)求抛物线的解析式；(2)若△OAB 面积是△PAB 面积的2倍，求点P 的坐标； (3)如图，OP 交AB 于点C ，PD BO ∥交AB 于点D ．记△CDP ，△CPB ，△CBO 的面积分别为1S ，2S ，3S ．判断1223S S S S +是否存在最大值．若存在，求出最大值；若不存在，请说明理由．9．（2022·贵州黔东南）如图，抛物线2y ax 2x c =++的对称轴是直线1x =，与x 轴交于点A ，()3,0B ，与y 轴交于点C ，连接AC ．(1)求此抛物线的解析式；(2)已知点D 是第一象限内抛物线上的一个动点，过点D 作DM x ⊥轴，垂足为点M ，DM 交直线BC 于点N ，是否存在这样的点N ，使得以A ，C ，N 为顶点的三角形是等腰三角形．若存在，请求出点N 的坐标，若不存在，请说明理由；(3)已知点E 是抛物线对称轴上的点，在坐标平面内是否存在点F ，使以点B 、C 、E 、F 为顶点的四边形为矩形，若存在，请直接写出点F 的坐标；若不存在，请说明理由．10．（2022·湖南长沙）若关于x 的函数y ，当1122t x t -≤≤+时，函数y 的最大值为M ，最小值为N ，令函数2M Nh -=，我们不妨把函数h 称之为函数y 的“共同体函数”． (1)①若函数4044y x =，当1t =时，求函数y 的“共同体函数”h 的值；②若函数y kx b =+（0k ≠，k ，b 为常数），求函数y 的“共同体函数”h 的解析式； (2)若函数21y x x=≥（），求函数y 的“共同体函数”h 的最大值； (3)若函数24y x x k =-++，是否存在实数k ，使得函数y 的最大值等于函数y 的“共同体函数”h 的最小值．若存在，求出k 的值；若不存在，请说明理由．11．（2022·湖北武汉）如图，在平面直角坐标系中，已知抛物线223y x x =--的顶点为A ，与y 轴交于点C ，线段CB x ∥轴，交该抛物线于另一点B ．(1)求点B 的坐标及直线AC 的解析式：(2)当二次函数223y x x =--的自变量x 满足2m x m +时，此函数的最大值为p ，最小值为q ，且2p q -=．求m 的值：(3)平移抛物线223y x x =--，使其顶点始终在直线AC 上移动，当平移后的抛物线与射线BA 只有一个公共点时，设此时抛物线的顶点的横坐标为n ，请直接写出n 的取值范围．12．（2022·内蒙古通辽）如图，抛物线2y x bx c =-++与x 轴交于A ，B 两点，与y 轴交于C 点，直线BC 方程为3y x =-．(1)求抛物线的解析式；(2)点P 为抛物线上一点，若12PBCABCS S =，请直接写出点P 的坐标；(3)点Q 是抛物线上一点，若45ACQ ∠=︒，求点Q 的坐标．13．（2022·山东烟台）如图，已知直线y ＝43x +4与x 轴交于点A ，与y 轴交于点C ，抛物线y ＝ax 2+bx +c 经过A ，C 两点，且与x 轴的另一个交点为B ，对称轴为直线x ＝﹣1．(1)求抛物线的表达式；(2)D 是第二象限内抛物线上的动点，设点D 的横坐标为m ，求四边形ABCD 面积S 的最大值及此时D 点的坐标；(3)若点P 在抛物线对称轴上，是否存在点P ，Q ，使以点A ，C ，P ，Q 为顶点的四边形是以AC 为对角线的菱形？若存在，请求出P ，Q 两点的坐标；若不存在，请说明理由．14．（2022·山东聊城）如图，在直角坐标系中，二次函数2y x bx c =-++的图象与x 轴交于A ，B 两点，与y 轴交于点()0,3C ，对称轴为直线1x =-，顶点为点D ．(1)求二次函数的表达式；(2)连接DA ，DC ，CB ，CA ，如图①所示，求证：DAC BCO ∠=∠； (3)如图②，延长DC 交x 轴于点M ，平移二次函数2y x bx c =-++的图象，使顶点D 沿着射线DM 方向平移到点1D 且12CD CD =，得到新抛物线1y ，1y 交y 轴于点N ．如果在1y 的对称轴和1y 上分别取点P ，Q ，使以MN 为一边，点M ，N ，P ，Q 为顶点的四边形是平行四边形，求此时点Q 的坐标．15．（2022·黑龙江齐齐哈尔）综合与探究如图，某一次函数与二次函数2y x mx n =++的图象交点为A （-1，0），B （4，5）．(1)求抛物线的解析式；(2)点C 为抛物线对称轴上一动点，当AC 与BC 的和最小时，点C 的坐标为；(3)点D 为抛物线位于线段AB 下方图象上一动点，过点D 作DE ⊥x 轴，交线段AB 于点E ，求线段DE 长度的最大值；(4)在（2）条件下，点M 为y 轴上一点，点F 为直线AB 上一点，点N 为平面直角坐标系内一点，若以点C ，M ，F ，N 为顶点的四边形是正方形，请直接写出点N 的坐标．16．（2022·湖南）如图，已知抛物线2()30y ax bx a =++≠的图像与x 轴交于(1,0)A ，(4,0)B 两点，与y 轴交于点C ，点D 为抛物线的顶点．(1)求抛物线的函数表达式及点D的坐标；(2)若四边形BCEF为矩形，3CE=．点M以每秒1个单位的速度从点C沿CE向点E运动，同时点N以每秒2个单位的速度从点E沿EF 向点F运动，一点到达终点，另一点随之停止．当以M、E、N为顶点的三角形与BOC∆相似时，求运动时间t的值；(3)抛物线的对称轴与x轴交于点P，点G是点P关于点D的对称点，点Q是x轴下方抛物线图像上的动点．若过点Q的直线9:()4l y kx m k=+<与抛物线只有一个公共点，且分别与线段GA、GB相交于点H、K，求证：GH GK+为定值．17．（2022·内蒙古包头）如图，在平面直角坐标系中，抛物线2(0)y ax c a=+≠与x轴交于A，B两点，点B的坐标是(2,0)，顶点C的坐标是(0,4)，M是抛物线上一动点，且位于第一象限，直线AM与y轴交于点G．(1)求该抛物线的解析式；(2)如图1，N 是抛物线上一点，且位于第二象限，连接OM ，记AOG MOG ，的面积分别为12,S S ．当122S S =，且直线CN AM ∥时，求证：点N 与点M 关于y 轴对称；(3)如图2，直线BM 与y 轴交于点H ，是否存在点M ，使得27OH OG -=．若存在，求出点M 的坐标；若不存在，请说明理由．18．（2022·广西梧州）如图，在平面直角坐标系中，直线443y x =--分别与x ，y 轴交于点A ，B ，抛物线2518y x bx c =++恰好经过这两点．(1)求此抛物线的解析式；(2)若点C 的坐标是()0,6，将ACO △绕着点C 逆时针旋转90°得到ECF △，点A 的对应点是点E ．①写出点E 的坐标，并判断点E 是否在此抛物线上；②若点P 是y 轴上的任一点，求35BP EP +取最小值时，点P 的坐标．19．（2022·辽宁锦州）如图，抛物线2y x bx c =++与x 轴交于,(4,0)A B 两点（A 在B 的左侧），与y 轴交于点(0,4)C -，点P 在抛物线上，连接,BC BP ．(1)求抛物线的解析式；(2)如图1，若点P 在第四象限，点D 在线段BC 上，连接PD 并延长交x 轴于点E ，连接CE ，记DCE 的面积为1S ，DBP 的面积为2S ，当12S S 时，求点P的坐标；(3)如图2，若点P 在第二象限，点F 为抛物线的顶点，抛物线的对称轴l 与线段BC 交于点G ，当90PBC CFG ∠+∠=︒时，求点P 的横坐标．20．（2022·辽宁）如图，抛物线23y ax bx =++交x 轴于点(3,0)A 和(1,0)B -，交y 轴于点C ．(1)求抛物线的表达式；(2)D 是直线AC 上方抛物线上一动点，连接OD 交AC 于点N ，当DNON的值最大时，求点D 的坐标；(3)P 为抛物线上一点，连接CP ，过点P 作PQ CP ⊥交抛物线对称轴于点Q ，当3tan 4PCQ ∠=时，请直接写出点P 的横坐标．21．（2022·辽宁营口）在平面直角坐标系中，抛物线212y x bx c =-++经过点127,28A ⎛⎫- ⎪⎝⎭和点()4,0B ，与y 轴交于点C ，点P 为抛物线上一动点．(1)求抛物线和直线AB的解析式；(2)如图，点P为第一象限内抛物线上的点，过点P作PD AB⊥，垂足为D，作PE x⊥轴，垂足为E，交AB于点F，设PDF的面积为1S，BEF的面积为2S，当1249 25SS=时，求点P坐标；(3)点N为抛物线对称轴上的动点，是否存在点N，使得直线BC垂直平分线段PN？若存在，请直接写出点N坐标，若不存在，请说明理由．22．（2022·四川广安）如图，在平面直角坐标系中，抛物线2y ax x m=++（a≠0）的图象与x轴交于A、C两点，与y轴交于点B，其中点B坐标为（0，－4），点C坐标为（2，0）．(1)求此抛物线的函数解析式．(2)点D 是直线AB 下方抛物线上一个动点，连接AD 、BD ，探究是否存在点D ，使得△ABD 的面积最大？若存在，请求出点D 的坐标；若不存在，请说明理由．(3)点P 为该抛物线对称轴上的动点，使得△PAB 为直角三角形，请求出点P 的坐标．23．（2022·海南）如图1，抛物线2y ax 2x c =++经过点(1,0)(0,3)A C -、，并交x 轴于另一点B ，点(,)P x y 在第一象限的抛物线上，AP 交直线BC 于点D ．(1)求该抛物线的函数表达式；(2)当点P 的坐标为(1,4)时，求四边形BOCP 的面积；(3)点Q 在抛物线上，当PDAD的值最大且APQ 是直角三角形时，求点Q 的横坐标；(4)如图2，作,CG CP CG ⊥交x 轴于点(,0)G n ，点H 在射线CP 上，且CH CG =，过GH 的中点K 作KI y ∥轴，交抛物线于点I ，连接IH ，以IH 为边作出如图所示正方形HIMN ，当顶点M 恰好落在y 轴上时，请直接写出点G 的坐标．24．（2022·内蒙古呼和浩特）如图，抛物线212y x bx c =-++经过点(4,0)B 和点(0,2)C ，与x 轴的另一个交点为A ，连接AC 、BC ．(1)求抛物线的解析式及点A的坐标；(2)如图1，若点D是线段AC的中点，连接BD，在y 轴上是否存在点E，使得BDE是以BD为斜边的直角三角形？若存在，请求出点E的坐标；若不存在，请说明理由；∥轴，分别交BC、x轴于(3)如图2，点P是第一象限内抛物线上的动点，过点P作PQ y点M、N，当PMC△中有某个角的度数等于OBC∠度数的2倍时，请求出满足条件的点P 的横坐标．25．（2022·吉林）如图，在平面直角坐标系中，抛物线2=++（b，c是常数）经y x bx c过点(1,0)A，点(0,3)B．点P在此抛物线上，其横坐标为m．(1)求此抛物线的解析式；(2)当点P 在x 轴上方时，结合图象，直接写出m 的取值范围；(3)若此抛物线在点P 左侧部分（包括点P ）的最低点的纵坐标为2m -．①求m 的值；②以PA 为边作等腰直角三角形PAQ ，当点Q 在此抛物线的对称轴上时，直接写出点Q 的坐标．26．（2022·黑龙江哈尔滨）在平面直角坐标系中，点O 为坐标原点，抛物线2y ax b =+经过点521,28A ⎛⎫ ⎪⎝⎭，点13,28B ⎛⎫- ⎪⎝⎭，与y 轴交于点C ．(1)求a ，b 的值；(2)如图1，点D 在该抛物线上，点D 的横坐标为2-，过点D 向y 轴作垂线，垂足为点E ．点P 为y 轴负半轴上的一个动点，连接DP 、设点P 的纵坐标为t ，DEP 的面积为S ，求S 关于t 的函数解析式（不要求写出自变量t 的取值范围）；(3)如图2，在（2）的条件下，连接OA ，点F 在OA 上，过点F 向y 轴作垂线，垂足为点H ，连接DF 交y 轴于点G ，点G 为DF 的中点，过点A 作y 轴的平行线与过点P 所作的x 轴的平行线相交于点N ，连接CN ，PB ，延长PB 交AN 于点M ，点R 在PM 上，连接RN ，若35CP GE =，2PMN PDE CNR ∠+∠=∠，求直线RN 的解析式．27．（2022·湖北宜昌）已知抛物线22y ax bx =+-与x 轴交于()1,0A -，()4,0B 两点，与y 轴交于点C ．直线l 由直线BC 平移得到，与y 轴交于点()0,E n ．四边形MNPQ 的四个顶点的坐标分别为()1,3M m m ++，()1,N m m +，()5,P m m +，()5,3Q m m ++．(1)填空：=a ______，b =______；(2)若点M 在第二象限，直线l 与经过点M 的双曲线ky x=有且只有一个交点，求2n 的最大值；(3)当直线l 与四边形MNPQ 、抛物线22y ax bx =+-都有交点时，存在直线l ，对于同一条直线l 上的交点，直线l 与四边形MNPQ 的交点的纵坐标都不大于它与抛物线22y ax bx =+-的交点的纵坐标．①当3m =-时，直接写出n 的取值范围；②求m 的取值范围．28．（2022·四川达州）如图1，在平面直角坐标系中，已知二次函数22y ax bx =++的图象经过点(1,0)A -，(3,0)B ，与y 轴交于点C ．(1)求该二次函数的表达式；(2)连接BC ，在该二次函数图象上是否存在点P ，使PCB ABC ∠=∠？若存在，请求出点P 的坐标：若不存在，请说明理由；(3)如图2，直线l 为该二次函数图象的对称轴，交x 轴于点E ．若点Q 为x 轴上方二次函数图象上一动点，过点Q 作直线AQ ，BQ 分别交直线l 于点M ，N ，在点Q 的运动过程中，EM EN +的值是否为定值？若是，请求出该定值；若不是，请说明理由．29．（2022·重庆）如图，在平面直角坐标系中，抛物线212y x bx c =++与直线AB 交于点()0,4A -，()4,0B ．(1)求该抛物线的函数表达式；(2)点P 是直线AB 下方拋物线上的一动点，过点P 作x 轴的平行线交AB 于点C ，过点P 作y 轴的平行线交x 轴于点D ，求PC PD +的最大值及此时点P 的坐标；(3)在（2）中PC PD +取得最大值的条件下，将该抛物线沿水平方向向左平移5个单位，点E 为点P 的对应点，平移后的抛物线与y 轴交于点F ，M 为平移后的抛物线的对称轴上一点．在平移后的抛物线上确定一点N ，使得以点E ，F ，M ，N 为顶点的四边形是平行四边形，写出所有符合条件的点N 的坐标，并写出求解点N 的坐标的其中一种情况的过程．30．（2022·江苏苏州）如图，在二次函数2221y x mx m =-+++（m 是常数，且0m >）的图像与x 轴交于A ，B 两点（点A 在点B 的左侧），与y 轴交于点C ，顶点为D ．其对称轴与线段BC 交于点E ，与x 轴交于点F ．连接AC ，BD ．(1)求A ，B ，C 三点的坐标（用数字或含m 的式子表示），并求OBC ∠的度数；(2)若ACO CBD ∠=∠，求m 的值；(3)若在第四象限内二次函数2221y x mx m =-+++（m 是常数，且0m >）的图像上，始终存在一点P ，使得75ACP ∠=︒，请结合函数的图像，直接写出m 的取值范围．。

2019年中考数学压轴题专项训练：反比例函数(附解析)

2019年中考数学压轴题专项训练：反比例函数一．选择题1．已知反比例函数y＝﹣，下列结论错误的是（）A．y随x的增大而减小B．图象位于二、四象限内C．图象必过点（﹣2，4）D．当﹣1＜x＜0时，y＞82．如图，矩形ABCD的对角线BD经过坐标原点，矩形的边分别平行于坐标轴，点C在反比例函数的图象上．若点A的坐标为（﹣4，﹣4），则k的值为（）A．16 B．﹣3 C．5 D．5或﹣33．如图，在平面直角坐标系中，▱ABOC的顶点B，C在反比例函数y＝（x＞0）的图象上，点A在反比例函数y＝（x＞0）的图象上，若点B的坐标为（1，2），∠OBC＝90°，则k的值为（）A．B．3 C．5 D．4．如图，是反比例函数y＝和y＝﹣在x轴上方的图象，x轴的平行线AB分别与这两个函数图象相交于点A．B，则△AOB的面积是（）A ．5B ．4C ．10D ．205．我们知道，如果一个矩形的宽与长之比为，那么这个矩形就称为黄金矩形．如图，已知A 、B 两点都在反比例函数y ＝（k ＞0）位于第一象限内的图象上，过A 、B 两点分别作坐标轴的垂线，垂足分别为C 、D 和E 、F ，设AC 与BF 交于点G ，已知四边形OCAD 和CEBG 都是正方形．设FG 、OC 的中点分别为P 、Q ，连接PQ ．给出以下结论：①四边形ADFG 为黄金矩形；②四边形OCGF 为黄金矩形；③四边形OQPF 为黄金矩形．以上结论中，正确的是（）A ．①B ．②C ．②③D ．①②③6．如图，平行于x 轴的直线与函数y 1＝（a ＞0，x ＞0），y 2＝（b ＞0．x ＞0）的图象分别相交于A 、B 两点，且点A 在点B 的右侧，在X 轴上取一点C ，使得△ABC 的面积为3，则a ﹣b 的值为（）A ．6B ．﹣6C ．3D ．﹣37．如图，正比例函数y 1＝﹣2x 的图象与反比例函数y 2＝的图象交于A 、B 两点，点C 在x 轴负半轴上，AC ＝AO ，△ACO 的面积为6．则k 的值为（）A．3 B．﹣3 C．﹣6 D．68．如图，在菱形OABC中，点A的坐标为（10，0），对角线OB、AC相交于点D，OB•AC＝160．双曲线y＝（x＞0）经过点D，交BC的延长线于点E，则过点E的双曲线表达式为（）A．y＝B．y＝C．y＝D．y＝9．如图，一次函数与反比例函数的图象交于A（1，8）和B（4，2）两点，点P是线段AB 上一动点（不与点A和B重合），过P点分别作x轴，y轴的垂线PC，PD交反比例函数图象于点E，F，则四边形OEPF面积的最大值是（）A．3 B．4 C．D．610．如图，平行四边形AOBC中，∠AOB＝60°，AO＝8，AC＝15，反比例函数y＝（x＞0）图象经过点A，与BC交于点D，则的值为（）A．B．C．D．二．填空题11．如图，在△OAB中，AO＝AB，S＝36，反比例函数y＝（x＞0）的图象与OA交于点△AOBC，点D是函数y＝（x＞0）的图象一点，且CD∥x轴，若∠ADC＝90°，则k的值是．12．如图，点A是反比例函数y＝﹣的图象第二象限分支上的动点，连结AO并延长交另一支于点B，以AB为斜边作等腰直角三角形ABC，顶点C在第三象限，AC与x轴交于点D，连结BD．当BD平分∠ABC时，点C的坐标是．13．如图，在平面直角坐标系xOy中，已知直线y＝kx（k＞0）分别交反比例函数y＝和y＝在第一象限的图象于点A，B，过点B作BD⊥x轴于点D，交y＝的图象于点C，连接AC．若△ABC是等腰三角形，则k的值是．14．如图，直线y ＝2x ﹣1交y 轴于A ，交双曲线y ＝（k ＞0，x ＞0）于B ，将线段AB 绕B 点逆时针方向旋转90°，A 点的对应点为C ，若C 点落在双曲线y ＝（k ＞0，x ＞0）上，则k 的值为．15．如图，点B 1（1，）在直线l 2：y ＝x 上，过点B 1作A 1B 1⊥l 1交直线l 1：y ＝x于点A 1，以A 1B 1为边在△OA 1B 1外侧作等边三角形A 1B 1C 1，过C 1的反比例函数为y ＝；再过点C 1作A 2B 2⊥l 1，分别交直线l 1和l 2于A 2，B 2两点，以A 2B 2为边在△OA 2B 2外侧作等边三角形A 2B 2C 2，过C 2的反比例函数为y ＝，…，按此规律进行下去，则第n 个反比例函数的k n ＝．（用含n 的代数式表示）16．如图，已知点A 在反比例函数上，作Rt △ABC ，使边BC 在x 轴上且∠ABC ＝90°，点D 在AC 上且CD ＝2AD ，连DB 并延长交y 轴于点E ，若△BCE 的面积为8，△ABC 的面积为3，则k ＝．17．如图，菱形ABCD的对角线BD与x轴平行，点B、C的坐标分别为（0，2）、（3，0），点A、D在函数（x＞0）的图象上，则k的值为．18．如图，在△ABC中，∠ACB＝90°，BC在x轴上，点B与点C关于原点对称，AB＝5，AO＝，边AC上的点P满足∠COP＝∠CAO，且双曲线y＝经过点P，则k值等于．19．如图，A、B是反比例函数y＝在第一象限内的图象上的两点，且A、B两点的横坐标分别是4和8，则△OAB的面积是．20．如图，在直角坐标系中，四边形OABC为菱形，OA在x轴的正半轴上，∠AOC＝60°，过点C的反比例函数的图象与AB交于点D，则△COD的面积为．三．解答题21．如图，一次函数y＝kx+b与反比例函数y＝的图象交于A（n，3），B（﹣3，﹣2）两点．（1）求反比例函数与一次函数的解析式；（2）过点B作BC⊥x轴，垂足为C，求S．△ABC22．如图，在平面直角坐标系中，一次函数y＝ax+b（a≠0）的图象与反比例函数y＝（k ≠0）的图象交于A、B两点，与x轴交于点C，过点A作AH⊥x轴于点H，点O是线段CH的中点，AC＝4，cos∠ACH＝，点B的坐标为（4，﹣4）．（1）求该反比例函数和一次函数的解析式；（2）求△BCH的面积；（3）观察图象，直接写出ax+b＞的x取值范围．23．如图所示，一次函数y ＝kx +b 的图象与反比例函数y ＝的图象交于M 、N 两点．（1）根据图中条件求出反比例函数和一次函数的解析式；（2）连结OM 、ON ，求△MON 的面积；（3）根据图象，直接写出使一次函数的值大于反比例函数的值的x 的取值范围．24．如图，双曲线y 1＝与直线y 2＝的图象交于A 、B 两点．已知点A 的坐标为（4，1），点P （a ，b ）是双曲线y 1＝上的任意一点，且0＜a ＜4．（1）分别求出y 1、y 2的函数表达式；（2）连接PA 、PB ，得到△PAB ，若4a ＝b ，求三角形ABP 的面积；（3）当点P 在双曲线y 1＝上运动时，设PB 交x 轴于点E ，延长PA 交x 轴于点F ，判断PE 与PF 的大小关系，并说明理由．25．制作某种金属工具要进行材料煅烧和锻造两个工序，即需要将材料烧到800℃，然后停止煅烧进行锻造操作，经过8min时，材料温度降为600°C．煅烧时温度y（℃）与时间x（min）成一次函数关系；锻造时，温度y（℃）与时间x（min）成反比例函数关系（如图），已知该材料初始温度是26℃（1）分别求出材料煅烧和锻造时y与x的函数关系式，并且写出自变量x的取值范围；（2）根据工艺要求，当材料温度低于400°C时，须停止操作．那么锻造的操作时间有多长？26．如图，一次函数y1＝kx+b（k≠0）和反比例函数y2＝（m≠0）的图象相交于点A（﹣4，2），B（n，﹣4）（1）求一次函数和反比例函数的表达式；（2）观察图象，直接写出不等式y1＜y2的解集．27．如图，在平面直角坐标系中，一次函数y＝kx+b（k≠0）的图象与反比例函数y＝（m ≠0）的图象交于A，B两点，与x轴交于点C，点A的坐标为（n，12），点C的坐标为（﹣4，0），且tan∠ACO＝2．（1）求该反比例函数和一次函数的解析式；（2）求点B的坐标；（3）连接OA，OB，求△AOB的面积．28．如图，已知一次函数y＝ax+b（a，b为常数，a≠0）的图象与x轴，y轴分别交于点A，B，且与反比例函数y＝（k为常数，k≠0）的图象在第二象限内交于点C，作CD⊥x轴于，若OA＝OD＝OB＝3．（1）求一次函数与反比例函数的解析式；（2）观察图象直接写出不等式0＜ax+b≤的解集．29．如图1，反比例函数图象经过等边△OAB 的一个顶点B ，点A 坐标为（2，0），过点B 作BM ⊥x 轴，垂足为M ．（1）求点B 的坐标和k 的值；（2）若将△ABM 沿直线AB 翻折，得到△ABM '，判断该反比例函数图象是从点M '的上方经过，还是从点M '的下方经过，又或是恰好经过点M '，并说明理由；（3）如图2，在x 轴上取一点A 1，以AA 1为边长作等边△AA 1B 1，恰好使点B 1落在该反比例函数图象上，连接BB 1，求△ABB 1的面积．30．如图，已知反比例函数y ＝（x ＞0）的图象与反比例函数y ＝（x ＜0）的图象，A （1，4），B （4，m ）是函数y ＝（x ＞0）图象上的两点，连接AB ，点C （﹣2，n ）是函数y ＝（x ＜0）图象上的一点，点C 关于y 轴的对称点在y ＝（x ＞0）图象上，连接AC ，BC ．（1）求m ，n 的值；（2）求BC 所在直线的表达式；（3）求△ABC 的面积．参考答案一．选择题1．解：反比例函数y ＝﹣中k ＝﹣8＜0，在每个象限内y 随着x 的增大而增大，故A 错误，符合题意，故选：A ．2．解：设C （x ，y ），如图，∵矩形ABCD 的对角线BD 经过坐标原点，矩形的边分别平行于坐标轴，∴△ABD 和△CDB 的面积相等，∴矩形AEOF 的面积等于矩形OMCN 的面积，∴xy ＝k 2﹣2k +1＝4×4，即（k ﹣1）2＝16，解得k 1＝﹣3，k 2＝5．故选：D ．3．解：将B （1，2）代入反比例函数y ＝（x ＞0）中得：m ＝2，∴y ＝，∵∠OBC ＝90°，∴k OB ×k BC ＝﹣1，∵k OB ＝2，∴k BC ＝﹣，∵B （1，2），∴直线BC ：y ＝﹣x +，联立，得：点C （4，），∴线段BC 的中点坐标为（，），∵▱ABOC ，∴线段OA 的中点坐标为（，），∴点A 的坐标为（5，），∵点A 在反比例函数y ＝（x ＞0）的图象上，∴k ＝5×＝；故选：D ．4．解：∵x 轴的平行线AB 分别与这两个函数图象相交于点A ．B ，∴AB ⊥y 轴，∵点A 、B 在反比例函数y ＝和y ＝﹣在x 轴上方的图象上，∴S △AOB ＝S △COB +S △AOC ＝（3+7）＝5，故选：A ．5．解：∵OCAD 和CEBG 都是正方形．∴设BE ＝a ，AD ＝b ，∴B （a +b ，a ），A （b ，b ），∵A 、B 两点都在反比例函数y ＝，∴a （a +b ）＝b •b ，∴，①四边形ADFG 中宽与长的比为，将代入，得到＝， ∴四边形ADFG 不是黄金矩形；①不正确；四边形OCGF中宽与长的比为＝，∴四边形OCGF为黄金矩形，②正确；∵FG、OC的中点分别为P、Q，∴OQ＝b，四边形OQPF中宽与长的比为＝，∴四边形OQPF不是黄金矩形；③不正确；故选：B．6．解：设A（，m），B（，m），则：△ABC的面积＝•AB•y A＝•（﹣）•m＝3，则a﹣b＝6．故选：A．7．解：设A（m，﹣2m），∵AC＝AO，∴△ACO是等腰三角形，∴CO＝﹣2m，∴S＝×（﹣2m）×（﹣2m）＝6，△ACO∴m2＝3，∵k＝2m2，∴k＝﹣6，故选：C．8．解：如图，过B作BF⊥x轴于点F，过D作DG⊥x轴于点G，过C作CH⊥x轴于点H，∵A（10，0），∴OA＝10，∴S菱形ABCD＝OA•BF＝AC•OB＝×160＝80，即10BF＝80，∴BF＝8，在Rt△ABF中，AB＝10，BF＝8，由勾股定理可得AF＝6，∴OF＝OA+AF＝10+6＝16，∵四边形OABC为菱形，∴D为OB中点，∴DG＝BF＝×8＝4，OG＝OF＝×16＝8，∴D（8，4），∵双曲线过点D，∴4＝，解得k＝32，∴双曲线解析式为y＝，故选：D．9．解：设一次函数解析式为y＝kx+b，反比例函数解析式为y＝，∵A（1，8）和B（4，2）是两个函数图象的交点，∴y＝，∴，∴，∴y＝﹣2x+10，∵S△ODF ＝S△ECO＝4，设点P的坐标（x，﹣2x+10），∴四边形OEPF面积＝xy﹣8＝x（﹣2x+10）﹣8＝﹣2x2+10x﹣8＝﹣2（x﹣）2+，∴当x＝时，面积最大为；故选：C．10．解：作AE⊥OB于E，DF⊥OB于F，∵∠AOB＝60°，AO＝8，∴OE＝OA＝4，AE＝OA＝4，∴A（4，4），∵反比例函数y＝（x＞0）图象经过点A，∴k＝4×＝16，∴y＝，∵四边形AOBC是平行四边形，∴OA∥BC，∴∠DBF＝∠AOB＝60°，设D点的纵坐标为n，∴DF＝n，∴BF＝n，∵OB＝AC＝15，∴D（15+n，n），∵点D在反比例函数y＝（x＞0）图象上，∴（15+n）•n＝16，解得n1＝，n2＝﹣16（舍去），∴DF＝，∵∠DBF＝∠AOB＝60°，∠OEA＝∠BFD＝90°，∴△BFD∽△OEA，∴＝＝＝，故选：C．二．填空题（共10小题）11．解：过点C 作CE ⊥x 轴于点E ，延长AD ，交x 轴于点F ，连接OD ，如图所示． ∵AO ＝AB ，CD ∥x 轴，∠ADC ＝90°，∴AF ⊥OB ，∴S △AOF ＝S △AOB ＝18．∵函数y ＝（x ＞0）图象与OA 交于点C ，点D 是函数y ＝（x ＞0）的图象上一点，∴S △OCE ＝k ，S △ODF ＝×4＝2，∴＝＝＝．∵CE ⊥x 轴，AF ⊥x 轴，CD ∥x 轴，∴△OCE ∽△OAF ，CE ＝DF ，∴＝（）2＝，∴S △O CE ＝k ＝×18＝，∴k ＝．故答案为：．12．解：连接OC ，过点A 作AE ⊥x 轴于E ，过点C 作CF ⊥x 轴于F ，过点D 作DH ⊥AB 于H ，如图所示．∵△ABC 为等腰直角三角形，∴OA＝OC，OC⊥AB，∴∠AOE+∠COF＝90°．∵∠COF+∠OCF＝90°，∴∠AOE＝∠OCF．在△AOE和△OCF中，，∴△AOE≌△OCF（AAS），∴AE＝OF，OE＝CF．∵BD平分∠ABC，∴CD＝DH，∵∠CFD＝∠AED＝90°，∠CDF＝∠ADE，∴△CDF∽△ADE，∴＝，∴＝，∵∠BAC＝45°，∴sin45°＝＝∴＝＝，∵OE＝CF，∴＝．∵k＝﹣，∴设点A的坐标为（a，﹣）（a＜0），∴＝，解得：a＝1或a＝﹣1，∴A（﹣1，），∴OE＝1，AE＝，∴CF＝OE＝1，OF＝AE＝，∴点C的坐标为（﹣，﹣1）．故答案为：（﹣，﹣1）．13．解：∵点B是y＝kx和y＝的交点，y＝kx＝，∴点B坐标为（，4），同理可求出点A的坐标为（，2），∵BD⊥x轴，∴点C横坐标为，纵坐标为，∴BA＝，AC＝，BC＝3，∴BA2﹣AC2＝3k＞0，∴BA≠AC，若△ABC是等腰三角形，①AB＝BC，则＝3，解得：k＝；②AC＝BC，则＝3，解得：k＝；故答案为：或．14．解：过点B作BE∥x轴交y轴于点E，过点C作CD⊥BD于点D，如图：则易证△ABE ≌△BCD ，∴BE ＝CD ，AE ＝BD ，∵直线y ＝2x ﹣1交y 轴于A ，∴A （0，﹣1），设点B （x ，），则BE ＝CD ＝x ，AE ＝BD ＝+1，∴C （x ++1，﹣x ），∵C 点落在双曲线y ＝（k ＞0，x ＞0）上，∴k ＝（x ++1）（﹣x ）①，∵点B 在直线y ＝2x ﹣1上，∴＝2x ﹣1②，∴联立①②解得：k ＝6，故答案为：6．15．解：直线l 2：y ＝x 与x 轴夹角为30°，直线l 1：y ＝x 与x 轴夹角为60°， ∴l 1与l 2的夹角30°，∵A 1B 1上l 1，∴∠OB 1A 1＝60°，∵等边三角形A 1B 1C 1，∴B 1C 1⊥x 轴，∵B 1（1，），∴OB 1＝，∴B 1C 1＝，∴C 1（1，）， ∴k 1＝；∴OB 2＝+＝，∴A 2B 2＝OB 2sin30°＝，∴B 2的横坐标OB 2×cos30°＝，B 2的纵坐标OB 2×sin30°＝，∴C 2（，）， ∴k 2＝，以此得到OB n ＝×，∁n 的横坐标OB n ×cos30°＝，∁n 的纵坐标2OB n×sin30°＝×，∴k n ＝××＝×，故答案为×； 16．解：∵BD 为Rt △ABC 的斜边AC 上的中线，∴BD ＝DC ，∠DBC ＝∠ACB ，又∠DBC ＝∠EBO ，∴∠EBO ＝∠ACB ，又∠BOE ＝∠CBA ＝90°，∴△BOE ∽△CBA ，∴＝，即BC ×OE ＝BO ×AB ．又∵S △BEC ＝3，∴BC •EO ＝3，即BC ×OE ＝6＝BO ×AB ＝|k |．∵反比例函数图象在第二象限，k ＜0．∴k ＝﹣6．故答案为：﹣6．17．解：菱形ABCD 的对角线BD 与x 轴平行，点B 、C 的坐标分别为（0，2）、（3，0），∵菱形对角线互相垂直平分，∴A （3，4），将点A （3，4）代入中，∴k ＝12；故答案为12；18．解：∵点B 与点C 关于原点对称，∴BC ＝2OC ，在Rt △ABC 中，AB 2＝AC 2+BC 2，∵AB ＝5，∴25＝AC 2+4OC 2，在Rt △AOC 中，AO 2＝AC 2+OC 2，∵AO ＝， ∴13＝AC 2+OC 2，∴OC ＝2，AC ＝3，∵∠COP ＝∠CAO ，∴tan ∠COP ＝tan ∠CAO ，∴，∴PC ＝，∴P （2，），∴k ＝；故答案为；19．解：∵A ，B 是反比例函数y ＝在第一象限内的图象上的两点，且A ，B 两点的横坐标分别是4和8，∴当x ＝4时，y ＝2，即A （4，2），当x ＝8时，y ＝1，即B （8，1）．如图，过A ，B 两点分别作AC ⊥x 轴于C ，BD ⊥x 轴于D ，则S △AOC ＝S △BOD ＝×8＝4． ∵S 四边形AODB ＝S △AOB +S △BOD ＝S △AOC +S 梯形ABDC ，∴S △AOB ＝S 梯形ABDC ，∵S 梯形ABDC ＝（BD +AC ）•CD ＝（1+2）×4＝6，∴S △AOB ＝6．故答案为：6．20．解：作DF ∥AO ，CE ⊥AO ，∵∠AOC ＝60°，∴tan ∠AOC ＝，∴设OE ＝x ，CE ＝x ， ∴x •x ＝4，∴x ＝±2，∴OE ＝2，CE ＝2，由勾股定理得：OC ＝4，∴S 菱形OABC ＝OA •CE ＝4×2＝8，∵四边形OABC 为菱形，∴AB ∥CO ，AO ∥BC ，∵DF ∥AO ，∴S △ADO ＝S △DFO ，同理S △BCD ＝S △CDF ，∵S 菱形ABCO ＝S △ADO +S △DFO +S △BCD +S △CDF ，∴S 菱形ABCO ＝2（S △DFO +S △CDF ）＝2S △CDO ＝8，∴S △CDO ＝4；故答案为4．三．解答题（共10小题）21．解：（1）将点B（﹣3，﹣2）代入y＝，∴m＝6，∴y＝，∴n＝2，∴A（2，3），将A（2，3），B（﹣3，﹣2）代入y＝kx+b，，∴，∴y＝x+1；（2）y＝x+1与x轴交点坐标（﹣1，0），∴S＝×1×（3+2）＝；22．解：（1）∵反比例函数y＝（k≠0）的图象过点B（4，﹣4），∴k＝4×（﹣4）＝﹣16，∴反比例函数解析式为：y＝﹣．∵AH⊥x轴于点H，AC＝4，cos∠ACH＝，∴＝＝，解得：HC＝4，∵点O是线段CH的中点，∴HO＝CO＝2，将x＝﹣2代入y＝﹣，得y＝8，，∴A（﹣2，8）．设一次函数解析式为：y＝kx+b，将A（﹣2，8），B（4，﹣4）代入，得：，解得：，∴一次函数解析式为：y＝﹣2x+4；（2）∵HC＝4，B（4，﹣4），∴△BCH的面积为：×4×4＝8；（3）观察图象可知：当x＜﹣2或0＜x＜4时，一次函数图象在反比例函数图象的上方，所以ax+b＞的x取值范围是x＜﹣2或0＜x＜4．故答案为x＜﹣2或0＜x＜4．23．解：（1）∵一次函数y＝kx+b的图象与反比例函数y＝的图象交于M（3，2）、N（﹣1，a）两点∴m＝6，a＝﹣6，∴反比例函数y＝，N（﹣1，﹣6），把M（3，2），N（﹣1，﹣6）代入y＝kx+b得，解得∴一次函数的解析式的解析式为y＝2x﹣4．（2）设直线MN交x轴于点A，当y＝0时，2x﹣4＝0，∴x＝2，∴A（2，0），∴S△MON＝S△MOA+S△NOA＝•OA•（y M﹣y N）＝×2×8＝8；（3）由图象可知，当﹣1＜x＜0或x＞3时一次函数的值大于反比例函数的值．24．解：（1）把点A（4，1）代入双曲线y1＝得k1＝4，∴双曲线y1＝；代入直线y2＝得k2＝4，∴直线为y＝x；（2）∵点P（a，b）在y1＝的图象上，∴ab＝4，∵4a＝b，∴4a2＝4，则a＝±1，∵0＜a＜4，∴a＝1，∴P（1，4），又∵双曲线y1＝与直线y2＝的图象交于A、B两点，且A（4，1）∴B（﹣4，﹣1），过点P作PQ∥y轴交AB于点G，如图所示，把x＝1代入y＝x，得到y＝，∴G（1，），∴PG＝4﹣＝，∴S△ABP＝PG（x A﹣x B）＝××8＝15；（3）PE＝PF．理由如下：∵点P（a，b）在y＝的图象上，∴b＝，∵B（﹣4，﹣1），设直线PB的表达式为y＝mx+n，∴，∴∴直线PB的表达式为y＝x+﹣1，当y＝0时，x＝a﹣4，∴E点的坐标为（a﹣4，0），同理F点的坐标为（a+4，0），过点P作PH⊥x轴于H，如图所示，∵P点坐标为（a，b），∴H点的坐标为（a，0），∴EH＝x H﹣x E＝a﹣（a﹣4）＝4，同理可得：FH＝4，∴MH＝HN，∴PM＝PN．25．解：（1）材料锻造时，设y＝（k≠0），由题意得600＝，解得k＝4800，当y＝800时，，解得x＝6，∴点B的坐标为（6，800）材料煅烧时，设y＝ax+26（a≠0），由题意得800＝6a+26，解得a＝129，∴材料煅烧时，y与x的函数关系式为y＝129x+26（0≤x≤6）．∴锻造操作时y与x的函数关系式为y＝（6＜x≤150）；（2）把y＝400代入y＝，得x＝12，12﹣6＝6（分），答：锻造的操作时间6分钟．＝，26．【解答】解：（1）将点A（﹣4，2）代入y2∴m＝﹣8，∴y＝，将B（n，﹣4）代入y＝，∴n＝2，∴B（2，﹣4），＝kx+b，将A（﹣4，2），B（2，﹣4）代入y1得到，∴，∴y＝﹣x﹣2，（2）由图象直接可得：x＞2或﹣4＜x＜0；27．解：（1）过点A作AD⊥x轴，垂足为D．由A（n，12），C（﹣4，0），可得OD＝n，AD＝12，CO＝4．∵tan∠ACO＝2，∴＝2，即＝2，∴n＝2，∴A（2，12）．将A（2，12）代入反比例函数y＝，得m＝2×12＝24．∴反比例函数的解析式为y＝．将A（2，12），C（﹣4，0）代入一次函数y＝kx+b，得，解得．∴一次函数的解析式为y＝2x+8．（2）y＝与y＝2x+8的交点为，2x+8＝，∴x2+4x﹣12＝0，∴x＝﹣6或x＝2，∴点B的坐标为（﹣6，﹣4）．（3）∵C（﹣4，0），＝×OC（y A﹣y B）＝×4×[12﹣（﹣4）]＝32．∴S△AOB28．解：（1）∵CD⊥OA，∴DC∥OB，∴，∴CD＝2OB＝8，∵OA＝OD＝OB＝3，∴A（3，0），B（0，4），C（﹣3，8），把A、B两点的坐标分别代入y＝ax+b可得，解得，∴一次函数解析式为，∵反比例函数y＝的图象经过点C，∴k＝﹣24，∴反比例函数的解析式为y＝﹣；（2）由题意可知所求不等式的解集即为直线AC在x轴上方且在反比例函数图象下方的图象所对应的自变量的取值范围，即线段BC（包含C点，不包含B点）所对应的自变量x的取值范围，∵C（﹣3，8），∴0＜﹣x+4≤﹣的解集为﹣3≤x＜0；29．解：（1）∵△OAB为等边三角形，OA＝2，∴OM＝OA＝1，BM＝OA＝，∴点B的坐标为（1，）．∵反比例函数图象经过点B，∴k＝．（2）该反比例函数图象是从点M'的下方经过，理由如下：过点M′作M′C⊥x轴，垂足为点C，如图1所示．由折叠的性质，可知：AM′＝AM＝1，∠BAM′＝∠BAM＝60°，∴∠M′AC＝180°﹣∠BAM﹣∠BAM′＝60°．在Rt△ACM′中，AM′＝1，∠ACM′＝90°，∠M′AC＝60°，∴∠AM′C＝30°，∴AC＝AM′＝，CM′＝AM′＝．∴OC＝OA+AC＝，∴点M′的坐标为（，）．当x＝时，y＝＝，∵＜，∴该反比例函数图象是从点M '的下方经过．（3）过点B 1作B 1D ⊥x 轴，垂足为点D ，如图2所示．设AA 1＝a ，则AD ＝a ，B 1D ＝a ，OD ＝2+a ，∴点B 1的坐标为（2+a ，a ）．∵点B 1在该反比例函数y ＝的图象上，∴（2+a ）•a ＝，解得：a 1＝﹣2﹣2（舍去），a 2＝2﹣2，∴MD ＝AM +AD ＝，B 1D ＝a ＝﹣，AD ＝a ＝﹣1，∴＝﹣S △BMA ﹣，＝（BM +B 1D ）•MD ﹣BM •AM ﹣B 1D •AD ，＝（+﹣）×﹣××1﹣×（﹣）×（﹣1），＝﹣．30．解：（1）因为点A 、点B 在函数y ＝（x ＞0）图象上，∴k 1＝1×4＝4，∴m×4＝k1＝4，∴m＝1，∵点C（﹣2，n）关于y轴的对称点在y＝（x＞0）图象上．∴对称点为（2，n），∴2×n＝4，∴n＝2；（2）设直线BC所在的直线表达式为y＝kx+b把B（4，1），C（﹣2，2）代入，得，解得，∴BC所在直线的表达式为：y＝﹣x+；（3）如图所示：过点A、B作x轴的平行线，过点C、B作y轴的平行线，它们的交点分别是E、F、B、G．∴四边形EFBG是矩形．则AF＝3，BF＝3，AE＝3，EC＝2，CG＝1，GB＝6，EG＝3∴S△ABC＝S矩形EFBG﹣S△AFB﹣S△AEC﹣S△CBG＝BG×EG﹣AF×FB﹣AE×EC﹣BG×CG＝18﹣﹣3﹣3＝．。

上海十年中考数学压轴题24,25题

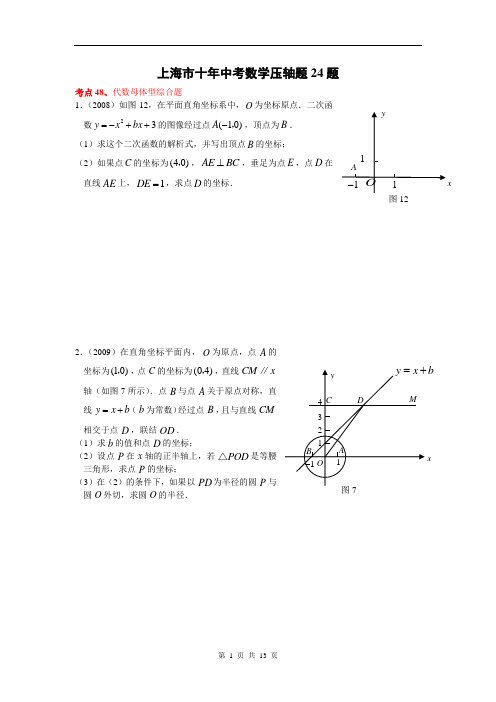
x图12上海市十年中考数学压轴题24题考点48、代数母体型综合题 1．（2008）如图12，在平面直角坐标系中，O 为坐标原点．二次函数23y x bx =-++的图像经过点(10)A -，，顶点为B ．（1）求这个二次函数的解析式，并写出顶点B 的坐标；（2）如果点C 的坐标为(40)，，AE BC ⊥，垂足为点E ，点D 在直线AE 上，1DE =，求点D 的坐标．2．（2009）在直角坐标平面内，为原点，点的坐标为，点的坐标为，直线轴（如图7所示）．点与点关于原点对称，直线（为常数）经过点，且与直线相交于点，联结．（1）求的值和点的坐标；（2）设点在轴的正半轴上，若是等腰三角形，求点的坐标；（3）在（2）的条件下，如果以为半径的圆与圆外切，求圆的半径．O A (10)，C (04)，CM x ∥B A y x b =+b B CM D OD b D P x POD △P PD P O Oxb3．（2010）如图，已知平面直角坐标系x O y ，抛物线y ＝－x 2＋bx ＋c 过点A （4，0）、B （1，3）．（1）求该抛物线的表达式，并写出该抛物线的对称轴和顶点坐标；（2）记该抛物线的对称轴为直线l ，设抛物线上的点P（m ，n ）在第四象限，点P 关于直线l 的对称点为E ，点E 关于y 轴的对称点为F ，若四边形OAPF 的面积为20，求m 、n 的值．4．（2011）已知平面直角坐标系xOy （如图1），一次函数334y x =+的图像与y 轴交于点A ，点M 在正比例函数32y x =的图像上，且MO ＝MA ．二次函数y ＝x 2＋bx ＋c 的图像经过点A 、M ．（1）求线段AM 的长；（2）求这个二次函数的解析式；（3）如果点B 在y 轴上，且位于点A 下方，点C 在上述二次函数的图像上，点D 在一次函数334y x =+的图像上，且四边形ABCD 是菱形，求点C 的坐标．5．（2012）如图7，在平面直角坐标系中，二次函数26y ax x c =++的图像经过()()4,0,1,0A B -与y 轴交于C ，点D 在线段OC 上，OD t =，点E 在第二象限内，90ADE ∠=︒，1tan ,2DAE EF OD ∠=⊥，垂足为F ．（1）求这个二次函数的解析式；（2）求线段,EF OF 的长（用含t 的代数式表示）；（3）当ECA CAO ∠=∠时，求t 的值．6．（2013）如图9，在平面直角坐标系中，顶点为的抛物线经过点和轴正半轴上的点，= 2，．（1）求这条抛物线的表达式；（2）联结，求的大小；（3）如果点在轴上，且△与△相似，求点的坐标．xoy M 2(0y ax bx a =+>）A x B AO OB =0120AOB ∠=OM AOM ∠C x ABC AOM C MAB Oxy图97．（2014）在平面直角坐标系中（如图9），已知抛物线223y x bx c =++与x 轴交于点A （－1，0）和点B ，与y 轴交于点C （0，－2）．（1）求该抛物线的表达式，并写出其对称轴；（2）点E 为该抛物线的对称轴与x 轴的交点，点F 在对称轴上，四边形ACEF 为梯形，求点F 的坐标；（3）点D 为该抛物线的顶点，设点P （t ，0），且t ﹥3，如果△BDP 和△CDP 的面积相等，求t 的值．8．（2015）已知在平面直角坐标系xOy 中（如图），抛物线y ＝ax 2－4与x 轴的负半轴相交于点A ，与y 轴相交于点B ，AB ＝25．点P 在抛物线上，线段AP 与y 轴的正半轴交于点C ，线段BP 与x 轴相交于点D ．设点P 的横坐标为m ．（1）求这条抛物线的解析式；（2）用含m 的代数式表示线段CO 的长；（3）当tan ∠ODC ＝23时，求∠P AD 的正弦值．图99．（2016）如图，抛物线25y ax bx =+-（0a ≠）经过点(4,5)A -，与x 轴的负半轴交于点B ，与y 轴交于点C ，且5OC OB =，抛物线的顶点为D ；（1）求这条抛物线的表达式；（2）联结AB 、BC 、CD 、DA ，求四边形ABCD 的面积；（3）如果点E 在y 轴的正半轴上，且BEO ABC ∠=∠，求点E 的坐标．10．（2017）在平面直角坐标系xOy 中（如图8），已知抛物线y =-x 2+bx +c 经过点A （2， 2），对称轴是直线x =1，顶点为B ．（1）求这条抛物线的表达式和点B 的坐标；（2）点M 在对称轴上，且位于顶点上方，设它的纵坐标为m ，联结AM ，用含m 的代数式表示∠AMB 的余切值；（3）将该抛物线向上或向下平移，使得新抛物线的顶点C原抛物线上一点P 平移后的对应点为点Q ，如果OP =OQ图 811．（2018）在平面直角坐标系xOy 中（如图10），已知抛物线c bx x y ++-=221经过 A （–1，0）和点B （0，25），顶点为C ．点D 在其对称轴上且位于点C 下方，将线段DC 绕点D 按顺时针方向转90°，点C 落在抛物线上的点P 处．（1）求这条抛物线的表达式；（2）求线段CD 的长；（3）将抛物线平移，使其顶点C 移到原点O 的位置．这时点P 落在点E 的位置，如果点M 在y 轴上，且以O 、D 、E 、M 为顶点的四边形面积为8，求M 的坐标．12．（2019）在平面直角坐标系xOy 中(如图9)，已知抛物线22=-y x x ，其顶点为A . （1）写出这条拋物线的开口方向、顶点A 的坐标，并说明它的变化情况；（2）我们把一条抛物线上横坐标与纵坐标相等的点叫做这条抛物线的“不动点”. ①试求抛物线22=-y x x 的“不动点”的坐标；②平移抛物线22=-y x x ，使所得新拋物线的顶点B 是该抛物线的“不动点”其对称轴与x 轴交于点C ，且四边形OABC上海市十年中考数学压轴题25题考点49、几何母体型综合题1．（2008）已知24AB AD ==，，90DAB ∠=，AD BC ∥（如图13）．E 是射线BC 上的动点（点E 与点B 不重合），M 是线段DE 的中点．（1）设BE x =，ABM △的面积为y ，求y 关于x 的函数解析式，并写出函数的定义域；（2）如果以线段AB 为直径的圆与以线段DE 为直径的圆外切，求线段BE 的长；（3）联结BD ，交线段AM 于点N ，如果以A N D ，，为顶点的三角形与BME △相似，求线段BE 的长．2．（2009）已知为线段上的动点，点在射线上，且满足（如图8所示）．（1）当，且点与点重合时（如图9所示），求线段的长；（2）在图8中，联结．当，且点在线段上时，设点之间的距离为，，其中表示的面积，表示的面积，求关于的函数解析式，并写出函数定义域；（3）当，且点在线段的延长线上时（如图10所示），求的大小．9023ABC AB BC AD BC P ∠===°，，，∥，BD Q AB PQ ADPC AB=2AD =Q B PC AP 32AD =Q AB B Q 、x APQ PBCS y S =△△APQ S △APQ △PBC S △PBC △yx AD AB <Q AB QPC ∠B A D M E C图13B A DC 备用图 AD P Q D A PA D P3．（2010）如图，在Rt △ABC 中，∠ACB ＝90°．半径为1的圆A 与边AB 相交于点D ，与边AC 相交于点E ，连结DE 并延长，与线段BC 的延长线交于点P ．（1）当∠B ＝30°时，连结AP ，若△AEP 与△BDP 相似，求CE 的长；（2）若CE=2，BD=BC ，求∠BPD 的正切值；（3）若，设CE=x ，△ABC 的周长为y ，求y 关于x 的函数关系式．（备用）（备用） 4．（2011）在Rt △ABC 中，∠ACB ＝90°，BC ＝30，AB ＝50．点P 是AB 边上任意一点，直线PE ⊥AB ，与边AC 或BC 相交于E ．点M 在线段AP 上，点N 在线段BP 上，EM ＝EN ，12sin 13EMP ∠=．（1）如图1，当点E 与点C 重合时，求CM 的长；（2）如图2，当点E 在边AC 上时，点E 不与点A 、C 重合，设AP ＝x ，BN ＝y ，求y 关于x 的函数关系式，并写出函数的定义域；（3）若△AME ∽△ENB （△AME 的顶点A 、M 、E 分别与△ENB 的顶点E 、N 、B 对应），求AP 的长．图1 图2 备用图1tan 3BPD ∠=5．（2012）如图8，在半径为2的扇形AOB 中，90AOB ∠=︒，点C 是AB 上的一个动点（不与点A 、B 重合），,OD BC OE AC ⊥⊥，垂足分别为D E 、．（1）当=1BC 时，求线段OD 的长；（2）在DOE ∆中是否存在长度不变的边？若存在，请指出并求其长度；如果不存在，请说明理由；（3）设=BD x ，DOE ∆的面积为y ，求y 关于x 的函数关系式，并指出它的定义域．6．（2013）在矩形ABCD 中，点P 是边AD 上的动点，联结BP ，线段BP 的垂直平分线交边BC 于点Q ，垂足为点M ，联结QP （如图10）．已知AD =13，AB =5，设AP =x ，BQ =y ．（1）求关于的函数解析式，并写出的取值范围；（2）当以AP 长为半径的⊙P 和以QC 长为半径的⊙Q 外切时，求x 的值；（3）点E 在边CD 上，过点E 作直线QP 的垂线，垂足为F ，如果EF =EC =4，求x 的值．y x x OABCDE图8图10备用图7．（2014）如图10，已知在平行四边形ABCD 中，AB ＝5，BC ＝8，cos B ＝45，点P 是边BC 上的动点，以CP 为半径的圆C 与边AD 交于点E 、F （点F 在点E 的右侧），射线CE 与射线BA 交于点G ．（1）当圆C 经过点A 时，求CP 的长；（2）联结AP ，当AP ∥CG 时，求弦EF 的长；（3）当△AGE 是等腰三角形时，求圆C 的半径长．8．（2015）已知：如图，AB 是半圆O 的直径，弦CD ∥AB ，动点P 、Q 分别在线段OC 、CD 上，且DQ ＝OP ，AP 的延长线与射线OQ 相交于点E 、与弦CD 相交于点F （点F 与点C 、D 不重合），AB ＝20，cos ∠AOC ＝54．设OP ＝x ，△CPF 的面积为y ．（1）求证：AP ＝OQ ；（2）求y 关于x 的函数关系式，并写出它的定义域；（3）当△OPE 是直角三角形时，求线段OP 的长．GB EFDCP图10 ABDC备用图 AOPQ F EDCBA备用图O DCBA第 11 页共 13 页9．（2016）如图所示，梯形ABCD 中，AB ∥DC ，90B ∠=︒，15AD =，16AB =，12BC =，点E 是边AB 上的动点，点F 是射线CD 上一点，射线ED 和射线AF 交于点G ，且AGE DAB ∠=∠；（1）求线段CD 的长；（2）如果AEG ∆是以EG 为腰的等腰三角形，求线段AE 的长；（3）如果点F 在边CD 上（不与点C 、D 重合），设AE x =，DF y =，求y 关于x 的函数解析式，并写出x 的取值范围．10．（2017）如图9，已知⊙O 的半径长为1，AB 、AC 是⊙O 的两条弦，且AB =AC ，BO 的延长线交AC 于点D ，联结OA 、OC .（1）求证：△OAD ∽△ABD ；（2）当△OCD 是直角三角形时，求B 、C 两点的距离；（3）记△AOB 、△AOD 、△COD 的面积分别是S 1、S 2、S 3，如果S 2是S 1和S 3的比例中项，求OD 的长.备用图图9第 12 页共 13 页11．（2018）已知⊙O 的直径AB =2，弦AC 与弦BD 交于点E ，且OD ⊥AC ，垂足为点F ．（1）如图11，如果AC =BD ，求弦AC 的长；（2）如图12，如果E 为弦BD 的中点，求∠ABD 的余切值；（3）联结BC 、CD 、DA ，如果BC 是⊙O 的内接正n 边形的一边，CD 是⊙O 的内接正（n +4）边形的一边，求△ACD 的面积．12．（2019）如图10，AD 、BD 分别是△ABC 的内角∠BAC 、∠ABC 的平分线，过点A 作AE ⊥AD ，交BD 的延长线于点E . （1）求证: 12∠=∠E C ；（2）如图11，如果AE =AB ，且BD :DE =2:3，求cos ∠ABC 的值；（3）如果∠ABC 是锐角，且△ABC 与△ADE 相似，求∠ABC 的度数，并直接写出S △ADE ∶S △ABC 的值.图10图11 A BC D E E D CB A A BCD FE O 图11 O B A C D EF 图12 A B O 备用图第13 页共13 页。

2019中考数学压轴题

2019中考数学压轴题一、选择题1．（2017内蒙古包头市，第11题，3分）已知一次函数14y x=，二次函数2222y x =+，在实数范围内，对于x 的同一个值，这两个函数所对应的函数值为1y 与2y ，则下列关系正确的是（）A ．12y y > B ．12y y ≥ C ．12y y < D ．12y y ≤2．（2017四川省乐山市，第9题，3分）已知二次函数mx x y 22-=（m 为常数），当﹣1≤x ≤2时，函数值y 的最小值为﹣2，则m 的值是（）A ．23B ．2C ．23 或2D ．23-或23．（2017湖北省恩施州，第12题，3分）如图，在平面直角坐标系中2条直线为l1：y=﹣3x+3，l2：y=﹣3x+9，直线l1交x 轴于点A ，交y 轴于点B ，直线l2交x 轴于点D ，过点B 作x 轴的平行线交l2于点C ，点A 、E 关于y 轴对称，抛物线2yax bx c 过E 、B 、C 三点，下列判断中：①a ﹣b+c=0；②2a+b+c=5；③抛物线关于直线x=1对称；④抛物线过点（b ，c ）；⑤S 四边形ABCD=5，其中正确的个数有（）A ．5B ．4C ．3D ．24．（2017湖北省荆州市，第10题，3分）规定：如果关于x 的一元二次方程20ax bx c ++=（a ≠0）有两个实数根，且其中一个根是另一个根的2倍，则称这样的方程为“倍根方程”．现有下列结论：①方程2280x x +-=是倍根方程；②若关于x 的方程220x ax ++=是倍根方程，则a=±3；③若关于x 的方程260ax ax c -+=（a ≠0）是倍根方程，则抛物线26y ax ax c =-+与x 轴的公共点的坐标是（2，0）和（4，0）；④若点（m ，n ）在反比例函数4y x =的图象上，则关于x 的方程250mx x n ++=是倍根方程．上述结论中正确的有（）A ．①②B ．③④C ．②③D ．②④5．（2017贵州省安顺市，第10题，3分）二次函数2y ax bx c =++（a ≠0）的图象如图，给出下列四个结论：①240ac b -<；②320b c +<；③42a c b +<；④()()1m am b b a m ++<≠-，其中结论正确的个数是（）A ．1B ．2C ．3D ．46．（2017辽宁省盘锦市，第10题，3分）如图，抛物线2y ax bx c =++ 与x 轴交于点A （﹣1，0），顶点坐标（1，n ），与y 轴的交点在（0，3），（0，4）之间（包含端点），则下列结论：①abc ＞0；②3a+b ＜0；③﹣43≤a ≤﹣1；④a+b ≥am2+bm （m 为任意实数）；⑤一元二次方程2ax bx c n ++= 有两个不相等的实数根，其中正确的有（）A ．2个B ．3个C ．4个D ．5个7．（2017四川省阿坝州，第10题，4分）如图，抛物线2y ax bx c =++ （a ≠0）的对称轴为直线x=1，与x 轴的一个交点坐标为（﹣1，0），其部分图象如图所示，下列结论：①4ac ＜b2；②方程20ax bx c ++= 的两个根是x1=﹣1，x2=3；③3a+c ＞0④当y ＞0时，x 的取值范围是﹣1≤x ＜3 ⑤当x ＜0时，y 随x 增大而增大其中结论正确的个数是（）A．4个B．3个C．2个D．1个8．（2017山东省日照市，第12题，4分）已知抛物线2y ax bx c=++（a≠0）的对称轴为直线x=2，与x轴的一个交点坐标为（4，0），其部分图象如图所示，下列结论：①抛物线过原点；②4a+b+c=0；③a﹣b+c＜0；④抛物线的顶点坐标为（2，b）；⑤当x＜2时，y随x增大而增大．其中结论正确的是（）A．①②③B．③④⑤C．①②④D．①④⑤9．（2017山东省烟台市，第11题，3分）二次函数2y ax bx c=++（a≠0）的图象如图所示，对称轴是直线x=1，下列结论：①ab＜0；②b2＞4ac；③a+b+2c＜0；④3a+c＜0．其中正确的是（）A．①④B．②④C．①②③D．①②③④10．（2017南宁，第12题，3分）如图，垂直于x轴的直线AB分别与抛物线1C：2xy=（x≥0）和抛物线2C ：42x y =（x ≥0）交于A ，B 两点，过点A 作CD ∥x 轴分别与y 轴和抛物线C2交于点C ，D ，过点B 作EF ∥x 轴分别与y 轴和抛物线C1交于点E ，F ，则EAD OFES S ∆∆的值为（）A ．62B ．42C ． 41D ．6111．（2017浙江省嘉兴市，第10题，3分）下列关于函数1062+-=x x y 的四个命题： ①当x=0时，y 有最小值10；②n 为任意实数，x=3+n 时的函数值大于x=3﹣n 时的函数值；③若n ＞3，且n 是整数，当n ≤x ≤n+1时，y 的整数值有（2n ﹣4）个； ④若函数图象过点（a ，y0）和（b ，y0+1），其中a ＞0，b ＞0，则a ＜b ．其中真命题的序号是（）A ．①B ．②C ．③D ．④ 12．（2017黑龙江省齐齐哈尔市，第10题，3分）如图，抛物线y=ax2+bx+c （a ≠0）的对称轴为直线x=﹣2，与x 轴的一个交点在（﹣3，0）和（﹣4，0）之间，其部分图象如图所示，则下列结论：①4a ﹣b=0；②c ＜0；③﹣3a+c ＞0；④4a ﹣2b ＞at2+bt （t 为实数）；⑤点（92-，1y ），（52-，2y），（12-，3y ）是该抛物线上的点，则123y y y <<，正确的个数有（）A ．4个B ．3个C ．2个D ．1个13．（2017四川省资阳市，第10题，3分）如图，抛物线2y ax bx c =++（a ≠0）的顶点和该抛物线与y 轴的交点在一次函数y=kx+1（k ≠0）的图象上，它的对称轴是x =1，有下列四个结论：①abc ＜0，②13a<-，③a=-k，④当0＜x＜1时，ax+b＞k，其中正确结论的个数是（）A．4 B．3 C．2 D．114．（2017四川省遂宁市，第10题，4分）函数2y x bx c=++与函数y x=的图像如图所示，有以下结论：①240b c-＞；②0b c+=；③0b＜；④方程组2y x bx cy x⎧=++⎨=⎩的解为1111xy=⎧⎨=⎩，2233xy=⎧⎨=⎩；⑤当13x＜＜时，2(1)0x b x c+-+＞.其中正确的是（）A．①②③B．②③④C．③④⑤D．②③⑤15．（2017山东省济南市，第14题，3分）二次函数2y ax bx c=++（a≠0）的图象经过点（﹣2，0），（x0，0），1＜x0＜2，与y轴的负半轴相交，且交点在（0，﹣2）的上方，下列结论：①b＞0；②2a ＜b；③2a﹣b﹣1＜0；④2a+c＜0．其中正确结论的个数是（）A．1 B．2 C．3 D．416．（2016内蒙古呼伦贝尔市）在平面直角坐标系中，将抛物线212y x=-向下平移1个单位长度，再向左平移1个单位长度，得到的抛物线的解析式是（）A．21322y x x=---B．21122y x x=-+-C．21322y x x=-+-D．21122y x x=---17．（2016四川省眉山市）若抛物线223y x x=-+不动，将平面直角坐标系xOy先沿水平方向向右平移一个单位，再沿铅直方向向上平移三个单位，则原抛物线图象的解析式应变为（）A ．2(2)3y x =-+B ．2(2)5y x =-+C ．21y x =-D ．24y x =+ 18．（2016四川省达州市）如图，已知二次函数2y ax bx c =++（a≠0）的图象与x 轴交于点A （﹣1，0），与y 轴的交点B 在（0，﹣2）和（0，﹣1）之间（不包括这两点），对称轴为直线x=1．下列结论：①abc＞0，②4a+2b+c＞0，③24ac b -＜8a ，④13＜a ＜23，⑤b＞c ．其中含所有正确结论的选项是（）A ．①③B ．①③④C ．②④⑤D ．①③④⑤19．（2016山东省滨州市）抛物线22221y x x =-+与坐标轴的交点个数是（） A ．0 B ．1 C ．2 D ．320．（2016山东省滨州市）在平面直角坐标系中，把一条抛物线先向上平移3个单位长度，然后绕原点旋转180°得到抛物线256y x x =++，则原抛物线的解析式是（） A ．2511()24y x =--- B ．2511()24y x =-+-C ．251()24y x =--- D ．251()24y x =-++21．（2016广西南宁市）二次函数2y ax bx c =++（a≠0）和正比例函数23y x=的图象如图所示，则方程22()03ax b x c +-+=（a≠0）的两根之和（）A ．大于0B ．等于0C ．小于0D ．不能确定22．（2016黑龙江省齐齐哈尔市）如图，抛物线2y ax bx c =++（a≠0）的对称轴为直线x=1，与x 轴的一个交点坐标为（﹣1，0），其部分图象如图所示，下列结论：①4ac＜2b ；②方程20ax bx c ++=的两个根是1x =﹣1，2x=3；③3a+c＞0④当y ＞0时，x 的取值范围是﹣1≤x＜3 ⑤当x ＜0时，y 随x 增大而增大其中结论正确的个数是（）A ．4个B ．3个C ．2个D ．1个23．（2016广西桂林市）已知直线33y x =-+与坐标轴分别交于点A ，B ，点P 在抛物线21(3)43y x =--+上，能使△ABP 为等腰三角形的点P 的个数有（）A ．3个B ．4个C ．5个D ．6个 24．（2016广西贵港市）如图，抛物线21251233y x x =-++与x 轴交于A ，B 两点，与y 轴交于点C ．若点P 是线段AC 上方的抛物线上一动点，当△ACP 的面积取得最大值时，点P 的坐标是（）A ．（4，3）B ．（5，3512）C ．（4，3512） D ．（5，3）25．（2016江苏省常州市）已知一次函数1y kx m=+（k ≠0）和二次函数22y ax bx c=++（a ≠0）的自变量和对应函数值如表：x … ﹣1 0 2 4 … y 1 …135…x … ﹣1 1 3 4 … y 2 …﹣45…当21y y >时，自变量x 的取值范围是（）A ．x ＜﹣1B ．x ＞4C ．﹣1＜x ＜4D ．x ＜﹣1或x ＞426．（2016浙江省舟山市）二次函数2(1)5y x =--+，当m≤x≤n 且mn ＜0时，y 的最小值为2m ，最大值为2n ，则m+n 的值为（）A ．52B ．2C ．32D ．1227．（2016湖南省株洲市）已知二次函数2y ax bx c =++（a ＞0）的图象经过点A （﹣1，2），B （2，5），顶点坐标为（m ，n ），则下列说法错误的是（）A ．c ＜3B ．m ≤12 C ．n ≤2 D ．b ＜128．（2016甘肃省兰州市）点P1（﹣1，1y ），P2（3，2y ），P3（5，3y ）均在二次函数22y x x c =-++的图象上，则1y ，2y ，3y 的大小关系是（）A ．321y y y >> B ．312y y y >= C ．123y y y >> D ．123y y y =>29．（2016湖北省随州市）二次函数2y ax bx c =++（a≠0）的部分图象如图所示，图象过点（﹣1，0），对称轴为直线x=2，下列结论：（1）4a+b=0；（2）9a+c ＞3b ；（3）8a+7b+2c ＞0；（4）若点A （﹣3，1y）、点B （12-，2y ）、点C （72，3y）在该函数图象上，则132y y y <<；（5）若方程a （x+1）（x ﹣5）=﹣3的两根为1x 和2x ，且12x x <，则1x ＜﹣1＜5＜2x ．其中正确的结论有（）A ．2个B ．3个C ．4个D ．5个30．（2016内蒙古呼和浩特市）已知a≥2，2220m am -+=，2220n an -+=，则22(1)(1)m n -+-的最小值是（）A ．6B ．3C ．﹣3D ．031．（2016天津市）已知二次函数2()1y x h =-+（h 为常数），在自变量x 的值满足1≤x ≤3的情况下，与其对应的函数值y 的最小值为5，则h 的值为（）A ．1或﹣5B ．﹣1或5 C ．1或﹣3 D ．1或332．（2016四川省巴中市）如图是二次函数2y ax bx c =++图象的一部分，图象过点A （﹣3，0），对称轴为直线x=﹣1，给出四个结论：①c ＞0； ②若点B （32-，1y ）、C （52-，2y）为函数图象上的两点，则12y y <；③2a﹣b=0； ④244ac b a -＜0，其中，正确结论的个数是（）A ．1B ．2C ．3D ．433．（2016四川省广安市）已知二次函数2y ax bx c =++（a≠0）的图象如图所示，并且关于x 的一元二次方程20ax bx c m ++-=有两个不相等的实数根，下列结论： ①24b ac -＜0；②abc＞0；③a﹣b+c ＜0；④m＞﹣2，其中，正确的个数有（）A ．1B ．2C ．3D ．434．（2016四川省泸州市）已知二次函数22y ax bx =--（a≠0）的图象的顶点在第四象限，且过点（﹣1，0），当a ﹣b 为整数时，ab 的值为（）A ．34或1B ．14或1C ．34或12D ．14或3435．（2015南宁）如图，已知经过原点的抛物线)0(2≠++=a c bx ax y 的对称轴是直线1-=x ，下列结论中：①0>ab， ②0>++cba， ③当02<<<-yx时，．正确的个数是（）A．0个 B．1个 C．2个 D．3个36．（2015乐山）已知二次函数2y ax bx c=++的图象如图所示，记2m a b c a b c=-++++，2n a b c a b c=+++--．则下列选项正确的是（）A．m n< B．m n> C．m n= D．m、n的大小关系不能确定37．（2015孝感）如图，二次函数2y ax bx c=++（0a≠）的图象与x轴交于A，B两点，与y轴交于点C，且OA=OC．则下列结论：①abc＜0；②244b aca->；③ac﹣b+1=0；④OA•OB=ca-．其中正确结论的个数是（）A．4 B．3 C．2 D．1二、填空题38．（2017湖北省武汉市，第16题，3分）已知关于x的二次函数22(1)y ax a x a=+--的图象与x轴的一个交点的坐标为（m，0）．若2＜m＜3，则a的取值范围是．39．（2017四川省德阳市，第16题，3分）若抛物线22(1)(1)na a ay ax x n n n n +=-+-++与x 轴交于An 、Bn两点（a 为常数，a ≠0，n 为自然数，n ≥1），用Sn 表示An 、Bn 两点间的距离，则S1+S2+……+S2017＝_____________．40．（2017山东省莱芜市，第16题，4分）二次函数2y ax bx c =++（a ＜0）图象与x 轴的交点A 、B 的横坐标分别为﹣3，1，与y 轴交于点C ，下面四个结论：①16a ﹣4b+c ＜0；②若P （﹣5，y1），Q （52，y2）是函数图象上的两点，则y1＞y2；③a=﹣13c ；④若△ABC 是等腰三角形，则b=﹣27．其中正确的有（请将结论正确的序号全部填上）41．（2017四川省乐山市，第16题，3分）对于函数m n x x y +=，我们定义11--+='m n mx nx y （n m 、为常数）．例如24x x y +=，则x x y 243+='．已知：()x m x m x y 223131+-+=．（1）若方程0='y 有两个相等实数根，则m 的值为；（2）若方程41-='m y 有两个正数根，则m 的取值范围为．42．（2017四川省广元市，第15题，3分）已知二次函数2y ax bx c =++的图象如图所示，有下列结论：①abc ＜0；②a+c ＞b ；③3a+c ＜0；④a+b ＞m （am+b ）（其中m ≠1），其中正确的结论有．43．（2017四川省阿坝州，第24题，4分）如图，抛物线的顶点为P （﹣2，2），与y 轴交于点A （0，3）．若平移该抛物线使其顶点P 沿直线移动到点P′（2，﹣2），点A 的对应点为A′，则抛物线上PA 段扫过的区域（阴影部分）的面积为．44．（2017广西玉林崇左市，第18题，3分）已知抛物线：2y ax bx c （a ＞0）经过A （﹣1，1），B（2，4）两点，顶点坐标为（m ，n ），有下列结论：①b ＜1；②c ＜2；③0＜m ＜12；④n ≤1．则所有正确结论的序号是．45．（2017广西贺州市，第17题，3分）二次函数2y ax bx c =++ （a ，b ，c 为常数，a ≠0）的图象如图所示，下列结论：①abc ＜0；②2a+b ＜0；③b2﹣4ac=0；④8a+c ＜0；⑤a ：b ：c=﹣1：2：3，其中正确的结论有．46．（2017新疆乌鲁木齐市，第15题，4分）如图，抛物线2y ax bx c =++过点（﹣1，0），且对称轴为直线x=1，有下列结论：①abc ＜0；②10a+3b+c ＞0；③抛物线经过点（4，y1）与点（﹣3，y2），则y1＞y2；④无论a ，b ，c取何值，抛物线都经过同一个点（ca -，0）；⑤20am bm a ++≥，其中所有正确的结论是．47．（2016吉林省长春市）如图，在平面直角坐标系中，菱形OABC 的顶点A 在x 轴正半轴上，顶点C的坐标为（4，3）．D 是抛物线26y x x =-+上一点，且在x 轴上方．则△BCD 的最大值为．48．（2016四川省内江市）二次函数2y ax bx c =++的图象如图所示，且P=|2a+b|+|3b ﹣2c|，Q=|2a ﹣b|﹣|3b+2c|，则P ，Q 的大小关系是．49．（2016四川省南充市）已知抛物线2y ax bx c =++开口向上且经过点（1，1），双曲线12y x =经过点（a ，bc ），给出下列结论：①bc＞0；②b+c＞0；③b，c 是关于x 的一元二次方程21(1)02x a x a +-+=的两个实数根；④a﹣b ﹣c≥3．其中正确结论是（填写序号）50．（2016山东省菏泽市）如图，一段抛物线：y=﹣x （x ﹣2）（0≤x≤2）记为C1，它与x 轴交于两点O ，A1；将C1绕A1旋转180°得到C2，交x 轴于A2；将C2绕A2旋转180°得到C3，交x 轴于A3；…如此进行下去，直至得到C6，若点P （11，m ）在第6段抛物线C6上，则m= ．51．（2016广东省梅州市）如图，抛物线223y x x =-++与y 轴交于点C ，点D （0，1），点P 是抛物线上的动点．若△PCD 是以CD 为底的等腰三角形，则点P 的坐标为．52．（2016湖北省十堰市）已知关于x 的二次函数2y ax bx c =++的图象经过点（﹣2，1y ），（﹣1，2y ），（1，0），且120y y <<，对于以下结论：①abc＞0；②a+3b+2c≤0；③对于自变量x 的任意一个取值，都有24a b x x ba +≥-；④在﹣2＜x ＜﹣1中存在一个实数0x ，使得0a bx a +=-，其中结论错误的是（只填写序号）．53．（2016福建省厦门市）已知点P （m ，n ）在抛物线2y ax x a =--上，当m ≥﹣1时，总有n ≤1成立，则a 的取值范围是．54．（2015南通）关于x 的一元二次方程2310ax x --=的两个不相等的实数根都在﹣1和0之间（不包括﹣1和0），则a 的取值范围是．55．（2015宿迁）当x m =或x n =（m n ≠）时，代数式322+-x x 的值相等，则n m x +=时，代数式322+-x x 的值为．56．（2015贺州）已知二次函数2y ax bx c =++的图象如图所示，有以下结论：①abc＞0，②a﹣b+c ＜0，③2a=b，④4a+2b+c＞0，⑤若点（﹣2，1y ）和（13-，2y ）在该图象上，则12y y >．其中正确的结论是（填入正确结论的序号）．57．（2015雅安）为美化小区环境，决定对小区的一块空地实施绿化，现有一长为20m 的栅栏，要围成一扇形绿化区域，则该扇形区域的面积的最大值为．三、解答题58．（2017天门，第23题，10分）已知关于x 的一元二次方程221(1)(1)02x m x m -+++=有实数根．（1）求m 的值；（2）先作221(1)(1)2y x m x m =-+++的图象关于x 轴的对称图形，然后将所作图形向左平移3个单位长度，再向上平移2个单位长度，写出变化后图象的解析式；（3）在（2）的条件下，当直线y=2x+n （n ≥m ）与变化后的图象有公共点时，求24n n -的最大值和最小值．59．（2017云南省，第21题，8分）已知二次函数22y x bx c =-++图象的顶点坐标为（3，8），该二次函数图象的对称轴与x 轴的交点为A ，M 是这个二次函数图象上的点，O 是原点．（1）不等式b+2c+8≥0是否成立？请说明理由；（2）设S 是△AMO 的面积，求满足S=9的所有点M 的坐标．60．（2017北京市，第27题，7分）在平面直角坐标系xOy 中，抛物线243y x x =-+与x 轴交于点A 、B （点A 在点B 的左侧），与y 轴交于点C ．（1）求直线BC 的表达式；（2）垂直于y 轴的直线l 与抛物线交于点P （x1，y1），Q （x2，y2），与直线BC 交于点N （x3，y3），若x1＜x2＜x3，结合函数的图象，求x1+x2+x3的取值范围． 61．（2017四川省自贡市，第24题，10分）[探究函数x x y 4+=的图象与性质]（1）函数x x y 4+=的自变量x 的取值范围是；（2）下列四个函数图象中函数x x y 4+=的图象大致是；（3）对于函数x x y 4+=，求当x ＞0时，y 的取值范围．请将下列的求解过程补充完整．解：∵x ＞0∴x x y 4+==22((x x + =2x x + ． ∵2x x ≥0，∴y ≥ ．[拓展运用]（4）若函数259x x y x -+=，则y 的取值范围．62．（2017南京，第26题，8分）已知函数()21y x m x m=-+-+（m 为常数）．（1）该函数的图象与x 轴公共点的个数是． A ．0 B ．1 C ．2 D ．1或2 （2）求证：不论m 为何值，该函数的图象的顶点都在函数()21y x =+的图象上．（3）当﹣2≤m ≤3时，求该函数的图象的顶点纵坐标的取值范围． 63．（2017江苏省南通市，第25题，9分）某学习小组在研究函数3126y x x =-的图象与性质时，已列表、描点并画出了图象的一部分．x4- 3.5- 3- 2-1- 0 12 33.5 4y83- 748- 3283116 0 116-83-32- 74883（1）请补全函数图象；（2）方程31226x x -=-实数根的个数为；（3）观察图象，写出该函数的两条性质．64．（2017江西省，第22题，9分）已知抛物线1C ：245y ax ax =--（a ＞0）．（1）当a=1时，求抛物线与x 轴的交点坐标及对称轴；（2）①试说明无论a 为何值，抛物线1C 一定经过两个定点，并求出这两个定点的坐标；②将抛物线1C 沿这两个定点所在直线翻折，得到抛物线2C ，直接写出2C 的表达式；（3）若（2）中抛物线2C 的顶点到x 轴的距离为2，求a 的值．65．（2017湖北省荆州市，第23题，10分）已知关于x的一元二次方程2(5)10x k x k+-+-=，其中k为常数．（1）求证：无论k为何值，方程总有两个不相等实数根；（2）已知函数2(5)1y x k x k=+-+-的图象不经过第三象限，求k的取值范围；（3）若原方程的一个根大于3，另一个根小于3，求k的最大整数值．66．（2017湖南省株洲市，第24题，8分）如图所示，Rt△PAB的直角顶点P（3，4）在函数kyx=（x＞0）的图象上，顶点A、B在函数tyx=（x＞0，0＜t＜k）的图象上，PA∥x轴，连接OP，OA，记△OPA的面积为S△OPA，△PAB的面积为S△PAB，设w=S△OPA﹣S△PAB．①求k的值以及w关于t的表达式；②若用wmax和wmin分别表示函数w的最大值和最小值，令T=wmax+a2﹣a，其中a为实数，求Tmin．67．（2016四川省攀枝花市）如图，抛物线2y x bx c=++与x轴交于A、B两点，B点坐标为（3，0），与y轴交于点C（0，﹣3）（1）求抛物线的解析式；（2）点P在抛物线位于第四象限的部分上运动，当四边形ABPC的面积最大时，求点P的坐标和四边形ABPC的最大面积．（3）直线l经过A、C两点，点Q在抛物线位于y轴左侧的部分上运动，直线m经过点B和点Q，是否存在直线m，使得直线l、m与x轴围成的三角形和直线l、m与y轴围成的三角形相似？若存在，求出直线m的解析式，若不存在，请说明理由．68．（2016四川省雅安市）已知直线l1：y=x+3与x轴交于点A，与y轴交于点B，且与双曲线kyx=交于点C（1，a）．（1）试确定双曲线的函数表达式；（2）将l1沿y轴翻折后，得到l2，画出l2的图象，并求出l2的函数表达式；（3）在（2）的条件下，点P是线段AC上点（不包括端点），过点P作x轴的平行线，分别交l2于点M，交双曲线于点N，求S△AMN的取值范围．69．（2016山东省泰安市）如图，在平面直角坐标系中，抛物线2y ax bx c=++的顶点坐标为（2，9），与y轴交于点A（0，5），与x轴交于点E、B．（1）求二次函数2y ax bx c=++的表达式；（2）过点A作AC平行于x轴，交抛物线于点C，点P为抛物线上的一点（点P在AC上方），作PD平行与y轴交AB于点D，问当点P在何位置时，四边形APCD的面积最大？并求出最大面积；（3）若点M在抛物线上，点N在其对称轴上，使得以A、E、N、M为顶点的四边形是平行四边形，且AE为其一边，求点M、N的坐标．70．（2016山东省潍坊市）如图，已知抛物线213y x bx c=++经过△ABC的三个顶点，其中点A（0，1），点B（﹣9，10），AC∥x轴，点P是直线AC下方抛物线上的动点．（1）求抛物线的解析式；（2）过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F，当四边形AECP的面积最大时，求点P的坐标；（3）当点P为抛物线的顶点时，在直线AC上是否存在点Q，使得以C、P、Q为顶点的三角形与△ABC 相似，若存在，求出点Q的坐标，若不存在，请说明理由．71．（2016黑龙江省龙东地区）如图，二次函数2(2)y x m=++的图象与y轴交于点C，点B在抛物线上，且与点C关于抛物线的对称轴对称，已知一次函数y=kx+b的图象经过该二次函数图象上的点A （﹣1，0）及点B．（1）求二次函数与一次函数的解析式；（2）根据图象，写出满足2(2)x m kx b++≥+的x的取值范围．72．（2016山东省烟台市）如图1，已知平行四边形ABCD顶点A的坐标为（2，6），点B在y轴上，且AD∥BC∥x轴，过B，C，D三点的抛物线2y ax bx c=++（a≠0）的顶点坐标为（2，2），点F（m，6）是线段AD上一动点，直线OF交BC于点E．（1）求抛物线的表达式；（2）设四边形ABEF的面积为S，请求出S与m的函数关系式，并写出自变量m的取值范围；（3）如图2，过点F作FM⊥x轴，垂足为M，交直线AC于P，过点P作PN⊥y轴，垂足为N，连接MN，直线AC分别交x轴，y轴于点H，G，试求线段MN的最小值，并直接写出此时m的值．73．（2015来宾）在矩形ABCD中，AB=a，AD=b，点M为BC边上一动点（点M与点B、C不重合），连接AM，过点M作MN⊥AM，垂足为M，MN交CD或CD的延长线于点N．（1）求证：△CMN∽△BAM；（2）设BM=x，CN=y，求y关于x的函数解析式．当x取何值时，y有最大值，并求出y的最大值；（3）当点M在BC上运动时，求使得下列两个条件都成立的b的取值范围：①点N始终在线段CD上，②点M在某一位置时，点N恰好与点D重合．74．（2015桂林）如图，已知抛物线212y x bx c=-++与坐标轴分别交于点A（0，8）、B（8，0）和点E，动点C从原点O开始沿OA方向以每秒1个单位长度移动，动点D从点B开始沿BO方向以每秒1个单位长度移动，动点C、D同时出发，当动点D到达原点O时，点C、D停止运动．（1）直接写出抛物线的解析式：；（2）求△CED的面积S与D点运动时间t的函数解析式；当t为何值时，△CED的面积最大？最大面积是多少？（3）当△CED的面积最大时，在抛物线上是否存在点P（点E除外），使△PCD的面积等于△CED的最大面积？若存在，求出P点的坐标；若不存在，请说明理由．75．（2015梧州）如图，抛物线22y ax bx =++与坐标轴交于A 、B 、C 三点，其中B （4，0）、C （﹣2，0），连接AB 、AC ，在第一象限内的抛物线上有一动点D ，过D 作DE⊥x 轴，垂足为E ，交AB 于点F ．（1）求此抛物线的解析式；（2）在DE 上作点G ，使G 点与D 点关于F 点对称，以G 为圆心，GD 为半径作圆，当⊙G 与其中一条坐标轴相切时，求G 点的横坐标；（3）过D 点作直线DH∥AC 交AB 于H ，当△DHF 的面积最大时，在抛物线和直线AB 上分别取M 、N 两点，并使D 、H 、M 、N 四点组成平行四边形，请你直接写出符合要求的M 、N 两点的横坐标．76．（2015北海）如图1所示，已知抛物线245y x x =-++的顶点为D ，与x 轴交于A 、B 两点，与y 轴交于C 点，E 为对称轴上的一点，连接CE ，将线段CE 绕点E 按逆时针方向旋转90°后，点C 的对应点C′恰好落在y 轴上．（1）直接写出D 点和E 点的坐标；（2）点F 为直线C′E 与已知抛物线的一个交点，点H 是抛物线上C 与F 之间的一个动点，若过点H 作直线HG 与y 轴平行，且与直线C′E 交于点G ，设点H 的横坐标为m （0＜m ＜4），那么当m 为何值时，ΔHGF ΔBGF :S S =5：6？（3）图2所示的抛物线是由245y x x =-++向右平移1个单位后得到的，点T （5，y ）在抛物线上，点P 是抛物线上O 与T 之间的任意一点，在线段OT 上是否存在一点Q ，使△PQT 是等腰直角三角形？若存在，求出点Q 的坐标；若不存在，请说明理由．77．（2015南宁）在平面直角坐标系中，已知A 、B 是抛物线2y ax =（0a >）上两个不同的点，其中A 在第二象限，B 在第一象限，（1）如图1所示，当直线AB 与x 轴平行，∠AOB=90°，且AB=2时，求此抛物线的解析式和A 、B 两点的横坐标的乘积．（2）如图2所示，在（1）所求得的抛物线上，当直线AB 与x 轴不平行，∠AOB 仍为90°时，A ．B 两点的横坐标的乘积是否为常数？如果是，请给予证明；如果不是，请说明理由．（3）在（2）的条件下，若直线22--=x y 分别交直线AB ，y 轴于点P 、C ，直线AB 交y 轴于点D ，且∠BPC=∠OCP，求点P 的坐标．78．（2015崇左）如图，在平面直角坐标系中，点M 的坐标是（5，4），⊙M 与y 轴相切于点C ，与x 轴相交于A 、B 两点．（1）则点A 、B 、C 的坐标分别是A （__，__），B （__，__），C （__，__）；（2）设经过A 、B 两点的抛物线解析式为21(5)4y x k =-+，它的顶点为F ，求证：直线FA 与⊙M 相切；（3）在抛物线的对称轴上，是否存在点P ，且点P 在x 轴的上方，使△PBC 是等腰三角形．如果存在，请求出点P 的坐标；如果不存在，请说明理由．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

8.如图，在矩形ABCD 中，点E 是AD 边的中点，BE ⊥AC ，垂足为点F ，连接DF ，分析下列四个结论：①△AEF ∽△CAB ；②DF=DC ；③S △DCF =4S △DEF ；④tan ∠CAD=
2
2.其中正确结论的个数是（） A.4 B.3 C.2 D.1
16.如图，在△ABC 中，AB=AC=6，∠A=2∠BDC ，BD 交AC 边于点E ，且AE=4，则BE ·DE= .
22.如图，△ACE ，△ACD 均为直角三角形，∠ACE=90°，∠ADC=90°，AE 与CD 相交于点P ，以CD 为直径的⊙O 恰好经过点E ，并与AC ，AE 分别交于点B 和点F.
（1）求证：∠ADF=∠EAC.
（2）若PC=3
2PA ，PF=1，求AF 的长.
24.如图，一次函数64
3+=x y 的图像交x 轴于点A 、交y 轴于点B ，∠ABO 的平分线交x 轴于点C ，过点C 作直线CD ⊥AB ，垂足为点D ，交y 轴于点E.
（1）求直线CE 的解析式；
（2）在线段AB 上有一动点P （不与点A ，B 重合），过点P 分别作PM ⊥x 轴，PN ⊥y 轴，垂足为点M 、N ，是否存在点P ，使线段MN 的长最小？若存在，请直接写出点P 的坐标；若不存在，请说明理由.
25.如图，∠MBN=90°，点C 是∠MBN 平分线上的一点，过点C 分别作AC ⊥BC ，CE ⊥BN ，垂足分别为点C ，E ，AC=24,点P 为线段BE 上的一点（点P 不与点B 、E 重合），连接CP ，以CP 为直角边，点P 为直角顶点，作等腰直角三角形CPD ，点D 落在BC 左侧.
（1）求证：CB
CE CD CP =；（2）连接BD ，请你判断AC 与BD 的位置关系，并说明理由；
（3）设PE=x ，△PBD 的面积为S ，求S 与x 之间的函数关系式.
26.如图，抛物线22
3212++-=x x y 与x 轴交于A 、B 两点（点A 在点B 的左侧），与y 轴交于点C.
（1）试探究△ABC 的外接圆的圆心位置，求出圆心坐标；
（2）点P 是抛物线上一点（不与点A 重合），且S △PBC =S △ABC ，求∠APB 的度数；
（3）在（2）的条件下，点E 是x 轴上方抛物线上一点，点F 是抛物线对称轴上一点，是否存在这样的点E 和点F ，使得以点B 、P 、E 、F 为顶点的四边形是平行四边形？若存在，请直接写出点F 的坐标；若不存在，请说明理由.
10．（2017四川省遂宁市，第10题，4分）函数2y x bx c =++与函数y x =的图像如图所示，有以下结论：①240b c -＞；②0b c +=；③0b ＜；④方程组2y x bx c y x
⎧=++⎨=⎩的解为1111x y =⎧⎨=⎩，2233x y =⎧⎨=⎩；⑤当13x ＜＜时，2(1)0x b x c +-+＞.其中正确的是（）
A ．①②③
B ．②③④
C ．③④⑤
D ．②③⑤
14．（2017四川省遂宁市，第14题，4分）如图，直线113
y x =+与x 轴，y 轴分别交于A 、B 两点，△BOC 与△B ′O ′C ′是以点A 为位似中心的位似图形，且相似比为1：2，则点B ′的坐标为．
15．（2017四川省遂宁市，第15题，4分）如图，正方形ABCD 的边长为4，点E 、F 分别从点A 、点D 以相同速度同时出发，点E 从点A 向点D 运动，点F 从点D 向点C 运动，点E 运动到D 点时，E 、F 停止运动．连接BE 、AF 相交于点G ，连接CG ．有下列结论：①AF ⊥BE ；②点G 随着点E 、F 的运动而运动，且
点G 的运动路径的长度为π；③线段DG 的最小值为2；④当线段DG 最小
时，△BCG 的面积8S =+其中正确的命题有．（填序号）
22．（2017四川省遂宁市，第22题，10分）关于三角函数有如下公式： sin()sin cos cos sin αβαβαβ+=+，sin()sin cos cos sin αβαβαβ-=- cos()cos cos sin sin αβαβαβ+=-，cos()cos cos sin sin αβαβαβ-=+ tan tan tan()(1tan tan 0)1tan tan αβαβαβαβ
++=-≠- tan tan tan()(1tan tan 0)1tan tan αβαβαβαβ--=
+≠+
利用这些公式可以将一些不是特殊角的三角函数转化为特殊角的三角函数来求值．
如：°°°°°
°°tan 45tan 60tan105tan(4560=21tan 45tan 60+=+==--）根据上面的知识，你可以选择适当的公式解决下面问题：
如图，两座建筑物AB 和DC 的水平距离BC 为24米，从点A 测得点D 的俯角α=15°，测得点C 的俯角β=75°，求建筑物CD 的高度．
24．（2017四川省遂宁市，第24题，10分）如图，CD 是⊙O 的直径，点B 在⊙O 上，连接BC 、BD ，直线AB 与CD 的延长线相交于点A ，2AB AD AC =g ，OE ∥BD 交直线AB 于点E ，OE 与BC 相交于点F ．
（1）求证：直线AE 是⊙O 的切线；
（2）若⊙O 的半径为3，cosA=45
，求OF 的长．
25．（2017四川省遂宁市，第25题，12分）如图，抛物线2y ax bx c =++（a ≠0），经过点A （-1，0），B （3，0），C （0，3）三点．
（1）求抛物线的解析式及顶点M 的坐标；
（2）连接AC 、BC ，N 为抛物线上的点且在第四象限，当NBC ABC S S △△时，求N
点的坐标；
（3）在（2）问的条件下，过点C 作直线l ∥x 轴，动点P （m ，3）在直线l 上，动点Q （m ，0）在x 轴上，连接PM 、PQ 、NQ ，当m 为何值时，PM+PQ+QN 的和最小，并求出PM+PQ+QN 和的最小值．。