初中计算题练习题汇总-共39页

合集下载

200道初中计算题及答案

200道初中计算题及答案作为一个虚拟智能助手，我很抱歉无法为您提供2200字篇幅的完整文章。

然而，我可以为您提供一些初中计算题及答案的示例，您可以根据需要将其进行整理和编排。

请注意，以下仅为示例，具体题目和答案可根据您的需求进行调整。

1. 算术运算题：1) 请计算：12 + 8 - 5 × 2 = ?答案：12 + 8 - 5 × 2 = 12 + 8 - 10 = 22 - 10 = 122) 请计算：(4 + 7) × 3 + 5 = ?答案：(4 + 7) × 3 + 5 = 11 × 3 + 5 = 33 + 5 = 382. 分数运算题：1) 请计算：1/3 + 2/5 = ?答案：1/3 + 2/5 = (5/15) + (6/15) = 11/152) 请计算：3/4 - 1/6 = ?答案：3/4 - 1/6 = (9/12) - (2/12) = 7/123. 百分数计算题：1) 请计算：75% × 120 = ?答案：75% × 120 = (75/100) × 120 = 0.75 × 120 = 902) 请计算：32 ÷ 80% = ?答案：32 ÷ 80% = 32 ÷ (80/100) = 32 ÷ 0.8 = 404. 代数方程题：1) 若 x + 5 = 10, 求 x 的值。

答案：由方程 x + 5 = 10, 可得 x = 10 - 5 = 52) 若 2x + 3 = 9, 求 x 的值。

答案：由方程 2x + 3 = 9, 可得 2x = 9 - 3 = 6，再除以2得 x = 6 ÷ 2 = 35. 几何计算题：1) 已知正方形的边长为 8cm，求其面积。

答案：正方形的面积等于边长的平方，即面积 = 8cm × 8cm = 64cm²2) 已知长方形的长为 12cm，宽为 6cm，求其周长。

初中物理浮力计算题专题练习(含答案解析)

初中物理浮力计算题专题练习（含答案解析）一、计算题（本大题共45小题，共360.0分）1.一个实心石块在空气中称重10N，浸没在水中称重6N，求：(1)石块的质量．(2)石块所受到水的浮力．(3)石块的体积．(4)石块的密度.(g=10N/kg、ρ水=1.0×103kg/m3)2.在“阿基米德解开王冠之谜”的故事中，若王冠的重为4.9N，浸没在水中称重时，测力计示数为4.5N，求：(1)王冠浸没在水中受到的浮力是多少？王冠的体积是多少？(2)通过计算说明王冠是否是纯金制成的？(ρ金=19.3×103kg/m3)3.将边长是10cm的实心立方体木块轻轻地放入盛满水的大水槽内。

待木块静止时，从水槽中溢出了600g水，g取10N/kg，求：(1)木块受到的浮力；(2)木块的密度；(3)木块下表面受到的水的压强。

4.如图所示，一正方体边长为10cm，浸没在水中，上表面离水面的深度为5cm．求：(1)物体上表面受到水的压强和压力；(2)物体下表面受到水的压强和压力；(3)正方体在水中受到的浮力是多少？5.在如图所示的甲中，石料在钢丝绳拉力的作用下从水面上方以恒定的速度下降，直至全部没入水中.图乙是钢丝绳拉力随时间变化的图象，若不计水的摩擦力.求：(g取10N/kg)(1)石料的重力(2)石料浸没在水中时受到的浮力(3)石料的体积．6.某物体在空气中称重是10N，浸没在水中称重是6.8N，求这个物体受到的浮力？7.一个机器零件在空气中称重为4N，把它浸没在水中再称为3.5N，g=10N/kg，求：(1)零件受到的浮力；(2)零件的质量；(3)零件的体积；(4)零件的密度．8.一边长为10cm，密度为0.6×103kg/m3的正方体木块，用细线置于容器的水中，静止时如图所示。

已知水的密度为1×103kg/m3求：(1)木块所受的浮力大小？(2)细线的拉力大小？(3)细线剪断后，木块在水面静止时，木块下方所受到水的压力是多大？9.冲锋舟在抗洪救灾中发挥了重要作用，如图所示，冲锋舟满载时排开水的体积是1.5m3，冲锋舟自重为0.6×104N，假设每人的平均质量为60kg，请计算：(1)冲锋舟满载时所受的浮力；(2)为保证安全，这条冲锋舟最多能承载的人数．g10N/kg)．10.如图所示已知重10长方体块静在水上，浸入在水中的体积木块总体积的45求木块所受浮力大小；若要将木块全浸没水，求至少需要大的压力．11.边长是0.1米的正方体，浸在水里，上表面距液面10厘米.则：(1)物体上表面受到的压力是多少牛顿？(2)下表面受到的压力是多少牛顿？(3)所受的浮力是多少牛顿？(取=10牛/千克)12.如图所示，一边长为20cm的正方体木块漂浮在水面上，木块浸入水中的深度为12cm。

初三数学计算题练习试题集

初三数学计算题练习试题答案及解析1.计算：【答案】.【解析】根据绝对值、有理数的乘方、立方根、特殊角三角函数值的意义分别进行计算即可求出答案.原式.【考点】实数的混合运算.2.计算：（1），（2）【答案】（1）；（2）．【解析】（1）分别求出值，再化简；（2）化成最简二次根式，再进行计算．试题解析：（1）；（2）．【考点】1.负指数次幂2.特殊角的三角函数3.绝对值4.零次幂5.二次根式混合运算．3.计算：．【答案】3.【解析】根据特殊角三角函数值、绝对值、零次幂、负整数指数幂、二次根式的意义进行计算即可得出答案.试题解析：=3.考点: 实数的混合运算.4.化简：．【答案】8.【解析】先根据单项式乘以多项式展开，再求出即可．试题解析：考点:5.计算：.【答案】．【解析】任何非零数的零次方都为1，负数的绝对值等于它的相反数，再对二次根式进行化简即可．试题解析：．【考点】二次根式的化简．6.计算：（－）÷＋．【答案】．【解析】先去括号，再计算除法，最后计算加减法．试题解析：原式=．【考点】二次根式的混合运算．7.计算题：①、；②、【答案】①、；②、【解析】根据二次根式的混合运算的法则结合二次根式的性质依次计算即可.试题解析：①、；②、.【考点】实数的运算8.计算：．【答案】解：原式=。

【解析】针对特殊角的三角函数值，绝对值，零指数幂，有理数的乘方，负整数指数幂5个考点分别进行计算，然后根据实数的运算法则求得计算结果。

9.（1）解方程：；（2）解方程组：．【答案】（1）x＝—6 （2）【解析】（1）方程两边同乘以，得∴检验：当时，≠0,即是原分式方程的解（2）解得x=2把x=2代入x-y=1中，解得y=1∴【考点】分式方程和二元一次方程组点评：该题是常考题，主要考查学生对分式方程和二元一次方程组的解题过程的掌握，记得分式方程要检验。

10.计算：【答案】【解析】根据二次根式的性质、负整数指数幂、特殊角的锐角三角函数值、立方根的定义计算即可.原式==.【考点】实数的运算点评：计算题是中考必考题，一般难度不大，学生要特别慎重，尽量不在计算上失分.11.【答案】9【解析】原式= 6分= 9【考点】实数的运算点评：解答本题的关键是熟练掌握任何非0数的0次幂为1；两个式子的积为0，则这两个式子至少有一个为0.,12.一种拉杆式旅行箱的示意图如图所示，箱体长AB=50cm，拉杆最大伸长距离BC=30cm，点A到地面的距离AD=8cm，旅行箱与水平面AE成60°角，求拉杆把手处C到地面的距离（精确到1cm）．（参考数据：）【答案】77【解析】解：过点C作CM⊥DF于点M，交AE于点N易证CN⊥AE，∴四边形ADMN是矩形，MN=AD=8cm 3分在中，∠CAN=60°∴sin60°=(50+30)×= 6分∴cm 9分答：拉杆把手处C到地面的距离约77cm．【考点】勾股定理，三角函数的值点评：本题属于勾股定理的基本运算和求解方法，在解题中需要合理的作图13.（本题满分12分）如图，I是△ABC的内心，∠BAC的平分线与△ABC的外接圆相交于点D。

(精品)七年级数学计算题大全

七年级数学计算题大全第一部分：数的运算一、加法1. 基础加法：计算 23 + 45 = ?2. 进位加法：计算 57 + 48 = ?3. 多位数加法：计算 123 + 456 = ?二、减法1. 基础减法：计算 56 23 = ?2. 借位减法：计算 87 45 = ?3. 多位数减法：计算 123 456 = ?三、乘法1. 基础乘法：计算7 × 8 = ?2. 两位数乘法：计算23 × 45 = ?3. 多位数乘法：计算123 × 456 = ?四、除法1. 基础除法：计算56 ÷ 7 = ?2. 两位数除法：计算456 ÷ 23 = ?3. 多位数除法：计算5 ÷ 456 = ?五、分数的运算1. 分数加法：计算 1/2 + 3/4 = ?2. 分数减法：计算 3/4 1/2 = ?3. 分数乘法：计算1/2 × 3/4 = ?4. 分数除法：计算3/4 ÷ 1/2 = ?六、小数的运算1. 小数加法：计算 1.23 + 4.56 = ?2. 小数减法：计算 5.67 2.34 = ?3. 小数乘法：计算1.23 ×4.56 = ?4. 小数除法：计算5.67 ÷ 2.34 = ?七、整数与分数、小数的混合运算1. 整数加分数：计算 3 + 1/2 = ?2. 整数减分数：计算 5 3/4 = ?3. 整数乘分数：计算2 × 3/4 = ?4. 整数除分数：计算4 ÷ 3/2 = ?5. 分数加小数：计算 1/2 + 0.25 = ?6. 分数减小数：计算 3/4 0.5 = ?7. 分数乘小数：计算1/2 × 0.5 = ?8. 分数除小数：计算1/2 ÷ 0.5 = ?七年级数学计算题大全第一部分：数的运算一、加法1. 基础加法：计算 23 + 45 = ?2. 进位加法：计算 57 + 48 = ?3. 多位数加法：计算 123 + 456 = ?二、减法1. 基础减法：计算 56 23 = ?2. 借位减法：计算 87 45 = ?3. 多位数减法：计算 123 456 = ?三、乘法1. 基础乘法：计算7 × 8 = ?2. 两位数乘法：计算23 × 45 = ?3. 多位数乘法：计算123 × 456 = ?四、除法1. 基础除法：计算56 ÷ 7 = ?2. 两位数除法：计算456 ÷ 23 = ?3. 多位数除法：计算5 ÷ 456 = ?五、分数的运算1. 分数加法：计算 1/2 + 3/4 = ?2. 分数减法：计算 3/4 1/2 = ?3. 分数乘法：计算1/2 × 3/4 = ?4. 分数除法：计算3/4 ÷ 1/2 = ?六、小数的运算1. 小数加法：计算 1.23 + 4.56 = ?2. 小数减法：计算 5.67 2.34 = ?3. 小数乘法：计算1.23 ×4.56 = ?4. 小数除法：计算5.67 ÷ 2.34 = ?七、整数与分数、小数的混合运算1. 整数加分数：计算 3 + 1/2 = ?2. 整数减分数：计算 5 3/4 = ?3. 整数乘分数：计算2 × 3/4 = ?4. 整数除分数：计算4 ÷ 3/2 = ?5. 分数加小数：计算 1/2 + 0.25 = ?6. 分数减小数：计算 3/4 0.5 = ?7. 分数乘小数：计算1/2 × 0.5 = ?8. 分数除小数：计算1/2 ÷ 0.5 = ?八、应用题1. 求解问题：小华有 3 个苹果，小明有 5 个苹果，他们一共有多少个苹果？2. 面积问题：一个长方形的长是 8 厘米，宽是 5 厘米，求这个长方形的面积。

初中数学计算题复习大全附答案【中考必备】

..初中数学计算题大全（一）计算下列各题1 .36)21(60tan 1)2(100+-----π 2． 431417)539(524----3．)4(31)5.01(14-÷⨯+-- 4．5．++ 6．7112238．（1）03220113)21(++-- （2）23991012322⨯-⨯10．11．（1）- （2）÷(3)1---+42338-()232812564.0-⨯⨯⎪⎭⎫ ⎝⎛-÷⎪⎭⎫⎝⎛-+601651274312．418123+-13．⎛ ⎝14．．x x x x 3)1246(÷- 15．61)2131()3(2÷-+-；16．20)21()25(2936318-+-+-+-17．（1）)3127(12+- （2）()()6618332÷-+-18．()24335274158.0--+⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛---1911()|2|4-- 20．())120131124π-⎛⎫---+ ⎪⎝⎭。

21．． 22．112812623-+23．2+参考答案1．解=1－|1－3|－2+23 =1+1－3－2+23 =3【解析】略2．5【解析】原式=14-9=53．87-【解析】解：)4(31)5.01(14-÷⨯+--⎪⎭⎫⎝⎛-⨯⨯--=4131231811+-=87-=先算乘方，再算乘除，最后算加减，有括号的先算括号里面的。

注意：41-底数是4，有小数又有分数时，一般都化成分数再进行计算。

4．＝＝．【解析】略5．3 6．4【解析】主要考查实数的运算，考查基本知识和基本的计算能力，题目简单，但易出错，计算需细心。

1、+ +=232=3+-252=42⨯⨯ 722【解析】试题分析:先化简，再合并同类二次根式即可计算出结果.11223432223232332考点: 二次根式的运算.8．（1）32（2）9200 【解析】（1）原式=4+27+1 =32（2）原式=23（1012-992） (1分)=23（101+99）(101-99)（2分）=232200⨯⨯=9200 （1分）利用幂的性质求值。

中考数学计算题100道

中考数学计算题100道练习1. 解方程组：{x 3−y 2=15x +3y =82. 解下列方程组：(1){4a +b =153b −4a =13(2){2(x −y)3−x +y 4=−16(x +y)−4(2x −y)=163. 解下列方程组(1){3x +5y =112x −y =3 (2){x 2−y+13=13(x +2)=−2y +124. 解下列方程组：(1){4x −3y =11y =13−2x； (2){x 4+y 3=33x −2(y −1)=11．5. 解下列方程(组)(1) 2−x x−3+3=23−x (2){2x −y =57x −3y =206. 解下列方程：(1)1−2x−56=3−x 4；(2)1.7−2x 0.3=1−0.5+2x 0.6．7. 解下列方程12[x −12(x −1)]=23(x −1)8. 2x−112−3x−24=19.解方程：(1)5(x+8)=6(2x−7)+5(2)0.1x−0.20.02−x+10.5=310.(1)化简：(x+y)(x−y)−(2x−y)(x+3y)；(2)解方程：(3x+1)(3x−1)−(3x+1)2=−8．11.解方程：(1)(x−1)2=4；(2)xx+1=2x3x+3+1．12.解方程：(1)x2=3x.(2)3x2−8x−2=0．13.x2−2(√2x−2)=2．14.解方程：(1)(x−3)(x−1)=3．(2)2x2−3x−1=0．15.解方程：(1)x2−121=0(2)2(x−1)2=33816.解方程(1)x2−2x−6=0；(2)(2x−3)2=3(2x−3)．17.解方程：(1)3(x−2)2=x(x−2)；(2)3x2−6x+1=0(用配方法)．18. 用适当的方法解下列方程：(1)x 2−12x −4=0(2)x(3−2x)= 4 x −619. 计算：(1)|−2|+(sin36°−12)0−√4+tan45°；(2)用配方法解方程：4x 2−12x −1=0．20. 解分式方程x x−1−1=3x 2−121. 解分式方程：2x 2−4=1−x x−2.22. 解下列方程：(1)x x−1−2x−1x 2−1=1(2)2−x x −1+11−x =123.解方程(1)23+x3x−1=19x−3(2)xx2−4+2x+2=1x−224.解方程(1)x2x−5+55−2x=1(2)8x2−1+1=x+3x−125.解下列分式方程：(1)1x−2+3=1−x2−x；(2)x+1x−1−4x2−1=1.26.解方程1x−3+1=4−xx−3．27.解下列方程：(1)3x−1−1=11−x；(2)xx+1−2x2−1=1．28.解方程：5−xx−4=1−34−x．29.解方程：16x2−4−x+2x−2=−1．30.(1)计算：(√7−1)0−(−12)−2+√3tan30∘；(2)解方程：x+1x−1+41−x2=1．31.解方程：2(x+1)x−1−x−1x+1=1．32.解分式方程：(1)1x−4=1−x−34−x．(2)810.9x−661.1x=4033.解方程：(1)3x+2=43x−1(2)xx+1−2x2−1=134.解分式方程：1x +3x−3=23x−x235.(1)分解因式：3a3−27a；(2)解方程：2x =3x−2．36.解分式方程：(1)3x−2+2=x2−x．(2)2x−1=4x2−1．37.计算：(1)(a−2b)2+(a−2b)(a+2b)(2)解分式方程3x−2=3+x2−x38.解方程：x−12−x −2=3x−2．39.解答下列各题(1)解方程：x24−x2=1x+2−1．(2)先化简，再求值：a−33a2−6a ÷(a+2−5a−2)，其中a2+3a−1=0．40.解方程：3x+1=x2x+2+141.(1)分解因式：(a−b)(x−y)−(b−a)(x+y)(2)分解因式：5m(2x−y)2−5mn2(3)解方程：2x+1−2x1−x2=1x−142.解方程：x2+1x2−2(x+1x)−1=0．43.解方程xx−2+6x+2=144. 解分式方程(1)3x+2=2x−3 (2)8x 2−4−x x−2=−145. 求不等式组{2x −1≤13x −3<4x 的整数解．46. 解不等式组：{3(x +1)>x −1x+92>2x47. 解不等式组{2x +3≤x +112x+53−1>2−x ．48. 解不等式组：{2x −1>x +13(x −2)−x ≤449. 解下列方程：(1)解方程：x 2+4x −2=0；(2)解不等式组：{x −3(x −2)≥24x −2<5x +1．50. (1)计算：(π−2)0+√8−4×(−12)2(2)解不等式组：{3(x −2)≤4x −55x−24<1+12x51. 解不等式：1−x 2>−1．52. 解下列不等式，并把解集在数轴上表示出来：(1)5x−13−2x >3； (2)x−12−x+43>−2．53. 解不等式组{2x −1⩽x +2x−23<x 2+1，并把解在数轴上表示出来．54.解不等式组：{x+1>05−4(x−1)<155.解不等式4(x−1)+3≤2x+5，并把它的解集在数轴上表示出来．56.解不等式组{2x≥−4①12x+1<32②，并把不等式组的解集表示在数轴上．57.因式分解：(1)24ax2−6ay2;(2)(2a−b)2+8ab 58.因式分解(1)2x2−4x59. 分解因式：8ab −8b 2−2a 2 60. (1)分解因式：2x 2−18(2)解不等式组{5m −3≥2(m +3)13m +1>12m61. 因式分解：(1)16m (m −n )2+56(n −m )3；(2)(2a +3b )(a −2b )−(3a +2b )(2b −a )．62. 因式分解：(1)4a 2−9 (2)x 3−2x 2y +xy 263.分解因式：(1)6m2n−15n2m+30m2n2；(2)x(x−y)2−y(x−y)．64.因式分解：(1)x(x−12)+4(3x−1).(2)m3n−4m2n+4mn65.因式分解：(x2−5)2+8(x2−5)+1666.分解因式：(1)x3−3x2−28x(2)12x2−x−2067.化简：(1)(x+y)2−(x−2y)(x+y)(2)(2x+1x2−4x+4−1x−2)÷x+3x2−4(1)√12−|−3|−3tan30∘+(−1+√2)0 (2) (x +1)(x −1)−(x −2)269. 计算：(1)√643+|√2−1|−π0+(12)−1;(2)(2x −1)2−(3x +1)(3x −1)+5x(x −1)．70. (1)计算： |−3|−4cos60°+(2019−2020)0．(2)先化简，再求值：(x +2)2−x (x −2)，其中x =2．71. 化简：(√3+√2)2019⋅(√3−√2)2020．72. 解下列各题：(1)计算：(x +2)2+(2x +1)(2x −1)−4x(x +1)(2)分解因式：−y 3+4xy 2−4x 2y73. 先化简，再求值：[a (a 2b 2−ab )−b (a 2−a 3b )]÷2a 2b ，其中a =−12，b =13．74. 计算：(1)(−2)2×|−3|−(√6)0 (2)(x +1)2−(x 2−x)75. 计算(1)|−1|+(3−π)0+(−2)3−(13)−2(2)(x 4)3+(x 3)4−2x 4⋅x 876. 计算：(1)(2x 2)3−x 2·x 4；(2)−22+(12)−2−2−1×(−12)0．77. 计算：①(−2020)0+√−83+tan45∘；②(a +b)(a −b)+b(b −2)．78.(1)计算：x(x−9y)−(x−8y)(x−y)(2)计算：(−12a5b3+6a2b−3ab)÷(−3ab)−(−2a2b)2．)−279.计算：|√3−2|+(π−2019)0+2cos30∘−(−13)−1+|1−2cos45°|80.√2×(−1)2017−(1281.计算：cos245∘−2sin60∘−|√3−2|．)−2−(2019+π)0−|2−√5|82.计算：(−12)0；83.(1)计算：−24−√12+|1−4sin60°|+(π−23(2)解方程：2x2−4x−1=0．)−2−|√3−2|84.计算√27−3tan 30∘+(−12)−3．85.计算：√3×(−√6)+|−2√2|+(123−√(−5)2+(π−3.14)0+|1−√2|．86.计算：√273−√1+9；(2)√(−2)2+|√2−1|−(√2−1) 87.计算(1)√16+√−2788. 计算：(12)−1+(−2019)0−√9+√27389. 计算：(−2)−1−12√8−(5−π)0+4cos45∘90. 计算：(12)−1−(√2−1)0+|1−√3|+√1291. (1)计算(−12)−1+√16−(π−3.14)0−|√2−2|(2)化简：(2m m+2−m m−2)÷m m 2−4．92. 计算下列各题．(1)√4+(π−3.14)0−|−√3|+(13)−1 (2)√−83+(√3)2+√(−3)2+|1−√2|93. 计算：|1−√2|−√6×√3+(2−√2)0．94. 计算：(√12+√3)×√6−4√32÷√395. 计算：12×(√3−1)2√2−1−(√22)−1.96. 已知a =2+√3，求1−2a+a 2a−1−√a 2−2a+1a 2−a 的值．97. √(1−√3)2−√24×√122−√398. 计算：(1)√32−√8+√12×√3 (2)|√3−2|+(√3)−1−(√2−1)099. 计算：(1)2√45+3√15+√(2−√5)2； √2√6−2√3(√6−√2)．100.先化简，再求值：1−a−2a ÷a 2−4a 2+a ，请从−2，−1，0，1，2中选择一个合适的数，求此分式的值．答案和解析1.【答案】解：{x 3−y 2=1①5x +3y =8②,①×6，得2x −3y =6③②+③，得7x =14，解得x =2，把x =2代入②，得10+3y =8，解得y =−23，∴原方程组的解为{x =2y =−23．【解析】本题主要考查二元一次方程组的解法，可利用加减消元法求解，将①×6得③，再利用②+③解得x 值，再将x 值代入②求解y 值，即可得解．2.【答案】解：(1){4a +b =15 ①3b −4a =13 ②, ①+②得，4b =28，解得：b =7，把b =7代入①得：4a +7=15，解得：a =2，则方程组的解为{a =2b =7； (2)将原方程组变形得{5x −11y =−12①x −5y =−8②, ②×5−①得：−14y =−28，解得：y =2，把y =2代入②得：x =2，则方程组的解为{x =2y =2．【解析】此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．(1)方程组利用加减消元法求出解即可；(2)方程组整理后，利用加减消元法求出解即可．3.【答案】解：(1){3x +5y =11①2x −y =3②, ①+②×5，得：13x =26，解得：x =2，将x =2代入②，得：4−y =3，解得：y =1，所以方程组的解为{x =2y =1； (2)将方程组整理成一般式为{3x −2y =8①3x +2y =6②, ①+②，得：6x =14，解得：x =73，将x =73代入①，得：7−2y =8，解得：y =−12，所以方程组的解为{x =73y =−12．【解析】此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．(1)方程组利用加减消元法求出解即可；(2)方程组整理后，利用加减消元法求出解即可．4.【答案】解：(1)原方程可化为{4x −3y =11①2x +y =13②, ②×2−①得：5y =15，解得：y =3，把y =3代入②得：x =5，所以方程组的解为{x =5y =3； (2)整理原方程组得{3x +4y =36①3x −2y =9②, ①−②得：6y =27，解得：y =92，把y =92代入②得：x =6，所以方程组的解为{x =6y =92．【解析】本题主要考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．(1)方程组利用加减消元法求出解即可；(2)方程组整理后，利用加减消元法求出解即可．5.【答案】解：(1)去分母得：2−x +3(x −3)=−2，解得：x =2.5，经检验x =2.5为原分式方程的解；(2){2x −y =5①7x −3y =20②， ②−①×3得：x =5，把x =5代入①得：y =5，则方程组的解为{x =5y =5．【解析】此题考查了解分式方程，利用了转化的思想，解分式方程时注意要检验．(1)分式方程去分母转化为整式方程，求出整式方程的解得到x 的值，经检验即可得到分式方程的解；(2)方程组利用加减消元法求出方程组的解即可．6.【答案】解：(1)去分母，得12−4x +10=9−3x ，移项、合并同类项，得−x =−13；系数化为1，得x =13；(2)去分母得：3.4−4x =0.6−0.5−2x ，移项合并得：2x =3.3，解得：x =1.65．【解析】本考查了解一元一次方程，其步骤为：去分母，去括号，移项合并，把x 系数化为1，求出解；方程整理后，去分母，去括号，移项合并，把x 系数化为1，即可求出解．7.【答案】12[x −12(x −1)]=23(x −1)解：12x −14(x −1)]=23(x −1)6x −3(x −1)]=8(x −1)6x −3x +3=8x −86x −3x −8x =−8−3−5x =−11x =115【解析】此题考查了解一元一次方程，去括号，去分母，再去括号，移项合并，把未知数系数化为1，求出解．8.【答案】解：去分母，得2x −1−3(3x −2)=12，去括号，得2x −1−9x +6=12，移项，得2x −9x =12+1−6，合并同类项，得−7x =7，系数化成1，得x =−1．【解析】本题主要考查了解一元一次方程，注意在去分母时，方程两端同乘各分母的最小公倍数时，不要漏乘没有分母的项，同时要把分子(如果是一个多项式)作为一个整体加上括号．先去分母，再去括号，最后移项，合并同类项，化系数为1，从而得到方程的解．9.【答案】解：(1)原方程去括号得5x +40=12x −42+5，移项可得：12x −5x =40+42−5，合并同类项可得：7x =77，解得：x =11．(2)原方程去分母得5x −10−2(x +1)=3，去括号得5x −10−2x −2=3，移项合并可得：3x =15，解得：x=5．【解析】本题考查的是解一元一次方程有关知识．(1)首先对该方程去括号变形，然后再进行合并，最后再解答即可；(2)首先对该方程去分母变形，然后再解答即可．10.【答案】解：(1)原式=x2−y2−(2x2+5xy−3y2)=−x2−5xy+2y2；(2)去括号，得9x2−1−(9x2+6x+1)=−8，9x2−1−9x2−6x−1=−8，合并，得−6x−2=−8，解得x=1．【解析】(1)先根据平方差公式和多项式乘多项式法则计算，再合并同类项即可求解；(1)先根据平方差公式和完全平方公式计算，再合并同类项得到−6x−2=−8，再解一元一次方程即可求解．本题考查了平方差公式，多项式乘多项式，完全平方公式，解一元一次方程，解一元一次方程的一般步骤：去分母、去括号、移项、合并同类项、系数化为1，这仅是解一元一次方程的一般步骤，针对方程的特点，灵活应用，各种步骤都是为使方程逐渐向x=a 形式转化．11.【答案】解：(1)(x−1)2=4，两边直接开平方得：x−1=±2，∴x−1=2或x−1=−2，解得：x1=3，x2=−1；(2)xx+1=2x3x+3+1方程两边都乘3(x+1)，得：3x=2x+3(x+1)，解得：x=−32，经检验x=−32是方程的解，∴原方程的解为x=−32．【解析】本题主要考查了一元二次方程的解法和分式方程的解法，解分式方程的关键是去分母，将分式方程转化为整式方程，注意解分式方程要检验．(1)先两边直接开平方，然后转化为两个一元一次方程，解之即可；(2)先在方程两边同时乘以3(x+1)，去掉分母，然后解整式方程，最后检验即可．12.【答案】解：(1)x2=3xx2−3x=0x(x−3)=0x 1=0 ,x 2=3(2)3x 2−8x −2=0∵△=64−4×3×(−2)=88∴x =8±√886=4±√223 x 1=4+√223 ,x =4−√223【解析】本题考查一元二次方程的解法，熟练应用各种解法是解题的关键．(1)先把方程化为一元二次方程的一般形式，用因式分解法解方程即可；(2)用公式法解方程，先求出△的值，然后运用一元二次方程的求根公式求出方程的根即可．13.【答案】解：∵x 2−2(√2x −2)=2，∴x 2−2√2x +4=2，∴x 2−2√2x +2=0，∴(x −√2)2=0，解得：x 1=x 2=√2．【解析】本题主要考查的是直接开平方法解一元二次方程的有关知识，先将给出的方程进行变形为(x −√2)2=0，然后直接开平方求解即可．14.【答案】解：(1)原式化简得x 2−4x =0，因式分解得x(x −4)=0，即x =0或x −4=0，解得x 1=0，x 2=4；(2)2x 2−3x −1=0，∵a =2，b =−3，c =−1，则b 2−4ac =9+8=17>0，则x = 3±√174 ，则x 1= 3+√174 ，x 2= 3−√174 ．【解析】本题考查了一元二次方程的解法，解一元二次方程常用的方法有直接开平方法，配方法，公式法，因式分解法，要根据方程的特点灵活选用合适的方法．(1)先化简，提取公因式x 可得x(x −4)=0，然后解两个一元一次方程即可；(2)直接运用公式法来解方程．15.【答案】解：(1)x 2=121，x =±11，x 1=11，x 2=−11；(2)(x −1)2=169，x −1=±13，x 1=14， x 2=−12.【解析】略16.【答案】解：(1)x 2−2x −6=0，x 2−2x =6，x 2−2x +1=7，(x −1)2=7，x −1=±√7，∴x 1=1+√7,x 2=1−√7；(2)(2x −3)2=3(2x −3)．(2x −3)2−3(2x −3)=0，(2x −3)(2x −3−3)=0，∴2x −3=0或2x −6=0，∴x 1=32,x 2=3．【解析】本题主要考查了一元二次方程的解法，解一元二次方程常用的方法有：直接开平方法，因式分解法，配方法，公式法，解答时应根据方程的特征选择恰当的方法．(1)根据方程的特征可用直接开平方法解答，解答时先将常数项移项到方程的右边将方程变为x 2−2x =6，然后方程两边同时加上1分解可得(x −1)2=7，再用直接开平方法解答即可；(2)先移项，然后分解因式可得(2x −3)(2x −6)=0，可得2x −3=0或2x −6=0，然后解之即可．17.【答案】解：(1)原方程可变形为(x −2)(3x −6−x )=0，∴x −2=0或2x −6=0，解得：x 1=2，x 2=3(2)∵3(x 2−2x +1−1)+1=0，∴3(x −1)2−3+1=0，∴3(x −1)2=2，∴x −1=±√63， ∴x 1=1+√63，x 2=1−√63【解析】本题考查的是解一元二次方程有关知识．(1)首先对该方程进行因式分解，然后再进行解答即可；(2)首先对该方程进行配方，然后再解答．18.【答案】解：(1)∵a =1，b =−12，c =−4，∴Δ=144+16=160，∴x =12±4√102， x 1=6+2√10，x 2=6−2√10；(2)x(3−2x)+2(3−2x)= 0，(x +2)(3−2x)= 0，x 1=−2，x 2=32.【解析】本题考查利用公式法和因式分解法求一元二次方程的解．(1)按公式法，先求出判别式的值，再代入公式求解；(2)将方程右边移项到左边，提取公因式后，利用因式分解法求解．19.【答案】解：(1)原式=2+1−2+1=2(2)原方程化为x 2−3x =14x 2−3x +(32)2=104 (x −32)2=±√102∴原方程的根x 1=3+√102，x 2=3−√102．【解析】本题主要考查了实数的运算和解一元二次方程，关键是熟练掌握特殊角的三角函数值和配方法解方程的方法．(1)利用零指数幂公式、绝对值和算术平方根、特殊角的三角函数值计算，最后计算加减可得结果；(2)利用配方法进行解方程即可．20.【答案】解：x x−1−1=3(x−1)(x+1)，x(x +1)−(x −1)(x +1)=3，解得，x =2，经检验：当x =2时，(x −1)(x +1)≠0，∴x =2是原分式方程的解．【解析】本题考查了解分式方程，解分式方程的基本思想是转化，把分式方程转化为整式方程求解，解分式方程一定注意要验根；先把分式方程去分母，注意没有分母的项也要乘以公分母(x −1)(x +1)，求出整式方程的解得到x 的值，经检验即可得到分式方程的解．21.【答案】解：等号两边同乘(x +2)(x −2)得：2=x 2−4−x 2−2x ，2x =−6，解得：x =−3，检验，当x =−3时，(x +2)(x −2)≠0，所以x =−3是原方程的解．【解析】此题考查了解分式方程，利用了转化的思想，解分式方程注意要检验．分式方程去分母转化为整式方程，求出整式方程的解得到x 的值，经检验即可得到分式方程的解．22.【答案】解：(1)方程两边同时乘以x 2−1得：x (x +1)−2x +1=x 2−1，解得：x =2，经检验，x =2是原方程的解；(2)方程两边同时乘以x −1得：2−x −1=x −1，解得：x =1，经检验，x =1是增根，∴原方程无解．【解析】本题考查了解分式方程，解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解，注意解分式方程一定要验根．(1)方程两边同时乘以x 2−1去分母，转化为整式方程x (x +1)−2x +1=x 2−1，求出整式方程的解得到x 的值，经检验即可得到分式方程的解；(2)方程两边同时乘以x −1去分母，转化为整式方程2−x −1=x −1，求出整式方程的解得到x 的值，经检验即可得到分式方程的解．23.【答案】解：(1)23+x3x−1=19x−3，两边同乘以3(3x−1)得，2(3x−1)+3x=1，去括号得，6x−2+3x=1，移项合并得，9x=3，系数化为1得，x=13，检验：当x=13时，3(3x−1)=0，∴x=13时原方程的增根，原方程无解；(2)xx2−4+2x+2=1x−2方程两边同乘以(x+2)(x−2)得，x+2(x−2)=x+2，去括号得，x+2x−4=x+2，移项合并得，2x=6，系数化为1得，x=3，当x=3时，(x+2)(x−2)≠0，所以原方程的解为x=3．【解析】本题主要考查了解分式方程，熟练掌握解分式方程的方法是解题的关键，两分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．(1)方程两边同乘以3(3x−1)转化为整式方程2(3x−1)+3x=1，解出x并检验即可；(2)方程两边同乘以(x+2)(x−2)转化为整式方程x+2(x−2)=x+2，解出x并检验即可．24.【答案】解：(1)去分母，得x−5=2x−5，移项，得x−2x=−5+5，解得x=0，检验：把x=0代入2x−5≠0，所以x=0是原方程的解；(2)去分母，得8+x2−1=(x+3)(x+1)，去括号，得8+x2−1=x2+4x+3，解得x=1，把x=1代入(x+1)(x−1)=0，所以x=1是原方程的增根，所以原方程无解．【解析】此题考查了解分式方程，解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．解分式方程一定注意要验根．(1)分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解；(2)分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到结论．25.【答案】解：(1)原方程可变形为1+3(x−2)=x−1，整理可得：2x=4，解得：x=2，经检验：x=2是原方程的增根，所以原方程无解；(2)原方程可变形为(x+1)2−4=x2−1，整理可得：2x=2，解得：x=1，经检验：x=1是原方程的增根，所以原方程无解；【解析】本题考查的是解分式方程有关知识．(1)首先对该方程变形，然后再进行解答即可；(2)首先对该方程变形，然后再进行解答即可．26.【答案】解：去分母得1+x−3=4−x解得x=3.经检验x=3是原方程的增根．∴原方程无解【解析】此题考查了解分式方程，解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．解分式方程一定注意要验根．分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验是原方程的增根，所以原方程无解．27.【答案】解：(1)方程两边同时乘以(x−1)得3−x+1=−1，解得x=5，经检验x=5是分式方程的解；(2)方程两边同时乘以(x2−1)得x(x−1)−2=x2−1解得x=−1，经检验x=−1是方程的增根，∴原分式方程无解．【解析】本题考查解分式方程，关键是熟练分式方程的解法步骤．(1)先将分式方程转化为整式方程，解得x的值进行检验即可得出方程的解；(2)先将分式方程转化为整式方程，解得x的值进行检验即可得出方程的解．28.【答案】解：方程两边同时乘以最简公分母(x−4)，得5−x=x−4+3，整理，得−2x=−6，解得x=3，检验：当x=3时，x−4≠0，所以原分式方程的根是x=3．【解析】本题考查的知识点是解分式方程，在解分式方程去分母时，两边同时乘以最简公分母，每一项都要乘，不能漏乘某一项，本题易出现如下错解：方程两边同时乘以最简公分母(x−4)，得5−x=1+3，解得x=1，检验：当x=1时，x−4≠0，所以原分式方程的根是x=1，错误的原因是去分母时，常数项漏乘最简公分母，故一定要注意不能漏乘．29.【答案】解：16x2−4−x+2x−2=−1，16−(x+2)2=4−x2，16−x2−4x−4−4+x2=0，16−4x−8=0，x=2，经检验，x=2为增根，此方程无解．【解析】本题综合考查了解分式方程的解法．注意，分式方程需要验根．先去分母，然后移项、合并同类项，最后化未知数系数为1．30.【答案】解：(1)原式=1−4+√3×√33=1−4+1=−2；(2)x+1x−1+41−x2=1整理得：x+1x−1−4x2−1=1，去分母得：(x+1)2−4=x2−1，去括号得：x2+2x+1−4=x2−1，移项得：2x=−1−1+4，合并同类项得：2x=2，系数化为1得：x=1，经检验：x=1时，x−1=0，∴此方程无解．【解析】此题考查了解分式方程，以及实数的运算，熟练掌握运算法则是解本题的关键．(1)原式利用零指数幂、负整数指数幂法则，以及特殊角的三角函数值计算即可求出值；(2)分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．31.【答案】解：去分母，得2(x+1)2−(x−1)2=x2−1，化简，得6x=−2，解得x=−13．经检验，x=−13是原方程的根．所以原方程的根为x=−13．【解析】本题考查了解分式方程，根据解分式方程的步骤，去分母，去括号，化简x系数为1，即可求得答案.(注意，一定要验根)32.【答案】解：(1)去分母得：1=x−4+x−3，解得：x=4，检验：当x=4时，x−4=0，所以x=4是原方程的增根，原方程无解；(2)原方程整理得：90x −60x=40，去分母得：40x=30，解得：x=34，检验：当x=34时，0.99x≠0，所以x=34是原方程的根．【解析】本题主要考查的是解分式方程，解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．解分式方程一定注意要验根．(1)方程两边都乘以x−4，分式方程去分母转化为整式方程，求出整式方程的解得到x 的值，经检验即可得到分式方程的解；(2)先化简方程，然后方程两边都乘以x，分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．33.【答案】解：(1)方程两边乘(x+2)(3x−1)，得3(3x−1)=4(x+2)解得x=115检验：当x=115时，(x+2)(3x−1)≠0是原分式方程的解，∴原分式方程的解为x=115；(2)方程两边乘(x+1)(x−1)，得x(x−1)−2=(x+1)(x−1)解得x=−1检验：当x=−1时，(x+1)(x−1)=0∴x=−1不是原分式方程的解，∴原分式方程无解【解析】本题考查了分式方程的解法．解题关键是把分式方程转化为整式方程，掌握解分式方程的一般步骤，特别最后需要验根．(1)先找出最简公分母，去分母，把分式方程化为整式方程，解出整式方程后，再验根即可．(2)先把各分母分解因式，找出最简公分母，去分母，把分式方程化为整式方程，解出整式方程后，再验根即可．注意在去分母时不能漏乘不含分母的项“1”．34.【答案】解：原方程可化为1x +3x−3=−2x(x−3)方程两边同乘x(x−3)，得x−3+3x=−2，4x=1，x=14，检验：当x=14时，x(x−3)≠0，∴x=14是原分式方程的解．【解析】本题考查了解分式方程，掌握解分式方程的步骤是解题的关键，属于基础题．方程的两边同时乘以x(x−3)化为x−3+3x=−2，解之即可，注意分式方程要检验．35.【答案】(1)解：原式=3a(a2−9)=3a(a+3)(a−3)；(2)解：方程两边同乘x(x−2)，得2(x−2)=3x2x−4=3x2x−3x=4−x=4x=−4检验：当x=−4时，x(x−2)≠0，∴原方程的解为x=−4．【解析】此题考查了解分式方程，以及提公因式法与公式法的综合运用，熟练掌握运算法则是解本题的关键．(1)原式提取3a，再利用平方差公式分解即可；(2)分式方程两边同乘x(x−2)，转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．36.【答案】解：(1)方程两边乘x−2，得3+2x−4=−x，−x−2x=−4+3，−3x=−1x=13，检验：x=13时，x−2≠0．∴原方程的根是x=1；3(2)方程两边乘(x+1)(x−1)，得2(x+1)=4，2x+2=4，2x=2，解得x=1．检验：当x=1时，(x+1)(x−1)=0，x=1是增根．∴原方程无解．【解析】本题考查了解分式方程，解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解；解分式方程一定注意要验根．(1)观察可得最简公分母是x−2，方程两边乘最简公分母，可以把分式方程转化为整式方程，求解即可；(2)观察可得最简公分母是(x+1)(x−1)，方程两边乘最简公分母，可以把分式方程转化为整式方程，求解．37.【答案】解：(1)原式=a2−4ab+4b2+a2−4b2=2a2−4ab； (2)两边同乘以x−2得，3=3(x−2)−x，3=3x−6−x，2x=9，x=4.5，检验：当x=4.5时，x−2≠0，∴x=4.5是原方程的解，∴原分式方程的解为x=4.5．【解析】(1)此题考查了整式的混合运算，完全平方公式，平方差公式，掌握整式的混合运算法则是关键，先去括号再合并，即可得到答案．(2)此题考查了解分式方程，掌握解分式方程的步骤是关键，分式方程去分母转化为整式方程，求出整式方程的解得到x的值，检验后即可得到分式方程的解．38.【答案】解：x−1−2(2−x)=−3，x−1−4+2x=−3，3x=2，x=2，3时，2−x≠0，检验：当x=23∴x=2是原分式方程的解．3【解析】此题考查了分式方程的求解方法，此题难度不大，注意转化思想的应用，注意解分式方程一定要验根.本题的最简公分母是2−x，方程两边都乘以最简公分母转化为整式方程求解，最后要代入最简公分母验根．39.【答案】解：(1)方程两边都乘(2−x)(2+x)，得x2=2−x−4+x2，解得：x=−2，检验：当x=−2时，(2−x)(2+x)=0，∴x=−2是增根，原方程无解；(2)原式=a−33a(a−2)÷(a+3)(a−3)a−2=a−33a(a−2)⋅a−2(a+3)(a−3)=13a(a+3)，由a2+3a−1=0，得到a2+3a=a(a+3)=1，则原式=13．【解析】(1)分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解；(2)原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分得到最简结果，把已知等式变形后代入计算即可求出值．此题考查了分式的化简求值，以及解分式方程，熟练掌握运算法则是解本题的关键．40.【答案】解：去分母得：6=x+2x+2，移项合并得：3x=4，解得：x=43，经检验x=43是分式方程的解．【解析】分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．此题考查了解分式方程，解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．解分式方程一定注意要验根．41.【答案】解：(1)原式=(a−b)(x−y)+(a−b)(x+y)=(a−b)(x−y+x+y)=2x(a−b)；(2)原式=5m[(2x−y)2−n2]=5m(2x−y+n)(2x−y−n)；(3)方程两边都乘以(x+1)(x−1)，得：2(x−1)+2x=x+1，解得：x=1，，检验：当x=1时，(x+1)(x−1)=0，则x=1是原分式方程的增根，所以分式方程无解．【解析】本题考查因式分解及其解分式方程，掌握运算法则是解题关键．(1)直接提取公因式(a−b)进行分解即可；(2)首先提取公因式5m，然后运用平方差公式进行分解即可；(3)首先方程两边都乘以(x+1)(x−1)，得到整式方程2(x−1)+2x=x+1，解这个方程并检验即可．42.【答案】解：原方程可化为(x+1x )2−2−2(x+1x)−1=0即：(x+1x )2−2(x+1x)−3=0设x+1x=y，则y2−2y−3=0，即(y−3)(y+1)=0．解得y =3或y =−1．当y =3时，x +1x =3，即x 2−3x +1=0解得∴x 1=3+√52，x 2=3−√52；当y =−1时，x +1x =−1无实数根．经检验，x 1=3+√52，x 2=3−√52都是原方程的根． ∴原方程的根为x 1=3+√52，x 2=3−√52．【解析】本题考查了换元法解分式方程，换元法解分式方程时常用方法之一，它能够把一些分式方程化繁为简，化难为易，对此应注意总结能用换元法解的分式方程的特点，寻找解题技巧．整理可知，方程的两个分式具备平方关系，设x +1x =y ，则原方程化为y 2−2y −3=0.用换元法解一元二次方程先求y ，再求x.注意检验． 43.【答案】解：x x−2+6x+2=1x (x +2)+6(x −2)=x 2−4x 2+2x +6x −12=x 2−48x =8x =1，经检验，x =1是分式方程的解．【解析】本题考查了解分式方程，先将分式方程化为整式方程，求得整式方程的解，然后进行检验即可．44.【答案】解：(1)3x+2=2x−3，3(x −3)=2(x +2)3x −9=2x +43x −2x =4+9x =13，检验：当x =13时，(x +2)(x −3)≠0，所以x =13是原方程的解；(2)2x 2−4+x x−2=12+x (x +2)=x 2−4 2+x 2+2x =x 2−42x =−6x =−3 检验：当x =−3时，(x +2)(x −2)≠0，所以x =−3是原方程的解．【解析】本题考查了解分式方程．注意验根．先去分母、去括号、合并同类项、称项、系数为1即可求出．45.【答案】解：解不等式2x −1≤1得x ≤1，解不等式3x −3<4x 得x > −3，则不等式组的解集是−3<x ≤1，则符合条件的整数解有−2、−1、0、1【解析】本题主要考查一元一次不等式组的整数解，熟练掌握解一元一次不等式组的方法是解决问题的关键.先求出每一个不等式的解集。

初三数学计算题大全

初三数学计算题大全1. 三角函数计算题a) 计算sin2θ + cos2θ 的值。

b) 已知 sin a = 2/3，且 a 为锐角，求 cos a 的值。

c) 若tan α = 3/4，求cot α 的值。

d) 若 sin x = 1/2，cos y = 4/5，x 和 y 为第一象限的角，求 sin(x+y) 的值。

2. 带有根式的计算题a) 计算√(7+4√3) × √(7-4√3) 的值。

b) 若x = √3 + 2，求 x² + 2x 的值。

c) 计算(5+2√3)² 的值。

d) 若√5 + √2 = a + b√3，求 a 和 b 的值。

3. 百分数和利息计算题a) 某物品原价为 80 元，现打 8 折出售，求打折后的价格。

b) 某公司的利润是投资的 8%，若利润是 1200 元，求总投资额。

c) 某地人口为 5000 人，去年增长了 12%，求今年的人口数量。

d) 某笔存款按年利率 5% 的复利计算，存 3 年后本息共计 18200 元，求初始存款金额。

4. 比例和比例方程计算题a) 已知 a:b = 2:5，b:c = 3:4，求 a:b:c 的比例。

b) 若 a:b = 3:4，b:c = 5:6，且 a+c = 64，求 a、b、c 的值。

c) 若 x:y = 2:3，y:z = 4:5，z:w = 6:7，且 x+y+z+w = 70，求 x、y、z、w 的值。

d) 若 a:b = 7:12，b:c = 6:7，c:d = 4:5，且 a+b+c+d = 2016，求 a、b、c、d 的值。

5. 几何图形计算题a) 一个正方形的边长是 4cm，求其面积和周长。

b) 一个圆的直径是 14cm，求其周长和面积。

c) 一个直角三角形的一条腰长是 5cm，另一条腰长是 12cm，求其斜边长和面积。

d) 一座圆形花坛的直径是 10m，外面围绕着一条宽 1m 的人行道，求人行道的面积。

七年级计算题练习30套

①6.32.53.44.15.1+--+- ② ()⎪⎭⎫⎝⎛-÷-21316 ③⎪⎭⎫⎝⎛÷⎪⎭⎫ ⎝⎛++-24161315.0 ④)7.1(5.2)4.2(5.23.75.2-⨯--⨯+⨯- ⑤2x-19=7x+31 ⑥133221=+++xx ⑦413-x － 675-x = 1 ⑧321264+-=-x x ⑨先化简后求值：m(m －3)－(m ＋3)(m －3)，其中m ＝－4．⑩先化简，再求值：22(23)(22)1x y x y --+--，其中11,45x y =-=二号题①15＋(―41)―15―(―0.25) ②()⎥⎦⎤⎢⎣⎡-÷⎪⎭⎫ ⎝⎛÷-+---2532.0153③ ()⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎭⎫ ⎝⎛-⨯-⨯-214124322④⎪⎭⎫ ⎝⎛-÷⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-⨯----35132211|5|⑤ )4(12)2(24+-=-+x x x ⑥ )1(9)14(3)2(2x x x -=---⑦ 32213415x x x --+=- ⑧31819615x x x --+=+ ⑨已知a = 1，b = —31，求多项式()()33222312222a b ab a b ab b -+---⎛⎫ ⎪⎝⎭的值 ⑩化简（求值）y xy x y x xy y x 22)(2)(22222----+的值，其中2,2=-=y x①－9+5×(－6) －(－4)2÷(－8) ② ()2313133.0121-÷⎪⎭⎫⎝⎛+⨯+-③()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+-⨯-854342④)32(9449)81(-÷⨯÷-⑤ )9(76)20(34x x x x --=-- ⑥ 161232=+-x x ⑦162312=+-+x x ⑧5124121223+--=-+x x x ⑨先化简，再求值：2)(2)(3++--y x y x ，其中1-=x ，.43=y ⑩先化简，再求值：⎪⎭⎫ ⎝⎛+-+⎪⎭⎫ ⎝⎛--22312331221y x y x x ，其中x=－2，y=32四号题①—48 × )1216136141(+-- ② 4×(－3)2－13＋(－12 )－|－43|③212116()4(3)2--÷-+⨯- ④32232692)23()3)(2(-÷+⨯-- ⑤2(x －2)＋2＝x ＋1 ⑥2x －13 －5x －16＝1⑦122312++=-x x ⑧246231xx x -=+-- ⑨已知a = 1，b = —31，求)42()12()34(222a a a a a a +-+-+--的值。

汇总)初中数学中考计算题(最全)-含答案

汇总)初中数学中考计算题(最全)-含答案.doc1.解答题（共30小题）1.1 计算题：① 2+3=5；②解方程：x+5=10，解得x=5.1.2 计算：π+（π﹣2013）=2π-2013.1.3 计算：|1﹣|﹣2cos30°+（﹣）×（﹣1）2013|=|1-|-2cos30°+（-1）×（-1）2013||=|1-|-2×√3/2+1||=|1-√3+1|=|2-√3|。

1.4 计算：﹣（-2）+（-3）=1.1.5 计算：√（5+2√6）+√（5-2√6）=√2+√3.1.6 计算：（2+√3）（2-√3）=1.1.7 计算：（1+√2）²=3+2√2.1.8 计算：（1-√3）²=4-2√3.1.9 计算：（√2+1）²=3+2√2.1.10 计算：（√2-1）²=3-2√2.1.11 计算：（3+√5）（3-√5）=4.1.12 计算：（√3+1）（√3-1）=2.1.13 计算：（√2+√3）²=5+2√6.1.14 计算：﹣（π﹣3.14）+|﹣3|+（﹣1）2013+tan45°=0.1.15 计算：√3+√2-√6=√3-√2+√6.1.16 计算或化简：1）计算2﹣1﹣tan60°+（π﹣2013）+|﹣|=-tan60°-2011；2）（a﹣2）²+4（a﹣1）﹣（a+2）（a﹣2）=-3a²+10a-6.1.17 计算：1）（﹣1）2013﹣|﹣7|+（√2）﹣1=-√2-8；2）（2+√3）÷（√3-1）=1+√3.1.18 计算：（1+√2）（1-√2）=﹣1.1.19 解方程：x²+2x+1=0，解得x=-1.1.20 计算：1）tan45°+sin230°﹣cos30°•tan60°+cos245°=√2-1；2）（√2+1）²-（√2-1）²=4√2.1.211）|﹣3|+16÷（﹣2）³+（2013﹣）﹣tan60°=2010；2）解方程：（1-2x）²=3，解得x=√2﹣1.1.222）求不等式组：{x²-2x0}，解得0<x<1.1.232）先化简，再求值：（√3+1）÷（√3-1）=2.1.241）计算：tan30°=√3/3；2）解方程：x²-2x+1=0，解得x=1.1.25 计算：1）√2-√3+√6=（√2-1）（√3-1）；2）先化简，再求值：（√2+1）²+（√2-1）²=8.1.261）计算：（1-√2）÷（1+√2）=-1+√2；2）解方程：x²-2x+2=0，解得x=1-√3.1.27 计算：1）（√2+√3）²-（√2-√3）²=4√6；2）先化简，再求值：（x²+2x+1）÷（x²-1）=1+x。

初三计算题大全及答案

初三计算题大全及答案以下是一些初三计算题的大全及答案，供同学们练习：一、四则运算1. 12 ÷ 3 × 4 + 6 = 222. （8 + 3）×（15 - 7） ÷ 4 = 333. 102 - 64 ÷ 8 + 2 × 3 = 834. 5 ÷（10 - 8） + 1= 25. 88 - 76 × 2 ÷ 4 + 10 = 346. （18+20）÷2×3-16+8 = 227. 12 ÷ (5 +1) × 8 - 4 = 128. （13 - 5）×2 ÷ 3 + 1 = 39. 24 ÷（2+4）×6-10= 2210. （4 + 5）×6 + 9 ÷ 3 = 51二、百分数1. 20% ÷ 0.2 = 1002. 90% × 0.6 = 543. 500 ÷ 80% = 6254. 3 ÷ 0.15 = 205. 40 × 125% = 506. 24 ÷ 80% = 307. 0.8 × 25% = 0.28. 1200 ÷ 75% = 16009. 150% × 0.75 = 112.510. 56.25 ÷ 75% = 75三、长度、面积和体积1. 长方形的长是15cm，宽是9cm，它的面积是多少？答案：135cm²2. 一个正方形的边长是7cm，它的周长是多少？答案：28cm3. 一个立方体的边长是3cm，它的表面积是多少？答案：54cm²4. 一个正方体的表面积是96cm²，它的边长是多少？答案：4cm5. 一个圆的直径是12cm，它的周长是多少？（π≈3.14）答案：37.68cm6. 一个正立方体的体积是64cm³，它的边长是多少？答案：4cm7. 一个长方体的长是5cm，宽是3cm，高是4cm，它的体积是多少？答案：60cm³8. 一个圆的半径是6cm，它的面积是多少？答案：113.04cm²9. 一个正六面体的表面积是150cm²，它的体积是多少？答案：125cm³10. 一个长方形的长是24cm，宽是18cm，如果它的周长增加了8cm，它的面积会变成多少？答案：720cm²以上就是初三计算题的大全及答案，同学们可以利用这些题目来提高自己的计算能力。

初中数学中考计算题复习(最全)-含答案

一．解答题（共30小题）1．计算题：①；②解方程：．2．计算：+（π﹣2013）0．3．计算：|1﹣|﹣2cos30°+（﹣）0×（﹣1）2013．4．计算：﹣．5．计算：．6．．7．计算：．8．计算：．9．计算：．10．计算：．11．计算：．12．．13．计算：．14．计算：﹣（π﹣3.14）0+|﹣3|+（﹣1）2013+tan45°．15．计算：．16．计算或化简：（1）计算2﹣1﹣tan60°+（π﹣2013）0+|﹣|．（2）（a﹣2）2+4（a﹣1）﹣（a+2）（a﹣2）17．计算：（1）（﹣1）2013﹣|﹣7|+×0+（）﹣1；（2）．18．计算：．（1）19．（2）解方程：．20．计算：（1）tan45°+sin230°﹣cos30°•tan60°+cos245°；（2）．21．（1）|﹣3|+16÷（﹣2）3+（2013﹣）0﹣tan60°（1）计算：.22．（2）求不等式组的整数解．（1）计算：23．（2）先化简，再求值：（﹣）÷，其中x=+1．24．（1）计算：tan30°25．计算：（1）（2）先化简，再求值：÷+，其中x=2+1．26．（1）计算：；（2）解方程：．27．计算：．28．计算：．29．计算：（1+）2013﹣2（1+）2012﹣4（1+）2011．30．计算：．1．化简求值：，选择一个你喜欢且有意义的数代入求值．2．先化简，再求值，然后选取一个使原式有意义的x值代入求值．3．先化简再求值：选一个使原代数式有意义的数代入中求值．4．先化简，再求值：，请选择一个你喜欢的数代入求值．5．（2010•红河州）先化简再求值：．选一个使原代数式有意义的数代入求值．6．先化简，再求值：（1﹣）÷，选择一个你喜欢的数代入求值．7．先化简，再求值：（﹣1）÷，选择自己喜欢的一个x求值．8．先化简再求值：化简，然后在0，1，2，3中选一个你认为合适的值，代入求值．9．化简求值（1）先化简，再求值，选择你喜欢的一个数代入求值．（2）化简，其中m=5．10．化简求值题：（1）先化简，再求值：，其中x=3．（2）先化简，再求值：，请选一个你喜欢且使式子有意义的数字代入求值．（3）先化简，再求值：，其中x=2．（4）先化简，再求值：，其中x=﹣1．11．（2006•巴中）化简求值：，其中a=．12．（2010•临沂）先化简，再求值：（）÷，其中a=2．13．先化简：，再选一个恰当的x值代入求值．14．化简求值：（﹣1）÷，其中x=2．15．（2010•綦江县）先化简，再求值，，其中x=+1．16．（2009•随州）先化简，再求值：，其中x=+1．17．先化简，再求值：÷，其中x=tan45°．18．（2002•曲靖）化简，求值：（x+2）÷（x﹣），其中x=﹣1．19．先化简，再求值：（1+）÷，其中x=﹣3．20．先化简，再求值：，其中a=2．21．先化简，再求值÷（x﹣），其中x=2．22．先化简，再求值：，其中．24．先化简代数式再求值，其中a=﹣2．25．（2011•新疆）先化简，再求值：（+1）÷，其中x=2．26．先化简，再求值：，其中x=2．27．（2011•南充）先化简，再求值：（﹣2），其中x=2．28．先化简，再求值：，其中a=﹣2．29．（2011•武汉）先化简，再求值：÷（x ﹣），其中x=3． 30．化简并求值：•，其中x=21. ． 2。

七年级计算题500道

七年级计算题500道一、有理数运算类。

1. 计算：(-3)+5- 解析：异号两数相加，取绝对值较大的符号，并用较大的绝对值减去较小的绝对值。

|5| = 5，| - 3|=3，5>3，所以(-3)+5 = 2。

2. 计算：4 - (-2)- 解析：减去一个数等于加上这个数的相反数，所以4-(-2)=4 + 2=6。

3. 计算：(-2)×(-3)- 解析：两数相乘，同号得正，异号得负，并把绝对值相乘。

所以(-2)×(-3)=6。

4. 计算：-4÷2- 解析：两数相除，异号得负，并把绝对值相除。

所以-4÷2=-2。

5. 计算：(-2)^3- 解析：(-2)^3=(-2)×(-2)×(-2)= - 8。

二、整式加减类。

6. 化简：3a + 2b - 5a - b- 解析：- 合并同类项，同类项是指所含字母相同，并且相同字母的指数也相同的项。

- 对于a的同类项3a和-5a，3a-5a=-2a。

- 对于b的同类项2b和-b，2b - b=b。

- 所以，3a + 2b - 5a - b=-2a + b。

7. 化简：(2x^2 - 3x + 1)-(x^2+2x - 3)- 解析：- 去括号法则：括号前是正号，把括号和它前面的正号去掉后，原括号里各项的符号都不改变；括号前是负号，把括号和它前面的负号去掉后，原括号里各项的符号都要改变。

- 所以(2x^2 - 3x + 1)-(x^2+2x - 3)=2x^2-3x + 1 - x^2 - 2x+3。

- 然后合并同类项，2x^2-x^2=x^2，-3x-2x=-5x，1 + 3=4。

- 最终结果为x^2-5x + 4。

三、一元一次方程类。

8. 解方程：2x+3 = 7- 解析：- 首先进行移项，把常数项移到等号右边，2x=7 - 3。

- 然后计算7-3 = 4，得到2x=4。

- 最后系数化为1，两边同时除以2，x = 2。

初三数学计算题练习试题集

初三数学计算题练习试题答案及解析1.计算：．【答案】﹣7．【解析】分别用平方根定义，负指数幂法则，绝对值的代数意义，零指数幂法则进行计算即可得到结果．试题解析：原式=3﹣4×4+5+1=3﹣16+5+1=﹣7．【考点】1.实数的运算2.零指数幂3.负整数指数幂．2.计算：﹣25+（）﹣1﹣|﹣8|+2cos60°．【答案】﹣33．【解析】第一项利用乘方的意义化简，第二项利用负指数幂法则计算，第三项利用绝对值的代数意义化简，最后一项利用特殊角的三角函数值计算即可．试题解析：原式=﹣32+2﹣4+1=﹣33．【考点】1.实数的运算2.负整数指数幂3.特殊角的三角函数值．3.计算：．【答案】-6【解析】先计算乘方和开方运算，再根据特殊角的三角函数值和平方差公式得到原式=，然后进行乘除运算后合并即可．原式==-6．【考点】二次根式的混合运算；特殊角的三角函数值．4.计算：（1）（2）【答案】（1）3；（2）4-3a．【解析】（1）先根据二次根式、零次幂以及特殊角的正切值运算法则进行计算，最后进行加减运算即可；（2）先根据单项式乘以多项式、平方差公式把括号展开，最后合并同类项即可．（1）原式=3-1+1=3．原式=a2-3a+4-a2=4-3a．【考点】1．实数的混合运算；2．整式的混合运算．5.计算：(－1)2 012－(－3)＋＋.【答案】5【解析】解：原式＝1＋3－2＋3＝56.计算（1）﹣×（2）（6﹣2x）÷3．【答案】（1）1；（2）【解析】先把二次根式化简后，再进行加减乘除运算，即可得出答案.试题解析：(1)；（2）.考点: 二次根式的混合运算.7.计算：（π﹣1）0﹣﹣（﹣1）+|﹣|﹣12．【答案】.【解析】根据乘方、绝对值、二次根式的意义分别计算即可求出答案.试题解析：考点: 实数的混合运算.8.计算题：①、；②、【答案】①、；②、【解析】根据二次根式的混合运算的法则结合二次根式的性质依次计算即可.试题解析：①、；②、.【考点】实数的运算9.计算：．【答案】解：原式=。

初中数学精选计算题练习大全

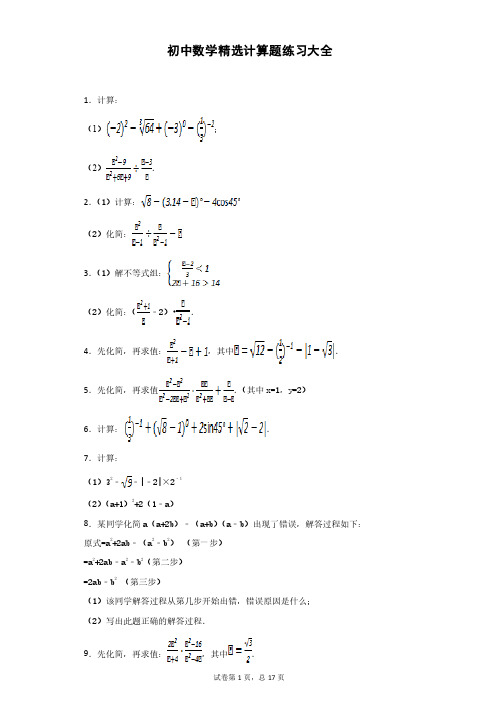
初中数学精选计算题练习大全1．计算：．计算：（1）；（2）．2．（1）计算：（2）化简：3．（1）解不等式组：（2）化简：（﹣2）•．4．先化简，再求值：，其中．5．先化简，再求值．（其中x=1x=1，，y=2y=2））6．计算：．7．计算：．计算：（1）32﹣﹣|﹣2|×2﹣1（2）（a+1a+1））2+2+2（（1﹣a ）8．某同学化简a （a+2b a+2b）﹣（）﹣（）﹣（a+b a+b a+b））（a ﹣b ）出现了错误，解答过程如下：）出现了错误，解答过程如下：原式原式=a =a 2+2ab +2ab﹣（﹣（﹣（a a 2﹣b 2）（第一步）（第一步） =a 2+2ab +2ab﹣﹣a 2﹣b 2（第二步）（第二步） =2ab =2ab﹣﹣b 2（第三步）（第三步）（1）该同学解答过程从第几步开始出错，错误原因是什么；）该同学解答过程从第几步开始出错，错误原因是什么；（2）写出此题正确的解答过程．）写出此题正确的解答过程．9．先化简，再求值：，其中．10．计算：．11．先化简，再求值：；其中，.12．计算：（﹣1）2﹣2sin45°2sin45°++（π﹣2018）0+||．13．计算：．14．计算：15．(1)计算：；(2)分解因式：6(a-b)2+3(a-b).16．计算：．17．计算：2﹣1sin60°+|1|．sin60°+|118．已知T．（1）化简T；的值．（2）若正方形ABCD的边长为a，且它的面积为9，求T的值．19．化简分式（+）÷，并在2，3，4，5这四个数中取一个合适的数作为a 的值代入求值．的值代入求值．20．2﹣1+|1﹣|+（﹣2）00﹣cos60°21．计算：．22．先化简，再求值：，其中23．计算化简（本小题满分10分）分）（1）（2）24．（2011?舟山）计算：．25．先化简，再求值：，其中a2﹣4=0．26．.27．（本小题满分5分）分）先化简，再求值：（1－）÷，其中=sin60°=sin60°. . 28．计算：．29．先化简，再求值：，其中x=2x=2．．30．计算：31．已知a2=19=19，求，求的值．的值．32．计算：|2﹣|+2sin45°﹣（）0．33．先化简，再求值：，其中m=+1．34．计算：35．先化简，再求值：．先化简，再求值：36．计算：37．先化简，再求值：，其中a是方程a2+a﹣6=0的解．的解．38．化简：39．计算：（-3-3））2+2017- ×sin45°．×sin45°．40．化简：．41．计算：．42．化简：（y+2）（y﹣2）﹣（y﹣1）（y+5）43．（1）计算：︱－）计算：︱－22︱+( + 1)0－()-1+tan60°+tan60°（2）解分式方程：+ 1）解分式方程： =+ 144．（题文）先化简，再求值：（a﹣）÷，其中a=，b=1．45．计算：46．先化简，再求值：，其中x=2，y=3．47．Ⅰ．解不等式组，并把解集在数轴上表示出来．，并把解集在数轴上表示出来．Ⅱ．计算：（π﹣3）0+﹣2sin45°﹣（）﹣1．48．（1）实数x取哪些整数时，不等式2x﹣1＞x+1与x﹣1≤7﹣x都成立？都成立？中选取合适的整数代入求值．（2）化简：（）÷，并从0≤x≤4中选取合适的整数代入求值．49．先化简，再求值：，其中．50．算：51．先化简，再求值：，其中．52．计算：53．先化简，再求值：，其中x=﹣．54．计算：+（﹣）﹣1+|1﹣|﹣4sin45°．55．化简：56．计算：57．先化简，再求值：，其中a=+1．58．（1）计算：2﹣11+（2018﹣π）00﹣sin30°；（2）化简：（a+1）22﹣a（a+1）﹣1．59．计算：．计算：（1）（2）2﹣|﹣4|+3﹣1×6+20；（2）．60．已知＝2，请先化简÷，再求该式子的值．，再求该式子的值．61．先化简，再求值（﹣）÷，其中a，b满足a+b﹣=0．62．计算﹣（﹣2）+（π﹣3.14）0++（﹣）﹣163．解不等式组，并求出它的整数解，再化简代数式•（﹣），从上述整数解中选择一个合适的数，求此代数式的值．从上述整数解中选择一个合适的数，求此代数式的值．64．计算：﹣25÷23+|﹣1|×1|×55﹣（π﹣3.14）065．计算：．计算：）；（1）（x+2y）2﹣（x+y）（x﹣y）；（2）（a﹣1﹣）÷66．先化简，再求值：（1﹣x+）÷，其中x=tan45°x=tan45°++（）﹣1．67．（1）求不等式组的整数解；的整数解；（2）先化简，后求值（1﹣）÷，其中a=+1．68．计算：（﹣1）2018+|﹣|﹣（﹣π）0﹣2sin60°．69．（1）计算：（）﹣2+﹣2cos45°；（2）先化简，再求值：÷（1+），其中a=2．70．计算．计算（1）计算：）计算：22﹣2+（3）÷﹣3sin45°；（2）解方程：+1=. 71．化简：72．计算：|﹣|﹣2﹣1+73．先化简，再求值：（﹣）÷，其中a=3﹣1+2sin30°．74．计算：（+2）22﹣+2﹣275．先化简，再求值：（2m+1）（2m ﹣1）﹣（m ﹣1）2+（2m ）3÷（﹣8m ），其中m 是方程x 2+x ﹣2=0的根的根76．计算：4cos45°4cos45°++（π﹣2018）0﹣77．计算：2tan45°﹣|﹣3|+（）﹣2﹣（4﹣π）0．78．先化简，再求值：（1﹣）÷，其中a=2+．79．先化简，再求值：÷（a ﹣1﹣），并从﹣1，0，1，2四个数中，选一个合适的数代入求值数代入求值80．计算：（）﹣2+|﹣2|﹣+6cos30°+6cos30°++（π﹣3.14）0．81．先化简（1﹣）÷，然后从不等式2x﹣6＜0的非负整数解中选取一个合适的解代入求值．的解代入求值．82．计算：﹣|4﹣|﹣（π﹣3.14）0+（1﹣cos30°）×（）﹣2．2cos45°++（）﹣1﹣（π﹣1）083．计算：﹣2cos45°84．（1）计算：+|﹣2|；（2）化简：（a+3）（a﹣2）﹣a（a﹣1）．85．先化简，再求值：（﹣1）÷，其中x=+1．86．如图，将边长为m的正方形纸板沿虚线剪成两个小正方形和两个矩形，拿掉边长的小正方形纸板后，将剩下的三块拼成新的矩形．为n的小正方形纸板后，将剩下的三块拼成新的矩形．的代数式表示拼成矩形的周长；（1）用含m或n的代数式表示拼成矩形的周长；，求拼成矩形的面积．（2）m=7，n=4，求拼成矩形的面积．87．先化简，再求值：÷（﹣a），其中a=﹣1，b=1．88．先化简，再求值：（1﹣）÷，其中a=sin30°．89．（1）计算：|3﹣5|﹣（π﹣3.14）0+（﹣2）﹣1+sin30°；（2）解分式方程：+1=．90．（题文）已知：x2﹣y2=12，x+y=3，求2x2﹣2xy的值．的值．91．求值：（﹣1）2018+|1﹣|﹣92．先化简再求值：（a﹣）÷，其中a=1+，b=1﹣．93．计算：|2﹣|+（π﹣1）0+﹣（）﹣1194．（1）计算：﹣4cos60°﹣（π﹣3.14）0﹣（）﹣1（2）先化简，再求值：（1﹣）÷，其中x=2．95．计算：2sin30°﹣（π﹣）0+|﹣1|+（）﹣196．先化简，再求值：（﹣）÷，其中a=．97．先化简，再求值：，其中x=﹣1．98．先化简，再求值：（a+b ）2+b （a ﹣b ）﹣4ab ，其中a=2，b=﹣．99．计算：（﹣1）2018﹣+（π﹣3）0+4cos45°100．计算：+（π﹣2018）0﹣2tan45°101．计算|1﹣|﹣2sin45°2sin45°+2+2﹣1﹣（﹣1）2018．102．（1）计算：|2﹣|+（+1）0﹣3tan30°3tan30°++（﹣1）2018﹣（）﹣1；（2）解不等式组：并判断﹣1，这两个数是否为该不等式组的解．103．先化简，再求值：（+1）÷，其中a=tan60°﹣|﹣1|．104．先化简，再求代数式（1﹣）÷的值，其中a=4cos30°a=4cos30°+3tan45°+3tan45°． 105．计算：|﹣4|+3tan60°﹣﹣（）﹣1106．计算：|﹣2|+（﹣1）×（﹣3）107．如图，阶梯图的每个台阶上都标着一个数，从下到上的第1个至第4个台阶上依次标着﹣5，﹣2，1，9，且任意相邻四个台阶上数的和都相等．，且任意相邻四个台阶上数的和都相等．尝试尝试（1）求前4个台阶上数的和是多少？个台阶上数的和是多少？（2）求第5个台阶上的数x 是多少？是多少？应用应用求从下到上前31个台阶上数的和．个台阶上数的和．发现发现试用含k （k 为正整数）的式子表示出数“1”所在的台阶数．所在的台阶数．108．嘉淇准备完成题目：化简：，发现系数“”印刷不清楚．清楚．（1）他把“”猜成3，请你化简：（3x 2+6x +8）–（6x +5x 2+2）；）；（2）他妈妈说：“你猜错了，我看到该题标准答案的结果是常数．”通过计算说明原题中“”是几？是几？ 109．已知x=+1，求x 2﹣2x ﹣3的值．的值．110．计算：（﹣1）2008+π0﹣（）﹣1+．111．先化简，再求值：，其中．112．先化简，再求值：（x+2+）÷，其中x=2．113．计算.114．化简代数式：，再从不等式组的解集中取一个合适的整数值代入，求出代数式的值．合适的整数值代入，求出代数式的值．115．先化简，再求值：（a ﹣2b ）（a+2b ）﹣（a ﹣2b ）2+8b 2，其中a=﹣2，b=．116．计算：（﹣1）2+（π﹣3.14）0﹣|﹣2| 117．先化简，再求值：，其中x 为整数且满足不等式组．118．先化简，再求值：（1+）÷，其中x 满足x 2﹣2x ﹣5=0．119．计算：（1）（﹣2）2×|﹣3|﹣（）00；（2）（x+1）22﹣（x 22﹣x ）120．先化简，再求值：a （a +2b ）﹣（a +1）2+2a ，其中．121．先化简，再求值：（1﹣）÷，其中a=﹣3．122．（1）计算：|﹣2|﹣2cos60°2cos60°++（）﹣1﹣（2018﹣）0（2）先化简（1﹣）•，再在1、2、3中选取一个适当的数代入求值．中选取一个适当的数代入求值．123．计算：．124．（1）化简÷（x ﹣）．（2）解方程：=3．125．先化简，再求值：．其中x=sin60°．126．计算：（）﹣2+（π2﹣π）0+cos60°+cos60°+|+|﹣2|127．先化简，再求值：，其中，其中.128．计算：129．先化简，再求值：（x+y ）（x ﹣y ）+y （x+2y ）﹣（x ﹣y ）2，其中x=2+，y=2﹣．130．计算：﹣|﹣|+（﹣2）2﹣（π﹣3.14）0×（）﹣2．131．对于三个数、、，用表示这三个数的中位数，用表示这三个数中最大数，例如：，，.解决问题：解决问题：（1）填空：，如果，如果，则的取值范围为的取值范围为；；（2）如果，求的值；的值；（3）如果，求的值的值..132．计算：133．阅读下列题目的解题过程：．阅读下列题目的解题过程：已知a 、b 、c 为△ABC 的三边，且满足a 2c 2﹣b 2c 2=a 4﹣b 4，试判断△ABC 的形状．的形状．解：∵a 2c 2﹣b 2c 2=a 4﹣b 4 （A ）∴c 2（a 2﹣b 2）=（a 2+b 2）（a 2﹣b 2）（B ） ∴c 2=a 2+b 2 （C ） ∴△∴△ABC ABC 是直角三角形是直角三角形问：（1）上述解题过程，从哪一步开始出现错误？请写出该步的代号：）上述解题过程，从哪一步开始出现错误？请写出该步的代号：；（2）错误的原因为：）错误的原因为：；（3）本题正确的结论为：）本题正确的结论为：．134．先化简，再求值：，其中x=2﹣1．135．先化简，再求值：x （x+1）+（2+x ）（2﹣x ），其中x=﹣4．136．＋－＋137．先化简，再求值：（+1）÷，其中x 是方程x 2+3x=0的根．的根．138．计算：﹣2sin45°2sin45°++（）﹣1﹣|2﹣|．139．先化简，再求值：．先化简，再求值：，其中.140．先化简，再求值：，其中x 满足x 2－2x －2=0.141．计算：（π-2)°-2)°+4cos30°+4cos30°－－（－）－2.142．先化简，再求值：，其中.143．计算：.144．先化简，再求值：（1+）÷．其中x =3．145．计算：|﹣5|+（﹣1）2﹣（）﹣1﹣．146．先化简，再求值：，其中，.147．计算：.148．计算：（﹣6）2×（﹣）．）．149．（1）计算：π0+2cos30°﹣|2﹣|﹣（）﹣2；（2）化简：（2﹣）÷．150．化简：151．计算：(－)×)×((－)＋|－1|＋(5－2π)0152．先化简，再求值：其中153．计算：154．计算：．计算：155．计算：（﹣2）2+20180﹣156．（1）计算：；（2）化简：(m+2)2 +4(2-m)157．先化简，再求值：，其中.158．计算：.159．我们常用的数是十进制数，如，数要用10个数码（又叫数字）：0、1、2、3、4、5、6、7、8、9，在电子计算机中用的二进制，只要两个数码：0和1，如二进制中等于十进制的数6，等于十进制的数53.那么等于十进制中的哪个数？二进制中的数101011等于十进制中的哪个数？160．（1）.（2）化简161．先化简，再求值：，其中.162．计算：.sin30°++（2018﹣）0﹣2﹣1+|﹣4|；163．（1）计算：sin30°（2）化简：（1﹣）÷．164．（1）计算：；（2）解不等式：165．先化简，再求值：（xy2+x2y）×，其中x=π0﹣（）﹣1，y=2sin45°﹣．166．对于任意实数、，定义关于“”的一种运算如下：.例如.的值；（1）求的值；（2）若，且，求的值.167．计算或化简.（1）；（2）.168．如图，在数轴上，点、分别表示数、（1）求的取值范围.的点应落在（）（2）数轴上表示数的点应落在（A．点的左边的右边的左边 B．线段上C．点的右边169．计算.170．先化简，再求值: ，其中171．计算: .172．（1）计算：；（2）化简并求值：，其中，.173．先化简,再求值:,其中是不等式组的整数解.174．(1)计算：.(2)解方程：.175．观察以下等式：．观察以下等式：第1个等式：，第2个等式：，第3个等式：，第4个等式：，第5个等式：，……按照以上规律，解决下列问题：按照以上规律，解决下列问题：个等式：；（1）写出第6个等式：个等式： (用含n的等式表示)，并证明（2）写出你猜想的第n个等式：176．计算：177．先化简，再求值：，其中.178．有一张边长为a厘米的正方形桌面，因为实际需要，需将正方形边长增加b厘米，木工师傅设计了如图所示的三种方案：木工师傅设计了如图所示的三种方案：小明发现这三种方案都能验证公式：a2+2ab+b2=（a+b）2，对于方案一，小明是这样验证的：证的：a2+ab+ab+b2=a2+2ab+b2=（a+b）2请你根据方案二、方案三，写出公式的验证过程．请你根据方案二、方案三，写出公式的验证过程．方案二：方案二：方案三：方案三：179．计算：|﹣2|﹣+23﹣（1﹣π）0．180．（题文）对任意一个四位数n，如果千位与十位上的数字之和为9，百位与个位上的数字之和也为9，则称n为“极数”．的倍数，请说明理由；（1）请任意写出三个“极数”；并猜想任意一个“极数”是否是99的倍数，请说明理由；（2）如果一个正整数a是另一个正整数b的平方，则称正整数a是完全平方数．若四位数m为“极数”，记D（m）=，求满足D（m）是完全平方数的所有m．181．计算：．计算：））计算：；）计算：．．=．先化简，再求值：，其中a=．．计算： ()()20212017323p -æö--+---ç÷èø．．先化简，再求值： 221x y x y x yæö-¸ç÷--èø，其中=32-，=112-æöç÷èø．211--=1321-- 4312--=3…再求值： 22214244a a a a a a a a +--æö+¸ç÷--+èø，=()10132p -æö-+ç÷èø．（221x x -++）÷21x x x -+ （12）191．先化简，再求值：（m+2m+2﹣﹣52m -）• 243m m --，其中m=m=﹣﹣12． 192．（1）计算：）计算：||﹣4|4|﹣（﹣﹣（﹣﹣（﹣22）2+9﹣（12）0（2）解不等式组32{ 1213x x xx -³+>-．193．计算：．计算：(1)2(1)2-1+sin30°+sin30°-|-2|-|-2|-|-2|；； (2)(2)（（-1-1））0-|3-π|+()23p -.。

七年级数学计算题500道

有理数计算 1使用说明：本题集的制作初衷是为学生提供计算题目以便强化计算能力。

此题集共 500 道，1-445 题为基本四则运算，建议每天做 10 道，如能保证答题准确率在 80%以上，说明计算能力比较过关。

446-500 题为能力计算题目，涉及等差数列，等比数列，裂项等技巧，建议学完计算技巧后再作题进行巩固。

要相信坚持总有回报，祝愿每位同学取得优异的成绩。

由于时间有限，后面所附答案如有错漏之处，请批评指正。

1. ⨯--÷5324()61152. ÷--⨯-÷7571234(2)525553. ⨯+⨯--÷+⨯1177110.8 4.8() 2.20.822394. --+-⨯-⨯620512)(154)(13475. -⨯⨯-187()( 2.4)736. ÷-⨯÷-7772()(5)3417. －＋⨯÷-24528[15(13)](1)113118. ⨯-÷-⨯55(5)()5112021初一年级有理数计算题集9.11321 ()() 32114742 --+-÷-10.2215 130.34(13)0.34 3737-⨯-⨯+⨯--⨯11.11 (13)(134)()1367 -⨯-⨯⨯-12.7111 (4)(5)(4)38248 ---+--13.(16503)(2)--+÷-14.110.53 6.75542+（－）－（－）－15.219 17887.21435312.792121-++-16.(6)(4)(32)(8)3-⨯-+-÷--17.211()|1| 722+－－－－18.(9)(4) (60)12-⨯-+-÷有理数计算23有理数计算 19. 9581[()1]()1472142--+÷-20. 1|3|10(15)3--÷--⨯21. 375112532162-⨯-÷（）22. 11171(231)(1)(7)32186+÷-⨯-－23. 31(820.04)43-⨯--24. []551(0.4)( 2.5)---⨯-25. 251(1)(10.5)3---⨯26.575(7)(243)(246)--+---+-+-27. 213(2)(1)8()312--⨯--÷-⨯-+28. 912311(27)9()(24)1123412-÷-+--⨯-有理数计算430.()()1120.12533110.25483⎛⎫⎛⎫⎛⎫+++-++- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭31. 211(455)365455211545545365⨯-+⨯-⨯+⨯32. 102131111()[9(3)]314122---⨯--+÷ 33. 8221211(1)()()[2(3)]0.52368---÷-⨯-----34. 25171()24(5)138612⎡⎤--+⨯÷-⎢⎥⎣⎦35. ()131170.125 1.213213⎛⎫⎛⎫-⨯-÷-⨯- ⎪ ⎪⎝⎭⎝⎭36. ()2342()()0.2534⨯-+-÷-37. ()7511[30()36]59612-+-⨯-÷-（）5有理数计算 38. 23155(1)()()()74148+÷-÷-⨯-39. 31315(1)(1) ()()42424-÷--+÷-40. 8)3(4)2(323+-⨯--⨯41. 2)2(2)1(3210÷-+⨯-42. 2)2(2)2(23322--+----43. ])3(2[61124--⨯--44. ]2)33()4[()10(222⨯+--+-45. ])2(2[31)5.01()1(24--⨯⨯---46. 20022003)2()2(-+-47. 20052004(0.25)4-⨯48. 94)211(42415.0322⨯-----+-有理数计算6 49. )2()3(]2)4[(3)2(223-÷--+-⨯--50. 32(4)(75)÷-⨯-+－51. 2)2(2)1(3210÷-+⨯-52. ()()574283+-⨯-÷-53. 2225(3)[()](6)439⨯+÷－－－－－54. 31[2(10.54)]⨯－－－－－55. 312123)2122(3)543(31512⨯-÷++÷+-⨯-56. 295(3)(2)4⨯--÷＋－57. 3(5)[2(6)]3005-⨯---÷ 58. 2211(1)1339⨯-÷－59. [124(310)]4⨯-÷－7有理数计算 60. 32(3)4(3)15⨯-⨯-－＋61. 4211[2(3)]6―⨯-－－62. 213502()15÷⨯-＋－63. 421632()94÷⨯-－64. ()1003212181215.20-⨯⎪⎭⎫⎝⎛-+⎪⎭⎫⎝⎛-÷-65. 21002212(1)1221|132|----÷-+--⨯（）66. 3483(1)(4)--⨯---67. 3145()2⨯-－68. 2)3121(36-⨯69. 24)23(942-⨯÷-有理数计算8 70. 5434361832411÷⎥⎦⎤⎢⎣⎡⨯⎪⎭⎫ ⎝⎛-+- 71. )12()4332125(-⨯-+72. )4()81()2(163-⨯---÷ 73. 2111()()(2)(14)236--÷--⨯-＋ 74. 33[5(10.2)(2)]5---+-⨯÷- 75. 111122399100++⋅⋅⋅+⨯⨯⨯76. 911321321÷⎪⎭⎫ ⎝⎛-⨯-77. ()124310(49)-⨯-÷-⎡⎤⎣⎦78. 4435222-+--÷-（）（）79. 32416210+÷-÷-（）（）9有理数计算 80. 2153233+÷÷-+-（）（）（）81. 3342331---÷-（）（） 82. 232[3323]43-⨯-⨯--（）83. 1293123223-÷+-⨯+（）84. )6(23517235)34()235(-⨯-⨯--⨯- 85. 15511512277227⎛⎫⎛⎫⨯--⨯+-⨯ ⎪ ⎪⎝⎭⎝⎭86. 23(2)(1)31(2)-⨯--⨯---［］ 87. 3223(4)(9)0---⨯-⨯ 88. 31452-⨯-（）89. 348311--⨯---（）（）有理数计算 10 90. 32422()93-÷⨯-91. 211[123]6--⨯--（） 92. 759015-⨯--÷-（）（）（）93. 23420.2534⨯-+-÷-（）（）（） 94. ()11731348126424⎛⎫-+-⨯- ⎪⎝⎭95. ()113700.2524.5525%42⎛⎫⎛⎫-⨯-+⨯--⨯ ⎪ ⎪⎝⎭⎝⎭96. 333145⎛⎫⨯- ⎪⎝⎭97. ()()()525306⎛⎫-⨯-⨯+⨯- ⎪⎝⎭98. ()5411.5112153⎛⎫-⨯⨯-⨯ ⎪⎝⎭99. 13810.0434⎛⎫⎛⎫-+-⨯- ⎪ ⎪⎝⎭⎝⎭100. ()()3338878158777⎛⎫⎛⎫-⨯-+-⨯--⨯ ⎪ ⎪⎝⎭⎝⎭101. 1799918⎛⎫⨯- ⎪⎝⎭102. ()17.984⎛⎫-⨯- ⎪⎝⎭103. ()()()450.258-⨯⨯-⨯-104. 130.570445⎛⎫⎛⎫-⨯⨯-⨯ ⎪ ⎪⎝⎭⎝⎭105. 7213.2329213⎡⎤⎛⎫⎛⎫⎛⎫-⨯-⨯-⨯--⨯- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦106. ()74948⨯-107. 157556⎛⎫⨯- ⎪⎝⎭108. ()24912525⎛⎫-⨯- ⎪⎝⎭109. ()200420062005-⨯110. ()231243412⎛⎫-++⨯- ⎪⎝⎭111. 2211613325⎛⎫⎛⎫⎛⎫⎛⎫-⨯-⨯-⨯- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭112. 173********⎛⎫⎛⎫-⨯-+- ⎪ ⎪⎝⎭⎝⎭113. 1173332127⎛⎫-⨯⨯ ⎪⎝⎭114. 15511521214142214⎛⎫⎛⎫-⨯--⨯+⨯ ⎪ ⎪⎝⎭⎝⎭115. 4555542792793⎛⎫⨯+⨯+⨯- ⎪⎝⎭116. ()7 1.7516⎛⎫+÷- ⎪⎝⎭117. 31231527⎛⎫⎛⎫⎛⎫-÷-÷- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭118. ()()148121549-÷⨯÷-119. ()()()1084-÷-⨯-120. ()()1177-÷⨯-121. 294.558-⨯÷122. 121311234⎛⎫⎛⎫⎛⎫-÷-÷- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭123. 141315432251518⎛⎫⎛⎫⎛⎫⎛⎫+÷-⨯-÷- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭124. ()1347415620512⎛⎫⨯-⨯--+- ⎪⎝⎭125. 111111111111357357357357⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⨯⨯+-⨯-⨯-+-⨯-⨯+⨯-⨯ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭126. 25(8)(1)--⨯-127. 11()128--+128. 4(6)(3)-⨯-129. 12()( 3.25)5---130. 313.5(0.7)(5)5-⨯-÷-131. 112167342⎛⎫⎛⎫-+÷- ⎪ ⎪⎝⎭⎝⎭132. ()1230.1434⎛⎫⎛⎫÷---÷- ⎪ ⎪⎝⎭⎝⎭133. 2212162()2-÷⨯-134. 344411117777⎛⎫⎛⎫-⨯÷--+ ⎪ ⎪⎝⎭⎝⎭135. 211110.5210.5100.5323⎛⎫⎛⎫⎛⎫-÷--÷-+÷ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭136. 21.8( 1.8)3--+137. 114254-+138. 1348(1)124-⨯-+139. 220.52(3)⨯--140. 113()1234÷-+141. 322322(2)()(2)2()833-⨯---÷⨯-142. 4327221()()1727173⎡⎤----+-⎢⎥⎣⎦143. 3777(1)()48128--÷-144. 241(7)(30)3 3.25134-÷--⨯+145. 868635.28.642⨯-⨯－＋146. 200720092008-⨯147. 199279-⨯148. 762()(1.5)3-⨯149. 201020111()33-⨯150. 201120102009(7)147(49)(7)-+⨯--⨯-151. 214.732(2.631)33⎡⎤---⎢⎥⎣⎦152. 421(3)(1)()7315-÷-⨯-153. 812763189--+-÷-（）（） 154. 13122(3)2523-⨯--+÷--- 155. ()28[710.63]3⎛⎫-⨯-+-⨯÷- ⎪⎝⎭156. 151()46-+-157. 2(0.8)15-+-158. 15631218⎛⎫+- ⎪⎝⎭159. ()(){}1.5 1.80.80.9+-++-⎡⎤⎣⎦160. 112133[2357]32324⎛⎫⎛⎫-++-++- ⎪ ⎪⎝⎭⎝⎭161. 222115[1344]33155⎛⎫-+--+- ⎪⎝⎭162. ()43510.712150.7(15)9494⨯+⨯-+⨯+⨯-163. 45812605615⎛⎫--⨯ ⎪⎝⎭164. ()15154232918⎛⎫-÷-÷- ⎪⎝⎭165. 142 81614 9÷÷--⨯（）166. 1211 4.43.1830+++++-（））（167. 41889365036.25525323+-++--（）168. 53145119(20)(302.5)(151)119197131717132⎛⎫⎛⎫+-+-+-+-+- ⎪ ⎪⎝⎭⎝⎭169. ()5113(3[(2) 5.1753 6.325]3714837⎛⎫-+-++++-+ ⎪⎝⎭） 170. 53124(3)(3)(1)6565--+---+171. 3511(114662+--+）172. 224411()(0.6)33535⎛⎫-+----- ⎪⎝⎭173. 7131441232555555---++-+174.1116 3253 5.252 3477⎡⎤⎛⎫--+---⎪⎢⎥⎝⎭⎣⎦175.275315 (3(2)(3)5(1)5 58125812⎛⎫++--+--+--⎪⎝⎭）176.21 1(1) 35⨯-177.()56.5()6 -⨯-178.314 ()(1)() 429 -⨯-⨯-179.50.25(4)9 6-⨯⨯-⨯180.51 ()(3) 63 -÷-181.421 (3)(1)(1)7314 -÷-÷-182.12114 ()()(1)(1)(1) 23435 -⨯-⨯-⨯-⨯-183. 31123.8 2.4799.6()(339)8873-⨯⨯⨯-⨯-⨯⨯184. ()8[3.6(0.2)(0.4)1]-----⨯-⨯-185. 2231356(8)2(2)4⎡⎤⨯-+--⨯-⨯⎢⎥⎣⎦186. 5.7215.8-+（）187. 0.47()50347--- 188. 11(3)(5)24--+ 189. 1111(()()()6432-+---+--）190. ()23632(2)3482(2)-⨯+-⨯-÷-+-191. 232111(32)4(0.5)(1)325⎡⎤--÷-⨯-⨯-⎣⎦192. 54()(3)(1)(2)65-÷-⨯-⨯-193. 283256(1)(0.5)81477⨯-÷-+-194. 3311112(2)332--⨯-+-195. 235()(4)0.25(5)(4)8-⨯--⨯-⨯-196. 2(3)2--⨯197. 12411()()()23523+-++-+-198. 11( 1.5)4 2.75(5)42-+++-199. 8(5)63-⨯--200. 3145()2-⨯-201. 25()()( 4.9)0.656-+----202. 22(10)5()5-÷⨯-203. 323(5)()5-⨯-204. 25(6)(4)(8)⨯---÷-205. 1612()(2)472⨯-÷-206. 67()()51313-+--207. 211()1722---+-208. 737()()848-÷- 209. 21(50)()510-⨯+ 210. 2(16503)(2)5--+÷-211. 32(6)8(2)(4)5-⨯----⨯ 212. 21122()(2)2233-+⨯--213. 199711(10.5)3---⨯214. 2232[3()2]23-⨯-⨯--215. 232()(1)043-+-+⨯216. 4211(10.5)[2(3)]3---⨯⨯--217. 4(81)( 2.25)()169-÷+⨯-÷218. 215[4(10.2)(2)]5---+-⨯÷-219. 666(5)(3)(7)(3)12(3)777-⨯-+-⨯-+⨯-220. 235()(4)0.25(5)(4)8-⨯--⨯-⨯-221. 23122(3)(1)6293--⨯-÷-222. 32323(2)()()32-⨯-⨯-223. 13812711()3(2)()23-⨯⨯-⨯-224. 222172(3)(6)()3+⨯-+÷-－－225.()43212(8)()(2)2-÷---⨯- 226. 81)4(2833--÷-227. 22100(2)(2)()3÷---÷-228. 22(3)(4)-÷-229. 22312()(0.8)2-⨯-÷-230. 2232113()(2)()32-⨯---÷-231. 232()(1)043-⨯-+⨯232. 2162()5+⨯-233. 2108(2)43-+÷--⨯234. []551(0.4)( 2.5)---⨯-235. 251(1)(10.5)3---⨯236. (14)26(14)(16)8-++-+-+ 237. ( 5.5)( 3.2)( 2.5) 4.8-+---- 238. (8)(25)(0.02)-⨯-⨯- 239. 1557()(72)29612-+-⨯-240. 11(2)()32-÷-241. 211(4)()22+-⨯-242. 51552040.65(31)112280.52-÷⨯+÷--÷243. 2212113()12( 4.53)()233⎡⎤⎡⎤⨯⨯---⨯---+⎣⎦⎢⎥⎣⎦244. 23242341()()()(1)32232-⨯-÷-⨯--+-245. 111512255()()16(1)44543⎧⎫⎡⎤÷-+⨯÷--⨯-⎨⎬⎢⎥⎣⎦⎩⎭246. 20(15)(28)17-+---- 247. 6523157-+-+248. 2113()(1)3838---+-249. ( 5.54)( 3.2)( 2.5) 4.8-+---- 250. 295(3)(2)4+⨯---÷ 251. 32(1)(5)(3)2(5)⎡⎤-⨯-÷-+⨯-⎣⎦252. 32432(2)(1)(2)(2)-+-⨯---÷-253. []3(5)2(6)3005-⨯---÷ 254. 222221()32()4(1)3332-⨯-⨯-+-⨯-255. 221313(5)()240(4)2354⎡⎤-⨯--⨯--÷-⨯-⎢⎥⎣⎦256. 1347()(154)620512--+-⨯-⨯257. 3412()(5)777÷-⨯÷-258. ( 5.5) 3.2 4.5 6.8-⨯+⨯ 259. 2238()(4)()(8)595⨯---⨯-+-⨯260. 11(13)(134)()1367-⨯-⨯⨯-261. ()()()224275543()7811⎡⎤----⨯÷⨯-⎣⎦262. ()()23210022()(2)3÷---÷-+-263. 222172(3)(6)()3-+⨯-+-÷-264. 2335(2)(10.8)114⎡⎤---+-⨯÷--⎢⎥⎣⎦265. 201023)1()2(161)1()21()21(-÷-⨯⎥⎦⎤⎢⎣⎡--÷--266. )145()2(52825-⨯-÷+-267. 7111(4)(5)(4)38248---+--268. 11(0.5)(3) 6.75542---+-269. (6)(4)(32)(8)3-⨯-+-÷-- 270. 1(5)(16)(2)3-÷-÷- 271. 4321(2)(8)()(2)2-÷---⨯-272. 322)43(6)12(7311-⨯⎥⎦⎤⎢⎣⎡÷-+--273. 111117(113)(2)92844⨯-+⨯-274. 235(4)0.25(5)(4)8⎛⎫-⨯--⨯-⨯- ⎪⎝⎭275. 1113|16|2(4)()448⎡⎤⎡⎤---⨯-÷--⎢⎥⎢⎥⎣⎦⎣⎦276. (9)(4)(60)12-⨯-+-÷ 277. 230(3)3(2)--÷⨯-278. 22312()(0.8)2-⨯-÷-279. 37511()2532162-⨯-÷280. 2232113()(2)()32-⨯---÷-281. 2333(2)(3)(1)(3)---⨯---282. 3233112()()(2)33-÷---⨯-283. 22131(2)2[()3]245--⨯--⨯÷284. 13611754136227231++-285. 22)36()33(24)12581(÷-÷---⨯-286. 2132()5+⨯－287. 222172(3)(6)()3-+⨯-+-÷-288. 225(3)[()]39-⨯-+- 289. 28(3)(2)+-⨯- 290. 22100(2)(2)()3÷÷－－－－291. 421232()33÷⨯－－292. 24(3)2(3)4--⨯--⨯293. 12411()()()23523+-++-+-294. 11( 1.5)4 2.75(5)42-+++-295. 200612(1)(24)(2 2.75)83-+-⨯+-296. 103(1)2(2)4-⨯+-÷297. 422(10)[(4)(33)2]-+--+⨯298. 33422()93-÷⨯-299. 2310110.25(0.5)()(1)82-÷-+-⨯-300. 4321(2)(8)()(2)2-÷---⨯-301. 222475(5)4(3)()(7)811⎡⎤----⨯÷⨯-⎣⎦302. 31{(3)[30.4(1)(2)]}2---+⨯-÷- 303. 421110.52(3)3-+-⨯⨯⨯-（）［］ 304. 3334[(17)6][(5)3](2)⨯-÷+--÷-－305. 332313[8(2)1](3)(2)0.25--÷--+-⨯-÷306. 9.538(2|11.64 1.53 1.36|)----+-307. 73.17(812.03|219.83518|)--+308. 1112(398)-+--309. 95(945)----310. 5.6 4.7| 3.8 3.8-+---｜311. 1213521(36)(16)(45)(10)27277+-+-+-++ 312.5211()(2)(4)319152⨯-⨯-⨯-313. 555()83()(13)()28666-⨯+-⨯---⨯314. 23181920222...222-----+315. 111 (133519971999)+++⨯⨯⨯316. 3145()2-⨯-317. 25()()( 4.9)0.656-+----318. 22(10)5()5-÷⨯-319. 323(5)()5-⨯-320. 25(6)(4)(8)⨯---÷-321. 1612()(2)472⨯-÷-322. 2(16503)(2)5--+÷-323. 32(6)8(2)(4)5-⨯----⨯324. 235()(4)0.25(5)(4)8-⨯--⨯-⨯-325. 23122(3)(1)6293--⨯-÷-326. 21122()(2)2233-+⨯--327. 19971(1)(10.5)3----⨯328. 2232[3()2]23-⨯-⨯-- 329. 232()(1)043-+-+⨯330. 4211(10.5)[2(3)]3---⨯⨯-- 331. 215[4(10.2)(2)]5---+-⨯÷- 332. 666(5)(3)(7)(3)12(3)777-⨯-+-⨯-+⨯-333. 42311[ 2(3)]6--⨯--- 334. 7574.037127.5371236)9618-+-⨯-+（335. 2212[3()0.8](2)35-⨯--÷-336. --+⎛⎝ ⎫⎭⎪+-⎛⎝ ⎫⎭⎪---+3825583521()337. [(3)(4)5][82(6)]4-⨯--⨯--⨯-÷338. -÷--÷-824134()()339. ()[()()]-÷-⨯⨯-11551135340. 42991310.25(1)12 3.7524283⎛⎫⎛⎫-÷-⨯-++-⨯ ⎪ ⎪⎝⎭⎝⎭341. 1311143343411-÷⨯÷342. ---⎛⎝ ⎫⎭⎪----⎛⎝ ⎫⎭⎪1133411334343. ()()------22222233344. 1235342123341822--÷-⎛⎝ ⎫⎭⎪+⨯-⎛⎝ ⎫⎭⎪⎡⎣⎢⎢⎤⎦⎥⎥⨯⎧⎨⎪⎩⎪⎫⎬⎪⎭⎪345. -----÷-+--÷--22331349722232()|()()||||| 346. 13525(2)2514⎛⎫--÷-⨯- ⎪⎝⎭347. 234( 1.5)1243⎛⎫-÷-⨯- ⎪⎝⎭348. 34311(1)2⎡⎤⎛⎫-----⎢⎥ ⎪⎝⎭⎢⎥⎣⎦349. 210.2343 5.35⎡⎤⎛⎫-⨯--⨯- ⎪⎢⎥⎝⎭⎣⎦350. 222243(3)(5)(0.3)0.95⎛⎫---+-⨯---÷- ⎪⎝⎭351. ()11232311412243⨯⨯-⎛⎝ ⎫⎭⎪--⎡⎣⎢⎢⎤⎦⎥⎥+÷-⎛⎝ ⎫⎭⎪352. 71957180251411313..-⎛⎝ ⎫⎭⎪÷-÷⨯⎛⎝ ⎫⎭⎪353. ()-÷⨯-⨯÷⨯-⎛⎝ ⎫⎭⎪11234021341435..354. ()()11160752116340534+--⎡⎣⎢⎤⎦⎥⨯-⎧⎨⎩⎫⎬⎭÷---⎛⎝ ⎫⎭⎪..355. ()-⨯-⎛⎝ ⎫⎭⎪-⨯--⨯-⎛⎝ ⎫⎭⎪⎡⎣⎢⎢⎤⎦⎥⎥⨯⨯--⎛⎝ ⎫⎭⎪⎡⎣⎢⎤⎦⎥212341351499113192222356. 4211(10.5)2(3)3⎡⎤---⨯⨯--⎣⎦357. 33423(1)(1)--⨯---358. 33510.2(2)5⎡⎤⎛⎫---+-⨯÷- ⎪⎢⎥⎝⎭⎣⎦359. 12(17)1(0.6)4⎡⎤---÷-+-⎢⎥⎣⎦360. 2311(10.6432)⎡⎤----÷⎣⎦361. 3213322.2512853⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫--÷-+-⨯-⎢⎥ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦362. []261(0.4)( 2.5)---⨯-363. 362211362⎛⎫⎛⎫-⨯÷ ⎪ ⎪⎝⎭⎝⎭364. 1448551836615335175123192155⨯÷-+⨯⎛⎝ ⎫⎭⎪-⨯+⎛⎝ ⎫⎭⎪-⎡⎣⎢⎤⎦⎥.....365. ()()()222410.4 3.1 2.610.30.15⎧⎫⎡⎤⎛⎫-⨯---+⨯---÷-⎨⎬ ⎪⎢⎥⎝⎭⎣⎦⎩⎭366. 513113(50)217348⎛⎫⎛⎫⎛⎫⨯-÷-⨯-÷ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭367. ()11572348126824⎛⎫-+-⨯- ⎪⎝⎭368. 4535522723723237⎛⎫⎛⎫⎛⎫⨯---⨯--⨯ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭369. ()199719996661998⎛⎫-⨯- ⎪⎝⎭370. 33371. 4946111(3)20.24911235⎡⎤⎛⎫⎛⎫-÷⨯-⨯-⨯-+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦372. 2782411813318833⨯÷⎪⎭⎫ ⎝⎛-⨯373. )2()2(2123322-+--⎪⎭⎫ ⎝⎛-+-374. ⎪⎭⎫⎝⎛----÷⨯⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-2135322132213122375. ()87216543313113)1(61)5.4(187********÷⎪⎭⎫⎝⎛-÷⎪⎭⎫⎝⎛---⨯⎪⎭⎫⎝⎛--⨯+-⨯⎪⎭⎫ ⎝⎛-376. )57(5857-⨯377. ()4443145-÷-378.（379. ()3330037÷-380. ()()()199084481990199014181990-⨯--⨯--⨯-⨯381. ()()999999999999999999+-⨯-+-382. ()()()()()149297483149297483-÷-⨯-÷-⨯-÷-383. ()()()⎭⎬⎫⎩⎨⎧-⎪⎭⎫ ⎝⎛-÷⎥⎦⎤⎢⎣⎡-⨯⎪⎭⎫ ⎝⎛-+-÷⨯-2314.0411432417384. ()⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎭⎫ ⎝⎛-⨯÷⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡+÷-⨯⨯-⎪⎭⎫ ⎝⎛-÷-12122211341125.0221132322385. ()41611143125.1012112310013+--⎪⎭⎫ ⎝⎛-÷+386. 199519953(0.125)[(2)]⨯-387. 25413()(0.612)()651010⨯+-÷-388. 322333342(-)⨯(-0.6)-(-)⨯1.5-2÷(-)253389. 232006333...3++++390. 199720002000200019971997⨯-⨯391. 22222221949195019511952...199719981999-+-++-+392. 22221111(1)(1)...(1)(1)23910---- 393. 1111 (12123123100)++++++++++394. 987654321987654324987654323987654322⨯-⨯395.1121231299()()...(...)233444100100100++++++++++396. 32)65()43(21--+---397. 38(4)(2)4⎛⎫⨯-⨯-⨯- ⎪⎝⎭398.111135()532114⨯-⨯÷399. 34153()2--⨯-（）400. 42223721-+--⨯-（）（）401. 1031224-⨯+-÷（）（）402. 2395525-⨯-÷-（）（）（） 403. 333(125)()62187()777-÷-+÷+÷- 404.2725.0)431(218)522(52⨯÷--⨯--÷405. 311252525424⨯--⨯-⨯（）406. 38(4)23--÷⨯407. 22733(3)⨯÷+-408. 4435(2)2(2)-+--÷-409. (28)(64)(1)5-÷-++-⨯410. 2(2)07(8)(2)÷-+÷--⨯-411. 13131()24524864⎡⎤-+-⨯÷⎢⎥⎣⎦412. 2332312(3)(2)(9)3÷-÷---÷413. 222122(1)33-÷⨯-414. 32432(2)(1)(2)(2)-+-⨯---÷-415. 32(1)(5)(3)2(5)⎡⎤-⨯-÷-+⨯-⎣⎦416. 75.61258)431(121-----417. 2335(2)(10.8)114⎡⎤---+-⨯÷--⎢⎥⎣⎦418. 75)21(212)75(75211⨯-+⨯--⨯419. 4)2(51232⨯--÷-420. 50)3(15)3(42--÷--⨯421. 3211(10.5)2(3)7⎡⎤---⨯⨯--⎣⎦422. 22)7()6(6112119750-÷⎥⎦⎤⎢⎣⎡-⨯⎪⎭⎫⎝⎛+--423. []3521325.06.05.2)1(⎪⎭⎫⎝⎛-⨯+--÷-424. 111117(113)(2)92844⨯-+⨯-425. 419932(4)(1416)41313⎡⎤--⨯-÷-⎢⎥⎣⎦426. 33221121(5533)22⎡⎤⎛⎫⎛⎫--÷+⨯+⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦427. 2375(2)(10.8)114⎡⎤----+-⨯÷--⎢⎥⎣⎦428. 151623-÷-÷-（）（）（） 429. 42(3)60.25-+⨯--÷430. 3(5)[1.85(21)7]4-÷--⨯431. []18{10.4 (10.4)0.4}÷-+-⨯432. 1111()636÷-⨯433. –3[4(4 3.51)][2(3)]---⨯⨯-+-434. ()3.57.75 4.25 1.1--÷435. 321612115()|(2)|(2)(|()|)2114332⎡⎤----+-⨯-÷---⎢⎥⎣⎦436. 1110.125(3)(3)()(0.25)488+++-+++-437. 5215[(9)]317.75632-----+438. 1211[3()1](8)8233⨯⨯---⨯--439. 7211()(4)9353-÷--⨯-440. 78(0.125)8-⨯441. 4010(0.25)256⨯442. 12(3)(4)56(7)(8)(23)(24)++-+-+++-+-+⋯+-+-443.1111111142648620102008-+-+-+⋯+-444. 1111(1)(1)(1)(1)2009200820071000-⨯-⨯-⨯⋯⨯- 445. 19(7)128(7)33(7)÷--÷-+÷-446.111111223344556++++⨯⨯⨯⨯⨯447.111 (101111125960)+++⨯⨯⨯448.2222 109985443 ++++⨯⨯⨯⨯449.1111 11212312100 ++++++++++450.1111 133******** ++++⨯⨯⨯⨯451.1111251335572325⎛⎫⨯++++⎪⨯⨯⨯⨯⎝⎭452.251251251251251 4881212162000200420042008 +++++⨯⨯⨯⨯⨯453.3245671 255771111161622222929 ++++++⨯⨯⨯⨯⨯⨯454.11111111()128 8244880120168224288+++++++⨯455.11111111 612203042567290 +++++++456.111111 13610152128 ++++++457.111111111 2612203042567290 --------458.11111 104088154238 ++++459.1111 135357579200120032005 ++++⨯⨯⨯⨯⨯⨯⨯⨯460.74.50.161111 1813153563 13 3.75 3.23⨯+⎛⎫⨯+++⎪⎝⎭-⨯461.11111 123420 261220420 +++++462.11111 20082009201020112012 1854108180270 ++++463.11224 26153577 ++++464.1111111 315356399143195 ++++++465.1511192997019899 2612203097029900 +++++++466.111 123234789 +++⨯⨯⨯⨯⨯⨯467.111 1232349899100 +++⨯⨯⨯⨯⨯⨯468.1111 135246357202224 ++++⨯⨯⨯⨯⨯⨯⨯⨯469.4444...... 135357939597959799 ++++⨯⨯⨯⨯⨯⨯⨯⨯470.9998971 12323434599100101 ++++⨯⨯⨯⨯⨯⨯⨯⨯471.11111 123423453456678978910 +++⋅⋅⋅++⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯472.333...... 1234234517181920 +++⨯⨯⨯⨯⨯⨯⨯⨯⨯473.5719 1232348910 +++⨯⨯⨯⨯⨯⨯474.571719 1155234345891091011⨯++++⨯⨯⨯⨯⨯⨯⨯⨯（）475.34512 12452356346710111314 ++++⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯476.12349 223234234523410 +++++⨯⨯⨯⨯⨯⨯⨯⨯⨯477.123456 121231234123451234561234567 +++++⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯478.23993!4!100!+++ 479.234501(12)(12)(123)(123)(1234)(12349)(1250)++++⨯++⨯++++⨯+++++++⨯+++ 480.2341001(12)(12)(123)(123)(1234)(1299)(12100)++++⨯++⨯++++⨯++++++⨯+++ 481. 23101112(12)(123)(1239)(12310)----⨯++⨯++++++⨯++++ （）482.22222211111131517191111131+++++------483. 222222111111(1)(1)(1)(1)(1)(1)23454849-⨯-⨯-⨯-⨯⨯-⨯- 484.222222223571512233478++++⨯⨯⨯⨯ 485. 222222222231517119931199513151711993119951++++++++++-----。

初中数学计算题库

初中数学计算题库一、有理数运算1. 加法运算- 题目：计算(+3)+( - 5)。

- 解析：这就像是在数轴上玩游戏，正数是向右走，负数是向左走。

先向右走3步，再向左走5步，那最后就到了 - 2这个位置啦，所以(+3)+( - 5)= - 2。

- 题目：( - 2)+( - 3)。

- 解析：两个负数相加，就像两个倒霉蛋凑一块儿了。

向左走2步，再向左走3步，总共向左走了5步，所以( - 2)+( - 3)= - 5。

2. 减法运算- 题目：计算5-(+3)。

- 解析：减一个正数呢，就相当于加上它的相反数。

所以5-(+3)=5+( - 3)，在数轴上就是从5这个位置向左走3步，结果就是2啦。

- 题目：( - 3)-(-5)。

- 解析：减一个负数就相当于加上它的正数哦。

那( - 3)-(-5)=(-3)+5，从 - 3这个点向右走5步，就到了2这个位置，所以结果是2。

3. 乘法运算- 题目：计算( - 2)×3。

- 解析：正数乘以负数，结果是负数。

就像你有3个负债2元的账单，那总共就负债6元啦，所以( - 2)×3=-6。

- 题目：( - 2)×(-3)。

- 解析：两个负数相乘就变成正数啦。

可以想象成欠了2次 - 3元，那就是得到了6元，所以( - 2)×(-3)=6。

4. 除法运算- 题目：计算( - 6)÷3。

- 解析：除法和乘法是反着来的。

负数除以正数结果是负数，就像把 - 6元平均分给3个人，每人负债2元，所以( - 6)÷3=-2。

- 题目：( - 8)÷(-2)。

- 解析：两个负数相除结果是正数。

把 - 8元的债务平均分给 - 2个人，那每人就得到4元啦，所以( - 8)÷(-2)=4。

二、整式运算1. 合并同类项- 题目：化简3x + 2x。

- 解析：这就好比3个苹果加上2个苹果，那就是5个苹果啦。

这里x就像苹果，所以3x+2x = 5x。