最新表面张力和表面能
合集下载
第三章表面张力及表面能
H ( A)S,P,nB
(FA)T,V,nB
(G A)T,P,nB
表面自由能与表面张力
对于表面相，我们从“能”和“力”的角度引出了两个 不同的概念：表面自由能与表面张力。事实上这两个概念有 着密切的联系
一、两者量纲相同
J Nm N m2 m2 m
表面自由能的量纲
表面张力量纲
表面自由能与表面张力
• For a rough estimate we picture the liquid as being arranged in a cubic structure. Each molecule is surrounded by 6 nearest neighbors. Thus each bond contributes roughly ΔvapU/6 = 5.08 kJ/mol. At the surface one neighbor and hence one bond is missing. Per mole we therefore estimate a surface tension of 5.08 kJ/mol.
硝基苯 20
苯
20
苯
30
甲苯 20
四氯化 22 碳
表面张力 (mN/m) 26.67
20.14
22.50
22.39 43.35 28.22 27.56 28.52 26.76
一些油水界面张力（20℃）
界面 苯－水
界面张力 (mN/m)
35.0
四氯化碳
45.1
－水
正己烷－
51.1
水
正辛烷－
50.8
水
作用于单位边界线上的这种力称为表面张力，用 表 示，单位是N·m-1。
表面张力和表面能 课件
膜的透过性能和抗污染性能。
在大气污染控制中，表面张力用于颗粒 物的沉降和去除，从而降低大气中的颗 粒物浓度。例如，在湿法脱硫中，表面 张力用于控制液滴的粒径和分布，从而
提高脱硫效率。
THANKS
感谢观看
表面张力的物理意义
表面张力是液体表面所具有的 一种特性，它反映了液体表面 分子间相互作用的强弱。
表面张力决定了液体表面的形 状、大小以及液滴的形状和稳 定性。
表面张力在许多物理现象中起 着关键作用，如毛细现象、润 湿现象、气泡形成和破裂等。
表面张力的影响因素
温度
温度升高，表面张力降低；温 度降低，表面张力增大。
阳能电池板的效率。
在燃料电池的液态水管理中，表 面张力用于控制水分的分布和迁 移，从而影响燃料电池的性能和
寿命。
在环境保护中的应用
表面张力和表面能在环境保护中也有着 重要的应用，如水处理、大气污染控制
、土壤修复等。
在水处理中，表面张力用于控制水的表 面张力，从而提高水处理的效率。例如 ，在超滤膜过滤中，表面张力用于控制
在石油工业中，表面张力用于油水分离、油泥清洁等，以提高采收率和 生产效率。
在化学工业中，表面张力用于化学反应的速率控制、化学物质的分离和 提纯等。
在能源开发中的应用
表面张力在能源开发中也有着重 要的应用，如太阳能电池板的清 洗、燃料电池的液态水管理、核
反应堆的冷却剂管理等。
在太阳能电池板的清洗中，表面 张力起着重要作用，清洗剂的选 择和清洗工艺的优化可以提高太
物质种类
不同物质具有不同的表面张力 ，同一物质在不同温度和压力 下也具有不同的表面张力。
压力
压力对表面张力影响较小，但 在高压下也会引起表面张力的 变化。
在大气污染控制中，表面张力用于颗粒 物的沉降和去除，从而降低大气中的颗 粒物浓度。例如，在湿法脱硫中，表面 张力用于控制液滴的粒径和分布，从而
提高脱硫效率。
THANKS
感谢观看
表面张力的物理意义
表面张力是液体表面所具有的 一种特性，它反映了液体表面 分子间相互作用的强弱。
表面张力决定了液体表面的形 状、大小以及液滴的形状和稳 定性。
表面张力在许多物理现象中起 着关键作用，如毛细现象、润 湿现象、气泡形成和破裂等。
表面张力的影响因素
温度
温度升高，表面张力降低；温 度降低，表面张力增大。
阳能电池板的效率。
在燃料电池的液态水管理中，表 面张力用于控制水分的分布和迁 移，从而影响燃料电池的性能和
寿命。
在环境保护中的应用
表面张力和表面能在环境保护中也有着 重要的应用，如水处理、大气污染控制
、土壤修复等。
在水处理中，表面张力用于控制水的表 面张力，从而提高水处理的效率。例如 ，在超滤膜过滤中，表面张力用于控制
在石油工业中，表面张力用于油水分离、油泥清洁等，以提高采收率和 生产效率。
在化学工业中，表面张力用于化学反应的速率控制、化学物质的分离和 提纯等。
在能源开发中的应用
表面张力在能源开发中也有着重 要的应用，如太阳能电池板的清 洗、燃料电池的液态水管理、核
反应堆的冷却剂管理等。
在太阳能电池板的清洗中，表面 张力起着重要作用，清洗剂的选 择和清洗工艺的优化可以提高太
物质种类
不同物质具有不同的表面张力 ，同一物质在不同温度和压力 下也具有不同的表面张力。
压力
压力对表面张力影响较小，但 在高压下也会引起表面张力的 变化。
表面张力和表面能 课件
表面张力和表面能的应用
表面张力在生活中的应用
01
02
03
露珠呈球形
由于表面张力，水滴在荷 叶或树叶上呈球形，不易 散开。
气泡形成
在洗衣服、洗碗时，表面 张力使气泡在水中形成并 保持。
防水表面
表面张力可以用于创造防 水表面，如荷叶的自洁效 应。
表面能在工业中的应用
涂层附着
表面能的大小影响涂层与 基材的附着力，选择合适 的涂层材料和工艺可以提 高附着力。
表面能与物质性质的关系
物质性质对表面能的影响
物质的化学性质、晶体结构、分子间作用力等都会影响其表 面能。例如，极性分子具有较大的表面能，因为它们具有更 强的分子间相互作用力。
表面能的应用
在化学、物理、工程等领域中，表面能具有广泛的应用，如 润湿现象、自组装单层膜、晶体生长等都与表面能密切相关 。
04
力等因素有关。
表面能
表面能是固体表面的能量，它是 由于固体表面原子或分子的排列 不规整而引起的。表面能的大小 与表面的粗糙度、化学组成、温
度等因素有关。
实验方法
通过测量液体在固体表面上展开 的角度或测量液体在固体表面上 的接触角，可以计算出表面张力
和表面能。
实验步骤
准备实验器材
测量液体在固体表面上的接触角
表面张力计、表面能计、待测液体和固体 样品等。
将待测液体滴在固体表面上，观察液滴的 形状，并测量接触角。
计算表面张力和表面能
分析实验结果
根据接触角的大小，利用相关公式计算出 表面张力和表面能。
分析实验结果，了解表面张力和表面能与 物质性质的关系，并得出结论。
06
相关理论介绍
杨氏方程
总结词
杨氏方程是描述表面张力和表面分子 间的相互吸引程度。
表面张力在生活中的应用
01
02
03
露珠呈球形
由于表面张力，水滴在荷 叶或树叶上呈球形，不易 散开。
气泡形成
在洗衣服、洗碗时，表面 张力使气泡在水中形成并 保持。
防水表面
表面张力可以用于创造防 水表面，如荷叶的自洁效 应。
表面能在工业中的应用
涂层附着
表面能的大小影响涂层与 基材的附着力，选择合适 的涂层材料和工艺可以提 高附着力。
表面能与物质性质的关系
物质性质对表面能的影响
物质的化学性质、晶体结构、分子间作用力等都会影响其表 面能。例如，极性分子具有较大的表面能，因为它们具有更 强的分子间相互作用力。
表面能的应用
在化学、物理、工程等领域中，表面能具有广泛的应用，如 润湿现象、自组装单层膜、晶体生长等都与表面能密切相关 。
04
力等因素有关。
表面能
表面能是固体表面的能量，它是 由于固体表面原子或分子的排列 不规整而引起的。表面能的大小 与表面的粗糙度、化学组成、温
度等因素有关。
实验方法
通过测量液体在固体表面上展开 的角度或测量液体在固体表面上 的接触角，可以计算出表面张力
和表面能。
实验步骤
准备实验器材
测量液体在固体表面上的接触角
表面张力计、表面能计、待测液体和固体 样品等。
将待测液体滴在固体表面上，观察液滴的 形状，并测量接触角。
计算表面张力和表面能
分析实验结果
根据接触角的大小，利用相关公式计算出 表面张力和表面能。
分析实验结果，了解表面张力和表面能与 物质性质的关系，并得出结论。
06
相关理论介绍
杨氏方程
总结词
杨氏方程是描述表面张力和表面分子 间的相互吸引程度。
表面张力和表面能
表面自由能(surface free energy)
广义的表面自由能定义：
保持相应的特征变量不变，每增加单位表面积 时，相应热力学函数的增值。
狭义的表面自由能定义：
(G) A
p,T,nB
保持温度、压力和组成不变，每增加单位表面 积时，Gibbs自由能的增加值称为表面Gibbs自由
能，或简称表面自由能或表面能，用符号 或
可见达到nm级的超细微粒具有巨大的比表面积， 因而具有许多独特的表面效应，成为新材料和多相 催化方面的研究热点。如铂黑电极及多孔电极由于 其表面积较大，电流密度小，因而极化小；再如， 由超细微粒制备的催化剂由于具有很高的比表面因 而催化活性较普通催化剂高；此外，将药物磨成细 粉以提高药效、将金属做成超细微粒以降低熔点都 说明了超细微粒具有独特的表面效应。
体，k =2.2×10-7 J·K-1 。
影响表面张力的因素
（1）分子间相互作用力的影响 对纯液体或纯固体，表面张力决定于分子间形成
的化学键能的大小，一般化学键越强，表面张力越大。
(金属键)> (离子键)> (极性共价键)> (非极性共价键)
两种液体间的界面张力，界于两种液体表面张力之间。
（2）温度的影响 温度升高，表面张力下降。
（3）压力的影响 表面张力一般随压力的增加而下降。因为压力增
加，气相密度增加，表面分子受力不均匀性略有好转。 另外，若是气相中有别的物质，则压力增加，促使表 面吸附增加，气体溶解度增加，也使表面张力下降。
压力的影响
压力与表面张力关系的实验研究不易进行，一般说来，压 力对表面张力的影响可以从下面三个方面考虑
称为表面张力，用 表示，单位是
N·m-1。
将一含有一个活动边框的金属 线框架放在肥皂液中，然后取出悬 挂，活动边在下面。由于金属框上 的肥皂膜的表面张力作用，可滑动 的边会被向上拉，直至顶部。
表面能与表面张力系数
R0
内其他分子对该分子的作用力是相
互抵消的。
• 但在液体表面层内 却并非如此。
• 若液体与它的蒸气相 接触，其表面层内分 子作用球的情况示于 图。
表面层分子的作用球中或多或少总有一部分是密度 很低的气体，使表面层内任一分子所受分子力不平衡， 其合力是垂直于液体表面并指向液体内部的。
在这种分子力合力作用下，液体有尽量缩小它的表面 积的趋势，使液体表面像拉紧的膜一样。表面张力就 这样产生的。
(二) 表面能与表面张力系数
• 表面张力是由于液体表面的过渡区域(称为表面层)内
分子力作用的结果。
• 表面层厚度大致等于分子引力的有效作用距离的数
倍，其数量级约为10-9 m，即2～4个分子直径的大小。
设分子互作用势能是球对称的，以任一分子为中心画
出以 R0 为半径的分子作用球。
显然,在液体内部，其分子作用球
• 当外力F 在等温条件下拉伸铁丝(见下图)以扩大肥 皂膜的表面积ΔA 时,
力F 做的功为ΔW = FΔx，因为
F = 2σL,ΔA = 2LΔx，W = σΔA
在扩大液体表面积过程中，一部分液体内部的分子 要上升到表面层中，而进入表面层的每一个分子都需 克服分子力的合力做功。 合力方向指向液体内部。
也可写成两种不同的形式：N·m-1及J·m-2。
表面张力产生原因另一种解释: 既然表面能是表面层中分子
比液体内部分子多出来的分子 互作用(吸引力)势能。 可见在表面层中分子的平均间 距要比液体内部大，为什么?
说明在表面层中分子排列要比 液体内部疏松些(而且越是沿液 面向外，其排列越疏松)。
从分子间作用力曲线可估 计到，平均说来，在表面层 中分子间的吸引力明显大于 液体内部。为什么?
第三章表面张力及表面能
• 2 × 0.01 m × 0.072 Jm−2 = 1.44 × 10−3N
That corresponds to a weight of 0.15 g.
How can we interpret the concept of surface tension on the molecular level?
For molecules it is energetically favorable to be surrounded by other molecules. Molecules attract each other by different interactions such as van der Waals forces or hydrogen bonds.
乙醚
甲醇 乙醇 硝基苯 苯 苯 甲苯 四氯化 碳
25
20 20 20 20 30 20 220.1422.50 22.39 43.35 28.22 27.56 28.52 26.76
一些油水界面张力（20℃）
界面 界面张力(mN/m) 界面 界面张力(mN/m)
苯－水
35.0
正辛醇－水
8.5
四氯化碳－水
一些液体的表面张力
液体 全氟戊 烷 温度／ ℃ 20 表面张力 (mN/m) 9.89 液体 三氟甲 烷 温度 /℃ 25 表面张力 (mN/m) 26.67
全氟庚 烷
全氟环 己烷 正己烷 正庚烷 正辛烷 水 水 水
20
20 20 20 20 20 25 30
13.19
15.70 18.43 20.30 21.8 72.8 72.0 71.2
AS 4 r 2 4 4 / 3 cm2 4.84 104 cm2
表面能和表面张力
表面能和表面张力1. 介绍表面能和表面张力是物理学中关于液体和固体界面性质的重要概念。
表面能描述了液体分子的吸引力和固体界面分子之间的相互作用能力，而表面张力则指液体表面的弹性和抵抗外部扩展的能力。
本文将详细介绍表面能和表面张力的含义、计算方法以及相关应用领域。
2. 表面能2.1 含义表面能是描述液体表面性质的重要参数，通常用符号γ表示。
它是指单位面积内液体分子的吸引力能量。
液体表面分子与内部分子相比，周围没有同种液体分子的引力作用，因此表面的分子受到的吸引力较大，导致表面能较高。
2.2 计算方法常用的计算液体表面能的方法有两种：Young-Laplace方法和相对法。
Young-Laplace方法是基于气泡和液滴的理论推导，通过测量气泡或液滴的形态参数来计算表面能。
将Young-Laplace方程应用于液滴或气泡的变形，可以得到表面能与液滴半径或气泡半径的关系。
相对法则是通过比较液体与不同材料的表面能差异，来计算液体自身的表面能。
可以借助表面张力平衡法或液体浸润法实现。
3. 表面张力3.1 含义表面张力是指液体表面上液体分子之间的相互作用力。
液体分子因互相吸引而紧密排列，使得液体表面呈现较高的张力，能够抵制外界对液体表面的扩展力。
3.2 计算方法表面张力的计算主要通过测量液体静态平衡或动态平衡状态下的力的大小来实现。
常用的实验方法有杨氏静水压力法和浊度法。
杨氏静水压力法是一种通过测量不同高度的水柱在液体表面产生的压力差来计算表面张力的方法。
该方法利用液体表面张力的平衡原理，得出表面张力与液体柱高之间的关系。
浊度法是基于光的折射原理，通过测量液体的浊度变化来计算表面张力。
浊度测量方法适合浑浊液体或液面上有液滴的情况。
4. 应用领域表面能和表面张力的研究在许多领域具有重要的应用价值：•材料科学：表面能对于材料的附着、涂覆、打印和涂料的均匀性都具有重要影响，因此在材料科学中有广泛的应用。
•纳米科技：纳米材料表面能和表面张力的研究对于纳米材料的制备、传输和应用具有重要意义。
表面张力及表面能
第三十四页，共95页
• Example:Estimate the surface tension of cyclohexane from the energy of vaporization ΔvapU = 30.5 kJ/mol at 25◦C. The density of cyclohexane is ρ = 773 kg/m3, its molecular weight is M = 84.16 g/mol.
第十一页，共95页
表面自由能(Surface Free Energy)
1. 狭义定义：保持体系温度、压力、组成不变时，增
加单位表面积，体系吉布斯自由能的增量。
G
(
) A
p,T,nB
也称为比表面吉布斯自由能
第十二页，共95页
表面自由能(Surface Free Energy)
表面化学基本热力学关系式：
• 2 × 0.01 m × 0.072 Jm−2 = 1.44 × 10−3N
That corresponds to a weight of 0.15 g.
第三十页，共95页
How can we interpret the concept of surface tension on the molecular level?
• 表面自由能（surface free energy）：是恒 温恒压下增加单位表面积时体系自由能的增 量，称作比表面自由能，简称表面自由能。 单位：mJ/m2（毫焦/米2）
第二十六页，共95页
dW •2bd x •dA
Figure 2.2: Schematic set-up to verify Eq. (2.2) and define the surface tension
• Example:Estimate the surface tension of cyclohexane from the energy of vaporization ΔvapU = 30.5 kJ/mol at 25◦C. The density of cyclohexane is ρ = 773 kg/m3, its molecular weight is M = 84.16 g/mol.
第十一页，共95页
表面自由能(Surface Free Energy)
1. 狭义定义：保持体系温度、压力、组成不变时，增
加单位表面积，体系吉布斯自由能的增量。
G
(
) A
p,T,nB
也称为比表面吉布斯自由能
第十二页，共95页
表面自由能(Surface Free Energy)
表面化学基本热力学关系式：
• 2 × 0.01 m × 0.072 Jm−2 = 1.44 × 10−3N
That corresponds to a weight of 0.15 g.
第三十页，共95页
How can we interpret the concept of surface tension on the molecular level?
• 表面自由能（surface free energy）：是恒 温恒压下增加单位表面积时体系自由能的增 量，称作比表面自由能，简称表面自由能。 单位：mJ/m2（毫焦/米2）
第二十六页，共95页
dW •2bd x •dA
Figure 2.2: Schematic set-up to verify Eq. (2.2) and define the surface tension
表面张力与表面能_2023年学习资料
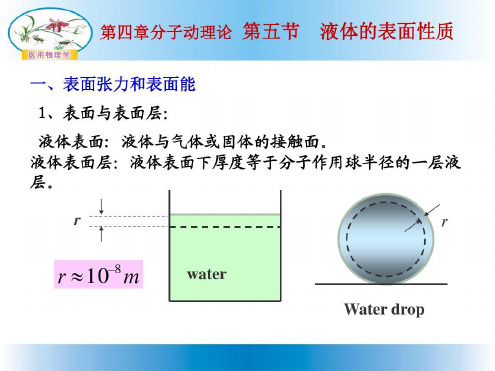
医用物理学-2肺组织中的表面活性物质：-*肺组织结构；-*肺泡内壁分泌某种磷脂是表面活-性物质；它的重要作
：维持正常-呼吸。-吸气过程：-R个→活性物质密度↓→粘液的α 个→P内个-图5-1呼吸系统全貌-呼气过程： R↓→活性物质密度个→粘液的α ↓→P↓-3表面非活性物质：-*尽量离开表面层而进入液体内部，使表面张力系数 大。-举例：水中的盐份等
医用物理学-浸湿现象：-不浸湿现象：-当f附>f内时，-当f附<f内时，-附着层扩展，-附着层收缩，-液体 湿固体：-液体不浸湿固体；-0<900-0>900-的-水-水银-7777-玻璃-LVTFFRBJKFFF 8EF85558888
2.毛细现象：-医用物理学-液体浸湿毛细管壁时，管内液面上升；液体不浸湿毛细-管壁时，管内液面下降。-液面 升的原因：〈卫A-平衡时，=PA-R-r Rcos 0-■■■■-h-h=-2-2oc0s0-PgR-pg -B-当090时，为完全浸湿。-对于下降同样适用
医用物理学-0-凸面-D=p+-△A-凹面-B=p-B--20-P。=P+-R-R>P。-P=P-P=-凸 ：-R<P-凹面：-=-B=2%>0-2a-<0-P=P-P。=-
球形液膜的附加压强：-医用物理学-对外表面：PB一PA=-20x-Ri-对内表面：-PB-PC=-肥皂泡2-4a-PC-PA=-R=R2=R
演示实验：（大泡小泡-医用物理学-对大泡：-P--40-+P-R-对小泡：-2-40+P-肥皂泡-P2=2-Po-因为-R>R,所以卫<P.-结果：大泡变大，小泡变小。
三、毛细现象和气体栓塞-医用物理学-1.接触角：-附着层（即与固体接触的一薄层液体）内-液体分子的运动主要 到两个力影响：-f附：固体分子对液体分子的吸引力称-为附着力。-f内：〉-液体分子对液体分子的吸引力称-为 聚力。
表面张力和表面能
2、若采用吉布斯界面模型，且体系为纯液体。则
有 Vs0,ns0 =Gs As
AA
可见，对纯液体， γ是单位面积等效表面所具有的 自由能。
2021/10/10
21
表面张力（surface tension）
在两相(特别是气-液)界面上，处 处存在着一种张力，它垂直于表面的 边界，指向液体方向并与表面相切。
温度、压力和组成恒定时，可逆使表面积增加dA 所需要对体系作的功，称为表面功。用公式表示为：
W ' dA
式中 为比例系数，它在数值上等于当T，P及组
成恒定的条件下，增加单位表面积时所必须对体 系做的可逆非膨胀功。
2021/10/10
16
表面自由能(surface free energy)
考虑了 表面功，热 力学基本公 式中应相应
1、严格讲，界面是“界”而不是“面”。因客观存在的界面 是物理面而非几何面，是一个准三维的区域。
2、目前，常用于处理界面的模型有两种：一为古根海姆 （Guggenheim）模型。其处理界面的出发点是：界面是 一个有一定厚度的过渡区，它在体系中自成一相—界面相。 界面相是一个既占有体积又有物质的不均匀区域。该模型 能较客观地反映实际情况但数学处理较复杂。另一个模型 是吉布斯（Gibbs）的相界面模型。该模型认为界面是几 何面而非物理面，它没有厚度，不占有体积，对纯组分也 没有物质存在。该模型可使界面热力学的处理简单化。
边长l/m
1×10-2 1×10-3 1×10-5 1×10-7 1×10-9
立方体数
1 103 109 1015 1021
比表面Av/（m2/m3） 6 ×102 6 ×103 6 ×105 6 ×107 6 ×109
2021/10/10
有 Vs0,ns0 =Gs As
AA
可见，对纯液体， γ是单位面积等效表面所具有的 自由能。
2021/10/10
21
表面张力（surface tension）
在两相(特别是气-液)界面上，处 处存在着一种张力，它垂直于表面的 边界，指向液体方向并与表面相切。
温度、压力和组成恒定时，可逆使表面积增加dA 所需要对体系作的功，称为表面功。用公式表示为：
W ' dA
式中 为比例系数，它在数值上等于当T，P及组
成恒定的条件下，增加单位表面积时所必须对体 系做的可逆非膨胀功。
2021/10/10
16
表面自由能(surface free energy)
考虑了 表面功，热 力学基本公 式中应相应
1、严格讲，界面是“界”而不是“面”。因客观存在的界面 是物理面而非几何面，是一个准三维的区域。
2、目前，常用于处理界面的模型有两种：一为古根海姆 （Guggenheim）模型。其处理界面的出发点是：界面是 一个有一定厚度的过渡区，它在体系中自成一相—界面相。 界面相是一个既占有体积又有物质的不均匀区域。该模型 能较客观地反映实际情况但数学处理较复杂。另一个模型 是吉布斯（Gibbs）的相界面模型。该模型认为界面是几 何面而非物理面，它没有厚度，不占有体积，对纯组分也 没有物质存在。该模型可使界面热力学的处理简单化。
边长l/m
1×10-2 1×10-3 1×10-5 1×10-7 1×10-9
立方体数
1 103 109 1015 1021
比表面Av/（m2/m3） 6 ×102 6 ×103 6 ×105 6 ×107 6 ×109
2021/10/10
基材表面能和表面张力区别
基材表面能和表面张力是两个不同的概念，它们在物理学中有着重要的应用。
首先，我们来了解一下什么是表面能。
表面能是指物体表面所具有的能量，它是由于物体内部的分子或原子与物体表面的分子或原子之间的相互作用力而产生的。
这种相互作用力可以是引力、斥力或其他类型的力。
表面能的大小取决于物体的性质和表面条件。
例如，对于液体来说，表面能通常表现为液体表面分子之间的相互吸引力；而对于固体来说，表面能则可能包括固体内部分子与表面分子之间的相互作用力以及固体表面分子之间的相互吸引力。
接下来，我们来了解一下什么是表面张力。
表面张力是指液体表面上的分子受到的来自内部的拉力。
这种拉力是由于液体内部的分子对液体表面的分子施加的压力不均匀所导致的。
具体来说，液体内部的分子对液体表面的分子施加的压力比液体内部的分子对液体内部的分子施加的压力要大，因此液体表面的分子会受到一个向内的拉力，这就是表面张力。
总之，基材表面能和表面张力是两个不同的概念。
基材表面能是指物体表面所具有的能量，而表面张力是指液体表面上的分子受到的来自内部的拉力。
虽然它们都与物体的表面有关，但它们描述的是不同类型的物理现象。
表面能和表面张力的关系【详解】
1、表面张力：表面张力是指液体内部分子的吸引力使表面上的分子处于向内一种力作用下，这种力使液体尽量缩小其表面积而形成平行于表面的力；或者说是液体表面相邻两部分间单位长度内的相互牵引力，它是分子力的一种表现。
表面张力的单位是N／m。
表面张力的大小与液体的性质、纯度和温度有关。
2、表面能：表面能是恒温、恒压、恒组成情况下，可逆地增加物系表面积须对物质所做的非体积功。
表面能的另一种定义是，表面粒子相对于内部粒子所多出的能量。
表面张力乘表面的面积即为表面能。
表面张力越大，表面积越大，所具有的表面能也越大。
扩展资料：水的表面张力原理：表面张力由于环境不同，处于界面的分子与处于相本体内的分子所受力是不同的。
在水内部的一个水分子受到周围水分子的作用力的合力为0，但在表面的一个水分子却不如此。
因上层空间气相分子对它的吸引力小于内部液相分子对它的吸引力，所以该分子所受合力不等于零，其合力方向垂直指向液体内部，结果导致液体表面具有自动缩小的趋势，这种收缩力称为表面张力，表面张力(surface tension)是物质的特性，其大小与温度和界面两相物质的性质有关。
表面能的产生原因：物体表面的粒子和内部粒子所处的环境不同，因而所具有的能量不同。
例如，在液体内部，每个离子都均匀地被邻近粒子包围着，使来自不同方向的吸引力相互抵消，处于力平衡状态。
处于液体表面的粒子却不同，液体的外部是气体，气体的密度小于液体，故表面离子受到来自气体分子的吸引力较小，而受到液体内部粒子吸引力较大，使它在向内向外两个方向受到的力不平衡。
这样是表面分子受到一个指向液体内部的拉力，因此，液体表面有自动收缩到最小的趋势。
表面张力和什么因素有关:内因：无机液体的表面张力比有机液体的表面张力大的多；水的表面张力72.8mN/m(20℃)；有机液体的表面张力都小于水；含氮、氧等元素的有机液体的表面张力较大；含F、Si的液体表面张力最小；分子量大表面张力的；水溶液：如果含有无机盐，表面张力比水大；含有有机物，表面张力比水小。
表面张力和表面能
其过程是如果在一封闭容器中有曲率大小不同的液面与它们的蒸气相共存由于在相同温度下不同液面的平衡蒸气压力不同体系中自发进行液体分子从大块液相通过气相转移到曲64开尔文公式的应用65六表面张力的测定方法1毛细管上升法如图将一洁净的半径为r的均匀毛细管插入能润湿该毛细管的液体中则由于表面张力所引起的附加压力将使液柱上升达平衡时附加压力与液柱所形成的压力大小相等方向相反
（1）分子间相互作用力的影响 对纯液体或纯固体，表面张力决定于分子间形成 的化学键能的大小，一般化学键越强，表面张力越大。
(金属键)>
3.1 表面吉布斯自由能和表面张力
表面和界面
界面现象的本质
比表面 分散度与比表面 表面功 表面自由能 表面张力 界面张力与温度的关系 影响表面张力的因素
一、表面和界面(surface and interface)
在一个非均匀的体系中,至少存在着两个性质不同的相。两 相共存必然有界面。可见，界面是体系不均匀性的结果。 一般指两相接触的约几个分子厚度的过渡区，若其中一相 为气体，这种界面通常称为表面。 严格讲表面应是液体和固体与其饱和蒸气之间的界面， 但习惯上把液体或固体与空气的界面称为液体或固体的表 面。 常见的界面有：气-液界面，气-固界面，液-液界面， 液-固界面，固-固界面。
G
,
n
,
i
表面自由能模型
可见，表面自由能是单位表面上的自由能相对于本 体相自由能的过剩量。这也是为什么称γ为比表 面过剩自由能的原因。 2、若采用吉布斯界面模型，且体系为纯液体。则 s s 有 G A V s 0, n s 0 =
A A
可见，对纯液体， γ是单位面积等效表面所具有的 自由能。
表面张力（surface tension）
（1）分子间相互作用力的影响 对纯液体或纯固体，表面张力决定于分子间形成 的化学键能的大小，一般化学键越强，表面张力越大。
(金属键)>
3.1 表面吉布斯自由能和表面张力
表面和界面
界面现象的本质
比表面 分散度与比表面 表面功 表面自由能 表面张力 界面张力与温度的关系 影响表面张力的因素
一、表面和界面(surface and interface)
在一个非均匀的体系中,至少存在着两个性质不同的相。两 相共存必然有界面。可见，界面是体系不均匀性的结果。 一般指两相接触的约几个分子厚度的过渡区，若其中一相 为气体，这种界面通常称为表面。 严格讲表面应是液体和固体与其饱和蒸气之间的界面， 但习惯上把液体或固体与空气的界面称为液体或固体的表 面。 常见的界面有：气-液界面，气-固界面，液-液界面， 液-固界面，固-固界面。
G
,
n
,
i
表面自由能模型
可见，表面自由能是单位表面上的自由能相对于本 体相自由能的过剩量。这也是为什么称γ为比表 面过剩自由能的原因。 2、若采用吉布斯界面模型，且体系为纯液体。则 s s 有 G A V s 0, n s 0 =
A A
可见，对纯液体， γ是单位面积等效表面所具有的 自由能。
表面张力（surface tension）
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Am A / m 或 AV A /V
式中，m和V分别为固体的质量和体积，A为其表 面积。目前常用的测定表面积的方法有BET法和 色谱法。
表面张力和表面能
分散度与比表面
把物质分散成细小微粒的程度称为分散度。
把一定大小的物质分割得越小，则分散度越高， 比表面也越大。
例如，把边长为1cm的立方体1cm3逐渐分割 成小立方体时，比表面增长情况列于下表：
表面张力和表面能
表面和界面(surface and interface)
常见的界面有： 1.气-液界面
表面张力和表面能
表面和界面(surface and interface)
2.气-固界面
表面张力和表面能
表面和界面(surface and interface)
3.液-液界面
表面张力和表面能
表面和界面(surface and interface)
是物理面而非几何面，是一个准三维的区域。 2、目前，常用于处理界面的模型有两种：一为古根海姆
（Guggenheim）模型。其处理界面的出发点是：界面是 一个有一定厚度的过渡区，它在体系中自成一相—界面相。 界面相是一个既占有体积又有物质的不均匀区域。该模型 能较客观地反映实际情况但数学处理较复杂。另一个模型 是吉布斯（Gibbs）的相界面模型。该模型认为界面是几 何面而非物理面，它没有厚度，不占有体积，对纯组分也 没有物质存在。该模型可使界面热力学的处理简单化。
3.1 表面吉布斯自由能和表面张力
❖表面和界面 ❖界面现象的本质 ❖比表面 ❖分散度与比表面 ❖表面功 ❖表面自由能 ❖表面张力 ❖界面张力与温度的关系
❖影响表面张力的因素
表面张力和表面能
一、表面和界面(surface and interface)
在一个非均匀的体系中,至少存在着两个性质不同的相。两 相共存必然有界面。可见，界面是体系不均匀性的结果。 一般指两相接触的约几个分子厚度的过渡区，若其中一相
为气体，这种界面通常称为表面。
严格讲表面应是液体和固体与其饱和蒸气之间的界面， 但习惯上把液体或固体与空气的界面称为液体或固体的表 面。
常见的界面有：气-液界面，气-固界面，液-液界面， 液-固界面，固-固界面。
表面张力和表面能
1.1表面和界面(surface and interface)
几点说明： 1、严格讲，界面是“界”而不是“面”。因客观存在的界面
边长l/m
1×10-2 1×10-3 1×10-5 1×10-7 1×10-9
立方体数
1 103 109 1015 1021
比表面Av/（m2/m3） 6 ×102 6 ×103 6 ×105 6 ×107 6 ×109
表面张力和表面能
分散度与比表面
从表上可以看出，当将边长为10-2m的立方体分 割成10-9m的小立方体时，比表面增长了一千万倍。
由此可得：
dU TdS PdV dA BdnB
B
dH TdS VdP dA BdnB
B
dF SdT PdV dA BdnB
B
dG SdT VdP dA BdnB
B
(
U A
)S
,V
,nB
(
H A
)
S
,
P
,nB
(
F A
)T
4.液-固界面
表面张力和表面能
表面和界面(surface and interface)
5.固-固界面
表面张力和表面能
二、比表面（specific surface area）
比表面通常用来表示物质分散的程度，有两 种常用的表示方法：一种是单位质量的固体所具 有的表面积；另一种是单位体积固体所具有的表 面积。即：
表面张力和表面能
三、表面张力与表面自由能
表面层分子与内部分子相比，它们所处的环境不同。
体相内部分子所受四周邻近相同分子的作用力是对称 的，各个方向的力彼此抵销(各向同性)；
但是处在界面层的分子，一方面受到体相内相同 物质分子的作用，另一方面受到性质不同的另一相中 物质分子的作用，其作用力不能相互抵销，因此，界 面层分子由于其处在一不均匀对称的力场会显示出一 些独特的性质。
可见达到nm级的超细微粒具有巨大的比表面积， 因而具有许多独特的表面效应，成为新材料和多相 催化方面的研究热点。如铂黑电极及多孔电极由于 其表面积较大，电流密度小，因而极化小；再如， 由超细微粒制备的催化剂由于具有很高的比表面因 而催化活性较普通催化剂高；此外，将药物磨成细 粉以提高药效、将金属做成超细微粒以降低熔点都 说明了超细微粒具有独特的表面效应。
表面张力和表面能
例题
例1、将1g水分散成半径为1 0 9 m的小水滴（视为球形）， 其表面积增加了多少倍？
解：对大水滴 对小水滴
A S4r24 4/1 3 2 /3c m 24 .8 4 1 0 4c m 2
As1
4/1306 r13
4r12
3106 r1
3.0103m2
As1 3.0 107m2 6.2106 As 4.84
这种作用力使表面有自动收缩到最小的趋势，并 使表面层显示出一些独特性质，如表面张力、表面吸 附、毛细现象、过饱和状态等。
表面张力和表面能
界面现象的本质
表面张力和表面能
表面功（surface work）
由于表面层分子的受力情况与本体中不同，因此 如果要把分子从内部移到界面，或可逆的增加表面积， 就必须克服体系内部分子之间的作用力，对体系做功。
对于单组分体系，这种特性主要来自于同一物质在 不同相中的密度不同；对于多组分体系，则特性来自 于界面层的组成与任一相的组成均不相同。
表面张力和表面能
界面现象的本质
最简单的例子是液体及其蒸气组成的表面。
液体内部分子所受的力可以 彼此抵销，但表面分子受到体相 分子的拉力大，受到气相分子的 拉力小（因为气相密度低），所 以表面分子受到被拉入体相的作 用力。
温度、压力和组成恒定时，可逆使表面积增加dA 所需要对体系作的功，称为表面功。用公式表示为：
W ' dA
式中 为比例系数，它在数值上等于当T，P及组
成恒定的条件下，增加单位表面积时所必须对体 系做的可逆非rface free energy)
考虑了 表面功，热 力学基本公 式中应相应 增加 dA一 项，即：
式中，m和V分别为固体的质量和体积，A为其表 面积。目前常用的测定表面积的方法有BET法和 色谱法。
表面张力和表面能
分散度与比表面
把物质分散成细小微粒的程度称为分散度。
把一定大小的物质分割得越小，则分散度越高， 比表面也越大。
例如，把边长为1cm的立方体1cm3逐渐分割 成小立方体时，比表面增长情况列于下表：
表面张力和表面能
表面和界面(surface and interface)
常见的界面有： 1.气-液界面
表面张力和表面能
表面和界面(surface and interface)
2.气-固界面
表面张力和表面能
表面和界面(surface and interface)
3.液-液界面
表面张力和表面能
表面和界面(surface and interface)
是物理面而非几何面，是一个准三维的区域。 2、目前，常用于处理界面的模型有两种：一为古根海姆
（Guggenheim）模型。其处理界面的出发点是：界面是 一个有一定厚度的过渡区，它在体系中自成一相—界面相。 界面相是一个既占有体积又有物质的不均匀区域。该模型 能较客观地反映实际情况但数学处理较复杂。另一个模型 是吉布斯（Gibbs）的相界面模型。该模型认为界面是几 何面而非物理面，它没有厚度，不占有体积，对纯组分也 没有物质存在。该模型可使界面热力学的处理简单化。
3.1 表面吉布斯自由能和表面张力
❖表面和界面 ❖界面现象的本质 ❖比表面 ❖分散度与比表面 ❖表面功 ❖表面自由能 ❖表面张力 ❖界面张力与温度的关系
❖影响表面张力的因素
表面张力和表面能
一、表面和界面(surface and interface)
在一个非均匀的体系中,至少存在着两个性质不同的相。两 相共存必然有界面。可见，界面是体系不均匀性的结果。 一般指两相接触的约几个分子厚度的过渡区，若其中一相
为气体，这种界面通常称为表面。
严格讲表面应是液体和固体与其饱和蒸气之间的界面， 但习惯上把液体或固体与空气的界面称为液体或固体的表 面。
常见的界面有：气-液界面，气-固界面，液-液界面， 液-固界面，固-固界面。
表面张力和表面能
1.1表面和界面(surface and interface)
几点说明： 1、严格讲，界面是“界”而不是“面”。因客观存在的界面
边长l/m
1×10-2 1×10-3 1×10-5 1×10-7 1×10-9
立方体数
1 103 109 1015 1021
比表面Av/（m2/m3） 6 ×102 6 ×103 6 ×105 6 ×107 6 ×109
表面张力和表面能
分散度与比表面
从表上可以看出，当将边长为10-2m的立方体分 割成10-9m的小立方体时，比表面增长了一千万倍。
由此可得：
dU TdS PdV dA BdnB
B
dH TdS VdP dA BdnB
B
dF SdT PdV dA BdnB
B
dG SdT VdP dA BdnB
B
(
U A
)S
,V
,nB
(
H A
)
S
,
P
,nB
(
F A
)T
4.液-固界面
表面张力和表面能
表面和界面(surface and interface)
5.固-固界面
表面张力和表面能
二、比表面（specific surface area）
比表面通常用来表示物质分散的程度，有两 种常用的表示方法：一种是单位质量的固体所具 有的表面积；另一种是单位体积固体所具有的表 面积。即：
表面张力和表面能
三、表面张力与表面自由能
表面层分子与内部分子相比，它们所处的环境不同。
体相内部分子所受四周邻近相同分子的作用力是对称 的，各个方向的力彼此抵销(各向同性)；
但是处在界面层的分子，一方面受到体相内相同 物质分子的作用，另一方面受到性质不同的另一相中 物质分子的作用，其作用力不能相互抵销，因此，界 面层分子由于其处在一不均匀对称的力场会显示出一 些独特的性质。
可见达到nm级的超细微粒具有巨大的比表面积， 因而具有许多独特的表面效应，成为新材料和多相 催化方面的研究热点。如铂黑电极及多孔电极由于 其表面积较大，电流密度小，因而极化小；再如， 由超细微粒制备的催化剂由于具有很高的比表面因 而催化活性较普通催化剂高；此外，将药物磨成细 粉以提高药效、将金属做成超细微粒以降低熔点都 说明了超细微粒具有独特的表面效应。
表面张力和表面能
例题
例1、将1g水分散成半径为1 0 9 m的小水滴（视为球形）， 其表面积增加了多少倍？
解：对大水滴 对小水滴
A S4r24 4/1 3 2 /3c m 24 .8 4 1 0 4c m 2
As1
4/1306 r13
4r12
3106 r1
3.0103m2
As1 3.0 107m2 6.2106 As 4.84
这种作用力使表面有自动收缩到最小的趋势，并 使表面层显示出一些独特性质，如表面张力、表面吸 附、毛细现象、过饱和状态等。
表面张力和表面能
界面现象的本质
表面张力和表面能
表面功（surface work）
由于表面层分子的受力情况与本体中不同，因此 如果要把分子从内部移到界面，或可逆的增加表面积， 就必须克服体系内部分子之间的作用力，对体系做功。
对于单组分体系，这种特性主要来自于同一物质在 不同相中的密度不同；对于多组分体系，则特性来自 于界面层的组成与任一相的组成均不相同。
表面张力和表面能
界面现象的本质
最简单的例子是液体及其蒸气组成的表面。
液体内部分子所受的力可以 彼此抵销，但表面分子受到体相 分子的拉力大，受到气相分子的 拉力小（因为气相密度低），所 以表面分子受到被拉入体相的作 用力。
温度、压力和组成恒定时，可逆使表面积增加dA 所需要对体系作的功，称为表面功。用公式表示为：
W ' dA
式中 为比例系数，它在数值上等于当T，P及组
成恒定的条件下，增加单位表面积时所必须对体 系做的可逆非rface free energy)
考虑了 表面功，热 力学基本公 式中应相应 增加 dA一 项，即：