信息学奥赛NOIP普及组历届试题分析(课堂PPT)
合集下载
历年noip普及组提高组试题分析
历年NOIP(普及组)难度分析by Climber.pI
数学： 5 图论：4
搜索： 4 构造：3
贪心：2 【动态规划】平均难度系数：0.55
此项为历届NOIP考察次数最多的知识点。
主要有 1.区间模型 2.子序列模型 3.资源分配模型以及一些简单的多维状态设计技巧。
动态规划可以与图,树,高精度等知识点配合出题。
【模拟】平均难度系数：0.76 平均每届NOIP都会出现1个模拟题。
这种题一般算法很简单，需要选手细心理解题目意思，注意细节。
考察选手的代码实现能力。
【数学】平均难度系数：0.46
需要掌握质数及其性质，基础的实属操作，加法原理和乘法原理。
此类题需要选手对数学规律的灵感。
【图论】平均难度系数：0.50
历届考察点基本上都是1.最短路问题和2.特殊图的性质。
特殊图包括树，拓扑图，二分图等。
历届NOIP在图论上的考察并不是很多。
【搜索】平均难度系数：0.38
历届搜索题一般都比较难，搜索算法本身简单，于是题目会提高选手对其他方面的要求。
主要有搜索优化和模拟。
写搜索题时应该以尽量多得分为目标。
【构造】平均难度系数：0.27
构造类题目一般没有明确的算法，需要选手仔细分析题目的实质，并得出解法。
这个解法通常不是唯一的。
有时一个好的贪心可以得相当多的分。
有时搜索剪枝可以很大的提高效率。
同样以多得分为目标。
【
【贪心】平均难度系数：0.75
此类题需要选手对算法的直觉，贪
心正确性一旦被证明，通常题目就
简单了。
【通用】信息学奥赛NOIP普及组历届试题分析.ppt
枚举法其实是最简单的搜索算法。
.,.,
4
珠心算测验 (noip2014普及组第一题)
珠心算是一种通过在脑中模拟算盘变化来完成快 速运算的一种计算技术。珠心算训练，既能够开 发智力，又能够为日常生活带来很多便利，因而 在很多学校得到普及。
某学校的珠心算老师采用一种快速考察珠心算加 法能力的测验方法。他随机生成一个正整数集合， 集合中的数各不相同，然后要求学生回答：其中 有多少个数，恰好等于集合中另外两个（不同的） 数之和？ 最近老师出了一些测验题，请你帮忙求 出答案。
不过，如果把调查结果就以这种方式呈现出来，大 多数人肯定不会满意。因为这个比例的数值太大， 难以一眼看出它们的关系。对于上面这个例子，如 果把比例记为 5:3，虽然与 真实结果有一定的误差， 但依然能够较为准确地反映调查结果，同时也显得 比较直观。
现给出支持人数 A，反对人数 B，以及一个上限 L， 请你将 A 比 B 化简为 A’比 B’，要求在 A’和 B’均 不大于 L 且 A’和 B’互质（两个整数的最大公约数 是 1）的前提下，A’/B’ ≥ A/B 且 A’/B’ - A/B 的值 尽可能小。
输入样例 2 23 ?*? *??
输出样例 2 mine.out 2*1 *21
对于 100%的数据，1≤n≤100，1≤m≤100
.,.,
10
比例简化 (noip2014普及组第二题)
在社交媒体上，经常会看到针对某一个观点同意与 否的民意调查以及结果。例如，对某 一观点表示 支持的有 1498 人，反对的有 902 人，那么赞同与 反对的比例可以简单的记为1498:902。
.,.,
11
比例简化 (noip2014普及组第二题)
输入格式 输入共一行，包含三个整数 A，B，L，每两个整
.,.,
4
珠心算测验 (noip2014普及组第一题)
珠心算是一种通过在脑中模拟算盘变化来完成快 速运算的一种计算技术。珠心算训练，既能够开 发智力，又能够为日常生活带来很多便利，因而 在很多学校得到普及。
某学校的珠心算老师采用一种快速考察珠心算加 法能力的测验方法。他随机生成一个正整数集合， 集合中的数各不相同，然后要求学生回答：其中 有多少个数，恰好等于集合中另外两个（不同的） 数之和？ 最近老师出了一些测验题，请你帮忙求 出答案。
不过，如果把调查结果就以这种方式呈现出来，大 多数人肯定不会满意。因为这个比例的数值太大， 难以一眼看出它们的关系。对于上面这个例子，如 果把比例记为 5:3，虽然与 真实结果有一定的误差， 但依然能够较为准确地反映调查结果，同时也显得 比较直观。
现给出支持人数 A，反对人数 B，以及一个上限 L， 请你将 A 比 B 化简为 A’比 B’，要求在 A’和 B’均 不大于 L 且 A’和 B’互质（两个整数的最大公约数 是 1）的前提下，A’/B’ ≥ A/B 且 A’/B’ - A/B 的值 尽可能小。
输入样例 2 23 ?*? *??
输出样例 2 mine.out 2*1 *21
对于 100%的数据，1≤n≤100，1≤m≤100
.,.,
10
比例简化 (noip2014普及组第二题)
在社交媒体上，经常会看到针对某一个观点同意与 否的民意调查以及结果。例如，对某 一观点表示 支持的有 1498 人，反对的有 902 人，那么赞同与 反对的比例可以简单的记为1498:902。
.,.,
11
比例简化 (noip2014普及组第二题)
输入格式 输入共一行，包含三个整数 A，B，L，每两个整
NOIP普及组历届试题分析
对于100%的数据，3 ≤ n ≤ 100 测验题给出的正整数大小不超过10,000。
试题分析
题意大意：给你n个数，在这n个数中，找 到满足A+B=C的C的个数，注意不是这个 等式的个数。
样例中，1,2,3,4有1+2=3，1+3=4两个。
由于本题数据规模n<=100，我们可以直接
枚举C, A, B，三层循环解决问题。
扫雷游戏 (noip2015普及组第二题)
输入样例 1 33 *?? ??? ?*? 输入样例 2 23 ?*? *??
输出样例 1 mine.out *10 221 1*1 输出样例 2 mine.out 2*1 *21
对于 100%的数据，1≤n≤100，1≤m≤100
问题分析：
本题也是简单的枚举类试题。 我们从雷区的第一行第一列(1,1)开始，判断它周围 有多少个地雷。 由于本题读入的是字符，读入时需要注意： readln(n,m); for i=1 to n do begin for j=1 to m do read(a[i][j]); readln; end;
比例简化 (noip2014普及组第二题)
在社交媒体上，经常会看到针对某一个观点同意与 否的民意调查以及结果。例如，对某 一观点表示 支持的有 1498 人，反对的有 902 人，那么赞同与 反对的比例可以简单的记为1498:902。 不过，如果把调查结果就以这种方式呈现出来，大 多数人肯定不会满意。因为这个比例的数值太大， 难以一眼看出它们的关系。对于上面这个例子，如 果把比例记为 5:3，虽然与 真实结果有一定的误差， 但依然能够较为准确地反映调查结果，同时也显得 比较直观。 现给出支持人数 A，反对人数 B，以及一个上限 L， 请你将 A 比 B 化简为 A’比 B’，要求在 A’和 B’均 不大于 L 且 A’和 B’互质（两个整数的最大公约数 是 1）的前提下，A’/B’ ≥ A/B 且 A’/B’ - A/B 的值 尽可能小。
信息学奥林匹克竞赛基础知识-PPT课件
二十多年来逐步演变和发展的Internet网络，已为信息 高速公路勾画出一个雏形，并为整个信息基础设施打下 了一定的基础。在美国政府提出信息高速公路发展计划 之后，全球许多国家纷纷制订了本国的信息计划，以期 在新世纪来临之际，占领有利位置，谋求国家的长远利 益，一时间信息高速公路热席卷全球。
我国的“三金”工 程
数据库
现在比较流行的大中型关系型数据库有IBM DB2、Oracle、SQL Server、 SyBase、Informix等，常用的小型数据库有Access、Pradox、Foxpro等， 现在个人用户比较常用的主要是基于中小型数据库MS SQL Server和Access 的，所以在以下的篇幅中我们介绍这两种数据库系统的简单操作。
处理速度
（指令数/秒）
几千条
几百万条几千万条源自研制中的第五代计算机至目前为止，各种类型的计算机都属于冯· 诺依曼型计算机， 即采用存储程序方式进行工作。随着计算机应用领域的扩大， 冯· 诺依曼型的工作方式逐渐显露出其局限性，所以科学家提出了 制造非冯· 诺依曼式计算机。正在开发研制中的第五代智能计算机， 将具有自动识别自然语言、图形、图像的能力，具有理解和推理 的能力，具有知识获取、知识更新的能力，可望能够突破当前的 计算机的结构模式。 研制朝两个方向努力： 1、创建非冯· 诺依曼式语言 2、创建以人脑神经系统处理信息原理为基础的非冯· 诺依曼 的计算机模型， 如：生物计算机、光子计算机、量子计算机
存储器有内存（主存）和外存（辅存）之分。外存是存放程序和数据“仓库”， 可以长时间的保存大量信息。但程序必须调入到内存方可执行，待处理的数据也 只有进行内存后才能被程序加工。所以内存和外存之间的严格的分工。 存储器采取按地址存（写）、取（读）的工作方式。一个内存体内包括许多的存 储单元，每个单元可以存放适当单位的信息，全部存储单元按一定的顺序编号， 这种编号就称为存储器的地址。 存储器按其读写性可以分为：RAM（随机存储器）、ROM（只读存储器） 当电源关闭时RAM不能保留数据，如果需要保存数据，就必须把它们写入到 一个长期的存储器中（例如硬盘）。
1995-2008 历届NOIP试题及详解
② 由编码求原数组：共 15 分（5%+5%+5%）
a 输入：N=5 B=（0，0，0，0，0）
输出： A=（4，3，2，1，0）
b 输入：N=10 B=（0，1，2，3，4，5，6，7，8，9）
输出： A=（0，1，2，3，4，5，6，7，8，9）
c 输入：N=7 B=（0，0，0，0，4，5，6）
R
Y Y
P2=B R N2R=2
Y
P3=Y R N3=R1
Y
Q
RR
Y
排列方案： 排列总数： 105×2=210
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y BB
① 输10入5×2=210 3 4R 4 R4 4R 3 4 B B
1 2R 2 R2 2R 2 1 3B B
应打印出完整的图形R：（R12 分R）
BB
15 1R6 1R6 1R5 4 B B
Y Y Y Y Y
7 8 R 8R 8 R 7 7
BB
Y
3 4 R4 R4 R4 3 4 B B
Y
1 2 2R 2 R 2 R 2 1
19 18 17 16 15 14 13 12 11 10 <3> 本题 14 分
a 输入：N=5 B=（0，0，0，0，0）
输出： A=（4，3，2，1，0）
b 输入：N=10 B=（0，1，2，3，4，5，6，7，8，9）
输出： A=（0，1，2，3，4，5，6，7，8，9）
c 输入：N=7 B=（0，0，0，0，4，5，6）
R
Y Y
P2=B R N2R=2
Y
P3=Y R N3=R1
Y
Q
RR
Y
排列方案： 排列总数： 105×2=210
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y BB
① 输10入5×2=210 3 4R 4 R4 4R 3 4 B B
1 2R 2 R2 2R 2 1 3B B
应打印出完整的图形R：（R12 分R）
BB
15 1R6 1R6 1R5 4 B B
Y Y Y Y Y
7 8 R 8R 8 R 7 7
BB
Y
3 4 R4 R4 R4 3 4 B B
Y
1 2 2R 2 R 2 R 2 1
19 18 17 16 15 14 13 12 11 10 <3> 本题 14 分
普及组近5年NOIP试题分析试题分析
1≤ L ≤ R≤10000。
NOIP2010——数字统计
从L到R枚举每一个数i,对i进行分离数字，直接
统计有多少个2......
分离数字的过程
void count(int n)
{while (n>0) {if (n%10==2) ans++; n/=10; }
}
NOIP2010——接水问题
NOIP2012——寻宝
藏宝楼共有N+1层，最上面一层是顶层，顶层有一个 房间里面藏着宝藏。除了顶层外，藏宝楼另有 N层， 每层M个房间，这M个房间围成一圈并按逆时针方向 依次编号为0，…，M-1。其中一些房间有通往上一 层的楼梯，每层楼的楼梯设计可能不同。每个房间里 有一个指示牌，指示牌上有一个数字x，表示从这个 房间开始按逆时针方向选择第x个有楼梯的房间（假 定该房间的编号为k），从该房间上楼，上楼后到达 上一层的k号房间。比如当前房间的指示牌上写着2， 则按逆时针方向开始尝试，找到第2个有楼梯的房间， 从该房间上楼。如果当前房间本身就有楼梯通向上层， 该房间作为第一个有楼梯的房间。
NOIP2010——三国
输入样例
输出样例
8
42 24 10 29 27 12 58
1
77
31 8 16 26 80 6
25 3 36 11 5 33 20 17 13 15 77 9 4 50
19
NOIP2010——三国
显然每个武将对应的最大默契值都无法选到，
但是可以保证能选到次大的。所以就在次大的 中选一个最大的作为答案咯。这样计算机肯定 也得不到更大的值所以一定是可以获胜的。
NOIP2012——质因数分解
历届NOIP试题及详解
间的整数，且 A[i]≠A[j]（当 i≠j 时）。
例如：N=6 时，有：
A=（4，3，0，5，1，2）
此时，数组 A 的编码定义如下：
A[0]的编码为 0；
A[i]的编码为：在 A[0]，A[1]，……A[i-1]中比 A[i]的值小的个数（i=1，2……N-1）
∴上面数组 A 的编码为：
B=（0，0，0，3，1，2）
输出： A=（3，2，1，0，4，5，6）
<5> 本题共 30 分（10%+10%+10%）
① 数据输入： N=6
P1=R
N1=1
Q
排列方案： R ② 排数列据总输数入=：6 N=6 R
P1=R
NR1=2
P2=Y
N2=1 R
Q
R
排列方案： R ③ 排数列据总输数入=：12N=1R2
P1=RR
R
Y
R R N1= 3
③ 同一种颜色的灯不能分开；
④ 不同颜色的灯之间至少要有一个空位置。
例如：N=8（格子数） R=2（红灯数） B=3（蓝灯数）
放置的方法有：
R-B 顺序
RR
BBB
RR
BBB
RR
BBB
RR
BBB
RR
BBB
B-R 顺序
RR
BBB
BBB
RR
BBB
RR
BBB
RR
BBB
RR
BBB
RR
放置的总数为 12 种。 数据输入的方式为：
提示：文档已分节，可用 word 跳转节功能 本文为本人将 1995-2008 年历届 NOIP 试题、研究成果整理而成，由于“年代久远”所以有不少 资料没有找到。但本人都尽量整理最有价值的信息记录于此。 资料来源皆为网络，若引用请注明出处 一不注意就 208 页了呢~ 其实最初只是想方便自己，看着一下午的成果，就忍不住放到了网络 上。由于赶时间，质量不太好，而且历届 NOIP 的排版也不一样，只是做了粗略的整理、排 版，若有错误之处，敬请谅解。 回首历届 NOIP，甚至比我自己出生的还早的老题，一代代 OIer 就从这条路上走过，作为一个 不大努力的 OIer，我甚至为自己感到愧疚。总之，为了报答一代代出题人、教师、主办方以及 OIer 们，在努力一把也不迟啊。
NOIP初赛复习-普及组PPT课件
B. 高速缓存
C.内存
D.中央处理器
• 有人认为，在个人电脑送修前，将文件放入回收站中就是已经将其删除了。这种想法是（ ）。
A. 正确的，将文件放入回收站意味着彻底删除、无法恢复
C
B. 不正确的，只有将回收站清空后，才意味着彻底删除、无法恢复
C. 不正确的，即使将回收站清空，文件只是被标记为删除，仍可能通过恢复软件找回
存空间为（ ）。 D
A．128KB
B．1MB
C．1GB
D．4GB
• 蓝牙和 Wi-Fi 都是（）设备。 C
A．无线广域网 B．无线城域网 C．无线局域网 D．无线路由器
11
• 一片容量为 8GB 的 SD 卡能存储大约（）张大小为 2MB 的数码照片。 C
A. 1600
B. 2000
C. 4000
A. exe
B. com
C. dll
D. 以上都不是
• 提出“存储程序”的计算机工作原理的是（ ）。D
冯·诺依曼思想：二进制数、存储程 序和程序控制、硬件由五大部件构 成。
计算机的工作原理就是“存储程序
和程序控制”，也称冯·诺依曼工作
原理。
John von Neumann
冯诺依曼
5
计算机硬件系统
计算机硬件系统均由运算器、控制器、存储器、 输入设备和输出设备五大部分构成。他们之间的逻辑
关系如下图所示:
• 断电后会丢失数据的存储器是（） 。a
A. RAM
B. ROM
C. 硬盘
D. 光盘
• 下列对操作系统功能的描述最为完整的是（） 。c
A. 负责外设与主机之间的信息交换 B. 负责诊断机器的故障 C. 控制和管理计算机系统的各种硬件和软件资源的使用 D. 将源程序编译成目标程序
普及组NOIP初赛复习(二)PPT教学课件
• 常用图分为：有向图、无向图
B
A
D
C E
2020/12/09
A
B
C
D
7
图ห้องสมุดไป่ตู้
• 有向图结点的入度和出度 • 无向图的度
B
A
D
C E
2020/12/09
A
B
C
D
8
图的遍历
• 图的深度遍历 • 图的广度遍历
B
A
D
B
C E
2020/12/09
A C
D
9
PPT精品课件
谢谢观看
Thank You For Watching
NOIP初赛复习（二）
2020/12/09
1
集合
• 集合的概念 • 集合的运算： • 交集 • 并集 • 补集 • 全集
A B
2020/12/09
2
树
• 树形结构是一种非线性结构，它的特点 是：每个结点最多只有1个前驱，但可以 有多个后继
• 概念：双亲和孩子、祖先和子孙、兄弟、 分支结点和树叶
A
B
C
D
2020/12/09
E
F
G
3
树
• 树的宽度和高度
• 结点的度
• 结点的层
A
B
C
D
2020/12/09
E
F
G
H
I
4
二叉树
• 二叉树定义 • 区别二叉树的左孩子和右孩子 • 二叉树的性质： • 性质1：在二叉树的第i层上最多有2i-1个结点 • 性质2：在高度为h的二叉树中最多有 2h-1个
结点
• 性质3：在非空二叉树中，叶子结点个数等于 度为2的分支结点个数加1
B
A
D
C E
2020/12/09
A
B
C
D
7
图ห้องสมุดไป่ตู้
• 有向图结点的入度和出度 • 无向图的度
B
A
D
C E
2020/12/09
A
B
C
D
8
图的遍历
• 图的深度遍历 • 图的广度遍历
B
A
D
B
C E
2020/12/09
A C
D
9
PPT精品课件
谢谢观看
Thank You For Watching
NOIP初赛复习（二）
2020/12/09
1
集合
• 集合的概念 • 集合的运算： • 交集 • 并集 • 补集 • 全集
A B
2020/12/09
2
树
• 树形结构是一种非线性结构，它的特点 是：每个结点最多只有1个前驱，但可以 有多个后继
• 概念：双亲和孩子、祖先和子孙、兄弟、 分支结点和树叶
A
B
C
D
2020/12/09
E
F
G
3
树
• 树的宽度和高度
• 结点的度
• 结点的层
A
B
C
D
2020/12/09
E
F
G
H
I
4
二叉树
• 二叉树定义 • 区别二叉树的左孩子和右孩子 • 二叉树的性质： • 性质1：在二叉树的第i层上最多有2i-1个结点 • 性质2：在高度为h的二叉树中最多有 2h-1个
结点
• 性质3：在非空二叉树中，叶子结点个数等于 度为2的分支结点个数加1
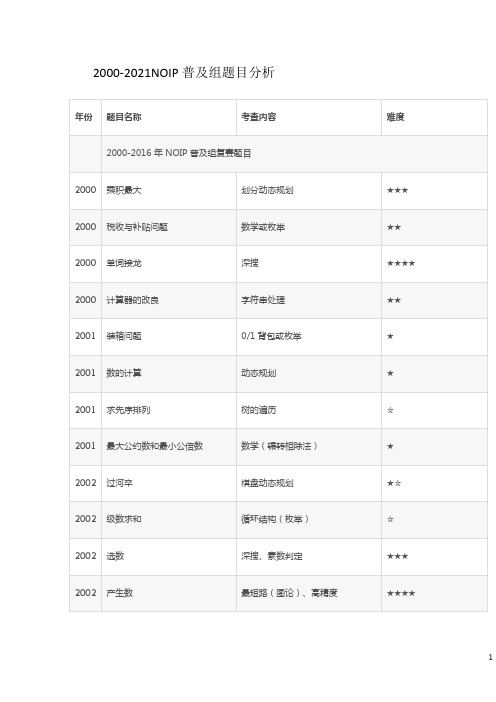
NOIP大纲整理：历年2000-2021NOIP普及组题目分析
★★★
2008
排座椅
贪心
★★
2008
ISBN 号码
字符串处理
★
2008
立体图
字符输出
★★★
2009
道路游戏
动态规划
★★★★★
2009
分数线划定
快速排序（双关键字）
★
2009
细胞分裂
数论
★★★★
2009
多项式输出
字符串处理
★
2010
数字统计
枚举
★
2010
接水问题
模拟
★★
2010
导弹拦截
排序+枚举，贪心
★★★★
2010
三国游戏
贪心
★★★
2011
瑞士轮
模拟、快拍、归并排序
★★★
2011
数字反转
模拟、字符串
★
2011
统计单词数
模拟、字符串函数
★
2011
表达式的值
栈、表达式计算、递推
★★★★★
2012
摆花
动态规划
★★★★
2012
质因数分解
枚举
★
2012
寻宝
模拟，模运算
★★★
2012
文化之旅
搜索、最短路(图论)、动规
数学（卡特兰数）
★★
2003
乒乓球
字符串处理
★☆
2004
FBI 树
二叉树的遍历
★★
2004
不高兴的津津
枚举
☆
2004
火星人
数学(排列)、stl
★★★
2004
花生采摘
贪心
★
2008
排座椅
贪心
★★
2008
ISBN 号码
字符串处理
★
2008
立体图
字符输出
★★★
2009
道路游戏
动态规划
★★★★★
2009
分数线划定
快速排序（双关键字）
★
2009
细胞分裂
数论
★★★★
2009
多项式输出
字符串处理
★
2010
数字统计
枚举
★
2010
接水问题
模拟
★★
2010
导弹拦截
排序+枚举，贪心
★★★★
2010
三国游戏
贪心
★★★
2011
瑞士轮
模拟、快拍、归并排序
★★★
2011
数字反转
模拟、字符串
★
2011
统计单词数
模拟、字符串函数
★
2011
表达式的值
栈、表达式计算、递推
★★★★★
2012
摆花
动态规划
★★★★
2012
质因数分解
枚举
★
2012
寻宝
模拟，模运算
★★★
2012
文化之旅
搜索、最短路(图论)、动规
数学（卡特兰数）
★★
2003
乒乓球
字符串处理
★☆
2004
FBI 树
二叉树的遍历
★★
2004
不高兴的津津
枚举
☆
2004
火星人
数学(排列)、stl
★★★
2004
花生采摘
贪心
★
信息学奥赛普及组1-18届问题求解题解析
历届“问题求解”解析（2013竞赛辅导）问题求解是信息学竞赛初赛中常见题型，它共两题，每题5分，共10分，十六届增加了比重，有三题，占15分。
诸如寻找假币、博弈原理、抽屉原理、容斥问题、排列组合、逻辑推理、递推关系等问题出现在问题求解中。
（相关问题的具体讲解根据需要考虑发讲义） 第一届（逻辑推理问题）1. 有标号为A 、B 、C 、D 和1、2、3、4的8个球，每两个球装一盒，分装4盒。
标号为字母的球与标号为数字的球有着某种一一对应的关系（称为匹配），并已知如下条件： ① 匹配的两个球不能在一个盒子内。
② 2号匹配的球与1号球在一个盒子里。
③ A 号和2号球在一个盒子里。
④ B 匹配的球和C 号球在一个盒子里。
⑤ 3号匹配的球与A 号匹配的球在一个盒子里。
⑥ 4号是A 或B 号球的匹配球。
⑦ D 号与1号或2号球匹配。
请写出这四对球匹配的情况。
第四届（递推、树、图）1. 已知一个数列U 1，U 2，U 3，…，U N ，… 往往可以找到一个最小的K 值和K 个数a 1，a 2，…,a n 使得数列从某项开始都满足： U N+K =a 1U N+K-1+a 2U N+K-2+……+a k U N (A)例如对斐波拉契数列1，1，2，3，5，…可以发现：当K=2，a 1 =1，a 2 =1时，从第3项起（即N>=1）都满足U n+2 =U n+1+U n 。
试对数列13，23，33，…，n 3,…求K 和a 1,a 2, …,a K 使得（A ）式成立。
当K= 4，a 1,a 2,…,a k 为a 1=4, a 2=6, a 3=4，a 4=-1对数列132333,…,n 3,…（A ）成立。
2．给出一棵二叉树的中序遍历：DBGEACHFI 与后序遍历：DGEBHIFCA 画出此二叉树。
3．用邻接矩阵表示下面的无向图：表示该无向图的邻接矩阵为 0 1 0 0 0 0 0 1 0 1 1 0 0 0 0 1 0 1 0 0 0 0 1 1 0 1 1 1 0 0 0 1 0 0 1 0 0 0 1 0 0 1 0 0 0 1 1 1 0第五届（递推）将Ln 定义为求在一个平面中用n 条直线所能确定的最大区域数目。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
NOIP普及组历届试题分析
2021/3/29
1
NOIP普及组题型分布
题型 枚举
模拟
题目
扫雷游戏(2015p2)、珠心算测验(2014p1) 数字统计(2010p1)、比例简化(2014p2)
金币(2015p1)、 螺旋方阵(2014p3)、计数问题(2013p1)、
字符串
数字反转(2011p1)、统计单词个数(2011p2)
贪心
2021/3/29
2
NOIP普及组题型分布
题型
简单 动态规划
题目 子矩阵(2014p4)、小朋友的数字(2013p3)
数学/数论 数据结构 图论（提高组）
表达式求值(2013p2)、 车站分级(2013p4 拓扑排序)
2021/3/29
3
一、枚举类试题
枚举法的基本思想是根据提出的问题枚举所 有可能的解，并用问题给定的条件检验哪些 解是需要的，哪些解是不需要的。能使条件 成立，即为其解。
不过，如果把调查结果就以这种方式呈现出来，大 多数人肯定不会满意。因为这个比例的数值太大， 难以一眼看出它们的关系。对于上面这个例子，如 果把比例记为 5:3，虽然与 真实结果有一定的误差， 但依然能够较为准确地反映调查结果，同时也显得 比较直观。
现给出支持人数 A，反对人数 B，以及一个上限 L， 请你将 A 比 B 化简为 A’比 B’，要求在 A’和 B’均 不大于 L 且 A’和 B’互质（两个整数的最大公约数 是 1）的前提下，A’/B’ ≥ A/B 且 A’/B’ - 金币 (noip2015普及组第一题)
国王将金币作为工资，发放给忠诚的骑士。第一天，骑士收到一枚金 币；之后两天（第二天和第三天），每天收到两枚金币；之后三天 （第四、五、六天），每天收到三枚金币；之后四天（第七、八、九、 十天），每天收到四枚金币……；这种工资发放模式会一直这样延续 下去：当连续N天每天收到N枚金币后，骑士会在之后的连续N+1天 里，每天收到N+1枚金币。 请计算在前K天里，骑士一共获得了多少金币。
枚举法其实是最简单的搜索算法。
2021/3/29
4
珠心算测验 (noip2014普及组第一题)
珠心算是一种通过在脑中模拟算盘变化来完成快 速运算的一种计算技术。珠心算训练，既能够开 发智力，又能够为日常生活带来很多便利，因而 在很多学校得到普及。
某学校的珠心算老师采用一种快速考察珠心算加 法能力的测验方法。他随机生成一个正整数集合， 集合中的数各不相同，然后要求学生回答：其中 有多少个数，恰好等于集合中另外两个（不同的） 数之和？ 最近老师出了一些测验题，请你帮忙求 出答案。
4
2
1234
对于100%的数据，3 ≤ n ≤ 100
测验题给出的正整数大小不超过10,000。
2021/3/29
6
试题分析
题意大意：给你n个数，在这n个数中，找 到满足A+B=C的个数，注意不是这个等式 的个数。
样例中，1,2,3,4有1+2=3，1+3=4两个。
由于本题数据规模n<=100，我们可以直接 枚举C, A, B，三层循环解决问题。
2021/3/29
11
比例简化 (noip2014普及组第二题)
输入格式 输入共一行，包含三个整数 A，B，L，每两个整
数之间用一个空格隔开，分别表示支持人数、反对 人数以及上限。 输出格式 输出共一行，包含两个整数 A’，B’，中间用一个 空格隔开，表示化简后的比例。 样例输入
1498 902 10 样例输出
现在给出n行m列的雷区中的地雷分布， 要 求计算出每个非地雷格周围的地雷格数。
注：一个格子的周围格子包括其上、下、左、 右、左上、右上、左下、右下八个方向上与之 直接相邻的格子。
2021/3/29
9
扫雷游戏 (noip2015普及组第二题)
输入样例 1 33 *?? ??? ?*?
输出样例 1 mine.out *10 221 1*1
输入样例 2 23 ?*? *??
输出样例 2 mine.out 2*1 *21
对于 100%的数据，1≤n≤100，1≤m≤100
2021/3/29
10
比例简化 (noip2014普及组第二题)
在社交媒体上，经常会看到针对某一个观点同意与 否的民意调查以及结果。例如，对某 一观点表示 支持的有 1498 人，反对的有 902 人，那么赞同与 反对的比例可以简单的记为1498:902。
2021/3/29
5
珠心算测验 (noip2014普及组第一题)
【输入】
输入共两行，第一行包含一个整数n，表示测试 题中给出的正整数个数。
第二行有n个正整数，每两个正整数之间用一个 空格隔开，表示测试题中给出的正整数。
【输出】 输出共一行，包含一个整数，表示测验题答案。
【样例输入】
【样例输出】
输入格式
输入共一行，为两个正整数L和R，之间用一个空格隔 开。
输出格式 输出共1行，表示数字2出现的次数。
样例输入：2 22
样例输出：6
2021/3/29
8
扫雷游戏 (noip2015普及组第二题)
扫雷游戏是一款十分经典的单机小游戏。 在 n 行 m 列的雷区中有一些格子含有地雷 （称之为地雷格） ，其他格子不含地雷（称之 为非地雷格） 。玩家翻开一个非地雷格时，该 格将会出现一个数字——提示周围格子中有多 少个是地雷格。 游戏的目标是在不翻出任何地 雷格的条件下，找出所有的非地雷格。
2021/3/29
7
数字统计 (noip2010普及组第一题)
请统计某个给定范围[L, R]的所有整数中，数字2出现 的次数。
比如在给定范围[2, 22]，数字2在数2中出现了1次，在 数12中出现了1次，在数20中出现了1次，在数21中出 现了1次，在数22中出现了2次，所以数字2在该范围内 一共出现了6次。
53
2021/3/29
12
二、模拟类试题
有些问题，我们很难建立数学模型，或者很难 用计算机建立递推、递归、枚举、回溯法等算 法。在这种情况下，一般采用模拟策略。
所谓模拟策略就是模拟某个过程，通过改变数 学模型的各种参数，进而观察变更这些参数所 引起过程状态的变化，由此展开算法设计。
2021/3/29
输入格式： 输入文件只有1行，包含一个正整数K，表示发放金币的天数。
2021/3/29
1
NOIP普及组题型分布
题型 枚举
模拟
题目
扫雷游戏(2015p2)、珠心算测验(2014p1) 数字统计(2010p1)、比例简化(2014p2)
金币(2015p1)、 螺旋方阵(2014p3)、计数问题(2013p1)、
字符串
数字反转(2011p1)、统计单词个数(2011p2)
贪心
2021/3/29
2
NOIP普及组题型分布
题型
简单 动态规划
题目 子矩阵(2014p4)、小朋友的数字(2013p3)
数学/数论 数据结构 图论（提高组）
表达式求值(2013p2)、 车站分级(2013p4 拓扑排序)
2021/3/29
3
一、枚举类试题
枚举法的基本思想是根据提出的问题枚举所 有可能的解，并用问题给定的条件检验哪些 解是需要的，哪些解是不需要的。能使条件 成立，即为其解。
不过，如果把调查结果就以这种方式呈现出来，大 多数人肯定不会满意。因为这个比例的数值太大， 难以一眼看出它们的关系。对于上面这个例子，如 果把比例记为 5:3，虽然与 真实结果有一定的误差， 但依然能够较为准确地反映调查结果，同时也显得 比较直观。
现给出支持人数 A，反对人数 B，以及一个上限 L， 请你将 A 比 B 化简为 A’比 B’，要求在 A’和 B’均 不大于 L 且 A’和 B’互质（两个整数的最大公约数 是 1）的前提下，A’/B’ ≥ A/B 且 A’/B’ - 金币 (noip2015普及组第一题)
国王将金币作为工资，发放给忠诚的骑士。第一天，骑士收到一枚金 币；之后两天（第二天和第三天），每天收到两枚金币；之后三天 （第四、五、六天），每天收到三枚金币；之后四天（第七、八、九、 十天），每天收到四枚金币……；这种工资发放模式会一直这样延续 下去：当连续N天每天收到N枚金币后，骑士会在之后的连续N+1天 里，每天收到N+1枚金币。 请计算在前K天里，骑士一共获得了多少金币。
枚举法其实是最简单的搜索算法。
2021/3/29
4
珠心算测验 (noip2014普及组第一题)
珠心算是一种通过在脑中模拟算盘变化来完成快 速运算的一种计算技术。珠心算训练，既能够开 发智力，又能够为日常生活带来很多便利，因而 在很多学校得到普及。
某学校的珠心算老师采用一种快速考察珠心算加 法能力的测验方法。他随机生成一个正整数集合， 集合中的数各不相同，然后要求学生回答：其中 有多少个数，恰好等于集合中另外两个（不同的） 数之和？ 最近老师出了一些测验题，请你帮忙求 出答案。
4
2
1234
对于100%的数据，3 ≤ n ≤ 100
测验题给出的正整数大小不超过10,000。
2021/3/29
6
试题分析
题意大意：给你n个数，在这n个数中，找 到满足A+B=C的个数，注意不是这个等式 的个数。
样例中，1,2,3,4有1+2=3，1+3=4两个。
由于本题数据规模n<=100，我们可以直接 枚举C, A, B，三层循环解决问题。
2021/3/29
11
比例简化 (noip2014普及组第二题)
输入格式 输入共一行，包含三个整数 A，B，L，每两个整
数之间用一个空格隔开，分别表示支持人数、反对 人数以及上限。 输出格式 输出共一行，包含两个整数 A’，B’，中间用一个 空格隔开，表示化简后的比例。 样例输入
1498 902 10 样例输出
现在给出n行m列的雷区中的地雷分布， 要 求计算出每个非地雷格周围的地雷格数。
注：一个格子的周围格子包括其上、下、左、 右、左上、右上、左下、右下八个方向上与之 直接相邻的格子。
2021/3/29
9
扫雷游戏 (noip2015普及组第二题)
输入样例 1 33 *?? ??? ?*?
输出样例 1 mine.out *10 221 1*1
输入样例 2 23 ?*? *??
输出样例 2 mine.out 2*1 *21
对于 100%的数据，1≤n≤100，1≤m≤100
2021/3/29
10
比例简化 (noip2014普及组第二题)
在社交媒体上，经常会看到针对某一个观点同意与 否的民意调查以及结果。例如，对某 一观点表示 支持的有 1498 人，反对的有 902 人，那么赞同与 反对的比例可以简单的记为1498:902。
2021/3/29
5
珠心算测验 (noip2014普及组第一题)
【输入】
输入共两行，第一行包含一个整数n，表示测试 题中给出的正整数个数。
第二行有n个正整数，每两个正整数之间用一个 空格隔开，表示测试题中给出的正整数。
【输出】 输出共一行，包含一个整数，表示测验题答案。
【样例输入】
【样例输出】
输入格式
输入共一行，为两个正整数L和R，之间用一个空格隔 开。
输出格式 输出共1行，表示数字2出现的次数。
样例输入：2 22
样例输出：6
2021/3/29
8
扫雷游戏 (noip2015普及组第二题)
扫雷游戏是一款十分经典的单机小游戏。 在 n 行 m 列的雷区中有一些格子含有地雷 （称之为地雷格） ，其他格子不含地雷（称之 为非地雷格） 。玩家翻开一个非地雷格时，该 格将会出现一个数字——提示周围格子中有多 少个是地雷格。 游戏的目标是在不翻出任何地 雷格的条件下，找出所有的非地雷格。
2021/3/29
7
数字统计 (noip2010普及组第一题)
请统计某个给定范围[L, R]的所有整数中，数字2出现 的次数。
比如在给定范围[2, 22]，数字2在数2中出现了1次，在 数12中出现了1次，在数20中出现了1次，在数21中出 现了1次，在数22中出现了2次，所以数字2在该范围内 一共出现了6次。
53
2021/3/29
12
二、模拟类试题
有些问题，我们很难建立数学模型，或者很难 用计算机建立递推、递归、枚举、回溯法等算 法。在这种情况下，一般采用模拟策略。
所谓模拟策略就是模拟某个过程，通过改变数 学模型的各种参数，进而观察变更这些参数所 引起过程状态的变化，由此展开算法设计。
2021/3/29
输入格式： 输入文件只有1行，包含一个正整数K，表示发放金币的天数。