高中数学学业水平必背公式定理知识点默写
学考考前必备1 必记公式归纳-备战2020年冬季山东省高中数学学业水平考试(考前全攻略)
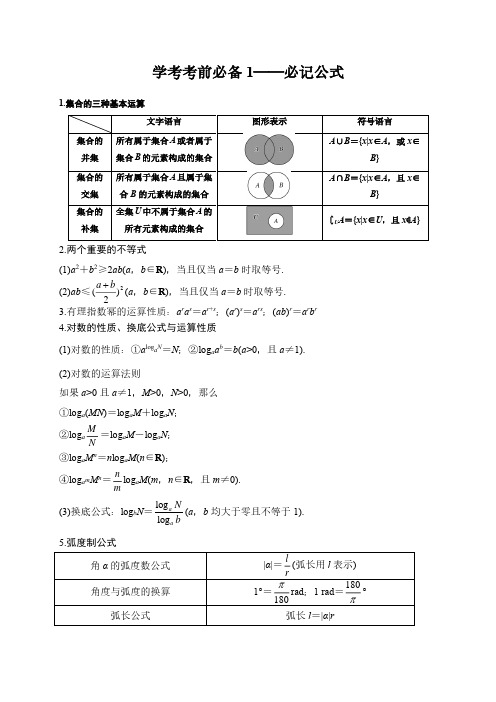
公式三: sin(− ) = −sin cos( − )= cos tan( − )= − tan
公式四: sin( − ) = sin cos( − )= − cos tan( − )= − tan
公式五:
sin
2
−
=
cos
cos
2
−
=
sin
8.两角和与差的正弦、余弦和正切
S(+ ) : sin( + ) = sin cos +cos sin
名称
直棱柱
正棱锥
圆柱
圆锥
球
面积
S 侧=ch
S 侧= 1 ch ' 2
体积 V=S 底·h
V=
1 3
S底
h
15.向量的长度公式、夹角公式
S 侧=2πrh V=πr2h
S 侧=πrl
V= 1 πr2h 3
S 球面=4πR2
V= 4 R3 3
(1)向量的长度:设 a = (x, y) ,则 | a |2 = x2 + y2,| a |= x2 + y2 ; 若 A(x1, y1) , B(x2, y2 ) ,则
2
2
2
cos2 = 1+ cos 2 = 1 cos 2 + 1
2
2
2
11.函数 y=Asin(ωx+φ)的有关概念
振幅 周期
频率
y=Asin(ωx+φ)(A>0,ω>0), x∈[0,+∞)表示一个振动量时 A
T= 2
f= 1 = T
2
12.解三角形
(1)三角形面积公式:S△ABC= 1 ab sin C = 1 ac sin B= 1 bc sin A
高二数学学业水平考试必背公式

高二数学学业水平考试必背公式一、二次函数y = ax 2 +bx + c 的性质1、顶点坐标公式:24,24b ac b a a ⎛⎫-- ⎪⎝⎭24b ac =- 对称轴:2b x a=- 最大(小)值:244ac b a -2、若一元二次方程()002≠=++a c bx ax 中,两根为1x ,2x 。
则abx x -=+21,12c x x a ⋅=。
二、指数与指数函数1、幂的运算法则: (1)m n m na a a+⋅= (2)m n m na a a-÷= (3)()nm mn a a = (4)()n n n ab a b =(5) nnn a a b b ⎛⎫= ⎪⎝⎭(6)01a = (a ≠0) (7) 1n n a a-= (8)n ma =2、指数函数y = a x (a > 0且a ≠1)的性质:(1)定义域:R ; 值域:( 0 , +∞) (2)图象过定点(0,1)2三、对数与对数函数1、对数的运算法则:(1)a b = N ⇔b = log a N (2)log a 1 = 0 (3)log a a = 1 (4)log a Na N=(5)log a (MN ) = log a M + log a N (6)log a (NM ) = log a M — log a N(7)log log n ma a mb b n = (8)换底公式:log a N = a Nb b log log (9)log a N = a Nlog 12、对数函数y = log a x (a > 0且a ≠1)的性质:(1)定义域:( 0 , +∞) ; 值域:R (2)图象过定点(1,0)四、幂函数:一般地,函数y x α=叫做幂函数.其中x 为自变量,α为常数.3【零点存在性原理】如果函数()y f x =在区间[],a b 上的图象是连续不断的一条曲线,并且有()()0f a f b ⋅<,那么,函数()y f x =在区间(),a b 内有零点,即存在(),c a b ∈,使得()0f c =,这个c 也就是方程()0f x =的根。
高中数学学业水平考试复习必背知识点

高中数学会考复习必背知识点第一章 集合与简易逻辑 1、含n 个元素的集合的所有子集有n 2个 第二章 函数 1、求)(x f y =的反函数:解出)(1y f x -=,y x ,互换,写出)(1x fy -=的定义域;2、对数:①:负数和零没有对数,②、1的对数等于0:01log =a ,③、底的对数等于1:1log =a a ,④、积的对数:N M MN a a a log log )(log +=, 商的对数:N M NMa a alog log log -=,幂的对数:M n M a n a log log =;b mnb a na m log log =, 第三章 数列1、数列的前n 项和:n n a a a a S ++++= 321; 数列前n 项和与通项的关系:⎩⎨⎧≥-===-)2()1(111n S S n S a a n n n2、等差数列 :(1)、定义:等差数列从第2项起,每一项与它的前一项的差等于同一个常数; (2)、通项公式:d n a a n )1(1-+= (其中首项是1a ,公差是d ;) (3)、前n 项和:1.2)(1n n a a n S +=d n n na 2)1(1-+=(整理后是关于n 的没有常数项的二次函数)(4)、等差中项: A 是a 与b 的等差中项:2ba A +=或b a A +=2,三个数成等差常设:a-d ,a ,a+d3、等比数列:(1)、定义:等比数列从第2项起,每一项与它的前一项的比等于同一个常数,(0≠q )。
(2)、通项公式:11-=n n q a a (其中:首项是1a ,公比是q )(3)、前n 项和:⎪⎩⎪⎨⎧≠--=--==)1(,1)1(1)1(,111q q q a qq a a q na S nn n(4)、等比中项: G 是a 与b 的等比中项:Gb a G =,即ab G =2(或ab G ±=,等比中项有两个)第四章 三角函数1、弧度制:(1)、π=180弧度,1弧度'1857)180( ≈=π;弧长公式:r l ||α= (α是角的弧度数)2、三角函数 (1)、定义:yr x r y x x y r x r y ======ααααααcsc sec cot tan cos sin 4、同角三角函数基本关系式:1cos sin22=+αα ααc o st a n =1c o t t a n =αα 5、诱导公式:(奇变偶不变,符号看象限) 正弦上为正;余弦右为正;正切一三为正 公式二: 公式三: 公式四: 公式五:ααααααtan )180tan(cos )180cos(sin )180sin(-=-︒-=-︒=-︒ ααααααt a n )180tan(cos )180cos(sin )180sin(=+︒-=+︒-=+︒ ααααααt a n )t a n (c o s )c o s (s i n )s i n (-=-=--=- 6、两角和与差的正弦、余弦、正切)(βα+S :βαβαβαsin cos cos sin )sin(+=+ )(βα-S :βαβαβαsin cos cos sin )sin(-=-)(βα+C :βαβαβsin sin cos cos )cos(-=+a )(βα-C :βαβαβsin sin cos cos )cos(+=-a )(βα+T : βαβαβαtan tan 1tan tan )tan(-+=+)(βα-T : βαβαβαtan tan 1tan tan )tan(+-=-7、辅助角公式:⎪⎪⎭⎫⎝⎛++++=+x b a b x b a a b a x b x a cos sin cos sin 222222 )sin()sin cos cos (sin 2222ϕϕϕ+⋅+=⋅+⋅+=x b a x x b a8、二倍角公式:(1)α2S : αααcos sin 22sin =α2C : ααα22sin cos 2cos -= 1cos 2sin 2122-=-=ααα2T : ααα2t a n 1t a n22t a n -=ααααααtan )360tan(cos )360cos(sin )360sin(-=-︒=-︒-=-︒ (2)、降次公式:(多用于研究性质)ααα2sin 21cos sin =212cos 2122cos 1sin 2+-=-=ααα212cos 2122cos 1cos 2+=+=ααα10、解三角形:(1)、三角形的面积公式:A bc B ac C ab S sin 2sin 2sin 2===∆ (2)正弦定理:sin 2sin 2,sin 2,2sin sin sin R c B R b A R a R CcB b A a ======, 边用角表示: (3)余弦定理:)1(2)(cos 2cos 2cos 22222222222cocC ab b a C ab b a c Bac c a b A bc c b a +-+=-+=⋅-+=⋅-+=求角:abc b a C ac b c a B bc a c b A 2cos 2cos 2cos 222222222-+=-+=-+= 第五章、平面向量1、坐标运算:(1)设()()2211,,,y x b y x a ==→→,则()2121,y y x x b a ±±=±→→ 数与向量的积:λ()()1111,,y x y x a λλλ==→,数量积:2121y y x x b a +=⋅→→(2)、设A 、B 两点的坐标分别为(x 1,y 1),(x 2,y 2),则()1212,y y x x AB --=→.(终点减起点)221221)()(||y y x x -+-=;向量a 的模|a |:⋅=2||22y x +=;(3)、平面向量的数量积: θcos →→→→⋅=⋅b a b a , 注意:00=⋅→→a ,→→=⋅00a ,)(=-+(4)、向量()()2211,,,y x b y x a ==→→的夹角θ,则222221212121cos y x y x y y x x +++=θ,2、重要结论:(1)、两个向量平行: →→→→=⇔b a b a λ// )(R ∈λ,⇔→→b a //01221=-y x y x(2)、两个非零向量垂直0=⋅⇔⊥→→→→b a b a ,02121=+⇔⊥→→y y x x b a(3)、P 分有向线段21P P 的:设P (x ,y ) ,P 1(x 1,y 1) ,P 2(x 2则定比分点坐标公式⎪⎪⎩⎪⎪⎨⎧++=++=λλλλ112121y y y x x x , 中点坐标公式⎪⎪⎩⎪⎪⎨⎧==y x 第六章:不等式1、 均值不等式:(1)、 ab b a 222≥+ (222b a ab +≤) (2)、a >0,b >0;ab b a 2≥+或2)2(b a ab +≤ 2、解指数、对数不等式的方法:同底法,同时对数的真数大于第七章:直线和圆的方程1、斜 率:αtan =k ,),(+∞-∞∈k ;直线上两点),(),,(222111y x P y x P ,则斜率为1212x x y y k --=2、直线方程:(1)、点斜式:)(11x x k y y -=-;(2)、斜截式:b kx y +=; (3)、一般式:0=++C By Ax (A 、B 不同时为0) 斜率B A k -=,y 轴截距为BC- 3、两直线的位置关系(1)、平行:212121//b b k k l l ≠=⇔且 212121C C B B A A ≠= 时 ,21//l l ;垂直: 21211l l k k ⊥⇔-=⋅ 2121210l l B B A A ⊥⇒=+;(2)、到角范围:()π,0 到角公式 : 12121tan k k k k +-=θ 21k k 、都存在,0121≠+k k夹角范围:]2,0(π夹角公式:12121tan k k k k +-=α 21k k 、都存在,0121≠+k k(3)、点到直线的距离公式2200B A C By Ax d +++=(直线方程必须化为一般式)6、圆的方程:(1)、圆的标准方程 222)()(r b y a x =-+-,圆心为),(b a C ,半径为r (2)圆的一般方程022=++++F Ey Dx y x(配方:44)2()2(2222F E D E y D x -+=+++)0422>-+F E D 时,表示一个以)2,2(E D --为圆心,半径为F E D 42122-+的圆;第八章:圆锥曲线 1、椭圆标准方程:)0(12222>>=+b a by a x ,半焦距:222b a c -= , 离心率的范围:10<<e ,准线方程:ca x 2±=, 参数方程:⎩⎨⎧==ϕϕsin cos b y a x 2、 双曲线标准方程:)0,0(,12222>>=-b a by a x ,半焦距:222b a c +=,离心率的范围:1>e准线方程:c a x 2±=,渐近线方程用02222=-by a x 求得:x a b y ±=,等轴双曲线离心率2=e3、抛物线:p 是焦点到准线的距离0>p ,离心率:1=epx y 22=:准线方程2p x -=焦点坐标)0,2(p ;px y 22-=:准线方程2p x = 焦点坐标)0,2(p-py x 22=:准线方程2p y -=焦点坐标)2,0(p ;py x 22-=:准线方程2p y = 焦点坐标)2,0(p-第九章 直线 平面 简单的几何体1、长方体的对角线长2222c b a l ++=;正方体的对角线长a l 3=2、两点的球面距离求法:球心角的弧度数乘以球半径,即R l ⋅=α;3、球的体积公式:334 R V π=,球的表面积公式:24 R S π= 4、柱体h s V ⋅=,锥体h s V ⋅=31,锥体截面积比:222121h h S S =A A‘O BαβAA‘OBαβ第十章 排列 组合 二项式定理1、排列:(1)、排列数公式: mn A =)1()1(+--m n n n =!!)(m n n -.(n ,m ∈N *,且m n ≤).0!=1(3)、全排列:n 个不同元素全部取出的一个排列;!n A nn =)!1(123)2)(1(-⋅=⋅⋅⋅⋅--=n n n n n ; 2、组合:(1)、组合数公式: mnC =m n m mA A =m m n n n ⨯⨯⨯+-- 21)1()1(=!!!)(m n m n -⋅(n ,m ∈N *,且m n ≤);10=n C ;(3)组合数的两个性质:mn C =mn n C - ;m n C +1-m nC =mn C 1+;3、二项式定理 :(1)、定理:nn n r r n r n n n n n n n n b C b a C b a C b a C a C b a ++++++=+--- 222110)( ;(2)、二项展开式的通项公式(第r +1项):r r n r n r b a C T -+=1)210(n r ,,, =各二项式系数和:C n 0+C n 1+C n 2+ C n 3+ C n 4+…+C n r +…+C n n =2n(表示含n 个元素的集合的所有子集的个数)。
高中必背的数学公式(完整归纳)

高中必背的数学公式(完整归纳)高中必背的数学公式(一)两角和公式1、sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-sinBcosA2、cos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinB3、tan(A+B)=(tanA+tanB)/(1-tanAtanB)tan(A-B)=(tanA-tanB)/(1+tanAtanB)4、ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA)ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA)(二)倍角公式1、cos2A=cos2A-sin2A=2cos2A-1=1-2sin2A2、tan2A=2tanA/(1-tan2A)ctg2A=(ctg2A-1)/2ctgA(三)半角公式1、sin(A/2)=√((1-cosA)/2)sin(A/2)=-√((1-cosA)/2)2、cos(A/2)=√((1+cosA)/2)cos(A/2)=-√((1+cosA)/2)3、tan(A/2)=√((1-cosA)/((1+cosA))tan(A/2)=-√((1-cosA)/((1+cosA))4、ctg(A/2)=√((1+cosA)/((1-cosA))ctg(A/2)=-√((1+cosA)/((1-cosA))(四)和差化积公式1、2sinAcosB=sin(A+B)+sin(A-B) 2cosAsinB=sin(A+B)-sin(A-B)2、2cosAcosB=cos(A+B)-sin(A-B) -2sinAsinB=cos(A+B)-cos(A-B)3、sinA+sinB=2sin((A+B)/2)cos((A-B)/2cosA+cosB=2cos((A+B)/2)sin((A-B)/2)4、tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosB5、ctgA+ctgBsin(A+B)/sinAsinB -ctgA+ctgBsin(A+B)/sinAsinB(五)几何体表面积和体积公式1、圆柱体:表面积:2πRr+2πRh体积:πR2h(R为圆柱体上下底圆半径,h为圆柱体高)2、圆锥体:表面积:πR2+πR[(h2+R2)的平方根]体积:πR2h/3(r为圆锥体低圆半径,h为其高)3、正方体:表面积:S=6a2,体积:V=a3(a-边长)4、长方体:表面积:S=2(ab+ac+bc)体积:V=abc(a-长,b-宽,c-高)5、棱柱:体积:V=Sh(S-底面积,h-高)6、棱锥:体积:V=Sh/3(S-底面积,h-高)7、棱台:V=h[S1+S2+(S1S2)^1/2]/3(S1上底面积,S2下底面积,h-高)8、拟柱体:V=h(S1+S2+4S0)/6(S1-上底面积,S2-下底面积,S0-中截面积,h-高)9、圆柱:S底=πr2,S侧=Ch,S表=Ch+2S底,V=S底h=πr2h(r-底半径,h-高,C—底面周长,S底—底面积,S侧—侧面积,S表—表面积)10、空心圆柱:V=πh(R^2-r^2)(R-外圆半径,r-内圆半径,h-高)11、直圆锥:V=πr^2h/3(r-底半径,h-高)12、圆台:V=πh(R2+Rr+r2)/3(r-上底半径,R-下底半径,h-高)13、球:V=4/3πr^3=πd^3/6(r-半径,d-直径)14、球缺:V=πh(3a2+h2)/6=πh2(3r-h)/3(h-球缺高,r-球半径,a-球缺底半径)15、球台:V=πh[3(r12+r22)+h2]/6(r1球台上底半径,r2-球台下底半径,h-高)16、圆环体:V=2π2Rr2=π2Dd2/4(R-环体半径,D-环体直径,r-环体截面半径,d-环体截面直径)(六)椭圆公式1、椭圆周长公式:l=2πb+4(a-b)2、椭圆周长定理:椭圆的周长等于该椭圆短半轴,长为半径的圆周长(2πb)加上四倍的该椭圆长半轴长(a)与短半轴长(b)的差3、椭圆面积公式:s=πab4、椭圆面积定理:椭圆的面积等于圆周率(π)乘该椭圆长半轴长(a)与短半轴长(b)的乘积如何提高高中数学成绩1、记数学笔记,特别是对概念理解的不同侧面和数学规律,教师在课堂中拓展的课外知识。
高中数学学业水平考试必备公式

一、1、定义域:〔1〕根号: 〔2〕分母: 〔3〕对数: 2、对数与指数互换:725log 8x a =⇔=⇔()a b a b a b x x x x x =÷==3、奇函数:f(x)与f(-x)_____ 偶函数:f(x)与f(-x)_____二、1、诱导公式:sin ()πα+= cos ()πα+= tan ()πα+=sin () πα-= cos () πα-= tan () πα-=sin ()2πα+= cos ()2πα+=sin ()2πα-= cos ()2πα-= sin 2) (πα+= cos 2) (πα+= tan 2) (πα+=sin (2)πα-= cos (2)πα-= tan (2)πα-= sin ( )α-= cos ( )α-= tan ( )α-= 2、两角和与差公式: Sin: Cos: Tan:3、二倍角: sin2α=cos2α= = = tan2α=4、正弦定理: 余弦定理:log log log log a a a a M N M N +=-=6、sin()y A x ωϕ=+的周期是: cos()y A x ωϕ=+的周期是:tan()y A x ωϕ=+的周期是:7、同角三角函数关系:〔1〕 〔2〕三、等差数列通项公式: 前n 项和公式: 等差中项:〔a,b,c 〕等比数列通项公式: 前n 项和公式: 等比中项:〔a,b,c 〕四、直线:1.〔k 与倾斜角〕k= 两点的斜率公式k=2.3.直线Ax+By+C=0的斜率:4.点到直线距离公式:5.平行线间的距离公式:6.圆的标准方程: 圆心: 半径:7.圆的一般方程: 〔方程表示圆的条件: 〕 圆心: 半径:8.直线与圆相切,则:9.直线与圆相交的弦长公式:12//l l ⇔12l l ⊥⇔220x yDx Ey F ++++=公式答案:一、1、定义域:〔1〕根号:大于或等于0 〔2〕分母:不等于0 〔3〕对数:真数>0 2、对数与指数互换:2725log 5log 878x ax a =⇔==⇔=()a b a b a b a b a b a bx x x x x x x x +-=÷== 3、奇函数:f(x)与f(-x)_相反____ 偶函数:f(x)与f(-x)__相同___二、1、诱导公式:sin ()πα+= —sin α cos ()πα+=—cos α tan ()πα+=tan αsin () πα-=sin α cos () πα-=—cos α tan () πα-=—tan αsin ()2πα+=cos α cos ()2πα+=—sin αsin ()2πα-= cos α cos ()2πα-= sin α sin 2) (πα+=sin α cos 2) (πα+=cos α tan 2) (πα+= tan αsin (2)πα-=sin α cos (2)πα-=cos α tan (2)πα-= tan α sin ( )α-= —sin α cos ( )α-=cos α tan ( )α-=—tan α 2、两角和与差公式:()()()sin sin cos cos sin cos cos cos sin sin tan tan tan 1tan tan αβαβαβαβαβαβαβαβαβ±=±±=±±=3、二倍角:22222sin 22sin cos cos 2cos sin 2cos 112sin 2tan tan 21tan ααααααααααα==-=-=-=-4、正弦定理:2sin sin sin a b cR A B C===〔R 为外接圆半径〕余弦定理:log log log ()log log log a a a a a aM N MN M M N N+=-=2222222222cos 2cos 2cos a b c bc A b a c ac Bc a b ab C=+-=+-=+-6、sin()y A x ωϕ=+的周期是:T ω=cos()y A x ωϕ=+的周期是:T ω=tan()y A x ωϕ=+的周期是:T πω=7、同角三角函数关系:〔1〕22sin cos 1αα+= 〔2〕sin tan cos ααα=三、等差数列通项公式: 前n 项和公式: 等差中项:〔a,b,c 〕 :2b=a+c等比数列通项公式: 前n 项和公式: 等比中项:〔a,b,c 〕:四、直线:1.〔k 与倾斜角〕k=两点的斜率公式k= 2.3.直线Ax+By+C=0的斜率:4.点到直线距离公式:5.平行线间的距离公式:6.圆的标准方程:圆心:〔a,b 〕 半径:r 7.圆的一般方程:圆心: 半径:8.直线与圆相切,则:d=r 〔d 为圆心到直线距离〕 9.直线与圆相交的弦长公式:2121y y x x --1(1)n a a n d =+-11()(1)22n n a a n n n d S na +-==+11n n a a q -=111,1(1),111n n n na q S a a q a q q q q =⎧⎪=--⎨=≠⎪--⎩2b a c =tan α1212//l l k k ⇔=12121l l k k ⊥⇔=-d =Ay =-d =222()()x a y b r -+-=22220(40)x y Dx Ey F D E F ++++=+->(,)22D E --2r =AB =。
高中数学学业水平考知识点总结(8篇)

高中数学学业水平考知识点总结(8篇)高中数学学业水平考知识点总结(8篇)高中数学学业水平考知识点总结11、向量的加法向量的加法满足平行四边形法则和三角形法则。
AB+BC=AC。
a+b=(某+某',y+y')。
a+0=0+a=a。
向量加法的运算律:交换律:a+b=b+a;结合律:(a+b)+c=a+(b+c)。
2、向量的减法如果a、b是互为相反的向量,那么a=-b,b=-a,a+b=0.0的反向量为0 AB-AC=CB.即“共同起点,指向被减”a=(某,y)b=(某',y')则a-b=(某-某',y-y').4、数乘向量实数λ和向量a的乘积是一个向量,记作λa,且∣λa∣=∣λ∣·∣a∣。
当λ>0时,λa与a同方向;当λ当λ=0时,λa=0,方向任意。
当a=0时,对于任意实数λ,都有λa=0。
注:按定义知,如果λa=0,那么λ=0或a=0。
实数λ叫做向量a的系数,乘数向量λa的几何意义就是将表示向量a的有向线段伸长或压缩。
当∣λ∣>1时,表示向量a的有向线段在原方向(λ>0)或反方向(λ当∣λ∣0)或反方向(λ数与向量的乘法满足下面的运算律结合律:(λa)·b=λ(a·b)=(a·λb)。
向量对于数的分配律(第一分配律):(λ+μ)a=λa+μa.数对于向量的分配律(第二分配律):λ(a+b)=λa+λb.数乘向量的消去律:①如果实数λ≠0且λa=λb,那么a=b。
②如果a≠0且λa=μa,那么λ=μ。
3、向量的的数量积定义:两个非零向量的夹角记为〈a,b〉,且〈a,b〉∈[0,π]。
定义:两个向量的数量积(内积、点积)是一个数量,记作a·b。
若a、b 不共线,则a·b=|a|·|b|·cos〈a,b〉;若a、b共线,则a·b=+-∣a∣∣b∣。
高中数学学业水平考试必背公式 (1)

水平考试必背公式及定义1.有理指数幂的含义及其运算性质:①rsr sa a a+⋅=;②()r s rs a a =;③()(0,0,,)r r rab a b a b r s Q =>>∈2.对数的定义:b N N a a b =⇔=log 01log =a 1log =a a )10(≠>a a 且3.对数的运算性质:如果a > 0 , a ≠ 1 , M > 0 , N > 0,那么:①N M MN a a a log log log +=; ②N M NMa a alog log log -=; ③)(log log R n M n M a na ∈=。
4换底公式:)0,10,10(log log log >≠>≠>=b c c a a abb c c a 且且 常取10=c 得: gbab a 1lg log =5.幂函数函数αx y =叫做幂函数(只考虑21,1,3,2,1-=α的图象)。
6. 直线的斜率(1) αtan =k (α为直线的倾斜角)(2) 经过两个定点 P 1(x 1,y 1) , P 2(x 2,y 2) 的直线: 若x 1≠x 2,则直线P 1P 2 的斜率存在,k=tan θ=1212x x y y --若x 1=x 2,则直线P 1P 2的斜率不存在,其倾斜角为900。
7.直线方程的五种形式及适用范围⑴一般式Ax+By+C=0 (A 、B 不同时为0):对坐标平面内的任何直线都适用 。
⑵点斜式Y- Y 0=k (X- X 0)、斜截式Y=kX+b 不能表示无斜率(垂直于x 轴)的直线.⑶两点式121y y y y --=121x x x x --不能表示平行或重合于两坐标轴的直线.⑷截距式a x +by=1不能表示平行或重合于两坐标轴的直线及过原点的直线8.两条直线“平行或垂直”的判定直线l 1∥l 2 或重合⇔倾斜角α1=α2⇔有斜率时k 1=k 2 ,或都无斜率; 直线l 1∥l 2 ⇔有斜率时k 1=k 2且y 轴上的截距不同,或都无斜率且x 轴上的截距不同; 直线l 1⊥l 2 ⇔有斜率时k 1×k 2=-1,或一条有斜率k 1=0另一条无斜率。
高二数学会考必背公式知识点

高二数学会考必背公式知识点在高中数学的学习中,必背公式是提高解题效率和准确性的基础。
掌握了这些公式,能够快速、准确地解决各类数学问题。
以下是高二数学会考必背公式知识点:1. 二次函数相关公式:- 一般式:$y = ax^2 + bx + c$- 根的判别式:$\Delta = b^2 - 4ac$- 顶点坐标:$(h, k)$,其中$h = -\frac{b}{2a}$,$k = f(h) =\frac{\Delta}{4a}$- 对称轴:$x = -\frac{b}{2a}$- 平移变换:$y = a(x - h)^2 + k$2. 三角函数相关公式:- 正弦定理:$\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}$- 余弦定理:$c^2 = a^2 + b^2 - 2ab\cos C$- 正切定理:$\tan A = \frac{\sin A}{\cos A}$- 三角和差公式:$\sin(A \pm B) = \sin A \cos B \pm \cos A \sin B$$\cos(A \pm B) = \cos A \cos B \mp \sin A \sin B$$\tan(A \pm B) = \frac{\tan A \pm \tan B}{1 \mp \tan A \tan B}$3. 平面几何相关公式:- 任意三角形面积公式:$S = \frac{1}{2} \cdot a \cdot b \cdot \sin C$- 直角三角形勾股定理:$c^2 = a^2 + b^2$- 中线定理:三角形三条中线交于一点且平分彼此的长度- 高线定理:三角形三条高线交于一点,且交点到三边的距离相等4. 概率与统计相关公式:- 排列公式:$A_n^m = \frac{n!}{(n-m)!}$- 组合公式:$C_n^m = \frac{n!}{m!(n-m)!}$- 事件的概率:$P(A) = \frac{N(A)}{N(S)}$- 条件概率:$P(A|B) = \frac{P(A \cap B)}{P(B)}$- 独立事件概率:$P(A \cap B) = P(A) \cdot P(B)$5. 数列与级数相关公式:- 等差数列通项公式:$a_n = a_1 + (n-1)d$- 等差数列前n项和公式:$S_n = \frac{n}{2}(a_1 + a_n)$- 等差数列求和公式:$S_n = \frac{n}{2}(2a_1 + (n-1)d)$- 等比数列通项公式:$a_n = a_1 \cdot q^{n-1}$- 等比数列前n项和公式(当$|q| < 1$):$S_n = a_1 \cdot \frac{1-q^n}{1-q}$以上是高二数学会考必背的公式知识点,掌握并熟练运用这些公式,能够在数学问题的解答中更加得心应手。
(完整版)高中数学公式总结-默写版

高中数学公式默写一、集合1、 若集合A 中有n )(N n ∈个元素,则集合A 的所有不同的子集个数为______,所有非空真子集的个数是______。
2、 若AB A A B B =⇔=⇔_________________3、 真值表4、常见结论的否定形式5、充要条件(1)充分条件:____________________ (2)必要条件:____________________ (3)充要条件:____________________. 二、函数1、 二次函数c bx ax y ++=2的图象的对称轴方程是______________,顶点坐标是___________。
用待定系数法求二次函数的解析式时,解析式的设法有3种形式,即____________________,____________________和____________________ .2、0)(2>++=c bx ax x f 恒成立的充要条件是_________________;0)(2<++=c bx ax x f 恒成立的充要条件是_____________________; 0)(2≥++=c bx ax x f 恒成立的充要条件是_________________; 0)(2≤++=c bx ax x f 恒成立的充要条件是_________________;3、单调性单调增:①_________________________________________;②___________________________; 单调减:①_________________________________________;②___________________________; 4、奇偶性 (1)前提:(2)奇函数:______________________________________;其图像_______________________; 偶函数:______________________________________;其图像_______________________; (3)若函数)(x f y =是奇函数,且在0=x 处有定义,则_____________;(4) 多项式函数110()n n n n P x a x a x a --=+++的奇偶性:多项式函数()P x 是奇函数⇔______________________________________;. 多项式函数()P x 是偶函数⇔______________________________________;.5、定义域:6、相同函数:_________________________,_____________________;7、函数图象: (1)指数函数:(2)对数函数:(3)幂函数: (4)三角函数8、对称性与周期性:(1)若)()(x a f x a f -=+,则_______________;若)()(x b f x a f -=+,则_______________; (2)若)()(a x f a x f -=+,则_______________;若)()(a x f x f += ,则_______________;(3)若)(1)(x f a x f =+, 则_______________;若)()(x f a x f -=+ ,则_______________; 9、计算:(1)=nm a________________;=n n a _____________________(2)=sr a a _______________;=s r a )(_______________;=rab )(_______________.(3)=+N M a a log log _____________;=-N M a a log log _____________;=m a M n log _____________;(4)=oa _____________;=Na a log _____________;0______log =a ;1______log =a .10、导数:(1) ='C __________;(2)=')(n x ____________;(3) =')(sin x _____________;.(4) =')(cos x _____________;(5) =')(ln x _____________;(6)=')(log xa _____________;. (7) =')(xe _____________;(8)=')(xa _____________; 11、图像变化(1))()(a x f x f +→:___________________________________; (2)a x f x f +→)()(:___________________________________; (3)|)(|)(x f x f →:___________________________________; (4)|)(|)(x f x f →:___________________________________;三、三角函数1、 若点),(y x P ,点P 到原点的距离记为r ,则sin α=_____,cos α=_____,tan α=____。
高中数学学考复习知识点

相品用口仪数学学业水平考试常用公式及结论一、集合与函数:集合1、集合中元素的特征:确定性,互异性,无序性A B2、集合相等:若:A B,B A,则3.元素与集合的关系:属于不属于:空集:4.集合{a1,a2,L ,a n}的子集个数共有2n个;真子集有2n - 1个;非空子集有2n - 1个;5.常用数集:自然数集: N正整数集:N 整数集:Z 有理数集:Q 实数集:R函数的奇偶性1、定义:奇函数 <=> f (- X)= -f ( X),偶函数 <=> f (i) = f ( X )(注意定义域)2、性质:(1)奇函数的图象关于原点成中心对称图形;(2)偶函数的图象关于 y轴成轴对称图形;(3)如果一个函数的图象关于原点对称,那么这个函数是奇函数;(4)如果一个函数的图象关于y轴对称,那么这个函数是偶函数.函数的单调性1、定义:对于定义域为D的函数f ( X ),若任意的X1, X2C D,且X1< X2① f ( X1 ) < f ( X 2 ) <=> f ( X1 ) - f ( X2 ) < 0 <=> f ( X )是增函数② f ( X1 ) > f ( X 2 ) <=> f ( X1 ) - f ( X2 ) > 0 <=> f ( X )是减函数二次函数y = aX2+bX + c (a 0)的性质y … —一 b 4ac b2 b …।… 4ac b21、顶点坐标公式:—, --------- , 对称车由:x —,取大(小)值:------------------2a 4a 2a 4a2.二次函数的解析式的三种形式(I)一般式f(x) ax2bx c(a 0); (2)顶点式f(x) a(x h)2k(a 0);(3)两根式f (x) a(x x1)(x x2)(a 0).指数与指数函数 1、哥的运算法则:(1。
高中数学必考公式定律与知识梳理

高中数学必考公式定律与知识梳理
以下是高中数学必考公式、定律和知识点的梳理:
1. 三角函数:
正弦定理:a/sin A = b/sin B = c/sin C
余弦定理:a² = b² + c² - 2bc cos A
正切定义:tan A = sin A / cos A
余切定义:cot A = cos A / sin A
常见三角函数值(0°、30°、45°、60°、90°)
2. 数列:
通项公式:an = a1 + (n-1)d
等差数列求和公式:Sn = n(a1+an)/2
通项公式:an = a1 * r^(n-1)
等比数列求和公式:Sn = a1(1-r^n)/(1-r)
3. 圆:
圆的面积公式:S = πr²
圆的周长公式:C = 2πr
圆锥/圆柱侧面积公式:S = πrl
4. 平面几何:
平行四边形面积公式:S = bh
矩形面积公式:S = lw
梯形面积公式:S = (a+b)h/2
直角三角形勾股定理:a² + b² = c²
5. 解析几何:
两点之间的距离公式:AB = √[(x2-x1)² + (y2-y1)²]
直线的一般式:Ax+By+C=0
直线的斜截式:y=kx+b
直线的点斜式:y-y1=k(x-x1)
圆的一般式:(x-a)² + (y-b)² = r²
以上是高中数学必考公式、定律和知识点的梳理,希望对您有所帮助。
数学学考必考知识点高中公式

数学学考必考知识点高中公式高中数学学考必考知识点公式引言高中数学学考是学生们进入大学的重要关卡,掌握必考知识点公式对于顺利通过考试至关重要。
本文旨在为学生们整理和梳理高中数学学考必考知识点公式,帮助大家复习和备考。
知识点一:函数与极限•函数求导法则:(u±v)′=u′±v′,(uv)′=u′v+uv′,(k×u)′= k×u′•高中常用极限公式:lim x→0sinxx =1,lim x→∞(1+1x)x=e,lim x→0(1+x)1x=e知识点二:数列与级数•通项与前n项和:a n=a1+(n−1)d,S n=n2(a1+a n)•等差数列公式:a n=a1+(n−1)d,S n=n2(a1+a n)•等比数列公式:a n=a1⋅q n−1,S n=a1⋅q n−1q−1知识点三:解析几何•点到直线的距离公式:d=00√A2+B2•两点间的距离公式:d=√(x2−x1)2+(y2−y1)2•直线的斜率公式:k=y2−y1x2−x1•圆的标准方程:(x−a)2+(y−b)2=r2知识点四:概率与统计•排列组合公式:A n m=n!(n−m)!,C n m=n!m!(n−m)!•二项式定理:(a+b)n=C n0a n b0+C n1a n−1b1+...+C n n a0b n知识点五:三角函数•基本三角函数公式:sin2x+cos2x=1,tanx=sinxcosx•三角函数的周期性:sin(x+2π)=sinx,cos(x+2π)=cosx结语本文仅列举了高中数学学考中的一部分必考知识点公式,希望对大家的复习和备考有所帮助。
在复习过程中,建议结合习题进行练习,加深对知识点公式的理解和运用。
祝愿大家取得优异的成绩!。
高中数学学业水平必背公式定理知识点默写

高中数学学业水平测试必背公式定理知识点1、空集定义:_____________________________________;空集是任何集合的______________。
N ____________ Z __________ Q ___________ R ___________〔常用集合字母表示〕2、含n 个元素的集合其子集个数为_____________________。
3、函数定义:对定义域内任意x ,都有___________y 值与之对应,称y 是x 的函数。
4、求函数定义域三种根本形式:①分式要求:__________________;②根式,开偶次方根,那么_______________________;③对数式那么要求__________________________。
5、①指数函数定义:__________________________________________;其定义域为_____________;值域为_________________;当_______________时函数单调递增;当_______________函数单调递减。
其图像恒过定点______________。
②对数函数定义:__________________________________。
其定义域为_____________;值域为_________________;当_______________时函数单调递增;当_______________函数单调递减。
其图像恒过定点______________。
③幂函数定义:_______________________________________。
当0>α时,图像恒过______________和_______________;在第一象限内单调_________; 当0<α时,图像恒过______________;在第一象限内单调_________;6、如果函数是奇偶函数,其定义域一定关于_______________对称;如果对定义域内任意x ,当________________时,函数为奇函数;如果对定义域内任意x ,当________________时,函数为偶函数;7、函数单调性定义:在区间D 内任取两个值1x 、2x ,设21x x <,如果______________,那么函数在此区间内单调递增;如果______________,那么函数在此区间内单调递减。
高级中学数学必背数学公式定理(学业水平考试)

老师寄语是花就要绽放,是树就要撑出绿荫,是水手就要搏击风浪,是雄鹰就要展翅飞翔. 很难说什么事情是难以办到的,昨天的梦想就是今天的希望和明天的辉煌. 我们要以坚定的信心托起昨天的梦想,以顽强的斗志,耕耘今天的希望,那我们一定能用我们的智慧和汗水书写明天的辉煌!高中学业水平考试复习必背数学公式必修一1.★元素与集合的关系如果a 是集合A 的元素,就说a 属于集合A ,记作:a A ∈; 如果a 不是集合A 的元素,就说a 不属于集合A ,记作:a A ∉.2. ★集合的运算:{}A B x x A x B =∈∈I 且;{}A B x x A x B =∈∈U 或;{}U C A x x U x A =∈∉且. 3. 子集的个数问题:若集合A 有n 个元素,则集合A 有2n 个子集,有21n -个真子集. 4. ★函数定义域:①分母不为0;②开偶次方被开方数0≥;③对数真数0> 5.★奇偶性(1)奇函数的定义:一般地,对于函数()f x 定义域内的任意一个x ,都有()()f x f x -=-,那么函数 ()f x 叫奇函数.(2)偶函数的定义:一般地,对于函数()f x 定义域内的任意一个x ,都有()()f x f x -=,那么函数 ()f x 叫偶函数.(3)奇(偶)函数图像的特点:奇函数图象关于原点对称;偶函数图象关于y 对称. 6.★函数的单调性(1)增函数:设函数()f x 的定义域为I ,如果对于定义域I 内某个区间D 上的任意两个自变量的 值12,x x ,当12x x <时,都有12()()f x f x <,那么就说函数()f x 在区间D 上是增函数, 区间D 称为函数()f x 的单调增区间.(2)减函数:设函数()f x 的定义域为I ,如果对于定义域I 内某个区间D 上的任意两个自变量的 值12,x x ,当12x x <时,都有12()()f x f x >,那么就说函数()f x 在区间D 上是减函数, 区间D 称为函数()f x 的单调减区间. (3)一次函数()0y kx b k =+≠,当0k >时,y 随x 的增大而增大,当0k <时,y 随x 的增大而减小; (4)反比例函数()0ky k x=≠ , 当0k >时,在每个区间内y 随x 的增大而增大,当0k <时,在每个区间内y 随x 的增大而减小;(5)二次函数()20y ax bx c a =++≠,当0a >时,在对称轴的左侧,y 随x 的增大而减小,在对称轴的右侧,y 随x 的增大而增大. 当0a <时,在对称轴的左侧,y 随x 的增大而增大,在对称轴的右侧,y 随x 的增大而减小. (6)指数函数(0,1)xy a a a =>≠当1a >时,y 随x 的增大而增大,当01a <<时,y 随x 的增大而减小. (7)对数函数log (0,1)a y x a a =>≠当1a >时,y 随x 的增大而增大,当01a <<时,y 随x 的增大而减小. 7. ★指数及指数函数(1)根式与指数幂互化nm nma a =()1,,,0*>∈>n N n m a ; pp a a 1=-()0,0>>p a (2) 指数幂的运算性质(),,0,0R s r b a ∈>> ①rsr sa a a+⋅=;②()r srsa a =;③()(0,0,,)rr rab a b a b r s Q =>>∈(3) 函数()1,0≠>=a a a y x叫做指数函数,其中x 是自变量. (x a y =01a << 1a >图 象性 质定义域 R值域 ()+∞,0定点过定点()1,0函数值的变化 当0x >时,()1,0∈y ; 当0x <时,()+∞∈,1y . 当0x >时,()+∞∈,1y ; 当0x <时,()1,0∈y . 单调性 在R 上是减函数在R 上是增函数对称性x y a =和x y a -=关于y 轴对称8. (1)对数与指数之间的互化:N x N a a xlog =⇔=(01)a a >≠且.(2) 对数log a N (01)a a >≠且的简单性质:01log =a ;1log =a a ; (3) 以10为底的对数叫做常用对数;记作lg ;以e (71828,2≈e )为底的对数叫做自然对数 ;记作ln ; (4)★★对数的运算性质:0,0,1,0>>≠>N M a a ①N M MN a a a log log log +=; ②N M NMa a alog log log -=;③)(log log R n M n M a n a ∈=. (5)函数()1,0log ≠>=a a x y a 叫做对数函数,其中x 是自变量.(6) 对数函数的图像及其性质x y a log =01a << 1a >图 象性 质定义域 ()+∞,0值域 R定点 过定点()0,1函数值的变化 当1x >时,()0,∞-∈y ; 当01x <<时,()+∞∈,0y . 当1x >时,()+∞∈,0y ; 当01x <<时,()0,∞-∈y . 单调性 在R 上是减函数在R 上是增函数对称性log a y x =和1log ay x =关于x 轴对称9.幂函数:函数αx y =叫做幂函数(只考虑21,1,3,2,1-=α的图象). 10.★函数的零点(1) 对于函数)(x f y =,把使0)(=x f 的实数x 的值叫做函数)(x f y =的零点.(2)方程0)(=x f 的根⇔函数)(x f y =的图像与x 轴交点的横坐标⇔函数)(x f y =的零点.(3)零点存在性定理:若连续函数()f x 在区间(,)a b 上满足()()0f a f b <,则函数()f x 在(,)a b 上至少有一个 零点.必修二1.3214=,==;=433V Sh V Sh V R S R ππ柱体椎体球球;2.★★线面平行的判定定理:平面外一条直线与此平面内的一.条直线平行,则该直线与此平面平行. 符号语言:////a b a a b ααα⎫⎪⊄⇒⎬⎪⊂⎭3.★★线面垂直的判定定理:一条直线与平面内的两.条相交直线垂直,则该直线与此平面垂直. 符号语言:,,l a l b a b l a b P ααα⊥⊥⎫⎪⊂⊂⇒⊥⎬⎪=⎭I4.★异面直线所成角:平移到一起求平移后的夹角.★直线与平面所成角:直线和它在平面内的射影所成的角.(如右图)αbaαabP lθαPHl5.两点的直线的斜率公式:)(211212x x x x y y k ≠--=6.直线方程的五种形式及适用范围(1)一般式:0Ax By C ++= (A 、B 不同时为0),对坐标平面内的任何直线都适用; (2)点斜式:()00y y k x x -=-,不能表示无斜率(垂直于x 轴)的直线; (3)斜截式:y kx b =+不能表示无斜率(垂直于x 轴)的直线; (4)两点式121y y y y --=121x x x x --不能表示平行或重合于两坐标轴的直线;(5)截距式a x +by=1不能表示平行或重合于两坐标轴的直线及过原点的直线. 6.★★两直线平行与垂直的判定7.两条直线的交点:0:1111=++C y B x A l 0:2222=++C y B x A l 相交交点坐标即方程组⎩⎨⎧=++=++0222111C y B x A C y B x A 的一组解.8.★距离公式:(1)两点间距离公式:设1122(,),A x y B x y ,()是平面直角坐标系中的两个点,则 ||AB (2)点到直线距离公式: ()00,y x P 到直线0:1=++C By Ax l 的距离2200BA CBy Ax d +++=9.★圆的方程:标准方程()()222r b y a x =-+-,圆心()b a ,,半径为r ;一般方程220x y Dx Ey F ++++=,22(40)D E F +->10.★线与圆的位置关系:设直线0:=++C By Ax l ,圆()()222:r b y a x C =-+-,圆心()b a C ,到l 的距离 为22B A C Bb Aa d +++=,d r l C >⇔与相离; d r l C =⇔与相切; d r l C <⇔与相交.必修三1.★★分层抽样:一般地,若从容量为N 的总体中抽取容量为n 的样本,则抽样比为nNλ=,若第i 层含有的 个体数为i N 个,则第i 层抽取的入样个体数为i i i nn N N Nλ==⋅. 2.★★频率分布直方图: =频率小矩形面积(注意:不是小矩形的高度) 计算公式: =频数频率样本容量;=⨯频数样本容量频率;==⨯频率频率小矩形面积组距组距;各组频数之和=样本容量;各组频率之和=1 3.茎叶图:茎表示高位,叶表示低位. 4.★古典概型的概率公式:()A m P A n==事件包含的基本事件个数实验中基本事件的总数5.★几何概型的概率公式:()A P A =事件构成的区域的长度(面积或体积)实验的全部结果构成的区域的长度(面积或体积)必修四1.弧度:lrα=,l 为α所对的弧长,r 为半径,正负号的确定:逆时针为正,顺时针为负. 2.弧度制与角度制的互化:0180=π,01801⎪⎭⎫ ⎝⎛=πrad ,rad 18010π=.3. 三角函数的定义: 设角α是一个任意角,(),P x y 是终边上的任意一点,点P 与原点的距离r = 那么sin y r α=;cos x r α=;tan yxα=. 4.★同角三角函数的基本关系:平方关系:22sin cos 1αα+=;商数关系:sin tan cos ααα=. 5. 三角函数诱导公式:()2kk z απ+∈与α之间函数值的关系,主要有:公式一:sin(2)k απ+⋅=sin α; 公式二:sin()πα+=sin α-; cos(2)k απ+⋅=cos α; cos()πα+=cos α-; tan(2)k απ+⋅=tan α. tan()πα+=tan α. 公式三:sin()α-=sin α-; 公式四:sin()πα-=sin α; cos()α-=cos α; cos()πα-=cos α-; tan()α-=tan α-. tan()πα-=tan α-. 公式五:sin()2πα-=cos α; 公式六:sin()2πα+=cos α;cos()2πα-=sin α. cos()2πα+=sin α-.其规律(口诀)是“ 奇变偶不变,符号看象限”.6.★三角和差公式:βαβαβαsin cos cos sin )sin(±=±;βαβαβαsin sin cos cos )cos(μ=±; tan tan tan()1tan tan αβαβαβ±±=m .7.★三角二倍角公式:αααcos sin 22sin =;ααααα2222sin 211cos 2sin cos 2cos -=-=-=;22tan tan 21tan ααα=-.8.★ 三角降幂公式:22cos 1sin 2αα-=;22cos 1cos 2αα+=.9.正弦函数sin y x =,余弦函数cos y x =,正切函数tan y x =的图象与性质 性质sin y x =cos y x = tan y x =图象定义域R R,2x x k k Z ππ⎧⎫≠+∈⎨⎬⎩⎭值域[]1,1-[]1,1-R最值当()22x k k Z ππ=+∈时,max 1y =;当()22x k k Z ππ=-∈时,min 1y =-.当()2x k k Z π=∈时,max 1y =;当()2x k k Z ππ=+∈时,min 1y =-.既无最大值,也无最小值周期性 2π 2ππ奇偶性()sin sin x x -=-,奇函数 ()cos cos x x -=偶函数 ()tan tan x x -=-奇函数单调性()2,222k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦上是增函数;()32,222k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦上是减函数.[]()2,2k k k Z πππ-∈上是增函数;π[]()2,2k k k Z πππ+∈上是减函数. (),22k k k Z ππππ⎛⎫-+∈ ⎪⎝⎭上是增函数.对称性对称中心()(),0k k Z π∈对称轴()2x k k Z ππ=+∈,既是中心对称又是轴对称图形对称中心(),02k k Z ππ⎛⎫+∈⎪⎝⎭ 对称轴()x k k Z π=∈,既是中心对称又是轴对称图形对称中心(),02k k Z π⎛⎫∈⎪⎝⎭无对称轴,是中心对称但不是轴对称图形10.★★()(0;0)y Asin x A ωϕω=+>>的最大值为A ,最小值为A -,最小正周期为2T ω=,由(0,0)y Asin x A ωω=>>向左平移ϕω个单位可得到()(0,0)y Asin x A ωϕω=+>>. 11.向量的模:线段AB 的长度叫向量AB u u u r 的长度,记为|AB u u u r|或|a r |;(1)若 (,)a x y =r,则 |a r |22x y =+(2)若1122(,),(,)A x y B x y ,则2121(,)AB x x y y =--u u u r , |AB u u u r |222121()()x x y y =-+-运 算图形语言运算性质坐标语言加法(平行四边形法则) (三角形法则)AB BC AC +=u u u r u u u r u u u ra b b a ρϖρρ+=+ )()(c b a c b a ρϖρρρρ++=++1122(,),(,)a x y b x y ==r r1212(,)a b x x y y +=++r r减法(三角形法则)“指向被减向量”AB AC CB AB CB AC-=-=u u u r u u u r u u u r u u u r u u u r u u u r )(b a b a ρρρρ-+=-1122(,),(,)a x y b x y ==r r1212(,)a b x x y y -=--r r数乘 向量a a ρρ)()(λμμλ=a a a ρρρμλμλ+=+)(b a b a ρρρρλλλ+=+)((,)(,)a x y a x y λλλ==rr数量积★cos a b a b θ⋅=⋅⋅r r r rcos a b a b θ⋅=⋅⋅r r r ra b b a ⋅=⋅r r r r ; ()a b c a c b c +⋅=⋅+⋅r r r r r r r()()()a b a b a b λλλ⋅=⋅=⋅r r r r r r1122(,),(,)a x y b x y ==r r★1212a b x x y y ⋅=+r r(1) 向量共线定理①a ρ∥b ρ(a r ≠0ρ)⇔存在惟一的实数λ使得b a λ=r r ;②若),,(),,(2211y x b y x a ==ρρ则a ρ∥b ρ⇔1221y x y x =(a ρ可以为0ρ).(2)两个向量垂直的充要条件①a b ⊥r r ⇔0a b ⋅=r r;②设1122(,),(,)a x y b x y ==r r,则a b ⊥r r ⇔12120x x y y +=.必修五1.★正弦定理:在ABC ∆中,a ,b ,c 分别为角,,A B C 的对边,则有:2sin sin sin a b cR A B C===.(其中R 为ABC ∆的外接圆的半径) 2.★余弦定理:在ABC ∆中,有①2222cos a b c bc A =+-,2222cos b a c ac B =+-,2222cos c a b ab C =+-.②222cos 2b c a A bc +-=,222cos 2a c b B ac+-=,222cos 2a b c C ab +-=.3.三角形面积公式:111sin sin sin 222ABC S bc A ab C ac B ∆===. 4.★等差数列(1) 定义:d a a n n =-+1(d 为常数); (2)通项公式:d n a a n )1(1-+=;(3)等差中项:若,,a A b 成等差数列,则A 叫做a 与b 的等差中项,且2b a A +=;(4)性质:若()*,,,m n p q m n p q N +=+∈,则m n p q a a a a +=+; (5)求和公式: 1()2n n n a a S += 或1(1)2n n n S na d -=+. 5.★等比数列 (1) 定义:q a a nn =+1(q 为常数); (2)通项公式:11-=n n q a a ;(3)等比中项:若,,a G b 成等比数列,则G 叫做a 与b 的等比中项,且ab G ±=; (4)性质:若()*,,,m n p q m n p q N +=+∈,则m n p q a a a a ⋅=⋅;(5)等比数列求和公式:⎪⎩⎪⎨⎧≠≠--=--==)10(11)1()1(111q q q q a a qq a q na S n n n且. 6. ★数列{}n a 的前n 项和n S 与项n a 之间的关系:⎩⎨⎧≥-==-2,1,11n S S n S a n nn .7. y kx b <+表示直线y kx b =+下方区域;y kx b >+表示直线y kx b =+上方区域. 8.★基本不等式: 若0a >,0b >,则a b +≥a b =时取到等号.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学学业水平测试必背公式定理知识点1、空集定义:_____________________________________;空集是任何集合的______________。
N ____________ Z __________ Q ___________ R ___________(常用集合字母表示)2、含n 个元素的集合其子集个数为_____________________。
3、函数定义:对定义域内任意x ,都有___________y 值与之对应,称y 是x 的函数。
4、求函数定义域三种基本形式:①分式要求:__________________;②根式,开偶次方根,则_______________________;③对数式则要求__________________________。
5、①指数函数定义:__________________________________________; 其定义域为_____________;值域为_________________;当_______________时函数单调递增;当_______________函数单调递减。
其图像恒过定点______________。
②对数函数定义:__________________________________。
其定义域为_____________;值域为_________________;当_______________时函数单调递增;当_______________函数单调递减。
其图像恒过定点______________。
③幂函数定义:_______________________________________。
当0>α时,图像恒过______________和_______________;在第一象限内单调_________; 当0<α时,图像恒过______________;在第一象限内单调_________;6、如果函数是奇偶函数,其定义域一定关于_______________对称;如果对定义域内任意x ,当________________时,函数为奇函数; 如果对定义域内任意x ,当________________时,函数为偶函数;7、函数单调性定义:在区间D 内任取两个值1x 、2x ,设21x x <,如果______________,则函数在此区间内单调递增;如果______________,则函数在此区间内单调递减。
8、空间两直线位置关系:_____________、________________、_________________; 空间两平面位置关系:________________、______________;空间直线与平面位置关系_____________、_____________、___________________;9、空间两直线所成角的范围:____________________;直线与平面所成角的范围:____________________;两异面直线所成角的范围:_____________________;10、线面平行判定定理:_________________________________________________________; 线面平行性质定理:_________________________________________________________; 线面垂直判定定理:_________________________________________________________; 线面垂直性质定理:_________________________________________________________; 面面平行判定定理:_________________________________________________________; 面面平行性质定理:_________________________________________________________;面面垂直判定定理:_________________________________________________________; 面面垂直性质定理:_________________________________________________________;11、圆锥的侧面展开图是_________________;体积公式为___________________;圆柱的侧面展开图是_________________;体积公式为___________________;锥体的体积公式是:V =_______________,柱体的体积公式为:V =_______________; 圆的表面积公式是:___________________;圆的体积公式为:___________________。
12、直线斜率三个常用公式:①已知直线倾斜角为α,则k =_____________;②已知直线经过两点(1x ,1y )、(2x ,2y ),则k =_____________;③直线0=++C By Ax 的斜率k =_____________;13、直线五种形式:①点斜式:__________________ ②斜截式:________________③两点式:__________________ ④截距式:________________⑤一般式:__________________14、最常用三个距离公式:①点(0x ,0y )到直线0=++C By Ax 的距离:______________________; ②两点(1x ,1y )、(2x ,2y )之间的距离公式:_______________________;③两平行线之间01=++C By Ax 和02=++C By Ax 之间的距离为________________。
15、圆的标准方程为____________________,其圆心坐标为___________,半径为_______; 圆的一般方程为_____________________,其圆心坐标为___________,半径为__________;16、圆的弦长公式:|AB |=__________________;直线和圆相切,则__________到直线的距离等于__________。
直线和圆相交,则__________到直线的距离__________半径。
17、诱导公式:=)sin(α-______________;=)cos(α-______________;=)tan(α-______________;)sin(απ+=____________;)cos(απ+=____________;)tan(απ+=____________;)sin(απ-=____________;)cos(απ-=____________;)tan(απ-=____________; =)2sin(απ-______________;=)2cos(απ-______________; =)2sin(απ+______________;=)2cos(απ+______________; 同角三角函数基本关系式:平方关系______________ 商数关系_______________;18、扇形弧长公式l =_________________;面积公式为S =___________________;19、①正弦函数x y sin =定义域为___________,值域为____________;最小正周期为______;图像为_____________________________________,奇偶性为____________;单调增区间为_____________________;单调减区间为___________________;②余弦函数x y cos =定义域为___________,值域为____________;最小正周期为______;图像为_____________________________________,奇偶性为____________;单调增区间为_____________________;单调减区间为___________________;③正切函数x y tan =定义域为______________,值域为______________;图像为_____________________________________,奇偶性为____________;单调增区间为_____________________;最小正周期为______;④函数)sin(ϕω+=x A y (A>0,0>ω)最大值为__________,最小值为_________ 最小正周期为T =_______________;20、三角函数定义:角α的终边过点(x ,y ),设22y x r +=,则αsin =________________;αcos =______________;αtan =______________;21、平面向量公式①零向量概念:长度为_________,方向__________的向量。
②若),(y x a =,则=||a ________________; ③若),(11y x a =,),(22y x b =则=+b a _________________;=-b a ______________b a ⋅=_______________(用模和夹角表示)=________________;④ a a ⋅=______________=______________;⑤ =+||b a _______________=_________________;⑥ 两个向量b a =,则其坐标对应为:_______________;⑦ a ∥b ,则其坐标满足________________;如果b a λ=,则a ___b ;⑧ a ⊥b ,则其坐标满足________________;22、三角恒等变换①两角和与差的三角函数值=+)sin(βα________________________,=-)sin(βα________________________, =+)cos(βα________________________,=-)cos(βα________________________, =+)tan(βα________________________,=-)tan(βα________________________, ②二倍角公式α2sin =_________________; α2tan =______________;α2cos =_________________=________________=____________________;③降次公式 α2sin =_______________ ,α2cos =______________;23、正弦定理:________=____________=___________=________;三角形面积公式:ABC S ∆=______________=______________=________________; 余弦定理:2a =___________________________ A cos =_____________________; 2b =___________________________ B cos =_____________________;2c =___________________________ C cos =_____________________;24、若一元二次方程02=++c bx ax 两根为1x ,2x 且1x <2x ,则02>++c bx ax 的解集为:______________________;02<++c bx ax 的解集为:______________________;25、基本不等式:①若a ,b 为两个正数,则b a +≥____________,当且仅当_______取等号;② ≥+22b a ___________,当且仅当______________取等号; ③ ≥+222b a __________________,且仅当______________取等号。
