高考数学必背公式与知识点过关检测
最新高考数学必背公式与知识点过关检测(精华版)

高考数学必背公式与知识点过关检测姓名 班级第一部分:集合与常用逻辑用语1.子集个数:含n 个元素的集合有 个子集,有 个真子集,有 个非空子集,有 个非空真子集2.常见数集:自然数集: 正整数集: 或 整数集: 有理数集: 实数集:3.空集:φ是任何集合的 ,是任何非空集合的 .4.元素特点: 、 、 确定性5.集合的的运算: 集运算、 集运算、 集运算6.四种命题:原命题:若p ,则q ;逆命题:若 ,则 ;否命题:若 ,则 ;逆否命题:若 ,则 ; 原命题与逆命题,否命题与逆否命题互 ;原命题与否命题、逆命题与逆否命题互 ;原命题与逆否命题、否命题与逆命题互为 。
互为逆否的命题7.充要条件的判断:p q ⇒,p 是q 的 条件;p q ⇒,q 是p 的 条件;p q ⇔,,p q 互为 条件;若命题p 对应集合A ,命题q 对应集合B ,则p q ⇒等价于 ,p q ⇔等价于 注意区分:“甲是乙的充分条件(甲⇒乙)”与“甲的充分条件是乙(乙⇒甲)”; 8.逻辑联结词:或命题:p q ∨,,p q 有一为真即为 ,,p q 均为假时才为 ;且命题:p q ∧,,p q 均为真时才为 ,,p q 有一为假即为 ;非命题:p ⌝和p 为一真一假两个互为对立的命题 9.全称量词与存在量词:⑴全称量词-------“所有的”、“任意一个”等,用∀表示;全称命题p :)(,x p M x ∈∀;全称命题p 的否定⌝p : ; ⑵存在量词--------“存在一个”、“至少有一个”等,用∃表示;特称命题p :)(,x p M x ∈∃;特称命题p 的否定⌝p : ;第二部分:函数与导数及其应用1.函数的定义域:分母 0;偶次被开方数 0;0次幂的底数 0 ;对数函数的真数 0;指数与对数函数的底数 0且 1 2.分段函数:值域(最值)、单调性、图象等问题,先分段解决,再下结论; 分段函数是一个函数,其定义域是各段定义域的 、值域是各段值域的3.函数的单调性:设1x ,2[,]x a b ∈(1⇔[]1212()()0(),f x f x f x a b x x ->⇔-在上是 函数;(2)[]1212()()()0x x f x f x --<⇔[]1212()()0(),f x f x f x a b x x -<⇔-在上是 函数;(3)如果0)(>'x f ,则)(x f 为 函数;0)(<'x f ,则)(x f 为 函数; (4)复合函数的单调性:根据“同 异 ”来判断原函数在其定义域内的单调性. 4.函数的奇偶性: ⑴函数的定义域关于 对称是函数具有奇偶性的前提条件.... ⑵)(x f 是 函数)()(x f x f -=-⇔;)(x f 是 函数)()(x f x f =-⇔. ⑶奇函数)(x f 在0处有定义,则⑷在关于原点对称的单调区间内:奇函数有 的单调性,偶函数有 的单调性⑸偶函数图象关于 轴对称、奇函数图象关于坐标 对称 5.函数的周期性:周期有关的结论:(约定a >0)(1))()(a x f x f +=,则)(x f 的周期T= ; (2))()(x f a x f -=+,或)0)(()(1)(≠=+x f x f a x f ,或1()()f x a f x +=-(()0)f x ≠, 则)(x f 的周期T=(3))()(a x f a x f -=+或)0)(()2(>=-a x f a x f ⇒)(x f 的周期为 6.函数的对称性:①()y f x =的图象关于直线 对称()()f a x f a x ⇔+=-(2)()f a x f x ⇔-=; ②()y f x =的图象关于直线 对称()()f a x f b x ⇔+=-()()f a b x f x ⇔+-=;7.对数运算规律:(1)对数式与指数式的互化:(2)对数恒等式:log 1a = ,log a a = ,log ba a = .lg 2+lg5= ,=lne(3)对数的运算性质:①加法:log log a a M N += ②减法: log aM N= ③数乘: log ()na M n R =∈ ④恒等式:log a N a =⑤log m n a b = ⑥换底公式:log log log m a m N N a=8.二次函数:二次函数c bx ax y ++=2(a ≠0)的图象的对称轴方程是 ,顶点坐标是 判别式ac b 42-=∆;0>∆时,图像与x 轴有 个交点;0=∆时,图像与x 轴有 个交点;0<∆时,图像与x 轴没有交点;9. 韦达定理:若x 1, x 2是一元二次方程)0(02≠=++a c bx ax 的两个根,则:x 1+x 2= ,x 1x 2= .10.零点定理:若y=f(x)在[a ,b ]上满足 , 则y=f(x)在(a ,b )内至少有一个零点11.常见函数的导数公式:①'()C = ;②'(n x =) ;'(nx =) ③'(sin x =) ; ④'(cos x =) ; ⑤'(x e =) ; ⑥ '(x a =) ; ⑦'(ln x =) ; ⑧'=(logx ) . 12.导数运算法则:()()f x g x '⋅=⎡⎤⎣⎦(1) ;()()2f x g x '⎡⎤=⎢⎥⎣⎦() .13.曲线的切线方程:函数)(x f y =在点0x 处的导数是曲线)(x f y =在))(,(00x f x P 处的切线的斜率为)(0x f ',相应的切线方程是 . 14.微积分基本定理:如果()f x 是[],a b 上的连续函数,并且有()()F x f x '=,则第三部分:三角函数、三角恒等变换与解三角形1.角度制与弧度制互化:360°= rad ,180°= rad ,1°= ≈ rad ,1rad= ≈ 2.若扇形的圆心角为()αα为弧度制,半径为r ,弧长为l ,周长为C ,面积为S ,则l = ,C = ,S= = .3.三角函数定义式:角α终边上任一点(非原点)P ),(y x ,设r OP =|| 则sin α= ,cos α= ,tan α=4.同角三角函数的基本关系:()1平方关系:()2tan =α商数关系: . 5.函数的诱导公式:口诀: .()()1sin 2sin k παα+=, , .(k ∈Z )(2) , ,()tan tan παα+=. (3) , ,()tan tan αα-=-. (4) , ,()tan tan παα-=-.()5sin cos 2παα⎛⎫-=⎪⎝⎭, .(6) ,cos sin 2παα⎛⎫+=- ⎪⎝⎭.8.几个常见三角函数的周期: ①x y sin =与x y cos =的周期为 .②)sin(ϕω+=x y 或)cos(ϕω+=x y (0≠ω)的周期为 . ③2tan x y =的周期为 .④x y cos =的周期为9. 两角和与差的正弦、余弦和正切公式:()1cos αβ-=() ; ()2cos αβ+=() ; ()3sin αβ-=() ; ()4sin αβ+=() ; ()5tan αβ-=() ; ()6tan αβ+=() .10. 二倍角的正弦、余弦和正切公式:sin 2α=cos2α= = =2cos α⇒=降次公式: ,2sin α= , sin cos αα=tan 2α=11.引入辅助角公式: sin cos a b αα+= . (其中,辅助角ϕ所在象限由点(,)a b 所在的象限决定,tan b aϕ= ).12. 正弦定理: . (R 是ABC ∆外接圆直径) 注:①C B A c b a sin :sin :sin ::=;②C R c B R b A R a sin 2,sin 2,sin 2===;③C B A cb a Cc B b A a sin sin sin sin sin sin ++++=== 13. 余弦定理: ⇔ .(变式)(以A 角和其对边来表示)14. 三角形面积公式:ABC S ∆= = = . (用边与角的正弦值来表示) 三角形面积导出公式:ABC S ∆= (r 为ABC ∆内切圆半径)= (R 外接圆半径)15. 三角形内切圆半径r = 外接圆直径2R = = =第四部分:平面向量、数列与不等式1. 平面向量的基本运算:设11(,)a x y =,22(,)b x y =;(0b ≠)= ;a b -= ;a b ⋅= (定义公式)= (坐标公式).a 在b 方向上的投影为. = (坐标公式) a b ⊥⇔ (一般表示) ⇔ (坐标表示) .a ∥b ⇔ (一般表示)⇔ (坐标表示).cos θ=夹角公式: = (坐标公式).2.若G 为ABC ∆的重心,则 =0;且G 点坐标为 ( , )3.三点共线的充要条件:P ,A ,B 三点共线⇔ →OP =x →OA +y →OB 且 =14.三角形的四心重心:三角形三条 交点.外心:三角形三边 相交于一点. 内心:三角形三 相交于一点.垂心:三角形三边上 的相交于一点.5. 数列{n a }中n a 与n S 的关系n a =2.n S =2.n S =性质1.,,a b c ⇒成等差数列称b 为a 与c 的等差中项 2.若m n p q +=+, 则1.,,a b c ⇒成等比数列 称b 为a 与c 的等比中项 2.若m n p q +=+, 则7.常见数列的和:①1+2+3+……+n=②12+22+32+……+n 2=③13+23+33+……+n 3=8.一元二次不等式解的讨论.0>∆0=∆0<∆二次函数c bx ax y ++=2(0>a )的图象一元二次方程()的根002>=++a c bx ax的解集)0(02>>++a c bx ax的解集)0(02><++a c bx ax9. 均值不等式: 若0a >,0b >,则 ⇔ ; 10. 重要不等式: 11.极值定理:已知y x ,都是正数,则有:(1)如果积xy 是定值p ,那么当y x =时和y x +有最小值 ; (2)如果和y x +是定值s ,那么当y x =时积xy 有最大值 .12.两个著名不等式:(1)平均不等式: 如果a ,b 都是正数,那么(当仅当a =b 时取等号)即:平方平均≥算术平均≥几何平均≥调和平均(a 、b 为正数) 特别地,222()22a b a b ab ++≤≤(当a = b 时,222()22a b a b ab ++==)),,,(332222时取等c b a R c b a c b a c b a ==∈⎪⎭⎫ ⎝⎛+++≥++ ⇒幂平均不等式:22122221)...(1...n n a a a na a a +++≥+++ (2)柯西不等式: .(当且仅当ad=bc 时取等号)第五部分:立体几何与解析几何1. 三视图与直观图:原图形与直观图面积之比为 2. 常见几何体表面积公式:圆柱的表面积 S= 圆锥的表面积S=圆台的表面积 S= 球的表面积 S= 3.常见几何体体积公式:柱体的体积 V= 锥体的体积 V=台体的体积 V= 球体的体积 V= 4. 常见空间几何体的有关结论:⑴棱锥的平行截面的性质:如果棱锥被平行于底面的平面所截,那么所得的截面与底面 ,截面面积与底面面积的比等于顶点到截面距离与棱锥高的 ;相应小棱锥与小棱锥的侧面积的比等于顶点到截面距离与棱锥高的 . ⑵长方体从一个顶点出发的三条棱长分别为a ,b ,c ,则体对角线长为 ,全面积为 ,体积V= ⑶正方体的棱长为a ,则体对角线长为 ,全面积为 ,体积V= ⑷球与长方体的组合体: 长方体的外接球的直径=长方体的 长.球与正方体的组合体:正方体的内切球的直径=正方体的 , 正方体的棱切球的直径=正方体的 长, 正方体的外接球的直径=正方体的体 长. ⑸正四面体的性质:设棱长为a ,则正四面体的:① 高: ;②对棱间距离: ;③内切球半径: ;④外接球半径: 5. 空间向量中的夹角和距离公式:(1)空间中两点A 111(,,)x y z ,B 222(,,)x y z 的距离d = (2)异面直线夹角:(0,]2πθ∈cosθ= (两直线方向向量为,a b )(3)线面角:[0,]2πθ∈,且sin θ= (l ,n 为直线的方向向量与平面的法向量)(4)二面角:[0,]θπ∈,且cos θ= (两平面的法向量分别为1n 和2n )(5)点到面的距离:平面α的法向量为n ,平面α内任一点为N ,点M 到平面α的距离d =6.直线的斜率:k = =(θ为直线的倾斜角,11(,)A x y 、22(,)B x y 为直线上的两点) 7. 直线方程的五种形式:直线的点斜式方程: (直线l 过点111(,)P x y ,且斜率为k ). 直线的斜截式方程: (b 为直线l 在y 轴上的截距).直线的两点式方程: (111(,)P x y 、222(,)P x y 12x x ≠,12y y ≠).直线的截距式方程: (a 、b 分别为直线在x 轴、y 轴上的截距,且0,0≠≠b a ).直线的一般式方程: (其中A 、B 不同时为0). 8.两条直线的位置关系:(1)若111:l y k x b =+,222:l y k x b =+,则:① 1l ∥2l ⇔ 且 ; .(2)若1111:0l A x B y C ++=,2222:0l A x B y C ++=,则:①1l ∥2l ⇔ 且 ;②. 12l l ⊥⇔ . 9.距离公式:(1)点111(,)P x y ,222(,)P x y 之间的距离: (2)点00(,)P x y 到直线0Ax By C ++=的距离:(3)平行线间的距离:10Ax By C ++=与20Ax By C ++=的距离:10.圆的方程:(1)圆的标准方程:(2)圆的一般方程: ()0422>-+F E D 11.直线与圆的位置关系:判断圆心到直线的距离d 与半径R 的大小关系 (1)当 时,直线和圆 (有两个交点);(2)当 时,直线和圆 (有且仅有一个交点); (3)当 时,直线和圆 (无交点);12. 圆与圆的位置关系:判断圆心距d 与两圆半径和12R R +,半径差12R R -(12R R >)的大小关系:(1)当 时,两圆 ,有4条公切线; (2)当 时,两圆 ,有3条公切线; (3)当 时,两圆 ,有2条公切线; (4)当 时,两圆 ,有1条公切线; (5)当 时,两圆 ,没有公切线;13. 直线与圆相交所得弦长|AB|= (d 为直线的距离r 为半径) 14.椭圆的定义:(1)第一定义:平面内与两个定点21F F 、的距离和等于常数 的点的轨迹叫椭圆.这两个定点叫椭圆的焦点,两焦点间的距离叫焦距.(222c b a +=)(2)标准方程:焦点在x 轴上: ;焦点在y 轴上: .15.双曲线的定义:(1)第一定义:平面内与两个定点21F F 、的距离之差的绝对值等于常数: 的点的轨迹叫双曲线.这两个定点叫双曲线的焦点,两焦点间的距离叫焦距.(222a b c +=)(2)标准方程:焦点在x 轴上: ;焦点在y 轴上: . 16.抛物线的定义:(1)平面内与一个定点F 和一条定直线l (点F 不在l 上)的距离的 的点的轨迹叫做双曲线.这个定点是抛物线的焦点,定直线是抛物线的准线.(2)标准方程:焦点在x 轴上: ;焦点在y 轴上: .17.离心率:e = (椭圆的离心率 ,双曲线的离心率 ,抛物线的离心率 )18.双曲线的渐近线:22221x y a b -=(0a >,0b >)的渐近线方程为 ,且与22221x y a b -=具有相同渐近线的双曲线方程可设为2222x y a bλ-=. 19.过抛物线焦点的直线:倾斜角为θ的直线过抛物线22y px =的焦点F 且与抛物线交于11(,)A x y 、22(,)B x y 两点(10y >):|AF|= |BF|= |AB|= = x 1x 2= y 1y 2=1|AF| +1|BF|= 20.焦点三角形的面积:(1)椭圆:S= ;(2)双曲线:S= (12F PF θ∠=) 21.几何距离:(1)椭圆双曲线特有距离:①长轴(实轴): ; ②短轴(虚轴): ; ③两焦点间距离: .(2)焦准距:①椭圆、双曲线: ; ②抛物线: . (3)通径长:①椭圆、双曲线: ; ②抛物线: . 22.直线被曲线所截得的弦长公式:若弦端点为A ),(),,(2211y x B y x ,则|AB|= = = 23. 中点弦问题: 椭圆:k AB k OP = 双曲线:k AB k OP =第六部分:统计与概率1. 总体特征数的估计:⑴样本平均数⎺x= = ;⑵样本方差;S 2= = ; ⑶样本标准差S= 2.概率公式:⑴互斥事件(有一个发生)概率公式:P(A+B)=⑵古典概型:基本事件的总数数为N ,随机事件A 包含的基本事件个数为M ,则事件A 发生的概率为:P(A)= ⑶几何概型:等)区域长度(面积或体积试验的全部结果构成的积等)的区域长度(面积或体构成事件A A P =)(3.离散型随机变量:⑴随机变量的分布列:①随机变量分布列的性质:p i ≥ , i=1,2,3,…; p 1+p 2+…=均值(又称期望):EX =方差:DX = 注:DX a b aX D b aEX b aX E 2)(;)(=++=+;③二项分布(独立重复试验):若X ~B (n , p ),则EX = , DX =注:k n k k n p p C k X P --==)1()(⑵条件概率: P (B|A )=注:0≤P (B|A )≤1⑶独立事件同时发生的概率:P (AB )=第七部分:复数与计数原理1. 复数的基本概念:z a bi =+(a ,b R ∈)(1)实部: ;虚部: ; 虚数单位:i 2=(2)模:|z |= =(3)共轭复数:-z= (4)在复平面内对应的点为 (5)复数相等:a+bi=c+di (a ,b ,c ,d ∈R )⇔2. 复数的基本运算: (1)加减法:(a+bi )+(c+di )= (a+bi )-(c+di )= (2)乘法:(a+bi )×(c+di )=(3)除法:(a+bi )÷(c+di )= 注:对虚数单位i ,有1 , ,1,4342414=-=-==+++n n n n i i i i i i.3.分类计数原理(加法原理)与分步计数原理(乘法原理):.(1)完成一件事有n 类不同方案,在第1类方案中有1m 种不同的方法,在第2类方案中有2m 种不同的方法,…,在第n 类方案中有n m 种不同的方法.那么完成这件事共有 N= 种不同的方法.(2)完成一件事情,需要分成n 个步骤,做第1步有1m 种不同的方法,做第2步有2m 种不同的方法……做第n 步有n m 种不同的方法.那么完成这件事共有N= 种不同的方法. 4.排列数公式:= = ;=(m≤ n, m 、n ∈N*) 规定0!1=5.组合数公式: = (n ,m N *∈,且m n ≤);6. 组合数性质: ;7.二项式定理:(a+b )n = (rn C 叫做二项式系数)8.二项展开式的通项公式:T r+1= (r=0,1,2……,n )第八部分:坐标系与参数方程1. 极坐标→直角坐标cos sin x y ρθρθ=⎧⎨=⎩直角坐标→极坐标tan (0)y x x ρθ⎧=⎪⎨=≠⎪⎩2. 圆的极坐标方程:①以极点为圆心,a 为半径的圆的极坐标方程是 ; ②以(,0)a )0(>a 为圆心, a 为半径的圆的极坐标方程是 ; ③以(,)2a π)0(>a 为圆心,a 为半径的圆的极坐标方程是 ;④以(),(0)a a π>为圆心,a 为半径的圆的极坐标方程是 ; ⑤以3,(0)2a a π⎛⎫> ⎪⎝⎭为圆心,a 为半径的圆的极坐标方程是 3. 常见曲线的参数方程:。
考点巩固卷12 等差、等比数列(七大考点)(学生版) 2025年高考数学一轮复习考点通关卷(新高考
考点巩固卷12 等差等比数列(七大考点)考点01:单一变量的秒解当数列的选择填空题中只有一个条件时,可将数列看成常数列,即每一项均设为x ,(注意:如果题目中出现公差不为0或公比不为1,则慎用此法)1.已知等差数列{}n a 的前n 项和为123456,6,12n S a a a a a a ++=++=,则12S =( )A .18B .36C .54D .602.已知等差数列{}n a 满足12318a a a ++=,则2a =( )A .5B .6C .7D .83.若{}n a 是正项无穷的等差数列,且396a a +=,则{}n a 的公差d 的取值范围是( )A .[)12,B .305æöç÷èø,C .35¥æö+ç÷èø,D .305éö÷êëø,4.等差数列{}n a 前n 项和为7,4n S a =,则13S =( )A .44B .48C .52D .565.已知等差数列{}n a 满足25815a a a ++=,记{}n a 的前n 项和为n S ,则9S =( )A .18B .24C .27D .456.在等差数列{}n a 中,若354a a +=,则其前7项和为( )A .7B .9C .14D .187.已知等差数列{}n a 的前n 项和为n S ,若91S =,则37a a +=( )A .2-B .73C .1D .298.在等比数列{}n a 中,25,a a 是方程2780x x --=的两个根,则16a a =( )A .7B .8C .8-或8D .8-9.已知等差数列{}n a 的前n 项和为S n ,若5414a a a +=+,则15S =( )A .4B .60C .68D .13610.设等差数列{}n a 的前n 项和为n S ,已知2410268a a a ++=,则9S =( )A .272B .270C .157D .153考点02:秒解等差数列的前n 项和等差数列中,有()⇒-=-n n a n S 1212奇偶有适用.()()()()nn n n an n a n a a 12212221212112-=-=-+=--⇒将12-n 换为n 11.在等差数列{}n a 中,公差3d =,n S 为其前n 项和,若89S S =,则17S =( )A .2-B .0C .2D .412.已知n S 是等差数列{}n a 的前n 项和,且7287026S a a =+=,,则{}n a 的公差d =( )A .1B .2C .3D .4.13.已知等差数列{}n a 的公差为d ,前n 项和为n S ,若12413,22a a S +==,则d =( )A .7B .3C .1D .1-14.等差数列 {}n a 中,n S 是其前 n 项和,53253S S -=,则公差 d 的值为( )A .12B .1C .2D .315.记n S 为等差数列{}n a 的前n 项和,已知510S S =,51a =,则1a =( )A .72B .73C .13-D .711-16.已知等差数列{}n a 的前15项之和为60,则313a a +=( )A .4B .6C .8D .1017.已知等差数列{}n a 的前n 项和为n S ,23a =,221n n a a =+,若1100n n S a ++=,则n =( )A .8B .9C .10D .1118.n S 是等差数列{}n a 的前n 项和,若1236a a a ++=,7916+=a a ,则9S =( )A .43B .44C .45D .4619.已知n S 是等差数列{}n a 的前n 项和,若23a =,525S =,则442S a a =-( )A .1B .2C .3D .420.已知n S 为等差数列{}n a 的前n 项和,已知848,16S S =-=,则56223839a a a a a ++++=( )A .215B .185C .155D .135考点03:数列片段和问题k k k k k S S S S S 232,,--这样的形式称之为“片段和”①当}{n a 是等差数列时:k k k k k S S S S S 232,,--也为等差数列,且公差为d k 2.②当}{n a 是等比数列时:k k k k k S S S S S 232,,--也为等比数列,且公比为kq .21.已知等差数列{}n a 的前n 项和为n S ,36S =,()*3164,n S n n -=³ÎN ,20n S =,则n 的值为( )A .16B .12C .10D .822.已知等差数列{}n a 的前n 项和为n S ,若330S =,651S =,则9S =( )A .54B .63C .72D .13523.已知等差数列{}n a 的前n 项和为n S ,且365,15S S ==,则9S =( )A .35B .30C .20D .1524.记n S 为等差数列{}n a 的前n 项和,若4127,45S S ==.则8S =( )A .28B .26C .24D .2225.已知等差数列{}n a 的前n 项和为n S ,若42S =,812S =,则20S =( )A .30B .58C .60D .9026.在等差数列{}n a 中,若363,24S S ==,则12S =( )A .100B .120C .57D .1827.等差数列{}n a 的前n 项和为n S .若10111012101310148a a a a +++=,则2024S =( )A .8096B .4048C .4046D .202428.若正项等比数列{}n a 的前n 项和为n S ,且8426S S -=,则9101112a a a a +++的最小值为( )A .22B .24C .26D .2829.设n S 是等比数列{}n a 的前n 项和,若23S =,346a a +=,则108S S =( )A .157B .3115C .2D .633130.在正项等比数列{}n a 中,n S 为其前n 项和,若301010303,80S S S S =+=,则20S 的值为( )A .10B .20C .30D .40考点04:秒杀和比与项比结论1:若两个等差数列}{n a 与}{n b 的前n 项和分别为n n T S ,,若DCn B An T S n n ++=,则()()Dn C B n A T S b a n n n n +-+-==--12121212结论2:若两个等差数列}{n a 与}{n b 的前n 项和分别为n n T S ,,若DCn B An T S n n ++=,则()()Dm C B n A b a m n +-+-=121231.已知等差数列{}n a 与{}n b 的前n 项和分别为,n n S T ,且231n n S n T n +=+,则19119a ab b ++的值为( )A .1311B .2110C .1322D .212032.已知等差数列{}n a 和{}n b 的前n 项和分别为n S 和n T ,且335n n S n T n +=+,则526a b b =+( )A .1417B .417C .313D .1533.已知数列{}{}n n a b ,均为等差数列,其前n 项和分别为n n S T ,,满足(23)(31)n n n S n T +=-,则789610a a ab b ++=+( )A .2B .3C .5D .634.设数列{}n a 和{}n b 都为等差数列,记它们的前n 项和分别为n S 和n T ,满足21n n n a b n =+,则55S T =( )A .12B .37C .59D .3535.已知等差数列{}n a 和{}n b 的前n 项和分别为,n n S T ,若342n n S n T n +=+,则58211a a b b +=+( )A .1713B .3713C .207D .37736.等差数列{}{},n n a b 的前n 项和分别是,n n S T ,若542n n S n T n +=+,则44a b = .37.设等差数列{}n a ,{}n b 的前n 项和分别为n S ,n T ,若对任意正整数n 都有2343n n S n T n -=-,则839457a ab b b b +=++ .38.已知n S ,n T 分别是等差数列{}n a ,{}n b 的前n 项和,且2131n n S n T n +=-,那么44a b = .39.两个等差数列{}n a 和{}n b 的前n 项和分别为n S 、n T,且523n n S n T n +=+,则220715a a b b ++等于40.已知等差数列{}n a , {}n b 的前n 项和分别为n S ,n T ,且214n nS n T n +=,则537a b b =+ .考点05:等差数列奇偶规律结论()*ÎNn n 2则1,+==-n n a aS S nd S S 偶奇奇偶n 2,则它的奇数项分别为135721,,,......n a a a a a -则它的偶数项分别为24682,,,......na a a a a 则奇数项之和()1212=22n nnn a a n a S na -+×==奇则偶数项之和()22+1+12=22n n n n a a n a S na +×==偶代入公式得1-S =n( )n n S a a nd +-=奇偶,11=S n n n n S na ana a ++=奇偶()*Î+Nn n 12则()()111,11,+++=+=+==-n n n na S a n S nn S S a S S 偶奇偶奇偶奇∵12-n 项,则它的奇数项为127531,,,+n a a a a a 则它的偶数项分别为na a a a 2642,, 则奇数项之和()()()1121112+++=+×+=n n an n a a S 奇则偶数项之和()1222+=×+=n n nan a a S 偶代入公式得()1111+++=-+=-n n n a na a n S S 偶奇()nn na a n S S n n 1111+=+=++偶奇说明:偶奇,S S 分别表示所有奇数项与所有偶数项的和41.已知等差数列{}n a 的项数为()21Ν,m m *+Î其中奇数项之和为140, 偶数项之和为 120,则m =( )A .6B .7C .12D .1342.一个等差数列共100项,其和为80,奇数项和为30,则该数列的公差为( )A .14B .2C .13D .2543.已知等差数列{}n a 的前30项中奇数项的和为A ,偶数项的和为B ,且45B A -=,2615A B =+,则n a =( )A .32n -B .31n -C .31n +D .32n +44.已知数列{}n a 的前n 项和为n S ,且11a =,22a =,13++=n n a a n ,则( )A .45a =B .20300S =C .31720S =D .n 为奇数时,2314+=n n S 45.已知等差数列{}n a 共有21n -项,奇数项之和为60,偶数项之和为54,则n =.46.已知数列{}n a 满足11a =,12,3,n n na n a a n ++ì=í+î为奇数为偶数,则{}n a 的前40项和为.47.已知等差数列{}n a 的项数为21m +()*m ÎN ,其中奇数项之和为140,偶数项之和为120,则数列{}n a 的项数是 .48.数列{}n a 满足:2212212121,2,2n n n na a a a a a ++-==-==,数列{}n a 的前n 项和记为n S ,则23S = .49.在等差数列{}n a 中,已知公差12d =,且1359960+++×××+=a a a a ,求12399100a a a a a +++×××++的值.50.已知{}n a 是等差数列,其中222a =,610a =.(1)求{}n a 的通项公式;(2)求24620a a a a ++++ 的值.考点06: 等差数列前n 项和最值规律方法一:函数法⇒利用等差数列前n 项和的函数表达式,通过配方或借助图象求二次函数最值的方法求解.bn an S n +=2模型演练()n d a n d S d n n na S n n ×÷øöçèæ-+=⇒×-+=222112121122222÷÷÷÷øöççççèæ--÷÷÷÷øöççççèæ-+=⇒d d a d d d a n d S n 2121212212÷øöçèæ--⎥⎦⎤êëé÷øöçèæ--=⇒d a d d a n d S n 由二次函数的最大值、最小值可知,当n 取最接近da 121-的正整数时,n S 取到最大值(或最小值)注意:最接近da 121-的正整数有时1个,有时2个51.已知等差数列{}n a 的前n 项和为n S ,10a >,且316=S S ,则n S 取最大值时,n =( ).A .9B .10C .9或10D .10或1152.已知等差数列{}n a 的前n 项和为n S ,若50a <,380a a +>,则当n S 取得最小值时,n =( )A .4B .5C .6D .753.设数列{}n a 的前n 项和为11,1,321n nn S S S S n n+-=-=+,则下列说法正确的是( )A .{}n a 是等比数列B .36396,,S S S S S --成等差数列,公差为9-C .当且仅当17n =时,n S 取得最大值D .0n S ³时,n 的最大值为3354.数列{}n a 的前n 项和211n S n n =-,则( )A .110a =B .32a a >C .数列{}n S 有最小项D .n S n ìüíýîþ是等差数列55.已知等差数列{}n a 的首项为1a ,公差为d ,前n 项和为n S ,若1089S S S <<,则下列说法正确的是( )A .1a d>B .使得0n S >成立的最大正整数18n =C .891011a a a a +<+D .n n S a ìüíýîþ中最小项为1100S a 56.等差数列 {}n a 的前 n 项和为 1214,0,0n S a a a >+=,则( )A .80a =B .1n na a +<C .79S S <D .当 0n S < 时, n 的最小值为 1657.已知无穷数列{}n a 满足:110a =-,12n n a a +=+()*N n Î.则数列{}n a 的前n 项和最小值时n 的值为 .58.设等差数列{}n a 的公差为d ,其前n 项和为n S ,且满足991,27a S =-=.(1)求d 的值;(2)当n 为何值时n S 最大,并求出此最大值.59.已知数列{}n a 是公差不为零的等差数列,111a =-,且256,,a a a 成等比数列.(1)求{}n a 的通项公式;(2)设n S 为{}n a 的前n 项和,求n S 的最小值.60.记n S 为等差数列{}n a 的前n 项和,已知17a =-,315S =-.(1)求{}n a 的通项公式;(2)求n S ,并求n S 的最小值.考点07:等比数列奇偶规律结论()*ÎNn n 2则qS S =奇偶n 2,则它的奇数项分别为135721,,,......n a a a a a -则它的偶数项分别为24682,,,......na a a a aq a a q a a q a a ×=×=×=342312,,∵()q a a a a a a a a a a q a a a a a a a a a a n n n n n n n n =++++++++=++++++++∴-------123253112325311232531222642()*Î+Nn n 12则q S a S =-偶奇112+n ,则它的奇数项分别为13572+1,,,......n a a a a a 则它的偶数项分别为24682,,,......na a a a a q a a q a a q a a ×=×=×=453423,,∵q S a S q a a a a a a a a a a a a a a a a a a a n n n n n n n n =-⇒=+++++++=++++++++∴-+--+-偶奇12226421212532226421212531 说明:偶奇,S S 分别表示所有奇数项与所有偶数项的和61.已知等比数列{}n a 有21n +项,11a =,所有奇数项的和为85,所有偶数项的和为42,则n =( )A .2B .3C .4D .562.已知等比数列{}n a 的前n 项和为n S ,其中10a >,则“31a a >”是“n S 无最大值”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件63.已知一个等比数列的项数是是偶数,其奇数项之和1011,偶数项之和为2022,则这个数列的公比为( ).A .8B .2-C .4D .264.已知等比数列{}n a 的公比为13-,其前n 项和为n S ,且1a ,243a +,3a 成等差数列,若对任意的*n ÎN ,均有2nnA SB S £-£恒成立,则B A -的最小值为( )A .2B .76C .103D .5365.已知一个项数为偶数的等比数列{}n a ,所有项之和为所有偶数项之和的4倍,前3项之积为64,则1a =( )A .1B .4C .12D .3666.已知数列}{n a 的前n 项和121n n S -=+,则数列}{n a 的前10项中所有奇数项之和与所有偶数项之和的比为( )A .12B .2C .172341D .34117267.等比数列{}n a 的首项为2,项数为奇数,其奇数项之和为8532,偶数项之和为2116,则这个等比数列的公比q = .68.等比数列的性质已知{}n a 为等比数列,公比为q ,n S 为其前n 项和.(1)若()0,0,1n n S Aq B A q q =+¹¹¹,则A B += ;(2)当0n S ¹时,n S , ,32,n n S S - 为等比数列;(3)若等比数列{}n a 共2k 项,记S 奇为诸奇数项和,S 偶为诸偶数项和,则S S =奇偶 ;69.已知首项均为32的等差数列{}n a 与等比数列{}n b 满足32a b =-,43a b =,且{}n a 的各项均不相等,设n S 为数列{}n b 的前n 项和,则n S 的最大值与最小值之差为 .70.(1)在等比数列{}n a 中,已知248,60n n S S ==,求3n S ;(2)一个等比数列的首项是1,项数是偶数,其奇数项的和为85,偶数项的和为170,求此数列的公比和项数.。
高考数学一轮复习课时过关检测五十椭圆的定义标准方程及简单几何性质含解析

课时过关检测(五十) 椭圆的定义、标准方程及简单几何性质A 级——基础达标1.与椭圆9x 2+4y 2=36有相同焦点,且满足短半轴长为25的椭圆方程是( ) A .x 225+y 220=1 B .x 220+y 225=1 C .x 220+y 245=1 D .x 280+y 285=1 解析:B 由9x 2+4y 2=36可得x 24+y 29=1,所以所求椭圆的焦点在y 轴上,且c 2=9-4=5,b =25,a 2=25,所以所求椭圆方程为x 220+y 225=1.2.“(log a 2)x 2+(log b 2)y 2=1表示焦点在y 轴上的椭圆”的一个充分不必要条件是( )A .0<a <bB .1<a <bC .2<a <bD .1<b <a解析:C 若(log a 2)x 2+(log b 2)y 2=1表示焦点在y 轴上的椭圆,则需⎩⎪⎨⎪⎧ log a 2>0,log b 2>0,log a 2>log b 2,即⎩⎪⎨⎪⎧a >1,b >1,a <b ,所以1<a <b ,所以“(log a 2)x 2+(log b 2)y 2=1表示焦点在y 轴上的椭圆”的一个充分不必要条件是2<a <b ,故选C .3.如图,P 是椭圆x 29+y 24=1上的一点,F 是椭圆的左焦点且PQ ―→=-FQ ―→,|OQ ―→|=2,则|PF |=( )A .2B . 5C .3D .4解析:A 由x 29+y 24=1可得a =3.因为PQ ―→=-FQ ―→,所以点Q 是线段PF 的中点,设椭圆的右焦点为F ′,则O 是FF ′的中点,所以|PF ′|=2|OQ |=4,由椭圆的定义可知:|PF |+|PF ′|=2a =6,所以|PF |=2,故选A .4.已知椭圆C :x 225+y 29=1的左、右焦点分别为F 1,F 2,点M 在椭圆C 上,当△MF 1F 2的面积最大时,△MF 1F 2内切圆半径为( )A .3B .2C .53D .43解析:D 因为椭圆为x 225+y 29=1,所以a =5,b =3,c =a 2-b 2=4.当△MF 1F 2的面积最大时,点M 为椭圆C 短轴的顶点,不妨设点M 为椭圆C 的上顶点,点O 为坐标原点,△MF 1F 2内切圆半径为r ,则|MF 1|=|MF 2|=a =5,|F 1F 2|=2c =8,|OM |=b =3,S △MF 1F 2=12(|MF 1|+|MF 2|+|F 1F 2|)·r =12|F 1F 2|·|OM |,所以r =43,故选D .5.过椭圆C :x 2a 2+y 2b2=1(a >b >0)的右焦点作x 轴的垂线,交C 于A ,B 两点,直线l 过C的左焦点和上顶点.若以AB 为直径的圆与l 存在公共点,则C 的离心率的取值范围是( )A .⎝ ⎛⎦⎥⎤0,55 B .⎣⎢⎡⎭⎪⎫55,1 C .⎝⎛⎦⎥⎤0,22 D .⎣⎢⎡⎭⎪⎫22,1 解析:A 由题设知,直线l :x -c +yb=1,即bx -cy +bc =0,以AB 为直径的圆的圆心为(c,0),根据题意,将x =c 代入椭圆C 的方程,得y =±b 2a ,即圆的半径r =b 2a .又圆与直线l 有公共点,所以2bcb 2+c 2≤b 2a,化简得2c ≤b ,平方整理得a 2≥5c 2,所以e =c a ≤55.又0<e <1,所以0<e ≤55.故选A . 6.(多选)对于曲线C :x 24-k +y 2k -1=1,下面四个说法正确的是( )A .曲线C 不可能是椭圆B .“1<k <4”是“曲线C 是椭圆”的充分不必要条件C .“曲线C 是焦点在y 轴上的椭圆”是“3<k <4”的必要不充分条件D .“曲线C 是焦点在x 轴上的椭圆”是“1<k <2.5”的充要条件解析:CD 对于A ,当1<k <4且k ≠2.5时,曲线C 是椭圆,所以A 错误;对于B ,当k =2.5时,4-k =k -1,此时曲线C 是圆,所以B 错误;对于C ,若曲线C 是焦点在y 轴上的椭圆,则⎩⎪⎨⎪⎧4-k >0,k -1>0,k -1>4-k ,解得2.5<k <4,所以“曲线C 是焦点在y 轴上的椭圆”是“3<k <4”的必要不充分条件,所以C 正确;对于D ,若曲线C 是焦点在x 轴上的椭圆,则⎩⎪⎨⎪⎧k -1>0,4-k >0,4-k >k -1,解得1<k <2.5,所以D 正确.7.(多选)如图,两个椭圆x 225+y 29=1,y 225+x 29=1内部重叠区域的边界记为曲线C ,P 是曲线C 上的任意一点,下列四个说法正确的为( )A .P 到F 1(-4,0),F 2(4,0),E 1(0,-4),E 2(0,4)四点的距离之和为定值B .曲线C 关于直线y =x ,y =-x 均对称 C .曲线C 所围区域面积必小于36D .曲线C 总长度不大于6π解析:BC 易知F 1(-4,0),F 2(4,0)分别为椭圆x 225+y 29=1的两个焦点,E 1(0,-4),E 2(0,4)分别为椭圆y 225+x 29=1的两个焦点.若点P 仅在椭圆x 225+y 29=1上,则P 到F 1(-4,0),F 2(4,0)两点的距离之和为定值,到E 1(0,-4),E 2(0,4)两点的距离之和不为定值,故A 错误;两个椭圆关于直线y =x ,y =-x 均对称,则曲线C 关于直线y =x ,y =-x 均对称,故B 正确;曲线C 所围区域在边长为6的正方形内部,所以面积必小于36,故C 正确;曲线C 所围区域在半径为3的圆外部,所以曲线的总长度大于圆的周长6π,故D 错误.故选B 、C .8.若椭圆x 2m +y 22=1的离心率为22,则该椭圆的长轴长为________.解析:由椭圆x 2m +y 22=1的离心率为22,当m >2时,椭圆焦点在x 轴上,c a =22=m -2m,解得m =4,所以椭圆的长轴长为4,当0<m <2时,椭圆焦点在y 轴上,ca=22=2-m 2,得m =1,所以椭圆的长轴长为22.答案:4或2 29.设F 1,F 2分别为椭圆C :x 2a 2+y 2a 2-1=1(a >1)的左、右焦点,P (1,1)为C 内一点,Q为C 上任意一点.现有四个结论:①C 的焦距为2;②C 的长轴长可能为10; ③|QF 2|的最大值为a +1;④若|PQ |+|QF 1|的最小值为3,则a =2. 其中所有正确结论的编号是________.解析:对于①:因为c 2=a 2-(a 2-1)=1,所以椭圆C 的焦距为2c =2,故①正确;对于②:若椭圆C 的长轴长为10,则a 2=52,所以椭圆C 的方程为x 252+y 232=1,则152+132>1,从而点P 在C 的外部,这与P 在C 内矛盾,所以②不正确;对于③:因为c =1,Q 为C 上任意一点,由椭圆的几何性质可知,|QF 2|的最大值为a +c =a +1,故③正确;对于④:由椭圆定义可知,|PQ |+|QF 1|=|PQ |-|QF 2|+2a ,因为||PQ |-|QF 2||≤|PF 2|=1,所以|PQ |-|QF 2|≥-1,所以|PQ |-|QF 2|+2a ≥2a -1=3,此时a =2,故④正确.答案:①③④10.(2019·全国Ⅱ卷)已知F 1,F 2是椭圆C :x 2a 2+y 2b2=1(a >b >0)的两个焦点,P 为C 上的点,O 为坐标原点.(1)若△POF 2为等边三角形,求C 的离心率;(2)如果存在点P ,使得PF 1⊥PF 2,且△F 1PF 2的面积等于16,求b 的值和a 的取值范围. 解:(1)连接PF 1(图略).由△POF 2为等边三角形可知在△F 1PF 2中,∠F 1PF 2=90°,|PF 2|=c ,|PF 1|=3c ,于是2a =|PF 1|+|PF 2|=(3+1)c ,故C 的离心率为e =ca=3-1.(2)由题意可知,满足条件的点P (x ,y )存在当且仅当 12|y |·2c =16,y x +c ·y x -c =-1,x 2a 2+y 2b 2=1, 即c |y |=16,①x 2+y 2=c 2,② x 2a 2+y 2b 2=1.③ 由②③及a 2=b 2+c 2得y 2=b 4c2.又由①知y 2=162c2,故b =4.由②③及a 2=b 2+c 2得x 2=a 2c2(c 2-b 2),所以c 2≥b 2,从而a 2=b 2+c 2≥2b 2=32,故a ≥42. 当b =4,a ≥42时,存在满足条件的点P .所以b =4,a 的取值范围为[42,+∞).B 级——综合应用11.如图是5号篮球在太阳光照射下的影子,已知篮球的直径为22 cm ,现太阳光与地面的夹角为60°,则此椭圆形影子的离心率为( )A .13B .12C .22D .32解析:B 由图可得,椭圆的短轴长2b =22⇒b =11,长轴长2a =22sin 60°=2232⇒a =223,∴e =ca =⎝ ⎛⎭⎪⎫2232-112223=1-34=12.故选B .12.明朝的一个葡萄纹椭圆盘如图①所示,清朝的一个青花山水楼阁纹饰椭圆盘如图②所示,北宋的一个汝窑椭圆盘如图③所示,这三个椭圆盘的外轮廊均为椭圆.已知图①、②、③中椭圆的长轴长与短轴长的比值分别为139,5645,107,设图①、②、③中椭圆的离心率分别为e 1,e 2,e 3,则( )A .e 1>e 3>e 2B .e 2>e 3>e 1C .e 1>e 2>e 3D .e 2>e 1>e 3解析:A 因为椭圆的离心率e =ca =c 2a 2=a 2-b 2a 2=1-b 2a2= 1-⎝ ⎛⎭⎪⎫2b 2a 2,所以椭圆的长轴长与短轴长的比值越大,离心率越大.因为139≈1.44,5645≈1.24,107≈1.43,则139>107>5645,所以e 1>e 3>e 2.故选A .13.(多选)数学家称5-12为黄金比,记为ω,定义:若椭圆的短轴与长轴之比为黄金比ω,则称该椭圆为“黄金椭圆”,以椭圆中心为圆心,半焦距长为半径的圆称为焦点圆.若黄金椭圆x 2a 2+y 2b2=1(a >b >0)与它的焦点圆在第一象限的交点为Q ,则下列结论正确的有( )A .ω2+ω=1B .黄金椭圆的离心率e =ωC .设直线OQ 的倾斜角为θ,则sin θ=ωD .交点Q 的坐标为(b ,ωb )解析:AC 方程ω2+ω-1=0的根为ω=-1±52,故A 正确;由题意可知,b a =5-12=ω,则e =ca=1-⎝ ⎛⎭⎪⎫b a 2=1-ω2=ω≠ω,故B 错误;易知QF 1⊥QF 2,且∠QF 1F 2=θ2,则|QF 2|=2c ·sin θ2,|QF 1|=2c ·cos θ2,所以|QF 1|+|QF 2|=2c ⎝⎛⎭⎪⎫sin θ2+cos θ2=2a ,即sin θ2+cos θ2=a c =1ω,两边平方,可得sin θ+1=1ω=25-1=5+12,即sin θ=5+12-1=5-12=ω,故C 正确;由C 知,sin θ=ω,所以tan θ≠ω,即D 错误.故选A 、C .14.(2021·浙江高考)已知椭圆x 2a 2+y 2b2=1(a >b >0),焦点F 1(-c,0),F 2(c,0)(c >0).若过F 1的直线和圆⎝ ⎛⎭⎪⎫x -12c 2+y 2=c 2相切,与椭圆的第一象限交于点P ,且PF 2⊥x 轴,则该直线的斜率是________,椭圆的离心率是________.解析:设过F 1的直线与圆的切点为M ,圆心A ⎝ ⎛⎭⎪⎫12c ,0,则|AM |=c ,|AF 1|=32c ,所以|MF 1|=52c ,所以该直线的斜率k =|AM ||MF 1|=c 52c =255.因为PF 2⊥x 轴,所以|PF 2|=b2a ,又|F 1F 2|=2c ,所以k =255=b 2a 2c =a 2-c 22ac =1-e 22e ,得e =55.答案:255 5515.已知直线x -3y +3=0经过椭圆C :x 2a 2+y 2b2=1(a >b >0)的左顶点和上顶点.(1)求椭圆C 的方程;(2)若A ,B 为椭圆上除上下顶点之外的关于原点对称的两个点,已知直线y =3-x 上存在一点P ,使得三角形PAB 为正三角形,求AB 所在直线的方程.解:(1)因为直线x -3y +3=0与x 轴交于点(-3,0),与y 轴交于点(0,1),又直线x -3y +3=0经过椭圆C :x 2a 2+y 2b2=1(a >b >0)的左顶点和上顶点,可得a =3,b =1,所以椭圆C 的方程为x 23+y 2=1.(2)设A (x 1,y 1),则B (-x 1,-y 1), 由题意知直线AB 的斜率存在,当直线AB 的斜率为0时,AB 的垂直平分线就是y 轴,y 轴与直线l :x +y -3=0的交点为P (0,3),因为|AB |=23,PO =3可得∠PAO =60°,以△PAB 为等边三角形,故得直线AB 的方程为y =0.当直线AB 的斜率不为0时, 设AB 的方程为y =kx ,代入椭圆方程消去y ,得(3k 2+1)x 2=3, 所以|x 1|=33k 2+1,则|AO |=1+k 2·33k 2+1=3k 2+33k 2+1, 设AB 的垂直平分线为y =-1kx ,设它与直线l :x +y -3=0的交点为P (x 0,y 0),则x 0=3k k -1,y 0=-3k -1,所以|PO |=9k 2+9k -12,因为△PAB 为正角形,所以应有|PO |=3|AO |, 可得9k 2+9k -12=3·3k 2+33k 2+1,解得k =0(舍)或k =-1, 故直线AB 的方程为y =0或x +y =0.。
2020新高考数学(文)二轮专题培优新方案检测:主攻36个必考点 函数与导数 考点过关检测二十七

考点过关检测(二十七)1.函数f (x )=Error!的零点个数为( )A .3 B .2C .1D .0解析:选C ①若x >0,则2x +1=0,无解.②若x ≤0,则x 2-x -2=0,解得x =-1或x =2(舍去).所以函数f (x )=Error!的零点个数为1.2.函数f (x )=2x +3x -7的零点所在的区间是( )A. B.(0,12)(12,1)C.D.(1,32)(32,2)解析:选C 函数f (x )=2x +3x -7是连续递增函数,∵f (1)=2+3-7<0,f =2+3×-7=2+4.5-7>0,(32)32322∴f (1)·f <0,故选C.(32)3.(2019·郑州模拟)已知函数f (x )=Error!(a ∈R ),若函数f (x )在R 上有两个零点,则实数a 的取值范围是( )A .(0,1]B .[1,+∞)C .(0,1)D .(-∞,1]解析:选A 因为函数f (x )在(-∞,0]和(0,+∞)上均为单调函数且在R 上有两个零点,所以f (x )在(-∞,0]和(0,+∞)上各有一个零点.当x ≤0时,f (x )有一个零点,需0<a ≤1;当x >0时,f (x )有一个零点,需-a <0,即a >0.综上,0<a ≤1.故选A.4.(2019·石家庄质检)已知M 是函数f (x )=|2x -3|-8sin πx (x ∈R )的所有零点之和,则M 的值为( )A .3B .6C .9D .12解析:选D 将函数f (x )=|2x -3|-8sin πx 的零点转化为函数h (x )=|2x -3|与g (x )=8sin πx 图象交点的横坐标.在同一平面直角坐标系中画出函数h (x )与g (x )的图象如图所示,因为函数h (x )与g (x )的图象都关于直线x =对称,两个函数的图象共有8个交点,32所以函数f (x )的所有零点之和M =8×=12.325.(2019·宣城二模)已知a ,b ,c ,d 都是常数,a >b ,c >d .若f (x )=2 019-(x -a )(x -b )的零点为c ,d ,则下列不等式正确的是( )A .a >c >b >dB .a >b >c >dC .c >d >a >bD .c >a >b >d解析:选D 因为f (x )=2 019-(x -a )(x -b ),所以f (a )=f (b )=2 019,又c ,d 为函数f (x )的零点,且a >b ,c >d ,所以可在平面直角坐标系中作出函数f (x )的大致图象如图所示,由图可知c >a >b >d ,故选D.6.(2019·泉州检测)设函数y =f (x )满足f (x +2)=f (x ),且当x ∈[-1,1]时,f (x )=|x |,则函数g (x )=f (x )-sin x 在区间[-π,π]上的零点的个数为( )A .2B .3C .4D .5解析:选B 要求函数g (x )=f (x )-sinx 的零点个数,即求方程f (x )-sinx =0的根的个数,可转化为函数y =f (x )与函数y =sin x 的图象的交点个数.在同一平面坐标系内作出y =f (x )与y =sin x 的图象如图所示,可知在区间[-π,π]上,图象有3个交点.故选B.7.已知f (x )=Error!若关于x 的方程a =f (x )恰有两个不同实根,则实数a的取值范围是( )A.∪[1,2)B.∪[1,2)(-∞,12)(0,12)C .(1,2)D .[1,2)解析:选B 关于x 的方程a =f (x )恰有两个不同实根等价于y =a ,y =f (x )的图象有两个不同的交点,画出y =a ,y =f (x )的图象,如图,由图可知,当a ∈∪[1,2)时,(0,12)y =a ,y =f (x )的图象有两个不同的交点,此时,关于x 的方程a =f (x )恰有两个不同实根,所以实数a 的取值范围是∪[1,2).故选B.(0,12)8.(2019·西安二模)已知函数f (x )=Error!又函数g (x )=f 2(x )+tf (x )+1(t ∈R )有4个不同的零点,则实数t 的取值范围是( )A.B.(-∞,-e2+1e )(e2+1e ,+∞)C.D.(-e2+1e ,-2)(2,e2+1e )解析:选A 由f (x )=(x ≥0),得f ′(x )=,xe x 1-x e x 当0≤x <1时,f ′(x )>0;当x >1时,f ′(x )<0,所以f (x )在[0,1)上为增函数,在(1,+∞)上为减函数,且f (x )max =.1e 设m =f (x ),则h (m )=m 2+tm +1,设h (m )=m 2+tm +1的零点为m 1,m 2,则g (x )=f 2(x )+tf (x )+1(t ∈R )有4个不同的零点等价于m =f (x )的图象与直线m =m 1,m =m 2的交点有4个,函数m =f (x )的图象与直线m =m 1,m =m 2的位置关系如图所示,由图知,0<m 2<<m 1,1e要满足题意,则需h <0即可,解得t <-,(1e )e2+1e 故选A.9.若函数f (x )=ax +1-2a 在区间(-1,1)上存在一个零点,则实数a 的取值范围是________.解析:当a =0时,函数f (x )=1在(-1,1)上没有零点,所以a ≠0.因为函数f (x )是单调函数,要满足题意,只需f (-1)f (1)<0,所以(-3a +1)(1-a )<0,即(a -1)·(3a -1)<0,解得<a <1,所以实数a 的取值范围是.13(13,1)答案:(13,1)10.设a ∈Z ,函数f (x )=e x +x -a ,若x ∈(-1,1)时,函数f (x )有零点,则a 的取值个数为________.解析:因为函数f (x )=e x +x -a ,易得函数f (x )在(-1,1)上为增函数,则-1-a <f (x )<e +1-a ,1e 由函数f (x )=e x +x -a 有零点,得Error!解得-1<a <e +1.1e 又a ∈Z ,所以a =0或a =1或a =2或a =3,故a 的取值个数有4个.答案:411.已知函数f (x )=x |x -4|+2x ,存在x 3>x 2>x 1≥0,使得f (x 1)=f (x 2)=f (x 3),则x 1+x 2=________,x 1x 2·f (x 3)的取值范围是________.解析:f (x )=x |x -4|+2x =Error!作出f (x )的图象如图所示.由图象可知,x 1+x 2=6,且2<x 1<3,∴x 1x 2f (x 3)=x 1(6-x 1)f (x 1)=x 1(6-x 1)·(-x +6x 1)21=(-x +6x 1)221=[-(x1-3)2+9]2,∵2<x1<3,∴-(x1-3)2+9∈(8,9),∴x1x2f(x3)∈(64,81).答案:6 (64,81)12.已知在区间(0,2]上的函数f(x)=Error!且g(x)=f(x)-mx在区间(0,2]内有且仅有两个不同的零点,则实数m的取值范围是________.解析:由函数g (x )=f (x )-mx 在(0,2]内有且仅有两个不同的零点,得y =f (x ),y =mx 在(0,2]内的图象有且仅有两个不同的交点.当y =mx 与y =-3在(0,1]内相切时,1x mx 2+3x -1=0,Δ=9+4m =0,m =-,结合图象可得当-<m ≤-2或94940<m ≤时,函数g (x )=f (x )-mx 在(0,2]内有且仅有两个不同的零点.12答案:∪(-94,-2](0,12]。
新教材高考数学考点过关检测15三角恒等变换1含解析

考点过关检测15 三角恒等变换(1)一、单项选择题1.[2022·广东顺德模拟]cos1875°=( ) A.6-22 B.2+64 C.2-64 D.6-242.若点M (-32,12)在角α的终边上,则tan2α=( ) A.33B .-33C.3D .- 33.已知cos θ=-13(θ∈(0,π)),则cos ⎝ ⎛⎭⎪⎫3π2-θ=( )A .-223B .-13C.223D.134.[2022·江苏东海月考]计算:2sin10°-cos20°sin20°=( )A .-1B .-2C .-2D .- 35.[2022·辽宁实验中学月考]已知cos α=-53,则sin ⎝ ⎛⎭⎪⎫3π2+2α=( ) A .-19B.19C .-23D.236.[2022·福建永安三中月考]已知α的终边在第四象限,若sin α=-45,则sin ⎝⎛⎭⎪⎫α+π4=( ) A .-210B.210C .-7210D.72107.已知sin ⎝ ⎛⎭⎪⎫π2+α=12,-π2<α<0,则cos ⎝ ⎛⎭⎪⎫α-π3的值是( )A.12B .-12 C.23D .1 8.[2022·河北邯郸模拟]若sin ⎝ ⎛⎭⎪⎫π2-2α=-45,则cos4α的值为( ) A.425B.725C.35D.31509.[2021·新高考Ⅰ卷]若tan θ=-2,则sin θ()1+sin2θsin θ+cos θ=( )A .-65B.-25C.25D.6510.已知sin α+cos α=52,且α∈⎝ ⎛⎭⎪⎫π4,π2,则cos α-sin α=( ) A.32B .-32 C .±32D.12二、多项选择题11.[2022·山东实验中学月考]下列式子正确的是( ) A .sin15°+cos15°=62B .cos75°=6+24C .23tan15°+tan 215°=1D .tan12°+tan33°+tan12°tan33°=112.已知θ∈(0,π),sin θ+cos θ=15,则下列结论正确的是( )A .θ∈⎝ ⎛⎭⎪⎫π2,πB .cos θ=-35C .tan θ=-34D .sin θ-cos θ=75三、填空题13.[2022·福建福州模拟]已知tan(π-α)=-34,则sin2α的值为________.14.[2022·湖南师大附中月考]已知sin(π+α)=23sin ⎝ ⎛⎭⎪⎫π2+α,则tan ⎝ ⎛⎭⎪⎫α-π3的值为________.15.[2022·广东湛江月考]已知x ∈⎝⎛⎭⎪⎫0,π2,2sin2x =3sin x ,则cos2x =________.16.[2022·浙江丽水模拟]已知角α的顶点与原点O 重合,始边与x 轴的非负半轴重合,它的终边过点P (-55,255),则tan α=________,sin ⎝⎛⎭⎪⎫α+π4=________.考点过关检测15 三角恒等变换(1)1.答案:D解析:cos1875°=cos(360°×5+75°)=cos75°=cos(45°+30°)=cos45°cos30°-sin45°sin30°=22×32-22×12=6-24. 2.答案:D解析:由已知tan α=12-32=-33,所以tan2α=2tan α1-tan 2α=2×⎝⎛⎭⎪⎫-331-⎝⎛⎭⎪⎫-332=- 3.3.答案:A解析:因为cos θ=-13(θ∈(0,π)),所以sin θ=1-cos 2θ=223,故cos ⎝⎛⎭⎪⎫3π2-θ=-sin θ=-223.4.答案:D 解析:2sin10°-cos20°sin20°=2sin 30°-20°-cos20°sin20°=2⎝ ⎛⎭⎪⎫12cos20°-32sin20°-cos20°sin20°=-3sin20°sin20°=- 3.5.答案:A 解析:sin ⎝⎛⎭⎪⎫3π2+2α=-cos2α=1-2cos 2α=1-2×59=-19.6.答案:A解析:α的终边在第四象限,sin α=-45,所以cos α=1-⎝ ⎛⎭⎪⎫-452=35, 则sin ⎝ ⎛⎭⎪⎫α+π4=22()sin α+cos α=22×⎝ ⎛⎭⎪⎫-45+35=-210. 7.答案:B解析:由sin ⎝ ⎛⎭⎪⎫π2+α=12可得cos α=12,因为-π2<α<0,所以sin α=-1-cos 2α=-1-⎝ ⎛⎭⎪⎫122=-32,所以cos ⎝ ⎛⎭⎪⎫α-π3=cos αcos π3+sin αsin π3=12×12-32×32=-12.8.答案:B解析:由sin ⎝ ⎛⎭⎪⎫π2-2α=-45,得cos2α=-45,则cos4α=2cos 22α-1=2×⎝ ⎛⎭⎪⎫-452-1=725. 9.答案:C解析:将式子进行齐次化处理得:sin θ()1+sin2θsin θ+cos θ=sin θ()sin 2θ+cos 2θ+2sin θcos θsin θ+cos θ=sin θ()sin θ+cos θ=sin θ()sin θ+cos θsin 2θ+cos 2θ=tan 2θ+tan θ1+tan 2θ=4-21+4=25.故选C. 10.答案:B解析:∵(sin α+cos α)2=1+2sin αcos α=54,∴2sin αcos α=14,∵(cos α-sin α)2=1-2sin αcos α=1-14=34,∴cos α-sin α=±32,又∵α∈⎝ ⎛⎭⎪⎫π4,π2,∴0<cos α<sin α,即cos α-sin α=-32.故选B. 11.答案:ACD解析:因为sin15°=sin(45°-30°)=sin45°cos30°-cos45°sin30°=6-24, cos15°=cos(45°-30°)=cos45°cos30°+sin45°sin30°=6+24, 所以sin15°+cos15°=62,所以A 正确, 因为cos75°=cos(45°+30°)=cos45°cos30°-sin45°sin30°=6-24,所以B 错误,因为tan15°=tan(45°-30°)=1-tan30°1+tan30°=1-331+33=2-3,所以23tan15°+tan 215°=23×(2-3)+(2-3)2=1,所以C 正确; 因为tan45°=tan(33°+12°)=tan33°+tan12°1-tan33°tan12°=1,所以tan33°+tan12°=1-tan33°tan12°,所以tan12°+tan33°+tan12°tan33°=1,所以D 正确. 12.答案:ABD解析:∵sin θ+cos θ=15 ①,∴(sin θ+cos θ)2=⎝ ⎛⎭⎪⎫152,即sin 2θ+2sin θcos θ+cos 2θ=125,∴2sin θcos θ=-2425.∵θ∈(0,π),∴sin θ>0,cos θ<0,∴θ∈⎝ ⎛⎭⎪⎫π2,π,故A 正确.(sin θ-cos θ)2=1-2sin θcos θ=4925,∴sin θ-cos θ=75 ②,故D 正确.①+②得sin θ=45,①-②得cos θ=-35,故B 正确.tan θ=sin θcos θ=45-35=-43,故C 错误.13.答案:2425解析:因tan(π-α)=-34,则tan α=34,sin2α=2sin αcos α=2sin αcos αsin 2α+cos 2α=2tan αtan 2α+1=2·34⎝ ⎛⎭⎪⎫342+1=2425. 14.答案:335解析:由题意知,-sin α=23cos α,则tan α=-23,所以tan ⎝ ⎛⎭⎪⎫α-π3=tan α-31+3tan α=-331-6=335. 15.答案:18解析:因为x ∈⎝⎛⎭⎪⎫0,π2,所以sin x ≠0,因此由2sin2x =3sin x ⇒4sin x cos x =3sin x ⇒cos x =34,所以cos2x =2cos 2x -1=2×⎝ ⎛⎭⎪⎫342-1=18.16.答案:-21010解析:由三角函数定义知:tan α=255-55=-2;|OP |=⎝ ⎛⎭⎪⎫-552+⎝ ⎛⎭⎪⎫2552=1,则sin α=255,cos α=-55, sin ⎝ ⎛⎭⎪⎫α+π4=sin αcos π4+cos αsin π4=255·22-55·22=1010.。
高考数学一轮复习课时过关检测二十九数列的概念与表示含解析

课时过关检测(二十九) 数列的概念与表示A 级——基础达标1.已知数列{a n }的前4项依次为2,6,12,20,则数列{a n }的通项公式可能是( ) A .a n =4n -2 B .a n =2n+2(n -1) C .a n =n 2+nD .a n =3n -1+2n -1解析:C 对于A ,a 3=10≠12,故A 错误;对于B ,a 4=16+6=22≠20,故B 错误;对于C ,a 1=12+1=2,a 2=22+2=6,a 3=32+3=12,a 4=42+4=20,故C 正确;对于D ,a 3=9+5=14≠12,故D 错误.故选C .2.(2022·潍坊一模)已知S n 为数列{a n }的前n 项和,且满足S n =n 2+4n +1,则a 1+a 3+a 5=( )A .27B .28C .29D .30解析:B 因为S n =n 2+4n +1,当n =1时,a 1=S 1=6,当n ≥2时,a n =S n -S n -1=2n+3.经检验,当n =1时不符合,所以a n =⎩⎪⎨⎪⎧6,n =1,2n +3,n ≥2,所以a 1+a 3+a 5=28.故选B .3.已知数列{a n }的前n 项和为S n ,且a 1=2,a n +1=S n +1(n ∈N *),则S 5=( ) A .31 B .42 C .37D .47解析:D 由题意,得S n +1-S n =S n +1(n ∈N *),所以S n +1+1=2(S n +1)(n ∈N *),又S 1+1=3,故数列{S n +1}是首项为3,公比为2的等比数列,则S 5+1=3×24,所以S 5=47.4.已知递增数列{a n },a n ≥0,a 1=0.对于任意的正整数n ,不等式t 2-a 2n -3t -3a n ≤0恒成立,则正数t 的最大值为( )A .1B .2C .3D .6解析:C 因为数列{a n }是递增数列,又t 2-a 2n -3t -3a n =(t -a n -3)(t +a n )≤0,t +a n >0,所以t ≤a n +3恒成立,即t ≤(a n +3)min =a 1+3=3,所以t max =3.5.(多选)(2022·泰安模拟)大衍数列来源于《乾坤谱》中对易传“大衍之数五十”的推论.主要用于解释中国传统文化中的太极衍生原理.数列中的每一项,都代表太极衍生过程中曾经经历过的两仪数量总和,其前10项依次是0,2,4,8,12,18,24,32,40,50,…,则下列说法正确的是( )A .此数列的第20项是200B .此数列的第19项是182C .此数列偶数项的通项公式为a 2n =2n 2D .此数列的前n 项和为S n =n (n -1)解析:AC 观察此数列,偶数项通项公式为a 2n =2n 2,奇数项是后一项减去后一项的项数,a 2n -1=a 2n -2n ,由此可得a 20=2×102=200,A 、C 正确;a 19=a 20-20=180,B 错误;S n =n (n -1)=n 2-n 是一个等差数列的前n 项和,而题中数列不是等差数列,不可能有S n =n (n -1),D 错误.故选A 、C .6.(多选)(2022·潍坊一模)已知数列{a n }的通项公式为a n =⎩⎪⎨⎪⎧3n +1,n 为奇数,2-2n ,n 为偶数,则( )A .a 6=19B .a 7>a 6C .S 5=22D .S 6>S 5解析:BC 因为a n =⎩⎪⎨⎪⎧3n +1,n 为奇数,2-2n ,n 为偶数,所以a 1=4,a 2=-2,a 3=10,a 4=-6,a 5=16,a 6=-10,a 7=22,所以A 错误,B 正确;S 5=a 1+a 2+a 3+a 4+a 5=4+(-2)+10+(-6)+16=22,故C 正确;因为a 6=-10,所以S 6-S 5=a 6<0,所以S 6<S 5,故D 错误.故选B 、C .7.已知数列{a n }的通项公式a n =632n ,若a 1·a 2·…·a n ≤a 1·a 2·…·a k 对n ∈N *恒成立,则正整数k 的值为________.解析:a n =632n ,当n ≤5时,a n >1;当n ≥6时,a n <1,由题意知,a 1·a 2·…·a k 是{a n }的前n 项乘积的最大值,所以k =5.答案:58.已知数列{a n }中,a 1=1,a n +1=a n +n (n ∈N *),则a 4=________,a n =________. 解析:由题意可得a 1=1,a n +1-a n =n ,则当n ≥2时,a n =a 1+(a 2-a 1)+(a 3-a 2)+…+(a n -a n -1)=1+[1+2+3+…+(n -1)]=1+n n -12=n 2-n +22,又a 1=1也适合上式,故a n =n 2-n +22,则a 4=42-4+22=7.答案:7n 2-n +229.(2022·北京质检)已知数列{a n }满足21·a 1+22·a 2+23.a 3+ (2)·a n =(n -1)·2n +1+2(n ∈N *),则数列{a n }的通项公式a n =________.解析:∵2a 1+22a 2+23a 3+…+2n -1a n -1+2n a n =(n -1)·2n +1+2,∴2a 1+22a 2+23a 3+…+2n -1a n -1=(n -2)·2n +2(n ≥2),两式相减,得2n a n =n ·2n ,即a n =n (n ≥2),当n =1时,a 1=1,适合a n =n ,故a n =n (n ∈N *).答案:n10.如果连续自然数数列a 1,a 2,…,a n ,…满足lg 2+lg ⎝⎛⎭⎪⎫1+1a 1+lg ⎝ ⎛⎭⎪⎫1+1a 2+…+lg ⎝⎛⎭⎪⎫1+1a n =lg n ,那么这个数列最多有几项?并求数列的前n 项和S n . 解:由已知得:2·⎝⎛⎭⎪⎫1+1a 1·⎝⎛⎭⎪⎫1+1a 2·…·⎝ ⎛⎭⎪⎫1+1a n =n ,即2·a 1+1a 1·a 2+1a 2·a 3+1a 3·…·a n +1a n=n . ∵a 1,a 2,…,a n ,…为连续自然数, ∴上式可化简为2·a n +1a 1=n ,即2·a 1+na 1=n , ∴2n +2a 1=na 1,即(n -2)(a 1-2)=4.若要n 最大,且n ∈N *,则只能有⎩⎪⎨⎪⎧n -2=4,a 1-2=1,∴⎩⎪⎨⎪⎧n =6,a 1=3,∴该数列最多有6项,首项为3, ∴S 6=3+4+5+6+7+8=33.B 级——综合应用11.设数列{a n }的前n 项和为S n ,满足S n =(-1)na n +12n ,则S 1+S 3+S 5=( )A .0B .1764C .564D .2164解析:D 数列{a n }的前n 项和为S n ,满足S n =(-1)na n +12n ,当n 为偶数时,S n =S n -S n -1+12n ,即有S n -1=12n ,所以S 1+S 3+S 5=14+116+164=2164.故选D .12.在数列{a n }中,a 1=2,a n +1n +1=a n n +ln ⎝ ⎛⎭⎪⎫1+1n ,则a n =( ) A .2+n ln n B .2+(n -1)ln n C .1+n +ln n D .2n +n ln n解析:D 由题意得,a n +1n +1=a n n +ln n +1n ,则a n n =a n -1n -1+ln n n -1,a n -1n -1=a n -2n -2+ln n -1n -2,…,a 22=a 11+ln 21,由累加法得,a n n =a 11+ln n n -1+ln n -1n -2+…+ln 21,即a nn=a 1+ln ⎝⎛⎭⎪⎫n n -1·n -1n -2·…·21,则a n n =2+ln n ,所以a n =2n +n ln n ,故选D .13.请写出一个符合下列要求的数列{a n }的通项公式:①{a n }为无穷数列;②{a n }为单调递增数列;③0<a n <2.这个数列的通项公式可以是________.解析:因为函数a n =2-1n 的定义域为N *,且a n =2-1n 在N *上单调递增,0<2-1n<2,所以满足3个条件的数列的通项公式可以是a n =2-1n.答案:a n =2-1n(答案不唯一)14.(2022·绵阳模拟)在数列{a n }中,a 1=1,a 1+2a 2+3a 3+…+na n =n +12a n +1.(1)求数列{a n }的通项公式;(2)若存在n ∈N *,使得a n ≤(n +1)λ成立,求实数λ的最小值. 解:(1)∵a 1+2a 2+3a 3+…+na n =n +12a n +1,∴当n ≥2时,a 1+2a 2+3a 3+…+(n -1)a n-1=n2a n , 两式相减得na n =n +12a n +1-n 2a n ,即n +1a n +1na n=3(n ≥2), ∵a 1=1,∴1=1+12a 2,即a 2=1,∴2·a 21·a 1=2≠3.∴数列{na n }是从第二项开始的等比数列, ∴当n ≥2时,有na n =2×3n -2,∴a n =⎩⎪⎨⎪⎧1,n =1,2n×3n -2,n ≥2.(2)存在n ∈N *使得a n ≤(n +1)λ成立⇔λ≥a nn +1有解,①当n =1时,a 12=12,则λ≥12,即λmin =12;②当n ≥2时,a nn +1=2×3n -2n n +1,设f (n )=2×3n -2n n +1,∴f n +1f n =3nn +2>1,∴f (n )单调递增,∴f (n )min =f (2)=13,∴实数λ的最小值是13.由①②可知实数λ的最小值是13.C 级——迁移创新15.(多选)已知数列{a n }满足a n =n ·k n(n ∈N *,0<k <1),下列命题正确的有( ) A .当k =12时,数列{a n }为递减数列B .当k =45时,数列{a n }一定有最大项C .当0<k <12时,数列{a n }为递减数列D .当k1-k为正整数时,数列{a n }必有两项相等的最大项解析:BCD 当k =12时,a 1=a 2=12,知A 错误;当k =45时,a n +1a n =45·n +1n,当n <4时,a n +1a n >1,当n >4时,a n +1a n <1,所以可判断{a n }一定有最大项,B 正确;当0<k <12时,a n +1a n =k n +1n<n +12n ≤1,所以数列{a n }为递减数列,C 正确;当k 1-k 为正整数时,1>k ≥12,当k =12时,a 1=a 2>a 3>a 4>…,当1>k >12时,令k 1-k =m ∈N *,解得k =m m +1,则a n +1a n =m n +1n m +1,当n =m时,a n +1=a n ,结合B ,数列{a n }必有两项相等的最大项,故D 正确.故选B 、C 、D .16.(2022·益阳一模)设曲线f (x )=xn +1(n ∈N *)在点(1,1)处的切线与x 轴的交点的横坐标为x n ,求x 1·x 2·x 3·x 4·…·x 2 020的值.解:由f (x )=xn +1得f ′(x )=(n +1)x n,切线方程为y -1=(n +1)(x -1),令y =0得x n =n n +1 ,故x 1·x 2·x 3·x 4·…·x 2 020=12 ×23 ×…×2 0202 021 =12 021.。
新教材高考数学考点过关检测3一元二次不等式含解析

考点过关检测3 一元二次不等式一、单项选择题1.[2022·湖北九师联盟]不等式x 2-2x -8≤0的解集为( ) A .{x |-4≤x ≤2} B .{x |-2≤x ≤4} C .{x |x ≥4或x ≤-2} D .{x |x ≥2或x ≤-4}2.已知不等式x 2-2x -3<0的解集为A ,不等式x 2+x -6<0的解集为B ,不等式x 2+ax +b <0的解集为A ∩B ,则a +b =( )A .1B .0C .-1D .-33.[2022·广东普师高级中学月考]函数y =log 0.54x 2-3x 的定义域为( )A.⎣⎢⎡⎭⎪⎫-14,0∪⎝ ⎛⎦⎥⎤34,1B.⎝ ⎛⎭⎪⎫-14,0∪⎝ ⎛⎦⎥⎤34,1C.⎣⎢⎡⎭⎪⎫-14,0∪⎝ ⎛⎭⎪⎫34,1D.⎝ ⎛⎭⎪⎫-14,0∪⎝ ⎛⎭⎪⎫34,1 4.[2022·山东新泰一中月考]若不等式ax2-x -c >0的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪-1<x <12,则函数y =cx 2-x -a 的图象可以为( )5.[2022·广东深圳月考]若不等式ax 2+bx +2>0的解集为{x |-2<x <1},则二次函数y =2bx 2+4x +a 在区间[0,3]上的最大值、最小值分别为( )A .-1,-7B .0,-8C .1,-1D .1,-76.在R 上定义运算⊗:M ⊗N =(1+M )(1-N ),若不等式(x -a )⊗(x +a )<1对任意实数x 均成立,则实数a 的取值范围是( )A .(-1,1)B .(0,2)C.⎝ ⎛⎭⎪⎫-12,32D.⎝ ⎛⎭⎪⎫-32,12 7.[2022·浙江五校联考]已知关于x 的不等式ax 2-2x +3a <0在(0,2]上有解,则实数a 的取值范围是( )A .-∞,33B.⎝⎛⎭⎪⎫-∞,47C.33,+∞D.⎝ ⎛⎭⎪⎫47,+∞8.设函数f (x )=mx 2-mx -1,若对于任意的x ∈{x |1≤x ≤3},f (x )<-m +4恒成立,则实数m 的取值范围为( )A .m <57B .0≤m <57C .m <0或0<m <57D .m ≤0二、多项选择题9.已知关于x 的不等式kx 2-2x +6k <0(k ≠0),则下列说法正确的是( ) A .若不等式的解集为{x |x <-3或x >-2},则k =-25B .若不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ∈R ,x ≠1k ,则k =66C .若不等式的解集为R ,则k <-66D .若不等式的解集为∅,则k ≥6610.已知关于x 的不等式ax 2+bx +c >0的解集为(-∞,-2)∪(3,+∞),则( ) A .a >0B .不等式bx +c >0的解集是{x |x <-6}C .a +b +c >0D .不等式cx 2-bx +a <0的解集为(-∞,-13)∪(12,+∞)11.[2022·福建龙岩模拟]已知函数f (x )=x 2-2(a -1)x +a ,若对于区间[-1,2]上的任意两个不相等的实数x 1,x 2都有f (x 1)≠f (x 2),则实数a 的取值范围可以是( )A .(-∞,0]B .[0,3]C .[-1,2]D .[3,+∞)12.[2022·湖南长郡中学月考]已知不等式x 2+ax +b >0(a >0)的解集是{}x |x ≠d ,则下列四个结论中正确的是( )A .a 2=4b B .a 2+1b≥4C .若不等式x 2+ax -b <0的解集为(x 1,x 2),则x 1x 2>0D .若不等式x 2+ax +b <c 的解集为(x 1,x 2),且|x 1-x 2|=4,则c =4 三、填空题13.[2022·福建福清西山学校月考]x 2+2(m -1)x +m 2-2≥0对x ∈R 恒成立,则m 的取值范围为________.14.[2022·江苏苏州十中月考]已知不等式ax 2+bx +c >0的解集为(2,4),则不等式cx 2+bx +a <0的解集为________.15.[2022·北京101中学模拟]若关于x 的不等式x 2-2ax -8a 2<0(a >0)的解集为{x |x 1<x <x 2},且x 2-x 1=15,则a 的值为________.16.[2022·河北石家庄二中月考]若一个集合是另一个集合的子集,则称这两个集合构成“全食”;若两个集合有公共元素但不互为对方的子集,则称两个集合构成“偏食”.已知集合A ={x |-t <x <t ,t >0}和集合B ={x |x 2-x -2<0},若集合A ,B 构成“偏食”,则实数t 的取值范围为________.考点过关检测3 一元二次不等式1.答案:B解析:由x 2-2x -8≤0,得(x -4)(x +2)≤0,所以-2≤x ≤4. 2.答案:D解析:由题意得,不等式x 2-2x -3<0的解集A =(-1,3),不等式x 2+x -6<0的解集B =(-3,2),所以A ∩B =(-1,2),即不等式x 2+ax +b <0的解集为(-1,2),所以a =-1,b =-2,所以a +b =-3.3.答案:A解析:由题可知,log 0.5(4x 2-3x )≥0,由对数函数的单调性,可得0<4x 2-3x ≤1,解得:-14≤x <0或34<x ≤1,所以y =log 0.54x 2-3x 的定义域为⎣⎢⎡⎭⎪⎫-14,0∪⎝ ⎛⎦⎥⎤34,1. 4.答案:C解析:由题可得-1和12是方程ax 2-x -c =0的两个根,且a <0,∴⎩⎪⎨⎪⎧-1+12=1a -1×12=-ca,解得a =-2,c =-1,则y =cx 2-x -a =-x 2-x +2=-(x +2)(x -1),则函数图象开口向下,与x 轴交于(-2,0),(1,0).5.答案:D解析:ax 2+bx +2>0的解集为{x |-2<x <1},∴-2,1是方程ax 2+bx +2=0的根,且a <0,∴⎩⎪⎨⎪⎧-2+1=-ba-2×1=2a,∴a =-1,b =-1,则二次函数y =2bx 2+4x +a =-2x 2+4x -1开口向下,对称轴x =1,在区间[0,3]上,当x =1时,函数取得最大值1,当x =3时,函数取得最小值-7.6.答案:B解析:因为(x -a )⊗(x +a )<1对任意实数x 均成立,所以(1+x -a )(1-x -a )<1对任意实数x 恒成立,即(1-a )2-x 2<1恒成立,所以(1-a )2<1+x 2恒成立,所以只需(1-a )2<(1+x 2)min ,又因为(1+x 2)min =1,所以(1-a )2<1,解得0<a <2.7.答案:A解析:因为x ∈(0,2],所以不等式可化为ax +3ax<2.当a =0时,不等式为0<2,满足题意;当a >0时,不等式化为x +3x <2a ,则x +3x≥2x ·3x=23,当且仅当x =3时取等号,所以2a >23,即0<a <33;当a <0时,x +3x >2a 在x ∈(0,2]时恒成立.综上所述,实数a 的取值范围是⎝ ⎛⎭⎪⎫-∞,33. 8.答案:A解析:若对于任意的x ∈{x |1≤x ≤3},f (x )<-m +4恒成立,即可知:mx 2-mx +m -5<0在x ∈{x |1≤x ≤3}上恒成立,令g (x )=mx 2-mx +m -5,对称轴为x =12.当m =0时,-5<0恒成立,当m <0时,有g (x )开口向下且在[1,3]上单调递减,∴在[1,3]上g (x )max =g (1)=m -5<0,得m <5,故有m <0.当m >0时,有g (x )开口向上且在[1,3]上单调递增,∴在[1,3]上g (x )max =g (3)=7m -5<0,∴0<m <57.综上,m 的取值范围为m <57.9.答案:ACD解析:对于A,∵不等式的解集为{x |x <-3或x >-2},∴k <0,且-3与-2是方程kx2-2x +6k =0的两根,∴(-3)+(-2)=2k ,解得k =-25.故A 正确;对于B,∵不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ∈R ,x ≠1k ,∴⎩⎪⎨⎪⎧k <0,Δ=4-24k 2=0,解得k =-66,故B 错误;对于C,由题意,得⎩⎪⎨⎪⎧k <0,Δ=4-24k 2<0,解得k <-66,故C 正确;对于D,由题意,得⎩⎪⎨⎪⎧k >0,Δ=4-24k 2≤0,解得k ≥66,故D 正确. 10.答案:ABD解析:关于x 的不等式ax 2+bx +c >0的解集为(-∞,-2)∪(3,+∞),∴a >0,A 选项正确;且-2和3是关于x 的方程ax 2+bx +c =0的两根,由韦达定理得⎩⎪⎨⎪⎧-2+3=-ba -2×3=c a,则b =-a ,c =-6a ,则a +b +c =-6a <0,C 选项错误;不等式bx +c >0即为-ax -6a >0,解得x <-6,B 选项正确;不等式cx 2-bx +a <0即为-6ax 2+ax +a <0,即6x 2-x -1>0,解得x <-13或x >12,D 选项正确.11.答案:AD解析:二次函数f (x )=x 2-2(a -1)x +a 图象的对称轴为直线x =a -1,∵任意x 1,x 2∈[-1,2]且x 1≠x 2,都有f (x 1)≠f (x 2),即f (x )在区间[-1,2]上是单调函数,∴a -1≤-1或a -1≥2,∴a ≤0或a ≥3,即实数a 的取值范围为(-∞,0]∪[3,+∞).12.答案:ABD解析:对于A,由题意,Δ=a 2-4b =0,∴b =a 24,所以A 正确;对于B,a 2+1b =a 2+4a2≥2a 2·4a 2=4当且仅当a 2=4a2,即a =2时等号成立,所以B 正确;对于C,由韦达定理,知x 1x 2=-b =-a 24<0,所以C 错误;对于D,由韦达定理,知x 1+x 2=-a ,x 1x 2=b -c =a 24-c ,则|x 1-x 2|=x 1+x 22-4x 1x 2=a 2-4⎝ ⎛⎭⎪⎫a 24-c =2c =4,解得c =4,所以D 正确.13.答案:⎣⎢⎡⎭⎪⎫32,+∞解析:由題意可知Δ=4(m -1)2-4(m 2-2)≤0,即-8m +12≤0,得m ≥32,故m 的取值范围为⎣⎢⎡⎭⎪⎫32,+∞. 14.答案:⎩⎪⎨⎪⎧ x ⎪⎪⎪ x >12或⎭⎬⎫x <14解析:因为不等式ax 2+bx +c >0的解集为(2,4),所以a <0且2和4是ax 2+bx +c =0的两根.所以⎩⎪⎨⎪⎧2+4=-ba2×4=ca可得:⎩⎪⎨⎪⎧b =-6ac =8a,所以cx 2+bx +a <0可化为:8ax 2-6ax+a <0,因为a <0,所以8ax 2-6ax +a <0可化为8x 2-6x +1>0,即(2x -1)(4x -1)>0,解得:x >12或x <14,所以不等式cx 2+bx +a <0的解集为⎩⎪⎨⎪⎧ x ⎪⎪⎪ x >12或⎭⎬⎫x <14.15.答案:52解析:关于x 的不等式x 2-2ax -8a 2<0(a >0)的解集为{x |x 1<x <x 2},所以x 1,x 2是一元二次方程x 2-2ax -8a 2=0(a >0)的实数根,所以Δ=4a 2+32a 2=36a 2>0,且x 1+x 2=2a ,x 1x 2=-8a 2.又因为x 2-x 1=15,所以152=(x 1+x 2)2-4x 1x 2=4a 2+32a 2=36a 2,又a >0,解得a =52.16.答案:{t |1<t <2}解析:由题意,可知集合A ={x |-t <x <t ,t >0},集合B ={x |-1<x <2},因为集合A ,B 构成“偏食”,所以⎩⎪⎨⎪⎧ -t <-1<t 2>t 或⎩⎪⎨⎪⎧-t <2<t -1<-t,解不等式组⎩⎪⎨⎪⎧-t <-1<t2>t,得1<t <2;解不等式组⎩⎪⎨⎪⎧-t <2<t-1<-t ,得⎩⎪⎨⎪⎧t >2t <1,此时无解.所以实数t 的取值范围为1<t <2.。
高中学业水平考试复习必背数学公式过关检测

高中学业水平考试复习必背数学公式过关检测班级 姓名 评价必修一1.★元素与集合的关系如果a 是集合A 的元素,就说a 属于集合A ,记作:; 如果a 不是集合A 的元素,就说a 不属于集合A ,记作:. 2. ★集合的运算:A B = ;A B = ;补集:U C A =.3.子集的个数问题:若集合A 有n 个元素,则集合A 有个子集,有个真子集.4.★函数定义域:①;②;③.5.★奇偶性(1)奇函数的定义:一般地,对于函数()f x 定义域内的任意一个x ,都有,那么函数()f x 叫奇函数.(2)偶函数的定义:一般地,对于函数()f x 定义域内的任意一个x ,都有,那么函数()f x 叫偶函数.(3)奇(偶)函数图像的特点:奇函数图象关于原点对称;偶函数图象关于y 对称. 6.★函数的单调性(1) 增函数:设函数()f x 的定义域为I ,如果对于定义域I 内某个区间D 上的任意两个自变量的 值12,x x ,当12x x <时,都有,那么就说函数()f x 在区间D 上是增函数, 区间D 称为函数()f x 的单调区间.(2)减函数:设函数()f x 的定义域为I ,如果对于定义域I 内某个区间D 上的任意两个自变量的 值12,x x ,当12x x <时,都有,那么就说函数()f x 在区间D 上是减函数, 区间D 称为函数()f x 的单调区间. (3)一次函数()0y kx b k =+≠,当0k >时,y 随x 的增大而,当0k <时,y 随x 的增大而; (4)反比例函数()0ky k x=≠, 当0k >时,在每个区间内y 随x 的增大而,当0k <时,在每个区间内y 随x 的增大而; (5)二次函数()20y ax bx c a =++≠,当0a >时,在对称轴的左侧,y 随x 的增大而,在对称轴的右侧,y 随x 的增大而. 当0a <时,在对称轴的左侧,y 随x 的增大而,在对称轴的右侧,y 随x 的增大而.(6)指数函数(0,1)x y a a a =>≠当1a >时,y 随x 的增大而,当01a <<时,y 随x 的增大而. (7)对数函数log (0,1)a y x a a =>≠当1a >时,y 随x 的增大而,当01a <<时,y 随x 的增大而. 7. 指数及指数函数 (1)根式与指数幂互化=nm a ()1,,,0*>∈>n N n m a ; =-p a ()0,0>>p a (2) 指数幂的运算性质(),,0,0R s r b a ∈>>=s r a a ;=s r a )(; =r ab )(.(3) 函数 叫做指数函数,其中x 是自变量.(4) 指数函数的图像及其性质(1)对数与指数之间的互化:=⇔=x N a x(01)a a >≠且. (2)对数log a N (01)a a >≠且的简单性质:=1log a ;=a a log ; (3) 以10为底的对数叫做 ;记作 ; 以e 为底的对数叫做 ;记作 ;(4)对数的运算性质:0,0,1,0>>≠>N M a a=⋅)(log N M a ;=NMalog ;=n a M log . (5)函数 叫做对数函数,其中x 是自变量.(6) 对数函数的图像及其性质9.幂函数:函数叫做幂函数(只考虑21,1,3,2,1-=α的图象). 10.★函数的零点(1) 对于函数)(x f y =,把使叫做函数)(x f y =的零点.(2)方程0)(=x f 的⇔函数)(x f y =的⇔函数)(x f y =的零点.(3)零点存在性定理:若连续函数()f x 在区间(,)a b 上满足,则函数()f x 在(,)a b 上至少有一个 零点.必修二1. =柱V ;=椎体V ;=球V ;=球表S ;2.★★线面平行的判定定理:平面外一条直线与此平面内的一.条直线平行,则该直线与此平面平行. 符号语言:.3.★★线面垂直的判定定理:一条直线与平面内的两.条相交直线垂直,则该直线与此平面垂直. 符号语言:.4. 两点的直线的斜率公式:;5. ★★两直线平行与垂直的判定6.★直线方程的形式(1)一般式: (A 、B 不同时为0),; (2)点斜式:; (3)斜截式:; 7.★距离公式:(1)两点间距离公式:设1122(,),A x y B x y ,()是平面直角坐标系中的两个点,则AB =.(2)点到直线距离公式: ()00,y x P 到直线0:1=++CBy Ax l 的距离=d . 8. ★圆的方程:标准方程,圆心()b a ,,半径为r ;一般方程220x y Dx Ey F ++++=,半径为 ,圆心坐标.9. ★线与圆的位置关系:设直线0:=++C By Ax l ,圆()()222:r b y a x C =-+-,圆心()b a C ,到l 的距离=d ,⇔相离与C l ; ⇔相切与C l ; ⇔相交与C l .必修三1.★★分层抽样:一般地,若从容量为N 的总体中抽取容量为n 的样本,则抽样比为λ=,若第i 层含有a的个体数为i N 个,则第i 层抽取的入样个体数为i i i nn N N Nλ==⋅. 2.★★频率分布直方图: =频率小矩形面积(注意:不是小矩形的高度) 计算公式: =频数频率样本容量;=⨯频数样本容量频率;==⨯频率频率小矩形面积组距组距;各组频数之和=样本容量;各组频率之和=1 3.茎叶图:茎表示高位,叶表示低位. 4.★古典概型的概率公式:()A m P A n==事件包含的基本事件个数实验中基本事件的总数5.★几何概型的概率公式:()A P A =事件构成的区域的长度(面积或体积)实验的全部结果构成的区域的长度(面积或体积)必修四1.弧度:=α,l 为α所对的弧长,r 为半径,正负号的确定:逆时针为,顺时针为.2.弧度制与角度制的互化:=π,=rad 1,=01.3. 三角函数的定义:设角α是一个任意角,(),P x y 是终边上的任意一点,点P 与原点的距离r =, 那么sin α=;cos α=;tan α=;4. 三角函数诱导公式:()2kk z απ+∈与α之间函数值的关系,主要有:公式一:sin(2)k απ+⋅=()k z ∈;公式二:sin()πα+=()k z ∈; cos(2)k απ+⋅=()k z ∈; cos()πα+=()k z ∈; tan(2)k απ+⋅=()k z ∈.tan()πα+=()k z ∈. 公式三:sin()α-=;公式四:sin()πα-=; cos()α-=;cos()πα-=; tan()α-=.tan()πα-=.公式五:sin()2πα-=;公式六:sin()2πα+=;cos()2πα-=.cos()2πα+=.其规律(口诀)是“ ”.5.★同角三角函数的基本关系:平方关系:;商数关系:.6.★三角和差公式:()=±βαsin ;()=±βαcos ;()=±βαtan .7.★三角二倍角公式:=α2sin ;=α2cos ==;tan 2α=.8.★ 三角降幂公式:=α2sin ;=α2cos .9. 正弦函数sin y x =,余弦函数cos y x =,正切函数tan y x =的图象与性质10.★★()(0;0)y Asin x A ωϕω=+>>的最大值为,最小值为,最小正周期为; 由(0,0)y Asin x A ωω=>>向左平移个单位可得到()(0;0)y Asin x A ωϕω=+>>.11. 向量的模:线段AB 的长度叫向量AB 的长度,记为|AB|或|a |; (1)若 (,)a x y =,则 |a |= .(2)若1122(,),(,)A x y B x y ,则AB = ,|AB|=.12. ★向量的线性运算:(平行四边形法则) (三角形法则)13. ★★向量的平行与垂直的判定 (1) 向量共线定理①a ∥b (a ≠0)⇔存在惟一的实数λ使得;②若),,(),,(2211y x b y x a ==则a ∥b ⇔(a 可以为0 ).(2)两个向量垂直的充要条件①a b ⊥⇔;②设1122(,),(,)a x y b x y ==,则a b ⊥ ⇔ .必修五1.★正弦定理:在ABC ∆中,在ABC ∆中,a ,b ,c 分别为角,,A B C 的对边, 则有:.(其中R 为的半径)2.★余弦定理:在ABC ∆中,若a ,b ,c 分别为角,,A B C 的对边,则有①=2a .=2b .=2c .②=A cos .=B cos .=C cos .3.三角形面积公式:=∆ABC S ==.4.★等差数列{}n a (1) 定义:(d 为常数); (2)通项公式:;(3)等差中项:若,,a A b 成等差数列,则A 叫做a 与b 的等差中项,且=A ;(4)性质:若()*,,,m n p q m n p q N +=+∈,则;(5)求和公式: n S =或n S =. 5.★等比数列 (1) 定义:(q 为常数); (2)通项公式:;(3)等比中项:若,,a G b 成等比数列,则G 叫做a 与b 的等比中项,且=G ;(4)性质:若()*,,,m n p q m n p q N +=+∈,则;(5)求和公式:=n S .6.★数列{}n a 的前n 项和n S 与项n a 之间的关系:=n a .7.★y kx b <+表示直线y kx b =+的区域;表示直线y kx b =+上方区域. 8.★基本不等式: 若0a >,0b >,则,当且仅当a b =时取到等号.。
2023年新教材高考数学全程考评特训卷考点过关检测9函数的应用含解析

考点过关检测9 函数的应用一、单项选择题1.[2022·湖北襄阳五中月考]下列函数在(0,+∞)上单调递增且存在零点的是( ) A .y =x 2-x -3B .y =-0.2xC .y =sin2xD .y =x -1x2.函数f (x )=ex -1-2的零点所在的区间是( )A .(0,1)B .(1,2)C .(2,3)D .(3,4)3.[2022·山东临沂一中月考]方程log 4x =2-1x的解所在的区间是( )A.⎝ ⎛⎭⎪⎫14,13B.⎝ ⎛⎭⎪⎫13,12C.⎝ ⎛⎭⎪⎫12,23D.⎝ ⎛⎭⎪⎫23,34 4.函数f (x )=2x-2x-a 的一个零点在区间(1,2)内,则实数a 的取值范围是( )A .(1,3)B .(1,2)C .(0,3)D .(0,2)5.[2022·辽宁朝阳模拟]某服装店开张第一周进店消费的人数每天都在变化,设第x (1≤x ≤7,x ∈N )天进店消费的人数为y ,且y 与⎣⎢⎡⎦⎥⎤5xx 2([t ]表示不大于t 的最大整数)成正比,第1天有10人进店消费,则第4天进店消费的人数为( )A .74B .76C .78D .806.[2022·江苏省镇江中学月考]已知函数f (x )是定义在R 上的奇函数,对任意的x ∈R ,均有f (x +2)=f (x )且f (1)=0,当x ∈[0,1)时,f (x )=2x-1,则方程f (x )-lg|x |=0的实根个数为( )A .6B .8C .10D .127.[2022·北京丰台模拟]已知函数f (x )=⎩⎪⎨⎪⎧|x +m |,x ≤m x 2,x >m,若存在实数b ,使得关于x 的方程f (x )=b 有三个不同的根,则实数m 的取值范围是( )A .(0,2)B .(-∞,-2)∪(0,2)C .(-2,0)D .(-2,0)∪(2,+∞)8.[2022·福建福州月考]根据《民用建筑工程室内环境污染控制标准》,文化娱乐场所室内甲醛浓度≤0.1mg/m 3为安全范围.已知某新建文化娱乐场所施工中使用了甲醛喷剂,处于良好的通风环境下时,竣工1周后室内甲醛浓度为 6.25mg/m 3,3周后室内甲醛浓度为1mg/m 3,且室内甲醛浓度ρ(t )(单位:mg/m 3)与竣工后保持良好通风的时间t (t ∈N *)(单位:周)近似满足函数关系式ρ(t )=eat +b,则该文化娱乐场所竣工后的甲醛浓度若要达到安全开放标准,至少需要放置的时间为( )A .5周B .6周C .7周D .8周 二、多项选择题9.已知f (x )是定义域为R 的偶函数,在(-∞,0)上单调递减,且f (-3)·f (6)<0,那么下列结论中正确的是( )A .f (x )可能有三个零点B .f (3)·f (-4)≥0C .f (-4)<f (6)D .f (0)<f (-6)10.[2022·广东揭阳一中月考]函数f (x )=a x -cos x ⎝ ⎛⎭⎪⎫13≤a ≤1的零点个数可能为( )A .1B .3C .4D .511.[2022·河北衡水中学月考]地震震级根据地震仪记录的地震波振幅来测定,一般采用里氏震级标准.里氏震级的计算公式为M =lgA maxA 0(其中常数A 0是距震中100公里处接收到的0级地震的地震波的最大振幅,A max 是指我们关注的这次地震在距震中100公里处接收到的地震波的最大振幅).地震的能量E (单位:焦耳)是指当地震发生时,以地震波的形式放出的能量.已知E =104.8×101.5M,其中M 为地震震级.下列说法正确的是( )A .若地震震级M 增加1级,则最大振幅A max 增加到原来的10倍B .若地震震级M 增加1级,则放出的能量E 增加到原来的10倍C .若最大振幅A max 增加到原来的100倍,则放出的能量E 也增加到原来的100倍D .若最大振幅A max 增加到原来的100倍,则放出的能量E 增加到原来的1000倍 12.[2022·海南昌茂花园学校月考]已知函数f (x )={ kx +1,x ≤0log 2x ,x >0,下列是关于函数y =f [f (x )+1]的零点个数的判断,其中不正确的是( )A .当k >0时,有3个零点B .当k <0时,有2个零点C .当k >0时,有4个零点D .当k <0时,有1个零点 三、填空题13.设函数f (x )=a x+b ,其中a >0,a ≠1,b ∈R .若f (x )无零点,则b 的取值范围是________.14.[2022·广东肇庆一中月考]若函数f (x )=x 2-ax +1在区间⎝ ⎛⎭⎪⎫12,3上有零点,则实数a 的取值范围是________.15.有一座大桥既是交通拥挤地段,又是事故多发地段,为了保证安全,交通部门规定,大桥上的车距d (m)与车速v (km/h)和车长l (m)的关系满足:d =kv 2l +12l (k 为正的常数),假定车身长为4m ,当车速为60(km/h)时,车距为2.66个车身长.应规定车速为________km/h 时,才能使大桥上每小时通过的车辆最多?16.[2022·湖南师大附中模拟]设f (x )=⎩⎪⎨⎪⎧log 2x 2-3x +1,x <0,2-|2-x |,x ≥0,且关于x 的方程f (x )=m (m ∈R )恰有三个互不相等的实数根x 1,x 2,x 3,则①m 的取值范围是__________;②x 1x 2x 3的取值范围是________.四、解答题17.[2022·河北张家口模拟]已知函数f (x )=ln x -m .(1)若函数g (x )=f (x )+e x 在区间⎝ ⎛⎭⎪⎫1e ,1内存在零点,求实数m 的取值范围;(2)若关于x 的方程f ()e x+1=x2有实数根,求实数m 的取值范围.18.[2022·北京四中月考]已知每投放1个单位的洗衣液在一定量水的洗衣机中,它在水中释放的浓度y (克/升)随着时间x (分钟)变化的函数关系式近似为y =f (x ),其中f (x )=⎩⎪⎨⎪⎧248-x-1,0≤x ≤47-12x ,4<x ≤14.某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和.根据经验,当水中洗衣液的浓度不低于3克/升时,它能起到有效去污的作用.(1)若只投放一次1个单位的洗衣液,求三分钟后水中洗衣液的浓度; (2)若只投放一次1个单位的洗衣液,则有效去污时间可达几分钟?(3)若第一次投放2个单位的洗衣液,10分钟后再投放1个单位的洗衣液,则在第12分钟时(从第一次投放算起),洗衣液是否还能起到有效去污的作用?请说明理由.考点过关检测9 函数的应用1.答案:D解析:y =x 2-x -3在⎝ ⎛⎭⎪⎫0,12上单调递减,不合题意,A 错误;令-0.2x=0,方程无解,不合题意,B 错误;y =sin2x 在⎝ ⎛⎭⎪⎫π4,3π4上单调递减,不合题意,C 错误;y =x 与y =-1x 在(0,+∞)上均单调递增,∴y =x -1x 在(0,+∞)上单调递增;令x -1x=0,解得:x =±1,则y =x -1x在(0,+∞)上存在零点x =1,D 正确.2.答案:B解析:因为函数f (x )为单调递增函数,且f (2)=e -2>0,f (1)=-1<0,所以零点所在的区间是(1,2).3.答案:B解析:令f (x )=log 4x +1x -2,则f (x )为连续函数,又因为f ⎝ ⎛⎭⎪⎫13=log 413+3-2=log 413+1>0,f ⎝ ⎛⎭⎪⎫12=log 412+2-2=log 412<0,f ⎝ ⎛⎭⎪⎫13f ⎝ ⎛⎭⎪⎫12<0,所以方程的解所在区间为⎝ ⎛⎭⎪⎫13,12.4.答案:C解析:由题得f (1)f (2)=(0-a )(3-a )<0,即a (a -3)<0,解得0<a <3,故选C. 5.答案:C解析:由题可设y =k ⎣⎢⎡⎦⎥⎤5x x 2(k ≠0),当x =1时,y =10代入可得10=k ⎣⎢⎡⎦⎥⎤5112=5k ,解得k=2,所以y =2⎣⎢⎡⎦⎥⎤5xx 2,令x =4,则y =2⎣⎢⎡⎦⎥⎤5442=2⎣⎢⎡⎦⎥⎤62516=2×39=78.6.答案:D解析:函数f (x )是定义在R 上的奇函数,对任意的x ∈R ,均有f (x +2)=f (x ),可得f (x )为周期为2的奇函数,可得f (-x +2)=f (-x )=-f (x ),又f (1)=0,∴f (2k -1)=0(k ∈N ), 画出函数y =f (x )与y =lg|x |的图象,如图所示,当x >0时,y =f (x )与y =lg|x |有5个交点, 当x <0时,y =f (x )与y =lg|x |有7个交点, 故方程f (x )-lg|x |=0有12个实数根,故D 正确. 7.答案:B解析:分情况讨论,当m >0时,要使f (x )=b 有三个不同的根,则⎩⎪⎨⎪⎧|2m |>m2m >0⇒0<m <2;当m <0时,要使f (x )=b 有三个不同的根,同理可知,需要⎩⎪⎨⎪⎧m 2>|2m |m <0⇒m <-2.当m =0时,两个分段点重合,不可能有三个不同的根,故舍去. ∴m 的取值范围是(-∞,-2)∪(0,2). 8.答案:B解析:由题意可知,ρ(1)=ea +b=6.25,ρ(3)=e3a +b=1,ρ3ρ1=e 2a =425,解得ea=25.设该文化娱乐场所竣工后放置t 0周后甲醛浓度达到安全开放标准,则ρ(t 0)=e at 0+b =ea +b·e a (t 0-1)=6.25×⎝ ⎛⎭⎪⎫25t 0-1≤0.1,整理得62.5≤⎝ ⎛⎭⎪⎫52t 0-1,设62.5=⎝ ⎛⎭⎪⎫52m -1,因为⎝ ⎛⎭⎪⎫524<62.5<⎝ ⎛⎭⎪⎫525,所以4<m -1<5,即5<m <6,则t 0-1≥m -1,即t 0≥m .故至少需要放置的时间为6周.9.答案:AC解析:因为f (x )是定义域为R 的偶函数,又f (-3)·f (6)<0,所以f (3)·f (6)<0.又f (x )在(0,+∞)上单调递增,所以函数f (x )在(0,+∞)上有一个零点,且f (3)<0,f (6)>0,所以函数f (x )在(-∞,0)∪(0,+∞)上有两个零点.但是f (0)的值没有确定,所以函数f (x )可能有三个零点,故A 正确;又f (-4)=f (4),4∈(3,6),所以f (-4)的符号不确定,故B 不正确;C 项显然正确;由于f (0)的值没有确定,所以f (0)与f (-6)的大小关系不确定,所以D 不正确.10.答案:AB解析:因为f (x )=a x -cos x 的零点个数即函数y =a x ,y =cos x 图象交点的个数, 由图可知,当a =1时,交点只有1个;当a =13时,交点有3个.正数a 越大,交点个数越少.故零点个数可能为1,或2,或3. 11.答案:AD解析:因为M ′=M +1=lg A max A 0+1=lg 10A max A 0=lg A ′maxA 0,所以A ′max =10A max ,故A 正确;因为E ′=104.8×101.5(M +1)=104.8×101.5M +1.5=104.8×101.5M×101.5=101.5E ,所以B 错误;因为M ′=lg 100A max A 0=2+lg A max A 0=2+M ,E ′=104.8×101.5(M +2)=104.8×101.5M +3=103E ,所以C 错误,D正确.12.答案:AB解析:函数y =f [f (x )+1]的零点个数,即方程f [f (x )+1]=0的解的个数,x ≤0时, 由kx +1=0得x =-1k ,k ≠0,若k >0,则x =-1k是f (x )=0的一个解,k <0时,x =-1k不是f (x )=0的解,x >0时,由f (x )=log 2x =0,得x =1是f (x )=0的一个解.所以若k <0,则由f [f (x )+1]=0得f (x )+1=1得f (x )=0,x =1,D 正确; 若k >0,则由f [f (x )+1]=0得f (x )+1=1,或f (x )+1=-1k,f (x )+1=1即f (x )=0⇒x =1或x =-1k,f (x )+1=-1k 即f (x )=-1k -1,-1k -1<0,log 2x =-1k -1有一解x =2-1k -1,kx +1=-1k -1,x =-1k 2-2k是一解, 综上方程f [f (x )+1]=0共4个解.C 正确. 13.答案:[0,+∞)解析:因为指数函数y =a x的值域为(0,+∞),故函数f (x )=a x+b 的值域为(b ,+∞), 因为函数f (x )无零点,则0∉(b ,+∞),所以,b ≥0.14.答案:⎣⎢⎡⎭⎪⎫2,103解析:由题意知方程ax =x 2+1在⎝ ⎛⎭⎪⎫12,3上有解,即a =x +1x 在⎝ ⎛⎭⎪⎫12,3上有解.设t =x+1x ,x ∈⎝ ⎛⎭⎪⎫12,3,则t 的取值范围是⎣⎢⎡⎭⎪⎫2,103,所以实数a 的取值范围是⎣⎢⎡⎭⎪⎫2,103.15.答案:50解析:由题设,2.66×4=4×602k +12×4,解得k =6×10-4,∴d =2.4×10-3v 2+2,要使大桥上每小时通过的车辆最多,则使y =1000v d +l 最大,∴由题意,y =1000v0.0024v 2+6=10000.0024v +6v ≤100020.0024v ·6v=10000.24,当且仅当0.0024v =6v ,即v =50km/h 时等号成立.16.答案:①0<m <2 ②2(3-21)<x 1x 2x 3<0解析:当x <0时,由复合函数的单调性知:y =log 2(x 2-3x +1)单调递减,作出函数f (x )的图象,如图所示:由图可知,当0<m <2时,f (x )=m (m ∈R )恰有三个互不相等的实数根x 1,x 2,x 3,不妨设x 1<x 2<x 3,易知x 2>0,且x 2+x 3=2×2=4≥2x 2x 3,∴0<x 2x 3<4.令log 2(x 2-3x +1)=2,解得x =3+212(舍去)或x =3-212.∴3-212<x 1<0,∴2(3-21)<x 1x 2x 3<0.17.解析:(1)因为函数f (x )=ln x -m 与y =e x 在⎝ ⎛⎭⎪⎫1e ,1都是增函数,所以函数g (x )=f (x )+e x =ln x +e x -m 在⎝ ⎛⎭⎪⎫1e ,1也是增函数, 因为函数g (x )在区间⎝ ⎛⎭⎪⎫1e ,1内存在零点,所以⎩⎪⎨⎪⎧ln 1e+1-m <0,ln1+e -m >0,解得0<m <e.所以实数m 的取值范围为(0,e).(2)关于x 的方程f ()e x+1=x2有实数根等价于关于x 的方程2m =2ln(e x+1)-x 有实数根,所以存在实数x 使2m =ln(e x+1)2-lne x=ln e x +12ex=ln(e x+1ex +2)成立.因为e x+1e x ≥2e x ·1e x =2(当且仅当e x=1ex ,x =0时取等号),所以ln(e x+1e x +2)≥ln ⎝⎛⎭⎪⎫2+2e x·1e x =2ln2,所以实数m 的取值范围是[ln2,+∞).18.解析:(1)因为每投放1个单位的洗衣液在一定量水的洗衣机中,它在水中释放的浓度y (克/升)随着时间x (分钟)变化的函数关系式近似为y =f (x ),其中f (x )=⎩⎪⎨⎪⎧248-x -1,0≤x ≤47-12x ,4<x ≤14.所以若只投放1个单位的洗衣液,则三分钟后水中洗衣液的浓度f (3)=248-3-1=3.8(克/升);(2)若只投放一次1个单位的洗衣液,且当水中洗衣液的浓度不低于3(克/升)时,它能起到去污的作用.当0≤x ≤4时,248-x -1≥3,解得2≤x ≤4,当4≤x ≤14,7-12x ≥3,解得4<x ≤8,综上所述,有效去污时间为6分钟;(3)若第一次投放2个单位的洗衣液,10分钟后再投放1个单位的洗衣液,则在第12分钟时,水中洗衣液的浓度为2×⎝ ⎛⎭⎪⎫7-12×12+1×⎝ ⎛⎭⎪⎫248-2-1=5>3,所以在第12分钟起(从第一次投放算起),洗衣液能起到有效去污的作用.。
高考数学课时过关检测(二十三) 两角和与差的正弦、余弦、正切公式及二倍角公式

课时过关检测(二十三) 两角和与差的正弦、余弦、正切公式及二倍角公式A 级——夯基保分练1.下列式子的运算结果为3的是( ) ①tan 25°+tan 35°+3tan 25°tan 35°; ②2(sin 35°cos 25°+cos 35°cos 65°); ③1+tan 15°1-tan 15°;④tan π61-tan 2π6. A .①②④ B .③④ C .①②③D .②③④解析:选C 对于①,tan 25°+tan 35°+3tan 25°tan 35°=tan(25°+35°)(1-tan 25°tan 35°)+3tan 25°tan 35°=3-3tan 25°tan 35°+3tan 25°tan 35°=3;对于②,2(sin 35°cos 25°+cos 35°cos 65°)=2(sin 35°cos 25°+cos 35°sin 25°)=2sin 60°=3;对于③,1+tan 15°1-tan 15°=tan 45°+tan 15°1-tan 45°tan 15°=tan 60°=3;对于④,tan π61-tan 2π6=12×2tanπ61-tan 2π6=12×tan π3=32.综上,式子的运算结果为3的是①②③.故选C. 2.已知α∈⎝⎛⎭⎫0,π2,cos ⎝⎛⎭⎫α+π3=-23,则cos α=( ) A.5+23 B.15-26 C.5-23D.15+26解析:选B 因为α∈⎝⎛⎭⎫0,π2,所以α+π3∈⎝⎛⎭⎫π3,5π6, 所以sin ⎝⎛⎭⎫α+π3= 1-cos 2⎝⎛⎭⎫α+π3= 1-49=53,所以cos α=cos ⎣⎡⎦⎤⎝⎛⎭⎫α+π3-π3=cos ⎝⎛⎭⎫α+π3cos π3+sin ⎝⎛⎭⎫α+π3sin π3=-23×12+53×32=15-26. 3.tan 18°+tan 12°+33tan 18°tan 12°=( ) A. 3 B . 2 C.22D .33解析:选D ∵tan 30°=tan(18°+12°)=tan 18°+tan 12°1-tan 18°tan 12°=33,∴tan 18°+tan 12°=33(1-tan 18°tan 12°),∴原式=33. 4.若α∈⎝⎛⎭⎫π2,π,且3cos 2α=sin ⎝⎛⎭⎫π4-α,则sin 2α的值为( ) A .-118 B .118 C .-1718D .1718解析:选C 由3cos 2α=sin ⎝⎛⎭⎫π4-α,可得3(cos 2α-sin 2α)=22(cos α-sin α),又由α∈⎝⎛⎭⎫π2,π,可知cos α-sin α≠0,于是3(cos α+sin α)=22,所以1+2sin αcos α=118,故sin 2α=-1718.5.已知sin 2θ=23,则tan 2⎝⎛⎭⎫θ-π4=( ) A.15 B .56C .5D .6解析:选A ∵sin 2θ=cos ⎝⎛⎭⎫2θ-π2=cos ⎣⎡⎦⎤2⎝⎛⎭⎫θ-π4=23,∴2cos 2⎝⎛⎭⎫θ-π4-1=23,即cos 2⎝⎛⎭⎫θ-π4=56, sin 2⎝⎛⎭⎫θ-π4=16, ∴tan 2⎝⎛⎭⎫θ-π4=sin 2⎝⎛⎭⎫θ-π4cos 2⎝⎛⎭⎫θ-π4=15.6.设α,β为锐角,且2α-β=π2,tan αcos βx +sin β=1,则x =( )A .1B .2 C. 3D . 2解析:选A ∵2α-β=π2,∴β=2α-π2,∴tan αcos ⎝⎛⎭⎫2α-π2x +sin ⎝⎛⎭⎫2α-π2=1,即tan αsin 2αx -cos 2α=1,∴x =cos 2α+tan αsin 2α=cos 2α+2sin 2α=1,故选A. 7.3cos 15°-4sin 215°cos 15°=________.解析:3cos 15°-4sin 215°cos 15°=3cos 15°-2sin 15°·2sin 15°·cos 15°=3cos 15°-2sin 15°sin 30°=3cos 15°-sin 15°=2cos(15°+30°)= 2.答案: 28.sin 10°sin 50°sin 70°=________.解析:sin 10°sin 50°sin 70°=sin 10°cos 40°cos 20° =sin 10°cos 10°cos 20°cos 40°cos 10°=18sin 80°cos 10°=18.答案:189.已知sin 10°-m cos 10°=2cos 140°,则m =________. 解析:由题意得m =sin 10°-2cos 140°cos 10°=sin 10°+2cos 40°cos 10°=sin 10°+2cos (30°+10°)cos 10°=sin 10°+2×32cos 10°-2×12sin 10°cos 10°= 3. 答案: 310.已知sin β=35,β∈⎝⎛⎭⎫π2,π,且sin(α+β)=cos α,则tan(α+β)=__________.解析:因为sin β=35,β∈⎝⎛⎭⎫π2,π,所以cos β=-45. 由sin(α+β)=cos α=cos [(α+β)-β]=cos(α+β)cos β+sin(α+β)sin β=-45cos(α+β)+35sin(α+β), 得25sin(α+β)=-45cos(α+β),所以tan(α+β)=-2. 答案:-2 11.已知tan α=2. (1)求tan ⎝⎛⎭⎫α+π4的值; (2)求sin 2αsin 2α+sin αcos α-cos 2α-1的值. 解:(1)tan ⎝⎛⎭⎫α+π4=tan α+tanπ41-tan αtanπ4=2+11-2=-3. (2)sin 2αsin 2α+sin αcos α-cos 2α-1 =2sin αcos αsin 2α+sin αcos α-(2cos 2α-1)-1=2sin αcos αsin 2α+sin αcos α-2cos 2α=2tan αtan 2α+tan α-2=2×222+2-2=1. 12.已知α,β为锐角,tan α=43,cos(α+β)=-55.(1)求cos 2α的值; (2)求tan(α-β)的值.解:(1)因为tan α =43,tan α =sin α cos α ,所以sin α =43cos α.因为sin 2α+cos 2α =1,所以cos 2α=925,所以cos 2α =2cos 2α-1=-725.(2)因为α,β 为锐角,所以α+β∈(0,π).又因为cos(α+β )=-55, 所以sin(α+β )=1-cos 2(α+β )=255, 所以tan(α+β )=-2. 因为tan α=43,所以 tan 2α=2tan α1-tan 2α=-247.所以tan(α-β )=tan [2α-(α+β) ] =tan 2α-tan (α+β )1+tan 2αtan (α+β )=-211.B 级——提能综合练13.若α为第一象限角,且sin 2α=sin ⎝⎛⎭⎫α-π2cos(π+α),则 2cos ⎝⎛⎭⎫2α-π4的值为( ) A .-75B .75C.13D .-73解析:选B 由sin 2α=sin ⎝⎛⎭⎫α-π2cos(π+α), 得2sin αcos α=cos 2 α.∵α为第一象限角,∴cos α≠0,∴tan α=12,∴2cos ⎝⎛⎭⎫2α-π4=2⎝⎛⎭⎫cos 2αcos π4+sin 2αsin π4 =cos 2α+sin 2α=cos 2α-sin 2α+2sin αcos α =1-tan 2α+2tan α1+tan 2α=1-14+2×121+14=75.故选B.14.设α,β∈[0,π],且满足sin αcos β-cos αsin β=1,则sin(2α-β)+sin(α-2β)的取值范围为________.解析:由sin αcos β-cos αsin β=1, 得sin(α-β)=1, 又α,β∈[0,π],∴-π<α-β<π,∴α-β=π2,∴⎩⎪⎨⎪⎧0≤α≤π,0≤β=α-π2≤π,即π2≤α≤π, ∴sin(2α-β)+sin(α-2β) =sin ⎝⎛⎭⎫2α-α+π2+sin(α-2α+π) =cos α+sin α=2sin ⎝⎛⎭⎫α+π4. ∵π2≤α≤π,∴3π4≤α+π4≤5π4, ∴-1≤2sin ⎝⎛⎭⎫α+π4≤1, 即sin(2α-β)+sin(α-2β)的取值范围为[-1,1]. 答案:[-1,1]15.已知cos ⎝⎛⎭⎫π6+αcos ⎝⎛⎭⎫π3-α=-14,α∈⎝⎛⎭⎫π3,π2. (1)求sin 2α的值; (2)求tan α-1tan α的值. 解:(1)cos ⎝⎛⎭⎫π6+αcos ⎝⎛⎭⎫π3-α=cos ⎝⎛⎭⎫π6+αsin ⎝⎛⎭⎫π6+α=12sin ⎝⎛⎭⎫2α+π3=-14, 即sin ⎝⎛⎭⎫2α+π3=-12. ∵α∈⎝⎛⎭⎫π3,π2, ∴2α+π3∈⎝⎛⎭⎫π,4π3, ∴cos ⎝⎛⎭⎫2α+π3=-32, ∴ sin 2α=sin ⎣⎡⎦⎤⎝⎛⎭⎫2α+π3-π3=sin ⎝⎛⎭⎫2α+π3cos π3-cos ⎝⎛⎭⎫2α+π3sin π3 =-12×12-⎝⎛⎭⎫-32×32=12.(2)∵α∈⎝⎛⎭⎫π3,π2,∴2α∈⎝⎛⎭⎫2π3,π, 又由(1)知sin 2α=12,∴cos 2α=-32.∴tan α-1tan α=sin αcos α-cos αsin α=sin 2α-cos 2αsin αcos α=-2cos 2αsin 2α=-2×-3212=2 3.C 级——拔高创新练16.如图,在平面直角坐标系xOy 中,以x 轴正半轴为始边的锐角α与钝角β的终边与单位圆分别交于A ,B 两点,x 轴正半轴与单位圆交于点M ,已知S △OAM =55,点B 的纵坐标是210,则cos(α-β)=________,2α-β=________.解析:由题意,OA =OM =1, 因为S △OAM =55和α为锐角,所以sin α=255,cos α=55. 又点B 的纵坐标是210,所以sin β=210,cos β=-7210, 所以cos(α-β)=cos αcos β+sin αsin β=55×⎝⎛⎭⎫-7210+255×210=-1010. 因为cos 2α=2cos 2α-1=2×⎝⎛⎭⎫552-1=-35, sin 2α=2sin αcos α=2×255×55=45,所以2α∈⎝⎛⎭⎫π2,π.因为β∈⎝⎛⎭⎫π2,π, 所以2α-β∈⎝⎛⎭⎫-π2,π2. 因为sin(2α-β)=sin 2αcos β-cos 2αsin β=-22, 所以2α-β=-π4.答案:-1010 -π4。
高考数学一轮复习课时过关检测二十七余弦定理和正弦定理含解析

课时过关检测(二十七) 余弦定理和正弦定理A 级——基础达标1.(2022·泰安模拟)在△ABC 中,AC =3,BC =2,cos C =34,则tan A =( )A .56 B .76 C .53D .73解析:D 由余弦定理得AB 2=AC 2+BC 2-2BC ·AC cos C =32+22-2×3×2×34=4,所以AB =2,因为AB =BC ,所以A =C ,所以cos A =cos C =34,tan A =73,故选D .2.在△ABC 中,A =π6,AB =3,AC =4,则BC 边上的高的长度为( )A .2217B . 2C . 3D .213解析:A 由A =π6,AB =3,AC =4,得S △ABC =12×4×3×12=3,由余弦定理得:BC =3+16-2×4×3×32=7,BC 边上的高的长度为2×37=2217.故选A . 3.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若a =b cos C 且c =6,A =π3,则△ABC 的面积为( )A .36 3B .27C .20 3D .18 3解析:D 在△ABC 中,a =b cos C ,所以sin A =sin B cos C ,又因为sin A =sin(B +C )=sin B cos C +cos B sin C ,所以cos B sin C =0,因为B ,C ∈⎝⎛⎭⎪⎫0,2π3,所以sin C ≠0,所以cos B =0,所以B =π2,又因为c =6,a =6tan A =63,所以△ABC 的面积为S △ABC =12ac =183,故选D .4.(2022·耀华模拟)已知△ABC 的面积为S =14(b 2+c 2)(其中b ,c 为△ABC 的边长),则△ABC 的形状为( )A .等边三角形B .是直角三角形但不是等腰三角形C .是等腰三角形但不是直角三角形D .等腰直角三角形解析:D 依题意△ABC 的面积为S =14(b 2+c 2),则12bc sin A =14(b 2+c 2),2bc sin A =b2+c 2,由于0<A <π,0<sin A ≤1,所以0<2bc sin A ≤2bc ,由基本不等式可知b 2+c 2≥2bc ,当且仅当b =c 时等号成立,所以sin A =1,A =π2,△ABC 是等腰直角三角形.故选D .5.已知△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,b =3c =6,A ∈⎝⎛⎭⎪⎫0,π2.△ABC面积为42,则sin C =( )A .16 B .13 C .69D .223解析:B 因为b =3c =6,△ABC 的面积为42=12bc sin A =6sin A ,解得sin A =223,因为A ∈⎝ ⎛⎭⎪⎫0,π2,所以cos A =13,在△ABC 中,由余弦定理可得a =b 2+c 2-2bc cos A =42,因为42223=2sin C,所以sin C =13.故选B .6.(多选)在△ABC 中,下列说法正确的是( ) A .若a cos A =b cos B ,则△ABC 为等腰三角形 B .若a =40,b =20,B =25°,则△ABC 必有两解 C .若△ABC 是锐角三角形,则sin A >cos BD .若cos 2A +cos 2B -cos 2C <1,则△ABC 为锐角三角形解析:BC 对于A ,由正弦定理可得sin A cos A =sin B cos B ,∴sin 2A =sin 2B ,∴A =B 或A +B =90°,∴△ABC 为等腰或直角三角形,故A 错误;对于B ,a sin B =40sin 25°<40sin 30°=40×12=20,即a sin B <b <a ,∴△ABC 必有两解,故B 正确;对于C ,∵△ABC 是锐角三角形,∴A +B >π2,即π2>A >π2-B >0,由正弦函数性质结合诱导公式得sin A >sin ⎝⎛⎭⎪⎫π2-B =cos B ,故C 正确;对于D ,利用二倍角的余弦公式可得1-2sin 2A +1-2sin 2B -1+2sin 2C <1,即sin 2A +sin 2B -sin 2C >0,即a 2+b 2-c 2>0,∴cos C >0,即C 为锐角,不能说明△ABC 为锐角三角形,故D 错误.故选B 、C .7.(多选)在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c .若a sin A =4b sin B ,ac =5(a 2-b 2-c 2),则下列选项正确的是( )A .a =2bB .cos A =55C .sin B =55D .△ABC 为钝角三角形解析:ACD 因为a sin A =4b sin B ,所以a 2=4b 2,所以a =2b ,故A 正确;因为ac =5(a 2-b 2-c 2)=5·(-2bc cos A ),且a =2b ,所以2bc =-25bc cos A ,所以cos A =-55,故B 错误;因为A ∈(0,π),所以sin A >0,所以sin A =1-cos 2A =255,又因为a =2b ,所以sin A =2sin B ,所以sin B =55,故C 正确;由cos A =-55<0可知A ∈⎝ ⎛⎭⎪⎫π2,π,所以△ABC 为钝角三角形,故D 正确;故选A 、C 、D .8.(2021·北京模拟)赵爽是我国古代数学家,大约在公元222年,他为《周髀算经》一书作序时,介绍了“赵爽弦图”——由四个全等的直角三角形与一个小正方形拼成的一个大正方形,如图①所示.类比“赵爽弦图”,可构造如图②所示的图形,它是由3个全等的三角形与中间一个小等边三角形拼成的一个大等边三角形.在△ABC 中,若AF =1,FD =2,则AB =________.解析:由题意△EFD 为等边三角形,则∠EDA =π3,所以∠BDA =2π3,根据条件△AFC 与△BDA 全等,所以AF =BD =1在△ABD 中,AD =3,BD =1,AB 2=AD 2+BD 2-2×AD ×BD ×cos∠BDA =32+12-2×1×3×⎝ ⎛⎭⎪⎫-12=13,所以AB =13.答案:139.在△ABC 中,角A ,B ,C 的对边分别是a ,b ,c ,已知A =60°,b +c =6,且△ABC 的面积为3,则△ABC 的内切圆的半径为________.解析:由题意得△ABC 的面积S =12bc sin A =34bc =3,故bc =4.因为A =60°,b+c =6,由余弦定理得,a 2=b 2+c 2-bc =(b +c )2-3bc =24,所以a =26,△ABC 的周长为6+26,设△ABC 的内切圆的半径为r ,则12(a +b +c )r =12×()6+26r =3,所以r=3-2.答案:3- 210.在①(a -c )(sin A +sin C )=b (sin A -sin B );②2c cos C =a cos B +b cos A ;③△ABC 的面积为12c (a sin A +b sin B -c sin C )这三个条件中任选一个,补充在下面的问题中,并加以解答.已知△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,且________. (1)求角C ;(2)若D 为AB 的中点,且c =2,CD =3,求a ,b 的值. 注:如果选择多个条件分别解答,则按第一个解答计分. 解:(1)选择①,根据正弦定理得(a -c )(a +c )=b (a -b ), 整理得a 2-c 2=ab -b 2,即a 2+b 2-c 2=ab ,所以cos C =a 2+b 2-c 22ab =12.因为C ∈(0,π),所以C =π3. 选择②,根据正弦定理有sin A cos B +sin B cos A =2sin C cos C , 所以sin(A +B )=2sin C cos C ,即sin C =2sin C cos C . 因为C ∈()0,π,所以sin C ≠0,从而有cos C =12,故C =π3.选择③,因为12ca sin B =12c (a sin A +b sin B -c sin C ),所以a sin B =a sin A +b sin B -c sin C ,由正弦定理得ab =a 2+b 2-c 2,由余弦定理,得cos C =a 2+b 2-c 22ab =ab 2ab =12,又因为C ∈(0,π),所以C =π3.(2)在△ACD 中,AC 2=AD 2+CD 2-2AD ·CD cos ∠ADC , 即b 2=1+3-23cos ∠ADC .在△BCD 中,BC 2=BD 2+CD 2-2BD ·CD cos ∠BDC , 即a 2=1+3-23cos ∠BDC . 因为∠ADC +∠BDC =π,所以cos ∠ADC =-cos ∠BDC , 所以a 2+b 2=8.由C =π3及c =2,得a 2+b 2-4=ab ,所以ab =4,从而a 2+b 2-2ab =0, 所以a =b =2.B 级——综合应用11.(多选)(2022·长治模拟)在Rt △ABC 中,C =90°,角A 的平分线交BC 于点D ,AD =1,cos ∠BAC =18,以下结论正确的是( )A .AB =8 B .CD BD =18C .AB =6D .△ABD 的面积为374解析:BCD 如图所示,因为AD 是角平分线,设∠CAD =∠DAB =α,则∠BAC =2α,根据二倍角公式得cos 2α=2cos 2α-1=18,且0<α<π2,所以cos α=34,在Rt △ACD 中,AD =1,所以AC =AD cos α=34,在Rt △ACB 中,AB =ACcos 2α=34×8=6,故A 错误,C 正确;根据角平分线定理,CD BD =AC AB =34×16=18,故B 正确;因为cos α=34,且0<α<π2,所以sin α=74,所以S △ABD =12AD ·AB ·sin α=12×6×74=374,故D 正确,故选B 、C 、D . 12.(2022·合肥模拟)北京大兴国际机场(如图所示)位于中国北京市大兴区和河北省廊坊市交界处,为4F 级国际机场、世界级航空枢纽.如图,天安门在北京大兴国际机场的正北方向46 km 处,北京首都国际机场在北京大兴国际机场北偏东16.28°方向上,在天安门北偏东47.43°的方向上,则北京大兴国际机场与北京首都国际机场的距离约为(参考数据:sin 16.28°≈0.28,sin 47.43°≈0.74,sin 31.15°≈0.52)( )A .65.46 kmB .85.09 kmC .74.35 kmD .121.12 km解析:A 如图所示,由题意可得AC =46 km ,∠ACB =16.28°,∠BAC =132.57°,由正弦定理可得BCsin A =AC sin B ,即BC sin 132.57°=46sin 31.15°,解得BC =46sin 31.15°·sin 132.57°≈460.52×0.74≈65.46.故选A .13.(2022·淮安模拟)已知△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,那么当b =________时,满足条件“a =1,A =30°”的△ABC 有两个.(仅写出一个b 的具体数值即可)解析:由正弦定理a sin A =bsin B ,得sin B =b sin A a =12b ,若满足条件的△ABC 有两个,则12b <1且1=a <b ,所以1<b <2. 答案:32((1,2)内任一数即可)14.(2022·济南模拟)已知a ,b ,c 分别为△ABC 的内角A ,B ,C 的对边,(3b -a )cosC =c cos A ,c 是a ,b 的等比中项,且△ABC 的面积为32,则ab =________,a +b =________.解析:∵(3b -a )cos C =c cos A ,∴利用正弦定理可得3sin B cos C =sin A cos C +sinC cos A =sin(A +C )=sin B .又∵sin B ≠0,∴cos C =13,则C 为锐角,∴sin C =223.由△ABC 的面积为32,可得12ab sin C =32,∴ab =9.由c 是a ,b 的等比中项可得c 2=ab ,由余弦定理可得c 2=a 2+b 2-2ab cos C ,∴(a +b )2=113ab =33,∴a +b =33.答案:93315.在△ABC 中,角A ,B ,C 所对的边分别是a ,b ,c ,且3b 2c -3a =cos Bcos A .(1)求角B 的大小;(2)若b =2,求△ABC 的面积的最大值. 解:(1)已知3b 2c -3a =cos Bcos A,则由正弦定理可得3sin B 2sin C -3sin A =cos Bcos A ,即3sin B cos A =(2sin C -3sin A )cos B ,即3sin(A +B )=2sin C cos B ,即3sin C =2sin C cos B , ∵sin C ≠0,∴cos B =32,又0<B <π,则B =π6. (2)由余弦定理可得b 2=a 2+c 2-2ac cos B , 即22=a 2+c 2-2ac cos π6,即4=a 2+c 2-3ac ≥2ac -3ac ,当且仅当a =c 时,等号成立,ac ≤42-3=4(2+3),∴△ABC 的面积为S =12ac sin B ≤12×4(2+3)×12=2+3.∴△ABC 的面积的最大值为2+3.C 级——迁移创新16.(2022·大庆模拟)已知锐角△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,若a =3,b 2+c 2-bc =3,则△ABC 面积的取值范围是( )A .⎝ ⎛⎦⎥⎤32,334B .⎝ ⎛⎭⎪⎫32,334C .⎝⎛⎭⎪⎫34,334D .⎝⎛⎦⎥⎤34,334解析:A 由于a =3,b 2+c 2-bc =3,cos A =b 2+c 2-a 22bc =12,且A ∈(0,π),所以A=π3,那么外接圆半径为R =12×332=1,所以S △ABC =12bc sin A =34·2R sin B ·2R sin ⎝ ⎛⎭⎪⎫2π3-B =3sin B ⎝⎛⎭⎪⎫32cos B +12sin B =32sin B cos B +32sin 2B =34sin 2B +32⎝ ⎛⎭⎪⎫12-12cos 2B =32⎝ ⎛⎭⎪⎫32sin 2B -12cos 2B +34=32sin ⎝ ⎛⎭⎪⎫2B -π6+34.由于△ABC 为锐角三角形,所以0<B<π2,0<C =π-A -B =2π3-B <π2,所以π6<B <π2,所以π6<2B -π6<5π6,12<sin ⎝⎛⎭⎪⎫2B -π6≤1,故32<S △ABC ≤334.故选A . 17.(2022·济南三模)已知在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,满足sin ⎝⎛⎭⎪⎫A -π6sin ⎝⎛⎭⎪⎫A +5π6=-14. (1)求角A 的大小;(2)若△ABC 为锐角三角形,a =1,求△ABC 周长的取值范围. 解:(1)因为sin ⎝ ⎛⎭⎪⎫A -π6sin ⎝ ⎛⎭⎪⎫A +5π6=-14,所以⎝⎛⎭⎪⎫32sin A -12cos A ⎝ ⎛⎭⎪⎫-32sin A +12cos A =-14,即32sin A cos A -34sin 2A -14cos 2A =-14,所以34sin 2A -38(1-cos 2A )-18(1+cos 2A )=-14,整理可得34sin 2A +14cos 2A =14, 所以可得sin ⎝ ⎛⎭⎪⎫2A +π6=12, 因为A ∈(0,π),可得2A +π6∈⎝ ⎛⎭⎪⎫π6,13π6,所以2A +π6=5π6,可得A =π3.(2)由正弦定理a sin A =b sin B =c sin C ,且a =1,A =π3,所以b =233sin B ,c =233sin C ;所以a +b +c =1+233(sin B +sin C )=1+233⎣⎢⎡⎦⎥⎤sin B +sin ⎝ ⎛⎭⎪⎫2π3-B =1+2sin ⎝⎛⎭⎪⎫B +π6.因为△ABC 为锐角三角形, 所以得⎩⎪⎨⎪⎧0<B <π2,0<2π3-B <π2,解得π6<B <π2,所以π3<B +π6<2π3,所以1+2sin ⎝⎛⎭⎪⎫B +π6∈(1+3,3],即△ABC 周长的取值范围是(1+3,3].。
高考数学滚动过关检测三 集合、常用逻辑用语、不等式、函数与导数、三角函数与解三角形
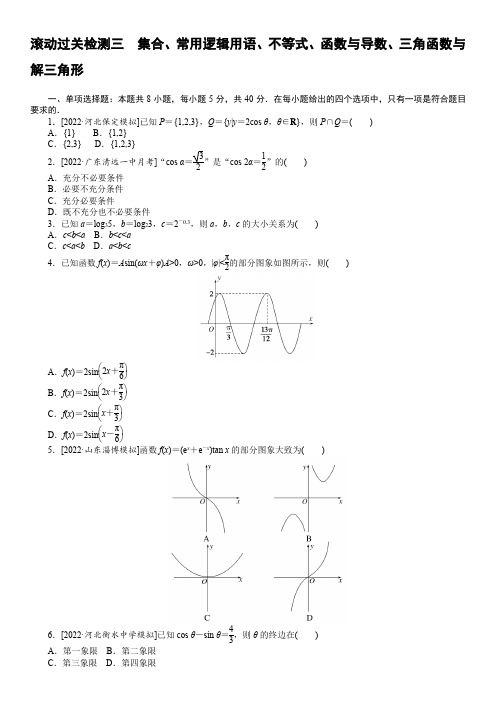
滚动过关检测三 集合、常用逻辑用语、不等式、函数与导数、三角函数与解三角形一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.[2022·河北保定模拟]已知P ={1,2,3},Q ={y |y =2cos θ,θ∈R },则P ∩Q =( )A .{1}B .{1,2}C .{2,3}D .{1,2,3}2.[2022·广东清远一中月考]“cos α=32”是“cos 2α=12”的( ) A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件3.已知a =log 35,b =log 23,c =2-0.3,则a ,b ,c 的大小关系为( )A .c <b <aB .b <c <aC .c <a <bD .a <b <c4.已知函数f (x )=A sin(ωx +φ)A >0,ω>0,|φ|<π2的部分图象如图所示,则( )A .f (x )=2sin ⎝⎛⎭⎫2x +π6 B .f (x )=2sin ⎝⎛⎭⎫2x +π3 C .f (x )=2sin ⎝⎛⎭⎫x +π3 D .f (x )=2sin ⎝⎛⎭⎫x -π6 5.[2022·山东淄博模拟]函数f (x )=(e x +e -x )tan x 的部分图象大致为( )6.[2022·河北衡水中学模拟]已知cos θ-sin θ=43,则θ的终边在( ) A .第一象限 B .第二象限C .第三象限D .第四象限7.[2022·湖南株洲模拟]在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,若23a cos C -3b cos C =3c cos B ,则角C 的大小为( )A.π6B.π4C.π3D.2π38.[2022·皖南八校联考]已知函数f (x )=(3a )x -x 3a (a >1),当x ≥2e 时,f (x )≥0恒成立,则实数a 的取值范围为 A.⎝⎛⎭⎫e 3,+∞ B.⎣⎡⎭⎫2e 3,+∞ C .(1,e) D.⎝⎛⎦⎤1,2e 3 二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,有选错的得0分,部分选对的得2分.9.下列说法正确的有( )A .终边在y 轴上的角的集合为θ⎪⎪ θ=π2+2k π,k ∈Z B .已知3a =4b =12,则1a +1b=1 C .已知x ,y ∈R +,且1x +4y=1,则x +y 的最小值为8 D .已知幂函数f (x )=kx a 的图象过点(2,4),则k +a =310.[2022·辽宁丹东模拟]已知a ,b ∈R ,且3a <3b <1,则( )A .a 2<b 2B .ln|a |>ln|b |C.b a +a b>2 D .a +b +2ab >0 11.[2022·河北石家庄一中月考]对于△ABC ,有如下判断,其中正确的判断是( )A .若cos A =cosB ,则△ABC 为等腰三角形B .若△ABC 为锐角三角形,有A +B >π2,则sin A >cos B C .若a =8,c =10,B =60°,则符合条件的△ABC 有两个D .若sin 2A +sin 2B <sin 2C ,则△ABC 是钝角三角形12.[2022·辽宁沈阳模拟]函数f (x )为定义在R 上的偶函数,且在[0,+∞)上单调递增,函数g (x )=x [f (x )-f (2)],则( )A .函数h (x )=f (x )cos x 为奇函数B .f (x )的解析式可能是f (x )=e x +e -x -x 2C .函数g (x )有且只有3个零点D .不等式g (x )≤0的解集为[-2,2]三、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中的横线上.13.设函数f (x )=⎩⎪⎨⎪⎧2x ,x ≤0log 2x ,x >0,则f ⎝⎛⎭⎫f ⎝⎛⎭⎫12=________. 14.[2022·湖北石首一中月考]在△ABC 中,已知sin A sin B sin C =357,则此三角形最大内角度数为________.15.已知cos ⎝⎛⎭⎫π6-x =13,则cos ⎝⎛⎭⎫5π6+x -sin 2⎝⎛⎭⎫x -π6=________. 16.[2022·浙江杭州模拟]函数f (x )=2x -x 2的零点个数为________,若函数f (x )=a x -x 2(a >1)恰有两个零点,则a =________.四、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.17.(10分)[2022·北京海淀模拟]设△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,且a sin B =3b cos A .(1)求角A 的大小;(2)再从以下三组条件中选择一组条件作为已知条件,使三角形存在且唯一确定,并求△ABC 的面积. 第①组条件:a =19,c =5;第②组条件:cos C =13,c =42; 第③组条件:AB 边上的高h =3,a =3.18.(12分)[2022·山东日照模拟]已知函数f (x )=cos(πx +φ)⎝⎛⎭⎫0<φ<π2的部分图象如图所示.(1)求φ及图中x 0的值;(2)设g (x )=f (x )+f ⎝⎛⎭⎫x +13,求函数g (x )在区间⎣⎡⎦⎤-12,13上的最大值和最小值.19.(12分)[2021·新高考Ⅰ卷]记△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .已知b 2=ac ,点D 在边AC 上,BD sin ∠ABC =a sin C .(1)证明:BD = b ;(2)若AD =2DC ,求cos ∠ABC .20.(12分)已知:f (x )=3sin(π+x )sin ⎝⎛⎭⎫x -π2+cos 2⎝⎛⎭⎫π2+x -12. (1)求函数f (x )的单调递增区间;(2)在△ABC 中,A ,B ,C 的对边分别为a ,b ,c ,若f (A )=1,a =2,求△ABC 面积的最大值.21.(12分)[2022·湖北九师联盟]已知函数f (x )=ln x ,g (x )=x 2-x +1.(1)求函数h (x )=f (x )-g (x )的极值;(2)证明:有且只有两条直线与函数f (x ),g (x )的图象都相切.22.(12分)[2022·广东茂名五校联考]已知函数f (x )=ln x +x 2-ax .(1)当a =3时,求曲线y =f (x )在点P (1,f (1))处的切线方程;(2)若x 1,x 2(x 1<x 2)是函数f (x )的两个极值点,证明:f (x 1)-f (x 2)>ln a 28+64-a 416a 2.。
2021年高考数学常用公式及重要知识记忆检查(8份)

12
1
2
(xx)f(x)f(x)0
x1x2 f(x1)f(x2)0
f(x)在a,b上是减函数.
12
1
2
x1x2
(2)设函数 yf(x)在某个区间内可导,如果 f(x)0,则 f(x)为增函数;如果 f(x)0, 则 f(x)为减函数.
⑶单调性性质:
①增函数+增函数=增函数;②减函数+减函数=减函数;③增函数-减函数=增函数;④减函数-
虑
yf(u)与
小结:同增异
ug(x)的单调性,从而得出 yf[g(x)]的单调性。
减。研究函数 的单调性,定
yfu
增函数
ugx
增函数
yf gx
增函数
义域优先考 虑,且复合函 数的单调区间
增函数 减函数
减函数
减函数
增函数 减函数
减函数 减函数 增函数
是它的定义域 的某个子区 间。
16. 函数的奇偶性(注:奇.偶.函.数.大.前.提.:.定.义.域.必.须.关.于.原.点.对.称.)
(2)当 a<0时b,
①若 x2ap,q,则有 f(x)minminf(p),f(q),
②若
xb p,q,则有
2a
f(x)maxmaxf(p),f(q),
f(x)minminf(p),f(q).
8.afxafxmax;afxafxmin
9.由不.等.导.相.等.的.有.效.方.法.:若ab且 ab,则 ab.
10. 真值表
表1
pq 真真 真假 假真 假假
非p 假 假 真 真
p或q 真 真 真 假
p且q 真 假 假 假
同真为 真同假 为假真 假相对
高考数学复习专题过关检测—立体几何(含解析)

高考数学复习专题过关检测—立体几何一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(2021·山东济宁二模)“直线m垂直于平面α内的无数条直线”是“m⊥α”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件2.(2021·重庆八中月考)已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则异面直线CD与PB所成角的余弦值为()A.√55B.2√55C.√510D.√95103.(2021·江西上饶三模)在正方体ABCD-A1B1C1D1中,G是线段BC1上一点,且A1G⊥B1D,则()A.BG=12BC1B.BC1=3GC1C.BG=3GC1D.G为线段BC1上任意一点4.(2021·辽宁葫芦岛一模)某保鲜封闭装置由储物区与充氮区(内层是储物区,用来放置新鲜易变质物品,充氮区是储物区外的全部空间,用来向储物区输送氮气从而实现保鲜功能)构成.如图,该装置外层上部分是半径为2的半球,下面大圆刚好与高度为3的圆锥的底面圆重合,内层是一个高度为4的倒置小圆锥,小圆锥底面平行于外层圆锥的底面,且小圆锥顶点与外层圆锥顶点重合,为了保存更多物品,充氮区的体积最小为()A.4πB.16π3C.28π3D.4π35.(2021·天津三模)在圆柱O1O2内有一个球O,球O分别与圆柱O1O2的上、下底面及母线均有且只有一个公共点.若O1O2=2,则圆柱O1O2的表面积为() A.4π B.5πC.6πD.7π6.(2021·广东深圳模拟)已知球O与棱长为2的正方体ABCD-A1B1C1D1的各个面都相切,M为棱DD1的中点,则平面AMC截球O所得截面的面积为()A.π3B.2π3C.πD.4π37.(2021·福建师大附中模拟)过正方形ABCD的顶点A作PA⊥平面ABCD,若AB=AP,则平面ABP与平面CDP的夹角的余弦值为()A.13B.√22C.√32D.√338.(2021·山东滨州二模)在正方体ABCD-A1B1C1D1中,M是棱DD1的中点,P是底面ABCD内(包括边界)的一个动点,若MP∥平面A1BC1,则异面直线MP与A1C1所成角的取值范围是()A.(0,π3] B.[π6,π3]C.[π3,π2] D.[π3,π)二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.(2021·广东广州三模)对于空间中的两条不同直线a,b和两个不同平面α,β,下列说法正确的是()A.若a⊥α,b⊥α,则a∥bB.若a⊥b,b⊥β,则a∥βC.若a⊥α,b⊥β,α⊥β,则a⊥bD.若a∥α,α⊥β,则a⊥β10.(2021·湖北荆门月考)如图,在正方体ABCD-A1B1C1D1中,点P在线段BC1上运动,下列结论正确的是()A.三棱锥A-D1PC的体积不变B.直线AP与平面ACD1所成角的大小不变C.直线AP与直线A1D所成角的大小不变D.二面角P-AD1-C的大小不变11.(2021·福建龙岩三模)在意大利,有一座满是“斗笠”的灰白小镇阿尔贝罗贝洛,这些圆锥形屋顶的奇特小屋名叫Trullo,于1996年被收入世界文化遗产名录.现测量一个Trullo的屋顶,得到圆锥SO(其中S为顶点,O为底面圆心),母线SA的长为6 m,C是母线SA上靠近点S的三等分点.从点A到点C绕屋顶侧面一周安装灯光带,灯光带的最小长度为2√13 m.下面说法正确的是()A.圆锥SO 的侧面积为12π m 2B.过点S 的平面截此圆锥所得截面面积最大值为18 m 2C.圆锥SO 的外接球的表面积为72π m 2D.棱长为√3 m 的正四面体在圆锥SO 内可以任意转动12.(2021·新高考Ⅰ,12)在正三棱柱ABC-A 1B 1C 1中,AB=AA 1=1,点P 满足BP ⃗⃗⃗⃗⃗ =λBC ⃗⃗⃗⃗⃗ +μBB 1⃗⃗⃗⃗⃗⃗⃗ ,其中λ∈[0,1],μ∈[0,1],则( )A.当λ=1时,△AB 1P 的周长为定值B.当μ=1时,三棱锥P-A 1BC 的体积为定值C.当λ=12时,有且仅有一个点P ,使得A 1P ⊥BP D.当μ=12时,有且仅有一个点P ,使得A 1B ⊥平面AB 1P三、填空题:本题共4小题,每小题5分,共20分.13.(2021·辽宁大连期中)已知一个圆锥的底面半径为6,其体积为30π,则该圆锥的侧面积为 .14.(2021·河北石家庄期末)如图,已知二面角A-EF-D 的大小为45°,四边形ABFE 与四边形CDEF 都是边长为1的正方形,则B ,D 两点间的距离是 .15.(2021·浙江绍兴二模)如图,在棱长为4的正方体ABCD-A 1B 1C 1D 1中,M 是棱A 1A 上的动点,N 是棱BC 的中点.当平面D 1MN 与平面ABCD 的夹角最小时,A 1M= .16.(2021·广东汕头二模)在菱形ABCD 中,AB=2,∠DAB=60°,E 为AB 的中点,将△ADE 沿DE 翻折成△A 1DE ,当三棱锥A 1-DEC 的体积最大时,三棱锥A 1-DEC 的外接球的表面积为 .四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(10分)(2021·广东韶关期中)如图,在直三棱柱ABC-A 1B 1C 1中,侧面ABB 1A 1,BCC 1B 1,ACC 1A 1的面积依次为16,12,20,E ,F 分别为A 1C 1,BC 的中点.求证:(1)平面ABE⊥平面BB1C1C;(2)C1F∥平面ABE.18.(12分)(2021·河北张家口一模)如图,四边形ABCD是正方形,PA⊥平面ABCD,PA∥EB,且PA=PB=3.(1)求证:CE∥平面PAD;PA,求直线PD与平面PCE所成角的正弦值.(2)若BE=1319.(12分)(2021·北京石景山区模拟)如图,四棱锥P-ABCD的底面为矩形,PD⊥底面ABCD,M为BC的中点,PB⊥AM.(1)求证:平面PAM⊥平面PBD;(2)若PD=DC=1,求四棱锥P-ABCD的体积.20.(12分)(2021·山东淄博三模)如图①,在平面图形ABCD中,△ABD是边长为4的等边三角形,DB是∠ADC的平分线,且BD⊥BC,M为AD的中点,沿BM将△ABM折起,得到四棱锥A1-BCDM,如图②.图①图②(1)设平面A1BC与平面A1DM的交线为l,在四棱锥A1-BCDM的棱A1C上求一点N,使直线BN∥l;(2)若二面角A1-BM-D的大小为60°,求平面A1BD与平面A1CD的夹角的余弦值.21.(12分)(2021·湖南长沙模拟)如图,C是以AB为直径的圆上异于点A,B的点,平面PAC⊥平面ABC,PA=PC=AC=2,BC=4,E,F分别是PC,PB的中点,设平面AEF与平面ABC的交线为直线l.(1)求证:直线l⊥平面PAC.(2)直线l上是否存在点Q,使直线PQ分别与平面AEF,直线EF所成的角互余?若存在,求出AQ的值;若不存在,请说明理由.22.(12分)(2021·重庆蜀都中学月考)如图①,在菱形ABCD 中,∠ABC=120°,动点E ,F 分别在边AD ,AB 上(不含端点),且存在实数λ,使EF ⃗⃗⃗⃗⃗ =λBD ⃗⃗⃗⃗⃗⃗ ,沿EF 将△AEF 向上折起得到△PEF ,使得平面PEF ⊥平面BCDEF ,如图②所示.图①图②(1)若BF ⊥PD ,设三棱锥P-BCD 和四棱锥P-BDEF 的体积分别为V 1,V 2,求V1V 2.(2)当点E 的位置变化时,二面角E-PF-B 是否为定值?若是,求出该二面角的余弦值;若不是,说明理由.答案及解析1.B解析由直线m垂直于平面α内的无数条直线不能推出m⊥α,但是由m⊥α一定能推出直线m垂直于平面α内的无数条直线,所以“直线m垂直于平面α内的无数条直线”是“m⊥α”的必要不充分条件.故选B.2.C解析连接AE,BE(图略),设AB=1,则PA=2,AE=√12+12-2×1×1×cos120°=√3,PE=√4+3=√7,BE=√3+1=2,PB=√4+1=√5.易知CD∥BE,所以∠PBE是直线CD与PB所成的角(或其补角).又cos∠PBE=2×2×√5=√510,所以直线CD与PB所成角的余弦值为√510.故选C.3.D解析如图,∵AD⊥平面ABB1A1,∴AD⊥A1B.又AB1⊥A1B,AB1∩AD=A,∴A1B⊥平面AB1D,∴A1B⊥B1D.同理BC1⊥B1D.又A1B∩BC1=B,∴B1D⊥平面A1BC1.又A1G⊂平面A1BC1,∴A1G⊥B1D.故G为线段BC1上任意一点.故选D.4.B解析由题意可知内层小圆锥底面半径最大为√22-12=√3,所以充氮区的体积最小为12×43π×23+13π×22×3-13π×(√3)2×4=16π3.故选B.5.C解析依题意,圆柱O1O2的底面半径r=1,高h=2,所以圆柱O1O2的表面积S=2πr·h+2πr2=4π+2π=6π.故选C.6.A解析设球心O到截面的距离为d,截面圆的半径为r,由V O-ACM=V M-AOC,得1 3·S△ACM·d=√23S△AOC.因为S△ACM=12×2√2×√3=√6,S△AOC=12×2√2×1=√2,所以d=√63.又d2+r2=1,所以r=√33,所以平面AMC截球O所得截面的面积为πr2=π3.故选A.7.B 解析 设AP=AB=1,以A 为原点,AB ,AD ,AP 所在直线分别为x 轴、y 轴、z 轴,建立空间直角坐标系如图所示,则P (0,0,1),D (0,1,0),C (1,1,0),所以PC ⃗⃗⃗⃗⃗ =(1,1,-1),PD ⃗⃗⃗⃗⃗ =(0,1,-1). 设平面CDP 的法向量m =(x ,y ,z ),则{m ·PC⃗⃗⃗⃗⃗ =x +y -z =0,m ·PD ⃗⃗⃗⃗⃗ =y -z =0,取y=1,则x=0,z=1,所以m =(0,1,1)为平面CDP 的一个法向量.易知n =(0,1,0)为平面ABP 的一个法向量.设平面ABP 与平面CDP 的夹角为θ,则cos θ=|m ·n ||m ||n |=√2×1=√22.故选B .8.C 解析 如图,以D 为原点,DA ,DC ,DD 1所在直线分别为x 轴、y 轴、z 轴,建立空间直角坐标系,设AB=2,则B (2,2,0),A 1(2,0,2),C 1(0,2,2),M (0,0,1),取AD 的中点E ,DC 的中点F ,连接ME ,EF ,MF ,则E (1,0,0),F (0,1,0).因为ME ⃗⃗⃗⃗⃗⃗ =(1,0,-1),C 1B ⃗⃗⃗⃗⃗⃗⃗ =(2,0,-2)=2ME ⃗⃗⃗⃗⃗⃗ ,所以C 1B ∥ME.同理EF ∥A 1C 1.又ME ⊄平面A 1BC 1,C 1B ⊂平面A 1BC 1,所以ME ∥平面A 1BC 1.同理MF ∥平面A 1BC 1.又MF ∩ME=M ,所以平面MEF ∥平面A 1BC 1.因为P 是底面ABCD 内(包括边界)的一个动点,MP ∥平面A 1BC 1,所以点P 在线段EF 上.因为EF ∥A 1C 1,所以异面直线MP 与A 1C 1所成的角即是直线MP 与EF 所成的角.当MP ⊥EF 时,异面直线MP 与A 1C 1所成的角最大为π2,当点P 与点E 或点F 重合时,异面直线MP 与A 1C 1所成的角最小为π3.故所求角的取值范围为[π3,π2].9.AC 解析 对于A,由线面垂直的性质定理知A 正确;对于B,若a ⊥b ,b ⊥β,则a ∥β或a ⊂β,所以B 错误;对于C,由a ⊥α,α⊥β,可知a ∥β或a ⊂β,又b ⊥β,所以a ⊥b ,所以C 正确;对于D,若a ∥α,α⊥β,则a ∥β或a ⊂β或a 与β相交,所以D 错误.故选AC .10.ACD 解析 对于A,因为BC 1∥平面AD 1C ,所以BC 1上任意一点到平面AD 1C 的距离都相等,所以三棱锥A-D 1PC 的体积不变,故A 正确;对于B,因为BC 1∥平面AD 1C ,所以点P 到平面ACD 1的距离不变,但AP 的长度随着点P 的移动而变化,所以直线AP 与平面ACD 1所成角的大小会改变,故B 错误;对于C,因为直线A 1D ⊥平面ABC 1D 1,AP ⊂平面ABC 1D 1,所以A 1D ⊥AP ,所以直线AP 与直线A 1D 所成角的大小不变;故C 正确;对于D,二面角P-AD 1-C 也就是二面角B-AD 1-C ,其大小不变,故D 正确.故选ACD .11.AD 解析 如图,设圆锥底面半径为r m,将圆锥侧面展开得到扇形ASA',在△A'SC 中,A'S=6 m,SC=2 m,A'C=2√13 m,则cos ∠A'SC=36+4-522×6×2=-12,所以∠A'SC=2π3,所以2πr=2π3×6=4π,r=2,所以圆锥的侧面积为π×2×6=12π(m 2),故A 正确.在△ASB 中,cos ∠ASB=SA 2+SB 2-AB 22SA ·SB=79,sin ∠ASB=√1-4981=4√29,易知过点S 的平面截此圆锥所得截面面积最大为S △SAB =12SA·SB·sin ∠ASB=12×6×6×4√29=8√2(m 2),故B 错误.设圆锥SO 的外接球的半径为R m,则R 2=(SO-R )2+r 2,又SO=√SA 2-r 2=√36-4=4√2,所以R 2=(4√2-R )2+4,解得R=9√24,所以圆锥SO 的外接球的表面积为4πR 2=81π2(m 2),故C 错误.设圆锥SO 的内切球的半径为t m,则4√2-t=13,解得t=√2,设棱长为√3 m 的正四面体的外接球的半径为r 1 m,将该正四面体放在棱长为√62的正方体中,可知该正四面体的外接球也是该正方体的外接球,易知r 1=12√3×(√62)2=3√24,因为r 1<t ,所以棱长为√3 m 的正四面体在圆锥SO 内可以任意转动,故D 正确.故选AD . 12.BD 解析图①A 项中,当λ=1时,BP ⃗⃗⃗⃗⃗ =BC ⃗⃗⃗⃗⃗ +u BB 1⃗⃗⃗⃗⃗⃗⃗ ⇒BP ⃗⃗⃗⃗⃗ −BC ⃗⃗⃗⃗⃗ =CP ⃗⃗⃗⃗⃗ =u BB 1⃗⃗⃗⃗⃗⃗⃗ ,则CP ⃗⃗⃗⃗⃗ 与BB 1⃗⃗⃗⃗⃗⃗⃗ 共线,故点P 在线段CC 1(包括端点)上,如图①所示.在△AB 1P 中,|AB 1|=√2,|AP|=√1+u 2,|B 1P|=√1+(1-u )2, 故△AB 1P 的周长L=|AB 1|+|AP|+|B 1P|不为定值,故A 错误;图②B 项中,当u=1时,BP ⃗⃗⃗⃗⃗ =λBC ⃗⃗⃗⃗⃗ +BB 1⃗⃗⃗⃗⃗⃗⃗ ⇒BP ⃗⃗⃗⃗⃗ −BB 1⃗⃗⃗⃗⃗⃗⃗ =B 1P ⃗⃗⃗⃗⃗⃗⃗ =λBC ⃗⃗⃗⃗⃗ ,则B 1P ⃗⃗⃗⃗⃗⃗⃗ 与BC⃗⃗⃗⃗⃗ 共线,故点P 在线段B 1C 1(包括端点)上,如图②所示.由图②可知B 1C 1∥平面A 1BC ,即B 1C 1上的每一点到平面A 1BC 的距离都相等,因此三棱锥P-A 1BC 的体积为定值,故B 正确;图③C 项中,当λ=12时,分别取线段BC ,B 1C 1的中点D ,D 1,连接DD 1,可知点P 在线段DD 1(包括端点)上,如图③所示.取AC 的中点O ,建立如图所示的空间直角坐标系Oxyz ,则B √32,0,0,C 0,12,0,A 10,-12,1,P (√34,14,u),从而A 1P ⃗⃗⃗⃗⃗⃗⃗ =(√34,34,u -1),BP ⃗⃗⃗⃗⃗ =(-√34,14,u), 由A 1P ⃗⃗⃗⃗⃗⃗⃗ ·BP⃗⃗⃗⃗⃗ =u (u-1)=0,得u=0或u=1. 当点P 与点D 或D 1重合时,满足A 1P ⊥BP ,故C 错误;D 项中,当u=12时,分别取线段BB 1,CC 1的中点M ,N ,连接MN ,可知点P 在线段MN (包括端点)上,如图④所示.图④建系同选项C,则A 0,-12,0,A 10,-12,1,B √32,0,0,P √32−√32λ,λ2,12,从而A 1B ⃗⃗⃗⃗⃗⃗⃗ =√32,12,-1,AP ⃗⃗⃗⃗⃗ =√32−√32λ,λ2+12,12,四边形ABB 1A 1为正方形,显然A 1B ⊥AB 1. 要使A 1B ⊥平面AB 1P ,只需A 1B ⊥AP ,即A 1B ⃗⃗⃗⃗⃗⃗⃗ ·AP⃗⃗⃗⃗⃗ =12−λ2=0,解得λ=1. 当且仅当点P 与点N 重合时,A 1B ⊥平面AB 1P ,故D 正确. 综上所述,选BD .13.39π 解析 ∵体积V=13π×62·h=30π,∴高h=52,∴母线长l=√ℎ2+r 2=√(52)2+62=132,∴S 侧=πrl=π×6×132=39π. 14.√3-√2 解析 ∵BD ⃗⃗⃗⃗⃗⃗ =BF ⃗⃗⃗⃗⃗ +FE ⃗⃗⃗⃗⃗ +ED ⃗⃗⃗⃗⃗ ,∴|BD ⃗⃗⃗⃗⃗⃗ |2=|BF ⃗⃗⃗⃗⃗ |2+|FE ⃗⃗⃗⃗⃗ |2+|ED ⃗⃗⃗⃗⃗ |2+2BF ⃗⃗⃗⃗⃗ ·FE ⃗⃗⃗⃗⃗ +2FE ⃗⃗⃗⃗⃗ ·ED ⃗⃗⃗⃗⃗ +2BF ⃗⃗⃗⃗⃗ ·ED ⃗⃗⃗⃗⃗ .由题意可知|BF ⃗⃗⃗⃗⃗ |=|FE ⃗⃗⃗⃗⃗ |=|ED ⃗⃗⃗⃗⃗ |=1,BF ⃗⃗⃗⃗⃗ ·FE ⃗⃗⃗⃗⃗ =0,FE ⃗⃗⃗⃗⃗ ·ED ⃗⃗⃗⃗⃗ =0,BF ⃗⃗⃗⃗⃗ ·ED ⃗⃗⃗⃗⃗ =1×1×cos 135°=-√22,∴|BD⃗⃗⃗⃗⃗⃗ |=√3-√2.故B ,D 两点间的距离是√3-√2. 15.85 解析 如图,建立空间直角坐标系,则N (2,4,0),D 1(0,0,4),设M (4,0,a )(0≤a ≤4),所以MN ⃗⃗⃗⃗⃗⃗⃗ =(-2,4,-a ),D 1N ⃗⃗⃗⃗⃗⃗⃗⃗ =(2,4,-4).设平面D 1MN 的法向量为n =(x ,y ,z ),则{n·MN⃗⃗⃗⃗⃗⃗⃗ =0,n·D1N⃗⃗⃗⃗⃗⃗⃗⃗ =0,即{-2x+4y-az=0,2x+4y-4z=0,解得{x=(4-a)z4,y=(a+4)z8,令z=8,则x=8-2a,y=a+4,所以n=(8-2a,a+4,8)为平面D1MN的一个法向量.易知m=(0,0,1)为平面ABCD的一个法向量.设平面D1MN与平面ABCD的夹角为θ,则cos θ=|m·n||m||n|=√(8-2a)+(a+4)+64=√5a2-24a+144,当a=125时,cos θ取最大值,则θ取最小值,所以A1M=4-125=85.16.8π解析如图,由余弦定理,得DE=√AD2+AE2-2AD·AEcos60°=√3,CE=√BE2+BC2-2BE·BCcos(180°-60°)=√7,所以AE2+DE2=AD2,DC2+DE2=CE2,即AE⊥DE,DC⊥DE.分别取CE,A1C的中点F,M,连接FM,则F为Rt△DEC的外心,因为△DEC的面积为定值,所以当平面A1DE⊥平面DEC时,点A1到平面DEC的距离最大,此时三棱锥A1-DEC的体积最大,又A1E⊥DE,所以A1E⊥平面DEC.由F,M分别为CE,A1C的中点,得FM∥A1E,所以FM⊥平面DEC,易知M是三棱锥A1-DEC的外接球的球心.因为A1C2=A1E2+CE2=1+7=8,所以所求外接球的表面积S=4π(A1C2)2=8π.17.证明(1)在直三棱柱ABC-A1B1C1中,BB1⊥平面ABC,AB⊂平面ABC,∴BB1⊥AB.∵侧面ABB1A1,BCC1B1,ACC1A1的面积依次为16,12,20,∴AB∶BC∶AC=4∶3∶5,∴AB2+BC2=AC2,即AB⊥BC.又BB1∩BC=B,∴AB⊥平面BB1C1C,又AB⊂平面ABE,∴平面ABE⊥平面BB1C1C.(2)如图,取AB的中点G,连接EG,GF.∵G,F分别为AB,BC的中点,∴GF∥AC,GF=12AC.∵E为A1C1的中点,∴EC1=12A1C1=12AC.又A 1C 1∥AC ,∴EC 1∥GF ,EC 1=GF ,∴四边形EGFC 1为平行四边形,∴C 1F ∥EG.又C 1F ⊄平面ABE ,EG ⊂平面ABE ,∴C 1F ∥平面ABE. 18.(1)证明 因为四边形ABCD 是正方形,所以BC ∥AD.又AD ⊂平面PAD ,BC ⊄平面PAD ,所以BC ∥平面PAD. 同理EB ∥平面PAD.又BC ∩EB=B ,所以平面EBC ∥平面PAD. 又CE ⊂平面EBC ,所以CE ∥平面PAD.(2)解 以A 为原点,AD ,AB ,AP 所在直线分别为x 轴、y 轴、z 轴,建立空间直角坐标系如图所示.因为PA=AB=3,所以BE=13PA=1,所以P (0,0,3),D (3,0,0),C (3,3,0),E (0,3,1), 所以PD ⃗⃗⃗⃗⃗ =(3,0,-3),PC ⃗⃗⃗⃗⃗ =(3,3,-3),PE⃗⃗⃗⃗⃗ =(0,3,-2). 设平面PCE 的法向量为m =(x ,y ,z ),则{m ·PC ⃗⃗⃗⃗⃗ =3x +3y -3z =0,m ·PE ⃗⃗⃗⃗⃗ =3y -2z =0,得{x =z3,y =2z 3,令z=3,则x=1,y=2,所以m =(1,2,3)为平面PCE 的一个法向量. 设直线PD 与平面PCE 所成的角为θ, 则sin θ=|cos <PD ⃗⃗⃗⃗⃗ ,m >|=|PD⃗⃗⃗⃗⃗⃗⃗ ·m ||PD ⃗⃗⃗⃗⃗⃗⃗||m |=3√2×√14=√77,所以直线PD 与平面PCE 所成角的正弦值为√77. 19.(1)证明 因为PD ⊥底面ABCD ,AM ⊂平面ABCD ,所以PD ⊥AM.又PB ⊥AM ,PB ∩PD=P ,所以AM ⊥平面PBD. 又AM ⊂平面PAM ,所以平面PAM ⊥平面PBD. (2)解 由(1)可知AM ⊥平面PBD ,所以AM ⊥BD ,所以△DAB ∽△ABM.设BM=x ,则AD=2x ,由BMAB =ABAD ,即x1=12x ,得2x 2=1,解得x=√22,所以AD=√2.因为PD ⊥底面ABCD ,所以四棱锥P-ABCD 的体积为13×1×√2×1=√23.20.解 (1)如图,延长CB ,DM 相交于点E ,连接A 1E.因为点A 1,E 既在平面A 1BC 内,又在平面A 1DM 内,所以直线A 1E 即为平面A 1BC 与平面A 1DM 的交线l.因为DB 是∠ADC 的平分线,且BD ⊥BC ,所以B 为EC 的中点. 取A 1C 的中点N ,连接BN ,则BN ∥A 1E ,即BN ∥l. 故当N 为棱A 1C 的中点时,BN ∥l.(2)由题意可知BM ⊥A 1M ,BM ⊥MD ,则∠A 1MD 为二面角A 1-BM-D 的平面角,所以∠AMD=60°.又A 1M=MD ,所以△A 1MD 为等边三角形. 取MD 的中点O ,连接A 1O ,则A 1O ⊥MD.由BM ⊥A 1M ,BM ⊥MD ,A 1M ∩MD=M ,可知BM ⊥平面A 1MD ,所以BM ⊥A 1O. 又BM ∩MD=M ,所以A 1O ⊥平面BCDM. 如图,建立空间直角坐标系.则D (-1,0,0),A 1(0,0,√3),C (-5,4√3,0),B (1,2√3,0),所以DA 1⃗⃗⃗⃗⃗⃗⃗⃗ =(1,0,√3),DC ⃗⃗⃗⃗⃗ =(-4,4√3,0),DB⃗⃗⃗⃗⃗⃗ =(2,2√3,0). 设平面A 1CD 的法向量m =(x ,y ,z ),则{m ·DA 1⃗⃗⃗⃗⃗⃗⃗⃗ =0,m ·DC ⃗⃗⃗⃗⃗ =0,即{x +√3z =0,-4x +4√3y =0, 令z=-√3,则x=3,y=√3,所以m =(3,√3,-√3)为平面A 1CD 的一个法向量. 设平面A 1BD 的法向量为n =(a ,b ,c ),则{n ·DA 1⃗⃗⃗⃗⃗⃗⃗⃗ =0,n ·DB ⃗⃗⃗⃗⃗⃗ =0,即{x +√3c =0,2a +2√3b =0, 令c=-√3,则a=3,b=-√3,所以n =(3,-√3,-√3)为平面A 1BD 的一个法向量. 设平面A 1BD 与平面A 1CD 的夹角为θ, 则cos θ=|cos <m ,n >| =√3×√3)√3)√3)|√3+(√3)+(-√3)×√3+(-√3)+(-√3)=35,所以平面A 1BD 与平面A 1CD 的夹角的余弦值为35.21.(1)证明 ∵E ,F 分别是PC ,PB 的中点,∴BC ∥EF.又EF ⊂平面AEF ,BC ⊄平面AEF ,∴BC ∥平面AEF. 又BC ⊂平面ABC ,平面AEF ∩平面ABC=l ,∴BC ∥l.∵BC ⊥AC ,平面PAC ∩平面ABC=AC ,平面PAC ⊥平面ABC ,BC ⊂平面ABC ,∴BC ⊥平面PAC.∴l ⊥平面PAC.(2)解 如图,建立空间直角坐标系,则A (2,0,0),B (0,4,0),P (1,0,√3),E 12,0,√32,F 12,2,√32.所以AE ⃗⃗⃗⃗⃗ =(-32,0,√32),EF⃗⃗⃗⃗⃗ =(0,2,0). 由题意可设Q (2,y ,0),平面AEF 的法向量为m =(x ,y ,z ), 则{AE⃗⃗⃗⃗⃗ ·m =-32x +√32z =0,EF ⃗⃗⃗⃗⃗ ·m =2y =0,取z=√3,则x=1,y=0,所以m =(1,0,√3)为平面AEF 的一个法向量. 又PQ ⃗⃗⃗⃗⃗ =(1,y ,-√3),所以|cos <PQ ⃗⃗⃗⃗⃗ ,EF⃗⃗⃗⃗⃗ >|=2√4+y =√4+y ,|cos <PQ ⃗⃗⃗⃗⃗ ,m >|=2√4+y =√4+y ,依题意,|cos <PQ ⃗⃗⃗⃗⃗ ,EF ⃗⃗⃗⃗⃗ >|=|cos <PQ ⃗⃗⃗⃗⃗ ,m >|,解得y=±1.故直线l 上存在点Q ,使直线PQ 分别与平面AEF ,直线EF 所成的角互余,此时AQ=1.22.解 (1)取EF 的中点G ,连接PG.因为EF⃗⃗⃗⃗⃗ =λBD ⃗⃗⃗⃗⃗⃗ ,所以EF ∥BD ,所以PE=PF , 所以PG ⊥EF.又平面PEF ⊥平面BCDEF ,平面PEF ∩平面BCDEF=EF ,PG ⊂平面PEF ,所以PG ⊥平面BCDEF.连接GC ,由题意可知GC ⊥EF.以G 为坐标原点,GF ,GC ,GP 所在直线分别为x 轴、y 轴、z 轴,建立空间直角坐标系如图所示.设菱形的边长为2,则F (λ,0,0),B (1,√3(1-λ),0),P (0,0,√3λ),D (-1,√3(1-λ),0),所以FB ⃗⃗⃗⃗⃗ =(1-λ,√3(1-λ),0),DP ⃗⃗⃗⃗⃗ =(1,-√3(1-λ),√3λ).因为BF ⊥PD ,所以FB ⃗⃗⃗⃗⃗ ·DP ⃗⃗⃗⃗⃗ =1-λ-3(1-λ)2=0,解得λ=23或λ=1(舍去).设△BCD 的面积为S ,则S △AEF =49S ,所以S 四边形BDEF =59S.所以V 1V 2=S △BCD S 四边形BDEF=S 59S =95.(2)二面角E-PF-B 是定值.证明如下:由(1)知n 1=(0,1,0)为平面PEF 的一个法向量. 设平面PFB 的法向量为n 2=(x ,y ,z ),因为FB ⃗⃗⃗⃗⃗ =(1-λ,√3(1-λ),0),FP⃗⃗⃗⃗⃗ =(-λ,0,√3λ), 所以{n 2·FB ⃗⃗⃗⃗⃗ =0,n 2·FP⃗⃗⃗⃗⃗ =0,即{(1-λ)x +√3(1-λ)y =0,-λx +√3λz =0,取y=1,则x=-√3,z=-1,所以n 2=(-√3,1,-1)为平面PFB 的一个法向量. 设二面角E-PF-B 的平面角为θ,所以|cos θ|=|cos <n 1,n 2>|=1×√5=√55.由图可知θ为钝角,所以二面角E-PF-B 为定值,其余弦值来为-√55.。
高考数学一轮复习课时过关检测(十四) 导数的概念及运算

课时过关检测(十四) 导数的概念及运算A 级——基础达标1.曲线y =e x -ln x 在点(1,e)处的切线方程为( ) A .(1-e)x -y +1=0 B .(1-e)x -y -1=0 C .(e -1)x -y +1=0D .(e -1)x -y -1=0解析:选C 由于y ′=e -1x ,所以y ′|x =1=e -1,故曲线y =e x -ln x 在点(1,e)处的切线方程为y -e =(e -1)·(x -1),即(e -1)x -y +1=0.2.已知函数f (x )的导函数为f ′(x ),且满足关系式f (x )=x 2+3xf ′(2)+ln x ,则f ′(2)的值等于( )A .-2B .2C .-94D .94解析:选C 因为f (x )=x 2+3xf ′(2)+ln x ,所以f ′(x )=2x +3f ′(2)+1x,所以f ′(2)=2×2+3f ′(2)+12,解得f ′(2)=-94.3.(2021·益阳、湘潭调研)已知函数f (x )在R 上可导,其部分图象如图所示,设错误!=a ,则下列不等式正确的是( )A .f ′(1)<f ′(2)<aB .f ′(1)<a <f ′(2)C .f ′(2)<f ′(1)<aD .a <f ′(1)<f ′(2)解析:选B 由图象可知,在(0,+∞)上,函数f (x )单调递增,且曲线切线的斜率越来越大, ∵错误!=a ,∴易知f ′(1)<a <f ′(2).4.(2021·湖北八校第一次联考)已知曲线C :f (x )=x 3-3x ,直线l :y =ax -3a ,则a =6是直线l 与曲线C 相切的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件解析:选A 因为曲线C :f (x )=x 3-3x ,所以f ′(x )=3x 2-3.设直线l 与曲线C 相切,且切点的横坐标为x 0,则切线方程为y =(3x 20-3)x -2x 30,所以⎩⎪⎨⎪⎧3x20-3=a ,2x30=3a ,解得⎩⎪⎨⎪⎧x0=3,a =6或⎩⎪⎨⎪⎧x0=-32,a =-34,所以a =6是直线l 与曲线C 相切的充分不必要条件,故选A .5.(多选)如图所示的是物体甲、乙在时间0到t 1范围内路程的变化情况,下列说法不正确的是( )A .在0到t 0范围内,甲的平均速度大于乙的平均速度B .在0到t 0范围内,甲的平均速度小于乙的平均速度C .在t 0到t 1范围内,甲的平均速度大于乙的平均速度D .在t 0到t 1范围内,甲的平均速度小于乙的平均速度解析:选ABD 在0到t 0范围内,甲、乙的平均速度都为v =s0t0,故A 、B 错误;在t 0到t 1范围内,甲的平均速度为s2-s0t1-t0,乙的平均速度为s1-s0t1-t0.因为s 2-s 0>s 1-s 0,t 1-t 0>0,所以s2-s0t1-t0>s1-s0t1-t0,故C 正确,D 错误.6.(多选)若函数f (x )的导函数f ′(x )的图象关于y 轴对称,则f (x )的解析式可能为( ) A .f (x )=3cos x B .f (x )=x 3+x C .f (x )=x +1xD .f (x )=e x +x解析:选BC 对于A ,f (x )=3cos x ,其导数f ′(x )=-3sin x ,其导函数为奇函数,图象不关于y 轴对称,不符合题意;对于B ,f (x )=x 3+x ,其导数f ′(x )=3x 2+1,其导函数为偶函数,图象关于y 轴对称,符合题意;对于C ,f (x )=x +1x ,其导数f ′(x )=1-1x2,其导函数为偶函数,图象关于y 轴对称,符合题意;对于D ,f (x )=e x +x ,其导数f ′(x )=e x +1,其导函数不是偶函数,图象不关于y 轴对称,不符合题意.7.(2021·江西南昌一模)设函数f (x )在(0,+∞)内可导,其导函数为f ′(x ),且f (ln x )=x +ln x ,则f ′(1)= .解析:因为f (ln x )=x +ln x ,所以f (x )=x +e x , 所以f ′(x )=1+e x ,所以f ′(1)=1+e 1=1+e. 答案:1+e8.如图,y =f (x )是可导函数,直线l :y =kx +2是曲线y =f (x )在x =3处的切线,令g (x )=xf (x ),则曲线g (x )在x =3处的切线方程为 .解析:由题图可知曲线y =f (x )在x =3处的切线斜率等于-13,即f ′(3)=-13.又g (x )=xf (x ),所以g ′(x )=f (x )+xf ′(x ),g ′(3)=f (3)+3f ′(3),由题图可知f (3)=1,所以g (3)=3f (3)=3,g ′(3)=1+3×⎝ ⎛⎭⎪⎫-13=0,则曲线g (x )在x =3处的切线方程为y -3=0.答案:y -3=09.(2021·开封市模拟考试)已知函数f (x )=mx 3+6mx -2e x ,若曲线y =f (x )在点(0,f (0))处的切线与直线4x +y -2=0平行,则m = .解析:f ′(x )=3mx 2+6m -2e x,则f ′(0)=6m -2=-4,解得m =-13.答案:-1310.若函数y =2x 3+1与y =3x 2-b 的图象在一个公共点处的切线相同,则实数b = . 解析:设公共切点的横坐标为x 0,函数y =2x 3+1的导函数为y ′=6x 2,y =3x 2-b 的导函数为y ′=6x ,由图象在一个公共点处的切线相同,可得6x 20=6x 0且1+2x 30=3x 20-b ,解得x 0=0,b =-1或x 0=1,b =0.故实数b =0或-1.答案:0或-111.已知曲线y =x 3+x -2在点P 0处的切线l 1平行于直线4x -y -1=0,且点P 0在第三象限.(1)求P 0的坐标;(2)若直线l ⊥l 1,且l 也过切点P 0,求直线l 的方程. 解:(1)由y =x 3+x -2,得y ′=3x 2+1, 由已知令3x 2+1=4,解得x =±1. 当x =1时,y =0;当x =-1时,y =-4. 又∵点P 0在第三象限, ∴切点P 0的坐标为(-1,-4). (2)∵直线l ⊥l 1,l 1的斜率为4, ∴直线l 的斜率为-14.∵l 过切点P 0,点P 0的坐标为(-1,-4), ∴直线l 的方程为y +4=-14(x +1),即x +4y +17=0.12.设函数f (x )=ax -bx ,曲线y =f (x )在点(2,f (2))处的切线方程为7x -4y -12=0.(1)求f (x )的解析式;(2)证明:曲线y =f (x )上任一点处的切线与直线x =0和直线y =x 所围成的三角形的面积为定值,并求此定值.解:(1)方程7x -4y -12=0可化为y =74x -3.当x =2时,y =12.又f ′(x )=a +bx2,于是⎩⎪⎨⎪⎧2a -b 2=12,a +b 4=74,解得⎩⎪⎨⎪⎧a =1,b =3.故f (x )=x -3x .(2)设P (x 0,y 0)为曲线上任一点,由y ′=1+3x2,知曲线在点P (x 0,y 0)处的切线方程为y -y 0=⎝ ⎛⎭⎪⎫1+3x20(x -x 0),即y -⎝⎛⎭⎪⎫x0-3x0=⎝ ⎛⎭⎪⎫1+3x20(x -x 0).令x =0,得y =-6x0,从而得切线与直线x =0的交点坐标为⎝⎛⎭⎪⎫0,-6x0.令y =x ,得y =x =2x 0,从而得切线与直线y =x 的交点坐标为(2x 0,2x 0).所以在点P (x 0,y 0)处的切线与直线x =0,y =x 所围成的三角形的面积为S =12⎪⎪⎪⎪⎪⎪-6x0·|2x 0|=6.故曲线y =f (x )上任一点处的切线与直线x =0,y =x 所围成的三角形的面积为定值,且此定值为6.B 级——综合应用13.(2021·甘肃、青海、宁夏联考)过点M (-1,0)引曲线C :y =2x 3+ax +a 的两条切线,这两条切线与y 轴分别交于A 、B 两点,若|MA |=|MB |,则a = .解析:设切点坐标为(t,2t 3+at +a ),∵y ′=6x 2+a ,∴6t 2+a =2t3+at +at +1,即4t 3+6t 2=0,解得t =0或t =-32,∵|MA |=|MB |,∴两切线的斜率互为相反数,即2a +6×⎝ ⎛⎭⎪⎫-322=0,解得a =-274. 答案:-27414.(2021·江西五校联考)已知函数f (x )=x +a2x,若曲线y =f (x )存在两条过(1,0)点的切线,则a 的取值范围是 .解析:f ′(x )=1-a2x2,设切点坐标为⎝ ⎛⎭⎪⎫x0,x0+a 2x0,则切线方程为y -x 0-a2x0=⎝ ⎛⎭⎪⎫1-a 2x20(x -x 0),又切线过点(1,0),所以-x 0-a2x0=⎝ ⎛⎭⎪⎫1-a 2x20(1-x 0),整理得2x 20+2ax 0-a =0,又曲线y =f (x )存在两条过(1,0)点的切线,故方程有两个不等实根,即满足Δ=4a 2-8(-a )>0,解得a >0或a <-2.答案:(-∞,-2)∪(0,+∞)15.已知函数f (x )=ax 3+3x 2-6ax -11,g (x )=3x 2+6x +12和直线m :y =kx +9,且f ′(-1)=0.(1)求a 的值;(2)是否存在k ,使直线m 既是曲线y =f (x )的切线,又是曲线y =g (x )的切线?如果存在,求出k 的值;如果不存在,请说明理由.解:(1)由已知得f ′(x )=3ax 2+6x -6a ,因为f ′(-1)=0,所以3a -6-6a =0,所以a =-2.(2)存在.由已知得,直线m 恒过定点(0,9),若直线m 是曲线y =g (x )的切线,则设切点为(x 0,3x 20+6x 0+12).因为g ′(x 0)=6x 0+6,所以切线方程为y -(3x 20+6x 0+12)=(6x 0+6)(x -x 0), 将(0,9)代入切线方程,解得x 0=±1.当x0=-1时,切线方程为y=9;当x0=1时,切线方程为y=12x+9.由(1)知f(x)=-2x3+3x2+12x-11,①由f′(x)=0得-6x2+6x+12=0,解得x=-1或x=2.在x=-1处,y=f(x)的切线方程为y=-18;在x=2处,y=f(x)的切线方程为y=9,所以y=f(x)与y=g(x)的公切线是y=9.②由f′(x)=12得-6x2+6x+12=12,解得x=0或x=1.在x=0处,y=f(x)的切线方程为y=12x-11;在x=1处,y=f(x)的切线方程为y=12x-10,所以y=f(x)与y=g(x)的公切线不是y=12x+9.综上所述,y=f(x)与y=g(x)的公切线是y=9,此时k=0.。
高考数学必背公式与知识点过关检测(精华版)

第一部分:集合与常用逻辑用语1.子集个数:含n 个元素的集合有 个子集,有 个真子集,有 个非空子集,有 个非空真子集2.常见数集:自然数集: 正整数集: 或 整数集: 有理数集: 实数集:3.空集:φ是任何集合的 ,是任何非空集合的 .4.元素特点: 、 、 确定性5.集合的的运算: 集运算、 集运算、 集运算6.四种命题:原命题:若p ,则q ;逆命题:若 ,则 ;否命题:若 ,则 ;逆否命题:若 ,则 ; 原命题与逆命题,否命题与逆否命题互 ;原命题与否命题、逆命题与逆否命题互 ;原命题与逆否命题、否命题与逆命题互为 。
互为逆否的命题7.充要条件的判断:p q ⇒,p 是q 的 条件;p q ⇒,q 是p 的 条件;p q ⇔,,p q 互为 条件;若命题p 对应集合A ,命题q 对应集合B ,则p q ⇒等价于 ,p q ⇔等价于 注意区分:“甲是乙的充分条件(甲⇒乙)”与“甲的充分条件是乙(乙⇒甲)”; 8.逻辑联结词:或命题:p q ∨,,p q 有一为真即为 ,,p q 均为假时才为 ;且命题:p q ∧,,p q 均为真时才为 ,,p q 有一为假即为 ;非命题:p ⌝和p 为一真一假两个互为对立的命题 9.全称量词与存在量词:⑴全称量词-------“所有的”、“任意一个”等,用∀表示;全称命题p :)(,x p M x ∈∀;全称命题p 的否定⌝p : ; ⑵存在量词--------“存在一个”、“至少有一个”等,用∃表示;特称命题p :)(,x p M x ∈∃;特称命题p 的否定⌝p : ;第二部分:函数与导数及其应用1.函数的定义域:分母 0;偶次被开方数 0;0次幂的底数 0 ;对数函数的真数 0;指数与对数函数的底数 0且 1 2.分段函数:值域(最值)、单调性、图象等问题,先分段解决,再下结论; 分段函数是一个函数,其定义域是各段定义域的 、值域是各段值域的3.函数的单调性:设1x ,2[,]x a b ∈(1⇔[]1212()()0(),f x f x f x a b x x ->⇔-在上是 函数;(2)[]1212()()()0x x f x f x --<⇔[]1212()()0(),f x f x f x a b x x -<⇔-在上是 函数;(3)如果0)(>'x f ,则)(x f 为 函数;0)(<'x f ,则)(x f 为 函数; (4)复合函数的单调性:根据“同 异 ”来判断原函数在其定义域内的单调性.4.函数的奇偶性: ⑴函数的定义域关于 对称是函数具有奇偶性的前提条件.... ⑵)(x f 是 函数)()(x f x f -=-⇔;)(x f 是 函数)()(x f x f =-⇔. ⑶奇函数)(x f 在0处有定义,则⑷在关于原点对称的单调区间内:奇函数有 的单调性,偶函数有 的单调性⑸偶函数图象关于 轴对称、奇函数图象关于坐标 对称 5.函数的周期性:周期有关的结论:(约定a >0)(1))()(a x f x f +=,则)(x f 的周期T= ; (2))()(x f a x f -=+,或)0)(()(1)(≠=+x f x f a x f ,或1()()f x a f x +=-(()0)f x ≠, 则)(x f 的周期T=(3))()(a x f a x f -=+或)0)(()2(>=-a x f a x f ⇒)(x f 的周期为 6.函数的对称性:①()y f x =的图象关于直线 对称()()f a x f a x ⇔+=-(2)()f a x f x ⇔-=; ②()y f x =的图象关于直线 对称()()f a x f b x ⇔+=-()()f a b x f x ⇔+-=;7.对数运算规律:(1)对数式与指数式的互化:(2)对数恒等式:log 1a = ,log a a = ,log ba a = .lg 2+lg5= ,=lne(3)对数的运算性质:①加法:log log a a M N += ②减法: log aM N= ③数乘: log ()na M n R =∈ ④恒等式:log a N a =⑤log m n a b = ⑥换底公式:log log log m a m N N a=8.二次函数:二次函数c bx ax y ++=2(a ≠0)的图象的对称轴方程是 ,顶点坐标是 判别式ac b 42-=∆;0>∆时,图像与x 轴有 个交点;0=∆时,图像与x 轴有 个交点;0<∆时,图像与x 轴没有交点;9. 韦达定理:若x 1, x 2是一元二次方程)0(02≠=++a c bx ax 的两个根,则:x 1+x 2= ,x 1x 2= .10.零点定理:若y=f(x)在[a ,b ]上满足 , 则y=f(x)在(a ,b )内至少有一个零点11.常见函数的导数公式:①'()C = ;②'(n x =) ;'(nx =) ③'(sin x =) ; ④'(cos x =) ; ⑤'(x e =) ; ⑥ '(x a =) ; ⑦'(ln x =) ; ⑧'=(logx ) . 12.导数运算法则:()()f x g x '⋅=⎡⎤⎣⎦(1) ;()()2f x g x '⎡⎤=⎢⎥⎣⎦() .13.曲线的切线方程:函数)(x f y =在点0x 处的导数是曲线)(x f y =在))(,(00x f x P 处的切线的斜率为)(0x f ',相应的切线方程是 .第三部分:三角函数、三角恒等变换与解三角形1.角度制与弧度制互化:360°= rad ,180°= rad ,1°= ≈ rad ,1rad= ≈ 2.若扇形的圆心角为()αα为弧度制,半径为r ,弧长为l ,周长为C ,面积为S ,则l = ,C = ,S= = .3.三角函数定义式:角α终边上任一点(非原点)P ),(y x ,设r OP =|| 则sin α= ,cos α= ,tan α=4.同角三角函数的基本关系:()1平方关系:()2tan =α商数关系: . 5.函数的诱导公式:口诀: .()()1sin 2sin k παα+=, , .(k ∈Z )(2) , ,()tan tan παα+=. (3) , ,()tan tan αα-=-. (4) , ,()tan tan παα-=-.()5sin cos 2παα⎛⎫-=⎪⎝⎭, .(6) ,cos sin 2παα⎛⎫+=- ⎪⎝⎭.8.几个常见三角函数的周期: ①x y sin =与x y cos =的周期为 .②)sin(ϕω+=x y 或)cos(ϕω+=x y (0≠ω)的周期为 .③2tan x y =的周期为 .④xy cos =的周期为9. 两角和与差的正弦、余弦和正切公式:()1cos αβ-=() ; ()2cos αβ+=() ; ()3sin αβ-=() ; ()4sin αβ+=() ; ()5tan αβ-=() ; ()6tan αβ+=() .10. 二倍角的正弦、余弦和正切公式:sin 2α=cos2α= = =2cos α⇒=降次公式: ,2sin α= , sin cos αα=tan 2α=11.引入辅助角公式: sin cos a b αα+= . (其中,辅助角ϕ所在象限由点(,)a b 所在的象限决定,tan b aϕ= ).12. 正弦定理: . (R 是ABC ∆外接圆直径) 注:①C B A c b a sin :sin :sin ::=;②C R c B R b A R a sin 2,sin 2,sin 2===;③C B A cb a Cc B b A a sin sin sin sin sin sin ++++=== 13. 余弦定理: ⇔ .(变式)(以A 角和其对边来表示)14. 三角形面积公式:ABC S ∆= = = . (用边与角的正弦值来表示) 三角形面积导出公式:ABC S ∆= (r 为ABC ∆内切圆半径)= (R 外接圆半径)15. 三角形内切圆半径r = 外接圆直径2R = = =第四部分:平面向量、数列与不等式1. 平面向量的基本运算:设11(,)a x y =,22(,)b x y =;(0b ≠)= ;a b -= ;a b ⋅= (定义公式)= (坐标公式). a 在b 方向上的投影为. = (坐标公式) a b ⊥⇔ (一般表示) ⇔ (坐标表示) .a ∥b ⇔ (一般表示)⇔ (坐标表示).cos θ=夹角公式: = (坐标公式).2.若G 为ABC ∆的重心,则 =0;且G 点坐标为 ( , )3.三点共线的充要条件:P ,A ,B 三点共线⇔ →OP =x →OA +y →OB 且 =14.三角形的四心重心:三角形三条 交点.外心:三角形三边 相交于一点. 内心:三角形三 相交于一点.垂心:三角形三边上 的相交于一点.5. 数列{n a }中n a 与n S 的关系n a =7.常见数列的和:①1+2+3+……+n=②12+22+32+……+n 2=③13+23+33+……+n 3=8.一元二次不等式解的讨论.0>∆0=∆0<∆二次函数c bx ax y ++=2(0>a )的图象一元二次方程()的根002>=++a c bx ax的解集)0(02>>++a c bx ax的解集)0(02><++a c bx ax9. 均值不等式: 若0a >,0b >,则 ⇔ ; 10. 重要不等式: 11.极值定理:已知y x ,都是正数,则有:(1)如果积xy 是定值p ,那么当y x =时和y x +有最小值 ; (2)如果和y x +是定值s ,那么当y x =时积xy 有最大值 .12.两个著名不等式:(1)平均不等式: 如果a ,b 都是正数,那么 (当仅当a =b 时取等号)即:平方平均≥算术平均≥几何平均≥调和平均(a 、b 为正数) 特别地,222()22a b a b ab ++≤≤(当a = b 时,222()22a b a b ab ++==)),,,(332222时取等c b a R c b a c b a c b a ==∈⎪⎭⎫ ⎝⎛+++≥++ 第五部分:立体几何与解析几何1. 三视图与直观图:原图形与直观图面积之比为 2. 常见几何体表面积公式:圆柱的表面积 S= 圆锥的表面积S=圆台的表面积 S= 球的表面积 S= 3.常见几何体体积公式:柱体的体积 V= 锥体的体积 V=台体的体积 V= 球体的体积 V= 4. 常见空间几何体的有关结论:⑴棱锥的平行截面的性质:如果棱锥被平行于底面的平面所截,那么所得的截面与底面 ,截面面积与底面面积的比等于顶点到截面距离与棱锥高的 ;相应小棱锥与小棱锥的侧面积的比等于顶点到截面距离与棱锥高的 . ⑵长方体从一个顶点出发的三条棱长分别为a ,b ,c ,则体对角线长为 ,全面积为 ,体积V= ⑶正方体的棱长为a ,则体对角线长为 ,全面积为 ,体积V= ⑷球与长方体的组合体: 长方体的外接球的直径=长方体的 长.球与正方体的组合体:正方体的内切球的直径=正方体的 , 正方体的棱切球的直径=正方体的 长, 正方体的外接球的直径=正方体的体 长. ⑸正四面体的性质:设棱长为a ,则正四面体的:① 高: ;②对棱间距离: ;③内切球半径: ;④外接球半径: 5. 空间向量中的夹角和距离公式:(1)空间中两点A 111(,,)x y z ,B 222(,,)x y z 的距离d = (2)异面直线夹角:(0,]2πθ∈cosθ= (两直线方向向量为,a b )(3)线面角:[0,]2πθ∈,且sin θ= (l ,n 为直线的方向向量与平面的法向量)(4)二面角:[0,]θπ∈,且cos θ= (两平面的法向量分别为1n 和2n )(5)点到面的距离:平面α的法向量为n ,平面α内任一点为N ,点M 到平面α的距离d =6.直线的斜率:k = = (θ为直线的倾斜角,11(,)A x y 、22(,)B x y 为直线上的两点) 7. 直线方程的五种形式:直线的点斜式方程: (直线l 过点111(,)P x y ,且斜率为k ). 直线的斜截式方程: (b 为直线l 在y 轴上的截距).直线的两点式方程: (111(,)P x y 、222(,)P x y 12x x ≠,12y y ≠). 直线的截距式方程: (a 、b 分别为直线在x 轴、y 轴上的截距,且0,0≠≠b a ).直线的一般式方程: (其中A 、B 不同时为0). 8.两条直线的位置关系:(1)若111:l y k x b =+,222:l y k x b =+,则: ① 1l ∥2l ⇔ 且 ;.(2)若1111:0l A x B y C ++=,2222:0l A x B y C ++=,则:①1l ∥2l ⇔ 且 ;②. 12l l ⊥⇔ . 9.距离公式:(1)点111(,)P x y ,222(,)P x y 之间的距离: (2)点00(,)P x y 到直线0Ax By C ++=的距离:(3)平行线间的距离:10Ax By C ++=与20Ax By C ++=的距离: 10.圆的方程:(1)圆的标准方程:(2)圆的一般方程: ()0422>-+F E D 11.直线与圆的位置关系:判断圆心到直线的距离d 与半径R 的大小关系 (1)当 时,直线和圆 (有两个交点); (2)当 时,直线和圆 (有且仅有一个交点); (3)当 时,直线和圆 (无交点);12. 圆与圆的位置关系:判断圆心距d 与两圆半径和12R R +,半径差12R R -(12R R >)的大小关系:(1)当 时,两圆 ,有4条公切线; (2)当 时,两圆 ,有3条公切线; (3)当 时,两圆 ,有2条公切线; (4)当 时,两圆 ,有1条公切线; (5)当 时,两圆 ,没有公切线;13. 直线与圆相交所得弦长|AB|= (d 为直线的距离r 为半径) 14.椭圆的定义:(1)第一定义:平面内与两个定点21F F 、的距离和等于常数 的点的轨迹叫椭圆.这两个定点叫椭圆的焦点,两焦点间的距离叫焦距.(222c b a +=)(2)标准方程:焦点在x 轴上: ;焦点在y 轴上: .15.双曲线的定义:(1)第一定义:平面内与两个定点21F F 、的距离之差的绝对值等于常数: 的点的轨迹叫双曲线.这两个定点叫双曲线的焦点,两焦点间的距离叫焦距.(222a b c +=)(2)标准方程:焦点在x 轴上: ;焦点在y 轴上: . 16.抛物线的定义:(1)平面内与一个定点F 和一条定直线l (点F 不在l 上)的距离的 的点的轨迹叫做双曲线.这个定点是抛物线的焦点,定直线是抛物线的准线.(2)标准方程:焦点在x 轴上: ;焦点在y 轴上: .17.离心率:e = (椭圆的离心率 ,双曲线的离心率 ,抛物线的离心率 )18.双曲线的渐近线:22221x y a b -=(0a >,0b >)的渐近线方程为 ,且与22221x y a b -=具有相同渐近线的双曲线方程可设为2222x y a bλ-=. 19.过抛物线焦点的直线:倾斜角为θ的直线过抛物线22y px =的焦点F 且与抛物线交于11(,)A x y 、22(,)B x y 两点(10y >):|AF|= |BF|= |AB|= = x 1x 2= y 1y 2=1|AF| +1|BF|= 20.焦点三角形的面积:(1)椭圆:S= ;(2)双曲线:S= (12F PF θ∠=) 21.几何距离:(1)椭圆双曲线特有距离:①长轴(实轴): ; ②短轴(虚轴): ; ③两焦点间距离: .(2)焦准距:①椭圆、双曲线: ; ②抛物线: . (3)通径长:①椭圆、双曲线: ; ②抛物线: . 22.直线被曲线所截得的弦长公式:若弦端点为A ),(),,(2211y x B y x ,则|AB|= = = 23. 中点弦问题: 椭圆:k AB k OP = 双曲线:k AB k OP =第六部分:统计与概率1. 总体特征数的估计:⑴样本平均数⎺x= = ;⑵样本方差;S 2= = ; ⑶样本标准差S= 2.概率公式:⑴互斥事件(有一个发生)概率公式:P(A+B)=⑵古典概型:基本事件的总数数为N ,随机事件A 包含的基本事件个数为M ,则事件A 发生的概率为:P(A)=⑶几何概型:等)区域长度(面积或体积试验的全部结果构成的积等)的区域长度(面积或体构成事件A A P =)( 3.离散型随机变量: ⑴随机变量的分布列:①随机变量分布列的性质:p i ≥ , i=1,2,3,…; p 1+p 2+…=均值(又称期望):EX =方差:DX =注:DX a b aX D b aEX b aX E 2)(;)(=++=+;③二项分布(独立重复试验):若X ~B (n , p ),则EX = , DX =注:k n k k n p p C k X P --==)1()( ⑵条件概率: P (B|A )=注:0≤P (B|A )≤1⑶独立事件同时发生的概率:P (AB )=第七部分:复数与计数原理1. 复数的基本概念:z a bi =+(a ,b R ∈) (1)实部: ;虚部: ; 虚数单位:i 2=(2)模:|z |= =(3)共轭复数:-z= (4)在复平面内对应的点为 (5)复数相等:a+bi=c+di (a ,b ,c ,d ∈R )⇔2. 复数的基本运算:(1)加减法:(a+bi )+(c+di )= (a+bi )-(c+di )=(2)乘法:(a+bi )×(c+di )=(3)除法:(a+bi )÷(c+di )=注:对虚数单位i ,有1 , ,1,4342414=-=-==+++n n n n i i i i i i .3.分类计数原理(加法原理)与分步计数原理(乘法原理):.(1)完成一件事有n 类不同方案,在第1类方案中有1m 种不同的方法,在第2类方案中有2m 种不同的方法,…,在第n 类方案中有n m 种不同的方法.那么完成这件事共有N=种不同的方法.(2)完成一件事情,需要分成n个步骤,做第1步有1m种不同的方法,做第2步有2m种m种不同的方法.那么完成这件事共有N=种不同的方法……做第n步有n不同的方法.4.排列数公式:= = ;==(m≤ n, m、n∈N*) 规定0!1∈,5.组合数公式:= (n,m N*≤);且m n6. 组合数性质:;7.二项式定理:(a+b)n=C叫做二项式系数)(rn8.二项展开式的通项公式:T r+1=(r=0,1,2……,n)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
[],a b 上是 函数;
[],a b 上是 函数;
为 函数;
. 前提条件.... )()(x f x f =-.
的单调性,偶函数有 的单调性
1)()
a f x +=-(()0)f x ≠, 的周期为 (2)()f a x f x -=; ()()f a
b x f x +-=; ()b x -
___________. AB OB OA
=-=设
11
(,)
a x y
=,
22
(,)
b x y
=(0
b≠)
=;a b
-=a=
a b⋅=(定义公式)坐标公式).
a在b方向上的投影为.=
a b
⊥⇔(一般表示).
a∥b⇔.
cos
夹角公式:坐标公式).
2.若G为ABC
∆=0;
且G点坐标为)
(1)
OP xOA x OB
=+-
,
n
a为末项.
,
n
a为末项.
.
(2)若{}n a 、{}n b 为等差数列,则{}n n a b ±为等差数列.
(3){}n a 为等差数列,n S 为其前n 项和,则232,,m m m m m S S S S S --也成等差数列. (4),,0p q p q a q a p a +===则 ; ★2.等比数列:
通项公式:(1) ________.n a = ,其中1a 为首项,n 为项数,q 为公比.
(2)推广:_________.n a =
前n 项和:__________________.n S == 常用性质:(1)若m+n=p+q ,则有
_______________________
;
注:若,m n p a a a 是的等比中项,则有 2
m n p a a a =⋅⇔n 、m 、p 成等比. (2)若{}n a 、{}n b 为等比数列,则{}n n a b ⋅为等比数列. 7.常见数列的和:
①1+2+3+……+n= ②12
+22
+32
+……+n 2
= ③13
+23
+33
+……+n 3
= 8.一元二次不等式解的讨论.
0>∆
0=∆
0<∆
二次函数
c bx ax y ++=2
(0>a )的图象
一元二次方程
()的根
00
2>=++a c bx ax
的解集)0(02>>++a c bx ax
的解集
)0(02><++a c bx ax
9. 重要不等式:
基本不等式: 若0,0a b >>则 ⇔ ; 11.极值定理:已知y x ,都是正数,则有:
(1)如果积xy 是定值p ,那么当y x =时和y x +有最小值 ; (2)如果和y x +是定值s ,那么当y x =时积xy 有最大值 .
12.均值不等式链:
如果a ,b 都是正数,那么 (当仅当a =b 时取等号) 即:平方平均≥算术平均≥几何平均≥调和平均(a 、b 为正数)
特别地,22
2
()22
a b a b ab ++≤≤(当a = b 时,222()22a b a b ab ++==)
),,,(332
222时取等c b a R c b a c b a c b a ==∈⎪⎭
⎫
⎝⎛+++≥++ ⇒幂平均不等式:2212
22
21)...(1
...n n a a a n
a a a +++≥+++ 13.均值定理:已知y x ,都是正数,则有 (1)已知,,,a
b x y R +
∈,若1ax by +=则有
21111()()2()by ax ax by a b a b ab a b x y x y x y
+=++=+++≥++=+. (2)已知,,,a b x y R +
∈,若1a b x y
+=则有
2
()()2()a b ay bx
x y x y a b a b ab a b x y x y +=++=+++≥++=+
第五部分:立体几何与解析几何
1. 三视图与直观图:
原图形与直观图面积之比为
2. 常见几何体表面积公式:
圆柱的表面积S= 圆锥的表面积S=
圆台的表面积S= 球的表面积S=
3.常见几何体体积公式:
柱体的体积V= 锥体的体积V=
台体的体积V= 球体的体积V=
4. 常见空间几何体的有关结论:
⑴棱锥的平行截面的性质:如果棱锥被平行于底面的平面所截,那么所得的截面与底面,截面面积与底面面积的比等于顶点到截面距离与棱锥高的;相应小棱锥与小棱锥的侧面积的比等于顶点到截面距离与棱锥高的.
⑵长方体从一个顶点出发的三条棱长分别为a,b,c,则体对角线长为,全面
积为,体积V=
⑶正方体的棱长为a,则体对角线长为 ,全面积为,体积V=
⑷球与长方体的组合体: 长方体的外接球的直径=长方体的长.
球与正方体的组合体:正方体的内切球的直径=正方体的,
正方体的棱切球的直径=正方体的长, 正方体的外接球的直径=正方体的体长.
⑸正四面体的性质:设棱长为a,则正四面体的:
①高:;②对棱间距离:;③内切球半径:;④外接球半径:
5.立体几何常用的六个定理(三种语言)
(1)直线和平面平行的判定定理
(2)直线和平面平行的性质定理
(3)平面和平面平行的判定定理(4)直线和平面垂直的判定定理
(5)平面和平面垂直的判断定理
(6)平面和平面垂直的性质定理
6.直线的斜率:k= =
(α为直线的倾斜角,
11
(,)
A x y、
22
(,)
B x y为直线上的两点)
7. 直线方程的五种形式:
直线的点斜式方程:(直线l过点
111
(,)
P x y,且斜率为k).
直线的斜截式方程:(b为直线l在y轴上的截距).
直线的两点式方程:(
111
(,)
P x y、
222
(,)
P x y
12
x x
≠,
12
y y
≠).
直线的截距式方程:(a、b分别为直线在x轴、y轴上的截距,且0
,0≠
≠b
a). 直线的一般式方程:0
Ax By C
++= (其中A、B不同时为0).
直线0
Ax By C
++=的法向量:(,)
l A B
'=,方向向量:(,)
l B A
=-
8.两条直线的位置关系:
(1)若
111
:l y k x b
=+,
222
:
l y k x b
=+,则:
①
1
l∥
2
l⇔且;.
(2)若
1111
:0
l A x B y C
++=,
2222
:0
l A x B y C
++=,则:
①
1
l∥
2
l⇔且;②.
12
l l
⊥⇔.
9.距离公式:
(1)点
111
(,)
P x y,
222
(,)
P x y之间的距离:。
