专项复习测试卷

合集下载

中考数学复习《反比例函数》专项测试卷(带答案)

中考数学复习《反比例函数》专项测试卷(带答案)学校:___________班级：___________姓名：___________考号：___________一、单选题1．若点()1,2A x ，()2,1B x -和()3,4C x 都在反比例函数8y x=的图像上，则1x ，2x 和3x 的大小关系是( ) A.123x x x <<B.231x x x <<C.132x x x <<D.213x x x <<2．若点()26-，在反比例函数ky x=的图象上，则下列说法正确的是( ) A.该函数的图象经过点()34--，B.该函数的图象位于第一、三象限C.当0x >时，y 的值随x 值的增大而增大D.当1x >-时，4y >3．如图，在同一平面直角坐标系中函数y ax a =+与函数ay x=的图象可能是( ) A. B. C. D.4．如图，点A 是双曲线()160y x x =-<上的一点，点B 是双曲线()60y x x=-<上的一点，AB 所在直线垂直x 轴于点C ，点M 是y 轴上一点，连接MA 、MB ，则MAB △的面积为( )A.5B.6C.10D.165．如图，点A ，B 为反比例函数()0ky x x=>的图象上的两点，且满足45AOB ∠=︒，若点A 的坐标为()3,5，则点B 的坐标是( ).A.15215,2⎛⎫ ⎪ ⎪⎝⎭B.1010,2⎛ ⎝⎭C.()8,2D.()8,36．如图，已知点A 、B 分别在反比例函数y ＝1x （x ＞0），y ＝－4x（x ＞0）的图象上，且OA⊥OB ，则OBOA的值为( )A.4B.2C.14D.127．如图,在ABC 中2AC BC == 90ACB ∠=︒ AC x ∥轴点D 是AB 的中点点C 、D 在(k 0,x 0)ky x=≠>的图象上则k 的值为( )A.1-B.2-C.1D.28．已知蓄电池的电压为定值（电压三星近总度阻）使用蓄电池时电流（单位：A ）与电阻尺（单位：Ω）是反比例函数关系它的图象如图所示下列说法不正确的是( )A.函数解析式为60I R=B.蓄电池的电压是C.当6ΩR =时 8A I =D.当10A I ≤时 6R ≥Ω9．如图在平面直角坐标系中直线24y x =-+与x 轴、y 轴分别交于A 、B 两点以AB 为边在第一象限作正方形ABCD 点D 在双曲线()0ky k x=≠上.将正方形沿x 轴负方向平移a 个单位长度后点C 恰好落在该双曲线上则a 的值( )A.1B.2C.3D.410．如图直线22y x =-与x 轴 y 轴分别交于点A B 与反比例函数()0ky k x=>图像交于点C .点D 为x 轴上一点（点D 在点A 右侧）连接BD 以BA BD 为边作ABDE E 点刚好在反比例函数图像上设(),E m n 连接EC DC 若1()2ACED S AD AD n =+四边形则k 的值为( )A.8B.10C.12D.1611．如图直线y kx =与双曲线3y x -=在同一坐标系中如图所示则不等式3x-<的解集为( )A.01x <<B.1x <-C.1x <-或01x <<D.10x -<<或1x >12．智能手机已遍及生活中的各个角落手机拍照功能也越来越强高档智能手机还具有调焦（调整镜头和感光芯片的距离）的功能.为了验证手机摄像头的放大率（摄像头的放大率是指成像长度与实物长度的比值也可计算为像距与物距的比值）小明用某透镜进行了模拟成像实验得到如图所示的像距v 随物距u 变化的关系图像下列说法不正确的是( )A.当物距为45.0cm 时像距为13.0cmB.当像距为15.0cm 时透镜的放大率为2C.物距越大像距越小D.当透镜的放大率为1时物距和像距均为20cm13．某商家设计了一个水箱水位自动报警仪其电路图如图1所示其中定值电阻110ΩR =2R 是一个压敏电阻用绝缘薄膜包好后放在一个硬质凹形绝缘盒中放入水箱底部受力面水平承受水压的面积S 为0.012m 压敏电阻的阻值随所受液体压力F 的变化关系如图2所示（水深h 越深压力F 越大）电源电压保持6V 不变当电路中的电流为0.3A 时报警器（电阻不计）开始报警水的压强随深度变化的关系图象如图3所示（参考公式：UI R=1000Pa 1kPa =）.则下列说法中不正确的是( )2R F pS =A.当水箱未装水（）时压强p 为0kPaB.当报警器刚好开始报警时水箱受到的压力F 为40NC.当报警器刚好开始报警时水箱中水的深度h 是0.8mD.若想使水深1m 时报警应使定值电阻1R 的阻值为二、填空题14．一个圆柱形蓄水池的底面半径为x cm 蓄水池的侧面积为40π2cm 则这个蓄水池的高h （cm ）与底面半径x （cm ）之间的函数关系式为_____.15．在反比例函数12my x-=的图象上的图象在二、四象限则m 的取值范围是_______. 16．若点()11,A y -、21,4B y ⎛⎫- ⎪⎝⎭、()31,C y 都在反比例函数21x k y +=（k 为常数）的图象上则1y 、2y 、3y 的大小关系为_____.17．如图点(3,1)P -是反比例函数m y x =的图象上的一点设直线y kx =与双曲my x=的两个交点分别为P 和P 当mkx x>时写出x 的取值范围_____.18．如图在平面直角坐标系xOy 中正方形OABC 的边OC 、OA 分别在x 轴和y 轴上 OA ＝10 点D 是边AB 上靠近点A 的三等分点将⊥OAD 沿直线OD 折叠后得到⊥OA ′D 若反比例函数y kx=（k ≠0）的图象经过A ′点则k 的值为_____. 0m h =12Ω19．如图在平面直角坐标系中直线12y k x =+与x 轴交于点A 与y 轴交于点B 与双曲线2(0)k y x x=>交于点C 连接OC .若52,sin 5OBC S BOC =∠=△ 则12k +的值是______.20．如图点1A 2A 3A …在反比例函数()10y x x=>的图象上点1B 2B 3B … n B 在y 轴上且11212323B OA B B A B B A ∠=∠=∠=直线y x =与双曲线1y x=交于点1A 111B A OA ⊥ 2221B A B A ⊥ 3323B A B A ⊥ … 则2023B 的坐标是________.三、解答题21．如图所示一次函数y kx b =+的图象与反比例函数my x=的图象相交于两点(1),A n (2,1)B -- 与y 轴相交于点C .(1)求反比例函数和一次函数解析式； (2)直接写出：不等式mkx b x+>解集是______； (3)依据相关数据求AOB 的面积.22．如图菱形OABC 的边OA 在y 轴正半轴上点B 的坐标为()48，.反比例函数11k y x=的图象经过菱形对角线AC OB ，的交点D 设直线OC 的解析式为22y k x =.(1)求反比例函数的解析式； (2)求菱形OABC 的边长；(3)请结合图象直接写出不等式120k k x x-<的解集. 23．如图▱OABC 的顶点O 与坐标原点重合边OA 在x 轴正半轴上 60AOC ∠=︒2OC = 反比例函数()0ky x x=>的图像经过顶点C 与边AB 交于点D.(1)求反比例函数的表达式.(2)尺规作图：作OCB ∠的平分线交x 轴于点E.（保留作图痕迹不写作法） (3)在（2）的条件下连接DE 若DE CE ⊥ 求证：AD AE =. 24．如图已知一次函数26y x =+与反比例函数()0ky x x=>的图象交于点()1,A m 与x 轴交于点B .(1)填空：m 的值为______ 反比例函数的解析式为______； (2)直接写出当0x >时 26kx x+<的解集； (3)点P 是线段AB 上一动点（不与A 、B 点重合）过P 作直线PM x ∥轴交反比例函数的图象于点M 连接BM .若PMB △的面积为S 求S 的取值范围.25．如图已知抛物线2y x bx =+与x 轴交于O (4,0)A 两点点B 的坐标为(0,3)-. （1）求抛物线的对称轴；（2）已知点P 在抛物线的对称轴上连接OP BP .若要使OP BP +的值最小求出点P 的坐标；（3）将抛物线在x 轴下方的部分沿x 轴翻折其余部分保持不变得到一个新的图象.当直线(0)y x m m =+≠与这个新图象有两个公共点时在反比例函数y mx=的图象中y 的值随x 怎样变化？判断并说明理由.26．如图在平面直角坐标系中正六边形ABCDEF 的对称中心P 在反比例函数()10,0ky k x x=>>的图象上边AB 在x 轴上点F 在y 轴上已知23AB =.（1）判断点E 是否在该反比例函数的图象上请说明理由；（2）求出直线EP ：()20y ax b a =+≠的解析式并根据图象直接写出当0x >时不等式kax b x+>的解集. 27．如图① 有一块边角料ABCDE 其中AB BC DE EA 是线段曲线CD 可以看成反比例函数图象的一部分.测量发现：90A E ∠=∠=︒ 5AE = 1AB DE == 点C 到AB AE 所在直线的距离分别为2 4.（1）小宁把A B C D E 这5个点先描到平面直角坐标系上记点A 的坐标为()1,0-；点B 的坐标为()1,1-.请你在图②中补全平面直角坐标系并画出图形ABCDE ；（2）求直线BC 曲线CD 的函数表达式；（3）小宁想利用这块边角料截取一个矩形MNQP 其中M N 在AE 上（点M 在点N 左侧）点P 在线段BC 上点Q 在曲线CD 上.若矩形的面积是53则=_________.参考答案1．答案：B解析：将三点坐标分别代入函数解析式8y x=得： 182x = 解得14x =； 28-1x =解得28x =-； 384x =解得； 824-<<故选：B. 2．答案：C解析：⊥点()26-，在函数ky x=的图象上 ⊥2(6)120k =⨯-=-< ⊥函数ky x=位于第二、四象限在每个象限内 y 的值随x 的增大增大 ⊥()341212-⨯-=≠-⊥该函数的图象不经过点()34--，把=1x -代入12y x=求得12y = ⊥当10x -<<时 12y > 综上只有选项C 说法正确故选：C. 3．答案：A解析：当0a ＞时一次函数图像经过第一、二、三象限反比例函数图像位于一、三象限可知A 符合题意；32x =231x x x ∴<<当0a ＜时一次函数图像经过第二、三、四象限反比例函数图像位于二、四象限可知B C D 不符合题意.故选：A.4．答案：A解析：如图所示作MN BA ⊥交BA 的延长线于N则12AMB S BA MN =⋅设点A 的坐标为16a a ⎛⎫- ⎪⎝⎭， <0aAB 所在直线垂直x 轴于点CB ∴点坐标为6a a ⎛⎫- ⎪⎝⎭，16610AB a a a ⎛⎫∴=---=- ⎪⎝⎭ MN a =()11101105222ABM S AB MN a a a a ⎛⎫⎛⎫∴=⋅=⨯-⨯=⨯-⨯-= ⎪ ⎪⎝⎭⎝⎭故选：A.5．答案：A解析：将OA 绕O 点顺时针旋转90︒到OC 连接AB 、CB作AM y ⊥轴于MCN x ⊥轴于N点A 的坐标为()3,53AM ∴= 5OM =45AOB ∠=︒45BOC ∠=︒∴在AOB 和COB △中OA OC AOB COBOB OB =⎧⎪∠=∠⎨⎪=⎩(SAS)AOB COB ∴△≌△AB CB ∴=90AOM AON CON AON ∠+∠=︒=∠+∠AOM CON ∴∠=∠ 在AOM 和CON 中AOM CON AMO ONCOA OC ∠=∠⎧⎪∠=∠⎨⎪=⎩ (AAS)AOM CON ∴△≌△3CN AM ∴== 5ON OM == (5,3)C ∴-点A 为反比例函数(0)k y x x=>图象上的点 3515k ∴=⨯= 15y x ∴=设B 点的坐标为15(,)m m AB CB =22221515(3)(5)(5)(3)m m m m ∴-+-=-++解得215m =（负数舍去）15215,B ⎛∴ ⎝⎭故选A.6．答案：B解析：作AC y ⊥轴于C BD y ⊥轴于D 如图点A 、B 分别在反比例函数1(0)y x x => 4(0)y x x=->的图象上 11122OAC S ∆∴=⨯= 1|4|22OBD ∆=⨯-=OA OB ⊥90AOB ∠=︒∴90AOC BOD ∴∠+∠=︒AOC DBO ∴∠=∠Rt AOC Rt OBD ∴∆∆∽ ∴212()2AOC OBD S OA S OB ∆∆== ∴12OA OB =. ∴2OB OA=. 故答案为B. 7．答案：B解析：设(0,)A b 根据题意(2,)C b - (2,2)B b -+点D 是AB 的中点(1,1)D b ∴-+点C 、D 在(k 0,x 0)k y x=≠>的图象上 2(1)k b b ∴=-=-+解得1b =22k b ∴=-=-故选：B.8．答案：C解析：设图象过蓄电池的电压是A 、B 选项正确不符合题意；当=6ΩR 时 (A 6010)6I ==∴C 选项错误符合题意；当10I =时 6R =由图象知：当10A I ≤时 6R ≥Ω∴D 选项正确不符合题意；故选：C.9．答案：B解析：作CE y ⊥轴于点E 交双曲线于点G 作DF x ⊥轴于点F在24y x =-+中令0x = 解得4y =∴B 的坐标是(0,4)令0y = 解得2x =∴A 的坐标是(2,0)kI R =(5,12)60k ∴=60I R ∴=∴60V ∴4OB ∴= 2OA =90BAD ∠=︒90BAO DAF ∴∠+∠=︒直角ABO △中90BAO OBA ∠+∠=︒DAF OBA ∴∠=∠在OAB △和FDA △中DAF OBA BOA AFD AD AD ∠=∠⎧⎪∠=∠⎨⎪=⎩(AAS)OAB FDA ∴≌△△同理 OAB FDA BEC ≌≌△△△ 4AF OB EC ∴=== 2DF OA BE ===∴D 的坐标是(6,2) C 的坐标是(4,6)点D 在双曲线(0)k y k x=≠上 6212k ∴=⨯=∴函数的解析式是：12y x =把6y =代入12y x=得：2x = 422a ∴=-=故选B.10．答案：C解析：直线与x 轴 y 轴分别交于点A B(1,0)A ∴ (0,2)B -作EF x ⊥轴于F 如图所示：22y x =-四边形是平行四边形在和中E 点刚好在反比例函数图像上设C 的纵坐标为hABDE AE BD ∴=//DE AB DAE ADB ∴∠=∠AEF △DBO △EAF BDO AFE DOB AE BD ∠=∠⎧⎪∠=∠⎨⎪=⎩(AAS)AEF DBO ∴≌△△2EF OB ∴==AF OD =1DF OA ∴==(,)E m n 2m AD ∴=+2n =2(2)k mn AD ∴==+122AD k ∴=-//DE BC AED CED S S ∴=△△()11122222ACD CED ACD AED ACED S S S S S AD h AD AD h ∴=+=+=⋅+⋅=+四边形△△△△()12ACED S AD AD n =+四边形122h AD k ∴==-C 的纵坐标为代入得解得反比例函数图像经过点C 解得 20k =（舍去） 12k∴=故选：C.11．答案：D解析：有题意可知当3y =时 33x= 解得=1x - ∴直线y kx =与双曲线3y x=在第二象限交点的坐标为1,3)- 由中心对称可得直线y kx =与双曲线3y x=在第四象限交点的坐标为3)- ∴观察图象可得不等式3kx x<的解集为10x <<或1x >. 故选：D.12．答案：B解析：由函数图象可知：当物距为45.0cm 时像距为13.0cm 故选项A 说法正确；由函数图象可知：当像距为15.0cm 时物距为300cm ．放大率为15.00.530.0= 故选项B 说法错误；由函数图象可知：物距越大像距越小故选项C 说法正确；由题意可知：当透镜的放大率为1时物距和像距均为20cm 故选项D 说法正确故选：B.13．答案：B解析：A.由图3得：当0h =时 0p = 故此项说法正确；122-22y x =-12222x -=-14x k =11(,2)42C k k ∴-(0)k y k x=>11(2)42k k k ∴-=112k =B.当报警器刚好开始报警时 260.310R =+ 解得210R =Ω 由图2可求得：2800R F =80010F∴= 解得80F N = 故此项说法错误； C.当报警器刚好开始报警时由上得80F N = 则有800.01p =⨯ 8P p k a ∴= 由图3求得10p h = 810h = 解得：0.8h = 故此项说法正确；D.当报警器刚好开始报警时：1260.3R R =+ 1220R R ∴+=Ω 当1h =时 10110kPa p =⨯= 100000.01100F N ∴=⨯= 28008100R ==Ω 120812R ∴=-=Ω 故此项说法正确. 故选：B.14．答案：20h x = 解析：根据题意得240x h ππ⋅= ⊥20h x=. 故答案为：20h x=. 15．答案：12m > 解析：由题意得反比例函数12m y x -=的图象在二、四象限内则120m -< 解得12m >. 故答案为12m >. 16．答案：213y y y << 解析：反比例函数2(1k k y x+=为常数） 210k +> ∴该函数图象在第一、三象限在每个象限内y 随x 的增大而减小点1(1,)A y -、1(4B 2)y 、3(1,)C y 都在反比例函数2(1k k y x +=为常数）的图象上 114-<- 点A 、B 在第三象限点C 在第一象限213y y y ∴<<故答案为：213y y y <<.17．答案：-3＜x ＜0或x ＞3 解析：⊥直线y =kx 与双曲线y =m x的两个交点分别为P 和P ′ P （-3 1） ⊥P ′的坐标为（3 -1）当mx ＞kx 时 x 的取值范围为-3＜x ＜0或x ＞3故答案为：-3＜x ＜0或x ＞3. 18．答案：48解析：如图所示：过A '作EF OC ⊥于F 交AB 于E⊥90OA D '∠=︒90OA F DA E ∴∠'+∠'=︒⊥90A F AOF O ∠'+∠'=︒D AOF AE ∴'=∠'∠D A FO AE '=∠∠'A OF DA E ∴''∠△△设A '（m n ）OF m ∴= A F n '=.正方形OABC 的边OC 、OA 分别在x 轴和y 轴上 OA ＝10点D 是边AB 上靠近点A 的三等分点∴ 103DE m = 10A E n '=-.310103m n m m ==-- 解得：m =6 n =8. ∴A '（6,8） ∴ 反比例函数中k =xy （0k ≠）=48 故答案为：48.19．答案：9解析：据题意可知(0,2)B 设(,)Cx y 52,sin OBC S BOC =∠=△1222x ∴⨯= 52xOC = 解得2,25x OC ==2225OC x y =+=即2425y +=得4y = 故(2,4)C 将(2,4)C 代入直线12y k x =+ 双曲线2(0)k y x x => 得到 121,8k k == 故12189k k +=+= 故答案为：9.20．答案：(0,22023解析：联立1y xy x =⎧⎪⎨=⎪⎩解得1x =由题意可知145AOB ∠=︒111B A OA ⊥11OA B ∴△为等腰直角三角形1122OB OA ∴==过2A 作22A H OB ⊥交y 轴于H 则容易得到21A H B H = 设21A H B H x == 则()2,2A x x +()21x x ∴+=解得121x = 221x =-（舍去）2121A H B H ∴== 1212222B B B H ==2222222OB ∴=+=同理可得323OB =则2n OB n =即(0,2n B n(20230,22023B ∴故答案为：(0,22023. 21．答案：(1)2y x = 1y x =+ (2)1x >或20x -<<(3)32解析：（1）反比例函数m y x =的图象过(2,1)--∴反比例函数的解析式为：2y x = 点(1),A n 在反比例函数图象上∴12n ⨯=∴2n =∴点A 的坐标为(1,2)将点A B 坐标代入一次函数y kx b =+中得221k b k b +=⎧⎨-+=-⎩解得11k b =⎧⎨=⎩∴一次函数的解析式为：1y x =+.（2）根据图象可知不等式0m kx b x+>>的解集是：1x >或20x -<<. 故答案为：1x >或20x -<<；（3）过点A 作AG y ⊥轴于点G 过点B 作BH y ⊥轴于点H 如下图所示：一次函数1y x =+与y 轴相交于点C∴C 点坐标为(0,1)∴1OC =A 点坐标为(1,2)∴1AG =B 点坐标为(2,1)--∴2BH =∴11123222AOB AOC BOC S S S ⨯⨯=+=+=△△△. 22．答案：(1)18y x = (2)5 (3)463x <或63x << 解析：（1）⊥菱形OABC 的对角线交于点D⊥OD DB =⊥点B 的坐标为()48，⊥点D 的坐标为()24，又⊥反比例函数11k y x=经过点D ⊥1248k =⨯= ⊥18y x =；（2）过点B 作BE y ⊥轴于点E设OA AB a == 则8AE a =- 4BE =在Rt ABE 中222BE AE AB += 即()22248x x +-= 解得：5x =⊥菱形OABC 的边长为5；（3）⊥点B 的坐标为()48， 5BC =⊥点C 的坐标为()43，代入22y k x =得：234k = 解得：234k =⊥234y x =令1y y = 则834x x = 解得：63x =±结合图象不等式120k k x x -<的解集为463x <或463x <<.23．答案：(1))30y x =>(2)见解析(3)见解析解析：（1）过点C 作CF OA ⊥于点F 如解图所示.在Rt COF △中2OC = 60COF ∠=︒30sin 6023CF C ∴=⋅==︒1cos60212OF OC =⋅︒=⨯=.(1,3C ∴. 把(3C 代入反比例函数()0ky x x =>中得3k =∴反比例函数的表达式为)30y x =>.（2）如解图所示所作射线CE 即为所求.（3）证明：在OABC 中//OC AB //CB OA .60AOC ∠=︒120OCB OAB ∴∠=∠=︒. CE 平分OCB ∠60OCE BCE OEC ∴∠=∠=∠=︒.DE CE ⊥90CED ∴∠=︒.180609030AED ∴∠=︒-︒-︒=︒.1801203030ADE ∴∠=︒-︒-︒=︒.AED ADE ∴∠=∠.AD AE ∴=.24．答案：(1)8 8y x= (2)01x << (3)S 的取值范围是2504S <≤ 解析：（1）⊥一次函数26y x =+的图象经过点()1,A m ⊥268m =+=⊥点()18A ，⊥反比例函数()0k y x x =>的图象经过点()18A ， ⊥188k =⨯=⊥反比例函数的解析式为8y x=；故答案为：8 8y x =；（2）观察图象得 26k x x+<的解集为1x <<；（3）设点P 的纵坐标为n ⊥点P 在线段AB 上点M 在8y x =的图象上 ⊥0n << 点P 的横坐标为62n -⊥PM x ∥轴⊥点M 的坐标为8n n ⎛⎫ ⎪⎝⎭， ⊥862n MP n -=. ⊥()21186125322244PMBn S MP n n n n -⎛⎫=⨯⨯=⨯-⨯=--+ ⎪⎝⎭. ⊥08n << 且104-<⊥当03n <<时 S 随n 的增大而增大当38n ≤<时 S 随n 的增大而减小. ⊥当3n =时 △的面积最大最大值为254 ⊥S 的取值范围是2504S <≤. 25．答案：（1）抛物线的对称轴为直线2x =（2）点P 的坐标为32,2⎛⎫- ⎪⎝⎭ （3）y 的值随x 的增大而增大解析：（1）由题意得：2440b +=4b ∴=-∴函数关系式为：24y x x =-∴对称轴为：4222b x a -=-=-=；（2）由题意得：OP PB +的值最小实际就是在同一直线一旁有两点在直线上求点只要取O 点关于直线2x =对称的点过AB 的直线与直线的交点就是点P设过AB 的直线为由在上()4,0A 2x =3y kx =-()4,0B 3y kx =-得34k =334AB y x =-P 在直线2x =上332342y ∴=⨯-=-32,2P ⎛⎫∴- ⎪⎝⎭；（3）24y x x =-在x 轴下方的部分沿x 轴翻转当直线()0y x m m =+≠有两个不相同的解0∴∆> 2340m -⨯> 得94m <又0> 904m ∴<< 在反比例函数m y x=中 904m k <=< y 随x 的增大而减小. 26．答案：（1）点E 在该反比例函数的图象上理由见解析（2）39y x =+ 323x <<解析：（1）六边形ABCDEF 为正六边形 23AB =23AB AF ∴== 60FAO =︒cos 603OA AF ∴=⋅︒= sin603AF =⋅︒=()0,3F ∴ )3,0A 连接PF PA六边形ABCDEF 为正六边形PE PF PA PB ∴=== 60EPF FPA APB ∠=∠=∠=︒EFP ∴△ FAP △ ABP △为等边三角形23AF PF ∴==()23,3P ∴ 把()23,3P 代入1k y x =得：23=解得：63k =043k ∴=-∴反比例函数表达式为163y x=. EFP △ FAP △为等边三角形∴点E 和点A 关于PF 对称)3,6E ∴ 把3x =代入163y x =得：13663y == ∴点E 在该反比例函数的图象上；（2）把()3,6E ()23,3P 代入()20y ax b a =+≠得： 6333a b a b ⎧=+⎪⎨=+⎪⎩ 解得：39a b ⎧=-⎪⎨=⎪⎩∴直线EP 的解析式为：39y x =+()3,6E ()23,3P由图可知当323x <<时 k b x +>. 27．答案：（1）见解析（2）直线BC 的函数表达式3522y x =曲线的函数表达式4y x= （3）72 解析：（1）根据点A 的坐标为()1,0- 点B 的坐标为()1,1- 补全x 轴和y 轴 90A E ∠︒∠== 5AE = 1AB DE == 点C 到AB AE 所在直线的距离分别为2 4 ()1,4C ∴ ()4,1D根据AB BC DE EA 是线段曲线CD 是反比例函数图象的一部分画出图形ABCDE如图所示（2）设线段BC 的解析式为y kx b =+ 把()1,1B - ()1,4C 代入得 14k b k b -+=⎧⎨+=⎩解得 3252k b ⎧=⎪⎪⎨⎪=⎪⎩3522y x ∴=+设曲线CD 的解析式为'k y x =把()1,4C 代入得 '41k = '4= 4y x ∴=；（3）设(),0M m 则35,22P m m ⎛⎫+ ⎪⎝⎭ 435,352222Q m m ⎛⎫ ⎪+ ⎪ ⎪+⎝⎭3522PM m ∴=+ 43522m m =-+354352222PM PQ m m m ⎛⎫ ⎪⎛⎫⋅=+- ⎪ ⎪⎝⎭ ⎪+⎝⎭23554223m m ∴--= 2915140m m ∴+-= 23m ∴= 或73m =-（舍去） 32572322PM ∴=⨯+=. 故答案为：72.。

中考化学专项复习测试卷：物质推断题测试卷(含解析)

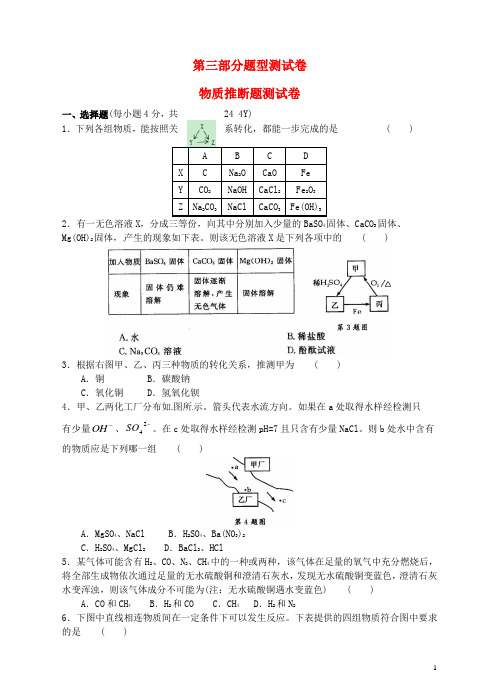
第三部分题型测试卷物质推断题测试卷一、选择题(每小题4分，共24 4Y)1．下列各组物质，能按照关系转化，都能一步完成的是 ( )2．有一无色溶液X，分成三等份，向其中分别加入少量的BaSO4固体、CaCO3固体、Mg(OH)2固体，产生的现象如下表。

则该无色溶液X是下列各项中的 ( )3．根据右图甲、乙、丙三种物质的转化关系，推测甲为 ( )A．铜 B．碳酸钠C．氧化铜 D．氢氧化钡4．甲、乙两化工厂分布如图所示。

箭头代表水流方向。

如果在a处取得水样经检测只SO。

在c处取得水样经检测pH=7且只含有少量NaCl。

则b处水中含有有少量OH-、-24的物质应是下列哪一组 ( )A．MgSO4、NaCl B．H2SO4、Ba(NO3)2C．H2SO4、MgCl2 D．BaCl2、HCl5．某气体可能含有H2、CO、N2、CH4中的一种或两种，该气体在足量的氧气中充分燃烧后，将全部生成物依次通过足量的无水硫酸铜和澄清石灰水，发现无水硫酸铜变蓝色，澄清石灰水变浑浊，则该气体成分不可能为(注：无水硫酸铜遇水变蓝色) ( )A．CO和CH4 B．H2和CO C．CH4 D．H2和N26．下图中直线相连物质间在一定条件下可以发生反应。

下表提供的四组物质符合图中要求的是 ( )二、非选择题(本题共6小题，共76分)7．(7分)A 、D 是两种常见的固体，其中D 为亮红色；B 、E 是两种常见的气体，其中气体E 有剧毒。

它们之间有如下关系：试推断：(1)A 、E 的化学式分别为：A_____________，E __________。

(2)写出A —D 的化学方程式：__________________________。

8．(10分)下图中，A 由两种元素组成且相对分子质量为120，B 中氧元素的质量分数为 30％，C 是具有刺激性气味的气体，B 、C 、D 、X 、Y 均是氧化物，F 是常见的金属。

(1)写出E 的化学式：_______________；(2)写出下列反应的化学方程式：反应①：____________，反应②：_____________； (3)图中X 与C 在一定条件下反应生成Y 和另一种物质M ，该反应的化学方程式可表示为：3X+C=2Y+M ，则M 中含有的元素是 _____________(填元素符号)。

中考数学复习《实数》专项测试卷(带答案)

中考数学复习《实数》专项测试卷(带答案)学校:___________班级：___________姓名：___________考号：___________一、单选题 1．与2(9)-结果相同的是( )A.3±B.|3|C.23D.方程281x =的解2．下列说法正确的是( )A.81-平方根是-B.81的平方根是9C.平方根等于它本身的数是1和0D.21a +一定是正数3．一个正方体的棱长为a ，体积为b ，则下列说法正确的是( )A.b 的立方根是a ±B.a 是b 的立方根C.a b =D.b a =4．下列关于5说法错误的是( ) A.5是无理数 B.数轴上可以找到表示5的点C.5相反数是5-D.53>5．估计11832的运算结果介于( )A.2与3之间B.3与4之间C.4与5之间D.5与6之间6．若实数a ，b 满足13a b +=( )A.a ，b 都是有理数B.a b -的结果必定为无理数C.a ，b 都是无理数D.a b -的结果可能为有理数7．如图，在ABC △中90ACB ∠=︒，AC=3，BC=1，AC 在数轴上，点A 所表示的数为1，以点A 为圆心，AB 长为半径画弧，在点A 左侧交数轴于点D ，则点D 表示的数是( )10 B.10- C.110-1018．若1014M -=，12N =则M ，N 的大小关系是( )A.M N <B.M N =C.M N >D.无法比较9．已知实数tan30sin 45cos60a b c =︒=︒=︒，，，则下列说法正确的是( )A.b a c >>B.a b c >>C.b c a >>D.a c b >>10．定义运算：若，则，例如328=，则2log 83=.运用以上定义，计算：53log 125log 81-=( )A.1-B.2C.1D.411．在下列计算中,正确的是( )A.()56+-=-B.122=C.()26⨯-=D.3sin 30︒= 12．式子52的倒数是( ) A.52 B.52- C.25+ D.52213．对于实数a 、b ，定义22()*2()a b ab a b a b ab a b a b +-≥⎧=⎨--<⎩，则结论正确的有( )①5*31=；②22272(1)*(21)451(1)m m m m m m m m ⎧-+-<-=⎨-+≥⎩； ③若1x ，2x 是方程2560x x --=的两个根，则12*16x x =或17-；④若1x ，2x 是方程210x mx m +--=的两个根12*4x x =，则m 的值为3-或.A.1个B.2个C.3个D.4个二、填空题14．在实数：中无理数有______个.15a 是一个无理数，且13a <<，请写出一个满足条件的a 值_____.16．011|3|(3π)()tan 45162--+-+-+︒+=______. 17．若m 为7的整数部分，n 为7的小数部分，则)7m n =______. 18．实数a ，b ，c 在数轴上的点如图所示，化简222()()a a b b c +-=____________.三、解答题19．计算m a b =log (0)a b m a =>6-（1）11233- （2）12632322⨯- （3）2245tan 30cos60︒+⋅︒︒20．计算：)102cos6031(16)27--︒-+-. 21．设5a 是一个两位数，其中a 是十位上的数字（9a ≤≤）.例如，当a =时5a 表示的两位数是45.尝试：①当1a =时2152251210025=⨯⨯+=；①当2a =时2256252310025==⨯⨯+；①当3a =时2351225==______；…… 归纳：()25a 与()100125a a ++有怎样的大小关系？验证：请论证“归纳”中的结论正确.22．若正整数a 是4的倍数，则称a 为“四倍数”，例如：8是4的倍数，所以8是“四倍数”.（1）已知p 是任意三个连续偶数的平方和，设中间的数为2n （n 为整数），判断p 是不是“四倍数”，并说明理由；（2）已知正整数k 是一个两位数，且10k x y =+（19x y ≤<≤，其中x ，y 为整数），将其个位上的数字与十位上的数字交换，得到新数m .若m 与k 的差是“四倍数”，求出所有符合条件的正整数k . 参考答案1．答案：C 解析：2(9)819-==33=239=方程281x =的解为9x =±. 故选C.2．答案：D解析：A 、81-是负数，负数没有平方根，不符合题意；B 、819= 9的平方根是3±，不符合题意；C 、平方根等于它本身的数是0，1的平方根是1±，不符合题意；D 、21>0a + 正数的算术平方根大于0，符合题意.故选：D.3．答案：B 解析：一个正方体的棱长为a ，体积为b∴3b a =，即：3a b =∴a 是b 的立方根故选：B.4．答案：D 解析：①5 2.2365857......≈属于无限不循环小数 ①5是无理数，故A 选项正确；①数轴上可以表示任意实数 ①数轴上可以找到表示5的点，故B 选项正确；①5相反数是5，故C 选项正确； ①5 2.2365857......≈①53<，故D 选项错误，符合题意故选：D.5．答案：C 解析：1183232223=+33=+； 132<<4335∴<<；故选：C.6．答案：D解析：A 、当2a =时13213b ==--a 是有理数，b 是无理数，故A 错误；B 、当1322a b ==-，那么0a b -=，所以B 错误； C 、当2a =时13b =-，a 是有理数，故选项C 错误；D 、当1322a b ==-，那么0a b -=，所以选项正确，D 正确. 故选：D.7．答案：C 解析：在Rt ABC △中3AC =，BC=1 22223110AB AC BC ∴=++=∴点D 表示的数为：110故选：C.8．答案：C 解析：1014M -=12= 1011103424M N ∴-=-=103> 0M N ∴->M N ∴>.故选C.9．答案：A 解析：321tan 30sin 45cos 602a b c =︒==︒==︒= 132232<< ∴b a c >> 故选：A.10．答案：A解析：35125= 4381=5log 1253∴= 3log 814=53log 125log 81∴-34=-1=-.故选：A.11．答案：A解析：A 、5(6)561+-=-=-正确,符合题意; B 、1222=原计算错误,不符合题意; C 、3(2)6⨯-=-原计算错误,不符合题意;D 、1sin 302=︒原计算错误,不符合题意. 故选: A.12．答案：A 解析:()()1521 52525252⨯==--+式子5的倒数是52式子5的倒数是52,故选:A.13．答案：C 解析：①5*32523531=⨯+⨯-⨯=，故①正确；②当21m m ≥-时即1m ≤时()()()22*212221212422272m m m m m m m m m m m m -=+---=+--+=-+-当21m m <-时即1m >时 ()()()22*21221214221451m m m m m m m m m m m m -=----=---+=-+()()222721*21451(1)m m m m m m m m ⎧-+-≤∴-=⎨-+>⎩，故②错误； ③1x ，2x 是方程2560x x --=的两个根 125x x ∴+= 126x x =-当12x x ≥时()()121212*225616x x x x x x =+-=⨯--= 当12x x <时()()121212*226517x x x x x x =-+=⨯--=-，故③正确；④1x ，2x 是方程210x mx m +--=的两个根12x x m ∴+=- 121x x m =--当12x x ≥时()()121212*22114x x x x x x m m m =+-=----=-+= 解得：3m =-当12x x <时()()121212*221()24x x x x x x m m m =-+=⨯----=--=解得：6m =-综上可知：①③④正确故选：C.14．答案：4 解析：3644= 其中8 ⋯ π -2是无理数，共4个故答案为：4.15．答案：2解析：2123<< 2a ∴=.故答案：2（答案不唯一）.16．答案：7 解析：0113(3π)()tan 45162-+-+-+︒+31(2)14=++-++7=.17．答案：3 解析：479<<273∴<2m ∴= 72n = )7(72)(72)743m n ==-=∴故答案为3.18．答案：0解析：由数轴可知0b c a <<<则0a b +< 0b c -<222()||()a a b c b c +---()()a a b c b c =-+++-a abc b c =--++-0=.故答案为：0.19．答案：（1）1（2）5 （3）76解析：（1）(133********===；（2）12632322⨯- 22126322⨯=+632=-+5=；（3）2245tan 30cos60︒+⋅︒︒2312222=+⨯⎝⎭ 21113=+⨯ 76=. 20．答案：532 解析：)102cos6031(16)27--︒-+- 1113133222=-+=53.21．答案：尝试3410025⨯⨯+ 归纳()()25100125a a a =++ 验证：见解析解析：尝试：当3a =时2351225==3410025⨯⨯+；归纳：()()25100125a a a =++；验证：等号左边222(5)(105)10010025a a a a =+=++ 等号右边2100(1)2510010025a a a a ++=++ 所以，等号左边＝等号右边，等式成立，即证.22．答案：（1）p 是“四倍数”；理由见解析（2）15，19，26，37，48，59解析：（1）p 是“四倍数”，理由如下：①()()()22222222p n n n ++=+-()22128432n n =+=+①p 是“四倍数”；（2）由题意得10m y x =+，则()()10109m k y x x y y x -=+-+=-． ①19x y ≤<≤，其中x ,y 为整数①18y x ≤-≤.若()9y x -．是4的倍数，则4y x -=或8y x -=.当4y x -=时符合条件的k 是15，26，37，48，59；当8y x -=时符合条件的k 是19.①所有符合条件的正整数k 是15，19，26，37，48，59.。

中考数学总复习《二元一次方程组》专项测试卷(附答案)

中考数学总复习《二元一次方程组》专项测试卷(附答案)一、单选题(共12题；共24分)1．方程组 {y =2x 3x +y =15,的解是（） A ．{x =3y =6,B ．{x =4y =3, C ．{x =4y =8,D ．{x =2y =3,2．以下是方程3x +2y =12的一个解的是（）A ．{x =−1y =2B ．{x =2y =−1C ．{x =2y =3D ．{x =3y =23．如图，在某张桌子上放相同的木块， R =32 ， S =96 ，则桌子的高度是（）A ．63B ．58C ．60D ．644．已知{x =1，y =−2是关于x ，y 的二元一次方程ax +y =1的一个解，那么a 的值为（） A ．3B ．1C ．-1D ．-35．已知关于x 、y 的方程组 {x +y =1−ax −y =3a +5 ，满足 x ≥12y ，则下列结论：①a ≥−2 ；②a =−53时， x =y ；③当 a =−1 时，关于x 、y 的方程组{x +y =1−ax −y =3a +5 的解也是方程 x +y =2 的解；④若 y ≤1 ，则 a ≤−1 ，其中正确的有（） A ．1个B ．2个C ．3个D ．4个6．一个长方形的长减少3cm ，宽增加2cm ，就成为一个正方形，并且长方形的面积与正方形的面积相等.如果设这个长方形的长为xcm ，宽为ycm ，那么所列方程组正确的是（）A ．{x +3=y −2(x +3)(y −2)=xyB ．{x −3=y +2(x −3)(y +2)=xyC ．{3−x =y +2(3−x)(y +2)=xyD ．{x −2=y +3(x −2)(y +3)=xy7．若 |b +2|+(a −3)2=0 ，则 b a 的值为（）A ．﹣bB ．−18C ．﹣8D ．88．已知关于 x,y 的二元一次方程组 {3x +y =−4m +2x −y =6 的解满足 x +y <3 ，则m 的取值范围是（） A ．m >−52B ．m <−52C ．m >52D ．m <529．已知关于x ，y 的二元一次方程ax +b =y ，当x 取不同值时，对应y 的值分别如下表所示：x … －1 0 1 2 3 … y…321－1…A ．x <0B ．x >0C ．x <2D ．x >210．《九章算术》是我国东汉初年编订的一部数学经典著作．在它的“方程”一章里，一次方程组是由算筹布置而成的．《九章算术》中的算筹图是竖排的，为看图方便，我们把它改为横排，如图1、图2（见下页）．图中各行从左到右列出的算筹数分别表示未知数x ，y 的系数与相应的常数项．把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来，就是{3x +2y =19x +4y =23，类似地，图2所示的算筹图我们可以表述为A ．{2x +y =114x +3y =27B ．{2x =y =114x +3y =22C ．{3x +2y =19x +4y =23D ．{2x +y =64x +3y =2711．一个两位数，个位数字与十位数字的和是9，如果将个位数字与十位数字对调后所得的新数比原数大9，则原来的两位数为（） A ．54B ．45C ．27D ．7212．用代入消元法解方程组 {3x −y =2，①y =1−2x ，② 时，把②代入①，得（）A ．3x-1-2x= 2B ．3x-（1-2x ）= 2C ．3x+（1-2x ）=2D ．3（1-2x ）-y=2二、填空题(共6题；共6分)13．若 (a −1)2+|b −2|=5 ，则以a 、b 为边长的等腰三角形的周长为 14．如图，将长方形ABCD 分割成1个灰色长方形与148个面积相等的小正方形．若灰色长方形的长与宽之比为5：3，则AD ：AB=15．为了开展阳光体育活动，某班计划购买毽子和跳绳两种体育用品（必须保证买两种），共花35元．毽子单价3元，跳绳单价5元，关于购买毽子和跳绳两种体育用品的数量购买的方案共有种．16．如果√x−2+（2y+1）2=0，那么xy=17．方程x2-y2=31的正整数解为。

部编版六年级语文上册古诗文专项复习测试卷(一)含答案

部编版六年级语文上册古诗文专项复习测试卷(一)含答案古诗文专项复测评卷（一）一、看拼音，写词语。

到得喜雀鸣二、查字典。

崖”字用音序查字法应该先查大写字母Y，再查音节Á；用部首查字法应该查山部，再查崖画。

可以组成词语：悬崖、峭壁。

三、想一想，写出相关诗句。

1.读一读《宿建德江》，写出两句你知道的描写秋天愁思的其他诗句：秋思悠悠雨濛濛，XXX归来兮秋未穷。

2.《六月二十七日望湖楼醉书》中的“黑云翻墨未遮山，白雨跳珠乱入船”是描写XXX的。

请你回忆平时读过的关于春雨、夏雨、秋雨的诗句，各写出两句：春雨斜风破晚霞，乱点梨花满地花。

夏日炎炎烈日高，暑气蒸腾天地烤。

秋雨绵绵湿衣裳，枯叶落时秋意长。

3.观察词句“池上碧苔三四点，叶底黄鹂一两声”的特点，写出你联想到的《西江月·夜行黄沙道中》中的词句。

翠峰如簇，玉洞琼池。

飞泉瀑布，激流奔注。

”四、选择题。

（给加点字词选择正确的解释）1．浪淘风簸自天涯。

（颠簸）2．水村山郭酒旗风。

（依山而建的城）3．书湖阴先生壁。

（一本书）4．两山排闼送青来。

（门）5．下列各句与“XXX，通国之善弈者也”句式不同的一项是（莲，花之君子者也）6．“金沙水拍云崖暖，大渡桥横铁索寒。

”对于句中的一“暖”一“寒”，下面理解正确的有（A、B、C）。

A．一“暖”一“寒”不仅写出了当时的天气情况，还写出了人们的心理感受。

B．从“暖”和“寒”可以看出巧渡金沙江和飞夺泸定桥两次战役是在不同季节发生的，从侧面反映出红军长征历时之长。

C．“暖”字形象地概括出巧渡金沙江后热烈沸腾的景象和战士们喜悦的心情；“寒”字形象地写出了强渡大渡河、飞夺泸定桥的艰苦激烈、惊心动魄。

D．作者将两种截然相反的心理感觉进行对比，突出了红军英勇顽强的战斗精神。

7．下面是对朗读这首诗歌的理解，其中说法错误的一项是（没有明显的错误）。

一、根据拼音写词语。

到得喜雀鸣二、使用字典查找字词。

崖”字使用音序查字法应该先查大写字母Y，再查音节Á；使用部首查字法应该查山部，再查崖画。

人教版三年级数学下期末专项复习测试卷(应用题)

4.比39的54倍新160的数是多少?四、（8分）期末专项复习测试卷（应用题）（时间：60分钟分值：100一、列式计算。

（24分）二、每班分了多少本？（7分） 1.一个数除以6,商是132,余数是5,这个数是多少?封2. 一个数比94的18倍多319,这个数是多少?三、（8分）150千克共有324本《优秀作文》, 平均;平均每箱装8千克，能装几箱？还剩几千克？3.比438与6的商多217的数是多少?15筐重多少千克？每筐56元每筐38千克买24筐需要多少元钱？五、学生和老师的体重相差多少千克？一共重多少千克？（8分）我的体重尾18.4蒔」［我的体戴49.8千克J六、学校要买11个排球,12个足球，1000元钱够用吗？八、（9分）九、1〜3年级共捐书625本,4*6年级12个班平均每附加题。

（10分）丹丹家住6楼，一层楼有18级台阶。

如果丹丹每天上下楼共4次，她一天走了多少级台阶。

（7分）排球©38元足球45元6月份上半月平均每科菜花了18元，下半归平均每天买菜花了14元。

十、（12 分）七、今年暑假共放了多少天？（8分）班捐了85本，全校共捐了多少本书？（9分）期末专项复习测试卷（应用题）一、1. 132X6+5 = 7972.94X18+319 = 20113.438 + 6 + 217 = 2904.39X54+160=2266二、324-6=54（本）三、150+8 = 18（箱）……6（千克）四、15X38=570（千克）56X24 = 1344（元）五、49. 8 — 18.4 = 31.4（千克）49.8+18.4=68.2（千克）六、38X11+45X12 = 958（元），958<1000 够七、31 — 16 + 1+28 = 44（天）八、15X18+15X14=480（元）九、625+12X85 = 1645（本）十、85X8 = 680（米）340+290=630（米）630<680能走到630+360+280 = 1270（米）冬冬从家里出发，向南走290米到医院.然后向东南走340米到邮局.再向东北走360 米到广场.最后向东走280米到学校。

中考化学专项复习测试卷：综合实验题测试卷(含解析)

综合实验题测试卷1．(10分)根据下列装置图，回答有关问题：(1)写出装置图中标号仪器的名称：①_____________；②_____________。

(2)写出实验室用大理石和稀盐酸制取二氧化碳的化学方程式：_____________。

并据此选择上图中_____________ (填字母)组装一套制取干燥二氧化碳的装置。

(3)如选用装置A作为制取氧气的发生装置，其化学方程式可以为__________________________。

2．(12分)在做盐跟盐反应的分组实验时，第一组学生进行BaCl2与Na2CO3溶液的反应，第二组学生进行BaCl2与Na2SO4溶液的反应。

实验结束后，两组同学将全部的浊液集中倒进一个废液缸中。

浊液中白色沉淀物质是 _________ 和_________。

化学兴趣小组对浊液进行过滤，探究滤液的成分。

【提出问题】滤液里除了NaCl外，还有什么物质?【提出猜想】猜想①：_________；猜想②：Na2SO4；猜想③：Na2CO3；猜想④：Na2CO3、Na2SO4【实验探究】若现象a只有白色沉淀，则猜想_________成立；若现象a只有气泡产生，则猜想_____________可能成立；若现象b产生白色沉淀，然后加稀硝酸沉淀部分溶解，并产生气泡，则猜想_________成立，若沉淀全部不溶解，则猜想_________成立。

3．(12分)某兴趣小组对固体酒精充分燃烧后残留的白色固体的成分进行如下探究。

【查阅资料】(1)醋酸钙[Ca(Ac)2]，不可燃，不助燃，易溶于水，溶于水时温度无显著变化；(2)醋酸钙受热分解生成碳酸钙和有特殊气味的丙酮；【猜想与假设】假设l：白色固体中含有Ca(Ac)2假设2：白色固体中含有CaCO3假设3：白色固体中含有CaO假设4：白色固体中含有Ca(OH)2【实验探究】实验①：取少量白色固体溶于足量蒸馏水中，过滤，得到溶液和白色不溶物；实验②：取①中滤液于试管中，滴入2滴酚酞试液，溶液变为红色；实验③：取①中滤液于试管中，滴加碳酸钠溶液，有白色沉淀生成。

中考数学总复习《一次函数》专项测试卷带答案

中考数学总复习《一次函数》专项测试卷带答案学校:___________班级：___________姓名：___________考号：___________A层·基础过关1.(2024·南宁模拟)若直线y=kx(k是常数,k≠0)经过第一、第三象限,则k的值可为( )A.-2B.-1C.-1D.222.(2024·玉林模拟)将直线y=5x+1向下平移2个单位长度,所得直线的解析式为( )A.y=5x-2B.y=5x-1C.y=5x+3D.y=5(x-1)3.(2024·崇左模拟)已知一次函数y=(m+1)x+5,y随x的增大而减小,则m的取值范围是( )A.m≤-1B.m>-1C.m≥-1D.m<-14.(2024·桂林模拟)如图,直线y=ax+b过点A(0,2)和点B(-3,0),则方程ax+b=0的解是( )A.x=2B.x=0C.x=-1D.x=-35.(2024·北海模拟)直线y=kx+3经过点A(2,1),则不等式kx+3≥0的解集是( )A.x≤3B.x≥3C.x≥-3D.x≤06.(2024·青海)如图,一次函数y=2x-3的图象与x轴相交于点A,则点A关于y轴的对称点是( )A .(-32,0) B .(32,0) C .(0,3) D .(0,-3)7.对于某个一次函数y =kx +b (k ≠0),根据两位同学的对话得出的结论,错误的是( )A .k >0B .kb <0C .k +b >0D .k =-12b8.一种弹簧秤最大能称不超过10 kg 的物体,不挂物体时弹簧的长为12 cm,每挂重1 kg 物体,弹簧伸长0.5 cm,在弹性限度内,挂重后弹簧的长度y (cm)与所挂物体的质量x (kg)之间的函数关系式为( )A.y =12-0.5xB.y =12+0.5xC.y =10+0.5xD.y =0.5x9.(2024·包头)在平面直角坐标系中,若一次函数的图象经过第一、二、三象限,请写出一个符合该条件的一次函数的解析式 .10.(2024·包头)如图是1个碗和4个整齐叠放成一摞的碗的示意图,碗的规格都是相同的.小亮尝试结合学习函数的经验,探究整齐叠放成一摞的这种规格的碗的总高度y(单位: cm)随着碗的数量x(单位:个)的变化规律.下表是小亮经过测量得到的y与x之间的对应数据:x/个1234y/cm68.410.813.2(1)依据小亮测量的数据,写出y与x之间的函数解析式,并说明理由;(2)若整齐叠放成一摞的这种规格的碗的总高度不超过28.8 cm,求此时碗的数量最多为多少个?B层·能力提升x+3分别与x轴,y轴交于点A,B,将△OAB绕着11.(2024·桂林模拟)如图,直线y=-32点A顺时针旋转90°得到△CAD,则点B的对应点D的坐标为( )A.(2,5)B.(3,5)C.(5,2)D.(√13,2)12.(2024·柳州模拟)在平面直角坐标系中,点A1,A2,A3,A4…在x轴的正半轴上,点B1,B2,B3…在直线y=√3x(x≥0)上,若点A1的坐标为(2,0),且3△A1B1A2,△A2B2A3,△A3B3A4…均为等边三角形,则点B2 025的坐标为.13.在“探索一次函数y=kx+b的系数k,b与图象的关系”活动中,老师给出了直角坐标系中的三个点:A(0,2),B(2,3),C(3,1).同学们画出了经过这三个点中每两个点的一次函数的图象,并得到对应的函数解析式y1=k1x+b1,y2=k2x+b2,y3=k3x+b3.分别计算k1+b1,k2+b2,k3+b3的值,其中最大的值等于.C层·挑战冲A+14.(2024·广州)一个人的脚印信息往往对应着这个人某些方面的基本特征.某数学兴趣小组收集了大量不同人群的身高和脚长数据,通过对数据的整理和分析,发现身高y和脚长x之间近似存在一个函数关系,部分数据如表:脚长x(cm)…232425262728…身高y(cm)…156163170177184191…(1)在图1中描出表中数据对应的点(x,y);(2)根据表中数据,从y=ax+b(a≠0)和y=k(k≠0)中选择一个函数模型,使它能近似地x反映身高和脚长的函数关系,并求出这个函数的解析式(不要求写出x的取值范围);(3)如图2,某场所发现了一个人的脚印,脚长约为25.8 cm,请根据(2)中求出的函数解析式,估计这个人的身高.参考答案A层·基础过关1.(2024·南宁模拟)若直线y=kx(k是常数,k≠0)经过第一、第三象限,则k的值可为(D)A.-2B.-1C.-1D.222.(2024·玉林模拟)将直线y=5x+1向下平移2个单位长度,所得直线的解析式为(B)A.y=5x-2B.y=5x-1C.y=5x+3D.y=5(x-1)3.(2024·崇左模拟)已知一次函数y=(m+1)x+5,y随x的增大而减小,则m的取值范围是(D)A.m≤-1B.m>-1C.m≥-1D.m<-14.(2024·桂林模拟)如图,直线y=ax+b过点A(0,2)和点B(-3,0),则方程ax+b=0的解是(D)A .x =2B .x =0C .x =-1D .x =-35.(2024·北海模拟)直线y =kx +3经过点A (2,1),则不等式kx +3≥0的解集是(A) A .x ≤3 B .x ≥3 C .x ≥-3 D .x ≤06.(2024·青海)如图,一次函数y =2x -3的图象与x 轴相交于点A ,则点A 关于y 轴的对称点是(A)A .(-32,0) B .(32,0) C .(0,3) D .(0,-3)7.对于某个一次函数y =kx +b (k ≠0),根据两位同学的对话得出的结论,错误的是(C)A .k >0B .kb <0C .k +b >0D .k =-12b8.一种弹簧秤最大能称不超过10 kg 的物体,不挂物体时弹簧的长为12 cm,每挂重1 kg 物体,弹簧伸长0.5 cm,在弹性限度内,挂重后弹簧的长度y (cm)与所挂物体的质量x (kg)之间的函数关系式为(B)A.y=12-0.5xB.y=12+0.5xC.y=10+0.5xD.y=0.5x9.(2024·包头)在平面直角坐标系中,若一次函数的图象经过第一、二、三象限,请写出一个符合该条件的一次函数的解析式y=x+1(答案不唯一).10.(2024·包头)如图是1个碗和4个整齐叠放成一摞的碗的示意图,碗的规格都是相同的.小亮尝试结合学习函数的经验,探究整齐叠放成一摞的这种规格的碗的总高度y(单位: cm)随着碗的数量x(单位:个)的变化规律.下表是小亮经过测量得到的y与x之间的对应数据:x/个1234y/cm68.410.813.2(1)依据小亮测量的数据,写出y与x之间的函数解析式,并说明理由;【解析】(1)由表中的数据,x的增加量不变∴y是x的一次函数设y=kx+b由题意得:{k+b=62k+b=8.4,解得:{k=2.4 b=3.6∴y与x之间的函数解析式为y=2.4x+3.6;(2)若整齐叠放成一摞的这种规格的碗的总高度不超过28.8 cm,求此时碗的数量最多为多少个?【解析】(2)设碗的数量有x个,则:2.4x+3.6≤28.8,解得:x≤10.5,∴x的最大整数解为10答:碗的数量最多为10个.B层·能力提升x+3分别与x轴,y轴交于点A,B,将△OAB绕着11.(2024·桂林模拟)如图,直线y=-32点A顺时针旋转90°得到△CAD,则点B的对应点D的坐标为(C)A.(2,5)B.(3,5)C.(5,2)D.(√13,2)12.(2024·柳州模拟)在平面直角坐标系中,点A1,A2,A3,A4…在x轴的正半轴上,点B1,B2,B3…在直线y=√3x(x≥0)上,若点A1的坐标为(2,0),且3△A1B1A2,△A2B2A3,△A3B3A4…均为等边三角形,则点B2 025的坐标为(3×22 024,√3×22 024).13.在“探索一次函数y=kx+b的系数k,b与图象的关系”活动中,老师给出了直角坐标系中的三个点:A(0,2),B(2,3),C(3,1).同学们画出了经过这三个点中每两个点的一次函数的图象,并得到对应的函数解析式y1=k1x+b1,y2=k2x+b2,y3=k3x+b3.分别计算k1+b1,k2+b2,k3+b3的值,其中最大的值等于5.C层·挑战冲A+14.(2024·广州)一个人的脚印信息往往对应着这个人某些方面的基本特征.某数学兴趣小组收集了大量不同人群的身高和脚长数据,通过对数据的整理和分析,发现身高y和脚长x之间近似存在一个函数关系,部分数据如表:脚长x(cm)…232425262728…身高y(cm)…156163170177184191…(1)在图1中描出表中数据对应的点(x,y);【解析】(1)描点如图所示:(2)根据表中数据,从y=ax+b(a≠0)和y=k(k≠0)中选择一个函数模型,使它能近似地x反映身高和脚长的函数关系,并求出这个函数的解析式(不要求写出x的取值范围);【解析】(2)∵y=kx(k≠0)转化为k=xy=23×156≠24×163≠25×170≠…∴y与x的函数不可能是y=kx故选一次函数y=ax+b(a≠0),将点(23,156),(24,163)代入解析式得:{23a+b=15624a+b=163,解得{a=7 b=−5∴一次函数解析式为y=7x-5.(3)如图2,某场所发现了一个人的脚印,脚长约为25.8 cm,请根据(2)中求出的函数解析式,估计这个人的身高.【解析】(3)当x=25.8时,y=7×25.8-5=175.6.答:脚长约为25.8 cm时,估计这个人的身高为175.6 cm.。

中考数学总复习《三角形与全等三角形》专项测试卷(带有答案)

中考数学总复习《三角形与全等三角形》专项测试卷(带有答案)时间：45分钟满分：100分学校:___________班级：___________姓名：___________考号：___________ 1．(2023·长沙)下列长度的三条线段，能组成三角形的是( )A．1，3，4 B．2，2，7C．4，5，7 D．3，3，62．(2023·凉山州)如图，点E，点F在BC上，BE＝CF，∠B＝∠C，添加一个条件，不能证明△ABF≌△DCE的是( )第2题图A．∠A＝∠D B．∠AFB＝∠DECC．AB＝DC D．AF＝DE3．(2023·济宁)如图，在正方形方格中，每个小正方形的边长都是一个单位长度，点A，B，C，D，E均在小正方形方格的顶点上，线段AB，CD相交于点F，若∠CFB＝α，则∠ABE等于( )第3题图A．180°－α B．180°－2αC．90°＋α D．90°＋2α4．(2023·巴中)如图，在Rt△ABC中，AB＝6 cm，BC＝8 cm，点D，E分别为AC，BC中点，连接AE，BD，相交于点F，点G在CD上，且DG∶GC＝1∶2，则四边形DFEG的面积为( )第4题图A．2 cm2B．4 cm2C．6 cm2D．8 cm25．(2023·浙江)如图，点P是△ABC的重心，点D是边AC的中点，PE∥AC交BC于点E，DF∥BC交EP于点F.若四边形CDFE的面积为6，则△ABC的面积为( )第5题图A．12 B．14 C．18 D．246．一个三角形的两边长分别是3和3，则第三边长可以是．(只填一个即可) 7．(2023·丽水)如图，在△ABC中，AC的垂直平分线交BC于点D，交AC于点E，∠B＝∠ADB.若AB＝4，则DC的长是．第7题图8．(2022·南京)在平面直角坐标系中，正方形ABCD如图所示，点A的坐标(－1，0)，点D的坐标是(－2，4)，则点C的坐标是．第8题图9．(2023·遂宁)如图，以△ABC的边AB，AC为腰分别向外作等腰直角△ABE，△ACD，连接ED，BD，EC，过点A的直线l分别交线段DE，BC于点M，N.以下说法：①当AB＝AC＝BC时，∠AED＝30°②EC＝BD ③若AB＝3，AC＝4，BC＝6，则DE＝2 3 ④当直线l⊥BC时，点M为线段DE的中点．正确的有．(填序号)第9题图10．(2023·苏州)如图，在△ABC中，AB＝AC，AD为△ABC的角平分线．以点A 为圆心，AD长为半径画弧，与AB，AC分别交于点E，F，连接DE，DF.第10题图(1)求证：△ADE≌△ADF；(2)若∠BAC＝80°，求∠BDE的度数．11．(2023·大连)如图，在△ABC和△ADE中，延长BC交DE于点F，BC＝DE，AC＝AE，∠ACF＋∠AED＝180°.求证：AB＝AD.第11题图12．(2023·聊城)如图，在四边形ABCD中，点E是BC边上一点，且BE＝CD，∠B＝∠AED＝∠C.第12题图(1)求证：∠EAD＝∠EDA；(2)若∠C＝60°，DE＝4，求△AED的面积．参考答案1．(2023·长沙)下列长度的三条线段，能组成三角形的是( C)A．1，3，4 B．2，2，7C．4，5，7 D．3，3，62．(2023·凉山州)如图，点E，点F在BC上，BE＝CF，∠B＝∠C，添加一个条件，不能证明△ABF≌△DCE的是( D)第2题图A．∠A＝∠D B．∠AFB＝∠DECC．AB＝DC D．AF＝DE3．(2023·济宁)如图，在正方形方格中，每个小正方形的边长都是一个单位长度，点A，B，C，D，E均在小正方形方格的顶点上，线段AB，CD相交于点F，若∠CFB＝α，则∠ABE等于( C)第3题图A．180°－α B．180°－2αC．90°＋α D．90°＋2α4．(2023·巴中)如图，在Rt△ABC中，AB＝6 cm，BC＝8 cm，点D，E分别为AC，BC中点，连接AE，BD，相交于点F，点G在CD上，且DG∶GC＝1∶2，则四边形DFEG的面积为( B)第4题图A．2 cm2B．4 cm2C．6 cm2D．8 cm25．(2023·浙江)如图，点P是△ABC的重心，点D是边AC的中点，PE∥AC交BC于点E，DF∥BC交EP于点F.若四边形CDFE的面积为6，则△ABC的面积为( C)第5题图A．12 B．14 C．18 D．246．一个三角形的两边长分别是3和3，则第三边长可以是(示例)3．(只填一个即可)7．(2023·丽水)如图，在△ABC中，AC的垂直平分线交BC于点D，交AC于点E，∠B＝∠ADB.若AB＝4，则DC的长是4．第7题图8．(2022·南京)在平面直角坐标系中，正方形ABCD如图所示，点A的坐标(－1，0)，点D的坐标是(－2，4)，则点C的坐标是(2，5)．第8题图9．(2023·遂宁)如图，以△ABC的边AB，AC为腰分别向外作等腰直角△ABE，△ACD，连接ED，BD，EC，过点A的直线l分别交线段DE，BC于点M，N.以下说法：①当AB＝AC＝BC时，∠AED＝30°②EC＝BD ③若AB＝3，AC＝4，BC＝6，则DE＝2 3 ④当直线l⊥BC时，点M为线段DE的中点．正确的有①②④．(填序号)第9题图10．(2023·苏州)如图，在△ABC中，AB＝AC，AD为△ABC的角平分线．以点A 为圆心，AD长为半径画弧，与AB，AC分别交于点E，F，连接DE，DF.第10题图(1)求证：△ADE≌△ADF；(2)若∠BAC＝80°，求∠BDE的度数．解：(1)证明：∵AD是△ABC的角平分线由作图知，AE ＝AF. 在△ADE 和△ADF 中 ⎩⎪⎨⎪⎧AE ＝AF ，∠BAD ＝∠CAD ，AD ＝AD ，∴△ADE ≌△ADF(SAS)；(2)∵∠BAC ＝80°，AD 为△ABC 的角平分线 ∴∠EAD ＝12∠BAC ＝40°由作图知，AE ＝AD. ∴∠AED ＝∠ADE∴∠ADE ＝12×(180°－40°)＝70°∵AB ＝AC ，AD 为△ABC 的角平分线 ∴AD ⊥BC.∴∠BDE ＝90°－∠ADE ＝20°.11．(2023·大连)如图，在△ABC 和△ADE 中，延长BC 交DE 于点F ，BC ＝DE ，AC ＝AE ，∠ACF ＋∠AED＝180°.求证：AB ＝AD.第11题图证明：∵∠ACB ＋∠ACF ＝∠ACF ＋∠AED ＝180°在△ABC 和△ADE 中 ⎩⎪⎨⎪⎧BC ＝DE ，∠ACB ＝∠AED ，AC ＝AE ，∴△ABC ≌△ADE(SAS) ∴AB ＝AD.12．(2023·聊城)如图，在四边形ABCD 中，点E 是BC 边上一点，且BE ＝CD ，∠B ＝∠AED＝∠C.第12题图(1)求证：∠EAD＝∠EDA；(2)若∠C＝60°，DE ＝4，求△AED 的面积．解：(1)证明：∵∠B ＝∠AED ＝∠C ，∠AEC ＝∠B ＋∠BAE ＝∠AED ＋∠CED ∴∠BAE ＝∠CED 在△ABE 和△ECD 中 ⎩⎪⎨⎪⎧∠BAE ＝∠CED ，∠B ＝∠C ，BE ＝CD ，∴△ABE ≌△ECD(AAS) ∴AE ＝ED ∴∠EAD ＝∠EDA ；(2)∵∠AED ＝∠C ＝60°，AE ＝ED ∴△AED 为等边三角形 ∴AE ＝AD ＝ED ＝4 过A 点作AF ⊥ED 于点F.第12题图∴EF ＝12ED ＝2∴AF ＝AE 2－EF 2＝42－22＝2 3 ∴S △AED ＝12ED ·AF ＝12×4×23＝4 3.。

中考数学总复习《二次函数的动态几何问题》专项测试卷-含参考答案

中考数学总复习《二次函数的动态几何问题》专项测试卷-含参考答案一、单选题(共12题；共24分)1．如图，在四边形ABCD中，AB∥CD，∥B=90°，AB=AD=5，BC=4，M、N、E分别是AB、AD、CB上的点，AM=CE=1，AN=3，点P从点M出发，以每秒1个单位长度的速度沿折线MB﹣BE向点E运动，同时点Q从点N出发，以相同的速度沿折线ND﹣DC﹣CE向点E运动，当其中一个点到达后，另一个点也停止运动．设∥APQ的面积为S，运动时间为t秒，则S与t函数关系的大致图象为（）A．B．C．D．2．如图，在平面直角坐标系中，M、N、C三点的坐标分别为（12，1），（3，1），（3，0），点A为线段MN上的一个动点，连接AC，过点A作AB⊥AC交y轴于点B，当点A从M运动到N时，则点B随之运动，设点B的坐标为（0，b），则b的取值范围是（）A．−14≤b≤1B．−54≤b≤1C．−94≤b≤12D．−94≤b≤13．如图所示，∥ABC为等腰直角三角形，∥ACB=90°，AC=BC=2，正方形DEFG边长也为2，且AC 与DE在同一直线上，∥ABC从C点与D点重合开始，沿直线DE向右平移，直到点A与点E重合为止，设CD的长为x，∥ABC与正方形DEFG重合部分（图中阴影部分）的面积为y，则y与x之间的函数关系的图象大致是（）A．B．C．D．4．二次函数y=﹣（x﹣1）2+2的顶点坐标是（）A．（1，﹣2）B．（1，2）C．（﹣1，2）D．（﹣1，﹣2）5．如图，等腰Rt∥ABC（∥ACB=90°）的直角边与正方形DEFG的边长均为2，且AC与DE在同一直线上，开始时点C与点D重合，让∥ABC沿这条直线向右平移，直到点A与点E重合为止．设CD的长为x，∥ABC与正方形DEFG重合部分（图中阴影部分）的面积为y，则y与x之间的函数关系的图象大致是（）A．B．C．D．6．如图，矩形ABCD中，AB=4cm，AD=5cm，点E在AD上，且AE=3cm，点P、Q同时从点B出发，点P沿BE→ED→DC运动到点C停止，点Q沿BC运动到点C停止，它们的运动速度都是1cm/s，设P、Q出发t秒，∥BPQ的面积为y cm2．则y与t的函数关系图象大致是（）A．B．C．D．7．如图，∥ABC是边长为4cm的等边三角形，动点P从点A出发，以2cm/s的速度沿A→C→B运动，到达B点即停止运动，过点P作PD∥AB于点D，设运动时间为x（s），∥ADP的面积为y （cm2），则能够反映y与x之间函数关系的图象大致是（）A．B．C．D．8．如图，动点P从点A出发，沿线段AB运动至点B后，立即按原路返回，点P在运动过程中速度不变，则以点B为圆心，线段BP长为半径的圆的面积S与点P的运动时间t的函数图象大致为（）A．B．C．D．9．如图1，在四边形ABCD中，AD∥BC，∥B=∥C=60°，P、Q同时从B出发，以每秒1单位长度分别沿B﹣A﹣D﹣C和B﹣C﹣D方向运动至相遇时停止，设运动时间为t（秒），∥BPQ的面积为S （平方单位），S与t的函数图象如图2所示，则下列结论错误的个数（）①当t=4秒时，则S=4 √3②AD=4③当4≤t≤8时，则S=2 √3t ④当t=9秒时，则BP平分四边形ABCD的面积．A．1个B．2个C．3个D．4个10．如图，直线l1:y=−x+4与x轴和y轴分别相交于A、B两点，平行于直线l1的直线l2从原点O出发，沿x轴的正方向以每秒1个单位长度的速度运动，它与x轴和y轴分别相交于C、D两点，运动时间为t秒(0≤t≤4).以CD为斜边作等腰直角ΔCDE（E、O两点分别在CD两侧），若ΔCDE和ΔOAB的重合部分的面积为S，则S与t之间的函数关系的图象大致是（）A．B．C．D．11．如图，在菱形ABCD中，∠ABC=120°，AB=2.动点P从点A出发，以每秒2个单位的速度沿折线AD→DC运动到点C，同时动点Q也从点A出发，以每秒√3个单位的速度沿AC 运动到点C，当一个点停止运动时，则另一个点也随之停止.设△APQ的面积为y，运动时间为x秒，则下列图象能大致反映y与x之间函数关系的是（）A．B．C．D．12．点C是线段AB上的一点，AB=1，分别以AC和CB为一边作正方形，用S表示这两个正方形的面积之和，下列判断正确的是（）A．当C是AB的中点时，则S最小B．当C是AB的中点时，则S最大C．当C为AB的三等分点时，则S最小D．当C是AB的三等分点时，则S最大二、填空题(共6题；共7分)13．如图，抛物线y = 13x2−23x−83的图象与坐标轴交于A、B、D，顶点为E，以AB为直径画半圆交y轴的正半轴于点C，圆心为M，P是半圆上的一动点，连接EP，N是PE的中点，当P沿半圆从点A运动至点B时,点N运动的路径长是．14．如图，在平面直角坐标系中，点A、B的坐标分别为（﹣5，0）、（﹣2，0）．点P在抛物线y=﹣2x2+4x+8上，设点P的横坐标为m．当0≤m≤3时，则∥PAB的面积S的取值范围是．15．如图，抛物线y=（x-1）2-1与直线y=x交于点O，点B为线段OA上的动点，过点B作BC∥y 轴，交交抛物线于点C，则线段BC长度的最大值为16．如图，在∥ABC中，∥B=90°，AB=12mm，BC=24mm，动点P从点A开始沿边AB向B以2mm/s的速度移动（不与点B重合），动点Q从点B开始沿边BC向C以4mm/s的速度移动（不与点C重合）．如果P、Q分别从A、B同时出发，那么经过秒，四边形APQC的面积最小．17．如图，在边长为6cm的正方形ABCD中，点E、F、G、H分别从点A、B、C、D同时出发，均以1cm/s的速度向点B、C、D、A匀速运动，当点E到达点B时，则四个点同时停止运动，在运动过程中，当运动时间为s时，则四边形EFGH的面积最小，其最小值是cm2．18．如图，抛物线y=13x2+83x−3与x轴交于点A和点B两点，与y轴交于点C，D点为拋物线上第三象限内一动点，当∠ACD+2∠ABC=180∘时，则点D的坐标为.三、综合题(共6题；共73分)19．如图，抛物线y =ax 2+bx +3与x 轴交于A(−2，0)，B(6，0)两点，与y 轴交于点C 直线l ：y =12x +n 与抛物线交于A ，D 两点，与y 轴交于点E ．（1）求抛物线的解析式；（2）若点P 是抛物线上的点且在直线l 上方，连接PA ，PD ，求当△PAD 面积最大时点P 的坐标及该面积的最大值；（3）y 轴上是否存在点Q ，使∠ADQ =45°，若存在请求点Q 的坐标；若不存在说明理由． 20．在平面直角坐标系中，已知抛物线y ＝ax 2+bx ﹣4经过A （﹣4，0），C （2，0）两点．（1）求抛物线的解析式；（2）若点M 为第三象限内抛物线上一动点，点M 的横坐标为m ，∥AMB 的面积为S ．求S 关于m 的函数关系式，并求出S 的最大值．21．如图，抛物线y=﹣x 2+6x 与x 轴交于点O ，A ，顶点为B ，动点E 在抛物线对称轴上，点F 在对称轴右侧抛物线上，点C 在x 轴正半轴上，且EF =//OC ，连接OE ，CF 得四边形OCFE ．（1）求B点坐标；（2）当tan∥EOC= 43时，则显然满足条件的四边形有两个，求出相应的点F的坐标；（3）当0＜tan∥EOC＜3时，则对于每一个确定的tan∥EOC值，满足条件的四边形OCFE有两个，当这两个四边形的面积之比为1：2时，则求tan∥EOC．22．如图，在△ABC中，∠B=90°，AB=6cm，BC=8cm，点P从A点开始沿AB边向点B以1cm/秒的速度移动，同时点Q从B点开始沿BC边向点C以2cm/秒的速度移动，且当其中一点到达终点时，则另一个点随之停止移动．设P，Q两点移动的时间为t秒，△PBQ的面积为Scm2．（1）BP=cm；（2）求S与t的函数关系式，并求出△PBQ面积的最大值．23．如图，平面直角坐标系中，四边形OABC为矩形，点A、B的坐标分别为（6，0），（6，8）、动点M、N分别从O、B同时出发，都以每秒1个单位的速度运动、其中，点M沿OA向终点A运动，点N沿BC向终点C运动、过点N作NP∥BC，交AC于P，连结MP、已知动点运动了t秒、（1）P点的坐标为（，）（用含t的代数式表示）;（2）试求∥MPA面积的最大值，并求此时t的值;（3）请你探索：当t为何值时，则∥MPA是一个等腰三角形？24．已知抛物线y=ax2+bx+3经过点A(−1，0)、B(3，0)，与y轴交于点C，连接BC．（1）求抛物线的解析式；（2）在直线BC上方抛物线上取一点P，过点P作PQ⊥x轴交BC边于点Q，求PQ的最大值；（3）在直线BC上方抛物线上取一点D，连接OD，CD．OD交BC于点F，当S△COF：S△CDF=3：2时，则求点D的坐标．参考答案1．【答案】D2．【答案】B3．【答案】A4．【答案】B5．【答案】A6．【答案】B7．【答案】B8．【答案】B9．【答案】C10．【答案】C11．【答案】A12．【答案】A13．【答案】1.5π14．【答案】3≤S≤1515．【答案】9416．【答案】317．【答案】3；1818．【答案】(−7，−163) 19．【答案】（1）解：将A （-2，0）、B （6，0）代入y=ax 2+bx+3得：{4a −2b +3＝036a +6b +3＝0解得{a ＝−14b ＝1∴抛物线的解析式为y=-14x 2+x+3 （2）解：∵y =12x +n 过点于A(−2，0)，所以n =1 ∴点D 的坐标为(4，3)．如图1中，过点P 作PK ∥y 轴交AD 于点K ．设P(m ，−14m 2+m +3)，则K(m ，12m +1)． ∵S △PAD =12⋅(x D −x A )⋅PK =3PK ∴PK 的值最大值时，则△PAD 的面积最大PK =−14m 2+m +3−12m −1=−14m 2+12m +2=−14(m −1)2+94∵−14<0∴m =1时，则PK 的值最大，最大值为94此时△PAD 的面积的最大值为274，P(1，154)．（3）解：存在如图2中，将线段AD 绕点A 逆时针旋转90°得到AT ，则T(−5，6)设DT 交y 轴于点Q ，则∥∠ADQ =45°∵D(4，3)∴直线DT 的解析式为y =−13x +133∴Q(0，133) 作点T 关于AD 的对称点T ′(1，−6)则直线DT ′的解析式为y =3x −9设DQ ′交y 轴于点Q ′，则∠ADQ ′=45°∴Q ′(0，−9)综上所述，满足条件的点Q 的坐标为(0，133)或(0，−9)． 20．【答案】（1）解：将A （﹣4，0），C （2，0）代入y ＝ax 2+bx ﹣4，得：{16a −4b −4=04a +2b −4=0 ，解得：{a =12b =1∴抛物线解析式为：y =12x 2+x −4 （2）解：如图，过点M 作MN∥AC 于点N∵抛物线y =12x 2+x −4与y 轴交于点B 当x =0 时，则y =−4∴B(0，−4) ，即OB=4∵点M 为第三象限内抛物线上一动点，点M 的横坐标为m∴M(m ，12m 2+m −4) ∴ON =−m ，MN =−(12m 2+m −4)=−12m 2−m +4 ∴AN =m −(−4)=m +4∴S △ABM =S △ANM +S 梯形MNOB −S △AOB =12(4+m)(−12m 2−m +4)+12(−12m 2−m +4+4)(−m)−12×4 =−m 2−4m =−(m +2)2+4(−4<m <0)∴当m =−2 时，则S 有最大值，最大值为4∴S 关于m 的函数关系式为S =−m 2−4m ， S 的最大值为4．21．【答案】（1）解：∵y=﹣x 2+6x=﹣（x ﹣3）2+9∴B （3，9）（2）解：抛物线的对称轴为直线x=3，直线x=3交x 轴于H ，如图∵tan∥EOC= 43 ，即tan∥EOH= 43∴EH OH = 43∴EH=4∴E 点坐标为（3，4）或（3，﹣4）当y=4时，则﹣（x ﹣3）2+9=4，解得x 1=3﹣ √5 （舍去），x 2=3+ √5当y=﹣4时，则﹣（x ﹣3）2+9=﹣4，解得x 1=3﹣ √13 （舍去），x 2=3+ √13∴F 点坐标为（3+ √5 ）或（3+ √13 ，﹣4）（3）解：如图，∵平行四边形OEFC 和平行四边形OE′F′C′等高∴这两个四边形的面积之比为1：2时，则OC′=2OC 设OC=t，则OC′=2t∴F点的横坐标为3+t，F′点的横坐标为3+2t而点F和F′的纵坐标互为相反数∴﹣（3+t﹣3）2+9+[﹣（3+2t﹣3）2+9]=0，解得t1= 3√105，t2=﹣3√105（舍去）∴F点坐标为（3+ 3√105，275）∴E（3，27 5）∴tan∥EOC= 2753= 95．22．【答案】（1）（6-t）（2）解：经过t秒后∴S=12×PB×BQ=12×(6－t)×2t=－t2+6t=−(t−3)2+9∴在移动过程中，△PBQ的最大面积是9cm2．23．【答案】（1）解：6－t；43t（2）解：延长NP交x轴于Q，则有PQ∥QA．设∥MPA的面积为SS＝12MA·PQ＝12（6—t）43t＝— 23t2＋4t （0≤t≤6）∴当t ＝3时，则S的最大值为6（3）解：①若MP＝PA ∵PQ∥MA ∴ MQ＝QA＝t ∴3t＝6 即t＝2②若MP＝MA 则MQ＝6—2t PQ＝43t PM＝MA＝6—t在Rt∥PMQ 中∵PM2＝MQ2＋PQ2 ∴（6—t）2＝（6—2t）2＋（43t）2∴t ＝10843③若PA＝AM ∵PA＝t AM＝6—t ∴t＝6—t ∴t＝94综上所述， t ＝2或t ＝ 10843 或t ＝ 9424．【答案】（1）解：∵抛物线y =ax 2+bx +3经过点A(−1，0)、B(3，0)∴{a −b +3=09a +3b +3=0解得{a =−1b =2∴抛物线的解析式为：y =−x 2+2x +3（2）解：∵抛物线的解析式为：y =−x 2+2x +3 令x =0，则y =3∴C(0，3)∵B(3，0)设直线BC 的解析式为y =kx +b则{b =33k +b =0解得{k =−1b =3直线BC 的解析式为：y =−x +3过点P 作PQ∥x 轴交BC 于点Q ，设P 点坐标为(x ，−x 2+2x +3)则Q 点坐标为(x ，−x +3)则PQ =(−x 2+2x +3)−(−x +3)=−x 2+3x=−(x −32)2+94∴PQ 的最大值是94．（3）解：∵∆COF 与∆CDF 共高，面积比转化为底边比 OF ：DF=S∥COF ：S∥CDF ＝3：2过点D 作BC 的平行线交x 轴于G ，交y 轴于E根据平行线分线段成比例OF：FD=OC：CE=3：2∵OC=3∴OE=5∴E（0，5）∴直线EG解析式为：y= -x+5联立方程，得：−x2+2x+3=−x+5解得：x1=1则点D的坐标为（1，4）或（2，3）；。

中考物理第一轮专项复习测试卷：作图(含答案)

专题八作图题一、光学部分(25分)1．(4分)物体AB放在平面镜前，AB的像．2．(3分)物体AB放在平面镜前，画出能看到AB像的范围．3．(3分)在图中画出合适的透镜．4．(3分)利用三种不同的光学透镜改变光线OA的方向，在图中画出合适的光学元件．5．(4分)图中S为发光点，从它发出的两条光线经平面镜反射后的两条反射光线分别与虚线a、b重合，根据平面镜成像规律在图中画出平面镜，并找出S在平面镜里的像S′．6．(8分)在“观察凸透镜所成的像”的实验中，保持凸透镜的位置不变，先后把烛焰放在．a、b、c、d和e点，如图所示，同时调整光屏的位置，那么(1)把烛焰放在______点，图上出现的像最小；(2)把烛焰放在______点，屏上出现的像最大；(3)把烛焰放在______点，屏上不出现烛焰的像；(4)如果把烛焰从a点移到d点，像到凸透镜的距离______，像的大小______．(填“变大”“变小”或“不变”)二、力学部分(35分)7．(5分)沿斜面用50 N的力拉重为100 N的小车，用力的图示法表示所受的拉力和重力．8．(5分)如图所示，O是杠杆的支点，画出力的力臂，并用字母L表示．9．(5分)一个质量为2 kg的木球漂浮在水面上，用力的图示法画出木球静止时的受力情况．(g＝10 N/kg)10．(5分)重15 N的小球，用细绳拴在墙上，已知球对墙面的压力为6 N，用力的图示法画出小球受到的重力和墙受的压力．11．(5分)小强想把一货物吊到楼上去，已知货物重1000 N，小强最大的拉力为300 N，如果使用滑轮组，至少需要几个滑轮？如何装配？12．(5分)要想用一个最小的力，推着一个圆筒越过障碍物，试在图上画出此力的作用点和方向．13．(5分)在杠杆上的A点挂一重物，在C点对杠杆施加一个最小的力，使杠杆平衡在图中所示的位置．试画出这个力的示意图和力臂．三、电学部分(电和磁、家用电路设计题) (40分)14．(5分)请在图中标出条形磁体的两极．15．(5分)已知通电螺线管中的电流方向，标出小磁针的N极．16．(5分)图中小磁针静止在通电螺线管旁，请你在图上标明：(1)电源的正负极；(2)通电螺线管的N、S极；(3)磁感线的方向．17．(5分)将电磁铁连入你设计的电路中(在方框内完成)，要求：使小磁针静止时如图所示．18．(5分)把螺口灯泡、开关和保险丝正确地接入家庭电路中去．19．(5分)根据图中所示的电路图连接右图中的实物图，要求导线不允许交叉，元件要与电路图对应．20．(5分)画出如图所示实物图的电路图．21．(5分)下图是伏安法测电阻的实验电路图，根据电路图，以笔画线代替导线，将实物图连成实验电路．(电压表用0～15 V的量程电流表用0～0.6 A的量程)专题八答案1．略 2．略3．4．5．6．(1)a (2)d (3)e (4)变大变小7．8．9．10．11．3个，装配图如下12．13．14．15． 16．17．18．19．20．21．。

中考数学专题复习《直线、射线、线段》测试卷(附带答案)

中考数学专题复习《直线射线线段》测试卷（附带答案)学校:___________班级:___________姓名:___________考号:___________知识点1. 定义与性质：线段：线段是由两个端点及其之间的所有点组成的。

它有一个固定的长度并且可以在数轴上表示一个区间。

例如线段AB表示从点A到点B的所有点的集合。

射线：射线有一个起点（称为端点）并从该点沿一个方向无限延伸。

射线有一个端点和一个方向但没有固定的长度。

例如射线AB表示从点A出发沿AB方向无限延伸的线的集合。

直线：直线由无数个点组成没有端点并且向两端无限延伸。

直线没有固定的长度并且可以通过任意两个不重合的点来确定。

例如通过点A和点B可以确定一条直线。

2. 表示方法：线段：通常使用两个端点的字母来表示如线段AB。

在数轴上也可以使用一个区间来表示如[A, B]。

射线：使用起点和另一个点的字母来表示并指明方向如射线AB（从A出发经过B）。

直线：可以通过两点来表示如直线AB。

在数轴上直线可以用一个小写字母或两个不等的点来表示。

3. 几何特性：线段：是有限长的可以度量其长度。

线段是构成其他几何图形（如三角形四边形等）的基本元素。

射线：有一个端点和一个方向因此是无限长的不能度量其长度。

射线在几何学和物理学中有应用如光线和雷达波的传播。

直线：没有端点因此是无限长的也不能度量其长度。

直线是构成平面图形和立体图形的基本元素如平行四边形圆等。

4. 轴对称性：线段：线段是轴对称图形其对称轴是垂直于线段并通过其中点的直线。

射线：射线也是轴对称图形其对称轴是包含其端点的直线。

直线：直线是轴对称图形有无数条垂直于它的直线可以作为对称轴。

专项练一单选题1．下列说法错误的是（）A．两点之间线段最短B．对顶角相等C．同角的补角相等D．过一点有且只有一条直线与已知直线平行2．我们知道若线段上取一个点（不与两个端点重合以下同）则图中线段的条数为++=条若线段上取三个点123+=条若线段上取两个点则图中线段的条数为1236+++=条……请用你找到的规律解决下列实际问题：杭甬铁路则图中线段的条数为123410（即杭州—宁波）上有萧山绍兴上虞余姚4个中途站则车站需要印的不同种类的火车票为（）A ．6种B ．15种C ．20种D ．30种3．下列命题中是假命题的是（）A ．三个角对应相等的两个三角形全等B ．﹣3a 3b 的系数是﹣3C ．两点之间线段最短D ．若|a |＝|b | 则a ＝±b4．在下列说法①联接两点的线中线段最短 ①相等的角是对顶角 ①过直线外一点有且只有一条直线与已知直线平行 ①两点间的线段是这两点的距离 ①20.196精确到百分位得20.2中正确的是（）A ．①①B ．①①C ．①①D ．①①5．已知线段AB 长2cm ．现延长AB 到点C 使3BC AB =．取线段AB 的中点D 线段CD 的长为（）A ．5cmB ．3cmC ．7cmD ．1cm6．如图以A B C D E 为端点图中共有线段（）A ．7条B ．8条C ．9条D ．10条7．如图所示下列说法正确的个数是（）①射线AB 和射线BA 是同一条射线 ①图中有两条射线 ①直线AB 和直线BA 是同一条直线 ①线段AB 和线段BA 是同一条线段．A ．4B ．3C ．2D ．18．如图在菱形ABCD 中 60ABC ∠=︒ E 是边BC 的中点 P 是对角线BD 上的一个动点连接AE AM 若12AP BP +的最小值恰好等于图中某条线段的长则这条线段是（）A ．AB B ．AEC ．BD D ．BE9．如图点C 是线段AB 的中点点D 是线段CB 上任意一点则下列表示线段关系的式子不正确的是（）A ．AB =2ACB ．AC +CD +DB =ABC ．CD =AD -12ABD ．AD =12（CD +AB ） 10．若将点A （－1 3）向右平移2个单位再向下平移4个单位得到点B 则点B 在第（）象限A ．一B ．二C ．三D ．四二填空题11．绷紧的琴弦人行横道都可以近似地看做它有个端点手电筒探照灯所射出的光线可以近似地看做它有个端点笔直的铁轨可以近似地看做它有端点．12．A B C 三点在同一条直线上若BC=2AB 且AB=m 则AC= ． 13．如图已知线段12AB = 延长线段AB 至点C 使得12BC AB =点D 是线段AC 的中点则线段BD 的长是．14．如图等边ABC 的边长为4 AD 是BC 边上的中线 F 是AD 边上的动点 E 是AC 边上一点若2AE = 当EF CF +取得最小值时则ECF ∠= ．15．若O 的半径为33 圆心O 为坐标系的原点点P 的坐标是()3,5 点P 在O ．16．已知线段AB=18cm P Q 是线段AB 上的两个点线段AQ=12cm 线段BP=14cm 则线段PQ= ．17．如图直线243y x =+与x 轴 y 轴分别交于点A 和点B 点C D 分别为线段AB OB 的中点点P 为OA 上一动点 PC PD +最小值是．18．菱形OBCD 在平面直角坐标系中的位置如图所示顶点B （2 0） ①DOB ＝60° 点P是对角线OC 上一个动点 E （0 则EP +BP 的最小值为．19．如图 C 为线段AD 上一点点B 为CD 的中点且8cm AD = 2cm BD =．若点E 在AD 上且EA=3cm BE 的长为．20．如图 AD 为等边ABC 的高 E F 分别为线段AD AC 上的动点且AE CF = 当BF CE +取得最小值时 AFB ∠的度数为．三解答题21．线段和角是我们初中数学常见的平面几何图形它们的表示方法和差计算以及线段的中点角的平分线的概念等有很多相似之处所以研究线段或角的问题时可以运用类比的方法．(1)特例感知：如图1 已知10cm AB = 点D 是线段AC 的中点点E 是线段BC 的中点．若6cm BC 则线段DE =________cm ．(2)数学思考：如图1 已知10cm AB = 若C 是线段AB 上的一个动点点D 是线段AC 的中点点E 是线段BC 的中点线段DE 的长会发生变化吗？说明理由．(3)知识迁移：如图2 OB 是AOC ∠内部的一条射线把三角尺中60︒角的顶点放在点O 处转动三角尺当三角尺的边OD 平分AOB ∠时在角尺的另一边OE 也正好平分BOC ∠ 求AOC ∠的度数．22．如图 C 为线段AB 的中点点D 在线段CB 上.（1）图中共有_________条线段（2）图中AD AC CD =+ BC AB AC =- 类似地请你再写出两个有关线段的和与差的关系式：①_________ ①_________（3）若8AB = 1.5DB = 求线段CD 的长.23．补全解题过程已知：如图点C 是线段AB 的中点 2CD =cm 8BD =cm 求AD 的长.解：①2CD=cm 8BD=cm①CB CD=+______＝______cm①点C是线段AB的中点①AC CB==______cm①AD AC=+_______＝_______cm24．（1）已知线段8AB=点C在线段AB的延长线上M N分别是线段AC与线段BC 的中点求线段MN的长（2）已知线段8cmAB=点C在线段AB的反向延长线上M N分别是线段AC与线段BC的中点则线段MN的长为cm．25．如图线段1134BD AB CD==点M N分别是线段AB CD的中点且20cmMN=求AC的长．参考答案：1．D2．D3．A4．A5．C6．D7．C8．B9．D10．D11．线段两射线 1 直线0个. 12．m或3m13．314．30︒15．外16．8cm17．5183119．3或9cm20．105︒/105度21．(1)5(2)不会(3)120︒22．（1）6 （2）(2)①BC=CD+DB ①AD=AB−DB (答案不唯一)（3）CD=2.5．23．BD10 10 CD12．24．（1）4 （2）425．48cm。

中考数学总复习《二次函数》专项测试卷-附参考答案

中考数学总复习《二次函数》专项测试卷-附参考答案学校:___________姓名：___________班级：___________考号：___________一、单选题(共12题；共24分)1．二次函数y＝﹣x2+2x﹣4，当﹣1＜x＜2时，y的取值范围是（）A．﹣7＜y＜﹣4B．﹣7＜y≤﹣3C．﹣7≤y＜﹣3D．﹣4＜y≤﹣3 2．已知二次函数y=3(x−2)2+ℎ，当自变量x分别取-2，2，5时，对应的值分别为y1，y2和y 3则y1，y2和y3的大小关系正确的是()A．y3<y2<y1B．y1<y2<y3C．y2<y3<y1D．y3<y1<y23．小敏在今年的校运动会跳远比赛中跳出了满意一跳，函数ℎ=3.5t−4.9t2（的单位：秒，h的单位：米）可以描述他跳跃时重心高度的变化，则他起跳后到重心最高时所用的时间是（）A．0.71B．0.70C．0.63D．0.364．对于二次函数y=−14(x+2)2−1，下列说法正确的是（）A．当x>−2时，y随x的增大而增大B．当x=−2时，y有最大值−1C．图象的顶点坐标为(2，−1)D．图象与x轴有两个交点5．抛物线y=2x2−12x+22的顶点是（）A．(3,−4)B．(−3,4)C．(3,4)D．(2,4)6．如图，二次函数y＝ax2＋bx＋c（a≠0）的图像的顶点在第一象限，且过点（0，1）和（－1，0）下列结论：①ab＜0，②b2-4ac＞0，③a-b+c＜0，④c=1，⑤当x＞－1时，y＞0.其中正确结论的个数是（）A．2个B．3个C．4个D．5个7．如图是二次函数y＝ax2+bx+c图象的一部分，其对称轴是x＝﹣1，且过点（﹣3，0），下列说法：①abc＜0；②2a﹣b＝0；③4a+2b+c＜0；④若（﹣5，y1），（3，y2）是抛物线上两点，则y1＜y2，其中说法正确的是（）A．①②B．②③C．①②④D．②③④8．关于二次函数y=-（x -2）2＋3，以下说法正确的是（）A．当x＞-2时，y随x增大而减小B．当x＞-2时，y随x增大而增大C．当x＞2时，y随x增大而减小D．当x＞2时，y随x增大而增大9．如图，双曲线y= k x经过抛物线y=ax2+bx（a≠0）的顶点（﹣1，m）（m＞0），则下列结论中，正确的是（）A．a+b=k B．2a+b=0C．b＜k＜0D．k＜a＜010．如图，抛物线y=ax2+bx+c交x轴于(−1，0)，(3，0)两点，则下列判断中，不正确的是（）A．图象的对称轴是直线x=1B．当x>2时，y随x的增大而减小C ．当−1<x <1时D ．一元二次方程ax 2+bx +c =0的两个根是−1和311．已知点(x 1，y 1)，(x 2，y 2)(x 1<x 2)在y =−x 2+2x +m 的图象上，下列说法错误的是（）A ．当m >0时，二次函数y =−x 2+2x +m 与x 轴总有两个交点B ．若x 2=2，且y 1>y 2，则0<x 1<2C ．若x 1+x 2>2，则y 1>y 2D ．当−1≤x ≤2时，y 的取值范围为m −3≤y ≤m12．从底面竖直向上抛出一小球，小球的高度h （单位：m ）与小球运动时间t （单位：s ）之间的关系式是：h ＝30t ﹣5t 2这个函数图象如图所示，则小球从第3s 到第5s 的运动路径长为（）A ．15mB ．20mC ．25mD ．30m二、填空题(共6题；共6分)13．在二次函数 y =−x 2+bx +c 中，函数y 与自变量x 的部分对应值如下表：则m 、n 的大小关系为 m n ．（填“＜”，“＝”或“＞”）14．已知一个二次函数的图象开口向上，顶点坐标为（0，﹣1 ），那么这个二次函数的解析式可以是．（只需写一个）15．二次函数 y =ax 2+bx +c 的图象与 x 轴相交于 (−1, 0) 和 (5, 0) 两点，则该抛物线的对称轴是 .16．函数y= {x 2+2x −3(x <0)x 2−4x −3(x ≥0) 的图象与直线y=﹣x+n 只有两个不同的公共点，则n 的取值为．17．已知二次函数y ＝﹣x 2+2mx+1，当﹣2≤x≤1时最大值为4，则m 的值为． 18．若函数y=（m ﹣2）x m 2−2+3是二次函数，则m=三、综合题(共6题；共70分)19．已知抛物线 y =a(x −4)2+2 经过点 (2,−2) ．（1）求a 的值；（2）若点A(m,y1),B(n,y2)(m<n<4)都在该抛物线上，试比较y1与y2的大小．20．宁波地区最近雾霾天气频繁，使得空气净化器得以畅销，某商场代理销售某种空气净化器，其进价是500元/台，经过市场销售后发现，在一个月内，当售价是1000元/台时，可售出50台，且售价每降低20元，就可多售出5台．若供货商规定这种空气净化器售价不能低于600元/台，代理销售商每月要完成不低于60台的销售任务．（1）试确定月销售量y（台）与售价x（元/台）之间的函数关系式；并求出自变量x的取值范围；（2）当售价x（元/台）定为多少时，商场每月销售这种空气净化器所获得的利润w（元）最大？最大利润是多少？21．某服装超市购进单价为30元的童装若干件，物价部门规定其销售单价不低于每件30元，不高于每件60元.销售一段时间后发现：当销售单价为60元时，平均每月销售量为80件，而当销售单价每降低10元时，平均每月能多售出20件.同时，在销售过程中，每月还要支付其他费用450元.设销售单价为x元，平均月销售量为y件.（1）求出y与x的函数关系式，并写出自变量x的取值范围.（2）当销售单价为多少元时，销售这种童装每月可获利1800元？（3）当销售单价为多少元时，销售这种童装每月获得利润最大？最大利润是多少？22．如图，是一座古拱桥的截面图，拱桥桥洞上沿是抛物线形状，抛物线两端点与水面的距离都是1m，拱桥的跨度为10m，桥洞与水面的最大距离是5m，桥洞两侧壁上各有一盏距离水面4m 的景观灯，把拱桥的截面图放在平面直角坐标系中。

中考数学总复习《函数》专项测试卷-附参考答案

中考数学总复习《函数》专项测试卷-附参考答案一、单选题(共12题；共24分)1．如图所示，抛物线L：y=ax2+bx+c（a<0）的对称轴为x=5，且与x轴的左交点为（1,0）则下列说法正确的有（）①C（9,0）；②b+c＞-10；③y的最大值为-16a；④若该抛物线与直线y=8有公共交点，则a的取值范围是a≤ 1 2．A．①②③④B．①②③C．①③④D．①④2．若y+3与x-2成正比例，则y是x的()A．正比例函数B．不存在函数关系C．一次函数D．以上都有可能3．关于函数y＝2x﹣1，下列结论成立的是（）A．当x＜0时，则y＜0B．当x＞0时，则y＞0C．图象必经过点（0，1）D．图象不经过第三象限4．关于一次函数y＝x＋2，下列说法正确的是（）A．y随x的增大而减小B．经过第一、三、四象限C．与y轴交于（0，2）D．与x轴交于（2，0）5．点P(3，y1)、Q (4，y2)是二次函数y=x2−4x+5的图象上两点，则y1与y2的大小关系为（）A．y1>y2B．y1<y2C．y1=y2D．无法确定6．快、慢两车分别从甲、乙两地同时出发，相向匀速行驶，两车在途中相遇时都停留了一段时间，然后分别按原速度原方向匀速行驶，快车到达乙地后休息半小时后，再以另一速度原路匀速返回甲地（掉头的时间忽略不计），慢车到达甲地以后即停在甲地等待快车．如图所示为快、慢两车间的距离y （千米）与快车的行驶时间x（小时）之间的函数图象．则下列说法：①两车在途中相遇时都停留了1小时；②快车从甲地去乙地时每小时比慢车多行驶40km；③快车从乙地返回甲地的速度为120km/h；④当慢车到达甲地的时候，快车与甲地的距离为400km．其中正确的有（）A．4B．3C．2D．17．如图，动点A在抛物线y=−x2+2x+3(0≤x≤3)上运动，直线l经过点（0,6），且与y轴垂直，过点A做AC⊥ l于点C，以AC为对角线作矩形ABCD，则另一对角线BD的取值范围正确的是（）A．2≤BD≤3B．3≤BD≤6C．1≤BD≤6D．2≤BD≤68．如图，在平面直角坐标系中，函数y=kx,y=−2x的图像交于A,B两点，过A作y轴的垂线，交函数y=3x的图像于点C，连接BC，则ΔABC的面积为（）A．2B．3C．5D．69．如图是抛物线y1＝ax2+bx+c（a≠0）图象的一部分，抛物线的顶点是A，对称轴是直线x＝1，且抛物线与x轴的一个交点为B（4，0）；直线AB的解析式为y2＝mx+n（m≠0）．下列结论：①2a+b＝0；②abc＞0；③方程ax2+bx+c＝mx+n有两个不相等的实数根；④抛物线与x轴的另一个交点是（﹣1，0）；⑤当1＜x＜4时，则则y1＞y2，其中正确的是（）A．①②B．①③⑤C．①④D．①④⑤10．如图，矩形ABCD中，AB=3，BC=4，点P从A点出发，按A→B→C的方向在AB和BC上移动，记PA=x，点D到直线PA的距离为y，则y关于x的函数大致图象是（）A．B．C．D．11．如图，在平面直角坐标系中，ΔA1A2A3，ΔA3A4A5，ΔA5A6A7，…都是等边三角形，其边长依次为2，4，6，…，其中点A1的坐标为(2，0)，点A2的坐标为(1，−√3)，点A3的坐标为(0，0)，点A4的坐标为(2，2√3)，…，按此规律排下去，则点A2020的坐标为()A．(1，−1009√3)B．(1，−1010√3)C．(2，1009√3)D．(2，1010√3)12．如图，二次函数y=-x2+bx+c 图象上有三点A(-1，y1 )、B(1，y2) 、C（2，y3），则y1，y2，y3大小关系为（）A．y1＜y3＜y2B．y3＜y1＜y2C．y1＜y2＜y3D．y2＜y1＜y3二、填空题(共6题；共6分)13．点P(1,1)向左平移两个单位后恰好位于双曲线y=k x上，则k=．14．将二次函数y=−x2+3的图像向下平移5个单位长度，所得图像对应的函数表达式为．15．如图，已知A1（1，0），A2（1，1），A3（﹣1，1），A4（﹣1，﹣1），A5（2，﹣1）…，则点A2021的坐标为.16．请写出一个二次函数，使它的图象同时满足下列两个条件：①开口向下，②与y轴的交点是（0，1），你写出的函数表达式是．17．若点P(n，1)，Q(n+6，3)在正比例函数图象上，请写出正比例函数的表达式. 18．在−3，−2，−1，4，5五个数中随机选一个数作为一次函数y=kx−3中k的值，则一次函数y=kx−3中y随x的增大而减小的概率是.三、综合题(共6题；共67分)19．3−√(−3)2+|√3−2|（1）计算：(−1)2021+√16+√−27（2）如图所示的是某学校的平面示意图，已知旗杆的位置是(−1，2)，实验室的位置是(2，3)．①根据所给条件建立适当的平面直角坐标系，并用坐标表示食堂，宿舍楼和大门的位置．②已知办公楼的位置是(−2，1)，教学楼的位置是(3，1)，在①中所画的图中标出办公楼和教学楼的位置．20．汽车出发1小时后油箱里有油40L，继续行驶若干小时后，在加油站加油若干升（加油时间忽略不计）．图象表示出发1小时后，油箱中剩余测量（y）与行驶时间t（h）之间的关系．（1）汽车行驶h后加油，中途加油L；（2）求加油前油箱剩余量y与行驶时间t的函数关系式；（3）若加油前后汽车都以80km/h匀速行驶，则汽车加油后最多能行驶多远？21．凤凰单丛（枞）茶，是潮汕的名茶，已有九百余年的历史．潮汕人将单丛茶按香型分为黄枝香、芝兰香、桃仁香、玉桂香、通天香、鸭屎香等多种．清明采茶季后，某茶叶店准备购买通天香和鸭屎香两种单丛茶进行销售，已知若购买4千克通天香单丛和3千克鸭屎香单丛需要2500元，购买2千克通天香单丛和5千克鸭屎香单丛需要2300元．（1）求通天香、鸭屎香两种茶叶的单价分别为多少元？（2）茶叶专卖店计划购买通天香、鸭屎香两种单丛茶共80千克，总费用不多于26000元，并且要求通天香茶叶数量不能低于10千克，那么应如何安排购买方案才能使总费用最少，最少费用应为多少元？22．为落实“双减”政策，丰富课后服务的内容，某学校计划到甲、乙两个体育专卖店购买一批新的体育用品，两个商店的优惠活动如下：甲：所有商品按原价8.5折出售；乙：一次购买商品总额不超过300元的按原价付费，超过300元的部分打7折．设需要购买体育用品的原价总额为x元，去甲商店购买实付y甲元，去乙商店购买实付y乙元，其函数图象如图所示.（1）分别求y甲，y乙关于x的函数关系式；（2）两图象交于点A，求点A坐标；（3）请根据函数图象，直接写出选择去哪个体育专卖店购买体育用品更合算．23．直线y=kx+b经过A（0，-3）)和B（-3，0）两点．（1）求这个一次函数的解析式；（2）画出图象，并根据图象说明不等式kx+b<0的解集．24．“龟兔首次赛跑”之后，输了比赛的兔子没有气馁，总结反思后，和乌龟约定再赛一场，下面的函数图象表示“龟兔再次赛跑”时，则乌龟所走路程y1（米）和兔子所走的路程y2（米）分别与乌龟从起点出发所用的时间x（分）之间的函数图象，根据图象解答下列问题：（1）“龟兔再次赛跑”的路程是米，兔子比乌龟晚走了分钟，乌龟在途中休息了分钟，“龟兔再次赛跑”获胜的是．（2）分别求出乌龟在途中休息前和休息后所走的路程y1关于时间x的函数解析式，并写出自变量x的取值范围．（3）乌龟和兔子在距离起点米处相遇．参考答案1．【答案】B 2．【答案】C 3．【答案】A 4．【答案】C 5．【答案】B 6．【答案】B 7．【答案】D 8．【答案】C 9．【答案】B 10．【答案】C 11．【答案】D 12．【答案】A 13．【答案】-114．【答案】y =−x 2−2 15．【答案】（506，﹣505）16．【答案】y =−x 2+x +1 （不唯一） 17．【答案】y =13x 18．【答案】3519．【答案】（1）解：原式=−1+4−3−3+2−√3=−1−√3（2）解：①根据题意，建立如图所示的平面直角坐标系，如下：∴食堂(−4，4)，宿舍楼（-5，1），大门(1，−1) ②办公楼和教学楼的位置如图所示．20．【答案】（1）4；35（2）解：设y 与x 的函数关系式为y ＝kt+b 把（1，40）和（4，10）代入得{k +b =404k +b =10解得 {k =−10b =50∴加油前油箱剩余油量y 与行驶时间t 的函数关系式y ＝﹣10t+50（3）解：由图象知，汽车加油前行驶了3小时，则用油40﹣10＝30（L ） ∴汽车行驶1小时耗油量为 303＝10（L/h ）加油后邮箱中剩余油量45L ，可以行驶 4510 ×80＝360（km ）．∴汽车加油后最多能行驶360km ．21．【答案】（1）解：设通天香茶叶每千克为x 元，鸭屎香茶叶每千克为y 元，根据题意，得{4x +3y =25002x +5y =2300解得{x =400y =300∴通天香茶叶每千克为400元，鸭屎香茶叶每千克为300元．（2）解：设购买通天香茶叶m 千克，鸭屎香茶叶（80－m ）千克，总费用w 元根据题意，得400m +300(80−m)≤26000 解得m ≤20 ∵m ≥10∴m 的取值范围是：10≤m ≤20总费用w =400m +300(80−m)=100m +24000 ∵100>0∴w 随着m 的增大而增大∴当m ＝10时，则w 最少，w 最少＝1000＋24000＝25000（元）∴通天香茶叶购进10千克，鸭屎香茶叶购进70千克，总费用最少为25000元．22．【答案】（1）解：由题意可得，y 甲=0.85x ；乙商店：当0≤x≤300时，则y 乙与x 的函数关系式为y 乙=x ；当x ＞300时，则y 乙=300+（x-300）×0.7=0.7x+90 由上可得，y 乙与x 的函数关系式为y 乙={x(0≤x ≤300)0.7x +90(x ＞300)（2）解：由{y 甲＝0.85xy 乙＝0.7x +90，解得{x ＝600y 乙＝510点A 的坐标为（600，510）；（3）解：由点A 的意义，当买的体育商品标价为600元时，则甲、乙商店优惠后所需费用相同，都是510元结合图象可知当x ＜600时，则选择甲商店更合算；当x=600时，则两家商店所需费用相同；当x ＞600时，则选择乙商店更合算．23．【答案】（1）解：将A(0，−3)，B(−3，0)代入y =kx +b 得{b =−3−3k +b =0解得：k =−1，b =−3∴y =−x −3一次函数的解析式为：y =−x −3．（2）解：作图如下：由图象可知：直线从左往右逐渐下降，即y 随x 的增大而减小当x =−3时∴kx +b <0的解集为：x >−3．24．【答案】（1）1000；40；10；兔子（2）解：设乌龟在途中休息前所走的路程y 1关于时间x 的函数解析式为y 1＝kx ∴600＝30k ，解得k ＝20∴乌龟在途中休息前所走的路程y 1关于时间x 的函数解析式为y 1＝20x （0≤x≤30）设乌龟在途中休息后所走的路程y 1关于时间x 的函数解析式为y 1＝k′x+b∴{40k ′+b =60060k ′+b =1000，解得{k ′=20b =−200∴乌龟在途中休息后所走的路程y1关于时间x的函数解析式为y1＝20x﹣200（40≤x≤60）；（3）750第11页共11。

中考化学专项复习测试卷：信息给予题测试卷(含解析)

信息给予题测试卷一、选择题(每题4分，共24分)1．已知“由同种元素组成的不同单质互称同素异形体”，下列各组物质互为同素异形体的是( )A．液氢、氢气 B．金刚石、刚玉C．氧气、臭氧(O3) D．SO2、SO32．钛和钛合金是21世纪的重要金属材料，它们具有优良的性能，如：熔点高，密度小，可塑性好，机械性能好，抗腐蚀能力强，钛合金与人体有很好的相容性。

根据它们的主要性能下列不合实际的是 ( )A．用于核潜艇设备的制造 B．用于制造航天设备C．用来做保险丝 D．可用来制造人造骨3．如图是氧元素在周期表中的信息，下列说法正确的是 ( )A．氧元素原子序数为8 B．氧原子核内质子数为l6C．氧元素属于金属元素 D．氧元素在地壳的含量为16％4．意大利科学家成功合成了一种新型氧分子——O4，这种氧分子把更多氧原子集中在同样大小的空间里，因此它液化后的能量密度将高于普通液态氧，可用作更强力的’火箭推进氧化剂。

以下关于O4的说法中错误的是 ( )A．一个O4分子由4个氧原子构成 B．O4和O2之间的转化属于物理变化C．O4的相对分子质量是64 D．O2、O3、O4都是由氧元素组成的单质5．自来水生产中通常使用少量氯气杀菌消毒，氯气与水反应的产物之一是盐酸。

市场上有些不法商贩为牟取暴利，用自来水冒充纯净水(蒸馏水)出售。

为辨别真假，可用下列一种化学试剂来鉴别，该试剂是 ( )A．酚酞试液 B．氯化钡溶液C．氢氧化钠溶液 D．硝酸银溶液6．二氧化硫是有刺激性的有毒的气体，其水溶液叫亚硫酸(H2SO3)。

硫化氢(H2S)是一种具有剧毒的臭鸡蛋气味的气体，其水溶液叫氢硫酸(H2S)。

又知相同条件下H2S的酸性小于H2SO3，现在室温下向饱和H2S03溶液通入过量H2S气体，反应方程式为：2 H2S +H2S03=3S↓+3H2O，则溶液的pH值随通入H2S体积的变化曲线示意图正确的是( )二、非选择题(本题共6小题，共76分)7．(4分)淡黄色固体氮化镁(Mg3N2)遇水反应生成一种碱和一种无色、有刺激性气味，能使湿润的红色石蕊试纸变蓝，写出该反应方程式：_______________________________。

专项复习测试卷(一)—数与代数(一)

２分)
＝２５２÷７
＝３６（分）……（１分）
答：小华平均每天阅读名著３６分。 ……（１分）
３７
(× )
(× )
(× )
三我会选. (将正确答案的序号填在括号里)(５分)
１
下面( C )中横线上的数是近似数.
A 四年级有１３２人
B
中心小学共有图书４６５８７本
C
正常人心脏一天大约跳动１０００００次
２
下面各数中,一个“
０”也不读出来的是( B ).
A５００００５ B
２在( 百 )位上,表示( ２个百 ).
２
－５．
０５读作( 负五点零五 ),零下２℃ 写作( －２℃ ).
３
最小的八位数是( １０００００００ ),比它小１的数是( ９９９９９９９ ),最大的八位数是
( ９９９９９９９９ ),比它大１的数是( １００００００００ ).
写作( ５２８０００３ )
２
读出下列各数.(
６分)
＋５读作: 正五
－１８℃
读作: 零下十八摄氏度
４００５３６２００读作: 四亿零五十三万六千二百
２００００５８０９０: 负三十六
３２６０００读作: 三十二万六千
３９
７００８３５０００
六下表记录的是小华上周阅读名著的情况. (共１１分)
星期一
星期二
星期三
星期四
星期五
星期六
星期日
３０分
３３分
３５分
３２分
３６分
４２分
４４分
－６分
－３分
－１分

中考化学专项复习测试卷：物质的变化测试卷(含解析)

物质的变化测试卷一、单项选择题(每小题只有一个选项符合题意，每题2分，共30分)1．下列变化中，发生了化学变化的是 ( )A．用木材做成桌椅 B．冰融化成水C．蜡烛燃烧 D．苹果榨汁2．下列变化中，没有新物质生成的是 ( )3．铁、稀硫酸、石灰水和氯化铜溶液之间的反应关系如图所示，图中两圆相交部分(A、B、C、D)表示物质间反应的类型或主要实验现象。

下列说法错误的是 ( )A．A处发生置换反应 B．B处发生复分解反应C．C处产生气泡 D．D处生成白色沉淀4．对反应x+3NaOH——3Y+Fe(OH)3↓的分析，错误的是( )A．X中含有三价元素 B．X可能是Fe2(SO4)3C．Y中一定含有Na元素 D．Y可能是NaNO35．在一定条件下，下列转化不能由一步反应实现的是 ( )A．H2O2→O2 B．CO2→COC．S→H2 SO4 D．P→P2 O56．已知某两种物质在一定条件下能发生化学反应，其反应的微观示意图如下，则下列说法中，正确的是 ( )A．图中的反应物都是化合物 B．该反应属于置换反应C．该反应属于复分解反应 D．该反应不符合质量守恒定律7．化学家在当今环境问题上的最新构想是“变废为宝，资源循环”。

例如，燃料』墼燃烧产物』堡塑燮堕竺坚燃料，这样既可解决能源问题，又能消除污染。

上述构想中的两个转化过程的变化为 ( )A．(1)为物理变化，(2)为化学变化B．均为物理变化C．(1)为化学变化，(2)为物理变化D．均为化学变化8．物质X是一种重要的阻燃剂，工业上用三氧化二锑(Sb2O3)生成X，反应的化学方式为：Sb2O3+2H2O2一X+2H2O (已配平)，则X的化学式为 ( )A．Sb2O3 B．SbO2 C．HSbO3 D．H3SbO49．科学家发现由C 60制取的化合物M 有抑制艾滋病毒的作用，下列叙述不正确的是( ) A ．厦大化学家制得了C 50，它与C 60都是单质B ．某物质含有C 50分子和C 60分子，该物质是化合物C ．由C 60制取化合物M 的过程，发生了化学变化D ．C 60在空气中燃烧生成二氧化碳的反应是化合反应10．在空气中发生的燃烧、爆炸、缓慢氧化和自燃的共同点是 ( )①都需要达到着火点 ②都发光③都很剧烈④都属于氧化反应A ．①②③④ B．②③④C ．③④D ．只有④11．人类生活需要能量。

中考化学专项复习测试卷：身边的化学物质测试卷(A)(含解析)

身边的化学物质测试卷(A)一、单项选择题(每小题只有一个选项符合题意，每题2分，共30分)1．学习化学可以防止走人生活和学习的误区。

你认为下列说法不正确的是 ( ) A．水银不是银，而是金属汞B．于冰不是冰，而是固体二氧化碳C．纯碱不是碱，而是盐D．苛性钠不是钠，而是一种常见的盐2．生活中常见的物质属于溶液的是 ( )A．八宝粥 B．珍珠奶茶C．矿泉水 D．蒸馏水3．下列“家庭小实验”不能达到预期目的的是 ( )A．用柠檬酸、果汁、白糖、水、小苏打等制汽水B．用空塑料瓶、小卵石、石英沙、活性炭、膨松棉等制作简易净水器C．向洗净的碎鸡蛋壳中加入食盐水可制二氧化碳D．用酒精浸泡捣烂的某些植物的花瓣可制酸碱指示剂4．下列物质中可作为复合肥料的是 ( )A．K2SO4 B．NH4HCO3C．NH4 H2PO4 D．CO(NH2)25．下列现象的产生，与空气中的水蒸气无关的是 ( )A．酥脆的饼干放置在空气中变软B．夏天从冰箱取出的冰糕冒“白气”C．冬季的早晨看到窗户的玻璃上有“冰花”D．进入久未开启的菜窖或乇涸深井使人感到气闷、头昏6．下列关于水的说法错误的是 ( )A．水是一种常用的溶剂B．我国的人均水量居世界第一C．加入肥皂水并搅拌，可区分硬水和软水D．水是人体必需的营养素之一7．下列生活经验和知识原理的叙述中，不正确的是 ( )A．铝合金比铁制品耐腐蚀的原理是：铁的化学性质比铝活泼B．用汽油洗涤衣服上的油渍的原理是：油渍易溶于汽油C．用含氢氧化铝的药物治疗胃酸过多的原理是：胃酸会和氢氧化铝发生中和反应D．食醋除水垢原理是:食醋中的醋酸和水垢中的物质发生化学反应生成可溶于水的物质8．下列各组物质分别加入足量的水中，能得到无色透明溶液的是 ( )A．FeCl3、NaOH、NaClB．Na2SO4、HCl、BaCl2C．CuSO4、KCl、HClD．Na2CO3、NaCl、Na2SO49．甲、乙两物质的溶解度曲线如图所示，下列叙述中正确的是 ( )A．t1℃时，甲、乙各30g分别加入70g水中均恰好饱和B．t1℃时，甲、乙两物质形成的溶液溶质的质量分数相等C．t2℃时，在100g水中放入l00g甲，所得溶液溶质的质量分数为50％D．t2℃时，分别在100g水中各溶解20g甲、乙，同时降低温度，甲先达到饱和10．水与我们息息相关，下列关于水的认识正确的是 ( )A．水电解产生氢气和氧气，说明水分子中含有氢分子和氧分子B．物质溶解于水时都会放出热量C．利用活性炭吸附水中的杂质可以使水软化D．使用无磷洗衣粉有利于防止水体富营养化11．根据物质的用途体现物质的性质这一关系，下列用途体现该物质的性质的说法错误的是 ( )A．金刚石可以刻划玻璃，说明金刚石的硬度大B．二氧化碳能使紫色石蕊试液变红，说明二氧化碳具有碱性C．氧气可用排水法收集，说明氧气不易溶于水D．活性炭可用于防毒面具，说明活性炭具有吸附性12．下列实验现象的描述错误的是 ( )A．铁丝在氧气中燃烧火星四射．B．镁条在空气中燃烧发出耀眼的强光C．锌片伸入硫酸铜溶液中表面有红色物质析出D．铜片投入稀硫酸中产生大量气泡13．如图是实验室加热高锰酸钾制取氧气的装置图，下列有关实验操作的分析错误的是 ( )A．气密性检查：用手握紧试管，观察到水中导气管有气泡冒出，说明装置不漏气B．试管略向下倾斜：防止试管壁上的水流入试管底部，导致试管炸裂C．加热：先用酒精灯预热，再直接对准药品所在位置加热D．停止加热：先熄灭酒精灯，再把导管移出水面14．下列有关二氧化碳的检验、制备和用途能达到目的的是 ( )A．干冰用于人工降雨B．二氧化碳气体通入紫色石蕊试液中，溶液变蓝C．用块状石灰石和稀硫酸迅速制备大量二氧化碳D．将燃着的木条伸入集气瓶，火焰立即熄灭，证明瓶内原有气体就是二氧化碳15．为证明Al、Fe．Cu三种金属的活动顺序，可选用的一组物质是 ( )A．Cu、AlCl3溶液、FeCl2溶液B．Cu、Fe、AlCl3溶液C．CuSO4溶液、Fe、AICl3溶液D．CuSO4溶液、AlCl3溶液、FeCl2溶液二、非选择题(本题共6小题，共70分)16．(9分)如图所示是A、B两种固体溶解度曲线(1)在t1℃时，A的溶解度比B _____(填“大”或“小”)；(2)在t2℃时______(填“能”或“不能”)配成40％的A溶液；(3)在t2℃时，将A、B两种物质的饱和溶液降温到t1℃时，A的饱和溶液中溶质的质量分数比B的饱和溶液中溶质的质量分数_______(填“大”或“小”)。

中考化学专项复习测试卷：化学与生活测试卷(含解析)

化学与生活测试卷一、单项选择题(每小题只有一个选项符合题意，每题2分，共30分)1．人体缺少必需的微量元素会影响健康，贫血通常需要补充的元素是 ( )A ．钙B ．铁C ．氟D ．碘2．下列富含糖类的食物是 ( )①鱼 ②牛肉 ③馒头 ④鸡蛋 ⑤玉米A ．①② B．③⑤ C．②④ D．④⑤3．某饮料的配料表：纯净水、蔗糖、苹果汁，维生素C 、维生素A 、乳酸钙。

此饮料不含有的营养素 ( )A ．糖类B ．维生素C ．水D ．油脂4．有机高分子合成材料的出现是材料发展吏上的一次重大突破，下列属于有机高分子合成材料的一组是 ( )①家用保鲜袋 ②不锈钢 ③淀粉④尼龙⑤汽车轮胎A ．①④⑤B ．②③④ C．②③⑤ D．只有①⑤5．下列物质在灼烧时能发出烧焦羽毛味的是 ( )A ．纯棉布料B ．羊毛纤维C ．腈纶面料D ．塑料袋6．下列说法错误的是 ( )A ．明矾既能净水又能杀菌消毒B ．利用洗洁精的乳化作用可以洗去餐具上的油污C ．误食重金属盐，可立即服用蛋清或牛奶解毒D ．蛋白质、糖类、油脂、维生素等是人体必需的营养素，但应注意膳食平衡7．下列说法正确的是 ( )A ．用灼烧的方法可鉴别：聚乙烯和聚氯乙烯；棉线和羊毛线；葡萄糖和蔗糖、B ．淀粉、油脂都是由碳、氢、氧元素组成，都属于糖类C ．维生素大多数不能在体内合成，需不断补充D ．大豆、花生遇到碘水变蓝8．近几年来，我国塑料废弃物总量已超过5 000万吨，为保护生存环境，下列对塑料废弃物的处理方法中，不正确的是 ( )A ．通过回收再生等途径直接用作材料B ．填埋、直接焚烧或倾倒于海洋中C ．降解后，再聚合成高分子材料D ．制成燃油和燃气，用作燃料9．下列对有关主题知识的归纳错误的是 ( )A ．认识元素B ．元素与人体健康C ．生活常识D ．环保与物质的利用10．今年世界地球日主题为“珍惜地球资源转变发展方式”。

下列做法违背该主题的是( ) A．利用秸杆、垃圾发电 B．利用太阳能、地热能等清洁能源C．回收利用废旧金属 D．大量开采、使用化石燃料11．下列叙述不正确的是 ( )A．凡是糖类都有甜昧B．人摄入蛋白质的量不足，会使人生长发育迟缓C．大豆、花生和谷物被霉菌污染，人不可食用，也不可喂家畜D．食用凉拌蔬菜，能获得较多的维生素12．“一杯牛奶强壮一个民族”是因为牛奶中富含人体所需要的 ( )A．铁元素 B．碘元素 C．锌元素 D．钙元素13．蛋白质是构成生命的基础物质。

中考数学总复习《尺规作图》专项测试卷带答案

中考数学总复习《尺规作图》专项测试卷带答案学校:___________班级：___________姓名：___________考号：___________A层·基础过关1.(2024·深圳中考)在如图的三个图形中,根据尺规作图的痕迹,能判断射线AD平分∠BAC的是( )A.①②B.①③C.②③D.只有①2.(2024·呼伦贝尔、兴安盟中考)如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,适当长为半径画弧分别交AB,AC于点M和点N,再分别以点M,N为圆心,大于1MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D.若△ACD的面2积为8,则△ABD的面积是( )A.8B.16C.12D.243.(2024·广西中考)如图,在△ABC中,∠A=45°,AC>BC.(1)尺规作图:作线段AB的垂直平分线l,分别交AB,AC于点D,E;(要求:保留作图痕迹,不写作法,标明字母)(2)在(1)所作的图中,连接BE,若AB=8,求BE的长.4.(2024·浙江中考)尺规作图问题:如图1,点E是▱ABCD边AD上一点(不包含A,D),连接CE.用尺规作AF∥CE,F是边BC上一点.小明:如图2以C为圆心,AE长为半径作弧,交BC于点F,连接AF,则AF∥CE.小丽:以点A为圆心,CE长为半径作弧,交BC于点F,连接AF,则AF∥CE.小明:小丽,你的作法有问题.小丽:哦…我明白了!(1)证明:AF∥CE;(2)指出小丽作法中存在的问题.B层·能力提升AC的5.(2024·济南莱芜区模拟)如图,在矩形ABCD中,分别以点A,C为圆心,大于12长为半径画弧,两弧相交于M,N两点;作直线MN,分别交AD,BC于点E,F,连接AF 和CE.已知DE=3,AB=4,则以下四个结论中正确的是( )AC·EF;②AE=5;①S四边形AFCE=12③∠F AC=∠ACF=30°;④EF=2√5.A.①②③B.①②④C.②③④D.①②6.(2024·武汉中考)如图是由小正方形组成的3×4网格,每个小正方形的顶点叫格点.△ABC三个顶点都是格点.仅用无刻度的直尺在给定网格中完成四个画图任务,每个任务的画线不得超过三条.(1)在图(1)中,画射线AD交BC于点D,使AD平分△ABC的面积;(2)在(1)的基础上,在射线AD上画点E,使∠ECB=∠ACB;(3)在图(2)中,先画点F,使点A绕点F顺时针旋转90°到点C,再画射线AF交BC 于点G;(4)在(3)的基础上,将线段AB绕点G旋转180°,画对应线段MN(点A与点M对应,点B与点N对应).7.(2024·绥化中考)已知:△ABC.(1)尺规作图:画出△ABC的重心G.(保留作图痕迹,不要求写作法和证明)(2)在(1)的条件下,连接AG,BG.已知△ABG的面积等于5 cm2,则△ABC的面积是_________cm2.C层·素养挑战8.(2024·淄博淄川区二模)如图,在四边形ABCD中,AB=AD,AB⊥AD,顶点(k>0,x>0)的图象经过C(4,n),D两A(0,2),B(1,0)分别在y轴、x轴上反比例函数y=kx点.(1)求反比例函数的解析式;(2)请用无刻度的直尺和圆规作出线段BC的垂直平分线;(要求:不写作法,保留作图痕迹)(3)线段BC与(2)中所作的垂直平分线分别与BC,AD交于点M,N两点.求点M的坐标.参考答案A层·基础过关1.(2024·深圳中考)在如图的三个图形中,根据尺规作图的痕迹,能判断射线AD平分∠BAC的是(B)A.①②B.①③C.②③D.只有①2.(2024·呼伦贝尔、兴安盟中考)如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,适当长为半径画弧分别交AB,AC于点M和点N,再分别以点M,N为圆心,大于1MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D.若△ACD的面2积为8,则△ABD的面积是(B)A.8B.16C.12D.243.(2024·广西中考)如图,在△ABC中,∠A=45°,AC>BC.(1)尺规作图:作线段AB的垂直平分线l,分别交AB,AC于点D,E;(要求:保留作图痕迹,不写作法,标明字母)【解析】(1)图形如图所示:(2)在(1)所作的图中,连接BE,若AB=8,求BE的长.【解析】(2)∵DE垂直平分线段AB,∴EB=EA∴∠EBA=∠A=45°,∴∠BEA=90°AB=4∵BD=DA,∴DE=DB=DA=12∴BE=√2BD=4√2.4.(2024·浙江中考)尺规作图问题:如图1,点E是▱ABCD边AD上一点(不包含A,D),连接CE.用尺规作AF∥CE,F是边BC上一点.小明:如图2以C为圆心,AE长为半径作弧,交BC于点F,连接AF,则AF∥CE.小丽:以点A为圆心,CE长为半径作弧,交BC于点F,连接AF,则AF∥CE.小明:小丽,你的作法有问题.小丽:哦…我明白了!(1)证明:AF∥CE;【解析】(1)根据小明的作法知,CF=AE∵四边形ABCD是平行四边形∴AD∥BC,又∵CF=AE∴四边形AFCE是平行四边形∴AF∥CE;(2)指出小丽作法中存在的问题.【解析】(2)以A为圆心,EC为半径画弧,交BC于点F,此时可能会有两个交点,只有其中之一符合题意.故小丽的作法有问题.B层·能力提升AC的5.(2024·济南莱芜区模拟)如图,在矩形ABCD中,分别以点A,C为圆心,大于12长为半径画弧,两弧相交于M,N两点;作直线MN,分别交AD,BC于点E,F,连接AF 和CE.已知DE=3,AB=4,则以下四个结论中正确的是(B)AC·EF;②AE=5;①S四边形AFCE=12③∠F AC=∠ACF=30°;④EF=2√5.A.①②③B.①②④C.②③④D.①②6.(2024·武汉中考)如图是由小正方形组成的3×4网格,每个小正方形的顶点叫格点.△ABC三个顶点都是格点.仅用无刻度的直尺在给定网格中完成四个画图任务,每个任务的画线不得超过三条.(1)在图(1)中,画射线AD交BC于点D,使AD平分△ABC的面积;(2)在(1)的基础上,在射线AD上画点E,使∠ECB=∠ACB;(3)在图(2)中,先画点F,使点A绕点F顺时针旋转90°到点C,再画射线AF交BC 于点G;(4)在(3)的基础上,将线段AB绕点G旋转180°,画对应线段MN(点A与点M对应,点B与点N对应).【解析】(1)如图(1)中,线段AD即为所求;(2)如图(1)中,点E即为所求;(3)如图(2)中,点C,射线AF,点G即为所求;(4)如图(2)中,线段MN即为所求.7.(2024·绥化中考)已知:△ABC.(1)尺规作图:画出△ABC的重心G.(保留作图痕迹,不要求写作法和证明)【解析】(1)分别作出AB边和BC边的垂直平分线,与AB和BC边分别交于点N 和点M连接AM和CN如图所示,点G即为所求作的点.(2)在(1)的条件下,连接AG,BG.已知△ABG的面积等于5 cm2,则△ABC的面积是_________cm2.答案:15【解析】(2)∵点G是△ABC的重心∴AG=2MG∵△ABG的面积等于5 cm2∴△BMG的面积等于2.5 cm2∴△ABM的面积等于7.5 cm2.又∵AM是△ABC的中线∴△ABC的面积等于15 cm2.C层·素养挑战8.(2024·淄博淄川区二模)如图,在四边形ABCD中,AB=AD,AB⊥AD,顶点A(0,2),B(1,0)分别在y轴、x轴上反比例函数y=k(k>0,x>0)的图象经过C(4,n),D两x点.(1)求反比例函数的解析式;【解析】(1)过点D作DT⊥OA于点T.∵A(0,2),B(1,0)∴OA=2,OB=1∵AB⊥AD,DT⊥OT∴∠DTA=∠DAB=∠AOB=90°∵∠DAT+∠OAB=90°,∠OAB+∠ABO=90°,∴∠DAT=∠ABO ∵AD=AB∴△DTA≌△AOB(AAS)∴AT=OB=1,DT=AO=2∴OT=OA+AT=3∴D(2,3)∵反比例函数y=kx (k>0,x>0)的图象经过D点,∴3=k2,∴k=6∴反比例函数解析式为y=6x;(2)请用无刻度的直尺和圆规作出线段BC的垂直平分线;(要求:不写作法,保留作图痕迹)【解析】(2)如图,直线MN即为所求;(3)线段BC与(2)中所作的垂直平分线分别与BC,AD交于点M,N两点.求点M的坐标.【解析】(3)∵C(4,n)在y=6x的图象上∴n=32∴C(4,32)∵BM=CM,B(1,0)∴M(4+12,32+02)即M(52,34).第11页共11页。