第十五章物理化学(第五版、胡英)课后答案
物理化学上册的答案第五版上册

气体pVT 性质1. 1-1物质的体膨胀系数V α与等温压缩系数T κ的定义如下:1 1T T p V p V V T V V⎪⎪⎭⎫ ⎝⎛∂∂-=⎪⎭⎫⎝⎛∂∂=κα试导出理想气体的V α、T κ与压力、温度的关系? 解:对于理想气体,pV=nRT111 )/(11-=⋅=⋅=⎪⎭⎫⎝⎛∂∂=⎪⎭⎫ ⎝⎛∂∂=T TVV p nR V T p nRT V T V V p p V α 1211 )/(11-=⋅=⋅=⎪⎪⎭⎫ ⎝⎛∂∂-=⎪⎪⎭⎫ ⎝⎛∂∂-=p p V V pnRT V p p nRT V p V V T T T κ 1-2 气柜内有、27℃的氯乙烯(C 2H 3Cl )气体300m 3,若以每小时90kg 的流量输往使用车间,试问贮存的气体能用多少小时?解:设氯乙烯为理想气体,气柜内氯乙烯的物质的量为mol RT pV n 623.1461815.300314.8300106.1213=⨯⨯⨯== 每小时90kg 的流量折合p 摩尔数为 133153.144145.621090109032-⋅=⨯=⨯=h mol M v Cl H C n/v=(÷)=小时1-3 0℃、的条件常称为气体的标准状况。
试求甲烷在标准状况下的密度。
解:33714.015.273314.81016101325444--⋅=⨯⨯⨯=⋅=⋅=m kg M RT p M V n CH CH CHρ 1-4 一抽成真空的球形容器,质量为。
充以4℃水之后,总质量为。
若改用充以25℃、的某碳氢化合物气体,则总质量为。
试估算该气体的摩尔质量。
解:先求容器的容积33)(0000.10010000.100000.250000.1252cm cm V l O H ==-=ρn=m/M=pV/RTmol g pV RTm M ⋅=⨯-⨯⨯==-31.301013330)0000.250163.25(15.298314.841-5 两个体积均为V 的玻璃球泡之间用细管连接,泡内密封着标准状况条件下的空气。
第五版物理化学课后习题答案 (2)

第三章 热力学第二定律3-1 卡诺热机在T 1=600K 的高温热源和T 2=300K 的低温热源间工作。
求: (1) 热机效率η;(2) 当向环境做功-W =100kJ 时,系统从高温热源吸收的热Q 1与Q2 解:(1) 卡诺热机的效率为: η=121T T T - =600300600-(2) η=1WQ - Q 1=2×100=200 kJ -Q 2=Q 1+W =200-100=100kJ3-2 某地热水的温度为65℃,大气温度为20℃。
若分别用一可逆热机和一不可逆热机从地热水中取出1000J 的热量。
(1) 分别计算两热机对外所做的功。
已知不可逆热机效率是可逆热机效率的80%; (2) 分别计算两热机向大气中放出的热。
解:(1) ∵ 1211338.15293.15338.15R W T T Q T ---==∴ W R =451000338.15-⨯J W IR =80% W R J (2) ∵ Q 1=-W -Q 2∴ 可逆热机 Q 1=133.1-1000=-866.9 J不可逆热机 Q 1=106.5-1000=-893.5 J3-3 卡诺热机在T 1=900K 的高温热源和T 2=300K 的低温热源间工作。
求: (1) 热机效率η;(2) 当向低温热源放热-Q 2=100kJ 时,系统从高温热源吸热Q 1及对环境作的功-W 。
解:(1) 卡诺热机的效率为: η=121T T T - =900300900-(2) η=1-21Q Q Q 1=122TQ T -=900100300⨯=21Q η-=1000.66671--kJ -W =ηQ 1×300=Q 1+Q 2=300.03-100=200.03 kJ3-4 冬季利用热泵从室外0℃的环境吸热,向室内18℃的房间供热。
若每分钟100 kJ 的功开动热泵,试估算热泵每分钟最多能向室内供热多少? 解: η=121T T T - =273.15291.15273.15--Q 2=1000.06950Wη-=kJ3-5 高温热源温度T 1=600K ,低温热源温度T 2=300K 。
(NEW)傅献彩《物理化学》(第5版)笔记和课后习题(含考研真题)详解

目 录第1章 气 体1.1 复习笔记1.2 课后习题详解1.3 名校考研真题详解第2章 热力学第一定律2.1 复习笔记2.2 课后习题详解2.3 名校考研真题详解第3章 热力学第二定律3.1 复习笔记3.2 课后习题详解3.3 名校考研真题详解第4章 多组分系统热力学及其在溶液中的应用4.1 复习笔记4.2 课后习题详解4.3 名校考研真题详解第5章 相平衡5.1 复习笔记5.2 课后习题详解5.3 名校考研真题详解第6章 化学平衡6.1 复习笔记6.2 课后习题详解6.3 名校考研真题详解第7章 统计热力学基础7.1 复习笔记7.2 课后习题详解7.3 名校考研真题详解第8章 电解质溶液8.1 复习笔记8.2 课后习题详解8.3 名校考研真题详解第9章 可逆电池的电动势及其应用9.1 复习笔记9.2 课后习题详解9.3 名校考研真题详解第10章 电解与极化作用10.1 复习笔记10.2 课后习题详解10.3 名校考研真题详解第11章 化学动力学基础(一)11.1 复习笔记11.2 课后习题详解11.3 名校考研真题详解第12章 化学动力学基础(二)12.1 复习笔记12.2 课后习题详解12.3 名校考研真题详解第13章 表面物理化学13.1 复习笔记13.2 课后习题详解13.3 名校考研真题详解第14章 胶体分散系统和大分子溶液14.1 复习笔记14.2 课后习题详解14.3 名校考研真题详解第1章 气 体1.1 复习笔记一、气体分子动理论1.理想气体理想气体:在任何压力、任何温度下都符合理想气体状态方程pV=nRT 的气体。
理想气体状态方程中,p为气体压力,单位是Pa;V为气体的体积,单位是m3;n为物质的量,单位是mol;T为热力学温度,单位是K;R是摩尔气体常数,。
2.气体分子动理论的基本公式(1)气体分子运动的微观模型①气体是大量分子的集合体;②气体分子不断地作无规则的运动,均匀分布在整个容器之中;③分子彼此的碰撞以及分子与器壁的碰撞是完全弹性的。
物理化学第五版复习题答案

物理化学第五版复习题答案物理化学是化学学科中的一个重要分支,它涉及到物质的物理性质和化学性质之间的相互关系。
以下是物理化学第五版复习题的一些答案,供参考:1. 什么是热力学第一定律?热力学第一定律,也称为能量守恒定律,表述为:在一个封闭系统中,能量既不能被创造也不能被消灭,只能从一种形式转换为另一种形式,或者从一个系统转移到另一个系统。
在热力学中,能量的总量保持不变。
2. 描述熵的概念及其物理意义。
熵是一个物理量,用来描述系统的无序程度。
在热力学中,熵的增加表示系统趋向于更加无序的状态。
熵的物理意义在于,它与系统的微观状态数有关,微观状态数越多,系统的熵就越大。
3. 什么是理想气体状态方程?理想气体状态方程是描述理想气体状态的方程,其形式为:\[ PV = nRT \],其中\( P \)是压力,\( V \)是体积,\( n \)是摩尔数,\( R \)是理想气体常数,\( T \)是绝对温度。
4. 简述化学平衡的概念。
化学平衡是指在一个封闭系统中,正向反应和反向反应进行得同样快,使得反应物和生成物的浓度保持不变的状态。
在化学平衡状态下,系统的宏观性质不随时间变化。
5. 什么是电化学电池的工作原理?电化学电池的工作原理基于氧化还原反应。
在电池中,一个物质在阳极上发生氧化,释放电子;另一个物质在阴极上发生还原,吸收电子。
电子的流动形成了电流,从而实现化学能向电能的转换。
6. 描述表面张力的概念及其影响因素。
表面张力是液体表面分子之间的相互吸引力,它使得液体表面尽可能地减小其表面积。
表面张力的大小受温度、压力和液体的化学性质等因素影响。
7. 什么是相变?相变是指物质从一种相态(如固态、液态或气态)转变为另一种相态的过程。
例如,冰融化成水是固态向液态的相变,水蒸发成蒸汽是液态向气态的相变。
8. 解释什么是阿伏伽德罗定律。
阿伏伽德罗定律指出,在相同的温度和压力下,等体积的任何气体都包含相同数量的分子。
物理化学上册的答案_第五版上册

气体pVT 性质1. 1-1物质的体膨胀系数V α与等温压缩系数T κ的定义如下:1 1T T p V p V V T V V⎪⎪⎭⎫ ⎝⎛∂∂-=⎪⎭⎫⎝⎛∂∂=κα试导出理想气体的V α、T κ与压力、温度的关系 解:对于理想气体,pV=nRT111 )/(11-=⋅=⋅=⎪⎭⎫⎝⎛∂∂=⎪⎭⎫ ⎝⎛∂∂=T TVV p nR V T p nRT V T V V p p V α 1211 )/(11-=⋅=⋅=⎪⎪⎭⎫ ⎝⎛∂∂-=⎪⎪⎭⎫ ⎝⎛∂∂-=p p V V pnRT V p p nRT V p V V T T T κ 1-2 气柜内有、27℃的氯乙烯(C 2H 3Cl )气体300m 3,若以每小时90kg 的流量输往使用车间,试问贮存的气体能用多少小时解:设氯乙烯为理想气体,气柜内氯乙烯的物质的量为mol RT pV n 623.1461815.300314.8300106.1213=⨯⨯⨯== 每小时90kg 的流量折合p 摩尔数为 133153.144145.621090109032-⋅=⨯=⨯=h mol M v Cl H Cn/v=(÷)=小时1-3 0℃、的条件常称为气体的标准状况。
试求甲烷在标准状况下的密度。
解:33714.015.273314.81016101325444--⋅=⨯⨯⨯=⋅=⋅=m kg M RT p M V n CH CH CHρ 1-4 一抽成真空的球形容器,质量为。
充以4℃水之后,总质量为。
若改用充以25℃、的某碳氢化合物气体,则总质量为。
试估算该气体的摩尔质量。
解:先求容器的容积33)(0000.10010000.100000.250000.1252cm cm V l O H ==-=ρn=m/M=pV/RTmol g pV RTm M ⋅=⨯-⨯⨯==-31.301013330)0000.250163.25(15.298314.841-5 两个体积均为V 的玻璃球泡之间用细管连接,泡内密封着标准状况条件下的空气。
胡英版物化练习题答案(不分章)
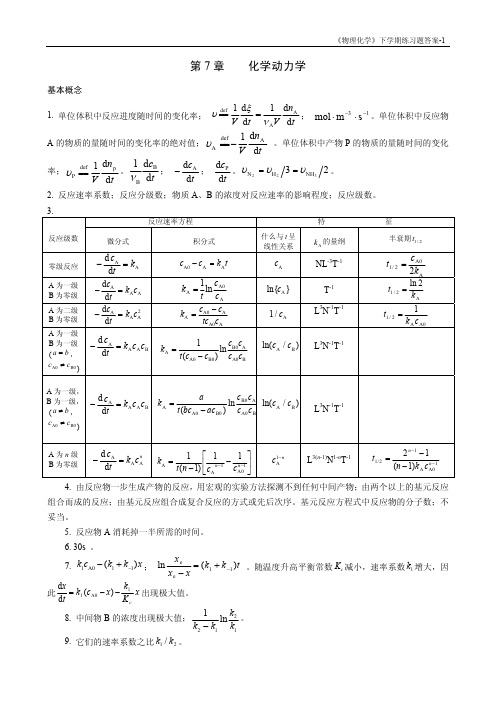
自由度不开放,只有平动和转动的贡献。
19. S = k lnΩ ;系统混乱程度的度量。 ⎛ ∂ lnq ⎞ ⎛ ∂ lnq ⎞ q 20. S = N k lnq + NkT ⎜ ⎜ ∂T ⎟ ⎟ + Nk 。 ⎜ ∂T ⎟ ⎟ ; S = Nkln N + NkT ⎜ ⎝ ⎠V , N ⎝ ⎠V , N 21. 物质在升温或降温过程中所能“吞吐”的那部分熵,与分子热运动能相对应;平动、转动和振动。
16. 链产生;链传递;链终止。
计算题
1. 解:(1)
A → B + C
t =t α α 1−α y A 1 − 01085 − 1 1 − α . 可得 = y ,α = = = 0.8042 。 A 1+ α . 1 + y A 1 + 01085
(2) t = 1/ 2
1 1 = = 146 s 。 k A c A0 1559 . × 4.39 × 10 − 3 p py . (3) p = p (1 − α ) ,∴ p = A = A = 24.58 × 01085 = 13.62 kPa 。 A0 A0 A 1− α 1− α 1 − 0.8042 p 13.62 × 10 3 = 4.39 mol ⋅ m − 3 = 4.39 × 10 − 3 mol ⋅ dm − 3 , cA0 = A0 = . RT 8.314 × 37315 0.8042 α kA = = = 1559 . mol −1 ⋅ dm 3 ⋅ s −1 t c A0 (1 − α ) (10 × 60) × 4.39 × 10 − 3 × (1 − 0.8042)
⎛ k1 ⎞ ⎜ ⎜k ⎟ ⎟ ⎝ 2 ⎠T2 E − E a 2 T1 − T 2 1⎛ 1 1⎞ ln = −( E a 1 − E a 2 ) ⎜ − ⎟ = − a1 ⋅ ⎜ ⎟ R ⎝ T 2 T1 ⎠ R T 2 ⋅ T1 ⎛ k1 ⎞ ⎜ ⎜k ⎟ ⎟ ⎝ 2 ⎠T
物理化学课后答案解析(傅献彩_第五版)

范文范例 精心整理 word 完美格式
范文范例 精心整理 word 完美格式
范文范例 精心整理 word 完美格式
范文范例 精心整理 word 完美格式
范文范例 精心整理 word 完美格式
范文范例 精心整理 word 完美格式
范文范例 精心整理 word 完美格式
范文范例 精心整理 word 完美格式
范文范例 精心整理 word 完美格式
范文范例 精心整理
第三章 热力学第二定律
word 完美格式
范文范例 精心整理 word 完美格式
范文范例 精心整理 word 完美格式
范文范例 精心整理 word 完美格式
范文范例 精心整理 word 完美格式
范文范例 精心整理 word 完美格式
范文范例 精心整理 word 完美格式
范文范例 精心整理 word 完美格式
范文范例 精心整理 word 完美格式
范文范例 精心整理 word 完美格式
范文范例 精心整理 word 完美格式
范文范例 精心整理 word 完美格式
范文范例 精心整理 word 完美格式
范文范例 精心整理 word 完美格式
范文范例 精心整理 word 完美格式
范文范例 精心整理 word 完美格式
范文范例 精心整理 word 完美格式
范文范例 精心整理 word 完美格式
范文范例 精心整理 word 完美格式
范文范例 精心整理 word 完美格式
范文范例 精心整理 word 完美格式
范文范例 精心整理
第二章 热力学第一定律
word 完美格式
范文范例 精心整理 word 完美格式
范文范例 精心整理 word 完美格式
物理化学第五版全册课后习题答案

n H 2O nC H 2 2 n H 2O nC H 2 2
p H 2O 进 p C2 H 2 p H 2O 出 p C 2 H 2
3.17 0.02339(mol ) 进 138.7 3.17 123 0.008947(mol ) 出 138.7 123
可见,隔板抽去前后,H2 及 N2 的摩尔体积相同。 (3) y H 2
3n N 2 n N 2 3n N 2
3 , 4
y N2
1 4
3 1 p; p N 2 y N 2 p p 4 4
pH2 yH2 p
所以有
p H2 : p N2 3 1 p : p 3 :1 4 4
3
VO2 y O2 V
n pV 101325 200 10 6 0.008315mol RT 8.314 293.15
3
M
m 0.3897 y AM A yB M B 46.867 g mol 1 n 0.008315 30.0694 y A 58.123 y B
(1)
第七章 电化学
余训爽
1-8 如图所示一带隔板的容器中, 两侧分别有同温同压的氢气与氮气, 二者均克视为理 想气体。 H2 p 3dm T
3
N2 p
1dm T
3
(1)保持容器内温度恒定时抽去隔板,且隔板本身的体积可忽略不计,试求两种气体 混合后的压力。 (2)隔板抽去前后,H2 及 N2 的摩尔体积是否相同? (3)隔板抽去后,混合气体中 H2 及 N2 的分压力之比以及它们的分体积各为若干? 解: (1)抽隔板前两侧压力均为 p,温度均为 T。 n H RT n N RT (1) p H 2 2 3 p N2 2 3 p 3dm 1dm 得: nH 3n N
物理化学(天大第五版全册)课后习题答案

资料范本本资料为word版本,可以直接编辑和打印,感谢您的下载物理化学(天大第五版全册)课后习题答案地点:__________________时间:__________________说明:本资料适用于约定双方经过谈判,协商而共同承认,共同遵守的责任与义务,仅供参考,文档可直接下载或修改,不需要的部分可直接删除,使用时请详细阅读内容气体pVT性质1-1物质的体膨胀系数与等温压缩系数的定义如下:试导出理想气体的、与压力、温度的关系?解:对于理想气体,pV=nRT1-5 两个体积均为V的玻璃球泡之间用细管连接,泡内密封着标准状况条件下的空气。
若将其中一个球加热到100℃,另一个球则维持0℃,忽略连接管中气体体积,试求该容器内空气的压力。
解:方法一:在题目所给出的条件下,气体的量不变。
并且设玻璃泡的体积不随温度而变化,则始态为终态(f)时1-8 如图所示一带隔板的容器中,两侧分别有同温同压的氢气与氮气,二者均克视为理想气体。
(1)保持容器内温度恒定时抽去隔板,且隔板本身的体积可忽略不计,试求两种气体混合后的压力。
(2)隔板抽去前后,H2及N2的摩尔体积是否相同?(3)隔板抽去后,混合气体中H2及N2的分压力之比以及它们的分体积各为若干?解:(1)抽隔板前两侧压力均为p,温度均为T。
(1)得:而抽去隔板后,体积为4dm3,温度为,所以压力为(2)比较式(1)、(2),可见抽去隔板后两种气体混合后的压力仍为p。
(2)抽隔板前,H2的摩尔体积为,N2的摩尔体积抽去隔板后所以有,可见,隔板抽去前后,H2及N2的摩尔体积相同。
(3)所以有*1-17 试由波义尔温度TB的定义式,试证范德华气体的TB可表示为TB=a/(bR)式中a、b为范德华常数。
解:先将范德华方程整理成将上式两边同乘以V得求导数当p→0时,于是有当p→0时V→∞,(V-nb)2≈V2,所以有 TB= a/(bR)第二章热力学第一定律2-1 1mol理想气体于恒定压力下升温1℃,试求过程中气体与环境交换的功W。
物理化学第五版上册习题答案

物理化学第五版上册习题答案10-1 请回答下列问题:(1) 常见的亚稳定状态有哪些?为什么产生亚稳态?如何防止亚稳态的产生?(2) 在一个封闭的钟罩内,有大小不等的两个球形液滴,问长时间放置后,会出现什么现象?(3) 下雨时,液滴落在水面上形成一个大气泡,试说明气泡的形状和理由? (4) 物理吸附与化学吸附最本质的区别是什么?(5) 在一定温度、压力下,为什么物理吸附都是放热过程?答: (1) 常见的亚稳态有:过饱和蒸汽、过热液体、过冷液体、过饱和溶液。
产生这些状态的原因就是新相难以生成,要想防止这些亚稳状态的产生,只需向体系中预先加入新相的种子。
(2) 一断时间后,大液滴会越来越大,小液滴会越来越小,最终大液滴将小液滴“吃掉”,根据开尔文公式,对于半径大于零的小液滴而言,半径愈小,相对应的饱和蒸汽压愈大,反之亦然,所以当大液滴蒸发达到饱和时,小液滴仍未达到饱和,继续蒸发,所以液滴会愈来愈小,而蒸汽会在大液滴上凝结,最终出现“大的愈大,小的愈小”的情况。
(3) 气泡为半球形,因为雨滴在降落的过程中,可以看作是恒温恒压过程,为了达到稳定状态而存在,小气泡就会使表面吉布斯函数处于最低,而此时只有通过减小表面积达到,球形的表面积最小,所以最终呈现为球形。
(4) 最本质区别是分子之间的作用力不同。
物理吸附是固体表面分子与气体分子间的作用力为范德华力,而化学吸附是固体表面分子与气体分子的作用力为化学键。
43331432r133r2r13a1222r2-r12)(1?10)1?10?9?33-10-6)2?r2?r4?r=2?58.91?100.1?10 ?6?32?58.91?100.1?10 ?6?34?58.91?100.1?10 ?6?3----2?r=2?22.3?105?10 ?5?3=892 pa?3h=2?cos?r?g=2?22.3?105?10 ?5?1?789.4?9.8=0.1153 m-时,计算(1) 开始形成水滴的半径;(2) 每个水滴中所含水分子的个数。
物理化学答案_上册_高教_第五版(Answer _ _ on physical chemistry of higher education _ Fifth Edition)

物理化学答案_上册_高教_第五版(Answer _ _ on physical chemistry of higher education _ Fifth Edition)Chapter 1 gasPVTNature1.1 material expansion coefficientIsothermal compression rateThe definition is as followsTest the introduction of ideal gas,Relationship with pressure and temperature.According to the ideal gas equation1.5 two glass balls with V volume are connected by a small tube, and the bubbles are sealed with standard air. If soA ball is heated to 100 degrees C, while the other ball is maintained at 0 degrees C. The volume of the gas in the pipe is neglected and the container is soughtInternal air pressure.Solution: from the question to the condition, (1) the total mass of the system is constant; (2) the pressure remains the same in the two ball.Standard state:Therefore,As figure 1.9 shows, the container area partition, both sides are at the same pressure of hydrogen and nitrogen, two are regarded as idealGas.Page(1) when the temperature in the container is kept constant, the separator is removed and the volume of the barrier itself is negligibleSeek the pressure of two gases mixed.(2) is the molar volume of H2 and N2 equal before and after the separation of the separator?(3) after the separation of the separator, the partial pressure of H2 and N2 in the mixture gas and the volume of their respective parts are severalSolution: (1) after isothermal mixingThat is, under the above conditions, the mixing pressure of the system is considered.(2) how is the molar volume of a component in a mixed gas defined?(3) according to the definition of volumeFor partial pressure1.11 atmospheric pressure air in a autoclave at room temperature for safety during the experiment and the use of pure nitrogen at the same temperatureThe steps are as follows: nitrogen is sent to the kettle until it is 4 times as high as the air, and then the mixture gas is discharged from the tank until it is recoveredCompound atmospheric pressure. Repeat three times. The mole fraction of oxygen contained in the gas is obtained when the final exhaust gas reaches the normal atmospheric pressure.Analysis: every time after the nitrogen gas, the gas returned to the atmospheric pressure P, and the mole fraction of the mixed gas remained unchanged.Before the first charge of nitrogen, the mole fraction of oxygen in the system isAfter nitrogen, the mole fraction of oxygen in the systembyThen,. Repeat the process above, nAfter secondary nitrogen, the mole fraction of the system is,therefore.1.13 there are 0 degrees C, 40.530 kPa N2 gas, using ideal gas equation of state and van, der, Waals equation calculationIts molar volume. The experimental value is.Solution: the equation of state of ideal gas is usedPageUsing van, der, and Waals calculations, look-up tables are known for N2 gas (Appendix seven)MatLab fzero function is used to obtain the solution of the equationDirect iteration can also be used,Take initial valueIterate ten timesAt 1.1625 degrees C, saturated acetylene gas saturated with water (i.e., the partial pressure of the steam in the mixture is saturated at the same temperature)And vapor pressure) the total pressure is 138.7 kPa and is cooled to 10 DEG C at constant total pressure, which condenses some of the water vapor into water. Try to seek forThe amount of material that condenses in the cooling process of each mole of dry acetylene gas. Saturated vapor of water at 25 C and 10 degrees CThe pressures are 3.17 kPa and 1.23 kPa, respectively.Solution: the process is illustrated as followsIf the system is an ideal gas mixture, then1.17 a tightly packed rigid container filled with air and witha small amount of water. But containers are in great balance at 300 K conditions, containersThe internal pressure is 101.325 kPa. If the container is moved to boiling water of 373.15 K, try to achieve a new equilibrium in the containerSome pressure. There is always water in the container, and any volume change of water can be neglected. 300 K the saturated vapor pressure of waterFor 3.567 kPa.Solution: when gas phase is regarded as ideal gas, at 300 K, the partial pressure of air isPageAs the volume is constant (ignoring any change in volume of water), the partial pressure of the air at 373.15 K isSince there is always water present in the container, the saturated vapor pressure of water at 373.15 K is 101.325 kPaThe partial pressure of water vapor is 101.325 kPa, so the total pressure of the systemPageThe second chapter is the first law of thermodynamics2.5 the initial state is 25 ~ C, 200 kPa, 5 mol of an ideal gas, by way of a, B two different ways to the same final.By way of a, the adiabatic expansion to -28.47 degrees C, 100 kPa, the steps of the workThe constant volume heats up to the pressure200 kPa the final step of heat. Pathway B is a constant pressure heating process. Seeking ways of Band.Solution: first determine the initial and final systemFor the way B, his work isAccording to the first law of thermodynamics2.64 mol of an ideal gas, the temperature increased by 20 degrees CValue.Solution: according to the definition of enthalpy2.102 mol an ideal gas,.The initial state is 100 kPa, 50 DMThreeThe constant volume heating increases the volume of pressure As large as 150 DMThreeConstant pressure cooling reduced the volume to 25 DMThree. Seeking the whole process.Solution: the process is illustrated as followsPageBecauseThen,Yes, ideal gasandIt's just a function of temperatureThe approach involves only constant volume and constant pressure processes, so it is convenient to calculate the workAccording to the first law of thermodynamicsThe 2.13 known 20 DEG C liquid ethanol (C2H5OH, l) of the expansion coefficientIsothermal compression rateDensityMolar heat capacity at constant pressure. Seek 20 DEG C, liquid ethanol.Solution: the second law of thermodynamics can prove that the relationship between constant pressure molar heat capacity and constant volume molar heat capacity is as follows2.14 volume is 27 mThreeA small heating element is arranged in the insulating container, and a small hole is communicated with the atmosphere of the 100 kPa,To maintain constant air pressure in the vessel. The heating device is used to heat the air in the apparatus from 0 DEG C to 20 DEG CHow much heat is given to the air in the container?. Known air.If the air is an ideal gas, the temperature of the air in the container will be uniform during heating.Solution: in this problem, the pressure of the air in the container is constant, but the mass of the material varies with the temperaturePageNote: cannot be applied in the above questionsAlthough the volume of the container is constant. This is because, fromThe air out of the hole will do the work to the environment. The work done is as follows:When the temperature is T, the system temperature is increased by dT, and the mass of the air discharged from the container isWork doneThat's exactly what it's worthandThe difference in heat calculated.2.15 volume is 0.1 MThreeAn insulating partition board is arranged in the constant volume closed container, wherein the sides are respectively 0 DEG C, 4 mol Ar (g) and150 degrees C, 2 mol Cu (s). The partition removed, the system reaches heat balance, temperature and process for final t.Known: molar heat capacity at constant pressure of Ar (g) and Cu (s)Respectively asandAnd assume that they do not change with temperature.Here is the diagram belowIt is assumed that the insulation wall is in close contact withthe copper block, and the volume of copper block varies with temperatureThe process can be viewed as a constant volume process, thereforePageIt is assumed that gas can be regarded as an ideal gas,Then,The temperature of the water gas at the outlet of the 2.16 water gas producer is 1100 degrees C, and the mole fractions of CO (g) and H2 (g) are 0.5.If 300 kg of water gas is cooled from 1100 C to 100 C per hour, and heated by the recovered heat, the water temperature is caused by25 degrees C rise to 75 degrees C. Seek the quality of hot water produced per hour. Molar constant heat capacity of CO (g) and H2 (g)TemperatureFunction relations, book, appendix, waterSpecific heat capacity at constant pressure.Interpretation: the mass fraction of CO (g) and H2 (g) in 300 kg water gas is respectively300 kg of water gas from 1100 degrees C to 100 degrees C cooling heatThe quality of producing hot water is m2.18 monatomic ideal gas A in a mixture of diatomic ideal gas B, a total of 5 mol, mole fractionInitial statetemperaturePressure. The mixture is insulated against constant external pressureExpand toEquilibrium state. For the final temperatureAnd process.Solution: the process is illustrated as followsAnalysis: because of the adiabatic process, the change ofthermodynamic energy in process is equal to the form of work between the system and environmentThe energy exchanged by the potential. Therefore,PageMonatomic moleculeDiatomic moleculeSince the ideal gases, U and H, are only functions of temperature, so2.19 there is an insulating partition in the insulated container of the piston in the vicinity. The sides of the bulkhead are 2 mol and 0 C respectivelyGas A and 5 mol, 100 degrees C diatomic ideal gas B, two gas pressure is 100 kPa. Pressure dimension outside the pistonRemain unchanged at 100 kPa. This will be removed from the container plate, the two kinds of gas mixture to reach an equilibrium state. The temperature for the final and TProcedural.Solution: the process is illustrated as followsIt is assumed that the insulation partition plate is replaced by a heat conduction baffle plate, then the heat balance is removed, and then the clapboard is removed to make the mixture mixedPageThe work is convenient because of the constant external pressureSince the cylinder is insulated,2.20 there is a fixed insulated partition in the insulated container of the piston in the area. The bulkhead is single C with 2 mol and 0 DEG C on the piston sideThe sub ideal gas A is equal to the constant ambient pressure; the other side of the barrier is 6 mol, 100 C diatomicThink of gas B, whose volume is constant. The insulating layer of the insulating partition is removed so that it becomes a heat conducting plate and the system is T when it reaches equilibriumAnd process.Solution: the process is illustrated as followsObviously, in the process, A is constant voltage, and B is constant volume, thereforePageIbid., first seeking meritSimilarly, due to cylinder insulation, the first law of thermodynamics2.235 mol diatomic gas from the initial state of 300 K, 200 kPa, first reversibly reversibly expanded to a pressure of 50 kPa, at adiabaticThe inverse compression pressure of 200 kPa to the final state. For the final temperature and the whole process of Tand.Solution: the process is illustrated as followsBe sureThe adiabatic equation of state can be applied to second steps onlyPairs of diatomic gasesthereforeSince the U and H of ideal gases are only functions oftemperature,PageThe whole process is convenient because the second step is adiabatic. The first step is constant temperature reversible2.24 it is proved that the absolute value of the slope of the adiabatic reversible line is greater than that of the constant temperature reversible line at the point where the ideal gas p-V diagram takes placeRight value.According to the adiabatic equation of ideal gas,have toTherefore. Therefore, the hot wireThe slope isConstant temperature lineThe slope is. BecauseTherefore, adiabatic reversibleThe absolute value of the slope of the line is greater than the absolute value of the constant temperature reversible line.2.25, the insulated and constant volume cylinder is provided with an adiabatic ideal piston without friction, and the left and the right sides of the piston are respectively50 DMThreeThe monatomic ideal gases A and 50 DMThreeDiatomic ideal gas B. The two gases are 0 C, 100 kPa. A gasAn electric heating wire with negligible volume and heat capacity is arranged in the inner part. Now, after energized, slowly heating the left gas A, so that the push pistonCompress the right gas B to the final pressure to 200 kPa. O:(1) the final temperature of gas B.Page(2) the work obtained by gas B;.(3) the final temperature of gas A.(4) the heat obtained by the gas A from the electric wire.Solution: the process is illustrated as followsBecause of the slow heating, B can be regarded as undergoing an adiabatic reversible processSolution of the first law of thermodynamicsThe final A gas temperature is the ideal gas state equation solving,Treat A and B as whole, W = 0, therefore2.25 in an insulated vessel with a piston, there is a solid substance of 4.25 mol and 5 mol, a monatomic ideal gas, B, substance APageA. Initial temperaturePressure. This is gas BFor systems, reversible expansion toSystematicAnd process.Solution: the process is illustrated as followsWhen A and B are regarded as systems, the process is an adiabatic reversible process. Assume the following (1) solidsThe volume of B does not vary with temperature; (2) for solid BThen,thusFor gas BPage2.26 known water (H2OlSaturation vapor pressure at 100 CAt this temperature and pressureEnthalpy of vaporization. Make the 1 kg water vapor coagulate at 100 degrees C and 101.325 kPaForming liquid water. Set up ideal gas equation of state.Solution: the process is reversible phase change2.28 it is known that the melting point of ice under 100 kPa is 0 degrees C, at this point the specific enthalpy of heat of ice is hotJ - G-1.Average waterheat capacity at constant pressure. 0.1 kg, 0 degrees C in 1 kg, 50 degrees C, in an adiabatic vesselThe ice after the final temperature system. The heat capacity of the vessel is not considered in the calculation.Solution: the rough estimate shows that the final temperature of T system should be higher than 0 DEG Ctherefore2.29 it is known that the melting point of ice under 100 kPa is 0 degrees C, at this point the specific enthalpy of heat of ice is hotJ - G-1.Water and iceAverage heat capacity at constant pressureRespectively asand. Present 1 kg 50 in an adiabatic vesselWater C degrees C degrees kg degrees -20 ice 0.8 degrees. O:(1) the final temperature.(2) the quality of the final water and ice.Solution: 1 kg, 50 degrees C water cooling, 0 degrees C exothermic0.8 kg -20 degrees C ice warming caused by 0 degrees C endothermicHeat is needed when melted completelyPageTherefore, only part of the ice melted. So the final temperature is 0 ~ C. AIce melting of g,Is thereThe quality of the system ice and water, respectively2.30 steam boilers are continuously injected with water of 20 degrees C, heated and evaporated to 180 degrees C, saturated steam pressure as1.003 MPa of water vapor. The amount of heat needed to produce 1 kg of water vapor.Known: waterMolar enthalpy of vaporization at 100 CWater levelMean molar heat capacity at constant pressureSteamMolar constant heat capacity and temperatureSee Appendix for function.Solution: the process is considered as a constant pressure processThe initial and final system), respectively.and. Insertion of equilibrium phase change pointWhen the steam is regarded as an ideal gas, the enthalpy of the process becomes10 DEG C by the following three differentThe process heats up to 100 degrees C of water, asking for a process.(1) the system contacts with the heat source of 100 C.(2) the system contacts the heat source of the 55 degree C to the heat balance, and then contacts with the heat source of 100 C.(3) the system contacts the heat source of 40 degrees C and 70 degrees C to the heat balance, and then contacts with the heat source of 100 C.Solution: the entropy is the state function, and the entropy of the system changes the same in three casesIn the process, the heat obtained by the system is heat released by a heat source, so that3.8 known nitrogen (N2gThe molar heat at constant pressure is a function of temperatureThe initial state is 300 K, 100 kPa, the 1 mol N2 (g) is placed in the heat source of 1000 K, and the following is requiredPageProcess (1) by constant pressure process; (2) when the constant volume process reaches equilibrium state.Solution: in the case of constant pressureIn constant volume, nitrogen (N2gAs ideal gasbodytakeInstead of all of the aboveYou can obtain the required quantitiesThe 3.9 initial state is,A diatomic ideal gas, 1 mol, changed in the following waysTo,The final. Seek steps and ways.(1) reversible expansion at constant temperature;(2) cool down the constant volume until the pressure drops to 100 kPa, and then heat up to the constant pressure;(3) expand first by adiabatic expansion until the pressure drops to 100 kPa, and then heat up to constant pressure.Solution: (1) reversible expansion of an ideal gas at constant temperature, DU = 0, thereforePage(2) calculate constant volume cooling until the pressure drops to 100 kPa, the temperature of the system is T:(3) similarly, the heat expands reversibly to a temperature of T: when the pressure drops to 100 kPaAccording to the equation of state of ideal gas adiabatic process,The thermodynamic quantities are calculated as follows2.122 mol diatomic ideal gas from the initial state 300 K, 50 DMThreeHeat the constant volume to 400 K, then heat it up to a constant pressureVolume increased to 100 DMThreeAsking for the whole process.Solution: the process is illustrated as followsPageFirst calculate the final temperatureTherefore,Two important formulasIdeal gas3.17 consists ofThe monatomic gas A is a mixture of 10 mol with ideal gas mixtures of diatomic gas B,Beginning stateAdiabatic reversible compression toEquilibrium state. Process seeking.Solution: the process is illustrated as followsPageThe adiabatic reversible equation of state for a mixed ideal gas is derived as followsEasy to getPage3.18 ideal mixture of monatomic gas A and diatomic gas B, 8 mol, consisting ofBeginning.state. Irreversible expansion to the final volume of this insulation against the constant pressureTheEquilibrium state. Process seeking.Solution: the process is illustrated as followsTo determine the final temperature, adiabatic processTherefore3.19 atmospheric pressure, 100 g, 27 C of water and 200 g, 72 degrees C of water in an insulated container mixed, the final water temperature TEntropy change of process. Specific heat at constant pressure of known water.Solution: the procedure is illustrated as followsPageIn the 321 adiabatic constant volume vessel, there is an insulating pressure bulkhead, with 200 K of 2 mol and 50 DM on the side of the partition boardThreeMonatomicThink gas A, and the other side is 3 mol, 400 K, 100 DMThreeDiatomic ideal gas B. Insulating partitions in a container todayThe way, A and B mixed gas gas balance. Process seeking.Solution: the process is illustrated as followsThe final temperature of the T system can be solved as followsEntropy change of the systemPageNote: for ideal gases, the presence of one component does not affect the other components. The final A and BVolume is the volume of the container.In the 322 adiabatic constant volume vessel, there is an insulating pressure bulkhead, with N2 (g) on both sides of the bulkhead. One side volume was 50 DMThreeThere is200 K N2 (g) 2 mol; the other side volume was 75 DMThreeWithin 500 K of N2 (g) 4 mol; N2 (g) can be considered as idealgas.This will be removed from the adiabatic partition in the container, allowing the system to achieve the equilibrium state. Process seeking.Solution: the process is illustrated as followsThe same problem, the final temperature of T is determined as followsAfter the first step, the volume of the two part isThat is, in addition to the partition, the 2 and final state of the same, soPagePay attention to the comparison between the 21 and the 22 questions.3.23 at atmospheric pressure, the melting point of ice is 0 degrees C, than the enthalpy of fusionConstant pressure hot melt of water. In an insulated vessel, there is 1 kg, 25 degrees C water, and 0.5 kg, 0 DEG C are added to the vesselThis is the beginning of the system. Seeking the equilibrium of a system; a process.Solution: the process is illustrated as followsThe process is considered as a constant pressure adiabatic process. As a result of 1 kg, water of 25 degrees C is cooled to 0 degrees CCan only lead toThe ice melts, therefore3.27 it is known that the melting point of ice at normal pressure is 0 degrees C, and the molar enthalpy of meltingBenzeneMelting point is 5.51 degrees C, molar melting enthalpy. Molar determination of liquid water and solid benzeneThe heat capacities areand. Today there are two containers surrounded by insulation, 0 C in a containerPageThe 8 mol H2O (s) is balanced with 2 mol H2O (L) and another container is 5.51 mol C6H6 (L) and 5 mol C6H6 (s) into 5 CBalance. The two containers are contacted to remove an insulating layer between the two containers so that the two container reaches a new equilibrium state. Process seeking.Solution: a rough estimate shows that 5 mol C6H6 (L) is completely solidified and will cause the 8 mol H2O (s) to melt completelyThe process is illustrated as followsThe total process is constant pressure adiabatic process,Therefore3.28 put a small glass bottle containing 0.1 mol ether (C2H5) 2O (L) into the volume of 10 DMThreeVacuum container with constant volume and airtightPageConstant temperature in the constant temperature trough at35.51 C. 35.51 C is the boiling point of ether at 101.325 kPa. Given this conditionMolar enthalpy of vaporization of diethyl ether. Now break the small glass bottle and the ether evaporates to equilibrium.seek(1) the pressure of ether vapor;(2) process.Solution: ether vapor is regarded as ideal gas due to constant temperatureThe changes in the state functions are calculated as followsIgnore the volume of the liquid etherThe 3.30. volume was 20 DMThreeThe closed vessel has 2 mol H2O gas liquid equilibrium. 80 degrees C, 100 degrees C saturation of the waterAnd vapor pressure, respectivelyandMolar enthalpy of vaporization of water at 25 CThe average pressure and molar heat capacities of water and water vapor at 25 ~ 100 degrees C are respectivelyand. Modern systemThe constant volume heating from 80 C to 100 C. Process seeking.Solution: first estimate 100 degrees C, whether there is liquid water in the system. There is only water vapor in the final stateThe quality is nbeObviously, only a portion of the water evaporation, the final is still the gas-liquid equilibrium. Therefore, the following process:Set the following channelsPageThe first and fourth steps are reversible phase change, the second step is constant temperature change of liquid water, and the third step is constant of liquid waterPressure changing temperature. The molar evaporation heat of water at 80 degrees C and 100 degrees C is first obtained3.31. O2 (g) is a function of the molar heat at constant pressure with temperaturePageThe standard molar entropy of O2 (g) under 25 degrees C is known. Seek O2 (g)Moore's entropy at 100 C and 50 kPa.Solution: by formulaknow3.32. if the molar heat capacity of each substance in the chemical reaction is expressed asTry to deduce the chemical reactionStandard molar reaction entropyAnd temperature T。
【物理化学上册完整习题答案】第五版

物理化学上册完整习题答案第五版第一章热力学基础习题一(a)热容量定义为物体单位质量或单位物质量的温度升高所需的热量。
它的单位是J/(g·°C)。
(b)热容量可以用以下公式来计算:Q = mcΔT,其中Q表示热量,m表示物体的质量,c表示物质的比热容,ΔT表示温度变化。
(c)水的比热容是4.18 J/(g·°C)。
(a)焓的定义是在恒定压力下,物体单位质量的温度升高所需的热量。
焓可以用以下公式来计算:H =Q/m,其中H表示焓,Q表示热量,m表示物体的质量。
(b)焓变是指在化学反应或物理过程中,物体单位质量的焓的变化。
1.辅助函数的作用是简化热力学计算过程。
它可以帮助我们计算焓、熵和自由能等。
习题二1.当物体从低温区域向高温区域传递热量时,热量会按照热流从高温区域传递到低温区域。
这个现象符合热力学第一定律,即能量守恒定律。
2.传送速率可以通过热传导定律来计算。
热传导定律可以用以下公式表示:Q = kA(ΔT/Δx),其中Q是传输的热量,k是热传导系数,A是传输的面积,ΔT是温度差,Δx是传输的距离。
3.传热的三种途径是热传导、热对流和热辐射。
习题三1.升华是指固体直接从固体相转变为气体相的过程,而不经过液体相。
凝华是指气体直接从气体相转变为固体相的过程。
2.溶解度是指溶质在溶剂中溶解所达到的最大浓度。
溶解度可以受到温度、压力和溶剂性质等因素的影响。
3.相变是指物质在一定条件下从一个相态转变为另一个相态的过程。
常见的相变包括融化、凝固、汽化、液化、升华和凝华。
第二章热力学函数习题一(a)熵是描述系统无序程度的物理量。
它的单位是J/(mol·K)。
(b)熵的变化可以通过以下公式计算:ΔS = Q/T,其中ΔS表示熵的变化,Q表示热量,T表示温度。
(a)熵增定律是指在孤立系统中,系统熵总是增加或至少保持不变。
(b)熵增定律可以用以下公式表示:ΔStotal =ΔSsystem + ΔSsurroundings ≥ 0,其中ΔStotal表示系统和周围环境的总熵变化,ΔSsystem表示系统的熵变化,ΔSsurroundings表示周围环境的熵变化。
物理化学第五版课后习题答案解析

第五章 化学平衡5-1.在某恒定的温度和压力下,取n 0﹦1mol 的A (g )进行如下化学反应:A (g )垐?噲? B (g ) 若0B μ﹦0A μ,试证明,当反应进度﹦时,系统的吉布斯函数G 值为最小,这时A ,B 间达到化学平衡。
解: 设反应进度为变量A (g )垐?噲?B (g )t ﹦0 n A , 0﹦n 0 0 0﹦0 t ﹦t 平 n A n B ﹦BBn ν n B ﹦B ,n A ﹦n 0-n B ﹦n 0-B ,n ﹦n A +n B ﹦n 0气体的组成为:y A ﹦A n n ﹦00B n n νξ-﹦01n ξ-,y B ﹦B nn﹦0n ξ各气体的分压为:p A ﹦py A ﹦0(1)p n ξ-,p B ﹦py B ﹦p n ξ各气体的化学势与的关系为:0000ln ln (1)A A AA p p RT RT p p n ξμμμ=+=+- 0000lnln B B B B p p RT RT p p n ξμμμ=+=+⋅ 由 G =n AA +n BB =(n A 0A μ+n B 0B μ)+00ln(1)A p n RT p n ξ-+00ln B p n RT p n ξ⋅ =[n 0-0A μ+0B μ]+n 00lnpRT p +00()ln(1)n RT n ξξ--+0ln RT n ξξ 因为 0B μ﹦0A μ,则G =n 0(0A μ+0lnpRT p)+00()ln(1)n RT n ξξ--+0ln RT n ξξ ,0()ln T p G RT n ξξξ∂=∂- 20,20()()T p n RT Gn ξξξ∂=-∂-<0 令 ,()0T p Gξ∂=∂011n ξξξξ==-- ﹦ 此时系统的G 值最小。
5-2.已知四氧化二氮的分解反应 N 2O 4 (g )垐?噲? 2 NO 2(g )在 K 时,0r m G ∆=·mol -1。
物理化学第五版课后习题答案

第十章 界面现象10-1 请回答下列问题:(1) 常见的亚稳定状态有哪些?为什么产生亚稳态?如何防止亚稳态的产生?(2) 在一个封闭的钟罩内,有大小不等的两个球形液滴,问长时间放置后,会出现什么现象?(3) 下雨时,液滴落在水面上形成一个大气泡,试说明气泡的形状和理由? (4) 物理吸附与化学吸附最本质的区别是什么?(5) 在一定温度、压力下,为什么物理吸附都是放热过程?答: (1) 常见的亚稳态有:过饱和蒸汽、过热液体、过冷液体、过饱和溶液。
产生这些状态的原因就是新相难以生成,要想防止这些亚稳状态的产生,只需向体系中预先加入新相的种子。
(2) 一断时间后,大液滴会越来越大,小液滴会越来越小,最终大液滴将小液滴“吃掉”, 根据开尔文公式,对于半径大于零的小液滴而言,半径愈小,相对应的饱和蒸汽压愈大,反之亦然,所以当大液滴蒸发达到饱和时,小液滴仍未达到饱和,继续蒸发,所以液滴会愈来愈小,而蒸汽会在大液滴上凝结,最终出现“大的愈大,小的愈小”的情况。
(3) 气泡为半球形,因为雨滴在降落的过程中,可以看作是恒温恒压过程,为了达到稳定状态而存在,小气泡就会使表面吉布斯函数处于最低,而此时只有通过减小表面积达到,球形的表面积最小,所以最终呈现为球形。
(4) 最本质区别是分子之间的作用力不同。
物理吸附是固体表面分子与气体分子间的作用力为范德华力,而化学吸附是固体表面分子与气体分子的作用力为化学键。
(5) 由于物理吸附过程是自发进行的,所以ΔG <0,而ΔS <0,由ΔG =ΔH -T ΔS ,得 ΔH <0,即反应为放热反应。
10-2 在293.15K 及101.325kPa 下,把半径为1×10-3m 的汞滴分散成半径为1×10-9m 的汞滴,试求此过程系统表面吉布斯函数变(ΔG )为多少?已知293.15K 时汞的表面张力为0.4865 N ·m -1。
解: 3143r π=N ×3243r π N =3132r rΔG =21A A dA γ⎰=γ(A 2-A 1)=4πγ·( N 22r -21r )=4πγ·(312r r -21r )=4π×0.47×(339(110)110--⨯⨯-10-6)=5.9062 J10-3 计算时373.15K 时,下列情况下弯曲液面承受的附加压力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课 后 答 案 网
w. p/kPa
8.70
a 13.64
22.11
d 29.93
38.91
V / cm3
115.6 126.3 150.7 166.4 184.4
p p∗
0.0878 0.1376 0.2231 0.3020 0.3926
( ) ( ) p∗ − p / kPa
p ×103 V p∗ − p
15
30
65
80 120
k ×102 min−1 1.24 1.29 1.30 1.31 1.26
k k = 1.28×10−2 min−1
11. 生产聚氯乙烯塑料的原料氯乙烯可由乙炔与氯化氢气体在
www. HgCl2(s)催化下得到:
·224·
思考题和习题解答
C2H 2 + HCl ⎯⎯→ C2H3Cl
= 496 m 2
m As0
=
As m
=
496 m 2 1g
= 496 m 2
⋅ g −1
o 10. 1173 K 时测得 N2O 在 Au 上的分解数据如下(x 为分解的 N2O
t / min 15
30
65
80 120 ∞
c x
0.17 0.32 0.57 0.65 0.78 1.00
. 量与反应开始的 N2O 量之比):
www. 问乙醇能否在汞表面上铺展?
第 15 章 界面现象
·221·
解: ϕ = σ 气,液II σ − 液I,液II − σ 气,液I
= (471.6 − 364.3 − 22.0)×10−3 N ⋅ m −1
= 85.3×10 −3 N ⋅ m −1 > 0
故能铺展。
7. 473 K 时研究 O2 在某催化剂上的吸附作用,当气态 O2 的平衡压 力为 0.1 及 1 MPa 时,测得每克催化剂吸附 O2 的量分别为 2.5 及
cm −3
90.40 85.46 76.99 69.17 60.19
0.833 1.264 1.906 2.600 3.506
h ( ) 解: V
p p∗ − p
=
1 V∞ c
+
c −1⋅ V∞ c
p p∗
k ( ) 以 p /V p∗ − p 为纵坐标, p 为横坐标作图,得一直线,其
www.cm−3
bHCl pHCl
1 + bHCl pHCl + bC2H3Cl pC2H3Cl
aw ≈
k1 k −1
p HCl
1+ k1 k −1
p HCl
d ∴
( ) υ = k2 k1 / k−1 p p HCl C2H2 ( ) 1 + k1 / k−1 pHCl
h (2) 当 HCl 强吸附或 HCl 分压很高时
4.2 1 1 + b × 0.1 MPa
解得 b = 12.2 MPa −1
a Γ
Γ ∞
=
bp 1 + bp
=
1 2
hd p
=
1 b
=
12.2
1 MPa
−1
=
0.082 MPa
= 82 kPa
8. 已 知 某 硅 胶 的 表 面 为 单 分 子 覆 盖 时 每 克 硅 胶 需 N2 体 积 为
k 129cm3 (STP) 。若 N2 分子所占面积为 0.162 nm2 ,试计算此硅胶的比表 www. 面。
−3 × 0.200 × 103 10−3 × 0.200 × 103
⎤ ⎥
mol
⋅
m
−
2
⎦
= 4.30 × 10−6 mol ⋅ m −2
k 6. 已知 293 K 时乙醇的表面张力为 22.0 ×10−3 N ⋅ m−1 ,汞的表面张
力为 471.6 ×10−3 N ⋅ m−1 ,汞与乙醇的界面张力为 364.3 ×10−3 N ⋅ m−1 ,试
m σ = 28.9×10−3 N ⋅ m−1 。
o 解: p(l)
−
p (g)
=
2σ r
=
2 × 28.9 ×10−3 1 × 10− 6
Pa
= 57.8 Pa
c ln
p
∗ r
p∗
=
2σM RTρr
=
MΔp RTρ
= 78.11×10−3 × 57.8 ×103 = 2.11×10−3
. 8.3145× 293× 0.879×103
N2 平衡压力的关系如下:
m p / kPa o V /cm3
8.70 13.64 22.11 29.93 38.91 115.6 126.3 150.7 166.4 184.4
试用 BET 吸附等温式求该催化剂的比表面。已知 77.2 K 时 N 2 的饱和蒸
c 气压为 99.10 kPa, N2 分子所占面积为 0.162 nm2 。
w 解:(1)
⎜⎜⎝⎛
∂σ ∂ c2
⎟⎟⎠⎞
=
⎜⎛ ⎝
∂σ ∂c
⎟⎞ ⎠
=
− 1
ab + bc
a Γ(1) 2
=
−
c2 RT
⎜⎜⎝⎛
∂σ ∂ c2
⎟⎟⎠⎞
=
abc
RT (1 + bc)
hd( ) (2)
Γ (1) 2
=
⎡ 13.1×10−3 ×19.6 ×10 ⎢⎣8.3145 × 292 × 1 + 19.6 ×
已知反应机理为:
HCl + HgCl2
k1 k-1
HgCl2 ⋅ HCl
①
C2H 2 + HgCl2 ⋅ HCl k2 HgCl2 ⋅ C2H3Cl
②
HgCl2 ⋅ C2H3Cl k3 HgCl2 + C2H3Cl
③
其中①和③进行得很快,即 HCl 在催化剂上的吸附和解吸保持平衡,
m 产物 C2H3Cl 在催化剂上的解吸也很迅速,所以反应②是整个反应过程
( ) 解:W R' = ΔG(σ ) = σΔAs = 72.0 ×10−3 ×1 J = 72.0 ×10−3 J
a 对纯物质,恒压下有
dG (σ ) = −S (σ )dT + σdAs
d 由全微分性质得
h ⎜⎜⎝⎛
∂S (σ ∂As
)
⎟⎟⎠⎞T , p
=
−⎜⎛ ⎝
∂σ ∂T
⎟⎞ ⎠ p, As
www.kh 试计算浓度为 0.5 mol ⋅ dm−3 时的单位界面吸附量Γ(21) 。
·220·
思考题和习题解答
解: ⎜⎜⎝⎛
∂σ ∂c2
⎟⎟⎠⎞
=
⎜⎛ ⎝
∂σ ∂c
⎟⎞ ⎠
= ⎜⎛ − 0.50 ×10−6 ⎝
+
0.40 × 10−9
c mol ⋅ m −3
⎟⎞ ⎠
N ⋅m2
⋅ mol−1
( ) = − 0.50 ×10−6 + 0.40 ×10−9 × 0.50 ×103 N ⋅ m 2 ⋅ mol−1
pr∗
w p∗
= 1.002
课 后 答 案 网
pr∗ − p∗
a p∗
=
0.002 =
0.2%
4. 298K 时,乙醇水溶液的表面张力与浓度 c 的关系为:
d σ
N ⋅ m −1
= 72 × 10−3
− 0.50 ×10−6
c mol ⋅ m −3
+
0.20
×
10
−9
⎜⎛ ⎝
mol
c ⋅
m
−3
⎟⎞ 2 ⎠
k⎜⎜⎝⎛
k1 k −1
⎟⎟⎠⎞ pHCl
>> 1
www. υ=k2pC2H2
第 15 章 界面现象
表现为一级反应。
·225·
课 后 答 案 网
c 其中σ ∗ 为纯水的表面张力,a、b 为常数。 (1) 导出Γ(21) 与 c 的关系式;
(2) 若已知 a = 13.1×10−3 N ⋅ m−1 , b = 19.6 ×10−3mol−1 ⋅ m3 ,试计算浓度
课 后 答 案 网
. 为 0.2 mol⋅ dm−3 时的单位界面吸附量Γ(21) 。
第 15 章 界面现象
习题解答
1. 将1cm3 的油分散到水中,形成油滴半径为1 μm 的乳状液,求所
m 需的最小功。设油水之间界面张力为 62×10−3 N ⋅ m−1。
解:W 'R
= σΔAs
≈ σAs
=σ
V 4 πr 3
⋅ 4πr 2
=
3σV r
o 3
c =
⎜⎜⎝⎛
3×
62
×10−3 ×1×10−6 1×10−6
的速率控制步骤。若 HCl 在 HgCl2 (s) 上的吸附服从兰缪尔吸附等温式,
课 后 答 案 网
o (1) 为反应 C2H2 + HCl ⎯⎯→C2H3Cl 建立反应速率方程; c (2) 指出在什么条件下,该反应表现为一级反应。
解:(1) υ = k2 p θ C2H2 HCl
. θ HCl
=
m 4.2 cm3 (STP) 。设吸附作用服从兰缪尔吸附等温式,计算当 O2 的吸附
量为饱和吸附量的一半时,相应的 O2 的平衡压力。
co 解:
Γ=
Γ∞
1
bp + bp
Γ 1
. Γ 2
=
p1 p2
× 1 + bp2 1 + bp1
