人工智能实验产生式系统解决汉诺塔(有代码)
汉诺塔问题c语言实现

汉诺塔问题c语言实现汉诺塔问题是一种经典的递归问题,也是计算机算法中的重要问题之一。
本文将介绍如何使用C语言实现汉诺塔问题。
汉诺塔问题的规则是:有三根柱子A、B、C,其中A柱子上有n 个盘子,这些盘子大小不等,大的在下面,小的在上面。
现在要把这n个盘子从A柱子移动到C柱子上,但是每次只能移动一个盘子,并且在移动过程中,任何时候都不能让大盘子放在小盘子上面。
最终要求把所有盘子都移动到C柱子上。
下面是汉诺塔问题的C语言实现代码:#include <stdio.h>void hanoi(int n, char A, char B, char C) {if (n == 1) {printf('%c -> %c', A, C);} else {hanoi(n-1, A, C, B);printf('%c -> %c', A, C);hanoi(n-1, B, A, C);}}int main() {int n;printf('请输入盘子的个数:');scanf('%d', &n);printf('移动的步骤如下:');hanoi(n, 'A', 'B', 'C');return 0;}在上面的代码中,hanoi函数是一个递归函数,用来实现汉诺塔问题的移动过程。
当n等于1时,直接将A柱子上的盘子移动到C柱子上;当n大于1时,将A柱子上的n-1个盘子移动到B柱子上,再将A柱子上的最后一个盘子移动到C柱子上,最后将B柱子上的n-1个盘子移动到C柱子上。
在main函数中,先输入要移动的盘子个数n,然后调用hanoi 函数进行移动,最后输出移动的步骤。
通过上面的代码,我们可以很方便地实现汉诺塔问题的求解。
汉诺塔程序

实现输出汉诺塔问题盘子个数为4时的移动步骤程序代码:void move(char X,int n,char Z){cout<<"将编号为"<<n<<"的盘子"<<"从"<<X<<"移到"<<Z<<endl;}void hanoi(int n,char X,char Y,char Z){if(n==1)move(X,1,Z);else{hanoi(n-1,X,Z,Y);move(X,n,Z);hanoi(n-1,Y,X,Z);}}int main(){int m;cout<<"请输入盘子的个数:";cin>>m;cout<<m<<"个盘子的移动步骤为: "<<endl;hanoi(m,'A','B','C');return 0;}数据测试:输入盘子个数为4时,盘子的移动步骤如下分析过程:要将4个盘子从A移到C,首先须借助C将A上的三个盘子移到B,将A上最大的盘子从A移到C后,接着将三个盘子借助A从B移到C;而将三个盘子从A移到B,则应借助C将上面的两个盘从A移到C,然后将A上最下面的盘移到B,再将C上的盘借助A移到B。
以此类推。
用算法实现时声明函数hanoi()和move(),hanoi函数是在需要借助辅助盘时才调用,同时调用该函数时会递归调用move函数;而每次调用move函数时,则输出每一次的移动步骤。
问题:写算法前思路虽然清晰,但写程序要使用到递归调用时还是没能运用自如。
另外,不懂得将本章学习的栈的内容运用到程序上。
《人工智能》课后答案

《人工智能》课后答案第一章课后习题1、对N=5、k≤3时,求解传教士和野人问题的产生式系统各组成部分进行描述(给出综合数据库、规则集合的形式化描述,给出初始状态和目标条件的描述),并画出状态空间图。
2、对量水问题给出产生式系统描述,并画出状态空间图。
有两个无刻度标志的水壶,分别可装5升和2升的水。
设另有一水缸,可用来向水壶灌水或倒出水,两个水壶之间,水也可以相互倾灌。
已知5升壶为满壶,2升壶为空壶,问如何通过倒水或灌水操作,使能在2升的壶中量出一升的水来。
3、对梵塔问题给出产生式系统描述,并讨论N为任意时状态空间的规模。
相传古代某处一庙宇中,有三根立柱,柱子上可套放直径不等的N个圆盘,开始时所有圆盘都放在第一根柱子上,且小盘处在大盘之上,即从下向上直径是递减的。
和尚们的任务是把所有圆盘一次一个地搬到另一个柱子上去(不许暂搁地上等),且小盘只许在大盘之上。
问和尚们如何搬法最后能完成将所有的盘子都移到第三根柱子上(其余两根柱子,有一根可作过渡盘子使用)。
求N=2时,求解该问题的产生式系统描述,给出其状态空间图。
讨论N为任意时,状态空间的规模。
4、对猴子摘香蕉问题,给出产生式系统描述。
一个房间里,天花板上挂有一串香蕉,有一只猴子可在房间里任意活动(到处走动,推移箱子,攀登箱子等)。
设房间里还有一只可被猴子移动的箱子,且猴子登上箱子时才能摘到香蕉,问猴子在某一状态下(设猴子位置为a,箱子位置为b,香蕉位置为c),如何行动可摘取到香蕉。
5、对三枚钱币问题给出产生式系统描述及状态空间图。
设有三枚钱币,其排列处在"正、正、反"状态,现允许每次可翻动其中任意一个钱币,问只许操作三次的情况下,如何翻动钱币使其变成"正、正、正"或"反、反、反"状态。
6、说明怎样才能用一个产生式系统把十进制数转换为二进制数,并通过转换141.125这个数为二进制数,阐明其运行过程。
【C语言程序设计】汉诺塔问题,用C语言实现汉诺塔!
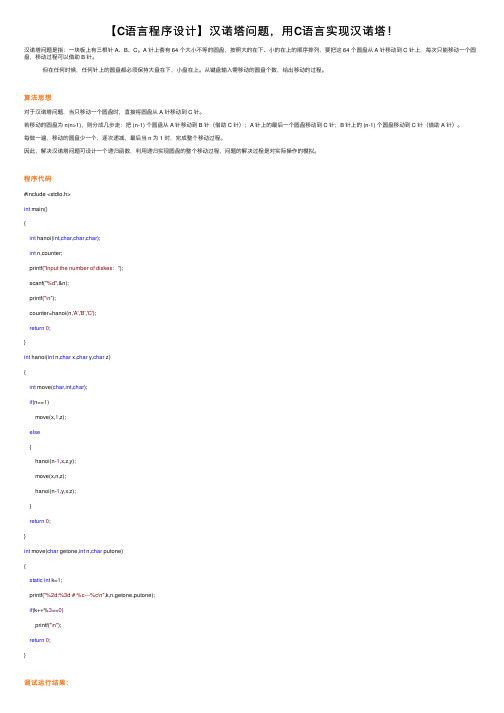
【C语⾔程序设计】汉诺塔问题,⽤C语⾔实现汉诺塔!汉诺塔问题是指:⼀块板上有三根针 A、B、C。
A 针上套有 64 个⼤⼩不等的圆盘,按照⼤的在下、⼩的在上的顺序排列,要把这 64 个圆盘从 A 针移动到 C 针上,每次只能移动⼀个圆盘,移动过程可以借助 B 针。
但在任何时候,任何针上的圆盘都必须保持⼤盘在下,⼩盘在上。
从键盘输⼊需移动的圆盘个数,给出移动的过程。
算法思想对于汉诺塔问题,当只移动⼀个圆盘时,直接将圆盘从 A 针移动到 C 针。
若移动的圆盘为 n(n>1),则分成⼏步⾛:把 (n-1) 个圆盘从 A 针移动到 B 针(借助 C 针);A 针上的最后⼀个圆盘移动到 C 针;B 针上的 (n-1) 个圆盘移动到 C 针(借助 A 针)。
每做⼀遍,移动的圆盘少⼀个,逐次递减,最后当 n 为 1 时,完成整个移动过程。
因此,解决汉诺塔问题可设计⼀个递归函数,利⽤递归实现圆盘的整个移动过程,问题的解决过程是对实际操作的模拟。
程序代码#include <stdio.h>int main(){int hanoi(int,char,char,char);int n,counter;printf("Input the number of diskes:");scanf("%d",&n);printf("\n");counter=hanoi(n,'A','B','C');return0;}int hanoi(int n,char x,char y,char z){int move(char,int,char);if(n==1)move(x,1,z);else{hanoi(n-1,x,z,y);move(x,n,z);hanoi(n-1,y,x,z);}return0;}int move(char getone,int n,char putone){static int k=1;printf("%2d:%3d # %c---%c\n",k,n,getone,putone);if(k++%3==0)printf("\n");return0;}调试运⾏结果:当移动圆盘个数为 3 时,具体移动步骤如下所⽰:Input the number of diskes:31: 1 # A---C2: 2 # A---B3: 1 # C---B4: 3 # A---C5: 1 # B---A6: 2 # B---C7: 1 # A---C总结:本实例中定义的 hanoi() 函数是⼀个递归函数,它有四个形参"n""x""y""z"。
scratch汉诺塔递归算法

Scratch汉诺塔递归算法1. 引言汉诺塔(Hanoi Tower)是一种经典的数学问题,它可以帮助我们理解递归算法的原理和应用。
在这个任务中,我们将使用Scratch编程语言来实现汉诺塔递归算法。
2. 汉诺塔问题简介汉诺塔问题源于印度传说中的一个故事。
据说,在一个庙里有三根针,第一根针上套着64个不同大小的金盘子,大的在下面,小的在上面。
庙里的和尚每天都要将这些金盘子从第一根针移动到第三根针上,但是移动时必须遵守以下规则:1.每次只能移动一个盘子;2.每次移动必须将较小的盘子放在较大的盘子上面;3.可以借助第二根针作为中转。
3. 算法设计思路要解决汉诺塔问题,我们可以使用递归算法。
递归是一种函数调用自身的方法。
对于汉诺塔问题来说,我们可以将其分解为三个步骤:1.将n-1个盘子从第一根针移动到第二根针(借助第三根针作为中转);2.将第n个盘子从第一根针移动到第三根针;3.将n-1个盘子从第二根针移动到第三根针(借助第一根针作为中转)。
这样,我们可以通过递归调用这三个步骤来解决汉诺塔问题。
4. Scratch实现在Scratch中实现汉诺塔递归算法,我们需要创建以下角色和代码块:4.1 角色设计我们需要创建三个角色来表示三根针,以及一个角色来表示金盘子。
每个角色都应该有一个变量来表示当前所在的位置。
4.2 代码块设计我们需要设计以下代码块来实现汉诺塔递归算法:4.2.1 初始化代码块在初始化时,我们需要将金盘子放置在第一根针上,并设置好每个金盘子的大小。
当绿旗被点击时把金盘子放置在第一根针上设置金盘子大小4.2.2 移动代码块移动一个金盘子的过程可以分为以下几步:1.判断当前金盘子是否在目标针上;2.如果在目标针上,结束移动;3.如果不在目标针上,找到下一个需要移动到的位置(借助另外一根针);4.将当前金盘子移动到下一个位置;5.递归调用移动代码块,将剩余的金盘子移动到目标针上。
当收到 [移动金盘子 v] 消息时如果 [当前位置 v] = [目标位置 v] ?那么结束此脚本否则设置 [下一个位置 v] 为 (3 - [当前位置 v] - [目标位置 v])把金盘子放置在第 [下一个位置 v] 根针上把金盘子移到第 [目标位置 v] 根针上发送消息 (移动金盘子) 给自己并等待 (0.5) 秒4.2.3 触发移动代码块为了触发整个移动过程,我们可以创建一个按钮,并在其点击事件中调用移动代码块。
python实现汉诺塔游戏

python实现汉诺塔游戏汉诺塔(Hanoi Tower)是一种经典的益智游戏,起源于中国。
它的规则很简单,但是解决它的问题却需要一定的智力和耐心。
下面我将用Python实现一个汉诺塔游戏。
汉诺塔游戏的规则如下:-有三根柱子,分别为A、B、C。
开始时,所有的盘子都堆在柱子A 上,从大到小依次摆放。
-目标是把所有的盘子从柱子A移动到柱子C上。
-移动盘子时,每次只能移动一个盘子,且必须保证大盘子在小盘子下面。
我们可以使用递归算法来解决这个问题。
具体实现如下:```pythondef hanoi(n, source, target, auxiliary):if n > 0:# 先将n-1个盘子从source柱子移动到auxiliary柱子上hanoi(n-1, source, auxiliary, target)# 将第n个盘子从source柱子移动到target柱子上print("Move disk", n, "from", source, "to", target)# 将n-1个盘子从auxiliary柱子移动到target柱子上hanoi(n-1, auxiliary, target, source)#测试hanoi(3, 'A', 'C', 'B')```上述代码中的`hanoi`函数用来实现递归的移动盘子操作。
参数`n`表示当前要移动的盘子数量,`source`表示源柱子,`target`表示目标柱子,`auxiliary`表示辅助柱子。
在代码中,我们首先判断`n`是否大于0,如果是,则进行递归操作。
首先将`n-1`个盘子从源柱子移动到辅助柱子上,然后将第`n`个盘子从源柱子移动到目标柱子上,最后将`n-1`个盘子从辅助柱子移动到目标柱子上。
我们可以通过调用`hanoi`函数来测试代码。
汉诺塔问题的程序实现

汉诺塔问题的程序实现汉诺塔问题的程序实现实验⽬的:运⽤程序解决汉诺塔(hanoi)问题。
汉诺塔问题:假设有3个分别命名为A,B,C的塔座,在塔座A上插有n个直径⼤⼩各不相同,依⼩到⼤编号为1,2....,n的圆盘。
现要求将A轴上的n个圆盘移到C并仍按同样顺序叠排,圆盘按以下规则(1)每次只能⼀动⼀个盘⼦(2)圆盘可以插在A,B,C中任⼀个塔座上(3)任何时刻都不能将⼀个较⼤的圆盘压在较⼩的圆盘之上。
A B C实验分析:汉诺塔问题可以规划为⼀个递归的问题予以分析,将n个盘⼦从A针移动到C 针可进⾏3个步骤:(1)将A上n-1的个盘⼦移到B针上;(2)把A针最后1个盘⼦移到C针上;(3)再把B盘⼦上的n-1个移到C针上。
实验过程:#includeusing namespace std;void main(){void hanoi(int m,char A,char B,char C); //A代表初始柱⼦,B代表辅助柱⼦,C代表⽬标柱⼦int m;printf("请输⼊盘⼦的个数:");scanf("%d", &m);printf("当盘⼦的个数为%d时移动的步骤是:\n",m);hanoi(m,'A','B','C');}void hanoi(int n,char X,char Y,char Z){void move(char X,char Z );if(n==1)move(X,Z);else{hanoi(n-1,X,Z,Y);move(X,Z);hanoi(n-1,Y,X,Z);}}void move(char x,char y){printf("%c-->%c\n",x,y);}过程:A代表初始柱⼦,B代表辅助柱⼦,C代表⽬标柱⼦。
⽽a代表第⼀根柱⼦,b代表第⼆根柱⼦,c代表第三根柱⼦。
汉诺塔综合实践报告

一、引言汉诺塔问题是一种经典的递归问题,起源于印度的一个古老传说。
该问题涉及三个柱子和若干个大小不一的盘子,要求按照一定的规则将盘子从第一个柱子移动到第三个柱子。
在解决汉诺塔问题的过程中,我们可以锻炼逻辑思维、递归算法设计以及编程能力。
本报告将详细介绍汉诺塔问题的背景、解决方法、实践过程及心得体会。
二、汉诺塔问题背景汉诺塔问题最早由法国数学家卢卡斯在1883年提出。
传说在古印度有一个名为汉诺塔的庙宇,庙里有一个汉诺塔塔,塔上有64个盘子,每个盘子大小不同,且按照从小到大的顺序叠放。
为了拯救世界,僧侣们需要将所有盘子从第一个柱子移动到第三个柱子,同时每次只能移动一个盘子,且在移动过程中,大盘子不能放在小盘子上面。
三、汉诺塔问题解决方法1. 递归算法汉诺塔问题可以通过递归算法来解决。
递归算法的基本思想是将大问题分解为若干个小问题,然后逐一解决小问题,最终解决大问题。
对于汉诺塔问题,我们可以将其分解为以下三个步骤:(1)将n-1个盘子从第一个柱子移动到第二个柱子;(2)将第n个盘子从第一个柱子移动到第三个柱子;(3)将n-1个盘子从第二个柱子移动到第三个柱子。
递归算法如下:```function hanoi(n, start, end, auxiliary) {if (n == 1) {console.log(`移动盘子1从${start}到${end}`);return;}hanoi(n - 1, start, auxiliary, end);console.log(`移动盘子${n}从${start}到${end}`);hanoi(n - 1, auxiliary, end, start);}```2. 动态规划除了递归算法,我们还可以使用动态规划的方法来解决汉诺塔问题。
动态规划的思想是将问题分解为若干个子问题,然后求解子问题,最后将子问题的解合并成原问题的解。
对于汉诺塔问题,我们可以定义一个二维数组dp[i][j],表示将i个盘子从第一个柱子移动到第j个柱子的最小移动次数。
人工智能汉诺塔实验报告

汉诺塔实验报告
一、实验目的:
1、掌握产生式系统解决汉诺塔算法的基本思想。
2、熟悉和掌握问题规约法的原理、实质和规约过程。
3、理解规约图的表示方法。
二、实验原理:
1、在移动盘子时,每次只移动A/B/C柱子上可以移动的盘子中最大的盘子。
2、如果上一次已经移动了某个盘子,则下一次不能继续移动,即:一个盘子不能被连续移动两次。
如:某次操作将1号盘子由A柱子移动到B柱子,那么在选择下一个要移动的盘子时应不在考虑1号盘。
3、当某个可以移动的盘子摆放位置不唯一时要将当前状态入栈,并选择盘子移动前所在的柱子的左侧(同理:反方向选择也可)柱子作为移动的目标柱子。
为提高程序运行过程中的空间利用率,产生式规则在汉诺塔移动过程中依据以上规则自动生成。
三、实验条件:
1、必须要有三个柱子A,B,C。
2、盘子的数量不能太多。
3、应该用自己熟悉的语言写程序。
四、实验步骤:
第一次移动之后:
第二次移动之后:
第三次移动之后:
五、实验内容:
利用c/c++语言编写汉诺塔程序,并实现盘子的移动过程。
六、实验小结:
通过本次实验我掌握了汉诺塔的算法和移动的过程,同时也更好的运用了c++的知识解决了这个问题,在做的过程中确实有不懂的地
方,但是查资料还是解决了,希望自己以后会更好的利用c++/c这们高级程序编写语言。
汉诺塔问题解决及游戏方案

汉诺塔问题的解决及游戏设计班级:数学与应用数学0901姓名:何文坤黄骏指导老师:王玉英随着时代的不断发展进步,计算机已经融入我们的日常生活。
很多时候,很多的问题想通过人的手来亲自解决已变得十分困难了,这时我们就要运用计算机来帮我们解决这些复杂的问题。
汉诺塔问题就是这类较复杂的问题。
汉诺塔游戏规则:有三根针A,B,C。
A针上有n个盘子,盘子大小不等,大的在下,小的在上。
要求把这n个盘子移到C针,在移动过程中可以借助B针,每次只允许移动一个盘子,且在移动过程中在三根针上的盘子都保持大盘在下,小盘在上。
此次,我们通过VisualC++软件运用递归算法来解决汉诺塔问题。
程序运行后会出现一个界面,界面上有各种操作提示,按照提示进行各种操作后会得到汉诺塔游戏的运行过程及结果。
关键词:汉诺塔;Visual C++;递归算法;问题描述------------------------------------------------------------------------------1开发平台------------------------------------------------------------------------------2变量命名规则------------------------------------------------------------------------3程序中主要类或函数的描述------------------------------------------------------4程序流程-----------------------------------------------------------------------------------------6设计难点及难点处理---------------------------------------------------------------7运行结果及结果分析---------------------------------------------------------------8程序需要完善的地方---------------------------------------------------------------10自己的心得体会---------------------------------------------------------------------11一、问题描述汉诺塔<又称河内塔)问题是起源于印度的一个古老的传说。
python 汉诺塔 非递归方法解题

python 汉诺塔非递归方法解题---随着编程语言的发展,算法问题解决的方式也在不断变化。
汉诺塔问题就是一个经典的算法问题,通常采用递归的方法来解决。
但是,非递归的方法同样可以解决汉诺塔问题,下面就让我们来看看如何用Python实现非递归方法解决汉诺塔问题。
汉诺塔问题的基本概念是这样的:给定三个柱子A、B、C,每个柱子上都放了若干个按照一定顺序排列的盘子,每个盘子都由一个数字标记,表示盘子的位置和大小。
任务是将所有的盘子从一个柱子移动到另一个柱子,移动过程中需要遵守以下规则:1. 每个盘子只能移动到比它小的柱子上;2. 三个柱子上的盘子不能重叠;3. 移动过程中不能使用柱子C。
非递归方法解决汉诺塔问题通常采用回溯法。
这种方法的基本思路是尝试将问题分解为更小的子问题,通过回溯不同的子问题的解来找到最终的解。
在汉诺塔问题中,我们可以将任务分解为将最大的盘子从柱子A移到柱子B,然后将中间大小的盘子从柱子A移到柱子C,最后将最小的盘子从柱子C移到柱子B。
通过这种方式,我们可以逐步解决汉诺塔问题。
下面是用Python实现非递归方法解决汉诺塔问题的代码:```pythondef hanoi(n, source, target, auxiliary):if n > 0:# 将n-1个盘子从source柱子移动到auxiliary柱子,再将最大的盘子从source移动到targ et柱子hanoi(n-1, source, auxiliary, target)# 将最大的盘子从auxiliary移动到target柱子print(f'Move disk {n} from {source} to {target}')# 将n-1个盘子从auxiliary柱子移动到target柱子hanoi(n-1, auxiliary, target, source)```在这个函数中,参数n表示盘子的数量,source表示起始柱子,target表示目标柱子,auxiliary表示辅助柱子。
Python递归算法实现汉诺塔(附代码+运行情况)

Python 递归算法实现汉诺塔(附代码+运⾏情况)⾸先你要知道汉诺塔是通过递归函数来解决的,递归函数,通俗易懂讲就是⾃⼰调⽤⾃⼰,类似于猫抓⾃⼰的尾巴,然后你可以脑⼦⾥把他想象成⼀个圈了。
汉诺塔的规则我就不说了,只给⼤家讲讲怎么理解代码为了讲解清楚,我给代码标记了⾏号。
①如果圆盘只有1,那就随便移动,直接把A 移动到C, A->C②就是圆盘数量不是1的时候,代码中第四⾏开始。
在讲之前,我们看第三⾏代码我们可以看到,在代码实现中A 直接移动到C ,是(a ‘>’ c )我们在看第⑤⾏代码,意思是A 移动B ,那么代码就是(A B )A 指向B就是A 在左,B 在最后,缓冲柱就在中间,⼤家可以观察观察是不是这样,到底是怎么做缓冲的,⼤家可以把这三个柱⼦想象成我前⾯说的⼀个圆圈举个例⼦哦,如果C 移动到B ,那么就是(C A B )C 在左 B 在右 中间是缓冲柱,现在⼀想就很清楚了。
代码+运⾏结果1 def move(n,a,b,c): #n 代表圆盘数,a,b,c 分别代表初始柱,缓冲柱,⽬标柱2 if n==1:3 print (a,'-->',c)4 else :5 move(n-1,a,c,b)#将 N-1 个圆盘从A 移动到B (A C B)6 print (a,'-->',c) 将最⼤的圆盘从A 直接移动到C (A C )因为不需要任何缓冲,直接移过去,所以是没有缓冲柱7 move(n-1,b,a,c) 将 N-1 个圆盘从B 移动到C (B A C )print (a,'-->',c)move(n-1,a,c,b)。
人工智能实验

实验一利用问题归约法实现Hanoi塔问题(一)教学要求理解问题归约法的原理和方法,掌握用问题归约表示问题的步骤,并能够对实际问题给出具体的实现。
(二)知识点提示主要知识点:分解、归约、本原问题、与树、或树、与或树、等价变换、用与或树表示问题的步骤。
重点:用与或树表示问题的步骤、Hanoi塔问题的实现。
难点:问题归约法的实现。
(三)教学内容利用问题归约法实现Hanoi塔,主要包括主函数、函数hanoi与搬移函数move,要求在主函数中接收盘子数目并调用hanoi函数。
(四)思考题1. 当盘子数目越来越多时,运行时间有何变化?2. 什么是本原问题?实验二利用状态空间搜索法实现八数码问题(一)教学要求理解状态空间知识表示方法,掌握搜索方法的基本原理,并能够对八数码问题给出具体的实现。
(二)知识点提示主要知识点:状态、状态空间、算符、用状态空间表示问题的步骤、用状态空间求解问题的过程、搜索、宽度优先搜索、有界深度优先搜索、启发式搜索。
重点:状态空间、用状态空间求解问题的过程、宽度优先搜索、有界深度优先搜索、启发式搜索。
难点:用状态空间法求解八数码问题的实现过程。
(三)教学内容用状态空间搜索法求解问题的基本思想是将适用的算符作用于初始状态,以产生新的状态;然后再把一些适用的算符作用于新的状态,重复该过程,直至产生的状态为目标状态为止。
实验内容包括:1.定义状态的描述形式,并给出初始状态和目标状态;2.定义一组算符;3. 利用搜索算法对状态不断扩展,直至得到目标状态为止。
(四)思考题1. 如何使用产生式表示该问题中的算符?2. 使用不同搜索算法求解该问题的性能如何?实验三机器人搬盒子问题(一)教学要求理解谓词逻辑知识表示的方法,掌握一阶谓词逻辑知识表示的基本原理,能够利用归结原理求解简单问题。
(二)知识点提示主要知识点:谓词、原子公式、谓词公式、子句、子句集、空子句、归结原理。
重点:谓词公式、子句集和归结原理的实现。
C语言递归调用实例——汉诺塔问题动画实现(附完整代码)

二、程序框架
古人云,不谋全局者,不足谋一域。同样,在编写代码之前,我们必 须得有个大体的思路和整体上的把握。不能一上来就稀里糊涂地乱敲一通。 当然,这里我也只能仅仅谈自己的个人想法,不一定就是最优的解决方案, 还希望能和大家一起相互交流,共同进步。整个程序的框架,我把它分为 动画效果和核心算法两大部分。我首先实现的是动画效果部分,等能够实 现盘子的随意移动后,我才开始研究核心算法的实现。这样一来,在核心 算法部分,我们正好可以利用前面的动画效果来直观地反映出我们的思路, 有助于代码的调试和缩短程序的开发周期。为了尽量减少废话,我们可以 用一张图来进行表示:
图 1-1 移动第一个圆盘..................................................................................................................... 4 图 1-2 移动第二个圆盘...................................................................................................................... 5 图 1-3 移动最后一个圆盘................................................................................................................. 6
能移动一个圆盘,且圆盘在放到棒上时,大的不能放在小的上面。中间的一根
棒作为辅助移动用。” 事实上,对此曾经有人作过分析,按这个规则,众僧耗尽毕生精力也
不可能完成圆盘的移动,因为需要移动圆盘的次数是一个天文数字 18446744073709551615(64 个圆盘需要移动的次数为 2 的 64 次方)。假设 1us 进行一次移动,也需要约一百万年的时间,使用计算机也很难解决 64
hanoi塔递归算法c语言

hanoi塔递归算法c语言Hanoi塔是一种经典的数字益智游戏,它来源于法国数学家Lucas的BrainVita游戏,被称为“汉诺威塔问题”或“汉诺塔问题”。
该游戏由三个柱子和几个圆盘组成,最初时,圆盘按半径从大到小依次放在一个柱子上(逆序排列),游戏的目标则是将这些圆盘移动到另一个柱子上,最终使得其按半径从小到大依次排列。
在移动整个圆盘的过程中,必须遵循以下规定:1. 每次只能移动一个圆盘;2. 圆盘可以放置在任何柱子上;3. 不能将一个大的圆盘放在较小的圆盘之上。
为了解决这一难题,Hanoi塔问题引入了递归算法,这也是大多数编程语言中最常使用的算法之一。
在C语言中,Hanoi塔问题可以用以下代码实现:```c#include<stdio.h>void move(int n, char x, char y, char z){if(n == 1){printf("%c-->%c\n", x, z);}else{move(n-1, x, z, y);printf("%c-->%c\n", x, z);move(n-1, y, x, z);}}int main(){int n;printf("请输入盘子数:");scanf("%d", &n);printf("移动的步骤如下:\n");move(n, 'A', 'B', 'C');return 0;}```在这个程序中,我们首先定义了一个函数`move()`,该函数接受四个参数:圆盘的数量`n`和字母标识符`x`、`y`、`z`,它们分别代表三个柱子。
在函数中,我们使用了条件判断语句,如果只有一个圆盘,我们直接将其从柱子`x`移动至柱子`z`上。
否则,我们需要进行3个步骤:1. 将n-1个圆盘从柱子`x`移动至柱子`y`上;2. 将第n个圆盘从柱子`x`移动至柱子`z`上;3. 将n-1个圆盘从柱子`y`移动至柱子`z`上。
汉诺塔程序实验报告

竭诚为您提供优质文档/双击可除汉诺塔程序实验报告篇一:汉诺塔程序实验报告实验题目:hanoi塔问题一、问题描述:假设有三个分别命名为A,b和c的塔座,在塔座b上插有n个直径大小各不相同、从小到大编号为1,2,…,n 的圆盘。
现要求将塔座b上的n个圆盘移至塔座A上并仍按同样顺序叠排,圆盘移动时必须遵守以下规则:(1)每次只能移动一个圆盘;(2)圆盘可以插在A,b和c中任一塔上;(3)任何时刻都不能将一个较大的圆盘压在较小的圆盘之上。
要求:用程序模拟上述问题解决办法,并输出移动的总次数,圆盘的个数从键盘输入;并想办法计算出程序运行的时间。
二、算法思路:1、建立数学模型:这个问题可用递归法解决,并用数学归纳法又个别得出普遍解法:假设塔座b上有3个圆盘移动到塔座A上:(1)"将塔座b上2个圆盘借助塔座A移动到塔座c上;(2)"将塔座b上1个圆盘移动到塔座A上;(3)"将塔座c上2个圆盘借助塔座b移动到塔座A上。
其中第2步可以直接实现。
第1步又可用递归方法分解为:1.1"将塔座b上1个圆盘从塔座x移动到塔座A;1.2"将塔座b上1个圆盘从塔座x移动到塔座c;1.3"将塔座A上1个圆盘从塔座Z移动到塔座c。
第3步可以分解为:3.1将塔座c上1个圆盘从塔座Y移动到塔座b;3.2将塔座c上1个圆盘从塔座Y移动到塔座A;3.3将塔座b上1个圆盘从塔座x移动到塔座A。
综上所述:可得到移动3个圆盘的步骤为b->A,b->c,A->c,b->A,c->b,c->A,b->A,2、算法设计:将n个圆盘由b依次移到A,c作为辅助塔座。
当n=1时,可以直接完成。
否则,将塔座b顶上的n-1个圆盘借助塔座A移动到塔座c上;然后将圆盘b上第n个圆盘移到塔座A上;最后将塔座c上的n-1个圆盘移到塔座A上,并用塔座b作为辅助塔座。
三、原程序#include#include#includeinttimes=0;voidmove(chara,charb){printf("%c---->%c\n",a,b);}voidhno(intn,chara,charb,charc){if(n==1){move(a,c);times++;}else{hno(n-1,a,c,b);move(a,c);times++;hno(n-1,b,a,c);}}voidmain(){unsignedstart,finish;intn;printf("请输入汉诺塔的层数:");scanf("%d",start=getTickcount();//hno(n,b,c,A);finish=getTickcount();floattime=(finish-start)/1000.0;printf("共移动了%d次!\n",times);cout }四:五.结论分析通过对上述递归在hanoi塔问题上的应用分析,可以得出如下结论:递归应用中的hanoi塔问题分析递归应用中的1、hanoi塔问题中函数调用时系统所做工作一个函数在运行期调用另一个函数时,在运行被调用函数之前,系统先完成3件事:1将所有的实参、返回地址等信息传递给被调用函数保存。
汉诺塔c语言程序代码

汉诺塔c语言程序代码(通过vc++6.0验证)(附讲解)让我们先看看代码吧#include <stdio.h>int hj(int a,int b, int c,int i){int t;if(i==1)printf("%d->%d\n",a,c);else{t=c;c=b;b=t;hj(a,b,c,i-1);printf("%d->%d\n",a,b);t=a;a=c;c=t;t=b;b=c;c=t;hj(a,b,c,i-1);return 0;}}main(){int a,b,c,i;a=1;b=2;c=3;printf("请输入汉诺塔的盘数");scanf("%d",&i);hj(a,b,c,i);return 0;}以上是汉诺塔的代码,该程序主要是运用了递归的思想,比如数学中的f(x)=f(x-1)+f(x-2),在本程序中为:int hj(int a,int b, int c,int i){int t;if(i==1)printf("%d->%d\n",a,c);else{t=c;c=b;b=t;hj(a,b,c,i-1);也就是说,我们在这个函数中再次调用这个函数,相当于一个循环,而在再次调用的过程中,i的值变成i-1,就类似于f(x-1),这样层层调用,最终就变成当i=1的时候的值,然后通过运算,计算出想要得到的值。
汉诺塔的数值分析:我们可以发现,当只有一个盘的时候,我们只需要做1->3(就是把第一个柱子上的最顶端的盘移动到第三根柱子,以下不再解释)当有两个盘的时候,是1->2 1->3 2->3三个盘子是:1->3 1->2 3->2 1->3 2->1 2->3 1->3分析一下可以得出以下结论:初始值a=1 b=2 c=3一个盘子就是a->c两个盘子与一个盘子的关系是:第一步:b与c交换值,然后打印a->c第二步:打印a->b第三步:a与c交换值,b与c交换值,打印a->c进一步分析,便可以得出以下结论只要盘子数量为i(i大于1),那么它就有三部分第一部分,b与c交换值,然后运行i-1第二部分,打印a->b第三部分,a与c交换值,b与c交换值,然后运行i-1程序表示便是:if(i==1)printf("%d->%d\n",a,c);else{t=c;c=b;(交换值)b=t;hj(a,b,c,i-1);printf("%d->%d\n",a,b);t=a;a=c;c=t;(a c交换)t=b;b=c;c=t;(b c交换)hj(a,b,c,i-1);。
汉诺塔问题的程序实现(hanoi塔)

汉诺塔问题的程序实现(hanoi塔)问题重述:有三根柱A、B、C,在柱A上有N块盘⽚,所有盘⽚都是⼤的在下⾯,⼩⽚能放在⼤⽚上⾯。
现要将A上的N块盘⽚移到C柱上,每次只能移动⼀⽚,⽽且在同⼀根柱⼦上必须保持上⾯的盘⽚⽐下⾯的盘⽚⼩,输⼊任意的N,输出移动⽅法。
(注意:这是⼀个古⽼的传说,传说是如果把64个盘⼦由A柱移到了C柱的话,那么世界末⽇就到了,事实上如果要把64个盘⼦从A柱移到C柱的话,即使⽤计算机运算,也要计算数亿年,所以这个预⾔未必不是真实。
)【分析】我们可以这样考虑,当n=1时,我们只要直接将A柱的盘⼦移到C柱,当n>1时,我们可以先把n-1个盘⼦由A柱通过C柱移到B 柱,此时就可以把A柱剩下的最后⼀个盘⼦直接移到C柱,这样接下来只要把n-1个盘⼦通过A柱移到C 柱即可,如果就构成了递归的思路,我们可以定义个移动过程mov(n,a,b,c)表⽰将n个盘⼦从a通过b移到c1.只要求输出搬运的次数#includeusing namespace std;int m=0;void move(){m++;}void I(int n){if(n==1)move();else{I(n-1);move();I(n-1);}}int main(){I(3);cout<cout<<"输出完毕!"<return 0;}更加简单的⽅法!#includeusing namespace std;int fact(int n){if(n==1)return(1);elsereturn((2*fact(n-1)+1));}int main(){cout<}2.不仅要求输出搬运的次数,⽽且要输出每个步骤的详细搬运#includeusing namespace std;int m=0;void Move(int n,char x,char y){cout<<"把"<m++;}void Hannoi(int n,char a,char b,char c){if(n==1)Move(1,a,c);else{Hannoi(n-1,a,c,b);Move(n,a,c);Hannoi(n-1,b,a,c);}}int main(){int i;cout<<"请输⼊圆盘数"<cin>>i;Hannoi(3,'a','b','c');cout<<"总的搬运次数"<cout<<"输出完毕!"<return 0;}}另外⼀种不利⽤递归的解法(很抱歉,我⾃⼰也没调出来,实在太复杂了)#includeusing namespace std;//圆盘的个数最多为64const int MAX = 1;//⽤来表⽰每根柱⼦的信息struct st{int s[MAX]; //柱⼦上的圆盘存储情况int top; //栈顶,⽤来最上⾯的圆盘char name; //柱⼦的名字,可以是A,B,C 中的⼀个int Top()//取栈顶元素{return s[top];}int Pop()//出栈{return s[top--];}void Push(int x)//⼊栈{s[++top] = x;}} ;long Pow(int x, int y); //计算x^yvoid Creat(st ta[], int n); //给结构数组设置初值void Hannuota(st ta[], long max); //移动汉诺塔的主要函数int main(void){int n;cin >> n; //输⼊圆盘的个数st ta[3]; //三根柱⼦的信息⽤结构数组存储Creat(ta, n); //给结构数组设置初值long max = Pow(2, n) - 1;//动的次数应等于2^n - 1 Hannuota(ta, max);//移动汉诺塔的主要函数system("pause");return 0;}void Creat(st ta[], int n){ta[0].name = 'A';ta[0].top = n-1;//把所有的圆盘按从⼤到⼩的顺序放在柱⼦A 上for (int i=0; ita[0].s[i] = n - i;//柱⼦B,C 上开始没有没有圆盘ta[1].top = ta[2].top = 0;for (int j=0; jta[1].s[j] = ta[2].s[j] = 0;//若n 为偶数,按顺时针⽅向依次摆放A B Cif (n%2 == 0){ta[1].name = 'B';ta[2].name = 'C';}else //若n 为奇数,按顺时针⽅向依次摆放A C B {ta[1].name = 'C';ta[2].name = 'B';}}long Pow(int x, int y){long sum = 1;for (int i=0; isum *= x;return sum;}void Hannuota(st ta[], long max){int k = 0; //累计移动的次数int i = 0;int ch;while (k < max){//按顺时针⽅向把圆盘1 从现在的柱⼦移动到下⼀根柱⼦ch = ta[i%3].Pop();ta[(i+1)%3].Push(ch);cout << ++k << ": " <<"Move disk " << ch << " from " << ta[i%3].name <<" to " << ta[(i+1)%3].name << endl;i++;//把另外两根柱⼦上可以移动的圆盘移动到新的柱⼦上if (k < max){ //把⾮空柱⼦上的圆盘移动到空柱⼦上,当两根柱⼦都为空时,移动较⼩的圆if (ta[(i+1)%3].Top() == 0 ||ta[(i-1)%3].Top() > 0 &&ta[(i+1)%3].Top() > ta[(i-1)%3].Top()){ch = ta[(i-1)%3].Pop();ta[(i+1)%3].Push(ch);cout << ++k << ": " << "Move disk "<< ch << " from " << ta[(i-1)%3].name<< " to " << ta[(i+1)%3].name << endl;}else{ch = ta[(i+1)%3].Pop();ta[(i-1)%3].Push(ch);cout << ++k << ": " << "Move disk " << ch << " from " << ta[(i+1)%3].name << " to " << ta[(i-1)%3].name << endl; }}}}补充知识:【典型例题1】求阶乘n!#includeusing namespace std;int fact(int n){if(n==0)return(1);elsereturn(n*fact(n-1)); }int main(){cout<。
python汉诺塔问题

python汉诺塔问题⼀、汉诺塔问题汉诺塔(⼜称河内塔)问题是源于印度⼀个古⽼传说的益智玩具。
⼤梵天创造世界的时候做了三根柱⼦,在⼀根柱⼦上从下往上按照⼤⼩顺序摞着64⽚黄⾦圆盘。
⼤梵天命令婆罗门把圆盘从下⾯开始按⼤⼩顺序重新摆放在另⼀根柱⼦上。
并且规定,在⼩圆盘上不能放⼤圆盘,在三根柱⼦之间⼀次只能移动⼀个圆盘⼆、汉诺塔问题分析我们可以将问题简化描述为:n个盘⼦和3根柱⼦:A(源)、B(备⽤)、C(⽬的),盘⼦的⼤⼩不同且中间有⼀孔,可以将盘⼦“串”在柱⼦上,每个盘⼦只能放在⽐它⼤的盘⼦上⾯。
起初,所有盘⼦在A柱上,问题是将盘⼦⼀个⼀个地从A柱⼦移动到C柱⼦。
移动过程中,可以使⽤B 柱,但盘⼦也只能放在⽐它⼤的盘⼦上⾯。
因此我们得出汉诺塔问题的以下⼏个限制条件:1.在⼩圆盘上不能放⼤圆盘。
2.在三根柱⼦之间⼀回只能移动⼀个圆盘。
3.只能移动在最顶端的圆盘。
⾸先,我们从简单的例⼦开始分析,然后再总结出⼀般规律。
当n = 1的时候,即此时只有⼀个盘⼦,那么直接将其移动⾄C即可。
移动过程就是 A -> C当n = 2的时候,这时候有两个盘⼦,那么在⼀开始移动的时候,我们需要借助B柱作为过渡的柱⼦,即将A柱最上⾯的那个⼩圆盘移⾄B柱,然后将A柱底下的圆盘移⾄C柱,最后将B柱的圆盘移⾄C柱即可。
那么完整移动过程就是A-> B , A -> C , B -> C当n = 3的时候,那么此时从上到下依次摆放着从⼩到⼤的三个圆盘,根据题⽬的限制条件:在⼩圆盘上不能放⼤圆盘,⽽且把圆盘从A柱移⾄C柱后,C柱圆盘的摆放情况和刚开始A柱的是⼀模⼀样的。
所以呢,我们每次移⾄C柱的圆盘(移⾄C柱后不再移到其他柱⼦上去),必须是从⼤到⼩的,即⼀开始的时候,我们应该想办法把最⼤的圆盘移⾄C柱,然后再想办法将第⼆⼤的圆盘移⾄C柱......然后重复这样的过程,直到所有的圆盘都按照原来A柱摆放的样⼦移动到了C柱。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验一一、实验目的:掌握产生式系统解决汉诺塔算法的基本思想。
二、问题描述:如图所示放置3根柱子,其中一根从上往下按由小到大顺序串有若干个圆盘,要求通过3根柱子移动圆盘。
若规定每次只能移动1片,且不许大盘放在小盘之上,最后要将圆盘从一根柱子移动到另一根柱子上。
三、问题分析及基本思想:汉诺塔(也被称为梵塔)问题有很多解决方法,比较典型的是使用递归算法,而本次设计的算法则是应用人工智能中产生式相关知识进行的求解。
数学模型描述如下:1、设计该问题的状态。
使用了二维数组描述汉诺塔的状态,对n个盘子由大到小分别用数组n、n-1...2、1描述。
例如:当n=4时,二维数组为:1002003004002、定义目标状态。
当n=4时,这里是:001002003004依据如下规则定义产生式规则:1、在移动盘子时,每次只移动A\B\C柱子上可以移动的盘子中最大的盘子。
2、如果上一次已经移动了某个盘子,则下一次不能继续移动,即:一个盘子不能被连续移动两次。
如:某次操作将1号盘子由A柱子移动到B柱子,那么在选择下一个要移动的盘子时应不在考虑1号盘。
3、当某个可以移动的盘子摆放位置不唯一时要将当前状态入栈,并选择盘子移动前所在的柱子的左侧(同理:反方向选择也可)柱子作为移动的目标柱子。
为提高程序运行过程中的空间利用率,产生式规则在汉诺塔移动过程中依据以上规则自动生成。
控制策略依据如下:1、根据以上产生式规则依据,在每次移动盘子时可选择产生式唯一,所以不需要考虑路径选择。
2、当移动的是一组盘子中的最大盘子(即:在要移动的一组盘子中的最下面的盘子)时,观察目标柱子是否是C柱子(最终结果所在柱子),如果是则表示当前盘子移动成功,并清空栈,转移问题(即减小一层盘子);如果移动目标错误(即移动到了A或B柱子)则执行回溯:栈顶状态出栈,向右选择目标柱子产生新的产生式规则,并按此执行移动操作。
3、如果要移动的一组盘子中最大的是1号盘(最后一个盘子),执行的移动操作是将盘子移动到C柱子,则算法结束。
四、主要功能流程图如下:(注意:本设计控制盘子为九个)。
五、源程序:package Hanoi;import java.util.Arrays;import java.util.Scanner;import java.util.Stack;public class Hanoi {public static void main(String[] args) {Scanner in = new Scanner(System.in);System.out.println("请输入汉诺塔盘子的个数:");int n = in.nextInt();// 定义初始状态int[][] first = new int[n][3];System.out.println("初始状态:");for (int i = 0; i < n; i++) {first[i][0] = i + 1;System.out.println(Arrays.toString(first[i]));}// 定义目标状态int[][] end = new int[n][3];for (int i = 0; i < n; i++) {end[i][2] = i + 1;// System.out.println(Arrays.toString(end[i]));}int maxValue = n;// 定义可以移动的最大盘子的值,初值Disk before = null;// 定义上一个移动的盘子,初始值为nullStack<int[][]> stack = new Stack<int[][]>();// 定义存放盘子状态的栈Stack<Disk> bs = new Stack<Disk>();b: while (true) {System.out.println("before:" + before);Disk canMoveDisk = Hanoi.findMoveDisk(first, before);// 找出当前可移动盘子// System.out.println("canMoveDisk:" + canMoveDisk);Disk[] movePlace = Hanoi.movePlace(first,Hanoi.findMoveDisk(first, before));// 返回当前可移动去的位置数组// System.out.println("locateionNumber:" +movePlace.length);Disk right = movePlace[0];// 如果可移动位置有两个,right 为右侧位置Disk left = movePlace[0];// 如果可移动位置有两个,left为左侧位置if (movePlace.length == 2) {if(movePlace[0].y==(canMoveDisk.y+1)%3){right=movePlace[0];left=movePlace[1];}else if(movePlace[0].y==(canMoveDisk.y+2)%3){right=movePlace[1];left=movePlace[0];}int[][] a = new int[n][3];for (int i = 0; i < n; i++)for (int j = 0; j < 3; j++)a[i][j] = first[i][j];stack.push(a);// 把当前状态入栈if (before == null)bs.push(null);else {Disk x = new Disk(before.x, before.y);bs.push(x);}System.out.println("入栈");}// System.out.println("right:" + right);Hanoi.move(canMoveDisk, right, first);before = right;if (maxValue == 1 && Hanoi.findDiskPrice(right, first) == 1&& right.y == 2)break b;if (Hanoi.findDiskPrice(right, first) == maxValue) {// 如果移动了要移动的最大盘子// 如果是则判断目标柱子是否是最终结果所在柱子if (right.y == 2) {// 如果是// 清空栈while(!stack.isEmpty()){stack.pop();}while(!bs.isEmpty()){bs.pop();}System.out.println("清空栈");maxValue =maxValue-1;// 要移动的最大盘子减1} else {for (int i = 0; i < n; i++)for (int j = 0; j < 3; j++)first[i][j] = stack.peek()[i][j];stack.pop();// 出栈恢复System.out.println("出栈恢复");Hanoi.print(first);Disk x = null;if (bs.peek() != null)x = new Disk(bs.peek().x, bs.peek().y);Disk canMoveDisk2 = Hanoi.findMoveDisk(first, x);bs.pop();Disk[] movePlace2 = Hanoi.movePlace(first, canMoveDisk2);// System.out.println("canMoveDisk:" + canMoveDisk2);// System.out.println("locateionNumber:" + movePlace2.length);Disk r = movePlace2[0];// 如果可移动位置有两个,right为右侧位置Disk l = movePlace2[0];// 如果可移动位置有两个,left为左侧位置if (movePlace2.length == 2) {if(movePlace2[0].y==(canMoveDisk2.y+1)%3){r=movePlace2[0];l=movePlace2[1];}elseif(movePlace2[0].y==(canMoveDisk2.y+2)%3){r=movePlace2[1];l=movePlace2[0];}}Hanoi.move(canMoveDisk2, l, first);// 选择左侧位置移动盘子// System.out.println("canMoveDisk:" + canMoveDisk2);// System.out.println("locateionNumber:" + movePlace.length);// System.out.println("left:" + l);before = l;if (maxValue == 1 && Hanoi.findDiskPrice(left, first) == 1&& l.y == 2)break b;}}}}// 找出可移动的盘子private static Disk findMoveDisk(int[][] a, Disk before) { Disk[] d = new Disk[3];// 柱子1,2,3的顶部盘子for (int i = 0; i < 3; i++) {d[i] = Hanoi.findTopDisk(i + 1, a);}for (int i = 0; i < 3; i++) {if (before == null)return d[0];else if ((!before.equals(d[i]))&& Hanoi.findDiskPrice(d[i], a) != 0&& ((Hanoi.findDiskPrice(d[i], a) <Hanoi.findDiskPrice(d[(i + 1) % 3], a)|| Hanoi.findDiskPrice(d[i], a) < Hanoi.findDiskPrice(d[(i + 2) % 3], a)|| Hanoi.findDiskPrice(d[(i + 1) % 3], a) == 0 || Hanoi.findDiskPrice(d[(i + 2) % 3], a) == 0))) // System.out.println(d[i]);return d[i];}return null;}// 找出可以移动的位置坐标private static Disk[] movePlace(int[][] a, Disk canMoveDisk) {Disk[] d = new Disk[2];int h = 0;// h是数组Disk的下标int i = canMoveDisk.y;// 当前可移动盘子的柱子纵坐标Disk d1 = findTopDisk((i + 1) % 3 + 1, a);Disk d2 = findTopDisk((i + 2) % 3 + 1, a);if (Hanoi.findDiskPrice(d1, a) == 0) {d[h] = d1;h++;} else if ((Hanoi.findDiskPrice(canMoveDisk, a) <Hanoi.findDiskPrice(d1, a))) {if (d1.x != 0) {Disk d0 = new Disk(d1.x - 1, d1.y);d[h] = d0;h++;}}if (Hanoi.findDiskPrice(d2, a) == 0) {d[h] = d2;h++;} else if ((Hanoi.findDiskPrice(canMoveDisk, a) < Hanoi.findDiskPrice(d2, a))) {if (d2.x != 0) {Disk d0 = new Disk(d2.x - 1, d2.y);d[h] = d0;h++;}}Disk[] d3;if(d[1]!=null){d3 = new Disk[2];d3[0] = d[0];d3[1] = d[1];}else{d3 = new Disk[1];d3[0] = d[0];}return d3;}// 找出一个Disk对应坐标的盘子值private static int findDiskPrice(Disk d, int[][] a) { return a[d.x][d.y];}// 找出柱子i的顶部盘子private static Disk findTopDisk(int i, int[][] a) { int j;for (j = 0; j < a.length; j++) {if (a[j][i - 1] == 0)continue;else {Disk d = new Disk(j, i - 1);return d;}}if (j >= a.length) {Disk d = new Disk(a.length - 1, i - 1);return d;}return null;}// 移动盘子,将盘子d1移至d2位置private static void move(Disk d1, Disk d2, int[][] a) { System.out.println("将盘子" + Hanoi.findDiskPrice(d1, a) + "从位置" + d1+ "移至位置" + d2 + " " + (d1.y + 1) + "号柱子-->" + (d2.y + 1)+ "号柱子");a[d2.x][d2.y] = a[d1.x][d1.y];a[d1.x][d1.y] = 0;Hanoi.print(a);}// 打印当前盘子位置分布private static void print(int[][] a) {for (int i = 0; i < a.length; i++)System.out.println(Arrays.toString(a[i]));}}package Hanoi;//定义一个盘子的位置class Disk {int x;// 盘子的横坐标int y;// 盘子的纵坐标public Disk(int x, int y) {this.x = x;this.y = y;}public boolean equals(Disk d) {if (this.x == d.x && this.y == d.y)return true;return false;}@Overridepublic String toString() {return"Disk" + "(" + this.x + "," + this.y + ")";}}六、运行结果(9层汉诺塔结果):......一层汉诺塔:二层汉诺塔:三层汉诺塔:七、结果分析:汉诺塔问题通过我们都知道的递归算法来实现很简单,而本实验中采用了产生式系统解决汉诺塔问题,确定要移动的盘子,确定盘子移去的位置都只要根据所给出的规则就能够确定了,整个实现过程看起来很复杂,其实根据给出的产生式规则都可以很好的解决。
