五年级奥数-一半模型

合集下载

一半模型经典例题

一半模型经典例题
题目一
【例题】甲、乙、丙三人分一堆桃子。

甲分得桃子数是乙的2倍，丙最少，但也多于10个，三个人不能分完，且每次分的时候都是丙先拿，然后甲、乙两人拿。

这堆桃子共有多少个？
【解析】因为甲是乙的2倍，所以先分乙的，乙1份，甲2份，还剩5份。

而且丙先拿，拿的数量最少也要占总数量的(1/8)，所以5份是总数的(1-1/8)=7/8，丙拿一份，是总数的1/8。

所以总数是5÷(7/8)=40/7的倍数。

因为丙拿的还要多于10个，所以总数的1/8要大于10，小于40/7。

所以总数是88。

题目二
【例题】有一堆围棋子，黑子和白子混在了一块，黑棋和白棋各有150颗，那么从中间摸出白子的可能性的大小是多少？
【解析】这道题目考查的是一半模型中的等可能性问题。

因为黑棋和白棋各有150颗，所以总共有300颗棋子。

从中随机摸出一颗棋子，摸到白棋的可能性是150/300=1/2。

小学奥数题库《几何》-直线型-一半模型-4星题(含解析)

几何-直线型几何-一半模型-4星题课程目标知识提要一半模型•平行四边形的一半模型•梯形的一半模型•任意四边形一半模型精选例题一半模型1. 如图，四边形ABCD是正方形，ABGF和FGCD都是长方形，点E在AB上，EC交FG于点M，假设AB=6，△ECF的面积是12，那么△BCM的面积是．【答案】6【分析】根据一半模型，S△EFM+S△BMG=S÷2,长方形AFBG÷2S△FMC+S△CMG=S长方形FDCG所以÷2=6×6÷2=18.S△ECF+S△BMC=S正方形所以S△BMC=18−12=6.2. 如下列图所示，过平行四边形ABCD内的一点P作边的平行线EF、GH．假设△PAC的面积为6，求平行四边形PGDF的面积比平行四边形PEBH的面积大．【答案】12【分析】根据差不变原理，要求平行四边形PGDF的面积与平行四边形PEBH的面积差，相当于求平行四边形DAEF的面积与平行四边形ABHG的面积差．如下列图所示，连接BP、DP．根据一半模型．由于S△ADP+S△BCP=S△ABP+S△ACP+S△BCP=12S ABCD,所以S△ADP−S△ABP=S△ACP.而S△ADP=12S DAEF,S△ABP=12S ABHG,所以S DAEF−S ABHG=2(S△ADP−S△ABP)=2S△ACP=12.即平行四边形PGDF的面积比平行四边形PEBH的面积大12．3. 正方形ABCD的面积为9平方厘米，正方形EFGH的面积为64平方厘米．如下图，边BC 落在EH上．三角形ACG的面积为6.75平方厘米，那么三角形ABE的面积为平方厘米．【答案】 2.25【分析】连接EG，EG是正方形EFGH的对角线，∠GEH=45∘；AC是正方形ABCD的对角线，∠ACB=45∘．∠GEH=∠ACB，可以知道AC∥EG．所以△ACG与△AEC面积相等，都是6.75平方厘米，那么△ABE的面积是：6.75−9÷2= 2.25(平方厘米).4. 如下图，矩形ABCD的面积为36平方厘米，四边形PMON的面积是3平方厘米，那么阴影局部的面积是平方厘米．【答案】12【分析】因为三角形ABP面积为矩形ABCD的面积的一半，即18平方厘米，三角形ABO 面积为矩形ABCD的面积的1，即9平方厘米，又四边形PMON的面积为3平方厘米，所以4三角形AMO与三角形BNO的面积之和是18−9−3=6(平方厘米)．又三角形ADO与三角形BCO的面积之和是矩形ABCD的面积的一半，即18平方厘米，所以阴影局部面积为18−6=12(平方厘米)．5. 长方形ABCD的面积是40平方厘米，E、F、G、H分别为AD、AH、DH、BC的中点；三角形EFG的面积是平方厘米．【答案】5【分析】三角形 EFG 的面积是三角形 AHD 的 14，三角形 AHD 的面积是长方形 ABCD 面积的 12，故三角形 EFG 的面积是长方形 ABCD 面积的 18，三角形 EFG 的面积为 40×18=5(平方厘米)．6. 如图，阴影局部四边形的外接图形是边长为 10cm 的正方形，那么阴影局部四边形的面积是 cm 2．【答案】 48【分析】如下图，分别过阴影四边形 EFGH 的四个顶点作正方形各边的平行线，相交得长方形 MNPQ ，易知长方形 MNPQ 的面积为4×1=4(平方厘米).从图中可以看出，原图中四个空白三角形的面积之和的 2 倍，等于 AENH 、BFME 、CGQF 、DHPG 四个长方形的面积之和，等于正方形 ABCD 的面积加上长方形 MNPQ 的面积，为10×10+4=104(平方厘米),所以四个空白三角形的面积之和为104÷2=52(平方厘米),那么阴影四边形 EFGH 的面积为100−52=48(平方厘米).7. 四边形ABCD是平行四边形，BC:CE=3:2，三角形ODE的面积为6平方厘米．那么阴影局部的面积是平方厘米．【答案】21平方厘米【分析】连接AC．由于ABCD是平行四边形，BC:CE=3:2，所以CE:AD=2:3,根据梯形蝴蝶模型，S△COE:S△AOC:S△DOE:S△AOD=22:2×3:2×3:32=4:6:6:9,所以S△AOC=6(平方厘米),S△AOD=9(平方厘米),又S△ABC=S△ACD=6+9=15(平方厘米),阴影局部面积为6+15=21(平方厘米)．8. 如图，长方形ABCD中，AB=67，BC=30．E、F分别是AB、BC边上的两点，BE+ BF=49．那么，三角形DEF面积的最小值是．【答案】717【分析】由于长方形ABCD的面积是一定的，要使三角形DEF面积最小，就必须使△ADE、△BEF、△CDF的面积之和最大．由于△ADE、△BEF、△CDF都是直角三角形，可以分别过E、F作AD、CD的平行线，可构成三个矩形ADME、CDNF和BEOF，如下图．容易知道这三个矩形的面积之和等于△ADE、△BEF、△CDF的面积之和的2倍，而这三个矩形的面积之和又等于长方形ABCD的面积加上长方形MDNO的面积．所以为使△ADE、△BEF、△CDF的面积之和最大，只需使长方形MDNO的面积最大．长方形MDNO的面积等于其长与宽的积，而其长DM=AE，宽DN=CF，由题知AE+CF=(AB+BC)−(BE+BF)=67+30−49=48，根据〞两个数的和一定，差越小，积越大〞，所以当AE与CF的差为0，即AE与CF相等时它们的积最大，此时长方形MDNO的面积也最大，所以此时三角形DEF面积最小．当AE与CF相等时，AE=CF=48÷2=24，此时三角形DEF的面积为：67×30−(67×30+24×24)÷2=717．9. 下列图ABCD是一个长方形，其中有三块面积分别为12、47、33，那么图中阴影局部为．【答案】92【分析】如下列图所示，设阴影局部面积为S，其他未知局部的面积为a、b、x和y．那么÷2x+S+y=a+S+b=S长方形ABCD(a+S+b)+(x+S+y)=S长方形ABCD根据覆盖的方法，那么阴影局部S=33+47+12=92．10. 如图，四边形ABCD中，DE:EF:FC=3:2:1，BG:GH:AH=3:2:1，AD:BC=1:2，四边形ABCD的面积等于4，那么四边形EFHG的面积=．【答案】43【分析】运用三角形面积与底和高的关系解题．连接AC、AE、GC、GE，因为DE:EF:FC=3:2:1,BG:GH:AH=3:2:1,所以，在△ABC中，S△BCG=12S△ABC,在△ACD中，S△AED=12S△ACD,在△AEG中，S△AEH=12S△HEG,在△CEG中，S△CFG=12S△EFG.因为S△BCG+S△AED=12S△ABC+12S△ACD=12(S△ABC+S△ACD)=12S ABCD=2S△BCG.所以S AGCE=S ABCD−(S△BCG+S△AED)=4−2=2.又因为S AGCE=S△AEH+S△HEG+S△CFG+S△EFG=12S△HEG+S△HEG+12S△EFG+S△EFG=32(S△HEG+S△EFG)=32S EFGH,所以S EFGH=2÷32=43.11. 如下列图所示，梯形ABCD的面积是48，E是下底BC上的一点，F是腰CD的中点，并且甲、乙、丙三个三角形面积相等，那么图中阴影局部的面积是．【答案】19.2【分析】因为三角形乙、丙的面积相等，且DF=FC，所以三角形乙、丙的高相等，于是AE∥DC，四边形AECD是平行四边形，易知S乙+S丙=S阴影=12S四边形AECD，因此，阴影局部的面积是48÷5×2=19.2．12. 正方形的边长为10，EC=3，BF=2，那么S四边形ABCD=．【答案】53【分析】如图，作BM⊥AE于M，CN⊥BM于N．那么四边形ABCD分为4个直角三角形和中间的一个长方形，其中的4个直角三角形分别与四边形ABCD周围的4个三角形相等，所以它们的面积和相等，而中间的小长方形的面积为3×2=6，所以S四边形ABCD =10×10−3×22+3×2=53．13. 如图，三角形ABC的面积为60平方厘米，D、E、F分别为各边的中点，那么阴影局部的面积是平方厘米．【答案】12.5【分析】阴影局部是一个不规那么的四边形，不方便直接求面积，可以将其转化为两个三角形的面积之差．而从图中来看，既可以转化为△BEF与△EMN的面积之差，又可以转化为△BCM与△CFN的面积之差．〔法一〕如图，连接DE．由于D、E、F分别为各边的中点，那么BDEF为平行四边形，且面积为三角形ABC面积的一半，即30平方厘米；那么△BEF的面积为平行四边形BDEF面积的一半，为15平方厘米．根据几何五大模型中的相似模型，由于DE为三角形ABC的中位线，长度为BC的一半，那么EM:BM=DE:BC=1:2,所以EM=13 EB;EN:FN=DE:FC=1:1,所以EN=12 EF.那么△EMN的面积占△BEF面积的12×13=16，所以阴影局部面积为15×(1−16)=12.5(平方厘米).〔法二〕如图，连接AM．根据燕尾定理，S△ABM:S△BCM=AE:EC=1:1,S△ACM:S△BCM=AD:DB=1:1,所以S△BCO=13S△ABC=13×60=20(平方厘米),而S△BDC=12S△ABC=12×60=30(平方厘米),所以S△FCN=14S△BDC=7.5(平方厘米),那么阴影局部面积为20−7.5=12.5(平方厘米).【总结】求三角形的面积，一般有三种方法：〔1〕利用面积公式：底×高÷2；〔2〕利用整体减去局部；〔3〕利用比例和模型．14. 如图，正方形的边长为12，阴影局部的面积为60，那么四边形EFGH的面积是．【答案】6【分析】如下图，设AD上的两个点分别为M、N．连接CN．根据面积比例模型，△CMF与△CNF的面积是相等的，那么△CMF与△BNF的面积之和，等于△CNF与△BNF的面积之和，即等于△BCN的面积．而△BCN的面积为正方形ABCD面积的一半，为122×12=72．又△CMF与△BNF的面积之和与阴影局部的面积相比拟，多了2个四边形EFGH的面积，所以四边形EFGH的面积为：(72−60)÷2=6．15. 下列图中，四边形ABCD都是边长为1的正方形，E、F、G、H分别是AB，BC，CD，DA的中点，如果左图中阴影局部与右图中阴影局部的面积之比是最简分数mn，那么，(m+n)的值等于．【答案】5【分析】左、右两个图中的阴影局部都是不规那么图形，不方便直接求面积，观察发现两个图中的空白局部面积都比拟好求，所以可以先求出空白局部的面积，再求阴影局部的面积．如下列图所示，在左图中连接EG．设AG与DE的交点为M．左图中AEGD为长方形，可知△AMD的面积为长方形AEGD面积的14，所以三角形AMD的面积为12×12×14=18．又左图中四个空白三角形的面积是相等的，所以左图中阴影局部的面积为1−18×4=12．如上图所示，在右图中连接AC、EF．设AF、EC的交点为N．可知EF∥AC且AC=2EF．那么三角形BEF的面积为三角形ABC面积的14，所以三角形BEF的面积为12×12×14=18，梯形AEFC的面积为12−18=38．在梯形AEFC中，由于EF:AC=1:2，根据梯形蝴蝶定理，其四局部的面积比为：12:1×2:1×2:22=1:2:2:4，所以三角形EFN的面积为38×11+2+2+4=124，那么四边形BENF的面积为18+124=16．而右图中四个空白四边形的面积是相等的，所以右图中阴影局部的面积为1−16×4=13．那么左图中阴影局部面积与右图中阴影局部面积之比为12:13=3:2，即mn=32，那么m+n=3+2=5．16. 如图，正方形ABCD的边长为10，AE＝2，CF＝3．长方形EFGH的面积为．【答案】94．【分析】连接DE，DF．在正方形ABCD中，S△DEF=S△ABCD−S△ADE−S△EBF−S△DFC,在长方形DEFG中，S△DEF=12S△EFGH,因为BE=10−2=8,BF=10−3=7,所以S△DEF=10×10−2×10÷2−8×7÷2−3×10÷2=47,所以S△EFGH=47×2=94.17. ABCD是边长为12的正方形，如下图，P是内部任意一点，BL=DM=4、BK=DN=5，那么阴影局部的面积是．【答案】34【分析】〔方法一〕特殊点法．由于P是内部任意一点，不妨设P点与A点重合〔如下列图〕，那么阴影局部就是△AMN和△ALK．而△AMN的面积为(12−5)×4÷2=14，△ALK的面积为(12−4)×5÷2=20，所以阴影局部的面积为14+20=34．〔方法二〕寻找可以利用的条件，连接AP、BP、CP、DP可得下列图所示：那么有：S△PDC+S△PAB=12S ABCD=12×122=72.同理可得：S△PAD+S△PBC=72;而S△PDM:S△PDC=DM:DC=4:12=1:3,即S△PDM=13S△PDC;同理：S△PBL=13S△PAB,S△PND=512S△PDA,S△PBK=512S△PBC;所以：(S△PDM+S△PBL)+(S△PND+S△PBK)=13(S△PDC+S△PAB)+512(S△PDA+S△PBC)而(S△PDM+S△PBL)+(S△PND+S△PBK)=(S△PNM+S△PLK)⏟阴影面积+(S△DNM+S△BLK);S△DNM=S△BLK=12×4×5=10;所以阴影局部的面积是：S△PNM+S△PLK=13(S△PDC+S△PAB)+512(S△PDA+S△PBC)−(S△DNM+S△BLK),即为：1 3×72+512×72−10×2=24+30−20=34.18. 下列图中，ABCD是平行四边形，E为CD的中点，AE和BD的交点为F，AC和BE的交点为H，AC和BD的交点为G，四边形EHGF的面积是15平方厘米，那么ABCD的面积是平方厘米．【答案】 180【分析】解法一：蝴蝶模型与一半模型．〔1〕E 是 CD 的中点，DE:AB =1:2，所以S △DEF :S △DAF :S △BEF :S △ABF =1:2:2:4.〔2〕设平行四边形面积为“1〞．E 是 CD 的中点，所以 S △ABG 、S △ADG 、S △BEC 占平行四边形面积的 14，梯形 S ABED 占平行四边形面积的 34；〔3〕所以S △DAF =34×21+2+2+4=16,S △GAF =14−16=112, 同理可知 S △GHB =112．〔4〕根据一半模型，S △ABE =12，S 四边形EHGF =12−14−112−112=112;〔5〕ABCD 的面积是15÷112=180(cm 2).解法二：相似模型、等积变形与一半模型．〔1〕E 是 CD 的中点，DE:AB =1:2，所以 DF:FB =1:2，而 DG =GB ，DF:FG =11+2:(12−11+2)=2:1;〔2〕设平行四边形面积为“1〞．E 是 CD 的中点，所以 S △ABG 、S △ADG 占平行四边形面积的 14，所以S △GAF =14×12+1=112,同理可知 S △GHB =112．〔3〕根据一半模型，S △ABE =12，S 四边形EHGF =12−14−112−112=112;〔4〕ABCD 的面积是15÷112=180(cm 2).解法三：燕尾模型与一半模型．〔1〕设平行四边形面积为“1〞．S △ADC =12．〔2〕E 是 CD 的中点，G 为 AC 的中点，连接 FC ，设 S △DEF 为 1 份，S △ECF 也为 1 份，根据燕尾 S △ADF 为 2 份，再根据燕尾 S △ACF 也为 2 份，根据按比例分配，S △AGF 、S △GCF 都为 1 份，所以S △GAF =12÷(2+1+1+1+1)=112,同理可知 S △GHB =112．〔3〕根据一半模型，S △ABE =12，S 四边形EHGF =12−14−112−112=112;〔4〕ABCD 的面积是15÷112=180(cm 2).解法四：风筝模型与一半模型．连接 EG 同样可解．19. 如图，正方形ABCD的边AD上有一点E，边BC上有一点F，G是BE的中点，H是CE 的中点，如果正方形的边长是2，那么阴影局部的面积是．【答案】1【分析】2×2÷2÷2=1.20. 如下列图所示，在长方形内画出一些直线，边上有三块面积分别是13，35，49．那么图中阴影局部的面积是多少？【答案】97【分析】三角形ABC的面积+三角形CDE的面积+(13+35+49) =长方形面积+阴影部分面积;又因为三角形ABC的面积=三角形CDE的面积=12长方形面积,所以可得：阴影部分面积=13+35+49=97.21. 如下列图所示长方形ADEH由上、中、下三个小长方形组成，AB+CD=BC，三角形ABI的面积为3，四边形GIJF的面积为12，求四边形CDEJ的面积．【答案】9【分析】因为AB+CD=BC，所以长方形BCFG的面积等于长方形ADEH面积的一半，即S梯形BCJI +S梯形IJFG=12S长方形ADEH，又S△ABI+S梯形BCJI+S梯形CDEJ=12S长方形ADEH，所以S△ABI+S梯形CDEJ =S梯形IJFG，故四边形CDEJ的面积是12−3=9．22. 如下图，O是长方形ABCD一条对角线的中点，图中已经标出两个三角形的面积3和4，那么阴影直角三角形的面积是多少？【答案】 318【分析】由 S △AOD =4 可知 S △BCD =12×S 长方形ABCD =12×4×S △AOD =8．而 △CDF 与 △CDB 从 C 出发的高相同，那么 DF DB =S △CDF S △CDB=58．由于 EF ∥CD ，把线段的比例转移到 BC 上，那么有 CE BC =DF DB =38，从而得到 BE BC =1−38=58，所以阴影 △BEF 的面积是 △BCF 面积的 58．于是阴影三角形的面积是58×S △BCF =58×(S △BCD −S △CDF )=58×(8−3)=258.23. 如图，正六边形的面积为 120，P 是其内任意一点，求 △PBC 和 △PEF 的面积之和．【答案】 40【分析】由一半模型，两个三角形面积和等于四边形 BCEF 面积的一半，而这个四边形的面积又是六边形面积的 23，所以所求面积和就是正六边形面积的 13，为 40．24. 如下图，E、H、F、G是四边形ABCD的AD、BC边上的三等分点，四边形ABCD的面积为18平方厘米，那么四边形EFGH的面积是平方厘米．【答案】6【分析】首先连接BE、DG、BD，如下列图所示：可以看出，三角形ABD的面积是三角形ABE面积的3倍，三角形BCD的面积是三角形GCD 的面积的3倍，所以三角形ABE与三角形GCD的面积和是6平方厘米，那么四边形BGDE 的面积是12平方厘米．再利用不规那么四边形中的一半模型可得，EFGH的面积是BFDG的一半，也就是6平方厘米．25. 如图，在三角形ABC中，BC＝8厘米，BC边对应的高是6厘米，E、F分别为AB和AC 的中点，那么三角形EBF的面积是多少平方厘米？【答案】6【分析】S△ABC=8×6÷2=24(平方厘米)，因为F是中点，所以S△AFB=S△FBC=24÷2=12(平方厘米),因为E是中点，所以S△BEF=S△EFA=12÷2=6(平方厘米).26. 如下图，P为长方形ABCD内的一点．三角形PAB的面积为5，三角形PBC的面积为13请问：三角形PBD的面积是多少？【答案】8【分析】图1阴影局部的面积是整个长方形的一半，而图2阴影局部的面积也是整个长方形的一半，两个阴影局部有一块公共局部，那就是△APD．去掉这块公共局部之后，剩下的阴影局部仍然应该相等，因此就有S1=S2+S3．由题意，S1=13，S2=5，所以S3=13−5= 8．27. 一张面积为7.17平方厘米的平行四边形纸片WXYZ放在另一张平行四边形纸片EFGH上面，如下列图所示，得出A、C、B、D四个交点，并且AB∥EF，CD∥WX．问纸片EFGH的面积是多少平方厘米？说明理由．【答案】7.17【分析】连接AC、CB、BD、DA如下列图所示，因为AB∥EF∥GH，所以△ABC的面积是平行四边形AEFB面积的一半，△ABD的面积是平行四边形AHGB的面积的一半，因此四边形ACBD的面积是平行四边形EFGH面积的一半．同理可证，四边形ACBD的面积也是平行四边形WXYZ面积的一半．因此，平行四边形EFGH的面积=平行四边形WXYZ的面积=7.17平方厘米．28. 如下列图所示，在平行四边形ABCD中，三角形ABP、BPC的面积分别是73、100，求三角形BPD的面积．【答案】27【分析】根据平行四边形的一半模型可知，S△APD+S△BPC=S△APD+S△APB+S△BPD=1 2S平行四边形ABCD，所以有S△BPC=S△APB+S△BPD，那么三角形BPD的面积等于100−73=27．29. 如图，ABCD为正方形，AM=NB=DE=FC=1cm且MN=2cm，请问四边形PQRS 的面积为多少？【答案】23cm2【分析】〔法1〕由AB∥CD，有MP MN = PC DC,所以PC=2PM,又MQ QC = MB EC,所以MQ=QC=12 MC,所以PQ=12MC−13MC=16MC,所以S SPQR占S AMCF的16，得到S SPQR=16×1×(1+1+2)=23(cm2).〔法2〕如图，连结AE，那么S△ABE=12×4×4=8(cm2),而RB AB = ER EF,所以RB EF =ABEF=2,S△ABR=23S△ABE=23×8=163(cm2).而S△MBQ=S△ANS=12×3×4×12=3(cm2),因为MN DC = MP PC,所以MP=13 MC,那么S△MNP=12×2×4×13=43(cm2),阴影局部面积等于S△ABR−S△ANS−S△MBQ+S△MNP=163−3−3+43=23 (cm2).30. 在长方形ABCD内部有一点O，形成等腰△AOB的面积为16，等腰△DOC的面积占长方形面积的18%，那么阴影△AOC的面积是多少？【分析】先算出长方形面积，再用其一半减去 △DOC 的面积〔长方形面积的 18%〕，再减去 △AOD 的面积，即可求出 △AOC 的面积．根据模型可知 S △COD +S △AOB =12S ABCD , 所以 S ABCD =16÷(12−18%)=50,又 △AOD 与 △BOC 的面积相等，它们的面积和等于长方形面积的一半，所以 △AOD 的面积等于长方形面积的 14，所以 S △AOC=S △ACD −S △AOD −S △COD =12S ABCD −25%S ABCD −18%S ABCD =25−12.5−9=3.5.31. 如下列图所示，点 P 及点 Q 在正方形 ABCD 之内部，假设 △ABP 与 △DPC 的面积比为 3:2，△ADP 与 △BCP 的面积比为 3:7，△ABQ 与 △CDQ 的面积比为 3:5，并且 △ADQ 与 △BCQ 的面积比为 4:1．请问四边形 APCQ 的面积〔阴影局部〕与正方形 ABCD 的面积比是多少？【分析】根据一半模型，△ABP与△DPC的面积和为正方形面积的一半，△ADP与△BCP的面积和为正方形面积的一半，△ABQ与△CDQ的面积和为正方形面积的一半，△ADQ与△BCQ的面积和也为正方形面积的一半，那么△DPC的面积占整个图形的25×12=15，△ADP的面积占整个图形的310×12=320，△ABQ的面积占整个图形的38×12=316，△BCQ的面积占整个图形的15×12=110，那么阴影局部占正方形面积的1−15−320−316−110=2980．32. 如图，有一个长6cm，宽4cm的长方形ABCD．在各边上取点E,F,G,H，再连接H,F的线上取点P，与点E和点G相连．当四边形AEPH的面积是5cm2时，求四边形PFCG的面积．【答案】8cm2．【分析】连结EH,EF,FG,GH，题目中的线段长度如右图所示．所求四边形的面积可以化为三角形FGP与FCG的面积和．易见中间的四边形EFGH是平行四边形．根据一半模型，S△EHP+S△FGP=12S EFGH.S平行四边形EFGH=4×6−2×3÷2×2−1×4÷2×2=14(cm2),那么S△EHP+S△FGP=14÷2=7(cm2).S△EHP=5−3=2(cm2),所以S△FGP=7−2=5(cm2).因此四边形PFCG的面积是5+2×3÷2=8(cm2)33. 在图中，正方形ADEB和正方形ECFG底边对齐，两个正方形边长分别为6和4．三角形BDF的面积是多少？【答案】18【分析】连接FE，那么三角形BFO的面积与三角形DOE的面积相等．那么图中阴影局部的面积为正方形ABDE面积的一半，为6×6÷2=18．34. 如图，阴影局部四边形的外接图形是边长为12厘米的正方形，那么阴影局部四边形的面积是多少平方厘米？【答案】68【分析】如下图，分别过阴影四边形EFGH的四个顶点作正方形各边的平行线，相交得长方形MNPQ，易知长方形MNPQ的面积为4×2=8平方厘米．从图中可以看出，原图中四个空白三角形的面积之和的2倍，等于AENH、BFME、CGQF、DHPG四个长方形的面积之和，等于正方形ABCD的面积加上长方形MNPQ的面积，为12×12+8=152平方厘米，所以四个空白三角形的面积之和为152÷2=76平方厘米，那么阴影四边形EFGH的面积为144−76=68平方厘米．35. 一个长方形分成4个不同的三角形，绿色三角形面积占长方形面积的15%，黄色三角形面积是21cm2．问：长方形的面积是多少平方厘米？【答案】60．【分析】由一半模型知：黄+绿=长方形的面积一半，所以绿占长方形面积的：12−15%=720，所以长方形的面积为：21÷720=60〔平方厘米〕．36. 如下图，长方形ABCD的长是12厘米，宽是8厘米，三角形CEF的面积是32平方厘米，那么OG=厘米．【答案】4【分析】由于AD与FG平行，因此S△FDO+S△CFO=S△CEF=32(平方厘米).而S△CFD=12×8÷2=48(厘米),所以S△CDO=S△CFD−S△FDO−S△CFO=48−32=16(平方厘米),故OG=2S△CDO÷CD=2×16÷8=4(厘米).37. 图中ABCD是梯形，三角形ADE面积是1.8，三角形ABF的面积是9，三角形BCF的面积是27．那么阴影局部面积是多少？【答案】 4.8【分析】设△ADF的面积为“上〞，△BCF的面积为“下〞，△ABF的面积为“左〞，△DCF 的面积为“右〞．左=右=9；上×下=左×右=9×9=81，而下=27，所以上=81÷27=3．△ADE的面积为1.8，那么△AEF的面积为1.2，那么EF:DF=S△AEF:S△AED=1.2:3=0.4.△CEF与△CDF的面积比也为EF与DF的比，所以有\[ {S}_{\vartriangle {{ACE }}}=0.4\times{S}_{\vartriangle {{ACD}}} $ =0.4\times(3+9)=4.8. \]即阴影局部面积为4．8．38. 如图，ABCD是一个直角梯形．以AD为边长向外做一个长方形ADEF，其面积是10平方厘米，连结BE交AD于P，再连接PC，那么图中阴影局部的面积是多少平方厘米？【答案】5平方厘米【分析】连结BD，如下列图．因为AD∥BC，所以S△PCD=S△PBD，所以阴影局部的面积等于S△EBD，再根据FB∥ED，所以阴影的面积就是长方形AFED面积的一半，即10÷2=5(平方厘米)．39. 有一个边长为16厘米的正方形，连接每边的中点构成第二个正方形，再连接每边的中点构成第三个正方形，第四个正方形．求图中阴影局部的面积？【答案】80cm2【分析】如下列图左所示，S阴①=4S1．S阴①=16×16÷2=128(cm2)如下列图中所示，此时斜放的正方形面积为128cm2，S=S阴②．S=S阴②=128÷2=64(cm2)如图右所示，此时外面正方形面积为64，图中S阴③=64÷2÷2=16(cm2)所以，图中阴影局部总面积为：S阴②+S阴③=64+16=80(cm2)40. 如图，四边形ABCD中，DE=4FC，EF=3FC，BG=4AH，GH=3AH，四边形ABCD 的面积等于24，那么四边形EFHG的面积=．【答案】9【分析】首先连接AE、CG、AC，由条件看出E、G分别为CD和AB的中点，那么根据所学的一半模型，四边形AECG的面积占ABCD的一半，也就是面积为12．接下来连结EG，又可看出HEG面积是HEA的3倍，以及FGE面积是FGC的3倍，所以推出四边形EFGH的面积是12÷(1+3)×3=9．41. 如图，长方形被其内的一些直线划分成了假设干块，边上有3块面积分别是13，35，49．那么图中阴影局部的面积是多少？【答案】97【分析】如下列图所示，为了方便表达，将局部区域标上序号，设阴影局部面积为“阴〞：(49+①+35)+(13+②)=12矩形的面积①+阴+②=12矩形的面积.比拟上面两个式子可得阴影局部的面积为97．42. 如图，将平行四边形ABCD的边DC延长一倍至点E，三角形BCE的面积是10平方厘米，阴影局部面积是多少平方厘米？【答案】10【分析】连接AC．因为DC=CE=AB，且AB∥CE，所以四边形ABEC是平行四边形．推知S△ABF=S△BEF，因为DC=CE，所以S△DCF=S△CEF，可得S△ABF+S△DCF=S△BEF+S△CEF．那么阴影局部的面积是10平方厘米．43. 如图，平行四边形ABCD的面积为36，三角形AOD的面积为8．三角形BOC的面积为多少？【答案】10．−8=10．【分析】由根本一半模型知：三角形BOC的面积为36×1244. 如图，四边形ABCD中，DE=3FC，EF=2FC，BG=3AH，GH=2AH，四边形ABCD 的面积等于24，那么四边形EFGH的面积=．【答案】8．【分析】首先连接AE、CG、AC，由条件看出E、G分别为CD和AB的中点，那么根据所学的一半模型，四边形AECG的面积占四边形ABCD面积的一半，也就是面积为12．接下来连结EG，又可看出HEG面积是HEA的2倍，以及FGE面积是FGC的2倍，所以推出四边形EFGH的面积是12÷(1+2)×2=8．45. 如下列图，正方形ABCD的面积是20，正三角形△BPC的面积是15，求阴影△BPD的面积．【答案】10【分析】连接AC交BD于O点，并连接PO．如上图所示，可得PO∥DC，所以△DPO与△CPO面积相等〔同底等高〕，所以有：S△BPO+S△CPO=S△BPO+S△PDO=S△BPD,因为S△BOC=14S ABCD=14×20=5,所以S△BPD=15−5=10.46. 如图，在一个梯形内有两个三角形的面积分别为10与12，梯形的上底长是下底长的23．那么余下阴影局部的面积是多少？【答案】23【分析】不妨设上底长2，那么下底长3，那么上面局部的三角形的高为10÷2×2=10，下面局部的三角形的高为12÷3×2=8，那么梯形的高为10+8=18．所以梯形的面积为1 2×(2+3)×18=45,所以余下阴影局部的面积为45−10−12=23.47. 如下图，BD、CF将长方形ABCD分成4块，△DEF的面积是5平方厘米，△CED的面积是10平方厘米．问：四边形ABEF的面积是多少平方厘米？【答案】25厘米【分析】连接BF，根据梯形模型，可知三角形BEF的面积和三角形DEC的面积相等，即其面积也是10平方厘米，再根据蝴蝶定理，三角形BCE的面积为10×10÷5=20(平方厘米),所以长方形的面积为(20+10)×2=60(平方厘米),四边形ABEF的面积为60−5−10−20=25(平方厘米).48. 如图，正六边形ABCDEF的面积为1，那么阴影局部的面积是多少？【答案】14【分析】把三角形EGD移到三角形CHB的位置，那么长方形DHBG面积为六边形面积一半，阴影面积又为此长方形面积一半，因此为1÷2÷2=1 4 .49. 下列图中的大正方形ABCD的面积是1，其他点都是它所在的边的中点．请问：阴影三角形的面积是多少？【答案】 332【分析】图中有大、中、小三个正方形，每个面积是前一个的 12，所以小正方形面积是 14，将小正方形各顶点标上字母，如下列图所示，很容易看出 $\triangle JFG\text{面积}=\triangle IHG\text{面积}=\dfrac 1 4\times \text{正方形$ EFGH $面积}$，$\triangle EJI\text{面积}=\dfrac 1 4\times \triangle EFH\text{面积}=\dfrac 1 8\times \text{正方形$ EFGH $面积}$．所以阴影 △JGI 面积=(1−14−14−18)×小正方形面积=38×小正方形面积=332．50. 三角形 ABC 中，BD =CD ，三角形 ABD 的面积为 20 平方厘米，AD =8 厘米，求高 CE 的长是多少厘米？【答案】5【分析】因为三角形ACD的面积=20平方厘米，同时三角形ACD的面积=AD×CE÷2，所以CE=20×2÷8=5〔厘米〕．51. 平行四边形内有一个点N，连接这个点和平行四边形的四个顶点，把平行四边形分成几块，各块的面积如下图，那么阴影局部的面积应该是多少？【答案】6【分析】平行四边形中也有一半模型．8+2−4=6就是阴影的面积．52. 如图是由5个大小不同的正方形叠放而成的，如果最小的正方形〔阴影局部〕的周长是8，那么最大的正方形的边长是多少？【答案】8厘米【分析】最小正方形的面积是2×2=4(平方厘米)最大的正方形的面积是4×2×2×2×2=64(平方厘米)那么最大的正方形的边长是8厘米．53. 如图，长方形ABCD的边上有两点E、F，线段AF、BF、CE、BE把长方形分成假设干块，其中三个小木块的面积标注在图上，阴影局部面积是多少平方米？【答案】97【分析】运用等积变换，S DFA+S FCB=12S ABCD,S BCE=12S ABCD=S DAF+S FCB,因此，阴影面积为15+36+46=97(平方米).54. 如图，正方形ABCD的边长为8，AE=2，CF=3．长方形EFGH的面积为．【答案】58【分析】连接DE，DF，正方形ABCD的面积为8×8=64，三角形AED的面积为8×2÷2=8,三角形DFC的面积为8×3÷2=12,三角形BEF的面积为(8−2)×(8−3)÷2=15,那么三角形DEF的面积为64−8−12−15=29,长方形EFGH的面积为29×2=58.55. 一个长方形分成4个不同的三角形，黄色的三角形面积是50平方厘米，绿色三角形的面积占长方形面积的20%，那么长方形的面积是多少平方厘米？【答案】5003【分析】由一半模型知：黄+绿=长方形的面积一半,所以绿占长方形面积的：1 2−20%=310,所以长方形的面积为：50÷310=5003(平方厘米).56. 如图，正方形ABCD的边长为6，AE＝1.5，CF＝2．长方形EFGH的面积是多少？【答案】33．【分析】连接DE，DF．在正方形ABCD中，S△DEF=S△ABCD−S△ADE−S△EBF−S△DFC,在长方形DEFG中，S△DEF=12S△EFGH,因为BE=6−1.5=4.5,BF=6−2=4,所以S△DEF=6×6−1.5×6÷2−2×6÷2−4.5×4÷2=16.5,。

五年级奥数一半模型

一、三角形当中的一半模型由于三角形的面积公式S=底×高÷2，决定于底和高的长度，所以我们有了等高模型和等底模型。

在等高模型中，（图1）当BD=CD 时，阴影部分，SΔABD=SΔABC÷2特别地如图2，当BE=ED ，DF=FC ，阴影部分面积，SΔAEF=SΔABC÷2在等底模型中（图3），当AE=DE 时，阴影部分，SΔEBC=SΔABC÷2二、平行四边形中的一半模型由于三角形的面积公式S=底×高÷2，平行四边行的面积公式S=底×高所以与平行四边形同底等高的三角形是它面积的一半！同时，长方形是特殊的平行四边行，再根据平行线间的等积变形，可以得到如下诸图，阴影部分面积是四边形面积的一半：知识结构五年奥数一半模型【巩固练习】判断下面的图形中阴影部分的面积是不是整个图形面积的一半。

是打“√”，不是打“×”。

三、梯形中的一半模型在梯形中，当三角形的底边是梯形的一个腰，顶点在另一个腰的中点处，那么三角形是梯形面积的一半。

如图4，在梯形ABCD中，BE=CE，则SΔADE=SABCD÷2如图5，是它的变形，注意其中AF=DF，BE=CE。

四、任意四边形中的一半模型如图6，在四边形ABCD中，AE=EB，DF=CF，则SEBFD=SABCD÷2【能力提升】【巩固练习】【例1】如图，已知长方形ABCD 的面积为24平方厘米，且线段EF,GH 把它分成四个小长方形，求阴影部分的面积。

24÷2=12（平方厘米）答：阴影部分的面积是12平方厘米。

【巩固】已知大长方形的长是6厘米，宽是4厘米，求阴影部分的面积。

6×4÷2=12（平方厘米）答：阴影部分的面积是12平方厘米。

【例2】如图所示，平行四边形的面积是 50 平方厘米，阴影部分面积是（）平方厘米．例题精讲4【例3】如图,长方形AFEB 和长方形FDCE 拼成了长方形ABCD,长方形ABCD 的长是20，宽是12，则它内部阴影部分的面积是多少？A BF ED C【巩固】如图，正方形ABCD的边长为4，矩形EDFG的边EF过A点，G点在BC上，若DG=5，则矩形EDGF的宽DE=_____；EA DFB C G【巩固】如图所示，正方形 A B C D的边长为8厘米，长方形 E B G F的长 B G为1 0厘米，那么长方形的宽为几厘米？EA BFD G C【例4】【巩固】如右图所示，在长方形内画出一些直线，已知边上有三块面积分别是11,32,57．那么图中阴影部分的面积是多少？A D325711B C【例4】如图所示，长方形ABCD内的阴影面积之和为65，AB=8，AD=15,四边形EFGD的面积是？【思考题】提示：构造一半模型（很多时候，需要我们构造一半模型来解决一些问题。

五年级公开课一半模型

几何中的一半模型一、导入图形的变化是多种多样的，但是无论是怎么样的变化都有着它的基本模型，今天我们就来一起学习众多模型中的一个基本模型---------一半模型二、新课教学图1引导学生思考图中阴影部分的面积与长方形的关系。

此图中阴影部分的面积学生马上可以看出是长方形面积的一半。

图2 此图中阴影部分的面积与长方形又是怎样的关系呢？学生一眼看不出来，遮住其中的一部分，引导学生发现和图1的联系。

作一条辅助线后，分成了左右两个长方形，并且左边的一部分和图1相似，左边阴影部分的面积等于空白部分；右边的长方形中阴影部分也是等于空白部分，所以阴影部分的总面积是等于空白部分的总面积，是长方形的一半。

图3 此图中阴影部分的面积与长方形又是怎样的关系呢？有了图2做基础，学生很容易想到需要做辅助线来分析图形，可以让学生自己先尝试一下，然后请学生来回答分析过程。

横着做一条辅助线，把图形分成了上下两个长方形。

长方形的下半部分就和图2相似了，那么直接得出结论，阴影部分的面积是长方形的一半；上半部分也一样，所以所以阴影部分的总面积是等于空白部分的总面积，是长方形的一半。

总结：我们刚刚所分析的3个图形中，阴影部分的面积都等于长方形面积的一半。

练习：判断下面的图形中阴影部分的面积是不是整个图形面积的一半。

是打“√”，不是打“×”。

（√）（X）（X）（√）（√）（X）小结：只有在长方形，正方形，平行四边形里面才存在一半模型现在我们已经清楚地了解了三个基本的一半模型，再一起来学习一半模型的综合运用。

例1.如图，已知长方形ABCD 的面积为24平方厘米，且线段EF,GH 把它分成四个小长方形，求阴影部分的面积。

24÷2=12（平方厘米）答：阴影部分的面积是12平方厘米。

练习：已知大长方形的长是6厘米，宽是4厘米，求阴影部分的面积。

6×4÷2=12（平方厘米）答：阴影部分的面积是12平方厘米。

例2：如图，正方形ABCD 的边长是4㎝，矩形DEFG 的长DG 为5㎝，求它的宽DE 等于多少厘米？4×4÷5=3.2（厘米）答：宽DE 等于3.2厘米。

五年级奥数-一半模型-

一、三角形当中的一半模型由于三角形的面积公式S=底×高÷2，决定于底和高的长度，所以我们有了等高模型和等底模型。

在等高模型中，（图1）当BD=CD时，阴影部分，SΔABD=SΔABC÷2特别地如图2，当BE=ED，DF=FC，阴影部分面积，SΔAEF=SΔABC÷2在等底模型中（图3），当AE=DE时，阴影部分，SΔEBC=SΔABC÷2二、平行四边形中的一半模型由于三角形的面积公式S=底×高÷2，平行四边行的面积公式S=底×高所以与平行四边形同底等高的三角形是它面积的一半！同时，长方形是特殊的平行四边行，再根据平行线间的等积变形，可以得到如下诸图，阴影部分面积是四边形面积的一半：知识结构一半模型【巩固练习】判断下面的图形中阴影部分的面积是不是整个图形面积的一半。

是打“√”，不是打“×”。

（）（）（）（）（）（）三、梯形中的一半模型在梯形中，当三角形的底边是梯形的一个腰，顶点在另一个腰的中点处，那么三角形是梯形面积的一半。

如图4，在梯形ABCD中，BE=CE，则SΔADE=SABCD÷2如图5，是它的变形，注意其中AF=DF，BE=CE。

四、任意四边形中的一半模型如图6，在四边形ABCD中，AE=EB，DF=CF，则SEBFD=SABCD÷2【能力提升】【巩固练习】【例1】如图，已知长方形ABCD的面积为24平方厘米，且线段EF,GH把它分成四个小长方形，求阴影部分的面积。

【巩固】已知大长方形的长是6厘米，宽是4厘米，求阴影部分的面积。

【例2】如图所示，平行四边形的面积是50 平方厘米，阴影部分面积是（）平方厘米．【例3】如图,长方形AFEB和长方形FDCE拼成了长方形ABCD,长方形ABCD的长是20，宽是12，则它部阴影部分的面积是多少？例题精讲4A BF ED C【巩固】如图，正方形ABCD的边长为4，矩形EDFG的边EF过A点，G点在BC上，若DG=5，则矩形EDGF的宽DE=_____；EA DFB C G【巩固】如图所示，正方形 A B C D的边长为8厘米，长方形 E B G F的长 B G为1 0厘米，那么长方形的宽为几厘米？EA BFD G C【例4】如右图所示，在长方形画出一些直线，已知边上有三块面积分别是1 3，3 5，4 9．那么图中阴影部分的面积是多少A D3549E13B C【巩固】如右图所示，在长方形画出一些直线，已知边上有三块面积分别是11,32,57．那么图中阴影部分的面积是多少？A D325711B C【例5】如图所示，长方形ABCD的阴影面积之和为65，AB=8，AD=15,四边形EFGD的面积是？【思考题】提示：构造一半模型（很多时候，需要我们构造一半模型来解决一些问题。

五年级奥数-一半模型-学生版-1

一半模型知识结构一、三角形当中的一半模型由于三角形的面积公式S=底×高÷2，决定于底和高的长度，所以我们有了等高模型和等底模型。

在等高模型中，（图1）当BD=CD时，阴影部分，SΔABD=SΔABC÷2特别地如图2，当BE=ED，DF=FC，阴影部分面积，SΔAEF=SΔABC÷2在等底模型中（图3），当AE=DE时，阴影部分，SΔEBC=SΔABC÷2二、平行四边形中的一半模型由于三角形的面积公式S=底×高÷2，平行四边行的面积公式S=底×高所以与平行四边形同底等高的三角形是它面积的一半！同时，长方形是特殊的平行四边行，再根据平行线间的等积变形，可以得到如下诸图，阴影部分面积是四边形面积的一半：【巩固练习】判断下面的图形中阴影部分的面积是不是整个图形面积的一半。

是打“√”，不是打“×”。

如图4，在梯形ABCD中，BE=CE，则SΔADE=SABCD÷2如图5，是它的变形，注意其中AF=DF，BE=CE。

四、任意四边形中的一半模型如图6，在四边形ABCD中，AE=EB，DF=CF，则SEBFD=SABCD÷2【能力提升】【巩固练习】例题精讲【例1】如图，已知长方形ABCD的面积为24平方厘米，且线段EF,GH把它分成四个小长方形，求阴影部分的面积。

【巩固】已知大长方形的长是6厘米，宽是4厘米，求阴影部分的面积。

4【例2】如图所示，平行四边形的面积是50 平方厘米，阴影部分面积是（）平方厘米．【例3】如图,长方形AFEB和长方形FDCE拼成了长方形ABCD,长方形ABCD的长是20，宽是12，则它内部阴影部分的面积是多少？A BF ED C【巩固】如图，正方形ABCD的边长为4，矩形EDFG的边EF过A点，G点在BC上，若DG=5，则矩形EDGF的宽DE=_____；EA DFB C G【巩固】如图所示，正方形 A B C D的边长为8厘米，长方形 E B G F的长 B G为1 0厘米，那么长方形的宽为几厘米？EA BFD G C【例4】如右图所示，在长方形内画出一些直线，已知边上有三块面积分别是1 3，3 5，4 9．那么图中阴影部分的面积是多少A D3549E13B C【巩固】如右图所示，在长方形内画出一些直线，已知边上有三块面积分别是11,32,57．那么图中阴影部分的面积是多少？A D325711B C【例5】如图所示，长方形ABCD内的阴影面积之和为65，AB=8，AD=15,四边形EFGD的面积是？【思考题】提示：构造一半模型（很多时候，需要我们构造一半模型来解决一些问题。

五年级上册第11讲一半模型

14
【课堂精练】
6.正方形ABCD的边长为8厘米，长方形EBGF的长BG为10厘米，那么长方形的宽为几厘米？长方形的面积=三角形面积×2倍
E A F D
10cm
B
8cm
正方形的面积=三角形面积×2倍长方形的面积=正方形的面积
面积： 8×8=64cm2 宽： 64÷10=6.4cm 答：长方形的宽为6.4厘米。
第11讲一半模型
五年级奥数班
【知识点拨】
(1)规则四边形如平行四边形、长方形、正方形的对角线把整个四边形的面积平分。
(2)规则四边形如平行四边形、长方形、正方形中选取三角形，其中三角形的底边落在四边形的某条边上，另外一个顶点在对边上。
【知识点拨】
(3)规则四边形内部取一点，连结该点与四个顶点的连线，讲四边形分成上下左右四块。
G
C
15
【课堂精练】
7．如图，正方形ABCD的面积是12 ，正三角形BPC 的面积是5，求阴影△BPD 的面积．
A
s4
D P
s3 s2
s阴 =s1+ s2－长方形面积的一半 s2+ s4=长方形面积的一半 s2 ： 12÷2÷2=3cm2
6
6
s1
B
C
s阴：
5+3－6=2cm2
答：阴影△BPD 的面积2cm2。
10cm 6cm
10cm
6cm 6×6÷2=18cm2 答：阴影部分的面积是18cm2。
13
【课堂精练】
5. 如图，阴影部分四边形的外接图形是边长为10cm的正方形，则阴影部分四边形的面积是多少平方厘米？长方形： 4×1=4cm2 正方形： 10×10=100cm2 剩下面积： 100－4=96cm2 阴影面积： 96÷2=48cm2 答：阴影部分四边形的面积是48平方厘米。

级奥数一半模型学生版

一半模型知识结构一、三角形当中的一半模型由于三角形的面积公式S=底×高÷2，决定于底和高的长度，所以我们有了等高模型和等底模型。

在等高模型中，（图1）当BD=CD时，阴影部分，SΔABD=SΔABC÷2特别地如图2，当BE=ED，DF=FC，阴影部分面积，SΔAEF=SΔABC÷2?在等底模型中（图3），当AE=DE时，阴影部分，SΔEBC=SΔABC÷2二、平行四边形中的一半模型由于三角形的面积公式S=底×高÷2，平行四边行的面积公式S=底×高所以与平行四边形同底等高的三角形是它面积的一半！同时，长方形是特殊的平行四边行，再根据平行线间的等积变形，可以得到如下诸图，阴影部分面积是四边形面积的一半：【巩固练习】判断下面的图形中阴影部分的面积是不是整个图形面积的一半。

是打“√”，不是打“×”。

如图4，在梯形ABCD中，BE=CE，则SΔADE=SABCD÷2如图5，是它的变形，注意其中AF=DF，BE=CE。

【巩固】已知大长方形的长是6厘米，宽是4厘米，求阴影部分的面积。

【例2】如图所示，平行四边形的面积是 50 平方厘米，阴影部分面积是（）平方厘米．【例3】如图,长方形 AFEB 和长方形FDCE 拼成了长方形 ABCD ,长方形 ABCD 的长是 20，宽是 12，则它内部阴影部分的面积是多少？例题精讲4 6A BF EDC【巩固】如图，正方形ABCD的边长为4，矩形EDFG的边EF过A点，G点在BC上，若DG=5，则矩形EDGF的宽DE=_____；EA DFB CG【巩固】如图所示，正方形 A B C D的边长为8厘米，长方形 E B G F的长 B G为1 0厘米，那么长方形的宽为几厘米？EA BFD G C【例4】如右图所示，在长方形内画出一些直线，已知边上有三块面积分别是1 3，3 5，4 9．那么图中阴影部分的面积是多少AD3549E13B C【巩固】如右图所示，在长方形内画出一些直线，已知边上有三块面积分别是11,32,57．那么图中阴影部分的面积是多少？A D325711CB【例5】如图所示，长方形ABCD内的阴影面积之和为65，AB=8，AD=15,四边形EFGD的面积是？【思考题】提示：构造一半模型（很多时候，需要我们构造一半模型来解决一些问题。

一半模型之答案详解版

4.如图，三角形 AEF 的面积是 17 ， DE 、 BF 的长度分别为 11、3．求长方形 ABCD 的面积．
A
B F
A H
G M
B F
D
E
C
D
E
C
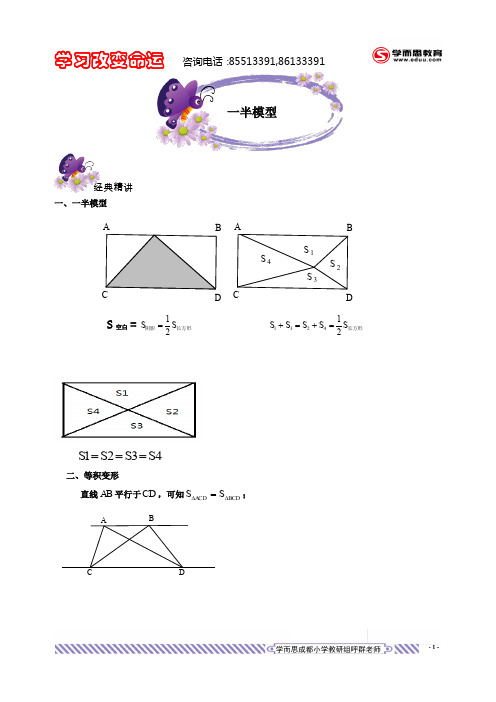
答案：如图，过 F 作 FH ∥ AB ，过 E 作 EG ∥ AD ， FH 、 EG 交于 M ，连接 AM ．则
S矩形ABCD S矩形AGMH S矩形GBFM S矩形MFCE S矩形HMED
A E P F G D
E A P F G D
B
H
C
B
H
C
答案： ( 法 1) 设 PGD 的 GD 边上的高为 h1 ， PEB 的 PE 1 1 1 h1 h2 AG GD AG h1 GD h1 PE h2 SPBD 8 ，整理得 2 2 2 1 1 S PHCF S PGAE 8 ，所以 S PHCF S PGAE 16 (平方分米)． 2 2 四边形 BCFE 的面积与平行四边形 ABHG 的面积差．如右上图，连接 CP 、 AP ．由于 SBCP SADP SABP SBDP SADP 而 SBCP
SBCE 1 S 2
ABCD
1 S 2
ABCD
，
SDAF SFCB ，
所以 S阴影 15 36 46 97 （平方米）。
例4
(2008 年” 华杯赛” 初赛)如图所示，长方形 ABCD 的面积为 24 平方厘米．三角形 ADM 与三角形 BCN 的面积之和为 7.8 平方厘米，则四边形 PMON 的面积是平方厘米．
1 S ABCD ，所以 SBCP SABP SBDP ． 2

小学奥数一半模型

小学奥数一半模型
小学奥数一半模型：
一、数学/逻辑类：
1. 解决问题技巧：此技术首先要求学生根据问题的提示，归纳概括出正确的解决思路，并根据问题采取最优解策略。

2. 推理解决：这种技术需要利用已知信息，借助逻辑技术，求解出未知信息。

3. 抽象理解能力：需要根据学生对各种抽象图形的概念的理解程度，来决定解决问题的套路。

4. 计算能力：要求学生在解决问题中，在有限的时间内，必须计算出准确的答案，这需要加强小学生学习计算术知识的学习。

二、文学/想象能力：
1. 说故事能力：要求学生能够根据提供的资料，把它们结合起来，进行完整的说故事，来表达自己的想法。

2. 小说阅读：此技术要求学生熟练阅读书、研究典型的作文格式，用
自己的话重讲故事情节，牢记优秀小说的架构。

3. 观察分析能力：要求学生能够仔细观察事物，在观察到的特点中，
进行分析总结，以求找出其中的联系和规律。

4. 想象力：要求学生根据不同环境背景，运用小说想象力，进行情节
发展的创新，让小说塑造一个精彩的故事世界。

三、语言/求解能力：
1. 文字的理解和逻辑推断：此技术要求学生能够通过句法结构，把句
子分解成更小的单位，用自己的思想去辩证地思考，从而分析求解问题。

2. 口头表达能力：要求学生能够利用良好的语言和文字表达能力，让
列数更加清晰、简单、准确地叙述出一件事物的真实状态。

3. 单词拼写能力：本技术要求学生熟练掌握单词的正确拼写及其意义，并能准确地使用其表达自己的思想。

4. 语法：要求学生能够准确的使用语法，灵活处理句子，建立正确的
语言思维，以及使用不同的句式。

五年级奥数一半模型教师版-1

一半模型知识结构一、三角形当中的一半模型由于三角形的面积公式S=底×高÷2，决定于底和高的长度，所以我们有了等高模型和等底模型。

在等高模型中，（图1）当BD=CD时，阴影部分，SΔABD=SΔABC÷2特别地如图2，当BE=ED，DF=FC，阴影部分面积，SΔAEF=SΔABC÷2在等底模型中（图3），当AE=DE时，阴影部分，SΔEBC=SΔABC÷2二、平行四边形中的一半模型由于三角形的面积公式S=底×高÷2，平行四边行的面积公式S=底×高所以与平行四边形同底等高的三角形是它面积的一半！同时，长方形是特殊的平行四边行，再根据平行线间的等积变形，可以得到如下诸图，阴影部分面积是四边形面积的一半：【巩固练习】判断下面的图形中阴影部分的面积是不是整个图形面积的一半。

是打“√”，不是打“×”。

如图4，在梯形ABCD中，BE=CE，则SΔADE=SABCD÷2如图5，是它的变形，注意其中AF=DF，BE=CE。

24÷2=12（平方厘米）答：阴影部分的面积是12平方厘米。

【巩固】已知大长方形的长是6厘米，宽是4厘米，求阴影部分的面积。

46×4÷2=12（平方厘米）答：阴影部分的面积是12平方厘米。

【例2】如图所示，平行四边形的面积是50 平方厘米，阴影部分面积是（）平方厘米．【例3】A BF ED C【巩固】如图，正方形ABCD的边长为4，矩形EDFG的边EF过A点，G点在BC上，若DG=5，则矩形EDGF的宽DE=_____；EA DFB C G【巩固】如图所示，正方形 A B C D的边长为8厘米，长方形 E B G F的长 B G为1 0厘米，那么长方形的宽为几厘米？EA BFD G C【例3】A D3549E13B C【巩固】如右图所示，在长方形内画出一些直线，已知边上有三块面积分别是11,32,57．那么图中阴影部分的面积是多少？A D325711B C【例4】如图所示，长方形ABCD内的阴影面积之和为65，AB=8，AD=15,四边形EFGD的面积是？【思考题】提示：构造一半模型（很多时候，需要我们构造一半模型来解决一些问题。

小学五年级奥数思维训练一半模型练习题

一半模型练习题1. 如图，E是平行四边形ABCD中的任意一点，已知△ABE的面积是20平方厘米，△EBC的面积25平方厘米，△ECD的面积是32平方厘米，那么△ADE的面积是多少平方厘米？2.如图，长方形ABCD被分成四个小长方形，边上各点均为任意点，已知长方形ABCD的面积是24平方厘米，求图中阴影部分的面积.3.如图，已知平行四边形ABCD的面积是120平方厘米，E是其中的任意一点，那么图中阴影部分面积是多少平方厘米？4.如图，长方形ABCD的面积是64平方厘米，四边形边上各点均为所在边的中点，求图中阴影部分的面积.BADC5. 如图，在平行四边形ABCD中，三角形AEF的面积为9平方厘米，三角形BCE的面积为13平方厘米，那么三角形DFC的面积是多少平方厘米？6. 如图，在长方形ABCD中，三角形ADE的面积为18平方厘米，三角形BEF的面积为11平方厘米，那么三角形DFC的面积是多少平方厘米？7.如图，正方形ABCD的边长是8厘米，G为BC边上一点，已知DG长是10厘米，且四边形DEFG是长方形，求长方形DEFG的宽.8.如图，长方形被分割成若干小块，其中三小块的面积分别是10、20、30，求图中阴影部分的面积.9.如图，长方形被分割成若干小块，其中三小块的面积分别是30、40、50，求图中阴影部分的面积.10.如图，梯形ABCD中，E、F为AB、CD的中点，G为EF上一点，若三角形AEG的面积是12，三角形CFG的面积是10，求图中阴影部分的面积.11.如图，大正方形的边长是8厘米，小正方形的边长是6厘米。

请问：两个阴影部分的面积分别是多少平方厘米？12.下图是由大、小两个正方形组成的，小正方形的边长是4厘米，求三角形ABC的面积。

13. 已知四边形ABCD和CEFG都是正方形，且正方形ABCD的边长为10厘米，那么图中阴影三角形BFD的面积为多少平方厘米?14.如图，有三个正方形ABCD，BEFG和CHIJ，其中正方形ABCD的边长是10，正方形BEFG的边长是6，那么三角形DFI的面积是．15.正方形ABCD、正方形BEFG和正方形RKPF的位置如图所示，点G在线段DK上，正方形BEFG的边长为4，则△DEK的面积为多少？16.如下图，每个小正方形的边长都是1厘米，阴影部分的面积是大长方形面积的几分之几？。

五年级奥数一半模型教师版-

一、三角形当中的一半模型由于三角形的面积公式S=底×高÷2，决定于底和高的长度，所以我们有了等高模型和等底模型。

在等高模型中，（图1）当BD=CD 时，阴影部分，SΔABD=SΔABC÷2特别地如图2，当BE=ED ，DF=FC ，阴影部分面积，S ΔAEF=S ΔABC ÷2在等底模型中（图3），当AE=DE 时，阴影部分，S ΔEBC=S ΔABC ÷2二、平行四边形中的一半模型由于三角形的面积公式S=底×高÷2，平行四边行的面积公式S=底×高所以与平行四边形同底等高的三角形是它面积的一半！同时，长方形是特殊的平行四边行，再根据平行线间的等积变形，可以得到如下诸图，阴影部分面积是四边形面积的一半：知识结构一半模型【巩固练习】判断下面的图形中阴影部分的面积是不是整个图形面积的一半。

是打“√”，不是打“×”。

（）（）（）（）三、梯形中的一半模型在梯形中，当三角形的底边是梯形的一个腰，顶点在另一个腰的中点处，那么三角形是梯形面积的一半。

如图4，在梯形ABCD中，BE=CE，则SΔADE=SABCD÷2如图5，是它的变形，注意其中AF=DF，BE=CE。

24÷2=12（平方厘米）答：阴影部分的面积是12平方厘米。

【巩固】已知大长方形的长是6厘米，宽是4厘米，求阴影部分的面积。

6×4÷2=12（平方厘米）答：阴影部分的面积是12平方厘米。

例题精讲4【例2】如图所示，平行四边形的面积是 50 平方厘米，阴影部分面积是（）平方厘米．【例3】A BF ED C【巩固】如图，正方形ABCD的边长为 4，矩形EDFG的边EF过A点，G点在BC上，若DG=5，则矩形EDGF的宽DE=_____；EA DFB C G【巩固】如图所示，正方形 A B C D的边长为8厘米，长方形 E B G F的长 B G为1 0厘米，那么长方形的宽为几厘米？EA BFD G C【例3】A D3549E13B C【巩固】如右图所示，在长方形内画出一些直线，已知边上有三块面积分别是 11,32,57．那么图中阴影部分的面积是多少？A D325711B C【例4】如图所示，长方形ABCD内的阴影面积之和为 65，AB=8，AD=15,四边形EFGD的面积是？【思考题】提示：构造一半模型（很多时候，需要我们构造一半模型来解决一些问题。

五年级奥数-一半模型

一半模型经典例题

小学奥数题库《几何》-直线型-一半模型-4星题(含解析)

五年级奥数一半模型

五年级公开课 一半模型

五年级奥数-一半模型-

五年级奥数-一半模型-学生版-1

五年级上册第11讲 一半模型

级奥数一半模型学生版

一半模型之答案详解版

小学奥数一半模型

五年级奥数一半模型教师版-1

小学五年级奥数 思维训练 一半模型 练习题

五年级奥数一半模型教师版-

五年级公开课一半模型

五年级上册第11讲一半模型

小学五年级奥数思维训练一半模型练习题