五年级奥数一半模型教师版
五年级奥数-比例模型(教师版)

比例模型1鸟头模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形.鸟头模型:有相等(或互补)的内角的两个三角形,其面积比等于相等(或互补)内角的夹边乘积之比.ADD AE EB C B C即有关系式S ADE AD AES ABC AB AC∆∆⨯=⨯存在。
2、风筝模型 (蝶形定理)任意四边形中的比例关系:①1243::S S S S =或者1324S S S S ⨯=⨯ ②()()1243::AO OC S S S S =++蝶形定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系.梯形中比例关系①2213::S S a b =②221324::::::S S S S a b ab ab =; ③S 的对应份数为()2a b +. 3相似模型GF E ABCD①AD AE DE AFAB AC BC AG===;A BCDO ba S 3S 2S 1S 4②22:ADE ABC S S AF AG =△△:正确识别各种图形所属的模型,并正确熟练运用比例模型中的关系例1如图在ABC △中,,D E 分别是,AB AC 上的点,且:2:5AD AB =,:4:7AE AC =,16ADE S =△平方厘米,求ABC △的面积.EDCBA答案 70平方厘米解析连接BE ,::2:5(24):(54)ADE ABE S S AD AB ===⨯⨯△△,::4:7(45):(75)ABE ABC S S AE AC ===⨯⨯△△,所以:(24):(75)ADE ABC S S =⨯⨯△△,设8ADE S =△份,则35ABC S =△份,16ADE S =△平方厘米,所以1份是2平方厘米,35份就是70平方厘米,ABC △的面积是70平方厘米例2 已知DEF △的面积为7平方厘米,,2,3BE CE AD BD CF AF ===,求ABC △的面积.FED CBA答案24平方厘米 解析:():()(11):(23)1:6BDE ABC S S BD BE BA BC =⨯⨯=⨯⨯=△△,:():()(13):(24)3:8CEF ABC S S CE CF CB CA =⨯⨯=⨯⨯=△△:():()(21):(34)1:6ADF ABC S S AD AF AB AC =⨯⨯=⨯⨯=△△设24ABC S =△份,则4BDE S =△份,4ADF S =△份,9CEF S =△份,244497DEF S =---=△份,恰好是7平方厘米,所以24ABC S =△平方厘米例3 如图,长方形ABCD 的面积是36,E 是AD 的三等分点,2AE ED =,则阴影部分的面积为.BB答案 2.7解析如图,连接OE .根据蝶形定理,1:::1:12COE CDE CAE CDE ON ND S S S S ∆∆∆∆===,所以12OEN OEDS S ∆∆=;1:::1:42BOE BAE BDE BAE OM MA S S S S ∆∆∆∆===,所以15OEM OEA S S ∆∆=.又11334OED ABCD S S ∆=⨯=矩形,26OEA OED S S ∆∆==,所以阴影部分面积为:1136 2.725⨯+⨯=.例4 如图,已知5CD =,7DE =,15EF =,6FG =,线段AB 将图形分成两部分,左边部分面积是38,右边部分面积是65,那么三角形ADG 的面积是.GFE DC BAABC DE FG答案 40解析连接AF ,BD .根据题意可知,571527CF =++=;715628DG =++=; 所以,1527BE CBF F S S ∆∆=,1227BE CBF C S S ∆∆=,2128AEG ADG S S ∆∆=,728AED ADG S S ∆∆=, 于是:2115652827ADG CBFS S ∆∆+=;712382827ADG CBF S S ∆∆+=; 可得40ADG S ∆=.故三角形ADG 的面积是40.例5 四边形ABCD 的对角线AC 与BD 交于点O (如图所示).如果三角形ABD 的面积等于三角形BCD 的面积的13,且2AO =,3DO =,那么CO 的长度是DO 的长度的_________倍.ABCDO答案 2:1解析∵::1:3ABD BDC AO OC S S ∆∆==,∴236OC =⨯=,∴:6:32:1OC OD ==例6 如图, ABC △中,DE ,FG ,BC 互相平行,AD DF FB ==,则::ADEDEGF FGCB S S S =△四边形四边形 .EGF A D CB答案 1:3:5解析设1ADE S =△份,根据面积比等于相似比的平方,所以22::1:4ADE AFG S S AD AF ==△△,22::1:9ADE ABC S S AD AB ==△△, 因此4AFG S =△份,9ABC S =△份, 进而有3DEGF S =四边形份,5FGCB S =四边形份,所以::1:3:5ADE DEGF FGCB S S S =△四边形四边形A1如图,三角形ABC 的面积为3平方厘米,其中:2:5AB BE =,:3:2BC CD =, 三角形BDE 的面积是多少?AB ECDDC E B A答案 12.5平方厘米解析由于180ABC DBE ︒∠+∠=,所以可以用共角定理,设2AB =份,3BC =份,则5BE =份, 325BD =+=份,由共角定理:():()(23):(55)6:25ABC BDE S S AB BC BE BD =⨯⨯=⨯⨯=△△,设6ABC S =△份,恰好是3平方厘米,所以1份是0.5平方厘米,25份就是250.512.5⨯=平方厘米,三角形BDE 的面积是12.5平方厘米2 如图,平行四边形ABCD ,BE AB =,2CF CB =,3GD DC =,4HA AD =,平行四边形ABCD 的面积是2, 求平行四边形ABCD 与四边形EFGH 的面积比.HGAB CD EFHGAB CD EF答案 1/18解析连接AC 、BD .根据共角定理∵在ABC △和BFE △中,ABC ∠与FBE ∠互补,∴111133ABC FBE S AB BC S BE BF ⋅⨯===⋅⨯△△. 又1ABC S =△,所以3FBE S =△.同理可得8GCF S =△,15DHG S =△,8AEH S =△.所以8815+3+236EFGH AEH CFG DHG BEF ABCD S S S S S S =++++=++=△△△△. 所以213618ABCD EFGH S S ==.3如图,三角形ABC 的面积是1,E 是AC 的中点,点D 在BC 上,且:1:2BD DC =,AD 与BE 交于点F .则四边形DFEC 的面积等于.FED CBA33321F E DC BAABCDEF答案 5/12解析方法一:连接CF ,根据燕尾定理,12ABF ACF S BD S DC ==△△,1ABF CBF S AES EC==△△, 设1BDFS =△份,则2DCF S =△份,3ABF S =△份,3AEF EFC S S ==△△份,如图所标所以551212DCEF ABC S S ==△ 方法二:连接DE ,由题目条件可得到1133ABD ABCS S ==△△, 11212233ADE ADC ABC S S S ==⨯=△△△,所以11ABD ADE S BF FE S ==△△, 111111122323212DEF DEB BEC ABC S S S S =⨯=⨯⨯=⨯⨯⨯=△△△△,而211323CDE ABC S S =⨯⨯=△△.所以则四边形DFEC 的面积等于512.4 如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知, 求:⑴三角形BGC 的面积;⑵:AG GC =?B答案 6 1:3解析⑴根据蝶形定理,123BGCS ⨯=⨯V ,那么6BGC S =V ;⑵根据蝶形定理,()():12:361:3AG GC =++=.5 如图,平行四边形ABCD 的对角线交于O 点,CEF △、OEF △、ODF △、BOE △的面积依次是2、4、4和6.求:⑴求OCF △的面积;⑵求GCE △的面积.OGF EDCBA答案 4 2/3解析⑴根据题意可知,BCD △的面积为244616+++=,那么BCO △和CDO ∆的面积都是1628÷=,所以OCF △的面积为844-=;⑵由于BCO △的面积为8,BOE △的面积为6,所以OCE △的面积为862-=, 根据蝶形定理,::2:41:2COE COF EG FG S S ∆∆===,所以::1:2GCE GCF S S EG FG ∆∆==,那么11221233GCE CEF S S ∆∆==⨯=+. B6如图,长方形ABCD 中,:2:3BE EC =,:1:2DF FC =,三角形DFG 的面积为2平方厘米,求长方形ABCD 的面积.ABCDEF GABCD EF G答案 72平方厘米 解析连接AE ,FE .因为:2:3BE EC =,:1:2DF FC =,所以3111()53210DEF ABCD ABCD S S S =⨯⨯=V 长方形长方形.因为12AED ABCDS S=V长方形,11::5:1210AG GF==,所以510AGD GDFS S==V V平方厘米,所以12AFDS=V平方厘米.因为16AFD ABCDS S=V长方形,所以长方形ABCD的面积是72平方厘米.7 如图,正方形ABCD面积为3平方厘米,M是AD边上的中点.求图中阴影部分的面积.CBA答案 1平方厘米解析因为M是AD边上的中点,所以:1:2AM BC=,根据梯形蝶形定理可以知道22:::1:12:12:21:2:2:4AMG ABG MCG BCGS S S S=⨯⨯=△△△△()(),设1AGMS=△份,则123MCDS=+=△份,所以正方形的面积为1224312++++=份,224S=+=阴影份,所以:1:3S S=阴影正方形,所以1S=阴影平方厘米.8 在下图的正方形ABCD中,E是BC边的中点,AE与BD相交于F点,三角形BEF的面积为1平方厘米,那么正方形ABCD面积是平方厘米.AB CDEF答案 12平方厘米解析连接DE,根据题意可知:1:2BE AD=,根据蝶形定理得2129S=+=梯形()(平方厘米),3ECD S =△(平方厘米),那么12ABCD S =W (平方厘米).9 已知ABCD 是平行四边形,:3:2BC CE =,三角形ODE 的面积为6平方厘米.则阴影部分的面积是平方厘米.BB答案 21平方厘米 解析 连接AC .由于ABCD 是平行四边形,:3:2BC CE =,所以:2:3CE AD =,根据梯形蝶形定理,22:::2:23:23:34:6:6:9COE AOC DOE AOD S S S S =⨯⨯=V V V V ,所以6AOC S =V (平方厘米),9AOD S =V (平方厘米),又6915ABC ACD S S ==+=V V (平方厘米),阴影部分面积为61521+=(平方厘米).10右图中ABCD 是梯形,ABED 是平行四边形,已知三角形面积如图所示(单位:平方厘米)阴影部分的面积是平方厘米.BB答案 6平方厘米解析 连接AE .由于AD 与BC 是平行的,所以AECD 也是梯形,那么OCD OAE S S ∆∆=.根据蝶形定理,4936OCD OAE OCE OAD S S S S ∆∆∆∆⨯=⨯=⨯=,故236OCD S ∆=,所以6OCDS ∆=(平方厘米).C11右图中ABCD 是梯形,ABED 是平行四边形,已知三角形面积如图所示(单位:平方厘米),阴影部分的面积是平方厘米.1682ABCDO 1682ABCD答案 4平方厘米解析连接AE .由于AD 与BC 是平行的,所以AECD 也是梯形,那么OCD OAE S S ∆∆=.根据蝶形定理,2816OCD OAE OCE OAD S S S S ∆∆∆∆⨯=⨯=⨯=,故216OCD S ∆=,所以4OCD S ∆=(平方厘米).另解:在平行四边形ABED 中,()111681222ADE ABED S S ∆==⨯+=Y (平方厘米), 所以1284AOE ADE AOD S S S ∆∆∆=-=-=(平方厘米), 根据蝶形定理,阴影部分的面积为8244⨯÷=(平方厘米).12 在四边形ABCD 中,其对角线AC 、DB 交于E 点。
五年级奥数一半模型

一、三角形当中的一半模型由于三角形的面积公式S=底×高÷2,决定于底和高的长度,所以我们有了等高模型和等底模型。
在等高模型中,(图1)当BD=CD 时,阴影部分,SΔABD=SΔABC÷2特别地如图2,当BE=ED ,DF=FC ,阴影部分面积,SΔAEF=SΔABC÷2在等底模型中(图3),当AE=DE 时,阴影部分,SΔEBC=SΔABC÷2二、平行四边形中的一半模型由于三角形的面积公式S=底×高÷2,平行四边行的面积公式S=底×高所以与平行四边形同底等高的三角形是它面积的一半!同时,长方形是特殊的平行四边行,再根据平行线间的等积变形,可以得到如下诸图,阴影部分面积是四边形面积的一半:知识结构五年奥数一半模型【巩固练习】判断下面的图形中阴影部分的面积是不是整个图形面积的一半。
是打“√”,不是打“×”。
三、梯形中的一半模型在梯形中,当三角形的底边是梯形的一个腰,顶点在另一个腰的中点处,那么三角形是梯形面积的一半。
如图4,在梯形ABCD中,BE=CE,则SΔADE=SABCD÷2如图5,是它的变形,注意其中AF=DF,BE=CE。
四、任意四边形中的一半模型如图6,在四边形ABCD中,AE=EB,DF=CF,则SEBFD=SABCD÷2【能力提升】【巩固练习】【例1】如图,已知长方形ABCD 的面积为24平方厘米,且线段EF,GH 把它分成四个小长方形,求阴影部分的面积。
24÷2=12(平方厘米)答:阴影部分的面积是12平方厘米。
【巩固】已知大长方形的长是6厘米,宽是4厘米,求阴影部分的面积。
6×4÷2=12(平方厘米)答:阴影部分的面积是12平方厘米。
【例2】如图所示,平行四边形的面积是 50 平方厘米,阴影部分面积是( )平方厘米.例题精讲4【例3】如图,长方形AFEB 和长方形FDCE 拼成了长方形ABCD,长方形ABCD 的长是20,宽是12,则它内部阴影部分的面积是多少?A BF ED C【巩固】如图,正方形ABCD的边长为4,矩形EDFG的边EF过A点,G点在BC上,若DG=5,则矩形EDGF的宽DE=_____;EA DFB C G【巩固】如图所示,正方形 A B C D的边长为8厘米,长方形 E B G F的长 B G为1 0厘米,那么长方形的宽为几厘米?EA BFD G C【例4】【巩固】如右图所示,在长方形内画出一些直线,已知边上有三块面积分别是11,32,57.那么图中阴影部分的面积是多少?A D325711B C【例4】如图所示,长方形ABCD内的阴影面积之和为65,AB=8,AD=15,四边形EFGD的面积是?【思考题】提示:构造一半模型(很多时候,需要我们构造一半模型来解决一些问题。
五年级奥数-一半模型

一、 三角形当中的一半模型由于三角形的面积公式S=底×高÷2,决定于底和高的长度,所以我们有了等高模型和等底模型。
在等高模型中,(图1)当BD=CD 时,阴影部分,SΔABD=SΔABC÷2特别地如图2,当BE=ED ,DF=FC ,阴影部分面积,SΔAEF=SΔABC÷2在等底模型中(图3),当AE=DE 时,阴影部分,SΔEBC=SΔABC÷2二、平行四边形中的一半模型由于三角形的面积公式S=底×高÷2,平行四边行的面积公式S=底×高所以与平行四边形同底等高的三角形是它面积的一半!同时,长方形是特殊的平行四边行,再根据平行线间的等积变形,可以得到如下诸图,阴影部分面积是四边形面积的一半: 知识结构一半模型【巩固练习】判断下面的图形中阴影部分的面积是不是整个图形面积的一半。
是打“√”,不是打“×”。
三、梯形中的一半模型在梯形中,当三角形的底边是梯形的一个腰,顶点在另一个腰的中点处,那么三角形是梯形面积的一半。
如图4,在梯形ABCD中,BE=CE,则SΔADE=SABCD÷2如图5,是它的变形,注意其中AF=DF,BE=CE。
四、任意四边形中的一半模型如图6,在四边形ABCD中,AE=EB,DF=CF,则SEBFD=SABCD÷2【能力提升】【巩固练习】【例1】如图,已知长方形ABCD 的面积为24平方厘米,且线段EF,GH 把它分成四个小长方形,求阴影部分的面积。
【巩固】已知大长方形的长是6厘米,宽是4厘米,求阴影部分的面积。
【例2】如图所示,平行四边形的面积是 50 平方厘米,阴影部分面积是( )平方厘米.【例3】例题精讲4。
第八讲 一半模型

第八讲 一半模型--感谢潘莹老师【知识点】一、本质:同底等高的三角形面积为平行四边形面积的一半二、常见一半模型1.平行四边形中的一半模型(同底)(1)顶点与顶点重合(2)顶点与底边重合(3)顶点在内部 相对△面积和(4)顶点在外部两对边之间 和一半两对边之外 差一半2.梯形中的一半模型模型底为一侧腰,顶点为另一侧腰中点【周周测】练习1 如图,长方形ABCD 中,长AB 为53厘米, 宽为38厘米,其中所有三角形的顶点均在长方形的边上,那么两个阴影三角形的面积之和是( )平方厘米.练习2 如图,ABCD 是长方形,EF 与宽平行,GH 与长平行,AB 的长是8厘米,BC 的长是6厘米,那么图中阴影部分的面积是( )平方厘米.练习3 如图,平行四边形的面积为100,阴影部分的面积为40,那么四边形EFGH 的面积是( ).练习4已知长方形ABCD ,四边形AEFG 是梯形,且GB BF ,已知长方形的面积是2014,梯形AEFG 的面积是( )练习5 如下图,E 、F 分别是梯形ABCD 的下底BC 和腰CD 上的点,DF=FC ,并且甲、乙、丙3个三角形面积相等.已知梯形ABCD 的面积是32平方厘米.图中阴影部分的面积是( )平方厘米HF D BF E GFDC BA BC练习6 如图,长方形ABCD 的边上有两点E 、F ,线段 AF 、BF 、CE 、BE 把长方形分成若干块,其中三个小木块的面积标注在图上,阴影部分面积是( )平方米练习7 如图所示,平行四边形 ABCD 的面积为36平方厘米.三角形 ADM 与三角形BCN 的面积之和为15平方厘米,则四边形 PMON 的面积是( )平方厘米.EA OB A N MC P D。
五年级公开课 一半模型

几何中的一半模型一、导入图形的变化是多种多样的,但是无论是怎么样的变化都有着它的基本模型,今天我们就来一起学习众多模型中的一个基本模型---------一半模型二、新课教学图1引导学生思考图中阴影部分的面积与长方形的关系。
此图中阴影部分的面积学生马上可以看出是长方形面积的一半。
图2 此图中阴影部分的面积与长方形又是怎样的关系呢?学生一眼看不出来,遮住其中的一部分,引导学生发现和图1的联系。
作一条辅助线后,分成了左右两个长方形,并且左边的一部分和图1相似,左边阴影部分的面积等于空白部分;右边的长方形中阴影部分也是等于空白部分,所以阴影部分的总面积是等于空白部分的总面积,是长方形的一半。
图3 此图中阴影部分的面积与长方形又是怎样的关系呢?有了图2做基础,学生很容易想到需要做辅助线来分析图形,可以让学生自己先尝试一下,然后请学生来回答分析过程。
横着做一条辅助线,把图形分成了上下两个长方形。
长方形的下半部分就和图2相似了,那么直接得出结论,阴影部分的面积是长方形的一半;上半部分也一样,所以所以阴影部分的总面积是等于空白部分的总面积,是长方形的一半。
总结:我们刚刚所分析的3个图形中,阴影部分的面积都等于长方形面积的一半。
练习:判断下面的图形中阴影部分的面积是不是整个图形面积的一半。
是打“√”,不是打“×”。
(√)(X)(X)(√)(√)(X)小结:只有在长方形,正方形,平行四边形里面才存在一半模型现在我们已经清楚地了解了三个基本的一半模型,再一起来学习一半模型的综合运用。
例1.如图,已知长方形ABCD 的面积为24平方厘米,且线段EF,GH 把它分成四个小长方形,求阴影部分的面积。
24÷2=12(平方厘米)答:阴影部分的面积是12平方厘米。
练习:已知大长方形的长是6厘米,宽是4厘米,求阴影部分的面积。
6×4÷2=12(平方厘米)答:阴影部分的面积是12平方厘米。
例2:如图,正方形ABCD 的边长是4㎝,矩形DEFG 的长DG 为5㎝,求它的宽DE 等于多少厘米?4×4÷5=3.2(厘米)答:宽DE 等于3.2厘米。
五年级奥数一半模型教师版

一半模型知识结构一、三角形当中的一半模型由于三角形的面积公式S=底×高÷2,决定于底和高的长度,所以我们有了等高模型和等底模型;在等高模型中,图1当BD=CD时,阴影部分,SΔABD=SΔABC÷2特别地如图2,当BE=ED,DF=FC,阴影部分面积,SΔAEF=SΔABC÷2在等底模型中图3,当AE=DE时,阴影部分,SΔEBC=SΔABC÷2二、平行四边形中的一半模型由于三角形的面积公式S=底×高÷2,平行四边行的面积公式S=底×高所以与平行四边形同底等高的三角形是它面积的一半同时,长方形是特殊的平行四边行,再根据平行线间的等积变形,可以得到如下诸图,阴影部分面积是四边形面积的一半:巩固练习判断下面的图形中阴影部分的面积是不是整个图形面积的一半;是打“√”,不是打“×”;三、梯形中的一半模型在梯形中,当三角形的底边是梯形的一个腰,顶点在另一个腰的中点处,那么三角形是梯形面积的一半;如图4,在梯形ABCD中,BE=CE,则SΔADE=SABCD÷2如图5,是它的变形,注意其中AF=DF,BE=CE;四、任意四边形中的一半模型如图6,在四边形ABCD中,AE=EB,DF=CF,则SEBFD=SABCD÷2能力提升巩固练习例题精讲例1如图,已知长方形ABCD的面积为24平方厘米,且线段EF,GH把它分成四个小长方形,求阴影部分的面积;24÷2=12平方厘米答:阴影部分的面积是12平方厘米;巩固已知大长方形的长是6厘米,宽是4厘米,求阴影部分的面积;46×4÷2=12平方厘米答:阴影部分的面积是12平方厘米;例2如图所示,平行四边形的面积是50 平方厘米,阴影部分面积是平方厘米.例3如图,长方形AFEB和长方形FDCE拼成了长方形ABCD,长方形ABCD的长是20,宽是12,则它内部阴影部分的面积是多少A BF ED C巩固如图,正方形ABCD的边长为4,矩形EDFG的边EF过A点,G点在BC上,若DG=5, 则矩形EDGF的宽DE=_____;EA DFB C G巩固如图所示,正方形 A B C D的边长为8厘米,长方形 E B G F的长 B G为1 0厘米,那么长方形的宽为几厘米EA BFD G C例3A D3549E13B C巩固如右图所示,在长方形内画出一些直线,已知边上有三块面积分别是11,32,57.那么图中阴影部分的面积是多少A D325711B C例4如图所示,长方形ABCD内的阴影面积之和为65,AB=8,AD=15,四边形EFGD的面积是思考题提示:构造一半模型很多时候,需要我们构造一半模型来解决一些问题;1.如图7,已知正方形ABCD面积为50,求长方形DEFG面积;解析:通过连结AG,可以得到三角形ADG,分别是正方形ABCD和长方形DEFG面积的一半,所以长方形DEFG 与正方形ABCD面积相等,为50;2.如图8,已知长方形ABCD面积是50,梯形ABFE的腰上ED=DF,求梯形ABFE的面积;解析:连结BD,可以得到三角形ABD分别是长方形ABCD和梯形ABFE面积的一半,所以梯形ABFE与长方形ABCD面积相等,为50;3.如图9,长方形ABCD中,SΔEGH=5,SΔIBC=20,SΔIFGI=8,求阴影部分面积;解析:从图中我们可以找到一半模型,SΔEBC与SΔFCD都是长方形ABCD的一半,故SΔEBC=SΔFCD,S阴=20+5-8=1745如图所示,正方形ABCD的边长是10厘米,BO长8厘米,求AE的长enjoy the trust of 得到...的信任have / put trust in 信任in trust 受托的,代为保管的take ...on trust对...不加考察信以为真trust on 信赖give a new turn to对~~予以新的看法turn a round / round 转身,转过来,改变意见turn back折回,往回走turn …away 赶走……,辞退……,把……打发走,转脸不睬,使转变方向turn to…转向……,for help向……求助,查阅,变成;着手于think thr ough…思考……直到得出结论,想通think of想到,想起,认为,对……有看法/想法。
五年级奥数-一半模型-

一、三角形当中的一半模型由于三角形的面积公式S=底×高÷2,决定于底和高的长度,所以我们有了等高模型和等底模型。
在等高模型中,(图1)当BD=CD时,阴影部分,SΔABD=SΔABC÷2特别地如图2,当BE=ED,DF=FC,阴影部分面积,SΔAEF=SΔABC÷2在等底模型中(图3),当AE=DE时,阴影部分,SΔEBC=SΔABC÷2二、平行四边形中的一半模型由于三角形的面积公式S=底×高÷2,平行四边行的面积公式S=底×高所以与平行四边形同底等高的三角形是它面积的一半!同时,长方形是特殊的平行四边行,再根据平行线间的等积变形,可以得到如下诸图,阴影部分面积是四边形面积的一半:知识结构一半模型【巩固练习】判断下面的图形中阴影部分的面积是不是整个图形面积的一半。
是打“√”,不是打“×”。
()()()()()()三、梯形中的一半模型在梯形中,当三角形的底边是梯形的一个腰,顶点在另一个腰的中点处,那么三角形是梯形面积的一半。
如图4,在梯形ABCD中,BE=CE,则SΔADE=SABCD÷2如图5,是它的变形,注意其中AF=DF,BE=CE。
四、任意四边形中的一半模型如图6,在四边形ABCD中,AE=EB,DF=CF,则SEBFD=SABCD÷2【能力提升】【巩固练习】【例1】如图,已知长方形ABCD的面积为24平方厘米,且线段EF,GH把它分成四个小长方形,求阴影部分的面积。
【巩固】已知大长方形的长是6厘米,宽是4厘米,求阴影部分的面积。
【例2】如图所示,平行四边形的面积是50 平方厘米,阴影部分面积是()平方厘米.【例3】如图,长方形AFEB和长方形FDCE拼成了长方形ABCD,长方形ABCD的长是20,宽是12,则它部阴影部分的面积是多少?例题精讲4A BF ED C【巩固】如图,正方形ABCD的边长为4,矩形EDFG的边EF过A点,G点在BC上,若DG=5,则矩形EDGF的宽DE=_____;EA DFB C G【巩固】如图所示,正方形 A B C D的边长为8厘米,长方形 E B G F的长 B G为1 0厘米,那么长方形的宽为几厘米?EA BFD G C【例4】如右图所示,在长方形画出一些直线,已知边上有三块面积分别是1 3,3 5,4 9.那么图中阴影部分的面积是多少A D3549E13B C【巩固】如右图所示,在长方形画出一些直线,已知边上有三块面积分别是11,32,57.那么图中阴影部分的面积是多少?A D325711B C【例5】如图所示,长方形ABCD的阴影面积之和为65,AB=8,AD=15,四边形EFGD的面积是?【思考题】提示:构造一半模型(很多时候,需要我们构造一半模型来解决一些问题。
五年级上册第11讲 一半模型

14
【课堂精练】
6.正方形ABCD的边长为8厘米,长方形EBGF的长BG为10厘米,那么长方形 的宽为几厘米? 长方形的面积=三角形面积×2倍
E A F D
10cm
B
8cm
正方形的面积=三角形面积×2倍 长方形的面积=正方形的面积
面积: 8×8=64cm2 宽: 64÷10=6.4cm 答:长方形的宽为6.4厘米。
第11讲 一半模型
五年级奥数班
【知识点拨】
(1)规则四边形如平行四边形、长方形、正方形的对角线把整个四边形 的面积平分。
(2)规则四边形如平行四边形、长方形、正方形中选取三角形,其中 三角形的底边落在四边形的某条边上,另外一个顶点在对边上。
【知识点拨】
(3)规则四边形内部取一点,连结该点与四个顶点的连线,讲四边形分成上 下左右四块。
G
C
15
【课堂精练】
7.如图,正方形ABCD的面积是12 ,正三角形BPC 的面积是5,求阴影△BPD 的面积.
A
s4
D P
s3 s2
s阴 =s1+ s2-长方形面积的一半 s2+ s4=长方形面积的一半 s2 : 12÷2÷2=3cm2
6
6
s1
B
C
s阴 :
5+3-6=2cm2
答:阴影△BPD 的面积2cm2。
10cm 6cm
10cm
6cm 6×6÷2=18cm2 答:阴影部分的面积是18cm2。
13
【课堂精练】
5. 如图,阴影部分四边形的外接图形是边长为10cm的正方形,则阴影部分四 边形的面积是多少平方厘米? 长方形: 4×1=4cm2 正方形: 10×10=100cm2 剩下面积: 100-4=96cm2 阴影面积: 96÷2=48cm2 答:阴影部分四边形的面积是48平方厘米。
小学数学几何模型之一半模型 PPT带答案

解答: 10×10÷2=50(cm²)
阴影
例题2
如图所示,正方形ABCD的边长为10厘米,BO长8厘米,BO垂 直于AE,求AE的长。
连接BE 正方形面积:10×10=100(cm²) 三角形ABE面积:100÷2=50(cm²) AE:50×2÷8=12.5(cm)
练习2
如图所示,正方形ABCD的边长为12厘米,DE=16厘米,AF 垂直于DE,则AF的长度是多少?
+△CDE的面积 △AEK是公共部分 所以△AKF的面积+△ADG的面积=△BEK的
面积+△CDE的面积 △AKF的面积+△ADG的面积=5cm² △CDE的面积:3×3÷2=4.5(cm²) △BEK的面积:5-4.5=0.5(cm²)
例题6
如图,ABCD是长方形,图中的数字是各部分的面积数,则图 中阴影部分面积是多少?
解析:连接AG 正方形面积:4×4=16(cm²)
△AGD面积=正方形面积 一半=长方形面积一半 长方形面积=16(cm²)
DE:16×2÷5=3.2(cm)
练习4
如图,ABFE和CDEF都是矩形,AB的长是4厘米,BC的长是3 厘米,那么图中阴影部分面积为?
阴影 阴影
阴影 阴影
阴影
阴影 阴影
解析:一半模型: 3×4÷2=6(cm²)
65 20
②
50
阴影
70 ①
15
解析:将图上空白标准①②
△ADE的面积=△ADF的面积+△BCF的 面积=长方形面积的一半
65+阴影部分面积+②面积 =65+20+50+②面积+15
阴影部分面积=85
小学奥数几何五大模型短期班第一讲教师版讲义

7 / 14
【解析】 A
4 2
B
C
将正六角星等分为 12 个相同的等边三角形,其中三角形 ABC 由 9 个组成,占总体 的 9 3.
12 4 A
4 D
11
B
13
E 2C
根据鸟头模型,
SBDE
1113 15 15
SABC
143 225
3 4
S总
=
143 300
S总
,
S阴影
SABC
C
G Q
F
P
O
H
K
G Q
F
P
O
H
K
A
B
E
A
B
E
【解析】 对于这种几个正方形并排放在一起的图形,一般可以连接正方形同方向的对角线, 连得的这些对角线互相都是平行的,从而可以利用面积比例模型进行面积的转化. 如右图所示,连接 FK 、GE 、 BD ,则 BD / /GE / /FK ,根据几何五大模型中的面 积比例模型,可得 SDGE SBGE , SKGE SFGE ,所以阴影部分的面积就等于正方 形 GFEB 的面积,即为102 100 平方厘米.
1.已知正方形 ABCD 边长为10,正方形 BEFG 边长为6,求阴影部分的面积.
A
D
A
D
F G
F G
J
I
J
I
B
ECH
B
E
C
H
【解析】如果注意到 DF 为一个正方形的对角线(或者说一个等腰直角三角形的斜边),那么 容易想到 DF 与 CI 是平行的.所以可以连接 CI 、 CF ,如上图. 由于 DF 与 CI 平行,所以 DFI 的面积与 DFC 的面积相等.而 DFC 的面积为 10 4 1 20 ,所以 DFI 的面积也为 20. 2
经典几何模型一半模型

知识点:【例1】如图所示,长方形的面积为36平方厘米,四边形RMON的面积是3平方厘米,则阴影部分的面积是平方厘米.【例2】(2008年”华杯赛”初赛)如图所示,长方形屋8的面积为24平方厘米.三角形与三角形BCN 的面积之和为7.8平方厘米,则四边形PMON的面积是________________ 平方厘米.【例3】如图所示,长方形488内的阴影部分的面积之和为70, AB = 8, 40 = 15,四边形EFGO的面积为,【巩固1】如图所示,正方形斜8的边长为8厘米,长方形EBG产的长5G为10厘米,那么长方形的宽为几厘米?D G C【巩固2] (2011华杯赛决赛试题)已知长方形488,四边形4EFG是梯形,且GB = BF ,已知长方形的面积是2011,求梯形且EFG的面积。
放心做自己想做的图2中,48co 是长方形,£尸平行于8a 四边形4EC 尸的面积是17.5, 三角形4ED的面积是20,三角形的面积是15,三角形CDF 的面积 是12.5,问三角形4BE 的面积是多少?7.如图,在梯形血D 中.三角用皿?的面积是6平方厘米,且3的性是.邨的2倍.梯格应0的 面积是 平方1M 米.放心做自己想做的10. 2.如图,长方形48co 的长和宽分别为6和4, E 、F 分别为刀。
、C 。
的中点,阴影部分面积为18.如下图,已知:梯形且君S 的面积为160G/,E为月B边上中点,DF: FC= 3:5,那么阴影部分的面积为切儿如图,是长方形,EF与宽平行,GH与长平行,的长是K厘米,的长是6厘米,那么图中阴影部分的面积是平方厘米.放心做自己想做的QOOS年春蕾杯五年级决赛)如图,长方形38的边上有两点E、尸,线段CF、DF. CE. BE把长方形分成若干块,其中三个小木块的面积标注在图上,阴影部分面积是平方米。
(2008年仁华考题)如图,正方形的边长为10,四边形EFG口的面积为5,那么阴影部分的面积是.1.(成都外国语学校2006年“德瑞杯”知识竞赛)如图,平行四边形源8的周长为75厘米以me为底时高是14厘米,以8为底时高是16厘米。
一半模型之答案详解版
A
B F
A H
G M
B F
D
E
C
D
E
C
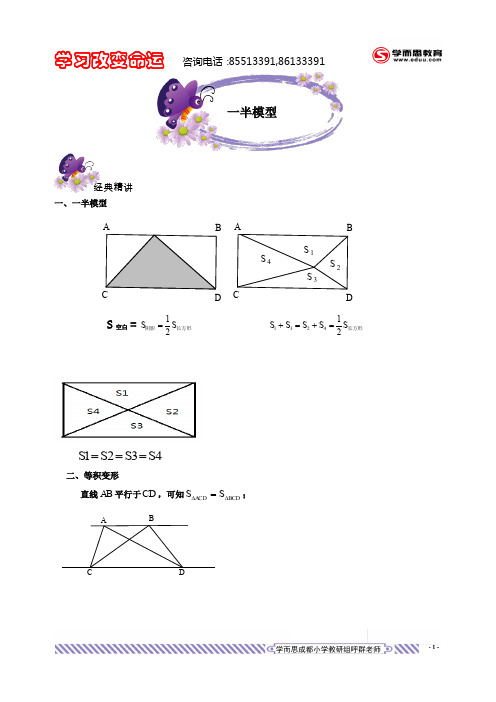
答案:如图,过 F 作 FH ∥ AB ,过 E 作 EG ∥ AD , FH 、 EG 交于 M ,连接 AM . 则
S矩形ABCD S矩形AGMH S矩形GBFM S矩形MFCE S矩形HMED
A E P F G D
E A P F G D
B
H
C
B
H
C
答案: ( 法 1) 设 PGD 的 GD 边 上 的 高 为 h1 , PEB 的 PE 1 1 1 h1 h2 AG GD AG h1 GD h1 PE h2 SPBD 8 ,整理得 2 2 2 1 1 S PHCF S PGAE 8 ,所以 S PHCF S PGAE 16 (平方分米). 2 2 四边形 BCFE 的面积与平行四边形 ABHG 的面积差. 如右上图,连接 CP 、 AP . 由于 SBCP SADP SABP SBDP SADP 而 SBCP
SBCE 1 S 2
ABCD
1 S 2
ABCD
,
SDAF SFCB ,
所以 S阴影 15 36 46 97 (平方米) 。
例4
(2008 年” 华杯赛” 初赛)如图所示, 长方形 ABCD 的面积为 24 平方厘米. 三角形 ADM 与三角形 BCN 的面积之和为 7.8 平方厘米,则四边形 PMON 的面积是 平方厘米.
1 S ABCD ,所以 SBCP SABP SBDP . 2
五年级春季班第6讲(几何模型)教师版

第六讲 几何模型一.等积变形(等积变形模型或比例模型):等积变形这里的积指的是面积,因为任何直线型图形都可以分解成若干个三角形,所以三角形是最基本图形,等积变形里主要研究的是三角形面积变换. 三角形面积=底⨯高÷2 1、等底等高:面积相等2、等底:面积之比等于高之比3、等高:面积之比等于底之比(注:夹在平行线之间的三角形等高) 常见模型:::ABD ADC S S BD DC ∆∆= ::ABC DBC S S AE DE ∆∆= ABC DBC S S ∆∆= 4.一半模型:一个三角形的面积是与其等底等高的平行四边形的面积的一半. 常见模型:1==2S S S 阴白平行四边形二.鸟头模型(共角模型)两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形.即形成鸟头模型. 常见模型:ADE ABC S AD AES AB AC∆∆⨯=⨯三.蝴蝶模型:蝴蝶模型为我们提供了解决不规则四边形的面积问题的一个途径,通过构造模型,一方面可以使不规则四边形的面积与四边形内的三角形之间建立相关的联系,另一方面还可得到与面积对应的对角线的比例关系. 常见模型:1.任意四边形中蝴蝶模型:①1243::S S S S =或者1324S S S S ⨯=⨯ ②1234:():()AO OC S S S S =++四.梯形中蝴蝶模型:① 2213::S S a b = ②221234::::::S S S S a ab b ab = ③S 的对应份数为2()a b +五.燕尾模型:从三角形一个顶点向对边上任意一点画线段,在线段上任取一点组成的图形面积之比等于与其所对底边之比.常见模型::::AOB AOC BFO CFO S S S S BF CF ∆∆∆∆== :::AOC BOC AOD BOD S S S S AD BD ∆∆∆∆==:::BOC AOB COE AOE S S S S CE AE ∆∆∆∆==六.沙漏、金字塔模型 所谓的沙漏、金字塔模型,就是指形状相同,大小不同的两个三角形,所有对应的线段长度成比例的模型. 常见模型: 1.沙漏模型AB 平行于CD ,则有:::.AB CD AO OC BO OD ==22::DCO ABO S S DC AB ∆∆= 2.金字塔模型DE 平行于BC ,则有:::.AD AB DE BC AE AC ==22::ADE ABC S S DE BC ∆∆=例题1【提高】三条边长分别为5,12,13的直角三角形如图所示,将它的短直角边对折到斜边上去,与斜边相重合,问图中阴影部分的面积是多少?【分析403(2013年五春第六讲例7)【集训】如图所示,已知在边长为10的正方形中,E 是AB 的中点,F 是EC 的中点,G 是DF 的中点,求阴影部分的面积.(单位:米)【分析】48(2013年五春第七讲练习5)例题2【提高】如图,四边形ABCD 的面积是20平方厘米,,,,EF EB HA HE GH GD FG FC ====,求四边形EFGH的面积.【分析】4平方厘米.(2013年五春第六讲例8)【集训】如图,梯形ABCD ,下底BC 上有一点E ,梯形空白处的面积比阴影ADE ∆的面积多200平方厘米,又知梯形下底BC 比上底AD 长20厘米.求这个梯形的高是多少?【分析】20厘米(小学奥数总复习上册77页例3)例题3【提高】【集训】如图,有一个长6cm ,宽4cm 的长方形ABCD .在各边上取点,,,E F G H ,在连接,H F 的线上取点P ,与点E 和点G 相连.当四边形AEPH 的面积是25cm 时,求四边形PFCG 的面积.【分析】28cm (2013年五春第七讲例6)例题4【提高】如图,已知111,,546AE AC CD BC BF AB ===,那么________DEF ABC S S ∆∆÷=【分析】61120.(2013年五秋第六讲尖1)【集训】如图,三角形ABC 中,延长BA 到D ,使DA AB =,延长CA 到E ,使2EA AC =,延长CB 到F ,使3FB BC =.如果三角形ABC 的面积是1,那么三角形DEF 的面积是________.【分析】7(2013年五春第七讲补充2)例题5【提高】如图,ABCD 是长方形,阴影部分的面积是多少平方厘米?【分析9平方厘米(2013年五春第七讲例1)【集训】如图所示,有边长为4厘米的49个小正方形,三角形DCE 的面积是_______【分析】35.(2013年五春第七讲例2)例题6【提高】【集训】(2007年香港圣公会数学竞赛)如图所示,在ABC △中,12CP CB =,13CQ CA =,BQ 与AP相交于点X ,若ABC △的面积为6,则ABX △的面积等于 .XQPABC【分析】方法一:连接PQ .由于12CP CB =,13CQ CA =,所以23ABQ ABC SS =,1126BPQ BCQABCS S S ==.由蝴蝶定理知,21:::4:136ABQ BPQ ABC ABC AX XP S S S S ===,所以441226 2.455255ABX ABP ABC ABC S S S S ==⨯==⨯=.例题7【提高】【集训】如图,三角形ABC 的面积是12,E 是AC 的中点,点D 在BC 上,且:1:2BD DC =,AD 与BE 交与点F .则四边形DFEC 的面积等于________.【分析】5(2013年五春第七讲例3)例题8【提高】如图,平行四边形ABCD 中,点,M N 分别在边,AD AB 上,且2,2AM MD AN NB ==,线段DN 与BM 相交于点O .已知四边形ABCD 的面积为260cm ,请问NBO ∆与MDO ∆的面积总和为多少平方厘米?【分析】28cm (2013年五春第七讲例3)【集训】如图,ABC ∆中,2BD D A =,2CE EB =,2AF FC =,那么ABC ∆的面积是阴影三角形面积的_________倍.【分析】7倍(小学奥数总复习上册80页例7)例题9【提高】【集训】如图,三角形ABC 被分成6个三角形,已知其中4个三角形的面积,问三角形ABC 的面积是多少?35304084O FED CBA【分析】设BOF S x =△,由题意知:4:3BD DC =根据燕尾定理,得::4:3ABO ACO BDO CDO S S S S ==△△△△,所以33(84)6344ACO S x x =⨯+=+△,再根据::ABO BCO AOE COE S S S S =△△△△,列方程3(84):(4030)(6335):354x x ++=+-解得56x =:35(5684):(4030)AOE S =++△,所以70AOE S =△所以三角形ABC 的面积是844030355670315+++++=.例题10【提高】【集训】三角形ABC 的面积为15平方厘米,D 为AB 中点,E 为AC 中点,F 为BC 中点,求阴影部分的面积.F CBAF CB【解析】 令BE 与CD 的交点为M ,CD 与EF 的交点为N ,连接AM ,BN .在ABC △中,根据燕尾定理,::1:1ABM BCM S S AE CE ==△△,::1:1ACM BCM S S AD BD ==△△,所以13ABM ACM BCN ABC S S S S ===△△△△由于1122AEM AMC ABM S S S ==△△△S ,所以:2:1BM ME =在EBC △中,根据燕尾定理,::1:1BEN CEN S S BF CF ==△△::1:2CEN CBN S S ME MB ==△△ 设1CEN S =△(份),则1BEN S =△(份),2BCN S =△(份),4BCE S =△(份),所以1124BCN BCE ABC S S S ==△△△,1148BNE BCE ABC S S S ==△△△,因为:2:1BM ME =,F 为BC 中点,所以221133812BMN BNE ABC ABC S S S S ==⨯=△△△△,11112248BFN BNC ABC S S S ==⨯=△△△,所以115515 3.1251282424ABC ABC S S S ⎛⎫=+==⨯= ⎪⎝⎭△△阴影(平方厘米)练习1如图,在三角形ABC中,D为BC的中点,,E F是AC的三等分点.已知三角形ABF的面积是108平方厘米,求三角形CDE的面积.【分析】54平方厘米.(2013年五春第七讲练习2)练习2如图所示,两个正方形并排放在一起,已知它们的面积相差96平方厘米,那么图中阴影四边形的面积是_______平方厘米.【分析】48.(2013年五春第六讲提3)练习3将长16厘米,宽9厘米的长方形的长和宽都分成三等份,长方形内任意一点O与分点及顶点连接,如图,则阴影部分的面积是_________平方厘米.【分析】72平方厘米.(小学奥数总复习上册78页例4)练习4如图,大长方形由面积是12平方厘米、24平方厘米、36平方厘米、48平方厘米的四个小长方形组合而成.求阴影部分的面积.【分析】如图,将大长方形的长的长度设为1,则12112364AB ==+,24124483CD ==+,所以1113412MN =-=,阴影部分面积为211(12243648)5(cm )212+++⨯⨯=.练习5如图所示,在梯形ABCD 中,//AB CD ,对角线,AC BD 相交于点O .已知5,3AB CD ==,梯形ABCD 的面积为4,求三角形OAB 的面积.【分析】9116.(2013年五春第七讲练习3)练习6如图,正方形ABCD 的面积是120平方厘米,E 是AB 的中点,F 是BC 的中点,四边形BGHF 的面积是______平方厘米.【分析】14平方厘米(2013年五春第七讲练习4)练习7(2009年清华附中入学测试题)如图,四边形ABCD 是矩形,E 、F 分别是AB 、BC 上的点,且13AE AB =,14CF BC =,AF 与CE 相交于G ,若矩形ABCD 的面积为120,则AEG ∆与CGF ∆的面积之和为 .BE【分析】.(法1)如图,过F 做CE 的平行线交AB 于H ,则::1:3EH HB CF FB ==,所以122AE EB EH ==,::2AG GF AE EH ==,即2AG GF =,所以122311033942AEG ABF ABCD S S S ∆∆=⨯⨯=⨯⨯=.且22313342EG HF EC EC ==⨯=,故CG GE =,则1152CGF AEG S S ∆∆=⨯⨯=.所以两三角形面积之和为10515+=.H BEBE(法2)如上右图,连接AC 、BG .根据燕尾定理,::3:1ABG ACG S S BF CF ∆∆==,::2:1BCG ACG S S BE AE ∆∆==,而1602ABC ABCD S S ∆==,所以3321ABG S ∆=++,160302ABC S ∆=⨯=,2321BCG S ∆=++,160203ABC S ∆=⨯=,则1103AEG ABG S S ∆∆==,154CFG BCG S S ∆∆==,所以两个三角形的面积之和为15.练习8如右图,三角形ABC 中,:4:9BD DC =,:4:3CE EA =,求:AF FB .O F EDCBA【分析】根据燕尾定理得::4:912:27AOB AOC S S BD CD ===△△ ::3:412:16AOB BOC S S AE CE ===△△(都有AOB △的面积要统一,所以找最小公倍数) 所以:27:16:AOC BOC S S AF FB ==△△【点评】本题关键是把AOB △的面积统一,这种找最小公倍数的方法,在我们用比例解题中屡见不鲜,如果能掌握它的转化本质,我们就能达到解奥数题四两拨千斤的巨大力量!。
小学奥数一半模型

小学奥数一半模型
小学奥数一半模型:
一、数学/逻辑类:
1. 解决问题技巧:此技术首先要求学生根据问题的提示,归纳概括出正确的解决思路,并根据问题采取最优解策略。
2. 推理解决:这种技术需要利用已知信息,借助逻辑技术,求解出未知信息。
3. 抽象理解能力:需要根据学生对各种抽象图形的概念的理解程度,来决定解决问题的套路。
4. 计算能力:要求学生在解决问题中,在有限的时间内,必须计算出准确的答案,这需要加强小学生学习计算术知识的学习。
二、文学/想象能力:
1. 说故事能力:要求学生能够根据提供的资料,把它们结合起来,进行完整的说故事,来表达自己的想法。
2. 小说阅读:此技术要求学生熟练阅读书、研究典型的作文格式,用
自己的话重讲故事情节,牢记优秀小说的架构。
3. 观察分析能力:要求学生能够仔细观察事物,在观察到的特点中,
进行分析总结,以求找出其中的联系和规律。
4. 想象力:要求学生根据不同环境背景,运用小说想象力,进行情节
发展的创新,让小说塑造一个精彩的故事世界。
三、语言/求解能力:
1. 文字的理解和逻辑推断:此技术要求学生能够通过句法结构,把句
子分解成更小的单位,用自己的思想去辩证地思考,从而分析求解问题。
2. 口头表达能力:要求学生能够利用良好的语言和文字表达能力,让
列数更加清晰、简单、准确地叙述出一件事物的真实状态。
3. 单词拼写能力:本技术要求学生熟练掌握单词的正确拼写及其意义,并能准确地使用其表达自己的思想。
4. 语法:要求学生能够准确的使用语法,灵活处理句子,建立正确的
语言思维,以及使用不同的句式。
五年级奥数一半模型教师版-1

一半模型知识结构一、三角形当中的一半模型由于三角形的面积公式S=底×高÷2,决定于底和高的长度,所以我们有了等高模型和等底模型。
在等高模型中,(图1)当BD=CD时,阴影部分,SΔABD=SΔABC÷2特别地如图2,当BE=ED,DF=FC,阴影部分面积,SΔAEF=SΔABC÷2在等底模型中(图3),当AE=DE时,阴影部分,SΔEBC=SΔABC÷2二、平行四边形中的一半模型由于三角形的面积公式S=底×高÷2,平行四边行的面积公式S=底×高所以与平行四边形同底等高的三角形是它面积的一半!同时,长方形是特殊的平行四边行,再根据平行线间的等积变形,可以得到如下诸图,阴影部分面积是四边形面积的一半:【巩固练习】判断下面的图形中阴影部分的面积是不是整个图形面积的一半。
是打“√”,不是打“×”。
()()()()()()三、梯形中的一半模型在梯形中,当三角形的底边是梯形的一个腰,顶点在另一个腰的中点处,那么三角形是梯形面积的一半。
如图4,在梯形ABCD中,BE=CE,则SΔADE=SABCD÷2如图5,是它的变形,注意其中AF=DF,BE=CE。
四、任意四边形中的一半模型如图6,在四边形ABCD中,AE=EB,DF=CF,则SEBFD=SABCD÷2【能力提升】【巩固练习】例题精讲【例1】如图,已知长方形ABCD的面积为24平方厘米,且线段EF,GH把它分成四个小长方形,求阴影部分的面积。
24÷2=12(平方厘米)答:阴影部分的面积是12平方厘米。
【巩固】已知大长方形的长是6厘米,宽是4厘米,求阴影部分的面积。
46×4÷2=12(平方厘米)答:阴影部分的面积是12平方厘米。
【例2】如图所示,平行四边形的面积是50 平方厘米,阴影部分面积是()平方厘米.【例3】A BF ED C【巩固】如图,正方形ABCD的边长为4,矩形EDFG的边EF过A点,G点在BC上,若DG=5,则矩形EDGF的宽DE=_____;EA DFB C G【巩固】如图所示,正方形 A B C D的边长为8厘米,长方形 E B G F的长 B G为1 0厘米,那么长方形的宽为几厘米?EA BFD G C【例3】A D3549E13B C【巩固】如右图所示,在长方形内画出一些直线,已知边上有三块面积分别是11,32,57.那么图中阴影部分的面积是多少?A D325711B C【例4】如图所示,长方形ABCD内的阴影面积之和为65,AB=8,AD=15,四边形EFGD的面积是?【思考题】提示:构造一半模型(很多时候,需要我们构造一半模型来解决一些问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、
三角形当中的一半模型 由于三角形的面积公式S=底×高÷2,决定于底和高的长度,所以我们有了等高模型和等底模型。
在等高模型中,(图1)当BD=CD 时,阴影部分,SΔABD=SΔABC÷2
特别地如图2,当BE=ED ,DF=FC ,阴影部分面积,SΔAEF=SΔABC÷2
在等底模型中(图3),当AE=DE 时,阴影部分,SΔEBC=SΔABC÷2
二、平行四边形中的一半模型
由于三角形的面积公式S=底×高÷2,
平行四边行的面积公式S=底×高
所以与平行四边形同底等高的三角形是它面积的一半!
同时,长方形是特殊的平行四边行,再根据平行线间的等积变形,可以得到如下诸图,阴影部分面积是四边形面积的一半:
【巩固练习】判断下面的图形中阴影部分的面积是不是整个图形面积的一半。
是打“√”,不是打“×”。
() () () ()
() ()
三、 梯形中的一半模型
在梯形中,当三角形的底边是梯形的一个腰,顶点在另一个腰的中点处,那么三角形是梯形面积的一半。
如图4,在梯形ABCD 中,BE=CE ,则SΔADE=SABCD÷2
如图5,是它的变形,注意其中AF=DF ,BE=CE 。
四、任意四边形中的一半模型
如图6,在四边形ABCD 中,AE=EB ,DF=CF ,则SEBFD=SABCD÷2
【能力提升】
【巩固练习】
知识结构
一半模型
【例1】如图,已知长方形ABCD 的面积为24平方厘米,且线段EF,GH 把它分成四个小长方形,求阴影部分的面积。
24÷2=12(平方厘米)
答:阴影部分的面积是12平方厘米。
【巩固】已知大长方形的长是6厘米,宽是4厘米,求阴影部分的面积。
6×4÷2=12(平方厘米) 答:阴影部分的面积是12平方厘米。
【例2】如图所示,平行四边形的面积是 50 平方厘米,阴影部分面积是( )平方厘米.
【例3】
如图,长方形 AFEB 和长方形 FDCE 拼成了长方形 ABCD ,长方形 ABCD 的长是 20,宽是 12,则它内
部阴影部分的面积是多少?
例题精讲
4 6
A B
F E
D
C
【巩固】如图,正方形ABCD的边长为4,矩形EDFG的边EF过A点,G点在BC上,若DG=5,则矩形EDGF的宽DE=_____;
E
A D
F
B C
G
【巩固】如图所示,正方形 A B C D的边长为8厘米,长方形 E B G F的长 B G为1 0厘米,那么长方形的宽为几厘米?
E
A B
F
D G C
【例3】
A
D
35
49
E
13
B C
【巩固】如右图所示,在长方形内画出一些直线,已知边上有三块面积分别是11,32,57.那么图中
阴影部分的面积是多少?
A D
32
57
11
C
B
【例4】如图所示,长方形ABCD内的阴影面积之和为65,AB=8,AD=15,四边形EFGD的面积是?
【思考题】
提示:构造一半模型
(很多时候,需要我们构造一半模型来解决一些问题。
)
1.如图7,已知正方形ABCD面积为50,求长方形DEFG面积。
解析:通过连结AG,可以得到三角形ADG,分别是正方形ABCD和长方形DEFG面积的一半,所以长方形DEFG与正方形ABCD面积相等,为50。
2.如图8,已知长方形ABCD面积是50,梯形ABFE的腰上ED=DF,求梯形ABFE的面积。
解析:连结BD,可以得到三角形ABD分别是长方形ABCD和梯形ABFE面积的一半,所以梯形ABFE与长方形ABCD面积相等,为50。
3.如图9,长方形ABCD中,SΔEGH=5,SΔIBC=20,SΔIFGI=8,求阴影部分面积。
解析:从图中我们可以找到一半模型,SΔEBC与SΔFCD都是长方形ABCD的一半,故SΔEBC=SΔFCD,S阴=20+5-8=17
4
5如图所示,正方形ABCD的边长是10厘米,BO长8厘米,求AE的长?。
