第二组阳离子分析
b2)分析化学(第四版)高等教育出版社2)_第三章-定性分析-2-3-4

小,在三种氯化物沉淀上加水并加热,则PbCl2溶解,趁热将它分离。
离心冷却液后,即可析出PbCl2的白色针状结晶; 以HAc酸化溶液,加K2CrO4鉴定,如析出黄色PbCrO4沉淀,示有铅。 • ⑵ 银与亚汞的分离及亚汞的鉴定 分出PbCl2后的沉淀应以热水洗涤干净,加入氨水,此时AgCl溶解, 生成Ag(NH3)2+,分出后另行签定。Hg2Cl2与氨水作用,生成HgNH2Cl+Hg, 残渣变黑,表示汞的存在。 银的鉴定:在分出的Ag(NH3)2+溶液中加入HNO3酸化,可以重新得到AgCl 白色沉淀: Ag(NH3)2++C1-+2H+=AgCl+2NH4+ 此现象说明有银的存在。
3.2 阳离子分析 要求:
1、掌握常见阳离子的硫化氢系统分组
方案的依据和分组方法
2、掌握常见阳离子与常用试剂的反应 3、掌握阳离子的分组
总体思路是将下列24种离子:Ag+、Hg22+、Hg2+、Pb2+、 Bi3+ 、Cu2+ 、Cd2+ 、As(Ⅲ,Ⅴ)、Sb(Ⅲ,Ⅴ)、Sn(Ⅱ,Ⅳ)、 Al3+ 、Cr3+ 、Fe3+ 、Fe2+ 、Mn2+ 、Zn2+ 、Co2+ 、Ni2+ 、Ba2+ 、
• 2、铜组中各离子如何分离?如何鉴定? • 3、锡组中各离子如何分离?如何鉴定? • 4、第二组阳离子分离时为何将As(V)、Sb(V)还原为As(III)、 Sb(III),而将Sn(II)氧化Sn(IV)?如何实现这一氧化还原过程?
• 5、解释铜组、锡组分离和鉴定过程中加入各试剂的作用?
四、第三组阳离子的分析
《无机与分析化学基础》第九章:定性分析概述

1.空白试验 :用蒸馏水代替试液,用同样 1.空白试验 的方法进行试验,称为空白试验。空白试 验用于检验试剂或蒸馏水中是否含有被检 验的离子。 • 2.对照试验 :用已知离子的溶液代替试液, 2.对照试验 用同样的方法进行鉴定,称为对照试验。 对照试验用于检验试剂是否失效,或是否 正确控制反应条件。
19:46
二、反应的选择性
在大多数情况下,一种试剂往往可以与 多种离子作用。如果一种试剂只与为数不 多的离子起反应,这种试剂称为选择试剂, 相应的反应称为选择性反应。与选择试剂 起反应的离子种类越少,则这一反应的选 择性越高。如果加入的试剂只与一种离子 起反应,则这一反应的选择性最高,称为 该离子的特效反应,该试剂称为特效试剂。
19:46
二、阴离子的个别鉴定反应
7. Cl-、Br-、I-的鉴定 (3)Br-、I-的鉴定 取处理好的溶液加H 取处理好的溶液加H2SO4和CCl4,并逐滴加入氯水, 振荡,CCl 层显紫色,表示有I 。因为I 是比Br 振荡,CCl4层显紫色,表示有I-。因为I-是比Br-强的还原 剂,首先被氧化: 2 I-+Cl2=I2+2Cl继续加入氯水,I 被氧化为IO ,紫色消失,CCl 继续加入氯水,I2被氧化为IO3-,紫色消失,CCl4层出现 Br2的红棕色,表示有Br-存在。 的红棕色,表示有Br 2 Br-+Cl2=Br2+2ClI2+5Cl2+6H2O=2IO3-+10Cl-+12H+
19:46
二、阴离子的个别鉴定反应
9. NO2-的鉴定 (1)试液用HAc酸化,加入KI溶液和CCl4,振荡。 )试液用HAc酸化,加入KI溶液和CCl 若试液中含有NO ,则会有I 产生,CCl 若试液中含有NO2-,则会有I2产生,CCl4层显紫 色。 2 NO2-+2 I-+4H+=2 NO+I2+2H2O NO+ (2)在微酸性溶液中,NO2-与加入的对氨基苯磺酸 )在微酸性溶液中,NO 和α–萘胺作用,形成红色氮染料,这是鉴定NO2萘胺作用,形成红色氮染料,这是鉴定NO 的特效反应。
第二组阳离子分析
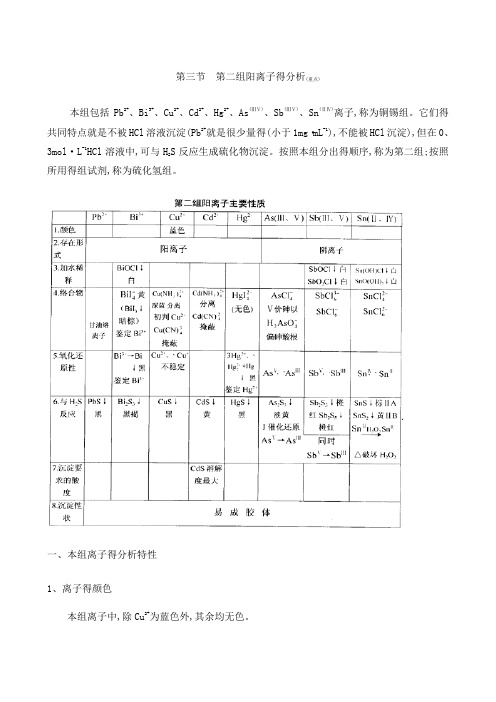
第三节第二组阳离子得分析(重点)本组包括Pb2+、Bi3+、Cu2+、Cd2+、Hg2+、As(ⅢⅤ)、Sb(ⅢⅤ)、Sn(ⅡⅣ)离子,称为铜锡组。
它们得共同特点就是不被HCl溶液沉淀(Pb2+就是很少量得(小于1mg·mL-1),不能被HCl沉淀),但在0、S反应生成硫化物沉淀。
按照本组分出得顺序,称为第二组;按照3mol·L-1HCl溶液中,可与H2所用得组试剂,称为硫化氢组。
一、本组离子得分析特性1、离子得颜色本组离子中,除Cu2+为蓝色外,其余均无色。
2、离子得存在形式铅、铋、铜、镉、汞具有显著得金属性质,在水溶液中主要以金属阳离子得形式存在;而砷、锑、锡三种元素则表现出不同程度得非金属性质,它们在溶液中得主要存在形式随酸碱环境而不同,主要以阴离子形式存在于溶液中。
但由于存在下述平衡AsO33-+6H+=As3++3H2OSbCl63-= Sb3++ 6C1-SnCl42-=Sn2++4Cl-溶液中也或多或少地存在着简单阳离子,并能生成相应得硫化物(如SnS2、As2S3等),所以这些元素还就是作为阳离子来研究。
鉴定时并不严格区分它们得存在形式,只就是泛指该元素,书写时只标出其氧化数,而不具体指明其存在形式。
3、加水稀释Bi3+、Sb(ⅢⅤ)、Sn(ⅡⅣ)离子(见前表)4、络合物本组离子一般都能生成多种络合物。
其中最常见得就是氯络离子,因而大量Cl-存在时可影响到各简单离子得浓度。
另外,Cu2+、Cd2+等能生成氨或氰络离子:Cu(NH3)42+、Cd(NH3)42+、Cu(CN)42+、Cd(CN)42+,它们在Cu2+、Cd2+得分离与鉴定上有很多应用。
Bi3+与I-生成黄色得BiI4-;用于铋得鉴定。
Cu2+、Pb2+与Bi3+能与甘油生成络离子;Hg2+与I-生成无色得HgI42-,它与KOH一起得溶液,可用于NH4+得鉴定,称为奈氏试剂。
这些都具有一定得分析应用价值。
阳离子的分离与鉴定

阳离子的分离与鉴定一. 实验目的1. 掌握用两酸三碱系统分析法对常见阳离子进行分组分离的原理和方法。
2. 掌握分离、鉴定的基本操作与实验技能。
二. 实验原理阳离子的种类较多,常见的有二十多种,个别检出时,容易发生相互干扰,所以一般阳离子分析都是利用阳离子某些共同特性,先分成几组,然后再根据阳离子的个别特性加以检出。
凡能使一组阳离子在适当的反应条件下生成沉淀而与其它组阳离子分离的试剂称为组试剂,利用不同的组试剂把阳离子逐组分离再进行检出的方法叫做阳离子的系统分析。
在阳离子系统分离中利用不同的组试剂,有很多不同的分组方案。
如硫化氢分组法,两酸、两碱系统分组法。
下面介绍一种以氢氧化物酸碱性与形成配合物性质不同为基础,以HCl、H2SO4、NH3 H2O、NaOH、(NH4)2S为组试剂的两酸三碱分组方法。
本方法将常见的二十多种阳离子分为六组。
第一组:盐酸组Ag+,Hg22+,Pb2+第二组:硫酸组Ba2+,Ca2+,Pb2+第三组:氨合物组Cu2+,Cd2+,Zn2+,Co2+,Ni2+第四组:易溶组Na+,NH4+,Mg2+,K+第五组:两性组Al3+,Cr3+,Sb III、V,Sn II、IV第六组:氢氧化物组Fe2+,Fe3+, Bi3+,Mn2+,Hg2+用系统分析法分析阳离子时,要按照一定的顺序加入组试剂,将离子一组一组沉淀下来,具体分离方法如下表。
表阳离子分组步骤试液(用个别检出法鉴定NH4+、Fe2+、Fe3+)(Hg)(两性组) (氢氧化物组) (第三组硫化物) (第四组易溶组)AlO2−、Cr O42−Fe(OH)3、K+、Na+、Mg2+、NH4+SbO43−、SnO32−MnO(OH)2、NaBiO3、HgNH2Cl每组分出后,继续再进行组内分离,直至鉴定时相互不发生干扰为止。
在实际分析中,如发现某组离子整组不存在(无沉淀产生)、这组离子的分析就可省去。
从而大大简化了分析的手续。
实验十常见无机阳离子的分离与鉴

2、物质检验的方法
物质的检验一般包括取样、操作、现象、结论四个部分:
①“先取样,后操作”。如果样品是固体,一般先用水 溶解,配成溶液后再检验;
②要“各取少量溶液分别加入几支试管中”进行检验, 不得在原试剂瓶中进行检验;
③要“先现象,后结论”,如向Na2CO3溶液中滴加盐酸, 所观察到的现象应记录为“有气泡产生”或“有无色气体放 出”,不能说成“碳酸钠和盐酸反应,放出二氧化碳”,或 “有无色二氧化碳气体放出”。
.
3. 银与亚汞的分离及亚汞的鉴定
分出PbCl2后的沉淀应以热水洗涤干净,然后 加入氨水,此时AgCl溶解,生成Ag(NH3)2+,分出后 另行鉴定。Hg2Cl2与氨水作用,生成HgNH2Cl+Hg, 残渣变黑,表示汞的存在。
4. 银的鉴定
在分出的Ag(NH3)2+溶液中加入HNO3酸化,可 以重新得到AgCl白色沉淀:
此种情况在溶液的酸度低于1.2—1.5mol/L时发生。 为防止它们水解,应使上述平衡向左移。为此,要 保 证 溶 液 有 足 够 的 H+ 浓 度 。 本 组 组 试 剂 所 以 采 用 HCl,就是考虑到它既含有C1-,又含有防止水解所 需要的H+。
.
3. 防止生成胶性沉淀
本组氯化银沉淀很容易生成难以分离的胶性沉淀。为 防止此种现象发生,加入适当过量的沉淀剂,以便提供使胶 体凝聚的电解质。
进 行消去实验 (4)对未消去的离子选择合适的方法加以确证。
.
阳离子分析
一、 常见阳离子的分组
常见的阳离子有二十几种,我们讨论的是下列24 种 : Ag+ 、 Hg22+ 、 Hg2+ 、 Pb2+ 、 Bi3+ 、 Cu2+ 、 Cd2+ 、 As(Ⅲ,Ⅴ) 、 Sb(Ⅲ,Ⅴ) 、 Sn(Ⅱ,Ⅳ) 、 Al3+ 、 Cr3+ 、 Fe3+、Fe2+、Mn2+、Zn2+、Co2+、Ni2+、Ba2+、Ca2+、 Mg2+、K+、Na+、NH4+ 。
阴阳离子系统分析

阳离子系统分析:常见阳离子:Ag +、Hg 2+、Hg 22+、Pb 2*、Bi 3+、Cu 2+、Cd 2+、As (3 价和 5 价卜 Sb (3 价和 5 价)、Sn (2 价和 4 价)、Al 3+、Cr 3+、Fe (2 价和 3 价)、Mn 2+、Zn 2+、Co 2+、Ni 2+、Ba 2+、Ca 2+、 Mg 2+、 K +、 Na +、 NH 4+系统分析步骤: 第一组、检验铅离子、亚汞离子、银离子。
1. 加入盐酸至有 0.6mol/L -1 的氯离子剩余,补加稀硝酸至氢离子约 2.0mol/L -1,如有白色沉淀,则为氯化铅(溶解度较大,下组仍要除去铅离子)、氯化亚汞、氯化银,剩余 滤液A 用 于下组分析。
2. 验铅离子: 沉淀加水加热并趁热过滤, 加入醋酸酸化, 加入铬酸钾产生黄色沉淀铬酸铅则 有铅离子; 3. 验银离子:以上剩余沉淀用热水洗净,加入氨水,分离滤液并用硝酸酸化,滤液产生白色沉淀氯化银则有银离子; 4. 验亚汞离子:以上第 3步剩余残渣如变黑则有 Hg 22+(HgNH 2Cl+Hg )。
第二组、检验铅离子、铋离子、铜离子、镉离子、三价砷、汞离子、三价锑、四价锡。
1.往滤液A 中加入0.3mol/L -1的盐酸,通入硫化氢,加热,产生沉淀:PbS CuS HgS 均为 黑色,黑褐色Bi 2$、黄色的CdS 和SnS 、淡黄色AS 2S 3、橙红色S6S 3,剩余滤液B 用于下组 分析。
2 (铅、铋、铜、镉离子的检验)•过滤以上沉淀,加入过量硫化钠,得 沉淀A (组成有硫化 2- 3- 3-2- 铅、三硫化二铋、硫化铜、硫化镉 )和滤液C (组成有HgS -、AsS s -、SbS -、Sn S -)。
3 (铅、铋、铜、镉离子的检验)•往沉淀A 中加入6摩尔每升硝酸,沉淀溶解,在加入 1:1的甘油和过量的浓氢氧化钠,如有黄色沉淀为氢氧化镉,分离出 滤液 D 待检验,沉淀用 3 摩尔每升盐酸溶解,再稀释3倍,加入硫代乙酰胺(CHCSNH )加热,生成黄色沉淀硫化镉则有镉离子。
常见阳离子的检验实验报告doc

常见阳离子的检验实验报告篇一:常见离子检验1.常见阳离子的检验检验操作1.检验溶液中含有Fe3+的实验操作:取少量溶液置于试管中,滴加几滴KSCN溶液,若溶液变红,则证明溶液中含有Fe。
2.检验溶液中含有Fe的实验操作是:取少量溶液置于试管中,滴加几滴KSCN溶液,溶液不变色,在加入几滴氯水后溶液变红,则证明溶液中含有Fe。
3.验证溶液中有铁元素的实验操作是:取少量溶液置于试管中,滴加几滴KSCN溶液,溶液不变色,在加入几滴氯水后溶液不变红,则证明溶液中不含+铁元素。
4.检验溶液中含有NH4的实验操作是:+2+2+3+取少量溶液置于试管中,加入氢氧化钠后加热,将湿润的红色石蕊试纸放在试管口,若试纸变蓝则证明溶液中含有NH4+。
5.如何检验SO42-取少量溶液置于试管中,加入盐酸无现象,在加入BaCl2溶液产生白色沉淀则证明溶液中有SO42-。
(补充:加入盐酸的作用防止Agcl 干扰) 6.如何检验Cl-取少量溶液置于试管中,加入AgNO3溶液有白色沉淀产生,再加入H NO3后沉淀不溶解则证明溶液中含有Cl-。
二、实验室常见操作1.气密性检验(1)装置形成封闭体系→操作(微热、手捂、热毛巾捂、加水等) →描述现象→得出结论; (2)微热法检查的关键词是封闭、微热、气泡、水柱; (3)液差法的关键词是封闭、形成液差。
甲①实验开始前,某同学对甲实验装置进行了气密性检查,方法是:关闭活塞,从长颈漏斗加水至浸没长颈漏斗的下端,继续加水形成一段水柱,一段时间水柱无变化则证明装置气密性良好。
①实验开始前,某同学对乙实验装置进行了气密性检查,方法是:关闭分液漏斗活塞,将导管插入水中用酒精灯微热烧瓶,导管口有气泡冒出,停止加热导管内出现一段水柱,证明气密性良好。
2.气体的收集依据:根据气体的溶解性或密度①②③④⑤⑥3.气体的净化、干燥4、尾气处理直接吸收燃烧处理袋装防倒吸吸收 ? 防倒吸装置4.溶液中晶体析出的方法:如何从NaCl溶液中得到NaCl晶体 ----------蒸发结晶如何从KNO3溶液中得到KNO3晶体 ------蒸发浓缩→冷却结晶蒸发结晶(溶解度随温度变化很小,如:NaCl)、蒸发浓缩、冷却结晶(溶解度随温度变化比较大,如:KNO3)5.沉淀的洗涤向漏斗内加蒸馏水至浸没沉淀,使水自然流出,重复操作2—3次6.中学化学常见的试纸:PH试纸、KI淀粉试纸、红色石蕊试纸、蓝色石蕊试纸①红色石蕊试纸:定性检验碱性。
分析化学 第2章定性分析1-2节

K+、Na+、NH4+
可溶组, 可溶组,钠组
2011-11-29
二、 第一组阳离子分析
(一)本组离子的分析特性 1. 离子的存在形式 ⑴本组三种离子均无色。 本组三种离子均无色。 ⑵银和铅主要以Ag+、Pb2+形式存在, 形式存在, 银和铅主要以 ⑶ 亚汞离子是以共价键结合的双聚离子 +Hg:Hg+, 故记为Hg 故记为 22+ 在水溶液中有如下的平衡: 在水溶液中有如下的平衡:Hg22+= Hg2++ Hg↓ 溶液中有如下的平衡
• ⑵ 银与亚汞的分离及亚汞的鉴定
3. 防止生成胶性沉淀
氯化银沉淀易生成难以分离的胶性沉淀
2011-11-29
(三)本组离子的系统分析
1. 本组离子沉淀 本组离子 离子沉淀 分析试液 性 检查其酸 检查其酸碱性 以HCl和HNO3中和至微酸 和
加入适当过量的盐酸( 浓度应为0.5mol/L,H+浓度 加入适当过量的盐酸(C1-浓度应为 , 大于2.0mol/L)此时如有白色沉淀产生,表示本组存在。 )此时如有白色沉淀产生,表示本组存在。 大于 离心管以流水冷却 1mol/lHCl洗涤作鉴定分析。 洗涤作鉴定分析。 洗涤作鉴定分析 问题:本组离子沉淀条件? 浓度过大的后果 过大的后果? 问题:本组离子沉淀条件? C1-浓度过大的后果? H+浓度过小 的后果? 如何控制? 的后果 H+如何控制?
2011-11-29
2. 难溶化合物
本组离子具有18或18+2的电子外壳,所以都有很强的极化作 本组离子具有 或 的电子外壳, 的电子外壳 用和变形性,能同易变形的阴离子如 用和变形性,能同易变形的阴离子如C1-、Br-、I-、CN-、 CO32-、SO42-、PO43-等生成共价化合物,难溶于水。 等生成共价化合物,难溶于水。
阳离子分析方法PPT课件

.
32
.
33
• 四、第三组阳离子的分析
• 本组包括由7种元素形成的8种离子:称为铁组 。
•
Al3+、Cr3+、Fe3+、Fe2+、
•
Mn2+、Zn2+、Co2+、Ni2+
• 分组依据: NH3—NH4Cl存在下与(NH4)2S生成硫化物 或氢氧化物沉淀
• 组试剂:NH3—NH4Cl存在下的(NH4)2S
Hg22+
Hg2Cl2 ↓(白色粉末状)
Pb2+
PbCl2 ↓ (白色针状或片状结晶)
氯化物的溶解度(25℃)
.
17
• 本组离子沉淀分离的关键是:
•
确保Ag+、Hg22+沉淀完全,适当降低PbCl2的溶解
度,防止第二组的Bi3+、Sb3+水解。
• 本组氯化物沉淀的条件是:
在室温下的酸性试液中,加入适当过量的稀HCl。
.
11
3. 第三组(氨组):分离一、二组后,氢 氧化物难溶于水,也难溶于NH3·H2O的离子有: Al3+、Cr3+、Fe3+、Fe2+、Mn2+、Bi3+、Hg2+、Sb Ⅲ,Ⅴ、SnⅡ,Ⅳ。
4. 第四组(碱组):分离一、二、三组后, 氢氧化物难溶于水,也难溶于过量NaOH溶液 的离子,包括:Cu2+、Cd2+、Co2+、Ni2+、Mg2+。
•
离子性质上的差异进行组内离子的分离与鉴定。
• 2. 根据ⅡA组和ⅡB组硫化物酸碱性的不同,分离
•
ⅡA组和ⅡB
Hale Waihona Puke • 3. ⅡB组As、Hg与Sb、Sn的分离
定性分析综合实验报告

定性分析综合实验报告一.实验目的1)掌握化学分析法的基本操作技能和初步运用的能力;2)掌握常见离子的个性、共性、反应条件和鉴定方法; 3)通过综合实验分析混合试液的各阳离子及其性质。
二.实验仪器和试剂仪器: 离心管若干、玻璃棒、离心机、量筒、滴管、电炉、烧杯、石棉网、试管架、试管夹、黑白点滴板、PH 试纸、药匙、表面皿、滤纸、红色石蕊试纸、坩埚试剂: 6mol/LHCL 、3mol/LHCL 、1mol/LHCL 、0.6mol/LHCL 、6mol/LHAC 、3mol/L HAC 、K 2CrO 4溶液、3mol/LH 2SO 4、6mol/LNaOH 、6mol/L 氨水、蒸馏水、6mol/LHNO 3、 3mol/LHNO 3、0. 6mol/LHCL 、稀氨水、TAA 、NH 4CL 、KCLO 3、甘油溶液(1:1)、 NaAc 、K 4Fe (CN )6、浓HAC 、SnCL 2、浓HCL 、(NH 4)2CO 3、浓HNO 3、铝片、 锡粒、新配制的NaBrO 、K 3Fe(CN)6、NH 4SCN 、0.1mol/LHCL 、NaBiO 3、H 2O 2、戊 醇、浓(NH 4)2HPO 4、丁二酮肟、氨气、(NH 4)2Hg(SCN)4、CoCl 2、(NH 4)2C 2O 4、四苯 硼化钠、醋酸铀酰锌、乙醇、浓NaOH 、镁试剂、NH 4NO 3三.实验步骤1. 被测溶液的PH 值大于7,显碱性,初步判定试液中可能有NH4+2. NH 4+的鉴定 水浴被测试液1滴(下表面皿)+湿润的红色石蕊试纸(上表面皿)+浓NaOH 红色石蕊试纸变蓝 示有NH 4+ 3.阳离子第一组(银组)的分析(1)本组的沉淀在试液中加2滴6mol/LHCL ,充分搅拌,约2min ,离心沉降,吸出离心液,留作第二组测定,沉淀以3滴1mol/LHCL 洗涤2次,然后按(2)研究(2)向所得氯化物沉淀上加水1ML ,然后在水浴中加热近沸,搅拌,约1-2min 后,趁热离心沉淀,并迅速吸出离心液于另一只离心管中①铅的鉴定离心液+6mol/LHAC +3滴K 2CrO 4 PbCrO 4(黄) 示有Pb 2+ ②Hg 2+的鉴定在(2)残渣+6mol/L 氨水 无现象 没有Hg 2+ ③Ag +的鉴定离心液+ 3 无白色沉淀+ AgCl ,Hg 2Cl 2 ,PbCl 2 II -IV 组Pb 2+,Cl -AgCl ,Hg 2Cl 2 6mol/LHAc6mol/L 氨水4(黄)无现象 示有Pb 2+4. 阳离子第二组(铜锡组)的分析向上述溶液中加6mol/L 氨水,使其呈碱性,再加3mol/LHCl(沉淀溶解,溶液蓝色透明)至酸度为PH=0.6.在该溶液中加TAA ,加热(褐色沉淀产生),离心沉降,保留沉淀,离心液继续处理。
分析化学教案设计

教案2013~2014学年课程名称分析化学院(系)化学与环境科学学院教研室(实验室) 化学系授课班级主讲教师职称副教授使用教材华中师大等编《分析化学(上册)》兰州城市学院化学与环境科学学院制教案(首页)注:课程类别:公共基础课、专业基础课、专业必修课、专业选修课、集中实践环节、实验课、公共选修课教学内容:第一章绪论一、分析化学的任务和作用1.分析化学的任务分析化学是研究关于物质的化学结构、化学组成及测定方法的一门学科。
它是化学科学的一个重要分支。
定性分析的任务:就是鉴定物质的化学结构和化学组成。
定量分析的任务:就是测定物质中各组分的相对含量。
2.分析化学的作用分析化学作为一门学科,对于化学本身的发展起过重大作用。
化学上的基本定律都是依靠大量的分析实验数据才得以创立和发展起来的,而其它各门学科的发展又进一步推动了分析化学的发展。
分析化学对工业、农业、国防和科学技术的发展都有重要的作用。
分析化学在高等学校理、工、农、医、师范各有关专业中,是一门重要的化学基础课。
三、定量分析的方法1.按对象分2.按操作方法分类3.按试样用量分类4.根据被测组分含量分类5.其它专有名词四、分析化学的发展趋势(一)分析化学的发展简史(二)当前的发展趋势第二章定性分析教学内容:§2-1 概述一、定性分析的任务和方法1.任务:鉴定物质中所含有的组分。
2.方法⑴干法:指分析反应在固体之间进行。
⑵湿法:指分析反应在溶液之间进行。
(主要学习湿法分析)二、定性分析反应进行的条件共5点三、鉴定方法的灵敏度和选择性1.鉴定方法的灵敏度鉴定反应的灵敏度常用“最低浓度”和“检出限量”来表示。
⑴最低浓度⑵检出限量⑶检出限量和最低浓度之间的关系2.鉴定反应的选择性四、空白试验和对照试验空白试验:用配制试液用的蒸馏水代替试液,用同样的方法和条件重做试验进行鉴定,就叫做空白试验。
对照试验:用已知溶液代替试液,用同样方法进行鉴定,就叫做对照试验。
(完整版)阳离子和阴离子的定性分析

铬酸钡黄色↓
SrCrO4↓黄色
铬酸钾+乙酸
铬酸钡黄色↓
硫酸铵
硫酸钡白色↓
SnSO4↓白色
CaSO4↓白色
草酸铵
草酸钡白色↓
SrC204↓白色
CaC2O4↓白色
磷酸氢二钠
磷酸氢钡白色↓
SrHPO4↓白色
CaHPO4↓白色
玫瑰红酸钠
红褐色↓
红褐色↓
焰色反应
黄绿色
洋红色
砖红色
硝酸盐+丙酮或乙醇
不溶
不溶
CrO42黄色
磷酸铁淡黄色↓
磷酸铁白色↓
磷酸锰白色↓
磷酸锌白色↓
磷酸钴紫色↓
磷酸镍绿色↓
K4【Fe(CN)6】
Fe4【Fe(CN)6】3↓普氏兰
Fe3【Fe(CN)6】2↓滕氏兰
Mn2【Fe(CN)6】白色↓
Zn2【Fe(CN)6】白色↓
Co2【Fe(CN)6】绿色↓
Ni2【Fe(CN)6】淡绿色↓
HSbO3白色↓
H4SnO4白色↓
Sn(OH)2白色↓
HgO黄色↓
适量
SbO2-
SbO3-
SnO32-
SnO32-
氢氧化铵、碳酸铵或碳酸钠
HSbO2白色↓
HSbO3白色↓
H4SnO4白色↓
Sn(OH)2白色↓
*(NH2Hg)Cl白色↓
碱盐红褐色
*若离子溶液是Hg(NO3)2则生成(NH2Hg)NO3白色↓
阳离子和阴离子的定性分析
表1.阳离子的分组
分
组
(族)
根
据
硫化物溶于水
硫化物不溶于水
碳酸盐溶于水
碳酸盐不溶于水
阳离子分析

I组 银 组 盐酸组
II组 铜 锡 组 硫化氢组
Ag+ Hg22+ Pb2+
IIA Pb2+ Bi3+ Cu2+ Cd2+
IIB Hg2+ As(III, V) Sb(III, V) Sn(II, IV)
Al3+ Cr3+ Fe3+ Fe2+
Mn2+ Zn2+ Co3+ Ni2+
Ba2+ K+ Ca2+ Na+ Mg2+ NH4+
3 2 的氨性液
AgCl (白)
B 10g m L 1
HNO 酸化 3
m 0.5g
Ag( NH 3 ) Cl 2 H AgCl 2 NH 4 2
本组混合物的系统分析见下表:
银组混合物的分析
试 液
6 mol · -1 HCl L
二、第一组阳离子的分析
(一)本组离子的分析特性
Ag 2 银组 : Hg2 HCl 白色 Pb2 第一组 盐酸组
1. 离子的存在形式
离子的颜色:均无色
存 在 形 式:Ag+、Pb2+,Hg22+ 以双聚离子 Hg+ :Hg+存在,水溶液中:
Hg22+
平衡时: ⑴若向溶液通H2S: ⑵若在溶液中+ KI:
[Cd 2 ][S 2 ] 0.11.021021 1.021022 K sp ,CdS , 生成CdS沉淀. [ Zn 2 ][S 2 ] 0.11.02 10 21 1.0210 22 K sp , ZnS , 不生成ZnS沉淀. 体系中残余的 Cd 2 ]应为 : [ 8 10 27 [Cd ] 8 106 105 (m ol L1 ) [ S 2 ] 1.0210 21
阴阳离子系统分析

阳离子系统分析:常见阳离子:Ag+、Hg2+、Hg22+、Pb2+、Bi3+、Cu2+、Cd2+、As(3价和5价)、Sb(3价和5价)、Sn(2价和4价)、Al3+、Cr3+、Fe(2价和3价)、Mn2+、Zn2+、Co2+、Ni2+、Ba2+、Ca2+、Mg2+、K+、Na+、NH4+系统分析步骤:第一组、检验铅离子、亚汞离子、银离子。
1.加入盐酸至有0.6mol/L-1的氯离子剩余,补加稀硝酸至氢离子约2.0mol/L-1,如有白色沉淀,则为氯化铅(溶解度较大,下组仍要除去铅离子)、氯化亚汞、氯化银,剩余滤液A用于下组分析。
2.验铅离子:沉淀加水加热并趁热过滤,加入醋酸酸化,加入铬酸钾产生黄色沉淀铬酸铅则有铅离子;3.验银离子:以上剩余沉淀用热水洗净,加入氨水,分离滤液并用硝酸酸化,滤液产生白色沉淀氯化银则有银离子;4.验亚汞离子:以上第3步剩余残渣如变黑则有Hg22+(HgNH2Cl+Hg)。
第二组、检验铅离子、铋离子、铜离子、镉离子、三价砷、汞离子、三价锑、四价锡。
1.往滤液A中加入0.3mol/L-1的盐酸,通入硫化氢,加热,产生沉淀:PbS、CuS、HgS均为黑色,黑褐色Bi2S3、黄色的CdS和SnS2、淡黄色As2S3、橙红色Sb2S3,剩余滤液B用于下组分析。
2(铅、铋、铜、镉离子的检验).过滤以上沉淀,加入过量硫化钠,得沉淀A(组成有硫化铅、三硫化二铋、硫化铜、硫化镉)和滤液C(组成有HgS22-、AsS33-、SbS33-、SnS32-)。
3(铅、铋、铜、镉离子的检验).往沉淀A中加入6摩尔每升硝酸,沉淀溶解,在加入1:1的甘油和过量的浓氢氧化钠,如有黄色沉淀为氢氧化镉,分离出滤液D待检验,沉淀用3摩尔每升盐酸溶解,再稀释3倍,加入硫代乙酰胺(CH3CSNH2)加热,生成黄色沉淀硫化镉则有镉离子。
4(铅、铋、铜、镉离子的检验).滤液D加入醋酸酸化,再加亚铁氰化钾变红棕色(Cu2Fe (CN)6)则有铜离子。
定性分析(共72张PPT)

同理可得: m = V× ρB
一般来说,检出量愈小,最低浓度愈低,则 此鉴定反应愈灵敏。
检出限量和最低浓度均由实验测得。
注意的几个问题: 1) 表示鉴定反应的灵敏度是对具体的鉴定反应而
言的。因此,同一离子的不同鉴定反应有不同的灵敏度
在系统分析法中,用某些试剂按一定的程序把 离子分成若干组,然后组内再细分,一直分到彼 此不再干扰为止。
适用于未知试液(或共存离子干扰较大的试液) 的分析。
§2 - 2 阳离子分析
一、常见阳离子的分组
阳离子定性分析仅讨论常见的二十四种离子, 。
它们是:Ag+、Hg22+、Hg2+、Pb2+、Bi3+、Cu2+、Cd2+、 AsⅢ、Ⅴ SbⅢ、Ⅴ、SnⅡ、Ⅳ、Al3+、Cr3+、Fe3+、Fe2+、 Mn2+、Zn2+、Co2+、Ni2+、Ba2+、Ca2+、Mg2+、K+、Na+、
水中
戊醇萃取
在A13+、Cr3+的浓度都低于10-2mol/L时,Al(OH)3在pH=4时沉淀,在10-12时溶解;
很快分解 稳定 第二组中,硫化物溶解度最大的是CdS( KSP×10-28),后面其它组中,硫化物溶解度最小的是ZnS(KSP×10-23)
在上述硫化物沉淀上加8mol/LHCl并加热,HgS与As2S3不溶解,而锑和锡的硫化物则生成氯合络离子而溶解:
CrO + 4 H O + 2H = 2 H CrO + 3 H O 也酸砷可度、用 是 锑鉴一、定个锡反很三应重种来要元鉴的素定反则。应出条不件同,程表度现的为非7:金2-属性质。
2第二章1-2-2 阳离子分析

第二讲 第二章 定性分析 2-1
漳 州 师 范 学 院
2-2 阳离子分析
一, 常见阳离子的分组
在湿法分析中, 直接检出的是溶液中的离子. 常见的阳离 化 在湿法分析中 , 直接检出的是溶液中的离子 . 讨论的是下列24种 子有二十几种, 我们讨论的是下列 子有二十几种 , 我们 讨论的是下列 种 : Ag+ , Hg22+ , Hg2+ , 学 系 2+ , Bi3+ , Cu2+ , Cd2+ , As(Ⅲ,Ⅴ) , Sb(Ⅲ,Ⅴ) , Sn(Ⅱ,Ⅳ) , Pb ⅢⅤ ⅢⅤ ⅡⅣ 】 3+,Cr3+,Fe3+,Fe2+,Mn2+,Zn2+,Co2+,Ni2+,Ba2+,Ca2+, 【 Al 分 Mg2+,K+,Na+,NH4+ . 析 化 学 课 硫化氢系统是目前应用最广泛, 硫化氢系统是目前应用最广泛,且较为完善的一种分组方 是目前应用最广泛 件 主要依据各离子硫化物溶解度的显著差异, 】 案 , 主要依据各离子硫化物溶解度的显著差异 , 将常见的阳离 子分成四组. 子分成四组.
硫化铵组, 硫化铵组,铁组 可溶组,钙钠组 可溶组,
-
Ba2+,Ca2+ ,Mg2+ K+,Na+,NH4+
用系统分析法分析阳离子时, 用系统分析法分析阳离子时,要按照一定的 顺序加入若干种试剂, 顺序加入若干种试剂,将离子按组逐一地沉淀出 这些分组用的试剂称为组试剂 组试剂. 来.这些分组用的试剂称为组试剂.
【 漳 州 师 范 学 院 化 学 系 】
【
第二讲 第二章 定性分析 2-5
分析化学实验思考题答案

分析化学实验思考题答案实验⼀阳离⼦第⼀组(银组)的分析思考题:1.沉淀第⼀组阳离⼦为什么要在酸性溶液中进⾏?若在碱性条件下进⾏,将会发⽣什么后果?答:在系统分析中,为了防⽌易⽔解离⼦的⽔解⽣成沉淀⽽进⼊第⼀组,所以沉淀第⼀组阳离⼦时要在酸性溶液中进⾏。
若在碱性条件下进⾏,第⼀组以后的⼤部分阳离⼦将⽣成沉淀,这样就不到分离的⽬的。
2.向未知溶液中加⼊第⼀组组试剂HCl时,未⽣成沉淀,是否表⽰第⼀组阳离⼦都不存在?答:向未知试液中加⼊第⼀组组试剂时,未⽣成沉淀,只能说明Ag+,Hg22+不存在,⽽不能说明Pb2+不存在,因为当试液中Pb2+的浓度⼩于1mg?ml-1,或温度较⾼时,Pb2+将不在第⼀组沉淀,⽽进⼊第⼆组。
3.如果以KI代替HCl作为第⼀组组试剂,将产⽣哪些后果?答:如果以KI代替HCl作为第⼀组组试剂时,酸度太⼩,第⼆组易⽔解的阳离⼦将⽔解进⼊第⼀组,达不到分离的⽬的。
另外具有氧化性阳离⼦将与I-发⽣氧化还原反应,使这些离⼦的浓度降低不能鉴出。
实验⼆阳离⼦第⼆组(铜锡组)的分析思考题:1.沉淀本组硫化物时,在调节酸度上发⽣了偏⾼或偏低现象,将会引起哪些后果?答:沉淀本组硫化物,若酸度偏低时,第三组阳离⼦Zn2+将⽣成ZnS 沉淀进⼊第⼆组。
若酸度偏⾼时,本组的Cd2+不⽣成硫化物沉淀⽽进⼊第三组。
2.在本实验中为沉淀硫化物⽽调节酸度时,为什么先调⾄0.6mol·L-1HCl酸度,然后再稀释⼀倍,使最后的酸度为0.2 mol·L-1?答:因As(III)的硫化物完全沉淀需在0.6 mol·L-1HCl酸度下,Cd2+的硫化物完全沉淀需在0.2 mol·L-1HCl酸度下。
因此为了使本组离⼦完全⽣成硫化物沉淀⽽与第三组阳离⼦分离,所以在调节酸度时,先调⾄0.6 mol·L-1HCl酸度,然后再稀释⼀倍,使最后的酸度为0.2mol·L-1。
第二组阳离子分析

H S
2
H HS
HS
H S
2
H HS K a1 H 2S
S 2 H K a2 HS
2
K K
a1
a2
2 HS S H S H H H 2S H 2S HS
Pb2+ Cu2+ Bi3+ Cu2+ Bi3+ Bi3+
Na2S 过量(NH4)2S 过量NaOH 过量NH3 · 2O H Na2S 过量(NH4)2S 过量NaOH 过量NH3 · 2O H Na2S 过量(NH4)2S 过量NH3 · 2O H 适量NaOH NH3 · 2O H 加水稀释 过量NaOH 加水稀释 NaOH NH3 · 2O H
0.1 9.210 S
2 23 2
9.210 S 2
9.210 S
810 H H
22
2 21 mol l S 2.510 mol l 23
9.210 S
Hg2Cl2 + SnCl42ˉ = 2Hg ↓黑 + SnCl62ˉ
SnCl62ˉ + Fe = SnCl42ˉ + 2Clˉ+ Fe 2+
2Cu2++Fe(CN)6 4ˉ =Cu2[Fe(CN)6] ↓红棕色 Sx2ˉ+ 2H+ = H2S ↑ + (X-1)S↓
2SbS33ˉ+ 6H+ = 3 H2S ↑ + Sb2S3 ↓ 硫代亚锑酸根离子 SnS32ˉ+ 2H+ = H2S ↑ + SnS2 ↓ 硫代锡酸根离子
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三节第二组阳离子的分析(重点)本组包括Pb2+、Bi3+、Cu2+、Cd2+、Hg2+、As(ⅢⅤ)、Sb(ⅢⅤ)、Sn(ⅡⅣ)离子,称为铜锡组。
它们的共同特点是不被HCl溶液沉淀(Pb2+是很少量的(小于1mg·mL-1),不能被HCl沉淀),但在S反应生成硫化物沉淀。
按照本组分出的顺序,称为第二组;0.3mol·L-1HCl溶液中,可与H2按照所用的组试剂,称为硫化氢组。
一、本组离子的分析特性1.离子的颜色本组离子中,除Cu2+为蓝色外,其余均无色。
2.离子的存在形式铅、铋、铜、镉、汞具有显著的金属性质,在水溶液中主要以金属阳离子的形式存在;而砷、锑、锡三种元素则表现出不同程度的非金属性质,它们在溶液中的主要存在形式随酸碱环境而不同,主要以阴离子形式存在于溶液中。
但由于存在下述平衡AsO33-+6H+=As3++3H2OSbCl63-= Sb3++ 6C1-SnCl42-=Sn2++4Cl-溶液中也或多或少地存在着简单阳离子,并能生成相应的硫化物(如SnS2、As2S3等),所以这些元素还是作为阳离子来研究。
鉴定时并不严格区分它们的存在形式,只是泛指该元素,书写时只标出其氧化数,而不具体指明其存在形式。
3.加水稀释Bi3+、Sb(ⅢⅤ)、Sn(ⅡⅣ)离子(见前表)4.络合物本组离子一般都能生成多种络合物。
其中最常见的是氯络离子,因而大量Cl-存在时可影响到各简单离子的浓度。
另外,Cu2+、Cd2+等能生成氨或氰络离子:Cu(NH3)42+、Cd(NH3)42+、Cu(CN)42+、Cd(CN)42+,它们在Cu2+、Cd2+的分离和鉴定上有很多应用。
Bi3+与I-生成黄色的BiI4-;用于铋的鉴定。
Cu2+、Pb2+和Bi3+能与甘油生成络离子;Hg2+与I-生成无色的HgI42-,它与KOH一起的溶液,可用于NH4+的鉴定,称为奈氏试剂。
这些都具有一定的分析应用价值。
5.氧化还原性质砷、锑、锡三元素的离子具有两种比较稳定的价态,它们在分析上都具有重要的意义。
例如,As(V)在冷而稀的HCl溶液中,与H2S通过一系列的反应,最终得到的是As2S3↓,但这个过程速率较慢,为了加速反应,先将As(V)还原为As(Ⅲ)。
通常使用NH4I来还原。
另外,Sn(Ⅱ)还原性较强,很容易被氧化为Sn(Ⅳ)。
而且SnS不溶于Na2S,而SnS2能溶于Na2S,这样在进一步分组时,把一种元素分在两个组中,将Sn(Ⅱ)归于ⅡA而Sn(Ⅳ)归于ⅡB组,将使操作不便,故一般在进行沉淀之前加入H2O2将Sn(Ⅱ)全部氧化成Sn(Ⅳ),并加热将剩余的H2O2除去。
锑的罗丹明B试法只对Sb(Ⅴ)有效,若溶液中的锑为三价则必须事先氧化。
此外,将Bi3+还原为金属Bi是铋的重要鉴定反应之一。
6.与H2S的反应及本组硫化物性质PbS Bi2S3CuS CdS HgS As2S3Sb2S3SnS SnS2颜色黑黑褐黑黄黑黄桔红棕黄稀硝酸√√√√王水√√√√浓盐酸√√√√稀盐酸√(△)√Na2S HgS22-AsS33-SbS33-SnS32-(NH4)2S √√√NaOH AsO33-+AsS33-√√氨水√极微溶(NH4)2CO3√沉淀的性状:易成胶体。
沉淀的溶解度:CdS最大。
二、组试剂与分离条件本组与第三、四组离子分离的依据是其硫化物溶解度有显著的差异。
事实上,除本组能形成MS沉淀,第三组大多数离子也能沉淀为硫化物。
如何使本组沉淀完全,又不使第三组离子混入?这就是要讨论的分离条件――组试剂的作用条件。
通过对溶解度进行比较可以得出,第二组中溶解度最大的硫化物沉淀是CdS(KSP=7.1×10-28),第三组中溶解度最小的硫化物沉淀是ZnS(KSP=1.2×10-23),比第二组大了大约五个数量级,因此,按照沉淀规律,溶解度小的首先沉淀,溶解度大的不沉淀而留在溶液中,从而达到分离的目的。
也就是说:当第二组中最难沉淀的CdS都沉淀完全时,第二组其它离子也就沉淀完全,第三组中最容易沉淀的ZnS没有开始沉淀,第三组其它离子也就没开始沉淀。
由此可见,分离第二组、第三组的关键是使CdS沉淀完全,ZnS不沉淀。
从平衡关系来看,这点可通过调整酸度、控制S2-来实现。
为了将本组比较完全地同第三组分开,我们需要讨论以下几个问题。
(一)沉淀要求的酸度1.适宜的酸度范围要达到这个目的,根据溶度积关系:KSP=[M2+][S2-],在金属离子浓度一定的情况下,是否发生沉淀反应,取决于溶液中[S2-],由于H2S是弱酸,[S2-]是随溶液酸度变化而变化,因此,可以通过调节酸度来控制溶液中S2-的浓度,从而达到分步沉淀的目的。
根据平衡:H2S=H++HS2- K1=1.3×10-7HS-=H++S2- K2=7.1×10-15K 1K2=[H+]2[S2-]/[H2S]=9.2×10-22室温下,饱和H2S溶液中[H2S]≈0.1mol·L-1所以,[H+]2[S2-]=9.2×10-23[S2-]=9.2×10-23/[H+]2结论:①稍改变H+,便可大幅度改变[S2-],如H+改变10倍,[S2-]将改变100倍。
②直接控制[S2-]难办到,但改变H+易办到。
③由[H+]2[S2-]=9.2×10-23和[M][S]=Ksp,可求出理论上的分离条件。
[H+]=Ksp 109.2[M]-23⨯⋅关键1:使第二组的Cd2+沉淀完全,即要求[Cd2+]=10-5mol·L-1,溶液中应达到[H+]= 2723-510 8109 10--⨯⨯⨯2.=0.34mol/L意味着只要酸度小于0.34mol·L-1,就能使第二组离子沉淀完全。
若溶液的酸度过高,第二组中溶解度较大的CdS、SnS和PbS将沉淀不完全或者不沉淀而进入第三组中。
关键2:使第三组Zn2+不沉淀,第三组中最容易沉淀的是ZnS。
在一般鉴定反应中,离子的浓度在0.1mol·L-1左右,所以设定[Zn2+]=0.1mol·L-1[H+]= 222310 2109--⨯⨯⨯2.1.=0.21mol/L意味着只要酸度大于0.21mol·L-1,第三组离子就没有一个能沉淀。
如果酸度太低第三组溶解度最小的硫化物ZnS(KSP=1.2×10-23)则可能析出沉淀而进入第二组中。
结论:①综合起来考虑,理论上酸度应控制在0.21~0.34mol ·L -1。
事实上,沉淀本组硫化物的最适宜的酸度,是通过实验方法测得的,实验证明,分离第二组与第三组最适宜的酸度是0.3mol ·L -1HCl 。
②实验中必须认真查对酸度。
2.酸度对砷、锑和锡的硫化物的影响酸度过低对形成砷、锑和锡的硫化物很不利。
这是因为:(1)它们只有在酸性环境中才能产生出生成硫化物所必需的简单阳离子。
以砷为例: AsO 33-+6H +=As 3++3H 2O 锑盐和锡盐的情况与此类似。
(2)在中性或碱性溶液中,上述三种离子砷、锑和锡同S 2-生成硫代酸盐,而不是生成硫化物沉淀。
3.沉淀的后期处理需要指出的是,在硫化物沉淀的过程中会不断有H +释放出来,例如 Cu 2++H 2S =CuS ↓+2H +使得后期溶液的酸度有所增高。
为了抵消这个变化,在通H 2S 的后期应将溶液适当地加以稀释,稀释的程度与沉淀量有关,一般稀释1倍即可。
(二) 五价砷的沉淀在冷的稀HCl 溶液中,三价砷可以很快地同H 2S 生成As 2S 3沉淀, 2As 3++H 2S =As 2S 3↓而五价砷却并不直接与H 2S 生成As 2S 5沉淀,而是通过下列三个步骤最后以As 2S 3的形式析出:H 3AsO 4+H 2S =H 3AsO 3S+H 2O H 3AsO 3S =H 3AsO 3+S ↓ 2H 3AsO 3+3H 2S =As 2S 3+6H 2O这个过程是很慢的。
为了加速反应,可以把溶液加热或在溶液中加入I -,先使五价砷还原为三价砷:AsO 43-+2I -+2H +=AsO 33-+I 2+H 2OI-转变为I2后,与H2S反应还可再生出来:I2+H2S=2I-+2H++S↓可见,不需要加得太多。
一般使用NH4I,没有NH4I时也可以用碘酒来代替,后者可被H2S还原为I-。
若改用TAA,就不必另NH4I,TAA可还原五价砷。
(三) 防止硫化物生成胶体(沉淀时的温度)硫化物,特别是IIB组硫化物生成胶体的倾向较大,为了防止这一现象发生,第一,要保持溶液的适当酸度,以促进胶体的凝聚(这个目的在调节酸度时即已达到);第二,硫化物沉淀要在热溶液中进行。
其目的是促进胶体凝聚和加速五价砷的还原。
但加热也会降低H2S 的溶解度从而使S2-浓度减小,不利于溶解度较大的PbS、CdS等沉淀生成,所以最后还要把溶液冷却至室温,再通H2S。
(四) 二价锡的氧化本组内部分离时,SnS不溶于Na2S,SnⅡ属于IIA组;SnS2溶于Na2S,SnⅣ属于IIB组,同一元素的不同价态分属两个组,组分析带来不便。
为使SnⅡ全部转化SnⅣ,可在通人H2S之前加H2O2将SnⅡ氧化为SnⅣ然后将过剩的H2O2加热分解,以免以后与H2S发生作用。
综上所述,本组离子沉淀的详细步骤如下:1.在酸性溶液中先加H2O2将SnⅡ→SnⅣ,然后,加热使过量H2O2分解;2.用NH3·H2O(在系统分析中,由于分出第一组阳离子的氯化物沉淀后,溶液的酸性较强,故需先用氨水中和,再用盐酸调至所需酸度)和HCl调节[H+]=0.3mol·L-1;3.加入少许NH4I,还原AsⅤ、SbⅤ为AsⅢ、SbⅢ;4.加热,通H2S,防止生成胶体;5.冷却,将试液稀释一倍,然后通H2S至沉淀完全。
(使用硫代乙酰胺时,将试液稀释一倍后酸度应为0.2mol/L)。
(五) 硫代乙酰胺CH3CSNH2由于H2S气体毒性较大,制备也不方便,故近年来已不再使用,而改用其替代品—硫代乙酰胺CH3CSNH2(通常简写为TAA)的水溶液代替H2S作沉淀剂。
硫代乙酰胺在酸性溶液中水解产生H2S。
硫代乙酰胺水溶液在常温下比较稳定,可长期存放,只有在加热时才能发生水解反应。
硫代乙酰胺水溶液在不同的介质中加热时发生不同的水解反应,可以分别代替H 2S 、(NH 4)2S 或Na 2S 。
在酸性溶液中水解产生H 2S ,可代替H 2S: CH 3CSNH 2+H ++2H 2O =CH 3COOH+NH 4++H 2S ↑在氨性溶液中水解生成HS -,相当于(NH 4)2S 的作用:-+++=-∆+HS NH NH C CH NH CSNH CH 433232NH 2在碱性溶液中水解生成S 2-,可代替Na 2S 使用:---+++∆+2233233S O H NH COO CH OH CSNH CH以硫代乙酰胺代替硫化氢作为组试剂具有以下特点:(1)由于水解过程较慢,同时硫代乙酰胺的沉淀作用属于均相(匀)沉淀,故所得硫化物一般具有良好的晶形,易于分离和洗涤,共沉淀现象较少。
