频繁子图模式挖掘
频繁子图挖掘算法的应用分类

频繁子图挖掘算法的应用分类作者:吴成凤来源:《电脑知识与技术》2020年第29期摘要:频繁子图挖掘属于数据挖掘领域的一部分,越来越受到研究学者的广泛应用,目前已经成功应用于生物学、化学、社会学等领域。
频繁子图算法的操作是从给定的图数据库中,根据同构测试及支持度计算判断出频繁子图。
本文整理出国内外学者基于频繁子图的应用文献。
根据文献,对这些应用进行分类,列表整理出各个应用领域的数据集的开源地址和图的顶点及边的标识含义。
关键词:频繁子图挖掘;应用场景;顶点;边中图分类号:TP311.12 文献标识码:A文章编号:1009-3044(2020)29-0040-021 引言在数据挖掘的领域中,频繁子图挖掘算法越来越受到国内外研究学者的关注。
频繁子图将各种数据处理成顶点到顶点的逻辑关系的表示,在该模型[1]中,顶点和对应的边关系可以具有与它们相关联的标签,这些标签不是唯一的。
使用这样的图表示,频繁模式的问题变成了在整个图上寻求频繁出现子图的问题,运用频繁子图算法挖掘其潜在的价值。
频繁子图挖掘算法即在给定的图中根据设定的支持度阈值,寻找出同构子图大于等于给定支持度阈值的子图。
频繁子图算法的发展历经二十年,基于频繁子图的应用也越来越广泛。
2 运用场景在由顶点和边构成的图中,顶点有其分类的标识,边亦有其分类的标识,我们需要在给定的图数据库中寻找出顶点标识和标识对应一致的子图,计算出支持度,若一旦支持度超过给定的阈值,便输出其子图,其子图便是一个频繁子图。
Lin W[2]等人认为频繁子图挖掘问题分为两个方面:在一个大图的不同区域挖掘子图适用于社交网络分析等领域;在大规模图集中挖掘子图适用于生物信息学和计算药理学等领域。
图集上的挖掘是指在多张图的图数据库中挖掘这些图中共现的子图。
在一张大图上的挖掘则是在一张图上挖掘图内出现的子图。
基于图事务集合的频繁子图挖掘算法与基于单个大图的频繁子图挖掘算法不同,在计算候选子图支持度的时候,基于图事务集合的频繁子图挖掘算法只需要计算候选子图与图事务集合中满足子图同构的小图的个数,而基于单个大图的频繁子图挖掘算法需要在这个大图中找出候选子图所有的同构的子图,计算用同构的子图的候选子图支持度[3]。
频繁子图挖掘算法

频繁子图挖掘算法一.算法定义与分类编辑按照模式挖掘算法的输入数据类型进行分类:分为graph-transaction和singie-graph两种类型。
graph-transaction型模式挖掘所处理的输入数据是由许多规模相对较小的图构成的集合,每个图可能只包含几十到几百个顶点;而single-graph型模式挖掘的对象则只有-个大图,这个大图包含成千上万个顶点。
这两种类型的区别还在于它们计算候选子图频度时所使用的策略。
graph-transaction型计算模式在图集合每个图中是否出现,不管它在同-个图中出现了多少次均计数-次,而single-graph型则计算模式在这个大图中不同位置出现的总次数。
根据两种类型的特征,解决graph-transaction类型的算法不能用来解决single-graph类型模式挖掘,但是Single-graph类型的算法却能方便应用于graph-transaction类型。
按照采用度量的不同进行分类:分为支持度(support)、支持度-置信度、MDL(minimumdescri-Ptionlength)三种。
支持度型挖掘是以子图在输入图中出现的次数来作为度量的,大部分算法都是基于支持度的;MDL型挖掘是以压缩输入数据的程度来度量,-般采用公式valuo(s,g)=dl(g)/(dl(g1)+dl(g2))来计算,其中:是子图,g是输入的图集合,dl(g)表示图集合g的存储空间,dl(g2)表示把g中所有出现:的地方都用同-个顶点替换后的图形所需的存储空间;支持度-置信度型挖掘是以既要满足最小支持度又要满足最小置信度来衡量的。
还有其它-些度量方法,这里就不再介绍了。
按照挖掘出的频繁子图的类型进行分类:分为一般子图、连通子图、诱导子图等。
二.算法思路编辑算法的思路比较简单,以递归计数为基础,可以挖掘出所有频繁子图。
但是对于包含较多图的输入集合来说执行效率非常低,主要是因为挖掘算法在生成候选子图时要判断是否存在相同的k-1子图,当川尺大时,这需要花费很长时间。
一种基于局部重构树的改进频繁子图挖掘算法

是一种高效的经典算 法 , 然而两遍数据库扫描不
能 适应 数据 流 的无 限性 和流 动性 的特 点 。为了克
服该局限性 , 需要设计一种有效的全局数据结构 , 通过一次扫描就能包含所有数据库信息。 笔 者提 出 了一种 新 的一 次 扫 描前 缀 树 结 构 , 称为局部重构 O P F 。该 结构是一种类 似于 F P—
根, 路径 上所 有能 与 O连通 的节 点或 者 能 与 O连 L t 通 的节 点 将 构 成 O条 件 图库 中 的一 个 图 。这 样 L 可 以剔 除 那 些 既 不 与 连 通 , 不 与 O连 通 的 又 l 点 。也 可 以避 免 同 时 考 虑 与 连 通 的边 和 与
含一个点的频繁图集 的标号顶点表 , 笔者 引入 了
为 [ I ]其中 t T t, 为第一个元素 , 为剩余元素 而
的表 , 递归调用 I e —re( I ,r ) n r t Te 函数实现 st e T e 将元 组对 应 的信 息加 入 到 Te r e中, 成 树 的 完
De 2 1 c. 01
文章编号 :0 7—14 2 1 )6— 8 4— 4 10 4 X( 0 1 0 06 0
文献标志码 : A
一
种 基 于局 部 重 构 树 的 改进 频 繁 子 图挖 掘算 法
蒋廷耀 , 廖 强
( 三峡大学 计算机与信息学 院, 湖北 宜昌 43 0 ) 4 0 2
关键词 : 频繁 子图 ; 图挖掘 ; s 表 ; P—t e Hah F r e
中 图分 类 号 :P 9 T 31 D I1 .93 ji n 10 O :0 3 6 /.s .07—14 2 1.6 O 4 s 4 X.0 10 .0
数据挖掘中的频繁模式发现

数据挖掘中的频繁模式发现数据挖掘是一种从大量数据中发现并提取有价值信息的过程。
频繁模式发现是数据挖掘领域中的一项重要任务,它帮助我们发现数据中经常出现的模式或关联规则,从而为决策和预测提供有力支持。
本文将介绍数据挖掘中频繁模式发现的基本概念、常用方法和实际应用。
一、频繁模式发现的概念在数据挖掘中,频繁模式指的是在数据集中经常出现的模式或子集。
这些模式可以是项集、序列或子图等形式。
频繁模式发现任务的目标是寻找在数据集中出现频率高于预设阈值的模式。
二、频繁模式发现的常用方法1. Apriori算法Apriori算法是频繁模式发现中最经典的方法之一。
该算法基于一种称为Apriori原则的性质,即如果一个模式是频繁的,那么它的所有子集也必须是频繁的。
Apriori算法通过迭代地生成候选项集,并在每一次迭代中利用Apriori原则剪枝,从而减少模式发现的搜索空间,提高算法的效率。
2. FP-Growth算法FP-Growth算法是另一种常用的频繁模式发现方法。
该算法通过构建一种称为FP树的数据结构来表示数据集,然后利用树的结构和属性,高效地挖掘频繁模式。
与Apriori算法相比,FP-Growth算法不需要生成候选项集,因此在一些情况下可以提供更好的性能。
三、频繁模式发现的应用频繁模式发现在各个领域都有广泛的应用。
以下是几个例子:1. 超市销售分析超市拥有大量的交易数据,通过频繁模式发现可以找到经常同时被购买的商品,从而帮助超市制定促销策略、调整商品陈列和优化供应链。
2. 社交网络分析在社交网络中,频繁模式发现可以用于发现用户之间的关联规则,例如朋友推荐、用户相似性分析和社群发现。
3. 生物信息学频繁模式发现可以在基因表达数据中发现共同出现的基因模式,从而帮助生物学家理解基因的功能和相互作用。
4. Web点击分析通过分析用户的点击行为,可以发现用户经常访问的网页或点击的广告,从而改进网站的推荐系统和广告投放策略。
图数据处理中的图挖掘与关键节点识别技术研究

图数据处理中的图挖掘与关键节点识别技术研究图数据处理是指对图结构的数据进行分析、挖掘和可视化的过程,其中图挖掘和关键节点识别是图数据处理中的重要技术。
一、图挖掘技术图挖掘是指从图数据中发现潜在的模式、规律和知识的过程。
图挖掘技术可以分为图模式挖掘和图分类挖掘两个方面。
1. 图模式挖掘图模式挖掘主要是从图数据中发现频繁出现的子图结构,如图中的子图、路径、圈等。
这些子图结构可能代表了一些重要的模式或特征,在社交网络分析、生物信息学、计算机视觉等领域有广泛的应用。
常用的图模式挖掘算法包括Apriori算法、FP-Growth算法和GSpan算法等。
Apriori算法是一种基于频繁项集的挖掘方法,通过迭代的方式挖掘出频繁子图;FP-Growth算法是一种基于前缀树的挖掘方法,通过构建频繁子图的树形结构来提高挖掘效率;GSpan算法是一种基于图搜索的挖掘方法,通过遍历图数据中的所有可能子图来发现频繁子图。
2. 图分类挖掘图分类挖掘主要是将图数据进行分类,即根据图的属性和拓扑结构将其归类到不同的类别中。
图分类挖掘可应用于推荐系统、网络安全和图像识别等领域。
常用的图分类挖掘算法包括最近邻算法、支持向量机和神经网络等。
最近邻算法通过将待分类图与已知类别图进行相似度计算,将其归类到最相似的类别中;支持向量机采用超平面划分图数据空间,实现分类目标;神经网络通过训练神经元之间的权值来实现图分类。
二、关键节点识别技术关键节点识别是指从图数据中识别出对整个网络结构具有重要影响力的节点。
关键节点的识别对于理解网络的拓扑结构、控制网络的传播过程以及防止网络攻击具有重要意义。
关键节点的识别可以基于节点的度中心性、介数中心性、紧密中心性和特征向量中心性等指标进行。
1. 度中心性度中心性指节点的度数,即与该节点相连接的边的数量。
度中心性高的节点在图中具有很大的影响力,通常被认为是关键节点。
2. 介数中心性介数中心性指节点在所有最短路径中作为中间节点的频率。
频繁子图挖掘算法的若干问题

1 频繁子 图挖掘算 法
1 1 图的存 储 .
用相 应 的 l , ’… , ’ ’ 2 , 替换 。如果 节
关 于 图的存 储也 可 以称 为 图 的表 示 (rp e— gahrp rsnai ) 目前 图 的表 示 有 邻 接 数 组 (  ̄aec eettn 。 o A cny
点i 和 之间存在边 E i ) 则生成 B D b E (, , . 『 D b : ()八 ’ , G 的所 有 关 联 关 系 可 表 示 如 下 : i () 图 ( )=Vb G 其 中 i 取 遍 1到 。如 果 i _ 相 , 和『 不
邻 , b . s。此 时 B D T( 已经 能 够 把 无 权 则 = e / D G)
图 G表示 出来 。 1 2 图数据 库 的预处理 .
Ar s 、 r y) 邻接链表 ( d cnyL t 、 a A j ec is 邻接矩阵 ( d a s) A— j ec a i 、 a nyM tx 隐式表示 ( s ao 其 中邻 接数 组主 要 用来 描 述 静 态 数 组 , 接 链 表 主 邻
要用 来 表示 动态 图 , 接矩 阵在 表 示 稠 密 图 上有 很 邻
大优 势 。本 文主 要介绍 以下 2种 隐式 表示 方式 。
( )区间 图 表 示 方 法 。 区 间 图 由 一 系 列 区 1
原 来 的各 种 算 法 中 , 了没 有讨 论 图的存 储 形 除 式外 , 也都 没有 对 数 据 库 中的 图进 行 预 处 理 。本 文
数量出现 , 通常是海量信息 。当进行频繁子图的挖 掘时 , 就会存在如下问题。
( )图数据库中存在某些图是另外一些图的子 1
图 。将 表示 结点 的区 间 的端 点 按 序 排 列 , 后 按序 然
频繁序列模式挖掘算法pbwl算法

频繁序列模式挖掘算法PBWL算法1. 简介频繁序列模式挖掘是数据挖掘领域中的一项重要任务,它用于发现数据集中频繁出现的序列模式。
序列模式是指在一个时间序列数据集中,经常以特定顺序出现的事件或行为。
PBWL(Prefix-Based Window Level)算法是一种用于频繁序列模式挖掘的有效算法。
它通过将时间序列划分为窗口,并使用前缀树来存储和搜索频繁序列模式。
本文将详细介绍PBWL算法的原理、步骤和优势,并通过示例说明其应用和效果。
2. PBWL算法原理2.1 窗口划分PBWL算法首先将时间序列划分为多个窗口,每个窗口包含固定数量的事件或行为。
窗口大小可以根据实际需求进行调整。
2.2 前缀树构建接下来,PBWL算法使用前缀树(Prefix Tree)来存储和搜索频繁序列模式。
前缀树是一种多叉树结构,其中每个节点表示一个事件或行为,路径表示事件之间的顺序关系。
2.3 频繁序列模式挖掘PBWL算法通过遍历每个窗口,将窗口中的事件序列插入到前缀树中。
在插入过程中,PBWL算法会记录每个节点的计数信息,以便后续的频繁模式挖掘。
当所有窗口都被处理完毕后,PBWL算法从前缀树中提取频繁序列模式。
频繁序列模式是指在整个时间序列数据集中经常出现的序列。
3. PBWL算法步骤PBWL算法的主要步骤如下:1.将时间序列划分为多个窗口,确定窗口大小和滑动步长。
2.初始化前缀树,并设置根节点。
3.遍历每个窗口:–将窗口中的事件序列插入到前缀树中。
–更新前缀树节点的计数信息。
4.从前缀树中提取频繁序列模式:–使用深度优先搜索(DFS)遍历前缀树。
–对于每个节点,检查其计数是否满足最小支持度要求。
–对于满足要求的节点,将其作为频繁序列模式输出。
4. PBWL算法优势PBWL算法相对于其他频繁序列模式挖掘算法具有以下优势:•高效性:PBWL算法通过窗口划分和前缀树存储结构,减少了搜索的空间和时间复杂度,提高了算法的效率。
【国家自然科学基金】_频繁子图挖掘_基金支持热词逐年推荐_【万方软件创新助手】_20140803
科研热词 频繁子图 数据挖掘 频繁模式挖掘 频繁hamilton子图 邻接矩阵 规范编码 节点支持度 相对支持度 生物网络 图的同构 图的匹配 图 同构 关联矩阵 不平衡性 hamilton子图 hamilton回路 apriori算法
推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2014年 序号 1 2 3 4
2014年 科研热词 推荐指数 频繁子图挖掘 1 预处理 1 recomputed embedding技术 1 ffsm算法 1
推荐指数 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
科研热词 频繁子图 数据挖掘 图数据库 图挖掘 频繁路径 频繁模式 跳跃模式 规范编码 联机分析处理 联合熵 算法 生物网络 物流 最大频繁子图 射频识别 子图搜索 子图同构 决策树 信息增益 代表模式
推荐指数 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
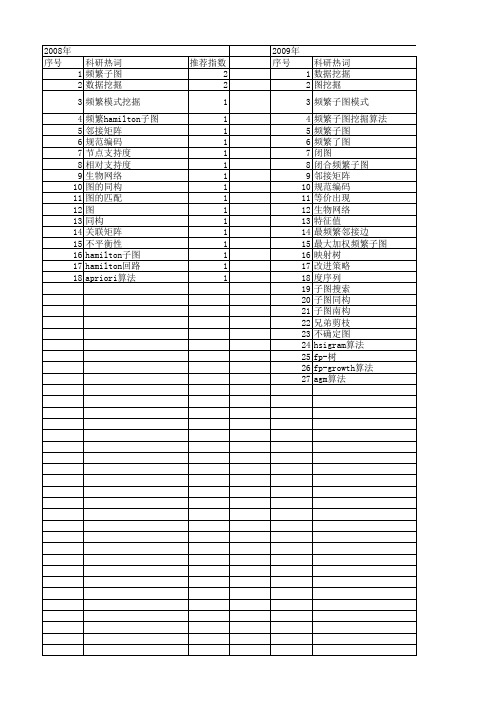
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
科研热词 数据挖掘 图挖掘 频繁子图模式 频繁子图挖掘算法 频繁子图 频繁了图 闭图 闭合频繁子图 邻接矩阵 规范编码 等价出现 生物网络 特征值 最频繁邻接边 最大加权频繁子图 映射树 改进策略 度序列 子图搜索 子图同构 子图南构 兄弟剪枝 不确定图 hsigram算法 fp-树 fp-growth算法 agm算法
一种新的频繁子图挖掘算法

1 概述
数据挖掘是指在 数据 中发现有效的、新颖的、潜在有用
Vuv , ∈V, “ v ∈E) (_(),()∈E’ ( ,) ( { ( “ , v) 厂 )
V u v ∈E L uv :L , , () (,) , ( , ) ( ) v) ,
的、可理解模式 的非平 凡过程 。图结构能够模拟几乎 所有 事 物之间的联系 ,如在 We b挖掘、药物分子设 计及 其功能预测 等领域都有广泛应用 。作为 图挖掘 中一个重 要分支 ,频繁 子
第3 7卷 第 2 期 0
、_ . 7 , 13 0
・
计
算
机
工
程
21 0 1年 1 0月
Oc o e t b r 201 1
No2 .0
Comp e g n e i utrEn i e rng
软 件 技术 与数 据 库 ・
一
文章编号t10.32( 12-o2—0 文献标识码: 0o一48 010-07 3 2 )_ A
[ ywod lApirag r m; a nn ;u gahio rhs f q e tu ga h Ke r s r i o t d t miig sb rp mo i r u n b rp o i l h a s p m; e s D0I 1.9 9jsn10 —4 82 1.00 0 : 03 6 /i . 03 2 . 1 .1 .s 0 0 2
的挖掘效率更高 。
关蝴
:A r r算法 ;数据挖掘 ;子 图同构 ;频繁子图 pi i o
Ne Al o ih o i i gFr q e tS b r p w g rt m f n n e u n u g a h M
・
数据挖掘之关联分析六(子图模式)

数据挖掘之关联分析六(⼦图模式)⼦图模式频繁⼦图挖掘(frequent subgraph mining):在图的集合中发现⼀组公共⼦结构。
图和⼦图图是⼀种⽤来表⽰实体集之间联系的数据结构。
⼦图,图G′=(V′,E′)是另⼀个图G=(V,E)的⼦图,如果它的顶点集V'是V的⼦集,并且它的边集E'是E的⼦集,⼦图关系记做G′⊆sG。
⽀持度,给定图的集族ς, ⼦图g的⽀持度定义为包含它的所有图所占的百分⽐。
s(g)=|G i|g⊆sG i,G i⊆ς||ς|频繁⼦图挖掘频繁⼦图挖掘给定集合ς和⽀持度阈值minsup,频繁⼦图挖掘的⽬标是找出使得所有s(g)≥minsup的⼦图g.该定义适⽤于所有类型的图,但是本章主要关注⽆向连通图(undirected,connected graph)。
定义如下1. ⼀个图是连通你的,如果图中每对顶点之间都存在⼀条路径。
2. ⼀个图是⽆向的,如果它只包含⽆向边。
挖掘频繁⼦图的是计算量很⼤的任务,对于d个实体的数据集,⼦图总数为d∑i=1C i d×2i(i−1)/2其中,C i d是选择i个顶点形成的⼦图⽅法数,2i(i−1)/2是⼦图的顶点之间边的最⼤值。
候选的⼦图很多,但不连通的⼦图通常被忽略,因为它们没有连通⼦图令⼈感兴趣。
频繁⼦图挖掘的⼀种蛮⼒⽅法是,产⽣所有连通⼦图作为候选,并计算各⾃的⽀持度。
候选⼦图⽐传统的候选项集的个数⼤得多的原因为1. 项在项集中之多出现⼀次,⽽某个标号可能在⼀个图中出现多次。
2. 相同的顶点标号对可以有多重边标号选择。
给定⼤量候选⼦图,即使对于规模适应的图,蛮⼒⽅法也可能垮掉类Apriori⽅法1.数据变换,⼀种⽅法是将图变换为类似事务的形式,使得我们可以使⽤诸如Apriori等已有的算法。
在这种情况下,边标号和对应的顶点标号(l(v i),l(v j))组合被映射到⼀个项。
事务的宽度由图的边数决定。
但是,只有当图中每⼀条边都具有唯⼀的顶点和边标号组合时,该⽅法才可⾏。
频繁子图挖掘算法的比较研究

频繁子图挖掘算法的比较研究在大数据时代,数据挖掘技术成为了人们研究数据的重要手段之一。
频繁子图挖掘算法是挖掘图数据中潜在关系的一种常用手段。
它可以挖掘出图数据中频繁出现的子图,如社交网络中的社区结构、生物信息学中的蛋白质相互作用网络等。
在实践中,频繁子图挖掘算法被广泛地应用于数据挖掘、机器学习等领域。
当前,随着研究的深入,频繁子图挖掘算法也在不断地发展和创新。
本文将对目前主流的几种频繁子图挖掘算法进行比较研究。
一、背景介绍频繁子图挖掘是指在给定的大规模无向或有向图中,挖掘出满足支持度和置信度要求的子图,其中支持度指的是子图在图中出现的次数,置信度指的是满足支持度的子图在图中出现的比例。
频繁子图挖掘算法可以在无需精确查询的前提下,对图中的隐含模式进行发现和分析。
目前,有很多种不同的频繁子图挖掘算法,其中最常用的是基于Apriori算法的频繁子图挖掘算法。
随着研究的深入,越来越多的算法被提出来,并逐渐成为了主流,如GSpan、FSG等算法。
本文将对这几种算法进行比较研究。
二、Apriori算法Apriori算法最早由Agrawal和Srikant在1994年提出。
该算法适用于一般的数据挖掘任务,可用于频繁项集挖掘、关联规则挖掘、分类和聚类等任务。
该算法的基本思想是通过多次扫描事务数据库来寻找频繁项集,通过候选项集的生成和筛选来减少扫描次数,从而提高算法的效率。
在频繁子图挖掘领域,Apriori算法也有相应的改进。
例如,Menardi和Torelli 等人提出了一种改进版本的Apriori算法——RapidMiner,在速度上有了显著的提升。
另外,Apriori算法还有很多种变种,例如Eclat、FP-Growth等,这里不再赘述。
三、GSpan算法GSpan算法是一种高效的频繁子图挖掘算法。
GSpan算法以图的邻接矩阵及其迭代的方式,满足Apriori性质,通过对子图的遍历,不断生成候选子图并判断其是否频繁,从而提高算法的效率。
数据分析知识:数据挖掘中的频繁模式挖掘

数据分析知识:数据挖掘中的频繁模式挖掘数据挖掘中的频繁模式挖掘数据挖掘是一个复杂的过程,需要从庞大的数据集中提取出有价值的信息,这些信息可以用于业务分析、决策支持、市场营销等方面。
而频繁模式挖掘,就是在大量数据中寻找频繁出现的组合,从而发现数据集中的一些结构、规律和特征,帮助人们更好地理解数据,作出可靠的决策。
本文将介绍频繁模式挖掘的概念、算法和应用,并探讨其在实践中的优势和不足之处。
一、频繁模式挖掘的概念频繁模式挖掘是数据挖掘中的一种技术,它通过数据集中的项集来寻找频繁出现的组合,从而发现数据集中的一些规律、结构和特征。
在频繁模式挖掘中,一个项集是指包含若干个属性(或特征)的集合,而频繁项集指在数据集中出现频率较高的项集。
举个例子,某超市的销售数据表格中,每一行代表一次购物,每一列代表某种商品,如果某些商品常常同时被购买,那么这些商品就组成了一个频繁项集。
对于频繁项集的挖掘,可以应用一些经典的算法,如Apriori算法、FP-growth算法等。
这些算法可以从数据集中提取出频繁项集,并进行支持度和置信度的计算,从而评估每个项集的重要性和关联性。
而支持度指项集在数据集中出现的概率,而置信度则是指在包含某项集的条件下,另一个项集出现的概率。
二、频繁模式挖掘的算法1、Apriori算法Apriori算法是频繁项集挖掘领域中的经典算法,它最早由R. Agrawal和R. Srikant于1994年提出。
该算法是基于Apriori原理的,即如果一个项集是频繁的,那么它的所有子集必须也是频繁的。
具体而言,Apriori算法的流程包括:(1)对数据集中的单个项进行扫描,统计每个项的出现次数,得到一个项集L1;(2)对于项集L1中的每一项,计算其支持度,只保留支持度大于等于设定阈值minsup的项,得到一个新的项集L2;(3)对于项集L2中的每两个项,判断它们是否能够组合成一个新的项集,如果满足条件,则进行计数,并得到一个新的项集L3;(4)重复第二步和第三步,直到无法生成新的项集为止。
一种快速的频繁子图挖掘算法

一种快速的频繁子图挖掘算法摘要:提出了一种基于关联矩阵的频繁子图挖掘算法。
该算法通过对关联矩阵的标准化,有效地降低了子图同构判断的代价。
在此基础上,算法利用深度优先的思想,通过逐步扩展频繁边找出所有频繁子图。
实验结果表明,该算法比其他同类算法具有更快的速度和更好的稳定性。
关键词:图;关联矩阵;同构;数据挖掘Abstract:Analgorithmforminingfrequentsubgraphsbasedonassociatedmatrixwasproposed.Bynorm alizingtheassociatedmatrixofthegraph,thecomputationalcostonverifyingtheisomorphismofthesubgr aphswaseffectivelyreduced.Basedonthedepth2firstsearchingmethod,allthefrequentsubgraphscouldb esearchedbyaddingedgesprogressively.Experimentalresultsshowthatthealgorithmhashigherspeedan dbetterstabilitythanothersimilarones.Keywords:graph;associatedmatrix;isomorphism;datamining一引言伴随着生物信息学、社会网络学、XML文档分析的发展,传统的针对非结构型数据的挖掘方法[1]诸如频繁项集和序列模式的挖掘,已经不能胜任对半结构型、结构型数据的挖掘。
图作为结构型数据中的一个重要数据类型,能够表示诸如化学分子(化学原子表示为图中的节点,原子与原子之间的化学键表示为节点之间的边)、蛋白质结构、社会网络等众多应用领域的数据。
对于图挖掘方法的研究,可以有效地解决这些领域的难题。
因此,对于半结构型、结构型数据挖掘的研究已经具有越来越高的应用价值。
一种基于前缀节点的频繁子图挖掘算法

在化学信息学 、 生物信息学 、 网络结构分析 等领域 , 频繁 子 图挖掘算法是一个热点研 究问题 。与其他 的频繁模式挖 掘算 法类似 , 一般 的频繁子图挖掘算法都分为候选模式生成和模式
频 繁判 定 两 步 … 。在 频 繁 子 图 的 挖 掘 过 程 中 , 生 成 大 黾 的 会 候选 模 式 图 。对 每 一 个 新产 生 的候 选 模 式 图 , 在进 行 频 繁判 定
d i1 .9 9 ji n 10 —65 2 1 . 7 00 o:0 3 6/ . s.0 13 9 .0 0 0 .2 s
F e u n u g a h n n lo i m a e n p e x n d r q e ts b r p s mi i g ag rt h b s d o rf o e i
m ii g i mp o e y CBE ag rt n n si r v d b lo i hm. Ke y wor s: d t nig;fe u n u r p d a a mi n r q e ts bga h;io r im l s s mophs ca s;c n ne lf r ;p e i o e a o ia om r fx n d
C E算法 。对 在分 支上扩展得 到的候选 模 式 图, B B C E算 法能 够在 常数 时 间 内完成 规 范化 判 定。通 过 实验 证 明
C E算法 的子图挖掘效 率有显著提 高 B 关键 词 :数据挖 掘 ;频 繁子 图 ;同构类 ;规 范化 形式 ;前缀 节点 中图分类号 :T 3 1 P 0 文献标 志码 :A 文章编号 :10 —6 5 2 1 ) 7 2 7 — 3 0 139 (0 0 0 —4 6 0
树也成为该 同构类的规范形式 。同构类 的规范形式有多 种不
频繁模式挖掘算法综述

结 构 以及 设 置广 告 页 面 等 。 因此 挖 掘 邻 近 序 列 模 式 有 实 际 意 义 。
为 了 提 高 算 法 效 率 , 们 提 出 了 散 列 项 集 计 数 1 划 分I、 人 9 1 、 , 选 O l 目前 人 们 已 经 提 出 了许 多 邻 近 序 列 模式 挖 掘算 法 . 如 ail rw提 出 的 P M 算 法fI 算 法 先 把所 有 的 序 列 串 联 在 D 3. 0该 样 I和 动 态 项 集 1等 技 术 来 对 A r r算 法 进 行 优 化 。 但 这 些 算 D ne C o I U 1 2 l pi i o 起 组 成 一 个 长 字符 串 .然 后 通 过 在 长 字 符 串 中 删 除 低 阶 邻 近 法 都 是 在 A f r算 法 基 础 上 进 行 的 改 进 . 可 能 改 变 A f f算 p oi i 不 po ii
2 频 繁 项 集挖 掘 、
要 多 次 扫 描 数 据 库 . 致 算 法 性 能 不 佳 。算 法 F S a 导 me pn和 Pe r. i a f P n虽 然 不 用 多 次 扫描 数 据 库 .但 往 往 会 构 造 很 多 投 影 或 者 x
关 联 规 则 是 数 据 挖 掘 的 众 多 模式 中最 为 重 要 的 一 种 .它 主 伪 投 影 数 据 库 . 此算 法 的 效率 也 不 理想 Pi 对 We 日志 的 因 e针 b 要 用 来揭 示数 据库 中项 目或 属 性 之 间 的相 关 性 。 关 联 规 则 经 常 特 点设 计 了一 个 称 为 WA — n P Mie的 算 法 . 算 法 首 先 扫 描 两 该
算法 , 并指 出 了频 繁 模 式 未 来的 研 究 方 向 。
基于确定图的频繁子图挖掘技术概述

基于确定图的频繁子图挖掘技术概述摘要:化学信息学、生物信息学、医学和社会科学等领域的科学研究的迅速发展积累了大量的图数据,如何从复杂和庞大的图数据中挖掘出有效信息成为数据挖掘领域的热点。
通过介绍现阶段图数据挖掘技术的进展,特别是确定图挖掘技术中有代表性的频繁子图挖掘技术研究,讨论并预测了频繁子图挖掘研究的发展趋势。
关键词:确定图;频繁子图挖掘;子图同构中图分类号:tp311.13 文献标识码:a 文章编号:1007-9599 (2012) 17-0000-021 引言广泛应用于描述化学信息学、生物信息学、医学和社会科学等领域的图数据挖掘技术是目前数据库研究领域的重要研究方向。
在生物技术领域,图数据挖掘技术可以帮助生物学家减轻蛋白质结构匹配实验的代价;在小世界(社会)网络分析中,对小部分节点的高度局部聚类的挖掘,有助于理解如何能接触到其他人、设计网络,有利于信息或其他资源的有效传输,从而不用太多的冗余连接使网络过载[1]。
在进行确定图数据挖掘技术的讨论之前,先给出确定图数据的基本定义。
确定图是一个五元组, =(,,,,)。
其中是图的顶点集合;是图边的集合;是图的顶点标号集合;是图的边标号集合;是用来对顶点和边分配标号的函数。
本文将对国内外基于确定图的频繁子图挖掘技术研究进行介绍和总结,并对未来的发展趋势和研究热点进行展望。
2 确定图的数据挖掘技术一段时间以来,确定图的频繁子图挖掘问题得到了一定的研究,确定图的频繁子图挖掘是指在确定图集合中挖掘出公共子结构。
常见的频繁子图挖掘算法可以分为4类:基于模式增长的算法、基于的算法、基于模式规约的算法以及基于最小描述长度的近似算法。
2.1 基于的频繁子结构挖掘算法基于的频繁子结构挖掘算法,包括算法和算法等。
akihiro inokuchi、takashi washio和hiroshi motoda提出的算法以递归统计的方法为基础,图的顶点相当于传统频繁项集挖掘算法中的项集,通过每次增加一个图节点来实现子结构规模的增大,该算法可以挖掘出所有频繁子图,对集成的密集数据集具有良好性能。
复杂网络数据挖掘方法

复杂网络数据挖掘方法随着互联网的快速发展,网络中积累了海量的复杂数据。
这些数据包含了丰富的信息和相互之间的复杂关联关系,如社交网络中的用户关系、电子商务中的用户购买行为、互联网搜索引擎中的链接关系等。
为了从这些复杂网络数据中发现有价值的知识和模式,研究者们提出了各种复杂网络数据挖掘方法。
一、节点挖掘方法节点挖掘方法通过分析网络中节点的属性和连接关系,发现节点的特征和节点之间的关联模式。
其中,社区发现是一种常见的节点挖掘方法,用于发现网络中具有紧密联系的节点群体。
社区发现方法通常基于节点之间的连接紧密度或共同的属性特征,如标签、兴趣等来划分社区。
二、链路挖掘方法链路挖掘方法主要关注网络中的边或链接关系,通过分析边的属性、权重或连接模式等,发现边的特征和边之间的规律。
链路预测是一种常见的链路挖掘方法,用于预测网络中可能存在但尚未建立的连接关系。
链路预测方法通常基于图结构中已有的边和节点属性,利用机器学习、统计模型等技术来预测未知的边。
三、图模式挖掘方法图模式挖掘方法旨在发现网络中的重复子结构和模式。
这些模式可以帮助我们理解网络的组织结构、功能特征等。
图模式挖掘方法通常基于频繁子图挖掘技术,通过寻找网络中出现频率较高的子图来发现模式。
这些子图可以是简单的三角形、环形结构,也可以是复杂的星形或其他特定形状。
四、流动性挖掘方法流动性挖掘方法关注网络中数据的流动和传播过程,通过分析节点和边的属性以及它们之间的交互关系,挖掘数据的传播路径和传播模式。
这些方法可以应用于社交网络中的信息传播、疾病传播模型等领域。
流动性挖掘方法通常基于图中的消息传播、扩散模型或随机游走等算法,并结合机器学习算法来对传播过程进行建模和预测。
总结起来,复杂网络数据挖掘方法主要包括节点挖掘、链路挖掘、图模式挖掘和流动性挖掘。
这些方法可以帮助我们从复杂网络中发现隐藏在数据背后的有价值的知识和模式。
通过应用这些方法,我们可以更好地理解和分析互联网中的各种网络结构,并提供科学依据和决策支持,促进社会、经济等领域的发展。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数据挖掘与商务智能读书报告Using Association Rules for Product Assortment英文标题:gSpan: Graph-Based Substructure Pattern Mining中文标题:频繁子图模式挖掘文献来源:ICDM 2002一、主要内容(2000~2500字):(1)论文研究的问题概述数据挖掘技术及其算法是目前国际上数据库和信息决策领域最前沿的研究方向之一,本文就数据挖掘中基于图结构的gSpan挖掘算法及其应用进行了研究。
本文研究了频繁字图挖掘在图数据集的新方法,提出了一种新的算法gSpan,它在没有候选集的情况下发现了频繁子结构。
gSpan在图中建立了一种新的字典序,和各图形映射到一个唯一的最小DFS代码作为它的规范的标签。
基于这种字典顺序,gSpan采用深度优先的搜索策略高效的挖掘频繁连通子图。
研究表明,gSpan大大优于以前的算法。
gSpan算法是图挖掘邻域的一个算法,而作为子图挖掘算法,又是其他图挖掘算法的基础,所以gSpan算法在图挖掘算法中还是非常重要的。
gSpan算法在挖掘频繁子图的时候,用了和FP-grown中相似的原理,就是模式增长方法,也用到了最小支持度计数作为一个过滤条件。
图算法在程序上比其他的算法更加的抽象,在实现时更加需要空间想象能力。
如果整个数据集图中可以容纳主存,gSpan可以直接应用,否则人们要首先执行基于图的数据投影仪,然后应用gSpan。
gSpan是第一个在频繁子图挖掘中使用深度优先搜索的算法。
本文介绍DFS字典序和最小DFS码这两种技术,它们形成一种新的规范的标识系统来支持DFS搜索。
gSpan在一个步骤里结合了频繁子图的增长和检查,从而加速挖掘过程。
(2)论文研究的理论意义及其应用前景频繁图挖掘是数据挖掘中一个非常广泛的应用。
频繁图挖掘可以理解为从大量的图中挖掘出一些满足给定支持度的频繁图,同时算法需要保证这些频繁图不是重复的。
gSpan是一个非常高效的算法,它利用dfs-code序列对搜索树进行编码,并且制定一系列比较规则,从而保证最后只得到序列“最小”的频繁图集合。
由于大部分图挖掘算法都需要利用频繁子图,频繁子图挖掘逐渐成为了数据挖掘领域中的热点研究内容。
目前,很多高效的频繁子图挖掘算法已经被提出。
其中,gSpan算法是目前公认的最好的频繁子图挖掘算法。
然而,在化合物数据集上,还可以利用化合物的特殊结构进一步优化gSpan算法的性能。
文献利用了化合物分子结构的对称性和原子类型分布的不均衡性,提出了一些新的优化策略,进一步改进了gSpan 的性能。
鉴于gSpan 算法在图挖掘领域乃至整个数据挖掘领域的重要性,设计并实现gSpan 算法。
同时,采用优化策略,进一步提高gSpan 算法在化合物数据集上的运行效率。
(3)论文所述系统或算法的过程描述为了遍历图,gSpan 算法采用深度优先搜索。
初始,随机选择一个起始顶点,并且对图中访问过的顶点做标记。
被访问过的顶点集合反复扩展,直到建立一个完全的深度优先搜索 (DFS) 树。
在构造DFS 树时,顶点的访问顺序形成了一个线性序。
使用下标来记录这一次序,其中i<j 意味着在进行深度优先搜索的时候i V 在j V 之前被访问。
用DFS 树做下标的图G 记作T G ,T 称为G 的一个DFS 下标。
给定一棵DFS 树T ,称T 的起始节点0V 为根。
最后访问的节点n V 称作最右节点。
从 0V 到n V 的直接路径称作最右路径。
给定图G 和G 的DFS 树T ,一条新边e 可以添加到最右节点和最右路径上另一个节点之间(后向扩展);或者可以引进一个新的节点并且连接到最右路径上的节点(前向扩展)。
由于这两种扩展都发生在最右路径上,因此称为最右扩展。
我们把每个加下标的图转换为边序列,称作DFS 编码,以便建立这些序列之间的序,目的是选择产生最小序列的下标作为基本下标。
在转换过程中有两种类型的序:(1)边序,将下标图中的边映射到一个序列;(2)序列序,它建立边序列(即图)之间的序。
基于边序,如果用5元组()()j j i i l l l j ,,,,i ,表示边,其中i l 和j l 分别是i V 和j V 的标记,而),(j i l 是连接它们的边的标记。
一个图可能有几个DFS 编码,我们想在这些编码之间建立序列并选择一个编码来代表图。
此时通过标记信息来进行排序。
令边序关系T 拥有第一优先级,节点的标记i l 拥有第二优先级,边标记),(j i l 拥有第三优先级,节点标记j l 拥有第四优先级,来决定两条边的次序。
基于上规则的序称作DFS 词典序(DFS Lexicographic Order)。
基于DFS 词典序,给定图G 的最小DFS 编码记作dfs(G),是所有编码中的最小者。
产生最小DFS 编码的下标称为基本下标。
同时,还有给定两个图G 和G ',G 和G '同构当且仅当dfs(G )=dfs(G ')。
基于这个性质,为了挖掘频繁子图,只需要对最小DFS 编码执行最右扩展,因为这种扩展将确保挖掘结果的完全性。
算法:gSpan 。
基于模式增长的频繁子结构挖掘算法,减少复制图的产生输入:DFS 编码s图数据集D最小支持度阈值min_sup输出:频繁图的集合S方法:φ←S 调用gSpan(s ,D ,min_sup ,S )procedure gSpan(s ,D ,min_sup ,S )(1) if then)(s dfs s ≠(3) 将s 插入S(5) 扫描D 一次,找出所有使s 可以最右扩展为的边e 将插入C 并计算它的频度e s r ◊(7) for each C 中频繁的do (8) gSpan( ,D ,min_sup ,S )(9) return(2) return(4) 设置C 为φe s r ◊(6) 按DFS 词典序对C 排序e s r ◊e s r ◊(4)论文的主要创新之处频繁子模式挖掘一直是许多科学和商业应用中新兴的数据挖掘问题。
作为一个一般的数据结构,可以使用标记图来建模数据中复杂的子结构模式。
频繁子图挖掘的核心是子图同构 试验。
开发了很多知名的成对的同构测试算法。
然而,频繁的子图挖掘问题并没有很好探索。
近日,Inokuchi 提出了一种基于Apriori 的算法,叫做AGM ,发现所有的频繁(同时连接和 断开)子结构。
Kuramochi 和Karypis 使用邻接表图形和一个边生长的策略进一步发展了这个思想。
他们的算法,被称为FSG ,对于相同的数据集,我们的新算法可以在10秒内完成相同的任务。
AGM 和FSG 都采用了Apriori 逐层方法的优势。
在频繁子图挖掘中,AMG 算法面临两个挑战:候选集,k 个频繁子图生成的(k+1)个候选子图更加复杂,代价更大;修剪错误肯定,子图同构测试是一个NP 完全问题,因此修剪的代价十分大。
在本文中,我们研究gSpan ,它的目标是减少或避免了以上提到的较大成本。
二、实验评价(500~1000字):(1)实验数据集综合数据集:使用所相似方法来生成合成数据集,Kuramochi 在图数据合成的时候采用了一个简化的程序。
我们使用他们的数据生成器,gSpan 在使用不同的参数的各种合成数据集下进行测试,N (可能的标签数),I (潜在频繁核心子图的平均大小),T (图中的边缘的的平均大小),K D 10=(生成图形的总数),200=L (潜在频繁核心数量),D Sup ⨯=01.0min ,在下图中表示在6和30之间加速Runtime: Synthetic data化合物数据集:数据集包含340个化合物,24个不同的原子,66个原子类型。
数据集是稀疏的,每张图平均包含27个结点、28个边缘。
最大的图包含214个结点和214个边缘。
所以发现模式很像一棵树,虽然他们包含了一些周期。
我们使用原子类型作为标记,目的是找到相同的化合物子结构,下图阐述了minSup 从2%到30%之间gSpanh 和FSG 的运行时间。
gSpan 的总内存消耗低于100M ,当minSup 低于5%时,程序由于主存耗尽或运行时间过长而退出。
下图也表明了gSpan 相较于FSG 实现了更高的性能Runtime: Chemical data(2)评价指标和性能分析在我们的实验中已经对合成和真实世界的数据集进行一种综合性能的研究。
我们使用由Kuramochi和Karypis提供了一种合成的数据产生器。
我们测试的真实数据集是一种化学化合物的数据集。
gSpan的所有实验都是在500MHz的Intel Pentium III处理器的PC机的448MB 主内存上完成,运行小红帽Linux6.2。
我们还实现了文章中报道的具有类似性能的FSG版本。
如示于上图所示,如果结果可用,我们比较gSpan与FSG,否则我们基于相同的数据集展示自己的实现结果,在具有类似配置的Linux机器上做了试验。
(3)本文方法的优点总结在本文中,我们引入了一个新的词典序列系统,并且在大型图形数据库中研发了一个用于频繁子图的有效挖掘的深度优先搜索的挖掘算法gSpan。
我们的研究表明,相比于以往研究,gSpan优于FSG一个数量级,而且gSpan能够在具有较低的最小支持度下的较大子图中挖掘更大的频繁子图。
gSpan算法比AGM、FSG算法计算更高效,而且它采取从内存到磁盘交换数据,减少了内存的消耗。
gSpan和FSG算法能够找到所有符合用户要求的子图,但是都产生大量的子结构。
(4)本文方法的缺点和局限性在后来实现完算法之后,对于其中的小的过程进行了分析,发现这个算法在2个深度优先遍历的过程中还存在问题,就是DFS判断是否最小编码和对原图进行寻找相应编码的时候,都只是限于Edge中边是连续的情况,如果不连续了,会出现判断出错的情况,因为在最右路径上添加边,就是会出现在前面的点中多扩展一条边,就不会是连续的,这里用栈的方式,将节点压入栈中实现应该可以解决。
