微电子器件公式表
微电子器件公式表

微电子器件公式: 部分物理常数:191412S 1031412G i S 13314G i O X 1.610C,0.026V (300k ),(Si)11.88.854101.04510F cm ,(Si) 1.09eV ,(Si) 1.510cm,(G e)168.854101.41710F cm ,(G e)0.66eV ,(G e)2.410cm ,3.98.854103.45q kT q T E n E n εεε--------=⨯===⨯⨯=⨯==⨯=⨯⨯=⨯==⨯=⨯⨯=13310F cm-⨯第1章 半导体器件基本方程 1. 泊松方程D A sd ()d E qp n N N xε=-+-2. 电流密度方程n nnp ppd d d d nJ q n E q D x p J q p E q D xμμ=+=-3. 电荷控制方程n nn n p pp pd d d d Q Q I t Q Q I tττ∆=--∆=--第2章 PN 结 2.1 PN 结的平衡状态1.平衡多子p 0A in 0D i ()p Nn n N n =>>=>>P 区(N 区)2.平衡少子22iip 0i p 0A 22iin 0in0D()n n n n P p N nnp n n N ==<<==<<区(N 区)3.内建电势 A Dbi 2ilnN N kT V qn =4.最大电场强度 120maxb i s 2qN E V ε⎛⎫= ⎪⎝⎭5.N 区耗尽区宽度 12s s An maxbi DD A D 2()N xE V qN q N N N εε⎡⎤==⋅⎢⎥+⎣⎦6.P 区耗尽区宽度 12s s D p maxbi AA A D 2()N x E V qN q N N N εε⎡⎤==⋅⎢⎥+⎣⎦7.总耗尽区宽度 12b is d n p b i ma x 022V x x x V E qN ε⎡⎤=+==⎢⎥⎣⎦2.2 PN 结的直流电流电压方程1.在N 型区与耗尽区的边界处,即 n x 处 n n n0()e x p qV p x pkT ⎛⎫= ⎪⎝⎭在P 型区与耗尽区的边界处,即 –p x 处 p p p 0()exp qV n x n kT ⎛⎫-= ⎪⎝⎭2.PN 结总的扩散电流密度 d Jp p 2n n d dp dnn0p 0i p n p D n A 0exp 1exp 1exp 1D D D D qV qV J J J q p n qn L L kT L N L N kT qV J kT ⎛⎫⎛⎫⎡⎤⎡⎤⎛⎫⎛⎫=+=+⋅-=+⋅- ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎣⎦⎣⎦⎝⎭⎝⎭⎡⎤⎛⎫=- ⎪⎢⎥⎝⎭⎣⎦3.势垒区产生复合电流 n pi d grd exp 1d 2exp 12x x qV qn x kT J q U x qU x qV kT τ-⎛⎫- ⎪⎝⎭===⋅⎛⎫+ ⎪⎝⎭⎰ 4.薄基区二极管扩散电流 22p i n i dp dn B D E A exp 1...exp 1qD n qD n qV qV J J W N kT W N kT ⎡⎤⎡⎤⎛⎫⎛⎫=-=- ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦2.3 准费米能级与大注入效应1.转折电压i i D K N K P 2ln ()2ln kT V N q n kT V qn ⎛⎫=⎪ ⎪⎝⎭⎛=⎝⎭区P 区) 2.大注入下结定律()()n n i p p i exp 2exp 2qV p x n kT qV n x n kT ⎛⎫= ⎪⎝⎭⎛⎫-= ⎪⎝⎭2.4 PN 结的击穿1.雪崩倍增因子 d i 011d x M xα=-⎰2.雪崩击穿近似计算120C B s 2qN E V ε⎛⎫= ⎪⎝⎭2.5 PN 结的势垒电容 ()()11223s 0sT T bi bi()...212qN aq C A C A V V V V εε⎡⎤⎡⎤==⎢⎥⎢⎥--⎣⎦⎣⎦均匀(缓变)2.6 PN 结的交流小信号特性与扩散电容 1. PN 结的直流增量电导 F D qI g kT=2. PN 结的扩散电容 F D D 22qI g C kTττ==2.7 PN 结的开关特性 1.反向恢复时间r t f r r p r ln I I t I τ⎛⎫+= ⎪⎝⎭第3章 双极结型晶体管3.1 双极结型晶体管基础 电流放大系数关系:C B.........11I I αββααβ===-+3.2 均匀基区晶体管的电流放大系数 1.基区输运系 2pC B pE B 112J W J L β*⎛⎫==- ⎪⎝⎭bB 1ττ=- 2.基区度越时间 2B bB2W D τ=B B pE pC Q Q J J =≈ 3.基区少子寿命 B B prQ J τ=4.注入效率 B EE B1W W ργρ=-11E B R R =-口口5.共基极电流放大系数 22E E B B22B B1B B1111122R R W W L R L R αδ⎛⎫⎛⎫=--≈--=- ⎪ ⎪⎝⎭⎝⎭口口口口 6.共发射极电流放大系数 1121E b E B 2BB1BB112R RW L R R τδβδδτ---⎛⎫⎛⎫-=≈=+=+ ⎪ ⎪⎝⎭⎝⎭口口口口7.异质结双极晶体管(HBT ) E G B11exp R E R kT γ∆⎛⎫=- ⎪⎝⎭口异口3.4 双极晶体管的直流电流电压方程1.埃伯斯-莫尔方程BC BE E ES R C SBC BE C ES C Sexp 1exp 1exp 1exp 1qV qV I I I kT kT qV qV I I I kT kT αα⎡⎤⎡⎤⎛⎫⎛⎫=--- ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦⎡⎤⎡⎤⎛⎫⎛⎫=--- ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦2.共发射极电流方程BC BE B ES R C SBC BE C ES C S(1)exp 1(1)exp 1exp 1exp 1qV qV I I I kT kT qV qV I I I kT kT ααα⎡⎤⎡⎤⎛⎫⎛⎫=--+-- ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦⎡⎤⎡⎤⎛⎫⎛⎫=--- ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦3.厄尔利电压 B B B B 0A dB B B B B BC BC E d d d d ()()d d W W N xN x V x W N W N W V V ≡=⎛⎫- ⎪⎝⎭⎰⎰4.共发射极增量输出电阻 C E A o CCV V r I I ∂≡=∂ 5.均匀基区厄尔利电压 B biA dB2,W V V x =3.5 双极晶体管的反向特性 1.浮空电势 BE ln(1)0kT V qα=-< 2.基区穿通电压 2B ptC B B s C ()2N q V N N W N ε⎛⎫=+ ⎪⎝⎭3.击穿电压 CBO B BV V = (共基极)C EO BV =(共发射极)3.6 基极电阻 b e bb B 3B 2B1b26212S S C d r R R R lS lllΩ'=+++口口口3.8 电流放大系数与频率的关系 1.特征频率 ()T ece bb d c1122f πτπττττ==+++0βf β=T||,()ff f f ωββ=<<2dc Bec T E cs T C TEBm ax1211222x W kT C r C f qI D v τπηη⎛⎫==+⋅-++ ⎪⎝⎭ 3.10 功率增益和最高振荡频率1.最大功率增益 o max Tp max 2inbb TC 8P f K P r C fπ'==2.高频优值 2Tp m ax bb T C8f M K fr C π'≡=3.最高振荡频率 112T 2Mbb T C 8f f Mr C π'⎛⎫== ⎪⎝⎭第 5 章 绝缘栅场效应晶体管5.2 MOSFET 的阈电压1.P 型衬底的费米势 A FP i F i1ln0N kT E E q qn ϕ=-=>() N 型衬底 D FN iln0N kT qn ϕ=-<2.阈值电压()()()1O X 2T M S FP FPO X12B FB FP S B FP S B 1O X 2M S FP S B FP SO X222222Q V K C V V K V V V V Q K V V V C ϕϕϕϕϕϕϕϕ=-++=+++-++-=-++-++ 5.3 MOSFET 的直流电流电压方程1.电流电压方程 ()2D G S T D S D S p O XD sat G S T22D sat G S T D sat D sat G S T 1()()....211()22Z I V V V V C L V V V I V V V V V V ββμββ⎡⎤=--=⎢⎥⎣⎦=-⎡⎤=--=-⎢⎥⎣⎦非饱和区(饱和区)5.5 MOSFET 的直流参数与温度特性 1.通导电阻 on R D S on DG S T n O X G S T 1()()V LR I V V Z C V V βμ===--5.6 MOSFET 的小信号参数、高频等效电路及频率特性1.跨导mg m D S m s G S T D sat ()()g V g V V V βββ==-=非饱和区(饱和区)2.漏源电导ds gd s G ST DSDs a td s s a tD Sg VV V I g V β=--∂==∂()()3.跨导的截止角频率 m n G S T g 2g s g s()1154V V R CLμω-==⋅ 4.本征最高工作频率 msn G S TT 2gs()13222g V V f C L μππ-⎡⎤==⋅⎢⎥⎣⎦5.高频功率增益为 22o max ms ds ms dsp max 2222igs gsgs gs44(2)P g r g r K P C R f C R ωπ===6.最高振荡频率M f 1122m s ds dsM T gsgs gs 244g r rf f C RRπ⎛⎫⎛⎫== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭。
微电子器件(2-1)

s
qN D
Emax Emax
1 2
(2-6)
s
qN A
(2-7)
Emax
2qN 0 Vbi s
(2-10)
但是有 4 个未知数,即 xn 、 p 、Emax 和 Vbi 。下面用另一种方法 x 来求 Vbi 。
已知在平衡状态下,净的空穴电流密度为零,故由空穴的
电流密度方程可得
代入载流子浓度表达式中,得
q ( x) n0 ( x) nn 0 exp kT
qVbi q ( x) p0 ( x) pp0 exp kT
2.1.4 线性缓变结
在线性缓变结中,杂质分布为 ND - NA = ax , 耗尽近似下的泊松方程为
2
2 x 2 1 xd
xd 2
0
xd 2
x
上式中, Emax 内建电势 Vbi 为
2 aqxd 8 s
Vbi
xd 2 x d 2
2 NA ND kT E ( x) dx Emax xd ln q ni2 3
将上面关于 Emax 与 xd 的两个方程联立,可解得
pp0
ni2 ni2 由于 pp0 N A ,pn0 ,故得 nn0 N D
kT N A N D Vbi ln q ni2
(2-13)
Vbi 与掺杂浓度、温度及半导体的种类有关。在通常的掺杂 范围和室温下,硅的 Vbi 约为 0.75V,锗的 Vbi 约为 0.35V。
最后可得
2 s s NA xn Emax Vbi qN D q ND ( NA ND ) 2 s s ND xp Emax Vbi qN A q NA ( NA ND )
微电子器件原理总结

三种管子的工作原理、符号、结构、电流电压方程、电导、跨导、频率然后还有集边效应,二次击穿双极型晶体管:发射极电流集边效应:(1)定义:由于p-n 结电流与结电压的指数关系,发射结偏压越高,发射极边缘处的电流较中间部位的电流越大(2)原因:基区体电阻的存在引起横向压降所造成的(3)影响:增大了发射结边缘处的电流密度,使之更容易产生大注入效应或有效基区扩展效应,同时使发射结面积不能充分利用(4)限制:限制发射区宽度,定义发射极中心到边缘处的横向压降为kT /q 时所对应的发射极条宽为发射极有效宽度,记为2S eff 。
S eff 称为有效半宽度。
发射极有效长度 :(1)定义:沿极条长度方向,电极端部至根部之间压降为kT/q 时所对应的发射极长度称为发射极有效长度(2)作用:类似于基极电阻自偏压效应,但沿Z 方向,作用在结的发射区侧二次击穿和安全工作区:(1)现象:当晶体管集电结反偏增加到一定值时,发生雪崩击穿,电流急剧上升。
当集电结反偏继续升高,电流I c 增大到某—值后,cb 结上压降突然降低而I c 却继续上升,即出现负阻效应。
(2)分类:基极正偏二次击穿(I b >0)、零偏二次击穿和(I b =0)、反偏二次击穿(I b <0)。
(3)过程:①在击穿或转折电压下产生电流不稳定性;②从高电压区转至低电压区,即结上电压崩落,该击穿点的电阻急剧下降;③低压大电流范围:此时半导体处于高温下,击穿点附近的半导体是本征型的;④电流继续增大,击穿点熔化,造成永久性损坏。
(4)指标:在二次击穿触发时间t d 时间内,消耗在晶体管中的能量 ⎰=dt SB IVdt E 0称为二次击穿触发能量(二次击穿耐量)。
晶体管的E SB (二次击穿触发功率P SB )越大,其抗二次击穿能力越强。
(5)改善措施:1、电流集中二次击穿①由于晶体管内部出现电流局部集中,形成“过热点”,导致该处发生局部热击穿。
②导致电流局部集中的原因:1.大电流下I e的高度集边。
微电子器件(3-10)
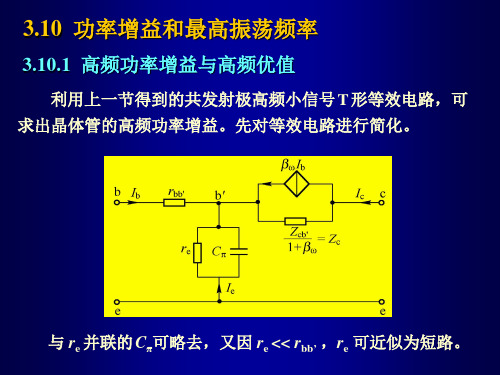
fT M ≡ K p max f = 8 π rbb′ CTC
2
高频优值也称为 功率增益-带宽乘积,是综合衡量晶体管的 功率放大能力与频率特性的重要参数。
3.10.2 最高振荡频率
定义:当 Kpmax 下降到 1 时的频率称为 最高振荡频率,记 为 fM 。 令 Kpmax = 1 ,可得
要使 τb↓,应: (1) WB↓( 但会使 rbb’↑,VA↓,且受工艺限制) (2) η↑ ( 采用平面工艺 ) 要使 τd↓,应:xdc↓ →NC↑( 但会使 BVCBO↓ , CTC↑) 要使 τc↓,应: ① NC↑( 但会使 BVCBO↓ , CTC↑) (1) rcs↓ ② 集电区厚度 dc↓ ③ AC↑( 但会使 CTC↑) (2) CTC↓ ① AC ↓ ② NC ↓( 但会使 rcs↑)
可见,Zc 相当于电阻() 2π f T CTC
−1
和电容 CTC 的并联。
于是原 T 形等效电路
经简化并接上共轭匹配负载后,成为
当负载阻抗 ZL 等于 Zc 的共轭复数 Zc* 时,可得到最大输出 功率。这时电流源 βω I b 的电流中有一半流经负载。
| Ic | | = | = 2
βω I b
re 1 1 = + jω CμDE ≈ jω TC C Z cbμ ′o r r
β0
+C TC ≈ jω C
fT 当 f >> f β 时,βω = ≈ =−j f jf f 1+ j fβ
β0 f β
fT 1 1 + βω jωCTC + 2π f T CTC = = 1 − j jωCTC = Zc Z cb′ f
微电子器件基础第一章补充共17页PPT资料

Jn
qnnE
qDn
dn dx
Jp
qp
pE
qDp
dp dx
(1-10) (1-11)
1.1.3 连续性方程
n t
1 q
Jn x
Un
p t
1 q
Jp x
Up
(1-12) (1-13)
1.2 基本方程的简化与应用举例
例 1.1 对于方程 ( 1-9 )
ddE xqspnNDNA
在耗尽区中,可假设 p = n = 0 ,又若在 N 型耗尽区中,则还可 忽略 NA ,得
dE dx
q
s
ND
(1-14)
若在 P 型耗尽区中,则得
dE dx
q
s
NA
例 1.2 对于方程(1-10),
式中的 Un 和 Up 分别代表电子和空穴的 净复合率。当 U > 0 时表示净复合,当 U < 0 时表示净产生。
所谓连续性是指载流子浓度在时空上的连续性,即:造成 某体积内载流子增加的原因,一定是载流子对该体积有净流入 和载流子在该体积内有净产生。
1.1.4 方程的积分形式
以上各方程均为微分形式。其中泊松方程和连续性方程可 根据场论中的积分变换公式而变为积分形式。
Jn
qnnEqDn
dn dx
当载流子浓度和电场很小而载流子浓度的梯度很大时,则
漂移电流密度远小于扩散电流密度,可以忽略漂移电流密度,
方程(1-10)简化为
Jn
qDn
微电子器件(24)解读
所以 对积分起主要作用的 只是 电场峰值附近很小一部分区域。 这个区域内 Emax 几乎不变,因 此可以近似认为,当 Emax 达到 某 临界电场 EC 时,即满足击穿 条件,从而发生雪崩击穿。
EC 与结的形式和掺杂浓度稍微有关,硅 PN 结的典型值为
EC 2105 V cm
Jp0
N区
0
x x dx
P区
xd
单位时间内流过位于 x 处单位面积的空穴数目为
1 q
Jp (x)
Jp0
由于这些空穴的碰撞电离而在 dx 距离内新增的流出 ( x+dx )
面的空穴数目为
1 q
J
p
(
x)
J
p
0
ipdx
同理,由于电子的碰撞电离在 dx 距离内新增的流出 ( x+dx )
面的空穴数目为
2.4 PN 结的击穿
击穿现象
VB
I
V
I0
击穿机理: 雪崩倍增 隧道效应 热击穿
电击穿
2.4.1 碰撞电离率和雪崩倍增因子
电子(或空穴)在两次碰撞之间从电场 E 获得的能量为
l
E q0 Edx
在耗尽区中,反向电压 , E , E , 当 E EG 时,
就会使被碰撞的价带电子跃迁到导带,从而产生一对新的电子 空穴对,这叫做 碰撞电离。
实际扩散结的击穿电压 硅平面工艺中,常采用杂质扩散工艺制造 PN 结。从表面 到冶金结面的距离,称为 结深,用 xj 表示。
P xj
N(0)
N(x)
N x
N0
0 xj
x
由扩散工艺形成的实际扩散结,其杂质分布既非突变结, 也非线性缓变结,而是 余误差分布 或 高斯分布。
模电公式总结

模电公式总结1. 基本电路参数1.1 电流公式•电流公式:$$I = \\frac{V}{R}$$–其中,I为电流,V为电压,R为电阻。
1.2 电压公式•电压公式:$$V = I \\cdot R$$–其中,V为电压,I为电流,R为电阻。
1.3 功率公式•功率公式:$$P = V \\cdot I$$–其中,P为功率,V为电压,I为电流。
2. 放大电路2.1 电压放大倍数•电压放大倍数:$$A_v = \\frac{V_o}{V_i}$$–其中,A_v为电压放大倍数,V_o为输出电压,V_i为输入电压。
2.2 增益•增益:$$G = \\frac{V_o - V_i}{V_i}$$–其中,G为增益,V_o为输出电压,V_i为输入电压。
3. 滤波电路3.1 截止频率•截止频率:$$f_c = \\frac{1}{2\\pi RC}$$–其中,f_c为截止频率,R为电阻,C为电容。
4. 频率响应4.1 相位差•相位差:$$\\phi = \\arctan(\\frac{X_L - X_C}{R})$$–其中,X_L为电感的电抗,X_C为电容的电抗,R为电阻。
4.2 增益•增益:$$|A_v| = \\sqrt{\\frac{X_L - X_C}{R}^2 + 1}$$–其中,|A_v|为增益,X_L为电感的电抗,X_C为电容的电抗,R为电阻。
5. 脉冲响应5.1 集成电路•脉冲响应:$$h(t) = V_i(t) \\ast g(t)$$–其中,h(t)为脉冲响应,V_i(t)为输入信号,g(t)为脉冲响应函数。
6. 非线性电路6.1 二极管方程•二极管方程:$$I_D = I_s(e^{\\frac{V_D}{V_t}} - 1)$$–其中,I_D为二极管正向电流,I_s为饱和电流,V_D为二极管正向电压,V_t为温度标准电压。
7. 反馈电路7.1 闭环增益•闭环增益:$$A_f = \\frac{A}{1 + A\\beta}$$–其中,A为开环增益,$\\beta$为反馈系数。
微电子器件(3-2)

均匀基区pnp晶体管能带图 放大状态:EFn − EFp = qV饱和状态:截止状态:倒向放大状态: 平衡态均匀基区pnp晶体管的各边界上少子浓度⎛ qVEB ⎞ nE = nE0 exp ⎜ ⎟ kT ⎝ ⎠E Emitter P⎛ qVEB ⎞ pB = pB0 exp ⎜ ⎟ ⎝ kT ⎠Base N Collector P CnE = nE0BnC = nC0⎛ qVCB ⎞ pB = pB0 exp ⎜ ⎟ ⎝ kT ⎠⎛ qVCB ⎞ nC = nC0 exp ⎜ ⎟ ⎝ kT ⎠均匀基区pnp晶体管的少子分布图: 放大状态:饱和状态:截止状态:倒向放大状态:忽略势垒区产生复合电流, 处于放大状态的晶体管内部的 各电流成分如下图所示:I pEI pCI prI nEI nrI ncI E = I pE + I nE , I B = I nE + I nr − I nc ≈ I nE + I nr , I C = I pc + I nc ≈ I pC = I pE − I pr = I E − I nE − I nrI pEI pCI prI nEI nr从 IE 到 IC ,发生了两部分亏损(PNP): InE 与 In r 。
要减小 InE ,就应使NE >> NB ; 要减小In r ,就应使WB << LB 。
§ 3-2 均匀基区晶体管的放大系数均匀基区晶体管:基区掺杂为均匀分布。
少子在基区中主 要作扩散运动,又称为 扩散晶体管。
(本节以pnp为例)均匀基区晶体管(理想晶体管)• 发射区、基区、集电区均匀非简并掺杂,发射结与集 电结为突变结; • 晶体管在一维稳态条件下工作; • 中性区满足小注入水平; • 发射结与集电结的耗尽区内复合-产生可以忽略不 计; • 发射区与集电区的中性区宽度远大于少子扩散长度, 而基区的中性区宽度则远小于少子扩散长度。
大学物理下册公式大全

大学物理第二学期公式集电磁学1.定义:①E 和B :F =q(E +V ×B)洛仑兹公式②电势:⎰∞⋅=rr d E U电势差:⎰-+⋅=l d E U电动势:⎰+-⋅=l d K ε(qF K 非静电 =)③电通量:⎰⎰⋅=S d E eφ磁通量:⎰⎰⋅=S d B Bφ磁通链:ΦB =N φB 单位:韦伯(Wb ) 磁矩:m =I S=IS nˆ ④电偶极矩:p =q l⑤电容:C=q/U 单位:法拉(F )*自感:L=Ψ/I单位:亨利(H ) *互感:M=Ψ21/I 1=Ψ12/I 2 单位:亨利(H ) ⑥电流:I =dtdq ; *位移电流:I D =ε0dtd e φ 单位:安培(A )⑦*能流密度: B E S⨯=μ12.实验定律①库仑定律:0204r r Qq F πε=②毕奥—沙伐尔定律:204ˆr r l Id B d πμ⨯=③安培定律:d F =I l d ×B④电磁感应定律:ε感= –dtd Bφ 动生电动势:⎰+-⋅⨯=l d B V)(ε感生电动势:⎰-+⋅=l d E iε(E i 为感生电场)E =F/q 0 单位:N/C =V/mB=F max /qv ;方向,小磁针指向(S →N );单位:特斯拉(T )=104高斯(G )Θ ⊕-q l +q*⑤欧姆定律:U=IR (E =ρj)其中ρ为电导率3.*定理(麦克斯韦方程组)电场的高斯定理:⎰⎰=⋅0εq S d E ⎰⎰=⋅0εq S d E 静(E静是有源场)⎰⎰=⋅0S d E感 (E 感是无源场)磁场的高斯定理:⎰⎰=⋅0S d B⎰⎰=⋅0S d B(B 稳是无源场) ⎰⎰=⋅0S d B(B 感是无源场)电场的环路定理:⎰-=⋅dtd l d EB φ⎰=⋅0l d E静(静电场无旋) ⎰-=⋅dtd l d E B φ感(感生电场有旋;变化的磁场产生感生电场)安培环路定理:d I I l d B 00μμ+=⋅⎰⎰=⋅I l d B 0μ稳(稳恒磁场有旋) dtd l d Be φεμ00⎰=⋅ 感(变化的电场产生感生磁场)4.常用公式①无限长载流导线:r I B πμ20= 螺线管:B=nμ0I②带电粒子在匀强磁场中:半径qBmV R =周期qBm T π2=磁矩在匀强磁场中:受力F=0;受力矩B m M⨯=③电容器储能:W c =21CU 2 *电场能量密度:ωe =21ε0E 电磁场能量密度:ω=21ε0E 2+021μB 2*电感储能:W L =21LI 2 *磁场能量密度:ωB =021μB 2电磁场能流密度:S=ωV④ *电磁波:C=001εμ=3.0×108m/s 在介质中V=C/n,频率f=ν=021εμπ波动学1.定义和概念简谐波方程: x 处t 时刻相位 振幅简谐振动方程:ξ=Acos(ωt+φ) 波形方程:ξ=Acos(2πx/λ+φ′)相位Φ——决定振动状态的量振幅A ——振动量最大值 决定于初态 x0=Acos φ 初相φ——x=0处t=0时相位 (x 0,V 0) V 0= –A ωsin φ 频率ν——每秒振动的次数圆频率ω=2πν 决定于波源如: 弹簧振子ω=m k / 周期T ——振动一次的时间 单摆ω=l g /波速V ——波的相位传播速度或能量传播速度。
微波常用公式

常用公式
1.常用公式
⑴交流电压有效值V e=电压最大值V m/
交流电压峰峰值V pp= 2 V m = 2 V e
功率P= V e2/ R(负载电阻)= V pp2/ 8R
dBm=10 log(P/mW)
⑵波长λ与频率f的乘积等于光速,即λf=3×108m/s,
或λ=300(m)/f(MHz)。
后面有频段划分与波长对照表。
⑶同轴线特性阻抗,式中D为外导体内径,d为内导体外径,为有效介电
常数。
Z C泛指一般特性阻抗,而Z C=50Ω时,通常称为Z0。
⑷反射系数,这是最基本的公式,矢量网络分析仪能测量
反射系数的幅值|Γ|与相位角∠,然后经过计算得到其他参数。
⑸驻波比是一个最常见的指标,它表征了线上最大电压与最小电压的比值。
这是
以往测量线时代留下来的一个名词,大家已经习惯了。
⑹回损RL=20 ㏒|Γ|。
微电子器件 (附答案) (第三版)

kT ln ND= NA
q
ni2
=q 1.6 ×10−19 C,= εS 1.045×10−12 F cm ,
代入 | Emax |中,得:| Em= ax | 1.52 ×104 V cm
shanren
0.757 V,
8、(1)
N
I
P
−xi1 − xn −xi1 0 xi2
xi2 + xp
在 N型区,= dE1 dx
shanren
6、
ND2
ND1
由平衡时多子电流为零
Jn
=
qDn
dn dx
+
qµn nE
=
0
得: E =− Dn ⋅ 1 ⋅ dn =− kT ⋅ 1 ⋅ dn =− kT ⋅ d ln n
µn n dx
q n dx
q dx
∫ Vbi
= − ND1 Edx ND2
= kT ln n | q
ND1 ND2
− Emax
+
E
(
x)
= q N
εs
D
x
当 x = xn 时,E(x) = 0,因此
Emax
=
−q
εs
ND xn ,于是得:
E ( x=)
q
εs)
ND
(0 ≤ x ≤ xn )
shanren
(2-5a)
3、
(1)
Vbi
= kT ln N q
A ND ni2
= 0.026× ln
5 ×1032 2.25 ×1020
2
=
3.40×10−5 cm
shanren
4、
微电子器件(3-4)
基区穿通时的 BVCBO与Vpt是否相等?为什么?
在进行BVCBO的测试时,发射结上 存在浮空电势,它使其反偏,发生 穿通时,由于发射结反偏,所以并 未发生击穿,直到发射结达到击穿 电压才发生击穿。
BVCBO V pt BVEBO
3)基区穿通时的 BVCEO
BVCEO V pt VF V pt
例: 若 0.99,则VBE 0.12V, n p (0) 9.9 10-3 n po
2、反向截止电流 1)IEBO和ICBO
n
p
n
n
p
n
定 义
ICBO表示集电极 IEBO表示集电极 开路时发射结的 开路时发射结的 反向饱和漏电流。 反向饱和漏电流。
ICBO ICS 1 R
但因 IE = 0 ,基区少子得不到 补充,使在靠近发射结一侧,
有:np(0) < npo ,根据边界条件,
这说明发射结上存在一个反向 电压,这就是 浮空电势 。 已知 NPN 管的共基极电流-电压方程为:
qVBE I E I ES exp kT
qVBC - 1 - R I CS exp kT qVBC - 1 - I CS exp kT
- 1
(1)
qVBE I C I ES exp kT
- 1
(2)
将 IE = 0 代入方程 ① , 得:
I CS qVBE exp kT 1 R I ES
考虑到 VBC
ICBO的测 试电路
ICBO ICS 1 R I EBO I ES 1 R
2)ICEO
微电子器件公式

微电子器件公式: 部分物理常数:191412S 1031412G i S 13314G i O X 1.610C,0.026V (300k ),(Si)11.88.854101.04510F cm ,(Si) 1.09eV ,(Si) 1.510cm,(G e)168.854101.41710F cm ,(G e)0.66eV ,(G e)2.410cm ,3.98.854103.45q kT q T E n E n εεε--------=⨯===⨯⨯=⨯==⨯=⨯⨯=⨯==⨯=⨯⨯=13310F cm-⨯第1章 半导体器件基本方程 1. 泊松方程D A sd ()d E qp n N N xε=-+-2. 电流密度方程n nnp ppd d d d nJ q n E q D x p J q p E q D xμμ=+=-3. 电荷控制方程n nn n p pp pd d d d Q Q I t Q Q I tττ∆=--∆=--第2章 PN 结 2.1 PN 结的平衡状态1.平衡多子p 0A in 0D i ()p Nn n N n =>>=>>P 区(N 区)2.平衡少子22iip 0i p 0A 22iin 0in0D()n n n n P p N nnp n n N ==<<==<<区(N 区)3.内建电势 A Dbi 2ilnN N kT V qn =4.最大电场强度 120maxb i s 2qN E V ε⎛⎫= ⎪⎝⎭5.N 区耗尽区宽度 12s s An maxbi DD A D 2()N xE V qN q N N N εε⎡⎤==⋅⎢⎥+⎣⎦6.P 区耗尽区宽度 12s s D p maxbi AA A D 2()N x E V qN q N N N εε⎡⎤==⋅⎢⎥+⎣⎦7.总耗尽区宽度 12b is d n p b i ma x 022V x x x V E qN ε⎡⎤=+==⎢⎥⎣⎦2.2 PN 结的直流电流电压方程1.在N 型区与耗尽区的边界处(即n x 处)少子浓度 n n n0()e x p qV p x pkT ⎛⎫= ⎪⎝⎭在P 型区与耗尽区的边界处(即 –p x 处)少子浓度 p p p 0()exp qV n x n kT ⎛⎫-= ⎪⎝⎭2.PN 结总的扩散电流密度 d Jp p 2n n d dp dnn0p 0i p n p D n A 0exp 1exp 1exp 1D D D D qV qV J J J q p n qn L L kT L N L N kT qV J kT ⎛⎫⎛⎫⎡⎤⎡⎤⎛⎫⎛⎫=+=+⋅-=+⋅- ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎣⎦⎣⎦⎝⎭⎝⎭⎡⎤⎛⎫=- ⎪⎢⎥⎝⎭⎣⎦3.薄基区二极管小子分布关系:n n0B ()exp 11qV x p x p kT W ⎛⎫⎡⎤⎛⎫∆=-⋅-⎪ ⎪⎢⎥⎝⎭⎣⎦⎝⎭ 2.4 PN 结的击穿1.雪崩倍增因子 d i 011d x M xα=-⎰2.雪崩击穿近似计算120C B s 2qN E V ε⎛⎫= ⎪⎝⎭3.突变结果的临界电场 131247G 8C 0s 1.110 1.1E q E N ε⎛⎫⎛⎫=⨯ ⎪ ⎪⎝⎭⎝⎭4.突变结外加反向电压时的最大电场强度112200m axbi s s 22||()qN qN E V V V εε⎡⎤⎛⎫=-≈ ⎪⎢⎥⎣⎦⎝⎭5.突变结果的雪崩击穿电压 33213s24B CG 05.2102V E E N qN ε-==⨯2.5 PN 结的势垒电容 ()()11223s 0sT T bi bi ()...212qN aq C A C A V V V V εε⎡⎤⎡⎤==⎢⎥⎢⎥--⎣⎦⎣⎦均匀(缓变)2.6 PN 结的交流小信号特性与扩散电容 1. PN 结的直流增量电导 F D qI g kT= 2. PN 结的扩散电容 F D D 22qI g C kTττ==第3章 双极结型晶体管3.1 双极结型晶体管基础 电流放大系数关系:C B.........11I I αββααβ===-+3.2 均匀基区晶体管的电流放大系数 1.基区输运系 2pC B pE B 112J W J L β*⎛⎫==- ⎪⎝⎭bB1ττ=- 2.基区度越时间 2B bB 2W D τ=B B pE pC Q Q J J =≈ 3.基区少子寿命 B B prQ J τ=4.注入效率 B EE B1W W ργρ=-11E B R R =-口口 5.共基极电流放大系数 22E E BB22BB1B B1111122R R W W L R L R αδ⎛⎫⎛⎫=--≈--=- ⎪ ⎪⎝⎭⎝⎭口口口口6.共发射极电流放大系数 121E B 2B B 112R W L R δβδδ--⎛⎫-=≈=+ ⎪⎝⎭口口7.异质结双极晶体管(HBT ) E G B11exp R E R kT γ∆⎛⎫=- ⎪⎝⎭口异口3.4 双极晶体管的直流电流电压方程1.埃伯斯-莫尔方程BC BE E ES R C SBC BE C ES C Sexp 1exp 1exp 1exp 1qV qV I I I kT kT qV qV I I I kT kT αα⎡⎤⎡⎤⎛⎫⎛⎫=--- ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦⎡⎤⎡⎤⎛⎫⎛⎫=--- ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦2.共发射极电流方程BC BE B ES R C SBC BE C ES C S(1)exp 1(1)exp 1exp 1exp 1qV qV I I I kT kT qV qV I I I kT kT ααα⎡⎤⎡⎤⎛⎫⎛⎫=--+-- ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦⎡⎤⎡⎤⎛⎫⎛⎫=--- ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦3.厄尔利电压 B B B B 0A dB B B B B BC BC E d d d d ()()d d W W N xN x V x W N W N W V V ≡=⎛⎫- ⎪⎝⎭⎰⎰4.共发射极增量输出电阻 C E A o CCV V r I I ∂≡=∂ 5.均匀基区厄尔利电压 B biA dB2,W V V x =3.5 双极晶体管的反向特性 1.浮空电势 BE ln(1)0kT V qα=-< 2.基区穿通电压 2B ptC B B s C ()2N q V N N W N ε⎛⎫=+ ⎪⎝⎭3.击穿电压 CBO B BV V = (共基极)C EO BV =(共发射极)3.6 基极电阻 b e bb B 3B 2B1b26212S S C d r R R R lS lllΩ'=+++口口口3.8 电流放大系数与频率的关系 1.特征频率 ()T ece bb d c1122f πτπττττ==+++0βf β=T||,()ff f f ωββ=<<2dc Bec T E cs T C TEBm ax1211222x W kT C r C f qI D v τπηη⎛⎫==+⋅-++ ⎪⎝⎭ 3.10 功率增益和最高振荡频率 1.最大功率增益 o max Tp max 2inbb TC 8P f K P r C fπ'==2.高频优值 2Tp m ax bb T C8f M K fr C π'≡=3.最高振荡频率 112T 2Mbb T C 8f f M r C π'⎛⎫== ⎪⎝⎭第 5 章 绝缘栅场效应晶体管 5.2 MOSFET 的阈电压1.P 型衬底的费米势 A FP i F i1ln0N kT E E q qn ϕ=-=>() N 型衬底 D FN iln0N kT qn ϕ=-<2.阈值电压()()()1O X 2T M S FP FPO X12B FB FP S B FP S B 1O X 2M S FP S B FP SO X222222Q V K C V V K V V V V Q K V V V C ϕϕϕϕϕϕϕϕ=-++=+++-++-=-++-++ 5.3 MOSFET 的直流电流电压方程1.电流电压方程 ()2D G S T D S D S p O XD sat G S T22D sat G S T D sat D sat G S T 1()()....211()22Z I V V V V C L V V V I V V V V V V ββμββ⎡⎤=--=⎢⎥⎣⎦=-⎡⎤=--=-⎢⎥⎣⎦非饱和区(饱和区)5.5 MOSFET 的直流参数与温度特性 1.通导电阻 on R D S on DG S T n O X G S T 1()()V LR I V V Z C V V βμ===--5.6 MOSFET 的小信号参数、高频等效电路及频率特性1.跨导mg m D S m s G S T D sat ()()g V g V V V βββ==-=非饱和区(饱和区)2.漏源电导ds gd s G ST DSDs a td s s a tD Sg VV V I g V β=--∂==∂()()3.跨导的截止角频率 m n G S T g 2g s g s()1154V V R CLμω-==⋅ 4.本征最高工作频率 msn G S TT 2gs()13222g V V f C L μππ-⎡⎤==⋅⎢⎥⎣⎦5.高频功率增益为 22o max ms ds ms dsp max 2222igsgsgsgs44(2)P g r g r K P C R f C R ωπ===6.最高振荡频率M f 1122m s ds dsM T gsgs gs 244g rrf f C RRπ⎛⎫⎛⎫== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭。
外围元件标称含义和它们取值的计算公式

外围元件标称含义和它们取值的计算公式:Vout(输出电压)=1.25V(1+R1/R2 )Ct( 定时电容):决定内部工作频率。
Ct=0.000 004*Ton(工作频率)Ipk=2*Iomax*T/toffRsc( 限流电阻):决定输出电流。
Rsc=0.33/IpkLmin (电感):Lmin=(Vimin-Vces)*Ton/ IpkCo(滤波电容):决定输出电压波纹系数,Co=Io*ton/Vp-p(波纹系数)固定值参数:ton/toff=(Vo+Vf-Vimin)/(Vimin-Vces)Vces=1.0VVimin:输入电压范围的最小值Vf=1.2V 快速开关二极管正向压降在实际应用中的注意:1、快速开关二极管可以选用IN4148,在要求高效率的场合必须使用IN5819(贴片为SS14);2、34063能承受的电压,即输入输出电压绝对值之和不能超过40V,否则不能安全稳定的工作;3、输出功率达不到要求的时候,比如>1A时,可以通过外接扩功率管的方法扩大输出电流,三极管、双极型或MOS管均可,一般的芯片PDF资料上都会有典型扩流电路介绍;MC34063斩波型电源结构图1 中,T 为开关管,L1 为储能电感,C1 为滤波电容,D1 为续流二极管。
当开关管导通时,电感被充磁,电感中的电流线性增加,电能转换为磁能存储在电感中。
设电感的初始电流为iL0,则流过电感的电流与时间t 的关系为:iLt= iL1+(Vi-Vo-Vs)t/L,Vs 为T 的导通电压。
当T 关断时,L1 通过 D1 续流,从而电感的电流线性减小,设电感的初始电流为 iL1,则则流过电感的电流与时间t 的关系:iLt=iL1-(Vo+Vf)t/L,Vf 为 D1 的正向饱和电压。
MC34063的扩展输出电流的应用DC/DC 转换器 34063 开关管允许的峰值电流为 1.5A,超过这个值可能会造成34063 永久损坏。
由于通过开关管的电流为梯形波,所以输出的平均电流和峰值电流间存在一个差值。
微电子器件(3-5)

微电子器件(3-5)3.5 双极晶体管的反向特性3.5.1 反向截止电流各种反向截止电流的小结(1) IES :VBE < 0 、VBC = 0 时的 IE ,即单个发射结的反向饱和电流。
IESEN+PBNCVBE(2) ICS :VBC < 0 、VBE = 0 时的 IC ,即单个集电结的反向饱和电流。
N+ PBENICSCVBC(3) ICBO :VBC < 0 、IE = 0 时的 IC , I CBO (1 R ) I CS 在共基极电路放大区中,I C I E I CBOEN+PBNICBOCVBC(4) ICEO :VBC < 0 、IB = 0 时的 IC ,I CEO 在共发射极电路放大区中,I CI B I CEO ICEOCI CBO 1I CBOEN+PBNVCE(5) IEBO :VBE < 0 、IC = 0 时的 IE ,I EBO (1 R ) I ES IEBOEN+PBNCVBE3.5.2 共基极接法中的雪崩击穿电压已知 PN 结的雪崩倍增因子 M 可以表示为M 1 1 i dx0 xd在工程实际中常用下面的经验公式来表示当已知击穿电压时 M 与外加电压之间的关系:M 1 V 1 V B S当 |V | = 0 时,M = 1; 当|V | → VB 时,M → ∞ 。
对于硅 PN 结,S = 2 ( PN+ ) S = 4 ( P+N )对于晶体管,在共基极接法的放大区,I C I E I CBO ,当发生雪崩倍增效应时,IC 成为 I C M I E M I CBO AI E I CBO 式中, A M ,I CBO M I CBO ,分别代表计入雪崩倍增效应后的放大系数与反向截止电流。
例 3.1 某硅 NPN 管的 0.98 ,0.99 , 则 0.9702, 取 S 4 。
当 V BC 0.4V B 时, M 1 1-(0.4)41.0263, 这时 A M 0.9955,A与 I CBO 均比与 I CBO 增大了0.0263 倍。
金属电热元件的计算
金属电热元件的计算计算电热元件前,应给出炉子的安装功率、供电线路电压、电热元件材料和电热元件的联接方式。
一、计算公式电热元件的尺寸按下表所列顺序进行计算。
电热元件尺寸计算表注:a------电阻带厚度(mm);b------电阻带宽度(mm);d------电阻丝直径(mm);m------b/a=5~18;g------每米元件重量(kg/m);U------线电压(V);P------安装功率(kW);W y ------元件允许的单位表面功率(W/cm2);ρ20、ρt------20℃及t℃时元件的电阻系数(Ω•mm2/m)。
电热元件有螺旋线、波形线、波形带三种不同结构形式。
1.螺旋线电热元件尺寸每圈螺旋线长度l q=πD (mm)每相电热元件圈数n=1000L x/l q螺旋节距S=L l/n (mm)式中:L l ------螺旋线长度,即炉内安装每相螺旋线的总长度(mm);L x------每相电热元件的长度(m),见上表;D------螺旋平均直径(mm)。
2.波形线电热元件尺寸每一波纹长度l b=2(πh/cosθ+H-2h/ cosθ) (mm)每相电热元件波纹数n=1000L x/l b波形线波距S=L b/n (mm)式中:H------波纹高度(mm);h------波纹弧高(mm);L b------波形线长度,即炉内安装每相波形线的总长度(mm)。
3.波形带电热元件尺寸每一波纹长度l b=2(πr+H-2r)(mm)每相电热元件波纹数n=1000L x/l b波形带波距S=L b/n (mm)式中:H------波纹高度(mm);r------波纹弯曲半径(mm);L b------波形带长度,即炉内安装每相波形带的总长度(mm)。
二、例题室式电阻炉炉膛尺寸为:长×宽×高=1200mm×850mm×800mm,最高工作温度950℃,安装功率为66kW,采用0Cr25Al5螺旋线电热元件,星形接法,供电线路电压380V,求电热元件尺寸。
微电子器件(2-2)

外加反向电压 V (V < 0 ) 后,xd 与 Emax 都增大, PN 结的
势垒高度由 qVbi 增高到 q(Vbi -V )。
外加电场 内建电场
P
N
E
外加反向电压时 平衡时
面积为 Vbi -V
面积为 Vbi
0
x
多子面临的势垒提高了,更不能扩散到对方区域中去了, 但少子面临的势阱也更深了,所以更容易被反向电场拉入对方 区域,从而形成反向电流。 由于反向电流的电荷来源是少子, 所以反向电流很小。
Vbi
kT ln q
pp0 pn0
可知平衡时在 N 型区与耗尽区的边界处即 xn 处的空穴浓度为
pn0
pp0
exp
qVbi kT
外加电压 V 后, Vbi Vbi V
pn0 pn
pp0 pp pp0 (小 注 入 )
从而得:pn
pp0
exp
exp
qV kT
1,
pn x 0 np x 0
当外加正向电压且 V >> kT/q ( 室温下约为 26 mV ) 时,非 平衡少子的边界条件可简化为,
pn (xn )
pn0
e
x
p
qV kT
,
np ( xp )
np0
2.2 PN 结的直流电流电压方程
PN 结在正向电压下电流很大 ,在反向电压下电流很小 , 这说明 PN 结具有单向导电性,可作为二极管使用。
PN 结二极管的直流电流电压特性曲线,及二极管在电路 中的符号为
微电子器件(4-3)

Qn COX VG VB VFB S,inv QA
当外加 VD ( > VS ) 后,沟道中将产生电势 V (y),V (y) 随 y 而 增加 ,从源极处的 V (0) = VS 增加到漏极处的 V (L) = VD 。这样
S,inv 、xd 与 QA 都成为 y 的函数,分别为
S,inv ( y) 2FP VB V ( y)
1、有效沟道长度调制效应 已知当 VDS = VDsat 时,V (L) = VDsat ,Qn (L) = 0 。 当 VDS > VDsat 后,沟道中满足 V = VDsat 和 Qn = 0 的位置向左 移动 L,即
V (L L) VDsat Qn (L L) 0
这意味着有效沟道长度缩短了。
nCOX
写作
,称为
MOSFET
的
增益因子,则
ID
(VGS
VT )VDS
1 2
VD2S
(4-51)
式(4-51)表明,ID 与 VDS 成 抛物线关系,即 ID
IDsat
0
VDsat
VDS
式(4-51)只在抛物线的左半段有物理意义。
由 Qn 的表达式可知,在 y = L 的漏极处,
Qn (L) COX VGS VT VDS
COX
VGS
VFB
2FP
V
(
y)
2sq NA 2FP
COX
1
2
COX VGS VT V ( y)
(4-50)
将此 Qn 代入式(5-37)的 ID 中,并经积分后得
ID
Z L
n
C VDS
0
OX
VGS VT V ( y)
微电子器件(3-6)
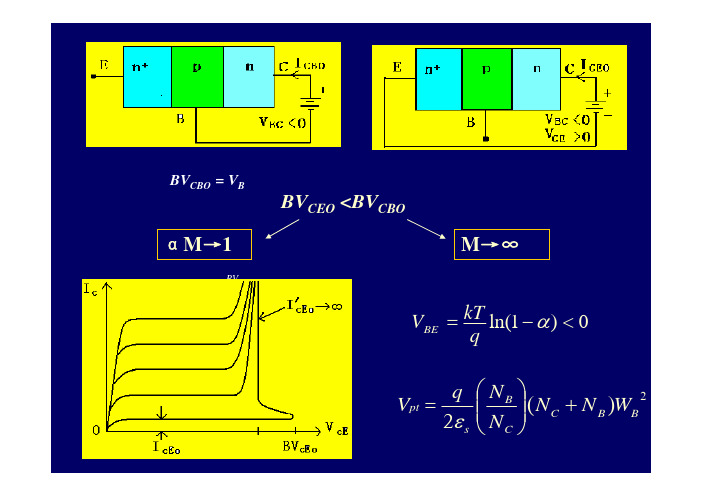
NE NB
N
+ B
R口B 3
x
+ jC
NC
IB
y
0
Sb
∫ R口B 3
=
qμn
1
N dx X
+ jC
+
0
B
用类似于求 rb’ 的方法,
得:
rcb=Βιβλιοθήκη Sb 3lR口 B 3
2) 双基极条
− Se 2
Ib ( y) IB 2
0
Se 2
Ib(y) =
1 2
I
B
1 2
S
e
=
IB Se
y,
∫ Pb′
=
2
1 2
Se
d
2 S
−
d
2 B
)
dr 段上的电阻为:
dr
2π r
R口 B 2
,
∫ rb =
dB
2 se
2
R口 B 2 dr
2π r
= R口 B 2 ln d B
2π
Se
3、工作基区电阻 rb’ 与基极接触区下的电阻 rcb
在产生电阻 rb’ 与 rcb 的基区 内,基极电流是随距离变化的分 布电流 Ib(y) ,因此这个区域内 的基极电阻是分布参数而不是集 中参数。
分布电流为 Ib ( y)
dy 段上的电阻为
= dy l
IB y, Se R口B1
,
Ib ( y) 在 dy 段电阻上消耗的功率
为: 于是有:
I
2 b
(
y
)
dy l
R口B1
=
(IB Se
)2
y2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
微电子器件公式: 部分物理常数:191412S 1031412G i S 13314G i OX 1.610C,0.026V (300k),(Si)11.88.85410 1.04510F cm,(Si) 1.09eV,(Si) 1.510cm ,(Ge)168.85410 1.41710F cm,(Ge)0.66eV,(Ge) 2.410cm , 3.98.85410 3.45q kT q T E n E n εεε--------=⨯===⨯⨯=⨯==⨯=⨯⨯=⨯==⨯=⨯⨯=13310F cm-⨯第1章 半导体器件基本方程 1. 泊松方程D A sd ()d E qp n N N x ε=-+- 2. 电流密度方程 n n np p pd d d d n J q nE qD xpJ q pE qD xμμ=+=- 3. 电荷控制方程n nn np pp pd d d d Q Q I t Q Q I t ττ∆=--∆=--第2章 PN 结2.1 PN 结的平衡状态 1.平衡多子p0A i n0D i ()p N n n N n =>>=>>P 区(N 区)2.平衡少子22i i p0i p0A 22iin0i n0D()n n n n P p N n n p n n N ==<<==<<区(N 区)3.内建电势 A Dbi 2i ln N N kT V q n =4.最大电场强度 120max bi s 2qN E V ε⎛⎫= ⎪⎝⎭5.N 区耗尽区宽度 12ss An max bi D D A D 2()N x E V qN q N N N εε⎡⎤==⋅⎢⎥+⎣⎦6.P 区耗尽区宽度 12ss Dp max bi A A A D 2()N x E V qN q N N N εε⎡⎤==⋅⎢⎥+⎣⎦7.总耗尽区宽度 12bi sd n p bi max 022V x x x V E qN ε⎡⎤=+==⎢⎥⎣⎦2.2 PN 结的直流电流电压方程1.在N 型区与耗尽区的边界处,即 n x 处 n n n0()exp qV p x p kT⎛⎫=⎪⎝⎭在P 型区与耗尽区的边界处,即 –p x 处 p p p0()exp qV n x n kT ⎛⎫-=⎪⎝⎭2.PN 结总的扩散电流密度 d Jp p 2n n d dp dn n0p0i p n p D n A 0exp 1exp 1exp 1D D D D qVqVJ J J q p n qn L L kT L N L N kT qVJ kT ⎛⎫⎛⎫⎡⎤⎡⎤⎛⎫⎛⎫=+=+⋅-=+⋅- ⎪ ⎪⎪ ⎪⎢⎥⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎣⎦⎣⎦⎝⎭⎝⎭⎡⎤⎛⎫=-⎪⎢⎥⎝⎭⎣⎦3.势垒区产生复合电流 n p i d gr d exp 1d 2exp 12x x qV qn x kT J q U x qU x qV kT τ-⎛⎫- ⎪⎝⎭===⋅⎛⎫+ ⎪⎝⎭⎰4.薄基区二极管扩散电流 22p i n i dp dn B D E A exp 1...exp 1qD n qD n qV qVJ J W N kT W N kT ⎡⎤⎡⎤⎛⎫⎛⎫=-=- ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦2.3 准费米能级与大注入效应1.转折电压i i D KN A KP2ln ()2ln kT V N q n kT V q n ⎛⎫=⎪ ⎪⎝⎭⎛⎫= ⎪ ⎪⎝⎭区(P 区) 2.大注入下结定律()()n n i p p i exp 2exp 2qV p x n kT qV n x n kT ⎛⎫= ⎪⎝⎭⎛⎫-= ⎪⎝⎭2.4 PN 结的击穿1.雪崩倍增因子 di 011d x M xα=-⎰ 2.雪崩击穿近似计算120C B s 2qN E V ε⎛⎫= ⎪⎝⎭2.5 PN 结的势垒电容 ()()11223s 0s T T bi bi()...212qN aq C A C A V V V V εε⎡⎤⎡⎤==⎢⎥⎢⎥--⎣⎦⎣⎦均匀(缓变)2.6 PN 结的交流小信号特性与扩散电容 1. PN 结的直流增量电导 F D qI g kT =2. PN 结的扩散电容 F D D 22qI g C kT ττ== 2.7 PN 结的开关特性 1.反向恢复时间r t f rr p r ln I I t I τ⎛⎫+=⎪⎝⎭第3章 双极结型晶体管3.1 双极结型晶体管基础 电流放大系数关系:C B .........11I I αββααβ===-+ 3.2 均匀基区晶体管的电流放大系数1.基区输运系 2pC B pEB 112J W J L β*⎛⎫==- ⎪⎝⎭bB1ττ=-2.基区度越时间 2B b B 2W D τ=B B pE pCQ Q J J =≈ 3.基区少子寿命 B B pr Q J τ=4.注入效率 B E E B 1W W ργρ=-11E B R R =-口口5.共基极电流放大系数 22E EB B 22B B1B B1111122R R W W L R L R αδ⎛⎫⎛⎫=--≈--=- ⎪ ⎪⎝⎭⎝⎭口口口口 6.共发射极电流放大系数 1121E b E B 2B B1B B112R R W L R R τδβδδτ---⎛⎫⎛⎫-=≈=+=+ ⎪ ⎪⎝⎭⎝⎭口口口口7.异质结双极晶体管(HBT ) E GB11exp R E R kTγ∆⎛⎫=- ⎪⎝⎭口异口 3.4 双极晶体管的直流电流电压方程1.埃伯斯-莫尔方程BC BE E ES R CS BC BE C ES CS exp 1exp 1exp 1exp 1qV qV I I I kT kT qV qV I I I kT kT αα⎡⎤⎡⎤⎛⎫⎛⎫=--- ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦⎡⎤⎡⎤⎛⎫⎛⎫=--- ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦2.共发射极电流方程BC BE B ES R CS BC BE C ES CS (1)exp 1(1)exp 1exp 1exp 1qV qV I I I kT kT qV qV I I I kT kT ααα⎡⎤⎡⎤⎛⎫⎛⎫=--+-- ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦⎡⎤⎡⎤⎛⎫⎛⎫=--- ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦3.厄尔利电压 BBB B 0A dBB B B B B CBCE d d d d ()()d d W W N xN xV xW N W N W V V ≡=⎛⎫- ⎪⎝⎭⎰⎰4.共发射极增量输出电阻 CE A o C C V V r I I ∂≡=∂5.均匀基区厄尔利电压 B biA dB2,W V V x = 3.5 双极晶体管的反向特性 1.浮空电势 BE ln(1)0kT V q α=-< 2.基区穿通电压 2B ptC B B s C ()2N q V N N W N ε⎛⎫=+ ⎪⎝⎭3.击穿电压 CBO B BV V = (共基极) CEO BV =(共发射极)3.6 基极电阻 b e bb B3B2B1b 26212S S C dr R R R lS l l lΩ'=+++口口口3.8 电流放大系数与频率的关系1.特征频率()T eceb b d c 1122f πτπττττ==+++0βf β=T ||,()f f f f ωββ=<<2dc B ec TE cs TC T E B max1211222x W kTC r C f qID v τπηη⎛⎫==+⋅-++ ⎪⎝⎭3.10 功率增益和最高振荡频率 1.最大功率增益omax Tpmax 2in bb TC 8P f K P r C f π'== 2.高频优值2T pmax bb TC8f M K f r C π'≡=3.最高振荡频率 112T2M bb TC 8f f M r C π'⎛⎫== ⎪⎝⎭第 5 章 绝缘栅场效应晶体管 5.2 MOSFET 的阈电压1.P 型衬底的费米势 A FP i F i 1ln 0N kT E E qq n ϕ=-=>()N 型衬底 DFN iln 0N kT q n ϕ=-< 2.阈值电压()()()1OX2T MS FP FPOX12B FB FP S B FP S B 1OX2MS FP S B FP SOX222222Q V K C V V K V V V V Q K V V V C ϕϕϕϕϕϕϕϕ=-++=+++-++-=-++-++5.3 MOSFET 的直流电流电压方程1.电流电压方程 ()2D GS T DS DS p OXDsat GS T22Dsat GS T Dsat Dsat GS T 1()()....211()22Z I V V V V C L V V V I V V V V V V ββμββ⎡⎤=--=⎢⎥⎣⎦=-⎡⎤=--=-⎢⎥⎣⎦非饱和区(饱和区)5.5 MOSFET 的直流参数与温度特性 1.通导电阻 on R DS on D GS T n OX GS T 1()()V LR I V V Z C V V βμ===-- 5.6 MOSFET 的小信号参数、高频等效电路及频率特性 1.跨导mg m DS ms GS T Dsat ()()g V g V V V βββ==-=非饱和区(饱和区)2.漏源电导ds gds GS T DS Dsatds sat DS0g V V V I g V β=--∂==∂()()3.跨导的截止角频率 m n GS T g 2gs gs ()1154V V R C Lμω-==⋅4.本征最高工作频率 ms n GS T T 2gs ()13222g V V f C L μππ-⎡⎤==⋅⎢⎥⎣⎦5.高频功率增益为 22omax ms ds ms dspmax2222i gs gs gs gs44(2)P g r g r K P C R f C R ωπ=== 6.最高振荡频率M f 1122ms ds ds M T gs gs gs 244g r r f f C R R π⎛⎫⎛⎫== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭(注:本资料素材和资料部分来自网络,仅供参考。
请预览后才下载,期待你的好评与关注!)。
