基于MATLAB的PID控制器设计说明

合集下载

基于matlabsimulink的pid控制器设计 -回复

基于matlabsimulink的pid控制器设计-回复基于Matlab Simulink的PID控制器设计引言：在自动化控制工程中，PID控制器（Proportional-Integral-Derivative Controller）是一种常见且经典的控制算法。

它通过根据当前误差的大小调整控制器的输出，使得被控对象的反馈变量尽可能地接近期望值。

Matlab Simulink是一个广泛应用于工程和科学领域的仿真软件，它提供了一个直观且交互式的设计平台，可以用于设计、建模和仿真各种控制系统。

本文将详细介绍基于Matlab Simulink 的PID控制器设计的步骤。

第一步：建立模型首先，我们需要建立被控对象的数学模型。

设被控对象的输入信号为u，输出信号为y。

可以通过实验测量或根据系统的物理原理来获得被控对象的传递函数。

传递函数可以表示为：G(s) = Y(s)/U(s)其中，G(s)为被控对象的传递函数，s为复平面上的复数变量。

在Simulink中，可以使用Transfer Fcn或State-Space等模块来表示被控对象。

根据具体情况选择适当的模块，并设置传递函数的系数。

第二步：设计PID控制器在Simulink中，可以使用PID Controller模块来表示一个PID控制器。

PID控制器的输入为误差e和时间变量t，输出为控制信号u。

控制信号u根据以下公式计算：u(t) = Kp * e(t) + Ki * ∫e(t) dt + Kd * de(t)/dt其中，Kp、Ki、Kd分别为比例、积分和微分增益。

选择合适的增益参数是PID控制器设计的关键。

通常，可以通过试验、Ziegler-Nichols 方法或基于频域特性的方法来确定这些增益参数。

第三步：模拟系统响应为了分析和评估PID控制器的性能，我们可以通过仿真系统来模拟系统的响应。

在Simulink中，可以使用Scope或To Workspace等模块来显示被控对象和控制器的输入输出变量。

基于matlab的pid控制仿真课程设计

这篇文章是关于基于Matlab的PID控制仿真课程设计的，主要内容包括PID控制的基本原理、Matlab的应用、课程设计的目的和意义、课程设计的具体步骤和具体操作步骤。

文章采用客观正式的语气，结构合理，旨在解释基于Matlab的PID控制仿真课程设计的重要性和实施方法。

1. 简介PID控制是一种常见的控制算法，由比例项（P）、积分项（I）和微分项（D）组成，可以根据被控对象的实际输出与期望输出的偏差来调整控制器的输出，从而实现对被控对象的精确控制。

Matlab是一种强大的数学建模与仿真软件，广泛应用于工程领域，尤其在控制系统设计和仿真方面具有独特优势。

2. PID控制的基本原理PID控制算法根据被控对象的实际输出与期望输出的偏差来调整控制器的输出。

具体来说，比例项根据偏差的大小直接调整输出，积分项根据偏差的积累情况调整输出，微分项根据偏差的变化速度调整输出。

三者综合起来，可以实现对被控对象的精确控制。

3. Matlab在PID控制中的应用Matlab提供了丰富的工具箱，其中包括控制系统工具箱，可以方便地进行PID控制算法的设计、仿真和调试。

利用Matlab，可以快速建立被控对象的数学模型，设计PID控制器，并进行系统的仿真和性能分析，为工程实践提供重要支持。

4. 课程设计的目的和意义基于Matlab的PID控制仿真课程设计，旨在帮助学生深入理解PID控制算法的原理和实现方法，掌握Matlab在控制系统设计中的应用技能，提高学生的工程实践能力和创新思维。

5. 课程设计的具体步骤（1）理论学习：学生首先需要学习PID控制算法的基本原理和Matlab在控制系统设计中的应用知识，包括控制系统的建模、PID控制器的设计原理、Matlab的控制系统工具箱的基本使用方法等。

（2）案例分析：学生根据教师提供的PID控制实例，在Matlab环境下进行仿真分析，了解PID控制算法的具体应用场景和性能指标。

（3）课程设计任务：学生根据所学知识，选择一个具体的控制对象，如温度控制系统、水位控制系统等，利用Matlab建立其数学模型，设计PID控制器，并进行系统的仿真和性能分析。

基于MATLAB的PID控制器设计资料

基于MATLAB的PID控制器设计资料PID控制器是一种经典控制器，可用于控制各种线性和非线性系统。

本文将介绍基于MATLAB的PID控制器的设计资料。

首先，我们需要了解PID控制器的工作原理。

PID控制器由三个主要组成部分组成：比例（P）项、积分（I）项和微分（D）项。

比例项根据目标值和实际输出之间的误差进行控制；积分项对误差进行积分，以消除累积的误差；微分项根据误差的变化率来调整控制输出。

在MATLAB中，我们可以使用pid函数来设计PID控制器。

pid函数的基本用法如下：```matlabKp=1;%比例增益Ki=1;%积分增益Kd=1;%微分增益controller = pid(Kp, Ki, Kd); % 创建PID控制器对象```要使用PID控制器，我们需要知道系统的传递函数或状态空间模型。

传递函数模型可以通过tf函数表示，状态空间模型可以通过ss函数表示。

```matlabs = tf('s');H=1/(s^2+2*s+1);%创建传递函数模型```接下来，我们可以使用feedback函数将PID控制器与系统模型相连，并进行闭环控制。

```matlabsys = feedback(controller*H, 1); % 创建闭环系统模型```通过对PID控制器参数的调整，我们可以实现系统的稳定性、快速响应和抗干扰性。

使用MATLAB的pidTuner工具箱可以帮助我们自动调整PID控制器的参数。

另外，MATLAB还提供了一些其他用于控制系统设计和分析的函数，例如step函数用于绘制系统的阶跃响应曲线，bode函数用于绘制系统的频率响应曲线。

```matlabstep(sys); % 绘制系统的阶跃响应曲线bode(sys); % 绘制系统的频率响应曲线```以上是基于MATLAB的PID控制器设计的一些基本资料。

在实际应用中，还有很多高级技术和方法可以用于更精确地设计和调整PID控制器。

Matlab控制系统工具箱的PID控制设计指南

Matlab控制系统工具箱的PID控制设计指南导言控制系统工具箱是Matlab提供的一个用于分析和设计控制系统的工具包。

其中，PID控制是最常用且广泛应用的一种控制算法。

本文将介绍Matlab控制系统工具箱中PID控制的设计指南，帮助读者快速掌握PID控制的原理和实践技巧。

一、PID控制简介PID控制是一种基于比例、积分和微分的控制方法，适用于各种不确定性和变化的系统。

PID控制器通过实时测量系统的误差（e），并计算比例项（P）、积分项（I）和微分项（D）的乘积和，调整输出控制信号（u），进而实现对系统的稳定控制。

二、PID控制的数学模型PID控制器可以用以下的数学模型表示：u(t) = Kp * e(t) + Ki * ∫e(t)dt + Kd * △e(t)/dt其中，u(t)表示控制器的输出，e(t)表示误差，Kp、Ki和Kd分别代表比例、积分和微分控制器的增益参数。

PID控制的目标是调整这些参数以使误差最小化。

三、PID控制器的参数调节PID控制器的性能和稳定性取决于增益参数的设置。

Matlab控制系统工具箱提供了多种方法来自动或手动地调节这些参数。

1. 自动调参方法Matlab提供了一些自动调参的函数，如pidtune和pidtool。

这些函数可以根据系统的频率响应和稳定性指标，自动选择合适的PID参数。

使用这些方法可以节省调试时间，但需要注意调参结果的合理性和系统实际需求的匹配性。

2. 手动调参方法手动调参是一种通过试验和调整来寻找最佳PID参数的方法。

Matlab中可以使用step函数或PID Controller Tuner App来进行手动调参。

这种方法需要对系统的特性和动态响应有一定的了解，并经过多次试验和优化来寻找最佳参数。

四、PID控制器的性能分析在设计PID控制器时，除了调节参数之外，还需要进行性能分析来评估控制质量和稳定性。

Matlab控制系统工具箱提供了一些常用的性能指标和分析工具。

基于MATLAB的PID控制器设计

基于MATLAB的PID控制器设计PID控制器是一种常见的反馈控制器，广泛应用于工业控制系统中。

它通过测量被控变量与目标值之间的差异，根据比例、积分和微分三个参数对控制输入进行调整，以实现对系统的稳定性、精度和响应速度的控制。

MATLAB是一个功能强大的数学计算软件，提供了丰富的工具和功能，可以方便地进行PID控制器设计。

下面将介绍基于MATLAB的PID控制器设计步骤和方法。

1.确定被控对象：首先需要确定需要控制的对象，即被控变量。

可以是温度、速度、位置等物理变量。

2.建立数学模型：在进行PID控制器设计之前，需要建立被控对象的数学模型。

可以使用系统辨识方法或根据物理原理进行建模。

3.设计PID控制器：PID控制器由比例（P）、积分（I）和微分（D）三个参数组成。

这些参数的合理选择对于控制器性能的好坏至关重要。

a.比例参数P：控制器输出的比例与误差的关系决定了控制器的灵敏度。

通过调整P参数的大小可以实现控制系统的稳定性和响应速度之间的折衷。

b.积分参数I：控制器积分误差的能力可以用来补偿系统误差和消除静态误差。

但是过大的积分参数可能导致系统震荡。

c.微分参数D：微分参数用来预测系统的变化趋势，通过减小过度调整和减少超调现象。

PID控制器的输出可以表示为：u(t) = Kp * e(t) + Ki * ∫e(t)dt + Kd * de(t)/dt其中，u(t)为控制器的输出信号，e(t)为目标值与被控变量之间的差异，Kp、Ki、Kd为比例、积分和微分参数。

4. 参数调整：PID控制器的性能取决于参数的选择和调整。

在MATLAB中，可以使用PID Tuner工具进行参数调整。

该工具可以自动化地对PID参数进行优化，以达到系统的最佳稳定性和性能。

5.控制器实现：设计好PID控制器后，需要将其应用于实际控制系统中。

在MATLAB中，可以使用控制系统工具箱提供的函数和命令来实现控制器的设计和实现。

总结而言，基于MATLAB的PID控制器设计可以通过确定被控对象、建立数学模型、设计PID控制器、参数调整和控制器实现等步骤来完成。

matlab实验四基于Matlab的PID控制器实验

实验四基于Matlab 的PID 控制器实验一、实验目的1、掌握使用MATLAB 进行根轨迹法的控制系统设计2、掌握使用MATLAB 进行Bode 图法的系统的控制系统设计3、掌握使用MATLAB 进行PID 控制器设计二、实验内容和要求1. 实验内容（1）练习MATLAB6.5或以上版本（2）练习掌握MATLAB 进行控制系统的设计 2. 实验要求：每位学生独立完成。

三、实验主要仪器设备和材料装有MATLAB6.5或以上版本的PC 机一台。

四、实验方法、步骤及结果测试1．实验方法：上机练习。

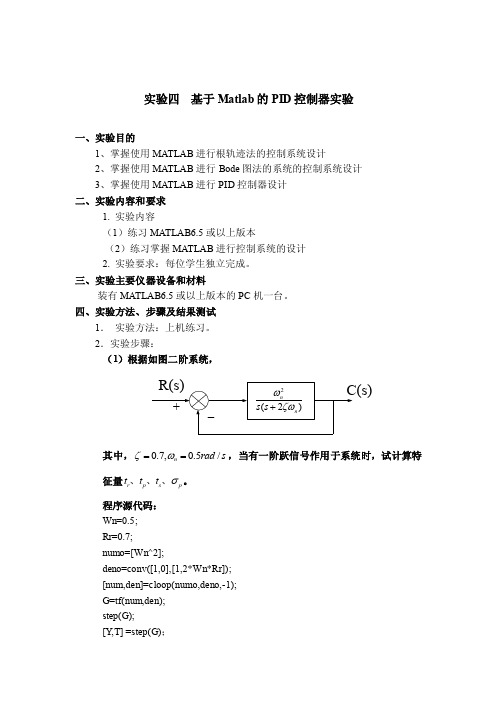
2．实验步骤：（1）根据如图二阶系统，其中，0.7,0.5/n rad s ζω==，当有一阶跃信号作用于系统时，试计算特征量r p s p t t t σ、、、。

程序源代码： Wn=0.5; Rr=0.7; numo=[Wn^2];deno=conv([1,0],[1,2*Wn*Rr]); [num,den]=cloop(numo,deno,-1); G=tf(num,den); step(G); [Y ,T] =step(G)；[pos,tp,tr,ts2]=stepchar(Y,T);pos =4.7092tp =8.8343tr =4.2594ts2 =11.8317其中stepchar函数如下function [pos,tp,tr,ts2]=stepchar(y,t)%find pos and tp%返回阶跃响应输出y列向量的最大值mp及对应下标值ind [mp,ind]=max(y);%求取时间向量的长度dimtdimt=length(t);%确定最终的稳定值yssyss=y(dimt);pos=100*(mp-yss)/yss;tp=t(ind);% find rise time tr%确定输出为0.1时的时刻i=1;j=1;k=1;q=1;while y(i)<0.1i=i+1;endt1=t(i);%确定输出为0.9时的时刻 while y(j)<0.9 j=j+1; end t2=t(j); tr=t2-t1; % find ts2 i=dimt+1; n=0; while n==0 i=i-1; if i==1 n=1; elseif y(i)>=1.02 n=1; end endt1=t(i);i=dimt+1;n=0; while n==0 i=i-1; if y(i)<=0.98 n=1; end t2=t(i); if t1>t2 ts2=t1; else ts2=t2; end end（2）设被控对象的传递函数为0()(1)(0.51)kG s s s s =++试其设计要求：1v K s -=10，相角裕度为50度，幅值裕度为10dB ，试确定一个校正装置，以满足性能指标。

基于matlab的pid控制器设计

基于Matlab的PID控制器设计引言PID控制器是一种常用的闭环控制器，可以通过调整控制系统的输出，使其迅速、准确地响应给定的参考输入。

在Matlab中，我们可以利用其强大的控制系统工具箱来设计和实现PID控制器。

本文将详细介绍基于Matlab的PID控制器设计的步骤和方法，并结合示例演示其应用。

PID控制器概述什么是PID控制器PID控制器是一种比例-积分-微分控制器，可以通过对误差信号的比例、积分和微分操作来调整控制系统的输出。

其中，比例项负责反馈控制误差，积分项用于消除静态误差，微分项则用于抑制振荡和提高系统的响应速度。

PID控制器的基本原理PID控制器的输出由以下三个部分组成： - 比例项：比例项与控制误差成正比，生成一个与误差成比例的控制信号。

- 积分项：积分项计算误差的积分累加值，用于消除控制系统的静态误差。

- 微分项：微分项计算误差的导数，用于抑制振荡和提高系统的响应速度。

PID控制器的输出计算公式如下：u(t) = K_p \cdot e(t) + K_i \cdot \int e(t) \, dt + K_d \cdot \frac{de(t)}{dt}其中，u(t)为控制器的输出，K_p、K_i、K_d分别为比例、积分和微分增益，e(t)为控制误差。

基于Matlab的PID控制器设计步骤1. 系统建模在设计PID控制器之前，我们首先需要对控制系统进行建模。

使用Matlab的控制系统工具箱，可以通过输入系统的传递函数或状态空间模型来进行建模。

示例：建模一个二阶惯性系统我们以一个简单的二阶惯性系统为例，其传递函数为：G(s) = \frac{1}{s^2 + 2s + 1}在Matlab中，我们可以使用tf函数来定义系统的传递函数模型：s = tf('s');G = 1/(s^2 + 2*s + 1);2. 设计PID控制器设计PID控制器的关键是选择合适的增益参数。

基于matlab的pid控制器设计

基于matlab的pid控制器设计一、PID控制器的介绍PID控制器是工业控制领域中常用的控制器之一，也是最常见、最基础的控制器之一。

PID全称为Proportional-Integral-Differential，即比例-积分-微分控制器。

该控制器通过对目标系统的输入量进行比例、积分、微分处理，从而提高目标系统的稳定性和响应速度。

二、控制器设计的前提在进行PID控制器的设计之前，需要对被控对象的数学模型有一定的了解，包括传递函数和状态方程等。

同时，在PID控制器的设计过程中要有清晰的控制目标，比如控制系统的稳态误差、系统的响应速度等等。

三、基于MATLAB的PID控制器设计MATLAB是一个功能强大的数学计算软件，也是工程控制领域中常用的分析工具。

在MATLAB中，我们可以利用内置的PID工具箱来进行PID控制器的设计。

1. 设计PID控制器实际上，在MATLAB中设计PID控制器只需一行代码即可完成：>> C = pid(kp, ki, kd);其中，kp、ki、kd分别代表比例系数、积分系数和微分系数。

我们可以根据PID控制的要求来调整这些参数以获得最好的性能。

2. 仿真PID控制器在设计了PID控制器之后，我们需要将其嵌入到目标系统中进行仿真。

首先，我们要对被控对象进行建模，可以采用MATLAB提供的SIMULINK工具。

接着，将PID控制器与被控对象进行连接，并进行仿真。

>> sim('pid_controller');最后，我们可以通过结果分析工具来评估PID控制器在目标系统上的表现情况，从而进行参数调整和优化。

四、参考文献1. Skogestad, S. (2003). PID control: developments and directions. IEEE Control Systems Magazine, 23(2), 57-67.2. Astrom, K. J., & Hagglund, T. (1995). PID controllers: theory, design,and tuning. Instrument Society of America.3. Ljung, L. (1999). System identification: Theory for the user. Prentice-Hall.。

基于MATLAB的PID控制器设计

基于MATLAB的PID 控制器设计基于MATLAB的PID 控制器设计一、PID控制简介PID控制是最早发展起来的经典控制策略, 是用于过程控制最有效的策略之一。

由于其原理简单、技术成，在实际应用中较易于整定, 在工业控制中得到了广泛的应用。

它最大的优点是不需了解被控对象精确的数学模型,只需在线根据系统误差及误差的变化率等简单参数, 经过经验进行调节器参数在线整定, 即可取得满意的结果, 具有很大的适应性和灵活性。

积分作用:可以减少稳态误差, 但另一方面也容易导致积分饱和, 使系统的超调量增大。

微分作用:可提高系统的响应速度, 但其对高频干扰特别敏感, 甚至会导致系统失稳。

所以, 正确计算控制器的参数, 有效合理地实现PID控制器的设计,对于PID 控制器在过程控制中的广泛应用具有重要的理论和现实意义。

在PID控制系统中, PID控制器分别对误差信号e（t）进行比例、积分与微分运算, 其结果的加权和构成系统的控制信号u（t），送给对象模型加以控制。

PID控制器的数学描述为其传递函数可表示为:从根本上讲, 设计PID控制器也就是确定其比例系数Kp、积分系数T i 和微分系数T d , 这三个系数取值的不同, 决定了比例、积分和微分作用的强弱。

控制系统的整定就是在控制系统的结构已经确定、控制仪表和控制对象等处在正常状态的情况下, 适当选择控制器参数使控制仪表的特性和控制对象的特性相配合, 从而使控制系统的运行达到最佳状态, 取得最好的控制效果。

二、MATLAB的Ziegler-Nichols算法PID控制器设计。

1、PID控制器的Ziegler-Nichols参数整定在实际的过程控制系统中, 有大量的对象模型可以近似地由一阶模型来表示。

这个对象模型可以表示为sL-esT1KG(s)+=如果不能建立起系统的物理模型, 可通过试验测取对象模型的阶跃响应, 从而得到模型参数。

当然, 我们也可在已知对象模型的情况下, 利用MATLAB，通过使用step ( ) 函数得到对象模型的开环阶跃响应曲线。

《MATLAB控制系统仿真》PID控制系统校正设计

《MATLAB控制系统仿真》PID控制系统校正设计引言1.PID校正装置PID校正装置也称为PID控制器或PID调节器。

这里P，I，D分别表示比例、积分、微分,它是最早发展起来的控制方式之一。

2.PID校正装置的主要优点原理简单，应用方便，参数整定灵活。

适用性强，在不同生产行业或领域都有广泛应用。

鲁棒性强，控制品质对受控对象的变化不太敏感，如受控对象受外界扰动时，无需经常改变控制器的参数或结构。

在科学技术迅速发展的今天，出现了许多新的控制方法，但PID由于其自身的的优点仍然在工业过程控制中得到最广泛的应用。

PID控制系统校正设计1.设计目的1.1 熟悉常规PID控制器的设计方法1.2掌握PID参数的调节规律1.3学习编写程序求系统的动态性能指标2.实验内容2.1在SIMULINK窗口建立方框图结构模型。

2.2设计PID控制器，传递函数模型如下。

()⎪⎭⎫⎝⎛++=s T s T k s G d i p c 112.3修改PID 参数p K 、i T 和d T ，讨论参数对系统的影响。

3.4利用稳定边界法对PID 参数p K 、i T 和d T 校正设计。

2.5根据PID 参数p K 、i T 和d T 对系统的影响，调节PID 参数实现系统的超调量小于10%。

3. 实验操作过程3.1在SIMULINK 窗口建立模型图1 设计模型方框图3.2设计PID 控制器图2 PID控制器模型3.3利用稳定边界法对PID参数p K、i T和d T校正设计: 表1 PID稳定边界参数值校正后的响应曲线图3（a）校正后的响应曲线图3（b）校正后的响应曲线3.4调节PID参数实现系统的超调量小于10%:表2 PID 参数图4 响应曲线图4.规律总结1.P控制规律控制及时但不能消除余差,I控制规律能消除余差但控制不及时且一般不单独使用,D控制规律控制很及时但存在余差且不能单独使用。

2.比例系数越小，过渡过程越平缓，稳态误差越大;反之，过渡过程振荡越激烈，稳态误差越小;若p K过大，则可能导致发散振荡。

基于MATLAB的PID控制器设计报告

MATLAB论文--基于控制系统的PID调节基于MATLAB的PID 控制器摘要：本论文主要研究PID控制器。

PID控制是迄今为止最通用的控制方法，大多数反馈回路用该方法或其较小的变形来控制。

PID控制器（亦称调节器）及其改进型因此成为工业过程控制中最常见的控制器(至今在全世界过程控制中用的84%仍是纯PID调节器，若改进型包含在内则超过90%)。

在PID控制器的设计中，参数整定是最为重要的,随着计算机技术的迅速发展，对PID参数的整定大多借助于一些先进的软件，例如目前得到广泛应用的MATLAB仿真系统。

本论文主要介绍PID的原理及简单的用法，探究控制器中各个参数对系统的影响，就是利用《自动控制原理》和《MATLAB》所学的内容利用简单的方法研究PID控制器的设计方法，并通过MATLAB中的虚拟示波器观察系统完善后在阶跃信号下的输出波形。

关键字：PID控制简介PID控制器原理MATLAB仿真PID参数的设定正文：一、PID控制简介PID控制器又称PID调节器，是工业过程控制系统中常用的有源校正装置。

长期以来，工业过程控制系统中多采用气动式PID控制器。

由于气动组件维修方便，使用安全可靠，因此在某些特殊场合，例如爆炸式环境，仍然使用气动式PID控制器。

随着运算放大器的发展和集成电路可靠性的日益提高，电子式PID控制器已逐渐取代了气动式PID控制器。

目前，已在开发微处理器PID控制器。

这里，仅简要介绍PID控制器的主要特性。

PID调节器是一种线性调节器，它根据给定值)(t r与实际输出值)(t c构成的控制偏差：)(t e=)(t r－)(t c将偏差的比例、积分、微分通过线性组合构成控制量，对控制对象进行控制，故称为PID调节器。

在实际应用中，常根据对象的特征和控制要求，将P、I、D基本控制规律进行适当组合，以达到对被控对象进行有效控制的目的。

例如，P 调节器，PI调节器，PID调节器等。

所以, 正确计算控制器的参数, 有效合理地实现PID控制器的设计,对于PID 控制器在过程控制中的广泛应用具有重要的理论和现实意义。

基于MATLAB的温度控制系统的PID控制器设计

基于MATLAB的温度控制系统的PID控制器设计摘要本论文以温度控制系统为研究对象设计一个PID控制器PID控制是迄今为止最通用的控制方法大多数反馈回路用该方法或其较小的变形来控制PID控制器亦称调节器及其改进型因此成为工业过程控制中最常见的控制器至今在全世界过程控制中用的84仍是纯PID调节器若改进型包含在内则超过90 在PID控制器的设计中参数整定是最为重要的随着计算机技术的迅速发展对PID参数的整定大多借助于一些先进的软件例如目前得到广泛应用的MATLAB仿真系统本设计就是借助此软件主要运用Relay-feedback法线上综合法和系统辨识法来研究PID控制器的设计方法设计一个温控系统的PID控制器并通过MATLAB中的虚拟示波器观察系统完善后在阶跃信号下的输出波形关键词 PID参数整定 PID控制器 MATLAB仿真冷却机AbstractThis paper regards temperature control system as the research object to design a pid controller Pid control is the most common control method up until now the great majority feedback loop is controlled by this method or its small deformation Pid controller claim regulator also and its second generation so become the most common controllers in the industry process control so far about 84 of the controller being used is the pure pid controller itll exceed 90 if the second generation included Pid parameter setting is most important in pid controller designing and with the rapid development of the computer technology it mostly recurs to some advanced software for example mat lab simulation software widely used now this design is to apply that soft mainly use Relay feedback law and synthetic method on the line to study pid controller design method design a pid controller of temperature control system and observe the output waveform while input step signal through virtual oscilloscope after system completedKeywords PID parameter setting PID controller MATLAB simulationcooling machine摘要Ibstract II第一章绪论 1课题来源及PID控制简介 1com 课题的来源和意义 1com PID控制简介1国内外研究现状及MATLAB简介 3二章控制系统及PID调节 5控制系统构成 5PID控制 5com积分微分 5com控制7三章系统辨识9系统辨识9系统特性图10系统辨识方法11PID最佳调整法与系统仿真1441 PID参数整定法概述14针对无转移函数的PID调整法15comay feedback调整法15com Relay feedback 在计算机做仿真15 com整法19com 在线调整法在计算机做仿真20针对有转移函数的PID调整方法23 com识法24com法及根轨迹法27五章油冷却机系统的PID控制器设计28 油冷却机系统28com机 28com转换器29com 控制组件30油冷却机系统之系统辨识31油冷却机系统的PID参数整定3340致谢41参考文献42第一章绪论11 课题来源及PID控制简介com 课题的来源和意义任何闭环的控制系统都有它固有的特性可以有很多种数学形式来描述它如微分方程传递函数状态空间方程等但这样的系统如果不做任何的系统改造很难达到最佳的控制效果比如快速性稳定性准确性等为了达到最佳的控制效果我们在闭环系统的中间加入PID控制器并通过调整PID参数来改造系统的结构特性使其达到理想的控制效果com PID控制简介当今的自动控制技术都是基于反馈的概念反馈理论的要素包括三个部分测量比较和执行测量关心的变量与期望值相比较用这个误差纠正调节控制系统的响应这个理论和应用自动控制的关键是做出正确的测量和比较后如何才能更好地纠正系统PID 比例 - 积分 - 微分控制器作为最早实用化的控制器已有 50多年历史现在仍然是应用最广泛的工业控制器 PID 控制器简单易懂使用中不需精确的系统模型等先决条件因而成为应用最为广泛的控制器PID 控制器由比例单元 P 积分单元 I 和微分单元 D 组成其输入 e t 与输出 u t 的关系为公式1-1公式1-1 公式1-2 比例调节作用是按比例反应系统的偏差系统一旦出现了偏差比例调节立即产生调节作用用以减少偏差比例作用大可以加快调节减少误差但是过大的比例使系统的稳定性下降甚至造成系统的不稳定积分调节作用是使系统消除稳态误差提高无差度因为有误差积分调节就进行直至无差积分调节停止积分调节输出一个常值积分作用的强弱取决与积分时间常数TiTi越小积分作用就越强反之Ti大则积分作用弱加入积分调节可使系统稳定性下降动态响应变慢积分作用常与另两种调节规律结合组成PI调节器或PID调节器微分调节作用微分作用反映系统偏差信号的变化率具有预见性能预见偏差变化的趋势因此能产生超前的控制作用在偏差还没有形成之前已被微分调节作用消除因此可以改善系统的动态性能在微分时间选择合适情况下可以减少超调减少调节时间微分作用对噪声干扰有放大作用因此过强的加微分调节对系统抗干扰不利此外微分反应的是变化率而当输入没有变化时微分作用输出为零微分作用不能单独使用需要与另外两种调节规律相结合组成PD或PID控制器PID控制器由于用途广泛使用灵活已有系列化产品使用中只需设定三个参数 Kp Ki 和 Kd 即可在很多情况下并不一定需要全部三个单元可以取其中的一到两个单元但比例控制单元是必不可少的首先PID应用范围广虽然很多控制过程是非线性或时变的但通过对其简化可以变成基本线性和动态特性不随时间变化的系统这样PID就可控制了其次PID参数较易整定也就是PID参数KpKi和Kd可以根据过程的动态特性及时整定如果过程的动态特性变化例如可能由负载的变化引起系统动态特性变化 PID 参数就可以重新整定第三PID控制器在实践中也不断的得到改进下面两个改进的例子在工厂总是能看到许多回路都处于手动状态原因是很难让过程在自动模式下平稳工作由于这些不足采用 PID 的工业控制系统总是受产品质量安全产量和能源浪费等问题的困扰PID参数自整定就是为了处理PID参数整定这个问题而产生的现在自动整定或自身整定的PID控制器已是商业单回路控制器和分散控制系统的一个标准在一些情况下针对特定的系统设计的PID控制器控制得很好但它们仍存在一些问题需要解决如果自整定要以模型为基础为了PID参数的重新整定在线寻找和保持好过程模型是较难的闭环工作时要求在过程中插入一个测试信号这个方法会引起扰动所以基于模型的 PID 参数自整定在工业应用不是太好如果自整定是基于控制律的经常难以把由负载干扰引起的影响和过程动态特性变化引起的影响区分开来因此受到干扰的影响控制器会产生超调产生一个不必要的自适应转换另外由于基于控制律的系统没有成熟的稳定性分析方法参数整定可靠与否存在很多问题因此许多自身整定参数的PID控制器经常工作在自动整定模式而不是连续的自身整定模式自动整定通常是指根据开环状态确定的简单过程模型自动计算PID 参数但仍不可否认 PID 也有其固有的缺点PID 在控制非线性时变耦合及参数和结构不确定的复杂过程时工作地不是太好最重要的是如果 PID 控制器不能控制复杂过程无论怎么调参数都没用虽然有这些缺点PID控制器是最简单的有时却是最好的控制器12 国内外研究现状及MATLAB简介PID控制中最重要的是对其参数的控制所以当今国内外PID控制技术的研究主要是围绕如何对其参数整定进行的自Ziegler和Nichols提出PID参数整定方法起有许多技术已经被用于PID控制器的手动和自动整定根据发展阶段的划分可分为常规PID参数整定方法及智能PID参数整定方法按照被控对象个数来划分可分为单变量PID参数整定方法及多变量PID参数整定方法前者包括现有大多数整定方法后者是最近研究的热点及难点按控制量的组合形式来划分可分为线性PID参数整定方法及非线性PID 参数整定方法前者用于经典PID调节器后者用于由非线性跟踪-微分器和非线性组合方式生成的非线性PID控制器Astrom在1988年美国控制会议ACC上作的《面向智能控制》〔〕自整定和自适应为智能PID控制的发展奠定了基础他认为自整定控制器和自适应控制器能视为一个有经验的仪表工程师的整定经验的自动化在文〔〕中继续阐述了这种思想PI或PID控制即自整定调节器应具有推理能力自适应PID的应用途径的不断扩大使得对其整定方法的应用研究变得日益重要目前在众多的整定方法中主要有两种方法在实际工业过程中应用较好一种是由福克斯波罗Foxboro公司推出的基于模式识别的参数整定方法基于规则另一种是基于继电反馈的参数整定方法基于模型前者主要应用于Foxboro的单回路EXACT控制器及其分散控制系统IA Series的PIDE功能块其原理基于Bristol在模式识别方面的早期工作〔〕这些技术极大地简化了PID控制器的使用显着改进了它的性能它们被统称为自适应智能控制技术〔〕〔〕PID参数整定方法和非线性PID参数整定方法PID控制算法是迄今为止最通用的控制策略有许多不同的方法以确定合适的控制器参数这些方法区分于复杂性灵活性及使用的过程知识量一个好的整定方法应该基于合理地考虑以下特性的折衷负载干扰衰减测量噪声效果过程变化的鲁棒性设定值变化的响应所需模型计算要求等我们需要简单直观易用的方法它们需要较少的信息并能够给出合适的性能我们也需要那些尽管需要更多的信息及计算量但能给出较好性能的较复杂的方法从目前PID参数整定方法的研究和应用现状来看以下几个方面将是今后一段时间内研究和实践的重点〔〕PID参数整定方法使其在初始化抗干扰和鲁棒性能方面进一步增强使用最少量的过程信息及较简单的操作就能较好地完成整定②对于多入多出被控对象需要研究针对具有显着耦合的多变量过程的多变量PID参数整定方法进一步完善分散继电反馈方法尽可能减少所需先验信息量使其易于在线整定〔〕PID控制技术有待进一步研究将自适应自整定和增益计划设定有机结合使其具有自动诊断功能结合专家经验知识直觉推理逻辑等专家系统思想和方法对原有PID控制器设计思想及整定方法进行改进将预测控制模糊控制和PID控制相结合进一步提高控制系统性能都是智能PID控制发展的极有前途的方向〔〕Matrix Laboratory 缩写为Mat lab 软件包是一种功能强效率高便于进行科学和工程计算的交互式软件包其中包括一般数值分析矩阵运算数字信号处理建模和系统控制和优化等应用程序并将应用程序和图形集于便于使用的集成环境中在此环境下所解问题的Mat lab语言表述形式和其数学表达形式相同不需要按传统的方法编程并能够进行高效率和富有创造性的计算同时提供了与其它高级语言的接口是科学研究和工程应用必备的工具目前在控制界图像信号处理生物医学工程等领域得到广泛的应用本论文设计中PID参数的整定用到的是Mat lab中的 SIMULINK它是一个强大的软件包在液压系统仿真中只需要做数学模型的推导工作用 SIMULINK对设计好的系统进行仿真可以预知效果检验设计的正确性为设计人员提供参考其仿真结果是否可用取决于数学模型正确与否因此要注意模型的合理及输入系统的参数值要准确〔〕PID调节21 控制系统构成对控制对象的工作状态能进行自动控制的系统称为自动控制系统一般由控制器与控制对象组成控制方式可分为连续控制与反馈控制即一般所称开回路与闭回路控制连续控制系统的输出量对系统的控制作用没有任何影响也就是说控制端与控制对象为单向作用这样的系统亦称开回路系统反馈控制是指将所要求的设定值与系统的输出值做比较求其偏差量利用这偏差量将系统输出值使其与设定值调为一致反馈控制系统方块图一般如图2-1所示图2-1反馈控制系统方块图22 PID控制将感测与转换器输出的讯号与设定值做比较用输出信号源 2-10v或4-20mA 去控制最终控制组件在工程实际中应用最为广泛的调节器控制规律为比例积分微分控制简称PID控制又称PID调节PID控制器问世至今已有近60年的历史了它以其结构简单稳定性好工作可靠调整方便而成为工业控制主要和可靠的技术工具当被控对象的结构和参数不能完全掌握或得不到精确的数学模型时控制理论的其它设计技术难以使用系统的控制器的结构和参数必须依靠经验和现场调试来确定这时应用PID控制技术最为方便即当我们不完全了解一个系统和被控对象，或不能通过有效的测量手段来获得系统的参数的时候便最适合用PID控制技术com 比例积分微分比例图2-2 比例电路公式2-1积分器图2-3 积分电路公式2-2图2-4微分电路微分器式2-3实际中也有PI和PD控制器PID控制器就是根据系统的误差利用比例积分微分计算出控制量控制器输出和控制器输入误差之间的关系在时域中如公式2-4和2-5u t Kp e t Td 公式2-4U s ]E s 公式2-5公式中U s 和E s 分别为u t 和e t 的拉氏变换其中分别为控制器的比例积分微分系数〔〕com ＰＩＤP控制比例控制是一种最简单的控制方式其控制器的输出与输入误差讯号成比例关系当仅有比例控制时系统输出存在稳态误差Steady-state error 积分I控制在积分控制中控制器的输出与输入误差讯号的积分成正比关系对一个自动控制系统如果在进入稳态后存在稳态误差则称这个控制系统是有稳态误差的或简称有差系统System with Steady-state Error为了消除稳态误差在控制器中必须引入积分项积分项对误差取关于时间的积分随着时间的增加积分项会增大这样即便误差很小积分项也会随着时间的增加而加大它推动控制器的输出增大使稳态误差进一步减小直到等于零因此比例积分 PI 控制器可以使系统在进入稳态后无稳态误差微分D控制在微分控制中控制器的输出与输入误差讯号的微分即误差的变化率成正比关系自动控制系统在克服误差的调节过程中可能会出现振荡甚至失稳其原因是由于存在有较大惯性的组件环节和或有滞后 delay 的组件使力图克服误差的作用其变化总是落后于误差的变化解决的办法是使克服误差的作用的变化要有些超前即在误差接近零时克服误差的作用就应该是零这就是说在控制器中仅引入比例项往往是不够的比例项的作用仅是放大误差的幅值而目前需要增加的是微分项它能预测误差变化的趋势这样具有比例微分的控制器就能够提前使克服误差的控制作用等于零甚至为负值从而避免了被控量的严重地冲过头所以对有较大惯性和或滞后的被控对象比例微分 PD 的控制器能改善系统在调节过程中的动态特性〔〕31 系统辨识1 所谓系统辨识即是在不知道系统转移函数时根据系统特性辨识出来2 若被控对象的数学模式相当线性 linear 且各项参数都可知道则可用控制理论来设计PID控制器的系数大小但实际的被控对象往往是非线性系统且系统复杂难以精确地用数学式表达所以工业上设计PID控制器时常常使用实验方法而较少用理论来设计调整PID控制器的方法中最有名的是Ziegler-Nichols所提出的二个调整法则这个调整法测是基于带有延迟的一阶传递函数模型提出的这种对象模型可以表示为公式3-1在实际的过程控制系统中有大量的对象模型可以近似的由这样的一阶模型来表示如果不能物理的建立起系统的模型我们还可以由实验提取相应的模型参数[5]3 将大小为1的阶跃信号加到被控对象如图3-1所示图3-1 将阶跃信号加到被控对象对大多数的被控对象若输入为阶跃信号则其输出c t 大多为S状曲线如下图3-2所示这个S状曲线称之为过程反应曲线process reaction curve 图3-2被控对象的阶跃响应图4 系统转移函数空调方面图3-3空调系统示意图图3-4 空调系统方块图由图3-3及图3-4可得知此系统的转移函数推导如下公式3-232 系统特性图1 系统为制热使用最大信号去控制系统直到稳定之后也就是热到达无法再上升时此时系统特性就会出现如下图3-5所示图3-5 系统制热的特性图2 系统为制冷使用最大信号去控制系统直到稳定之后也就是冷到达无法再下降时此时系统特性就会出现如下图3-6所示图3-6 系统制冷的特性图33 系统辨识方法1一阶系统带有延迟特性图3-7 一阶系统带有延迟特性图一阶系统加一个传递来近似被控对象则其近似转移函数如公式3-3所示公式3-3其中KTL可由上图3-7求得K稳态时的大小T时间常数※注系统越大时间常数越大L延迟时间2 KTL的求法K如上图3-31所示K值相当于C t 在稳态时的大小T与L求T及L必须在S形状曲线划一条切线最大斜率画出切线之后T及L值可以直接从图上得知T及L值与C t 及切线的关系如上图3-7所示第四章PID最佳调整法与系统仿真41 PID参数整定法概述1PID参数整定方法1 Relay feedback 利用Relay 的 on-off 控制方式让系统产生一定的周期震荡再用Ziegler-Nichols调整法则去把PID值求出来2 在线调整实际系统中在PID控制器输出电流信号装设电流表调P值观察电流表是否有一定的周期在动作利用Ziegler-Nichols把PID求出来PID值求法与Relay feedback一样3 波德图跟轨迹在MATLAB里的Simulink绘出反馈方块图转移函数在用系统辨识方法辨识出来之后输入指令算出PID值[13]2PID调整方式图4-1 PID调整方式如上描述之PID调整方式分为有转函数和无转移函数一般系统因为不知转移函数所以调PID值都会从Relay feedback和在线调整去着手波德图及根轨迹则相反一定要有转移函数才能去求PID值那这技巧就在于要用系统辨识方法辨识出转移函数出来再用MATLAB里的Simulink画出反馈方块图调出PID值〔〕PID 值的方法有在线调整法Relay feedback波德图法根轨迹法前提是要由系统辨识出转移函数才可以使用波德图法和根轨迹法如下图4-2所示42 针对无转移函数的PID调整法在一般实际系统中往往因为过程系统转移函数要找出之后再利用系统仿真找出PID值但是也有不需要找出转移函数也可调出PID值的方法以下一一介绍com Relay feedback4-3所示将PID控制器改成Relay利用Relay的On-Off 控制将系统扰动可得到该系统于稳定状态时的震荡周期及临界增益Tu及Ｋu在用下表4-4 的Ziegler-Nichols第一个调整法则建议PID调整值即可算出该系统之ＫpTiTv之值Controller P 05Ｋu PI 045Ｋu 083Tu PID 06Ｋu 05Tu 0125Tu 〔〕com Relay feedback 在计算机做仿真Step 1 以MATL AB里Simulink绘出反馈方块如下图4-5所示图4-5 Simulink绘出的反馈方块图Step 2让Relay做On-Off动作将系统扰动On-Off动作将以±１做模拟如下图4-6所示图4-6Step 3即可得到系统的特性曲线如下图4-7所示图4-7 系统震荡特性曲线Step 4取得Tu及a带入公式3-1计算出Ｋu以下为Relay feedback临界震荡增益求法公式4-1ａ振幅大小ｄ电压值com 在线调整法图4－８在线调整法示意图在不知道系统转移函数的情况下以在线调整法直接于PID控制器做调整亦即PID控制器里的I值与D值设为零只调P值让系统产生震荡这时的P值为临界震荡增益Ｋv之后震荡周期也可算出来只不过在线调整实务上与系统仿真差别在于在实务上处理比较麻烦要在PID控制器输出信号端在串接电流表即可观察所调出的P值是否会震荡虽然比较上一个Relay feedback法是可免除拆装Relay 的麻烦但是就经验而言在实务上线上调整法效果会较Relay feedback 差在线调整法也可在计算机做出仿真调出PID值可是前提之下如果在计算机使用在线调整法还需把系统转移函数辨识出来但是实务上与在计算机仿真相同之处是PID 值求法还是需要用到调整法则Ziegler-Nichols经验法则去调整与Relay feedback的经验法则一样调出PID值com 在线调整法在计算机做仿真Step 1以MATLAB里的Simulink绘出反馈方块如下图4-9所示图4-9反馈方块图PID方块图内为图4-10 PID方块图Step 2将Td调为0Ti无限大让系统为P控制如下图4-11所示图4-11Step 3调整KP使系统震荡震荡时的KP即为临界增益KU震荡周期即为TV 使在线调整时不用看a求KU如下图4-12所示图4-12 系统震荡特性图Step 4再利用Ziegler-Nichols调整法则即可求出该系统之ＫpTiTd之值43 针对有转移函数的PID调整方法com系统反馈方块图在上述无转移函数PID调整法则有在线调整法与Relay feedback调整法之外也可利用系统辨识出的转移函数在计算机仿真求出PID值至于系统辨识转移函数技巧在第三章已叙述过接下来是要把辨识出来的转移函数用在反馈控制图之后应用系统辨识的经验公式Ziegler-Nichols第二个调整法求出PID值〔〕4-14所示controllerPPI33LPID2L 表4-14 Ziegler-Nichols第二个调整法则建议PID调整值〔〕为本专题将经验公式修正后之值※comL为延迟时间可com b※coma的解法可有以下2种解一如下图4-15中可先观察系统特性曲线图辨识出a值解二利用三角比例法推导求得图4-15利用三角比例法求出a值公式4-2用Ziegler-Nichols第一个调整法则求得之PID控制器加入系统后一般闭环系统阶跃响应最大超越的范围约在1060之间所以PID控制器加入系统后往往先根据Ziegler-Nichols第二个调整法则调整PID值然后再微调PID值至合乎规格为止com 波德图法及根轨迹法利用系统辨识出来的转移函数使用MATLAB软件去做系统仿真由于本设计中PID参数的整定主要是基于系统辨识及Ziegler-Nichols调整法则所以在此不用波德图法及根轨迹法第五章油冷却机系统的PID控制器设计51 油冷却机系统本论文设计以油冷却机温度控制系统为被控对象进行PID控制器的参数整定及其设计下面介绍一下油冷却机系统以及各个组成部分com 油冷却机图5-1 油冷却机实物图图5-2 油冷却机系统循环图油冷却机系统循环主要可分为冷媒循环系统以及油循环系统冷媒循环系统即为一般常见之制冷循环而油循环则是将油打出后经过负载加热再与冷媒循环的蒸发器作热交换再流回油槽做冷却用[16]com 感测与转换器图5-3 PT100实物图电阻式温度检测器 RTDResistance Temperature Detector －一种物质材料作成的电阻它会随温度的上升而改变电阻值如果它随温度的上升而电阻值也跟着上升就称为正电阻系数如果它随温度的上升而电阻值反而下降就称为负电阻系数[6]PT100温度传感器是一种以白金 Pt 作成的电阻式温度检测器属于正电阻系数其电阻和温度变化的关系式如下R Ro 1αT其中α 000392Ro为100Ω 0℃的电阻值 T为摄氏温度Vo 255mA ×100 1000392T 0255T1000 电源是带噪声的因此我们使用齐纳二极管作为稳压零件由于72V齐纳二极管的作用使得1K电阻和5K可变电阻之电压和为65V靠5K可变电阻的调整可决定晶体管的射集极极电流而我们须将集极电流调为255mA使得量测电压V如箭头所示为0255T1000其后的非反向放大器输入电阻几乎无限大同时又放大10倍使得运算放大器输出为255T100 6V齐纳二极管的作用如72V齐纳二极管的作用我们利用它调出255V因此电压追随器的输出电压V1亦为255V其后差动放大器之输出为Vo 10 V2-V1 10 255T100-255 T10如果现在室温为25℃则输出电压为25V。

基于MATLAB的PID控制器设计说明

基于MATLAB的PID控制器设计说明PID控制是一种广泛应用于工业控制系统中的常用控制方法。

其主要思想是通过对系统输出和系统期望值之间的误差进行反馈调节，从而实现对系统的精确控制。

PID控制器的设计主要包括三个方面：比例控制、积分控制和微分控制。

下面将对MATLAB中的PID控制器设计进行详细说明。

第一步，确定系统模型：在设计PID控制器之前，首先需要获得被控对象的数学模型。

可以通过实验测量、建立数学模型或者系统辨识等方法来获取系统模型。

一般而言，常用的系统模型有传递函数模型和状态空间模型。

第二步，选择控制器类型：在MATLAB中，可以使用pid函数来构造PID控制器对象。

pid函数有多个重载形式，可以根据系统的实际情况选择适合的函数。

通常有两种常见的方式，一种是使用系统传递函数作为输入参数，另一种是使用系统状态空间模型作为参数。

例如，可以使用以下形式调用pid函数来构造一个PID控制器对象：pid_controller = pid(P, I, D)其中P、I和D分别表示比例增益、积分增益和微分增益。

根据系统的实际需求，可以调整这三个参数来获得更好的控制效果。

通常可以通过试探法或者经验法来选取合适的参数值。

第三步，闭环控制：在得到PID控制器对象后，可以通过MATLAB中的反馈函数来实现闭环控制。

反馈函数的基本形式如下：sys_cl = feedback(sys, pid_controller)其中sys为被控对象的传递函数或状态空间模型。

反馈函数可以自动生成闭环传递函数或闭环状态空间模型，并返回新的系统模型sys_cl。

第四步，性能评估和调试：在实际应用中，需要对系统的控制性能进行评估和调试。

MATLAB提供了一系列功能强大的工具和函数用于控制系统分析和调试，如step函数、bode函数、nyquist函数等。

这些工具可以帮助分析系统的响应特性、稳定性和鲁棒性，并通过调整PID控制器的参数来获得更好的控制效果。

基于MATLAB的PID控制器设计说明

基于MATLAB的PID控制器设计说明PID控制器是一种经典的控制算法，被广泛应用于工业自动化领域。

本文将详细介绍基于MATLAB的PID控制器设计说明。

首先，我们需要明确PID控制器的基本原理。

PID控制器由比例（P）、积分（I）和微分（D）三部分组成。

比例部分根据当前偏差与设定值之间的关系进行调节；积分部分通过累积误差来消除系统的稳态偏差；微分部分根据当前误差与前一次误差的差异来预测系统的未来状态。

在MATLAB中，我们可以使用pid函数来设计PID控制器。

pid函数的基本语法如下：C = pid(Kp, Ki, Kd)其中，Kp、Ki、Kd分别表示PID控制器的比例增益、积分时间常数和微分时间常数。

根据实际需求，我们可以通过调整这三个参数来优化控制器的性能。

接下来，我们需要明确控制系统的传递函数。

传递函数是描述系统输入与输出之间关系的函数，通常用一个分子多项式除以一个分母多项式的比值来表示。

在MATLAB中，我们通过tf函数来创建传递函数。

tf函数的基本语法如下：G = tf(num, den)其中，num表示分子多项式的系数，den表示分母多项式的系数。

通过tf函数创建的传递函数可以方便地进行各种运算和分析。

设计PID控制器的一种常见方法是将传递函数G(s)与控制器C(s)串接起来。

通过串接两个传递函数，我们可以得到一个闭环传递函数，用于描述控制器对系统的影响。

MATLAB提供了series函数来实现传递函数的串接。

series函数的基本语法如下：H = series(G, C)设计好闭环传递函数后，我们可以使用feedback函数来创建一个反馈控制系统。

feedback函数的基本语法如下：Sys = feedback(H, 1)其中，H表示闭环传递函数，1表示反馈路径的增益。

通过feedback函数创建的反馈控制系统可以方便地进行稳定性分析和性能评估。

在设计PID控制器时，我们需要确保控制器参数的合理性。

基于MATLAB的PID控制器设计报告

MATLAB论文--基于控制系统的PID调节基于MATLAB 的PID 控制器摘要：本论文主要研究PID 控制器。

PID 控制是迄今为止最通用的控制方法，大多数反馈回路用该方法或其较小的变形来控制。

PID 控制器（亦称调节器）及其改进型因此成为工业过程控制中最常见的控制器 (至今在全世界过程控制中用的84%仍是纯PID 调节器，若改进型包含在内则超过90%)。

在PID 控制器的设计中，参数整定是最为重要的,随着计算机技术的迅速发展，对PID 参数的整定大多借助于一些先进的软件，例如目前得到广泛应用的MATLAB 仿真系统。

本论文主要介绍PID 的原理及简单的用法，探究控制器中各个参数对系统的影响，就是利用《自动控制原理》和《MATLAB 》所学的内容利用简单的方法研究PID 控制器的设计方法，并通过MATLAB 中的虚拟示波器观察系统完善后在阶跃信号下的输出波形。

关键字：PID 控制简介 PID 控制器原理 MATLAB 仿真 PID 参数的设定正文：一、PID 控制简介PID 控制器又称PID 调节器，是工业过程控制系统中常用的有源校正装置。

长期以来，工业过程控制系统中多采用气动式PID 控制器。

由于气动组件维修方便，使用安全可靠，因此在某些特殊场合，例如爆炸式环境，仍然使用气动式PID 控制器。

随着运算放大器的发展和集成电路可靠性的日益提高，电子式PID 控制器已逐渐取代了气动式PID 控制器。

目前，已在开发微处理器PID 控制器。

这里，仅简要介绍PID 控制器的主要特性。

PID 调节器是一种线性调节器，它根据给定值)(t r 与实际输出值)(t c 构成的控制偏差： )(t e =)(t r －)(t c 将偏差的比例、积分、微分通过线性组合构成控制量，对控制对象进行控制，故称为PID 调节器。

在实际应用中，常根据对象的特征和控制要求，将P 、I 、D 基本控制规律进行适当组合，以达到对被控对象进行有效控制的目的。

基于matlabsimulink的pid控制器设计

基于matlabsimulink的pid控制器设计1.引言1.1 概述概述部分：PID控制器是一种常用的控制算法，它通过不断地调整系统的输出来使其尽量接近所期望的目标值。

在工业控制领域，PID控制器被广泛应用于各种工艺过程和自动化系统中。

本文将以MATLAB/Simulink为工具，探讨基于PID控制器的设计方法。

PID控制器以其简单易实现、稳定性好的特点，成为许多控制系统的首选。

在文章的正文部分，我们将对PID控制器的基本原理进行详细介绍，并结合MATLAB/Simulink的应用，展示如何使用这一工具来设计和实现PID控制器。

在控制系统设计中，PID控制器通过测量系统的误差，即期望输出值与实际输出值之间的差异，并根据三个控制参数：比例项（Proportional）、积分项（Integral）和微分项（Derivative）来调整系统的输出。

比例项控制系统的响应速度，积分项消除系统的稳态误差，微分项抑制系统的震荡。

MATLAB/Simulink作为一款功能强大的仿真软件，提供了丰富的控制系统设计工具。

它不仅可以帮助我们直观地理解PID控制器的工作原理，还可以实时地模拟和分析系统的响应。

通过使用MATLAB/Simulink，我们可以轻松地进行PID控制器参数调整、系统性能评估和控制算法的优化。

总之，本文旨在介绍基于MATLAB/Simulink的PID控制器设计方法，通过理论介绍和实例演示，帮助读者深入理解PID控制器的原理和应用，并为读者在实际工程项目中设计和实施PID控制器提供参考。

在结论部分，我们将总结所得结论，并对未来进一步研究的方向进行展望。

文章结构部分的内容可以描述文章的整体架构和各个部分的内容大纲。

以下是对文章1.2部分的内容补充:1.2 文章结构本文主要由以下几个部分构成：第一部分是引言部分，包括概述、文章结构和目的等内容。

在概述中，将简要介绍PID控制器在自动控制领域的重要性和应用背景。

基于matlab的pid控制仿真课程设计

基于matlab的pid控制仿真课程设计PID（比例-积分-微分）控制器是一种常见的控制算法，被广泛应用于工业控制系统中。

在本文中，我们将介绍基于MATLAB的PID控制仿真课程设计。

首先，我们将简要介绍PID控制器的原理和特点，然后介绍如何使用MATLAB进行PID控制的仿真。

PID控制器是一种反馈控制器，可以通过比例、积分和微分三部分来调节控制系统的输出。

比例部分根据误差的大小进行调节，积分部分用于消除稳态误差，微分部分用于抑制系统振荡。

通过调节PID控制器的参数，可以使系统的稳定性、响应速度和稳态误差达到预期的要求。

在MATLAB中，可以使用控制系统工具箱来进行PID控制的仿真。

首先，我们需要定义一个系统模型，可以是连续时间系统或离散时间系统。

然后，我们可以使用PID控制器对象来创建一个PID控制器。

PID控制器的参数可以通过试错法、模型辨识等方法进行调节。

一旦系统模型和PID控制器被定义，我们可以使用MATLAB中的仿真工具来进行PID控制器的仿真。

通常，我们将输入信号作为控制器的参考信号，将输出信号作为系统的输出，并将控制器的输出作为系统的输入。

然后，我们可以观察系统的响应，并根据需要调整控制器的参数。

在进行PID控制仿真实验时，我们可以通过选择不同的控制器参数、改变控制器的结构、调整参考信号等方式来研究控制系统的性能。

例如，我们可以改变比例增益来改变系统的稳定性和响应速度，增加积分时间常数来减小稳态误差，增加微分时间常数来抑制系统振荡等。

在课程设计中，我们可以设计不同的控制实验，并分析不同参数对系统性能的影响。

例如，可以研究比例增益对系统稳定性和响应速度的影响，或者研究积分时间常数对稳态误差的影响等。

同时，我们还可以通过比较PID控制和其他控制算法（如PI控制、PD控制等）来评估PID控制的优势和局限性。

在进行PID控制仿真实验时，我们应该注意以下几点。

首先，选择合适的系统模型，确保模型能够准确地描述实际系统的行为。

毕业设计--基于MATLAB的PID控制算法的实现

摘要目前工业自动化水平已成为衡量各行各业现代化水平的一个重要标志。

PID 控制及其控制器已在工程实际中得到了广泛的应用。

本文介绍了PID控制的基础知识和工作原理，并讨论PID控制器的类型以及各种控制器的优缺点，为进行数字PID的算法研究和仿真提供理论基础。

在简单介绍工业过程控制中经常使用到的位置式和增量式PID控制后主要讨论了两种改进的数字PID控制算法：积分分离PID算法与不完全微分PID算法，比较传统控制算法与改进的算法的优缺点，并基于MATLAB对其进行仿真，讨论仿真结果。

仿真结果表明：积分分离控制算法和不完全微分控制算法可以提高控制精度和消除系统高频干扰等。

证明改进的PID控制算法相比一般PID控制算法有很多优点。

关键词：数字PID；积分分离；不完全微分；MATLAB仿真AbstractAt present the level of industrial automation has become an important sign of the modernization of every industries.PID control and controllers now have been worked in a wide range of engineering applications.This paper briefly introduces and discusses the types and the advantages or disadvantages of the PID controllers.These konwledge lay the foundation for the arithmetical research and the simulation.It mainly discusses two improved PID control algorithms: Integral separation PID control algorithm and Not completely differential PID control algorithm after introducing the Incremental PID control and the Position control algorithm used in the industrial process paring the advantage and diadvantage of the traditional PID control algorithm to the improved PID control algorithm and discussing the results of MATLAB simulation.The simulation results show that the Integral separation PID control algorithm and Not completely differential PID control algorithm can improve the control accuracy and eliminate the high frequency interference ,etc.This article proves that the improved PID control algorithm have more advantages than normal PID control algorithm.Key words:digital PID; Integral separation; Not completely differential simulation; MATLAB simulation目录第1章概述 (1)1.1设计的目的和意义 (1)1.2国内外研究发展现状 (1)1.3本次设计的研究内容 (2)第2章 PID控制基本理论 (3)2.1PID的工作原理 (3)2.2PID控制器类型分类 (4)2.4PID控制器参数确定 (6)2.5PID控制器优缺点 (10)2.6本章小结 (10)第3章数字PID控制算法及仿真意义 (11)3.1数字PID控制算法 (11)3.2MATLAB简介 (19)3.3PID仿真的意义 (21)3.4本章小结 (22)第4章改进型PID控制算法及仿真 (23)4.1积分分离式PID控制算法 (23)4.2不完全微分PID控制算法 (27)4.3本章小结 (32)结论 (33)参考文献 (34)致谢 (35)附录 (36)第1章概述1.1 设计的目的和意义PID控制由于结构简单、工作稳定、鲁棒性好等因素在当今的工业过程控制中仍占有主导地位。