基于AMESim的气动系统建模与仿真技术研究
基于AMESim注塑机快速合模系统的建模仿真及节能研究

的建 模 、仿 真 及 动 力 学 分 析 的 优 秀 软 件 ,至 今 已经 历 了 十 多 年 的 丰 富 和 完 善 。该 软件 包 含 了 I GI E 的专 门技 术 .并 为 工 程 设 计 提 供 交 互 MA N
能 力 。 它 具 有 完 全 图 形 界 面 ,在 整 个 仿 真 过 程 中 , 系 统 都 是 以 图形 的 形 式 显 示 的 。 在 表 示 元
c mp n n u cin, a d v rf h o rcn s fte mo e a e ne p rme t h tc mp r dt esmuain rs lsa d e p rme tl o o e tfn t o n eiyte c re te so d lb sd o x e h i nsta o ae h i lto eut n x e i na d t o v rf e c re te so h d e;so te e eg t h ciae n e fc mp n ns a d u ig te o t z t n to aa t e y t orcn s fte mo l h w h n ry wi te a tv td id x o o o e t, n sn h pi ai o l i h h mi o
为 重要 的作 用 。其液 压 传 动 系 统 的 主要 任 务是 依
靠 液 体压 力 克 服 负 载 阻 力进 行 动 力 传 动 , 以完成 预定 动作 。然而人们 往往侧 重其 性能及 可靠 性 ,对 其 能耗 控 制 和 效 率 重视 不 足 。造 成 液 压 系 统 的运
行 效率 较 低 ,系统 能耗 较 大 。本 文 将 基 于 AM S E. i m仿 真 软 件 建 立 某 注 塑 机 快 速 合 模 回路 的模 型 , 将 模 型仿 真 结 果 与 实验 数 据 对 比 .验证 模 型 的正 确性 ;而后 对模 型进 行优 化分 析 ,降低 系 统能耗 。
基于AMESim平台的轨道车辆空气弹簧系统气动力学仿真模型研究

整阀、差压阀等部件的作用[ 1 。
本 文基 于空气 动力 学 、流体 力学 和热力 学 的理 论 ,在 建立 空气 弹 簧 气 动力 学 微 分 方程 的基 础 上 , 基 于 AME S i m 平 台建 立 空 气 弹 簧 系统 气 动 力 学 模 型 ,并将 其 引入 车辆 动力学 仿 真 中研 究空气 弹簧 的
果 对 比,验证了该模型能够很好反映实际空气 弹簧 的静 态和 动态特性 。仿 真计算 结果表 明 :该模型解 决 了常规
车辆动力学模型不能模拟空气弹簧刚度变化和高度 调整 阀在 有些 工况下会 打开 的问题 ,从 而提高 了车 辆动力学
仿 真的计算精度 。
关键词 :空气弹簧 ;刚度 ;气动力学 ;车辆动力学 ;AME S i m
Ma y, 2 01 3
基 于 AME S i m 平 台 的轨 道 车 辆 空气 弹 簧 系统 气 动 力 学 仿 真模 型研 究
戚 壮 ,李 芾 ,黄运华 ,虞大联
6 1 0 0 3 1 ; 2 6 6 1 1 1 ) ( 1 .西南交通大学 机械工程学 院 ,四川 成都
作者简介 :戚
壮 ( 1 9 8 8 一) ,男 ,河北 石家庄人 ,博 士研究生 。
8 0
中
国
铁
道
科
学
第 3 4 卷
如图 1 所示 。 图 中:m 为半 车体 的质 量 ;D 为两 侧 空气 弹簧 的横 向跨 距 。由图看 出 :橡 胶气囊 、附 加 空气 室和节 流孔组 成空气 弹簧 ,高度 调整 阀和差 压 阀与 空气 弹簧组成 空气 弹簧 系统 。橡 胶气囊 与 附 加 空气 室之 间的节流 孔 ,起 到一 定 的阻尼作 用 。差 压 阀连接 两侧 空气 弹簧 的附加 空气室 ,当两侧 空气 弹 簧压差 超 出预定范 围后 ,差压 阀 自动打开 ,两侧 附 加空气 室连 通 ,使 气体从 高压 侧流 向低压侧 。高 度 调整 阀的作 用是 ,当车体 高度 超过 预定值 时 ,高 度 调整 阀使 气 囊 向 大 气 排 气 ,降 低 车 体 高 度 ,反 之 ,高度 调 整 阀使 风 源 向气 囊 充 气 ,提 升 车体 高 度 。高 度调 整阀具有 一定 范 围的无感 区 ,当车体 高 度 变化 在此无 感 区范 围以 内时 ,高度 调整 阀不会 作 用 。此 外 ,高 度 调 整 阀 还 具 有 一 定 的 动 作 延 迟
基于AMESim电控空气悬架系统性能仿真研究

基于AMESim电控空气悬架系统性能仿真研究董威望;郑泉【摘要】基于AMESim软件建立1/4空气悬架系统模型,利用Matlab软件设计空气悬架系统控制器,使用Matlab和AMESim对空气悬架系统进行联合仿真.白噪声路面信号输入下的联合仿真结果分析表明,安装主动空气悬架系统车辆的最大振动加速度与振动加速度均方根、平均车身高度、动载荷均比安装被动空气悬架系统的车辆小,该仿真结果符合有关主动空气悬架系统的一般研究结论,该控制方法可以有效提高车辆的平顺性.【期刊名称】《山东交通学院学报》【年(卷),期】2014(022)004【总页数】5页(P1-4,19)【关键词】电控空气悬架;AMESim;控制器;联合仿真【作者】董威望;郑泉【作者单位】安徽农业大学工学院,安徽合肥230036;安徽农业大学工学院,安徽合肥230036【正文语种】中文【中图分类】U463.33车辆电控空气悬架系统作为主动悬架系统的重要组成形式,其结构形式、性能参数与控制策略的选择,对汽车的行驶平顺性有着直接的影响[1]。
目前,对电控空气悬架系统的主要研究对象是带有附加气室的空气弹簧,通过建立数学及物理模型进行仿真。
文献[2]基于工程热力学和空气动力学理论分别建立了带附加气室空气弹簧系统各部件的状态方程和动力学方程,利用空气弹簧动刚度模型,计算了弹簧动刚度和各因素之间的动态变化关系。
文献[3]利用自由衰减振动的方法研究了簧上质量、节流孔直径等因素对悬架系统等效刚度、等效阻尼等力学特性参数的影响。
文献[4]基于能量守恒方程、理想气体状态方程和孔隙流量方程指出了附加气室容积、节流孔开度对空气弹簧动刚度的影响。
这些研究内容没有考虑到带附加气室空气弹簧的刚度变化具有非线性的特点,所建数学模型欠准确,降低了仿真结果的正确性[5]。
本文以电控空气悬架系统为研究对象,基于AMESim建立车辆二自度1/4电控空气悬架系统模型,利用Matlab/simulink设计悬架的控制系统,通过Matlab/simulink和AMESim对电控空气悬架系统进行联合仿真。
基于AMESim的减压阀建模与仿真

智者论道智库时代 ·241·减压阀是机车空气管路系统的重要部件,本文利用AMESim 软件对减压阀进行建模并仿真分析,得到减压阀各关键参数的最优取值范围,为减压阀的选型提供依据。
一、减压阀结构及工作原理图1为减压阀结构原理图[1]。
如图所示,初始状态时,低压腔室p2中无压力,调压弹簧2推动膜片4和阀杆5下移,阀杆5再推动阀芯7下移,阀口打开,此时高压腔室p1中压力空气输入到低压腔室p2中。
低压腔室p2压力逐渐上升,同时经阻尼孔6流向膜片4下表面腔室。
当膜片4下表面气体向上推力F2等于调压弹簧向下推力F1时,阀芯7在复位弹簧8的作用下向上移动,阀口关闭,高压腔室p1中压力空气输入到低压腔室p2中的通道关闭,低压腔室p2中的气压不再上升,此时低压腔室p2中即有稳定压力输出。
通过调节调压弹簧2、3的预紧力,即可调节减压阀的输出压力[2]。
图1 直动式减压阀结构原理图1、手柄;2、调压弹簧;3、溢流阀;4、膜片;5、阀杆;6、阻尼孔;7、阀芯;8、复位弹簧二、减压阀AMESim 模型建立A M E S i m (A d v a n c e d M o d e l i n g Environment for performing Simulationof engineering systems)为多学科领域复杂系统建模仿真平台。
用户可以在这个单一平台上建立复杂的多学科领域的系统模型,并在此基础上进行仿真计算和深入分析,也可以在这个平台上研究任何元件或系统的稳态和动态性能。
AMESim 软件采用基于物理化图形建模方法,因此对于气动减压阀来说,利用AMESim 软件建模仿真更加方便与准确[3]。
减压阀的AMESim 模型如图2。
调压弹簧3推动阀芯质量块5向右移动,阀芯6打开,高压腔室9内压力空气通过阀口进入低压腔室12中,进一步经过阻尼孔11进入膜片下腔室10。
当膜片下腔室10中压力作用在膜片上推力F2等于调压弹簧3对膜片下推力F1时,阀芯6向左移动,阀口关闭,高压腔室9中压力空气通向低压腔室12的通道关闭,低压腔室12中压力稳定在设定压力值。
AMESim论文仿真研究论文:基于AMESim软件的液压控制仿真技术研究

AMESim论文仿真研究论文:基于AMESim软件的液压控制仿真技术研究摘要imagine公司推出的amesim软件在液压控制建模方面拥有强大的分析和仿真能力,介绍了amesim软件的基本特征,以电液伺服阀为例进行了建模及仿真分析。
关键词amesim;液压控制;仿真研究随着仿真技术的发展,极大缩短了开发周期、减小了科研成本及风险。
amesim是法国imagine公司研究开发的仿真平台,它集机械、流体、气动、控制、电控、热力学等多学科于一体,可以构建比较真实的仿真系统。
amesim软件在仿真开发中,为企业技术人员节省了时间,比较适用于液压控制系统的建模与仿真。
1amesim软件具有的特点1)建模仿真平台。
amesim软件提供了充足的模型数据库,包括了液压、控制、机械、电磁、电工电子等领域。
2)图形建模化。
图形化物理建模方法可使用户专注于物理系统本身的开发。
建模的语言是工程术语,仿真模型的扩展是通过图形用户界面来完成,无需编制程序代码。
3)智能求解数学模型。
可以在多种算法中优选积分方法;同时在不同的仿真时期结合系统的特征动态地调节积分步长和变换积分算法提高仿真精度和缩短仿真时间,同时嵌式数学不连续性处理工具可以解决数值仿真的“间断点问题”。
4)计算准确迅速。
amesim采用变阶数、变步长、鲁棒性强、变类型的智能求解器,结合所建模型自动地优选积分方法。
2amesim在液压控制控制仿真中的应用电液伺服阀是电液伺服系统中的关键部件。
在电液伺服阀中力反馈两级电液伺服阀是最基本、应用最广泛的伺服阀。
为此,以它为例进行分析。
1)建立四通四边功率级滑阀的模型,如图1所示。
图1功率级滑阀仿真模型2)建立前置放大级双喷嘴挡板阀的模型,如图2所示。
图2双喷嘴挡板阀的仿真模型3)建立永磁动铁式力矩马达的模型,如图3所示。
图3力矩马达的仿真模型4)伺服阀的仿真压力曲线,如图4所示。
图4伺服阀的仿真压力曲线根据仿真结果可知,仿真曲线和实际情况相符。
基于AMESim的电控天然气针口阀喷嘴仿真设计

天然气喷射器由电磁阀,控制室,针阀偶件组成,其工作原理如图(1)所示,发动机ECU接受经过滤波,整形,放大后的前向电路中的曲轴位置传感器和凸轮轴位置传感器(在顺序喷射中需要该传感器)所测得的模拟信号,经过其处理与计算,判断出符合该工况的喷射正时与喷射脉宽,发送PWM波信号控制电磁线圈的通断电,其中通电时刻决定喷射正时,而通电时间的长短则决定该工况下的喷气量。在整个机构中高压天燃气经过减压与调压后进入喷射器中分为两部分,一部分气体进入喷射针阀,一部分气体则进入喷射器气腔中,当进入喷射气体的压力和流量较小的时候电磁阀处于关闭状态。气体进入了喷射器气腔,由于控制活塞上的面积大于喷射器针阀的作用面积,加上针阀弹簧的作用力,使得喷射器的喷射针阀处于关闭状态。而当电磁线圈通电时产生一个磁场,顶杆(衔铁)在电磁力的作用下,克服天然气背压和复位弹簧的预紧力而升起,打开喷嘴阀门,天然气喷出。顶杆在未达到最大升程前,由于流通面积不断增大,引起喷孔处压力降低,导致了喷嘴环形腔因压力波动而使气体不稳定流动,直到顶杆(衔铁)由于机械限位挡板的作用达到最大升程,喷嘴环形腔内气体流动趋于稳定。当电磁线圈断电后,顶杆(衔铁)所受电磁力也立即消失,并在复位弹簧和天然气背压的作用下,落回并压紧阀座,切断喷气动作,从而可以根据该原理对天然气这一特殊燃料的喷射机理进行研究,以期发现天然气的喷射规律,改进喷射方式。
注意:由于气体的泄漏,部件传热与管路设计长度等在实际的使用过程中对喷射的影响是很小的,为了方便建模同时考虑到实际情况所以均把它们作为理想化的模型处理。下图4为电控天燃气的AMESim模型:
图 4 电控天然气喷嘴模型
1—天然气特征参数 2—电磁特性参数 3—重力参数 4—气隙 5—复位弹簧 6—铁芯
7—限位挡板 8—PWM占控比 9—PWM波 10—驱动电路 11—电磁线圈 12—天然气喷嘴阀门 13—理想气源 14—低压腔 15—可变器腔体积 16—节流孔 17—燃烧室18—高压枪19—喷孔体积
基于AMESim的新型油气弹簧建模与仿真

(. 1 武汉理工大学 汽车工程学院 , 湖北 武汉 40 7 2 吉林大学 汽 车仿真与控制 国家重点实验室 , 30 0; . 吉林 长春 10 2 ) 3 0 2
摘 要 : 对传统 气 室外置 式 油气弹 簧存在 的 结构复 杂 、 间布 置较 难等 问题 , 出了一种 新 型单 气 针 空 提 室 油气弹簧 结构 . 绍 了该 油 气弹 簧 的结 构 和 工 作 原 理 , 介 简化 得 到 了其 物 理模 型 , 在 仿 真 软 件 并 A Sm 下搭 建 了其动 力 学模 型 , 时对 油 气弹 簧 样 件进 行 了外特 性 试 验 , ME i 同 验证 了仿 真 模 型 的 精
moi i lt na dC nrl J i nv r t,C a g h n in 1 0 2 ,C ia t eSmua o n o t , in U ie i v i o l s y h n e u ,J i 3 0 2 hn ) l
Ab t a t s r c :To s le t e df c l f s c s e ln o r d to lh d o p e ov h i u t o pa e a s mb i g f r ta iina y r — n umai p i g u o t e i f y tc s rn s d e t h c mp e tu t e ,a n v lh d o p e mai p i g wih snge g sc l wa r p s d.Th tu t r n o lx sr cur s o e y r — n u t s rn t i l a el sp o o e c e sr c u e a d prn i e o he p o o e y r - ne ma i prn r n rdu e a d smpl e o o t i h sc l mo i cpl ft r p s d h d o- u tc s i g we e i to c d n i i d t b a n p y ia — p i f de .Th y a c 1 e d n mi mo e s sa ls e b d l wa e tb ih d y AMESi m s f r . An e t r a c a a t rsi ts fr t e ot e wa xe n l h r ce t e t o h i c h d o- n u tc s rn s c n u td t e f h c u a y o y a c mo e .On u  ̄e ft e v h . y r p e ma i p g wa o d c e o v r y t e a c r c fd n mi d 1 i i e q a ro h e i
基于AMESim双筒叠加阀片式充气减振器建模与仿真_马天飞

密度; ε 为小孔的流量系数; h1 为带孔节流阀片厚 度; lA 为孔的宽度。 1.2.2 减振器复原阀初次开阀
随着活塞相对工作缸运动速度的增加,减振器
上腔的压力也随之增大,当作用在复原阀片的压力
Fup 达到弹性阀片预紧力时,复原阀打开。此时有
Fup = pud1 + pud 2
(6)
与开阀前相似,油液经活塞孔、开阀后形成的
活塞上下压差 pud (t) 可看成由两部分组成:① 活塞孔的节流作用产生的压差 pud1(t) ;②复原阀上 的常通节流孔产生的压差 pud 2 (t) ,即
pud (t) = pud1(t) + pud 2 (t)
(3)
测量得活塞孔长与孔径的比值大于 4,故减振
器油液在此孔中的流动可视为细长孔中的流动,而
关键词:减振器 AMESim 气体反弹力 叠加阀片 阻尼特性
中图分类号:U463
Modeling and Simulating of the Gas-precharged Dual-sleeve Shock Absorber with Multiple Valve Plates Using AMESim
(吉林大学汽车仿真与控制国家重点实验室 长春 130022)
摘要:以某乘用车前悬架双筒叠加阀片式充气液压减振器为研究对象,通过对其工作原理进行分析,建立该减振器在各种工 况下的数学模型。基于该减振器的数学模型,在多领域系统仿真分析软件 AMESim 中搭建其详细的仿真草图模型。考虑到 叠加阀片的非线性弹性特性,根据叠加阀片的等效厚度计算公式,在有限元分析软件 Abaqus 中建立阀片的有限元模型,仿 真得出阀片受力与变形曲线,再将曲线数据导入 AMESim 模型中进行系统仿真。仿真结果表明,减振器速度特性曲线和示 功图与试验数据吻合良好,符合工程实际要求,证明所建 AMESim 模型的正确性。基于 AMESim 模型研究该减振器的气体 反弹力、活塞缝隙和常通节流孔等几个关键设计参数对减振器阻尼特性的影响,并得出几个重要的结论。仿真模型可用于指 导减振器的关键参数的设计与性能预测。
simulink与AMESim联合仿真

Simulink与AMSIM联合仿真的方法虽然随着新材料、电机技术、控制学和先进制造技术等的发展,出现了用以取代目前所依赖的功率液压传动的功率电传技术,但是在现阶段,液压伺服作动系统仍然占据航空作动系统的主导地位。
主要原因是液压伺服作动系统具有其它伺服作动系统无法比拟的优势,具有容易得到大功率输出、高功率/重量比、响应快和低俗特性好的特点。
航空液压作动系统是目前飞机上最成熟的液压作动方式,大多直接采用飞机的中央液压源提供的恒压油,通过(伺服)阀来控制执行机构的双腔流量完成指令动作,精度高、响应快。
航空也要作动系统根据其发展历程一般分为以下四类:液压助力器、电液指令作动器、复合式伺服作动器和直接驱动阀式伺服作动器。
本文将主要对其关键技术进行深入分析,并提出关键技术的解决途径。
1 建模仿真技术由于对航空液压作动系统自身结构比较复杂,对其自身的性能要求比较高,需要满足包括输出载荷、中立位置、额定行程、最大行程、行程余量、额定速度、最大速度、极限载荷、主控阀剪切力、门限、位置精度和滞环等的静态特性,满足包括频率响应和阶跃响应的动态特性,以及稳定性和阻抗特性要求。
银次,在研制航空液压作动系统的过程中,对其进行建模仿真非常重要。
通过仿真,可以对所设计的作动器性能有全面的了解,便于改进和完善设计。
传统的建模仿真分析手短一般采用数学推到加Simulink仿真的方式进行。
Simulink是美国Match Works公司开发的MA TLAB软件的可视化仿真环境,具有丰富的线性/非线性、连续/离散等控制系统仿真功能模块,具备神经网络、模糊控制等一系列先进的智能控制工具箱,非常适合进行航空液压作动系统的建模与分析,但其前提是基于用户建立的数学模型和其自身提供的结构参数化的功能模块。
而这已无法满足现在对仿真高精度和高准确度的要求。
而且Simulink本身没有专门针对液压流体仿真的工具箱,用户使用时要自己建立模型。
AMESim是法国Imagine公司推出的基于功率键合图的液压/机械系统建模、仿真机动力学分析软件,采用图形化的物理建模方式,具有复杂液压元件结构参数化的功能模块,也同样非常适合进行航空液压作动系统的结构参数化建模与分析,但是他的控制系统仿真功能模块相对较少,不具备神经网络、模糊控制等一系列先进的智能控制工具箱。
基于AMESim恒功率泵的动静态特性仿真分析

2010年7月第38卷第13期机床与液压MACH I NE TOOL &HYDRAUL I CSJul 2010V ol 38No 13DO I :10.3969/j issn 1001-3881 2010 13 037收稿日期:2010-04-23基金项目:国家 863 高技术产业化研究资助项目(2007AA041803);上海市数字化汽车车身工程重点实验室开放课题基金资助(MS V 2009 02);十一五科技支撑计划资助项目(2006B AF01B03 01)作者简介:文哲(1985 ),男,硕士研究生,主要研究方向为轴向柱塞泵变量控制。
通讯作者:徐兵,E -m ai:l bxu @zju edu cn 。
基于AMES im 恒功率泵的动静态特性仿真分析文哲,徐兵(浙江大学流体传动及控制国家重点实验室,浙江杭州310027)摘要:以压力流量功率复合控制泵的功率控制部分为研究对象,利用AM ESi m 搭建压力流量功率复合控制泵的整体仿真模型,针对影响其功率控制部分动静态特性的几个关键因素 流量阀弹簧刚度、功率阀阀芯三角槽数进行变参分析。
仿真结果表明:增大流量阀弹簧刚度,可以改善功率控制范围内斜盘摆角的动态特性;增加功率阀阀芯三角槽个数,可以减小最小功率值,从一定程度上增大功率控制范围。
关键词:恒功率;轴向柱塞泵;动态特性;静态工作曲线中图分类号:TH137 51!!文献标识码:A !!文章编号:1001-3881(2010)13-122-6Dyna m ic and Static Sim ulation Analysis of ConstantPower Pu mp Based on Am esi mW E N Zhe ,XU B ing(State Key Lab of Flui d Po w er Trans m i s si o n and Contro l of Zhe jiang Un i v ersity ,H angzhou Zhe jiang 310027,Ch i n a)Abstrac t :T he po w er con tro l pa rt o f pressure /flow /powe r con tro l pump as the st udy object ,t he m ode l of t he pump w as co m pletely bu ilt i n AM ESi m for s i m u l a tion .A lter i ng para m eter ana l ys i s was perfor m ed for several key factors that i nfl uence t he dynam ic and sta ti c cha racte ristics o f the power control part of t he pu m p ,such as spr i ng stiff ness of flow ra te v alve and the nu m ber o f the tr iangu l a r g rooves o f the powe r va l ve spoo.l T he si m ulati on resu lts sho w tha t t he dynam ic and static character istics of the s w ash p l a te ang le i n rang e o f pow er contro l are i m proved by i ncreasi ng the spri ng stiffness o f flow ra te v alve ;the m i ni m u m pow er va l ue is reduced and the rang e o f pow er contro l i s broadened to a cer tai n ex tent by i ncreas i ng the number of t he triangular grooves of t he pow er valve spoo.lK eyword s :Constant pow er ;A x ial pist on pu m p ;Dyna m i c charac teristi c ;Static curve!!恒功率控制泵是提高液压系统节能效率的关键元件,可以在特定工况下减少原动机功率的浪费,具有良好的节能效果。
基于AMESim的气动系统建模与仿真技术研究.

基于AMESim的气动系统建模与仿真技术研究(版本A)本文主要内容如下(1)推导气体的流量、温度和压力方程。
(2)基于AMESim对普通气动回路进行仿真分析。
并推导气动系统常用元件的数学方程,在此基础上对气动元件及系统进行模型仿真分析。
(3)对气动比例位置系统进行建模与仿真研究,在系统仿真模型基础上进行故障仿真研究。
最后探讨基于 AMESim 的气动比例位置系统实时仿真研究。
1.气动系统建模的理论基础气动系统和元件建模的首要任务就是要充分的明确空气的物理性质和空气的热力学性质,为准确的元件建模和系统仿真奠定基础。
气动元件的结构是十分复杂的,但其中的基本规律和数学描述一般还是比较清楚的。
经过前人的大量研究发现,气动系统的动态特性从本质上讲可以抽象为由一些基本环节所组成,比如放气环节、惯性环节和气容充气环节等等。
而它们之间又是通过压力、力、位移、容积等参数相互关联相互影响的。
1.1 流量方程流量特性表示元件的空气流通能力,将直接影响气动系统的动态特性。
所有的压力降取决于下面两个基本参数:a)声速流导 C(Sonic Conductance)——[null]b)临界压力比b(Critical Pressure Ratio)[S*m4/kg]ISO6358标准孔口——标准体积流量设绝对温度T ,绝对压力p的工况下的体积流量为Q,基准状态和标准状态下的体积流量可表示为:空气压缩机的输出流量通常用换算到吸入口的大气状态下的体积流量来表示。
以上公式同样适用于从吸入口的大气状态到基准或标准状态的换算。
气动孔口流量在气动系统中,一般需要计算通过节流口的气体压力、流量、温度等参数,但是由于气体的可压缩性,气体在通过节流口时是个很复杂的过程,节流口前后的流道突然收缩或扩张,气体在孔口前后均会形成涡流,产生强烈的摩擦,因而机械能变成热能具有不可逆过程。
同时,由于流体运动的极不规则,同一界面上的各点参数极不均匀。
为了研究气体的流量特性,基本上可将阀中的节流口理想地等价为一个小孔或收缩喷嘴,并用小孔或者收缩喷嘴的流量特性来表示其流量特性。
(整理)基于AMESIM的ABS液压系统建模与仿真本科生论文

第 1 章绪论1.1 研究目的与意义随着我国汽车工业的发展,就必须进行汽车关键零部件的自主研发。
汽车制动过程中的安全性也已成为人们关注的焦点。
汽车防抱死制动系统(ABS),关系着汽车制动的安全性。
目前国内许多汽车公司已经开始进行汽车自主研发,要在商业的竞争中脱颖而出,要拥有自主知识产权的汽车,要使我国由一个汽车大国变为一个汽车强国,就必须进行汽车关键零部件的自主研发。
汽车制动过程中的安全性也已成为人们关注的焦点,防抱死制动系统ABS是汽车关键的零部件之一,因此国家、企业和高校都投入了大量的人力和资源对ABS进行自主研发。
汽车动力性能的提高和高速公路的延伸对汽车安全提出了越来越高的要求,许多国家都为此颁布了严厉的汽车安全法规,汽车在制动过程中的方向稳定性和转向操纵能力,已成为人们关注的焦点。
因此,探讨各种高性能的制动系统和完善制动系统的性能是减少交通事故和促进汽车工业发展的重要举措[1]。
而ABS可以在制动过程中自动、高频地对制动系统压力进行调节,从而对制动力进行调节,使车轮滑移率保持在理想滑移率附近,既防止车轮抱死,又充分利用了车轮与路面的附着能力,缩短了制动距离,提高了汽车制动过程中的方向稳定性和转向操作能力,达到了最佳制动效果的目的。
ABS控制的关键之一就是控制制动过程中的滑移率,从而提高路面附着系数的利用率,缩短制动距离,提高制动的稳定性。
然而,滑移率和路面附着系数的关系又受到很多因素的影响,如车辆本身的结构参数、车速、轮胎充气压力、轮胎垂直载荷、路面状况等等[2]。
因此,要求ABS保证汽车在短时间内在各种路面上,各种情况下都能安全制动的难度是相当大的。
还需要针对不同车型进行大量的参数匹配试验,大概需要一年半到两年的时间,并且需要大量的经验,不仅耗资巨大,而且延长了产品的开发周期。
目前国内外也有人应用新的控制理论,进行ABS控制的探讨。
根据汽车制动过程的物理实质及动力学分析,对ABS控制器的结构原理、控制方法等方面进行分析和研究,利用AMESim软件建立车辆防抱死制动系统模型,可以很容易分析液压系统元件对整个系统的影响。
AMESim动力传动系统建模、仿真和分析解决方案
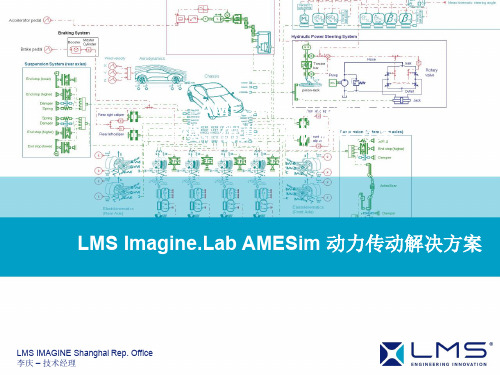
- 扭矩的变化及其齿接触力 - 换档品质 - 液压系统正常工作, 失效安全分析 - 元件性能分析 - 功率流 - 传动损失 - 热交换及其油冷却器的尺寸确定
Performances&losses Passenger Comfort NVH
以下应用的完美方案: - 手动/手动自动变速器 - DCT (Dual Clutch Transmission) - 自动变速器 - 静液传动 - 复合传动 - CVT / IVT (Continuous或Infinitely variable)
应用
- 扭矩变化及其最大值 (驱动链阻力特性分析) - 车辆运动的舒适性 (SUV和卡车发动机纵置的jerk和roll分析), 考虑驱动链的动态特性,包括发
动机在支座上的运动。 - 设计和优化作动和主动控制系统: TCC (变矩器离合器), 分动器, 主动差速器, 发动机支座
定位…
发动机 – 详述
机械模型:主要包括齿轮模型(定轴齿轮和行星齿轮), 惰轮, 差速器模型, 同步器
模型, 片式离合器模型, 片式制动器模型, 带式制动器模型, 单向轮模型, 变矩器 模型, 无级变速器模型等。同时在模型中需要考虑回转元件的回转惯性, 齿轮的间隙 撞击效应, 传动轴的扭转刚度等现象。 因此对仿真软件需要有专门的动力传动方面应 用库来支持自动变速器机械模型的建立, 同时为了能够实现硬件在环仿真, 仿真软件 建立的机械模型必须支持实时代码的产生, 从而能够通过实时仿真平台跟事物连接起来 仿真。
Driveline
2D/3D Modeling U-joints, Tires ESP / ASR Piloted Differential
Transmission
Robotized / Automatics DCT/Hybrid IVT/CVT
空气悬架气动系统的AMESim研究

01
空气悬架系统广泛应用于商用车 、客车和特种车辆等领域,能够 提高车辆的行驶舒适性和安全性 ,降低车辆维护成本。
02
在高速公路、城市道路、崎岖山 路等不同路况下,空气悬架系统 都能提供良好的减震效果,提高 车辆的行驶稳定性和可靠性。
空气悬架系统的研究现状
目前,国内外学者对空气悬架系统的研究主要集中在系统设计、动态特性分析、 控制策略优化等方面。
研究不足与展望
01
虽然AMESim软件为空气悬架气动系统的模拟提供了有力支持,但仍 存在一定的局限性,如无法完全模拟真实世界的复杂环境。
02
在研究中,未能充分考虑实际应用中的多种不确定性因素,如气源压 力波动、温度变化等。
03
未来研究可以进一步优化AMESim模型,提高模拟精度,并考虑更多 实际工况下的不确定性因素。
等。
AMESim具有强大的库和元件库, 用户可以根据需要选择和组合元
件来构建复杂的系统模型。
AMESim软件的应用领域
汽车工程
用于汽车动力系统、底盘系统 、排放系统等的建模和仿真。
航空航天
用于飞行器、卫星、火箭等的 流体动力学、热力学、机构运 动等的建模和仿真。
液压传动
用于液压系统、气动系统等的 建模和仿真。
参数设定
根据实际系统参数,设定仿真模 型的参数,如气体的状态方程、 气动控制阀的流量系数、弹簧的 刚度等。
边界条件
设定仿真模型的边界条件,如初 始压力、温度、流量等,确保仿 真结果的准确性。
仿真结果分析
01
动态响应
分析仿真模型的动态响应,包括 气体的压力、流量、温度等参数 随时间的变化情况。
稳态性能
AMESim作为一种多学科领域复杂系统仿真软件,为空气悬架气动系统的研究提供 了强大的工具。
AMESim与MATLAB_Simulink联合仿真接口配置

AMESim—MATLAB(64位)联合仿真设置详细步骤说明:现以AMESimR12、MATLAB2014b为例说明,其他版本类似。
1、版本要求2、辅助软件VS2013若要使用 AMESim 与 Simulink 的接口,则需要在本机安装编译器,高版本软件需要高版本的编译器,这里以VS2013为例设置。
一般推荐先安装VS编译器,然后安装 Matlab,最后安装 AMESim的顺序。
若后安装VS编译器,将VS编译器安装目录下如 D:\ Microsoft Visual Studio 12.0 \VC\bin 目录中的nmake.exe 文件和vcvars32.bat 以及D:\Microsoft Visual Studio 12.0\VC\bin\amd64下的vcvars64.bat(64位版本的MATLAB)文件拷贝至 AMESim 安装目录,如D:\AMESim\v1200下。
3、环境变量设置定义Windows 系统环境变量:1)选择“控制面板-系统”或者在“我的电脑”图标上点右键,选择“属性”;2)在弹出的“系统属性”窗口中选择“高级”页,选择“环境变量”;3)用户变量中添加HOME D:\MATLAB D:\MATLAB\R2014bPath D:\ Microsoft Visual Studio 12.0\Common7\Tools; D:\ Microsoft Visual Studio 12.0\VC\bin; D:\Program Files\MATLAB\R2014b\bin; D:\ProgramFiles\MATLAB\R2014b\bin\win644) 在系统变量中添加在Path 环境变量中加入(以分号与其它已经存在的变量值隔开)路径:Matlab_Root(如 D:\Matlab\R2010a)\bin 和Matlab_Root(如D:\Matlab\R2010a)\bin\win32 ,以及%windir%\System32,其中%windir%指的是 Windows 的安装路径,如 C:\WINNTPath D:\Program Files (x86)\Microsoft Visual Studio 10.0; D:\AMESim\v1000; D:\AMESim\v1000\win64;D:\AMESim\v1000\sys\mingw32\bin;D:\AMESim\v1000\s ys\mpich\mpd\bin;D:\AMESim\v1000\sys\cgns;%SystemRoot%\system32;%SystemR oot%;%SystemRoot%\System32\Wbem;D: \MATLAB\R2014b\bin\win64;C:\WINDOWS\system32;C:\WINNT (该处很重要一定要添加,而且一定要包含C:\WINDOWS\system32,不然会有引起很多错误)4、AMESim与MATLAB设置启动AMESim并确认 AMESim 使用的是 MS C++编译器。
AMESIM介绍

第二章 AMESim的应用方法2.1 AMESim简介AMESim表示系统工程高级建模和仿真平台(Advanced Modeling Environment for Simulations of engineering systems)。
它能够从元件设计出发,可以考虑摩擦、油液、和气体的本身特性、环境温度等非常难以建模的部分,直到组成部件和系统进行功能性能仿真和优化,并能够联合其他优秀软件进行联合仿真和优化,还可以考虑控制器在环构成闭环系统进行仿真,使设计出的产品完全满足实际应用环境的要求。
AMESim软件共由四个功能模块组成:AMESim、AMESet、AMECustom、AMERun,另外还有软件帮助模块AMEHelp。
其中,AMESim用于面向对象的系统建模、参数设置、仿真运行和结果分析,是该工具软件的主功能模块,主要工作模式为:按系统原理图建模一确定元件子模型一设定元件参数一仿真运行一结果观测和分析。
AMEest用于构建符合用户个人需求的元件子模型,主要通过两步进行:先设定子模型外部参数情况,系统自动生成元件代码框架,再通过用户的算法编程实现满足用户需要的元件,程序使用C或Fortnar77实现;AMECustom用于对软件提供的元件库中的元件进行改造,但不能深入到元件代码层次,只适用于元件的外部参数特性的改造;AMERun是提供给最终用户的只运行模块,最终用户可以修改模型的参数和仿真参数,执行稳态或动态仿真,输出结果图形和分析仿真结果,但不能够修改模型结构,不能够访问或修改元件代码等涉及技术敏感性的信息。
2.2AMESim的特点1.多学科的建模平台AMESim在统一的平台上实现了多学科领域的系统工程的建模和仿真,模型库丰富,涵盖了机械、液压、控制、液压管路、液压元件设计、液压阻力、气动、热流体、冷却、动力传动等领域,且采用易于识别的标准ISO图标和简单直观的多端口框图,方便用户建立复杂系统及用户所需的特定应用实例。
AMESim个人学习心得

AMESim个人学习心得LMS旗下的AMESim软件是一款性能很强大的系统仿真软件,能够实现对机械、液压、气动、电气、热等多个领域的仿真计算。
作为一名在读研究生,我想把我这段时间使用AMESim的感受和经验教训分享一下,希望能对那些初学AMESim的或者正在头疼的人们有所帮助。
首先,我想告诉大家什么是仿真。
仿真说白了就是用数学公式来简化物理实际,再用电脑软件来模拟这些数学公式,用一些基本的模块来实现这些复杂的过程。
给出输入量,记过计算,得到结果,用之代替实际结果。
这样能减少实际设计之中的时间周期,以及原料浪费和成本投入。
那么仿真是否可行,一个很关键的参数就是仿真结果和实际结果的差异,谁也无法用数学公式来精确代替实际物理过程。
但是只要在大方向上和实际结果差不多就行,许多的仿真软件在这方面就做的很好。
在工程仿真领域,有许多的仿真软件,其中较熟悉的一个当属MA TLAB/simulink,汽车方面还有什么Cruis、carsim、trucsim等等,其实MATLAB 更加偏向于工程计算,如果要用MA TLAB来做仿真的话,需要你对物理实际很了解,然后在simulink之中搭建其物理模型。
但是这对一般初学者来讲比较困难,而且仿真结果容易和实际出入太大。
Cruis和其他汽车仿真软件虽然能够实现不错的仿真效果,但是功能有限,不能实现机械和电、热等多个领域之间的仿真。
因此,我后来选择了使用AMESim,虽然其比一般软件要难点,但是用熟悉之后,能够实现很强大功能,不得不说是一款强大的仿真软件。
其次,我想告诉大家,AMESim如何入门的问题,这应该是很多初学AMESim的用户最大的困难吧,我当时也经历了这个困难的过程。
很多人可能会在网上下载一大堆资料,或者去书店买本书,然后埋头看啊看。
其实我想说这样的效果并不好,软件是要在使用之中去学习和熟练的。
当你初学时,你可以找一个会用此软件的人给你做一个简单的例子,在制作例子之中就会告诉此软件的一般步骤。
基于AMESim的飞机环控系统建模与仿真

202022/3160引言为体现新型民用客机“更经济、更安全、更舒适、更环保”的设计思想[1],民用飞机逐渐朝多电化方向发展,四轮升压式高压除水电动环控系统具有取消发动机做功影响、节省燃油以及防止涡轮冰堵等优点[2-3],越来越受到研究人员的重视。
国内对飞机环控系统仿真研究始于20世纪90年代,李俊杰[4]、董素君[5]等人采用easy5软件建立起空气循环制冷系统和蒸发循环制冷系统仿真模型,具有一定的实用性和推广价值。
董素君[6]、宋俊虓[7]、赵俊茹[8]等人利用Matlab/Simulink 建立起环控系统各主要部件的数学模型,对系统进行了仿真研究,Matlab/Simulink 属于通用仿真软件,具有强大的编程计算语言和图形化建模方式,但是在复杂系统的仿真研究,易产生代数环问题,对计算结果精度和效率影响较大。
AMESim 属于一维多学科复杂系统建模仿真平台,可实现气动、热流体、液压、机械和电磁等多学科领域的联合建模仿真,可以实现机电系统中多个分系统的耦合工作[9]。
本文通过建立环控系统仿真模型,得到了在给定状态下各部件出口的稳态仿真结果与理论计算值的对比结果,以及给定在飞行高度和飞行马赫数扰动下的二级涡轮出口温度的动态响应曲线,可为系统设计优化以及整机环境控制系统的控制规律设计提供模型和数据支持[10]。
1AMESim 仿真模型四轮升压式高压除水电动环控系统主要部件有:热交换器、压气机、涡轮冷却器、风扇、转轴等,通过气体能量传递方向将部件各仿真模块连接起来,构成整机系统进行仿真。
四轮升压式高压除水电动环控系统原理图见图1。
AMESim 搭建空气循环制冷系统基于AMESim 的飞机环控系统建模与仿真刘征崔燚周琼瑶戴铮王宇迪摘要为获得四轮升压式高压除水电动环控系统性能及动态变化过程,校核计算结果是否满足系统设计要求,本文基于模块化结构搭建了AMESim 环控系统仿真模型进行了稳态仿真研究,并对系统在飞行高度和飞行马赫数扰动下的动态响应进行了仿真分析,仿真结果表明所建模型具有较高的精度,满足设计指标的要求,而且能够很好反应系统的动态变化情况,为系统的校核优化以及整机环控系统的控制律设计提供支持。
浅析基于AMESim的气液联合式液压破碎锤建模与仿真

式中,m是活塞质量;x是活塞位移;动速度;1A、2A、3A是活塞前后腔和氮气室有效作用面积;1P、2P、3P是活塞前后腔和氮气室压力。
氮气室 2.后腔 3.信号口 4.活塞 5.前腔 6.7.阀上腔 8.控制阀阀芯 9.阀下腔图1 气液联合式液压破碎锤工作原理瞬间,短暂停滞时间约为0.03s,撞击后活塞反弹速度较小,能量传递效果好,冲击力约为1.7×103N,如图4所示。
阀芯的行程为30mm,运动到极限位置有稳定的停留,没有出现抖动现象,工作过程稳定。
图4 岩石受到的冲击力随时间变化曲线在工作过程中,活塞前腔压力保持在8MPa左右,活塞在不同位置时,前腔压力有轻微波动,活塞后腔压力在冲程时为8MPa,其他阶段为0MPa,氮气室受到活塞回程的影响最大压力为1.23MPa,反作用协助推动活塞向下加速运动,实现活塞冲程运动。
2.3 系统压力与稳定性分析不同的液压系统压力对气液联合式液压破碎锤的冲图5 不同系统压力对稳定性的影响如图5所示,系统压力从6MPa以1MPa为步长增加到23MPa时,活塞位移逐渐增大、频率逐渐增高。
系统压力6MPa时,几乎没有产生碰撞瞬间停滞现象;系统压力7~8MPa时,明显产生了碰撞瞬间停滞现象,活塞有了冲击作用;系统压力19MPa后,曲线幅值和周期变化不明显,基本上趋于极限,因此,分别以8MPa、19MPa、23MPa的系统压力为条件,考查破碎锤的冲击功、冲击力和冲击频率的变化情况。
图6 8MPa、19MPa、23MPa时活塞的速度曲线如图6、图7所示,当液压系统压力为8MPa时,最大冲击速度为4.6m/s,冲击频率约660bpm,冲击力超过1.7×103N,冲击功为158.7J左右;当液压系统压力为19MPa时,最大冲击速度为8.2m/s,冲击频率约1200bpm,冲击力超过7.5×103N,冲击功为504.3J左右;当液压系统压力为23MPa时,最大冲击速度为8.7m/s,冲击频率约1380bpm,冲击力超过9.6×103N,冲击功为567.7J左右。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于AMESim的气动系统建模与仿真技术研究(版本A) 本文主要内容如下(1)推导气体的流量、温度与压力方程。
(2)基于AMESim对普通气动回路进行仿真分析。
并推导气动系统常用元件的数学方程,在此基础上对气动元件及系统进行模型仿真分析。
(3)对气动比例位置系统进行建模与仿真研究,在系统仿真模型基础上进行故障仿真研究。
最后探讨基于 AMESim 的气动比例位置系统实时仿真研究。
1、气动系统建模的理论基础气动系统与元件建模的首要任务就就是要充分的明确空气的物理性质与空气的热力学性质,为准确的元件建模与系统仿真奠定基础。
气动元件的结构就是十分复杂的,但其中的基本规律与数学描述一般还就是比较清楚的。
经过前人的大量研究发现,气动系统的动态特性从本质上讲可以抽象为由一些基本环节所组成,比如放气环节、惯性环节与气容充气环节等等。
而它们之间又就是通过压力、力、位移、容积等参数相互关联相互影响的。
1、1 流量方程流量特性表示元件的空气流通能力,将直接影响气动系统的动态特性。
所有的压力降取决于下面两个基本参数:a)声速流导 C(Sonic Conductance)——[null]b)临界压力比b(Critical Pressure Ratio)[S*m4/kg]ISO6358标准孔口——标准体积流量设绝对温度T ,绝对压力p的工况下的体积流量为Q,基准状态与标准状态下的体积流量可表示为:空气压缩机的输出流量通常用换算到吸入口的大气状态下的体积流量来表示。
以上公式同样适用于从吸入口的大气状态到基准或标准状态的换算。
气动孔口流量在气动系统中,一般需要计算通过节流口的气体压力、流量、温度等参数,但就是由于气体的可压缩性,气体在通过节流口时就是个很复杂的过程,节流口前后的流道突然收缩或扩张,气体在孔口前后均会形成涡流,产生强烈的摩擦,因而机械能变成热能具有不可逆过程。
同时,由于流体运动的极不规则,同一界面上的各点参数极不均匀。
为了研究气体的流量特性,基本上可将阀中的节流口理想地等价为一个小孔或收缩喷嘴,并用小孔或者收缩喷嘴的流量特性来表示其流量特性。
式中 u——缩流处的流速k ——空气的比热ρ0 ——喷嘴上游空气密度(kg/m3)p0 ——上游压力(bar)p1——下游压力(bar)因为就是等熵流动,将绝热过程公式带入替换密度ρ1可得流经收缩喷嘴的质量流量:式中 R ——气体常数(J/(kgK))T0——上游空气的绝对温度(K)A1——喷嘴出口面积(mm2)这里A1比喷嘴入口处截面积A 0小,两者的比就是:称之为缩流系数。
缩流系数根据收缩喷嘴入口的形状及尺寸不同,一般在0、85~0、95 之间的范围内。
当质量流量达到最大时,即流量达到饱与,此时的压力比P1/P0就就是临界压力比。
根据气体绝热过程的能量方程式可得临界压力比b为:压力比P1/P0比临界压力小时,流动为声速流。
将临界压力比代入质量流量计算式则:实际上气体流过复杂的内部元件时,流动损失就是不能忽略的。
在一定的上游条件与一定的压差条件下,实际通过元件的质量流量将小于按理论公式计算出来的理论质量流量。
则实际流量应为:(重要公式)式中 Cq流量系数:实际流量与理论流量之比当进口的流量系数就是一个定值时,那么流过收缩喷嘴的焓流量如下式:式中 Cq ——等压比热(Nm/kg/K)h ——单位质量流量的焓(J/s/kg)注意到在收缩喷嘴处的气体音速表达式就是:式中 Tvc——喷嘴下游温度(K)结合质量流量计算式可以推导出:流量系数(重要公式)实际的气动系统中,由于气动元件的节流方程可知节流孔的面积不等于其气流的节流面积,要知道小孔的节流面积就是十分困难的,因而流量系数的测定很难做到精确。
而且在实际工程中,不可能逐一的用实验来测定其流量系数,实际上流量系数就是一个不断变化的量,因为它不仅跟阀口或者小孔的上下游压力差有关,而且还与阀口或者小孔的类型、开度及气流的流动方向等因素有关。
然而我们在工程设计与仿真时,经常把流量系数瞧作一个常数,但这样必定会给系统的最终计算结果带来一定的误差,因此针对不同类型的阀口,选取合适的流量系数能真实的反映实际情况,这在建模过程中就是十分必要的。
实际的气动元件不同于单个喷嘴,因为每个实际元件并非就是单个节流口,而就是与流通界面面积相串联的、任意形式收缩的一串喷嘴群,显然,当气体通过串联的两个喷嘴时,当其中任何一个喷嘴达到临界状态时,气流都会发生阻塞而得到最大流量。
然而由于总压力比的原因,因此任何时候的临界压力比都应该小于 0、5283。
在利用 AMESim 软件进行气动元件建模时可以充分利用相关流量系数的曲线图与相关点的数值,只要把这些数值通过 AMESim 中的 Table 编辑器后即可生成“、data”数据文件如图所示,图中显示的就是流量系数随上下游压力比与阀口开度关系的二维线性样条变化曲线,该文件可以很方便的在元件模型系统仿真时调用,这样一来可以保证元件流量系数的准确性同时也确保了流量计算的正确。
(打开方式:tools-table editor)1、2 温度压力方程根据热力学第一定律与能量守恒定律推知一个系统(开口或闭口、与外界发生或不发生热交换)的内部能量变化方程为:式中 dQ/dt——外界加入控制体的热量的变化(J/s)dW/dt——控制体内气体对外做功的变化(J/s)dV/dt——腔室体积变化(m3/s)Aex ——元件的热交换面积(m2)T ext——外界温度(K)T ——腔室内气体温度(K)K ——气体热交换系数(J/m2/s)假设单位质量气体的内能就是u ,所以气体的内能为:联立dU/dt与U方程得:对于理想气体,单位气体的内能也就是温度的函数所以有:式中C V——比定容热容(Nm/kg/K)因为理想气体的状态方程为:上式两边对时间t微分即可求得压力的一阶微分方程式:然而对于变体积的热气动腔室来说,由于气体自身的温度在不断的变化,所以单位气体的内能也就是不断的变化,用公式表示即为:综合方程式,可得变体积气动腔室温度变化的一阶微分方程通式:(重要公式)在此公式中,m i、h i表示的就是在一开口或闭口系统之中气体带入控制体的焓与气体流出控制体的焓之与,流入的为正值,流出的为负值。
上述所推导的流量、温度与压力方程在气动系统中建模时普遍适用,但针对个别具体的气动元件还有一些个别相关的方程需要计算。
小结:本节针对气体的流量、常见类型的小孔与喷嘴状阀口的流量系数以及温度压力方程进行了详细的分析论述,得出如下结论:(1)通过对流量、温度压力方程推导所得到的相关一阶微分方程在气动元件建模中普遍实用。
(2)流量系数本身就是一个不断变化的值,其值的变化情况不仅与阀口处上下游的静压力比有关而且还与阀口的开度大小有关。
通常情况下流量系数都就是随阀口的上下游压力的比值增大而增加的,阀口的开度越大时相应的流量系数也就是越大的。
通过对一些类型的小孔与喷嘴状阀口的流量系数的分析后,从方便应用的角度出发对它们的流量系数的取值给出了一个合适的取值范围以供使用时作为参考。
根据需要可以将流量系数随变量的变化关系通过 AMESim 设置成数据文件的形式,在进行元件模型系统仿真时能够调用该文件或者直接调用表达式,保证了流量系数或其它相关参数的正确性。
2、气动主要元件及系统的建模与仿真2、1 AMESim介绍AMESim 环境下的气动控制系统建模常采用自上而下的建模方法,把复杂的系统模块化,使得抽象的系统具体化,AMESim 仿真机构框架如图所示。
AMESim 具有丰富的模型库,用户可以采用基本元素法,按照实际物理系统来构建自定义模块或仿真模型,不需要推导复杂的数学模型。
在AMESim 中,用于气动系统建模的气动库中包括了一些在气动系统中经常使用的气动元件图标,这些图标直观形象地表现了气动元件的功能,每个图标有一个或多个数学模型与之对应,用于描述气动元件的特性,以便更真实地模拟气动系统的参数并进行仿真研究。
以PCD中的带环形孔口的滑阀设计一个三通阀为例进行说明。
在完成草图后,在子模型模式中可以更换子模型,然后在参数模式中中设置各个参数,最后进行运行仿真。
在 AMESim 中,每一个子模型都就是由语言程序代码编写的。
在建模过程中,如果遇到AMESim 标准库中没有的子模型,可以通过 AMEset(模型、文档生成器)编辑子模型,来扩充AMESim 应用库。
以下就是方波信号的c语言代码:气动元件的数学模型就是依据气体状态方程与质量守恒定律以及等熵方程等建立,同时也考虑到了一些元件的动态特性,为了方便地建立数学型,一般都会做一些假设,比如:(1)气体流过阀口或其它限流孔时,均为等熵流动;(2)腔室内气体的压力场与温度场均匀;(3)气体粘度小时,忽略控制截面处粘性阻力的影响;(4)不考虑引力场对气流的作用;等等。
2、2 气体回路分析以列车中一个简单的气动回路为例进行说明。
该回路描述的就是两个压力储能容器释放气体进入到第三个储能器中。
这个系统中三个储能器的体积分别为(800L、400L 与100L)通过两个截面积分别就是500mm2与 20mm2的节流口与气管连接而成的,它们的初始压力分别就是12bar、7bar 与1 bar,而初始温度就是293、15 K,所采用的仿真时间就是20秒,步长为0、01秒。
经过仿真之后,可知在第三个腔室达到稳定之前,两个较高压力的腔室首先达到了稳定状态,这个最终的稳定压力大概就是 8、7bar 在仿真时间进行到 18 秒左右时到达。
气体由节流口面积为500mm2与20mm2的节流口进入储能器 2 与 3,因而气体流量因为较大的节流口面积而较快达到稳定,通过小的节流口时候,节流口达到稳定过程就需要耗费较长的时间,同时也因为储能器之间的高压力比而导致了音速饱与流,而这种情况可以通过质量流参数Cm来反映。
这个例子,需要设置的参数不多,但对于一些复杂的系统来说,需要设置的参数十分庞大,要得到满意的结果往往需要反复不断的试值才能找到一个满意的结果。
2、3 调压阀PCD模型调压阀在气动系统中起到稳定系统压力的作用,AMESim对元件进行仿真,可以模拟调压阀在气源压力波动与负载变化的情况下的稳压效果。
比如B10调压阀可以类似地瞧为这种调压阀。
通过一个可变节流孔来控制气源压力的变化,另外一个可变节流孔来控制负载的变化,气源为一个简单的温度压力源。
在建模过程中最重要的就是对各个子模块设置参数,准确的参数使得系统模型更加精确。
下图所示为气体喷嘴平板阀子模型PNAPO32-1 的参数列表。
设置阀口的开口量为零,表明在没有气源通过时,阀芯处于关闭状态。
再通过阀芯质量的参数列表设置阀芯的最大位移为 2 mm。
在 0~1 秒内控制气源的可变节流孔逐渐打开并在 1 秒后保持恒定,这时控制负载的可变节流口开始逐渐打开,并在 2 秒时保持稳定。
