三角函数知识点总结及同步练习
三角函数知识点整理+练习

三角函数知识点一,看看这些,你记住了吗?1. 角的分类:任意角可按旋转方向分为 , , 。
2. 终边相同的角:与角α终边相同的角的集合为 。
3. 象限角:第一象限角的集合为: 。
第二象限角的集合为: 。
第三象限角的集合为: 。
第四象限角的集合为: 。
练一练会更牢固:已知α是第三象限角,则2α是第几象限角?4. 轴线角:终边落在x 轴上的角的集合为: 。
终边落在y 轴上的角的集合为: 。
终边落在坐标轴上的角的集合为: 。
5. 弧度制:1rad 的定义: 。
特殊角的弧度数及三角函数值:6.角度与弧度的换算:360︒= rad ,180︒= rad ,1︒= rad ,1rad ≈ ︒。
7.弧长,扇形面积公式:设扇形的弧长为l ,圆心角大小为α(弧度),半径为r , 则弧长l = ,S 扇形= = 。
来个小练习:(1)已知扇形的周长为10,面积是4,求该扇形的圆心角。
(2)已知扇形的周长为40,当它的半径和圆心角取何值时,才能使扇形面积最大?P-,求α的正弦,余弦,正切值。
你一定可以的:已知角α的终边经过点(2,3)9.三角函数线:当角α的终边在不同象限时,分别作出其三角函数线:正弦线: ;余弦线: ;正切线: 。
试试这个:求定义域:(1)y = (2)2lg(34sin )y x =-10.同角三角函数的基本关系:(1)平方关系: 。
(2)商数关系: 。
11.诱导公式:公式一:sin(2)k απ+= 公式二:sin()α-= cos(2)k απ+= cos()α-= tan(2)k απ+= tan()α-= 公式三:sin()πα-= 公式四:sin()πα+= cos()πα-= cos()πα+=tan()πα-= tan()πα+=公式五:sin()2πα+= 公式六:sin()2πα-=cos()2πα+= cos()2πα-= 记忆口诀:奇变偶不变,符号看象限 再试试这两个:1、已知3sin(3)2sin()2ππαα+=+,求下列各式的值: (1)sin 4cos 5sin 2cos αααα-+ (2)2sin sin 2αα+2、已知1sin(3)3πθ+=,试求: []cos()cos cos()1πθθπθ+--+()cos(2)33sin()cos sin()22θπππθθπθ----+的值。
三角函数的概念(原卷版)

5.2.1 三角函数的概念【知识点梳理】 知识点一:三角函数定义设α是一个任意角,它的终边与半径是r 的圆交于点(,)P x y ,则22r x y +,那么: (1)y r 做α的正弦,记做sin α,即sin y r α=; (2) x r 叫做α的余弦,记做cos α,即cos x rα=; (3)y x叫做α的正切,记做tan α,即tan (0)yx x α=≠.知识点诠释:(1)三角函数的值与点P 在终边上的位置无关,仅与角的大小有关.我们只需计算点到原点的距离22r x y +,那么22sin x y α=+22cos x y α=+,tan yxα=. (2)三角函数符号是一个整体,离开α的sin 、cos 、tan 等是没有意义的,它们表示的是一个比值,而不是sin 、cos 、tan 与α的积.知识点二:三角函数在各象限的符号 三角函数在各象限的符号:在记忆上述三角函数值在各象限的符号时,有以下口诀:一全正,二正弦,三正切,四余弦. 知识点诠释:口诀的含义是在第一象限各三角函数值为正;在第二象限正弦值为正,在第三象限正切值为正,在第四象限余弦值为正.知识点三:诱导公式一由三角函数的定义,可以知道:终边相同的角的同一三角函数的值相等,由此得到诱导公式一: sin(2)sin k απα+= cos(2)cos k απα+=tan(2)tan k απα+=,其中k Z ∈注意:利用诱导公式一,可以把求任意角的三角函数值,转化为求02π~(或0360︒︒~)范围内角的三角函数值.知识点四、特殊角的三角函数值 0° 30°45°60°90°120°135°150°180°270°6π 4π 3π 2π 23π 34π 56π π32π sin α 0 12 22 3213222 12 0 1-cos α132 2212 012- 22- 32- 1- 0tan α0 331 33-1- 33- 0【题型归纳目录】 题型一:三角函数的定义 题型二:判断三角函数值的符号 题型三:确定角所在象限 题型四:诱导公式(一)的应用 题型五:圆上的动点与旋转点 【典型例题】题型一:三角函数的定义例1.(2022·陕西·蒲城县蒲城中学高三阶段练习(文))设α是第二象限角,(),8P x 为其终边上的一点,且4sin 5α,则x =( ) A .3- B .4-C .6-D .10-例2.(2022·北京市西城外国语学校高三阶段练习)角α的终边上有一点(2,2)P -,则sin α=( ) A .22B .22-C .2D .1例3.(2022·河南·高三阶段练习(文))已知角α的终边经过点()()4,30P m m m -≠,则2sin cos αα+的值为( ) A .35 B .25C .1或25-D .25或25-变式1.(2022·山西大附中高三阶段练习(文))已知角x 的终边上一点的坐标为55sin ,cos 66ππ⎛⎫⎪⎝⎭,则角x 的最小正值为( ) A .56πB .53π C .6π D .3π变式2.(2022·江西·崇仁县第二中学高三阶段练习(文))已知点2π(cos ,1)3P 是角α终边上一点,则cos α=( )A 5B .5C 25D .3变式3.(2022·全国·高三专题练习)已知角α的终边经过点()3,4P -,则sin cos 11tan ααα--+的值为( )A .65-B .1C .2D .3变式4.(2022·全国·高三专题练习)已知角θ的终边经过点(,3)M m m -,且1tan 2θ=,则m =( ) A .12B .1C .2D .52变式5.(2022·全国·高一课时练习)已知顶点在原点,始边与x 轴非负半轴重合的角α的终边上有一点()3,P m ,且()2sin 0m α=≠,求m 的值,并求cos α与tan α的值.变式6.(2022·全国·高一课时练习)已知角α的终边在函数()102y x x =->的图像上,求sin α,cos α的值.【方法技巧与总结】利用三角函数的定义求值的策略(1)已知角α的终边在直线上求α的三角函数值时,常用的解题方法有以下两种:方法一:先利用直线与单位圆相交,求出交点坐标,然后再利用正、余弦函数的定义求出相应三角函数值.方法二:在α的终边上任选一点(,)P x y ,P 到原点的距离为r (0r >).则sin y rα=,cos xr α=.已知α的终边求α的三角函数值时,用这几个公式更方便.(2)当角α的终边上点的坐标以参数形式给出时,要根据问题的实际情况对参数进行分类讨论. (3)若终边在直线上时,因为角的终边是射线,应分两种情况处理. 题型二:判断三角函数值的符号例4.(2022·全国·高一课时练习)已知α为第二象限角,则( ) A .sin 0α< B .tan 0α> C .cos 0α< D .sin cos 0αα>例5.(2022·湖北·高一阶段练习)下列各式的符号为正的是( ) A .cos3 B .5ππsin cos 36⎛⎫- ⎪⎝⎭C .sin2cos2-D .7πtan8例6.(2022·甘肃·静宁县第一中学高一阶段练习(文))sin 4tan7⋅的值( ) A .大于0 B .小于0 C .等于0 D .不大于0变式7.(2022·江西省万载中学高一期中)设02πα≤<,如果sin 0α<且cos20α<,则α的取值范围是( ) A .π<α<3π2B .3π2<α<2π C .π4<α<34π D .5π4<α<7π4【方法技巧与总结】三角函数值在各象限内的符号也可以用下面的口诀记忆:“一全正二正弦,三正切四余弦”,意为:第一象限各个三角函数均为正;第二象限只有正弦为正,其余两个为负;第三象限正切为正,其余两个为负;第四象限余弦为正,其余两个为负.题型三:确定角所在象限例7.(2022·全国·高一课时练习)点()cos2018,sin 2018P ︒︒所在的象限是( ) A .一B .二C .三D .四例8.(2022·福建·莆田二中高三阶段练习)设α角属于第二象限,且cos cos22αα=-,则2α角属于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限例9.(2022·陕西汉中·高一期中)若cos tan 0αα<,且sin cos 0αα<,则α是( ) A .第一象限角 B .第二象限角 C .第三象限角 D .第四象限角变式8.(2022·全国·高三专题练习)若sin 0θ<且tan 0θ<,则角θ所在的象限是( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限变式9.(2022·江苏·无锡市教育科学研究院高一期末)已知角α的顶点为坐标原点,始边为x 轴的非负半轴,若点(sin ,tan )P αα在第四象限,则角α的终边在( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限变式10.(2022·辽宁·高一期末)坐标平面内点P 的坐标为()sin5,cos5,则点P 位于第( )象限. A .一 B .二 C .三 D .四【方法技巧与总结】 确定角所在象限的步骤(1)判断该角的某些三角函数值的符号;(2)根据角的 三角函数值的符号,确定角所在象限. 题型四:诱导公式(一)的应用例10.(2022·天津市红桥区教师发展中心高一期末)17sin 4π=____________.例11.(2022·广西·桂林十八中高一开学考试)13sin 3π=_________.例12.(2022·湖南·高一课时练习) 17tan()3π-=______.变式11.(2022·云南民族大学附属中学模拟预测(理))()cos 300-︒=______.变式12.(2022·湖南·()3tan330sin 60︒+︒+-︒.【方法技巧与总结】利用诱导公式一化简或求值的步骤(1)将已知角化为·360k α︒+(k 为整数,0360α︒≤<︒)或2k πβ+(k 为整数,02βπ≤<)的形式.(2)将原三角函数值化为角α的同名三角函数值.(3)借助特殊角的三角函数值或任意角的三角函数的定义达到化简求值的目的. 题型五:圆上的动点与旋转点例13.(2022·湖南益阳·高一期末)在直角坐标系xOy 中,一个质点在半径为2的圆O 上,以圆O 与x 正半轴的交点0P 为起点,沿逆时针方向匀速运动到P 点,每5s 转一圈,则2s 后0P P 的长为( ) A .42sin 5πB .42cos 5πC .24sin 5π D .24cos5π例14.(2022·全国·高一专题练习)点P 从()1,0出发,沿单位圆按逆时针方向运动263π弧长到达Q 点,则Q 的坐标为( ) A .13,22B .312⎛⎫- ⎪ ⎪⎝⎭C .13,2⎛- ⎝⎭D .321⎛⎫ ⎪ ⎪⎝⎭例15.(2022·江西师大附中高一期末)在平面直角坐标系xOy 中,若点P 从()2,0出发,沿圆心在原点,半径为2的圆按逆时针方向运动43π弧长到达点Q ,则点Q 的坐标是( ) A .(3- B .(1,3--C .(3D .(1,3-变式13.(2022·江西·模拟预测(文))已知单位圆上第一象限一点P 沿圆周逆时针旋转3π到点Q ,若点Q 的横坐标为12-,则点P 的横坐标为( )A.13B.12C2D3变式14.(2022·全国·高三专题练习)如图所示,滚珠P,Q同时从点(2,0)A出发沿圆形轨道匀速运动,滚珠P按逆时针方向每秒钟转π3弧度,滚珠Q按顺时针方向每秒钟转6π弧度,相遇后发生碰撞,各自按照原来的速度大小反向运动.(1)求滚珠P,Q第一次相遇时所用的时间及相遇点的坐标;(2)求从出发到第二次相遇滚珠P,Q各自滚动的路程.【方法技巧与总结】利用三角函数的定义求解【同步练习】一、单选题1.(2022·全国·高三专题练习)已知角α的终边与单位圆交于点132P⎛-⎝⎭,则sinα的值为()A.3B.12-C3D.122.(2022·江西赣州·高一期末)在3世纪中期,我国古代数学家刘徽在《九章算术注》中提出了割圆术:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣”这可视为中国古代极限观念的佳作.割圆术可以视为将一个圆内接正n边形等分成n个等腰三角形(如图所示),当n越大,等腰三角形的面积之和越近似等于圆的面积.运用割圆术的思想,可得到sin9︒的近似值为(π取近似值3.14)()A .0.039B .0.157C .0.314D .0.0793.(2022·四川省平昌中学高一阶段练习)如图,角α的终边与单位圆O 的交点34(,)55A -,则4cos 2sin 5cos 3sin αααα-=+( )A .203B .23C .45D .203-4.(2022·全国·高三专题练习)已知角α的终边与单位圆交于点1,3P m ⎛⎫- ⎪⎝⎭,则sin α=( )A .223B .13C .22D .13±5.(2022·江西上饶·高一阶段练习)赵爽是我国古代数学家、天文学家,约公元222年,赵爽在注解《周髀算经》一书时介绍了“勾股圆方图”,亦称“赵爽弦图”,它是由四个全等的直角三角形与一个小正方形拼成的大正方形.如图所示的是一张弦图,已知大正方形的面积为100,小正方形的面积为20,若直角三角形较小的锐角为α,则sin αcos α的值为( )A .15B .25C 5D 256.(2022·北京市第五中学高一期末)在直角坐标系xOy 中,已知43sin ,cos 55αα=-=,那么角α的终边与单位圆O 坐标为( ) A .34,55⎛⎫- ⎪⎝⎭B .43,55⎛⎫- ⎪⎝⎭C .34,55⎛⎫- ⎪⎝⎭D .43,55⎛⎫- ⎪⎝⎭7.(2022·江西·景德镇一中高一期中)已知α是第二象限角,则( ) A .2α是第一象限角 B .sin02α>C .sin 20α<D .2α是第三或第四象限角8.(2022·四川省内江市第六中学高一阶段练习(理))在平面直角坐标系xOy 中,P (x ,y )(xy ≠0)是角α终边上一点,P 与原点O 之间距离为r ,比值rx叫做角α的正割,记作sec α;比值r y 叫做角α的余割,记作csc α;比值xy叫做角α的余切,记作cot α.四名同学计算同一个角β的不同三角函数值如下:甲:5sec 4β=-;乙:5csc 3β=;丙:3tan 4β=-;丁:4cot 3β=.如果只有一名同学的结果是错误的,则错误的同学是( ) A .甲 B .乙C .丙D .丁二、多选题9.(2022·江苏·南京市第一中学高一阶段练习)已知α是第一象限角,则下列结论中正确的是( ) A .sin20α>B .cos20α>C .cos02α> D .tan02α>10.(2022·全国·高一单元测试)下列结论正确的是( ) A .76π-是第三象限角 B .若圆心角为3π的扇形的弧长为π,则该扇形的面积为32πC .若角α的终边上有一点()3,4P -,则3cos 5α=-D .若角α为锐角,则角2α为钝角11.(2022·辽宁朝阳·高一阶段练习)已知角θ的终边经过点(2,3)--,且θ与α的终边关于x 轴对称,则( ) A .21sin 7θ=-B .α为钝角C .27cos α= D .点(tan θ,tan α)在第四象限12.(2022·全国·高一)以原点为圆心的单位圆上一点P 从()1,0出发,沿逆时针方向运动133π弧长到达点Q ,则点Q 的坐标不可能的是( )A .312⎛⎫- ⎪ ⎪⎝⎭B .312⎫⎪⎪⎝⎭C .132⎛ ⎝⎭D .13,2⎛ ⎝⎭三、填空题13.(2022·上海理工大学附属中学高一期中)角α的终边上有一点()()3,40P a a a ->,则sin α的值为______;14.(2022·全国·高一课时练习)已知角α的终边在射线3(0)y x x =≥上,则角α的正弦值为______,余弦值为______.15.(2022·全国·高一课时练习)已知角α的终边上有一点()3,P m -,且2sin 4α=,则m 的值为______.16.(2022·全国·高一课时练习)若角θ是第四象限角,则sin cos tan sin cos tan y θθθθθθ=++=______. 17.(2022·江苏盐城·高一期末)已知角α为第一象限角,其终边上一点(),P x y 满足()()222ln 2ln x y x y -=+,则2cos α-sin α=________.四、解答题18.(2022·江苏·高一专题练习)已知角α的终边经过点()()4,30P a a a -≠,求2sin cos αα+的值.19.(2022·江苏·高一专题练习)已知α角的终边经过点()3,P m ,且满足2sin 4m α=. (1)若α为第二象限角,求sin α值; (2)求cos tan αα+的值.20.(2022·全国·高一课时练习)已知11sin sin αα=-,且lg cos α有意义. (1)试判断角α是第几象限角;(2)若角α的终边上有一点3,5M m⎛⎫⎪⎝⎭,且1OM=(O为坐标原点),求实数m的值及sinα的值.21.(2022·全国·高一课前预习)计算下列各式的值:(1)tan405sin450cos750︒-︒+︒;(2)t 15s25ann3i4ππ⎛⎫-⎝+⎪⎭.。
三角函数知识点及典型例题

三角函数知识点及典型例题三角函数知识点及典型例题§1.1.1、任意角1、正角、负角、零角、象限角的概念.2、与角α终边相同的角的集合:{}|360,S k k Z ββα==+?∈.§1.1.2、弧度制1、把长度等于半径长的弧所对的圆心角叫做1弧度的角.2、 rl =α.3、弧长公式: R4、扇形面积公式: S=21 lr=21αr 2.§1.2.1、任意角的三角函数1、设α是一个任意角,它的终边与单位圆交于点()y x P ,,那么:xyx y ===αααtan ,cos ,sin . 2、设点()00,y x A 为角α终边上任意一点,那么:(设2020y x r +=)_______sin r y =α,________cos rx=α,_____tan x y =α.3、αsin ,αcos ,αtan 在四个象限的符号一正二正弦三切四余和三角函数线的画法. 4、诱导公式一:()()()_tan _2tan _cos _2cos _sin _2sin απααπααπα=+=+=+kk k (Z k ∈)5、特殊角0°,30°,45°,60°,90°,180°,270°的三角函数值. §1.2.2、同角三角函数的基本关系式1、平方关系:22sin cos 1αα+=.2、商数关系:sin tan cos ααα=. §1.3、三角函数的诱导公式1、诱导公式二:()()()._tan _tan _,cos _cos _,sin _sin ααπααπααπ=+-=+-=+2、诱导公式三:()()()._tan _tan _____,cos _cos _,sin _sin αααααα-=-=--=-3、诱导公式四:()()()._tan _tan _,cos _cos _,sin _sin ααπααπααπ-=--=-=-4、诱导公式五:._sin _2cos _,cos _2sin ααπααπ=??-=-5、诱导公式六:._sin _2cos _,cos _2sin ααπααπ-=??+=+ §1.4.1、正弦、余弦函数的图象1、记住正弦、余弦函数图象:2、能够对照图象讲出正弦、余弦函数的相关性质:定义域、值域、最大最小值、对称轴、对称中心、奇偶性、单调性、周期性. 3、会用五点法作图.§1.4.2、正弦、余弦函数的性质1、周期函数定义:对于函数()x f ,如果存在一个非零常数T ,使得当x 取定义域内的每一个值时,都有()()x f T x f =+,那么函数()x f 就叫做周期函数,非零常数T 叫做这个函数的周期.§1.4.3、正切函数的图象与性质 1、记住正切函数的图象:2、能够对照图象讲出正切函数的相关性质:定义域、值域、对称中心、奇偶性、单调性、周期性. §1.5、函数()?ω+=x A y sin 的图象1、能够讲出函数x y sin =的图象和函数()b x A y ++=?ωsin 的图象之间的平移伸缩变换关系.2、对于函数:()()0,0sin >>++=ω?ωA b x A y 有:振幅A ,周期ωπ2=T ,初相?,相位?ω+x ,频率πω21==f .第三章、三角恒等变换两角和与差的正弦、余弦、正切公式cos()cos cos sin sin αβαβαβ-=+cos()cos cos sin sin αβαβαβ+=-sin()αβ+=sin cos cos sin αβαβ+sin()sin cos cos sin αβαβαβ-=-tan()αβ-tan tan 1tan tan αβαβ-=+ . tan()αβ+tan tan 1tan tan αβαβ+=-二倍角的正弦、余弦、正切公式1、_cos sin 2_2sin ααα=,变形:cos α=ααsin 22sin .2、22cos2cossin ααα=-22cos 1α=-212sin α=-变形1:21cos 2cos 2αα+=,变形2:21cos 2sin 2αα-=. 3、22tan tan 21tan ααα=- 1、注意正切化弦、平方降次. 解三角形 1、正弦定理R CcB b A a 2sin sin sin === 2、余弦定理a A bc c b cos 222-+=变形 cosA=bca cb 2222-+b B ac c a cos 2222-+=变形 cosB=acb c a 2222-+c C ab b a cos 2222-+=变形cosC=abc b a 2222-+3、三角形面积公式: S =21absinC=21bcsinA=21acsinB 课本题(必修4)1.(P 11 习题13)若扇形的周长为定值l ,则该扇形的圆心角为多大时,扇形的面积最大?22.(P 23 练习4)已知sin (4π-x )=-51,且0<x<="">623.( P 24 习题9(2))设tan α=-21,计算αααα22cos 2cos sin sin 1--。
三角函数_知识点(含例题)

一、三角函数_____目录:1、任意角的三角函数;2、同角三角函数的基本关系式及诱导公式;3、三角函数的图象与性质;4、函数y=A sin(ωx+φ)的图象及三角函数模型的简单应用;5、两角和与差的正弦、余弦和正切公式;6、简单的三角恒等变换;7、正弦定理和余弦定理;8、正弦定理和余弦定理应用举例;1、任意角的三角函数;自主梳理1.任意角的概念角可以看成平面内一条射线OA绕着端点从一个位置旋转到另一个位置OB所成的图形.旋转开始时的射线OA叫做角的________,射线的端点O叫做角的________,旋转终止位置的射线OB叫做角的________,按______时针方向旋转所形成的角叫做正角,按______时针方向旋转所形成的角叫做负角.若一条射线没作任何旋转,称它形成了一个________角.(1)象限角使角的顶点与原点重合,角的始边与x轴的非负半轴重合,角的终边落在第几象限,就说这个角是__________角.(2)象限界角(即终边在坐标轴上的角)终边在x轴上的角表示为____________________;终边在y轴上的角表示为__________________________________________;终边落在坐标轴上的角可表示为____________________________.(3)终边相同的角所有与角α终边相同的角,连同角α在内,可构成一个集合______________________或__________________________,前者α用角度制表示,后者α用弧度制表示.(4)弧度制把长度等于________长的弧所对的__________叫1弧度的角.以弧度作为单位来度量角的单位制,叫做________,它的单位符号是________,读作________,通常略去不写.(5)度与弧度的换算关系360°=______ rad;180°=____ rad;1°=________ rad;1 rad=_______________≈57.30°.(6)弧长公式与扇形面积公式l=________,即弧长等于_________________________________________________.S扇=________=____________.2.三角函数的定义任意角的三角函数定义:设α是一个任意角,它的终边与单位圆交于点P(x,y),那么①____叫做α的正弦,记作sin α,即sin α=y;②____叫做α的余弦,记作cos α,即cos α=x;③________叫做α的正切,记作tan α,即tan α=yx(x≠0).(1)三角函数值的符号各象限的三角函数值的符号如下图所示,三角函数正值歌:一全正,二正弦,三正切,四余弦.(2)三角函数线下图中有向线段MP,OM,AT分别表示__________,__________________和____________.探究点一 角的概念例1 (1)如果角α是第三象限角,那么-α,π-α,π+α角的终边落在第几象限; (2)写出终边落在直线y =3x 上的角的集合;(3)若θ=168°+k ·360° (k ∈Z ),求在[0°,360°)内终边与θ3角的终边相同的角.变式迁移1 若α是第二象限的角,试分别确定2α,α2的终边所在位置.探究点二 弧长与扇形面积 例2 (2014·金华模拟)已知一个扇形的圆心角是α,0<α<2π,其所在圆的半径是R . (1)若α=60°,R =10 cm ,求扇形的弧长及该弧所在弓形的面积;(2)若扇形的周长是一定值C (C >0),当α为多少弧度时,该扇形有最大面积?变式迁移2(1)已知扇形的周长为10,面积为4,求扇形中心角的弧度数;(2)已知扇形的周长为40,当它的半径和中心角取何值时,才能使扇形的面积最大?最大面积是多少?探究点三 三角函数的定义例3 已知角α的终边在直线3x +4y =0上,求sin α,cos α,tan α的值.变式迁移3 已知角α的终边经过点P (-4a,3a ) (a ≠0),求sin α,cos α,tan α的值.2、同角三角函数的基本关系式及诱导公式;1.同角三角函数的基本关系(1)平方关系:____________________.(2)商数关系:______________________________. 2.诱导公式(1)sin(α+2k π)=________,cos(α+2k π)=__________,tan(α+2k π)=__________,k ∈Z .(2)sin(π+α)=________,cos(π+α)=________,tan(π+α)=________. (3)sin(-α)=________,cos(-α)=__________,tan(-α)=________.(4)sin(π-α)=__________,cos(π-α)=__________,tan(π-α)=________.(5)sin ⎝⎛⎭⎫π2-α=________,cos ⎝⎛⎭⎫π2-α=________. (6)sin ⎝⎛⎭⎫π2+α=__________,cos ⎝⎛⎭⎫π2+α=____________________________________. 3.诱导公式的作用是把任意角的三角函数转化为锐角三角函数,一般步骤为:上述过程体现了化归的思想方法.探究点一 利用同角三角函数基本关系式化简、求值例1 已知-π2<x <0,sin x +cos x =15.(1)求sin 2x -cos 2x 的值;(2)求tan x2sin x +cos x 的值.变式迁移1 已知sin(3π+α)=2sin ⎝⎛⎭⎫3π2+α,求下列各式的值. (1)sin α-4cos α5sin α+2cos α;(2)sin 2α+sin 2α.探究点二 利用诱导公式化简、求值例2 (2014·合肥模拟)已知sin ⎝⎛⎭⎫α+π2=-55,α∈(0,π). (1)求sin ⎝⎛⎭⎫α-π2-cos ⎝⎛⎭⎫3π2+αsin (π-α)+cos (3π+α)的值;(2)求cos ⎝⎛⎭⎫2α-3π4的值.变式迁移2 设f (α)=2sin (π+α)cos (π-α)-cos (π+α)1+sin 2α+cos ⎝⎛⎭⎫3π2+α-sin 2⎝⎛⎭⎫π2+α (1+2sin α≠0),则f ⎝⎛⎭⎫-23π6=________. 探究点三 综合应用例3 在△ABC 中,若sin(2π-A )=-2sin(π-B ),3cos A =-2co s(π-B ),求△ABC 的三个内角.变式迁移3 (2014·安阳模拟)已知△ABC 中,sin A +cos A =15,(1)求sin A ·cos A ;(2)判断△ABC 是锐角三角形还是钝角三角形; (3)求tan A 的值.3、三角函数的图象与性质;1.三角函数的图象和性质 函数 y =sin xy =cos xy =tan x图象定义域 值域 周期性 奇偶性单调性在______________________上增,在__________________________________上减在__________________________上增,在______________________________上减在定义域的每一个区间________________________________内是增函数2.正弦函数y =sin x当x =____________________________________时,取最大值1; 当x =____________________________________时,取最小值-1. 3.余弦函数y =cos x当x =__________________________时,取最大值1; 当x =__________________________时,取最小值-1.4.y =sin x 、y =cos x 、y =tan x 的对称中心分别为____________、___________、______________.5.y =sin x 、y =cos x 的对称轴分别为______________和____________,y =tan x 没有对称轴.探究点一 求三角函数的定义域例1 (2014·衡水月考)求函数y =2+log 12x +tan x 的定义域.变式迁移1 函数y =1-2cos x +lg(2sin x -1)的定义域为________________________.探究点二 三角函数的单调性例2 求函数y =2sin ⎝⎛⎭⎫π4-x 的单调区间.变式迁移2 (2014·南平月考)(1)求函数y =sin ⎝⎛⎭⎫π3-2x ,x ∈[-π,π]的单调递减区间; (2)求函数y =3tan ⎝⎛⎭⎫π6-x 4的周期及单调区间.探究点三 三角函数的值域与最值例3 已知函数f (x )=2a sin(2x -π3)+b 的定义域为[0,π2],函数的最大值为1,最小值为-5,求a 和b 的值.变式迁移3 设函数f (x )=a cos x +b 的最大值是1,最小值是-3,试确定g (x )=b sin(ax +π3)的周期.4、函数y =A sin(ωx +φ)的图象及三角函数模型的简单应用1.用五点法画y =A sin(ωx +φ)一个周期内的简图用五点法画y =A sin(ωx +φ)一个周期内的简图时,要找五个特征点.如下表所示.XΩx +φy =A sin(ωx +φ)0 A 0 -A2.图象变换:函数y =A sin(ωx +φ) (A >0,ω>0)的图象可由函数y =sin x 的图象作如下变换得到:(1)相位变换:y =sin x →y =sin(x +φ),把y =sin x 图象上所有的点向____(φ>0)或向____(φ<0)平行移动__________个单位.(2)周期变换:y =sin (x +φ)→y =sin(ωx +φ),把y =sin(x +φ)图象上各点的横坐标____(0<ω<1)或____(ω>1)到原来的________倍(纵坐标不变).(3)振幅变换:y =sin (ωx +φ)→y =A sin(ωx +φ),把y =sin(ωx +φ)图象上各点的纵坐标______(A >1)或______(0<A <1)到原来的____倍(横坐标不变).3.当函数y =A sin(ωx +φ) (A >0,ω>0),x ∈(-∞,+∞)表示一个振动量时,则____叫做振幅,T =________叫做周期,f =______叫做频率,________叫做相位,____叫做初相.函数y =A cos(ωx +φ)的最小正周期为____________.y =A tan(ωx +φ)的最小正周期为________.例1 已知函数y =2sin ⎝⎛⎭⎫2x +π3. (1)求它的振幅、周期、初相;(2)用“五点法”作出它在一个周期内的图象;(3)说明y=2sin ⎝⎛⎭⎫2x +π3的图象可由y =sin x 的图象经过怎样的变换而得到.变式迁移1 设f (x )=12cos 2x +3sin x cos x +32sin 2x (x ∈R ).(1)画出f (x )在⎣⎡⎦⎤-π2,π2上的图象; (2)求函数的单调增减区间;(3)如何由y =sin x 的图象变换得到f (x )的图象?探究点二 求y =A sin(ωx +φ)的解析式例2 已知函数f (x )=A sin(ωx +φ) (A >0,ω>0,|φ|<π2,x ∈R )的图象的一部分如图所示.求函数f (x )的解析式.变式迁移2 (2014·宁波模拟)已知函数f (x )=A sin(ωx +φ) (A >0,ω>0,|φ|<π2)的图象与y轴的交点为(0,1),它在y 轴右侧的第一个最高点和第一个最低点的坐标分别为(x 0,2)和(x 0+2π,-2).(1)求f (x )的解析式及x 0的值;(2)若锐角θ满足cos θ=13,求f (4θ)的值.探究点三 三角函数模型的简单应用例3 已知海湾内海浪的高度y (米)是时间t (0≤t ≤24,单位:小时)的函数,记作y =f (t ).下表是某日各时刻记录的浪高数据:t 0 3 6 9 12 15 18 21 24 y 1.5 1.0 0.5 1.0 1.5 1.0 0.5 0.99 1.5经长期观测,y =f (t )的曲线可近似地看成是函数y =A cos ωt +b .(1)根据以上数据,求函数y =A cos ωt +b 的最小正周期T ,振幅A 及函数表达式;(2)依据规定,当海浪高度高于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的上午8∶00至晚上20∶00之间,有多少时间可供冲浪者进行运动?变式迁移3 交流电的电压E (单位:伏)与时间t (单位:秒)的关系可用E =2203sin ⎝⎛⎭⎫100πt +π6表示,求: (1)开始时的电压;(2)最大电压值重复出现一次的时间间隔;(3)电压的最大值和第一次取得最大值时的时间.5、两角和与差的正弦、余弦和正切公式;自主梳理1.(1)两角和与差的余弦cos(α+β)=_____________________________________________, cos(α-β)=_____________________________________________. (2)两角和与差的正弦sin(α+β)=_____________________________________________, sin(α-β)=_____________________________________________. (3)两角和与差的正切tan(α+β)=_____________________________________________, tan(α-β)=_____________________________________________.(α,β,α+β,α-β均不等于k π+π2,k ∈Z )其变形为:tan α+tan β=tan(α+β)(1-tan αtan β), tan α-tan β=tan(α-β)(1+tan αtan β). 2.辅助角公式a sin α+b cos α=a 2+b 2sin(α+φ), 其中⎩⎪⎨⎪⎧cos φ= ,sin φ= ,tan φ=ba,角φ称为辅助角.探究点一 给角求值问题(三角函数式的化简、求值) 例1 求值: (1)[2sin 50°+sin 10°(1+3tan 10°)]2sin 280°; (2)sin(θ+75°)+cos(θ+45°)-3·cos(θ+15°).变式迁移1 求值:(1)2cos 10°-sin 20°sin 70°;(2)tan(π6-θ)+tan(π6+θ)+3tan(π6-θ)tan(π6+θ).探究点二 给值求值问题(已知某角的三角函数值,求另一角的三角函数值)例2 已知0<β<π4<α<3π4,cos ⎝⎛⎭⎫π4-α=35, sin ⎝⎛⎭⎫3π4+β=513,求sin(α+β)的值.变式迁移2 (2014·广州模拟)已知tan ⎝⎛⎭⎫π4+α=2,tan β=12.(1)求tan α的值;(2)求sin (α+β)-2sin αcos β2sin αsin β+cos (α+β)的值.探究点三 给值求角问题(已知某角的三角函数值,求另一角的值)例3 已知0<α<π2<β<π,tan α2=12,cos(β-α)=210.(1)求sin α的值; (2)求β的值.变式迁移3 (2014·岳阳模拟)若sin A =55,sin B =1010,且A 、B 均为钝角,求A +B的值.6、简单的三角恒等变换;1.二倍角的正弦、余弦、正切公式 (1)sin 2α=________________;(2)cos 2α=______________=________________-1=1-________________;(3)tan 2α=________________________ (α≠k π2+π4且α≠k π+π2).2.公式的逆向变换及有关变形(1)sin αcos α=____________________⇒cos α=sin 2α2sin α;(2)降幂公式:sin 2α=________________,cos 2α=________________; 升幂公式:1+cos α=________________,1-cos α=_____________; 变形:1±sin 2α=sin 2α+cos 2α±2sin αcos α=________________________. 探究点一 三角函数式的化简例1 求函数y =7-4sin x cos x +4cos 2x -4cos 4x 的最大值和最小值.变式迁移1 (2014·泰安模拟)已知函数f (x )=4cos 4x -2cos 2x -1sin ⎝⎛⎭⎫π4+x sin ⎝⎛⎭⎫π4-x .(1)求f ⎝⎛⎭⎫-11π12的值; (2)当x ∈⎣⎡⎭⎫0,π4时,求g (x )=12f (x )+sin 2x 的最大值和最小值.探究点二 三角函数式的求值例2 已知sin(π4+2α)·sin(π4-2α)=14,α∈(π4,π2),求2sin 2α+tan α-1tan α-1的值.变式迁移2 (1)已知α是第一象限角,且cos α=513,求sin (α+π4)cos (2α+4π)的值.(2)已知cos(α+π4)=35,π2≤α<3π2,求cos(2α+π4)的值.探究点三 三角恒等式的证明 例3 (2014·苏北四市模拟)已知sin(2α+β)=3sin β,设tan α=x ,tan β=y ,记y =f (x ). (1)求证:tan(α+β)=2tan α;(2)求f(x)的解析表达式;(3)若角α是一个三角形的最小内角,试求函数f(x)的值域.变式迁移3求证:sin 2x(sin x+cos x-1)(sin x-cos x+1)=1+cos x sin x.7、正弦定理和余弦定理;1.三角形的有关性质(1)在△ABC 中,A +B +C =________; (2)a +b ____c ,a -b <c ;(3)a >b ⇔sin A ____sin B ⇔A ____B ;(4)三角形面积公式:S △ABC =12ah =12ab sin C =12ac sin B =_________________;(5)在三角形中有:sin 2A =sin 2B ⇔A =B 或________________⇔三角形为等腰或直角三角形;sin(A +B )=sin C ,sin A +B 2=cos C2.2.正弦定理和余弦定理 定理 正弦定理 余弦定理内容 ________________=2Ra 2=____________,b 2=____________,c 2=____________.变形形式①a =__________, b =__________, c =__________; ②sin A =________, sin B =________, sin C =________; ③a ∶b ∶c =__________;④a +b +c sin A +sin B +sin C =asin Acos A =________________;cos B =________________;cos C =_______________. 解决的问题①已知两角和任一边,求另一角和其他两条边. ②已知两边和其中一边的对角,求另一边和其他两角.①已知三边,求各角;②已知两边和它们的夹角,求第三边和其他两个角. 探究点一 正弦定理的应用例1 (1)在△ABC 中,a =3,b =2,B =45°,求角A 、C 和边c ; (2)在△ABC 中,a =8,B =60°,C =75°,求边b 和c .变式迁移1 (1)在△ABC 中,若tan A =13,C =150°,BC =1,则AB =________;(2)在△ABC 中,若a =50,b =256,A =45°,则B =________.探究点二 余弦定理的应用 例2 (2014·咸宁月考)已知a 、b 、c 分别是△ABC 中角A 、B 、C 的对边,且a 2+c 2-b 2=ac .(1)求角B 的大小;(2)若c =3a ,求tan A 的值.变式迁移2 在△ABC 中,a 、b 、c 分别为A 、B 、C 的对边,B =2π3,b =13,a +c =4,求a .探究点三 正、余弦定理的综合应用例3 在△ABC 中,a 、b 、c 分别表示三个内角A 、B 、C 的对边,如果(a 2+b 2)sin(A -B )=(a 2-b 2)sin(A +B ),试判断该三角形的形状.变式迁移3 (2013·天津)在△ABC 中,AC AB =cos Bcos C.(1)证明:B =C ;(2)若cos A =-13,求sin ⎝⎛⎭⎫4B +π3的值.8、正弦定理和余弦定理应用举例;1.仰角和俯角与目标视线同在一铅垂平面内的水平视线和目标视线的夹角,目标视线在水平视线上方时叫仰角,目标视线在水平视线下方时叫俯角.(如图所示)2.方位角一般指北方向线顺时针到目标方向线的水平角,如方位角45°,是指北偏东45°,即东北方向.3.方向角:相对于某一正方向的水平角.(如图所示)①北偏东α°即由指北方向顺时针旋转α°到达目标方向. ②北偏西α°即由指北方向逆时针旋转α°到达目标方向. ③南偏西等其他方向角类似. 4.坡角坡面与水平面的夹角.(如图所示)5.坡比坡面的铅直高度与水平宽度之比,即i =hl=tan α(i 为坡比,α为坡角).6.解题的基本思路运用正、余弦定理处理实际测量中的距离、高度、角度等问题,实质是数学知识在生活中的应用,要解决好,就要把握如何把实际问题数学化,也就是如何把握一个抽象、概括的问题,即建立数学模型.探究点一 与距离有关的问题 例1 (2013·陕西)如图,A ,B 是海面上位于东西方向相距5(3+3)海里的两个观测点,现位于A 点北偏东45°,B 点北偏西60°的D 点有一艘轮船发出求救信号,位于B 点南偏西60°且与B点相距203海里的C点的救援船立即前往营救,其航行速度为30海里/时,该救援船到达D点需要多长时间?变式迁移1某观测站C在目标A的南偏西25°方向,从A出发有一条南偏东35°走向的公路,在C处测得与C相距31千米的公路上B处有一人正沿此公路向A走去,走20千米到达D,此时测得CD为21千米,求此人在D处距A还有多少千米?探究点二测量高度问题例2如图所示,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D,现测得∠BCD=α,∠BDC=β,CD=s,并在点C测得塔顶A的仰角为θ,求塔高AB.变式迁移2某人在塔的正东沿着南偏西60°的方向前进40米后,望见塔在东北方向,若沿途测得塔的最大仰角为30°,求塔高.探究点三三角形中最值问题例3(2013·江苏)某兴趣小组要测量电视塔AE的高度H(单位:m),示意图如图所示,垂直放置的标杆BC的高度h=4 m,仰角∠ABE=α,∠ADE=β.(1)该小组已测得一组α、β的值,算出了tan α=1.24,tan β=1.20,请据此算出H的值;(2)该小组分析若干测得的数据后,认为适当调整标杆到电视塔的距离d(单位:m),使α与β之差较大,可以提高测量精度.若电视塔实际高度为125 m,试问d为多少时,α-β最大?变式迁移3(2014·宜昌模拟)如图所示,已知半圆的直径AB=2,点C在AB的延长线上,BC=1,点P为半圆上的一个动点,以DC为边作等边△PCD,且点D与圆心O分别在PC的两侧,求四边形OPDC面积的最大值.。
(完整版)初中三角函数知识点总结及典型习题含答案)

( 1)2009
3
10. 计算:
2. 原式 = 2
3 3
2
3 1 1=0. 3
依据:①边的关系: a 2 b2 c2 ;②角的关系: A+B=90°;③边角关系:三角函数的定义。 ( 注意:
尽量避免使用中间数据和除法 ) 2、应用举例: (1) 仰角:视线在水平线上方的角;俯角:视线在水平线下方的角。
铅垂线
视线
仰角 俯角
水平线
h
i h:l
视线
α
l
(2) 坡面的铅直高度 h 和水平宽度 l 的比叫做坡度 ( 坡比 ) 。用字母 i 表示,即 i 的形式,如 i 1:5 等。
80 .
3
BC CD BD 240 80=160. 答:这栋大楼的高为 160 米.
8. 如图所示,城关幼儿园为加强安全管理,决定将园内的滑滑板的倾斜角由 45°降为 30°,已知 原滑滑板 AB的长为 4 米,点 D、B、C在同一水平面上.
(1)改善后滑滑板会加长多少米? (2)若滑滑板的正前方能有 3 米长的空地就能保证安全,原滑滑板的前方有 6 米长的空地,像这 样改造是否可行?请说明理由. (参考数据: 2 1.141, 3 1.732 , 6 2.449 ,以上结果均保留到小数点后两位. )
线,∠ ABC=150°, BC的长是 8m,则乘电梯从点 B到点 C上升的高度 h
是( B )
CD
A. 8 3 m
3
B
.4 m
1
h
C. 4 3 m
D
.8 m
A
B
B
4. 河堤横断面如图所示,堤高 BC=5米,迎水坡 AB的坡比是 1: 3 (坡比是坡
三角函数知识点总结及练习题

三角函数知识点总结及练习题高中数学必修4三角函数知识点总结一、角的概念和弧度制1.在直角坐标系内讨论角:当角的终边在坐标轴上时,这个角不属于任何象限,称为象限界角。
2.与角α终边相同的角的集合:β|β=360k+α。
k∈Z}或{β|β=2kπ+α。
k∈Z}与角α终边在同一条直线上的角的集合、与角α终边关于x轴对称的角的集合、与角α终边关于y轴对称的角的集合、与角α终边关于y=x轴对称的角的集合。
3.区间角的表示:象限角:第一象限角、第四象限角、第一、三象限角。
写出图中所表示的区间角。
4.由α的终边所在的象限,来判断α所在的象限,来判断α所在的象限,其中l为以角α为圆心角时所对圆弧的长。
5.弧度制:正角的弧度数为正数,负角的弧度数为负数,零角的弧度数为零。
任一角α的弧度数的绝对值|α|=απ/180.6.弧长公式、半径公式、扇形面积公式。
练:已知扇形AOB的周长是6cm,该扇形的中心角是1弧度,求该扇形的面积(2cm)。
二、任意角的三角函数1.任意角的三角函数定义:以角α的顶点为坐标原点,始边为x轴正半轴建立直角坐标系。
I。
在角α的终边上任取一个异于原点的点P(x,y),点P到原点的距离记为r,则sinα=y/r,cosα=x/r,tanα=y/x(注意r>0)。
练:已知角α的终边经过点P(5,-12),则sinα+cosα的值为-7/13.角α的终边上一点(a,-3a),则cosα+2sinα=-3a/r。
II。
作单位元交角α的终边上点P(x,y),则sinα=y,cosα=x,tanα=y/x。
2.在图中画出角α的正弦线、余弦线、正切线。
练:1)若α为锐角,则α,sinα,tanα的大小关系为sinα<α<tanα。
2)函数y=1+2cosx+lg(2sinx+3)的定义域是{x|x≤π/2 或x>π}。
3)特殊角的三角函数值:sin0=0,sinπ/6=1/2,sinπ/4=√2/2,sinπ/3=√3/2,sinπ/2=1cos0=1,cosπ/6=√3/2,cosπ/4=√2/2,cosπ/3=1/2,cosπ/2=0tan0=0,tanπ/6=1/√3,tanπ/4=1,tanπ/3=√3,tanπ/2=无穷大。
(完整版)高考数学三角函数知识点总结及练习

三角函数总结及统练一。
教学内容:三角函数总结及统练(一)基础知识1。
与角α终边相同的角的集合},2{Z k k S ∈+==απβ2。
三角函数的定义(六种)-—三角函数是x 、y 、r 三个量的比值 3. 三角函数的符号—-口诀:一正二弦,三切四余弦。
4. 三角函数线 正弦线MP=αsin 余弦线OM=αcos 正切线AT=αtan5. 同角三角函数的关系平方关系:商数关系:倒数关系:1cot tan =⋅αα 1csc sin =⋅αα 1sec cos =⋅αα 口诀:凑一拆一;切割化弦;化异为同。
6。
α απ+k 2 α- απ- απ+απ-2 απ-2 απ+2 正弦 αsin αsin - αsin αsin - αsin - αcos αcos 余弦 αcos αcos αcos - αcos - αcos αsin αsin - 正切 αtan αtan - αtan - αtan αtan - αcot αcot - 余切 αcotαcot -αcot -αcotαcot -αtanαtan -7。
⎪⎪⎩⎪⎪⎨⎧⋅+-=-⋅-+=+⇒⎪⎪⎩⎪⎪⎨⎧⋅+⋅=-⋅-⋅=+⋅-⋅=-⋅+⋅=+βαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαtan tan 1tan tan )tan(tan tan 1tan tan )tan(sin sin cos cos )cos(sin sin cos cos )cos(sin cos cos sin )sin(sin cos cos sin )sin( 8。
二倍角公式——代换:令αβ=⎪⎪⎩⎪⎪⎨⎧-=-=-=-=⋅=ααααααααααα22222tan 1tan 22tan sin cos sin 211cos 22cos cos sin 22sin降幂公式⎪⎪⎩⎪⎪⎨⎧+=-=22cos 1cos 22cos 1sin 22αααα半角公式:2cos 12sinαα-±=;2cos 12cos αα+±=;αααcos 1cos 12tan +-±= αααααcos 1sin sin cos 12tan+=-=9。
高中数学必修五三角函数知识点+练习题含答案解析(很详细)

高中数学必修五三角函数知识点+练习题含答案解析(很详细)第一部分必修五三角函数知识点整理第一章解三角形1、三角形的性质:①.A+B+C=π,? 222A B C π+=-?sin cos 22A B C += ②.在ABC ?中, a b +>c , a b -<c ; A >B ?sin A >sinB ...........................A >B ?cosA <cosB, a >b ? A >B③.若ABC ?为锐角?,则A B +>2π,B+C >2π,A+C >2π; 22a b +>2c ,22b c +>2a ,2a +2c >2b2、正弦定理与余弦定理:①.(2R 为ABC ?外接圆的直径)2s i n a R A =、2sin b R B =、2sin c R C =sin 2a A R =、 sin 2b B R =、 sin 2c C R= 面积公式:111sin sin sin 222ABC S ab C bc A ac B ?=== ②.余弦定理:2222cos a b c bc A =+-、2222cos b a c ac B =+-、2222cos c a b ab C =+-222cos 2b c a A bc +-=、222cos 2a c b B ac +-=、222cos 2a b c C ab+-= 补充:两角和与差的正弦、余弦和正切公式:⑴()cos cos cos sin sin αβαβαβ-=+;⑵()cos cos cos sin sin αβαβαβ+=-;⑶()sin sin cos cos sin αβαβαβ-=-;⑷()sin sin cos cos sin αβαβαβ+=+;⑸()tan tan tan 1tan tan αβαβαβ --=+ ? (()()tan tan tan 1tan tan αβαβαβ-=-+);⑹()tan tan tan 1tan tan αβαβαβ++=- ? (()()tan tan tan 1tan tan αβαβαβ+=+-).二倍角的正弦、余弦和正切公式:⑴sin 22sin cos ααα=.222)cos (sin cos sin 2cos sin 2sin1ααααααα±=±+=±?⑵2222cos2cos sin 2cos 112sin ααααα=-=-=-升幂公式2sin 2cos 1,2cos 2cos 122αααα=-=+ ?落幂公式2cos 21cos 2αα+=,21cos 2sin 2αα-=.第二部分必修五练习题含答案解析第一章解三角形1.在△ABC 中,AB =5,BC =6,AC =8,则△ABC 的形状是( )A .锐角三角形B .直角三角形C .钝角三角形D .非钝角三角形解析:最大边AC 所对角为B ,则cosB =52+62-822×5×6=-320B>CB .B>A>C C .C>B>AD .C>A>B解析由正弦定理a sinA =b sinB ,∴sinB =bsinA a =32.∵B 为锐角,∴B =60°,则C =90°,故C>B>A. 答案 C3.在△ABC 中,已知a =8,B =60°,C =75°,则b 等于( )A .4 2B .4 3C .4 6 D.323解:由A +B +C =180°,可求得A =45°,由正弦定理,得b =asinB sinA =8×sin60°sin45°=8×3222=4 6. 答案 C4.在△ABC 中,AB =5,BC =7,AC =8,则BA →·BC → 的值为( )A .5B .-5C .15D .-15解析在△ABC 中,由余弦定理得:cosB =AB 2+BC 2-AC 22AB ·BC =25+49-642×5×7=17. ∴BA →·BC →=|BA →|·|BC →|cosB =5×7×17=5. 答案 A5.若三角形三边长之比是1:3:2,则其所对角之比是( )A .1:2:3B .1:3:2C .1:2: 3 D.2:3:2解析设三边长分不为a ,3a,2a ,设最大角为A ,则cosA =a 2+3a 2-2a 22·a ·3a =0,∴A =90°.设最小角为B ,则cosB =2a 2+3a 2-a 22·2a ·3a =32,∴B =30°,∴C =60°. 所以三角之比为1:2:3. 答案 A6.在△ABC 中,若a =6,b =9,A =45°,则此三角形有( )A .无解B .一解C .两解D .解的个数别确定解析由b sinB =a sinA ,得sinB =bsinA a =9×226=3 24>1.∴此三角形无解.答案 A7.已知△ABC 的外接圆半径为R ,且2R(sin 2A -sin 2C)=(2a -b)sinB(其中a ,b 分不为A ,B 的对边),这么角C 的大小为( )A .30°B .45°C .60°D .90°解析依照正弦定理,原式可化为2R ? ??a 24R 2-c 24R 2=(2a -b)·b 2R ,∴a 2-c 2=(2a -b)b ,∴a 2+b 2-c 2=2ab ,∴cosC =a 2+b 2-c 22ab =22,∴C =45°. 答案 B8.在△ABC 中,已知sin 2A +sin 2B -sinAsinB =sin 2C ,且满脚ab =4,则该三角形的面积为( )A .1B .2 C. 2 D. 3解析由a sinA =b sinB =c sinC=2R ,又sin 2A +sin 2B -sinAsinB =sin 2C ,可得a 2+b 2-ab =c 2.∴c osC =a 2+b 2-c 22ab =12,∴C =60°,sinC =32. ∴S △ABC =12absinC = 3. 答案 D9.在△ABC 中,A =120°,AB =5,BC =7,则sinB sinC 的值为( ) A.85 B.58 C.53 D.35解析由余弦定理,得 cosA =AB 2+AC 2-BC 22AB ·AC,解得AC =3. 由正弦定理sinB sinC =AC AB =35. 答案 D10.在三角形ABC 中,AB =5,AC =3,BC =7,则∠BAC 的大小为( )A.2π3B.5π6C.3π4D.π3解析由余弦定理,得cos ∠BAC =AB 2+AC 2-BC 22AB ·AC =52+32-722×5×3=-12,∴∠BAC =2π3. 答案 A11.有一长为1 km 的歪坡,它的倾歪角为20°,现要将倾歪角改为10°,则坡底要加长( )A .0.5 kmB .1 kmC .1.5 km D.32km 解析如图,AC =AB ·sin20°=sin20°,BC =AB ·cos20°=cos20°,DC =AC tan10°=2cos 210°,∴DB =DC -BC =2cos 210°-cos20°=1.答案 B12.已知△ABC 中,A ,B ,C 的对边分不为a ,b ,c.若a =c =6+2,且A =75°,则b 为( )A .2B .4+2 3C .4-2 3 D.6- 2解析在△ABC 中,由余弦定理,得a 2=b 2+c 2-2bccosA ,∵a =c ,∴0=b 2-2bccosA =b 2-2b(6+2)cos75°,而cos75°=cos(30°+45°)=cos30°cos45°-sin30°sin45°=22? ????32-12=14(6-2),∴b 2-2b(6+2)cos75°=b 2-2b(6+2)·14(6-2)=b 2-2b =0,解得b =2,或b =0(舍去).故选A. 答案 A 13.在△ABC 中,A =60°,C =45°,b =4,则此三角形的最小边是____________.解析由A +B +C =180°,得B =75°,∴c 为最小边,由正弦定理,知c =bsinC sinB =4sin45°sin75°=4(3-1).答案 4(3-1)14.在△ABC 中,若b =2a ,B =A +60°,则A =________.解析由B =A +60°,得 sinB =sin(A +60°)=12sinA +32cosA. 又由b =2a ,知sinB =2sinA.∴2sinA =12sinA +32cosA. 即32sinA =32cosA.∵cosA ≠0,∴tanA =33.∵0°<A<180°,∴A =30°. 答案30° 15.在△ABC 中,A +C =2B ,BC =5,且△ABC 的面积为103,则B =_______,AB =_______.解析由A +C =2B 及A +B +C =180°,得B =60°.又S =12AB ·BC ·sinB ,∴10 3=12AB ×5×sin60°,∴AB =8. 答案60° 816.在△ABC 中,已知(b +c):(c +a):(a +b)=8:9:10,则sinA :sinB :sinC =________.解析设b +c =8k ,c +a =9k ,a +b =10k ,可得a :b :c =11:9:7.∴sinA :sinB :sinC =11:9:7.答案 11:9:717.在非等腰△ABC 中,角A ,B ,C 所对的边分不为a ,b ,c ,且a 2=b(b +c).(1)求证:A =2B ;(2)若a =XXX ,试推断△ABC 的形状.解 (1)证明:在△ABC 中,∵a 2=b ·(b +c)=b 2+bc ,由余弦定理,得cosB =a 2+c 2-b 22ac =bc +c 22ac =b +c 2a =a 2b =sinA 2sinB ,∴sinA =2sinBcosB =sin2B.则A =2B 或A +2B =π.若A +2B =π,又A +B +C =π,∴B =C.这与已知相矛盾,故A =2B.(2)∵a =XXX ,由a 2=b(b +c),得XXX 2=b 2+bc ,∴c =2b.又a 2+b 2=4b 2=c 2.故△ABC 为直角三角形.18.锐角三角形ABC 中,边a ,b 是方程x 2-23x +2=0的两根,角A ,B 满脚2sin(A +B)-3=0.求:(1)角C 的度数;(2)边c 的长度及△ABC 的面积.解 (1)由2sin(A +B)-3=0,得sin(A +B)=32. ∵△ABC 为锐角三角形,∴A +B =120°,∴∠C =60°.(2)∵a ,b 是方程x 2-23x +2=0的两个根,∴a +b =23,ab =2.∴c 2=a 2+b 2-2abcosC =(a +b)2-3ab =12-6=6.∴c = 6.S △ABC =12absinC =12×2×32=32. 19.已知△ABC 的角A ,B ,C 所对的边分不是a ,b ,c ,设向量m =(a ,b),n =(sinB ,sinA),p =(b -2,a -2).(1)若m ∥n ,求证:△ABC 为等腰三角形;(2)若m ⊥p ,边长c =2,角C =π3,求△ABC 的面积.解 (1)证明:∵m ∥n ,∴asinA =bsinB.由正弦定得知,sinA =a 2R ,sinB =b 2R (其中R 为△ABC 外接圆的半径),代入上式,得a ·a 2R =b ·b 2R,∴a =b.故△ABC 为等腰三角形.(2)∵m ⊥p ,∴m ·p =0,∴a(b -2)+b(a -2)=0,∴a +b =ab.由余弦定理c 2=a 2+b 2-2abcosC 得4=(a+b)2-3ab,即(ab)2-3ab-4=0. 解得ab=4,ab=-1(舍去).∴△ABC的面积S=12absinC=12×4×sinπ3= 3.。
三角函数例题和知识点总结

三角函数例题和知识点总结三角函数是数学中的一个重要分支,在几何、物理、工程等领域都有广泛的应用。
下面我们将通过一些例题来加深对三角函数知识点的理解,并对相关知识点进行总结。
一、三角函数的基本概念1、角的概念角可以看作是平面内一条射线绕着端点从一个位置旋转到另一个位置所形成的图形。
按旋转方向不同,角可分为正角、负角和零角。
2、弧度制把长度等于半径长的弧所对的圆心角叫做 1 弧度的角。
用弧度作为单位来度量角的制度叫做弧度制。
弧度与角度的换算关系为:180°=π 弧度。
3、任意角的三角函数设角α的终边上任意一点 P 的坐标为(x, y),它到原点的距离为 r(r =√(x²+ y²)),则角α的正弦、余弦、正切分别为:sinα = y/r ,cosα = x/r ,tanα = y/x (x ≠ 0)二、三角函数的图像和性质1、正弦函数 y = sin x图像:正弦函数的图像是一个周期为2π,振幅为 1 的波浪线。
性质:定义域为 R,值域为-1, 1,是奇函数,在π/2 +2kπ, π/2 +2kπ (k∈Z)上单调递增,在π/2 +2kπ, 3π/2 +2kπ (k∈Z)上单调递减。
2、余弦函数 y = cos x图像:余弦函数的图像是一个周期为2π,振幅为 1 的波浪线。
性质:定义域为 R,值域为-1, 1,是偶函数,在π +2kπ, 2kπ(k∈Z)上单调递增,在2kπ, π +2kπ (k∈Z)上单调递减。
3、正切函数 y = tan x图像:正切函数的图像是由无数个周期为π的分支组成,其定义域为{ x |x ≠ π/2 +kπ, k∈Z }。
性质:值域为 R,是奇函数,在(π/2 +kπ, π/2 +kπ )(k∈Z)上单调递增。
三、三角函数的诱导公式1、同角三角函数的基本关系sin²α +cos²α = 1 ,tanα =sinα /cosα2、诱导公式sin( α )=sinα ,cos( α )=cosα ,tan( α )=tanαsin( π α )=sinα ,cos( π α )=cosα ,tan( π α )=tanαsin( π +α )=sinα ,cos( π +α )=cosα ,tan( π +α )=tanαsin( 2π α )=sinα ,cos( 2π α )=cosα ,tan( 2π α )=tanα四、三角函数的和差公式1、两角和与差的正弦公式sin(α +β) =sinαcosβ +cosαsinβsin(α β) =sinαcosβ cosαsinβ2、两角和与差的余弦公式cos(α +β) =cosαcosβ sinαsinβcos(α β) =cosαcosβ +sinαsinβ3、两角和与差的正切公式tan(α +β) =(tanα +tanβ) /(1 tanαtanβ)tan(α β) =(tanα tanβ) /(1 +tanαtanβ)五、例题解析例 1:已知sinα = 3/5,且α为第二象限角,求cosα 和tanα 的值。
三角函数例题和知识点总结

三角函数例题和知识点总结一、三角函数的基本概念在数学中,三角函数是一类重要的函数,它们描述了三角形中边与角之间的关系。
首先,我们来了解一下角度的度量。
角度可以用度(°)或弧度来表示。
一个完整的圆周对应的角度是 360°,而用弧度表示则是2π 弧度。
接下来,我们认识一下常见的三角函数:正弦函数(sin)、余弦函数(cos)、正切函数(tan)。
正弦函数sinθ 表示在直角三角形中,对边与斜边的比值;余弦函数cosθ 表示邻边与斜边的比值;正切函数tanθ 则是对边与邻边的比值。
二、三角函数的基本公式1、同角三角函数的基本关系sin²θ +cos²θ = 1tanθ =sinθ /cosθ2、诱导公式例如:sin(π θ) =sinθ ,cos(π θ) =cosθ 等三、三角函数的图像和性质1、正弦函数 y = sin x 的图像是一个周期为2π 的波形,其值域为-1, 1,在 x =π/2 +2kπ (k 为整数)时取得最大值 1,在 x =3π/2 +2kπ (k 为整数)时取得最小值-1。
2、余弦函数 y = cos x 的图像也是一个周期为2π 的波形,值域同样为-1, 1,在 x =2kπ (k 为整数)时取得最大值 1,在 x =π +2kπ (k 为整数)时取得最小值-1。
3、正切函数 y = tan x 的图像其周期为π,定义域为x ≠ π/2 +kπ (k 为整数),值域为 R 。
四、三角函数的例题例 1:已知sinθ = 08,且θ 在第一象限,求cosθ 和tanθ 的值。
因为sin²θ +cos²θ = 1,所以cosθ =√(1 sin²θ) =√(1 08²) =06 。
tanθ =sinθ /cosθ = 08 / 06 = 4 / 3 。
例 2:求函数 y = 2sin(2x +π/3) 的周期和振幅。
三角函数性质与应用例题和知识点总结

三角函数性质与应用例题和知识点总结一、三角函数的基本定义在直角三角形中,正弦(sin)、余弦(cos)和正切(tan)分别定义为:正弦:对边与斜边的比值,即sinθ =对边/斜边。
余弦:邻边与斜边的比值,即cosθ =邻边/斜边。
正切:对边与邻边的比值,即tanθ =对边/邻边。
二、三角函数的性质1、周期性正弦函数和余弦函数的周期都是2π,即 sin(x +2π) = sin(x),cos(x +2π) = cos(x);正切函数的周期是π,即 tan(x +π) = tan(x)。
2、奇偶性正弦函数是奇函数,即 sin(x) = sin(x);余弦函数是偶函数,即cos(x) = cos(x)。
3、值域正弦函数和余弦函数的值域都是-1, 1,正切函数的值域是 R(全体实数)。
4、单调性正弦函数在π/2 +2kπ, π/2 +2kπ 上单调递增,在π/2 +2kπ, 3π/2 +2kπ 上单调递减(k∈Z)。
余弦函数在2kπ, π +2kπ 上单调递减,在π +2kπ, 2π +2kπ 上单调递增(k∈Z)。
正切函数在(π/2 +kπ, π/2 +kπ) 上单调递增(k∈Z)。
三、三角函数的应用例题例 1:已知一个直角三角形的一个锐角为 30°,斜边为 2,求这个直角三角形的两条直角边的长度。
解:因为一个锐角为 30°,所以 sin30°= 1/2,cos30°=√3/2。
设 30°角所对的直角边为 a,邻边为 b,则:a = 2×sin30°= 2×(1/2) = 1b = 2×cos30°= 2×(√3/2) =√3例 2:求函数 y = 2sin(2x +π/3) 的最大值和最小值,并求出取得最值时 x 的值。
解:因为正弦函数的值域为-1, 1,所以 2sin(2x +π/3) 的值域为-2, 2。
三角函数知识点归纳总结及例题

《三角函数》一、任意角的概念与弧度制1、将沿x 轴正向的射线,围绕原点旋转所形成的图形称作角. 逆时针旋转为正角,顺时针旋转为负角,不旋转为零角2、同终边的角可表示为{}()360k k Z ααβ︒=+∈x 轴上角:{}()180k k Z αα=∈ y 轴上角:{}()90180k k Z αα=+∈3、第一象限角:{}()036090360k k k Z αα︒︒+<<+∈第二象限角:{}()90360180360k k k Z αα︒︒+<<+∈第三象限角:{}()180360270360k k k Z αα︒︒+<<+∈第四象限角:{}()270360360360k k k Z αα︒︒+<<+∈4、区分第一象限角、锐角以及小于90的角 第一象限角:{}()036090360k k k Z αα︒︒+<<+∈锐角:{}090αα<< 小于90的角:{}90αα<例题 :1.下列各角中,与27︒角终边相同的是( ) A .63︒ B .153︒C .207︒D .387︒2.已知cos0,sin0,22αα<<且cos α<0,则角α为( )A .第一象限的角B .第二象限的角C .第三象限的角D .第四象限的角3.若角α为第二象限角,则角2α为( )象限角 A .第一 B .第一或第二C .第二D .第一或第三5、若α为第二象限角,那么2α为第几象限角? ππαππk k 222+≤≤+ππαππk k +≤≤+224,24,0παπ≤≤=k ,2345,1παπ≤≤=k 所以2α在第一、三象限 6、弧度制:弧长等于半径时,所对的圆心角为1弧度的圆心角,记作1rad . 7、角度与弧度的转化:01745.01801≈=︒π815730.571801'︒=︒≈︒=π9、弧长与面积计算公式 弧长:l R α=⨯;面积:21122S l R R α=⨯=⨯,注意:这里的α均为弧度制. 例题:4.512π=( ) A .70°B .75°C .80°D .85°5.300︒-化成弧度制为( ) A .103πB .56π-C .53π-D .73π二、任意角的三角函数1、正弦:sin y r α=;余弦cos x r α=;正切tan yxα=其中(),x y 为角α终边上任意点坐标,r =例6.已知角θ的顶点为坐标原点,始边为x 轴正半轴,若(4,3)P 是角θ终边上的一点,则cos θ=( )A .35B .45C .43D .347.已知角α的顶点在坐标原点,始边在x 轴非负半轴上,终边与单位圆交于12P ⎛- ⎝⎭,则sinα=()A.3-B.12-C.3-D.38.已知tan2α=,则2221sin2cossin2cosαααα++=-()A.32B.52C.4 D.52、三角函数值对应表:口诀:一全正,二正弦,三正切,四余弦.(简记为“全s t c”)sinαtanαcosα第一象限:0,0.>>yx sinα>0,cosα>0,tanα>0,第二象限:0,0.><yx sinα>0,cosα<0,tanα<0,第三象限:0,0.<<yx sinα<0,cosα<0,tanα>0,度030456090120135150180︒270360弧度06π4π3π2π23π34π56ππ32π2πsinα01222321322212010cosα132221212-22-32-1-01 tanα03313无3-1-33-0无0第四象限:0,0.<>y x sin α<0,cos α>0,tan α<0,4、同角三角函数基本关系式22sin cos 1αα+=sin tan tan cot 1cos ααααα=⇒= ααααcos sin 21)cos (sin 2+=+ ααααcos sin 21)cos (sin 2-=-(ααcos sin +,ααcos sin -,ααcos sin •,三式之间可以互相表示)5.诱导公式口诀:奇变偶不变,符号看象限(所谓奇偶指的是απ+2n 中整数n 的奇偶性,把α看作锐角)212(1)sin ,sin()2(1)s ,n n n n co n απαα-⎧-⎪+=⎨⎪-⎩为偶数为奇数;212(1)s ,s()2(1)sin ,nn co n n co n απαα+⎧-⎪+=⎨⎪-⎩为偶数为奇数. ①.公式(一):α与()2,k k Z απ+∈απαsin )2sin(=+k ;απαcos )2cos(=+k ;απαtan )2tan(=+k②.公式(二):α与α-()sin sin αα-=-;()cos cos αα-=;()tan tan αα-=-③.公式(三):α与πα+()sin sin παα+=-;()cos cos παα+=-;()tan tan παα+=④.公式(四):α与πα-()sin sin παα-=;()cos cos παα-=-;()tan tan παα-=-⑤.公式(五):α与2πα+sin cos 2παα⎛⎫+= ⎪⎝⎭;cos sin 2παα⎛⎫+=- ⎪⎝⎭; ⑥.公式(六):α与2πα-sin cos 2παα⎛⎫-= ⎪⎝⎭;cos sin 2παα⎛⎫-= ⎪⎝⎭;⑦.公式(七):α与32πα+ 3sin cos 2παα⎛⎫+=- ⎪⎝⎭;3cos sin 2παα⎛⎫+= ⎪⎝⎭; ⑧.公式(八):α与32πα- 3sin cos 2παα⎛⎫-=- ⎪⎝⎭;3cos sin 2παα⎛⎫-=- ⎪⎝⎭;例题:9.已知α为第三象限角,且sin α=,则cos α=( )A B .C D .10.在[]0,2π上满足1sin 2x ≥的x 的取值范围是( )A .06,π⎡⎤⎢⎥⎣⎦B .5,66ππ⎡⎤⎢⎥⎣⎦C .2,63ππ⎡⎤⎢⎥⎣⎦D .5,6ππ⎡⎤-⎢⎥⎣⎦11.若sin 3α=,2a ππ<<,则sin 2πα⎛⎫+= ⎪⎝⎭( )A .B .12-C .12 D12.已知1cos 2α=-,()0,απ∈,则α=( ).A .6πB .56πC .3π D .23π13.sin330︒等于( )A .2-B .12-C .12D .214.sin 3π⎛⎫- ⎪⎝⎭的值是( )A .12B .12-C .2D .15.若α是第三象限角,则点()()()tan 3,cos παπα-+在( )A .第一象限B .第二象限C .第三象限D .第四象限16.2sin 3π=( )A .12 B .12-C D . 17.sin 210︒的值为( )A .12B .12-C .2D .三、三角函数的图像与性质5、三角函数的图像与性质表格 sin y x =cos y x =tan y x =图像定义域 R R,2x x k k Z ππ⎧⎫≠+∈⎨⎬⎩⎭值域[]1,1-[]1,1-R最值当22x k ππ=+()k Z ∈时,max 1y =;当22x k ππ=-()k Z ∈时,min 1y =-.当()2x k k Z π=∈时,max 1y =;当2x k ππ=+()k Z ∈时,min 1y =-.既无最大值也无最小值周期性 2π 2ππ奇偶性奇函数 偶函数 奇函数单调性在2,222k k ππππ⎡⎤-++⎢⎥⎣⎦()k Z ∈上是增函数;在32,222k k ππππ⎡⎤++⎢⎥⎣⎦()k Z ∈上是减函数.在[]()2,2k k k Z πππ-+∈上是增函数; 在[]2,2k k πππ+()k Z ∈上是减函数.在,22k k ππππ⎛⎫-+⎪⎝⎭()k Z ∈上是增函数.对称性对称中心()(),0k k Z π∈ 对称轴()2x k k Z ππ=+∈对称中心(),02k k Z ππ⎛⎫+∈⎪⎝⎭ 对称轴()x k k Z π=∈对称中心(),02k k Z π⎛⎫∈⎪⎝⎭无对称轴函数 性 质21.已知函数()sin 022f x x ππϕϕ⎛⎫⎛⎫=+<< ⎪⎪⎝⎭⎝⎭的图象过点30,2⎛⎫ ⎪ ⎪⎝⎭,则()f x 图象的一个对称中心为( ) A .1,03⎛⎫ ⎪⎝⎭B .()1,0C .4,03⎛⎫ ⎪⎝⎭D .()2,022.已知函数()()sin 04f x x πωω⎛⎫=+> ⎪⎝⎭的最小正周期为π,则8f π⎛⎫= ⎪⎝⎭( ) A .1B .12C .1-D .12-23.函数sin 2y x =的图象的一条对称轴的方程是( ) A .2x π=-B .4πx =-C .8x π=D .58x π=24.若α,β为锐角,且2cos()sin()63ππαβ-=+,则( ) A .3παβ+=B .6παβ+=C .3παβ-= D .6παβ-=25.函数3cos 1()x f x x+=的部分图象大致是( ) A . B .C .D .26.函数cos(),[0,2]y x x π=-∈的简图是( )A .B .C .D .27.函数2cos 53y x π⎛⎫=+ ⎪⎝⎭的最小正周期是( )A .5πB .52πC .2πD .5π28.已知[]0,x π∈,则满足1cos 2x >-的x 的取值范围是( ) A .2,33ππ⎛⎫⎪⎝⎭B .20,,33πππ⎡⎤⎛⎤⎢⎥⎥⎣⎦⎝⎦C .50,6π⎡⎤⎢⎥⎣⎦D .20,3π⎡⎫⎪⎢⎣⎭29.函数3cos 28y x π⎛⎫=-⎪⎝⎭的一个对称中心是( ) A .,08π⎛⎫⎪⎝⎭B .5,016π⎛⎫⎪⎝⎭C .3,08π⎛⎫⎪⎝⎭D .7,016π⎛⎫⎪⎝⎭1、将函数sin y x =的图象上所有的点,向左(右)平移ϕ个单位长度,得到函数()sin y x ϕ=+的图象;再将函数()sin y x ϕ=+的图象上所有点的横坐标伸长(缩短)到原来的1ω倍(纵坐标不变),得到函数()sin y x ωϕ=+的图象;再将函数()sin y x ωϕ=+的图象上所有点的纵坐标伸长(缩短)到原来的A 倍(横坐标不变),得到函数()sin y A x ωϕ=+的图象。
三角函数知识点及典型例题
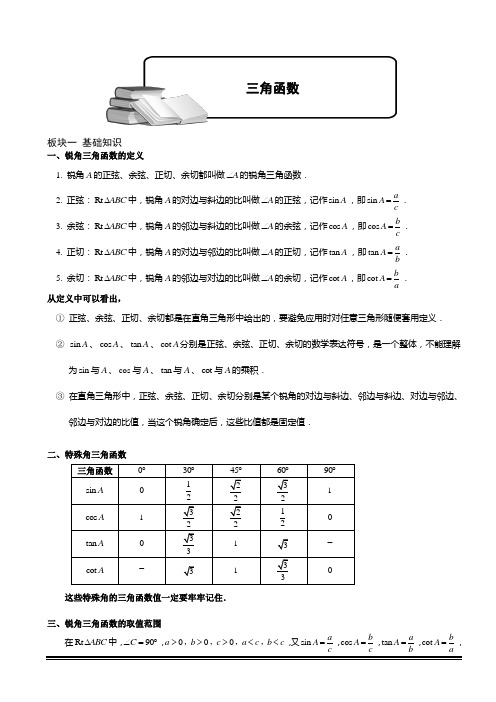
板块一 基础知识一、锐角三角函数的定义1. 锐角A 的正弦、余弦、正切、余切都叫做A ∠的锐角三角函数.2. 正弦:Rt ABC ∆中,锐角A 的对边与斜边的比叫做A ∠的正弦,记作sin A ,即sin aA c =. 3. 余弦:Rt ABC ∆中,锐角A 的邻边与斜边的比叫做A ∠的余弦,记作cos A ,即cos b A c =. 4. 正切:Rt ABC ∆中,锐角A 的对边与邻边的比叫做A ∠的正切,记作tan A ,即tan a A b =. 5. 余切:Rt ABC ∆中,锐角A 的邻边与对边的比叫做A ∠的余切,记作cot A ,即cot b A a=. 从定义中可以看出,① 正弦、余弦、正切、余切都是在直角三角形中给出的,要避免应用时对任意三角形随便套用定义. ② sin A 、cos A 、tan A 、cot A 分别是正弦、余弦、正切、余切的数学表达符号,是一个整体,不能理解为sin 与A 、cos 与A 、tan 与A 、cot 与A 的乘积.③ 在直角三角形中,正弦、余弦、正切、余切分别是某个锐角的对边与斜边、邻边与斜边、对边与邻边、邻边与对边的比值,当这个锐角确定后,这些比值都是固定值.二、特殊角三角函数这些特殊角的三角函数值一定要牢牢记住.三、锐角三角函数的取值范围在Rt ABC ∆中,90C ∠=︒,000a b c a c b c >>><<,,,,,又sin a A c =,cos b A c =,tan a A b =,cot bA a=,三角函数 0︒ 30︒45︒60︒90︒sin A 012 22 321cos A 132 22 12 0tan A 03313-cot A - 3 1 33三角函数所以0sin 10cos 1tan 0cot 0A A A A <<<<>>,,,.四、三角函数关系 1. 同角三角函数关系: 22sin cos 1A A +=,sin tan cos AA A=,tan cot 1A A ⋅= 2. 互余角三角函数关系:⑴ 任意锐角的正弦值等于它的余角的余弦值:()sin cos 90A A =︒-; ⑵ 任意锐角的余弦值等于它的余角的正弦值:()cos sin 90A A =︒-; ⑶ 任意锐角的正切值等于它的余角的余切值:()tan cot 90A A =︒-;⑷ 任意锐角的余切值等于它的余角的正切值:()cot tan 90A A =︒-. 3. 锐角三角函数值的变化规律:令1c =,锐角A ∠越小,则a 越小,则b 越大;当A ∠越大,则a 就越大,b 就越小,且a c b c <<,,所以当角度在0~90︒︒范围内变化时,正弦值随角度的增大(或减小)而增大(或减小);余弦值随角度的增大(或减小)而减小(或增大).而正切值也是随角度的增大(或减小)而增大(或减小);余切值随角度的增大(或减小)而减小(或增大).可以应用0~90︒︒间的正弦值、余弦值、正切值、余切值的增减性来比较角的正弦、余弦、正切、余切值的大小,其规律是:⑴A B 、为锐角且A B >,则sin sin A B >,cos cos A B <,tan tan A B >,cot cot A B <;⑵A B 、为锐角且A B <,则sin sin A B <,cos cos A B >,tan tan A B <,cot cot A B >.该规律反过来也成立.板块二 常用公式1. 和角公式:cos()cos cos sin sin αβαβαβ+=-,sin()sin cos cos sin αβαβαβ+=+,tan tan tan()1tan tan αβαβαβ++=-⋅;2. 差角公式:cos()cos cos sin sin αβαβαβ-=+,sin()sin cos cos sin αβαβαβ-=-,tan tan tan()1tan tan αβαβαβ--=+⋅;3. 倍角公式:2222cos2cos sin 2cos 112sin ααααα=-=-=-,sin22sin cos ααα=,22tan tan 21tan ααα=-; 4. 半角公式:21cos cos 22αα+=,21cos sin 22αα-=,sin 1cos tan 21cos sin ααααα-==+; 5. 万能公式:22tan2sin 1tan 2ααα=+,221tan 2cos 1tan 2ααα-=+,22tan2tan 1tan 2ααα=-;6. 积化和差公式:1cos cos [cos()cos()]2αβαβαβ=++-,1cos sin [sin()sin()]2αβαβαβ=+--,1sin cos [sin()sin()]2αβαβαβ=++-,1sin sin [cos()cos()]2αβαβαβ=-+--.7. 和差化积公式:cos cos 2cos cos22αβαβαβ+-+=,cos cos 2sin sin22αβαβαβ+--=-,sin sin 2sin cos22αβαβαβ+-+=,sin sin 2cossin22αβαβαβ+--=.板块一、三角函数基础【例1】 已知如图:在Rt ABC ∆中,810BC AC ==,.求sin A 和sin B 的值。
高考数学三角函数知识点及典型例题讲解

――概念、方法、题型、易误点及应试技巧总结三角函数1、角的概念的推广:平面内一条射线绕着端点从一个位置旋转到另一个位置所的图形。
按逆时针方向旋转所形成的角叫正角,按顺时针方向旋转所形成的角叫负角,一条射线没有作任何旋转时,称它形成一个零角。
射线的起始位置称为始边,终止位置称为终边。
2、象限角的概念:在直角坐标系中,使角的顶点与原点重合,角的始边与x 轴的非负半轴重合,角的终边在第几象限,就说这个角是第几象限的角。
如果角的终边在坐标轴上,就认为这个角不属于任何象限。
3. 终边相同的角的表示:(1)α终边与θ终边相同(α的终边在θ终边所在射线上)⇔2()k k αθπ=+∈Z ,注意:相等的角的终边一定相同,终边相同的角不一定相等.如与角 1825-的终边相同,且绝对值最小的角的度数是___,合___弧度。
(答:25-;536π-)(2)α终边与θ终边共线(α的终边在θ终边所在直线上) ⇔()k k αθπ=+∈Z . (3)α终边与θ终边关于x 轴对称⇔2()k k αθπ=-+∈Z . (4)α终边与θ终边关于y 轴对称⇔2()k k απθπ=-+∈Z . (5)α终边与θ终边关于原点对称⇔2()k k απθπ=++∈Z .(6)α终边在x 轴上的角可表示为:,k k Z απ=∈;α终边在y 轴上的角可表示为:,2k k Z παπ=+∈;α终边在坐标轴上的角可表示为:,2k k Z πα=∈.如α的终边与6π的终边关于直线x y =对称,则α=____________。
(答:Z k k ∈+,32ππ)4、α与2α的终边关系:由“两等分各象限、一二三四”确定.如若α是第二象限角,则2α是第_____象限角 (答:一、三)5.弧长公式:||l R α=,扇形面积公式:211||22S lR R α==,1弧度(1rad)57.3≈. 如已知扇形AOB 的周长是6cm ,该扇形的中心角是1弧度,求该扇形的面积。
(完整版)三角函数知识点及练习题含答案,推荐文档

y
++
o -
-x
y
-+
o -
+
x
y
-+
o +
-
x
、、 、、、
、、 、、、
、、 、、、
6、三角函数线 正弦线:MP; 余弦线:OM;
正切线: AT.
a的 的 的 P、 x,y) r
x
y T
P O M Ax
7. 三角函数的定义域: 三角函数 f (x) sinx f (x) cosx f (x) tanx
8.如果 π <θ< π ,那么下列各式中正确的是( )
4
2
A.cosθ<tanθ<sinθ
B.sinθ<cosθ<tanθ
C.tanθ<sinθ<cosθ
D.cosθ<sinθ<tanθ
9.若 A、B 是锐角△ABC 的两个内角,则 P(cosB-sinA,sinB-cosA)在( )
A.第一象限
任意角
1.D 2.C 3.A 4.D
三角函数
1.B 2.A 3. C 4.D 5. A 6. C 7.B
11.A
12.±4
4 ±
5
13. [ π , 3π ] 14. 0 22
15.二
16.[0, π ]∪( π , π ]∪( 3π ,2π) 17.( π , 3π
4
24
2
44
8.D
9. D
10. D
③终边不相同,它们的同名三角函数值一定不相同;
④不相等的角,同名三角函数值也不相同.
其中正确的个数是( )
A.0
B.1
C.2
D.3
2.若角 α、β 的终边关于 y 轴对称,则下列等式成立的是( )
初中三角函数知识点+题型总结+课后练习

锐角三角函数知识点1、勾股定理:直角三角形两直角边a 、b 的平方和等于斜边c 的平方; 222c b a =+2、如下图,在Rt △ABC 中,∠C 为直角,则∠A 的锐角三角函数为∠A 可换成∠B :定 义表达式取值范围关 系正弦斜边的对边A A ∠=sin c aA =sin 1sin 0<<A∠A 为锐角B A cos sin =B A sin cos =1cos sin 22=+A A余弦斜边的邻边A A ∠=cos c bA =cos 1cos 0<<A∠A 为锐角正切的邻边的对边A tan ∠∠=A A b aA =tan 0tan >A∠A 为锐角B A cot tan =B A tan cot =AA cot 1tan =倒数 1cot tan =⋅A A余切的对边的邻边A A A ∠∠=cot a bA =cot 0cot >A∠A 为锐角3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦值;4、任意锐角的正切值等于它的余角的余切值;任意锐角的余切值等于它的余角的正切值;5、0°、30°、45°、60°、90°特殊角的三角函数值重要三角函数 0° 30°45°60°90° αsin 0 21 22 23 1 αcos1 23 2221 0 αtan 0 33 1 3 不存在αcot不存在3133 0)90cot(tan A A -︒=)90tan(cot A A -︒= B A cot tan =B A tan cot =)90cos(sin A A -︒=)90sin(cos A A -︒= BA cos sin =BA sin cos =A90B 90∠-︒=∠︒=∠+∠得由B A 对边 邻斜边 ABba c A 90B 90∠-︒=∠︒=∠+∠得由B A锐角三角函数题型训练类型一:直角三角形求值1.已知Rt △ABC 中,,12,43tan ,90==︒=∠BC A C 求AC 、AB 和cos B .2.已知:如图,⊙O 的半径OA =16cm,OC ⊥AB 于C 点,⋅=∠43sin AOC 求:AB 及OC 的长.3.已知:⊙O 中,OC ⊥AB 于C 点,AB =16cm,⋅=∠53sin AOC1求⊙O 的半径OA 的长及弦心距OC ; 2求cos ∠AOC 及tan ∠AOC .4.已知A ∠是锐角,178sin =A ,求A cos ,A tan 的值类型二. 利用角度转化求值:1.已知:如图,Rt △ABC 中,∠C =90°.D 是AC 边上一点,DE ⊥AB 于E 点.DE ∶AE =1∶2.求:sin B 、cos B 、tan B .2. 如图4,沿AE 折叠矩形纸片ABCD ,使点D 落在BC 边的点F 处.已知8AB =,10BC =,则tan EFC ∠的值为 A.34 B.43C.35D.453. 如图6,在等腰直角三角形ABC ∆中,90C ∠=︒,6AC =,D 为AC 上一点,若1tan 5DBA ∠= ,则AD 的长为 A .2 B .2 C .1 D .224. 如图6,在Rt △ABC 中,∠C =90°,AC =8,∠A 的平分线AD =3316求∠B 的度数及边BC 、AB 的长.A D E CB FA类型三. 化斜三角形为直角三角形例1 2012•安徽如图,在△ABC 中,∠A=30°,∠B=45°,AC=23,求AB 的长.例2.已知:如图,△ABC 中,AC =12cm,AB =16cm,⋅=31sin A 1求AB 边上的高CD ; 2求△ABC 的面积S ; 3求tan B .例3.已知:如图,在△ABC 中,∠BAC =120°,AB =10,AC =5.求:sin ∠ABC 的值.对应训练1.2012•重庆如图,在Rt △ABC 中,∠BAC=90°,点D 在BC 边上,且△ABD 是等边三角形.若AB=2,求△ABC 的周长.结果保留根号2.已知:如图,△ABC 中,AB =9,BC =6,△ABC 的面积等于9,求sin B .类型四:利用网格构造直角三角形例1 2012•内江如图所示,△ABC 的顶点是正方形网格的格点,则sinA 的值为 A .12 B .55 C .1010 D .255对应练习:1.如图,△ABC 的顶点都在方格纸的格点上,则sin A =_______.特殊角的三角函数值例1.求下列各式的值CBA︒-︒+︒30cos 245sin 60tan 2=. 计算:3-1+2π-10-33tan30°-tan45°=30tan 2345sin 60cos 221⎪⎪⎭⎫ ⎝⎛︒-︒+︒+= ︒-︒+︒60tan 45sin 230cos 2 tan 45sin 301cos 60︒+︒-︒=在ABC ∆中,若0)22(sin 21cos 2=-+-B A ,B A ∠∠,都是锐角,求C ∠的度数.例2.求适合下列条件的锐角α . 121cos =α 233tan =α 3222sin =α433)16cos(6=- α5已知α 为锐角,且3)30tan(0=+α,求αtan 的值6在ABC ∆中,若0)22(sin 21cos 2=-+-B A ,B A ∠∠,都是锐角,求C ∠的度数.例3. 三角函数的增减性 1.已知∠A 为锐角,且sin A <21,那么∠A 的取值范围是 A. 0°< A < 30° B. 30°< A <60° C. 60°< A < 90° D. 30°< A < 90° 2. 已知A 为锐角,且030sin cos <A ,则A. 0°< A < 60°B. 30°< A < 60°C. 60°< A < 90°D. 30°< A < 90° 例4. 三角函数在几何中的应用1.已知:如图,在菱形ABCD 中,DE ⊥AB 于E ,BE =16cm,⋅=1312sin A 求此菱形的周长.2.已知:如图,Rt △ABC 中,∠C =90°,3==BC AC ,作∠DAC =30°,AD 交CB 于D 点,求:1∠BAD ;2sin ∠BAD 、cos ∠BAD 和tan ∠BAD .3. 已知:如图△ABC 中,D 为BC 中点,且∠BAD =90°,31tan =∠B ,求:sin ∠CAD 、cos ∠CAD 、tan ∠CAD .解直角三角形:1.在解直角三角形的过程中,一般要用的主要关系如下如图所示: 在Rt △ABC 中,∠C =90°,AC =b ,BC =a ,AB =c ,①三边之间的等量关系:________________________________.②两锐角之间的关系:__________________________________. ③边与角之间的关系:==B A cos sin ______;==B A sin cos _______;==BA tan 1tan _____;==B A tan tan 1______.④直角三角形中成比例的线段如图所示.在Rt △ABC 中,∠C =90°,CD ⊥AB 于D .CD 2=_________;AC 2=_________; BC 2=_________;AC ·BC =_________.类型一例1.在Rt △ABC 中,∠C =90°.1已知:a =35,235=c ,求∠A 、∠B ,b ;2已知:32=a ,2=b ,求∠A 、∠B ,c ;3已知:32sin =A ,6=c ,求a 、b ;4已知:,9,23tan ==b B 求a 、c ;5已知:∠A =60°,△ABC 的面积,312=S 求a 、b 、c 及∠B .例2.已知:如图,△ABC 中,∠A =30°,∠B =60°,AC =10cm .求AB 及BC 的长.例3.已知:如图,Rt △ABC 中,∠D =90°,∠B =45°,∠ACD =60°.BC =10cm .求AD 的长.例4.已知:如图,△ABC 中,∠A =30°,∠B =135°,AC =10cm .求AB 及BC 的长.类型二:解直角三角形的实际应用 仰角与俯角:例1.2012•福州如图,从热气球C 处测得地面A 、B 两点的俯角分别是30°、45°,如果此时热气球C 处的高度CD 为100米,点A 、D 、B 在同一直线上,则AB 两点的距离是 A . 200米 B . 200米 C . 220米 D . 100米例2.已知:如图,在两面墙之间有一个底端在A 点的梯子,当它靠在一侧墙上时,梯子的顶端在B 点;当它靠在另一侧墙上时,梯子的顶端在D 点.已知∠BAC =60°,∠DAE =45°.点D 到地面的垂直距离m 23=DE ,求点B 到地面的垂直距离BC .例3昌平19.如图,一风力发电装置竖立在小山顶上,小山的高BD =30m . 从水平面上一点C 测得风力发电装置的顶端A 的仰角∠DCA =60°, 测得山顶B 的仰角∠DCB =30°,求风力发电装置的高AB 的长.例4 .如图,小聪用一块有一个锐角为30︒的直角三角板测量树高,已知小聪和树都与地面垂直,且相距33米,小聪身高AB 为1.7米,求这棵树的高度.例5.已知:如图,河旁有一座小山,从山顶A 处测得河对岸点C 的俯角为30°,测得岸边点D 的俯角为45°,又知河宽CD 为50m .现需从山顶A 到河对岸点C 拉一条笔直的缆绳AC ,求山的高度及缆绳AC 的长答案可带根号.例5.2012•泰安如图,为测量某物体AB 的高度,在D 点测得A 点的仰角为30°,朝物体AB 方向前进20米,到达点C,再次测得点A 的仰角为60°,则物体AB 的高度为 A . 10米 B . 10米 C . 20米D . 米例6.2012•益阳超速行驶是引发交通事故的主要原因之一.上周末,小明和三位同学尝试用自己所学的知识检测车速.如图,观测点设在A 处,离益阳大道的距离AC 为30米.这时,一辆小轿车由西向东匀速行驶,测得此车从B 处行驶到C 处所用的时间为8秒,∠BAC=75°.A BCD E1求B 、C 两点的距离;2请判断此车是否超过了益阳大道60千米/小时的限制速度计算时距离精确到1米,参考数据:sin75°≈0.9659,cos75°≈0.2588,tan75°≈3.732,3≈1.732,60千米/小时≈16.7米/秒类型四. 坡度与坡角例.2012•广安如图,某水库堤坝横断面迎水坡AB 的坡比是1:3,堤坝高BC=50m,则应水坡面AB 的长度是 A .100m B .1003m C .150m D .503m类型五. 方位角1.已知:如图,一艘货轮向正北方向航行,在点A 处测得灯塔M 在北偏西30°,货轮以每小时20海里的速度航行,1小时后到达B 处,测得灯塔M 在北偏西45°,问该货轮继续向北航行时,与灯塔M 之间的最短距离是多少 精确到0.1海里,732.13≈综合题:三角函数与四边形:西城二模1.如图,四边形ABCD 中,∠BAD=135°,∠BCD=90°,AB=BC=2, tan∠BDC= 错误!.1 求BD 的长;2 求AD 的长.2011东一2.如图,在平行四边形ABCD 中,过点A 分别作AE ⊥BC 于点E ,AF ⊥CD 于点F . 1求证:∠BAE =∠DAF ; 2若AE =4,AF =245,3sin 5BAE ∠=,求CF 的长.三角函数与圆:1. 如图,直径为10的⊙A 经过点(05)C ,和点(00)O ,,与x 轴的正半轴交于点D ,B 是y 轴右侧圆弧上一点,则cos ∠OBC 的值为 D CB AOyx第8题图CB AA .12 BC .35D .45延庆19. 已知:在⊙O 中,AB 是直径,CB 是⊙O 的切线,连接AC 与⊙O 交于点D, (1) 求证:∠AOD=2∠C(2) 若AD=8,tanC=34,求⊙O 的半径;2013朝阳期末21.如图,DE 是⊙O 的直径,CE 与⊙O 相切,E 为切点.连接CD 交⊙O 于点B,在EC 上取一个点F,使EF=BF.1求证:BF 是⊙O 的切线; 2若54C cos =, DE =9,求BF 的长.作业:昌平1.已知21sin =A ,则锐角A 的度数是 A .75︒B .60︒C .45︒D .30︒西城北2.在Rt △ABC 中,∠ C =90°,若BC =1,AB则tan A 的值为ABC .12D .2 房山3.在△ABC 中,∠C =90°,sin A=53,那么tan A 的值等于 .A .35B . 45C . 34D . 43大兴4. 若sin α=32,则锐角α= . 石景山1.如图,在Rt △ABC 中,∠C =90°,BC =3,AC =2, 则tan B 的值是A .23 B .32CD丰台5.将∠α放置在正方形网格纸中,位置如图所示,则tan α的值是 A .21 B .2 C .25 D .552 大兴5. △ABC 在正方形网格纸中的位置如图所示,则sin α的值是AαA.35B.34C.43D.45通县4.如图,在直角三角形ABC 中,斜边AB 的长为m ,40B ∠=,则直角边BC 的长是 A .sin 40mB .cos 40mC .tan 40mD .tan 40m通州期末1.如图,已知P 是射线OB 上的任意一点,PM ⊥OA 于M , 且OM : OP =4 : 5,则cos α的值等于 A .34 B .43 C .45D .35西城6.如图,AB 为⊙O 的弦,半径OC ⊥AB 于点D ,若OB 长为10, 3cos 5BOD ∠=, 则AB 的长是 A . 20 B. 16 C. 12 D. 87.在Rt △ABC 中,∠C=90°,如果cosA=54,那么tanA 的值是 A .53 B .35 C .43 D .3411.如图,在△ABC 中,∠ACB =∠ADC= 90°,若sin A =35,则cos ∠BCD 的值为 .13.计算:︒-︒+︒60tan 45sin 230cos 2 13.计算︒+︒-︒-︒45tan 30tan 345cos 260sin 2.1322604cos 30+sin 45tan 60-⋅.14.如图,小聪用一块有一个锐角为30︒的直角三角板测量树高,已知小聪和树都与地面垂直,且相距33米,小聪身高AB 为1.7米,求这棵树的高度.15.已知在Rt △ABC 中,∠C =90°,a=64,b=212.解这个直角三角形DCBAA BCD E第1题图O M PBAα20. 如图,在Rt △ABC 中,∠CAB =90°,AD 是∠CAB 的平分线,tan B =21,求CDBD的值.延庆19. 已知:在⊙O 中,AB 是直径,CB是⊙O 的切线,连接AC 与⊙O 交于点D, (3) 求证:∠AOD=2∠C (4) 若AD=8,tanC=34,求⊙O 的半径;延庆期末19.如图,某同学在楼房的A 处测得荷塘的一端 B 处的俯角为30︒,荷塘另一端D 处C 、B 在 同一条直线上,已知32AC =米,16CD =米, 求荷塘宽BD 为多少米 结果保留根号18.6分如图,在△ABC 中,点O 在AB 上,以O 为圆心的圆经过A ,C 两点,交AB 于点D ,已知2∠A +∠B =90︒. 1求证:BC 是⊙O 的切线; 2若OA =6,BC =8,求BD 的长.西城15.如图,在Rt △ABC 中,∠C =90°,点D 在AC 边上.若DB =6,AD =12CD ,sin ∠CBD =23,求AD 的长和tan A 的值.18.如图,一艘海轮位于灯塔P 的南偏东45°方向,距离灯塔100海里的A 处,它计划沿正北方向航行,去往位于灯塔P 的北偏东30°方向上的B 处. 1B 处距离灯塔P 有多远2圆形暗礁区域的圆心位于PB 的延长线上,距离灯塔200海里的O 处.径为50海里,进入圆形暗礁区域就有触礁的危险.请判断若海轮到达B DBOACABCDD 第18题图OCBA危险,并说明理由22.已知,如图,在△ADC 中,90ADC ∠=︒,以DC 为直径作半圆O ,交边AC 于点F ,点B 在CD 的延长线上,连接BF ,交AD 于点E ,2BED C ∠=∠.1求证:BF 是O 的切线;2若BF FC =,3AE =,求O 的半径.15.如图,为了测量楼AB 的高度,小明在点C 处测得楼AB 的顶端A 的仰角为30º,又向前走了20米后到达点D ,点B 、D 、C 在同一条直线上,并在点D 测得楼AB 的顶端A 的仰角为60º,求楼AB 的高.14.2009·眉山中考海船以5海里/小时的速度向正东方向行驶,在A 处看见灯塔B 在海船的北偏东60°方向,2小时后船行驶到C 处,发现此时灯塔B 在海船的北偏西45方向,求此时灯塔B 到C 处的距离;15.2009·常德中考如图,某人在D 处测得山顶C 的仰角为30o ,向前走200米来到山脚A 处,测得山坡AC 的坡度为i=1∶0.5,求山的高度不计测角仪的高度,3 1.73≈,结果保留整数.16.2008·广安中考如图,某幼儿园为了加强安全管理,决定将园内的滑滑板的倾角由45º降为30º,已知原滑滑板AB的长为5米,点D 、B 、C 在同一水平地面上.1改善后滑滑板会加长多少 精确到0.01D O AC B FE2若滑滑板的正前方能有3米长的空地就能保证安全,原滑滑板的前方有6米长的空地,像这样改造是否可行 说明理由;参考数据:2 1.414,3 1.732,6 2.449===18. 在一次数学活动课上,海桂学校初三数学老师带领学生去测万泉河河宽,如图13所示,某学生在河东岸点A 处观测到河对岸水边有一点C ,测得C 在A 北偏西31︒的方向上,沿河岸向北前行20米到达B 处,测得C 在B 北偏西45︒的方向上,请你根据以上数据,帮助该同学计算出这条河的宽度.参考数值:tan31°≈53,sin31°≈21 .图13。
高一下册数学必修四第一章 三角函数.知识点及同步练习

巩固练习
1、 在直角坐标系中,若角α与角β的终边关于x轴对称,则α与β的
关系一定是 ( )
A.α=-β B.α+β=k·360°(k∈Z) C.α-β=k·360°(k∈Z)
D.以上答案都不对
2、圆内一条弦的长等于半径,这条弦所对的圆心角是
()
A.等于1弧度 B.大于1弧度 C.小于1弧度
D.无法
判断
(2) 角α + k·720 °与角α终边相同,但不能表示与角
α终边相同的所有角. 例4.写出终边在y轴上的角的集合(用0°到360°的角表示) . 例5.写出终边在上的角的集合S,并把S中适合不等式- 360°≤β<720°的元素β写出来. 思考题:已知α角是第三象限角,则α/2,α/3,α/4各是第 几象限角?
D.{α∣-270°+k·360°<α<-180°+k·360°,k∈Z}
11、下列命题是真命题的是( )
Α.三角形的内角必是一、二象限内的角 B.第一象限的角必是
锐角
C.不相等的角终边一定不同
D.=
12、已知A={第一象限角},B={锐角},C={小于90°的角},那么A、B、
C关系是( )
A.B=A∩C B.B∪C=C
度记做1rad.在实际运算中,常常将rad单位省略.
3.思考:
(1)一定大小的圆心角所对应的弧长与半径的比值是否是确
定的?与圆的半径大小有关吗?
弧度制的性质:
①半圆所对的圆心角为
②整圆所对的圆心角为
③正角的弧度数是一个正数.
④负角的弧度数是一
个负数.
⑤零角的弧度数是零.
⑥角α的弧度数的绝
对值|α|=
始边 终边 顶点 A O B
高考数学三角函数知识点总结及练习

高考数学三角函数知识点总结及练习三角函数总结及统练本文旨在总结和统练三角函数的基础知识,包括以下内容:一、基础知识1.集合S表示与角α终边相同的角的集合,其中β=2kπ+α,k∈Z。
2.三角函数是x、y、r三个量的比值,共有六种定义。
3.三角函数的符号口诀为“一正二弦,三切四余弦”。
4.三角函数线包括正弦线MP=sinα、余弦线OM=cosα和正切线AT=tanα。
5.同角三角函数的关系包括平方关系、商数关系和倒数关系,可以用“凑一拆一,切割化弦,化异为同”的口诀记忆。
6.诱导公式口诀为“奇变偶不变,符号看象限”,其中包括正弦、余弦、正切和余切的公式。
7.两角和与差的三角函数包括正弦、余弦、正切和余切的公式,以及三角函数的和差化积公式。
8.二倍角公式包括sin2α=2sinαcosα、cos2α=2cos2α-1=1-2sin2α=cosα-sinα、tan2α=2tanα/1-tan2α,以及对应的cos、tan公式。
9.三角函数的图象和性质,包括函数y=sinx、y=cosx和y=tanx的定义和定义域。
总之,三角函数是数学中的重要概念,掌握其基础知识对于研究高等数学和其他相关学科都有很大的帮助。
对于函数 $y=\sin x$,其定义域为 $[-\pi/2,\pi/2]$,值域为$[-1,1]$。
当 $x=2k\pi+\pi/2$ 时,函数取最大值 $1$;当$x=2k\pi-\pi/2$ 时,函数取最小值$-1$。
函数的周期为$2\pi$,是奇函数。
在区间 $[2k\pi-\pi/2,2k\pi+\pi/2]$ 上是增函数,在区间$[2k\pi-\pi,2k\pi]$ 上也是增函数,其中$k\in\mathbb{Z}$。
在区间 $[2k\pi,2k\pi+\pi]$ 上是减函数。
对于函数 $y=Asin(\omega x+\phi)$,当 $A>0$ 且$\omega>0$ 时,函数图像可以通过将横坐标缩短到原来的$\dfrac{1}{\omega}$ 倍,纵坐标伸长为原来的 $A$ 倍,再将图像左移$\dfrac{\phi}{\omega}$ 个单位得到。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
必修四第一章三角函数1.1任意角与弧度制一、任意角和弧度制1、角的概念的推广定义:一条射线OA由原来的位置,绕着它的端点O按一定的方向旋转到另一位置OB,就形成了角α,记作:角α或α∠可以简记成α。
注意:(1)“旋转”形成角,突出“旋转”(2)“顶点”“始边”“终边”“始边”往往合于x轴正半轴(3)“正角”与“负角”——这是由旋转的方向所决定的。
2、角的分类:由于用“旋转”定义角之后,角的围大扩大了。
可以将角分为正角、零角和负角。
正角:按照逆时针方向转定的角。
零角:没有发生任何旋转的角。
负角:按照顺时针方向旋转的角。
3、“象限角”为了研究方便,我们往往在平面直角坐标系中来讨论角,角的顶点合于坐标原点,角的始边合于x轴的正半轴。
角的终边落在第几象限,我们就说这个角是第几象限的角角的终边落在坐标轴上,则此角不属于任何一个象限,称为轴线角。
4、常用的角的集合表示方法<1>、终边相同的角:(1)终边相同的角都可以表示成一个0︒到360︒的角与)k∈个周角的和。
(Zk(2)所有与α终边相同的角连同α在可以构成一个集合{}Z k k S ∈⋅+==,360| αββ即:任何一个与角α终边相同的角,都可以表示成角α与整数个周角的和 注意:1、Z ∈k2、α是任意角3、终边相同的角不一定相等,但相等的角的终边一定相同。
终边相同的角有无数个,它们相差360°的整数倍。
4、一般的,终边相同的角的表达形式不唯一。
<2>、终边在坐标轴上的点:终边在x 轴上的角的集合: {}Z k k ∈⨯=,180| ββ 终边在y 轴上的角的集合:{}Z k k ∈+⨯=,90180| ββ 终边在坐标轴上的角的集合:{}Z k k ∈⨯=,90| ββ <3>、终边共线且反向的角:终边在y =x 轴上的角的集合:{}Z k k ∈+⨯=,45180| ββ 终边在x y -=轴上的角的集合:{}Z k k ∈-⨯=,45180| ββ <4>、终边互相对称的角:若角α与角β的终边关于x 轴对称,则角α与角β的关系:βα-=k 360 若角α与角β的终边关于y 轴对称,则角α与角β的关系:βα-+= 180360k 若角α与角β的终边在一条直线上,则角α与角β的关系:βα+=k 180 角α与角β的终边互相垂直,则角α与角β的关系: 90360±+=βαk 二、弧度与弧度制 <1>、弧度与弧度制:弧度制—另一种度量角的单位制, 它的单位是rad 读作弧度定义:长度等于 的弧所对的圆心角称为1弧度的角。
如图:∠AOB=1rad ,∠AOC=2rad , 周角=2πrad 注意:1、正角的弧度数是正数,负角的弧度数是负数,零角的弧度数是02、角α的弧度数的绝对值 rl=α(l 为弧长,r 为半径) 3、用角度制和弧度制来度量零角,单位不同,但数量相同(都是0) 用角度制和弧度制来度量任一非零角,单位不同,量数也不同。
4、在同一个式子中角度、弧度不可以混用。
<2>、角度制与弧度制的换算弧度定义:对应弧长等于半径所对应的圆心角大小叫一弧度 角度与弧度的互换关系:∵ 360︒= rad 180︒= rad∴ 1︒=rad rad 01745.0180≈π'185730.571801=≈⎪⎭⎫ ⎝⎛=πrad注意:正角的弧度数为正数,负角的弧度数为负数,零角的弧度数为零. 三、弧长公式和扇形面积公式r l α= ; 22121r lR S α==1.2 任意角的三角函数orC 2rad1rad r l=2r oB一、三角函数定义如图,设锐角α的顶点与原点O 重合,始边与x 轴的正半轴重合,那么它的终边在第一象限.在α的终边上任取一点),(b a P ,它与原点的距离2222(y x yx r r +=+=)。
(1)比值r y 叫做α的正弦,记作αsin ,即r y =αsin ; (2)比值r x 叫做α的余弦,记作αcos ,即rx=αcos ;(3)比值y 叫做α的正切,记作αtan ,即x y=αtan ;(4)比值y x 叫做α的余切,记作αcot ,即yx =αcot ; (5)比值x r 叫做α的正割,记作αsec ,即xr=αsec ;(6)比值y r 叫做α的余割,记作αcsc ,即yr =αcsc . 二、三角函数的定义域、值域①α的始边与x 轴的非负半轴重合,α的终边没有表明α一定是正角或负角,以及α的大小,只表明与α的终边相同的角所在的位置;②根据相似三角形的知识,对于确定的角α,六个比值不以点(,)P x y 在α的终边上的位置的改变而改变大小;③当()2k k Z παπ=+∈时,α的终边在y 轴上,终边上任意一点的横坐标x 都等于0,所以tan y x α=与sec r x α=无意义;同理,当()k k Z απ=∈时,x coy y α=与csc r y α=无意义; ④除以上两种情况外,对于确定的值α,比值y r 、x r 、y x 、x y 、rx 、r y 分别是一个确定的实数,所以正弦、余弦、正切、余切、正割、余割是以角为自变量,一比值为函数值的函数,以上六种函数统称为三角函数。
三角函数的定义域、值域三.三角函数的符号由三角函数的定义,以及各象限点的坐标的符号,我们可以得知:①正弦值yr 对于第一、二象限为正(0,0y r >>),对于第三、四象限为负(0,0y r <>); ②余弦值xr 对于第一、四象限为正(0,0x r >>),对于第二、三象限为负(0,0x r <>); ③正切值yx 对于第一、三象限为正(,x y 同号),对于第二、四象限为负(,x y 异号).说明:若终边落在轴线上,则可用定义求出三角函数值。
ααcsc sin 为正 全正 ααcot tan 为正 ααsec cos 为正四、诱导公式1、由三角函数的定义,就可知道:终边相同的角三角函数值相同。
正切、余切余弦、正割正弦、余割即有:sin(2)sin k απα+=,cos(2)cos k απα+=,其中k Z ∈. tan(2)tan k απα+=,这组公式的作用是可把任意角的三角函数值问题转化为0~2π间角的三角函数值问题.2、三角函数诱导公式(2kπα+)的本质是:奇变偶不变(对k 而言,指k 取奇数或偶数),符号看象限(看原函数,同时可把α看成是锐角).诱导公式的应用是求任意角的三角函数值,其一般步骤:(1)负角变正角,再写成2k π+α,02απ≤<;(2)转化为锐角三角函数 五、三角函数线的定义:设任意角α的顶点在原点O ,始边与x 轴非负半轴重合,终边与单位圆相交与点P (,)x y ,过P 作x(1,0)A α的终边或其反向延长线交与点T .由四个图看出:当角α的终边不在坐标轴上时,有向线段,OM x MP y ==,于是有(Ⅳ)(Ⅱ)(Ⅰ)(Ⅲ)sin 1y y y MP r α====, cos 1x x x OM r α====, tan y MP AT AT x OM OA α====.我们就分别称有向线段,,MP OM AT 为正弦线、余弦线、正切线。
①三条有向线段的位置:正弦线为α的终边与单位圆的交点到x 轴的垂直线段;余弦线在x 轴上;正切线在过单位圆与x 轴正方向的交点的切线上,三条有向线段中两条在单位圆,一条在单位圆外。
②三条有向线段的方向:正弦线由垂足指向α的终边与单位圆的交点;余弦线由原点指向垂足;正切线由切点指向与α的终边的交点。
③三条有向线段的正负:三条有向线段凡与x 轴或y 轴同向的为正值,与x 轴或y 轴反向的为负值。
④三条有向线段的书写:有向线段的起点字母在前,终点字母在后面。
注:(1)三角函数线的特征是:正弦线MP “站在x 轴上(起点在x 轴上)”、余弦线OM “躺在x 轴上(起点是原点)”、正切线AT “站在点(1,0)A 处(起点是A )”.(2)三角函数线的重要应用是比较三角函数值的大小和解三角不等式。
六、同角三角函数的基本关系式:(1)平方关系:222222sin cos 1,1tan sec ,1cot csc αααααα+=+=+= (2)倒数关系:sin αcsc α=1,cos αsec α=1,tan αcot α=1, (3)商数关系:sin cos tan ,cot cos sin αααααα== 同角三角函数的基本关系式的主要应用是,已知一个角的三角函数值,求此角的其它三角函数值。
在运用平方关系解题时,要根据已知角的围和三角函数的取值,尽可能地压缩角的围,以便进行定号;在具体求三角函数值时,一般不需用同角三角函数的基本关系式,而是先根据角的围确定三角函数值的符号,再利用解直角三角形求出此三角函数值的绝对值。
1.3三角函数的诱导公式知识点1:诱导公式(二)(2)结构特征:①函数名不变,符号看象限(把α看作锐角时) ②把求(180°+α)的三角函数值转化为求α的三角函数值。
知识点2:诱导公式(三)结构特征:①函数名不变,符号看象限(把α看作锐角) ②把求(-α)的三角函数值转化为求α的三角函数值 知识点3:诱导公式(四) Sin(π-α)=Sin α Cos(π-α)=-cos α Ten(π-α)=-tan α 知识点4:诱导公式(五) sin()cos ;cos()sin 22ππαααα-=-=知识点5:诱导公式(六)sin()cos ;cos()sin 22ππαααα+=+=1.4三角函数的图像与性质 一、正弦函数余弦函数的图象 (1)函数y=sinx 的图象第一步:在直角坐标系的x 轴上任取一点1O ,以1O 为圆心作单位圆,从这个圆与x 轴的交点A 起把圆分成n(这里n=12)等份.把x 轴上从0到2π这一段分成n(这里n=12)等份.(预备:取自变量x 值—弧度制下角与实数的对应). 第二步:在单位圆中画出对应于角6,0π,3π,2π,…,2π的正弦线正弦线(等价于“列表” ).把角x 的正弦线向右平行移动,使得正弦线的起点与x 轴上相应的点x 重合,则正弦线的终点就是正弦函数图象上的点(等价于“描点” ).第三步:连线.用光滑曲线把这些正弦线的终点连结起来,就得到正弦函数y=sinx ,x ∈[0,2π]的图象.根据终边相同的同名三角函数值相等,把上述图象沿着x 轴向右和向左连续地平行移动,每次移动的距离为2π,就得到y=sinx ,x ∈R 的图象.把角x ()x R ∈的正弦线平行移动,使得正弦线的起点与x 轴上相应的点x 重合,则正弦线的终点的轨迹就是正弦函数y=sinx 的图象.(2)余弦函数y=cosx 的图象用几何法作余弦函数的图象,可以用“反射法”将角x 的余弦线“竖立”[把坐标轴向下平移,过1O 作与x 轴的正半轴成4π角的直线,又过余弦线1O A 的终点A 作x 轴的垂线,它与前面所作的直线交于A ′,那么1O A 与AA ′长度相等且方向同时为正,我们就把余弦线1O A “竖立”起来成为AA ′,用同样的方法,将其它的余弦线也都“竖立”起来.再将它们平移,使起点与x 轴上相应的点x 重合,则终点就是余弦函数图象上的点.] 也可以用“旋转法”把角 的余弦线“竖立”(把角x 的余弦线O 1M 按逆时针方向旋转2π到O 1M 1位置,则O 1M 1与O 1M 长度相等,方向相同.)根据诱导公式cos sin()2x x π=+,还可以把正弦函数x=sinx 的图象向左平移2π单位即得余弦函数y=cosx 的图象.(1) 正切函数y=tanx 的图像:二、五点法作图用五点法作正弦函数和余弦函数的简图(描点法): 正弦函数y=sinx ,x ∈[0,2π]的图象中,五个关键点是:(0,0) (2π,1) (π,0) (23π,-1) (2π,0) 余弦函数y=cosx x ∈[0,2π]的五个点关键是(0,1) (2π,0) (π,-1) (23π,0) (2π,1)只要这五个点描出后,图象的形状就基本确定了.因此在精确度不太高时,常采用五点法作正弦函数和余弦函数的简图,要求熟练掌握. 三、奇偶性请同学们观察正、余弦函数的图形,说出函数图象有怎样的对称性?其特点是什么? (1)余弦函数当自变量取一对相反数时,函数y 取同一值。
