华师一附中历年招生考试题型及分数分布
武汉华师一附中高中招生数学试题

武汉华师一附中高中招生数学试题华中师大一附中高中招生理科素质测试数学部分考试时间75分钟,卷面满分100分一,选择题:(4`X10=40`)1,如果-3<x<4,化简|x-4|+|x+3|得< p="">A.7B.-7C.1-2XD.2X-12.如果两圆心都在X轴上,⊙O1的圆心坐标为(7,0),半径为1;⊙O2的圆心坐标为(X,0),半径为2,当2<x<4时,两圆的位置关系是:< p="">A.相交B.相切C.外离D.内含3.在同一坐标系内,如果正比例函数Y=MX的图象与反比例函数Y=P/X的图象没有交点,那么M 与P的关系一定是A.M<0,P>0B.M>0,P>0C.MP>0D.MP<04.已知X=1+sin30°/cos30°,且tgα=x,0<α<90,则α的值是A.30°B.45°C.60°D.75°5.二次函数y=ax2+bx+c的图象如图所示,则a-b-c的值A.大于零B.小于零C.等于零D.正负不能确定6.若等腰梯形的对角线互相垂直,且它的中位线等于m,则此梯形的高等于A.m/2B.mC./2D.2m7.已知|xy+4|+=0,则x+y的值是A.2B.3C.2,-2D.3,-38.如图,在直角三角型ABC中,∠C=60°,以AB为直径的半圆交斜边于D,则△ACD与△ABD的面积之比为A.1:2B.1:3C.2:3D.3:49.某项工程,甲,乙两队合作需要X天完成,甲队单独做需要Y天完成,那么乙队单独做需要的时间是____A.y-xB.xy/x-yC.1/y-xD.xy/y-x10.设实数a,x满足x/x2-ax+1 =1,则x2/x4-a2x2+1的值是A.1B.1/2a2+1C.1/2a-1D.1/2a+1二.填空题(4`X4=16)11.将(a+b)(a-b)+4(b-1)因式分解的结果是_______12.关于的方程2x2+x+m+1/4=0有两个不相等的负数根,则m的取值范围是_____13.已知半径为R 的扇型面积为πR2/4,将此扇型围成一个原锥的侧面,则此圆锥的高为______14.设a<0,-1<b<0,则四个数a,ab,ab2,ab3中最大的一个数是______.< p="">三.解答题15.(本题满分6分)已知=1/2-,求3x+5-2/3-1的值16.(本小题满粉8分)如图,AB为O的直径,O为圆心,COAB,E是圆上的一点,F是BA延长线上的一点,FC交O于P,EC 交AB于G,EP交AB于H 求证:PH·EH=FH·GH17.(本小题满粉8分)已知x1,x2是x2+px+q2=0的两个根,且满足x1-2x2=0,又4p2-9q=27,求p,q的值.18.(本小题满粉10分)如图,△A BC中,AB=5,BC=6,BD=BC/3,AD⊥BC于D,E为AB延长线上的一点,且EC交AD的延长线于F,(1)设BE为X,DF为Y,试用X的式子表示Y.(2)当∠ACE=90时,求此时X的值.19.(本小题满粉12分)已知二次函数的图象与Y轴交于点C(0,2),且过点N(1,2-3P),对称轴是直线X=2,(1)求此二次函数的解析式,并求顶点D的坐标.(2)若此函数的图象与X轴交于A,B两点且两点间的距离为2 ,求P 的值;并求此时△DAB外接圆的面积.</b<0,则四个数a,ab,ab2,ab3中最大的一个数是______.<></x<4时,两圆的位置关系是:<> </x<4,化简|x-4|+|x+3|得<>。
2022年湖北省武汉市华中师范大学第一附属中学自主招生数学试题(专县生)

2022年华师一附中专县生数学试卷理科综合测试题时限:100分钟满分:150分数学部分(100分)一、选择题(共6小题,每小题5分,共30分)1.新冠疫情对某地区的经济发展造成了巨大影响,为了改善该地区经济发展的现状,政府部门对该地区的经济进行了为期一年的宏观调控,使得该地区的经济收入增加了一倍,实现翻番.为更好地了解调控前后该地区的经济收入变化情况,统计了该地区宏观调控前后的经济收入构成比例,得到如下饼图:则下面结论中不正确的是()。
A.宏观调控后,服务业收入减少B.宏观调控后,农业收入增加了一倍以上C.宏观调控后,工业收入增加了一倍D.宏观调控后,工业收入与其它收入的总和超过了经济收入的一半2.已知a=√2023−√2022,b=√2022−√2021,c=√2021−√2020,则a,b,c的大小关系为()。
A.a>b>cB.c>b>aC.b>a>cD.b>c>a(k⟩0)的图象的交点的横坐标为2,则关于x的不等3.已知二次函数y=ax²+1(a>0)的图象与反比例函数y=kx+ax2+1<0的解集是()。
式kxA.x < -2B.-2< x< 0C.0<x<2D.x>24. 如图,四边形ABCD 中,∠A=∠C=90°,,32,2,30,90===∠=∠=∠CD AD ABC C A oo则BD=()。
A.338 B.3394 C.74 D.845、如图1,点G 是BC 上靠近点C 的三等分点,点H 在AF 上,动点P 以每秒1cm 的速度沿图1的边线运动,运动路径为:G-C-D-E-F-H,相应的△ABP 的面积y(cm²)关于运动时间t(s)的函数图象如图2,若AB=4cm ,则下列四个结论中正确的个数有()。
①图1中的BC 长是9cm;②图2中的M 点表示第6秒时y 的值为18cm²;③图1中的CD 长是3cm;④图2中的N 点表示第19秒时y 的值为14cm².A.1个B.2个C.3个D.4个6、如图,△ABC中∠ACB=90°,点D 在CA 上,CD=1,AD=4,∠BDC=3∠BAC,则BC=()。
华师一附中初中部招生试题

华师一附中初中部招生试题一、填空题(4分×10=40分)1. 计算:211×555+445×789+555×789+211×445=______.2. 纽约时间是香港时间减13小时,你与一位在纽约的朋友约定,纽约时间4月1日晚上8时与他通话,那么在香港你应____月____日____时给他打电话.3. 3名工人5小时加工零件90件,要在10小时完成540个零件的加工,需要工人____人.4. 大于100的整数中,被13除后商与余数相同的数有____个.5. 移动循环小数5.085836的前一个循环点后,使新的循环小数尽可能大.这个新的循环小数是______.6. 在1998的约数(或因数)中有两位数,其中最大的数是______.7. 狗追狐狸,狗跳一次前进1.8米,狐狸跳一次前进1.1米.狗每跳两次时狐狸恰好跳3次,如果开始时狗离狐狸有30米,那么狗跑_____米才能追上狐狸.8. 在下面(1)、(2)两排数字之间的“□”内,选择四则运算中的符号填入,使(1)、(2)两式的运算结果之差尽可能大.那么差最大是_____. (1)1□2□3□4□5□6□7= (2)7□6□5□4□3□2□1=9. 下图中共有____个长方形(包括正方形).10. 有一个号码是六位数,前四位是2857,后两位记不清,即2857□□.但是我记得,它能被11和13整除,那么这个号码是_____.二、解答题(15分×4=60分)11. 有一池泉水,泉底不断涌出泉水,而且每分钟涌出的泉水一样多.如果用8部抽水机10小时能把全池泉水抽干,如果用12部抽水机6小时能把全池泉水抽干,那么用14部抽水机多少小时能把全池泉水抽干?12. 如图,ABCD是长方形,其中AB=8,AE=6,ED=3.并且F是线段BE 的中点,G是线段FC的中点.求三角形DFG(阴影部分)的面积. 13. 从7开始,把7的倍数依次写下去,一直994,成为一个很大的数: 71421……987994.这个数是几位数?如果从这个数的末位数字开始,往前截去160个数字,剩下部分的最末一位数字是多少?14. 两人做一种游戏:轮流报数,报出的数只能是1,2,3,4,5,6,7,8.把两人报出的数连加起来,谁报数后,加起来的数是123,谁就获胜,让你先报,就一定会赢,那么你就第一个数报几?。
武汉华师一附中高中招生试题(语文、数学)

武汉华师一附中高中招生试题(语文、数学)华中师大一附中高中招生文科素质测试卷语文部分考试时间80分钟,卷面满分75分一、选择题(11分)1、选出下列句子中加点的词语的书写及注音、解释全都正确的一项(2分)答案[ ]A、校团委、校学生会组织同学们向河北省张家口市张北、尚义两县地震灾区捐款振灾[振:振济,用钱或衣服、粮食等救灾(灾民)振,音zhèn。
]B、华中理工大学博导王能超教授于1998年3月15日下午莅临我校作学术报告,题为“千古绝技割圆术”。
[莅临:书面语,来到;来临(多用于贵宾)。
莅,音lì]C、在当代,信息在不断“激增”,要学要懂的东西越来越使人眼花缭乱,目不暇接。
[目不暇接:东西太多,眼睛看不过来。
暇,音jiá]D、1997年11月24日,国务院副总理李岚清第二次到华师一附中视察。
在校电视演播室,李副总理以赞赏的眼光观看同学们娴熟地操作摄像机等设备。
[娴熟:熟练,文雅。
娴,音xián]2、选出下列没有语病、句意明确的一项(3分)A、雅琪将士用不屈的斗志和协作的团队精神化作战斗力,使得劲旅申花怏怏而归。
B、梨园绿化广场是武汉市创建山水园林城市的重要项目之一。
该广场位于武昌徐东路、东湖路、环湖路三条交通干道的交汇处。
C、1970年3月18日凌晨,“诺曼底”号邮船在英伦海峡沉没。
船上有28名船员,1名女服务员,31名乘客,12名妇女。
D、外国朋友来武汉作客,往往会盛情约请他们品尝一下汉味小吃。
3、选出文言句子翻译正确的一项(3分)A、“吾与汝毕力平险,指通豫南,达于汉阴,可乎?”译文:“我和你们尽全力铲除险峻的大山,一直通向豫州的南部,到达汉水北岸,可以吗?”B、斯是陋室,惟吾德罄。
译文:这是简陋的屋子,只是我(住屋的人)的品德好(就不感到简陋了)。
C、小大之狱,虽不能察,必以情。
译文:大大小小的监狱,虽然不能一一察看,但一定按照实情处理。
D、孰知赋敛之毒有甚是蛇者乎?译文:谁知道搜刮百姓的毒害有的如同蛇一样厉害呀。
湖北省武汉华中师范大学第一附属中学自主招生考试数学试题-word版含解析知识讲解

华师一附中2015年高中招生考试数学测试题详解考试时间:80分钟 卷面满分:150分一.选择题(6分×6=36分)1,如果实数,,a b c 在数轴上的位置如图所示,2222a a b c ac a +-+可以化简为....A a b c B a b cC a b cD a b c--+-----+-【解析】由图知0b c a <<<,()222,2a a a a b a b c ac a c a a c ==-+=-+-+=-=-2222a a b c ac a +-+()()a a b a c a b c =-+++-=+-,选D .2.反比例函数4y x =-的图象与直线y kx b =-+交于()()1,,,1A m B n -两点,则△OAB 的面积为111513..4..222A B C D 【解析】(补形)()4.1,:-4,4;xy A m m m =--=-∴=Q 代入(),1:4B n n =-代入.故有A (-1,4),B (-4,1).作AE ⊥y 轴于E ,BD ⊥x 轴于D .可知: △AOE ≌△BOD .且11422AOE BOD S S ∆∆==⨯⨯=. 延长EA ,DB 交于C ,则四边形CDOE 是边长为4的正方形,且2416,CDOE S ==W △ABC 是腰长为3的等腰直角三角形,且219322ABC S ∆=⨯=.于是△OAB 的面积为915162222ABC S ∆=-⨯-= 3.设12,x x 是一元二次方程230x x +-=的两根,则3212415x x -+等于A.-4B.8C.6D.0【解析】(降次)由韦达定理:221212112211.3,3x x x x x x x x +=-⇒=--+=+=Q()()()2322212111111141534115341215x x x x x x x x x ∴-+=----+=--+++()2115344x x =-+--=-,故选A .4.已知,,ABC a b c ∆分别是的三边长,且满足44422222222a b c a c b c ++-+,则△ABC 是A.等腰三角形B.等腰直角三角形C.直角三角形D.等腰三角形或直角三角形注:原题条件不完整(是代数式而不是条件等式),故无法解出.为试卷完整起见,将原题条件调整为:已知,,ABC a b c ∆分别是的三边长,且满足444222222220a b c a c b c ++--=,则△ABC 是⋯.【解析】由条件得: 4442222442440,a b c a c b c ++--=()()222222222222220,22,a cbcc a b a b a b c -+-=∴===+=即或且.故△ABC 是等腰直角三角形,选B .5.在一节3数学实践活动课上,老师拿出三个边长都为40mm 的正方形硬纸板,他向同学们提出了这样一个问题:若将三个正方形纸板不重叠地放在桌面上,用一个圆形硬纸板将其盖住,这样的圆形硬纸板的 最小直径为(单位:mm )210.2517.100A B C D【解析】当3个正方形按如图排列时,其外接圆直径最小.显然,这个圆是等腰梯形ABCD 的外接圆O ,这里AB ∥CD 且CD =40,AB =80.设此等腰梯形的对称轴交AB 于M ,交CD 于N ,则MN =80. ∵AB >CD ,∴OM <ON .设OM =40-x ,ON =40+x ,圆半径为r . △AOM 中,()()22240401r x =+- △DON 中,()()22220402r x =++(1)-(2):1512001600,2x x -=∴=,代入(2)29025106256251725400,17.4442r r ⨯=+==∴= 故所求最小圆的直径为2257r =故选C .6.如图,△ABC 内接于圆O ,BC =36,∠A =60°,点D 为»BC 上一动点,BE ⊥直线OD 于E ,当点D 由B 点沿»BC运动到点C 时,点E 经过的路线长为 3.83.273.54A B C D ππ【解析】(轨迹法)如解图,连结OB ,分别在»BC 上取123,,,,,B D D D C 其中2OD BC ⊥,则相应的动点 依次为123,,,,.B E E E N12390BE O BE O BE O BNO ∠=∠=∠=∠=︒Q .故点E 的轨迹是OB为直径的优弧¼2BE N . 已知BC =36,∴2218.BE BOE =∆是含30°角的直角三角形,∴123OB =.设M 为OB 的中点(优弧圆心),连MN .则圆M 的半径MB =63注意到∠BOC =120°,∴∠BON =60°,∠BMN =120°, 优弧¼2BE N 之长为圆M 周长的¼222,26383.33BE Nl ππ∴=⨯⋅=,故选B . 二.填空题(7×7=49分)7.方程()31641x x x +=+的所有根的和为【解析1】3244160x x x --+=.根据广义韦达定理,此方程3根之和为4. 即123,1,4b x x x a b a ⎛⎫++=-==- ⎪⎝⎭这里 【解析2】由原方程得:()()()124220,4,2,x x x x x -+-=∴==-31232.4x x x x =++=.8.在5瓶饮料中,有2瓶已过了保质期,随机地从这5瓶饮料中取2瓶,取到至少有1瓶过保质期饮料的概率为【解析】(正繁则反)由于从这5瓶饮料中任取2瓶,没有过期饮料的概率为3,5故取2瓶,取到至少有1瓶过保质期饮料的概率为32155-= 9.关于x 的方程211aa x =--无解,则a 的值是【解析】由原方程得:()()()2111a a x =--关于x 的方程(1)只有唯一解1x =,代入(1)得0a =,此时原方程无解; 又在方程(1)中令1,a =得0a =.矛盾.此时方程(1)无解,从而原方程无解. 故若原方程无解,则必01a =或.10.一辆快车从甲地开往乙地,一辆慢车从乙地开往甲地,两车同时出发,分别以各自的速度在甲乙两地间匀速行驶,1小时后,快车司机发现有重要文件遗忘在出发地,便立即返回拿上文件(取文件时间不计)后再从甲地开往乙地,结果快车先到达乙地.慢车继续行驶到甲地.设慢车行驶速度为x (h ),两车之间的距离为y (km ),y 与x 的函数图象如图所示,则a =【解析】慢车12.5小时走完全程,()12.5100080x x km =⇒=设快车速度为t (h ) ∵1小时后两车相距800km ,即 1小时两车共行200km ,∴t =120km (h )∵a 小时后两车相遇,此时慢车走80akm ,快车走120(a -1)km ,故有:()()80120110002001120, 5.6a a a a h +-=⇒=∴=11.已知24,13,234a x y x ax ≥≤≤=-+当时函数的最小值为-23,则a =【解析】原式配方得:2392448y x a a ⎛⎫⎛⎫=-+- ⎪ ⎪⎝⎭⎝⎭,抛物线开口向上且对称轴为34x a =.当34,34a a ≥≥时,故当13x ≤≤时,y 随x 增大而减小.故当x =3时有:22333423945, 5.a a a ⨯-⋅+=-⇒=∴=12.如图,在单位为1的正方形的网格纸上,123345567A A A ,A A A ,A A A ,,∆∆∆L 都是斜边在x 轴上,且斜边长分别为2,4,6,⋯的等腰直角三角形.若123A A A ∆的顶点分别为()()()123A 2,0,A 1,-1,A 0,0,则依图中的规律,2015A 的坐标为【解析】注意到点13521,,,,n A A A A +L 全在x 轴上,设其横坐标依次为1352015,,,,x x x x L ..继续分析.点41A n +都在原点右边,其横坐标取正值,点41A n -都在原点左边(其中3A 为原点),其横坐标取0或负值(其中仅3A 横坐标为0).∵2015=4×504-1,故2015A 必在原点左边,其横坐标必为负值.易求()()34117421114310,021,0224,x x x x x x ⨯-⨯-⨯-====+-⨯==+-⨯=-L()201545041025031006x x ⨯-==+-⨯=-,故所求点A 的坐标为:()20151006,0A -.13.有一张矩形风景画,长为90cm ,宽为60cm ,现对该风景画进行装裱,得到一个新的矩形,要求其长,宽之比与原风景画的长,宽之比相同,且面积比原风景画的面积大44%.若装裱后的上,下边衬的宽都为a cm ,左,右边衬都为b cm ,那么ab =【解析】依题意有:9029032360260222a ab b +==⇒=+(据等比定理)故()231a b=又:()()1449026029060100a b ++=⨯⨯()120180454442a b ab ⇒++=⨯(1)代入(2):2260318065444603960.b b b b b ⋅++=⨯⇒+-=解得:()666b b ==-或舍,从而9,54a ab =∴=.三.解答题14.(14分)已知m ,n 是方程2310x x ++=的两根, (1)求162102553m m m m m-⎛⎫+-⋅- ⎪--⎝⎭的值; (233m n n m的值 【解析】(1)∵2310,m m ++=故()()()()551625162102255353m m m m m m m m m m m +-+--⎛⎫+-⋅-=⋅- ⎪-----⎝⎭ ()()2229223123203m m m m m m m m-++=--=-+-=-⋅=-. (2)m ,n 是方程2310x x ++=的两根,31m n mn +=-⎧∴⎨=⎩设33m n x n m =则33334422222m n m n m n x m n n m n m mn +=++⋅=+()()()2222222221,2229249mn x m nm n m n mn ⎡⎤=∴=+-+=+-=-=⎣⎦Q7,x ∴=即33m n n m15.(15分)如图,△ABC 中,AC =BC ,I 为△ABC 的内心,O 为BC 上一点,过B ,I 两点的圆O 交BC 于D 点,1tan ,6,3CBI AB ∠== (1)求线段BD 的长; (2)求线段BC 的长【解析】(1)如解图,I 为△ABC 内心,故BI 平分 ∠ABC .设∠ABI =∠CBI =α.连CI ,并延长交AB 于E ,∵CA =CB ,∴CE ⊥AB ,且 AE =BE =3.于是221IE=BE tan 31,31103BI α⋅=⨯==+=连DI ,∵BD 为圆O 的直径,∴∠BID =90°.于是101010tan 10393DI BI BD α=⋅==+=. (2)连OI ,∵OI =OB =53,∴∠DOI =2α,故OI ∥AB , △COI ∽△CBE ,5533,539353OI CO CO COBE CB CO CO =⇒=⇒=++2525515,121234CO BC ∴==+=.16.(18分)如图,四边形ABCD中,AD ∥BC ,∠BCD =90°,AD =6,BC =3,DE ⊥AB 于E ,AC 交DE 于F ,(1)求AE ·AB 的值; (2)若CD =4,求AFFC的值; (3)若CD =6,过A 点作 AM ∥CD ,交CE 的延长线于M , 求MEEC的值. 【解析】(1)如解图1,作AG ∥BC ,交 CB 延长线于G ,则四边形AGCD 为矩形. ∴GC =AD =6,但BC =3,∴GB =3.已知DE ⊥AB 于E ,∴△AGB ∽△DEA . 于是18.AB BGAB AE AD BG AD AE=⇒⋅=⋅= (2)延长AB ,DC 交于H .∵AD ∥BC ,且AD =2BC ,∴BC 为△AHD 的中位线,故 CH =DC =4.由勾股定理知AH =10,AB =BH =5.沿DE ,CB 交于T ,有△AED ∽△BTE .Rt △ADH 中,DE ⊥AH ,23618,105AD AE AH ∴=== 187555BE AB AE =-=-=.于是 775,186185BT BE BT AD AE =⇒==7716,3333BT CT ∴==+=由△AFD ∽△CFT ,知69168AF AD FC CT ===. (3)如解图3有35,AB BH ==6565555AE EH ==∴== ∵△AEM ∽△HEC ,651.2445ME AE EC EH ∴=== 17.(18分)二次函数242y x mx n =-+的图象与x 轴交于()()()1212,0,,A x B x o x x <两点,与y 轴交于c 点.(1)若AB =2,且抛物线的顶点在直线y =-x -2上,试确定m ,n 的值;(2)在(1)中,若点P 为直线BC 下方抛物线上一点,当△PBC 的面积最大时,求P 点坐标;(3)是否存在整数m ,n ,使得1212,12,x x <<<<同时成立?请证明你的结论. 【解析】(1)()2212121AB=2244x x x x x x ⇒-=⇒+-=.由韦达定理:121224m x x n x x ⎧+=⎪⎪⎨⎪=⎪⎩,故有:()2414m n -=抛物线的顶点为24,44m n m ⎛⎫- ⎪⎝⎭,代入y =-x -2:()2242224444n m m m mn -=--⇒=--代入(1): 20,8,4mm -=∴=从而12n =. (2)在(1)的条件下,有:241612y x x =-+此抛物线的顶点为(2,-4),交x 轴于A (1,0),B (3,0),交y 轴于C (0,12)易求直线BC 的解析式为412y x =-+.为使△PBC 面积最大,只需点P 与直线BC 距离最远.设过P 且平行于BC 的直线解析式为4y x b =-+,代入抛物线解析式;22416124412120.x x x b x x b -+=-+⇒-+-=()14416120912,3b b b ∆=--=⇒=-∴=令.此时有33,43 3.22x y ==-⨯+=-即所求点的坐标为3,32P ⎛⎫-⎪⎝⎭. (3)(反证法)假如存在这样的整数m ,n ,使得方程2420x mx n -+=之2根满足121,2x x <<.那么:()122<<4,4<8,,5,6,7;12mx x m m m +=∴<∴=为整数()121<<4,416,,5,6,7,,15;24nx x n n n =∴<<∴=L 为整数()224160,34m m n n ∆=->∴<方程之2根为:x ==由()221481642444m m m m m n n m >⇒->-+>-⇒>-由()2228464164165m m n m m n m <⇒<-⇒-<-+⇒>-当m =5时,2m -4=6>4m -16=4,根据(3),(4),取2m -4<24m n <,即1664n <<,无整数解,舍去;当m =6时, 2m -4=8=4m -16, 根据(3),(4),取2m -4<24m n <,即89,n <<无整数解,舍去;当m =7时, 2m -4=10<4m -16=12. 根据(5),(4),取2416,4m m n -<<即112124n <<无整数解,舍去.据上分析,不存在整数m ,n ,使得1212,12,x x <<<<同时成立.。
华师一附中2020年自主招生(分配生)数学试题(word版附答案)

华中师大一附中2020年自主招生(分配生)数学试题考试时间:90分钟卷面满分:100分说明:所有答案一律书写在答题卡上,写在试卷上作答无效,其中,将所有选择题答案用2B铅笔也相应位置涂黑。
一、选择题(本大题共6小题,每小题4分,共24分,在每小题给出的四个选项中,有且只有一个是正确的)1.在数轴上和有理数a,b,c对应的点的位置如图所示,有下列四个结论:①a2﹣a﹣2<0;②|a﹣b|+|b﹣c|=|a﹣c|;③(a+b)(b+c)(c+a)>0;④|a|<1﹣bc.其中正确的结论有()个A.4 B.3 C.2 D.12.已知a,b,c分别是Rt△ABC的三条边长,c为斜边长,∠C=90°,我们把关于x的形如y=x+的一次函数称为“勾股一次函数”.若点P(﹣1,)在“勾股一次函数”的图象上,且Rt△ABC的面积是4,则c的值是()A.2B.24 C.2D.123.5G时代悄然来临,为了研究中国手机市场现状,中国信通院统计了2019年手机市场每月出货量以及与2018年当月同比增长的情况,得到如图统计图:根据该统计图,下列说法错误的是()A.2019年全年手机市场出货量中,5月份出货量最多B.2019年下半年手机市场各月份出货量相对于上半年各月份波动小C.2019年全年手机市场总出货量低于2018年全年总出货量D.2018年12月的手机出货量低于当年8月手机出货量4.已知函数y=x2+x﹣1在m≤x≤1上的最大值是1,最小值是﹣,则m的取值范围是()A.m≥﹣2 B.0≤m≤C.﹣2≤m≤﹣D.m≤﹣5.如图,△AOB中,∠AOB=90°,AO=4,BO=8,△AOB绕点O逆时针旋转到△A'OB'处,此时线段A'B'与BO的交点E为BO的中点,则线段B'E的长度为()A.3B.C.D.第5题图第6题图6.如图1,在矩形ABCD中,动点M从点A出发,沿A→B→C方向运动,当点M到达点C时停止运动,过点M作MN⊥AM交CD于点N,设点M的运动路程为x,CN=y,图2表示的是y与x的函数关系的大致图象,则矩形ABCD的面积是()A.24 B.20 C.12 D.10二、填空题(本大题共6小题,每小题4分,共24分)7.2020年某校将迎来70周年校庆,学校安排3位男老师和2位女老师一起筹办大型文艺晚会,并随机地从中抽取2位老师主持晚会,则最后确定的主持人是一男一女的概率为________.8.在△ABC中,AB=AC,若cosA=,则=________.9.如图1是个轴对称图形,且每个角都是直角,长度如图所示,小王按照如图2所示的方法玩拼图游戏,两两相扣,相互不留空隙,那么小王用2020个这样的图形(图1)拼出来的图形的总长度是________.(结果用m,n表示)10.如图,以正六边形ABCDEF的对角线BD为边,向右作等边三角形BDG,若四边形BCDG(图中阴影部分)的面积为6,则五边形ABDEF的面积为________.第10题图第11题图第12题图11.如图,在菱形ABCD中,AB=4,∠BAD=120°,点E、F分别是边AB、BC边上的动点,沿EF折叠△BEF,使点B的对应点B′始终落在边CD上,则A、E两点之间的最大距离为________.12.如图,点A 是反比例函数y =kx 的图象上位于第一象限的点,点B 在x 轴的正半轴上,过点B 作BC ⊥x 轴,与线段OA 的延长线交于点C ,与反比例函数的图象交于点D ,若直线AD 垂直OC ,且使得AC=2OA ,则sinC =________.三、解答题(本大题共4小题,共52分,解答题应写出文字说明、证明过程和演算过程) 13.(本小题满分12分)(1)已知关于x 的方程x 2﹣(2k ﹣1)x+k 2=0有两个实根x 1,x 2,且满足x 1x 2﹣|x 1|﹣|x 2|=2,求实数k 的值;(2)已知a <b <0,且+=6,求()3的值.14.(本小题满分14分)如图,在ABC ∆中,BA BC =,90ABC ∠=︒,以AB 为直径的半圆O 交AC 于点D ,点E 是弧BD 上不与点B ,D 重合的任意一点,连接AE 交BD 于点F ,连接BE 并延长交AC 于点G .(1)求证:ADF BDG ∆≅∆;(2)取弧AE 的中点H ,若四边形OBEH 为菱形,求EAB ∠的大小;(3)若4AB =,且点E 是弧BD 上靠近点B 的一个三等分点,求线段DG 的长.15.(本小题满分12分)习总书记强调,实行垃圾分类,关系广大人民群众生活环境,关系节约使用资源,也是社会文明水平的一个重要体现.为改善城市生态环境,某市决定从6月1日起,在全市实行生活垃圾分类处理,某街道计划建造垃圾初级处理点20个,解决垃圾投放问题.有A、B两种类型垃圾处理点,其占地面积、可供使用居民楼幢数及造价见表:类型占地面积可供使用幢数造价(万元)A 15 18 1.5B 20 30 2.1(1)已知该街道可供建造垃圾初级处理点的占地面积不超过370m2,如何分配A、B两种类型垃圾处理点的数量,才能够满足该街道490幢居民楼的垃圾投放需求,且使得建造方案最省钱?(2)当建造方案最省钱时,经测算,该街道垃圾月处理成本y(元)与月处理量x(吨)之间的函数关系可以近似的表示为:y=,若每个B型处理点的垃圾月处理量是A型处理点的1.2倍,该街道建造的每个A型处理点每月处理量为多少吨时,才能使该街道每吨垃圾的月处理成本最低?(精确到0.1)16.(本小题满分14分)如图①,已知抛物线y=ax2+x+c(a≠0)与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点A坐标为(﹣1,0),点C坐标为(0,),点D是点C关于抛物线对称轴的对称点,连接CD,过点D作DH⊥x轴于点H,过点A作AE⊥AC交DH的延长线于点E.(1)求a,c的值;(2)求线段DE的长度;(3)如图②,试在线段AE上找一点F,在线段DE上找一点P,且点M为直线PF上方抛物线上的一点,求当△CPF的周长最小时,△MPF面积的最大值是多少?华中师大一附中2020年自主招生(分配生)数学试题参考答案与试题解析一、选择题(本大题共6小题,每小题4分,共24分,在每小题给出的四个选项中,有且只有一个是正确的)1.解:根据题意得:a<﹣1<0<b<c<1,则①a2﹣a﹣2=(a﹣2)(a+1)>0;②∵|a﹣b|+|b﹣c|=﹣a+b﹣b+c=﹣a+c,|a﹣c|=﹣a+c,∴|a﹣b|+|b﹣c|=|a﹣c|;③∵a+b<0,b+c>0,c+a<0,∴(a+b)(b+c)(c+a)>0;④∵|a|>1,1﹣bc<1,∴|a|>1﹣bc;故正确的结论有②③,一共2个.故选:C.2.解:∵点P(﹣1,)在“勾股一次函数”y=x+的图象上,∴=﹣+的一次函数,即a﹣b=﹣c,又∵a,b,c分别是Rt△ABC的三条变长,∠C=90°,Rt△ABC的面积是4,∴ab=4,即ab=8,又∵a2+b2=c2,∴(a﹣b)2+2ab=c2,∴(﹣c)2+2×8=c2,解得c=2,故选:A.3.解:对于A,由柱状图可得5月份出货量最高,故A正确;对于B,根据曲线幅度可得下半年波动比上半年波动小,故B正确;对于C,根据曲线上数据可得仅仅4月5月比同比高,其余各月均低于2018,且明显总出货量低于2018年,故C正确;对于D,可计算得2018年12月出货量为:3044.4÷(1﹣14.7%)=3569.05,8月出货量为:3087.5÷(1﹣5.3%)=3260.3,因为3260.3<3569.05,故12月更高,故D错误.故选:D.4.解:∵函数y=x2+x﹣1的对称轴为直线x=﹣,∴当x=﹣时,y有最小值,此时y=﹣﹣1=﹣,∵函数y=x2+x﹣1在m≤x≤1上的最小值是﹣,∴m≤﹣;∵当x=1时,y=1+1﹣1=1,对称轴为直线x=﹣,∴当x=﹣﹣[1﹣(﹣)]=﹣2时,y=1,∵函数y=x2+x﹣1在m≤x≤1上的最大值是1,且m≤﹣;∴﹣2≤m≤﹣.故选:C.5.解:∵∠AOB=90°,AO=4,BO=8,∴AB ===4,∵△AOB 绕顶点O 逆时针旋转到△A ′OB ′处, ∴AO =A ′O =4,A ′B ′=AB =4, ∵点E 为BO 的中点,∴OE =BO =×8=4,∴OE =A ′O =4,过点O 作OF ⊥A ′B ′于F , S △A ′OB ′=×4•OF =×4×8,解得OF =, 在Rt △EOF 中,EF ===, ∵OE =A ′O ,OF ⊥A ′B ′,∴A ′E =2EF =2×=,∴B ′E =A ′B ′﹣A ′E =4﹣=;故选:B .6.解:由图2知:AB+BC =10,设AB =m ,则BC =10﹣m ,如图所示,当点M 在BC 上时,则AB =m ,BM =x ﹣m ,MC =10﹣x ,NC =y , ∵MN ⊥AM ,则∠MAB =∠NMC ,tan ∠MAB =tan ∠NMC ,即,即,化简得:y =﹣x 2+x ﹣10,当x =﹣=时,y =﹣(10+m 2)2+·﹣10=23,解得:m =6,则AM =6,BC =4,故ABCD 的面积=24,故选:A . 二、填空题(本大题共6小题,每小题4分,共24分) 7.解:根据题意画图如下:共有20种等可能的情况数,其中最后确定的主持人是一男一女的有12种, 则最后确定的主持人是一男一女的概率为=.故答案为:.8.解:过B 点作BD ⊥AC 于点D , ∵cosA =,∴,设AD =4x ,则AB =5x ,∴, ∵AB =AC ,∴AC =5x ,∴CD =5x ﹣4x =x , ∴BC =,∴,故答案为:.9.解:由图可得,2个这样的图形(图1)拼出来的图形中,重叠部分的长度为m ﹣n , ∴用2020个这样的图形(图1)拼出来的图形的总长度 =2020m ﹣2019(m ﹣n)=m+2019n ,故答案为:m+2019n . 10.解:如图,连接GC 并延长交BD 于点H ,连接AE , ∵ABCDEF 正六边形,∴AB =BC =CD =DE =EF =AF ,∠F =∠FAB =∠ABC =∠BCD =∠CDE =∠DEF =120°,∴∠CBD =∠CDB =30° ∵△BDG 是等边三角形,∴BG =DG =BD ,∠GBD =∠GDB =60°, 又CG =CG ,∴△BCG ≌△DCG (SSS ), ∵∠GBC =∠DBC =60°﹣30°=30°,∴△GBC ≌△DBC (SAS ),∴S △BCG =S △DCG =S △BCD =3,∴S △AEF =3, 设CH =x ,则BC =CG =2x ,BH =√3x ,∴BD =2√3x ,∴12CG •BH =3, 即12×2x ·√3x =3,∴√3x 2=3,∴S 四边形ABDE =AB •BD =2x •2√3x =4√3x 2=12, ∴五边形ABDEF 的面积为:3+12=15. 11.解:如图,作AH ⊥CD 于H .∵四边形ABCD 是菱形,∠BAD =120°,∴AB ∥CD , ∴∠D+∠BAD =180°,∴∠D =60°, ∵AD =AB =4,∴AH =AD •sin60°=2√3, ∵B ,B ′关于EF 对称,∴BE =EB ′, 当BE 的值最小时,AE 的值最大,根据垂线段最短可知,当EB ′=AH =2√3时,BE 的值最小, ∴AE 的最大值=4−2√3,故答案为4−2√3. 12.解:如图,作AE ⊥BC 于点E ,设A (a ,b ),则C (3a ,3b ),∴OB =3a ,BC =3b , ∴D (3a ,13b ),∴AE =2a ,CE =2b ,DE =23b ,又∵AD ⊥AC ,∴AE 2=CE ·DE ,∴(2a)2=2b ·23b ,∴b 2=3a 2, 又∵Rt △BOC 中,OC =√OB 2+BC 2=3√a 2+b 2, ∴sinC =OBOC =3a 3√a 2+3a 2=3a 3×2a =12.故答案为:12.三、解答题(本大题共4小题,共52分,解答题应写出文字说明、证明过程和演算过程) 13.解:(1)根据题意得△=(2k ﹣1)2﹣4k 2≥0,解得k ≤;(2)x 1+x 2=2k ﹣1,x 1x 2=k 2, ∵k ≤,∴x 1+x 2=2k ﹣1≤0,而x 1x 2=k 2≥0,∴x 1≤0,x 2≤0,∵x 1x 2﹣|x 1|﹣|x 2|=2,∴x 1•x 2+x 1+x 2=2,即k 2+(2k ﹣1)=2, 整理得k 2+2k ﹣3=0,解得k 1=﹣3,k 2=1,而k ≤,∴k =﹣3;(3)∵+=6,∴a 2+b 2=6ab ,∴(a+b)2=8ab ,∴(b ﹣a)2=(a+b)2﹣4ab =4ab ,∴()2==2,∴=±, ∵a <b <0,∴a+b <0,b ﹣a >0,∴<0,∴=﹣,∴()3=﹣2.答:()3的值为﹣2.14.解:(1)证明:如图1,BA BC =,90ABC ∠=︒,45BAC ∴∠=︒ ∵AB 是⊙O 的直径,90ADB AEB ∴∠=∠=︒,90ADF BDG ∴∠=∠=︒, 90DAF BGD DBG BGD ∴∠+∠=∠+∠=︒,DAF DBG ∴∠=∠,90ABD BAC ∠+∠=︒,45ABD BAC ∴∠=∠=︒,AD BD ∴=,()ADF BDG ASA ∴∆≅∆;(2)连接OH ,EH ,点H 是弧AE 的中点,OH AE ∴⊥,90AEB ∠=︒,BE AE ∴⊥, //BE OH ∴,四边形OBEH 为菱形,12BE OH OB AB ∴===, 1sin 2BE EAB AB ∴∠==,30EAB ∴∠=︒. (3)如图2,连接OD 、OE ,点E 是弧BD 上靠近点B 的三等分点,∴∠DOE =23∠DOB , 由(1)知△ADB 是等腰直角三角形,∴∠DOB =2∠DAB =90°,∴∠DOE =60°,∴∠DBE =30°,∴DG =BD ·tan30°, 又∵AB =4,∴BD =2√2,∴DG =2√2×√33=23√6.15.解:(1)设建造A 型处理点x 个,则建造B 型处理点(20﹣x )个. 依题意得:,解得6≤x ≤9.17,∵x 为整数,∴x =6,7,8,9有四种方案;设建造A 型处理点x 个时,总费用为y 万元.则:y =1.5x+2.1(20﹣x )=﹣0.6x+42, ∵﹣0.6<0,∴y 随x 增大而减小,当x =9时,y 的值最小,此时y =36.6(万元), ∴当建造A 型处理点9个,建造B 型处理点11个时最省钱; (2)由题意得:每吨垃圾的处理成本为(元/吨),当0≤x <144时,=(x 3﹣80x 2+5040x )=x 2﹣80x+5040,∵0,故有最小值,当x =﹣=﹣=120(吨)时,的最小值为240(元/吨),当144≤x <300时,=(10x+72000)=10+,当x =300(吨)时,=250,即>250(元/吨),∵240<250,故当x =120吨时,的最小值为240元/吨,∵每个B 型处理点的垃圾月处理量是A 型处理点的1.2倍且A 型处理点9个,建造B 型处理点11个,∴每个A 型处理点每月处理量=×120×≈5.4(吨),故每个A 型处理点每月处理量为5.4吨时,才能使该街道每吨垃圾的月处理成本最低. 16.解:(1)将A(﹣1,0),C(0,)代入抛物线y =ax 2+x+c(a ≠0),,∴a =﹣,c = (2)由(1)得抛物线解析式:y =﹣x 2+x+, ∵点D 是点C 关于抛物线对称轴的对称点,C(0,),∴D(2,),∴DH =,令y =0,即﹣x 2+x+=0,得x 1=﹣1,x 2=3,∴A(﹣1,0),B(3,0),∵AE ⊥AC ,EH ⊥AH ,∴△ACO ∽△EAH ,∴,即,解得:EH=2,则DE=2;(3)找点C关于DE的对称点N(4,),找点C关于AE的对称点G(﹣2,﹣),连接GN,交AE于点F,交DE于点P,即G、F、P、N四点共线时,△CPF周长=CF+PF+CP=GF+PF+PN最小,∴直线GN的解析式:y=x﹣,由(2)得E(2,﹣),A(﹣1,0),∴直线AE的解析式:y=﹣x﹣,联立解得,∴F(0,﹣),∵DH⊥x轴,∴将x=2代入直线GN的解析式:y=x﹣,∴P(2,)∴F(0,﹣)与P(2,)的水平距离为2过点M作y轴的平行线交FP于点Q,设点M(m,﹣m2+m+),则Q(m,m﹣)(<m<);∴S△MFP=S△MQF+S△MQP=MQ×2=MQ=(﹣m2+m+)﹣(m﹣),S△MFP==∵对称轴为:直线m=,又∵开口向下,<m<,∴m=时,△MPF面积有最大值为.。
华师一附中分配生考试试题精析和高分策略

华一分配生考试试题精析和高分策略纵观近三年的华一分配生考试试题,语文共占45分,主要考查内容有三:一、基础。
主要考察范围为初一至初三的古诗文默写。
其中,《书愤》、《蜀相》、《过零丁洋》、《望月怀远》、《酹江月》、《孟子》、《邹忌讽齐王纳谏》是初三的内容;《陋室铭》、《爱莲说》、《商山早行》、《古朗月行》《桃花源记》、《与朱元思书》是初二的内容;《渡者之言》是初一的内容;故推测今年古诗文考察的热点为:初三:古诗:《醉花阴》、《行路难》、《满江红》(秋瑾)、《水调歌头》、《蒹葭》、《关雎》、《龟虽寿》、《浣溪沙》、《山居秋暝》、《破阵子》、《临江仙》、《宣州谢朓楼饯别校书叔云》;文言:《岳阳楼记》、《醉翁亭记》、《曹刿论战》(一鼓作气,再而衰,三而竭)、《子鱼论战》、《送东阳马生序》、《李将军列传》、《生于忧患,死于安乐》、《公输》、《出师表》;初二:古诗:《鲁山山行》、《对酒》、《己亥杂诗》、《相见欢》、《武陵春》、《春望》、《白雪歌送武判官归京》、《酬乐天扬州初逢席上见赠》、《渔家傲秋思》、《天净沙秋思》、《游山西村》、《使至塞上》;文言:《愚公移山》(子子孙孙无穷匮也,而山不加增,何苦而不平?)、《三峡》、《小石潭记》、《湖心亭看雪》、《记承天寺夜游》;初一:文言:《卖油翁》(熟能生巧)、《南辕北辙》、《塞翁失马》(祸兮福之所倚,福兮祸之所伏)、《黔之驴》(黔驴技穷、庞然大物)、《论语八则》(温故知新、见贤思齐、“三人行,必有我师”、不耻下问);补充说明:1、初三的古诗和课文大家都比较熟悉,初一初二的还要巩固一下。
要特别注意:(1)、包含成语的名篇;(2)、对偶句;(3)、古诗名句;2、2013年的病句修改,是平时天天都在训练的题,得分不难;3、2014年考课内翻译,因为是课内的,所以扣得会更严,要做到字字落实,连词成句,特别是省略的成分要补进去,做到“信”“达”“雅”;4、2015年考过排序,但中考也淡化了这一题型。
2020年湖北省武汉华师一附中高中招生分配生考试英语语文5.31

语文、英语试题考试时间:90分钟卷面满分:120分说明:1.本试卷为英语、语文合卷,其中英语50分,语文70分。
2.所有答案一律书写在答题卡上,在试卷上作答无效。
其中,将所有选择题答案用2B铅笔在相应位置涂黑。
英语部分一、完形填空(共15小题;每小题l分,满分15分)阅读下面的短文,从短文后各题所给的A、B、C和D四个选项中,选出可以填入空白处的最佳选项,并在答题卡上将该项涂黑。
I grew up in a small town where the elementary school was a ten-minute walk from my house and in an age when children could go home for lunch and find their mothers 1 .At that time, I didn’t consider this a luxury(奢望), 2 today it certainly would be. I never 3 that this smart woman, who had had a job before I was born and would finally 4 a job, would spend almost every 5 hour throughout my elementary school years just with me.I only knew that when the noon bell rang, I would 6 breathlessly home. My mother would be standing at the top of the 7 , smiling down at me with a look that suggested I was the only important thing she had on her mind. For this, I am forever8 .One lunchtime when I was in the third grade will 9 with me always. I had been picked to be the princess in the school 10 , and for weeks my mother had practiced my lines with me. But no matter how 11 I remembered them at home, as soon as I stepped on 12 , every word disappeared from my head.At last, my teacher took me aside. She 13 that she had written a narrator’s(旁白的) part to the play, and asked me to change roles. Her words, 14 said, still stung(刺痛), especially when I saw my part go to another girl.I didn’t tell my mother what had happened when I went home for lunch that day. But she 15 my unease(心神不定), and instead of suggesting we practice my lines, she asked if I wanted to walk in the yard.1. A. working B. waiting C. reading D. shopping2. A. if B. unless C. although D. so3. A. questioned B. expected C. guessed D. decided4. A. take up B. deal with C. care for D. return to5. A. breakfast B. lunch C. supper D. study6. A. race B. walk C. leave D. ride7. A. hill B. tree C. stairs D. table8. A. relaxed B. joyful C. thankful D. sorry9. A. agree B. stay C. argue D. fight10. A. concert B. event C. festival D. play11. A. hopefully B. easily C. hardly D. luckily12. A. boat B. playground C. stage D. top13. A. realized B. understood C. imagined D. explained14. A. publicly B. sadly C. surprisedly D. kindly15. A. sensed B. caused C. forgot D. hid二、阅读理解(共10小题;每小题2分,满分20分)阅读下面的短文,从每题所给的四个选项(A、B、C和D)中,选出最佳选项,并在答题卡上将该项涂黑。
2015华师一附中自主招生考试

2015年华师一附中自主招生考试考试时间:80分钟卷面满分:150分一、选择题(本大题共有6小题,每小题6分,共36分)1.如果实数a,b,c 在数轴上的位置如图所示,那么代数式2222a ac c b a a +-++-可以化简为 ( ) A.c b a +-- B.c b a -- C.c b a --- D.c b a -+2.如图,反比例函数xy 4=的图像与直线b kx y +=交于A(-1,m),B(n ,1)两点,则ABC ∆的面积为() A. 512 B. 4 C. 215 D. 2133.设21,x x 是一元二次方程032=-+x x 的两根,则1542231+-x x 等于()A. -4B. 8C. 6D. 04.已知c b a ,,分别是ABC ∆的三边长,且满足22224442222c b c a c b a +=++,则ABC ∆是()A. 等腰三角形B. 等腰直角三角形C. 直角三角形D. 等腰三角形或直角三角形5.在一节数学实践活动课上,老师拿出三个边长都是40mm 的正方形硬纸板,他向同学们提出了这样一个问题:若将三个正方形纸板不重叠的放在桌面上,用一个圆形硬纸板将其盖住,这样的圆形硬纸板最小直径为(单位:mm )()A. 280B. 1040C.1725D. 1006.如图,ABC ∆为圆O 的内接三角形,BC=36,60=∠A ,点D 是弧BC 上一动点,⊥BE 直线OD于E ,当点D 由B 点沿弧BC 运动到点C 时,点E 经过的路径长为()A. π312B. π38C. 327D. 54二、填空题(本大题共7小题,每小题7分,共49分) 7.方程)1(4163+=+x x x 的所有根的和为。
8.在5瓶饮料中,有2瓶已过了保质期,随机的从这5瓶饮料中取2瓶,取到至少有一瓶过保质期的概率为。
9.关于x 的方程112-=-a x a无解,则a 的值为。
10.一辆快车从甲地开往乙地,一辆慢车从乙地开往甲地,两车同时出,分别以各自的速度在甲乙两地间匀速行驶,行驶1小时后,快车司机发现有重要文件遗忘在出发地,便立即返回出发地,拿上文件后(取文件时间不计)立即再从甲地开往乙地,结果快车先到达乙地,慢车继续行驶到甲地,设慢车行驶时间为x (h ),两车之间的距离为y (km ),y 与x 的函数图像如图所示,则a=。
华师一附中历年招生考试题型及分数分布
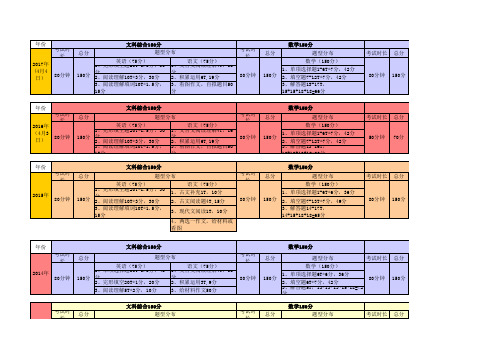
总分
题型分布
英语(75分) 1、完形填空题20T*1.5分,30 150分 分 2、阅读理解10T*3分,30分 3、阅读理解填词10T*1.5分, 15分
语文(75分) 1、文言文阅读理解4T,16 分 2、积累运用6T,19分 3、看图作文,自拟题目50 分
考试时 长ห้องสมุดไป่ตู้
80分钟
数学150分
总分 150分
考试时长 总分 50分钟 70分
考试时长 总分 80分钟 150分
年份 2014年
考试时 长
80分钟
文科综合150分
总分
题型分布
英语(75分) 1、单项选择题30T*1.5分,45 150分 分 2、完形填空20T*1分,20分
语文(75分) 1、文言文阅读理解4T,16 分 2、积累运用3T,9分
3、阅读理解5T*2分,10分
3、给材料作文50分
考试时 长
80分钟
数学150分
总分 150分
题型分布
考试时长
数学(150分)
1、单项选择题6T*6分,36分
2、填空题6T*7分,42分 3、解答题5T,13+13+13+15+18=72 分
80分钟
总分 150分
考试时 长
2013年
总分
文科综合150分 题型分布
80分钟
150分
2011年 (4月 24日)
考试时 长
90分钟
文科综合150分
总分
题型分布
英语(75分) 1、完形填空题20T*1.5分,30 150分 分 2、阅读理解15T*2分,30分
3、短文填词15T*1分,15分
华附入学考试

华附入学考试
华附入学考试通常包括笔试和面试两个部分。
笔试部分:笔试通常包括英语和数学两个科目,这两个科目是国际班或国际学校入学考试的基本组成部分。
英语考试满分为100分,考查学生的英语语言能力。
数学考试则检测学生的数学知识和解题技能。
面试部分:面试则是评价学生综合素质和沟通能力的重要环节。
面试可能涉及学生的个人背景、学习经历、兴趣爱好等方面,考官通过面试来了解学生的个性和潜力。
需要注意的是,每年的入学考试时间和具体要求可能会有所不同,因此建议考生和家长提前关注华附官方网站或相关教育平台上发布的最新招生信息,以确保准备充分。
整合湖北省武汉华中师范大学第一附属中学自主招生考试数学试题word版含解析名师精品资料

2华师一附中 2015 年高中招生考试数学测试题详解考试时间 :80 分钟 卷面满分 :150 分一.选择题( 6 分×6=36 分)2221, 如果实数 a,b, c 在数轴上的位置如图所示,那么代数式aa b c2ac a可以化简为A. a b cB.a b cC. a b cD.a b c【解析】由图知b c a 0 ,故a2a a, ab a b , c22ac a2c a a ca 2a bc242ac a 2a ab a ca b c ,选 D .2. 反比例函数 y的图象与直线 ykx b 交于 A x 1,m , B n,1两点 ,则△ OAB 的面积为A.11B.4C.15 D. 13 222【解析】(补形)xy 4.A 1, m 代入:-m 4, m 4;B n,1 代入:n4 .故有 A (- 1,4),B (- 4,1) .作 AE ⊥y 轴于 E,BD ⊥ x 轴于 D .可知:△AOE ≌△ BOD .且 S AOE S BOD1 1 42 .2延长 EA,DB 交于 C,则四边形 CDOE 是边长为4 的正方形 ,且 S CDOE416, △ ABC 是腰长为 3 的等腰直角三角形 ,且S ABC1 329 .22于是△ OAB 的面积为S ABC16 2 29 15 223. 设 x , x 是一元二次方程 x2x 3 0 的两根 ,则 x34x215 等于1212A. - 4B.8C.6D.0【解析】(降次)由韦达定理: x x 1 x 1 x . x2 x 3, x2 x 31 2 1 2 1 1 2 2x3 4x2 15 x 3 x 24 1 x 15 3x x2 4 1 2x x2 151 2 1 1 1 1 1 1 15 x2 x 3 4 4 ,故选 A.1 14 4 4 2 2 2 24. 已知a, b,c分别是ABC 的三边长,且满足2a2b c 2 a c 2b c ,则△ABC 是A. 等腰三角形B.等腰直角三角形C.直角三角形D.等腰三角形或直角三角形注: 原题条件不完整(是代数式而不是条件等式),故无法解出.为试卷完整起见,将原题条件调整为:已知a,b,c分别是ABC 的三边长, 且满足2a 42b 4 c42a 2c22b 2c20 , 则△ABC 是?.【解析】由条件得: 4a 44b 42c44a 2c24b 2c2 0,即2a 2 c22b 2 c20, c2 2 a22b 2, 或a b且a 2 b2c2 .故△ABC 是等腰直角三角形,选B.5. 在一节 3 数学实践活动课上,老师拿出三个边长都为40mm 的正方形硬纸板,他向同学们提出了这样一个问题:若将三个正方形纸板不重叠地放在桌面上,用一个圆形硬纸板将其盖住, 这样的圆形硬纸板的最小直径为(单位:mm)A.80 2B.40 10C.25 17D.100【解析】当 3 个正方形按如图排列时,其外接圆直径最小.显然,这个圆是等腰梯形ABCD 的外接圆O,这里AB∥CD 且CD =40,AB =80.设此等腰梯形的对称轴交AB 于M,交CD 于N,则MN =80.∵AB >CD ,∴OM<ON.设OM=40 -x,ON=40+ x,圆半径为r .△AOM 中, r 2△DON 中, r 2402202240 x 1240 x 2(1)-(2):1200 160 x0, x 15,代入(2)22 2r 2 400 9025 10625 625 17 , r 2517.4 4 4 2故所求最小圆的直径为2r 25 7 ,故选C.6. 如图,△ABC 内接于圆O,BC=36, ∠A=60 °,点D 为BC 上一动点,BE⊥直线OD 于E,当点D 由B 点沿BC 运动到点 C 时,点E 经过的路线长为A.12 3B.8 3C.27 3D.54【解析】(轨迹法)如解图,连结OB,分别在BC 上取B, D1 , D2 , D3 , C, 其中OD2BC ,则相应的动点依次为B, E1 , E2 , E3 , N .BE1O BE2O BE3O BNO 90 .故点E 的轨迹是OB为直径的优弧BE2 N .已知BC=36, ∴BE218. BOE 2 是含30°角的直角三角形,∴OB 12 3 .设M 为OB 的中点(优弧圆心),连MN .则圆M 的半径MB= 6 3 .注意到∠ BOC=120°,∴∠ BON =60°,∠BMN =120°, 优弧BE2N 之长为圆M 周长的2, l3 BE2 N 22 63 8 3 . ,故选B. 3二.填空题(7×7=49 分)7. 方程x3 16 4x x 1 的所有根的和为【解析1】x3 4 x2 4 x 16 0 .根据广义韦达定理,此方程 3 根之和为 4.即x1 x2 x3b, 这里aa1,b 4【解析2】由原方程得: x 4x 2 x 2 0, x14, x22,x3 2.x1 x2 x3 4 .8. 在5 瓶饮料中,有2 瓶已过了保质期,随机地从这 5 瓶饮料中取 2 瓶,取到至少有 1 瓶过保质期饮料的概率为【解析】(正繁则反)由于从这5 瓶饮料中任取 2 瓶,没有过期饮料的概率为3 , 故取 2 瓶,取到至少有 1 瓶过保质期饮料的概率为 513 2 5 5 2 a9. 关于 x 的方程 a 1 无解,则 a 的值是x 1【解析】由原方程得 : 2a a 1 x 1 1关于 x 的方程( 1)只有唯一解 x 1 ,代入( 1)得 a 0 ,此时原方程无解 ;又在方程( 1)中令 a 1, 得 a 0 .矛盾.此时方程( 1)无解 ,从而原方程无解 . 故若原方程无解 ,则必 a0或1 .10. 一辆快车从甲地开往乙地,一辆慢车从乙地开往甲地 ,两车同时出发 ,分别以各自的速度在甲乙两地间匀速行驶 ,1 小时后 ,快车司机发现有重要文件遗忘在出发地,便立即返回拿上文件(取文件时间不计)后再从甲地开往乙地 ,结果快车先到达乙地 .慢车继续行驶到甲地 .设慢车行驶速度为 x ( h ),两车之间的距离为 y ( km ) ,y 与 x 的函数图象如图所示 ,则 a 【解析】慢车 12.5 小时走完全程 ,12.5x 1000 x 80 km设快车速度为 t ( h )∵ 1 小时后两车相距 800km,即1 小时两车共行 200km,∴ t=120km (h )∵ a 小时后两车相遇 ,此时慢车走 80akm,快车走 120( a-1) km,故有 :80a 120 a 1 1000200a 1120, a 5.6 h11. 已知 a4,当1 x 3时,函数 y 22 x3ax 4 的最小值为- 23,则 a =【解析】 原式配方得 : y22 x3 a4 9a ,抛物线开口向上且对称轴为x 3 a .当 a 4时, 3 a 43 ,故当 1 x4 843 时,y 随 x 增大而减小 .故当 x=3 时有:2 323a 3 423 9a 45, a 5.12. 如 图 , 在 单 位 为 1 的 正 方 形 的 网 格 纸上 , A 1A 2 A 3, A 3 A 4A 5 , A 5A 6 A 7 ,, 都是斜边在x轴上 ,且斜边长分别为2,4,6,? 的等腰直角三角形. 若A 1A 2A 3 的顶点分别为 A 1 2,0 ,A 2 1,-1 ,A 30,0 ,则依图中的规律 , A 2015 的坐标为【解析】注意到点A 1 , A 3 , A 5, , A 2 n 1 全在 x 轴上 ,设其横坐标依次为 x 1 , x 3 , x 5 ,, x 2015 ..继续分析 .点 A 4 n 1 都在原点右边 ,其横坐标取正值 ,点 A 4 n 1 都在原点左边(其中A 3 为原点) ,其横坐标取 0 或负值(其中仅 A 3 横坐标为 0) .∵ 2015=4×504- 1,故 A 2015 必在原点左边 ,其横坐标必为负值 .易求 x 3x 4 1 1 0, x 7 x 4 2 1 02 1, x 11 x 43 10 2 2 4,x 2015x 4 504 1 0 2 5031006,故所求点 A 的坐标为 : A 20151006,0 .13. 有一张矩形风景画 ,长为 90cm,宽为 60cm,现对该风景画进行装裱 ,得到一个新的矩形 ,要求其长 ,宽之比与原风景画的长 ,宽之比相同 ,且面积比原风景画的面积大 44%.若装裱后的上,下边衬的宽都为 a cm,左 ,右边衬都为b cm,那么 ab【解析】依题意有 :90 2 a 60 2b90 3 2a 6022b3 (据等比定理)2故 2a又: 3b 90 2a 160 2b90 60144 100120a 180b 4ab 54 442( 1)代入( 2): 60 3b 180b 6b254 44 b260b 396 0.解得: b 6或b 66 舍 ,从而 a 9, ab 54 .33 三.解答题14.( 14 分)已知 m,n 是方程x23 x1 0 的两根 ,( 1)求 m 5162m 10 2 的值 ;5 m 3 m m( 2)求mn的值n m【解析】( 1)∵ 2m3m 1 0, 故m 516 2m 10 2 m 5 m 5 16 2 m 52 5 m3 mmm 5m 3m2 m292 2 m23m 1 2 m 320 .m 3mmm( 2) m,n 是方程 x23 x 1 0 的两根 ,m n 3mn 1m3n3m3n3m3n3m4n4设 x, 则 x2nm2 2 nmn m mn m 2n 2mn 1, x2m2n2 2m 2n 2222m n2mn29 249x 7,即 mn3=7.nm15.( 15 分)如图 ,△ ABC 中,AC=BC,I 为△ ABC 的内心 ,O 为 BC 上一点 ,过 B,I 两点的圆 O交 BC 于 D 点, tan CBI1, AB 6, 3( 1)求线段 BD 的长 ;( 2)求线段 BC 的长【解析】( 1)如解图 ,I 为△ ABC 内心,故 BI 平分∠ABC .设∠ ABI =∠ CBI =α.连 CI ,并延长交 AB 于 E,∵ CA=CB,∴ CE ⊥ AB,且AE=BE=3.于是 IE=BE tan31 1, B I3321210 .连 DI ,∵ BD 为圆 O 的直径 ,∴∠ BID =90°.于是2310 10 10 DI BI tan , BD 10 .3 9 3(2)连OI ,∵OI =OB= 5,∴∠ DOI =2α,故OI ∥AB, 3△COI ∽△CBE,OI COBE CB 53 CO3 CO 535 3CO,9 3CO 5CO 25, B C 25 5 15 .12 12 3 416.(18 分)如图,四边形ABCD中,AD∥BC,∠BCD =90°,AD =6,BC=3,DE ⊥AB 于E,AC 交DE 于F,(1)求AE·AB 的值;(2)若CD =4,求AFFC的值;(3)若CD =6,过A 点作MEAM∥CD ,交CE 的延长线于M , 求EC的值.【解析】(1)如解图1,作AG∥BC ,交CB 延长线于G,则四边形AGCD 为矩形.∴GC=AD=6, 但BC=3,∴GB=3.已知DE⊥AB 于E,∴△ AGB∽△ DEA.于是AB BGAB AE AD BGAD AE18. (2)延长AB ,DC 交于H.∵AD ∥BC,且AD =2BC,∴BC 为△ AHD 的中位线,故CH =DC =4. 由勾股定理知AH =10,AB=BH =5.沿DE ,CB 交于T,有△ AED∽△ BTE.Rt△ADH 中,DE ⊥AH, AE2AD 36 18,BE AB AEAH18 75 .于是5 510 5BT BE BT 75 7 7 7 16AD AE, BT6 18 185,CT 33 3 3由△ AFD ∽△ CFT ,知AF AD FCCT6 9.16 3 8( 3)如解图 3 有 ABBH 3 5,AE36 6, EH 6 56 246 5 555∵△ AEM ∽△ HEC ,ME AE ECEH6 5 1 .24 4517. ( 18分 ) 二 次 函 数 y 4 x22 m x n 的 图 象 与 x 轴 交 于A x 1,0 ,B x 2 ,o 两点 x 1 x 2 ,与 y 轴交于 c 点.( 1)若 AB=2,且抛物线的顶点在直线y=- x - 2 上,试确定 m,n 的值 ;( 2)在( 1)中 ,若点 P 为直线 BC 下方抛物线上一点 ,当△ PBC 的面积最大时 ,求 P 点坐标;( 3)是否存在整数 m,n,使得 1 x 12,1 x 22, 同时成立 ?请证明你的结论 .【解析】( 1) AB=2x 1 x 2x 2 x 12m2 m2x 2x 14 x 2 x 14 .由韦达定理 :x 1 x 2,故有 :n 44n 4 1抛物线的顶点为m 4n m 2, ,代入 y=-x - 2:4 44n m 2m m2m 2n2 2 代入( 1):4 4442m 0, m 48, 从而 n 12 .( 2)在( 1)的条件下 ,有: y24 x16x 12此抛物线的顶点为( 2,- 4),交 x 轴于 A ( 1,0) ,B ( 3,0) ,交 y 轴于 C(0,12)易求直线 BC 的解析式为 y4 x 12 .为使△ PBC 面积最大 ,只需点 P 与直线 BC 距离最远 .2设过P 且平行于BC 的直线解析式为y 4 x b ,代入抛物线解析式;4 x216x 12 4 x b 4 x212x 12 b 0.令144 16 12 b 0 9 12 b, b 3 .此时有x 3, y 433 3.即所求点的坐标为2 2 P3, 3 .2(3)(反证法)假如存在这样的整数m,n, 使得方程4x22mx n 0 之 2 根满足1 x , x2 .那么: 2< x x m<4, 4< m8, m为整数, m 5,6,7; 11 2 1 221<x1x2n<4, 44n 16, n为整数, nm25,6,7, ,15; 24m216n 0, n 34方程之 2 根为: x2m4m2 16n m m2 4n8 4由m m2 4n1 m 44m2 4n m28m 16 m24n n 2m 4 4由m m2 4n24m2 4 n8 m m2 4n 64 16m m2n 4m 16 5m2当m=5 时,2m-4=6>4 m-16=4,根据(3),(4),取2m-4< n ,即46 n 614,无整数解,舍去;m2当m=6 时, 2m-4=8=4 m-16, 根据(3),(4),取2m-4< n ,即48 n 9, 无整数解,舍去;2当 m=7 时, 2m - 4=10<4 m -16=12. 根据( 5)(,4),取 4m 16 n m, 即 12 4n 12 14无整数解 ,舍去 .据上分析 ,不存在整数 m,n,使得 1 x 1 2,1 x 22, 同时成立 .。
2018年华师一附中招生试题
2018年武汉华师一附中招生试题时间:70分钟 卷面分:120分 制作人:安陆实中一、 选择题(5*7=35分,单选题)1、 二次函数y=x 2+2x+c 的图象与x 轴的两个交点为A (x 1,0),B (x 2,0),x 1<x 2,点P (m,n )是图象上一点,那么下列判断正确的是( )A 当n>0时,m<x 1B 当n>0时,m>x 2C 当n<0时,m<0D 当n<0时,x 1<m<x 22、 已知实数a,b,c 满足a<b<c,并且111k a b b c c a=++---,则直线y=-kx+k 一定经过( ) A 第一三四象限 B 第一二四象限 C 第一二三象限 D 第二三四象限 3、 下边程序框图的算法思路源于我国古代数学名著《九章算术》中“更相减损术”,执行该程序框图,若输入的a 、b 分别为16、22,则输出的a =(a ←a-b 的含义:将a-b 的结果赋给a )A 、0B 、2C 、4D 、144、直线l:kx-y-2k-1=0被以A (1 ,0)为圆心 ,2为半径的⊙A 所截得最短弦长为()A B 2 C D 、45如图,△ABC 中,AB =AC =8,BC =4,BF ⊥AC 于F ,D 是AB 的中点,E 为AC 上一点,且2EF =AC ,则tan ∠DEF =( )ABC D 14二、.填 空题(本题5小题,每小题7分,共35分) 6、若521332412---=----+c c b a b a ,则(b-c)a 的值为_____ 7、△ABC 的一边长为4,另外两边长恰是方程2x 2-12x+m+1=0的两实根,则实数m 的取值范围是______8、如图,D 是△AB C的边AB上的一点,且AB=3AD,P是△ABC外接园上一点,使得∠ADP=∠ACB ,则PB:PD =______9、有十张正面分别标有数字1、2、3、4、5、6、7、8、9、10的不透明卡片,它们除数字不同外其余全部相同,将它们背面朝上,洗匀后从中任取一张,以卡片上的数字作为关于的不等式5x-a ≤5,中的系数a ,使得该不等式的正整数解只有1和2的概率为______a>bb←b-aa←a-b是否是否a≠b?10,若四个互不相等的正实数a 、b 、c 、d 满足20182018201820182018201820182018(a )(a )2018,()()2018c d b c b d --=--=则20182018()()ab cd -的值为_________三、解答题(本大题共3小题,共50分) 11、(本题16分)如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE,(1)求证:CE=CF(2)在图1中,若G在AD上,且∠GCE=45°,则GE、BE、GD有什么数量关系?说明理由。
华师一附中2019年自主招生数学试题(word版附答案)

华中师大一附中2019年高中招生考试数学试题2019.3.31考试时间:70分钟卷面满分:120分说明:所有答案一律书写在答题卡上,在试卷上作答无效.一、选择题(本大题共6小题,每小题6分,共36分.在每小题给出的四个选项中,有且只有一项是正确的.)1.若关于x 的一元二次方程(m -2)x 2+4x -1=0有实数根,则实数m 的取值范围是() A .m ≥-2 B .m>-2或m ≠2 C .m ≥-2且m ≠2 D .m ≠22.已知过点(2,3)的直线y=ax +b(a ≠0)不经过第四象限,设s=a +2b ,则s 的取值范围是() A .32≤s <6B .-6<s ≤−32C .-6≤s ≤32D .32≤s ≤63.已知√(x +1)2+|3-x|=4,则y=2x -1的最大值与最小值的和是() A .1B .2C .3D .44.古希腊数学家欧几里德的《几何原本》记载,形如x 2+2bx=a 2的方程的图解法是:如图,画Rt △ACB ,∠ACB=90°,BC=a ,AC=b ,在斜边AB 上截取AD=b ,则该方程的一个正根是() A .AC 的长B .BC 的长C .CD 的长D .BD 的长5.如图,正方形ABCD 中,E ,F 分别是AB ,BC 上的点,DE 交AC 于点M ,AF 交BD 于点N ;若AF 平分∠BAC ,DE ⊥AF ;记x=BNON,y=CFBF,z=BE OM,则有()A .x >y >zB .x=y=zC .x=y <zD .x=y >z6.设a ,b 为整数,关于x 的一元二次方程x 2+(2a +b +3)x +(a 2+ab +6)=0有两相等实根α,关于x 的一元二次方程2a x 2+(4a -2b -2)x +(2a -2b -1)=0有两相等实根β;那么以α,β为实根的整系数一元二次方程是() A .2x 2+7x +6=0 B .x 2+x -6=0 C .x 2+4x +4=0D .x 2+(a +b)x +ab=0二、填空题(本大题共6小题,每小题6分,共36分) 7.ΔABC 是⊙O 的内接三角形,∠BAC=60°,劣弧BC 的长是4π3,则⊙O 的半径是 .8.若m ,n 是方程x 2-x -2019=0的两实根,则m 2-2m -n 的值为 .9.一组“数值转换机”按下面的程序计算,如果输入的数是36,则输出的结果为106,要使输出的结果为127,则输入的最小正整数是 .10.当a ,b 是正实数,且满足a +b=ab 时,就称点M(a ,ab )为“完美点”;已知点A 是“完美点”且在直线y=-x +5上,则点A 的坐标为 .11.从-3,-2,-1,-12,0,12,1,2,3这9个数中随机抽取一个数,记为m .若数m 使关于x 的不等式组{13(2x +7)≥3x −m <0无解,且使关于x 的分式方程x x +3+m−2x +3=-1有整数解,那么从这9个数中抽到满足条件的m 的概率是 . 12.如图,ΔABC 中,∠ACB=90°,sinA=513,AC=12,将ΔABC 绕点C 顺时针旋转90°得到ΔA'B'C ,P 为线段A'B'上的动点,以点P 为圆心,PA'长为半径作⊙P ,当⊙P 与ΔABC 的边相切时,⊙P 的半径为 .三、解答題(本大题共3小題,共48分,解答应写出文字说明、证明过程和演算步骤.) 13.(本小题满分16分)已知:如图,Rt ΔABC 的三边满足(AB -4)2+|AB -BC|=0,∠ABC=90°. (1)若M 是边AB 上一点,N 是边BC 延长线上一点,且线段AM=CN=m ,mAB−m=ABBC +2,求m 的值;(2)若M 是边AB 上一动点,N 是边BC 延长线上一动点,且线段AM=CN ,判断线段DM 与DN 的大小关系,并说明你的理由;(3)若M 、N 分别是边AB 、BC 延长线上的动点,D 为线段MN 与边AC 延长线的交点,线段AM=CN ,判断线段DM 与DN 的大小关系,并说明你的理由.AMB C DNAM B CD N14.(本小题满分16分)在平面直角坐标系xOy中,对于任意两点P1(x1,y1)与P2(x2,y2)的“特别距离”,给出如下定义:若|x1-x2|≥|y1-y2|,则点P1与点P2的“特别距离”为|x1-x2|;若|x1-x2|<|y1-y2|,则点P1与点P2的“特别距离”为|y1-y2|.例如:点P1(1,2),点P2(3,5),因为|1-3|<|2-5|,所以点P1与点P2的“特别距离”为|2−5|=3,也就是图1中线段P1Q与线段P2Q长度的较大值(点Q为垂直于y轴的直线P1Q与垂直于x 轴的直线P2Q交点).,0),B为y轴上的一个动点.(1)已知点A(-12①若点A与点B的“特别距离”为3,写出一个满足条件的点B的坐标;②直接写出点A与点B的“特别距离”的最小值.x+4上的一个动点,如图2,点D的坐标是(0,1),求点C与点D (2)已知C是直线y=43的“特别距离”的最小值及相应的点C的坐标.15.(本小题满分16分)如图,已知抛物线y=x2+2bx+2c(b,c是常数,且c<0)与x轴分别交于点A、B(点A位于点B的左侧),与y轴的负半轴交于点C,点A的坐标为(-1,0).(1)点B的坐标为____(结果用含c的代数式表示);(2)连接BC,过点A作直线AE∥BC,与抛物线y=x2+2bx+2c交于点E,点D是x轴上的一点,其坐标为(2,0).当C,D,E三点在同一直线上时,求抛物线的解析式;(3)在(2)条件下,点P是x轴下方的抛物线上的一个动点,连接PB,PC,设所得ΔPBC 的面积为S.①S的取值范围;②若ΔPBC的面积S为整数,则这样的ΔPBC共有____个.华中师大一附中2019年高中招生考试数学试题参考答案与试题解析一、选择题1.C .由△≥0,且m -2≠0,得m ≥-2且m ≠2. 2.A .由题意得a >0,b ≥0,且3=2a +b ,当b=0时,s=a=32;当b >0时,s=a +2(3-2a)=6-3a <6.3.B .由题意得x +1≥0,3-x ≥0,∴-1≤x ≤3,当x=-1时,y=2x -1有最小值为-3,当x=3时,y=2x -1有最大值为5,∴和是2.法2:由题意得|x +1|+|3−x |=4,即数轴上一点x 到点(-1,0)、(3,0)的距离之和为4,当x=-1时,y=2x -1有最小值为-3,当x=3时,y=2x -1有最大值为5,∴和是2. 4.D .由勾股定理得AB=√b 2+a 2,∴BD=√b 2+a 2-b ,由求根公式得x=−2b±√(2b)2−4×1×(−a 2)2=±√b 2+a 2-b ,∴该方程的一个正根是BD 的长. 5.C .如图,由角平分线,2BN AB AC CFON AO AB BF====,即x=y=√2,又AME ∆的角分线与高重合,则AME ∆为等腰三角形,AM AE =,作OP ∥AB ,交ED 于P ,则OP 为DBE ∆的中位线,OMP AME ∆∆∽,z=BE OM =BE OP=2,∴x=y <z .6.A .由题意得,(2a +b +3)2-4(a 2+ab +6)=0,即(b +3)2=12(2-a)①, 又(4a -2b -2)2-4×2a(2a -2b -1)=0,即(b +1)2=2a ②, 由①②得,7b 2+18b −9=0,其整根为b=-3,∴a=2;两个方程分别是:x 2+4x +4=0和4x 2+12x +9=0,∴α=−2,β=−32, ∴以α,β为实根的整系数一元二次方程是2x 2+7x +6=0. 二、填空题7.解:连接OB 、OC .,劣弧BC 的长是, ,.故答案为2. 8.解:由题意得:m 2-m -2019=0,m +n=1,∴m 2-m=2019, ∴m 2-2m -n=m 2-m -(m +n)=2019-1=2018.2120BOC BAC ∠=∠=︒43π∴12041803r ππ⋅⋅=2r ∴=9.解:当3x -2=127时,x=43,当3x -2=43时,x=15,当3x -2=15时,x=173,不是整数;所以输入的最小正整数为15.故答案为15.10.解:∵a ,b 是正实数,且满足a +b=ab ,∴a b+1=a ,即ab=a -1,∴M(a ,a -1),即“完美点”A 在直线y=x -1上,又∵点A 是“完美点”且在直线y=-x +5上, ∴{y =x −1y =-x +5,∴{x =3y =2,∴点A 的坐标为(3,2).11.解:整理不等式组得:{x ≥1x <m ,由不等式组无解,得m ≤1,即m 为-3,-2,-1,-12,0,12,1;分式方程去分母得:x +m -2=-x -3,∴x=−m +12,由分式方程有整数解,∴m 为-3,-1,1,3,∴满足条件的m 为-3,-1,1,∴m 的概率是13. 12.解:如图1中,当⊙P 与直线AC 相切于点Q 时,连接PQ . 设PQ=PA'=r ,∵PQ ∥CA',∴,,.如图2中,当⊙P 与AB 相切于点T 时,易证A'、B'、T 三点共线, △,,,,.综上所述,⊙P 的半径为或.13.解:(1)∵(AB -4)2+|AB -BC|=0,∴AB -4=0,且AB -BC=0,∴AB=BC=4,∵mAB−m= AB BC+2,∴m 4−m=3,∴m=3,经检验得,m=3.(注:未检验扣1分)(2)∵DM=DN .理由如下:过M 作ME ⊥AB 交AC 于E , ∴∠AME=∠B=90°,∴ME ∥BC ,∴∠EMD=∠N , ∵AB=BC ,∠B =90°,∴∠A =∠ACB=45°, ∴∠AEM=∠ACB=45°,∴AM=ME ,∵AM=CN , ∴ME=CN ,又∵∠MDE=∠NDC , ∴△MED ≌△NCD(AAS),∴DM=DN .(3)∵DM=DN .理由如下:过M 作MH ⊥AB 交AC 的延长线于H ,同(2)可证△MHD ≌△NCD(AAS),∴DM=DN .(注:其它解法酌情给分,(2)、(3)问只有结论而无证明过程各得1分).PQ PB CA A B '='''∴131213r r -=15625r ∴=A BT ABC '∆∽∴A T AB AC AB''=∴171213A T '=20413A T ∴'=1102213r A T ∴='=1562510213 AM B CD NEAMB C D NH14.解:(1)①∵点B 为y 轴上的一个动点,∴设点B 的坐标为(0,y).∵|−12−0|=12≠3,∴|0−y |=3,∴y=3或y=-3,∴点B 点的坐标为(0,3)或(0,-3).②点A 与B 点的“特别距离”的最小值为12.故答案是:12.(2)设点C(x ,43x +4),D(0,1),则|x 1-x 2|=x ,|y 1-y 2|=|43x +3|,①当|x |≥|43x +3|时,(i)若x ≤-94,则-x ≥−43x −3,x ≥-9,∴-9≤x ≤-94,(ii)若-94<x ≤0,则-x ≥43x +3,73≤x ≤-3,x ≤-94,∴-94<x ≤-97,(iii)若x >0,则x ≥43x +3,x ≤-9(舍),综上,-9≤x ≤-97,∴当x=-97时,|x|min =|-97|=97,②当|x |<|43x +3|时,同理可得,x <-9或x >-97, (i)若x <-9,则|43x +3|=−43x −3,|43x +3|>9, (ii)若x >-97,则|43x +3|=43x +3,|43x +3|>97,综合①②得,点C 与点D 的“特别距离”的最小值为97.相应的点C(-97,167).(注:其它解法酌情给分)15.(1)∵抛物线y=x 2+2bx +2c 过点A(-1,0),∴1-2b +2c=0,∴2b=1+2c , ∵抛物线y=x 2+2bx +2c 与x 轴分别交于点A(-1,0)、B(x B ,0),∴−1、x B 是一元二次方程x 2+2bx +2c 的两个根,∴−1+x B =-2b=-1-2c , ∴x B =-2c ,∴点B 的坐标为(-2c ,0);(2)∵抛物线y=x 2+2bx +2c 与y 轴的负半轴交于点C , ∴当x=0时,y=2c ,即点C 的坐标为(0,2c).设直线BC 的解析式为y=kx +2c ,∵点B 的坐标为(-2c ,0),∴-2ck +2c=0, ∵c ≠0,∴k=1,∴直线BC 的解析式为y=x +2c , ∵AE ∥BC ,∴可设直线AE 的解析式为y=x +m ,∵点A 的坐标为(-1,0),∴-1+m=0,解得m=1,∴直线AE 的解析式为y=x +1. ∵抛物线y=x 2+2bx +2c 过点A(-1,0),∴1-2b +2c=0,∴2b=1+2c ,∴y=x 2+(1+2c)x +2c ,与y=x +1联立,解得x=-1,y=0或x=1-2c ,y=2-2c , ∴E(-1,0)(与点A 重合,舍去),E(1-2c ,2-2c).∵点C 的坐标为(0,2c),点D 的坐标为(2,0),∴直线CD 的解析式为y=-cx +2c . ∵点C ,D ,E 三点在同一直线上,∴2-2c=-c(1-2c)+2c ,∴2c 2+3c -2=0, ∴c 1=12(与c <0矛盾,舍去),c 2=-2,∴b=−32,∴抛物线的解析式为y=x 2-3x -4;(3)①∵A(-1,0),B(4,0),C(0,-4), ∴AB=5,OC=4,直线BC 的解析式为y=x -4, 分两种情况: (i)当-1<x <0时,0<S <S △ACB ,∵S △ACB =12AB ·OC=10,∴0<S <10;(ii)当0<x <4时,过点P 作PG ⊥x 轴于点G ,交CB 于点F , 设PF=y F −y P =(x -4)-(x 2-3x -4)=−x 2+4x ,∴S △PCB =S △PFC +S △PFB =12PF ·OB=12(−x 2+4x)×4=−2x 2+8x=−2(x −2)2+8, ∴当x=2时,S 最大值=8,∴0<S ≤8; 综合(i)(ii)可知:S 的取值范围为0<S <10.②∵S 的取值范围为0<S <10,且S 为整数.∴S=1,2,3,4,5,6,7,8,9. 分两种情况:(i)当-1<x <0时,设△PBC 中BC 边上的高为h .∵B(4,0),C(0,-4),∴BC =4√2,∴S=12BC ·h=2√2h ,∴h =√24S ,又∵0<S <10,即0<2√2h <10,∴0<h <5√22, ∴当S=1,2,3,4,5,6,7,8,9时,√24≤h ≤9√24,此时,满足条件的ΔPBC 有9个;(ii)当0<x <4时,∵S △PCB =−2x 2+8x ,且0<S ≤8;∴当S=1,2,3,4,5,6,7时,均有∆>0,此时P 点共有7×2=14个, 当S=8,有∆=0,此时P 点只有1个;综上可知,满足条件的ΔPBC 共有9+14+1=24个.D A B Oyx ECPFG。
华中师大一附中2013年高中招生考试(物理及详解)(王涛2014自己的备课)

华中师大一附中2013年高中招生考试理科综合测试考试时间:80分钟卷面满分150分说明:1.本试卷为物理、化学合卷,其中物理100分,化学50分。
2.所有答案一律书写在答题卡上,在试卷上作答无效。
一、选择题(本题共13小题,1一8题每小题5分,9一招题每小题4分,共60分。
每小题给出的四个选项中,只有一个选项符合题意。
)l.下列说法错误的是A.夏天,我们要喝冰凉的饮料,往往会在饮料中加上几个冰块,这是因为不仅冰块的温度低,而且冰块熔化成水时吸热B.人们在高温的天气里大汗淋漓,是人体自我保护的生理现象,汗液蒸发吸热使体温不致升得太高C.我国北方冬季树枝上出现的雾淞是凝华现象D.在运输食品时,为了防止食品腐烂变质,可以利用干冰的熔化来吸热降温。
解:D2.如图a,蜡烛在光屏上能成一清晰的像。
如果沿直径对称地切除透镜很小的一部分,如图6所求,再把上半截透镜A和下半截透镜B向原主光轴位置合拢,则下列说法中正确的是( )A.在a图中,如果一只小飞虫恰好落在透镜上的P点,不会在光屏上留下小飞虫的影子B.在a图中,如果蜡烛向透镜不断靠近,则所成的像一直变大C.在b图中,A, B.合拢后,所成像情况与a图相同,只是亮度变低D.在b图中,A, B合拢后,无论怎样移动光屏,在光屏上都不能成像解:正选A。
因为这个点无法成像。
只是亮度变低B说得不太清晰,在一倍焦距以内时,越近所成像越小。
CD 若切了再合拢后则f减小,如图相当于在上半部分的主光轴上升。
3.有一个上细下粗的筒,下端用一薄片盖住后浸入水中(不计薄片重),薄片因受水的压力而不下落,如图所示。
这时向筒内轻轻注入150克水后,恰能使薄片下落,那么下列做法中同样可使薄片下落的是( B )A.在筒内轻轻注入150克水银B.往筒内轻轻注入150克酒精C. 在筒内轻轻注入150克砝码D.以上三种方法都可以解:注入150克水时,有侧壁在压水,所以底部受到的压力大于150克力,用砝码没有借助侧壁的压力一定不行。
华师一附中自主招生考试物理试题及详细解析

华师一附中自主招生考试物理试题及详细解析华师大一附中高中招生考试理科综合测试物理试题及详细解析一.选择题(共5小题)1.完全相同的物体,分别以相同的速度,从A点和A′点进入并通过光滑圆弧轨道和到达C点和C′点,如图所示.如果两圆弧轨道的半径相同,物体到达C点和C′点的速度分别记为v1、v2,物体在和轨道运动的时间分别记为t1、t2,则()A.v1=v2;t1<t2B.v1>v2;t1=t2C.v1<v2;t1>t2D.v1=v2;t1>t2解答:由速度公式V=可知,由于两个物体的运动路程是相同的,要比较物体的运动时间,只要比较出两物体的运动速度的关系,就可以比较出时间的关系即路程一定,时间与速度成反比.故答案为:D2.如图所示,一个木块A放在长木板B上,长木板B放在水平地面上,在恒力F作用下,长木板B以速度v匀速运动,水平弹簧秤的示数为T.下列关于摩擦力的说法正确的是()A.木块A受到的滑动摩擦力的大小等于TB.木块A受到的静摩擦力的大小等于TC.若长木板B以2v的速度匀速运动时,木块A受到的摩擦力的大小等于2TD.若用2F的力作用在长木板上,木块A受到的摩擦力的大小等于2T解答:A、B稳定时,A保持静止.A水平方向受到弹簧的拉力和B对A的滑动摩擦力,由平衡条件得到,木块A 受到的滑动摩擦力的大小等于弹簧的拉力T.故A正确,B错误.C、若长木板B以2v的速度匀速运动时,AB间动摩擦因数不变,A对B的压力不变,则木块A受到的滑动摩擦力的大小不变,仍等于T.故C错误.D、若用2F的力作用在长木板上,木板加速运动,而木块A受到的滑动摩擦力的大小不变,仍等于T,与F无关.故D错误.故选A3.一物体从某一高度自由落下,落在直立于地面的轻弹簧上,如图所示,在A点物体开始与弹簧接触,到B点时物体速度为零,然后被弹回,下列说法中正确的是()A.物体从A下降到B的过程中,动能不断变小B.物体从A下降到B,以及从B上升到A的过程中,动能都是先增大,后减小C.物体从B上升到A的过程中,动能不断变大D.物体在B点时,所受合力为零解答:首先分析一下,从A点接触弹簧开始到将弹簧压缩到最短B点的过程中,物体的运动过程:在物体刚接触弹簧的时候,弹簧的弹力小于物体的重力,合力向下,小球还是向下加速,当弹簧的弹力和物体的重力相等时,小球的速度达到最大,之后弹力大于了重力,小球开始减速,直至减为零.弹簧从压缩到最短B点到弹簧弹回原长A点的过程中,物体的运动过程:弹簧压缩到最短时弹力最大,大于重力,合力方向向上,物体加速上升,当弹簧的弹力和物体的重力相等小球的速度达到最大,之后弹力小于重力,小球开始减速.A、根据以上分析,物体从A下降到B的过程中,物体的速度先变大后变小,所以动能也是先变大后变小,故A错误.B、由A、C分析知B正确.C、物体从B上升到A的过程中,速度先变大,后变小,所以动能先增大后减小,故C错误.D、物体在B时,弹性形变最大,故物体受到的弹力大于重力,合力向上,故D错误.故选B.4.为了连续改变反射光的方向,并多次重复这个过程,方法之一是旋转由许多反射镜组成的多面体棱镜(简称镜鼓),如图所示.当激光束从固定方向入射到镜鼓上的一块反射镜上时,由于反射镜绕竖直轴旋转,反射光就可在屏幕上扫出一条水平线.每块反射镜都将轮流扫描一次.如果要求扫描的范围θ=45°且每秒钟扫描48次,那么镜鼓的反射镜的数目和镜鼓旋转的转速分别为()A.8;360 r/min B.16;360 r/min C.16;180 r/min D.32;180 r/min解答:已知入射光线不变,根据反射光线转过的角度求出法线转过的角度,然后利用转过一圈的角度和法线转过的角度即可求出镜面的个数;又知道每秒钟扫描的次数和镜面的个数,求出每秒转的圈数,最后转化为一分钟转的圈数即可.故选C.5.图中,电阻R1与R3相等,电阻R2与R4相等.现有一个两端电压为10V的电源,当把该电源接在A、B两个接线端时,电压表的示数为7.5V,电阻R1两端电压为U1.当把该电源接在C、D两个接线端时,电压表的示数为5V,电阻R2两端电压为U2.则下列选项不正确的是()A.R1:R5=1:3 B.U1:U2=1:2 C.R2:R5=1:2 D.R1:R2=1:3解答:分析电路图可知接在A、B两个接线端时,电阻R1与R3,R5串联在电路中,接在C、D两个接线端时,电阻R2与R4、R5串联在电路中,电压表都测R5的电压.根据串联电路电压特点结合欧姆定律可计算电阻R1两端的电压与电阻R2两端的电压和电阻之比.故选A.二.非选择题(共3小题)6.如图为测量电阻的电路,R x为待测电阻,R的阻值已知;R’为滑动变阻器,且滑片位置固定不动;电源电压U 未知.S1、S2均为单刀双掷开关,A为电流表,其内阻不计,测量R x的步骤为:将S2向d闭合,S1向闭合,记下电流表读数I1;再将S2向c闭合,S1向闭合,记下电流表读数I2.计算R x的数学表达式为R x=_____ .解答:①将S2向d闭合、S1向a闭合时,R X与R并联,电流表测通过R X的电流,记下电流表读数I1;②将S2向c闭合,S1向b闭合,R X与R并联,电流表测通过R的电流,记下电流表读数I2.滑动变阻器滑片位置固定不动,滑动变阻器接入电路的阻值不变,两次实验时,R X与R并联的并联电压不变,设并联电压为U,∵I=,∴由②得,并联电压U=I2R,由①得:R X==;故答案为:a;b;.7.小明将一只铝制的水桶浸没在水深为1.3m的大水池中,然后用测力计提着满桶水缓慢离开水面.在此过程中,分别测出对应的弹簧测力计的示数以及水桶上端到水面的距离(水面处记为0,水面下记为负).然后将记录的数据绘成如图所示图象,铝的密度为2.7×103k g/m3,水的密度为1.0×103k g/m3,g=10N/kg.(连接桶和测力计的绳子和受到的浮力不计)。
2021年华师大一附中自主招生数学试题含详解

2021年华师大一附中自主招生数学试题含详解XXX高中数学招生考试详解本文为XXX高中数学招生考试的题目解析。
考试时间为80分钟,卷面满分为150分。
一、选取题(共6题,每题6分,共36分)1.如果实数a、b、c在数轴上的位置如图所示,那么代数式a-a+b+c-2ac+a可以化简为什么?解析:由图可知b<c<a,因此a=a'=-a,a+b=-(a+b'),c-2ac+a=c-a。
将代数式代入化简得到a^2-a+b+c^2-2ac+a^2=-a+(a+b)+(a-c)=a+b-c,因此选D。
2.反比例函数y=-4x的图像与直线y=-kx+b交于A(-1,m)和B(n,1)两点,那么△OAB的面积是多少?解析:将A(-1,m)代入y=-4x得到-m=-4,因此m=4;将B(n,1)代入y=-4x得到n=-4,因此A(-1,4)、B(-4,1)。
作AE⊥y 轴于E,BD⊥x轴于D,则△AOE≌△BOD,且S△AOE=S△BOD=1×4/2=2.延长EA、DB交于C,则四边形CDOE是边长为4的正方形,且SCDOE=4×4=16.△ABC是腰长为3的等腰直角三角形,且S△ABC=3×2/2=3.因此,△OAB的面积为S△OAB=16-2×2-3/22=323/22.3.设x1、x2是一元二次方程x^2+x-3的两根,那么x1-4x2+15等于多少?解析:由韦达定理,x1+x2=-1,因此x1=-1-x2.又因为x1x2=-3,所以x2^2+(-1-x2)x2-3=0,即x2^2-x2-3=0.解得x2=(1-√13)/2或x2=(1+√13)/2.代入x1=-1-x2得到x1=-(3+√13)/2或x1=-(3-√13)/2.因此,x1-4x2+15=-5(x2+x1^2+x1x2)-4=-4,因此选A。
4.已知a、b、c分别是△ABC三边长,且满足2a+2b+c-2ac+2bc,那么△ABC是什么?解析:将2a+2b+c-2ac+2bc分解得到2(a+b)+c(1-2a+2b),由于a、b、c为三角形的三条边长,因此a+b>c,即2(a+b)>c。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2、填空实验题4T,30分 (6+6+5+13)
分)
理科综合200分
题型分布
物理(60分)
化学(40分)
1、单项选择题6-10T*5分,25分
1、单项选择题11-14T*3分,12分
2、实验填空题1T,8分 3、计算题(浮力13分、电学14分;27
2、填空实验题3T,28分 (5+13+10)
分)
理科综合200分
题型分布
物理(60分)
化学(40分)
1、单项选择题7-11T*4分,20分
1、单项选择题12-15T*4分,16分
2、实验填空题2T,16分(10+6) 3、计算题(压力12分、密度12分;24
2、填空实验题4T,24分 (10+6+6+2)
分)
理科综合200分 题型分布 物理(60分)
1、单项选择题5T*5分,25分 2、实验填空题1T,14分(电学) 3、计算题(浮力9分、电学12分;21 分)
2、填空题6T,31分 3、计算题(电学14分、力学15分;29
2、填空实验题4T,30分 (6+6+5+13)
分)
理科综合150分
题型分布
物理(100分)
化学(50分)
1、单项选择题8T*6分,48分
1、单项选择题5T*4分,20分
2、实验填空题2T,20分 3、计算题(速度16分、电学16分;32
分)
考试时 长
120分钟
总分 200分
数学(100分) 1、单项选择题1-5T*5分,25分 2、填空题6-8T*6分,18分 3、解答题9-12T,13+14+14+16=57分
题型分布
理科综合100分
题型分布
物理(70分)
化学(30分)
1、单项选择题1-8T*5分,40分
1、单项选择题9-13T*4分,20分
化学(40分)
1、单项选择题4T*3分,12分 2、填空实验题3T,28分 (8+6+14)
理科综合200分
题型分布
物理(60分)
化学(40分)
1、单项选择题5T*5分,25分
1、单项选择题4T*3分,12分
2、实验填空题1T,8分(电学) 3、计算题(压力12分、电学15分;27
2、填空实验题3T,28分 (5+10+13)
化学(50分)
1、单项选择题8T*5分,40分
1、单项选择题5T*4分,20分
2、填空题6T,31分 3、计算题(电学14分、热学15分;29
2、填空实验题4T,30分 (6+7+7+10)
分)
理科综合150分 题型分布
物理(100分)
化学(50分)
1、单项选择题8T*5分,40分
1、单项选择题5T*4分,20分
考试时 长
总分
数学150分 题型分布
考试时长 总分
理科综合100分 理科综合(物理)70分
理科综合150分 理科综合150分 理科综合150分
2013年
80分钟
英语(75分) 1、单项选择题30T*1.5分,45 150分 分 2、完形填空20T*1分,20分
3、阅读理解5T*2分,10分
语文(75分) 1、文言文阅读理解4T,16 分 2、积累运用3T,9分
15分
分
考试时 长
80分钟
总分 150分
数学150分 题型分布
数学(150分) 1、单项选择题1-6T*7分,42分 2、填空题7-12T*7分,42分 3、解答题13-17T, 15+15+18+18=66分
考试时长 总分 80分钟 150分
年份
2016年 (4月3
日)
考试时 长
80分钟
文科综合150分
考试时 长
120分钟
总分 200分
数学(100分) 1、单项选择题1-5T*5分,25分 2、填空题3T*6分,18分 3、解答题4T,13+14+14+16=57分
理科综合200分 题型分布
2010年 (5月1
日)
考试时 长
90分钟
文科综合150分
总分
题型分布
英语(75分) 1、完形填空题20T*1.5分,30 150分 分 2、阅读理解15T*2分,30分
考试时 长
90分钟
总分
题型分布
英语(75分)
语文(75分)
150分
1、单项选择题15T*1分,15分 2、完形填空题20T*1.5分,30
分 3、阅读理解10T*2分,20分
4、短文填词题10T*1分,10分
1、积累运用2T,10分 2、现代文阅读理解6T,15 分3、给材料命题作文(寻找 理想)50分
2、填空题13-16T,39分
2、填空实验题3T,32分 (6+10+16)
3、计算题17-18(电学6分、密度压强
15分;21分)
理科综合(物理)70分
题型分布 物理(70分) 1、单项选择题1-6T*4分,24分 2、填空题7-9T,20分 3、计算题10-11T,13+13=26分
化学(0分)
考试时 长
120分钟
总分 200分
数学(100分) 1、单项选择题1-5T*5分,25分 2、填空题6-8T*6分,18分 3、解答题9-12T,13+14+14+16=57分
理科综合200分 题型分布
理科综合150分
2008年 (5200分
2008年 (5月1
日)
语文(75分) 1、古文补充1T,10分 2、古文阅读题4T,15分
3、阅读理解填词10T*1.5分, 15分
3、现代文阅读1T,10分
4、两选一作文,给材料或 看图
考试时 长
80分钟
数学150分
总分 150分
题型分布 数学(150分) 1、单项选择题1-6T*6分,36分 2、填空题7-13T*7分,49分 3、解答题14-17T, 14+15+18+18=65分
年份
2017年 (4月4 日)
考试时 长
80分钟
文科综合150分
总分
题型分布
英语(75分) 1、完形填空题20T*1.5分,30
150分
分 2、阅读理解10T*3分,30分
语文(75分) 1、文言文阅读理解4T,16 分 2、积累运用6T,19分
3、阅读理解填词10T*1.5分, 3、看图作文,自拟题目50
理科综合150分
题型分布
物理(100分)
化学(50分)
1、单项选择题1-8T*5分,40分
1、单项选择题9-13T*4分,20分
2、填空题13-16T,39分
2、填空实验题3T,32分 (6+10+16)
3、计算题17-18(电学6分、密度压强
15分;21分)
理科综合150分
题型分布
物理(100分)
题型分布 数学(150分) 1、单项选择题1-6T*7分,42分 2、填空题7-12T*7分,42分 3、解答题13-16T, 16+16+16+18=66分
年份 2015年
考试时 长
80分钟
文科综合150分
总分
题型分布
英语(75分) 1、完形填空题20T*1.5分,30
150分
分 2、阅读理解10T*3分,30分
3、完成句子10T*1.5分,15分
语文(75分)
1、积累运用2T,14分 2、现代文阅读理解3T,11 分 3、给材料作文50分
考试时 长
120分钟
总分 200分
数学(100分) 1、单项选择题1-6T*4分,24分 2、填空题3T*6分,18分 3、解答题4T,12+15+15+16=58分
理科综合200分 题型分布
3、阅读理解5T*2分,10分
语文(75分) 1、文言文阅读理解4T,15 分 2、积累运用2T,10分 3、命题作文(这也是一笔 财富)50分
考试时 长
80分钟
数学150分
总分
题型分布
考试时长 总分
数学(150分)
150分
1、单项选择题6T*6分,36分
2、填空题6T*7分,42分 3、解答题5T,13+13+13+15+18=72 分
80分钟
150分
2011年 (4月 24日)
考试时 长
90分钟
文科综合150分
总分
题型分布
英语(75分) 1、完形填空题20T*1.5分,30 150分 分 2、阅读理解15T*2分,30分
3、短文填词15T*1分,15分
语文(75分)
1、积累运用2T,13分 2、现代文阅读理解3T,12 分3、命题作文(站在高处) 50分
3、给材料作文50分
80分钟
150分
数学(150分) 1、单项选择题6T*6分,36分 2、填空题6T*7分,42分 3、解答题5T,13+13+13+15+18=72 分
80分钟
150分
2012年 (4月4
日)
考试时 长
80分钟
文科综合150分
总分
题型分布
英语(75分) 1、单项选择题30T*1.5分,45 150分 分 2、完形填空20T*1分,20分
考试时长 总分 50分钟 70分
考试时长 总分 80分钟 150分
