西安交通大学数字图像处理第二次作业
(完整版)数字图像处理课后题答案

1. 图像处理的主要方法分几大类?答:图字图像处理方法分为大两类:空间域处理(空域法)和变换域处理(频域法)。
空域法:直接对获取的数字图像进行处理。
频域法:对先对获取的数字图像进行正交变换,得到变换系数阵列,然后再进行处理,最后再逆变换到空间域,得到图像的处理结果2. 图像处理的主要内容是什么?答:图形数字化(图像获取):把连续图像用一组数字表示,便于用计算机分析处理。
图像变换:对图像进行正交变换,以便进行处理。
图像增强:对图像的某些特征进行强调或锐化而不增加图像的相关数据。
图像复原:去除图像中的噪声干扰和模糊,恢复图像的客观面目。
图像编码:在满足一定的图形质量要求下对图像进行编码,可以压缩表示图像的数据。
图像分析:对图像中感兴趣的目标进行检测和测量,从而获得所需的客观信息。
图像识别:找到图像的特征,以便进一步处理。
图像理解:在图像分析的基础上得出对图像内容含义的理解及解释,从而指导和规划行为。
3. 名词解释:灰度、像素、图像分辨率、图像深度、图像数据量。
答:像素:在卫星图像上,由卫星传感器记录下的最小的分立要素(有空间分量和谱分量两种)。
通常,表示图像的二维数组是连续的,将连续参数 x,y ,和 f 取离散值后,图像被分割成很多小的网格,每个网格即为像素 图像分辨率:指对原始图像的采样分辨率,即图像水平或垂直方向单位长度上所包含的采样点数。
单位是“像素点/单位长度”图像深度是指存储每个像素所用的位数,也用于量度图像的色彩分辨率.图像深度确定彩色图像的每个像素可能有的颜色数,或者确定灰度图像的每个像素可能有的灰度级数.它决定了彩色图像中可出现的最多颜色数,或灰度图像中的最大灰度等级(图像深度:位图图像中,各像素点的亮度或色彩信息用二进制数位来表示,这一数据位的位数即为像素深度,也叫图像深度。
图像深度越深,能够表现的颜色数量越多,图像的色彩也越丰富。
)图像数据量:图像数据量是一幅图像的总像素点数目与每个像素点所需字节数的乘积。
西安交大数字图像处理第一次作业

数字图像处理第一次作业姓名:班级:学号:提交日期:2015年3月13日摘要本次报告首先简单阐述了BMP图像格式及其相关数据结构,随后主要完成了作业要求中关于图像处理与计算的各项任务。
本次作业以Matlab 2014为平台,通过对lena.bmp,elain.bmp图像文件的编程处理,分别得到了lena.bmp图像的8到1级灰度逐级递减显示,lena.bmp图像的均值和方差,通过近邻、双线性和双三次插值法对lena.bmp进行4倍放大后得到的2048×2048尺寸图像,和对lena.bmp、elain.bmp图像分别进行水平偏移变换和旋转变换后的图像及其4倍插值放大图像。
以上任务完成后均得到了预期的结果。
1.Bmp图像格式简介。
1.1 BMP格式概述BMP(全称Bitmap)是Windows操作系统中的标准图像文件格式,可以分成两类:设备相关位图(DDB)和设备无关位图(DIB),使用非常广。
它采用位映射存储格式,除了图像深度可选以外,不采用其他任何压缩,因此,BMP文件所占用的空间很大。
BMP文件的图像深度可选lbit、4bit、8bit及24bit。
BMP文件存储数据时,图像的扫描方式是按从左到右、从下到上的顺序。
1.2 BMP格式组成典型的BMP图像文件由四部分组成:(1)位图头文件数据结构,它包含BMP图像文件的类型、显示内容等信息;(2)位图信息数据结构,它包含有BMP图像的宽、高、压缩方法,以及定义颜色等信息;(3)调色板,这个部分是可选的,有些位图需要调色板,有些位图,比如真彩色图(24位的BMP)就不需要调色板;(4)位图数据,这部分的内容根据BMP位图使用的位数不同而不同,在24位图中直接使用RGB,而其他的小于24位的使用调色板中颜色索引值。
1.3 BMP格式对应数据结构BMP文件由文件头、位图信息头、颜色信息和图形数据四部分组成。
1.3.1 BMP文件头(14字节)BMP文件头数据结构含有BMP文件的类型、文件大小和位图起始位置等信息。
关于第2次作业(49布置,423截止)
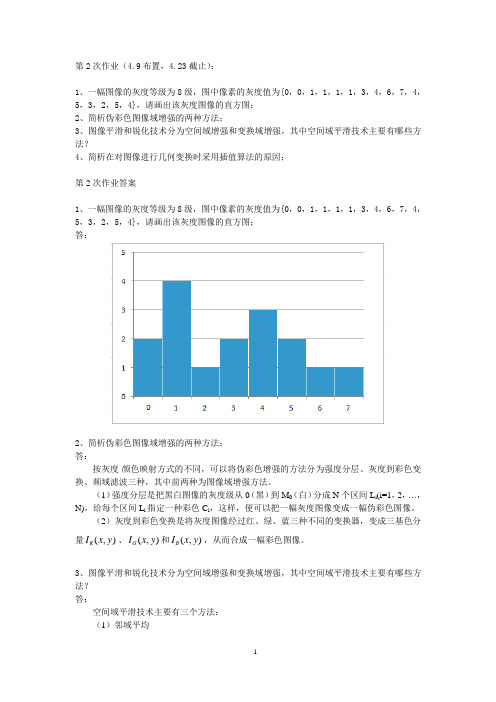
第2次作业(4.9布置,4.23截止):1、一幅图像的灰度等级为8级,图中像素的灰度值为{0,0,1,1,1,1,3,4,6,7,4,5,3,2,5,4},请画出该灰度图像的直方图;2、简析伪彩色图像域增强的两种方法;3、图像平滑和锐化技术分为空间域增强和变换域增强,其中空间域平滑技术主要有哪些方法?4、简析在对图像进行几何变换时采用插值算法的原因;第2次作业答案1、一幅图像的灰度等级为8级,图中像素的灰度值为{0,0,1,1,1,1,3,4,6,7,4,5,3,2,5,4},请画出该灰度图像的直方图;答:2、简析伪彩色图像域增强的两种方法;答:按灰度-颜色映射方式的不同,可以将伪彩色增强的方法分为强度分层、灰度到彩色变换、频域滤波三种,其中前两种为图像域增强方法。
(1)强度分层是把黑白图像的灰度级从0(黑)到M 0(白)分成N 个区间L i (i=1,2,…,N),给每个区间L i 指定一种彩色C i ,这样,便可以把一幅灰度图像变成一幅伪彩色图像。
(2)灰度到彩色变换是将灰度图像经过红、绿、蓝三种不同的变换器,变成三基色分量(,)R I x y 、(,)G I x y 和(,)B I x y ,从而合成一幅彩色图像。
3、图像平滑和锐化技术分为空间域增强和变换域增强,其中空间域平滑技术主要有哪些方法?答:空间域平滑技术主要有三个方法:(1)邻域平均假设图像是由许多灰度恒定的小块组成,相邻像素间存在很高的空间相关性,而噪声则是统计独立的。
因此,可用当前像素邻域内各像素的灰度平均值代替该像素原来的灰度值,实现图像的平滑去噪。
(2)中值滤波对一个滑动窗口内各个像素的灰度值进行排序,用其中值代替窗口中心像素的原来灰度值,因此是一种非线性的图像平滑法。
(3)图像间运算对图像进行相减运算,可以把两图的差异显示出来,常用于去除背景和运动检测。
图像平均常用于在图像采集中去除加性噪声,随着平均图像数量的增加,噪声在每个像素位置的影响将逐渐减小。
西安交通大学数字图像处理第二次作业知识分享

数字图像处理的基本数学工具的使用摘要本报告主要介绍了运用编程软件MATLAB对图像灰度级进行变换、求取图像均值与方差、采用不同的内插方法对图像进行缩放及利用仿射变换对图像进行空间变换处理的方法。
同时,对最近邻内插法、双线性内插法、双三次内插法进行图像处理的效果进行了详细的对比,并对出现差异的原因做出了简要分析。
姓名: X X X班级:学号:提交日期:年月日2_1. 把lena 512*512图像灰度级逐级递减8-1显示;(1)问题分析:所要实现的功能是:在不改变图像大小的前提下,使得整幅图像的灰度级逐级递减并将图像显示出来;即对所有像素点的灰度依次进行除2操作;(2)实验过程:工具:MATLAB软件;利用imread()函数将图像读入MATLAB,利用imshow()对原图像进行显示,再利用循环体对整幅图像的灰度级逐级递减并一一进行显示。
源代码附于本报告最后一部分。
(3)实验结果:备注:在大小为512X512的途中观察更为方便,但此处为了便于排版以及将结果进行对比对所有图像做了一定的缩小。
a bc de fg h图2_1 (a)大小为512X512的256灰度级图像;(b)~(h)保持图像大小不变的同时以灰度级128,62,32,16,8,4,2显示的图像。
(4)结果分析:对图2_1中的(a)~(h)图像进行对比可知,256级、128级、64级以及32级灰度的图像几乎没有太大的区别;然而在灰度级为16的图(e)中出现了较为明显的伪轮廓,这种效果是由数字图像的平滑区域中的灰度级数不足引起的。
(说明:此分析为本人肉眼的观察结果,对细节的观察难免存在疏漏之处,还请批评指正。
)2_2. 计算lena图像的均值方差;(1)问题分析:所要实现的功能是:计算图像‘lena.bmp’的均值与方差;(2)实验过程:工具:MATLAB软件;利用imread()函数将图像读入MATLAB,由于二维数字图像使用二维阵列表示的,因而可以直接利用MATLAB中的mean2()及std2()分别求整幅图像的均值于方差;源代码附于本报告最后一部分。
西安交大自动化专业多传感器信息融合作业2

上的高斯白噪声,标准差为 10 。 目标初始状态为 X 1 = [10000 −100 10000 0] ,雷达本身位置分别
T
为 ( 0 0 ) 和 (10000m 0 ) 。用 Matlab 语言,完成以下功能,要求附上全 部源代码并做简要分析。 (1)在同一张图上,画出目标真实轨迹、雷达 1 量测的目标轨 迹和雷达 2 量测的目标轨迹。 (2 ) 用蒙特卡洛法仿真 500 次, 并用扩展卡尔曼滤波算法 (EKF) ,
分别计算出雷达 1 估计的目标状态和雷达 2 估计的目标状态。并将 2 个雷达量测的距离均方根误差、2 个雷达估计的距离均方根误差画在 一张图上。 距离均方根误差定义如下:
RMSE position (k ) =
1 M ˆ x ∑⎡ ⎣(
i =1 M k
2 2 ˆ k − yk ) ⎤ − xk ) + ( y ⎦
+ vr ,k ⎤ ⎥ ⎥, ⎛ y − yi ⎞ ⎥ v arctan ⎜ k + ⎟ θ ,k ⎥ ⎝ xk − xi ⎠ ⎦
2
i = 1, 2
其中 ( xi yi ) 为雷达本身的坐标, ( xk
yk ) 为目标在 k 时刻的位置。
vr 为距离量测上的零均值高斯白噪声,标准差为 10m。 vθ 为角度量测
⎡ wx ,k ⎤ 2 wk = ⎢ ⎥ , wx , k , wy , k 均为零均值高斯白噪声,标准差为 1 m s w ⎣ y ,k ⎦
第 i 个雷达的量测方程为:
⎡ r ⎡ k ,i ⎤ ⎢ =⎢ ⎥=⎢ ⎣θ k ,i ⎦ ⎢ ⎢ ⎣
( xk − xi ) + ( yk − yi )
2
Z k ,i
作业 2 非线性量测滤波与分布式融合
西南交大数字图像处理第二次试验

西南交⼤数字图像处理第⼆次试验数字图像处理第⼆次实验注意提交实验报告的⽂件名格式(姓名+学号+实验报告⼆.doc)实验三灰度变换增强⼀、实验⽬的1.熟悉matlab图像处理⼯具箱及直⽅图函数的使⽤;2.了解灰度变换增强的Matlab实现⽅法3.掌握直⽅图灰度变换⽅法4.理解和掌握直⽅图原理和⽅法;⼆、实验内容1. 线段上像素灰度分布读⼊灰度图像'peppers_gray.bmp',采⽤交互式操作,⽤improfile绘制⼀条线段的灰度值。
imshow(rgb2gray(imread('peppers.bmp')))Improfile读⼊RGB图像‘flowers.tif’,显⽰所选线段上红、绿、蓝颜⾊分量的分布imshow('flowers.tif')Improfile2. 直⽅图变换A)直⽅图显⽰在matlab环境中,程序⾸先读取图像'cameraman.tif',然后调⽤直⽅图函数,设置相关参数,再输出处理后的图像。
I=imread('cameraman.tif'); %读取图像subplot(1,2,1),imshow(I) %输出图像title('原始图像') %在原始图像中加标题subplot(1,2,2),imhist(I) %输出原图直⽅图title('原始图像直⽅图') %在原图直⽅图上加标题读⼊图像‘rice.png’,在⼀个窗⼝中显⽰灰度级n=64,128和256的图像直⽅图。
I=imread('rice.png');imshow(I)I=imread('rice.png');subplot(1,3,1),imhist(I,64)title('n=64')subplot(1,3,2),imhist(I,128)title('n=128')subplot(1,3,3),imhist(I,256)title('n=256')B)直⽅图灰度调节利⽤函数imadjust调解图像灰度范围,观察变换后的图像及其直⽅图的变化。
数字图像处理大作业(DOC)

大作业指导书题目:数字图像处理院(系):物联网工程学院专业: 计算机班级:计算机1401-1406指导老师:学号:姓名:设计时间: 2016-2017学年 1学期摘要 (3)一、简介 (3)二、斑点数据模型.参数估计与解释 (4)三、水平集框架 (5)1.能量泛函映射 (5)2.水平集传播模型 (6)3.随机评估方法 (7)四、实验结果 (8)五、总结 (11)基于水平集方法和G0模型的SAR图像分割Abstract(摘要)这篇文章提出了一种分割SAR图像的方法,探索利用SAR数据中的统计特性将图像分区域。
我们假设为SAR图像分割分配参数,并与水平集模型相结合。
分布属于G分布中的一种,处于数据建模的目的,它们已经成功的被用于振幅SAR图像中不同区域的建模。
这种统计数据模型是驱动能量泛函执行区域映射的基础,被引用到水平集传播数值方案中,将SAR 图像分为均匀、异构和极其异构区域。
此外,我们引入了一个基于随机距离和模型的评估过程,用于量化我们方法的鲁棒性和准确性。
实验结果表明,我们的算法对合成和真实SAR 数据都具有准确性。
+简介1、Induction(简介)合成孔径雷达系统是一种成像装置,采用相干照明比如激光和超声波,并会受到斑点噪声的影响。
在SAR图像处理过程中,返回的是斑点噪声和雷达切面建模在一起的结果。
这个积性模型(文献[1])因包含大量的真实SAR数据,并且在获取过程中斑点噪声被建模为固有的一部分而被广泛应用。
因此,SAR图像应用区域边界和目标检测变得更加困难,可能需要斑点去除。
因此,斑点去除是必需的,有效的方法可以在文献[2][3][4][5][6][7][8][9][10]中找到。
对于SAR图像分割,水平集方法构成一类基于哈密顿-雅克比公式的重要算法。
水平集方法允许有效的分割标准公式,从文献[12]中讨论的传播函数项可以得到。
经典方法有着昂贵的计算成本,但现在的水平集的实现配置了有趣的低成本的替换。
西安交大数字图像处理第一次作业.

数字图像处理第一次作业姓名:班级:学号:提交日期:2015年3月13日摘要本次报告首先简单阐述了BMP图像格式及其相关数据结构,随后主要完成了作业要求中关于图像处理与计算的各项任务。
本次作业以Matlab 2014为平台,通过对lena.bmp,elain.bmp图像文件的编程处理,分别得到了lena.bmp图像的8到1级灰度逐级递减显示,lena.bmp图像的均值和方差,通过近邻、双线性和双三次插值法对lena.bmp进行4倍放大后得到的2048×2048尺寸图像,和对lena.bmp、elain.bmp图像分别进行水平偏移变换和旋转变换后的图像及其4倍插值放大图像。
以上任务完成后均得到了预期的结果。
1.Bmp图像格式简介。
1.1 BMP格式概述BMP(全称Bitmap)是Windows操作系统中的标准图像文件格式,可以分成两类:设备相关位图(DDB)和设备无关位图(DIB),使用非常广。
它采用位映射存储格式,除了图像深度可选以外,不采用其他任何压缩,因此,BMP文件所占用的空间很大。
BMP文件的图像深度可选lbit、4bit、8bit及24bit。
BMP文件存储数据时,图像的扫描方式是按从左到右、从下到上的顺序。
1.2 BMP格式组成典型的BMP图像文件由四部分组成:(1)位图头文件数据结构,它包含BMP图像文件的类型、显示内容等信息;(2)位图信息数据结构,它包含有BMP图像的宽、高、压缩方法,以及定义颜色等信息;(3)调色板,这个部分是可选的,有些位图需要调色板,有些位图,比如真彩色图(24位的BMP)就不需要调色板;(4)位图数据,这部分的内容根据BMP位图使用的位数不同而不同,在24位图中直接使用RGB,而其他的小于24位的使用调色板中颜色索引值。
1.3 BMP格式对应数据结构BMP文件由文件头、位图信息头、颜色信息和图形数据四部分组成。
1.3.1 BMP文件头(14字节)BMP文件头数据结构含有BMP文件的类型、文件大小和位图起始位置等信息。
数字图像处理第二次作业

2014301220040李进华Problem 3.13The purpose of this simple problem is to make the student think of the meaningof histograms and arrive at the conclusion that histograms carry no informationabout spatial properties of images. Thus, the only time that the histogram of the images formed by the operations shown in the problem statement can be determined in terms of the original histograms is when one (both) of the imagesis (are) constant. In (d) we have the additional requirement that none of thepixels of g(x, y) can be 0. Assume for convenience that the histograms are not normalized, so that,for example,h f (r k )is the number of pixels in f (x, y) havingIn tensity level r k. Assume also that all the pixels in g(x, y)have constant value c.The pixels of both images are assumed to be positive. Finally, let u k denote the intensity levels of the pixels of the images formed by any of the arithmetic operations given in the problem statement. Under the preceding set of conditions,the histograms are determined as follows:(a) We obtain the histogram h sum (u k ) of the sum by letting u k =r k +c, and alsoh sum (u k ) = h f (r k ) for all k. In other words, the values (height) of the components of h sum are the same as the components of h f , but their locations on the intensity axis are shifted right by an amount c.(b) Similarly, the histogram h diff (u k ) of the difference has the same componentsas h f but their locations are moved left by an amount c as a result of the sub-traction operation.(c) Following the same reasoning, the values (heights) of the components of histogram h prod (u k ) of the product are the same as h f , but their locations are atu k = c ×r k . Note that while the spacing between components of the resulting histograms in (a) and (b) was not affected, the spacing between components ofh prod (u k ) will be spread out by an amount c.(d) Finally, assuming that c ≠0, the components of h div (u k ) are the same asthose of h f , but their locations will be at u k = r k /c. Thus, the spacing between components of h div (u k ) will be compressed by an amount equal to 1/c. The preceding solutions are applicable if image f (x, y) is constant also. In this casethe four histograms just discussed would each have only one component. Their location would be affected as described (a) through (d).Problem 3.14(a)Thenumberofboundarypointsbetweentheblackandwhiteregionsismuchlarger in the image on the right. When the images are blurred, the boundarypoints will give rise to a larger number of different values for the image on theright, so the histograms of the two blurred images will be different.(b) To handle the border effects, we surround the image with a border of 0s. We assume that image is of size N ×N (the fact that the image is square is evident from the right image in the problem statement). Blurring is implemented bya 3×3 mask whose coefficients are 1/9. Figure P3.14 shows the different typesof values that the blurred left image will have (see image in the problem statement). The values are summarized in Table P3.14-1. It is easily verified that thesum of the numbers on the left column of the table is N 2 . A histogram is easily constructed from the entries in this table. A similar (tedious) procedure yieldsthe results in Table P3.14-2.Problem 3.16(a)The key to solving this problem is to recognize (1) that the convolution resultat any location (x,y) consists of centering the mask at that point and then formingthesumoftheproductsofthemaskcoefficientswiththecorrespondingpixels in the image; and (2) that convolution of the mask with the entire image results in every pixel in the image being visited only once by every element ofthe mask (i.e., every pixel is multiplied once by every coefficient of the mask). Because the coefficients of the mask sum to zero, this means that the sum of the products of the coefficients with the same pixel also sum to zero. Carrying outthis argument for every pixel in the image leads to the conclusion that the sumof the elements of the convolution array also sum to zero.(b) The only difference between convolution and correlation is that the maskis rotated by 180 ◦. This does not affect the conclusions reached in (a), so cor- relating an image with a mask whose coefficients sum to zero will produce acorrelation image whose elements also sum to zero.Problem 3.17One of the easiest ways to look at repeated applications of a spatial filter is to use superposition. Let f (x, y) and h(x, y) denote the image and the filter function, respectively. Assuming square images of size N ×N for convenience, we can express f (x, y) as the sum of at most N 2 images, each of which has only one nonzero pixel (initially, we assume that N can be infinite). Then, the process of running h(x, y) over f (x, y) can be expressed as the following convolution:h(x,y) ★f (x,y) =h(x,y) ★[f1 (x,y)+ f 2 (x,y)+···+ f N 2 (x,y)]Suppose for illustrative purposes that f i (x,y) has value 1 at its center, while the other pixels are valued 0, as discussed above (see Fig. P3.17a). If h(x,y) is a3×3 mask of 1/9’s (Fig. P3.17b), then convolving h(x,y) with f i (x,y) will produce an image with a 3×3 array of 1/9’s at its center and 0s elsewhere, as Fig.P3.17(c) shows. If h(x,y) is now applied to this image, the resulting image willbe as shown in Fig. P3.17(d). Note that the sum of the nonzero pixels in both Figs. P3.17(c) and (d) is the same, and equal to the value of the original pixel. Thus, it is intuitively evident that successive applications of h(x,y) will ”diffuse”the nonzero value of f i (x,y) (not an unexpected result, because h(x,y)is a blurring filter). Since the sum remains constant, the values of the nonzero elements will become smaller and smaller, as the number of applications of the filter increases. The overall result is given by adding all the convolved f k (x,y),for k =1,2,...,N 2 .It is noted that every iteration of blurring further diffuses the values out- wardly from the starting point. In the limit, the values would get infinitely small, but, because the average value remains constant, this would require an image of infinite spatial proportions. It is at this junction that border conditions become important. Although it is not required in the problem statement, it is instructive to discuss in class the effect of successive applications of h(x,y) to an image of finite proportions. The net effect is that, because the values cannot diffuse out- ward past the boundary of the image, the denominator in the successive appli- cationsofaveragingeventuallyoverpowersthepixelvalues, driving the image to zero in the limit. A simple example of this is given in Fig. P3.17(e), which shows an array of size 1×7 that is blurred by successive applications of the 1×3 mask h(y) =13 [1,1,1]. We see that, as long as the values of the blurred 1 can diffuseout, the sum,S, of the resulting pixels is 1. However, when the boundary is met, an assumption must be made regarding how mask operations on the border are treated. Here, we used the commonly made assumption that pixel value imme- diately past the boundary are 0. The mask operation does not go beyond the boundary, however. In this example, we see that the sum of the pixel values be- gins to decrease with successive applications of the mask. In the limit, the term 1/(3) n would overpower the sum of the pixel values, yielding an array of 0s.Problem 3.21From Fig. 3.33 we know that the vertical bars are 5 pixels wide, 100 pixels high, and their separation is 20 pixels. The phenomenon in question is related to the horizontal separation between bars, so we can simplify the problem by consid- ering a single scan line through the bars in the image. The key to answering this question lies in the fact that the distance (in pixels) between the onset of one bar and the onset of the next one (say, to its right) is 25 pixels.Consider the scan line shown in Fig. P3.21. Also shown is a cross sectionof a 25×25 mask. The response of the mask is the average of the pixels that it encompasses. We note that when the mask moves one pixel to the right, it loses one value of the vertical bar on the left, but it picks up an identical one on the right, so the response doesn’t change. In fact, the number of pixels belonging to the vertical bars and contained within the mask does not change, regardless of where the mask is located (as long as it is contained within the bars, and not near the edges of the set of bars).The fact that the number of bar pixels under the mask does not change is dueto the peculiar separation between bars and the width of the lines in relationto the 25-pixel width of the mask This constant response is the reason why no white gaps are seen in the image shown in the problem statement. Note that this constantresponsedoesnothappenwiththe23×23orthe45×45masksbecause they are not ”synchronized”with the width of the bars and their separation.Problem 3.23The student should realize that both the Laplacian and the averaging process are linear operations, so it makes no difference which one is applied first.。
数字图像处理作业题目

数字图像处理作业班级:Y100501姓名:雷锋学号:000000001一、编写程序完成不同滤波器的图像频域降噪和边缘增强的算法并进行比较,得出结论。
频域降噪。
对图像而言,噪声一般分布在高频区域,而图像真是信息主要集中在低频区,所以,图像降噪一般是利用低通滤波的方法来降噪。
边缘增强。
图像的边缘信息属于细节信息,主要由图像的高频部分决定,所以,边缘增强一般采取高通滤波,分离出高频部分后,再和原频谱进行融合操作,达到边缘增强,改善视觉效果,或者为进一步处理奠定基础的目的。
1频域降噪,主程序如下:I=imread('lena.bmp'); %读入原图像文件J=imnoise(I,'gaussian',0,0.02);%加入高斯白噪声A=ilpf(J,0.4);%理想低通滤波figure,subplot(222);imshow(J);title('加噪声后的图像');subplot(222);imshow(A);title('理想低通滤波');B=blpf(J,0.4,4);%巴特沃斯低通滤波subplot(223);imshow(B);title('巴特沃斯低通滤波');C=glpf(J,0.4);%高斯低通滤波subplot(224);imshow(C);title('高斯低通滤波');用到的滤波器函数的程序代码如下:function O=ilpf(J,p) %理想低通滤波,p是截止频率[f1,f2]=freqspace(size(J),'meshgrid');hd=ones(size(J));r=sqrt(f1.^2+f2.^2);hd(r>p)=0;y=fft2(double(J));y=fftshift(y);ya=y.*hd;ya=ifftshift(ya);ia=ifft2(ya);O=uint8(real(ia));function O=blpf(J,d,n) %巴特沃斯低通滤波器,d是截止频率,n是阶数[f1,f2]=freqspace(size(J),'meshgrid');hd=ones(size(J));r=f1.^2+f2.^2;for i=1:size(J,1)for j=1:size(J,2)t=r(i,j)/(d*d);hd(i,j)=1/(t^n+1);endendy=fft2(double(J));y=fftshift(y);ya=y.*hd;ya=ifftshift(ya);ia=ifft2(ya);O=uint8(real(ia));function O=glpf(J,D) %高斯滤波器,D是截止频率[f1,f2]=freqspace(size(J),'meshgrid');r=f1.^2+f2.^2;Hd=ones(size(J));for i=1:size(J,1)for j=1:size(J,2)t=r(i,j)/(D*D);Hd(i,j)=exp(-t);endendY=fft2(double(J));Y=fftshift(Y);Ya=Y.*Hd;Ya=ifftshift(Ya);ia=ifft2(Ya);O=uint8(real(ia));运行结果如图1所示。
数字图像处理期末大作业
数字图像处理期末大作业一、问题描述实现第十章中采用Hough变换来检测图像中圆的过程。
,通过包括平滑(把细节去除),边缘检测(得到轮廓)以及Hough变换得到的圆,并把结果叠加到原来的灰度图像上。
给出具体的过程,中间结果,最后结果,实现的代码,并写出报告。
二、图片的获取以及预处理针对老师提供的一副硬币图片,要求检测出其中的hough圆,并叠加到原图像上以便增强图像。
在检测hough圆之前,首先要对图像进行平滑处理,进行拉普拉斯变换,然后检测垂直方向,水平方向,+45度和-45度方向的边缘,将四个方向的边缘叠加起来,得到总的边缘,对该图像进行二值化,然后对得到的图像检测其hough圆,得到圆形边缘,将该图像叠加到原图像上,就实现了图像边缘增强的目的。
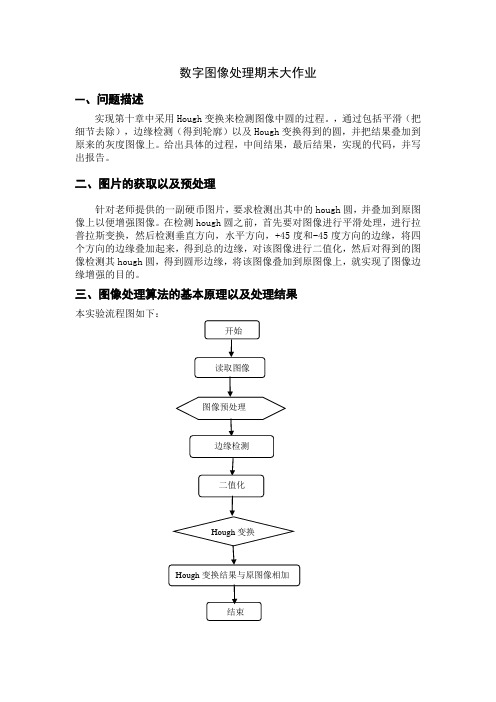
三、图像处理算法的基本原理以及处理结果本实验流程图如下:1.读取图像图像处理的第一步就是对所采集的图像进行读入,本次实验的输入图像是一幅灰度图像,不需要将图像转换成为灰度图像,直接利用函数imread ()完成。
原图像如下所示:原图像2.图像预处理在图像预处理中,我们完成了两步工作,首先使用方差为1的高斯噪声对图像进行平滑,然后进行拉普拉斯变换,即)],(*)([2y x f r h ∇,222r 2e 21)(σσ-=πr h 为方差为2σ的高斯噪声,本实验中12=σ。
又),(*)]([)],(*)([22y x f r h y x f r h ∇=∇,其中2224222]2[)(σσσr er r h --=∇,将)(2r h ∇和),(y x f 分别进行傅里叶别换,将其逐点相乘,再进行傅里叶反变换,就得到了预处理后的图像。
3.边缘检测对水平,垂直,+45度,-45度方向进行边缘检测,本实验中我们采用了Prewitt 梯度算子,它用于检测水平方向,垂直方向,+45度方向和-45度方向的掩膜分别如下:水平掩膜 垂直掩膜 +45度掩膜 -45度掩膜使用这四个掩膜分别对上一步得到的图像逐点进行处理,就可以得到四个方向的边缘了(本实验中边缘的一个像素都不处理),再将它们加起来,就得到了总的边缘,实验结果如下:水平边缘垂直边缘-45度边缘总的边缘如下图所示:4.二值化对上图得到的图像进行二值化,这里我采用的是循环方式确定图像全局阈值,即首先以图像的平均值作为阈值,将图像分成两部分,分别求两部分的平均值,新的阈值为这两个平均值的均值,重复上述过程,直到两次阈值之差小于特定的值时停止,并以最后一次得到的阈值对图像进行二值化,本实验中我要求两次阈值之差小于0.5时停止,最后得到的全局阈值为 -102.1332,二值化后的图像如下所示:二值化后的图像5.Hough变换检测圆形边界Hough 变换的原理就是利用图像全局特征将边缘像素连接起来组成区域封闭边界,它将图像空间转换到参数空间,在参数空间对点进行描述,达到检测图像边缘的目的。
西安交大数字图像处理第二次实验报告

数字图像处理第二次作业摘要本次报告主要记录第二次作业中的各项任务完成情况。
本次作业以Matlab 2013为平台,结合matlab函数编程实现对lena.bmp,elain1.bmp图像文件的相关处理:1.分别得到了lena.bmp 512*512图像灰度级逐级递减8-1显示,2.计算得到lena.bmp图像的均值和方差,3.通过近邻、双线性和双三次插值法将lena.bmp zoom到2048*2048,4. 把lena和elain图像分别进行水平shear(参数可设置为1.5,或者自行选择)和旋转30度,并采用用近邻、双线性和双三次插值法zoom到2048*2048。
以上任务完成后均得到了预期的结果。
1.把lena 512*512图像灰度级逐级递减8-1显示(1)实验原理:给定的lena.bmp是一幅8位灰阶的图像,即有256个灰度色。
则K位灰阶图像中某像素的灰度值k(x,y)(以2k阶色为基准)与原图同像素的灰度值v(x,y)(以256阶色为基准)的对应关系为:k(x,y)=floor(v(x,y))28−k式中floor函数为向下取整操作。
取一确定k值,对原图进行上式运算即得降阶后的k位灰阶图像矩阵。
(2)实验方法首先通过imread()函数读入lena.bmp得到图像的灰度矩阵I,上式对I矩阵进行灰度降阶运算,最后利用imshow()函数输出显示图像。
对应源程序为img1.m。
(3)处理结果8灰度级7灰度级6灰度级5灰度级4灰度级3灰度级2灰度级(4)结果讨论:由上图可以看出,在灰度级下降到5之前,肉眼几乎感觉不出降阶后图像发生的变化。
但从灰度级4开始,肉眼明显能感觉到图像有稍许的不连续,在灰度缓变区常会出现一些几乎看不出来的非常细的山脊状结构。
随着灰度阶数的继续下降,图像开始出现大片的伪轮廓,灰度级数越低,越不能将图像的细节刻画出来,最终的极端情况是退化为只有黑白两色的二值化图像。
由此可以得出,图像采样的灰度阶数越高,灰度范围越大,细节越丰富,肉眼看去更接近实际情况。
图像处理第二次作业

图像处理第二次作业一. 几何畸变的图像如何被复原?为什么灰度插值是必要的?(15分) 答:先创建一个与畸变图像大小相同的空数字矩阵,然后用这个矩阵存放校正后的图像.接着给这个矩阵中的每个元素赋予灰度值,可以通过两步运算来实现,第一步插入灰度值, 第二步空间转换,灰度插值是必要:二. 下图中的网格图是几何畸变图像,阿拉伯数字是灰度值。
已知像素点ABCD 畸变前的位置分别是(0,0),(3,0),(0,3),(3,3)。
假设ABCD 的畸变可以由双线性插值来建模。
求畸变前点(2,2)处的灰度值。
灰度插值采用最近邻插值。
(15分)4 3 2 5 1 3 3 4 2 40 5 5 3 3 0 4 2 1 22 1 0 3 5三. 假设当摄录静态场景时,相机沿平行于图像平面(x,y)的平面移动。
相机延时从t=0到t=T (T 是常数)。
请利用传递函数对由相机移动产生的图像退化过程建模。
(15分)四. 设某一幅图像共有8个灰度级,各灰度级出现的概率分别为:P1=0.20,P2=0.09,P3=0.11,P4=0.13,P5=0.07,P6=0.12,P7=0.08,P8=0.20。
试对此图像进行霍夫曼编码,并计算信源的熵、平均码长、编码效率及冗余度。
(15分)5.图像编码有哪些国际标准?它们的基本应用对象分别是什么?(15分)答: 1、JPEG (Joint Photographic Expert Group )AB C DJPEG是ISO/IEC联合图像专家组制定的静止图像压缩标准,是适用于连续色调(包括灰度和彩色)静止图像压缩算法的国际标准。
JPEC算法共有4种运行模式,其中一种是基于空间预测(DPCM)的无损压缩算法,另外3种是基于DCT的有损压缩算法。
1)无损压缩算法,可以保证无失真地重建原始图像。
2)基于DCT的顺序模式,按从上到下,从左到右的顺序对图像进行编码,称为基本系统。
3)基于DCT的递进模式,指对一幅图像按由粗到细对图像进行编码。
数字图像处理第二次作业
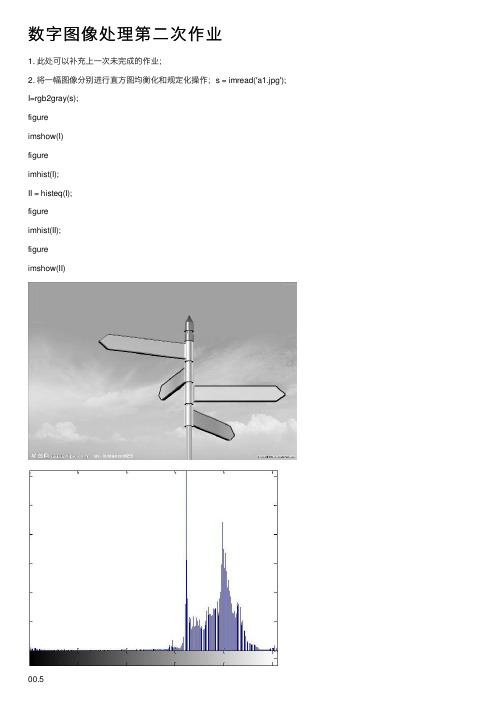
数字图像处理第⼆次作业1. 此处可以补充上⼀次未完成的作业;2. 将⼀幅图像分别进⾏直⽅图均衡化和规定化操作;s = imread('a1.jpg'); I=rgb2gray(s);figureimshow(I)figureimhist(I);II = histeq(I);figureimhist(II);figureimshow(II)2.5 3 4 50 100 150 200 250200250s = imread('a1.jpg'); I=rgb2gray(s); [m,n] = size(I); for i=1 :8:257 count(i)=i;endN = histeq(I,count);figureimshow(N)figureimhist(N);00.511.522.533.54501001502002503. 将⼀幅被椒盐噪声影响的图像分别使⽤3×3、5×5和7×7的模版进⾏均值滤波,将原图像和滤波之后的图像显⽰出来。
并总结说明模版尺⼨对图像效果的影响; i = imread('c1.png'); i=rgb2gray(i);j=imnoise(i,'salt & pepper',0.02); subplot(231), imshow(i);title('?-í?')subplot(232), imshow(j);title('ìí?óá??·éù'); K1 = filter2(fspecial('average',3),j); K2 = filter2(fspecial('average',5),j); K3 = filter2(fspecial('average',7),j);subplot(233), imshow(uint8(K1));title('3X32¨') subplot(234), imshow(uint8(K2));title('5X52¨') subplot(235), imshow(uint8(K3));title('7X72¨')原图添加了椒盐噪声3X3平滑滤波5X5平滑滤波7X7平滑滤波当所⽤平板模板尺⼨增⼤时,对噪声的消除有所增强,但同时所得到的图像便得更加模糊,细节的锐化部分逐步减弱。
数字图像处理每章课后题参考答案

数字图像处理每章课后题参考答案第一章和第二章作业:1.简述数字图像处理的研究内容?答:数字图像处理的主要研究内容,根据其主要的处理流程与处理目标大致可以分为图像信息的描述、图像信息的处理、图像信息的分析、图像信息的编码以及图像信息的显示等几个方面,将这几个方面展开,具体有以下的研究方向:1.图像数字化,2.图像增强,3.图像几何变换,4.图像恢复,5.图像重建,6.图像隐藏,7.图像变换,8.图像编码,9.图像识别与理解。
2.什么是图像工程?根据抽象程度和研究方法等的不同,图像工程可分为哪几个层次?每个层次包含哪些研究内容?答:图像工程是一门系统地研究各种图像理论、技术和应用的新的交叉科学。
根据抽象程度、研究方法、操作对象和数据量等的不同,图像工程可分为三个层次:图像处理、图像分析、图像理解。
图像处理着重强调在图像之间进行的变换。
比较狭义的图像处理主要满足对图像进行各种加工以改善图像的视觉效果。
图像处理主要在图像的像素级上进行处理,处理的数据量非常大。
图像分析则主要是对图像中感兴趣的目标进行检测和测量,以获得它们的客观信息从而建立对图像的描述。
图像分析处于中层,分割和特征提取把原来以像素描述的图像转变成比较简洁的非图形式描述。
图像理解的重点是进一步研究图像中各目标的性质和它们之间的相互联系,并得出对图像内容含义的理解以及对原来客观场景的解释,从而指导和规划行为。
图像理解主要描述高层的操作,基本上根据较抽象地描述进行解析、判断、决策,其处理过程与方法与人类的思维推理有许多相似之处。
第三章图像基本概念1.图像量化时,如果量化级比较小时会出现什么现象?为什么?答:当实际场景中存在如天空、白色墙面、人脸等灰度变化比较平缓的区域时,采用比较低的量化级数,则这类图像会在画面上产生伪轮廓(即原始场景中不存在的轮廓)。
图像的量化等级反映了采样的质量,数字图像的量化级数随图像的内容及处理的目的差别而不同,低的量化级数只满足于处理简单的线条而对于图像,若线条不明显时,则会产生伪轮廓。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数字图像处理的基本数学工具的使用摘要本报告主要介绍了运用编程软件MATLAB对图像灰度级进行变换、求取图像均值与方差、采用不同的内插方法对图像进行缩放及利用仿射变换对图像进行空间变换处理的方法。
同时,对最近邻内插法、双线性内插法、双三次内插法进行图像处理的效果进行了详细的对比,并对出现差异的原因做出了简要分析。
姓名: X X X班级:学号:提交日期:年月日2_1. 把lena 512*512图像灰度级逐级递减8-1显示;(1)问题分析:所要实现的功能是:在不改变图像大小的前提下,使得整幅图像的灰度级逐级递减并将图像显示出来;即对所有像素点的灰度依次进行除2操作;(2)实验过程:工具:MATLAB软件;利用imread()函数将图像读入MATLAB,利用imshow()对原图像进行显示,再利用循环体对整幅图像的灰度级逐级递减并一一进行显示。
源代码附于本报告最后一部分。
(3)实验结果:备注:在大小为512X512的途中观察更为方便,但此处为了便于排版以及将结果进行对比对所有图像做了一定的缩小。
a bc de fg h图2_1 (a)大小为512X512的256灰度级图像;(b)~(h)保持图像大小不变的同时以灰度级128,62,32,16,8,4,2显示的图像。
(4) 结果分析:对图2_1中的(a)~(h)图像进行对比可知,256级、128级、64级以及32级灰度的图像几乎没有太大的区别;然而在灰度级为16的图(e)中出现了较为明显的伪轮廓,这种效果是由数字图像的平滑区域中的灰度级数不足引起的。
(说明:此分析为本人肉眼的观察结果,对细节的观察难免存在疏漏之处,还请批评指正。
)2_2. 计算lena 图像的均值方差;(1) 问题分析:所要实现的功能是:计算图像‘lena.bmp ’的均值与方差; (2) 实验过程:工具:MATLAB 软件;利用imread()函数将图像读入MATLAB ,由于二维数字图像使用二维阵列表示的,因而可以直接利用MATLAB 中的mean2()及std2()分别求整幅图像的均值于方差; 源代码附于本报告最后一部分。
(3) 实验结果:均值 m =99.0512 方差 =52.8776。
2_3. 把lena 图像用近邻、双线性和双三次插值法zoom 到2048*2048;(1)问题分析:分别用三种内插方法将图像‘lena.bmp’由512X512放大到2048X2048;(2)实验过程:工具:MATLAB软件;函数B=imresize(A,[numrows,numcols],’method’)功能说明:‘method’指所采用的内插方法,一般默认为’nearest’(最近邻内插法),还可指定为’bilinear’(双线性内插法)、’bicubic’(双三次内插法);A指原图像;numrows用于指定变换后的图像的行数,numcols用于指定变换后的图像的列数;源代码附于本报告最后一部分。
(3)实验结果:图2_31 (a) 大小为512*512的原图像;(b)~(d) 分别为采用最近邻、双线性、双三次内插法进行内插后得到的大小为2048*2048的图像(4)结果分析:abcd图2_32 (a)~(d)分别为图2_31中(a)~(d)的部分截取将图2_32中的(a)~(d)进行对比可知:原图像与经过最近邻内插所得的图像的肩膀以及脸颊部分的曲线呈现锯齿状;采用双线性内插法所得的图像的肩膀以及脸颊部分的曲线则比较平滑,基本没有锯齿出现;而采用双三次内插法所得的图像的曲线均非常平滑。
原因分析:最近邻内插法把原图像中最近邻的灰度赋给了每个新位置,这种方法简单,但有产生不希望的人为缺陷的倾向;双线性内插法用4个最近邻去估计给定位置的灰度,通常所给出的内插效果会比最近邻法好,但计算量也相对有所增加;双三次内插法用16个最近邻点的灰度去估计给定位置的灰度,因而在保持细节方面比双线性内插法要好。
2_4. 把lena和elain图像分别进行水平shear(参数可设置为1.5,或者自行选择)和旋转30度,并采用用近邻、双线性和双三次插值法zoom到2048*2048;(1)问题分析:先将lena和elain分别进行水平偏移变换、旋转变换,再讲变换后的图像利用最近邻内插法、双线性内插法、双三次内插法缩放为大小为2048*2048的图像,并进行显示。
(2)实现过程:先读入图像I=imread(),再根据需要输入矩阵T=[],再创建仿射矩阵tform=maketform(‘affine’,T);,其次进行空间变换II=imtrasform(I,tform);,最后再进行内插并进行图像显示;源代码附于本报告最后一部分。
(3)实验结果:abcd图2_4_1 (a)512*512的lena原图像;(b)将图(a)进行水平偏移变换()并采用最近邻内插法zoom到2048*2048后的图像;(c)将图(a)进行水平偏移变换()并采用双线性内插法zoom到2048*2048后的图像;(d)将图(a)进行水平偏移变换()并采用双三次内插法zoom到2048*2048后的图像。
abcd图2_4_2 (a)512*512的elain1原图像;(b)将图(a)进行水平偏移变换()并采用最近邻内插法zoom到2048*2048后的图像;(c)将图(a)进行水平偏移变换()并采用双线性内插法zoom到2048*2048后的图像;(d)将图(a)进行水平偏移变换()并采用双三次内插法zoom到2048*2048后的图像。
abcd图2_4_3 (a)512*512的lena原图像;(b)将图(a)进行旋转变换()并采用最近邻内插法zoom到2048*2048后的图像;(c)将图(a)进行旋转变换()并采用双线性内插法zoom到2048*2048后的图像;(d)将图(a)进行旋转变换()并采用双三次内插法zoom到2048*2048后的图像。
abcd图2_4_4 (a)512*512的elain原图像;(b)将图(a)进行旋转变换()并采用最近邻内插法zoom到2048*2048后的图像;(c)将图(a)进行旋转变换()并采用双线性内插法zoom到2048*2048后的图像;(d)将图(a)进行旋转变换()并采用双三次内插法zoom到2048*2048后的图像。
(4)结果分析:将图2_4_4中的图(b)、(c)、(d)中的局部进行放大得到图2_4_5 (a)~(c);将图2_4_5 (a)~(c)进行对比可得:最近邻内插产生了最大的锯齿边缘,双线性内插得到了极大地改善,双三次内插产生了稍微清晰一些的结果;且图2_4_5(c)中的垂直灰度块数量要比图2_4_5(d)的相应垂直灰度块数量多,这说明图像的边缘更加清晰。
abc图2_4_5 (a) 图2_4_4(a)的局部边缘放大图;(b) 图2_4_4(b)的局部边缘放大图;(c) 图2_4_4(c)的局部边缘放大图。
参考文献:百度百科、维基百科❖源代码:2_1:close all;clear all;clc;I=imread('lena.bmp');%导入图像“lena.bmp”figure(1)imshow(I);title('image of 8 bits');%显示k=8的原图像[x,y]=size(I);%读取图像“lena.bmp”的长宽img7=zeros(x,y);%产生一个名为img7的512X512的0矩阵img6=zeros(x,y);img5=zeros(x,y);img4=zeros(x,y);img3=zeros(x,y);img2=zeros(x,y);img1=zeros(x,y);for i=1:xfor j=1:yimg7(i,j)=floor(I(i,j)/2);%将原图像的每个像素的灰度级除以2,并用函数floor进行下取整endendfigure(2)imshow((img7),[0,127]);title('image of 7 bits');for i=1:xfor j=1:yimg6(i,j)=floor(img7(i,j)/2);%将原图像的每个像素的灰度级除以2,并用函数floor进行下取整endendfigure(3)imshow((img6),[0,63]);title('image of 6 bits');for i=1:xfor j=1:yimg5(i,j)=floor(img6(i,j)/2);%将原图像的每个像素的灰度级除以2,并用函数floor进行下取整endendfigure(4)imshow((img5),[0,31]);title('image of 5 bits');for i=1:xfor j=1:yimg4(i,j)=floor(img5(i,j)/2);%将原图像的每个像素的灰度级除以2,并用函数floor进行下取整endendfigure(5)imshow((img4),[0,15]);title('image of 4 bits');for i=1:xfor j=1:yimg3(i,j)=floor(img4(i,j)/2);%将原图像的每个像素的灰度级除以2,并用函数floor进行下取整endendfigure(6)imshow((img3),[0,7]);title('image of 3 bits');for i=1:xfor j=1:yimg2(i,j)=floor(img3(i,j)/2);%将原图像的每个像素的灰度级除以2,并用函数floor进行下取整endendfigure(7)imshow((img2),[0,3]);title('image of 2 bits');for i=1:xfor j=1:yimg1(i,j)=floor(img2(i,j)/2);%将原图像的每个像素的灰度级除以2,并用函数floor进行下取整endendfigure(8)imshow((img1),[0,1]);title('image of 1 bits')2_2:close all;clear all;clc;I=imread('lena.bmp');m=mean2(I)d2=std2(I)2_3:法(1):采用imresize()close all;clear all;clc;I=imread('lena.bmp');IN=imresize(I,[2018,2048],'nearest');IB=imresize(I,[2048,2048],'bilinear');IC=imresize(I,[2048,2048],'bicubic');subplot(2,2,1);imshow(I);title('(a) 原图像');subplot(2,2,2);imshow(IN);title('(b) 最近邻内插法所得图像');subplot(2,2,3);imshow(IB);title('(c) 双线性内插法所得图像');subplot(2,2,4);imshow(IC);title('(d) 双三次内插法所得图像')法(2):采用几何空间变换close all;clear all;clc;I=imread('lena.bmp');T=[4 0 0;0 4 0;0 0 1];tform=maketform('affine',T);IN=imtransform(I,tform,'nearest');IB=imtransform(I,tform,'bilinear');IC=imtransform(I,tform,'bicubic');figure(1)imshow(I);title('原图像');figure(2)imshow(IN);title('最近邻内插');figure(3)imshow(IB);title('双线性内插');figure(4)imshow(IC);title('双三次内插')2_4:(1)水平偏移变换:close all;clear all;clc;I1=imread('lena.bmp');I2=imread('elain1.bmp');T=[1 1.5 0;0 1 0;0 0 1];tform=maketform('affine',T);I11=imtransform(I1,tform);I1N=imresize(I11,[2048 2048],'nearest'); I1B=imresize(I11,[2048 2048],'bilinear'); I1C=imresize(I11,[2048 2048],'bicubic'); I22=imtransform(I2,tform);I2N=imresize(I22,[2048 2048],'nearest');I2B=imresize(I22,[2048 2048],'bilinear');I2C=imresize(I22,[2048 2048],'bicubic');figure(1);imshow(I1);title('lena原图像');figure(2);imshow(I1N);title('lena最近邻');figure(3);imshow(I1B);title('lena双线性');figure(4);imshow(I1C);title('lena双三次');figure(5);imshow(I2);title('elain1原图像');figure(6);imshow(I2N);title('elain1最近邻');figure(7);imshow(I2B);title('elain1双线性');figure(8);imshow(I2C);title('elain1双三次')(2)旋转变换:close all;clear all;clc;I1=imread('lena.bmp');I2=imread('elain1.bmp');T=[cosd(30) sind(30) 0;-sind(30) cos(30) 0;0 0 1]; tform=maketform('affine',T);I11=imtransform(I1,tform);I1N=imresize(I11,[2048 2048],'nearest');I1B=imresize(I11,[2048 2048],'bilinear');I1C=imresize(I11,[2048 2048],'bicubic');I22=imtransform(I2,tform);I2N=imresize(I22,[2048 2048],'nearest');I2B=imresize(I22,[2048 2048],'bilinear');I2C=imresize(I22,[2048 2048],'bicubic');figure(1);imshow(I1);title('lena原图像');figure(2);imshow(I1N);title('lena最近邻'); figure(3);imshow(I1B);title('lena双线性'); figure(4);imshow(I1C);title('lena双三次'); figure(5);imshow(I2);title('elain1原图像'); figure(6);imshow(I2N);title('elain1最近邻'); figure(7);imshow(I2B);title('elain1双线性'); figure(8);imshow(I2C);title('elain1双三次')。
