多元尺度分析1
多尺度几何分析详解

多尺度几何分析详解一、从小波分析到多尺度几何分析小波分析取在从多学科领域中取得巨大成功的一个关键原因在于它比傅里叶分析能更“稀疏”地表示一维分段光滑或者有界变差函数。
遗憾的是,小波分析在一维时所具有的优异特性并不能简单的推广到二维或更高维。
这是因为一维小波张成的可分离小波(Separable wavelet)只具有有限的方向,不能“最优”表示含线或者面奇异的高维函数,但事实上具有线或面奇异的函数在高维空间中非常普遍,例如,自然物体光滑边界使得自然图像的不连续性往往体现为光滑曲线上的奇异性,而并不仅仅是点奇异。
换句话说,在高维情况下,小波分析并不能充分利用数据本身特有的几何特征,并不是最优的或者说“最稀疏”的函数表示方法;而继小波分析之后发展起来的多尺度几何分析(Multiscale Geometric Analysis,MGA)发展的目的和动力正是要致力于发展一种新的高维函数的最优表示方法,为了检测、表示、处理某些高维空间数据,这些空间的主要特点是:其中数据的某些重要特征集中体现于其低维子集中(如曲线、面等)。
比如,对于二维图像,主要特征可以由边缘所刻画,而在3-D图像中,其重要特征又体现为丝状物(filaments)和管状物(tubes)。
由一维小波张成的二维小波基具有正方形的支撑区间,不同的分辨率下,其支撑区间为不同尺寸大小的正方形。
二维小波逼近奇异曲线的过程最终表现为用“点”来逼近线的过程。
在尺度j,小波支撑区间的边长近似为2-j,幅值超过2-j的小波系数的个数至少为O(2j)阶,当尺度变细时,非零小波系数的数目以指数形式增长,出现了大量不可忽略的系数,最终表现为不能“稀疏”表示原函数。
因此,我们希望某种变换在逼近奇异曲线时,为了能充分利用原函数的几何正则性,其基的支撑区间应该表现为“长条形”,以达到用最少的系数来逼近奇异曲线。
基的“长条形”支撑区间实际上是“方向”性的一种体现,也称为这种基具有“各向异性(anisotropy)”。
CH10+多元尺度法

10.2 資料編碼與SPSS輸入
要使受試者對若干個品牌建立其偏好次序,最簡 單的方法就是要他們排出次序。但是品牌數目一 多時,受試者便不易排出次序了。這時候,我們 可用成對比較法或三比法(三個、三個比較), 來評定他們的偏好次序。這種比較的缺點是在於 當品牌數目很多時,必須做很多的比較,使得受 試者失去耐心
10.3 非計量多元尺度法
大海行銷公司受委託進行四種品牌的定位 分析,並在產品空間中做出偏好圖,以作 為行銷定位策略的參考
圖10-5 「Multidimensional Scaling: Data Format」視窗設定
按〔Define〕(界定),出現「Multidimensional Scaling(Proximities in Matrices Across Columns)」視窗, 如圖10-4所示。將左邊的變數(甲牌、乙牌、丙牌、丁牌) 選入「Proximities」(相近性)下方的方格內。此視窗的目 的是要讓我們選擇變數,並對於Model(模式)、 Restrictions(限制)、Options(選項)、Plots(繪圖)、 Output(輸出)做交代。
圖10-5 「Multidimensional Scaling: Model」視窗設定
限制 在「Multidimensional Scaling(Proximities in Matrices Across Columns)」視窗中按 〔Restrictions〕,就會出現「Multidimensional Scaling: Restrictions」視窗,如圖10-6所示。 此視窗的目的是要我們設定一些限制條件。我們依 照SPSS的內定值作為現制條件,故選擇「No restrictions」(無限制)。
多维尺度分析

例如;希望研究消费者对自己公司某个品牌的产品和另外几个 主要竞争对手产品的认可程度,则使用多维尺度分析可以回答 下列问题:
1、消费者认为那些品牌的产品类似与我们的产品?
2、在这些品牌中消费者用于评价相似性的是哪些特征?
分析原理:将观察数据分配到“概念空间”(二、三维)的特 殊位臵,数据点间的距离由计算出的不相似性决定,从而可以 在低度空间描述相似性和不相似性,以得到对象关系的“空间” 理解。
多维尺度分析
多维尺度分析是市场调查、分析数据的统计方法之一 。 通过多维尺度分析,可以将消费者对商品相似性的判断产生一 张能够看出这些商品间相关性的图形。 例如:有十个百货商场,让消费者排列出对这些百货商场两两 间相似的感知程度,根据这些数据,用多维尺度分析,可以判 断消费者认为哪些商场是相似的,从而可以判断竞争对手。 用于反映多个研究事物间相似(不相似)程度,通过适当 的降维方法,将这种相似(不相似)程度在低维度空间中用点 与点之间的距离表示出来,并有可能帮助识别那些影响事物间 相似性的潜在因素。这种方法在市场研究中应用得非常广泛。 它使用的数据是消费者对一些商品相似程度(或差异程度 的评分,通过分析产生一张能够看出这些商品间相关性的图形 (感知图)。
1、所有饮料分成两类: yukon、可口可乐、百事可乐、shasta、 rc、pepper为一类 无糖pepper、无糖可口可乐、无糖百事 可乐、tab为一类 2、第一维度方向上: 两种pepper在最右侧,两种百事可乐在中 间, (饮料自身口味) 两种可口可乐靠左,除RC和百事可乐比较 接近外,另外三种饮料均比较靠左。 第二维度方向上: 三种无糖饮料在上方,而对应的原始饮料 在下方。 (饮料对健康 的有益程度)
例:对七种彩电品牌的相似程度评价情况: 1、对七种彩电品牌两两组合(21对) 2、对这些对子相似程度打分(1分—10分,1分——最相似) 3、分值平均 4、形成七种品牌相似评分矩阵 5、多维尺度分析可以对该矩阵进行分析,用图形化将结果 呈现出来。(哪些品牌靠得比较近)
彩色图像多尺度多元图像的检测分析

彩色图像多尺度多元图像的检测分析1引言近几年来随着彩色图像传感器成本的降低和机器视觉应用的发展,彩色机器视觉检测需求变得越来越多,已经成为机器视觉理论和应用发展的重要方向。
但目前彩色机器视觉检测理论还不够成熟,检测方法的应用不能只是简单的从灰度图像扩展到多通道彩色图像,彩色图像视觉检测方法有着自己的特点,有必要进一步的深入研究。
本文在前面高斯多尺度多元图像分析的基础上,从灰度图像分析扩展到彩色图像,提出彩色图像的多尺度多元图像表示及其多元图像分析理论。
通过对人眼视觉系统结构和感知特性的分析,可以发现彩色图像的多尺度表示及多元图像分析方法有着深刻的视觉仿生理论基础,能够模拟人眼对颜色纹理的三基色多尺度视觉感知和感受野拮抗信息处理过程。
本文首先从人眼视网膜结构和信息传递特性出发,对颜色和纹理的神经生理学感知和处理机制进行了分析,提出多尺度颜色纹理视觉感知和拮抗色信息处理的模型,从视觉仿生角度,对彩色图像颇色纹理多尺度多元图像表示及其多元图像分析方法进行了论述。
多尺度多元图像分析方法,将颜色纹理彩色图像的多尺度表示投影到本征空间,能够获得非常符合人眼颜色纹理感知的本征特征。
在此基础上,提出了颇色纹理彩色图像的去噪算法,通过在本征空间上滤波消除噪声。
实验结果表明,提出的彩色图像去噪算法更符合人对图像质量的主观评价。
2人眼颜色和纹理感知机制分析颜色和纹理是人类视觉系统感知的两种最主要信息,也是彩色机器视觉和图像分析的重要内容。
为了获得有效的颜色纹理图像分析方法,有必要对人眼视觉系统的神经生理学结构和颜色纹理感知及信息处理机制进行深入的认识和分析。
2.1视觉通路和视网膜生理结构外界光线通过人眼的角膜,经过瞳孔进入眼球,通过晶状体的聚焦调节,穿过玻璃体投影到眼球后部的视网膜上,在视网膜上由感光细胞完成光到生物电信号的转换,并进行信息的初级处理,视网膜输出的信号经过视神经向下一级传递,左右两眼的视神经信息在视交叉处经过交叉,通过视束将信息分别传递到位于间脑的左右两个侧膝体(外侧膝状体),侧膝体本身作为一种信息中转结构,最终将信息通过视辐射传递到大脑视皮层。
多维尺度分析-SPSS例析资料讲解

多维尺度分析多维尺度分析(multidimensional scaling ,MDS )又称ALSCALE(alternative least-square SCALing),还有人称之为多维量表分析;它是将一组个体间的相异数据经过MDS 转换成空间构图,且保留原始数据的相对关系。
1多维尺度分析的目的假设给你一张中国台湾省地图,要你算出基隆,台北,新竹,台中,台南,嘉义,高雄,花莲,台东,枋寮,苏澳,恒春等地间的距离,你可以用一把刻度尺根据比例测算出一个12x12de 距离矩阵;反之,如果给你一份12个城市间的距离矩阵,要你画出12个城市相对位置的二维台湾地图,且要他们与现实尽量保持一致,那就是一件不容易的工作了,多为尺度分析就为此工作提供了一个有效地分析手段。
2多为尺度分析与因子分析和聚类分析的异同多为尺度分析和因子分析都是维度缩减技术,但是因子分析一般使用相关系数进行分析,使用的是相似性矩阵;而多为尺度分析采用的是不相似的评分数据或者说相异性数据来进行分析;与因子分析不同,多为尺度分析中维度或因素的含义不是分析的中心,各数据点在空间中的位置才是分析解释的核心内容;多为尺度分析与聚类分析也有相似之处,两者都可以检验样品或者变量之间的近似性或距离,但聚类分析中样品通常是按质分组的;多维分析不是将分组或聚类作为最终结果,而是以一个多维尺度图作为最终结果,比较直观。
若你的目的是要把一组变量缩减成几个因素来代表,可考虑使用因素分析;若目的是变量缩减后以呈现在空间图上,则可以使用MDS 。
如果你是想要却仍相似观测值得组别,请考虑以聚类分析来补充多为尺度分析,聚类分析虽可以确认组别,但无法在空间图中标示出观测。
3.定性的和定量的MDSMDS 分析测量的尺度不可以是nominal 的,但可以是顺序的ordinal,等距的interval,比率的ratio 。
顺序量表只可以用于质的分析,又称为定性多维量表分析;它以个体间距离排序为主;而interval 和ratio 量表称为定量多维量表分析(定量多维尺度分析)。
【办公自动化】SPSS(第十章):多元尺度法

如图10-9所示。此窗口的目的是要我们决定输出报表要呈 现什么。选「Common space coordinates」(共同空间 坐标)以及「Multiple stress measures」(多种压力测 量)。如果想要将有关数据储存起来,可在「Save to New File」方盒下的选项中勾选。
在SPSS内的甲牌就是甲牌与乙牌的相似度,乙牌就是乙 牌与丙牌的相似度,以此类推。何以上述没有甲牌与丙牌、 乙牌与丁牌的相似比较?因为比较甲牌与乙牌、乙牌与丙 牌就可以推断甲牌与丙牌;比较甲牌与乙牌、甲牌与丁牌 就可以推乙牌与丁牌。例如,如果小明认为甲牌与乙牌相 似、乙牌与丙牌相似,就可以推断甲牌与丙牌相似;如果 小明认为甲牌与乙牌相似、甲牌与丁牌相似,就可以推断 乙牌与丁牌相似。
在SPSS中,按〔Analyze〕、〔Scale〕、〔Multidimensional Scaling(PROXSCAL)〕(〔分析〕〔量尺法〕〔PROXSCAL多元尺 度方法〕),在所产生的「Multidimensional Scaling: Data Format」窗口中,我们所做的设定如图10-11所示
多维尺度分析

2.3MDS算法
• MDS是一系列算法的总称,都是从刺激物间的相似性或相异性 数据出发,用低维空间中的点关系表示研究的客体,从而发现 数据之间的潜在结构。目前,最常见的算法有ALSCAL、 INDSCAL、 MDPREF、MDSCAL、ASCAL、KYST和 PREFMAP,研究者需要基于不同的研究特点选择适当的研究 方法。 • KYST主要用于可用于识别两点之间的距离,辨别刺激物的相 似性与非相似性; • MDPREF可以最直接的显示刺激点与属性之间的关系,但是它 没有模型效度方面的指标; • ALSCAL也可用于探讨刺激点与属性之间的关系,而且提供了 很多选项,不仅可以分析感知图,而且可以显示模型有效性指 标。ALSACL是应用最广泛的MDS模型,已经成为SPSS统计 软件包中的内嵌部分。它不但对分析数据的规模没有限制,例 如可以是任何形式的,连续的或离散的,也可以有缺失值;而 且也有大量的选项以供数据分析的需要。
•
•
•
2. MDS分析步骤
• 多维尺度分析与其他多元统计方法一样,首先需要对所研究的问题进行准确 界定;由于MDS允许多种类型数据的输入,所以,需要根据问题决定获取数 据的形式和方法;并在多种MDS算法中选择一种符合研究目的的方法;处理 分析结果的一个重要方面就是确定适当的空间图维数;之后需要基于空间结 构的解释,对空间图的坐标轴进行命名;最后要对评估所用方法的可靠性和 有效性。具体的分析步骤如图所示:
– 对于直接法获取的数据:可以图相联系,继而为各维度 命名 – 对于间接法获取的数据:可以直接用回归等统计方法对这些属性 的矢量在空间图中进行拟合,然后用最接近的属性命名坐标轴。 (属性之间的夹角也是判断相似性的重要标准,属性间的角度越 小,调查对象认为这两个属性的相似性越高 )
多维尺度分析

多维尺度分析多维尺度分析(MultiDimensional Scaling)是分析研究对象的相似性或差异性的一种多元统计分析方法。
采用MDS可以创建多维空间感知图,图中的点(对象)的距离反应了它们的相似性或差异性(不相似性)。
一般在两维空间,最多三维空间比较容易解释,可以揭示影响研究对象相似性或差异性的未知变量-因子-潜在维度。
在市场研究领域主要研究消费者的态度,衡量消费者的知觉及偏好。
涉及的研究对象非常广泛,例如:汽车、洗头水、饮料、快餐食品、香烟和国家、企业品牌、政党候选人等。
通过MDS分析能够为市场研究提供有关消费者的知觉和偏好信息。
MDS一般需要借助SPSS或SAS统计分析软件,输入有关消费者对事物的知觉或偏好数据,转换为一组对象或对象特征构成的多维空间知觉或偏好图——感知图。
应用MDS,收集的数据值大小必须能够反应两个研究对象的相似性或差异性程度。
这种数据叫做邻近数据,所有研究对象的邻近数据可以用一个邻近矩阵表示。
反映邻近的测量方式:•相似性-数值越大对应着研究对象越相似。
•差异性-数值越大对应着研究对象越不相似。
测量邻近性数据的类型:•两个地点(位置)之间的实际距离。
(测量差异性)•两个产品之间相似性或差异性的消费者心理测量。
(差异性或相似性)•两个变量的相关性测量。
(相关系数测量相似性)•从一个对象过渡到另一个对象的转换概率。
例如概率反应了消费者对品牌或产品偏好的变化。
(测量相似性)•反映两种事物在一起的程度。
例如:用早餐时人们经常将哪两种食品搭配在一起。
(测量相似性)•谁喜欢谁,谁是谁的领导,谁传递给谁信息,谁是谁的上游或下游等等社会网络数据等(测量相似性)邻近数据即可以直接测量(距离),也可以通过计算得到(变量间的相关系数)。
MDS最经典的案例就是用感知图表现美国主要城市的航空距离!我们采用SAS进行分析,选择Market模块,选择MDS方法,SAS可以直接处理矩阵数据!非常简单得到结果:你可以对着美国的地图和各个城市的地理位置,是否能够看出MDS给你的方位和差异感觉!请大家自己试一试用MDS分析中国主要省会城市之间航空距离的MDS分布。
多维尺度分析结果解读_SPSS数据处理与分析_[共6页]
![多维尺度分析结果解读_SPSS数据处理与分析_[共6页]](https://img.taocdn.com/s3/m/ad7a1539aeaad1f347933f85.png)
第十三章数据的多维尺度分析1.形象测定比较组织的支持者与非支持者对组织形象的感知,并与组织自身的初衷相对照比较,如企业、社会机构、政府部门形象测定等。
2.细分对象分析不同对象在相同维度空间上的位置,确定他(它)们在感知方面相对同质的群体。
3.寻找业务空间图上的空档通常意味着潜在机会。
通过空间图的分析,可以对现有业务进行评估,了解人们对新业务概念的感觉和偏好,以便找到新业务并为其准确定位。
4.确定态度量表的结构可以用来确定态度空间的合适维度和结构。
在考虑产品研发和形象设计时,可通过调查获取描述自身产品与竞争对手产品的感知相似性数据,将这些近似性与自变量(如价格)相对接,可尝试确定哪些变量对于人们如何看待这些产品至关重要,从而对产品形象做出相应的调整。
第三节多维尺度分析结果解读 本节阐述导入问题用SPSS的ALSCAL、PROXSCAL方法分析后所得结果的解读。
一、ALSCAL的结果解读与分析第一节各选项设置完毕后,单击图13-3中的“确定”按钮,即得到ALSCAL的各项输出结果。
包括表13-3的文本及图13-16、图13-17、图13-18、图13-19。
表13-3由以下三部分构成。
第一部分说明降为二维空间时的迭代进程,经过4次迭代后,S-stress改变量为0.000 62,小于0.001的迭代标准,模型迭代停止。
第二部分说明模型的拟合效果,RSQ是不相似性在二维空间中能够解释部分占总变异的比例,而Stress是依据Kruskal’s应力公式1计算所得,显示了每个个体和样本整体的应力值,样本的应力平均值为0.398 94>0.2,且RSQ=0.376 64,表示用二维空间只能解释10个消费者评价饮料差异性的37.7%,模型拟合效果较差。
第三部分输出模型结果。
(1)10种品牌的饮料投影到二维空间上的坐标值,绘制在二维坐标系下的散点如图13-16所示。
它是评价对象(客体)在二维空间的直观呈现。
多元尺度分析与联合分析
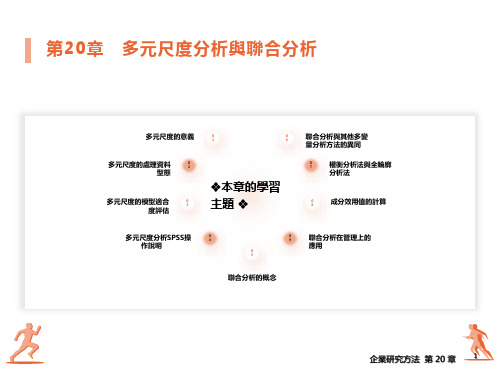
企業研究方法 第 20 章 3
01
02
( d d ) 壓 力 係 數 是 由 K r u s k a l ( 1 9 6 4 )
所提出,其計算公式如下:
S=
ij
2 ij
( d ij ) 2
d ij
03
S:
壓力係數
dij: 成對事物在構 面中之距離
:
dij 之估計值,
通常是以簡單迴歸
(monotone
問項 利用類比、象徵來使知識具體化 利用專家取得及移轉知識 人工智慧系統 教育訓練 利用網路聊天室、討論群組 建立操作手冊 公司內 / 外部網際網路網頁 建立專家資料庫 利用師徒制來傳承知識 利用腦力激盪 利用跨部門的工作輪調 利用跨部門的合作計畫案 實地考察 由操作中學習 利用在職訓練 透過觀察來進行學習 透過面對面會議
企業研究方法 第 20 章 11
表 20 - 3 十七項研究變數在知覺屬性空間之座標
變數名稱 Kcp 1 Kcp 2 Kcp 3 Kcp 4 Kcp 5 Kcp 6 Kcp 7 Kcp 8 Kcp 9 Kcp 10 Kcp 11 Kcp 12 Kcp 13 Kcp 14 Kcp 15 Kcp 16 Kcp 17
regression)之方法求得,
壓力係數愈小
代表dij與之差異不大,
即代表模式之適合度很高。
企業研究方法 第 20 章 4
20.3 多元尺度的模型適合度評估
進行 MDS 分析時通常以壓力係數(stress)作為衡量標 準,根據Kruskal (1964)的解釋,不同的壓力係數水 準,有其代表的配適程度 。
5.5455
5.1731
5.0606
4.8462
5.6970
多尺度几何分析详解

多尺度几何分析详解一、从小波分析到多尺度几何分析小波分析取在从多学科领域中取得巨大成功的一个关键原因在于它比傅里叶分析能更“稀疏”地表示一维分段光滑或者有界变差函数。
遗憾的是,小波分析在一维时所具有的优异特性并不能简单的推广到二维或更高维。
这是因为一维小波张成的可分离小波(Separable wavelet)只具有有限的方向,不能“最优”表示含线或者面奇异的高维函数,但事实上具有线或面奇异的函数在高维空间中非常普遍,例如,自然物体光滑边界使得自然图像的不连续性往往体现为光滑曲线上的奇异性,而并不仅仅是点奇异。
换句话说,在高维情况下,小波分析并不能充分利用数据本身特有的几何特征,并不是最优的或者说“最稀疏”的函数表示方法;而继小波分析之后发展起来的多尺度几何分析(Multiscale Geometric Analysis,MGA)发展的目的和动力正是要致力于发展一种新的高维函数的最优表示方法,为了检测、表示、处理某些高维空间数据,这些空间的主要特点是:其中数据的某些重要特征集中体现于其低维子集中(如曲线、面等)。
比如,对于二维图像,主要特征可以由边缘所刻画,而在3-D图像中,其重要特征又体现为丝状物(filaments)和管状物(tubes)。
由一维小波张成的二维小波基具有正方形的支撑区间,不同的分辨率下,其支撑区间为不同尺寸大小的正方形。
二维小波逼近奇异曲线的过程最终表现为用“点”来逼近线的过程。
在尺度j,小波支撑区间的边长近似为2-j,幅值超过2-j的小波系数的个数至少为O(2j)阶,当尺度变细时,非零小波系数的数目以指数形式增长,出现了大量不可忽略的系数,最终表现为不能“稀疏”表示原函数。
因此,我们希望某种变换在逼近奇异曲线时,为了能充分利用原函数的几何正则性,其基的支撑区间应该表现为“长条形”,以达到用最少的系数来逼近奇异曲线。
基的“长条形”支撑区间实际上是“方向”性的一种体现,也称为这种基具有“各向异性(anisotropy)”。
多元尺度法MultiDimensional课件

b.所有樣本加權評分 包裝行銷研究之加權評分表,是多元尺度分析
之主要投入資料。 ❖ 包裝咖啡加權評分表
多元尺度法MultiDimensional课件
方法說明
1. MDS的目erence)判斷轉化成在一多構面空間 (即知覺圖)上的距離。
2. 發展知覺圖的方法
5. 多元尺度法有計量多元尺度法(metric multidimentional scaling)和非計量多元尺度法 (nonmetric multidimentional scaling)之分。前 者以相似(距離)的實際數值為投入資料,後 者則以順序尺度的資料為投入資料。不論是計 量或非計量的多元尺度法,都能導出計量的產 出結果。
多元尺度法MultiDimensional课件
處理流程
多元尺度法MultiDimensional课件
p295 圖11-2
運算步驟
知覺圖之產生 1.構建加權均值矩陣 2.構建標準化均值矩陣 3.構建距離平方矩陣 4.構建中心化距離矩陣 5.構建雙重中心化距離矩陣 6.計算座標矩陣 7.配適準則軸 8.計算方向餘弦 9.決定準則軸方向 10.構建競爭群
2. CA是根據事物和一組研究人員所設定的敘述 性特徵或屬性間的關聯來發展出知覺圖。它可 描述變數(特別是名目尺度的變數)之類別的 「一致性」(correspondence),然後以此一致 性為基礎來發展知覺圖,並能將事物和屬性同 時展示在一聯合空間中。
多元尺度法MultiDimensional课件
2.客體點(Object Point) 知覺圖中之M個客體點,分別表示M個接受評 估的客體,如圖中之A、B、C等。知覺圖之構 建及客體點之相對位置,取決於兩兩客體點間 之實際距離。
多元尺度法MultiDimensional课件
市场研究定量分析:多维尺度分析

重要指标的统计含义
1.接近程度 接近程度(proximities)表示亊物相似或相异的 程度值。人们常用各种距离和相似系数来表示接近 程度,与聚类分析中所用的统计量类似。 2.空间图 空间图(spatial map)又称为感知图( perception map),它可以用图形直观地显示各个亊 物乊间的相似程度,是通过反复的迭代计算,使图 形中点与点乊间的分布结构与原始数据所表示的亊 物乊间距离或相似系数尽可能一致得到的。
(8)回到主画面乊后点击右侧的“选项”,如 图9-7所示。
(9)在“输出”中勾选“组图”、“数据矩阵 ”和“模型和选项摘要”;“标准”中设定值为迭 代求解的过程当中的收敛条件,“S-应力收敛性” 、“最小s应力值”和“最大迭代”的默认值分别为 0.001,0.005与30,分析时通常不刻意去修改这些内 定值, S-应力收敛性、“s最小应力值”越小或最大 迭代的值越大,迭代的次数就越多,所求得的解误 差也越小。勾选完毕以后点击“继续”,如图9-8所 示。
(3)在SP键幵选择“粘贴”,如 图9-2所示。
(4)数据粘贴后再“变量视图”中赋予新的变 量名称,以ck,c,cd,ga,g,nr分别代表上述六 种香水。于“标签”中给予完整品牌名称的注解, 如图9-3所示。
(6)将所有品牌变量放入“变量列表”乊中, 在“距离”中点选“从数据创建距离”,因为比例 是直接对原始数据作分析,所以点选此项。如果数 据为不相似(或相似)矩阵数据,则必须选取“数 据为距离数据”,如图9-5所示。
多维尺度分析可以看成因子分析的一种替代。 一般而言,多维尺度分析的目的是识别潜在的有意 义的维度,使得研究者能够解释被调查对象乊间的 相似性或不相似性。在因子分析中,个体(或变量 )乊间的相似性是用相关系数矩阵表示的。但在多 维尺度分析里,研究者可以分析仸何形式的相似矩 阵或不相似矩阵,包括相关系数矩阵,因为距离测 度可以通过仸何途径获得。这也是多维尺度分析的 优点乊一。一般,多维尺度分析允许研究者问相对 不明显的问题,如品牌A和品牌B如何相似。研究者 可以从这些问题中得到想要的结果,而被调查者却 不知道研究者的真正目的。
07 多维尺度分析方法

第七讲 多维尺度分析多维尺度分析(MultiDimensional Scaling)是分析研究对象的相似性或差异性的一种多元统计分析方法。
采用MDS可以创建多维空间感知图,图中的点(对象)的距离反应了它们的相似性或差异性(不相似性)。
一般在两维空间,最多三维空间比较容易解释,可以揭示影响研究对象相似性或差异性的未知变量-因子-潜在维度。
在市场研究领域主要研究消费者的态度,衡量消费者的知觉及偏好。
涉及的研究对象非常广泛,例如:汽车、洗头水、饮料、快餐食品、香烟和国家、企业品牌、政党候选人等。
通过MDS分析能够为市场研究提供有关消费者的知觉和偏好信息。
MDS一般需要借助SPSS或SAS统计分析软件,输入有关消费者对事物的知觉或偏好数据,转换为一组对象或对象特征构成的多维空间知觉或偏好图——感知图。
应用MDS,收集的数据值大小必须能够反应两个研究对象的相似性或差异性程度。
这种数据叫做邻近数据,所有研究对象的邻近数据可以用一个邻近矩阵表示。
反映邻近的测量方式:z相似性-数值越大对应着研究对象越相似。
z差异性-数值越大对应着研究对象越不相似。
测量邻近性数据的类型:z两个地点(位置)之间的实际距离。
(测量差异性)z两个产品之间相似性或差异性的消费者心理测量。
(差异性或相似性)z两个变量的相关性测量。
(相关系数测量相似性)z从一个对象过渡到另一个对象的转换概率。
例如概率反应了消费者对品牌或产品偏好的变化。
(测量相似性)z反映两种事物在一起的程度。
例如:用早餐时人们经常将哪两种食品搭配在一起。
(测量相似性)z谁喜欢谁,谁是谁的领导,谁传递给谁信息,谁是谁的上游或下游等等社会网络数据等(测量相似性)邻近数据即可以直接测量(距离),也可以通过计算得到(变量间的相关系数)。
MDS最经典的案例就是用感知图表现美国主要城市的航空距离!我们采用SAS进行分析,选择Market模块,选择MDS方法,SAS可以直接处理矩阵数据!(原博文图片缺失)非常简单得到结果:你可以对着美国的地图和各个城市的地理位置,是否能够看出MDS给你的方位和差异感觉!(原博文图片缺失)请大家自己试一试用MDS分析中国主要省会城市之间航空距离的MDS分布。
多维尺度分析

我们知道对应分析是一种图示分析技术,通过对应分析图能够简单直观的将变量间的关系加以呈现,多维尺度分析和对应分析类似,也是将变量间的关系通过图形进行展现,关于二者的区别后面会做论述。
一、多维尺度分析简介多维尺度分析Multidimensional Scaling,简称MDS,是一种探索性数据分析技术,主要是用适当的降维方法,将多个变量通过坐标定位在低维空间中(二维或三维),变量之间的欧氏距离就可以反映它们之间的差异性和相似性。
多维尺度分析根据数据集特征分为:1.不考虑个体差异MDS模型2.考虑个体差异MDS模型MDS模型允许多种类型的数据输入,并且在实际应用中,也有多种测量相似性或差异性的方法,根据分析数据的类型分为:1.度量化MDS模型:也称为古典MDS模型,所输入的数据是直接反映变量间差异或相似的距离或比率,例如城市间的距离就是现成的反映差异的数据。
2.非度量化MDS模型:输入的数据不是直接反映变量间的差异,而是通过对其属性的评分,间接的反映变量间的差异或相似性。
二、多维尺度分析的分析步骤1.界定问题明确研究的问题和范畴,确定相关的变量种类和数量2.获取数据根据实际情况获取分析数据3.选择MDS模型根据获得的数据类型,选择相应的MDS模型4.确定维度MDS模型是为了生成一个用尽可能小的维度对数据进行最佳拟合的空间感知图,因此要确定一个合适的维度,维度太高不易于解读,维度太低会影响拟合度,通常采用二维或三维。
5.模型评价考察应力系数Stress和拟合指数RSQ,应力系数越小越好,RSQ越大越好6.解读图表多维尺度分析最重要的结果是感知图,图中各点之间的距离直接反映了各变量的相似或差异程度,除了查看差异程度之外,如果要对图表进行整体的分析解读,还需要对每个维度进行解释。
三、多维尺度分析与对应分析的异同相同点:1.都是可以得出有直观的图形结果,并且也都常用在市场分析中2.都具有降维,数据浓缩的思想,实际上,多元统计分析都是基于将高维空间的数据压缩至低维空间进行分析。
多元尺度分析1

计量与非计量多元尺度比较
计量多元尺度
输入 数据
优点
非计量多元尺度
距离排序矩阵,为顺序尺度的数据
1,简便,按超常评估客体差异即 可; 2,可从中导出计量分析结果,已 成为目前较常用的MDS; 3,可集合聚类分析、方差分析、 误差分析等生成多种分析结果
评分表或距离平方矩阵,为定距或 定比尺度的数据
1,精确,可据多个准则评估客体间 差异; 2,可集合聚类分析、方差分析、误 差分析等生成多种分析结果
竞争态势分析(competitive situation analysis)
根据个别客体在P个评估准则上的表现,找 出客体的优势与劣势 客体表现明显较佳的准则称为优势点,表 现明显较弱的准则称为弱势点
王老师 竞争力 属性 评分 竞争力
李老师 属性 评分 竞争力
陈老师 属性 评分 优势点 进度掌控 75 弱势点 教材内容 80 评分公正 75 课程内容 74 表达能力 70 课堂气氛 70
多维标度分析 (多元尺度分析)
Multidimensional Scaling Analysis, MDS
聚类分析与多元尺度分析,都是减少case个 数的统计方法 聚类分析进行个案缩减 多元尺度分析同时进行个案与准则变量双 重缩减
为什么需要这种技术?
多维标度可以看成是因子分析的一种替代。一般 而言,多维标度分析的目的是识别潜在的有意义 的维度,使得研究者能够解释被调查对象之间的 相似性或不相似性。在因子分析中,个体(或变 量)之间的相似性是用相关系数矩阵表示的。但 在多维标度里,研究者可以分析任何形式的相似 矩阵或不相似矩阵,包括相关系数矩阵,因为距 离测度可以通过任何途径获得。这也是多维标度 的优点之一。一般地,MDS允许研究者问相对不 明显的问题,如,品牌A和品牌B如何相似,然后 研究者可以从这些问题中得到想要的结果,而被 调查者却不知道研究者的真正目的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
关健因 素评估
准则
找出比较重要的 准则,形成客体 未来定位策略的 依据
知觉分析的要点(续)
分析方法 评价对象 分析内容 分析目的
准则相关 准则 分析
策略分析 准则
探讨两准则间的相 关程度
探讨客体在准则上 的表现,以及准则 本身的权重 探讨M个客体的预 测绩效与实际绩效 的差异程度 探讨N个主体对特 定客体、特定准则 上评分的变异程度
拟合优度(goodness-of-fit)
拟合优度用于判断迭代 算法对模型的拟合程度, stress 拟合优度 多维标度分析按照使拟 20% 差 合优度达到最大的准则 一般 来确定点的空间位置的。 10% 5% 好 一般用克鲁斯卡压迫公 式(Kruskal’s stress formula 2.5% 非常好 0 完美 L)值衡量
个别绩效指标的权重,由学生自行按重视程度 设定
每个学生的权重,由教育研究人员给定,通常 是等权重1/N
财务研究
财务研究的分析要素
分析要素 客体 主体 准则 准则权重 主体权重 内容 股票名称,如三一重工、招商银行等 证券分析师,假定有若干位 股票属性,如收益性、成长性、风险性等 个别股票属性的权重,由个别证券分析师自定 个别证券分析的权重,由财务研究人员给定, 通常视分析师的获利能力而定
择偶研究
择偶研究的分析要素
分析要素 客体 主体 准则 准则权重 主体权重 内容 男朋友,设有三位备选者 女孩及其亲友团,如父母、朋友、亲戚等 男友条件,如经济基础、学历、外貌、人品等 个别条件的权重,由女孩及其亲友团自行按条 件重要性给出 女孩本人权重最高,甚至可达100%;其他人的 权重按女孩重视意见的程度赋予权重
策略分析(strategy analysis)
根据准则评分及准则权重,针对个别客体 分别研拟诉求、改善、放弃、改变等四种 策略
教师评价三教师的策略分析
略。可见一教师、属性与策略建议的三维 表
误差分析(error analysis)
客体的知觉绩效与实际绩效间的差距 误差分析只适用于主体只有一个的情形 通常利用符号检验,探讨评估结果与实际 结果间的误差是否达达显著水平。
多维标度分析 (多元尺度分析)
Multidimensional Scaling Analysis, MDS
聚类分析与多元尺度分析,都是减少case个 数的统计方法 聚类分析进行个案缩减 多元尺度分析同时进行个案与准则变量双 重缩减
为什么需要这种技术?
多维标度可以看成是因子分析的一种替代。一般 而言,多维标度分析的目的是识别潜在的有意义 的维度,使得研究者能够解释被调查对象之间的 相似性或不相似性。在因子分析中,个体(或变 量)之间的相似性是用相关系数矩阵表示的。但 在多维标度里,研究者可以分析任何形式的相似 矩阵或不相似矩阵,包括相关系数矩阵,因为距 离测度可以通过任何途径获得。这也是多维标度 的优点之一。一般地,MDS允许研究者问相对不 明显的问题,如,品牌A和品牌B如何相似,然后 研究者可以从这些问题中得到想要的结果,而被 调查者却不知道研究者的真正目的。
考虑删除重叠 性高的准则
将P个准则分成 诉求重点等四 种策略方向 评估单一主体 的预测能力 找出离群点
误差分析 主体
变异分析 主体
基准分析(benchmarking analysis)
目的在于找出特定准则表现最佳的客体,客 体评分的优劣取决于加权评分内所得评分 如前例教师评价中,课程内容基准为王老师 的评分,表达能力为王老师与李老师,教材 内容为王老师,进度掌控为李老师与陈老师, 评分公正为王老师课堂气氛为王老师。每一 准则下其他教师的评分为非基准评分
计量与非计量多元尺度比较
计量多元尺度
输入 数据
优点
非计量多元尺度
距离排序矩阵,为顺序尺度的数据
1,简便,按超常评估客体差异即 可; 2,可从中导出计量分析结果,已 成为目前较常用的MDS; 3,可集合聚类分析、方差分析、 误差分析等生成多种分析结果
评分表或距离平方矩阵,为定距或 定比尺度的数据
1,精确,可据多个准则评估客体间 差异; 2,可集合聚类分析、方差分析、误 差分析等生成多种分析结果
计量与非计量多元尺度法
计量多元尺度分析
输入数据为定距尺度或定比尺度
非计量多元尺度分析
输入数据属于顺序尺度
知觉图(perceptual map) 又称空间图(spatial map )
知觉图
评分表或加权评分表经由多元尺度分析后所产 生的图 常见的形式由两个参照轴所构成之平面图,内 容包含M个客体点、一个理想点、数个竞争群、 P个准则轴等
变异分析(variation analysis)
探讨所有主体对特定客体在特定准则上评分的变异 程度,进而了解主体评估的公正性 变异数系数大于0.1则需重新评估
S ( xmp ) | xmp | 100%
CV
评分公正 10 课堂气氛 5
非关健
非关健 非关健
准则相关分析(criterion correlation analysis)
探讨两两准则变量间的相关程度,以研判 准则间的重迭性 准则变量的相关程度,可以由知觉图中两 两准则轴之间的夹角加以衡量,夹角越小, 表示两两准则变量间越趋于正相关,越趋 于90度,则表示无关,超过90度则为负相 关 越成正相关或负相关的准则,其间重迭性 越高,可以考虑舍弃其中之一
相依关系
多元尺度应用到变量相依与个案相依两个 观念 输入数据包括五大要素
客体 主体 准则 准则权重 主体权重
多元尺度分析要素
分析要素
客体
意义
被评估的对象,可以是人、事、物等,共有M个
主体
准则
评估客体的单位,通常是人,有N个
研究者根据研究目的自行设定的,用以评估客体 优劣的标准,共有K个,以(x1, x2,…xk)表示
客体点(object point)
知觉图中M个客体点,分别表示M个接受评估的 客体,如图中的A、B、C 知觉图的建构与客体点的相对位置,取决于两 两客体点间的实际距离
理想点(idea point)
根据加权准则所构建的特定客体点 平均而言,理想点在主体心目中的评价最高、 绩效也最高
基本概念
多元尺度分析(MDS, multidimensional scaling analysis)系指N个主体(subjects) 根据P个准则(criterion)评估M个客体 (object)的统计分法 多元尺度分析之目的在于应用知觉图进行 知觉定位分析,包含评估分析、竞争分析; 绩效分析、误差分析、变异分析等
知觉定位分析
探讨产品在消费者心目中的形象,以知觉定位 图为基础,比较不同品牌之间的差异,进而为 自有品牌拟定未来的定位策略
探讨哪些产品属性可有效刺激消费者需求,提 升市场占有率,进而拟定自有品牌之关键成功 因素策略 探讨自有品牌在消费者心目中的价值,形成价 格策略的依据
关键成功因素评估
竞争态势分析(competitive situation analysis)
根据个别客体在P个评估准则上的表现,找 出客体的优势与劣势 客体表现明显较佳的准则称为优势点,表 现明显较弱的准则称为弱势点
王老师 竞争力 属性 评分 竞争力
李老师 属性 评分 竞争力
陈老师 属性 评分 优势点 进度掌控 75 弱势点 教材内容 80 评分公正 75 课程内容 74 表达能力 70 课堂气氛 70
准则权重
主体权重
主体在权衡准则的重要性后,分别对P个准则所 赋予的相对权重,以(w1, w2,…wp)表示 研究者在权衡主体的重要性后,分别对N个主体 所赋予的权重。以(v1, v2,…vn)表示据此可产 生加权评分表
应用举例
市场营销方面
消费可以按照几个决定属性来评估几个不同包 装咖啡品牌的表现,评估结果是探讨知觉定位 的依据 学生可以按照多个教学绩效指针,评估教师的 表现,评估结果是决定最佳师资阵容策略的依 据
竞争群(competitive cluster)
数个距离相近的客体点,可并成一个竞争群, 如理想群、群B、群C等 距离相近的客体点,准则表现比较一致,替代 性高
准则轴(criterion axes)
自原点出发的射线 客体点与准则轴的相对位置可以反映客体点的 绩效表现,越靠近某一准则轴的箭头处,则表 示该准则评分越高
理想点分析(idea point analysis)
以客体点与理想点的接近程度,衡量客体 的知觉绩效,客体与理想点越近,则客体 绩效越佳,越远绩效越差 在实务上常以客体点至理想点间的距离的 倒数占倒数总和的百分比,作为衡量客体 绩效的指标
1 d mi 客体绩效=
2
100% M 1 1 d m mi
知觉分析的要点
分析方法 评价对象 分析内容 基准分 析 理想点 分析 竞争态 势评估 客体 客体 客体 探讨M个客体在某 一准则上的表现 探讨M个客体在P个 准则上的综合表现 探讨客体在P个准则 上的表现 探讨P个准则的相对 重要性 分析目的 订立个别准则的 基准 预估客体的绩效 描述个别客体的 特征
优势点 课程内容 94 优势点 表达能力 80 教材内容 90 表达能力 85 评分公正 80 弱势点 进度掌控 70 进度掌控 75 课程内容 84 课堂气氛 80 评分公正 70 课堂气氛 90 弱势点 教材内容 85
王老师的优势点:课程内容、教材内容、课堂气氛 表达能力、平分公正 弱势点:进度掌控
