后缀表达式求值的算法及代码

合集下载

计算后缀表达式的过程（C#）

计算后缀表达式的过程（C#）
计算后缀表达式的过程是⼀个很好玩的过程，⽽且很简单哦！这⾥呢，有个计算的技巧，就是：遇到数字直接⼊栈，遇到运算符就计算！
后缀表达式也叫逆波兰表达式，求值过程可以⽤到栈来辅助存储；
假定待求值的后缀表达式为：12 4 + 13 - 6 2 * + =
求计算出最终结果：
（1）⾸先我们看到在第⼀个运算符之前呢，有两个数字，那么我们就先把它放⼊栈中：
注：我们可以看到，下标是从下⽅开始读的，⼀定要注意哦，不要弄反了
（2）读到“+”，则弹出12和4，执⾏相加，12+4,=16，并把16放进栈中：（先弹12，再弹4，顺序不能弄错了!!）
（3）读到数字“13”，则直接把13放⼊栈内：
（4）读到运算符“-”，则弹出16和13，执⾏相减，那么16-13=3，并把3放⼊到栈中：
注：在这⾥我们可以看到，如果我们把弹出的顺序弄反了，那么得到的数字就会完全不同，那后⾯的结算也会完全不⼀样，所以，弹出的顺序不能弄反了
（5）读到数字“6”，直接⼊栈：
（6）读到数字“2”，直接⼊栈：
（7）读到运算符“*”，弹出6和2，执⾏相乘，6*2=12，并把12放⼊到栈中：
（8）读到运算符“+”，则弹出3和12，执⾏相加，3+12=15，并把15放⼊栈中：
（9）到了这⾥，我们已经把后缀表达式都已经执⾏了⼀遍，那么得到的最后结果为15，故：
12 4 + 13 - 6 2 * + = 15
这就是运算过程，是不是很简单
END。

基于栈的后缀算术表达式求值c语言

基于栈的后缀算术表达式求值c语言1. 引言1.1 概述本文将讨论基于栈的后缀算术表达式求值的实现过程。

后缀算术表达式（也称为逆波兰表达式）是一种无需括号即可进行运算的表达式表示方法，它将操作符置于操作数之后。

相较于传统的中缀表达式，在计算机程序中处理后缀表达式更为高效和简洁。

1.2 文章结构文章分为五个主要部分：引言、栈的概念及原理、后缀算术表达式的定义和转换、基于栈的后缀算术表达式求值算法实现以及结论与总结。

在引言部分，我们将首先介绍本文的概述和目标，对后续内容进行简要说明。

1.3 目的通过本文，我们旨在让读者了解栈数据结构的基本概念和原理，并且掌握如何利用栈来实现对后缀算术表达式进行求值的算法。

同时，我们将介绍后缀算术表达式的定义和转换方法，并给出基于栈实现该计算方式的详细步骤与示例代码。

通过深入研究并学习这些内容，读者可以加深对栈数据结构和后缀算术表达式的理解，并且能够应用所学知识解决实际问题。

本文不仅适用于计算机科学或相关专业的学生，也适合对数据结构和算法感兴趣的读者阅读和学习。

2. 栈的概念及原理2.1 栈的定义栈是一种具有特定限制条件的线性数据结构，它具备“先进后出”（Last-In-First-Out，LIFO）的特性。

栈可以看作是一个容器，其中可以存储各种类型的数据。

与实际生活中的堆栈类似，栈只允许在其末尾进行插入和删除操作。

在栈中，最后加入的元素首先被访问和处理。

这是由于栈内元素之间的相对位置关系决定的。

插入操作称为“压栈”（Push），删除操作称为“弹栈”（Pop），而从栈顶读取元素或获取栈顶元素但不删除它称为“查看”（Peek）。

2.2 栈的基本操作推入元素：将一个元素添加到栈顶。

如果已经存在满员条件，则无法执行此操作。

弹出元素：从栈顶移除一个元素，并返回移除的值。

如果没有任何元素存在，则无法执行此操作。

查看栈顶元素：获取位于栈顶处的元素值，但不对其进行删除。

判断是否为空：检查栈是否为空。

用栈对后缀表达式求值的算法（五种）

⽤栈对后缀表达式求值的算法（五种）转载出处：第⼀种/* 此程序的功能是求出⽤户输⼊的整形表达式的值*//*输⼊的表达式请⽤#结尾，⽐如：2+3+5，应输⼊：2+3+5#。

*/#include <stdio.h>#define MAXSIZE 16typedef struct{int data[MAXSIZE];int top;int base;}seqstack; /* 顺序栈的定义*//*以下为函数声明*/void InitStack(seqstack *);int Empty(seqstack *);void Push(seqstack *, int );int Pop(seqstack *);int GetTop(seqstack *);int Operate(int ,char ,int );char Proceed(char ,char );int In(char );int EvalExpres(void);/* 定义两个栈分别存放运算符和操作数*/seqstack StackR,StackD;/*主函数*/int main(){int v;char ch;while(1){printf("end with #,for example 2+3+5 input:2+3+5#\n");printf("calculate:") ;v = EvalExpres();printf("The result is:%d",v);/*以下为程序控制*/printf("\nInput 'q' to quit and ENTER run again:");do{scanf("%c",&ch);if(ch == 'q' || ch == 'Q')exit(0);}while(ch!='\n');system("cls");}return 0;}void InitStack(seqstack *s){ s->top = 0;s->base = 0;} /* 初始化栈*/int Empty(seqstack *s){ if(s->top == s->base)return 1;elsereturn 0;} /* 判断栈是否为空*/void Push(seqstack *s, int x){if(s->top == MAXSIZE){ printf("OVER FLOW!\n");exit(0);}else{ s->data[s->top] = x;s->top++;}} /* 进栈 */int Pop(seqstack *s){ int e;if(Empty(s)){ printf("Under flow!\n");return 0;} /* 下溢*/else{ s->top--;e = s->data[s->top];return e;}} /* 出栈*/int GetTop(seqstack *s) /*取栈顶元素*/{if(Empty(s)){ printf("Under flow!\n");return 0;}elsereturn s->data[s->top-1];}int EvalExpres(void) /* 表达式求解函数*/{int a,b,i=0,s=0;char c[80],r;InitStack(&StackR);Push(&StackR,'#');InitStack(&StackD);printf(" end with #");gets(c);while(c[i]!='#' || GetTop(&StackR)!='#'){if(!In(c[i])) /* 判断读⼊的字符不是运算符是则进栈*/{ if(c[i] >= '0' && c[i] <= '9'){s += c[i]-'0';while(!In(c[++i])) /*此处实现的功能为当输⼊的数字为多位数时*/{ s*=10;s += c[i]-'0';}Push(&StackD,s+'0');s = 0;}else{printf("wrong!\n");return 0;}}elseswitch(Proceed(GetTop(&StackR),c[i])) /* 此函数⽤来⽐较读取的运算符和栈顶运算符的优先级*/ {case '<': /* 栈顶的元素优先级⾼*/i++;break;case '=': /* 遇到匹配的⼩括号时则去掉他*/Pop(&StackR);i++;break;case '>': /* 栈顶的优先级低则出栈并将结果写⼊栈内*/r = Pop(&StackR);a = Pop(&StackD)-'0';b = Pop(&StackD)-'0';Push(&StackD,Operate(a,r,b)) ;break;}}return (GetTop(&StackD)-'0'); /* 返回运算结果*/}int In(char c) /*问题2：解决In函数问题:判断C是否为运算符是返回1否则返回0*/{char ch[7]={'+','-','*','/','#','(',')'};int i;for(i = 0; i < 7; i++)if(c == ch[i])return 1;return 0;}char Proceed(char op,char c) /*op为栈顶元素，c为当前读⼊的运算符,⽐较⼆者的优先级*/ { /*问题1：解决Proceed函数*/char ch;if(op=='(' && c==')' || op=='#' && c=='#' )ch = '=';elseif(op=='+' || op=='-') /*栈顶元素为‘+’或‘-’的时候*/switch(c){case '+':case '-':case ')':case '#': ch = '>'; break;case '*':case '/':case '(': ch = '<';}elseif(op=='*' || op=='/') /*栈顶元素为‘*’或‘/’的时候*/switch(c){case '+':case '-':case '*':case '/':case ')':case '#': ch = '>'; break;case '(': ch = '<';}elseif(op=='(') /*栈顶元素为‘(’的时候*/switch(c){case '+':case '-':case '*':case '/':case '#': printf("Error!\n"); exit(0);}elseif(op==')') /*栈顶元素为‘)’的时候*/switch(c){case '+':case '-':case '*':case '/':case '#': ch = '>'; break;case '(': printf("Error!\n"); exit(0);}elseif(op=='#') /*栈顶元素为‘#’的时候*/ switch(c){case '+':case '-':case '*':case '/':case '(': ch = '<'; break;case ')': printf("Error!\n"); exit(0);}return ch;}/* 问题3：解决Operate函数*/int Operate(int a,char r,int b) /*返回由aRb的值 */ {int s;int d1 = a;int d2 = b; /*把字符ab变为对应数字*/switch(r){case '+': s = d1+d2; break;case '-': s = d2-d1; break;case '*': s = d1*d2; break;case '/': s = d2/d1;}return (s+'0');}第⼆种#include <stdio.h>#include <malloc.h>#define MaxSize 50void trans(char *exp,char *postexp){struct{char data[MaxSize];int top;} op;int i=0;op.top=-1;while(*exp!='\0'){switch(*exp){case '(':op.top++;op.data[op.top]=*exp;exp++;break;case ')':postexp[i++]=op.data[op.top];op.top--;}op.top--;exp++;break;case '+':case '-':while(op.top!=-1&&op.data[op.top]!='('){postexp[i++]=op.data[op.top];op.top--;}op.top++;op.data[op.top]=*exp;exp++;break; case '*':case '/':while(op.data[op.top]=='*'||op.data[op.top]=='/') {postexp[i++]=op.data[op.top];op.top--;}op.top++;op.data[op.top]=*exp;exp++;break; case ' ':break;default:while(*exp>='0'&&*exp<='9'){postexp[i++]=*exp;exp++;}postexp[i++]='#';}}while(op.top!=-1){postexp[i++]=op.data[op.top];op.top--;}postexp[i]='\0';}float compvalue(char *postexp){struct{float data[MaxSize];int top;} st;float a,b,c,d;st.top=-1;while(*postexp!='\0'){switch(*postexp){case '+':a=st.data[st.top];st.top--;b=st.data[st.top];st.top--;c=b+a;st.top++;st.data[st.top]=c;break;case '-':a=st.data[st.top];st.top--;b=st.data[st.top];st.top--;c=b-a;break;case '*':a=st.data[st.top];st.top--;b=st.data[st.top];st.top--;c=b*a;st.top++;st.data[st.top]=c;break;case '/':a=st.data[st.top];st.top--;b=st.data[st.top];st.top--;if(a!=0){c=b/a;st.top++;st.data[st.top]=c;}else{printf("\n\t除零错误!\n");exit(0);}break;default:d=0;while(*postexp>='0'&&*postexp<='9'){d=10*d+*postexp-'0';postexp++;}st.top++;st.data[st.top]=d;break;}postexp++;}return st.data[st.top];}int main(){char exp[MaxSize],postexp[MaxSize];while(scanf("%s",&exp)!=EOF){trans(exp,postexp);printf("zhongzhuibiaodashi: %s\n",exp);printf("houzuibiaodashi: %s\n",postexp);printf("zhi: %g\n",compvalue(postexp)); }return 0;}第三种#include<stdio.h>#include<stdlib.h>#define add 43#define subs 45#define mult 42#define div 47#define MAXSIZE 100int data[MAXSIZE];int top;}seqstack;seqstack *s;seqstack *Init() /*栈的初始化*/{seqstack *s;s=(seqstack *)malloc(sizeof(seqstack)); if(!s){printf("FULL!");return NULL;}else{s->top=-1;return s;}}int Empty(seqstack *s) /*栈空的判断*/{if(s->top==-1) return 1;else return 0;}int Push(seqstack *s,int x) /*⼊栈*/{if(s->top==MAXSIZE-1) return 0;else{s->top++;s->data[s->top]=x;return 1;}}int Pop(seqstack *s,int *x) /*出栈的算法*/ {if (Empty(s)) return 0;else{*x=s->data[s->top];s->top--;return 1;}}int Top(seqstack *s) /*取栈顶元素*/ {if(Empty(s)) return 0;else return s->data[s->top];}int eval(char t,int a1,int a2){switch(t){case add:return(a1+a2);case subs:return(a1-a2);case mult:return(a1*a2);case div:return(a1/a2);}}void main(){char c;int op1,op2,temp,c1;s=Init();printf("Input:(end with #)\n");while((c=getchar())!='#'){if(c=='')continue;if(c>47&&c<58){putchar(c);c1=c-48;}else if(c==add||c==subs||c==mult||c==div){putchar(c);Pop(s,&op1);Pop(s,&op2);temp=eval(c,op2,op1);Push(s,temp);}else printf("It's wrong!\n");}Pop(s,&op1);printf("=%d\n",op1);getch();}第四种#include<stdio.h>#include<stdlib.h>#define add 43#define subs 45#define mult 42#define div 47#define MAXSIZE 100typedef struct{int data[MAXSIZE];int top;}STKzone;typedef STKzone *STK;typedef enum{ture=1,false=0} bool;typedef enum{ok,error} status;STKzone expSTKzone;STK expSTK;STK initSTK(STKzone *stkzone) /*栈的初始化*/{STK p;p=stkzone;p->top=0;}status push(int *term,STK pstk) /*⼊栈*//*term前可以没有*，同时将第28、71、81⾏稍作修改即可 */ {if(pstk->top==MAXSIZE) return error;pstk->data[pstk->top]=*term;pstk->top++;return ok;}bool emptySTK(STK pstk) /*栈空的判断*/{return (pstk->top==0);}status pop(int *pdata,STK pstk) /*出栈的算法*/{if (emptySTK(pstk)) return error;(pstk->top)--;*pdata=pstk->data[pstk->top];return ok;}void synerror(){printf("\nyu fa cuo wu!");}{switch(tag){case add:return(a1+a2);case subs:return(a1-a2);case mult:return(a1*a2);case div:return(a1/a2);}}main(){ char c;int op1,op2,temp,c1;expSTK=initSTK(&expSTKzone);printf("Input:\n");while((c=getchar())!='\n'){if(c=='')continue;if(c>47&&c<58){putchar(c);c1=c-48;if(push(&c1,expSTK)==error){printf("\n too long!\n");}}else if(c==add||c==subs||c==mult||c==div) {putchar(c);if(pop(&op1,expSTK)==error)synerror(); if(pop(&op2,expSTK)==error)synerror(); temp=eval(c,op2,op1);push(&temp,expSTK);}else synerror();}if(pop(&op1,expSTK)==error) synerror();if(!(emptySTK(expSTK))) synerror();printf("=%d\n",op1);getch();}第五种#include<stdio.h>#include<stdlib.h>#define add 43#define subs 45#define mult 42#define div 47#define MAXSIZE 100typedef struct{int stkdata[MAXSIZE];int top;}stack;int init_stack(stack *s){ s=(stack *)malloc(sizeof(stack));if(!s){printf("FULL!\n");return 0;}else{s->top=-1;return 1;}}int push(stack *s,int x){ printf("over flow\n");return 0;}else{s->top++;s->stkdata[s->top]=x;return 1;}}char pop(stack *s){ char e;if(s->top==-1){printf("under flow \n");return 0;}e=s->stkdata[(s->top)--];return e;}void main(){stack *s1;int length,i,num1,num2,result,sum;char s[100];init_stack(s1);printf("please input \n");printf("warning:must less than 100\n");gets(s);length=strlen(s);for(i=0;i<=length-1;i++){ if(s[i]>='1'&&s[i]<='9')push(s1,s[i]-48);else{ num1=pop(s1);num2=pop(s1);switch(s[i]){case add: {sum=num1+num2;push(s1,sum);break;}case subs:{sum=num2-num1;push(s1,sum);break;}case div:{sum=num2/num1;push(s1,sum);break;}case mult:{sum=num1*num2;push(s1,sum);break;}}}}result=s1->stkdata[s1->top];printf("result is %d\n",result);getch();}在研究表达式。

栈应用之后缀表达式计算（python版）

栈应⽤之后缀表达式计算（python版）栈应⽤之后缀表达式计算（python 版）后缀表达式特别适合计算机处理1. 中缀表达式、前缀表达式、后缀表达式区别中缀表达式：(3 - 5) * (6 + 17 * 4) / 3 17 * 4 + 6前缀表达式：/ * - 3 5 + 6 * 17 4 3 * 17 4 + 6后缀表达式：3 5 - 6 17 4 * + * 3 / 17 4 * 6 +2. 算法核⼼假定 st 是⼀个栈（栈的特点：后进先出 LIFO）　⽐如【3 / 5】即【3 5 / 】； 3 先压⼊栈，⽽后 5 出栈；元素在栈⾥⾯的顺序应该是【5，3】； 5 先出栈，⽽后 3 出栈。

所以第⼆个运算对象先出栈，第⼀个运算对象后出栈。

1# 扩充栈的⽅法计算栈元素个数2class ESStack(SStack):3"""docstring for ESS"""4def depth(self):5return len(self._elems)1def auf_exp_evaluator(exp):2 operatora = '+-*/'3 st = ESStack() # 扩充功能的栈，可⽤depth()检查元素个数45for x in exp:6if x not in operatora:7 st.push(flaot(x))8continue# 跳过本次for循环910if st.depth() < 2 :11raise SyntaxError{"Short of operand(s)"}12 a = st.pop() # 取出第⼆个运算对象13 b = st.pop() # 取出第⼀个运算对象1415if x == "+"：16 c = b + a17elif x == "-":18 c = b - a19elif x == "*"：20 c = b * a21elif x == "/" : # 这⾥可能引发异常 ZeroDivisionError22 c = b / a23else :24break# 这⼀步不可能出现，只是为了⽅便看、理解2526 st.push(c) # 将本次运算结果压⼊栈2728if st.depth() == 1 # 如果栈⾥⾯只有⼀个元素，表⽰计算完成29return st.pop()30raise SyntaxError{"Extra operand(s) ."}。

后缀表达式求值的算法及代码

#include<stdlib.h>#include<stdio.h>struct node // 栈结构声明{int data; // 数据域struct node *next; // 指针域};typedef struct node stacklist; // 链表类型typedef stacklist *link; // 链表指针类型link operand=NULL; // 操作数栈指针link push(link stack,int value) // 进栈{link newnode; // 新结点指针newnode=new stacklist; // 分配新结点if (!newnode){printf("分配失败！");return NULL;}newnode->data=value; // 创建结点的内容newnode->next=stack;stack=newnode; // 新结点成为栈的开始return stack;}link pop(link stack,int *value) // 出栈{link top; // 指向栈顶if (stack !=NULL){top=stack; // 指向栈顶stack=stack->next; // 移动栈顶指针*value=top->data; // 取数据delete top; // 吸收结点return stack; // 返回栈顶指针}else*value=-1;}int empty(link stack) // 判栈空{if (stack!=NULL)return 1;elsereturn 0;}int isoperator(char op) // 判运算符{switch (op){case'+':case'-':case'*':return 1; // 是运算符,返回1case'/':return 0; // 不是运算符,返回0}}int getvalue(int op,int operand1,int operand2) // 计算表达式值{switch((char)op){case'*':return(operand1*operand2);case'/':return(operand1/operand2);case'+':return(operand1+operand2);case'-':return(operand1-operand2);}}void main() // 主函数{char exp[100];int operand1=0; // 定义操作数1int operand2=0; // 定义操作数2int result=0; // 定义操作结果int pos=0;printf("\t\n 请输入后缀表达式：");gets(exp); // 读取表达式printf("\t\n\n 后缀表达式[%s]的计算结果是：",exp);while (exp[pos] !='\0' && exp[pos] !='\n') // 分析表达式字符串{if (isoperator(exp[pos])) // 是运算符，取两个操作数{operand=pop(operand,&operand1);operand=pop(operand,&operand2);operand=push(operand,getvalue(exp[pos],operand1,operand2));// 计算结果入栈}elseoperand=push(operand,exp[pos]-48); // 是操作数，压入操作数栈pos++; // 移到下一个字符串位置}operand=pop(operand,&result); // 弹出结果printf("%d\n",result); // 输出}。

C#算术表达式求值（后缀法），看这一篇就够了

C#算术表达式求值（后缀法），看这⼀篇就够了⼀、种类介绍算术表达式有三种：前缀表达式、中缀表达式和后缀表达式。

⼀般⽤的是中缀，⽐如1+1，前后缀就是把操作符移到前⾯和后⾯，下⾯简单介绍⼀下这三种表达式。

1、前缀表⽰法前缀表⽰法⼜叫波兰表⽰法，他的操作符置于操作数的前⾯（例：+ 1 2），是波兰数学家扬·武卡谢维奇1920年代引⼊的，⽤于简化命题逻辑。

因为我们⼀般认为操作符是在操作数中间的，所以在⽇常⽣活中⽤的不多，但在计算机科学领域占有⼀席之地。

⼀般的表⽰法对计算机来说处理很⿇烦，每个符号都要考虑优先级，还有括号这种会打乱优先级的存在，将使计算机花费⼤量的资源进⾏解析。

⽽前缀表⽰法没有优先级的概念，他是按顺序处理的。

举个例⼦：9-2*3这个式⼦，计算机需要先分析优先级，先乘后减，找到2*3，再进⾏减操作；化成前缀表⽰法就是：- 9 * 2 3，计算机可以依次读取，操作符作⽤于后⼀个操作数，遇到减就是让9减去后⾯的数，⽽跟着9的是乘，也就是说让9减去乘的结果，这对计算机来说很简单，按顺序来就⾏了。

2、中缀表⽰法这也就是我们⼀般的表⽰法，他的操作符置于操作数的中间（例：1 + 2），前⾯也说过这种⽅法不容易被计算机解析，但他符合⼈们的普遍⽤法，许多编程语⾔也就⽤这种⽅法了。

在中缀表⽰法中括号是必须有的，要不然运算顺序会乱掉。

3、后缀表⽰法后缀表⽰法⼜叫逆波兰表⽰法，他的操作符置于操作数的后⾯（例：1 2 +），他和前缀表⽰法都对计算机⽐较友好，但他很容易⽤堆栈解析，所以在计算机中⽤的很多。

他的解释过程⼀般是：操作数⼊栈；遇到操作符时，操作数出栈，求值，将结果⼊栈；当⼀遍后，栈顶就是表达式的值。

因此逆波兰表达式的求值使⽤堆栈结构很容易实现，且能很快求值。

注意：逆波兰记法并不是简单的波兰表达式的反转。

因为对于不满⾜交换律的操作符，它的操作数写法仍然是常规顺序，如，波兰记法/ 6 3的逆波兰记法是6 3 /⽽不是3 6 /；数字的数位写法也是常规顺序。

前缀后缀算数运算编程

一、设计思想1、中缀转化为后缀算法过程中要使用一个栈和两个数组，（栈用来存放运算符，一个数组用来存放中缀表达式，两一个则是存放后缀表达式）表达式的转换过程如下：（1）、将表达式开始符“#“压入运算符栈，作为栈底元素。

（2）、从左到右依次扫描中缀表达式的每一个字符。

（3）、如果遇到的是开括号“（”，则将它们压入一个操作符栈（不需要与栈顶操作符相比较），它表明一个新的计算层次的开始，在遇到和它匹配的闭括号“）”时，将栈中的元素弹出来并放入后缀表达式中，直到栈顶元素为“(”时，将栈顶元素“（”弹出（不需要加入后缀表达式），表明这一层括号内的操作处理完毕（4）、即将进栈的操作符要与栈顶的操作符进行优先级比较，若当所遇到的操作符的优先级大于栈顶元素时，进栈，否则是将栈顶元素一次弹栈放入后缀数组，直到比较操作符小于或等于栈顶元素时为止。

重复以上操作，最后将栈内所有操作符放进后缀数组内。

（5）、重复上述步骤直到缀表达式的结束符标记“#“，弹出栈中所有元素并放入后缀表达，转换结束。

中缀表达式为：17-3*4+（8/2）# 后缀表达式为：17 3 4 * - 8 2/+2、中缀转化为前缀算法过程中要使用三个数组，（一个栈数组，一个存放中缀表达式，一个存放前缀表达式）表达式的转换过程如下：（1）将表达式开始符“#“压入运算符栈数组，作为栈底元素。

（2）、从右到左依次扫描中缀表达式的每一个字符。

（3）、如果遇到的是开括号“）”，则将它们放进栈数组内（不需要与栈顶操作符相比较），它表明一个新的计算层次的开始，在遇到和它匹配的闭括号“（”时，将栈中的元素弹出来并放入前缀表达式中，直到栈顶元素为“）”时，将栈顶元素“）”弹出（不需要加入后缀表达式），表明这一层括号内的操作处理完毕（4）、如果遇到的是操作符，则将该操作符和操作符栈顶元素比较：当所遇到的操作符的优先级小于栈顶元素的优先级时，则取出栈顶元素放入后缀表达式，并弹出该栈顶元素，反复执行直到操作符的优先级大于或等于栈顶元素的优先级的时则将它压入栈中。

中缀表达式变后缀表达式、后缀表达式（逆波兰）求值（python版本）

中缀表达式变后缀表达式、后缀表达式（逆波兰）求值（python版本）定义：中缀表达式：在通常的表达式中，⼆元运算符总是置于与之相关的两个运算对象之间，这种表⽰法也称为中缀表达式后缀表达式：⼜叫逆波兰表达式，不包含括号，放在两个运算对象的后⾯，所有的计算按运算符出现的顺序，严格从左向右进⾏（不再考虑运算符的优先规则，如：(2 + 1) * 3 ，即2 1 + 3 *⼀个字符串表达式s = “9 + ( 3 - 1 ) * 3 + 10 / 2”）求值的过程分为两步(⼀) 将中缀表达式s变为后缀表达式s_after = "9 3 1 - 3 * + 10 2 / +",具体的规则如下：⾸先维护两个空栈，（stack_exp）存放逆波兰表达式，(stack_ops)暂存操作符，运算结束后stack_ops必为空循环遍历字符串(将表达式分为四种元素 1、数值; 2、操作符; 3、左括号; 4、右括号)，具体情况如下1、遇到数值，将该值⼊栈stack_exp2、遇到左括号，将左括号⼊栈stack_ops3、遇到右括号，将stack_ops中的操作符从栈顶依次出栈并⼊栈stack_exp，直到第⼀次遇到左括号终⽌操作（注意：该左括号出栈stack_ops但不⼊栈stack_exp）⾄此消除表达式中的⼀对括号4、遇到四则运算操作符号（+ - * /）4-1、如果stack_ops为空，操作符⼊栈stack_ops4-2、如果stack_ops不空，将stack_ops栈顶操作符与遍历到的操作符(op)⽐较：4-2-1：如果stack_ops栈顶操作符为左括或者op优先级⾼于栈顶操作符优先级， op⼊栈stack_ops，当前遍历结束4-2-2：如果op优先级⼩于或者等于stack_ops栈顶操作符， stack_ops栈顶操作符出栈并⼊栈stack_exp，重复4-1、 4-2直到op⼊栈stack_ops5、字符串遍历结束后如果stack_ops栈不为空，则依次将操作符出栈并⼊栈stack_exppython代码实现如下：ops_rule = {'+': 1,'-': 1,'*': 2,'/': 2}def middle_to_after(s):expression = []ops = []ss = s.split('')for item in ss:if item in ['+', '-', '*', '/']:while len(ops) >= 0:if len(ops) == 0:ops.append(item)breakop = ops.pop()if op == '('or ops_rule[item] > ops_rule[op]:ops.append(op)ops.append(item)breakelse:expression.append(op)elif item == '(':ops.append(item)elif item == ')':while len(ops) > 0:op = ops.pop()if op == '(':breakelse:expression.append(op)else:expression.append(item)while len(ops) > 0:expression.append(ops.pop())return expression(⼆) 将后缀表达式s_after = "9 3 1 - 3 * + 10 2 / +" 求值,具体的规则如下：初始化⼀个空栈stack_value，⽤于存放数值循环s_after1、如果遇到数字，⼊栈stack_value;2、如果遇到运算符，从stack_value中依次出栈两个数（先出栈的在右，后出栈的在左）连同遍历到的运算符组成⼆⽬运算，求值后将结果压栈stack_value3、继续遍历下⼀个元素，直到结束遍历完后stack_value中的结果便是表达式的值python代码实现如下：def expression_to_value(expression):stack_value = []for item in expression:if item in ['+', '-', '*', '/']:n2 = stack_value.pop()n1 = stack_value.pop()result = cal(n1, n2, item)stack_value.append(result)else:stack_value.append(int(item))return stack_value[0]def cal(n1, n2, op):if op == '+':return n1 + n2if op == '-':return n1 - n2if op == '*':return n1 * n2if op == '/':return n1 / n2if __name__ == '__main__':expression = middle_to_after('9 + ( 3 * ( 4 - 2 ) ) * 3 + 10 / 2')value = expression_to_value(expression)print value。

表达式求值（后缀表达式求值）

表达式求值（后缀表达式求值）表达式求值时间限制：3000 ms | 内存限制：65535 KB难度：4描述ACM队的mdd想做⼀个计算器，但是，他要做的不仅仅是⼀计算⼀个A+B的计算器，他想实现随便输⼊⼀个表达式都能求出它的值的计算器，现在请你帮助他来实现这个计算器吧。

⽐如输⼊：“1+2/4=”，程序就输出1.50（结果保留两位⼩数）输⼊第⼀⾏输⼊⼀个整数n，共有n组测试数据（n<10)。

每组测试数据只有⼀⾏，是⼀个长度不超过1000的字符串，表⽰这个运算式，每个运算式都是以“=”结束。

这个表达式⾥只包含+-*/与⼩括号这⼏种符号。

其中⼩括号可以嵌套使⽤。

数据保证输⼊的操作数中不会出现负数。

数据保证除数不会为0输出每组都输出该组运算式的运算结果，输出结果保留两位⼩数。

样例输⼊21.000+2/4=((1+2)*5+1)/4=样例输出1.504.00题解：求后缀表达式，⽤后缀表达式，求解；AC代码：#include<cstdio>#include<iostream>#include<cmath>#include<algorithm>#include<cstring>#include<queue>#include<stack>using namespace std;const int INF=0x3f3f3f3f;#define mem(x,y) memset(x,y,sizeof(x))#define SI(x) scanf("%d",&x)#define PI(x) printf("%d",x)typedef long long LL;const int MAXN=1010;char s[MAXN];char work(char a,char b){if(a=='#')return'<';if(a=='+'||a=='-'){if(b=='*'||b=='/'||b=='(')return'<';else return'>';}if(a=='*'||a=='/'){if(b=='(')return'<';else return'>';}if(a=='('||a=='='){if( (a=='('&&b==')')||(a=='='&&b=='=') ) return'=';else return'<';}}int main(){int T;SI(T);while(T--){double temp,p,a,b;scanf("%s",s);stack<char>S;stack<double>s2;S.push('#');for(int i=0;s[i];){// printf("%c\n",s[i]);if(isdigit(s[i])||s[i]=='.'){temp=0,p=10;while(isdigit(s[i])||s[i]=='.'){if(s[i]=='.'){p=0.1;i++;continue;}if(p==10)temp=temp*p+s[i]-'0';else temp=temp+(s[i]-'0')*p,p*=0.1;i++;}// printf("%lf\n",temp);s2.push(temp);}//s2.push(s[i++]);else{switch(work(S.top(),s[i])){case'<':S.push(s[i]);i++;break;case'>':a=s2.top();s2.pop();b=s2.top();s2.pop();if(S.top()=='+')s2.push(a+b);else if(S.top()=='-')s2.push(b-a);else if(S.top()=='*')s2.push(a*b);else s2.push(b/a);//printf("%lf\n",s2.top());S.pop();break;case'=':S.pop();i++;break;}}}//printf("%d %d %lf\n",S.size(),s2.size(),s2.top()); printf("%.2lf\n",s2.top());}return0;}。

C语言下表达式的自动计算(两种方式)(报告+源代码)

一、设计思想第一种算法：将中缀表达式转为后缀表达式，然后通过后缀表达式计算出算术表达式的结果。

核心思想：第一步：中缀变后缀。

首先，我们做出一个统一的Node结构体，结构体内部包含四个属性，分别是操作符的字符‘op’，char类型；操作符的优先级‘level’，int 类型；数字的浮点数数值‘od’，float类型；Node的标识符，int类型。

然后，定义一个Node结构体类型的数组*listNode，这里的*listNode用的是全局变量，为了方便在得到后缀表达式后，不需再传递给计算的方法。

定义一个存放操作符的栈，遍历用户输入的算术表达式（不考虑错误情况），在遍历的过程中如果遇到数字，直接将数字存放在*listNode里面；如果遇到了操作符，则判断操作符栈目前是不是为空，如果为空，直接将遇到的操作符放入操作符栈中，如果操作符栈不为空，那么观察操作符栈中栈顶的操作符，然后再次判断当前遇到的操作符的优先级是不是比栈顶的操作符的优先级高，如果是，那么将当前的操作符入操作符栈；如果不是，那么将操作符栈的栈顶操作符取出，追加到*listNode中，然后继续观察栈顶操作符，直到当前的操作符的优先级比栈顶操作符的优先级高或者操作符栈为空时，将当前操作符入操作符栈。

如果遇到了左括号，那么定义其优先级为最低，然后直接将左括号入操作符栈。

如果遇到了右括号，那么开始从操作符栈中取出操作符追加到*listNode中，直到遇到了与之对应的左括号，然后将左括号和右括号一起销毁。

当遍历完成了算术表达式之后，这时判断操作符栈是否为空，如果不为空，那么从操作符栈中依次取出栈顶操作符追加到*listNode中，直到操作符栈为空，那么就代表我们将中缀表达式转变成为了后缀表达式。

第二步：通过得到的后缀表达式，计算算术表达式。

首先，定义一个数字栈用来存放数值。

然后，遍历*listNode中的每一个Node，如果Node是一个数字，那么就将数字入数字栈，如果Node是一个操作符，那么就从数字栈中依次取出栈顶的两个数字，然后根据操作符计算这两个数字，将得到的结果再次入数字栈，直到遍历*listNode完成，最终数字栈中会只剩下一个Node，那就是我们计算出算术表达式的结果，将结果返回给main 函数用来输出。

数据结构代码中缀转后缀表达式算法及源代码

数据结构代码中缀转后缀表达式算法及源代码#include<stdio.h>#include<stdlib.h>#include<math.h>#define MAX 100 /* 表达式最大长度 */ #define true 1#define false 0/* 定义数据栈 */typedef struct LinkStack1{float data;struct LinkStack1 *next; }LinkStack1,*Top1; nt initStack1(Top1 *t) /*数据栈初始化*/ i{*t=NULL;return true;}int push1(Top1 *t,float val) /*数据栈插入元素*/{Top1 p=(Top1)malloc(sizeof(LinkStack1));/* 开内存 */if(p==NULL)return false;p->data=val;p->next=*t;*t=p;return true;}float getTop1(Top1 *t) /*取数据栈元素*/ {return (*t)->data; }int pop1(Top1 *t,float *val) /*推出数据栈元素并存到*val中*/ {Top1 p=*t;if(p==0)return false;*t=p->next;*val=p->data;free(p); /* 释放所占内存 */return true;}/* 定义操作符栈 */typedef struct LinkStack2{int data;struct LinkStack2 *next; LinkStack2,*Top2; }int initStack2(Top2 *t) /*数据栈初始化*/ {*t=NULL;return true;}int push2(Top2 *t,char val) /*操作符栈插入元素*/ {Top2 p=(Top2)malloc(sizeof(LinkStack2)); /* 开内存 */ if(p==0)return false;p->data=val;p->next=*t;*t=p;return true;}int getTop2(Top2 *t) /*取操作符栈元素*/ {return (*t)->data; }int pop2(Top2 *t,char *val)Top2 p=*t;if(p==0)return false;*t=p->next;*val=p->data;free(p); /* 释放所占内存 */return true;}/* 计算 */float calc(float a, char op, float b) { int d,e; switch(op){case '+':return a+b; /* 计算+ */case '-':return a-b; /* 计算- */case '*':return a*b; /* 计算* */case '/': /* 计算/，若被除数为零，报错 */if(b==0){printf("Error Divisor is 0\n");return false;}return a/b;case '%': /* 计算%，若被取余数为零报错 */d=(int)a;e=(int)b;if(e==0){printf("Error Divisor is 0\n");return false;}return (float)(d%e);default:printf("Error !! not oprater\n"); /* 非操作符报错 */ return false;}}/* 判断操作符优先级 */char priority(char a,char b) {if(a=='='&&b=='\n')return'*'; /* '*' 表示结束 */if(a=='('&&b==')')return'#'; /* '#' 表示左右括号相遇 */ /* '<'、'>'、'=' 分别表示优先级:小于、大于、相等 */if(a=='=')return'<';if(b=='\n')return'>';if(a==')')return'>';if(a=='(')return'<';if(b=='(')return'<';if(b==')'&&a!='(')return'>';if((a=='+'||a=='-')&&(b=='/'||b=='*'||b=='%'))return'<';if((b=='+'||b=='-')&&(a=='/'||a=='*'||a=='%'))return'>';if((a=='+'||a=='-')&&(b=='+'||b=='-'))return'=';if((a=='*'||a=='/'||a=='%')&&(b=='*'||b=='/'||b=='%'))return'='; } /* 是否操作符 */int isOp(char m){if(m=='*'||m=='/'||m=='%'||m=='('||m==')'||m=='+'||m=='-'||m=='\n') return true;return false;}/* 中缀变后缀 */void Infix(char a[],char b[]) {char c,p,x;int i=0,j=0;Top2 op;initStack2(&op); /*初始化操作符栈*/push2(&op,'='); /* '='作为栈底元素 */while(a[i]!='\0'){if(!isOp(a[i])) /*是操作数，直接输出*/{b[j++]=a[i];}else{b[j++]=' '; /* 数字和数字用空格隔开 */switch(priority(getTop2(&op),a[i])) /*比较两个算符的优先级*/ {case'<':push2(&op,a[i]);/*当前算符优先级高，将其入操作符栈*/break;case'>':case'=':while((priority(getTop2(&op),a[i])=='=')||(priority(getTop2(&op),a[i])=='>')){pop2(&op,&c); /*当前算符优先级低，则取栈顶*/b[j++]=c;}if(priority(getTop2(&op),a[i])=='<')push2(&op,a[i]); /*出栈*/else{if(priority(getTop2(&op),a[i])=='#'){pop2(&op,&c); /*当前算符优先级低，则取栈顶*/i++;break;}else break;}break;case'#':/*左右括号相遇，则推出栈顶，并原表达式数组下标加1*/ pop2(&op,&c);i++;break;case'*': /*结束*/break;}}i++;}if(a[i]=='\0'){while(op->data!='=')/* 字符栈元素全都放到b数组中 */ {pop2(&op,&p);b[j++]=p;i++;}for(i=0;i<j;i++) /* 输出后缀表达式 */printf("%c",b[i]);}b[j]='\0'; /*为字符数组置结束标志 */}/*将数字字符转变成相应的数*/float charToNum(char a[],int *i) {float x=0.0;int k=0;while(a[*i]>='0'&&a[*i]<='9') /* 整数部分 */{x=x*10+a[*i]-'0';(*i)++;}if(a[*i]=='.') /*小数部分*/{(*i)++;while(a[*i]>='0'&&a[*i]<='9'){x=x*10+a[*i]-'0';(*i)++;k++; /*记录多少小数位数*/}}while(k!=0){x=x/10;k=k-1;}return x;}/* 第一种:后缀表达式计算 */float the_fir_Exp(char c[]){int i=0;float a,b,n;Top1 dig;initStack1(&dig); /*初始化操作数栈*/ push1(&dig,0);while(c[i]!='\0') /*为表达式的结束标志*/{if(!isOp(c[i])&&c[i]!=' ') /*为操作数*/{n=charToNum(c,&i);i=i-1; /*转换后 i值应该减一否则丢掉一个字符*/ push1(&dig,n);}else if(isOp(c[i])) /*为操作符*/{pop1(&dig,&a);/*取一操作数*/pop1(&dig,&b); /*取另一操作数*/push1(&dig,(calc(b,c[i],a))); /*计算，并压入栈*/ }i++;}return getTop1(&dig);}/* 第二种计算方法 */float the_sec_Exp(char a[]) {int i=0,j;char b[MAX],c;float m,n;Top2 op;Top1 dig;initStack2(&op); /*初始化操作符栈*/push2(&op,'=');initStack1(&dig); /*初始化操作数栈*/push1(&dig,0);while(a[i]!='\0'){if(!isOp(a[i])) /*是操作数*/{j=0;for(;!isOp(a[i])&&a[i]!='\0';i++)b[j++]=a[i];b[j]='+'; /*‘+’结束*/j=0;push1(&dig,(charToNum(b,&j))); /*转换，并压入栈*/}else{switch(priority(getTop2(&op),a[i]))/*比较两个算符的优先级*/ {case'<':push2(&op,a[i]); i++;break;case'>':case'=':pop2(&op,&c); /*取出操作符*/pop1(&dig,&m);/*取一操作数*/pop1(&dig,&n); /*取另一操作数*/push1(&dig,(calc(n,c,m))); /*计算，并压入栈*/ break;case'#':pop2(&op,&c);i++;break;case'*':break;}}}pop2(&op,&c); /*取出操作符*/while(c!='=') /*‘=’为操作符栈的结束标志*/ {pop1(&dig,&m); /*取一操作数*/pop1(&dig,&n); /*取另一操作数*/push1(&dig,(calc(n,c,m))); /*计算，并压入栈*/ pop2(&op,&c); /*取出操作符*/}return getTop1(&dig); /*返回值为数字栈栈顶*/ } /* 主函数 */void main(){loop: /* 确定再次输入数据计算，及输入错误时循环 */{int i,k,j;int z[MAX],y[MAX];char a[MAX]={""},b[MAX],ch;float m;z[MAX]="";y[MAX]=""; /* 初始化a[]/,z[],y[]*/printf("\nInput:");scanf("%s",&a); /* 输入表达式 *//* 容错四种情况 */for(i=0;a[i]!='\0';i++){if(!(a[i]>='0'&&a[i]<='9'||isOp(a[i])||a[i]=='.'))/* 1 非数字、小数点和操作符 */{printf("------");for(j=0;j<i;j++)printf("-");printf("^\n");printf("input wrong!!! intput again.\n");goto loop;}if(i>=MAX-1) /* 2 表达式越界 */{printf("input too long!!! intput again.\n");goto loop;}}for(i=0,j=0,k=0;a[i]!='\0';i++){if(a[i]=='(') z[k++]=i; /*z[k]为记录'('的位置 k表示(的数目*/ if(a[i]==')') y[j++]=i; /*y[k]为记录')'的位置 y表示 )的数目*/ }if(k!=j)/* 3 左右括号不相等 */{printf("------");if(k>j){for(i=0;i<z[k-1];i++)printf("-"); }elseif(k<j){ for(i=0;i<y[j-1];i++)printf("-");}printf("^\n");printf("input wrong!!! the NO. of '(' != ')'intput again:\n"); goto loop;}k=0; j=0; i=0;for(;a[i]!='\0';i++) /* 4 左括号在右括号右面 */{if(z[k++]>y[j++]){printf("------");for(i=0;i<z[k-1];i++)printf("-");printf("^\n");printf("input wrong!!! ')'first then '(' intput again:\n"); goto loop;}}/* 中缀变后缀,再计算 */printf("postfix expressions is:");Infix(a,b); /* 中缀变后缀 */m=the_fir_Exp(b); /* 后缀表达式计算 */printf("\nthe first method result is :%lf\n",m);/* 直接计算 */m=the_sec_Exp(a);printf("the second method result is :%lf\n",m);/* 是否再次输入数据计算 */printf("again?(y or n)\ninput:");loop_1:{ch=getch();if(ch=='y') /* y 再次输入 */goto loop;else if(ch=='n') /* n 退出 */exit(0);else /* 都不是提示输入错误 */{printf("\ninput wrong!again please!!!\ninput:"); goto loop_1;}}getch();}}。

递归版后缀表达式

后缀表达式也称为逆波兰表达式，使用递归可以比较简便地进行计算。

具体的后缀表达式计算递归算法如下：1. 定义一个栈，用于存储操作数。

2. 从左到右扫描后缀表达式，每次取出一个操作符或操作数。

3. 如果是操作数，则将其压入栈中。

4. 如果是操作符，则从栈中取出两个操作数，将操作符应用于这两个操作数，并将计算结果压入栈中。

5. 重复上述步骤，直到扫描完整个后缀表达式。

6. 最后栈中存放的就是表达式的计算结果。

下面是一个使用递归计算后缀表达式的示例Python 代码：```pythondef calculate(expression):# 定义操作符映射表operators = {'+': lambda x, y: x + y,'-': lambda x, y: x - y,'*': lambda x, y: x * y,'/': lambda x, y: x / y}# 定义递归函数def helper(stack):# 取出栈顶元素item = stack.pop()if item in operators:# 如果是操作符，递归计算出栈顶的两个操作数y = helper(stack)x = helper(stack)# 计算结果，并压入栈中stack.append(operators[item](x, y))else:# 如果是操作数，直接压入栈中stack.append(float(item))# 返回栈顶元素return stack[-1]# 将表达式按照空格划分为单词tokens = expression.split()# 创建一个空栈，递归计算表达式的值value = helper(tokens)# 返回计算结果return value```。

后缀算术表达式求值

实验名称：后缀算术表达式求值背景描述：表达式求值是程序设计语言编译中的一个最基本的问题。

因为任何程序设计语言都必须具有表达式求值的功能，同时表达式的计算应用也相当广泛，比如电力调度系统中的计算遥测、车站票务系统中的票价类型计算公式等。

通常，我们所说的表达式是由运算符、操作数、界限符所组成。

而算术表达式中最常见的表示法形式有中缀、前缀和后缀表示法。

中缀表示法是书写表达式的常见方式，而前缀和后缀表示法主要用于计算机科学领域。

一、表达式表示法1、中缀表达式---将运算符放在两操作数的中间。

在运算中存在运算符的优先权与结合性的问题。

例如运算：a*b+(c-d/e)*f 时，编译器即自左向右逐一检查，当检查到第一个运算符"*"时还无法知道是否执行；待检查到第二个运算符" + "时，因为知道"*"的优先级别高于" + "时，才知道执行"a*b"；当继续检查到" ( "时，可知道先执行括号以内部分等。

2、前缀表达式---将运算符放在两操作数的前面。

这种表示法经常用于计算机科学，特别是编译器设计方面。

为纪念其发明家-Jan Lukasiewicz，这种表示法也称波兰表示法。

3、后缀表达式---将运算符放在两操作数的后面。

后缀表达式也称逆波兰表达式，因其使表达式求值变得轻松，所以被普遍使用。

前缀和后缀表示法有三项公共特征：（1）操作数的顺序与等价的中缀表达式中操作数的顺序一致；（2）不需要括号；（3）操作符的优先级不相关。

问题描述：读入一个后缀表达式表达式，利用堆栈来计算该表达式的值，同时要效验后缀表达式是否正确。

输入输出格式：第一种方式：输入：在字符界面上输入一个后缀表达式，其中两相邻操作数之间利用空格隔开。

以"#"表示结束。

输出：如果该后缀表达式正确，那么在字符界面上输出其结果，计算结果小数点后面保留两位有效数字，如果不正确，请在字符界面上输出表达式错误提示。

c语言中缀、后缀算术表达式求值用栈实现

c语言中缀、后缀算术表达式求值用栈实现下面是用栈实现中缀表达式求值的示例代码：#include <stdio.h>#include <stdlib.h>#include <ctype.h>#define MAX_STACK_SIZE 100typedef struct {int top;int data[MAX_STACK_SIZE];} Stack;void init(Stack *s) {s->top = -1;}int is_empty(Stack *s) {return s->top == -1;}int is_full(Stack *s) {return s->top == MAX_STACK_SIZE - 1;}void push(Stack *s, int x) {if (is_full(s)) {printf("Error: stack overflow\n");exit(EXIT_FAILURE);}s->data[++s->top] = x;}int pop(Stack *s) {if (is_empty(s)) {printf("Error: stack underflow\n");exit(EXIT_FAILURE);}return s->data[s->top--];}int peek(Stack *s) {if (is_empty(s)) {printf("Error: stack underflow\n");exit(EXIT_FAILURE);}return s->data[s->top];}int precedence(char op) {switch (op) {case '+':case '-':return 1;case '*':case '/':return 2;default:return 0;}}int evaluate(int op1, int op2, char op) {switch (op) {case '+':return op1 + op2;case '-':return op1 - op2;case '*':return op1 * op2;case '/':return op1 / op2;default:printf("Error: invalid operator\n");exit(EXIT_FAILURE);}}int evaluate_infix(char *expr) {Stack op_stack, val_stack;init(&op_stack);init(&val_stack);while (*expr != '\0') {if (isdigit(*expr)) {int val = 0;while (isdigit(*expr)) {val = val * 10 + (*expr - '0');expr++;}push(&val_stack, val);} else if (*expr == '+' || *expr == '-' || *expr == '*' || *expr == '/') {while (!is_empty(&op_stack) && precedence(peek(&op_stack)) >= precedence(*expr)) {int op2 = pop(&val_stack);int op1 = pop(&val_stack);char op = pop(&op_stack);push(&val_stack, evaluate(op1, op2, op));}push(&op_stack, *expr);expr++;} else if (*expr == '(') {push(&op_stack, '(');expr++;} else if (*expr == ')') {while (peek(&op_stack) != '(') {int op2 = pop(&val_stack);int op1 = pop(&val_stack);char op = pop(&op_stack);push(&val_stack, evaluate(op1, op2, op));}pop(&op_stack);expr++;} else {printf("Error: invalid character\n");exit(EXIT_FAILURE);}}while (!is_empty(&op_stack)) {int op2 = pop(&val_stack);int op1 = pop(&val_stack);char op = pop(&op_stack);push(&val_stack, evaluate(op1, op2, op));}return peek(&val_stack);}int main() {char expr[100];printf("Enter infix expression: ");scanf("%[^\n]", expr);printf("Result = %d\n", evaluate_infix(expr));return 0;}下面是用栈实现后缀表达式求值的示例代码：#include <stdio.h>#include <stdlib.h>#include <ctype.h>#define MAX_STACK_SIZE 100typedef struct {int top;int data[MAX_STACK_SIZE];} Stack;void init(Stack *s) {s->top = -1;}int is_empty(Stack *s) {return s->top == -1;}int is_full(Stack *s) {return s->top == MAX_STACK_SIZE - 1;}void push(Stack *s, int x) {if (is_full(s)) {printf("Error: stack overflow\n");exit(EXIT_FAILURE);}s->data[++s->top] = x;}int pop(Stack *s) {if (is_empty(s)) {printf("Error: stack underflow\n");exit(EXIT_FAILURE);}return s->data[s->top--];}int peek(Stack *s) {if (is_empty(s)) {printf("Error: stack underflow\n");exit(EXIT_FAILURE);}return s->data[s->top];}int evaluate(int op1, int op2, char op) {switch (op) {case '+':return op1 + op2;case '-':return op1 - op2;case '*':return op1 * op2;case '/':return op1 / op2;default:printf("Error: invalid operator\n");exit(EXIT_FAILURE);}}int evaluate_postfix(char *expr) {Stack stack;init(&stack);while (*expr != '\0') {if (isdigit(*expr)) {int val = 0;while (isdigit(*expr)) {val = val * 10 + (*expr - '0');expr++;}push(&stack, val);} else if (*expr == '+' || *expr == '-' || *expr == '*' || *expr == '/') { int op2 = pop(&stack);int op1 = pop(&stack);push(&stack, evaluate(op1, op2, *expr));expr++;} else {printf("Error: invalid character\n");exit(EXIT_FAILURE);}}return peek(&stack);}int main() {char expr[100];printf("Enter postfix expression: ");scanf("%[^\n]", expr);printf("Result = %d\n", evaluate_postfix(expr));return 0;}。

C语言利用栈实现对后缀表达式的求解

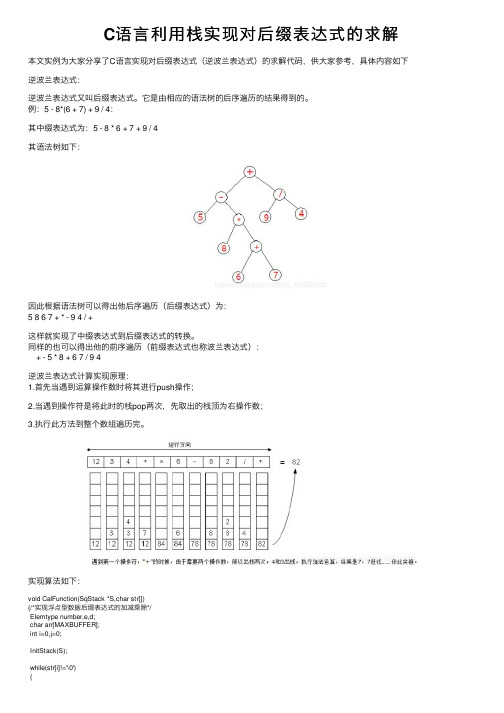
C语⾔利⽤栈实现对后缀表达式的求解本⽂实例为⼤家分享了C语⾔实现对后缀表达式（逆波兰表达式）的求解代码，供⼤家参考，具体内容如下逆波兰表达式：逆波兰表达式⼜叫后缀表达式。

它是由相应的语法树的后序遍历的结果得到的。

例：5 - 8*(6 + 7) + 9 / 4：其中缀表达式为：5 - 8 * 6 + 7 + 9 / 4其语法树如下：因此根据语法树可以得出他后序遍历（后缀表达式）为：5 867 + * - 9 4 / +这样就实现了中缀表达式到后缀表达式的转换。

同样的也可以得出他的前序遍历（前缀表达式也称波兰表达式）：　+ - 5 * 8 + 6 7 / 9 4逆波兰表达式计算实现原理：1.⾸先当遇到运算操作数时将其进⾏push操作；2.当遇到操作符是将此时的栈pop两次，先取出的栈顶为右操作数；3.执⾏此⽅法到整个数组遍历完。

实现算法如下：void CalFunction(SqStack *S,char str[]){/*实现浮点型数据后缀表达式的加减乘除*/Elemtype number,e,d;char arr[MAXBUFFER];int i=0,j=0;InitStack(S);while(str[i]!='\0')while(isdigit(str[i])||str[i]=='.') //过滤数字{arr[j++]=str[i++];arr[j]='\0';if( j >= MAXBUFFER ){printf("输⼊单个数据过⼤！\n");return ;}if(str[i]==' '){number=atof(arr); //利⽤atof函数将数字字符串转化为double型数据PushStack(S,number); //将转换的数进⾏压栈j=0; //这⾥不要忘记将j重新初始化进⾏下个数据的转化break;}}/*如果遇到操作运算符则，弹出两个数据进⾏运算，然后将得出的结果重新⼊栈*/ switch(str[i]){case '+':PopStack(S,&e);PopStack(S,&d);PushStack(S,d+e);break;case '-':PopStack(S,&e);PopStack(S,&d);PushStack(S,d-e);break;case '*':PopStack(S,&e);PopStack(S,&d);PushStack(S,d*e);break;case '/':PopStack(S,&e);PopStack(S,&d);if(e == 0){printf("输⼊出错，分母为零！\n");return ;}PushStack(S,d/e);break;}i++; //继续遍历直到遍历字符串结束}PopStack(S,&e);printf("计算结果为：%lf",e);}完整代码如下：#include<stdio.h>#include<stdlib.h>#include<assert.h>#include<ctype.h>#define INITSIZE 20#define INCREMENT 10#define MAXBUFFER 10#define LEN sizeof(Elemtype)/*栈的动态分配顺序存储结构*/typedef double Elemtype;typedef struct{Elemtype *base;Elemtype *top;int StackSize;}SqStack;void InitStack(SqStack *S)S->base=(Elemtype*)malloc(LEN*INITSIZE);assert(S->base != NULL);S->top=S->base;S->StackSize=INITSIZE;}void PushStack(SqStack *S,Elemtype e){if(S->top - S->base >= S->StackSize){S->base=(Elemtype*)realloc(S->base,(S->StackSize+INCREMENT)*LEN); assert(S->base !=NULL);S->top=S->base+S->StackSize;S->StackSize+=INCREMENT;}*S->top =e;S->top++;}void PopStack(SqStack *S,Elemtype *e){*e=*--S->top;}void CalFunction(SqStack *S,char str[]){Elemtype number,e,d;char arr[MAXBUFFER];int i=0,j=0;InitStack(S);while(str[i]!='\0'){while(isdigit(str[i])||str[i]=='.') //过滤数字{arr[j++]=str[i++];arr[j]='\0';if( j >= MAXBUFFER ){printf("输⼊单个数据过⼤！\n");return ;}if(str[i]==' '){number=atof(arr); //利⽤atof函数将数字字符转化为double型数据PushStack(S,number); //将转换的数进⾏压栈j=0;break;}}switch(str[i]){case '+':PopStack(S,&e);PopStack(S,&d);PushStack(S,d+e);break;case '-':PopStack(S,&e);PopStack(S,&d);PushStack(S,d-e);break;case '*':PopStack(S,&e);PopStack(S,&d);PushStack(S,d*e);break;case '/':PopStack(S,&e);PopStack(S,&d);if(e == 0){return ;}PushStack(S,d/e);break;}i++;}PopStack(S,&e);printf("计算结果为：%lf",e);}int main(){char str[100];SqStack S;printf("请按逆波兰表达式输⼊数据,每个数据之间⽤空格隔开:");gets(str);CalFunction(&S,str);return 0;}// 检测⽤例 5 - (6 + 7) * 8 + 9 / 4// 输⼊：5 8 6 7 + * - 9 4 / + #// 输出： - 96.750000运⾏效果截图如下：以上就是本⽂的全部内容，希望对⼤家的学习有所帮助，也希望⼤家多多⽀持。

数据结构实验四后缀表达式的计算

实验四后缀表达式的计算实验目的：熟练掌握栈和队列的存储结构设计及基本操作的实现；学会分析实际问题中具有栈特点的数据结构；了解表达式的前缀、中缀、后缀等计算机内表示形式。

实验内容与要求：按常规形式输入算术表达式（例如：输入2*(6-4)+8/4），要求能够：（1）基于表达式的中缀表示，对该表达式求值；（2）生成表达式的后缀表示，并输出；（3）基于表达式的后缀表示，对该表达式求值；（4）编写一个主程序对中序和后序表达式求值函数进行测试。

源程序：#include<stdio.h>#include<string.h>#include<stdlib.h>char s1[20],s2[20],a;int x,y,z,n,m,i,j=0;typedef struct node //数据结构常用类型{char data;int num;struct node *next;}sqstack;sqstack *InitSqStack()//创建栈并实现输入{sqstack *top;top=(sqstack *)malloc(sizeof(sqstack));top->data='#';top->num=0;top->next=NULL;return top;}sqstack *Push(sqstack *s)//实现表达式的后序表达{sqstack *p,*top;top=s;gets(s1);m=strlen(s1);for(i=0;i<=m;i++){a=s1[i];if('0'<=s1[i]&&s1[i]<='9'){s2[j]=s1[i];j++;} else{switch(a){case '(':{p=(sqstack *)malloc(sizeof(sqstack));p->data=a;p->next=top;top=p;break;}case '*':case '/':s2[j]=' ';j++;if((top->data=='*')||(top->data=='/')){s2[j]=top->data;j++;top->data=a;break;} else{p=(sqstack *)malloc(sizeof(sqstack));p->data=a;p->next=top;top=p;break;}case '+':case '-':{s2[j]=' ';j++;if(top->data=='+'||top->data=='-'||top->data=='*'||top->data=='/'){s2[j]=top->data;j++;top->data=a;break;} else{p=(sqstack *)malloc(sizeof(sqstack));p->data=a;p->next=top;top=p;break;}}case ')':{s2[j]=' ';j++;if(top->data=='#'){printf("input error");break;}while(top->data!='('){s2[j]=top->data;j++;p=top;top=top->next;free(p);}p=top;top=top->next;free(p);break;}}}}while(top->data!='#')//外部加入的输出函数{s2[j]=top->data;j++;p=top;top=top->next;free(p);}s2[j]='#';printf("后缀表达式为:%s\n",s2);return top;}sqstack *Calcolate(sqstack *s)//中序求值法{sqstack *top,*p;char *q;top=s;for(i=0;i<=j;i++){if(s2[i]>='0'&&s2[i]<='9'){q=&s2[i];z=atoi(q);for(n=i;s2[n]>='0'&&s2[n]<='9';n++)p=(sqstack *)malloc(sizeof(sqstack));p->num=z;p->next=top;top=p;i=n-1; elseif(s2[i]=='#')printf("表达式求值结果为:%d\n",top->num); else{if(s2[i]==' ') else{y=top->num;p=top;top=top->next;free(p);x=top->num;p=top;top=top->next;free(p);switch(s2[i]){case '+':{z=x+y;p=(sqstack *)malloc(sizeof(sqstack));p->num=z;p->next=top;top=p;break;}case '-':{z=x-y;p=(sqstack *)malloc(sizeof(sqstack));p->num=z;p->next=top;top=p;break;}case '*':{z=x*y;p=(sqstack *)malloc(sizeof(sqstack));p->num=z;p->next=top;top=p;break;}case '/':{z=x/y;p=(sqstack *)malloc(sizeof(sqstack));p->num=z;p->next=top;top=p;break;}}}}}return 0;}void main()//主函数部分{sqstack *top,*head;top=InitSqStack();printf("请输入表达式：");head=Push(top);Calcolate(head);}测试结果：心得体会：这个程序极为复杂，算法都不会，没有写出来，这个程序是根据同学的程序改了一些形式而已，没有内部算法的改动，盯着电脑看了一整天大致看懂了。

c语言中缀后缀算术表达式求值用栈实现

c语言中缀、后缀算术表达式求值用栈实现#include<stdio.h>#include<string.h>#include<malloc.h>#include<stdlib.h>#define MaxSize 50typedef struct{float data[MaxSize];int top;}OpStack;typedef struct{char data[MaxSize];int top;}SeqStack;void InitStack(SeqStack *S);//初始化栈int StackEmpty(SeqStack S);//判断栈是否为空int PushStack(SeqStack *S,char e);//进栈int PopStack(SeqStack *S,char *e);//删除栈顶元素int GetTop(SeqStack S,char *e);//取栈顶元素void TranslateExpress(char s1[],char s2[]);//将中缀表达式转化为后缀表达式float ComputeExpress(char s[]);//计算后缀表达式的值void main(){char a[MaxSize],b[MaxSize];float f;printf("请输入一个算术表达式:\n");gets(a);printf("中缀表达式为：%s\n",a);TranslateExpress(a,b);printf("后缀表达式为：%s\n",b);f=ComputeExpress(b);printf("计算结果：%f\n",f);}void InitStack(SeqStack *S)//初始化栈{S->top=0;}int StackEmpty(SeqStack S)//判断栈是否为空{if(S.top ==0)return 1;elsereturn 0;}int PushStack(SeqStack *S,char e)//进栈{if(S->top>=MaxSize){printf("栈已满，不能进栈!"); return 0;}else{S->data[S->top]=e;S->top++;return 1;}}int PopStack(SeqStack *S,char *e)//删除栈顶元素{if(S->top==0){printf("栈已空\n");return 0;}else{S->top--;*e=S->data[S->top];return 1;}}int GetTop(SeqStack S,char *e)//取栈顶元素{if(S.top<=0){printf("栈已空");return 0;}else{*e=S.data[S.top-1];return 1;}}void TranslateExpress(char str[],char exp[])//把中缀表达式转换为后缀表达式{SeqStack S;char ch;char e;int i=0,j=0;InitStack(&S);ch=str[i];i++;while(ch!='\0') //依次扫描中缀表达式{switch(ch){case'(':PushStack(&S,ch);break;case')':while(GetTop(S,&e)&&e!='('){PopStack(&S,&e);exp[j]=e;j++;}PopStack(&S,&e);break;case'+':case'-':while(!StackEmpty(S)&&GetTop(S,&e)&&e!='(') {PopStack(&S,&e);j++;}PushStack(&S,ch);break;case'*':case'/':while(!StackEmpty(S)&&GetTop(S,&e)&&e=='/'||e==&# 39;*'){PopStack(&S,&e);exp[j]=e;j++;}PushStack(&S,ch);break; //是空格就忽略case' ':break;default:while(ch>='0'&&ch<='9'){exp[j]=ch;j++;ch=str[i];i++;}i--;exp[j]=' ';j++;}ch=str[i];i++;}while(!StackEmpty(S)) //将栈中剩余运算符出栈{PopStack(&S,&e);exp[j]=e;j++;}exp[j]='\0';}float ComputeExpress(char a[])//计算后缀表达式的值{int i=0;float x1,x2,value;float result;S.top=-1;while(a[i]!='\0') //依次扫描后缀表达式{if(a[i]!=''&&a[i]>='0'&&a[i]<='9')//如果是数字{value=0;while(a[i]!=' ') //如果不是空格{value=10*value+a[i]-'0';i++;}S.top++;S.data[S.top]=value; //处理后进栈}else //如果是运算符{switch(a[i]){case'+':x1=S.data[S.top];S.top--;x2=S.data[S.top];S.top--;result=x1+x2;S.top++;S.data[S.top]=result;break;case'-':x1=S.data[S.top];S.top--;x2=S.data[S.top];S.top--;result=x2-x1;S.top++;S.data[S.top]=result;break;case'*':x1=S.data[S.top];S.top--;x2=S.data[S.top];S.top--;result=x1*x2;S.top++;S.data[S.top]=result;break;case'/':x1=S.data[S.top];S.top--;x2=S.data[S.top];S.top--;result=x2/x1;S.top++;S.data[S.top]=result;break;}i++;}}if(!S.top!=-1) //如果栈不空，将结果出栈并返回{result=S.data[S.top];S.top--;if(S.top==-1)return result;else{printf("表达式错误");exit(-1);}}return 0;}。

c++ 后缀中表达式求值

#include"stdio.h"#include"stdlib.h"#include"malloc.h"typedef struct {char *base;char *top;int stacksize;}SqStackchar;typedef struct {float *base;float *top;int stacksize;}SqStackint;//构造空栈SqStackchar InitStackchar(){SqStackchar S;S.base=(char *)malloc(sizeof(char));if(S.base==NULL) exit(-1);S.top=S.base;S.stacksize=100;return S;}SqStackint InitStackint(){SqStackint S;S.base=(float *)malloc(sizeof(float));if(S.base==NULL) exit(-1);S.top=S.base;S.stacksize=100;return S;}//进栈SqStackchar Pushchar(SqStackchar &S,char c){if((S.top-S.base)==S.stacksize){S.base=(char *)realloc(S.base,110*sizeof(char));if(S.base==NULL) exit(-1);S.top=S.base+S.stacksize;}*S.top++=c;return S;}SqStackint Pushint(SqStackint &S,float c){if((S.top-S.base)==S.stacksize){S.base=(float *)realloc(S.base,110*sizeof(float));if(S.base==NULL) exit(-1);S.top=S.base+S.stacksize;}*S.top++=c;return S;}//获得栈顶元素char GetTopchar(SqStackchar S){char e;if(S.top==S.base) exit(-1);e=*(S.top-1);return e;}float GetTopint(SqStackint S){float e;if(S.top==S.base) exit(-1);e=*(S.top-1);return e;}//出栈操作char Popchar(SqStackchar &S){if(S.top==S.base) exit(-1);char e;e=*--S.top;return e;}float Popint(SqStackint &S){if(S.top==S.base) exit(-1);float e;e=*--S.top;return e;}//判断该字符是数字的还是操作符int In(char c){if(c=='0'||c=='1'||c=='2'||c=='3'||c=='4'||c=='5'||c=='6'||c=='7'||c=='8' ||c=='9') return 1;else return 0;}//运算函数float Operate(float a,char theta,float b){switch(theta){case '+':return (a+b);case '-':return (a-b);case '*':return (a*b);case '/':return (a/b);default:exit(-1);}}//判断操作符的优先级char Precede(char a,char b){if((a=='('&&b!=')')||(a=='#'&&b!='#'))return '<';if(a==')')if((a=='('&&b==')')||(a=='#'&&b=='#'))return '=';if((a=='+'||a=='-')&&(b=='+'||b=='-'||b==')'||b=='#'))return '>';if((a=='+'||a=='-')&&(b=='*'||b=='/'||b=='('))return '<';if((a=='*'||a=='/')&&(b=='('))return '<';if((a=='*'||a=='/')&&(b=='+'||b=='-'||b=='*'||b=='/'||b==')'||b=='#')) return '>';}//主函数int main(){SqStackchar OPRT;SqStackint OPND;OPRT=InitStackchar();Pushchar(OPRT,'#');OPND=InitStackint();printf("请输入表达式：\n");c=getchar();float a,b;char theta;while(c!='#'||GetTopchar(OPRT)!='#'){if(In(c)){Pushint(OPND,c-48);c=getchar();while(In(c)){float e;e=GetTopint(OPND)*10+(int)(c)-48;Popint(OPND);Pushint(OPND,e);c=getchar();}}elseswitch(Precede(GetTopchar(OPRT),c)){ case '<':Pushchar(OPRT,c);c=getchar();break;case '=':Popchar(OPRT);c=getchar();break;case '>':theta=Popchar(OPRT);b=Popint(OPND);a=Popint(OPND);Pushint(OPND,Operate(a,theta,b));break;}//switch}//whileprintf("结果为：%f\n",GetTopint(OPND));return 0;}Ps.此文章来自网络，供大家学习交流。

计算后缀表达式的值：JAVA-Stack实现

计算后缀表达式的值：JAVA-Stack实现计算⼀个后缀表达式的值，⾸先想到就是可以利⽤栈来实现。

当见到⼀个数时，就把数推⼊到栈中去。

当见到⼀个运算符时，就把栈顶的两个元素即数字弹出并删除，计算出结果后，再结果这个数推⼊到栈中。

注意就是，先弹出的数（即代码中的a）在运算符的右边，后弹出的数（即代码中的b）在运算符的左边，这样⼦进⾏计算。

⽽加减乘除幂+-*/^这五个运算符都符合这样的逻辑。

package three;import java.util.Scanner;import java.util.Stack;public class postfix {//The following function evaluates a postfix expression, using+, −, ∗, /, and ^ ending in =. It requires//spaces between all operators and =.static double evalPostFix(){Stack<Double> s = new Stack<Double>();String token;Double a, b, result=0.0;//ab是计算过程的中间变量，result是⼊栈时的变量boolean isNumber;Scanner sc = new Scanner(System.in);token = sc.next();//后缀表达式⼀个⼀个输⼊，当输⼊了=时，循环结束while (token.charAt(0) != '=')//每次输⼊检测字符串的第⼀个字符是否为={try{isNumber = true;result = Double.parseDouble(token);//若输⼊字符不是数字，肯定报异常，即让布尔类型为false}catch (Exception e){isNumber = false;}if (isNumber)//如果是数字，那么就⼊栈s.push(result);else//如果是运算符，那么就栈顶出两个数字，计算后再⼊栈{switch (token.charAt(0)){//每个case后⾯都应该有breakcase '+': a = s.pop(); b = s.pop();s.push(b+a); break;case '-': a = s.pop(); b = s.pop();s.push(b-a); break;case '*': a = s.pop(); b = s.pop();s.push(b*a); break;case '/': a = s.pop(); b = s.pop();s.push(b/a); break;case '^': a = s.pop(); b = s.pop();s.push(Math.exp(a*Math.log(b)));//这⾥就相当于b^abreak;}}token = sc.next();}//当循环结束时，栈⾥只剩下⼀个元素return s.peek();//返回栈顶元素，并不删除}public static void main(String[] args) {// TODO Auto-generated method stubSystem.out.println(evalPostFix());}}程序运⾏过程注释已经解释得很清楚了。

后缀表达式求值的算法及代码

计算后缀表达式的过程（C#）

基于栈的后缀算术表达式求值c语言

用栈对后缀表达式求值的算法（五种）

栈应用之后缀表达式计算（python版）

后缀表达式求值的算法及代码

C#算术表达式求值（后缀法），看这一篇就够了

前缀后缀算数运算编程

中缀表达式变后缀表达式、后缀表达式（逆波兰）求值（python版本）

表达式求值（后缀表达式求值）

C语言下表达式的自动计算(两种方式)(报告+源代码)

数据结构代码中缀转后缀表达式算法及源代码

递归版 后缀表达式

后缀算术表达式求值

c语言中缀、后缀算术表达式求值用栈实现

C语言利用栈实现对后缀表达式的求解

数据结构实验四后缀表达式的计算

c语言中缀后缀算术表达式求值用栈实现

c++ 后缀中表达式求值

计算后缀表达式的值：JAVA-Stack实现

递归版后缀表达式