第二次模拟考试试题(理)参考答案
2024学年山东省新泰市第二中学高三下学期第二次模拟考试数学试题理试卷

2024学年山东省新泰市第二中学高三下学期第二次模拟考试数学试题理试卷 注意事项1.考生要认真填写考场号和座位序号。
2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。
第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。
3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.若复数z 满足2(13)(1)i z i +=+,则||z =( ) A .54 B .55 C .102 D .1052.若复数()()31z i i =-+,则z =( )A .22B .25C .10D .203.已知向量()()1,2,2,2a b λ==-,且a b ⊥,则λ等于( )A .4B .3C .2D .14.已知12,F F 是双曲线222:1(0)x C y a a-=>的两个焦点,过点1F 且垂直于x 轴的直线与C 相交于,A B 两点,若2AB =,则2ABF ∆的内切圆半径为( )A .23B .33C .323D .2335.已知数列满足:.若正整数使得成立,则( )A .16B .17C .18D .196.已知复数z 满足(3)1i z i +=+,则z 的虚部为( )A .i -B .iC .–1D .17.第七届世界军人运动会于2019年10月18日至27日在中国武汉举行,中国队以133金64银42铜位居金牌榜和奖牌榜的首位.运动会期间有甲、乙等五名志愿者被分配到射击、田径、篮球、游泳四个运动场地提供服务,要求每个人都要被派出去提供服务,且每个场地都要有志愿者服务,则甲和乙恰好在同一组的概率是( )A .110B .15C .140D .9408.设i 为数单位,z 为z 的共轭复数,若13z i =+,则z z ⋅=( ) A .110 B .110i C .1100 D .1100i 9.命题“20,(1)(1)∀>+>-x x x x ”的否定为( )A .20,(1)(1)∀>+>-x x x xB .20,(1)(1)∀+>-x x x xC .20,(1)(1)∃>+-x x x xD .20,(1)(1)∃+>-x x x x10.已知不等式组y x y x x a ≤⎧⎪≥-⎨⎪≤⎩表示的平面区域的面积为9,若点, 则的最大值为( )A .3B .6C .9D .12 11.若函数()3cos 4sin f x x x =+在x θ=时取得最小值,则cos θ=( )A .35B .45-C .45D .3512.如图,正方体1111ABCD A B C D -的棱长为1,动点E 在线段11A C 上,F 、M 分别是AD 、CD 的中点,则下列结论中错误的是( )A .11//FM AC ,B .存在点E ,使得平面//BEF 平面11CCD D C .BM ⊥平面1CC F D .三棱锥B CEF -的体积为定值二、填空题:本题共4小题,每小题5分,共20分。
2020年普通高等学校招生全国统一考试理科数学模拟测试试题(二)(含答案)

2020年普通高等学校招生考试数学模拟测试一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若集合A={0,1,2,3},B={2,3,4,5},则A ∪B= A.{1,2,3,4,5}B.{0,1,4,5}C.{2,3}D.{0,1,2,3,4,5}2.i 是虚数单位,z=2—i,则|z|=B.23.已知向量a =(1,2),b =(-1,λ),若a ∥b ,则实数λ等于 A.-1B.1C.-2D.24.设命题p:∀x ∈R ,x 2>0,则p ⌝为A.∀x ∈R ,x 2≤0B.∀x ∈R ,x 2>0C.∃x ∈R ,x 2>0D.∃x ∈R ,x 2≤05.51(1)x-展开式中含x -2的系数是 A.15B.-15C.10D.-106.若双曲线22221(0,x y a b a b -=>>)的左、右焦点分别为F 1、F 2,离心率为53,点P(b,0),为则12||||PF PF =A.6B.8C.9D.107.图为祖冲之之子祖暅“开立圆术”中设计的立体模型.祖暅提出“祖氏原理”,他将牟合方盖的体积化成立方体与一个相当于四棱锥的体积之差,从而求出牟合方盖的体积等于32(3d d 为球的直径),并得到球的体积为16V d π=,这种算法比外国人早了一千多年,人们还用过一些类似的公式,根据π=3.1415926…,判断下列公式中最精确的一个是A.d ≈3B .d ≈√2V 3C.d≈√300157V3D .d≈√158V 38.已知23cos cos ,2sin sin 2αβαβ-=+=则cos(a+β)等于 A.12B.12-C.14D.14-二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分.9.第18届国际篮联篮球世界杯(世界男子篮球锦标赛更名为篮球世界杯后的第二届世界杯)于2019年8月31日至9月15日在中国的北京广州、南京、上海、武汉、深圳、佛山、东莞八座城市举行.中国队12名球员在第一场和第二场得分的茎叶图如图所示,则下列说法正确的是A.第一场得分的中位数为52 B.第二场得分的平均数为193C.第一场得分的极差大于第二场得分的极差D.第一场与第二场得分的众数相等10.已知正方体的外接球与内切球上各有一个动点M 、N,若线段MN 1,则 A.正方体的外接球的表面积为12π B.正方体的内切球的体积为43πC.正方体的边长为2D.线段MN 的最大值为11.已知圆M 与直线x 十y +2=0相切于点A(0,-2),圆M 被x 轴所截得的弦长为2,则下列 结论正确的是A.圆M 的圆心在定直线x-y-2=0上B.圆M 的面积的最大值为50πC.圆M 的半径的最小值为1D.满足条件的所有圆M 的半径之积为1012.若存在m,使得f(x)≥m 对任意x ∈D 恒成立,则函数f(x)在D 上有下界,其中m 为函数f(x)的一个下界;若存在M,使得f(x)≤M 对任意x ∈D 恒成立,则函数f(x)在D 上有上界,其中M 为函数f(x)的一个上界.如果一个函数既有上界又有下界,那么称该函数有界.下列说法正确的是A.1不是函数1()(0)f x x x x=+>的一个下界 B.函数f(x)=x l nx 有下界,无上界C.函数2()xe f x x=有上界有,上无界下,界无下界D.函数2sin ()1xf x x =+有界 三、填空题:本题共4小题,每小题5分,共20分.把答案填在答题卡中的横线上. 13.设f(x)是定义在R 上的函数,若g(x)=f(x)+x 是偶函数,且g(-2)=-4,则f(2)=___. 14.已知函数f(x)=sin(ωx+φ)(ω>0),点2(,0)3π和7(,0)6π是函数f(x)图象上相邻的两个对称中心,则ω=___.15.已知F 1,F 2分别为椭圆的221168x y +=左、右焦点,M 是椭圆上的一点,且在y 轴的左侧,过点F 2作∠F 1MF2的角平分线的垂线,垂足为N,若|ON|=2(О为坐标原点),则|MF 2|-|MF 1|=___,|OM|=__.(本题第一空2分,第二空3分)16.在正三棱柱ABC-A 1B 1C 1中,AB =1=2,E,F 分别为AB 1,A 1C 1的中点,平面α过点C 1,且平面α∥平面A 1B 1C ,平面α∩平面A 1B 1C 1=l ,则异面直线EF 与l 所成角的余弦值为__·四、解答题:本题共6小题,共70分。
陕西省铜川市2023届高三下学期第二次模拟考试(铜川二模)理综答案

铜川市2023年高三第二次质量检测理综生物参考答案1-6A B D C C A29.(除标注外,每空1分,共10分)(1)C5、PEP和C5ATP和NADPH(答ATP也给分)叶绿体类囊体薄膜C、D (2)主动运输细胞呼吸夜间[H]是细胞呼吸第一、二阶段产生的,只能用于第三阶段,且光合作用产生的[H]是NADPH,而细胞呼吸产生的[H]是NADH(3)取等体积的透光玻璃瓶甲、乙和不透光玻璃瓶丙,同时从桃曲坡水库水深1m处的同一位置取满水样,立即测定甲瓶中氧气的含量,并将乙、丙瓶密封后沉回原处。
一昼夜后取出玻璃瓶,分别测定两瓶中的氧气含量。
乙瓶氧气含量减去丙瓶氧气含量,差值为该处自养生物一昼夜的实际光合速率。
若乙瓶氧气含量大于甲瓶初始氧气含量,则该水层自养生物产氧量能维持本层水体生物呼吸耗氧所需,反之不能。
(答案合理即可给分)(2分)30.(每空1分,共9分)(1)微量、高效(由体液运输,作用于靶细胞和靶器官等)不对胰腺包括内分泌腺和外分泌腺,外分泌腺产生的与糖类等物质分解有关的酶可以反复利用,内分泌腺分泌的激素具有发挥作用后被灭活的特点(2)血糖浓度和神经递质促进使葡萄糖及时被组织细胞摄取并氧化分解产生能量(3)体温、水盐(4)自身免疫病丙、甲、乙31.(每空1分,共9分)(1)水平结构等距取样法(2)直接间接(3)①乙8.0②12.5%单向流动、逐级递减③不完全相同32.(除标注外,每空2分,共11分)(1)DNA分子中发生碱基的替换、增添或缺失,而引起的基因结构的改变随机(1分)(2)野生型:突变型=9:14中突变型个体与野生型个体杂交预期结果及结论:若子代表型及比实验思路:①让F1例为突变型:野生型=1:1,则其基因型为MmNn;若子代表型只有突变型,则其基因型为MMNN或MmNN或MMNn37.(15分)(1)①灭菌③最大(2)聚丙烯纤维选择在微生物学中,将允许特定种类的微生物生长,同时抑制或阻止其他种类微生物生长的培养基,称为选择培养基(3)稀释涂布平板法 6.6×108当两个或多个细胞连在一起时平板上观察到的只是一个菌落38.(除标注外,每空2分,共15分)(1)核酸(RNA)(1分)(血浆中)新冠病毒的抗体(2)组织液大脑皮层(3)限制酶和DNA 连接(4)刺突蛋白(或S 蛋白)杂交瘤克隆化培养和抗体检测(抗原抗体检测)铜川市2023年高三第二次质量检测理综物理参考答案题号1415161718192021选项BDAACBDABAC23.实验二(1)红(2)大(3)1602879.6(4)10002v =s =设碰撞刚结束时,两物块整体的速度为2()12mv m m v =+解得2v =(2)设物块整体到达D 点时的速度为3v ,物块整体从B 运动到D 的过程,由动能定理得22321122222222d mg mg R mv mv μ-⋅-⋅=⋅-⋅从D 点平抛,竖直方向满足2122R gt =设水平方向位移为s ,则3s v t=解得s =25.(1)B =2)2mv x vt F=-;(3)254Q Fvt mv=-(1)设磁感应强度为B ,对ab 棒由受力平衡 F BIL =02BLv I R =解得B =(2)撤力前,棒ab 前进的距离为x ,对ab 棒达到最大速度v 的过程,由动量定理Ft BILt mv-=02E I R =BLx E t=解得2mv x vt F=-(3)解除锁定后两棒相互作用过程动量守恒,最后共同运动速度为v 共2mv mv =共对全过程由功能关系2122Q Fx mv =-⋅共解得254Q Fvt mv =-A A A A得Δx =L A -L A ′=5cm②对B 中气体p B ′=p A ′=43×105Pa 由查理定律得出'B B 'B B P P T T =T B ′='B BP P T B =400K即t =127℃34.(1)【答案】BDE(2)【答案】①n ②94at c=【详解】①单色光在棱镜中的光路如图所示,由几何关系可知,CD a 、△OCD 为等边三角形,故α=β=60°根据折射定律有()00sin60sin 90n α=-解得n②由于sin β=2>1n,故单色光在D 点发生全反射,由几何关系可知,反射光垂直BC 边从BC 边射出棱镜,故γ=β=60°光在棱镜中的传播速度为解得4t c=铜川市2023年高三第二次质量检测理综化学参考答案7.答案:D 解析:A.不同金属元素的焰色试验可以发出不同颜色的光,喷涂碱金属目的是利用焰色试验让火焰可视,故A 正确;B.晶体硅为良好的半导体材料,是制造光电池的主要原料,故B 正确;C.“84”消毒液、二氧化氯泡腾片都具有强的氧化性,能够使蛋白质变性,能够用于环境杀菌消毒,故C 正确;D.玻璃纤维是一种性能优异的无机非金属材料,,故D 错误;8.答案A解析:A.只有羧基能和氢氧化钠反应,且羧基和氢氧化钠以1:1反应,则1mol 脱落酸能与1mol 的氢氧化钠发生反应,故A 错误;B.该分子中含有羰基、碳碳双键、醇羟基和羧基,具有酮、烯烃、醇、羧酸性质,醇羟基和羧基能发生酯化反应、碳碳双键能发生加聚反应、碳碳双键能发生氧化反应,故B 正确;C.该分子中含有4个甲基,具有甲烷结构特点,所以该分子中所有原子不可能位于同一个平面上,故C 正确;D.根据结构简式确定分子式为C 15H 20O 4,故D 正确;9.答案D解析:A .向Na 2SO 3溶液中滴加稀HNO 3溶液,二者发生氧化还原反应,正确的离子反应为:23NO -+323SO -+2H +═324SO -+2NO↑+H 2O ,故A 错误;B.用过量氨水吸收SO 2气体,反应生成亚硫酸铵:2NH 3·H 2O +SO 2=2+4NH +2-3SO +H 2O,选项B 错误;C.电解MgCl 2水溶液的离子方程式:Mg 2++2Cl -+2H 2O=====通电H 2↑+Cl 2↑+Mg(OH)2D.酸性K 2Cr 2O 7溶液具有强氧化性,可以氧化NaNO 2变成NaNO 3,Cr 2O 27-还原成Cr 3+现绿色,离子方程式为:Cr 2O 2-7+3NO -2+8H +==3NO -3+2Cr 3++4H 2O故D正确。
江西省新余市2022届高三数学下学期第二次模拟考试试题理

1江西省新余市2022届高三数学下学期第二次模拟考试试题 理一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知全集,集合,集合,则( )A .B .C .D .2.已知复数,且,则( )A .B .C .1D .23.执行如图所示的程序框图,则可以输出函数的为( )A .B .C .D .4.下列函数是奇函数,且函数值恒小于1的是( )A .B .C .D .5.在的展开式中,所有二项式系数和为64,则该展开式中常数项为( ){}1,234,5,6U =,,{}1,25A =,{}1,3,4B =U A B ⋂=ð{}1{}3,4{}2,5{}1,2,3,4,5()i ,z a b a b R =+∈()31i 2iz +=+a b +=1232()sin f x x =()x f x e =()ln 2f x x x =++()2f x x =()2121x xf x -=+()2f x x x=-+()sin f x x=()1133f x x x-=+213nx x ⎛⎫- ⎪⎝⎭2A .90B .135C .D .6.已知命题p :,;命题q :,.则下列命题中为真命题的是( )A .p 且q B .且qC .p 且D .且7.设等差数列的前n 项和为,且,,则当最大时,( )A .1011B .1010C .1009D .10128.已知圆:与圆:有且仅有两条公共切线,则正数a 的取值范围为( )A .(0,1)B .(0,3)C .(1,3)D .9.三棱锥的体积为,底面ABC ,且的面积为4,三边AB ,BC ,CA 的乘积为16,则三棱锥的外接球的表面积为( )A .B .C .D .10.已知数列满足,,数列满足,,则数列的最小值为( )A .B .C .D .11.若存在两个正数x ,y ,使得不等式成立,其中,其中e 为自然对数的底数,则实数a 的取值范围为( )90-135-()0x ∃∈+∞,sin 2xx =()0x ∀∈+∞,1ln x x -≥()p ⌝()q ⌝()p ⌝()q ⌝{}n a n S 20200S >20210S <n S n =1O 222210x ax y a -++-=2O 224x y +=()3+∞,83PA ⊥ABC △P ABC -4π8π16π32π{}n a 121n n n a a a +=+11a ={}n b 11b =()112n n nb b n a --=≥13n b n +⎧⎫⎨⎬⎩⎭294223436()()324ln ln 0x a y ex y x +--≤0a >3A .B .C .D .12.已知函数在区间上有且仅有4条对称轴,给出下列四个结论:①在区间上有且仅有3个不同的零点;②的最小正周期可能是;③的取值范围是;④在区间上单调递增.其中所有正确结论的序号是( )A .①④B .②③C .②④D .②③④二、填空题(本大题共4小题,每题5分,共20分.请将正确答案填在答题卷相应位置.)13.已知实数x ,y 满足约束条件,则的最大值为___________.14.若一个三位数的各位数字之和为10,则称这个三位数“十全十美数”,如208,136都是“十全十美数”,现从所有三位数中任取一个数,则这个数恰为“十全十美数”的概率是___________.15.如图是数学家GerminalDandelin 用来证明一个平面截圆锥得到的截口曲线是椭圆的模型(称为“Dandelin 双球”);在圆锥内放两个大小不同的小球,使得它们分别与圆锥的侧面、截面相切,设图中球,球的半径分别为3和1,球心距离,截面分别与球,球切于点E ,F ,(E ,F 是截口椭圆的焦点),则此椭圆的离心率等于___________.()0,2e 3,22e e ⎡⎫⎪⎢⎣⎭3,2e ⎡⎫+∞⎪⎢⎣⎭[)2,e +∞()()sin 04f x x πωω⎛⎫=+> ⎪⎝⎭[]0π,()f x ()0,π()f x 2πω1317,44⎡⎫⎪⎢⎣⎭()f x 0,15π⎛⎫ ⎪⎝⎭2202201x y x y y +-≥⎧⎪--≤⎨⎪≤⎩3z x y =-1O 2O 128O O =1O 2O416.右图是由两个有一个公共边的正六边形构成的平面图形,其中正六边形边长为1.设,则______;P 是平面图形边上的动点,则的取值范围是___________.(本题第一空2分,第二空3分).三、解答题(本大题共6小题,共70分解答应写出必要的文字说明、证明过程及演算步骤)17.(本小题满分12分)在①,②.这三个条件中任选一个,补充在下面的横线上,并解答.在中,角A ,B ,C 所对的边分别为a ,b ,c 且_________.(1)求角C 的大小;(2)若,求AB 的中线CD 长度的最小值.18.(本小题满分12分)如图,已知直三棱柱中,侧面为正方形,,D ,E ,F 分别为AC ,BC ,的中点,,G 为线段DE 上的点且.ΓAG xAB y AI =+ x y +=ΓAC BP ⋅2sin sin 1sin sin A B c B A ab ++=()2cos cos 0a b C c A ++=sin sin 2A Bc A +=ABC △4c =111A B C ABC-11AA B B2ABBC ==1B B111C F A B ⊥2EG GD =5(1)证明:;(2)求二面角的余弦值.19.(本小题满分12分)学习强国中有两项竞赛答题活动,一项为“双人对战”,另一项为“四人赛”.活动规则如下:一天内参与“双人对战”活动,仅首局比赛可获得积分,获胜得2分,失败得1分:一天内参与“四人赛”活动,仅前两局比赛可获得积分,首局获胜得3分,次局获胜得2分,失败均得1分.已知李明参加“双人对战”活动时,每局比赛获胜的概率为,参加“四人赛”活动(每天两局)时,第一局和第二局比赛获胜的概率分别为P ,.李明周一到周五每天都参加了“双人对战”活动和“四人赛”活动(每天两局),各局比赛互不影响.(1)求李明这5天参加“双人对战”活动的总得分X 的分布列和数学期望:(2)设李明在这5天的“四人赛”活动(每天两局)中,恰有3天每天得分不低于3分的概率为.求p为何值时,取得最大值.20.(本小题满分12分)已知双曲线.(1)过点的直线与双曲线交于S ,T 两点,若点N 是线段ST 的中点,求直线ST 的方程;(2)直线l :与双曲线有唯一的公共点M ,过点M 且与l 垂直的直线分别交x 轴、y 轴11C F A G⊥111C AG B --1213()f p ()f p 221416x y -=()1,4N ()y kx m k =+≠±26于,两点.当点M 运动时,求点的轨迹方程,并说明该轨迹是什么曲线.21.(本小题满分12分)已知函数.(1)讨论函数的单调性:(2)设,为两个不等的正数,且,若不等式恒成立,求实数的取值范围.选做题:(本小题满分10分).请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.22.【选修4-4:坐标系与参数方程】在平面直角坐标系xOy 中,直线l 的参数方程为(t 为参数,),以O 为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 的极坐标方程为.(1)求直线l 和曲线C 的普通方程;(2)直线l 和曲线C 相交A ,B 两点,若,且,求直线l 的方程.23.【选修4-5:不等式选讲】已知函数.(1)求满足不等式的最大整数a ;(2)在(1)的条件下,对任意,若,求的最小值.()0,0A x ()00,B y ()00,P x y ()()1x f x e x -=+()f x 1t2t ()21121212ln ln t t t t t t t t -=-<12ln ln 0t t λ+>λ2cos sin x t y t αα=-+⎧⎨=⎩02πα<<22843cos ρθ=-()2,0M -2MA MB MA MB -=()121f x x x =---()1f x ≥-()x y a ∈+∞,,4x y +=2211y x z x y =+--7数学参考答案一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)题号123456789101112答案BDCABBBCBACB二、填空题(本大题4小题,每小题5分,共20分)13.1114.15.16.1和三、解答题17.(1)选择条件①:由及正弦定理,得:,即,由余弦定理,得;因为,所以,选择条件②:由及正弦定理,得:,即.即.350533,2⎡⎤-⎢⎥⎣⎦2sin sin 1sin sin A B c B Aab ++=21a b c b a ab ++=222a b c ab +-=-2221cos 222a b c ab C ab ab +--===-0C π<<23C π=()2cos cos 0a b C c A ++=()sin 2sin cos sin cos 0A B C C A ++=sin cos cos sin 2sin cos A C A C B C +=-()sin 2sin cos A C B C+=-8在中,,所以,即,因为,所以,所以因为,所以,及正弦定,因为.在中,,则,因为,所以,则,故(2)因为,所以,整理得,在三角形ABC 中,由余弦定理得;因为,当且仅当时取等号,所以,即所以,即,即CD 长度的最小值为(也可转化为平面向量解答)18.(1)在直三棱柱中,侧面为正方形,ABC △A B C π++=()()sin sin sin A C B Bπ+=-=sin 2cos sin B C B =-0B π<<sin 0B ≠1cos 2C =-0C π<<23C π=sinsin 2A B c A +=sin sin sin 2A BA C A +=sin 0A ≠sinC 2AB +=ABC △A B C π++=sin cos 22A B C+=2sin cos 222C C C=0Cπ<<cos02C≠sin 22C =23C π=ADC BDC π∠+∠=22224402222CD b CD a CD CD +-+-+=⨯⨯⨯⨯22228CD a b =+-22222242cos3a b ab a b ab π=+-=++222a b ab +≤a b =()()22222222131622a b ab a b a b a b =++≤+++=+22323a b +≥22232828833CD a b =+-≥-=3CD ≥3111A B C ABC-11AA B B9所以,,而,,,平面,所以平面,所以平面,平面,所以,故以B 为坐标原点,以BA 为x 轴,以BC 为y 轴,以为z 轴,建立空间直角坐标系,如图:,,,,∴,∴所以,即;方法二:在正方形中.∵.∴又∵,∴.∴.又∵,.∴平面又∵平面.∴11AB A B ∥111A B B B⊥111C F A B ⊥11B B C F F⋂=1B B1C F ⊂11BB C C11A B ⊥11BB C CAB ⊥11BB C CBC ⊂11BB C CAB BC ⊥1BB ()12,0,2A ()10,2,2C ()0,0,1F ()10,0,2B 2,1,03G ⎛⎫⎪⎝⎭()10,2,1C F =--14,1,23AG ⎛⎫=-- ⎪⎝⎭ 110C F AG ⋅= 11C F AG ⊥11C F AG ⊥ 11BCC B 111Rt B C F Rt BB E≌△△111BB E B C F∠=∠11112B C F B FC π∠+∠=1112BB E B FC π∠+∠=11B E C F ⊥111C F A B ⊥1111B E A B B ⋂=1C F ⊥11A B ED1A G ⊂11A B ED11C F A G⊥10(2)由(1)可知:,,,设平面的法向量为,则,即令,则,则.设平面的法向量为,则即则,令,则,则故设二面角的平面角为,结合图形,为锐角,故19.(1)X 可取5,6,7,8,9,10,,,()112,2,0AC =- 14,1,23AG ⎛⎫=-- ⎪⎝⎭ ()112,0,0A B =- 11C A G (),,m x y z = 11100m A C m A G ⎧⋅=⎪⎨⋅=⎪⎩ 2204203x y x y z -+=⎧⎪⎨-+-=⎪⎩6x =6y =1z =-()6,6,1m =- 11AGB (),,n a b c = 11100n A B n A G ⎧⋅=⎪⎨⋅=⎪⎩204203a a b c -=⎧⎪⎨-+-=⎪⎩0a =1c =2b =()0,2,1n = 111C A G B --θθcos cos 365m n θ=⋅==()505115232P X C ⎛⎫==⋅= ⎪⎝⎭()41511262232P X C ⎛⎫==⨯⨯=⎪⎝⎭11,,,,分布列如下:X 5678910P所以(分);(2)解:设一天得分不低于3分为事件A ,则,则恰有3天每天得分不低于3分的概率,()则.当时,.当时所以函数在递增,在递减所以当时,取得最大值.()232511572216P X C ⎛⎫⎛⎫==⨯⨯= ⎪ ⎪⎝⎭⎝⎭()323511582216P X C ⎛⎫⎛⎫==⨯⨯=⎪ ⎪⎝⎭⎝⎭()44511592232P X C ⎛⎫==⨯⨯= ⎪⎝⎭()5551110232P X C ⎛⎫==⨯= ⎪⎝⎭132532516516532132()15555156789107.5323216163232E x =⨯+⨯+⨯+⨯+⨯+⨯=()()()122111111333p P A p p ⎡⎤+⎛⎫=---=--=⎪⎢⎥⎝⎭⎣⎦()()()323235212140121133243p p f p C p p ++⎛⎫⎛⎫=⋅-=+- ⎪⎪⎝⎭⎝⎭01p <<()()()()()()22340403212121211243243f p p p p p =⨯+⋅⋅-+⨯+⋅⋅--()()()240211410243p p p =+--205p <<()0f x >215p <<()0f x <()f x 20,5⎛⎫⎪⎝⎭2,15⎛⎫⎪⎝⎭25p =()f p1220.(1)设,,则两式相减得,即若N 为ST 的中点,则,即直线ST 的斜率为1所以直线ST 的方程为,即联立方程组得,满足,故直线ST 的方程为.(2)联立方程组,得,因为,且M 是双曲线与直线l 唯一的公共点,所以,得,所以点M 的坐标为,其中.因为过点M 且与直线l 垂直的直线为,令,得,令,得,所以,()11,S x y ()22,T x y 2211222214161416x y x y ⎧-=⎪⎪⎨⎪-=⎪⎩22221212416x x y y --=121212124y y x x x x y y -+=⨯-+1212214124y y x x -⨯=⨯=-⨯41y x -=-3y x =+2231416y x x y =+⎧⎪⎨-=⎪⎩236250x x --=0∆>30x y -+=221416x y y kx m ⎧-=⎪⎨⎪=+⎩()()22242160k x kmx m ---+=2k ≠±()()()222244160km k m ∆=-+-+=()2244m k =-416,k mm ⎛⎫-- ⎪⎝⎭0m ≠1614k y x m k m ⎛⎫+=-+ ⎪⎝⎭0y =020k x m =-0x =020y m =-2222002224004001600410010044k m x y m m m ⎛⎫==+=+=+ ⎪⎝⎭13故P 的轨迹方程为,其中,P 的轨迹是焦点在x 轴上,实轴长为20,虚轴长为10的双曲线去掉两个顶点后的图形.21.(1)因为所以当,,在上单调递增,当,,在上单调递减.(2)令,,则,依题意得实数,满足且不等式恒成立,由及(1)知,法1:不等式恒成立知,所以,∴,又函数在单调递减,∴,又,所以,即,两边取对数得对恒成立设,,22110025x y -=0y ≠()xf x xe -'=-(),0x ∈-∞()0f x '>()f x (),0-∞()0,x ∈+∞()0f x '<()f x ()0,+∞11ln x t =22ln x t =211212122112121211ln ln x x x x x x x x t t t t t t e x e x e e e e ++-=-⇔-=-⇔=1x 2x ()()12f x f x =120x x λ+>12x x <1210x x -<<<<+∞120x x λ+>21x x λ>-0λ>120x x λ>->()f x ()0,+∞()12x f x f λ⎛⎫<- ⎪⎝⎭()()12f x f x =()11x f x f λ⎛⎫<- ⎪⎝⎭111111x x x x e e λλ--++<=()()111ln 1ln 110x x x λλλλ⎛⎫+---+< ⎪⎝⎭()11,0x ∈-()()()ln 1ln 11x F x x xλλλλ⎛⎫=+---+ ⎪⎝⎭()1,0x ∈-14则①当时,对恒成立,此时在上单调递增,故恒成立,符合题意,②当时,,则,,此时在上单调递减,故,不符合题意.综上所述,所求取值范围是法2:由令(),则,,所以不等式令,依题意恒成立.,①当时,,递增,从而,所以在上递增,故恒成立.②当时,由得,所以在上递减,所以,,在上递减.()()()()()()1111111x x F x x x x x λλλλλλ++-'=+-+=++--1λ≥()0F x '>()1,0x ∈-()F x ()1,0x ∈-()()00F x F <=()0,1λ∈()11,0λ-∈-()1,0x λ∈-()0F x '<()F x ()1,0λ-()()00F x F >=[)1,+∞211212211111x x x x x x x e e e x -+++=⇒=+21y x x =-0t >111t t t e x e +-=-()2111tt t e x e -+=-()()12111011011t t t tt tt e t e x x t e e t e e λλλλ-++-+>⇔+>⇔--+++>--()()()110t t h t t e e t t λλ=--+++>()0h t >()()1t t g t h t te e λ'==-+()()()11t t tg t t e e t e λλλ'=+-=+-1λ≥()0g t '≥()h t '()()00h t h ''≥=()h t ()0,+∞()0h t >01λ<<()0g t '<10t λλ-<<()h t '10,λλ-⎛⎫ ⎪⎝⎭10,t λλ-⎛⎫∈ ⎪⎝⎭()()00h t h ''<=()h t 10,λλ-⎛⎫⎪⎝⎭15故,,,不合题意.③当时,由,知,不合题意.综上所述,所求取值范围是22.(1)直线l 的参数方程为(t 为参数,),消去参数t 得,,令,,可得曲线C 的普通方程是(2)将直线l 的参数方程代入曲线C 的直角坐标方程中,整理得关于t 的方程,显然,设点A ,B 所对应的参数分别为,,由根与系数的关系,得,,所以,由直线参数方程的几何意义得:,,所以,化简得,,∴所以,直线l 的方程是10,t λλ-⎛⎫∈ ⎪⎝⎭()()00h t h <=0λ≤10x <20x >120x x λ+<[)1,+∞2cos sin x t y t αα=-+⎧⎨=⎩02πα<<()tan 2y x α=+22843cos ρθ=-cos x ρθ=sin y ρθ=22182x y +=()2213sin 4cos 40tt αα+--=0∆>1t2t 1221224cos 13sin 413sin t t t t ααα⎧+=⎪⎪+⎨-⎪=⎪+⎩120t t <121224cos 13sin MA MB t t t t αα-=-=+=+122413sin MA MB t t α-==+222413sin 13sin αα-=++1cos 2α=02πα<<3πα=)2y x =+1623.(1)当时,原不等式可转化为,所以;当时,原不等式可转化为,解得,所以当时,原不等式可转化为,解得(舍),综上所述,原不等式的解集为,所以满足不等式的最大整数.(2)由(1)得,因为,所以,当且仅当,即时等号成立,故的最小值为8.12x ≤1x ≥-112x -≤≤112x <≤231x -≥-1x ≤112x <≤1x >1x -≥-1x ≤[]1,1-()1f x ≥-1a =()1x y ∈+∞,,4x y +=()()()()2222222211111111211211y y x x y x y x z x y x y x y x y x y ⎛⎫--⎛⎫=+=-+-+=+++⎡⎤ ⎪⎪⎣⎦------⎝⎭⎝⎭()()222112822x y xy x y ≥++=+=()()221111y y x x x y --=--2x y ==2211y x z x y =+--。
高中物理:2024年山东省聊城市普通高中学业水平等级考试第二次模拟卷物理试题(含参考答案)

聊城市2024年普通高中学业水平等级考试模拟卷物理(二)注意事项:1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷的指定位置。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、单项选择题:本题共8小题,每小题3分,共24分。
每小题只有一个选项符合题目要求。
1.某实验小组利用如图所示的实验装置探究光的干涉现象。
单色点光源S 发出的光波长为λ,平面镜M 水平放置,光源S 到平面镜的竖直距离为a 、到平面镜左端的水平距离为b ,平面镜左端到光屏的水平距离为c 。
光源S 发出的光和由S 发出经过平面镜反射的光照在竖直放置的光屏上,形成明暗相间的条纹,则相邻两条亮纹之间的距离为( )A .2b c a λ+BC .2c a λD .c aλ 2.如图所示,甲图为研究光电效应规律的实验装置,乙图为a 、b 、c 三种光照射下得到的三条电流表与电压表读数之间的关系曲线,丙图为氢原子的能级图,丁图给出了几种金属的逸出功和极限频率。
下列说法正确的是( )A .若b 光为绿光,c 光不可能是紫光B .图甲所示的电路中,滑动变阻器滑片右移时,电流表示数一定增大C .若用能量为0.66eV 的光子照射某一个处于3n =激发态的氢原子,最多可以产生6种不同频率的光D .若用能使金属铷发生光电效应的光直接照射处于3n =激发态的氢原子,可以使该氢原子电离3.如图所示,某创新实验小组制作了一个半径为12cm 的圆环,将3个相同的轻弹簧一端等间距地连接在圆环上的A 、B 、C 三点,另外一端连接于同一点,结点恰好在圆心O 处。
将圆环水平放置,在结点O 处悬挂一瓶矿泉水,缓慢释放直至平衡时测得结点下降了5cm 。
已知轻弹簧的自然长度为9cm ,矿泉水的重力为6N ,则弹簧的劲度系数为( )A .390N /mB .130N /mC .3.90N /mD .1.30N /m4.2023年12月15日我国在文昌航天发射场使用长征五号遥六运载火箭,成功将遥感四十一号卫星发射升空,卫星顺利进入预定轨道,该星在距地面高度为h 的轨道做圆周运动,已知地球的半径为R ,自转周期为0T ,地球表面的重力加速度为g ,引力常量为G 。
山西省临汾市2023届高三下学期高考考前适应性训练考试(二)理综答案
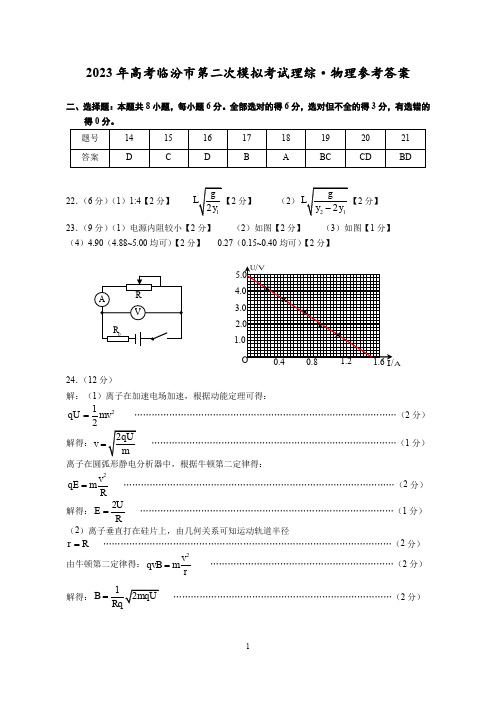
2023年高考临汾市第二次模拟考试理综·物理参考答案二、选择题:本题共8小题,每小题6分。
全部选对的得6分,选对但不全的得3分,有选错的得0分。
22.(6分)(1)1:4【2分】 2分】 (2)2分】 23.(9分)(1)电源内阻较小【2分】 (2)如图【2分】 (3)如图【1分】 (4)4.90(4.88~5.00均可)【2分】 0.27(0.15~0.40均可)【2分】24.(12分)解:(1)离子在加速电场加速,根据动能定理可得:212qU mv =………………………………………………………………………………(2分) 解得:v =…………………………………………………………………………(1分) 离子在圆弧形静电分析器中,根据牛顿第二定律得:2v qE m R = …………………………………………………………………………………(2分)解得:2UE R= ……………………………………………………………………………(1分) (2)离子垂直打在硅片上,由几何关系可知运动轨道半径r R = ………………………………………………………………………………………(2分)由牛顿第二定律得:2vqvB m r= ………………………………………………………(2分)解得:B = …………………………………………………………………(2分)A解:(1)未用毛刷擦冰面时对冰壶A ,根据动能定理:210102mgx mv μ-=- ………………………………………………………………………(2分) 解得:10.02μ= …………………………………………………………………………(2分) (2)设运动员擦冰面的长度为L ,冰壶A 与冰壶B 碰前的速度为v 1,根据动能定理:22121011()22mg x L mgL mv mv μμ---=- ………………………………………………(3分) 冰壶A 与冰壶B 弹性碰撞,设它们碰后的速度分别为A v 、B v ,根据动量守恒和机械能守恒定律:1A B mv mv mv =+ ……………………………………………………………………(2分)2221111222A B mv mv mv =+ …………………………………………………………………(2分) 碰后,冰壶B 要离开营垒区,至少应该满足:21102B mgR mv μ-=- ……………………………………………………………………(2分)联立解得擦冰面的长度至少为7.2m L = ………………………………………………(2分) 【用牛顿第二定律与运动学公式结合求解也可参照给分。
2023届宁夏回族自治区银川一中高三下学期第二次模拟考试 数学(理)答案

银川一中2023届高三第二次模拟数学(理科)参考答案一、单选题1.【答案】A【分析】根据给定条件,求出复数z 及z ,再利用复数除法运算求解作答.【详解】依题意,12z i =+,则12i z =-,所以12i (12i)(12i)34i 34i 12i (12i)(12i)555z z +++-+====-+--+.故选:A2.【答案】D 【分析】由已知可推得2B ∈,代入即可解得2m =-,代入即可得出答案.【详解】由题意可知,2B ∈,即2220m -+=,所以2m =-,所以,{}{}2202,1B x x x =--==-.故选:D.3.【答案】C【分析】根据含量词命题的否定形式可得到原命题,通过反例可说明原命题为假命题.【详解】 命题P 的否定为特称命题,P ∴:x ∀∈R ,211x +>,当0x =时,211x +=,P ∴为假命题,ABD 错误,C 正确.故选:C.4.【答案】B【分析】求出基本事件总数,再求出和为奇数事件所包含的基本事件个数,根据古典概型求解.【详解】不超过17的质数有:2,3,5,7,11,13,17,共7个,随机选取两个不同的数,基本事件总数27C 21n ==,其和为奇数包含的基本事件有:(2,3),(2,5),(2,7),(2,11),(2,13),(2,17),共6个,所以62217P ==.故选:B 5.【答案】B【分析】执行程序即可算出其输出值结果.【详解】由题意可知,流程图的功能为计算111111223344556S =++++⨯⨯⨯⨯⨯的值,裂项求和可得:111111111122334455566S ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-+-+-= ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭.故选:B.6.【答案】D【分析】根据一次函数、反比例函数、幂函数和分段函数的性质,逐个选项进行判断即可得到答案.【详解】对于A :函数2y x =-+的定义域为R ,值域也为R ,不符合题意;对于B:函数y =的定义域和值域都为[)0,∞+,不符合题意;对于C :2y x =的定义域和值域都为{}0x x ≠,不符合题意;对于D :2,02,0x x y x x -≤⎧=⎨+>⎩的定义域为R ;当0x ≤时,22y x =-≤-;当0x >时,22y x =+>;所以值域为(](),22,∞∞--⋃+,定义域和值域不相同,符合题意;故选:D .7.【答案】A【分析】利用向量垂直的坐标表示,结合数量积公式,即可求解.【详解】因为()2cos 75cos152sin 75sin152cos 15750a b ⋅=-=+=,2a = ,1b = .所以()()222280a b a b a b λλλ+⋅-=-=-= .所以8λ=.故选:A 8.【答案】A 【分析】由题意求出双曲线的一条渐近线的倾斜角,可得渐近线的斜率,根据离心率的计算公式可得答案.【详解】由题意设一条渐近线的倾斜角为π,(0,)2αα∈,则另一条渐近线的倾斜角为5α,由双曲对称性可得π5π,=6ααα+=∴,则一条渐近线的斜率为πtan 6=设双曲线的长半轴长为a ,短半轴长为b,则b a =,故离心率为3e ==,故选:A 9.【答案】C 【分析】根据已知条件求得123R h =,243R h =,代入体积公式计算即可.【详解】设小球缺的高为1h ,大球缺的高为2h ,则122h h R +=,①由题意可得:122π12π2Rh Rh =,即:212h h =,②所以由①②得:123R h =,243R h =,所以小球缺的体积23112228ππ333381R R R V R ⎛⎫⎛⎫=-⨯= ⎪ ⎝⎭⎝⎭,大球缺的体积23214480ππ333381R R R V R ⎛⎫⎛⎫=-⨯= ⎪ ⎪⎝⎭⎝⎭,所以小球缺与大球缺体积之比为313228π78180π2081R V R V ==.故选:C.10【答案】B 【分析】由判别式可解得6k ,由根与系数关系可得121212111331x x k x x x x k k ++===++ ,由k 的范围结合不等式的性质变形可得答案.【详解】由题意可得∆2()4(3)0k k =--+,解得6k 或2k ≤-,设两个为1x ,2x ,由两根为正根可得12120·30x x k x x k +=>⎧⎨=+>⎩,解得0k >,综上知,6k .故两个根的倒数和为12121211x x x x x x ++=1331kk k==++,6k ,∴1106k <,3102k <,故33112k <+,∴12331k+,故两个根的倒数和的最小值是23.故选:B 11.【答案】B 【分析】根据二倍角公式得到11tan 10γ=,代入式子得到22111061410hhD d ==++,解得答案.【详解】10sin 211cos 21γγ=+,即220sin cos 10tan 112cos γγγγ==,所以11tan 10γ=,22111061410h h D d ==++,解得66h =,故选:B.12.【答案】B【分析】结合229x y +≥可确定曲线上的点的位置,结合双曲线和圆的图象可确定曲线Γ的图象,采用数形结合的方式可求得结果.【详解】由题意得:2290x y +-≥,即229x y +≥,即曲线Γ上的点(),x y 为圆229x y +=上或圆229x y +=外的点,由221033x y ⎛⎫-- ⎪⎝⎭得:22133y x -=或229x y +=,由22221339x y x y ⎧-=⎪⎨⎪+=⎩得:xy ⎧=⎪⎨=⎪⎩x y ⎧=⎪⎨=⎪⎩x y ⎧⎪⎨⎪⎩x y ⎧=⎪⎨=⎪⎩由此可得曲线Γ的图象如下图所示,由图象可知:当()3,m ∈- 时,直线y m =与曲线Γ有四个不同交点;∴实数m的取值范围为()3,- .故选:B.二、填空题13.【答案】11【分析】根据题设的抽取方式,结合随机表法依次写出所得编号,即可得答案.【详解】由题设,依次取出的编号为08、02、14、07、11、05,所以第5个个体的编号为11.故答案为:1114.【答案】2【分析】由题,利用导数及韦达定理可得37a a,后利用等比中项性质可得答案.【详解】()284f x x x '=-+,由题37a a ,是方程2840x x -+=的两个不等实根,则由韦达定理373740,80a a a a =>+=>,所以370,0a a >>又5a 是37a a ,的等比中项且5a 与37a a ,同号,则2555402a a a =>⇒=,.故答案为:2.15.【答案】60︒【分析】把展开图恢复到原正方体,得到AE //DC ,从而得到∠BAE 或其补角是异面直线AB 与CD 所成的角,从而可解.【详解】如图所示,把展开图恢复到原正方体.连接AE ,BE .由正方体可得//CE AD 且CE AD =,∴四边形ADCE 是平行四边形,∴AE //DC .∴BAE ∠或其补角是异面直线AB 与CD 所成的角.由正方体可得:AB AE BE ==,∴ABE 是等边三角形,∴60=︒∠BAE .∴异面直线AB 与CD 所成的角是60°.故答案为:60°16.【答案】1【分析】构造函数()x f x e =,设切点为11(,)x y ,设()ln g x x =,设切点为22(,)x y ,结合条件得到12,x x 是函数()f x e x =和()ln g x x =的图象与曲线1y x =交点的横坐标,利用对称性得出1122(,),(,)x y x y 关于直线y x =对称,从而得出12e x x =,12ln x x =,然后计算出12k k .【详解】设()x f x e =,则()e x f x '=,设切点为11(,)x y ,则11e x k =,则切线方程为111e ()x y y x x -=-,即111e e ()x x y x x -=-,直线1(1)1y k x =+-过定点(1,1)--,所以1111e e (1)x x x --=--,所以11e 1x x =,设()ln g x x =,则1()g x x '=,设切点为22(,)x y ,则221k x =,则切线方程为2221()y y x x x -=-,即2221ln ()y x x x x -=-,直线1(1)1y k x =+-过定点(1,1)--,所以22211ln (1)x x x --=--,所以22ln 1x x =,则12,x x 是函数()f x e x =和()ln g x x =的图象与曲线1y x =交点的横坐标,易知()f x 与()g x 的图象关于直线y x =对称,而曲线1y x =也关于直线y x =对称,因此点1122(,),(,)x y x y 关于直线y x =对称,从而12e x x =,12ln x x =,所以1122e 1x k k x ==.故答案为:1.三、解答题17.【答案】(1)21n a n =+;(2)详见解析.【分析】(1)设数列{}n a 的公差为d ,将已知条件转化为1,a d 关系,即可求解;(2)根据{}n b 通项公式,用裂项相消法求出和n T ,即可证明结论.【详解】(1)由设数列{}n a 的公差为d ,则11393315a d a d +=⎧⎨+=⎩解得2d =,13a =,所以{}n a 是首项为3,公差为2的等差数列,所以21n a n =+;(2)由21n a n =+,可得111111()(21)(23)22123n n n b a a n n n n +===-++++,所以12n n T b b b =+++ 1111111()()()235572123n n ⎡⎤=-+-++-⎢⎥++⎣⎦11111()2323646n n =-=-++,又1046n >+,故.18.【答案】(1)12(2)分布列见解析,()87E X =(3)3月3日【分析】(1)根据古典概型公式求解即可.(2)根据题意得到0,1,2X =,()2327C 10C 7P X ===,()113427C C 41C 7P X ===,()2427C 22C 7PX ===,再写出分布列数学期望即可.(3)根据折线图和频率分布直方图求解即可.【详解】(1)令时间A 为“职工甲和职工乙微信记步数都不低于10000”,从3月2日至3月7日这6天中,3月2日、5日、7日这3天中,甲乙微信记步数都不低于10000,故()3162P A ==.(2)由(1)知:0,1,2X =,()2327C 10C 7P X ===,()113427C C 41C 7P X ===,()2427C 22C 7P X ===,X的分布列为:X 012P 174727()14280127777E X =⨯+⨯+⨯=(3)根据频率分步直方图知:微信记步数落在[]20,25,[)15,20,[)10,15,[)5,10,[)0,5(单位:千步)区间内的人数依次为2000.1530⨯=人,2000.2550⨯=人,2000.360⨯=人,2000.240⨯=人,2000.120⨯=人,由甲微信记步数排名第68,可知当天甲微信记步数在15000到20000万之间,根据折线图知:只有3月2日,3月3日,3月7日.由乙微信记步数排名第142,可知当天乙微信记步数在5000到10000万之间,根据折线图知:只有3月3日和3月6日,所以3月3日符合要求.19.【答案】(1)26y x =(2)证明见解析【分析】(1)将(6,6)M -代入抛物线即可求解;(2)设()()1122,,,A x y B x y ,直线l 的方程为,(0)my x t t =-≠,将直线l 与抛物线进行联立可得12126,6y y m y y t +==-,结合OA OB ⊥可得6t =,即可求证【详解】(1)因为抛物线C 过点(6,6)M -,∴2(6)26p -=⨯,解得3p =,∴抛物线C 的标准方程为26y x =.(2)设()()1122,,,A x y B x y ,直线l 的方程为,(0)my x t t =-≠,联立26my x ty x =-⎧⎨=⎩,化为2660y my t --=,236240m t ∆=+>,∴12126,6y y m y y t +==-,∵OA OB ⊥,∴()212121236y y OA OB x x y y ⋅=+= 12661036t y y t -⎛⎫+=-+= ⎪⎝⎭,0t ≠,16n T <解得6t =,满足236240m t ∆=+>,∴直线l的方程为6my x =-,∴直线过定点()6,0.20.【答案】(1)存在,理由见解析【分析】(1)根据面面平行的判定定理、性质定理分析证明;(2)根据题意结合长方体的外接球可得12AA =,建系,利用空间向量求二面角.【详解】(1)当点D 为AB 的中点时,1O D 平面1A AC ,证明如下:取AB 的中点D ,连接OD ,∵O ,D 分别为BC ,AB 的中点,则OD AC ,OD ⊄平面1A AC ,AC ⊂平面1A AC ,∴OD 平面1A AC ,又∵1OO 1AA ,1OO ⊄平面1A AC ,1AA ⊂平面1A AC ,∴1OO 平面1A AC ,1O O OD O ⋂=,1,O O OD ⊂平面1OO D ,∴平面1OO D 平面1A AC ,由于1O D ⊂平面1OO D ,故1O D ∥平面1A AC .(2)∵BC 是O 的直径,可得90BAC ∠=︒,即AB AC ⊥,且2BC =,30ABC ∠=︒,故AB =1AC =,又∵1AA ⊥平面ABC ,且,AB AC 平面ABC ,∴11,AA AB AA AC ⊥⊥,即AB ,AC ,1AA 两两垂直,且点1A ,A ,B ,C 可知该球为以AB 、AC 、1AA 则(22221AB AC AA ++=,可得12AA =,以A为原点,AB ,AC ,1AA 所在直线分别为x ,y ,z 轴建立直角坐标系,则()0,0,0A,)B ,()0,1,0C ,()10,0,2A ,得)12A B =- ,()10,1,2AC=- ,设(),,n x y z =r 为平面1A BC 的一个法向量,则112020n A B z n A C y z ⎧⋅=-=⎪⎨⋅=-=⎪⎩ ,令2x=,则y z =,可得(2,=r n ,且()0,1,0AC = 为平面1A AB 的一个法向量,设二面角1C A B A--为θ,则cos cos ,19AC n AC n AC n θ⋅===uuu r r uuu r r uuu r r ,所以二面角1C A B A --的余弦值为19.21.【答案】(1)存在,22m -≤≤;(2)①证明见解析;②证明见解析.【分析】(1)根据微积分基本定理求得()f x ,由()10f '=,求得参数a ;利用导数求函数的在区间上的最值,结合一次不等式在区间上恒成立问题,即可求得参数m 的范围;(2)①求得()F x ',利用导数求得()F x 的单调性,即可容易证明;②由①中所求,可得12ln()11k k k +>++,利用对数运算,即可证明.【详解】由题可知2()ln(1)(1)f x a x x =+++,∴()221a f x x x '=+++.(1)由()01f '=,可得2202a ++=,8a =-.又当8a =-时,()()()2311x x f x x +'-=+,故()f x 在区间()0,1单调递减,在()1,+∞单调递增.故函数()f x 在1x =处取得极值,所以8a =-.∵11e <-,82(1)(3)()2211x x f x x x x --+'=++=++.∴()0f x '>,当[]1,x e e ∈-时,由上述讨论可知,()f x 单调递增,故2min ()(1)8f x f e e =-=-+不等式2214()m tm e f x ++-≤对任意[]1,x e e ∈-及[]1,1t ∈-恒成立,即:22222min 14()148m tm e f x m tm e e ++-≤⇔++-≤-+,即:260m tm +-≤对[]1,1t ∈-恒成立,令2()6g t m mt =+-,(1)0g ⇒-≤,(1)0g ≤即260m m --≤,且260m m +-≤,整理得()()320m m -+≤,且()()320m m +-≤,解得:22m -≤≤,即为所求.(2)①∵2()()(1)ln(1)F x f x x x x x =-+-=+-,∴()1xF x x-'=+当0x >时,()0F x '<,∴()F x 在(0,)+∞上单调递减,()(0)0F x F ∴<=即证.②由①可得:ln(1)(0)x x x +<>令:11x k =+,得11ln(111k k +<++,即:12ln()11k k k +>++∴1112322ln ln ln 12(1)1221n n n n n n n n n n +++++⋅⋅⋅+>++⋅⋅⋅++++++++=ln 2即证.【点睛】本题考查由极值点求参数值,利用导数由恒成立问题求参数范围,以及利用导数证明不等式以及数列问题,属压轴题.22.【答案】(1)C 的极坐标方程为2sin22ρθλ=,ππ,Z 2k k θ≠+∈,l的直角坐标方程为40x +=(2)1λ=【分析】(1)消去参数得到C 的普通方程,再利用公式得到极坐标方程,注意定义域,再求出l 的直角坐标方程;(2)将()π12θρ=∈R 代入C 的极坐标方程,求出,A B 的坐标,得到AB 为直径的圆的圆心和半径,根据相切关系得到方程,求出答案.【详解】(1)将曲线C 的参数方程x ty tλ=⎧⎪⎨=⎪⎩消去t ,得C 的普通方程为xy λ=,且因为0t ≠,所以0x ≠,将cos ,sin x y ρθρθ==,ππ,Z 2k k θ≠+∈,代入xy λ=,得2sin cos ρθθλ=,即2sin22ρθλ=,ππ,Z 2k k θ≠+∈,即为C 的极坐标方程,由直线l 的方程πsin 26ρθ⎛⎫-= ⎪⎝⎭化简得1sin cos 222ρθρθ-=,化简得40x +=,即为l 的直角坐标方程.(2)将直线π12θ=代入2sin22ρθλ=,得24ρλ=,即12ρρ==-故以AB 为直径的圆圆心为O,半径r =圆心O 到直线l的距离2d =,由已知得2=,解得1λ=.23.【答案】(1)(0,4)【分析】(1)根据零点分区间,分类求解即可,(2)根据绝对值三角不等关系可得21a =,进而结合基本不等式即可求解.【详解】(1)当1a =-时,()4f x <等价于|1||3|4x x -+-<,当1x ≤时,13420x x x -+-<⇒-<,则01x <≤,当13x <<时,13424x x -+-<⇒<,则13x <<,当3x ≥时,134244x x x -+-<⇒-<,则34x ≤<,综上所述,不等式()4f x <的解集为(0,4).(2)()3(3)2f x x a x a x a x a a =+++≥+-+= ,当且仅当()(3)0x a x a ++≤等号成立,min ()|2|2f x a ∴==,即21a =,24()()a m a m n -+= ,∴22241a m n =+=,∴2222222211445()59()n n m mn m m n mn ⎛⎫⎛⎫+=++=++≥+ ⎪⎪⎝⎭⎝⎭,当且仅当224()()mn mn =,即2()2mn =,即213m =,26n =时,等号成立,故221n m +的最小值为9。
2023年安徽安庆市中考第二次模拟考试物理试题(含答案)

2023年安徽中考第二次模拟考试物理试题注意事项:1、物理试卷共四大题23小题,满分70分.物理与化学的考试时间共120分钟.2、试卷包括“试题卷”和“答题卷”,请务必在“答题卷”上答题,在“试题卷”上答题无效。
3、本卷试题中g值均取10N/kg。
一、填空题(每空2分,共20分)1.唐代诗人王之焕在《登鹳雀楼》中写到“白日依山尽,黄河入海流”。
其中“白日依山尽”是以______为参照物的。
2.如图是一种“鸣音水壶”,当壶中的水烧开时会产生大量水蒸气,这些高压水蒸气通过壶盖内的簧片,使簧片振动发出尖细而清脆的报警声音。
“尖细而清脆”是指声音的______(填写声音的特性)。
3.一台电风扇的额定功率是60W,它所表示的物理意义是______。
4.当条形磁铁靠近电磁铁左端时,它们之间的磁感线如图,请在图中标出电源的正、负极。
5.摄像机相当于一台可变焦距的照相机,它的镜头实质上是一个凸透镜。
在视频会议中,如果要让拍摄的像更大一些,镜头焦距应该调得______(选填“较大”或“较小”)些。
6.在实践活动中,小明利用滚轴和绳子组装成一种简易的滑轮组(如图),借助这种简易的滑轮组也可以将较重的物体搬运到高处。
如果利用该简易滑轮组吊起一辆重为800N的摩托车,所用拉力为250N,则该简易滑轮组的机械效率是______。
7.经常用热水泡脚是养生的方式之一。
现有质量为5kg、初温为90℃的热水和质量为5kg、初温为20℃的冷水,则可配制成温度为______℃的温水(不计热损失),[已知()34.210J/kg c =⨯⋅水℃]8.如图所示,轻质杠杆OAB 可绕支点O 自由转动。
将重为100N 的物块用细线挂在轻质杠杆的A 点处,在杠杆的B 端施加竖直向上、大小为30N 的力F 时,杠杆在水平位置平衡,已知OA =0.3m ,0.6m AB =,则此时物块对水平地面的压力为______N 。
9.在如图所示的电路中,13R =Ω,39R =Ω,电流表A 的示数为1.2A ,电流表1A 的示数为0.8A ,则电阻2R 的阻值是______Ω。
江苏省南京市2024届高三下学期第二次模拟考试物理试卷(含答案)

江苏省南京市2024届高三下学期第二次模拟考试物理试卷学校:___________姓名:___________班级:___________考号:___________一、单选题1.常见的气压式水枪玩具内部原理如图所示。
从储水罐充气口充入气体,达到一定压强后,关闭充气口。
扣动扳机将阀门M打开,水立即从枪口喷出。
若在水不断喷出的过程中,罐内温度始终保持不变,则罐内气体( )A.压强变大B.内能减少C.对外做功D.对外放热2.龙年首发,“长征5号”遥七运载火箭搭载通信技术试验卫星十一号发射成功,卫星进入地球同步轨道后,主要用于开展多频段、高速率卫星通信技术验证。
下列说法正确的是( )A.同步卫星的加速度大于地球表面的重力加速度B.同步卫星的运行速度小于7.9km/sC.所有同步卫星都必须在赤道平面内运行D.卫星在同步轨道运行过程中受到的万有引力不变3.为了装点夜景,常在喷水池水下安装彩灯。
如图甲所示,空气水下有一点光源S,同时发出两种不同颜色的a光和b光,在水面上形成了一个有光射出的圆形区域,俯视如图乙所示,环状区域只有b光,中间小圆为复色光,下列说法正确的是( )A.a光发生全反射的临界角大B.a光的频率小于b光C.水对a光的折射率大于对b光的折射率D.用同一装置做双缝干涉实验,b光条纹间距更小4.把带铁芯的线圈L(电阻忽略不计)、电容器、小灯泡、开关、直流恒压电源DC 和交流电源AC(直流恒压电源的电压与交流电源电压的有效值相等),分别组成如下电路,其中小灯泡最亮的是( )A. B.C. D.5.如图所示为模拟气体压强产生机理的实验,在一定时间内将100颗豆粒从秤盘上方20cm高度处均匀连续倒在秤盘上,观察指针摆动情况。
关于该实验下列说法正确的是( )A.仅将释放位置升高,指针示数不变B.仅将释放位置升高,可模拟温度升高对气体压强的影响C.仅增加豆粒数量,可模拟温度降低对气体压强的影响D.仅增加豆粒数量,可模拟体积增大对气体压强的影响6.如图所示,一带正电的小球用绝缘细绳悬于O点,将小球拉开较小角度后静止释放,其运动可视为简谐运动,下列操作能使周期变小的是( )A.增大摆长B.初始拉开的角度更小一点C.在悬点O处放置一个带正电的点电荷D.在此空间加一竖直向下的匀强电场7.如图甲所示是一种静电除尘装置,在金属板A与金属棒B间加恒定高压,烟气从一端进入静电除尘区经过净化后从另一端排出。
2023届内蒙古包头市高三第二次模拟考试 理综化学答案

2023年普通高等学校招生全国统一考试化学参考答案78910111213B D B A BC A26.(15分)(1)搅拌(1分);CuS(硫化铜)(2分)(2)2Fe3++H2S=S↓+2Fe2++2H+(2分)(3)加入Ni(OH)2后消耗H+,使Fe3++3H2O Fe(OH)3+3H+平衡正向移动,有利于Fe3+形成Fe(OH)3沉淀而被除去(2分)(4)蒸发皿(1分)出现少量晶膜(1分)(5)0.003(2分)(6)H2SO4(2分).pH太小,锌的萃取率低,pH太大,镍可能以Ni(OH)2的形式沉出,不利于硫酸镍晶体的生成(2分)27.(14分)(1)防止X和Y被氧化(2分)(2)500(2分)恒压滴液漏斗(2分)(3)FeHClL2+Na[B(C6H5)4]+N2=NaCl+[FeH(N2)L2][B(C6H5)4](2分)(4)石油醚(2分)61.8%(2分)(5)2N2+6H2O4NH3+3O2(2分)28.(14分)(1)-124.38(2分)(2)①90.2(2分)②温度高于580℃,异丙烯收集效率变化不大,经济效益不高(2分)(3)①0.0075(2分)②>(2分)(4)0.01(2分)<(2分)35.[化学——选修3:物质结构与性质](15分)(1)3(1分);哑铃形(1分);(2)D(2分)(3)sp3(1分)2(1分);石墨烯同层碳原子中,1个碳原子和周围3个碳原子结合后,还剩1个价电子,单层磷烯同层磷原子中,1个磷原子和周围3个磷原子结合后,还剩2个价电子;(在同一层内磷原子的剩余价电子数比碳原子多)(2分)(2) PCl6-(1分);大于(1分)(3)YPO4(2分)SO42-、ClO4-、BrO4-、IO4-、SiO44-(1分)213214(8931164m4(8931164ρ0.690.690.60100.690.690.6010AAgNV cm N--⨯++⨯⨯++⨯===⨯⨯⨯⨯⨯⨯))(2分)36.[化学——选修5:有机化学基础](15分)(1)对二甲苯(2分)HOCH2CH2Br(2分)(2)AB(2分)(3)+4NaOH2H OΔ→+2+2NaBr(2分)(4)碳碳三键(三键)、酯基(2分)(或、、)(2分)(5)(3分)。
安徽省2024届高三第二次模拟考试物理试卷含解析

2024年高考物理模拟试卷注意事项:1.答卷前,考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。
用2B 铅笔将试卷类型(B )填涂在答题卡相应位置上。
将条形码粘贴在答题卡右上角"条形码粘贴处"。
2.作答选择题时,选出每小题答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案。
答案不能答在试题卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。
不按以上要求作答无效。
4.考生必须保证答题卡的整洁。
考试结束后,请将本试卷和答题卡一并交回。
一、单项选择题:本题共6小题,每小题4分,共24分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1、如图所示,一轻绳跨过固定在竖直杆下端的光滑定滑轮O ,轻绳两端点A 、B 分别连接质量为m 1和m 2两物体。
现用两个方向相反的作用力缓慢拉动物体,两个力方向与AB 连线在同一直线上。
当∠AOB =90︒时,∠OAB =30︒,则两物体的质量比m 1 :m 2为( )A .1:1B .1:2C .1:2D .1:32、一定质量的理想气体由状态A 沿平行T 轴的直线变化到状态B ,然后沿过原点的直线由状态B 变化到状态C ,p -T 图像如图所示,关于该理想气体在状态A 、状态B 和状态C 时的体积V A 、V B 、V C 的关系正确的是( )A .ABC V V V ==B .A BC V V V <=C .A B C V V V >>D .A B C V V V <<3、已知光速为 3 × 108 m/s 电子的质量为 9.1 × 10−31 kg ,中子的质量为1.67 ×10−27 kg ,质子的质量为1.67 ×10−27 kg 。
高三物理第二次模拟考试试题(含解析)

南宁三中2018届高三第二次模拟考试理综试题二、选择题:本大题共8小题,每小题6分。
在每小题给出的四个选项中,第14~18题只有一项是符合题目要求,第19~21题有多项符合题目要求。
全部选对的得6分,选对但不全的得3分。
有选错的得0分。
1. 某金属被光照射后产生了光电效应现象,测得光电子的最大初动能与入射光频率v之间的关系如图所示。
已知h为普朗克常量,电子的电荷量的绝对值为e,则当入射光频率为3v0时,其遏止电压为A. hv0B. 3hv0C.D.【答案】C【解析】由爱因斯坦光电效应方程可知,当时,有,故当入射光的频率为时,光电子的最大初动能为,又因为,所以此时遏止电压,C正确.【点睛】由爱因斯坦光电效应方程去分析图象中所包含的对解题有用的物理信息,图象与纵轴和横轴交点分别表示普朗克常量和金属的极限频率.2. 如图所示,水平固定的圆环带正电荷,且电荷均匀分布,圆环圆心为O,MN为过O点的竖直线,且,四边形abcd是以O为中心、MN为对称轴的正方形,其边长小于圆环的直径。
则下列说法正确的是A. a、d两点处的电场强度相同B. 将一试探电荷由d点沿dc边移动到c点的过程中电场力始终不做功C. 若将一重力不计的负试探电荷从M点由静止释放,则试探电荷运动到N点时速度恰好为0D. 若将一重力不计的负试探电荷从M点由静止释放后能运动到N点,则过O点时试探电荷的加速度最大【答案】C【解析】根据对称性可知,a、d两点的电场强度大小相等,方向不同,故A错误;将一试探电荷由d点沿dc移动到c点的过程中,只有过cd的中点时电场力与速度垂直,其他位置均不垂直,电场力并非始终不做功,B错误;O点电场强度为零,若一重力不计的负试探电荷从M点由静止释放后能运动到N点,则试探电荷先做加速运动,在O点时加速度为零,后做减速运动,由运动的对称性可知,到达N点时速度减为0,C正确D错误.3. 汽车在高速公路上超速是非常危险的,为防止汽车超速,高速公路都装有测汽车速度的装置。
2022年成人高考第二次模拟考试高起点《数学(理工农)》试卷及参考答案

春华教育集团2022年成人高考第二次模拟考试高起点 《数学(理工类)》试题 本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分,满分150分。
考试时间120分钟。
第I 卷(选择题,共85分) 一、选择题(本大题共17小题,每小题5分,共85分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1. 设集合M ={x|−1≤x ≤1},N ={x|0<x <1},则集合M ∩N =( ) A. {x|x ≥−1} B. {x|0<x <1} C. {x|0<x ≤1} D. {x|−1≤x ≤1} 2. 设cos α=−12,α为第三象限角,则sin α=( ) A. −√32 B. −√22 C. 12 D. √32 3. 下列函数中,既是偶函数又是周期函数的为( ) A. y =log 3x B. y =x 2 C. y =tan x D. y =cos3x 4. 不等式|x −2|≥3的解集是( ) A. {x|x ≤−5或x ≥1} B. {x |−5≤x ≤1} C. {x|x ≤−1或x ≥5} D. {x |−1≤x ≤5} 5. 函数y =cos 23x 的最小正周期是( ) A. 13π B. 23π C. 2π D. π 6. 设甲:直线倾斜角为π2;乙:直线斜率不存在,则( ) A. 甲是乙的充要条件 B. 甲是乙的充分非必要条件 C. 甲是乙的必要非充分条件 D. 甲跟乙既非充分又非必要 7. 下列函数中,在(0,+∞)为增函数的是( )A. y=log12x B. y=x2+xC. y=(14)x D. y=cos x8. log28−(12)=()A.3B.2C.0D.49. 函数f(x)=3x+1的反函数f−1(x)=()A.x−13B.x+13C.3x−1D. 1-3x10. 从5位同学中任意选出3位参加公益活动,不同的选法共有()A. 5种B. 10种C. 15种D. 20种11. 已知向量a=(2,4),b=(m,−1),且a⊥b,则实数m=()A. 2B. 1C. −1D. −212. 双曲线x 24−y29=1的渐近线方程为()A. x4±y9=0 B. x9±y4=0C. x2±y3=0 D. x3±y2=013. 函数f(x)=log3(x2−2x)的定义域是()A. (−∞,0)∪(2,+∞)B.(−∞,−2)∪(0,+∞)C. (0,2)D. (−2,0)14. 过点(1,1)且与直线x+2y−1=0平行的直线方程为()A. 2x−y−1=0B. 2x−y−3=0C. x+2y−3=0D. x−2y+1=015. 甲,乙两人射击的命中率都是0.6,他们对着目标各射击一次,两人都击中目标的概率是()A. 0.36B. 0.48C. 0.84D. 116. 顶点在原点准线为x=2的抛物线方程是下面哪个()A. y2=8xB. y2=−8xC. x2=8yD. x2=−8y17.数列{a n}是等差数列,若a1+a5=6,则a2+a3+a4=()A.18B. 12C.9D.10第Ⅱ卷(非选择题,共65分)二、填空题(本大题共4小题,每小题4分,共16分)18. (x+2)4=a0x4+a1x3+a2x2+a3x+a4,则a4=.19. 已知函数f(2x)=4x+1,则f(x)= .20. 已知f (x )=ax 3,若f′(3)=9则a = .21. 已知 射击运动员一枪射中环数ξ分布列如下表:则a =____________.三、解答题(本大题共4小题,共49分。
2022年北京市大兴区初三(第二次)模拟考试物理试题及答案解析

2022年北京市大兴区初三(第二次)模拟考试物理试卷一、单选题(本大题共12小题,共24.0分)1. 在国际单位制中,功的单位是( )A. 牛顿B. 帕斯卡C. 瓦特D. 焦耳2. 下列四种发电方式中,利用可再生能源发电的是( )A. 煤炭发电B. 核能发电C. 天然气发电D. 太阳能发电3. 如图所示的光现象中,由于光的反射形成的是( )A. 露珠把叶脉放大了B. 利用后视频扩大视野C.D.4. 下列措施中,能使蒸发变快的是( )A. 把刚栽种的禾苗覆盖上塑料膜B. 把水果放进冰箱冷藏室内C. 酒精灯使用完要盖上盖子D. 用扫帚把路面上的积水扫开5. 如图所示的实例中,目的是为了减小压强的是( )A. B.C. D.6. 如图所示的实例中,目的是为了增大摩擦的是( )A. B.C. D.7. 在如图所示的实例中,可以用流体的压强与流速的关系解释的是( )A. B.C. D.8. 工人推着箱子在水平地面上匀速前进,如图所示。
下列关于力对箱子是否做功的判断,其中正确的是( )A. 重力对箱子做了功B. 地面的支持力对箱子做了功C. 工人对箱子的推力对箱子做了功D. 箱子对工人的推力对箱子做了功9. 电吹风机的电路主要由电风扇、电热丝、导线、开关和电源组成。
为了使电吹风机不会因为温度过高而发生危险,要求接通电源后电风扇既可以单独工作,也可以跟电热丝一起工作,但电热丝不能单独工作。
用表示电风扇,用表示电热丝,则图所示的电路图中符合设计要求的是( )A. B.C. D.10. 踢毽子是一项集健身、娱乐、表演于一体的活动,拥有非常广泛的群众基础,如图所示为两个小朋友正在踢毽子的情景。
若不计空气阻力,下列说法中正确的是( )A. 毽子向上运动时速度变小,它的动能在增大B. 毽子向上运动时速度变小,是把势能转化成了动能C. 被踢出去的毽子能继续向上运动,是因为毽子有惯性D. 毽子向上运动时速度变小,是因为毽子受到向上的力越来越小11. 如图所示的电路中,电源两端的电压保持不变,闭合开关S后小灯泡L正常发光。
广西柳州市2023届高三第二次模拟考试数学(理)试题(含答案解析)

16.① 0.35 log3 5 ,② ln
2
2 2
2
,③ e3
2
,④
2
ln
sin
1 8
cos
1 8
1 4
,上述不等式
正确的有______(填序号)
三、解答题 17.第 24 届冬季奥运会将于 2022 年 2 月在北京举办,为了普及冬奥知识,某校组织全 体学生进行了冬奥知识答题比赛,从全校众多学生中随机选取了 10 名学生,得到他们 的分数统计如下表:
减区间即可对选项一一验证.
【详解】由 f (x) Asin x 的图像可知,相邻两条对称轴的距离为最小正周期的一半,
T ,即T , 22
2
,即
2,
f x sin 2x ,
对任意
x R ,都有
f
(x)
f
7 12
,
当 x 7 时, f x sin 2x 取最小值,
4 5
QF1
,则椭圆 C 的标准方程为(
)
A. 5x2 5y2 1 23
B. x2 y2 1 2
C. x2 y2 1 23
D. x2 y2 1
45
11.在 ABC 中,角 A,B,C 的对边分别为 a,b,c,已知 a b sinA sinB c sinC sinB ,
试卷第 2页,共 5页
【详解】 A B 1, 0,1, 2 ,共有 4 个元素, A B 的子集有 24 16 个.
故选:C.
3.D
【分析】由平面向量基本定理求解即可
【详解】因为在 ABC 中,点 D 在边 AC 上, DC 2DA ,
所以
2025年浙江省温州市高中毕业班第二次模拟考试物理试题含解析

2025年浙江省温州市高中毕业班第二次模拟考试物理试题注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.答题时请按要求用笔。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、单项选择题:本题共6小题,每小题4分,共24分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1、伽利略通过斜面理想实验得出了( )A .力是维持物体运动的原因B .物体的加速度与外力成正比C .物体运动不需要力来维持D .力是克服物体惯性的原因2、如图所示,两个质量均为m 的小球A 、B 套在半径为R 的圆环上,圆环可绕竖直方向的直径旋转,两小球随圆环一起转动且相对圆环静止。
已知OA 与竖直方向的夹角θ=53°,OA 与OB 垂直,小球B 与圆环间恰好没有摩擦力,重力加速度为g ,s in 53°=0.8,co s53°=0.6。
下列说法正确的是( )A 45g RB 53g RC .小球A 与圆环间摩擦力的大小为75mg D .小球A 与圆环间摩擦力的大小为15mg 3、某行星为质量分布均匀的球体,半径为R ,质量为M 。
科研人员研究同一物体在该行星上的重力时,发现物体在“两极”处的重力为“赤道”上某处重力的1.1倍。
已知引力常量为G ,则该行星自转的角速度为( )A 310GM RB 311GM RC 31.1GM RD GM R4、如图甲所示,沿波的传播方向上有六个质点a 、b 、c 、d 、e 、f ,相邻两质点之间的距离均为1m ,各质点均静止在各自的平衡位置,t =0时刻振源a 开始做简谐运动,取竖直向上为振动位移的正方向,其振动图像如图乙所示,形成的简谐横波以2m/s 的速度水平向左传播,则下列说法正确的是( )A.此横波的波长为1mB.质点e开始振动的方向沿y轴负方向C.从t=0至t=3s内质点b运动的路程为10cmD.从t=2s至t=2.5s内质点d的加速度沿y轴正向逐渐减小5、由于空气阻力的影响,炮弹的实际飞行轨迹不是抛物线,而是“弹道曲线”,如图中实线所示。
20234湘豫高三联考理数答案

解析#"!$年至#"##年生产的纪录影片时长的中位数为#'"#0#*"2#(&分 钟. 选 项 错 误#"!$ 年 至 #"##
年生产的科教影片时长的平均数 大 于%""0(""0'""0!"""0&""!"0*""0'""0'""0&""0)""2''" 分 钟
- 选项错误由方差的定义可知科教影片时长的 方 差 大 于 纪 录 影 片 时 长 的 方 差所 以 科 教 影 片 时 长 的 标 准
解析方法一因为)2678%&26688%&%!*2 !#678#'2678%'26688'%%)"#+2
! #
"!'
#!所 以*%)%+!故
选 .!
方法二因为)2678%&*2 !#678#'2678%'所以!#)#*!又"#+2
! #
"!'
#!所以*%)%+!故选 .!
"" <""
2!<1""""
"1""!将
")代
入
切
线
方
程
得
)1<""""
2!<1""""
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
宁夏石嘴山市回民高级中学xx ~xx 学年第二学期高三第二次模拟考试理科数学参考答案及评分标准一.选择题:题号 1 2 3 4 5 6 7 8 9 10 11 12 答案DBBDCDABAACB二.填空题:13. 214.1.415. 216.①②④三.解答题:17、解:(1)()2sin()2cos 2sin cos 2cos sin 2cos 666f x a b x x x x x πππ=⋅=+-=+-r r …2分3sin cos 2sin()6x x x π=-=-.…………………………………………5分 由22262k x k πππππ-+≤-≤+ 得 22233k x k ππππ-+≤≤+ …………………………………………7分所以2[2,2]33x k k ππππ∈-++( k Z ∈)时, ()f x 为增函数………………8分(Ⅱ)由(Ⅰ)知6()2sin()65f x x π=-=,即3sin()65x π-=,.……………………………10分∴27cos(2)12sin ()3625x x ππ-=--=-。
………………………………………12分18、解:(Ⅰ)记“恰好选到1个曾经参加过数学研究性学习活动的同学”为事件的A ,则其概率为.74)(271314==C C C A P …………………………………4分 (Ⅱ)随机变量X=2,3,4。
24272(2);7C P X C === ……………………6分 1143274(3);7C C P X C === …………………………8分23271(4);7C P X C === ………………………………10分∴随机变量X 的分布列为X 234P72 74 71 ∴2347777EX =⨯+⨯+⨯=…………………………12分 19、解:如图,以A 为坐标原点建立空间直角坐标系A xyz -,设1BC =,则1(0,0,0),(0,0,2),(2,0,0),(2,1,0),(1,,1),(0,2,0)2A PBC MD .…………………………3分(I ) 因为3(2,0,2)(1,,1)2PB DM ⋅=-⋅-u u u r u u u u r 0=,所以.PB DM ⊥…………………………6分(II ) 因为(2,0,2)(0,2,0)PB AD ⋅=-⋅u u u r u u u r 0=, 所以PB AD ⊥,又因为PB DM ⊥,所以PB ⊥平面.ADMN …………………………8分 设CD 与平面ADMN 所成的角为θ, 则sinθ=|cos ,|||||||PB DCPB DC PB DC ⋅<>=⋅u u u r u u u ru u u r u u u r u u u r u u u r 10=,…………11分所以CD 与平面ADMN 所成的角正弦值为10。
…………………………12分 20、解:(Ⅰ)由框图,知数列2,1}{11+==+n n n x x x x 中,∴)2007,(12)1(21≤*∈-=-+=n N n n n x n …………3分 (Ⅱ)y 1=2,y 2=8,y 3=26,y 4=80。
由此,猜想).2007,(13≤*∈-=n N n y nn …………5分证明:由框图,知数列{y n }中,y n+1=3y n +2 ∴)1(311+=++n n y y ∴.3,31111==+++y y y n n∴数列{y n +1}是以3为首项,3为公比的等比数列。
∴n y +1=3·3n -1=3n ∴n y =3n -1(2007,≤*∈n N n ) ……………8分(Ⅲ)(理)z n =n n y x y x y x +++Λ2211=1×(3-1)+3×(32-1)+…+(2n -1)(3n -1) =1×3+3×32+…+(2n -1)·3n -[1+3+…+(2n -1)] 记S n =1×3+3×32+…+(2n -1)·3n ,①则3S n =1×32+3×33+…+(2n -1)×3n+1 ② ……………10分 ①-②,得-2S n =3+2·32+2·33+…+2·3n -(2n -1)·3n+1=2(3+32+…+3n )-3-(2n -1)·3n+1=2×13·)12(331)31(3+-----n nn =113·)12(63++---n n n 63·)1(21--=+n n ……………12分∴.33·)1(1+-=+n n n S 又1+3+…+(2n -1)=n 2 ∴)2007,(33·)1(21≤*∈-+-=+n N n n n z n n …………14分 21、解:(1)设M (x ,y )是所求曲线上的任意一点,P (x 1,y 1)是方程x 2 +y 2 =4的圆上的任意一点, 则).,0(1y P ' 则有:4,2,222211111=+⎩⎨⎧==⎪⎪⎩⎪⎪⎨⎧+==y x y y x x y y y x x 代入即得, 轨迹C 的方程为.1422=+y x …………………………………………4分 (2)当直线l 的斜率不存在时,与椭圆无交点.所以设直线l 的方程为y = k (x +2),与椭圆交于A (x 1,y 1)、B (x 2,y 2)两点,N 点所在直线方程为.0174=+x 由.0444)4()2(14222222=-+++⎪⎩⎪⎨⎧+==+k x k x k x k y y x 得 由△= 42224164(4)(44)0,.3k k k k -+->∴<即k << …………………………………………………6分 .4)1(4,4422212221k k x x k k x x +-=+-=+ ,+=Θ即=,∴四边形OANB 为平行四边形 …………7分 假设存在矩形OANB ,则0=⋅OB OA ,即02121=+y y x x , 即04)(2)1(2212212=++++k x x k x x k ,于是有0441622=+-k k 得.21±=k …………………………………………10分 设17444),,(2221000-=+-=+=+=k k x x x y x N 得由, …………12分即点N 在直线174-=x 上. ∴存在直线l 使四边形OANB 为矩形, 直线l 的方程为).2(21+±=x y ………………………………………………………14分四、选做题:22、A 、选修4—1:几何证明选讲证明: ①连结OD . ∵DE 切⊙O 于点D ,∴DE ⊥OD, ∴∠ODE=900又∵AD=DC, AO=OB ,∴OD//BC∴∠DEC=∠ODE=900, ∴DE ⊥BC …………………………………5分②连结BD . ∵AB 是⊙O 的直径, ∴∠ADB=900∴BD ⊥AC, ∴∠BDC=900又∵DE ⊥BC, Rt △CDB ∽Rt △CED∴CE DC DC BC =, ∴BC=3163422==CE DC 又∵OD=21BC ,∴OD=3831621=⨯, 即⊙O 的半径为38.…………………………10分 B 、选修4—4:坐标系与参数方程B 、1、解:()3cos 2sin 10P P θθ设,,则到定点(,)的距离为: ()d θ===∴当时,取最小值cos )θθ=(35455d .…………………………………5分 2、解:5sin ρθθ=-可表示为2cos 5sin ρθρθ=-,化为直角坐标方程为2250x y y +-+=,即225(()252x y ++=,因此该圆的半径为5,圆心的直角坐标为5()22-, 所以圆的半径为5,圆心的极坐标为(5,6π-)。
…………………………………10分 C 、选修4—5:不等式选讲C 、证法1:由已知条件和均值不等式有:321111a a a ++)111)((1321321a a a a a a m ++++= ⎥⎥⎦⎤⎢⎢⎣⎡++++++=)()()(31133123321221a a a a a a a a a a a a m mm 9)2223(1=+++≥, 当且仅当3321ma a a ===时,等号成立.…………………………………10分 证法2:由已知条件和柯西不等式有:321111a a a ++)111)((1321321a a a a a a m ++++=21m ≥9m=,当且仅当3321ma a a ===时,等号成立.…………………………………10分。
