实验一 数据的多元线性回归分析
计量经济实验报告多元(3篇)

第1篇一、实验目的本次实验旨在通过多元线性回归模型,分析多个自变量与因变量之间的关系,掌握多元线性回归模型的基本原理、建模方法、参数估计以及模型检验等技能,提高运用计量经济学方法解决实际问题的能力。
二、实验背景随着经济的发展和社会的进步,影响一个变量的因素越来越多。
在经济学、管理学等领域,多元线性回归模型被广泛应用于分析多个变量之间的关系。
本实验以某地区居民消费支出为例,探讨影响居民消费支出的因素。
三、实验数据本实验数据来源于某地区统计局,包括以下变量:1. 消费支出(Y):表示居民年消费支出,单位为元;2. 家庭收入(X1):表示居民家庭年收入,单位为元;3. 房产价值(X2):表示居民家庭房产价值,单位为万元;4. 教育水平(X3):表示居民受教育程度,分为小学、初中、高中、大专及以上四个等级;5. 通货膨胀率(X4):表示居民消费价格指数,单位为百分比。
四、实验步骤1. 数据预处理:对数据进行清洗、缺失值处理和异常值处理,确保数据质量。
2. 模型设定:根据理论知识和实际情况,建立多元线性回归模型:Y = β0 + β1X1 + β2X2 + β3X3 + β4X4 + ε其中,Y为因变量,X1、X2、X3、X4为自变量,β0为截距项,β1、β2、β3、β4为回归系数,ε为误差项。
3. 模型估计:利用统计软件(如SPSS、R等)对模型进行参数估计,得到回归系数的估计值。
4. 模型检验:对估计得到的模型进行检验,包括以下内容:(1)拟合优度检验:通过计算R²、F统计量等指标,判断模型的整体拟合效果;(2)t检验:对回归系数进行显著性检验,判断各变量对因变量的影响是否显著;(3)方差膨胀因子(VIF)检验:检验模型是否存在多重共线性问题。
5. 结果分析:根据模型检验结果,分析各变量对因变量的影响程度和显著性,得出结论。
五、实验结果与分析1. 拟合优度检验:根据计算结果,R²为0.812,F统计量为30.456,P值为0.000,说明模型整体拟合效果较好。
多元线性回归模型实验报告
多元线性回归模型一、实验目的通过上机实验,使学生能够使用Eviews 软件估计可化为线性回归模型的非线性模型,并对线性回归模型的参数线性约束条件进行检验。
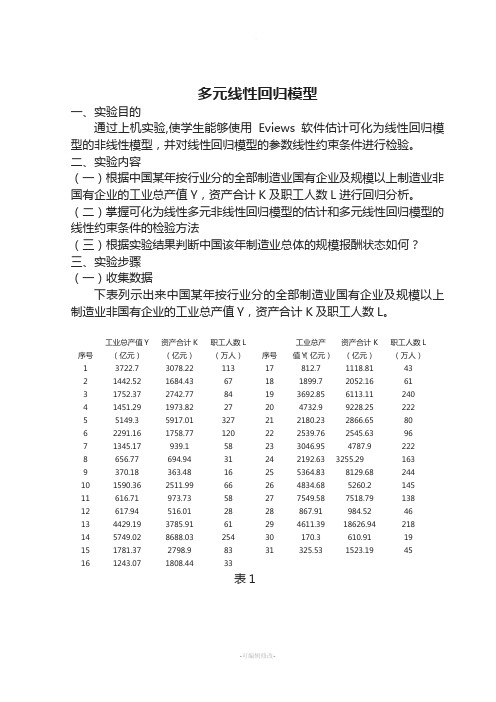
二、实验内容(一)根据中国某年按行业分的全部制造业国有企业及规模以上制造业非国有企业的工业总产值Y,资产合计K及职工人数L进行回归分析。
(二)掌握可化为线性多元非线性回归模型的估计和多元线性回归模型的线性约束条件的检验方法(三)根据实验结果判断中国该年制造业总体的规模报酬状态如何?三、实验步骤(一)收集数据下表列示出来中国某年按行业分的全部制造业国有企业及规模以上制造业非国有企业的工业总产值Y,资产合计K及职工人数L。
序号工业总产值Y(亿元)资产合计K(亿元)职工人数L(万人)序号工业总产值Y(亿元)资产合计K(亿元)职工人数L(万人)1 3722.7 3078.22 113 17 812.7 1118.81 432 1442.52 1684.43 67 18 1899.7 2052.16 613 1752.37 2742.77 84 19 3692.85 6113.11 2404 1451.29 1973.82 27 20 4732.9 9228.25 2225 5149.3 5917.01 327 21 2180.23 2866.65 806 2291.16 1758.77 120 22 2539.76 2545.63 967 1345.17 939.1 58 23 3046.95 4787.9 2228 656.77 694.94 31 24 2192.63 3255.29 1639 370.18 363.48 16 25 5364.83 8129.68 24410 1590.36 2511.99 66 26 4834.68 5260.2 14511 616.71 973.73 58 27 7549.58 7518.79 13812 617.94 516.01 28 28 867.91 984.52 4613 4429.19 3785.91 61 29 4611.39 18626.94 21814 5749.02 8688.03 254 30 170.3 610.91 1915 1781.37 2798.9 83 31 325.53 1523.19 4516 1243.07 1808.44 33表1(二)创建工作文件(Workfile)。
多元线性回归计量经济学实验报告-V1

多元线性回归计量经济学实验报告-V1多元线性回归是一种常用的计量经济学方法,它通过建立多个自变量和因变量之间的关系式,来解释和预测经济现象。
在本次实验中,我们利用多元线性回归方法,对GDP、人口、教育程度和失业率这四个变量之间的关系进行了分析和探讨。
一、数据收集和处理本实验采用的数据来源于世界银行官方网站,数据时间跨度为1990年至2018年。
我们通过Excel软件进行了数据处理和分析,包括数据清洗、变量筛选和数据转换等,以保证数据可靠性和分析准确性。
二、变量解释和关系建立我们选取了GDP、人口、教育程度和失业率这四个变量,其中GDP作为因变量,人口、教育程度和失业率作为自变量。
我们分别解释了这四个变量:1. GDP:即国内生产总值,反映了一个国家或地区的经济规模和发展水平。
2. 人口:反映了一个国家或地区的人口规模和结构。
3. 教育程度:反映了一个国家或地区的人力资本水平和教育资源状况。
4. 失业率:反映了一个国家或地区的劳动力市场状况和社会稳定性。
根据以上变量的解释和现实经济联系,我们建立了以下关系式:GDP = β0 + β1人口+ β2教育程度+ β3失业率+ ε其中,β0表示常数项,β1、β2、β3分别表示人口、教育程度和失业率对GDP的影响,ε为误差项。
三、实验结果分析我们利用Stata软件进行了多元线性回归分析,得到以下结果:1. 回归方程的拟合程度通过F检验可以得出,本回归方程的拟合程度显著,F统计量为XXX,P值为XXX<0.05,说明该模型拟合程度良好。
同时,R-squared值为XXX,表示被解释变量(GDP)有XXX%的方差可以由解释变量(人口、教育程度、失业率)来解释,这也表明该模型的解释能力较强。
2. 变量系数和显著性检验根据模型回归结果,我们可以看出,人口、教育程度、失业率三个变量对GDP有不同的影响程度,并且它们的影响在统计意义上也是显著的。
具体地,我们可以看出教育程度的系数估计值为XXX,p<0.05,说明教育程度与GDP呈现正相关关系,即教育程度越高,GDP水平越高。
多元线性回归实验报告
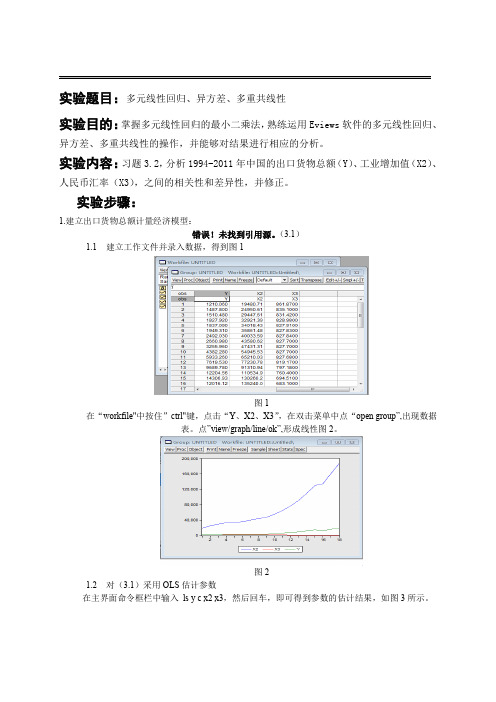
实验题目:多元线性回归、异方差、多重共线性实验目的:掌握多元线性回归的最小二乘法,熟练运用Eviews软件的多元线性回归、异方差、多重共线性的操作,并能够对结果进行相应的分析。
实验内容:习题3.2,分析1994-2011年中国的出口货物总额(Y)、工业增加值(X2)、人民币汇率(X3),之间的相关性和差异性,并修正。
实验步骤:1.建立出口货物总额计量经济模型:错误!未找到引用源。
(3.1)1.1建立工作文件并录入数据,得到图1图1在“workfile"中按住”ctrl"键,点击“Y、X2、X3”,在双击菜单中点“open group”,出现数据表。
点”view/graph/line/ok”,形成线性图2。
图21.2对(3.1)采用OLS估计参数在主界面命令框栏中输入ls y c x2 x3,然后回车,即可得到参数的估计结果,如图3所示。
图 3根据图3中的数据,得到模型(3.1)的估计结果为(8638.216)(0.012799)(9.776181)t=(-2.110573) (10.58454) (1.928512)错误!未找到引用源。
错误!未找到引用源。
F=522.0976从上回归结果可以看出,拟合优度很高,整体效果的F检验通过。
但当错误!未找到引用源。
=0.05时,错误!未找到引用源。
=错误!未找到引用源。
2.131.有重要变量X3的t检验不显著,可能存在严重的多重共线性。
2.多重共线性模型的识别2.1计算解释变量x2、x3的简单相关系数矩阵。
点击Eviews主画面的顶部的Quick/Group Statistics/Correlatios弹出对话框在对话框中输入解释变量x2、x3,点击OK,即可得出相关系数矩阵(同图4)。
相关系数矩阵图4由图4相关系数矩阵可以看出,各解释变量相互之间的相关系数较高,证实解释变量之间存在多重共线性。
2.2多重共线性模型的修正将各变量进行对数变换,在对以下模型进行估计。
多元线性回归

多元线性回归方程
Y=a+b1X1+b2X2+…+bkXk
自变量
自变量是指研究者主动操纵,而引起因变量发生变化的因素或条件,因此 自变量被看作是因变量的原因。自变量有连续变量和类别变量之分。如果实 验者操纵的自变量是连续变量,则实验是函数型实验。如实验者操纵的自变 量是类别变量,则实验是因素型的。 在心理实验中,自变量是由实验者操纵、掌握的变量。自变量一词来自数 学。在数学中,y=f(x)。在这一方程中自变量是x,因变量是y。将这个方 程运用到心理学的研究中,自变量是指研究者主动操纵,而引起因变量发生 变化的因素或条件,因此自变量被看作是因变量的原因。自变量有连续变量 和类别变量之分。如果实验者操纵的自变量是连续变量,则实验是函数型实 验。如实验者操纵的自变量是类别变量,则实验是因素型的。在心理学实验 中,一个明显的问题是要有一个有机体作为被试(符号O)对刺激(符号S) 作反应(符号R),即S-O—R。显然,这里刺激变量就是自变量。
多元回归分析数据格式
例号 X1 1 X11 2 X21 ┇ ┇ n Xn1 X2 … X m X12 X22 ┇ Xn2 … … … … X1m X2m ┇ Xnm Y Y1 Y2 ┇ Yn
条件
(1)Y 与X1 , X2 ,…, Xm 之间具有线性关系。 (2)各例观测值Yi (i = 1,2,,n)相互独立。 (3)残差 e服从均数为 0﹑方差为σ2 的正态分布,它等价于对任意 一组自变量X1 , X 2,…, Xm 值,应变量 Y 具有相同方差,并且服从正态 分布。
10个50mL的容量瓶中分别加人不 同体积的Ca2+、Mg2+标准溶液 (所加入的体积数由计算机随机函数计算得到 ),2.00 mLHg(Ⅱ)一 EDTA溶液,5.0rnL的三乙醇溶液和1mLNa2S溶液,用水稀释至刻度。 溶液转入电解池后插入电极,用EDTA标准溶液滴定并记录滴定曲线。
计量地理学实验报告

《计量地理学》实验报告学院:班级:学号:姓名:指导老师:实验地点:目录一、第一次实验(1)多元线性回归分析··3(2)逐步回归分析··6二、第二次实验(1)主成分回归分析··10(2)方差分析··13三、第三次实验(1)非线性回归分析··17(2)聚类分析··20四、第四次实验趋势面分析··22第一次实验1.实验名称:多元线性回归分析实验目的:通过探讨自变量与因变量之间变动的比例关系,建立模型,揭示地理要素之间的线性相关关系。
实验内容:以《贵州省遵义市海龙坝水源地供水水文地质详查报告》中的数据资料为例,对该地区地下水流量进行预测。
从详查报告可以看出,该区地下水流量的动态变化主要受降雨量及人工开采两个因素的影响,因此主要通过研究区降雨量及人工开采用水资料来预测地下水各观测孔流量的变化,而不考虑其它因素的影响,则模型可简化为:22110x x y ∂+∂+∂=式中,y 为观测孔地下水流量的变化;21,x x 分别为降雨量和人工开采量。
年份 降雨量1x /mm人工开采量2x /3m观测孔流量y/(L/s)1990 954 658.8 51.54 1991 1389.5 723.1 63.71 1992 864 701.9 54.44 1993 1193.2 689.5 56.78 1994 841 734.6 53.45 1995 1378.4 699.2 65.92 19961686.9685.467.581997 1592.1 704.7 64.591998 1956.7 613.7 75.31实验步骤:(1)在DPS系统中对原始数据进行回归分析,将上表中数据编辑、定义成数据块;(2)在“多元分析”菜单下选择“回归分析”中的“线性回归”,系统给出下图界面点击右下角的“返回编辑”,得到以下数据:多元线性回归分析结果:方差来源平方和df 均方F值p值相关系数R=0.962768 决定系数RR=0.926923 调整相关R'=0.950034press=117.3509 剩余标准差sse= 2.4622 预测误差标准差MSPE=4.4225 Durbin-Watson d=2.2597回 归461.39792230.6989 38.0527 0.0004剩 余36.3757 6 6.0626总 的497.77368 62.2217变量 回归系数 标准系数 偏相关 标准误t 值p-值 b0 26.3907 21.6685 1.21790.2627b1 0.0201 0.9914 0.9523 0.0026 7.6450 0.0001 b2 0.01250.05680.17600.02840.43790.6746序号观察值拟合值残差标准残差 学生残差cook 距离成果处理:经过以上分析,由上表可知,该区地下水流量计算模型为:210125.00201.03907.26x x y ++=通过对回归方程进行F 显著性检验,该地下水流量预测模型显著性很好,符合1 51.5400 53.7836 -2.2436 -0.9112 -1.3434 0.7061 2 63.7100 63.3429 0.3671 0.1491 0.1774 0.00443 54.4400 52.5106 1.92940.78360.93320.12144 56.7800 58.9766 -2.1966 -0.8921 -0.9563 0.04545 53.4500 52.4554 0.9946 0.4039 0.5048 0.0477 6 65.9200 62.8219 3.09811.25821.35180.09407 67.5800 68.8541 -1.2741 -0.5175 -0.5965 0.0390 8 64.5900 67.1881 -2.5981 -1.0552 -1.2416 0.1976 975.3100 73.3868 1.92320.78111.48581.9270通径系数分析直接作用 通过x1通过x2 x1 0.9914 -0.0298x20.0568-0.5206剩余通径系数=0.270327该地区的实际情况,因此可以通过该模型对研究区地下水流量进行预测。
生物统计学:第10章 多元线性回归分析及一元非线性回归分析

H0 : 1 2 k 0 H A : 至少有一个i 0
拒绝H0意味着至少有一个自变量对因变量是有影 响的。
检验的程序与一元的情况基本相同,即用方差
胸围X2 186.0 186.0 193.0 193.0 172.0 188.0 187.0 175.0 175.0 185.0
体重Y 462.0 496.0 458.0 463.0 388.0 485.0 455.0 392.0 398.0 437.0
序号 体长X1 胸围X2 体重Y 11 138.0 172.0 378.0 12 142.5 192.0 446.0 13 141.5 180.0 396.0 14 149.0 183.0 426.0 15 154.2 193.0 506.0 16 152.0 187.0 457.0 17 158.0 190.0 506.0 18 146.8 189.0 455.0 19 147.3 183.0 478.0 20 151.3 191.0 454.0
R r Y•1,2,,k
yp yˆ p
,
p 1,2,, n
对复相关系数的显著性检验,相当于对整个回 归的方差分析。在做过方差分析之后,就不必再检 验复相关系数的显著性,也可以不做方差分析。
例10.1的RY·1,2为:
RY •1,2
24327 .8 0.9088 29457 .2
从附表(相关系数检验表)中查出,当独立
表示。同样在多元回归问题中,可以用复相关系数表 示。对于一个多元回归问题,Y与X1,X2,… ,Xk 的线性关系密切程度,可以用多元回归平方和与总平 方和的比来表示。因此复相关系数由下式给出,
多元线性回归模型实验报告

多元线性回归模型实验报告
关于多元线性回归模型实验报告,我可以向您提供以下信息:多元线性回归模型是一种常用的统计分析方法,用于研究多个自变量对一个因变量的影响。
在实验中,我们首先需要确定自变量和因变量之间的关系,然后使用回归分析方法拟合出一个多元线性回归模型,最后通过模型的参数估计和显著性检验来评估自变量对因变量的影响。
在实验中,我们需要收集一定量的数据,并对数据进行预处理和清洗,以确保数据的准确性和可靠性。
然后,我们可以使用统计软件(如SPSS、R等)来进行多元线性回归分析,得出模型的参数估计和显著性检验结果。
在分析结果中,我们需要关注自变量的系数估计值、标准误、置信区间和显著性水平等指标,以评估自变量对因变量的影响。
最后,我们需要对模型的拟合效果进行评估,可以使用拟合优度、残差分析等方法来判断模型的拟合程度和预测能力。
如果模型的拟合效果不佳,我们可以考虑调整模型的自变量或者采用其他的回归分析方法。
希望以上信息能够对您有所帮助。
上机实验指导(多元线性回归模型)

实验一多元线性回归模型一实验目的:1.理解多元线性回归分析的方法原理。
2.熟练掌握多元回归分析的Eviews操作。
3.掌握多元线性回归模型的估计方法。
4.掌握模型方程的F检验,参数的t检验。
5.掌握如何利用回归模型进行预测。
6.培养运用多元线性回归模型解决实际经济问题的能力。
二实验要求:通过案例对多元线性回归模型估计,对回归方程和回归参数进行检验并做出预测与预测置信区间三预备知识:回归系数的参数估计,最小二乘法估计原理、t检验、F检验和预测四实验内容:为了确定Woody’s餐厅(Wo ody’s 是一个价格适中,24小时营业的家庭式连锁餐厅)下一个连锁店的最佳位置,研究者决定建立回归模型来描述各个连锁店的总销售量。
每家连锁店的总销售量都是地理位置相关属性的函数,经过分析,研究者选定:被解释变量y:已存在的连锁店的顾客数量解释变量:N:竞争,当地Woody’s 的方圆2英里内的直接对手数量;P:人口,当地Woody’s 的方圆3英里内的居住人口;I:收入,当地Woody’s 的方圆3英里内的居住人口的平均收入水平。
数据文件:woody3.xls,样本量:33,下表为部分数据用Eviews做多元线性回归分析。
1. 估计回归方程的参数及随机干扰项的标准误差,计算2R及2R。
写出回归方程,解释回归系数的含义。
2. 对方程进行F检验,对参数进行t检验,并构造参数95%的置信区间.3. 预测y0:如果N=4,P=90000,I=15000,构造y0的95%的预测置信区间。
五实验步骤:1.建立工作文件并录入全部数据,如图1所示:图 12. 建立多元线性回归模型33,2,1,3210 =++++=i u I P N y i ββββ回归方程:I P N y 3210ˆˆˆˆˆββββ+++=点击主界面菜单Quick\Estimate Equation 选项,在弹出的对话框中输入:Y C N P I点击确定即可得到回归结果,如图2所示图 2根据图2的信息,得到回归方程为:758.1,649.15,679.0,3337.288.442.4)543.0()073.0()2053(288.1355.09075102192ˆ2====-=++-=DW F R N t IP N y随机干扰项的标准误差为78.14542ˆ=σ3方程和回归系数显著性检验 方程的F 检验3,2,1,0至少一个:0:i 3210=≠===i H H A ββββ回归模型的F 值为:15.649, F 分布的自由度为(3,29)p-value=0.000003在5%的显著性水平下,p-value 小于0.05, 拒绝原假设,回归方程的F 检验显著。
统计预测与决策实验报告

实验一:多元线性回归模型实验目的与要求:熟练掌握建立多元线性回归模型的方法。
实验内容:问题:国际旅游外汇收入是国民经济发展的重要组成部分,影响一个国家或地区旅游收入的因素包括自然、文化、社会、经济、交通等多方面的因素,本例研究第三产业对旅游外汇收入的影响。
《中国统计年鉴》把第三产业划分为12个组成部分,分别为1x 农林牧渔服务业,2x 地质勘查水利管理业,3x 交通运输仓储和邮电通信业,4x 批发零售贸易和餐饮业,5x 金融保险业,6x 房地产业,7x 社会服务业,8x 卫生体育和社会福利业,9x 教育文化艺术和广播,10x 科学研究和综合艺术,11x 党政机关,12x 其他行业。
选取1998年我国31个省、市、自治区的数据(见实验一数据.xls )。
自变量单位为亿元人民币,以国际旅游外汇收入为因变量y (百万美元)。
试建立线性回归模型。
(要求用MATLAB 的stepwise 函数解决问题。
取05.0=进α,1.0=出α。
)解:Matlab 操作步骤1、将excel 文件中的数据导入Matlab 文件中(1)在Matlab 的“Command Window ”窗口中输入“A=[]”,点击回车键; (2)在Matlab 的“Workspace ”窗口中双击“A ”,打开“Variable Editor ”窗口,将保存在excel 中的实验一的数据复制到“Variable Editor ”窗口中,保存为“sy1_sj.mat ”。
2、建立M 文件打开一个空白的M 文件,并在其中输入程序: (1)后退法clear;clc load sy1_sj.mat [n,m]=size(A); X=A(:,1:m-1);y=A(:,m);stepwise(X,y,[1 2 3 4 5 6 7 8 9 10 11 12],0.05,0.1)保存在数据保存的位置,命名为“sy1_ht.m ”。
(2)前进法clear;clc load sy1_sj.mat [n,m]=size(A); X=A(:,1:m-1);y=A(:,m); stepwise(X,y,[],0.05,0.1)保存在数据保存的位置,命名为“sy1_qj.m ”。
计量经济学实验指导

计量经济学实验指导实验一多元线性回归模型【实验目的】通过本实验,了解Eviews软件,熟悉软件建立工作文件,文件窗口操作,数据输入与处理等基本操作。
掌握多元线性回归模型的估计方法,学会用Eiews 软件进行多元回归分析。
通过本实验使得学生能够根据所学知识,对实际经济问题进行分析,建立计量模型,利用Eiews软件进行数据分析,并能够对输出结果进行解释说明。
【实验内容及步骤】本实验选用美国金属行业主要的27家企业相关数据,如下表,其中被解释变量Y表示产出,解释变量L表示劳动力投入,K表示资本投入。
试建立三者之间的回归关系。
【实验内容及步骤】1.数据的输入STEP1:双击桌面上Eviews快捷图标,打开Eviews,如图1.图1STEP2:点击Eviews主画面顶部按钮file/new/Workfile ,如图2,弹出workfile create对话框如图3。
在frequency中选择integer data,在start date 和end date 中分别输入1和27,点击OK,出现图如4画面,Workfile 定义完毕。
在新建的workfile中已经存在两个objects,即c和residual。
c 是系数向量、residual是残差序列,当估计完一个模型后,该模型的系数、残差就分别保存在c和residual中。
图2图3图4STEP3:在workfile空白部分单击右键,选择New object,在Type of object 中选择Series,将该对象命名为Y,如图5.单击ok,得到图6。
图5图6STEP4:双击图6中的图标“y”,得到如下图7,是关于序列“y”的工作表。
点击表示命令栏中的“Edit+/-”即可进入数据输入状态,利用给定的数据逐步输入27个数值。
图7STEP5:重复上面的数据输入步骤,依次输入序列“L”和“K”.如下图8所示.图82数据描述(1).数据的查看方式。
Eviews可以有多种不同数据的查看方式,在数据输入时用的表格形式,即Spreadsheet。
《应用回归分析 》---多元线性回归分析实验报告

《应用回归分析》---多元线性回归分析实验报告
二、实验步骤:
1、计算出增广的样本相关矩阵
2、给出回归方程
Y=-65.074+2.689*腰围+(-0.078*体重)3、对所得回归方程做拟合优度检验
4、对回归方程做显著性检验
5、对回归系数做显著性检验
三、实验结果分析:
1、计算出增广的样本相关矩阵相关矩阵
2、给出回归方程
回归方程:Y=-65.074+2.689*腰围+(-0.078*体重)
3、对所得回归方程做拟合优度检验
由表可知x与y的决定性系数为r2=0.800,说明模型的你和效果一般,x与y 线性相关系数为R=0.894,说明x与y有较显著的线性关系,当F=33.931,显著性Sig.p=0.000,说明回归方程显著
4、对回归方程做显著性检验
5、对回归系数做显著性检验
Beta的t检验统计量t=-6.254,对应p的值接近0,说明体重和体内脂肪比重对腰围数据有显著影响
6、结合回归方程对该问题做一些基本分析
从上面的分析过程中可以看出腰围和脂肪比重以及腰围和体重的相关性都是很大的,通过检验可以看出回归方程、回归系数也很显著。
其次可以观察到腰围、脂肪比重、体重的数据都是服从正态分布的。
第4章 回归分析

r=1
r=-1
y
y
x
x
r<0:x与y负线性相关(negative linear correlation) r>0:x与y正线性相关(positive linear correlation)
-1<r<0
0<r<1
y y
x
② 自由度
SST的自由度 :dfT=n-1 SSR的自由度 :dfR=1 SSe的自由度 :dfe=n-2 三者关系: dfT= dfR +dfe
③ 均方
MSR
SSR dfR
MSe
SSe dfe
④ F检验
F MSR MSe
F服从自由度为(1,n-2)的F分布
给定的显著性水平α下 ,查得临界值: Fα(1,n-2)
① 离差平方和
总离差平方和:
n
SST ( yi y)2 Lyy
i 1
回归平方和(regression sum of square) :
n
SSR ( $yi y)2 b2 Lxx bLxy i 1
残差平方和 : n SSe ( yi $yi )2 i 1
三者关系:
SST SSR SSe
性回归方程,其中b1,b2,…,bm 称为偏回归系数。。
设变量 x1, x2 , xm , y 有N组试验数据:
x11, x21, xm1, y1 x12 , x22 , xm2 , y2
回归系
数?
x1k , x2k , xmk , yk (k 1,2, , N )( N m)
回归系数的确定
根据最小二乘法原理 :求偏差平方和最小时的回归系数。
多元线性回归模型实验报告 计量经济学

多元线性回归模型实验报告计量经济学多元线性回归模型是一种比较常见的经济学建模方法,其可用于对多个自变量和一个因变量之间的关系进行分析和预测。
在本次实验中,我们将使用一个包含多个自变量的数据集,对其进行多元线性回归分析,并对分析结果进行解释。
数据集介绍本次实验使用的数据集来自于UCI Machine Learning Repository,数据集包含有关汽车试验的多个自变量和一个连续因变量。
数据集中包含了204条记录,其中每条记录包含了一辆汽车的14个属性,分别是:MPG(燃油效率),气缸数(Cylinders)、排量(Displacement)、马力(Horsepower)、重量(Weight)、加速度(Acceleration)、模型年(Model Year)、产地(Origin)等。
模型建立在进行多元线性回归分析之前,我们首先需要对数据进行预处理。
为了确保数据的可用性,我们需要先检查数据是否存在缺失值和异常值。
如果有,需要进行相应的处理,以确保因变量和自变量之间的关系受到了正确地分析。
在对数据进行预处理之后,我们可以使用Python中的statsmodels包来对数据进行多元线性回归分析。
具体建模过程如下:```import statsmodels.api as sm# 准备自变量和因变量数据X = data[['Cylinders', 'Displacement', 'Horsepower', 'Weight', 'Acceleration', 'Model Year', 'Origin']]y = data['MPG']# 添加常数项X = sm.add_constant(X)# 拟合线性回归模型model = sm.OLS(y, X).fit()# 输出模型摘要print(model.summary())```在上述代码中,我们首先通过data[['Cylinders', 'Displacement', 'Horsepower', 'Weight', 'Acceleration', 'Model Year', 'Origin']]选择了所有自变量列,用于进行多元线性回归分析;然后,我们又通过`sm.add_constant(X)`,向自变量数据中添加了一列全为1的常数项,用于对截距进行建模;最后,我们使用`sm.OLS(y, X).fit()`来拟合线性回归模型,并使用`model.summary()`输出模型摘要。
计量经济学实验报告1

一.预期Y和各个解释变量之间的关系
家庭书刊年支出(Y)与家庭月收入(X),户主受教育程度(T)呈线性相关关系
二. Y对X的回归
1.建立经济模型
2.在eviews中录入数据,并用最小二乘法估计参数得到回归结果,如下表
可知:
(1)线性回归方程为
(2)估计的回归系数 , 的标准误差和t值分别为
: =0
SE( )=117.1579 ;t( )=1.604113取
查t分布表得自由度为n-2=18-2=16的临界值 (16)=2.120>t( )=1.60411
未落在了拒绝域内,故假设成立
:=0
SE( )=0.056922;t( )=5.128460取
查t分布表得自由度为n-2=18-2=16的临界值 (16)=2.120<t( )=5.128460
SE( )=117.1579 ;t( )=1.604113;
SE( )=0.056922;t( )=5.128460
(3) =0.621759 F=26.30110 n=18
经济意义解释:
当家庭月平均收入每变动一单位时,家庭书刊年消费支出就同向变动0.291923个单位
4.参数显著性检验(对回归系数的t检验)
四.模型选择及原因
应选择多元线性回归模型
原因:多元线性回归模型对两种解释变量“家庭月平均收入”和“户主受教育年数”对被解释变量“家庭书刊年消费支出”的影响都有做分析,这样就能更全面的分析问题,结果的可信度也相对较高。
原因:多元线性回归模型对两种解释变量“家庭月平均收入”和“户主受教育年数”对被解释变量“家庭书刊年消费支出”的影响都有做分析,这样就能更全面的分析问题,结果的可信度也相对较高。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验一数据的多元线性回归分析
[实验目的和要求]
1、熟练运用计算机和Eviews软件进行分析,并对数据进行预处理,进行初步描述性分析,然后估计出相关系数,写出估计方程,并进行检验,需要用到R方、调整R方,F、T、置信区间检验,然后分析其经济意义;
2、建立的工作文件以“组-姓名”,如“第一组-王诚.wf1”;
3、独立完成实验,并得到正确结果。
[实验内容]
对64个国家的婴儿死亡率、女性文盲率、人均GNP、总生育率进行分析考察婴儿死亡的影响因素。
[实验数据]
附表:table 1,给出了64个国家的数据,其中CM表示婴儿死亡率,FLR表示女性文盲率、PGNP表示人均GNP,TFR表示总生育率。
[实验过程]
1.先验地预期CM和各个变量之间的关系。
2.做CM对各个变量之间的回归,并写出估计方程。
3.对估计方程作检验
4.写出经济意义
5、实验总结。
