多元线性回归模型案例分析.doc
多元线性回归分析范例

多元线性回归分析范例多元线性回归是一种用于预测因变量和多个自变量之间关系的统计分析方法。
它假设因变量与自变量之间存在线性关系,并通过拟合一个多元线性模型来估计因变量的值。
在本文中,我们将使用一个实际的数据集来进行多元线性回归分析的范例。
数据集介绍:我们选取的数据集是一份汽车销售数据,包括了汽车的价格(因变量)和多个与汽车相关的特征(自变量),如车龄、行驶里程、汽车品牌等。
我们的目标是通过这些特征来预测汽车的价格。
数据集包括了100个样本。
数据集的构成如下:车龄(年),行驶里程(万公里),品牌,价格(万元)----------------------------------------5,10,A,153,5,B,207,12,C,10...,...,...,...建立多元线性回归模型:我们首先需要将数据集划分为自变量矩阵X和因变量向量y。
其中,自变量矩阵X包括了车龄、行驶里程和品牌等特征,因变量向量y包括了价格。
在Python中,我们可以使用NumPy和Pandas库来处理和分析数据。
我们可以使用Pandas的DataFrame来存储数据集,并使用NumPy的polyfit函数来拟合多元线性模型。
首先,我们导入所需的库并读取数据集:```pythonimport pandas as pdimport numpy as np#读取数据集data = pd.read_csv('car_sales.csv')```然后,我们将数据集划分为自变量矩阵X和因变量向量y:```python#划分自变量矩阵X和因变量向量yX = data[['车龄', '行驶里程', '品牌']]y = data['价格']```接下来,我们使用polyfit函数来拟合多元线性模型。
我们将自变量矩阵X和因变量向量y作为输入,并指定多项式的次数(线性模型的次数为1):```python#拟合多元线性模型coefficients = np.polyfit(X, y, deg=1)```最后,我们可以使用拟合得到的模型参数来预测新的样本。
多元线性回归模型案例(DOC)

多元线性回归模型案例分析——中国人口自然增长分析一·研究目的要求中国从1971年开始全面开展了计划生育,使中国总和生育率很快从1970年的5.8降到1980年2.24,接近世代更替水平。
此后,人口自然增长率(即人口的生育率)很大程度上与经济的发展等各方面的因素相联系,与经济生活息息相关,为了研究此后影响中国人口自然增长的主要原因,分析全国人口增长规律,与猜测中国未来的增长趋势,需要建立计量经济学模型。
影响中国人口自然增长率的因素有很多,但据分析主要因素可能有:(1)从宏观经济上看,经济整体增长是人口自然增长的基本源泉;(2)居民消费水平,它的高低可能会间接影响人口增长率。
(3)文化程度,由于教育年限的高低,相应会转变人的传统观念,可能会间接影响人口自然增长率(4)人口分布,非农业与农业人口的比率也会对人口增长率有相应的影响。
二·模型设定为了全面反映中国“人口自然增长率”的全貌,选择人口增长率作为被解释变量,以反映中国人口的增长;选择“国名收入”及“人均GDP”作为经济整体增长的代表;选择“居民消费价格指数增长率”作为居民消费水平的代表。
暂不考虑文化程度及人口分布的影响。
从《中国统计年鉴》收集到以下数据(见表1):表1 中国人口增长率及相关数据设定的线性回归模型为:1222334t t t t t Y X X X u ββββ=++++三、估计参数利用EViews 估计模型的参数,方法是:1、建立工作文件:启动EViews ,点击File\New\Workfile ,在对话框“Workfile Range ”。
在“Workfile frequency ”中选择“Annual ” (年度),并在“Start date ”中输入开始时间“1988”,在“end date ”中输入最后时间“2005”,点击“ok ”,出现“Workfile UNTITLED ”工作框。
其中已有变量:“c ”—截距项 “resid ”—剩余项。
多元线性回归模型案例

多元线性回归模型案例多元线性回归是统计学中常用的一种回归分析方法,它可以用来研究多个自变量与因变量之间的关系。
在实际应用中,多元线性回归模型可以帮助我们理解不同自变量对因变量的影响程度,从而进行预测和决策。
下面,我们将通过一个实际案例来介绍多元线性回归模型的应用。
案例背景:某电商公司希望了解其产品销售额与广告投入、季节因素和竞争对手销售额之间的关系,以便更好地制定营销策略和预测销售额。
数据收集:为了分析这一问题,我们收集了一段时间内的产品销售额、广告投入、季节因素和竞争对手销售额的数据。
这些数据将作为我们多元线性回归模型的输入变量。
模型建立:我们将建立一个多元线性回归模型,以产品销售额作为因变量,广告投入、季节因素和竞争对手销售额作为自变量。
通过对数据进行拟合和参数估计,我们可以得到一个多元线性回归方程,从而揭示不同自变量对产品销售额的影响。
模型分析:通过对模型的分析,我们可以得出以下结论:1. 广告投入对产品销售额有显著影响,广告投入越大,产品销售额越高。
2. 季节因素也对产品销售额有一定影响,不同季节的销售额存在差异。
3. 竞争对手销售额对产品销售额也有一定影响,竞争对手销售额越大,产品销售额越低。
模型预测:基于建立的多元线性回归模型,我们可以进行产品销售额的预测。
通过输入不同的广告投入、季节因素和竞争对手销售额,我们可以预测出相应的产品销售额,从而为公司的营销决策提供参考。
结论:通过以上分析,我们可以得出多元线性回归模型在分析产品销售额与广告投入、季节因素和竞争对手销售额之间关系时的应用。
这种模型不仅可以帮助我们理解不同因素对产品销售额的影响,还可以进行销售额的预测,为公司的决策提供支持。
总结:多元线性回归模型在实际应用中具有重要意义,它可以帮助我们理解复杂的变量关系,并进行有效的预测和决策。
在使用多元线性回归模型时,我们需要注意数据的选择和模型的建立,以确保模型的准确性和可靠性。
通过以上案例,我们对多元线性回归模型的应用有了更深入的理解,希望这对您有所帮助。
案例2多元线性回归模型的计算过程及

多元线性回归模型的计算过程及案例分析计算过程(1) 根据n组观察样本的原始数据,12(,,,)t t t kt y x x x(1,2,,)t n = 写出如下矩阵:1112112212221211,1k k n nnkn y x x x y x x x Y X y x x x ⎛⎫⎛⎫⎪ ⎪⎪⎪== ⎪⎪ ⎪ ⎪⎝⎭⎝⎭(2) 计算1)X X X X -'''、(、X Y 。
(3) 计算参数向量B 的最小二乘法估计1ˆˆ:()BB X X X Y -''=。
(4) 计算应变量观测值向量Y 的拟合值向量ˆˆˆ:YY XB =。
(5) 计算残差平方和2t e ∑及残差的标准差ˆ:σˆσ=(6) 计算多重决定系数2R 和修正的多重系数2R ,作拟合检验。
2221;()tt e R y y =--∑∑222/(1)1;()/(1)tte n k Ry y n --=---∑∑(7)计算参数估计ˆ(0,1,2,,)j b j k =的标准差:ˆ();js b σ=其中jj c 是矩阵1)X X -'(中第j 行第j 列位置上的元素。
(8)计算检验统计量t 和F 的值,作回归参数及回归方程的显著性检验。
在原假设0:0(0,1,2,,)j H b j k == 下的t 统计量为ˆˆ/jt b σ= 在原假设001:0k H b b b === 下的F 统计量为22()1tty y n k F ke---=⋅∑∑。
(9)若模型未通过检验,则重新建立模型并重复上述步骤;若模型通过检验,且满足模型的古典假设,则可利用此模型进行结构分析或经济预测等实际应用案例分析某种商品的需求量(y,吨)、价格(1x ,元/千克)、和消费者收入(2x ,元)观测值如表所示:商品的需求量(y,吨)、价格(1x ,元/千克)、和消费者收入(2x ,元)观测值(1) 建立需求函数:01122t t t t y b b x b x u =+++; (2) 估计12b b 、的置信区间(置信度为95%); (3) 在5%显著水平上检验模型的有效性。
多元线性回归分析范例

国际旅游外汇收入是国民经济发展的重要组成部分, 影响一个国家或地区旅游收入的因素包 括自然、文化、社会、经济、交通等多方面的因素,本例研究第三产业对旅游外汇收入的影响。
《中国统计年鉴》 把第三产业划分为12个组成部分, 分别为 x 农林牧渔服务业 ,x 21地质勘查水利 管理业 ,x 交通运输仓储和邮电通信业 ,x 批发零售贸易和餐饮业 ,x 金融保险 534业,x 房地产业 ,x 社会服务业 ,x 卫生体育和社会福利业, x 教育文化艺术和广播 ,x 科学研106987究和综合艺术 ,x 党 政机关, x 其他行业。
采用 1998年我国 31 个省、市、自治区的数据, 1211以国际旅游外汇收入 (百 万美元)为因变量 y ,以如上 12 个行业为自变量做多元线性回归,其中自变量单位为亿元人民 币。
即样本量n=31,变量 p=12。
利用 SPSS 软件对数据进行处理,输出:图1 输入/移除变量图 1 即输入了所有模型中的变量,分别为x :农林牧渔服务业 1x :地质勘查水利管理业 2x 电通信业 3x :批发零售贸易和餐饮业 4x :金融保险业 6x :社会服务业 7x :卫生体育和社会福利业 8x 播 9 x :科学研究和综合艺术 10x :党政机关 11x12 .图2 模型概述2=0.935R 。
由决 即回归方程对样本观测值的拟合程度,复相关系数R=0.875,决定系数2决定,得出回归拟合的效果较好,但是并不能作为严格的显著性检验。
由R 定系数接近 1 模型优劣时需慎重,尤其是样本量与自变量个数接近时。
:交通运输仓储和邮5x :房地产业 :教育文化艺术和广 :其他行业图3 回归方程显著性的F检验F=10.482,F(n,n-p-1)=F(30,18)=2.11(α =0.05),P值=0.000,表明回归方程高度显著,αα即12 个自变量整体对因变量y 产生显著线性影响。
但是并不能说明回归方程中所有自变量都对因变量y 有显著影响,因此还要对回归系数进行检验。
多元线性回归模型的案例分析

多元线性回归模型的案例分析年份 Y/千克 X/元 P 1/(元/千克)P 2/(元/千克)P 3/(元/千克)年份 Y/千克 X/元 P 1/(元/千克)P 2/(元/千克)P 3/(元/千克)1980 397 1992 911 1981 413 1993 931 1982 439 1994 1021 1983 459 1995 1165 1984 492 1996 1349 1985 528 1997 1449 1986 560 1998 1575 1987 624 1999 1759 1988 666 2000 1994 1989 717 2001 2258 1990 768 2002 24781991843(1)求出该地区关于家庭鸡肉消费需求的如下模型:01213243ln ln ln ln ln Y X P P P u βββββ=+++++ (2)请分析,鸡肉的家庭消费需求是否受猪肉及牛肉价格的影响。
先做回归分析,过程如下:输出结果如下:所以,回归方程为:123ln 0.73150.3463ln 0.5021ln 0.1469ln 0.0872ln Y X P P P =-+-++由上述回归结果可以知道,鸡肉消费需求受家庭收入水平和鸡肉价格的影响,而牛肉价格和猪肉价格对鸡肉消费需求的影响并不显著。
验证猪肉价格和鸡肉价格是否有影响,可以通过赤池准则(AIC )和施瓦茨准则(SC )。
若AIC 值或SC 值增加了,就应该去掉该解释变量。
去掉猪肉价格P 2与牛肉价格P 3重新进行回归分析,结果如下:VariableCoefficient Std. Error t-Statistic Prob. C LOG(X) LOG(P1)R-squaredMean dependentvarAdjusted R-squared . dependent var . of regression Akaike info criterionSum squared resid Schwarz criterion Log likelihood F-statistic Durbin-Watson stat Prob(F-statistic )通过比较可以看出,AIC 值和SC 值都变小了,所以应该去掉猪肉价格P 2与牛肉价格P 3这两个解释变量。
(完整word版)多元线性回归模型案例分析

多元线性回归模型案例分析——中国人口自然增长分析一·研究目的要求中国从1971年开始全面开展了计划生育,使中国总和生育率很快从1970年的5.8降到1980年2.24,接近世代更替水平。
此后,人口自然增长率(即人口的生育率)很大程度上与经济的发展等各方面的因素相联系,与经济生活息息相关,为了研究此后影响中国人口自然增长的主要原因,分析全国人口增长规律,与猜测中国未来的增长趋势,需要建立计量经济学模型。
影响中国人口自然增长率的因素有很多,但据分析主要因素可能有:(1)从宏观经济上看,经济整体增长是人口自然增长的基本源泉;(2)居民消费水平,它的高低可能会间接影响人口增长率。
(3)文化程度,由于教育年限的高低,相应会转变人的传统观念,可能会间接影响人口自然增长率(4)人口分布,非农业与农业人口的比率也会对人口增长率有相应的影响。
二·模型设定为了全面反映中国“人口自然增长率”的全貌,选择人口增长率作为被解释变量,以反映中国人口的增长;选择“国名收入”及“人均GDP”作为经济整体增长的代表;选择“居民消费价格指数增长率”作为居民消费水平的代表。
暂不考虑文化程度及人口分布的影响。
从《中国统计年鉴》收集到以下数据(见表1):表1 中国人口增长率及相关数据设定的线性回归模型为:1222334t t t t t Y X X X u ββββ=++++三、估计参数利用EViews 估计模型的参数,方法是:1、建立工作文件:启动EViews ,点击File\New\Workfile ,在对话框“Workfile Range ”。
在“Workfile frequency ”中选择“Annual ” (年度),并在“Start date ”中输入开始时间“1988”,在“end date ”中输入最后时间“2005”,点击“ok ”,出现“Workfile UNTITLED ”工作框。
其中已有变量:“c ”—截距项 “resid ”—剩余项。
多元线性回归模型案例分析报告

多元线性回归模型案例分析——中国人口自然增长分析一·研究目的要求中国从1971年开始全面开展了计划生育,使中国总和生育率很快从1970年的5.8降到1980年2.24,接近世代更替水平。
此后,人口自然增长率(即人口的生育率)很大程度上与经济的发展等各方面的因素相联系,与经济生活息息相关,为了研究此后影响中国人口自然增长的主要原因,分析全国人口增长规律,与猜测中国未来的增长趋势,需要建立计量经济学模型。
影响中国人口自然增长率的因素有很多,但据分析主要因素可能有:(1)从宏观经济上看,经济整体增长是人口自然增长的基本源泉;(2)居民消费水平,它的高低可能会间接影响人口增长率。
(3)文化程度,由于教育年限的高低,相应会转变人的传统观念,可能会间接影响人口自然增长率(4)人口分布,非农业与农业人口的比率也会对人口增长率有相应的影响。
二·模型设定为了全面反映中国“人口自然增长率”的全貌,选择人口增长率作为被解释变量,以反映中国人口的增长;选择“国名收入”及“人均GDP”作为经济整体增长的代表;选择“居民消费价格指数增长率”作为居民消费水平的代表。
暂不考虑文化程度及人口分布的影响。
从《中国统计年鉴》收集到以下数据(见表1):表1 中国人口增长率及相关数据设定的线性回归模型为:1222334t t t t t Y X X X u ββββ=++++三、估计参数 利用EViews 估计模型的参数,方法是:1、建立工作文件:启动EViews ,点击File\New\Workfile ,在对话框“Workfile Range ”。
在“Workfile frequency ”中选择“Annual ” (年度),并在“Start date ”中输入开始时间“1988”,在“end date ”中输入最后时间“2005”,点击“ok ”,出现“Workfile UNTITLED ”工作框。
其中已有变量:“c ”—截距项 “resid ”—剩余项。
—多元线性回归分析案例

t=(2.184942) (3.849318) (12.80847)
(7.130844)
R2 0.963517 R 2 0.959307 F 228.2846 df 26
模型检验:拟合优度可决系数 R2 0.963517 较高, 修正的可决系数 R 2 0.959307 也较高,表明模型 拟合较好。
t0025260684因为各解释变量的参数对应的t统计量均大于0684这说明在5的显著水平下斜率系数均显著不为零表明三大产业的增长率对gdp增长都有显著影响
多元线性回归分析 案例
目录
• 1.建立模型 • 2.模型参数估计 • 3.检验 • 4.预测 • 5.软件操作
1.建立模型
考察三大产业的增长对我国经济增长 的贡献
F检验: 针对H0: b1=b2=b3=0
F 228.2846
给定 0.05,得临界值F0.0(5 k,n k 1) F0.05(3,26) 2.98 由于228.2846>2.98,故拒绝H0 回归方程是显著的。
t检验: 给定 0.05,查自由度t分布表得:t0.025(26)=0.684 因为各解释变量的参数对应的t统计量均大于0.684, 这说明在5%的显著水平下,斜率系数均显著不为零, 表明三大产业的增长率对GDP增长都有显著影响。
8.3
2.8
8.4
10.3
1987 11.6
4.7
13.7
14.4 2002
9.1
2.9
9.8
10.4
1988 11.3
2.5
14.5
13.2 2003 10.0
2.5
—多元线性回归分析案例

—多元线性回归分析案例多元线性回归分析是一种广泛使用的统计分析方法,用于研究多个自变量对一个因变量的影响程度。
在实际应用中,多元线性回归可以帮助我们理解变量之间的相互关系,并预测因变量的数值。
下面我们将以一个实际案例来介绍多元线性回归分析的应用。
假设我们是一家电子产品制造商,我们想研究影响手机销量的因素,并尝试通过多元线性回归模型来预测手机的销量。
我们选择了三个自变量作为影响因素:广告投入、价格和市场份额。
我们收集了一段时间内的数据,包括这三个因素以及对应的手机销量。
现在我们将利用这些数据来进行多元线性回归分析。
首先,我们需要将数据进行预处理和清洗。
我们检查数据的完整性和准确性,并去除可能存在的异常值和缺失值。
然后,我们对数据进行描述性统计分析,以了解数据的整体情况和变量之间的关系。
接下来,我们将建立多元线性回归模型。
我们将销量作为因变量,而广告投入、价格和市场份额作为自变量。
通过引入这些自变量,我们可以预测手机销量,并分析它们对销量的影响程度。
为了进行回归分析,我们需要估计模型的系数。
这可以通过最小二乘法来实现,该方法将使得模型的预测结果与实际观测值之间的残差平方和最小化。
接下来,我们将进行统计检验,以确定自变量对因变量的显著影响。
常见的统计指标包括回归系数的显著性水平、t值和p值。
在我们的案例中,假设多元线性回归模型的方程为:销量=β0+β1×广告投入+β2×价格+β3×市场份额+ε。
其中,β0、β1、β2和β3为回归系数,ε为误差项。
完成回归分析后,我们可以进行模型的诊断和评估。
我们可以检查模型的残差是否呈正态分布,以及模型的拟合程度如何。
此外,我们还可以通过交叉验证等方法评估模型的准确性和可靠性。
最后,我们可以利用训练好的多元线性回归模型来进行预测。
通过输入新的广告投入、价格和市场份额的数值,我们可以预测手机的销量,并根据预测结果制定相应的市场策略。
综上所述,多元线性回归分析是一种强大的统计工具,可用于分析多个自变量对一个因变量的影响。
多元线性回归模型案例
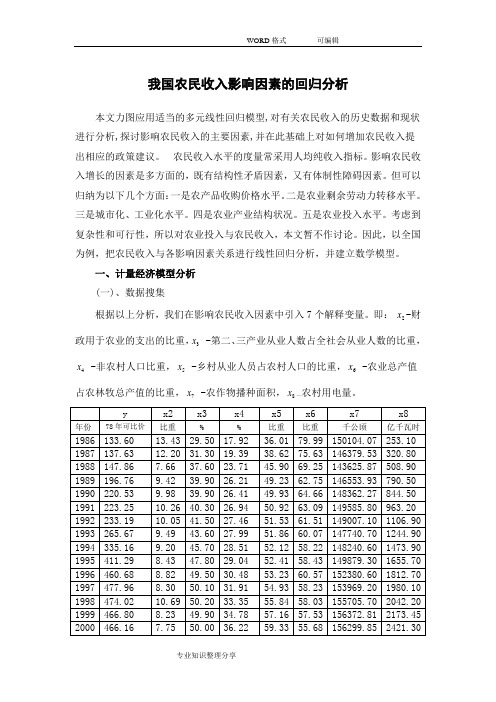
我国农民收入影响因素的回归分析本文力图应用适当的多元线性回归模型,对有关农民收入的历史数据和现状进行分析,探讨影响农民收入的主要因素,并在此基础上对如何增加农民收入提出相应的政策建议。
农民收入水平的度量常采用人均纯收入指标。
影响农民收入增长的因素是多方面的,既有结构性矛盾因素,又有体制性障碍因素。
但可以归纳为以下几个方面:一是农产品收购价格水平。
二是农业剩余劳动力转移水平。
三是城市化、工业化水平。
四是农业产业结构状况。
五是农业投入水平。
考虑到复杂性和可行性,所以对农业投入与农民收入,本文暂不作讨论。
因此,以全国为例,把农民收入与各影响因素关系进行线性回归分析,并建立数学模型。
一、计量经济模型分析 (一)、数据搜集根据以上分析,我们在影响农民收入因素中引入7个解释变量。
即: 2x -财政用于农业的支出的比重,3x -第二、三产业从业人数占全社会从业人数的比重,4x -非农村人口比重,5x -乡村从业人员占农村人口的比重,6x -农业总产值占农林牧总产值的比重,7x -农作物播种面积,8x —农村用电量。
资料来源《中国统计年鉴2006》。
(二)、计量经济学模型建立 我们设定模型为下面所示的形式:122334455667788t t Y X X X X X X X u ββββββββ=++++++++ 利用Eviews 软件进行最小二乘估计,估计结果如下表所示:Dependent Variable: Y Method: Least Squares Sample: 1986 2004 C -1102.373 375.8283 -2.933184 0.0136 X1 -6.635393 3.781349 -1.754769 0.1071 X3 18.22942 2.066617 8.820899 0.0000 X4 2.430039 8.370337 0.290316 0.7770 X5 -16.23737 5.894109 -2.754847 0.0187 X6 -2.155208 2.770834 -0.777819 0.4531 X7 0.009962 0.002328 4.278810 0.0013 R-squared0.995823 Mean dependent var 345.5232 Adjusted R-squared 0.993165 S.D. dependent var 139.7117 S.E. of regression 11.55028 Akaike info criterion 8.026857 Sum squared resid 1467.498 Schwarz criterion 8.424516 Log likelihood -68.25514 F-statistic 374.6600 表1 最小二乘估计结果回归分析报告为:()()()()()()()()()()()()()()()()23456782ˆ -1102.373-6.6354X +18.2294X +2.4300X -16.2374X -2.1552X +0.0100X +0.0634X 375.83 3.7813 2.066618.37034 5.8941 2.77080.002330.02128 -2.933 1.7558.820900.20316 2.7550.778 4.27881 2.97930.99582i Y SE t R ===---=230.99316519 1.99327374.66R Df DW F ====二、计量经济学检验(一)、多重共线性的检验及修正①、检验多重共线性(a)、直观法从“表1 最小二乘估计结果”中可以看出,虽然模型的整体拟合的很好,但是x4 x6的t统计量并不显著,所以可能存在多重共线性。
(实验2)多元回归分析实验报告.doc

⑩陕&科技丈嗲实验报告成绩一、实验预习:1.多元回归模型。
2.多元回归模型参数的检验。
3.多元回归模型整体的检验。
二、实验的目的和要求:通过案例分析掌握多元回归模型的建立方法和检验的标准;并掌握分析解决实际金融问题的能力。
三、实验过程:(实验步骤、原理和实验数据记录等)软件:Eviews3.1数据:给定美国机动车汽油消费量研究数据。
1.实验步骤1)在Eviews7.0中,新建文件,并将给定的数据输入新建的文件中;2)分析变量间的相关关系;3)进行时间序列的平稳性检验,根据序列趋势图,对原序列进行ADF平稳性检验,再对时间序列数据的一阶差分进行ADF检验,并对结果进行分析讨论。
2.实验原理对于只有一个解释变量的模型,其参数估计方法是最简单的,一般形式如下:y t= A)+ +其中&称为被解释变量,人称为解释变量,%称为随机误差项。
模型可分为两部分:1)回归方程部分,2)随机误差部分,义㈣归分析就是根据样本观察值寻求从和成的估计值。
图一0 Series: S Torkfile: ADF::Adf\| VeA- J Proc: Object Properties ^nnt Name {Freeze J Default-n x| Options | Sample [Gerr j图二2)建立回归模型如卜:四、实验总结:(实验数据处理和实验结果讨论等)1.实验数据处理1)数据的预处理:通过绘制动态曲线、绘制散点图、计算变量之间的相关 关系为正式建模做准备。
可以画出美国汽车各项研究数据的趋势图如下:QMG = c(l) + c(2) * MOB + c(3) * PMG + c(4) * POP + c(5) * GNP 回归结果如下:Dependent Variable: QMG Method: LeastSquares Date: 06/10/14 Time: 16:19 Sample:1950 1987 Included observations: 38QMG=C(1)+C(2)*MOB+C(3)*PMG+C(4)*POP+C(5)*GNP由表中数据带入公式可写出线性回归表达式为:QMG = 24553723 + 1.418520 * MOB- 27995762 * PMG- 59.8748 * POP- 30540.88 * GNP3)进行模型检验从表Prob列的数据中发现c(0)与c(4)的值T检验未通过,可以考虑删除相应的自变量。
多元线性回归实例分析

SPSS--回归—多元线性回归模型案例解析!(一)多元线性回归,主要是研究一个因变量与多个自变量之间的相关关系,跟一元回归原理差不多,区别在于影响因素(自变量)更多些而已,例如:一元线性回归方程为:毫无疑问,多元线性回归方程应该为:上图中的x1, x2, xp分别代表“自变量”Xp截止,代表有P个自变量,如果有“N组样本,那么这个多元线性回归,将会组成一个矩阵,如下图所示:那么,多元线性回归方程矩阵形式为:其中:代表随机误差,其中随机误差分为:可解释的误差和不可解释的误差,随机误差必须满足以下四个条件,多元线性方程才有意义(一元线性方程也一样)1:服成正太分布,即指:随机误差必须是服成正太分别的随机变量。
2:无偏性假设,即指:期望值为03:同共方差性假设,即指,所有的随机误差变量方差都相等4:独立性假设,即指:所有的随机误差变量都相互独立,可以用协方差解释.今天跟大家一起讨论一下,SPSS—-—多元线性回归的具体操作过程,下面以教程教程数据为例,分析汽车特征与汽车销售量之间的关系。
通过分析汽车特征跟汽车销售量的关系,建立拟合多元线性回归模型.数据如下图所示:点击“分析”——回归——线性——进入如下图所示的界面:将“销售量”作为“因变量"拖入因变量框内,将“车长,车宽,耗油率,车净重等10个自变量拖入自变量框内,如上图所示,在“方法”旁边,选择“逐步”,当然,你也可以选择其它的方式,如果你选择“进入”默认的方式,在分析结果中,将会得到如下图所示的结果:(所有的自变量,都会强行进入)如果你选择“逐步”这个方法,将会得到如下图所示的结果:(将会根据预先设定的“F统计量的概率值进行筛选,最先进入回归方程的“自变量”应该是跟“因变量”关系最为密切,贡献最大的,如下图可以看出,车的价格和车轴跟因变量关系最为密切,符合判断条件的概率值必须小于0.05,当概率值大于等于0.1时将会被剔除)“选择变量(E)" 框内,我并没有输入数据,如果你需要对某个“自变量”进行条件筛选,可以将那个自变量,移入“选择变量框”内,有一个前提就是:该变量从未在另一个目标列表中出现!,再点击“规则”设定相应的“筛选条件”即可,如下图所示:点击“统计量"弹出如下所示的框,如下所示:在“回归系数”下面勾选“估计,在右侧勾选”模型拟合度“ 和”共线性诊断“ 两个选项,再勾选“个案诊断”再点击“离群值”一般默认值为“3",(设定异常值的依据,只有当残差超过3倍标准差的观测才会被当做异常值)点击继续。
多元线性回归模型案例分析报告

多元线性回归模型案例分析报告多元线性回归模型是一种用于预测和建立因变量和多个自变量之间关系的统计方法。
它通过拟合一个线性方程,找到使得回归方程和实际观测值之间误差最小的系数。
本报告将以一个实际案例为例,对多元线性回归模型进行案例分析。
案例背景:公司是一家在线教育平台,希望通过多元线性回归模型来预测学生的学习时长,并找出对学习时长影响最大的因素。
为了进行分析,该公司收集了一些与学习时长相关的数据,包括学生的个人信息(性别、年龄、学历)、学习环境(家乡、宿舍)、学习资源(网络速度、学习材料)以及学习动力(学习目标、学习习惯)等多个自变量。
数据分析方法:通过建立多元线性回归模型,我们可以找到与学习时长最相关的因素,并预测学生的学习时长。
首先,我们将根据实际情况对数据进行预处理,包括数据清洗、过滤异常值等。
然后,我们使用逐步回归方法,通过逐步添加和删除自变量来筛选最佳模型。
最后,我们使用已选定的自变量建立多元线性回归模型,并进行系数估计和显著性检验。
案例分析结果:经过数据分析和模型建立,我们得到了如下的多元线性回归模型:学习时长=0.5*年龄+0.2*学历+0.3*学习资源+0.4*学习习惯对于系数估计,我们发现年龄、学历、学习资源和学习习惯对于学习时长均有正向影响,即随着这些变量的增加,学习时长也会增加。
其中,年龄和学习资源的影响较大,学历和学习习惯的影响较小。
在显著性检验中,我们发现该模型的拟合度较好,因为相关自变量的p值均小于0.05,表明它们对学习时长的影响具有统计学意义。
案例启示:本案例的分析结果为在线教育平台提供了重要的参考。
公司可以针对年龄较大、学历高、学习资源丰富和有良好学习习惯的学生,提供个性化的学习服务和辅导。
同时,公司也可以通过提供更好的学习资源和培养良好的学习习惯,来提升学生的学习时长和学习效果。
总结:多元线性回归模型在实际应用中具有广泛的应用价值。
通过对因变量和多个自变量之间的关系进行建模和分析,我们可以找到相关影响因素,并预测因变量的取值。
多元线性回归分析实例
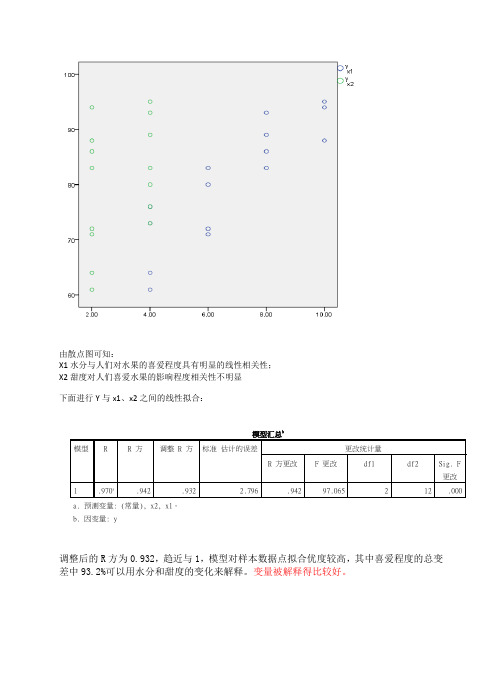
由散点图可知:
X1水分与人们对水果的喜爱程度具有明显的线性相关性;
X2甜度对人们喜爱水果的影响程度相关性不明显
下面进行Y与x1、x2之间的线性拟合:
调整后的R方为0.932,趋近与1,模型对样本数据点拟合优度较高,其中喜爱程度的总变差中93.2%可以用水分和甜度的变化来解释。
变量被解释得比较好。
H0:β
=0 (水果甜度和人们对水果的喜爱程度无显著线性关系)
2
H1:β
≠0(水果甜度和人们对水果的喜爱程度有显著线性关系)
2
P值0.000,小于0.05,拒绝原假设,接受对立假设,即水果甜度和人们对水果的喜爱程度有显著线性关系
线性回归方程:
Y=4.395x1+4.326x2+37.955
方程的解释:
在水果甜度不变的前提下,水果水分每增加1个单位,人们对水果的喜爱程度增加4.395个单位
在水果水分不变的前提下,水果甜度每增加1个单位,人们对水果的喜爱程度增加4.326个单位
残差的正态性检验:
H0:该模型的误差项符合正态性检验
H1:该模型的误差项不符合正态性检验
K-S检验的P值为0.763,大于0.05,接受原假设,该模型符合正态性检验,说明误差项的正态性假设是合理的。
残差的方差齐性检验:
上述散点图水果水分与误差近似分布在一条水平的带状线中,那么就可以认为残差的齐性假设是合理的。
散点图水果甜度与误差近似分布在一条垂直的带状线中,可以认为残差的齐性假设是不合理的。
多元线性回归模型案例

多元线性回归模型案例在统计学中,多元线性回归是一种用于研究多个自变量与一个因变量之间关系的方法。
它可以帮助我们了解各个自变量对因变量的影响程度,并预测因变量的取值。
本文将通过一个实际案例来介绍多元线性回归模型的应用。
案例背景:假设我们是一家房地产公司的数据分析师,公司希望通过分析房屋的各项特征来预测房屋的销售价格。
我们收集了一批房屋的数据,包括房屋的面积、卧室数量、浴室数量、地理位置等多个自变量,以及每套房屋的销售价格作为因变量。
数据准备:首先,我们需要对收集到的数据进行清洗和处理。
这包括处理缺失值、异常值,对数据进行标准化等操作,以确保数据的质量和可靠性。
在数据准备阶段,我们还需要将数据分为训练集和测试集,以便后续模型的建立和验证。
模型建立:接下来,我们使用多元线性回归模型来建立房屋销售价格与各项特征之间的关系。
假设我们的模型为:Y = β0 + β1X1 + β2X2 + ... + βnXn + ε。
其中,Y表示房屋销售价格,X1、X2、...、Xn表示房屋的各项特征,β0、β1、β2、...、βn表示模型的系数,ε表示误差项。
模型评估:建立模型后,我们需要对模型进行评估,以验证模型的拟合程度和预测能力。
我们可以使用各项统计指标如R方、均方误差等来评估模型的拟合程度和预测能力,同时也可以通过绘制残差图、QQ图等来检验模型的假设是否成立。
模型优化:在评估模型的过程中,我们可能会发现模型存在欠拟合或过拟合的问题,需要对模型进行优化。
优化的方法包括添加交互项、引入多项式项、进行特征选择等操作,以提高模型的拟合程度和预测能力。
模型应用:最后,我们可以使用优化后的模型来预测新的房屋销售价格。
通过输入房屋的各项特征,模型可以给出相应的销售价格预测值,帮助公司进行房地产市场的决策和规划。
结论:通过本案例,我们了解了多元线性回归模型在房地产数据分析中的应用。
通过建立、评估、优化和应用模型的过程,我们可以更好地理解各项特征对房屋销售价格的影响,并进行有效的预测和决策。
多元线性回归模型案例

多元线性回归模型案例多元线性回归模型是一种用于分析多个自变量和一个因变量之间关系的统计方法。
它可以帮助我们理解不同自变量对因变量的影响程度,以及它们之间的相互关系。
在本文中,我们将通过一个实际案例来演示多元线性回归模型的应用。
假设我们想要研究某个地区的房屋价格与房屋面积、房间数量和地理位置之间的关系。
我们收集了一些数据,包括不同房屋的面积、房间数量、地理位置和售价。
我们希望利用这些数据建立一个多元线性回归模型,以预测房屋价格。
首先,我们需要对数据进行预处理。
这包括检查数据是否存在缺失值、异常值或离群点。
如果发现这些问题,我们需要进行相应的处理,例如删除缺失值、调整异常值或使用合适的方法进行离群点处理。
在数据预处理完成后,我们可以开始建立多元线性回归模型。
建立多元线性回归模型的第一步是选择自变量。
在本例中,我们选择房屋面积、房间数量和地理位置作为自变量,售价作为因变量。
接下来,我们需要检验自变量之间是否存在多重共线性。
如果存在多重共线性,我们需要进行相应的处理,例如删除一些自变量或使用主成分分析等方法进行处理。
一旦确定了自变量,我们可以利用最小二乘法来估计回归系数。
最小二乘法是一种常用的估计方法,它可以帮助我们找到使得观测数据和模型预测值之间残差平方和最小的回归系数。
通过最小二乘法,我们可以得到每个自变量的回归系数,从而建立多元线性回归模型。
建立好多元线性回归模型后,我们需要对模型进行检验。
这包括检验模型的拟合优度、残差的正态性和独立性等。
如果模型通过了检验,我们就可以利用该模型进行预测和推断。
例如,我们可以利用模型来预测某个房屋的售价,或者利用模型来推断不同自变量对售价的影响程度。
在实际应用中,多元线性回归模型可以帮助我们理解复杂的数据关系,进行预测和推断。
然而,我们也需要注意模型的局限性和假设条件。
例如,多元线性回归模型假设自变量和因变量之间是线性关系,如果实际情况并非如此,我们需要考虑使用其他模型进行分析。
多元线性回归模型的案例分析

多元线性回归模型的案例分析在实际生活中,多元线性回归模型可以广泛应用于各个领域。
以下是一个案例分析,以说明多元线性回归模型的应用。
案例:房价预测背景:城市的房地产公司想要推出一款房屋估价服务,帮助人们预测房屋的销售价格。
他们收集了一些相关数据,如房屋的面积、房间的数量、地理位置等因素,并希望通过建立一个多元线性回归模型来实现房价的预测。
步骤:1.数据收集:收集相关数据。
在本案例中,我们收集到了50个样本数据,每个样本包含了房屋的面积、房间的数量和房屋的销售价格。
2.数据预处理:对数据进行预处理,包括缺失值处理、异常值处理等。
在本案例中,我们假设数据已经经过清洗,没有缺失值和异常值。
3.特征选择:选择合适的特征变量。
在本案例中,我们选择房屋的面积和房间的数量作为特征变量,房屋的销售价格作为目标变量。
4.模型建立:建立多元线性回归模型。
根据特征变量和目标变量的关系,建立多元线性回归方程。
在本案例中,假设多元线性回归方程为:房价=β0+β1×面积+β2×房间数量+ε,其中β0、β1和β2分别为回归系数,ε为误差项。
5.模型训练:使用样本数据对模型进行训练。
通过最小二乘法等方法,估计出回归系数的取值。
6.模型评估:评估模型的性能。
通过计算模型的均方误差(MSE)、决定系数(R²)等指标,评估模型的拟合效果和预测能力。
7.模型应用:将模型用于房价的预测。
当有新的房屋数据输入时,通过模型的预测方程,可以得到该房屋的预测销售价格。
通过上述步骤,我们可以建立一个多元线性回归模型,并通过该模型对房价进行预测。
这个模型可以帮助房地产公司提供房价估价服务,也可以帮助购房者了解合理的房价范围。
多元线性回归案例分析

多元线性回归案例分析案例背景:我们假设有一家制造业公司,想要研究员工的工作效率与其工作经验、教育水平和工作时间之间的关系。
公司收集了100名员工的数据,并希望通过多元线性回归模型来分析这些变量之间的关系。
数据收集:公司收集了每个员工的工作效率(因变量)、工作经验、教育水平和工作时间(自变量)的数据。
假设工作效率由工作经验、教育水平和工作时间这三个因素决定。
根据所收集的数据,我们可以建立如下的多元线性回归模型:工作效率=β0+β1*工作经验+β2*教育水平+β3*工作时间+ε在这个模型中,β0、β1、β2和β3分别是待估参数,代表截距和自变量的系数;ε是误差项,代表模型中未被解释的因素。
模型参数的估计:通过最小二乘法可以对模型中的参数进行估计。
最小二乘法的目标是让模型的预测值与观测值之间的残差平方和最小化。
模型诊断:在对模型进行参数估计后,我们需要对模型进行诊断,以评估模型的质量和稳定性。
常见的模型诊断方法包括:检查残差的正态分布、残差与自变量的无关性、残差的同方差性等。
模型解释和预测:根据参数估计结果,可以对模型进行解释和预测。
例如,我们可以解释每个自变量与因变量之间的关系,并分析它们的显著性。
我们还可以通过模型进行预测,比如预测一位具有一定工作经验、教育水平和工作时间的员工的工作效率。
结果分析:根据对模型的诊断和解释,我们可以对结果进行分析。
我们可以得出结论,一些自变量对因变量的影响显著,而其他自变量对因变量的影响不显著。
这些结论可以帮助公司更好地理解员工工作效率与工作经验、教育水平和工作时间之间的关系,并采取相应的管理措施来提高工作效率。
总结:通过以上的案例分析,我们可以看到多元线性回归在实际中的应用。
它可以帮助我们理解多个自变量与一个因变量之间的关系,并对因变量进行预测和解释。
通过多元线性回归分析,我们可以更好地了解因素对于结果的作用,并根据分析结果进行决策和管理。
然而,需要注意的是,多元线性回归的结果可能受到多种因素的影响,我们需要综合考虑所有的因素来做出准确的分析和决策。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
多元线性回归模型案例分析
——中国人口自然增长分析一·研究目的要求
中国从1971年开始全面开展了计划生育,使中国总和生育率很快从1970年的5.8降到1980年2.24,接近世代更替水平。
此后,人口自然增长率(即人口的生育率)很大程度上与经济的发展等各方面的因素相联系,与经济生活息息相关,为了研究此后影响中国人口自然增长的主要原因,分析全国人口增长规律,与猜测中国未来的增长趋势,需要建立计量经济学模型。
影响中国人口自然增长率的因素有很多,但据分析主要因素可能有:(1)从宏观经济上看,经济整体增长是人口自然增长的基本源泉;(2)居民消费水平,它的高低可能会间接影响人口增长率。
(3)文化程度,由于教育年限的高低,相应会转变人的传统观念,可能会间接影响人口自然增长率(4)人口分布,非农业与农业人口的比率也会对人口增长率有相应的影响。
二·模型设定
为了全面反映中国“人口自然增长率”的全貌,选择人口增长率作为被解释变量,以反映中国人口的增长;选择“国名收入”及“人均GDP”作为经济整体增长的代表;选择“居民消费价格指数增长率”作为居民消费水平的代表。
暂不考虑文化程度及人口分布的影响。
从《中国统计年鉴》收集到以下数据(见表1):
表1 中国人口增长率及相关数据
设定的线性回归模型为:
1222334t t t t t Y X X X u ββββ=++++
三、估计参数
利用EViews 估计模型的参数,方法是:
1、建立工作文件:启动EViews ,点击File\New\Workfile ,在对
话框“Workfile Range ”。
在“Workfile frequency ”中选择“Annual ” (年度),并在“Start date ”中输入开始时间“1988”,在“end date ”中输入最后时间“2005”,点击“ok ”,出现“Workfile UNTITLED ”工作框。
其中已有变量:“c ”—截距项 “resid ”—剩余项。
在“Objects ”菜单中点击“New Objects”,在“New Objects”对话框中选“Group”,并在“Name for Objects”上定义文件名,点击“OK ”出现数据编辑窗口。
年份 人口自然增长率
(%。
) 国民总收入(亿元) 居民消费价格指数增长
率(CPI )% 人均GDP (元) 1988 15.73 15037 18.8 1366 1989 15.04 17001 18 1519 1990 14.39 18718 3.1 1644 1991 12.98 21826 3.4 1893 1992 11.6 26937 6.4 2311 1993 11.45 35260 14.7 2998 1994 11.21 48108 24.1 4044 1995 10.55 59811 17.1 5046 1996 10.42 70142 8.3 5846 1997 10.06 78061 2.8 6420 1998 9.14 83024 -0.8 6796 1999 8.18 88479 -1.4 7159 2000 7.58 98000 0.4 7858 2001 6.95 108068 0.7 8622 2002 6.45 119096 -0.8 9398 2003 6.01 135174 1.2 10542 2004 5.87 159587 3.9 12336 2005 5.89 184089 1.8 14040 2006
5.38 213132 1.5 16024
2、输入数据:点击“Quik ”下拉菜单中的“Empty Group ”,出现“Group”窗口数据编辑框,点第一列与“obs ”对应的格,在命令栏输入“Y ”,点下行键“↓”,即将该序列命名为Y ,并依此输入Y 的数据。
用同样方法在对应的列命名X 2、X
3、X 4,并输入相应的数据。
或者在EViews 命令框直接键入“data Y 2X X 3 X 4 … ”,回车出现“Group”窗口数据编辑框,在对应的Y 、X 2、X 3、X 4下输入响应的数据。
3、估计参数:点击“Procs “下拉菜单中的“Make Equation ”,在出现的对话框的“Equation Specification ”栏中键入“Y C X 2 X 3 X 4”,在“Estimation Settings ”栏中选择“Least Sqares ”(最小二乘法),点“ok ”,即出现回归结果: 表3.4
根据表3.4中数据,模型估计的结果为:
432005109.0047918.0000332.060851.15X X X Y t -++=Λ
(0.913842) (0.000134) (0.033919) (0.001771)
t= (17.08010) (2.482857) (1.412721) (-2.884953) 930526.02
=R 915638.02
=R F=62.50441 四、模型检验
1、经济意义检验
模型估计结果说明,在假定其它变量不变的情况下,当年国民总收入每增长1亿元,人口增长率增长0.000332%;在假定其它变量不变的情况下,当年居民消费价格指数增长率每增长 1%,人口增长率增长0.047918%;在假定其它变量不变的情况下,当年人均GDP 没增加一元,人口增长率就会降低0.005109%。
这与理论分析和经验判断相一致。
2、统计检验
(1)拟合优度:由表3.4中数据可以得到:930526.02
=R ,修正
的可决系数为915638
.02
=R
,这说明模型对样本的拟合很好。
(2)F 检验:针对0234:0H βββ===,给定显著性水平0.05α=,在F 分布表中查出自由度为k-1=3和n-k=14的临界值34.3)14,3(=αF 。
由表3.4中得到F=62.50441 ,由于F=62.50441 >(3,21) 3.075F α=,应拒绝原假设0234:0H βββ===,说明回归方程显著,即“国民总收入”、“居民消费价格指数增长率”、“人均GDP ”等变量联合起来确实对“人口自然增长率”有显著影响。
(3)t 检验:分别针对0H :0(1,2,3,4)j j β==,给定显著性水平0.05α=,
查t 分布表得自由度为n-k=14临界值145.2)(2/=-k n t α。
由表3.4中数据可得,与^
1β、^
2β、^
3β、^
4β对应的t 统计量分别为17.08010、2.482857 、1.412721、-2.884953
除^
3β,其绝对值均大于145.2)(2/=-k n t α,这说明分别都应当拒
绝0H :)4,2,1(0==j j β,也就是说,当在其它解释变量不变的情况下,
解释变量“国民总收入”、“人均GDP ”分别对被解释变量“人口自
然增长率”Y 都有显著的影响。
^
3β的绝对值小于145.2)(2/=-k n t α,:这说明接受0H :03=β,X3系数对t 检验不显著,这表明很可能存在多重共线性。
所以计算各解释变量的相关系数,选择X2、X3、X4数据,
点”view/correlations ”得相关系数矩阵(如表4.4):
表4.4
由相关系数矩阵可以看出:各解释变量相互之间的相关系数较高,证实确实存在严重多重共线性。
五、消除多重共线性
采用逐步回归的办法,去检验和解决多重共线性问题。
分别作Y 对X2、X3、X4的一元回归,结果如表4.5所示:
表4.5
变量 X2
X3 X4 参数估计值 0.000134 0.033919 0.001771 t 统计量
2.482857
1.412721 -
2.88495
0.873915
0.388495
0.886412
按2R 的大小排序为:X4、X2、X3
以X2为基础,顺次加入其他变量逐步回归。
首先加入X2回归结果为:
40005397.02000350.035540.16ˆX X Y
-+= t=(2.542529) (-2.970874) 920622.02
=R
当取05.0=α时,131
.2)318(025
.0)(2
/=-=-t
t k n α,X2参数的t 检验显
著,加入X3回归得
432005109.0047918.0000332.060851.15X X X Y t -++=Λ
t= (17.08010) (2.482857) (1.412721) (-2.884953)
930526.02
=R 915638.02
=R F=62.50441
当取05.0=α时, 145.2)418(2/=-αt ,X3参数的t 检验不显著,予以剔除
即40005397.02000350.035540.16ˆX X Y
-+=,这是最后消除多重共线性的结果。
在假定其它变量不变的情况下,当年国民总收入每增长1亿元,人口增长率增长0.000332%;在假定其它变量不变的情况下,在假定其它变量不变的情况下,当年人均GDP 没增加一元,人口增长率就会降低0.005109%。
金服131 王亚平
13019122。
