线性系统的时域分析与校正习题及答案
线性系统分析_习题答案

专业课习题解析课程西安电子科技大学844信号与系统专业课习题解析课程第1讲第一章信号与系统(一)专业课习题解析课程第2讲第一章信号与系统(二)1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t et f t,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f kε= (10))(])1(1[)(k k f kε-+=解:各信号波形为 (2)∞<<-∞=-t et f t,)((3))()sin()(t t t f επ=(4))(sin )(t t f ε=(5))(sin )(t r t f =(7))(2)(k t f k ε=(10))(])1(1[)(k k f k ε-+=1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f (5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε (11))]7()()[6sin()(--=k k k k f εεπ (12))]()3([2)(k k k f k---=εε解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k---=εε1-3 写出图1-3所示各波形的表达式。
第3章 线性系统的时域分析与校正

第3章线性系统的时域分析与校正3.1 概述系统的数学模型建立后,便可对系统进行分析和校正。
分析和校正是自动控制原理课程的两大任务。
系统分析是由已知的系统模型确定系统的性能指标;校正是根据需要在系统中加入一些机构和装置并确定相应的参数,用以改善系统性能,使其满足所要求的性能指标。
系统分析的目的在于“认识”系统,系统校正的目的在于“改造”系统。
系统的分析校正方法一般有时域法、根轨迹法和频域法,本章介绍时域法。
3.1.1 时域法的作用和特点时域法是一种直接在时间域中对系统进行分析校正的方法,具有直观,准确的优点,它可以提供系统时间响应的全部信息,但在研究系统参数改变引起系统性能指标变化的趋势这一类问题,以及对系统进行校正设计时,时域法不是非常方便。
时域法是最基本的分析方法,该方法引出的概念、方法和结论是以后学习复域法、频域法等其他方法的基础。
3.1.2 时域法常用的典型输入信号要确定系统性能的优劣,就要在同样的输入条件激励下比较系统的行为。
为了在符合实际情况的基础上便于实现和分析计算,时域分析法中一般采用如表3-1中的典型输入信号。
3.1.3 系统的时域性能指标如第一章所述,对控制系统的一般要求归纳为稳、准、快。
工程上为了定量评价系统性能好坏,必须给出控制系统的性能指标的准确定义和定量计算方法。
稳定是控制系统正常运行的基本条件。
系统稳定,其响应过程才能收敛,研究系统的性能(包括动态性能和稳态性能)才有意义。
实际物理系统都存在惯性,输出量的改变是与系统所储有的能量有关的。
系统所储有的能量的改变需要有一个过程。
在外作用激励下系统从一种稳定状态转换到另一种稳定状态需要一定的时间。
一个稳定系统的典型阶跃响应如图3-1所示。
响应过程分为动态过程(也称为过渡过程)和稳态过程,系统的动态性能指标和稳态性能指标就是分别针对这两个阶段定义的。
表3-1 时域分析法中的典型输入信号名称)(tr时域关系时域图形)(sR复域关系例单位脉冲函数⎩⎨⎧≠=∞=)(tttδ⎰=1)(dttδdtd1s⨯撞击作用后坐力电脉冲单位阶跃函数⎩⎨⎧<≥=1)(1ttts1开关输入单位斜坡函数⎩⎨⎧<≤=)(ttttf21s等速跟踪信号单位加速度函数⎪⎩⎪⎨⎧<≥=21)(2ttttf31s1 动态性能系统动态性能是以系统阶跃响应为基础来衡量的。
第三章 线性系统的时域分析与校正 习题及答案

第三章 线性系统的时域分析与校正习题及答案3-1 已知系统脉冲响应t e t k 25.10125.0)(-=试求系统闭环传递函数)(s Φ。
解 Φ()()./(.)s L k t s ==+00125125 3-2 设某高阶系统可用下列一阶微分方程T c t c t r t r t ∙∙+=+()()()()τ近似描述,其中,1)(0<-<τT 。
试证系统的动态性能指标为 T T T t d ⎥⎦⎤⎢⎣⎡⎪⎭⎫⎝⎛-+=τln 693.0t T r =22. T T T t s ⎥⎦⎤⎢⎣⎡-+=)ln(3τ 解 设单位阶跃输入ss R 1)(=当初始条件为0时有:11)()(++=Ts s s R s C τ 11111)(+--=⋅++=∴Ts T s s Ts s s C ττC t h t T Te t T()()/==---1τ 1) 当 t t d = 时h t T Te t td ()./==---051τ12=--T T e t T d τ/ ; T t T T d -⎪⎭⎫ ⎝⎛-=-τln 2ln ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+=∴T T T t d τln 2ln2) 求t r (即)(t c 从1.0到9.0所需时间)当 Tt e TT t h /219.0)(---==τ; t T T T 201=--[ln()ln .]τ 当 Tt e TT t h /111.0)(---==τ; t T T T 109=--[ln()ln .]τ 则 t t t T T r =-==21090122ln ... 3) 求 t sTt s s e TT t h /195.0)(---==τ ]ln 3[]20ln [ln ]05.0ln [ln TT T T T T T T T t s τττ-+=+-=--=∴3-3 一阶系统结构图如图3-45所示。
要求系统闭环增益2=ΦK ,调节时间4.0≤s t s ,试确定参数21,K K 的值。
线性系统的时域分析习题答案.doc

第 3 章线性系统的时域分析学习要点1控制系统时域响应的基本概念,典型输入信号及意义;2控制系统稳定性的概念、代数稳定判据及应用;3控制系统的时域指标,一阶二阶系统的阶跃响应特性与时域指标计算;4高阶系统时域分析中主导极点和主导极点法;5控制系统稳态误差概念、计算方法与误差系数,减小稳态误差的方法。
思考与习题祥解题思考与总结下述问题。
(1)画出二阶系统特征根在复平面上分布的几种情况,归纳值对二阶系统特征根的影响规律。
(2)总结和n 对二阶系统阶跃响应特性的影响规律。
(3)总结增加一个零点对二阶系统阶跃响应特性的影响规律。
(4)分析增加一个极点可能对二阶系统阶跃响应特性有何影响(5)系统误差与哪些因素有关试归纳减小或消除系统稳态误差的措施与方法。
(6)为减小或消除系统扰动误差,可采取在系统开环传递函数中增加积分环节的措施。
请问,该积分环节应在系统结构图中如何配置,抗扰效果是否与扰动点相关答:( 1)二阶系统特征根在复平面上分布情况如图所示。
Im③j n (0)p1③j n 1 2(0 1)p1 ③( 1) ( 1) n p③③ 20 ( 2 1) n ( 2 1) Ren n n np2③j n1 / 2j n③图二阶系统特征根在复平面上的分布当0 ,二阶系统特征根是一对共轭纯虚根,如图中情况①。
当 01,二阶系统特征根是一对具有负实部的共轭复数根,变化轨迹是以n为半径的圆弧,如图中情况②。
当1 ,二阶系统特征根是一对相同的负实根,如图中情况③。
当1 ,二阶系统特征根是一对不等的负实根,如图中情况④。
(2)和n 是二阶系统的两个特征参量。
是系统阻尼比,描述了系统的平稳性。
当0 ,二阶系统特征根是一对共轭纯虚根,二阶系统阶跃响应为等幅振荡特性,系统临界稳定。
当 01,二阶系统特征根是一对具有负实部的共轭复数根,二阶系统阶跃响应为衰减振荡特性,系统稳定。
越小,二阶系统振荡性越强,平稳性越差;越大,二阶系统振荡性越弱,平稳性越好。
信号与线性系统分析复习题及答案

信号与线性系统复习题单项选择题。
1. 已知序列3()cos()5f k k π=为周期序列,其周期为 ( C ) A . 2 B. 5 C. 10 D. 12 2. 题2图所示()f t 的数学表达式为 ( B )图题2A .()10sin()[()(1)]f t t t t πεε=+- B. ()10sin()[()(1)]f t t t t πεε=-- C.()10sin()[()(2)]f t t t t πεε=-- D. ()10sin()[()(2)]f t t t t πεε=+-3.已知sin()()()t f t t dt tπδ∞-∞=⎰,其值是 ( A )A .π B. 2π C. 3π D. 4π4.冲激函数()t δ的拉普拉斯变换为 ( A ) A . 1 B. 2 C. 3 D. 45.为了使信号无失真传输,系统的频率响应函数应为 ( D ) A . ()djwt H jw e= B. ()djwt H jw e-= C. ()djwt H jw Ke = D. ()djwt H jw Ke-=6.已知序列1()()()3k f k k ε=,其z 变换为 ( B )A .13z z + B.13z z - C.14z z + D.14z z -7.离散因果系统的充分必要条件是 ( A ) A .0,0)(<=k k h B. 0,0)(>=k k hC.0,0)(<<k k h D. 0,0)(>>k k h8.已知()f t 的傅里叶变换为()F jw ,则(3)f t +的傅里叶变换为 ( C )A .()jwF jw eB. 2()j wF jw eC. 3()j wF jw eD. 4()j wF jw e9.已知)()(k k f kεα=,)2()(-=k k h δ,则()()f k h k *的值为( B )A .)1(1--k k εαB. )2(2--k k εαC. )3(3--k k εαD. )4(4--k k εα10.连续时间系统的零输入响应的“零”是指( A ) A. 激励为零 B. 系统的初始状态为零 C. 系统的冲激响应为零 D. 系统的阶跃响应为零11. 已知序列kjek f 3)(π=为周期序列,其周期为 ( )A . 2 B. 4 C. 6 D. 812. 题2图所示()f t 的数学表达式为 ( )A .)1()1()(--+=t t t f εε B.)1()1()(-++=t t t f εε C. )1()()(--=t t t f εε D. )1()()(-+=t t t f εε13.已知)2()(),1()(21-=-=t t f t t f εδ,则 12()()f t f t *的值是 ( ) A .)(t ε B.)1(-t ε C. )2(-t ε D. )3(-t ε14.已知ωωj j F =)(,则其对应的原函数为 ( ) A .)(t δ B.)('t δ C. )(''t δ D. )('''t δ15.连续因果系统的充分必要条件是 ( ) A . 0,0)(==t t h B. 0,0)(<=t t h C. 0,0)(>=t t h D. 0,0)(≠=t t h16.单位阶跃序列)(k ε的z 变换为 ( )A .1,1<+z z z B. 1,1>+z z z C. 1,1<-z z z D. 1,1>-z z z 17.已知系统函数ss H 1)(=,则其单位冲激响应()h t 为 ( )A .)(t ε B. )(t t ε C. )(2t t ε D. )(3t t εt18.已知()f t 的拉普拉斯变换为()F s ,则)5(t f 的拉普拉斯变换为 ( ) A .)5(s F B. )5(31s F C. )5(51s F D. )5(71s F 19.已知)2()(2-=-k k f k εα,)2()(-=k k h δ,则()()f k h k *的值为( )A .)1(1--k k εα B. )2(2--k k εαC.)3(3--k k εα D. )4(4--k k εα20.已知)(t f 的傅里叶变换为)(ωj F ,则)(jt F 的傅里叶变换为( ) A.)(ωπ-f B. )(ωπf C. )(2ωπ-f D. )(2ωπf21. 下列微分或差分方程所描述的系统是时变系统的是 ( ) A . )(2)()(2)(''t f t f t y t y -=+ B. )()(sin )('t f t ty t y =+ C. )()]([)(2't f t y t y =+ D. )()2()1()(k f k y k y k y =--+22. 已知)()(),()(21t t f t t t f εε==,则)()(21t f t f *的值是 ( ) A .)(1.02t tε B. )(3.02t t ε C. )(5.02t t ε D. )(7.02t t ε23.符号函数)sgn(t 的频谱函数为 ( )A .ωj 1 B. ωj 2 C. ωj 3 D. ωj 4 24.连续系统是稳定系统的充分必要条件是 ( ) A . M dt t h ≤⎰∞∞-)( B. M dt t h ≥⎰∞∞-)(C.M dt t h ≤⎰∞∞-)( D.M dt t h ≥⎰∞∞-)(25.已知函数)(t f 的象函数)5)(2()6()(+++=s s s s F ,则原函数)(t f 的初值为 ( )A . 0 B. 1 C. 2 D. 3 26.已知系统函数13)(+=s s H ,则该系统的单位冲激响应为 ( ) A .)(t etε- B.)(2t e t ε- C.)(3t e t ε- D. )(4t e t ε-27.已知)2()(),1()(1-=-=-k k h k k f k δεα,则)()(k h k f *的值为( )A .)(k kεαB.)1(1--k k εαC.)2(2--k k εαD. )3(3--k k εα28. 系统的零输入响应是指( ) A.系统无激励信号 B. 系统的初始状态为零C. 系统的激励为零,仅由系统的初始状态引起的响应D. 系统的初始状态为零,仅由系统的激励引起的响应 29.偶函数的傅里叶级数展开式中 ( )A .只有正弦项 B.只有余弦项 C. 只有偶次谐波 D. 只有奇次谐波10. 已知信号()f t 的波形,则)2(tf 的波形为 ( ) A .将()f t 以原点为基准,沿横轴压缩到原来的12B. 将()f t 以原点为基准,沿横轴展宽到原来的2倍C. 将()f t 以原点为基准,沿横轴压缩到原来的14D. 将()f t 以原点为基准,沿横轴展宽到原来的4倍 填空题1. 已知象函数223()(1)s F s s +=+,其原函数的初值(0)f +为___________________。
哈尔滨工程大学答案自动控制原理A卷试题答案及平分标准-07A
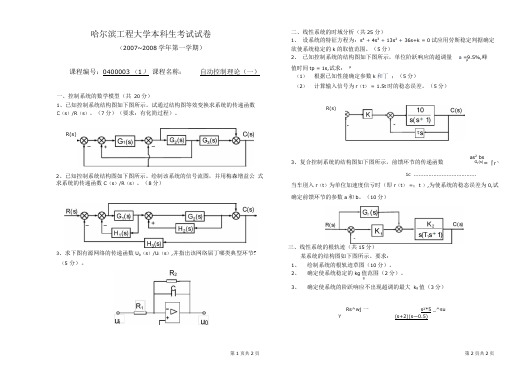
哈尔滨工程大学本科生考试试卷(2007~2008学年第一学期)课程编号:0400003 (1)课程名称:自动控制理论(一)二、线性系统的时域分析(共25分)1、设系统的特征方程为:s4+ 4s3+ 13s2+ 36s+k = 0试应用劳斯稳定判据确定欲使系统稳定的k的取值范围。
(5分)2、已知控制系统的结构图如下图所示,单位阶跃响应的超调量 a =9.5%,峰p值时间tp = 1s,试求:p(1)根据已知性能确定参数k和丁;(5分)2、已知控制系统结构图如下图所示。
绘制该系统的信号流图,并用梅森增益公式求系统的传递函数C(s)/R(s)。
(8分)1c ......................................当车刖入r(t)为单位加速度信亏时(即r(t) =;t ),为使系统的稳态误差为0,试确定前馈环节的参数a和b。
(10分)三、线性系统的根轨迹(共15分)某系统的结构图如下图所示。
要求:1、绘制系统的根轨迹草图(10分)。
2、确定使系统稳定的kg值范围(2分)。
g3、确定使系统的阶跃响应不出现超调的最大k g值(3分)一、控制系统的数学模型(共20分)1、已知控制系统结构图如下图所示。
试通过结构图等效变换求系统的传递函数C(s)/R(s)。
(7分)(要求:有化简过程)。
R(s)(2)计算输入信号为r(t) = 1.5t时的稳态误差。
(5分)R(s)3、复合控制系统的结构图如下图所示,前馈环节的传递函数as2 bsG r(s)=『r ‘Rs^wj 一s2*5 _^suY (s+2)(s—0.5)3、求下图有源网络的传递函数U0(s)/U i(s),并指出该网络届丁哪类典型环节?(5 分)。
第1页共2页第2页共2页第3页共4页 第4页 共4页四、线性系统的频域分析(共10分)1、已知最小相位系统的 Bode 图如下图所示。
求该系统的传递函数 G (s )。
(5分)L()A 10 一 0__ 1六、非线性控制系统分析(共15分)非线性控制系统如下图所示。
自动控制原理胡寿松第五版第三章答案

第三章 线性系统的时域分析与校正习题及答案3-1 已知系统脉冲响应t 25.1e 0125.0)t (k -=,试求系统闭环传递函数)s (Φ。
解 [])25.1s /(0125.0)t (k L )s (+==Φ3-2 设某高阶系统可用下列一阶微分方程)t (r )t (r )t (c )t (c T +τ=+∙∙近似描述,其中,1)T (0<τ-<。
试求系统的调节时间s t 。
解 设单位阶跃输入ss R 1)(=当初始条件为0时有:1T s 1s )s (R )s (C ++τ= 1Ts T s 1s 11Ts 1s )s (C +τ--=⋅++τ=∴ T/t e T T 1)t (h )t (c -τ--== T )0(h τ=,1)(h =∞,20T T )]0(h )(h [05.0τ-=-∞=∆求 s tT/t s s e TT 1)0(h )]0(h )(h [95.0)t (h -τ--=+-∞= 3T 05.ln0T t s ==∴3-2 一阶系统结构如图所示。
要求单位阶跃输入时调节时间4.0t s ≤s (误差带为5%),稳态 输出为2,试确定参数21k ,k 的值。
解 由结构图写出闭环系统传递函数1k k sk 1k k s k sk k 1s k )s (212211211+=+=+=Φ闭环增益2k 1k 2==Φ, 得:5.0k 2= 令调节时间4.0k k 3T 3t 21s ≤==,得:15k 1≥。
3-4 在许多化学过程中,反应槽内的温度要保持恒定, 下图(a )和(b )分别为开环和闭环温度控制系统结构图,两种系统正常的K 值为1。
解 (1)对(a )系统: 1s 1011s 10K )s (G a +=+=, 时间常数 10T =632.0)T (h = (a )系统达到稳态温度值的63.2%需要10秒;对(b )系统:1s 10110101100101s 10100)s (b+=+=Φ, 时间常数 10110T = 632.0)T (h = (b )系统达到稳态温度值的63.2%需要0.099秒。
自动控制原理卢京潮主编课后习题答案西北工业大学出版社

自动控制原理卢京潮主编课后习题答案西北工业大学出版社SANY标准化小组 #QS8QHH-HHGX8Q8-GNHHJ8-HHMHGN#第五章 线性系统的频域分析与校正习题与解答5-1 试求题5-75图(a)、(b)网络的频率特性。
(a) (b)图5-75 R-C 网络解 (a)依图:⎪⎪⎪⎩⎪⎪⎪⎨⎧+==+=++=++=2121111212111111221)1(11)()(R R C R R T C R RR R K s T s K sC R sC R R R s U s U r c ττ (b)依图:⎩⎨⎧+==++=+++=C R R T CR s T s sCR R sC R s U s U r c)(1111)()(2122222212ττ 5-2 某系统结构图如题5-76图所示,试根据频率特性的物理意义,求下列输入信号作用时,系统的稳态输出)(t c s 和稳态误差)(t e s(1) t t r 2sin )(=(2) )452cos(2)30sin()(︒--︒+=t t t r 解 系统闭环传递函数为: 21)(+=Φs s 图5-76 系统结构图 频率特性: 2244221)(ωωωωω+-++=+=Φj j j 幅频特性: 241)(ωω+=Φj相频特性: )2arctan()(ωωϕ-=系统误差传递函数: ,21)(11)(++=+=Φs s s G s e 则 )2arctan(arctan )(,41)(22ωωωϕωωω-=++=Φj j e e(1)当t t r 2sin )(=时, 2=ω,r m =1则 ,35.081)(2==Φ=ωωj 45)22arctan()2(-=-=j ϕ (2) 当 )452cos(2)30sin()(︒--︒+=t t t r 时: ⎩⎨⎧====2,21,12211m m r r ωω5-3 若系统单位阶跃响应 试求系统频率特性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章 线性系统的时域分析与校正习题及答案3-1 已知系统脉冲响应t25.1e0125.0)t (k -=,试求系统闭环传递函数)s (Φ。
解 [])25.1s /(0125.0)t (k L )s (+==Φ3-2 设某高阶系统可用下列一阶微分方程)t (r )t (r )t (c )t (c T +τ=+••近似描述,其中,1)T (0<τ-<。
试求系统的动态性能指标s r d t ,t ,t 。
解 设单位阶跃输入ss R 1)(= 当初始条件为0时有:1Ts 1s )s (R )s (C ++τ= 1Ts T s 1s 11Ts 1s )s (C +τ--=⋅++τ=∴ T/t e T T 1)t (h )t (c -τ--==T )0(h τ=,1)(h =∞,20T T )]0(h )(h [05.0τ-=-∞=∆1) 当 d t t = 时2TT e T T 1)]0(h )(h [5.0)0(h )t (h t /t d τ+=τ--=-∞+=-T /t d e 21-= ; 693T .0t d = 2) 求r t (即)t (c 从1.0)(h ∞到9.0)(h ∞所需时间)当T/t 2eTT 1)0(h )]0(h )(h [9.0)t (h -τ--=+-∞=; 当T/t 1eTT 1)0(h )]0(h )(h [1.0)t (h -τ--=+-∞=; )T 1(.0T lnT t 2τ+τ-=, τ+τ-=)T 9(.0T ln T t 1则 2T .29ln T t t t 12r ==-=3) 求 s tT/t s s eTT 1)0(h )]0(h )(h [95.0)t (h -τ--=+-∞= 3T 05.ln0T t s ==∴3-3 一阶系统结构如图所示。
要求系统闭环增益2k =Φ,调节时间4.0t s ≤s ,试确定参数21k ,k 的值。
解 由结构图写出闭环系统传递函数1k k sk 1k k s k sk k 1s k )s (212211211+=+=+=Φ闭环增益2k 1k 2==Φ, 得:5.0k 2= 令调节时间4.0k k 3T 3t 21s ≤==,得:15k 1≥。
3-4 在许多化学过程中,反应槽内的温度要保持恒定, 下图(a )和(b )分别为开环和闭环温度控制系统结构图,两种系统正常的K 值为1。
解 (1)对(a )系统:1s 1011s 10K )s (G a +=+=, 时间常数 10T = 632.0)T (h = (a )系统达到稳态温度值的%需要10个单位时间;对(b )系统:1s 10110101100101s 10100)s (b +=+=Φ, 时间常数 10110T =632.0)T (h = (b )系统达到稳态温度值的%需要个单位时间。
(2)对(a )系统: 1)s (N )s (C )s (G n ==1.0)t (n =时,该扰动影响将一直保持。
对(b )系统: 101s 101s 101s 1010011)s (N )s (C )s (n ++=++==Φ 1.0)t (n =时,最终扰动影响为001.010111.0≈⨯。
3-5 给定典型二阶系统的设计指标:超调量0<%5%≤σ,调节时间 s 3t s <,峰值时间s 1t p <,试确定系统极点配置的区域,以获得预期的响应特性。
解 依题 %5%≤σ, )45(707.0︒≤≥⇒βξ;35.3<=ns t ωξ, 17.1>⇒n ωξ;(1) 若)t (1)t (r =,0)t (n =两种系统从响应开始达到稳态温度值的%各需 多长时间(2) 当有阶跃扰动1.0)t (n =时,求扰动对两种系统的温度的影响。
np t ωξπ21-=1<, 14.312>-⇒n ωξ综合以上条件可画出满足要求的特征根区域如图所示。
3-6 电子心脏起博器心律控制系统结构如图所示,其中模仿心脏的传递函数相当于一纯积分环节。
解 依题,系统传递函数为 2n n 22n2s 2s 05.0K s 05.01s 05.0K)s (ω+ξω+ω=++=Φ ⎪⎪⎩⎪⎪⎨⎧ω⨯=ξ=ωn n 205.0105.0K令 5.0=ξ可解出 ⎩⎨⎧=ω=2020K n将 s 1t =代入二阶系统阶跃响应公式()β+ωξ-ξ--=ξω-t 1sin 1e 1)t (h n 22t n可得 m in 00145.60s 000024.1)1(h 次次==5.0=ξ时,系统超调量 %3.16%=σ,最大心速为 min 78.69s 163.1163.01t (h p 次次)==+=3-7 机器人控制系统结构如图所示, 试确定 参数21k ,k 值,使系统阶跃响应的峰值时间5.0t p =s ,超调量%2%=σ。
解 依题,系统传递函数为12122212121(1)G()(1)(1)21(1)n n n K K K s s s K K s s K K s K s s s s ωξωωΦ+===++++++++ (1) 若5.0=ξ对应最佳响应,问起博器增益K 应取多大 (2) 若期望心速为60次/min ,并突然接通起博器,问1s 钟后实际心速为多少瞬时最大心速多大由 ⎪⎩⎪⎨⎧=ωξ-π=≤=σξ-πξ-5.01t 02.0e n 2p 1oo 2 联立求解得 ⎩⎨⎧=ω=ξ1078.0n比较)(s Φ分母系数得⎪⎩⎪⎨⎧=-ξω==ω=146.0K 12K 100K 1n 22n 1 3-8 下图(a)所示系统的单位阶跃响应如图(b)所示。
试确定系统参数,k 12k ,a 和闭环传递函数)s (Φ。
解 由系统阶跃响应曲线有⎪⎩⎪⎨⎧=-=σ==∞oo o op 3.333)34(1.0t 3)(h系统闭环传递函数为2nn 22n21221s 2s K K as s K K )s (ω+ξω+ω=++=Φ (1) 由 ⎪⎩⎪⎨⎧==σ=ωξ-π=ξ-ξπ-o o 1oo n2p 3.33e 1.01t 2联立求解得 ⎩⎨⎧=ω=ξ28.3333.0n 由式(1)⎩⎨⎧=ξω==ω=222a 1108K n 2n 1另外 3K K as s K K lim s 1)s (s lim )(h 212210s 0s ==++=⋅Φ=∞→→ 56.110796s .21s 68.3322)s (2++=Φ3-9 已知系统的特征方程为D(s),试判别系统的稳定性,并确定在右半s 平面根的个数及纯虚根。
(1) 0100s 24s 8s )s (D 23=+++= (2) 02s s 5s 10s 3)s (D 234=++++=(3) 010s 11s 4s 2s 2s )s (D 2345=+++++= (4) 048s 32s 24s 12s 3s )s (D 2345=+++++= (5) 05s 2s 4s 2s )s (D 234=-++-= 解 (1) 0100s 24s 8s )s (D 23=+++=Routh : s 31 24 s2 8 100 s 1 92 s0 100 第一列同号,所以系统稳定。
(2) 02s s 5s 10s 3)s (D 234=++++=Routh : s 43 5 2s 3 10 1s 2 47 20 s 1 -153 s 0 20第一列元素变号两次,有2个正实部根。
(3)1011422)(2345+++++=s s s s s s D =0 Routh : S 5 1 2 11 S 4 2 4 10 S 3 ε 6 S 2 ε124- 10S 6 S 0 10第一列元素变号两次,有2个正实部根。
(4)483224123)(2345+++++=s s s s s s D =0Routh : s 5 1 12 32s 4 3 24 48s 33122434⨯-= 32348316⨯-= 0 s 2424316412⨯-⨯= 48 s 1216448120⨯-⨯= 辅助方程 124802s +=,s 24 辅助方程求导:024=ss 0 48第一列没有变号,系统没有正实部根。
对辅助方程求解,得到系统一对虚根 2j s 2,1±=,系统不稳定。
(5) 05s 2s 4s 2s )s (D 234=-++-= Routh : s 41 4 -5s 3 -2 2s 2 10 -10s 1 0 辅助方程 010s 102=-s 120 辅助方程求导 0s 20= s 0-10第一列元素变号3次,有3个正实部根,系统不稳定。
. 解辅助方程得:s 1=-1,s 2=+1,由长除法得s 3=+1+j2,s 4=+1-j23-10 单位反馈系统的开环传递函数)5s )(3s (s k)s (G ++=,试判断系统稳定性;若要求系统特征根的实部不大于1-,试确定k 的取值范围。
解 特征方程为:0k s 15s 8s )s (D 23=+++= Routh : S 3 1 15 S 2 8 k S 120-kS 0 k120k 0<<时系统稳定。
做代换 1s s -'= 有:0)8k (s 2s 5s k )1s (15)1s (8)1s ()s (D 2323=-+'+'+'=+-'+-+-'='Routh : S 3 1 2 S 2 5 k-8 S 18-k 18k <⇒S 0 k-8 8k >⇒系统特征根的实部不大于1-的k 值范围为: 18k 8≤≤3-11 下图是船舶横摇镇定系统结构图,为增加船只的阻尼引入了内环速度反馈。
(1) 动力矩对船只倾斜角的传递函数)s (M )s (N Θ;(2) 单位阶跃时倾斜角θ的终值不超过,且系统的阻尼比为,求2k 、1k 和3k 应满足的方程。
解 (1))K K 5.01(s )K K 5.02.0(s 5.01s 2.0s K K 5.01s 2.0s s K K 5.011s 2.0s 5.0)s (M )s (213222a 12322N ++++=++++++++=Θ(2)由题意知: 1.0K K 5.015.0)s (M )s (s 1s lim )s (M )s ()s (M s lim )(21N 0s N N 0s ≤+=Θ⋅⋅=Θ⋅=∞θ→→ 得8K K 21≥。
由 )s (M )s (N Θ 有: ⎪⎩⎪⎨⎧=ω+=ξ+=ω5.02K K 5.02.0K K 5.01n 3231n , 可得 2132K K 5.01K K 25.02.0+=+3-12 温度计的传递函数为11+Ts ,用其测量容器内的水温,1min 才能显示出该温度的98%的数值。
