西南交大电路分析谭永霞版习题答案-习题11 一阶电路习题答案3
西南交大电路分析谭永霞版习题答案-习题8

= ∠0°A
= ∠-210°
=22∠150°A=-22∠-30°A
= ∠30°A
= + +
=22+(-22∠-30°)-22∠30°
=22-(19.1-j11)-(19.1+j11)
=22-19.1+j11-19.1-j11
=-16.2∠0°A
三相有功功率,即电阻吸收功率之和。
P=R =10×222=4840W
= ×(- )∠-30°
∴ = = =-4.7∠–10°A
(2)P= cos = ×380×16.1 cos(-48°)
= ×380×16.1×0.669
=7089W
8—11某三相电动机绕组为三角形连接,它的输出功率为60kW,满负载时的功率因数为0.82(滞后),电机的效率为87%,电源的线电压为415V。试计算电机在满负载运行情况下的线电流It及相电流IP。
(1)线电流 、 、 及中线电流 ;
(2)电压 的瞬时表达式。
题8—2图
解
设
= = =6.85∠(-16.8°)A
=6.85∠(-136.8°)A =6.85∠103.2°A
=0A
∵ =Z =(20+j10 )×6.85∠–16.8°
=30∠48.2°×6.85∠–16.8°
=205.5∠31.4°
解:取 为参考正弦量:
三相电动机实际吸收有功功率P=60
=117A
由于电动机绕组是三角形联接,所以
8—12已知对称三相电源的线电压Ut为380V,井在三相四线制系统中,一组为三相对称负载,每相阻抗为Z=31.35∠30°Ω;另一组为三相不对称电阻性负载,如题8—12图所示.试求三个功率表的读数。
《电路分析》西南交大 习题解答 第4章 一阶电路的时域分析

第4章 一阶电路的时域分析基础与提高题P4-1 uF 2电容器的端电压是V 10时,存储电荷是多少? 解:uC 20101026=⨯⨯==-CU qP4-2 充电到V 150的uF 20电容器,通过一个M Ω3电阻器放电,需要多长时间?何时的放电电流最大?最大值多少?解:s RC 60102010366=⨯⨯⨯==-τ,放电完毕约等于s 3005=τ 刚开始放电时电流最大,最大电流为uA 501031506=⨯ P4-3 当uF 2电容器电压如图P4-3所示时,画出流过此电容器的电流波形图。
假设电压与电流为关联参考方向。
图P4-3 图1解:关联参考方向,则电容电流dtt du C t i c c )()(=,分段求解如下: (1)A t i V t u ust c c 0)(,0)(,0=∴=≤(2)()A t i Vt t u us t c c 401020102)(,1020)(,10666=⨯⨯⨯=∴⨯=≤≤-(3)A t i V t u us t c c 0)(,20)(,41=∴=≤≤(4)()A t i V t t u us t c c 40)1020(102)(,1001020)(,64666-=⨯-⨯⨯=∴+⨯-=≤≤-(5)()A t i Vt t u us t c c 201010102)(,801010)(,86666=⨯⨯⨯=∴-⨯=≤≤-(6)A t i V t u ust c c 0)(,0)(,8=∴=≥ 电容的电流如图1所示。
P4-4 0.32tA 电流流过150mH 电感器,求s t 4=时,电感器存储的能量。
解:电感器存储的能量()23232.0101502121t Li W ⨯⨯⨯==- 当s t 4=时,电感器存储的能量为P4-5 由20V 电源与Ω2电阻、H 6.3电感组成的串联电路,合上开关后经过多长时间电流达到其最大值,最大值多少?设合上开关前电感无初始储能。
西南交大电路分析谭永霞版习题答案-习题15

习题十五15-1 某非线性电阻的伏安特性为252i i u +=,求该电阻在工作点A I Q 2.0=处的静态电阻和动态电阻。
解: 静态电阻 Ω=+===3)52(2.0A i i i uR 动态电阻 Ω=+===4)102(2.0A i d i diduR 15-2 画出题15-2图示电路端口的伏安特性曲线。
其中D 为理想二极管,并假设0,0>>s s I U 。
+ - -+uU s RDi -+uI sRDi-+uRDi I s-+uI sRDi(a)(b)(c)(d)题15-2图解:(a )图:各元件上电压、电流的参考方向如图(1),其伏安特性曲线如图(2)、(3)、(4)所示。
二极管D 与电压源U s 串联后的伏安特性如图(5)所示。
再并电阻R 后,电路端口的伏安特性曲线如图(6)所示。
0 + - -+uu 2=U sRDi(1)+ -i 1 u 1 i 2 uU sR 的伏安特性D 的伏安特性u 1i 1i 1 u 2U s 的伏安特性(2)(3) (4)ui 1(5)U s i 2ui(6)U s各元件上电压、电流的参考方向如图(1),其伏安特性曲线如图(2)、(3)、(4)所示。
二极管D 与电阻R 串联后的伏安特性如图(5)所示。
再并电流源I s 后,电路端口的伏安特性曲线如图(6)所示。
I sD 的伏安特性u 1i 1 uI s 的伏安特性(2) (3) (4)u(5)ui(6)-+uI sRD i (1)i 1i 2+ + - -u 1 u 2 i 2R 的伏安特性i 2u 2i 2I s各元件上电压、电流的参考方向如图(1),其伏安特性曲线如图(2)、(3)、(4)所示。
电流源I s 与电阻R 并联后的伏安特性如图(5)所示。
再并二极管D 后,电路端口的伏安特性曲线如图(6)所示。
-I suI s 的伏安特性 (2)(3) (4)0 u(5)(6)(1)R 的伏安特性i 2u-+uRDi I si 1i 2i 3D 的伏安特性ui 1i 3-I si 4i 4u-I si各元件上电压、电流的参考方向如图(1),其伏安特性曲线如图(2)、(3)、(4)所示。
西交《电路》参考答案西安交大11春

第一章 参考答案一、单项选择题1、 (b) ;2、 (d) ;3、 (d) ;4、 (a);5、(d);6、 (c) ;7、(d) ;8、 (a) ;9、(d) ; 10、(a) ;11、(b) ;12、(b) ;13、(c) ;14、(a) ;15、(c) ;16、(d) ;17、(a) 。
二、填空题1、某种确定的电磁性能;2、不变;3、高10V ;4、吸收,40W ;5、开路;6、短路;7、短路;8、开路;9、短路;10、开路;11、相等;12、通过原点的直线;13、韦安;14、库伏;15、u =Ri ;16、dt di Lu=;17、dtdu C i =;18、一定为零;19、不一定为零;20、电阻,电容和电感;21、一类是元件特性造成的约束,另一类是元件的相互连接造成的约束;22、集总电路;23、在集总电路中,任何时刻,沿任一回路,所有支路电压的代数和等于零;24、在集总电路中,任何时刻,对任一结点,所有流出结点的支路电流的代数和等于零;25、相互连接,性质。
三、分析计算题1、 A c o s 2)(t t i =W cos 8)(2t t p =2、 A 455.0=I Ω=484R 3、 221111=⨯==I U P W (发出)()623122-=⨯-==I U P W (发出)1628133=⨯==I U P W (消耗) ()414244-=⨯-==I U P W (发出) ()717355-=-⨯==I U P W (发出)()()313366-=-⨯-==I U P W (消耗)4、解: u S (t)的函数表示式为:⎪⎪⎩⎪⎪⎨⎧≥<≤+-<≤<=s20s 2s 142s10200)(t t t t t t t u S故电流:==t u C t i s d d )(⎪⎪⎩⎪⎪⎨⎧≥<≤-<≤<s20s 2s 11s1010t t t t功率:==)()()(t i t u t p ⎪⎪⎩⎪⎪⎨⎧≥<≤-<≤<s20s 2s 142s10200t t t t t t能量:==)(21)(2t Cu t W C ⎪⎪⎩⎪⎪⎨⎧≥<≤-<≤<s20s 2s 1)2(s100022t t t t t t5、电阻消耗的功率为: W 50=R P6、解:已知电流:==t u C t i s d d )(⎪⎪⎩⎪⎪⎨⎧≥<≤-<≤<s 20s 2s 11s 10100t t t ts 10<≤t t t d C d C t u tC 2201101)(00=+=+=⎰⎰∞-ξξs 21≤≤t t d u t u tC 24)1(5.01)1()(1-=-+=⎰ξ s 2≥t 005.01)2()(2=+=⎰ξd u t u tC 8、 W 10V 10=P (发出)W 5V 5-=P (发出)W 5=R P (吸收)10、 W 10A 2=P (发出)W 10V 5-=P (发出)11、 V 42-=u 12、 V 15-=u 13、 A 3=i 14、 V 12=u 15、 A 3-=I 16、 V 10=U 17、 -2V =U 18、解:由欧姆定律知12aI R U -=根据KCL : 111R U aI I S =+,从而解得: )1(11a R U I S+=所以 )1(12a R U aR U S+-=电源发出的功率为:)1(121a R U I U P SS S +==,输出功率为:221222)1(a R U a R P So += 输出电压与电源电压的比值为: )1(||22a aR R U U S += 输出功率与电源发出功率的比值为: )1(||2220a a R R P P S += 19、解:控制变量:A 110101S ===R U I 受控电压源电压:V 10110=⨯=γIR 3上电压: V 5γ332=⨯+=R R R IU20、解:A ===110102R Us I 211I I I =+γ 当ϒ =2时,A =+=+=31211121γI I 当ϒ =0时,A =+=+=1011121γI I 当ϒ = -2时,A -=-=+=1211121γI I 特别当ϒ = -1时, I 1为无穷大,电路无解。
电子电路(1-10)习题参考答案
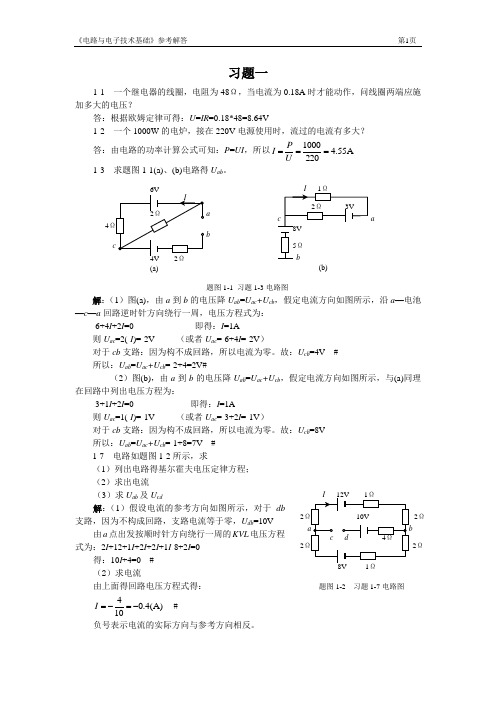
习题一1-1 一个继电器的线圈,电阻为48Ω,当电流为0.18A 时才能动作,问线圈两端应施加多大的电压?答:根据欧姆定律可得:U =IR =0.18*48=8.64V1-2 一个1000W 的电炉,接在220V 电源使用时,流过的电流有多大?答:由电路的功率计算公式可知:P =UI ,所以A 55.42201000===U P I 1-3 求题图1-1(a)、(b)电路得U ab 。
解:(1)图(a),由a 到b 的电压降U ab =U ac +U cb ,假定电流方向如图所示,沿a —电池—c —a 回路逆时针方向绕行一周,电压方程式为: -6+4I +2I =0 即得:I =1A则U ac =2(-I )=-2V (或者U ac =-6+4I =-2V )对于cb 支路:因为构不成回路,所以电流为零。
故:U cb =4V # 所以:U ab =U ac +U cb =-2+4=2V #(2)图(b),由a 到b 的电压降U ab =U ac +U cb ,假定电流方向如图所示,与(a)同理在回路中列出电压方程为:-3+1I +2I =0 即得:I =1A则U ac =1(-I )=-1V (或者U ac =-3+2I =-1V )对于cb 支路:因为构不成回路,所以电流为零。
故:U cb =8V 所以:U ab =U ac +U cb =-1+8=7V #1-7 电路如题图1-2所示,求(1)列出电路得基尔霍夫电压定律方程; (2)求出电流(3)求U ab 及U cd解:(1)假设电流的参考方向如图所示,对于db支路,因为不构成回路,支路电流等于零,U db =10V由a 点出发按顺时针方向绕行一周的KVL 电压方程式为:2I +12+1I +2I +2I +1I -8+2I =0得:10I +4=0 #(2)求电流 由上面得回路电压方程式得:)A (4.0104-=-=I # 负号表示电流的实际方向与参考方向相反。
电工学_第三版_唐介_课后答案(免费下载)

返回主页
下一页
1.5.1 试根据理想电压源和理想电流源的特点分析图示的 两电路:当 R 变化时,对其余电路(虚线方框内的电路)的 电压和电流有无影响? R 变化时所造成的影响是什么? + US_
ww
1.6.1 图示电路中,已知 US =6 V ,IS=2 A , R1=2 Ω, R2 =1 Ω。求开关S 断开时开关两端 的电压 U 和开关 S 闭合时通过开 关的电流 I(不必用支路电流 法)。
.k hd aw .c om
R2 R1
案 网
+ US _
S I
+ U _
IS
返回练习题集
上一题
下一题
1.6.3 求图示电路中通过恒压 源的电流 I1、I2 及其功率,并说明 是起电源作用还是起负载作用。
[解] 设 2 Ω 电阻上电流为 I3, 如图。
ww
该电阻与 10 V恒压源并联,故其上电压为 10 V,所以 I3 = (10/2) A = 5 A 。 右回路: 5I1+2I3-40 = 0,则 I1= 6 A 或外回路: 5I1+10-40 = 0,有 I1= 6 A 再用 KCL 求得 I2= I1-I3= 1 A, 左恒压源的功率 P1=240 W,由于其电压和电流的实际方 ,故起 电源 作用; 向符合电源关联参考方向 向符合电源关联参考方向,故起 ,故起电源 电源作用; 右恒压源的功率 P2=10 W,由于其电压和电流的实际方向 ,故起 负载 作用。 符合负载关联参考方向 符合负载关联参考方向,故起 ,故起负载 负载作用。
课
R1
R3
2Ω
1Ω
6V
+ US1 R2 _
2 Ω
R4
1Ω
电路分析课后答案谭永霞西南交通大学

60Ω 30Ω
Ri
10Ω
K
30Ω
60Ω
题 2-3 图
解:K 打开,电路图为
60Ω
30Ω
10Ω
Ri
30Ω
60Ω
∴ Ri
= 10 //(60 + 30) //(60 + 30)
= 10 // 90 // 90
= 10 // 45
=
10 × 45 10 + 45
= 8.18(Ω)
K 闭合,电路图为
30Ω
1-12 电路如题 1-12(a)、(b)所示。iL(0)=0,如电容电压uC电感电压uL的波形如图(c) 所示,试求电容电流和电感电流。
iC +
uc 0.5F
(a)
iL +
uL
0.5H
(b)
uc,uL/V 1
t/s
0
1
2
(c)
题 1-12 图
⎧− 0.5 0 < t < 1s
解:
iC
(t)
=
−C
U cd = −U s3 + U ab = −10 + 15 = 5V
(2)
Q U cd = −U s3 + U ab = 0
∴ U s3 = U ab = 15V
1-5 电路如题 1-5 图所示。设 is (t) = Asin ωt (A), us(t) = Be-α t (V), 求 uR1(t) 、 uL (t) 、
iC (t) 和 iR2 (t) 。
R1
L
+
-+
-
uR1
uL
iR2
is(t)
西南交1112考试批次《电路分析AI》复习题及参考答案

电路分析AI第1次作业(本次作业是本门课程本学期的第1次作业,注释如下:一、单项选择题(只有一个选项正确,共2道小题)1.题1-3图示电路所示结点的KCL方程正确的是()。
(A)(B)(C)(D)正确答案:B解答参考:2.题1-4图示电路所示结点的KCL方程正确的是()(A)(B)(C)(D)正确答案:D解答参考:二、不定项选择题(有不定个选项正确,共1道小题)3.题1-5图示电路所示回路的KVL方程正确的是()[不选全或者选错,不算完成](A)(B)(C)(D)正确答案:A C解答参考:(四、主观题(共5道小题)4.根据题1-1图中给定的数值,计算各元件吸收的功率。
参考答案:(a)(b)(c)(d)5.题1-2图示电路,已知各元件发出的功率分别为,,。
求各元件上的电压U1、U2及U3。
参考答案:6.题1-7图示电路,已知求图中标出的各支路电流。
参考答案:7.试分别求出题1-9图示独立电压源和独立电流源发出的功率。
参考答案:解:设独立电流源上的电压u2、独立电压源上的电流i1如图8.题1-14图示电路中,已知求I3、I4、I5和I6。
参考答案:解:电路分析AI第2次作业(本次作业是本门课程本学期的第2次作业,注释如下:一、单项选择题(只有一个选项正确,共2道小题)1.电路如图2-3(a)所示。
对外电路的等效电路正确的是。
(A)图(b)(B) 图(c)(C) 图(b)、图(c)均不是正确答案:A解答参考:2.电路如图2-4(a)所示。
对外电路的等效电路正确的是(A) 图(b)(B) 图(c)(C) 图(d)(D) 以上三个均不是正确答案:C解答参考:(四、主观题(共7道小题)3.题2-3图示电路。
求开关K打开和闭合情况下的输入电阻R i。
参考答案:4.求题2-5图示电路的等效电阻R ab。
参考答案:5.化简题2-7图示各电路参考答案:解:(注:与电流源串联的元件略去,与电压源并联的元件略去)(a)图等效为:6.用电源等效变换法求题2-8图示电路中负载R L上的电压U.参考答案:解:电路等效为:7.求题3-5图示电路的结点电压u1和u2。
电路分析试题和答案(全套),DOC

电路分析试题(Ⅰ)二.填空(每题1分,共10分)1.KVL体现了电路中守恒的法则。
2.电路中,某元件开路,则流过它的电流必为。
3.若电路的支路数为b,节点数为n,则独立的KCL方程数为。
457T 89三.求下图单口网络的诺顿等效电路,并画等效电路图。
ab四.用结点分析法,求各结点电位和电压源功率。
12五.一阶电路如图,t=0开关断开,断开前电路为稳态,求电流i L(t),并画出波形。
(15分)电路分析试题(Ⅱ)123.含U S和I S两直流电源的线性非时变电阻电路,若I S单独作用时,R上的电流为I′,当U S单独作用时,R上的电流为I",(I′与I"参考方向相同),则当U S和I S共同作用时,R上的功率应为。
4.若电阻上电压u与电流i为非关联参考方向,则电导G的表达式为。
5.实际电压源与理想电压源的区别在于实际电压源的内阻。
6.电感元件能存储能。
9.正弦稳态电路中,某电感两端电压有效值为20V,流过电流有效值为2A,正弦量周期T=πS,则电感的电感量L=。
10.正弦稳态L,C串联电路中,电容电压有效值为8V,电感电压有效值为12V,则总电压有效值为。
11.正弦稳态电路中,一个无源单口网络的功率因数为0.5,端口电压u(t)=10cos(100t+ψu)V,端口电流i(t)=3cos(100t-10°)A(u,i为关联参考方向),则电压的初相ψu为。
*三.求下图电路中,负载电阻R 获得的最大功率。
(15分)分)12345I67U的极坐标式8.正弦电流的有效值10A,初相30°,周期20ms,写出用cos表示此电流的瞬时式为。
9.正弦稳态电路中,电流超前电压-90°的元件是。
10.正弦稳态电路中,电容的电压有效值为10V,电流有效值为2A,电容吸收的平均功率是。
*11.若正弦稳态无源单口网络端口电压u(t)=100+100cost V,端口电流i(t)=1+10cos(t-60°)+50cos2t A,(设u,i为关联参考方向)2则网络吸收的平均功率是。
西南交大电路分析谭永霞版习题答案习题11一阶电路习题答案3
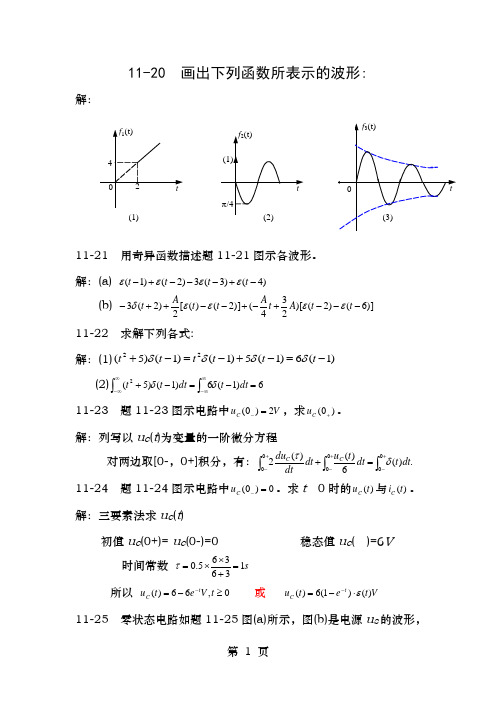
11-20 画出下列函数所表示的波形:解:2 4 tf 1(t) 0t(1)-π/4(1)(2)t(3)f 2(t)f 3(t)11-21 用奇异函数描述题11-21图示各波形。
解:(a) )4()3(3)2()1(-+---+-t t t t εεεε(b) )]6()2()[234()]2()([2)2(3---+-+--++-t t A t A t t At εεεεδ 11-22 求解下列各式:解:(1))1(6)1(5)1()1()5(22-=-+-=-+t t t t t t δδδδ(2)6)1(6)1()5(2=-=-+⎰⎰∞∞-∞∞-dt t dt t t δδ11-23 题11-23图示电路中V u C 2)0(=-,求)0(+C u 。
解:列写以u C (t )为变量的一阶微分方程对两边取[0-,0+]积分,有:.)(6)()(2000000⎰⎰⎰+-+-+-=+dt t dt t u dt dt du C C δτ11-24 题11-24图示电路中0)0(=-C u 。
求t 0时的)(t u C 与)(t i C 。
解:三要素法求u C (t )初值u C (0+)= u C (0-)=0 稳态值u C ()=6V时间常数 s 136365.0=+⨯⨯=τ 所以 0,66)(≥-=-t V e t u t C 或 V t e t u t C )()1(6)(ε⋅-=-11-25 零状态电路如题11-25图(a)所示,图(b)是电源u S 的波形,求电感电流i L (分别用线段形式与一个表达式来描述)。
解:当)(t u S ε=时电感电流.)()1(201)()(20A t e t i t s t L ε--== 图(b)中u s 的表达式为:由线性电路的延时性,可知电感电流的表达式为: 分段:0 t <2s 时A e i t L )1(5.020--= i L (2-)=0.5A 2st <3s时 i L (2+)= i L (2-)=0.5Ai L ()=-0.25At 3s 时i L (3+)= i L (3-)=-0.25A A e t i t L )3(2025.0)(---=11-26 题11-26图(a)电路中N R 纯电阻网络,其零状态响应V e u t C )44(25.0--=。
电子电路(1-10)习题参考答案

习题一1-1 一个继电器的线圈,电阻为48Ω,当电流为0.18A 时才能动作,问线圈两端应施加多大的电压?答:根据欧姆定律可得:U =IR =0.18*48=8.64V1-2 一个1000W 的电炉,接在220V 电源使用时,流过的电流有多大?答:由电路的功率计算公式可知:P =UI ,所以A 55.42201000===U P I 1-3 求题图1-1(a)、(b)电路得U ab 。
解:(1)图(a),由a 到b 的电压降U ab =U ac +U cb ,假定电流方向如图所示,沿a —电池—c —a 回路逆时针方向绕行一周,电压方程式为: -6+4I +2I =0 即得:I =1A则U ac =2(-I )=-2V (或者U ac =-6+4I =-2V )对于cb 支路:因为构不成回路,所以电流为零。
故:U cb =4V # 所以:U ab =U ac +U cb =-2+4=2V #(2)图(b),由a 到b 的电压降U ab =U ac +U cb ,假定电流方向如图所示,与(a)同理在回路中列出电压方程为:-3+1I +2I =0 即得:I =1A则U ac =1(-I )=-1V (或者U ac =-3+2I =-1V )对于cb 支路:因为构不成回路,所以电流为零。
故:U cb =8V 所以:U ab =U ac +U cb =-1+8=7V #1-7 电路如题图1-2所示,求(1)列出电路得基尔霍夫电压定律方程; (2)求出电流(3)求U ab 及U cd解:(1)假设电流的参考方向如图所示,对于db支路,因为不构成回路,支路电流等于零,U db =10V由a 点出发按顺时针方向绕行一周的KVL 电压方程式为:2I +12+1I +2I +2I +1I -8+2I =0得:10I +4=0 #(2)求电流 由上面得回路电压方程式得:)A (4.0104-=-=I # 负号表示电流的实际方向与参考方向相反。
西南交大电路分析谭永霞版习题答案-习题9
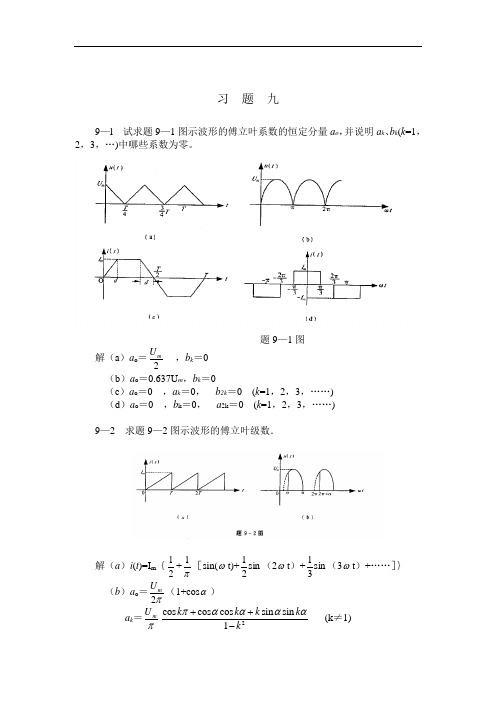
))))))))习 题 九9—l 试求题9—1图示波形的傅立叶系数的恒定分量a o ,并说明a k 、b k (k =1,2,3,…)中哪些系数为零。
题9—1图解(a )a o =2mU ,b k =0 (b )a o =0.637U m ,b k =0(c )a o =0 ,a k =0, b 2k =0 (k =1,2,3,……) (d )a o =0 ,b k =0, a 2k =0 (k =1,2,3,……)9—2 求题9—2图示波形的傅立叶级数.解(a )i (t )=I m {21+π1[sin(ωt)+sin 21(2ωt )+sin 31(3ωt )+……]} (b )a o =π2mU (1+cos α) a k =πm U 2cos cos cos sin sin 1k k k k kπαααα++- (k ≠1)a 1=πmU -sin 2αb k =πm U 2cos()sin sin()cos 1k k k k αααα-- (k ≠1) 1b =π2m U(-πα+sin αcos α)9—3 试求题9—2图(a)所示波形的平均值,有效值与绝对平均值(设I m =10A)。
解:(1)平均值 av I =⎰Tdt t i T 0)(1=m I T2本题绝对平均值:⎰=Tdt t i T 0)(1I av =m I T2(2)有效值I =⎰Tdt i T 021 i (t)=t T I m(0≤t ≤T) =⎰T m dt t T I T 02221 3231t dt t ⎰= =322311TT I T m =3m I9—4 题9—2图(b)所示波形为可控硅整流电路的电压波形,图中不同控制角a 下的电压的直流分量大小也不同。
现已知a =π/3,试确定电压的平均值和有效值。
解: 由9-2题知,当3πα=时,付立叶系数如下:0112233(1cos )0.239230.1190.4020.2390.1380.060.103m m mm m mmmU a U a U b U a U b U a U b U ππ=+==-==-=-==- (1)∴u (t )的平均值(0)00.239m U a U == (2)一次谐波1(1)1())a U t t arctgb ω=+))))))))一次谐波有效值(1)0.422mU U=同理,二次谐波有效值2222(2)0.27622ma bU U+==三次谐波有效值(3)0.1192mU U=∴略去四次以上高次谐波,电压u(t)的有效值为2222 (0)(1)(2)(3)0.44mU U U U U U=+++≈9—5 一半波整流电路的原理图如题9—5图所示。
西南交大电路分析谭永霞版习题答案-习题11 一阶电路习题答案1

11-1 题11-1图示电路原已达到稳态,当t=0时开关K 动作,求t=0+时各元件的电流和电压。
12A V+ -K解:(a) i L (0-) = 6A ,i L (0+) = i L (0-)= 6AA i R 46966636)0(2=⨯=⨯+=+, i R 3(0+) = 2Ai R 1(0+) =12 i L (0+)= 6A(b) V u C 41052)0(=⨯=-, u C (0+) = 4Vi C (0+) =A 23410=- (R 2与u C 串联)11-2 题11-2图示电路原处于稳态,t=0时开关K 闭合,求u C 1(0+)、u C 2(0+)、u L 1(0+)、u L 2(0+)、i (0+)。
5A题11-2图C1 L 22Ω解: u C 1 (0-) = u C 2 (0-) =V 632=⨯, i L 1 (0-) = i L 2 (0-)=A 5由换路定则,有u C 1 (0+) = u C 1 (0-)=V 6, u C 2 (0+) = u C 2 (0-) =V 6L 2(0+) +2Ω V -+0+网络列网孔电流i (0+)方程:2 i (0+) + 6 + 3(-5-5 + i (0+))+6 = 05 i (0+) = 30 – 12 = 18i (0+) = A 6.3518=Vi u L 2.1362.76)0(2)0(1-=--=--=++V i u L 2.136)0(2)0(2-=--=++11-3 求题11-3图示电路的初始值u C (0+)、i L (0+)、i R (0+)、+0dtdi L 。
开关K 打开前电路处于稳态。
题11-3图5L解:A i L 5.2)0(=-,Vu C 5.125.25)0(=⨯=-由换路定则,有 A i L 5.2)0(=+,V uC 5.12)0(=+5i L (0+)+0+网络0)5)0((5)5.2)0((55.12=-+-+++i i 25)0(10=+i0)0(0)0(5.2)0(0===∴=++++Lu dtdi i A i L LR11-4 题11-4图示电路原处于稳态,求开关开打开后瞬间的i L1(0+)、i L2(0+)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
11-20 画出下列函数所表示的波形:。
;;)(4sin )()3()](4[cos )()2()2(2)()1(2321t t e t f t t dt d t f t t t f t εεπε⋅=⋅=-⋅=- 解:(1)11-21 用奇异函数描述题11-21图示各波形。
题11-21图解:(a) )4()3(3)2()1(-+---+-t t t t εεεε(b) )]6()2()[234()]2()([2)2(3---+-+--++-t t A t A t t A t εεεεδ 11-22 求解下列各式:?)1()5()2(?)1()5)(1(22=-+=-+⎰∞∞-dt t t t t δδ 解:(1))1(6)1(5)1()1()5(22-=-+-=-+t t t t t t δδδδ(2)6)1(6)1()5(2=-=-+⎰⎰∞∞-∞∞-dt t dt t t δδ11-23 题11-23图示电路中V u C 2)0(=-,求)0(+C u 。
C+ -6Ω题11-23图解:列写以u C (t )为变量的一阶微分方程).(62t udt du C C δ=+ 对两边取[0-,0+]积分,有:.)(6)()(2000000⎰⎰⎰+-+-+-=+dt t dt t u dt dt du C C δτ1)]0()0([2=--+C C u uV u u C C 5.22412)0(21)0(=+=+=∴-+ 11-24 题11-24图示电路中0)0(=-C u 。
求t ≥0时的)(t u C 和)(t i C 。
9ε(t )V+ -6Ω解:三要素法求u C (t )初值u C (0+)= u C (0-)=0 稳态值u C (∞)=6V时间常数 s 136365.0=+⨯⨯=τ所以 0,66)(≥-=-t V e t u t C 或 V t e t u t C )()1(6)(ε⋅-=-A t e dtdu Ct i t CC )(3)(ε-== 11-25 零状态电路如题11-25图(a)所示,图(b)是电源u S 的波形,求电感电流i L (分别用线段形式和一个表达式来描述)。
题11-25图L解:当)(t u S ε=时电感电流.)()1(201)()(20A t e t i t s t L ε--== 图(b)中u s 的表达式为: )3(5)2(15)(10)]3()2([5)]2()([10-+--=-----+=t t t t t t t u S εεεεεεε由线性电路的延时性,可知电感电流的表达式为:A t e t e t e t i t t t L )3()1(25.0)2()1(75.0)()1(5.0)()3(20)2(2020--+----=-----εεε 分段:0≤ t <2s 时A e i t L )1(5.020--= i L (2-)=0.5A 2s ≤ t <3s 时 i L (2+)= i L (2-)=0.5A i L (∞)=-0.25AA e e t i t t L )2(20)2(2075.025.0)25.05.0(25.0)(----+-=++-=t ≥3s 时i L (3+)= i L (3-)=-0.25A A et i t L )3(2025.0)(---=⎪⎩⎪⎨⎧≥-<≤+-<≤-=∴-----s t A e s t s A es t A e t i t t t L 3 25.032 75.025.020 )1(5.0)()3(20)2(2020 11-26 题11-26图(a)电路中N R 纯电阻网络,其零状态响应V e u t C )44(25.0--=。
如用L =2H 的电感代替电容,如图(b)所示,求零状态响应i L 。
题11-26图C+ -K ε(t )+-LK ε(t )+ -解:图(a)电路中N R 纯电阻网络,其零状态响应V e u t C )44(25.0--=由以上条件可知:电容处的开路电压为4V ,时间常数s 425.01==τ 从电容向左看的等效电阻Ω===2240CR τ图(b)的电路等效为图示2HL于是s R LL 10==τ i L (∞)=2A.0,22)(≥-=∴-t A e t i t L11-27 求题11-27图示电路的电感电流i L 。
ε (-t )A10Ω解:t <0时,i L =1A .所以 i L (0+)= i L (0-)=1AsR L A i L 1001202.05.22050)(===-=-=∞τ0 5.35.2)5.21(5.2)(100100>+-=++-=∴--t A e e t i t t L 故A t e t t i t L )()5.35.2()()(100εε-+-+-=11-28 题11-28图示电路,已知0)0(=+C u ,求)(t u C 。
(t -2)Aδ(t )+-题11-28图解:用叠加定理求1、电压源δ(t )单独作用时,电容电压为u'C (t ), 列写以u'C (t )为变量的一阶微分方程08)(85.0=-'+'+'t u u dt u d C C C δ8)(45.0t u dt u d C C δ='+' 方程两边取-+0~0积分,有:⎰⎰⎰+-+-+-='+'0000008)(4)(5.0dt t dt u dt dt u d CC δτ 81)0(5.0='+Cu V t e u tC)(41)0(2ε-+='∴ 2、电流源单独作用时,电容电压为Cu '' )1(4)(2)2(---=''t Ce t u s t 2≥V t e t )2()1(42)2(--=--ε3、结果.)2()1(4)(25.0)(")(')()2(5.05.0V t e t e t u t u t u t t C C C --+=+=---εε11-29 求题11-29图示电路的电感电流)(t i L 和电阻电压)(t u R 。
L题11-29图2ε (-t )解:i L (0-)=1At ≥0时,列写以i L (t )为变量的一阶微分方程).(22t i dt diL L δ=+ 方程两边取-+0~0积分,有:.)(2)(2000000⎰⎰⎰+-+-+-=+dt t dt i dt dtdi L L δτ1)]0()0([2=--+L L i i.5.1221)0(A i L =+=+ 所以 ..5.1)(A e t i t L -=结果:.)(5.1)()(A t e t t i t L εε-+-= .)(5.1)()(1)(V t e t t i t u t L R εε---=⨯-== 11-30 求题11-30图示电路的零状态响应i L (t )和i (t )。
题11-30图3δ (t )Ω解:1、当电流源为ε(t )时,求解对应量的响应分别为s 1(t)、s 2(t)sR L R 515.01.0.213/613/43/2100===Ω==+=τ初值 s 1(0+)=0,s 2(0-)=1A 稳态值 s 1(∞)=1A ,s 2(∞)=0A t e t s t )()1()(51ε--=∴ .)()(52A t e t s t ε-= 2、当电流源为3δ(t)A 时At t e dt ds t i A t e dtds t i t t L )(3)(153)()(153)(5251δεε+-====--11-31 题11-31图示电路。
求零状态响应i L (t )。
已知输入V t u S )(ε=。
L 题11-31图解: S O u R R u 12-= A t e R R RR R R t i t L R L )(][)()/(3123123ε-+-= 11-32 电路如题11-32图(a)所示,求:(1) 电阻电压的单位冲击响应h(t );(2) 如果u S 的波形如图(b)所示,用卷积积分法求零状态响应)(t u R 。
(b)(a)题11-32图u u R+ -/s解:(1) 列写以u C (t)为变量的一阶微分方程)(1.020t dtduu C C δ=⨯⨯+)(2t u dtduC C δ=+ 由方程的系数可知:21)0(=+C u而s 21.020=⨯=τV t e t u tC)(21)(21ε-=∴ )()()(t t h t u C δ=+,)(21)()(21t e t t h tεδ--=∴(2) )()3(2)2()(t f t t t u S =---+=εεε)(21)()(21t e t t h tεδ--=)(*)()(t h t f t u R =∴而)()2()()]1(1[)()21)(()(*)(2202t e t e t d e t t t h tt t εεετδετ----=-+=⨯-=⎰-由卷积延时性质可得:V t et et e t f t h t u t t t R )3()2(2)2()2()()2()(*)()(23222-----+-==-----εεε11-33 f 1(t )、f 2(t )的波形如题11-33图所示,用图解法求f 1(t )*f 2(t )。
题11-33图解:⎰+∞∞--=τττd f t f t f t f )()()(*)(21210≤ t <1s 时f202021|2)(*)(t d t f t f t t===⎰τττ1s ≤ t <2s 时2422)1(1||22)(*)(22111211121-+-=-+--=+=+=--⎰⎰t t t t d d t f t f t t tt τττττ2s ≤ t <3s 时62)1(24|22)(*)(212121+-=--===--⎰t t d t f t f t t ττt ≥3s 时波形没有重合部分,所以0)(*)(21=t f t f 结果:⎪⎪⎪⎩⎪⎪⎪⎨⎧≥<≤+-<≤-+-<≤<=s t s t s t s t s t t s t t t t f t f 30326221,241000)(*)(2221。
