扫描线填充算法讲解
扫描线填充算法讲解

扫描线算法(S c a n-L i n e F i l l i n g)扫描线算法适合对矢量图形进行区域填充,只需要直到多边形区域的几何位置,不需要指定种子点,适合计算机自动进行图形处理的场合使用,比如电脑游戏和三维CAD软件的渲染等等。
对矢量多边形区域填充,算法核心还是求交。
《计算几何与图形学有关的几种常用算法》一文给出了判断点与多边形关系的算法――扫描交点的奇偶数判断算法,利用此算法可以判断一个点是否在多边形内,也就是是否需要填充,但是实际工程中使用的填充算法都是只使用求交的思想,并不直接使用这种求交算法。
究其原因,除了算法效率问题之外,还存在一个光栅图形设备和矢量之间的转换问题。
比如某个点位于非常靠近边界的临界位置,用矢量算法判断这个点应该是在多边形内,但是光栅化后,这个点在光栅图形设备上看就有可能是在多边形外边(矢量点没有大小概念,光栅图形设备的点有大小概念),因此,适用于矢量图形的填充算法必须适应光栅图形设备。
2.1扫描线算法的基本思想扫描线填充算法的基本思想是:用水平扫描线从上到下(或从下到上)扫描由多条首尾相连的线段构成的多边形,每根扫描线与多边形的某些边产生一系列交点。
将这些交点按照x坐标排序,将排序后的点两两成对,作为线段的两个端点,以所填的颜色画水平直线。
多边形被扫描完毕后,颜色填充也就完成了。
扫描线填充算法也可以归纳为以下4个步骤:(1)求交,计算扫描线与多边形的交点(2)交点排序,对第2步得到的交点按照x值从小到大进行排序;(3)颜色填充,对排序后的交点两两组成一个水平线段,以画线段的方式进行颜色填充;(4)是否完成多边形扫描?如果是就结束算法,如果不是就改变扫描线,然后转第1步继续处理;整个算法的关键是第1步,需要用尽量少的计算量求出交点,还要考虑交点是线段端点的特殊情况,最后,交点的步进计算最好是整数,便于光栅设备输出显示。
对于每一条扫描线,如果每次都按照正常的线段求交算法进行计算,则计算量大,而且效率底下,如图(6)所示:图(6)多边形与扫描线示意图观察多边形与扫描线的交点情况,可以得到以下两个特点:(1)每次只有相关的几条边可能与扫描线有交点,不必对所有的边进行求交计算;(2)相邻的扫描线与同一直线段的交点存在步进关系,这个关系与直线段所在直线的斜率有关;第一个特点是显而易见的,为了减少计算量,扫描线算法需要维护一张由“活动边”组成的表,称为“活动边表(AET)”。
案例10 扫描线种子填充算法

程序代码
PointTemp.x=xleft;PointTemp.y=PointTemp.y-2; //处理下一条扫描线 while(PointTemp.x<xright) { bSpanFill=FALSE; while(pDC->GetPixel(Round(PointTemp.x),Round(PointTemp.y))!=BoundaryClr && pDC->GetPixel(Round(PointTemp.x),Round(PointTemp.y))!=SeedClr) { bSpanFill=TRUE; PointTemp.x++; } if(bSpanFill) { if(PointTemp.x==xright && pDC->GetPixel(Round(PointTemp.x), Round(PointTemp.y))!=BoundaryClr && pDC->GetPixel(Round(PointTemp.x),Round(PointTemp.y))!=SeedClr) PopPoint=PointTemp; else PopPoint.x=PointTemp.x-1;PopPoint.y=PointTemp.y; Push(PopPoint); bSpanFill=FALSE; } while((pDC->GetPixel(Round(PointTemp.x),Round(PointTemp.y))==BoundaryClr && PointTemp.x<xright) || (pDC->GetPixel(Round(PointTemp.x),Round(PointTemp.y)) ==SeedClr && PointTemp.x<xright)) PointTemp.x++; } }
图形学中的光栅化与三角形填充算法

图形学中的光栅化与三角形填充算法光栅化和三角形填充算法是图形学中常用的技术,用于在计算机图形学中将2D或3D场景转换为最终在屏幕上呈现的图像。
本文将介绍光栅化和三角形填充算法的原理、应用和实现。
一、光栅化算法光栅化算法是指将连续的几何图形转化为离散的像素点的过程。
在计算机图形学中,屏幕被划分为一个个像素点的网格,每个像素点的颜色值由计算机确定。
通过光栅化算法,可以将几何图形的顶点信息转化为像素点的颜色值,从而实现图形的显示。
常用的光栅化算法有扫描线光栅化算法和射线光栅化算法。
1.扫描线光栅化算法扫描线光栅化算法逐行扫描图形,通过判断扫描线与几何图形的交点,确定像素点的颜色值。
这种算法适用于任意形状的几何图形。
在扫描线光栅化算法中,一般需要考虑图形的边界条件、插值计算和像素点的填充等问题。
2.射线光栅化算法射线光栅化算法通过从特定点向几何图形发射射线,并计算射线与几何图形的交点,确定像素点的颜色值。
这种算法适用于封闭的几何图形,如圆、椭圆等。
在射线光栅化算法中,常用的算法有中点画圆算法、Bresenham算法等。
光栅化算法广泛应用于计算机图形学中,用于生成点、线、多边形等几何图形的像素点的颜色值,从而实现图像的显示。
光栅化算法在计算机游戏、计算机辅助设计等领域有着广泛的应用。
二、三角形填充算法三角形填充算法是指将一个给定的三角形填充为实心或渐变颜色的过程。
在计算机图形学中,三角形是最基本的几何图形,通过三角形填充算法可以实现更复杂图形的显示和渲染。
常用的三角形填充算法有扫描线填充算法和边缘填充算法。
1.扫描线填充算法扫描线填充算法是通过遍历三角形内的每一行像素点,并判断像素点是否在三角形内部,从而确定像素点的颜色值。
该算法简单直观,但对于复杂的三角形可能效率较低。
2.边缘填充算法边缘填充算法是通过扫描三角形的边缘,并根据每个像素点的位置关系确定颜色值。
常用的边缘填充算法有中点边缘填充算法、贝塞尔曲线填充算法等。
扫描线多边形填充算法

扫描线多边形填充算法扫描线多边形填充算法(Scanline Polygon Fill Algorithm)是一种计算机图形学中广泛使用的算法,用于将一个封闭的多边形形状涂色填充。
它通过扫描线的方式,从上到下将多边形内的像素按照预设的填充颜色来进行填充。
本文将详细介绍扫描线多边形填充算法的原理、流程和实现细节。
1.算法原理:扫描线多边形填充算法基于扫描线的思想,在水平方向上扫描每一行像素,并检测多边形边界与扫描线的交点。
通过将扫描线从上到下扫过整个多边形,对于每一行像素,找出与多边形边界交点的水平线段,然后根据填充颜色将像素点进行填充。
2.算法流程:-找出多边形的最小和最大Y坐标,确定扫描线的范围。
-从最小Y坐标开始,到最大Y坐标结束,逐行进行扫描。
-对于每一行,找出与多边形边界交点的水平线段。
-根据填充颜色,为每个水平线段上的像素点进行填充。
3.算法实现:-首先,需要根据给定的多边形描述边界的顶点坐标,计算出每条边的斜率、最小和最大Y值以及每条边的X坐标交点。
-然后,对于每一扫描线,找出与多边形边界交点的水平线段,即找出交点的X坐标范围。
-最后,根据填充颜色,将该范围内的像素点进行填充。
4.算法优化:- 针对复杂多边形,可以使用活性边表(AET,Active Edge Table)来管理边界信息,加快查找交点的速度。
-可以使用桶排序来排序边界事件点,提高扫描速度。
-根据多边形边的特征,对算法进行优化,减少不必要的计算和内存消耗。
5.算法应用:-扫描线多边形填充算法广泛应用于计算机图形学中的图形渲染、图像处理等领域。
-在游戏开发、CAD绘图、虚拟现实等应用中,扫描线多边形填充算法被用于快速绘制和渲染复杂多边形。
总结:扫描线多边形填充算法是一种经典的计算机图形学算法,通过扫描线的方式对多边形进行填充。
它可以高效地处理各种形状的多边形,包括凸多边形和凹多边形。
算法虽然简单,但在实际应用中具有广泛的用途。
实验2:多边形区域扫描线填充或种子填充

实验2:多边形区域扫描线填充或种子填充计科102 蓝广森 1007300441一、实验目的通过实验,进一步理解和掌握几种常用多边形填充算法的基本原理掌握多边形区域填充算法的基本过程掌握在C/C++环境下用多边形填充算法编程实现指定多边形的填充。
二、实验内容及要求实现多边形区域扫描线填充的有序边表算法,并将实现的算法应用于任意多边形的填充,要求多边形的顶点由键盘输入或鼠标拾取,填充要准确,不能多填也不能少填。
要求掌握边形区域扫描线填充的有序边表算法的基本原理和算法设计,画出算法实现的程序流程图,使用C或者VC++实现算法,并演示。
三、实验原理种子填充算法又称为边界填充算法。
其基本思想是:从多边形区域的一个内点开始,由内向外用给定的颜色画点直到边界为止。
如果边界是以一种颜色指定的,则种子填充算法可逐个像素地处理直到遇到边界颜色为止。
种子填充算法常用四连通域和八连通域技术进行填充操作。
四向连通填充算法:a)种子像素压入栈中;b)如果栈为空,则转e);否则转c);c)弹出一个像素,并将该像素置成填充色;并判断该像素相邻的四连通像素是否为边界色或已经置成多边形的填充色,若不是,则将该像素压入栈;d)转b);e)结束。
扫描线填充算法的基本过程如下:当给定种子点(x,y)时,首先填充种子点所在扫描线上的位于给定区域的一个区段,然后确定与这一区段相连通的上、下两条扫描线上位于给定区域内的区段,并依次保存下来。
反复这个过程,直到填充结束。
区域填充的扫描线算法可由下列四个步骤实现:(1)初始化:堆栈置空。
将种子点(x,y)入栈。
(2)出栈:若栈空则结束。
否则取栈顶元素(x,y),以y作为当前扫描线。
(3)填充并确定种子点所在区段:从种子点(x,y)出发,沿当前扫描线向左、右两个方向填充,直到边界。
分别标记区段的左、右端点坐标为xl和xr。
(4)并确定新的种子点:在区间[xl,xr]中检查与当前扫描线y上、下相邻的两条扫描线上的象素。
颜色填充算法

颜色填充算法颜色填充算法是计算机图形学中非常常见的一种算法,它可以根据用户指定的起始点和填充颜色,自动填充其中的封闭区域。
在绘制图形、编辑图片等方面都有着广泛应用。
一、算法原理颜色填充算法的实现原理通常可以分为两种,一种是递归算法,另一种是扫描线算法。
1.递归算法递归算法是最基本的实现方式之一,其核心思想是从起始点开始,递归地填充相邻的像素,直到遇到边界或者不需要填充的像素为止。
具体步骤如下:1)从指定起始点开始,判断当前像素是否需要进行填充,如果需要则填充颜色,否则结束填充。
2)判断当前像素的4个相邻像素是否需要进行填充,如果需要则递归调用步骤1,否则结束该像素的填充。
递归算法的优点是实现简单直观,但由于递归的特性,对于大型区域可能会产生栈溢出的问题。
2.扫描线算法扫描线算法相对于递归算法更加优化,它通过扫描线的方式,一行一行地扫描像素,并判断是否需要进行填充。
具体步骤如下:1)从指定起始点开始,将该点入栈。
2)当栈非空时,弹出栈顶元素,填充当前像素,然后判断其上下左右是否需要进行填充。
3)如果需要填充的像素没有入栈,则将其入栈。
4)重复步骤2-3,直到栈为空,表示填充结束。
扫描线算法相对于递归算法来说,对于大型区域的填充效率更高,同时也避免了栈溢出的问题。
二、实现思路无论是递归算法还是扫描线算法,颜色填充算法的实现思路都是一样的,主要包括以下几个步骤:1.初始化:根据用户指定的起始点和填充颜色,确定起始点的位置和颜色值。
2.像素填充:从起始点开始,根据算法原理递归地或者按扫描线的方式填充相邻像素。
3.边界判断:对于非封闭区域,可能会存在边界问题,需要在像素填充过程中进行边界判断,避免填充超出边界。
4.停止条件:在填充过程中,需要设定填充的停止条件,可以是遇到边界、遇到指定颜色或者其他条件。
5.优化:根据实际应用场景,可以对算法进行优化,比如使用数据结构如队列或栈来辅助实现。
三、应用场景颜色填充算法在计算机图形学和图像处理中广泛应用,以下是一些常见的应用场景:1.图像编辑:在图像编辑软件中,用户可以通过选定区域填充工具,进行颜色填充,实现图像涂鸦、填充背景颜色等功能。
计算机图形学扫描线种子填充算法

2.1 深度递归的种子填充算法
2.2 扫描线种子填充算法
2.1 深度递归的种子填充算法
种子填色又称边界填色(Boundary Filling)。 它的功能是,给出多边形光栅化后的边界位置及边 界色代码oundary_color,以及多边形内的一点(x, y)位置,要求将颜色fill_color填满多边形。
动画演示
扫描线种子填充算法特点
1. 该算法考虑了扫描线上象素的相关性,种子象 素不再代表一个孤立的象素,而是代表一个尚 未填充的区段。 2. 进栈时,只将每个区段选一个象素进栈(每个 区段最右边或最左边的象素),这样解决了堆 栈溢出的问题。 3. 种子出栈时,则填充整个区段。 4. 这样有机的结合:一边对尚未填充象素的登记 (象素进栈),一边进行填充(象素出栈), 既可以节省堆栈空间,又可以实施快速填充。
3. 已知有一个5边形如下。建立新边表 NET,并写出每一条扫描线经过时活性边 表AET中的数据状态。
X ΔX Ymax
第1项存当前扫描线与边的交点坐标x值; 第2项存从当前扫描线到下一条扫描线间x的增量Dx; 第3项存该边所交的最高扫描线号ymax; 第4项存指向下一条边的指针。
假定当前扫描线与多边形某一条边的交点的x 坐标为x,则下一条扫描线与该边的交点不要重计 算,只要加一个增量△x。(连贯性) 设该边的直线方程为:ax+by+c=0; 若y=yi,x=x i;则当y = y i+1时, x i+1=xi-b/a 其中ΔX= -b/a为常数, 另外使用增量法计算时,我们需要知道一条边 何时不再与下一条扫描线相交,以便及时把它从 活性边表中删除出去。
建立或调整AET(ActiveEdgeList);
扫描线种子填充算法

扫描线种子填充算法扫描线种子填充算法的基本过程如下:当给定种子点(x, y)时,首先分别向左和向右两个方向填充种子点所在扫描线上的位于给定区域的一个区段,同时记下这个区段的范围[xLeft, xRight],然后确定与这一区段相连通的上、下两条扫描线上位于给定区域内的区段,并依次保存下来。
反复这个过程,直到填充结束。
扫描线种子填充算法可由下列四个步骤实现:(1) 初始化一个空的栈用于存放种子点,将种子点(x, y)入栈;(2) 判断栈是否为空,如果栈为空则结束算法,否则取出栈顶元素作为当前扫描线的种子点(x, y),y是当前的扫描线;(3) 从种子点(x, y)出发,沿当前扫描线向左、右两个方向填充,直到边界。
分别标记区段的左、右端点坐标为xLeft和xRight;(4) 分别检查与当前扫描线相邻的y - 1和y + 1两条扫描线在区间[xLeft, xRight]中的像素,从xLeft开始向xRight方向搜索,若存在非边界且未填充的像素点,则找出这些相邻的像素点中最右边的一个,并将其作为种子点压入栈中,然后返回第(2)步;这个算法中最关键的是第(4)步,就是从当前扫描线的上一条扫描线和下一条扫描线中寻找新的种子点。
如果新扫描线上实际点的区间比当前扫描线的[xLeft, xRight]区间大,而且是连续的情况下,算法的第(3)步就处理了这种情况。
如图所示:新扫描线区间增大且连续的情况假设当前处理的扫描线是黄色点所在的第7行,则经过第3步处理后可以得到一个区间[6,10]。
然后第4步操作,从相邻的第6行和第8行两条扫描线的第6列开始向右搜索,确定红色的两个点分别是第6行和第8行的种子点,于是按照顺序将(6, 10)和(8, 10)两个种子点入栈。
接下来的循环会处理(8, 10)这个种子点,根据算法第3步说明,会从(8, 10)开始向左和向右填充,由于中间没有边界点,因此填充会直到遇到边界为止,所以尽管第8行实际区域比第7行的区间[6,10]大,但是仍然得到了正确的填充。
扫描线填充算法讲解

扫描线算法(Scan-Line F illing)扫描线算法适合对矢量图形进行区域填充,只需要直到多边形区域的几何位置,不需要指定种子点,适合计算机自动进行图形处理的场合使用,比如电脑游戏和三维CAD软件的渲染等等。
对矢量多边形区域填充,算法核心还是求交。
《计算几何与图形学有关的几种常用算法》一文给出了判断点与多边形关系的算法――扫描交点的奇偶数判断算法,利用此算法可以判断一个点是否在多边形内,也就是是否需要填充,但是实际工程中使用的填充算法都是只使用求交的思想,并不直接使用这种求交算法。
究其原因,除了算法效率问题之外,还存在一个光栅图形设备和矢量之间的转换问题。
比如某个点位于非常靠近边界的临界位置,用矢量算法判断这个点应该是在多边形内,但是光栅化后,这个点在光栅图形设备上看就有可能是在多边形外边(矢量点没有大小概念,光栅图形设备的点有大小概念),因此,适用于矢量图形的填充算法必须适应光栅图形设备。
扫描线算法的基本思想扫描线填充算法的基本思想是:用水平扫描线从上到下(或从下到上)扫描由多条首尾相连的线段构成的多边形,每根扫描线与多边形的某些边产生一系列交点。
将这些交点按照x坐标排序,将排序后的点两两成对,作为线段的两个端点,以所填的颜色画水平直线。
多边形被扫描完毕后,颜色填充也就完成了。
扫描线填充算法也可以归纳为以下4个步骤:(1)求交,计算扫描线与多边形的交点(2)交点排序,对第2步得到的交点按照x值从小到大进行排序;(3)颜色填充,对排序后的交点两两组成一个水平线段,以画线段的方式进行颜色填充;(4)是否完成多边形扫描?如果是就结束算法,如果不是就改变扫描线,然后转第1步继续处理;整个算法的关键是第1步,需要用尽量少的计算量求出交点,还要考虑交点是线段端点的特殊情况,最后,交点的步进计算最好是整数,便于光栅设备输出显示。
对于每一条扫描线,如果每次都按照正常的线段求交算法进行计算,则计算量大,而且效率底下,如图(6)所示:图(6)多边形与扫描线示意图观察多边形与扫描线的交点情况,可以得到以下两个特点:(1)每次只有相关的几条边可能与扫描线有交点,不必对所有的边进行求交计算;(2)相邻的扫描线与同一直线段的交点存在步进关系,这个关系与直线段所在直线的斜率有关;第一个特点是显而易见的,为了减少计算量,扫描线算法需要维护一张由“活动边”组成的表,称为“活动边表(AET)”。
计算机图形学5多边形扫描转换和区域填充

多边形分为凸多边形、凹多边形、含内环的多边 形等:
(1)凸多边形 任意两顶点间的连线均在多边形内。
(2)凹多边形
任意两顶点间的连线有不在多边形内的部分。
凸多边形
凹多边形
含内环的多边形
有关概念
1) 区域:一组相邻而且又相连的像素,而且具有 相同属性的封闭区域。 2)种类:①单域 ②复合域
3) 区域填充:以某种属性对整个区域进行设置的过 程。
另外使用增量法计算时,我们需要知道一条边何时不再与下 一条扫描线相交,以便及时把它从有效边表中删除出去,避免 下一步进行无谓的计算。 综上所述,有效边表AET的每个结点存放对应边的有关信息 如下:
x
△x
ymax
next
其中x为当前扫描线与边的交点,ymax是边所在的最大扫描 线值,通过它可以知道何时才能“抛弃”该边,△x表示从 当前扫描线到下一条扫描线之间的x增量即斜率的倒数。 next为指向下一条边的指针
P6(2,7)
P4(11,8) F G B P5(5,5) P3(11,3) C D
A
1
0 1
P1(2,2) P2(5,1) 2 3 4 5 6 7
E
8
9
10
11
一个多边形与若干扫描线
7
把多边形所有 的边全部填成这 样的结构,插到 这个指针数组里 面来。
计算机图形学——区域填充算法(基本光栅图形算法)

计算机图形学——区域填充算法(基本光栅图形算法)⼀、区域填充概念区域:指已经表⽰成点阵形式的填充图形,是象素的集合。
区域填充:将区域内的⼀点(常称【种⼦点】)赋予给定颜⾊,然后将这种颜⾊扩展到整个区域内的过程。
区域填充算法要求区域是连通的,因为只有在连通区域中,才可能将种⼦点的颜⾊扩展到区域内的其它点。
1、区域有两种表⽰形式1)内点表⽰:枚举出区域内部的所有象素,内部所有象素着同⼀个颜⾊,边界像素着与内部象素不同的颜⾊。
2)边界表⽰:枚举出区域外部的所有象素,边界上的所有象素着同⼀个颜⾊,内部像素着与边界象素不同的颜⾊。
21)四向连通区域:从区域上⼀点出发可通过【上、下、左、右】四个⽅向移动的组合,在不越出区域的前提下,到达区域内的任意象素。
2)⼋向连通区域:从区域上⼀点出发可通过【上、下、左、右、左上、右上、左下、右下】⼋个⽅向移动的组合,在不越出区域的前提下,到达区域内的任意象素。
⼆、简单种⼦填充算法给定区域G⼀种⼦点(x, y),⾸先判断该点是否是区域内的⼀点,如果是,则将该点填充为新的颜⾊,然后将该点周围的四个点(四连通)或⼋个点(⼋连通)作为新的种⼦点进⾏同样的处理,通过这种扩散完成对整个区域的填充。
这⾥给出⼀个四连通的种⼦填充算法(区域填充递归算法),使⽤【栈结构】来实现原理算法原理如下:种⼦像素⼊栈,当【栈⾮空】时重复如下三步:这⾥给出⼋连通的种⼦填充算法的代码:void flood_fill_8(int[] pixels, int x, int y, int old_color, int new_color){if(x<w&&x>0&&y<h&&y>0){if (pixels[y*w+x]==old_color){pixels[y*w+x]== new_color);flood_fill_8(pixels, x,y+1,old_color,new_color);flood_fill_8(pixels, x,y-1,old_color,new_color);flood_fill_8(pixels, x-1,y,old_color,new_color);flood_fill_8(pixels, x+1,y,old_color,new_color);flood_fill_8(pixels, x+1,y+1,old_color,new_color);flood_fill_8(pixels, x+1,y-1,old_color,new_color);flood_fill_8(pixels, x-1,y+1,old_color,new_color);flood_fill_8(pixels, x-1,y-1,old_color,new_color);}}}简单种⼦填充算法的不⾜a)有些像素会多次⼊栈,降低算法效率,栈结构占空间b)递归执⾏,算法简单,但效率不⾼,区域内每⼀像素都要进/出栈,费时费内存c)改进算法,减少递归次数,提⾼效率三、扫描线种⼦填充算法基本思想从给定的种⼦点开始,填充当前扫描线上种⼦点所在的⼀区段,然后确定与这⼀段相邻的上下两条扫描线上位于区域内的区段(需要填充的区间),从这些区间上各取⼀个种⼦点依次把它们存起来,作为下次填充的种⼦点。
多边形的扫描转换算法、区域填充算法

贵州大学计算机图形学实验报告学院:计算机科学与信息学院专业:软件工程班级:反映)根据扫描线的连贯性可知:一条扫描线与多边形的交点中,入点和出点之间所有点都是多边形的内部点。
所以,对所有的扫描线填充入点到出点之间的点就可填充多边形。
如何具体实现(如何找到入点、出点)?根据区域的连贯性,分为3个步骤:(1)求出扫描线与多边形所有边的交点;(2)把这些交点按x坐标值以升序排列;(3)对排序后的交点进行奇偶配对,对每一对交点间的区域进行填充。
步骤(3)如上图:对y=8的扫描线,对交点序列按x坐标升序排序得到的交点序列是(2,4,9,13),然后对交点2与4之间、9与13之间的所有象素点进行填充。
求交点、排序、配对、填色利用链表:与当前扫描线相交的边称为活性边(Active Edge),把它们按与扫描线交点x坐标递增的顺序存入一个链表中,称为活性边表AEL (AEL, Active Edge List)。
它记录了多边形边沿扫描线的交点序列。
AEL中每个对象需要存放的信息:ymax:边所交的最高扫描线;x:当前扫描线与边的交点;Δx:从当前扫描线到下一条扫描线之间的x增量next:指向下一对象的指针。
伪码:建立ET,置y为ET中非空桶的最小序号;置AEL表为空,且把y桶中ET表的边加入AEL表中;while AEL表中非空do begin对AEL表中的x、Δx按升序排列;按照AEL表中交点前后次序,在每对奇偶交点间的x段予以填充;计算下一条扫描线:y=y+1;if 扫描线y=ymax then 从AEL表中删除这些边;对在AEL表中的其他边,计算与下一条扫描线的交点:x=x +Δx 按照扫描线y值把ET表中相应桶中的边加入AEL表中;endend of algorithm二、区域填充算法:区域可采用两种表示形式:内点表示枚举区域内部的所有像素;内部的所有像素着同一个颜色;边界像素着不同的颜色。
边界表示:枚举出边界上所有的像素;边界上的所有像素着同一颜色;内部像素着不同的颜色。
实验六 扫描线填充算法

实验六扫描线填充算法一、实验目的编写多边形的扫描线填充算法程序,加深对扫描线算法的理解,验证算法的正确性。
二、实验任务(2学时)编写多边形的扫描线填充算法程序,利用数组实现AET,考虑与链表实现程序的不同。
三、实验内容1、算法对一条扫描线的填充一般分为以下4个步骤:(1)求交:计算扫描线与多边形各边的交点;(2)排序:把扫描线上所有交点按递增顺序进行排序;(3)配对:将第一个交点与第二个交点,第三个交点与第四个交点等等进行配对,每对交点代表扫描线与多边形的一个相交区间。
(4)着色:把区间内的像素置为填充色。
2、成员函数的关系主程序名为fill_area(count, x, y),其中参数x, y是两个一维数组,存放多边形顶点(共c ount个)的x和y坐标。
它调用8个子程序,彼此之间的调用关系图1所示为:图1 fill_area的程序结构3、算法的程序设计步骤1:创建“S_L_Fill”工程文件;步骤2:创建类class:“EACH_ENTRY”。
在工作区“S_L_Fill classes”单击右键-→“new class”-→选择类型“Generic Class”名称为“EACH_ENTRY”,添加成员变量(添加至“class EACH_ENTRY { public:”之内):int y_top;float x_int;int delta_y;float x_change_per_scan;步骤3:包含头文件,同时初始化定义多边形顶点数目。
在“class CS_L_FillView : public Cview……”之前添加代码“#include EACH_ENTRY.h”及“#define MAX_POINT 9”。
#define MAX_POINT 9#include "EACH_ENTRY.h"步骤4:在类“class CS_L_FillView”中添加成员变量(鼠标双击工作区“CS_L_FillView”,代码添加至“class CS_L_FillView : public Cview {protected: ……public:之后”):EACH_ENTRY sides[MAX_POINT];int x[MAX_POINT],y[MAX_POINT];int side_count,first_s,last_s,scan,bottomscan,x_int_count;步骤5:利用构造函数“CS_L_FillView::CS_L_FillView()”初始化顶点坐标(鼠标双击工作区“CS_L_FillView”,代码添加至“CS_L_FillView()之内”):x[0]=200;y[0]=100;x[1]=240;y[1]=160;x[2]=220;y[2]=340;x[3]=330;y[3]=100;x[4]=400;y[4]=180;x[5]=300;y[5]=400;x[6]=170;y[6]=380;x[7]=120;y[7]=440;x[8]=100;y[8]=220;步骤6:在“class CS_L_FillView”下添加实现不同功能的成员函数。
扫描线算法
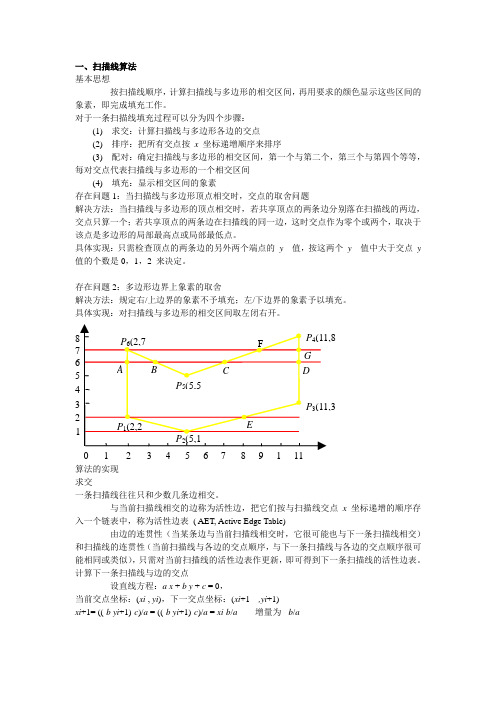
一、扫描线算法基本思想按扫描线顺序,计算扫描线与多边形的相交区间,再用要求的颜色显示这些区间的象素,即完成填充工作。
对于一条扫描线填充过程可以分为四个步骤:(1) 求交:计算扫描线与多边形各边的交点(2) 排序:把所有交点按x 坐标递增顺序来排序(3) 配对:确定扫描线与多边形的相交区间,第一个与第二个,第三个与第四个等等,每对交点代表扫描线与多边形的一个相交区间(4) 填充:显示相交区间的象素存在问题1:当扫描线与多边形顶点相交时,交点的取舍问题解决方法:当扫描线与多边形的顶点相交时,若共享顶点的两条边分别落在扫描线的两边,交点只算一个;若共享顶点的两条边在扫描线的同一边,这时交点作为零个或两个,取决于该点是多边形的局部最高点或局部最低点。
具体实现:只需检查顶点的两条边的另外两个端点的y值,按这两个y值中大于交点y 值的个数是0,1,2 来决定。
存在问题2:多边形边界上象素的取舍解决方法:规定右/上边界的象素不予填充;左/下边界的象素予以填充。
具体实现:对扫描线与多边形的相交区间取左闭右开。
算法的实现求交一条扫描线往往只和少数几条边相交。
与当前扫描线相交的边称为活性边,把它们按与扫描线交点x 坐标递增的顺序存入一个链表中,称为活性边表( AET, Active Edge Table)由边的连贯性(当某条边与当前扫描线相交时,它很可能也与下一条扫描线相交)和扫描线的连贯性(当前扫描线与各边的交点顺序,与下一条扫描线与各边的交点顺序很可能相同或类似),只需对当前扫描线的活性边表作更新,即可得到下一条扫描线的活性边表。
计算下一条扫描线与边的交点设直线方程:a x + b y + c = 0,当前交点坐标:(xi , yi),下一交点坐标:(xi+1,yi+1)xi+1=((-b yi+1)-c)/a = ((-b yi+1)-c)/a = xi-b/a 增量为-b/a故在活性边表中需要存放的信息: x :当前扫描线与边的交点△x = -b /a :从当前扫描线到下一条扫描线之间的 x 增量 ymax :该边所交的最高扫描线P PA BCD△x y maxP P P P P PFGP 4P 5P 3P 4上图为扫描线 6 的活性边表 左图为扫描线 7 的活性边表 活性边表的更新为方便活性边表的更新,建立另一个表。
扫描线区域填充算法

扫描线区域填充算法算法步骤如下:1.找到图形区域的上下边界:-遍历图形的所有边界点,找到最大纵坐标和最小纵坐标,确定扫描线的上下边界。
2.初始化扫描线列表:-从上到下依次生成扫描线,建立一个扫描线列表。
3.计算扫描线与图形的交点:-遍历扫描线列表中的每个扫描线,与图形的所有边界进行求交。
-如果与边界有交点,将交点的横坐标存入一个集合中,集合中的数据按从小到大排序。
4.进行填充:-遍历扫描线列表中的每个扫描线,找到对应的交点集合。
-将集合中的每两个横坐标之间的像素点进行填充。
以下是对算法的详细解释:首先,我们需要遍历所有边界点,找到最大纵坐标和最小纵坐标。
这样就确定了我们需要扫描的区域范围,也就是扫描线的上下边界。
接下来,我们生成一个扫描线列表。
从上到下依次生成每一条扫描线,将其存储在扫描线列表中。
然后,对于每一条扫描线,我们需要计算该扫描线与图形的交点。
我们遍历图形的所有边界,并与当前扫描线进行求交。
如果与边界有交点,我们将交点的横坐标存入一个集合中。
这个集合中的数据按从小到大排序,以便后续的填充操作。
最后,我们对于每一条扫描线,找到对应的交点集合。
我们遍历集合中的每两个横坐标之间的像素点,将其进行填充。
这可以通过修改像素的颜色或设置像素的属性来实现。
总结一下,扫描线区域填充算法通过逐行扫描图形区域,计算每行与区域内部的交点,然后进行填充。
该算法的优点是简单、高效,适用于填充简单凸多边形等闭合图形。
然而,该算法对于非凸多边形或包含内孔的图形表现较差,可能需要额外的处理逻辑。
计算机图形学第3章二维基本图(4)

二、扫描线种子填充算法实现
借助于堆栈,上述算法实现步骤如下:
1、初始化堆栈。 2、种子压入堆栈。 3、while(堆栈非空) { (1)从堆栈弹出种子象素。 (2)如果种子象素尚未填充,则:
a.求出种子区段:xleft、xright; b.填充整个区段。 c.检查相邻的上扫描线的xleft≤x≤xright区间内, 是否存在需要填充的新区段,如果存在的话, 则把每个新区段在xleft≤x≤xright范围内的最 右边的象素,作为新的种子象素依次压入堆栈。 d.检查相邻的下扫描线的xleft≤x≤xright区间内, 是否存在需要填充的新区段,如果存在的话, 则把每个新区段在 xleft≤x≤xright范围内的 最右边的象素,作为新的种子象素依次压入堆 栈。 }
扫描线种子填充算法步骤 (1)种子象素入栈。 (2)栈非空时象素出栈,否则结束。 (3)对出栈象素及左、右两边象素填充,直到遇边界XL、XR。 (4)在(XL ,XR) 内查相临的上、下两条扫描线是否为边界或已填充, 如不是,则将每区间的最右边的象素入栈。回到(2)。
练习: 用扫描线种子填充算法,写出图中顺序进栈的种子坐标及 所需最大栈空间
2、国标码 我国除了采用ASCII码外,还制定了汉字编 码的国家标准字符集:中华人民共和国国家标准 信息交换编码,代号为“GB2312-80”。该字符 集共收录常用汉字6763个,图形符号682个。 它规定所有汉字和图形符号组成一个94×94 的矩阵,在此方阵中,每一行称为“区”,用区 码来标识;每一列称为“位”,用位码来标识, 一个符号由一个区码和一个位码共同标识。 区码和位码分别需要7个二进制位,同样, 为了方便,各采用一个字节表示。所以在计算机 中,汉字(符号)国标码占用两个字节。
多边形扫描线填充算法的概念和步骤

多边形扫描线填充算法的概念和步骤嘿,咱今儿个就来聊聊多边形扫描线填充算法。
你知道不,这就像是给多边形这个大拼图上色一样有趣呢!多边形啊,它可不是个乖乖待着的主儿,有好多边和角呢。
那这扫描线填充算法呢,就是来搞定怎么把这些多边形填满颜色的。
想象一下,有一条线就像个小刷子似的,从这头刷到那头,把多边形的每一块都照顾到。
这就是扫描线啦。
它一格一格地走,每到一个地方,就看看和多边形有啥关系。
那具体步骤呢,咱可得好好说说。
首先得确定这个多边形的边啊,知道它们在哪儿,长啥样。
然后呢,这条扫描线就开始工作啦,它会和多边形的边相交,这就像它们在打招呼呢。
接着,就根据这些交点来算出要填充的区域。
这就好比是知道了要给哪块地播种一样。
然后啊,就开开心心地把颜色填上。
你说这神奇不神奇?就这么一步一步的,一个多边形就被漂亮地填满啦。
这可不比画画简单哦,这里面可有大学问呢。
比如说吧,要是交点算错了,那颜色可就填错地方啦,那就成大花脸啦!所以每一步都得仔细着点呢。
而且啊,这算法就像个小魔法师,能让那些奇奇怪怪形状的多边形都变得漂漂亮亮的。
它能让我们在屏幕上看到各种好看的图形,这可都是它的功劳呀。
你再想想,要是没有这个算法,那我们看到的图形不就干巴巴的,一点都不生动啦。
多边形扫描线填充算法,虽然名字听起来有点拗口,但它真的超级重要呢。
它就像一个默默工作的小工匠,为我们打造出美丽的图形世界。
怎么样,现在对这个多边形扫描线填充算法是不是有点感觉啦?它可不简单哦,是计算机图形学里的一个宝贝呢!以后再看到那些好看的图形,可别忘了背后有它的功劳哟!。
计算机图形学课件:6 边缘填充算法

(b) Outline of house icon
(c) Brick pattern
(d)
(e)
(f)
(g)
(d) Bitmap for solid version of house icon. (e) Clearing the scene by writing background (f) Brick pattern applied to house icon (g) Writing the screen transparently with patterned house icon
以边为中心的边缘填充算法
边缘填充算法特点
优点:与扫描线算法相比,边缘填充算法的 数据结构和程序结构简单。
缺点:但该算法需要对帧缓存的大量象素反 复赋值,速度较慢。
栅栏填充算法
栅栏:一条与扫描线垂直的直线,过多边形的某个 顶点,并把多边形分为左右两半。
基本思想: 对于每条扫描线与多边形边的交点,仅将交点
Be suitable to characters, icons and application symbols
An example: Writing a patterned object in opaque mode
with two transparent writes
(a) Mountain scene
To consider the entire screen as being tiled with the pattern and to think of the primitive as consisting of an outline or filled area of transparent bits that let the pattern show through value[x][y]=pattern[x%M][y%N]
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
扫描线算法(Scan-Line F illing)扫描线算法适合对矢量图形进行区域填充,只需要直到多边形区域的几何位置,不需要指定种子点,适合计算机自动进行图形处理的场合使用,比如电脑游戏和三维CAD软件的渲染等等。
对矢量多边形区域填充,算法核心还是求交。
《计算几何与图形学有关的几种常用算法》一文给出了判断点与多边形关系的算法――扫描交点的奇偶数判断算法,利用此算法可以判断一个点是否在多边形内,也就是是否需要填充,但是实际工程中使用的填充算法都是只使用求交的思想,并不直接使用这种求交算法。
究其原因,除了算法效率问题之外,还存在一个光栅图形设备和矢量之间的转换问题。
比如某个点位于非常靠近边界的临界位置,用矢量算法判断这个点应该是在多边形内,但是光栅化后,这个点在光栅图形设备上看就有可能是在多边形外边(矢量点没有大小概念,光栅图形设备的点有大小概念),因此,适用于矢量图形的填充算法必须适应光栅图形设备。
2.1扫描线算法的基本思想扫描线填充算法的基本思想是:用水平扫描线从上到下(或从下到上)扫描由多条首尾相连的线段构成的多边形,每根扫描线与多边形的某些边产生一系列交点。
将这些交点按照x坐标排序,将排序后的点两两成对,作为线段的两个端点,以所填的颜色画水平直线。
多边形被扫描完毕后,颜色填充也就完成了。
扫描线填充算法也可以归纳为以下4个步骤:(1)求交,计算扫描线与多边形的交点(2)交点排序,对第2步得到的交点按照x值从小到大进行排序;(3)颜色填充,对排序后的交点两两组成一个水平线段,以画线段的方式进行颜色填充;(4)是否完成多边形扫描?如果是就结束算法,如果不是就改变扫描线,然后转第1步继续处理;整个算法的关键是第1步,需要用尽量少的计算量求出交点,还要考虑交点是线段端点的特殊情况,最后,交点的步进计算最好是整数,便于光栅设备输出显示。
对于每一条扫描线,如果每次都按照正常的线段求交算法进行计算,则计算量大,而且效率底下,如图(6)所示:图(6)多边形与扫描线示意图观察多边形与扫描线的交点情况,可以得到以下两个特点:(1)每次只有相关的几条边可能与扫描线有交点,不必对所有的边进行求交计算;(2)相邻的扫描线与同一直线段的交点存在步进关系,这个关系与直线段所在直线的斜率有关;第一个特点是显而易见的,为了减少计算量,扫描线算法需要维护一张由“活动边”组成的表,称为“活动边表(AET)”。
例如扫描线4的“活动边表”由P1P2和P3P4两条边组成,而扫描线7的“活动边表”由P1P2、P6P1、P5P6和P4P5四条边组成。
第二个特点可以进一步证明,假设当前扫描线与多边形的某一条边的交点已经通过直线段求交算法计算出来,得到交点的坐标为(x, y),则下一条扫描线与这条边的交点不需要再求交计算,通过步进关系可以直接得到新交点坐标为(x+ △x, y + 1)。
前面提到过,步进关系△x是个常量,与直线的斜率有关,下面就来推导这个△x。
假设多边形某条边所在的直线方程是:ax + by + c = 0,扫描线y i和下一条扫描线y i+1与该边的两个交点分别是(x i,y i)和(x i+1,y i+1),则可得到以下两个等式:ax i + by i + c = 0 (等式 1)ax i+1 + by i+1 + c = 0 (等式 2)由等式1可以得到等式3:x i = -(by i + c) / a (等式 3)同样,由等式2可以得到等式4:x i+1 = -(by i+1 + c) / a (等式 4)由等式 4 –等式3可得到x i+1– x i = -b (y i+1 - y i) / a由于扫描线存在y i+1 = y i + 1的关系,将代入上式即可得到:x i+1– x i = -b / a即△x = -b / a,是个常量(直线斜率的倒数)。
“活动边表”是扫描线填充算法的核心,整个算法都是围绕者这张表进行处理的。
要完整的定义“活动边表”,需要先定义边的数据结构。
每条边都和扫描线有个交点,扫描线填充算法只关注交点的x坐标。
每当处理下一条扫描线时,根据△x直接计算出新扫描线与边的交点x坐标,可以避免复杂的求交计算。
一条边不会一直待在“活动边表”中,当扫描线与之没有交点时,要将其从“活动边表”中删除,判断是否有交点的依据就是看扫描线y是否大于这条边两个端点的y坐标值,为此,需要记录边的y坐标的最大值。
根据以上分析,边的数据结构可以定义如下:65typedef struct tagEDGE66{67double xi;68double dx;69int ymax;74}EDGE;根据EDGE的定义,扫描线4和扫描线7的“活动边表”就分别如图(7)和图(8)所示:图(7)扫描线4的活动边表图(8)扫描线7的活动边表前面提到过,扫描线算法的核心就是围绕“活动边表(AET)”展开的,为了方便活性边表的建立与更新,我们为每一条扫描线建立一个“新边表(NET)”,存放该扫描线第一次出现的边。
当算法处理到某条扫描线时,就将这条扫描线的“新边表”中的所有边逐一插入到“活动边表”中。
“新边表”通常在算法开始时建立,建立“新边表”的规则就是:如果某条边的较低端点(y坐标较小的那个点)的y坐标与扫描线y相等,则该边就是扫描线y的新边,应该加入扫描线y的“新边表”。
上例中各扫描线的“新边表”如下图所示:图(9)各扫描线的新边表讨论完“活动边表(AET)”和“新边表(NET)”,就可以开始算法的具体实现了,但是在进一步详细介绍实现算法之前,还有以下几个关键的细节问题需要明确:(1)多边形顶点处理在对多边形的边进行求交的过程中,在两条边相连的顶点处会出现一些特殊情况,因为此时两条边会和扫描线各求的一个交点,也就是说,在顶点位置会出现两个交点。
当出现这种情况的时候,会对填充产生影响,因为填充的过程是成对选择交点的过程,错误的计算交点个数,会造成填充异常。
假设多边形按照顶点P1、P2和P3的顺序产生两条相邻的边,P2就是所说的顶点。
多边形的顶点一般有四种情况,如图(10)所展示的那样,分别被称为左顶点、右顶点、上顶点和下顶点:图(10)多边形顶点的四种类型左顶点――P1、P2和P3的y坐标满足条件:y1 < y2 < y3;右顶点――P1、P2和P3的y坐标满足条件:y1 > y2 > y3;上顶点――P1、P2和P3的y坐标满足条件:y2 > y1 && y2 > y3;下顶点――P1、P2和P3的y坐标满足条件:y2 < y1 && y2 < y3;对于左顶点和右顶点的情况,如果不做特殊处理会导致奇偶奇数错误,常采用的修正方法是修改以顶点为终点的那条边的区间,将顶点排除在区间之外,也就是删除这条边的终点,这样在计算交点时,就可以少计算一个交点,平衡和交点奇偶个数。
结合前文定义的“边”数据结构:EDGE,只要将该边的ymax修改为ymax – 1就可以了。
对于上顶点和下顶点,一种处理方法是将交点计算做0个,也就是修正两条边的区间,将交点从两条边中排除;另一种处理方法是不做特殊处理,就计算2个交点,这样也能保证交点奇偶个数平衡。
(2)水平边的处理水平边与扫描线重合,会产生很多交点,通常的做法是将水平边直接画出(填充),然后在后面的处理中就忽略水平边,不对其进行求交计算。
(3)如何避免填充越过边界线边界像素的取舍问题也需要特别注意。
多边形的边界与扫描线会产生两个交点,填充时如果对两个交点以及之间的区域都填充,容易造成填充范围扩大,影响最终光栅图形化显示的填充效果。
为此,人们提出了“左闭右开”的原则,简单解释就是,如果扫描线交点是1和9,则实际填充的区间是[1,9),即不包括x坐标是9的那个点。
2.2扫描线算法实现扫描线算法的整个过程都是围绕“活动边表(AET)”展开的,为了正确初始化“活动边表”,需要初始化每条扫描线的“新边表(NET)”,首先定义“新边表”的数据结构。
定义“新边表”为一个数组,数组的每个元素存放对应扫描线的所有“新边”。
因此定义“新边表”如下:510 std::vector< std::list<EDGE>> slNet(ymax - ymin +1);ymax和ymin是多边形所有顶点中y坐标的最大值和最小值,用于界定扫描线的范围。
slNet 中的第一个元素对应的是ymin所在的扫描线,以此类推,最后一个元素是ymax所在的扫描线。
在开始对每条扫描线处理之前,需要先计算出多边形的ymax和ymin并初始化“新边表”:503void ScanLinePolygonFill(const Polygon& py,int color)504{505 assert(py.IsValid());506507int ymin =0;508int ymax =0;509 GetPolygonMinMax(py, ymin, ymax);510 std::vector< std::list<EDGE>> slNet(ymax - ymin +1);511 InitScanLineNewEdgeTable(slNet, py, ymin, ymax);512//PrintNewEdgeTable(slNet);513 HorizonEdgeFill(py, color);//水平边直接画线填充514 ProcessScanLineFill(slNet, ymin, ymax, color);515}InitScanLineNewEdgeTable()函数根据多边形的顶点和边的情况初始化“新边表”,实现过程中体现了对左顶点和右顶点的区间修正原则:315void InitScanLineNewEdgeTable(std::vector< std::list<EDGE>>& slNet,316const Polygon& py,int ymin,int ymax)317{318 EDGE e;319for(int i =0; i < py.GetPolyCount(); i++)320{321const Point& ps = py.pts[i];322const Point& pe = py.pts[(i +1)% py.GetPolyCount()];323const Point& pss = py.pts[(i -1+ py.GetPolyCount())%py.GetPolyCount()];324const Point& pee = py.pts[(i +2)% py.GetPolyCount()];325332if(pe.y != ps.y)//不处理水平线333{334 e.dx =double(pe.x - ps.x)/double(pe.y - ps.y);335if(pe.y > ps.y)336{337 e.xi = ps.x;338if(pee.y >= pe.y)339 e.ymax = pe.y -1;340else341 e.ymax = pe.y;342343 slNet[ps.y - ymin].push_front(e);344}345else346{347 e.xi = pe.x;348if(pss.y >= ps.y)349 e.ymax = ps.y -1;350else351 e.ymax = ps.y;352 slNet[pe.y - ymin].push_front(e);353}354}355}356}多边形的定义Polygon和本系列第一篇《计算几何与图形学有关的几种常用算法》一文中的定义一致,此处就不再重复说明。
