初中几何基本图形归纳(基本图形+常考图形)
初中数学几何知识点和题型归纳总复习

图 形
平
线段,射线,直线
面
角的度量
两点之间 线段最短
图 形角
角
角的大小比较
平
余角补角
分
线
按柱、锥、球划分 (1) (2) 是一类,是柱体 (3)(4)是锥体 (5) 是球体
圆柱
柱体
三棱柱
四棱柱 棱柱
五棱柱
六棱柱
圆锥
锥体
三棱锥
棱锥
四棱锥 五棱锥
六棱锥
认识多面体
若围成立体图形的面是平的面,这样的立体图形又称为多面体
l
l
AB
直线AB、直
线BA、直线l
延伸性 端点个数 作图叙述
无
2 连接AB
沿OC方向 向两方无限
延伸
延伸
1
0
以点O为端 过A、B两点 点作射线OC 作直线AB
下面的知识点你掌握了吗?
知识点1:线段 (1)线段的概念:它是直线的一部分,它的
长度是有限的,它有两个端点. (2)线段的表示方法:可用它的两个端点
▪ (2)直线的表示方法:可用这条直线上 的两个点表示,也可以用一个小写字母 表示.
▪ (3)直线的基本性质:经过两点有一条 直线,并且只有一条直线.
▪ (4)直线的特点:没有端点,向两方无限 延伸,不可度量,不能比较大小.
你能解决下列问题吗?
1、图中共有几条线段?几条射线?几 条直线?能用字母表示出来的分别用 字母表示出来。
知识点2:射线
(1)射线的概念:把线段向一方无限延伸 所形成的图形叫做射线.
(2)射线的表示方法:可用两个大写字母 表示,第一个大写字母表示它的端点; 也可用一个小写字母表示.
(3)射线的特点:只有一个端点,向一方无 限延伸,无法度量,不能比较长短.
初中数学几何知识点和题型归纳总复习

49
一.平行线的定义: 在同一平面内,不相交的两条直线 叫做平行线。
结论:在同一平面内,两直线的位置 关系有平行与相交两种。
经过直线外一点,有且只有一条 直线与这条直线平行.(平行公理)
整理ppt
50
平行公理的推论:
如果两条直线都和第三条直线平行, 那么这两条直线也互相平行
几何语言表达:
a//c , c//b(已知) a c b
正方体
长方体
三棱柱
四棱锥
三棱柱
整理ppt
五棱锥
8
归纳:正方体 的表面展开图 有以下11种。你能看 出有什么规律吗?
一
二
阶
四
三
梯
一
一
型
型
型
整理ppt
9
当将这个图案折起来组成一 个正方体时,数字____会3 与数字2 所在的平面相对的平面上。
12 34 56
整理ppt
10
点和线
A 点A — 用一个大写字母表示。
AB
C
整理ppt
24
探究二:画一画,数一数,再找规律
1.在平面内有n个点(n≥3),其中没有任 何三个点在一条直线上,如果过任意两点 画一条直线,这n个点可以画多少条直线?
n(n-1)/2 (n2+n+2)/2
2.一条直线将平面分成两部分,两条直 线将平面分成四部分,那么三条直线将 平面最多分成几部分?四条直线将平面 最多分成几部分?n条直线呢?
离。(垂线段) A.
.
B
l
整理ppt
47
交两 条 直 线 相
况一 般 情
对顶角:相等 邻补角:互补
特殊
情况 垂线 相交成
初中几何知识点总结分类

初中几何知识点总结分类一、平面几何知识点总结1. 平面上的基本图形a. 点、线、线段和射线b. 三角形、矩形、正方形、平行四边形、梯形、菱形、圆2. 点、线和面的关系a. 由点确定一条直线b. 由直线确定一个平面3. 角a. 角的概念b. 角的种类和性质c. 同位角、对顶角、内错角的关系4. 相交线和平行线a. 相交线b. 平行线及判定条件二、空间几何知识点总结1. 空间几何体的基本概念a. 点、线、面和体的概念及性质2. 空间几何体的展开和折叠a. 空间几何体的展开图b. 箱体的展开图3. 空间几何体的表达和判定a. 立体图形的表达方法b. 立体图形的判定方法三、初中几何知识点详解1. 点、线和面的关系a. 由点确定一条直线:两点确定一条直线,三点不共线确定一条圆锥曲线。
b. 由直线确定一个平面:两点确定一条直线,一直线和一点确定一个平面。
2. 角a. 角的概念:由两条相交的线段,所形成的交点称为顶点,两条线段分别为边,夹角为两边的非公共部分。
b. 角的种类和性质:锐角、直角、钝角,顶角为180°,对顶角相等。
c. 同位角、对顶角、内错角的关系:同位角相等、对顶角相等、内错角互补。
3. 相交线和平行线a. 相交线:两条线相交于一点;b. 平行线及判定条件:两条直线的交角等于180°,则这两条直线互相平行。
4. 三角形a. 三角形的定义和构造:三条线段构成的图形;b. 三角形的分类和性质:等边三角形、等腰三角形、直角三角形;c. 三角形边长和角度关系:勾股定理,三角形内角和为180°。
5. 四边形a. 四边形的定义和构造:四条线段构成的图形;b. 四边形的分类和性质:矩形、正方形、平行四边形、菱形、梯形;c. 四边形的性质:对角线互相平分,相对角互补。
四、初中几何实际应用1. 几何知识在建筑工程中的应用a. 地平线和垂直线的概念b. 地基深度的计算c. 地板和瓷砖的铺设2. 几何知识在工艺制作中的应用a. 切割和焊接的角度计算b. 圆形工件的切割c. 立体工件的展开和装配3. 几何知识在日常生活中的应用a. 房屋装饰和家具的摆放b. 购物时的大小尺寸判断c. 旅行中的地图导航和方向判断五、初中几何学习方法1. 强化基础知识a. 认真理解点、线、面和体的概念、性质及相互关系;b. 熟练掌握角的性质,深入理解角的分类及其所具有的性质;2. 多做几何题a. 多做几何题,注重发现规律和解题方法;b. 针对不同难度的几何题,掌握基本解题技巧;3. 多进行几何实践a. 多进行几何实践,参与建筑、制作、生活等实际活动;b. 运用几何知识分析和解决实际生活中的问题;4. 合理利用工具a. 合理使用尺规等绘图工具,加深对图形构造的理解;b. 利用计算工具进行角度计算和尺寸测量。
几何图形初步讲解

初中精品数学精选精讲学科:数学任课教师:授课时间: 年月日4。
直线、射线、线段区别:直线没有距离.射线也没有距离。
因为直线没有端点,射线只有一个端点,可以无限延长.5。
尺规作图;几何里把限定用直尺和圆规来画图,称为尺规作图,最基本最常用的尺规作图,称基本作图6.线段的中点:把一条线段分成两条相等的线段的点,叫做线段的中点。
3、角1。
定义:由两条有公共端点的射线组成的几何对象。
这两条射线叫做角的边,它们的公共端点叫做角的顶点。
注意:角的两条边是射线,所以角的大小与边的长短无关。
2。
角的表示::(1)用三个大写字母表示,这种表示方法表示角时顶点字母必须写在中间;(2)用一个大写字母表示,这种表示方法表示角时必须分清楚表示的是哪个角;(3)用数字或希腊字母表示。
3。
角的度量:度量仪器:量角器度量单位:度、分、秒1°=60′1′=60〃1周角等于360度。
1平角等于180度。
4。
角的比较与运算:(1)角的比较:量角器直接量出,比较大小;把它们叠合在一起比较大小。
(2)角的平分线:静态:一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线。
动态:从一个角的顶点引出一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线。
5.角平分线的定理:在角平分线上的点到这个角的两边的距离相等。
角平分线的逆定理:在一个角的内部(包括顶点)且到角的两边距离相等的点,在这个角的平分线上。
6。
余角,补角(1)余角概念:如果两个角的和是一个直角,那么称这两个角互为余角,简称互余,也可以说其中一个角是另一个角的余角。
(2)补角概念:如果两个角的和是一个平角,那么这两个角叫互为补角.其中一个角叫做另一个角的补角(3)余角的性质:同角的余角相等.比如:∠A+∠B=90°,∠A+∠C=90°,则:∠C=∠B。
等角的余角相等。
比如:∠A+∠B=90°,∠D+∠C=90°,∠A=∠D则:∠C=∠B。
32华东师大版初中数学七年级上册 几何图形(基础)知识讲解

华东师大版初中数学七年级上册几何图形(基础)知识讲解【学习目标】1.理解几何图形的概念,并能对具体图形进行识别或判断;2. 掌握立体图形从不同方向看得到的平面图形及立体图形的平面展开图,在平面图形和立体图形相互转换的过程中,初步培养空间想象能力;3. 理解点线面体之间的关系,掌握怎样由平面图形旋转得到几何体,能够借助平面图形剖析常见几何体的形成过程.【要点梳理】要点一、几何图形1.定义:把从实物中抽象出的各种图形统称为几何图形.要点诠释:几何图形是从实物中抽象得到的,只注重物体的形状、大小、位置,而不注重它的其它属性,如重量,颜色等.2.分类:几何图形包括立体图形和平面图形(1)立体图形:图形的各部分不都在同一平面内,这样的图形就是立体图形,如长方体,圆柱,圆锥,球等.(2)平面图形:有些几何图形(如线段、角、三角形、圆等)的各部分都在同一平面内,它们是平面图形.要点诠释:(1)常见的立体图形有两种分类方法:(2) 常见的平面图形有圆和多边形,其中多边形是由线段所围成的封闭图形,生活中常见的多边形有三角形、四边形、五边形、六边形等.(3)立体图形和平面图形是两类不同的几何图形,它们既有区别又有联系.要点二、从不同方向看从不同的方向看立体图形,往往会得到不同形状的平面图形.一般是从以下三个方向:(1)从正面看;(2)从左面看;(3)从上面看.从这三个方向看到的图形分别称为正视图(也称主视图)、左视图、俯视图.要点三、简单立体图形的展开图有些立体图形是由一些平面图形围成,将它们的表面适当剪开,可以展开成平面图形,这样的平面图形称为相应立体图形的展开图.要点诠释:(1)不是所有的立体图形都可以展成平面图形.例如,球便不能展成平面图形.(2)不同的立体图形可展成不同的平面图形;同一个立体图形,沿不同的棱剪开,也可得到不同的平面图.要点四、点、线、面、体长方体、正方体、圆柱、圆锥、球、棱柱、棱锥等都是几何体,几何体也简称体;包围着体的是面,面有平的面和曲的面两种;面和面相交的地方形成线,线也分为直线和曲线两种;线和线相交的地方形成点.从上面的描述中我们可以看出点、线、面、体之间的关系. 此外,从运动的观点看:点动成线,线动成面,面动成体.【典型例题】类型一、几何图形1.如图所示,请写出下列立体图形的名称.【思路点拨】可以联系生活中常见的图形及基本空间想象能力,描述各种几何体的名称.【答案与解析】解:(1)五棱柱;(2)圆锥;(3)四棱柱或长方体;(4)圆柱;(5)四棱锥.【总结升华】先根据立体图形的底面的个数,确定它是柱体、锥体还是球体,再根据其侧面是否为多边形来判断它是圆柱(锥)还是棱柱(锥).举一反三:【变式】如图所示,下列各标志图形主要由哪些简单的几何图形组成?【答案】(1)由圆组成;(2)长方形和正方形;(3)菱形(或四边形);(4)由圆和圆弧组成(或由一个圆和两个小半圆组成).类型二、从不同方向看2.如图所示的是一个三棱柱,试着把从正面、左面、上面观察所得到的图形画出来.【思路点拨】注意观察的角度和方向.【答案与解析】解:从正面观察这个三棱柱,看到的图形是长方形;从左面观察它,看到的图形是长方形;从上面观察,看到的图形是三角形.因此,从三个方向看,得到的图形如图所示.【总结升华】若要画出从不同方向观察物体所得的图形,方向、角度一定要选准.因为从不同方向观察得到的图形往往不同.举一反三:【变式1】画出下列几何体的主视图、左视图与俯视图.【答案】主视图左视图俯视图【变式2】如图所示的工件的主视图是()A.B.C.D.【答案】B【解析】从物体正面看,看到的是一个横放的矩形,且一条斜线将其分成一个直角梯形和一个直角三角形.3.已知一个几何体的三视图如图所示,则该几何体是( )A.棱柱 B.圆柱 C.圆锥 D.球【答案】B【解析】此题可采用排除法.棱柱的三视图中不存在圆,故A不对;圆锥的主视图、左视图是三角形,故C不对;球的三视图都是圆,故D不对,因此应选B.【总结升华】平面展开图中,含有三角形,一般考虑棱锥或棱柱;如果只有两个三角形,必是三棱柱;如果含长方形,一般考虑棱柱;如果含有圆和长方形,一般考虑圆柱;如果含有扇形和圆,一般考虑圆锥.举一反三:【变式】右图是某个几何体的三视图,该几何体是()A.长方体 B.正方体 C.圆柱 D.三棱柱【答案】D类型三、展开图4.(2016•徐州)下列图形中,不可以作为一个正方体的展开图的是()A.B. C.D.【思路点拨】利用不能出现同一行有多于4个正方形的情况,不能出现田字形、凹字形的情况进行判断也可.【答案】C【解析】正方体沿着不同棱展开,把各种展开图分类,可以总结为如下11种情况:故选:C.【总结升华】本题考查了正方体的展开图,熟记展开图的11种形式是解题的关键,利用不是正方体展开图的“一线不过四、田凹应弃之”(即不能出现同一行有多于4个正方形的情况,不能出现田字形、凹字形的情况)判断也可.举一反三:【变式】(2015•宜昌)下列图形中可以作为一个三棱柱的展开图的是()A.B.C.D.【答案】 A .类型四、点、线、面、体5.分别指出下列几何体各有多少个面?面与面相交形成的线各有多少条?线与线相交形成的点各有多少个? 如图所示.【答案与解析】解:(1)4个面,6条线,4个顶点;(2)6个面,12条线,8个顶点;(3) 9个面,16条线,9个顶点.【总结升华】(1)数几何体中的点、线、面数时,要按一定顺序数,做到不重不漏.(2)一般地,n棱柱有(n+2)个面(其中2为两个底面),n棱锥有(n+1)个面(其中1为一个底面).6.如图,上面的平面图形绕轴旋转一周,可以得出下面的立方图形,请你把有对应关系的平面图形与立体图形连接起来.【答案与解析】连线如下:【总结升华】“面动成体”,要充分发挥空间想象能力判断立体图形的形状.举一反三:【变式】将如图所示的Rt△ABC绕直角边AC旋转一周,所得几何体从正面看到的图形是( ).【答案】A。
初中几何基本图形归纳(基本图形+常考图形)

初中几何基本图形归纳(基本图形+常考图形)初中几何常见基本图形1.基本图形及结论A、B、C、D分别为四边形的顶点,AC=BD,AD=BC,∠AOC=∠BOD,∠AOD=∠BOC。
2.直角三角形在直角三角形ABC中,∠C=90°,OA为斜边的中线,OD⊥XXX。
3.等腰三角形在等腰三角形ABC中,AB=AC,AD为角A的平分线,BD=CD。
4.三角形的面积公式在三角形ABC中,AB2=BD×BC,AC2=CD×BC。
5.三角形内角和公式在三角形ABC中,∠A+∠B+∠C=180°。
6.平行四边形在平行四边形ABCD中,∠A+∠B=∠C+∠D,AC平分∠BAD。
7.直角三角形的斜边中线在直角三角形ABC中,BD为斜边AC的中线,∠B=∠D。
8.直角三角形的高线在直角三角形ABC中,PA⊥AB,PB⊥AC,PC⊥BC,且PA=PB+PC,∠P=∠A/2.9.直角三角形的内心在直角三角形ABC中,∠P=∠A/2,PD为角A的平分线,AD=BD=AC=DC。
10.直角三角形的外心在直角三角形ABC中,∠P=90°-∠A/2,以AB的中点O为圆心,AB为半径作圆,交AC于点P,则P为三角形ABC的外心。
11.等腰三角形的中线在等腰三角形ABC中,AB=CB,BD为角B的平分线,且BC∥AD。
12.等边三角形在等边三角形ABC中,AB=AC=BC。
13.等角三角形在等角三角形ABC中,∠A=∠B=∠C。
14.三角形的相似在三角形ABC和DEF中,如果∠A=∠D,∠B=∠E,∠C=∠F,则称三角形ABC与DEF相似。
15.圆的基本性质在圆O中,AB为直径,则∠C=90°,且AC=BC=OD。
16.圆的切线在圆O中,以点A为圆心,AB为半径作圆,则CD为圆O的切线。
17.圆的割线在圆O中,以点A为圆心,AC为半径作圆,则BD为圆O的割线。
18.圆的弦在圆O中,AB为圆O的弦,R为圆O的半径,则弦长公式为AB2=BD×BC,且弦AB平分∠AOB。
初中数学几何图形知识点掌握归纳

初中数学几何图形知识点掌握归纳初一上册数学几何图形初步知识点归纳1.几何图形:点、线、面、体这些可帮助人们有效的刻画错综复杂的世界,它们都称为几何图形。
从实物中抽象出的各种图形统称为几何图形。
有些几何图形的各部分不在同一平面内,叫做立体图形。
有些几何图形的各部分都在同一平面内,叫做平面图形。
虽然立体图形与平面图形是两类不同的几何图形,但它们是互相联系的。
2.几何图形的分类:几何图形一般分为立体图形和平面图形。
3.直线:几何学基本概念,是点在空间内沿相同或相反方向运动的轨迹。
从平面解析几何的角度来看,平面上的直线就是由平面直角坐标系中的一个二元一次方程所表示的图形。
求两条直线的.交点,只需把这两个二元一次方程联立求解,当这个联立方程组无解时,二直线平行;有无穷多解时,二直线重合;只有一解时,二直线相交于一点。
常用直线与X轴正向的夹角(叫直线的倾斜角)或该角的正切(称直线的斜率)来表示平面上直线(对于X轴)的倾斜程度。
4.射线:在欧几里德几何学中,直线上的一点和它一旁的部分所组成的图形称为射线或半直线。
5.线段:指一个或一个以上不同线素组成一段连续的或不连续的图线,如实线的线段或由“长划、短间隔、点、短间隔、点、短间隔”组成的双点长划线的线段。
线段有如下性质:两点之间线段最短。
6. 两点间的距离:连接两点间线段的长度叫做这两点间的距离。
7. 端点:直线上两个点和它们之间的部分叫做线段,这两个点叫做线段的端点。
线段用表示它两个端点的字母或一个小写字母表示,有时这些字母也表示线段长度,记作线段AB或线段BA,线段a。
其中AB表示直线上的任意两点。
8.直线、射线、线段区别:直线没有距离。
射线也没有距离。
因为直线没有端点,射线只有一个端点,可以无限延长。
9.角:具有公共端点的两条不重合的射线组成的图形叫做角。
这个公共端点叫做角的顶点,这两条射线叫做角的两条边。
一条射线绕着它的端点从一个位置旋转到另一个位置所形成的图形叫做角。
初中数学基本几何图形大全
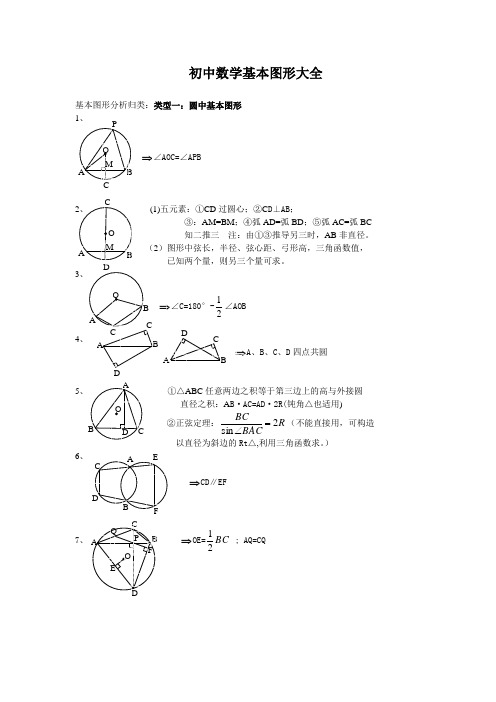
初中数学基本图形大全基本图形分析归类:类型一:圆中基本图形D⊥AB;弧BD;⑤弧AC=弧BCAB非直径。
、C、D四点共圆·2R(钝角△也适用)=(不能直接用,可构造R2)8、(弧AC=弧EC ) ⇒AM=CM=FM ;AC=EC;AE CD 21=; ABAD AE AM AC ⋅=⋅=2;BF OM 21=9∽CDE, △ABD ∽△AEC ∽BED,·AC=AD ·AE,AE ·DE=BE ·CEBAD ∠cos 2 关注∠BAC 为特殊角时图形的 10 AC 、AB 的对称点在⊙O 上,11DC 切⊙O 于C 点 知二推一12 ,BO ⊥DE , ∠DEF=90°-21∠A 13 14CE 切⊙O 于点E,知二推一15⇒C △PDE=PA+PB ∠DOE=)180(21P ∠-16 ①EA 切⊙O 于点A AE ∥CF ③AP=EP 知二推一17、 △ABD 、△ACE 为等边△⇒ BE=CD,BE 、CD 相交所成锐角为60° 18、正方形ABDE 、正方形ACFG ⇒EC=BG ,BG ⊥CE注:条件可为等腰Rt △19、①AD 平分∠CAB, ②DE ∥AC,③AE=DE 知二推一20、 △ABC 为等腰Rt △,AE 平分∠CAB ,BD ⊥AD⇒AE=2BD21、⇒C △ADE=AB+ACA B C DEA B C D E F G A B CD E A B C D E A B C D E M22、 △ACD 、△BCE 为等边△,A 、C 、B 三点共线⇒ △ACE ≌△DCB , △ACM ≌△DCN , △MCE ≌△NCB AE=BD,AM=DN,EM=BN,CM=CN,AE 、BD 相交所成锐角为60° AO=DO+CO,BO=EO+CO,OM+ON=OC,OC 平分∠AOB 注:△BCE 旋转时,结论有变化。
图形的计数知识点总结

图形的计数知识点总结图形的计数是数学中的一个重要内容,它涉及到几何形状的种类、性质以及应用,是数学学习的一个基础知识点。
在初中阶段,学生开始系统学习图形的知识,包括基本图形的性质、图形的分类、图形的计数等内容。
本文将对图形的计数知识点进行总结,帮助学生更好地理解和掌握这一知识点。
1. 基本图形的性质在图形的计数中,首先要了解基本图形的性质。
基本图形包括点、线、线段、射线、角、三角形、四边形、多边形等。
这些图形有各自的定义、性质及特点,对于学生来说,需要对这些基本图形有一个清晰、完整的理解。
(1)点:点是几何中最基本的概念,它没有长度、宽度和高度,只有位置。
点在几何图形中起到连接线段、构建图形等作用。
(2)线:线是由一组点按照一定规律排列而成,没有宽度和厚度。
线在几何图形中起到连接点、构成图形等作用。
(3)线段:线段是由两个端点和这两个端点之间的所有点组成的,有一定的长度,但没有宽度和厚度。
(4)射线:射线是由一个端点和这个端点上的一条直线上的所有点组成的,有一定的长度,但在一个方向上是无限长的。
(5)角:角是由两条射线的公共端点所确定的,角的度量单位通常是度。
角分为锐角、直角、钝角等。
(6)三角形:三角形是一个有三个顶点和三条边的几何图形,根据边长和角度的不同,可分为等边三角形、等腰三角形、直角三角形、等腰直角三角形等。
(7)四边形:四边形是一个有四个顶点和四条边的几何图形,根据边长和角度的不同,可分为矩形、正方形、平行四边形、菱形、梯形等。
(8)多边形:多边形是一个有多个顶点和边的几何图形,根据边的个数和边长的不同,可分为五边形、六边形、七边形等。
以上是基本图形的性质和特点,这些知识是图形计数的基础,学生需要通过实际操作和练习,充分理解和掌握这些内容。
2. 图形的分类图形的分类是图形计数中的重要内容之一,它涉及到几何图形的形状、性质和特点,对于学生来说,需要对各种分类有一个清晰、准确的认识。
(1)按形状分类:常见的图形按照形状可以分为圆形、三角形、四边形、多边形等。
图形与几何初中知识点总结

图形与几何初中知识点总结图形与几何是数学中的一个重要分支,主要涉及平面图形的性质、图形的相似关系、几何变换等内容。
通过学习图形与几何,可以培养学生的空间想象力、逻辑思维和解决问题的能力。
以下是对初中图形与几何知识点的总结:一、基本概念1. 点、线、面的概念:- 点:没有长度、宽度和高度,只有位置的概念。
- 线:由无数个点组成,没有宽度和高度,只有方向和长度的概念。
- 面:由无数条线组成,有长度和宽度,没有高度。
2. 平面图形的分类:- 线段:由两个端点确定的线段。
- 射线:有一个端点和一个方向的线段。
- 直线:无限延伸的线段。
- 角:由两条射线共享一个端点组成。
- 三角形:由三条线段组成的图形。
- 四边形:由四条线段组成的图形。
- 多边形:由多条线段组成的图形。
二、图形的性质1. 三角形的性质:- 内角和:任意三角形的三个内角之和为180度。
- 外角和:任意三角形的三个外角之和为360度。
- 等边三角形:三条边相等的三角形,三个角也相等。
- 等腰三角形:两条边相等的三角形,两个对角线也相等。
2. 直角三角形的性质:- 直角三角形:有一个直角(90度)的三角形。
- 勾股定理:直角三角形的两条直角边的平方和等于斜边的平方。
3. 平行四边形的性质:- 对角线:平行四边形的对角线互相平分。
- 对边和角:平行四边形的对边相等,对角线之间的角相等。
4. 正方形和长方形的性质:- 正方形:具有四条相等边和四个直角的四边形。
- 长方形:具有四个直角的四边形。
三、图形的相似关系1. 相似三角形的性质:- 对应角相等:两个三角形的对应角相等。
- 边比例相等:两个相似三角形的对应边的比例相等。
2. 相似四边形的性质:- 对应角相等:两个四边形的对应角相等。
- 边比例相等:两个相似四边形的对应边的比例相等。
四、几何变换1. 平移变换:- 定义:平移变换是指在平面上将图形按照一定的方向和距离进行移动。
- 性质:平移前后,图形的形状、大小和方向不变。
初中数学几何知识点归纳

初中数学几何知识点归纳1 过两点有且只有一条直线2 两点之间线段最短3 同角或等角的补角相等4 同角或等角的余角相等5 过一点有且只有一条直线和已知直线垂直6 直线外一点与直线上各点连接的所有线段中,垂线段最短7 平行公理经过直线外一点,有且只有一条直线与这条直线平行8 如果两条直线都和第三条直线平行,这两条直线也互相平行9 同位角相等,两直线平行10 内错角相等,两直线平行11 同旁内角互补,两直线平行12 两直线平行,同位角相等13 两直线平行,内错角相等14 两直线平行,同旁内角互补15 定理三角形两边的和大于第三边16 推论三角形两边的差小于第三边17 三角形内角和定理三角形三个内角的和等于180°18 推论1 直角三角形的两个锐角互余19 推论2 三角形的一个外角等于和它不相邻的两个内角的和20 推论3 三角形的一个外角大于任何一个和它不相邻的内角21 全等三角形的对应边、对应角相等22 边角边公理(SAS) 有两边和它们的夹角对应相等的两个三角形全等23 角边角公理( ASA)有两角和它们的夹边对应相等的两个三角形全等24 推论(AAS) 有两角和其中一角的对边对应相等的两个三角形全等25 边边边公理(SSS) 有三边对应相等的两个三角形全等26 斜边、直角边公理(HL) 有斜边和一条直角边对应相等的两个直角三角形全等27 定理1 在角的平分线上的点到这个角的两边的距离相等28 定理2 到一个角的两边的距离相同的点,在这个角的平分线上29 角的平分线是到角的两边距离相等的所有点的集合30 等腰三角形的性质定理等腰三角形的两个底角相等(即等边对等角)31 推论1 等腰三角形顶角的平分线平分底边并且垂直于底边32 等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合33 推论3 等边三角形的各角都相等,并且每一个角都等于60°34 等腰三角形的判定定理如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边)35 推论1 三个角都相等的三角形是等边三角形36 推论2 有一个角等于60°的等腰三角形是等边三角形37 在直角三角形中,如果一个锐角等于30°那么它所对的直角边等于斜边的一半38 直角三角形斜边上的中线等于斜边上的一半39 定理线段垂直平分线上的点和这条线段两个端点的距离相等40 逆定理和一条线段两个端点距离相等的点,在这条线段的垂直平分线上41 线段的垂直平分线可看作和线段两端点距离相等的所有点的集合42 定理1 关于某条直线对称的两个图形是全等形43 定理2 如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线44定理3 两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上45逆定理如果两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称46勾股定理直角三角形两直角边a、b的平方和、等于斜边c的平方,即a^2+b^2=c^2 47勾股定理的逆定理如果三角形的三边长a、b、c有关系a^2+b^2=c^2 ,那么这个三角形是直角三角形48定理四边形的内角和等于360°49四边形的外角和等于360°50多边形内角和定理n边形的内角的和等于(n-2)×180°51推论任意多边的外角和等于360°52平行四边形性质定理1 平行四边形的对角相等53平行四边形性质定理2 平行四边形的对边相等54推论夹在两条平行线间的平行线段相等55平行四边形性质定理3 平行四边形的对角线互相平分56平行四边形判定定理1 两组对角分别相等的四边形是平行四边形57平行四边形判定定理2 两组对边分别相等的四边形是平行四边形58平行四边形判定定理3 对角线互相平分的四边形是平行四边形59平行四边形判定定理4 一组对边平行相等的四边形是平行四边形60矩形性质定理1 矩形的四个角都是直角61矩形性质定理2 矩形的对角线相等62矩形判定定理1 有三个角是直角的四边形是矩形63矩形判定定理2 对角线相等的平行四边形是矩形64菱形性质定理1 菱形的四条边都相等65菱形性质定理2 菱形的对角线互相垂直,并且每一条对角线平分一组对角66菱形面积=对角线乘积的一半,即S=(a×b)÷267菱形判定定理1 四边都相等的四边形是菱形68菱形判定定理2 对角线互相垂直的平行四边形是菱形69正方形性质定理1 正方形的四个角都是直角,四条边都相等70正方形性质定理2正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角71定理1 关于中心对称的两个图形是全等的72定理2 关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分73逆定理如果两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点对称74等腰梯形性质定理等腰梯形在同一底上的两个角相等75等腰梯形的两条对角线相等76等腰梯形判定定理在同一底上的两个角相等的梯形是等腰梯形77对角线相等的梯形是等腰梯形78平行线等分线段定理如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等79 推论1 经过梯形一腰的中点与底平行的直线,必平分另一腰80 推论2 经过三角形一边的中点与另一边平行的直线,必平分第三边81 三角形中位线定理三角形的中位线平行于第三边,并且等于它的一半82 梯形中位线定理梯形的中位线平行于两底,并且等于两底和的一半L=(a+b)÷2 S=L×h83 (1)比例的基本性质如果a:b=c:d,那么ad=bc如果ad=bc,那么a:b=c:d84 (2)合比性质如果a/b=c/d,那么(a±b)/b=(c±d)/d85 (3)等比性质如果a/b=c/d=…=m/n(b+d+…+n≠0),那么(a+c+…+m)/(b+d+…+n)=a/b86 平行线分线段成比例定理三条平行线截两条直线,所得的对应线段成比例87 推论平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例88 定理如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边89 平行于三角形的一边,并且和其他两边相交的直线,所截得的三角形的三边与原三角形三边对应成比例90 定理平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似91 相似三角形判定定理1 两角对应相等,两三角形相似(ASA)92 直角三角形被斜边上的高分成的两个直角三角形和原三角形相似93 判定定理2 两边对应成比例且夹角相等,两三角形相似(SAS)94 判定定理3 三边对应成比例,两三角形相似(SSS)95 定理如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似96 性质定理1 相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比97 性质定理2 相似三角形周长的比等于相似比98 性质定理3 相似三角形面积的比等于相似比的平方99 任意锐角的正弦值等于它的余角的余弦值,任意锐角的余弦值等于它的余角的正弦值100任意锐角的正切值等于它的余角的余切值,任意锐角的余切值等于它的余角的正切值101圆是定点的距离等于定长的点的集合102圆的内部可以看作是圆心的距离小于半径的点的集合103圆的外部可以看作是圆心的距离大于半径的点的集合104同圆或等圆的半径相等105到定点的距离等于定长的点的轨迹,是以定点为圆心,定长为半106和已知线段两个端点的距离相等的点的轨迹,是着条线段的垂直平分线107到已知角的两边距离相等的点的轨迹,是这个角的平分线108到两条平行线距离相等的点的轨迹,是和这两条平行线平行且距离相等的一条直线109定理不在同一直线上的三点确定一个圆。
七年级数学几何知识点梳理

七年级数学几何知识点梳理数学几何是初中数学的重要组成部分之一。
在初中阶段,学生们需要学习并掌握基本的几何知识和技能,为高中和大学学习打下坚实基础。
本文将为大家梳理七年级数学几何知识点,帮助同学们更好地学习和掌握数学几何。
一、点、线、面的基本概念点是几何的基本要素,它是没有长、宽、高的,用大写字母表示。
线是由无数个点在同一方向上依次排列组成,用小写字母表示。
面是由无数个点和线在同一平面上组成的,用大写字母表示。
二、角的概念和性质角是由两条射线公共端点组成的图形,用小写希腊字母表示。
角是几何中的重要概念,学习角的概念和性质是初中几何学习的重点之一。
(1)角的度量单位是度,在逆时针方向旋转一度可以使一条线段的一端向前移动约0.0015个单位长度。
(2)对顶角的度数相等,即∠ABC=∠DEF。
(3)平分线所分割的角相等,即∠ABD=∠CBD。
(4)相邻角互补,即∠ABC和∠CBD互补,它们的和为90度。
(5)邻补角相等,即∠ABC和∠CBD邻补,它们的和为180度。
三、三角形的性质三角形的性质是初中几何的重点之一,它是几何中最基本的图形之一。
根据三角形内角和定理,三角形的三个内角和为180度,可以推出以下性质:(1)等腰三角形的两个底角相等。
(2)等边三角形的三个内角相等。
(3)直角三角形的两条直角边上的直角角平分三角形的直角角。
(4)全等三角形对应的边和角相等。
(5)相似三角形对应的角相等。
四、正方形、长方形和平行四边形的性质正方形、长方形和平行四边形是初中几何中的基本图形,学习它们的性质对于初中学生而言非常重要。
(1)正方形的特点是四条边相等、四个角相等、对角线相等垂直相交。
(2)长方形的特点是两对相等的边、四个角都是直角。
(3)平行四边形的特点是两组对边分别平行、对边相等、对角线互相平分。
五、圆的性质圆是初中几何中的另一个重要图形,学习圆的性质可以帮助初中学生更好地理解圆的概念。
(1)圆的直径是圆上任意两个点之间的最长线段,其长度等于圆的半径的两倍。
初中数学立体几何知识点归纳

初中数学立体几何知识点归纳立体几何是数学中的一个重要分支,涉及到空间中的图形、体积和表面积等概念。
在初中数学中,学生将会接触到一些基本的立体几何知识点。
本文将对初中数学中的立体几何知识点进行归纳和介绍。
1. 空间几何体空间几何体是指在空间中存在的具有一定形状和大小的物体。
常见的空间几何体包括立方体、球体、长方体、圆柱体等。
这些几何体具有不同的性质和特点,对于初中学生来说,需要了解它们的名称、形状和基本性质。
2. 平面与直线在立体几何中,平面和直线是两个重要的概念。
平面是一个无限延伸的二维几何图形,由无数的点组成。
直线是由无数个点延伸而成的一维图形,没有宽度和厚度。
初中学生需要掌握平面和直线的基本定义,并能够通过给定的条件进行判断和绘制。
3. 点、线、面、棱、角在空间几何中,点、线、面、棱、角是常见的基本概念。
点是空间中最基本的要素,它没有长度、宽度和厚度。
线是由无数个点连接而成的图形,具有长度但没有宽度和厚度。
面是由无数个连续的点组成的平面形状,它具有长度和宽度但没有厚度。
棱是由二维图形的边界上的相邻点连接而成的线段,它具有长度但没有宽度和厚度。
角是由两条相交的线段组成的图形,它具有大小和形状。
4. 体积和表面积在立体几何中,体积和表面积是两个重要的指标,用来描述立体几何体的大小。
体积是一个三维图形所包含的空间的大小,通常用立方单位(如立方厘米)来表示。
初中学生需要掌握计算简单几何体(如立方体、长方体)的体积的方法,并能够应用到实际问题中。
表面积是一个三维图形外部的总面积,通常用平方单位(如平方厘米)来表示。
初中学生需要了解计算简单几何体的表面积的方法,并能够应用到实际问题中。
5. 空间图形的展开与还原空间图形的展开是指将一个立体图形展开成一个平面图形,以便于计算其面积或进行其他几何运算。
还原则是将展开后的平面图形重新折叠成原来的立体图形。
初中学生需要理解展开和还原的概念,并能够应用到实际问题中。
初中数学几何常见基本图形归纳总结大全

6、如图 AB=AC,∠A=360,则:BC= 5 1 AB。 2
7、如图 AB=AC,D 是 BC 上一点,AE=AD,则: 1 ∠BAD=∠EDC。 2
8、 如图,D、E 是△ABC 边 BC 上两点,AC=CD,BE=BA,则当:①∠BAC=1000 时,∠
A D
C E
A
D
A
E
G
H
D
E
F
A
D
B
B
C
F
B
C
B
C
G
13、如图,正方形 ABCD 对角线交于 O,E 是 OB 上一点,EF∥BC: ①△AOE≌△BOF; ②AE⊥BF。 14、如图,E 是正方形 ABCD 对角线上一点,EF⊥CD,EG⊥BC: ①AE=FG;②AE⊥FG。 15、如图,将矩形 ABCD 顶点 B 沿某直线翻折可与 D 点重合:
B
D
O
F
C
B
F
C
E
17、如图,B 是直线 DF 上一点,∠ABC=Rt∠,过 A、C 做直线的垂线,D、E 是垂足:① △ABD∽△BCE; ②当 AB=BC 时,△ABD≌△BCE。 18、如图,以△ABC 两边向形外作正方形 ABED,ACFG,H 是 BC 中点:
①AH= 1 DG;②E、F 到 BC 所在直线的距离和等于 A 到直线 BC 的距离;③当∠BAC=Rt 2
13
P
A
C
A
12
14
B
D
C
A
PB=PC
① AB=AC ② BD=CD ③ ADBC ④ 1=2
“二推二”
初中数学几何图形初步全集汇编附解析
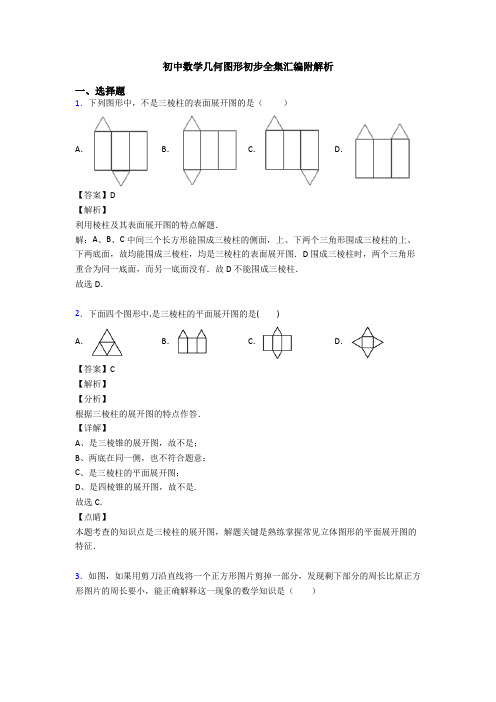
初中数学几何图形初步全集汇编附解析一、选择题1.下列图形中,不是三棱柱的表面展开图的是()A.B.C.D.【答案】D【解析】利用棱柱及其表面展开图的特点解题.解:A、B、C中间三个长方形能围成三棱柱的侧面,上、下两个三角形围成三棱柱的上、下两底面,故均能围成三棱柱,均是三棱柱的表面展开图.D围成三棱柱时,两个三角形重合为同一底面,而另一底面没有.故D不能围成三棱柱.故选D.2.下面四个图形中,是三棱柱的平面展开图的是()A.B.C.D.【答案】C【解析】【分析】根据三棱柱的展开图的特点作答.【详解】A、是三棱锥的展开图,故不是;B、两底在同一侧,也不符合题意;C、是三棱柱的平面展开图;D、是四棱锥的展开图,故不是.故选C.【点睛】本题考查的知识点是三棱柱的展开图,解题关键是熟练掌握常见立体图形的平面展开图的特征.3.如图,如果用剪刀沿直线将一个正方形图片剪掉一部分,发现剩下部分的周长比原正方形图片的周长要小,能正确解释这一现象的数学知识是()A.线段比曲线短B.经过一点有无数条直线C.经过两点,有且仅有一条直线D.两点之间,线段最短【答案】D【解析】【分析】如下图,只需要分析AB+BC<AC即可【详解】∵线段AC是点A和点C之间的连线,AB+BC是点A和点C经过弯折后的路径又∵两点之间线段最短∴AC<AB+BC故选:D【点睛】本题考查两点之间线段最短,在应用的过程中,要弄清楚线段长度表示的是哪两个点之间的距离4.如图,是一个正方体的表面展开图,将其折成正方体后,则“扫”的对面是()A.黑B.除C.恶D.☆【答案】B【解析】【分析】正方体的空间图形,从相对面入手,分析及解答问题.【详解】解:将其折成正方体后,则“扫”的对面是除.故选B.【点睛】本题考查了正方体的相对面的问题.能够根据正方体及其表面展开图的特点,找到相对的面是解题的关键.5.如图,三角形ABC中,AD平分∠BAC,EG⊥AD,且分别交AB、AD、AC及BC的延长线于点E、H、F、G,下列四个式子中正确的是()A.∠1=12(∠2﹣∠3)B.∠1=2(∠2﹣∠3)C.∠G=12(∠3﹣∠2)D.∠G=12∠1【答案】C【解析】【分析】根据角平分线得,∠1=∠AFE,由外角的性质,∠3=∠G+∠CFG=∠G+∠1,∠1=∠2+∠G,从而推得∠G=12⨯(∠3﹣∠2).【详解】解:∵AD平分∠BAC,EG⊥AD,∴∠1=∠AFE,∵∠3=∠G+∠CFG,∠1=∠2+∠G,∠CFG=∠AFE,∴∠3=∠G+∠2+∠G,∠G=12⨯(∠3﹣∠2).故选:C.【点睛】本题考查了三角形中角度的问题,掌握角平分线的性质、三角形外角的性质是解题的关键.6.一个立方体的表面展开图如图所示,将其折叠成立方体后,“你”字对面的字是()A.中B.考C.顺D.利【答案】C【解析】试题解析:正方体的表面展开图,相对的面之间一定相隔一个正方形,“祝”与“考”是相对面,“你”与“顺”是相对面,“中”与“立”是相对面.故选C.考点:正方体展开图.7.如果圆柱的母线长为5cm,底面半径为2cm,那么这个圆柱的侧面积是()A.10cm2B.10πcm2C.20cm2D.20πcm2【答案】D【解析】【分析】根据圆柱的侧面积=底面周长×高.【详解】根据圆柱的侧面积计算公式可得π×2×2×5=20πcm2,故选D.【点睛】本题考查了圆柱的计算,解题的关键是熟练掌握圆柱侧面积公式.8.已知:在Rt△ABC中,∠C=90°,BC=1,AC=3,点D是斜边AB的中点,点E是边AC 上一点,则DE+BE的最小值为()A.2B31C3D.23【答案】C【分析】作B 关于AC 的对称点B',连接B′D ,易求∠ABB'=60°,则AB=AB',且△ABB'为等边三角形,BE+DE=DE+EB'为B'与直线AB 之间的连接线段,其最小值为B'到AB 的距离=AC=3,所以最小值为3.【详解】解:作B 关于AC 的对称点B',连接B′D ,∵∠ACB=90°,∠BAC=30°,∴∠ABC=60°,∵AB=AB',∴△ABB'为等边三角形,∴BE+DE=DE+EB'为B'与直线AB 之间的连接线段,∴最小值为B'到AB 的距离=AC=3,故选C .【点睛】本题考查的是最短线路问题及等边三角形的性质,熟知两点之间线段最短的知识是解答此题的关键.9.将一副三角板如下图放置,使点A 落在DE 上,若BC DE P ,则AFC ∠的度数为( )A .90°B .75°C .105°D .120°【答案】B【解析】【分析】 根据平行线的性质可得30E BCE ==︒∠∠,再根据三角形外角的性质即可求解AFC ∠的度数.【详解】∴30E BCE ==︒∠∠∴453075AFC B BCE =+=︒+︒=︒∠∠∠故答案为:B .【点睛】本题考查了三角板的角度问题,掌握平行线的性质、三角形外角的性质是解题的关键.10.如图,在Rt ABC V 中,90C ∠=︒,以顶点A 为圆心,适当长为半径画弧,分别交AC 、AB 于点M 、N ,再分别以点M 、N 为圆心,大于12MN 的长为半径画弧,两弧交于点P ,作射线AP 交边BC 于点D ,若4CD =,15AB =,则ABD △的面积是( )A .15B .30C .45D .60 【答案】B【解析】【分析】作DE AB ⊥于E ,根据角平分线的性质得4DE DC ==,再根据三角形的面积公式求解即可.【详解】作DE AB ⊥于E由尺规作图可知,AD 是△ABC 的角平分线∵90C ∠=︒,DE AB ⊥∴4DE DC ==∴△ABD 的面积1302AB DE =⨯⨯= 故答案为:B .【点睛】本题考查了三角形的面积问题,掌握角平分线的性质、三角形面积公式是解题的关键.11.将下面平面图形绕直线l 旋转一周,可得到如图所示立体图形的是( )A .B .C .D .【答案】B【解析】分析:根据面动成体,所得图形是两个圆锥体的复合体确定答案即可.详解:由图可知,只有B 选项图形绕直线l 旋转一周得到如图所示立体图形. 故选:B .点睛:本题考查了点、线、面、体,熟悉常见图形的旋转得到立体图形是解题的关键.12.如图,一副三角板按如图所示的位置摆放,其中//AB CD ,45A ∠=︒,60C ∠=°,90AEB CED ∠=∠=︒,则AEC ∠的度数为( )A .75°B .90°C .105°D .120°【答案】C【解析】【分析】 延长CE 交AB 于点F ,根据两直线平行,内错角相等可得∠AFE =∠C ,再根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.【详解】解:如图,延长CE 交AB 于点F ,∵AB ∥CD ,∴∠AFE =∠C =60°,在△AEF 中,由三角形的外角性质得,∠AEC =∠A +∠AFE =45°+60°=105°.故选:C .【点睛】本题考查了平行线的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记相关性质并作出正确的辅助线是解题的关键.13.如图,直线 a ∥b ∥c ,直角三角板的直角顶点落在直线 b 上,若∠1=30°,则∠2 等于( )A .40°B .60°C .50°D .70° 【答案】B【解析】【分析】根据两直线平行内错角相等得1324==∠∠,∠∠,再根据直角三角板的性质得341290+=+=︒∠∠∠∠,即可求出∠2的度数.【详解】∵a ∥b ∥c∴1324==∠∠,∠∠∵直角三角板的直角顶点落在直线 b 上∴341290+=+=︒∠∠∠∠∵∠1=30°∴290160=︒-=︒∠∠故答案为:B .【点睛】本题考查了平行线和三角板的角度问题,掌握平行线的性质、三角板的性质是解题的关键.14.如图,在ABC V 中,90C ∠=︒,30B ∠=︒,如图:(1)以A 为圆心,任意长为半径画弧分别交AB 、AC 于点M 和N ;(2)分别以M 、N 为圆心,大于MN 的长为半径画弧,两弧交于点P ;(3)连结AP 并延长交BC 于点D .根据以上作图过程,下列结论中错误的是( )A .AD 是BAC ∠的平分线B .60ADC ∠=︒ C .点D 在AB 的中垂线上D .:1:3DAC ABD S S =△△【答案】D【解析】【分析】 根据作图的过程可以判定AD 是∠BAC 的角平分线;利用角平分线的定义可以推知∠CAD=30°,则由直角三角形的性质来求∠ADC 的度数;利用等角对等边可以证得△ADB 的等腰三角形,由等腰三角形的“三线合一”的性质可以证明点D 在AB 的中垂线上;利用30度角所对的直角边是斜边的一半、三角形的面积计算公式来求两个三角形的面积之比.【详解】解:A 、根据作图方法可得AD 是∠BAC 的平分线,正确;B 、∵∠C=90°,∠B=30°,∴∠CAB=60°,∵AD 是∠BAC 的平分线,∴∠DAC=∠DAB=30°,∴∠ADC=60°,正确;C 、∵∠B=30°,∠DAB=30°,∴AD=DB ,∴点D 在AB 的中垂线上,正确;D 、∵∠CAD=30°,∴CD=12AD , ∵AD=DB ,∴CD=12DB , ∴CD=13CB , S △ACD =12CD•AC ,S △ACB =12CB•AC , ∴S △ACD :S △ACB =1:3,∴S △DAC :S △ABD ≠1:3,错误,故选:D .【点睛】本题考查了角平分线的性质、线段垂直平分线的性质以及作图—基本作图.解题时,需要熟悉等腰三角形的判定与性质.15.下列说法中,正确的个数为( )①过同一平面内5点,最多可以确定9条直线;②连接两点的线段叫做两点的距离;=,则点B是线段AC的中点;③若AB BC④三条直线两两相交,一定有3个交点.A.3个B.2个C.1个D.0个【答案】D【解析】【分析】根据直线交点、两点间距离、线段中点定义分别判断即可得到答案.【详解】①过同一平面内5点,最多可以确定10条直线,故错误;②连接两点的线段的长度叫做两点的距离,故错误;=,则点B不一定是线段AC的中点,故错误;③若AB BC④三条直线两两相交,可以都交于同一点,故错误;故选:D.【点睛】此题考查直线交点、两点间距离定义、线段中点定义,正确理解定义是解题的关键.16.一个角的补角比这个角的余角3倍还多10°,则这个角的度数为()A.140° B.130° C.50° D.40°【答案】C【解析】【分析】根据互为余角的两个角的和等于90°,互为补角的两个角的和等于180°,列出方程,然后解方程即可.【详解】设这个角为α,则它的余角为90°-α,补角为180°-α,根据题意得,180°-α=3(90°-α)+10°,180°-α=270°-3α+10°,解得α=50°.故选C.【点睛】本题考查了互为余角与补角的性质,表示出这个角的余角与补角然后列出方程是解题的关键.17.下列说法中不正确的是()①过两点有且只有一条直线②连接两点的线段叫两点的距离③两点之间线段最短④点B在线段AC上,如果AB=BC,则点B是线段AC的中点A.①B.②C.③D.④【答案】B【解析】【分析】依据直线的性质、两点间的距离、线段的性质以及中点的定义进行判断即可.【详解】①过两点有且只有一条直线,正确;②连接两点的线段的长度叫两点间的距离,错误③两点之间线段最短,正确;④点B在线段AC上,如果AB=BC,则点B是线段AC的中点,正确;故选B.18.小张同学的座右铭是“态度决定一切”,他将这几个字写在一个正方体纸盒的每个面上,其平面展开图如图所示,那么在该正方体中,和“一”相对的字是()A.态B.度C.决D.切【答案】A【解析】【分析】正方体的平面展开图中,相对面的特点是之间一定相隔一个正方形,据此可得和“一”相对的字.【详解】正方体的平面展开图中,相对面的特点是之间一定相隔一个正方形,所以和“一”相对的字是:态.故选A.【点睛】注意正方体的空间图形,从相对面入手,分析及解答问题.19.如图,小慧从A处出发沿北偏东60°方向行走至B处,又沿北偏西20°方向行走至C 处,此时需要将方向调整到与出发时一致,则方向的调整应为()A.左转80°B.右转80°C.左转100°D.右转100°【答案】B【解析】【分析】如图,延长AB到D,过C作CE//AD,由题意可得∠A=60°,∠1=20°,根据平行线的性质可得∠A=∠2,∠3=∠1+∠2,进而可得答案.【详解】如图,延长AB到D,过C作CE//AD,∵此时需要将方向调整到与出发时一致,∴此时沿CE方向行走,∵从A处出发沿北偏东60°方向行走至B处,又沿北偏西20°方向行走至C处,∴∠A=60°,∠1=20°,AM∥BN,CE∥AB,∴∠A=∠2=60°,∠1+∠2=∠3∴∠3=∠1+∠2=20°+60°=80°,∴应右转80°.故选B.【点睛】本题考查了方向角有关的知识及平行线的性质,解答时要注意以北方为参照方向,进行角度调整.20.一把直尺和一块三角板ABC(含30°,60°角)的摆放位置如图,直尺一边与三角板的两直角边分别交于点D、点E,另一边与三角板的两直角边分别交于点F、点A,且∠CED =50°,那么∠BAF=()A.10°B.50°C.45°D.40°【答案】A【解析】【分析】先根据∠CED=50°,DE∥AF,即可得到∠CAF=50°,最后根据∠BAC=60°,即可得出∠BAF的大小.【详解】∵DE∥AF,∠CED=50°,∴∠CAF=∠CED=50°,∵∠BAC=60°,∴∠BAF=60°﹣50°=10°,故选:A.【点睛】此题考查平行线的性质,几何图形中角的和差关系,掌握平行线的性质是解题的关键.。
2023年中考数学常见几何模型全归纳之模 相似模型-母子型(共角共边模型)和A(X)字型(解析版)

∴∠BCD=∠ACD=45°,∠BCE=∠ACF= 90°,∴∠DCE=∠DCF= 135°
∵在△DCE与△DCF中,
,∴ ,∴DE=DF;
(2)证明∶∵∠DCE= ∠DCF= 135°∴∠CDF+∠F=180°-135°=45°,
∵∠CDF+∠CDE=45°,∴∠F=∠CDE,
【详解】∵∠B=∠ACD,∠A=∠A,
∴△ACD∽△ABC,∴ ,
∵ ,∴ ,
∴ ,
∴△ADC与△ACB的周长比1:2,故选:B.
【点睛】本题主要考查了相似三角形的判定与性质,证明△ACD∽△ABC是解答本题的关键.
2.(2022·陕西汉中·九年级期末)如图, 是等腰直角 斜边 的中线,以点 为顶点的 绕点 旋转,角的两边分别与 、 的延长线相交,交点分别为点 、 , 与 交于点 , 与 交于点 ,且 .(1)如图1,若 ,求证: ;(2)如图2,若 ,求证: ;
1.(2022·湖南怀化·中考真题)如图,△ABC中,点D、E分别是AB、AC的中点,若S△ADE=2,则S△ABC=_____.
【答案】8
【分析】根据三角形中位线定理求得DE∥BC, ,从而求得△ADE∽△ABC,然后利用相似三角形的性质求解.
【详解】解:∵D、E分别是AB、AC的中点,则DE为中位线,
∴ ,∴ ∴ ,
∵ ,DE=BF,∴ ,
∴ ,∴ ,
∵ , ,∴ ,
∵ ,∴ ,
∴ .
【点睛】本题考查了相似三角形,熟练掌握相似三角形的面积比等于相似比的平方、灵活运用平行条件证明三角形相似并求出相似比是解题关键.
3.(2022·浙江宁波·中考真题)(1)如图1,在 中,D,E,F分别为 上的点, 交 于点G,求证: .
七年级立体图形的知识点

七年级立体图形的知识点立体图形是初中数学中比较重要的一个内容,也是有具体的知识点和考核标准的。
在七年级阶段,学生需要掌握立体图形的基本概念和相关计算方法,下面就来对七年级立体图形的知识点进行详细的介绍。
一、基本概念立体图形是由平面图形按一定规律排列而成的具有空间形态的几何体。
与平面图形不同,立体图形不仅有面积,还有体积和表面积的概念。
学习立体图形首先需要掌握几何体的基本概念,如正方体、长方体、棱锥、棱台、球等。
1、正方体正方体是六个正方形组成的立体图形,它的六个面都是正方形,每个面都平行于另外两个相邻的面。
正方体有以下重要特点:(1)正方体的长、宽、高相等,记为a;(2)正方体的棱长、对角线长、表面积、体积都有特定的计算公式。
2、长方体长方体是六个矩形组成的立体图形,也就是一个长宽高都不相等的立方体。
长方体也有其特点:(1)长方体的长、宽、高分别为l、w、h;(2)长方体的棱长、对角线长、表面积、体积都有特定的计算公式。
3、棱锥棱锥是底为多边形,侧面都是三角形的立体图形,其中最常见的是四棱锥。
棱锥的基本特点为:(1)棱锥的底面为n边形,n为自然数;(2)每条侧棱的顶点与底面任一点连线构成的直线在底面上的交点连成的点要么都相同,要么都在同一直线上。
4、棱台棱台是底面为n边形,顶面为n边形,侧面为n个台面的立体图形,其中最常见的是四棱台。
棱台的特点为:(1)棱台的底面和顶面分别为n边形;(2)棱台的侧面都是梯形,有n个。
5、球球是由一条不动点绕着一个确定平面的轨迹不断旋转而成的几何体。
它的特点为:(1)球的表面是全部与中心点等距离的点的集合;(2)球有半径和直径的概念,有特定的计算公式。
二、相关计算了解几何体的基本概念后,就需要了解它们的相关计算方法,包括棱长、对角线长、表面积和体积的计算公式。
1、棱长正方体和长方体的棱长分别为正方体边长a和长方体的三条棱。
棱锥和棱台的棱长需要根据图形的不同确定,通常利用勾股定理和正弦定理等方法来计算。
初中几何模型及常见结论的总结归纳

初中几何模型及常见结论的总结归纳一、引言在初中数学学习中,几何是一个重要的部分,它不仅涉及到图形的性质和特点,还涉及到一些基本的几何模型和常见结论。
掌握这些模型和结论,有助于更好地理解和应用几何知识,提高解题能力和数学素养。
二、初中几何模型总结1. 全等三角形模型:两个三角形全等,则它们的边相等或角相等。
2. 相似三角形模型:两个三角形相似,则它们的对应边成比例。
3. 直角三角形模型:直角三角形的两个锐角互余。
4. 平行线模型:两直线平行,同位角相等,内错角相等,同旁内角互补。
5. 三角形内角和定理:三角形内角和为180度。
6. 多边形内角和定理:n边形内角和等于(n-2) × 180度。
7. 三角形重心性质模型:三角形的重心是三边中线的交点,重心到顶点的距离是它到对边中点距离的2倍。
三、常见结论归纳1. 等腰三角形的特点:等腰三角形两底角相等,顶角平分线垂直平分底边。
2. 直角三角形的特点:直角三角形斜边上的中线等于斜边的一半;勾股定理的逆定理适用;两个锐角互余。
3. 平行线的判定和性质:平行线的判定主要是依据平行线的定义和两直线夹角相等;平行线的性质主要有两直线平行,同位角相等;三角形内角和定理的推论等。
4. 辅助线常见位置和方法:在添加辅助线时,常常用到截长补短、垂直平分线、对顶角相等、平行线的性质等。
四、应用举例1. 利用全等三角形模型解决实际问题:例如测量旗杆高度或河流宽度等问题,需要用到全等三角形的性质。
2. 利用相似三角形模型解决实际问题:例如测量河对岸的建筑物高度或篮球架高度等问题,需要用到相似三角形的性质。
3. 利用平行线模型解决实际问题:例如求两直线的距离问题,需要用到平行线的判定和性质。
4. 利用勾股定理解决实际问题:例如求斜坡的长度等问题,需要用到勾股定理的性质。
五、总结通过总结归纳初中几何模型和常见结论,可以更好地理解和应用几何知识,提高解题能力和数学素养。
在应用时,需要根据具体情况选择合适的几何模型和结论,并结合辅助线等方法解决问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
9 2初 中 几 何 常 见 基 本 图 形序号1基 本 图 形A C D B基 本 结 论23子母型①② 2· C B4③ 2·④ 2·5CCA6DBD7D890+2APBCD16()/2∥∥18ADD E∥20AD AE DE== AB AC BC1090-211①平分②③∥“二推一”⊕⊕→⊕12 13为中线1:3:2平分14A12B D CA①“二推二”②③⊕⊕→⊕⊕④1=15D E D、E为中点2∥B CA DE、F为中点E F17B H D CE、F、G、HA为中点GEB F C四边形为平行四边形A型AAE AD AE DE===BD CD AB AC BC19B CX型EDA∥AD AE AD AE DE===BD CD AB AC BCB C假A型AEDB CdB④O∠90°25AD P A PD==BC PC PB O26P A PD ADPC PB BC P29∠∠∠∠180°假子母型A21D2·B B C221:1:2A CC①过圆心二推三23A ORE a/2②垂直于弦③平分弦平分弦所对的优弧⑤平分弦所对的劣弧⊕⊕→⊕⊕⊕R22+(2)224A D C为直径B蝶型DAPBC规型AB== ODC27A型AOBDP·PB PD BD==PC P A ACCA28OD BAB BC AC==BD AB AD2·CD AO30B C E①过圆心“二推一”O②过切点③垂直于切线A C B33AOOO1 O1 CO ①::2:1:3②内切圆半径 3 O2 ②当是角平分线时,长为 4 - 2 2 a 。
⊕⊕→⊕A31OP∠∠32P2BA1CB∠1=∠P ∠2=∠CA1O 1、O 2、A 三点共线A34O 1⊥O 22B几何基本图形1、如图,正三角形中,,、交于 F : ①△≌△ ②∠600 ③△∽△2、如图,正三角形中,F 是△中心,正三角形边长为 a :3a ③外接圆半径 a6 3△3、如图 中,∠900,∠300,,D 是上的点:①内切圆半径为 3 - 12a ②外接圆半径为 a△4、如图 中,∠900,,D 是上的点:①当 D 是中点时,长为A5 a ; AAAFEEDFBD CBD C30 0C B B C2ax - x 2△5、如图,如图 中,∠900,,E 、D 是、上的点,且∠450:①∽ ②设,则 。
a6、如图,∠360,则: 5 - 1。
27、如图,D 是上一点,,则:1∠∠。
28、 如图,D 、E 是△边上两点,,,则当:①∠1000 时,∠400;②当∠0 时,∠180 - x 20。
AAA ADBE45CB CEB D CB D E C△9、如图, 中,D 是三角形内一点,①当点 D 是外心时,∠ 1 180 + ∠A∠A ;②当点 D 是内心时,∠2 210、如图,∠900,是中垂线,则①,若 3,4,设,有 (4 - x )2 + 32 = x 2 ; ②△∽△。
11、如图,E 是正方形对角线上一点,交延长线于点 F ,H 是中点:①△≌△; ②△∽; ③ ⊥; ④是以为直径的圆的切线。
△12、如图,、是正方形:①≌; ②⊥。
ACEAEDGA DDABCD BHB C FBE FC G13、如图,正方形对角线交于 O ,E 是上一点,∥: ①△≌△; ②⊥。
14、如图,E 是正方形对角线上一点,⊥,⊥: ①;②⊥。
15、如图,将矩形顶点 B 沿某直线翻折可与 D 点重合: ①是中垂线; ②,若 3,5,设,则 32 + (5 - x )2 = x 2 。
16、将矩形顶点 A 沿翻折,A 落在 E 处,如图: ①是中垂线,;②△≌△;③。
AO D AEDFAEDAODEFOB F CBCB GCBFCEAF BD BD, AD等腰 A B CB17、如图,B 是直线上一点,∠∠,过 A 、C 做直线的垂线,D 、E 是垂足:①△∽△; ② 当时,△≌△。
△18、如图,以 两边向形外作正方形,,H 是中点:① 12;②E 、F 到所在直线的距离和等于 A 到直线的距离;③当∠∠时,⊥;19、如图,E 是正方形对角线上一点,F 是边上一点∠900:则。
20、如图,H 是矩形对角线上一点 E 、F 是矩形两边上的点,∠900,则过 H 作⊥,⊥,就 有 17 题基本图形。
CAD DGAEDAED B EFEHFB H CB F CB C△21、如图,是 角平分线,⊥,作出常用辅助线(延长与相交即可),并体会结果。
利用角 平分线翻折。
22、如图,E 是中点,F 是中点,当 8 时:则 2。
注:可作多种辅助线,有利于提高转比能 力。
23、如图,D 是△边上一点,:1:2,E 是中点: ①:1:3 ②:2:1 ③:7:1224、如图,D 是中点,E 是上一点:3:2:①:3:1 ②:3:5 ③:9:11。
AAAAFEEFEE F CCBDCBDC25、如图:梯形中,∥,,则,可利用①平移——过 D 作∥交延长线于 M ;②分割——过 A 、D 作垂线。
26、如图为对角线相等的四边形(例如矩形),则连结四边中点形成的四边形是菱形。
27、如图为对角线互相垂直的四边形(例如菱形) 则该四边形中点围成的四边形是矩形。
28、如图,对边,相等的四边形中,E 、H 、F 是边对角线中DD 点,则△是EDAAO三B OCC B角形。
HF CBC DE CO r△29、如图 中,∠900,⊥,则①2:2:;② 1 1 1= +AC 2 AB 2 AD 230、如图,F 是正方形边中点,①2·;②2·。
1 4:则△31、如图,、是高线:①中点在中垂线上;② ∽ ;③当∠△600 时,AD AC CD= =32、如图 D 是中点, 2 ;①△∽;②ABBC ACA1 2。
AD AAFD EBD CBB C33、如图,D 是△直角边上中点,⊥则:△∽△。
34、如图,梯形中,∥,已知:2:3;①S △:S △4:9 ②:2:3;③:4:25。
35、如图,梯形中,∥,是中位线,已知:2:3;①②:1:6; ③S △:1:100。
36、如图,E 是平行四边形边上一点,:3:1,则:S △19:56。
ADADADCEDE EB C BOG H FC BFE CAB37、如图,直角梯形中,⊥,∥,,E 是中点:①、是角平分线 ②∠∠。
△38、如图, 中,∠900,点 O 在直角边上,当以 O 为圆心的圆与、相切时:①②2· ③△∽;④当 3,4 时,⊙O 半径为 3 2;⑤当∠300,时。
3 3 a 。
39、如图,∠∠, 是斜边上一点,以 O 为圆心的圆与、相切, 是⊙O 半径:①r r+ = 1 ; AC BC②当 4,3 时, 12 7。
40、如图,∠∠,O 是斜边上一点,以 O 为圆心的圆过点 B ,且与相切,r 是⊙O 半径:①BCOD5 2= ; ②当 4,3 时, r , r ,2·。
AC AD 3 3CFAG k AADEEBDCED CEAFOAO G BF OBBC41、如图⊙O 是△内切圆,①,,, r = a + b - c242、如图,⊙O 切△直角边与斜边于 C 、D ,⊥,、是垂线,⊥:①△≌△ ;②△≌△ ; ③∠∠;④是、比例中项;⑤是、比例中项;⑥△≌△;⑦△≌△…… 43、如图,以为直径的⊙O 切于 E ,、是垂线:①;②是矩形。
44、如图,以为直径的⊙O 中,、是弦的垂线:①;②是矩形;③连结,,∠∠∠……AAHDOE BDE F O CF OAB GOBBF CCE D CE F D△45、如图,在直径所在直线上,⊥:①∠∠;② ∽△∽△∽△。
46、如图,⊙O 是△外接圆,⊥,⊥,⊥:①是平行四边形;②47、如图是⊙O 切线,C 是中点,是割线,则△∽△。
1 2。
48、如图,∥,、交于 O ,∥,则,A1 1 1 + =AD BC OE。
FEG DA BGEC AOOHOCBH DB F ECDDFCOAE B49、如图,点 B 在⊙O 上,以 B 为圆心的圆与⊙A 的公切线是,切点是 D 、E ,若交于 C ; 当⊙B 半径是⊙A 的一半时;①∠300;50、如图,两圆内切于 P ,大圆弦、交小圆于 A 、B ,则∥。
51、如图,⊙O 与⊙O 1 内切于 P ,⊙O 的弦切⊙O 1 于 C ,连结交⊙O 于 D ,则: 。
1C F O O E AE D 1O52、已知⊙A 的圆心在⊙O 上,⊙O 的弦与⊙A 切于 P ,若两圆半径为 R ,r ,则•2。
PDEABD P OO ABA PCA B CCDOB53、如图,⊙O 1 与⊙O 2 内切于 A ,⊙O 1 的弦经过 O 2,交⊙O 2 于 D 、E ,若⊙O 1 的直径为 6,:: 3:4:2,则可设 3k ,在利用相交弦定理求⊙O 2 半径。
54、如图,半圆 O 与⊙O 1 内切于 E ,⊙O 1 与半圆直径切于 D ,连结 1 交半圆于 C ,若 32, ⊙O 1 直径为 12,可将半圆补全,利用相交弦定理求长。
55、如图,两圆相交于 A 、B ,一直线分别交⊙O 1,⊙O 2 于 D 、E 、F 、G ,与交于 C ,则::。
56、如图⊙O 与⊙A 交于 B 、C ,过点 A 作直线交⊙O 于 E ,交⊙A 于 D ,交于 F ,则:2•。
ABD O2E CE CAGBO1AO 1 D O B D O 1B2 F CB57、如图,两圆外切于 A ,是两圆公切线,①∠900;②∠2=∠B ,∠1=∠C 。
CBO1AO 258、如图,两圆外切于 A ,是两圆公切线,、是直径,①在同一直线上; 在同一直线上;②2•;③2•r ;④若过点 D 作⊙O 2 的切线,则该切线长等于。
CO1AO259、如图,两圆外切于 A ,是两圆公切线,与 O 1O 2 交于 P ,①△∽△;②当 R :3:1 时,∠300,∠300。
60、如图,两圆外切于 A ,是⊙O 1 的切线,①△∽△;② ∠∠1800;③2•。
OBADC 2 BCEPE增补:DO1AO2△61、如图 中,,,①当∠400 时,∠700,②当∠0 时,∠180 - x 2。
△62、如图 中,,,①当∠400 时,∠1000,②当∠0 时,∠ 180 - 2 x 。
△63、如图, 边、中垂线交于 D 、E ,①当∠1000 时,∠200;②当∠0(x >900)时,∠2x、如图,是△64内接矩形,则AK;当△是直角三角形时,经常用–1800。
AFDE DG BD==AH BC AH ABA。
