初二数学特殊平行四边形压轴:几何证明题1
初二数学压轴几何证明题(含答案)

1.四边形ABCD是正方形,△BEF是等腰直角三角形,∠BEF=90°,BE=EF,连接DF,G 为DF的中点,连接EG,CG,EC.ﻫ(1)如图1,若点E在CB边的延长线上,直接写出EG与GC 的位置关系及的值;ﻫ(2)将图1中的△BEF绕点B顺时针旋转至图2所示位置,请问(1)中所得的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;(3)将图1中的△BEF绕点B顺时针旋转α(0°<α<90°),若BE=1,AB=,当E,F,D三点共线时,求DF的长及tan∠ABF的值.解:(1)EG⊥CG,=,ﻫ理由是:过G作GH⊥EC于H,ﻫ∵∠FEB=∠DCB=90°,∴EF∥GH∥DC,ﻫ∵G为DF中点,ﻫ∴H为EC中点,ﻫ∴EG=GC,GH=(EF+DC)=(EB+BC),ﻫ即GH=EH=HC,ﻫ∴∠EGC=90°,即△EGC是等腰直角三角形,∴=;ﻫ(2)ﻫ解:结论还成立,ﻫ理由是:如图2,延长EG到H,使EG=GH,连接CH、EC,过E作BC的垂线EM,延长CD,∵在△EFG和△HDG中ﻫ∴△EFG≌△HDG(SAS),∴DH=EF=BE,∠FEG=∠DHG,∴EF∥DH,ﻫ∴∠1=∠2=90°-∠3=∠4,ﻫ∴∠EBC=180°-∠4=180°-∠1=∠HDC,在△EBC和△HDC中ﻫ∴△EBC≌△HDC.ﻫ∴CE=CH,∠BCE=∠DCH,∴∠ECH=∠DCH+∠ECD=∠BCE+∠ECD=∠BCD=90°,∴△ECH是等腰直角三角形,ﻫ∵G为EH的中点,ﻫ∴EG⊥GC,=,ﻫ即(1)中的结论仍然成立;ﻫﻫ(3)ﻫ解:连接BD,∵AB=,正方形ABCD,ﻫ∴BD=2,ﻫ∴cos∠DBE==,∴∠DBE=60°,ﻫ∴∠ABE=∠DBE-∠ABD=15°,ﻫ∴∠ABF=45°-15°=30°,∴tan∠ABF=,∴DE=BE=,∴DF=DE-EF=-1.解析: (1)过G作GH⊥EC于H,推出EF∥GH∥DC,求出H为EC中点,根据梯形的中位线求出EG=GC,GH=(EF+DC)=(EB+BC),推出GH=EH=BC,根据直角三角形的判定推出△EGC是等腰直角三角形即可;ﻫ(2)延长EG到H,使EG=GH,连接CH、EC,过E作BC的垂线EM,延长CD,证△EFG≌△HDG,推出DH=EF=BE,∠FEG=∠DHG,求出∠EBC=∠HDC,证出△EBC≌△HDC,推出CE=CH,∠BCE=∠DCH,求出△ECH是等腰直角三角形,即可得出答案;3(ﻫ)连接BD,求出cos∠DBE==,推出∠DBE=60°,求出∠ABF=30°,解直角三角形求出即可.2.已知正方形ABCD和等腰直角三角形BEF,BE=EF,∠BEF=90°,按图1放置,使点E在BC上,取DF的中点G,连接EG,CG.(1)延长EG交DC于H,试说明:DH=BE.ﻫ(2)将图1中△BEF绕B点逆时针旋转45°,连接DF,取DF中点G(如图2),莎莎同学发现:EG=CG且EG⊥CG.在设法证明时他发现:若连接BD,则D,E,B三点共线.你能写出结论“EG=CG且EG⊥CG”的完整理由吗?请写出来.ﻫ(3)将图1中△BEF绕B点转动任意角度α(0<α<90°),再连接DF,取DF的中点G(如图3),第2问中的结论是否成立?若成立,试说明你的结论;若不成立,也请说明理由.(1)证明:∵∠BEF=90°,∴EF∥DH,ﻫ∴∠EFG=∠GDH,ﻫ而∠EGF=∠DGH,GF=GD,ﻫ∴△GEF≌△GHD,ﻫ∴EF=DH,而BE=EF,ﻫ∴DH=BE;ﻫ(2)连接DB,如图,ﻫ∵△BEF为等腰直角三角形,∴∠EBF=45°,ﻫ而四边形ABCD为正方形,∴∠DBC=45°,ﻫ∴D,E,B三点共线.ﻫ而∠BEF=90°,∴△FED为直角三角形,ﻫ而G为DF的中点,∴EG=GD=GC,∴∠EGC=2∠EDC=90°,∴EG=CG且EG⊥CG;ﻫﻫ(3)第2问中的结论成立.理由如下:连接AC、BD相交于点O,取BF的中点M,连接OG、EM、MG,如图,ﻫ∵G为DF的中点,O为BD的中点,M为BF的中点,ﻫ∴OG∥BF,GM∥OB,ﻫ∴四边形OGMB为平行四边形,∴OG=BM,GM=OB,而EM=BM,OC=OB,∴EM=OG,MG=OC,∵∠DOG=∠GMF,而∠DOC=∠EMF=90°,∴∠EMG=∠GOC,ﻫ∴△MEG≌△OGC,∴EG=CG,∠EGM=∠OCG,ﻫ又∵∠MGF=∠BDF,∠FGC=∠GDC+∠GCD,∴∠EGC=∠EGM+∠MGF+∠FGC=∠BDF+∠GDC+∠GCD+∠OCG=45°+45°=90°,ﻫ∴EG=CG且EG⊥CG.解析:(1)由∠BEF=90°,得到EF∥DH,而GF=GD,易证得△GEF≌△GHD,得EF=DH,而BE=EF,即可得到结论.ﻫ(2)连接DB,如图2,由△BEF为等腰直角三角形,得∠EBF=45°,而四边形ABCD为正方形,得∠DBC=45°,得到D,E,B三点共线,而G为DF的中点,根据直角三角形斜边上的中线等于斜边的一半得到EG=GD=GC,于是∠EGC=2∠EDC=90°,即得到结论.ﻫ(3)连接AC、BD相交于点O,取BF的中点M,连接OG、EM、MG,由G为DF的中点,O为BD的中点,M为BF的中点,根据三角形中位线的性质得OG∥BF,GM∥OB,得到OG=BM,GM=OB,而EM=BM,OC=OB,得到EM=OG,MG=OC,又∠DOG=∠GMF,而∠DOC=∠EMF =90°,得∠EMG=∠GOC,则△MEG≌△OGC,得到EG=CG,∠EGM=∠OCG,而∠MGF=∠BD F,∠FGC=∠GDC+∠GCD,所以有∠EGC=∠EGM+∠MGF+∠FGC=∠BDF+∠GDC+∠GCD+∠OCG=45°+45°=90°.3.已知正方形ABCD和等腰Rt△BEF,BE=EF,∠BEF=90°,按图①放置,使点F在BC上,取DF的中点G,连接EG、CG.ﻫ(1)探索EG、CG的数量关系和位置关系并证明;ﻫ(2)将图①中△BEF绕B点顺时针旋转45°,再连接DF,取DF中点G(如图②),问(1)中的结论是否仍然成立.证明你的结论;(3)将图①中△BEF绕B点转动任意角度(旋转角在0°到90°之间),再连接DF,取DF的中点G(如图③),问(1)中的结论是否仍然成立,证明你的结论.ﻫ解:(1)EG=CG且EG⊥CG.ﻫ证明如下:如图①,连接BD.∵正方形ABCD和等腰Rt△BEF,∴∠EBF=∠DBC=45°.∴B、E、D三点共线.ﻫ∵∠DEF=90°,G为DF的中点,∠DCB=90°,∴EG=DG=GF=CG.ﻫ∴∠EGF=2∠EDG,∠CGF=2∠CDG.ﻫ∴∠EGF+∠CGF=2∠ED C=90°,ﻫ即∠EGC=90°,∴EG⊥CG.ﻫﻫ(2)仍然成立,证明如下:如图②,延长EG交CD于点H.ﻫ∵BE⊥EF,∴EF∥CD,∴∠1=∠2.ﻫ又∵∠3=∠4,FG=DG,ﻫ∴△FEG≌△DHG,∴EF=DH,EG=GH.∵△BEF为等腰直角三角形,∴BE=EF,∴BE=DH.ﻫ∵CD=BC,∴CE=CH.∴△ECH为等腰直角三角形.又∵EG=GH,∴EG=CG且EG⊥CG.ﻫ(3)仍然成立.证明如下:如图③,延长CG至H,使GH=CG,连接HF交BC于M,连接EH、EC.∵GF=GD,∠HGF=∠CGD,HG=CG,ﻫ∴△HFG≌△CDG,ﻫ∴HF=CD,∠GHF=∠GCD,∴HF∥CD.∵正方形ABCD,∴HF=BC,HF⊥BC.∵△BEF是等腰直角三角形,∴BE=EF,∠EBC=∠HFE,∴△BEC≌△FEH,ﻫ∴HE=EC,∠BEC=∠FEH,ﻫ∴∠BEF=∠HEC=90°,ﻫ∴△ECH为等腰直角三角形.又∵CG=GH,∴EG =CG 且EG ⊥C G.解析:(1)首先证明B 、E、D三点共线,根据直角三角形斜边上的中线等于斜边的一半,即可证明EG=DG=GF=CG,得到∠EGF=2∠EDG ,∠CGF=2∠CDG,从而证得∠EGC=90°;ﻫ(2)首先证明△FE G≌△DHG,然后证明△ECH 为等腰直角三角形.可以证得:EG=CG 且EG ⊥C G.ﻫ(3)首先证明:△BEC ≌△FEH,即可证得:△ECH 为等腰直角三角形,从而得到:EG=C G且EG ⊥CG.已知,正方形A BCD 中,△BEF 为等腰直角三角形,且BF 为底,取DF 的中点G,连接EG 、C G.ﻫ(1)如图1,若△B EF 的底边B F在BC 上,猜想E G和CG 的数量关系为______;ﻫ(2)如图2,若△B EF 的直角边BE 在BC 上,则(1)中的结论是否还成立?请说明理由;(3)如图3,若△B EF 的直角边BE 在∠DB C内,则(1)中的结论是否还成立?说明理由. 解:(1)GC=EG,(1分)理由如下:ﻫ∵△BEF 为等腰直角三角形,ﻫ∴∠DEF=90°,又G为斜边DF 的中点, ∴EG= DF,∵A BCD 为正方形,ﻫ∴∠BCD=90°,又G为斜边DF 的中点,∴CG= DF,ﻫ∴G C=EG;ﻫ(2)成立.如图,延长EG 交CD 于M,D,∵∠BEF =∠FEC=∠BCD=90°,∴EF ∥C1 2 1 2∴∠EFG=∠MD G,ﻫ又∠E GF=∠DGM ,D G=FG ,∴△G EF ≌△GMD,ﻫ∴EG=MG,即G 为EM 的中点.∴CG为直角△EC M的斜边上的中线,ﻫ∴CG=G E= EM;(3)成立.ﻫ取BF 的中点H,连接EH ,GH ,取BD 的中点O,连接O G,OC . ∵CB=CD,∠DCB=90°,∴C O= BD .ﻫ∵DG=G F,ﻫ∴GH ∥BD ,且GH= BD ,ﻫOG ∥BF,且OG= B F,ﻫ∴CO =GH .∵△BEF 为等腰直角三角形. B F∴EH=∴EH=OG . ∵四边形O BHG 为平行四边形, ∴∠BOG =∠BH G.∵∠B OC=∠BH E=90°. ∴∠GOC=∠EHG .ﻫ∴△GOC ≌△E HG .ﻫ∴EG=GC .此题考查了正方形的性质,以及全等三角形的判定与性质.要求学生掌握直角三角形斜边上的中线等于斜边的一半,以及三角形的中位线与第三边平行且等于第三边的一半.掌握这些性质,熟练运用全等知识是解本题的关键.解析:(1)E G=CG,理由为:根据三角形BEF 为等腰直角三角形,得到∠DEF 为直角,又G 为DF 中点,根据在直角三角形中,斜边上的中线等于斜边的一半,得到EG 为DF 的一半,同理在直角三角形DC F中,得到CG 也等于DF 的一半,利用等量代换得证;ﻫ(2)成立.理由为:延长EG 交CD 于M,如图所示,根据“A SA ”得到三角形E FG 与三角形GDM 全等,由全等三角形的对应边相等得到EG 与MG 相等,即G 为EM 中点,根据直角三角形斜边上的中线等于斜边的一半得到E G与CG相等都1212 1 2 1 2。
初二数学证明题(精选多篇)

初二数学证明题(精选多篇)第一篇:初二数学证明题初二数学证明题1、如图,ab=ac,∠bac=90°,bd⊥ae于d,ce⊥ae于e.且bd>ce,证明bd=ec+ed.解答:证明:∵∠bac=90°,ce⊥ae,bd⊥ae,∴∠abd+∠bad=90°,∠bad+∠dac=90°,∠adb=∠aec=90°.∴∠abd=∠dac.又∵ab=ac,∴△abd≌△cae(aas).∴bd=ae,ec=ad.∵ae=ad+de,∴bd=ec+ed.2、△abc是等要直角三角形。
∠acb=90°,ad是bc边上的中线,过c 做ad的垂线,交ab于点e,交ad于点f,求证∠adc=∠bde解:作ch⊥ab于h交ad于p,∵在rt△abc中ac=cb,∠acb=90°,∴∠cab=∠cba=45°.∴∠hcb=90°-∠cba=45°=∠cba.又∵中点d,∴cd=bd.又∵ch⊥ab,∴ch=ah=bh.又∵∠pah+∠aph=90°,∠pcf+∠cpf=90°,∠aph=∠cpf,∴∠pah=∠pcf.又∵∠aph=∠ceh,在△aph与△ceh中∠pah=∠ech,ah=ch,∠pha=∠ehc,∴△aph≌△ceh(asa).∴ph=eh,又∵pc=ch-ph,be=bh-he,∴cp=eb.在△pdc与△edb中pc=eb,∠pcd=∠ebd,dc=db,∴△pdc≌△edb(sas).∴∠adc=∠bde.2证明:作oe⊥ab于e,of⊥ac于f,∵∠3=∠4,∴oe=of.(问题在这里。
理由是什么埃我有点不懂)∵∠1=∠2,∴ob=oc.∴rt△obe≌rt△ocf(hl).∴∠5=∠6.∴∠1+∠5=∠2+∠6.即∠abc=∠acb.∴ab=ac.∴△abc是等腰三角形过点o作od⊥ab于d过点o作oe⊥ac于e再证rt△aod≌rt△aoe(aas)得出od=oe就可以再证rt△dob≌rt△eoc(hl)得出∠abo=∠aco再因为∠obc=∠ocb得出∠abc=∠abc得出等腰△abc41.e是射线ab的一点,正方形abcd、正方形defg有公共顶点d,问当e在移动时,∠fbh的大小是一个定值吗?并验证(过f作fm⊥ah于m,△ade全等于△mef证好了)2.三角形abc,以ab、ac为边作正方形abmn、正方形acpq1)若de⊥bc,求证:e是nq的中点2)若d是bc的中点,∠bac=90°,求证:ae⊥nq3)若f是mp的中点,fg⊥bc于g,求证:2fg=bc3.已知ad是bc边上的高,be是∠abc的平分线,ef⊥bc于f,ad与be交于g求证:1)ae=ag(这个证好了)2)四边形aefg是菱形第二篇:初二数学证明题测试例1、如图,ab∥cd,且∠abe=120°,∠cde=110°,求∠bed的度数。
专题06 平行四边形解答题压轴训练(解析版)八年级数学下期(人教版)

专题06 平行四边形解答题压轴训练(时间:60分钟 总分:120) 班级 姓名 得分一、解答题1.如图1,在ABCD 中,BAD ∠的平分线交BC 于点E ,交DC 的延长线于点F ,以EC ,CF 为邻边作ECFG .(1)求证:ECFG 是菱形.(2)如图2,若90ABC ∠=︒,8AB =,12AD =,M 是EF 的中点,求DM 的长. (3)如图3,若120ABC ∠=︒,连结BD ,BG ,CG ,DG ,求BDG ∠的度数.【答案】(1)见解析;(2);(3)60°【分析】(1)由平行四边形的性质可得AD ∥BC ,AB ∥CD ,再根据平行线的性质证明∥CEF =∥CFE ,根据等角对等边可得CE =CF ,再有条件四边形ECFG 是平行四边形,可得四边形ECFG 为菱形,即可解决问题;(2)首先证明四边形ECFG 为正方形,再证明∥BME ∥∥DMC 可得DM =BM ,∥DMC =∥BME ,再根据∥BMD =∥BME +∥EMD =∥DMC +∥EMD =90°可得到∥BDM 是等腰直角三角形,由等腰直角三角形的性质可求解.(3)延长AB 、FG 交于H ,连接HD ,求证平行四边形AHFD 为菱形,得出∥ADH ,∥DHF 为全等的等边三角形,证明∥BHD ∥∥GFD ,即可得出答案.【详解】解:(1)∥AF 平分∥BAD ,∥∥BAF =∥DAF ,∥四边形ABCD 是平行四边形,∥AD ∥BC ,AB ∥CD ,∥∥DAF =∥CEF ,∥BAF =∥CFE ,∥∥CEF =∥CFE ,∥CE =CF ,又∥四边形ECFG 是平行四边形,∥四边形ECFG 为菱形;(2)如图,连接BM ,MC ,∥∥ABC =90°,四边形ABCD 是平行四边形,∥四边形ABCD 是矩形,又由(1)可知四边形ECFG 为菱形,∥ECF =90°,∥四边形ECFG 为正方形.∥∥BAF =∥DAF ,∥BE =AB =DC ,∥M 为EF 中点,∥∥CEM =∥ECM =45°,∥∥BEM =∥DCM =135°,在∥BME 和∥DMC 中,BE CD BEM DCM EM CM =⎧⎪∠=∠⎨⎪=⎩,∥∥BME ∥∥DMC (SAS ),∥DMC=∥BME.∥∥BMD=∥BME+∥EMD=∥DMC+∥EMD=90°,∥∥BMD是等腰直角三角形.∥AB=8,AD=12,∥BDBD=;∥DM=2(3)∥BDG=60°,延长AB、FG交于H,连接H D.∥AD∥GF,AB∥DF,∥四边形AHFD为平行四边形,∥∥ABC=120°,AF平分∥BAD,∥∥DAF=30°,∥ADC=120°,∥DF A=30°,∥∥DAF为等腰三角形,∥AD=DF,∥平行四边形AHFD为菱形,∥∥ADH,∥DHF为全等的等边三角形,∥DH=DF,∥BHD=∥GFD=60°,∥FG=CE,CE=CF,CF=BH,∥BH=GF,在∥BHD与∥GFD中,BHD GFD BH GF ⎪∠=∠⎨⎪=⎩,∥∥BHD ∥∥GFD (SAS ),∥∥BDH =∥GDF∥∥BDG =∥BDH +∥HDG =∥GDF +∥HDG =60°.【点睛】此题是四边形综合题,主要考查平行四边形的判定方法,全等三角形的判定与性质,等边三角形的判定与性质,菱形的判定与性质等知识点,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法.2.如图,在四边形ABCD 中,连接AC ,BD 交于点O ,∠ADO =∠CBO ,且AO =CO ,E 为线段OC 上一点,连接DE 并延长交BC 于点F .(1)求证:四边形ABCD 为平行四边形;(2)若∠ADE =45°,AD ∠AC ,AE =3,CE =2,求三角形AOD 的面积.【答案】(1)见解析;(2)154【分析】 (1)依据∥AOD ∥∥COB (AAS ),即可得出AD =BC ,再根据∥ADO =∥CBO ,即可得到AD ∥BC ,进而判定四边形ABCD 是平行四边形;(2)依据∥ADE 是等腰直角三角形,即可得到AD 的长,由平行四边形的性质可得OA 的长,再根据三角形面积计算公式,即可得出∥AOD 的面积.【详解】(1)∥AC ,BD 交于点O ,∥∥AOD =∥COB ,在∥AOD 和∥COB 中,ADO CBO AOD COB AO CO ∠=∠⎧⎪∠=∠⎨⎪=⎩,∥∥AOD ∥∥COB (AAS ),∥AD =BC ,∥∥ADO =∥CBO ,∥AD ∥BC ,∥四边形ABCD 是平行四边形;(2)∥∥ADE =45°,AD ∥AC ,∥∥AED =45°,∥AD =AE =3,又∥CE =2,∥AC =3+2=5,∥在平行四边形ABCD 中,AO =12AC =52, ∥Rt∥AOD 的面积=12×AD ×AO =12×3×52=154.【点睛】本题考查了平行四边形的判定与性质、全等三角形的判定与性质、等腰三角形的判定. 3.定义:一组邻角相等的凸四边形叫做“友好四边形”.(1)写出我们所学过的特殊四边形中是“友好四边形”的图形的名称____(写一个) (2)在探究“友好四边形”性质时:∠小明画了一个“友好四边形”ABCD (如图),其中A B ∠=∠,AD BC =,此时他发现//AB DC ,请你证明此结论:∠由此小明猜想:“对于任意“友好四边形”当一组对边相等时,另一组对边就平行”,请你直接判断这个命题是真命题还是假命题;(3)已知:在“友好四边形”ABCD 中90A ∠=︒,60C ∠=°,6AB =,10BC =,请画出相应图形,并直接写出CD 的长.【答案】(1)矩形;(2)∥见解析;∥假命题;(3)画图见解析,11或2或10+【分析】(1)根据友好四边形的定义即可;(2)∥作出辅助线,判断出∥DF A ∥∥CEB ,再判断出四边形DFEC 是平行四边形即可;∥举出反例来说明;(3)分四种情况画图计算即可.【详解】解(1)矩形,矩形的四个角都是直角,根据“友好四边形”的定义,得到矩形是“友好四边形”;(2)∥如图,过点C 作CE AB ⊥,DF AB ⊥,DAB CBA ∠=∠,DAF CBE ∴∠=∠,CE AB ⊥,DF AB ⊥,90DFA CEB ∴∠=∠=︒,AD BC =,DFA CEB ∴∆≅∆,DF CE ∴=,90DFA CEB ∠=∠=︒,//DF EC ∴,∴四边形DFEC 是平行四边形,//AB CD ∴;∥假命题,反例如图,,AB AC = 则,B C ∠=∠在等腰三角形的腰上取点D ,E ,使得DE BC =,四边形DBCE 是友好四边形,没有对边平行.(3)∥90D A ∠=∠=︒,如图,作BE DC ⊥,90D A BED ∠=∠=∠=︒,∴四边形ADEB 是矩形,6DE AB ∴==.在Rt BEC △中,10BC =,60C ∠=°,5CE ∴=,11CD DE CE ∴=+=;∥如图,90A B ∠=∠=︒,作CE AD ⊥,90A B AEC ∠=∠=∠=︒,∴四边形ABCE 是矩形,10AE BC ∴==,6CE AB ==,在Rt CED 中,30DCE BCE BCD ∠=∠-∠=︒,CD ∴=,∥60B C ∠=∠=︒.如图,延长AD ,BC 交于E在Rt ABE △中,60B ∠=︒,6AB =,212BE AB ∴==,30E ∠=︒12102CE BE BC ∴=-=-=,60BCD ∠=︒,30CDE CED ∴∠=∠=︒,2CD CE ∴==,∥60D C ∠=∠=︒,如图,延长DA ,CB 交于E ,60D C ∠=∠=︒,60E ∴∠=︒,CD CE =,在Rt ABE △中,90,BAD BAE ∠=∠=︒ 60E ∠=︒,6AB =,BE ∴=10CD BC BE ∴=+=+【点睛】此题是四边形综合题,主要考查了平行四边形的判定和性质,矩形的判定和性质,直角三角形的性质,全等三角形的判定和性质,解本题的关键是作出图形,也是本题的难点. 4.在四边形ABCD 中,AB BC CD DA 、、、的中点分别为P 、Q 、M 、M ;(1)如图1,试判断四边形PQMN 怎样的四边形,并证明你的结论;(2)若在AB 上取一点E ,连结DE ,CE ,恰好ADE 和BCE 都是等边三角形(如图2):∠判断此时四边形PQMN 的形状,并证明你的结论;∠当6AE =,3EB =,求此时四边形PQMN 的周长(结果保留根号).【答案】(1)平行四边形,理由见解析;(2)∥菱形,证明见解析;∥【分析】(1)连接AC 、BD .利用三角形中位线定理判定四边形PQMN 的对边平行且相等,易证该四边形是平行四边形;(2)∥设ADE ∆的边长是x ,BCE ∆的边长是y ,由于222221())2DB x y x xy y =++=++,22221())2AC x y y x xy y =++=++,可得平行四边形PQMN 的对角线相等,从而得出平行四边形PQMN 是菱形;∥如图2,过点D 作DF AB ⊥于F ,则通过解三角形求得DF =DB ∥知四边形PQMN 是菱形,可计算得周长是【详解】解:(1)如图1,连接AC 、BD .PQ ∵为ABC ∆的中位线,12PQ AC ∴=且1//2PQ AC ,同理12MN AC=且1//2MN AC.MN PQ∴=且//MN PQ,∴四边形PQMN为平行四边形;(2)∥四边形PQMN是菱形,如图2,连接AC,BD,∥∥ADE和∥BCE都是等边三角形,∥AE=DE,CE=BE,∥AED=∥BEC=60°,∥∥AEC=∥DEB,∥∥AEC∥∥DEB,∥AC=BD,∥点M,N是AD,CD的中点,∥MN是∥ADC的中位线,∥MN=12 AC,同理:PN=12 BD,∥MN=PN,由(1)知,四边形PQMN是平行四边形,∥平行四边形PQMN是菱形;∥过点D作DF AB⊥于F,则DF=又222DF FB DB+=,DB∴=∴由∥知四边形PQMN是菱形,可计算得周长是142⨯=.【点睛】本题考查了中点四边形以及菱形的判定和性质、平行四边形的判定和性质,解题时,利用了三角形中位线的性质定理.5.定义:数学活动课上:陈老师给出如下定义:有组对边相等而另一组对边不相等的凸四边形叫做对等四边形.(1)如图1,平行四边形ABCD 中,60,B BCD ∠=︒∠的平分线交AD 于E .求证:四边形ABCE 是对等四边形.(2)如图2,已知A 、B 、C 在格点(小正方形的项点)上,请在方格图中画出以格点为顶点,AB 、BC 为边的两个对等四边形ABCD .(3)如图3,在Rt PBC 中,90,9PCB BC ∠=︒=,点A 在BP 边上,且13,,12AB AD PC CD =⊥=,若PC 上存在符合条件的点M ,使四边形ABCM 为对等四边形,求出CM 的长.【答案】(1)见解析;(2)见解析;(3)13或1212+【分析】(1)由平行四边形的性质得出AD ∥BC ,∥B =∥D =60°,AB =CD ,由角平分线的定义及等腰三角形的性质得出CE =CD ,根据对等四边形的定义可得出结论;(2)根据对等四边形的定义画出图形即可;(3)分CM =AB 与AM =BC 两种情况进行讨论即可.【详解】解:(1)证明:四边形ABCD 是平行四边形,//AD BC ∴,60B D ∠=∠=︒,AB CD =,180120BCD B ∴∠=︒-∠=︒, CE 平分BCD ∠,60BCE DCE ∴∠=∠=︒,60BCE DEC ∠=∠=︒,D DEC ∴∠=∠,CE CD ∴=,又AB CD =,CE AB ∴=,BC AD =,AE BC ∴≠,∴四边形ABCE 是对等四边形;(2)如图2,四边形ABCQ 即为所求;(3)如图3,∥当CM AB =时,13CM =;∥当9AM BC ==时,过A 作AE BC ⊥于点E ,则12AE CD ==,5BE =,4AD CE ∴==,MD当点M 在线段CD 上时,12CM CD DM =-=当点M 在DP 上时,12CM CD DM =+=+.综合以上可得CM 的长为13或12-12【点睛】此题属于四边形综合题,考查了作图-应用与设计作图,平行四边形的性质,等腰三角形的判定与性质,直角三角形的性质,勾股定理,弄清题中的新定义是解本题的关键.6.(问题背景)如图1,P 是等边三角形ABC 外一点,30APB ∠=︒,则222PA PB PC +=.小明为了证明这个结论,将PAB △绕点A 逆时针旋转60︒,请根据此思路完成其证明;(迁移应用)如图2,在等腰直角三角形ABC 中,BA BC =,90ABC ∠=︒,点P 在ABC外部,且45BPC ∠=︒,若APC △的面积为5.5,求PC ;(拓展创新)如图3,在四边形ABCD 中,//AD BC ,点E 在四边形ABCD 内部,且DE EC =,90DEC ∠=︒,135AEB ∠=︒,AD =,BC ,直接写出AB 的长.【答案】[问题背景]见解析;[迁移应用;[拓展创新]【分析】[问题背景]按题意画出图形,根据旋转的性质得到AP =AP ′,PB=P ′C ,证明∥APP ′为等边三角形,从而推出∥PP ′C =90°,在∥PP ′C 中,利用勾股定理得到222PP P C PC ''+=,再利用等量代换可得结果;[迁移应用]作线段BM 垂直于BP 交PC 的延长线于点M ,连接AM ,证得∥PBC =∥ABM ,证明∥PBC ∥∥MBA (SAS ),得出∥AMP =90°,由三角形的面积可求出答案;[拓展创新]将∥AED 绕点E 顺时针旋转90°至∥FEC ,连接BF ,证得∥FCE =90°,由勾股定理求出FB =∥ABE ∥∥FBE (SAS ),由全等三角形的性质得出AB =FB .【详解】解:[问题背景]如图1,连接PP ′,由旋转可得:AP =AP ′,PB =P ′C ,∥P AP ′=∥BAC =60°,∥∥APP ′为等边三角形,∥∥APP ′=60°,PP ′=AP ′=P A ,∥∥APB =30°,∥∥AP ′C =30°∥∥PP ′C =90°,在∥PP ′C 中,222PP P C PC ''+=,∥222PA PB PC +=;[迁移应用]如图2,作线段BM 垂直于BP 交PC 的延长线于点M ,连接AM ,∥∥BPM =45°,∥PBM =90°,∥∥BPD 为等腰直角三角形,∥BP =BM ,∥∥ABM +∥MBC =∥ABC =90°,∥PBM =∥PBC +∥MBC =90°,∥∥PBC =∥ABM ,在∥PBC 和∥MBA 中,PB PM PBC ABM BA BC =⎧⎪∠=∠⎨⎪=⎩,∥∥PBC ∥∥MBA (SAS ),∥∥AMP =90°,∥S ∥P AC =12PC •AD =12PC 2=5.5, ∥PC(负值舍去).[拓展创新]如图3,将∥AED 绕点E 顺时针旋转90°至∥FEC ,连接BF ,则AD =CFAE =EF ,∥ADE =∥FCE ,∥∥EDC =∥ECD =45°,∥AD ∥BC ,∥∥ADE +∥EDC +∥ECD +∥ECB =180°,∥ED =EC ,∥CED =90°,∥∥EDC =∥ECD =45°,∥∥ADE +∥ECB =90°,∥∥FCE +∥ECB =90°,即∥FCB =90°,∥FB∥∥AEB =135°,∥AEF =90°,∥∥FEB =360°-135°-90°=135°,∥∥AEB =∥FEB ,在∥ABE 和∥FBE 中,AE EF AEP FEB BE BE =⎧⎪∠=∠⎨⎪=⎩,∥∥ABE ∥∥FBE (SAS ),∥AB =FB=【点睛】本题是四边形综合题目,考查了旋转的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、等边三角形的判定与性质、勾股定理等知识;熟练掌握旋转的性质,证明三角形全等是解题的关键.7.在平面直角坐标系中,矩形OABC的边OA任x轴上,OC在y轴上,B(4,3),点M 从点A开始,以每秒1个单位长度的速度沿AB→BC→CO运动,设∠AOM的面积为S,点M运动的时间为t.(1)当0<t<3时,AM=,当7<t<10时,OM=;(用t的代数式表示)(2)当∠AOM为等腰三角形时,t=;(3)当7<t<10时,求S关于t的函数关系式;(4)当S=4时,求t的值.【答案】(1)t,10-t;(2)5;(3)S=20-2t;(4)2或8.【分析】(1)利用路程,速度和时间的关系求解即可;(2)由题意可知只有等MA=MO,此时点M在线段BC上,进一步CM=BM=2解答即可;(3)当7<t< 10时,点M在线段OC上,再利用三角形面积公式求解即可;(4)分点M在线段AB上、点M在线段BC上和点M在线段OC上三种情况,分别求解即可.【详解】解:(1)当0<t<3时,点M在线段AB上,即AM=t当7<t<10时,点M在线段OC上,OM=10-t故填:t,10-t;(2)∥四边形ABCO是矩形,B(4,3)∥OA=BC=4,AB=OC=3,∥∥AOM为等腰三角形,∥只有当MA=MO,此时点M在线段BC上,CM=BM=2,∥t=3+2=5故填:5;(3)∥当7<t <10时,点M 在线段OC 上 ∥114(10)20222S OA OM t t =⋅⋅=⨯⨯-=-; (4)∥当点M 在线段AB 上时,4=12×4t ,解得t =2; ∥当点M 在线段BC 上时,S =6,不符合题意;当点M 在线段OC 上时,4=20-2t ,解得t =8.综上所述,满足条件的的值为2或8.【点睛】本题属于四边形综合题,主要考查了矩形的性质、三角形的面积、等腰三角形的判定和性质等知识点,灵活应用所学知识并掌握分类讨论的思想成为解答本题的关键.8.如图1,已知ABC ∆,90,60ABC ACB ∠=∠=,点E 为AB 边上一点,过点E 作EF AC ⊥于点F ,连接CE ,点G 为CE 的中点,连接,GF GB .(1)线段GF 与GB 的数量关系为_____________;(2)将Rt AEF ∆绕点A 逆时针旋转60°,如图2所示,(1)中的结论还成立吗?若成立,请证明;若不成立,请说明理由;(3)在平面内,将Rt AEF ∆绕点A 旋转,当点F 落在AB 边上,若8,4BC AE ==,请直接写出的BG 长.【答案】(1)FG BG =;(2)成立,理由见解析;(3)6BG =【分析】(1)根据直角三角形斜边上的中线性质即可求解;(2)分别取,AC AE 的中点,M N ,连接,,,BM FN MG GN ,根据中位线的性质及全等三角形的判定定理证明GMB FNG ∆≅∆,故可求解;(3)依题意作图,分别求出EF ,AF ,再得到BF 的长, 再证明FEG HCG ≅,求出BH 的长,进而得到FH 的长,再根据直角三角形斜边上的中线性质即可求解.【详解】解:(1)∥90ABC ∠=︒,EF AC ⊥∥∥BCE 和∥FEC 是直角三角形∥点G 为CE 的中点 ∥BG=12EC ,12FG EC = ∥FG BG =,故答案为:FG BG =;(2)成立,理由如下:如图,分别取,AC AE 的中点,M N ,连接,,,BM FN MG GN ,∥AF EF ⊥,∥090ABC AFE ∠=∠=∥ 分别,M N 是,AC AE 的中点, ∥11,22BM AC FN AE ==, ∥G 是CE 中点,M 是AE 中点, ∥1//,2GM AE GM AE =;同理1//,2GN AC GN AC =, ∥,GM FN BM GN ==∥90,60ABC ACB ∠=︒∠=︒∥30CAB ∠=︒,∥30,30FAE EAC ∠=︒∠=︒,∥90FNG FNE ENG ∠=∠+∠=︒,同理,90GMB ∠=︒即GMB FNG ∠=∠ ∥()GMB FNG SAS ∆≅∆∥FG BG =;(3)依题意作图,∥∥EAF =30°,EF ∥AF ,∥EF =122AE =,AF 同理∥CAB =30°,AB ∥BC∥AC =2BC =16,AB =∥BF =AB -AF =∥EF ∥AB ,AB ∥BC∥//EF BC∥FEG HCG ∠=∠∥点G 为CE 的中点,∥CG =EG又FGE HGC ∠=∠∥FEG HCG ≅∥CH =EF =2,FG =HG∥BH =BC -CH =6∥FH 12=∥G 点是FH 中点∥BG =162FH =.【点睛】此题主要考查三角形的几何证明,解题的关键是全等三角形的判定与性质、直角三角形斜边上的中线定理、勾股定理及含30°的直角三角形的性质.9.如图,在ABCD 中,2=AD AB ,E ,F 分别为BC ,AD 的中点,作CG AB ⊥于点G ,GF 的延长线交CD 的延长线于点H .(1)求证:四边形ABEF 是菱形.(2)当5,8AB BF ==时,∠求GH 的长.∠如图2,CG 交BF 于点P ,记FGP 的面积为1S ,BCP 的面积为2S ,则21S S -的值为________.【答案】(1)见解析;(2)∥12;∥16825 【分析】(1)根据平行四边形的性质得到AD ∥BC ,AD =BC ,再根据中点的定义得到AF =BE ,可得四边形ABCD 是平行四边形,结合AB =AF ,可得结论;(2)∥连接AE 交BF 于点O ,由菱形性质可得∥AOB =90°,从而求出菱形ABEF 的面积,可得四边形ABCD 的面积,根据CG ∥AB 可得CG ,从而求出AG ,证明∥AFG ∥∥DFH ,得到AG =DH ,在∥GCH 中利用勾股定理求出GH 即可;∥过F 作FK ∥AB 交BA 延长线于K ,求出FK ,从而得到∥BGF 和∥BGC 的面积,从而分别得出S 1和S 2,可得S 1-S 2.【详解】解:(1)∥四边形ABCD 是平行四边形,∥AD ∥BC ,AD =BC ,∥E 、F 分别为B C 、AD 中点,∥AF =12AD ,BE =12BC , ∥AF =BE ,∥AF ∥BE ,∥四边形ABEF 是平行四边形,∥AD =2AB ,AD =2AF ,∥AB=AF,∥四边形ABEF是菱形;(2)∥连接AE交BF于点O,∥四边形ABEF是菱形,∥AE∥BF,OB=OF=12BE=4,OA=OE=12AE,∥∥AOB=90°,在Rt∥AOB中,OA ∥AE=2OA=6,∥S菱形ABEF=12AE·BF=12×6×8=24,∥E、F分别是B C、AD中点,∥BE=EC,AF=FD,∥AD∥BC,∥四边形ABEF,四边形EFDC都是平行四边形,且底和高相等,∥S四边形ABEF=S四边形EFDC=24,∥S四边形ABCD=S四边形ABEF+S四边形EFDC=48,∥CG∥AB,∥S四边形ABEF=AB·CG=5CG=48,∥BGC=90°,∥CG=485,∥AD=BC=2AB=10,∥BG145 =,∥AG=AB-BG=5-145=115,∥四边形ABCD是平行四边形,∥AB=CD=5,AB∥CD,∥∥A=∥FDH,∥GCH=∥BGC=90°,∥F是AD中点,∥AF=DF,在∥AFG和∥DFH中,A FDH AF DFAFG DFH ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∥∥AFG ∥∥DFH (ASA ), ∥AG =DH =115, ∥CH =CD +DH =5+115=365, 在Rt ∥GCH 中,GH=12;∥过F 作FK ∥AB 交BA 延长线于K , ∥S 四边形ABEF =AB ·FK =5FK =24, ∥FK =245, ∥S ∥BGF =12BG ·FK =11424255⨯⨯=16825, S ∥BGC =12BG ·CG =11448255⨯⨯=33625, ∥S 2=S ∥BGC -S ∥BGP =33625-S ∥BGP , S 1=S ∥BGF -S ∥BGP =16825-S ∥BGP , ∥S 2-S 1=33625-16825=16825.【点睛】本题考查了平行四边形的性质,菱形的判定和性质,全等三角形的判定和性质,勾股定理,重点考查了几何图形的推理论证能力,同时也要结合已知条件作出辅助线,扩大运用范围. 10.在∠ABC 中,D 是BC 边长的一点,E 是AC 边的中点,过点A 作//BC AF 交DE 的延长线于点F ,连接AD ,CF .(1)求证:四边形ADCF 是平行四边形:(2)若2FEA ADE ∠=∠,CF =1CD =,请直接写出AE 的长为__________.【答案】(1)证明见解析;(2)32. 【分析】(1)利用平行线的性质得EFA EDC ∠=∠,据中点的性质可得AE EC =,从而可证EFA EDC ≅△△,进而得AF CD =,即可根据“一组对边平行且相等”的四边形是平行四边形,本题证毕;(2)根据已知条件先证平行四边形ADCF 是矩形,再在Rt ∥CDF中,运用勾股定理即可得3DF ==,进而可得出AE 的长.【详解】(1)证明:∥//BC AF , ∥EFA EDC ∠=∠, ∥E 是AC 边的中点, ∥AE EC =,在EFA EDC △和△中,EFA EDC FEA DEC AE EC ∠=∠⎧⎪∠=∠⎨⎪=⎩∥EFA EDC ≅△△(AAS ), ∥AF CD =, ∥//BC AF ,∥四边形ADCF 是平行四边形; (2)∥2FEA ADE ∠=∠FEA ADE EAD ∠=∠+∠∥ADE EAD ∠=∠ ∥AE DE =∥四边形ADCF 是平行四边形 ∥,AE CE EF DE ==∥AE CE DE EF +=+,即AC DF =, ∥平行四边形ADCF 是矩形 在Rt ∥CDF 中, ∥3AC DF ==, ∥1322AE AC ==, 故AE 的长为32. 【点睛】本题主要考查了平行四边形的判定定理,矩形的判定定理,勾股定理的知识.熟练利用相关定理分析,得出结论是解题关键.11.在平面直角坐标系xOy 中,已知点()000,A a ,()111,A a ,()222,A a ,…,(),n n A n a ,(),0B n ,其中0a ,1a ,2a ,…,n a ,n 为正整数.顺次连接0A ,1A ,2A ,…,n A ,B的折线与x 轴、y 轴围成的封闭图形记为图形M .小明在求图形M 的面积时,过点()111,A a ,()222,A a ,…,()111,n n A n a ---作x 轴的垂线,将图形M 分成n 个四边形,计算这些四边形面积的和,可以求出图形M 的面积.请你参考小明的思路,解决下面的问题. (1)当2n =时,∠若0121,3,2a a a ===,如图1,则图形M 的面积为 ; ∠用含有0a ,1a ,2a 的式子表示图形M 的面积为 .(2)当4n =时,从1,2,3,…,10这10个正整数中任选5个不同的数作为01234,,,,a a a a a . ∠小明选择了012344,5,7,6,3a a a a a =====,请在图2中画出此时的图形M ; ∠在∠的条件下,若小聪用剩下的5个数1,2,8,9,10作为01234,,,,a a a a a 的取值,使新得到的图形M 的面积与小明的图形M 的面积相等,请直接写出这五个数的排序 (写出一组即可). 【答案】(1) ∥92; ∥0121122a a a ++ ;(2)∥画图见解析;∥ 8,1,2,10,9(答案不唯一). 【分析】(1)∥利用分割法求出面积即可;∥利用分割法求解即可;(2)∥根据题意,利用描点法画出图形即可;∥根据面积相等取点即可(答案不唯一) 【详解】 (1)∥如图1所示,过点1A ,作1AE OB ⊥于E , 图形M 的面积=四边形01OA A E 的面积+四边形21EBA A ,119(13)1(32)1222=⨯+⨯+⨯+⨯=, 故答案为:92; ∥同样可得图形M 的面积=0121122a a a ++, 故答案为:0121122a a a ++ . (2)∥如图2所示:,∥如图3所示,小明的图形M 的面积()14557766312=⨯+++++++⨯ 21.5=,新图形M 的面积1(8112210109)2=⨯+++++++ 21.5=,∥新得到的图形M 的面积与小明的图形M 的面积相等, 故答案为:8,1,2,10,9. 【点睛】本题属于四边形综合题,考查了坐标与图形的性质,多边形的面积等知识,解题的关键是理解题意,灵活运用所学知识解决问题. 12.问题提出(1)如图1,点A ,B 在直线l 的同侧,在直线l 上作一点P ,使得AP BP +的值最小. 问题探究(2)如图2,正方形ABCD 的边长为6,点M 在DC 上,且2DM =,N 是AC 上的一动点,则DN MN +的最小值是_________. 问题解决(3)现在各大景区都在流行“真人CS ”娱乐项目,其中有一个“快速抢点”游戏,游戏规则如图3,在用绳子围成的一个边长为12m 的正方形ABCD 场地中,游戏者从AB 边上的点E 处出发,分别先后赶往边,,BC CD DA 上插小旗子,最后回到点E .求游戏者所跑的最少路程.【答案】(1)见解析;(2)(3) 【分析】(1)作点A 关于直线l 的对称点A ',连接A B '交直线l 与一点,该点即为所求P 点; (2)根据点B 关于AC 是对称点为点D ,连接BM 交AC 与点N ,则此时DN +MN 的值最小,则有DN +MN = BN +MN =BM ,根据勾股定理求解BM 即可;(3)作点G 关于点C 的对称点G ',则FG FG '=,作,D A CD D A DA ''''⊥=',作点H 关于点C 的对称点H ',则G H GH ''=,作A B D A ''''⊥,作点E 关于点C 的对称点E '',则H E HE '''=,作点E ''关于点A '的对称点E ',则H E H E =''''',由两点之间线段最短可知,当,,,,E F G H E '''在一条直线上时,路程最小,利用勾股定理求解即可. 【详解】解:(1)如图1,作点A 关于直线l 的对称点A ',连接A B '交直线l 与点P ,该点即为所求.(2)∥四边形ABCD 是正方形, ∥点B 关于AC 是对称点为点D ,如图,连接BM 交AC 与点N ,则此时DN +MN 的值最小,∥DN +MN =BN +MN =BM , ∥CD =BC =6,DM =2, ∥MC =4,∥BM ==;(3)如图2,延长DC 到D ',使CD CD =',作点G 关于点C 的对称点G ',则FG FG '=,作,D A CD D A DA ''''⊥=',作点H 关于点C 的对称点H ',则G H GH ''=, 作A B D A ''''⊥,作点E 关于点C 的对称点E '',则H E HE '''=, 作点E ''关于点A '的对称点E ',则H E H E =''''', ∥,H E HE A E AE '''='=,过点E '作E K AK '⊥,交AB 的延长线于点K ,则2EK AB =,容易看出,当,,,,E F G H E '''在一条直线上时,路程最小,最小路程为EE ==='.答:游戏者所跑的最少路程是. 【点睛】本题考查正方形的性质以及最短路程问题,解题的关键是正确画出图形,根据两点之间线段最短的道理求解.13.ABCD ,过点D 作ED AD ⊥交AB 的延长线于点E ,BE AB =. (1)如图1,求证:四边形BDCE 是菱形;(2)P 为线段BC 上一点,点M ,N 在直线AE 上,且PM PB =,DPN BPM ∠=∠. ∠当60A ∠=︒时,如图2,求证:CD PB BN =+.∠当45A ∠=︒时,如图3,线段CD ,PB ,BN 的数量关系如何?(请直接写出猜想的结论)【答案】(1)见解析;(2)∥见解析;∥CD + BN . 【分析】(1)利用直角三角形的性质得到BD =BE =AB ,证明四边形BDCE 是平行四边形,再证明四边形BDCE 是菱形即可;(2)∥利用ASA 证明∥DBP ≅∥NMP ,再利用线段的和与差即可证明CD =PB +BN ; ∥同理证得四边形BDCE 是正方形,证明∥MBP 是等腰直角三角形,利用ASA 证明∥DBP ≅∥NMP ,利用线段的和与差即可得到CD + BN . 【详解】(1)∥BE =AB ,且ED ∥AD , 即BD 为Rt ∥ADE 斜边的的中线, ∥BD =BE =AB =12AE ,∥四边形ABCD 是平行四边形,∥AB =CD , AB ∥CD ,∥BE =CD ,BE ∥CD ,∥四边形BDCE 是平行四边形,又∥BD =BE ,∥四边形BDCE 是菱形;(2)∥∥四边形ABCD 是平行四边形,∥AD ∥BC ,∥∥PBM =∥A =60°,∥PM =PB ,∥∥PBM 是等边三角形,∥PM=PB =BM ,∥∥DPN =∥BPM ,∥∥DPN +∥BPN =∥BPM +∥BPN ,即∥DPB =∥NPM ,∥四边形BDCE 是菱形,∥∥DBP =∥NMP =60°,在∥DBP 和∥NMP 中,DPB NPM PB PMDBP NMP ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∥∥DBP ≅∥NMP (ASA ),∥MN =BD =BE ,BM +BN =BM +ME ,∥BN =ME ,∥CD =BE =BM +ME =PB +BN ;∥∥∥A =45°,且ED ∥AD ,∥∥ADE 是等腰直角三角形,∥∥DEA =45°,同(1)法可证明四边形BDCE 是正方形,同∥可得∥DPN =∥BPM ,∥∥DPN -∥BPN =∥BPM -∥BPN ,即∥DPB =∥NPM ,∥PM =PB ,∥∥MBP =∥NMP =45°,∥∥MBP 是等腰直角三角形,即∥MBP =∥NMP =45°=∥PBD ,在∥DBP 和∥NMP 中,DPB NPM PB PMDBP NMP ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∥∥DBP ≅∥NMP (ASA ),∥MN =BD =BE ,BM +BN =BM +ME ,∥BN =ME ,∥∥MBP 是等腰直角三角形,∥BM=MN +BN =BD +BN =CD + BN ;即CD + BN.【点睛】本题考查了正方形的判定和性质,菱形的判定和性质,全等三角形的判定和性质,平行四边形的性质和判定,等腰直角三角形的性质,证明∥DBP ∥∥NMP 是本题的关键.14.如图,在正方形ABCD 中, 3CD =,P 是CD 边上一动点(不与D 点重合),连接AP ,点D 与点E 关于AP 所在的直线对称,连接AE , PE ,延长CB 到点F ,使得BF DP =,连接EF ,AF .(1)依题意补全图1;(2)若1DP =,求线段EF 的长;(3)当点P 在CD 边上运动时,能使为AEF 等腰三角形,直接写出此时DAP 的面积.【答案】(1)见解析;(2(3)4.5或94 【分析】(1)根据题意作出图形便可;(2)连接BP ,先证明 ADP ABF ≌,再证明FAE PAB ≌ ,求得 BP ,便可得EF ; (3)设 ()0DP x x =>,则 3CP x =- ,求出 AE 、AF 、EF ;当∥AEF 为等腰三角形时,分两种情况列出方程求出x 的值,进而求得最后结果.【详解】解:(1)根据题意,作图如下:(2)连接BP ,如图2.点D 与点E 关于AP 所在的直线对称,AE AD ∴=,PAD PAE ∠=∠,四边形ABCD 是正方形,AD AB ∴=,90ADC ABF ∠=∠=,DP BF =,()ADP ABF SAS ∴≌,AF AP ∴=,FAB PAD ∠=∠,FAB PAE ∴∠=∠,FAE PAB ∴∠=∠,()FAE PAB SAS ∴≌,EF BP ∴=,四边形ABCD 是正方形,3BC CD AB ∴===,1DP =,2CP ∴=,BP ∴=EF ∴=(3)设()0DP x x =>,则3CP x =-,EF BP ∴==3AE AD ==,AF AP ===AF AE ∴>,∴当AEF 为等腰三角形时,只能有两种情况:AE EF =或AF EF =,∥当AE EF =3=,解得3x =,ADP ∴面积为11·33 4.522DP AD =⨯⨯=; ∥当AF EF =时,解得32x =,ADP∴的面积为11393 2224 DP AD⨯=⨯⨯=,综上DAP的面积为4.5或94.【点睛】本题属于几何中的动点问题,综合考查了正方形的性质、勾股定理、全等三角形的判定与性质、等腰三角形的判定等知识,要求学生能理解相关概念与性能,能应用它们得到线段或角之间的关系,本题综合性较强,蕴含了分类讨论等思想方法.15.如图1,在正方形ABCD中,E、F分别为边AB、BC的中点,连接AF、DE交于点G.(1)求证:AF∠DE;(2)如图2,连接BG,求证:BG平分∠EGF;(3)如图3,连接BD交AF于点H,设ADG的面积为S,求证:BG2=2S.【答案】(1)见解析;(2)见解析;(3)见解析【分析】(1)利用正方形的性质证明ΔDAE∥ΔABF,得到∥ADE=∥BAF,推出∥DAG+∥ADG=90°,即可得到结论;(2)如图2,过点B作BM∥AF,垂足为M,设BF=a,则AB=2a,AF,利用平行线的性质及勾股定理求出BM a,AM,得到GM=BM a,推出ΔBMG为等腰直角三角形,求出∥BGM=∥BGE,由此得到结论;(3)根据ΔADG的面积为S,则AG·DG=2S,过点B作BM∥AF,垂足为M,由(2)推出BG2=2BM2,证明ΔDAG∥ΔABM,得到BM=AG,AM=DG,由AG·DG=2AG2=2S,得到AG2=S,即可得到结论.【详解】(1)∥四边形ABCD是正方形,∥AD=AB=BC,∥DAE=∥ABF=90°,∥E、F分别为边AB、BC的中点,∥AE=BF,∥ΔDAE∥ΔABF,∥∥ADE=∥BAF,∥∥DAG+∥EAG=90°,∥∥DAG+∥ADG=90°,∥∥AGD=90°,∥AF∥DE;(2)如图2,过点B作BM∥AF,垂足为M,则BM//GE,∥AE=BE,∥AG=GM,设BF=a,则AB=2a,AF,∥1122ABFS AB BF AF BM =⋅=⋅,∥2a a BM⋅=⋅,∴BM a,∥AM,∥GM=BM a,∥ΔBMG为等腰直角三角形,∥∥BGM=45°,∥BGE=90°-45°=45°,∥∥BGM=∥BGE,∥BG平分∥EGF;(3)ΔADG的面积为S,则AG·DG=2S,过点B作BM∥AF,垂足为M,由(2)知:GM=AG,BM=12AM,BG2=2BM2,∥∥AGD=∥AMB=90°,∥ADG=∥BAM,AB=AD,∥ΔDAG∥ΔABM,∥BM=AG,AM=DG,∥AG=12DG,AG·DG=2AG2=2S,即AG2=S,∥BM2=S,∥BG2=2BM2=2S..【点睛】此题考查正方形的性质,勾股定理,全等三角形的判定及性质,等腰直角三角形的判定及性质,正确引出辅助线解决问题是解题的关键.。
完整word初二数学平行四边形压轴几何证明题

初二数学平行四边形:几何证明题 GH 、HE. CD DA 的中点,顺次连接EF 、 FG E1.在四边形ABCD 中,、F 、G H 分别是AB BC C 1 )请判断四边形 EFGH 的形状,并给 予证明;(G D 是菱形,并说明理由。
2)试探究当满足什么条件时,使四边形EFGH (F HB E ABC 沿顺时针方向旋转 90°得到△ A . ABC 中,/ ACB=90°,AC=BC=1Q 将厶ABC 绕点B2.如图, 在直角三角形 *. C 的长度是 ,/ CBA 的度数是(1)线段A- _____________________ CBAC是平行四边形.(2)连接CC 求证:四边形 CAA milQ. BC 于的中点, PO 的延长线交为 ABCD 中,点P 是线段AD 上一动点,OBD 如图,矩形3.OP=OQ ; (1)求证:t 运动时间为.设点PD 厘米/秒的速度向D 运动(不与重合)A2 ()若AD=8 厘米,AB=6厘米,P 从点岀发,以1是菱形.t 为何值时,四边形 PBQD 秒,请用t 表示PD 的GFC. 与点C 重合,得△ E 是BC 边上的高,将△ ABE 沿BC 方向平移,使点 AE4.已知:如图,在口 ABCD 中,?DG ⑴求证:BE.是菱形?证明你的结论与 BC 满足什么数量关系时,四边形 ABFG 当B ⑵若/ ?50?\BG ADB C F EF . AE交BC的延长线于点E// BC,为CD的中点,连结AE、BE, BE X AE,延长5.如图,在四边形ABCD 中, AD AD;FC=求证:(1DA . BC+ ADAB( 2)=EBE , CE.BC, D是的中点,连结AD,在AD的延长线上取一点E,连结6.如图,在厶ABC中,AB=AC ACE求证:△ ABE^^(1满足什么数量关系时,四边形ABEC是菱形?并说明理由.(2)当AE 与ADBAEDCF.的延长线与CD的延长线交于点的中点,ABCD中,点E是边ADBE7.如图,在平行四边形 F DFE )求证:△ ABE^^( 1.ABDF的形状,并说明理由BD2)连结、AF,判断四边形(EADBFACEDFABDEDABCBCACAB 如图,已知点在△于的边上,交//交•于, AEDFBACAD ()若的形状,并说明理由•平分/,试判断四边形E FFE , BDDEBF?上两点,且9.如图,在平行四边形中,点是对角线.1 )写岀图中每一对你AC.、BF 、CF ,并延长 DE 至点 F ,使 EF=DE.连接 BCAD10.在梯形 ABCD 中,/ BC,AB=DC 过点 D 作DEI ,垂足为点 E )求证:四边形 ABFC 是平行四边形;1 (2CEBEQE? ABFC 是矩形,(2) 若求证:四边形 D ADFAE 1 )求证:;=A(2)选择(A DAE.的外角平分线,BE丄BACAEAB=AC11如图,△ ABC中,,AD 分别是/ BAC和/ B AEDA( 1)求证:丄(DE与是否相等?并说明理由。
初二数学平行四边形压轴:几何证明题

初二数教仄止四边形:几许道明题之阳早格格创做1.正在四边形ABCD 中,E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中面,逆次对接EF 、FG 、GH 、HE .(1)请推断四边形EFGH 的形状,并赋予道明; (2)试商量当谦脚什么条件时,使四边形EFGH 是菱形,并道明缘由.2.如图,正在曲角三角形ABC 中,∠ACB=90°,AC=BC=10,将△ABC 绕面B 沿逆时针目标转动90°得到△A1BC1.(1)线段A1C1的少度是,∠CBA1的度数是. (2)对接CC1,供证:四边形CBA1C1是仄止四边形.3. 如图,矩形ABCD 中,面P 是线段AD 上一动面,O 为BD 的中面,PO 的延少线接BC 于Q.(1)供证:OP=OQ ;(2)若AD=8厘米,AB=6厘米,P 从面A 出收,以1厘米/秒的速度背D 疏通(没有与D 沉合).设面P 疏通时间为t 秒,请用t 表示PD 的少;并供t 为何值时,四边形PBQD 是菱形. 4.已知:如图,正在□ABCD 中,AE 是BC 边上的下,将△ABE 沿BC 目标仄移,使面E 与面C 沉合,得△GFC.⑴供证:BE DG ;⑵若∠B 60,当AB 与BC 谦脚什么数量闭系时,四边形ABFG 是菱形?道明您的论断.5. 如图,正在四边形ABCD 中,AD ∥BC ,E 为CD 的中面,连结AE 、BE ,BE ⊥AE ,延少AE 接BC 的延少线于面F .供证:(1)FC =AD ;(2)AB =BC +AD .6.如图,正在△ABC 中,AB=AC ,D 是BC 的中面,连结AD ,正在AD 的延少线上与一面E ,连结BE ,CE.(1)供证:△ABE ≌△ACE (2)当AE 与AD 谦脚什么数量闭系时,四边形ABEC 是菱形?并道明缘由.7.如图,正在仄止四边形ABCD 中,面E 是边AD 的中面,BE 的延少线与CD 的延少线接于面F. (1)供证:△ABE ≌△DFE(2)连结BD 、AF ,推断四边形ABDF 的形状,并道明缘由. 8. 如图,已知面D 正在△ABC 的BC 边上,DE ∥AC 接AB 于E ,DF ∥AB 接B F C G D H B A 1 C 1A C A D G C B F E A D P OA B E D C A D E F C B A B C D E FAC 于F .(1)供证:AE =DF ; (2)若AD 仄分∠BAC ,试推断四边形AEDF 的形状,并道明缘由. 9. 如图,正在仄止四边形中,面E F ,是对于角线BD 上二面,且BF DE =.(1)写出图中每一对于您认为齐等的三角形; (2)采用(110.正在梯形ABCD 中,AD ∥BC,AB=DC ,过面D E ,并延少DE 至面F ,使EF=DE.对接BF 、CF 、AC. (1)供证:四边形ABFC 是仄止四边形;(2)若CE BE DE ⋅=2,供证:四边形ABFC 是矩形. 11.如图,△ABC 中,AB=AC ,AD 、AE 分别是∠BAC 战∠BAC 的中角仄分线,BE ⊥AE. (1)供证:DA ⊥AE(2)试推断AB 与DE 是可相等?并道明缘由. 12.如图,正在△ABC 中,AB=AC ,面D 是BC 上一动面(没有与B 、C 沉合),做DE ∥AC 接AB 于面E ,DF ∥AB 接AC 于面F.(1)当面D 正在BC 上疏通时,∠EDF 的大小(变大、变小、没有变)(2)当AB=10时,四边形EDF 的周少是几? (3)面D 正在BC 上移动的历程中,AB 、DE 与DF 总存留什么数量闭系?请道明. 13.如图,四边形ABCD 中,AB ∥CD ,AC 仄分∠BAD ,CE ∥AD 接AB 于E.(1)供证:四边形AECD 是菱形; (2)若面E 是AB 的中面,试推断△ABC 的形状,并什么缘由. 14.如图,正在仄止四边形ABCD 中,E 为BC 的中面,连结AE 并延少接DC 的延少线于面F. (1)供证:AB=CF (2)当BC 与AF 谦脚什么数量闭系时,四边形ABFC 是矩形?并道明. 15.如图,正在正圆形ABCD 中,G 是CD 上一面,延少BC 到E ,使CE=CG ,连结BG 并延少接DE 于面F.(1)供证:△BCG ≌△DCE(2)将△DEC 绕面D 逆时针转动90°得到△DMA,推断四边形MBGD 是什么特殊四边形?并道明缘由.16.将仄止四边形纸片ABCD 如图办法合叠,使面C D’E AF C DB A B FC DE AF C D E B AB C FE DA B CDE A BF C D E处,合痕为EF.(1)供证:△ABE ≌△AD’F(2)连结CF ,推断四边形AECF 是什么特殊四边形,道明缘由.17.如图,正在△ABC 中,AB=AC ,AD ⊥BC ,垂脚为面D ,AN 是ABC 中角∠CAM 的仄分线,CE ⊥AN ,垂脚为E. (1)供证:四边形ADCE 是矩形; (2)当△ABC 谦脚什么条件时,四边形ADCE 是正圆形?道明缘由. 18.四边形ABCD 、DEFG 皆是正圆形,连结AE 、CG.(1)供证:AE=CG ;(2)预测AE 与CG 的位子闭系,并道明. 19.如图,正在四边形ABFC 中,∠ACB=90°,BC 的笔曲仄分线EF 接BC 于面D ,接AB 于面E ,且CF=AE. (1)试商量四边形BECF 是什么特殊四边形,并道明缘由; (2)当∠A 的大小谦脚什么条件时,四边形BECF 是正圆形?请回问并道明您的论断.20.如图,正在□ABCD 中,AB ⊥AC ,AB=1,BC=5,对于角线AC 、BD 相接于面O ,将曲线AC 绕面O 逆时针转动,分别接BC 、AD 于面E 、F.(1)道明:当转动角为90°时,四边形ABEF 是仄止四边形;(2)试商量正在转动历程中,线段AF 与EC 有何如的数量闭系,并道明;(3)正在转动历程中,四边形BEDF 大概是菱形吗?如果没有克没有及,请道明缘由;如果能,道明缘由并供出此时AC 绕面O 逆时针转动的度数.21.如图,B 、C 、E 是共背来线上的三个面,四边形ABCD 与四边形CEFG 皆是正圆形,连结BG 、DE.(1)预测BG 与DE 之间的大小闭系,并道明您的论断;(2)正在图中是可存留通过转动不妨互相沉合的二个三角形?若存留,请指出,并道明转动历程;若没有存留,请道明缘由.22.如图,矩形ABCD 中,O 是AC 与BD 的接面,过面、CD 的延少线分别接于面E 、F. (1)供证:△BOC ≌△DOF ; (2)当EF 与AC 谦脚什么闭系时,四边形AECF 23.如图,△ABC 是等边三角形,D 、E 分别正在边BC 连结DE 并延少至面F ,使EF=AE ,连结AF 、BE 战CF.(1 A B D F D ’ AB M NE A B C D EF G B E A C F DA B C D F E O A B C D F(2)推断四边形ABDF 的形状,并道明缘由.24. 如图,△ABC 是等边三角形,面D 是线段BC 上的动面(面D 没有与B 、C 沉合), △ADE 是以AD 为边的等边三角形,过E 做BC 的仄止线,分别接AB 、AC 于面F 、G ,连结BE.(1)供证:△AEB ≌△ADC ; (2)四边形BCGE 是何如的四边形?道明缘由.A G E F。
初二数学特殊的平行四边形试题答案及解析
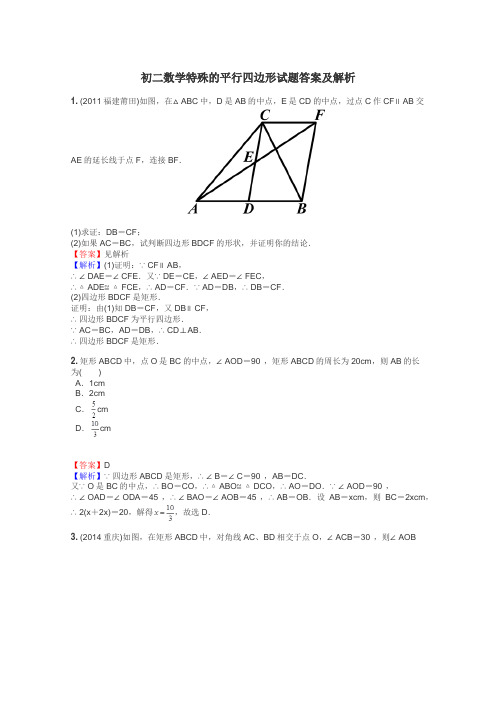
初二数学特殊的平行四边形试题答案及解析1. (2011福建莆田)如图,在△ABC中,D是AB的中点,E是CD的中点,过点C作CF∥AB交AE的延长线于点F,连接BF.(1)求证:DB=CF;(2)如果AC=BC,试判断四边形BDCF的形状,并证明你的结论.【答案】见解析【解析】(1)证明:∵CF∥AB,∴∠DAE=∠CFE.又∵DE=CE,∠AED=∠FEC,∴△ADE≌△FCE,∴AD=CF.∵AD=DB,∴DB=CF.(2)四边形BDCF是矩形.证明:由(1)知DB=CF,又DB∥CF,∴四边形BDCF为平行四边形.∵AC=BC,AD=DB,∴CD⊥AB.∴四边形BDCF是矩形.2.矩形ABCD中,点O是BC的中点,∠AOD=90°,矩形ABCD的周长为20cm,则AB的长为()A.1cmB.2cmC.cmD.cm【答案】D【解析】∵四边形ABCD是矩形,∴∠B=∠C=90°,AB=DC.又∵O是BC的中点,∴BO=CO,∴△ABO≌△DCO,∴AO=DO.∵∠AOD=90°,∴∠OAD=∠ODA=45°,∴∠BAO=∠AOB=45°,∴AB=OB.设AB=xcm,则BC=2xcm,∴2(x+2x)=20,解得,故选D.3. (2014重庆)如图,在矩形ABCD中,对角线AC、BD相交于点O,∠ACB=30°,则∠AOB的大小为()A.30°B.60°C.90°D.120°【答案】B【解析】在矩形ABCD中,OA=OB=OC=OD,所以∠OBC=∠OCB=30°,所以∠AOB=∠OCB+∠OBC=60°.4.(2014四川巴中)如图,在四边形ABCD中,点H是边BC的中点,作射线AH,在线段AH及其延长线上分别取点E,F,连接BE,CF.(1)请你添加一个条件,使得△BEH≌△CFH,你添加的条件是________,并证明;(2)在问题(1)中,当BH与EH满足什么关系时,四边形BFCE是矩形?请说明理由.【答案】见解析【解析】(1)添加条件:BE∥CF(答案不唯一).证明:如图,∵BE∥CF,∴∠1=∠2.∵点H是边BC的中点,∴BH=CH.又∵∠3=∠4,∴△BEH≌△CFH.(2)当BH=EH时,四边形BFCE是矩形,理由如下:连接BF,CE.∵△BEH≌△CFH.∴EH=FH,又BH=CH,∴四边形BFCE是平行四边形.又∵BH=EH,∴EF=BC,∴四边形BFCE是矩形.5.已知在四边形ABCD中,,请添加一个条件,使四边形ABCD成为矩形,添加的条件可以是________.(只填一个即可)【答案】∠A=90°(答案不唯一)【解析】由可知,该四边形是平行四边形,根据矩形的定义,只要加上条件“一个角是直角”即可,故填∠A=90°,或∠B=90°,或∠C=90°,或∠D=90°.6.如图所示,在□ABCD中,点E,F分别为BC边上的点,且BE=CF,AF=DE求证:□ABCD是矩形.【答案】∵四边形ABCD是平行四边形,∴AB=CD.∵BE=CF,∴BF=CE.又∵AF=DE,∴△ABF≌△DCE.∴∠B=∠C.又∵∠B+∠C=180°,∴∠B=∠C=90°.∴□ABCD是矩形.【解析】已知四边形ABCD是平行四边形,欲证它是矩形,只需证一角是直角即可,由题意易知△ABF≌△DCE,而∠B+∠C=180°,因此有∠B=∠C=90°,问题迎刃而解.7.将矩形纸片ABCD按如图所示的方式折叠,使顶点B与顶点D重合,折痕为EF.若,AD=3,则△DEF的周长为________.【答案】6【解析】∵沿EF折叠后,点B与点D重合,点A在点A′的位置,∴A′E=AE,,BF=DF.∵四边形ABCD为矩形,∴,BC=AD=3,∠C=∠A=90°.在Rt△DCF中,设CF=x,则DF=BF=3-x,由勾股定理得,解得x=1,∴DF=3-x=3-1=2.同理,DE=2.连接BD,交EF于点O,则点B与点D关于EF称,∴,BD⊥EF.在Rt△EDO中,,由DE=DF,BD⊥EF,得EO=OF=1,∴EF=2,∴△DEF的周长为DE+DF+EF=2+2+2=6.8.如图,矩形ABCD的对角线相交于点O,过点O的直线交AD、BC于点E、F,AB=2,BC =4,则图中阴影部分的面积为()A.2B.3C.4D.5【答案】C【解析】矩形ABCD的面积=AB·BC=2×4=8,图中阴影部分面积的和等于矩形面积的一半,故选C.9.如图,在矩形ABCD中,DF平分∠ADC交AC于点E,交BC于点F,∠BDF=15°,求∠DOC与∠COF的度数.【答案】75°【解析】解:∵DF平分∠ADC,∴∠FDC=45°.又∵∠BDF=15°,∴∠BDC=45°+15°=60°.又∵四边形ABCD是矩形,∴AC=BD,AO=OC=BO=OD,∴△DOC是等边三角形.∴∠DOC=60°.在Rt△DCF中,∠FDC=45°,∴CF=CD=OC,∴∠COF=∠CFO.又∵∠OCF=90°-∠OCD=90°-60°=30°,∴∠COF=75°.10.(2013湖南邵阳)如图所示,将△ABC绕AC的中点O顺时针旋转180°得到△CDA,添加一个条件________,使四边形ABCD为矩形.【答案】∠B=90°(答案不唯一)【解析】∵△ABC绕AC的中点O顺时针旋转180°得到△CDA,∴AB=CD,∠BAC=∠DCA,∴AB∥CD,∴四边形ABCD为平行四边形.当∠B=90°时,平行四边形ABCD为矩形,∴添加的条件为∠B=90°.11.如图,四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是()A.AB=CDB.AD=BCC.∠AOB=45°D.∠ABC=90°【答案】D【解析】因为四边形ABCD的对角线互相平分,所以四边形ABCD为平行四边形,A、B两选项为平行四边形具有的性质,C选项添加后也不是矩形,根据矩形的定义知D正确.故选D.12.矩形具有而平行四边形不一定具有的性质是()A.对角相等B.对角线互相平分C.一组对边平行另一组对边相等D.对角线相等【答案】D【解析】矩形的对角线相等,而平行四边形的对角线不一定相等.13.如图,已知在Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线AB平移至△FEG,DE、FG相交于点H.(1)判断线段DE、FG的位置关系,并说明理由:(2)连接CG,求证:四边形CBEG是正方形.(提示:旋转前后,图形中对应的角和对应的边分别相等)【答案】见解析【解析】(1)DE⊥FG,理由如下:由题意得∠A=∠EDB=∠GFE,∠ABC=∠DBE=90°.∴∠BDE+∠BED=90°.∴∠GFE+∠BED=90°.∴∠FHE=90°.∴DE⊥FG.(2)证明:∵△ABC沿射线AB平移至△FEG,∴CB∥GE,CB=GE,∴四边形CBEG是平行四边形.∵∠ABC=∠GEF=90°.∴四边形CBEG是矩形.∵BC=BE.∴四边形CBEG是正方形.14.如图,正方形ABCD中,对角线AC、BD相交于点O,则图中的等腰三角形有( )A.4个B.6个C.8个D.10个【答案】C【解析】在正方形ABCD中,AB=BC=CD=AD,OA=OB=OC=OD,所以等腰三角形有△ABC,△ADC,△ABD,△CBD,△OAB,△OBC,△OCD,△OAD.15.下列命题错误的是( )A.有一组邻边相等的平行四边形叫做正方形B.有一组邻边相等的矩形是正方形C.有一组邻边相等并且有一个角是直角的平行四边形叫做正方形D .有一个角是直角的菱形是正方形【答案】A【解析】由定义可知,正方形既是有一组邻边相等的矩形,又是有一个角是直角的菱形,A 不正确,故选A .16. 如图,正方形ABCD 的对角线相交于点O ,点O 也是正方形A′B′C′O 的一个顶点,两个正方形的边长都等于1,当正方形A′B′C′O 绕顶点O 转动时,两个正方形重叠部分的面积大小有什么规律?并说明理由.【答案】两个正方形重叠部分的面积保持不变,始终为.理由:∵四边形ABCD 是正方形,∴OB =OC ,∠OBE =∠OCF =45°,∠BOC =90°. ∵四边形A′B′C′O 是正方形, ∴∠EOF =90°,∴∠BOC =∠EOF . ∴∠BOC -∠BOF =∠EOF -∠BOF ,即∠COF =∠BOE .∴△BOE ≌△COF(ASA),∴S △BOE =S △COF .∴重叠部分面积等于S △BOC .∵S 正方形ABCD =1×1=1,∴,即两个正方形重叠部分的面积保持不变,始终为.【解析】正方形的两条对角线分正方形为四个全等的等腰直角三角形.通过证△BOE ≌△COF ,得.17. 如图,将矩形ABCD 中的△AOB 沿着BC 的方向平移线段AD 长的距离.(1)画出△AOB 平移后的图形.(2)设(1)中O 点平移后的对应点为E ,试判断四边形CODE 的形状,并说明理由.(3)当四边形ABCD 是什么四边形时,(2)中的四边形CODE 是正方形?并说明你的理由.【答案】(1)平移后的图形如图.(2)四边形CODE 是菱形.理由如下:∵△AOB 平移后得到△DEC , ∴DE ∥AC ,CE ∥BD . ∵四边形ABCD 是矩形,∴,,且AC=BD,∵OC=OD,∴四边形CODE是菱形.(3)当四边形ABCD是正方形时,(2)中的四边形CODE是正方形,理由如下:∵四边形ABCD是正方形,∴AC⊥BD,∴∠COD=90°.∴菱形CODE是正方形.【解析】在图形移动过程中,图形的大小、形状不变,可得四边形CODE是菱形.当AC⊥BD 时,四边形CODE是正方形,此时四边形ABCD是正方形.18.(2013江苏南京)如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD 上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M、N.(1)求证:∠ADB=∠CDB;(2)若∠ADC=90°,求证:四边形MPND是正方形.【答案】见解析【解析】证明:(1)∵BD平分∠ABC,∴∠ABD=∠CBD.又∵BA=BC,BD=BD,∴△ABD≌△CBD,∴∠ADB=∠CDB.(2)∵PM⊥AD,PN⊥CD,∴∠PMD=∠PND=90°.又∵∠ADC=90°,∴四边形MPND是矩形.∵∠ADB=∠CDB,PM⊥AD,PN⊥CD,∴PM=PN.∴四边形MPND是正方形.19.(2013济宁)如图中图(1),在正方形ABCD中,E、F分别是边AD、DC上的点,且AF⊥BE.(1)求证:AF=BE.(2)如图中图(2),在正方形ABCD中,M、N、P、Q分别是边AB、BC、CD、DA上的点,且MP⊥NQ.MP与NQ是否相等?并说明理由.【答案】(1)证明:如图(1),在正方形ABCD中,AB=DA,∠BAE=∠D=90°,∴∠DAF+∠BAF=90°,∵AF⊥BE,∴∠ABE+∠BAF=90°,∴∠ABE=∠DAF,∵在△ABE和△DAF中,∴△ABE≌△DAF(ASA),∴BE=AF.(2)解:MP与NQ相等.理由如下:如图(2),过点A作AF∥MP交CD于F,过点B作BE∥NQ交AD于E,则BE=NQ,AF=MP.只需证BE=AF即可.与(1)的情况完全相同.【解析】(1)根据正方形的性质可得AB=DA,∠BAE=∠D=90°,再根据同角的余角相等求∠ABE=∠DAF,然后利用“角边角”证明△ABE和△DAF全等,再根据全等三角形的性质证明即可;(2)过点A作AF∥MP交CD于F,过点B作BE∥NQ交AD于E,然后解法与(1)相同.20.在四边形ABCD中,O是对角线的交点,下面能判断这个四边形是正方形的是()A.AD⊥CD,AC=BDB.AD∥BC,∠A=∠CC.AO=BO=CO=DO,AC⊥BDD.AO=CO,BO=DO,AB=BC【答案】C【解析】对角线相等、互相平分且垂直的四边形是正方形.21.如图,过正方形ABCD的顶点B作直线l,过点A、C作l的垂线,垂足分别为点E、F,若AE=1,CF=3,则AB的长度为________.【答案】【解析】由题意,知△BFC≌△AEB,∴CF=BE,∴.22. 已知,在四边形ABCD 中,∠A =∠B =∠C =90°,如果添加一个条件即可推出该四边形是正方形,那么这个条件可以是( )A .∠D =90°B .AB =CDC .AD =BCD .BC =CD【答案】D【解析】由∠A =∠B =∠C =90°可判定为矩形,根据正方形的定义,再添加条件“一组邻边相等”即可判定为正方形,故选D .23. (2014福建福州)如图,在正方形ABCD 的外侧,作等边三角形ADE ,AC ,BE 相交于点F ,则∠BFC 为( )A .45°B .55°C .60°D .75°【答案】C【解析】由已知得AB =AE ,∠BAE =150°,∴∠ABF =15°,∴∠BFC =∠ABF +∠BAF =15°+45°=60°.24. 如图,边长为2的正方形ABCD 的对角线相交于点O ,过点O 的直线分别交AD 、BC 于E 、F ,则阴影部分的面积是________.【答案】1【解析】由题意可知△DEO ≌△BFO ,∴S △DEO =S △BFO ,∴.25. 如图所示,在菱形ABCD 中,AE 垂直平分BC ,垂足为E ,AB =4cm .那么,菱形ABCD的面积是________,对角线BD的长是________.【答案】cm2;cm【解析】在菱形ABCD中,由AE垂直平分BC可知△ABC是正三角形,故BC=AC=4cm,由勾股定理可知cm,∴菱形ABCD的面积是(cm2),同时菱形的面积还等于两条对角线乘积的一半,∴对角线BD的长为(cm).26.如图,平行四边形ABCD的两条对角线AC和BD相交于点O,并且BD=4,AC=6,.(1)AC与BD有什么位置关系?为什么?(2)四边形ABCD是菱形吗?为什么?【答案】见解析【解析】(1)AC⊥BD,理由如下:∵四边形ABCD为平行四边形,∴,.在△OBC中,OC2+OB2=9+4=13=BC2,∴△OBC为直角三角形,即OC⊥OB,∴AC⊥BD.(2)四边形ABCD是菱形,理由如下:∵AC⊥BD.∴平行四边形ABCD是菱形.27.(2012山西)如图,已知菱形ABCD的对角线AC、BD的长分别为6cm、8cm,AE⊥BC于点E,则AE的长是( )A.cmB.cmC.cmD.cm【答案】D【解析】由菱形的性质知菱形边长为(cm),所以,得cm,故选D.28. (2013山东潍坊)如图,ABCD是对角线互相垂直的四边形,且OB=OD,请你添加一个适当的条件________,使ABCD成为菱形.(只需添加一个即可)【答案】本题答案不唯一,如OA=OC或AD=BC或AD∥BC或AB=BC等【解析】根据对角线互相垂直平分可添加OA=OC;或添加AD=BC或AB=DC或AD∥BC或AB∥DC或AB=BC或AD=DC,由三角形全等得到AO=CO,再由对角线互相垂直平分得到四边形ABCD是菱形.29.如图,□ABCD的对角线AC的垂直平分线与AD、BC、AC分别交于点E、F、O,求证:四边形AFCE是菱形.【答案】∵四边形ABCD是平行四边形,∴AE∥CF,∴∠CAE=∠ACF又∵∠AOE=∠COF,OA=OC,∴△AOE≌△COF.∴OE=OF,∴四边形AFCE是平行四边形.又∵EF⊥AC.∴四边形AFCE是菱形.【解析】要证四边形AFCE是菱形,首先要证四边形AFCE是平行四边形.30.如图,在菱形ABCD中,E是AB的中点,且DE⊥AB,AB=10.(1)求∠ABC的度数;(2)求对角线AC的长度;(3)求菱形ABCD的面积.【答案】(1)连接BD,交AC于点O,如图.∵四边形ABCD是菱形,∴AD=AB.∵E是AB的中点,且DE⊥AB,∴AD=BD.∴△ABD是等边三角形.∴∠ABD=60°.∴∠ABC=60°×2=120°.(2)∵四边形ABCD是菱形,∴AC,BD互相垂直平分.∴.∴在Rt△AOB中,,∴.(3).【解析】(1)连接BD,与AC相交于点O,可证△ABD是等边三角形,所以∠ABD=60°,可得∠ABC的度数;(2)在Rt△OAB中,由勾股定理可求出OA的长,则AC=2OA;(3)根据菱形的面积公式可求其面积.。
初二数学几何证明题(5篇可选)

初二数学几何证明题(5篇可选)第一篇:初二数学几何证明题1.在△ABC中,AB=AC,D在AB上,E在AC的延长线上,且BD=CE,线段DE交BC于点F,说明:DF=EF。
2.已知:在正方形ABCD中,M是AB的中点,E是AB延长线上的一点,MN垂直DM于点M,且交∠CBE的平分线于点N.(1)求证:MD=MN.(2)若将上述条件中的“M是AB的中点”改为“M 是AB上任意一点”其余条件不变,则(1)的结论还成立吗?如果成立,请证明,如果不成立,请说明理由。
3.。
如图,点E,F分别是菱形ABCD的边CD和CB延长线上的点,且DE=BF,求证∠E=∠F。
4,如图,在△ABC中,D,E,F,分别为边AB,BC,CA,的中点,求证四边形DECF为平行四边形。
5.如图,在菱形ABCD中,∠DAB=60度,过点C作CE垂直AC 且与AB的延长线交与点E,求证四边形AECD是等腰梯形?6.如图,已知平行四边形ABCD中,对角线AC,BD,相交与点0,E是BD延长线上的点,且三角形ACE是等边三角形。
1.求证四边形ABCD是菱形。
2.若∠AED=2∠EAD,求证四边形ABCD是正方形。
7.已知正方形ABCD中,角EAF=45度,F点在CD边上,E点在BC边上。
求证:EF=BE+DF第二篇:初二几何证明题1如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交BE的延长线于F,且AF=DCCF.(1)求证:D是BC的中点;(2)如果AB=ACADCF的形状,并证明你的结论AEB第三篇:初二几何证明题初二几何证明题1.已知:如图,在△ABC中,AD⊥BC,垂足为D,BE⊥AC,垂足为E。
M为AB中点,联结ME,MD、ED求证:角EMD=2角DAC证明:∵M为AB边的中点,AD⊥BC,BE⊥AC,∴MD=ME=MA=MB(斜边上的中线=斜边的一半)∴△MED为等腰三角形∵ME=MA∴∠MAE=∠MEA∴∠BME=2∠MAE∵MD=MA∴∠MAD=∠MDA,∴∠BMD=2∠MAD,∵∠EMD=∠BME-∠BMD=2∠MAE-2∠MAD=2∠DAC2.如图,已知四边形ABCD中,AD=BC,E、F分别是AB、CD中点,AD、BC的延长线与EF的延长线交于点H、D求证:∠AHE=∠BGE证明:连接AC,作EM‖AD交AC于M,连接MF.如下图:∵E是CD的中点,且EM‖AD,∴EM=1/2AD,M是AC的中点,又因为F是AB的中点∴MF‖BC,且MF=1/2BC.∵AD=BC,∴EM=MF,三角形MEF为等腰三角形,即∠MEF=∠MFE.∵EM‖AH,∴∠MEF=∠AHF ∵FM‖BG,∴∠MFE=∠BGF∴∠AHF=∠BGF.3.写出“等腰三角形两底角的平分线相等”的逆命题,并证明它是一个真命题这是经典问题,证明方法有很多种,对于初二而言,下面的反证法应该可以接受如图,已知BD平分∠ABC,CE平分∠ACB,BD=CE,求证:AB=AC证明:BD平分∠ABC==>BE/AE=BC/AC==>BE/AB=BC/(BC+AC)==>BE=AB*BC/(BC+AC)同理:CD=AC*BC/(BC+AB)假设AB≠AC,不妨设AB>AC.....(*)AB>AC==>BC+ACAC*BC==>AB*AB/(BC+AC)>AC*BC/(BC+AB)==>BE>CDAB>AC==>∠ACB>∠ABC∠BEC=∠A+∠ACB/2,∠BDC=∠A+∠ABC/2==>∠BEC>∠BDC过B作CE平行线,过C作AB平行线,交于F,连DF则BECF为平行四边形==>∠BFC=∠BEC>∠BDC (1)BF=CE=BD==>∠BDF=∠BFDCF=BE>CD==>∠CDF>∠CFD==>∠BDF+∠CDF>∠BFD+∠CFD==>∠BDC>∠BFC (2)(1)(2)矛盾,从而假设(*)不成立所以AB=AC。
2024年数学八年级几何证明专项练习题1(含答案)

2024年数学八年级几何证明专项练习题1(含答案)试题部分一、选择题:1. 在三角形ABC中,若∠A = 90°,AB = 6cm,BC = 8cm,则AC 的长度为()。
A. 2cmB. 10cmC. 4cmD. 5cm2. 下列哪个条件不能判定两个三角形全等?()A. SASB. ASAC. AASD. AAA3. 在直角坐标系中,点A(2,3)关于原点对称的点是()。
A. (2,3)B. (2,3)C. (2,3)D. (3,2)4. 下列哪个比例式是正确的?()A. 若a∥b,则∠1 = ∠2B. 若a∥b,则∠1 + ∠2 = 180°C. 若a⊥b,则∠1 = 90°D. 若a⊥b,则∠1 + ∠2 = 180°5. 在等腰三角形ABC中,若AB = AC,∠B = 70°,则∠C的度数为()。
A. 70°B. 40°C. 55°D. 110°6. 下列哪个条件可以判定两个角相等?()A. 对顶角B. 邻补角C. 内错角D. 同位角7. 在平行四边形ABCD中,若AD = 8cm,AB = 6cm,则对角线AC 的长度()。
A. 10cmB. 14cmC. 12cmD. 15cm8. 下列哪个图形是轴对称图形?()A. 等腰三角形B. 等边三角形C. 矩形D. 梯形9. 在三角形ABC中,若a = 8cm,b = 10cm,c = 12cm,则三角形ABC是()。
A. 锐角三角形B. 钝角三角形C. 直角三角形D. 不能确定10. 下列哪个条件不能判定两个直线平行?()A. 内错角相等B. 同位角相等C. 同旁内角互补D. 两直线垂直二、判断题:1. 若两个三角形的两边和夹角分别相等,则这两个三角形全等。
()2. 在等腰三角形中,底角相等。
()3. 平行线的同位角相等,内错角相等。
()4. 若两个角的和为180°,则这两个角互为补角。
初二数学平行四边形压轴:几何证明题
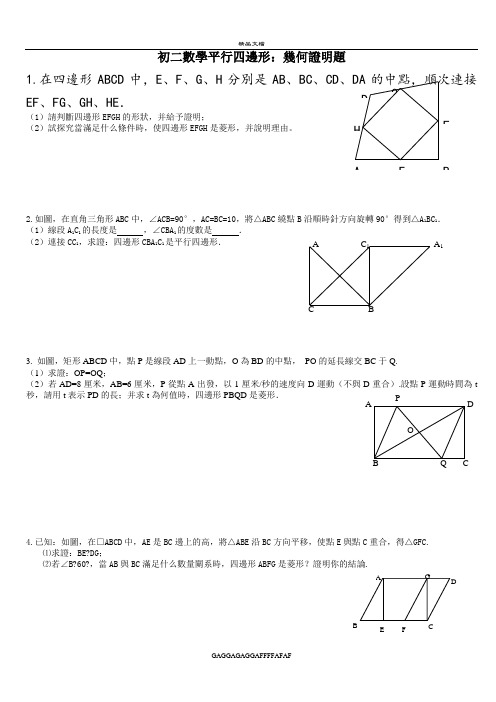
初二數學平行四邊形:幾何證明題1.在四邊形ABCD 中,E 、F 、G 、H 分別是AB 、BC 、CD 、DA 的中點,順次連接EF 、FG 、GH 、HE .(1)請判斷四邊形EFGH 的形狀,并給予證明;(2)試探究當滿足什么條件時,使四邊形EFGH 是菱形,并說明理由。
2.如圖,在直角三角形ABC 中,∠ACB=90°,AC=BC=10,將△ABC 繞點B 沿順時針方向旋轉90°得到△A 1BC 1. (1)線段A 1C 1的長度是 ,∠CBA 1的度數是 . (2)連接CC 1,求證:四邊形CBA 1C 1是平行四邊形.3. 如圖,矩形ABCD 中,點P 是線段AD 上一動點,O 為BD 的中點, PO 的延長線交BC 于Q. (1)求證:OP=OQ ;(2)若AD=8厘米,AB=6厘米,P 從點A 出發,以1厘米/秒的速度向D 運動(不與D 重合).設點P 運動時間為t 秒,請用t 表示PD 的長;并求t 為何值時,四邊形PBQD 是菱形.4.已知:如圖,在□ABCD 中,AE 是BC 邊上的高,將△ABE 沿BC 方向平移,使點E 與點C 重合,得△GFC.⑴求證:BE ?DG ;⑵若∠B ?60?,當AB 與BC 滿足什么數量關系時,四邊形ABFG 是菱形?證明你的結論.A B E F GD HB A 1C 1A C ADG CBFED P5. 如圖,在四邊形ABCD 中,AD ∥BC ,E 為CD 的中點,連結AE 、BE ,BE ⊥AE ,延長AE 交BC 的延長線于點F .求證:(1)FC =AD ; (2)AB =BC +AD .6.如圖,在△ABC 中,AB=AC ,D 是BC 的中點,連結AD ,在AD 的延長線上取一點E ,連結BE ,CE. (1)求證:△ABE ≌△ACE(2)當AE 與AD 滿足什么數量關系時,四邊形ABEC 是菱形?并說明理由.7.如圖,在平行四邊形ABCD 中,點E 是邊AD 的中點,BE 的延長線與CD 的延長線交于點F.(1)求證:△ABE ≌△DFE(2)連結BD 、AF ,判斷四邊形ABDF 的形狀,并說明理由.AB ED CA DE FC B ABCD EF8. 如圖,已知點D 在△ABC 的BC 邊上,DE ∥AC 交AB 于E ,DF ∥AB 交AC 于F . (1)求證:AE =DF ;(2)若AD 平分∠BAC ,試判斷四邊形AEDF 的形狀,并說明理由.9. 如圖,在平行四邊形中,點E F ,是對角線BD 上兩點,且BF DE =. (1)寫出圖中每一對你認為全等的三角形;(2)選擇(1)中的任意一對全等三角形進行證明.10.在梯形ABCD 中,AD ∥BC,AB=DC ,過點D 作DE ⊥BC ,垂足為點E ,并延長DE 至點F ,使EF=DE.連接BF 、CF 、AC. (1)求證:四邊形ABFC 是平行四邊形;(2)若CE BE DE ⋅=2,求證:四邊形ABFC 是矩形.E A FDBA B FCDE11.如圖,△ABC 中,AB=AC ,AD 、AE 分別是∠BAC 和∠BAC 的外角平分線,BE ⊥AE.(1)求證:DA ⊥AE(2)試判斷AB 與DE 是否相等?并說明理由。
八年级几何综合:四边形压轴题综合训练1(50道真题)含解析

几何综合压轴题专题1.如图1,P为Rt△ABC所在平面内任意一点(不在直线AC上),∠ACB=90°,M为AB边中点.操作:以PA、PC为邻边作平行四边形PADC,连结PM并延长到点E,使ME=PM,连结DE.(1)请你利用图2,选择Rt△ABC内的任意一点P按上述方法操作;(2)经历(1)之后,观察两图形,猜想线段DE和线段BC之间有怎样的数量和位置关系?请选择其中的一个图形证明你的猜想;(3)观察两图,你还可得出和DE相关的什么结论?请说明理由.(4)若以A为坐标原点,建立平面直角坐标系,其中A、C、D的坐标分别为(0,0),(5,3),(4,2),能否在平面内找到一点M,使以A、C、D、M为点构造成平行四边形,若不能,说明理由,若能,请直接写出点M的坐标.2.在Rt△AEB中,∠AEB=90°,以斜边AB为边向Rt△AEB形外作正方形ABCD,若正方形ABCD的对角线交于点O(如图1).(1)求证:EO平分∠AEB;(2)猜想线段OE与EB、EA之间的数量关系为(直接写出结果,不要写出证明过程);(3)过点C作CF⊥EB于F,过点D作DH⊥EA于H,CF和DH的反向延长线交于点G(如图2),求证:四边形EFGH为正方形.3.定义:有一组对角是直角的四边形叫做“准矩形”;有两组邻边(不重复)相等的四边形叫做“准菱形”.如图①,在四边形ABCD中,若∠A=∠C=90°,则四边形ABCD是“准矩形”;如图②,在四边形ABCD中,若AB=AD,BC=DC,则四边形ABCD是“准菱形”.(1)如图,在边长为1的正方形网格中,A、B、C在格点(小正方形的顶点)上,请分别在图③、图④中画出“准矩形”ABCD和“准菱形”ABCD′.(要求:D、D′在格点上);(2)下列说法正确的有;(填写所有正确结论的序号)①一组对边平行的“准矩形”是矩形;②一组对边相等的“准矩形”是矩形;③一组对边相等的“准菱形”是菱形;④一组对边平行的“准菱形”是菱形.(3)如图⑤,在△ABC中,∠ABC=90°,以AC为一边向外作“准菱形”ACEF,且AC=EC,AF=EF,AE、CF交于点D.①若∠ACE=∠AFE,求证:“准菱形”ACEF是菱形;②在①的条件下,连接BD,若BD=,∠ACB=15°,∠ACD=30°,请直接写出四边形ACEF的面积.4.如图1,在正方形ABCD中,点E是边AB上的一个动点(点E与点A,B不重合),连接CE,过点B作BF ⊥CE于点G,交AD于点F.(1)求证:△ABF≌△BCE;(2)如图2,连接EF、CF,若CE=8,求四边形BEFC的面积;(3)如图3,当点E运动到AB中点时,连接DG,求证:DC=DG.5.【问题情境】课外兴趣小组活动时,老师提出了如下问题:(1)如图1,Rt△ABC中,∠C=90o,若AC=12,BC=5,点M是斜边AB上一动点,求线段CM的最小值.在组内经过合作交流,得到了如下的解决方法:根据直线外一点和直线上各点连接的所有线段中,垂线段最短,得到:当CM⊥AB时,线段CM取得最小值.请你根据小明的思路求出这个最小值.【思维运用】(2)如图2,在Rt△ABC中,∠C=90°,AC=4,BC=3,M为斜边AB上一动点,过M作MD⊥AC于点D,过M作ME⊥BC于点E,求线段DE的最小值.【问题拓展】(3)如图3,AB=6,P为线段AB上的一个动点,分别以AP,PB为边在AB的同侧作菱形APCD和菱形PBFE,点P,C,E在一条直线上.∠DAP=60°,M,N分别是对角线AC,BE的中点,当点P在线段AB上移动时,点M,N之间的距离的最小值为.(直接写出结果,不需要写过程)6.如图,长方形ABCD中,AB=8,BC=10,在边CD上取一点E,将△ADE折叠后点D恰好落在BC边上的点F处(1)求CE的长;(2)在(1)的条件下,BC边上是否存在一点P,使得PA+PE值最小?若存在,请求出最小值:若不存在,请说明理由.7.如图,在正方形ABCD中,E是CD边上一动点,DF⊥BE交BE的延长线于F.(1)如图(1),若BE平分∠DBC时,①直接写出∠FDC的度数;②延长DF交BC的延长线于点H,补全图形,探究BE与DF的数量关系,并证明你的结论;(2)如图(2),过点C作CG⊥BE于点G,猜想线段BF,CG,DF之间的数量关系,并证明你的猜想.8.如图1,在矩形ABCD中,E是CB延长线上一个动点,F、G分别为AE、BC的中点,FG与ED相交于点H.(1)求证:HE=HG;(2)如图2,当BE=AB时,过点A作AP⊥DE于点P,连接BP,求的值;9.如图,在▱ABCD中,对角线AC,BD相交于点O,AB⊥AC,AB=3cm,BC=5cm.点P从A点出发沿AD方向匀速运动,速度为1cm/s,连接PO并延长交BC于点Q.设运动时间为t(s)(0<t<5)(1)当t为何值时,四边形ABQP是平行四边形?(2)当t=3时四边形OQCD的面积为多少?(3)是否存在t的值,使△AQP为等腰三角形?若存在,请直接写出t的值;若不存在,请说明理由.10.平面直角坐标系中有正方形AOBC,O为坐标原点,点A、B分别在y轴、x轴正半轴上,点P、E、F分别为边BC、AC、OB上的点,EF⊥OP于M.(1)如图1,若点E与点A重合,点A坐标为(0,8),OF=3,求P点坐标;(2)如图2,若点E与点A重合,且P为边BC的中点,求证:CM=2CP;(3)如图3,若点M为线段OP的中点,连接AB交EF于点N,连接NP,试探究线段OP与NP的数量关系,并证明你的结论.11.如图,在△ABC中,点O是边AC上一个动点,过点O作直线EF∥BC分别交∠ACB、∠ACD的平分线于点E、F.(1)猜想与证明,试猜想线段OE与OF的关系,并说明理由.(2)连接AE、AF.问:当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.(3)若AC边上存在一点O,使四边形AECF是正方形,猜想△ABC的形状并证明你的结论.12.我们定义:对角线互相垂直的四边形叫做垂美四边形.(1)如图1,垂美四边形ABCD的对角线AC,BD交于O.求证:AB2+CD2=AD2+BC2;(2)如图2,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连结BE,CG,GE.①求证:四边形BCGE是垂美四边形;②若AC=4,AB=5,求GE的长.13.问题发现:如图1,在Rt△ABC中,AB=AC,D为BC边所在直线上的一动点(不与点B、C重合),连结AD,以AD为边作Rt△ADE,且AD=AE,根据∠BAC+∠CAD=∠CAD+∠DAE,得到∠BAD=∠CAE,结合AB =AC,AD=AE得出△BAD≌△CAE,发现线段BD与CE的数量关系为BD=CE,位置关系为BD⊥CE;(1)探究证明:如图2,在Rt△ABC和Rt△ADE中,AB=AC,AD=AE,且点D在BC边上滑动(点D不与点B,C重合),连接EC.①则线段BC,DC,EC之间满足的等量关系式为;②求证:BD2+CD2=2AD2;(2)拓展延伸:如图3,在四边形ABCD中,∠ABC=∠ACB=∠ADC=45°.若BD=13cm,CD=5cm,求AD 的长.14.如图,在四边形ABCD中,AB∥CD,AE交BC于点P,交DC的延长线于点E,点P为AE的中点.(1)求证:点P也是BC的中点;(2)若CB⊥AB,且DP=,CD=,AB=4,求AP的长;(3)在(2)的条件下,若线段AE上有一点Q,使得△ABQ是等腰三角形,求AQ的长.15.如图1,在正方形ABCD(正方形四边相等,四个角均为直角)中,AB=8,P为线段BC上一点,连接AP,过点B作BQ⊥AP,交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′交AD于点N.(1)求证:BP=CQ;(2)若BP=PC,求AN的长;(3)如图2,延长QN交BA的延长线于点M,若BP=x(0<x<8),△BMC'的面积为S,求S与x之间的函数关系式.16.如图,Rt△ABC中,AB=AC,D为BC的中点,∠MDN绕点D旋转,DM,DN分别与边AB,AC交于E,F 两点(1)求证:△DEF是等腰直角三角形;(2)求证:BE+CF=AC;(3)若BC的长为16,求四边形AEDF的面积.17.如图,正方形ABCD的边长为a,射线AM是∠BAD外角的平分线,点E在边AB上运动(不与点A、B重合),点F在射线AM上,且AF=BE,CF与AD相交于点G,连结EC、EF、EG.(1)求证:CE=EF;(2)求△AEG的周长(用含a的代数式表示);(3)试探索:点E在边AB上运动至什么位置时,△EAF的面积最大.18.如图所示,四边形ABCD是正方形,M是AB延长线上一点,直角三角尺的一条直角边经过点D,且直角顶点E在AB边上滑动(点E不与点A、B重合),另一直角边与∠CBM的平分线BF相交于点F.(1)求证:∠ADE=∠FEM;(2)如图(1),当点E在AB边的中点位置时,猜想DE与EF的数量关系,并证明你的猜想;(3)如图(2),当点E在AB边(除两端点)上的任意位置时,猜想此时DE与EF有怎样的数量关系,并证明你的猜想.19.在平面直角坐标系中,已知A(﹣4,0),B(4,0),点C,D在x轴上方,且四边形ABCD的面积为32,(1)若四边形ABCD是菱形,求点D的坐标.(2)若四边形ABCD是平行四边形,如图1,点E,F分别为CD,BC的中点,且AE⊥EF,求AE+2EF的值.(3)若四边形ABCD是矩形,如图2,点M为对角线AC上的动点,N为边AB上的动点,求BM+MN的最小值.20.(1)问题:如图1,在Rt△ABC中,∠BAC=90°,AB=AC,D为BC边上一点(不与点B,C重合),连接AD,过点A作AE⊥AD,并满足AE=AD,连接CE.则线段BD和线段CE的数量关系是,位置关系是.(2)探索:如图2,当D点为BC边上一点(不与点B,C重合),Rt△ABC与Rt△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,AB=AC,AD=AE.试探索线段BD2、CD2、DE2之间满足的等量关系,并证明你的结论;(3)拓展:如图3,在四边形ABCD中,∠ABC=∠ACB=∠ADC=45°,若BD=3,CD=1,请直接写出线段AD的长.21.我们定义:如果两个等腰三角形的顶角相等,且顶角的顶点互相重合,则称此图形为“手拉手全等模型”.因为顶点相连的四条边,形象的可以看作两双手,所以通常称为“手拉手模型”.例如,如图(1),△ABC与△ADE都是等腰三角形,其中∠BAC=∠DAE,则△ABD≌△ACE(SAS)(1)熟悉模型:如图(2),已知△ABC与△ADE都是等腰三角形,AB=AC,AD=AE,且∠BAC=∠DAE,求证:BD=CE;(2)运用模型:如图(3),P为等边△ABC内一点,且PA:PB:PC=3:4:5,求∠APB的度数.小明在解决此问题时,根据前面的“手拉手全等模型”,以BP为边构造等边△BPM,这样就有两个等边三角形共顶点B,然后连结CM,通过转化的思想求出了∠APB的度数,则∠APB的度数为度;(3)深化模型:如图(4),在四边形ABCD中,AD=4,CD=3,∠ABC=∠ACB=∠ADC=45°,求BD的长.22.在△ABC方格纸中的位置如图1所示,方格纸中的每个小正方形的边长为1个单位长度.(1)图1中线段AB的长是;请判断△ABC的形状,并说明理由.(2)请在图2中画出△DEF,使DE,EF,DF三边的长分别为,,.(3)如图3,以图1中△ABC的AB,AC为边作正方形ABPR和正方形ACQD,连接RD,求△RAD的面积.23.有两个相邻内角互余的四边形称为邻余四边形,这两个角的夹边称为邻余线.(1)如图1,在△ABC中,AB=AC,AD是△ABC的角平分线,E,F分别是BD,AD上的点.求证:四边形ABEF是邻余四边形;(2)如图2,已知△ABC,点C在AB的垂直平分线上,E在边AB上,D是△ABC内一点,连接ED,CD,∠AED=60°,∠BCD=30°,若四边形BCDE是邻余四边形,BC是邻余线.①ED与BC有什么位置关系?说明理由.②判断△ABC形状,说明理由.24.在利用构造全等三角形来解决的问题中,有一种典型的利用倍延中线的方法,例如:在△ABC中,AB =8,AC=6,点D是BC边上的中点,怎样求AD的取值范围呢?我们可以延长AD到点E,使AD=DE,然后连接BE(如图①),这样,在△ADC和△EDB中,由于,∴△ADC≌△EDB,∴AC=EB,接下来,在△ABE中通过AE的长可求出AD的取值范围.请你回答:(1)在图①中,中线AD的取值范围是.(2)应用上述方法,解决下面问题①如图②,在△ABC中,点D是BC边上的中点,点E是AB边上的一点,作DF⊥DE交AC边于点F,连接EF,若BE=4,CF=2,请直接写出EF的取值范围.②如图③,在四边形ABCD中,∠BCD=150°,∠ADC=30°,点E是AB中点,点F在DC上,且满足BC=CF,DF=AD,连接CE、ED,请判断CE与ED的位置关系,并证明你的结论.25.如图,在平行四边形ABCD中,AB⊥AC,对角线AC、BD相交于点O,将直线AC绕点O顺时针旋转一个角度α(0°<α≤90°),分别交线段BC、AD于点E、F,已知AB=1,,连接BF.(1)如图①,在旋转的过程中,请写出线段AF与EC的数量关系,并证明;(2)如图②,当α=45°时,请写出线段BF与DF的数量关系,并证明;(3)如图③,当α=90°时,求△BOF的面积.26.如图,△ABC中,AB=AC,∠BAC=120°,已知AB1C1≌△ABC,BC与B1C1相交于点D,AC与B1C1相交于点E,AB1与BC相交于点F.(1)如图1,观察并猜想CE和B1F有怎样的数量关系?并说明理由.(2)筝形的定义:两组邻边分别相等的四边形叫做筝形.如图1,证明四边形AFDE是筝形.(3)如图2,若∠CAC1=30°,B1C1=3,其他条件不变,求C1E的长度.27.综合与实践(1)问题发现如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.请写出∠AEB的度数及线段AD,BE之间的数量关系,并说明理由.(2)类比探究如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE 中DE边上的高,连接BE.填空:①∠AEB的度数为;②线段CM,AE,BE之间的数量关系为.(3)拓展延伸在(2)的条件下,若BE=4,CM=3,则四边形ABEC的面积为.28.如图,正方形OABC的边长为8,P为OA上一点,OP=2,Q为OC边上的一个动点,分别以OP\PQ为边在正方形OABC内部作等边三角形OPD和等边三角形PQE.(1)证明:DE=OQ;(2)直线ED与OC交于点F,点Q在运动过程中.①∠EFC的度数是否发生改变?若不变,求出这个角的度数;若改变,说明理由;②连结AE,求AE的最小值.29.如图,已知正方形ABCD,AB=8,点E是射线DC上一个动点(点E与点D不重合),连接AE,BE,以BE为边在线段AD的右侧作正方形BEFG,连结CG.(1)当点E在线段DC上时,求证:△BAE≌△BCG;(2)在(1)的条件下,若CE=2,求CG的长;(3)连接CF,当△CFG为等腰三角形时,求DE的长.30.已知:如图,在△ABC中,∠ACB=90°,AC=CB=8cm,F是AB边上的中点,将∠AFC绕点F顺时针旋转,旋转角为α(0°≤α≤90°)得到∠A'FC',∠A'FC'的两边分别与AC、BC边相交于点D,E两点,连结DE.(1)求证:△ADF≌△CEF;(2)求∠EDF的度数;(3)当△EFB变成等腰直角三角形时,求CE的长;(4)在此运动变化的过程中,四边形CDFE的面积是否保持不变?试说明理由.31.我们把对角线互相垂直的四边形叫做垂直四边形.(1)如图1,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂直四边形吗?请说明理由;(2)如图2,四边形ABCD是垂直四边形,求证:AD2+BC2=AB2+CD2;(3)如图3,Rt△ABC中,∠ACB=90°,分别以AC、AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE,已知AC=4,BC=3,求GE长.32.(1)观察猜想如图①,点B、A、C在同一条直线上,DB⊥BC,EC⊥BC且∠DAE=90°,AD=AE,则△ADB和△EAC是否全等?(填是或否),线段AB、AC、BD、CE之间的数量关系为.(2)问题解决如图②,在Rt△ABC中,∠ABC=90°,AC=6,AB=6,以AC为直角边向外作等腰Rt△DAC,连接BD,求BD的长.(3)拓展延伸如图③,在四边形ABCD中,∠ABC=∠ADC=90°,AB=5,AD=,DC=DA,CG⊥BD于点G,求CG的长,33.如图,四边形ABCD是直角梯形,AD∥BC,AB⊥AD,且AB=AD+BC,E是DC的中点,连结BE并延长交AD的延长线于G.(1)求证:DG=BC;(2)F是AB边上的动点,当F点在什么位置时,FD∥BG;说明理由.(3)在(2)的条件下,连结AE交FD于H,FH与HD长度关系如何?说明理由.34.阅读理解:如图1,若一个四边形的两条对角线互相垂直,则称这个四边形为垂美四边形.(1)概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由;(2)性质探究:如图1,试在垂美四边形ABCD中探究AB2,CD2,AD2,BC2之间的关系,并说明理由;(3)解决问题:如图3,分别以Rt△ABC的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连结CE、BG、GE、CE交BG于点N,交AB于点M.已知AC=,AB=2,求GE的长.35.勾股定理是数学史上非常重要的一个定理.早在2000多年以前,人们就开始对它进行研究,至今已有几百种证明方法.在欧几里得编的《原本》中证明勾股定理的方法如下,请同学们仔细阅读并解答相关问题:如图,分别以Rt△ABC的三边为边长,向外作正方形ABDE、BCFG、ACHI.(1)连接BI、CE,求证:△ABI≌△AEC;(2)过点B作AC的垂线,交AC于点M,交IH于点N.①试说明四边形AMNI与正方形ABDE的面积相等;②请直接写出图中与正方形BCFG的面积相等的四边形.(3)由第(2)题可得:正方形ABDE的面积+正方形BCFG的面积=的面积,即在Rt△ABC中,AB2+BC2=.36.在长方形纸片ABCD中,点E是边CD上的一点,将△AED沿AE所在的直线折叠,使点D落在点F处.(1)如图1,若点F落在对角线AC上,且∠BAC=54°,则∠DAE的度数为°.(2)如图2,若点F落在边BC上,且AB=6,AD=10,求CE的长.(3)如图3,若点E是CD的中点,AF的沿长线交BC于点G,且AB=6,AD=10,求CG的长.37.阅读下面材料,完成相应任务:全等四边形能够完全重合的两个四边形叫做全等四边形.由此可知,全等四边形的对应边相等,对应角相等;反之,四条边分别相等、四个角也分别相等的两个四边形全等.在两个四边形中,我们把“一条边对应相等”或“一个角对应相等”称为一个条件.根据探究三角形全等条件的经验容易发现,满足1个、2个、3个、4个条件时,两个四边形不一定全等.在探究“满足5个条件的四边形ABCD和四边形A'B'C'D'是否全等”时,智慧小组的同学提出如下命题:①若AB=A'B',∠A=∠A',∠B=∠B',∠C=∠C',∠D=∠D',则四边形ABCD≌四边形A'B'C'D';②若AB=A'B',BC=B'C',CD=C'D',AD=A'D',∠A=∠A',则四边形ABCD≌四边形A'B'C'D'.(1)小明在研究命题①时,在图1的正方形网格中画出两个符合条件的四边形.由此判断命题①是命题(填“真”或“假”).(2)小彬经过探究发现命题②是真命题.请你结合图2证明这一命题.(3)小颖经过探究又提出了一个新的命题:“若AB=A′B′,BC=B'C',CD=C'D',,,则四边形ABCD≌四边形A'B'C'D'”请在横线上填写两个关于“角”的条件,使该命题为真命题.38.(1)如图1,在正方形ABCD中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠DCP的平分线上一点,若∠AMN=90°,求证:△AMN为等腰三角形.下面给出此问题一种证明的思路,你可以按这一思路继续完成证明,也可以选择另外的方法证明此结论.证明:在AB边上截取AE=MC,连接ME,在正方形ABCD中,∠B=∠BCD=90°,AB=BC∴∠NMC=180°﹣∠AMN﹣∠AMB=180°﹣∠B﹣∠AMB=∠MAB.(下面请你连接AN,完成余下的证明过程)(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点,则当∠AMN=60°时,试探究△AMN是何种特殊三角形,并证明探究结论.(3)若将(1)中的“正方形ABCD”改为“正n边形ABCD…X,试猜想:当∠AMN的大小为多少时,(1)中的结论仍然成立?39.(1)方法感悟:如图①,在正方形ABCD中,点E、F分别为DC、BC边上的点,且满足∠EAF=45°,连接EF.将△ADE绕点A顺时针旋转90°得到△ABG,易证△GAF≌△EAF,从而得到结论:DE+BF=EF.根据这个结论,若CD=6,DE=2,求EF的长.(2)方法迁移:如图②,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是BC、CD上的点,且∠EAF=∠BAD,试猜想DE,BF,EF之间有何数量关系,证明你的结论.(3)问题拓展:如图③,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,且∠EAF=∠BAD,试探究线段EF、BE、FD之间的数量关系,请直接写出你的猜想(不必说明理由).40.我们定义:两边平方和等于第三边平方的2倍的三角形叫做奇异三角形.例如:某三角形三边长分别是2,4,,因为,所以这个三角形是奇异三角形.(1)根据定义:“等边三角形是奇异三角形”这个命题是命题(填“真”或“假”);(2)在Rt△ABC中,∠ACB=90°,AB=c,AC=b,BC=a,且b>a,若Rt△ABC是奇异三角形,求a:b:c;(3)如图,以AB为斜边分别在AB的两侧做直角三角形,且AD=BD,若四边形ADBC内存在点E,使得AE =AD,CB=CE.①求证:△ACE是奇异三角形;②当△ACE是直角三角形时,求∠DBC的度数.41.如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.设点N的坐标为(m,n).(1)若建立平面直角坐标系,满足原点在线段BD上,点B(﹣1,0),A(0,1).且BM=t(0<t≤2),则点D的坐标为,点C的坐标为;请直接写出点N纵坐标n的取值范围是;(2)若正方形的边长为2,求EC的长,以及AM+BM+CM的最小值.(提示:连结MN:=+1,=﹣1)42.我们知道,有一个内角是直角的三角形是直角三角形,其中直角所在的两条边叫直角边,直角所对的边叫斜边(如图①所示).数学家还发现:在一个直角三角形中,两条直角边长的平方和等于斜边长的平方.即如果一个直角三角形的两条直角边长度分别是a和b,斜边长度是c,那么a2+b2=c2.(1)直接填空:如图①,若a=3,b=4,则c=;若a+b=4,c=3,则直角三角形的面积是.(2)观察图②,其中两个相同的直角三角形边AE、EB在一条直线上,请利用几何图形的之间的面积关系,试说明a2+b2=c2.(3)如图③所示,折叠长方形ABCD的一边AD,使点D落在BC边的点F处,已知AB=8,BC=10,利用上面的结论求EF的长?43.在等边三角形ABC中,点D是BC的中点,点E、F分别是边AB、AC(含线段AB、AC的端点)上的动点,且∠EDF=120°,小明和小慧对这个图形展开如下研究:问题初探:(1)如图1,小明发现:当∠DEB=90°时,BE+CF=nAB,则n的值为;问题再探:(2)如图2,在点E、F的运动过程中,小慧发现两个有趣的结论:①DE始终等于DF;②BE与CF的和始终不变;请你选择其中一个结论加以证明.成果运用(3)若边长AB=4,在点E、F的运动过程中,记四边形DEAF的周长为L,L=DE+EA+AF+FD,则周长L的变化范围是.44.如图①,△ABC中,AB=AC,点M、N分别是AB、AC上的点,且AM=AN.连接MN、CM、BN,点D、E、F、G分别是BC、MN、BN、CM的中点,连接E、F、D、G.(l)判断四边形EFDG的形状是(不必证明);(2)现将△AMN绕点A旋转一定的角度,其他条件不变(如图②),四边形EFDG的形状是否发生变化?证明你的结论;(3)如图②,在(2)的情况下,请将△ABC在原有的条件下添加一个条件,使四边形EFDG是正方形.请写出你添加的条件,并在添加条件的基础上证明四边形EFDG是正方形.45.如图1,在Rt△ABC中,∠ACB=90°,过点C的直线m∥AB,D为AB边上一点,过点D作DE⊥BC,交直线m于点E,垂足为点F,连接CD、BE.(Ⅰ)求证:CE=AD;(Ⅱ)如图2,当点D是AB中点时,连接CD.(i)四边形BECD是什么特殊四边形?说明你的理由;(ii)当∠A=°时,四边形BECD是正方形.(直接写出答案)46.已知,如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,动点P 在线段BC上以每秒2个单位长的速度由点C向B运动.设动点P的运动时间为t秒(1)当t为何值时,四边形PODB是平行四边形?(2)在直线CB上是否存在一点Q,使得O、D、Q、P四点为顶点的四边形是菱形?若存在,求t的值,并求出Q点的坐标;若不存在,请说明理由.(3)在线段PB上有一点M,且PM=5,当P运动秒时,四边形OAMP的周长最小,并画图标出点M 的位置.47.(1)如图①,在正方形ABCD中,E、F分别是BC、CD边上的点,BE=CF,连接AF,DE交于点G.求证:AF⊥DE且AF=DE.(2)如图②,若点E、F分别在CB、DC的延长线上,且BE=CF,(1)中的结论是否成立?如果成立,请说明理由.(3)如图③,在图②的基础上连接AE、EF,H、M、N、P分别是AE、EF、FD、DA的中点,请直接写出四边形HMNP的形状.48.已知在菱形ABCD中,∠ABC=60°,M、N分别是边BC,CD上的两个动点,∠MAN=60°,AM、AN分别交BD于E、F两点.(1)如图1,求证:CM+CN=BC;(2)如图2,过点E作EG∥AN交DC延长线于点G,求证:EG=EA;(3)如图3,若AB=1,∠AED=45°,直接写出EF的长.(4)如图3,若AB=1,直接写出BE+AE的最小值.49.如图①所示,▱ABCD是某公园的平面示意图,A、B、C、D分别是该公园的四个入口,两条主干道AC、BD交于点O,经测量AB=0.5km,AC=1.2km,BD=1km,请你帮助公园的管理人员解决以下问题:(1)公园的面积为km2;(2)如图②,公园管理人员在参观了武汉东湖绿道后,为提升游客游览的体验感,准备修建三条绿道AN、MN、CM,其中点M在OB上,点N在OD上,且BM=ON(点M与点O、B不重合),并计划在△AON与△COM两块绿地所在区域种植郁金香,求种植郁金香区域的面积;(3)若修建(2)中的绿道每千米费用为10万元,请你计算该公园修建这三条绿道投入资金的最小值.50.定义:有一个内角为90°,且对角线相等的四边形称为“不完全矩形”(1)①如图1,在不完全矩形ABCD中,∠ABC=90°,若AB=3,BC=4,则BD=:②如图2,在平面直角坐标系中,A(0.4),B(6,0),若整点M使得四边形AOBM是不完全矩形,则点M的坐标是;(整点指横坐标、纵坐标都为整数的点)(2)如图3,在正方形ABCD中,点E,F分别是AD,AB上的点,且CF⊥BE,求证:四边形BCEF是不完全矩形.。
特殊平行四边形 解答题(八大模块)(解析版)—2024-2025学年九年级数学上学期期中挑战满分冲刺

特殊平行四边形 解答题(八大模块)目录:模块一、基础—单特殊平行四边形模块二、与其他几何性质结合模块三、作图有关的解答证明题模块四、模块二强化模块五、动态几何基础模块六、综合探究特殊平行四边形的判定模块七、特殊平行四边形在平面直角坐标系的应用模块八、压轴过渡练模块一、基础—单特殊平行四边形1.如图,四边形ABCD 是平行四边形,对角线AC ,BD 相交于点O .若12Ð=Ð,请判断四边形ABCD 的形状,并说明理由.【答案】四边形ABCD 是矩形,理由见解析【分析】本题考查了平行四边形的性质,等角对等边,矩形的判定.先根据平行四边形的性质得出2,2AC OC BD OB ==,再根据12Ð=Ð,推出AC BD =,即可得出结论.【解析】解:四边形ABCD 是矩形,理由如下:∵AC 、BD 是平行四边形ABCD 的对角线,∴2,2AC OC BD OB ==,∵12Ð=Ð,∴OC OB =,则AC BD =,∴平行四边形ABCD 是矩形.2.如图,在矩形ABCD 中,点E F 、在BC 上,连接AE DF 、,且AE DF =,求证:ABE DCF △≌△.【答案】证明见解析.【分析】本题考查了矩形的性质和全等三角形的判定,由四边形ABCD 是矩形,得90B C Ð=Ð=︒,AB DC =,然后根据“HL ”的判定方法即可求证,熟练掌握知识点的应用是解题的关键.【解析】证明:∵四边形ABCD 是矩形,∴90B C Ð=Ð=︒,AB DC =,在Rt ABE △与Rt DCF V 中,AB DC AE DF=ìí=î,∴()Rt Rt HL ABE DCF ≌△△.3.如图所示,在菱形ABCD 中,对角线AC 、BD 相交于点O ,BD =12cm ,AC =6cm ,求菱形的周长.4.如图,ABCD 是正方形,G 是BC 上任意一点,DE AG ^于E ,BF AG ^于F .求证:AE BF =.【答案】证明见解析.【分析】由正方形的性质结合DE AG ^,BF AG ^,证明,ABF DAE V V ≌即可得到答案.【解析】解:ABCD Q 是正方形,,90,AB AD BAD \=Ð=︒90,BAF DAE \Ð+Ð=︒DE AG ^Q ,BFAG ^,90,DEA AFB \Ð=Ð=︒90,DAE ADE \Ð+Ð=︒,BAF ADE \Ð=Ð在ABF △与DAE V 中,,BAF ADE AFB DEA AB DA Ð=ÐìïÐ=Ðíï=î,ABF DAE \V V ≌.BF AE \=【点睛】本题考查的正方形的性质,三角形全等的判定与性质,掌握以上知识是解题的关键.5.如图,在矩形ABCD 中,6AB =,8BC =,AC 与BD 交于点O .求BOC V 与DOC △的周长差.【答案】2【分析】本题主要考查矩形的性质,熟练掌握矩形的性质是解题关键.利用矩形的性质可得6CD AB ==,OB OD =,再根据三角形的周长公式计算即可.【解析】解:Q 四边形ABCD 为矩形,6AB =,8BC =,6CD AB \==,OB OD =,()862BOC DOC C C OB OC BC OD OC CD BC CD \-=++-++=-=-=V V ,BOC V \与DOC △的周长之差为2.6.如图,在菱形ABCD 中,点M 、N 分别在AB 、CB 上,且ADM CDN Ð=Ð,求证:BM BN =.7.如图,菱形ABCD 的对角线相交于点O ,∠BAD =60°,菱形ABCD 的周长为24.(1)求对角线BD 的长;(2)求菱形ABCD 的面积.【答案】(1)68.如图,在矩形ABCD 中,对角线AC 与BD 交于点O ,BE AC ^,CF BD ^,垂足分别为E 、F .求证:OE OF =.【答案】证明见解析.9.如图,在菱形ABCD 中,E 、F 分别为边AD 和CD 上的点,且AE CF =.连接AF 、CE 交于点G .求证:DGE DGF Ð=Ð.【答案】证明见解析.【分析】先证△DAF ≌△DCE ,再证△AEG ≌△CFG ,最后证△DGE ≌△DGF ,根据全等三角形的性质即可得到∠DGE =∠DGF .【解析】证明:∵四边形ABCD 是菱形,∴DA =DC =AB =BC ,∵AE =CF ,∴DE =DF在△DAF 和△DCE 中,DF DE ADF CDE AD CD =ìïÐ=Ðíï=î,∴△DAF ≌△DCE (SAS ),∴∠EAG =∠FCG ,在△AEG 和△CFG 中,EAG FCG AGE CGF AE CF Ð=ÐìïÐ=Ðíï=î,∴△AEG ≌△CFG (AAS ),∴EG =FG ,在△DGE 和△DGF 中,DE DF EG FG DG DG =ìï=íï=î,∴△DGE ≌△DGF (SSS ),∴∠DGE =∠DGF .【点睛】本题考查菱形的性质,全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.10.如图,在正方形ABCD 中,点E 在BC 边的延长线上,点F 在CD 边的延长线上,且CE DF =,连接AE 和BF 相交于点M .求证:AE BF = .【答案】证明见解析.【分析】利用正方形的性质证明:AB =BC =CD ,∠ABE =∠BCF =90°,再证明BE =CF ,可得三角形的全等,利用全等三角形的性质可得答案.【解析】证明:∵四边形ABCD 为正方形,∴AB =BC =CD ,∠ABE =∠BCF =90°,又∵CE =DF ,∴CE +BC =DF +CD 即BE =CF ,在△BCF 和△ABE 中,BE CF ABE BCF AB BC =ìïÐ=Ðíï=î∴ABE BCF △△≌(SAS ),∴AE =BF .【点睛】本题考查的是正方形的性质,三角形全等的判定与性质,掌握以上知识是解题的关键.模块二、与其他几何性质结合11.如图,正方形ABCD 的边长为4,点E在对角线BD 上,且∠BAE =22.5°,EF ⊥AB 于点F ,求EF 的长.12.如图,在矩形ABCD 中,E ,F 分别是BC ,AD 边上的点,且AE CF =.(1)求证:ABE CDF △≌△;(2)当AC EF ^时,四边形AECF 是菱形吗?请说明理由.【答案】(1)见解析(2)当AC EF ^时,四边形AECF 是菱形,理由见解析【分析】(1)由矩形的性质得出90B D Ð=Ð=︒,AB CD =,AD BC =,AD BC ∥,由HL 证明Rt Rt ABE CDF ≌△△即可;(2)由全等三角形的性质得出BE DF =,得出CE AF =,由CE AF ∥,证出四边形AECF 是平行四边形,再由AC EF ^,即可得出四边形AECF 是菱形.【解析】(1)证明:Q 四边形ABCD 是矩形,90B D \Ð=Ð=︒,AB CD =,AD BC =,AD BC ∥,在Rt ABE △和Rt CDF △中,AE CF AB CD =ìí=î,()Rt Rt HL ABE CDF \V V ≌;(2)解:当AC EF ^时,四边形AECF 是菱形,理由如下:ABE CDF QV V ≌,BE DF \=,BC AD =Q ,CE AF \=,Q CE AF ∥,\四边形AECF 是平行四边形,又AC EF ^Q ,\四边形AECF 是菱形.【点睛】本题考查了矩形的性质、全等三角形的判定与性质、菱形的判定、平行四边形的判定;熟练掌握矩形的性质和菱形的判定,证明三角形全等是解题的关键.13.如图,已在ABCD Y 中,对角线AC 与BD 相交于点O ,E ,F 是BD 上两点,且BE DF =,2AC OE =,(1)求证: 四边形AECF 是矩形;(2)若90304BAC ACE AE Ð=︒Ð=︒=,,,求BC 的长.∴903060AEG Ð=︒-︒=︒,∴1206060,BEG Ð=︒-︒=︒∴906030,GBE Ð=︒-︒=︒14.在四边形ABCD 中,AD BC ∥,AD BC =,对角线AC BD 、交于点O ,BD 平分ABC Ð,延长AD 至点E ,使DE BO =,连接OE .(1)求证:四边形ABCD 是菱形;(2)若460AD DAB =Ð=︒,,求OE 的长.【答案】(1)见解析15.如图,在矩形ABCD 中,对角线AC 的垂直平分线分别与边AB ,CD 的延长线交于点M ,N ,与边AD 交于点E ,垂足为O .(1)求证:AOM CON △△≌;(2)若8AD =,4CD =,求AE 的长.【答案】(1)见解析(2)5AE =【分析】(1)根据矩形的性质得出AB CD ∥,求出M N Ð=Ð,AO CO =,再根据全等三角形的判定定理AAS 推出即可;(2)根据矩形的性质得出4AB CD ==,根据线段垂直平分线的性质得出AE CE =,再根据勾股定理求出即可.【解析】(1)证明:∵四边形ABCD 是矩形,∴AB CD ∥,∴M N Ð=Ð,∵AC 的垂直平分线是MN ,∴AO CO =,在AOM V 和CON V 中,AOM CON M NAO CO Ð=ÐìïÐ=Ðíï=î,∵AC 的垂直平分线是∴AE CE x ==,∵四边形ABCD 是矩形,∴90ADC Ð=︒,DC =在Rt CDE △中,由勾股定理,得即()22284x x -+=,解得16.如图,在四边形ABCD 中,AB DC P ,AB AD =,AC 平分DAB Ð.对角线AC ,BD 相交于点O ,过点D 作DE AB ^于点E ,连接OE .(1)求证:四边形ABCD 是菱形.(2)若AD =4AC =,求OE 的长.【答案】(1)见解析(2)1,,,,17.如图,在正方形ABCD中,E是BC边上的一点,连接AE,点B关于直线AE的对称点为F,连接EF并延长交CD 于点G ,连接AG .求证:GF GD =.【答案】证明见解析.【分析】连接AF ,根据对称得:△ABE ≌△AFE ,再由HL 证明Rt △AFG ≌Rt △ADG ,可得结论.【解析】证明:连接AF ,Q 四边形ABCD 是正方形,AB AD \=,90B D Ð=Ð=︒,Q 点B 关于直线AE 的对称点为F ,∴△ABE ≌△AFE ,AB AF AD \==,90AFE B Ð=Ð=︒,90AFG \Ð=︒,在Rt AFG V 和Rt ADG V 中,AG AG =Q ,AF AD =,∴Rt △AFG ≌Rt △ADG (HL ),GF GD \=.【点睛】本题考查了正方形的性质,全等三角形的判定与性质,对称的性质,解决本题的关键是利用正方形的性质得到相等的边和相等的角,证明三角形全等,作出辅助线也是解决本题的关键.18.如图,在矩形ABCD 中,AB BC <,E 为AD 上一点,且BE AD =.(1)请用无刻度的直尺和圆规作出CBE Ð的平分线.(保留作图痕迹,不写作法)(2)在(1)中所作的角平分线与AD 的延长线交于点F ,连接CF .猜想四边形BEFC 是什么四边形?并证明你的猜想.【答案】(1)见解析(2)四边形BEFC 是菱形.证明见解析【分析】本题考查作图—基本作图、矩形的性质、角平分线的定义、菱形的判定,熟练掌握矩形的性质、角平分线的定义、菱形的判定是解答本题的关键.(1)根据角平分线的作图方法作图即可.(2)结合矩形的性质、角平分线的定义、菱形的判定可得结论.【解析】(1)解:如图,BP 即为所求.(2)解:四边形BEFC 是菱形.证明:BF Q 平分CBE Ð,CBF EBF \Ð=Ð.Q 四边形ABCD 是矩形,AD BC \=,AF BC ∥,CBF EFB \Ð=Ð,EBF EFB \Ð=Ð,BE EF \=,BE AD =Q ,AD BC =,BC EF \=,\四边形BEFC 是平行四边形.BE EF =Q ,\四边形BEFC 是菱形.模块三、作图有关的解答证明题19.如图,四边形ABCD 是正方形,射线DP 交AB 于点,90,P PDQ DQ Ð=︒交BC 的延长线于点Q .(1)尺规作图:作PDQ Ð的平分线交BC 于E ;(保留作图痕迹,不写作法)(2)在(1)的基础上,连接PE ,求证:PE PA CE=+【答案】(1)见解析(2)见解析【分析】此题考查了正方形的性质、全等三角形的判定和性质角平分线的作图等知识.(1)按照角平分线的作图方法作图即可;(2)证明()ASA PDA QDC V V ≌,则AP CQ =,PD QD =,再证明()SAS PDE QDE V V ≌,则PE QE =,由QE CQ CE PA CE =+=+即可得到PE PA CE =+.【解析】(1)解:如图所示:(2)证明:∵四边形ABCD 是正方形,∴90PAD ADC BCD Ð=Ð=Ð=︒,AD CD =,∴90PDA CDP Ð+Ð=︒,90QCD Ð=︒∵90PDQ Ð=︒,∴90CDQ CDP Ð+Ð=︒∴PDA CDQ Ð=Ð,∵90QCD PAD Ð=Ð=︒,AD CD =,∴()ASA PDA QDC V V ≌∴AP CQ =,PD QD =,∵作PDQ Ð的平分线交BC 于E∴PDE QDE Ð=Ð,又∵,DE DE =∴()SAS PDE QDE V V ≌∴PE QE =,∵QE CQ CE PA CE=+=+∴PE PA CE=+20.如图,在由24个全等的正三角形组成的正六边形网格中,请画出符合要求的格点四边形(即顶点均在格点上的四边形).(1)在图中画出以AB 为对角线的矩形APBQ .(2)在图中画出一个邻边比为1)中的矩形不全等.(2)解:如图,矩形CDEF 即为所求作的矩形.设每个小正方形的边长为1,∵1AC CG DG AD ====,∴四边形ACGD 为菱形,∴1122AO GO AG ===,CD ^模块四、模块二强化21.如图,在正方形ABCD 中,E 是边CD 的中点,点P 是边AD 上一点(与点A ,D 不重合),射线PE 与BC 的延长线交于点Q .(1)求证:PDE QCE V V ≌;(2)过点E 作EF BC ∥交PB 于点F ,连接AF ,当PB PQ =时.求证:四边形AFEP 是平行四边形.由三角形内角和定理可得AFP FPEÐ=ÐPE AF \∥,EF AP Q ∥,\四边形AFEP 是平行四边形.【点睛】本题主要考查正方形的性质,平行四边形的判定,全等三角形的判定与性质,平行线分线段成比例,直角三角形性质,等腰三角形的判定与性质,三角形内角和定理,熟练掌握相关几何性质与判定是解题的关键.22.如图,在矩形ABCD 中,6AD =,8CD =,菱形EFGH 的三个顶点E 、G 、H 分别在矩形ABCD 的边AB 、CD 、DA 上,2AH =,连接CF .(1)当2DG =时,求证:四边形EFGH 是正方形;(2)当△FCG 的面积为2时,求CG 的值.则90FMG Ð=︒,90A FMG \Ð=Ð=︒,由矩形和菱形的性质,可得AEG MGE \Ð=Ð,HEG Ð23.如图,在ABC V 中,AB AC =,AD 平分BAC Ð,CE AD ∥且CE AD =.(1)求证:四边形ADCE 是矩形;(2)若ABC V 是边长为4的等边三角形,,AC DE 相交于点O ,在CE 上截取CF CO =,连接OF ,求线段FC 的长及四边形AOFE 的面积.则90OHC Ð=︒,∵30OCH Ð=︒,112OH OC \==,AEC COF AOFE S S S \=-=V V 四边形模块五、动态几何基础24.如图,在矩形纸片AEE D ¢中,5AD =,15AEE D S ¢=矩形,在EE ¢上取一点F ,使4EF =,剪下AEF △,将它平移至DE F ¢¢V 的位置,拼成四边形AFF D ¢.(1)求证∶四边形AFF D ¢是菱形;(2)求四边形AFF D ¢的两条对角线的长.∵4EF =,5FF AD ¢==,∴9EF EF FF ¢¢=+=,在Rt AEF ¢△中,22239AF AE EF ¢¢=+=+在Rt DFE ¢V 中,541FE FF E F ¢¢¢¢=-=-=,25.如图,把矩形ABCD 绕点A 按逆时针方向旋转得到矩形AEFG ,使点E 落在对角线BD 上,连接DG ,DF .(1)若50BAE Ð=︒,则DAG Ð= °;(2)求证:DF AB =.【答案】(1)50(2)见解析【分析】(1)根据矩形的性质,得到90BAD EAG Ð=Ð=︒,进而得到BAE DAG Ð=Ð,即可求出DAG Ð的度数;(2)根据旋转和矩形的性质,易证四边形ABDF 是平行四边形,即可证明结论.【解析】(1)解:Q 矩形ABCD 和矩形AEFG ,90BAD EAG \Ð=Ð=︒,BAD EAD EAG EAD -=-∴∠∠∠∠,BAE DAG \Ð=Ð,50BAE Ð=︒Q ,50DAG \Ð=︒,故答案为:50;(2)证明:连接AF ,由旋转的性质可知,AF BD =,FAE ABD Ð=Ð,AB AE =,ABE AEB \Ð=Ð,FAE AEB \Ð=Ð,AF BD \∥,\四边形ABDF 是平行四边形,DF AB \=;【点睛】本题考查了旋转的性质,矩形的性质,平行四边形的判定和性质,平行线的判定,等边对等角,熟练掌握旋转和矩形的性质是解题关键.26.如图,在矩形ABCD 中,2AB AD >,点E F ,分别在边AB CD ,上.将ADF △沿AF 折叠,点D 的对应点G 恰好落在对角线AC 上;将CBE △沿CE 折叠,点B 的对应点H 恰好也落在对角线AC 上.连接GE FH ,.求证:(1)AEH CFG △≌△;(2)四边形EGFH 为平行四边形.【答案】(1)证明见解析;(2)证明见解析.【分析】(1)由矩形的性质可得AD BC =,90B D Ð=Ð=︒,AB CD ∥,即得EAH FCG Ð=Ð,由折叠的性质可得AG AD =,CH CB =,90CHE B Ð=Ð=︒,90AGF D Ð=Ð=︒,即得CH AG =,90AHE CGF Ð=Ð=︒,进而得AH CG =,即可由ASA 证明AEH CFG △≌△;(2)由(1)得90AHE CGF Ð=Ð=︒,AEH CFG △≌△,即可得到EH FG ∥,EH FG =,进而即可求证;本题考查了矩形的性质,折叠的性质,全等三角形的判定和性质,平行线的判定和性质,掌握矩形和折叠的性质是解题的关键.【解析】(1)证明:∵四边形ABCD 是矩形,∴AD BC =,90B D Ð=Ð=︒,AB CD ∥,∴EAH FCG Ð=Ð,由折叠可得,AG AD =,CH CB =,90CHE B Ð=Ð=︒,90AGF D Ð=Ð=︒,∴CH AG =,90AHE CGF Ð=Ð=︒,∴AH CG =,在AEH △和CFG △中,90EAH FCG AH CGAHE CGF Ð=Ðìï=íïÐ=Ð=︒î,∴()ASA AEH CFG V V ≌;(2)证明:由(1)知90AHE CGF Ð=Ð=︒,AEH CFG △≌△,∴EH FG ∥,EH FG =,∴四边形EGFH 为平行四边形.27.如图,正方形ABCD 和正方形GECF ,点E 、F 分别在边BC 、上,将正方形GECF 绕点C 顺时针方向旋转,旋转角为0180a a ︒<<︒().(1)如图2,连接BE 、DF ,求证:BE DF =;(2)如图3,若1BC =+,1EC =,当点E 旋转到边上时,连接BE 、连接DF ,并将延长BE 交DF 于点H ,求证:BH 垂直平分DF .【答案】(1)见解析(2)见解析【分析】(1)根据四边形ABCD 和GECF为正方形可得BC DC =,EC FC =,BCE DCF Ð=Ð,再证明()SAS BCE DCF V V ≌即可得到结论;(2)证明BD BF =,=DE EF 即可得出结论.本题主要考查了正方形的性质,旋转的性质,线段垂直平分线的判断,全等三角形的判定与性质等知识,正确作出辅助线构造全等三角形是解答本题的关键.【解析】(1)证明:∵四边形ABCD 和GECF 为正方形,BC DC \=,EC FC =,90BCD ECF Ð=Ð=︒,BCE DCE DCF DCE \Ð+Ð=Ð+Ð,)解:连接, Q ()2221BD BC \==+22EF CE ==,CD BC =211BF BC CF \=+=++22,BF BD DE EF \==+=模块六、综合探究特殊平行四边形的判定28.如图,点O 是ABC V 内一点,连接OB 、OC ,并将AB 、OB 、OC 、AC 的中点D 、E 、F 、G 依次连接,得到四边形DEFG .(1)求证:四边形DEFG 是平行四边形;(2)连接AO①直接写出当AO 和BC 有怎样的位置关系时,四边形DEFG 是矩形;②直接写出当AO和BC有怎样的关系时,四边形DEFG是正方形.Q\∥DE AO,Q点E、F分别是OB、\BC EF∥,Q,AO BC^由①得当AO BC ^时,四边形Q 点D 、E 分别是AB 、\12DE AO =,Q 点E 、F 分别是OB 、(1)求证:四边形EFGH 是矩形;(2)如图二,连接FH ,P 为边FH 上一动点,PN EF ^于点N ,PM EH ^于点M ,3EF =,4EH =,求MN 的最小值.30.如图(1),在ABCD 中,对角线AC 与BD 相交于点O ,点E ,F 分别为OB ,OD 的中点,延长AE 至点G ,使EG AE =,连接CG ,延长CF 至点H ,使FH CF =,连接AH .(1)求证:四边形AGCH 是平行四边形;(2)如图(2),若2AC AB =,求证:四边形AGCH 是矩形;(3)如图(3),若AC AB ^,求证:四边形AGCH 是菱形.()SAS AEO CFO \△≌△,\Ð=Ð=,AEO CFO AE CF ,AE CF \∥,,==EG AE FH CF Q ,AG CH \=,\四边形AGCH 是平行四边形;(2)==Q ,EA EG OA OC ,EO \是AGC V 的中位线,∥\EO GC ,AE CF \∥,\四边形EGCF 是平行四边形,22==Q ,AC AB AC AO ,AB AO \=,E Q 是OB 的中点,AE OB \^,90OEG \Ð=︒,\四边形EGCF 是矩形;90AGC \Ð=︒,由(1)知,四边形AGCH 是平行四边形,\四边形AGCH 是矩形;(3)连接H G ,由(1)知,OA OC =,HG \过点O ,连接BG ,Q 点E 为OB 的中点,BE OE \=,AE EG =Q ,\四边形ABGO 是平行四边形,∥\AB OG ,AB AC ^Q ,\^HG AC ,\四边形AGCH 是菱形.【点睛】本题是四边形的综合题,考查了矩形的判定,菱形的判定,平行四边形的判定和性质,全等三角形的判定和性质,三角形的中位线定理,正确的识别图形是解题的关键.31.如图所示,在Rt ABC △中,90B =°,100cm AC =,60A Ð=︒,点D 从点C 出发沿CA 方向以4cm s 的速度向点A 匀速运动,同时点E 从点A 出发沿AB 方向以2cm s 的速度向点B 匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D 、E 运动的时间是t 秒()025t <£.过点D 作DF BC ^于点F ,连接DE ,EF .(1)求证:四边形AEFD 是平行四边形;(2)四边形AEFD 能够成为菱形吗?如果能,求出相应的t 值;如果不能,请说明理由;(3)当t 为何值时,DEF V 为直角三角形?请说明理由.【答案】(1)证明见解析Q 90CFD \Ð=︒,90B Ð=︒Q ,60A Ð=︒,30C \Ð=︒,114222DF CD t t \==´=,AE DF \=,若四边形AEFD 为菱形,则AE =100AC =Q ,4CD t =,1004AD AC CD t \=-=-,又2AE t =Q ,21004t t \=-,Q 90DFC DFB \Ð=Ð=︒,又90B Ð=︒Q ,\四边形DFBE 为矩形,DF BE \=,90B Ð=︒Q ,60A Ð=︒,由(1)可知:四边形AEFD 是平行四边形,\∥EF AD ,90ADE DEF \Ð=Ð=︒,在Rt ADE V 中,60A Ð=︒,2AE t =30AED \Ð=︒,11模块七、特殊平行四边形在平面直角坐标系的应用32.如图,已知OABC 是一张放在平面直角坐标系中的矩形纸片,O 为坐标原点,点(10,0)A ,点(0,6)C ,在边AB 上任取一点D ,将AOD △沿OD 翻折,使点A 落在BC 边上,记为点E .(1)EC 的长度为 ;(2)求D 点坐标;(3)若在x 轴正半轴上存在点P ,使得OEP V 为等腰三角形,则点P 的坐标为 .则6EM AB ==,在Rt OEM △中,OM OE =设OP a =,则PE a =,PM 在Rt PEM △中,2PE PM =222(8)6a a \=-+,\同②得8OM =,8MP \=,\点P 的坐标为(16,0);综上,点P 的坐标为(10,0)或25,04æöç÷èø【点睛】本题属于几何变换综合题,考查了翻折变换,矩形的性质,等腰三角形的性质,勾股定理,分类讨论思想的运用是解题的关键.33.如图1,在平面直角坐标系中,一次函数48y x =+的图象分别交x 轴,y 轴于A ,B 两点,将AOB V 绕点O 顺时针旋转90︒得COD △(点A 与点C 对应,点B 与点D 对应).(1)直接写出直线CD 的解析式;(2)点E 为线段CD 上一点,过点E 作EF y ∥轴交直线AB 于点F ,作EG x ∥轴交直线AB 于点G ,当EF EG AD +=时,求点E 的坐标;(3)如图2,若点M 为线段AB 的中点,点N 为直线CD 上一点,点P 为坐标系内一点.且以O ,M ,N ,P 为顶点的四边形为矩形,请直接写出所有符合条件的点N 的坐标,并写出其中一种求解点N 坐标的过程.∵,∵,()0,8B ,点M 为线段∴()1,4M -,12OM AM BM AB ===∵将AOB V 绕点O 顺时针旋转90∴AOB COD ≌△△,∴2OA OC ==,OAB OCD Ð=Ð∵ON OM ^,由(1)得,直线CD 的解析式为设1,24N n n æö-+ç÷èø,∵()1,4M -,∴2221417OM =+=,22ON n =+模块八、压轴过渡练34.如图,在ABC V 中,点O 是边AC 上一个动点,过点O 作直线MN BC ∥.设MN 交ACB Ð的平分线于点E ,交ABC V 的外角ACD Ð的平分线于点F .(1)求证:OE OF =;(2)若12CE =,5CF =,求OC 的长;(3)连接AE ,AF ,当点O 在边AC 上运动到什么位置时,四边形AECF 是矩形?请说明理由.【答案】(1)见解析(2) 6.5OC =(3)点O 在边AC 上运动到AC 的中点时,四边形AECF 是矩形.理由见解析【分析】(1)由角平分线的定义结合平行线的性质可证得ACE OEC Ð=Ð,则OE OC =,同理OC OF =,即可得出结论;(2)利用勾股定理可求得EF 的长,再结合(1)的结论可求得OC 的长;(3)只要保证四边形AECF 是平行四边形即可,则可知O 为AC 的中点时,满足条件.本题考查了矩形的判定、平行四边形的判定与性质、等腰三角形的判定以及勾股定理等知识,熟练掌握矩形的判定和等腰三角形的判定是解题的关键.【解析】(1)证明:CE Q 平分ACB Ð,ACE ECB \Ð=Ð,MN BC Q P ,ECB OEC \Ð=Ð,ACE OEC \Ð=Ð,OE OC \=,同理可得OC OF =,OE OF \=;35.如图,四边形ABCD 和BGEF 均为正方形,点E 恰好在线段AD 上,连接AF 、BE 、CG .(1)当点E 与A 、D 两点都不重合时,求证:ABF CBG V V ≌;(2)当点E 与A 点重合时,等式AB AE CG -=成立;当点E 与A 、D 两点都不重合时,等式AB AE CG -=是否仍然成立?请证明你的结论.Q 90EFB \Ð=︒,45FEB FBE Ð=Ð=︒,90AFE EFH BFH EFH \Ð+Ð=Ð+Ð=︒,AFE HFB \Ð=Ð.36.问题解决:如图①,在矩形ABCD 中,点E ,F 分别在AB BC ,边上,DE AF DE AF =^,于点G .(1)求证:四边形ABCD 是正方形;(2)延长CB 到点H ,使得BH AE =,连接AH ,判断AHF △的形状,并说明理由.类比迁移:如图②,在菱形ABCD 中,点E ,F 分别在AB BC ,边上,DE 与AF 相交于点G ,6072DE AF AED AE BF =Ð=︒==,,,,求DE 的长.【答案】(1)见解析;(2)等腰三角形,见解析;类比迁移:9【分析】本题主要考查了正方形的证明、菱形的性质、三角形全等的判断与性质等知识点,理解题意并灵活运用相关知识、正确做出辅助线构造三角形全等是解题的关键.(1)先说明90DE AF AGD ^Ð=︒,可得ADE BAF Ð=Ð,再证明()AAS ADE BAF V V ≌得到AD AB =,然后根据一组邻边相等的矩形是正方形即可证明结论;(2)由ADE BAF ≌△△可得AE BF =,再证明BH BF =可得AH AF =,从而得到等腰三角形;类比迁移:如图,延长CB 到点H ,使BH AE =,连接AH ,由菱形的性质可证明DAE ABH ≌V V ,再结合已知60AED Ð=︒可得AHF △是等边三角形,最后利用线段的和差即可解答.【解析】(1)解:证明:∵四边形ABCD 是矩形,∴90DAB ABC Ð=Ð=︒,∴90DE AF AGD ^Ð=︒,,∵9090BAF DAF ADE DAF Ð+Ð=︒Ð+Ð=︒,,∴ADE BAFÐ=Ð在ADE V 和BAF △中,90DAE ABF ADE BAFDE AF Ð=Ð=︒ìïÐ=Ðíï=î∴()AAS ADE BAF V V ≌,∴AD AB =,∴四边形ABCD 是正方形.(2)AHF △是等腰三角形,理由:由(1)得ADE BAF ≌△△,∴AE BF =,∵BH AE =,∴BH BF =,∵90ABH Ð=︒,∴AH AF =,。
初二数学证明题(精选多篇)

初二数学证明题(精选多篇)第一篇:初二数学证明题初二数学证明题1、如图,ab=ac,∠bac=90°,bd⊥ae于d,ce⊥ae于e.且bd>ce,证明bd=ec+ed.解答:证明:∵∠bac=90°,ce⊥ae,bd⊥ae,∴∠abd+∠bad=90°,∠bad+∠dac=90°,∠adb=∠aec=90°.∴∠abd=∠dac.又∵ab=ac,∴△abd≌△cae(aas).∴bd=ae,ec=ad.∵ae=ad+de,∴bd=ec+ed.2、△abc是等要直角三角形。
∠acb=90°,ad是bc边上的中线,过c做ad的垂线,交ab于点e,交ad于点f,求证∠adc=∠bde 解:作ch⊥ab于h交ad于p,∵在rt△abc中ac=cb,∠acb=90°,∴∠cab=∠cba=45°.∴∠hcb=90°-∠cba=45°=∠cba.又∵中点d,∴cd=bd.又∵ch⊥ab,∴ch=ah=bh.又∵∠pah+∠aph=90°,∠pcf+∠cpf=90°,∠aph=∠cpf,∴∠pah=∠pcf.又∵∠aph=∠ceh,在△aph与△ceh中∠pah=∠ech,ah=ch,∠pha=∠ehc,∴△aph≌△ceh(asa).∴ph=eh,又∵pc=ch-ph,be=bh-he,∴cp=eb.在△pdc与△edb中pc=eb,∠pcd=∠ebd,dc=db,∴△pdc≌△edb(sas).∴∠adc=∠bde.2证明:作oe⊥ab于e,of⊥ac于f,∵∠3=∠4,∴oe=of.(问题在这里。
理由是什么埃我有点不懂) ∵∠1=∠2,∴ob=oc.∴rt△obe≌rt△ocf(hl).∴∠5=∠6.∴∠1+∠5=∠2+∠6.即∠abc=∠acb.∴ab=ac.∴△abc是等腰三角形过点o作od⊥ab于d过点o作oe⊥ac于e再证rt△aod≌rt△aoe(aas)得出od=oe就可以再证rt△dob≌rt△eoc(hl)得出∠abo=∠aco再因为∠obc=∠ocb得出∠abc=∠abc得出等腰△abc41.e是射线ab的一点,正方形abcd、正方形defg有公共顶点d,问当e在移动时,∠fbh的大小是一个定值吗?并验证(过f作fm⊥ah于m,△ade全等于△mef证好了)2.三角形abc,以ab、ac为边作正方形abmn、正方形acpq1)若de⊥bc,求证:e是nq的中点2)若d是bc的中点,∠bac=90°,求证:ae⊥nq3)若f是mp的中点,fg⊥bc于g,求证:2fg=bc3.已知ad是bc边上的高,be是∠abc的平分线,ef⊥bc于f,ad与be交于g求证:1)ae=ag(这个证好了)2)四边形aefg是菱形第二篇:初二数学证明题测试例1、如图,ab∥cd,且∠abe=120°,∠cde=110°,求∠bed的度数。
经典初二数学几何证明题

A DB C EBCD FEFEBAC D最新(一)中考数学几何证明(平行四边形,菱形矩形正方形)经典1.(本题10分)如图,已知: ABCD 中,BCD ∠的平分线CE 交边AD 于E ,ABC∠的平分线BG 交CE 于F ,交AD 于G .求证:AE DG =.2.在正方形ABCD 中,AC 为对角线,E 为AC 上一点,连接EB 、ED . (1)求证:△BEC ≌△DEC ;(2)延长BE 交AD 于F ,当∠BED =120°时,求∠EFD 的度数.3.(本小题满分5分)如图,在△ABC 中,点D 、E 分别在边AC 、AB 上,BD=CE ,∠DBC=∠ECB 。
求证:AB=AC 。
4.(本小题满分7分)如图,在△ABC 中,AB=AC ,D 为BC 中点,四边形ABDE 是平行四边形。
求证:四边形ADCE 是矩形。
5.(10分)在□ABCD 中,AC 是一条对角线,∠B =∠CAD ,延长BC 至点E ,使CE =BC ,连接DE .(1)求证:四边形ABED 是等腰梯形.(2)若AB =AD =4,求梯形ABED 的面积. 6、(本小题7分)如图,点A 、E 、B 、D 在同一条直线上,AE=DB ,AC=DF ,AC ∥DF.请探索BC 与EF 有怎样的位置关系?并说明理由。
7.如图,已知BE ⊥AD ,CF ⊥AD ,且BE =CF .(1) 请你判断AD 是△ABC 的中线还是角平分线?请证明你的结论.(2)连接BF 、CE ,若四边形BFCE 是菱形,则△ABC 中应添加一个条件▲8.(广东广州,18,9分)如图5,在等腰梯形ABCD 中,AD ∥BC .求证:∠A +∠C =180°AB CD10.如图,C 是线段AB 的中点,CD 平分∠ACE ,CE 平分∠BCD ,CD=CE .(1)求证:△ACD≌△BCE;(2)若∠D=50°,求∠B 的度数.A B C E F GEB D AC F A FDE B C11.(本题6分)如图,在△ABC 中,D 是BC 边上的点(不与B ,C 重合),F ,E 分别是AD 及其延长线上的点,CF ∥BE. 请你添加一个条件,使△BDE ≌△CDF (不再添加其它线段,不再标注或使用其他字母),并给出证明.(1)你添加的条件是: ▲ ;(2)证明:.12.(8分)如图,请在下列四个关系中,选出两个恰当....的关系作为条件,推出四边形ABCD 是平行四边形,并予以证明.(写出一种即可)关系:①AD ∥BC ,②CD AB =,③C A ∠=∠,④︒=∠+∠180C B .已知:在四边形ABCD 中,,; 求证:四边形ABCD 是平行四边形. 13.(本题满分9分)将三角形纸片ABC (AB >AC )沿过点A 的直线折叠,使得AC 落在AB 边上,折痕为AD ,展平纸片,如图(1);再次折叠该三角形纸片,使得点A 与点D 重合,折痕为EF ,再次展平后连接DE 、DF ,如图2,证明:四边形AEDF 是菱形.14.如图10,已知ABC ADE Rt △≌Rt △,90ABC ADE ∠=∠=°,BC 与DE 相交于点F ,连接CD ,EB .(1)图中还有几对全等三角形,请你一一列举. (2)求证:.CF EF = 15.(本小题满分8分)如图,已知:点B 、F 、C 、E 在一条直线上,FB =CE ,AC =DF . A CBDFE (第11题)AB C(1) (2) 第13题图 ABDCCDBF AEABDFB CDE FAA EB FC DA GEB CF D 能否由上面的已知条件证明AB ∥ED ?如果能,请给出证明;如果不能,请从下列三个条件中选择一个合适的条件.......,添加到已知条件中,使AB ∥ED 成立,并给出证明. 供选择的三个条件(请从其中选择一个): ①AB =ED ; ②BC =EF ; ③∠ACB =∠DFE . 16.(6分)已知:正方形ABCD 中,E 、F 分别是边CD 、DA 上的点,且CE =DF ,AE 与BF 交于点M . (1)求证:△ABF ≌△DAE ;(2)找出图中与△ABM 相似的所有三角形(不添加任何辅助线).17.(6分)如图,在△ABC 中,BC >AC ,点D 在BC 上,且DC =AC ,∠ACB 的平分线CF 交AD 于点F .点E 是AB 的中点,连接EF .(1)求证:EF ∥BC ;(2)若△ABD 的面积是6,求四边形BDFE 的面积.18.(本小题满分8分) 如图,四边形ABCD 的对角线AC 、DB 相交于点O ,现给出如下三个条件:AB DC AC DB OBC OCB ==∠=∠①②③.(1)请你再增加一个..条件:________,使得四边形ABCD 为矩形(不添加其它字母和辅助线,只填一个即可,不必证明);(2)请你从①②③中选择两个条件________(用序号表示,只填一种情况),使得AOB DOC △≌△,并加以证明.19.如图,在直角梯形ABCD 中,AD ∥BC ,∠A =90º,AB =AD =6,DE ⊥CD交AB 于E ,DF 平分∠CDE 交BC 于F ,连接EF . (1)证明:CF =EF ; (2)当tan ∠ADE = 13时,求EF 的长.20.(10分)如图,在□ABCD 中,E 、F 分别是边AB 、CD的中点,AG ∥BD 交CB 的延长线于点G .(1)求证:△ADE ∽≌△CBF ;(2)若四边形BEDF 是菱形,则四边形AGBD 是什么特殊四边形?请说明你的理由. 21.(本题满分8分)如图,在ABCD 中,点E 、F 是对角线AC 上两点,且CF AE =.求证:FDE EBF =∠.22.(8分)如图,四边形ABCD 是矩形,∠EDC=∠CAB , ∠DEC=90°。
初二数学几何证明与推理练习题及答案20题

初二数学几何证明与推理练习题及答案20题1. 题目:已知ABCD是一个平行四边形,证明AC=BD。
证明:由平行四边形的定义,可知AB∥CD和AD∥BC。
在ABCD中,我们连接AC和BD,假设它们的交点为E。
因为AB∥CD,所以∠ABC+∠BCD=180°(内错角性质)。
又由于AD∥BC,所以∠BCD+∠CDE=180°(内错角性质)。
综上,∠ABC+∠CDE=180°,即△ABC与△CDE互补。
根据互补角的性质,△ABC与△CDE全等,因此AC=BD得证。
2. 题目:已知ABCD是一个矩形,证明BD是直径。
证明:由矩形的定义,可知AB∥CD和AD∥BC。
在矩形ABCD中,我们连接角BAD的角平分线BE和角BCD的角平分线CF,它们相交于点O。
因为角BAD和角BCD都是直角(矩形的性质),所以∠BAE=∠CFO=90°。
由于角平分线的性质,∠BAE=∠CAE,∠CFO=∠CDO。
因此,在△BAE和△CFO中,∠CAE=∠CDO,且∠BAE=∠CFO。
根据AA相似三角形的性质,△BAE与△CFO相似。
因此,AE/CF=BA/CO=1/2(相似三角形的对应边比例相等)。
由此可得,CO=2AE,即CO=2BO。
由于OC=OC(公共边),所以△BOC为等腰三角形,即BO=BC。
综上所述,BD=2BO=2BC,即BD是直径。
3. 题目:已知△ABC中,AB=AC,垂直平分线BM过点B交AC于点M,证明∠ABM=∠ACM。
证明:由题意可得AB=AC,BM⊥AC,且BM平分∠ABC。
连接AM和CM。
在△ABC中,由于AB=AC,所以∠ABC=∠ACB。
由垂直平分线的性质,BM平分了∠ABC,所以∠ABM=∠CBM。
同理,在△ACB中,由于AB=AC,所以∠ACB=∠ABC。
由垂直平分线的性质,BM平分了∠ACB,所以∠CBM=∠ACM。
综上所述,∠ABM=∠CBM=∠ACM得证。
初中数学特殊平行四边形的证明及详细答案

初中数学特殊平行四边形的证明一. 解答题(共30小题)1.(2019•泰安模拟)如图, 在△ABC中, ∠ACB=90°, BC的垂直平分线DE交BC于D, 交AB于E, F在DE上, 并且AF=CE.(1)求证: 四边形ACEF是平行四边形;(2)当∠B满足什么条件时, 四边形ACEF是菱形?请回答并证明你的结论.2.(2019•福建模拟)已知: 如图, 在△ABC中, D、E分别是AB.AC的中点, BE=2DE, 延长DE到点F, 使得EF=BE, 连接CF.求证: 四边形BCFE是菱形.3.(2019•深圳一模)如图, 四边形ABCD中, AB∥CD, AC平分∠BAD, CE∥AD交AB于E.(1)求证: 四边形AECD是菱形;(2)若点E是AB的中点, 试判断△ABC的形状, 并说明理由.4.(2019•济南模拟)如图, 四边形ABCD是矩形, 点E是边AD的中点.求证: EB=EC.5. (2019•临淄区校级模拟)如图所示, 在矩形ABCD中, DE⊥AC于点E, 设∠ADE=α, 且cosα= , AB=4, 则AC的长为多少?6. (2019春•宿城区校级月考)如图, 四边形ABCD是矩形, 对角线AC、BD相交于点O, BE ∥AC交DC的延长线于点E. 求证:BD=BE.7.(2019•雅安)如图:在▱ABCD中, AC为其对角线, 过点D作AC的平行线及BC的延长线交于E.(1)求证: △ABC≌△DCE;(2)若AC=BC, 求证: 四边形ACED为菱形.8.(2019•贵阳)如图, 在Rt△ABC中, ∠ACB=90°, D.E分别为AB, AC边上的中点, 连接DE, 将△ADE绕点E旋转180°得到△CFE, 连接AF, AC.(1)求证: 四边形ADCF是菱形;(2)若BC=8, AC=6, 求四边形ABCF的周长.9.(2019•遂宁)已知:如图, 在矩形ABCD中, 对角线AC、BD相交于点O, E是CD中点, 连结OE.过点C作CF∥BD交线段OE的延长线于点F, 连结DF.求证:(1)△ODE≌△FCE;(2)四边形ODFC是菱形.10. (2019•宁德)如图, 在梯形ABCD中, AD∥BC, 点E是BC的中点, 连接AC, DE, AC=AB, DE∥AB. 求证: 四边形AECD是矩形.11. (2019•钦州)如图, 在正方形ABCD中, E、F分别是AB、BC上的点, 且AE=BF. 求证:CE=DF.12.(2019•贵港)如图, 在正方形ABCD中, 点E是对角线AC上一点, 且CE=CD, 过点E 作EF⊥AC交AD于点F, 连接BE.(1)求证: DF=AE;(2)当AB=2时, 求BE2的值.13.(2019•吴中区一模)已知:如图, 菱形ABCD中, E、F分别是CB.CD上的点, ∠BAF=∠DAE.(1)求证: AE=AF;(2)若AE垂直平分BC, AF垂直平分CD, 求证: △AEF为等边三角形.14. (2019•新乡一模)小明设计了一个如图的风筝, 其中, 四边形ABCD及四边形AEFG都是菱形, 点C在AF上, 点E, G分别在BC, CD上, 若∠BAD=135°, ∠EAG=75°, AE=100cm, 求菱形ABCD的边长.15. (2019•槐荫区三模)如图, 菱形ABCD的边长为1, ∠D=120°. 求对角线AC的长.16. (2019•历城区一模)如图, 已知菱形ABCD的对角线AC.BD的长分别为6cm、8cm, AE ⊥BC于点E, 求AE的长.17.(2019•湖南校级模拟)如图, AE=AF, 点B.D分别在AE、AF上, 四边形ABCD是菱形, 连接EC、FC(1)求证: EC=FC;(2)若AE=2, ∠A=60°, 求△AEF的周长.18.(2019•清河区一模)如图, 在△ABC中, AB=AC, 点D.E、F分别是△ABC三边的中点.求证: 四边形ADEF是菱形.19. (2019春•防城区期末)如图, 已知四边形ABCD是平行四边形, DE⊥AB, DF⊥BC, 垂足分别是为E, F, 并且DE=DF. 求证:四边形ABCD是菱形.20.(2019•通州区一模)如图, 在四边形ABCD中, AB=DC, E、F分别是AD.BC的中点, G、H分别是对角线BD.AC的中点.(1)求证: 四边形EGFH是菱形;(2)若AB=1, 则当∠ABC+∠DCB=90°时, 求四边形EGFH的面积.21.(2019•顺义区二模)如图, 在△ABC中, D、E分别是AB.AC的中点, BE=2DE, 过点C 作CF∥BE交DE的延长线于F.(1)求证: 四边形BCFE是菱形;(2)若CE=4, ∠BCF=120°, 求菱形BCFE的面积.22.(2019•祁阳县校级模拟)如图, O为矩形ABCD对角线的交点, DE∥AC, CE∥BD.(1)求证: 四边形OCED是菱形.(2)若AB=6, BC=8, 求四边形OCED的周长.23. (2019•荔湾区校级一模)已知点E是矩形ABCD的边AD延长线上的一点, 且AD=DE, 连结BE交CD于点O, 求证:△AOD≌△BOC.24.(2019•东海县二模)已知:如图, 在正方形ABCD中, 点E、F在对角线BD上, 且BF=DE, (1)求证: 四边形AECF是菱形;(2)若AB=2, BF=1, 求四边形AECF的面积.25.(2019•玉溪模拟)如图, 正方形ABCD的边CD在正方形ECGF的边CE上, 连接BE、DG.求证: BE=DG.26.(2019•工业园区一模)已知:如图正方形ABCD中, E为CD边上一点, F为BC延长线上一点, 且CE=CF(1)求证: △BCE≌△DCF;(2)若∠FDC=30°, 求∠BEF的度数.27.(2019•深圳模拟)四边形ABCD是正方形, E、F分别是DC和CB的延长线上的点, 且DE=BF, 连接AE、AF、EF.(1)求证: △ADE≌△ABF;(2)若BC=8, DE=6, 求△AEF的面积.28. (2019•碑林区校级模拟)在正方形ABCD中, AC为对角线, E为AC上一点, 连接EB、ED. 求证:∠BEC=∠DEC.29.(2019•温州一模)如图, AB是CD的垂直平分线, 交CD于点M, 过点M作ME⊥A C, MF ⊥AD, 垂足分别为E、F.(1)求证: ∠CAB=∠DAB;(2)若∠CAD=90°, 求证: 四边形AEMF是正方形.30.(2019•湖里区模拟)已知:如图, △ABC 中, ∠ABC=90°, BD 是∠ABC 的平分线, DE⊥AB 于点E, DF ⊥BC 于点F .求证:四边形DEBF 是正方形.初中数学 特殊平行四边形的证明参考答案及试题解析一. 解答题(共30小题)1.(2019•泰安模拟)如图, 在△ABC 中, ∠ACB=90°, BC 的垂直平分线DE 交BC 于D, 交AB 于E, F 在DE 上, 并且AF=CE .(1)求证: 四边形ACEF 是平行四边形;(2)当∠B 满足什么条件时,四边形ACEF是菱形?请回答并证明你的菱形的判定;线段垂直平分线的性质;平行四边形的判定. 菁优网版权所有结论.考点:考点:专题:证明题.(1)ED是BC的垂直平分线, 根据中垂线的性质: 中垂线上的分析:点线段两个端点的距离相等, 则EB=EC, 故有∠3=∠4, 在直角三角形ACB中, ∠2及∠4互余, ∠1及∠3互余, 则可得到AE=CE, 从而证得△ACE和△EFA都是等腰三角形, 又因为FD⊥BC, AC⊥BC, 所以AC∥FE, 再根据内错角相等得到AF∥CE, 故四边形ACEF是平行四边形;(2)由于△ACE是等腰三角形, 当∠1=60°时△ACE是等边三角形, 有AC=EC, 有平行四边形ACEF是菱形.(2)由于△ACE是等腰三角形,当∠1=60°时△ACE是等边三角形,有AC=EC,有平行四边形ACEF是菱形.(2)由于△ACE是等腰三角形,当∠1=60°时△ACE是等边三角形,有AC=EC,有平行四边形ACEF是菱形.解: (1)∵ED是BC的垂直平分线解答:∴EB=EC, ED⊥BC,∴∠3=∠4,∵∠ACB=90°,∴FE∥AC,∴∠1=∠5,∵∠2及∠4互余, ∠1及∠3互余∴∠1=∠2,∴AE=CE,又∵AF=CE,∴△ACE和△EFA都是等腰三角形,∴∠5=∠F,∴∠2=∠F,∴在△EFA和△ACE中∵,∴△EFA≌△ACE(AAS),∴∠AEC=∠EAF∴AF∥CE∴四边形ACEF是平行四边形;(2)当∠B=30°时, 四边形ACEF是菱形. 证明如下: ∵∠B=30°, ∠ACB=90°∴∠1=∠2=60°∴∠AEC=60°∴AC=EC∴平行四边形ACEF是菱形.点评:本题综合利用了中垂线的性质、等边对等角和等角对等边、直角三角形的性质、平行四边形和判定和性质、菱形的判定求解, 有利于学生思维能力的训练.涉及的知识点有:有一组邻边相等的平行四边形是菱形.2. (2019•福建模拟)已知: 如图, 在△ABC中, D.E分别是AB.AC 的中点, BE=2DE, 延长DE到点F, 使得EF=BE, 连接CF.菱形的判定. 菁优网版权所有求证:四边形BCFE是菱形.考点:考点:专题:证明题.分析:由题意易得, EF 及BC 平行且相等, ∴四边形BCFE 是平行四边形.又EF=BE, ∴四边形BCFE 是菱形.解答: 解: ∵BE=2DE, EF=BE,∴EF=2DE. (1分)∵D.E 分别是AB.AC 的中点,∴BC=2DE 且DE ∥BC. (2分)∴EF=BC. (3分)又EF ∥BC,∴四边形BCFE 是平行四边形. (4分)又EF=BE,∴四边形BCFE 是菱形. (5分)∴四边形BCFE 是菱形.(5分)点评: 此题主要考查菱形的判定, 综合利用了平行四边形的性质和判定.3. (2019•深圳一模)如图, 四边形ABCD 中, AB ∥CD, AC 平分∠BAD, CE ∥AD 交AB 于E.(1)求证: 四边形AECD 是菱形;菱形的判定及性质. 菁优网版权所有(2)若点E是AB的中点,试判断△ABC的形状,并说明理由.考点:考点:几何图形问题.专题:(1)利用两组对边平行可得该四边形是平行四边形, 进而证明分析:一组邻边相等可得该四边形为菱形;(2)利用菱形的邻边相等的性质及等腰三角形的性质可得两组角相等, 进而证明∠ACB为直角即可.(2)利用菱形的邻边相等的性质及等腰三角形的性质可得两组角相等,进而证明∠ACB为直角即可.(2)利用菱形的邻边相等的性质及等腰三角形的性质可得两组角相等,进而证明∠ACB为直角即可.解: (1)∵AB∥CD, CE∥AD,解答:∴四边形AECD为平行四边形, ∠2=∠3,又∵AC平分∠BAD,∴∠1=∠2,∴∠1=∠3,∴AD=DC,∴四边形AECD是菱形;(2)直角三角形.理由: ∵AE=EC∴∠2=∠4,∵AE=EB,∴EB=EC,∴∠5=∠B,又因为三角形内角和为180°,∴∠2+∠4+∠5+∠B=180°,∴∠ACB=∠4+∠5=90°,∴△ACB为直角三角形.点评:考查菱形的判定及性质的应用;用到的知识点为:一组邻边相等的平行四边形是菱形;菱形的4条边都相等.4. (2019•济南模拟)如图, 四边形ABCD是矩形, 点E是边AD的中点.求证:矩形的性质;全等三角形的判定及性质. 菁优网版权所有EB=EC.考点:考点:专题: 证明题.分析: 利用矩形的性质结合全等三角形的判定及性质得出△ABE ≌△DCE(SAS), 即可得出答案.解答: 证明: ∵四边形ABCD是矩形,∴AB=DC, ∠A=∠D=90°,∵点E是边AD的中点,∴AE=ED,在△ABE和△DCE中,,∴△ABE≌△DCE(SAS),∴EB=EC.∴EB=EC.点评: 此题主要考查了全等三角形的判定及性质以及矩形的性质, 得出△ABE≌△DCE是解题关键.矩形的性质. 菁优网版权所有5. (2019•临淄区校级模拟)如图所示, 在矩形ABCD中, DE⊥AC于点E, 设∠ADE=α,且cosα= ,AB=4, 则AC的长为多少?考点:分析: 根据等角的余角相等, 得∠BAC=∠ADE=α;根据锐角三角函数定义可求AC的长.解答: 解: ∵四边形ABCD是矩形,∴∠ABC=90°, AD∥BC,∴∠EAD=∠ACB,∵在△ABC及△AED中,∵DE⊥AC于E, ∠ABC=90°∴∠BAC=∠ADE=α.∴cos∠BAC=cosα= ,∴AC= = .∴AC==.点评: 此题综合运用了锐角三角函数的知识、勾股定理、矩形的性质.矩形的性质;平行四边形的判定及性质. 菁优网版权所有6.(2019春•宿城区校级月图, 四边形ABCD是矩形, 对角线AC.BD相交于点O,BE∥AC交DC的延长线于点E. 求证:BD=BE.考点:考点:专题: 证明题.分析: 根据矩形的对角线相等可得AC=BD, 对边平行可得AB∥CD,再求出四边形ABEC 是平行四边形, 根据平行四边形的对边相等可得AC=BE, 从而得证.解答: 证明: ∵四边形ABCD 是矩形,∴AC=BD, AB ∥CD,又∵BE ∥AC,∴四边形ABEC 是平行四边形,∴AC=BE,∴BD=BE.∴BD=BE.点评: 本题考查了矩形的性质, 平行四边形的判定及性质, 熟记各性质并求出四边形ABEC 是平行四边形是解题的关键.7. (2019•雅安)如图: 在▱ABCD 中, AC 为其对角线, 过点D 作AC 的平行线及BC 的延长线交于E.(1)求证: △ABC ≌△DCE ;(2)若AC=BC, 求证:四边形ACED为菱菱形的判定;全等三角形的判定及性质;平行四边形的性质. 菁优网版权所有形.考点:考点:专题: 证明题.分析: (1)利用AAS判定两三角形全等即可;(2)首先证得四边形ACED为平行四边形, 然后证得AC=AD,利用邻边相等的平行四边形是菱形判定即可.(2)首先证得四边形ACED为平行四边形,然后证得AC=AD,利用邻边相等的平行四边形是菱形判定即可.(2)首先证得四边形ACED为平行四边形,然后证得AC=AD,利用邻边相等的平行四边形是菱形判定即可.解答: 证明: (1)∵四边形ABCD为平行四边形,∴AB∥CD, AB=CD,∴∠B=∠1,又∵DE∥AC∴∠2=∠E,在△ABC及△DCE中,,∴△ABC≌△DCE;(2)∵平行四边形ABCD中,∴AD∥BC,即AD∥CE,由DE∥AC,∴ACED为平行四边形,∵AC=BC,∴∠B=∠CAB,由AB∥CD,∴∠CAB=∠ACD,又∵∠B=∠ADC,∴∠ADC=∠ACD,∴AC=AD,∴四边形ACED为菱形.点评: 本题考查了菱形的判定等知识, 解题的关键是熟练掌握菱形的判定定理, 难度不大.8. (2019•贵阳)如图, 在Rt△ABC中, ∠ACB=90°, D.E分别为AB, AC边上的中点, 连接DE, 将△ADE绕点E旋转180°得到△CFE, 连接AF, AC.(1)求证: 四边形ADCF是菱形;(2)菱形的判定及性质;旋转的性质. 菁优网版权所有若BC=8,AC=6,求四边形ABCF的周长.考点:考点:几何综合题.专题:(1)根据旋转可得AE=CE, DE=EF, 可判定四边形ADCF是平行分析:四边形, 然后证明DF⊥AC, 可得四边形ADCF是菱形;(2)首先利用勾股定理可得AB长, 再根据中点定义可得AD=5, 根据菱形的性质可得AF=FC=AD=5, 进而可得答案.(2)首先利用勾股定理可得AB长,再根据中点定义可得AD=5,根据菱形的性质可得AF=FC=AD=5,进而可得答案.(2)首先利用勾股定理可得AB长,再根据中点定义可得AD=5,根据菱形的性质可得AF=FC=AD=5,进而可得答案.(1)证明: ∵将△ADE绕点E旋转180°得到△CFE,解答:∴AE=CE, DE=EF,∴四边形ADCF是平行四边形,∵D.E分别为AB, AC边上的中点,∴DE是△ABC的中位线,∴DE∥BC,∵∠ACB=90°,∴∠AED=90°,∴DF⊥AC,∴四边形ADCF是菱形;(2)解: 在Rt△ABC中, BC=8, AC=6,∴AB=10,∵D是AB边上的中点,∴AD=5,∵四边形ADCF是菱形,∴AF=FC=AD=5,∴四边形ABCF的周长为8+10+5+5=28.∴四边形ABCF的周长为8+10+5+5=28.此题主要考查了菱形的判定及性质, 关键是掌握菱形四边相点评:等, 对角线互相垂直的平行四边形是菱形.9. (2019•遂宁)已知: 如图, 在矩形ABCD中, 对角线AC.BD相交于点O, E是CD中点, 连结OE. 过点C作CF∥BD交线段OE的延长线于点F, 连结DF. 求证:(1)△ODE≌△FCE;(2)四边形ODFC是菱形. 考点: 考点:矩形的性质;全等三角形的判定及性质;菱形的判定. 菁优网版权所有专题: 证明题.分析: (1)根据两直线平行, 内错角相等可得∠ODE=∠FCE, 根据线段中点的定义可得CE=DE, 然后利用“角边角”证明△ODE和△FCE全等;(2)根据全等三角形对应边相等可得OD=FC, 再根据一组对边平行且相等的四边形是平行四边形判断出四边形ODFC是平行四边形, 根据矩形的对角线互相平分且相等可得OC=OD, 然后根据邻边相等的平行四边形是菱形证明即可.(2)根据全等三角形对应边相等可得OD=FC,再根据一组对边平行且相等的四边形是平行四边形判断出四边形ODFC是平行四边形,根据矩形的对角线互相平分且相等可得OC=OD,然后根据邻边相等的平行四边形是菱形证明即可.(2)根据全等三角形对应边相等可得OD=FC,再根据一组对边平行且相等的四边形是平行四边形判断出四边形ODFC是平行四边形,根据矩形的对角线互相平分且相等可得OC=OD,然后根据邻边相等的平行四边形是菱形证明即可.解答: 证明: (1)∵CF∥BD,∴∠ODE=∠FCE,∵E是CD中点,∴CE=DE,在△ODE和△FCE中,,∴△ODE≌△FCE(ASA);(2)∵△ODE≌△FCE,∴OD=FC,∵CF∥BD,∴四边形ODFC是平行四边形,在矩形ABCD中, OC=OD,∴四边形ODFC是菱形.∴四边形ODFC是菱形.点评: 本题考查了矩形的性质, 全等三角形的判定及性质, 菱形的判定, 熟记各性质及平行四边形和菱形的判定方法是解题的关键.10.矩形的判定. 菁优网版权所有(2019•宁德)如图, 在梯形ABCD中,AD∥BC,点E是BC的中点,连接AC,DE,AC=AB,DE∥AB.求证:四边形AECD是矩形.考点:考点:专题: 证明题.分析: 先判断四边形AECD为平行四边形, 然后由∠AEC=90°即可判断出四边形AECD是矩形.解答: 证明: ∵AD∥BC, DE∥AB,∴四边形ABED是平行四边形.∴AD=BE.∵点E是BC的中点,∴EC=BE=AD.∴四边形AECD是平行四边形.∵AB=AC, 点E是BC的中点,∴AE⊥BC, 即∠AEC=90°.∴▱AECD是矩形.∴▱AECD是矩形.点评: 本题考查了梯形和矩形的判定, 难度适中, 解题关键是掌握平行四边形和矩形的判定定理.正方形的性质;全等三角形的判定及性质. 菁优网版权所有11.(2019•钦州)如图,在正方形ABCD中, E、F分别是AB.BC上的点, 且AE=BF.求证:CE=DF.考点:考点:专题: 证明题.分析: 根据正方形的性质可得AB=BC=CD, ∠B=∠BCD=90°, 然后求出BE=CF, 再利用“边角边”证明△BCE和△CDF全等, 根据全等三角形对应边相等证明即可.解答: 证明: 在正方形ABCD中, AB=BC=CD, ∠B=∠BCD=90°, ∵AE=BF,∴AB﹣AE=BC﹣BF,即BE=CF,在△BCE和△CDF中,,∴△BCE≌△CDF(SAS),∴CE=DF.∴CE=DF.点评: 本题考查了正方形的性质, 全等三角形的判定及性质, 熟记性质并确定出三角形全等的条件是解题的关键.12. (2019•贵港)如图, 在正方形ABCD中, 点E是对角线AC上一点, 且CE=CD, 过点E作EF⊥AC交AD于点F, 连接BE.(1)求证: DF=AE;正方形的性质;角平分线的性质;勾股定理. 菁优网版权所有(2)当AB=2时,求BE2的值.考点:考点:(1)连接CF, 根据“HL”证明Rt△CDF和Rt△CEF全等, 根分析:据全等三角形对应边相等可得DF=EF, 根据正方形的对角线平分一组对角可得∠EAF=45°, 求出△AEF是等腰直角三角形, 再根据等腰直角三角形的性质可得AE=EF, 然后等量代换即可得证;(2)根据正方形的对角线等于边长的倍求出AC, 然后求出AE, 过点E作EH⊥AB于H, 判断出△AEH是等腰直角三角形, 然后求出EH=AH= AE, 再求出BH, 然后利用勾股定理列式计算即可得解.(2)根据正方形的对角线等于边长的倍求出AC,然后求出AE,过点E作EH⊥AB于H,判断出△AEH是等腰直角三角形,然后求出EH=AH= AE,再求出BH,然后利用勾股定理列式计算即可得解.(2)根据正方形的对角线等于边长的倍求出AC,然后求出AE,过点E作EH⊥AB于H,判断出△AEH是等腰直角三角形,然后求出EH=AH=AE,再求出BH,然后利用勾股定理列式计算即可得解.(1)证明: 如图, 连接CF,解答:在Rt△CDF和Rt△CEF中,,∴Rt△CDF≌Rt△CEF(HL),∴DF=EF,∵AC是正方形ABCD的对角线,∴∠EAF=45°,∴△AEF是等腰直角三角形,∴AE=EF,∴DF=AE;(2)解: ∵AB=2,∴AC= AB=2 ,∵CE=CD,∴AE=2 ﹣2,过点E作EH⊥AB于H,则△AEH是等腰直角三角形,∴EH=AH= AE= ×(2 ﹣2)=2﹣,∴BH=2﹣(2﹣)= ,在Rt△BEH中, BE2=BH2+EH2=()2+(2﹣)2=8﹣4 .本题考查了正方形的性质, 全等三角形的判定及性质, 等腰直点评:角三角形的判定及性质, 勾股定理的应用, 作辅助线构造出全等三角形和直角三角形是解题的关键.13. (2019•吴中区一模)已知: 如图, 菱形ABCD中, E、F分别是CB.CD上的点, ∠BAF=∠DAE.(1)求证: AE=AF ;(2)若AE 垂直平分BC, AF 垂直平分CD, 求证:△AEF 为等边三角形.考点:考点:菱形的性质;全等三角形的判定及性质;等边三角形的判定. 菁优网版权所有专题:证明题. 分析:(1)首先利用菱形的性质得出AB=AD, ∠B=∠D, 进而得出△ABE ≌△ADF (ASA ), 即可得出答案;(2)利用垂直平分线的性质得出△ABC 和△ACD 都是等边三角形, 进而得出∠EAF=∠CAE+∠CAF=60°, 求出△AEF 为等边三角形.(2)利用垂直平分线的性质得出△ABC 和△ACD 都是等边三角形,进而得出∠EAF=∠CAE+∠CAF=60°,求出△AEF 为等边三角形.(2)利用垂直平分线的性质得出△ABC 和△ACD 都是等边三角形,进而得出∠EAF=∠CAE+∠CAF=60°,求出△AEF 为等边三角形.解答: (1)证明: ∵四边形ABCD 是菱形,∴AB=AD, ∠B=∠D,又∵∠BAF=∠DAE,∴∠BAE=∠DAF,在△ABE和△ADF中,,∴△ABE≌△ADF(ASA),∴AE=AF;(2)解: 连接AC,∵AE垂直平分BC, AF垂直平分CD,∴AB=AC=AD,∵AB=BC=CD=DA,∴△ABC和△ACD都是等边三角形,∴∠CAE=∠BAE=30°, ∠CAF=∠DAF=30°,∴∠EAF=∠CAE+∠CAF=60°,又∵AE=AF,∴△AEF是等边三角形.点评: 此题主要考查了等边三角形的判定及性质以及全等三角形的判定及性质等知识, 熟练掌握全等三角形的判定方法是解题关键.14. (2019•新乡菱形的性质. 菁优网版权所有一模)小明设计了一个如图的风筝, 其中, 四边形ABCD及四边形AEFG都是菱形,点C在AF上, 点E, G分别在BC,CD上, 若∠BAD=135°, ∠EAG=75°,AE=100cm, 求菱形ABCD的边长.考点:考点:分析: 根据菱形的性质可得出∠BAE=30°, ∠B=45°, 过点E作EM⊥AB于点M, 设EM=x, 则可得出AB、AE的长度, 继而可得出的值, 求出AB即可.解答: 解: ∵∠BAD=135°, ∠EAG=75°, 四边形ABCD及四边形AEFG都是菱形,∴∠B=180°﹣∠BAD=45°, ∠BAE=∠BAC﹣∠EAC=30°,过点E作EM⊥AB于点M, 设EM=x,在Rt△AEM中, AE=2EM=2x, AM= x,在Rt△BEM中, BM=x,则= = ,∵AE=100cm, ∴AB=50(+1)cm,∴菱形ABCD的边长为:50(+1)cm.点评: 本题考查了菱形的性质及解直角三角形的知识, 属于基础题, 关键是掌握菱形的对角线平分一组对角.15. (2019菱形的性质. 菁优网版权所有•槐荫区三模)如图,菱形ABCD的边长为1, ∠D=120°.求对角线AC的长.考点:考点:分析: 连接BD及AC交于点O, 根据菱形的性质可得AB=AD, AC=2AO, ∠ADB= ∠ADC, AC⊥BD, 然后判断出△ABD是等边三角形, 根据等边三角形的性质求出AO, 再根据AC=2AO计算即可得解.解答: 解: 如图, 连接BD及AC交于点O,∵四边形ABCD是菱形,∴AB=AD, AC=2AO, ∠ADB= ∠ADC, AC⊥BD,∵∠D=120°,∴∠ADB=60°,∴△ABD是等边三角形,∴AO=AD×sin∠ADB= ,∴AC=2AO= .点评: 本题考查了菱形的性质, 等边三角形的判定及性质, 熟记性质并作辅助线构造出等边三角形是解题的关键.16.菱形的性质;勾股定理. 菁优网版权所有(2019•历城区一模)如图, 已知菱形ABCD的对角线AC.BD的长分别为6cm、8cm,AE⊥BC于点E, 求AE的长.考点:分析: 根据菱形的对角线互相垂直平分求出CO、BO, 再利用勾股定理列式求出BC, 然后利用菱形的面积等于底乘以高和对角线乘积的一半列出方程求解即可.解答: 解: ∵四边形ABCD是菱形,∴CO= AC=3cm, BO= BD=4cm, AO⊥BO,∴BC= = =5cm,∴S菱形ABCD= =BC•AE,即×6×8=5•AE,解得AE= cm.答:AE的长是cm.答: AE的长是cm.答:AE 的长是cm.点评: 本题考查了菱形的性质, 勾股定理, 熟记菱形的对角线互相垂直平分是解题的关键, 难点在于利用菱形的面积列出方程.17. (2019•湖南校级模拟)如图, AE=AF, 点B.D分别在AE、AF上, 四边形ABCD是菱形, 连接EC.FC(1)求证: EC=FC;(2)若菱形的性质;全等三角形的判定及性质. 菁优网版权所有∠A=60°,求△AEF的周长.考点:考点:分析: (1)连接AC, 根据菱形的对角线平分一组对角可得∠CAE=∠CAF, 然后利用“边角边”证明△ACE和△ACF全等, 根据全等三角形对应边相等可得EC=FC;(2)判断出△AEF是等边三角形, 然后根据等边三角形的三条边都相等解答.(2)判断出△AEF是等边三角形,然后根据等边三角形的三条边都相等解答.(2)判断出△AEF是等边三角形,然后根据等边三角形的三条边都相等解答.解答: (1)证明: 如图, 连接AC,∵四边形ABCD是菱形,∴∠CAE=∠CAF,在△ACE和△ACF中,,∴△ACE≌△ACF(SAS),∴EC=FC;(2)解: 连接EF,∵AE=AF, ∠A=60°,∴△AEF是等边三角形,∴△AEF的周长=3AE=3×2=6.点评: 本题考查了菱形的性质, 全等三角形的判定及性质, 等边三角形的判定及性质, 熟记各性质并作出辅助线是解题的关键.18. (2019•清河区一模)如图, 在△ABC中, AB=AC, 点D.E、F分别是△ABC三边的中点.求证:菱形的判定;三角形中位线定理. 菁优网版权所有四边形ADEF是菱形.考点:专题: 证明题.分析: 利用三角形中位线的性质得出DE AC, EF AB, 进而得出四边形ADEF 为平行四边形., 再利用DE=EF 即可得出答案.解答: 证明: ∵D.E 、F 分别是△ABC 三边的中点,∴DE AC, EF AB,∴四边形ADEF 为平行四边形.又∵AC=AB,∴DE=EF.∴四边形ADEF 为菱形.∴四边形ADEF 为菱形.点评: 此题主要考查了三角形中位线的性质以及平行四边形的判定和菱形的判定等知识, 熟练掌握菱形判定定理是解题关键.19. (2019春•防城区期末)如图, 已菱形的判定;全等三角形的判定及性质;平行四边形的性质. 菁优网版权所有形ABCD是平行四边形, DE⊥AB,DF⊥BC, 垂足分别是为E, F,并且DE=DF.求证:四边形ABCD是菱形.考点:考点:专题: 证明题.分析: 首先利用已知条件和平行四边形的性质判定△ADE≌△CDF, 再根据邻边相等的平行四边形为菱形即可证明四边形ABCD是菱形.解答: 证明: 在△ADE和△CDF中,∵四边形ABCD是平行四边形,∴∠A=∠C,∵DE⊥AB, DF⊥BC,∴∠AED=∠CFD=90°.又∵DE=DF,∴△ADE≌△CDF(AAS)∴DA=DC,∴平行四边形ABCD是菱形.∴平行四边形ABCD是菱形.点评: 本题考查了平行四边形的性质, 全等三角形的判定和性质以及菱形的判定方法, 解题的关键是熟练掌握各种图形的判定和性质.20. (2019•通州区一模)如图, 在四边形ABCD中, AB=DC, E、F分别是AD.BC的中点, G、H分别是对角线BD.AC的中点.(1)求证: 四边形EGFH是菱形;(2)若AB=1, 则当∠ABC+∠DCB=90°时, 求四边形EGFH 的面积.考点:考点:菱形的判定及性质;正方形的判定及性质;中点四边形. 菁优网版权所有分析: (1)利用三角形的中位线定理可以证得四边形EGFH 的四边相等, 即可证得;(2)根据平行线的性质可以证得∠GFH=90°, 得到菱形EGFH 是正方形, 利用三角形的中位线定理求得GE 的长, 则正方形的面积可以求得.(2)根据平行线的性质可以证得∠GFH=90°,得到菱形EGFH 是正方形,利用三角形的中位线定理求得GE 的长,则正方形的面积可以求得.(2)根据平行线的性质可以证得∠GFH=90°,得到菱形EGFH 是正方形,利用三角形的中位线定理求得GE 的长,则正方形的面积可以求得.解答: (1)证明: ∵四边形ABCD中, E、F、G、H分别是AD.BC.BD.AC 的中点,∴FG= CD, HE= CD, FH= AB, GE= AB.∵AB=CD,∴FG=FH=HE=EG.∴四边形EGFH是菱形.(2)解: ∵四边形ABCD中, G、F、H分别是BD.BC.AC的中点,∴GF∥DC, HF∥AB.∴∠GFB=∠DCB, ∠HFC=∠ABC.∴∠HFC+∠GFB=∠ABC+∠DCB=90°.∴∠GFH=90°.∴菱形EGFH是正方形.∵AB=1,∴EG= AB= .∴正方形EGFH的面积=()2= .点评: 本题考查了三角形的中位线定理, 菱形的判定以及正方形的判定, 理解三角形的中位线定理是关键.21. (2019•顺义区二模)如图, 在△ABC中, D.E分别是AB.AC的中点, BE=2DE, 过点C作CF∥BE交DE的延长线于F.(1)求证: 四边形BCFE是菱形;(2)若菱形的判定及性质. 菁优网版权所有CE=4, ∠BCF=120°,求菱形BCFE的面积.考点:考点:分析: (1)由题意易得, EF及BC平行且相等, 故四边形BCFE 是平行四边形. 又麟边EF=BE, 则四边形BCFE是菱形;(2)连结BF, 交CE于点O.利用菱形的性质和等边三角形的判定推知△BCE是等边三角形.通过解直角△BOC求得BO的长度, 则BF=2BO.利用菱形的面积= CE•BF进行解答.(2)连结BF,交CE于点O. 利用菱形的性质和等边三角形的判定推知△BCE是等边三角形. 通过解直角△BOC求得BO的长度,则BF=2BO. 利用菱形的面积= CE•BF进行解答.(2)连结BF,交CE于点O.利用菱形的性质和等边三角形的判定推知△BCE是等边三角形.通过解直角△BOC求得BO的长度,则BF=2BO.利用菱形的面积=CE•BF进行解答.解答: (1)证明: ∵D.E分别是AB.AC的中点,∴DE∥BC, BC=2DE.∵CF∥BE,∴四边形BCFE是平行四边形.∵BE=2DE, BC=2DE,∴BE=BC.∴□BCFE是菱形;(2)解: 连结BF, 交CE于点O.∵四边形BCFE是菱形, ∠BCF=120°,∴∠BCE=∠FCE=60°, BF⊥CE,∴△BCE是等边三角形.∴BC=CE=4.∴.∴.点评: 此题主要考查菱形的性质和判定以及面积的计算, 使学生能够灵活运用菱形知识解决有关问题.22. (2019•祁阳县校级模拟)如图, O为矩形ABCD对角线的交点, DE ∥AC, CE∥BD.矩形的性质;菱形的判定. 菁优网版权所有(1)求证: 四边形OCED是菱形.(2)若AB=6,BC=8,求四边形OCED的周长.考点:考点:分析: (1)根据矩形性质求出OC=OD, 根据平行四边形的判定得出四边形OCED是平行四边形, 根据菱形判定推出即可;(2)根据勾股定理求出AC, 求出OC, 得出OC=OD=CE=ED=5,相加即可.(2)根据勾股定理求出AC,求出OC,得出OC=OD=CE=ED=5,相加即可.(2)根据勾股定理求出AC,求出OC,得出OC=OD=CE=ED=5,相加即可.解答: (1)证明: ∵四边形ABCD是矩形,∴AC=2OC, BD=2OD, AC=BD,∴OD=OC,∵DE∥AC, CE∥BD,∴四边形OCED是菱形.(2)解: ∵四边形ABCD是矩形,∴∠ABC=90°,∵AB=6, BC=8,∴在Rt△ABC中, 由勾股定理得: AC=10,即OC= AC=5,∵四边形OCED是菱形,∴OC=OD=DE=CE=5,∴四边形OCED的周长是5+5+5+5=20.∴四边形OCED的周长是5+5+5+5=20.。
人教版初二数学8年级下册 第18章(平行四边形)证明题专题训练(含答案)

人教版八年级下册数学第十八章平行四边形证明题专题训练1.如图,在平行四边形ABCD中,E、F是对角线AC所在直线上的两点,且AE=CF.求证:四边形EBFD 是平行四边形.2.如图,在△ABC中,点D,E分别是BC,AC的中点,延长BA至点F,使得AF= 1AB,连接DE,AD,EF,DF.2(1)求证:四边形ADEF是平行四边形;(2)若AB=6,AC=8,BC=10,求EF的长.的对角线AC的垂直平分线与边AD,BC分别相交于点E,3.如图所示,ABCDF.求证:四边形AFCE是菱形.AC BD交于点,O过点O任作直线分别交4.如图,在平行四边形ABCD中,对角线,AB CD于点E F,、.求证:OE OF =.5.已知:如图,在ABCD 中,,E F 是对角线BD 上两个点,且BE DF =.求证:.AE CF =6.已知:如图,矩形ABCD 中,O 是AC 与BD 的交点,过O 点的直线EF 与AB 、CD 的延长线分别相交于点E 、F .(1)求证:△BOE ≌△DOF ;(2)当EF 与AC 满足什么关系时,以A 、E 、C 、F 为顶点的四边形是菱形?并给出证明.7.如图,菱形ABCD 的对角线AC 、BD 相交于点O ,//BE AC ,//AE BD ,OE 与AB 交于点F .(1)求证:四边形AEBO 的为矩形;(2)若OE =10,AC =16,求菱形ABCD 的面积.8.已知:如图,在ABC 中,中线,BE CD 交于点,,O F G 分别是,OB OC 的中点.求证:(1)//DE FG ;(2)DG 和EF 互相平分.9.如图,在平行四边形ABCD 中,AC 是对角线,且AB =AC ,CF 是∠ACB 的角平分线交AB 于点F ,在AD 上取一点E ,使AB =AE ,连接BE 交CF 于点P .(1)求证:BP =CP ;(2)若BC =4,∠ABC =45°,求平行四边形ABCD 的面积.10.如图,AB,CD相交于点O,AC∥DB,OA=OB,E、F分别是OC,OD中点.(1)求证:OD=OC.(2) 求证:四边形AFBE平行四边形.11.如图所示,在菱形ABCD中,E、F分别为AB、AD上两点,AE=AF.(1)求证:CE=CF;(2)若∠ECF=60°,∠B=80°,试问BC=CE吗?请说明理由.12.已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点.(1)求证:△ABM≌△DCM;(2)当AB:AD的值为多少时,四边形MENF是正方形?请说明理由.13.如图,在矩形ABCD中,过对角线AC的中点O作AC的垂线,分别交射线AD 和CB于点E,F连接AF,CE.(1)求证:OE=OF;(2)求证:四边形AFCE是菱形.14.如图,BD是△ABC的角平分线,过点作DE//BC交AB于点E,DF//AB交BC 于点F.(1)求证:四边形BEDF是菱形;(2)若∠ABC=60°,∠ACB=45°,CD=6,求菱形BEDF的边长.15.如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG.(1)求证:△ABG≌△AFG;(2)求∠EAG的度数;(3)求BG的长.16.如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D在AB边上一点.过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.(1)求证:CE=AD;(2)当点D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由.17.如图,在△ABC中,AB=AC,点D为边BC上一点,以AB,BD为邻边作▱ABDE,连接AD、EC.(1)求证:△ADC≌△ECD; (2)若BD=CD,求证:四边形ADCE是矩形.18.如图,在四边形ABCD中,AB=CD,BF=DE,AE⊥BD,CF⊥BD,垂足分别为E、F.(1)求证:△ABE≌△CDF;(2)若AC与BD交于点O,求证:AO=CO.19.在平行四边形ABCD中,点E在AD边上,连接BE、CE,EB平分∠AEC,(1)如图1,判断△BCE的形状,并说明理由;(2)如图2,若∠A=90°,BC=5,AE=1,求线段BE的长.20.如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于点F,连接DF.(1)求证:∠BAC=∠DAC,∠AFD=∠CFE;(2)若AB∥CD,试证明四边形ABCD是菱形;(3)在(2)的条件下,试确定E点的位置,使∠EFD=∠BCD,并说明理由.参考答案:1.解:证明:如图,连接BD交AC于点O,∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,又∵AE=CF,∴OA-AE=OC-CF,即OE=OF,∴四边形EBFD是平行四边形.2.(1)证明:∵点D,E分别是BC,AC的中点,∴DE是△ABC的中位线,∴DE∥AB,DE=12 AB,∵AF=12 AB,∴DE=AF,DE∥AF,∴四边形ADEF是平行四边形;(2)解:由(1)得:四边形ADEF是平行四边形,∴EF=AD,∵AB=6,AC=8,BC=10,∴AB2+AC2=BC2,∴△ABC是直角三角形,∠BAC=90°,∵点D是BC的中点,∴AD=12BC=5,∴EF=AD=5.3.证明:∵四边形ABCD 是平行四边形∴//AE FC ,AO CO =,∴EAC FCA ∠=∠,∵EF 是AC 的垂直平分线,∴EF AC ⊥,在AOE △与COF 中,EAO FCO AO COAOE COF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴()ASA AOE COF ≌△△,∴EO FO =,∴四边形AFCE 为平行四边形,又∵EF AC ⊥,∴四边形AFCE 为菱形.4.解:证明:∵四边形ABCD 是平行四边形,∴AD ∥BC ,OA =OC ,∴∠EAO =∠FCO ,在△AEO 和△CFO 中,OAE OCF OA OCAOE COF ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△AEO ≌△CFO (ASA ),∴OE =OF .5.证明:∵四边形ABCD 是平行四边形,∴AB =CD ,AB ∥CD .∴∠ABE =∠CDF .在△ABE 和△CDF 中AB CD ABE CDF BE DF =⎧⎪∠=∠⎨⎪=⎩∴△ABE ≌△CDF (SAS )∴AE =CF .6.(1)证明:∵四边形ABCD 是矩形,∴OB =OD ,∵AE //CF ,∴∠E =∠F ,∠OBE =∠ODF ,在△BOE 与△DOF 中,E F OBE ODF OB OD ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△BOE ≌△DOF (AAS );(2)当EF ⊥AC 时,四边形AECF 是菱形. 证明:∵△BOE ≌△DOF ,∴OE =OF ,∵四边形ABCD 是矩形,∴OA =OC ,∴四边形AECF 是平行四边形,∵EF ⊥AC ,∴四边形AECF 是菱形.7.解:(1)证明:∵//BE AC ,//AE BD ,∴四边形AEBO 为平行四边形,又∵四边形ABCD 为菱形,∴BD AC ⊥,∴90AOB ∠=︒,∴平行四边形AEBO 为矩形;(2)∵四边形AEBO 为矩形,∴AB =OE =10,又∵四边形ABCD 为菱形,∴AO =12AC =8,∴90AOB ∠=︒,∴6BO ==,∴BD =2BO =12,∴菱形ABCD 的面积=12121696⨯⨯=.8.(1)在△ABC 中,∵BE 、CD 为中线∴AD =BD ,AE =CE ,∴DE ∥BC 且DE =12BC .在△OBC 中,∵OF =FB ,OG =GC ,∴FG ∥BC 且FG =12BC .∴DE ∥FG(2)由(1)知:DE ∥FG ,DE =FG .∴四边形DFGE 为平行四边形.∴DG 和EF 互相平分9.解:(1)设AP 与BC 交于H ,∵在平行四边形ABCD 中,AD ∥BC ,∴∠AEB=∠CBE,∵AB=AE,∴∠ABE=∠AEB,∴∠ABE=∠CBE,∴BE平分∠ABC,∵CF是∠ACB的角平分线,BE交CF于点P,∴AP平分∠BAC,∵AB=AC,∴AH垂直平分BC,∴PB=PC;(2)∵AH垂直平分BC,∴AH⊥BC,BH=CH=12BC=2,∵∠ABH=45°,∴AH=BH=2,∴平行四边形ABCD的面积=4×2=8.10.证明:(1)∵AC∥DB,∴∠CAO=∠DBO,∵∠AOC=∠BOD,OA=OB,∴△AOC≌△BOD,∴OC=OD;(2)∵E是OC中点,F是OD中点,∴OE=12OC,OF=12OD,∵OC=OD,∴OE=OF,又∵OA=OB,∴四边形AFBE是平行四边形.11.(1)证明:∵ABCD是菱形,∴AB =AD ,BC =CD ,∠B =∠D ,∵AE =AF ,∴AB ﹣AE =AD ﹣AF ,∴BE =DF ,在△BCE 与△DCF 中,∵BE DF B D BC CD =⎧⎪∠=∠⎨⎪=⎩,∴△BCE ≌△DCF ,∴CE =CF ;(2)结论是:BC =CE .理由如下:∵ABCD 是菱形,∠B =80°,∴∠A =100°,∵AE =AF ,∴180100402AEF AFE ︒-︒∠=∠==︒由(1)知CE =CF ,∠ECF =60°,∴△CEF 是等边三角形,∴∠CEF =60°,∴∠CEB =180°﹣60°﹣40°=80°,∴∠B =∠CEB ,∴BC =CE .12.(1)证明:∵四边形ABCD 是矩形,∴AB =DC ,∠A =∠D =90°,∵M 为AD 中点,∴AM =DM ,在△ABM 和△DCM ,AM DM A D AB CD =⎧⎪∠=∠⎨⎪=⎩,∴△ABM ≌△DCM (SAS );(2)解:当AB :AD =1:2时,四边形MENF 是正方形,理由:当四边形MENF 是正方形时,则∠EMF =90°,∵△ABM ≌△DCM ,∴∠AMB =∠DMC =45°,∴△ABM 、△DCM 为等腰直角三角形,∴AM =DM =AB ,∴AD =2AB ,即当AB :AD =1:2时,四边形MENF 是正方形.13.解:(1)∵四边形ABCD 是矩形,∴//AD BC ,∴∠EAO =∠FCO ,∵AC 的中点是O ,∴OA =OC ,在EOA △和FOC 中,AOE COF AO COEAO FCO ∠=∠⎧⎪=⎨⎪∠=∠⎩,()EOA FOC ASA ∴ ≌,∴OE =OF ;(2)∵OE =OF ,AO =CO ,∴四边形AFCE 是平行四边形,∵EF ⊥AC ,∴四边形AFCE 是菱形.14.证明:(1)∵DE ∥BC ,DF ∥AB ,∴四边形DEBF 是平行四边形,∵DE ∥BC ,∴∠EDB =∠DBF ,∵BD平分∠ABC,∠ABC,∴∠ABD=∠DBF=12∴∠ABD=∠EDB,∴DE=BE,又∵四边形BEDF为平行四边形,∴四边形BEDF是菱形;(2)如图,过点D作DH⊥BC于H,∵DF∥AB,∴∠ABC=∠DFC=60°,∵DH⊥BC,∴∠FDH=30°,DF,DH,∴FH=12∵∠C=45°,DH⊥BC,∴∠C=∠HDC=45°,∴DC DH=6,∴DF=,∴菱形BEDF的边长为15.(1)证明;在正方形ABCD中,AD=AB=BC=CD,∠D=∠B=∠BCD=90°,∵将△ADE沿AE对折至△AFE,∴AD=AF,DE=EF,∠D=∠AFE=90°,∴AB=AF,∠B=∠AFG=90°,又∵AG=AG,在Rt △ABG 和Rt △AFG 中,AG=AG AB=AF ⎧⎨⎩,∴△ABG ≌△AFG (HL );(2)∵△ABG ≌△AFG ,∴∠BAG =∠FAG ,∴∠FAG =12∠BAF ,由折叠的性质可得:∠EAF =∠DAE ,∴∠EAF =12∠DAF ,∴∠EAG =∠EAF +∠FAG =12(∠DAF +∠BAF )=12∠DAB =12×90°=45°;(3)∵E 是CD 的中点,∴DE =CE =12CD =12×6=3,设BG =x ,则CG =6﹣x ,GE =EF +FG =x +3,∵GE 2=CG 2+CE 2∴(x +3)2=(6﹣x )2+32,解得:x =2,∴BG =2.16.(1)证明:∵DE ⊥BC ,∴∠DFB =90°,∵∠ACB =90°,∴∠ACB =∠DFB ,∴AC ∥DE ,∵MN ∥AB ,即CE ∥AD ,∴四边形ADEC 是平行四边形,∴CE =AD ;(2)解:四边形BECD 是菱形,理由是:∵D 为AB 中点,∴AD =BD ,∵CE =AD ,∴BD =CE ,∵BD ∥CE ,∴四边形BECD 是平行四边形,∵∠ACB =90°,D 为AB 中点,∴CD =BD ,∴四边形BECD 是菱形.17.(证明:(1)∵四边形ABDE 是平行四边形(已知),∴AB ∥DE ,AB =DE (平行四边形的对边平行且相等);∴∠B =∠EDC (两直线平行,同位角相等);又∵AB =AC (已知),∴AC =DE (等量代换),∠B =∠ACB (等边对等角),∴∠EDC =∠ACD (等量代换);∵在△ADC 和△ECD 中,AC ED ACD EDC DC CD =⎧⎪∠=∠⎨⎪=⎩,∴△ADC ≌△ECD (SAS );(2)∵四边形ABDE 是平行四边形(已知),∴BD ∥AE ,BD =AE (平行四边形的对边平行且相等),∴AE ∥CD ;又∵BD =CD ,∴AE =CD (等量代换),∴四边形ADCE 是平行四边形(对边平行且相等的四边形是平行四边形);在△ABC 中,AB =AC ,BD =CD ,∴AD ⊥BC (等腰三角形的“三合一”性质),∴∠ADC =90°,∴▱ADCE 是矩形.18.证明:(1)∵BF=DE ,∴BF EF DE EF -=-,即BE=DF ,∵AE ⊥BD ,CF ⊥BD ,∴∠AEB=∠CFD=90°,在Rt △ABE 与Rt △CDF 中,AB CD BE DF =⎧⎨=⎩,∴Rt ABE Rt CDF ∆∆≌(HL );(2)如图,连接AC 交BD 于O ,∵Rt ABE Rt CDF ∆∆≌,∴ABE CDF ∠=∠,∴//D AB C ,∵=D AB C ,∴四边形ABCD 是平行四边形,∴AO CO =.19.证明:∵四边形ABCD 是平行四边形,∴BC ∥AD ,∴∠CBE=∠AEB ,∵EB 平分∠AEC ,∴∠CBE=∠BEC ,∴CB=CE ,∴△CBE 是等腰三角形;(2)如图2中,∵四边形ABCD 是平行四边形,∠A=90°,∴四边形ABCD 是矩形,∴∠A=∠D=90°,BC=AD=5,在Rt △ECD 中,∵∠D=90°,ED=AD-AE=4,EC=BC=5,3AB CD ∴====,在Rt AEB 中,∵∠A=90°,AB=3.AE=1,BE ∴===20.(1)证明:在△ABC 和△ADC 中,AB AD CB CD AC AC =⎧⎪=⎨⎪=⎩∴△ABC ≌△ADC(SSS),∴∠BAC=∠DAC ,在△ABF 和△ADF 中,AB AD BAF DAF AF AF =⎧⎪∠=∠⎨⎪=⎩∴△ABF ≌△ADF(SAS),∴∠AFB=∠AFD ,∵∠CFE=∠AFB ,∴∠AFD=∠CFE ,∴∠BAC=∠DAC ,∠AFD=∠CFE ;(2)证明:∵AB ∥CD ,∴∠BAC=∠ACD ,∵∠BAC=∠DAC ,∴∠DAC=∠ACD,∴AD=CD,∵AB=AD,CB=CD,∴AB=CB=CD=AD,∴四边形ABCD是菱形;(3)BE⊥CD时,∠BCD=∠EFD;理由如下:∵四边形ABCD是菱形,∴BC=CD,∠BCF=∠DCF,∵CF=CF,∴△BCF≌△DCF,∴∠CBF=∠CDF,∵BE⊥CD,∴∠BEC=∠DEF=90°,∴∠BCD=∠EFD.。
特殊平行四边形证明及解答题--困难--教师版版

2015年初中数学中考特殊四边形证明及计算组卷参考答案与试题解析姓名______________学号_____________一.解答题(共30小题)1.(2012•威海)(1)如图①,▱ABCD的对角线AC,BD交于点O,直线EF过点O,分别交AD,BC于点E,F.求证:AE=CF.(2)如图②,将▱ABCD(纸片)沿过对角线交点O的直线EF折叠,点A落在点A1处,点B落在点B1处,设FB1交CD于点G,A1B1分别交CD,DE于点H,I.求证:EI=FG.,∴△2.(2011•贵阳)[阅读]在平面直角坐标系中,以任意两点P(x1,y1)、Q(x2,y2)为端点的线段中点坐标为.[运用](1)如图,矩形ONEF的对角线相交于点M,ON、OF分别在x轴和y轴上,O为坐标原点,点E的坐标为(4,3),则点M的坐标为(2,1.5).(2)在直角坐标系中,有A(﹣1,2),B(3,1),C(1,4)三点,另有一点D与点A、B、C构成平行四边形的顶点,求点D的坐标.,BC=,∵﹣AC=2BD=2AB=CD=3.(2007•黑龙江)在△ABC中,AB=AC,点P为△ABC所在平面内一点,过点P分别作PE∥AC交AB于点E,PF∥AB交BC于点D,交AC于点F.若点P在BC边上(如图1),此时PD=0,可得结论:PD+PE+PF=AB.请直接应用上述信息解决下列问题:当点P分别在△ABC内(如图2),△ABC外(如图3)时,上述结论是否成立?若成立,请给予证明;若不成立,PD,PE,PF与AB之间又有怎样的数量关系,请写出你的猜想,不需要证明.4.(2006•泰安)如图,矩形ABCD的对角线交于点O,AE⊥BD,CF⊥BD,垂足分别为E,F,连接AF,CE.OA=AC=5.(2006•陕西)如图,在Rt△ABC中,∠BAC=90°,E,F分别是BC,AC的中点,延长BA到点D,使AD=AB.连接DE,DF.EF=ABAD=BC=26.如图,以△ABC三边为边在BC同侧作三个等边△ABD、△BCE、△ACF.请回答下列问题:(1)求证:四边形ADEF是平行四边形;7.(2010•盘锦)如图,△ABC是等边三角形,点D是边BC上的一点,以AD为边作等边△ADE,过点C作CF∥DE 交AB于点F.(1)若点D是BC边的中点(如图①),求证:EF=CD;(2)在(1)的条件下直接写出△AEF和△ABC的面积比;(3)若点D是BC边上的任意一点(除B、C外如图②),那么(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.解答:BAD=∠8.(2011•海南)如图,在菱形ABCD中,∠A=60°,点P、Q分别在边AB、BC上,且AP=BQ.(1)求证:△BDQ≌△ADP;(2)已知AD=3,AP=2,求cos∠BPQ的值(结果保留根号).CBD=∠CBD=QE=QB•sin60°=2×,=1PQ==,BPQ==9.(2007•常德)如图1,已知四边形ABCD是菱形,G是线段CD上的任意一点时,连接BG交AC于F,过F作FH∥CD交BC于H,可以证明结论成立.(考生不必证明)(1)探究:如图2,上述条件中,若G在CD的延长线上,其它条件不变时,其结论是否成立?若成立,请给出证明;若不成立,请说明理由;(2)计算:若菱形ABCD中AB=6,∠ADC=60°,G在直线CD上,且CG=16,连接BG交AC所在的直线于F,过F作FH∥CD交BC所在的直线于H,求BG与FG的长.(3)发现:通过上述过程,你发现G在直线CD上时,结论还成立吗?)借助中间比进行证明,根据平行线分线段成比例定理分别证明两个比都等于)结论,.,可得,)知,,可得.BF=14×÷16=的延长线上时,,10.(2001•河北)如图,在菱形ABCD中,AB=10,∠BAD=60度.点M从点A以每秒1个单位长的速度沿着AD 边向点D移动;设点M移动的时间为t秒(0≤t≤10).(1)点N为BC边上任意一点,在点M移动过程中,线段MN是否一定可以将菱形分割成面积相等的两部分并说明理由;(2)点N从点B(与点M出发的时刻相同)以每秒2个单位长的速度沿着BC边向点C移动,在什么时刻,梯形ABNM的面积最大并求出面积的最大值;(3)点N从点B(与点M出发的时刻相同)以每秒a(a≥2)个单位长的速度沿着射线BC方向(可以超越C点)移动,过点M作MP∥AB,交BC于点P.当△MPN≌△ABC时,设△MPN与菱形ABCD重叠部分的面积为S,求出用t表示S的关系式,井求当S=0时的值.,5×=点外,所以不重合处面积为×S=25﹣,12.在平行四边形ABCD中,∠BAD的平分线交直线BC于点E,交直线DC的延长线于点F,以EC、CF为邻边作平行四边形ECFG.(1)如图1,证明平行四边形ECFG为菱形;(2)如图2,若∠ABC=90°,M是EF的中点,求∠BDM的度数;(3)如图3,若∠ABC=120°,请直接写出∠BDG的度数.,,13.如图1,在△ABC中,AB=BC=5,AC=6.△ECD是△ABC沿BC方向平移得到的,连接AE、AC和BE相交于点O.(1)判断四边形ABCE是怎样的四边形,说明理由;(2)如图2,P是线段BC上一动点(图2),(不与点B、C重合),连接PO并延长交线段AE于点Q,QR⊥BD,垂足为点R.四边形PQED的面积是否随点P的运动而发生变化?若变化,请说明理由;若不变,求出四边形PQED 的面积.ED=14.(2011•清远)如图,在矩形ABCD中,E是BC边上的点,AE=BC,DF⊥AE,垂足为F,连接DE.(1)求证:AB=DF;(2)若AD=10,AB=6,求tan∠EDF的值.=.15.(2010•大庆)已知:如图①,正方形ABCD与矩形DEFG的边AD、DE在同一直线l上,点G在CD上.正方形ABCD的边长为a,矩形DEFG的长DE为b,宽DG为3(其中a>b>3).若矩形DEFG沿直线l向左以每秒1个单位的长度的速度运动(点D、E始终在直线l上).若矩形DEFG在运动过程中与正方形ABCD的重叠部分的面积记作S,运动时间记为t秒(0≤t≤m),其中S与t的函数图象如图②所示.矩形DEFG的顶点经运动后的对应点分别记作D′、E′、F′、G′.(1)根据题目所提供的信息,可求得b=4,a=5,m=9;(2)连接AG′、CF′,设以AG′和CF′为边的两个正方形的面积之和为y,求当0≤t≤5时,y与时间t之间的函数关系式,并求出y的最小值以及y取最小值时t的值;(3)如图③,这是在矩形DEFG运动过程中,直线AG′第一次与直线CF′垂直的情形,求此时t的值.并探究:在矩形DEFG继续运动的过程中,直线AG′与直线CF′是否存在平行或再次垂直的情形?如果存在,请画出图形,并求出t的值;否则,请说明理由.),时,=,=,,=,,即16.(2005•淮安)已知:平行四边形ABCD的对角线交点为O,点E、F分别在边AB、CD上,分别沿DE、BF折叠四边形ABCD,A、C两点恰好都落在O点处,且四边形DEBF为菱形(如图).(1)求证:四边形ABCD是矩形;(2)在四边形ABCD中,求的值.,易求解则17.如图,已知矩形ABCD,AD=4,CD=10,P是AB上一动点,M、N、E分别是PD、PC、CD的中点.(1)求证:四边形PMEN是平行四边形;(2)请直接写出当AP为何值时,四边形PMEN是菱形;(3)四边形PMEN有可能是矩形吗?若有可能,求出AP的长;若不可能,请说明理由.PD ME=PN=DP=CP=18.如图:矩形ABCD中,AB=2,BC=5,E、P分别在AD、BC上,且DE=BP=1.(1)判断△BEC的形状,并说明理由?(2)判断四边形EFPH是什么特殊四边形?并证明你的判断;(3)求四边形EFPH的面积.CE===BE=2=﹣PF==,=EF•PF=,的面积是19.(2012•黑龙江)在△ABC中,∠BAC=90°,AB=AC,若点D在线段BC上,以AD为边长作正方形ADEF,如图1,易证:∠AFC=∠ACB+∠DAC;(1)若点D在BC延长线上,其他条件不变,写出∠AFC、∠ACB、∠DAC的关系,并结合图2给出证明;(2)若点D在CB延长线上,其他条件不变,直接写出∠AFC、∠ACB、∠DAC的关系式.,,20.(2012•常德)已知四边形ABCD是正方形,O为正方形对角线的交点,一动点P从B开始,沿射线BC运动,连接DP,作CN⊥DP于点M,且交直线AB于点N,连接OP,ON.(当P在线段BC上时,如图1:当P在BC 的延长线上时,如图2)(1)请从图1,图2中任选一图证明下面结论:①BN=CP;②OP=ON,且OP⊥ON;(2)设AB=4,BP=x,试确定以O、P、B、N为顶点的四边形的面积y与x的函数关系.,,=2+=2+=的函数关系是:21.(2011•来宾)已知正方形ABCD的对角线AC与BD交于点O,点E、F分别是OB、OC上的动点,(1)如果动点E、F满足BE=CF(如图1):①写出所有以点E或F为顶点的全等三角形(不得添加辅助线);②证明:AE⊥BF;(2)如果动点E、F满足BE=OF(如图2),问当AE⊥BF时,点E在什么位置,并证明你的结论.,==,AO====,BO==22.(2011•河北)如图,四边形ABCD是正方形,点E,K分别在BC,AB上,点G在BA的延长线上,且CE=BK=AG.(1)求证:①DE=DG;②DE⊥DG(2)尺规作图:以线段DE,DG为边作出正方形DEFG(要求:只保留作图痕迹,不写作法和证明);(3)连接(2)中的KF,猜想并写出四边形CEFK是怎样的特殊四边形,并证明你的猜想:(4)当时,请直接写出的值.)由已知表示出=.23.(2011•阜新)如图,点P是正方形ABCD对角线AC上一动点,点E在射线BC上,且PB=PE,连接PD,O 为AC中点.(1)如图1,当点P在线段AO上时,试猜想PE与PD的数量关系和位置关系,不用说明理由;(2)如图2,当点P在线段OC上时,(1)中的猜想还成立吗?请说明理由;(3)如图3,当点P在AC的延长线上时,请你在图3中画出相应的图形(尺规作图,保留作图痕迹,不写作法),并判断(1)中的猜想是否成立?若成立,请直接写出结论;若不成立,请说明理由.,24.(2006•内江)如图:四边形ABCD中,E、F、G、H分别为各边的中点,顺次连接E、F、G、H,把四边形EFGH 称为中点四边形.连接AC、BD,容易证明:中点四边形EFGH一定是平行四边形.(1)如果改变原四边形ABCD的形状,那么中点四边形的形状也随之改变,通过探索可以发现:当四边形ABCD 的对角线满足AC=BD时,四边形EFGH为菱形.当四边形ABCD的对角线满足AC⊥BD时,四边形EFGH为矩形;当四边形ABCD的对角线满足AC⊥BD且AC=BD时,四边形EFGH为正方形;(2)探索三角形AEH、三角形CFG与四边形ABCD的面积之间的等量关系,请写出你发现的结论,并加以证明;(3)如果四边形ABCD的面积为2,那么中点四边形EFGH的面积是多少?EF=AC BD=EF=BDSBDSS((S25.如图,四边形ABCD是正方形,点P是BC上任意一点,DE⊥AP于点E,BF⊥AP于点F,CH⊥DE于点H,BF的延长线交CH于点G.(1)求证:AF﹣BF=EF;(2)四边形EFGH是什么四边形?并证明;(3)若AB=2,BP=1,求四边形EFGH的面积.AP=×AP=BF×=1×2×,BF=====26.如图,在正方形ABCD中,点M在边AB上,点N在边AD的延长线上,且BM=DN.点E为MN的中点,DE的延长线与AC相交于点F.试猜想线段DF与线段AC的关系,并证你的猜想.ACACAC27.在图1到图3中,点O是正方形ABCD对角线AC的中点,△MPN为直角三角形,∠MPN=90°.正方形ABCD 保持不动,△MPN沿射线AC向右平移,平移过程中P点始终在射线AC上,且保持PM垂直于直线AB于点E,PN垂直于直线BC于点F.(1)如图1,当点P与点O重合时,OE与OF的数量关系为OE=OF;(2)如图2,当P在线段OC上时,猜想OE与OF有怎样的数量关系与位置关系?并对你的猜想结果给予证明;(3)如图3,当点P在AC的延长线上时,OE与OF的数量关系为OE=OF;位置关系为OE⊥OF.28.以△ABC的各边,在边BC的同侧分别作三个正方形.他们分别是正方形ABDI,BCFE,ACHG,试探究:(1)如图中四边形ADEG是什么四边形?并说明理由.(2)当△ABC满足什么条件时,四边形ADEG是矩形?(3)当△ABC满足什么条件时,四边形ADEG是正方形?ABABABAC=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初二数学平行四边形压轴:几何证明题
1.在四边形ABCD 中,E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点,顺次连接EF 、FG 、GH 、HE . (1)请判断四边形EFGH 的形状,并给予证明;
(2)试探究当满足什么条件时,使四边形EFGH 是菱形,并说明理由。
2.如图,在直角三角形ABC 中,∠ACB=90°,AC=BC=10,将△ABC 绕点B 沿顺时针方向旋转90°得到△A 1BC 1.
(1)线段A 1C 1的长度是 ,∠CBA 1的度数是 . (2)连接CC 1,求证:四边形CBA 1C 1是平行四边形.
3. 如图,矩形ABCD 中,点P 是线段AD 上一动点,O 为BD 的中点, PO 的延长线交BC 于Q.
(1)求证:OP=OQ ;
(2)若AD=8厘米,AB=6厘米,P 从点A 出发,以1厘米/秒的速度向D 运动(不与D 重合).设点P 运动时间为t 秒,请用t 表示PD 的长;并求t 为何值时,四边形PBQD 是菱形.
4.已知:如图,在□ABCD 中,AE 是BC 边上的高,将△ABE 沿BC 方向平移,使点E 与点C
重合,得△GFC. ⑴求证:BE =DG ;
⑵若∠B =60︒,当AB 与BC 满足什么数量关系时,四边形ABFG 是菱形?证明你的结论.
5. 如图,在四边形ABCD 中,AD ∥BC ,E 为CD 的中点,连结AE 、BE ,BE ⊥AE ,延长AE 交BC 的延长线于点F . 求证:(1)FC =AD ;
(2)AB =BC +AD .
A B
E F
C
G
D H B A 1
C 1
A C A
G
C
B
F
E
P
A D E
C
B
6.如图,在△ABC 中,AB=AC ,D 是BC 的中点,连结AD ,在AD 的延长线上取一点E ,连结BE ,CE.
(1)求证:△ABE ≌△ACE
(2)当AE 与AD 满足什么数量关系时,四边形ABEC 是菱形?并说明理由.
7.如图,在平行四边形ABCD 中,点E 是边AD 的中点,BE 的延长线与CD 的延长线交于点F. (1)求证:△ABE ≌△DFE
(2)连结BD 、AF ,判断四边形ABDF 的形状,并说明理由.
8. 如图,已知点D 在△ABC 的BC 边上,DE ∥AC 交AB 于E ,DF ∥AB 交AC 于F . (1)求证:AE =DF ;
(2)若AD 平分∠BAC ,试判断四边形AEDF 的形状,并说明理由.
9. 如图,在平行四边形中,点E F ,是对角线BD 上两点,且BF DE =. (1)写出图中每一对你认为全等的三角形;
(2)选择(1)中的任意一对全等三角形进行证明.
10.在梯形ABCD 中,AD ∥BC,AB=DC ,过点D 作DE ⊥BC ,垂足为点E ,并延长DE 至点F ,使EF=DE.连接BF 、CF 、AC.
(1)求证:四边形ABFC 是平行四边形;
(2)若CE BE DE ⋅=2
,求证:四边形ABFC 是矩形.
A
B E
D C
A
B
C
D E
E A F
C D
B A B
C E F A B F
C
D
E
11.如图,△ABC中,AB=AC,AD、AE分别是∠BAC和∠BAC的外角平分线,BE⊥AE. (1)求证:DA⊥AE
(2)试判断AB与DE是否相等?并说明理由。
12.如图,在△ABC中,AB=AC,点D是BC上一动点(不与B、C重合),作DE∥AC交AB于点E,DF∥AB交AC于点F.
(1)当点D在BC上运动时,∠EDF的大小(变大、变小、不变)
(2)当AB=10时,四边形EDF的周长是多少?
(3)点D在BC上移动的过程中,AB、DE与DF总存在什么数量关系?请说明. A F
C
D
E
B
A
B C
F
E
D。
