累加数列错位相减取大差法案例详解(骄阳教育)

数列求和公式错位相减法公式

数列求和公式错位相减法公式数列求和公式，听上去就有点儿复杂对吧？但别急，咱们慢慢来，今天就给大家讲讲一个超好用的技巧——错位相减法。

乍一听，可能有点懵，但你放宽心，一旦弄明白了，分分钟让你觉得数列求和其实没啥难度。

你想啊，谁不想让看似难搞的数学题变得简单呢？对吧？就像是你去超市买东西，拿到结账单时，发现所有打折的商品都给你算得特别清楚，省了不少钱。

今天这招，保准让你在求和的路上少走很多弯路。

咱们从最简单的数列讲起。

你想求一个简单的等差数列的和，通常大家都会背那些公式。

嗯，好像也不难，直接套用公式就行了。

但很多时候，公式也有它的局限，尤其是当数列比较复杂，或者我们想要更高效地解决问题的时候，就得学点儿新招数了。

而这招“错位相减法”，就像是给数列加了一双隐形的翅膀，飞起来不费劲。

说白了，错位相减法就是把两个数列“合并”在一起，然後相减，结果会让你大吃一惊。

听起来有点儿抽象？那就举个例子。

比如你有一个数列1 + 2 + 3 + … + n，咱们现在的目标就是求它的和。

你可以这样操作：写下这个数列，然后把它倒过来再写一次。

比如：1 +2 +3 + … + nn + (n1) + (n2) + … + 1。

好像没啥特别的对吧？但重点来了：你把它们相加——每一项的和都是一样的。

举个例子，第一项1加最后一项n，第二项2加倒数第二项(n1)，以此类推。

结果呢，每一对加起来的结果都是n+1。

那么你就可以轻松得出，整个数列的和是（n+1）乘以n，然后再除以2！是不是一下子就变得清晰明了，省时又省力。

是不是有点“豁然开朗”的感觉？这个方法简直就是数学的“撒手锏”，不仅效率高，而且其实背后的道理也不难理解。

你想，原本一个长长的数列，把它拆成两个“对称”的部分，再相加就能搞定。

多么聪明的招数！就像你去买东西，店员总会问你“要不要礼品包装”，一看就是已经帮你考虑好了怎么样更方便、更高效。

咱们可以稍微升级一下这个技巧。

假如你遇到的不是等差数列，而是更复杂一点的数列，怎么办呢？别怕！这时候错位相减法依然能派上用场。

累加数列错位相减取大差法案例详解

累加数列错位相减取大差法案例详解Last revision on 21 December 2020累加数列错位相减取大差法在非节奏流水施工中，通常采用累加数列错位相减取大差法计算流水步距。

由于这种方法是由潘特考夫斯基首先提出的，故又称为潘特考夫斯基法。

基本步骤：1. 对每一个施工过程在各施工段上的流水节拍依次累加，求得各施工过程流水节拍的累加数列；2. 将相邻施工过程流水节拍累加数列中的后者错后一位，相减后求得一个差数列；3. 在差数列中取最大值，即为这两个相邻施工过程的流水步距。

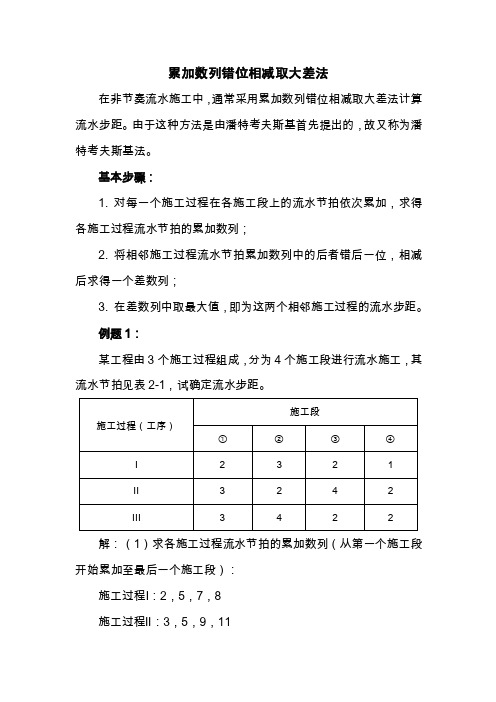
例题1：某工程由3个施工过程组成，分为4个施工段进行流水施工，其流水节拍见表2-1，试确定流水步距。

解：（1）求各施工过程流水节拍的累加数列（从第一个施工段开始累加至最后一个施工段）：施工过程Ⅰ：2，5，7，8施工过程Ⅱ：3，5，9，11施工过程Ⅲ：3，7，9，11（2）错位相减求得差数列：施工过程Ⅰ： 2，5，7，8施工过程Ⅱ： 3，5，9，11相减，得： 2，2，2，-1，-11施工过程Ⅱ： 3，5，9，11施工过程Ⅲ： 3，7，9，11相减，得： 3，2，2，2，-11（3）在求得的数列中取最大值求得流水步距：K1=max{2，2，2，-1，-11}=2K2=max{3，2，2，2，-11}=3表示：工序Ⅰ与工序Ⅱ之间的流水步距为2天，工序Ⅱ与工序Ⅲ之间的流水步距为3天。

例题2：某工程有5座通道，每座通道工序流水节拍如下：挖基2D，清基2D，浇基4D，台身8D，盖板4D，回填6D。

浇基后等4D才能施工台身，台身完成后要等2天才能进行盖板施工。

问题：（1）计算不窝工的流水工期；（2）计算无多余间歇流水工期；（3）有窝工且有多余间歇流水时的工期是多少解答：（1）本题中，5道相同的涵洞，说明有5个施工段，各施工段的施工工艺都一样，均为挖基、清基、浇基、台身、盖板、回填。

列入如例题1题干中的表格为：求各施工过程流水节拍的累加数列，为：挖基：2，4，6，8，10清基：2，4，6，8，10浇基：4，8，12，16，20台身：8，16，24，32，40盖板：4，8，12，16，20回填：6，12，18，24，30按照例题1的计算方法，错位相减求得差数列，得各工序之间的流水步距，为：K1=max{2，2，2，2，2，-10}=2K2=max{2，0，-2，-4，-6，-20}=2K3=max{4，0，-4，-8，-12，-40}=4K4=max{8，12，16，20，24，-20}=24K5=max{4，2，0，-2，-4，-30}=4接着计算不窝工的流水工期：不窝工的无节拍流水工期=流水步距和+最后一道工序流水节拍的和+技术间歇之和，即：T=ΣK+Σt+ΣZ=（2+2+4+24+4）+5×6+（4+2）=72（天）注：题中告诉“浇基后等4D才能施工台身，台身完成后要等2天才能进行盖板施工”，说明技术间歇为4+2=6天。

累加数列错位相减取大差法案例详解

累加数列错位相减取大差法案例详解累加数列错位相减取大差法是一种常用的数学方法，用于求解数列中的规律或者特征。

下面将通过十个案例来详解累加数列错位相减取大差法的应用。

案例一：斐波那契数列我们先来看一个经典的案例，斐波那契数列。

斐波那契数列的规律是每个数都是前两个数的和。

我们可以用累加数列错位相减取大差法来验证这个规律。

我们将斐波那契数列的前五项写出来：0, 1, 1, 2, 3。

然后，我们将这些数相邻两项相减得到新的数列：1, 0, 1, 1。

我们将这个新的数列再次相邻两项相减得到新的数列：-1, 1, 0。

我们将这个新的数列再次相邻两项相减得到新的数列：2, -1。

观察最后得到的数列，我们可以发现，它是一个循环数列，循环节为2, -1。

而斐波那契数列的规律就是循环节的第一个数的倒数。

案例二：等差数列接下来，我们来看一个等差数列的案例。

等差数列的规律是每个数都是前一个数加上一个固定的差值。

我们同样可以用累加数列错位相减取大差法来验证这个规律。

假设我们有一个等差数列的前五项为：1, 3, 5, 7, 9。

我们将这些数相邻两项相减得到新的数列：2, 2, 2, 2。

观察得到的新的数列，我们可以发现，它是一个恒定数列，每个数都是2。

而等差数列的规律就是恒定数列的差值。

案例三：等比数列接下来，我们来看一个等比数列的案例。

等比数列的规律是每个数都是前一个数乘以一个固定的比值。

同样，我们可以用累加数列错位相减取大差法来验证这个规律。

假设我们有一个等比数列的前五项为：1, 2, 4, 8, 16。

我们将这些数相邻两项相减得到新的数列：1, 2, 4, 8。

我们将这个新的数列再次相邻两项相减得到新的数列：1, 2, 4。

我们将这个新的数列再次相邻两项相减得到新的数列：1, 2。

观察得到的新的数列，我们可以发现，它也是一个恒定数列，每个数都是1。

而等比数列的规律就是恒定数列的比值。

案例四：平方数列接下来，我们来看一个平方数列的案例。

累加数列错位相减取大差法案例详细讲解

累加数列错位相减取大差法案例详细讲解
累加数列错位相减取大差法是一种常用于金融、统计等领域的分析方法，其主要目的是通过对一组数据的差值进行分析，从而得出对应的趋势变化情况。

下面我们就通过一个简单的案例来详细讲解这种方法的应用过程。

假设我们有以下一组数据：
10、14、18、22、26
我们要通过累加数列错位相减取大差法来分析这组数据的趋势变化情况。

首先，我们需要将这组数据按照顺序排列，并且计算出每一个数与前一个数的差值，得到如下结果：
10、4、4、4、4
接下来，我们需要将这个差值序列错位向下平移一位，得到新的序列：
最后，我们需要对这个差值序列取大值，即得到其中的最大值，从而得出整个数据序列所表示的趋势变化情况。

在这个例子中，最大值为6，意味着这组数据整体呈现出逐渐上升的趋势。

通过这个案例，我们可以看到，累加数列错位相减取大差法是一种非常简单有效的数据分析方法，能够帮助我们在金融、统计等领域快速准确地判断数据的变化趋势，从而更好地指导决策。

累加数列错位相减取大差法案例详解

累加数列错位相减取大差法案例详解
累加数列错位相减取大差法是数学中常用的算法，该方法可以用来快速计算某一个累加数列的和，从而减少计算时间。

本文将介绍累加数列错位相减取大差法的原理，并通过一个简单的例子来展示如何使用该方法。

累加数列错位相减取大差的原理是：将一系列的累加数列拆分成两个新的数列，称为A和B，把A中的每一项减去B中的相应项，取两个数中大者，然后用这些差的和来替代原累加数列的和。

例如，我们要计算a1+a2+a3+a4+a5+a6+a7的和。

我们可以把这个累加数列拆分成两个新的累加数列A和B，分别如下：
A：a1+a2+a3+a4
B：a4+a5+a6+a7
用A中的每一项分别减去B中的相应项，取出两个数中的大者，将这些差的和相加，就可以得到a1+a2+a3+a4+a5+a6+a7的和。

例如： (a1-a4)+(a2-a5)+(a3-a6)+(a4-a7) = a1+a2+a3+a4+a5+a6+a7 从这个例子中可以看出，用累加数列错位相减取大差法计算累加数列的和可以比直接累加节约计算时间。

- 1 -。

【最新精选】累加数列错位相减取大差法案例详解

累加数列错位相减取大差法在非节奏流水施工中，通常采用累加数列错位相减取大差法计算流水步距。

由于这种方法是由潘特考夫斯基首先提出的，故又称为潘特考夫斯基法。

基本步骤：1. 对每一个施工过程在各施工段上的流水节拍依次累加，求得各施工过程流水节拍的累加数列；2. 将相邻施工过程流水节拍累加数列中的后者错后一位，相减后求得一个差数列；3. 在差数列中取最大值，即为这两个相邻施工过程的流水步距。

例题1：某工程由3个施工过程组成，分为4个施工段进行流水施工，其流水节拍见表2-1，试确定流水步距。

解：（1）求各施工过程流水节拍的累加数列（从第一个施工段开始累加至最后一个施工段）：施工过程Ⅰ：2，5，7，8施工过程Ⅱ：3，5，9，11施工过程Ⅲ：3，7，9，11（2）错位相减求得差数列：施工过程Ⅰ：2，5，7，8施工过程Ⅱ：3，5，9，11相减，得：2，2，2，-1，-11施工过程Ⅱ：3，5，9，11施工过程Ⅲ：3，7，9，11相减，得：3，2，2，2，-11（3）在求得的数列中取最大值求得流水步距：K1=max{2，2，2，-1，-11}=2K2=max{3，2，2，2，-11}=3表示：工序Ⅰ与工序Ⅱ之间的流水步距为2天，工序Ⅱ与工序Ⅲ之间的流水步距为3天。

例题2：某工程有5座通道，每座通道工序流水节拍如下：挖基2D，清基2D，浇基4D，台身8D，盖板4D，回填6D。

浇基后等4D才能施工台身，台身完成后要等2天才能进行盖板施工。

问题：（1）计算不窝工的流水工期；（2）计算无多余间歇流水工期；（3）有窝工且有多余间歇流水时的工期是多少？解答：（1）本题中，5道相同的涵洞，说明有5个施工段，各施工段的施工工艺都一样，均为挖基、清基、浇基、台身、盖板、回填。

列入如例题1题干中的表格为：求各施工过程流水节拍的累加数列，为：挖基：2，4，6，8，10清基：2，4，6，8，10浇基：4，8，12，16，20台身：8，16，24，32，40盖板：4，8，12，16，20回填：6，12，18，24，30按照例题1的计算方法，错位相减求得差数列，得各工序之间的流水步距，为：K1=max{2，2，2，2，2，-10}=2K2=max{2，0，-2，-4，-6，-20}=2K3=max{4，0，-4，-8，-12，-40}=4K4=max{8，12，16，20，24，-20}=24K5=max{4，2，0，-2，-4，-30}=4接着计算不窝工的流水工期：不窝工的无节拍流水工期=流水步距和+最后一道工序流水节拍的和+技术间歇之和，即：T=ΣK+Σt+ΣZ=（2+2+4+24+4）+5×6+（4+2）=72（天）注：题中告诉“浇基后等4D才能施工台身，台身完成后要等2天才能进行盖板施工”，说明技术间歇为4+2=6天。

《错位相减大招》课件

步骤详解
通过图文并茂的方式，详细讲解错位相减大招的具体步骤，让学生清晰地了解如何运用该技巧。
实战演练
设计一些实战演练题目，以实例的形式让学生亲身体验错位相减大招的运用，加深他们对该技巧的理解和掌握。
思考题
提出几个思考题，鼓励学生深入思考和探究错位相减大招的应用，并激发他们的创造力和解决问题的能力。
《错位相减大招》PPT课件
通过这份PPT课件，我们将深入探究错位相减大招的应用，以图文并茂的方式让学生更好地理解该技巧，帮助他们更好地掌握和应用。
简介
介绍错位相减大招的概念和演示的主题，引起学生对该技巧的兴趣和好奇心。
基础概念
讲解错位相减大招的前置知识和一些基本概念，为学生理解该技巧的原理和应用打下基础。Fra bibliotek总结回顾
总结错位相减大招的优点和应用场景，帮助学生加深对该技巧的理解和应用，并激发他们的兴趣和学习动力。

累加数列错位相减取大差法案例详解.docx

累加数列错位相减取大差法在非节奏流水施工中，通常采用累加数列错位相减取大差法计算流水步距。

由于这种方法是由潘特考夫斯基首先提出的，故又称为潘特考夫斯基法。

基本步骤：1. 对每一个施工过程在各施工段上的流水节拍依次累加，求得各施工过程流水节拍的累加数列；2. 将相邻施工过程流水节拍累加数列中的后者错后一位，相减后求得一个差数列；3. 在差数列中取最大值，即为这两个相邻施工过程的流水步距。

例题1：某工程由3个施工过程组成，分为4个施工段进行流水施工，其流水节拍见表2-1，试确定流水步距。

解：（1）求各施工过程流水节拍的累加数列（从第一个施工段开始累加至最后一个施工段）：施工过程Ⅰ：2，5，7，8施工过程Ⅱ：3，5，9，11施工过程Ⅲ：3，7，9，11（2）错位相减求得差数列：施工过程Ⅰ： 2，5，7，8施工过程Ⅱ： 3，5，9，11相减，得： 2，2，2，-1，-11施工过程Ⅱ： 3，5，9，11施工过程Ⅲ： 3，7，9，11相减，得： 3，2，2，2，-11（3）在求得的数列中取最大值求得流水步距：K1=max{2，2，2，-1，-11}=2K2=max{3，2，2，2，-11}=3表示：工序Ⅰ与工序Ⅱ之间的流水步距为2天，工序Ⅱ与工序Ⅲ之间的流水步距为3天。

例题2：某工程有5座通道，每座通道工序流水节拍如下：挖基2D，清基2D，浇基4D，台身8D，盖板4D，回填6D。

浇基后等4D才能施工台身，台身完成后要等2天才能进行盖板施工。

问题：（1）计算不窝工的流水工期；（2）计算无多余间歇流水工期；（3）有窝工且有多余间歇流水时的工期是多少？解答：（1）本题中，5道相同的涵洞，说明有5个施工段，各施工段的施工工艺都一样，均为挖基、清基、浇基、台身、盖板、回填。

列入如例题1题干中的表格为：求各施工过程流水节拍的累加数列，为：挖基：2，4，6，8，10清基：2，4，6，8，10浇基：4，8，12，16，20台身：8，16，24，32，40盖板：4，8，12，16，20回填：6，12，18，24，30按照例题1的计算方法，错位相减求得差数列，得各工序之间的流水步距，为：K1=max{2，2，2，2，2，-10}=2K2=max{2，0，-2，-4，-6，-20}=2K3=max{4，0，-4，-8，-12，-40}=4K4=max{8，12，16，20，24，-20}=24K5=max{4，2，0，-2，-4，-30}=4接着计算不窝工的流水工期：不窝工的无节拍流水工期=流水步距和+最后一道工序流水节拍的和+技术间歇之和，即：T=ΣK+Σt+ΣZ=（2+2+4+24+4）+5×6+（4+2）=72（天）注：题中告诉“浇基后等4D才能施工台身，台身完成后要等2天才能进行盖板施工”，说明技术间歇为4+2=6天。

数列错位相减法

数列错位相减法形如An=BnCn，其中{Bn}为等差数列，通项公式为bn=b1+(n-1)*d；{Cn}为等比数列，通项公式为cn=c1*q^(n-1)；对数列An进展求和，首先列出Sn，记为式〔1〕；再把所有式子同时乘以等比数列的公比q，即q·Sn，记为式〔2〕；形如An=BnCn，其中{Bn}为等差数列，通项公式为bn=b1+(n-1)*d；{Cn}为等比数列，通项公式为cn=c1*q^(n-1)；对数列An进展求和，首先列出Sn，记为式〔1〕；再把所有式子同时乘以等比数列的公比q，即q·Sn，记为式〔2〕；然后错开一位，将式〔1〕与式〔2〕作差，对从而简化对数列An的求和。

这种数列求和方法叫做错位相减法。

经典例题数列{an}中，a1=3，点(an，an+1)在直线y=x+2上。

(1)求数列{an}的通项公式；(2)假设bn=an`3n，求数列{bn}的前n项和Tn。

解：(1)∵点〔an,an+1)在直线y=x+2上∴an+1=an+2,即an+1-an=2∴数列{an}是以3为首项，以2为公差的等差数列∴an=3+2(n-1)=2n+1(2)∵bn=an·3n∴bn=(2n+1)·3n∴Tn=3×3+5×32+7×33+…+(2n-1)·3n-1+(2n+1)·3n①3Tn=3×32+5×33+…+(2n-1)·3n+(2n+1)·3n+1②由①-②得-2Tn=3×3+2(32+33+…+3n)-(2n+1)·3n+1=9+2×9(1-3n-1)/(1-3)-(2n+1)·3n+1=-2n·3n+1∴Tn=n·3n+1。

【最新精选】累加数列错位相减取大差法案例详解

累加数列错位相减取大差法在非节奏流水施工中，通常采用累加数列错位相减取大差法计算流水步距。

由于这种方法是由潘特考夫斯基首先提出的，故又称为潘特考夫斯基法。

基本步骤：1. 对每一个施工过程在各施工段上的流水节拍依次累加，求得各施工过程流水节拍的累加数列；2. 将相邻施工过程流水节拍累加数列中的后者错后一位，相减后求得一个差数列；3. 在差数列中取最大值，即为这两个相邻施工过程的流水步距。

例题1：某工程由3个施工过程组成，分为4个施工段进行流水施工，其流水节拍见表2-1，试确定流水步距。

解：（1）求各施工过程流水节拍的累加数列（从第一个施工段开始累加至最后一个施工段）：施工过程Ⅰ：2，5，7，8施工过程Ⅱ：3，5，9，11施工过程Ⅲ：3，7，9，11（2）错位相减求得差数列：施工过程Ⅰ：2，5，7，8施工过程Ⅱ：3，5，9，11相减，得：2，2，2，-1，-11施工过程Ⅱ：3，5，9，11施工过程Ⅲ：3，7，9，11相减，得：3，2，2，2，-11（3）在求得的数列中取最大值求得流水步距：K1=max{2，2，2，-1，-11}=2K2=max{3，2，2，2，-11}=3表示：工序Ⅰ与工序Ⅱ之间的流水步距为2天，工序Ⅱ与工序Ⅲ之间的流水步距为3天。

例题2：某工程有5座通道，每座通道工序流水节拍如下：挖基2D，清基2D，浇基4D，台身8D，盖板4D，回填6D。

浇基后等4D才能施工台身，台身完成后要等2天才能进行盖板施工。

问题：（1）计算不窝工的流水工期；（2）计算无多余间歇流水工期；（3）有窝工且有多余间歇流水时的工期是多少？解答：（1）本题中，5道相同的涵洞，说明有5个施工段，各施工段的施工工艺都一样，均为挖基、清基、浇基、台身、盖板、回填。

列入如例题1题干中的表格为：求各施工过程流水节拍的累加数列，为：挖基：2，4，6，8，10清基：2，4，6，8，10浇基：4，8，12，16，20台身：8，16，24，32，40盖板：4，8，12，16，20回填：6，12，18，24，30按照例题1的计算方法，错位相减求得差数列，得各工序之间的流水步距，为：K1=max{2，2，2，2，2，-10}=2K2=max{2，0，-2，-4，-6，-20}=2K3=max{4，0，-4，-8，-12，-40}=4K4=max{8，12，16，20，24，-20}=24K5=max{4，2，0，-2，-4，-30}=4接着计算不窝工的流水工期：不窝工的无节拍流水工期=流水步距和+最后一道工序流水节拍的和+技术间歇之和，即：T=ΣK+Σt+ΣZ=（2+2+4+24+4）+5×6+（4+2）=72（天）注：题中告诉“浇基后等4D才能施工台身，台身完成后要等2天才能进行盖板施工”，说明技术间歇为4+2=6天。

累加数列错位相减取大差法案例详解

注：题中告诉“浇基后等4D才能施工台身，台身完成后要等2天才能进行盖板施工”，说明技术间歇为4+2=6天。最后一道工序为回填，需要6天，一共5道相同的涵洞，则最后一道工序流水节拍的和为5×6=30天。
（2）计算无多余间歇流水工期
各施工段之间的时间间隔计算，同段节拍累加错位相减取大差就等于流水节拍的最大值8。具体计算方法如下：
4
4
回填
6
6
6
6
6
求各施工过程流水节拍的累加数列，为：
挖基246810
清基246810
浇基48121620
台身816243240
盖板48121620
回填612182430
按照例题1的计算方法，错位相减求得差数列，得各工序之间的流水步距，为：
K1=max{2，2，2，2，2，-10}=2
K2=max{2，0，-2，-4，-6，-20}=2
先进行各段上工序节拍累加，这里并不同于第（1）步中那样将同一工序在各工段上累加（即表中横向数据累加），而是在一个工段上各工序节拍的累加（即表中竖向数据累加），由于5道涵洞的施工工序及持续时间都一致，因此，每段上节拍的累加都一样，即：
第①道涵洞248162026
第②道涵洞248162026
第③道涵洞248162026
3.在差数列中取最大值即为这两个相邻施工过程的流水步距。
例题1：
某工程由3个施工过程组成，分为4个施工段进行流水施工，其流水节拍见表，试确定流水步距。
施工过程
(工序)
施工段
1
2
3
4
Ⅰ
2
3
2
1
Ⅱ
3
2
4
2
Ⅲ
3

累加数列错位相减取大差法案例详解

累加数列错位相减取大差法案例详解案例：求解数列1，4，7，10，13，16，...的前n项和。

解析：首先，我们可以观察到这个数列是一个等差数列，公差为3、我们可以利用累加数列错位相减取大差法来求解。

我们将数列错位相减得到一个新的数列：4-1=37-4=310-7=313-10=3...可以发现，这个新的数列也是一个等差数列，同样的公差为3接下来，我们求这个新数列的前n-1项和，记为Sn-1根据等差数列求和公式，Sn-1 = n*(a1+an-1)/2，其中，n为项数，a1为首项，an-1为最后一项。

对于这个新数列，n-1项和可以表示为：Sn-1=(n-1)*(3+3(n-2))/2=(3n^2-9n+6)/2这样，我们就得到了新数列的前n-1项和。

接下来，我们计算原数列的前n项和Sn。

由于原数列是新数列错位相减得到的，所以原数列的第一项就是新数列的第二项，即a2=3又因为新数列是一个等差数列，所以原数列的公差也是3我们可以推出，原数列的第n项 an = a2 + 3(n-1)，即 an = 3n-1利用求和公式，我们可以计算出原数列的前n项和：Sn = n*(a1+an)/2 = n*(1+(3n-1))/2 = (3n^2+n)/2所以，数列1，4，7，10，13，16，...的前n项和可以表示为(3n^2+n)/2通过这个案例，我们可以看到，累加数列错位相减取大差法是一种简便而有效的数列求和方法。

它通过将数列错位相减得到一个新的数列，然后利用求和公式计算得到原数列的和。

这种方法在高中数学中经常会遇到，对于理解数列求和有很大的帮助。

【最新精选】累加数列错位相减取大差法案例详解

累加数列错位相减取大差法在非节奏流水施工中，通常采用累加数列错位相减取大差法计算流水步距。

由于这种方法是由潘特考夫斯基首先提出的，故又称为潘特考夫斯基法。

基本步骤：1. 对每一个施工过程在各施工段上的流水节拍依次累加，求得各施工过程流水节拍的累加数列；2. 将相邻施工过程流水节拍累加数列中的后者错后一位，相减后求得一个差数列；3. 在差数列中取最大值，即为这两个相邻施工过程的流水步距。

例题1：某工程由3个施工过程组成，分为4个施工段进行流水施工，其流水节拍见表2-1，试确定流水步距。

解：（1）求各施工过程流水节拍的累加数列（从第一个施工段开始累加至最后一个施工段）：施工过程Ⅰ：2，5，7，8施工过程Ⅱ：3，5，9，11施工过程Ⅲ：3，7，9，11（2）错位相减求得差数列：施工过程Ⅰ：2，5，7，8施工过程Ⅱ：3，5，9，11相减，得：2，2，2，-1，-11施工过程Ⅱ：3，5，9，11施工过程Ⅲ：3，7，9，11相减，得：3，2，2，2，-11（3）在求得的数列中取最大值求得流水步距：K1=max{2，2，2，-1，-11}=2K2=max{3，2，2，2，-11}=3表示：工序Ⅰ与工序Ⅱ之间的流水步距为2天，工序Ⅱ与工序Ⅲ之间的流水步距为3天。

例题2：某工程有5座通道，每座通道工序流水节拍如下：挖基2D，清基2D，浇基4D，台身8D，盖板4D，回填6D。

浇基后等4D才能施工台身，台身完成后要等2天才能进行盖板施工。

问题：（1）计算不窝工的流水工期；（2）计算无多余间歇流水工期；（3）有窝工且有多余间歇流水时的工期是多少？解答：（1）本题中，5道相同的涵洞，说明有5个施工段，各施工段的施工工艺都一样，均为挖基、清基、浇基、台身、盖板、回填。

列入如例题1题干中的表格为：求各施工过程流水节拍的累加数列，为：挖基：2，4，6，8，10清基：2，4，6，8，10浇基：4，8，12，16，20台身：8，16，24，32，40盖板：4，8，12，16，20回填：6，12，18，24，30按照例题1的计算方法，错位相减求得差数列，得各工序之间的流水步距，为：K1=max{2，2，2，2，2，-10}=2K2=max{2，0，-2，-4，-6，-20}=2K3=max{4，0，-4，-8，-12，-40}=4K4=max{8，12，16，20，24，-20}=24K5=max{4，2，0，-2，-4，-30}=4接着计算不窝工的流水工期：不窝工的无节拍流水工期=流水步距和+最后一道工序流水节拍的和+技术间歇之和，即：T=ΣK+Σt+ΣZ=（2+2+4+24+4）+5×6+（4+2）=72（天）注：题中告诉“浇基后等4D才能施工台身，台身完成后要等2天才能进行盖板施工”，说明技术间歇为4+2=6天。

一级建造师错位相减取大差

一级建造师错位相减取大差“错位相减取大差”，听起来是不是有点拗口？一开始，谁能理解这几个字到底是什么意思嘛？不过，别急，今天我们就来聊聊这个话题，保证让你听得懂，甚至能一笑而过。

好啦，咱们直奔主题，别绕弯子了。

这是一级建造师考试中的一道常见题型，看似复杂，实际上掌握了方法，轻松搞定，根本不需要慌张。

首先啊，你得知道，这个“错位相减取大差”，其实就是要你在两个数字之间比较，看哪个差值大。

简单来说，就是两个数对比，不是算一个普通的差，而是要特别注意它们在数字位置上的差异。

是不是有点像做数学题的时候，老师让你注意“看清楚题目”，别光算出来，搞错了就是白忙活。

你想，这个“错位相减”，跟咱们生活中的某些情况还挺像的吧？比如说，你买了两件衣服，一件是A牌，一件是B牌，A牌的价格是198元，B牌的价格是200元。

你一看价格，咦，好像差不多，觉得买哪件都差不多。

但，如果你换个角度看看，A牌198元背后有个优惠活动，实际付款150元，B牌200元什么优惠都没有，结果你差点就不小心白白多花了50元。

这个“错位相减”，就跟你看到的这些数字表面上相似，实际上差距却大得离谱。

所以啊，光看数字可不行，得学会抓住细节，尤其是在价格、数字背后的变动。

再说了，这道题的精髓就在于“取大差”。

嘿，这个取大差是关键，你得学会看到两个数字背后到底藏着多大的差距，不能被表面现象迷了眼。

就像你去餐馆点了两份一样的菜，结果端上来，你发现，一份特别丰盛，另一份却少得可怜。

你怎么看，能不觉得差距太大了吗？这个时候，我们不是单纯地看哪一份贵，而是看哪个份量更足，哪个菜更划算。

说起来，做这类题目就像在市场上买东西一样，眼尖一点，别让价格或者其他诱惑蒙蔽了眼。

你看，有的商家就会利用“错位”的策略，把一些小数字包装成大数字，吸引顾客。

要是你不小心上了当，那可就亏大了。

考试中的“错位相减”也是这么个道理。

你得时刻提醒自己，哪个数字看起来更高，哪个差距更大，不要只看一眼就得出结论。

累加数列错位相减取大差法案例详解【最新资料】

累加数列错位相减取大差法在非节奏流水施工中，通常采用累加数列错位相减取大差法计算流水步距。

由于这种方法是由潘特考夫斯基首先提出的，故又称为潘特考夫斯基法。

基本步骤：1. 对每一个施工过程在各施工段上的流水节拍依次累加，求得各施工过程流水节拍的累加数列；2. 将相邻施工过程流水节拍累加数列中的后者错后一位，相减后求得一个差数列；3. 在差数列中取最大值，即为这两个相邻施工过程的流水步距。

例题1：某工程由3个施工过程组成，分为4个施工段进行流水施工，其流水节拍见表2-1，试确定流水步距。

解：（1）求各施工过程流水节拍的累加数列（从第一个施工段开始累加至最后一个施工段）：施工过程Ⅰ：2，5，7，8施工过程Ⅱ：3，5，9，11施工过程Ⅲ：3，7，9，11（2）错位相减求得差数列：施工过程Ⅰ： 2，5，7，8施工过程Ⅱ： 3，5，9，11相减，得： 2，2，2，-1，-11施工过程Ⅱ： 3，5，9，11施工过程Ⅲ： 3，7，9，11相减，得： 3，2，2，2，-11（3）在求得的数列中取最大值求得流水步距：K1=max{2，2，2，-1，-11}=2K2=max{3，2，2，2，-11}=3表示：工序Ⅰ与工序Ⅱ之间的流水步距为2天，工序Ⅱ与工序Ⅲ之间的流水步距为3天。

例题2：某工程有5座通道，每座通道工序流水节拍如下：挖基2D，清基2D，浇基4D，台身8D，盖板4D，回填6D。

浇基后等4D才能施工台身，台身完成后要等2天才能进行盖板施工。

问题：（1）计算不窝工的流水工期；（2）计算无多余间歇流水工期；（3）有窝工且有多余间歇流水时的工期是多少？解答：（1）本题中，5道相同的涵洞，说明有5个施工段，各施工段的施工工艺都一样，均为挖基、清基、浇基、台身、盖板、回填。

列入如例题1题干中的表格为：求各施工过程流水节拍的累加数列，为：挖基：2，4，6，8，10清基：2，4，6，8，10浇基：4，8，12，16，20台身：8，16，24，32，40盖板：4，8，12，16，20回填：6，12，18，24，30按照例题1的计算方法，错位相减求得差数列，得各工序之间的流水步距，为：K1=max{2，2，2，2，2，-10}=2K2=max{2，0，-2，-4，-6，-20}=2K3=max{4，0，-4，-8，-12，-40}=4K4=max{8，12，16，20，24，-20}=24K5=max{4，2，0，-2，-4，-30}=4接着计算不窝工的流水工期：不窝工的无节拍流水工期=流水步距和+最后一道工序流水节拍的和+技术间歇之和，即：T=ΣK+Σt+ΣZ=（2+2+4+24+4）+5×6+（4+2）=72（天）注：题中告诉“浇基后等4D才能施工台身，台身完成后要等2天才能进行盖板施工”，说明技术间歇为4+2=6天。

累加数列错位相减取大差法

累加数列错位相减取大差法
累加数列错位相减取大差法，是一种常用于数据分析和统计学中的数
学方法。

该方法可以用来比较两个连续时间段内的数据变化程度，从
而判断变化趋势是否一致。

具体方法是将两个时间段内的数据分别累加成两个数列，然后对这两
个数列进行错位相减，并取绝对值。

最后将得到的结果按照大小排序，取其中的最大值作为比较的标准。

这种方法的优点是简便易行，不需要太多的复杂计算。

并且可以有效
区分数据的变化趋势。

然而，也存在一些缺点，比如不适用于数据集
比较小的情况，以及对于极端值的敏感性较高等。

因此，在实际应用过程中，需要结合具体情况进行分析和评估。

同时，在使用该方法时，也需要注意数据的质量和可靠性，以及应该将其作
为补充分析手段来使用，而不是单一的主要数据分析方法。

累加数列错位相减取大差法

累加数列错位相减取大差法累加数列错位相减取大差法是一种常用的数学方法，它可以用来求解一些复杂的数学问题。

这种方法的核心思想是将一个数列错位相减，然后取其中的最大值作为结果。

下面我们来详细介绍一下这种方法的具体应用。

我们需要明确一个概念，那就是累加数列。

累加数列是指一个数列中每个数都是前面所有数的和。

例如，1、3、6、10、15就是一个累加数列，其中第n项的值可以表示为n*(n+1)/2。

接下来，我们来看一下累加数列错位相减取大差法的具体步骤。

假设我们有一个数列a1、a2、a3、……、an，那么我们可以将它错位相减，得到一个新的数列b1、b2、b3、……、bn-1，其中bi=ai+1-ai。

然后，我们再从b1、b2、b3、……、bn-1中取出最大值，作为累加数列a1、a2、a3、……、an的最大差值。

这种方法的优点在于它的计算量比较小，而且可以很快地得到结果。

另外，它还可以用来解决一些实际问题，例如求解股票价格的最大涨幅、求解最长递增子序列等等。

下面我们来举一个例子，说明累加数列错位相减取大差法的具体应用。

假设我们有一个数列1、3、-2、4、-1、2、-5、7，我们要求这个数列中相邻两个数之差的最大值。

首先，我们将这个数列错位相减，得到一个新的数列2、-5、6、-5、3、-7、12。

然后，我们从这个数列中取出最大值12，作为原数列的最大差值。

因此，这个数列中相邻两个数之差的最大值为12。

累加数列错位相减取大差法是一种非常实用的数学方法，它可以用来解决一些复杂的数学问题。

在实际应用中，我们可以根据具体情况灵活运用这种方法，以便更好地解决问题。