数列思维导图教程文件
等比数列知识点归纳总结思维导图

等比数列知识点归纳总结思维导图思维导图是一种辅助思维和记忆的工具,通过图形化的方式将知识点有机地连接起来,可以帮助我们更好地理解和记忆复杂的信息。
在学习等比数列的过程中,绘制思维导图可以帮助我们整理和梳理知识点,更好地掌握与之相关的概念和公式。
下面是一个等比数列知识点的归纳总结思维导图:【思维导图】1. 等比数列的定义- 数列的前两个数之比等于后两个数之比- 通项公式:an = a1 * r^(n-1),其中a1为首项,r为公比2. 等比数列的性质- 公比大于1时,数列递增;公比小于1但大于0时,数列递减 - 若公比为负数,则与首项同号的项无法确定,通项公式仍成立 - 若公比为0,则数列中所有项均为0,通项公式成立3. 等比数列的前n项和- 首项为a1,公比为r的等比数列的前n项和Sn可表示为:Sn = (a1 * (1 - r^n)) / (1 - r) ,其中r不等于14. 等比数列的无穷项和- 若-1 < r < 1,则等比数列的无穷项和为S∞ = a1 / (1 - r)5. 判断数列是否为等比数列的方法- 相邻两项的比值是否相等- 若数列中任意三项的比值相等,则数列为等比数列6. 等比中项- 若a, b, c为等比数列中连续的三项,且b为等比中项,则b^2 = ac7. 等比数列的应用- 在财务、利润、人口统计等领域中的增长模型- 在几何图形中的应用,如等比放大、缩小等通过以上的等比数列知识点的归纳总结思维导图,我们可以更加直观地了解等比数列的基本定义、性质以及相关公式与应用。
希望这个思维导图能够帮助大家更好地掌握等比数列的概念,并在解题过程中起到参考和辅助的作用。
数列知识点思维导图

数列知识点思维导图├── 数列基础│ ├── 定义│ ├── 表示方法│ │ ├── 序列表示│ │ └── 递推表示│ ├── 有界数列│ └── 收敛与发散数列│ ├── 收敛数列│ └── 发散数列├── 等差数列 (Arithmetic Sequence)│ ├── 定义│ ├── 通项公式│ ├── 求和公式│ └── 性质│ ├── 奇偶性│ └── 等差中项├── 等比数列 (Geometric Sequence)│ ├── 定义│ ├── 通项公式│ ├── 求和公式│ └── 性质│ ├── 等比中项│ └── 无穷等比数列├── 级数 (Series)│ ├── 级数概念│ ├── 收敛性判断│ │ ├── 比较判别法│ │ ├── 比值判别法│ │ └── 根值判别法│ ├── 幂级数 (Power Series)│ │ ├── 泰勒级数 (Taylor Series)│ │ └── 劳朗级数 (Laurent Series)│ └── 傅里叶级数 (Fourier Series)├── 数列极限 (Limits of Sequences)│ ├── 极限定义│ ├── 极限存在性│ ├── 极限性质│ ├── 极限运算法则│ └── 极限的应用└── 数列求和技巧├── 裂项相消法├── 错位相减法├── 倒序相加法└── 综合法```这个概要提供了数列相关的主要知识点和子知识点。
在实际的思维导图中,这些内容将以图形化的方式展示,每个主要节点和子节点都用线条连接,形成树状结构。
这样的图形化表示有助于直观理解和记忆数列的概念和它们之间的关系。
请注意,这个概要是为了帮助理解和创建一个数列知识点的思维导图,而不是一个传统意义上的文章。
如果您需要一个实际的思维导图图形文件,您可能需要使用专门的软件或工具来创建它。
数学分析第二章极限与连续知识网络思维导图及复习
量求极限。 6、 理解函数连续的概念,会判断函数不连续点的类型。 7、 掌握用基本定理证明闭区间上连续函数的最大值、最小值、介值性定理的基本思路和方
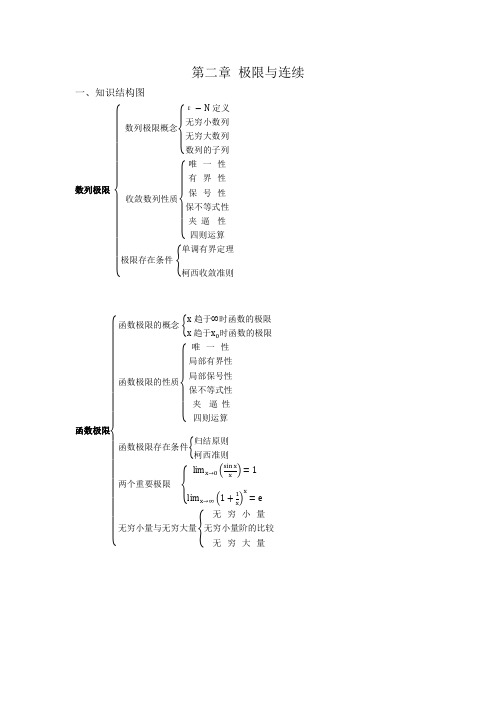
法。 8、 理解一致连续的概念,并会应用其证明相关命题。 三、知识点梳理 1、数列极限的概念、性质与定理
不一致连续: 0
0,
xn
,xn
,
lim(
n
xn
x)
0 ,而 lim( n
f
(xn )
f
( xn)
c
0.
四、典型例题分析
基本题型 I 利用定义证明数列的极限
例
证明
lim
n
n 2n
0
证 明 : 0, 要 使 得
n 2n
0
成立,只要
n 2n
0
n 2n
2 n
(这是因为
2n (11)n 1 n n(n 1) ... n2
(ii) 同 阶 无 穷 小 : lim f (x) a 0 , 则 称 f (x) 是 g(x) 的 同 阶 无 穷 小 , 记 为 xx0 g(x)
f (x) Og(x) x x0 ,
0
特别地,如果 f (x) 在 O(x0 ) 有界,记作 f (x) O(1), (x x0 )
③ 函数的不连续点
(i)第一类不连续点: f (x0 0), f (x0 0) 存在,但不相等。
(ii)第二类不连续点: f (x0 0), f (x0 0) 中至少有一个不存在.
(iii)可移不连续点:
f (x0
0)
f
(x0
数列-高中数列知识梳理思维导图脑图
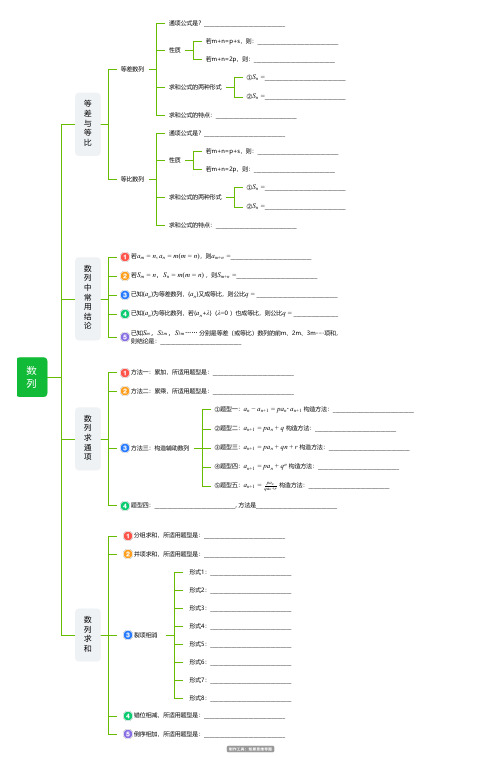
数列等差与等比等差数列通项公式是?_______________________________性质若m+n=p+s,则:_______________________________若m+n=2p,则:_______________________________求和公式的两种形式①_______________________________S=n②_______________________________S=n求和公式的特点:_______________________________等比数列通项公式是?_______________________________性质若m+n=p+s,则:_______________________________若m+n=2p,则:_______________________________求和公式的两种形式①_______________________________S=n②_______________________________S=n求和公式的特点:_______________________________数列中常用结论若,则_______________________________a=mn,a=nm(m= n)a=m+n若 ,则_______________________________S=mn,S=nm(m= n)S=m+n已知{}为等差数列,{}又成等比,则公比 _______________________________a n a n q=已知{}为等比数列,若{+}(0 )也成等比,则公比 _________________a n a nλλ= q=已知 分别是等差(或等比)数列的前m、2m、3m······项和,则结论是:_______________________________S,S,S⋅⋅⋅⋅⋅⋅m2m3m数列求通项方法一:累加,所适用题型是:_______________________________方法二:累乘,所适用题型是:_______________________________方法三:构造辅助数列①题型一: 构造方法:_______________________________a−n a=n+1pa⋅an n+1②题型二: 构造方法:_______________________________a=n+1pa+nq③题型三: 构造方法:_______________________________a=n+1pa+nqn+r④题型四: 构造方法:_______________________________a=n+1pa+nq n⑤题型五: 构造方法:_______________________________a=n+1qa+rnpa n题型四:_______________________________, 方法是_______________________________数列求和分组求和,所适用题型是:_______________________________并项求和,所适用题型是:_______________________________裂项相消形式1:_______________________________形式2:_______________________________形式3:_______________________________形式4:_______________________________形式5:_______________________________形式6:_______________________________形式7:_______________________________形式8:_______________________________错位相减,所适用题型是:_______________________________倒序相加,所适用题型是:_______________________________。
山东专升本高等数学思维导图

第五章 定积分
高等数学
第六章 常微分方程
基本概念
定义 阶数 次数
解
通解 特解
一阶微分方程
求解微分方程
高阶微分方程
可分离变量的微分方程 齐次微分方程 一阶线性微分方程
可降阶的高阶微分方程
二阶常系数线性微分方程
齐次 非齐次
y^(n)=f(x) 不显含y:y′′=f(x,y′) 不显含x:y′′=f(y,y′)
定义 几何意义 基本微分公式 基本微分法则 复合函数的微分法则
导数 微分
第二章 导数、微分
费马定理
罗尔中值定理
拉格朗日中值定理 洛必达法则求极限
判别函数的单调性
求函数的极值
求函数的最值
判别函数的凹凸性、求函数的拐点
水平渐近线
垂直渐近线
求函数的渐近线
斜渐近线
微中值定理 导数的应用
第三章 微分中值定理、导数的应用
第一类换元法 第二类换元法
分部积分 有理函数的积分
定义 性质 基本积分公式
计算不定积分
第四章 不定积分
求平面图形的面积
旋转体的体积 平行截面面积已知的立体的体积
求体积
求曲边梯形的面积 定积分的定义
定积分的几何意义 定积分的性质 变限积分函数
牛顿-莱布尼兹公式 计算定积分 广义积分 定积分证明
定积分的应用
齐次 非齐次
第七章 向量代数空解析几何
向量代数 空间解析几何
基本概念 线性运算 坐标表示的线性运算 向量的模 方向角与方向余弦 数量积 向量积
平面方程
直线方程
点法式方程 一般式方程 一般方程 对称式(点向式)方程 Subtopic 3
第八章 多元函数微积分学
数列知识框图—经典

数列知识网络111111(2)(2)(1)(1)()22()n n n n n n m p q n n n n a q n a a a q a a d n a a n d n n n S a a na d a a a a m n p q --=≥=⎧⎪←⎨⎪⎩-=≥⎧⎪=+-⎪⎪-⎨=+=+⎪⎪+=++=+⎪⎩两个基等比数列的定义本数列等比数列的通项公式等比数列数列数列的分类数列数列的通项公式函数角度理解的概念数列的递推关系等差数列的定义等差数列的通项公式等差数列等差数列的求和公式等差数列的性质1111(1)(1)11(1)()n n n n m p q a a q a q q q q S na q a a a a m n p q ---=≠--===+=+⎧⎪⎪⎪⎪⎪⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧⎪⎪⎨⎪⎨⎪⎪⎨⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎩⎩⎪⎧⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎩⎧⎨⎩⎩等比数列的求和公式等比数列的性质公式法分组求和错位相减求和数列裂项求和求和倒序相加求和累加累积归纳猜想证明分期付款数列的应用其他⎪⎪⎪⎪⎪⎪⎪⎪⎪一、考点回顾1.数列的概念,数列的通项公式与递推关系式差数列和等比数列的概念、有关公式和性质.2.判断和证明数列是等差(等比)数列常用三种方法:(1)定义法:对于n≥2的任意自然数,验证11(n n n n a a a a ---为同一常数。
(2)通项公式法:①若1(1)()n k a a n d a n k d =+-=+-,则{}n a 为等差数列;②若,则{}n a 为等比数列。
③中项公式法:验证都成立。
3.在等差数列{}n a 中,有关S n 的最值问题——常用邻项变号法求解:(1)当10a >,d<0时,满足的项数m 使得m S 取最大值.(2)当10a <,d>0时,满足的项数m 使得m S 取最小值。
在解含绝对值的数列最值问题时,注意转化思想的应用。
七年级数学[上册]思维导图
![七年级数学[上册]思维导图](https://img.taocdn.com/s3/m/76cb6c7fae45b307e87101f69e3143323868f550.png)
七年级数学[上册]思维导图第一章:数与代数1.1 实数1.1.1 实数的概念1.1.2 实数的分类1.1.3 实数的性质1.1.4 实数的运算1.2 代数式1.2.1 代数式的概念1.2.2 代数式的分类1.2.3 代数式的运算1.3 方程与不等式1.3.1 方程的概念1.3.2 一元一次方程1.3.3 不等式的概念1.3.4 一元一次不等式第二章:几何初步2.1 点、线、面2.1.1 点的概念2.1.2 线的概念2.1.3 面的概念2.2 平面图形2.2.1 线段2.2.2 角2.2.3 三角形2.2.4 四边形2.2.5 圆2.3 空间图形2.3.1 长方体2.3.2 正方体2.3.3 球第三章:统计与概率3.1 统计3.1.1 数据的收集与整理3.1.2 数据的表示3.1.3 数据的分析3.2 概率3.2.1 概率的概念3.2.2 概率的计算3.2.3 概率的运用第四章:数学思维与方法4.1 逻辑思维4.2 抽象思维4.3 创新思维4.4 数学方法七年级数学[上册]思维导图第五章:函数及其图像5.1 函数的概念5.2 函数的表示方法5.3 函数的性质5.4 函数图像的绘制第六章:数列与数列极限6.1 数列的概念6.2 等差数列与等比数列6.3 数列的求和6.4 数列极限的概念第七章:数学建模与实际问题7.1 数学建模的概念7.2 数学建模的方法7.3 实际问题的解决第八章:数学文化8.1 数学发展的历史8.2 数学家的故事8.3 数学文化的传播第九章:数学竞赛与挑战9.1 数学竞赛的种类9.2 数学竞赛的准备9.3 数学竞赛的挑战第十章:数学与生活10.1 数学在生活中的应用10.2 数学与科技的发展10.3 数学与艺术的结合七年级数学[上册]思维导图第十一章:数学与自然科学11.1 数学与物理的关系11.2 数学与化学的关系11.3 数学与生物的关系第十二章:数学与社会科学12.1 数学与经济学的关系12.2 数学与心理学的关系12.3 数学与历史的关系第十三章:数学与信息技术13.1 数学与计算机科学的关系13.2 数学与网络技术的关系第十四章:数学教育与发展14.1 数学教育的重要性14.2 数学教育的现状14.3 数学教育的发展趋势第十五章:数学与个人成长15.1 数学与思维能力15.2 数学与创新能力15.3 数学与人格培养第十六章:数学与团队合作16.1 数学与沟通能力16.2 数学与协作能力16.3 数学与领导力。
找规律思维导图知识点总结

找规律思维导图知识点总结
一、数列找规律
1. 等差数列的特点和求和公式
2. 等比数列的特点和求和公式
3. 通项公式和常项公式的确定方法
4. 数列的应用问题
二、图形找规律
1. 几何图形的特点和性质
2. 图形的对称性和相似性
3. 图形的旋转和平移规律
4. 图形的应用问题
三、排列组合找规律
1. 排列与组合的定义和区别
2. 排列组合的计算方法
3. 排列组合的应用问题
四、逻辑推理找规律
1. 数字逻辑推理
2. 关系逻辑推理
3. 条件逻辑推理
4. 逻辑推理的应用问题
五、综合运用
1. 数学、物理、化学等学科中的找规律问题
2. 生活中的找规律问题
3. 考试中的找规律题型
以上就是找规律思维导图知识点的总结,希望对大家有所帮助。
找规律是一个综合性很强的思维能力,在学习和生活中都会有很大的作用。
因此我们要多多练习,提高自己的找规律能力。
高中数学必修一第五章思维导图手写笔记

高中数学必修一第五章思维导图手写笔记
第五章数列
一、数列的定义
数列是按照一定规律排列的数的有限序列,它可以是有理数、无理数、自然数、整数等。
二、数列的性质
1. 通项公式:数列的每一项都可以用一个公式表示,这个公式就叫做通项公式。
2. 递推公式:数列的每一项都可以用前面几项的结果来推出,这个公式就叫做递推公式。
3. 数列的和:数列的和是指把数列中所有项的和加起来的结果,它可以用求和公式来表示。
4. 数列的等差:等差数列是指每一项与它的前一项之差都是相等的数列,它可以用通项公
式来表示。
5. 数列的等比:等比数列是指每一项与它的前一项之比都是相等的数列,它可以用通项公
式来表示。
三、数列的应用
1. 数列可以用来描述一些规律性的现象,如经济增长、人口增长等。
2. 数列可以用来解决一些实际问题,如投资问题、贷款问题等。
3. 数列可以用来求解一些数学问题,如求和、求积分等。
