第十章习题解答
第十章(含耦合电感的电路)习题解答

第十章(含耦合电感的电路)习题解答一、选择题1.图10—1所示电路的等效电感=eq L A 。
A.8H ; B.7H ; C.15H ; D.11H解:由图示电路可得 121 d d 2d d )63(u t i t i =++, 0d d 4d 221=+tit i d从以上两式中消去ti d d 2得t iu d d 811=,由此可见8=eq L H2.图10—2所示电路中,V )cos(18t u s ω=,则=2i B A 。
A.)cos(2t ω; B.)cos(6t ω; C.)cos(6t ω-; D.0解:图中理想变压器的副边处于短路,副边电压为0。
根据理想变压器原副边电压的关系可知原边的电压也为0,因此,有A )cos(29)cos(18 1t t i ω=ω=再由理想变压器原副边电流的关系ni i121= (注意此处电流2i 的参考方向)得A )cos(612t ni i ω==因此,该题应选B 。
3.将图10─3(a )所示电路化为图10—3(b )所示的等效去耦电路,取哪一组符号取决于 C 。
A.1L 、2L 中电流同时流入还是流出节点0;B.1L 、2L 中一个电流流入0,另一个电流流出节点0 ;C.1L 、2L 的同名端相对于0点是在同侧还是在异侧,且与电流参考方向无关;D.1L 、2L 的同名端相对于0点是在同侧还是在异侧,且与电流参考方向有关。
解:耦合电感去耦后电路中的M 前面是取“+”还是取“–”,完全取决于耦合电感的同名端是在同侧还是在异侧,而与两个电感中电流的参考方向没有任何关系。
因此,此题选C 。
4.图10—4所示电路中,=i Z B 。
A .Ω2j ; B.Ωj1; C.Ωj3; D.Ωj8解:将图10—4去耦后的等效电路如图10—4(a ),由图10—4(a )得j1 j6j6j6j6j2Ω=+⨯+-=i Z因此,该题选B。
5.在图10—5所示电路中,=i Z D 。
第十章_电荷和静电场课后习题答案

证:由库仑定律得 :
而:
∵ 角很小
∴
故:
即得: 证毕
10-4 在上题中, 如果l = 120 cm,m = 0.010 kg,x = 5.0 cm,问每个小
球所带的电量q为多大?
解:由上题得:
10-5 氢原子由一个质子和一个电子组成。根据经典模型,在正常状态
下,电子绕核作圆周运动,轨道半径是。质子的质量,电子的质量,
∴
10-16 一个半径为R的半球面均匀带电,面电荷密度为s。求球心的电 场强度。
解:由题9-14知:圆环的电场强度为: 10-17 回答下列问题: (1)处于高斯面内的任何位置上的电荷对该高斯面的电通量是否都有贡 献?是否只要电量相同,贡献就相等? (2)处于高斯面外的任何位置上的电荷对该高斯面的电通量是否都无贡 献? (3)假设一个点电荷正好处于高斯面上,那么这个点电荷对该高斯面的 电通量是否有贡献? 答:(1)是的。高斯面内的任何位置上电荷对高斯面的电通量都有贡 献。只要电量相同,电性相同,贡献就相同。
∴ 方向沿轴线方向
故:
∴
(2) ∴
∴
∴ 10-14 一个半径为R的圆环均匀带电,线电荷密度为l。求过环心并垂 直于环面的轴线上与环心相距a的一点的电场强度。 解:如图:圆环上一线元上产生的电场强度为:
与其对称的一线元产生的电场强度为 : ,
两个电场强度的合成为: ∴ 故:
10-15 一个半径为R的圆盘均匀带电,面电荷密度为。求过盘心并垂直 于盘面的轴线上与盘心相距的P点电场强度。 解:由上题知,圆环上电场强度
∴ 10-11 有两个点电荷,电量分别为5.0´10-7C和2.8´10-8C,相距15 cm。求:
(1)一个电荷在另一个电荷处产生的电场强度; (2)作用在每个电荷上的力 已知:点电荷 求: 解: (方向沿两电荷联线向外)
第十章 静电场中的导体和电介质习题解答
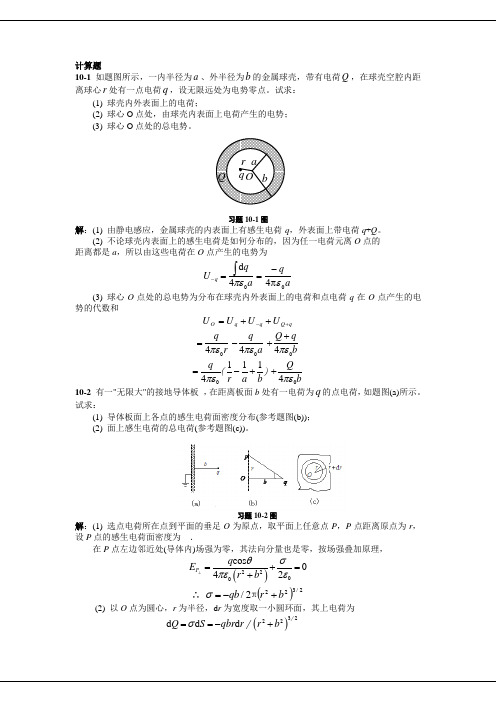
10-1 如题图所示,一内半径为a 、外半径为b 的金属球壳,带有电荷Q ,在球壳空腔内距离球心r 处有一点电荷q ,设无限远处为电势零点。
试求: (1) 球壳内外表面上的电荷;(2) 球心O 点处,由球壳内表面上电荷产生的电势;(3) 球心O 点处的总电势。
习题10-1图解:(1) 由静电感应,金属球壳的内表面上有感生电荷-q ,外表面上带电荷q +Q 。
(2) 不论球壳内表面上的感生电荷是如何分布的,因为任一电荷元离O 点的 距离都是a ,所以由这些电荷在O 点产生的电势为0d 4q qU aπε-=⎰aq04επ-=(3) 球心O 点处的总电势为分布在球壳内外表面上的电荷和点电荷q 在O 点产生的电势的代数和q Q q q O U U U U +-++=04qr πε=04qa πε-04Q qb πε++01114()q r a bπε=-+04Q bπε+ 10-2 有一"无限大"的接地导体板 ,在距离板面b 处有一电荷为q 的点电荷,如题图(a)所示。
试求:(1) 导体板面上各点的感生电荷面密度分布(参考题图(b)); (2) 面上感生电荷的总电荷(参考题图(c))。
习题10-2图解:(1) 选点电荷所在点到平面的垂足O 为原点,取平面上任意点P ,P 点距离原点为r ,设P 点的感生电荷面密度为.在P 点左边邻近处(导体内)场强为零,其法向分量也是零,按场强叠加原理,()220cos 024P q E r b θσεπε⊥=+=+ ∴ ()2/3222/b r qb +-=πσ (2) 以O 点为圆心,r 为半径,d r 为宽度取一小圆环面,其上电荷为 ()3222d d d //Q S qbr r r bσ==-+q Q a bO r()q brrr qb S Q S-=+-==⎰⎰∞2322d d /σ10-3 如题图所示,中性金属球A ,半径为R ,它离地球很远.在与球心O 相距分别为a 与b 的B 、C 两点,分别放上电荷为A q 和B q 的点电荷,达到静电平衡后,问: (1) 金属球A 内及其表面有电荷分布吗?(2) 金属球A 中的P 点处电势为多大?(选无穷远处为电势零点)B C R AP Oq A q Bba习题10-3图解:(1) 静电平衡后,金属球A 内无电荷,其表面有正、负电荷分布,净电荷为零. (2) 金属球为等势体,设金属球表面电荷面密度为. ()()000d 4=4////AP A B S U U S R q a q a σπεπε==⋅+⎰⎰∵d 0AS S σ⋅=⎰⎰∴ ()()04///P A B U q a q a πε=+10-4 三个电容器如题图联接,其中C 1 = 10×10-6 F ,C 2 = 5×10-6 F ,C 3 = 4×10-6 F ,当A 、B 间电压U =100 V 时,试求:(1) A 、B 之间的电容;(2) 当C 3被击穿时,在电容C 1上的电荷和电压各变为多少?ABC 1C 2 C 3U习题10-4图解:(1) =+++=321321)(C C C C C C C 3.16×10-6 F(2) C 1上电压升到U = 100 V ,电荷增加到==U C Q 111×10-3 C10-5 一个可变电容器,由于某种原因所有动片相对定片都产生了一个相对位移,使得两个相邻的极板间隔之比为2:1,问电容器的电容与原来的电容相比改变了多少?(a) (b)习题10-5图解:如图所示,设可变电容器的静片数为n ,定片数为1-n ,标准情况下,极板间的距离为d (图a ),极板相对面积为S 。
第十章中级无机化学课后习题答案

第10章习题1 简要回答问题(1) 什么叫稀土元素? 什么叫镧系元素?答:参见本书10.1节《概述》。
(2) 镧系收缩的原因是什么? 简述镧系收缩造成的影响。
答:关于镧系收缩的原因参见本书10.1.2节《原子半径和离子半径》。
由于镧系收缩的影响,使第二、三过渡系的Zr和Hf、Nb与Ta、Mo与W三对元素的半径相近,化学性质相似,分离困难。
(3) 为什么Eu、Yb原子半径比相邻元素大? 而Ce又小?答:① Eu、Yb元素参与形成金属键的电子数为2,Ce为3.1,其余为3.0;② Eu、Yb具碱土性;③ Eu、Yb的f7、f14的半充满和全充满的结构能量低、稳定、屏蔽大,核对外面的6s电子吸引较弱。
(4) 为什么镧系元素的电子结构在固态和气态不同?解:参见本书10.1.1节《镧系元素的价电子层结构》。
(5) 镧系离子的电子光谱同d区过渡金属离子相比有何不同? 为什么?解:除La3+、Lu3+离子的4f电子层是全空(4f0)和全满(4f14)之外,其余Ln3+离子4f轨道上的电子数由1到14,这些电子可以在7条4f简并轨道上任意排布,这样就会产生各种光谱项和能级。
4f 电子在不同能级间跃迁可以吸收或发射从紫外经可见直至红外区的各种波长的电磁辐射。
通常具有未充满的4f电子壳层的原子或离子,可以观察到的光谱线大约有30 000条,而具有未充满d电子壳层的过渡金属元素的谱线约有7 000条。
在理论上,f→f跃迁产生的谱线强度不大。
但是某些f→f跃迁的吸收带的强度,随镧系离子周围环境的变化而明显增大(这种跃迁称为超灵敏跃迁)。
这可能是由于配体的碱性、溶剂的极性、配合物的对称性以及配位数等多种因素的影响,亦即离子周围环境的变化,再加上镧系离子本身的性质等诸因素的综合作用所引起的。
镧系离子的吸收谱带范围较广且镧系离子光谱谱带狭窄,表明电子跃迁时并不显示激发分子振动,狭窄的谱带意味着电子受激发时分子势能面几乎没有变化,这与f 电子与配体只存在弱相互作用相一致。
第10章习题解答

第10章思考题及习题10参考答案一、填空1.对于电流输出型的D/A转换器,为了得到电压输出,应使用。
答:I/V转换电路2.使用双缓冲同步方式的D/A转换器,可实现多路模拟信号的输出。
答:同步3.一个8位A/D转换器的分辨率是 ,若基准电压为5V,该A/D转换器能分辨的最小的电压变化为。
答:1/28,20Mv4.若单片机发送给8位D/A转换器0832的数字量为65H,基准电压为5V,则D/A转换器的输出电压为 .答:1.973V5.若A/D转换器00809的基准电压为5V,输入的模拟信号为2.5V时,A/D转换后的数字量是。
答:80H二、判断对错1.“转换速度”这一指标仅适用于A/D转换器,D/A转换器不用考虑“转换速度"问题。
错2.ADC0809可以利用“转换结束"信号EOC向AT89S52单片机发出中断请求.对3.输出模拟量的最小变化量称为A/D转换器的分辨率。
错4.对于周期性的干扰电压,可使用双积分型A/D转换器,并选择合适的积分元件,可以将该周期性的干扰电压带来的转换误差消除。
对三、单选1.在【例10—5】中的应用程序中,第2条与第4条指令:MOV DPTR,#7FF8HMOVX @DPTR,A的作用是。
A。
使单片机的WR信号有效 B. 使ADC0809的片选信号有效C。
发送ADC当前的转换通道号并启动A/D转换 D.将A中的数据写入0809答:C2.对于图10—20,如果P2.7改为 P2.3,且A/D转换的通道号选为IN3,则DPTR的值为 .A. FBF3H B。
FBFCH C。
7BFCH D。
F7F3H答:D四、简答1.D/A转换器的主要性能指标都有哪些?设某DAC为二进制12位,满量程输出电压为5V,试问它的分辨率是多少?答:D/A转换器的主要技术指标如下:分辨率:D/A转换器的分辨率指输入的单位数字量变化引起的模拟量输出的变化,是对输入量变化敏感程度的描述。
第10章 习题解答
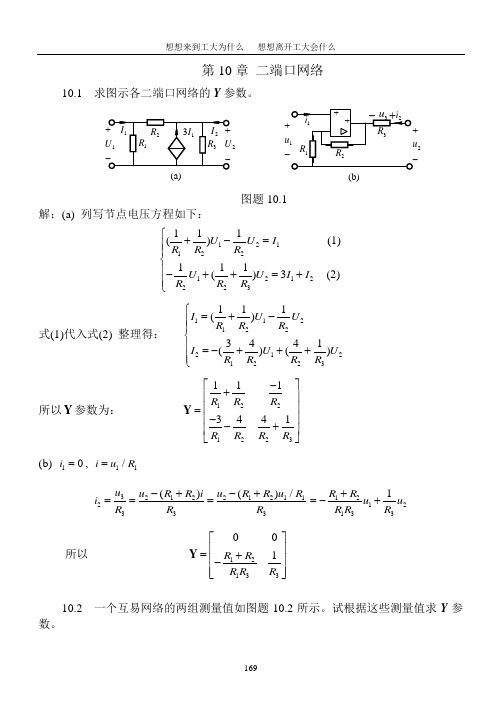
第10章 二端口网络10.1 求图示各二端口网络的Y 参数。
22u (b)图题10.1解:(a) 列写节点电压方程如下:1211221212223111() (1)111()3 (2)U U I R R R U U I I R R R ⎧+-=⎪⎪⎨⎪-++=+⎪⎩ 式(1)代入式(2) 整理得: 1121222121223111()3441()()I U U R R R I U U R R R R ⎧=+-⎪⎪⎨⎪=-+++⎪⎩所以Y 参数为:12212231113441R R R R RR R -⎡⎤+⎢⎥⎢⎥=-⎢⎥-+⎢⎥⎣⎦Y (b) 10i =, 11/i u R =3212212112333()()/u u R R i u R R u R i R R R -+-+===12121331R R u u R R R +=-+ 所以12133001R R R R R ⎡⎤⎢⎥=+⎢⎥-⎢⎥⎣⎦Y10.2 一个互易网络的两组测量值如图题10.2所示。
试根据这些测量值求Y 参数。
(a)(b)22-+U图题10.2解:图(a)中11222A,j2V 2j5j 10V j5A I U U I ===⨯==-,,由Y 参数方程得:11112221222j2j 10 (1)j5j2j 10 (2)I Y Y I Y Y ⎧==⨯+⨯⎨=-=⨯+⨯⎩ 由图(b)得 222jA 1V I Y ==⨯ (3) 对互易网络有:1221Y Y = (4)由式(3) 得: 22j 1S Y =,代入式(2) 得:2112( 2.5j5)S Y Y ==-- 再代入式(1)得:11(12.5j24)S Y =+ 所以12.5j2425j52.5j5j1.+--⎡⎤=⎢⎥--⎣⎦Y S 10.3 求图示各二端口网络的Z 参数。
(b)图题10.3解 (a):按网孔列写KVL 方程得1211221(2)2 (1)2(2)3 (2)R R I RI U RI R R I U U ++=⎧⎨++=+⎩ 将式(1)代入式(2)整理得1122123273U RI RI U RI RI =+⎧⎨=--⎩ 所以 3273RR R R ⎡⎤=⎢⎥--⎣⎦Z(b) 将∆联接的三个阻抗转换成Y 形联接,如图(c)所示,由此电路可直接写出Z 参数1j j j 0+⎡⎤=⎢⎥⎣⎦Z Ω10.4求图示各二端口网络的A 参数。
大学物理第十章有导体和电介质时的静电场习题解答和分析

第十章习题解答10-1 如题图10-1所示,三块平行的金属板A ,B 和C ,面积均为200cm 2,A 与B 相距4mm ,A 与C 相距2mm ,B 和C 两板均接地,若A 板所带电量Q =3.0×10-7C ,忽略边缘效应,求:(1)B 和C 上的感应电荷?(2)A 板的电势(设地面电势为零)。
分析:当导体处于静电平衡时,根据静电平衡条件和电荷守恒定律,可以求得导体的电荷分布,又因为B 、C 两板都接地,所以有AC AB U U =。
解:(1)设B 、C 板上的电荷分别为Bq 、C q 。
因3块导体板靠的较近,可将6个导体面视为6个无限大带电平面。
导体表面电荷分布均匀,且其间的场强方向垂直于导体表面。
作如图中虚线所示的圆柱形高斯面。
因导体达到静电平衡后,内部场强为零,故由高斯定理得:1A C q q =-2A B q q =-即 ()A B C q q q =-+ ① 又因为: AC AB U U = 而: 2AC AC d U E =⋅AB AB U E d =⋅∴ 2AC AB E E =于是:02C Bσσεε =⋅两边乘以面积S 可得:2C BS S σσεε =⋅即: 2C B q q = ②联立①②求得: 77210,110C B q C q C --=-⨯=-⨯题图10-1题10-1解图d(2) 00222C C A AC C AC AC q d d dU U U U E S σεε =+==⋅=⋅=⋅ 7334122102102.2610()200108.8510V ----⨯=⨯⨯=⨯⨯⨯⨯10-2 如题图10-2所示,平行板电容器充电后,A 和B 极板上的面电荷密度分别为+б和-б,设P 为两极板间任意一点,略去边缘效应,求: (1)A,B 板上的电荷分别在P 点产生的场强E A ,E B ; (2)A,B 板上的电荷在P 点产生的合场强E ; (3)拿走B 板后P 点处的场强E ′。
第10章 习题解答(联接)09

作业一
作业一
41.3 20358 15.9mm 133.3
式中: S 400 133.3MPa 螺栓选用45钢,不控制预紧力
S3
故取M20 d1=17.294>15.9mm
安全系数取3是正确的
四.根据螺栓间距和扳手空间确定分布圆直径D0
D0 D 2[d (3~6) 10] 160 2[20 (3~6) 10] 226~232mm
P11.522~24/01表.5 1012-.47305
177.8MPa
作业一
作业一
7.图示夹紧螺栓中,已知螺栓数为2,螺纹为M20,螺栓力学性能等
级为4.8级,轴径D=50mm,杠杆长L=400mm,f=0.15,求W的允许。
解:
不滑移条件:(f
F0
z
m)
D 2
CWL
W fzmDF 0 2CL
S
s
41.3 F0 d12
S
4 1.3 12923.1 3 13.8352
335.4MPa
式中: d1 13.835mm
查表10-5,选择螺栓力学性能等级为5.8,螺母为5级。
作业一
10.图示为一液压油缸,油压p=作业3一MPa,油缸内径D=160mm,为保证 气密性,螺栓间距≤4.5d,螺柱力学性能等级为5.8级,试计算 此螺栓联接和分布圆直径。
arctan P 3.17 d2
arctan f 6.59 cos
rf
dw d0 4
5.125mm
P148/表10-5,10-6,10-7
即得螺栓的拉应力为: Fa 24326 .95 N mm
第十章练习题答案

第十章 练习题一、 填空1、设区域D 由圆环2214x y ≤+≤所确定的闭区域,则二重积分⎰⎰Ddxdy = 3π ___2、 设是由直线所围成的闭区域,则 1 .3、改变二次积分的积分次序得 。
4、已知积分区域D 为单位圆,则=5、设是由所围成的闭区域,则= 0 .6、将改变积分次序7、设是矩形:,则( ) 二、选择1、 设积分区域D 由21,21==y x 所围成,则⎰⎰Dxyd σ=( A ). A. 0 B.41 C. 21D. 12、设函数),(y x f为连续函数,交换积分14(4)0(,)y dy f x y dx -⎰⎰的次序得( D )(A )24224(,)x x dy f x y dx --+⎰⎰(B )04224(,)xx dx f x y dy --+⎰⎰(C)11(,)dy f x y dx -⎰ (D )24224(,)x x dx f x y dy --+⎰⎰3、设函数),(y x f为连续函数,交换积分10(,)dy f x y dx ⎰的次序得( B )(A)20(,)xdy f x y dx ⎰ (B)11(,)dx f x y dy -⎰(C)11(,)dy f x y dx -⎰ (D )2022(,)yy dy f x y dx ⎰⎰4、设D 是由01,0x y π≤≤≤≤所围成的闭区域,则()cos Dy xy dxdy =⎰⎰( A );A .2B .2πC .1π+D .05、设为连续函数,=,则=( B )D 01,1==-=+x y x y x 及⎰⎰=Ddxdy ()dx y x f dy y ⎰⎰010,()⎰⎰110,x dy y x f dx ()d xdy y x D⎰⎰+222πD 2,1x y ==2Dxy dxdy ⎰⎰xydy dx x ⎰⎰121⎰⎰212y xydx dy D 11,11≤≤-≤≤-y x =⎰⎰Dydxdy x 32sin cos 0()x f ()t F ()dx x f dy ty t⎰⎰1()2'FA. B. C. D.6、设是由轴、轴及直线所围成的区域,则的面积为( C ) A 、 B 、 C 、 D 、7、( C ),其中。
《电路原理导论》第十章习题解答

习题1010-1 已知非线性电阻的电压、电流关系为32i i u +=(式中,u 的单位为V ,i 的单位为A ),试求工作点i =1A 和i =2A 处的静态电阻和动态电阻。
答案:A i 1=:Ω=Ω=5,3d R R ;A i 2=:Ω=Ω=14,6d R R解:i =1A :V 323=+=i i u ,Ω=+==322i iuR Q Ω=+===53221i di duR i d Ω=+===6222i iu R i QΩ=+===143222i di duR i d 10-2一非线性电感的磁链ψ与电流i 的关系为3ψψb a i +=,其中Wb A 0.1=a ,3A/Wb 1.0=b 。
试求它的静态电感L s 和动态电感L d 。
答()H L s 21.011ψ+=,()H L d 23.011ψ+=解:Li =ψ did L ψ=1.静态 2231.011ψψψψψψ+=+=+==b a b a i L 2.223.0131ψψψ+=+==b a d diL d 10-3 一非线性电容的电荷与电压的关系可表示为3Bu Au q +=。
在此电容两端加有电压t u ωsin 3=。
求电容中的电流()t i ,并把它表为其中所含谐波之和的形式。
若给定V C A /106-=, 37/10V C B -=,Rad/S 10000=ω,算出电流()t i 。
答: mA3cos 25.20cos 25.50t t i ωω-=解:()()tt t t t t t dt d t t dtd t dt d u dt d B dt du A Bu Au dt d dt dq i ωωωωωωωωωω3cos 1025.20cos 1025.503cos 1031075.6cos 1025.20cos 1033sin 41sin 431027cos 10103sin 310sin 31033473274637633---------⨯-⨯=⨯⨯⨯-⨯+⨯=⎪⎭⎫⎝⎛-⨯+⨯⨯=+=+=+==t t t ωωω3sin 4sin 33sin -= 3Bu Au q +=t t t ωωω3sin 41sin 43sin 3-=t u 10000sin 3=10-4 一非线性电阻电路的伏安特性如表10-1所示:表10-1 一非线性电阻的端口特性(a )将它接至电动势为,内电阻为的电压源上。
第10章习题与解答
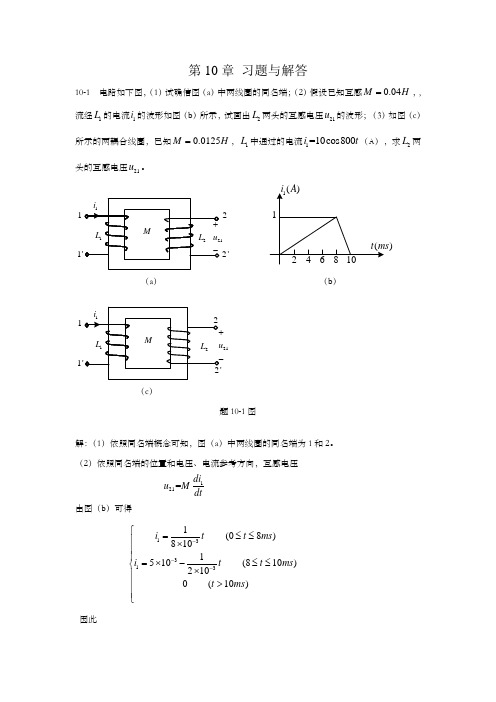
第10章 习题与解答10-1 电路如下图,(1)试确信图(a )中两线圈的同名端;(2)假设已知互感0.04M H =,,流经1L 的电流1i 的波形如图(b )所示,试画出2L 两头的互感电压21u 的波形;(3)如图(c )所示的两耦合线圈,已知0.0125M H =,1L 中通过的电流1=10cos800i t (A ),求2L 两头的互感电压21u 。
122')(a ) (b )121(c )题10-1图解:(1)依照同名端概念可知,图(a )中两线圈的同名端为1和2。
(2)依照同名端的位置和电压、电流参考方向,互感电压121=di u Mdt由图(b )可得133131(08)8101510(810)2100(10)i t t ms i t t ms t ms ---⎧=≤≤⎪⨯⎪⎪=⨯-≤≤⎨⨯⎪>⎪⎪⎩因此3131125(/)(08)8101500(/)(810)2100(10)A s t ms di A s t ms dt t ms --⎧=≤≤⎪⨯⎪⎪=-=-≤≤⎨⨯⎪>⎪⎪⎩则1210.041255()0.04(500)20()0V di u M V dt ⨯=⎧⎪==⨯-=-⎨⎪⎩21u 的波形图为)-题10-1 附图(3) 依照同名端概念可知,图(c )中两线圈的同名端为1和2',因此 1210.012510cos800di du Mt dt dt=-=-⨯ 0.012510(800sin800)100sin800100cos(80090)()t t t V =-⨯⨯-==-10-2有两组线圈,一组的参数为1=0.01L H ,2=0.04L H ,=0.01M H ;另一组的参数为1'=0.04L H ,2'=0.06L H ,'=0.02M H 。
别离计算每组线圈的耦合系数,通过比较说明,是不是互感大者耦合必紧?什么缘故?解:计算耦合系数0.5k == 0.41k ==比较:'M M <但'k k >,k 大者耦合较紧。
第10章习题答案

第10章习题答案习题101.(1)图G 的度数列为2、2、3、3、4,则G 的边数是多少(2)3、3、2、3和5、2、3、1、4能成为图的度数列吗为什么(3)图G 有12条边,度数为3的结点有6个,其余结点的度数均⼩于3,问图G 中⾄多有⼏个结点为什么解 (1)设G 有m 条边,由握⼿定理得2m =∑∈Vv v d )(=2+2+3+3+4=14,所以G 的边数7条。
(2)由于这两个序列中有奇数个是奇数,由握⼿定理的推论知,它们都不能成为图的度数列。
(3) 由握⼿定理得∑∈Vv v d )(=2m =24,度数为3的结点有6个占去18度,还有6度由其它结点占有,其余结点的度数可为0、1、2,当均为2时所⽤结点数最少,所以应由3个结点占有这6度,即图G 中⾄多有9个结点。
2.若有n 个⼈,每个⼈恰有3个朋友,则n 必为偶数。
证明设1v 、2v 、…、n v 表⽰任给的n 个⼈,以1v 、2v 、…、n v 为结点,当且仅当两⼈为朋友时其对应的结点之间连⼀条边,这样得到⼀个简单图G 。
由握⼿定理知∑=nk kv d 1)(=3n 必为偶数,从⽽n 必为偶数。
3.判断下列各⾮负整数列哪些是可图化的哪些是可简单图化的 (1)(1,1,1,2,3)。
(2)(2,2,2,2,2)。
(3)(3,3,3,3)。
(4)(1,2,3,4,5)。
(5)(1,3,3,3)。
解由于⾮负整数列d =(d 1,d 2,…,d n )是可图化的当且仅当∑=ni i d 1≡0(mod 2),所以(1)、(2)、(3)、(5)能构成⽆向图的度数列。
(1)、(2)、(3)是可简单图化的。
其对应的⽆向简单图如图所⽰。
(5)是不可简单图化的。
若不然,存在⽆向图G 以为1,3,3,3度数列,不妨设G 中结点为1v 、2v 、3v 、4v ,且d(1v )=1,d(2v )=d(3v )=d(4v )=3。
⽽1v 只能与2v 、3v 、4v 之⼀相邻,设1v 与2v相邻,于是d(3v )=d(4v )=3不成⽴,⽭盾。
第十章-曲线曲面积分(习题及解答)

<第十章 曲线曲面积分§10.1对弧长的曲线积分一、选择题1. 设曲线弧段AB 为,则曲线积分有关系( ).(A)(,)d (,)d ABBAf x y s f x y s =-⎰⎰; (B)(,)d (,)d ABBAf x y s f x y s =⎰⎰;(C)(,)d (,)d 0ABBAf x y s f x y s +=⎰⎰;(D)(,)d (,)d ABBAf x y s f x y s =--⎰⎰. 答(B).2. 设有物质曲线23:,,(01),23t t C x t y z t ===≤≤其线密度为ρ=它的质量M =( ).(A)10t ⎰; (B)10t t ⎰;(C)t ⎰; (D)t ⎰. 答(A).…3.设OM 是从(0,0)O 到(1,1)M 的直线段,则与曲线积分OMI s=⎰不相等的积分是( ).(A)10x ⎰; (B)10y ⎰;(C)d r r ⎰; (D)10e r ⎰答(D).4 .设L 是从(0,0)A 到(4,3)B 的直线段,则曲线积分()d Lx y s -=⎰( ).(A)403d 4x x x ⎛⎫- ⎪⎝⎭⎰; (B)303d 4y y y ⎛⎫- ⎪⎝⎭⎰;(C)3034y y y ⎛- ⎝⎰; (D)4034x x x ⎛- ⎝⎰. 答(D).5. 设L 为抛物线2y x =上从点(0,0)到点(1,1)的一段弧,则曲线积分s =⎰( ).(A)x ⎰; (B)y ⎰;}(C)10x ⎰; (D)y ⎰. 答(C).6. 设L 是从(1,0)A 到(1,2)B -的直线段,则曲线积分()d Lx y s +=⎰( ).(A); (B)2; (C)(D)答(D).二、填空题1. 设L 是圆周221x y +=,则31d LI x s =⎰与52d LI x s =⎰的大小关系是.答:12.I I =2. 设L 是连接(1,0)A 与(0,1)B 两点的直线段, 则()d Lx y s +=⎰.&.3. 设:cos ,sin (02),L x a t y a t t π==≤≤则22()d n Lx y s +=⎰. 答:212a a π+.4. 设:cos ,sin (02),L x a t y a t t π==≤≤则22()d Lx y s -=⎰.答:0.5. 设L 是圆周221x y +=,则2d LI x s ==⎰.答:π.6. 设:cos ,sin ,t t t x e t y e t z e Γ===,上相应于t 从0变到2的这段弧,则曲线积分22()d Lx y s -=⎰.答2)e --.7. 设L 为曲线24y x =上从点(0,0)A 到点(1,2)B 的弧段, ?则Ls =⎰.答:3. 三、解答题1.计算下列对弧长的曲线积分:(1) d Lx s ⎰其中为由直线y x =与抛物线2y x =所围区域的整个边界.答: 11)12.(2) 22d x y Les +⎰其中L 为圆周222x y a +=,直线y x =及x 轴在第一象限内所围成的扇形的整个边界.答: 2 2.4a a e π⎛⎫+- ⎪⎝⎭》(3) 2d x yz s Γ⎰,其中Γ为折线ABCD ,这里,,,A B C D 依次为点(0,0,0)、(0,0,2)、(1,0,2)、(1,3,2).答:9.(4) 2d Ly s ⎰其中L 为摆线一拱(sin ),(1cos )(02)x a t t y a t t π=-=-≤≤.答: 34232.53a ⋅⋅(5) 22()d L x y s +⎰其中L 为曲线(cos sin )(sin cos )x a t t t y a t t t =+⎧⎨=-⎩(02)t π≤≤.答: 2322(12).a ππ+§10.2对坐标的曲线积分一、选择题,1. 设AB 为由(0,)A π到(,0)B π的直线段,则sin d sin d ABy x x y +=⎰( ).(A)2; (B)1-; (C)0; (D)1. 答(C). 2. 设C 表示椭圆22221x y a b+=,其方向为逆时针,则2()d C x y x +=⎰( ).(A)ab π; (B)0; (C)2a b +; (D)1. 答(B). 3. 设C 为由(1,1)A 到(2,3)B 的直线段,则(3)d (2)d Cx y x y x y +++=⎰( ).(A)21[(2)(23)]d x x x x x +++⎰; (B)21[(21)(213)]d x x x x x +-+-+⎰ (C)21[(73)2(51)]d x x x -+-⎰; (D)21[(73)(51)]d x x x -+-⎰. 答(C).》4. 设曲线C 的方程为x y =(0)2t π≤≤,则22d d Cx y y y x x -=⎰( )(A)20[cos sin t π⎰; (B)2220(cos sin )d t t t π-⎰(C)220cos sin ππ-⎰⎰(D)201d 2t π⎰.答(D).5. 设()f u 连续可导,L 为以原点为心的单位圆,则必有( ).(A)22()(d d )0Lf x y x x y y ++=⎰;(B)22()(d d )0Lf x y x y y x ++=⎰ (C)22()(d d )0L f x y x y y ++=⎰; (D)22()(d d )0Lf x y x x y ++=⎰.答(A).6. 设C 是从(0,0)O 沿折线11y x =--到(2,0)A 到的折线段,则d d Cx y y x -=⎰( )】(A)0; (B)1-; (C)2-; (D)2. 答(C).二、填空题1. L 为xoy 平面内直线x a =上的一段,则(,)d LP x y x =⎰.答:0.2. 设L 为2y x =上从(0,0)O 到(2,4)A 的一段弧,则22()d Lx y x -=⎰.答:5615-. 3. 设L 为2y x =上从(0,0)O 到(2,4)A 的一段弧,则22()d Lx y y -=⎰.答:403-. *4.L 为圆弧y 上从原点到(2,2)A 的一段弧,则d Lxy y =⎰.答:43. 5.设L 为圆周222()(0)x a y a a -+=>及x 轴所围成的在第一象限的区域的整个边界(按逆时针方向绕行),则d Lxy y =⎰.答:32a π-.6.设(2)d (23)d 9Lx y x x y y -++=-⎰,其中L 为xoy 平面上简单闭曲线,方向为逆时针.则L 所围成的平面区域D 的面积等于.答:32. 三、解答题1.计算()d ()d Lx y x y x y ++-⎰,其中L 为:,(1) 抛物线2y x =上从(1,1)到(4,2)的一段弧; (2) 从点(1,1)到点(4,2)的一直线段;(3) 先沿直线从点(1,1)到点(1,2),然后再沿直线到点(4,2)的折线; (4) 曲线2221,1x t t y t =++=+上从点(1,1)到点(4,2)的一段弧. 答案:3432(1);(2)11;(3)14;(4).332.计算d d Ly x x y +⎰其中L 为圆周cos ,sin x R t y R t ==上对应t 从0到2π的一段弧.答:0. 3.计算22()d ()d Lx y x x y y x y+--+⎰,其中L 为圆周222x y a +=(方向按逆时针).—答:2π-.4.计算d d (1)d x x y y x y z Γ+++-⎰其中Γ为从点(1,1,1)到点(2,3,4)的直线段.答:13.5. 计算22(2)d (2)d Lx xy x y xy y -+-⎰,其中L 是2y x =上从点(1,1)-到点(1,1)的一段弧.答:1415-. §10.3 格林公式一、选择题1. 设C 是圆周222x y R +=,方向为逆时针方向,则22d d Cx y x xy y -+⎰用格林公式计算可化为( ).|(A)2300d d Rr r πθ⎰⎰; (B)220d d Rr r πθ⎰⎰;(C)230d 4sin cos d R r r πθθθ-⎰⎰; (D)220d d RR r r πθ⎰⎰. 答(A).2. 设L 是圆周222x y a +=,方向为负向, 则3223()d ()d Lx x y x xy y y -+-⎰= ( ).(A)323a π; (B)4a π-; (C); (D)42a π-. 答(D). 3. 设L 是从(0,0)O 沿折线22y x =--到(4,0)A 到的折线段,则d d Cx y y x -=⎰( )(A)8; (B)8-; (C)4-; (D)4. 答(B). 4. 设(,),(,)P x y Q x y 在单连通区域D 内具有一阶连续偏导数,则d d LP x Q y +⎰在D 内与路径无关的充分必要条件是在D 内恒有( ).<(A)0Q P x y ∂∂+=∂∂; (B)0Q Px y∂∂-=∂∂; (C)0P Q x y ∂∂-=∂∂; (D)0P Q x y∂∂+=∂∂. 答(B). 5. 设L 为一条不过原点,不含原点在内的简单闭曲线, 则22d d 4L x y y xx y -=+⎰( ).(A)4π; (B)π; (C)2π; (D)0. 答(D).6. 设L 为一条包含原点在内的简单闭曲线,则22d d 4L x y y xI x y -==+⎰( ).(A)因为Q P x y ∂∂=∂∂,所以0I =; (B)因为,Q Px y∂∂∂∂不连续,所以I 不存在;(C)2π; (D)因为Q Px y ∂∂≠∂∂,所以沿不同的L ,I 的值不同. 答(C).【7. 表达式(,)d (,)d P x y x Q x y y -为某函数(,)U x y 的全微分的充分心要条件是( ).(A)P Q x y ∂∂=∂∂; (B)P Q y x∂∂=∂∂; (C)P Q x y ∂∂=-∂∂; (D)P Q y x∂∂=-∂∂. 答(D). 8. 已知2()d d ()x ay x y yx y +++为某函数(,)U x y 的全微分,则a =( ).(A)0; (B)2; (C)1-; (D)1. 答(B). 9. 设L 是从点(1,1)A 到点(2,3)B 的直线段,则(3)d (3)d Lx y x y x y +++=⎰( ).(A)2311(3)d (6)d x x y y +++⎰⎰; (B)21[(6)(23)]d x x x x x +++⎰;,(C)23111(31)d (3)d 2y x x y y ++++⋅⎰⎰; (D)21[(31)(51)]d x x x -++⎰.答(A).10*. 设()f x 连续可导,且(0)1f =,曲线积分(,)43(0,0)()tan d ()d I yf x x x f x y ππ=-⎰与路径无关,则()f x =( ).(A)1cos x +; (B)1cos x -; (C)cos x ; (D)sin x . 答(C).二、填空题1. 设区域D 的边界为L ,方向为正向, D 的面积为σ. 则d d Lx y y x -=⎰.:答: 2σ.2. 设(,)f x y 在22:14x D y +≤上具有二阶连续偏导数, L 是D 的边界正向,则(,)d [3(,)]d y x Lf x y y y f x y x -+=⎰.答: 6π.3. 设L 是圆周229x y +=,方向为逆时针, 则2(2)d (4)d Lxy y x x x y -+-=⎰.答: 27π-.4. 设L 为闭曲线2x y +=方向为逆时针,,a b 为常数,则d d L ax y by x x y -+⎰=.【答: 4()a b +.5. 设ABCDA 为以点(1,0),(0,1),(1,0),(0,1)A B C D --为顶点的正方形逆时针方向一周,则d d Lx yx y++⎰=.答: 0.6. 设L 为圆周221x y +=上从(1,0)A 到(0,1)B 再到(1,0)C -的曲线段,则2d y Le y =⎰.答: 0. 7. (2,2)2(0,0)2d (3)d xy x x y +-=⎰.答: 2.8. 设L 为直线y x =从(0,0)O 到(2,2)A 的一段,)则22d 2d y y Le x xye y +=⎰.答: 42e .9*. 设L 为抛物线上一段弧,试将积分(,)d (,)d LP x y x Q x y y +⎰化为对弧长的曲线积分,其中(,),(,)P x y Q x y 在L 上连续.答: 22d 14L P xQs x ++⎰.10*. 设()f x 连续可导,且(0)0f =,曲线积分[()]sin d ()cos d x Lf x e y x f x y y --⎰与路径无关,则()f x =.答: 2x xe e --.三、解答题~1. 计算22d d 2()L y x x y x y -+⎰,其中L 为圆周22(1)2x y -+=的正向.答:π-. 2. 计算(24)d (536)d Lx y x y x y -+++-⎰,其中L 是顶点分别为(0,0)、(3,0)和(3,2)的三角形正向边界.答:12. 3. 计算3222(2cos )d (12sin 3)d Lxy y x x y x x y y -+-+⎰,其中L 为抛物线22x y π=上由点(0,0)到,12π⎛⎫⎪⎝⎭的一段弧.答:24π.4. 计算22()d (sin )d Lx y x x y y --+⎰,其中L 是圆周y =上由(0,0)到(1,1)的一段弧.答:7sin 264-+. )5. 证明下列曲线积分与路径无关,并计算积分值: (1) (2,3)(1,1)()d ()d x y x x y y ++-⎰.答:52. (2) (2,1)423(1,0)(23)d (4)d xy y x x xy y -++-⎰.答: 5.6. 验证下列(,)d (,)d P x y x Q x y y +在整个xoy 平面内是某函数(,)u x y 的全微分,并求函数(,)u x y .(1) (2)d (2)d x y x x y y +++. (2) 22d d xy x x y +.#(3) 22(2cos cos )d (2sin sin )d x y y x x y x x y y ++-.答: (1) 22222x y xy ++; (2) 2x y ; (3)22cos sin x y y x +.7. 用格林公式计算223()d (2)d Lx x y x xy y y -+-+⎰,其中L 是圆周y (2,0)A 到(0,0)O 的一段弧.答:324π-.8. 用格林公式计算423(23)d (4)d Lxy y x x x xy y -+++-⎰,其中L 是圆周y (1,0)A 到(1,0)B -的一段弧.答:62π-.·§10.4 对面积的曲面积分一、选择题1. 设∑是xoy 平面上的一个有界闭区域xy D ,则曲面积分(,,)d f x y z S ∑⎰⎰与二重积分(,)d d xyD f x y x y ⎰⎰的关系是 ( ).(A)(,,0)d f x y S ∑⎰⎰=(,)d d xyD f x y x y ⎰⎰;(B)(,,0)d f x y S ∑⎰⎰=(,)d d xyD f x y x y -⎰⎰;(C)(,,0)d f x y S ∑<⎰⎰(,)d d xyD f x y x y ⎰⎰;(D)(,,0)d f x y S ∑>⎰⎰(,)d d xyD f x y x y ⎰⎰.答(A).2. 设∑是抛物面22(04)z x y z =+≤≤,则下列各式正确的是( ).…(A)(,,)d f x y z S ∑⎰⎰=22224(,,)d d x y f x y x y x y +≤+⎰⎰;(B)(,,)d f x y z S ∑⎰⎰=22224(,,d x y f x y x y x y +≤+⎰⎰;(C)(,,)d f x y z S ∑=⎰⎰22224(,,d x y f x y x y x y +≤+⎰⎰;(D)(,,)d f x y z S ∑=⎰⎰22224(,,d x y f x y x y x y +≤+⎰⎰. 答(D).3.设2222:(0)x y z a z ∑++=≥,1∑是∑在第一卦限中的部分,则有( ).(A)1d 4d x S x S ∑∑=⎰⎰⎰⎰; (B)1d 4d y S x S ∑∑=⎰⎰⎰⎰;(C)1d 4d z S z S ∑∑=⎰⎰⎰⎰; (D)1d 4d xyz S xyz S ∑∑=⎰⎰⎰⎰. 答(C).4. 设∑是锥面1)z z =≤≤,则22()d x y S ∑+=⎰⎰( ).~(A)22()d x y S ∑+=⎰⎰2120d d r r r πθ⋅⎰⎰;(B)22()d x y S ∑+=⎰⎰1200d d r r r πθ⋅⎰⎰;(C)22()d xy S ∑+=⎰⎰21200d d r r πθ⎰;(D)22()d x y S ∑+=⎰⎰21200d d r r r πθ⋅⎰;. 答(D). 5. 设∑为平面1234x y z++=在第一卦限内的部分, 则42d 3z x y S ∑⎛⎫++= ⎪⎝⎭⎰⎰( ).(A)4d d xyD x y ⎰⎰;(B)4d d xyD x y ⎰⎰;(C)23004d d x y ⎰;(D)32004d d x y ⎰;. 答(B). [6. 设∑为曲面222()z x y =-+在xoy 平面上方的部分,则d z S ∑=⎰⎰( ).(A)22220d (2)d r r r r πθ--⋅⎰⎰;(B)2220d (2d r r r πθ-⎰⎰;(C)220d )d r r r πθ-⋅⎰;(D)220d d r r r πθ-⎰⎰. 答(D).7. 设∑为球面2222x y z z ++=,则下列等式错误的是( ).(A)22()d 0x y z S ∑+=⎰⎰; (B)22()d 0y y z S ∑+=⎰⎰;(C)22()d 0z x y S ∑+=⎰⎰; (D)2()d 0x y z S ∑+=⎰⎰. 答(C).二、填空题1. 设2222:x y z a ∑++=,则222()d x y z S ∑++=⎰⎰.…答: 44a π.2. 设∑为球面2222x y z a ++=,则222d xy z S ∑=⎰⎰.答: 0.3. 设∑为上半球面z ,则d z S ∑=⎰⎰.答: 3a π.4. 设∑为下半球面z =,则d z S ∑=⎰⎰.答: 3a π.5 设∑为球面2222x y z a ++=,则d z S ∑=⎰⎰.^答: 23a π.6. 设∑为上半球面z ,则d x S ∑=⎰⎰.答: 0.7. 设∑为平面1232x y z++=在第一卦限部分,则2d 3z y x S ∑⎛⎫++= ⎪⎝⎭⎰⎰.答:8. 设∑为平面1x y z ++=在第一卦限部分,则d z S ∑=⎰⎰.答. 9. 设∑为平面226x y z ++=在第一卦限部分, #则(522)d x y z S ∑---=⎰⎰.答: 272-. 三、解答题1. 计算曲面积分(,,)d f x y z S ∑⎰⎰,其中∑为抛物面222()z x y =-+在xoy面上方部分,(,,)f x y z 分别如下:(1) (,,)1f x y z =; (2) 22(,,)f x y z x y =+; (3) (,,)2f x y z z =. 答: (1) 136π; (2) 14930π; (3) 11110π. 2. 计算22()d x y S ∑+⎰⎰,其中∑是锥面z 1z =所围成的区域的整个边界曲面.答:12. ;3. 计算22()d x y S ∑+⎰⎰,其中∑是锥面222z x y =+被平面0z =和3z =所截得的部分.答: 9π.4. 计算42d 3z x y S ∑⎛⎫++ ⎪⎝⎭⎰⎰,其中∑为平面1234x y z ++=在第一卦限中的部分.答:5. 计算()d x y z S ∑++⎰⎰,其中∑为球面2222x y z a ++=上(0)z h h a ≥<<的部分.答: 22()a a h π-.§10.5 对坐标的曲面积分一、选择题`1. 设∑是球面2222x y z a ++=外侧,222:xy D x y a +≤,则下列结论正确的是( ).(A) 2d d z x y ∑=⎰⎰222()d d xyD ax y x y --⎰⎰;(B)2d d z x y ∑=⎰⎰2222()d d xyD a x y x y --⎰⎰; (C)2d d z x y ∑=⎰⎰0; (D) (A)(B)(C)都不对. 答(C). 2. 设∑为柱面222x y a +=被平面0z =及3z =所截得的部分外侧,则d d d d d d z x y x y z y x z ∑++=⎰⎰( ).(A) 3d d z x y ∑⎰⎰; (B)3d d x y z ∑⎰⎰;(C)3d d y x z ∑⎰⎰0; (D) d d d d x y z y x z ∑+⎰⎰. 答(D).3. 设∑为柱面222x y a +=被平面0z =及3z =所截得的部分外侧在第一卦限内的部分,则d d d d d d z x y x y z y x z ∑++=⎰⎰( ).·(A)303d y x ⎰⎰;(B)3002d z y ⎰⎰;(C)30d z x ⎰⎰; (D)3d z x ⎰⎰. 答(B).4. 设2222:x y z a ∑++=,1:z ∑=∑取外侧, 1∑取上侧.下列结论正确的是( ).(A) 12222()d d d d x y z x y a x y ∑∑++=⎰⎰⎰⎰; (B)12222()d d 2d d xy z x y a x y ∑∑++=⎰⎰⎰⎰;(C)2222222()d d 2d d x y axy z x y a x y ∑+≤++=⎰⎰⎰⎰; (D) 0. 答(D).5. 已知∑为平面1x y z ++=在第一卦限内的下侧,则d d z x y ∑=⎰⎰( ).(A) 110d (1)d x x x y y ----⎰⎰; (B) 110d (1)d x x x y y ---⎰⎰;\(C) 110d (1)d x y x y x ---⎰⎰; (D) 110d (1)d x y x y x ----⎰⎰. 答(A).6. 曲面积分2d d z x y ∑⎰⎰在数值上等于( ).(A)向量2z i 穿过曲面∑的流量;(B)密度为2z 的曲面∑的质量;(C)向量2z k 穿过曲面∑的流量;(D)向量2z j 穿过曲面∑的流量. 答(C).二、填空题1. 设∑是xoy 平面上的闭区域0101x y ≤≤⎧⎨≤≤⎩的上侧,则()d d x y z y z ∑++=⎰⎰.答: 0.》2. 设∑是xoy 平面上的闭区域0101x y ≤≤⎧⎨≤≤⎩的上侧,则()d d x y z x y ∑++=⎰⎰.答: 1. 3.设∑为球面2222x y z a ++=取外侧, 则222()d d xy z x y ∑++=⎰⎰..答: 0.4. 设∑为球面2222x y z a ++=取外侧, 则d d z x y ∑=⎰⎰..答: 343a π.5. 设∑为球面2222()()()x a y b z c R -+-+-=取外侧, 则曲面积分d d z x y ∑=⎰⎰..-答: 343R π.6. 设∑为球面2222x y z a ++=取外侧, 则222()d d x y z x y ∑++=⎰⎰.答: 0. 三、解答题1. 计算22d d x y z x y ∑⎰⎰,其中∑是球面2222x y z R ++=的下半部分的下侧.答:77426422453753105R R ππ⎛⎫⋅-⋅⋅= ⎪⎝⎭. 2. 计算d d d d d d z x y x y z y z x ∑++⎰⎰,其中∑是柱面221x y +=被平面0z =及3z =所截得的在第一卦限内的部分的前侧.答: 32π.】3. 计算d d d d d d xz x y xy y z yz z x ∑++⎰⎰,其中∑是平面0x =,0y =,0z =,及1x y z ++=所围成的空间区域的整个边界曲面的外侧.答: 18.4*. 把对坐标的曲面积分(,,)d d (,,)d d (,,)d d P x y z y z Q x y z z x R x y z x y∑++⎰⎰化成对面积的曲面积分,其中:(1) ∑是平面326x y ++=在第一卦限部分的上侧. (2) ∑是抛物面228()z x y =-+在xoy 面上方部分的上侧.答: (1) 32d 55P Q S ∑⎛⎫+ ⎪ ⎪⎝⎭⎰⎰; (2) S ∑. §10.6 高斯公式一、选择题(1. 设空间闭区域Ω的边界是分片光滑的闭曲面∑围成, ∑取外侧,则Ω的体积V =( ).(A)1d d d d d d 3y y z z z x x x y ∑++⎰⎰; (B)1d d d d d d 3x y z y z x z x y ∑++⎰⎰; (C)1d d d d d d 3z y z z z x y x y ∑++⎰⎰; (D) 1d d d d d d 3x y z z z x y x y ∑++⎰⎰.答(B).2.设∑是长方体{}:(,,)0,0,0,x y z x a y b z c Ω≤≤≤≤≤≤的整个表面的外侧,则222d d d d d d x y z y z x z x y ∑++=⎰⎰( ).(A) 2a bc ; (B)2ab c ; (C)2abc ; (D) ()a b c abc ++. 答(D).3. 在高斯定理的条件下,下列等式不成立的是( ).(A) d d d P Q R x y z x y z Ω⎛⎫∂∂∂++=⎪∂∂∂⎝⎭⎰⎰⎰(cos cos cos )d P Q R S αβγ∑++⎰⎰;(B)d d d d d d P y z Q z x R x y ∑++=⎰⎰d d d P Q R x y z x y z Ω⎛⎫∂∂∂++ ⎪∂∂∂⎝⎭⎰⎰⎰; 》(C)d d d d d d P y z Q z x R x y ∑++=⎰⎰d d d R Q P x y z x y z Ω⎛⎫∂∂∂++ ⎪∂∂∂⎝⎭⎰⎰⎰; (D)d d d d d d P y z Q z x R x y ∑++=⎰⎰(cos cos cos )d P Q R Sαβγ∑++⎰⎰.答(C).4. 若∑是空间区域Ω的外表面,下述计算用高斯公式正确的是( ).(A) 2d d (2)d d x y z z y x y ∑++=⎰⎰(22)d d d x x y z Ω+⎰⎰⎰;(B)3()d d 2d d d d x yz y z xy z x z x y ∑--+=⎰⎰2(321)d d d x x x y z Ω-+⎰⎰⎰; (C) 2d d (2)d d x y z z y z x ∑++=⎰⎰(21)d d d x x y z Ω+⎰⎰⎰;(D)2d d (2)d d x x y z y y z ∑++=⎰⎰(22)d d d x x y z Ω+⎰⎰⎰. 答(B).二、填空题,1. 设∑是球面2222x y z a ++=外侧, 则d d z x y ∑=⎰⎰.答: 343a π. 2.设∑是球面2222x y z a ++=外侧, 则333d d d d d d x y z y z x z x y ∑++=⎰⎰.答: 525a π.3. 设∑是长方体{}:(,,)0,0,0,x y z x a y b z c Ω≤≤≤≤≤≤的整个表面的外侧,则d d d d d d x y z y z x z x y ∑++=⎰⎰.答: 3abc .4. 设∑是长方体{}:(,,)0,0,0,x y z x a y b z c Ω≤≤≤≤≤≤的整个表面的外侧,则222d d d d d d x y z y z x z x y ∑++=⎰⎰.答: ()a b c abc ++.、5. 向量A yzi zxj xyk =++穿过圆柱222(0)x y a z h +=≤≤全表面∑流向外侧的通量Φ=.答: 0.6.向量2(23)()(2)A x z i xz y j y z k =+-+++穿过球面222(3)(1)(2)9x y z -+++-=∑流向外侧的通量Φ=.答: 108π. 三、解答题1. 计算222d d d d d d x y z y z x z x y ∑++⎰⎰,其中∑为平面0x =,0y =,0z =及x a =,y a =,z a =所围成的立体的表面外侧.【答: 43a . 2. 计算333d d d d d d x y z y z x z x y ∑++⎰⎰,其中∑为球面2222xy z a ++=外侧.答: 525a π.3. 计算2232d d ()d d (2)d d xz y z x y z z x xy y z x y ∑+-++⎰⎰,其中∑为上半球体222x y a +≤,0z ≤.答: 525a π.4. 计算d d d d d d x y z y z x z x y ∑++⎰⎰,其中∑是界于0z =和3z =之间的圆柱体223x y +≤的整个表面外侧. 答: 81π.5. 计算24d d d d d d xz y z y z x yz x y ∑-+⎰⎰,其中∑是平面0x =,0y =,0z =与平面1x =,1y =,1z =所围成的立方体的全表面外侧.(答:32. 6. 计算22d d (2)d d d d 2zx y z z xy z x x y ∑+-+⎰⎰,其中∑为曲面22z x y =+与平面1z =所围成的立体的表面外侧. 答:4π. 7. 计算曲面积分3333d d (2)d d ()d d x y z yz x z x x y ∑+++-⎰⎰,其中∑为曲面z =z .答: 326(1cos2)5π⋅⋅-. 8. 计算曲面积分222d d d d (1)d d xy y z z z x z xx y ∑++-⎰⎰,其中∑为由曲面z =0z =所围成的空间区域的整个边界表面外侧.答: 322161625335πππ⋅⋅-=. 9*.用Gauss 公式计算曲面积分2()d d d d z x y z z x y ∑+-⎰⎰,其中∑是旋转抛物面221()2z x y =+介于平面0z =及2z =之间部分的下侧. 答: 8π.§10.7 斯托克斯公式一、选择题1. 在斯托克斯定理的条件下,下列等式不成立的是( ).(A) d d d P x Q y R z Γ++=⎰d d d d d d y z z x x y x y z P Q R ∑∂∂∂∂∂∂⎰⎰; (B) d d d P x Q y R z Γ++=⎰cos cos cos d S x y z PQ Rαβγ∑∂∂∂∂∂∂⎰⎰; (C)d d d P x Q y R z Γ++=⎰{}cos ,cos ,cos d i j k S x y z P Q Rαβγ∑∂∂∂⋅∂∂∂⎰⎰; (D)d d d P x Q y R z Γ++=⎰{}d ,d ,d i j k x y z x y z PQR∑∂∂∂⋅∂∂∂⎰⎰. 答(D). 2. 设Γ是从点(,0,0)a 到点(0,,0)a 再到(0,0,)a 最后回到(,0,0)a 的三角形边界(0a >),则()d ()d ()d z y x x z y y x z Γ-+-+-=⎰( ).(A) 23a ; (B)26a ; (C)22a ; (D) 2a . 答(A).3. 设Γ为圆周2229,0x y z z ++==,若从z 轴正向看去, Γ为逆时针方向.则22d 3d d y x x y z z Γ+-=⎰( ).(A) π; (B)6π; 9π; (D) 0. 答(C).二、填空题1. 设Γ为圆周2222,0x y z a z ++==,若从z 轴正向看去, Γ为逆时针方向.22d 2d d y x x y z z Γ+-=⎰.答: 0.2. 设u xy yz zx xyz =+++, 则(1)grad u =.答: {},,y z yz z x xz x y xy ++++++(2) div(grad )u = .答: 0.(3) rot(grad )u = . 答: 0.3. 设向量场(23)(3)(2)A z y i x z j y x k =-+-+-,则rot A =.答: 246i j k ++.4. 设向量场22sin sin()sin(cos )A x yi y xz j xy z k =++, 则rot A =.答: 222[sin(cos )cos()]sin(cos )[cos()cos ]x z xy xz i y z j y z xz x y k --+-. 三、解答题1. 计算d d d y x z y x z Γ++⎰,其中Γ为圆周2222,0x y z a x y z ++=++=,若从z 轴正向看去, Γ为逆时针方向.答: 2a .2*. 计算()d ()d ()d yz x z x y x y z Γ+-+-⎰,其中Γ为椭圆222x y a +=,1(0,0)x ya b a b+=>>,若从x 轴正向看去, Γ为逆时针方向.答: π 3. 计算23d d d y x xz y yz z Γ-+⎰,其中Γ为圆周222,2x y z z +==,若从z 轴正向看去, Γ为逆时针方向.答: 20π-. 4. 计算22d 3d d y x x y z z Γ+-⎰,其中Γ为圆周2229,0x y z z ++==,若从z轴正向看去, Γ为逆时针方向.答: 9π.5*. 利用斯托克斯公式把曲面积分rot d A n S ∑⋅⎰⎰化为曲线积分,并计算积分值,其中A 、∑及n 分别如下:(1) 2A y i xyj xzk =++,∑为上半球面z , n 是∑的单位法向量.(2) ()A y z i yzj xzk =-+-,∑为{}(,,)02,02,02x y z x y z ≤≤≤≤≤≤的表面外侧去掉xoy 平面上的那个底面,, n 是∑的单位法向量.答: (1) 0. (2) 4-.。
习题解答10

第十章配位化合物和配位-离解平衡习题解答:1. 给以下各配离子命名(略):⑴Zn(NH3);⑵Co(NH3)3Cl3;⑶FeF;⑷Ag(CN);⑸[Fe(CN)5NO2] 3-。
2. Al2S3受潮时发出一种腐败气味,写出该反应的平衡化学方程式并用软硬酸碱理论讨论之。
(略)3. 对下列各组中的物质两两比较,哪一个可能存在?如都能存在,哪一个稳定性更大?简述理由。
答:⑴ Na2SO4 >Cu2SO4硬亲硬⑵ AlI63- 不存在,AlF63-硬亲硬⑶ HgI42- > HgF42-软亲软⑷ PbI42-> PbCl42-软亲软4. 用晶体场理论解释,为什么ZnCl42- 和NiCl42- 为四面体构型,而PtCl42-和CuCl42- 为平面正方形构型?答: Zn2+为3d10, CFSE =0, 所以ZnCl42-四面体构型; Cu2+为3d9, 弱场条件下正方形场的CFSE 最大, 所以CuCl42- 为平面正方形构型.d8构型的中心离子, 在强场条件下均形成正方形, 在弱场条件下可形成四面体或正方形. Ni2+和Pt2+均为d8构型, 与相同配体结合时, Pt2+的分裂能大于Ni2+的分裂能,所以Pt2+的8个d电子成对, PtCl42-为正方形构型; Ni2+的分裂能较小于电子成对能,故NiCl42-为四面体构型.附:Acta Cryst. (1974). A30, 484-486 [ doi:10.1107/S0567739474001161 ] Relation entre la symétrie des groupements CuCl42-tétraédriques et les propriétés physiques descupritétrachlorures. I. Moment magnétique moyenJ. Lamotte-Brasseur et G. van den BosscheAbstract: For some crystals, the structures of which have already been determined, the flattening, D, of the CuCl42- tetrahedra has been estimated. The paramagnetic susceptibilities of many tetrachlorocuprates have been measured by the Faraday method. The mean magnetic moment decreases linearly as D increases, if D is greater than 0.2. From the known meanmagnetic moment, it is therefore possible to estimate the D value of the CuCl42- tetrahedron.5. 氯化铜溶液随浓度的增大,颜色由浅兰色变为绿色再变为土黄色。
第十章毛概习题答案

第十章中国特色社会主义外交和国际战略一、单项选择题1.()是当今世界的两大主题。
A.和平与发展B.经济全球化与世界多极化C.开放与合作D.互惠与共存2.()是国家关系发展的必然结果和客观趋势。
A.霸权主义B.强权政治C.单边主义D.世界格局多极化3. 走()道路,是中国政府和人民根据时代发展潮流和自身根本利益作出的战略抉择。
A.和平发展B.强权政治C.单边主义D.霸权主义4.我国独立自主的和平外交政策,应坚持把()。
A.发展对外经济关系放在首位B.发展睦邻友好关系放在首位C.维护国家主权和安全放在首位D.反对霸权主义和强权政治放在首位5.我国处理对外关系的基本准则是()A.和平共处五项原则B.争取全球领导权C.自给自足D.广泛结盟6.当前国际间的经济竞争实质上是()A.社会制度的竞争B.科学技术的竞争C.经济资源的竞争D.军事力量的竞争7.1953年12月,周恩来在会见印度政府代表团时首次系统地提出了()。
A.不结盟战略B.一边倒战略C.一条线战略D.和平共处五项原则8.建立国际政治经济新秩序的长期斗争中,必须始终()A.以人权高于主权的原则为基础B.以不结盟原则为基础C.以和平共处五项原则为基础D.以自由、平等原则为基础9. 20世纪80年代以来,邓小平根据形势的变化,确定了()战略。
A.一边倒B.另起炉灶C.真正的不结盟D.打扫干净屋子再请客10.20世纪70年代,美苏争霸出现了苏攻美守的态势。
中国审时度势,提出了()的外交战略.A.一边倒B.另起炉灶C.打扫干净屋子再请客D.一条线11.当前国际间的经济竞争实质上是()A.产品质量的竞争B.经济资源的竞争C.产品价格的竞争D.科技和人才的竞争12.当今世界和平与发展的主要障碍是()A.领土争端B.民族矛盾C.宗教纷争D.霸权主义和强权政治13. 在处理国家之间的关系上,中国坚持的原则是()A.相互尊重主权和领土完整B.互不侵犯C.互不干涉内政D.平等互利和和平共处二、多项选择题1.()是当前和今后一个时期国际局势发展的基本态势。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
m2
, Pr 2.99
1.3 0.014 38075.3 0.478 106
f w
0.14
采用紊流换热关系式:
Nu f 0.027 Re f
0.8
Pr f
1
3
195.3
所以, Nu
d
9192
校核: Q1 Ftm 9192 0.014 2.5 49.33 49829.44W
2 0.45 3 0 . 022 331 0.8 0.4 0.0214 4103.2 100 0.6964 1 2.25 363 12.578
查附录水的物性表有:
983.1 kg
m3
, c p 4.179 kJ
2
kg0 C
, 0.659W
m 0 C
0.478 106 m s , f 469.9 106 N s 2 , m
w 259.0 106 N s
Re um d
当 x 0.2m 时, x 422.63 0.2 当 x 0.3m 时, x 422.63 0.3
1 2 1 2 1 2
945.032W 771.615W 668.239W
m 2 0 C m 2 0 C m 2 0 C
当 x 0.4m 时, x 422.63 0.4
f w
0.14
采用紊流换热关系式:
Nu f 0.027 Re f
0.8
Pr f
1
3
211.94
所以, Nu
d
10218.7
校核: Q1 Ftm 31338.9W
Q2 Gc p t f ' 't f '
d 2
4
c p t f ' 't f ' 31331.8W
Re u x
1 x 0.659 106
1 2 1 3 1 1 1
0.0276 1 x 2 x 0.332 Re Pr 0.332 0.699 3 1.975 x 2 6 x x 16.96 10
当 x 0.4m 时, x 1.975 0.4
1.13355 kg
m3
, c p 1.005 kJ
2
kg0 C
, 0.027465W
m 0 C
16.816 106 m s , f 19.025 106 N s 2 , Pr 0.6993 m
t w 580 C , w 20 106 N s
c p 1.005 kJ kg0 C
, 0.02886W
m 0 C
18.766 106 m s , f 20 106 N s 2 , Pr 0.6964 m
2
t w 900C , w 21.5 106 N s
m2
,
Re
um d
t ' 110 50 60 0 C ,
t m
t ' 't ' 10 60 27.90C t ' ' 10 ln ln t ' 60
t f t w tm 110 27.9 82.10 C
查附录水的物性表有:
970.4 kg
m3
, c p 4.197 kJ
tw t f 2 60 20 400 C 查附录 3 水的物性表得到: 2
2
63.5 102 W m K , 0.659 106 m s , Pr 4.31
Re u x
1 x 0.659 106
1
当 x=0.4 时,为旺盛湍流,不应再用那个公式。
10-1 水和空气都以速度 u 1 m/s 分别平行流过平板, 边界层的平均温度都 为 50 C,试求距平板前沿 100 mm 处流动边界层及热边界层的厚度。 解:对水:由 tm 500 C 查附录 3 水的物性表得到:
64.8 102 W m K , 0.556 106 m s , Pr 3.54
t Pr
1 3
x 5 0.05571 105
1 3
1 2
0.1 0.006699m 6.699mm
0.006699 0.698
0.007552m 7.552mm
10-2 试求水平行流过长度为 0.4 m 的平板时沿程 x 0.1 、 0.2 、 0.3 、 0.4 m 处 的局部表面传热系数。己知水的来流温度为 t 20 C,速度为 u 1 m/s,平板 的壁面温度 t w 60 C。 解:由 t m
所以, Nu
d
10218.7
校核: Q1 Ftm 31338.9W
Q2 Gc p t f ' 't f '
d 2
4
c p t f ' 't f ' 31331.8W
可见 Q1 和 Q2 相差很小,所以 t f ' ' 1000C 10-6 用内径为 0.016 m、长为 2.5 m 的不锈钢管进行管内对流换热实验,实 验时直接对不锈钢管通以直流电加热,电压为 5V,电流为 900A,水的进口温度 为 20 C ,流速为 0.5 m/s,管外用保温材料保温,忽略热损失。试求管内对流 换热的表面传热系数及换热温差。 解:假定出口温度为 400C,则有:
可见 Q1 和 Q2 相差很小,所以 t f ' ' 1000C
10-7 空气以 1.3 m/s 速度在内径为 22 mm、长为 2.25m 的管内流动,空气的 平均温度为 38.5 C,管壁温度为 58 C,试求管内对流换热的表面传热系数。 解: t f 38.50 C 查附录空气的物性表有:
w 259.0 106 N s
Re um d
m2
, Pr 2.155
1.3 0.014 50980.4 0.357 106
f Pr f 3 w
1 0.14
采用紊流换热关系式:
Nu f 0.027 Re f
0.8
211.94
t f t w tm 110 27.9 82.10 C
查附录水的物性表有:
970.4 kg
m3
, c p 4.197 kJ
2
kg0 C
, 0.675W
m 0 C
0.357 106 m s , f 347 106 N s 2 , m
10-3 如果将上题中的水改为空气, 其它参数保持不变, 试计算整个平板的平 均表面传热系数以及单位宽度平板的换热量,并对比这两种情况的计算结果。 解:由 t m
tw t f 2 60 20 400 C 查附录 2 空气的物性表得到: 2
2
2.76 102 W m K , 16.96 106 m s , Pr 0.699
3.5 0.022 4103.2 2300 为过渡流, 18.766 106
采用过渡流换热关系式:
2 0.45 3 Tf d 0.8 0.4 Nu f 0.0214 Re f 100 Pr f 1 L Tw
2.59 102 W m K , 15.06 106 m s
当空气温度为 2000C 时,
2
2
3.93 102 W m K , 34.85 106 m s
(1)由相似原理: Re Re' ,
u ' L' ' u L ' 6 5 15.06 所以有 u ' 12.964m / s L' 34.85
Q2 Gc p t f ' 't f '
d 2
4
c p t f ' 't f ' 12642.3W
重新假定出口温度为 1000C,则有:
t ' 110 50 600C , t ' ' 110 100 100C
t m t ' 't ' 10 60 27.90C t ' ' 10 ln ln t ' 60
t ' 110 50 600C , t ' ' 110 70 400C
t m t ' 't ' 40 60 49.330 C t ' ' 40 ln ln t ' 60
t f t w tm 110 49.33 60.670C
0.635 1 x 2 x 0.332 Re Pr 0.332 4.313 422.63x 2 6 x x 0.659 10
1 2
1 3
1
1
当 x 0.1m 时, x 422.63 0.1
1 2
1336.447 W
m 2 0 C
2
kg0 C
, 0.675W
m 0 C
0.357 106 m s , f 347 106 N s 2 , m
