时间序列分析 读书笔记
《时间序列分析及应用:R语言》读书笔记
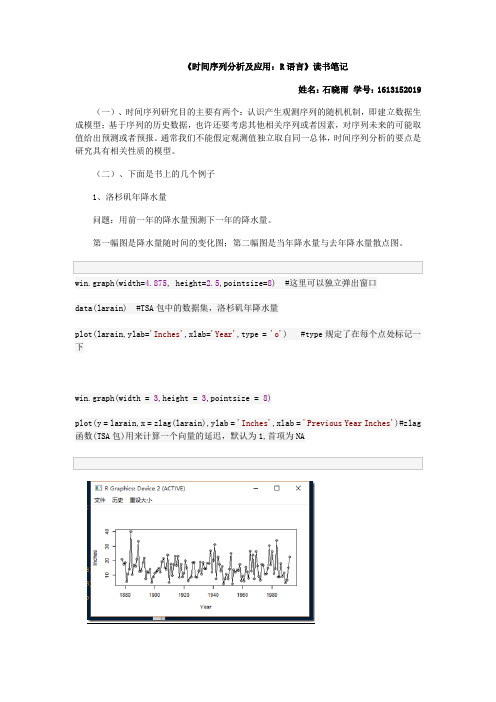
《时间序列分析及应用:R语言》读书笔记姓名:石晓雨学号:1613152019(一)、时间序列研究目的主要有两个:认识产生观测序列的随机机制,即建立数据生成模型;基于序列的历史数据,也许还要考虑其他相关序列或者因素,对序列未来的可能取值给出预测或者预报。
通常我们不能假定观测值独立取自同一总体,时间序列分析的要点是研究具有相关性质的模型。
(二)、下面是书上的几个例子1、洛杉矶年降水量问题:用前一年的降水量预测下一年的降水量。
第一幅图是降水量随时间的变化图;第二幅图是当年降水量与去年降水量散点图。
win.graph(width=4.875, height=2.5,pointsize=8) #这里可以独立弹出窗口data(larain) #TSA包中的数据集,洛杉矶年降水量plot(larain,ylab='Inches',xlab='Year',type = 'o') #type规定了在每个点处标记一下win.graph(width = 3,height = 3,pointsize = 8)plot(y = larain,x = zlag(larain),ylab = 'Inches',xlab = 'Previous Year Inches')#zlag 函数(TSA包)用来计算一个向量的延迟,默认为1,首项为NA从第二幅图看出,前一年的降水量与下一年并没有什么特殊关系。
2、化工过程win.graph(width = 4.875,height = 2.5,pointsize = 8)data(color)plot(color,ylab = 'Color Property',xlab = 'Batch',type = 'o')win.graph(width = 3,height = 3,pointsize = 8)plot(y = color,x = zlag(color),ylab = 'Color Property',xlab = 'Previous Batch Color Property')len <- length(color)cor(color[2:len],zlag(color)[2:len])#相关系数>0.5549第一幅图是颜色属性随着批次的变化情况。
《时间序列分析及应用:R语言》读书笔记

《时间序列分析及应用:R语言》读书笔记姓名:石晓雨学号:1613152019(一)、时间序列研究目的主要有两个:认识产生观测序列的随机机制,即建立数据生成模型;基于序列的历史数据,也许还要考虑其他相关序列或者因素,对序列未来的可能取值给出预测或者预报。
通常我们不能假定观测值独立取自同一总体,时间序列分析的要点是研究具有相关性质的模型。
(二)、下面是书上的几个例子1、洛杉矶年降水量问题:用前一年的降水量预测下一年的降水量。
第一幅图是降水量随时间的变化图;第二幅图是当年降水量与去年降水量散点图。
win.graph(width=4.875, height=2.5,pointsize=8) #这里可以独立弹出窗口data(larain) #TSA包中的数据集,洛杉矶年降水量plot(larain,ylab='Inches',xlab='Year',type = 'o') #type规定了在每个点处标记一下win.graph(width = 3,height = 3,pointsize = 8)plot(y = larain,x = zlag(larain),ylab = 'Inches',xlab = 'Previous Year Inches')#zlag 函数(TSA包)用来计算一个向量的延迟,默认为1,首项为NA从第二幅图看出,前一年的降水量与下一年并没有什么特殊关系。
2、化工过程win.graph(width = 4.875,height = 2.5,pointsize = 8)data(color)plot(color,ylab = 'Color Property',xlab = 'Batch',type = 'o')win.graph(width = 3,height = 3,pointsize = 8)plot(y = color,x = zlag(color),ylab = 'Color Property',xlab = 'Previous Batch Color Property')len <- length(color)cor(color[2:len],zlag(color)[2:len])#相关系数>0.5549第一幅图是颜色属性随着批次的变化情况。
统计学基础第五章时间数列分析笔记

统计学时间数列分析笔记
时间序列数据用于描述现象随时间发展变化的特征。
时间序列(timesseries)是同一现象在不同时间的相继观察值
排列而形成的序列。
经济数据大多数以时间序列的形式给出。
时间序列可以分为平稳序列和非平稳序列两大类。
平稳序列是基本上不存在趋势的序列。
这类序列中的各观察值基本上在某个固定的水平上波动,虽然在不同的时间段波动的程度不同,但并不存在某种规律,波动可以看成是随机的。
时间序列的成分可以分为四种:
趋势(T)、季节性或季节变动(S)、周期性或循环波动(C)、随机性或不规则波动(I)。
构成要素:长期趋势,季节变动,循环变动,不规则变动。
1)长期趋势(T)现象在较长时期内受某种根本性因素作用而形成的总的变动趋势。
2)季节变动(S)现象在一年内随着季节的变化而发生的有规律的周期性变动。
3)循环变动(C)现象以若干年为周期所呈现出的波浪起伏形态的有规律的变动。
4)不规则变动(I)是一种无规律可循的变动,包括严格的随机变动和不规则的突发性影响很大的变动两种类型。
时间序列笔记

通过定义日期变量将新的日期变量选进“时间轴”通常,时间序列经过两次差分变量就可以得到稳定了。
第一次差分结果,得到期望值不为零;第二次差分结果期望值大致为零,于是序列得到了平稳。
那么就可以开始做自相关函数和偏自相关函数了。
当期和之后16期的相关系数图,原假设是否为相关系数都为零。
当期序列和滞后十六期的相关系数。
Box-ljung统计量(值、自由度、原假设成立的概率值)在第一次结尾,不是依序衰减的。
(结合讲义)Eg:这种情况就有两个K,2或者是4.具体代入哪一个,需要进行检验。
Eg:第2个和第3个都行。
3.互相关的步骤先试一试,不加上任何对数变换和差分操作。
上图表示,最大互相关系数出现在滞后0处,为0.998.滞后0处的相关同简单的皮尔逊相关市一样的,说明两个变量之间按存在线性相关性。
而横轴上下的两根横4.利用时间序列进行模型建立。
由于使用专家选项的属于系统自我识别,所以应该自行定义差分自相关(ARIMA条件),会得到可能更为精确合理的结果。
以上为自我手动做出的结果。
(怎样看出比较准确适合)5.季节分析法再通过加法模型进行分解Err为随机误差项,SAS-1为季节校准(调整之后的)序列,SAF-1季节因素指数,季节趋势周期STC-1(STC-1趋势成分+ERR随机成分=季节校准序列SAS-1,SAS-1+SAF=实际的序列变量)。
如果使用的是乘法模型,则使得其更平滑但是加法模型更为直观。
(直接在该分析界面改成乘法模型就可以了)看原数据变化就可以知道预测的结果了。
课堂练习:利用中经网2000-2013年中国GDP 及全社会固定资产投资年度及月度数据,预测2014-2015年中国GDP及全社会固定资产投资年度及月度数据。
时间序列实验报告心得

在本次时间序列实验中,我深刻体会到了时间序列分析在解决实际问题中的重要作用。
通过对时间序列数据的收集、处理、分析和预测,我学会了如何运用时间序列分析方法解决实际问题,以下是我在实验过程中的心得体会。
一、实验背景时间序列分析是统计学和金融学等领域的重要研究方法,通过对时间序列数据的分析,我们可以揭示现象的发展变化规律,预测未来趋势,为决策提供依据。
本次实验以我国某地区1980年1月至1995年8月每月屠宰生猪数量为研究对象,运用时间序列分析方法进行建模和预测。
二、实验步骤1. 数据收集与处理:首先,收集了某地区1980年1月至1995年8月每月屠宰生猪数量数据。
然后,对数据进行初步处理,包括去除异常值、缺失值等。
2. 时间序列图绘制:运用Excel或R等软件绘制时间序列图,观察数据的变化趋势,为后续建模提供依据。
3. 平稳性检验:对时间序列数据进行平稳性检验,以确定是否可以直接进行建模。
常用的平稳性检验方法有ADF检验、KPSS检验等。
4. 模型选择与参数估计:根据时间序列图和平稳性检验结果,选择合适的模型进行拟合。
本次实验选择了ARIMA模型,并对模型参数进行估计。
5. 模型预测与结果分析:利用估计出的模型对未来的数据进行预测,并对预测结果进行分析,评估模型的准确性。
三、实验心得1. 时间序列分析的重要性:通过本次实验,我深刻认识到时间序列分析在解决实际问题中的重要性。
在实际工作中,许多现象都呈现出时间序列特征,运用时间序列分析方法可以揭示现象的发展变化规律,为决策提供依据。
2. 数据处理的重要性:在实验过程中,数据预处理是至关重要的。
只有保证数据的准确性和完整性,才能得到可靠的实验结果。
3. 平稳性检验的必要性:时间序列建模的前提是数据平稳。
通过对数据平稳性进行检验,可以确保模型的准确性。
4. 模型选择与参数估计的重要性:选择合适的模型和参数对于时间序列分析至关重要。
不同的模型适用于不同类型的数据,需要根据实际情况进行选择。
时间序列分析-读书笔记

时间序列分析模型~()()⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎩⎨⎧⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎪⎪⎩⎪⎪⎨⎧=-=-⎩⎨⎧∑∑-可变权数选点法固定权数选点法选点法曲线曲线如修正指数曲线曲线的模型参数主要用于估计一些增长三段求和法差分指数平法滑高次指数平滑法双参数线性指数平滑法单参数线性指数平滑法一次指数平滑法指数平滑法二次移动平均法一次移动平均法移动平均法折扣最小二乘法普通最小二乘法最小二乘法分段平均法全列平均法平均数法isticGompertzHoltBrownyyyyiiitlog,,,,,:minˆ:minˆ:22α1. 时间序列作用:描述系统运行规律预测对特殊政策或事件的影响加以估计2. 时间序列分类:确定时间序列,随机时间序列3. 确定时间序列的分析方法:它不计算时间序列的随机变动值,建模的目的是要消除随机变动的影响,揭示预测对象随时间变动的规律性用于预测,这是确定性时间序列和随机时间序列分析的区别。
趋势外推法:有明显上升或下降趋势,没有明显季节变动,能用函数表示%移动平均法:一次移动平均:大体成水平变动,平滑公式,预测公式两次移动平均:线性上升或下降,预测公式指数平滑法:一次指数平滑法:水平变动,平滑公式,预测公式Brown 单参数线性指数平滑法:线性上升或下降,平滑公式,预测公式Holt 双参数线性指数平滑法: 线性上升或下降,平滑公式,预测公式 参数选择主观性较强,不能提供置信区间信息季节调整术:试图度量序列中的季节变动,并利用这些指数剔除序列中的季节变动。
4.随机时间序列分析:平稳时间序列分析严平稳的概率分布与时间的平移无关。
宽平稳序列的均值随时间的平移而不变,自协方差仅与时间间隔有关*自回归模型、滑动平均模型和自回归滑动平均模型分析平稳的时间序列的规律。
自回归模型:如果时间序列() ,2,1=t X t 是平稳的且数据之间前后有一定的依存关系,即t X 与前面p t t t X X X --- ,,21有关与其以前时刻进入系统的扰动(白噪声)无关,具有p 阶的记忆,描述这种关系的数学模型就是p 阶自回归模型可用来预测:t p t p t t t a X X X X ++++=---ϕϕϕ 2211滑动平均模型:如果时间序列() ,2,1=t X t 是平稳的与前面p t t t X X X --- ,,21无关与其以前时刻进入系统的扰动(白噪声)有关,具有q 阶的记忆,描述这种关系的数学模型就是q 阶滑动平均模型可用来预测:q t q t t t t a a a a X ---+++-=θθθ 2211回归滑动平均模型:如果时间序列() ,2,1=t X t 是平稳的与前面p t t t X X X --- ,,21有关且与其以前时刻进入系统的扰动(白噪声)也有关,则此系统为自回归移动平均系统,预测模型为:=+++----p t p t t t X X X X ϕϕϕ 2211q t q t t t a a a a ---+++-θθθ 2211非平稳时间序列分析用模型来预测应是要把趋势和波动综合考虑进来,是它们的叠加。
《时间序列分析》(第部分)解读共46页文档

1
0
、
倚
南
窗
以
寄
傲
,
审
容
膝
之
易
安
。
16、业余生活要有意义,不要越轨。——华盛顿 17、一个人即使已登上顶峰,也仍要自强不息。——罗素·贝克 18、最大的挑战和突破在于用人,而用人最大的突破在于信任人。——马云 19、自己活着,就是为了使别人过得更美好。——雷锋 20、要掌握书,莫被书掌握;要为生而读,莫为读而生。——布尔沃
ENDLeabharlann 《时间序列分析》(第部分)解读
6
、
露
凝
无
游
氛
,
天
高
风
景
澈
。
7、翩翩新 来燕,双双入我庐 ,先巢故尚在,相 将还旧居。
8
、
吁
嗟
身
后
名
,
于
我
若
浮
烟
。
9、 陶渊 明( 约 365年 —427年 ),字 元亮, (又 一说名 潜,字 渊明 )号五 柳先生 ,私 谥“靖 节”, 东晋 末期南 朝宋初 期诗 人、文 学家、 辞赋 家、散
时间序列分析与预测心得报告

時間序列分析與預測心得報告所謂時間序列分析(Time Series Analysis),乃探討一串按時序列間的關係,並籍由此關係前瞻至未來。
時間序列分析模式是計量經濟模式的一般化,可分為狹義及廣義。
狹義的時間序列分析是Box and Jankins在1961年所提出的ARIMA模式和後人延伸的ARIMA相關系統;廣義的時間序列除了ARIMA及其相關體系外,還包括趨勢預測、時間序列分解、譜系分析及狀況空間分析等模式。
其中,ARIMA轉移函數為高度一般化的模式,其特例簡化為自我迴歸模式及多項式遞延落差模式;而向量ARIMA模式更可簡化為聯立方程式模式。
ARIMA、ARIMA轉移函數及向量ARIMA構成了ARIMA系統。
事實上,除了ARIMA模式外,尚有其他可用以預測外生變數之統計模式,但每種模式皆適用於不同的研究特性,如表4.1-1所示。
表中,依模式誤差、變數性質、資料特性,可產生六種不同情況的組合,每一組合的預測,均有適當的統計模式可用。
預測模式之適用場合資料特性模式特性變數特性連續性季節性非隨機性外生變數趨勢預測時間序列分解隨機性外生變數ARIMA SARIMA內生變數ARIMAT SARIMAT模式依特性可分為非隨機模式和隨機模式。
非隨機模式(Non-stochastic Model)的誤差項背後無隨機過程的假定,亦即時間序列不是由隨機過程產生。
典型的非隨機模式為趨勢預測模式。
這種模式非常單純,僅用一個數學函數,配適在所觀察到的時間序列上,再用函數的特性,產生未來的預測。
趨勢預測模式有誤差項,假定遵循NID(0, 2)。
非隨機模式的特例為確定性模式(Deterministic Model),模式中無誤差項,純為數學結構,不是統計推理的應用,沒有假說檢定,也沒有常態分配的觀念存在。
典型的確定性模式,就是時間序列分解模式。
這種模式用數學的方式,將時間序列分解成長期趨勢、循環變動、季節變動、不規則變動。
时间序列分析笔记

时间序列分析笔记总结一、主要概念经典的T 检验、f 检验隐含假定了所依据的时间序列是平稳的,若时间序列不平稳,我们做的T 值、F 值、R ²等是失效的。
弱平稳:如果一个随机过程的均值、方差和协方差在时间上是恒定的(不随时间的变化变化)。
平稳性检验可以通过图示简单判断,平稳时间序列的相关图会很快变平,非平稳时间序列消失缓慢;平稳性可以通过时间序列是否含有单位根来检查,如DF ,ADF 检验。
伪回归: 回归分析结果中,R ²>DW 就可能存在伪回归问题。
随机游走:如股票、汇率等价格为随机游走,是非平稳的。
随机游走分为带漂移的随机游走(不存在常数项或截距项)和不带漂移的随机游走(出现常数项)。
单整(单积随机过程):差分后平稳。
不带漂移的随机游走模型为一阶单整序列,记为I(1),如果进行两次差分后为平稳序列,为二阶单整, I (0),I (1),I (2)以此类推。
单位根过程:对于Y t= Y t-1+μt (-1≤ρ≤0),当ρ=1时是一个单位根过程。
两边同时减去一个Y t-1,式子变形为△Y=(ρ-1)Y t-1+μt ,然后看ρ-1的值。
当ρ <1时,我们说Y t 是一个平稳序列;而当ρ >1时, Y t 是非平稳的。
DF 检验:如果ρ=1或者δ=0, xt 就是最基本的单位根过程(随机游走),是非平稳的,然后用最小二乘法估计δ,但是得到的t 统计量不服从t 分布,所以DF 两人构造了专门的临界值分布表。
参数ρ或δ所对应的t 统计量服从DF 分布,若计算值小于临界值,拒绝原假设。
ADF 检验(增广DF ):在DF 基础上通过在三个方程中增加因变量△Yt 的滞后值控制εt 的自相关(差分)。
协整:把两个非平稳的波动相减或相加抵消掉,剩余的部分是平稳的,变成了有效的回归分析。
残差序列做平稳性检验。
二、主要模型ARMA 模型(Auto-Regressive and Moving Average Model )是研究时间序列的重要方法,由自回归模型(简称AR 模型)与滑动平均模型(简称MA 模型)相加构成。
时间序列分析实训报告心得

时间序列分析实训报告心得1. 引言时间序列分析是一种重要的统计分析方法,可以用于研究时间序列数据的变化规律、预测未来趋势以及分析影响因素等。
在本次时间序列分析实训中,我们通过实际数据的分析和建模,深入学习了时间序列的基本理论和方法,并运用所掌握的知识解决了实际问题。
在本文中,我将分享我的实训心得和体会。
2. 数据获取与初步分析在时间序列分析的实训中,首先需要获取相关的时间序列数据,并进行初步的数据分析。
我们可以使用Python编程语言和相关的库来获取和处理数据。
通过对实际数据的初步观察和描述性统计分析,可以对数据的特征有一个初步的了解。
3. 数据预处理时间序列数据可能存在缺失值、异常值以及非平稳性等问题,因此在进行时间序列分析之前需要对数据进行预处理。
我们可以使用插值法来填充缺失值,使用平滑法或者移动平均法来处理异常值,使用差分法来消除非平稳性等。
4. 时间序列模型的选择与建立选择适当的时间序列模型是时间序列分析的关键步骤之一。
常见的时间序列模型包括ARMA模型、ARIMA模型、ARCH模型等。
根据实验要求和数据特点,我们可以选择合适的模型,并通过参数估计来建立模型。
5. 模型诊断与验证建立时间序列模型后,需要进行模型的诊断和验证。
通过残差的自相关图和偏自相关图,可以判断模型是否符合ARMA(p, q)模型的要求。
同时,还可以通过计算残差的百分比误差、平均绝对百分比误差等指标来评估模型的拟合效果。
6. 模型用于预测与应用时间序列模型的主要应用之一是预测未来的数值。
在选定合适的模型后,可以使用模型对未来的数据进行预测。
同时,时间序列模型还可以用于分析影响因素、判断趋势变化等。
通过对模型的应用,可以得到一些有价值的结论和洞察。
7. 总结与展望通过本次时间序列分析实训,我不仅深入了解了时间序列分析的理论和方法,还学会了使用Python编程语言和相关的库对时间序列数据进行分析和建模。
实践中遇到的问题和挑战也锻炼了我的动手能力和解决问题的能力。
《时间序列分析——基于R》王燕,读书笔记

《时间序列分析——基于R》王燕,读书笔记笔记:⼀、检验:1、平稳性检验:图检验⽅法:时序图检验:该序列有明显的趋势性或周期性,则不是平稳序列⾃相关图检验:(acf函数)平稳序列具有短期相关性,即随着延迟期数k的增加,平稳序列的⾃相关系数ρ会很快地衰减向0(指数级指数级衰减),反之⾮平稳序列衰减速度会⽐较慢衰减构造检验统计量进⾏假设检验:单位根检验adfTest()——fUnitRoots包2、纯随机性检验、⽩噪声检验(Box.test(data,type,lag=n)——lag表⽰输出滞后n阶的⽩噪声检验统计量,默认为滞后1阶的检验统计量结果)1、Q统计量:type=“Box-Pierce”2、LB统计量:type=“Ljung-Box”⼆、模型1、ARMA平稳序列模型1.1平稳性检验1.2ARMA的p、q定阶——acf(),pacf(),auto.arima()⾃动定阶1.3建模arima()1.4模型显著性检验:残差的⽩噪声检验Box.test();参数显著性检验t分布2、⾮平稳确定性分析2.1趋势拟合:直线、曲线(⼀般是多项式,还有其它函数)2.2平滑法移动平均法:SMA()——TTR包指数平滑法:HoltWinters()3、⾮平稳随机性分析3.1ARIMA1平稳性检验,差分运算2拟合ARMA3⽩噪声检验3.2疏系数模型arima(p,d,f)3.3季节模型可以叠加的模型4、残差⾃回归模型:4.1建⽴线性模型4.2对滞后的因变量间拟合线性模型,对模型做残差⾃相关DW检验。
dwtest()——lmtest包,增加选项order.by指定延迟因变量4.3对残差建⽴ARIMA模型5、条件异⽅差模型:异⽅差检验:LM检验ArchTest()——FinTS包,⽤ARCH、GARCH模型建模第⼀章简介统计时序分析⽅法:1、频域分析⽅法2、时域分析⽅法步骤:1、观察序列特征2、根据序列特征选择模型3、确定模型的⼝径4、检验模型,优化模型5、推断序列其它统计性质或预测序列将来的发展时域分析研究的发展⽅向:1、AR,MA,ARMA,ARIMA(Box-Jenkins模型)2、异⽅差场合:ARCH,GARCH等(计量经济学)3、多变量场合:“变量是平稳”不再是必需条件,协整理论3、⾮线性场合:门限⾃回归模型,马尔科夫转移模型第⼆章时间序列的预处理预处理内容:对它的平稳性和纯随机性进⾏检验,最好是平稳⾮⽩噪声的序列1、特征统计量1.1概率分布分布函数或密度函数能够完整地描述⼀个随机变量的统计特征,同样⼀个随机变量族{Xt}的统计特性也完全由它们的联合分布函数或联合密度函数决定。
《数据分析实战-托马兹.卓巴斯》读书笔记第7章-时间序列技术(ARMA模型、ARIMA模型)

《数据分析实战-托马兹.卓巴斯》读书笔记第7章-时间序列技术(ARMA模型、ARIMA模型)第7章探索了如何处理和理解时间序列数据,并建⽴ARMA模型以及ARIMA模型。
注意:我在本章花的时间较长,主要是对dataframe结构不熟。
/*sh riverflows.webarchive*/邀⽉建议:安装cygwin巨⿇烦,还是⽤安装好的CentOS虚拟机执⾏⼀下。
7.2在Python中如何处理⽇期对象时间序列是以某个时间间隔进⾏采样得到的数据,例如,记录每秒的车速。
拿到这样的数据,我们可以轻松估算经过的距离(假设观测值加总并除以3600)或者汽车的加速度(计算两个观测值之间的差异)。
可以直接⽤pandas处理时间序列数据。
准备:需装好pandas、NumPy和Matplotlib。
1import numpy as np2import pandas as pd3import pandas.tseries.offsets as ofst4import matplotlib5import matplotlib.pyplot as plt67# change the font size8 matplotlib.rc('xtick', labelsize=9)9 matplotlib.rc('ytick', labelsize=9)10 matplotlib.rc('font', size=14)1112# files we'll be working with13 files=['american.csv', 'columbia.csv']1415# folder with data16 data_folder = '../../Data/Chapter07/'1718# colors19 colors = ['#FF6600', '#000000', '#29407C', '#660000']2021# read the data22 american = pd.read_csv(data_folder + files[0],23 index_col=0, parse_dates=[0],24 header=0, names=['','american_flow'])2526 columbia = pd.read_csv(data_folder + files[1],27 index_col=0, parse_dates=[0],28 header=0, names=['','columbia_flow'])2930# combine the datasets31 riverFlows = bine_first(columbia)3233# periods aren't equal in the two datasets so find the overlap34# find the first month where the flow is missing for american35 idx_american = riverFlows \36 .index[riverFlows['american_flow'].apply(np.isnan)].min()3738# find the last month where the flow is missing for columbia39 idx_columbia = riverFlows \40 .index[riverFlows['columbia_flow'].apply(np.isnan)].max()4142# truncate the time series43 riverFlows = riverFlows.truncate(44 before=idx_columbia + ofst.DateOffset(months=1),45 after=idx_american - ofst.DateOffset(months=1))Tips:/*Traceback (most recent call last):File "D:\Java2018\practicalDataAnalysis\Codes\Chapter07\ts_handlingData.py", line 49, in <module>o.write(riverFlows.to_csv(ignore_index=True))TypeError: to_csv() got an unexpected keyword argument 'ignore_index'D:\Java2018\practicalDataAnalysis\Codes\Chapter07\ts_handlingData.py:80: FutureWarning: how in .resample() is deprecatedthe new syntax is .resample(...).mean()year = riverFlows.resample('A', how='mean')*/解决⽅案:/*# year = riverFlows.resample('A', how='mean')year = riverFlows.resample('A').mean()# o.write(riverFlows.to_csv(ignore_index=True))o.write(riverFlows.to_csv(index=True))*/原理:⾸先,我们引⼊所有必需的模块:pandas和NumPy。
时间序列心得体会

时间序列心得体会时间序列分析是一种处理时间相关数据的方法,通过对数据进行分析和建模,可以揭示出数据中的趋势、季节性、周期性以及其他相关性等特征。
在学习和应用时间序列分析的过程中,我有以下一些心得体会。
首先,时间序列分析需要对数据进行预处理。
在进行模型建立之前,我们需要对数据进行查缺补漏、去除异常值、平滑处理等。
这是为了消除数据的噪声和异常,使得数据更具有可靠性和可预测性。
在预处理的过程中,我们需要运用一些统计方法和技巧,如平均值、中位数、滑动平均、指数平滑等。
其次,时间序列分析可以帮助我们发现数据中的趋势和周期性。
通过对时间序列数据的拟合和预测,我们可以了解数据的增长趋势以及周期性的变化。
这对于决策和规划具有重要意义。
例如,在经济领域中,我们可以通过时间序列分析来解读经济增长趋势,预测未来的经济发展方向,从而指导政策制定和市场调控。
另外,时间序列分析还可以用来检查模型的有效性和准确性。
通过建立合适的时间序列模型,我们可以对观测值进行预测,并与实际观测值进行比较。
如果预测值与实际值较为接近,并且误差较小,则说明所建立的模型是有效的。
如果误差较大,则可能需要进行模型的调整或采用其他方法。
在检验模型有效性的过程中,我们常用的指标有均方根误差、平均绝对百分比误差等。
此外,时间序列分析还可以用来进行预测和决策支持。
通过建立时间序列模型并预测未来的数值,我们可以为决策者提供依据和参考。
例如,在金融领域中,我们可以利用时间序列分析来预测股票价格的走势,从而为投资者提供投资建议。
在市场营销领域,我们可以通过时间序列分析来预测销售额的增长趋势,从而帮助企业进行销售策略的制定和调整。
最后,时间序列分析需要综合运用统计学、概率论、数学建模等多个学科的知识。
在学习和应用过程中,我们需要掌握时间序列模型的基本原理和方法,比如自回归移动平均模型(ARMA)、自回归条件异方差模型(ARCH)、季节性模型等。
同时,我们还需要利用各种统计软件和编程语言进行数据分析和模型建立,比如R、Python、MATLAB等。
现代时间序列分析读书报告

现代时间序列分析读书报告时间序列分析是一种通过对时间序列数据进行建模和分析来识别趋势、季节性和其他周期性变化的方法。
随着计算机和数据分析技术的发展,这一领域也在不断地进步和发展,在现代时间序列分析中,新的模型和技术正在被广泛应用。
书籍介绍《现代时间序列分析》是对时间序列分析基础和现代模型的介绍,作者为Jonathan D. Cryer和Kung-Sik Chan。
这本书概括了时间序列的基本理论和应用,并描述了一些常用的时间序列分析模型,如ARIMA、GARCH、VAR等。
在书中,作者通过讲解时间序列的基础知识、模型和实际应用,使读者能够理解和掌握时间序列分析方法的基本原理,并且能够将这些方法应用到具体的数据分析问题中。
时间序列的基本概念时间序列是指在一段时间内观察到的连续性随机变量序列,例如股票市场中每日的股票价格,气象数据中每日的温度和降雨量等。
基本概念包括自回归(AR)模型、移动平均(MA)模型、自回归移动平均(ARMA)模型、自回归积分移动平均(ARIMA)模型和广义自回归条件异方差(GARCH)模型等,这些模型都是经典的时间序列模型。
除了经典的时间序列模型之外,现代时间序列分析还包括如卡尔曼滤波器、状态空间模型、向量自回归(VAR)模型、脉冲响应模型等新的模型和方法,在实际应用中,这些模型已经得到了广泛的应用。
时间序列分析的应用时间序列分析可以用来描述数据中的趋势和周期性变化,例如用于股票市场数据的预测,预测某个企业的销售额和财务状况等。
在气象数据中,时间序列分析可以用来预测未来的温度和降雨情况,以及跟踪自然灾害的发展。
此外,时间序列分析还可以用于信号处理、控制系统等其他领域,例如用于分析脑电图(EEG)数据,以及用于机器人的控制系统。
总结《现代时间序列分析》这本书介绍了时间序列分析的基础知识和现代模型,通过讲解经典的时间序列模型和新的模型和方法,读者可以更加深入地了解时间序列分析的原理和应用。
时间序列分析-读书笔记
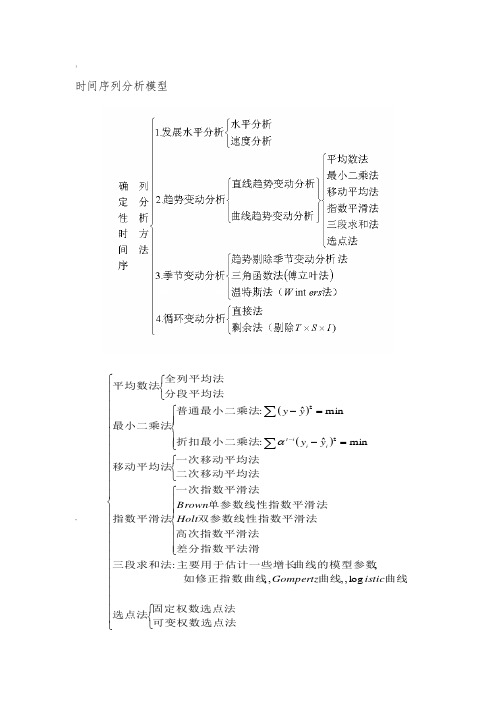
)时间序列分析模型~()()⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎩⎨⎧⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎪⎪⎩⎪⎪⎨⎧=-=-⎩⎨⎧∑∑-可变权数选点法固定权数选点法选点法曲线曲线如修正指数曲线曲线的模型参数主要用于估计一些增长三段求和法差分指数平法滑高次指数平滑法双参数线性指数平滑法单参数线性指数平滑法一次指数平滑法指数平滑法二次移动平均法一次移动平均法移动平均法折扣最小二乘法普通最小二乘法最小二乘法分段平均法全列平均法平均数法isticGompertzHoltBrownyyyyiiitlog,,,,,:minˆ:minˆ:22α1. 时间序列作用:描述系统运行规律预测对特殊政策或事件的影响加以估计2. ~3. 时间序列分类:确定时间序列,随机时间序列4. 确定时间序列的分析方法:它不计算时间序列的随机变动值,建模的目的是要消除随机变动的影响,揭示预测对象随时间变动的规律性用于预测,这是确定性时间序列和随机时间序列分析的区别。
趋势外推法:有明显上升或下降趋势,没有明显季节变动,能用函数表示移动平均法:一次移动平均:大体成水平变动,平滑公式,预测公式两次移动平均:线性上升或下降,预测公式指数平滑法:一次指数平滑法:水平变动,平滑公式,预测公式Brown 单参数线性指数平滑法:线性上升或下降,平滑公式,预测公式 ?Holt 双参数线性指数平滑法: 线性上升或下降,平滑公式,预测公式 参数选择主观性较强,不能提供置信区间信息季节调整术:试图度量序列中的季节变动,并利用这些指数剔除序列中的季节变动。
4.随机时间序列分析:平稳时间序列分析严平稳的概率分布与时间的平移无关。
宽平稳序列的均值随时间的平移而不变,自协方差仅与时间间隔有关自回归模型、滑动平均模型和自回归滑动平均模型分析平稳的时间序列的规律。
%自回归模型:如果时间序列() ,2,1=t X t 是平稳的且数据之间前后有一定的依存关系,即t X 与前面p t t t X X X --- ,,21有关与其以前时刻进入系统的扰动(白噪声)无关,具有p 阶的记忆,描述这种关系的数学模型就是p 阶自回归模型可用来预测:t p t p t t t a X X X X ++++=---ϕϕϕ 2211滑动平均模型:如果时间序列() ,2,1=t X t 是平稳的与前面p t t t X X X --- ,,21无关与其以前时刻进入系统的扰动(白噪声)有关,具有q 阶的记忆,描述这种关系的数学模型就是q 阶滑动平均模型可用来预测:q t q t t t t a a a a X ---+++-=θθθ 2211回归滑动平均模型:如果时间序列() ,2,1=t X t 是平稳的与前面p t t t X X X --- ,,21有关且与其以前时刻进入系统的扰动(白噪声)也有关,则此系统为自回归移动平均系统,预测模型为:=+++----p t p t t t X X X X ϕϕϕ 2211q t q t t t a a a a ---+++-θθθ 2211非平稳时间序列分析!用模型来预测应是要把趋势和波动综合考虑进来,是它们的叠加。
时间序列分析报告心得

时间序列分析报告心得一、引言时间序列分析是一门研究按一定时间顺序排列的数据并通过统计方法对其进行建模、预测和分析的方法。
在时间序列分析的过程中,我们运用了各种统计技术,比如平均数、标准差等,通过对历史数据的分析,我们可以预测未来一段时间内的数据变化趋势和规律。
本篇报告主要总结了我对时间序列分析的学习和实践的心得体会。
二、学习过程在学习时间序列分析的过程中,我首先了解了时间序列分析的基本概念和常用的方法。
我了解到,时间序列分析的目标是通过分析时间序列的内在规律,对未来的发展趋势进行预测。
同时,时间序列分析也可以揭示时间序列中的周期性变化、趋势性变化和季节性变化。
我学习了一些时间序列分析的基本概念,比如平稳性、自相关函数、移动平均、自回归等。
在学习过程中,我尝试了不同的学习方法。
首先,我阅读了一些经典的时间序列分析教材和文献,掌握了基本的理论知识。
其次,我通过在线课程和视频教程学习了时间序列分析的实践技巧。
最后,我参与了一些实际项目,应用时间序列分析模型对数据进行预测和分析。
三、实践应用在时间序列分析的实践应用中,我主要应用了Python编程语言和一些常用的时间序列分析工具包,比如pandas和statsmodels。
通过这些工具,我可以对时间序列数据进行读取、处理、分析和可视化。
我首先通过pandas库读取了时间序列数据,并进行了数据的预处理工作。
预处理包括填充缺失值、平滑数据、去除异常点等步骤,这可以使得模型更准确地反映数据的真实情况。
然后,我使用了statsmodels库来构建时间序列分析模型。
statsmodels库提供了丰富的时间序列模型类和函数,比如ARIMA模型、SARIMA模型等。
通过这些模型,我可以对时间序列数据进行建模和预测。
最后,我使用了matplotlib库对分析结果进行可视化。
可视化可以帮助我们更直观地理解数据的规律和趋势,以及模型的预测效果。
四、心得体会通过学习和实践时间序列分析,我深刻体会到了时间序列分析在实际应用中的重要性和价值。
时间序列分析学习心得体会

时间序列分析学习心得体会时间序列分析是一门涉及到时间序列的预测和分析的学科。
它涉及到一系列数据,按照时间顺序排列,我们可以通过这些数据来推测未来的走向以及过去的变化。
时间序列分析具有广泛的应用领域,比如股票的走势、天气的预报和经济的波动等等。
在我学习时间序列分析的过程中,我深深地感受到了它的优雅之处,并从中获得了许多经验和体会。
首先,时间序列分析需要对数据进行仔细检查。
对时间序列数据进行检查,可以发现一些异常和错误,比如重复的数据、异常的数据点或者缺失的数据点等等。
我们需要通过做出异常检验、趋势检验等来确定数据质量,以保证最终得到的结果是准确的。
其次,时间序列分析需要对数据进行变换。
对数据进行转化和变换可以使数据与所需的分析方法相适应,方便我们进行后续的处理。
可以采用加法模型或乘法模型,根据数据的性质的不同做出适当的选择。
通过对数据的变换,我们可以在保证数据的准确性的同时,更好地解读它们。
然后,时间序列分析需要选择恰当的模型。
时间序列分析涉及到的模型有很多种,比如滑动平均模型、指数平滑模型、ARIMA模型等等。
在选择模型的过程中,我们需要考虑数据的性质,比如是否有趋势和季节性。
同时,我们需要对各种模型进行比较,选出最适合的模型,以得到准确的预测结果。
最后,时间序列分析需要对模型进行评估和预测。
我们需要对模型进行验证,即检验模型在历史数据上的拟合情况。
同时,我们还需要对模型的预测结果进行评估,以确定模型的准确性和预测能力。
我们需要使用各种检验方法,比如平均绝对误差、平均绝对百分比误差等等,进行评估和比较。
在我学习时间序列分析的过程中,我深深地感受到了这门学科的复杂性和精妙性。
时间序列分析需要对数据进行仔细检查和变换,选择恰当的模型,进行预测和评估。
只有在这个过程中,我们才能够得到准确的预测结果,为我们的决策提供依据。
尽管这个过程可能会较为耗费时间和精力,但是当我们得到准确的结果时,我们会感到收获颇丰,也将带来实际应用领域的实际价值。
时间序列心得体会

时间序列心得体会时间序列我记得再学习时间序列时,花了整整一个星期,每天只看这个,终于在一天的下午给弄明白了,这是本人学习的时候的心得,只要开窍了比就会觉得很简单,事实上却是如此,我的好多同学,在考玩以后,都有这个体会,看样子估计你时大学生,不是研究生吧(弱弱的估计一下)。
本科生学习时间序列的时候我记得好像用不找SAS,不知道你们怎么样,现把我考试时的情况说一下,因为时间序列对于本科生有点吃力,这门科时在大四开,好多学生为了找工作,没有更多的时间学习,有的学校就是开卷考试,当然闭卷的话就相对简单了,老师都会画出范围的。
AMIAR不知道写没写对,值考一员的二元估计不可能,多元的估计时研究生要学的,所以别担心只要在考试前画上一个星期,我保障没有问题。
时间序列分析预测法优缺点时间序列分析预测法有两个特点:①时间序列分析预测法是根据市场过去的变化趋势预测未来的发展,它的前提是假定事物的过去会同样延续到未来。
事物的现实是历史发展的结果,而事物的未来又是现实的延伸,事物的过去和未来是有联系的。
市场预测的时间序列分析法,正是根据客观事物发展的这种连续规律性,运用过去的历史数据,通过统计分析,进一步推测市场未来的发展趋势。
市场预测中,事物的过去会同样延续到未来,其意思是说,市场未来不会发生突然跳跃式变化,而是渐进变化的。
时间序列分析预测法的哲学依据,是唯物辩证法中的基本观点,即认为一切事物都是发展变化的,事物的发展变化在时间上具有连续性,市场现象也是这样。
市场现象过去和现在的发展变化规律和发展水平,会影响到市场现象未来的发展变化规律和规模水平;市场现象未来的变化规律和水平,是市场现象过去和现在变化规律和发展水平的结果。
需要指出,由于事物的发展不仅有连续性的特点,而且又是复杂多样的。
因此,在应用时间序列分析法进行市场预测时应注意市场现象未来发展变化规律和发展水平,不一定与其历史和现在的发展变化规律完全一致。
随着市场现象的发展,它还会出现一些新的特点。
时序数据分析观后感

时序数据分析观后感1背景时序数据分析方法可以分为基于时域和基于频域的方法。
基于时域的方法将时序数据当作有序点的序列,然后分析这些点的相关性。
基于频域的方法利用一个转换算法(如离散傅里叶变换,Z变换等)将时序数据转换到频谱,然后将这些频谱数据作为特征来分析。
现有的基于深度学习的方法都是基于时域的方法。
小波分解是一种典型的将数据转换到同时带有时域和频域特征的方法,将原始的时间序列通过小波转换后得到特征,再送给神经网络,比直接利用神经网络的方法在性能上会更优。
2模型2.1多级离散小波分解一个小波函数(基函数)包含一个低通滤波器和一个高通滤波器。
将一条时序数据通过一次小波分解能得到一个低通分量和一个高通分量。
将得到的低通分量通过1/2下采样后,再进行一次小波分解同样可以得到一个低通分量和一个高通分量。
依次下去,最后可以得到一个高通分量和个低通分量。
2.2多级小波分解网络本文引入了多级小波分解网络,这也是本文最大的亮点之一。
如果没有这个网络,最简单的做法是先将时序数据做多级小波分解,分解得到的特征直接送给后续处理的神经网络。
这种做法的缺点是将小波分解和神经网络这两个过程分离,不能够互相影响,也就是说此时的小波分解是一个静态的过程,相当于预处理。
有了这个小波分解网络,可以将小波分解和后续处理的神经网络进行联合处理。
也就是说将小波分解的过程在神经网络框架中实现,原来的小波函数中的值变成神经网络中的参数,可以和后续处理的神经网络中的参数一起优化。
这样做的好处是,相比于原来的做好:给定一个小波函数,则函数中的滤波系数是固定不变的。
变得可调之后,相当于这些滤波系数是针对给定的数据集做过了优化,显然效果会更好。
接下来将如何将小波分解的过程在神经网络框架中实现。
其实小波分解就是小波函数以滑动窗口的形式和原始数据做点乘,和卷积的过程类似,如下图所示,其中矩阵中有颜色的部分填充小波函数的滤波系数,其他部分填充0。
在训练过程中,矩阵中所有值都可以调整。
时间序列与机器学习阅读札记

《时间序列与机器学习》阅读札记一、时间序列分析概述时间序列分析是一种统计学方法,用于研究随时间变化的数据点序列。
这些数据点可能是连续的值,如温度、股票价格或离散的事件,如网站访问次数或用户行为记录。
时间序列分析的主要目标是揭示数据中的模式、趋势和周期性变化,并基于这些信息进行预测。
时间序列分析在多个领域都有广泛应用,包括金融、气候学、生物学、经济学等。
随着机器学习的兴起,许多先进的方法和技术也被引入时间序列分析中,以提高分析的精度和效率。
在传统的时间序列分析方法中,通常依赖于统计模型如ARIMA模型或其变体进行预测。
随着大数据和机器学习技术的发展,研究者开始尝试使用更复杂的模型和方法来处理时间序列数据。
机器学习模型,特别是深度学习模型,如循环神经网络(RNN)和长短期记忆网络(LSTM),已被证明在处理复杂时间序列数据方面表现出强大的能力。
这些模型能够捕捉序列中的长期依赖关系和非线性模式,从而提供更准确的预测结果。
在机器学习中,时间序列数据通常被转化为监督学习任务,其中目标是预测未来的数据点或序列趋势。
为了有效地处理时间序列数据,通常需要考虑到数据的时序特性和依赖性。
在特征工程阶段,研究者会采取一系列技术来捕捉和编码这些数据特性,如时间窗口、周期性特征和趋势特征等。
处理时间序列数据时还需考虑到一些特有的挑战,如数据的季节性变化、异常值和缺失值等。
为了应对这些挑战,除了选择合适的机器学习模型外,还需要结合领域知识和数据特性进行模型调优和参数调整。
时间序列数据的解释性也是一项重要任务,需要确保模型的预测结果不仅准确,而且能够解释其背后的原因。
时间序列分析与机器学习的结合为处理复杂时序数据提供了强大的工具和方法。
随着技术的不断进步和新方法的出现,时间序列分析将继续在多个领域发挥重要作用,并推动相关领域的进步。
1. 时间序列定义及特点时间序列是一种按照时间顺序排列的数据点序列,这些数据点可能代表某一特定对象或系统的某种指标或观测值,它们随时间变化而变化。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
时间序列分析模型
()()⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩
⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎩⎨⎧⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎪⎪⎩⎪⎪⎨⎧=-=-⎩⎨⎧∑∑-可变权数选点法固定权数选点法选点法曲线曲线如修正指数曲线曲线的模型参数主要用于估计一些增长三段求和法差分指数平法滑高次指数平滑法双参数线性指数平滑法单参数线性指数平滑法一次指数平滑法指数平滑法二次移动平均法一次移动平均法移动平均法折扣最小二乘法普通最小二乘法最小二乘法分段平均法全列平均法平均数法istic Gompertz Holt Brown y y y y i i i t log ,,,,,:min ˆ:min ˆ:22α
1. 时间序列作用:描述系统运行规律
预测
对特殊政策或事件的影响加以估计
2. 时间序列分类:确定时间序列,随机时间序列
3. 确定时间序列的分析方法:
它不计算时间序列的随机变动值,建模的目的是要消除随机变动的影响,揭示预测对象随时间变动的规律性用于预测,这是确定性时间序列和随机时间序列分析的区别。
3.1趋势外推法:有明显上升或下降趋势,没有明显季节变动,能用函数表示
3.2移动平均法:一次移动平均:大体成水平变动,平滑公式,预测公式
两次移动平均:线性上升或下降,预测公式
3.3指数平滑法:一次指数平滑法:水平变动,平滑公式,预测公式
Brown 单参数线性指数平滑法:线性上升或下降,平滑公式,预测公式 Holt 双参数线性指数平滑法: 线性上升或下降,平滑公式,预测公式 参数选择主观性较强,不能提供置信区间信息
3.4季节调整术:试图度量序列中的季节变动,并利用这些指数剔除序列中的季节变动。
4.随机时间序列分析:
4.1 平稳时间序列分析
严平稳的概率分布与时间的平移无关。
宽平稳序列的均值随时间的平移而不变,自协方差仅与时间间隔有关
自回归模型、滑动平均模型和自回归滑动平均模型分析平稳的时间序列的规律。
自回归模型:如果时间序列() ,2,1=t X t 是平稳的且数据之间前后有一定的依存关系,即t X 与前面p t t t X X X --- ,,21有关与其以前时刻进入系统的扰动(白噪声)无关,具有p 阶的记忆,描述这种关系的数学模型就是p 阶自回归模型可用来预测:
t p t p t t t a X X X X ++++=---ϕϕϕ 2211
滑动平均模型:如果时间序列() ,2,1=t X t 是平稳的与前面p t t t X X X --- ,,21无关与其以前时刻进入系统的扰动(白噪声)有关,具有q 阶的记忆,描述这种关系的数学模型就是q 阶滑动平均模型可用来预测:
q t q t t t t a a a a X ---+++-=θθθ 2211
回归滑动平均模型:如果时间序列() ,2,1=t X t 是平稳的与前面p t t t X X X --- ,,21有关且与其以前时刻进入系统的扰动(白噪声)也有关,则此系统为自回
归移动平均系统,预测模型为:
=+++----p t p t t t X X X X ϕϕϕ 2211q t q t t t a a a a ---+++-θθθ 2211
4.2 非平稳时间序列分析
用模型来预测应是要把趋势和波动综合考虑进来,是它们的叠加。
用模型来描述:
t t t Y X +=μ
t μ表示t X 中随时间变化的均值(往往是趋势值),t Y 是t X 中剔除t μ后的剩余部分,表示零均值平稳过程,就可用自回归模型、滑动平均模型或自回归滑动平均模型来拟合。
要解模型t t t Y X +=μ,分以下两步:
(1)具体求出t μ的拟合形式,可以用上面介绍的确定性时序分析方法建模,求出t μ,得
到拟合值,记为t μ
ˆ。
(2)对残差序列{}t t X μ
ˆ-进行分析处理,使之成为均值为零的随机平稳过程,再用平稳随机时序分析方法建模求出t Y ,通过反运算,最后可得t t t Y X +=μ。
