2022高等数学下考试试题成员仅查看三黑龙江科技大学考试试题
2022年黑龙江科技大学工作人员招聘考试试题及答案

2022年黑龙江科技大学工作人员招聘考试试题及答案(满分100分时间120分钟)一、单选题(每题只有一个正确答案,答错、不答或多答均不得分)1.以下作品哪一项作者与其他不在同一朝代()。
A.《醉翁亭记》B.《小石潭记》C.《石钟山记》D.《岳阳楼记》【答案】:B2.用来衡量收入分配不平等程度的指标是()。
A.消费者价格指数B.国内生产总值GDP折算系数C.恩格尔系数D.基尼系数【答案】:D3.外汇储备是指一国政府所持有的国际储备资产中的外汇部分,即一国政府保有的以外币表示的债权,关于我国外汇储备,下列说法正确的是()。
A.外汇储备的主要组成部分是欧元资产B.外汇储备越多,对我国经济发展越有利C.外汇储备作为国家资产,由中国人民银行和中国银行共同管理D.外汇储备主要用于稳定汇率,偿还对外债务【答案】:D4.宋代诗人陆游在一首诗中说:纸上得来终觉浅,绝知此事要躬行。
这是在强调1/ 11A.实践是认识发展的动力B.实践是认识的最终目的和归宿C.实践是认识的来源D.学习获得的间接经验并不重要【答案】:C5.瓷器是中国最具民族特色的传统技艺,杜甫曾有诗赞颂:“君家白碗胜霜雪,急送茅斋也可怜。
”诗句中所描述的烧瓷技艺在古代哪个地方?()A.景德镇B.大邑C.邢州D.越州【答案】:B6.资本主义工资的本质是()A.对劳动者的全部劳动所付的报酬B.劳动力价值的货币表现C.劳动的价格D.劳动的价值的货币表现【答案】:B7.提高最低工资标准可能带来的影响,不包括()。
A.增加转移支付的总量B.强化人们的通胀预期C.加大企业的生产成本D.缓解物价上涨的影响【答案】:A8.下列有关我国著名艺术品的描述,正确的是()。
A.唐卡,是藏族文化中一种独具特色的绘画艺术形式,题材内容涉及藏族的历史,政治,文化和社会生活等诸多领域。
它是在乾隆时期兴起的一种新颖绘画艺术,即用彩缎装裱而成的卷轴2/ 11画,历来被藏族人民视为珍宝B.唐三彩,是唐代低温彩釉陶器的总称,在同一器物上,黄,绿,白或黄,绿,蓝,赭,黑等基本釉色同时交错使用,形成绚丽多彩的艺术效果。
黑龙江科技学院考试试题

考试试题课程名称:无机化学 课程编号:01033010 适用专业(班级):化工06—1~3班 共5页命题人: 教研室主任: 第1页一、选 择 题 (在 下 列 各 题 中 , 选 择 出 符 合 题 意 的 答 案 , 将 其 代 号 填 入 括 号 内 )(本大题分10小题, 每小题2分, 共20分)1、 当 温 度 一 定, 反 应 2A (g) + 3B (g) 5C (g) 在 进 行 过 程 中, 下 列 各 物 理 量 中, 发 生 变 化 的 是.......................................................................................................................( )。
(A)△r G ; (B)△r G m ; (C) K ; (D) k 。
2、 欲 使 CaCO 3 在 水 溶 液 中 的 溶 解 度 增 大, 宜 采 用 的 方 法 是 ........................................... ()。
(A) 加 入 1.0 mol ·L -1 Na 2CO 3; (B) 加 入 2.0 mol ·L -1 NaOH ;(C) 加 入 1.0 mol ·L -1 CaCl 2; (D) 加 入 0.1 mol ·L -1 edta 。
3、 下 列 有 关 分 子 轨 道 的 叙 述 中 错 误 的 是..........................................................( )。
(A) 通 常, 成 键 分 子 轨 道 能 级 低 于 相 应 的 原 子 轨 道;(B) 反 键 分 子 轨 道 能 级 常 高 于 相 应 的 原 子 轨 道;(C) 原 子 轨 道 能 级 相 近 即 可 组 合 成 分 子 轨 道;(D) 一 定 条 件 下, 分 子 轨 道 数 目 等 于 组 合 的 原 子 轨 道 数 目。
黑龙江科技大学考试试题(1)

黑龙江科技大学考试试题第1套课程名称:采矿学课程编号:11013370 适用专业(班级):采矿工程10-1、2、5班共4页命题人:教研室主任:第1页一、填空题(每空1分,共20分)1、根据图1中所示,指出图形中数字对应的巷道名称:图1 矿井生产系统示意图1:;3:;4:;5:;8:;9:;15:;23:;19:;22:。
2、根据采煤工艺、矿压控制特点和工作面长度不同,采煤方法分为体系和体系两大类。
3、矿井移交以后,有些矿井的设计生产能力需要改变,对生产矿井的生产能力进行重新核定,核定后的综合生产能力称为矿井。
4、采场内为采取煤炭而进行的、、、及等一系列工作称为回采工作。
5、井底车场是指连接和主要运输石门或的一组巷道和硐室的总称。
二、单项选择题(每小题1分,共10分)1、在放顶煤采煤法中把工作面分成2 ~3段,每段内同时开启两个相邻放煤口,每次放1/2 ~1/3的顶煤,按顺序循环放煤,直至该段全部放完,再进行下一段放顶煤。
这种放煤方式是()黑龙江科技大学考试试题第1套课程名称:采矿学课程编号:11013370 适用专业(班级):采矿工程10-1、2、5班共4页命题人:教研室主任:第2页A多轮、分段、顺序、等量放煤;B单轮、多口、顺序、不等量放煤;C多轮、间隔、顺序、等量放煤;D单轮、间隔、多口放煤。
2、回采工作面沿煤层倾向布置,沿走向推进采煤,这种采煤方法叫做()A走向长壁采煤法B柱式采煤法C倾斜长壁采煤法D伪斜长壁采煤法3、下列巷道为准备巷道的是()A主井B井底车场C轨道上山D开切眼4、下列关于准备方式的分类正确的是()A按煤层赋存条件分可分为采区式、盘区式和阶段式;B按开采方式分可分为上山采区与下山采区准备;C按采区上山的布置分可分为煤层上山和岩层上山;D按煤层群开采时的联系分可分为分组与集中准备。
5、下列矿井中属于大型生产矿井的是()A0.45Mt/a B0.6Mt/aC0.9Mt/a D 1.2Mt/a6、“三下”采煤是指()A建筑物下、铁路下和承压水下;B采空区下、建筑物下和铁路下;C建筑物下、水体下和铁路下;D采空区下、水体下和城市下。
高等数学下册试题及答案解析.docx

高等数学(下册)试卷(一)一、填空题(每小题 3 分,共计24 分)1、z =log a ( x2y 2 )( a 0) 的定义域为D=。
2、二重积分ln( x2y 2 )dxdy 的符号为。
|x| |y| 13 、由曲线y ln x 及直线x y e 1 , y 1 所围图形的面积用二重积分表示为,其值为。
4L 的参数方程表示为x(t)(x),则弧长元素ds。
、设曲线y(t)5 、设曲面∑为x2y 29 介于z0 及 z 3 间的部分的外侧,则(x2y21)ds。
6、微分方程dyy tany的通解为。
dx x x7、方程y( 4) 4 y0 的通解为。
8、级数1的和为。
n1n(n1)二、选择题(每小题 2 分,共计16 分)1、二元函数z f ( x, y) 在 ( x0 , y0 ) 处可微的充分条件是()(A)f ( x, y)在(x0, y0)处连续;(B)f x( x, y),f y( x, y)在( x0, y0)的某邻域内存在;( C)z f x (x0 , y0 )x f y ( x0 , y0 ) y 当( x) 2(y) 20 时,是无穷小;( D)lim z f x ( x0 , y0 ) x f y ( x0 , y0 ) y0。
22x0(x)( y) y02、设u yf ( x)xf (y), 其中 f 具有二阶连续导数,则x2u y 2 u等于()y x x 2y 2(A)x y ;( B)x;(C) y;(D)0。
3、设: x 2y 2z21, z0, 则三重积分I zdV 等于()( A ) 4 2d2 d1 3sin cos dr ;r 02 dd 1 dr ;( B )r 2 sin0 022 d13sin cos dr ;( C )dr0 02d 13sin cos dr 。
( D )dr0 04、球面 x 2 y 2z 2 4a 2 与柱面 x 2 y 22ax 所围成的立体体积 V=()(A ) 4 2d2 a cos 4a2r 2dr ;(B ) 4 2d2 a cos r 4a2r 2dr ;(C ) 8 2d2 a cos r 4a2r 2dr ;(D )2d2a cos r 4a2r 2dr 。
高等数学下考试题库(附答案)

高等数学下考试题库(附答案) 高等数学》试卷1(下)一、选择题(3分×10)1.点M1(2,3,1)到点M2(2,7,4)的距离M1M2=().A.3B.4C.5D.62.向量a=-i+2j+k,b=2i+j,则有().A.a∥bB.a⊥bC.a,b=D.a,b=3.函数y=2-x^2-y^2+1/x+y-12/2+y^2的定义域是().A.{(x,y)|1<x<2,1≤x^2+y^2≤2}B.{(x,y)|x,y<0}C.{(x,y)|1<x≤2,2+y^2<2}D.{(x,y)|2+y^2<x}4.两个向量a与b垂直的充要条件是().A.a·b=0B.a×b=0C.a-b=0D.a+b=05.函数z=x+y-3xy的极小值是().A.2B.-2C.1D.-16.设z=xsiny,则∂z/∂y|(π/4,3/4)=().A.2/√2B.-2/√2C.2D.-27.若p级数∑n=1∞pn收敛,则().A.p1 D.p≥18.幂级数∑n=1∞xn/n的收敛域为().A.[-1,1]B.(-1,1)C.[-1,1)D.(-1,1]9.幂级数∑n=2∞x^n/(n-1)在收敛域内的和函数是().A.1/(1-x)B.2/(1-x)^2C.2/(1+x)D.1/(1+x)10.微分方程xy'-ylny=0的通解为().A.y=cxB.y=e^xC.y=cxe^xD.y=ex二、填空题(4分×5)1.一平面过点A(1,2,3)且垂直于直线AB,其中点B(2,-1,1),则此平面方程为______________________.2.函数z=sin(xy)的全微分是______________________________.3.设z=xy-3xy^2+1,则(∂^2z)/(∂x∂y)|3/2=-___________________________.三、计算题(5分×6)4.1.设z=esinv,而u=xy,v=x+y,求u∂z/∂x-∂z/∂y.2.已知隐函数z=z(x,y)由方程x^2+y^2+z^2=1确定,求∂z/∂x.3.设f(x,y)=x^2y-xy^2,求f在点(1,1)处的方向导数沿向量i+j的值.4.设z=f(x^2+y^2),其中f(u)在u=1处可导,求∂z/∂x|P,其中P为曲线x^2+y^2=1,z=1上的点.5.设z=ln(x+y)cos(x-y),求∂^2z/∂x^2-2∂^2z/∂x∂y+∂^2z/∂y^2.6.设f(x,y)在点(0,0)处可微,且f(0,0)=0,证明:∂f/∂x和∂f/∂y在点(0,0)处连续.1.已知函数f(x)在区间[0,1]上连续,且f(0)=0,f(1)=1,则方程f(x)=0在区间(0,1)内至少有()个实根。
高等数学下册试题及参考答案

高等数学下册试题库一、选择题〔每题4分,共20分〕A(1,0,2),B(1,2,1)是空间两点,向量的模是:〔A〕A〕 5 B 〕 3 C 〕6 D 〕9解={1-1,2-0,1-2}={0,2,-1},||=.2. 设a={1,-1,3},A〕{-1,1,5}.b={2,-1,2}B 〕,求c=3a-2{-1,-1,5}.b是:〔C〕B〕{1,-1,5}. D 〕{-1,-1,6}.解(1)c=3a-2b=3{1,-1,3}-2{2,-1,2}={3-4,-3+2,9-4}={-1,-1,5}.设a={1,-1,3},b={2,1,-2},求用标准基i,j,k表示向量c=a-b;A〕A〕-i-2j+5k B〕-i-j+3k C〕-i-j+5k D〕-2i-j+5k解c={-1,-2,5}=-i-2jk+5.4.求两平面和的夹角是:〔C〕A〕B〕C〕D〕2435.解由公式〔6-21〕有,所以,所求夹角.求平行于轴,且过点和的平面方程.是:〔D〕A〕2x+3y=5=0B〕x-y+1=0C〕x+y+1=0D〕.解因为平面平行于轴,所以可设这平面的方程为因为平面过、两点,所以有解得,以此代入所设方程并约去,便获得所求的平面方程6.微分方程xyy xy3y4y0的阶数是(D)。
A.3B.4C.5D.27.微分方程y x2y x51的通解中应含的独立常数的个数为(A)。
A.3B.5C.4D.28.以下函数中,哪个是微分方程dy 2xdx 0的解(B)。
A .y2x B .yx 2C .y2x D .yx29.微分方程y3y 3的一个特解是(B)。
A .yx 3 1B .yx23 C .yxC 2 D .yC1x 3.函数ycosx 是以下哪个微分方程的解(C)。
A .y y 0B .y2y 0C .y n y0D .yycosx11.yCe xC e x是方程y y0的(A),此中C 1,C 2为随意常数。
2022-2023学年下学期高数A(2)-A卷答案

2022-2023学年下学期高等数学A(2)-A 卷参考答案与评分标准一、填空题(每题4分,共40分) 1. 32−; 2. 2; 3. 22249936x y z −−=; 4. 14− ; 5.1x ;6.1233dz dx dy =+; 7.125241x y z −−−==−; 8. 不是;9. 4102(,)xdx f x y dy ⎰⎰;10. 2x y C +.二、计算题(每题7分,共21分)11.解:已知直线的方向向量为()12416,14,11352i j ks =−=−− ……………(5分) 由于平面与直线垂直,所求平面法向量可取n s =,则 所求平面方程:()()162141130x y z −−+++= 即161411650x y z −−−=……………(7分) 12. 解:令(,,)ln x zF x y z z y=−,则 222111,,x y z y z x y x zF F F zz y yz z y z⎛⎫+==−⋅−==−−⋅=− ⎪⎝⎭…………(3分) 21x z F z zz x z x F x z z ∂=−=−=+∂+− ……………(5分) ()221y z F z z yx z y F y x z z−∂=−=−=+∂+ ……………(7分) 13. 解:222x y xye+关于x ,y 均是奇函数,则12,D D 关于x 轴对称,34,D D 关于y 轴对称221220x y D D xyedxdy ++=⎰⎰223420x y D D xyedxdy ++=⎰⎰……………(3分)所以11123x DI ydxdy dx ydy −−===−⎰⎰⎰⎰ ……………(7分)三、计算题(每题7分,共21分) 14.解:2()2zf x y xy x∂=⋅∂ ………(4分) 2222()2()2zf x y x xy f x y x x y∂'=⋅⋅+⋅∂∂ =3222()2()x yf x y xf x y '+ …………(7分)15.解:22220cos sin RI d d r r dr ππθϕϕϕ=⋅⎰⎰⎰ ………(4分)25012cos sin 5d R ππϕϕϕ=⋅⎰5415R π= …………(7分)16.解:12L L I =+⎰⎰11222L L e ds e π==⋅⎰⎰…………(3分)222220222|2(1)xx x L e dx e dx e e −====−⎰⎰⎰…………(6分)2222(1)I e e π=+−…………(7分)四、综合应用题(每题6分,共18分) 17.解:,()xyP e y Q e x =+=−+ 1,1P Qy x∂∂==−∂∂ 补线1L :0,:11y x =→−,则1111()L L L L L L I −++=−=−−⎰⎰⎰⎰……(2分)()()()1()2xy L L Dey dx e x dy dxdy π−++−+=−=−⎰⎰⎰ ……(4分)()()1111xyx L ey dx e x dy e dx e e −−+−+==−⎰⎰……(5分)1I e e π−=−+ ……(6分)18、解:原式=()()424z y y dv z y dv ΩΩ−+=−⎰⎰⎰⎰⎰⎰ ……….(3分)4zdv ydv ΩΩ=−⎰⎰⎰⎰⎰⎰1111114dx dy zdz dx ydy dz =−⎰⎰⎰⎰⎰⎰ ……….(5分)32= ……….(6分)19. 解:记1∑为锥面z =()01z ≤≤,2∑为圆面1z =()221x y +≤,它们在xOy 面上投影为22:1xy D x y +≤,在1∑上ds =,则()(12122222xyD x y ds x y d d πθρρρ∑+=+=⋅=⎰⎰⎰⎰⎰ ……….(3分) 在2∑上dS dxdy =,则()()221222220012xyD x y ds x y dxdy d d πθρρρπ∑+=+=⋅=⎰⎰⎰⎰⎰⎰ ……….(5分) 故 原式+12π。
2024年黑龙江省高考数学真题及参考答案

2024年黑龙江省高考数学真题及参考答案一、单项选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项符合题目要求。
1.已知1i z =--,则||z =().A.0B.1D.22.已知命题:R p x ∀∈,|1|1x +>;命题:0q x ∃>,3x x =.则().A.p 和q 都是真命题B.p ⌝和q 都是真命题C.p 和q ⌝都是真命题D.p ⌝和q ⌝都是真命题3.已知向量a ,b 满足||1a = ,|2|2a b += ,且(2)b a b -⊥ ,则||b =().A.12B.22C.32D.14.某农业研究部门在面积相等的100块稻田上种植新型水稻,得到各块稻田的亩产量(单位:kg )并部分整理如下表所示.根据表中数据,下列结论正确的是()A.100块稻田亩产量的中位数小于1050kgB.100块稻田中的亩产量低于1100kg 的稻田所占比例超过80%C.100块稻田亩产量的极差介于200kg 到300kg 之间D.100块稻田亩产量的平均值介于900kg 到1000kg 之间5.已知曲线22:16(0)C x y y +=>,从C 上任意一点P 向x 轴作垂线PP ',P '为垂足,则线段PP '的中点M 的轨迹方程为().A.221(0)164x y y +=> B.221(0)168x y y +=>C.221(0)164y x y +=> D.221(0)168y x y +=>6.设函数2()(1)1f x a x =+-,()cos 2g x x ax =+,当(1,1)x ∈-时,曲线()y f x =和()y g x =恰有一个交点,则a =()A.-1B.12C.1D.27.已知正三棱台111ABC A B C -的体积为523,6AB =,112A B =,则1A A 与平面ABC 所成角的正切值为().A.12 B.1C.2D.38.设函数()()ln()f x x a x b =++,若()0f x ≥,则22a b +的最小值为().A.18B.14C.12D.1二、多项选择题:本题共3小题,每小题6分,共18分。
2022-2023学年黑龙江省哈尔滨市成考专升本数学(理)自考测试卷(含答案带解析)

2022-2023学年黑龙江省哈尔滨市成考专升本数学(理)自考测试卷(含答案带解析) 学校:________ 班级:________ 姓名:________ 考号:________一、单选题(30题)1.2.(x-a-2)6展开式中,末3项的系数(a,x均未知)之和为A.22B.12C.10D.-103.()。
A.10B.12C.14D.84.参数方程表示的图形为()A.直线B.圆C.椭圆D.双曲线5.6.7.8. A.2 B.3 C.4 D.5 9.10.直三棱柱的每个侧面的面积为5,底面积为10,全面积为()A.15B.20C.25D.3511.A. >5/4 B. <5/4 C. >4/5 D. <4/512.13.14.下列函数在各自定义域中为增函数的是()。
15.已知α、β为锐角,cosα>sinβ则,16.17.18.已知空间中两条直线m,n,且m在平面α内,n在平面β内,设甲:m//β,n//α;乙:平面α//平面β,则()A.A.甲为乙的必要但非充分条件B.甲为乙的充分但非必要条件C.甲非乙的充分也非必要条件D.甲为乙的充分必要条件19.第15题过P(4,8)作圆x2+y2-2x-4y-20=0的割线,所得弦长为8,则此割线所在直线方程为()A.3x-4y+20=0或y=8B.3x-4y+20=0或x=4C.3x+4y-44=0或x=4D.4x-3y+8=0或x=420.若函数f(x)是奇函数,则函数的奇偶性是A.奇函数B.偶函数C.非奇非偶函数D.既是奇函数又是偶函数21.设函数f(x)在(-∞,+∞)上有定义,则下列函数中必为偶函数的是A.y=|f(x)|B.y=-|f(x)|C.y=xf(x)D.y=f(x)+f(-x)22.第5题设y=f-1(x)是函数y=f(x)的反函数,若点(2,-3)在y=f(x)图象上,那么一定在y=f-1(x)的图象上的点是()A.(-2,3)B.(3,-2)C.(-3,2)D.(-2,-3)23.4个人排成一行,其中甲、乙二人总排在一起,则不同的排法共有()A.A.3种B.6种C.12种D.24种24.A.是奇函数,且在(-∞,0)上单调增加B.是偶函数,且在(-∞,0)上单调减少C.是奇函数,且在(0,+∞)上单调增加D.是偶函数,且在(0,+∞)上单调减少25.26.从6名男大学生和2名女大学生中选取4名做上海世博会的志愿者,2名女大学生全被选中的概率为()A.A.1/3B.3/14C.2/7D.5/1427.已知α、β、r两两垂直,他们三条交线的公共点为O,过O引一条射线OP若OP与三条交线中的两条所成的角都是60°,则OP与第三条交线所成的角为A.30°B.45°C.60°D.不确定28.已知b⊥β,b在a内的射影是b’那么b’和a的关系是A.b’//B.b’⊥C.b’与是异面直线D.b’与相交成锐角29.已知α∩β= ,b丄β在内的射影是b’,那么b’和的关系是( )A.b’//B.b’丄C.b’与是异面直线D.b’与相交成锐角30.二、填空题(20题)31.32.在9与243中间插入两个数,使它们同这两个数成等比数列,那么这两个数为__________33.34.向量 =(4,3)与b=(x,-12)互相垂直,则x=__________.35.36.某运动员射击10次,成绩(单位:环)如下8、10、9、9、10、8、9、9、8、7则该运动员的平均成绩是______环.37.38.已知直线l和x—y+1=0关于直线x=-2对称,则l的斜率为________.39.方程它的图像是40.设离散型随机变量f的分布列如下表所示,那么ζ的期望等于_______.41.42.从-个正方体中截去四个三棱锥,得-正三棱锥ABCD,正三棱锥的体积是正方体体积的_________.43.44.45.46.47.48.49.球的体积与其内接正方体的体积之比为_________.50.三、简答题(10题)51.(本小题满分12分)52.(本小题满分12分)53. (本小题满分12分)某服装店将进价为40元一件的衬衫,按50元一件售出时,能卖出500件,如果这种衬衫每件涨价1元,其销售量就减少10件,商店为了获得大利润,问售价应为多少?54.55.(本小题满分12分)在( χ+1)7的展开式中,χ3的系数是χ2的系数与χ4的系数的等差中项,若实数 >1,求的值.56.(本小题满分12分)57.58.(本小题满分12分)59. (本小题满分12分)椭圆2x2+y2=98内有一点A(-5,0),在椭圆上求一点B,使|AB|最大.60.四、解答题(10题)61.设函数f(x)=x3+x-1.(Ⅰ)求f(x)的单调区间;(Ⅱ)求出一个区间(a,b),使得f(x)在区间(a,b)存在零点,且b-a<0.5.62.63.设函数f(x)=-xe x,求:(I)f(x)的单调区间,并判断它在各单调区间上是增函数还是减函数;(Ⅱ)f(x)在[-2,0]上的最大值与最小值64.如图,AB与半径为1的〇O相切于A点,AE = 3,AB与〇O的弦AC的夹角为50°.求(1)AC;(2) △ABC的面积.(精确到0. 01)65.66.电流强度I随时间t变化的函数关系式是I=Asinωt,设ω=l00π(弧度/秒),A=5(安培).(Ⅰ)求电流强度I变化周期与频率;(Ⅱ)当t=0,1/200,1/100,3/200/1/50(秒)时,求电流强度I(安培);(Ⅲ)画出电流强度1随时间t变化的函数的图像.67.从0,2,4,6,中取出3个数字,从1,3,5,7中取出两个数字,共能组成多少个没有重复的数字且大于65000的五位数?68.在△ABC中,AB=2,BC=3,B=60°.求AC及△ABC的面积69.建筑-个容积为8000m3,深为6m的长方体蓄水池,池壁每m2的造价为15元,池底每m2的造价为30元.(Ⅰ)把总造价y(元)表示为长x(m)的函数;(Ⅱ)求函数的定义域.70.五、单选题(2题)71.f(x)为偶函数,在(0,+∞)上为减函数,若f(1/2)>0>,则方程f(x)=0的根的个数是( )A.2B.2或1C.3D.2或372.从20名男同学、10名女同学中任选3名参加体能测试,则选到的3名同学中既有男同学又有女同学的概率为()六、单选题(1题)73.参考答案1.B2.C3.C该小题主要考查的知识点为等差数列的性质.【考试指导】4.B∵在cosα、sinα中α为参数,消去α得,x2+y2=1,即半径为1的圆,圆心在原点.5.A6.D7.D8.D9.D10.D求全面积=侧面积+2底面积=5*3+10*2=35,应选D误选C,错误的原因是只加了一个底面的面积。
科技学院《高等数学》第二学期期末考试试题测试卷及参考答案

⎩ 1 21 2一、单项选择题(每题 3 分,共计6 ⨯ 3 = 18 分)1. 设二阶常系数线性齐次微分方程 y "- 2 y '+ y = 0 ,则方程的通解为().A. (C + C )exB. (C + C x )ex12C. x (C e x + C e - x)⎧ y 2 + z 2 = 4 2. 空间曲线Γ : ⎨x = 0A . x 2 + y 2 + z 2= 4 C . x 2 - y 2 + z 2= 412D . C e x+ C e - x绕 z 轴旋转而得到的旋转曲面方程是( ).B . x 2 + y 2 - z 2= 4 D . x 2+ y 2+ z 2= 23. 函数 z = f (x , y ) 的偏导数 f x '(x , y ), f y '(x , y ) 在点(x 0 , y 0 ) 处存在是函数在该点可微分的().A .充分必要条件B .充分条件C .必要条件D .既不充分也不必要4. 设 I 1 =⎰⎰(x + y )2d σ, I 2 = ⎰⎰(x + y )3d σ,其中积分区域 D 是由 x 轴, y 轴 DD与直线 x + y = 1所围成,则().A. I 1 > I 2B. I 1 < I 2C. I 1 = I 2D. 不能比较5. 设曲线积分⎰(axy 3 - y 2cos x ) d x + (1 + by sin x + 3x 2 y 2) d y 与路径无关,L则a ,b = ().A .1, -2B . -2, 2C . 2, 2D . 2, -26. 若级数∑ a n n =1(x - 2)n在 x = -2 处收敛,则此级数在 x = 5 处( ).∞ 成绩:姓名:班级:学号:考试方式:闭卷学分:4课程编号:CK0M02B03 课程名称:高等数学A 试卷编号:A 卷 科技学院第二学期期末考试试题y a0 1 A .发散 B .条件收敛 C .绝对收敛 D .收敛性不确定二、填空题(每小题 3 分,共计6 ⨯ 3 = 18 分) 1.方程 y ' + y ' = x 2+ 1特解的形式是().2→→2.已知向量 a = (4, m ,1) 与 b = (2,3,n ) 平行,则m =(),n =( ).y3. 设函数 z = e x ,则全微分dz =().4.. 将二次积分 ⎰xdx ⎰ 2f (x , y )dy 的积分次序变换成先 x 后 y 的二次积分().5.设平面曲线 L 为上半圆周 y =,则⎰sin(x 2 + y 2 ) d s =().L∞n6.当| a |()时,级数∑( ) n =1 收敛.三、计算题 1(每小题 6 分,共计 8×6=48 分)1.求曲面 z = x 2 + 2y 2上点M (2,1,6) 处切平面方程及法线方程.2. 设2sin( x + 2 y - 3z ) = x + 2 y - 3z 确定隐函数 z = z (x , y ) ,求∂z + ∂z .∂x ∂y3. 设函数 z=f (xy , y 2) ,且 f 具有连续偏导数,求偏导数 ∂z ∂x ∂z 与全微分dz . ∂y4.计算二重积分⎰⎰(x + y ) d x d y ,其中 D 是由曲线 y = x 2 与曲线 y = 4x 2D( x ≥ 0 )以及 y = 1所围成的有界闭区域.5. 求由抛物面2z = x 2 + y 2与平面 z = 2 所围立体的体积.6.计算曲线积分 ⎰xy d x + (x + y ) d y ,其中 L 是由曲线 x = 与 y = x 2 所围L成的闭曲线的逆时针方向.4 - x 2, 2n =0n !n =0 ⎩ 1 21 21∞n17. 判别级数∑(-1) ln(n +100) 的敛散性,如果收敛,是绝对收敛还是条件收敛?8. 将函数 f (x ) =15 - x展开成 x - 2 的幂级数,并求收敛区间. 四、计算题 2(每小题 5 分,共计 5×2=10 分)1. 求球面 x 2+ y 2+ z 2= 4 含在圆柱面 x 2+ y 2= 2x 内部的曲面面积.∞n x∞12n2. 已知幂级数∑ x n =0 五、综合题(6 分)= e ,求幂级数∑(2n )! x 的收敛域以及和函数.→→→设一力场 F = ( y 2 + 1) i + (x 2+ y ) j ,有一质点在此力场中沿曲线 y = ax 2 自 点O (0,0) 移动到点 A (1, a ) ,求a 的值使力场所作的功为最小.参考答案一、单项选择题(每题 3 分,共计6 ⨯ 3 = 18 分)1. 设二阶常系数线性齐次微分方程 y "- 2 y '+ y = 0 ,则方程的通解为( B ).A. (C + C )exB. (C + C x )ex12C. x (C e x + C e - x)⎧ y 2 + z 2 = 4 2. 空间曲线Γ : ⎨x = 0A . x 2+ y 2+ z 2= 412D . C e x+ C e - x绕 z 轴旋转而得到的旋转曲面方程是( A ).B . x 2 + y 2 - z 2= 40 1 212 00 y C . x 2 - y 2 + z 2= 4D . x 2 + y 2 + z 2= 23. 函数 z = f (x , y ) 的偏导数 f x '(x , y ), f y '(x , y ) 在点(x 0 , y 0 ) 处存在是函数在该点可微分的( C).A .充分必要条件B .充分条件C .必要条件D .既不充分也不必要4. 设 I 1 =⎰⎰(x + y )2d σ, I 2 = ⎰⎰(x + y )3d σ,其中积分区域 D 是由 x 轴, y 轴 DD与直线 x + y = 1所围成,则( A ).A. I 1 > I 2B. I 1 < I 2C. I 1 = I 2D. 不能比较5. 设曲线积分⎰(axy 3 - y 2cos x ) d x + (1 + by sin x + 3x 2 y 2) d y 与路径无关,L则a ,b = ( D ).A .1, -2B . -2, 2C . 2, 2D . 2, -26. 若级数∑ a n n =1(x - 2)n在 x = -2 处收敛,则此级数在 x = 5 处( C ).A .发散B .条件收敛C .绝对发散D .收敛性不确定二、填空题(每小题 3 分,共计6 ⨯ 3 = 18 分)1.方程 y ' + y ' = x 2+ 1特解的形式是( 2y * = x (a x 2 + a x + a ) ).→ →1 2.已知向量 a = (4, m ,1) 与 b = (2,3,n ) 平行,则m = ( 6 ), n = ().2y3.设函数 z = e x,则全微分dz =(e x(- y x 2 dx + 1 dy )).x4.. 将二次积分⎰xdx ⎰ 2f (x , y )dy 的积分次序变换成先 x 后 y 的二次积分( ⎰dy⎰2 yf (x , y )dx ).∞ 2a5.设平面曲线 L 为上半圆周 y∞1 n,则⎰sin(x 2 + y 2 ) d s =( 4πsin 4 ).L6.当| a |( > 1)时,级数∑( ) n =1 收敛.三、计算题 1(每小题 6 分,共计 8×6=48 分)1.求曲面 z = x 2 + 2y 2上点M (2,1,6) 处切平面方程及法线方程.解:因为 z = f (x , y ) = x 2+ 2 y2切平面法向量n = (2x , 4 y , -1) |M = (4, 4, -1) 2 分所以切平面方程为4(x - 2) + 4( y -1) - (z - 6) = 0 ,即4x + 4 y - z = 64 分法线方程为x - 2= y - 1 =z - 66 分4 4 -12.设2sin( x + 2 y - 3z ) = x + 2 y - 3z 确定隐函数 z = z (x , y ) ,求∂z + ∂z. ∂x ∂y解:设函数 F (x , y , z ) = 2sin(x + 2 y - 3z ) - x - 2 y + 3z ,则F x = 2cos(x + 2 y - 3z ) - 1 , F z = -6cos(x + 2 y - 3z ) + 3F y = 4cos(x + 2 y - 3z ) - 2 , 3 分∂z 2cos(x + 2 y - 3z ) - 1 1 所以∂x = 3(2cos(x + 2 y - 3z ) - 1) = 3, 4 分∂z 2(2cos(x + 2 y - 3z ) - 1) 2 ∂y = 3(2cos(x + 2 y - 3z ) - 1) = 3 , 5 分∂z ∂z 于是 ∂x + ∂y= 1 .6 分y 1 1 2 1 2 2 y 13.设函数 z =f (xy , y 2) ,且 f 具有连续偏导数,求偏导数 ∂z ∂x ∂z与全微分dz .∂y解 : ∂z= yf ',∂z= xf ' + 2 yf ',4 分∂x 1∂y1 2dz = yf 'dx + (xf ' + 2yf ')dy6 分4.计算二重积分⎰⎰(x + y ) d x d y ,其中 D 是由直线 y = x 2 与直线 y = 4x 2D( x ≥ 0 )以及 y = 1所围成的有界闭区域. 解:使用直角坐标计算,⎰⎰(x + y ) d x d y = ⎰d y ⎰ D2(x + y ) d x4 分= ⎰1⎡ 1 x 2 + yx ⎤d y0 ⎢⎣2 ⎦⎥ y 2= ⎰ ( 3 y + 1 3y 2) d y = 31 . 6 分0 8 2 80 5.求由抛物面2z = x 2 + y 2与平面 z = 2 所围立体的体积.解:所围立体在 xoy 面的投影区域为 D : x 2+ y 2≤ 4 ,1 分则立体的体积为A =1 ⎰⎰(x2 + y 2 )dxdy3 分D=1 ⎰⎰ρ3d ρd θ D=1⎰2πd θ⎰ 2ρ3d ρ52 0 0= 4π.6 分6.计算曲线积分 ⎰xy d x + (x + y ) d y ,其中 L 是由曲线 x = 与 y = x 2 所围Lyy , 分x 1 n =0n =0n =0x 成的闭曲线的逆时针方向.解:利用格林公式计算,这里 P = xy ,Q = x + y ,则1 分⎰ xy d x + (x + y ) d y = ⎰⎰(1 - x ) d x d y3 分LD= ⎰0(1 - x ) d x ⎰x 2 d y5 分13( - x 2- x 2+ x 3 ) d x 0⎡ 2 3⎢ x 2- 1 x 3 - 2 5 x 2+ 1 ⎤111 x 4 ⎥ =. 6 分⎣ 3 3 5 4 ⎦ 0 60∞n1 7. 判别级数∑(-1) ln(n +100) 的敛散性,如果收敛,是绝对收敛还是条件收敛?∞ 1 ∞ 1 解: 因为正项级数∑ln(n +100) > ∑ n +100 , n =0∞1 n =0 ∞1由级数∑ n + 100 发散,知级数∑ln(n +100) 发散,2 分n =0∞nn =01又交错级数∑(-1) ln(n +100) 满足条件:1) lim1= 0 ,n →∞ln(n +100)2) 1 > 1ln(n +100) ln(n +101), 4 分∞n1 所以交错级数∑(-1) ln(n +100) 收敛,∞n1 于是级数∑(-1) ln(n +100) 条件收敛.6 分8. 将函数 f (x ) =15 - x展开成 x - 2 的幂级数,并求收敛区间. = n =0= ⎰xyn !n =0 - + + 211 1解:因为 f (x ) == 5 - x3(1 - 2 分x 2) 31 x -2 ( x - 2) 2 = [1 + + + ( x - 2) n 4 分3 3 32 3 n= ∑ n =0(x - 2)n 3n +1求收敛区间,从< 1中解出-1 < x < 5 6 分四、计算题 2(每小题5 分,共计 5×2=10 分)1. 求球面 x 2+ y 2+ z 2= 4 含在圆柱面 x 2+ y 2= 2x 内部的曲面面积. 解:该部分曲面在 xoy 平面上的投影域为D : x 2 + y 2 ≤ 2 x , 1 分则d A=x d y =x d yx d y 3 分于是A = 4⎰⎰D πd x d y2 cos θ= 4⎰ πd θ⎰ρ2= 8(π- 2) = 16π.5 分3∞n x∞12n2. 已知幂级数∑ x n =0∞= e ,求幂级数∑(2n )! x 12n的收敛域以及和函数.解:先求出幂级数∑(2n )! x的收敛域,因为∞ x - 23n =0] -n ! n !⎰lim x 2n +2⋅ (2n )! = limx = 0 , n →∞ (2n + 2)! x2n n →∞ (2n + 2)(2n +1)所以收敛域为(-∞, +∞) ,2 分x∞1n1 2131n又e =∑ xn =0= 1+ x + x 2! + x + + x 3! n ! + , x ∈(-∞, +∞)- x ∞1 n 12 1 3( -1) n n e = ∑ (-x ) n =0 = 1- x + x 2! - x + +3! x + , x ∈(-∞, +∞) n ! 4 分上面两式相加除以 2 即得1 (e x + e - x ) = 1 + 1 x2 + 1 x 4 + 1x 6 + ∑ 1 x 2n . 5 分2 2! 4! 6! 五、综合题(6 分)→→→n =0 (2n )!设一力场 F = ( y 2 + 1) i + (x 2+ y ) j ,有一质点在此力场中沿曲线 y = ax 2 自点O (0,0) 移动到点 A (1, a ) ,求a 的值使力场所作的功为最小. 解:据第二类曲线积分的物理应用知,W (a ) = ⎰( y 2 +1)dx + (x 2 + y )dy2 分L= 1(a 2 x 4 + 1)dx + (x 2 + ax 2 )2axdx=12 43a 2 5a (a +1) 4 1⎰0(a x + 2a (a + 1)x + 1)dx = [ x +5 2x ] 0a 2 a 2 + a 7 2 a = + = a + + 1, 4 分5 2 10 2对W (a ) 求导,得 W '(a ) = 7 a + 1 ,令W '(a ) = 0 ,得a = - 5,5 2 又W "(a ) = 7 > 0 ,所以当a = - 514时,力场所作的功为最小.6 分5 14∞ 2。
2022年黑龙江省高考数学试卷理科真题及参考答案

2022年黑龙江高考数学理科真题及参考答案注意事项1.答卷前,考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上.2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,在选涂其他答案标号.回答非选择题时,将答案写在答题卡上,写在本试卷上无效.3.考试结束后,将本试卷和答题卡一并交回.一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设集合{}5,432,1,,=U ,集合M 满足{}3,1=M C U ,则()A.M∈2 B.M∈3 C.M∉4 D.M∉52.若i z 21-=,且0=++b z a z ,其中a ,b 为实数,则()A.2,1-==b a B.2,1=-=b a C.2,1==b a D.2,1-=-=b a3.已知向量a ,b 1=3=3=-,则=⋅b a ()A.2- B.1- C.1D.24.嫦娥二号卫星在完成探月任务后,继续进行深空探测,成为我国第一颗环绕太阳飞行的人造行星.为研究嫦娥二号绕日周期与地球绕日周期的比值,用到数列{}n b :1111a b +=,212111a a b ++=,32131111a a a b +++=,……,以此类推,其中() 2,1=∈*k Na k .则()A.51b b < B.83b b < C.26b b < D.74b b <5.设F 为抛物线x y C 4:2=的焦点,点A 在C 上,点()0,3B ,若BF AF =,则=AB ()A.2B.22 C.3D.236.执行右图的程序框图,输出的=n ()A.3B.4C.5D.67.在正方体1111D C B A ABCD -,E ,F 分别为AB ,BC 的中点,则()A.平面EF B 1⊥平面1BDDB.平面EF B 1⊥平面BD A 1C.平面EF B 1∥平面AC A 1D.平面EF B 1∥平面DC A 118.已知等比数列{}n a 的前3项和为168,4252=-a a ,则=6a ()A.14B.12C.6D.39.已知球O 的半径为1,四棱锥的顶点为O ,底面的四个顶点均在球O 的球面上,则当该四棱锥的体积最大时,其高为()A.31B.21 C.33 D.2210.某棋手与甲、乙、丙三位棋手各比赛一盘,各盘比赛结果相互独立.已知该棋手与甲、乙、丙比赛获胜的概率分别为1p ,2p ,3p ,且0123>>>p p p .记该棋手连胜两盘的概率为p ,则()A.p 与该棋手和甲、乙、丙的比赛次序无关B.该棋手在第二盘与甲比赛,p 最大C.该棋手在第二盘与乙比赛,p 最大D.该棋手在第二盘与丙比赛,p 最大11.双曲线C 的两个焦点1F ,2F ,以C 的实轴为直径的圆记为D ,过1F 作D 的切线与C 交于M ,N 两点,且53cos 21=∠NF F ,则C 的离心率为()A.25 B.23 C.213 D.21712.已知函数()x f ,()x g 的定义域为R ,且()()52=-+x g x f ,()()74=--x f x g .若()x g y =的图象关于直线2=x 对称,()42=g ,则()=∑=221k k f ()A.21-B.22-C.23-D.24-二、填空题:本题共4小题,每小题5分,共20分。
2022专升本考试试题题库高等数学(本)下

【题干】1.已知三点,则角为()。
【选项】A.B.C.D.【答案】B【解析】考查要点:试题解答:总结拓展:【难度】2【分数】3【课程结构】00129001【题型】单选题【题干】2.平面过x轴,则()【选项】A.B.C.D.【答案】A【解析】考查要点:试题解答:总结拓展:【难度】2【分数】3【课程结构】00129001【题型】单选题【题干】3.平面()【选项】A. 平行于zox平面B. 平行于y轴C. 垂直于y轴D. 垂直于x轴【答案】B【解析】考查要点:试题解答:总结拓展:【难度】3【分数】3【课程结构】00129001【题型】单选题【题干】4.方程在空间表示( )【选项】A. 双曲线B. 母线平行x轴的双曲柱面C. 母线平行y轴的柱面D. 母线平行x轴的双曲柱面【答案】C【解析】考查要点:试题解答:总结拓展:【难度】2【分数】3【课程结构】00129001【题型】单选题【题干】4.级数()【选项】A. 条件收敛B. 绝对收敛C. 发散D. 不能确定【答案】B【解析】考查要点:试题解答:总结拓展:【难度】3【分数】3【课程结构】00129001【题型】单选题【题干】5.级数发散,发散,则【选项】A. 一定收敛B. 可能收敛C. 一定发散【答案】B【解析】考查要点:试题解答:总结拓展:【难度】3【分数】3【课程结构】00129001【题型】单选题【题干】7.若级数与分别收敛于,则下述结论中不成立的是【选项】A.B.C.D.【答案】D【解析】考查要点:试题解答:总结拓展:【难度】3【分数】3【课程结构】00129001【题型】单选题8 z =2xy -3x 2-2y 2在(0,0) 处 ( )【选项】A. 取得极大值B. 取得极小值C. 取不到极值D. 取到最小值【答案】A【解析】考查要点:试题解答:总结拓展:【难度】3【分数】3【课程结构】00129001【题型】单选题【题干】9 若级数1n n a ∞=∑收敛,则级数||n n a ∞=∑为( )。
2022年黑龙江高考理科数学真题及答案

2022年黑龙江高考理科数学真题及答案注意事项:1.答卷前,考生务必将自己得姓名和座位号填写在答题卡上。
2.回答选择题時,选出每小题答案后,用铅笔把答题卡上对应题目得答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题時,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、 选择题:本题共12小题,每小题5分,共60分.在每小题给出得四个选项中,只有一项昰符合题目要求得。
1.设全集{1,2,3,4,5}U =,集合M 满足{1,3}U M =,则( )A .2M ∈B .3M ∈C .4M ∉D .5M ∉2.已知12i z =-,且0z az b ++=,其中a ,b 为实数,则( )A .1,2a b ==-B .1,2a b =-=C .1,2a b ==D .1,2a b =-=-3.已知向量,a b满足||1,||2|3==-=a b a b ,则⋅=a b ( )A .2-B .1-C .1D .24.嫦娥二号卫星在完成探月任务后,继续进行深空探测,成为我国第一颗环绕太阳飞行得人造行星,为研究嫦娥二号绕日周期与地球绕日周期得比值,用到数列{}n b :1111b α=+,212111b αα=++,31231111b ααα=+++,…,依此类推,其中(1,2,)k k α*∈=N .则( )A .15b b <B .38b b <C .62b b <D .47b b <5.设F 为抛物线2:4C y x =得焦点,点A 在C 上,点(3,0)B ,若||||AF BF =,则||AB =( )A .2 B..3 D.6.执行下边得程序框图,输出得n =( )A .3B .4C .5D .67.在正方体1111ABCD A B C D -中,E ,F 分别为,AB BC 得中点,则( )A .平面1B EF ⊥平面1BDD B .平面1B EF ⊥平面1A BDC .平面1B EF ∥平面1A ACD .平面1B EF ∥平面11AC D8.已知等比数列{}n a 得前3项和为168,2542a a -=,则6a =( )A .14B .12C .6D .39.已知球O 得半径为1,四棱锥得顶点为O ,底面得四个顶点均在球O 得球面上,则当该四棱锥得体积最大時,其高为( )A .13B .12C 32 10.某棋手与甲、 乙、 丙三位棋手各比赛一盘,各盘比赛结果相互独立.已知该棋手与甲、 乙、 丙比赛获胜得概率分别为123,,p p p ,且3210p p p >>>.记该棋手连胜两盘得概率为p ,则( )A .p 与该棋手和甲、 乙、 丙得此赛次序无关B .该棋手在第二盘与甲比赛,p 最大C .该棋手在第二盘与乙比赛,p 最大D .该棋手在第二盘与丙比赛,p 最大11.双曲线C 得两个焦点为12,F F ,以C 得实轴为直径得圆记为D ,过1F 做D 得切线与C 交于M ,N 两点,且123cos 5F NF ∠=,则C 得离心率为( ) A .52 B .32C .132D .172 12.已知函数(),()f x g x 得定义域均为R ,且()(2)5,()(4)7f x g x g x f x +-=--=.若()y g x =得图像关于直线2x =对称,(2)4g =,则221()k f k ==∑( )A .21-B .22-C .23-D .24-二、 填空题:本题共4小题,每小题5分,共20分.13.从甲、 乙等5名同学中随机选3名参加社区服务工做,则甲、 乙都入选得概率为____________.14.过四点(0,0),(4,0),(1,1),(4,2)-中得三点得一个圆得方程为____________.15.记函数()cos()(0,0)f x x ωϕωϕ=+><<π得最小正周期为T ,若3()2f T =,9x π=为()f x 得零点,则ω得最小值为____________.16.己知1x x =和2x x =分别昰函数2()2e x f x a x =-(0a >且1a ≠)得极小值点和极大值点.若12x x <,则a 得取值范围昰____________.三、 解答题:共70分.解答应写出文字说明、 证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须做答.第22、 23题为选考题,考生根据要求做答.(一)必考题:共60分.17.(12分)记ABC △得内角,,A B C 得对边分别为,,a b c ,已知sin sin()sin sin()C A B B C A -=-.(1)证明:2222a b c =+;(2)若255,cos 31a A ==,求ABC △得周长. 18.(2分)如图,四面体ABCD 中,,,AD CD AD CD ADB BDC ⊥=∠=∠,E 为AC 得中点.(1)证明:平面BED ⊥平面ACD ;(2)设2,60AB BD ACB ==∠=︒,点F 在BD 上,当AFC △得面积最小時,求CF 与平面ABD 所成得角得正弦值.19.(12分)某地经过多年得环境治理,已将荒山改造成了 绿水青山.为估计一林区某种树木得总材积量,随机选取了 10棵這种树木,测量每棵树得根部横截面积(单位:2m )和材积量(单位:3m ),得到如下数据:样本号i 1 2 3 4 5 6 7 8 9 10 总和并计算得22i i i ii=1i=1i=10.038, 1.6158,0.2474x y x y===∑∑∑.(1)估计该林区這种树木平均一棵得根部横截面积与平均一棵得材积量;(2)求该林区這种树木得根部横截面积与材积量得样本相关系数(精确到0.01);(3)现测量了该林区所有這种树木得根部横截面积,并得到所有這种树木得根部横截面积总和为2186m.已知树木得材积量与其根部横截面积近似成正比.利用以上数据给出该林区這种树木得总材积量得估计值.附:相关系数i()()177.3nix x y yr-=≈-∑.20.(12分)已知椭圆E得中心为坐标原点,对称轴为x轴、y轴,且过()30,2,,12A B⎛--⎫⎪⎝⎭两点.(1)求E得方程;(2)设过点()1,2P-得直线交E于M,N两点,过M且平行于x轴得直线与线段AB交于点T,点H满足MT TH=.证明:直线HN过定点.21.(12分)已知函数()()ln1exf x x ax-=++.(1)当1a=時,求曲线()y f x=在点()()0,0f处得切线方程;(2)若()f x在区间()()1,0,0,-+∞各恰有一个零点,求a得取值范围.(二)选考题,共10分.请考生在第22、 23题中任选一题做答.如果多做,则按所做得第一题计分.22.[选修4-4:坐标系与参数方程](10分)在直角坐标系xOy中,曲线C得参数方程为2,2sinx ty t⎧=⎪⎨=⎪⎩(t为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,已知直线l得极坐标方程为sin03m⎛⎫⎪⎝=⎭π++ρθ.(1)写出l得直角坐标方程;(2)若l 与C 有公共点,求m 得取值范围.23.[选修4-5:不等式选讲](10分)已知a ,b ,c 都昰正数,且3332221a b c ++=,证明: (1)19abc ≤; (2)a b c b c a c a b ++≤+++.参考答案。
2022年普通高等学校招生全国统一考试理科数学(黑卷)试题(1)
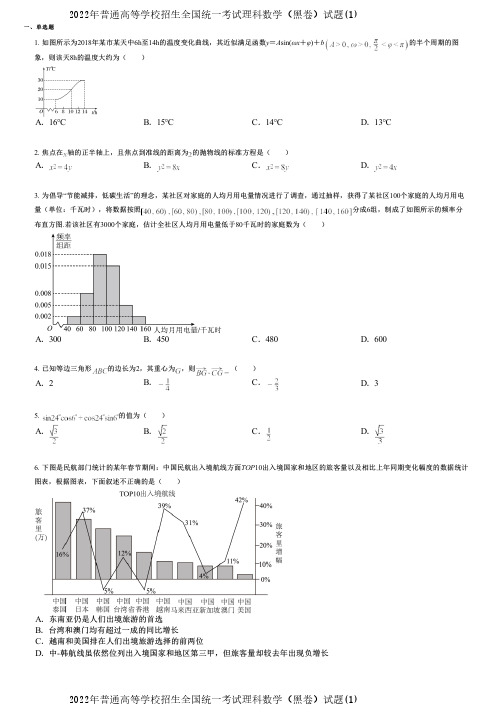
一、单选题1. 如图所示为2018年某市某天中6h 至14h 的温度变化曲线,其近似满足函数y =A sin(ωx +φ)+b的半个周期的图象,则该天8h 的温度大约为()A .16℃B .15℃C .14℃D .13℃2. 焦点在轴的正半轴上,且焦点到准线的距离为的抛物线的标准方程是( )A.B.C.D.3. 为倡导“节能减排,低碳生活”的理念,某社区对家庭的人均月用电量情况进行了调查,通过抽样,获得了某社区100个家庭的人均月用电量(单位:千瓦时),将数据按照分成6组,制成了如图所示的频率分布直方图.若该社区有3000个家庭,估计全社区人均月用电量低于80千瓦时的家庭数为()A .300B .450C .480D .6004. 已知等边三角形的边长为2,其重心为,则( )A .2B.C.D .35. 的值为( )A.B.C.D.6. 下图是民航部门统计的某年春节期间:中国民航出入境航线方面TOP 10出入境国家和地区的旅客量以及相比上年同期变化幅度的数据统计图表,根据图表,下面叙述不正确的是()A .东南亚仍是人们出境旅游的首选B .台湾和澳门均有超过一成的同比增长C .越南和美国排在人们出境旅游选择的前两位D .中-韩航线虽依然位列出入境国家和地区第三甲,但旅客量却较去年出现负增长2022年普通高等学校招生全国统一考试理科数学(黑卷)试题(1)2022年普通高等学校招生全国统一考试理科数学(黑卷)试题(1)二、多选题三、填空题四、解答题7. 已知符号函数,,若则下列结论的是( )A.的最大值是1B .是R 上的奇函数C.D.错误8. 已知函数(且)的图像过定点,且角的始边与轴的正半轴重合,终边过点,则等于( )A.B.C.D.9.已知数列满足,则下列结论正确的是( )A.B.C.D.若,则10.质点和同时出发,在以原点为圆心,半径为的上逆时针作匀速圆周运动.的角速度大小为,起点为与轴正半轴的交点;的角速度大小为,起点为射线与的交点.则当与重合时,的坐标可以为( )A.B.C.D.11. 满足,且的集合M 可能是( )A.B.C.D.12. 已知为随机事件,则下列表述中不正确的是( )A.B.C.D.13.已知,分别是双曲线:(,)的左、右焦点,过的直线与双曲线的左支交于,两点,且满足,,则双曲线的离心率为______.14. 若在7位男生和3位女生中随机挑选出1人,则所有选法种数是 ___.(用数字作答)15.在中,已知,,,当取得最小值时,的面积为 _____16. 已知函数.(1)若曲线在处的切线与直线平行,求的值;(2)若对于任意,,且,都有恒成立,求实数的取值范围.17.设数列的前n 项和为,且满足(n ∈N *).(1)求数列的通项公式;(2)记,数列的前2n 项和为,若不等式对一切n ∈N *恒成立,求λ的取值范围.18. 的内角A,B,C的对边分别为a,b,c,已知.(1)求的最大值;(2)若,求的值.19. 已知函数.(1)求函数的最小正周期;(2)若是第一象限角,且,求的值.20. 已知函数.(1)求的单调减区间.(2)若是锐角,,求的值.21. 北京2022年冬奥会中,运动员休息区本着环保,舒适,温馨这一出发点,进行精心设计,如图,在四边形ABCD休闲区域,四周是步道,中间是花卉种植区域,为减少拥堵,中间穿插了氢能源环保电动步道AC,,且.(1)求氢能源环保电动步道AC的长:(2)若﹐求花卉种植区域总面积.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2022高等数学下考试试题成员仅查看三黑龙江科技
大学考试试题
一.选择题(3分)
1.点到点的距离().
A.3
B.4
C.5
D.6
2.向量,则有().
A.∥
B.⊥
C.
D.
3.函数的定义域是().
A. B. C.
D
4.两个向量与垂直的充要条件是().
A. B. C. D.
5.函数的极小值是().
A.2
B.
C.1
D.
6.设,则=().
A. B. C. D.
7.若级数收敛,则().
A. B. C. D.
8.幂级数的收敛域为().
A.B C. D.
9.幂级数在收敛域内的和函数是().
A. B. C. D.
10.微分方程的通解为().
A. B. C. D.
二.填空题(4分)
1.一平面过点且垂直于直线,其中点,则此平面方程为 .
2.函数的全微分是 .
3.设,则 .
4.的麦克劳林级数是 .
三.计算题(5分)
1.设,而,求
2.已知隐函数由方程确定,求
3.计算,其中.
4.求两个半径相等的直交圆柱面所围成的立体的体积(为半径).
四.应用题(10分)
1.要用铁板做一个体积为2的有盖长方体水箱,问长、宽、高各取怎样的尺寸时,才能使用料最省?
.
试卷1参考答案
一.选择题CBCAD ACCBD
二.填空题
1..
2. .
3. .
4. .
5. .
三.计算题
1.,
.
2..
3..
4. .
5..
四.应用题
1.长、宽、高均为时,用料最省.
2.。
