北大张伟考研数学

合集下载

考研数学线性代数和概率论的复习重点

考研数学线性代数和概率论的复习重点考研数学线性代数和概率论的复习重点有许多表示刚一开始线性代数和概率论与数理统计有难处，认为看书举步维艰。

店铺为大家精心准备了考研数学线性代数和概率论的复习要点，欢迎大家前来阅读。

考研数学线性代数和概率论的复习难点▶难点事实上线性代数应该是数学三门课中最好拿分的，但是这门课有一个特点，就是入门难，但是一旦入门就一通百通。

这门课由于思维上与高数南辕北辙，所以一上来会很不适应。

总体而言，6章内容环环相扣，所以很多同学一上来看第一章发现内容涉及到第五章，看到第二章发现竟有第4章的知识点，无法形成完整的知识网络，自然无法入门。

▶学习规划总的来说，线性代数这本书6章内容应该分为三个部分逐个攻破：首先行列式和矩阵，第二向量与方程组，第三第5和第六章。

这三个内容联系得相当紧密，必须逐个攻破，这样以两章为单位，每个单位中出现的知识点定理罗列出来，找到他们彼此的关系。

最好是拿一张白纸，像C语言中的指针那样一个一个连起来，形成属于你的知识网络，这一部分有哪些板块，每个板块有哪些定义知识点，比如行列式的定义，矩阵的定义各是，你是怎么理解的，向量与方程组有什么联系与区别，这些最基础的一定要搞清。

对于概率论，第一章是整本书的思维基础，第二章与第三章的逻辑思维就好像一元积分与二元积分一样，难点在于二元积分的计算。

在学习的过程中还是要先思考这一章节有哪些部分，每个部分哪些定义，哪些知识点，自己要找一张大纸，将这些全部像C语言中二叉树一样，罗列成一个树形图，最后根据每一个知识点各个击破。

第5章不用细看，第六章第七章主要是记忆，在记忆的基础上尽可能的理解。

浙大版的书上每章的课后题相当经典，请同学们反复推敲，做过之后，请在总结一遍，比如说这几道题是属于离散型还是连续型，对应了哪些知识点。

▶视频学习法线性代数：不要一上来就看李永乐的视频，因为那个视频是强化阶段看的，建议听一下施光燕的线性代数12讲，这位老师讲的内容很基础，只有十二讲，但是全讲到重点上去了，这样你就会很容易入门了。

考研届数学名师大盘点,你pick谁

考研届数学名师大盘点，你pick谁摘要：跟一位适合自己、能为自己指点迷津的老师，无疑会大大提高数学水平，今日帮仔为大家盘考下考研届的数学老师，来看一看你pick谁？1、汤家凤老师►名师简介：老汤的基础班被认为是所有老师里最负责最踏实的！因为绝大部分老师都是一个样，收着讲，而不是全局概括，往往基础班讲高数上册的前三四章就匆匆了事。

汤老师是比较务实的人，他的基础班除了比较偏的几个知识点（三重积分、第二型曲线曲面积分等），从数一到数三的内容都会讲完，你要是看完高数课本，再把老汤的基础班看完，是极好的，你定会打一个不错的基础。

但是如果你不听他的基础课就直接奔着强化课去听，那么就会感觉比较吃力，因为老汤的强化班是建立在基础班上的，算是对基础班的一个延伸概括。

►当然，他老人家讲课有两个不足之处：（1）重视题量，对概念的讲解却不是特别深入！（这点和张宇正好相反）所以他的课适合基础差的同学打基础的，通过做题来深化对知识点的认识（2）口音问题，这是老汤被黑的重要原因，老汤的江苏南京人，讲话口音有点怪怪的，普通话讲得并不是太好，但是多听几节课，这也不是什么大问题。

►概括：所以考研的同学可以打基础的时候看完课本直接上手老汤的基础班！权当练习！2、张宇老师►名师简介：张宇，江湖人称宇哥，他独树一帜，是考研老师新生派的代表人物，其微博名字也为宇哥考研，为人风趣幽默，讲课就像讲故事，听起来毫不费力。

如果你对数学没兴趣，听宇哥的课会激发你对数学的热情，听宇哥的课就是一个感觉，上瘾！好听！有意思！相信绝大部分同学都听过他的sin狗（广义化）的公式，宇哥的一大能力就是他能将数学抽象问题形象化，复杂问题简单化。

例如，二重积分大面包切切切切切、狗减sin狗等于六分之一狗三、夹逼准则哪里跑、格林闭关七天研究出格林公式、欠阿贝尔两块钱以及普京题抓住重点、毛主席题举重若轻等等，这些本来在高数课本中枯燥繁琐的东西在张宇口中变得呼之欲出、极为生动，这都能反应宇哥的特色。

北大中文系考研数学

北大中文系考研数学北大中文系考研数学是指北大中文系的学生考研时需要面对的数学科目。

对于很多中文系的学生来说，数学一直都是一个相对较弱的学科，对于考研的数学科目的要求常常会让人感到有些吃力。

然而，作为一名北大中文系的学生，我们应该积极迎接这个挑战，并且努力提升自己的数学水平。

首先，学习数学需要调整好心态。

虽然我们可能对数学这门学科感到陌生或者害怕，但是我们不能抱有消极的态度，而是要积极主动地面对它。

我们要相信自己有能力学好数学，只要努力去做就一定能有好的结果。

其次，我们需要制定一个科学的学习计划。

学习数学需要持续的努力和时间投入。

我们可以根据自己的实际情况，合理地规划每天的学习时间，并且在规定的时间内专注地学习数学。

同时，我们还可以结合自己的学习进度，合理划定每个阶段的目标，逐步提高数学知识和能力。

此外，我们可以利用各种资源来帮助自己学好数学。

北大提供了丰富的学习资源，我们可以积极利用图书馆、教师的讲座以及网上的学习资料，扩展我们的数学知识。

同时，我们还可以参加数学学习小组或者数学辅导班，与同学们一起交流学习经验，共同解决问题。

最后，我们需要不断地做题来提高自己的数学水平。

练习题是检验我们对数学知识掌握程度的有效途径。

我们可以通过大量的练习来巩固和加深对数学知识的理解，提高解题能力和应用能力。

在做题的过程中，我们要注意理清思路，分析问题，有意识地总结解题经验，从而逐渐提高自己的数学能力。

总之，北大中文系考研数学对于我们来说确实是一个挑战，但是只要我们积极面对、科学学习，充分利用各种资源，不断做题，相信自己一定能够学好数学，进入自己理想的研究生院校。

毕竟，数学不仅是我们考研的必考科目，也是我们作为终身学习者需要具备的重要能力之一。

考研机构哪家好？八大机构新排名!

考研八大机构排名近年来，由于市场经济下行压力增大，就业压力越来越大，各行业的优质岗位对学历的要求越来越高，于是许多职场人士，大学毕业生都把考研，提升学历，专业能力放在了职业规划上最重要的位置。

考研学生逐年增加，于是市场上的各种考研培训机构层出不穷。

竞争激烈的程度的不断提升，使得许多学生更愿意为自己选择一个优质的辅导机构，保障自己的考研率。

老牌的考研培训机构面临更多的挑战，纷纷扩大市场规模，各个学科领域全面布局；部分机构专注于研发科学的课程体系，提高升学率；也有的机构为了招生虚假宣传，专注于坑蒙拐骗，损坏行业声誉。

错综复杂的市场环境，每个机构擅长的领域也不相同，选择考研辅导机构成为了考研生涯中的第一道选择题。

20考研已经结束，21考研的同学要准备起来，报辅导班，或是确定目标院校。

以下是我们通过对各个考研培训机构的的师资、品牌、授课方式等方面逐进行综合评价得出的排名。

希望能给考研学子在选择考研培训机构时做一个参考。

1.中域简介：成立于2011年，是集高端考研，在职考研一体的考研辅导机构。

主要师资：汪泽荃、崔简盛、于皇智、张远方、吴在望、王季钧、丛雅然、刘棋帅、曲京京等多位名师考研院校规划师：崔楠萍、李覃维等名师中域力量雄厚，考研教师都深谙考研命题规律，拥有多年考研备考辅导经验。

拿考研英语崔简盛老师来说，崔老师专注考研英语多年，拥有丰富的考研辅导经验。

经济学人杂志是考研英语试题的一个主要来源，考研英语崔简盛的课程便是针对考研命题规律，抓核心重点，让学员不盲目复习，精准复习。

培训体系：模式：面授、网络课程、集训综合评价：优点：中域考研领跑考研8年，拥有丰富的考研辅导经验。

中域考研是从考前择校，初试，复试，调剂，全流程服务的考研培训机构,高端考研班的客服都是24小时在线，随时答疑解惑，并且专业课和公共课都采用一对一的服务模式，从各个方面为学员服务，中域的高端考研班已经帮助众多学员实现名校梦。

缺点：中域是一个相对年轻的考研辅导机构，在品牌知名度上和文都、新东方有一定的差距，并且中域只有高端班次，没有低端班，因此中域考研口碑虽好，虽然通过率年年攀升，但因为学员相比文都较少，口碑在一时之间不能传播出去，也就不能大面积覆盖学生。

2011年北大研究生拟录取名单

北京大学北京大学北京大学中央民族大学天津大学中国农业大学北京大学北京大学北京大学北京大学北京大学北京大学北京大学北京大学北京理工大学北京大学北京大学北京大学北京理工大学北京大学兰州大学北京大学北京科技大学合肥工业大学北京大学北京大学北京大学河北大学山东大学北京大学华南理工大学郑州大学北京大学大连理工大学武汉大学四川大学南京农业大学厦门大学同济大学北京师范大学
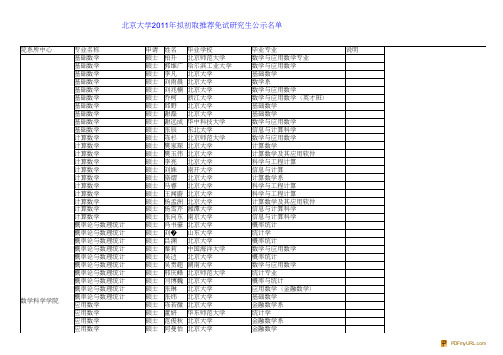
北京大学2011年拟初取推荐免试研究生公示名单
院系所中心专业名称基础数学基础数学基础数学基础数学基础数学基础数学基础数学基础数学基础数学基础数学计算数学计算数学计算数学计算数学计算数学计算数学计算数学计算数学计算数学计算数学计算数学概率论与数理统计概率论与数理统计概率论与数理统计概率论与数理统计概率论与数理统计概率论与数理统计概率论与数理统计概率论与数理统计概率论与数理统计概率论与数理统计应用数学应用数学应用数学应用数学申请硕士硕士硕士硕士硕士硕士硕士硕士硕士硕士硕士硕士硕士硕士硕士硕士硕士硕士硕士硕士硕士硕士硕士硕士硕士硕士硕士硕士硕士硕士硕士硕士硕士硕士硕士姓名柏升郭维广李凡刘雨晨刘兆楠乔柯邱野谢磊谢远成张辰陈杉樊家琛樊玉伟李亮刘姝骆熠马睿王闻蔚杨孟洲杨雪芹张向东冯书豪刘� 吕渊秦莉吴边吴贵超邢庆峰闫博巍张琳张炜陈若微董妍范俊秋何曼怡毕业学校北京师范大学哈尔滨工业大学北京大学北京大学北京大学浙江大学北京大学北京大学华中科技大学东北大学北京师范大学北京大学北京大学北京大学南开大学北京大学北京大学北京大学北京大学湘潭大学南京大学北京大学山东大学北京大学中国海洋大学北京大学湖南大学北京师范大学北京大学北京大学北京大学北京大学华东师范大学北京大学北京大学毕业专业数学与应用数学专业数学与应用数学基础数学数学系数学与应用数学数学与应用数学（英才班）基础数学基础数学数学与应用数学信息与计算科学数学与应用数学计算数学计算数学及其应用软件科学与工程计算信息与计算计算数学系科学与工程计算科学与工程计算计算数学及其应用软件信息与计算科学信息与计算科学概率统计统计学概率统计数学与应用数学概率统计数学与应用数学统计专业概率与统计应用数学（金融数学）基础数学金融数学系统计学金融数学系金融数学说明

北大ccer考研试题

北大ccer考研试题北大ccer考研试题一: 数学类1. 设函数 $f(x)=\sqrt{2x+1}+\sqrt{x-1}$，求 $f(x)$ 的极限值。

2. 已知三阶行列式$D=\begin{vmatrix}1&2&3\\4&5&6\\7&8&9\end{vmatrix}$，求其值。

3. 设数列 $\{a_n\}$ 满足 $a_1=2$，$a_2=3$，$a_n=a_{n-1}+a_{n-2}$（$n\geq3$），求 $a_{2023}$。

4. 已知三角形 $ABC$ 中，$\angle CAB=60^\circ$，$AC=2$，$BC=4$，求 $\sin(\angle ABC)$。

5. 函数 $f(x)$ 在区间 $[0,3]$ 上连续，且对任意 $x\in[0,3]$，有 $0\leq f(x)\leq2$。

证明：存在 $x_1,x_2\in[0,3]$，使得$f(x_1)=f(x_2)$。

北大ccer考研试题二: 英语类1. 根据下列句子，选择合适的词填空：I have been to China _______ times. (a few/few)2. 根据下列句子，选择正确的时态：He _______ to the gym every day last week. (go/went)3. 选择与下列单词划线部分发音不同的选项：A. clothesB. roughC. thoughD. thoughT4. 根据所给提示，完成下列句子：I am tired ______ I stayed up late last night. (so/because)5. 阅读下列短文，选择最佳答案：My sister and I _______ in the same school. She is in Grade 9and I am in Grade 12. We both have _______ best friends, Lucy and Lily. We often go shopping together on weekends. Last Saturday, _______ of us went to the mall to buy new clothes. My sister bought a beautiful dress, and I bought a pair of new shoes. Then we went to have lunch at our favorite restaurant. We had a great time!A. study - differentB. studies - the sameC. are studying - eachD. studied - both请注意，以上题目仅为示例，并非真实的北大ccer考研试题。

深入理解内容本质,做好全概率公式的教学

深入理解内容本质,做好全概率公式的教学
张伟;王绍锋
【期刊名称】《中国数学教育（高中版）》
【年(卷),期】2024()2
【摘要】全概率公式在求复杂事件的概率方面有重要作用,蕴含着重要的思想和方法.以具体案例引入,从特殊到一般给出全概率公式,在深入剖析全概率公式的基础上,分析使用公式的前提、蕴含的思想方法和实施步骤,给出全概率公式的应用和变形.【总页数】3页(P13-15)
【作者】张伟;王绍锋
【作者单位】人民教育出版社课程教材研究所;中国人民大学附属中学朝阳学校【正文语种】中文
【中图分类】G633.6
【相关文献】
1.从蒙提霍尔问题到全概率公式--关于全概率公式的教学设计
2.概率论与数理统计在线课程教学设计与创新--以“全概率公式与贝叶斯公式”为例
3.“概率论与数理统计”课程的教学创新探讨——以全概率公式和贝叶斯公式为例
4.吃透教材、领悟意图、设计教学--条件概率与全概率公式小节教学案例
5.数学建模视角下的概率专题复习探索——以“全概率公式与概率递推模型”的教学设计为例
因版权原因，仅展示原文概要，查看原文内容请购买。

张继平用有限人生发掘数学的无限魅力

他在北京大学数学课程改革方面大胆尝试，推出了数学类通识课程。

他深深陶醉于数学之美，并致力于让更多人体会到数学的乐趣，改变了他们对数学枯燥艰涩的印象。

他就是中国科学院院士、北京国际数学研究中心副主任、北京大学数学科学学院教授张继平老师。

一、恩师带领步入学科最前沿1958年，张继平出生在山西曲沃的小山村。

8岁那年，他回到了鲁西南的老家，家庭文化的熏陶使得张继平奠定了良好的学业基础。

1977年恢复高考，张继平被山东大学数学系录取。

本科期间，张继平的学业成绩门门拔尖，考研时，痴迷于代数研究的张继平下定决心要“考到最好的学校，找到最好的老师”。

功夫不负有心人，张继平来到了北京大学数学系投入著名数学家段学复院士的门下。

段学复先生是中国群表示论奠基人，1955年被选为中国科学院院士，他不但把张继平带到有限群表示论研究的前沿，其高尚伟大的人格魅力和品质更教育感染着朴实敦厚的张继平。

张继平动情地回忆，特别令他难忘的是段老师的“认真”与“达观”。

“老师的眼睛近视非常严重，看电视只能模模糊糊地看个影子，但在批改我的博士论文时，从英文拼写到标点符号，所有的问题都在手稿上改得清清楚楚”。

还有一次，张继平偶然看到了老师在1955年任系主任张继平登上北京大学与央视《开讲啦》节目联手打造的“一起开讲”北大专场课堂上的张继平差分(differential)定义：一种改进无线电导航系统定位精度的技术。

通过确定已知位置的定位误差，随后将该误差或校正因子发送给在相同地理区域内使用同一个无线电导航系统信号源的用户，求差后消除或减小其定位误差。

【北斗卫星·科技名词】张继平院士近照张继平院士与菲尔茨奖获得者Thompson 讨论问题的重要难题，被认为是模表示论十大公开问题之第6问题，Brauer第12问题的也主要与此相关。

1986年在美国Arcata举办的国际表示论会议上，研究生张继平关于亏零p-块存在性的工作由石生明老师报告后引起广泛的关注。

“数论大神”张伟

“数论大神”张伟作者：张静来源：《海外星云》2019年第17期“我就不陪你上去了，加上排队要一两个小时，我在附近的咖啡馆等你吧。

”在陪同学参观了哥大校园和美国自然博物馆之后，张伟在帝国大厦周边的咖啡馆里，拿起餐巾纸开始了数学演算，同学目瞪口呆：“没有人能够体会我当时震惊的心情，我的上颌与下颌估计跟自然历史博物馆那个恐龙骨架的头颅没拼合好之前是一样的。

”类似的场景还出现在回家的火车上，即使是路途中休息的时间他的大脑也从不停歇，“突然间，所有东西都能连接在一起，这绝对是一个让人感叹‘原来如此’的时刻。

”10年前在火车上的构想像是一块拼图，在经过这些年的“耐心拼装”之后，终于在最近完成了一篇论文。

不知道张伟的演算笔迹还被留在过什么地方的什么平面上，可能就是这些零零碎碎的推导验证造就了一代“数学大神”：在29岁荣获SASTRA拉马努金奖，34岁破格成为哥伦比亚大学数学系终身教授，35岁斩获晨兴数学奖，37岁担任MIT数学系正教授，并荣获科学突破奖。

近日，张伟因在算术几何与自守形式的算术面向上的突破性工作获得本年度克雷研究奖（Clay Research Awards），成为获此殊荣的首位华人数学家。

张伟就读的高中离他的家乡有500多公里，这并没有阻挡他追求数学的热情。

他出生在四川达州的偏远乡村。

小学四年级就开始感叹：“就是纯粹的好奇，一些数学问题怎么就被设置地那么精妙！这很美。

”五年级他转入大竹县天成乡小学，当时的数学老师看到了张伟的潜力，便开始让他精读课外习题书。

中学时期，他自己写了自荐信邮寄给成都七中校长，后来幸运地成为1997年成都七中招收的五名外地生之一。

高三那年，在申请北大保送的时候，张伟就决定未来要“成为数学家”。

2000年，Andrew Wiles早在五年前就证明了的“费马大定理”在当时仍然是相对新颖的课题，并引起了数学界很大的反响。

这一年张伟刚刚进入北大，北大的一位教授深谙教育之道，通过“深入浅出”的教学方式为张伟打开了数学新世界的大门，张伟在这一年就开始接触尖端科学和像“费马大定理”这样的前沿学术研究。

北大数学系考研复试概率论

北大数学系考研复试概率论
在北大数学系考研复试中，概率论是一个重要的科目。

概率论是数学的一个分支，研究随机事件和概率的理论。

考研复试中对概率论的要求主要包括以下几个方面。

首先，考生需要熟练掌握概率论的基本概念和基本定理。

例如，要清楚地理解概率的定义、条件概率、独立性等基本概念，掌握常用的概率分布如二项分布、正态分布等，并了解它们的性质和应用。

此外，还需要熟悉概率论的基本定理，如大数定律、中心极限定理等。

其次，考生需要掌握概率论的常用方法和技巧。

概率论是一门较为抽象的学科，需要运用一些具体的方法和技巧进行求解。

例如，在计算概率时，可以利用排列组合、条件概率的公式、贝叶斯公式等进行转换和计算；在计算期望和方差时，可以利用数学期望和方差的性质，以及线性性质等进行推导和计算。

此外，考生还需要具备一定的证明能力。

概率论中有一些重要的定理和命题，对于这些定理和命题，考生需要理解其证明过程，并且能够根据题目要求进行证明。

要注意的是，在进行证明时，要注意严谨性，避免逻辑错误和漏洞。

最后，考生还需能够运用概率论解决实际问题。

概率论是一门实用的学科，能够应用到生活和科学研究的各个领域。

考生需要掌握如何将概率论的知识应用到具体的问题中，进行分析和求解。

这就要求考生具备一定的数学建模能力和实际问题分析能力。

总之，北大数学系考研复试中的概率论是一个相对难度较大的科目，考生需要充分准备，掌握概率论的基本概念和定理，熟练掌握常用的方法和技巧，具备一定的证明能力，并能够将概率论的知识应用到实际问题中。

只有全面而扎实地掌握概率论的知识，才能在复试中取得好成绩。

概率论.pdf

考研数学问题咨询张伟老师新浪微博张伟老师仰望星空E-mail: zwpku@参考教材概率论与数理统计第四版（浙江大学主编）重要定理、性质、公式、结论经典例题、重要例题及不需要做的题目第一章概率论的基本概念（考小题）第一节随机试验（了解）第二节样本空间，随机事件（了解）第三节频率与概率（频率可以不用看，了解）第四节等可能概率（古典概论）（难点非重点，做一些基本题即可）第五节条件概率（重要，考小题为主，考大题有时会用到）第六节独立性（重要，考小题为主，大题经常会用到）第二章随机变量及其分布（至少考小题，考大题一定会用到）第一节随机变量（了解）第二节离散型随机变量及其分布律（重要，经常考）第三节随机变量的分布函数（重要，每年必考）第四节连续型随机变量及其概率密度（重要，每年必考）第五节随机变量的函数分布（重要，大题的命题点）第三章多维随机变量及其分布（考大题可能性极大）第一节二维随机变量（了解）第二节边缘分布（理解）第三节条件分布（理解）第四节概率独立的随机变量（重要，基本每年必考）第五节两个随机变量函数的分布（重要，大题的经典命题点）第四章随机变量的数字特征（重要）第一节数学期望（重要，每年必考）第二节方差（重要，每年必考）第三节协方差与相关系数（重要，经常考）第四节矩，协方差矩阵（矩，了解，协方差矩阵不用看）.第五章大数定律及中心极限定理(了解)第一节大数定律(了解,关注定律的前提条件与结论)第二节中心极限定理（了解，关注定理的前提条件与结论）考研数学问题咨询张伟老师新浪微博张伟老师仰望星空E-mail: zwpku@第六章样本及抽样分布（考小题为主）第一随机样本（了解，其中有重要概念，简单随机样本）第二直方图和箱线图（重要，考小题）第三抽样分布（重要，考小题）第七章参数估计（重要，考大题经典章节）第一节点估计（极其重要，矩估计：重点非难点，最大似然估计（重点且难点））第二节基于截尾样本的最大似然估计（不用看）第三节估计量的评选标准（数一重要，数三不用看）第四区间估计（数一理解，考的比较少）第五正态总体均值与方差的区间估计（数一理解，考的比较少）第六（０－１）分布参数的区间估计（不用看）第七单侧置信区间（理解，一般不考）（第四－第七，只有数一考，数三均不用看）第八章假设检验（理解，一般不考，只有数一有要求，数三不考）第一假设检验（理解）第二正态总体均值的假设检验（理解）第三正态总体方差的假设检验（理解）第四，第五，第六，第七，第八（均不用看）．考研数学问题咨询张伟老师新浪微博张伟老师仰望星空E-mail: zwpku@考研数学概率统计的重点难点必考点及重要例题和习题不用做的例题和习题第一章概率论的基本概念P３最后４行的小写字体不用看P５例３不用做（一）频率不用看P6-7 例 1 与例 2 均不用做，P7 概率重点看P9 等可能概率一般都不单独考，考大题经常会用到，P13 例 6 不用做，P14 例 8 不用做 P14 条件概率重点看，P15 例 2 不用做，P16 例 3 不用做，P17 例 4 重点做P17（三）全概率公式和贝叶斯公式为难点P19例5不用做，P20独立性为考研数学的绝对重点，P22例2与例3均不用做P23例4重点做P24-29 不用做的习题是 1、5、6、10、12、15、16、18、19、20、21、23、25、26、29、32、34、35、38、39、40第二章随机变量及其分布P30 例 1 不用看P37 泊松定理只需要记住结论，证明可以不用看P38 随机变量的分布函数为考研必考概念P42 连续性随机变量概率密度为考研必考点P50 随机变量的函数的分布是考大题的重要命题点P53 例 5 不用做P55-59 不用做的习题 1、5、6、7、9、10、11、13、15、16、19、22、27、28、30、31、38、39第三章多位随机变量及其分布P63 性质 4 的解释不用看P65 例 1 不用做，P66 例 3 重点做一下（提升计算能力）P68 例 1 不用做，P72 相互独立的随机变量为重点章节P76 两个随机变量的函数的分布为考大题的重要备考章节P78 例 3 不用做，P81 例 5 不用做P84-89 不用做的习题是 3、6、7、10、11、12、13、28、31第四章随机变量的数字特征P91 例 1 不用做，P92 例 3 与例 4 不用做，P93 例 5 不用做P95 中间的证明不用看，P96 例 8 与例 10 不用做P97 例 11 不用做，P100 例 13 不用做，P105 不用做P107 XY的两条重要性质的推导及含义不用看考研数学问题咨询张伟老师新浪微博张伟老师仰望星空E-mail: zwpku@考研数学问题咨询张伟老师新浪微博张伟老师仰望星空E-mail: zwpku@P108 只需要看前四行即只需要记住定理 4 证明可以不用看P109 例 2 重点做（提升计算能力）P110 矩为一般考点，协方差矩阵不用看P113-118 不用做的习题是 1.4.5.12.13.15.16.18.19.22.23.24.35.36.37.38第五章大数定律及中心极限定理（难点非重点）P124 例 1 不用做P126-127 不用做的习题是 2、4、5、10、11、13第六章样本及抽样分布（一般考点考小题）P130 第四行简单随机样本为重要概念P130 第二节直方图和箱线图不用看P135 第三节抽样分布（考小题），P136 统计量定义及几个常见统计量要重点看而且要牢记其表达式P137 经验分布函数只有数三同学稍微了解P138-141 数理统计所有的三大分布的典型模式要牢记但三种分布的概率密度表达式可以不用记P145-147 定理 2 的证明与推广均不用看P147-148 不用做的习题是 1、5、6、10、11第七章参数估计（数一数三的绝对的重点和难点）P149 点估计数一数三的绝对重点矩估计重点非难点，最大似然估计重点且难点P163-155 例 4 例 5 例 6 重点做P156-158 第二节基于截尾样本的最大似然估计不用看P158 估计量的评选标准数一重点看，数三大纲上虽然没有但建议数三看一下最好P161-168 区间估计，正态总体均值与方差的区间估计，只有数一看，为一般考点P168 0-1 分布参数的区间估计数一数三均不用看P169 单侧置信区间，只有数一看，为一般考点P193-177 数三不用做的习题为 4（3）、6、7、8、9、10、11-27 均不用做数一不用做的习题为4（3）、6、7、8、9、15、17、20、21、22、23、26、27第八章假设检验（数一特有的考点，难点非重点）数一只需要看前四节P178-193从第五节以后均不需要看P218-223 习题只需要做 1、2、3、4 其余的题目可以不用做考研数学问题咨询张伟老师新浪微博张伟老师仰望星空E-mail: zwpku@。

2012年研究生复试名单-公布版

李茂
数学科学学院
二〇一二年三月二日
2
100012012000009
刘松
3
100012012000029
楚天翔
4
100012012000018
李诗宇
5
100012012013798
邵长天
6
100012012010296
杨延展
7
100012012011011
李曦涛
8
100012012013662
孙治龙
9
100012012000017
胡涵
13
100012012000086
杨政
14
100012012000082
徐鸿毅
15
100012012014982
王磊
16
100012012010470
周志国
17
100012012000070
刘巍放
18
100012012015354
程超
应用统计专业硕士复试名单如下：
序号
考生编号
姓名
1
100012012008276
曹寅
5
100012012000064
梁磊
6
100012012000074
任泰
7
100012012000075
商震
8
100012012017268
景龙
9
100012012000063
李阳
10
100012012016499
张宁
11
100012012000083
鄢略峰
12
100012012012979
鲁绍非
数学学院关于2012年硕士生入学考试复试名单

北京大学1996-2021历年数学分析_考研真题试题(1)

x n a z ) d x d y d z 考试科目：数学分析一、（10 分）将函数 f (x ) = arctan2x1- x 2在 x = 0 点展开为幂级数，并指出收敛区间。

+∞ ln(1+ x )二、（10 分）判别广义积分的收敛性： ⎰0 d x 。

x p 三、（15 分）设 f (x ) 在(-∞, +∞) 上有任意阶导数 f (n ) (x ) ，且对任意有限闭区间[a , b ] ，f (n ) (x ) 在[a , b ] 上一致收敛于φ(x )(n → +∞) ，求证：φ(x ) = ce x ， c 为常数。

四、（15 分）设 x n > 0( n = 1, 2 ⋅⋅⋅) 及 lim x n = a ，用ε - N 语言证明： lim= 。

n →+∞n →+∞五、（15 分）求第二型曲面积分⎰⎰ (x d y d z + cos y d z d x + d x d y ) ，其中S 为Sx 2 + y 2 + z 2 = 1的外侧。

∂f ∂g 六、（20 分）设 x = f (u , v ) ， y = g (u , v ) ，w = w (x , y ) 有二阶连续偏导数，满足 ∂u = ∂v，∂f = - ∂g∂v ∂u ∂2w ， ∂x 2 ∂2w + = 0 ，证明： ∂y 2（1） ∂2( fg ) ∂u 2∂2( fg ) + = 0 ， ∂v 2（2） w (u , v ) = w ( f (u , v ), g (u , v )) 满足 ∂2w ∂u 2 ∂2w+ = 0 。

∂v 2七、（15 分）计算三重积分⎰⎰⎰Ω:x 2+ y 2 + z 2 ≤2 z(x 2 + y 2 +25/ 2。

n 1+ a nx ∞∑ ⎰ y+ x = = = 考试科目：数学分析一、（26 分）选一个最确切的答案，填入括号中：1.设 f (x ) 定义在[a , b ] 上，若对任意的 g ∈ R ([a , b ]) ，有 f ⋅ g ∈ R ([a , b ]) ，则（）A. f ∈ R ([a , b ]) ，B. g ∈ C ([a , b ]) ，C. f 可微，D. f 可导。

张伟概率讲义

学府考研培训学校
·2013 年强化班讲义·
【概率统计部分】
主讲：张伟
学府考研培训学校 2012 年 7 月

0
概率论与数理统计
概率论和数理统计六大类考点 (1) 随机事件和概率 (2) 一维随机变量及其分布 (3) 多维随机变量及其分布 (4) 随机变量的数字特征 (5) 大数定律和中心极限定理 (6) 数理统计的基本概念、参数估计和假设检验
( A) uα
2
(B)
u
1−
α
2
(C) u1−α
2
(D) u1−α
7
例18
设f1(x)为标准正态分布的概率密度, f2(x)为[−1,3]上的均匀分布的概率密度,
( A) 与a无关,随λ增大而增大;
(B) 与a无关,随λ增大而减小;
(C) 与λ无关,随a增大而增大;
(D) 与λ无关,随a增大而减小.
例10
⎧1 3,
设随机变量X的概率密度为f (x) = ⎪⎨2 9,
⎪ ⎩
0,
若x ∈[ 0,1 ], 若x ∈[ 3, 6 ],
其他.
若使得P{X ≥ k}= 2 , 则k的取值范围是 ______.
(B)若AB ≠ φ, 则A, B有可能独立. (D)若AB = φ, 则A, B一定不独立.
3
例18 对于任意二事件A和B,已知0 < P( A) < 1, 则 ( A)若A ⊂ B, 则A, B一定不独立. (B)若B ⊂ A, 则A, B一定不独立.
(C)若AB = φ, 则A, B一定不独立. (D)若A = B, 则A, B一定不独立.
(D)1− e−1
2
2
离散型随机变量的概率分布

北大数学考研试题及答案

北大数学考研试题及答案一、选择题（每题5分，共20分）1. 设函数 $ f(x) $ 在区间 $[a, b]$ 上连续，且 $ f(a) = f(b) $，则下列结论正确的是：A. $ f(x) $ 在 $[a, b]$ 上存在零点B. $ f(x) $ 在 $[a, b]$ 上单调递增C. $ f(x) $ 在 $[a, b]$ 上单调递减D. $ f(x) $ 在 $[a, b]$ 上至少存在一个极值点答案：D2. 若 $\lim_{x \to 0} \frac{\sin x}{x} = 1$，则下列说法正确的是：A. $\lim_{x \to 0} \frac{\sin 2x}{x} = 2$B. $\lim_{x \to 0} \frac{\sin 2x}{2x} = 1$C. $\lim_{x \to 0} \frac{\sin 2x}{2x} = 2$D. $\lim_{x \to 0} \frac{\sin 2x}{2x} = 0$答案：B3. 设 $ A $ 是 $ 3 \times 3 $ 矩阵，且 $ \text{det}(A) =1 $，则 $ A $ 的逆矩阵 $ A^{-1} $ 的行列式值为：A. 0B. 1C. -1D. 3答案：B4. 若 $\int_{0}^{1} f(x) \, dx = 2$，则 $\int_{0}^{1} xf(x) \, dx$ 的值为：A. 1B. 2C. 3D. 4答案：A二、填空题（每题5分，共20分）1. 设 $ f(x) = x^3 - 6x^2 + 11x - 6 $，求 $ f'(x) $ 的值为 $ x^2 - 4x + 11 $。

2. 若 $\lim_{x \to 0} \frac{e^x - 1}{x} = 1$，则 $\lim_{x\to 0} \frac{e^{2x} - 1}{2x} = $。

考研二人组完整版

考研二人组完整版
【实用版】
目录
1.考研二人组的概念和背景
2.考研二人组的成员和特点
3.考研二人组的创作过程和成果
4.考研二人组的影响和评价
正文
考研二人组是指由两名年轻人组成的一个考研团队，他们以幽默、搞笑的方式分享考研经验和知识，为广大考研学子提供了一个轻松愉快的学习平台。

考研二人组的成员是张伟和刘明，两人都是具有丰富考研经验的学长。

张伟擅长用生动形象的语言讲解复杂的知识点，而刘明则善于通过有趣的实例帮助大家理解和记忆。

他们的视频不仅内容丰富，而且形式多样，涵盖了考研的各个方面，如数学、英语、政治等。

考研二人组的创作过程可以说是充满艰辛和挑战的。

他们需要花费大量的时间和精力去整理资料、策划视频、拍摄和剪辑。

尽管如此，他们仍然坚持不懈地为大家提供高质量的学习资源。

正是这种坚持和付出，使得他们的作品在短时间内迅速获得了广泛的关注和认可。

考研二人组的成果无疑是显著的。

他们的视频在各大视频平台上收获了数百万的点击量，为无数考研学子提供了宝贵的学习资源。

不仅如此，他们还通过自己的努力和影响力，帮助了许多学子成功考上了理想的研究生院。

考研二人组的影响和评价也是颇高的。

他们的作品不仅受到了广大考研学子的喜爱，还得到了许多教育专家和学者的认可。

他们以自己的实际
行动，向大家展示了一个轻松愉快的学习方式，并激励着更多的人去追求自己的梦想。

总的来说，考研二人组是一个充满正能量的团队。

他们的作品不仅为大家提供了学习的便利，还传递了一种积极向上的人生态度。