数字信号处理实验二.doc

数字信号处理实验报告(实验二)

实验二时域采样与频域采样1. 实验目的：(1) 掌握模拟信号采样前后频谱的变化，以及如何选择采样频率才能使采样后的信号不丢失信息。

(2) 掌握频率域采样会引起时域周期化的概念，以及频率域采样定理及其对频域采样点数选择的指导作用。

(3) 会用MATLAB 语言进行时域抽样与信号重建的方法，以及频域抽样与恢复时程序的编写方法。

2. 实验原理：了解时域采样定理的要点，理解理想采样信号)(ˆt xa 和模拟信号)(t x a 之间的关系，了解频域采样定理的要点，掌握这两个采样理论的结论：“时域采样频谱周期延拓，频域采样时域信号周期延拓”。

3. 实验内容：（1）时域采样理论的验证。

给定模拟信号，)()sin()(0t u t Ae t x t a Ω=-α式中A=444.128，α=502π，0Ω=502πrad/s（2）用DFT(FFT)求该模拟信号的幅频特性，选取三种采样频率，以验证时域采样理论。

（3）编写实验程序，计算)(1n x 、)(2n x 和)(3n x 的幅度特性，并绘图显示。

观察分析频谱混叠失真。

（4）频域采样理论的验证。

给定信号如下：⎪⎩⎪⎨⎧≤≤-≤≤+=其它02614271301)(n n n n n x（5）编写程序分别对频谱函数()FT[()]j X e x n ω=在区间]2,0[π上等间隔采样32和16点，得到)()(1632k X k X 和，再分别对)()(1632k X k X 和进行32点和16点IFFT ，得到)()(1632n x n x 和。

（6）分别画出()j X e ω、)()(1632k X k X 和的幅度谱，并绘图显示x(n)、)()(1632n x n x 和的波形，进行对比和分析，验证总结频域采样理论。

4. 思考题：如果序列x(n)的长度为M ，希望得到其频谱()j X e ω在]2,0[π上的N 点等间隔采样，当N<M 时，如何用一次最少点数的DFT 得到该频谱采样？答：将长序列分段分段计算，这种分段处理方法有重叠相加法和重叠保留法两种。

数字信号处理实验报告

数字信号处理实验报告实验一：混叠现象的时域与频域表现实验原理：当采样频率Fs不满足采样定理，会在0.5Fs附近引起频谱混叠，造成频谱分析误差。

实验过程：考虑频率分别为3Hz，7Hz，13Hz 的三个余弦信号，即：g1(t)=cos(6πt), g2(t)=cos(14πt), g3(t)=cos(26πt),当采样频率为10Hz 时，即采样间隔为0.1秒，则产生的序列分别为：g1[n]=cos(0.6πn), g2[n]=cos(1.4πn), g3[n]=cos(2.6πn)对g2[n]，g3[n] 稍加变换可得：g2[n]=cos(1.4πn)＝cos((2π-0.6π)n)= cos(0.6πn)g3[n]=cos(2.6πn)= cos((2π+0.6π)n)=cos(0.6πn)利用Matlab进行编程：n=1:300;t=(n-1)*1/300;g1=cos(6*pi*t);g2=cos(14*pi*t);g3=cos(26*pi*t);plot(t,g1,t,g2,t,g3);k=1:100;s=k*0.1;q1=cos(6*pi*s);q2=cos(14*pi*s);q3=cos(26*pi*s);hold on; plot(s(1:10),q1(1:10),'bd');figuresubplot(2,2,1);plot(k/10,abs(fft(q1)))subplot(2,2,2);plot(k/10,abs(fft(q2)))subplot(2,2,3);plot(k/10,abs(fft(q3)))通过Matlab软件的图像如图所示：如果将采样频率改为30Hz，则三信号采样后不会发生频率混叠，可运行以下的程序，观察序列的频谱。

程序编程改动如下：k=1:300;q=cos(6*pi*k/30);q1=cos(14*pi*k/30);q2=cos(26*pi*k/30);subplot(2,2,1);plot(k/10,abs(fft(q)))subplot(2,2,2);plot(k/10,abs(fft(q1)))subplot(2,2,3);plot(k/10,abs(fft(q2)))得图像：问题讨论：保证采样后的信号不发生混叠的条件是什么？若信号的最高频率为17Hz，采样频率为30Hz，问是否会发生频率混叠？混叠成频率为多少Hz的信号？编程验证你的想法。

数字信号处理实验报告

《数字信号处理》—实验指导数字信号处理课程组电子与信息工程学院班级：姓名：学号：综合评定：成绩：指导教师签字：实验一典型离散信号及其MATLAB 实现一、实验目的1．掌握MATLAB 语言的基本操作，学习基本的编程功能。

2．掌握MATLAB 产生常用离散时间信号的编程方法。

3．掌握MATLAB 计算卷积的方法。

二、实验原理（一）MATLAB 常用离散时间信号1．单位抽样序列:⎩⎨⎧=01)(n δ 00≠=n n在MATLAB 中可以利用zeros()函数实现。

;1)1();,1(==x N zeros x如果)(n δ在时间轴上延迟了k 个单位，得到)(k n -δ即：⎩⎨⎧=-01)(k n δ 0≠=n kn2．单位阶跃序列:⎩⎨⎧01)(n u<≥n n 在MATLAB 中可以利用ones()函数实现。

);,1(N ones x =3．正弦序列:)/2sin()(ϕπ+=Fs fn A n x在MATLAB 中:)/***2sin(*1:0fai Fs n f pi A x N n +=-=4．复正弦序列:n j e n x ϖ=)(在MATLAB 中:)**ex p(1:0n w j x N n =-=5．指数序列:na n x =)(在MATLAB 中:na x N n .^1:0=-=6.y=fliplr(x)——信号的翻转； y=square(x)——产生方波信号y=sawtooth(x)——产生锯齿波信号； y=sinc(x)——产生sinc 函数信号。

（二）离散时间信号的卷积由于系统的零状态响应是激励与系统的单位取样响应的卷积，因此卷积运算在离散时间信号处理领域被广泛应用。

离散时间信号的卷积定义为∑∞-∞=-==m m n h m x n h n x n y )()()(*)()(可见，离散时间信号的卷积运算是求和运算，因而常称为“卷积和”。

MATLAB 求离散时间信号卷积和的命令为conv ，其语句格式为y=conv(x,h)其中，x 与h 表示离散时间信号值的向量；y 为卷积结果。

数字信号处理实验(吴镇扬)答案-2

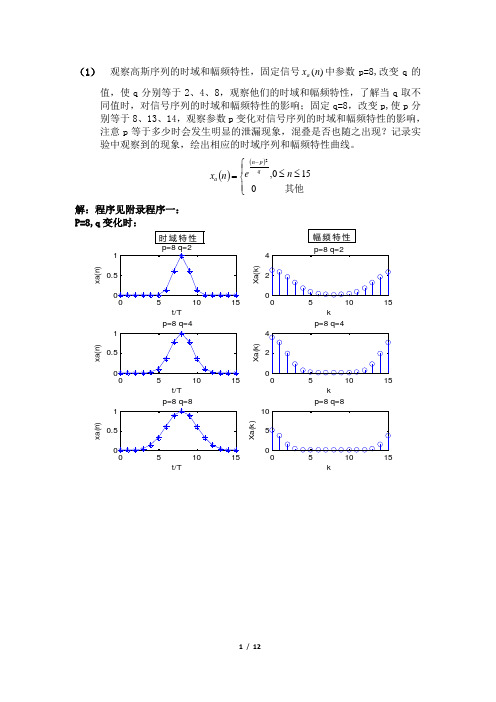
（1）观察高斯序列的时域和幅频特性，固定信号)(n x a 中参数p=8,改变q 的值，使q 分别等于2、4、8，观察他们的时域和幅频特性，了解当q 取不同值时，对信号序列的时域和幅频特性的影响；固定q=8，改变p,使p 分别等于8、13、14，观察参数p 变化对信号序列的时域和幅频特性的影响，注意p 等于多少时会发生明显的泄漏现象，混叠是否也随之出现？记录实验中观察到的现象，绘出相应的时域序列和幅频特性曲线。

()()⎪⎩⎪⎨⎧≤≤=-其他0150,2n e n x q p n a解：程序见附录程序一：P=8,q 变化时：t/T x a (n )k X a (k )t/T x a (n )p=8 q=4k X a (k )p=8 q=4t/Tx a (n )p=8 q=8kX a (k )p=8 q=8幅频特性时域特性t/T x a (n )p=8 q=8k X a (k )p=8 q=8t/T x a (n )51015k X a (k )p=13 q=8t/Tx a (n )p=14 q=851015kX a (k )p=14 q=8时域特性幅频特性分析：由高斯序列表达式知n=p 为期对称轴；当p 取固定值时，时域图都关于n=8对称截取长度为周期的整数倍，没有发生明显的泄漏现象；但存在混叠，当q 由2增加至8过程中，时域图形变化越来越平缓，中间包络越来越大，可能函数周期开始增加，频率降低，渐渐小于fs/2,混叠减弱；当q 值固定不变，p 变化时，时域对称中轴右移，截取的时域长度渐渐地不再是周期的整数倍，开始无法代表一个周期，泄漏现象也来越明显，因而图形越来越偏离真实值，p=14时的泄漏现象最为明显，混叠可能也随之出现；（2）观察衰减正弦序列的时域和幅频特性，a=0.1,f=0.0625,检查谱峰出现的位置是否正确，注意频谱的形状，绘出幅频特性曲线，改变f ，使f 分别等于0.4375和0.5625，观察这两种情况下，频谱的形状和谱峰出现的位置，有无混叠和泄漏现象？说明产生现象的原因。

数字信号处理实验报告一二

数字信号处理课程实验报告实验一离散时间信号和系统响应一. 实验目的1. 熟悉连续信号经理想采样前后的频谱变化关系，加深对时域采样定理的理解2. 掌握时域离散系统的时域特性3. 利用卷积方法观察分析系统的时域特性4. 掌握序列傅里叶变换的计算机实现方法，利用序列的傅里叶变换对离散信号及系统响应进行频域分析二、实验原理1. 采样是连续信号数字化处理的第一个关键环节。

对采样过程的研究不仅可以了解采样前后信号时域和频域特性的变化以及信号信息不丢失的条件，而且可以加深对离散傅里叶变换、Z 变换和序列傅里叶变换之间关系式的理解。

对连续信号()a x t 以T 为采样间隔进行时域等间隔理想采样，形成采样信号：式中()p t 为周期冲激脉冲，()a x t 为()a x t 的理想采样。

()a x t 的傅里叶变换为()a X j Ω：上式表明将连续信号()a x t 采样后其频谱将变为周期的，周期为Ωs=2π/T 。

也即采样信号的频谱()a X j Ω是原连续信号xa(t)的频谱Xa(jΩ)在频率轴上以Ωs 为周期，周期延拓而成的。

因此，若对连续信号()a x t 进行采样，要保证采样频率fs ≥2fm ，fm 为信号的最高频率，才可能由采样信号无失真地恢复出原模拟信号ˆ()()()a a xt x t p t =1()()*()21()n a a a s X j X j P j X j jn T π∞=-∞Ω=ΩΩ=Ω-Ω∑()()n P t t nT δ∞=-∞=-∑计算机实现时，利用计算机计算上式并不方便，因此我们利用采样序列的傅里叶变换来实现，即而()()j j n n X e x n e ωω∞-=-∞=∑为采样序列的傅里叶变换2. 时域中，描述系统特性的方法是差分方程和单位脉冲响应，频域中可用系统函数描述系统特性。

已知输入信号，可以由差分方程、单位脉冲响应或系统函数求出系统对于该输入信号的响应。

(完整版)数字信号处理实验二

xlabel('时间序号n'); ylabel('振幅');
y = filter(num,den,x,ic);
yt = a*y1 + b*y2;
d = y - yt;
subplot(3,1,1)
stem(n,y);
ylabel('振幅');
title('加权输入: a \cdot x_{1}[n] + b \cdot x_{2}[n]的输出');
subplot(3,1,2)
%扫频信号通过2.1系统：
clf;
n = 0:100;
s1 = cos(2*pi*0.05*n);
s2 = cos(2*pi*0.47*n);
a = pi/2/100;
b = 0;
arg = a*n.*n + b*n;
x = cos(arg);
M = input('滤波器所需的长度=');
num = ones(1,M);
三、实验器材及软件
1.微型计算机1台
2. MATLAB 7.0软件
四、实验原理
1.三点平滑滤波器是一个线性时不变的有限冲激响应系统，将输出延时一个抽样周期，可得到三点平滑滤波器的因果表达式，生成的滤波器表示为
归纳上式可得
此式表示了一个因果M点平滑FIR滤波器。
2.对线性离散时间系统，若y1[n]和y2[n]分别是输入序列x1[n]和x2[n]的响应，则输入
plot(n, y);
axis([0, 100, -2, 2]);
xlabel('时间序号 n'); ylabel('振幅');

数字信号处理实验报告二与三

实验二用FFT 进行谱分析一.实验目的：1 进一步加深DFT 算法原理和基本性质的理解（因为FFT 只是DFT 的一种快速算法，所以FFT 的运算结果必然满足DFT 的基本性质）。

熟悉FFT 程序结构及编程方法。

2 熟悉应用FFT 对确定信号进行谱分析方法，熟悉FFT 算法原理和FFT 子程序的应用。

3 学习用FFT 对连续信号和时域离散信号进行谱分析的方法，了解可能出现的分析误差及其原因，以便在实际中正确应有FFT 。

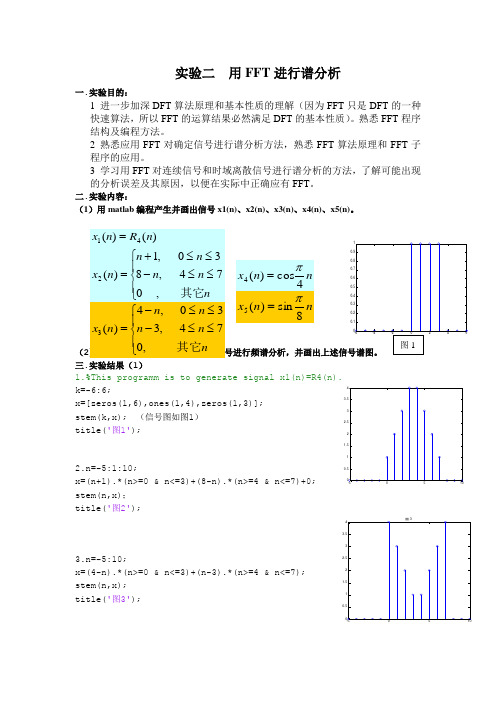
二.实验内容：（1）用matlab 编程产生并画出信号x1(n)、x2(n)、x3(n)、x4(n)、x5(n)。

（2）用matlab 编制FFT 函数对上述信号进行频谱分析，并画出上述信号谱图。

三.实验结果（1）1.%This programm is to generate signal x1(n)=R4(n).k=-6:6;x=[zeros(1,6),ones(1,4),zeros(1,3)];stem(k,x); （信号图如图1） title('图1');2.n=-5:1:10;x=(n+1).*(n>=0 & n<=3)+(8-n).*(n>=4 & n<=7)+0; stem(n,x)； title('图2');3.n=-5:10;x=(4-n).*(n>=0 & n<=3)+(n-3).*(n>=4 & n<=7); stem(n,x); title('图3');-6-4-2024600.10.20.30.40.50.60.70.80.91⎪⎩⎪⎨⎧≤≤-≤≤+==n n n n n n x n R n x 其它,074,830,1)()()(241⎪⎩⎪⎨⎧≤≤-≤≤-=n n n n n n x 其它,074,330,4)(3n n x 4cos )(4π=n n x 8sin )(5π=图1-5051000.511.522.533.54-5051000.511.522.533.54图34.n=-10:10; x=cos(pi/4*n); stem(n,x); title('图4');5.n=-10:10;x=sin(pi/8*n); stem(n,x); title('图5');实验结果（2）: FFT 算法function y=myditfft(x) % y=myditfft(x)% 本程序对输入序列 x 实现DIT-FFT 基2算法，点数取大于等于x 长度的2的幂次 % x 为给定时间序列% y 为x 的离散傅立叶变换m=nextpow2(x);N=2^m; % 求x 的长度对应的2的最低幂次m if length(x)<N;% 若x 的长度不是2的幂，补零到2的整数幂 x=[x,zeros(1,N-length(x))]; endnxd=bin2dec(fliplr(dec2bin([1:N]-1,m)))+1; % 求1:2^m 数列的倒序 y=x(nxd); % 将x 倒序排列作为y 的初始值 for mm=1:m; % 将DFT 作m 次基2分解,从左到右，对每次分解作DFT 运算 Nmr=2^mm;u=1; % 旋转因子u 初始化为WN^0=1WN=exp(-i*2*pi/Nmr); % 本次分解的基本DFT 因子WN=exp(-i*2*pi/Nmr) for j=1:Nmr/2; % 本次跨越间隔内的各次蝶形运算for k=j:Nmr:N; % 本次蝶形运算的跨越间隔为Nmr=2^mm kp=k+Nmr/2; % 确定蝶形运算的对应单元下标 t=y(kp)*u; % 蝶形运算的乘积项 y(kp)=y(k)-t; % 蝶形运算 y(k)=y(k)+t; % 蝶形运算 endu=u*WN; % 修改旋转因子,多乘一个基本DFT 因子WN end-10-8-6-4-2246810-1-0.8-0.6-0.4-0.200.20.40.60.81图4-10-8-6-4-2246810-1-0.8-0.6-0.4-0.200.20.40.60.81图5end 1.k=-6:6;x=[zeros(1,6),ones(1,4),zeros(1,3)]; y=myditfft(x); k=-6:9; stem(k,y); xlabel('m'); ylabel('X[M]');title('FFT 图');2.n=-5:1:10;x=(n+1).*(n>=0 & n<=3)+(8-n).*(n>=4 & n<=7)+0;y=myditfft(x); stem(n,y); xlabel('n'); ylabel('X[M]'); title('FFT 图'); 3.n=-5:10;x=(4-n).*(n>=0 & n<=3)+(n-3).*(n>=4 & n<=7); y=myditfft(x); stem(n,y); xlabel('n'); ylabel('X[M]'); title('FFT3'); 4.n=-10:10;x=cos(pi/4*n); y=myditfft(x); n=-10:21; stem(n,y); xlabel('n'); ylabel('X[M]'); title('FFT4'); 5.n=-10:10;x=sin(pi/8*n); y=myditfft(x); n=-10:21; stem(n,y); xlabel('n'); ylabel('X[M]'); title('FFT5');-6-4-20246810-4-3-2-101234m X [M ]FFT 图-5510-20-15-10-505101520nX [M ]FFT 图-5510-10-55101520nX M FFT3-10-50510152025-4-3-2-1012345n X [M ]FFT4-10-50510152025-6-4-22468nX [M ]FFT5四.简要回答以下问题：①在N=8时，x2(n)和x3(n)的幅频特性会相同吗？为什么？N=16呢？答：不相同。

数字信号处理实验报告一二

数字信号处理课程实验报告实验一离散时间信号和系统响应一. 实验目的1. 熟悉连续信号经理想采样前后的频谱变化关系，加深对时域采样定理的理解2. 掌握时域离散系统的时域特性3. 利用卷积方法观察分析系统的时域特性4. 掌握序列傅里叶变换的计算机实现方法，利用序列的傅里叶变换对离散信号及系统响应进行频域分析二、实验原理1. 采样是连续信号数字化处理的第一个关键环节。

对采样过程的研究不仅可以了解采样前后信号时域和频域特性的变化以及信号信息不丢失的条件，而且可以加深对离散傅里叶变换、Z 变换和序列傅里叶变换之间关系式的理解。

对连续信号()a x t 以T 为采样间隔进行时域等间隔理想采样，形成采样信号：式中()p t 为周期冲激脉冲，()a x t 为()a x t 的理想采样。

()a x t 的傅里叶变换为()a X j Ω：上式表明将连续信号()a x t 采样后其频谱将变为周期的，周期为Ωs=2π/T 。

也即采样信号的频谱()a X j Ω是原连续信号xa(t)的频谱Xa(jΩ)在频率轴上以Ωs 为周期，周期延拓而成的。

因此，若对连续信号()a x t 进行采样，要保证采样频率fs ≥2fm ，fm 为信号的最高频率，才可能由采样信号无失真地恢复出原模拟信号ˆ()()()a a xt x t p t =1()()*()21()n a a a s X j X j P j X j jn T π∞=-∞Ω=ΩΩ=Ω-Ω∑()()n P t t nT δ∞=-∞=-∑计算机实现时，利用计算机计算上式并不方便，因此我们利用采样序列的傅里叶变换来实现，即而()()j j n n X e x n e ωω∞-=-∞=∑为采样序列的傅里叶变换2. 时域中，描述系统特性的方法是差分方程和单位脉冲响应，频域中可用系统函数描述系统特性。

已知输入信号，可以由差分方程、单位脉冲响应或系统函数求出系统对于该输入信号的响应。

数字信号处理实验1--5含代码

数字信号处理实验1--5含代码实验一离散时间信号的时域分析 1. 在MATLAB中利用逻辑关系式n,,0来实现序列，显示范围。

(产生如下，，,n,nn,n,n012图所示的单位脉冲信号的函数为impseq(n0,n1,n2)，程序如示例所示),3,n,10并利用impseq函数实现序列:; ，，，，，，yn,2,n,3，,n,6，，xn1nnnn120源代码:impseq.mfunction y=impseq(n0,n1,n2)n=[n1:n2]y=[(n-n0)==0]exp01-1.mfunction impseq(n0,n1,n2)n=-3:1:10y=2*impseq(3,-3,10)+impseq(6,-3,10);stem(n,y)n,,0，，2. 在MATLAB中利用逻辑关系式来实现序列，显示范围。

(自己编写un,nn,n,n012产生单位阶跃信号的函数，函数命名为stepseq(n0,n1,n2)) 并利用编写的stepseq函数实现序列: ，，，，，，yn,un，2，un,2,5,n,10源代码:stepseq.mfunction y=stepseq(n0,n1,n2)n=n1:1:n2y=[(n-n0)>=0]exp01-2.mfunction stepseq(n0,n1,n2)n=-5:1:20y=stepseq(-2,-5,20)+stepseq(2,-5,20)stem(n,y)3. 在MATLAB中利用数组运算符“.^”来实现一个实指数序列。

如: n ，，，，xn,0.30,n,15源代码:n=0:1:15;x=0.3.^nstem(n,x)4. 在MATLAB中调用函数sin或cos产生正余弦序列，如:π,, ，，，，xn,3sin0.4πn，，5cos0.3πn0,n,20,,5,,源代码:n=0:1:20x=11*sin(0.3*pi*n+pi/5)+5*cos(0.3*pi*n)stem(n,x)思考题:1.在MATLAB环境下产生单位脉冲序列和单位阶跃序列各有几种方法,如何使用,2.在MATLAB环境下进行序列的相乘运算时应注意什么问题,实验二离散时间系统的时域分析1. 在MATLAB中利用内部函数conv来计算两个有限长序列的卷积。

数字信号处理实验(吴镇扬)答案-2

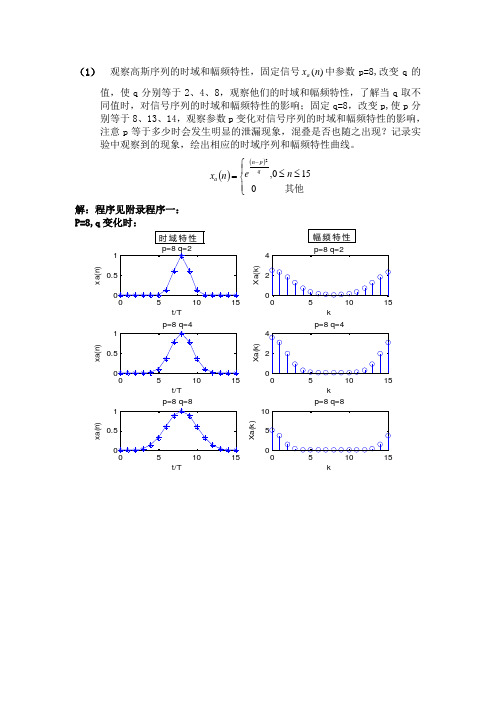
（1）观察高斯序列的时域和幅频特性，固定信号)(n x a 中参数p=8,改变q 的值，使q 分别等于2、4、8，观察他们的时域和幅频特性，了解当q 取不同值时，对信号序列的时域和幅频特性的影响；固定q=8，改变p,使p 分别等于8、13、14，观察参数p 变化对信号序列的时域和幅频特性的影响，注意p 等于多少时会发生明显的泄漏现象，混叠是否也随之出现？记录实验中观察到的现象，绘出相应的时域序列和幅频特性曲线。

()()⎪⎩⎪⎨⎧≤≤=-其他0150,2n e n x q p n a解：程序见附录程序一：P=8,q 变化时：t/T x a (n )p=8 q=2k X a (k )t/T x a (n )p=8 q=4k X a (k )p=8 q=4t/Tx a (n )p=8 q=8kX a (k )p=8 q=8幅频特性时域特性t/T x a (n )p=8 q=8k X a (k )p=8 q=8t/T x a (n )p=13 q=851015k X a (k )p=13 q=8t/Tx a (n )p=14 q=851015kX a (k )p=14 q=8时域特性幅频特性分析：由高斯序列表达式知n=p 为期对称轴；当p 取固定值时，时域图都关于n=8对称截取长度为周期的整数倍，没有发生明显的泄漏现象；但存在混叠，当q 由2增加至8过程中，时域图形变化越来越平缓，中间包络越来越大，可能函数周期开始增加，频率降低，渐渐小于fs/2,混叠减弱；当q 值固定不变，p 变化时，时域对称中轴右移，截取的时域长度渐渐地不再是周期的整数倍，开始无法代表一个周期，泄漏现象也来越明显，因而图形越来越偏离真实值，p=14时的泄漏现象最为明显，混叠可能也随之出现；（2）观察衰减正弦序列的时域和幅频特性，a=0.1,f=0.0625,检查谱峰出现的位置是否正确，注意频谱的形状，绘出幅频特性曲线，改变f ，使f 分别等于0.4375和0.5625，观察这两种情况下，频谱的形状和谱峰出现的位置，有无混叠和泄漏现象？说明产生现象的原因。

数字信号处理第2次实验

信号与系统实验报告（第二次实验）实验一：给定两个序列x1和x2,X1=[0,1,2,3,4,3,2,1,0],起始位置ns1=-2；X2=[2,2,0,0,0,-2,-2],起始位置ns2=2;求它们的和ya及乘积yp,并画出序列x1,x2,ya和yp的图实验要求：分析参考程序，写实验报告，说明编程思路。

参考程序中给出了中间序列y1和y2的计算及图示，握有关函数length、min、max、find的用法，以及有关逻辑操作运算和点乘运算。

掌握有关绘图函数的使用。

参考程序：% 离散信号序列相加和相乘参考程序如下：%x1=[0,1,2,3,4,3,2,1,0];ns1=-2; % 给定x1及ns1x2=[2,2,0,0,0,-2,-2]; ns2=2; % 给定x2及ns2nf1=ns1+length(x1)-1; nf2=ns2+length(x2)-1;ny= min(ns1,ns2):max(nf1,nf2); % y(n)的位置向量y1 = zeros(1,length(ny)); y2 = y1; % 延拓序列初始化y1(find((ny>=ns1)&(ny<=nf1)==1))=x1; % 给y1赋值x1y2(find((ny>=ns2)&(ny<=nf2)==1))=x2; % 给y2 赋值x2ya = y1 + y2; % 序列相加yp = y1.* y2; % 序列相乘subplot(4,2,1), stem(ns1:nf1,x1,'.') % 绘图xlabel('nx1'),ylabel('x1'),axis([-5,10,0,4])subplot(4,2,3), stem(ns2:nf2,x2,'.'),axis([-5,10,-2,2])xlabel('nx2'),ylabel('x2')subplot(4,2,2), stem(ny,y1,'.') % 绘图xlabel('ny'),ylabel('y1')subplot(4,2,4), stem(ny,y2,'.')xlabel('ny'),ylabel('y2')line([ny(1),ny(end)],[0,0]) % 画x轴subplot(4,2,6), stem(ny,ya,'.')xlabel('ny'),ylabel('ya')line([ny(1),ny(end)],[0,0]) % 画x轴subplot(4,2,8), stem(ny,yp,'.')xlabel('ny'),ylabel('yp')line([ny(1),ny(end)],[0,0]) % 画x轴set(gcf,'color','w') % 置图形背景色为白实验结果：编程思路：实验中给出的两个序列的起始位置和长度都不同，对该两个序列进行的操作实际上是对两个矩阵进行的操作，根据矩阵的运算性质可知，要想实现需要的操作，这两个序列起始位置和长度必须相等，所以先要对其进行序列的延拓之后才能进行相应的操作。

数字信号处理实现技术实验报告2

数字信号处理实现技术实验报告书2指导教师：周云学生姓名：实验组号：5实验时间：2016年4月8日一、实验名称：汇编语言-卷积运算 conv二、实验目的：1、学习卷积运算原理，学习卷积的汇编语言实现。

2、熟悉VDSP软件和MATALAB的使用。

三、实验内容：1、学习卷积的基本原理结构2、卷积程序的编写与改写3、数据源生成与测试(可产生正弦，方波，三角波等，进行自相关和互相关运算，记录卷积结果，点数和参数自拟)要求：数据源点数为：50+分组号*2波形类型：分组号%3：0：正弦，1：方波，2：三角波采样率，频率，占空比自定四、实验步骤步骤一使用VDSP打开工程文件conv.dpj选择运行这个project的session，编译及调试步骤二根据组号5，选择产生一个数据源点数为60的三角波利用MATLAB生成三角波和一个复杂波形观察波形，产生波形的数据文件步骤三将生成的数据文件写入VDSP程序中，再次对工程进行编译和调试利用plot功能观测输入、输出序列的波形五、实验结果（一）1、生成三角波和复杂波形源文件的MATLAB程序：clear all;close all;clc;M=60;N=60;x1=tripuls(-33:32,10);z8=conv(x1,x1);t=-2*pi/100:pi/1024:2*pi/100;x2=square(2*pi*30*t,50)x3=conv(x1,x2);x4=conv(x3,x3);figure(1)plot(x1);grid on;title('tripulse');figure(2)plot(z8);grid ontitle('convlution of tripulseanddtripulse');figure(3)plot(x3);grid ontitle('complicated wave');figure(4)plot(x4);grid ontitle('complicated wave andd complicated wave ');fid=fopen('C:\Users\jun\Desktop\code\conv\Conv\tripulse.dat','w'); fprintf(fid,'%15.10e\n',x1);fid=fopen('C:\Users\jun\Desktop\code\conv\Conv\complicatedwave.dat','w');fprintf(fid,'%15.10e\n',x3);z0=zeros(1,M+2*N-2);fid=fopen('C:\Users\jun\Desktop\code\conv\Conv\zeros.dat','w'); fprintf(fid,'%15.10e\n',z0);fclose('all');2、两个波形在MATLAB中的显示和他们的卷积（二）VDSP中程序部分#include "def21060.h"#define M 60#define N 60.section/dmdm_data;.varinputx[M]={0.0000000000e+00,0.0000000000e+00,0.0000000000e+00,0.0000000000e+00,0.000 0000000e+00,0.0000000000e+00,0.0000000000e+00,0.0000000000e+00,0.0000000000e+00,0.0 000000000e+00,0.0000000000e+00,0.0000000000e+00,0.0000000000e+00,0.0000000000e+00, 0.0000000000e+00,0.0000000000e+00,0.0000000000e+00,0.0000000000e+00,0.0000000000e+ 00,0.0000000000e+00,0.0000000000e+00,0.0000000000e+00,0.0000000000e+00,0.0000000000 e+00,0.0000000000e+00,0.0000000000e+00,0.0000000000e+00,0.0000000000e+00,0.00000000 00e+00,2.0000000000e-01,4.0000000000e-01,6.0000000000e-01,8.0000000000e-01,1.0000000 000e+00,8.0000000000e-01,6.0000000000e-01,4.0000000000e-01,2.0000000000e-01,0.000000 0000e+00,0.0000000000e+00,0.0000000000e+00,0.0000000000e+00,0.0000000000e+00,0.0000 000000e+00,0.0000000000e+00,0.0000000000e+00,0.0000000000e+00,0.0000000000e+00,0.00 00000000e+00,0.0000000000e+00,0.0000000000e+00,0.0000000000e+00,0.0000000000e+00,0. 0000000000e+00,0.0000000000e+00,0.0000000000e+00,0.0000000000e+00,0.0000000000e+00 ,0.0000000000e+00,0.0000000000e+00,0.0000000000e+00,0.0000000000e+00,0.0000000000e+ 00,0.0000000000e+00,0.0000000000e+00,0.0000000000e+00};.varinputy[M]={0.0000000000e+00,0.0000000000e+00,0.0000000000e+00,0.0000000000e+00,0.000 0000000e+00,0.0000000000e+00,0.0000000000e+00,0.0000000000e+00,0.0000000000e+00,0.0 000000000e+00,0.0000000000e+00,0.0000000000e+00,0.0000000000e+00,0.0000000000e+00, 0.0000000000e+00,0.0000000000e+00,0.0000000000e+00,0.0000000000e+00,0.0000000000e+ 00,0.0000000000e+00,0.0000000000e+00,0.0000000000e+00,0.0000000000e+00,0.0000000000 e+00,0.0000000000e+00,0.0000000000e+00,0.0000000000e+00,0.0000000000e+00,0.00000000 00e+00,2.0000000000e-01,4.0000000000e-01,6.0000000000e-01,8.0000000000e-01,1.0000000 000e+00,8.0000000000e-01,6.0000000000e-01,4.0000000000e-01,2.0000000000e-01,0.000000 0000e+00,0.0000000000e+00,0.0000000000e+00,0.0000000000e+00,0.0000000000e+00,0.0000 000000e+00,0.0000000000e+00,0.0000000000e+00,0.0000000000e+00,0.0000000000e+00,0.00 00000000e+00,0.0000000000e+00,0.0000000000e+00,0.0000000000e+00,0.0000000000e+00,0. 0000000000e+00,0.0000000000e+00,0.0000000000e+00,0.0000000000e+00,0.0000000000e+00 ,0.0000000000e+00,0.0000000000e+00,0.0000000000e+00,0.0000000000e+00,0.0000000000e+ 00,0.0000000000e+00,0.0000000000e+00,0.0000000000e+00};.section/pm pm_data;.varoutput[M+2*N-2]={0.0000000000e+00,……，0.0000000000e+00};.section/pm pm_rsti;jump start;.section/pm pm_code;start:i0=inputx;m0=1;i8=output+N-1;m8=1;lcntr=M, do label until lce;f0=dm(i0,m0);label: pm(i8,m8)=f0;conv:i10=output;m10=1;m1=-1;lcntr=M+N-1, do outer until lce;i1=inputy+N-1;i9=i10;f9=0;lcntr=N, do inner until lce;f0=dm(i1,m1), f5=pm(i9,m10);f12=f0*f5;inner: f9=f9+f12;outer: pm(i10,m10)=f9;end: idle;2、利用VDSP生成的图形六、实验分析本实验中生成的复杂波是有一个方波和三角波的卷积而成，自身卷积得到复杂波的卷积经过验证，实验最后，不论是用MATLAB还是用Visual DSP++软件进行画图比对，得到的输入、输出波形是基本一致的。

数字信号处理实验二

实验二快速傅里叶变换(FFT)及其应用一、思考题(1) 实验中的信号序列()c x n 和()d x n 在单位圆上的z 变换频谱()()c j j d X e X e ωω和会相同吗如果不同，说出哪一个低频分量更多一些，为什么答：设j Z r e ω=⨯ ()()n n G z g n z ∞-=-∞=⨯∑因为为单位圆，故r=1.因为()()j j n n G e g n eωω∞-=-∞=⨯∑，故3723456704()(8)23432j j n j n j j j j j j j c n n X e nen e e e e e e e e ωωωωωωωωωω---------===+-=++++++∑∑ 7235670()(4)43223j j n j j j j j j d n X e n ee e e e e e ωωωωωωωω-------==-=+++---∑比较可知频谱不相同，()c X n 的低频分量多。

(2) 对一个有限长序列进行DFT 等价于将该序列周期延拓后进行DFS 展开，因为DFS 也只是取其中一个周期来运算，所以FFT 在一定条件下也可以用以分析周期信号序列。

如果实正弦信号()sin(2),0.1x n fn f π== 用16点FFT 来做DFS 运算，得到的频谱是信号本身的真实谱吗为什么答：针对原来未经采样的连续时间信号来说，FFT 做出来的永远不会是信号本身的真实频谱，只能够是无限接近。

FFT 频谱泄露问题是一定会存在的，因为毕竟采样率再高，也不能完全达到原来的连续时间信号准确。

原题的采样率是1/10，就是将2*pi 分成10份，即每个正弦波周期进行10次采样，这样的采样率很低，而最后你只截取16个点来做分析，泄露一般会挺严重，看到的频谱，应该是一个上头尖，下面慢慢变宽的尖锥形，而纯正的正弦波的理想频谱应该是在某频点只有一个尖峰。

二．?实验原理：?（1）混叠：采样序列的频谱是被采样信号频谱的周期延拓，当采样频率不满足奈奎斯特采样定理的时候，就会发生混叠，使得刺痒后的序列信号的频谱不能真实的反映原采样信号的频谱。

数字信号处理实验文档

实验一：离散信号的MATLAB实现一、实验目的：1、掌握离散时间信号的一般表示方法。

2、熟悉连续信号经理想采样后的频谱变化关系，加深对时域采样定理的理解。

3、掌握离散信号序列的操作。

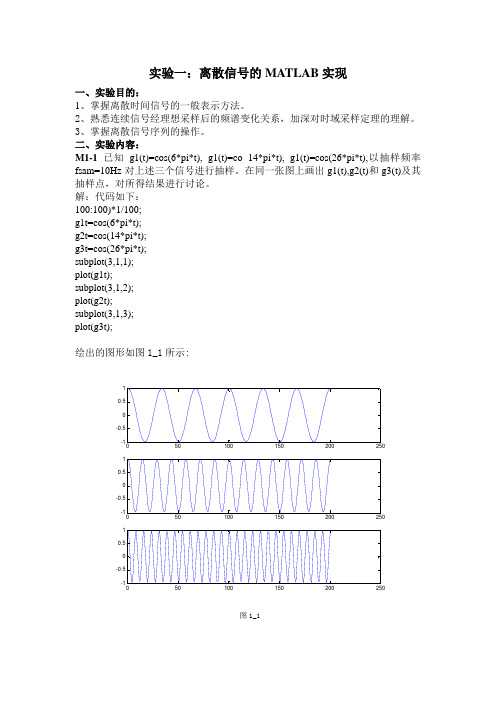
二、实验内容：M1-1 已知g1(t)=cos(6*pi*t), g1(t)=co 14*pi*t), g1(t)=cos(26*pi*t),以抽样频率fsam=10Hz对上述三个信号进行抽样。

在同一张图上画出g1(t),g2(t)和g3(t)及其抽样点，对所得结果进行讨论。

解：代码如下：100:100)*1/100;g1t=cos(6*pi*t);g2t=cos(14*pi*t);g3t=cos(26*pi*t);subplot(3,1,1);plot(g1t);subplot(3,1,2);plot(g2t);subplot(3,1,3);plot(g3t);绘出的图形如图1_1所示:图1_1采样频率为fsam=10Hz，采样时间为0.1s，而f1=3Hz，f2=7Hz，f3=13Hz，使得三个信号的采样图形相似，这样不能很好还原原来的信号图像。

所以对信号的采样频率应足够大，应满足fsam>=2fm.M1-2利用MATLAB的filter函数，求出下列系统的单位脉冲响应，并判断系统是否稳定。

讨论题所获得的结果。

代码1：k=1:300;x=zeros(1,300);x(1)=1;b1=[1];a1=[1,-1.845,0.850586];y1=filter(b1,a1,x);subplot(1,2,1);plot(k,y1);xlabel('k');ylabel('幅度y1');b2=[1];a2=[1,-1.85,0.85];y2=filter(b2,a2,x);subplot(1,2,2);plot(k,y2);xlabel('k');ylabel('幅度y2');图1_2_1代码2：x=zeros(1,500);x(1)=1;b1=[1];a1=[1,-1.845,0.850586];y1=filter(b1,a1,x);plot(k,y1);b2=[1];a2=[1,-1.85,0.85];y2=filter(b2,a2,x);plot(k,y1,k,y2,':');xlabel('k');ylabel('幅度');legend('y1''y2');图1_2_2结论：H1（z）的两个极点都在单位圆内，所以系统稳定，从图中可以看出响应曲线升高后有回落，系统最终趋向于0；H2（z）的一个极点在单位圆内，另一个在单位圆上，所以系统最终临界稳定，从图中可以看出响应曲线上升后没有回落，系统最终趋向于6.7左右。

数字信号处理第二次实验报告

2
% 设计Butterworth低通模拟滤波器 % 通带衰减小于1分贝、阻带（>0.6pi）衰减大于25分贝 % n: 阶数 % wn:低通模拟滤波器的3分贝通带截止频率 [B1,A1] = BUTTER(n,wn,'s'); % 设计Butterworth低通模拟滤波器 % B,A：模拟滤波器传递函数分子、分母多项式系数 [b1,a1]=impinvar(B1,A1,fs); % 用脉冲响应不变法将模拟低通滤波器转换为数字滤波器b,a：分子、分母多项式系数 % 双曲变换的预畸变 [B2,A2]=butter(n,2000*tan(pi/5),'s'); % 用双曲变换法将模拟低通滤波器转化为数字滤波器b,a:分子,分母多项式系数 [b2,a2]=bilinear(B2,A2,fs);
(3) 熟悉巴特沃思滤波器，切比雪夫滤波器和椭圆滤波器的频率特性。
二. 实验原理:
(1) 实验中有关变量的定义：fc 通带边界频率ห้องสมุดไป่ตู้fr 阻带边界频率，tao 通带波动，at 最小阻带衰减，fs 采样频率，t 采样周期。
(2) 设计一个数字滤波器一般包括以下两步： a.按照任务要求，确定滤波器性能指标 b.用一个因果稳定的离散时不变系统的系统函数去逼近这一性能要求
姓名:陈桐学号:04004316
实验日期:2006 年 11 月 14 日
一. 实验目的:
(1) 掌握双线形变换法及脉冲响应不变法设计 IIR 数字滤波器的具体设计方法及其原理，熟悉用双线形变换法及脉冲响应不变法设计低通，高通和带通 IIR 数字滤波器的计算机编程。
(2) 观察双线形变换法及脉冲响应不变法设计的滤波器的频域特性，了解双线形变换法及脉冲响应不变法的特点。

数字信号处理实验二时域采样和频域采样

实验二-时域采样和频域采样一、实验目的时域采样理论与频域采样理论是数字信号处理中的重要理论。

要求掌握模拟信号采样前后频谱的变化，以及如何选择采样频率才能使采样后的信号不丢失信息；要求掌握频率域采样会引起时域周期化的概念，以及频率域采样定理及其对频域采样点数选择的指导作用。

二、实验原理及方法1、时域采样定理的要点：a)对模拟信号)(t x a 以间隔T 进行时域等间隔理想采样，形成的采样信号的频谱)(ˆΩj X 是原模拟信号频谱()aX j Ω以采样角频率s Ω（T s /2π=Ω）为周期进行周期延拓b)采样频率s Ω必须大于等于模拟信号最高频率的两倍以上，才能使采样信号的频谱不产生频谱混叠。

利用计算机计算上式并不方便，下面我们导出另外一个公式，以便用计算机上进行实验。

2、频域采样定理的要点：a)对信号x(n)的频谱函数X(ej ω)在[0，2π]上等间隔采样N 点则N 点IDFT[()N X k ]得到的序列就是原序列x(n)以N 为周期进行周期延拓后的主值区序列。

三、实验内容及步骤1、时域采样理论的验证程序：clear;clcA=444.128;a=50*sqrt(2)*pi;w0=50*sqrt(2)*pi;Tp=50/1000;F1=1000;F2=300;F3=200;T1=1/F1;T2=1/F2;T3=1/F3;n1=0:Tp*F1-1;n2=0:Tp*F2-1;n3=0:Tp*F3-1;x1=A*exp(-a*n1*T1).*sin(w0*n1*T1);x2=A*exp(-a*n2*T2).*sin(w0*n2*T2);x3=A*exp(-a*n3*T3).*sin(w0*n3*T3);f1=fft(x1,length(n1));f2=fft(x2,length(n2)); %f3=fft(x3,length(n3)); %k1=0:length(f1)-1;fk1=k1/Tp; %k2=0:length(f2)-1;fk2=k2/Tp; % k3=0:length(f3)-1;fk3=k3/Tp; % subplot(3,2,1)stem(n1,x1,'.')title('(a)Fs=1000Hz');xlabel('n');ylabel('x1(n)');subplot(3,2,3)stem(n2,x2,'.')title('(b)Fs=300Hz');xlabel('n');ylabel('x2(n)');subplot(3,2,5)stem(n3,x3,'.')title('(c)Fs=200Hz');xlabel('n');ylabel('x3(n)');subplot(3,2,2)plot(fk1,abs(f1))title('(a) FT[xa(nT)],Fs=1000Hz'); xlabel('f(Hz)');ylabel('·ù¶È')subplot(3,2,4)plot(fk2,abs(f2))title('(b) FT[xa(nT)],Fs=300Hz'); xlabel('f(Hz)');ylabel('·ù¶È')subplot(3,2,6)plot(fk3,abs(f3))title('(c) FT[xa(nT)],Fs=200Hz'); xlabel('f(Hz)');ylabel('·ù¶È')结果分析：由图2.2可见，采样序列的频谱的确是以采样频率为周期对模拟信号频谱的周期延拓。