三角函数角度换算公式总结
三角函数公式凑角

三角函数公式凑角
三角函数公式凑角是指通过已知的三角函数值,利用三角函数的和差角公式、倍角公式、半角公式等,将给定的角度变换为易于计算的角度。
常见的凑角方法包括:
1.和差角公式:sin(α+β)=sinαcosβ+cosαsinβ;
cos(α+β)=cosαcosβ-sinαsinβ;tan(α+β)=(tanα+tanβ)/(1-tanαtanβ)。
2.倍角公式:sin2α=2sinαcosα;cos2α=cos²α-sin²α;
tan2α=(2tanα)/(1-tan²α)。
3.半角公式:sin(α/2)=±√[(1-cosα)/2];
cos(α/2)=±√[(1+cosα)/2];tan(α/2)=±√[(1-
cosα)/(1+cosα)]。
4.辅助角公式:sinx=(2tan(x/2))/(1+tan²(x/2));cosx=(1-
tan²(x/2))/(1+tan²(x/2));tanx=(2tan(x/2))/(1-tan²(x/2))。
通过这些公式,可以将给定的角度变换为易于计算的角度,例如将角度转换为正弦值、余弦值或正切值,或将角度转换为半角或辅助角等。
这样可以简化三角函数的计算,提高计算效率和准确性。
三角函数关系公式大全

三角函数关系公式大全一、同角三角函数的基本关系。
1. 平方关系。
- sin^2α+cos^2α = 1- 1+tan^2α=sec^2α(其中secα=(1)/(cosα))- 1 + cot^2α=csc^2α(其中cscα=(1)/(sinα))2. 商数关系。
- tanα=(sinα)/(cosα)- cotα=(cosα)/(sinα)二、诱导公式。
1. 关于α与-α的诱导公式。
- sin(-α)=-sinα- cos(-α)=cosα- tan(-α)=-tanα2. 关于α与π±α的诱导公式。
- sin(π+α)=-sinα- sin(π - α)=sinα- cos(π+α)=-cosα- cos(π-α)=-cosα- tan(π+α)=tanα- tan(π-α)=-tanα3. 关于α与(π)/(2)±α的诱导公式。
- sin((π)/(2)+α)=cosα- sin((π)/(2)-α)=cosα- cos((π)/(2)+α)=-sinα- cos((π)/(2)-α)=sinα- tan((π)/(2)+α)=-cotα- tan((π)/(2)-α)=cotα三、两角和与差的三角函数公式。
1. 两角和的正弦公式。
- sin(A + B)=sin Acos B+cos Asin B2. 两角差的正弦公式。
- sin(A - B)=sin Acos B-cos Asin B3. 两角和的余弦公式。
- cos(A + B)=cos Acos B-sin Asin B4. 两角差的余弦公式。
- cos(A - B)=cos Acos B+sin Asin B5. 两角和的正切公式。
- tan(A + B)=(tan A+tan B)/(1-tan Atan B)6. 两角差的正切公式。
- tan(A - B)=(tan A-tan B)/(1 + tan Atan B)四、二倍角的三角函数公式。
三角函数与角度的换算与应用

三角函数与角度的换算与应用三角函数是高中数学中的重要概念,广泛应用于物理、几何等学科。
本文将介绍三角函数与角度的换算方法,并探讨其在实际问题中的应用。
一、角度的度、弧度与百分度表示法角度可以用不同的单位表示,常见的有度(°)、弧度(rad)和百分度(%)。
三者之间的换算关系如下:1度= π/180 rad1 rad = 180/π° ≈ 57.296°1° = 1/360 × 100% ≈ 0.2778%角度的度数制是最常见的表示方法,常用于日常生活和初等数学中。
弧度制则在高等数学和物理学中使用较多,因为弧度制具有更好的计算性质和物理意义。
百分度则是商业运算和某些领域常用的表示方法。
二、角度转换公式1. 弧度与度的相互换算角度与弧度之间的转换公式已在上一部分中给出,可以根据需要灵活运用。
2. 百分度与度的相互换算令 x 为百分度,y 为度,则有 x% = y°。
两边同时除以100得到x/100 = y/1,即 x = y。
因此,百分度和度是相等的。
三、常用三角函数的计算与应用在三角函数中,最为常用的三个函数是正弦函数 sin,余弦函数 cos 和正切函数 tan。
它们的定义如下:1. 正弦函数 sin(x) = 对边/斜边2. 余弦函数 cos(x) = 邻边/斜边3. 正切函数 tan(x) = 对边/邻边其中,x 为角的度数或弧度,对边、邻边和斜边分别指与角 x 相关联的三角形的边。
三角函数在实际问题中具有广泛的应用。
以下是三角函数的几个常见应用场景:1. 三角测量:利用三角函数,我们可以测量无法直接测量的高度、距离等物理量。
例如,在测量一座高楼的高度时,可以利用三角函数计算出与视线相关的角度和斜边的长度,从而计算出楼的高度。
2. 机械振动:在研究机械振动时,三角函数可以描述物体振动的周期性变化。
例如,简谐振动可以用正弦函数来表示,根据振幅、频率等参数可以计算出振动物体的位置和速度。
三角函数角度公式

三⾓函数⾓度公式三⾓函数⾓度公式两⾓和公式sin(A+B)=sinAcosB+cosAsinBsin(A-B)=sinAcosB-sinBcosAcos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB)tan(A-B)=(tanA-tanB)/(1+tanAtanB)cot(A+B)=(cotAcotB-1)/(cotB+cotA)cot(A-B)=(cotAcotB+1)/(cotB-cotA)倍⾓公式tan2A=2tanA/[1-(tanA)^2]cos2a=(cosa)^2-(sina)^2=2(cosa)^2 -1=1-2(sina)^2sin2A=2sinA*cosA三倍⾓公式sin3a=3sina-4(sina)^3cos3a=4(cosa)^3-3cosatan3a=tana*tan(π/3+a)*tan(π/3-a)半⾓公式sin(A/2)=√((1-cosA)/2) sin(A/2)=-√((1-cosA)/2)cos(A/2)=√((1+cosA)/2) cos(A/2)=-√((1+cosA)/2)tan(A/2)=√((1-cosA)/((1+cosA)) tan(A/2)=-√((1-cosA)/((1+cosA))cot(A/2)=√((1+cosA)/((1-cosA)) cot(A/2)=-√((1+cosA)/((1-cosA))tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA)和差化积2sinAcosB=sin(A+B)+sin(A-B)2cosAsinB=sin(A+B)-sin(A-B) )2cosAcosB=cos(A+B)+cos(A-B)-2sinAsinB=cos(A+B)-cos(A-B)sinA+sinB=2sin((A+B)/2)cos((A-B)/2cosA+cosB=2cos((A+B)/2)sin((A-B)/2)tanA+tanB=sin(A+B)/cosAcosB积化和差公式sin(a)sin(b)=-1/2*[cos(a+b)-cos(a-b)]cos(a)cos(b)=1/2*[cos(a+b)+cos(a-b)]sin(a)cos(b)=1/2*[sin(a+b)+sin(a-b)]诱导公式sin(-a)=-sin(a)cos(-a)=cos(a)sin(pi/2-a)=cos(a)cos(pi/2-a)=sin(a)sin(pi/2+a)=cos(a)cos(pi/2+a)=-sin(a)sin(pi-a)=sin(a)cos(pi-a)=-cos(a)sin(pi+a)=-sin(a)cos(pi+a)=-cos(a)tgA=tanA=sinA/cosA万能公式sin(a)= (2tan(a/2))/(1+tan^2(a/2))cos(a)= (1-tan^2(a/2))/(1+tan^2(a/2))tan(a)= (2tan(a/2))/(1-tan^2(a/2))其它公式a*sin(a)+b*cos(a)=sqrt(a^2+b^2)sin(a+c) [其中,tan(c)=b/a]a*sin(a)-b*cos(a)=sqrt(a^2+b^2)cos(a-c) [其中,tan(c)=a/b]1+sin(a)=(sin(a/2)+cos(a/2))^21-sin(a)=(sin(a/2)-cos(a/2))^2其他⾮重点三⾓函数csc(a)=1/sin(a)sec(a)=1/cos(a)双曲函数sinh(a)=(e^a-e^(-a))/2cosh(a)=(e^a+e^(-a))/2tgh(a)=sinh(a)/cosh(a)公式⼀: 设α为任意⾓,终边相同的⾓的同⼀三⾓函数的值相等: sin(2kπ+α)= sinα cos(2kπ+α)= cosα tan(2kπ+α)= tanα cot(2kπ+α)= cotα 公式⼆: 设α为任意⾓,π+α的三⾓函数值与α的三⾓函数值之间的关系: sin(π+α)= -sinα cos(π+α)= -cosα tan(π+α)= tanα cot(π+α)= cotα 公式三: 任意⾓α与 -α的三⾓函数值之间的关系: sin(-α)= -sinα cos(-α)= cosα tan(-α)= -tanα cot(-α)= -cotα 公式四: 利⽤公式⼆和公式三可以得到π-α与α的三⾓函数值之间的关系: sin(π-α)= sinα cos(π-α)= -cosα tan(π-α)= -tanα cot(π-α)= -cotα 公式五: 利⽤公式-和公式三可以得到2π-α与α的三⾓函数值之间的关系: sin(2π-α)= -sinα cos(2π-α)= cosα tan(2π-α)= -tanα cot(2π-α)= -cotα 公式六: π/2±α及3π/2±α与α的三⾓函数值之间的关系: sin(π/2+α)= cosα cos(π/2+α)= -sinα tan(π/2+α)= -cotα cot(π/2+α)= -tanα sin(π/2-α)= cosα cos(π/2-α)= sinα tan(π/2-α)= cotα cot(π/2-α)= tanα sin(3π/2+α)= -cosα cos(3π/2+α)= sinα tan(3π/2+α)= -cotα cot(3π/2+α)= -tanα sin(3π/2-α)= -cosα cos(3π/2-α)= -sinα tan(3π/2-α)= cotα cot(3π/2-α)= tanα (以上k∈Z) A·sin(ωt+θ)+ B·sin(ωt+φ) = √{(A^2 +B^2 +2ABcos(θ-φ)}*sin{ ωt + arcsin[ (A*sinθ+B*sinφ) / √{A^2 +B^2; +2ABcos(θ-φ)} } √表⽰根号,包括{……}中的内容反三⾓函数公式⼀.⼀若sinx=a (-1≤a≤1 -∏/2≤x≤∏/2)x=arcsina⼆①sin(arcsina)=a (-1≤a≤1)②arcsin(sina)=a (-∏/2≤a≤∏/2)⼆.⼀若cosx=a (-1≤a≤1 0≤x≤∏)x=arccosa⼆①cos(arccosa)=a (-1≤a≤1)②arccos(cosa)=a (0≤a≤∏)三.⼀若tanx=a (-∏/2<x<∏/2)x=arctana⼆①arctan(-a)=-arctana a∈R②arctan(tana)=a (-∏/2<a<∏/2)③tan(arctana)=a a∈R已知dCosA dSinA,求A(0<= A <360)double dArccos=acos(dCosA);if((dSinA>0&&dCosA>0) || (dSinA>0&&dCosA<0) )//第⼀、⼆象限{A = dArccos;}else if((dSinA<0&&dCosA<0) || (dSinA<0&&dCosA>0) )//第三、四象限{ A=2*D3DX_PI - dArccos;}else if(dSinA==0&&dCos==1){ D3DXToRadian(0);}else if(dSinA==1&&dCos==0){ D3DXToRadian(90);}else if(dSinA==0&&dCos==-1){ D3DXToRadian(180);}else if(dSinA==-1&&dCos==0){ D3DXToRadian(270);}。
tansincos公式

tan sin cos公式
sin度数公式:sin30°= 1/2;sin45°=根号2/2;sin60°=根号3/2。
cos度数公式:cos30°=根号3/2;cos45°=根号2/2;cos60°=1/2。
tan度数公式:tan30°=根号3/3;tan45°=1;tan60°=根号3。
1、三角函数是基本初等函数之一,是以角度(数学上最常用弧度制,下同)为自变量,角度对应任意角终边与单位圆交点坐标或其比值为因变量的函数。
也可以等价地用与单位圆有关的各种线段的长度来定义。
2、三角函数在研究三角形和圆等几何形状的性质时有重要作用,也是研究周期性现象的基础数学工具。
在数学分析中,三角函数也被定义为无穷级数或特定微分方程的解,允许它们的取值扩展到任意实数值,甚至是复数值。
三角函数的公式
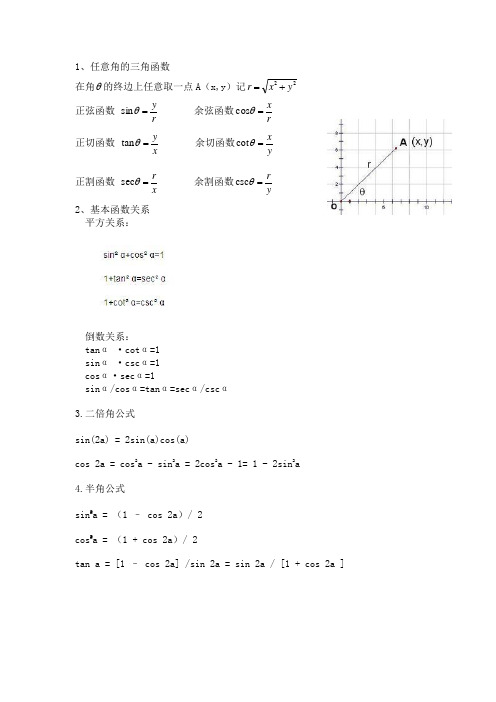
1、任意角的三角函数在角θ的终边上任意取一点A (x,y )记22y x r += 正弦函数 r y =θsin 余弦函数r x =θcos 正切函数 xy =θtan 余切函数y x =θcot 正割函数 x r =θsec 余割函数y r =θcsc 2、基本函数关系平方关系:倒数关系:tan α ·cot α=1sin α ·csc α=1cos α·sec α=1 sin α/cos α=tan α=sec α/csc α3.二倍角公式sin(2a) = 2sin(a)cos(a)cos 2a = cos 2a - sin 2a = 2cos 2a - 1= 1 - 2sin 2a4.半角公式sin 2a = (1 – cos 2a )/ 2cos 2a = (1 + cos 2a )/ 2tan a = [1 – cos 2a] /sin 2a = sin 2a / [1 + cos 2a ]5.万能公式sin(a) = 2tan(a/2) / [1+tan2(a/2)]cos(a) = [1-tan2(a/2)] / [1+tan2(a/2)]tan(a) = 2tan(a/2) / [1-tan2(a/2)]6、两角和三角函数的公式sin(a + b) = sin(a)cos(b) + cos(α)sin(b)cos(a + b) = cos(a)cos(b) - sin(a)sin(b)sin(a - b) = sin(a)cos(b) - cos(a)sin(b)cos(a - b) = cos(a)cos(b) + sin(a)sin(b)tan(a + b) = [tan(a) + tan(b)] / [1 - tan(a)tan(b)] tan(a - b) = [tan(a) - tan(b)] / [1 + tan(a)tan(b)] 7、诱导公式sin(-a) = - sin(a)cos(-a) = cos(a)sin(π/2 - a) = cos(a)cos(π/2 - a) = sin(a)sin(π/2 + a) = cos(a)cos(π/2 + a) = - sin(a)sin(π - a) = sin(a)cos(π - a) = - cos(a)sin(π + a) = - sin(a)cos(π + a) = - cos(a)8、和差化积公式sin(a) + sin(b) = 2sin[(a + b)/2]cos[(a - b)/2] sin(a) - sin(b) = 2sin[(a - b)/2]cos[(a + b)/2] cos(a) + cos(b) = 2cos[(a + b)/2]cos[(a - b)/2] cos(a) - cos(b) = - 2sin[(a + b)/2]sin[(a - b)/2]9、积化和差公式sin(a)sin(b) = - 1/2[cos(a + b) - cos(a - b)] cos(a)cos(b) = 1/2[cos(a + b) + cos(a -b)]sin(a)cos(b) = 1/2[sin(a + b) + sin(a - b)]。
三角函数的万能公式有哪些

三角函数积化和差公式
sinAsinB=-[cos(A+B)-cos(A-B)]/2
cosAcosB=[cos(A+B)+cos(A-B)]/2
sinAcosB=[sin(A+B)+sin(A-B)]/2
cosAsinB=[sin(A+B)-sin(A-B)]/2
sinA-sinB=2cos[(A+B)/2]sin[(A-B)/2]
cosA+cosB=2cos[(A+B)/2]cos[(A-B)/2]
cosA-cosB=-2sin[(A+B)/2]sin[(A-B)/2]
tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB)
熟练掌握三角函数的公式对我们解三角函数题有很大的帮助接下来给大家分享三角函数的万能公式以及三角函数的常用公式
三角函数的万能公式有哪些
熟练掌握三角函数的公式对我们解三角函数题有很大的帮助,接下来给大家分享三角函数的万能公式以及三角函数的常用公式。
三角函数的万能公式
sin(a)=[2tan(a/2)]/[1+tan2(a/2)]
cos(a)=[1-tan2(a/2)]/[1+tan2(a/2)]
tan(a)=[2tan(a/2)]/[1-tan2(a/2)]
三角函数的转化公式
sin(-α)=-sinα
cos(-α)=cosα
sin(π/2-α)=cosα
cos(π/2-α)=sinα
sin(π/2+α)=cosα
三角函数所有公式大全

三角函数所有公式大全三角函数是数学中的一个重要概念,它在几何学、物理学、工程学等领域都有着广泛的应用。
在学习和应用三角函数时,掌握各种公式是非常重要的。
本文将为大家详细介绍三角函数的所有公式,希望能够帮助大家更好地理解和运用三角函数。
首先,我们来看一下最基础的三角函数:正弦函数、余弦函数和正切函数。
这三个函数在直角三角形中有着重要的几何意义,它们的定义如下:正弦函数 sinθ = 对边/斜边。
余弦函数 cosθ = 邻边/斜边。
正切函数 tanθ = 对边/邻边。
在了解了三角函数的基本定义之后,我们可以进一步学习它们的各种公式。
首先是三角函数的基本关系式:sin²θ + cos²θ = 1。
1 + tan²θ = sec²θ。
1 + cot²θ = csc²θ。
这些基本关系式是我们学习三角函数的基础,通过它们我们可以推导出许多其他的三角函数公式。
比如,我们可以利用基本关系式推导出三角函数的和差化积公式:sin(α±β) = sinαcosβ± cosαsinβ。
cos(α±β) = cosαcosβ∓ sinαsinβ。
tan(α±β) = (tanα± tanβ) / (1 ∓ tanαtanβ)。
这些和差化积公式在解决三角函数的复杂运算中起着非常重要的作用,它们可以帮助我们简化计算,提高效率。
除了和差化积公式之外,三角函数还有许多其他重要的公式,比如倍角公式、半角公式、辅助角公式等等。
倍角公式是指将角度加倍后的三角函数关系,它们的形式如下:sin2θ = 2sinθcosθ。
cos2θ = cos²θ sin²θ。
tan2θ = 2tanθ / (1 tan²θ)。
而半角公式则是指将角度减半后的三角函数关系,它们的形式如下:sin(θ/2) = ±√((1 cosθ) / 2)。
高中数学三角函数应知应会必记公式汇总

高中数学三角函数应知应会必记公式汇总设是一个任意角,它的终边与单位圆交于点(,),那么正弦sinα=y,余弦cosα=x,正切tanα=(x≠0).设α是一个任意角,它的终边上任意一点P(x,y),记r=,那么正弦sinα=,余弦cosα=,正切tanα= (x≠0).3同角三角函数的基本关系式(必记)(1)平方关系:sin2α+cos2α=1.(2)商数关系:=tanα(α≠+kπ,k∈Z).记)5和角、差角公式(必记)6二倍角公式(必记)二倍角公式有以下常用变形结论:(规律:升幂缩角,降幂扩角)(会推导)1、升幂公式:2、降幂公式:3、正余弦的和差与积结构互化4、正切的和差与积结构互化5、倍半关系弦切互化7半角公式(熟悉其中一组即可)(会推导)8万能公式(可以理解为二倍角公式的另一种形式)(会推导)万能公式告诉我们,单角的三角函数都可以用半角的正切来表示。
万能公式推导思路:9和差化积公式(会推导)了解和差化积公式的推导,有助于我们理解并掌握好公式:10积化和差公式(会推导)我们可以把积化和差公式看成是和差化积公式的逆应用。
11辅助角公式(必记)12正弦定理(必记)13余弦定理(必记)14三角形的面积公式(必记)说明:三角问题解题思路的三个转化方向:1、转化角:分析角的和差倍半关系、异角化同角、非特殊角化特殊角。
2、转化函数名:异名化同名、弦切互化、正余弦互化。
3、转化结构:凑公式结构、和差与积结构的互化、升幂或降幂、因式分解、配完全平方、分式的合并与拆分,整式与分式的互化,出根号,分母有理化、通分、消项、去分母等代数式恒等变形方法与三角公式的分解合并的灵活结合。
中考数学知识点三角函数的公式

中考数学知识点三角函数的公式中考数学知识点三角函数的公式关于初中三角函数公式,在考试中用的最多的就是特殊三角度数的'特殊值。
下面一起来看看!三角函数的公式sin30°=1/2sin45°=√2/2sin60°=√3/2cos30°=√3/2cos45°=√2/2cos60°=1/2tan30°=√3/3tan45°=1tan60°=√3[1]cot30°=√3cot45°=1cot60°=√3/3其次就是两角和公式,这是在初中数学考试中问答题中容易用到的三角函数公式。
两角和公式sin(A+B)=sinAcosB+cosAsinBsin(A-B)=sinAcosB-sinBcosAcos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB)tan(A-B)=(tanA-tanB)/(1+tanAtanB)ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA)ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA)除了以上常考的初中三角函数公示之外,还有半角公式和和差化积公式也在选择题中用到。
所以同学们还是要好好掌握。
半角公式sin(A/2)=√((1-cosA)/2) sin(A/2)=-√((1-cosA)/2) cos(A/2)=√((1+cosA)/2) cos(A/2)=-√((1+cosA)/2) tan(A/2)=√((1-cosA)/((1+cosA))tan(A/2)=-√((1-cosA)/((1+cosA))ctg(A/2)=√((1+cosA)/((1-cosA))ctg(A/2)=-√((1+cosA)/((1-cosA))和差化积2sinAcosB=sin(A+B)+sin(A-B)2cosAsinB=sin(A+B)-sin(A-B)2cosAcosB=cos(A+B)-sin(A-B)-2sinAsinB=cos(A+B)-cos(A-B)sinA+sinB=2sin((A+B)/2)cos((A-B)/2cosA+cosB=2cos((A+B)/2)sin((A-B)/2)tanA+tanB=sin(A+B)/cosAcosBtanA-tanB=sin(A-B)/cosAcosBctgA+ctgBsin(A+B)/sinAsinB- ctgA+ctgBsin(A+B)/sinAsinB锐角三角函数公式sin α=∠α的对边 / 斜边cos α=∠α的邻边 / 斜边tan α=∠α的对边/ ∠α的邻边cot α=∠α的邻边/ ∠α的对边倍角公式Sin2A=2SinA.CosACos2A=CosA^2-SinA^2=1-2SinA^2=2CosA^2-1 tan2A=(2tanA)/(1-tanA^2)(注:SinA^2 是sinA的平方 sin2(A) )三倍角公式sin3α=4sinα·sin(π/3+α)sin(π/3-α)cos3α=4cosα·cos(π/3+α)cos(π/3-α)tan3a = tan a · tan(π/3+a)· tan(π/3-a)三倍角公式推导sin3a=sin(2a+a)=sin2acosa+cos2asina辅助角公式A sinα+Bcosα=(A^2+B^2)^(1/2)sin(α+t),其中sint=B/(A^2+B^2)^(1/2)cost=A/(A^2+B^2)^(1/2)tant=B/AAsinα+Bcosα=(A^2+B^2)^(1/2)cos(α-t),tant=A/B 降幂公式sin^2(α)=(1-cos(2α))/2=versin(2α)/2cos^2(α)=(1+cos(2α))/2=covers(2α)/2tan^2(α)=(1-cos(2α))/(1+cos(2α))推导公式tanα+cotα=2/sin2αtanα-cotα=-2cot2α1+cos2α=2cos^2α1-cos2α=2sin^2α1+sinα=(sinα/2+cosα/2)^2=2sina(1-sin2a)+(1-2sin2a)sina=3sina-4sin3acos3a=cos(2a+a)=cos2acosa-sin2asina=(2cos2a-1)cosa-2(1-sin2a)cosa=4cos3a-3cosasin3a=3sina-4sin3a=4sina(3/4-sin2a)=4sina[(√3/2)2-sin2a]=4sina(sin260°-sin2a)=4sina(sin60°+sina)(sin60°-sina)=4sina*2sin[(60+a)/2]cos[(60°-a)/2]*2sin[(60°-a)/2]cos[(60°-a)/2]=4sinasin(60°+a)sin(60°-a)cos3a=4cos3a-3cosa=4cosa(cos2a-3/4)=4cosa[cos2a-(√3/2)2]=4cosa(cos2a-cos230°)=4c osa(cosa+cos30°)(cosa-cos30°)=4cosa*2cos[(a+30°)/2]cos[(a-30°)/2]*{-2sin[(a+30°)/2]sin[(a-30°)/2]}=-4cosasin(a+30°)sin(a-30°)=-4cosasin[90°-(60°-a)]sin[-90°+(60°+a)]=-4cosacos(60°-a)[-cos(60°+a)]=4cosacos(60°-a)cos(60°+a)半角公式tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA);cot(A/2)=sinA/(1-cosA)=(1+cosA)/sinA.sin^2(a/2)=(1-cos(a))/2cos^2(a/2)=(1+cos(a))/2tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))三角和sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·sinβ·sinγcos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-sinα·sinβ·cosγtan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tanα·tanβ-tanβ·tanγ-tanγ·tanα)两角和差cos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβsin(α±β)=sinα·cosβ±cosα·sinβtan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)和差化积sinθ+sinφ = 2 sin[(θ+φ)/2] cos[(θ-φ)/2]sinθ-sinφ = 2 cos[(θ+φ)/2] sin[(θ-φ)/2]cosθ+cosφ = 2 cos[(θ+φ)/2] cos[(θ-φ)/2]cosθ-cosφ = -2 sin[(θ+φ)/2] sin[(θ-φ)/2]tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB) tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB) 积化和差sinαsinβ = [cos(α-β)-cos(α+β)] /2cosαcosβ = [cos(α+β)+cos(α-β)]/2sinαcosβ = [sin(α+β)+sin(α-β)]/2cosαsinβ = [sin(α+β)-sin(α-β)]/2诱导公式sin(-α) = -sinαcos(-α) = cosαtan (—a)=-tanαsin(π/2-α) = cosαcos(π/2-α) = sinαsin(π/2+α) = cosαcos(π/2+α) = -sinαsin(π-α) = sinαcos(π-α) = -cosαsin(π+α) = -sinαcos(π+α) = -cosαtanA= sinA/cosAtan(π/2+α)=-cotαtan(π/2-α)=cotαtan(π-α)=-tanαtan(π+α)=tanα诱导公式记背诀窍:奇变偶不变,符号看象限万能公式sinα=2tan(α/2)/[1+tan^(α/2)]cosα=[1-tan^(α/2)]/1+tan^(α/2)]tanα=2tan(α/2)/[1-tan^(α/2)]其它公式(1)(sinα)^2+(cosα)^2=1(2)1+(tanα)^2=(secα)^2(3)1+(cotα)^2=(cscα)^2证明下面两式,只需将一式,左右同除(sinα)^2,第二个除(cosα)^2即可(4)对于任意非直角三角形,总有tanA+tanB+tanC=tanAtanBtanC证:A+B=π-Ctan(A+B)=tan(π-C)(tanA+tanB)/(1-tanAtanB)=(tanπ-tanC)/(1+tanπtanC)整理可得tanA+tanB+tanC=tanAtanBtanC得证同样可以得证,当x+y+z=nπ(n∈Z)时,该关系式也成立由tanA+tanB+tanC=tanAtanBtanC可得出以下结论(5)cotAcotB+cotAcotC+cotBcotC=1(6)cot(A/2)+cot(B/2)+cot(C/2)=cot(A/2)cot(B/2)cot(C/2)(7)(cosA)^2+(cosB)^2+(cosC)^2=1-2cosAcosBcosC(8)(sinA)^2+(sinB)^2+(sinC)^2=2+2cosAcosBcosC(9)sinα+sin(α+2π/n)+sin(α+2π*2/n)+sin(α+2π*3/n)+……+si n[α+2π*(n-1)/n]=0cosα+cos(α+2π/n)+cos(α+2π*2/n)+cos(α+2π*3/n)+……+c os[α+2π*(n-1)/n]=0 以及sin^2(α)+sin^2(α-2π/3)+sin^2(α+2π/3)=3/2tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0。
三角函数常用公式表格

三角函数常用公式表格三角函数是数学中非常重要的一个部分,它在几何、物理、工程等多个领域都有广泛的应用。
为了更好地理解和运用三角函数,我们需要熟悉一些常用的公式。
以下是为大家整理的三角函数常用公式表格:一、基本关系1、平方关系sin²α +cos²α = 11 +tan²α =sec²α1 +cot²α =csc²α2、商数关系tanα =sinα /cosαcotα =cosα /sinα3、倒数关系sinα · cscα = 1cosα · secα = 1tanα · cotα = 1二、诱导公式1、终边相同的角的三角函数值相等sin(2kπ +α) =sinαcos(2kπ +α) =cosαtan(2kπ +α) =tanα2、关于 x 轴对称的角的三角函数值sin(α) =sinαcos(α) =cosαtan(α) =tanα3、关于 y 轴对称的角的三角函数值sin(π α) =sinαcos(π α) =cosαtan(π α) =tanα4、关于原点对称的角的三角函数值sin(π +α) =sinαcos(π +α) =cosαtan(π +α) =tanα5、函数名改变的诱导公式sin(π/2 α) =cosαcos(π/2 α) =sinαsin(π/2 +α) =cosαcos(π/2 +α) =sinα三、两角和与差的三角函数公式1、两角和的正弦公式sin(α +β) =sinαcosβ +cosαsinβ2、两角差的正弦公式sin(α β) =sinαcosβ cosαsinβ3、两角和的余弦公式cos(α +β) =cosαcosβ sinαsinβ4、两角差的余弦公式cos(α β) =cosαcosβ +sinαsinβ5、两角和的正切公式tan(α +β) =(tanα +tanβ) /(1 tanαtanβ) 6、两角差的正切公式tan(α β) =(tanα tanβ) /(1 +tanαtanβ)四、二倍角公式1、二倍角的正弦公式sin2α =2sinαcosα2、二倍角的余弦公式cos2α =cos²α sin²α =2cos²α 1 =1 2sin²α3、二倍角的正切公式tan2α =2tanα /(1 tan²α)五、半角公式1、半角的正弦公式sin(α/2) =±√(1 cosα) / 22、半角的余弦公式cos(α/2) =±√(1 +cosα) / 23、半角的正切公式tan(α/2) =±√(1 cosα) /(1 +cosα) =sinα /(1 +cosα) =(1 cosα) /sinα六、万能公式1、万能公式的正弦sinα =2tan(α/2) / 1 +tan²(α/2)2、万能公式的余弦cosα =1 tan²(α/2) / 1 +tan²(α/2)3、万能公式的正切tanα =2tan(α/2) /1 tan²(α/2)七、积化和差公式1、sinαcosβ =(1/2)sin(α +β) +sin(α β)2、cosαsinβ =(1/2)sin(α +β) sin(α β)3、cosαcosβ =(1/2)cos(α +β) +cos(α β)4、sinαsinβ =(1/2)cos(α +β) cos(α β)八、和差化积公式1、sinα +sinβ =2sin(α +β) /2cos(α β) / 22、sinα sinβ =2cos(α +β) /2sin(α β) / 23、cosα +cosβ =2cos(α +β) /2cos(α β) / 24、cosα cosβ =2sin(α +β) /2sin(α β) / 2这些三角函数公式在解决各种数学问题和实际应用中都非常重要。
已知三角函数求角度公式

已知三角函数求角度公式
已知三角函数求角度公式是指通过已知三角函数值,求解对应角度的公式。
根据三角函数的定义,正弦、余弦、正切分别是一个角的对边、邻边、斜边与该角的比值,而余割、正割、余切则是该角的补角的余弦、正弦、正切的倒数。
因此,在已知某个三角函数值的情况下,可以通过相应的三角函数公式计算出对应的角度。
具体而言,已知正弦、余弦、正切、余割、正割、余切的值,可以分别利用以下公式求解对应角度:
正弦值已知时,对应角度的正弦值为该值,即 sin(x) = y,则 x = arcsin(y)。
余弦值已知时,对应角度的余弦值为该值,即 cos(x) = y,则 x = arccos(y)。
正切值已知时,对应角度的正切值为该值,即 tan(x) = y,则 x = arctan(y)。
余割值已知时,对应角度的余割值为该值的倒数,即 csc(x) = 1/y,则 x = arccsc(1/y) = arcsin(1/y)。
正割值已知时,对应角度的正割值为该值的倒数,即 sec(x) = 1/y,则 x = arcsec(1/y) = arccos(1/y)。
余切值已知时,对应角度的余切值为该值的倒数,即 cot(x) = y,则 x = arccot(y)。
需要注意的是,在计算过程中需要考虑函数定义域和值域的限制以及角度的多解性。
三角函数的万能公式与和差角公式

三角函数的万能公式与和差角公式三角函数是数学中常见的一类函数,涉及到角度和三角比例的关系。
在解决各种三角函数问题时,我们可以利用万能公式和和差角公式来简化计算和推导过程。
本文将详细介绍三角函数的万能公式和和差角公式,并给出示例说明其在解决实际问题中的应用。
一、三角函数的万能公式三角函数的万能公式指的是正弦函数、余弦函数和正切函数之间的关系式。
具体而言,我们有以下三个公式:1. 正弦函数的万能公式:sinθ = 2 · sin(θ/2) · cos(θ/2)这个公式告诉我们,任意一个角的正弦值可以表示为两个半角的正弦值的乘积。
2. 余弦函数的万能公式:cosθ = cos²(θ/2) - sin²(θ/2)这个公式告诉我们,任意一个角的余弦值可以表示为两个半角的余弦值的差。
3. 正切函数的万能公式:tanθ = 2 · tan(θ/2) / (1 - tan²(θ/2))这个公式告诉我们,任意一个角的正切值可以表示为两个半角的正切值的比。
利用三角函数的万能公式,我们可以简化计算和推导过程,并在实际问题中应用。
二、和差角公式和差角公式将两个角的三角函数值联系了起来,是解决相关角的函数值问题的重要工具。
下面是三角函数的和差角公式:1. 正弦函数的和差角公式:sin(α ± β) = sinα · cosβ ± cosα · sinβ这个公式告诉我们,两个角的正弦函数值的和(差)等于分别对应的正弦函数值相乘后再进行加(减)的结果。
2. 余弦函数的和差角公式:cos(α ± β) = cosα · cosβ ∓ sinα · sinβ这个公式告诉我们,两个角的余弦函数值的和(差)等于分别对应的余弦函数值相乘后再进行减(加)的结果。
3. 正切函数的和差角公式:tan(α ± β) = (tanα ± tanβ) / (1 ∓ tanα · tanβ)这个公式告诉我们,两个角的正切函数值的和(差)等于分别对应的正切函数值相加(减)后再进行除以(乘以)一定项的结果。
三角函数像技巧总结

三角函数像技巧总结三角函数是数学中一种重要的函数类型,它在计算、建模和科学研究中具有广泛的应用。
掌握三角函数的性质和技巧,可以在解题和计算中起到极大的帮助。
本文将总结一些三角函数的常用技巧,以帮助读者更好地理解和应用三角函数。
一、角度与弧度的转换在三角函数的计算中,经常需要在角度和弧度之间进行转换。
角度是以度数来表示的,而弧度是以弧长比上半径的方式来度量的。
两者之间的转换关系为:弧度 = (角度× π) / 180角度 = (弧度× 180) / π这个转换关系十分重要,因为在计算中可能需要将角度转换为弧度或将弧度转换为角度。
二、正弦函数的性质与技巧正弦函数是三角函数中最基本的一种函数,它的定义为:sinθ = 对边 / 斜边其中,θ为角度,对边指的是角度θ对应的三角形中与θ相对的边,斜边是三角形的斜边。
正弦函数具有以下性质与技巧:1. 正弦函数的取值范围:正弦函数的取值范围为[-1, 1],即sinθ的值在这个范围内变化。
2. 正弦函数的周期性:正弦函数的周期为360度或2π弧度。
3. 角度的正负关系:正弦函数在180度对称,即sin(-θ) = -sin(θ),这一关系可用来简化计算。
三、余弦函数的性质与技巧余弦函数是三角函数中另一种常用的函数,它的定义为:cosθ = 邻边 / 斜边其中,邻边是与角度θ相邻的边。
余弦函数具有以下性质与技巧:1. 余弦函数的取值范围:余弦函数的取值范围也是[-1, 1],即cosθ的值在这个范围内变化。
2. 余弦函数的周期性:余弦函数的周期也是360度或2π弧度。
3. 角度的正负关系:余弦函数与正弦函数类似,在180度对称,即cos(-θ) = cos(θ)。
四、正切函数的性质与技巧正切函数是三角函数中非常重要的一种函数,它的定义为:tanθ = 对边 / 邻边其中,对边和邻边的含义与正弦函数和余弦函数相同。
正切函数具有以下性质与技巧:1. 正切函数的取值范围:正切函数的取值范围是全体实数,即tanθ的值可以是任意实数。
三角函数的公式归纳总结

三角函数的公式归纳总结三角函数是数学中重要的部分,它们涉及到三角形的各个方面,如角度的度量、边长的比例以及角的正弦、余弦和正切等。
我们首先来总结三角函数的角度度量法。
在数学中,角度可以用弧度来度量。
弧度是一个用于测量角度的标准单位,它是以半径长为1的圆的圆心角所对应的弧长。
为了方便使用角度制,我们引入了一个用于将角度转换为弧度的公式:弧度=角度×(π/180)。
同样地,我们也可以通过一个公式将弧度转换为角度:角度=弧度×(180/π)。
接下来,我们来看一下三角函数的定义及其公式。
1. 正弦函数(sine function)是一个一一对应的三角函数,表示一个角的正弦值与其对应的圆角中线段比例之间的关系。
在直角三角形中,它被定义为斜边与斜边上的对边比例。
正弦函数的公式为:sin(x) = 对边 / 斜边。
2. 余弦函数(cosine function)是一个一一对应的三角函数,表示一个角的余弦值与其对应的圆角中线段比例之间的关系。
在直角三角形中,它被定义为斜边与斜边上的邻边比例。
余弦函数的公式为:cos(x) = 邻边 / 斜边。
3. 正切函数(tangent function)是一个一一对应的三角函数,表示一个角的正切值与其对应的圆角中线段比例之间的关系。
在直角三角形中,它被定义为邻边与对边的比例。
正切函数的公式为:tan(x) = 邻边/ 对边。
上述公式只适用于直角三角形中的角度,但它们可以扩展到任意角度上。
通过一些几何证明,我们可以证明三角函数的周期性质和相关公式。
4. 余切函数(cotangent function)是一个辅助三角函数,它表示一个角的余切值与其对应的正切值的倒数之间的关系。
余切函数的公式为:cot(x) = 1 / tan(x) = 对边 / 邻边。
5. 正割函数(secant function)是一个辅助三角函数,它表示一个角的正割值与其对应的余弦值的倒数之间的关系。
三角函数公式总结

三角函数公式总结三角函数是高中数学中的重要内容之一。
它涉及到角度和三角形的关系,对于解决实际问题和几何分析具有重要意义。
在三角函数的学习中,我们会遇到各种各样的公式,这些公式可以帮助我们求解三角函数的值,或者是通过已知角度或边长来求解其他未知的角度或边长。
下面,我将对三角函数的常见公式进行总结。
首先是正弦函数(sin)和余弦函数(cos)的公式。
对于一个任意角度θ而言,我们可以得到以下公式:sinθ = 对边/斜边cosθ = 邻边/斜边其中,对边和邻边分别为三角形中与角度θ相关的两条边,而斜边则为三角形的斜边。
接下来是正切函数(tan)的公式。
我们可以得到以下公式:tanθ = 对边/邻边其中,对边和邻边的含义与前面提到的一致。
此外,我们还可以通过角度θ求解其余切函数(cot)、正割函数(sec)和余割函数(csc)的值。
这些函数的定义如下:cotθ = 1/tanθ = 邻边/对边secθ = 1/cosθ = 斜边/邻边cscθ = 1/sinθ = 斜边/对边这些公式可以帮助我们方便地求解不同角度的三角函数值,从而进行各种数学运算和几何分析。
除了单独的三角函数公式,我们还可以应用一些三角恒等式来推导和求解。
下面是一些常见的三角恒等式:1. 三角函数的互余关系:sinθ = cos(90° - θ)cosθ = sin(90° - θ)tanθ = 1/cotθcotθ = 1/tanθsecθ = 1/cscθcscθ = 1/secθ2. 三角函数的平方和差公式:sin²θ + cos²θ = 11 + tan²θ = sec²θ1 + cot²θ = csc²θ3. 三角函数的和差公式:sin(α ± β) = sinαcosβ ± cosαsinβcos(α ± β) = cosαcosβ ∓ sinαsinβtan(α ± β) = (tanα ± tanβ)/(1 ∓ tanαtanβ)除了上述的基本公式和恒等式,我们还可以应用三角函数的周期性质和特殊角的值来解决问题。
常用三角函数转换公式

常用三角函数转换公式三角函数转换公式汇总锐角三角函数公式sinα=∠α的对边/斜边cosα=∠α的邻边/斜边tanα=∠α的对边/∠α的邻边cotα=∠α的邻边/∠α的对边倍角公式Sin2A=2SinA?CosACos2A=CosA^2-SinA^2=1-2SinA^2=2CosA^2-1tan2A=(2tanA)/(1-tanA^2)(注:SinA^2是sinA的平方sin2(A))三倍角公式sin3α=4sinα·sin(π/3+α)sin(π/3-α)cos3α=4cosα·cos(π/3+α)cos(π/3-α)tan3a=tana·tan(π/3+a)·tan(π/3-a)一个特殊公式(sina+sinθ)*(sina-sinθ)=sin(a+θ)*sin(a-θ)证明:(sina+sinθ)*(sina-sinθ)=2sin[(θ+a)/2]cos[(a-θ)/2]*2cos[(θ+a)/2]sin[(a-θ)/2]=sin(a+θ)*sin(a-θ)坡度公式我们通常半坡面的铅直高度h与水平高度l的比叫做坡度(也叫坡比),用字母i表示,即i=h/l,坡度的一般形式写成l:m形式,如i=1:5.如果把坡面与水平面的夹角记作a(叫做坡角),那么i=h/l=tana.常用三角函数公式1.万能公式令tan(a/2)=tsina=2t/(1+t^2)cosa=(1-t^2)/(1+t^2)tana=2t/(1-t^2)2.辅助角公式asint+bcost=(a^2+b^2)^(1/2)sin(t+r) cosr=a/[(a^2+b^2)^(1/2)]sinr=b/[(a^2+b^2)^(1/2)]tanr=b/a3.两角和差公式:sin(AB)=sinAcosBcosAsinBcos(AB)=cosAcosBsinAsinBtan(AB)=(tanAtanB)/(1tanAtanB)cot(AB)=(cotAcotB1)/(cotBcotA)4.半角公式tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA); cot(A/2)=sinA/(1-cosA)=(1+cosA)/sinA. sin^2(a/2)=(1-cos(a))/2cos^2(a/2)=(1+cos(a))/2tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a)) 5.积化和差sina*cosb=[sin(a+b)+sin(a-b)]/2cosa*sinb=[sin(a+b)-sin(a-b)]/2cosa*cosb=[cos(a+b)+cos(a-b)]/2sina*sinb=-[cos(a+b)-cos(a-b)]/26.和差化积sina+sinb=2sin[(a+b)/2]cos[(a-b)/2]sina-sinb=2sin[(a-b)/2]cos[(a+b)/2]cosa+cosb=2cos[(a+b)/2]cos[(a-b)/2] cosa-cosb=-2sin[(a+b)/2]sin[(a-b)/2]。
