矩阵的LU分解(自编MATLAB)实验报告
matlab矩阵实验报告

matlab矩阵实验报告《MATLAB矩阵实验报告》摘要:本实验报告利用MATLAB软件进行了矩阵实验,通过对矩阵的运算、转置、逆矩阵、特征值等操作进行了分析和讨论。
实验结果表明,MATLAB在矩阵运算方面具有高效、准确的特点,能够满足工程和科学计算的需求。
引言:矩阵是线性代数中的重要概念,广泛应用于工程、物理、经济等领域。
MATLAB是一种强大的数学软件,能够对矩阵进行各种运算和分析。
本实验旨在利用MATLAB软件对矩阵进行实验,探讨其在矩阵运算中的应用和优势。
实验方法:1. 创建矩阵:利用MATLAB软件创建不同大小的矩阵,包括方阵和非方阵。
2. 矩阵运算:进行矩阵的加法、减法、乘法等运算,比较不同大小矩阵的计算效率和结果准确性。
3. 矩阵转置:对矩阵进行转置操作,观察转置后矩阵的性质和应用。
4. 逆矩阵:求解矩阵的逆矩阵,并分析逆矩阵在实际问题中的应用。
5. 特征值和特征向量:利用MATLAB软件求解矩阵的特征值和特征向量,分析其在物理、工程等领域的应用。
实验结果与讨论:通过实验发现,MATLAB软件在矩阵运算中具有高效、准确的特点。
对于大规模矩阵的运算,MATLAB能够快速进行计算并给出准确的结果。
在矩阵转置和逆矩阵求解方面,MATLAB也能够满足工程和科学计算的需求。
此外,通过求解矩阵的特征值和特征向量,可以得到矩阵的重要性质,为实际问题的分析和求解提供了有力支持。
结论:本实验利用MATLAB软件进行了矩阵实验,通过对矩阵的运算、转置、逆矩阵、特征值等操作进行了分析和讨论。
实验结果表明,MATLAB在矩阵运算方面具有高效、准确的特点,能够满足工程和科学计算的需求。
希望本实验能够对矩阵运算和MATLAB软件的应用有所启发,为相关领域的研究和应用提供参考。
MATLAB报告用LU分解法求解线性方程组
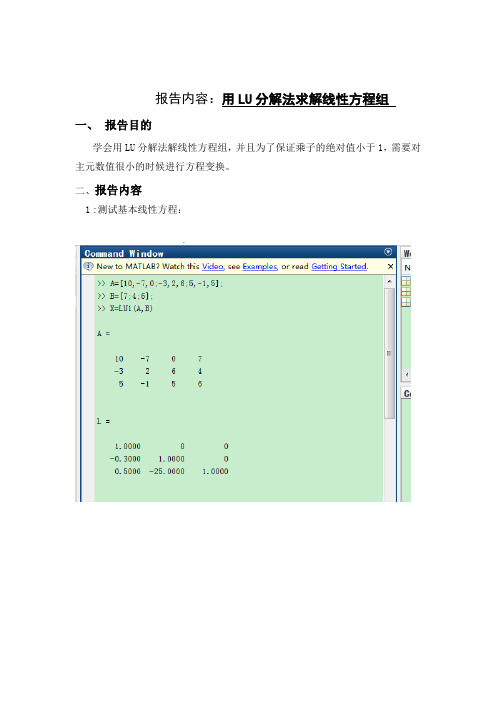
报告内容:用LU分解法求解线性方程组一、报告目的学会用LU分解法解线性方程组,并且为了保证乘子的绝对值小于1,需要对主元数值很小的时候进行方程变换。
二、报告内容1 :测试基本线性方程:可见程序运行结果正确。
2 :测试主元有接近于0的线性方程:可见程序运行结果正确。
3:测试矩阵维度大于5情况:可见程序运行结果正确。
三、源程序function X=LU1(A,B)B=B';A=[A';B]',n=length(B');X=zeros(n,1);y=zeros(n,1);U=zeros(n);L=eye(n);for k=1:nU(1,k)=A(1,k);L(k,1)=A(k,1)/U(1,1);endfor i=2:nfor k=i:nlu=0;lu1=0;for j=1:i-1lu=lu+L(i,j)*U(j,k);lu1=lu1+L(k,j)*U(j,i);endU(i,k)=A(i,k)-lu;L(k,i)=(A(k,i)-lu1)/U(i,i);endendLUfor i=1:nly=0;for j=1:ily=ly+L(i,j)*y(j);endy(i)=B(i)-ly;endfor i=n:-1:1ly1=0;for j=i+1:nly1=ly1+U(i,j)*X(j);endX(i)=(y(i)-ly1)/U(i,i);end四、报告分析与心得MATLAB编程和C编程一样需要仔细的逻辑和十分的细心,自己还有很多需要学习的地方。
矩阵数值计算实验报告

#### 一、实验目的本次实验旨在通过MATLAB软件,对矩阵进行数值计算,掌握矩阵的基本操作、运算函数的使用,以及解决实际问题的能力。
通过实验,加深对线性代数基本理论的理解,提高数值计算技能。
#### 二、实验环境软件:MATLAB R2020a硬件:****************************,8GB RAM#### 三、实验内容1. 矩阵的创建与操作(1)创建矩阵:通过MATLAB内置函数创建不同类型的矩阵,如`zeros`、`ones`、`rand`等。
```matlabA = zeros(3,3); % 创建3x3零矩阵B = ones(2,2); % 创建2x2单位矩阵C = rand(4,4); % 创建4x4随机矩阵```(2)矩阵的引用:使用矩阵的行和列索引访问矩阵元素。
```matlabE = A(1,1); % 访问矩阵A的第一个元素```(3)矩阵的运算:进行矩阵的加法、减法、乘法等运算。
```matlabD = A + B; % 矩阵A和B相加F = A . C; % 矩阵A和C对应元素相乘```2. 矩阵的基本运算(1)矩阵的逆:计算矩阵的逆矩阵。
```matlabA_inv = inv(A);```(2)矩阵的行列式:计算矩阵的行列式值。
```matlabdet_A = det(A);```(3)矩阵的秩:计算矩阵的秩。
```matlabrank_A = rank(A);```(4)矩阵的迹:计算矩阵的迹。
```matlabtrace_A = trace(A);```3. 矩阵分解(1)奇异值分解(SVD):对矩阵进行奇异值分解。
```matlab[U, S, V] = svd(A);```(2)LU分解:将矩阵分解为下三角矩阵和上三角矩阵。
```matlab[L, U] = lu(A);```4. 解线性方程组(1)使用矩阵的逆解方程组。
```matlabb = [1; 2; 3];x = A_inv b;```(2)使用矩阵分解方法解方程组。
实验一 矩阵的LU分解

实验一 矩阵的LU 分解1、原理设A ∈C n ×n 若A 可以表示成一个下三角矩阵和一个上三角矩阵的乘积A=LU ,则称其为矩阵A 的LU 分解(三角分解)。
矩阵的LU 分解在求解线性方程组时将十分简便。
如对线性方程组Ax=b ,设A=LU 是其LU 分解。
我们先求解方程组Ly=b 。
由于L 是下三角矩阵,则解向量y 可以通过依次求出其分量y 1,y 2,……,y n 而求出,再求解方程组Ux=y 。
解向量x 可以通过该方程组依次求出分量xn ,xn-1,……,x2,x1而快速得出。
于是由两个方程组Ux=y ,Ly=b 的求解而给出LUx=Ly=b=Ax 的解。
若矩阵A 非奇异,则A 能分解为LU 的充分必要条件是A 的顺序主子行列式不为0。
则存在惟一的主对角线上元素全为1的下三角阵L 与惟一的上三角阵U ,使得A=LU 。
2、算法因为当A=LU 时,由于L 可逆,故必存在可逆阵P 使PL=E ,即PA=PLU=U 。
也就是说,我们可以先对A 施行行变换得出上三角阵U ,而矩阵P 可以通过对单位阵E 进行同样的行初等变换得出。
既有P (A ,E )=(PA ,PE )=(U ,P )于是A=P -1U ,为保持P 为下三角阵(从而P -1也为下三角阵),在进行行初等变换时,不能进行行的对换,上行的倍数应加到下行的对应元。
3、程序矩阵的LU 分解在matlab 中有自己的指令,如:[L1,U1]=lu (A ),此指令在matlab 运行中得到的L 不是下三角阵,与所学的不太一样,程序运行如下图:因此,不能用方法来求解课本上的习题。
通过网络搜到符合课本上的LU 分解的程序,程序如下:022*******≠⎥⎦⎥⎢⎣⎢=∆a a a a 0111≠=∆a 0.........111≠=∆nn nz nn a a a a ,function[L U flag]= LU_Decom(A) [n,m]=size(A);if n~=merror('The rows and the columns of the matrix A must be equal!') return;endflag='OK'; L=eye(n);U=zeros(n);for k=1:nfor j=k:nz=0;for q=1:k-1z=z+L(k,q)*U(q,j);end U(k,j)=A(k,j)-z;endif abs(U(k,k))< epsflag='failure';return;endfor i=k+1:nz=0;for q=1:k-1z=z+L(i,q)*U(q,k);endL(i,k)=(A(i,k)-z)/U(k,k);endend4、例子以教材上矩阵A=[2 1 1;4 1 0;-2 2 1]为例说明上述程序的正确性,在matlab中输入以下指令:5、结果输入上述指令以后,得到如下的结果:此时可以说,上述程序是正确的。
matlab之UL分解实验报告

计算机上机实验报告课程名称:MA TLAB数值计算教师姓名:谭小球日期:2016年9月12日学号:150607116 学生姓名:李妙锋班级:Z15计算机院系:数理与信息学院实验题目:UL分解实验报告1、实验名称实现LU算法,并利用该算法求解线性方程组2、实验目的了解如何用LU三角分解法解线性方程组,利用LU三角分解法解线性方程组3、实验原理设无行交换变换的高斯消去法可求解一般线性方程组AX=B,则矩阵A可分解为一个下三角矩阵L和一个上三角矩阵U乘积:A=LU而且L的对角线元素为1,U的对角线元素非零。
得到L和U后,可通过如下步骤得到X:1.利用向前替换法对方程组L Y=B求解Y。
2.利用回带法对方程组UX=Y求解X。
4、实验步骤1.输入矩阵A2.LU分解A,得到L矩阵与U矩阵的值[L U]=LU_1(A)3.输入矩阵B,利用向前回带法求出Y值Y=upsub(L,B)4.利用回带发求出X值[X]=backsub(U,Y)5、实验程序1.LU分解代码:function [L U]=LU_1(A)n=length(A(1,:));L=eye(n);U=zeros(n);for j=1:nU(1,j)=A(1,j);endfor i=2:nL(i,1)=A(i,1)/U(1,1);endfor k=2:nfor j=k:nU(k,j)=A(k,j)-L(k,1:k-1)*U(1:k-1,j);endfor i=k+1:nL(i,k)=(A(i,k)-L(i,1:k-1)*U(1:k-1,k))/U(k,k);endend结果:2.向前回带法代码:%向前代入法function Y=upsub(A,B)n=length(B);Y=zeros(n,1);Y(1)=B(1)/A(1,1);for k=2:nY(k)=(B(k)-A(k,1:k-1)*Y(1:k-1))/A(k,k);end结果:3.回带法代码:%回代法function [X]=backsub(A,B)n=length(B);X=zeros(n,1);X(n)=B(n)/A(n,n);for k=n-1:(-1):1X(k)=(B(k)-A(k,k+1:n)*X(k+1:n))/A(k,k);end结果:6、实验分析LU分解法比较简便迅速,当解多个系数矩阵为A的线性方程做时,LU分解法就显得特别优越,只要对系数矩阵做一次LU分解,以后只要解三角形方程即可。
matlab 矩阵分解

Matlab矩阵分解矩阵分解是将一个复杂的矩阵拆分成更简单的矩阵的过程。
在Matlab中,我们可以使用不同的方法来进行矩阵分解,如LU分解、QR分解、奇异值分解(SVD)等。
这些方法可以帮助我们简化矩阵操作、求解线性方程组、计算特征值等。
本文将介绍Matlab中常用的矩阵分解方法,包括LU分解、QR分解和SVD分解,并提供相应的示例代码。
1. LU分解LU分解是将一个矩阵分解为一个下三角矩阵L和一个上三角矩阵U的乘积的过程。
LU分解可以用于求解线性方程组、计算矩阵的逆等。
在Matlab中,我们可以使用lu函数进行LU分解。
下面是一个示例代码:A = [1, 2, 3; 4, 5, 6; 7, 8, 9]; % 待分解的矩阵[L, U] = lu(A); % 进行LU分解在上面的代码中,我们定义了一个3x3的矩阵A,然后使用lu函数进行LU分解,并将结果保存在L和U中。
2. QR分解QR分解是将一个矩阵分解为一个正交矩阵Q和一个上三角矩阵R的乘积的过程。
QR分解可以用于求解最小二乘问题、计算矩阵的特征值等。
在Matlab中,我们可以使用qr函数进行QR分解。
下面是一个示例代码:A = [1, 2; 3, 4; 5, 6]; % 待分解的矩阵[Q, R] = qr(A); % 进行QR分解在上面的代码中,我们定义了一个3x2的矩阵A,然后使用qr函数进行QR分解,并将结果保存在Q和R中。
3. 奇异值分解(SVD)奇异值分解是将一个矩阵分解为一个正交矩阵U、一个对角矩阵Σ和一个正交矩阵V的乘积的过程。
奇异值分解可以用于求解最小二乘问题、降维、图像压缩等。
在Matlab中,我们可以使用svd函数进行奇异值分解。
下面是一个示例代码:A = [1, 2, 3; 4, 5, 6; 7, 8, 9]; % 待分解的矩阵[U, S, V] = svd(A); % 进行奇异值分解在上面的代码中,我们定义了一个3x3的矩阵A,然后使用svd函数进行奇异值分解,并将结果保存在U、S和V中。
解密Matlab中的矩阵分解算法

解密Matlab中的矩阵分解算法矩阵分解算法是一种将复杂的矩阵转化为简单的形式以便于分析和处理的数学技术。
在计算机科学和工程领域中,矩阵分解算法被广泛应用于数据处理、图像处理、机器学习以及信号处理等方面。
Matlab作为一种强大的数值计算软件,提供了许多内置的矩阵分解函数,帮助研究人员和工程师快速并且高效地解决问题。
在Matlab中,常用的矩阵分解算法包括LU分解、QR分解、特征值分解、奇异值分解等。
本文将对这些算法进行详细的解读,帮助读者更好地理解和应用它们。
一、LU分解LU分解是将一个矩阵分解为一个下三角矩阵和一个上三角矩阵的乘积的过程。
在Matlab中,我们可以使用lu()函数来进行LU分解。
假设我们有一个方阵A,将其进行LU分解的过程如下:[L, U] = lu(A)其中,L为下三角矩阵,U为上三角矩阵。
通过LU分解,我们可以方便地求解线性方程组,计算矩阵的逆等。
二、QR分解QR分解是将一个矩阵分解为一个正交矩阵和一个上三角矩阵的乘积的过程。
在Matlab中,我们可以使用qr()函数来进行QR分解。
假设我们有一个矩阵A,将其进行QR分解的过程如下:[Q, R] = qr(A)其中,Q为正交矩阵,R为上三角矩阵。
QR分解在解决线性方程组、最小二乘问题以及计算矩阵的秩等方面具有广泛的应用。
三、特征值分解特征值分解是将一个方阵分解为一个可对角化矩阵和一个相似变换矩阵的乘积的过程。
在Matlab中,我们可以使用eig()函数来进行特征值分解。
假设我们有一个方阵A,将其进行特征值分解的过程如下:[V, D] = eig(A)其中,V为相似变换矩阵,D为对角矩阵,对角线上的元素即为A的特征值。
特征值分解在信号处理、图像处理、降维等领域有着重要的应用。
四、奇异值分解奇异值分解是将一个矩阵分解为三个矩阵的乘积的过程,分别为左奇异矩阵、奇异值矩阵和右奇异矩阵。
在Matlab中,我们可以使用svd()函数来进行奇异值分解。
MATLAB中矩阵LU分解

一、 题目编写实现对N 阶非奇矩阵A 进行LU 分解的程序。
二、 算法组织若n 阶方阵的各阶顺序主子行列式不为零则存在唯一的单位上三角矩阵L 和上三角矩阵L 式的A=LU 。
其基本思想是GAUSS 消去法。
参照《计算方法》第38页L 、U 各项计算公式编写公式。
1. 输入带分解矩阵A 2. For i=1,2,……n2.1 将L 对角线元素赋值L (i ,i )=1;3. For j=1,2,……n3.1 将U 第一行元素赋值U (1,j )=A (1,j );4. For k=2,……n4.1 将L 第一列元素赋值L(k,1)=A(k,1)/U(1,1);5. For i=2,……n5.1 For j=i ,……n5.1.110k kj kiij kj i A LA U -=-⇒∑5.2 For k=i+1,……n5.2.1 10k jk ki ij kk jk i A L A U L -=⎛⎫-⇒ ⎪⎝⎭∑三、 程序实现clear all clcA=input('请输入一个方阵 ');%输入一个n 阶方阵[n,n]=size(A); L=zeros(n,n); U=zeros(n,n);for i=1:n %将L 的主对角线元素赋值1 L(i,i)=1; endfor j=1:n %求矩阵U 的第一行元素 U(1,j)=A(1,j); endfor k=2:n %求矩阵L 的第一列元素 L(k,1)=A(k,1)/U(1,1); endfor i=2:n %求L 、U 矩阵元素 for j=i:n s=0;for t=1:i-1 s=s+L(i,t)*U(t,j); endU(i,j)=A(i,j)-s; endfor k=i+1:n r=0;for t=1:i-1r=r+L(k,t)*U(t,i); endL(k,i)=(A(k,i)-r)/U(i,i); end end%输出矩阵L 、U L U四、计算与结果分析本题中根据GAUSS消去算法对任意一各阶顺序主子式不为零的n阶方阵A进行L分解。
矩阵的LU分解(自编MATLAB)实验报告

1矩阵的LU分解1.1 LU 分解原理定理:设A C?n?n,如果A的顺序主子式0, 0,…,则存在唯一的主对角线上元素全为1 的下三角矩阵L与唯一的上三角矩阵U,使得A=LU.证明:对矩阵A的阶数使用数学归纳法.显然,当n=1 时,=1就是唯一的分解式。
现假定对n-1 阶矩阵,定理的结论成立。
对A进行分块A=其中.由于n-1 阶矩阵的k 阶顺序主子式就是A的k阶主子式(k=1,2,…,n-2),故它们都不为零.从而由归纳法假设,有唯一的LU分解其中的主对角线上的元素都1.由于==0所以是n-1阶可逆矩阵先假设已有A=LU,其中L=,U=,==A 则,是n-1阶可逆矩阵,则由上式可惟一确定, 这就证明了A的LU分解的存在性和唯一性.1.2 LU分解算法当n 阶矩阵满足定理的条件时,可以用初等变换的方法求出L 和U.因为当A=LU时,由于L 可逆,故必存在可逆矩阵P 使得即PA=PLU=U.也就是说,可以先对A施行行的初等变换得出上三角矩阵U,而矩阵P可以通过对单位矩阵I进行相同的行初等变换得出,即P(A,I)(PA,PI)(U,P)于是,为保持P为下三角矩阵(从而也是下三角矩阵),在进行行初等变换时,不能进行行的对换,上行的倍数应加到下行的对应元.1.3 LU分解用于解方程组矩阵的三角分解在求解线性方程组时十分方便.如对线性方程组由于是下三角矩阵,则解向量可以通过依次求出其分量而求出,在求解方程组可以通过该方程组依次求出分量而快速得出.于是由两个方程组的求解而给出的解.1.4程序流程图1.5 MATLAB程序function f=LU_decom(A)[m,n]=size(A)if m~=nfprintf('Error:m and n must be equal!m=%d,n=%d\n',m,n) endfor i=1:n-1if (det(A(1:i,1:i))==0)fprintf('Error:det A(%d,%d)=0!\n',i,i)flag='failure'return;elseflag='ok';endendL=eye(n);U=zeros(n);for i=1:nU(1,i)=A(1,i);endfor r=2:nL(r,1)=A(r,1)/U(1,1);endfor i=2:nfor j=i:nz=0;for r=1:i-1z=z+L(i,r)*U(r,j);endU(i,j)=A(i,j)-z;endif abs(U(i,i))<epsflag='failure'return;endfor k=i+1:nm=0;for q=1:i-1m=m+L(k,q)*U(q,i);endL(k,i)=(A(k,i)-m)/U(i,i); end endLU1.6 实际数据计算已知矩阵A先对A进性LU分解,并求解方程A的解.(1)A的LU分解在MATLAB命令行中输入A=[2 1 1;4 1 0;-2 2 1];并调用以上函数可得如下结果>> A=[2 1 1;4 1 0;-2 2 1];LU_decom(A)m =3n =3L =1 0 02 1 0-1 -3 1U =2 1 10 -1 -20 0 -4(2)解方程组,程序及结果如下%-----用LU分解解线性方程组------y=zeros(n,1);y(1)=b(1);for i=2:ny(i)=b(i)-sum(L(i,1:i-1)'.*y(1:i-1));endyx(n)=y(n)/U(n,n);for i=n-1:-1:1x(i)=(y(i)-sum(U(i,i+1:n)'.*x(i+1)))/U(i,i);endx=x'运行结果如下:y =12x =-0.50001.0000-0.50001.7数据分析调用MATLAB固有的LU分解函数,以及解方程组相关函数对以上数据进行计算,运行结果如下:>> A=[2 1 1;4 1 0;-2 2 1];>> b=[1 2 1]';>> [L,U]=lu(A)L =0.5000 0.2000 1.00001.0000 0 0-0.5000 1.0000 0U =4.0000 1.0000 00 2.5000 1.00000 0 0.8000 >> X=inv(A)*bX =0.25001.0000-0.5000经比对结果相同,可见以上程序可行。
矩阵lu分解计算实例

矩阵lu分解计算实例矩阵LU分解(LUdecomposition)是一种数值计算技术,也被称为LU factorization或LU矩阵分解。
它的本质是将矩阵拆分为两个矩阵的乘积,其中一个矩阵是上三角矩阵,另一个是下三角矩阵。
在计算上也可以视作是将一个复杂的矩阵拆分为简单的形式进行操作,使得线性方程组更容易求解。
矩阵LU分解在线性代数中有着重要的意义。
它主要用于矩阵求逆、解线性方程组、求矩阵行列式等操作,在科学计算和理论计算中都有着广泛的应用。
此外,矩阵LU分解是一种很有效的计算技术,也用于解决稀疏系统的数值计算问题。
它的实质是将稀疏矩阵转换为密矩阵,然后进行LU分解,从而减少计算量,提高计算效率。
下面通过一个计算实例来讨论矩阵LU分解的具体操作流程和计算步骤:首先,给定系数矩阵A =begin{bmatrix}1 &2 & 32 & 5 & 73 & 7 & 8end{bmatrix},和方程右端b =begin{bmatrix}-178end{bmatrix},求其解:begin{equation}x = begin{bmatrix}x_1x_2x_3end{bmatrix}end{equation}设A = LU,其中L是一个单位下三角阵,U是一个上三角阵,此时可将等式A = LU拆分成两个等式:begin{equation}Lbegin{bmatrix}y_1y_2y_3end{bmatrix}=begin{bmatrix}1 & 0 & 02 & 1 & 03 &4 & 1end{bmatrix}begin{bmatrix} y_1y_2y_3end{bmatrix}=begin{bmatrix} -178end{bmatrix}end{equation} begin{equation} Ubegin{bmatrix} x_1x_2x_3end{bmatrix}=begin{bmatrix}1 &2 & 30 & 1 & 30 & 0 & 1end{bmatrix}begin{bmatrix}x_1x_2x_3end{bmatrix}=begin{bmatrix}y_1y_2y_3end{bmatrix}end{equation}解出上述两个方程,即可求出解x,即x = begin{bmatrix}211end{bmatrix}以上就是矩阵LU分解的具体操作步骤。
数值计算LU分解实验报告

数值计算LU分解实验报告实验目的:1.了解LU分解的原理和数值计算方法;2.掌握LU分解的算法实现过程;3.验证LU分解的正确性和数值稳定性。
实验器材:1.计算机;2.编程环境。
实验步骤:1.确定要进行LU分解的方阵A的大小;2.随机生成一个大小为nxn的方阵A;3.使用LU分解算法对方阵A进行分解;4. 验证LU分解的正确性,即计算得到的L和U是否满足L \cdot U = A;5. 计算方阵A的行列式det(A),并与分解得到的L和U的主对角线元素的乘积进行比较,验证LU分解的数值稳定性。
实验原理:LU分解是将一个n x n的矩阵A分解为一个下三角矩阵L和一个上三角矩阵U的乘积的过程,满足A = L \cdot U。
其中,L的主对角线元素全为1、LU分解的主要目的是为了简化线性方程组的求解过程,因为当A被分解为LU后,可以通过解两个三角线性方程组来求解原方程组。
实验结果与分析:1.随机生成一个3x3的矩阵A,如下所示:A=[[4,3,-2],[8,5,4],[1,-2,3]]2.对矩阵A进行LU分解,得到L和U矩阵分别为:L=[[1,0,0],[2,1,0],[0.25,0.1,1]]U=[[4,3,-2],[0,-1,8],[0,0,10.2]]3. 验证LU分解的正确性,计算L和U矩阵的乘积是否等于矩阵A。
结果为L \cdot U = [[4, 3, -2], [8, 5, 4], [1, -2, 3]],与矩阵A 一致,因此LU分解正确。
4. 计算矩阵A的行列式det(A)为 -95、计算分解得到的L和U的主对角线元素的乘积为 4 \cdot (-1) \cdot 10.2 = -40.8、由于det(A) ≠ 0,且det(A)≠-40.8,因此LU分解满足数值稳定性。
结果分析:通过对3x3方阵A进行LU分解的实验,验证了LU分解算法的正确性和数值稳定性。
LU分解可以将一个矩阵分解为一个下三角矩阵和一个上三角矩阵的乘积,从而简化线性方程组的求解过程。
三阶矩阵的lu分解法试验总结

三阶矩阵的lu分解法试验总结
LU分解是一种用于解决线性方程组的方法,可以将一个方阵分解为两个三角矩阵的乘积,其中一个为下三角矩阵(L),另一个为上三角矩阵(U)。
在实际应用中,原始方阵被分解为LU矩阵后,可以通过简化的计算方法求解线性方程组。
以下是对三阶矩阵的LU分解法试验的总结。
1. 实验目的:
掌握LU分解法在解决三阶线性方程组中的应用。
2. 实验步骤:
a. 给定一个三阶矩阵A和一个向量b,构成线性方程组
Ax=b。
b. 进行LU分解,将矩阵A分解为下三角矩阵L和上三角矩阵U。
c. 解方程组Ly=b得到向量y。
d. 解方程组Ux=y得到向量x。
3. 实验结果:
a. LU分解成功,得到下三角矩阵L和上三角矩阵U。
b. 成功解得方程组的解向量x。
4. 实验总结:
a. LU分解法可以有效地解决三阶线性方程组,避免了高斯消元法中的矩阵消元过程。
b. LU分解法的计算复杂度比高斯消元法低,对于大规模的线性方程组计算更加高效。
c. LU分解法的应用不仅仅局限于解线性方程组,还可以用于计算矩阵的行列式和逆矩阵等问题。
d. 在实际应用中,需要注意矩阵A是否可以进行LU分解,即矩阵是否可逆。
综上所述,LU分解法是一种有效解决线性方程组的方法,可以通过分解矩阵为下三角和上三角矩阵来简化计算过程,并得到方程组的解。
它具有高效、灵活和广泛适用的特点,在实际应用中得到了广泛的应用。
MATLAB中的矩阵分解方法及其应用

MATLAB中的矩阵分解方法及其应用概述矩阵分解是一种常用的数学工具,可以将一个复杂的矩阵分解为若干个简单的矩阵,从而简化计算和分析过程。
在MATLAB中,有多种矩阵分解方法可供选择,如LU分解、QR分解、特征值分解等。
本文将对这些方法进行详细介绍,并探讨它们在各个领域的应用。
LU分解LU分解(Lower-Upper factorization)是一种常用的矩阵分解方法,它将一个矩阵A分解为一个下三角矩阵L和一个上三角矩阵U的乘积,即A = LU。
在MATLAB中,可以使用“lu”函数进行LU分解。
LU分解的一个重要应用是求解线性方程组,通过LU分解可以将复杂的线性方程组转化为简单的求解过程。
QR分解QR分解是将一个矩阵分解为一个正交矩阵Q和一个上三角矩阵R的乘积,即A = QR。
在MATLAB中,可以使用“qr”函数进行QR分解。
QR分解在许多领域中都有广泛的应用,如信号处理、图像处理等。
例如,在图像处理中,QR分解可以用于计算图像的特征值和特征向量,从而实现图像压缩和增强的效果。
特征值分解特征值分解是将一个矩阵分解为一个对角矩阵D和一个由特征向量组成的矩阵V的乘积,即A = VDV^(-1)。
在MATLAB中,可以使用“eig”函数进行特征值分解。
特征值分解在谱分析、信号处理、系统控制等领域中有广泛的应用。
例如,在谱分析中,特征值分解可以用于分析音频信号的频谱成分,从而实现音频信号的滤波和降噪。
奇异值分解奇异值分解是将一个矩阵分解为一个正交矩阵U、一个对角矩阵S和另一个正交矩阵V的乘积,即A = USV^T。
在MATLAB中,可以使用“svd”函数进行奇异值分解。
奇异值分解在图像处理、数据压缩等领域中有广泛的应用。
例如,在图像处理中,奇异值分解可以用于图像的降噪和图像的压缩,从而减少图像的存储空间和传输带宽。
总结MATLAB提供了丰富的矩阵分解方法,包括LU分解、QR分解、特征值分解和奇异值分解等。
1、克劳特(Crout)(LU)分解法求解线性方程组的matlab实现

1、克劳特(Crout)(LU)分解法求解线性方程组的matlab实现1、克劳特(Crout)(LU)分解法求解线性方程组function [x,L,U]=Crout(A,b)%Crout分解法求解线性方程组%系数矩阵:AN=size(A);n=N(1);L=zeros(n,n); %下三角矩阵U=eye(n,n); %上三角矩阵L(1:n,1)=A(1:n,1); %L的第一列U(1,1:n)=A(1,1:n)/L(1,1); %U的第一行?for k=2:nfor i=k:nL(i,k)=A(i,k)-L(i,1:(k-1))*U(1:(k-1),k);%L的第k列endfor j=(k+1):nU(k,j)=(A(k,j)-L(k,1:(k-1))*U(1:(k-1),j))/(L(k,k));%U的第k行endend%y=inv(L)*b;%x=inv(U)*y;y=SolveDownTriangle(L,b);x=SolveUpTriangle(U,y); %求解线性方程组的解x%x=U\(L\b);function x=SolveUpTriangle(A,b)%求解上三角矩阵Ax=b的解N=size(A);n=N(1);for i=n:-1:1if(i<n)< p="">s=A(i,(i+1):n)*x((i+1):n,1);elses=0;endx(i,1)=(b(i)-s)/A(i,i);endfunction x=SolveDownTriangle(A,b) %求解下三角矩阵Ax=b的解N=size(A);n=N(1);for i=1:nif(i>n)s=A(i,1:(i-1))*x(1:(i-1),1);elses=0;endx(i,1)=(b(i)-s)/A(i,i);end%求解线性方程组的解clcclearA=[12 -3 3;-16 3 -1;1 1 1];b=[15;-13;6];%x=A\b[x,L,U]=Crout(A,b)解:123L =12.0000 0 0-16.0000 -1.0000 01.0000 1.2500 4.5000U =1.0000 -0.2500 0.25000 1.0000 -3.00000 0 1.0000列主元LU分解function [L,U,x]=lux(A,b)%LU 分解法解线性方程组(列主元LU分解)[n,n]=size(A);p=eye(n);%p记录了选择主元时候所进行的行变换for k=1:n-1[r,m]=max(abs(A(k:n,k))); %选列主元m=m+k-1;if(A(m,k)~=0)if(m~=k)A([k m],:)=A([m k],:);p([k m])=p([m k]);endfor i=k+1:nA(i,k)=A(i,k)/A(k,k);j=k+1:n;A(i,j)=A(i,j)-A(i,k)*A(k,j); endendL=tril(A,-1)+eye(n,n);U=triu(A);%解下三角矩阵 Ly=bnewb=p*b;y=zeros(n,1);for k=1:nj=1:k-1;y(k)=(newb(k)-L(k,j)*y(j))/L(k,k); end %解上三角方程组 Ux=yx=zeros(n,1);for k=n:-1:1j=k+1:n;x(k)=(y(k)-U(k,j)*x(j))/U(k,k);end</n)<>。
matlab实验十五 矩阵的分解

实验十五矩阵的分解【实验目的】1.了解矩阵LU,QR和Cholesky分解的基本概念。
2.学习,掌握MATLAB软件中有关命令。
【实验内容】矩阵分解的计算【实验准备】1.矩阵的LU分解2.矩阵的QR分解3.矩阵的Cholesky分解4.矩阵的MATLAB命令。
主要用lu,qr和chol分别完成矩阵的LU,QR和Cholesky分解。
【实验重点】1、矩阵的LU分解、QR分解、Cholesky分解【实验难点】1、矩阵分解的应用【实验方法与步骤】练习1 求矩阵123456780A⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦的LU分解。
相应的MATLAB代码和计算结果为A=[1 2 3;4 5 6;7 8 0];[L,U]=lu(A)L=0.14291.00000.57140.50001.00001.000000U=7.00008.000000.85713.0000004.5000练习2 求矩阵123456789101112A ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦的QR 分解。
实际上A 是一个亏损矩阵,中间列是其他两列的平均,秩和亏损值由QR 分解得出。
相应的MATLAB 代码和计算结果为A=[1 2 3;4 5 6;7 8 9;10 11 12]A=123456789101112[Q ,R]=qr(A)Q=0.07760.83310.26360.31050.45120.70930.44370.54330.06940.62780.55300.77620.31240.18210.5166----------- R=12.884114.5916101.04132.0826000.0000000------ 该练习表明,当矩阵为长方形时,R 矩阵的末行元素为0;当矩阵的纵横方向上的元素个数相差较大时,R 中的零元素将被压缩掉,Q 中相应的列也被压缩掉。
这种方法很有用,节省磁盘空间,节省内存。
【练习与思考】。
LU分解法实验

LU分解法实验LU 分解求解线性方程组【实验目的】1、实现LU 算法,并利用该算法求解线性方程组【实验内容】1. 编写LU 分解法程序LU_Decom.m ,调用该程序,求解方程组12341234123412342234124916148246336165110029x x x x x x x x x x x x x x x x +++=??+++=?+++=??+++=-?的根。
【算法流程说明】一、LU 分解,得到L 矩阵与U 矩阵的值111211112111,,1,,1,,,,11,2,,,1.U U ,,2.L ,,,.U 2L U 3L U r L r U L n 3.1,,,U ,3.1.13.2,,,,3.2j n i n r r r r r j r n r r j r j r kk jk r r r r i r n r U U L L L U U U a lU L L L L +-=++=-∑ 计算,的值;计算的值;3计算的第行和的第2列,的第行和的第三列,的第行和的第列,的第n 行和的第列计算U 的值计算的值11.1r ir ir ik kr rr k L a l U U -=?∑二、回代过程求y 值1123111.(1)2.,,,2.1()()()*(,)k n k j y b y y y y y k b k y j L k j -===-∑ 求的值:y 求的值三、回代过程求x 值12111.2.,,,,2.1()()()*(,)n n n k nj k x x x x x x k y k x j U k j --=+=-∑求的值求的值【C语言算法】//LU分解,得到L矩阵与U矩阵的值For(r=2;r<=n;r++){//计算U的第r行各元素的值For(j=r;j<=n;j++){For(k=1;k<=r-1;k++){a(r,j)=a(r,j)-L(r,k)*U(k,j);}U(r,j)=a(r,j);//计算L的第r列各元素的值For(i=r+1;r<=n;r++) {For(k=1;k<=r-1;k++) {a(i,r)=a(i,r)-L(i,k)*U(k,r);}L(i,r)=a(i,r)/U(r,r);}}//回代求y值y(1)=b(1);For(k=2;k<=n;k++){For(j=1;j<=k-1;j++){b(k)=b(k)-y(j)*L(k,j);}y(k)=b(k);}//回代求x值x(n)=y(n)/U(n,n);For(k=n-1;k>=1;k--){For(j=n;j>=k+1;j++) {y(k)=y(k)-x(j)*U(k,j);}x(k)=y(k)/U(k,k);2编写追赶法程序chase.m ,调用该程序,求解方程组12342111 3121112210x x x x ?????? ? ? ?= ? ? ? ? ? ??的根。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1矩阵的LU分解
1.1 LU 分解原理
定理:设A C n n,如果A的顺序主子式
A11≠0, |a11a12
a21a22|≠0,…,|
a11a12
a21a22
…a12
…a22
⋮⋮
a n−11a n−12
⋮
⋯a n−1n−1
|≠0
则存在唯一的主对角线上元素全为1 的下三角矩阵L与唯一的上三角矩阵U,使得
A=LU.
证明:对矩阵A的阶数使用数学归纳法.
显然,当n=1 时,A11=1 ∙A11就是唯一的分解式。
现假定对n-1 阶矩阵,定理的结论成立。
对A进行分块
A=(A n−1α1α2Tαnn
)
其中α1,α2∈C n−1.由于n-1 阶矩阵A n−1的k阶顺序主子式就是A的k阶主子式(k=1,2,…,n-2),故它们都不为零.从而由归纳法假设,A n−1有唯一的LU分解
A n−1=L n−1U n−1
其中L n−1的主对角线上的元素都1.由于
|A n−1|=|a11a12
a21a22
…a12
…a22⋮⋮
a n−11a n−12
⋮
⋯a n−1n−1
|=|L n−1U n−1|≠0
所以L n−1及U n−1是n-1阶可逆矩阵先假设已有A=LU,其中
L=(L n−10
γT1
),U= (
U n−1β
γT b nn
)
β,γ∈C n−1是待定向量。
作乘积
LU =(L n−1U n−1L n−1β
γT U n−1b nn+γTβ
)=(
A n−1α1
α2Tαnn
)=A
则β,γ必须满足
L n−1β=α1,γT U n−1=α2T ,b nn +γT β=αnn
注意到L n−1及U n−1都是n-1阶可逆矩阵,则由上式可惟一确定
β=L n−1−1α1,γT =α2T U n−1−1, b nn =αnn −γT β
这就证明了 A 的 LU 分解的存在性和唯一性.
1.2 LU 分解算法
当 n 阶矩阵满足定理的条件时,可以用初等变换的方法求出 L 和 U .
因为当 A=LU 时,由于 L 可逆,故必存在可逆矩阵 P 使得
PL =I
即 PA=PLU=U .也就是说,可以先对 A 施行行的初等变换得出上三角矩阵U ,而矩阵 P 可以通过对单位矩阵I 进行相同的行初等变换得出,即
P(A,I) =(PA,PI) =(U,P)
于是A =P −1U ,为保持P 为下三角矩阵(从而P −1也是下三角矩阵),在进行行初等变换时,不能进行行的对换,上行的倍数应加到下行的对应元.
1.3 LU 分解用于解方程组
矩阵的三角分解在求解线性方程组时十分方便.如对线性方程组 Ax =b,设A =LU.我们先求解方程组 Ly =b. 由于L 是下三角矩阵,则解向量y 可以通过依次求出其分量 y 1,y 2,⋯y n 而求出,在求解方程组Ux =y.解向量x 可以通过该方程组依次求出分量x n ,⋯,x 2,x 1而快速得出.于是由两个方程组Ux =y ,Ly =b 的求解而给出
LUx =Ly =b = Ax 的解.
1.4程序流程图
1.5 MATLAB程序
function f=LU_decom(A)
[m,n]=size(A)
if m~=n
fprintf('Error:m and n must be equal!m=%d,n=%d\n',m,n) end
for i=1:n-1
if (det(A(1:i,1:i))==0)
fprintf('Error:det A(%d,%d)=0!\n',i,i)
flag='failure'
return;
else
flag='ok';
end
end
L=eye(n);
U=zeros(n);
for i=1:n
U(1,i)=A(1,i);
end
for r=2:n
L(r,1)=A(r,1)/U(1,1);
end
for i=2:n
for j=i:n
z=0;
for r=1:i-1
z=z+L(i,r)*U(r,j);
end
U(i,j)=A(i,j)-z;
end
if abs(U(i,i))<eps
flag='failure'
return;
end
for k=i+1:n
m=0;
for q=1:i-1
m=m+L(k,q)*U(q,i);
end
L(k,i)=(A(k,i)-m)/U(i,i); end end
L
U
1.6 实际数据计算
已知矩阵A=(211 410
−221),b=(
1
2
1
),先对A进性LU分解,
并求解方程A x=b的解.
(1)A的LU分解
在MATLAB命令行中输入A=[2 1 1;4 1 0;-2 2 1];并调用以上函数可得如下结果
>> A=[2 1 1;4 1 0;-2 2 1];LU_decom(A)
m =
3
n =
3
L =
1 0 0
2 1 0
-1 -3 1
U =
2 1 1
0 -1 -2
0 0 -4
(2)解方程组,程序及结果如下
%-----用LU分解解线性方程组------
y=zeros(n,1);
y(1)=b(1);
for i=2:n
y(i)=b(i)-sum(L(i,1:i-1)'.*y(1:i-1));
end
y
x(n)=y(n)/U(n,n);
for i=n-1:-1:1
x(i)=(y(i)-sum(U(i,i+1:n)'.*x(i+1)))/U(i,i);
end
x=x'
运行结果如下:
y =
1
2
x =
-0.5000
1.0000
-0.5000
1.7数据分析
调用MATLAB固有的LU分解函数,以及解方程组相关函数对以上数据进行计算,运行结果如下:
>> A=[2 1 1;4 1 0;-2 2 1];
>> b=[1 2 1]';
>> [L,U]=lu(A)
L =
0.5000 0.2000 1.0000
1.0000 0 0
-0.5000 1.0000 0
U =
4.0000 1.0000 0
0 2.5000 1.0000
0 0 0.8000
>> X=inv(A)*b
X =
0.2500
1.0000
-0.5000
经比对结果相同,可见以上程序可行。
