7月浙江自考高等几何试题及答案解析
2005年7月浙江省自考高等几何试题试卷真题

做试题,没答案?上自考365,网校名师为你详细解答!浙江省2005年7月高等教育自学考试高等几何试题课程代码:10027一、填空题(每空2分,共20分)1.平面仿射变换由__________唯一决定。
2.在仿射几何里,四边形可以分成__________。
3.在欧氏平面上添加了__________以后,成为射影平面。
4.共线四点A,B,C,D若满足__________,则称它们是调和点列。
5.y轴上无穷远点的齐次坐标是__________。
6.两个射影线束成透视的充要条件是__________。
7.点列到自身的射影对应S若满足__________,则称S是对合。
8.二阶曲线的射影定义是__________。
9.有心二次曲线的中心是__________。
10.平面上的圆点是__________。
二、计算下列各题(每小题6分,共36分)1.经过A(-3,2)和B(6,1)的直线AB与直线x+3y-6=0相交于P,求(ABP)。
2.求连接两点A=(-2,1)与B=(3,2)所得直线的齐次坐标。
3.求射影对应,使点列l上三点1,2,3对应点列l′上三点4,3,2。
4.求四点(0,-2,1),(2,1,-1),(-6,1,1)与(2,-1,0)顺这次序的交比。
5.求点(1,-1,0)关于二阶曲线3x12+5x22+x32+7x1x2+4x1x3+5x2x3=0的极线。
6.求二次曲线x2+4xy-2y2+10x+4y=0的中心。
三、求作下列图形(写出作法,画出图形,每小题6分,共12分)1.已知共直线三点A,B,C,求作点D使A,B,C,D是调和点列。
作法:2.如图,求作点P关于二次曲线Γ的两条切线。
作法:四、证明下列各题(每小题10分,共20分)1.试用代沙格定理及其逆定理证明:若两个对应的完全四点形有五对对应边的交点在一条直线上,那么第六对对应边的交点也在这条直线上。
2.试用坐标法证明巴卜斯定理。
五、试用特殊仿射象证明几何题(12分)从双曲线上任何一点引两条直线各平行于两条渐近线。
最新7月浙江自考高等几何试题及答案解析

浙江省2018年7月自学考试高等几何试题课程代码:10027一、填空题(本大题共10小题,每小题2分,共20分)请在每小题的空格中填上正确答案。
错填、不填均无分。
1.平面到自身的有限回_________组成平面内的仿射变换。
2._________叫做完全四点形。
3.已知共线四点A ,B ,C ,D 的交比(AB ,CD)=2.则(AD ,BC)=_________。
4.一直线上点的射影变换是x ′=423++x x ,则其不变点是_________ 5.巴斯卡定理就是设一六角形内接于一条二次曲线,那末它的_________共线。
6.有公共渐近线的一切圆是_________圆。
7.无穷远点关于二次曲线的极线(极线为无穷远直线除外),称为二次曲线的_________。
8.凡不用欧氏公设V 就能证明的命题叫做_________命题。
9.明万历五年(1607年)_________和利玛窦合译《几何原本》前六卷于北京。
10.1872年克莱因宣读了现在大家叫做“_________”的演说,提出变换群和几何学的关系。
二、计算题(本大题共5小题,每小题6分,共30分)1.求直线(1,-1,2)与两点(3,4,-1)、(5,-3,1)之连线的交点坐标。
解:2.经过A(-3,2)和B(6,1)两点的直线被直线x+3y-6=0截于P 点,求简比(ABP).解:3.若直线l 1:2x 1+x 2-x 3=0,l 3:x 1-x 2+x 3=0,l 4:x 1=0.且(l 1l 2,l 3l 4)=-32.求l 2的方程. 解:4.试求直线x=0关于二阶曲线2x 2-4xy+5y 2-8x+6=0的极点.解:5.求二次曲线x 2+2xy-3y 2+2x-4y=0的渐近线方程.解:三、作图题(本大题共3小题,每小题6分,共18分)1.如图,在平面上给定二直线a 及b 及不在a ,b 上的一点P ,试问不先定出a 和b 的交点,如何用一只直尺作一直线连接P和这交点.作法:2.已知一直线上三点A、B、C,求作第四点D,使交比(AB,CD)=2.作法:3.如图,求作点P关于二次曲线Γ的极线.作法:四、证明题(本大题共3小题,第1、2题各10分,第3小题12分,共32分)1.设六角形的对边互相平行,求证这六角形内接于一二次曲线.证明:2.试证二阶曲线x21+x22+x23-2x2x3-2x1x2-2x1x3=0与坐标三角形的各边相切.证明:3.已知O是椭圆中心,ABCD是椭圆的外切四边形,试证下述面积关系成立.S△AOB+S△OCD=S△ODA+S△OBC(图甲).证明(按以下程序作业):第一步:经某仿射变换将椭圆变成圆(图乙),为什么这样的变换一定存在?第二步:在图乙中画出图甲的对应点和对应线段,叙述原来的命题对应地变成怎样的命题。
浙江月高等教育自学考试高等数学(工本)试题

浙江省2002年7月高等教育自学考试高等数学(工本)试题课程代码:00023一、单项选择题(在每小题的四个备选答案中,选出一个正确答案,并将正确答案的序号填在题干的括号内。
每小题2分,共40分) 1. xmxsin limx ∞→ (m 为常数)等于( )A. 0B. 1C.m1D. m 2. 函数f(x)=⎪⎩⎪⎨⎧=≠0x ,00x ,x1sin x 在x=0点处( ) A. 不连续B. 连续但不可导C. 可导D. 无定义3. f(x)=2x e --1+x 2, g(x)=x 2,当x →0时( ) A. f(x)是g(x)的高阶无穷小 B. f(x)是g(x)的低阶无穷小C. f(x)是g(x)的同阶但非等价无穷小D. f(x)与g(x)是等价无穷小4. 设f(x)=⎪⎩⎪⎨⎧≤≤-<≤<-2x 1,x 21x 0,x 0x ,1x 2,则f(x)在( )A. x=0,x=1处都间断B. x=0,x=1处都连续C. x=0处间断,x=1处连续D. x=0处连续,x=1处间断5. 若x 0为函数y=f(x)的极值点,则下列命题中正确的是( ) A. f ′(x 0)=0 B. f ′(x 0)≠0C. f ′(x 0)=0或f ′(x 0)不存在D. f ′(x 0)不存在6. 设f(x)=x(x-1)(x-2)(x-3)(x-4),则f ′(0)等于( ) A. 0 B. -4! C. 4 D. 4!7. 设函数y=sinx 2,则dy=( )A. cosx 2dx 2B. cosx 2dxC. cosxdx 2D. 2xsinxdx 8. 函数f(x)在[a,b ]上连续,且φ(x)=(x-b)⎰xaf(t)dt ,则在(a,b)内至少存在一点ξ,使ϕ′(ξ)=( )A. 0B. 1C.21D. 2 9. 若函数f(x)在点x=0的某一领域内一阶导函数连续,且f ′(0)=0,1e )x (f lim x 20x -'→ =-3则( )A. f ″(0)不存在B. 在点(0,f(0))为曲线y=f(x)的拐点C. f ″(0)存在但不等于-6D. f(x)在x=0处有极大值10. 函数y=sinx,x ∈[0,2π]的拐点为( ) A. (2π,1) B. (π,0) C. (23,-1) D. 不存在11. 设f(x)在[0,+∞]上连续,且⎰xf(t)dt=x(1+cosx),则f(2π)=( ) A. 1-2π B. 2πC. 1-πD. π 12. 已知6x 020x axdt t sin lim2⎰→ =1,则( )A. a=3B. a=31C. a=1D. a=6 13. 曲线x=cost+sin 2t,y=sint(1-cost),z=-cost 在t=2π的点处的切线方程是 ( )A. 1z 11y 11x =--=-B. 11z 12y 1x -=--= C. 1z 11y 11x -=-=- D. 11z 12y 1x -=-=- 14. 交换二次积分⎰⎰xx10dyf(x,y)dy 的积分次序,它等于( )A. ⎰⎰yy 102dy f(x,y)dx B. ⎰⎰2y y1dy f(x,y)dxC.⎰⎰yy1dyf(x,y)dx D.⎰⎰yy 12dyf(x,y)dy15. 设OM 是从O(0,0)到点M(1,1)的直线段,则与曲线积分I=⎰+OMy x 22eds 不等的积分是( ) A. ⎰1x22edx B.⎰10y22edyC.⎰2r e dr D.⎰1r2edr16. 设D={(x,y)|x 2+y 2≤a 2,a>0,y ≥0},在极坐标系中,二重积分⎰⎰+D22y x dxdy 可表示为( ) A.⎰⎰πθad rdr B.⎰⎰πθad r 2drC.⎰⎰ππ-θ22a0d rdr D.⎰⎰ππ-θ22a0d r 2dr17. 若级数∑∞=1n u n 收敛,则下列级数中不收敛的是( )A.∑∞=1n 2u n B.∑∞=1n (u n +2) C. 2+∑∞=1n u n D.∑∞=kn u n18. 若级数∑∞=1n c n (x+2)n 在x=-4处是收敛的,则此级数在x=1处是( )A. 发散B. 条件收敛C. 绝对收敛D. 收敛性不能确定 19. 微分方程y ″=y ′,的通解为( )A. y=c 1x+c 2e xB. y=c 1+c 2e xC. y=c 1+c 2xD. y=c 1x+c 2x 2 20. 微分方程ydx+(y 2x-e y )dy=0是( ) A. 可分离变量方程B. 可化为一阶线性的微分方程C. 全微分方程D. 齐次方程二、填空题(每小题2分,共20分)1. 若函数f(x)=⎪⎩⎪⎨⎧=≠--+0x ,k 0x ,x x 1x 1在x=0处连续,则k=______。
2004年7月浙江省自考高等几何试题试卷真题

做试题,没答案?上自考365,网校名师为你详细解答!浙江省2004年7月高等教育自学考试高等几何试题课程代码:10027一、填空题(每空2分,共20分)1.有公共渐近线的一切圆是_________________圆。
2.点坐标为(1,0,0)的方程是_________________。
3.2221u u -=0 代表点_________________的方程。
4.二阶曲线就是两个射影响_________________的全体。
5.平行四边形是_________________不变图形。
6.在配极对应下,点列与线束之间的对应是_________________的。
7.设共线四点A ,B ,C ,D ,交比(AB ,CD )定义为_________________。
8.射影平面上_________________线是不存在的。
9.平面内的透视仿射是由_________________完全决定。
10.罗氏几何的一个重要定理,任何三角形的内角和_________________两直角。
二、计算下列各题(每小题6分,共36分)1.求仿射变换⎩⎨⎧+='+='14213y-x y x-y x 的不变点。
2.求直线(2,3i ,2+3i )上的实点。
3.求二次曲线 2x 2+xy -3y 2+x -y =0的渐近线。
4.共线三点P 1,P 2,P 3在笛氏坐标下,已知的P 1,P 3非齐次坐标为(x 1,y 1),(x 3,y 3),且简比(P 1P 2P 3)=λ,求P 2的坐标。
5.求a 1x 1+a 2x 2+a 3x 3=0,b 1x 1+b 2x 2+b 3x 3=0的交点与直线 c 1x 1+c 2x 2+c 3x 3=0 的无穷远点连线的方程。
6.(ab ,cd )=λ(ad ,bc ),求(1)λ的取值范围;(2)若a,b,c,d 成调和共轭,求λ的值。
三、求作下列图形(写出作法,画出图形,每小题6分,共12分)1.给定点A ,B ,作出点C ,使(ABC)=5作法:2.如图,求作点P关于二次曲线Γ的极线。
微分几何浙江省月自考试题

浙江省2013年10月高等教育自学考试微分几何试题课程代码:10022一、单项选择题(本大题共5小题,每小题2分,共10分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其选出并将“答题纸”的相应代码涂黑.错涂、多涂或未涂均无分.1.如果在点P 有20LN M >-,则点P 称为曲面的 A .双曲点 B.椭圆点 C.抛物点D.平点2.球面上的大圆不可能是球面上的 A .测地线 B.曲率线 C.法截线D.渐近线 3.若曲线Γ的曲率、挠率都为非零常数,则曲线Γ是 A .平面曲线 B.球面曲线 C.圆柱螺线D.直线4.设曲面在一点的单位法向量n →,切向量为d r →,则d n →=λd r →的充分必要条件是 A.存在方向r δ→使d n →·r δ→=0 B.存在方向r δ→使·d r r δ→→=0C.存在方向r δ→使·d n r δ→→=0且·d r r δ→→=0 D.沿d r →有n k =05.曲面(),r r u v →→=上曲线(C)在P 点的基本向量为,,,αβγ→→→曲面在P 点的单位法向量为n →.则下列选项中不是曲线(C)在P 点的测地曲率的是 A.k n β→→⨯ B.(,,)k n αβ→→→C.(,,)r r n →→→D.(,,)k n αβ→→→二、填空题(本大题共10小题,每小题3分,共30分)6.若向量函数()r t 对于t 的每一个值有()()·r t r t '=0,且()|1|r =3,则()|5|r =________. 7.主法线与固定方向垂直的曲线是________.8.成为球面{cos cos , cos sin , sin }r R R R θϕθϕθ→=纬线的坐标曲线是________曲线.9.若曲面上非直线的曲线(C )在每一点的切平面是在这点的密切平面,则曲线(C )是曲面的________曲线.10.曲率恒等于零的曲线是________.11.曲线(C )上P 点处的三个基本向量是,,αβγ→→→,则过P 点由β→和γ→确定的平面叫曲线(C)在P 点的________.12.若00u v r r u v →→⨯在(,)点模不等于零,则00u v (,)为曲面的________点. 13.曲面上曲线是曲率线的充要条件是________组成可展曲面. 14.柱面的高斯曲率K=________.15.曲面上曲线(C )在一点P 的测地曲率g k =4,曲面在P 点沿(C )的切向的法曲率n k =3,则曲线(C )的曲率k =________.三、计算题(本大题共6小题,每小题7分,共42分)16.求曲线{} sin , cos ,t r t t t t te →=在原点的密切平面、法平面、切线方程. 17.求圆柱螺线{}2 cos ,2 sin ,2r t t t →=的曲率和挠率. 18.求正螺面{} cos , sin ,r u v u v bv →=的第二基本形式. 19.求在正螺面上{} cos , sin ,r u v u v bv →=的渐近线.20.求曲面(){(),,}222a b uvr u v u v →=+-上的曲率线的方程.21.求位于正螺面{} cos , sin ,r u v u v av →=上的圆柱螺线(C):{}00cos ,sin ,r u v u v av →=(0u =常数)的测地曲率.四、证明题(本大题共3小题,每小题6分,共18分) 22.向量函数()r t 平行于固定平面,则有(,,)r r r '''=0. 23.证明:球面与平面不存在等距对应.24.证明:若曲面上非直线的所有测地线均为平面曲线,则它必为曲率线.。
浙江7月自考高等数学(工本)试题及答案解析

浙江省 2018 年 7 月高等教育自学考试高等数学 (工本 )试题课程代码: 00023一、单项选择题 (在每小题的四个备选答案中,选出一个正确答案, 并将正确答案的序号填在题干的括号内。
每小题2 分,共 40 分)1. limsin x().xxA.1B. ∞C.- 1D.- ∞2.函数 f(x)=ln( a x 2), x 1在 x=1处可导,则常数 ().x b, x 1A. a=0,b= - 1B. a=3,b=(ln4) - 1C. a=2,b=(ln3) - 1D. a=1,b=(ln2) - 1 3.当 x → 0 时, tan 3x 是 sin(2x 3)的 ().A. 较高阶的无穷小B. 较低阶的无穷小C.等价无穷小D.同阶但不是等价无穷小4.曲线 y=x 3- 3x 上切线平行 x 轴的点是 ().A.(0 , 0)B.(1 , 2)C.( - 1, 2)D.( - 1,- 2)5.若 f(x) 的一个原函数是f ( x) f ( x h)).sinx ,则 lim(hhA.sinxB.cosxC.- sinxD.- cosx6.设 f (x1)dxcos x C ,则 f(x)=().A.sin(x - 1)B. - sin(x-1)C.sin(x+1)D.- sin(x+1)7.曲线 f(x)=e x 2在区间 ()上单调递减且向上凹 .A.(- ∞, - 1)B.( - 1, 0)C.(0, 1)D.(1 , +∞)8.交换积分次序,1y2 2 y ).dy f (x, y)dxdyf ( x, y) dx (11 x22 xA. dxf (x, y)dydxf (x, y)dy0 012xB.dx f ( x, y)dy 1 2 x112 x C.dx f ( x, y) dyx12 y D. dyyf (x, y)dx9.若 d(e - x f(x))=e x dx,且 f(0)=0 ,则 f(x)=().A.e 2x +e xB.e 2x - e xC.e 2x +e - xD.e 2x - e - x10.二重积分y ln xd=().1 x 20 y 11B.ln2A. -2C.ln2+1D.ln2 -12211.设二元函数 z=f(x,y) 在 (x 0,y 0)的某邻域内有连续的二阶偏导数,已知f x (x 0,y 0 )= f y (x 0,y 0)=0, f xx (x 0,y 0)>0, f xy (x 0,y 0)=0, f y y (x 0,y 0)>0, 则点 (x 0,y 0)( ).A. 是极小值点B. 是极大值点C.不是极值点D. 是否为极值点需进一步判定12.设 z=f(xy,x - y),则zz=().xyf fB.ffA.y(xy )(xy)xC.(x+y)fD.0(xy )13.已知△ ABC 的顶点为 A(3 , 2, - 1), B(5 ,- 4,7)和 C(- 1, 1, 2),则从顶点 C 所引中线长度为 ( ).A. 30B.30C.6D.514.设 D= { (x,y)| 1≤x 2 +(y- 2)2≤ 4} ,则 d=().DA. πB.2 πC.3πD.4 π15.已知直线 l:x3 y4 z和平面π: 4x- 2y- 2z=3,则 ().273A. l 在π内B. l 与π平行,但 l 不在π内C.l 与π垂直D. l 与π不垂直, l 与π不平行16.设 f 在 D 上连续,则xf ( x, y )d =().D2A.fB.fd dxdy DxDxC.0D.f(x,y)17.f(x)=ln(1 - x)的马克劳林级数展开式为().A. x x 2x 3B.xx 2x 32+, (- 1, 1]2- , (- 1,1] 33 2323C.x x x- ,[- 1,1)D.x x x+,[ - 1, 1)2323 18.下列级数中条件收敛的是().A.(1) n11B.(1) n 1nn1n n 13n 1sinn1 1 1C.(1)n1D.( 1)nn n nn 1n 119.幂级数n!x n的收敛半径 R=().n 0 2n1B.2A.2C.0D.+ ∞20.微分方程 y″ +y ′ =2x 的一个解为 ().A.y=cosxB.y=1+xC.y=x 2- 2xD.y=e - x二、填空题 (每小题 2 分,共 20分)1.设 f(x)=e ax a, x0为 ( - ∞, +∞ )上的连续函数,则 a=______. x a cos 2x, x02.设 f(1+x)-f(1)=2x+(x)2,则f(1)=______.3.f(x)=x 2+cosx 的递增区间为______.1dx=______.4.ln 2 x)0 x(15.设 z=f(x 2+y 2)满足 x zyz=1,其中 f 可微,则f (t)=______. x y6.与向量a={2,-1,2} 共线且满足方程a x18 的向量 x =______.2x 2y 247.要使 f(x,y)=22在点 (0, 0)处连续,则应定义 f(0,0)=______.x y8.C 为圆周 x2 +y2=1, 则( x 2y 2 ) 2 ds =______.C3x x9.f(x)=ee 的关于 x 的幂级数展开式为 ______.210.已知微分方程 y ″ - 2y ′ - 3y=e - x 有一特解 y *=1 xe x,则其通解为 ______.4三、计算题 (每小题 4 分,共 24分)1. lim x 2 (1 x sin 1 ).xx2.已知 e xyz +z- sin(xy)=6, 求 dz.13.计算 I=| x( 2x 1) | dx.4.计算二重积分1dxdy ,其中 D={ (x,y)|x 2+y 2≤ 1}.x 2D 1y 25.求 I=y 2 dx x 2 dy ,其中 +C 是逆时针方向的圆周x 2+y 2 =1.C6.求微分方程 x y +y=xe x满足 y(1)=1 的特解 .四、应用及证明题 (每小题 8 分,共 16 分)1.要造一个容积等于定数 k 的长方形无盖水池,应如何选择水池的尺寸,方可使它的表面积最小 .2.已知立体Ω是由 z= 2 x 2 y 2 与 z=x 2 +y 2 所围成,求Ω的体积 .4。
(最新整理)7月全国自考高等数学(工专)试题及答案解析

全国2018年7月自考高等数学(工专)试题课程代码:00022一、单项选择题(本大题共5小题,每小题2分,共10分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.函数111arcsin 22-+-=x x y 的定义域是( ) A .[-2,2]B .[-2,-1)∪(1,2]C .[2,2-]D .(-∞,-1)∪(1,+∞)2.在同一坐标系下,方程x y 2=与y x 2log =代表的图形( )A .关于x 轴对称B .关于y 轴对称C .是同一条曲线D .关于直线y =x 对称3.=+++++→∞)5454544(lim 1232n n n Λ( ) A .4B .5C .10D .20 4.函数)1ln(2x x y +-=的极值( )A .是-1-ln2B .是0C .是1-ln2D .不存在5.设A 为3阶方阵,且行列式|A |=1,则|-2A |之值为( )A .-8B .-2C .2D .8二、填空题(本大题共10小题,每小题3分,共30分)请在每小题的空格中填上正确答案。
错填、不填均无分。
6.xx x πsin lim ∞→=________. 7.曲线y =cos x 上点)21,3π(处的法线的斜率等于________. 8.设f (x )可导,则)6(2+x f dx d =________. 9.设xx y ln =,则dy =________. 10.曲线2sin 2-+=x x x y 的水平渐近线方程为________.11.已知⎩⎨⎧-=-=),cos 1(7),sin (7t y t t x 则dx dy =________. 12.如果⎰+=C x x dx x f ln )(,则f (x )________.13.设行列式1110212-k k=0,则k 的取值为________. 14.无穷限反常积分⎰+∞=e dx xx 2ln 1________. 15.设A =⎥⎦⎤⎢⎣⎡-2312,则A -1=________. 三、计算题(本大题共8小题,每小题6分,共48分)16.设⎪⎪⎪⎩⎪⎪⎪⎨⎧>--=<-=,1,11,1,0,1,cos 1)(x x x x x x x f π 问f (x )在x =1是否连续?若间断,指出间断点的类型.17.求极限.1cos )1(lim 0--→x e x x x 18.讨论曲线y =(x +1)4+e x 的凹凸性.19.求由方程y 2-2xy +9=0所确定的隐函数y =y (x )的导数dxdy . 20.一曲线通过点(1,1),且该曲线上任一点M (x ,y )处的切线垂直于此点与原点的连线,求这曲线的方程.21.求不定积分.⎰dx xe x22.计算定积分⎰-π053.sin sin xdx x23.当λ取何值时,线性方程组⎪⎩⎪⎨⎧=+-=+=++,0,02,0z y x y x z y x λ有非零解?在有非零解时求出它的通解.四、综合题(本大题共2小题,每小题6分,共12分)24.陆上C 处的货物要运到江边B 处,设江岸为一直线,C 到江岸的最近点为A ,C 到A 的距离为30公里,B 到A 的距离为100公里,已知每公里陆路运费为水路运费的2倍。
浙江7月自考高等数学(二)试题及答案解析

1浙江省2018年7月高等教育自学考试高等数学(二)试题课程代码:00021一、单项选择题(在每小题的四个备选答案中,选出一个正确答案,并将正确答案的序号填在题干的括号内。
每小题2分,共20分) 1.D=nnn n n a a a a a a ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-2112100000000000=( )。
A.0 B.a n1 C.(-1)n+1a 1a 2…a n-1a n1 D.(-1)n+1a 1a 2…a n-1a nn 2.设2003阶矩阵A ,满足A ′=-A ,则|A |=( )。
A.不确定 B.0 C.-1 D.13.若A 、B 均为n 阶方阵,则AB=0,则( )。
A.A=0或B=0B.|A |和|B |都等于零C.|A |和|B |中至少有一个等于零D.以上结论都不正确4.设A 是正交矩阵,则下列结论( )成立。
A.A 是对称矩阵B.A 中不同行的对应元素乘积之和等于1C.A 中不同行的对应元素乘积之和等于0D.A 不可逆5.若A 为m ×n 矩阵,r(A)=r<n 的充分必要条件是( )。
A.A 中非零子式的最高阶数等于r B.A 中非零子式的最高阶数小于r+1 C.A 中所有r+1阶子式全为0 D.A 中有r 阶子式不等于06.以A 表示事件“甲种产品畅销,乙种产品滞销”,则事件A 表示( )。
A.甲乙产品均畅销B.甲种产品滞销,乙种产品畅销2C.甲种产品滞销D.甲种产品滞销或乙种产品畅销7.随机变量ξ,η相互独立,ζ=2ξ-η+1,则D ζ等于( )。
A.4D ξ-D η B.4D ξ+D η C.4D ξ+D η+1 D.2D ξ+D η8.设一种零件的加工由两道工序组成,第一道工序的废品率为p ,第二道工序的废品率为q ,则该零件加工为成品的概率是( )。
A.1-p -q B.1-pq C.1-p -q+pq D.(1-p)+(1-q)9.设X 1,X 2,X 3是来自总体X 的样本,EX=μ,则( )是参数μ的较有效估计。
浙江7月高等教育自学考试结构力学(二)试题及答案解析
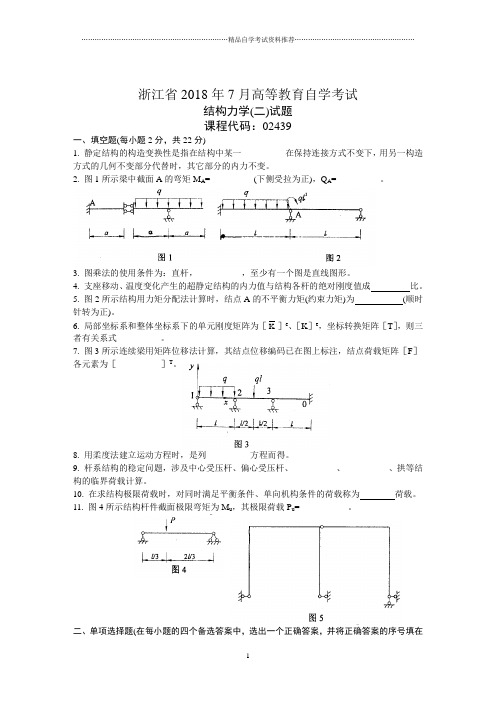
浙江省2018年7月高等教育自学考试结构力学(二)试题课程代码:02439一、填空题(每小题2分,共22分)1. 静定结构的构造变换性是指在结构中某一__________在保持连接方式不变下,用另一构造方式的几何不变部分代替时,其它部分的内力不变。
2. 图1所示梁中截面A的弯矩M A=__________(下侧受拉为正),Q A=__________。
3. 图乘法的使用条件为:直杆,__________,至少有一个图是直线图形。
4. 支座移动、温度变化产生的超静定结构的内力值与结构各杆的绝对刚度值成比。
5. 图2所示结构用力矩分配法计算时,结点A的不平衡力矩(约束力矩)为(顺时针转为正)。
6. 局部坐标系和整体坐标系下的单元刚度矩阵为[K]e、[K]e,坐标转换矩阵[T],则三者有关系式__________。
7. 图3所示连续梁用矩阵位移法计算,其结点位移编码已在图上标注,结点荷载矩阵[F]各元素为[__________]T。
8. 用柔度法建立运动方程时,是列__________方程而得。
9. 杆系结构的稳定问题,涉及中心受压杆、偏心受压杆、__________、__________、拱等结构的临界荷载计算。
10. 在求结构极限荷载时,对同时满足平衡条件、单向机构条件的荷载称为荷载。
11. 图4所示结构杆件截面极限弯矩为M u,其极限荷载P u=___________。
二、单项选择题(在每小题的四个备选答案中,选出一个正确答案,并将正确答案的序号填在题干的括号内。
每小题2分,共16分)1. 图5所示体系经几何组成分析为( )A. 无多余约束的几何不变体系B. 有多余约束的几何不变体系C. 瞬变体系D. 常变体系2. 图6所示刚架中M A和Q A为( )A. M A=Pl(下侧受拉) Q A=PB. M A=Pl(上侧受拉) Q A=PC. M A=Pl/2(下侧受拉) Q A=P/2D. M A=0 Q A=P3. 图7所示三铰拱,拉杆AB拉力为( )A. PB. P/2C. P/3D. P/44. 图8所示桁架中零杆数为( )A. 4B. 5C. 6D. 75. 用图9所示结构的超静定次数为( )A. 6B. 7C. 8D. 96. 图10所示结构用位移法计算,其结点的独立角位移和线位移未知量为( )A. 角位移=3 线位移=2B. 角位移=3 线位移=1C. 角位移=2 线位移=2D. 角位移=2 线位移=17. 图11所示结构用力矩分配法计算时,AB杆A端的分配系数μAB为( )A. 1/3B. 12/37C. 3/11D. 3/138. 图12所示体系略去杆件轴向变形,动力计算时体系自由度数为( )A. 3B. 4C. 5D. 6三、计算分析题(共62分)1.求作图13所示刚架的弯矩图、剪力图。
2011年7月浙江自考真题高等数学(工专)

2011年7月浙江自考真题高等数学(工专) 12一、单项选择题(在每小题的四个备选答案中,选出一个正确答案,并将正确答案的序号填在题干的括号内。
每小题2分,共40分)1. 函数f(x)=2x1x +在定义域内是( ) A.无界函数 B.有界函数C.上无界下有界D.上有界下无界2.设y=sin(7x+2),则=dxdy ( ) A.7sin(7x+2) B.7cos(7x+2)C.cos(7x+2)D.sin(7x+2)3.曲线y=3xx sin -的水平渐近线方程为( ) A.x=0 B.y=-3C.y=0D.y=-24.曲线y=ctgx 在点(1,4π)处的切线的斜率是( ) A.21- B.-2 C.22 D.-csc 21 5.在区间[-1,1]上满足罗尔定理条件的函数是( ) A.2x-1B.x 1C.x 2D.x 2/36.设f(x)=⎪⎩⎪⎨⎧<>0x x 1sin x 0x x 1sin ,则)x (f lim 0x →不存在的原因是( ) A.f(0)无定义B. )x (f lim 0x -→不存在C. )x (f lim 0x +→不存在D. )x (f lim 0x +→和)x (f lim 0x -→都存在但不等 7.⎰=b xdt )t (f dx d ( ) A.f(b)B.-f(x)C.f(b)-f(x)D.08.⎰=+dx )1x (x 10( ) A.C )1x (11111++ B.C )1x (111)1x (1211112++-+C.C )1x (111x 21112++⋅ D. C )1x (111)1x (1211112++++ 9.⎰-=+222dx )x 1(1( ) A.34- B.32- C.34D.不存在10.由曲线y=e x 和y=e -x 及直线x=1所围平面图形的面积等于( )A.e+e -1-2B.e+e -1C.2-e-e -1D.e-e -1-211.设=⨯-=-=→→→→b a },2,1,3{b },5,3,2{a 则( )A.{1,-19,-11}B.{0,19,11}C.{1,19,11}D.-712.过点(3,0,0)且平行于y=1的平面方程是( )A.x=0B.y=0C.z=0D.x=313.设f(x,y 0)和f(x 0,y)均在点P 0(x 0,y 0)处连续,则f(x,y)在点P 0处( )A.连续B.不连续C.没有意义D.可能连续,可能不连续14.设Z=x y e ,则=∂∂y z( )A. x y eB.y x x y eC.y x x y e lnyD.xy x-1x y e15.设曲线C :是从A (1,0)到B (-1,2)的直线段,则曲线积分=+⎰c ds )y x (() A.22 B.0 C.2 D.216.设积分区域B:x 2+y 22R ≤,则⎰⎰=σ+B22d )y x (x ( )A.2R πB.0C.22R πD.117.在下列级数中,发散的是( ) A.∑∞=1n n 32B.∑∞=--1n 1n n )1( C.∑∞=+1n 421n 3n D.∑∞=+1n 3)1n (n 118.级数∑∞=1n n )x (lg 的收敛区间是( )A.(-1,1)B.(-10,10)C.(101,101-) D.(10,101) 19.微分方程0y 4y =-''的通解是( ) A.y=C 1e 2x +C 2e -2x B.y=C 1+C 2e 4xC.y=C 1cos2x+C 2sin2xD.y=Ce 2x +e -2x20.微分方程0y ln y y x =-'的满足y(1)=e 的特解为( )A.y=exB.y=e xC.y=xe 2x-1D.y=elnx二、填空题(每小题2分,共20分)21.设f(x)=⎩⎨⎧>-≤+0x 1e 0x x sin a x 在x=0处连续,则常数a=_____________. 22.曲线y=lnx 在点(1,0)处的法线斜率为_____________.23.⎰=.______________xdx sec e 2tgx 2 24.⎰-=++113.______________________dx )1x cos x x 3(25.设⎩⎨⎧==-t t ey te x 则=dx dy ______________. 26.设f(x,y)=ln(x 2+y 2),g(x,y)=e (x+y),则f[x 2,g(x,y)]=__________.27.已知曲面z=4-x 2-y 2上点P 0处的切平面平行于平面2x+2y+z-1=0,则P 0点的坐标应为_____.28.设B :22224y x π≤+≤π,则⎰⎰=B._____________dxdy29.设常数项级数∑∞==1n n ,2002a则.__________a lim n n =∞→ 30.微分方程.__________0y 6y 5y 的通解是=+'-''三、计算题(每小题5分,共25分) 31.)x1)x 1ln(1(lim 0x -+→ 32.⎰xarctgxdx 33.求过点(2,0,-1)且与直线⎩⎨⎧=-+-=++-06z y 3x 209z 3y 2x 4 平行的直线方程. 34.计算二重积分⎰⎰σB 2d xy,其中B 是由y=x 2,y=x 所围成的区域.35.求幂级数∑∞=1n n nx的收敛区间(考虑端点).四、应用和证明题(每小题5分,共15分)36.证明:当x>0时,e x >1+x.37.用薄钢板做一体积为V 的有盖圆柱形桶。
7月浙江自考高等几何试题及答案解析试卷及答案解析真题

浙江省2019年7月高等教育自学考试高等几何试题课程代码:10027一、填空题(每空2分,共20分)1.平行四边形是______不变图形。
2.在仿射变换下,任何一对对应三角形面积之比等于______。
3.三角形的______心是仿射不变性。
4.斜率为k的直线上的无穷远点的齐次坐标是______。
5.点坐标(0,0,1)的方程是______。
6.设A、B、C、D为共线四点,交比(AB,CD)定义为______。
7.两个射影点列成透视的充要条件是______。
8.欧几里得几何是研究______群下图形的不变性质。
9.在配极对应下,点列与线束之间的对应是______的。
10.由罗巴切夫斯基平行公理出发,在罗氏平面上通过直线a外一点A有______条直线与a不相交。
二、计算题(每小题6分,共30分)1.求直线(2,i,3-4i)上的实点。
解:2.求a1x1+a2x2+a3x3=0, b1x1+b2x2+b3x3=0的交点与直线c1x1+c2x2+c3x3=0上的无穷远点连线的方程。
解:3.设P1,P2分别为y轴、x轴上的无穷远点,P3是斜率为1的直线上的无穷远点,又(P1P2,P3P4)=m.求P4的坐标.解:4.试求已知直线3x-y+6=0关于二阶曲线x2-2xy+y2+2x-6y=0的极点。
解:5.试求二次曲线x2+3xy-4y2+2x-10y=0的中心解:三、作图题(每小题6分,共18分)1.给定点A、B作出点C,使(ABC)=-1作法:2.如图,已知直线a∥b,限用直尺,过任一点P,作它们的平行线.作法:3.如图,求作点P关于二次曲线Γ的切线作法:四、证明题(第1、2题各10分,第3小题12分,共32分)1.设AD、BE、CF为△ABC的三高线,EF×BC=D′求证(BC,DD′)=-1,在等腰三角形AB=AC的情况下命题给出什么结论.证明:2.试证迷向直线与其本身所成的角是不定的。
证明:3.点A1、B1、C1为△ABC每边的三等分点,连接AA1、BB1、CC1,得点A2=BB1×CC1,B2=AA1×CC1,C2=AA1×BB1,求证:△ABC,△A1B1C1,△A2B2C2有共同的重心(图甲)证明:(按以下程序作业)第一步:将△ABC仿射变换为等边△A′B′C′(图乙),为什么这样变换存在?第二步:在图乙中画出图甲的对应点和线段,并叙述原来命题对应地变成怎样的命题?第三步:证明:变换后的相应命题成立,这样原命题也成立,为什么?。
浙江省普通高校招生学考科目考试立体几何多选题试题含答案

浙江省普通高校招生学考科目考试立体几何多选题试题含答案一、立体几何多选题1.如图①,矩形ABCD 的边2BC =,设AB x =,0x >,三角形BCM 为等边三角形,沿BC 将三角形BCM 折起,构成四棱锥M ABCD -如图②,则下列说法正确的有( )A .若T 为BC 中点,则在线段MC 上存在点P ,使得//PD 平面MATB .当)3,2x ∈时,则在翻折过程中,不存在某个位置满足平面MAD ⊥平面ABCDC .若使点M 在平面ABCD 内的射影落在线段AD 上,则此时该四棱锥的体积最大值为1 D .若1x =,且当点M 在平面ABCD 内的射影点H 落在线段AD 上时,三棱锥M HAB -6322++【答案】BCD 【分析】对于A ,延长AT 与DC 的延长线交于点N ,此时,DP 与MN 必有交点; 对于B ,取AD 的中点H ,表示出2223MH MT HT x --,验证当)3,2x ∈时,无解即可; 对于C ,利用体积公式21233V x x =⨯⨯-,借助基本不等式求最值即可; 对于D ,要求外接球半径与内切球半径,找外接圆的圆心,又内接圆半径为2323r =++【详解】对于A ,如图,延长AT 与DC 的延长线交于点N ,则面ATM ⋂面()MDC N MN =.此时,DP 与MN 必有交点,则DP 与面ATM 相交,故A 错误; 对于B ,取AD 的中点H ,连接MH ,则MH AD ⊥.若面MAD ⊥面ABCD ,则有2223MH MT HT x =-=- 当)3,2x ∈时,无解,所以在翻折过程中,不存在某个位置满足平面MAD ⊥平面ABCD故B 正确;对于C ,由题可知,此时面MAD ⊥面ABCD ,由B 可知,(3x ∈,所以()22222221223232331333232x x V x x x x ⎛⎫+-⎛⎫=⨯⨯-=-≤== ⎪ ⎪⎝⎭⎝⎭当且仅当223x x =-,即6x =时等号成立.故C 正确; 对于D ,由题可知,此时面MAD ⊥面ABCD ,且2MH =因为AHB ,MHB 都是直角三角形,所以M ABH -底面外接圆的圆心是中点,所以1R =,由等体积法,可求得内接圆半径为2323r =++,故61322R r ++=,故D 正确.故选:BCD . 【点睛】本题从多个角度深度考查了立体几何的相关内容,注意辅助线的作法,以及求内接圆半径的公式、基本不等式、构造函数等核心思想.2.如图,正方体1111ABCD A B C D -中的正四面体11A BDC -的棱长为2,则下列说法正确的是( )A .异面直线1AB 与1AD 所成的角是3πB .1BD ⊥平面11AC DC .平面1ACB 截正四面体11A BDC -3D .正四面体11A BDC -的高等于正方体1111ABCD A B C D -体对角线长的23【答案】ABD【分析】选项A ,利用正方体的结构特征找到异面直线所成的角;选项B ,根据正方体和正四面体的结构特征以及线面垂直的判定定理容易得证;选项C ,由图得平面1ACB 截正四面体11A BDC -所得截面面积为1ACB 面积的四分之一;选项D ,分别求出正方体的体对角线长和正四面体11A BDC -的高,然后判断数量关系即可得解. 【详解】A :正方体1111ABCD ABCD -中,易知11//AD BC ,异面直线1A B 与1AD 所成的角即直线1A B 与1BC 所成的角,即11A BC ∠,11A BC 为等边三角形,113A BC π∠=,正确;B :连接11B D ,1B B ⊥平面1111DC B A ,11A C ⊂平面1111D C B A ,即111AC B B ⊥,又1111AC B D ⊥,1111B B B D B ⋂=,有11A C ⊥平面11BDD B ,1BD ⊂平面11BDD B ,所以111BD AC ⊥,同理可证:11BD A D ⊥,1111AC A D A ⋂=,所以1BD ⊥平面11AC D ,正确;C :易知平面1ACB 截正四面体11A BDC -所得截面面积为134ACB S=,错误;D :易得正方体1111ABCD A B C D -()()()2222226++=2的正四面体11A BDC -22222262213⎛⎫--⨯ ⎪⎝⎭,故正四面体11A BDC -的高等于正方体1111ABCD A B C D -体对角线长的23,正确. 故选:ABD. 【点睛】关键点点睛:利用正方体的性质,找异面直线所成角的平面角求其大小,根据线面垂直的判定证明1BD ⊥平面11AC D ,由正四面体的性质,结合几何图形确定截面的面积,并求高,即可判断C 、D 的正误.3.在三棱柱111ABC A B C -中,ABC ∆是边长为343( )A .直线1A C 与直线1BB 之间距离的最大值为3B .若1A 在底面ABC 上的投影恰为ABC ∆的中心,则直线1AA 与底面所成角为60︒ C .若三棱柱的侧棱垂直于底面,则异面直线AB 与1A C 所成的角为30D .若三棱柱的侧棱垂直于底面,则其外接球表面积为64π 【答案】AD 【分析】建立空间直角坐标系,用向量法求解. 【详解】如图示,以A 为原点,AC 为y 轴正方向,Ax 为x 轴正方向,过A 点垂直于面ABC 的向上方向为z 轴正方向建系,则()()()0,0,0,3,0,0,23,0,A B C 设()()()100010001000,,,3,3,,,23,,A x y z B x y z C x y z ++所以()()()1000100011,23,,,,,3,3,0,AC x y z BB x y z A B =---== 对于A:设n 为直线1A C 与直线1BB 的公垂线的方向向量,则有:11·0·0AC n BB n ⎧=⎪⎨=⎪⎩,即()()0000002300x x y y zz x x y y zz ⎧-+-=⎪⎨++=⎪⎩解得:()00,0n z x =- 设直线1A C 与直线1BB 之间距离为d ,则22011222200009||||z A B nd d x z n x z ===++ 22009x d ≥∴≤,即3d ≤,故A 正确;对于B :若1A 在底面ABC 上的投影恰为ABC ∆的中心,则(13,211A 底面法向量()(10,0,1,1,3,211m AA ==,设直线 1AA 与底面所成角为θ,则:121133sin |cos ,|143AA n θ===⨯,故B 错误; 对于C : 三棱柱的侧棱垂直于底面时,则(((1110,0,43,3,43,0,23,43,A B C则()()13,3,0,0,23,43,AB AC ==- 设异面直线AB 与1A C 所成的角为θ,则11165cos |cos ,|||10||||23215AB AC AB AC AB AC θ====⨯,故C 错误;对于D :若三棱柱的侧棱垂直于底面时,外接球的球心O 为上下底面中心DD 1连线的中点,所以外接球的半径()222324R =+=,所以2464S R ππ==.故D 正确故选:AD 【点睛】向量法解决立体几何问题的关键: (1)建立合适的坐标系; (2)把要用到的向量正确表示; (3)利用向量法证明或计算.4.如图,正方体1111ABCD A B C D -的棱长为1,线段11B D 上有两个动点E ,F ,且2EF =.则下列结论正确的是( )A .三棱锥A BEF -的体积为定值B .当E 向1D 运动时,二面角A EF B --逐渐变小C .EF 在平面11ABB A 内的射影长为12D .当E 与1D 重合时,异面直线AE 与BF 所成的角为π4【答案】AC 【分析】对选项分别作图,研究计算可得. 【详解】选项A:连接BD ,由正方体性质知11BDD B 是矩形,1112212224BEF S EF BB ∆∴=⋅=⨯⨯=连接AO 交BD 于点O由正方体性质知AO ⊥平面11BDD B ,所以,AO 是点A 到平面11BDD B 的距离,即22AO =11221334212A BEF BEF V S AO -∆∴=⨯=⨯⨯=A BEF V -∴是定值.选项B:连接11A C 与11B D 交于点M ,连接11,AD AB , 由正方体性质知11AD AB =,M 是11B D 中点,AM EF ∴⊥ ,又1BB EF ⊥,11//BB AAA EFB ∴--的大小即为AM 与1AA 所成的角,在直角三角形1AA M 中,12tan 2MAA ∠=为定值. 选项C:如图,作1111,,,FH A B EG A B ET EG ⊥⊥⊥ 在直角三角形EFT 中,221cos 45222FT EF =⨯=⨯= 12HG FT ∴==选项D:当E 与1D 重合时,F 与M 重合,连接AC 与BD 交于点R ,连接1D R ,1//D R BM 异面直线AE 与BF 所成的角,即为异面直线1AD 与1D R 所成的角, 在三角形1AD R 中,22111132,2AD D R MB BB M B ===+=2AR = 由余弦定理得13cos AD R ∠= 故选:AC 【点睛】本题考查空间几何体性质问题.求解思路:关键是弄清(1)点的变化,点与点的重合及点的位置变化;(2)线的变化,应注意其位置关系的变化;(3)长度、角度等几何度量的变化.求空间几何体体积的思路:若所给定的几何体是柱体、锥体或台体等规则几何体,则可直接利用公式进行求解.其中,求三棱锥的体积常用等体积转换法;若所给定的几何体是不规则几何体,则将不规则的几何体通过分割或补形转化为规则几何体,再利用公式求解.5.如图所示,在长方体1111ABCD A B C D -中,11,2,AB BC AA P ===是1A B 上的一动点,则下列选项正确的是( )A .DP 35B .DP 5C .1AP PC +6D .1AP PC +的最小值为1705【答案】AD 【分析】DP 的最小值,即求1DA B △底边1A B 上的高即可;旋转11A BC 所在平面到平面11ABB A ,1AP PC +的最小值转化为求AC '即可.【详解】求DP 的最小值,即求1DA B △底边1A B 上的高,易知115,2A B A D BD ===,所以1A B 边上的高为355h =111,AC BC ,得11A BC ,以1A B 所在直线为轴,将11A BC 所在平面旋转到平面11ABB A ,设点1C 的新位置为C ',连接AC ',则AC '即为所求的最小值,易知11122,2,cos 10AA AC AAC ''==∠=-, 所以217042222()10AC '=+-⨯⨯⨯-= 故选:AD. 【点睛】本题考查利用旋转求解线段最小值问题.求解翻折、旋转问题的关键是弄清原有的性质变化与否, (1)点的变化,点与点的重合及点的位置变化;(2)线的变化,翻折、旋转前后应注意其位置关系的变化;(3)长度、角度等几何度量的变化.6.如图,已知矩形ABCD 中,2AB AD =,E 为边AB 的中点,将ADE ∆沿直线DE 翻折成1A DE ∆,若M 为线段1A C 的中点,则ADE ∆在翻折过程中,下列说法正确的是( )A .线段BM 的长是定值B .存在某个位置,使1DE AC ⊥C .点M 的运动轨迹是一个圆D .存在某个位置,使MB ⊥平面1A DE【答案】AC【分析】取CD 中点F ,连接BF ,MF ,根据面面平行的判定定理可得平面//BMF 平面1A DE ,由面面平行的性质定理可知//BM 平面1A DE ,可判断D ;在BFM ∆中,利用余弦定理可求得BM a =为定值,可判断A 和C ;假设1DE A C ⊥,由线面垂直的判定定理可得DE ⊥平面1A CE ,由线面垂直的性质定理可知1DE A E ⊥,与11DA A E ⊥矛盾,可判断B .【详解】解:取CD 的中点F ,连接BF ,MF ,∵M ,F 分别为1A C 、CD 中点,∴1MF A D ∥,∵1A D ⊂平面1A DE ,MF ⊄平面1A DE ,∴MF 平面1A DE ,∵DF BE ∥且DF BE =,∴四边形BEDF 为平行四边形,∴BF DE ,∵DE ⊂平面1A DE ,BF ⊄平面1A DE ,∴BF ∥平面1A DE ,又BF MF F =,BF 、MF ⊂平面BMF ,∴平面//BMF 平面1A DE ,∵BM ⊂平面BMF ,∴BM ∥平面1A DE ,即D 错误,设22AB AD a ==, 则112MF A D a ==,2BF DE a ==,145A DE MFB ︒∠=∠=, ∴222cos45BM MF BF MF BF a ︒=+-⋅⋅=,即BM 为定值,所以A 正确,∴点M 的轨迹是以B 为圆心,a 为半径的圆,即C 正确,∵2DE CE a ==,2CD AB a ==, ∴222DE CE CD +=, ∴DE CE ⊥,设1DE A C ⊥,∵1A C 、CE ⊂平面1A CE ,1AC CE C =, ∴DE ⊥平面1A CE ,∵1A E ⊂平面1A CE ,∴1DE A E ⊥,与11DA A E ⊥矛盾,所以假设不成立,即B 错误.故选:AC .【点睛】本题考查立体几何中的翻折问题,涉及到线段长度的求解、直线与平面位置关系的判定、点的轨迹的求解、反证法的应用等知识点,考查学生的空间立体感和推理论证能力.7.如图,在正方体ABCD ﹣A 1B 1C 1D 1中,点P 在线段B 1C 上运动,则( )A .直线BD 1⊥平面A 1C 1DB .三棱锥P ﹣A 1C 1D 的体积为定值C .异面直线AP 与A 1D 所成角的取值范用是[45°,90°]D .直线C 1P 与平面A 1C 1D 6 【答案】ABD【分析】在A 中,推导出A 1C 1⊥BD 1,DC 1⊥BD 1,从而直线BD 1⊥平面A 1C 1D ;在B 中,由B 1C ∥平面 A 1C 1D ,得到P 到平面A 1C 1D 的距离为定值,再由△A 1C 1D 的面积是定值,从而三棱锥P ﹣A 1C 1D 的体积为定值;在C 中,异面直线AP 与A 1D 所成角的取值范用是[60°,90°];在D 中,以D 为原点,DA 为x 轴,DC 为y 轴,DD 1为z 轴,建立空间直角坐标系,利用向量法能求出直线C 1P 与平面A 1C 1D所成角的正弦值的最大值为3. 【详解】解:在A 中,∵A 1C 1⊥B 1D 1,A 1C 1⊥BB 1,B 1D 1∩BB 1=B 1,∴A 1C 1⊥平面BB 1D 1,∴A 1C 1⊥BD 1,同理,DC 1⊥BD 1,∵A 1C 1∩DC 1=C 1,∴直线BD 1⊥平面A 1C 1D ,故A 正确;在B 中,∵A 1D ∥B 1C ,A 1D ⊂平面A 1C 1D ,B 1C ⊄平面A 1C 1D ,∴B 1C ∥平面 A 1C 1D ,∵点P 在线段B 1C 上运动,∴P 到平面A 1C 1D 的距离为定值,又△A 1C 1D 的面积是定值,∴三棱锥P ﹣A 1C 1D 的体积为定值,故B 正确;在C 中,异面直线AP 与A 1D 所成角的取值范用是[60°,90°],故C 错误;在D 中,以D 为原点,DA 为x 轴,DC 为y 轴,DD 1为z 轴,建立空间直角坐标系, 设正方体ABCD ﹣A 1B 1C 1D 1中棱长为1,P (a ,1,a ),则D (0,0,0),A 1(1,0,1),C 1(0,1,1),1DA =(1,0,1),1DC =(0,1,1),1C P =(a ,0,a ﹣1),设平面A 1C 1D 的法向量(),,n x y z =, 则1100n DA x z n DC y z ⎧⋅=+=⎪⎨⋅=+=⎪⎩,取x =1,得1,1,1n ,∴直线C 1P 与平面A 1C 1D 所成角的正弦值为: 11||||||C P n CP n ⋅⋅=∴当a =12时,直线C 1P 与平面A 1C 1D ,故D 正确. 故选:ABD .【点睛】求直线与平面所成的角的一般步骤:(1)、①找直线与平面所成的角,即通过找直线在平面上的射影来完成;②计算,要把直线与平面所成的角转化到一个三角形中求解;(2)、用空间向量坐标公式求解.8.如图,已知P 为棱长为1的正方体对角线1BD 上的一点,且()()10,1BP BD λλ=,下面结论中正确结论的有( )A .11A D C P ⊥;B .当1A P PD +取最小值时,23λ=; C .若()0,1λ∈,则7,312APC ππ⎛⎫∠∈ ⎪⎝⎭; D .若P 为1BD 的中点,四棱锥11P AA D D -的外接球表面积为94π. 【答案】ABD【分析】 以D 为坐标原点建立如图空间直角坐标系,利用向量关系可判断ABC ;根据几何体外接球关系建立方程求出球半径即可判断D.【详解】以D 为坐标原点建立如图空间直角坐标系,则()1,1,0B ,()10,0,1D ,设(),,P x y z ,()()10,1BP BD λλ=,1BP BD λ∴=,即()()1,1,1,1,1x y z λ--=--,则可解得()1,1,P λλλ--,对A ,()()()111,0,1,0,0,0,0,1,1A D C ,()11,0,1A D ∴=--,()11,,1C P λλλ=---,则()()()()11110110A D C P λλλ⋅=-⨯-+⨯-+-⨯-=,则11A D C P ⊥,故A 正确;对B ,()()()()()2222221111111A P PD λλλλλλ+=--+-+--+-+222223422333λλλ⎛⎫=-+=-+ ⎪⎝⎭ 则当23λ=时,1A P PD +取最小值,故B 正确; 对C ,()()1,0,0,0,1,0A C ,(),1,PA λλλ∴=--,()1,,PC λλλ=--,则222321cos 1321321PA PC APC PA PC λλλλλλ⋅-∠===--+-+⋅, 01λ<<,则2232123λλ≤-+<,则2111123212λλ-≤-<-+, 即11cos 22APC -≤∠<,则2,33APC ππ⎛⎤∠∈ ⎥⎝⎦,故C 错误; 对于D ,当P 为1BD 中点时,四棱锥11P AA D D -为正四棱锥,设平面11AA D D 的中心为O ,四棱锥11P AA D D -的外接球半径为R ,所以222122R R ⎛⎫-+= ⎪⎝⎭⎝⎭,解得34R =, 故四棱锥11P AA D D -的外接球表面积为94π,所以D 正确. 故选:ABD.【点睛】关键点睛:本题考查空间相关量的计算,解题的关键是建立空间直角坐标系,利用向量建立关系进行计算.。
《高等几何》考试练习题及参考答案

《高等几何》考试练习题及参考答案一、单选题1. 菱形的仿射对应图形是()A 、菱形B 、平行四边形C 、正方形D 、不等边四边形答案:B2. 圆经过中心射影之后的对应图形是()A 、圆B 、椭圆C 、二次曲线D 、二共点直线答案:C3. 射影平面上所有射影变换的集合构成群,称为射影变换群,它是()A 、8维群B 、6维群C 、4维群D 、3维群答案:A4. 正六边形经过中心射影后的对应图形是()A 、正六边形B 、二次曲线C 、二平行直线D 、内接于二次曲线的六边形答案:D5. 在射影平面上,两条相交直线可以把平面分成几个区域?()A 、1B 、2C 、3D 、4答案:B6. 欧式平面内所有正交变换的集合构成群,称为正交变换群,它是()A 、3维群B 、4维群C 、6维群D 、8维群答案:A7. 双曲型曲线与无穷远直线的关系是()A 、相交B 、相切C 、相离D 、相割答案:A8. 下面属于欧式几何学的是()A 、梯形B 、离心率C 、重心D 、塞瓦定理和麦尼劳斯定理答案:B9. 直角三角形经过中心射影后的对应图形是()A 、三角形B 、等腰三角形C 、直角三角形D 、四边形答案:A10. 共点的直线经过中心射影之后的对应图形是()A 、二直线B 、二垂直直线C 、共点的直线D 、二平行直线答案:C11. 在射影平面上二阶曲线可共分为()类.A 、2B 、3C 、4D 、5答案:D12. 双曲线有几条主轴?()A 、1B 、2C 、3D 、4答案:B13. 已知两点A(2,-1,1),B(3,1,-2),下列哪一个点与它们共线?()A 、(7 ,-1 ,0)B 、(7 ,-1 ,1)C 、(5 ,0 ,2)D 、(0 ,0 ,1)答案:A14. 等腰梯形的仿射对应图形是:()A 、等腰梯形B 、梯形C 、四边形D 、平行四边形答案:B15. 对于非恒等二维射影变换下列说法错误的是()A 、是非奇线性对应B 、保持共线四点的交比不变C 、不变直线不能超过三条D 、不共线的不变点至多有三个答案:C16. 下列哪些图形具有射影性质?()A 、平行直线B 、三点共线C 、两点间的距离D 、两直线的夹角答案:B17. 圆的仿射对应图形是:()A 、梯形B 、四边形C 、椭圆D 、平行四边形答案:C18. 矩形的仿射对应图形是:()A 、四边形B 、平行四边形C 、梯形D 、圆答案:B19. 下列名称或者定理不属于仿射几何学的是A 、三角形的垂心B 、梯形C 、在平面内无三线共点的四条直线有六个交点D 、椭圆答案:A二、判断题1. 一维基本形间的射影对应不保持对应四元素的交比. ()A 、正确B 、错误答案:错误2. 两全等三角形经仿射对应后得两全等三角形()A 、正确B 、错误答案:错误3. 射影平面的不共点三直线将平面分成四部分.()A 、正确B 、错误答案:正确4. 一个角的内外角平分线调和分离角的两边()A 、正确B 、错误答案:正确5. 共线三点的单比经中心射影后不变. ()A 、正确B 、错误答案:错误6. 二直线所成角度是相似群的不变量.()A 、正确B 、错误答案:正确7. 射影平面上的一直线能将射影平面剖分成两部分. ()A 、正确B 、错误答案:错误8. 三点形经中心射影之后还是三点形.()A 、正确B 、错误答案:正确9. 在一维射影变换中,若已知一对对应元素(非自对应元素)符合对合条件,则此射影变换一定是对合. ()A 、正确B 、错误答案:正确10. 在仿射变换下,等腰三角形的对应图形是三角形. ()A 、正确B 、错误答案:正确11. 仿射变换的基本不变量是单比. ()A 、正确B 、错误答案:正确12. 抛物线有一对主轴. ()A 、正确B 、错误答案:错误13. 三角形的垂心属于仿射几何学的范畴()A 、正确B 、错误答案:错误14. 在仿射变换下,正方形的对应图形是正方形.()A 、正确B 、错误答案:错误15. 共线点的极线必共点,共点线的极点必共线()A 、正确B 、错误答案:正确16. 椭圆和双曲线的四个焦点中有二实点二虚点.()A 、正确B 、错误答案:正确17. 配极变换是一种非奇线性对应,()A 、正确B 、错误答案:正确18. 两个三角形的面积之比是仿射不变量. ()A 、正确B 、错误19. 德萨格定理属于射影几何学的范畴. ()A 、正确B 、错误答案:正确20. 二阶曲线上任一点向曲线上四定点作直线,四直线的交比为常数. ()A 、正确B 、错误答案:正确21. 菱形的仿射对应图形是四边形. ()A 、正确B 、错误答案:错误22. 两点列的底只要相交构成的射影对应就是透视对应. ()A 、正确B 、错误答案:错误23.A 、正确B 、错误答案:正确24. 两个不同的无穷远点所决定的直线上可以含有有穷远点.()A 、正确B 、错误答案:错误三、名词解释1. 图形的仿射性质答案:图形经过任何仿射变换后都不变的性质称为图形的仿射性质.2. 二次曲线的直径答案:无穷远点关于二次曲线的有穷极线称为此二次曲线的直径.3. 二次曲线的中心答案:无穷远直线关于二次曲线的极点称为此二次曲线的中心.4. 配极原则答案:如果P点的极线通过Q点,则Q点的极线也通过P点.5. 二阶曲线答案:在射影平面上,成射影对应的两个线束对应直线的交点的集合称为二阶曲线.6. 二次曲线的渐近线答案:二次曲线上的无穷远点的切线,如果不是无穷远直线,则称为二次曲线的渐近线.7. 对偶原则答案:在射影平面里,如果一个命题成立,则它的对偶命题也成立.8. 完全四点形答案:由四个点(其中无三点共线)以及连结其中任意两点的六条直线所组成的图形称为完全四点形.四、问答题1. 下列图形的仿射对应图形是什么?(1)圆;(2)等腰三角形;(3)三角形的内心;(4)两个合同的矩阵;(5)三角形的重心;(6)相似三角形;(7)三角形的垂心;(8)矩形。
10027高等几何浙江省2013年7月自考试题

浙江省2013年7月高等教育自学考试高等几何试题课程代码:10027一、单项选择题(本大题共5小题,每小题2分,共10分)1.正方形的仿射对应图形是A.菱形B.平行四边形C.矩形D.正方形2.与点(1,1+i,1-i)是同一点的是A.(1+i,1-i,2)B.(i,1-i,1+i)C.(1-i,2,1+i)D.(i,-1+i,1+i)3.没有奇异点的二阶曲线可以分为A.2类B.3类C.4类D.5类4.以下齐次仿射坐标方程所表示的二次曲线是虚椭圆的是A.x2-y2-t2=0B.x2+y2-t2=0C.x2+y2+t2=0D.x2-y2+t2=05.通过两点(1,i,0),(1,-i,0)的二次曲线是A.两条直线B.圆C.双曲线D.抛物线二、填空题(本大题共5小题,每小题2分,共10分)6.过两点(1,2,1),(1,1,-1)的直线上的无穷远点的坐标是_____.7.若交比(AB,CD)=-3,则(BC,DA)=_____.8.射影几何的基本不变量是_____.9.一点关于二次曲线所有共轭点的轨迹称为该点的_____.10.在欧氏平面上,二次曲线的焦点的极线叫做_____.三、计算题(本大题共6小题,每小题6分,共36分)11.求一仿射变换,它使直线x+2y-1=0和2x+3y+2=0分别变为x轴和y轴,且使点(0,0)变为(2,3).12.求直线(1-i,2+i,3i)上的实点.13.求对合方程,两对对应点的参数各为2与2,1与4,并确定该对合所属类型.14.求射影变换的二重点.15.求直线x1-5x3=0关于二阶曲线+2--2x1x3+4x2x3=0的极点.16.求二次曲线x2-2xy-3y2+4x+2=0的渐近线方程.四、作图题(本大题共2小题,每小题8分,共16分)(写出作法)17.给定透视仿射的一对对应点A,Aʹ和透视轴g,求作给定三角形ABC的对应三角形.18.已知椭圆及其外一点P,求作它的两条切线.五、证明题(本大题共3小题,第19、20小题各10分,第21小题8分,共28分)19.设A,B,C,D为共线四点,O为CD中点,且OC2=OA·OB,证明(AB,CD)=-1.20.如果一个完全四角形内接于一条二次曲线,证明它的对角三角形是自极三角形.。
7月浙江自考机械制图(三)试题及答案解析

浙江省2018年7月自学考试机械制图(三)试题
课程代码:04107
一、填空题(本大题共4小题,每空2分,共10分)
请在每小题的空格中填上正确答案。
错填、不填均无分。
1.点划线、虚线和其他图线相交时,都应在______处相交,不应在______处相交。
2.图样中所标注的尺寸,为该图样所示机件的______尺寸,否则应另加说明。
3.若圆柱和圆锥的轴线相交、且公切于一球面时,它们的相贯线必为______。
4.当与圆锥轴线平行且不与圆锥顶点相交的平面截切圆锥时,截交线总是______,但根据平面与投影面的相对位置不同,截交线的投影也不同。
二、名词解释(本大题共2小题,每小题5分,共10分)
1.投影面垂直面
2.六个基本视图
三、简答题(本大题10分)
写出仪器绘图的5个步骤。
四、读懂机件形状,改正视图中的错误画法(本大题共2小题,每小题5分,共10分)
1.补画组合体视图中遗漏的线条。
1
2.补画剖视图中遗漏的线条。
五、补画第三视图(本大题共2小题,每小题5分,共10分)
1.根据主视图和左视图,补画俯视图。
2.根据主视图和俯视图,补画左视图。
2
六、用正确的剖视方法,补齐图中的视图(本大题共2小题,每小题5分,共10分)
1.根据上、下图给出的主视图和俯视图,用正确的剖视方法,补齐图中间的主视图。
3
2.根据主视图和俯视图,画出全剖的左视图。
4
七、几何作图(本大题40分)
按照题中给出的图形,在空白处按1∶1抄画该图形(尺寸需要标注)。
5。
浙江7月高等教育自学考试高等数学(工专)试题及答案解析

浙江省2018年7月高等教育自学考试高等数学(工专)试题课程代码:00022一、单项选择题(在每小题的四个备选答案中选出一个正确答案,并将其号码填在题后的括号内。
每小题2分,共20分)1. 设f(x)=⎩⎨⎧≤≤<-)3x 1(1)1|x (|x 2,则f(x-2)的定义域是( ) A. 〔-1,3〕 B. 〔1,5〕 C. (-1,3〕 D. (1,5〕2. 如果数列{x n }收敛,{y n }发散,则数列{x n +y n }一定( )A. 收敛B. 发散C. 有界D. 无界3. 设f(x)=⎪⎩⎪⎨⎧>-=<+)0x (x 21)0x (2)0x (1x 3, 则)x (f 0x →lim =( ) A. 1 B. 2 C. -1 D. 不存在4. 设f(x)在点x=0处可导,且f(0)=0,则:)h2(hf lim h ∞→=( ) A. f ′(0) B. 2f ′(0) C. 21f ′(0) D. 2 5. 设y 是由方程xy+x+y-2=0所确定的x 的隐函数,则:y ′(0)=( ) A. -21)(x 3+ B. -3 C. 3 D. -1x 1y ++ 6. 函数f(x)=x x -1在区间〔0,1〕上满足罗尔定理条件的C=( )A. 1/2B. 1/3C. 2/3D. 3/47. 如果广义积分⎰+∞-11P x dx 收敛,则( )A. P>1B. P<1C. P>0D. P<08. 过原点与平面x+2y+z=2垂直的直线方程为( )A. x+2y+z=0B.1z 2y 1x -==- C. x=2y =z D. x=-y=z 9. 设D :x 2+(y-1)2≤1,则:⎰⎰D dxdy )y ,x (f =( ) A.⎰⎰θππ-θcos 202/2/d f(rcos θ,rsin θ)rdrB. ⎰⎰θπ-θcos 200d f(rcos θ,rsin θ)rdrC.⎰⎰θππ-θsin 202/2/d f(rcos θ,rsin θ)rdr D. ⎰⎰θπθsin 200d f(rcos θ,rsin θ)rdr10. 方程y ′-x 1y=x 的通解为( ) A. Cx 2+x B. x 2+x+C C. x 2+Cx D. Cx 2-x二、填空题(每格2分,共20分)11. 设x 2x )xa x (lim +∞→=e -6,则a=_______. 12. )2x 3sin 2x 3sinx (lim x +∞→ =_______. 13. 设y=sin 22x ,则:y 0″=_______. 14. 曲线y 2=x 上点(1,1)处的切线方程为_______. 15. ⎰+dx x1x 332=_______. 16. 设⎰=+1023dx )ax x 3(,则:a=_______.17. 曲线y=7x 4x 1x 322++-的渐近线为_______.18. 函数z=x 2-3xy+y 2-3x+7y+5的驻点是_______.19. 设D 是由曲线x+y=1,x-y=1及x=0所围的区域,则:⎰⎰Ddxdy =_______. 20. 级数∑+∞=-+-1n n n 1n x 1n 2)1(的收敛半径R=_______. 三、计算题(每题6分,共42分)21. 求函数y=ln(x+22x a +)的导数.22. 求2x x 0x x 2e e lim -+-→.23. 设⎪⎩⎪⎨⎧==⎰t 0udu sin u y cost x 求:22dx y d ,dx dy .24. 求⎰x cos x2dx.25. 计算⎰⎰1y 210dx x cos dy . 26. 求微分方程y ′=y-2x 2y x +的通解.27. 将函数lnx 展开成(x-1)的幂级数,并确定其收敛域.四、应用和证明题(每小题6分,共18分)28. 欲建造一个容积为16m 3的长方体水箱。
浙江7月自考高等数学(工专)试题及答案解析

1浙江省2018年7月高等教育自学考试高等数学(工专)试题课程代码:00022一、单项选择题(在每小题的四个备选答案中,选出一个正确答案,并将正确答案的序号填在题干的括号内。
1—10每小题1分,11—20每小题2分,共30分)(一)每小题1分,共10分1.下列函数中为奇函数的是( ).A.x 2-xB.5x 5x ln-+ C.e x +e -x D.xsinx2.设α和β分别是同一变化过程中的无穷小量与无穷大量,则α+β是同一变化过程中的( ).A.无穷小量B.有界变量C.无界变量但非无穷大D.无穷大量3.在点x 处,当自变量有改变量Δx 时,函数y=5x 2的改变量Δy=( ).A.10x ΔxB.10+5ΔxC.10Δx+(Δx)2D.10x Δx+5(Δx)24.若f '(x 0)=0,则x 0一定是函数y=f(x)的( ).A.极值点B.驻点C.拐点D.零点 5.若C e 2dx )x (f 2x +=⎰,则f(x)=( ). A.2xeB.22x eC.212x eD.42xe 6.下列积分中为广义积分的是( ).A.⎰e 1x ln x dx B.⎰10dx x x sin C.⎰-1024x dxD.dx x x cot 242⎰ππ7.平面x+2y -6=0的位置是( ).A.平行xoy 平面B.平行z 轴C.垂直z 轴D.通过z 轴2 8.设u=x 2+3xy -y 2,则y x u2∂∂∂=( ).A.-2B.2C.3D.69.级数∑∞=1n n U 收敛的充要条件是( ).A.0U lim n n =∞→B.1r U U lim n1n n <=+∞→C.n n S lim ∞→存在(其中S n =U 1+U 2+…+U n )D.U n ≤2n 110.过点(1,2)且切线斜率为3x 的曲线方程y=y(x)应满足的关系是( ).A.y ′=3xB.y ″=3xC.y ′=3x;y(1)=2D.y ′=2x;y(1)=3(二)每小题2分,共20分11.函数y=ln(3x -1)在区间内有界的区间是( ).A.(1,+∞)B.(31,1)C.(31,+∞) D.(1,3)12.设f(x)=⎩⎨⎧=≠1x ,21x ,x 2,则)x (f lim 1x →=( ).A.3B.2C.1D.不存在13.用微分近似计算公式可求得e 0.05的近似值是( ).A.0.05B.1.05C.0.95D.114.设函数f(x)在[0,a ]上二阶导数存在,且x f ''(x)-f '(x)>0,则x )x (f '在区间(0,a)内是(). A.单调增加的 B.单调减少的C.不增的D.有增有减的15.设sinx 是f(x)的一个原函数,则⎰dx )x (xf =( ).A.xsinx+cosx+CB.-xsinx+cosx+CC.-xsinx -cosx+CD.xsinx -cosx+C3 16.⎰=x04x dt )t (f ,则=⎰dx )x (f x140( ). A.32B.512C.8D.256 17.坐标面yoz 截双曲抛物面x 4z 2y 22=-所得的截痕是( ). A.抛物线 B.双曲线C.两条平行直线D.两条相交直线18.若u=sin(y+x)+sin(y -x),则下列关系式中正确的是( ).A.yu x u ∂∂=∂∂ B.y x u x u 222∂∂∂=∂∂ C.2222y u x u∂∂=∂∂ D.222y u y x u ∂∂=∂∂∂ 19.下列级数中发散的是( ).A. ∑∞=--1n n )1n (n )1( B.)1|r (|r )1(1n n n >-∑∞= C. ∑∞=+1n )1n ln(1 D.∑∞=-1n 1n 3120.微分方程2ydy -3dx=0的通解是( ).A.y -3x=CB.y 2-3x=CC.2y+3x=CD.2y=3x+C二、填空题(每小题2分,共10分)21.已知f(x+1)=x(x -1),则f(x -2)=______.22.设y=xlnx+x 2,则dy=______.23.设f(x)=lnx,则⎰'dx )x 1(f x 12=______. 24.f(x,y)=x 2y 12-的定义域是______.25.微分方程2y x 3dy dx +-=0的通解是______. 三、计算题(每小题5分,共45分)26.求xsin e e lim xx 0x -→- 27.设f(x)可导,且y=f(sin 2x),求dxdy4 28.求⎰-dx )1x 3(x 629.求由曲线y=x 2与直线y=2x+3所围成图形的面积 30.设z=f(x 2,y+1),x=sint,y=t 3,求dtdz 31.求微分方程y ″+y ′+y=3x 2的通解. 32.求幂级数∑+∞=--1n 1n n n 3)x (的收敛区间(考虑端点)33.求过点M 0(2,9,-6),且与连接坐标原点及点M 0的线段OM 0垂直的平面方程.34.化二次积分⎰⎰-++20x 42x 222dy )y x (f dx 为极坐标形式的二次积分.四、证明与应用题(每小题5分,共15分)35.设b>a>e ,证明a b >b a36.证明:)a (f )x (f dt )t (f )t x (dx d x a-='-⎰37.设用两种原料A 、B 生产某产品的数量y 与A 、B 的用量x 1、x 2之间的函数为y=x 1x 22,已知A 的单价为1元,B 的单价为3元,现用180元购原料,问两种原料各购多少时可使产品的数量最多?。
浙江7月高等教育自学考试高等数学(二)试题及答案解析

浙江省2018年7月高等教育自学考试高等数学(二)试题课程代码:00021一、单项选择题(在每小题的四个备选答案中,选出一个正确答案,并将正确答案的 序号填在题干的括号内。
每小题2分,共20分)1.A 是n 阶对称阵,B 是n 阶方阵,则( )是对称阵 A. AB-BA B. ABA ′ C. BAB ′ D. AB+BA2.行列式|A |≠0是方阵A 可逆的( )A.充分条件B.必要条件C.充要条件D.非充要条件 3.下列矩阵中不是约当型矩阵的是( )A. ⎥⎦⎤⎢⎣⎡--1011B. ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-100100001C. ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡000100010D. ⎥⎦⎤⎢⎣⎡1011 4.二次型f(x 1,x 2,x 3)=Ax x '=x 1x 2-2x 1x 3中A 是( )A. ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡--00100211210B. ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡--10100211210 C. ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-000000210D. ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-0020010005.设试验成功概率是p(0<p<1),则在三次重复独立试验中至少失败一次的概率是( )A. (1-p)3B. 1-p 3C. 3(1-p)D. (1-p)3+p(1-p)2+p 2(1-p)件零件出次品数的概率分布为A. 一样B. 甲机床不如乙机床C. 乙机床不如甲机床D. 无法比较7.随机变量ξ服从正态分布N(μ,σ2),已知E ξ=-1,D ξ=4,P {ξ≤0}=0.6,则P {ξ<-2}=( )A. 0.1B. 0.3C. 0.4D. 0.2 8.由D(ξ+η)=D ξ+D η可断定ξ与η( ) A. 不相关 B. 相互独立C. 联合分布函数F(x,y)=F ξ(x)·F η(y)D. 相关系数ξηρ=-19.总体服从正态分布N(μ,σ2),其中μ未知,对检验H 0:σ2=20σ选用的统计量2n1i 2i)x x(σ-∑=服从( )分布。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
浙江省2018年7月自学考试高等几何试题
课程代码:10027
一、单项选择题(本大题共5小题,每小题2分,共10分)
在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.在三角形的以下性质中是仿射性质的是( ) A.垂心 B.重心 C.内心
D.外心
2.以下四条直线中所含的无穷远点与其他三条不同的是( ) A.x y x y 121)1(2+=++ B.11)(2=++x x y
C.x +2y =0
D.过点(1,3),(3,2)的直线
3.已知A ,B ,C ,D 四点是调和点列,任意调整它们次序后所得交比不会出现的是( ) A.1 B.2 C.-1
D.
2
1
4.椭圆型射影对应的自对应元素是( ) A.两个互异的实元素 B.两个互异的虚元素 C.两个重合的实元素
D.两个重合的虚元素 5.唯一决定一条二阶曲线需无三点共线的( ) A.3点 B.4点
C.5点
D.6点
二、填空题(本大题共5小题,每小题2分,共10分)
请在每小题的空格中填上正确答案。
错填、不填均无分。
6.两点-3u 1+u 2+2u 3=0,2u 1-u 2+3u 3=0连线的坐标是_________.
7.若对合a μμ′+b (μ+μ′)+c =0是椭圆型的,则系数满足_________.
8.完全四线形的每一条对角线上有一组调和点列,即这直线上的两个顶点和_________. 9.椭圆上四定点与其上任意第五点所联四直线的交比为_________.
2 10.平面上任一圆通过的两个固定点称为_________. 三、计算题(本大题共6小题,每小题6分,共36分)
11.求使三点A (0,0),B (1,1),C (1,-1)变到三点A ′(1,1),B ′(3,1),C (1,-1)的仿射变换. 12.已知平面上有点A (2,1),B (4,2),C (6,-3),D (-3,2),E (-5,1),求A (BC ,DE ).
13.求射影变换式,使它的不变元素的参数是λ1=-1,λ2=3,并且使λ3=1变为3
λ'=0. 14.求射影变换⎪⎩⎪
⎨⎧--='-='-='3213
212
211
36 4 x
x x x x x x x x x ρρρ的二重直线. 15.求两个成射影对应的线束x 1-λx 2=0,x 2-λ′x 3=0,(λ′=λ
λ
+1)所构成的二阶曲线的方程.
16.求二次曲线x 1x 2+x 1x 3+x 2x 3=0的中心.
四、作图题(本大题共2小题,每小题8分,共16分)(第18题写出作法) 17.作出下列图形的对偶图形:
题17图
18.已知二阶曲线上五点A ,B ,C ,D ,E ,求作该曲线上点A 处的切线.
题18图
五、证明题(本大题共3小题,第19小题和第20小题各10分,第21小题8分,共28分)
19.设三条定直线l1,l2,l3共点于M,A与B为二定点,其连线通过M.又R为l3上的动点,且RA,RB 分别交l1,l2于P,Q,证明PQ必过AB上一定点.
20.设A,B,C,A′,B,′C′是共线点,且
(AA′,BC)=(BB′,CA)=(CC′,AB)=-1,
求证:A,A′;B,B′;C,C′是同一对合的对应点.
21.四边形ABCD的四边AB,BC,CD,DA分别切一圆于E,F,G,H,求证AC,BH,DE共点.
题21图
3。
