电磁学PPT课件:习题课
合集下载
电磁学基本理论 ppt课件

2
0
0 I
4a
ˆz a
ppt课件
O点产生的磁感应强度: 0 I
B B1 B2 B3
ppt课件 2
3. 库仑定律
F21
q1q2 ˆR21 a 2 4π 0 R21
其中: 0为真空中介电常数。
0
1 109 8.85 1012 36 π
q1
R21
q2
F/m
q1
4. 电场强度的计算 q1qt2 ˆR21 F21 a 2 4π 0 R21
R21
q 2t
E
q 1 1 q R2 R1 4π 0 R1 R2 4π 0 R R 1 2
R1 R l cos 2 l R2 R cos 2
因为: l R 则: R2 R1 l cos
2 l R2 R1 R 2 cos2 R 2 4
15
(三) 磁场
Fm
产生磁场的源: a.永久磁铁 b.变化的电场 c.电流周围,即运动的电荷
v
B
1. 什么是磁场?
Fm qv B
存在于载流回路或永久磁铁周围空间,能对运动电荷 施力的特殊物质称为磁场。 ˆv Fm a B lim qt 0 2. 磁感应强度 B的定义 qt v
ˆv 和磁感应强度 B 三者相互 可见: 磁场力 Fm 、运动速度 a 垂直,且满足右手螺旋法则。
ppt课件 16
3. 磁感应强度的计算
安培力实验定律:
dF21 ˆR ) 0 I 2dl2 ( I1dl1 a 4π R
2
电流元
I1
I 2dl2
I2
I1dl1
0
0 I
4a
ˆz a
ppt课件
O点产生的磁感应强度: 0 I
B B1 B2 B3
ppt课件 2
3. 库仑定律
F21
q1q2 ˆR21 a 2 4π 0 R21
其中: 0为真空中介电常数。
0
1 109 8.85 1012 36 π
q1
R21
q2
F/m
q1
4. 电场强度的计算 q1qt2 ˆR21 F21 a 2 4π 0 R21
R21
q 2t
E
q 1 1 q R2 R1 4π 0 R1 R2 4π 0 R R 1 2
R1 R l cos 2 l R2 R cos 2
因为: l R 则: R2 R1 l cos
2 l R2 R1 R 2 cos2 R 2 4
15
(三) 磁场
Fm
产生磁场的源: a.永久磁铁 b.变化的电场 c.电流周围,即运动的电荷
v
B
1. 什么是磁场?
Fm qv B
存在于载流回路或永久磁铁周围空间,能对运动电荷 施力的特殊物质称为磁场。 ˆv Fm a B lim qt 0 2. 磁感应强度 B的定义 qt v
ˆv 和磁感应强度 B 三者相互 可见: 磁场力 Fm 、运动速度 a 垂直,且满足右手螺旋法则。
ppt课件 16
3. 磁感应强度的计算
安培力实验定律:
dF21 ˆR ) 0 I 2dl2 ( I1dl1 a 4π R
2
电流元
I1
I 2dl2
I2
I1dl1
大学物理《电磁学》PPT课件
欧姆定律
描述导体中电流、电压和电阻之间关系的 定律。
电场强度
描述电场强弱的物理量,其大小与试探电 荷所受电场力成正比,与试探电荷的电荷 量成反比。
恒定电流
电流大小和方向均不随时间变化的电流。
电势与电势差
电势是描述电场中某点电势能的物理量, 电势差则是两点间电势的差值,反映了电 场在这两点间的做功能力。
电介质的极化现象
1 2
电介质的定义 电介质是指在外电场作用下能发生极化的物质。 极化是指电介质内部正负电荷中心发生相对位移, 形成电偶极子的现象。
极化类型 电介质的极化类型包括电子极化、原子极化和取 向极化等。
3
极化强度
极化强度是描述电介质极化程度的物理量,用矢 量P表示。极化强度与电场强度成正比,比例系 数称为电介质的电极化率。
磁场对载流线圈的作用
对于载流线圈,其受力可分解为沿线圈平面的法向力和切线方 向的力,分别用公式Fn=μ0I²S/2πa和Ft=μ0I²a/2π计算。
05
电磁感应原理及技 术应用
法拉第电磁感应定律
法拉第电磁感应定律的内容
01
变化的磁场会产生感应电动势,感应电动势的大小与磁通量的
变化率成正比。
法拉第电磁感应定律的数学表达式
安培环路定理及其推广形式
安培环路定理
磁场中B沿任何闭合路径L的线积分, 等于穿过这路径所围面积的电流代数 和的μ0倍,即∮B·dl=μ0∑I。
推广形式
对于非稳恒电流产生的磁场,安培环路 定理可推广为 ∮B·dl=μ0∑I+ε0μ0∂/∂t∮E·dl。
磁场对载流导线作用力计算
载流导线在磁场中受力
当载流导线与磁场方向不平行时,会受到安培力的作用,其大 小F=BILsinθ,方向用左手定则判断。
电磁学基础知识ppt课件

Br •
时,铁心中的磁感应强度。
矫顽磁力Hc: 使 B = 0 所需的 H 值。
磁性物质不同,其磁滞回线 和磁化曲线也不同。
• O •Hc H •
磁滞回线
17
几种常见磁性物质的磁化曲线
B/T 1 2 3 4 5 6 7 8 9
1.8
1.6
1.4 1.2 c
b 1.0
0.8
0.6
0.4
0.2
a
O 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 a 铸铁 b 铸钢 c 硅钢片
电动势三者参考方向一致,则
电感的欧姆 定律
u e L di dt
注意
在直流电路中,由于电流变化率为零,所以电 感电压等于零,电感元件相当于短路。
13
3.2铁磁性材料
磁性材料主要指铁、镍、钴及其合金等。
3.2.1 高导磁性
磁性材料的磁导率通常都很高,即 r 1 (如坡 莫合金,其 r 可达 2105 ) 。
有效值
E
Em 2
2
fN m
2
4.44
fN m
由于线圈电阻 R 和感抗X(或漏磁通)较小,其
电压降也较小,与主磁电动势 E 相比可忽略,故有
U E
式中:BmU是铁E心中4磁.44感f应N强m度的4最.4大4 f值N,Bm单S位(V[T)];
S 是铁心截面积,单位[m2]。
非线
对于铁心线圈来说,电感L不为常数。
性电
感
若为线性电感元件
eL
d
dt
d(Li) L di
dt
dt
(2)
注
式(1)与式(2)是电动势的两种表达式,
电磁学--第三版--课件
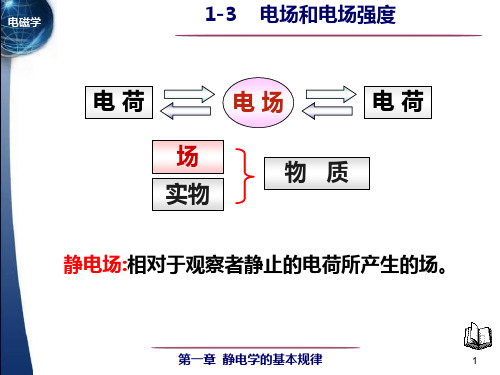
dEx
•
P
a
r
1
2
O x dx
x
由此得
d
Ex
4 π 0a
cos
d
d
Ey
4 π 0a
sin
d
将以上两式对整个带电细棒积分
第一章 静电学的基本规律
电磁学
1-3 电场和电场强度
y
dE dE y
dEx
•
P
ar
1
2
O x dx
x
Ex
4 π0a
2 cos d
1
4
π
0a
(sin
2
sin
1 )
Ey
4 π0a
12
电磁学
1-3 电场和电场强度
电偶极子是一个重要的物理模型,在研究电介质的极化、 电磁波的发射和吸收等问题时,都要用到这个模型。
在均匀外电场中,电偶极子所受 的合力为零,电偶极子在电场中 所受的力矩
M flsin qElsin
PEsin
M PE
+f
f
l
P
E
第一章 静电学的基本规律
F
i 1
i
Fi
E
F
qi 对 q0 的作用
q0
F1 F2 Fn
q0
q1
e1
q2
P
r1
e2 r2
e3
r3
q0
q3
E1 E2 En
第一章 静电学的基本规律
F3 F2 F1
8
电磁学
1-3 电场和电场强度
q1 q2
e1
r1
e2 r2
P
e3
大学物理《电磁学》PPT课件

电场和磁场都由电荷产生,也都由电荷的受力 情况来检验。那么,这两种场之间到底有什么本质 的区别呢?
众所周知,电荷的静止与运动都是相对观察者 而言的,我们对运动与静止的描述依赖于所选择的 参照系,这样看来,电场和磁场的区别,也只有相 对意义了。
具体地说:给定一试验电荷,在不同的参照系 上,测定该试验电荷的受力情况从而辨认其周围空 间的电场和磁场,所得描述结果是不同的。
作用于
运动电荷 B
产生
三、磁感应强度(Magnetic Induction)
1. 磁感应强度 B 的定义:
对比静电场场强的定义 F q0 E
将一实验电荷射入磁场,运动电荷在磁场中 会受到磁力作用。
实验表明
① Fm v
② Fm q0v sin
2
时Fm达到最大值
Fm
q0
v
θ=0 时Fm= 0,
①方向:
曲线上一点的切线
方向和该点的磁场方
B
向一致。②大小:ຫໍສະໝຸດ 磁感应线的疏密反映磁场的强弱。
③性质:
•磁感应线是无头无尾的闭合曲线,磁场中任
意两条磁感应线不相交。
•磁感应线与电流线铰链
通过无限小面元dS 的磁感应线数目dm与dS 的 比值称为磁感应线密度。我们规定磁场中某点的磁
感应强度的值等于该点的磁感应线密度。
i jk
F e 0 v y 0 e(v yBzi v yBxk )
Bx 0 Bz
Fz e v y Bx
Bx
Fz e vy
8.69 10-2 T
B
Bx2
B
2 y
0.1T
tan Bz 0.57
Bx
300
资料
原子核表面 中子星表面 目前最强人工磁场 太阳黑子内部 太阳表面 地球表面
第二章电磁学PPT课件

E10 (rR3)
-q
q
E24πq0r2 (R3rR2)
R3
E 30 (R 1rR 2)
E4 4π2q0r2
.
(R1r)
R2 R1
3U 8 O4π q0(R 1 3-R 1 2R 2 1)2.3 1 130 V
第二章 静电场中的导体和电介质
§2-1 静电场中的导体 §2-2 电容和电容器 §2-3 电介质 §2-4 电场的能量和能量密度
外表面所带的电量由电荷守恒定律决定。
.
31
三 静电屏蔽
1 屏蔽外电场
E
E
外电场
空腔导体屏蔽外电场
空腔导体可以屏蔽外电场, 使空腔内物体不受外电 场影响.这时,整个空腔导体和腔内的电势也必处处相等.
.
32
2 屏蔽腔内电场
接地空腔导体 将使外部空间不受 空腔内的电场影响.
接地导体电势为零
+
+
+
q
别带上电荷量q和Q.试求:
(1)小球的电势UR,球壳内、外表面的电势; (2)两球的电势差; (3)若球壳接地,再求小球与球壳的电势差。
解:小球在球壳内外表面感应出电荷-q、q
球壳外总电荷为q+Q。
Q
R2
q
R R1
.
35
(1)小球的电势UR,球壳内、外表面的电势
UR410(R q-R q1qR 2Q)
+
-+
R2
+
-
-
+-
R
1
+ +
-
+
+-*P-
R2 ,
C4π .
R 450 1
孤立导体球电容
例3 两半径为 R的平行长直导线中心间距为d ,
大学物理电磁学课件PPT
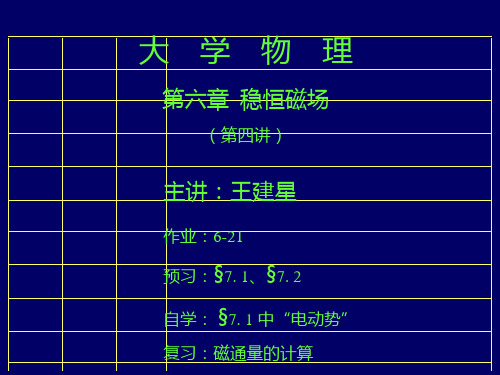
d f I1 d l B =BI1dlsin(90/2)
0I2 0I1I2 = ————————I1Rd cos(/2) = ———cot(/2)d 2[2Rsin(/2)] 4
df
N
俯视图
力偶矩
dM= ——— cot(—)d 2Rsin( ) = ——— 4 2 I I R 0I1I2R 2 0 1 2 M cos d = ———— 0 2 2
L
例1.在匀强磁场中,有一长为 L 的载流直导线,其与磁场夹角 I 为 ,求磁场对它的作用力 f 。 I dl 解:任取一 I d l d f BI d l sin B
方向: 垂直纸面向里。各 d f 同向
f BI d l sin BI L sin
f
f d f I dl B
L L
(6-39)
求
的思路: 1) 求任一 I d l 的d f ;
I dl
I
2) 分解 d f
3) 合成
f f xi f y j
d fx d f y fx d fx
L
B
fy d fy
I
L
dfx
B
R
4 B I
f x BI d y =0 f y BI d x = BI l
0
3
(6-J3)
若为通电闭合回路?
结论:在稳恒的均匀磁场中,任意形状的通电导线所受的磁力
等效为连接该导线两端点的直线电流所受的磁力。 f I d l B
L
例3.求载流直导线在非匀强磁场中所受安培力。
B
0I2 0I1I2 = ————————I1Rd cos(/2) = ———cot(/2)d 2[2Rsin(/2)] 4
df
N
俯视图
力偶矩
dM= ——— cot(—)d 2Rsin( ) = ——— 4 2 I I R 0I1I2R 2 0 1 2 M cos d = ———— 0 2 2
L
例1.在匀强磁场中,有一长为 L 的载流直导线,其与磁场夹角 I 为 ,求磁场对它的作用力 f 。 I dl 解:任取一 I d l d f BI d l sin B
方向: 垂直纸面向里。各 d f 同向
f BI d l sin BI L sin
f
f d f I dl B
L L
(6-39)
求
的思路: 1) 求任一 I d l 的d f ;
I dl
I
2) 分解 d f
3) 合成
f f xi f y j
d fx d f y fx d fx
L
B
fy d fy
I
L
dfx
B
R
4 B I
f x BI d y =0 f y BI d x = BI l
0
3
(6-J3)
若为通电闭合回路?
结论:在稳恒的均匀磁场中,任意形状的通电导线所受的磁力
等效为连接该导线两端点的直线电流所受的磁力。 f I d l B
L
例3.求载流直导线在非匀强磁场中所受安培力。
B
电磁学第二章习题课

C0
εo S C0 Q C V 1 l ε r 1 d 1 l ε r 1 d εr d εr
0S
d
特例 : 当l d时, C r C 0
S
d
0 SV Q CV l r 1 1 d d r
0 d1
r1 S2 r2 +D 1
B
+
+ S 1 + E1 E 2
d1 d2
S1
S2 D2
q = S
σ d1 d 2 ) E1d1 E2 d 2 ( ) ( 1 2 ε0 ε r 1 ε r 2
d1 d2
q ε r 1 ε r 2 ε0 S εr 1 εr 2 d 0S (3) C C0 VA VB d1 d 2 εr 2d1 εr 1d 2 εr 2d1 εr 1d 2
+Q1 +Q2
可见,若VAB不变,则E1=E2=E,D1<D2,Q1<Q2
(2)电量Q不变
VA + + + + + A 0 E D d 1 VB – – – – – B
–Q +Q
V'A + + + + + A E2 D d V'B – – – – – B
–Q
+Q
Q 由介质中的高斯定量得 D1 D2 D S D2 Q D1 Q E2d , VAB E1d , VAB E1 , E2 S 0 0S
例3、讨论平板电容器两极板间为真空和充满电介质 时的电位移和场强:(1)电势差不变;(2)电量不变。 解:(1)电势差不变:VAB= VA–VB
εo S C0 Q C V 1 l ε r 1 d 1 l ε r 1 d εr d εr
0S
d
特例 : 当l d时, C r C 0
S
d
0 SV Q CV l r 1 1 d d r
0 d1
r1 S2 r2 +D 1
B
+
+ S 1 + E1 E 2
d1 d2
S1
S2 D2
q = S
σ d1 d 2 ) E1d1 E2 d 2 ( ) ( 1 2 ε0 ε r 1 ε r 2
d1 d2
q ε r 1 ε r 2 ε0 S εr 1 εr 2 d 0S (3) C C0 VA VB d1 d 2 εr 2d1 εr 1d 2 εr 2d1 εr 1d 2
+Q1 +Q2
可见,若VAB不变,则E1=E2=E,D1<D2,Q1<Q2
(2)电量Q不变
VA + + + + + A 0 E D d 1 VB – – – – – B
–Q +Q
V'A + + + + + A E2 D d V'B – – – – – B
–Q
+Q
Q 由介质中的高斯定量得 D1 D2 D S D2 Q D1 Q E2d , VAB E1d , VAB E1 , E2 S 0 0S
例3、讨论平板电容器两极板间为真空和充满电介质 时的电位移和场强:(1)电势差不变;(2)电量不变。 解:(1)电势差不变:VAB= VA–VB
《电磁学电磁场》PPT课件_OK

) dS
t
D
dS
(S) t
d
D
dS
d
全电流在任何情况下都
I I0 Id dt S
dt
是2连021/续8/2的9 ,具有闭合性
2
安培环路定理的推广
• 非恒定情况下,全电流为
I I0
(S)
(S)
改写为 H
(L)
D t
dl
dS
=
(S)
( j0
(S)
j0 dS
8
L
I0 +
L内SD源自dSt微分形式 介质方程
D = e0
E
=
B
D 0r E
B 0rH
t
j0
E.
B = 0
H = j0
D t
j0 (E + v B)
介质以速
度v运动
如果有任何非静电力
j0 (E + K)
2021/8/29
6
• 电磁场的规律由Maxwell方程组和介质性质的方程 决定
n (D2 D1) 0 n (E2 E1) 0
体与真空的
界面 n H外 j0
以上设界面上没有自由电荷和无传导电流 Maxwell 方 程 组
n两 (种j2导体j界1)面上 ,j法t0 向连n 续(,E2E切E向1)连续0
的微分形式+ 介质方程+边 界条件,唯一 地确定解
2021/8/29
• 位移电流与涡旋电场两个假说具有十分重要 的意义,不仅为建立统一的电磁场理论奠定 了基础,而且预言了电磁波的存在
• 例题1
• 例题2
2021/8/29
5
麦克斯韦方程组各向性同介性质线
《电磁学》PPT课件

磁场
由运动电荷(电流)产生的特 殊物理场,描述磁极间的相互
作用。
电场性质
对放入其中的电荷有力的作用, 且力的方向与电荷的电性有关。
磁场性质
对放入其中的磁体或通电导线 有力的作用,且力的方向与电
流方向及磁场方向有关。
库仑定律与高斯定理
库仑定律
描述真空中两个静止点电荷之间的相 互作用力,与电荷量的乘积成正比, 与距离的平方成反比。
超导材料在电磁领域应用前景
01
超导材料的基本特 性
零电阻、完全抗磁性Fra bibliotek02超导材料在电磁领 域的应用
超导磁体、超导电缆、超导电机 等
03
超导材料应用前景 展望
高温超导材料、超导电子学器件 等
太赫兹技术发展现状和挑战
太赫兹技术的概念和特点
介于微波和红外之间的电磁波
太赫兹技术发展现状
太赫兹源、太赫兹探测器、太赫兹波谱仪等
05
电磁波传播与辐射理论
麦克斯韦方程组内容解读
麦克斯韦方程组的四个基本方程
01
高斯定律、高斯磁定律、麦克斯韦-安培定律、法拉第感应定律。
方程组的物理意义
02
揭示了电荷、电流与电场、磁场之间的内在联系,描述了电磁
场的产生、传播和变化规律。
方程组在电磁学中的地位
03
是电磁学的基石,为电磁波理论、电磁辐射和天线设计等领域
实例分析
通过具体磁路实例,如电磁铁、变压器等,分析磁路的结构、工作原理和性能特点。
铁磁材料特性及应用领域
铁磁材料特性
具有高磁导率、低矫顽力、高饱和磁感应 强度等特点,易于实现磁化和退磁。
VS
应用领域
广泛应用于电机、变压器、继电器、扬声 器等电气设备中,以及磁记录、磁放大等 领域。
2024年度电磁学全套ppt课件

VS
防止涡流的措施
为了减小涡流的影响,可以采取以下措施 :增加金属导体的电阻率、减小金属导体 的厚度、采用相互绝缘的薄片叠加而成的 导体等。这些措施可以有效地减小涡流的 大小,从而减小涡流对设备的影响。
2024/3/24
27
06
交流电产生、传输和转换过程Fra bibliotek析2024/3/24
28
正弦交流电产生原理和特点介绍
感应电动势的大小与磁通量变化的快慢成正比,即与磁通量对时间的导数成正比。
2024/3/24
法拉第电磁感应定律是电磁学的基本定律之一,揭示了电磁感应现象的本质和规律 。
24
动生和感生两种类型分析比较
2024/3/24
动生电动势
由于导体在磁场中运动而产生的感应 电动势。其大小与导体在磁场中的有 效长度、导体在磁场中的运动速度以 及磁场的磁感应强度有关。
由电荷产生的特殊物理场,描 述电荷间相互作用。
2024/3/24
磁场
由运动电荷(电流)产生的特 殊物理场,描述磁极间相互作 用。
电场性质
对放入其中的电荷有力的作用 ,且力的方向与电荷的正负有 关。
磁场性质
对放入其中的运动电荷(电流 )有力的作用,且力的方向与 电荷的运动方向及磁场方向有
关。
4
库仑定律与高斯定理
安培环路定理
磁场中沿任何闭合回路L的线积分,等 于穿过这回路的所有电流强度的代数 和的μ0倍。
2024/3/24
6
洛伦兹力与霍尔效应
洛伦兹力
运动于电磁场的带电粒子所受的力。根据洛伦兹力定律,洛伦兹力可以用方程 ,称为洛伦兹力方程。
霍尔效应
当电流垂直于外磁场通过半导体时,载流子发生偏转,垂直于电流和磁场的方 向会产生一附加电场,从而在半导体的两端产生电势差,这一现象就是霍尔效 应。
电磁学PowerPoint幻灯片

E E • d S E • d S E • d S E • d S
s
左底
右底
侧面
E
E
•
S
E
•
S
0
1
O(
dS
s)
S O
2E • S S E
O
2 O
▲ 例2 均匀带正电无限长圆柱面的电场
沿轴线方向单位长度带电量λ
解:场具有轴对称 高斯面:同轴圆柱面
(1)r<R
E E • d S E • d S E • d S E • d S
s
上底
下底
侧面
E 0 0 E • 2rl
qi 0
联立: E • 2rl 1 0
解得: E 0 o
▲ (2)r>R
E E • d S E • d S E • d S E • d S
s
上底
下底
侧面
E 0 0 E • 2rl
qi l 联立可得:E • 2rl 1 l
o
解得: E 2 Or
2.作高斯面,计算电通量及qi
注意要害:(1)首先寻找与E垂直的面,此面上 要求E大小相等,其次寻找E平行面作为补充面
(2)必要时,该高斯面可分裂为几个 局部,分别满足上述条件
3.利用高斯定理求解
三 例题实训
▲ 例1 无限大的均匀带点平面
正电荷电荷量面密度
解:场关于平面对称
高斯面 :垂直于面且关于面对称的圆柱面
高斯定理应用(二)
利用高斯定理计算具有 对称性质的电场
一 内容诠释
▲ 真空中若某静电场具有简单对称性(如中心对称,
轴对称或者面对称等),则可适当选择高斯面,使
得高斯定理中的E能以标量的形式从积分号内部提
电磁学PPT课件
开始
安培定则:用右手握螺线管,四指弯向螺线管中 电流的方向,大拇指所指的方向为螺线管的N极20年10月2日
4
1、通电螺线管的周围存在着磁场,其磁感 线的分布与条形磁体的十分相似。
2020年10月2日
5
通电螺线管有N、S极?
2020年10月2日
返回6
判断通电螺线管的N、S极
汇报人:XXX 汇报日期:20XX年10月10日
9
触接
2020年10月2日
1
8、2 电生磁
一、奥斯特的发现
1、通电导体周围存在磁场,既电流的磁效应。
2、通电导体周围磁场的方向与电流的方向有关。
2020年10月2日
2
二、通电螺线管的磁场
1、通电螺线管的周围存在着磁场,其磁感 线的分布与条形磁体的十分相似。 2、通电螺线管的极性与电流方向有关吗? 观察下面实验,判断通电螺丝管的N、S极。
2020年10月2日
7
给螺线管通电时小磁针处于静止状态,判断 此时小磁针的N、S极
2020年10月2日
返回 8
演讲完毕,谢谢观看!
Thank you for reading! In order to facilitate learning and use, the content of this document can be modified, adjusted and printed at will after downloading. Welcome to download!
安培定则:用右手握螺线管,四指弯向螺线管中 电流的方向,大拇指所指的方向为螺线管的N极20年10月2日
4
1、通电螺线管的周围存在着磁场,其磁感 线的分布与条形磁体的十分相似。
2020年10月2日
5
通电螺线管有N、S极?
2020年10月2日
返回6
判断通电螺线管的N、S极
汇报人:XXX 汇报日期:20XX年10月10日
9
触接
2020年10月2日
1
8、2 电生磁
一、奥斯特的发现
1、通电导体周围存在磁场,既电流的磁效应。
2、通电导体周围磁场的方向与电流的方向有关。
2020年10月2日
2
二、通电螺线管的磁场
1、通电螺线管的周围存在着磁场,其磁感 线的分布与条形磁体的十分相似。 2、通电螺线管的极性与电流方向有关吗? 观察下面实验,判断通电螺丝管的N、S极。
2020年10月2日
7
给螺线管通电时小磁针处于静止状态,判断 此时小磁针的N、S极
2020年10月2日
返回 8
演讲完毕,谢谢观看!
Thank you for reading! In order to facilitate learning and use, the content of this document can be modified, adjusted and printed at will after downloading. Welcome to download!
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
?
(B)
1/ r
OR
r
13
(5082)真空中一半径为R的球面均匀带电Q,在
球心O处有一电荷为q的点电荷,如图所示.设无穷
远处为电势零点,则在球内离球心O距离为r的P点处
的电势为
(A) q
4 0 r
(B)
1
4 0
q r
Q R
(C) q Q
4 0 r
(D)
1
4 0
q r
Q R
q
PQ
(B)
r
Oq R
p 沿径向指向球面,同时逆电力线
方向远离球面移动。 (D)沿顺时针方向旋转至
p沿径向朝外,同时沿电力线方向
向着球面移动 。
(B)
r
p
21
(1567)一半径为R的“无限长”均匀带电圆
柱面,其电荷面密度为s.该圆柱面内、外场
强分布r为( 表示在垂直于圆柱面的平面上,
从轴线处引出的矢径):
Er =______0________________(r<R ),
(A)电场强度的大小 E A EB
(B)电势 VA VB
B
(C)电势能 E pA E pB
A •
•
(D)电场力作的功 W 0
5
例 有一边长为 a 的正方形平面,其中垂线上距
正方形中心 o 点为 a 2处有一电量为 q的正点电荷,则
通过该正方形平面的电通量为:( )
o
q
a2
aq
4πq
(1) 6 0
盘中心O点的电势 U0 =_____.
s P
x
30
s
R
E2
O
x P E1
X
(1180) 一“无限大”平面,中部有一半径为R的
圆孔,设平面上均匀带电,电荷面密度s为 ,
试求通过小孔中心O并与平面垂直的直线上各 点的场强和电势(选O点的电势为零)。
31
(5100) 举例说明在选无穷远处为电势零点的
条件下,带正电的物体的电势是否一定为 正?电势等于零的物体是否一定不带电?
16
(1019)在点电荷+q的电场中,若取图中p点处 为电势零点,则M点的电势为
q
(A) 40a
q
q
(B) 8 0a
(C)
4 0 a
q
(D)
8 0 a
q
p
M
a
a
(D )
17
(1623)某电场的电力线分布情况如图所示,一 负电荷从M点移到N点,有人根据这个图作出 下面几点结论,其中哪点是正确的:
(A) 电场强度EM EN (C) 电势能 WM WN A>0
E
r
sR
=______0_r2_r______________(r>R ).
22
(1039) 如图所示,在边长为a的正方形平面的中垂线
上,距中心0点
1 2
a
处,有一电量为q的正点电荷,
则通过该平面的电场强度通量为__________。
a
1a
2
o
q
a
6 q q
0
6 0
23
(1498)如图,点电荷q和-q被包围在高斯面S
q0U D0
qq0
6π l020
(12其99电) 矩在p一的个方带向有如负图电所荷示的,均当匀电带偶电极球子外被,释放放置后一,电该偶电极偶子极,
( (AB子))将沿沿逆逆时时针针方方向向旋旋转转直至到p电沿矩径p向沿指径向向球指面向,球同面时而沿停电止力。线
方向向着球面移动。 (C)沿逆时针方向旋转至
dq 2πr dl 4 π 0r 0 4 π 0r
2πr
4 π0r
2 0
+
+
+
+
+++
9
例 在真空中,A 、B 两板相距 d,面积都为 S (平 板的尺寸远大于两板间距),A、B两板各带 q 、 q.
则两板间的相互作用力为:( )
q2
(1) 4π 0d 2
(3) q 2
2 0S
q2
(2)
0S
(4) 2q2
[1
4 0
9 109
N
m2
/ C 2,
1ev 1.6 1019 J ]
r
+e
-e
27
(0391)AC为一根长2L的带电细棒,左半部均匀带
有负电荷,右半部均匀带有正电荷,电荷线密度分
别为 和 ,如图所示。O点在棒的延长线上,距
A端的距离为L。P点在棒的垂直平分线上,到棒的
垂直距离为L。以棒的中点B为电势的零点,则O点
习题课
1
例 在静电场中,下列说法中正确的是 (A)带正电荷的导体其电势一定是正值 (B)等势面上各点的场强一定相等 (C)场强为零处电势也一定为零 (D)场强相等处电势不一定相等
2
例 在点电荷 +2q 的电场中,如果取图中P点处 为电势零点,则 M点的电势为
2q P M
a
a
(A) q
2π 0a
q
h
r
l P
33
(1501)在盖革计数器中有一直径为2.00 cm的金属长 圆筒,在圆筒轴线上有一条直径为0.134 mm的长导 线.如果在导线与圆筒之间加上850 V的电压,试分 别求: (1) 导线表面处 (2) 金属圆筒内表面处的电场 强度的大小.
书P87 3.2
34
(1008)如图所示,真空中一长为L的均匀带电 细直杆,总电荷为q,试求在直杆延长线上距杆 的一端距离为 d 的P点的电场强度.
(D)
q 5 1
4 0l 5 D l C l -q B l
E lF
A 一半径为R的薄金属球壳,带电荷
-Q.设无穷远处电势为零,则球壳内各点
的电势U可表示为
1 (K )
4 0
(A) U K Q (B) U K Q
R
R
(C) U K Q (D) K Q U 0
R
R
(B)
2L 3L
qdr
4π 0 r 2
q
24π 0 L
U AC
VA
VC
q
6π 0 L
19
例 如图所示的电场,点电荷q0 从 D 点沿弧形路
径 DCO 到达 0 点,求电场力所做的功.
解 V0 0
C
VD
q
4π0 (3l)
q
4π0l
q
Al
l lB
q 0 q
D
q0
6π0l
WD0
(q0V0
q0VD )
(C)
q
8π
0
a
q
(B)
4π 0a
(D) q
4π 0a
3
例 一球壳半径为 R ,带电量 q ,在离球心 O 为 r (r < R)处一点的电势为(设“无限远”处为电势零点)
(A) 0
(C) q
4π 0r
q
(B)
4π 0 R
(D) q
4π 0r
4
例 某电场的电力线分布如图,一负电荷从 A 点移至 B 点,则正确的说法为
E dS
s
v dv / 0
(A)适用于任何静电场。 (B)只适用于真空中的静电场。 (C)只适用于具有球对称性、轴对称性和平面对
称形的静电场。 (D)只适用于虽然不具有(C)中所述的对称性、
但可以找到合适的高斯面的静电场。
(A)
12
(1633) 图中所示曲线表示球对称或轴对称静电场的 某一物理量随径向距离r变化的关系,请指出该曲线可描 述下列哪方面内容(E为电场强度的大小,U为电势): (A)半径为R的无限长均匀带电圆柱体电场的E~r关系. (B)半径为R的无限长均匀带电圆柱面电场的E~r关系. (C) 半径为R的均匀带正电球体电场的U~r关系. (D) 半径为R的均匀带正电球面电场的U ~r关系.
q
r
R Q AB
32
(5273)电荷q均匀分布在长度为L的圆柱面上, 如图所示.有人在圆柱面外中部位置作了一个高 度为h(h<<L)半径为r的同轴圆柱面作为高斯面, 并根据高斯定理求得与轴相距r(r的大小比L小得 不多)处P点的电场强度的大小为 E q / l
2 0 r
以上推导方法与所得结论对不对?如有错误请指 出.
P
(3)场强分量 Ez 相等,电势相等.
oy
(4)场强分量 Ez 相等,电势不等.
x
8
例 真空中,有一均匀带电细环,电荷线密度为 ,
求圆心处的电场强度 E0 和电势U0 .(无穷远处电势为零)
解:
E0 0
dq dl
dU 0
4
dq
π 0r
dl 4 π 0r
dl + + +
+
+
+r +
U0
电势Uo _____ ;
3 ln
40 4
P点电U势p
0 ______.
p
l
O
A B C
l
l
l
28
(1024)有一电荷面密度为s 的“无限大”
均匀带电平面.若以该平面处为电势零点, 试求带电平面周围空间的电势分布.
29
(1407) 一半径为R的均匀带电圆盘,电荷面
密度为s ,设无穷远处为电势零点,则圆
q
P
L
d
书P40 1.9
35
0S
10
例 一封闭高斯面内有两个点电荷,电量为 +q 和 -q,封闭面外也有一带电 q 的点电荷(如图),则下 述正确的是
