最小元素法求运价最小
运筹学04_运输问题

基于以上思路,元素差额法求初始基本可行解的步骤是:
第 一 步 : 求 出 每 行 次 小 运 价 与 最 小 运 价 之 差 , 记 为 ui , i=1,2,…,m ;同时求出每列次小运价与最小运价之差,记为vj,j=1, 2,…,n ; 第二步:找出所有行、列差额的最大值,即L=max{ui,vi},差 额L对应行或列的最小运价处优先调运; 第三步:这时必有一列或一行调运完毕,在剩下的运价中再求 最大差额,进行第二次调运,依次进行下去,直到最后全部调运 完毕,就得到一个初始调运方案。 用元素差额法求得的基本可行解更接近最优解,所以也称为近 似方案。
1 1 1 1 1 1 A= 1 1 1 1 1 1
m行
n行
14
1 1
1 0 1 1 1 1 1 1
故r(A)=m+n-1所以运输问题有m+n-1个基变量。 为了在mn个变量中找出m+n-1个变量作为一组基变量,就是 要在A中找出m+n-1个线性无关的列向量,也即是在运输表格中 确定m+n-1个格的运输量不为零,而剩下的(m-1)(n-1)格为零。
TP 生产能力: 300单位
8
运输模型方法举例
从纳瑞多发货
DL 生产能力: 100单位
MD 需求: 300单位
OM 需求: 200单位
BS 需求: 200单位
LR 生产能力: 300单位
TP 生产能力: 300单位
9
运输模型方法举例
每条路线上应当运多少以 实现最低成本?
© 1984-1994 T/Maker Co.
DL 生产能力: 100单位 $3 $4 BS 需求: 200单位
最小元素法求解运输问题

最小元素法求解运输问题
运输问题是运筹学中经典的问题,其问题定义如下:给定若干由供应源和需求中心组成的网络,求出最优的组合,使得传输货物的成本最低。
最小元素法求解运输问题被认为是求解运输问题的最常用的方法之一。
最小元素法求解运输问题的过程分为四个步骤:
第一步,确定总的可用货物量和需求量;
第二步,找出当前的步数,记为t,以及向量c(t);
第三步,计算最小元素c0=min(c(t)),求出相应的路径;
第四步,删除或者增加每个占用元素最小的路径。
最小元素法求解运输问题的优点是比较简单易行,而且可以较为容易地找出最优解。
应用最小元素法可以有效地减少货物成本,使得传输货物的消耗最小化,这种方法充分考虑了各种约束条件。
最小元素法求解运输问题的缺点在于容易变成循环搜索的问题,可能容易陷入局部最优而不能找到系统最优解,因此当运输问题的约束条件增多时,很难找到最优解。
除此之外,最小元素法求解运输问题与运输图法求解运输问题相比,使用计算机资源也比较大。
总之,最小元素法求解运输问题是求解运输问题的一种有效的方法,可以有效地帮助我们找到最优解。
在实际应用中,需要控制条件,加以合理利用,才能避免陷入局部最优,帮助求解运输问题。
最小元素法

什么是最小元素法[1]最小元素法是找出运价表中最小的元素,在运量表内对应的格填入允许取得的最大数,若某行(列)的产量(销量)已满足,则把运价表中该运价所在行(列)划去;找出未划去的运价中的最小数值,按此办法进行下去,直至得到一个基本可行解的方法。
注:应用西北角法和最小元素法,每次填完数,都只划去一行或一列,只有最后一个元素例外(同时划去一行和一列)。
当填上一个数后行、列同时被满足(也就是出现退化现象)时,也只任意划去一行(列)。
需要填入“0”的位置不能任意确定,而要根据规则来确定。
所谓退化现象是指:当在平衡表中某一处填入一数字后,该数字所在的行和列同时被满足,即需方的需求得到满足,同时供方的供应数量也已经供完的现象。
最小元素法的基本思想是:运价最小的优先调运,即从单位运价中最小的运价开始确定供销关系,然后次小,一直到给出初始基本可行解为止。
[编辑]最小元素法的例子[1]第一步:列出运价表和调运物资平衡表。
运用表上作业法时,首先要列出被调运物资的运价表和供需平衡表(简称平衡表),如表1,2所示。
第二步:编制初始调运方案。
首先,在运价表中找出最小的数值(若几个同为最小,则任取其中一个),A2B1最小,数值为1,这表示先将A2产品供应给B1 是最便宜的,故应给C21所对应的变量x21以尽可能大的数值。
显然x21=min{4,3}=3。
在表4中的A2B1处填上“3”。
B1列被满足,已不需要A1和A3再向它供货,故运价表2中的第一列数字已不起作用,因此将原运价表1中的第一列划去,并标注①(见表3)。
然后,在运价表中未划去的元素中找最小运价A 2B 3 = 2,让A 2 尽量供应满足B 3的需要,由于A 2的4已经供应了3T 给B 1,最多只能供应1T 给B 3。
于是在平衡表的A 2B 3格中填上“1”;相应地由于A 2所生产的产品已全部供应完毕,因此,在运价表中与A 2 同行的运价也不再起作用,所以也将它们划去,并标注②。
第二节运输问题求解表上作业法

即从 Ai 向 Bj 运最大量(使行或列在 允许的范围内尽量饱和,即使一个约 束方程得以满足),填入 xij 的相应位 置; (2) 从 ai 或 bj 中分别减去 xij 的值,即调整 Ai 的拥有量及 Bj 的需 求量;
3
(3) 若 ai = 0 ,则划去对应的行(把 拥有的量全部运走),若 bj = 0 则划去 对应的列(把需要的量全部运来),且每 次只划去一行或一列(即每次要去掉且只 去掉一个约束);
—表上作业法
我们已经介绍过,可以通过增加虚 设产地或销地(加、减松弛变量)把问 题转换成产销平衡问题。
1.产量大于销量的情况
考虑 si > dj 的运输问题,得到的数学模 型为
i=1 j=1
39
m
n
2.运输问题求解
—表上作业法
Min f =
n m i=1 j=1
n
cij xij
s.t. xij si i = 1,2,…,m
10
应用西北角法、最小元素法和 Vogel法,每次填完数,都只划去一 行或一列,只有最后一个元例外(同 时划去一行和一列)。当填上一个数 后行、列同时饱和时,也应任意划去 一行(列),在保留的列(行)中没 被划去的格内标一个0。
11
表1
12
13
14
15
16
二、基本可行解的最优性检验
最优性检验就是检查所得到的方 案是不是最优方案。 检查的方法----计算检验数 由于目标要求极小,因此,当所 有的检验数都大于或等于零时该调运 方案就是最优方案;否则就不是最优, 需要进行调整。
第二节 运输问题求解 —表上作业法
运输问题的方法 —— 表上作业法: 1、确定一个初始基本可行解; 2 、根据最优性判别准则来检查这 个基本可行解是不是最优的。如果 是则计算结束;如果不是,则至3 3、换基,直至求出最优解为止。
运输问题(最小元素法+位势法)

运输问题教案某单位有三个工厂A1,A2,A3生产同一产品,有四个销售点,有四个销售点B1,B2,B3,B4进行销售。
各工厂的产量,各销售点的销量(吨)以及各加工厂到各销售点的单位运价(元/吨)见下表。
问:如何调运才能使总运费最少?解:第一步:确定初始方案(最小元素法)最小元素法:就近供应,即从单位运价表中最小的运价开始确定供销关系,依次类推,一直到给出全部方案为止。
产销平衡问题:∑(∑x ijnj=1)mi=1=总产量模型最多有m+n-1个独立约束方程第二步:解的最优性检验(位势法)检验数σij运费=现在的方案运费+非基变量*x ijσij意义:当从产地i调往销地j,1单位物资时,总运费的该变量。
若存在σij≤0,说明总费用有下降调整的空间。
位势法:对运输表上的每一行赋予一个数值u i,每一列赋予一个数值v j,使之满足:σij=C ij−(u i+u i)。
称u i为行位势,v j为列位势。
(1)基变量的检验数σij=0,填入。
(2)任取对偶问题变量为自由变量,设定其取值,不妨设u1=0。
(3)利用σij=C ij−(u i+u i),基变量检验数等于0,算出所有的u i和v j。
判断所有非基变量的检验数是否都大于等于零。
若是,为最优调运方案;否则,寻找下一个调运方案。
σij=C ij−(u i+u i)第三步解的调整优化,直至最优解调入格(入基变量):选择σij≤0的基变量入基,即x24调出格:偶数顶点小的那个改进方案表显然,检验数均大于等于0.因此,最佳调运方案即改进方案表中的调运方案。
即,A1运往B3地12吨,运往B4地4吨;A2运往B1地 8吨,运往B4地 2吨;A3运往B2地14吨,运往B4地8吨;。
运筹学07-运输问题

2 432
2
2
A3
4 3 8 553
2
1
运价列差额
1
需求量 3 2 3 2
10
29
伏格尔(Vogel)法
销地
产地
B1
B2
B3
B4
行差 供应 额量
A1
3 7 6 445
3
1
A2
2 432
2
2
A3
4 385
3
2
1
运价列差额
4
需求量 3 2 3 2
10
30
伏格尔(Vogel)法
销地
产地
B1
B2
B3
B4
19
最小元素法
销地 产地
B1 B2
B3
B4
供应 量
A1
3 7645
1
22
A2
24
32 2
2
A3
4 3853
21
需求量 3 2 3 2 10
20
最小元素法
销地 产地
B1
B2
B3
B4
供应 量
运量
A1
1
22 5
A2
2
2
A3
21
3
需求量 3
2
3
2 10
初始基 可行解
21
伏格尔(Vogel)法(推荐)
比较最小运费与次小运费的差额,在差额最大 处,采用最小运费调运。
(2) 运输问题的一般数学模型
运输问题的一般描述: m个产地Ai,I=1,2..,m,产量分别为ai个单位, n个产地Bj,j=1,2..,n, 产量分别为bj个单位; Ai与Bj之间的单位运价爲Cij ,问如何安排 运输方案,使总运费最少?
运筹学运输问题的三种算法

运筹学运输问题的三种算法
运筹学运输问题的三种算法包括最小元素法、付格尔法和闭回路法。
1. 最小元素法:先找出运费最小的元素,优先满足最小运费的需求,然后根据已满足的需求进行迭代计算,直到所有需求都得到满足。
2. 付格尔法:首先计算各行和各列的差额,然后优先满足差额最大的行或列中的需求,每次满足需求后更新差额,直到所有需求都得到满足。
3. 闭回路法:首先构造一个初始解,然后通过搜索和迭代的方式寻找可以改进的路径,并不断更新解,直到无法再找到可以改进的路径为止。
这三种算法各有特点,具体选择哪种算法取决于问题的特性和要求。
最优化理论——运输问题的案例
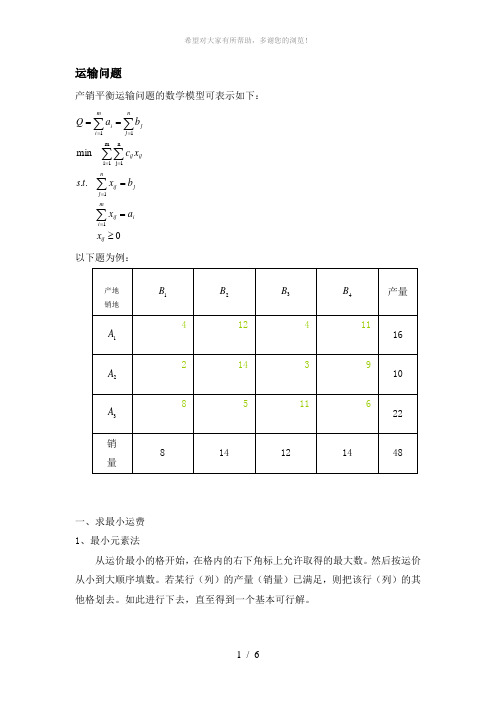
运输问题产销平衡运输问题的数学模型可表示如下:.. min 11m 1i n1j 11≥====∑∑∑∑∑∑======ij i mi ij j nj ij ijij nj jmi i x a x b x t s x c b a Q以下题为例:一、求最小运费 1、最小元素法从运价最小的格开始,在格内的右下角标上允许取得的最大数。
然后按运价从小到大顺序填数。
若某行(列)的产量(销量)已满足,则把该行(列)的其他格划去。
如此进行下去,直至得到一个基本可行解。
最小运费为:246⨯+++⨯⨯⨯+⨯+2=⨯866115814231042、西北角法从西北角(左上角)格开始,在格内的右下角标上允许取得的最大数。
然后按行(列)标下一格的数。
若某行(列)的产量(销量)已满足,则把该行(列)的其他格划去。
如此进行下去,直至得到一个基本可行解。
最小运费为:372=6×14+11×8+3×4+10×6+12×8+4×8 3、Vogel (沃格尔)法① 计算出各行各列中最小元素和次小元素差额(罚数),并标出。
② 在罚数最大的行和列中填上尽可能大的数(若有两个罚数最大,则选择最大罚数所在行或所在列运费最小的)。
若有行或列饱和,划去。
二、检验是否是最优解 1、闭回路法闭回路:从空格出发,遇到数字格可以旋转90度,最后回到空格所构成的回路;原理:利用检验数的经济含义;检验数:非基变量增加一个单位引起的成本变化量。
当所有非基变量的检验数均大于或等于零时,现行的调运方案就是最优方案,因为此时对现行方案作任何调整都将导致总的运输费用增加。
闭回路法的主要缺点是:当变量个数较多时,寻找闭回路以及计算两方面都会产生困难。
检验数14-32-4c c c c 1323211111=+=-+-=σ0134119c c c c 2313142424<-=-+-=-+-=σ,故知该最小元素法的解不是最优解。
《运筹学》第三章 运输问题

二、表上作业法
计算步骤:
(1) 找出初始调运方案。即在(m×n)产销平衡表 上给出m+n-1个数字格。(最小元素法、西北角法 或伏格尔法) 确定m+n-1个基变量 (2) 求检验数。(闭回路法或位势法) 判别是 否达到最优解。如已是最优解,则停止计算,否 则转到下一步。 空格 (3)对方案进行改善,找出新的调运方案。 (表上闭回路法调整) (4) 重复(2)、(3),直到求得最优调运方案。
B1 A1 A2 A3 销量 3 1
B2 2
B3 4
B4 3
产量 7 4
3
6 6
1
3 5 6
9
B1 A1 A2 A3 销量 3 1
B2 2
B3 4
B4 3
产量 7 4 9
3
6 6
1
-1
3
5
6
B1 A1 A2 A3 销量 3 1 3
B2 2 1 6 6
B3 4 1
B4 3 -1 3
产量 7 4 9
(ui+vj)
- B2 9 8 4 B3 3 2 -2 B4 10 9 5
A3 -3
σij
B1 = A1 A2 A3 1 0 10 B2 2 1 0 B3 B4 0 0 0 -1 12 0
表中还有负数,说明 还未得到最优解,应 继续调整。 用位势法与用闭回路法 算出的检验数? 相同
3、解的改进
——闭合回路调整法(原理同单纯形法一样) 上例: min( σ ij 0 ) pq
m
n
系数列向量的结构: A ij ( 0, 0, 0 ,, 0, 0 ) 1, 0 1,
第 i个
第 ( m j )个
运筹学 04 运输问题

位势法思路 令第1行的u1=0,在第1行有运输数量的地方根据cij-ui-vj=0计 算对应列的vj=cij-u1;其他ui和vj类推 根据λij=cij-ui-vj计算每一个空格的检验数 检验数>0,方案不能调整;检验数<0,必须调整方案;检 验数=0,调整与否均可
工厂 A1
A2 A3 销量 工厂 A1 A2
原问题变量xj的检验数 σj=cj-zj =cj-CBB-1Pj =cj-YPj 变量xij的检验数 σij=cij-zij =cij-YPij =cij-(u1,u2,…,um,v1,v2,…,vn)Pij =cij-(ui+vj)
2 运输问题的表上作业法
运输问题的数学模型及其约束方程组的系数矩阵结构具有特 殊性,使用表上作业法解决运输问题,比单纯形法更为简便 。 表上作业法的步骤: 第1步:确定初始基可行解 第2步:解的最优性检验 第3步:解的调整,转第2步
例3:设3个化肥厂供应4个地区的农用化肥。各化肥厂年产量 (万吨)、各地区年需求量(万吨)以及各化肥厂到各地区单位运 价(万元/万吨)见表。试求总运费最低的化肥调拨方案。 产地 A B C 最低需求 最高需求 Ⅰ 16 14 19 30 50 Ⅱ 13 13 20 70 70 Ⅲ 22 19 23 0 30 Ⅳ 17 15 M 10 ∞ 产量 50 60 50
工厂 A1
A2 A3 销量 工厂 A1 A2
B1
4 2 8 8 B1 1 8
B2
12 10 5 14 B2 2 1
B3
4 3 11 12 B3 10 2
B4
11 9 6 14 B4 6 -1
产量 (1)A1B1处检验数 闭合回路:A1B1-A1B3-A2B3-A2B1 16
运筹学 第04章 运输问题

2
最小元素法
例:运输问题如下表,请用最小元素法求解最初方案
销地 产地
B1 0.3 0.1 0.7 300
B2 1.1 0.9 0.4 600
B3 0.3 0.2 1.0 500
B4 1.0 0.8 0.5 600
产量 700 400 900
A1 A2 A3 销量
最小元素法:优先满足运价(或运距)最小的供销业务。
②
4
④
6
8 5 14
A3
销量
22 48
8
①
6
③
8
3
西北角法
销地
产地
B1
4
B2
12
B3
4 3
B4
11 9
产 量
A1
A2
8
2
8
10
16
10
②
④
6
8 5
4
11 6
14
A3
销量
x32
22
48
8
①
14
6
③
12
8
3
西北角法
销地 产地
B1
4
B2
12
B3
4
3
B4
11
9 6
产 量
A1
A2
8
2
8
10
16
10
② ④
6
2 8
16 8
8
10
22 48
A3
销 量
8
①
3
西北角法
销地
产地
B1
4
B2
x12
12 10
B3
4 3
运输与指派问题

x11 x12 x13 x14 10
x21
x22
x23
x24
8
min Z 3x11 2x12 6x13 3x14 5x21 3x22 8x23 2x24 4x31 x32 2x33 9x34
x31
x32 x33 x34 x11 x21 x31 5
5
运输单纯形法 Transportation Simplex Method
求检验数 求出一组基可行解后,判断其是否最优,仍然是用检验数来判断, 记xij的检验数为λij ,由第一章知,求最小值的运输问题的最优判 别准则是: 所有非基变量的检验数都非负,则运输方案最优(即为最优解)。
求检验数的方法有两种,闭回路法和位势法。
设平衡运输问题的数学模型为:
mn
min z
cij xij
i1 j 1
n
xij ai
j 1
m
xij bj
i 1
xij
0,
i 1,
i 1, , m j 1, , n , m; j 1, , n
运输单纯形法基本思路: 基可行解
最优否
是停
否
运输单纯形法 Transportation Simplex Method
地区
产粮区
B1
表1
B2
B3
运价表(元/吨)
B4
产量
A1
3
2
6
3
10
A2
A3
4
1
2
9
5
需要量
5
7
8
3
23
运输模型 Model of Transportation Problems
【解】设xij(i=1,2,3;j=1,2,3,4)为i个产粮地运往第j个需求地的运 量,这样得到下列运输问题的数学模型:
《运筹学》教材编写组《运筹学》笔记和课后习题(含考研真题)详解(运输问题)

第3章 运输问题3.1 复习笔记1.运输问题的数学模型运输问题:已知有m 个生产地点,1,2,,i A i m =…,可供应某种物资,其供应量(产量)分别为i a ,1,2,,i m =…,有n 个销地j B ,1,2,,j n =…,其需要量分别为j b ,1,2,,j n =…,从i A 到j B 运输单位物资的运价(单价)为ij c 。
如何安排运输,能使得总运输成本最小?(1)产销平衡运输问题的数学模型1111min ,1,2,,..,1,2,,0m nij iji j mij j i nij i j ijz c x x b j n s t x a i mx =====⎧==⎪⎪⎪==⎨⎪⎪≥⎪⎩∑∑∑∑ 模型特点:①该模型包含m n ⨯个变量,()m n +个约束方程;②该系数矩阵中对应于变量ij x 的系数向量ij P ,其分量中除第i 个和第m j +个为1外,其余的都为零。
即(01010)T ij i m j P e e +==+…………③对于产销平衡的运输问题,有以下关系式存在:111111n m n n m m j ij ij i j i j j i i b x x a ======⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭∑∑∑∑∑∑ 所以模型最多只有m+n-1个独立约束方程。
即系数矩阵的秩≤m+n -1。
注意:运输问题的基变量一定是m+n-1个,m+n-1个变量构成基变量的充要条件是它们不构成闭回路。
闭回路的特点:在运输产销平衡表中,每一条边都是水平或垂直的;每一行或每一列至多只有两个闭回路的顶点。
(2)产销不平衡运输问题的数学模型当产大于销,即11m n i j i j a b ==>∑∑时,运输问题的数学模型可写成:1111min ,1,2,,..,1,2,,0m n ij iji j mij j i nij i j ijz c x x b j n s t x a i mx =====⎧==⎪⎪⎪≤=⎨⎪⎪≥⎪⎩∑∑∑∑ 当产小于销,即11m n i j i j a b ==<∑∑时,运输问题的数学模型可写成:11min m n ij ij i j z c x ===∑∑11, (1,2,,), (1,2,,)0nij i j mij j i ij x a i m x b j n x ==⎧==⎪⎪⎪≤=⎨⎪⎪≥⎪⎩∑∑……2.表上作业法表上作业法是单纯形法在求解运输问题时的一种简化方法,其实质是单纯形法。
运筹学论文-产销不平衡运输

管理运筹学论文---产销不平衡运输摘要运输问题是运筹学中的一个重要问题,也是物流系统优化中常见的问题,同时也是一种特殊的线性规划问题。
怎么样尽可能的在产地与销地之间减少运输成本和降低运输费用是很多运输公司热切关注的话题。
本文涉及的是一个总产量大于总销量的产销不平衡运输问题,通过对产地与销售地车辆运输的建立模型,在运用表上作业迭代法(最小元素法)求解后,再根据模型用lingo软件编写程序进行求解。
然后对结果进行分析,以及运输问题的延伸。
最后证明用lingo 解决车辆运输的可行性。
关键字:运输问题,产销不平衡,表上作业法, lingo目录一、问题的提出与分析 (1)1.1问题提出 (1)1.2问题分析 (1)二、模型的建立与基本假设........................................................... . (1)2.1模型的建立 (1)2.2基本假设 (2)三、定义符号说明与表上作业法 (2)四、问题求解 (2)4.1、Lingo求解模型 (4)4.2、Lingo结果 (5)五、模型结果分析与改进 (10)参考文献 (11)一、问题的提出与分析1.1问题提出重庆有三家电子厂分别是新普,隆宇和恒华,生产的笔记本电脑将要运向北京,天津,广东,上海四个城市销售,其产量和销售量见下表:(单位:万台)表:1-1北京天津广东上海产量新普626730隆宇495325恒华881521销量15172212-问:哪种销售方案将会取得最少的运输费用,费用为多少?1.2问题分析图表数据显示产量总和为30+25+21=76万台,销量的总和为15+17+22+12=66万台,说明了此问题是一个总产量大于总销量的运输问题(76>66)。
该问题一方面要求满足北京,天津,广东,上海四个销售地的供货需求,而另一方面又要考虑新普,隆宇和恒华三个产地的运往销售地的运输费用,此外问题不但要求满足销售地分配要足,同时也要保证最大化的减少运输费用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
jp2.setVisible(false);
//jp3.setVisible(false);
jp4.setVisible(false);
try{
String ccmj1=cd.getText();//获取数值
String scsl1=xd.getText();
import java.awt.event.ActionListener;
import javax.swing.JButton;
import javax.swing.JFrame;
import javax.swing.JLabel;
import javax.swing.JOptionPane;
//JOptionPane.showMessageDialog(null,"产地"+ xd1+"个");
jp3 = new JPanel(new GridLayout(cd1+2,xd1+2));
jp3.setBackground(SystemColor.cyan);
import java.awt.BorderLayout;
import java.awt.FlowLayout;
import java.awt.GridLayout;
import java.awt.SystemColor;
import java.awt.event.ActionEvent;
{
jp3.add(new JLabel("产量"));
}
else
{
jp3.add(new JLabel("销地"+j));
System.out.println("i "+i+"j "+(cd1+2)+"ooo ");
}
a=1;
cz1();
//jp3.add(c1);
jp1.add(jp3);
cz2();
// jj.setText(jg);
cd1=Integer.parseInt(ccmj1);
xd1=Integer.parseInt(scsl1);
//double ccmj2=Double.parseDouble(ccmj1);//字符转换
//double scsl2=Double.parseDouble(scsl1);
}
class qudong implements ActionListener{
public void actionPerformed(ActionEvent e)
{
Object temp = e.getSource();
if(temp==s1)
{
String a=b[i][j].getText();
System.out.println(a);
System.out.println("分割线555555");
c[i][j]=Integer.parseInt(a);
s1=new JButton("生成图表");
s2=new JButton("计算");
s3=new JButton("重置");
s1.setBackground(SystemColor.PINK);
s2.setBackground(SystemColor.PINK);
}
System.out.println("测试");
sf();
System.out.println(jg1);
String jg2=jg1+"";
System.out.println(jg2+"测试");
import javax.swing.JPanel;
import javax.swing.JTextField;
public class min1 extends JFrame{
private JPanel jp1, jp2, jp3,jp4,jp5;
private JButton s1,s2,s3,s4;
jp1.setBackground(SystemColor.cyan);
jp1.setBackground(SystemColor.cyan);
jp2.setBackground(SystemColor.cyan);
jp4.setBackground(SystemColor.cyan);
// double jieguo=ccmj2+scsl2;
// double jieg=ccmj2-scsl2;
JOptionPane.showMessageDialog(null,"销地" +cd1+"个"+" "+"产地"+ xd1+"个");
}
}
a=2;
if(i==cd1+1)
{
jp3.add(new JLabel("销量"));
}
else
{
jp3.add(new JLabel("产地"+i));
}
}
for(int i=1;i<=xd1+1;i++)
{
b[cd1+2][i]=new JTextField();
}
for(int i=1;i<=xd1+1;i++)
{
jp3.add(b[cd1+2][i]);
{
jp1.add(jp4);
this.add(jp1);
this.setSize(400,600);
this.setTitle("最小元素法实现运输问题");
setLayout(null);
setVisible(true);
setLocationRelativeTo(null);
s1.addActionListener(new qudong());//计算按钮驱动
s2.addActionListener(new qudong());//计算按钮驱动
s3.addActionListener(new qudong());//计算按钮驱动
jp3.setSize(400, 400);
int a=1;
jp3.add(new JLabel());
for(int i=1;i<=cd1+2;i++)
{
for(int j=1;j<=xd1+1;j++)
{
b[i][j]=new JTextField();
private JTextField cd,xd,jg;
private JLabel c1,c2,c3,c4;
private int cd1,xd1;
public min1()
{
cz1();
//jp1.add(jp3);
cz2();
// c[i][j]=(b[i][j]).getText();
}
}
System.out.println("测试22222");
for(int j=1;j<=xd1+1;j++)
{
System.out.println("测试33333");
jp2.add(xd);
jp2.add(s1);
jp4.add(c4);
jp4.add(jg);
jp4.add(s2);
jp4.add(s3);
jp1.add(jp2);
}
public void cz2()
s3.setBackground(SystemColor.PINK);
c1=new JLabel("表格区域");
c2=new JLabel("产地");
c3=new JLabel("销地");
c4=new JLabel("结果");
cd = new JTextField(10);
}
}
for(int i=1;i<=cd1+1;i++)
{
for(int j=1;j<=xd1+1;j++)
{
if(a==1)
{
if(j==xd1+1)
}
}
else
{
System.out.println("i "+i+"j "+j);
jp3.Field[][] b=new JTextField[100][100];
private int[] d1=new int[10000];
private int a1=0,a2=0,jg1=0;
private int[][] c=new int[100][100];
String a=b[cd1+2][j].getText();
System.out.println(a);
