c语言中缀后缀算术表达式求值用栈实现
用栈对后缀表达式求值的算法(五种)

⽤栈对后缀表达式求值的算法(五种)转载出处:第⼀种/* 此程序的功能是求出⽤户输⼊的整形表达式的值*//*输⼊的表达式请⽤#结尾,⽐如:2+3+5,应输⼊:2+3+5#。
*/#include <stdio.h>#define MAXSIZE 16typedef struct{int data[MAXSIZE];int top;int base;}seqstack; /* 顺序栈的定义*//*以下为函数声明*/void InitStack(seqstack *);int Empty(seqstack *);void Push(seqstack *, int );int Pop(seqstack *);int GetTop(seqstack *);int Operate(int ,char ,int );char Proceed(char ,char );int In(char );int EvalExpres(void);/* 定义两个栈分别存放运算符和操作数*/seqstack StackR,StackD;/*主函数*/int main(){int v;char ch;while(1){printf("end with #,for example 2+3+5 input:2+3+5#\n");printf("calculate:") ;v = EvalExpres();printf("The result is:%d",v);/*以下为程序控制*/printf("\nInput 'q' to quit and ENTER run again:");do{scanf("%c",&ch);if(ch == 'q' || ch == 'Q')exit(0);}while(ch!='\n');system("cls");}return 0;}void InitStack(seqstack *s){ s->top = 0;s->base = 0;} /* 初始化栈*/int Empty(seqstack *s){ if(s->top == s->base)return 1;elsereturn 0;} /* 判断栈是否为空*/void Push(seqstack *s, int x){if(s->top == MAXSIZE){ printf("OVER FLOW!\n");exit(0);}else{ s->data[s->top] = x;s->top++;}} /* 进栈 */int Pop(seqstack *s){ int e;if(Empty(s)){ printf("Under flow!\n");return 0;} /* 下溢*/else{ s->top--;e = s->data[s->top];return e;}} /* 出栈*/int GetTop(seqstack *s) /*取栈顶元素*/{if(Empty(s)){ printf("Under flow!\n");return 0;}elsereturn s->data[s->top-1];}int EvalExpres(void) /* 表达式求解函数*/{int a,b,i=0,s=0;char c[80],r;InitStack(&StackR);Push(&StackR,'#');InitStack(&StackD);printf(" end with #");gets(c);while(c[i]!='#' || GetTop(&StackR)!='#'){if(!In(c[i])) /* 判断读⼊的字符不是运算符是则进栈*/{ if(c[i] >= '0' && c[i] <= '9'){s += c[i]-'0';while(!In(c[++i])) /*此处实现的功能为当输⼊的数字为多位数时*/{ s*=10;s += c[i]-'0';}Push(&StackD,s+'0');s = 0;}else{printf("wrong!\n");return 0;}}elseswitch(Proceed(GetTop(&StackR),c[i])) /* 此函数⽤来⽐较读取的运算符和栈顶运算符的优先级*/ {case '<': /* 栈顶的元素优先级⾼*/i++;break;case '=': /* 遇到匹配的⼩括号时则去掉他*/Pop(&StackR);i++;break;case '>': /* 栈顶的优先级低则出栈并将结果写⼊栈内*/r = Pop(&StackR);a = Pop(&StackD)-'0';b = Pop(&StackD)-'0';Push(&StackD,Operate(a,r,b)) ;break;}}return (GetTop(&StackD)-'0'); /* 返回运算结果*/}int In(char c) /*问题2:解决In函数问题:判断C是否为运算符是返回1否则返回0*/{char ch[7]={'+','-','*','/','#','(',')'};int i;for(i = 0; i < 7; i++)if(c == ch[i])return 1;return 0;}char Proceed(char op,char c) /*op为栈顶元素,c为当前读⼊的运算符,⽐较⼆者的优先级*/ { /*问题1:解决Proceed函数*/char ch;if(op=='(' && c==')' || op=='#' && c=='#' )ch = '=';elseif(op=='+' || op=='-') /*栈顶元素为‘+’或‘-’的时候*/switch(c){case '+':case '-':case ')':case '#': ch = '>'; break;case '*':case '/':case '(': ch = '<';}elseif(op=='*' || op=='/') /*栈顶元素为‘*’或‘/’的时候*/switch(c){case '+':case '-':case '*':case '/':case ')':case '#': ch = '>'; break;case '(': ch = '<';}elseif(op=='(') /*栈顶元素为‘(’的时候*/switch(c){case '+':case '-':case '*':case '/':case '#': printf("Error!\n"); exit(0);}elseif(op==')') /*栈顶元素为‘)’的时候*/switch(c){case '+':case '-':case '*':case '/':case '#': ch = '>'; break;case '(': printf("Error!\n"); exit(0);}elseif(op=='#') /*栈顶元素为‘#’的时候*/ switch(c){case '+':case '-':case '*':case '/':case '(': ch = '<'; break;case ')': printf("Error!\n"); exit(0);}return ch;}/* 问题3:解决Operate函数*/int Operate(int a,char r,int b) /*返回由aRb的值 */ {int s;int d1 = a;int d2 = b; /*把字符ab变为对应数字*/switch(r){case '+': s = d1+d2; break;case '-': s = d2-d1; break;case '*': s = d1*d2; break;case '/': s = d2/d1;}return (s+'0');}第⼆种#include <stdio.h>#include <malloc.h>#define MaxSize 50void trans(char *exp,char *postexp){struct{char data[MaxSize];int top;} op;int i=0;op.top=-1;while(*exp!='\0'){switch(*exp){case '(':op.top++;op.data[op.top]=*exp;exp++;break;case ')':postexp[i++]=op.data[op.top];op.top--;}op.top--;exp++;break;case '+':case '-':while(op.top!=-1&&op.data[op.top]!='('){postexp[i++]=op.data[op.top];op.top--;}op.top++;op.data[op.top]=*exp;exp++;break; case '*':case '/':while(op.data[op.top]=='*'||op.data[op.top]=='/') {postexp[i++]=op.data[op.top];op.top--;}op.top++;op.data[op.top]=*exp;exp++;break; case ' ':break;default:while(*exp>='0'&&*exp<='9'){postexp[i++]=*exp;exp++;}postexp[i++]='#';}}while(op.top!=-1){postexp[i++]=op.data[op.top];op.top--;}postexp[i]='\0';}float compvalue(char *postexp){struct{float data[MaxSize];int top;} st;float a,b,c,d;st.top=-1;while(*postexp!='\0'){switch(*postexp){case '+':a=st.data[st.top];st.top--;b=st.data[st.top];st.top--;c=b+a;st.top++;st.data[st.top]=c;break;case '-':a=st.data[st.top];st.top--;b=st.data[st.top];st.top--;c=b-a;break;case '*':a=st.data[st.top];st.top--;b=st.data[st.top];st.top--;c=b*a;st.top++;st.data[st.top]=c;break;case '/':a=st.data[st.top];st.top--;b=st.data[st.top];st.top--;if(a!=0){c=b/a;st.top++;st.data[st.top]=c;}else{printf("\n\t除零错误!\n");exit(0);}break;default:d=0;while(*postexp>='0'&&*postexp<='9'){d=10*d+*postexp-'0';postexp++;}st.top++;st.data[st.top]=d;break;}postexp++;}return st.data[st.top];}int main(){char exp[MaxSize],postexp[MaxSize];while(scanf("%s",&exp)!=EOF){trans(exp,postexp);printf("zhongzhuibiaodashi: %s\n",exp);printf("houzuibiaodashi: %s\n",postexp);printf("zhi: %g\n",compvalue(postexp)); }return 0;}第三种#include<stdio.h>#include<stdlib.h>#define add 43#define subs 45#define mult 42#define div 47#define MAXSIZE 100int data[MAXSIZE];int top;}seqstack;seqstack *s;seqstack *Init() /*栈的初始化*/{seqstack *s;s=(seqstack *)malloc(sizeof(seqstack)); if(!s){printf("FULL!");return NULL;}else{s->top=-1;return s;}}int Empty(seqstack *s) /*栈空的判断*/{if(s->top==-1) return 1;else return 0;}int Push(seqstack *s,int x) /*⼊栈*/{if(s->top==MAXSIZE-1) return 0;else{s->top++;s->data[s->top]=x;return 1;}}int Pop(seqstack *s,int *x) /*出栈的算法*/ {if (Empty(s)) return 0;else{*x=s->data[s->top];s->top--;return 1;}}int Top(seqstack *s) /*取栈顶元素*/ {if(Empty(s)) return 0;else return s->data[s->top];}int eval(char t,int a1,int a2){switch(t){case add:return(a1+a2);case subs:return(a1-a2);case mult:return(a1*a2);case div:return(a1/a2);}}void main(){char c;int op1,op2,temp,c1;s=Init();printf("Input:(end with #)\n");while((c=getchar())!='#'){if(c=='')continue;if(c>47&&c<58){putchar(c);c1=c-48;}else if(c==add||c==subs||c==mult||c==div){putchar(c);Pop(s,&op1);Pop(s,&op2);temp=eval(c,op2,op1);Push(s,temp);}else printf("It's wrong!\n");}Pop(s,&op1);printf("=%d\n",op1);getch();}第四种#include<stdio.h>#include<stdlib.h>#define add 43#define subs 45#define mult 42#define div 47#define MAXSIZE 100typedef struct{int data[MAXSIZE];int top;}STKzone;typedef STKzone *STK;typedef enum{ture=1,false=0} bool;typedef enum{ok,error} status;STKzone expSTKzone;STK expSTK;STK initSTK(STKzone *stkzone) /*栈的初始化*/{STK p;p=stkzone;p->top=0;}status push(int *term,STK pstk) /*⼊栈*//*term前可以没有*,同时将第28、71、81⾏稍作修改即可 */ {if(pstk->top==MAXSIZE) return error;pstk->data[pstk->top]=*term;pstk->top++;return ok;}bool emptySTK(STK pstk) /*栈空的判断*/{return (pstk->top==0);}status pop(int *pdata,STK pstk) /*出栈的算法*/{if (emptySTK(pstk)) return error;(pstk->top)--;*pdata=pstk->data[pstk->top];return ok;}void synerror(){printf("\nyu fa cuo wu!");}{switch(tag){case add:return(a1+a2);case subs:return(a1-a2);case mult:return(a1*a2);case div:return(a1/a2);}}main(){ char c;int op1,op2,temp,c1;expSTK=initSTK(&expSTKzone);printf("Input:\n");while((c=getchar())!='\n'){if(c=='')continue;if(c>47&&c<58){putchar(c);c1=c-48;if(push(&c1,expSTK)==error){printf("\n too long!\n");}}else if(c==add||c==subs||c==mult||c==div) {putchar(c);if(pop(&op1,expSTK)==error)synerror(); if(pop(&op2,expSTK)==error)synerror(); temp=eval(c,op2,op1);push(&temp,expSTK);}else synerror();}if(pop(&op1,expSTK)==error) synerror();if(!(emptySTK(expSTK))) synerror();printf("=%d\n",op1);getch();}第五种#include<stdio.h>#include<stdlib.h>#define add 43#define subs 45#define mult 42#define div 47#define MAXSIZE 100typedef struct{int stkdata[MAXSIZE];int top;}stack;int init_stack(stack *s){ s=(stack *)malloc(sizeof(stack));if(!s){printf("FULL!\n");return 0;}else{s->top=-1;return 1;}}int push(stack *s,int x){ printf("over flow\n");return 0;}else{s->top++;s->stkdata[s->top]=x;return 1;}}char pop(stack *s){ char e;if(s->top==-1){printf("under flow \n");return 0;}e=s->stkdata[(s->top)--];return e;}void main(){stack *s1;int length,i,num1,num2,result,sum;char s[100];init_stack(s1);printf("please input \n");printf("warning:must less than 100\n");gets(s);length=strlen(s);for(i=0;i<=length-1;i++){ if(s[i]>='1'&&s[i]<='9')push(s1,s[i]-48);else{ num1=pop(s1);num2=pop(s1);switch(s[i]){case add: {sum=num1+num2;push(s1,sum);break;}case subs:{sum=num2-num1;push(s1,sum);break;}case div:{sum=num2/num1;push(s1,sum);break;}case mult:{sum=num1*num2;push(s1,sum);break;}}}}result=s1->stkdata[s1->top];printf("result is %d\n",result);getch();}在研究表达式。
(完整版)数学表达式计算(c语言实现)

一、设计思想计算算术表达式可以用两种方法实现:1.中缀转后缀算法此算法分两步实现:先将算术表达式转换为后缀表达式,然后对后缀表达式进行计算.具体实现方法如下:(1)中缀转后缀需要建一个操作符栈op和一个字符数组exp,op栈存放操作符,字符数组用来存放转换以后的后缀表达式。
首先,得到用户输入的中缀表达式,将其存入str数组中。
对str数组逐个扫描,如果是数字或小数点,则直接存入exp数组中,当扫描完数值后,在后面加一个#作为分隔符。
如果是操作符,并且栈为空直接入栈,如果栈不为空,与栈顶操作符比较优先等级,若比栈顶优先级高,入栈;如果比栈顶优先级低或相等,出栈将其操作符存到exp数组中,直到栈顶元素优先等级低于扫描的操作符,则此操作符入栈;如果是左括号,直接入栈,如果是右括号,出栈存入exp数组,直到遇到左括号,左括号丢掉。
然后继续扫描下一个字符,直到遇到str中的结束符号\0,扫描结束。
结束后看op栈是否为空,若不为空,继续出栈存入exp数组中,直到栈为空.到此在exp数组最后加结束字符\0。
我们就得到了后缀表达式。
(2)后缀表达式计算此时需要一个数值栈od来存放数值。
对exp数组进行逐个扫描,当遇到数字或小数点时,截取数值子串将其转换成double类型的小数,存入od栈中。
当遇到操作符,从栈中取出两个数,进行计算后再放入栈中。
继续扫描,知道扫描结束,此时值栈中的数值就是计算的结果,取出返回计算结果。
2。
两个栈实现算法此算法需要两个栈,一个值栈od,一个操作符栈op。
将用户输入的数学表达式存入str数组中,对其数组进行逐个扫描。
当遇到数字或小数点,截取数值子串,将其转换成double类型的数值存入od栈中;当遇到左括号,直接入op栈;遇到右括号,op栈出栈,再从值栈od中取出两个数值,计算将其结果存入值栈中,一直进行此操作,直到操作符栈栈顶为左括号,将左括号丢掉。
如果遇到操作符,若op栈为空,直接入栈;若栈不为空,与栈顶元素比较优先等级,若比栈顶操作符优先等级高,直接入op栈,如果低于或等于栈顶优先等级,op栈出栈,再从值栈中取出两个数值,计算将其结果存入值栈中,一直进行此操作,直到栈顶优先等级低于扫描的操作符等级,将此操作符入op 栈。
算法笔记--中缀表达式转后缀表达式后缀表达式计算

算法笔记--中缀表达式转后缀表达式后缀表达式计算中缀表达式转后缀表达式规则中缀表达式a + b*c + (d * e + f) * g,转换成后缀表达式则为a b c * + d e * f + g * +转换过程需要⽤到栈,具体过程如下:1 如果遇到操作数,我们就直接将其输出。
2 如果遇到操作符,则我们将其放⼊到栈中,遇到左括号时我们也将其放⼊栈中。
3 如果遇到⼀个右括号,则将栈元素弹出,将弹出的操作符输出直到遇到左括号为⽌。
注意,左括号只弹出并不输出。
4 如果遇到任何其他的操作符,如+, *, (等,从栈中弹出元素直到遇到发现更低优先级的元素(或者栈为空)为⽌。
弹出完这些元素后,才将遇到的操作符压⼊到栈中。
有⼀点需要注意,只有在遇到 )的情况下我们才弹出( ,其他情况我们都不会弹出( 。
即:若操作符op的优先级⾼于栈顶操作符的优先级,则压⼊操作符栈若操作符op的优先级⼩于等于栈顶操作符的优先级,则将操作栈的操作符不断弹出到后缀表达式中,直到op的优先级⾼于栈顶操作符的优先级5 如果我们读到了输⼊的末尾,则将栈中所有元素依次弹出。
实例a +b *c + (d *e + f) * g1. ⾸先读到a,直接输出。
2. 读到“+”,将其放⼊到栈中。
3. 读到b,直接输出。
此时栈和输出的情况如下:4. 读到“*”,因为栈顶元素"+"优先级⽐" * " 低,所以将" * "直接压⼊栈中。
5. 读到c,直接输出。
此时栈和输出情况如下:6. 读到" + ",因为栈顶元素" * "的优先级⽐它⾼,所以弹出" * "并输出,同理,栈中下⼀个元素" + "优先级与读到的操作符" + "⼀样,所以也要弹出并输出。
然后再将读到的" + "压⼊栈中。
C语言下表达式的自动计算(两种方式)(报告+源代码)

一、设计思想第一种算法:将中缀表达式转为后缀表达式,然后通过后缀表达式计算出算术表达式的结果。
核心思想:第一步:中缀变后缀。
首先,我们做出一个统一的Node结构体,结构体内部包含四个属性,分别是操作符的字符‘op’,char类型;操作符的优先级‘level’,int 类型;数字的浮点数数值‘od’,float类型;Node的标识符,int类型。
然后,定义一个Node结构体类型的数组*listNode,这里的*listNode用的是全局变量,为了方便在得到后缀表达式后,不需再传递给计算的方法。
定义一个存放操作符的栈,遍历用户输入的算术表达式(不考虑错误情况),在遍历的过程中如果遇到数字,直接将数字存放在*listNode里面;如果遇到了操作符,则判断操作符栈目前是不是为空,如果为空,直接将遇到的操作符放入操作符栈中,如果操作符栈不为空,那么观察操作符栈中栈顶的操作符,然后再次判断当前遇到的操作符的优先级是不是比栈顶的操作符的优先级高,如果是,那么将当前的操作符入操作符栈;如果不是,那么将操作符栈的栈顶操作符取出,追加到*listNode中,然后继续观察栈顶操作符,直到当前的操作符的优先级比栈顶操作符的优先级高或者操作符栈为空时,将当前操作符入操作符栈。
如果遇到了左括号,那么定义其优先级为最低,然后直接将左括号入操作符栈。
如果遇到了右括号,那么开始从操作符栈中取出操作符追加到*listNode中,直到遇到了与之对应的左括号,然后将左括号和右括号一起销毁。
当遍历完成了算术表达式之后,这时判断操作符栈是否为空,如果不为空,那么从操作符栈中依次取出栈顶操作符追加到*listNode中,直到操作符栈为空,那么就代表我们将中缀表达式转变成为了后缀表达式。
第二步:通过得到的后缀表达式,计算算术表达式。
首先,定义一个数字栈用来存放数值。
然后,遍历*listNode中的每一个Node,如果Node是一个数字,那么就将数字入数字栈,如果Node是一个操作符,那么就从数字栈中依次取出栈顶的两个数字,然后根据操作符计算这两个数字,将得到的结果再次入数字栈,直到遍历*listNode完成,最终数字栈中会只剩下一个Node,那就是我们计算出算术表达式的结果,将结果返回给main 函数用来输出。
c两种方法实现表达式的计算 (1)

数据结构(双语)——项目文档报告用两种方式实现表达式自动计算专业:网络工程班级:网络1班指导教师:吴亚峰姓名:王嘉宇学号:201214620111目录一、设计思想 (01)二、算法流程图 (01)三、源代码 (04)四、运行结果 (12)五、遇到的问题及解决 (13)六、心得体会 (14)一、设计思想(1)先将中缀表达式转化为后缀表达式,再通过计算后缀表达式求表达式的值。
第一遍扫描中缀表达式,需要一个运算符栈和一个数组。
运算符栈用来存放运算符,数组用来存放转换成的后缀表达式。
首先将中缀表达式挨个扫描。
如果是数字,则直接放在后缀表达式数组中,依次存放。
如果扫描到的是运算符,则按照以下规则存放:栈空时,任何运算符可直接入栈。
栈不空是,如果栈中运算符的优先级高于或等于将要放入栈中的运算符的优先级,则将栈中运算符出栈,放入后缀表达式数组中,直到栈中运算符优先级低于将要放入栈中的运算符的优先级,此时将此运算符放入运算符栈中。
如果遇到左括号,则直接将左括号入栈,左括号入栈后优先级最低,其他运算符可直接放入。
如果遇到右括号,则将运算符栈中的运算符依次取出放到后缀表达式数组中,直到遇到左括号为止,此时将左括号从栈顶删除。
按此方法,直到后缀表达式转换成功。
第二遍扫描后缀表达式,此时需要一个数栈。
扫描时如果遇到数字,则直接放到数栈中。
如果遇到运算符,则将数栈中两个数取出,先取出的放在运算符后面,后取出的放在运算符前面,进行运算符运算。
将运算的结果放入栈中。
之后接着扫描后缀表达式。
另外因为运算数的位数不一定而且还有小数点,所以在扫到一个数时要判断这个数的位数,将这个完整的运算数字符串整个取出,这需要用到一个辅助索引。
当栈中只有一个数字时,这个数字就是我们要求的表达式的值。
(2)直接计算表达式的值。
这种方法需要两个栈,一个运算符栈,一个数栈。
只需扫描一遍中缀表达式,边运算边入栈。
当扫描到的为数字是,将其放入数栈中,然后扫描下一个字符。
c语言基于二叉树的表达式求值算法

c语言基于二叉树的表达式求值算法C语言中,基于二叉树的表达式求值算法主要包括两部分:中缀表达式转换为后缀表达式和后缀表达式求值。
1.中缀表达式转换为后缀表达式中缀表达式是我们常见的数学表达方式,例如3 + 4 * 2 - 5。
为了方便计算机求值,我们需要将中缀表达式转换为后缀表达式,也叫做逆波兰表达式。
转换的过程使用栈数据结构来实现。
具体算法如下:1.定义一个栈和一个结果字符串,栈用于存储操作符,结果字符串用于保存后缀表达式。
2.从左到右遍历中缀表达式的每一个字符。
3.如果当前字符是数字,直接将其加入结果字符串。
4.如果当前字符是左括号"(",将其入栈。
5.如果当前字符是右括号")",则依次将栈顶的操作符弹出并加入结果字符串,直到遇到左括号为止,同时将左括号从栈中弹出。
6.如果当前字符是操作符,需要将栈中优先级比当前操作符高或者相等的操作符弹出并加入结果字符串,然后将当前操作符入栈。
7.遍历完所有字符后,将栈中剩余的操作符依次弹出并加入结果字符串。
8.最终结果字符串就是后缀表达式。
例如,对于中缀表达式3 + 4 * 2 - 5,转换为后缀表达式为3 4 2 * + 5 -2.后缀表达式求值后缀表达式求值算法使用栈数据结构来实现。
具体算法如下:1.定义一个栈,用于存储操作数。
2.从左到右遍历后缀表达式的每一个字符。
3.如果当前字符是数字,则将其转换为对应的整数并入栈。
4.如果当前字符是操作符,则从栈中弹出两个操作数,先弹出的作为右操作数,后弹出的作为左操作数,根据操作符进行运算,得到结果后入栈。
5.遍历完所有字符后,栈顶的数字即为最终的结果。
例如,对于后缀表达式3 4 2 * + 5 -,求值的过程如下:1.入栈3。
2.入栈4。
3.入栈2。
4.弹出2和4,计算4 * 2 = 8,将8入栈。
5.弹出8和3,计算3 + 8 = 11,将11入栈。
6.入栈5。
7.弹出5和11,计算11 - 5 = 6,得到最终结果。
利用栈或二叉树将算术表达式输入串(只要求1位整数)转换为后缀式,然后计算该表达式

利用栈或二叉树将算术表达式输入串(只要求1位整数)转换为后缀式,然后计算该表达式利用栈或二叉树将算术表达式输入串(只要求1位整数)转换为后缀式,然后计算该表达式算术表达式的计算通常需要将中缀表达式转换为后缀表达式,然后使用栈或二叉树对后缀表达式进行计算。
首先,我们需要定义运算符的优先级。
在本例中,我们只考虑加法'+'和减法'-'两个运算符,其中加法的优先级较低。
接下来,我们可以使用栈来转换中缀表达式为后缀表达式。
具体步骤如下:1. 创建一个空栈和一个空字符串,用于存储后缀表达式。
2. 从左到右遍历中缀表达式的每个字符。
3. 对于每个字符,进行如下处理:- 如果是数字,则直接添加到后缀表达式字符串中。
- 如果是运算符,则比较其与栈顶运算符的优先级。
- 如果栈为空或栈顶运算符为'(',则直接将当前运算符入栈。
- 如果当前运算符的优先级大于栈顶运算符的优先级,则将当前运算符入栈。
- 如果当前运算符的优先级小于或等于栈顶运算符的优先级,则将栈顶运算符弹出并加入后缀表达式字符串中,直到栈为空或栈顶运算符为'(',然后将当前运算符入栈。
- 如果是左括号'(',则直接将其入栈。
- 如果是右括号')',则将栈顶运算符弹出并加入后缀表达式字符串中,直到遇到左括号'(',然后将左括号出栈但不加入后缀表达式字符串。
4. 遍历完中缀表达式后,将栈中剩余的运算符依次弹出并加入后缀表达式字符串中。
现在,我们已经将中缀表达式转换为后缀表达式。
接下来,我们可以使用栈或二叉树来计算后缀表达式。
1. 创建一个空栈,用于存储操作数。
2. 从左到右遍历后缀表达式的每个字符。
3. 对于每个字符,进行如下处理:- 如果是数字,则将其转换为整数并入栈。
- 如果是运算符,则从栈中弹出两个操作数,进行相应的运算,并将结果入栈。
4. 遍历完后缀表达式后,栈中最后剩下的元素即为计算结果。
用栈解决表达式求值问题的c语言代码

栈是一种常见的数据结构,用于解决许多算法和数据处理问题。
在编程中,栈通常用于处理表达式求值问题。
本篇文章将介绍如何使用栈解决表达式求值问题,并给出对应的C语言代码。
1. 表达式求值问题介绍表达式求值是指计算一个数学表达式的值,通常涉及到四则运算、括号和优先级等概念。
给定一个表达式“3 + 4 * 2”,我们需要得到其计算结果为11。
在编程中,需要将该表达式转换为计算机可识别的形式,并使用算法进行求值。
2. 中缀表达式、前缀表达式和后缀表达式在计算机中常见的表达式有三种形式:中缀表达式、前缀表达式和后缀表达式。
其中,中缀表达式是通常人们在日常生活中使用的表达式形式,如“3 + 4 * 2”。
前缀表达式是运算符位于操作数之前的形式,例如“+ 3 * 4 2”。
后缀表达式则是运算符位于操作数之后的形式,例如“3 4 2 * +”。
3. 使用栈解决表达式求值问题在解决表达式求值问题时,我们可以利用栈的特性来简化计算过程。
具体步骤如下:3.1 将中缀表达式转换为后缀表达式我们需要将中缀表达式转换为后缀表达式,这样可以简化表达式的计算顺序。
具体转换规则如下:- 从左至右扫描中缀表达式的每个数字或符号。
- 如果是操作数,则直接输出。
- 如果是运算符,则弹出栈中所有优先级大于或等于该运算符的运算符,并将其压入栈中,然后压入该运算符。
- 如果是括号,则根据括号的不同情况进行处理。
通过以上规则,我们可以将中缀表达式转换为后缀表达式。
3.2 计算后缀表达式的值得到后缀表达式后,我们可以利用栈来计算其值。
具体步骤如下:- 从左至右扫描后缀表达式的每个数字或符号。
- 如果是操作数,则压入栈中。
- 如果是运算符,则弹出栈中的两个操作数进行相应的运算,并将结果压入栈中。
- 继续扫描直到表达式结束,栈中的值即为所求结果。
通过以上步骤,我们可以使用栈来解决表达式求值问题。
4. C语言代码实现以下是使用C语言实现栈来解决表达式求值问题的代码示例:```c#include <stdio.h>#include <stdlib.h>#include <string.h>typedef struct {int top;int capacity;int* array;} Stack;Stack* createStack(int capacity) {Stack* stack = (Stack*)malloc(sizeof(Stack));stack->capacity = capacity;stack->top = -1;stack->array = (int*)malloc(stack->capacity * sizeof(int)); return stack;}int isFull(Stack* stack) {return stack->top == stack->capacity - 1; }int isEmpty(Stack* stack) {return stack->top == -1;}void push(Stack* stack, int item) {if (isFull(stack)) return;stack->array[++stack->top] = item;}int pop(Stack* stack) {if (isEmpty(stack)) return -1;return stack->array[stack->top--];}int evaluatePostfix(char* exp) {Stack* stack = createStack(strlen(exp)); for (int i = 0; exp[i]; i++) {if (isdigit(exp[i])) {push(stack, exp[i] - '0');} else {int val1 = pop(stack);int val2 = pop(stack);switch (exp[i]) {case '+':push(stack, val2 + val1); break;case '-':push(stack, val2 - val1); break;case '*':push(stack, val2 * val1); break;case '/':push(stack, val2 / val1); break;}}}return pop(stack);}int m本人n() {char exp[] = "34*2+";printf("The value of s is d\n", exp, evaluatePostfix(exp));return 0;}```以上代码实现了栈的基本功能,并利用栈来计算后缀表达式的值。
C语言实现中缀、后缀、前缀表达式 相互转化并求值

C语言实现中缀、后缀、前缀表达式相互转化并求值1.问题描述(1)表达式求值问题表达式是数据运算的基本形式。
人们的书写习惯是中缀式,如:11+22*(7-4)/3。
中缀式的计算按运算符的优先级及括号优先的原则,相同级别从左到右进行计算。
表达式还有后缀式(如:22 7 4 - * 3 / 11 +)和前缀式(如:+ 11 / * 22 –7 4 3)。
后缀表达式和前缀表达式中没有括号,给计算带来方便。
如后缀式计算时按运算符出现的先后进行计算。
本设计的主要任务是进行表达式形式的转换及不同形式的表达式计算。
2.数据结构设计(1)表达式求值问题由于表达式中有字符与数字两种类型,故定义结点一个标志域data,标志结点存储的为字符data=2还是数字data=1,再寻找结点中对应的存储位置,读取数字域data1,字符域data2。
而在前缀表达式时,存在表达式逆序,因表达式类型不统一,用栈逆序极不方便,选择构建双向链表,存储表达式。
typedef struct Node //定义存储中缀表达式的结点类型{int data;int data1;char data2;struct Node *next;}Lnode;typedef struct Node2 //定义存储前缀表达式的结点类型{int data;int data1;char data2;struct Node2 *next;struct Node2 *prior;}Lnode2;3.运行、测试与分析(1)表达式求值问题(1)按提示输入中缀表达式,如图1.1所示。
如输入中缀表达式不正确,提示输入有误,如图1.2,1.3所示。
图1.1图1.2图1.3(2)选择表达式转换并求值方式。
按“1”选择中缀表达式求值,如图1.4所示。
图1.4(3)按“2”选择中缀表达式转变为后缀表达式并求值,如图1.5所示。
图1.5(4)按“3”选择中缀表达式转变为前缀表达式并求值,如图1.6所示。
使用栈实现中缀转后缀表达式及计算结果完整源码

原创作者:/p/hky_bd2010?from=zhidaousing System;using System.Collections.Generic;using System.Linq;using System.Text;namespace RPN{class Program{static void Main(string[] args){string infix = "2+3*4"; // 中缀string suffix = InfixChangeSuffix(infix); // 中缀转后缀double result=CalcSuffix(suffix.Split(',').ToArray());Console.WriteLine(result);}///<summary>///中缀转后缀///</summary>///<param name="infixExpression">中缀表达式</param>///<returns></returns>static string InfixChangeSuffix(string infixExpression){string suffix = string.Empty;string completeDigits = string.Empty;Stack<char> stack = new Stack<char>();for (int i = 0; i < infixExpression.Length; i++){if (IsOperator(infixExpression[i])) // 是否是运算符{if (!String.IsNullOrWhiteSpace(completeDigits)){suffix += completeDigits + ","; // 把前面的数字加入到后缀表达式里completeDigits = string.Empty; // 清空,待下次继续使用}if (stack.Count>0) // 如果栈里有元素,则判断当前符号与栈顶元素的优先级{char stackTopSymbol;if (infixExpression[i] == '(') // 如果是左括号则直接进栈{stack.Push(infixExpression[i]);}else if (infixExpression[i] == ')') // 如果是右括号,则出栈直到遇到左括号为止{stackTopSymbol = stack.Pop(); // 弹出栈顶元素do{if (stackTopSymbol != '(') suffix +=Convert.ToString(stackTopSymbol) + ",";if (stack.Count > 0) stackTopSymbol = stack.Pop();else break; // 中缀表达式有异常即四则运算不符合数学规则} while (stackTopSymbol != '('); // 直到遇到左括号为止则停止出栈}else{stackTopSymbol = stack.Peek(); // 拿栈顶元素出来,但不移除int curPriority = Priority(infixExpression[i]);int stackTop = Priority(stackTopSymbol);if (curPriority <= stackTop){do{suffix += stackTopSymbol + ",";stack.Pop(); // 栈顶元素优先级高当前符号,则弹出来if (stack.Count > 0){stackTopSymbol = stack.Peek();// 拿栈顶元素出来,但不移除stackTop = Priority(stackTopSymbol);}else break; // 原理同上} while (curPriority<=stackTop);}stack.Push(infixExpression[i]); // 当前的运算符入栈 }}else{stack.Push(infixExpression[i]);}}else{completeDigits += Convert.ToString(infixExpression[i]);}}suffix += completeDigits+",";while (stack.Count>0){suffix += Convert.ToString(stack.Pop())+",";}return suffix;}///<summary>///运算符符号优先级///</summary>///<param name="symbol">运算符符号</param>///<returns></returns>static int Priority(char symbol){switch (symbol){case'*':case'/':return 2;case'+':case'-':return 1;}return -1;}static double Calc(double first, double second, char symbol){switch (symbol){case'*':return (double)first * second;case'/':return (double)first / second;case'+':return (double)first + second;case'-':return (double)first - second;}return 0.0d;}static bool IsOperator(char symbol){char[] symbols={'+','-','*','/','(',')'};return symbols.Contains(symbol);}///<summary>///计算后缀表达式结果///</summary>///<param name="suffixExpression"></param>///<returns></returns>static double CalcSuffix(string[] suffixExpression){Stack<double> stack = new Stack<double>();double temp;for (int i = 0; i < suffixExpression.Length; i++){if (String.IsNullOrWhiteSpace(suffixExpression[i])) break;if (double.TryParse(suffixExpression[i], out temp)) // 是数字 {stack.Push(temp);}else// 是运算符{double rightNum = stack.Pop();double leftNum = stack.Pop();double result = Calc(leftNum, rightNum, Convert.ToChar(suffixExpression[i]));stack.Push(result);}}return stack.Pop();}}}。
C语言简单计算器原理——表达式求值(采用逆波兰表达式和栈结合)

C语⾔简单计算器原理——表达式求值(采⽤逆波兰表达式和栈
结合)
表达式的求解的关键是将其转换成逆波兰表达式(即后缀表达式,如1+2*3它的逆波兰表达式为123*+),在后缀表达式中已经考虑了运算符的优先级,
没有括号,只有操作数和运算符。
算术表达式转换成后缀表达式⽅法如下:
依次从键盘输⼊表达式的字符ch,对于每个ch:
(1)若ch为数字则直接将其放⼊后缀数组exp中并以#号标记数值串结束。
(2)若ch为"(",则直接将其压⼊字符栈op中。
(3)若ch为")",则将栈中"("以前的字符依次全部删除并将其放⼊后缀数组exp中,然后再将字符ch放⼊字符栈op中。
(4)若ch为"+"."-",则将栈中"("以前的运算符依次全部删除并将其放⼊后缀数组exp中,然后再将ch放⼊op栈中。
(5)若ch为"*"."/",则将栈顶连续的"*"."/"删除,并放⼊后缀数组exp中,然后将ch放⼊op栈中。
(6)若字符串str扫描完毕,则将栈中所有运算符删除并放⼊后缀数组exp,最后在后缀数组exp中便可得到后缀表达式。
在对后缀表达式求值时要⽤到⼀个数值栈st,在后缀数组exp中从头开始扫描,若是数字则将其放⼊数值栈中,
若遇到字符就进⾏两次退栈,并将运算结果再放⼊栈中,如此重复下去,最后当后缀数组扫描完后数值栈st的栈顶元素便是所要求的表达式的值。
c语言表达式求值中缀表达式转后缀表达式求值

c语⾔表达式求值中缀表达式转后缀表达式求值中转后具体转换⽅式:1.从左到右遍历需要计算的字符串2.若是运算数,直接压⼊后缀表达式栈3.若是左括号,直接压⼊运算符栈,(括号是最⾼优先级,⽆需⽐较)(⼊栈后优先级降到最低,确保其他符号正常⼊栈)4.若是右括号,(意味着括号已结束)不断弹出运算符栈顶运算符并输出到后缀表达式栈直到遇到左括号(弹出但不输出)5.运算符,将该运算符与运算符栈顶运算符进⾏⽐较,如果优先级⾼于栈顶运算符则压⼊运算符栈(该部分运算还不能进⾏),如果优先级低于等于栈顶运算符则将栈顶运算符弹出到后缀表达式栈然后⽐较新的栈顶运算符.(低于弹出意味着前⾯部分可以运算,先输出到后缀表达式栈⼀定是⾼优先级运算符,等于弹出是因为同等优先级,从左到右运算)直到优先级⼤于栈顶运算符或者栈空,再将该运算符⼊运算符栈6.如果字符串处理完毕,则按顺序从运算符栈弹出所有运算符到后缀表达式栈使⽤后缀表达式计算的⽅法:1、按顺序取后缀表达式的每个值2、若是数字则⼊栈3、若是操作符则从栈取出两个数字进⾏运算运算之后再将结果⼊栈4、循环上述过程知道后缀表达式结束栈顶元素(栈中只有⼀个元素)即为结果1 #include <windows.h>2 #include <stdio.h>3 #include <string.h>4 #include <malloc.h>5#define NUM 06#define OPERATION 17 typedef struct {//栈中的结点8int val;9int type;10 } Node;11 typedef struct {//栈12const char* name;//栈名13 Node* sta;//结点14int size;//最多存储多少个元素15int cnt;//当前存储了多少个元素16 } MyStack;17void trace(MyStack* s)//栈的遍历18 {19int i;20 printf("%s栈中的元素为:", s->name);21for (i = 0; i < s->cnt; i++) {22if (s->sta[i].type == NUM) {//若是数字23 printf("%d ", s->sta[i].val);24 }25else {//若是字符26 printf("%c ", (char)s->sta[i].val);27 }28 }29 printf("\n");30 }31void sFree(MyStack* s)//释放栈32 {33if (s->sta != NULL) {34 free(s->sta);35 s->sta = NULL;36 }37return;38 }39int sInit(MyStack* s, const char* name, int size)//初始化栈40 {41 s->name = name;42 s->size = size;43 s->sta = (Node*)calloc(s->size, sizeof(Node));//calloc申请后其中存的都是044if (s->sta == NULL) {45return -1;//分配失败46 }47 s->cnt = 0;//当前栈中元素有0个48return0;//分配成功49 }50void sPush(MyStack* s, Node item)//⼊栈⼀个元素51 {52if (s->cnt == s->size) {53 printf("栈空间不⾜\n");54return;55 }56 s->sta[s->cnt] = item;57 s->cnt++;58return;59 }60bool sIsEmpty(MyStack* s)//判断栈是否为空61 {62return s->cnt == 0;63 }64void sPop(MyStack* s, Node* item)//删除栈顶元素并返回值到item65 {66if (sIsEmpty(s)) {67return;68 }69 *item = s->sta[s->cnt - 1];70 s->cnt--;71return;72 }73void sTop(MyStack* s, Node* item)//获得栈顶元素到item 不删除栈顶袁术74 {75if (sIsEmpty(s)) {76return;77 }78 *item = s->sta[s->cnt - 1];79return;80 }81bool myIsNum(char ch)//判断是否是数字82 {83return ch >= '0' && ch <= '9';84 }85bool myIsOper(char ch)//判断是否是运算符86 {87return ch == '+' || ch == '-' || ch == '*' || ch == '/'||ch=='('||ch==')';88 }89//处理数值90void procNum(MyStack* postfix_expression, char* s, int len, int* pi)91 {92int i = *pi;//令i等于当前在处理的元素的坐标93int num=0;//当前数字的值具体是多少94 Node item_num;95while (myIsNum(s[i]))96 {97 num = num * 10 + s[i]-'0';98 i++;99 }100//新建结点101 item_num.type = NUM;102 item_num.val = num;103//数字直接⼊后缀表达式的栈104 sPush(postfix_expression, item_num);105 *pi = i-1;//改变calculate_postfix_expression 中i的值106return;107 }108//处理运算符109void procOper(MyStack* postfix_expression, MyStack* s_oper, char* s, int len, int* pi) 110 {111int i = *pi;112 Node item;113 Node top_item;114 Node pop_item;115if (s[i] == '(')//如果是( 直接存⼊运算符栈116 {117 item.type = OPERATION;118 item.val = s[i];119 sPush(s_oper, item);120 }121else if (s[i] == ')')//若是) 则弹出到(为⽌122 {123int flag = 0;//是否找到了 (124while (!sIsEmpty(s_oper)) {125 sPop(s_oper, &pop_item);126if (pop_item.val == '(') {//若找到了左括号退出127 flag = 1;128break;129 }130 sPush(postfix_expression, pop_item);//若未找到左括号则⼀直从运算符栈中pop131 }132if (!flag)133 {134 printf("括号不匹配!");135 exit(0);136 }137 }138//如果是乘除139else if (s[i] == '*' || s[i] == '/')140 {141 item.type = OPERATION;142 item.val = s[i];143while (!sIsEmpty(s_oper)) {144 sTop(s_oper, &top_item);145//如果当前运算符栈的栈顶是+ - (146//则* /级别较⾼则跳出循环147if (top_item.val == '+' || top_item.val == '-' || top_item.val == '(') {148break;149 }150//若当前运算符栈顶不是+ - ( 则是* /151//则需先把* / pop完152 sPop(s_oper, &pop_item);153 sPush(postfix_expression, pop_item);154 }155//才能将当* /⼊栈156 sPush(s_oper, item);157 }158//如果是 + -159else if (s[i] == '+' || s[i] == '-')160 {161 item.type = OPERATION;162 item.val = s[i];163while (!sIsEmpty(s_oper)) {164 sTop(s_oper, &top_item);165//如果当前运算符栈的栈顶是 (166//则当前运算符级别较⾼则跳出循环167if (top_item.val == '(') {168break;169 }170//若当前运算符栈顶不是 ( 则是+ - * /171//则需先把+ - * /pop完172 sPop(s_oper, &pop_item);173 sPush(postfix_expression, pop_item);174 }175//才能将当+ - ⼊栈176 sPush(s_oper, item);177 }178else179 {180 printf("输⼊了⾮空格⾮数字⾮运算符的元素 %c\n", s[i]);181 exit(0);182 }183return;184 }185//计算后缀表达式存储在s_trans中186void calculate_postfix_expression(MyStack* postfix_expression, MyStack* s_oper, char* s, int len) 187 {188int i;189int ret;190int num;191 Node item;192for (i = 0; i < len; i++) {193if (s[i] == '') {//当前输⼊为空格时跳过194continue;195 }196if (myIsNum(s[i])) {//当前是数字时197 procNum(postfix_expression, s, len, &i);198continue;199 }200if (myIsOper(s[i])) {//当前是运算符时进⼊运算的处理程序201 procOper(postfix_expression, s_oper, s, len, &i);202continue;203 }204 printf("输⼊了⾮空格⾮数字⾮运算符的元素 %c\n", s[i]);205 exit(0);206 }207//若运算栈不为空依次pop出运算栈中的元素再push到后缀表达式栈208while (!sIsEmpty(s_oper)) {209 sPop(s_oper, &item);210 sPush(postfix_expression, item);211 }212return;213 }214int cal(MyStack* postfix_expression, MyStack* s_num)//进⾏计算215 {216int i;217 Node n1, n2;218 Node item;219//顺序取出栈中的每个元素220for (i = 0; i < postfix_expression->cnt; i++) {221//item为后缀表达式中顺序取的第i个元素222 item = postfix_expression->sta[i];223//若⼀直是数字则⼀直放进数字栈224if (item.type == NUM) {225 sPush(s_num, item);226continue;//开始下⼀次循环227 }228//执⾏到这⾥证明不是数字是运算符了229 sPop(s_num, &n2);//从栈中拿出两个元素到n2 n1中230 sPop(s_num, &n1);231if (item.val == '+') {232 n1.val += n2.val;233 }234else if (item.val == '-') {235 n1.val -= n2.val;236 }237else if (item.val == '*') {238 n1.val *= n2.val;239 }240else {241 n1.val /= n2.val;242 }243 sPush(s_num, n1);//再将此次运算结果⼊数字栈244 }245return s_num->sta[0].val;//最后数字栈中的第⼀个元素就是计算结果246 }247int calculate(char* s) {//进⾏计算248int ret;249int len;250if (s == NULL||(len=strlen(s))==0) {251return0;252 }253 MyStack s_num;//数字栈254 MyStack s_oper;//运算符栈255 MyStack postfix_expression;//后缀表达式栈256if (sInit(&s_num, "数字", len)==-1||257 sInit(&s_oper, "运算符", len)==-1||258 sInit(&postfix_expression, "后缀表达式", len)==-1259 ) //若初始化三个栈失败的话则释放内存 return 0260 {261 sFree(&s_num);262 sFree(&postfix_expression);263 sFree(&s_oper);264return0;265 }266//计算后缀表达式267 calculate_postfix_expression(&postfix_expression, &s_oper, s, len); 268//显⽰后缀表达式269 trace(&postfix_expression);270//使⽤后缀表达是进⾏计算271 ret = cal(&postfix_expression, &s_num);272//释放栈的空间273 sFree(&postfix_expression);274 sFree(&s_oper);275 sFree(&s_num);276//返回结果277return ret;278 }279int main()280 {281char str[10000];282 scanf("%[^\n]", str);//可以输⼊空格回车停⽌输⼊283 printf("计算结果为%d\n", calculate(str));284 }285//例⼦ (((50+20)+(2*3))/14)。
c 实现中缀表达式转后缀表达式比计算值

c 实现中缀表达式转后缀表达式比计算值C语言是一种广泛应用的编程语言,它具有高效、可移植、灵活等特点,在计算机科学领域有着广泛的应用。
中缀表达式是我们常见的数学表达方式,而将中缀表达式转换为后缀表达式是一项常见的任务。
本文将介绍如何使用C语言实现中缀表达式转后缀表达式,并计算其值。
我们需要了解中缀表达式和后缀表达式的概念。
中缀表达式是我们常见的数学表达方式,其中操作符位于操作数之间,如"3 + 4"。
而后缀表达式(也称为逆波兰表达式)是一种更加简洁的数学表达方式,其中操作符位于操作数之后,如"3 4 +"。
后缀表达式的计算更加简单直观,因此在计算机中更为常见。
接下来,我们需要实现一个函数来将中缀表达式转换为后缀表达式。
我们可以使用栈这一数据结构来辅助实现。
具体的步骤如下:1. 创建一个栈,用于存储操作符。
2. 遍历中缀表达式的每个字符。
3. 如果当前字符是操作数,直接输出。
4. 如果当前字符是操作符,并且栈为空,将操作符入栈。
5. 如果当前字符是操作符,并且栈不为空,比较当前操作符与栈顶操作符的优先级。
- 如果当前操作符的优先级大于栈顶操作符的优先级,将当前操作符入栈。
- 如果当前操作符的优先级小于等于栈顶操作符的优先级,将栈顶操作符出栈并输出,直到栈为空或者栈顶操作符的优先级小于当前操作符。
- 将当前操作符入栈。
6. 如果当前字符是左括号"(",将其入栈。
7. 如果当前字符是右括号")",将栈顶操作符出栈并输出,直到栈顶操作符为左括号"("。
8. 遍历结束后,将栈中剩余的操作符依次出栈并输出。
通过上述步骤,我们可以将中缀表达式转换为后缀表达式。
接下来,我们需要计算后缀表达式的值。
为了计算后缀表达式的值,我们可以使用另一个栈来辅助实现。
具体的步骤如下:1. 创建一个栈,用于存储操作数。
2. 遍历后缀表达式的每个字符。
c语言中缀、后缀算术表达式求值用栈实现

c语言中缀、后缀算术表达式求值用栈实现下面是用栈实现中缀表达式求值的示例代码:#include <stdio.h>#include <stdlib.h>#include <ctype.h>#define MAX_STACK_SIZE 100typedef struct {int top;int data[MAX_STACK_SIZE];} Stack;void init(Stack *s) {s->top = -1;}int is_empty(Stack *s) {return s->top == -1;}int is_full(Stack *s) {return s->top == MAX_STACK_SIZE - 1;}void push(Stack *s, int x) {if (is_full(s)) {printf("Error: stack overflow\n");exit(EXIT_FAILURE);}s->data[++s->top] = x;}int pop(Stack *s) {if (is_empty(s)) {printf("Error: stack underflow\n");exit(EXIT_FAILURE);}return s->data[s->top--];}int peek(Stack *s) {if (is_empty(s)) {printf("Error: stack underflow\n");exit(EXIT_FAILURE);}return s->data[s->top];}int precedence(char op) {switch (op) {case '+':case '-':return 1;case '*':case '/':return 2;default:return 0;}}int evaluate(int op1, int op2, char op) {switch (op) {case '+':return op1 + op2;case '-':return op1 - op2;case '*':return op1 * op2;case '/':return op1 / op2;default:printf("Error: invalid operator\n");exit(EXIT_FAILURE);}}int evaluate_infix(char *expr) {Stack op_stack, val_stack;init(&op_stack);init(&val_stack);while (*expr != '\0') {if (isdigit(*expr)) {int val = 0;while (isdigit(*expr)) {val = val * 10 + (*expr - '0');expr++;}push(&val_stack, val);} else if (*expr == '+' || *expr == '-' || *expr == '*' || *expr == '/') {while (!is_empty(&op_stack) && precedence(peek(&op_stack)) >= precedence(*expr)) {int op2 = pop(&val_stack);int op1 = pop(&val_stack);char op = pop(&op_stack);push(&val_stack, evaluate(op1, op2, op));}push(&op_stack, *expr);expr++;} else if (*expr == '(') {push(&op_stack, '(');expr++;} else if (*expr == ')') {while (peek(&op_stack) != '(') {int op2 = pop(&val_stack);int op1 = pop(&val_stack);char op = pop(&op_stack);push(&val_stack, evaluate(op1, op2, op));}pop(&op_stack);expr++;} else {printf("Error: invalid character\n");exit(EXIT_FAILURE);}}while (!is_empty(&op_stack)) {int op2 = pop(&val_stack);int op1 = pop(&val_stack);char op = pop(&op_stack);push(&val_stack, evaluate(op1, op2, op));}return peek(&val_stack);}int main() {char expr[100];printf("Enter infix expression: ");scanf("%[^\n]", expr);printf("Result = %d\n", evaluate_infix(expr));return 0;}下面是用栈实现后缀表达式求值的示例代码:#include <stdio.h>#include <stdlib.h>#include <ctype.h>#define MAX_STACK_SIZE 100typedef struct {int top;int data[MAX_STACK_SIZE];} Stack;void init(Stack *s) {s->top = -1;}int is_empty(Stack *s) {return s->top == -1;}int is_full(Stack *s) {return s->top == MAX_STACK_SIZE - 1;}void push(Stack *s, int x) {if (is_full(s)) {printf("Error: stack overflow\n");exit(EXIT_FAILURE);}s->data[++s->top] = x;}int pop(Stack *s) {if (is_empty(s)) {printf("Error: stack underflow\n");exit(EXIT_FAILURE);}return s->data[s->top--];}int peek(Stack *s) {if (is_empty(s)) {printf("Error: stack underflow\n");exit(EXIT_FAILURE);}return s->data[s->top];}int evaluate(int op1, int op2, char op) {switch (op) {case '+':return op1 + op2;case '-':return op1 - op2;case '*':return op1 * op2;case '/':return op1 / op2;default:printf("Error: invalid operator\n");exit(EXIT_FAILURE);}}int evaluate_postfix(char *expr) {Stack stack;init(&stack);while (*expr != '\0') {if (isdigit(*expr)) {int val = 0;while (isdigit(*expr)) {val = val * 10 + (*expr - '0');expr++;}push(&stack, val);} else if (*expr == '+' || *expr == '-' || *expr == '*' || *expr == '/') { int op2 = pop(&stack);int op1 = pop(&stack);push(&stack, evaluate(op1, op2, *expr));expr++;} else {printf("Error: invalid character\n");exit(EXIT_FAILURE);}}return peek(&stack);}int main() {char expr[100];printf("Enter postfix expression: ");scanf("%[^\n]", expr);printf("Result = %d\n", evaluate_postfix(expr));return 0;}。
C语言利用栈实现对后缀表达式的求解
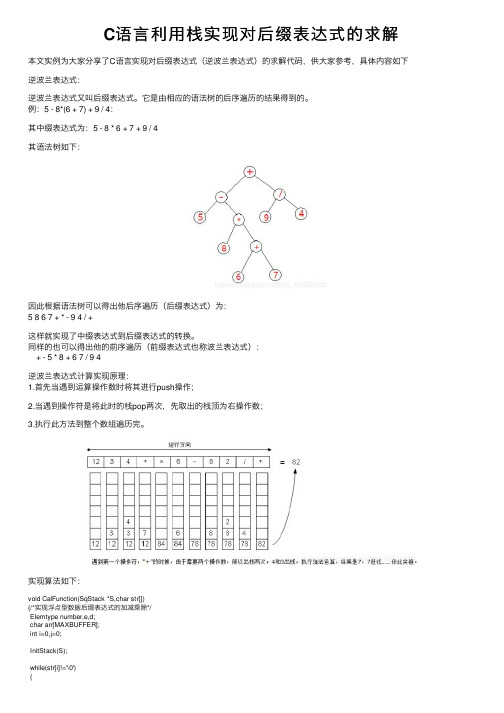
C语⾔利⽤栈实现对后缀表达式的求解本⽂实例为⼤家分享了C语⾔实现对后缀表达式(逆波兰表达式)的求解代码,供⼤家参考,具体内容如下逆波兰表达式:逆波兰表达式⼜叫后缀表达式。
它是由相应的语法树的后序遍历的结果得到的。
例:5 - 8*(6 + 7) + 9 / 4:其中缀表达式为:5 - 8 * 6 + 7 + 9 / 4其语法树如下:因此根据语法树可以得出他后序遍历(后缀表达式)为:5 867 + * - 9 4 / +这样就实现了中缀表达式到后缀表达式的转换。
同样的也可以得出他的前序遍历(前缀表达式也称波兰表达式): + - 5 * 8 + 6 7 / 9 4逆波兰表达式计算实现原理:1.⾸先当遇到运算操作数时将其进⾏push操作;2.当遇到操作符是将此时的栈pop两次,先取出的栈顶为右操作数;3.执⾏此⽅法到整个数组遍历完。
实现算法如下:void CalFunction(SqStack *S,char str[]){/*实现浮点型数据后缀表达式的加减乘除*/Elemtype number,e,d;char arr[MAXBUFFER];int i=0,j=0;InitStack(S);while(str[i]!='\0')while(isdigit(str[i])||str[i]=='.') //过滤数字{arr[j++]=str[i++];arr[j]='\0';if( j >= MAXBUFFER ){printf("输⼊单个数据过⼤!\n");return ;}if(str[i]==' '){number=atof(arr); //利⽤atof函数将数字字符串转化为double型数据PushStack(S,number); //将转换的数进⾏压栈j=0; //这⾥不要忘记将j重新初始化进⾏下个数据的转化break;}}/*如果遇到操作运算符则,弹出两个数据进⾏运算,然后将得出的结果重新⼊栈*/ switch(str[i]){case '+':PopStack(S,&e);PopStack(S,&d);PushStack(S,d+e);break;case '-':PopStack(S,&e);PopStack(S,&d);PushStack(S,d-e);break;case '*':PopStack(S,&e);PopStack(S,&d);PushStack(S,d*e);break;case '/':PopStack(S,&e);PopStack(S,&d);if(e == 0){printf("输⼊出错,分母为零!\n");return ;}PushStack(S,d/e);break;}i++; //继续遍历直到遍历字符串结束}PopStack(S,&e);printf("计算结果为:%lf",e);}完整代码如下:#include<stdio.h>#include<stdlib.h>#include<assert.h>#include<ctype.h>#define INITSIZE 20#define INCREMENT 10#define MAXBUFFER 10#define LEN sizeof(Elemtype)/*栈的动态分配顺序存储结构*/typedef double Elemtype;typedef struct{Elemtype *base;Elemtype *top;int StackSize;}SqStack;void InitStack(SqStack *S)S->base=(Elemtype*)malloc(LEN*INITSIZE);assert(S->base != NULL);S->top=S->base;S->StackSize=INITSIZE;}void PushStack(SqStack *S,Elemtype e){if(S->top - S->base >= S->StackSize){S->base=(Elemtype*)realloc(S->base,(S->StackSize+INCREMENT)*LEN); assert(S->base !=NULL);S->top=S->base+S->StackSize;S->StackSize+=INCREMENT;}*S->top =e;S->top++;}void PopStack(SqStack *S,Elemtype *e){*e=*--S->top;}void CalFunction(SqStack *S,char str[]){Elemtype number,e,d;char arr[MAXBUFFER];int i=0,j=0;InitStack(S);while(str[i]!='\0'){while(isdigit(str[i])||str[i]=='.') //过滤数字{arr[j++]=str[i++];arr[j]='\0';if( j >= MAXBUFFER ){printf("输⼊单个数据过⼤!\n");return ;}if(str[i]==' '){number=atof(arr); //利⽤atof函数将数字字符转化为double型数据PushStack(S,number); //将转换的数进⾏压栈j=0;break;}}switch(str[i]){case '+':PopStack(S,&e);PopStack(S,&d);PushStack(S,d+e);break;case '-':PopStack(S,&e);PopStack(S,&d);PushStack(S,d-e);break;case '*':PopStack(S,&e);PopStack(S,&d);PushStack(S,d*e);break;case '/':PopStack(S,&e);PopStack(S,&d);if(e == 0){return ;}PushStack(S,d/e);break;}i++;}PopStack(S,&e);printf("计算结果为:%lf",e);}int main(){char str[100];SqStack S;printf("请按逆波兰表达式输⼊数据,每个数据之间⽤空格隔开:");gets(str);CalFunction(&S,str);return 0;}// 检测⽤例 5 - (6 + 7) * 8 + 9 / 4// 输⼊:5 8 6 7 + * - 9 4 / + #// 输出: - 96.750000运⾏效果截图如下:以上就是本⽂的全部内容,希望对⼤家的学习有所帮助,也希望⼤家多多⽀持。
C语言计算器实现(中缀表示法后缀表示法)

C语⾔计算器实现(中缀表⽰法后缀表⽰法)————————————————————————————————————————————实现原理:每个操作数都被依次压⼊栈中,当⼀个运算符到达时,从栈中弹出相应数⽬的操作数(对于⼆元运算符来说是两个操作数),把该运算符作⽤于弹出的操作数,并把运算结果再压⼊栈中- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -计算器(后缀表达式)相关知识:后缀表达式(逆波兰表⽰法):在逆波兰中,所有运算符都跟在操作数后⾯,如下:(1 - 2) *(4 + 5) 采⽤逆波兰表⽰法表⽰为:1 2 - 4 5 + *,不需要圆括号,只要知道每个运算符需要⼏个操作数就不会引起歧义实现功能:输⼊后缀表达式,以换⾏结束,计算四则运算结果。
对于 1 2 - 4 5 + * 来说,⾸先把1和2压⼊到栈中,再⽤两者之差-1取代它们;然后将4和5压⼊到栈中,再⽤两者之和9取代它们。
最后从栈中取出栈顶的-1和9,并把它们的积-9压⼊到栈顶。
到达输⼊⾏的末尾时,把栈顶的值弹出来并打印。
伪代码:while 读⼊值不为换⾏时if 是数字压⼊栈中else if 是运算符弹出两个运算数,计算并压栈else 输⼊错误并退出end if读⼊值弹出最终结果并打印实现代码:1/* 实现功能:输⼊后缀表达式,以换⾏结束,计算四则运算结果 */2/* 这种后缀表⽰法只需要⼀个栈就可以了,遇到符号则弹运算数,但是中缀就不⼀样 */3 #include <stdio.h>4 #include <stdlib.h>5#define OK 16#define ERROR 07#define OVERFLOW -28#define STACK_INIT_SIZE 1009#define STACKINCREAMENT 1010 typedef int Status;11 typedef char SElemType;12 typedef struct13 {14 SElemType *top;15 SElemType *base;16int stacksize;17 } SqStack;18 Status InitStack(SqStack *s)19 {20 s->base = (SElemType *)malloc(STACK_INIT_SIZE * sizeof(SElemType));21if (!s->base) exit(OVERFLOW);22 s->top = s->base;23 s->stacksize = STACK_INIT_SIZE;24return OK;25 }26 Status Push(SqStack *s, SElemType e)27 {28if (s->top - s->base == s->stacksize)29 {30 s->base = (SElemType *)realloc(s->base, (s->stacksize + STACKINCREAMENT) * sizeof(SElemType)); 31if (!s->base) exit(OVERFLOW);32 s->top = s->base + s->stacksize;33 s->stacksize += STACKINCREAMENT;34 }35 s->top++;36 *(s->top) = e;37return OK;38 }39 Status Pop(SqStack *s, SElemType *e)40 {41if (s->top == s->base) exit(OVERFLOW);42 *e = *(s->top);43 s->top--;44return OK;45 }46 Status Empty(SqStack s)47 {48if (s.top - s.base == 0)49return OK;50else51return ERROR;52 }53int main()54 {55 SqStack OPND; //OPTR是运算符 OPND是运算数56char c, num1, num2;57 InitStack(&OPND);58while((c = getchar()) != '\n')59 {60switch(c)61 {62case'0':63case'1':64case'2':65case'3':66case'4':67case'5':68case'6':69case'7':70case'8':71case'9':72 Push(&OPND, c - '0');73break;74case'+':75 Pop(&OPND, &num2);76 Pop(&OPND, &num1);77 Push(&OPND, num1 + num2);78break;79case'-':80 Pop(&OPND, &num2);81 Pop(&OPND, &num1);82 Push(&OPND, num1 - num2);83break;84case'*':85 Pop(&OPND, &num2);86 Pop(&OPND, &num1);87 Push(&OPND, num1 * num2);88break;89case'/':90 Pop(&OPND, &num2);91 Pop(&OPND, &num1);92 Push(&OPND, num1 / num2);93break;94default:95break;96 }97 }98while(!Empty(OPND))99 {100 Pop(&OPND, &c);101 printf("%d ", c);102 }103return OK;104 }- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -计算器(中缀表⽰法)运算符优先级:+-*/()# +>><<<>>->><<<>>*>>>><>>/>>>><>>(<<<<<=0)>>>>0>>#<<<<<0=执⾏过程:在计算 #4+3*(5-10)/5# 时栈中的执⾏过程如下步骤输⼊字符执⾏操作OPTR OPND 1#Push(#)#24Push(4)#43+'#'<'+',Push(+)# +443Push(3)# + 4 35*'+'<'*',Push(*)# + * 4 36('*'<'(',Push(()# + * ( 4 375Push(5)# + * ( 4 3 58-'('<'-',Push(-)# + * ( - 4 3 5910Push(10)# + * ( - 4 3 5 1010)'-'>')',计算并压⼊结果# + * ( 4 3 -511'('=')',脱括号# + * 4 3 -5 12/'*'>'/'计算并压⼊结果# + 4 -1513'+'<'/',Push(/)# + / 4 -15145Push(5)# + / 4 -15 5 15#'/'>'#',计算并压⼊结果# + 4 -316'+'>'#',计算并压⼊结果#117'#'='#',脱括号1伪代码:初始化运算符栈;压⼊#;初始化运算数栈;获取输⼊;while 获取输⼊不为#或栈顶不为#if 输⼊的是数字压⼊运算数栈获取输⼊if 新输⼊的也是数字⼗位数百位数运算end ifelseswitch 运算符栈顶与当前输⼊优先级⽐较压⼊运算符栈获得输⼊弹出运算符栈顶(或#获得输⼊弹出运算符栈顶弹出两个运算数计算并将结果压⼊运算数栈//此时不获取新输⼊,该循环输⼊的运算符作为c重新进⼊循环end ifend while输出运算数栈中剩的运算数实现代码:1/* 只能运算-128~127之间的结果 */2 #include <stdio.h>3 #include <stdlib.h>4 #include <math.h>5#define OK 16#define ERROR 07#define SPILL -2 //math.h中已有OVERFLOW,则改⽤SPILL8#define STACK_INIT_SIZE 1009#define STACKINCREAMENT 1010 typedef char SElemType;11 typedef int Status;12 typedef struct13 {14 SElemType *top;15 SElemType *base;16int stacksize;17 } SqStack;18 Status InitStack(SqStack *s)19 {20 s->base = (SElemType *)malloc(STACK_INIT_SIZE * sizeof(SElemType));21if (!s->base)22 exit(SPILL);23 s->top = s->base;24 s->stacksize = STACK_INIT_SIZE;25return OK;26 }27 Status EmptyStack(SqStack s)28 {29if (s.top - s.base == 0)30return OK;31else32return ERROR;33 }34 Status Push(SqStack *s, SElemType e)35 {36if (s->top - s->base == s->stacksize)37 {38 s->base = (SElemType *)realloc(s->base, (s->stacksize + STACKINCREAMENT) * sizeof(SElemType)); 39if (!s->base)40 exit(SPILL);41 s->top = s->base + s->stacksize;42 s->stacksize += STACKINCREAMENT;43 }44 s->top ++;45 *(s->top) = e;46return OK;47 }48 Status Pop(SqStack *s, SElemType *e)49 {50if (s->top == s->base)51 exit(SPILL);52 *e = *(s->top);53 s->top--;54return OK;55 }56 SElemType GetTop(SqStack s)57 {58return *(s.top);59// *e = *(s.top);60// return OK;61 }62/* 判断如果是数字则返回OK,运算符返回ERROR,⾮法输⼊则退出 */63 Status InputJudge(SElemType c)64 {65switch(c)66 {67case'0':68case'1':69case'2':70case'3':71case'4':72case'5':73case'6':74case'7':75case'8':76case'9':77return OK;78break;79case'+':80case'-':81case'*':82case'/':83case'(':84case')':85case'#':86return ERROR;87break;88default:89 exit(SPILL);90break;91 }92 }93/* 当前输⼊的运算符和前⼀个运算符⽐较优先级 */94 SElemType PriorityJudge(SElemType optr1, SElemType optr2)95 {96int i, j;97char priorityTable[7][7] =98 {99 {'>', '>', '<', '<', '<', '>', '>'},100 {'>', '>', '<', '<', '<', '>', '>'},101 {'>', '>', '>', '>', '<', '>', '>'},102 {'>', '>', '>', '>', '<', '>', '>'},103 {'<', '<', '<', '<', '<', '=', '0'},104 {'>', '>', '>', '>', '0', '>', '>'},105 {'<', '<', '<', '<', '<', '0', '='}106 };107switch(optr1)108 {109case'+':110 i = 0;111break;112case'-':113 i = 1;114break;115case'*':116 i = 2;117break;118case'/':119 i = 3;120break;121case'(':122 i = 4;123break;124case')':125 i = 5;126break;127case'#':128 i = 6;129break;130 }131switch(optr2)132 {133case'+':134 j = 0;135break;136case'-':137 j = 1;138break;139case'*':140 j = 2;141break;142case'/':143 j = 3;144break;145case'(':146 j = 4;147break;148case')':149 j = 5;150break;151case'#':152 j = 6;153break;154 }155return priorityTable[i][j];156 }157/* 四则运算 */158 SElemType Calc(SElemType optr, SElemType num1, SElemType num2)159 {160switch(optr)161 {162case'+':163return (num1 + num2);164break;165case'-':166return (num1 - num2);167break;168case'*':169return (num1 * num2);170break;171case'/':172return (num1 / num2);173break;174 }175 }176int main()177 {178char c, optr, num1, num2, temp;179 SqStack OPND, OPTR;180 InitStack(&OPTR);181 Push(&OPTR, '#');182 InitStack(&OPND);183 c = getchar();184while(c != '#' || GetTop(OPTR) != '#')185// while(!EmptyStack(OPTR))186//严蔚敏⽼师书上的算法是判断输⼊⾮#或栈顶⾮#时循环,个⼈认为判断运算符栈不为空也可以,当初始化时压⼊的#闭合,结束运算187 {188if (InputJudge(c))189 {190 Push(&OPND, c - '0');191 c = getchar();192/* 当连续输⼊数字时,计算⼗位数和百位数 */193while(InputJudge(c))194 {195int i = 1;196 Pop(&OPND, &temp);197 Push(&OPND, temp * pow(10, i) + (c - '0'));198 i++;199 c = getchar();200 }201 }202else203switch(PriorityJudge(GetTop(OPTR), c))204 {205case'<':206 Push(&OPTR, c);207 c = getchar();208break;209case'=':210 Pop(&OPTR, &c);211 c = getchar();212break;213case'>':214 Pop(&OPTR, &optr);215 Pop(&OPND, &num2);216 Pop(&OPND, &num1);217 Push(&OPND, Calc(optr, num1, num2)); 218break;219 }220 }221while(!EmptyStack(OPND))222 {223 Pop(&OPND, &c);224 printf("%d\n", c);225 }226return OK;227 }。
用栈和二叉树实现中缀表达式转后缀表达式构建计算机并求值实验报告

实验报告姓名:黄雄镖学号:13331093院系专业:软件学院2013级教务4班完成日期:2014 年10 月20 日实验题目:实现一个较为通用的计算器需求分析:实现一个包含加减乘除运算的较为通用的计算器,操作数可能是负数,并且可能是多位数。
运算式中可以有括号和多余空格。
计算器对负号不敏感, 形如1+-1或者1+(-1)都是可以接受的。
概要设计思路: 将表达式的中缀表达式转换成后缀表达式,然后利用一个栈或者建立二叉树对后缀表达式进行求值。
由于多位数在转为后缀表达式时会分不清, 故在每个数和运算符后面加上一个空格作为区别在主程序中调用用栈求值的计算器类和用二叉树计算的计算器类, 输出算式的结果13331093_03.h里存放用栈求值的计算器类13331093_03_tree.h里存放用二叉树计算的计算器类13331093_03.h的类里主要包括:获得算术表达式的函数getexpression(string expression), expression为所要计算的算术表达式计算函数calculate(string num2, string num1, string op), 输入为两个数(字符串形式)和一个操作符, 返回值为计算结果(字符串形式)返回中缀表达式函数ShowMiddleExpression(), 返回的中缀表达式为字符串形式RidSpace(string origin)用于去除输入中多余的空格, 输入为要除去空格的算术表达式, 返回去掉空格的算术表达式MidToLast(string str)中缀表达式转后缀表达式获得后缀表达式函数GetLastExpression(), 返回的后缀表达式为字符串形式用栈执行计算后缀表达式函数exe(), 返回计算结果为字符串形式13331093_03_tree.h类里主要包括:获得算术表达式的函数getexpression(string expression), expression为所要计算的算术表达式计算函数calculate(string num2, string num1, string op), 输入为两个数(字符串形式)和一个操作符, 返回值为计算结果(字符串形式)返回中缀表达式函数ShowMiddleExpression(), 返回的中缀表达式为字符串形式RidSpace(string origin)用于去除输入中多余的空格, 输入为要除去空格的算术表达式, 返回去掉空格的算术表达式MidToLast(string str)中缀表达式转后缀表达式获得后缀表达式函数GetLastExpression(), 返回的后缀表达式为字符串形式生成一颗二叉树的函数makeTree(TNode *&p)后序遍历二叉树并计算的函数PostOrder(TNode *p), 返回计算结果为字符串形式a.调试过程遇到的问题与解决方案:遇到的问题:调试过程中出现程序崩溃的现象, 后来debug发现是没有考虑到执行运算过程中出现的-()的情况原因:没有考虑-()的情况, 导致栈为空的时候还弹出元素解决方案:特殊处理这种情况b.时间和空间复杂度:除去输入中空格的操作的时间复杂度为O(n),中缀表达式转后缀表达式的时间复杂度为O(n), 用栈执行运算的时间复杂度为O(n),后序遍历二叉树的时间复杂度为O(n) 所以用栈计算或者用二叉树计算的操作的时间复杂度为都是O(n)栈属于线性表, 故用栈计算的空间复杂度为O(n)用二叉树计算的空间复杂度也是O(n)主程序:输入一个整数m,代表有m个输入接下来有m行,每一行输入你要计算的式子13331093_03.h:含有用stack计算的计算器类用法:calculator c_stack 声明一个计算器对象c_stack.getexpression(expression) 把算术表达式存入计算器中expression为所要计算的算术表达式c_stack.GetLastExpression() 获取算术表达式的后缀表达式c_stack.exe() 获取计算结果13331093_03_tree.h:含有用二叉树计算的计算器类用法:calculator_tree c_tree 声明一个计算器对象c_tree.getexpression(expression) 把算术表达式存入计算器中expression为所要计算的算术表达式c_tree.GetLastExpression() 获取算术表达式的后缀表达式c_tree.makeTree(tree) 建立一棵二叉树c_tree.PostOrder(tree) 后序遍历二叉树并返回计算结果测试结果在主程序中调用用栈求值的计算器类和用二叉树计算的计算器类, 并对输入表达式进行两种方法所生成的后缀表达式和结果的对比测试代码在test.cpp中测试输入:11-(12.34)-11+-21+(-2)11 + 23 * 32/4-8-1.234/5 *(1 +3)2.333*4-(3+(-5))12345+5432.1/(-12345)-(100 ) * 0.5 -(-22.22)1234/-123+3.333-( 123*50 ) / 2.2测试结果如下:另外我用计算器算过, 结果是正确的实验心得通过这次实验, 我对栈和二叉树的理解加深了很多。
用栈实现中缀表达式转后缀表达式并构建计算机求值

#include <string>#include <stack>#include <iostream>#include <sstream>#include <iomanip>using namespace std;class calculator{public:calculator() {}calculator(string expression) {getexpression(expression);}//获得算术表达式void getexpression(string expression) {e = expression;}~calculator() {}//返回中缀表达式string ShowMiddleExpression() {return e;}//计算函数, 输入为两个数和一个操作符, 返回值为计算结果(字符串形式) string calculate(string num2, string num1, string op) {double n2, n1;string result;stringstream x;x << num2;x >> n2;x.clear();x << num1;x >> n1;x.clear();if (op == "+")x << (n2 + n1);if (op == "-")x << (n2 - n1);if (op == "*")x << (n2 * n1);if (op == "/")x << (n2 / n1);x >> result;x.clear();return result;}//判别符号的优先级int Priority(char a) {if (a == '(')return 0;else if (a == '+' || a == '-')return 1;else if (a == '*' || a == '/')return 2;return 0;}//用于去除输入中多余的空格输入为要除去空格的算术表达式返回去掉空格的算术表达式string RidSpace(string origin) {string transfer;for (int i = 0; i < origin.length(); i++) {if (origin[i] != ' ')transfer += origin[i];}return transfer;}//中缀表达式转后缀表达式, 因为要兼容多位数, 括号, 负数和小数等功能,//由于多位数在转为后缀表达式时会分不清, 故在每个数和运算符后面加上一个空格作为区别//expression为输出的后缀表达式string MidToLast(string str) {str = RidSpace(str);string expression = "";string number = "";char x;stack<char> op;for (int i = 0; i < str.length(); ) {//第一位做特殊处理判断是否为负号if (i == 0 && str[i] == '-') {number = "-";i++;}x = str[i];//录入数字if ((x >= '0' && x <= '9') || number == "-" || x == '.') {while ((str[i] >= '0' && str[i] <= '9') || str[i] == '.') {number += str[i];i++;}expression += number;//加空格以区别expression += " ";number = "";continue;} else {//判断是括号还是运算符if (x == '(') {op.push(x);//判断是否为负号if (str[i+1] == '-') {number = "-";i++;}} else {//遇到右括号直接弹出运算符栈里的运算符到表达式中运算符后加空格以区别if (x == ')') {while (op.top() != '(') {expression += op.top();expression += " ";op.pop();}//弹出右括号op.pop();} else {//弹出栈中优先级较高的运算符运算符后加空格以区别while (!op.empty() && (Priority(op.top()) >= Priority(x))) {expression += op.top();expression += " ";op.pop();}//判断是否为负号if (str[i+1] == '-') {number = "-";i++;}//将运算符压入栈op.push(x);}}}i++;}while (!op.empty()) {expression += op.top();expression += " ";op.pop();}return expression;}//获得后缀表达式string GetLastExpression() {return MidToLast(RidSpace(e));}string exe() {//获取后缀表达式string le = GetLastExpression();string tem = "";stack<string> num;for (int i = 0; i < le.length(); ) {while (le[i] != ' ') {tem += le[i];i++;}//若为数字, 压栈if (tem.length() > 1 || (tem.length() == 1 && tem[0] >= '0' && tem[0] <= '9')) { num.push(tem);} else {//若为运算符, 执行运算后压栈//处理如-()的情况if (num.empty()) {tem = "-";i++;continue;}string tem1 = num.top();num.pop();if (!num.empty()) {string tem2 = num.top();num.pop();num.push(calculate(tem2, tem1, tem));} else {tem1 = "-" + tem1;num.push(tem1);}}i++;tem = "";}return num.top();}private:string e;};。
c语言中缀后缀算术表达式求值用栈实现

c语言中缀、后缀算术表达式求值用栈实现#include<stdio.h>#include<string.h>#include<malloc.h>#include<stdlib.h>#define MaxSize 50typedef struct{float data[MaxSize];int top;}OpStack;typedef struct{char data[MaxSize];int top;}SeqStack;void InitStack(SeqStack *S);//初始化栈int StackEmpty(SeqStack S);//判断栈是否为空int PushStack(SeqStack *S,char e);//进栈int PopStack(SeqStack *S,char *e);//删除栈顶元素int GetTop(SeqStack S,char *e);//取栈顶元素void TranslateExpress(char s1[],char s2[]);//将中缀表达式转化为后缀表达式float ComputeExpress(char s[]);//计算后缀表达式的值void main(){char a[MaxSize],b[MaxSize];float f;printf("请输入一个算术表达式:\n");gets(a);printf("中缀表达式为:%s\n",a);TranslateExpress(a,b);printf("后缀表达式为:%s\n",b);f=ComputeExpress(b);printf("计算结果:%f\n",f);}void InitStack(SeqStack *S)//初始化栈{S->top=0;}int StackEmpty(SeqStack S)//判断栈是否为空{if(S.top ==0)return 1;elsereturn 0;}int PushStack(SeqStack *S,char e)//进栈{if(S->top>=MaxSize){printf("栈已满,不能进栈!"); return 0;}else{S->data[S->top]=e;S->top++;return 1;}}int PopStack(SeqStack *S,char *e)//删除栈顶元素{if(S->top==0){printf("栈已空\n");return 0;}else{S->top--;*e=S->data[S->top];return 1;}}int GetTop(SeqStack S,char *e)//取栈顶元素{if(S.top<=0){printf("栈已空");return 0;}else{*e=S.data[S.top-1];return 1;}}void TranslateExpress(char str[],char exp[])//把中缀表达式转换为后缀表达式{SeqStack S;char ch;char e;int i=0,j=0;InitStack(&S);ch=str[i];i++;while(ch!='\0') //依次扫描中缀表达式{switch(ch){case'(':PushStack(&S,ch);break;case')':while(GetTop(S,&e)&&e!='('){PopStack(&S,&e);exp[j]=e;j++;}PopStack(&S,&e);break;case'+':case'-':while(!StackEmpty(S)&&GetTop(S,&e)&&e!='(') {PopStack(&S,&e);j++;}PushStack(&S,ch);break;case'*':case'/':while(!StackEmpty(S)&&GetTop(S,&e)&&e=='/'||e==&# 39;*'){PopStack(&S,&e);exp[j]=e;j++;}PushStack(&S,ch);break; //是空格就忽略case' ':break;default:while(ch>='0'&&ch<='9'){exp[j]=ch;j++;ch=str[i];i++;}i--;exp[j]=' ';j++;}ch=str[i];i++;}while(!StackEmpty(S)) //将栈中剩余运算符出栈{PopStack(&S,&e);exp[j]=e;j++;}exp[j]='\0';}float ComputeExpress(char a[])//计算后缀表达式的值{int i=0;float x1,x2,value;float result;S.top=-1;while(a[i]!='\0') //依次扫描后缀表达式{if(a[i]!=''&&a[i]>='0'&&a[i]<='9')//如果是数字{value=0;while(a[i]!=' ') //如果不是空格{value=10*value+a[i]-'0';i++;}S.top++;S.data[S.top]=value; //处理后进栈}else //如果是运算符{switch(a[i]){case'+':x1=S.data[S.top];S.top--;x2=S.data[S.top];S.top--;result=x1+x2;S.top++;S.data[S.top]=result;break;case'-':x1=S.data[S.top];S.top--;x2=S.data[S.top];S.top--;result=x2-x1;S.top++;S.data[S.top]=result;break;case'*':x1=S.data[S.top];S.top--;x2=S.data[S.top];S.top--;result=x1*x2;S.top++;S.data[S.top]=result;break;case'/':x1=S.data[S.top];S.top--;x2=S.data[S.top];S.top--;result=x2/x1;S.top++;S.data[S.top]=result;break;}i++;}}if(!S.top!=-1) //如果栈不空,将结果出栈并返回{result=S.data[S.top];S.top--;if(S.top==-1)return result;else{printf("表达式错误");exit(-1);}}return 0;}。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
OpStack S; int i=0; float x1,x2,value; float result; S.top=-1; while(a[i]!='\0') //依次扫描后缀表达式 { if(a[i]!=' '&&a[i]>='0'&&a[i]<='9')//如果
exp[j]=e; j++; } PushStack(&S,ch); break; case'*': case'/': while(!StackEmpty(S)&&GetTop(S,&e)&&e=='/'||e==&# 39;*') { PopStack(&S,&e); exp[j]=e; j++; } PushStack(&S,ch); break; //是空格就忽略 case' ': break; default: while(ch>='0'&&ch<='9') { exp[j]=ch; j++; ch=str[i]; i++; } i--; exp[j]=' '; j++; } ch=str[i]; i++; } while(!StackEmpty(S)) //将栈中剩余运算符出栈 { PopStack(&S,&e); exp[j]=e; j++; } exp[j]='\0'; } float ComputeExpress(char a[])//计算后缀表达式的值 {
c 语言 中缀、后缀 算术表达式求值用栈实现
#include<stdio.h> #include<string.h> #include<malloc.h> #include<stdlib.h> #define MaxSize 50 typedef struct { float data[MaxSize]; int top; }OpStack; typedef struct { char data[MaxSize]; int top; }SeqStack; void InitStack(SeqStack *S);//初始化栈 int StackEmpty(SeqStack S);//判断栈是否为空 int PushStack(SeqStack *S,char e);//进栈 int PopStack(SeqStack *S,char *e);//删除栈顶元素 int GetTop(SeqStack S,char *e);//取栈顶元素 void TranslateExpress(char s1[],char s2[]);//将中缀表达式转化为后缀表达式 float ComputeExpress(char s[]);//计算后缀表达式的值 void main() { char a[MaxSize],b[MaxSize]; float f; printf("请输入一个算术表达式:\n"); gets(a); printf("中缀表达式为:%s\n",a); TranslateExpress(a,b); printf("后缀表达式为:%s\n",b); f=ComputeExpress(b); printf("计算结果:%f\n",f); } void InitStack(SeqStack *S)//初始化栈
ห้องสมุดไป่ตู้
{ S->top=0; } int StackEmpty(SeqStack S)//判断栈是否为空 { if(S.top ==0) return 1; else return 0; } int PushStack(SeqStack *S,char e)//进栈 { if(S->top>=MaxSize) { printf("栈已满,不能进栈!"); return 0; } else { S->data[S->top]=e; S->top++; return 1; } } int PopStack(SeqStack *S,char *e)//删除栈顶元素 { if(S->top==0) { printf("栈已空\n"); return 0; } else { S->top--; *e=S->data[S->top]; return 1; } } int GetTop(SeqStack S,char *e)//取栈顶元素 {
break; case'*': x1=S.data[S.top]; S.top--; x2=S.data[S.top]; S.top--; result=x1*x2; S.top++; S.data[S.top]=result; break; case'/': x1=S.data[S.top]; S.top--; x2=S.data[S.top]; S.top--; result=x2/x1; S.top++; S.data[S.top]=result; break; } i++; } } if(!S.top!=-1) //如果栈不空,将结果出栈并返回 { result=S.data[S.top]; S.top--; if(S.top==-1) return result; else { printf("表达式错误"); exit(-1); } } return 0; }
if(S.top<=0) { printf("栈已空"); return 0; } else { *e=S.data[S.top-1]; return 1; } } void TranslateExpress(char str[],char exp[])//把中缀表达式转换为后缀表达式 { SeqStack S; char ch; char e; int i=0,j=0; InitStack(&S); ch=str[i]; i++; while(ch!='\0') //依次扫描中缀表达式 { switch(ch) { case'(': PushStack(&S,ch); break; case')': while(GetTop(S,&e)&&e!='(') { PopStack(&S,&e); exp[j]=e; j++; } PopStack(&S,&e); break; case'+': case'-': while(!StackEmpty(S)&&GetTop(S,&e)&&e!='(') { PopStack(&S,&e);
是数字 { value=0; while(a[i]!=' ') //如果不是空格 { value=10*value+a[i]-'0'; i++; } S.top++; S.data[S.top]=value; //处理后进栈 } else //如果是运算符 { switch(a[i]) { case'+': x1=S.data[S.top]; S.top--; x2=S.data[S.top]; S.top--; result=x1+x2; S.top++; S.data[S.top]=result; break; case'-': x1=S.data[S.top]; S.top--; x2=S.data[S.top]; S.top--; result=x2-x1; S.top++; S.data[S.top]=result;
