瑞利分布

瑞利分布信道M A T L A B 仿真一、瑞利衰落原理在陆地移动通信中，移动台往往受到各种障碍物和其他移动体的影响，以致到达移动台的信号是来自不同传播路径的信号之和。

而描述这样一种信道的常用信道模型便是瑞利衰落信道。

定义:由于信号进行多径传播达到接收点处的场强来自不同传播的路径，各条路径延时时间是不同的，而各个方向分量波的叠加，又产生了驻波场强，从而形成信号快衰落称为瑞利衰落。

瑞利衰落信道（Rayleighfadingchannel）是一种无线电信号传播环境的统计模型。

这种模型假设信号通过无线信道之后，其信号幅度是随机的，表现为“衰落”特性，并且多径衰落的信号包络服从瑞利分布。

由此，这种多径衰落也称为瑞利衰落。

这一信道模型能够描述由电离层和对流层反射的短波信道，以及建筑物密集的城市环境。

瑞利衰落只适用于从发射机到接收机不存在直射信号的情况，否则应使用莱斯衰落信道作为信道模型。

假设经反射（或散射）到达接收天线的信号为N 个幅值和相位均随机的且统计独立的信号之和。

信号振幅为r,相位为,则其包络概率密度函数为P(r)=2222rr e(r 0)相位概率密度函数为：P()=1/2（20）二、仿真原理（1）瑞利分布分析环境条件：通常在离基站较远、反射物较多的地区，发射机和接收机之间没有直射波路径（如视距传播路径），且存在大量反射波，到达接收天线的方向角随机的（（0~2π）均匀分布），各反射波的幅度和相位都统计独立。

幅度与相位的分布特性：包络r 服从瑞利分布，θ在0～2π内服从均匀分布。

瑞利分布的概率分布密度如图1所示：00.51 1.52 2.530.10.20.30.40.50.60.70.80.9图1瑞利分布的概率分布密度（2）多径衰落信道基本模型离散多径衰落信道模型为()1()()()N t k kk y t r t x t%%(1)其中,()k r t 复路径衰落，服从瑞利分布;k是多径时延。

多径衰落信道模型框图如图2所示：图2多径衰落信道模型框图（3）产生服从瑞利分布的路径衰落r(t)利用窄带高斯过程的特性，其振幅服从瑞利分布，即22()()()c s r t n t n t （2）上式中()()c s n t n t 、，分别为窄带高斯过程的同相和正交支路的基带信号。

瑞利分布

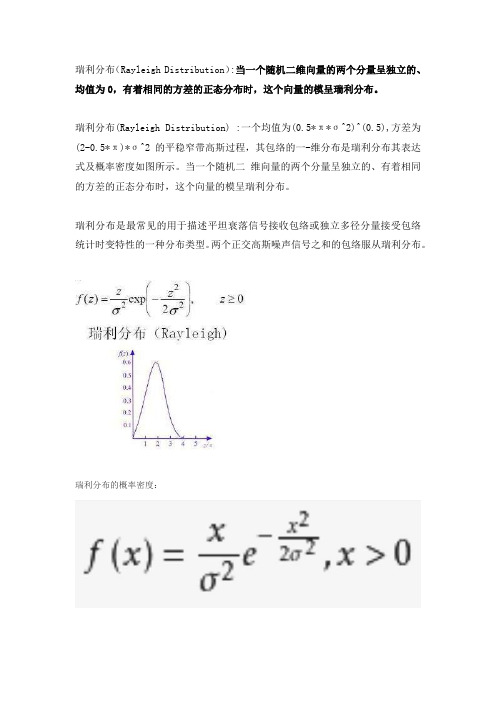
瑞利分布（Rayleigh Distribution）:当一个随机二维向量的两个分量呈独立的、均值为0，有着相同的方差的正态分布时，这个向量的模呈瑞利分布。

瑞利分布(Rayleigh Distribution) :一个均值为(0.5*π*σ^2)^(0.5),方差为(2-0.5*π)*σ^2的平稳窄带高斯过程，其包络的一-维分布是瑞利分布其表达式及概率密度如图所示。

当一个随机二维向量的两个分量呈独立的、有着相同的方差的正态分布时，这个向量的模呈瑞利分布。

瑞利分布是最常见的用于描述平坦衰落信号接收包络或独立多径分量接受包络统计时变特性的一种分布类型。

两个正交高斯噪声信号之和的包络服从瑞利分布。

瑞利分布的概率密度：。

几种衰落信道

⼏种衰落信道瑞利分布瑞利分布(Rayleigh distribution)是指当⼀个随机的⼆维向量的每个分量呈独⽴的、均值为0、⽅差为σ2并且有着相同的⽅差的正态分布时，这个向量的模呈瑞利分布。

它是⼀个均值为0，⽅差为σ2的平稳窄带⾼斯过程，其包络的⼀维分布是瑞利分布⼀、准静态平坦衰落信道⼀般来说，多路信号到达接收机的时间有先有后，即有相对时(间)延(迟)。

如果这些相对时延远⼩于⼀个符号的时间，则可以认为多路信号⼏乎是同时到达接收机的。

这种情况下多径不会造成符号间的⼲扰。

这种衰落称为平坦衰落，因为这种信道的频率响应在所⽤的频段内是平坦的。

相反地，如果多路信号的相对时延与⼀个符号的时间相⽐不可忽略，那么当多路信号迭加时，不同时间的符号就会重叠在⼀起，造成符号间的⼲扰。

这种衰落称为频率选择性衰落，因为这种信道的频率响应在所⽤的频段内是不平坦的。

⽽准静态平坦衰落信道(quasi-static frequency-flat fading)是指多径情况不会造成符号间的⼲扰，并且在每⼀个传输块内为常数。

⼆、瑞利衰落信道模型（Rayleigh）假设发送信号为单⼀频率正弦波，即若不考虑直射路径，多径信道共有n条路径，各条路径具有时变衰耗和时变传输时延，且从各条路径到达接收端的信号相互独⽴，则接收端接受到的合成波为式中，ai(t)为从第i条路径到达接收端的信号振幅，τi(t)为第i条路径的传输时延。

传输时延可以转换为相位的形式，即为从第i条路径到达接收端的信号的随机相位。

r(t)也可表⽰为如下形式：由于X(t)和Y(t)都是相互独⽴的随机变量之后，根据中⼼极限定理，⼤量独⽴随机变量之和的分布趋于正态分布。

因此，当n⾜够⼤时，X(t)和Y(t)都趋于正态分布。

通常情况下X(t)和Y(t)的均值为0（由于没有直射路径），⽅差相等。

这种表⽰⽅式也叫做同相-正交表⽰法。

r(t)也可以表⽰为如下形式：这种表达⽅式也称包络-相位表⽰法。

根据瑞利分布生成信道增益

根据瑞利分布⽣成信道增益瑞利衰落⼀、概念瑞利衰落是⼀种统计模型，⽤于传播环境对⽆线电信号的影响，例如⽆线设备使⽤的⽆线电信号。

瑞利衰落模型假设已经通过这种传输介质（也称为通信信道）的信号幅度将根据瑞利分布（两个不相关的⾼斯随机变量之和的径向分量）随机变化或衰减。

瑞利衰落被认为是对流层和电离层信号传播以及城市密集环境对⽆线电信号影响的合理模型。

在⽆线通信信道环境中，电磁波经过反射折射散射等多条路径传播到达接收机后，总信号的强度服从瑞利分布（Rayleigh distribution）。

同时由于接收机的移动及其他原因，信号强度和相位等特性⼜在起伏变化，故称为瑞利衰落。

如果收到的信号中除了经反射折射散射等来的信号外，还有从发射机直接到达接收机（如从卫星直接到达地⾯接收机）的信号，那么总信号的强度服从莱斯分布(Rician distribution)，故称为莱斯衰落。

如下图，若⽆直射信号（LOS），则对应的信道模型为瑞利衰落；若有⼀路直射信号，则对应的信道模型为莱斯衰落。

个⼈理解：直观地解释，因信号传输使⽤电磁波的形式，其特性必定为周期函数。

当在⾃由空间中，以不同路线达到接收端时，其相位相错，能量会存在相互抵消或增强，⽽该情况即信道衰落模型。

⼆、模型瑞利分布是⼀个均值为0，⽅差为σ^2的平稳窄带⾼斯过程，其包络的⼀维分布是瑞利分布。

其表达式及概率密度如图所⽰。

瑞利分布是最常见的⽤于描述平坦衰落信号接收包络或独⽴多径分量接受包络统计时变特性的⼀种分布类型。

两个正交⾼斯噪声信号之和的包络服从瑞利分布。

瑞利衰落能有效描述存在能够⼤量散射⽆线电信号的障碍物的⽆线传播环境。

若传播环境中存在⾜够多的散射，则冲激信号到达接收机后表现为⼤量统计独⽴的随机变量的叠加，根据中⼼极限定理，则这⼀⽆线信道的冲激响应将是⼀个⾼斯过程。

如果这⼀散射信道中不存在主要的信号分量，通常这⼀条件是指不存在直射信号（LOS），则这⼀过程的均值为0，且相位服从0 到2π的均匀分布。

iirct下瑞利分布参数多变点的贝叶斯估计

iirct下瑞利分布参数多变点的贝叶斯估计1. 引言1.1 iirct简介在了解瑞利分布参数多变点的贝叶斯估计之前，我们首先需要了解iirct（iterative individual response-controlled targeting）的基本概念。

iirct是一种基于个体反应的迭代方法，其核心思想是不断地根据个体的反应情况来调整治疗目标，从而实现个体化的治疗。

这种方法对于疾病治疗和药物研发具有重要意义。

1.2 瑞利分布简介瑞利分布是一种连续概率分布，广泛应用于信号处理、通信系统和无线通信等领域。

它的概率密度函数具有如下形式：f(x;σ)=xσ2e−x22σ2其中，σ是分布的尺度参数。

瑞利分布在实际问题中的应用非常广泛，因此对其参数的准确估计具有重要意义。

2. 贝叶斯估计贝叶斯估计是统计学中一种重要的参数估计方法，其基本思想是将参数看作是随机变量，通过观测数据来更新参数的分布。

对于瑞利分布参数多变点的贝叶斯估计，我们可以使用贝叶斯方法来不断地根据观测数据来调整参数的估计，从而获得更加准确的结果。

3. 瑞利分布参数多变点的贝叶斯估计方法3.1 先验分布的选择在进行贝叶斯估计之前，我们首先需要选择参数的先验分布。

对于瑞利分布的尺度参数σ，通常可以选择适当的分布作为先验分布，比如Gamma分布或者Inverse Gamma分布。

根据实际问题中的先验信息，选择合适的先验分布对于后续的参数估计非常重要。

3.2 参数的后验分布在确定了先验分布之后，我们通过观测数据来计算参数的后验分布。

根据贝叶斯定理，参数的后验分布可以表示为：f(σ|x1,x2,...,x n)∝f(x1,x2,...,x n|σ)f(σ)其中，f(x1,x2,...,x n|σ)表示给定参数σ下观测数据的似然函数，f(σ)表示参数σ的先验分布。

通过参数的后验分布，我们可以得到参数的点估计或者区间估计。

3.3 迭代更新参数在实际问题中，通常需要通过迭代的方式来更新参数的估计。

瑞利分布

瑞利分布：平稳的窄带高斯过程，平均值为（0.5*π*σ^2）^（0.5），方差为（2-0.5*π）*σ^2。

其包络的一维分布是瑞利分布。

其表达和概率密度如图所示。

当随机二维向量的两个分量独立且具有相同方差时，向量的模量为瑞利分布。

瑞利分布是最常见的分布类型，用于描述平坦衰落信号或独立多径分量的接收包络的统计时变特性。

两个正交高斯噪声信号之和的包络服从瑞利分布。

在概率论和统计学中，指数分布是连续的概率分布。

指数分布可用于表示独立随机事件的时间间隔，例如乘客进入机场的时间间隔，中文维基百科中新条目的时间间隔等。

许多电子产品的寿命分布通常遵循指数分布。

一些系统的寿命分布也可以通过指数分布来近似。

它是可靠性研究中最常用的分布形式。

指数分布是伽玛分布和威布尔分布的特例。

当产品的故障是偶然的时，其寿命遵循指数分布。

当威布尔分布的形状系数等于1时，可以将指数分布视为特殊分布。

指数分布的失效率是与时间t无关的常数，因此分布函数简单。

如果指数分布的参数为λ，则指数分布的期望值为1/λ，方差为（1//λ）的平方。

正态分布也称为高斯分布，在数学，物理和工程领域是非常重要的概率分布。

它对统计的许多方面都有很大的影响。

如果随机变量x服从具有数学期望μ和标准偏差σ2的高斯分布，则其概率密度函数为正态分布，期望值μ确定其位置，其标准偏差σ确定分布的幅度。

因为它的曲线是钟形的，所以人们经常称其为钟形曲线。

我们通常所指的标准正态分布是μ=0和σ=1的正态分布。

正态分布是具有两个参数μ和σ2的连续随机变量的分布。

第一个参数μ是服从正态分布的随机变量的平均值，第二个参数σ2是随机变量的方差，因此正态分布表示为n（μ，σ2）。

瑞利分布

瑞利分布信道M A T L A B 仿真一、瑞利衰落原理在陆地移动通信中，移动台往往受到各种障碍物和其他移动体的影响，以致到达移动台的信号是来自不同传播路径的信号之和。

而描述这样一种信道的常用信道模型便是瑞利衰落信道。

定义:由于信号进行多径传播达到接收点处的场强来自不同传播的路径，各条路径延时时间是不同的，而各个方向分量波的叠加，又产生了驻波场强，从而形成信号快衰落称为瑞利衰落。

瑞利衰落信道（Rayleighfadingchannel）是一种无线电信号传播环境的统计模型。

这种模型假设信号通过无线信道之后，其信号幅度是随机的，表现为“衰落”特性，并且多径衰落的信号包络服从瑞利分布。

由此，这种多径衰落也称为瑞利衰落。

这一信道模型能够描述由电离层和对流层反射的短波信道，以及建筑物密集的城市环境。

瑞利衰落只适用于从发射机到接收机不存在直射信号的情况，否则应使用莱斯衰落信道作为信道模型。

假设经反射（或散射）到达接收天线的信号为N 个幅值和相位均随机的且统计独立的信号之和。

信号振幅为r,相位为,则其包络概率密度函数为P(r)=2222rr e(r 0)相位概率密度函数为：P()=1/2（20）二、仿真原理（1）瑞利分布分析环境条件：通常在离基站较远、反射物较多的地区，发射机和接收机之间没有直射波路径（如视距传播路径），且存在大量反射波，到达接收天线的方向角随机的（（0~2π）均匀分布），各反射波的幅度和相位都统计独立。

幅度与相位的分布特性：包络r 服从瑞利分布，θ在0～2π内服从均匀分布。

瑞利分布的概率分布密度如图1所示：00.51 1.52 2.530.10.20.30.40.50.60.70.80.9图1瑞利分布的概率分布密度（2）多径衰落信道基本模型离散多径衰落信道模型为()1()()()N t k kk y t r t x t%%(1)其中,()k r t 复路径衰落，服从瑞利分布;k是多径时延。

多径衰落信道模型框图如图2所示：图2多径衰落信道模型框图（3）产生服从瑞利分布的路径衰落r(t)利用窄带高斯过程的特性，其振幅服从瑞利分布，即22()()()c s r t n t n t （2）上式中()()c s n t n t 、，分别为窄带高斯过程的同相和正交支路的基带信号。

matlab 瑞利分布函数

matlab 瑞利分布函数【原创实用版】目录1.MATLAB 简介2.瑞利分布函数简介3.MATLAB 中实现瑞利分布函数的方法4.应用实例正文1.MATLAB 简介MATLAB 是一种广泛使用的数学软件，主要用于科学计算、数据分析和可视化。

它有强大的矩阵计算能力和各种工具箱，可以方便地处理各种复杂的数学问题。

在信号处理、通信和概率论等领域都有广泛的应用。

2.瑞利分布函数简介瑞利分布是一种概率分布，它是指数分布的一种特殊形式。

瑞利分布的特征是具有一个参数，这个参数决定了分布的形状。

当参数为 1 时，瑞利分布就变成了均匀分布。

在通信和信号处理中，瑞利分布常用来描述信号的强度或者噪声的强度。

3.MATLAB 中实现瑞利分布函数的方法在 MATLAB 中，可以使用内置的函数或者自己编写函数来实现瑞利分布。

下面是两种常见的方法：（1）使用内置函数：MATLAB 中有一个叫做"rander"的函数，可以生成服从瑞利分布的随机数。

使用方法如下：```matlabx = rander(mu, sigma)```其中，mu 是瑞利分布的均值，sigma 是标准差。

（2）自己编写函数：你也可以自己编写一个函数来计算瑞利分布的值。

下面是一个简单的例子：```matlabfunction y = rayleigh(x, alpha)% alpha = 1 / sqrt(2)y = (alpha / sqrt(2)) * (x^2);end```这个函数的输入参数 x 是瑞利分布的平方，alpha 是瑞利分布的参数。

4.应用实例假设我们要模拟一个信号，这个信号的强度服从瑞利分布。

我们可以使用 MATLAB 的"rander"函数来生成一个服从瑞利分布的随机数，然后将这个随机数平方，就可以得到信号的强度。

matlab 瑞利分布函数

matlab 瑞利分布函数【原创版】目录1.瑞利分布函数的定义2.MATLAB 中瑞利分布函数的实现3.使用 MATLAB 计算瑞利分布的概率密度函数值4.使用 MATLAB 绘制瑞利分布的概率密度函数曲线正文瑞利分布是一种在概率论和统计学中常见的连续型概率分布，它是由英国数学家瑞利（Rayleigh）在 19 世纪末提出的。

瑞利分布函数的定义是：对于任意实数 x，如果 X~R(a)，则 P(X ≤ x) = 1 - e^(-ax)。

其中，a 是瑞利分布的参数，X 表示随机变量。

在 MATLAB 中，我们可以使用现成的函数来实现瑞利分布。

首先，我们需要导入 MATLAB 的统计工具箱，通过输入“stats”命令即可完成导入。

接着，我们可以使用“rpdf”函数来计算瑞利分布的概率密度函数值，使用“rccdf”函数来计算瑞利分布的累积分布函数值。

例如，假设我们想要计算瑞利分布的概率密度函数值，我们可以输入以下命令：```matlaba = 1; % 设定瑞利分布的参数x = 0:0.1:1; % 定义 x 的取值范围f = rpdf(x, a); % 计算概率密度函数值```同样，如果我们想要绘制瑞利分布的概率密度函数曲线，我们可以使用“plot”函数。

例如：```matlaba = 1;x = 0:0.1:1;f = rpdf(x, a);plot(x, f);xlabel("x");ylabel("f(x)");title("瑞利分布的概率密度函数曲线");```以上，就是我们如何使用 MATLAB 实现瑞利分布函数的方法。

瑞利分布在无线通信中的应用

瑞利分布在无线通信中的应用移动通信系统的性能主要受到无线信道的制约，无线信道不像有线信道那样固定并可预见，而是具有极度的随机性，从简单的视距传播，到遭遇各种复杂的地形、地物，甚至移动台的移动速度也会对信号电平的衰落产生影响。

因此，要对无线信道进行控制和预测是非常困难的，即便这样，我们可以通过对针对信道的某一统计特性来建立信道模型，从而达到对信号发射和接受进行研究的目的。

一、瑞利分布瑞利分布（Rayleigh Distribution ）:一个均值为2πσ，方差为222σπ⎪⎭⎫ ⎝⎛-的平稳窄带高斯过程，其包络的一维分布是瑞利分布.其表达式及概率密度为：()()()⎪⎩⎪⎨⎧<≥⎪⎪⎭⎫ ⎝⎛-=0002exp 222x x x x x f σσ 当一个随机二维向量的两个分量呈独立的、有着相同的方差的正态分布时，这个向量的模呈瑞利分布。

瑞利分布是最常见的用于描述平坦衰落信号接收包络或独立多径分量接受包络统计时变特性的一种分布类型。

两个正交高斯噪声信号之和的包络服从瑞利分布。

二、瑞利衰落信道通过相关的理论知识，我们知道在任何一点接收到的信号是由大量的建筑物或树木、山丘反射来的电波叠加而成的。

这些电波虽然都是从一个天线辐射出来的，但由于到达接收天线的路径不同，故其相位是随机的，从而导致合成信号的幅度急剧变化，即产生了衰落。

对于小尺度的多径衰落，我们分析它的一阶统计特性我们令任意t 时刻的包络为：()()()()()()[]t Z t Z t t Z t Z t C s s c /tan ,122-=+=θα所以，衰落特性可以通过对任意时刻t 包络()t α和相位()t θ的概率密度函数进行研究。

对于非视距的衰落信道因为不存在直接路径，我们可以建模为瑞利分布。

瑞利衰落信道（Rayleigh fading channel ）是一种无线电信号传播环境的统计模型。

这种模型假设信号通过无线信道之后，其信号幅度是随机的，即“衰落”，并且其包络服从瑞利分布。

复杂数据模型下瑞利及广义瑞利分布的拟合检验与统计推断

复杂数据模型下瑞利及广义瑞利分布的拟合检验与统计推断关键词：瑞利分布；广义瑞利分布；数据模型；拟合检验；统计推断1.引言随着科学技术的进步，数据的规模和复杂性不息增长。

在大数据时代，探究数据分布模型是分外重要的，并且对模型的拟合检验和统计推断也变得尤其关键。

瑞利分布及广义瑞利分布是常见的概率分布模型，其在信号处理、天文学、物理学等领域都有广泛的应用。

因此，对这两种概率分布模型的拟合检验和统计推断具有重要的探究价值。

2.瑞利分布及广义瑞利分布2.1瑞利分布瑞利分布是一种常见的概率分布模型，常用来描述射线、波和信号在随机震动的介质中传输的衰减状况，其概率密度函数为：$$f(x;\sigma)=\frac{x}{\sigma^2}\exp(-\frac{x^2}{2\sigma^2}),x\geq0$$其中，$\sigma$是瑞利分布的标准参数，它是随机过程振幅的方均值的平方根，也称为瑞利参数。

2.2广义瑞利分布广义瑞利分布是瑞利分布的推广形式，其概率密度函数为：$$f(x;k,\sigma)=\frac{2x}{\sigma^2}\left(\frac{x^2}{\sig ma^2}\right)^{\frac{k}{2}-1}\exp(-\frac{x^k}{\sigma^k}),x\geq0,k>0,$$其中，$\sigma$是广义瑞利分布的标准参数，$k$是广义瑞利分布的外形参数。

3.数据模型和预估方法在现实生活中，瑞利分布及广义瑞利分布往往作为复杂数据模型的子模型出现。

针对这种状况，本文介绍了最大似然预估法、贝叶斯预估法和矩预估法等统计方法，并详尽谈论了在复杂数据模型下的参数预估方法。

4.拟合检验为了验证瑞利分布及广义瑞利分布在复杂数据模型下的适用性，本文提出了适用于大样本的渐进理论检验方法和适用于小样本的Bootstrap检验方法。

通过这两种方法的试验结果，本文验证了瑞利分布及广义瑞利分布在复杂数据模型下的优越性。

瑞利数文档

瑞利数瑞利数的定义瑞利数（Raleigh number），也称为瑞利分布参数，是统计学中常用的一个概念。

瑞利数的定义如下：瑞利数是一种描述随机振荡或随机波动的现象的数学参数。

它在概率论和统计学中被广泛应用。

瑞利数的应用瑞利数在各个领域中都有广泛的应用，以下是几个常见的应用领域：1. 无线通信中的使用在无线通信中，瑞利数可以用来描述无线信号的衰落过程。

当无线信号穿过自由空间或其他介质时，由于多种多样的衰弱因素，信号的强度会随着距离的增加而下降。

瑞利数可以帮助我们理解信号衰减的过程，并对无线信号传输中的可靠性和性能进行评估。

2. 光学中的使用在光学中，瑞利数可以用来描述光的波动和干涉现象。

瑞利数可以衡量光波的相位差，从而帮助我们理解干涉条纹的形成原理，以及波前传播的特性。

3. 天文学中的使用在天文学中，瑞利数可以用来描述天体的扩散和分辨能力。

由于地球大气层的湍流和散射效应，观测到的天体图像往往会受到模糊和失真的影响。

瑞利数可以帮助天文学家评估天文望远镜的分辨能力，并优化观测条件。

4. 金融学中的使用在金融学中，瑞利数可以用来描述金融资产的价格波动。

股票、外汇和其他金融产品的价格通常呈现出随机波动的特征，而瑞利数可以帮助我们对金融市场的波动性进行建模和分析。

瑞利数的计算瑞利数的计算可以通过概率密度函数（PDF）来实现。

瑞利分布的概率密度函数是一个标准正态分布的平方根。

瑞利分布的概率密度函数如下：f(x;\\sigma) = \\frac{x}{\\sigma^2}e^{-\\frac{x^2}{2\\sigma^2}}其中，x表示变量，σ表示瑞利数的参数。

瑞利数的性质1. 平均值和方差瑞利数的平均值和方差可以通过以下公式计算：平均值（mean）：E(X) = σ√π/2方差（variance）：Var(X) = (4 - π)σ^2/22. 分布函数瑞利数的累积分布函数（CDF）可以通过以下公式计算：F(x;\\sigma) = 1 - e^{-\\frac{x^2}{2\\sigma^2}}其中，x表示变量，σ表示瑞利数的参数。

瑞利分布的概率密度函数

瑞利分布的概率密度函数
哎呀呀，这“瑞利分布的概率密度函数”可把我这个小学生难住啦！我连听都没听说过呢，这到底是个啥呀？
就好像我在玩拼图，可这瑞利分布的概率密度函数就像一块我怎么也找不到位置的拼图块。

老师讲的时候，同学们有的一脸迷茫，有的好像懂了，我就在心里想：“这难道是外星人的语言？”
我们数学老师在黑板上写那些奇怪的符号和公式，嘴里还不停地说着：“同学们，这个很重要哦！”我偷偷看了看同桌，他也是眉头紧皱，好像在说：“这都是啥呀？”我忍不住问他：“你懂了吗？”他摇摇头说：“完全不懂！”
我就琢磨啊，这瑞利分布的概率密度函数到底能用来干啥？难道能像魔法一样让我的玩具自己排好队？还是能让我一下子就知道明天考试的答案？
老师说它在通信里有用，可通信又是啥？难道就像我们传纸条那样？可传纸条哪用得着这么复杂的东西呀！
我回到家问爸爸妈妈，他们也是一脸懵，爸爸还说：“孩子，等你长大了就懂啦！”哼，我才不想等长大呢，我现在就想搞明白！
这瑞利分布的概率密度函数，就像是一个藏在迷雾里的神秘城堡，我怎么都走不进去。

难道我要一直被它挡在外面吗？不行，我一定要想办法弄清楚它！我相信，只要我努力，总有一天我能揭开它神秘的面纱！
我的观点是：虽然现在我对瑞利分布的概率密度函数一知半解，但是我不会放弃，我会一直努力去探索，直到完全明白它！。

iirct下瑞利分布参数多变点的贝叶斯估计

iirct下瑞利分布参数多变点的贝叶斯估计标题：贝叶斯估计在iirct下瑞利分布参数多变点的探索导言：在通信领域中，瑞利分布广泛应用于描述信号经过无线传播后的幅度衰减情况。

然而，传统的频域方法对瑞利分布参数的估计存在一定的局限性。

本文将探讨一种基于贝叶斯估计的方法，用于估计iirct下瑞利分布参数多变点，通过全面评估其深度和广度，帮助读者更好地理解这一方法。

正文：1. 瑞利分布的背景和重要性：瑞利分布是一种常用的概率分布函数，它常用于描述随机信号在无线传输中的幅度衰减。

瑞利分布函数主要依赖于两个重要的参数：幅度（也称为尺度参数）和相位（也称为位相参数）。

具体而言，幅度参数决定了随机信号的分布形状，而相位参数则是与信号的起始相位相关的。

准确估计瑞利分布的参数对于了解信号传输的特性至关重要。

2. 传统频域方法的局限性：在现实应用中，瑞利分布的参数通常是多变的，在不同的环境下可能会有所变化。

传统的频域方法对于参数多变的情况下的估计存在一定的局限性。

频域方法主要通过傅里叶变换来估计瑞利分布的参数，但这种方法往往要求信号满足严格的条件，可能难以满足实际场景下的要求。

我们需要探索一种更加有效的方法来进行瑞利分布参数的估计。

3. 贝叶斯估计在iirct下的应用：贝叶斯估计是一种基于贝叶斯理论的参数估计方法，在估计瑞利分布参数多变点的问题上具有较好的表现。

贝叶斯估计通过利用已有数据和先验知识来估计参数的后验概率分布，从而得到更准确的参数估计值。

在iirct (iterative interpolation-recombination technique)的框架下，贝叶斯估计可以得到更准确的瑞利分布参数估计。

4. iirct的框架与步骤：在使用贝叶斯估计进行瑞利分布参数多变点估计时，可以按照以下步骤进行：步骤 1：收集足够的样本数据，包括具有多变点的瑞利分布信号。

步骤 2：建立瑞利分布参数的后验概率模型，包括幅度参数和相位参数。

matlab 瑞利分布函数

matlab 瑞利分布函数
摘要：
1.瑞利分布函数简介
2.瑞利分布函数在MATLAB中的实现
3.MATLAB中瑞利分布函数的常见应用
4.总结
正文：
瑞利分布函数是描述光在各个方向上传播时的强度分布情况的一种函数，它在物理、光学、通信等领域有着广泛的应用。

MATLAB提供了丰富的瑞利分布函数的计算和绘图功能，方便用户进行相关研究和仿真。

在MATLAB中，瑞利分布函数可以通过以下命令实现：
```matlab
R = rice(x, y, z, lambda, theta, phi)
```
其中，`x`、`y`、`z` 是光束的传播方向，`lambda` 是波长，`theta` 和`phi` 是空间角坐标。

函数返回的`R`即表示瑞利分布函数值。

瑞利分布

瑞利分布我们所熟知的瑞利分布的定义是当一个随机二维向量的两个分量呈独立的、均值为0，有着相同的方差的正态分布时，这个向量的模呈瑞利分布。

瑞利分布是最常见的用于描述平坦衰落信号接收包络或独立多径分量接受包络统计时变特性的一种分布类型。

两个正交高斯噪声信号之和的包络服从瑞利分布。

瑞利分布的概率密度：期望（此处应为）瑞利分布均值方差举个例子便于理解一个均值为(0.5*π*σ^2)^(0.5)，方差为(2-0.5*π)*σ^2 的平稳窄带高斯过程，其包络的一维分布是瑞利分布。

当一个随机二维向量的两个分量呈独立的、有着相同的方差的正态分布时，这个向量的模呈瑞利分布。

瑞利分布是最常见的用于描述平坦衰落信号接收包络或独立多径简介分量接受包络统计时变特性的一种分布类型。

两个正交高斯噪声信号之和的包络服从瑞利分布。

瑞利分布DT--DriveTest--路测，专业术语中又把CQT 称之为“点测”无线网络性能测试包括CQT 和DT 两个方面。

CQT 包括呼叫建立测试、休眠重激活测试、传输时延测试等。

DT 主要测试用户吞吐量、FER、SCH 速率分布、手机发射功率等。

CQT 测试目前CQT 测试主要都是以人工测试的方式进行，一般的流程是，先制定一个测试计划交由测试人员到指定地点进行测试，测试工具一般为信号测试专用手机，这种测试过程中所得的数据都是由测试人员手工记录而来，再由他们来对数据进行统计整理，最后手工录入记录并制作出分析报告。

从流程中我们不难发现，在整个测试过程中人工成分占了绝大部分，导致测试数据存在很大的主观性缺乏真实性而且在测试中每次呼叫的采样数据只有一次又使数据缺乏准确性。

目前移动通信中基站架设的特点是数量大、分布广特别是在一些地形复杂的山区，想要对大量的基站和其覆盖的范围进行信号测试用目前的测试方法几乎是不可能的，以至于一些地方成为测试盲区。

瑞利分布均值：瑞利分布方差：莱斯分布正弦波加窄带高斯过程的包络概率密度函数分布称为莱斯（Rice）密度函数，也称广义瑞利分布。

瑞利分布

瑞利分布
气体瑞利分布双正正态解析。

瑞利为双正态分布合成。

电磁波的虚部为磁场。

原麦克斯韦分布为其中一个分布的近似值。

电磁波必须存在虚部磁波，否则叫库仑波，而且单库仑波是不存在的！i表示与速度垂直的另两个三维平面。

本次解析主要是针对辐射的电磁波的解析，同时确认热功当量的理论数据。

为4丌/3焦耳每卡。

1.热功当量实为三维均分球辐射的系数。

当到热平衡时刚好是声速均分球面。

解析后分布才是真实的，两个层面存在互补关系！。

瑞利分布和莱斯应用场景

瑞利分布和莱斯应用场景
莱斯应用
在无线信道中，莱斯分布是一种最常见的用于描述接收信号包络统计时变特性的分布类型。

其中莱斯因子是反映信道质量的重要参数，在计算信道质量和链路预算、移动台移动速度以及测向性能分析等方面都发挥着重要的作用。

信号在传输过程中由于多径效应，接收信号是直射信号（主信号）和多径信号的叠加，此时接收信号的包络服从莱斯分布。

瑞利分布
当一个随机二维向量的两个分量呈独立的、有着相同的方差的正态分布时，这个向量的模呈瑞利分布。

瑞利分布是最常见的用于描述平坦衰落信号接收包络或独立多径分量接受包络统计时变特性的一种分布类型。

两个正交高斯噪声信号之和的包络服从瑞利分布。

第一种理解：当一个随机二维向量的两个分量呈独立的、有着相同的方差的正态分布时，这个向量的模呈瑞利分布。

瑞利分布是最常见的用于描述平坦衰落信号接收包络或独立多径分量接受包络统计时变特性的一种分布类型。

两个正交高斯噪声信号之和的包络服从瑞利分布。

第二种理解：信号经过不同的路径到达接收端，接收信号若不包括直射信号，仅包含多条反射或折射等路径信号分量，此时接收
信号的包络服从瑞利分布。

瑞利衰落要求信道传输的物理环境中有足够多的散射体，且散射体的分布比较均匀，传输信号在不同物体上反射造成随机的时延，此时接收到的信号是一个复高斯随机过程，即两路正交的高斯随机过程信号合在一起，对应接收信号(包络服从瑞利分布，相位服从均匀分布)==(瑞利衰落信道)==(复高斯随机过程)。